[精品]2015-2016学年天津市河北区八年级(上)期末数学试卷与参考答案

合集下载

2015-2016人教版八年级数学第一学期期末考试试卷及答案

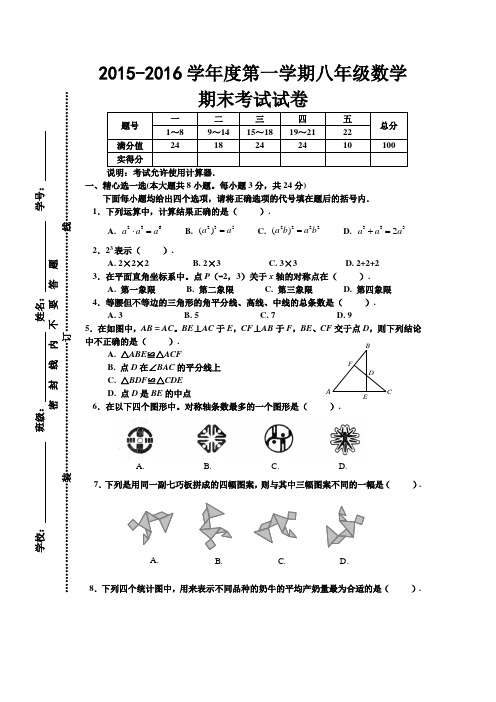
2015-2016学年度第一学期八年级数学期末考试试卷一、精心选一选(本大题共8小题。

每小题3分，共24分)下面每小题均给出四个选项，请将正确选项的代号填在题后的括号内． 1．下列运算中，计算结果正确的是（）.A. 236a a a ⋅=B. 235()a a =C. 2222()a b a b =D. 3332a a a += 2．23表示（）.A. 2×2×2B. 2×3C. 3×3D. 2+2+2 3．在平面直角坐标系中。

点P （-2，3）关于x 轴的对称点在（）.A. 第一象限B. 第二象限C. 第三象限D. 第四象限 4．等腰但不等边的三角形的角平分线、高线、中线的总条数是（）.A. 3B. 5C. 7D. 95．在如图中，AB = AC 。

BE ⊥AC 于E ，CF ⊥AB 于F ，BE 、CF 交于点D ，则下列结论中不正确的是（）. A. △ABE ≌△ACFB. 点D 在∠BAC 的平分线上C. △BDF ≌△CDED. 点D 是BE的中点 6．在以下四个图形中。

对称轴条数最多的一个图形是（）.7．下列是用同一副七巧板拼成的四幅图案，则与其中三幅图案不同的一幅是（）.D.C.B.A.8．下列四个统计图中，用来表示不同品种的奶牛的平均产奶量最为合适的是（）.FEDC BAA. B. C. D.二、细心填一填(本大题共6小题，每小题3分，共18分)9．若单项式23m a b 与n ab -是同类项，则22m n -= .l0．中国文字中有许多是轴对称图形，请你写出三个具有轴对称图形的汉字 . 11．如图是由三个小正方形组成的图形，请你在图中补画一个小正方形，使补画后的图形为轴对称图形．12．如图，已知方格纸中的每个小方格都是相同的正方形．∠AOB 画在方格纸上，请在小方格的顶点上标出一个点P 。

使点P 落在∠AOB 的平分线上．BOA13．数的运算中有一些有趣的对称，请你仿照等式“12×231=132×21”的形式完成：(1)18×891 = × ；(2)24×231 = × ．14．下列图案是由边长相等的灰白两色正方形瓷砖铺设的地面，则按此规律可以得到：（1）第4个图案中白色瓷砖块数是；（2）第n 个图案中白色瓷砖块数是 .第1个图案第2个图案第3个图案三、耐心求一求（本大题共4小题．每小题6分。

2015-2016年天津市南开区八年级上学期期末数学试卷和答案

2015-2016学年天津市南开区八年级（上）期末数学试卷一、选择题（每小题3分，共30分）1．（3分）下列图案中，是轴对称图形的是（）A．B．C． D．2．（3分）若代数式有意义，则x的取值范围是（）A．x＞1 B．x≥1 C．x≥1且D．x＞1且3．（3分）在△ABC和△A′B′C′中，已知∠A=∠A′，AB=A′B′，添加下列条件中的一个，不能使△ABC≌△A′B′C′一定成立的是（）A．AC=A′C′B．BC=B′C′C．∠B=∠B′D．∠C=∠C′4．（3分）下列各式中，正确的是（）A． B．C．D．5．（3分）若，则A为（）A．3x+1 B．3x﹣1 C．x2﹣2x﹣1 D．x2+2x﹣16．（3分）下列三角形：①有两个角等于60°；②有一个角等于60°的等腰三角形；③三个外角（每个顶点处各取一个外角）都相等的三角形；④一腰上的中线也是这条腰上的高的等腰三角形．其中是等边三角形的有（）A．①②③B．①②④C．①③D．①②③④7．（3分）已知等腰三角形的一边长为6，一个内角为60°，则它的周长是（）A．12 B．15 C．18 D．208．（3分）下列分解因式错误的是（）A．x2﹣2xy+y2=（x﹣y）2B．x3﹣x2+x=x（x2﹣x）C．x2y﹣xy2=xy（x﹣y） D．x2﹣y2=（x﹣y）（x+y）9．（3分）已知实数a，b，c在数轴上的位置如图所示，则化简﹣﹣﹣的结果是（）A．﹣3a B．﹣a+2b﹣2c C．2b D．a10．（3分）已知x2n=3，则（x3n）2•4（x2）2n的值是（）A．12 B．C．27 D．11．（3分）如图，直线l外不重合的两点A、B，在直线l上求作一点C，使得AC+BC的长度最短，作法为：①作点B关于直线l的对称点B′；②连接AB′与直线l相交于点C，则点C为所求作的点．在解决这个问题时没有运用到的知识或方法是（）A．转化思想B．三角形的两边之和大于第三边C．两点之间，线段最短D．三角形的一个外角大于与它不相邻的任意一个内角12．（3分）若（m﹣2016）2+（2014﹣m）2=2，则（2014﹣m）（m﹣2016）=（）A．2015 B．2016 C．1 D．2二、填空题（本大题有6小题，每小题3分，共18分）13．（3分）点P（，2）关于y轴对称点的坐标为．14．（3分）PM 2.5是指大气中直径小于或等于0.0000025m的颗粒物，将0.0000025用科学记数法表示为．15．（3分）若分式值为0，则q的值是．16．（3分）等腰三角形的两条边长分别为2和5，那么这个三角形的周长等于．17．（3分）如果ab＞0，a+b＜0，那么下面各式：①=，②=1，③÷=﹣b，其中正确的是（填序号）18．（3分）己知，如图，在△ABC中，∠C=90°，∠A=24°，请用直尺和圆规找到一条直线，把△ABC恰好分割成两个等腰三角形（不写作法，但需保留作图痕迹），直线即为所求．三、解答题（共46分）19．（12分）（1）计算：（﹣）2+（2+）（2﹣）（2）因式分解：9a2（x﹣y）+4b2（y﹣x）（3）先化简，再求值：÷（a﹣1﹣），其中a2﹣a﹣6=0．20．（5分）解方程：+1=21．（6分）如图，在直角坐标系中，B点的坐标为（a，b），且a，b满足b=（1）求B点的坐标；（2）点A为y轴上一动点，过B点作BC⊥AB交x轴正半轴于点C，求证：BA=BC．22．（7分）在平面直角坐标系xOy中，等腰三角形ABC的三个顶点A（0，1），点B在x轴的正半轴上，∠ABO=30°，点C在y轴上．（1）直接写出点C的坐标：；（2）点P关于直线AB的对称点P′在x轴上，AP=1，在图中标出点P的位置并说明理由．23．（8分）某书店老板去图书批发市场购买某种图书．第一次用1200元购书若干本，并按该书定价7元出售，很快售完．由于该书畅销，第二次购书时，每本书的批发价已比第一次提高了20%，他用1500元所购该书数量比第一次多10本．当按定价售出200本时，出现滞销，便以定价的4折售完剩余的书．试问该老板这两次售书总体上是赔钱了，还是赚钱了（不考虑其它因素）？若赔钱，赔多少？若赚钱，赚多少？24．（8分）在△ABC中，BC=AC，∠BCA=90°，P为直线AC上一点，过A作AD ⊥BP于D，交直线BC于Q．（1）如图1，当P在线段AC上时，求证：BP=AQ．（2）当P在线段AC的延长线上时，请在图2中画出图形，并求∠CPQ．（3）如图3，当P在线段AC的延长线上时，∠DBA=时，AQ=2BD．2015-2016学年天津市南开区八年级（上）期末数学试卷参考答案与试题解析一、选择题（每小题3分，共30分）1．（3分）下列图案中，是轴对称图形的是（）A．B．C． D．【解答】解：A、图形不是轴对称图形，B、图形不是轴对称图形，C、图形不是轴对称图形，D、图形是轴对称图形，故选D．2．（3分）若代数式有意义，则x的取值范围是（）A．x＞1 B．x≥1 C．x≥1且D．x＞1且【解答】解：∵代数式有意义，∴，解得x＞1．故选A．3．（3分）在△ABC和△A′B′C′中，已知∠A=∠A′，AB=A′B′，添加下列条件中的一个，不能使△ABC≌△A′B′C′一定成立的是（）A．AC=A′C′B．BC=B′C′C．∠B=∠B′D．∠C=∠C′【解答】解：A、∠A=∠A′，AB=A′B′AC=A′C′，根据SAS能推出△ABC≌△A′B′C′，故A选项错误；B、具备∠A=∠A′，AB=A′B′，BC=B′C′，不能判断△ABC≌△A′B′C′，故B选项正确；C、根据ASA能推出△ABC≌△A′B′C′，故C选项错误；D、根据AAS能推出△ABC≌△A′B′C′，故D选项错误．故选：B．4．（3分）下列各式中，正确的是（）A． B．C．D．【解答】解：∵=，故B选项说法正确．故选：B．5．（3分）若，则A为（）A．3x+1 B．3x﹣1 C．x2﹣2x﹣1 D．x2+2x﹣1【解答】解：=x+=，得到2x2+2x+1=2x2﹣x+A，则A=3x+1．故选A．6．（3分）下列三角形：①有两个角等于60°；②有一个角等于60°的等腰三角形；③三个外角（每个顶点处各取一个外角）都相等的三角形；④一腰上的中线也是这条腰上的高的等腰三角形．其中是等边三角形的有（）A．①②③B．①②④C．①③D．①②③④【解答】解：①两个角为60度，则第三个角也是60度，则其是等边三角形，故正确；②这是等边三角形的判定2，故正确；③三个外角相等则三个内角相等，则其是等边三角形，故正确；④根据等边三角形三线合一性质，故正确．所以都正确．故选D．7．（3分）已知等腰三角形的一边长为6，一个内角为60°，则它的周长是（）A．12 B．15 C．18 D．20【解答】解：∵三角形是等腰三角形，一个内角为60°，∴三角形是等边三角形，∵一边长为6，∴它的周长是6×3=18；故选C．8．（3分）下列分解因式错误的是（）A．x2﹣2xy+y2=（x﹣y）2B．x3﹣x2+x=x（x2﹣x）C．x2y﹣xy2=xy（x﹣y） D．x2﹣y2=（x﹣y）（x+y）【解答】解：A、x2﹣2xy+y2=（x﹣y）2，正确，不合题意；B、x3﹣x2+x=x（x2﹣x+1），故此选项错误，符合题意；C、x2y﹣xy2=xy（x﹣y），正确，不合题意；D、x2﹣y2=（x﹣y）（x+y），正确，不合题意．故选：B．9．（3分）已知实数a，b，c在数轴上的位置如图所示，则化简﹣﹣﹣的结果是（）A．﹣3a B．﹣a+2b﹣2c C．2b D．a【解答】解：由数轴可得：b＜a＜0＜c，∴a﹣b＞0，a﹣c＜0，b﹣c＜0，则原式=|a|﹣|a﹣b|﹣|a﹣c|﹣|b﹣c|=﹣a﹣a+b+a﹣c+b﹣c=﹣a+2b﹣2c．故选B．10．（3分）已知x2n=3，则（x3n）2•4（x2）2n的值是（）A．12 B．C．27 D．【解答】解：∵x2n=3，∴=（x2n）3•4（x2n）2=×33×4×32=12．故选：A．11．（3分）如图，直线l外不重合的两点A、B，在直线l上求作一点C，使得AC+BC的长度最短，作法为：①作点B关于直线l的对称点B′；②连接AB′与直线l相交于点C，则点C为所求作的点．在解决这个问题时没有运用到的知识或方法是（）A．转化思想B．三角形的两边之和大于第三边C．两点之间，线段最短D．三角形的一个外角大于与它不相邻的任意一个内角【解答】解：∵点B和点B′关于直线l对称，且点C在l上，∴CB=CB′，又∵AB′交l与C，且两条直线相交只有一个交点，∴CB′+CA最短，即CA+CB的值最小，将轴对称最短路径问题利用线段的性质定理两点之间，线段最短，体现了转化思想，验证时利用三角形的两边之和大于第三边．故选D．12．（3分）若（m﹣2016）2+（2014﹣m）2=2，则（2014﹣m）（m﹣2016）=（）A．2015 B．2016 C．1 D．2【解答】解：∵（m﹣2016）2+（2014﹣m）2=2，[（m﹣2016）+（2014﹣m）]2=（﹣2）2=4，∴（m﹣2016）2+2×（m﹣2016）×（2014﹣m）+（2014﹣m）2=4，∴2×（m﹣2016）×（2014﹣m）=4﹣2=2，∴（2014﹣m）（m﹣2016）=1，故选C．二、填空题（本大题有6小题，每小题3分，共18分）13．（3分）点P（，2）关于y轴对称点的坐标为（﹣，2）．【解答】解：点P（，2），则点P关于y轴对称点的坐标为：（﹣，2）．故答案为：（﹣，2）．14．（3分）PM 2.5是指大气中直径小于或等于0.0000025m的颗粒物，将0.0000025用科学记数法表示为 2.5×10﹣6．【解答】解：0.0000025=2.5×10﹣6，故答案为：2.5×10﹣6．15．（3分）若分式值为0，则q的值是5．【解答】解：依题意，得|q|﹣5=0，且q+5≠0，解得，q=5．故填：5．16．（3分）等腰三角形的两条边长分别为2和5，那么这个三角形的周长等于10+2．【解答】解：①若腰长为2，则有2×2＜5，故此情况不合题意，舍去；②若腰长为5，则三角形的周长=2×5+2=10+2．故答案为：10+2．17．（3分）如果ab＞0，a+b＜0，那么下面各式：①=，②=1，③÷=﹣b，其中正确的是②③（填序号）【解答】解：∵ab＞0，a+b＜0，∴a＜0，b＜0．①根号下必须非负，错误；②==1，正确；③÷===﹣b，正确．故答案为：②③．18．（3分）己知，如图，在△ABC中，∠C=90°，∠A=24°，请用直尺和圆规找到一条直线，把△ABC恰好分割成两个等腰三角形（不写作法，但需保留作图痕迹），直线CD即为所求．【解答】解：如图所示：直线CD即为所求，故答案为：CD．三、解答题（共46分）19．（12分）（1）计算：（﹣）2+（2+）（2﹣）（2）因式分解：9a2（x﹣y）+4b2（y﹣x）（3）先化简，再求值：÷（a﹣1﹣），其中a2﹣a﹣6=0．【解答】解：（1）原式=（）2﹣2××+（）2+（2）2﹣（）2=2﹣2+3+12﹣6=11﹣2；（2）原式=9a2（x﹣y）﹣4b2（x﹣y）=（x﹣y）（9a2﹣4b2）=（x﹣y）（3a+2b）（3a﹣2b）；（3）÷（a﹣1﹣）=÷=÷=•==，∵a2﹣a﹣6=0，∴a2﹣a=6，∴原式=．20．（5分）解方程：+1=【解答】解：方程两边同乘以（x2﹣1），得x2﹣4x+x2﹣1=2x（x﹣1），2x2﹣4x﹣1=2x2﹣2x，﹣2x=1，∴x=﹣．经检验：x=﹣是原方程的解，∴原方程的解为x=﹣．21．（6分）如图，在直角坐标系中，B点的坐标为（a，b），且a，b满足b=（1）求B点的坐标；（2）点A为y轴上一动点，过B点作BC⊥AB交x轴正半轴于点C，求证：BA=BC．【解答】解：（1）∵b=，∴a2﹣4≥0，4﹣a2≥0，解得：a=±2，∵a+2≠0，∴a=2，∴b=2，∴B（2，2）；（2）作BM⊥y轴于M，BN⊥x轴于N点，如图：∴∠MBN=90°．∵BC⊥AB，∴∠ABC=90°．∴∠ABM=∠CBN．∵B点坐标是（2，2），∴BM=BN，在△ABM和△CBN中，，∴△ABM≌△CBN（ASA），∴BA=BC．22．（7分）在平面直角坐标系xOy中，等腰三角形ABC的三个顶点A（0，1），点B在x轴的正半轴上，∠ABO=30°，点C在y轴上．（1）直接写出点C的坐标：（0，﹣1）或（0，3）；（2）点P关于直线AB的对称点P′在x轴上，AP=1，在图中标出点P的位置并说明理由．【解答】解：（1）根据题意完善图形，如图1所示．∵∠ABO=30°，点A（0，1），∴OA=1，tan∠ABO==，AB==2，∴点B的坐标为（，0）．∵点C在y轴上，∴设点C的坐标为（0，m）．∵三角形ABC为等腰三角形，∴分三种情况考虑：①当AC=AB时，由两点间的距离公式可知：=2，解得：m=﹣1，或m=3，即点C的坐标为（0，﹣1）或（0，3）；②当AC=BC时，由两点间的距离公式可知：=，解得：m=﹣1，即点C的坐标为（0，﹣1）；③当AB=BC时，由两点间的距离公式可知：2=，解得m=﹣1或m=1（舍去），即点C的坐标为（0，﹣1）．综上得：点C的坐标为：（0，﹣1）或（0，3）．故答案为：（0，﹣1）或（0，3）．（2）第一步：以A点为圆心，1为半径作圆，⊙A与x轴切与原点O，第二步：过点O作OP⊥AB交⊙A于点P，P点即为所求（图形如图2）．∵点P与点P′关于直线AB对称，且AP=1，∴AP′=AP=1．故用上面的画法寻找点P．23．（8分）某书店老板去图书批发市场购买某种图书．第一次用1200元购书若干本，并按该书定价7元出售，很快售完．由于该书畅销，第二次购书时，每本书的批发价已比第一次提高了20%，他用1500元所购该书数量比第一次多10本．当按定价售出200本时，出现滞销，便以定价的4折售完剩余的书．试问该老板这两次售书总体上是赔钱了，还是赚钱了（不考虑其它因素）？若赔钱，赔多少？若赚钱，赚多少？【解答】解：设第一次购书的单价为x元，∵第二次每本书的批发价已比第一次提高了20%，∴第二次购书的单价为1.2x元．根据题意得：．（4分）解得：x=5．经检验，x=5是原方程的解．（6分）所以第一次购书为1200÷5=240（本）．第二次购书为240+10=250（本）．第一次赚钱为240×（7﹣5）=480（元）．第二次赚钱为200×（7﹣5×1.2）+50×（7×0.4﹣5×1.2）=40（元）．所以两次共赚钱480+40=520（元）（8分）．答：该老板两次售书总体上是赚钱了，共赚了520元．（9分）24．（8分）在△ABC中，BC=AC，∠BCA=90°，P为直线AC上一点，过A作AD ⊥BP于D，交直线BC于Q．（1）如图1，当P在线段AC上时，求证：BP=AQ．（2）当P在线段AC的延长线上时，请在图2中画出图形，并求∠CPQ．（3）如图3，当P在线段AC的延长线上时，∠DBA=22.5°时，AQ=2BD．【解答】（1）证明：∵∠ACB=∠ADB=90°，∠APD=∠BPC，∴∠DAP=∠CBP，在△ACQ和△BCP中，∴△ACQ≌△BCP（ASA），∴BP=AQ；（2）解：如图2所示：∵∠ACQ=∠BDQ=90°，∠AQC=∠BQD，∴∠CAQ=∠DBQ，在△AQC和△BPC中，∴△AQC≌△BPC（ASA），∴QC=CP，∵∠QCD=90°，∴∠CQP=∠CPQ=45°；（3）解：当∠DBA=22.5°时，AQ=2BD；∵AC=BC，∠ACB=90°，∴∠BAC=45°，∴∠P=22.5°，∴∠DBA=∠P，∴AP=AB，∵AD⊥BP，∴AD=DP，∵∠ACQ=∠ADP=90°，∠PAD=∠QAC，∴∠P=∠Q，在△ACQ和△BCP中，∴△ACQ≌△BCP（ASA），∴BP=AQ，∴此时AQ=BP=2BD．故答案为：22.5°．赠送初中数学几何模型【模型一】“一线三等角”模型：图形特征：60°60°60°45°45°45°运用举例：1.如图，若点B 在x 轴正半轴上，点A (4，4)、C (1，－1)，且AB ＝BC ，AB ⊥BC ，求点B 的坐标；xyB CAO2.如图，在直线l 上依次摆放着七个正方形（如图所示），已知斜放置的三个正方形的面积分别是1、2、3，正放置的四个正方形的面积依次是1S 、2S 、3S 、4S ，则14S S += ．ls 4s 3s 2s 13213. 如图，Rt △ABC 中，∠BAC =90°，AB =AC =2，点D 在BC 上运动（不与点B ，C 重合），过D 作∠ADE =45°，DE 交AC 于E ．（1）求证：△ABD ∽△DCE ；（2）设BD =x ，AE =y ，求y 关于x 的函数关系式，并写出自变量x 的取值范围；（3）当△ADE 是等腰三角形时，求AE 的长．EB4.如图，已知直线112y x =+与y 轴交于点A ，与x 轴交于点D ，抛物线212y x bx c =++与直线交于A 、E 两点，与x 轴交于B 、C 两点，且B 点坐标为 (1，0)。

2015--2016学年天津市五区县八年级(上)期末数学试卷

2015-2016学年天津市五区县八年级（上）期末数学试卷一、选择题：本题包括12小题，每小题3分，共36分．1．（3分）（2015秋•天津期末）如果三角形的两边长分别为3cm和5cm，第三边是偶数，则此三角形的第三边长可为（）A．2cm B．3cm C．4cm D．8cm2．（3分）（2015秋•天津期末）若分式有意义，则a的取值范围是（）A．a=﹣5 B．a≠5 C．a=5 D．a≠﹣53．（3分）（2015秋•天津期末）在中，分式有（）A．1个B．2个C．3个D．4个4．（3分）（2015秋•天津期末）在△ABC中，如果，则这个三角形一定是（）A．直角三角形B．等腰三角形C．锐角三角形D．钝角三角形5．（3分）（2015秋•天津期末）若2x=3y，则的值是（）A．﹣1 B．C．1 D．6．（3分）（2015秋•天津期末）某病毒的直径是0.000000068m，这个数据用科学计数法表示为（）A．6.8×10﹣7m B．68×10﹣9m C．0.68×10﹣7m D．6.8×10﹣8m7．（3分）（2015秋•天津期末）若点P（m+5，2）与点Q（3，n﹣5）关于y轴对称，则m，n的值分别是（）A．﹣8，﹣7 B．8，﹣7 C．﹣8，7 D．8，78．（3分）（2015秋•天津期末）下列计算正确的是（）A．a5+a5=a10 B．3a5•2a3=6a8C．a10÷a2=a5D．（3a4）3=9a129．（3分）（2015秋•天津期末）观察如图所示图形，其中不是轴对称图形的有（）A．2个B．3个C．4个D．1个10．（3分）（2015秋•天津期末）把2ab2﹣4ba+2a分解因式的结果是（）A．2ab（b﹣2）+2a B．2a（b2﹣2b）C．2a（b+1）（b﹣1）D．2a（b﹣1）211．（3分）（2016春•山亭区期末）如图，△ABC中，AB=AC，D是BC中点，下列结论中不正确的是（）A．∠B=∠C B．AD⊥BC C．AD平分∠BAC D．AB=2BD12．（3分）（2015秋•天津期末）若（a+b）2=12，（a﹣b）2=6，则ab的值是（）A．B．C．5 D．﹣5二、填空题：本题包括6小题，每小题3分，共18分．13．（3分）（2015秋•天津期末）如图，已知△ABC≌△A1B1C1，∠A=45°，∠C1=60°，则∠B=．14．（3分）（2015秋•天津期末）若（2x﹣3y）•N=9y2﹣4x2，那么代数式N应该是．15．（3分）（2015秋•天津期末）分解因式：（x+4）（x﹣1）﹣3x=．16．（3分）（2016•梅州模拟）化简的结果是．17．（3分）（2015秋•天津期末）某多边形内角和与外角和共1080°，则这个多边形的边数是．18．（3分）（2007•赤峰）附加题：已知，则=．三、解答题：本题共46分。

河北区2014-2015学年度第一学期期末八年级质量检测

河北区2014-2015学年度第一学期期末八年级质量检测物理第Ⅰ卷（选择题共90分）一、单项选择（本题共10小题，在每题给出的四个选项中只有一项是符合题目要求的，每小题3分，1．下列数据中最接近实际的是（）A．成都三环路限速950km/hB．PM2.5是指空气中直径为2.5cm的固体颗粒C．一个鸡蛋的质量约为500gD．人体感觉适宜的温度约为23℃2．光学实验课时，小叶用激光灯对着光滑的大理石地面照射，无意中发现对面粗糙的墙壁上会出现一个明亮的光斑，而光滑地面上的光斑很暗，对此现象解释较合理的是（）A．地面吸收了所有的光B．墙壁对光发生漫反射C．地面对光发生漫反射D．墙壁对光发生镜面反射3．关于温度计的使用，下列说法中正确的是（）A．用酒精灯给体温计消毒B．测量液体温度时，温度计应紧贴容器的壁或底C．用寒暑表测量开水的温度D．使用体温计前，一般应先用力向下甩几下4．P Q，是同一直线上相距12米的两点，甲从P点向Q方向运动，乙从Q点同时沿直线与甲同向而行，它们运动的“s t ”图象如图所示，分析图象可知（）A．甲的速度小于乙的速度B．经过3秒，甲、乙相距3米C．甲、乙相遇时离Q点6米D．甲到达Q点时，乙离P点20米5．如图所示是“探究光的反射规律”的实验装置，一面可沿ON折叠的白色硬纸板垂直放置在平面镜上，使光线AO紧贴硬纸板射向镜面O点，为了研究反射角与入射角之间关系，实验时应进行的操作是（）A ．绕ON 前后转动板EB ．绕ON 前后转动板FC ．改变光线AO 与ON 之间的夹角D ．改变光线OB 与ON 之间的夹角6．下列现象发生的过程中，吸收热量的一组是（）（1）春天，冰雪融化汇成溪流（2）夏天，从冰箱里面拿出业的饮料罐“出汗” （3）秋天，清晨的雾在太阳出来后散去（4）冬天，室外草地上出现了霜 A ．（1）（2） B ．（1）（3） C ．（3）（4） D ．（2）（4）7．下列各组有关物理原理、现象及应用的连线中有错误的是（）8．在①小孔成像；②平面镜成像；③放大镜成像；④照相机成像；⑤幻灯机成像中（） A ．成实像的是①②③ B ．成虚像的是②③④ C ．属于反射成像的是② D ．属于折射成像的是①③④ 9．体积为3100cm 的冰熔化成水后，下列说法正确的是（330.910kg/m ρ=⨯冰）（） A ．质量不变，水的体积为390cm B ．质量变大，水的质量为100g C ．质量不变，水的体积为3100cm D ．质量变小，水的密度为31.0g/cm10．有密度分别为1ρ和2ρ的液体各kg m ，只用这两种液体最多可配成密度为122ρρρ+=的溶液的质量为（已知12ρρ>，且不计混合后体积变化）（） A ．12m ρρ B ．21m ρρ C ．121m ρρ⎛⎫+ ⎪⎝⎭D ．211m ρρ⎛⎫+ ⎪⎝⎭二、多项选择题（在下列列出的四个选项中，有多个选项是正确的，全选对的得3分，选对但不全的得1分，有选错或不答的得0分，共9分，请将答案填在下面表格中）11．在下图中，能用光的折射规律来解释的现象是（）12．老师上课时经常用到投影仪，如图所示，关于投影仪的使用以下做法中合理的是（）A ．投放到屏幕上的画面太靠上时，应减小平面镜与凸透镜的夹角使画面向下移动B ．若使屏幕上的画面大一些，可使投影仪靠近屏幕同时将凸透镜适当向下移动C ．若使屏幕上的画面大一些，可使投影仪远离屏幕同时将凸透镜适当向上移动D ．若使屏幕上的画面大一些，可使投影仪远离屏幕同时将凸透镜适当向下移动 13．体积和质量都相等的铜球、铁球和铝球，已知ρρρ>>铜铝铁，则（）A ．铜球若是实心的，则另外两球一定是空心的B ．铁球若是实心的，则另外两球一定是空心的C ．铝球若是实心的，则另外两球一定是空心的D ．三个球都有可能是空心的第Ⅱ卷（非选择题共61分）三、填空题（本题共6小题，每小题4分，共24分）14．家庭和实验室里常用的温度计是根据液体的热胀冷缩原理制成的，小明用温度计测量教室外的温度如图所示，其示数为________℃；小明想温度计的玻璃泡不装水的原因是________。

天津市五区县八级上期末数学试卷含答案解析

2015-2016学年天津市五区县八年级（上）期末数学试卷一、选择题：本题包括12小题，每小题3分，共36分．1．如果三角形的两边长分别为3cm和5cm，第三边是偶数，则此三角形的第三边长可为( )A．2cm B．3cm C．4cm D．8cm2．若分式有意义，则a的取值范围是( )A．a=﹣5 B．a≠5 C．a=5 D．a≠﹣53．在中，分式有( )A．1个B．2个C．3个D．4个4．在△ABC中，如果，则这个三角形一定是( )A．直角三角形B．等腰三角形C．锐角三角形D．钝角三角形5．若2x=3y，则的值是( )A．﹣1 B． C．1 D．6．某病毒的直径是0.000000068m，这个数据用科学计数法表示为( )A．6.8×10﹣7m B．68×10﹣9m C．0.68×10﹣7m D．6.8×10﹣8m7．若点P（m+5，2）与点Q（3，n﹣5）关于y轴对称，则m，n的值分别是( ) A．﹣8，﹣7 B．8，﹣7 C．﹣8，7 D．8，78．下列计算正确的是( )A．a5+a5=a10 B．3a5•2a3=6a8C．a10÷a2=a5D．（3a4）3=9a129．观察如图所示图形，其中不是轴对称图形的有( )A．2个B．3个C．4个D．1个10．把2ab2﹣4ba+2a分解因式的结果是( )A．2ab（b﹣2）+2a B．2a（b2﹣2b）C．2a（b+1）（b﹣1） D．2a（b﹣1）2 11．如图，△ABC中，AB=AC，D是BC中点，下列结论中不正确的是( )A．∠B=∠C B．AD⊥BC C．AD平分∠BAC D．AB=2BD12．若（a+b）2=12，（a﹣b）2=6，则ab的值是( )A．B． C．5 D．﹣5二、填空题：本题包括6小题，每小题3分，共18分．13．如图，已知△ABC≌△A1B1C1，∠A=45°，∠C1=60°，则∠B=__________．14．若（2x﹣3y）•N=9y2﹣4x2，那么代数式N应该是__________．15．分解因式：（x+4）（x﹣1）﹣3x=__________．16．化简的结果是__________．17．某多边形内角和与外角和共1080°，则这个多边形的边数是__________．18．附加题：已知，则=__________．三、解答题：本题共46分。

河北区2015-2016上学期8年级期中数学答案

22．（本小题满分 12 分） 2 解：（1）∵（a＋2）＋|b－4|＝0， ∴a＋2＝0，b－4＝0，解得：a＝－2，b＝4；故答案为：－2，4；………2 分（2）如图 1，过点 C 作 CE⊥y 轴于点 E，………3 分 ∵∠ABC＝90°， ∴∠CBE＋∠ABO＝90°， ∵∠ECB＋∠CBE＝90°， ∴∠ECB＝∠ABO，………4 分在△CBE 和△BAO 中，
河北区 2015－2016 学年度第一学期期中八年级质量检测
数学答案
一、选择题：（每题 3 分，共 24 分） 1．C ； 2．A； 3．B； 4．D； 5．C； 6．B； 7．A； 8．B．
二、填空题：（每题 3 分，共 24 分） 9．10:51； 10．15； 11．115° ； 12．AC ＝AD 或∠C＝∠D 或∠ABC＝∠ABD 或∠CBE＝∠DBE 13．13； 14．100° ； 15．1； 16．（1，4），（，5），（0，10）．
八年级数学答案第 3 页（共 4 页）
ECB ABO BEC AOB ， BC AB
∴△CBE≌△BAO（AAS），………7 分 ∴AO＝BE，BO＝EC， ∵a＝－2，b＝4， ∴BO＝CE＝4，AO＝BE＝2， ∴C（﹣4，6）；………9 分（3）如图 2， P1（﹣6，2），………10 分 P2（4，2），………11 分 P3（2，﹣2）．………12 分
DB DC ， DE DF
Rt△DBE≌Rt△DCF（HL）， ∴BE＝CF．……DF 中
AD AD DE DF
∴Rt△ADE≌Rt△ADF（HL）．………7 分 ∴AE＝AF．………8 分 ∵AC＋CF＝AF， ∴AE＝AC＋CF． ∵AE＝AB－BE， ∴AC＋CF＝AB－BE，………9 分 ∵AB＝6，AC＝4， ∴4＋BE＝6－BE， ∴BE＝1．………10 分

2015-2016学年度上学期期末考试八年级数学试卷(含答案)

2015—2016学年度上学期期末考试八年级数学试题注意事项：1．本卷满分120分，考试时间120分钟。

2．本卷是试题卷，不能答题。

答题必须写在答题卡上。

解题中的辅助线和需标注的角、字母、符号等务必添在答题卡的图形上。

3．在答题卡上答题，选择题必须用2B铅笔填涂，非选择题必须用0.5毫米黑色签字笔或黑色墨水钢笔作答。

★祝考试顺利★一、选择题（每小题3分,共30分）1．下列图形中轴对称图形是（）ＡＢＣＤ２,.已知三角形的三边长分别是3，8，x，若x的值为偶数，则x的值有( )A.6个B.5个C.4个D.3个３.一个多边形截去一个角后，形成的多边形的内角和是2520°，则原多边形的边数是( )A.15或16B.16或17C.15或17D.15.16或174.如图，△ACB≌△A'CB'，∠BCB'＝30°，则∠ACA'的度数为( )A.20°B.30°C.35°D.40°５, 等腰三角形的两边长分别为5cm 和10cm，则此三角形的周长是（）A.15cmB. 20cmC. 25cmD.20cm或25cm6.如图，已知∠CAB＝∠DAB，则添加下列一个条件不能使△ABC≌△ABD的是( )A.AC＝ADB.BC＝BDC.∠C＝∠DD.∠ABC＝∠ABD7.如图，已知在△ABC中，CD是AB边上的高，BE平分∠ABC，交CD于点E，BC＝5，DE ＝2，则△BCE的面积等于( )A.10B.7C.5D.4第９题图 8．若()22316m x x+-+是完全平方式,则m 的值等于( )A. 3B. -5C.7D. 7或-19．如图，在△ABC 中，AB =AC ，BE=CD ，BD =CF ，则∠EDF 的度数为（） A ．1452A ︒-∠ B ．1902A ︒-∠ C ．90A ︒-∠ D ．180A ︒-∠第10题 10．如上图，等腰Rt △ABC 中，∠BAC ＝90°，AD ⊥BC 于点D ，∠ABC 的平分线分别交AC 、AD 于E 、F 两点，M 为EF 的中点，AM 的延长线交BC 于点N ，连接DM ，下列结论：① DF ＝DN ；② △DMN 为等腰三角形；③ DM 平分∠BMN ；④ AE ＝32EC ；⑤ AE ＝NC ，其中正确结论的个数是（）A ．2个B ．3个C ．4个D ．5个二、填空题（每小题3分,共24分）11．计算:()()312360.1250.2522⨯-⨯⨯- = 12,在实数范围内分解因式:3234a ab - = 13.若2,3,mn xx ==则2m nx+=14．若A （x ，3）关于y 轴的对称点是B （﹣2，y ），则x=__________，y=__________，点A 关于x 轴的对称点的坐标是__________．15,如图，△ABC 中，DE 是AC 的垂直平分线，AE ＝3 cm ，△ABD 的周长是13 cm ，则△ABC 的周长为 _________第15题图第17题图16,已知等腰三角形一腰的垂直平分线与另一腰所在直线的夹角为40°，求此等腰三角形的顶角为17．如图，∠AOB ＝30°，点P 为∠AOB 内一点，OP ＝8．点M 、N 分别在OA 、OB 上，则△PMN 周长的最小值为__________2第18题图18. 如图所示，在△ABC 中，∠A =80°，延长BC 到D ，∠ABC 与∠ACD 的平分线相交于A 1点，∠A 1BC 与∠A 1CD 的平分线相交于A 2点，依此类推，∠A 4BC 与∠A 4CD 的平分线相交于A 5点，则∠A 5的度数是。

2018-2019学年天津市河北区八年级上册期末数学测试卷(含答案解析)

在△AED 与△DFB 中，
，
∴△AED≌△DFB（SAS），
∴∠ADE=∠DBF，
∵∠CDG=∠ADC﹣∠ADE=120°﹣∠ADE，∠CBM=120°﹣∠DBF，
∴∠CBM=∠CDG， ∵△DBC 是等边三角形， ∴CD=CB，
.
.
在△CDG 和△CBM 中， ∴△CDG≌△CBM， ∴∠DCG=∠BCM，CG=CM， ∴∠GCM=∠DCB=60°， ∴△CGM 是等边三角形， ∴CG=GM=BG+BM=BG+DG， ∵（a+b）2=a2+b2+2ab=9， ∴a+b=3， ∴CG=3， ∴GH= CG= ．故答案为：．
【解答】解：（A）x2+2x﹣1≠（x﹣1）2，故 A 不是因式分解，
（B）a2﹣b2=（a+b）（a﹣b），故 B 不是因式分解，
（D）a x2﹣a=a（x2﹣1）=a（x+1）（x﹣1），故 D 分解不完全，
故选：C．
3．（3 分）要使分式有意义，x 应满足的条件是（） A．x＞3 B．x=3 C．x＜3D．x≠3
【解答】解：如图，DF=DF′=DE； ∵BD 平分∠ABC，由图形的对称性可知： △BDE≌△BDF， ∴∠DFB=∠DEB； ∵DE∥AB，∠ABC=50°，
.
.
∴∠DEB=180°﹣50°=130°； ∴∠DFB=130°；当点 F 位于点 F′处时， ∵DF=DF′， ∴∠DF′B=∠DFF′=50°，故答案是：50°或 130°．
三、解答题（17、18、19、20 题各 8 分，21、22 题 10 分，共 52 分，解答应写出文字说明、证明过程或演算步骤） 17．（8 分）（1）（﹣2a）3﹣（﹣a）•（3a）2 （2）（2a﹣3b）2﹣4a（a﹣2b）【解答】解：（1 ）（﹣2a）3﹣（﹣a）•（3a）2 =﹣8a3﹣（﹣a）•9a2 =﹣8a3+9a3 =a3；

2015-2016年天津市河北区八年级(上)期末数学试卷含参考答案

2015-2016学年天津市河北区八年级（上）期末数学试卷一、选择题（本大题共8小题，每小题3分，共24分，在每小题给出的四个选项中，只有一项符合题目的要求的.）1．（3分）下列各式从左到右的变形中，是因式分解的是（）A．（a+3）（a﹣3）=a2﹣9 B．m（m﹣1）=m2﹣mC．a2﹣4a﹣5=a（a﹣4）﹣5 D．a2﹣4a+4=（a﹣2）22．（3分）下列能用完全平方公式因式分解的是（）A．x2+2xy﹣y2B．﹣xy+y2C．x2﹣2xy+y2D．x2﹣4xy+2y23．（3分）若多项式乘法（x+2y）（2x﹣ky﹣1）的结果中不含xy项，则k的值为（）A．4 B．﹣4 C．2 D．﹣24．（3分）下列各式正确的是（）A． B． C． D．5．（3分）下列从左到右的变形：①=；②=；③=；④=．其中，正确的是（）A．①②B．②④C．③④D．①②③④6．（3分）如果分式的值为零，那么x等于（）A．1 B．﹣1 C．0 D．±17．（3分）若关于x的分式方程=2的解为非负数，则m的取值范围是（）A．m＞﹣1 B．m≥1 C．m＞﹣1且m≠1 D．m≥﹣1且m≠18．（3分）如图，点P是△ABC外的一点，PD⊥AB于点D，PE⊥AC于点E，PF ⊥BC于点F，连接PB，PC．若PD=PE=PF，∠BAC=70°，则∠BPC的度数为（）A．25°B．30°C．35°D．40°二、填空题（本大题共8小题，每小题3分，共24分，请将答案填在题中横线上）9．（3分）若分式有意义，则x的取值范围是．10．（3分）PM 2.5是指大气中直径小于或等于0.0000025m的颗粒物，将0.0000025用科学记数法表示为．11．（3分）若a+3b﹣2=0，则3a•27b=．12．（3分）因式分解：x3﹣xy2=．13．（3分）计算（π﹣3.14）0+（）﹣2=．14．（3分）计算：（﹣3）2013•（﹣）2011=．15．（3分）如图，在△ABC中，∠C=90°，∠CAB=60°，按以下步骤作图：①分别以A，B为圆心，以大于AB的长为半径做弧，两弧相交于点P和Q．②作直线PQ交AB于点D，交BC于点E，连接AE．若CE=4，则AE=．16．（3分）如图，∠AOB=60°，OC平分∠AOB，如果射线OA上的点E满足△OCE 是等腰三角形，那么∠OEC的度数为．三、解答题（7题6分，18题10分，19、20题各8分，21、22题各10分，共52分，解答写出文字说明，演算步骤或推理过程）17．（6分）解方程：．18．（10分）（1）若a+b=5，ab=3，求+的值；（2）化简：÷（m+n﹣）19．（8分）如图，△ABC中BD、CD平分∠ABC、∠ACB，过D作直线平行于BC，交AB、AC于E、F，求证：EF=BE+CF．20．（8分）如图，△ABC为等边三角形，AE=CD，AD、BE相交于点P，BQ⊥AD 于点Q，PQ=3，PE=1．（1）求证：AD=BE；（2）求AD的长．21．（10分）李老师家距学校1900米，某天他步行去上班，走到路程的一半时发现忘带手机，此时离上班时间还有23分钟，于是他立刻步行回家取手机，随后骑电瓶车返回学校．已知李老师骑电瓶车到学校比他步行到学校少用20分钟，且骑电瓶车的平均速度是步行速度的5倍，李老师到家开门、取手机、启动电瓶车等共用4分钟．（1）求李老师步行的平均速度；（2）请你判断李老师能否按时上班，并说明理由．22．（10分）如图，在平面直角坐标系中，O为坐标原点，A、B两点的坐标分别为A（0，m）、B（n，0），且|m﹣n﹣3|+=0，点P从A出发，以每秒1个单位的速度沿射线AO匀速运动，设点P的运动时间为t秒．（1）求OA、OB的长；（2）连接PB，设△POB的面积为S，用t的式子表示S；（3）过点P作直线AB的垂线，垂足为D，直线PD与x轴交于点E，在点P运动的过程中，是否存在这样的点P，使△EOP≌△AOB？若存在，请求出t的值；若不存在，请说明理由．2015-2016学年天津市河北区八年级（上）期末数学试卷参考答案与试题解析一、选择题（本大题共8小题，每小题3分，共24分，在每小题给出的四个选项中，只有一项符合题目的要求的.）1．（3分）下列各式从左到右的变形中，是因式分解的是（）A．（a+3）（a﹣3）=a2﹣9 B．m（m﹣1）=m2﹣mC．a2﹣4a﹣5=a（a﹣4）﹣5 D．a2﹣4a+4=（a﹣2）2【解答】解：A、右边不是等式积的形式，不是因式分解，故本选项错误；B、右边不是等式积的形式，不是因式分解，故本选项错误；C、右边不是等式积的形式，不是因式分解，故本选项错误；D、符合因式分解的定义，故本选项正确．故选：D．2．（3分）下列能用完全平方公式因式分解的是（）A．x2+2xy﹣y2B．﹣xy+y2C．x2﹣2xy+y2D．x2﹣4xy+2y2【解答】解：A、不是两数的平方和加这两个数乘积的二倍，故A错误；B、不是两数的平方和减这两个数乘积的二倍，故B错误；C、两数的平方和减这两个数乘积的二倍，故C正确；D、不是两数的平方和减这两个数乘积的二倍，故D错误；故选：C．3．（3分）若多项式乘法（x+2y）（2x﹣ky﹣1）的结果中不含xy项，则k的值为（）A．4 B．﹣4 C．2 D．﹣2【解答】解：（x+2y）（2x﹣ky﹣1）=2x2﹣kxy﹣x+4xy﹣2ky2﹣2y=2x2+（4﹣k）xy﹣x﹣2ky2﹣2y，∵结果中不含xy项，∴4﹣k=0，解得，k=4，故选：A．4．（3分）下列各式正确的是（）A． B． C． D．【解答】解：A、=，故A正确；B、=，故B错误；C、=，故C错误；D、=﹣，故D错误．故选：A．5．（3分）下列从左到右的变形：①=；②=；③=；④=．其中，正确的是（）A．①②B．②④C．③④D．①②③④【解答】解：①=，当a=0时，该等式不成立，故①错误；②=，分式的分子、分母同时乘以b，等式仍成立，即=，故②正确；③=，当c=0时，该等式不成立，故③错误；④=，因为x2+1≠0，即分式的分子、分母同时乘以（x2+1），等式仍成立，即=成立，故④正确；综上所述，正确的②④．故选：B．6．（3分）如果分式的值为零，那么x等于（）A．1 B．﹣1 C．0 D．±1【解答】解：∵分式的值为零，∴，解得x=﹣1．故选：B．7．（3分）若关于x的分式方程=2的解为非负数，则m的取值范围是（）A．m＞﹣1 B．m≥1 C．m＞﹣1且m≠1 D．m≥﹣1且m≠1【解答】解：去分母得：m﹣1=2x﹣2，解得：x=，由题意得：≥0且≠1，解得：m≥﹣1且m≠1，故选：D．8．（3分）如图，点P是△ABC外的一点，PD⊥AB于点D，PE⊥AC于点E，PF ⊥BC于点F，连接PB，PC．若PD=PE=PF，∠BAC=70°，则∠BPC的度数为（）A．25°B．30°C．35°D．40°【解答】解：在Rt△BDP和Rt△BFP中，，∴Rt△BDP≌Rt△BFP（HL），∴∠ABP=∠CBP，在Rt△CEP和Rt△CFP中，，Rt△CEP≌Rt△CFP（HL），∴∠ACP=∠FCP，∵∠ACF是△ABC的外角，∴∠ABC+∠BAC=∠ACF，两边都除以2，得：∠ABC+∠BAC=∠ACF，即∠PBC+∠BAC=∠FCP，∵∠PCF是△BCP的外角，∴∠PBC+∠BPC=∠FCP，∴∠BPC=∠BAC=×70°=35°，故选：C．二、填空题（本大题共8小题，每小题3分，共24分，请将答案填在题中横线上）9．（3分）若分式有意义，则x的取值范围是x≠3的全体实数．【解答】解：∵3﹣x≠0，∴x≠3．10．（3分）PM 2.5是指大气中直径小于或等于0.0000025m的颗粒物，将0.0000025用科学记数法表示为 2.5×10﹣6．【解答】解：0.0000025=2.5×10﹣6，故答案为：2.5×10﹣6．11．（3分）若a+3b﹣2=0，则3a•27b=9．【解答】解：∵a+3b﹣2=0，∴a+3b=2，则3a•27b=3a×33b=3a+3b=32=9．故答案为：9．12．（3分）因式分解：x3﹣xy2=x（x﹣y）（x+y）．【解答】解：x3﹣xy2=x（x2﹣y2）=x（x﹣y）（x+y）．故答案为：x（x﹣y）（x+y）．13．（3分）计算（π﹣3.14）0+（）﹣2=10．【解答】解：原式=1+9=10，故答案为10．14．（3分）计算：（﹣3）2013•（﹣）2011=9．【解答】解：（﹣3）2013•（﹣）2011=（﹣3）2•（﹣3）2011•（﹣）2011=（﹣3）2•[﹣3×（﹣）]2011=（﹣3）2=9，故答案为：9．15．（3分）如图，在△ABC中，∠C=90°，∠CAB=60°，按以下步骤作图：①分别以A，B为圆心，以大于AB的长为半径做弧，两弧相交于点P和Q．②作直线PQ交AB于点D，交BC于点E，连接AE．若CE=4，则AE=8．【解答】解：由题意可得出：PQ是AB的垂直平分线，∴AE=BE，∵在△ABC中，∠C=90°，∠CAB=60°，∴∠CBA=30°，∴∠EAB=∠CAE=30°，∴CE=AE=4，∴AE=8．故答案为：8．16．（3分）如图，∠AOB=60°，OC平分∠AOB，如果射线OA上的点E满足△OCE 是等腰三角形，那么∠OEC的度数为120°或75°或30°．【解答】解：∵∠AOB=60°，OC平分∠AOB，∴∠AOC=30°，①当E在E1时，OE=CE，∵∠AOC=∠OCE=30°，∴∠OEC=180°﹣30°﹣30°=120°；②当E在E2点时，OC=OE，则∠OCE=∠OEC=（180°﹣30°）=75°；③当E在E3时，OC=CE，则∠OEC=∠AOC=30°；故答案为：120°或75°或30°．三、解答题（7题6分，18题10分，19、20题各8分，21、22题各10分，共52分，解答写出文字说明，演算步骤或推理过程）17．（6分）解方程：．【解答】解：方程两边同乘以（x﹣2），得：x﹣3+（x﹣2）=﹣3，解得x=1，检验：x=1时，x﹣2≠0，∴x=1是原分式方程的解．18．（10分）（1）若a+b=5，ab=3，求+的值；（2）化简：÷（m+n﹣）【解答】解：（1）原式==，当a+b=5，ab=3时，原式===；（2）原式=÷=÷=•=．19．（8分）如图，△ABC中BD、CD平分∠ABC、∠ACB，过D作直线平行于BC，交AB、AC于E、F，求证：EF=BE+CF．【解答】解：∵△ABC中BD、CD平分∠ABC、∠ACB，∴∠1=∠2，∠5=∠6，∵EF∥BC，∴∠2=∠3，∠4=∠6，∴∠1=∠3，∠4=∠5，根据在同一三角形中等角对等边的原则可知，BE=ED，DF=FC，故EF=ED+DF=BE+CF．20．（8分）如图，△ABC为等边三角形，AE=CD，AD、BE相交于点P，BQ⊥AD 于点Q，PQ=3，PE=1．（1）求证：AD=BE；（2）求AD的长．【解答】（1）证明：∵△ABC为等边三角形，∴AB=CA=BC，∠BAE=∠ACD=60°；在△ABE和△CAD中，，∴△ABE≌△CAD（SAS），∴AD=BE；（2）解：∵△ABE≌△CAD，∴∠CAD=∠ABE，∴∠BPQ=∠ABE+∠BAD=∠BAD+∠CAD=∠BAE=60°；∵BQ⊥AD，∴∠AQB=90°，∴∠PBQ=90°﹣60°=30°，∵PQ=3，∴在Rt△BPQ中，BP=2PQ=6，又∵PE=1，∴AD=BE=BP+PE=6+1=7．21．（10分）李老师家距学校1900米，某天他步行去上班，走到路程的一半时发现忘带手机，此时离上班时间还有23分钟，于是他立刻步行回家取手机，随后骑电瓶车返回学校．已知李老师骑电瓶车到学校比他步行到学校少用20分钟，且骑电瓶车的平均速度是步行速度的5倍，李老师到家开门、取手机、启动电瓶车等共用4分钟．（1）求李老师步行的平均速度；（2）请你判断李老师能否按时上班，并说明理由．【解答】解：（1）设李老师步行的平均速度为xm/分钟，骑电瓶车的平均速度为5xm/分钟，由题意得，﹣=20，解得：x=76，经检验，x=76是原分式方程的解，且符合题意，则5x=76×5=380，答：李老师步行的平均速度为76m/分钟，骑电瓶车的平均速度为380m/分；（2）由（1）得，李老师走回家需要的时间为：=12.5（分钟），骑车走到学校的时间为：=5，则李老师走到学校所用的时间为：12.5+5+4=21.5＜23，答：李老师能按时上班．22．（10分）如图，在平面直角坐标系中，O为坐标原点，A、B两点的坐标分别为A（0，m）、B（n，0），且|m﹣n﹣3|+=0，点P从A出发，以每秒1个单位的速度沿射线AO匀速运动，设点P的运动时间为t秒．（1）求OA、OB的长；（2）连接PB，设△POB的面积为S，用t的式子表示S；（3）过点P作直线AB的垂线，垂足为D，直线PD与x轴交于点E，在点P运动的过程中，是否存在这样的点P，使△EOP≌△AOB？若存在，请求出t的值；若不存在，请说明理由．【解答】解：（1）∵|m﹣n﹣3|+=0，且|m﹣n﹣3|≥0，≥0∴|m﹣n﹣3|==0，∴n=3，m=6，∴点A（0，6），点B（3，0）；（2）连接PB，t秒后，AP=t，OP=|6﹣t|，∴S=OP•OB=|6﹣t|；（t≥0）（3）作出图形，∵∠OAB+∠OBA=90°，∠OAB+∠APD=90°，∠OPE=∠APD，∴∠OBA=∠OPE，∴只要OP=OB，即可求证△EOP≌△AOB，∴AP=AO﹣OP=3，或AP′=OA+OP′=9∴t=3或9．。

8年级上期末数学试卷

河北区2014－2015学年度第一学期期末八年级质量检测数学本试卷满分100分，另附加题20分，考试时间70分钟一、选择题：本大题共8个小题，每小题3分，共24分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．下列式子，从左到右的变形中是因式分解的是(A)aaaa2)2(2-=-(B)4)4(442+-=+-aaaa(C)2(1)(1)1a a a+-=-(D))3)(3(92-+=-aaa2．下列图形中，不是轴对称图形的是(A) (B) (C) (D)3．下列变形正确的是(A)326x xx =(B)n n x x ππ=++ (C)y x yx y x +=++22(D)1-=-+-y x y x4．下列运算正确的是(A) 623a a a =⋅(B) 632)(a a -=- (C) 33)(ab ab =(D)428a a a =÷5．下列代数式中能用平方差公式分解因式的是(A) 22b a +(B) 22b a --(C) ac c a 222--(D)224b a +-6．如图，小明将一张三角形纸片（△ABC ），沿着DE 折叠（点D 、E 分别在边AB 、AC 上），并使点A 与点A ′重合，若∠A =70°，则∠1+∠2的度数为(A) 140° (B) 130° (C) 110°(D) 70°7．如图，点P 是∠AOB 外的一点，点M ，N 分别是∠AOB 两边上的点，点P 关于OA 的对称点Q 恰好落在线段MN 上，点P 关于OB 的对称点R 落在MN 的延长线上．若PM =2.5cm ， PN =3cm ，MN =4cm ，则线段QR 的长为(A) 4.5 cm (B) 5.5 cm (C) 6.5 cm(D) 7 cm8．如图，已知六边形ABCDEF 的每个内角都是120°，且AB =1，BC =CD =7，DE =3，则这个六边形周长为(A) 31 (B) 36 (C) 32 (D) 29二、填空题：本大题共8个小题，每小题3分，共24分．将答案填在题中横线上．9．若分式5-x 有意义，则实数x 的取值范围是． 10．若实数m ，n 满足|m ﹣2|+(n ﹣2014)2=0，则=+-01n m ．12．已知6=+y x ，4=xy ，则22xy y x +的值为．13．如图，在△ABC 中，AB =AC ，∠A =30°，以B 为圆心，BC 的长为半径画弧，交AC 于点D ，连接BD ，则∠ABD = ．14．如图为6个边长相等的正方形的组合图形，则∠1+∠2+∠3= ．15．一个大正方形和四个全等的小正方形按图①、②两种方式摆放，则图②的大正方形中未被小正方形覆盖部分的面积是（用a 、b 的代数式表示）． 16．姐妹两人在50米的跑道上进行短跑比赛，两人从出发点同时起跑，姐姐到达终点时，妹妹离终点还差3米，已知姐妹两人的平均速度分别为a 米/秒、b 米/秒．如果两人想同时到达终点，起跑时姐姐需后退米．三、解答题： 17、18、19、20题各8分，21、 22题各10分，共52分.解答应写出文字说明、证明过程或演算步骤.（2）先化简，再求值：2[(2)(2)(2)]4a b a b a b b --+-÷，其中2=a ，1-=b ．（1）解方程：1221+=+-x x ；（2）化简：)21()(2222abb a ab a b b ab a ++÷---．19．（本小题满分8分）如图，在△ABC中，AB=AC，点F在AC上，在BA的延长线上截取AE=AF，EF的延长线交BC于D点，求证：EF⊥BC．20．（本小题满分8分）AOB的顶点O在直线l上，且AO=AB．（1）画出△AOB关于直线l成轴对称的图形△COD，且使点A的对称点为点C；（2）在（1）的条件下，AC与BD的位置关系是；（3）在（1）、（2）的条件下，连接AD，如果∠ABD=2∠ADB，求∠AOC的度数．21．（本小题满分10分）队单独完成这项工程所需天数是甲队单独完成这项工程所需天数的2倍；该工程甲队计划用若干天完成，若在甲队独立工作6天后，乙队加入此项工作，结果比甲队计划时间提前8天完成任务．（1）求甲队计划完成这项工程需要多少天？（2）已知甲队每天的施工费用为0.67万元，乙队每天的施工费用为0.33万元，该工程预算的施工费用为19万元．为缩短工期，拟安排甲、乙两队同时开工合作完成这项工程，问：该工程预算的施工费用是否够用？若不够用，需要追加预算多少万元？请说明理由．22．（本小题满分10分），AC⊥AB，BD⊥AB，AC=BD=3cm．点P在线段AB上以1cm/s 的速度由点A向点B运动，同时，点Q在线段BD上由点B向点D运动．它们运动的时间为t（s）．（1）若点Q的运动速度与点P的运动速度相等，当t=1时，△ACP与△BPQ是否全等，请说明理由，并判断此时线段PC和线段PQ的位置关系；（2）如图（2），将图（1）中的“AC⊥AB，BD⊥AB”改为“∠CAB=∠DBA=60°”，其他条件不变．设点Q的运动速度为x cm/s，是否存在实数x，使得△ACP与△BPQ全等？若存在，求出相应的x、t的值；若不存在，请说明理由．附加题20分:（市重点学校：外大附校、二中、十四中、五十七中、扶抡中学、红光中学必答，其它学校选答）一、填空题：（本大题共4个小题，每小题3分，共12分．将答案填在题中横线上） 1．若x ＝20072007200720112007200820072010⨯-⨯，y ＝20072008200720122007200920072011⨯-⨯，x 、y 2．如果a 、b 是整数，且12-+x x 是13++bx ax 的因式，则b 的值为．3．已知x 为整数，且 222218339x x x x ++++-- 为整数，则所有符合条件的x 值的和（不与点A 、点D 重合）将正方形纸片折叠，使点B 落在P 处，点C 落在G 处， PG 交DC 于H ，折痕为EF ，连接BP 、BH ．（1）求证：∠APB =∠BPH ；（2）当点P 在边AD 上移动时，△PDH 的周长是否发生变化？并证明你的结论．。

河北区2015-2016 上学期8年级期中数学试卷

河北区2015－2016学年度第一学期期中八年级质量检测数学本试卷满分100分，考试时间70分钟一、选择题：（本大题共8个小题，每小题3分，共24分．在每小题给出的四个选项中，只有一项是符合题目要求的）1．下列图形是轴对称图形的是A ．B ．C ．D ．2．以下列各组数为长度的三条线段能组成三角形的是A ．5，5，8B ．4，5，9C ．3，5，8D ．4，4，93．点M （3，﹣4）关于y 轴的对称点的坐标是 A ．（3，4）B ．（﹣3，﹣4）C ．（﹣3，4）D ．（﹣4，3）4．已知一个多边形的内角和等于它的外角和的3倍，那么它的边数是 A ．5 B ．6 C ．7 D ．85．用同一种正多边形地砖不能镶嵌成平整的地面的是 A ．正三角形地砖 B ．正方形地砖 C ．正五边形地砖 D ．正六边形地砖 AC C ．6D ．57．长为l 的一根绳，恰好可围成两个全等三角形，则其中一个三角形的最长边x 的取值范围为 A ．61≤x ＜41 B ．81≤x ＜41C ．61＜x ＜41D ．81＜x ＜418．如图，△ABC 中，∠ABC 、∠EAC 的角平分线BP 、AP 交于点P ，下列结论： ① CP 平分∠ACF ； ②∠AB C ＋∠APC =180°；③若PM ⊥BE 于M ，PN ⊥BF 于N ，则A M ＋CN ＝AC ； ④∠BAC ＝2∠BPC ．其中正确的是 A ．①②③ B ．①③④ C ．②③④ D ．①③9．小明从镜子中看到对面电子钟如图所示，这时的时刻应是．10．等腰三角形两边长分别是3和6，则该三角形的周长为．11．如图，△ABC 中，BO ，CO 分别是∠ABC ，∠ACB 的平分线，∠A ＝50°，则∠BOC 等于________________．12．如图，点B在线段AE上，∠1＝∠2，如果添加一个条件，即可得到△ABC ≌△ABD，那么这个条件可以是．（要求：不在图中添加其他辅助线，写出一个条件即可）13．如图，AB＝AC，AB的垂直平分线MN交AC于点D，AB＝8cm，BC＝5cm，则△DBC的周长是cm．14．如图，∠1，∠2，∠3，∠4是五边形ABCDE的外角，且∠1＝∠2＝∠3＝∠4＝70°，则∠AED的度数是．15．如图所示，在△ABC中，已知点D、E、F分别为边BC、AD、CE的中点，且△ABC的面积是4cm2，则阴影部分面积等于cm2．16．如图，在平面直角坐标系中，矩形OABC的两边分别在x轴和y轴上，OA＝10cm，OC＝6cm．F是线段OA上的动点，从点O出发，以1cm/s的速度沿OA方向作匀速运动，点Q在线段AB上．已知A、Q两点间的距离是O、F两点间距离的a倍．若用（a，t）表示经过时间t（s）时，△OCF、△F AQ、△CBQ中有两个三角形全等．请写出（a，t）的所有可能情况．（备用图）三、解答题：（17题6分，18、19、20题各8分，21题10分，22题12分，共52分）17．（本小题满分6分）在边长为1的小正方形组成的正方形网格中建立如图片所示的平面直角坐标系，已知格点三角形ABC （三角形的三个顶点都在小正方形上）（1）画出△ABC 关于直线l ：x ＝﹣1的对称三角形△A 1B 1C 1；（2）写出A 1、B 1、C 1的坐标．18．（本小题满分8分）如图，已知在△ABC 中，AD 是BC 边上的高，AE 是∠BAC 的角平分线，若∠B ＝40°，∠C ＝62°．求∠DAE 的度数．lO 1 2 3 4-119．（本小题满分8分）如图，E，F在BC上，BE＝CF，AB＝CD，AB∥CD．求证：（1）△ABF ≌△DCE．（2）AF∥DE．21．（本小题满分10分）如图，在△ABC中，AD为∠BAC的平分线，DG⊥BC且平分BC，DE⊥AB于E，DF⊥AC交AC的延长线于F．（1）求证：BE＝CF；（2）如果AB＝6，AC＝4，求BE的长．22．（本小题满分12分）如图，已知点A（a，0），B（0，b），且（a＋2）2＋|b－4|＝0，以B点为直角顶点在第二象限作等腰直角△ABC．（1）填空：a＝，b＝；（2）求C点的坐标；（需要过程）（3）在坐标平面内是否存在点P（不与点C重合），使△P AB与△ABC全等？若存在，请直接写出满足条件的所有P点的坐标（不需要过程）；若不存在，请说明理由．。

2015-2016年天津市河西区八年级(上)期末数学试卷和参考答案

10．（3 分）如图，先将正方形纸片对折，折痕为 MN，再把 B 点折叠在折痕 MN 上，折痕为 AE，点 B 在 MN 上的对应点为 H，沿 AH 和 DH 剪下得到△ADH，则下列选项正确的个数为（）
①AE 垂直平分 HB；②∠HBN=15°；③DH=DC；④△ADH 是一个等边三角形．
A．1 个 B．2 个 C．3 个 D．4 个
C．（5，﹣1） D．（1，﹣5））
2．（3 分）下列图形中，可以看做是轴对称图形的是（
A．1 个 B．2 个 C．3 个 D．4 个 3．（3 分）下列等式不成立的是（ A．（ab）2=a2b2 B．a5÷a2=a3 4．（3 分）化简（ A． B． C．）
C．（a﹣b）2=（b﹣a）2 D．（a+b）2=（﹣a+b）2 ）÷ D．的结果为（）
5．（3 分）如图，地面上有三个洞口 A、B、C，老鼠可以从任意一个洞口跑出，猫为能同时最省力地顾及到三个洞口（到 A、B、C 三个点的距离相等），尽快抓到老鼠，应该蹲守在（）
A．△ABC 三边垂直平分线的交点 C．△ABC 三条高所在直线的交点
B．△ABC 三条角平分线的交点 D．△ABC 三条中线的交点）根木条．
6．（3 分）要使六边形木架不变形，至少要再钉上（ A．2 B．3 C．4 D．5
7．（3 分）纳米是非常小的长度单位，1nm=10﹣9m，那么，1mm3 的空间可以放多少个 1nm3 的物体（不计物体之间的间隙）（
第 1 页（共 17 页）
）
A．1018 B．10﹣9 C．10﹣18
D．109
22．（8 分）甲乙两人做某种机器零件，已知甲每小时比乙多做 6 个，甲做 90 个所用的时间与乙做 60 个所用的时间相等，求甲乙每小时各做多少个零件？ 23．（8 分）如图 1，直线 AB 交 x 轴于点 A（4，0），交 y 轴于点 B（0，﹣4），（1）如图，若 C 的坐标为（﹣1，0），且 AH⊥BC 于点 H，AH 交 OB 于点 P，试求点 P 的坐标；（2）在（1）的条件下，如图 2，连接 OH，求证：∠OHP=45°；（3）如图 3，若点 D 为 AB 的中点，点 M 为 y 轴正半轴上一动点，连结 MD，过点 D 作 DN⊥DM 交 x 轴于 N 点，当 M 点在 y 轴正半轴上运动的过程中，式子 S

[精品]2016-2017学年天津市部分区八年级(上)期末数学试卷与参考答案

2016-2017学年天津市部分区八年级（上）期末数学试卷一、选择题（本题包括12小题，每小题3分，共36分）1．（3分）下列式子是分式的是（）A．B． C．+y D．2．（3分）计算（﹣3a3）2的结果是（）A．﹣6a5B．6a5C．9a6D．﹣9a63．（3分）如果一个三角形的两边长分别为2和5，则此三角形的第三边长可能为（）A．2 B．3 C．6 D．74．（3分）下列平面图形中，不是轴对称图形的是（）A．B．C． D．5．（3分）下列运算正确的是（）A．﹣2（a+b）=﹣2a+2b B．x5+x5=x C．a6﹣a4=a2D．3a2•2a3=6a5 6．（3分）下列从左到右的变形是因式分解的是（）A．6a2b2=3ab•2ab B．﹣8x2+8x﹣2=﹣2（2x﹣1）2C．2x2+8x﹣1=2x（x+4）﹣1 D．a2﹣1=a（a﹣）7．（3分）下列说法正确的是（）A．形状相同的两个三角形全等B．面积相等的两个三角形全等C．完全重合的两个三角形全等D．所有的等边三角形全等8．（3分）下列多项式中，含有因式（y+1）的多项式是（）A．y2﹣2xy﹣3x2B．（y+1）2﹣（y﹣1）2C．（y+1）2﹣（y2﹣1）D．（y+1）2+2（y+1）+19．（3分）若一个多边形的内角和与它的外角和相等，则这个多边形是（）A．三角形B．四边形C．五边形D．六边形10．（3分）两组邻边分别相等的四边形叫做“筝形”，如图，四边形ABCD是一个筝形，其中AD=CD，AB=CB，在探究筝形的性质时，得到如下结论：①△ABD≌△CBD；②AC⊥BD；③四边形ABCD的面积=AC•BD，其中正确的结论有（）A．0个 B．1个 C．2个 D．3个11．（3分）八年级学生去距学校10千米的博物馆参观，一部分学生骑自行车先走，过了20分钟后，其余学生乘汽车出发，结果他们同时到达，已知汽车的速度是骑车学生速度的2倍．设骑车学生的速度为x千米/小时，则所列方程正确的是（）A．﹣=20 B．﹣=20 C．﹣=D．﹣=12．（3分）已知a、b、c是△ABC的三边的长，且满足a2+b2+c2=ab+bc+ac，关于此三角形的形状有下列判断：①是锐角三角形；②是直角三角形；③是钝角三角形；④是等边三角形，其中正确说法的个数是（）A．4个 B．3个 C．2个 D．1个二、填空题（本题包括6小题，每小题3分，共18分）13．（3分）若分式有意义，则x的取值范围是．14．（3分）若a2+ab+b2+M=（a﹣b）2，那么M=．15．（3分）在实数范围内分解因式：x2y﹣4y=．16．（3分）如图，已知AD所在直线是△ABC的对称轴，点E、F是AD上的两点，若BC=4，AD=3，则图中阴影部分的面积的值是．17．（3分）若关于x的方程无解，则m的值是．18．（3分）如图，在第一个△A1BC中，∠B=30°，A1B=CB，在边A1B上任取一D，延长CA2到A2，使A1A2=A1D，得到第2个△A1A2D，在边A2B上任取一点E，延长A1A2到A3，使A2A3=A2E，得到第三个△A2A3E，…按此做法继续下去，第n个等腰三角形的底角的度数是度．三、解答题（本题共46分）19．（6分）（1）计算（12a3﹣6a2+3a）÷3a；（2）计算（x﹣y）（x2+xy+y2）．20．（4分）解方程：﹣=21．（6分）如图，△ABC中，∠C=90°，AD是∠BAC的平分线，DE⊥AB于E，点F在AC上，BD=DF，求证：CF=BE．22．（6分）已知a+b=3，ab=2，求代数式a3b+2a2b2+ab3的值．23．（8分）（1）计算：+（2）先化简，再求值：（）÷，其中x=3．24．（8分）一项工程，若由甲、乙两公司合作18天可以完成，共需付施工费144000元，若甲、乙两公司单独完成此项工程，甲公司所用时间是乙公司的1.5倍，已知甲公司每天的施工费比乙公司每天的施工费少2000元．（1）求甲、乙两公司单独完成此项工程，各需多少天？（2）若由一个公司单独完成这项工程，哪个公司的施工费较少？25．（8分）如图，在△ABC中，已知AB=AC，AB的垂直平分线交AB于点N，交AC于点M，连接MB．（1）若∠ABC=70°，则∠NMA的度数是度．（2）若AB=8cm，△MBC的周长是14cm．①求BC的长度；②若点P为直线MN上一点，请你直接写出△PBC周长的最小值．2016-2017学年天津市部分区八年级（上）期末数学试卷参考答案与试题解析一、选择题（本题包括12小题，每小题3分，共36分）1．（3分）下列式子是分式的是（）A．B． C．+y D．【解答】解：A、分母中不含有字母的式子是整式，故A错误；B、分母中含有字母的式子是分式，故B正确；C、分母中不含有字母的式子是整式，故C错误；D、分母中不含有字母的式子是整式，故D错误；故选：B．2．（3分）计算（﹣3a3）2的结果是（）A．﹣6a5B．6a5C．9a6D．﹣9a6【解答】解：（﹣3a3）2=9a6．故选C．3．（3分）如果一个三角形的两边长分别为2和5，则此三角形的第三边长可能为（）A．2 B．3 C．6 D．7【解答】解：设第三边长为x，则由三角形三边关系定理得5﹣2＜x＜5+2，即3＜x＜7．故选：C．4．（3分）下列平面图形中，不是轴对称图形的是（）A．B．C． D．【解答】解：A、不是轴对称图形，故本选项正确；B、是轴对称图形，故本选项错误；C、是轴对称图形，故本选项错误；D、是轴对称图形，故本选项错误．故选A．5．（3分）下列运算正确的是（）A．﹣2（a+b）=﹣2a+2b B．x5+x5=x C．a6﹣a4=a2D．3a2•2a3=6a5【解答】解：A、﹣2（a+b）=﹣2a﹣2b，故此选项错误；B、x5+x5=2x5，故此选项错误；C、a6﹣a4，无法计算，故此选项错误；D、3a2•2a3=6a5，正确．故选：D．6．（3分）下列从左到右的变形是因式分解的是（）A．6a2b2=3ab•2ab B．﹣8x2+8x﹣2=﹣2（2x﹣1）2C．2x2+8x﹣1=2x（x+4）﹣1 D．a2﹣1=a（a﹣）【解答】解：把一个多项式在一个范围（如有理数范围内分解，即所有项均为有理数）化为几个整式的积的形式，称为多项式的因式分解故选（B）7．（3分）下列说法正确的是（）A．形状相同的两个三角形全等B．面积相等的两个三角形全等C．完全重合的两个三角形全等D．所有的等边三角形全等【解答】解：A、形状相同的两个三角形全等，说法错误，应该是形状相同且大小也相同的两个三角形全等；B、面积相等的两个三角形全等，说法错误；C、完全重合的两个三角形全等，说法正确；D、所有的等边三角形全等，说法错误；故选：C．8．（3分）下列多项式中，含有因式（y+1）的多项式是（）A．y2﹣2xy﹣3x2B．（y+1）2﹣（y﹣1）2C．（y+1）2﹣（y2﹣1）D．（y+1）2+2（y+1）+1【解答】解：A、y2﹣2xy﹣3x2=（y﹣3x）（y+x），故不含因式（y+1）．B、（y+1）2﹣（y﹣1）2=[（y+1）﹣（y﹣1）][（y+1）+（y﹣1）]=4y，故不含因式（y+1）．C、（y+1）2﹣（y2﹣1）=（y+1）2﹣（y+1）（y﹣1）=2（y+1），故含因式（y+1）．D、（y+1）2+2（y+1）+1=（y+2）2，故不含因式（y+1）．故选C．9．（3分）若一个多边形的内角和与它的外角和相等，则这个多边形是（）A．三角形B．四边形C．五边形D．六边形【解答】解：设多边形的边数为n，根据题意得（n﹣2）•180°=360°，解得n=4．故这个多边形是四边形．故选B．10．（3分）两组邻边分别相等的四边形叫做“筝形”，如图，四边形ABCD是一个筝形，其中AD=CD，AB=CB，在探究筝形的性质时，得到如下结论：①△ABD≌△CBD；②AC⊥BD；③四边形ABCD的面积=AC•BD，其中正确的结论有（）A．0个 B．1个 C．2个 D．3个【解答】解：在△ABD与△CBD中，，∴△ABD≌△CBD（SSS），故①正确；∴∠ADB=∠CDB，在△AOD与△COD中，，∴△AOD≌△COD（SAS），∴∠AOD=∠COD=90°，AO=OC，∴AC⊥DB，故②正确；四边形ABCD的面积==AC•BD，故③正确；故选D．11．（3分）八年级学生去距学校10千米的博物馆参观，一部分学生骑自行车先走，过了20分钟后，其余学生乘汽车出发，结果他们同时到达，已知汽车的速度是骑车学生速度的2倍．设骑车学生的速度为x千米/小时，则所列方程正确的是（）A．﹣=20 B．﹣=20 C．﹣=D．﹣=【解答】解：由题意可得，﹣=，故选C．12．（3分）已知a、b、c是△ABC的三边的长，且满足a2+b2+c2=ab+bc+ac，关于此三角形的形状有下列判断：①是锐角三角形；②是直角三角形；③是钝角三角形；④是等边三角形，其中正确说法的个数是（）A．4个 B．3个 C．2个 D．1个【解答】解：∵a2+b2+c2=ab+bc+ca，∴2a2+2b2+2c2=2ab+2bc+2ca，即（a﹣b）2+（b﹣c）2+（a﹣c）2=0，∴a=b=c，∴此三角形为等边三角形，同时也是锐角三角形．故选C．二、填空题（本题包括6小题，每小题3分，共18分）13．（3分）若分式有意义，则x的取值范围是x≠1．【解答】解：由题意得：x﹣1≠0，解得：x≠1，故答案为：x≠1．14．（3分）若a2+ab+b2+M=（a﹣b）2，那么M=﹣3ab．【解答】解：∵a2+ab+b2+M=（a﹣b）2=a2﹣2ab+b2，∴M=﹣3ab．故答案为：﹣3ab．15．（3分）在实数范围内分解因式：x2y﹣4y=y（x+2）（x﹣2）．【解答】解：原式=y（x2﹣4）=y（x+2）（x﹣2），故答案为：y（x+2）（x﹣2）16．（3分）如图，已知AD所在直线是△ABC的对称轴，点E、F是AD上的两点，若BC=4，AD=3，则图中阴影部分的面积的值是3．【解答】解：∵△ABC关于直线AD对称，∴B、C关于直线AD对称，∴△CEF和△BEF关于直线AD对称，∴S=S△CEF，△BEF∵△ABC的面积是：×BC×AD=×3×4=6，∴图中阴影部分的面积是S=3．△ABC故答案为：3．17．（3分）若关于x的方程无解，则m的值是2．【解答】解：关于x的分式方程无解即是x=1，将方程可转化为m﹣1﹣x=0，当x=1时，m=2．故答案为2．18．（3分）如图，在第一个△A1BC中，∠B=30°，A1B=CB，在边A1B上任取一D，延长CA2到A2，使A1A2=A1D，得到第2个△A1A2D，在边A2B上任取一点E，延长A1A2到A3，使A2A3=A2E，得到第三个△A2A3E，…按此做法继续下去，第n个等腰三角形的底角的度数是度．【解答】解：∵在△ABA1中，∠B=30°，AB=A1B，∴∠BA1A==75°，∵A1A2=A1D，∠BA1C是△A1A2D的外角，∴∠DA2A1=∠BA1C=×75°=37.5°；同理可得，∠EA3A2=，∠FA4A3=，∴第n个等腰三角形的底角的度数=．故答案为．三、解答题（本题共46分）19．（6分）（1）计算（12a3﹣6a2+3a）÷3a；（2）计算（x﹣y）（x2+xy+y2）．【解答】解：（1）（12a3﹣6a2+3a）÷3a=12a3÷3a﹣6a2÷3a+3a÷3a=4a2﹣2a+1（2）（x﹣y）（x2+xy+y2）=x3+x2y+xy2﹣x2y﹣xy2﹣y3=x3﹣y3．20．（4分）解方程：﹣=【解答】解：方程两边同乘以（x+1）（x﹣1），得2（x﹣1）﹣3（x+1）=6，∴2x﹣2﹣3x﹣3=6，∴x=﹣11．经检验：x=﹣11是原方程的根．21．（6分）如图，△ABC中，∠C=90°，AD是∠BAC的平分线，DE⊥AB于E，点F在AC上，BD=DF，求证：CF=BE．【解答】证明：∵∠C=90°，∴DC⊥AC．∵AD是∠BAC的平分线，DE⊥AB，∴DC=DE．在Rt△DCF和Rt△DEB中，，∴Rt△DCF≌Rt△DEB（HL），∴CF=EB．22．（6分）已知a+b=3，ab=2，求代数式a3b+2a2b2+ab3的值．【解答】解：a3b+2a2b2+ab3=ab（a2+2ab+b2）=ab（a+b）2，将a+b=3，ab=2代入得，ab（a+b）2=2×32=18．故代数式a3b+2a2b2+ab3的值是18．23．（8分）（1）计算：+（2）先化简，再求值：（）÷，其中x=3．【解答】解：（1）原式=+=+=；（2）原式=[﹣]•=•=，当x=3时，原式=．24．（8分）一项工程，若由甲、乙两公司合作18天可以完成，共需付施工费144000元，若甲、乙两公司单独完成此项工程，甲公司所用时间是乙公司的1.5倍，已知甲公司每天的施工费比乙公司每天的施工费少2000元．（1）求甲、乙两公司单独完成此项工程，各需多少天？（2）若由一个公司单独完成这项工程，哪个公司的施工费较少？【解答】解：（1）设乙公司单独完成此项工程需x天，则甲公司单独完成需要1.5x天．由题意，得=．解得：x=30经检验x=30是原方程的解．则1.5x=45．答：甲公司单独完成需要45天，乙公司单独完成需要30天．（2）设甲公司每天的施工费用为y元，则乙公司每天的施工费用为（y+2000）元．由题意，得18（y+y+2000）=144000．解得y=3000．则y+2000=5000．甲公司施工费为：3000×45=135000乙公司施工费为：5000×30=150000答：甲公司施工费用较少．25．（8分）如图，在△ABC中，已知AB=AC，AB的垂直平分线交AB于点N，交AC于点M，连接MB．（1）若∠ABC=70°，则∠NMA的度数是50度．（2）若AB=8cm，△MBC的周长是14cm．①求BC的长度；②若点P为直线MN上一点，请你直接写出△PBC周长的最小值．【解答】解：（1）∵AB=AC，∴∠C=∠ABC=70°，∴∠A=40°，∵AB的垂直平分线交AB于点N，∴∠ANM=90°，∴∠NMA=50°，故答案为：50；（2）①∵MN是AB的垂直平分线，∴AM=BM，∴△MBC的周长=BM+CM+BC=AM+CM+BC=AC+BC，∵AB=8，△MBC的周长是14，∴BC=14﹣8=6；②当点P与M重合时，△PBC周长的值最小，理由：∵PB+PB=PA+PC，PA+PC≥AC，∴P与M重合时，PA+PC=AC，此时PB+PC最小，∴△PBC周长的最小值=AC+BC=8+6=14．。

2015-2016学年度第一学期八年级数学上册期末考试试卷

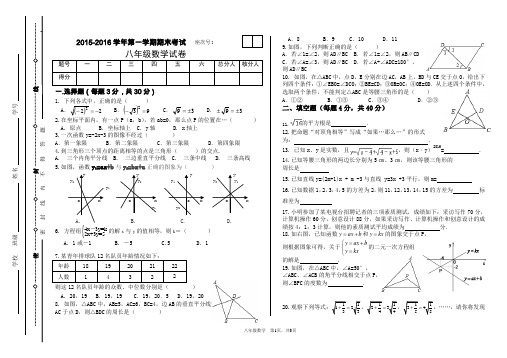
八年级数学第1页，共3页密学校班级姓名学号密封线内不得答题2015-2016学年第一学期期末考试座次号：八年级数学试卷一.选择题（每题3分，共30分）1. 下列各式中，正确的是（）A ．()222-=- B ．()932=- C ．39±= D ．39±=±2.在坐标平面内，有一点P （a ，b ），若ab=0，那么点P 的位置在…（） A. 原点 B. 坐标轴上 C. y 轴 D. x 轴上3.一次函数y=-2x-3的图像不经过（）A ．第一象限B ．第二象限C ．第三象限D ．第四象限 4.到三角形三个顶点的距离相等的点是三角形（）的交点.A. 三个内角平分线B. 三边垂直平分线C. 三条中线D. 三条高线 5.如图，函数y 1=ax +b 与y 2=bx+a 正确的图象为（）1 6. 方程组{4x 3y=k 2x+3y=5－的解x 与y 的值相等，则k ＝（）A. 1或－1B. －5C.5D. 1 则这12名队员年龄的众数、中位数分别是（） A. 20，19 B. 19，19 C. 19，20．5 D. 19，208. 如图，△ABC 中，AB=5，AC=6，BC=4，边AB 的垂直平分线交 AC 于点D ，则△BDC 的周长是（）A ．8B ．9C ．10D ．11 9.如图，下列判断正确的是（）A ．若∠1=∠2，则AD∥BCB ．若∠1=∠2，则AB∥CDC ．若∠A=∠3，则AD∥BCD ．若∠A+∠ADC=180°，则AD∥BC10. 如图，在△ABC 中，点D ，E 分别在边AC ，AB 上，BD 与CE 交于点O ，给出下列四个条件：①∠EBO=∠DCO ；②BE=CD ；③OB=OC ；④OE=OD ．从上述四个条件中，选取两个条件，不能判定△ABC 是等腰三角形的是（） A ．①② B ．①③ C ．③④ D ．②③二、填空题（每题4分，共40分）11.的平方根是．12.把命题“对顶角相等”写成“如果…那么…”的形式为：． 13. 已知x 、y 是实数，且，则（x ﹣y ）2016= ．14.已知等腰三角形的两边长分别为5㎝、3㎝，则该等腰三角形的周长是15.已知直线y=(2m+1)x + m -3与直线 y=3x +3平行，则m= 16.已知数据1，2，3，4，5的方差为2，则11，12，13，14，15的方差为标准差为17.小明参加了某电视台招聘记者的三项素质测试，成绩如下：采访写作70分，计算机操作60分，创意设计88分，如果采访写作、计算机操作和创意设计的成绩按4：1：3计算，则他的素质测试平均成绩为分． 18.如右图，已知函数y ax b =+和y kx =的图象交于点P ，则根据图象可得，关于y ax by kx =+⎧⎨=⎩的二元一次方程组的解是 .19.如图，在△ABC 中，∠A=50°， ∠ABC、∠ACB 的角平分线相交于点P ，则∠BPC 的度数为．20.==第2页，共3 页的规律用含自然数n(n≥1)的等式表示出来___________________。

2015-2016学年度第一学期期末八年级数学试题(含答案)

2015—2016学年度第一学期期末考试八年级数学试卷试卷说明:本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，共4页，满分120分，考试时间100分钟。

答题前，学生务必将自己的姓名和学校、班级、学号等填写在答题卷上；答案必须写在答题卷各题目指定区域内的相应位置上；考试结束后，只需将答题卷交回。

第Ⅰ卷（选择题）一、选择题（本大题共10小题，每小题3分，共30分，在每小题给出的四个选项中，只有一项正确） 1、9的平方根是( )．A ．3B ．－3C ．±3D ．±32、将下列长度的三根木棒首尾顺次连接，能组成直角三角形的是（）．A ．1、2、3B ． 2、3、4C ． 3、4、5D ．4、5、63、下列说法：①实数与数轴上的点一一对应；②2a 没有平方根；③任何实数的立方根有且只有一个；④平方根与立方根相同的数是0和1.其中正确的有（） A ．1个 B ．2个 C ．3个 D ．4个4、下列各组图形，可以经过平移变换由一个图形得到另一个图形的是（）．A B C D5、若一个多边形的内角和等于720°，则这个多边形的边数是（）． A ．5 B ．6 C ．7 D ．86、为筹备本班元旦联欢晚会，在准备工作中，班长对全班同学爱吃什么水果作了民意调查，再决定最终买哪种水果，下面的调查数据中，他最关注的是（） A ．中位数 B ．平均数 C ．加权平均数 D ．众数7、如图，已知棋子“车”的坐标为（-2，3），棋子“马” 的坐标为（1，3），则棋子“炮”的坐标为（）．A ．（3，1）B ．（2，2）C ．（3，2）D ．（-2，2）8．下列一次函数中，y 的值随着x 值的增大而减小的是( )． A ．y ＝x B ．y ＝－x C ．y ＝x ＋1 D ．y ＝ x －19、如图所示，两张等宽的纸条交叉重叠在一起，则重叠部分ABCD 一定是（）． A ．菱形 B ．矩形 C ．正方形 D ．梯形10、一水池蓄水20 m 3，打开阀门后每小时流出5 m 3，放水后池内剩下的水的立方数Q （m 3）与放水时间t （时）的函数关系用图表示为（）A B C D（第9题图）（第7题图）第Ⅱ卷（非选择题）二、填空题（本大题共5小题，每小题3分，共15分，将答案填写在题中横线上） 11、比较大小：32（填“＞”、“＜”、或“=”）．12、写出一个你所学过的既是轴对称又是中心对称图形的四边形：．13、如图，是用形状、大小完全相同的等腰梯形密铺成的图案，则这个图案中的等腰梯形的底角（指锐角）是度．14、如图，若直线l 1：32-=x y 与l 2：3+-=x y 相交于点P ，则根据图象可得，二元一次方程组⎩⎨⎧=+=-332y x y x 的解是． 15、如图，在直角坐标平面内的△ABC 中，点A 的坐标为（0，2），点C 的坐标为（5，5），要使以A 、B 、 C 、D 为顶点的四边形是平行四边形，且点D 坐标在第一象限，那么点D 的坐标是．三、解答题（本大题共10小题，共75分。

天津市河北区八年级上期末数学试卷(有答案)-精选

天津市河北区八年级（上）期末数学试卷一、选择题（本大题共8个小题，每小题3分，共24分，在每小题给出的四个选项中只有一项是符合题目要求的）1．（3分）下面四个图形分别是节能、节水、低碳和绿色食品标志，是轴对称图形的是（）A．B．C．D．2．（3分）下列等式从左到右的变形，属于因式分解的是（）A．x2+2x﹣1=（x﹣1）2B．（a+b）（a﹣b）=a2﹣b2C．x2+4x+4=（x+2）2D．ax2﹣a=a（x2﹣1）3．（3分）要使分式有意义，x应满足的条件是（）A．x＞3 B．x=3 C．x＜3 D．x≠34．（3分）计算x3•x2的结果是（）A．x6B．x5C．x2D．x5．（3分）已知点P（a，3）、Q（﹣2，b）关于y轴对称，则=（）A．﹣5 B．5 C．﹣ D．6．（3分）下列各式：①，②，③，④，其中是分式的有（）A．①②③④B．①④C．①②④D．②④7．（3分）小朱要到距家1500米的学校上学，一天，小朱出发10分钟后，小朱的爸爸立即去追小朱，且在距离学校60米的地方追上了他．已知爸爸比小朱的速度快100米/分，求小朱的速度．若设小朱速度是x米/分，则根据题意所列方程正确的是（）A．B．C．D．8．（3分）如图，等腰三角形ABC的底边BC长为4，面积是16，腰AC的垂直平分线EF分别交AC，AB边于E，F点．若点D为BC边的中点，点M为线段EF上一动点，则△CDM周长的最小值为（）A．6 B．8 C．10 D．12二、填空题（本大题共8个小题，每小题3分，共24分，将答案填在题中横线上）9．（3分）当x=时，分式的值为零．10．（3分）一种病毒的直径为0.000023m，这个数用科学记数法表示为．11．（3分）已知x m=6，x n=3，则x2m﹣n的值为．12．（3分）分解因式：27x2+18x+3=．13．（3分）若关于x的分式方程无解，则m的值是．14．（3分）如图，在等腰△ABC的两腰AB、BC上分别取点D和E，使DB=DE，此时恰有∠ADE=∠ACB，则∠B的度数是．15．（3分）如图，∠ABC=50°，BD平分∠ABC，过D作DE∥AB交BC于点E，若点F在AB上，且满足DF=DE，则∠DFB的度数为．16．（3分）如图，△ADB、△BCD都是等边三角形，点E，F分别是AB，AD上两个动点，满足AE=DF．连接BF与DE相交于点G，CH⊥BF，垂足为H，连接CG．若DG=a，BG=b，且a、b满足下列关系：a2+b2=5，ab=2，则GH=．三、解答题（17、18、19、20题各8分，21、22题10分，共52分，解答应写出文字说明、证明过程或演算步骤）17．（8分）（1）（﹣2a）3﹣（﹣a）•（3a）2（2）（2a﹣3b）2﹣4a（a﹣2b）18．（8分）先化简再求值：（1﹣）÷，其中x=（）﹣1+3019．（8分）解分式方程： +=1．20．（8分）已知，如图，△ABC为等边三角形，AE=CD，AD、BE相交于点P，BQ⊥AD于Q，求证：PQ=BP．21．（10分）某文具店老板第一次用1000元购进一批文具，很快销售完毕；第二次购进时发现每件文具进价比第一次上涨了2.5元．老板用2500元购进了第二批文具，所购进文具的数量是第一次购进数量的2倍，同样很快销售完毕，两批文具的售价为每件15元．（1）问第二次购进了多少件文具？（2）文具店老板第一次购进的文具有30元的损耗，第二次购进的文具有125元的损耗，问文具店老板在这两笔生意中是盈利还是亏本？请说明理由．22．（10分）如图，在平面直角坐标系中，点A的坐标为（1，0），以线段OA为边在第四象限内作等边三角形AOB，点C为x正半轴上一动点（OC＞1），连接BC，以线段BC为边在第四象限内作等边△CBD，连接DA并延长，交y轴于点E．①△OBC与△ABD全等吗？判断并证明你的结论；②当点C运动到什么位置时，以A，E，C为顶点的三角形是等腰三角形？2017-2018学年天津市河北区八年级（上）期末数学试卷参考答案与试题解析一、选择题（本大题共8个小题，每小题3分，共24分，在每小题给出的四个选项中只有一项是符合题目要求的）1．（3分）下面四个图形分别是节能、节水、低碳和绿色食品标志，是轴对称图形的是（）A．B．C． D．【解答】解：A、不是轴对称图形，故本选项错误；B、不是轴对称图形，故本选项错误；C、不是轴对称图形，故本选项错误；D、是轴对称图形，故本选项正确．故选：D．2．（3分）下列等式从左到右的变形，属于因式分解的是（）A．x2+2x﹣1=（x﹣1）2B．（a+b）（a﹣b）=a2﹣b2C．x2+4x+4=（x+2）2D．ax2﹣a=a（x2﹣1）【解答】解：（A）x2+2x﹣1≠（x﹣1）2，故A不是因式分解，（B）a2﹣b2=（a+b）（a﹣b），故B不是因式分解，（D）a x2﹣a=a（x2﹣1）=a（x+1）（x﹣1），故D分解不完全，故选：C．3．（3分）要使分式有意义，x应满足的条件是（）A．x＞3 B．x=3 C．x＜3 D．x≠3【解答】解：当x﹣3≠0时，分式有意义，即当x≠3时，分式有意义，故选：D．4．（3分）计算x3•x2的结果是（）A．x6B．x5C．x2D．x【解答】解：x3•x2=x3+2=x5．故选：B．5．（3分）已知点P（a，3）、Q（﹣2，b）关于y轴对称，则=（）A．﹣5 B．5 C．﹣ D．【解答】解：∵点P（a，3）、Q（﹣2，b）关于y轴对称，∴a=2，b=3，则==﹣．故选：C．6．（3分）下列各式：①，②，③，④，其中是分式的有（）A．①②③④B．①④C．①②④D．②④【解答】解：式子：①，②，③，④，其中是分式的有：①，④．故选：B．7．（3分）小朱要到距家1500米的学校上学，一天，小朱出发10分钟后，小朱的爸爸立即去追小朱，且在距离学校60米的地方追上了他．已知爸爸比小朱的速度快100米/分，求小朱的速度．若设小朱速度是x米/分，则根据题意所列方程正确的是（）A．B．C．D．【解答】解：设小朱速度是x米/分，则爸爸的速度是（x+100）米/分，由题意得：=+10，即：=+10，故选：B．8．（3分）如图，等腰三角形ABC的底边BC长为4，面积是16，腰AC的垂直平分线EF分别交AC，AB边于E，F点．若点D为BC边的中点，点M为线段EF上一动点，则△CDM周长的最小值为（）A．6 B．8 C．10 D．12【解答】解：连接AD，∵△ABC是等腰三角形，点D是BC边的中点，∴AD⊥BC，=BC•AD=×4×AD=16，解得AD=8，∴S△ABC∵EF是线段AC的垂直平分线，∴点C关于直线EF的对称点为点A，∴AD的长为CM+MD的最小值，∴△CDM的周长最短=（CM+MD）+CD=AD+BC=8+×4=8+2=10．故选：C．二、填空题（本大题共8个小题，每小题3分，共24分，将答案填在题中横线上）9．（3分）当x=﹣3时，分式的值为零．【解答】解：要使分式由分子x2﹣9=0解得：x=±3．而x=﹣3时，分母x﹣3=﹣6≠0．x=3时分母x﹣3=0，分式没有意义．所以x的值为﹣3．故答案为：﹣3．10．（3分）一种病毒的直径为0.000023m，这个数用科学记数法表示为 2.3×10﹣5．．【解答】解：0.000023=2.3×10﹣5，故答案为：2.3×10﹣5．11．（3分）已知x m=6，x n=3，则x2m﹣n的值为12．【解答】解：x2m﹣n=（x m）2÷x n=36÷3=12．故答案为：12．12．（3分）分解因式：27x2+18x+3=3（3x+1）2．【解答】解：27x2+18x+3，=3（9x2+6x+1），=3（3x+1）2．13．（3分）若关于x的分式方程无解，则m的值是3．【解答】解：去分母，得m﹣3=x﹣1，x=m﹣2．∵关于x的分式方程无解，∴最简公分母x﹣1=0，∴x=1，当x=1时，得m=3，即m的值为3．故答案为3．14．（3分）如图，在等腰△ABC的两腰AB、BC上分别取点D和E，使DB=DE，此时恰有∠ADE=∠ACB，则∠B的度数是20°．【解答】解：设∠B=x．∵DB=DE，∴∠DEB=∠B=x，∴∠ADE=∠DEB+∠B=2x，∴∠ACB=2∠ADE=4x．∵AB=BC，∴∠ACB=∠A=4x．在△ABC中，∵∠A+∠B+∠C=180°，∴4x+x+4x=180°，∴x=20°．即∠B的度数是20°．故答案为20°．15．（3分）如图，∠ABC=50°，BD平分∠ABC，过D作DE∥AB交BC于点E，若点F在AB上，且满足DF=DE，则∠DFB的度数为50°或130°．【解答】解：如图，DF=DF′=DE；∵BD平分∠ABC，由图形的对称性可知：△BDE≌△BDF，∴∠DFB=∠DEB；∵DE∥AB，∠ABC=50°，∴∠DEB=180°﹣50°=130°；∴∠DFB=130°；当点F位于点F′处时，∵DF=DF′，∴∠DF′B=∠DFF′=50°，故答案是：50°或130°．16．（3分）如图，△ADB、△BCD都是等边三角形，点E，F分别是AB，AD上两个动点，满足AE=DF．连接BF与DE相交于点G，CH⊥BF，垂足为H，连接CG．若DG=a，BG=b，且a、b满足下列关系：a2+b2=5，ab=2，则GH=．【解答】证明：延长FB到点M，使BM=DG，连接CM∵△ABD是等边三角形，∴AD=BD，∠A=∠ABD=60°，在△AED与△DFB中，，∴△AED≌△DFB（SAS），∴∠ADE=∠DBF，∵∠CDG=∠ADC﹣∠ADE=120°﹣∠ADE，∠CBM=120°﹣∠DBF，∴∠CBM=∠CDG，∵△DBC是等边三角形，∴CD=CB，在△CDG和△CBM中，∴△CDG≌△CBM，∴∠DCG=∠BCM，CG=CM，∴∠GCM=∠DCB=60°，∴△CGM是等边三角形，∴CG=GM=BG+BM=BG+DG，∵（a+b）2=a2+b2+2ab=9，∴a+b=3，∴CG=3，∴GH=CG=．故答案为：．三、解答题（17、18、19、20题各8分，21、22题10分，共52分，解答应写出文字说明、证明过程或演算步骤）17．（8分）（1）（﹣2a）3﹣（﹣a）•（3a）2（2）（2a﹣3b）2﹣4a（a﹣2b）【解答】解：（1）（﹣2a）3﹣（﹣a）•（3a）2=﹣8a3﹣（﹣a）•9a2=﹣8a3+9a3=a3；（2）（2a﹣3b）2﹣4a（a﹣2b）=4a2﹣12ab+9b2﹣4a2+8ab=﹣4ab+9b2．18．（8分）先化简再求值：（1﹣）÷，其中x=（）﹣1+30【解答】解：原式=•=，当x=（）﹣1+30=3+1=4时，原式==2．19．（8分）解分式方程： +=1．【解答】解：去分母得：x2﹣x﹣2=x2﹣3x，解得：x=1，经检验x=1是分式方程的解．20．（8分）已知，如图，△ABC为等边三角形，AE=CD，AD、BE相交于点P，BQ⊥AD于Q，求证：PQ=BP．【解答】解：AE=CD，AC=BC，∴EC=BD；∵△ABC为等边三角形，∴∠C=∠ABC=60°，AB=BC，在△BEC与△ADB中，，∴△BEC≌△ADB（SAS），∴∠EBC=∠BAD；∵∠ABE+∠EBC=60°，∴∠ABE+∠BAD=60°，∵∠BPQ是△ABP外角，∴∠ABP+∠BAP=60°=∠BPQ，又∵BQ⊥AD，∴∠PBQ=30°，∴PQ=BP．21．（10分）某文具店老板第一次用1000元购进一批文具，很快销售完毕；第二次购进时发现每件文具进价比第一次上涨了2.5元．老板用2500元购进了第二批文具，所购进文具的数量是第一次购进数量的2倍，同样很快销售完毕，两批文具的售价为每件15元．（1）问第二次购进了多少件文具？（2）文具店老板第一次购进的文具有30元的损耗，第二次购进的文具有125元的损耗，问文具店老板在这两笔生意中是盈利还是亏本？请说明理由．【解答】解：（1）设第一次购进x件文具，第二次就购进2x件文具，由题意得，=﹣2.5，解得：x=100，经检验，x=100是原方程的解，且符合题意，则2x=2×100=200．答：第二次购进200件文具；（2）第一次购进100件文具，利润为：（15﹣10）×100﹣30=470（元）；第二次购进200件文具，利润为：（15﹣12.5）×200﹣125=375（元），两笔生意是盈利：利润为470+375=845元．22．（10分）如图，在平面直角坐标系中，点A的坐标为（1，0），以线段OA为边在第四象限内作等边三角形AOB，点C为x正半轴上一动点（OC＞1），连接BC，以线段BC为边在第四象限内作等边△CBD，连接DA并延长，交y轴于点E．①△OBC与△ABD全等吗？判断并证明你的结论；②当点C运动到什么位置时，以A，E，C为顶点的三角形是等腰三角形？【解答】解：（1）△OBC≌△ABD．证明：∵△AOB，△CBD都是等边三角形，∴OB=AB，CB=DB，∠ABO=∠DBC，∴∠OBC=∠ABC，在△OBC和△ABD中，，∴△OBC≌△ABD（SAS）；（2）∵△OBC≌△ABD，∴∠BOC=∠BAD=60°，又∵∠OAB=60°，∴∠OAE=180°﹣60°﹣60°=60°，∴∠EAC=120°，∠OEA=30°，∴以A，E，C为顶点的三角形是等腰三角形时，AE和AC是腰，∵在Rt△AOE中，OA=1，∠OEA=30°，∴AE=2，∴AC=AE=2，∴OC=1+2=3，∴当点C的坐标为（3，0）时，以A，E，C为顶点的三角形是等腰三角形．。