(完整word)线面平行垂直知识点,推荐文档
直线平面平行、垂直的判定及其性质知识点
一、直线、平面平行的判定及其性质
知识点一、直线与平面平行的判定
ⅰ.直线和平面的位置关系(一条直线和一个平面的位置关系有且只有以下三种)
位置关系直线在平面内直线与平面相交直线与平面平行
公共点有无数个公共点有且只有一个公共点没有公共点
符号表示a⊂αa∩α=A a||α
图形表示
注:直线和平面相交或平行的情况统称为直线在平面外
ⅱ.思考:如图,设直线b在平面α内,直线a在平面α外,猜想在什么条件下直线a与平面α平行.(a||b)
判定
文字描述直线和平面在空间平面永无交点,则
直线和平面平行(定义)
平面外的一条直线一次平面内的一条直线
平行,则该直线与此平面平行
图形
条件a与α无交点
结论
a∥αb∥α
线线平行,则线面平行(线与面的平行问题一定要排除现在直线内的情况)
※判定定理的证明
知识点二、直线与平面平行的性质
性质
文字描述一条直线与一个平面平行,
则这条直线与该平面无交点
一条直线和一个平面平行,则
过这条直线的任一平面与此平
面相交,这条直线和交线平行.
图形
条件
a∥αa∥αa⊂βα∩β=b
结论
a∩α=∅a∥b
线面平行,则线线平行
特别提示
证明直线和平面的平行通常采用如下两种方法:①利用直线和平面平行的判定定理,通过“线线”平行,证得“线面”平行;②利用两平面平行的性质定理,通过“面面”平行,证得“线面”平行.
判定
文字描述如果两个平面无公共
点,责成这两个平面平
行一个平面内有两条相
交直线与另一个平面
平行,那么这两个平面
平行.
如果两个平面同时垂直于
一条直线,那么这两个平
面垂直。
图形
条件
α∩β=∅a,b⊂β
a∩b=P
a∥α
数学线面垂直的知识点总结归纳

数学线面垂直的知识点总结归纳
数学是一座高山,哪怕是高考数学这样的小山丘,也让无数学子望其背而心戚戚,更有人混淆知识点。下面是小编为大家整理的关于数学线面垂直的知识点,希望对您有所帮助!
数学直线与平面平行、垂直知识点
直线与平面垂直的判定定理一:如果一条直线和一个平面内的两条相交直线都垂直,那么这两条直线垂直于这个平面.(“线线垂直,线面垂直”)
直线与平面垂直的判定定理二:如果平行线中一条直线垂直于一个平面,那么另一条也垂直于这个平面.
推论:如果两条直线同垂直于一个平面,那么这两条直线平行.
注:①垂直于同一平面的两个平面平行.(×)(可能相交,垂直于同一条直线的两个平面平行)
②垂直于同一直线的两个平面平行.(√)(一条直线垂直于平行的一个平面,必垂直于另一个平面)
③垂直于同一平面的两条直线平行.(√)
5. ⑴垂线段和斜线段长定理:从平面外一点向这个平面所引的垂线段和斜线段中,
①射影相等的两条斜线段相等,射影较长的斜线段较长;
②相等的斜线段的射影相等,较长的斜线段射影较长;
③垂线段比任何一条斜线段短.
注:垂线在平面的射影为一个点. [一条直线在平面内的射影是一条直线.(×)]
⑵射影定理推论:如果一个角所在平面外一点到角的两边的距离相等,那么这点在平面内的射影在这个角的平分线上
高中数学线面垂直知识点
1)直线垂直于平面内两条非平行的线,则直线垂直于该平面
2)直线的两条不平行的垂线与平面平行,则直线垂直于该平面
3)有A、B两个面都与C平面垂直,则A、B两个面的交线也垂直于
C平面
4)直线垂直于与A平面平行的B平面,则直线垂直于A平面
高中数学直线与平面平行直线与平面垂直知识点总结

高中数学直线与平面平行直线与平面垂直知识点总结
1.空间直线与平面位置分三种:相交、平行、在平面内
2. 直线与平面平行判定定理:假如平面外一条直线和这个平面内一条直线平行,那么这条直线和这个平面平行.(“线线平行,线面平行”)
[注]:①直线与平面内一条直线平行,则∥. (×)(平面外一条直线)
②直线与平面内一条直线相交,则与平面相交. (×)(平面外一条直线)
③若直线与平面平行,则内必存在很多条直线与平行. (√)(不是任意一条直线,可利用平行的传递性证之)
④两条平行线中一条平行于一个平面,那么另一条也平行于这个平面. (×)(可能在此平面内)
⑤平行于同始终线的两个平面平行.(×)(两个平面可能相交)
⑥平行于同一个平面的两直线平行.(×)(两直线可能相交或者异面)
⑦直线与平面、所成角相等,则∥.(×)(、可能相交)
3.直线和平面平行性质定理:假如一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线和交线平行.(“线面平行,线线平行”)
4. 直线与平面垂直是指直线与平面任何一条直线垂直,过一点有且只有一条直线和一个平面垂直,过一点有且只有一个平面和一
条直线垂直.
若⊥,⊥,得⊥(三垂线定理),
得不出⊥. 由于⊥,但不垂直OA.
三垂线定理的逆定理亦成立.
直线与平面垂直的判定定理一:假如一条直线和一个平面内的两条相交直线都垂直,那么这两条直线垂直于这个平面.(“线线垂直,线面垂直”)
直线与平面垂直的判定定理二:假如平行线中一条直线垂直于一个平面,那么另一条也垂直于这个平面.
线线平行垂直,线面平行垂直,面面平行垂直判定与性质

线线平行垂直,线面平行垂直,面面平行垂直判定与性质
编辑整理:
尊敬的读者朋友们:
这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(线线平行垂直,线面平行垂直,面面平行垂直判定与性质)的内容能够给您的工作和学习带来便利。同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为线线平行垂直,线面平行垂直,面面平行垂直判定与性质的全部内容。
1.线线平行
判定:a用向量,方向向量平行b一条直线平行于另一个平面,则它平行于它所在平面与那个平面的交线。C若一平面与两平行平面相交,则两交线平行.D同时与一平面垂直的两直线平行.E同时平行于一条直线的两直线平行。
性质:貌似没啥性质,一般是证明线面关系的时候先证明线线关系。
2。线线垂直
判定:a向量,方向向量垂直b直线垂直于平面,则直线与平面中的任意直线都垂直c第一条直线与第二条直线平行,第一条垂直于第三条,则第二条也垂直于第三条d把两直线放在一个平面中,利用平面几何各种判定方法,如等腰三角形的底和高等。E(重点)三垂线定理:平面内的一条直线,如果和过平面的一条斜线在平面内的射影垂直,那么它就和这条斜线垂直。三垂线逆定理:在平面内的一条直线,如果和过平面的一条斜线垂直,那么它也垂直于斜线在平面内的射影。(这个比较重要,记不住的话找一下例题,多看看图就好了)
性质:貌似也没什么性质,一般也是要证明线面关系的时候用到它。注意:第一条直线垂直于第二条直线,第一条直线垂直于第三条直线,则第二条直线与第三条直线可垂直可平行也可普通相交。
立体几何平行和垂直知识点

立体几何的平行和垂直定理
一、空间中的平行问题
1、直线与平面平行的判定及其性质
1判定定理:平面外一条直线与此平面内一条直线平行,则该直线与此平面平行.线线平行⇒线面平行
符号表示:
2性质定理:如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线和交线平行.线面平行⇒线线平行
符号表示:
作用:利用该定理可解决直线间的平行问题.
2、平面与平面平行的判定及其性质
1判定定理:如果一个平面内的两条相交直线都平行于另一个平面,那么这两个平面平行线面平行→面面平行,
符号表示:
2性质定理:如果两个平行平面都和第三个平面相交,那么它们的交线平行.面面平行→线线平行
符号表示:
作用:可以由平面与平面平行得出直线与直线平行
3、在寻求平行关系时,利用中位线、平行四边形等知识是非常常见的手段.有时也可用“垂直于同一个平面的两条直线平行”进行证明.
二、空间中的垂直问题
1、线线、面面、线面垂直的定义
①两条异面直线的垂直:如果两条异面直线所成的角是直角,就说这两条异面直线互相垂直.
②线面垂直:如果一条直线垂直于一个平面内的任何一条直线垂直,就说这条直线和这个平面垂直.
③平面和平面垂直:如果两个平面相交,所成的二面角从一条直线出发的两个半平面所组成的图形是直二面角平面角是直角,就说这两个平面垂直.
2、线面垂直判定定理和性质定理
判定定理:如果一条直线垂直于一个平面内的两条相交直线,那么这条直线垂直这个平面.线线垂直→线面垂直
性质定理:垂直于同一个平面的两条直线平行.
3、面面垂直的判定定理和性质定理
判定定理:如果一个平面经过另一个平面的一条垂线,那么这两个平面互相垂直.性质定理:如果两个平面互相垂直,那么在一个平面内垂直于他们的交线的直线垂直于另一个平面.
(完整版)线面、面面平行和垂直的八大定理

线面、面面平行和垂直的八大定理
一、线面平行。
1、判定定理:平面外一条直线与平面内一条直线平行,那么这条直线与这个平面平行.符合表示:
β
ββ////a b a b a ⇒⎪⎭⎪⎬⎫⊂⊄
2、性质定理:如果一条直线与平面平行,经过这条直线的平面和这个平面相交,那么这条直线
和交线平行。 符号表示: b a b a a a ////⇒⎪⎪
⎭⎪⎪⎬⎫=⊂⊄βαβαα
二、面面平行。
1、判定定理:如果一个平面内有两条相交直线分别平行于另一个平面内的两条相交直线,那么这两个平面平行。
符号表示: β
α//////⇒⎪⎪⎪⎭⎪⎪⎪⎬⎫==N n m M b a a m b
n 2、性质定理:如果两个平面平行同时与第三个平面相交,那它们的交线平行。 符号表
示: d l d l ////⇒⎪⎭
⎪⎬⎫==γβγαβα (更加实用的性质:一个平面内的任一直线平行另一平面)
三、线面垂直。
1、判定定理:如果一条直线与一个平面内的两条相交直线都垂直,那么这条直线垂直这个平面.
符号表示: α⊥⇒⎪⎪⎪⎪⎭
⎪⎪⎪⎪⎬⎫=⊥⊥a M c b b a c a $:三垂线定理:(经常考到这种逻辑)在平面内的一条直线,如果它和这个平面的一条斜线的射
影垂直,那么它也和这条斜线垂直。
符号表示:
PA a A oA a po oA a ⊥⇒⎪⎪
⎭
⎪⎪⎬⎫=⊥⊥⊂⊂αα
α 2、性质定理:垂直同一平面的两条直线互相平行。(更加实用的性质是:一个平面的垂线垂直于该平面内任一直线.)
四、面面垂直.
1、判定定理:经过一个平面的垂线的平面与该平面垂直。
线面垂直、面面垂直知识点总结、经典例题及解析、高考题练习及答案

直线、平面垂直的判定与性质
【知识梳理】
一、直线与平面垂直的判定与性质
1、 直线与平面垂直
(1)定义:如果直线l 与平面α内的任意一条直线都垂直,我们就说直线l 与平面α互相垂直,记作l ⊥α,直线l 叫做平面α的垂线,平面α叫做直线l 的垂面。如图,直线与平面垂直时,它们唯一公共点P 叫做垂足。
(2)判定定理:一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直。
结论:如果两条平行直线中的一条垂直于一个平面,那么另一条也垂直于这个平面,记作.//a b b a αα⎫⇒⊥⎬⊥⎭
(3)性质定理:垂直于同一个平面的两条直线平行。即,//a b a b αα⊥⊥⇒.
由定义知:直线垂直于平面内的任意直线。
2、 直线与平面所成的角
平面的一条斜线和它在平面上的射影所成的锐角或者直角叫做这条直线和这个平面所成的
角。一条直线垂直于平面,该直线与平面所成的角是直角;一条直线和平面平行,或在平面内,则此直线与平面所成的角是00的角。
3、 二面角的平面角
从一条直线出发的两个半平面所组成的图形叫做二面角,这条直线叫做二面角的棱,这两个
半平面叫做二面角的面。如果记棱为l ,那么两个面分别为αβ、的二面角记作l αβ--.在二面角的棱上任取一点,以该点为垂足,在两个半平面内分别作垂直于棱的射线,则两射线所构成的角叫做叫做二面角的平面角。其作用是衡量二面角的大小;范围:000180θ≤≤.
二、平面与平面垂直的判定与性质
1、定义:一般地,两个平面相交,如果它们所成的二面角是直二面角,就说这两个平面垂直.
数学线面垂直知识点总结

数学线面垂直知识点总结
一、线面垂直关系的定义
1. 在平面几何中,两条线段或者两条直线如果所成的角度为90度,那么它们就是垂直的。具体来说,如果两条线段或者两条直线相交,并且它们所成的角度为90度,那么它们就
是垂直的。
2. 在空间几何中,两个平面如果它们的法向量垂直于彼此,那么这两个平面就是垂直的。
具体来说,如果两个平面的法向量的内积为0,那么这两个平面就是垂直的。
二、线面垂直关系的性质
1. 垂直线的性质
(1)垂直线的斜率乘积为-1
(2)垂直线的两条直线的斜率相乘等于-1。
2. 垂直平面的性质
(1)垂直平面的法向量垂直
(2)垂直平面的法向量的内积为0
(3)垂直平面的法向量可以确定平面的方向
三、线面垂直关系的判定方法
1. 通过角度判断
在平面几何中,可以通过计算两条直线所成的角度来判断它们是否垂直。如果两条直线所
成的角度为90度,那么这两条直线就是垂直的。
2. 通过斜率判断
在平面几何中,可以通过计算两条直线的斜率来判断它们是否垂直。如果两条直线的斜率
乘积为-1,那么这两条直线就是垂直的。
3. 通过向量判断
在空间几何中,可以通过计算两个平面的法向量来判断它们是否垂直。如果两个平面的法
向量的内积为0,那么这两个平面就是垂直的。
四、线面垂直关系的应用
1. 在几何中的应用
垂直关系在几何中有着广泛的应用。比如在平面几何中,通过垂直关系可以求解直角三角形的性质,可以求解平行四边形的性质,可以求解垂直线的交点等等。在空间几何中,通过垂直关系可以求解平面的交点,可以求解两个平面之间的夹角等等。
2. 在物理中的应用
直线平面平行、垂直的判定及其性质知识点

一、直线、平面平行的判定及其性质
知识点一、直线与平面平行的判定
ii.思考:如图,设直线b在平面a内,直线a在平面a外,猜想在什么条件下直线a与平面a平行.(a|| b)
直线与平面平行的判断
※判定定理的证明
特别提示
证明直线和平面的平行通常采用如下两种方法:①利用直线和平面平行的判定定理,通过“线线”平行,证得“线面”平行;②利用两平面平行的性质定理,通过“面面”平行,证得“线面”平行
、直线、平面垂直的判定及其性质知识点一、直线和平面垂直的定义与判定
要点诠释:定义中“平面
条直线”不同(线线垂直内的任意一条直线”就是
指“平面内的所有直线”,这与“无数
线面垂直)
知识点二、二面角
I.二面角::从一条直线出发的两个半平面所组成的图形叫二面角( dihedral angle ).这条直线叫做
二面角的棱,这两个半平面叫做二面角的面.记作二面角一AB —.(简记P — AB —Q)
.面角的平面角的三个特征:i .点在棱上
ii .线在面内
iii . 与棱垂直
n .二面角的平面角:在二面角一丨一的棱|上任取一点0,以点0为垂足,在半平面,内分别作垂直于棱I的射线0A和0B,则射线0A和0B构成的A0B叫做二面角的平面角.
作用:衡量二面角的大小;范围:0°180°.
(完整版)直线平面平行、垂直的判定及其性质知识点
一、直线、平面平行的判定及其性质知识点一、直线与平面平行的判定
ⅰ.直线和平面的位置关系(一条直线和一个平面的位置关系有且只有以下三种)
位置关系直线在平面内直线与平面相交直线与平面平行
公共点有无数个公共点有且只有一个公共点没有公共点
符号表示a⊂αa∩α=A a||α
图形表示
注:直线和平面相交或平行的情况统称为直线在平面外
ⅱ.思考:如图,设直线b在平面α内,直线a在平面α外,猜想在什么条件下直线a与平面α平行.(a||b)
判定
文字描述直线和平面在空间平面永无交点,则
直线和平面平行(定义)
平面外的一条直线一次平面内的一条直线
平行,则该直线与此平面平行
图形
条件a与α无交点
结论
a∥αb∥α
※判定定理的证明
知识点二、直线与平面平行的性质
性质
文字描述一条直线与一个平面平行,
则这条直线与该平面无交点
一条直线和一个平面平行,则
过这条直线的任一平面与此平
面相交,这条直线和交线平行.
图形
条件
a∥αa∥αa⊂βα∩β=b
结论
a∩α=∅a∥b
线面平行,则线线平行
特别提示
证明直线和平面的平行通常采用如下两种方法:①利用直线和平面平行的判定定理,通过“线线”平行,证得“线面”平行;②利用两平面平行的性质定理,通过“面面”平行,证得“线面”平行.
判定
文字描述如果两个平面无公共
点,责成这两个平面平
行一个平面内有两条相
交直线与另一个平面
平行,那么这两个平面
平行.
如果两个平面同时垂直于
一条直线,那么这两个平
面垂直。
图形
条件
α∩β=∅a,b⊂β
a∩b=P
a∥α
b∥α
l⊥α
l⊥β
结论
α∥βα∥βα∥β
性质
文字描述如果两个平行平面同时和第
直线平面平行、垂直的判定及其性质知识点上课讲义

、直线、平面平行的判定及其性质
知识点一、直线与平面平行的判定
)
ii.思考:如图,设直线b在平面a内,直线a在平面a外,猜想在什么条件下直线a与平面a平行.(a||b)
直线与平面平行的判断
※判定定理的证明
知识点二、直线与平面平行的性质
线面平行,则线线平行
特别提示
证明直线和平面的平行通常采用如下两种方法:①利用直线和平面平行的判定定理,通过“线线”平行,证得质定理,通过“面面”平行,证得“线面”平行
知识点三、平面与平面平行的判定
判定
、直线、平面垂直的判定及其性质
定义
判定
语言描述
如果直线1和平面a 内的任意一条直线都 垂直,我们就说直线1与平面①互相垂直, 记作1丄a
一条直线与一个平面内的两条相交直线都 垂直,则这条直线与该平面垂直
图形
I
/
条件 b 为平面a 内的任一直线,而I 对这 一直线总有I 丄a
I 丄 m , I 丄 n , m n n = B , m
,
n 结论
I 丄 1丄
要点诠释:定义中“平面 二内的任意一条直线”就是指“平面 内的所有直线”,这与“无数条直线”
.面角的平面角的三个特征 :i .点在棱上
ii .线在面内 iii . 与棱垂直
n .二面角的平面角:在二面角
一I — 的棱I 上任取一点0,以点0为垂足,在半平面 ,内分别作垂直于棱I 的射
成的 AOB 叫做二面角的平面角. 作用:衡量二面角的大小;范围:
0°
180°.
dihedral angle ).这条直线叫做二面角的棱,这两
知识点二、二面角
I •二面角::从一条直线出发的两个半平面所组成的图形叫二面角
( 角一
AB —.(简记 P — AB — Q )
平行与垂直知识点总结

直线和平面垂直的定义:如果一条直线a 和一个平面 内的任意一条直线都垂直,我们就说直线a 和平面 互相垂直.直线a 叫做平面 的垂线,平面 叫做直线a 的垂面。
直线与平面垂直的判定定理(线线垂直→线面垂直):如果一条直线和
一个平面内的两条相交直线都垂直,那么这条直线垂直于这个平面。
基础例题:1、求证在正方体ABCD-A 1B 1C 1D 1中,体对角线AC 1垂直于面对角线BD
2、AB 是圆O 的直径,C 是异于A 、B 的圆周上的任意一点,PA 垂直于圆O 所在的平面,证明:PAC BC 平面
直线与平面垂直的性质定理(线面垂直→线线垂直):如果一条直线垂
直于一个平面,那么他就和平面内的任意一条直线垂直。
基础例题1.已知:在空间四边形ABCD 中,AC =AD ,BC =BD ,中点为CD E ,求证:AB ⊥CD
推论1(线线平行→线面垂直)如果在两条平行线中,有一条垂直于平面,那么
另一条也垂直于这个平面。
C
C1
推论2(线面垂直→线线平行)如果两条直线同垂直于一个平面,那么这两条直
线平行。
正方体AC 1中,EF 与异面直线AC,A 1D 都 垂直相交,交点分别为E,F , 求证:EF//BD 1
2、直线和平面平行的定义:如果一条直线和一个平面没有公共点,那么我们就说这条直线和这个平面平行。
直线和平面平行的判定定理(线线平行→线面平行):如果平面外一条直
线和这个平面内的一条直线平行,那么这条直线和这个平面平行。
基本例题:1已知:空间四边形ABCD 中,F E ,分别是AD AB ,的中点
9.2线面平行、面面平行Microsoft Word 文档

9.2 线面平行、面面平行
一、明确复习目标
1.掌握空间直线和平面、平面和平面的位置关系;
2.掌握直线与平面、平面与平面平行的定义、判定和性质,并能运用这些知识进行论证或解题.
3.能灵活进行“线线平行,线面平行,面面平行”之间的相互转化.
二.建构知识网络
1.直线和平面的位置关系有:
(1)直线在平面内;
(2)直线和平面相交;
(3)直线和平面平行:
定义——.
2.线面平行的判定方法:
①a∩α=ф⇒a∥α(定义法)
②判定定理;
③b⊥a, b⊥α, a⊄α⇒a∥α;
④α∥β,a⊂α⇒a∥β
⑤空间向量证线面平行.
3线面平行的性质定理:如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线和交线平行.
4.判定平面平行的方法:
(1)根据定义——证明两平面没有公共点;
(2)判定定理——证明一个平面内的两条相交直线都平行于另一个平面;
(3)证明两平面同垂直于一条直线.
5.平行平面的主要性质:
⑴由定义知:“两平行平面没有公共点”.
⑵由定义推得:“两个平面平行,其中一个平面内的直线必平行于另一个平面。
⑶两个平面平行的性质定理:“如果两个平行平面同时和第三个平面相交,那么它们的交线平行”.
⑷一条直线垂直于两个平行平面中的一个平面,它也垂直于另一个平面.
⑸夹在两个平行平面间的平行线段相等.
⑹经过平面外一点只有一个平面和已知平面平行.
三、双基题目练练手
(2006重庆)对于任意的直线l与平面α,在平面α内必有直线m,使m与l()1.
A.平行B.相交C.垂直D.互为异面直线
2.一条直线同时平行于两个相交平面,那么这条直线与这两个平面的交线的位置关系是 ( ) A 异面 B 平行 C 相交 D 不能确定 3.(2005广东)给出下列关于互不相同的直线m 、l 、n 和平面α、β的四个命题: ①若,,m l A A m αα⊂⋂=∉点,则l 与m 不共面;
立体几何讲义(线面平行-垂直-面面垂直)
A B
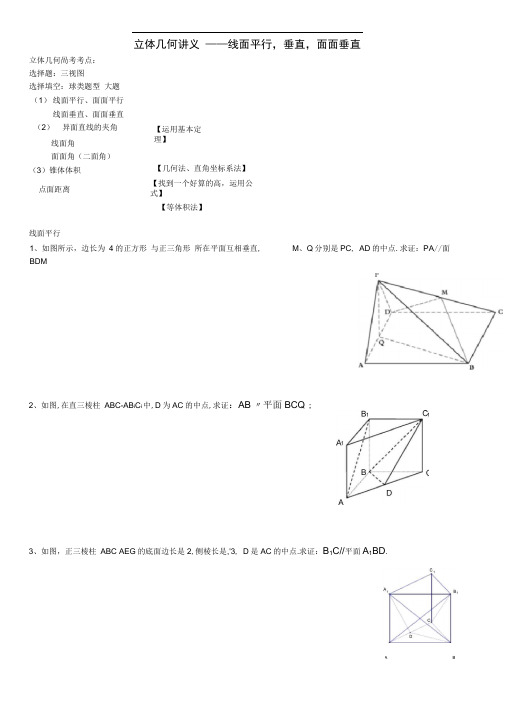
立体几何讲义 ——线面平行,垂直,面面垂直
2、如图,在直三棱柱 ABC-AB i C i 中,D 为AC 的中点,求证:AB 〃平面BCQ ;
3、如图,正三棱柱 ABC AEG 的底面边长是2,侧棱长是,'3, D 是AC 的中点.求证:B 1C//平面A 1BD .
立体几何咼考考点: 选择题:三视图 选择填空:球类题型 大题 (1) 线面平行、面面平行 线面垂直、面面垂直 (2) 异面直线的夹角 线面角 面面角(二面角) (3)锥体体积 点面距离 【运用基本定
理】
【几何法、直角坐标系法】 【找到一个好算的高,运用公式】
【等体积法】
线面平行 1、如图所示,边长为 4的正方形 与正三角形 所在平面互相垂直, M 、Q 分别是PC , AD 的中点.求证:PA //面
BDM P
4、如图,在四棱锥 P -ABCD 中 ABCD 是平行四边形, M N 分别是AB, PC 的中点,求证: MIN/平面PAD
B
/V
N
A
B
6、(2012)如图,直三棱
柱
7、【2015高考】 如图,三棱台 DEF ABC 中,AB 2DE , G , H 分别为AC , BC 的中点
)求证:BD //平面FGH
ABC — A ' B ' C ',/ BAC = 90 ° AB 证明:MN //平面A ' ACC
所在的平面,AD=PA=2 , CD=2 一 ?, E 、F 分别是 AB 、PD 的中点.求证: AF //
AC = .2 AA ' = 1,点M 、N 分别为A ' B 和B ' C '的中点 5、如图,PA 垂直于矩形 ABCD 平面PCE ;
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
立体几何知识点总结
一、平面
通常用一个平行四边形来表示.
平面常用希腊字母α、β、γ…或拉丁字母M、N、P来表示,也可用表示平行四边形的两个相对顶点字母表示,如平面AC.
在立体几何中,大写字母A,B,C,…表示点,小写字母,a,b,c,…l,m,n,…表示直线,且把直线和平面看成点的集合,因而能借用集合论中的符号表示它们之间的关系,例如:
a)A∈l—点A在直线l上;A∉α—点A不在平面α内;
b)l⊂α—直线l在平面α内;
c)a⊄α—直线a不在平面α内;
d)l∩m=A—直线l与直线m相交于A点;
e)α∩l=A—平面α与直线l交于A点;
f)α∩β=l—平面α与平面β相交于直线l.
二、平面的基本性质
公理1 如果一条直线上的两点在一个平面内,那么这条直线上所有的点都在这个平面内.
公理2 如果两个平面有一个公共点,那么它们有且只有一条通过这个点的公共直线.
公理3 经过不在同一直线上的三个点,有且只有一个平面.
根据上面的公理,可得以下推论.
推论1 经过一条直线和这条直线外一点,有且只有一个平面.
推论2 经过两条相交直线,有且只有一个平面.
推论3 经过两条平行直线,有且只有一个平面.
公理4 平行于同一条直线的两条直线互相平行
三、证题方法
四、空间线面的位置关系
共面平行—没有公共点
(1)直线与直线相交—有且只有一个公共点
异面(既不平行,又不相交)
直线在平面内—有无数个公共点
(2)直线和平面直线不在平面内平行—没有公共点
(直线在平面外) 相交—有且只有一公共点
(3)平面与平面相交—有一条公共直线(无数个公共点)
平行—没有公共点
五、异面直线的判定
证明两条直线是异面直线通常采用反证法.
有时也可用定理“平面内一点与平面外一点的连线,与平面内不经过该点的直线是异面直线”.
六、线面平行与垂直的判定
(1)两直线平行的判定
①定义:在同一个平面内,且没有公共点的两条直线平行.
②如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线和交线平行,即若a∥α,a ∥β
④垂直于同一平面的两直线平行,即若a⊥α,b⊥α,则a∥b(线面垂直的性质定理)
⑤两平行平面与同一个平面相交,那么两条交线平行,即若α∥β,α∩γ,β∩γ=b,则a∥b(面面平行的性质公理)
⑥中位线定理、平行四边形、比例线段……,α∩β=b,则a∥b.(线面平行的判定定理)
③平行于同一直线的两直线平行,即若a∥b,b∥c,则a∥c.(公理4)
(2)两直线垂直的判定
①定义:若两直线成90°角,则这两直线互相垂直.
②一条直线与两条平行直线中的一条垂直,也必与另一条垂直.即若b∥c,a⊥b,则a⊥c
③一条直线垂直于一个平面,则垂直于这个平面内的任意一条直线.即若a⊥α,b⊂α,a⊥b.
④三垂线定理和逆定理:在平面内的一条直线,若和这个平面的一条斜线的射影垂直,则它也和这条斜线垂直.
⑤如果一条直线与一个平面平行,那么这条直线与这个平面的垂线垂直.即若a∥α,b⊥α,则a⊥b.
(3)直线与平面平行的判定
①定义:若一条直线和平面没有公共点,则这直线与这个平面平行.
②如果平面外一条直线和这个平面内的一条直线平行,则这条直线与这个平面平行.即若a⊄α,b⊂α,a ∥b,则a∥α.(线面平行的判定定理)
③两个平面平行,其中一个平面内的直线平行于另一个平面,即若α∥β,l⊂α,则l∥β.
(4)直线与平面垂直的判定
①定义:若一条直线和一个平面内的任何一条直线垂直,则这条直线和这个平面垂直.
②如果一条直线和一个平面内的两条相交直线都垂直,那么这条直线垂直于这个平面.即若m⊂α,n⊂α,m∩n=B,l⊥m,l⊥n,则l⊥α.(线面垂直判定定理)
③如果两条平行线中的一条垂直于一个平面,那么另一条也垂直于同一平面.即若l∥a,a⊥α,则l⊥α.
④一条直线垂直于两个平行平面中的一个平面,它也垂直于另一个平面,即若α∥β,l⊥β,则l⊥α.
⑤如果两个平面互相垂直,那么在一个平面内垂直于它们交线的直线垂直于另一个平面,即若α⊥β,a∩β=α,l⊂β,l⊥a,则l⊥α.(面面垂直的性质定理)
(5)两平面平行的判定
①定义:如果两个平面没有公共点,那么这两个平面平行,即无公共点⇔α∥β.
②如果一个平面内有两条相交直线都平行于另一个平面,那么这两个平面平行,即若a,b⊂α,a∩b=P,a ∥β,b∥β,则α∥β.(面面平行判定定理)
推论:一个平面内的两条直线分别平行于另一平面内的两条相交直线,则这两个平面平行,即若a,b⊂α,c,d⊂β,a∩b=P,a∥c,b∥d,则α∥β.
(6)两平面垂直的判定
①定义:两个平面相交,如果所成的二面角是直二面角,那么这两个平面互相垂直,即二面角α-a-β=90°⇔α⊥β.
②如果一个平面经过另一个平面的一条垂线,那么这两个平面互相垂直,即若l⊥β,l⊂α,则α⊥β.
(面面垂直判定定理)
七、空间中的各种角
等角定理及其推论
定理若一个角的两边和另一个角的两边分别平行,并且方向相同,则这两个角相等.
推论若两条相交直线和另两条相交直线分别平行,则这两组直线所成的锐角(或直角)相等.
1、异面直线所成的角
(1)定义:a 、b 是两条异面直线,经过空间任意一点O ,分别引直线a ′∥a,b ′∥b,则a ′和b ′所成的锐角(或直角)叫做异面直线a 和b 所成的角.
(2)取值范围:0°<θ≤90°. (3)求解方法
①根据定义,通过平移,找到异面直线所成的角θ; ②解含有θ的三角形,求出角θ的大小. 2、直线和平面所成的角——斜线和射影所成的锐角 (1)取值范围0°≤θ≤90° (2)求解方法
①作出斜线在平面上的射影,找到斜线与平面所成的角θ. ②解含θ的三角形,求出其大小. 3、二面角及二面角的平面角
(1)半平面 直线把平面分成两个部分,每一部分都叫做半平面.
(2)二面角 条直线出发的两个半平面所组成的图形叫做二面角.这条直线叫做二面角的棱,这两个平面叫做二面角的面,即二面角由半平面一棱一半平面组成.
若两个平面相交,则以两个平面的交线为棱形成四个二面角.
二面角的大小用它的平面角来度量,通常认为二面角的平面角θ的取值范围是0°<θ≤180° (3)二面角的平面角
①以二面角棱上任意一点为端点,分别在两个面内作垂直于棱的射线,这两条射线所组成的角叫做二面角的平面角.
如图,∠PCD 是二面角α-AB-β的平面角.平面角∠PCD 的大小与顶点C 在棱AB 上的位置无关. ②二面角的平面角具有下列性质:
(i)二面角的棱垂直于它的平面角所在的平面,即AB ⊥平面PCD.
(ii)从二面角的平面角的一边上任意一点(异于角的顶点)作另一面的垂线,垂足必在平面角的另一边(或其反向延长线)上.
(iii)二面角的平面角所在的平面与二面角的两个面都垂直,即平面PCD ⊥α,平面PCD ⊥β. ③找(或作)二面角的平面角的主要方法.
(i)定义法 (ii)垂面法 (iii)三垂线法 (Ⅳ)根据特殊图形的性质 (4)求二面角大小的常见方法
先找(或作)出二面角的平面角θ,再通过解三角形求得θ的值. 八.空间的各种距离 点到平面的距离
(1)定义 面外一点引一个平面的垂线,这个点和垂足间的距离叫做这个点到这个平面的距离. (2)求点面距离常用的方法: 1)直接利用定义求
①找到(或作出)表示距离的线段;
②抓住线段(所求距离)所在三角形解之.
2)体积法其步骤是:①在平面内选取适当三点,和已知点构成三棱锥;②求出此三棱锥的体积V 和所取三点构成三角形的面积S ;③由V=
3
1
S ·h ,求出h 即为所求.这种方法的优点是不必作出垂线即可求点面距离.难点在于如何构造合适的三棱锥以便于计算.
直线和平面的距离、平行平面的距离
将线面、面面距离转化为点面距离,然后运用解三角形或体积法求解之.
