南京市数学高三上学期第理数一次模拟考试试卷C卷

合集下载

南京市高考数学一模试卷C卷

南京市高考数学一模试卷C卷姓名:________ 班级:________ 成绩:________一、填空题 (共12题；共12分)1. （1分） (2017高二下·濮阳期末) 设复数a+bi（a，b∈R）的模为，则（a+bi）（a﹣bi）=________．2. （1分） (2019高一上·嘉兴期中) 已知函数，若函数有四个零点，则实数m的取值范围为________．3. （1分） (2017高一下·南通期中) 设集合A={x|x2+2x﹣3＞0}，集合B={x|x2﹣2ax﹣1≤0，a＞0}．若A∩B 中恰含有一个整数，则实数a的取值范围是________．4. （1分）若抛物线y2=2px(p>0)的准线经过双曲线x2-y2=1的一个焦点，则p=________ ．5. （1分）(2017·衡阳模拟) 已知数列{an}是无穷等比数列，它的前n项的和为Sn ，该数列的首项是二项式展开式中的x的系数，公比是复数的模，其中i是虚数单位，则 =________．6. （1分） (2017高一下·扬州期末) 已知正数a，b满足 + = ，则ab的最小值为________．7. （1分） (2015高二上·新疆期末) 底面是菱形的棱柱其侧棱垂直于底面，且侧棱长为5，它的体对角线的长分别是9和15，则这个棱柱的侧面积是________．8. （1分）设二项式（x﹣）6（a≠0）的展开式中x2的系数为A，常数项为B，若B=44，则a=________9. （1分） (2018高二下·泰州月考) 函数和射线的交点从左至右依次记为，则 ________..10. （1分）将序号分别为1，2，3，4，5的5张参观券全部分给4人，每人至少1张，如果分给同一人的2张参观券连号，那么不同的分法种数是________11. （1分） (2018高二上·延边期中) 下列说法中错误的序号是： ________①已知恒成立，若为真命题，则实数的最大值为2；②已知三点共线，则的最小值为11；③已知是椭圆的为两个焦点，点在椭圆上,则使三角形为直角三角形的点个数4 个；④在圆内，过点有条弦的长度成等差数列，最小弦长为数列的首项，最大弦长为，若公差那么的取值集合为.12. （1分）已知正六边形A1A2…A6内接于圆O，点P为圆O上一点，向量与的夹角为θi（i=1，2，…，6），若将θ1 ，θ2 ，…，θ6从小到大重新排列后恰好组成等差数列，则该等差数列的第3项为________二、选择题 (共4题；共8分)13. （2分） (2017高一上·潮州期末) 已知函数f（x）是定义在（﹣8，8）上的偶函数，f（x）在[0，8）上是单调函数，且f（﹣3）＜f（2）则下列不等式成立的是（）A . f（﹣1）＜f（1）＜f（3）B . f（2）＜f（3）＜f（﹣4）C . f（﹣2）＜f（0）＜f（1）D . f（5）＜f（﹣3）＜f（﹣1）14. （2分）(2018·浙江) 已知平面α ，直线m ， n满足m α ， n α ，则“m∥n”是“m∥α”的（）A . 充分不必要条件B . 必要不充分条件C . 充分必要条件D . 既不充分也不必要条件15. （2分） (2017高二下·汪清期末) 设椭圆的左、右焦点分别为，上顶点为 .若 =2，则该椭圆的方程为（）A .B .C .D .16. （2分）(2018·内江模拟) 已知数列满足，，则（）A . 8B . 16C . 32D . 64三、解答题 (共5题；共40分)17. （5分）如图所示，在直二面角E﹣AB﹣C中，四边形ABEF是矩形，AB=2，AF=2，△ABC是以A为直角顶点的等腰直角三角形，点P是线段BF上的一点，PF=3．（1）证明：FB⊥平面PAC；（2）求异面直线PC与AB所成的角的余弦值．18. （5分）在某点B处测得建筑物AE的顶端A的仰角为θ，沿BE方向前进30m，至点C处测得顶端A的仰角为2θ，再继续前进10 m至D点，测得顶端A的仰角为4θ，求θ的大小和建筑物AE的高．19. （10分）(2014·浙江理) 如图，设椭圆C：（a＞b＞0），动直线l与椭圆C只有一个公共点P，且点P在第一象限．（1）已知直线l的斜率为k，用a，b，k表示点P的坐标；（2）若过原点O的直线l1与l垂直，证明：点P到直线l1的距离的最大值为a﹣b．20. （15分） (2015高二上·仙游期末) 函数f（x）定义在（0，+∞）上，f（1）=0，导函数f′（x）= v，g（x）=f（x）+af′（x）．（1）若a＜0，试判断g（x）在定义域内的单调性；（2）若g（x）在[1，e]上的最小值为，求a的值；（3）证明：当a≥1时，g（x）＞ln（x+1）在（0，+∞）上恒成立．21. （5分） (2018高一下·攀枝花期末) 已知数列满足，．（Ⅰ）求数列的通项公式；（Ⅱ）设，求．参考答案一、填空题 (共12题；共12分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、答案：略10-1、11-1、12-1、二、选择题 (共4题；共8分)13-1、14-1、15-1、16-1、三、解答题 (共5题；共40分) 17-1、18-1、19-1、19-2、20-1、20-2、20-3、21-1、。

江苏省南京市第一中学2023届高三上学期第一次模拟考试数学试题 (2)

一、单选题二、多选题1. 已知全集，则（）A．B．C．D．2. 某地的中学生中有的同学爱好滑冰，的同学爱好滑雪，的同学爱好滑冰或爱好滑雪.在该地的中学生中随机调查一位同学，若该同学爱好滑雪，则该同学也爱好滑冰的概率为（）A ．0.8B ．0.6C ．0.5D ．0.43. 已知函数的定义域为R，为偶函数，，当时，（且），且．则（）A ．16B ．20C ．24D ．284. 在正方体中，，分别为棱，的中点，则在直线，，，中，与异面且垂直的直线的条数为（）A．B．C．D．5. 设命题p ：，x若是真命题，则实数a 的取值范围是（）A．B．C ．(-D ．(-6. 已知函数，则下述结论中的是（）A ．若在有且仅有个零点，则在有且仅有个极小值点B．若在有且仅有个零点，则在上单调递增C ．若在有且仅有个零点，则的范围是D ．若图像关于对称，且在单调，则的最大值为错误7. 已知，不等式对任意的实数都成立，则实数的最小值为（）A．B ．C．D．8. 已知复数z满足，则z 为实数的一个充分条件是（）A．B．C．D．9. 已知函数的图象的对称轴方程为，则函数的解析式可以是（）A．B．C．D．10. 已知，函数，下列选项正确的有（）A．若的最小正周期，则B ．当时，函数的图象向右平移个单位长度后得到的图象C ．若在区间上单调递增，则的取值范围是D ．若在区间上只有一个零点，则的取值范围是11.已知函数，则下列说法正确的是（）A．的图像关于轴对称B．是周期为的周期函数江苏省南京市第一中学2023届高三上学期第一次模拟考试数学试题 (2)江苏省南京市第一中学2023届高三上学期第一次模拟考试数学试题 (2)三、填空题四、解答题C ．的值域为D ．不等式的解集为12. 随着时代与科技的发展，信号处理以各种方式被广泛应用于医学、声学、密码学、计算机科学、量子力学等各个领域.而信号处理背后的“功臣”就是正弦型函数，的图象就可以近似的模拟某种信号的波形，则下列说法正确的是（）A．函数的图象关于直线对称B．函数的图象关于点对称C．函数为周期函数，且最小正周期为D ．函数的导函数的最大值为313.在中，，，，线段在斜边上运动，且，设，则的取值范围是__________．14. 当，则_________．15.已知都是定义在R 上的函数,并满足以下条件:(1);(2);(3).且,则_________.16. 已知函数.(1)判断函数的单调性；(2)已知函数，其中，若存在，证明：.17. 如图，四棱锥P-ABCD 的底面ABCD 是矩形，O 是AC 与BD 的交点，E 为PB的中点．（Ⅰ）求证：平面PAD ；（Ⅱ）若平面ABCD ，，垂足为F ，，，求三棱锥P-DEF 的体积．18. 某校为调查高中生选修课的选修倾向与性别的关系，随机抽取50名学生，得到下面的数据表：倾向“平面几何选讲”倾向“坐标系与参数方程”倾向“不等式选讲”合计男生164626女生481224合计20121850（1）根据表中提供的数据，选择可直观判断“选课倾向与性别有关系”的两种，作为选修倾向变量的取值，并分析哪两种选择倾向与性别有关系的把握最大；（2）在抽取的50名学生中，按照分层抽样的方法，从倾向“平面几何选讲”与倾向“坐标系与参数方程”的学生中抽取8人进行问卷，若从这8人中任选3人，记倾向“平面几何选讲”的人数减去倾向“坐标系与参数方程”人数的差为，求的分布列及数学期望.附：19. 中国古代数学名著《九章算术》中记载了一种名为“堑堵”的几何体：“邪解立方，得二堑堵，邪解堑堵，其一为阳马，一为鳖臑”．“堑堵”其实就是底面为直角三角形的直棱柱．某“堑堵”如图所示，，点在线段上，平面．（Ⅰ）证明：；（Ⅱ）若点是底面内的动点，且，求三棱锥体积的最小值．20. 设数列的前项和为，在①，②，③这三个条件中任选一个，补充在下面问题中，并加以解答．问题：已知数列满足，______，若数列是等比数列，求数列的通项公式；若数列不是等比数列，说明理由．注：如果选择多个条件分别解答，按第一个解答计分．21. 已知数列的前项和为，且.(1)求的通项公式；(2)求数列的前项和.。

南京市、盐城市2022届高三年级第一次模拟考试数学试卷及答案

2022届高三年级第一次模拟考试(一)数学(满分150分，考试时间120分钟)一、选择题：本题共8小题，每小题5分，共40分。

在每小题给出的四个选项中，只有一项是符合题目要求的．1. 已知集合M ＝{y|y ＝sin x ，x ∈R }，N ＝{y|y ＝2x ，x ∈R }，则M ∩N 等于( )A. [－1，＋∞)B. [－1，0)C. [0，1]D. (0，1]2. 在等比数列{a n }中，公比为q.已知a 1＝1，则0<q<1是数列{a n }单调递减的( )A. 充分不必要条件B. 必要不充分条件C. 充要条件D. 既不充分又不必要条件3. 某中学高三(1)班有50名学生，在一次高三模拟考试中，经统计，得数学成绩X ～N(110，100)，则该班数学得分大于120分的学生人数约为( )(参考数据：P(|X －μ|<σ)≈0.68，P(|X －μ|<2σ)≈0.95) A. 16 B. 10 C. 8 D. 24. 若f(α)＝cos α＋isin α(i 为虚数单位)，则[f(α)]2等于( ) A. f(α) B. f(2α) C. 2f(α) D. f(α2)5. 已知直线2x ＋y ＋a ＝0与圆C ：x 2＋(y －1)2＝4相交于A ，B 两点，且△ABC 为等边三角形，则实数a 的值为( )A. －4或2B. －2或4C. －1±3D. －1±66. 在平面直角坐标系xOy 中，设点A(1，0)，B(3，4)，向量OC →＝xOA →＋yOB →，x ＋y ＝6，则|AC→|的最小值为( ) A. 1 B. 2 C. 5 D. 2 57. 已知α＋β＝π4(α>0，β>0)，则tan α＋tan β的最小值为( ) A. 22 B. 1 C. －2－2 2 D. －2＋2 28. 已知f(x)＝⎩⎨⎧e x －4，x ≤4，（x －16）2－143，x>4，则当x ≥0时，f(2x )与f(x 2)的大小关系是( )A. f(2x )≤f(x 2)B. f(2x )≥f(x 2)C. f(2x )＝f(x 2)D. 不确定二、选择题：本题共4小题，每小题5分，共20分。

南京市数学高三上学期理数期末教学质量检测试卷C卷

南京市数学高三上学期理数期末教学质量检测试卷C卷姓名:________ 班级:________ 成绩:________一、单选题 (共12题；共12分)1. （1分） (2019高一上·北京月考) 下列五个写法：① ；② ；③ ；④ ；⑤ .其中正确写法的个数为（）A . 1B . 2C . 3D . 42. （1分） (2019高二下·亳州月考) 设复数满足 ,则（）A .B .C .D .3. （1分）已知等比数列{an}中，各项都是正数，且a1 ，a3 ， 2a2成等差数列，则=（）A . 1+B . 1﹣C . 3+2D . 3﹣24. （1分） (2015高三上·广州期末) 一个几何体的三视图如图所示，其中正视图是正三角形，则几何体的外接球的表面积为（）A .B .C .D .5. （1分） (2017高三上·沈阳开学考) 某地区空气质量监测资料表明，一天的空气质量为优良的概率是0.75，连续两天为优良的概率是0.6，已知某天的空气质量为优良，则随后一天的空气质量为优良的概率是（）A . 0.8B . 0.75C . 0.6D . 0.456. （1分）由曲线y＝x2与直线y＝2x所围成的平面图形的面积为（）A .B .C .D .7. （1分） (2017高三上·长沙开学考) 已知等差数列{an}的前n项和为Sn ，若a4+a12﹣a8=8，a10﹣a6=4，则S23=（）A . 23B . 96C . 224D . 2768. （1分） ""是""的（）A . 充分不必要条件B . 必要不充分条件C . 充要条件D . 既不充分也不必要条件9. （1分）如图所示，M，N是函数（ω＞0）图像与x轴的交点，点P在M，N之间的图像上运动，当△MPN面积最大时，则ω＝（）A .B .C .D . 810. （1分） (2019高一上·兴仁月考) 已知函数在上是减函数，则，，的大小关系正确的是（）A .B .C .D .11. （1分）以下四个结论：①若a⊂α，b⊂β，则a，b为异面直线；②若a⊂α，b⊄α，则a，b为异面直线；③没有公共点的两条直线是平行直线；④两条不平行的直线就一定相交．其中正确答案的个数是（）A . 0个B . 1个C . 2个D . 3个12. （1分） (2017高一下·宜昌期中) 在△ABC中，边AC长为，| + |=2 ，D是BC边上的点，且 =2 ，• =0，则cos∠BAC=（）A .B .C .D .二、填空题 (共4题；共4分)13. （1分）已知在二项式（x2+ ）5的展开式中，含x4的项的二项式系数是________．14. （1分）若=(3,-1)，=(-3,2)，则=________15. （1分） (2017高一上·陵川期末) 某同学从区间[﹣1，1]随机抽取2n个数x1 ， x2 ，…，xn ， y1 ，y2 ，…，yn ，构成n个数对（x1 ， y1），（x2 ， y2），…（xn ， yn），该同学用随机模拟的方法估计n个数对中两数的平方和小于1（即落在以原点为圆心，1为半径的圆内）的个数，则满足上述条件的数对约有________个．16. （1分）(2020·海南模拟) 若曲线存在两条垂直于y轴的切线，则m的取值范围为________.三、解答题 (共7题；共8分)17. （2分） (2016高一上·武汉期末) 计算：（1）若cos = ，π＜x＜π，求的值．（2）已知函数f（x）=2 sinxcosx+2cos2x﹣1（x∈R），若f（x0）= ，x0∈[ ， ]，求cos2x0的值．18. （1分）(2018·广东模拟) 据某市地产数据研究院的数据显示，2016年该市新建住宅销售均价走势如图所示，为抑制房价过快上涨，政府从8月份采取宏观调控措施，10月份开始房价得到很好的抑制．参考数据：，（说明：以上数据为3月至7月的数据）回归方程中斜率和截距的最小二乘估计公式分别为：，（1）地产数据研究院研究发现，3月至7月的各月均价（万元/平方米）与月份之间具有较强的线性相关关系，试建立关于的回归方程（系数精确到 0.01），政府若不调控，依次相关关系预测第12月份该市新建住宅销售均价；（2）地产数据研究院在2016年的12个月份中，随机抽取三个月份的数据作样本分析，若关注所抽三个月份的所属季度，记不同季度的个数为X，求X的分布列和数学期望．19. （1分）如图，在正三棱柱ABC﹣A1B1C1中，点D是棱BC的中点．求证：（1）AD⊥C1D；（2）A1B∥平面ADC1 ．20. （1分） (2018高一下·福州期末) 已知向量，，且 .（1）求：及；（2）若的最小值是，求实数的值.21. （1分） (2019高三上·中山月考) 已知函数．（1）证明在区间内有且仅有唯一实根；（2）记在区间内的实根为，函数，若方程在区间有两不等实根，证明．22. （1分） (2017高三上·荆州期末) 在直角坐标系xOy中，圆C的参数方程（φ为参数），以O为极点，x轴的非负半轴为极轴建立极坐标系．（1）求圆C的极坐标方程；（2）直线l的极坐标方程是2ρsin（θ+ ）=3 ，射线OM：θ= 与圆C的交点为O、P，与直线l 的交点为Q，求线段PQ的长．23. （1分）(2018·佛山模拟) 设函数 .(Ⅰ)当时，求不等式的解集；(Ⅱ)若函数的图象与直线所围成的四边形面积大于20,求的取值范围.参考答案一、单选题 (共12题；共12分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、11-1、12-1、二、填空题 (共4题；共4分)13-1、14-1、15-1、16-1、三、解答题 (共7题；共8分) 17-1、17-2、18-1、18-2、19-1、20-1、20-2、21-1、21-2、22-1、22-2、23-1、。

江苏省南京市数学高三上学期理数第一次联考试卷

江苏省南京市数学高三上学期理数第一次联考试卷姓名:________ 班级:________ 成绩:________一、单选题 (共12题；共24分)1. （2分）(2020·晋城模拟) 已知是正项等比数列，，则（）A .B . 2C .D . 42. （2分） (2019高二上·沈阳月考) 若复数满足为虚数单位），则（）A .B .C .D .3. （2分） (2016高二上·山东开学考) 已知向量 =（x﹣5，3）， =（2，x），且⊥ ，则由x的值构成的集合是（）A . {2，3}B . {﹣1，6}C . {2}D . {6}4. （2分） (2019高三上·西安月考) 公元263年左右，我国数学家刘徽发现，当圆内接正多边形的边数无限增加时，多边形面积可无限逼近圆的面积，由此创立了割圆术，利用割圆术刘徽得到了圆周率精确到小数点后面两位的近似值3.14，这就是著名的徽率，下图是利用刘徽的割圆术设计的程序框图，则输出的值为（）（参考数据：，，）A . 3B . 4C . 5D . 65. （2分） (2019高三上·西安月考) 一个几何体的三视图如图所示，则该几何体的各个表面中，最大面的面积为（）A .B .C . 2D . 46. （2分） (2019高三上·西安月考) 已知函数，（为自然对数的底数）的图象与直线，轴围成的区域为E ，直线与围成的区域为F ，在区域F内任取一点，则该点落在区域E内的概率为（）A .B .C .D .7. （2分） (2019高三上·西安月考) 已知动点满足，且代数式的最小值为，则实数的取值为（）A .B .C .D . 48. （2分） (2019高三上·西安月考) 已知函数的部分图象如图所示，已知点，，若将它的图象向右平移个单位长度，得到函数的图象，则函数的图象的一条对称轴方程为（）A .B .C .D .9. （2分） (2019高三上·西安月考) 已知腰长为2的等腰直角ΔABC中，M为斜边AB的中点，点P为该平面内一动点，若，则的最小值为（）A .B .C .D .10. （2分） (2019高三上·西安月考) 已知、分别是具有公共焦点、的椭圆和双曲线的离心率，P是两曲线的一个公共点，O是的中点，且，则 =（）A .B .C .D . 211. （2分） (2019高三上·西安月考) 若数列的前项和满足：对都有（为常数）成立，则称数列为“和敛数列”，则数列，，，中是“和敛数列”的有（）A . 1个B . 2个C . 3个D . 4个12. （2分） (2019高三上·西安月考) 定义在R上的偶函数满足，且当时，，若函数有三个零点，则正实数的取值范围为（）A .B .C .D .二、填空题 (共4题；共4分)13. （1分）(2020·菏泽模拟) 已知直线（其中，）与圆交于点，，是坐标原点，则 ________， ________．14. （1分） (2017高三上·西安开学考) 已知幂函数y=xa的图象过点（3，9），则的展开式中x 的系数为________．15. （1分） (2018高三上·西安模拟) 从集合中任选一个元素，则满足的概率为________．16. （1分） (2019高三上·西安月考) 在四面体ABCD中，AB=AD=2 ，∠BAD=60° ，∠BCD=90°，二面角A-BD-C的大小为120°，则四面体ABCD外接球的半径为________三、解答题 (共7题；共65分)17. （10分）已知函数的图象（部分）如图所示．（I）求函数f（x）的解析式；（ II）求函数f（x）在区间上的最大值与最小值．18. （10分） (2018高二下·上海月考) 如图，在长方体中，、分别是棱、的中点，，，求：（1）与所成的角；（2）与平面所成的角．19. （10分） (2019高三上·西安月考) 2019年初，某市为了实现教育资源公平，办人民满意的教育，准备在今年8月份的小升初录取中在某重点中学实行分数和摇号相结合的录取办法．该市教育管理部门为了了解市民对该招生办法的赞同情况，随机采访了440名市民，将他们的意见和是否近三年家里有小升初学生的情况进行了统计，得到如下的2×2列联表.赞同录取办法人数不赞同录取办法人数合计近三年家里没有小升初学生18040220近三年家里有小升初学生14080220合计320120440（1）根据上面的列联表判断，能否在犯错误的概率不超过0.001的前提下认为是否赞同小升初录取办法与近三年是否家里有小升初学生有关；（2）从上述调查的不赞同小升初录取办法人员中根据近三年家里是否有小升初学生按分层抽样抽出6人，再从这6人中随机抽出3人进行电话回访，求3人中恰有1人近三年家里没有小升初学生的概率.附：，其中 .P（）0.100.050.0250.100.0050.0012.7063.841 5.024 6.6357.87910.82820. （10分）(2019高三上·西安月考) 在平面直角坐标系中，点，分别为椭圆C：的左右焦点，椭圆的离心率为，点在椭圆C上，不在轴上的动点P与动点Q关于原点O对称，且四边形的周长为 .（1）求动点P的轨迹方程；（2）在动点P的轨迹上有两个不同的点M ，N ，线段MN的中点为G ，已知点在圆上，求的最大值，并判断此时ΔOMN的形状.21. （5分） (2019高三上·西安月考) 己知函数 .( 是常数，且（）（Ⅰ）求函数的单调区间；22. （10分） (2019高三上·西安月考) 在平面直角坐标系中，直线的参数方程为（为参数）.在以坐标原点为极点，轴的正半轴为极轴的极坐标系中，曲线C的极坐标方程为 .（1）求直线的极坐标方程及曲线C的直角坐标方程；（2）若是直线上的一点，是曲线C上的一点，求的最大值.23. （10分） (2019高三上·西安月考) 已知函数 . （1）若，解不等式；（2）若不等式恒成立，求实数的取值范围.参考答案一、单选题 (共12题；共24分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、11-1、12-1、二、填空题 (共4题；共4分)13-1、14-1、15-1、16-1、三、解答题 (共7题；共65分) 17-1、18-1、18-2、19-1、19-2、20-1、20-2、21-1、22-1、22-2、23-1、23-2、。

高三南京数学一模试卷

高三南京数学一模试卷一、选择题（本大题共8小题，每小题5分，共40分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

）1. 函数f(x) = 2x^2 - 3x + 1的图像开口方向是：A. 向上B. 向下C. 向左D. 向右2. 已知集合A = {1, 2, 3}，B = {2, 3, 4}，则A∩B =：A. {1}B. {2, 3}C. {4}D. {1, 4}3. 已知圆的方程为x^2 + y^2 = 1，点P(2, 0)到圆心的距离是：A. 1B. 2C. √3D. 34. 函数y = ln(x+1)的定义域是：A. (-∞, 0)B. (-∞, -1)C. (-1, +∞)D. (0, +∞)5. 已知数列{a_n}满足a_1 = 1，a_n = 2a_{n-1} + 1，n≥2，那么a_3 =：A. 5B. 7C. 9D. 116. 函数y = sin(x) + cos(x)的周期是：A. πB. 2πC. 4πD. 6π7. 已知等差数列{a_n}的前n项和为S_n，且S_5 = 25，S_10 = 100，则a_6 + a_7 =：A. 14B. 20C. 26D. 328. 已知函数f(x) = x^3 - 3x^2 + 2x + 1，求f'(x) =：A. 3x^2 - 6x + 2B. 3x^2 - 6x + 3C. 3x^2 - 3x + 2D. 3x^2 - 3x + 1二、填空题（本大题共6小题，每小题5分，共30分。

）9. 已知函数f(x) = x^3 - 6x^2 + 11x - 6，求f'(2) = _______。

10. 已知函数y = x^2 - 4x + 4，求顶点坐标为 _______。

11. 已知等比数列{a_n}的公比为2，且a_1 = 1，则a_5 = _______。

12. 已知直线方程为y = 2x + 3，求与x轴的交点坐标为 _______。

南京市高三上学期期中数学试卷(理科)C卷(模拟)

南京市高三上学期期中数学试卷（理科）C卷姓名:________ 班级:________ 成绩:________一、选择题 (共12题；共24分)1. （2分）(2017·深圳模拟) 若集合A={2，4，6，8}，B={x|x2﹣9x+18≤0}，则A∩B=（）A . {2，4}B . {4，6}C . {6，8}D . {2，8}2. （2分）下列全称命题中假命题的个数是（）①2x+1是整数（x∈R）②对所有的x∈R ，x>3③对任意一个x∈z，2x2+1为奇数A . 0B . 1C . 2D . 33. （2分）定义2×2矩阵，若，则f（x）（）A . .图象关于（π，0）中心对称B . 图象关于直线对称C . 在区间上单调递增D . 周期为π的奇函数4. （2分） (2016高一下·湖南期中) 若l、m、n是互不相同的空间直线，α、β是不重合的平面，则下列命题中为真命题的是（）A . 若α∥β，l⊂α，n⊂β，则l∥nB . 若α⊥β，l⊂α，则l⊥βC . 若l⊥n，m⊥n，则l∥mD . 若l⊥α，l∥β，则α⊥β5. （2分）方程（x+y﹣1）=0所表示的曲线是（）A .B .C .D .6. （2分） (2018高一下·吉林期中) 设，，，则（）A .B .C .D .7. （2分） (2018高二下·南宁月考) 设实数满足不等式组，则的取值范围是（）A .B .C .D .8. （2分）设是两个不共线的非零向量，则“向量与共线”是“”的（）A . 充分非必要条件B . 必要非充分条件C . 充要条件D . 非充分非必要条件9. （2分）在三角形ABC中，E，F分别为边AB，AC上的点，且，，，则等于（）A .B .C .D .10. （2分）在椭圆中，记左焦点为F,右顶点为A，短轴上方的端点为B，若，则椭圆的离心率为（）A .B .C .D .11. （2分）已知a，b，c分别为△ABC三个内角A，B，C的对边，（sinA+sinB）（a﹣b）=（sinC﹣sinB）c，S△ABC= ，c=4b，则函数f（x）=bx2﹣ax+c的零点个数为（）A . 0B . 1C . 2D . 不确定12. （2分） (2016高一上·辽宁期中) 若x0是函数f（x）=2 的一个零点，x1∈（0，x0），x2∈（x0 ，+∞），则（）A . f（x1）＜0，f（x2）＜0B . f（x1）＞0，f（x2）＞0C . f（x1）＞0，f（x2）＜0D . f（x1）＜0，f（x2）＞0二、填空题 (共4题；共4分)13. （1分） (2018高一下·珠海月考) 已知，， ,则________.14. （1分）(2017·运城模拟) 四棱锥P﹣ABCD底面是一个棱长为2的菱形，且∠DAB=60°，各侧面和底面所成角均为60°，则此棱锥内切球体积为________．15. （1分） (2016高一上·宿迁期末) 函数f（x）=cos（ x+ ）的图象向右平移φ（φ＞0）个单位，所得函数图象关于y轴对称，则φ的最小值为________．16. （1分） (2016高二上·河北期中) 已知数列{an}的前n项和Sn=﹣ n2+kn（k∈NΦ），且Sn的最大值为8，则a2=________三、解答题 (共6题；共50分)17. （5分） (2018高二上·合肥期末) 已知，设命题：指数函数≠ 在上单调递增.命题：函数的定义域为．若“ ”为假，“ ”为真，求的取值范围．18. （10分） (2016高一下·辽宁期末) 在锐角△ABC中，a、b、c分别为角A、B、C所对的边，且 =2csinA（1）确定角C的大小；（2）若c= ，且△ABC的面积为，求a+b的值．19. （10分） (2016高二上·驻马店期中) 在四棱锥P﹣ABCD中，PA⊥面ABCD，∠DAB=90°，AB平行于CD，AD=CD=2AB=2，E，F分别为PC，CD的中点（1）求证：AB⊥面BEF；（2）设PA=h，若二面角E﹣BD﹣C大于45°，求h的取值范围．20. （5分）(2017·鹰潭模拟) 已知正项数列{an}的前n项和为Sn ，且是1与an的等差中项．（Ⅰ）求数列{an}的通项公式；（Ⅱ）设Tn为数列{ }的前n项和，证明：＜Tn＜1（n∈N*）21. （5分）(2017·汉中模拟) 已知在△ABC中，角A，B，C所对的边分别是a，b，c，且a、b、c成等比数列，c= bsinC﹣ccosB．（Ⅰ）求B的大小；（Ⅱ）若b=2 ，求△ABC的周长和面积．22. （15分）已知a∈R，函f（x）=x3﹣ax2+ax+a，g（x）=f（x）+（a﹣3）x．（1）求证：曲线y=f（x）在点（1，f（1））处的切线过定点；（2）若g（1）是g（x）在区间（0，3]上的极大值，但不是最大值，求实数a的取值范围；（3）求证：对任意给定的正数b，总存在a∈（3，+∞），使得g（x）在上为单调函数．参考答案一、选择题 (共12题；共24分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、11-1、12-1、二、填空题 (共4题；共4分)13-1、14-1、15-1、16-1、三、解答题 (共6题；共50分) 17-1、18-1、18-2、答案：略19-1、19-2、20-1、答案：略21-1、22-1、22-2、22-3、第11 页共11 页。

南京市一模高三数学试卷

南京市一模高三数学试卷一、选择题（本大题共10小题，每小题4分，共40分）1. 若函数f(x) = x^2 - 4x + c在区间[2, +∞)上为增函数，则c的取值范围是A. c ≥ 0B. c > 0C. c ≤ 4D. c < 42. 已知集合A = {x | x^2 - 5x + 6 = 0}，则A的元素个数是A. 1B. 2C. 3D. 43. 函数y = 2^x + 3^x的值域是A. (0, +∞)B. [1, +∞)C. [2, +∞)D. [3, +∞)4. 若a, b, c ∈ R，且a + b + c = 0，则下列不等式成立的是A. a^2 + b^2 + c^2 ≥ ab + bc + acB. a^2 + b^2 + c^2 ≤ ab + bc + acC. a^2 + b^2 + c^2 > ab + bc + acD. a^2 + b^2 + c^2 < ab + bc + ac5. 已知数列{an}满足a1 = 1，an = 2an-1 + 1，n ≥ 2，则a5的值为A. 17B. 33C. 65D. 1296. 已知向量a = (1, 2)，b = (3, -4)，则向量a与向量b的夹角θ满足A. 0° < θ < 90°B. 90° < θ < 180°C. θ = 90°D. θ = 180°7. 已知圆C：x^2 + y^2 - 6x + 8y - 24 = 0，圆心为C，半径为r，则r =A. 2B. 4C. 6D. 88. 已知直线l：x + y - 3 = 0与圆C：x^2 + y^2 = 9相交于A，B 两点，则|AB| =A. 3B. 4C. 5D. 69. 若方程x^2 - 4x + 4 = 0有实根，则实根的个数是A. 0B. 1C. 2D. 310. 已知等比数列{an}满足a1 = 2，公比q = 3，则a5的值为A. 96B. 162C. 486D. 729二、填空题（本大题共5小题，每小题4分，共20分）11. 若函数f(x) = x^3 - 3x在x = 1处取得极值，则该极值是_______。

南京市高考数学一模试卷(理科)C卷

南京市高考数学一模试卷（理科）C卷姓名:________ 班级:________ 成绩:________一、选择题 (共10题；共20分)1. （2分）在复平面内为坐标原点，复数与分别对应向量和，则（）A .B .C .D .2. （2分） (2016高一上·湖北期中) 已知集合U={x|x是小于6的正整数}，A={1，2}，B∩（C∪A）={4}，则∁∪（A∪B）=（）A . {3，5}B . {3，4}C . {2，3}D . {2，4}3. （2分）“a=1“是“直线ax+y+1=0与直线（a+2）x﹣3y﹣2=0垂直”的（）A . 充要条件B . 充分不必要条件C . 必要不充分条件D . 既不充分也不必要条件4. （2分） (2018高三下·滨海模拟) 设，则“ ”是“ ”的（）A . 充分不必要条件B . 必要不充分条件C . 充要条件D . 既不充分也不必要条件5. （2分）通过随机询问200名性别不同的大学生是否爱好“踢毽子运动”，计算得到统计量值k2的观测值k≈4.892，参照下表，得到的正确结论是（）P（k2≥k）0.100.050.010k 2.706 3.841 6.635A . 在犯错误的概率不超过5%的前提下，认为“爱好该运动与性别有关”B . 在犯错误的概率不超过5%的前提下，认为“爱好该运动与性别无关”C . 有99%以上的把握认为“爱好该运动与性有关”D . 有99%以上的把握认为“爱好该运动与性别无关”6. （2分） (2018高一上·湘东月考) 已知函数，函数．若函数恰好有2个不同的零点，则实数的取值范围是（）A .B .C .D .7. （2分） (2017高二下·咸阳期末) 已知方程x2﹣4x+1=0的两根是两圆锥曲线的离心率，则这两圆锥曲线是（）A . 双曲线、椭圆B . 椭圆、抛物线C . 双曲线、抛物线D . 无法确定8. （2分）(2019·呼和浩特模拟) 过坐标轴上一点作圆的两条切线，切点分别为、 .若，则的取值范围是（）A .B .C .D .9. （2分）(2017·雨花模拟) 秦九韶是我国南宋时期的数学家，他在所著的《数书九章》中提出的多项式求值的秦九韶算法，至今仍是比较先进的算法．如图所示的程序框图给出了利用秦九韶算法求某多项式值的一个实例，若输入n，x的值分别为3，3，则输出v的值为（）A . 16B . 18C . 48D . 14310. （2分）奇函数、偶函数的图像分别如图1、2所示，方程，的实根个数分别为，则（）A . 14B . 8C . 7D . 3二、填空题 (共5题；共5分)11. （1分） (2016高一下·咸阳期末) 设向量 =（m，﹣1）， =（1，2），若，则m=________．12. （1分） (2017高二下·南昌期末) 若某空间几何体的三视图如图所示，则该几何体的体积为________13. （1分） (2017高一下·怀仁期末) 若满足则的最小值为________．14. （1分）若（1﹣2x）2013=a0+a1x+…+a2013x2013（x∈R），则 + +…+ =________．15. （1分） (2016高一下·兰陵期中) 给出下列四个命题：①函数y=2sin（2x﹣）的一条对称轴是x= ；②函数y=tanx的图象关于点（，0）对称；③正弦函数在第一象限为增函数④存在实数α，使 sin（α+ ）=以上四个命题中正确的有________（填写正确命题前面的序号）三、解答题 (共6题；共50分)16. （10分） (2015高二上·东莞期末) 在△ABC中，a，b，c分别是A，B，C的对边，且2cosA= ．（1）若a2﹣c2=b2﹣mbc，求实数m的值；（2）若a=2，求△ABC面积的最大值．17. （5分）某工厂在试验阶段大量生产一种零件．这种零件有A、B两项技术指标需要检测，设各项技术指标达标与否互不影响．若A项技术指标达标的概率为，有且仅有一项技术指标达标的概率为．按质量检验规定：两项技术指标都达标的零件为合格品．（Ⅰ）求一个零件经过检测为合格品的概率；（Ⅱ）任意依次抽取该种零件4个，设ξ表示其中合格品的个数，求Eξ与Dξ．18. （5分）(2017·吉林模拟) 如图，在四棱锥P﹣ABCD中，底面ABCD是菱形，且∠ABC=120°．点E是棱PC的中点，平面ABE与棱PD交于点F．（Ⅰ）求证：AB∥EF；（Ⅱ）若PA=PD=AD=2，且平面PAD⊥平面ABCD，求平面PAF与平面AEF所成的二面角的正弦值．19. （10分） (2016高二下·安吉期中) 各项为正数的数列{an}的前n项和为Sn ，且满足：Sn= an2+ an+ （n∈N*）（1）求an（2）设数列{ }的前n项和为Tn，证明：对一切正整数n，都有Tn＜．20. （10分）(2018·吕梁模拟) 已知函数 .（1）求函数在点处的切线方程；（2）证明： .21. （10分）已知椭圆C：，右焦点，且离心率．（1）求椭圆C的方程．（2）过F且倾斜角为45°的直线l与椭圆交于不同的两点M，N，求△OMN（O为坐标原点）的面积．参考答案一、选择题 (共10题；共20分)1-1、答案：略2-1、答案：略3-1、答案：略4-1、5-1、答案：略6-1、7-1、答案：略8-1、9-1、10-1、答案：略二、填空题 (共5题；共5分)11-1、12-1、13-1、14-1、15-1、三、解答题 (共6题；共50分)16-1、答案：略16-2、答案：略17-1、答案：略18-1、答案：略19-1、答案：略19-2、答案：略20-1、答案：略20-2、答案：略21-1、答案：略21-2、答案：略。

南京市数学高三上学期理数第一次模拟考试试卷(II)卷

南京市数学高三上学期理数第一次模拟考试试卷（II）卷姓名:________ 班级:________ 成绩:________一、单选题 (共12题；共24分)1. （2分） (2019高一上·长春月考) 设集合，，则（）A .B .C .D .2. （2分） (2018高二上·山西月考) 平面向量与的夹角为60°，且 ,则（）A .B .C . 4D . 123. （2分） (2016高二上·郑州期中) 已知数列Sn为等比数列{an}的前n项和，S8=2，S24=14，则S2016=（）A . 2252﹣2B . 2253﹣2C . 21008﹣2D . 22016﹣24. （2分）(2017·武汉模拟) 设{an}是首项为正数的等比数列，公比为q，则“q＜0”是“对任意的正整数n，a2n﹣1+a2n＜0”的（）A . 充要条件B . 充分而不必要条件C . 必要而不充分条件D . 既不充分也不必要条件5. （2分） (2019高一上·杭州期中) 函数（其中常数e=2.71828……是一个无理数）的图像为（）A .B .C .D .6. （2分） (2016高一上·崇礼期中) 设a= ，b= ，c= ，则（）A . c＞b＞aB . a＞b＞cC . b＞a＞cD . b＞c＞a7. （2分）已知，则 =（）A . 2B . ﹣2C . 3D . ﹣38. （2分） (2018高一上·吉林期末) 圆台上、下底面面积分别是、，侧面积是，则这个圆台的体积是（）A .B .C .D .9. （2分） (2018高一上·西宁期末) 如图，是边的中点，则向量用表示为（）A .B .C .D .10. （2分）已知椭圆和双曲线有公共的焦点，那么双曲线的渐近线方程为（）A .B .C .D .11. （2分）圆绕直线旋转一周所得的几何体的体积为（）A .B .C .D .12. （2分）(2020·淮南模拟) 若函数有三个不同的零点，则实数a的取值范围是（）A .B .C .D .二、填空题 (共4题；共4分)13. （1分） (2017高二下·嘉兴期末) 已知圆C的方程为x2+y2﹣4x﹣6y+10=0，则过点（1，2）的最短弦的长度为________．14. （1分） (2016高三上·嘉兴期末) 设，实数满足若的最大值是0，则实数 =________，的最小值是________．15. （1分） (2018高三上·龙泉驿月考) 、分别为双曲线左、右支上的点，设是平行于轴的单位向量，则的最小值为________．16. （1分） (2018高一上·吉林期末) 已知将函数的图象向左平移个单位长度后得到的图象，则在上的值域为________．三、解答题 (共7题；共70分)17. （10分） (2020高二上·天津期末) 设数列的前项和为 ,且 ,等比数列满足.(I)求和的通项公式;(II)求数列的前项和.18. （10分）如图，在四棱锥中，，，是的中点，是棱上的点，，，， .（1）求证：平面底面；（2）设，若二面角的平面角的大小为，试确定的值.19. （10分） (2019高三上·宁德月考) 的内角的对边分别为，已知，.（1）求角C；（2）延长线段到点D，使，求周长的取值范围．20. （10分）(2017·东城模拟) 设函数f（x）=（x2+ax﹣a）•e﹣x（a∈R）．（Ⅰ）当a=0时，求曲线y=f（x）在点（﹣1，f（﹣1））处的切线方程；（Ⅱ）设g（x）=x2﹣x﹣1，若对任意的t∈[0，2]，存在s∈[0，2]使得f（s）≥g（t）成立，求a的取值范围．21. （10分）(2017·扬州模拟) 已知函数f（x）= ，g（x）=lnx，其中e为自然对数的底数．（1）求函数y=f（x）g（x）在x=1处的切线方程；（2）若存在x1，x2（x1≠x2），使得g（x1）﹣g（x2）=λ[f（x2）﹣f（x1）]成立，其中λ为常数，求证：λ＞e；（3）若对任意的x∈（0，1]，不等式f（x）g（x）≤a（x﹣1）恒成立，求实数a的取值范围．22. （10分）(2020·茂名模拟) 设为椭圆：上任意一点，以坐标原点为极点，轴的正半轴为极轴建立极坐标系，曲线的极坐标方程为，为上任意一点.（Ⅰ）写出参数方程和普通方程；（Ⅱ）求最大值和最小值.23. （10分）(2017·南阳模拟) 设函数f（x）=|2x﹣a|+|x+a|（a＞0）．（1）当a=1时，求f（x）的最小值；（2）若关于x的不等式在x∈[1，2]上有解，求实数a的取值范围．参考答案一、单选题 (共12题；共24分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、11-1、12-1、二、填空题 (共4题；共4分)13-1、14-1、15-1、16-1、三、解答题 (共7题；共70分) 17-1、18-1、18-2、19-1、19-2、21-1、21-2、21-3、22-1、23-1、23-2、。

2022届南京市高三年级第一次模拟考试数学试题(含答案解析)

2022届南京市高三年级第一次模拟考试数学试题一、单选题（本大题共8小题，共40.0分） 1.已知集合M ={y|y =sinx,x ∈R}，N ={y|y =2x ,x ∈R}，则M ∩N =( )A. [−1,+∞)B. [−1,0)C. [0,1]D. (0,1]2.在等比数列{a n }中，公比为q ，已知a 1=1，则0<q <1是数列{a n }单调递减的( )A. 充分不必要条件B. 必要不充分条件C. 充要条件D. 既不充分又不必要条件3.某中学高三(1)班有50名学生，在一次高三模拟考试中，经统计得：数学成绩X∽N(110,100)，则估计该班数学得分大于120分的学生人数为( )(参考数据：P(|X −μ|<σ)≈0.68 ，P(|X −μ|<2σ)≈0.95)A. 16B. 10C. 8D. 24. 若f(α)=cosα+isinα(i 为虚数单位)，则[f(α)]2=( )A. f(α) B. f(2α) C. 2f(α) D. f(α2)5. 已知直线√2x +y +a =0与⊙C ：x 2+(y −1)2=4相交于A ，B 两点，且ΔABC 为等边三角形，则实数a =( )A. −4或2B. −2或4C. −1±√3D. −1±√66. 在平面直角坐标系xOy 中，设A(1,0)，B(3,4)，向量OC⃗⃗⃗⃗⃗ =x OA ⃗⃗⃗⃗⃗ +y OB ⃗⃗⃗⃗⃗⃗ ，x +y =6，则|AC ⃗⃗⃗⃗⃗ |的最小值为( )A. 1B. 2C. √5D. 2√57. 已知α+β=π4(α>0,β>0)，则tanα+tanβ 的最小值为( )A. √22B. 1C. −2−2√2D. −2+2√28. 已知f(x)={e x−4,x ⩽4(x −16)2−143,x >4，则当x ≥0时，f(2x )与f(x 2)的大小关系是( ) A. f(2x )≤f(x 2) B. f(2x )≥f(x 2) C. f(2x )=f(x 2) D. 不确定二、多选题（本大题共4小题，共20.0分）9. 若函数f(x)=cos2x +sinx ，则关于f(x)的性质说法正确的有( )A. 偶函数B. 最小正周期为πC. 既有最大值也有最小值D. 有无数个零点10. 若椭圆C:x 29+y 2b 2=1(b >0)的左，右焦点分别为F 1,F 2，则下列b 的值，能使以F 1F 2为直径的圆与椭圆C 有公共点的有( )A. b =√2B. b =√3C. b =2D. b =√511. 若数列{a n }的通项公式为a n =(−1)n−1，记在数列{a n }的前项中任取两项都是正数的概率为P n ，则( )A. P 1=13 B. P 2n <P 2n+2 C. P 2n−1<P 2nD. P 2n−1+P 2n <P 2n+1+P 2n+212. 如图，在四棱锥P −ABCD 中，已知PA ⊥底面ABCD ，底面ABCD为等腰梯形，AD//BC ，AB =AD =CD =1，BC =PA =2，记四棱锥P −ABCD 的外接球为球O ，平面PAD 与平面PBC 的交线为l ，BC 的中点为E ，则( )A. l//BCB. AB ⊥PCC. 平面PDE ⊥平面PADD. l 被球O 截得的弦长为1三、填空题（本大题共4小题，共20.0分）13. 若f(x)=(x +3)5+(x +m)5是奇函数，则m = ．14. 在ΔABC 中，角A ，B ，C 的对边分别为a ，b ，c.若a =3b ，则cosB 的最小值是． 15. 计算机是二十世纪最伟大的发明之一，被广泛地应用于人们的工作与生活之中，计算机在进行数的计算处理时，使用的是二进制．一个十进制数n(n ∈N ∗)可以表示成二进制数(a 0a 1a 2…a k )2，k ∈N ，则n =a 0·2k +a 1·2k−1+a 2·2k−2+⋯+a k ·20，其中a 0=1，当i ≥1时，a i ∈{0,1}.若记a 0，a 1，a 2，…，a k 中1的个数为f(n)，则满足k =6，f(n)=3的n 的个数为．16. 已知：若函数f(x)，g(x)在R 上可导，f(x)=g(x)，则f′(x)=g′(x).又英国数学家泰勒发现了一个恒等式e 2x =a 0+a 1x +a 2x 2+⋯+a n x n +⋯，则a 0= ，∑ 10n=1 a n+1na n= ．四、解答题（本大题共6小题，共70.0分）17. 从①sin D =sin A ；②S △ABC =3S △BCD ；③DB ⃗⃗⃗⃗⃗⃗ ⋅DC ⃗⃗⃗⃗⃗ =−4，这三个条件中任选一个，补充在下面的问题中，并完成解答．已知点D 在△ABC 内，cos A >cos D ，AB =6，AC =BD =4，CD =2，若__________，求△ABC 的面积．注：如果选择多个条件分别解答，按第一个解答计分．18. 已知数列{a n }的通项公式为a n =2n +4，数列{b n }的首项为b 1=2．(1)若{b n }是公差为3的等差数列，求证：{a b n }也是等差数列； (2)若{a b n }是公比为2的等比数列，求数列{b n }的前n 项和．19. 佩戴头盔是一项对家庭与社会负责的表现，某市对此不断进行安全教育．下表是该市某主干路口连续4年监控设备抓拍到的驾驶员不戴头盔的统计数据：(1)请利用所给数据求不戴头盔人数y 与年度序号x 之间的回归直线方程y ̂=b ̂x +a ̂，并估算该路口2022年不戴头盔的人数；(2)交警统计2018∼2021年通过该路口的开电瓶车出事故的50人，分析不戴头盔行为与事故是否伤亡的关系，得到下表，能否有95%的把握认为不戴头盔行为与事故伤亡有关⋅参考公式：b ̂=i ni=1i −nxy ∑x 2n −nx2=ni=1i −x)(y i −y)∑(n x −x)2，a ̂=y −b ̂x ．χ2=n(ad−bc)2(a+b)(c+d)(a+c)(b+d)，其中n =a +b +c +d ．20. 在三棱柱ABC−A1B1C1中，AA1=13，AB=8，BC=6，AB⊥BC，AB1=B1C，D为AC中点，平面AB1C⊥平面ABC．(1)求证：B1D⊥平面ABC；(2)求直线C1D与平面AB1C所成角的正弦值．21. 设双曲线C:x2a2−y2b2=1(a,b>0)的右顶点为A，虚轴长为√2，两准线间的距离为2√63．(1)求双曲线C的方程；(2)设动直线l与双曲线C交于P、Q两点，若，设点A到动直线l的距离为d，求d的最大值．22. 设函数．(1)求函数f(x)在x=1处的切线方程；(2)若x1,x2为函数f(x)的两个不等于1的极值点，设P(x1,f(x1))，Q(x2,f(x2))，记直线PQ的斜率为k，求证：k+2<x1+x2．参考答案及解析1.答案：D解析：本题主要考查集合交集的运算，属于基础题．先化简集合M，N，再由交集运算得答案．解：∵M={y|y=sinx,x∈R}=[−1，1]，N={y|y=2x,x∈R}=(0,+∞)，∴M∩N=(0,1]．故选：D．2.答案：C解析：本题考查充要条件的判断，涉及等比数列的性质，属于基础题．根据等比数列的性质结合必要条件、充分条件的判断，即可得到答案．解：当0<q<1时，a n+1−a n=a1q n−a1q n−1=a1q n−1(q−1)<0，故a n+1<a n，即{a n}是单调递减数列，充分性成立．若{a n}是单调递减数列，则a n+1<a n，即a1q n<a1q n−1，∵a1=1,∴q n<q n−1，∴q n−1(q−1)<0对都成立，∴0<q<1，必要性成立．故当a1=1时，0<q<1是数列{a n}单调递减的充要条件．故选C．3.答案：C解析：本题考查正态分布的概率计算，属于基础题．由正态分布的概率计算即可求解．=0.16，解：P(X>120)=P(X>μ+σ)=1−P(|X−μ|<σ)250×0.16=8，故选：C．4.答案：B解析：本题考查复数的运算，二倍角正弦公式，属基础题．由复数的四则运算法则，结合二倍角公式即可求得结果．解：由f(α)=cosα+isinα可得，[f(α)]2=(cosα+isinα )2=cos 2α−sin 2α+2isinαcosα=cos2α+isin2α=f(2α)．故选B ．5.答案：A解析：本题考查了直线与圆的位置关系，点到直线的距离公式的应用，属于基础题．求出圆心到直线的距离，直接利用点到直线的距离公式求出结果．解：由于⊙C 的方程为x 2+(y −1)2=4，所以⊙C 的圆心为(0,1)，半径为2，由于ΔABC 为等边三角形，所以AB =AC =BC =2，圆心(0,1)到直线√2x +y +a =0的距离d =√22−1=√3，即√3=√3，解得a =−4或a =2．故选：A ．6.答案：D解析：本题考查向量的模和平面向量的坐标运算，属于基础题．由题意知 OC ⃗⃗⃗⃗⃗ =(x +3y,4y)，AC ⃗⃗⃗⃗⃗ =(x +3y −1,4y)=(5+2y,4y)，|AC ⃗⃗⃗⃗⃗ |=√(5+2y)2+16y 2=√20y 2+20y +25，根据二次函数的性质即可求其最值．解：由于A(1,0)，B(3,4)，向量OC⃗⃗⃗⃗⃗ =x OA ⃗⃗⃗⃗⃗ +y OB ⃗⃗⃗⃗⃗⃗ ，所以OA ⃗⃗⃗⃗⃗ =(1,0)，OB ⃗⃗⃗⃗⃗⃗ =(3,4)，OC ⃗⃗⃗⃗⃗ =(x +3y,4y)，AC ⃗⃗⃗⃗⃗ =OC ⃗⃗⃗⃗⃗ −OA ⃗⃗⃗⃗⃗ =(x +3y −1,4y)，又因为x +y =6，所以AC⃗⃗⃗⃗⃗ =(5+2y,4y)，所以|AC ⃗⃗⃗⃗⃗ |=√(5+2y)2+16y 2=√20y 2+20y +25=√20(y +12)2+20 故当y =−12时，|AC⃗⃗⃗⃗⃗ |取最小值2√5．故选：D ．7.答案：D解析：本题考查同角三角函数关系式及两角和与差的三角函数，属于中档题．根据题意利用同角三角函数之间的关系及两角和与差的三角函数可得cosαcosβ的最大值为12+√24，进而利用分母取最大值时分式值最小即可求得结果．解：，=√22cos 2α+√22cosα·sinα =√24(cos2α+1)+√24sin2α，，．所以cosαcosβ的最大值为12+√24，所以tanα+tanβ的最小值为√2212+√24=2√2−2．故选D ．8.答案：B解析：。

南京市数学高三上学期理数第一次模拟考试试卷C卷

18. （10分） (2017高一下·桃江期末) 设函数f（x）=cos（ωx+φ）（ω＞0，﹣ ＜φ＜0）的最小正周期为π．且f（） = ．
（1）求ω和φ的值；
（2）在给定坐标系中作出函数f（x）在[0，π]上的图象（3）若f（x）＞，求x的取值范围．
19. （10分）已知函数f（x）=ax2﹣|x|+2a﹣1（a为实常数）．
A .
B .
C .
D .
7. （2分） (2020·贵州模拟) 已知曲线，，则下面结论正确的是（）
A . 把上各点的横坐标伸长到原来的2倍，纵坐标不变，再把得到的曲线向左平移个单位长度，得到曲线；
B . 把上各点的横坐标伸长到原来的2倍，纵坐标不变，再把得到的曲线向右平移个单位长度，得到曲线；
C .
பைடு நூலகம்D .
9. （2分） (2018高一下·福州期末) 如图，在的内部，为的中点，且，则的面积与的面积的比值为（）
A . 3
B . 4
C . 5
D . 6
10. （2分）已知锐角α，β满足cosα= ，sin（α﹣β）=﹣ ，则sinβ的值为（）
A .
B .
C .
D .
11. （2分）若指数函数y=（2a﹣1）x在R上为单调递减函数，则a的取值范围是（）
南京市数学高三上学期理数第一次模拟考试试卷C卷
姓名:________班级:________ 成绩:________
一、单选题 (共12题；共24分)
1. （2分）已知集合则
A .
B .
C .
D . {—2，0}
2. （2分）复数z满足，则复数的实部与虚部之差为（）

南京市数学高三上学期理数期末考试试卷C卷

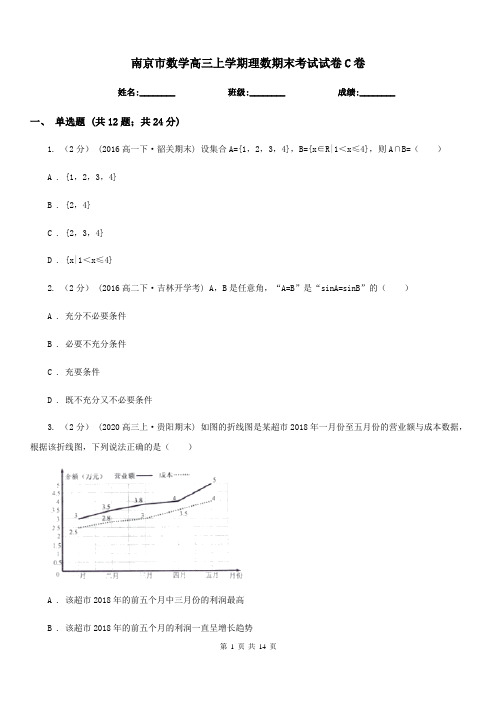
南京市数学高三上学期理数期末考试试卷 C 卷姓名:________班级:________成绩:________一、单选题 (共 12 题；共 24 分)1. （2 分） (2016 高一下·韶关期末) 设集合 A={1，2，3，4}，B={x∈R|1＜x≤4}，则 A∩B=（）A . {1，2，3，4}B . {2，4}C . {2，3，4}D . {x|1＜x≤4}2. （2 分） (2016 高二下·吉林开学考) A，B 是任意角，“A=B”是“sinA=sinB”的（）A . 充分不必要条件B . 必要不充分条件C . 充要条件D . 既不充分又不必要条件3. （2 分） (2020 高三上·贵阳期末) 如图的折线图是某超市 2018 年一月份至五月份的营业额与成本数据，根据该折线图，下列说法正确的是（）A . 该超市 2018 年的前五个月中三月份的利润最高B . 该超市 2018 年的前五个月的利润一直呈增长趋势第 1 页共 14 页C . 该超市 2018 年的前五个月的利润的中位数为 0.8 万元 D . 该超市 2018 年前五个月的总利润为 3.5 万元4. （2 分）若函数的图像与轴有公共点，则的取值范围是（）A.B.C.D.5. （2 分） (2016 高一下·郑州期末) 在直角△ABC 中，∠BCA=90°，CA=CB=1，P 为 AB 边上的点且 =λ ，若 • ≥ • ，则 λ 的取值范围是（）A . [ ，1]B.[，1]C.[ ，]D.[，]6. （2 分） (2016 高一下·益阳期中) 函数 y=sinxcosx 是（）A . 最小正周期为 π 的奇函数B . 最小正周期为 π 的偶函数C . 最小正周期为 2π 的奇函数D . 最小正周期为 2π 的偶函数7. （2 分）已知向量 =（λ+1，1）， =（λ+2，2），若（ + ）⊥（ ﹣ ），则 λ=（）A . -4第 2 页共 14 页B . -3C . -2D . -18. （2 分）已知公比为的等比数列的前项和为（1）成等比数列；，则下列结论中：（2）；（3）正确的结论为（） A . （1）（2）． B . （1）（3）． C . （2）（3）． D . （1）（2）（3）． 9. （2 分）将函数 y=sinx，x∈R 的图象上所有点的横坐标缩短为原来的一半，纵坐标不变，所得图象对应的函数解析式为（）A . y=sin ， x∈R B . y=sin2x，x∈RC . y= sinx，x∈R D . y=2sinx，x∈R10. （2 分） (2018·安徽模拟) 已知分别是双曲线的左右焦点，过的直线与双曲线左右两支分别交于两点，若是等边三角形，则该双曲线的离心率为（）A.第 3 页共 14 页B.C.D.11.（2 分）已知函数与函数的图像在是定义在实数集上的以 2 为周期的偶函数，当时，内恰有两个不同的公共点，则实数的值是（）A. 或； B . 0；C . 0或；D . 0或 ..若直线12. （2 分） (2019 高二上·扶余期中) 实轴长为的双曲线的点值范围为（满足），其中，分别是双曲线上恰有个不同的左、右顶点.则的离心率的取A.B. C. D.二、填空题 (共 4 题；共 4 分)第 4 页共 14 页13. （1 分） (2015 高二上·淄川期末) 已知实数 x，y 满足约束条件，则 x2+y2 的最小值是________14. （1 分） (2017 高二下·芮城期末) 在 ________．的展开式中，若第四项的系数为 84，则实数的值为15. （ 1 分） (2017 高二下 · 寿光期中 ) ∠AOB 在平面 α 内， OC 是平面 α 的一条斜线，若已知 ∠AOB=∠BOC=∠COA=60°，则 OC 与平面 α 所成的角的余弦值等于________．16. （ 1 分） (2019 高三上 · 吉林月考 ) 直线的圆心，则的最小值是________.（，）过圆：三、解答题 (共 7 题；共 70 分)17. （10 分） (2016 高三上·沈阳期中) 已知公差不为 0 的等差数列{an}中，a1=2，且 a2+1，a4+1，a8+1 成等比数列．（1）求数列{an}通项公式；（2）设数列{bn}满足 bn= ，求适合方程 b1b2+b2b3+…+bnbn+1= 的正整数 n 的值．18. （10 分）某中学为了了解全校学生的上网情况，在全校采用随机抽样的方法抽取了 40 名学生（其中男女生人数恰好各占一半）进行问卷调查，并进行了统计，按男女分为两组，再将每组学生的月上网次数分为 5 组：[0， 5），[5，10），[10，15），[15，20），[20，25]，得到如图所示的频率分布直方图：（I）写出 a 的值；第 5 页共 14 页（II）在抽取的 40 名学生中，从月上网次数不少于 20 次的学生中随机抽取 3 人，并用 X 表示其中男生的人数，求 X 的分布列和数学期望．19. （10 分） (2018 高三上·吉林月考) 如图，为圆的直径，点，在圆上，，矩形和圆所在的平面互相垂直，已知，．（Ⅰ）求证：平面平面；（Ⅱ）当的长为何值时，二面角的大小为．20. （10 分） (2019 高三上·广东月考) 已知函数（Ⅰ）求函数的极值；（Ⅱ）若实数为整数，且对任意的时，都有，.恒成立，求实数的最小值.21. （10 分） (2019 高三上·汕头期末) 设椭圆圆：的圆心.（1）求椭圆的方程；（2）已知过椭圆右焦点的直线交椭圆于两点，求四边形面积的取值范围.的左焦点为，离心率为，为两点，过且与垂直的直线与圆交于22. （10 分） (2018·长安模拟) 已知曲线 C：，直线：（t 为参数，）.（Ⅰ）求曲线 C 的直角坐标方程；（Ⅱ）设直线与曲线 C 交于 A、B 两点（A 在第一象限），当第 6 页共 14 页时，求的值.23. （10 分） (2018·鞍山模拟) 已知，（1）若且的最小值为 1，求的值；（2）不等式的解集为，不等式的解集为，. ，求的取值范围.第 7 页共 14 页一、单选题 (共 12 题；共 24 分)1-1、 2-1、 3-1、 4-1、 5-1、 6-1、 7-1、 8-1、 9-1、 10-1、 11-1、 12-1、二、填空题 (共 4 题；共 4 分)13-1、 14-1、参考答案第 8 页共 14 页15-1、 16-1、三、解答题 (共 7 题；共 70 分)17-1、17-2、第 9 页共 14 页18-1、第 10 页共 14 页19-1、20-1、21-1、21-2、22-1、23-1、23-2、。

南京市届高三第一次模拟考试数学卷-5页文档资料

南京市2019届高三第一次模拟考试数学2019．01 注意事项：1．本试卷共4页，包括填空题(第1题～第14题)、解答题(第15题～第20题)两部分．本试卷满分为l60分，考试时间为120分钟．2·答题前，请务必将自己的姓名、学校、班级、学号写在答题纸的密封线内-试题的答案写在答题纸上对应题目的答案空格内。

考试结束后，交回答题纸．参考公式，1．样本数据x1,x2,x3,…x n的方差其中是这组数据的平均数．2．柱体、锥体的体积公式：，其中s是柱(锥)体的底面面积，h 是高．一、填空题：本大题共l4小题，每小题5分，共70分．请把答案填写在答题纸相应的位置上．1．函数的定义域是 ___ ▲___．2．已知复数=满足(z--2)i=l+i(i为虚数单位)，则z的模为___ ▲___ ．3．已知实数x，y满足则Z＝2x+y的最小值是___ ▲___4 如图所示的流程图，若输入x＝-9.5，则输出的结果为___ ▲___5在集合A＝{2，3}中随机取一个元素m，在集合B＝{1，2，3}中随机取一个元素n，得到点P（m,n），则点P在圆x2+y2=9内部的概率为___ ▲___6．已知平面向量a,b满足|a|=1，|b|=2 n与b的夹角为．以a,b为邻边作平行四边形，则此平行四边形的两条对角线中较短的一条的长度为___ ▲___7．为了分析某篮球运动员在比赛中发挥的稳定程度，统计了该运动员在6场比赛中的得分，用茎叶图表示如右图，则该组数据的方差为 ___ ▲___．8．在△ABC中，角A，B，c所对的边分别为a,c,c 若，则角A的大小为__ ▲___．9．已知双曲线c： (a>0，b>o)的右顶点、右焦点分别为A，F，它的左准线与z轴的交点为B，若A是线段BF的中点，则双曲线C的离心率为__ ▲___·10．已知正数数列{a n)对任意．若a2=4，则a9=__ ▲___11．已知l,m是两条不同的直线，a，β是两个不同的平面．下列命题：[来源:Z#xx#k] 其中真命题是 _ ___▲___ (写出所有真命题的序号)．12．已知．若实数m，n满足，则m十n的最小值是_ ___▲__·13．在△ABC中，已知BC=2，，则△ABC面积的最大值是___▲__14．若直角坐标平面内两点P，Q满足条件：①P、Q都在函数的图象上；②P、Q关于原点对称，则称点对(P，Q)是函数的一个“友好点对’(点对(P，Q)与点对(Q，P)看作同一个“友好点对)．已知函数则的“友好点对”有___▲__个·二、解答题：本大翘共6小题，共计90分．请在答题纸指定区域内作答，解答时应写出文字说明、证明过程或演算步骤．15．(本题满分l4分)已知函数的最小正周期·16．(本题满分l4分)如图，在棱长均为4的三棱柱ABC—A1B1C1。