振动周期(秒),X、Y方向的平动因子及Z向扭转因子,振型质量参与系数
振型参与质量系数系数

抗震规范和高规都有这个系数,牵涉到其他几个概念,与大家分享有关振型的几个概念振型参与系数:每个质点质量与其在某一振型中相应坐标乘积之和与该振型的主质量(或者说该模态质量)之比,即为该振型的振型参与系数。
一阶振型自振频率最小(周期最长),二阶,三阶....振型的自振频率逐渐增大. 地震力大小和地面加速度大小成正比,周期越长加速度越小,地震力也越小。
自振振型曲线是在结构某一阶特征周期下算得的各个质点相对位移(模态向量)的图形示意.在形状上如实反映实际结构在该周期下的振动形态.振型零点是指在该振型下结构的位移反应为0。
振型越高,周期越短,地震力越大,但由于我们地震反应是各振型的迭代,高振型的振型参与系数小。
特别是对规则的建筑物,由于高振型的参与系数小,一般忽略高振型的影响。
振型的有效质量:这个概念只对于串连刚片系模型有效(即基于刚性楼板假定的,不适用于一般结构。
)。
某一振型的某一方向的有效质量为各个质点质量与该质点在该一振型中相应方向对应坐标乘积之和的平方((∑mx)2)。
一个振型有三个方向的有效质量,而且所有振型平动方向的有效质量之和等于各个质点的的质量之和,转动方向的有效质量之和等于各个质点的转动惯量之和。
有效质量系数:如果计算时只取了几个振型,那么这几个振型的有效质量之和与总质量之比即为有效质量系数。
这个概念是由WILSON E.L. 教授提出的,用于判断参与振型数足够与否,并将其用于ETABS程序。
振型参与质量:某一振型的主质量(或者说该模态质量)乘以该振型的振型参与系数的平方,即为该振型的振型参与质量。
振型参与质量系数:由于有效质量系数只实用于刚性楼板假设,现在不少结构因其复杂性需要考虑楼板的弹性变形,因此需要一种更为一般的方法,不但能够适用于刚性楼板,也应该能够适用于弹性楼板。
出于这个目的,我们从结构变形能的角度对此问题进行了研究,提出了一个通用方法来计算各地震方向的有效质量系数即振型参与质量系数,规范即是通过控制有效质量振型参与质量系数的大小来决定所取的振型数是否足够。
振型参与质量系数详解与解释

振型参与质量系数详解抗震规范和高规都有这个系数,牵涉到其他几个概念,与大家分享有关振型的几个概念振型参与系数:每个质点质量与其在某一振型中相应坐标乘积之和与该振型的主质量(或者说该模态质量)之比,即为该振型的振型参与系数。
一阶振型自振频率最小(周期最长),二阶,三阶....振型的自振频率逐渐增大. 地震力大小和地面加速度大小成正比,周期越长加速度越小,地震力也越小。
自振振型曲线是在结构某一阶特征周期下算得的各个质点相对位移(模态向量)的图形示意.在形状上如实反映实际结构在该周期下的振动形态.振型零点是指在该振型下结构的位移反应为0。
振型越高,周期越短,地震力越大,但由于我们地震反应是各振型的迭代,高振型的振型参与系数小。
特别是对规则的建筑物,由于高振型的参与系数小,一般忽略高振型的影响。
振型的有效质量:这个概念只对于串连刚片系模型有效(即基于刚性楼板假定的,不适用于一般结构。
)。
某一振型的某一方向的有效质量为各个质点质量与该质点在该一振型中相应方向对应坐标乘积之和的平方((∑mx)2)。
一个振型有三个方向的有效质量,而且所有振型平动方向的有效质量之和等于各个质点的的质量之和,转动方向的有效质量之和等于各个质点的转动惯量之和。
有效质量系数:如果计算时只取了几个振型,那么这几个振型的有效质量之和与总质量之比即为有效质量系数。
这个概念是由WILSON E.L. 教授提出的,用于判断参与振型数足够与否,并将其用于ETABS程序。
振型参与质量:某一振型的主质量(或者说该模态质量)乘以该振型的振型参与系数的平方,即为该振型的振型参与质量。
振型参与质量系数:由于有效质量系数只实用于刚性楼板假设,现在不少结构因其复杂性需要考虑楼板的弹性变形,因此需要一种更为一般的方法,不但能够适用于刚性楼板,也应该能够适用于弹性楼板。
出于这个目的,我们从结构变形能的角度对此问题进行了研究,提出了一个通用方法来计算各地震方向的有效质量系数即振型参与质量系数,规范即是通过控制有效质量振型参与质量系数的大小来决定所取的振型数是否足够。
对抗震规范GB5011-2010 中 (5.2.5) (楼层最小剪重比)的重新理解
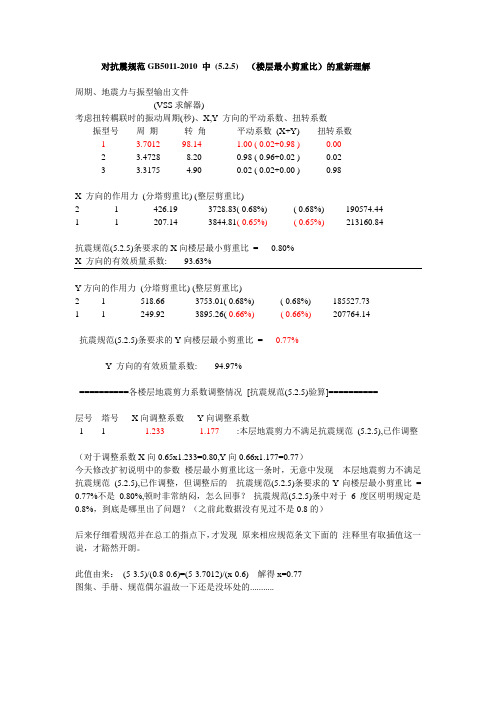
对抗震规范GB5011-2010 中(5.2.5) (楼层最小剪重比)的重新理解周期、地震力与振型输出文件(VSS求解器)考虑扭转耦联时的振动周期(秒)、X,Y 方向的平动系数、扭转系数振型号周期转角平动系数(X+Y) 扭转系数1 3.7012 98.14 1.00 ( 0.02+0.98 ) 0.002 3.4728 8.20 0.98 ( 0.96+0.02 ) 0.023 3.3175 4.90 0.02 ( 0.02+0.00 ) 0.98X 方向的作用力(分塔剪重比) (整层剪重比)2 1 426.19 3728.83( 0.68%) ( 0.68%) 190574.441 1 207.14 3844.81( 0.65%) ( 0.65%)213160.84抗震规范(5.2.5)条要求的X向楼层最小剪重比= 0.80%X 方向的有效质量系数: 93.63%Y方向的作用力(分塔剪重比) (整层剪重比)2 1 518.66 3753.01( 0.68%) ( 0.68%) 185527.731 1 249.92 3895.26( 0.66%) ( 0.66%) 207764.14抗震规范(5.2.5)条要求的Y向楼层最小剪重比= 0.77%Y 方向的有效质量系数: 94.97%==========各楼层地震剪力系数调整情况[抗震规范(5.2.5)验算]==========层号塔号X向调整系数Y向调整系数1 1 1.233 1.177 :本层地震剪力不满足抗震规范(5.2.5),已作调整(对于调整系数X向0.65x1.233=0.80,Y向0.66x1.177=0.77)今天修改扩初说明中的参数楼层最小剪重比这一条时,无意中发现本层地震剪力不满足抗震规范(5.2.5),已作调整,但调整后的抗震规范(5.2.5)条要求的Y向楼层最小剪重比= 0.77%不是0.80%,顿时非常纳闷,怎么回事?抗震规范(5.2.5)条中对于6度区明明规定是0.8%,到底是哪里出了问题?(之前此数据没有见过不是0.8的)后来仔细看规范并在总工的指点下,才发现原来相应规范条文下面的注释里有取插值这一说,才豁然开朗。
振动周期XY方向的平动因子及Z向扭转因子振型质量参与

振动周期XY方向的平动因子及Z向扭转因子振型质量参与振动周期是指一个物体从一个极端位置运动到另一个极端位置并返回到初始位置所需的时间。
它是描述物体振动特征的重要参数之一在振动过程中,物体可以沿着不同的方向发生平动和扭转。
平动是指物体在空间内沿直线方向移动,扭转是指物体围绕一些轴旋转。
因此,对于一个三维物体,我们可以将它的平动和扭转分为三个方向:XY方向的平动和Z向的扭转。
在振动系统中,物体的平动和扭转通常由振型来描述。
振型是指在一些振动系统中,使系统产生稳定振动的特定形式。
每个振型都有其对应的振型质量,即在该振型下各个部分参与振动的质量比例。
对于振动周期而言,当振动的频率较高时,周期就会变短;而当振动的频率较低时,周期就会变长。
在XY方向的平动中,平动因子用于描述物体沿XY方向上的运动特征。
它是由物体在该方向上的受力和质量之比得到的。
平动因子越大,表示该方向上的受力较大,物体在该方向上的振动较为明显。
在Z向的扭转中,扭转因子用于描述物体围绕Z轴旋转的特征。
扭转因子的大小取决于物体在该方向上的受力矩和惯性矩之比。
扭转因子越大,表示物体在Z向的扭转运动越明显。
振型质量参与描述了每个振型中各个部分参与振动的质量比例。
振型质量参与的大小取决于每个部分的质量和振型的特征。
振型质量参与越大,表示该部分在振动中的作用越显著。
总结起来,振动周期、XY方向的平动因子、Z向的扭转因子和振型质量参与是描述物体振动特征的重要参数。
通过对这些参数的分析,可以更好地理解和描述振动现象。
在实际应用中,这些参数可以用于设计振动系统、控制振动和评估振动的影响。
振型参与质量系数详解与解释

振型参与质量系数详解抗震规范和高规都有这个系数,牵涉到其他几个概念,与大家分享有关振型的几个概念振型参与系数:每个质点质量与其在某一振型中相应坐标乘积之和与该振型的主质量(或者说该模态质量)之比,即为该振型的振型参与系数。
一阶振型自振频率最小(周期最长),二阶,三阶....振型的自振频率逐渐增大. 地震力大小和地面加速度大小成正比,周期越长加速度越小,地震力也越小。
自振振型曲线是在结构某一阶特征周期下算得的各个质点相对位移(模态向量)的图形示意.在形状上如实反映实际结构在该周期下的振动形态.振型零点是指在该振型下结构的位移反应为0。
振型越高,周期越短,地震力越大,但由于我们地震反应是各振型的迭代,高振型的振型参与系数小。
特别是对规则的建筑物,由于高振型的参与系数小,一般忽略高振型的影响。
振型的有效质量:这个概念只对于串连刚片系模型有效(即基于刚性楼板假定的,不适用于一般结构。
)。
某一振型的某一方向的有效质量为各个质点质量与该质点在该一振型中相应方向对应坐标乘积之和的平方((∑mx)2)。
一个振型有三个方向的有效质量,而且所有振型平动方向的有效质量之和等于各个质点的的质量之和,转动方向的有效质量之和等于各个质点的转动惯量之和。
振型参与质量:某一振型的主质量(或者说该模态质量)乘以该振型的振型参与系数的平方,即为该振型的振型参与质量。
由此可见,有效质量系数与振型参与质量系数概念不同,但都可以用来确定振型叠加法所需的振型数。
注释:1)这里的“质量”的概念不同于通常意义上的质量。
离散结构的振型总数是有限的,振型总个数等于独立质量的总个数。
可以通过判断结构的独立质量数来了解结构的固有振型总数。
具体地说:每块刚性楼板有三个独立质量Mx,My,Jz;每个弹性节点有两个独立质量mx,my;根据这两条,可以算出结构的独立质量总数,也就知道了结构的固有振型总数。
2)若记结构固有振型总数是NM,那么参与振型数最多只能选NM个,选参与振型数大于NM 是错误的,因为结构没那么多。
振动周期(秒),X、Y方向的平动因子及Z向扭转因子,振型质量参与系数

振动周期(秒),X、Y方向的平动因子及Z向扭转因子,振型质量参与系数功能说明该文件主要输出与结构整体性能相关的一些内容。
输出内容如下:(1)振动周期(秒),X、Y方向的平动因子及Z向扭转因子,振型质量参与系数其格式如下:振型号,周期,X向平动因子,Y向平动因子,Z向扭转因子振型号,X向平动质量系数,Y向平动质量系数,Z向扭转质量系数最后输出:X向平动振型质量参与系数总计Y向平动振型质量参与系数总计Z向扭转振型质量参与系数总计结构的周期比(Tt/T1)最不利地震作用方向= (度)注意事項(1)有效质量系数是判断结构振型数够否的重要指标,也就是地震作用够否的重要指标。
当有效质量系数大于90%时,表示振型数、地震作用满足规范要求,否则应该增加计算振型数量;(2)《高规》第4.3.5条控制结构的扭转效应,对第一扭转周期Tt与第一平动周期T1之比给出明确规定。
程序中对于第一周期是这样判断的:X或Y向平动因子最大对应振型的周期为第一平动周期;Z向扭转因子最大,且扭转因子大于0.5对应振型的周期为第一扭转周期;(3)用户对于第一周期的判断还应该结合振型图的形状,查看结构在该振型作用下是否为整体振动,第一周期对应的振型必须是整体振动的振型,而不是局部振动的振型。
因此建议对于程序自动计算的周期比结果还应该人为核算一下是否合理;(4)输出的最不利地震作用方向为与整体坐标系X轴的夹角,逆时针为正,顺时针为负。
功能说明(2)各振型的地震力及基底剪力的输出输出用户定义的各个方向地震作用工况(RS_*)及最不利地震作用工况(RS_C(*))下的地震力。
其格式如下:【RS_*】振型**的地震力塔号,层号,F.x,F.y,F.t其中:F.x:X方向的地震力分量(kN);F.y:Y方向的地震力分量(kN);F.t :X(Y)方向的地震力的扭矩(kN.m)。
【RS_*】各振型的基底剪力振型,基底剪力(kN)【RS_*】各层地震作用(CQC(耦联)或SRSS(非耦联))塔号,层号,层地震力,楼层剪力,剪重比,倾覆弯矩最后输出:抗震规范(5.2.5条)中要求的最小剪重比(%)= x.xx%。
satwe结果分析

规范条文:新高规的 4.3.5条规定,结构扭转为主的第一周期Tt与平动为主的第一周期T1 之比,A级高度高层建筑不应大于0.9;B级高度高层建筑、混合结构高层建筑及复杂高层建筑不应大于0.85。
一旦出现周期比不满足要求的情况,一般只能通过调整平面布置来改善这一状况,这种改变一般是整体性的,局部的小调整往往收效甚微。
周期比不满足要求,说明结构的扭转刚度相对于侧移刚度较小,总的调整原则是要加强结构外圈,或者削弱内筒。
周期比:主要为限制结构的抗扭刚度不能太弱,使结构具有必要的抗扭刚度,减小扭转对结构产生的不利影响。
见高规4.3.5及相应的条文说明。
周期比不满足规范要求,说明结构的抗扭刚度相对于侧移刚度较小,扭转效应过大,结构抗侧力构件布置不合理。
周期比不满足规范要求时的调整方法(转):1、程序调整:SATWE程序不能实现。
2、结构调整:只能通过调整改变结构布置,提高结构的抗扭刚度。
由于结构外围的抗侧力构件对结构的抗扭刚度贡献最大,所以总的调整原则是加强结构外围墙、柱或梁的刚度,或适当削弱结构中间墙、柱的刚度。
利用结构刚度与周期的反比关系,合理布置抗侧力构件,加强需要减小周期方向(包括平动方向和扭转方向)的刚度,削弱需要增大周期方向的刚度。
当结构的第一或第二振型为扭转时,可按以下方法调整:1)SATWE程序中的振型是以其周期的长短排序的。
2)结构的第一、第二振型宜为平动,扭转周期宜出现在第三振型及以后。
见抗规3.5.3条3款及条文说明“结构在两个主轴方向的动力特性(周期和振型)宜相近”。
3)当第一振型为扭转时,说明结构的抗扭刚度相对于其两个主轴(第二振型转角方向和第三振型转角方向,一般都靠近X轴和Y轴)的抗侧移刚度过小,此时宜沿两主轴适当加强结构外围的刚度,并适当削弱结构内部的刚度。
4)当第二振型为扭转时,说明结构沿两个主轴方向的抗侧移刚度相差较大,结构的抗扭刚度相对其中一主轴(第一振型转角方向)的抗侧移刚度是合理的;但相对于另一主轴(第三振型转角方向)的抗侧移刚度则过小,此时宜适当削弱结构内部沿“第三振型转角方向”的刚度,并适当加强结构外围(主要是沿第一振型转角方向)的刚度。
结构第一周期扭转调整方法

结构第一周期扭转调整方法2011-04-21 16:34:10| 分类:默认分类| 标签:|字号大中小订阅规范条文:新高规的4.3.5条规定,结构扭转为主的第一周期Tt与平动为主的第一周期T1 之比,A级高度高层建筑不应大于0.9;B级高度高层建筑、混合结构高层建筑及复杂高层建筑不应大于0.85。
一旦出现周期比不满足要求的情况,一般只能通过调整平面布置来改善这一状况,这种改变一般是整体性的,局部的小调整往往收效甚微。
周期比不满足要求,说明结构的扭转刚度相对于侧移刚度较小,总的调整原则是要加强结构外圈,或者削弱内筒。
周期比:主要为限制结构的抗扭刚度不能太弱,使结构具有必要的抗扭刚度,减小扭转对结构产生的不利影响。
见高规4.3.5及相应的条文说明。
周期比不满足规范要求,说明结构的抗扭刚度相对于侧移刚度较小,扭转效应过大,结构抗侧力构件布置不合理。
周期比不满足规范要求时的调整方法(转):1、程序调整:SATWE程序不能实现。
2、结构调整:只能通过调整改变结构布置,提高结构的抗扭刚度。
由于结构外围的抗侧力构件对结构的抗扭刚度贡献最大,所以总的调整原则是加强结构外围墙、柱或梁的刚度,或适当削弱结构中间墙、柱的刚度。
利用结构刚度与周期的反比关系,合理布置抗侧力构件,加强需要减小周期方向(包括平动方向和扭转方向)的刚度,削弱需要增大周期方向的刚度。
当结构的第一或第二振型为扭转时,可按以下方法调整:1)SATWE程序中的振型是以其周期的长短排序的。
2)结构的第一、第二振型宜为平动,扭转周期宜出现在第三振型及以后。
见抗规3.5.3条3款及条文说明“结构在两个主轴方向的动力特性(周期和振型)宜相近”。
3)当第一振型为扭转时,说明结构的抗扭刚度相对于其两个主轴(第二振型转角方向和第三振型转角方向,一般都靠近X轴和Y轴)的抗侧移刚度过小,此时宜沿两主轴适当加强结构外围的刚度,并适当削弱结构内部的刚度。
4)当第二振型为扭转时,说明结构沿两个主轴方向的抗侧移刚度相差较大,结构的抗扭刚度相对其中一主轴(第一振型转角方向)的抗侧移刚度是合理的;但相对于另一主轴(第三振型转角方向)的抗侧移刚度则过小,此时宜适当削弱结构内部沿“第三振型转角方向”的刚度,并适当加强结构外围(主要是沿第一振型转角方向)的刚度。
新的抗震规范将结构分为规则结构、一般不规则结构、特别不规则结构和严重不规则结构,而严重不规则结构是禁

SATWE中,有效质量的计算适用于弹性板和刚性板.当有效质量系数不足时,也会发生剪重比不够的情况.
======================================================================
考虑扭转耦联时的振动周期(秒)、X,Y方向的平动系数、扭转系数
振型号周期转角平动系数(X+Y)扭转系数
1 1.4877 179.67 0.99 ( 0.99+0.00 ) 0.01
周期比,位移比是通过数据来分析结构布置的合理性,另外更重要的是强调抗震较大,原则是离刚心越远的地方增加抗侧力构件的刚度,可调整边框梁柱,剪力墙断面。同时可减小X,Y向侧向刚度,总之Tt/T1,从分母,分子两个方面着手即可。
另外,多层只需满足抗规的要求,只有位移比控制,没有周期比控制,但可参考分析。
==============================================
3-Dimensional Vibration Period (Seconds)
and Vibration coefficient in X, Y direction and torsion
Mode NoPeriodAngleMovementTorsion
注释:
1)这里的“质量”的概念不同于通常意义上的质量。离散结构的振型总数是有限的,振型总个数等于独立质量的总个数。可以通过判断结构的独立质量数来了解结构的固有振型总数。具体地说:
结构第一周期扭转调整方法

结构第一周期扭转调整方法2011-04-21 16:34:10| 分类:默认分类| 标签:|字号大中小订阅规范条文:新高规的4.3.5条规定,结构扭转为主的第一周期Tt与平动为主的第一周期T1 之比,A级高度高层建筑不应大于0.9;B级高度高层建筑、混合结构高层建筑及复杂高层建筑不应大于0.85。
一旦出现周期比不满足要求的情况,一般只能通过调整平面布置来改善这一状况,这种改变一般是整体性的,局部的小调整往往收效甚微。
周期比不满足要求,说明结构的扭转刚度相对于侧移刚度较小,总的调整原则是要加强结构外圈,或者削弱内筒。
周期比:主要为限制结构的抗扭刚度不能太弱,使结构具有必要的抗扭刚度,减小扭转对结构产生的不利影响。
见高规4.3.5及相应的条文说明。
周期比不满足规范要求,说明结构的抗扭刚度相对于侧移刚度较小,扭转效应过大,结构抗侧力构件布置不合理。
周期比不满足规范要求时的调整方法(转):1、程序调整:SATWE程序不能实现。
2、结构调整:只能通过调整改变结构布置,提高结构的抗扭刚度。
由于结构外围的抗侧力构件对结构的抗扭刚度贡献最大,所以总的调整原则是加强结构外围墙、柱或梁的刚度,或适当削弱结构中间墙、柱的刚度。
利用结构刚度与周期的反比关系,合理布置抗侧力构件,加强需要减小周期方向(包括平动方向和扭转方向)的刚度,削弱需要增大周期方向的刚度。
当结构的第一或第二振型为扭转时,可按以下方法调整:1)SATWE程序中的振型是以其周期的长短排序的。
2)结构的第一、第二振型宜为平动,扭转周期宜出现在第三振型及以后。
见抗规3.5.3条3款及条文说明“结构在两个主轴方向的动力特性(周期和振型)宜相近”。
3)当第一振型为扭转时,说明结构的抗扭刚度相对于其两个主轴(第二振型转角方向和第三振型转角方向,一般都靠近X轴和Y轴)的抗侧移刚度过小,此时宜沿两主轴适当加强结构外围的刚度,并适当削弱结构内部的刚度。
4)当第二振型为扭转时,说明结构沿两个主轴方向的抗侧移刚度相差较大,结构的抗扭刚度相对其中一主轴(第一振型转角方向)的抗侧移刚度是合理的;但相对于另一主轴(第三振型转角方向)的抗侧移刚度则过小,此时宜适当削弱结构内部沿“第三振型转角方向”的刚度,并适当加强结构外围(主要是沿第一振型转角方向)的刚度。
3.2风雨连廊YJKS结构计算书

风雨连廊YJKS结构计算书盈建科软件目录第1章设计依据............................................................................................................. 错误!未定义书签。
第2章设计参数 (2)2.1 结构总体信息 (2)2.2 计算控制信息 (2)2.3 风荷载信息 (3)2.4 地震信息 (3)2.5 设计信息 (3)2.6 活荷载信息 (4)2.7 构件设计信息 (4)2.8 材料信息 (4)2.9 钢筋强度 (5)2.10 荷载组合 (5)第3章结构基本信息 (5)3.1 楼层属性 (5)3.2 构件统计 (5)第4章周期、振型 (7)4.1 振型基本计算结果 (7)4.2 振型阻尼比 (7)4.3 X、Y向地震单振型楼层反应力 (7)4.3.1 仅考虑X 向地震作用时的地震力 (7)4.3.2 仅考虑Y 向地震作用时的地震力 (7)4.4 X、Y向地震单振型楼层剪力 (7)4.5 X、Y向地震CQC组合后结果 (7)第5章楼层风荷载、地震作用统计结果 (11)5.1 风荷载信息 (11)5.2 风荷载下框架剪力统计 (16)5.3 风荷载下框架倾覆弯矩统计(抗规方式) (17)5.4 风荷载外力、层剪力、倾覆弯矩统计 (18)5.5 规定水平力 (19)5.6 规定水平力下倾覆弯矩统计(抗规方式) (20)5.7 规定水平力下倾覆弯矩统计(轴力方式) (26)5.8 地震作用下框架剪力统计 (31)5.9 地震外力、层剪力、倾覆弯矩统计 ............................................................................................37第6章工况、组合. (40)6.1 工况设定 (40)6.2 荷载组合表 (41)第7章整体指标统计 (41)7.1 层刚度统计(各层刚心、偏心率、相邻层侧移刚度比等计算信息) (41)7.2 结构整体稳定验算 (48)7.3 结构整体抗倾覆验算 (48)7.4 位移角和位移比 (49)第8章结构分析及设计结果简图 (56)8.1 结构平面简图 (57)8.2 平面荷载简图 (59)8.3 配筋简图 (61)第2章设计参数2.1 结构总体信息结构体系框架结构结构材料信息钢筋混凝土结构所在地区全国地下室层数0嵌固端所在层号(层顶嵌固)0与基础相连构件最大底标高(m)-1.000裙房层数0转换层所在层号0加强层所在层号0恒活荷载计算信息施工模拟三风荷载计算信息一般计算方式地震作用计算信息不计算地震作用是否计算吊车荷载否是否计算人防荷载否是否考虑预应力等效荷载工况否是否生成传给基础的刚度否是否生成绘等值线用数据否是否计算温度荷载否竖向荷载砼墙轴向刚度考虑徐变收缩影响否上部结构计算考虑基础结构否施工模拟加载层步长12.2 计算控制信息水平力与整体坐标夹角(°)0.00梁刚度放大系数按2010《混凝土规范》取值是梁刚度放大系数上限 2.00边梁刚度放大系数上限 1.50连梁刚度折减系数(地震)0.50连梁刚度折减系数(风)0.70连梁按墙元计算控制跨高比 4.00普通梁连梁砼等级默认同墙是墙元细分最大控制长度(m) 1.00板元细分最大控制长度(m) 1.00短墙肢自动加密是弹性楼板荷载计算方式平面导荷膜单元类型经典膜元(QA4)考虑梁端刚域否考虑柱端刚域否墙梁跨中节点作为刚性楼板从节点是结构计算时考虑楼梯刚度否梁与弹性板变形协调是弹性板与梁协调时考虑梁向下相对偏移否刚性楼板假定不采用强制刚性楼板假定地下室楼板强制采用刚性楼板假定否是否自动划分多塔是自动划分多塔时不考虑地下室否可确定最多塔数的参考层号2计算现浇空心板否增加计算连梁刚度不折减模型下的地震位移否梁墙自重扣除与柱重叠部分否楼板自重扣除与梁墙重叠部分否是否输出节点位移否地震内力按全楼弹性板6计算否求解器设定内存2000是否考虑 P-Delt 效应否进行屈曲分析否自动计算现浇板自重是2.3 风荷载信息使用直接指定的风洞试验结果否执行规范GB50009-2012地面粗糙程度B修正后的基本风压(kN/m2)0.50风荷载计算用阻尼比(%) 5.0结构X向基本周期(s)0.53结构Y向基本周期(s)0.47承载力设计时风荷载效应放大系数 1.0用于舒适度验算的风压(kN/m2)0.50用于舒适度验算的结构阻尼比(%) 2.0考虑顺风向风振是多方向风角度考虑横向风振否考虑扭转风振否自动计算结构宽深是风荷载体型系数分段数1第一段最高层号2X迎风0.80X背风-0.50X侧风0.00X挡风 1.00Y迎风0.80Y背风-0.50Y侧风0.00Y挡风 1.002.4 地震信息砼框架抗震等级三级剪力墙抗震等级三级钢框架抗震等级三级抗震构造措施的抗震等级不改变框支剪力墙结构底部加强区剪力墙抗震等级自动提高一级是地下一层以下抗震构造措施抗震等级逐层降级及抗震措施4级是是否考虑性能设计否2.5 设计信息是否按抗震规范5.2.5调整楼层地震力是是否扭转效应明显否是否自动计算动位移比例系数否第一平动周期方向动位移比例(0~1)0.50第二平动周期方向动位移比例(0~1)0.50与柱相连的框架梁端M、V不调整否是否用户指定0.2V0调整系数否0.2V0调整规则Min(0.20*Vo, 1.50*Vfmax) 0.2V0调整时楼层剪力最小倍数0.200.2V0调整时各层框架剪力最大值的倍数 1.500.2V0调整分段数00.2V0调整上限 2.00考虑双向地震时内力调整方式先考虑双向地震再调整剪力墙端柱的面外剪力统计到框架部分0实配钢筋超配系数 1.15框支柱调整上限 5.00按层刚度比判断薄弱层方法高规和抗规从严底部嵌固楼层刚度比执行《高规》3.5.2-2否自动对层间受剪承载力突变形成的薄弱层放大调整否自动根据层间受剪承载力比值调整配筋至非薄弱否是否转换层指定为薄弱层是指定薄弱层层号0薄弱层地震内力放大系数 1.25梁端负弯矩调幅系数0.85框架梁调幅后不小于简支梁跨中弯矩的倍数0.50非框架梁调幅后不小于简支梁跨中弯矩的倍数0.33梁扭矩折减系数0.40支撑临界角(度) (与竖轴夹角小于此值的支撑将按柱考虑)20按竖向构件内力统计层地震剪力否位移角小于此值时,位移比设置为10.00020剪力墙承担全部地震剪力否2.6 活荷载信息柱、墙活荷载是否折减否楼面梁活荷载折减不折减考虑活荷不利布置的最高层号0梁活荷载内力放大系数 1.00 2.7 构件设计信息柱配筋计算原则双偏压连梁按对称配筋设计否抗震设计的框架梁端配筋考虑受压钢筋是矩形混凝土梁按T形梁配筋否按简化方法计算柱剪跨比(Hn/2h0)是墙柱配筋设计考虑端柱否墙柱配筋设计考虑翼缘墙否与剪力墙面外相连的梁按框架梁设计是验算一级抗震墙施工缝是梁压弯设计控制轴压比0.40梁端配筋内力取值位置(0-节点,1-支座边)0.00钢构件截面净毛面积比0.85X向钢柱计算长度是否按有侧移计算是Y向钢柱计算长度是否按有侧移计算是按《钢规》5.3.3-2自动判断强弱支撑否执行门规GB51022附录A.0.8否不计算地震作用时按重力荷载代表值计算柱轴压比否框架柱的轴压比限值按框架结构采用否梁保护层厚度(mm)20柱保护层厚度(mm)20剪力墙构造边缘构件的设计执行高规7.2.16-4否底部加强区全部设为约束边缘构件否归入阴影区的λ/2区最大长度否面外梁下生成暗柱边缘构件是边缘构件合并距离(mm)300短肢边缘构件合并距离(mm)600边缘构件尺寸取整模数(mm)50构造边缘构件尺寸设计依据《高规》JGJ3-2010 第7.2.16条约束边缘构件尺寸依据《广东高规》设计否按边缘构件轮廓计算配筋是组合梁施工荷载(kN/m2) 1.50型钢混凝土构件设计依据《组合结构设计规范》JGJ138-2016执行《高钢规》JGJ99-2015是按叠合柱设计的叠合比0.00执行《钢结构设计标准》(GB50017-2017)是按宽厚比等级控制局部稳定是截面宽厚比等级S3支撑杆件截面宽厚比等级S32.8 材料信息混凝土容重(kN/m3)25.00砌体容重(kN/m3)22.00钢材容重(kN/m3)78.00轻骨料混凝土容重(kN/m3)18.50轻骨料混凝土密度等级1800梁箍筋间距(mm)100柱箍筋间距(mm)100墙水平分布筋最大间距(mm)150墙竖向分布筋最小配筋率(%)0.30结构底部单独指定墙竖向分布筋配筋率的层号无结构底部NSW层的墙竖向分布配筋率0.602.9 钢筋强度HRB400钢筋强度设计值(N/mm2)3602.10 荷载组合结构重要性系数 1.00恒载分项系数 1.20活载分项系数 1.40活荷载组合值系数0.70活荷载频遇值系数0.60活荷载准永久值系数0.50考虑结构设计使用年限的活荷载调整系数 1.00风荷载分项系数 1.40风荷载组合值系数0.60风荷载频遇值系数0.40风荷载是否参与地震组合否水平地震力分项系数 1.30第3章结构基本信息3.1 楼层属性表3-1 楼层属性3.2 构件统计表3-2 各层构件数量、构件材料和层高(单位:m)表3-3 保护层(单位:mm)表3-4 混凝土构件表3-5 钢构件表3-6 箍筋(墙分布筋)第4章 周期、振型4.1 振型基本计算结果表4-1 考虑扭转耦联时的振动周期(秒)、X,Y 方向的平动系数、扭转系数表4-2 质量系数(Z 向扭转质量系数只在强制刚性板下有意义,对于非强制刚性板下的计算结果仅供参考) 根据《高规》5.1.13条,各振型的参与质量之和不应小于总质量的90%。
振型参与质量系数

【分享】振型参与质量系数详解【分享】振型参与质量系数详解抗震规范和高规都有这个系数,牵涉到其他几个概念,与大家分享有关振型的几个概念振型参与系数:每个质点质量与其在某一振型中相应坐标乘积之和与该振型的主质量(或者说该模态质量)之比,即为该振型的振型参与系数。
一阶振型自振频率最小(周期最长),二阶,三阶....振型的自振频率逐渐增大. 地震力大小和地面加速度大小成正比,周期越长加速度越小,地震力也越小。
自振振型曲线是在结构某一阶特征周期下算得的各个质点相对位移(模态向量)的图形示意.在形状上如实反映实际结构在该周期下的振动形态.振型零点是指在该振型下结构的位移反应为0。
振型越高,周期越短,地震力越大,但由于我们地震反应是各振型的迭代,高振型的振型参与系数小。
特别是对规则的建筑物,由于高振型的参与系数小,一般忽略高振型的影响。
振型的有效质量:这个概念只对于串连刚片系模型有效(即基于刚性楼板假定的,不适用于一般结构。
)。
某一振型的某一方向的有效质量为各个质点质量与该质点在该一振型中相应方向对应坐标乘积之和的平方((∑mx)2)。
一个振型有三个方向的有效质量,而且所有振型平动方向的有效质量之和等于各个质点的的质量之和,转动方向的有效质量之和等于各个质点的转动惯量之和。
有效质量系数:如果计算时只取了几个振型,那么这几个振型的有效质量之和与总质量之比即为有效质量系数。
这个概念是由WILSON E.L. 教授提出的,用于判断参与振型数足够与否,并将其用于ETABS程序。
振型参与质量:某一振型的主质量(或者说该模态质量)乘以该振型的振型参与系数的平方,即为该振型的振型参与质量。
振型参与质量系数:由于有效质量系数只实用于刚性楼板假设,现在不少结构因其复杂性需要考虑楼板的弹性变形,因此需要一种更为一般的方法,不但能够适用于刚性楼板,也应该能够适用于弹性楼板。
出于这个目的,我们从结构变形能的角度对此问题进行了研究,提出了一个通用方法来计算各地震方向的有效质量系数即振型参与质量系数,规范即是通过控制有效质量振型参与质量系数的大小来决定所取的振型数是否足够。
结构第一周期扭转调整方法

结构第一周期扭转调整方法[转帖]结构第一周期扭转调整方法2规范条文:新高规的4.3.5条规定,结构扭转为主的第一周期Tt与平动为主的第一周期T1之比,A级高度高层建筑不应大于0.9;B级高度高层建筑、混合结构高层建筑及复杂高层建筑不应大于0.85。
一旦出现周期比不满足要求的情况,一般只能通过调整平面布置来改善这一状况,这种改变一般是整体性的,局部的小调整往往收效甚微。
周期比不满足要求,说明结构的扭转刚度相对于侧移刚度较小,总的调整原则是要加强结构外圈,或者削弱内筒。
周期比:主要为限制结构的抗扭刚度不能太弱,使结构具有必要的抗扭刚度,减小扭转对结构产生的不利影响。
见高规4.3.5及相应的条文说明。
周期比不满足规范要求,说明结构的抗扭刚度相对于侧移刚度较小,扭转效应过大,结构抗侧力构件布置不合理。
周期比不满足规范要求时的调整方法(转):1、程序调整:SATWE程序不能实现。
2、结构调整:只能通过调整改变结构布置,提高结构的抗扭刚度。
由于结构外围的抗侧力构件对结构的抗扭刚度贡献最大,所以总的调整原则是加强结构外围墙、柱或梁的刚度,或适当削弱结构中间墙、柱的刚度。
利用结构刚度与周期的反比关系,合理布置抗侧力构件,加强需要减小周期方向(包括平动方向和扭转方向)的刚度,削弱需要增大周期方向的刚度。
当结构的第一或第二振型为扭转时,可按以下方法调整:1)SATWE程序中的振型是以其周期的长短排序的。
2)结构的第一、第二振型宜为平动,扭转周期宜出现在第三振型及以后。
见抗规3.5.3条3款及条文说明“结构在两个主轴方向的动力特性(周期和振型)宜相近”。
3)当第一振型为扭转时,说明结构的抗扭刚度相对于其两个主轴(第二振型转角方向和第三振型转角方向,一般都靠近某轴和Y轴)的抗侧移刚度过小,此时宜沿两主轴适当加强结构外围的刚度,并适当削弱结构内部的刚度。
4)当第二振型为扭转时,说明结构沿两个主轴方向的抗侧移刚度相差较大,结构的抗扭刚度相对其中一主轴(第一振型转角方向)的抗侧移刚度是合理的;但相对于另一主轴(第三振型转角方向)的抗侧移刚度则过小,此时宜适当削弱结构内部沿“第三振型转角方向”的刚度,并适当加强结构外围(主要是沿第一振型转角方向)的刚度。
振型参与质量系数详解与解释讲解学习

振型参与质量系数详解与解释振型参与质量系数详解抗震规范W高规都有这个系数,牵涉到其他几个概念,与大家分享有关振型的几个概念振型参与系数:每个质点质量与其在某一振型中相应坐标乘积之和与该振型的主质量(或者说该模态质量)之比,即为该振型的振型参与系数。
一阶振型自振频率最小(周期最长),二阶,三阶…•振型的自振频率逐渐增大•地震力大小和地面加速度大小成正比,周期越长加速度越小,地震力也越小。
自振振型曲线是在结构某一阶特征周期下算得的各个质点相对位移(模态向量)的图形示意•在形状上如实反映实际结构在该周期下的振动形态•振型零点是指在该振型下结构的位移反应为O0振型越高,周期越短,地震力越大,但由于我们地震反应是各振型的迭代,高振型的振型参与系数小。
特别是对规则的建筑物,由于高振型的参与系数小,一般忽略高振型的影响。
振型的有效质量:这个概念只对于串连刚片系模型有效(即基于刚性楼板假定的,不适用于一般结构。
)o某一振型的某一方向的有效质量为各个质点质量与该质点在该一振型中相应方向对应坐标乘积之和的平方((刀mx ) 2 )0—个振型有三个方向的有效质量,而且所有振型平动方向的有效质量之和等于各个质点的的质量之和,转动方向的有效质量之和等于各个质点的转动惯量之和。
有效质量系数:如果计算时只取了几个振型,那么这几个振型的有效质量之和与总质量之比即为有效质量系数。
这个概念是由WILSON E.L.教授提岀的,用于判断参与振型数足够与否,并将其用于ETABS程序。
振型参与质量:某一振型的主质量(或者说该模态质量)乘以该振型的振型参与系数的平方,即为该振型的振型参与质量振型参与质量系数:由于有效质量系数只实用于刚性楼板假设,现在不少结构因其复杂性需要考虑楼板的弹性变形,因此需要一种更为一般的方法,不但能够适用于刚性楼板,也应该能够适用于弹性楼板。
出于这个目的,我们从结构变形能的角度对此问题进行了研究,提出了 _个通用方法来计算各地震方向的有效质量系数即振型参与质量系数,规范即是通过控制有效质量振型参与质量系数的大小来决定所取的振型数是否足够。
结构特征参数控制

结构特征参数控制 1、周期比 A 、规范要求 [高规]4.3.5条规定,结构扭转为主的第一自振周期Tt 与平动为主的第一自振周期T1之比(即周期比),A 级高度高层建筑不应大于0.9;B 级高度高层建筑、混合结构高层建筑及复杂高层建筑不应大于0.85。
[高规]5.1.13条规定,高层建筑结构计算振型数不应小于9,抗震计算时,宜考虑平扭藕连计算结构的扭转效应,振型数不小于15,对于多塔楼结构的振型数不应小于塔楼数的9倍,且计算振型数应使振型参与质量不小于总质量的90%。
B 、名词解释 振型: 振型是指体系的一种固有的特性。
它与固有频率相对应,即为对应固有频率体系自身振动的形态。
每一阶固有频率都对应一种振型。
振型与体系实际的振动形态不一定相同。
振型对应于频率而言,一个固有频率对应于一个振型。
按照频率从低到高的排列来说第一振型,第二振型等等。
此处的振型就是指在该固有频率下结构的振动形态,频率越高则振动周期越小。
在实验中,我们就是通过用一定的频率对结构进行激振,观测相应点的位移状况,当观测点的位移达到最大时,此时频率即为固有频率。
实际结构的振动形态并不是一个规则的形状,而是各阶振型相叠加的结果。
振型参与质量: 在层刚性板的假设下,如果累计x,y 的振型有效的质量,都大于90%的时候,这时候我们就可以认为选了足够的振型了。
如果,有效质量系数不够90%,那可以说明后续的地震作用效应不能忽略。
如果不能保证这点,那将导致计算所考虑的地震作用偏小。
平动为主的第一自振周期T1: 根据各振型的两个平动系数和一个扭转系数(三者之和等于1)判别各振型分别是扭转为主的振型(也称扭振振型)还是平动为主的振型(也称侧振振型)。
一般来说,可以简单的以SA TWE 程序输出的“周期、地震力与振型输出文件”WZQ.OUT 文件中扭转因子比例来判断,即:扭转因子不大于50%的振型为第一个以平动为主的振型。
但是这里要注意,从概念上讲,并不能绝对地说只要排列在第一位且扭转因子不大于50%的振型,就一定是以平动为主的第一振型!尽管对多数一般结构来说不会出现这个问题,但是对于某些扭转不利的结构,还要看其X 、Y 两方向基底地震剪力大小才能判定。
3.4无障碍坡道YJKS结构计算书

无障碍坡道YJKS结构计算书盈建科软件目录第1章设计依据 (2)第2章设计参数 (2)2.1 结构总体信息 (2)2.2 计算控制信息 (2)2.3 风荷载信息 (3)2.4 地震信息 (3)2.5 设计信息 (3)2.6 活荷载信息 (4)2.7 构件设计信息 (4)2.8 包络设计 (5)2.9 材料信息 (5)2.10 钢筋强度 (5)2.11 荷载组合 (5)第3章结构基本信息 (5)3.1 楼层属性 (5)3.2 塔属性 (5)3.3 构件统计 (6)3.4 楼层质量 (6)3.5 楼层尺寸、单位质量 (7)第4章周期、振型 (7)4.1 振型基本计算结果 (7)4.2 振型阻尼比 (8)4.3 X、Y向地震单振型楼层反应力 (8)4.3.1 仅考虑X 向地震作用时的地震力 (8)4.3.2 仅考虑Y 向地震作用时的地震力 (8)4.4 X、Y向地震单振型楼层剪力 (8)4.5 X、Y向地震CQC组合后结果 (8)第5章楼层风荷载、地震作用统计结果 (9)5.1 风荷载信息 (9)5.2 风荷载下框架剪力统计 (10)5.3 风荷载下框架倾覆弯矩统计(抗规方式) (10)5.4 风荷载外力、层剪力、倾覆弯矩统计 (10)5.5 规定水平力 (10)5.6 规定水平力下倾覆弯矩统计(抗规方式) (10)5.7 规定水平力下倾覆弯矩统计(轴力方式) (11)5.8 地震作用下框架剪力统计 (12)5.9 地震外力、层剪力、倾覆弯矩统计 (13)第6章工况、组合 (13)6.1 工况设定 (13)6.2 荷载组合表 (14)第7章整体指标统计 (14)7.1 周期比 (14)7.2 层刚度统计(各层刚心、偏心率、相邻层侧移刚度比等计算信息) (14)7.3 结构整体稳定验算 (15)7.4 结构整体抗倾覆验算 (15)7.5 楼层抗剪承载力验算 (16)7.6 薄弱层信息 (16)7.7 剪重比调整系数 (16)7.8 位移角和位移比 (16)7.9 风振舒适度验算 (18)第8章结构分析及设计结果简图 (18)8.1 结构平面简图 (19)8.2 平面荷载简图 (22)8.3 配筋简图 (25)第1章设计依据本工程按照如下规范、规程进行设计:1、《荷载规范》:《建筑结构荷载规范》GB 50009 - 20122、《混凝土规范》或《混规》:《混凝土结构设计规范》GB 50010 - 20103、《抗震规范》或《抗规》:《建筑抗震设计规范》GB 50011 - 20104、《高规》:《高层建筑混凝土结构技术规程》JGJ 3 - 20105、《广东高规》:广东省标准《高层建筑混凝土结构技术规程》DBJ 15 - 92 - 20136、《上海抗规》:上海市工程设计规范《建筑抗震设计规范》DGJ 08 - 9 - 20137、《人防规范》:《人民防空地下室设计规范》GB 50038 - 20058、《钢结构规范》:《钢结构设计标准》GB 50017 - 20179、《高钢规》:《高层民用建筑钢结构技术规程》JGJ 99 - 201510、《门刚规程》:《门式刚架轻型房屋钢结构技术规程》GB51022-201511、《冷弯薄壁型钢规范》:《冷弯薄壁型钢结构技术规范》GB 50018 - 200212、《异形柱规程》:《混凝土异形柱结构技术规程》JGJ 149 - 201713、《组合规范》:《组合结构设计规范》JGJ 138 - 201614、《钢骨规程》:《钢骨混凝土结构技术规程》YB 9082 - 200615、《钢管规范》:《钢管混凝土结构技术规范》GB 50936 - 201416、《叠合柱规程》:《钢管混凝土叠合柱结构技术规程》CECS 188:200517、《矩形钢管规程》:《矩形钢管混凝土结构技术规程》CECS 159 : 200418、《空心楼盖规程》:《现浇混凝土空心楼盖结构技术规程》CECS 175 : 200419、《鉴定标准》:《建筑抗震鉴定标准》GB 50023 - 200920、《加固规范》:《混凝土结构加固设计规范》GB 50367 - 201321、《抗震加固规程》:《建筑抗震加固技术规程》JGJ 116 - 2009第2章设计参数2.1 结构总体信息结构体系框架结构结构材料信息钢筋混凝土结构所在地区全国地下室层数0嵌固端所在层号(层顶嵌固)0与基础相连构件最大底标高(m)0.000裙房层数0转换层所在层号0加强层所在层号0恒活荷载计算信息施工模拟三风荷载计算信息一般计算方式地震作用计算信息不计算地震作用是否计算吊车荷载否是否计算人防荷载否是否考虑预应力等效荷载工况否是否生成传给基础的刚度否是否生成绘等值线用数据否是否计算温度荷载否竖向荷载砼墙轴向刚度考虑徐变收缩影响否上部结构计算考虑基础结构否施工模拟加载层步长12.2 计算控制信息水平力与整体坐标夹角(°)0.00梁刚度放大系数按2010《混凝土规范》取值是梁刚度放大系数上限 2.00边梁刚度放大系数上限 1.50连梁刚度折减系数(地震)0.50连梁刚度折减系数(风)0.70连梁按墙元计算控制跨高比 4.00普通梁连梁砼等级默认同墙是墙元细分最大控制长度(m) 1.00板元细分最大控制长度(m) 1.00短墙肢自动加密是弹性楼板荷载计算方式平面导荷膜单元类型经典膜元(QA4)考虑梁端刚域否考虑柱端刚域否墙梁跨中节点作为刚性楼板从节点是结构计算时考虑楼梯刚度否梁与弹性板变形协调是弹性板与梁协调时考虑梁向下相对偏移否刚性楼板假定不采用强制刚性楼板假定地下室楼板强制采用刚性楼板假定否是否自动划分多塔是自动划分多塔时不考虑地下室否可确定最多塔数的参考层号1计算现浇空心板否增加计算连梁刚度不折减模型下的地震位移否梁墙自重扣除与柱重叠部分否楼板自重扣除与梁墙重叠部分否是否输出节点位移否地震内力按全楼弹性板6计算否求解器设定内存0是否考虑 P-Delt 效应否进行屈曲分析否自动计算现浇板自重是2.3 风荷载信息使用直接指定的风洞试验结果否执行规范GB50009-2012地面粗糙程度B修正后的基本风压(kN/m2)0.50风荷载计算用阻尼比(%) 5.0结构X向基本周期(s)0.53结构Y向基本周期(s)0.47承载力设计时风荷载效应放大系数 1.0用于舒适度验算的风压(kN/m2)0.50用于舒适度验算的结构阻尼比(%) 2.0考虑顺风向风振是多方向风角度考虑横向风振否考虑扭转风振否自动计算结构宽深是风荷载体型系数分段数1第一段最高层号3X迎风0.80X背风-0.50 X侧风0.00X挡风 1.00Y迎风0.80Y背风-0.50 Y侧风0.00Y挡风 1.00 2.4 地震信息砼框架抗震等级三级剪力墙抗震等级三级钢框架抗震等级三级抗震构造措施的抗震等级不改变框支剪力墙结构底部加强区剪力墙抗震等级自动提高一级是地下一层以下抗震构造措施抗震等级逐层降级及抗震措施4级是是否考虑性能设计否2.5 设计信息是否按抗震规范5.2.5调整楼层地震力是是否扭转效应明显否是否自动计算动位移比例系数否第一平动周期方向动位移比例(0~1)0.50第二平动周期方向动位移比例(0~1)0.50与柱相连的框架梁端M、V不调整否是否用户指定0.2V0调整系数否0.2V0调整规则Min(0.20*Vo, 1.50*Vfmax) 0.2V0调整时楼层剪力最小倍数0.200.2V0调整时各层框架剪力最大值的倍数 1.500.2V0调整分段数00.2V0调整上限 2.00考虑双向地震时内力调整方式先考虑双向地震再调整剪力墙端柱的面外剪力统计到框架部分0实配钢筋超配系数 1.15框支柱调整上限 5.00按层刚度比判断薄弱层方法高规和抗规从严底部嵌固楼层刚度比执行《高规》3.5.2-2否自动对层间受剪承载力突变形成的薄弱层放大调整否自动根据层间受剪承载力比值调整配筋至非薄弱否是否转换层指定为薄弱层是指定薄弱层层号0薄弱层地震内力放大系数 1.25梁端负弯矩调幅系数0.85框架梁调幅后不小于简支梁跨中弯矩的倍数0.50非框架梁调幅后不小于简支梁跨中弯矩的倍数0.33梁扭矩折减系数0.40支撑临界角(度) (与竖轴夹角小于此值的支撑将按柱考虑)20按竖向构件内力统计层地震剪力否位移角小于此值时,位移比设置为10.00020剪力墙承担全部地震剪力否2.6 活荷载信息柱、墙活荷载是否折减否楼面梁活荷载折减不折减考虑活荷不利布置的最高层号0梁活荷载内力放大系数 1.00 2.7 构件设计信息柱配筋计算原则双偏压连梁按对称配筋设计否抗震设计的框架梁端配筋考虑受压钢筋是矩形混凝土梁按T形梁配筋否按简化方法计算柱剪跨比(Hn/2h0)是墙柱配筋设计考虑端柱否墙柱配筋设计考虑翼缘墙否与剪力墙面外相连的梁按框架梁设计是验算一级抗震墙施工缝是梁压弯设计控制轴压比0.40梁端配筋内力取值位置(0-节点,1-支座边)0.00钢构件截面净毛面积比0.85 X向钢柱计算长度是否按有侧移计算是Y向钢柱计算长度是否按有侧移计算是按《钢规》5.3.3-2自动判断强弱支撑否执行门规GB51022附录A.0.8否不计算地震作用时按重力荷载代表值计算柱轴压比否框架柱的轴压比限值按框架结构采用否梁保护层厚度(mm)20柱保护层厚度(mm)20剪力墙构造边缘构件的设计执行高规7.2.16-4否底部加强区全部设为约束边缘构件否归入阴影区的λ/2区最大长度否面外梁下生成暗柱边缘构件是边缘构件合并距离(mm)300短肢边缘构件合并距离(mm)600边缘构件尺寸取整模数(mm)50构造边缘构件尺寸设计依据《高规》JGJ3-2010 第7.2.16条约束边缘构件尺寸依据《广东高规》设计否按边缘构件轮廓计算配筋是组合梁施工荷载(kN/m2) 1.50型钢混凝土构件设计依据《组合结构设计规范》JGJ138-2016执行《高钢规》JGJ99-2015是按叠合柱设计的叠合比0.00执行《钢结构设计标准》(GB50017-2017)是按宽厚比等级控制局部稳定是截面宽厚比等级S3支撑杆件截面宽厚比等级S32.8 包络设计是否分塔与整体分别计算,并取大否自动取框架和框架-抗震墙模型计算大值否是否与其它模型进行包络取大否2.9 材料信息混凝土容重(kN/m3)25.00砌体容重(kN/m3)22.00钢材容重(kN/m3)78.00轻骨料混凝土容重(kN/m3)18.50轻骨料混凝土密度等级1800梁箍筋间距(mm)100柱箍筋间距(mm)100墙水平分布筋最大间距(mm)150墙竖向分布筋最小配筋率(%)0.30结构底部单独指定墙竖向分布筋配筋率的层号无结构底部NSW层的墙竖向分布配筋率0.602.10 钢筋强度HRB400钢筋强度设计值(N/mm2)3602.11 荷载组合结构重要性系数 1.00恒载分项系数 1.20活载分项系数 1.40活荷载组合值系数0.70活荷载频遇值系数0.60活荷载准永久值系数0.50考虑结构设计使用年限的活荷载调整系数 1.00风荷载分项系数 1.40风荷载组合值系数0.60风荷载频遇值系数0.40风荷载是否参与地震组合否水平地震力分项系数 1.30第3章结构基本信息3.1 楼层属性表3-1 楼层属性3.2 塔属性表3-2 塔属性3.3 构件统计表3-3 各层构件数量、构件材料和层高(单位:m)表3-4 保护层(单位:mm)表3-5 混凝土构件表3-6 箍筋(墙分布筋)3.4 楼层质量表3-7 各层质心坐标(单位:m)根据《高规》3.5.6条的规定,楼层质量沿高度宜均匀分布,楼层质量不宜大于相邻下部楼层的1.5倍。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
功能说明
该文件主要输出与结构整体性能相关的一些内容。
输出内容如下:
(1)振动周期(秒),X、Y方向的平动因子及Z向扭转因子,振型质量参与系数
其格式如下:
振型号,周期,X向平动因子,Y向平动因子,Z向扭转因子
振型号,X向平动质量系数,Y向平动质量系数,Z向扭转质量系数
最后输出:
X向平动振型质量参与系数总计
Y向平动振型质量参与系数总计
Z向扭转振型质量参与系数总计
结构的周期比(Tt/T1)
最不利地震作用方向= (度)
注意事項
(1)有效质量系数是判断结构振型数够否的重要指标,也就是地震作用够否的重要指标。
当有效质量系数大于90%时,表示振型数、地震作用满足规范要求,否则应该增加计算振型数量;
(2)《高规》第4.3.5条控制结构的扭转效应,对第一扭转周期Tt与第一平动周期T1之比给出明确规定。
程序中对于第一周期是这样判断的:X或Y向平动因子最大对应振型的周期为第一平动周期;Z向扭转因子最大,且扭转因子大于0.5对应振型的周期为第一扭转周期;
(3)用户对于第一周期的判断还应该结合振型图的形状,查看结构在该振型作用下是否为整体振动,第一周期对应的振型必须是整体振动的振型,而不是局部振动的振型。
因此建议对于程序自动计算的周期比结果还应该人为核算一下是否合理;
(4)输出的最不利地震作用方向为与整体坐标系X轴的夹角,逆时针为正,顺时针为负。
功能说明
(2)各振型的地震力及基底剪力的输出
输出用户定义的各个方向地震作用工况(RS_*)及最不利地震作用工况(RS_C(*))下的地震力。
其格式如下:
【RS_*】振型**的地震力
塔号,层号,F.x,F.y,F.t
其中:
F.x:X方向的地震力分量(kN);
F.y:Y方向的地震力分量(kN);
F.t :X(Y)方向的地震力的扭矩(kN.m)。
【RS_*】各振型的基底剪力
振型,基底剪力(kN)
【RS_*】各层地震作用(CQC(耦联)或SRSS(非耦联))塔号,层号,层地震力,楼层剪力,剪重比,倾覆弯矩
最后输出:
抗震规范(5.2.5条)中要求的最小剪重比(%)= x.xx%。
