对面积曲面积分
对面积的曲面积分

3
3 : z 0,4 : x y x z 1
4
1
y
于是 Ò xyzdS xyzdS
1 2 3 4
由于在 1 : x 0, 2 : y 0,3 : z 0上,
f ( x, y, z) xyz 0
所以
xyzdS 0
1 2 3 1
x
z 1
2 1
O Dxy
3
4
1
y
在4上:z 1 x y,
)
r2 n (zx
,
zy
d
,1),
Q cos
1
, dS
1
z
2 x
z
2 y
1
z
2 x
z
2 y
d
的面积元素:
dS
1
z
2 x
z
2 y
d
计算对面积的曲面积分
——化为二重积分 向xoy面投影Dxy
f ( x, y, z)dS : z z(x, y)
z z(x, y)
(x, y, z)在上变化
f ( x, y, z) dS : x x( y, z)
f x y, z , y, z
1
x
2 y
xz2 d
D yz
f ( x, y, z) dS
: y y(x, z)
f x, y x, z , z
1
y
2 x
yz2 d
Dxz
例1 计算 1 dS,其中:x2 y2 z2 a2
且在第一卦限的部分.
解 由于 不能表示成 z=z(x,y) 的形式,
现写成 x R2 y2
z
这样就需投影到yoz面上, H
10曲线积分与曲面积分-2

线性性质.
∫∫∑ [k1 f (x, y, z) ± k2g(x, y, z)]d S = k1∫∫ f (x, y, z) dS ± k2 ∫∫ g(x, y, z) dS ∑ ∑
二,对面积的曲面积分的计算法
定理1: 定理 设有光滑曲面 f (x, y, z) 在 ∑ 上连续, 则曲面积分
z
其中, λ 表示 n 小块曲面的直径的
x
最大值 (曲面的直径为其上任意两点间距离的最大者).
定义: 定义: 设 ∑ 为光滑曲面, "乘积和式极限"
f (x, y, z) 是定义在 ∑ 上的一
个有界函数, 若对∑ 做任意分割和局部区域任意取点,
记作
∫∫ f (x, y, z)d S
∑
都存在, 则称此极限为函数 f (x, y, z) 在曲面 ∑ 上对面积 的曲面积分 或第一类曲面积分. 其中 f (x, y, z) 叫做被积 函数, ∑ 叫做积分曲面. 据此定义, 曲面形构件的质量为 曲面面积为
xdS ; xdS ;
( 2000 考研 )
1
1
备用题 1. 已知曲面壳
质量 M . 解: ∑ 在 xOy 面上的投影为
的面密度
求此曲面壳在平面 z =1以上部分∑ 的
Dx y : x2 + y2 ≤ 2 , 故
M = ∫∫ d S = ∫∫
∑
3 1+ 4( x2 + y2 ) d xdy Dx y z
解
积分曲面 ∑:z = 5 y ,
投影域 : D xy = {( x , y ) | x 2 + y 2 ≤ 25 }
dS = 1 + z ′x + z ′y dxdy
高数第四节.对面积的曲面积分 (1)

1. f ( x, y, z)dS f ( x, y, z)dS f ( x, y, z)dS.
1
2
当为闭曲面时, f ( x, y, z)dS 可写成 f ( x, y, z)dS.
2. 当 f ( x, y, z) 1时, dS 是曲面的面积.
复习:
z n
设光滑曲面
M
则面积 A 可看成曲面上各点 M (x, y, z) S dA
处小切平面的面积 d A 无限积累而成. o
设它在 D 上的投影为 d , 则
x
y
d
d cos d A n ( fx( x0 , y0 ), fy( x0 , y0 ), 1 )
cos
1
1 fx2 (x, y) f y2 (x, y)
d A 1 fx2 (x, y) f y2 (x, y) d
z
h
oD xy
ay
x
因为dS
1
z
2 x
z
2 y
dxdy
a
dxdy,
a2 x2 y2
dS
a
dxdy,
a2 x2 y2
ห้องสมุดไป่ตู้
dS z
Dxy
a2
adxdy x2
y2
add Dxy a2 2
a
2π
d
0
a2 h2 0
d a2 2
2πa
1 2
ln( a 2
2
) 0
a2
h2
2πa ln a . h
f (i ,i , i )Si
积分曲面
面积元素
积分和式
以上积分也称为第一类曲面积分或对面积的 曲面积分.
高等数学对面积曲面积分

1 z x 2 (k ,k ) z y 2 (k ,k ) ( k ) x y
f(x,y,z)dS
f(k,k,z(k,k))
1 z x 2 (k ,k ) z y 2 (k ,k )( k ) x y
f(k,k,z(k,k))
定理 设有光滑曲面
z
f (x, y, z) 在 上连续, 则曲面积分
O
y
f(x,y,z)dS存在, 且有
x Dxy
(k)xy (k,k,k)
f(x,y, Dxy
证明 由定义知
)
n
lim
0 k 1
而
(k)x y 1 zx 2 (x ,y ) zy2 (x ,y )d x d y
用球面坐标
zRcos
dSR2sindd
R3
2πd
π
2sincosd
0
0
R 2πd
π
2sind
0
0
思考题: 例 3 是否可用球面坐标计算 ?
例5 计算
z22(xyz).
其中 是球面 x2 y2
解 显然球心为 (1,1,1), 半径为 3
利用对称性可知
z
1
计算 I f(x,y,z)dS.
x Dxy y
解 锥面 z x2y2与上半球面 z a2x2y2的
交线为Βιβλιοθήκη 设1为上半球面夹于锥面间的部分,它在 xOy 面上的
投影域为 D x y (x ,y )x 2 y 2 1 2 a 2 ,则
I (x2y2)dS 1
O
y
其中, 表示 n 小块曲面的直径的 x
最大值 (曲面的直径为其上任意两点间距离的最大者).
曲线曲面积分公式总结

曲线曲面积分公式总结
以下是曲线曲面积分的一些基本公式:
1. 曲线积分公式:
- 第一类曲线积分(对弧长的曲线积分):∫(L) f(x,y) ds = ∫(a) (b)
f(x,y)√[(dx)^2 + (dy)^2]。
- 第二类曲线积分(对坐标的曲线积分):∫(L) P(x,y) dx + Q(x,y) dy = ∫(a) (b) [∫(L1) P(x,y) dx + Q(x,y) dy] dσ。
2. 曲面积分公式:
- 第一类曲面积分(对面积的曲面积分):∫∫(Σ) f(x,y,z) dS。
- 第二类曲面积分(对坐标的曲面积分):∫∫(Σ) P(x,y,z) dydz + Q(x,y,z) dzdx + R(x,y,z) dxdy。
其中,f(x,y,z)、P(x,y,z)、Q(x,y,z)、R(x,y,z) 是定义在曲面Σ 上的函数,Σ 是积分曲面,L 是积分曲线,a、b 是积分上下限,dS 是面积元,ds 是线段元,dxdy、dydz、dzdx 是面元。
这些公式是积分学中的基本公式,也是解决复杂积分问题的关键。
对于具体的问题,需要选择合适的积分公式和计算方法。
对面积的曲面积分公式

对面积的曲面积分公式1. 对面积的曲面积分的概念。
- 设曲面∑是光滑的,函数f(x,y,z)在∑上有界。
把∑任意分成n小块Δ S_i(Δ S_i同时也表示第i小块曲面的面积),设(ξ_i,eta_i,ζ_i)是Δ S_i上任意取定的一点,作乘积f(ξ_i,eta_i,ζ_i)Δ S_i,并作和∑_i = 1^nf(ξ_i,eta_i,ζ_i)Δ S_i。
- 如果当各小块曲面的直径的最大值λto0时,这和式的极限存在,则称此极限为函数f(x,y,z)在曲面∑上对面积的曲面积分或第一类曲面积分,记作∬_∑f(x,y,z)dS=limlimits_λto0∑_i = 1^nf(ξ_i,eta_i,ζ_i)Δ S_i。
2. 对面积的曲面积分的计算方法。
- 一、利用曲面的方程化为二重积分计算。
- 设曲面∑的方程为z = z(x,y),∑在xOy面上的投影区域为D_xy,函数z(x,y)在D_xy上具有连续偏导数,被积函数f(x,y,z)在∑上连续,则∬_∑f(x,y,z)dS=∬_D_{xy}f[x,y,z(x,y)]√(1 + z_x)^2+z_{y^2}dxdy。
- 类似地,如果曲面∑的方程为x = x(y,z),∑在yOz面上的投影区域为D_yz,则∬_∑f(x,y,z)dS=∬_D_{yz}f[x(y,z),y,z]√(1 + x_y)^2+x_{z^2}dydz。
- 如果曲面∑的方程为y = y(z,x),∑在zOx面上的投影区域为D_zx,则∬_∑f(x,y,z)dS=∬_D_{zx}f[x,y(z,x),z]√(1 + y_z)^2+y_{x^2}dzdx。
- 二、利用曲面的参数方程计算(略高于一般要求)- 设曲面∑的参数方程为<=ft{begin{array}{l}x = x(u,v) y = y(u,v) z =z(u,v)end{array}right.,(u,v)∈ D,且x(u,v),y(u,v),z(u,v)在D上具有连续偏导数,(∂(x,y))/(∂(u,v)),(∂(y,z))/(∂(u,v)),(∂(z,x))/(∂(u,v))不全为零,则dS=√(EG - F^2)dudv,其中E=x_u^2+y_u^2+z_u^2,F = x_ux_v+y_uy_v+z_uz_v,G=x_v^2+y_v^2+z_v^2。
对面积的曲面积分

M = lim∑ρ(ξi ,ηi ,ζ i )∆Si
0 λ→ i=1
n
∑
其中λ是n个小曲面 个小曲面 块的直径的最大值。 块的直径的最大值。
o x
y
2
2、对面积的曲面积分的定义 、 定义8.3.1 设曲面 是光滑的,函数 (x,y,z)在Σ上 设曲面Σ是光滑的 函数f 是光滑的, 定义 在 上 有界。 任意分成n小块 同时也代表第i小 有界 。 把 Σ任意分成 小块 ⊿ Si ( 同时也代表第 小 任意分成 小块⊿ 块的面积) 设 上任意取定的一点, 块的面积),设 (ξi ,ηi ,ζi)是⊿Si上任意取定的一点, 是 作乘积 f (ξi ,ηi ,ζi)∆si (i=1,2,3,…,n),并作和 , , , , ,
Σ
o
Dxy x
y
∫∫ f (x, y, z)dS Σ
Dxy
(∆σi )x y (ξi ,ηi ,ζ i )
)
= ∫∫
f (x, y,
7
说明 (1)计算方法可概括为“一代、二换、三投影” )计算方法可概括为“一代、二换、三投影” “一代” 将z=z(x,y)代入被积函数 (x,y,z), 一代” 代入被积函数f 一代 代入被积函数 , 得f [x,y,z(x,y)]; ; “二换”将dS换成相应的曲面面积元素的表达式: 二换” 换成相应的曲面面积元素的表达式: 二换 换成相应的曲面面积元素的表达式 如Σ:z=z(x,y),则 : ,
o x
13
y
I = 0 + 2∫∫ x x2 + y2 dxdy
Dxy
y
= 2∫ π dθ ∫
2 − 2
π
2acosθ
0
r cosθ ⋅ r ⋅ rdr
同济版大一高数第十一章第四节对面积曲面积分

∫∫Σ f (x, y, z) d S = ∫∫D
f (x , y , 0 ) d xdy
xy
26
P219 题4(1). ∑ 在 xoy 面上的投影域为
2
z
d S = 1+ zx2 + z y 2 dxdy
a −r
r dr
z∑
o x
1
Dx y
y
计算结果如何 ?
14
例5:计算 : 解:
I = ∫∫ xds ∑ : z = a2 − x2 − y2
∑
Q f ( x,y,z) = x 是关于x 的奇函数
又∑ 是关于 yoz 面对称。 ∴ I = 0
例6:计算 :
I = ∫∫ (x2 + y2 + z2 )ds ∑ : x2 + y2 + z2 = a2
dS = 1+ z′ + z′ dxdy x y
2 2
= 1+ 0 + (−1) dxdy = 2dxdy,
2
故
∫∫ (x + y + z)ds =
Σ
Dxy
2 ∫∫ (5 + x)dxdy
Dxy
= 2 ⋅ 5∫∫ dxdy =125 2π.
16
1 2 例8:设均匀抛物面壳 z = 2 − x + y2 : 2 其面密度为 ρ (常数),求 IZ
= −3∫
π
0
5 + 4cos2 t dcos t
23
内容小结
1. 定义:
高等数学第四节 曲 面 积 分

例 1 计算曲面积分 (xz2)dS, 其中 为
球面 x2 + y2 + z2 = 1.
解 球面方程为 z 1x2y2 与z 1x2y2.
上半球面记为 1,下半球面记为 2,则根据
对面积的曲面积分的性质,有
(xz2)dS(xz2)dS(xz2)dS.
设曲面 是双侧的. 例如方程 z = z(x, y) 表示的曲
面,有上侧与下侧之分;方程 y = y(x, z)表示的曲面.
有左侧与右侧之分;方程 x = x(y, z) 所表示的曲面, 有前侧与后侧之分;对于封闭曲面,有内侧与外侧之
分
z
上侧
z
外侧
Mo
内侧
下侧
内侧
O
y
x (a)
O
外侧 y
x (b)
P 1, Q 1,
x
y
所以由高斯公式,得
R 0. z
I(x1 )d yd zyd zd xd x d y
2dV
211111.
6
3
时,则曲面的法向量
n与
z
轴正向的夹角不大于 π
2
,
于是,曲面的面积元素 dS 在 xy 平面的投影 dxdy 不
为负值,如果 Dxy 表示曲面 在 xy 平面上的投影区
域,那么我们可将对坐标的曲面积分化成在 xy 平面
上区域 Dxy 的二重积分来计算,即
R(x, y,z)dxdy R[x,y,z(x,y)d ]xdy.
在曲面 上连续,则
f
(x,
y,
z)dS
10-4对面积的曲面积分33410
显 然 xdS xdx 0d , y
1
D 1
xdS x11dx d0,y
2
D 1
讨 论 3 时 ,将 投 影 域 选 在 x 上 . oz ( 注 意 : y1x2分 为 左 、 右 两 片 )
(左右两片投影相同)
xdSxdSxdS
3
31
32
2 x 1yx2yz2dxdz
Dxz
xoz
2 x
1 、 ( 2 xy 2 x 2 x z )ds , 其 中 为 平 面 2x 2y z 6在第一卦限中的部分;
2 、 ( xy yz zx )ds , 其 中 为 锥 面 z x 2 y 2 被 柱 面 x 2 y 2 2 ax 所 截 得 的 有 限 部 分 .
三 、 求 抛 物 面 壳 z 1 ( x 2 y 2 )( 0 z 1 ) 的 质 量 , 此 壳 2
关 于 坐 标 面 、 原 点 均 对 称 ,
积 分 曲 面 也 具 有 对 称 性 ,
故 原 积 分 8 ,
1
(其 中 1 表 示 第 一 卦 限 部 分 曲 面 )
1 : x y z a , 即 z a x y
dS 1zx2zy2dxd y3dxdy
(x2y2z2)dS8(x2y2z2)dS
2011
记 为 f(x,y,z)d.S
n
即 f(x,y,z)d S l i0im 1f(i, i, i) S i
其中 f(x, y,z)叫被积函数 叫积 ,分曲.面
2.对面积的曲面积分的性质
若可分为分片光 1及 滑 2,则 的曲面
f(x ,y ,z )d S f(x ,y ,z )d Sf(x ,y ,z )d.S
2 、 f ( x , y , z ) ds = f ( x ( y , z ), y , z ) _ _ _ _ _ _ _ _ dydz ;
对面积的曲面积分

被柱面
x y 25
所截得的部分.
2 2
解 曲面 : z 5 y 投影域: D xy {( x , y ) | x y 25 } 故 ( x
z
O
y z )d S
x
y
2 ( x y 5 y ) dxdy
D xy
dS
的二 对重 称积 性分
z a a x y
2 2 2
O
x
y
2
投影域 Dxy : x
y a
2
2
17
对面积的曲面积分
Σ 是球面 x y z 2 az
2 2 2
对上半球 z a
dS
2 2
a x y
2 2
2
1 z x z y dxdy
2
a a x y
2 2
2
若 可分为分片光滑的曲面
1及 2 , 则
f ( x , y , z )d S
1
f ( x , y , z )d S
2
f ( x , y , z )d S
5
对面积的曲面积分
补充:第一类面积分对称性
设分片光滑的 曲面Σ 关于yOz面对称,
则
f ( x , y , z )d S
1
O
1
x
16
对面积的曲面积分
计算曲面积分 I
( x y z )d S
2 2 2
的值.
2 2 2 其中Σ 是球面 x y z 2 az .
(a 0)
对面积的曲面积分.

o
y
x
2.定义:
设 为光滑曲面, f (x, y, z) 是定义在 上的一 个有界函数, 若对 做任意分割和局部区域任意取点, “乘积和式极限”
记作 f (x, y, z)d S
都存在, 则称此极限为函数 f (x, y, z) 在曲面 上对面积 的曲面积分 或第一类曲面积分. 其中 f (x, y, z) 叫做被积 函数, 叫做积分曲面.其中, 表示 n 小块曲面的直径 的最大值(曲面的直径为其上任意两点间距离的最大者).
(7) 积分中值定理
若f (x, y, z)在光滑曲面 上连续,则至少存在一点
( ,, ) ,使得
f (x, y, z)dS f (,, )S
(8) 对称性
若积分曲面 具有某种对称性 ,而被积函数 f (x, y, z)对于
该对称性是奇函数,则 f (x, y, z)dS 0.
例如:若关于xoy面是对称的,则当 f (x, y, z)对于变量
二重积分.
例33.1.计算曲面积分
其中是球面
被平面
截出的顶部.
解:
z
Dxy : x2 y2 a2 h2
1
z x2
z
2 y
h o
Dxy a y x
d S z
a dxdy
2
Dxy a2 x2 y2 a 0 d
a2 h2 rd r
0
a2 r2
2
a
1 ln(a2 2
r2)
1 zx2 (x, y) z y2 (x, y)dxdy
说明: 1) 如果曲面方程为
x x( y, z), ( y, z) Dyz 或 y y(x, z), (x, z) Dxz
对面积的曲面积分的可代入性和对称性

对面积的曲面积分的可代入性和对称性第十二章 曲面积分一、对面积的曲面积分的可代入性对面积的曲面积分中被积函数可代入性:是指可以将曲面的表达式代入被积函数。
所以x , y , z 满足曲面的方程.是定义在曲(,,)f x y z面 上的,也就是说以 f (x , y , z ) 的自变量x , y , z 为坐标的点P 就是曲面Σ上,比如:设 f (x , y , z )=xyz 是定义在曲面Σ:z = x 2 + y 2 上,从而 f (x ,y ,z ) 就可以写成 xy (x 2+y 2),即f (x ,y ,z ) = xy (x 2+y 2).因为 f 中的x , y , z 是约定在曲面之上的,所以 z 的取值为x 2 + y 2 , 而点的坐标必须满足曲面的方程,而二重积分计算时则不能把边界曲线的表达式代入被积函数,满足的关系式通过不等式描述,一般含有“≤”或“≥”。
因为被积函数中的x , y 是平面区域D 内部的点对应的x , y ,此时x , y +≤+⎰⎰22221()d ,x y x y x y σ比如:中的取值限定在圆内,满足的是x 2 + y 2 ≤ 1,所以22221()d x y x y σ+≤+⎰⎰+≤≠⎰⎰2211d .x y σ二、对面积的曲面积分的对称性定义1设曲面∑上任取一点P(x, y, z),若(x, y, – z)对应的点Q也在∑上,或者说:将∑的关系式中“z”换成“–z”,而关系式不变,则称曲面∑关于xOy面对称.【曲面还可以关于yOz面对称或zOx面对称。
】例如: Σ的关系式为:x2 + y2 + z2= a2 (z ≥ 0), 若将z改成-z,则关系式变成了: x2 + y2 +(-z)2= a2 (-z ≥0),即x2 + y2 + z2= a2 (z ≤ 0),关系式发生了变化,即曲面发生了变化,所以曲面不关于xOy面对称。
当然,如果大家把x改成-x,则关系式不变,所以曲面关于yOz面对称。
对面积的曲面积分

对面积的曲面积分
曲面积分是对一个曲面上某个标量函数的积分,它和常规的二重积分或三重积分类似,只不过积分的对象是曲面上的函数值。
对于一个曲面S,曲面积分的一般形式为:
∫∫S f(x,y,z) dS
其中f(x,y,z)是曲面S上的一个标量函数,dS是曲面S上的面积元素。
在实际计算过程中,需要将曲面分成小面元,然后对每个小面元进行积分,最终将所有小面元的积分累加起来得到整个曲面的积分值。
曲面积分在物理、工程、数学等领域中都有广泛的应用,例如计算电场、磁场、流体力学等。
在数学的研究中,曲面积分也是研究曲面上的微积分和几何学性质的重要工具。
需要注意的是,曲面积分的计算方法和结果与所采用的坐标系有关,通常需要根据具体问题选择合适的坐标系来计算。
- 1 -。
曲面积分
2,计算曲面积分 ,其中 是上半个球面 与平面 围成封闭曲面外侧.
解:
本题需用高斯公式计算,化为三重积分后,再用球坐标计算
=
=
=
3,计算曲面积分 ,其中 是长方体 的整个表面的外侧,
解:(1)直接计算法
将有向曲面分成以下六个部分
上侧;
下侧;
前侧;
后侧;
左侧;
右侧;
对于 ,需将 向xoy坐标面做投影.显然,除 外,其余四片曲面在xoy坐标面上的投影均为零,故
曲面积分
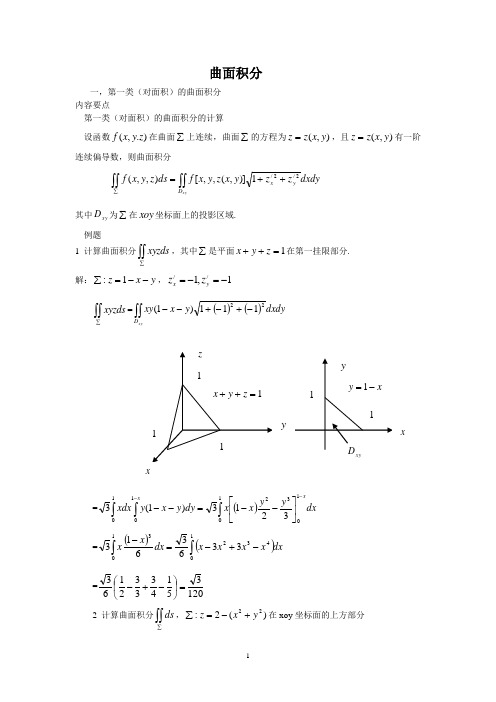
一,第一类(对面积)的曲面积分
内容要点
第一类(对面积)的曲面积分的计算
设函数 在曲面 上连续,曲面 的方程为 ,且 有一阶连续偏导数,则曲面积分
其中 为 在 坐标面上的投影区域.
例题
1计算曲面积分 ,其中 是平面 在第一挂限部分.
解: ,
=
=
=
=
2计算曲面积分 , 在xoy坐标面的上方部分
解:
=
=
=
= .
练习题
1设 为平面 在第一卦限部分,求
2设 为平面 在第一卦限部分,求
3计算曲面积分 , 在xoy坐标面的上方部分
[答案:1, ; 2, ; 3, .]
二,第二类(对坐标)的曲面积分
内容要点
1,第二类(对坐标)曲面积分的计算
对于曲面积分 的计算,首先应将 的方程表为 ,然后将 向xoy坐标面做投影,若投影区域为 ,则曲面积分便可化为二重积分
[答案:1, ; 2, 3, 4, 5, . ]
同理可得
总之
=
(2)高斯公式法
=
=
其中
一,对面积的曲面积分的概念与性质

f(x ,y ,z )d S f[x ,y ,z (x ,y )1 ] zx 2 (x ,y ) zy 2 (x ,y )dx . d
S
D x y
讨论: 如果积分曲面S由方程yy(z, x)给出或由xx(y, z)给出,那么
f(x, y, z)在S上对面积的曲线面积分如何计算?
例 1 计 算 曲 面 积 分 1 d , 其 S 中 S 是 球 面 x 2 y 2 z 2 a 2 被 平 面 S z zh(0<h<a)截出的顶部.
Mf(x,y,z)dS S
另一方面,设积分曲面S由方程zz(x, y)给出,S在xOy面上的 投影区域为Dxy,函数zz(x, y)在Dxy上具有连续偏导数,则光滑曲 面S的质量M也可用元素法来求: S上任意点(x, y, z)处的面积元素为dS 1zx2(x,y)zy2(x,y)dxd,y
Dxy 为圆形闭区域:x2y2a 2h 2. 又
z
1 z x 2 z y 2 a 2 a x 2 y 2 . h
于是 1 d S adxdy
S z D x a 2 y x 2 y 2
Dxy
a
2 a 2 h 2 rdr
d x ady
x 2 y 2
Dxy
1 1x
30xd 0 xy(1xy)dy
S1
S2
S4Oຫໍສະໝຸດ 11 Dxy y 3 0 1 x ( 1 6 x ) 3 d 1 3 . x 2 x 0S 3
质量元素为 d M f[x,y,z(x,y)]1zx 2(x,y)zy 2(x,y)d x,d y
于是质量 M f[x,y,z(x,y)]1zx 2(x,y)zy 2(x,y)dx.dy
对面积的曲面积分

第四节 对面积的曲面积分4.1 学习目标了解对面积的曲面积分的概念、 性质,掌握对面积的曲面积分的计算方法, 会用曲面积分求一些几何量与物理量 .4.2 内容提要1.定义 设函数f x, y,z 在光滑曲面上有界,将曲面任意分成n 小块 s ( S i也表示第i 小块曲面的面积),在 S i 上任取一点 M i ( i , i , J ,作乘积f( i , i , i ) S i n (i 1,2,L ,n ),并作和 f i , i , is i ,记各小曲面直径的最大值为,如果对曲i 1面的任一分法和点(i , i , i )的任意取法,当 0时,上述和式的极限都存在且相等,则称此极限值为函数 f x,y,z 在曲面上对面积的曲面积分或第一类曲面积分,记nf(x, y,z)dS lim 0 i 1 f ( i , i , i ) S •【注】定义中的“ S i ”是面积元素,因此,S i 0 .2•性质f(x,y,z)dS f(x,y,z)dS f(x, y,z)dS ;1 2②当被积函数为1时,积分结果在数值上等于曲面的面积S ,即f (x, y, z)dS S .3.对面积的曲面积分的计算在xoy 面上的投影区域为 D xy ,函数z z x, y 在Dxy同样地:x x y,zf (x, y, z)dSD yzD xy 上具有连续偏导数,被积函数f (x, y,z)在 上连续,则f (x,y,z)dSf(x, y,z(x,y)h 1dxdy①关于曲面具有可加性,若12,且1与2没有公共的内点,则设曲面 由z z x, y 给出,x y,z , y,z dydz ,:y y z,xf(x,y,z)dS f x, yz,x ,zD xz4•对面积的曲面积分的应用设曲面上任意一点x, y, z处的面密度是x, y,z①曲面的质量x, y, zdS.②曲面的质心x,y,z 2 dzdx .x,y,z dS, x,y,z dS③曲面的转动惯量I x x,y,z dS Iyx, y,zI z x,y,z dS, I o z x, y, z dSdS,x, y,zdS.4.3 典型例题与方法基本题型I :计算对面积的曲面积分1 填空题:x2y2z24,则Q(X2y2)dS由积分区域的对称性知乙x2dS y2dS? z2dS而积分在上进行,乙(x2故应填12832 选择题(A) xdS (C) zdS乙(X2y2)dS - (x23z24,y2)dSa2(z 0),代入上式得,z2)dS .22128在第一卦限中的部分,则有()4 xdS ;( B) ydS 4 xdS ;1 14 xdS ;( D) xyzdS 4 xyzdS解因为曲面是上半球面, 关于yoz 面对称且被积函数f i (x, y,z) x ,f 2(x, y, z) xyz 都是变量X 的奇函数,于是 xdS xyzdS ° .类似地, 关于xoz面对称且f 3(x, y,z) y 是变量y 的奇函数,于是 yds 0 .而 xdS 0, xyzdS 0 ,1 1故应选(C ).事实上,由对称性,zdS 4zdS ,zdS xdS, (0正确.1 1 1【方法点击】 在计算对面积的曲面积分时,应注意下列技巧: (1) 利用对称性,但要注意,曲面 关于某坐标面对称,被积函数关于相应变量具有 奇偶性,两者缺一不可.(2)利用积分曲面 的方程化简被积函数.例3计算曲面积分 (2x 2y z)ds ,其中 是平面2x 2y z 2 0被三个坐标面所截下的在第一卦限的部分D : 0 x 1,0 y22dSJ 1~x ~ dxdy ^ 2dxdy ,解法2x 2y,z x2,Z y 2.在xoy 平面上的投影是三角形,记为(2x 2y z)ds2g 1 z x 2 z y 2 dxdy6dxdy 3.D解法(2x 2y z)ds 2dS22 3 .【方法点击】在解法二中,将曲面方程代入到了曲面积分里, 形,最后用到了三角形的面积公式 .例 4 计算 | (x2y 2)dS ,因为积分曲面是一个三角为立体.x 2 y2z 1的边界.【分析】]根据积分曲面 的方程, 分转化为投影区域上的二重积分进行计算.确定投影区域,计算曲面面积微元dS ,将曲面积1为锥面zx 2 y 2 , 0 z 1,在 1 上,图4-12为z 1上x 2y 21部分,在 2上,dS dxdy ,2 2i, 2在xOy 面的投影区域为D :x y 1,所以图4-2【注】该题不能将积分曲面向xoy 面作投影,因为投影为曲线,不是区域•基本题型II :对面积的曲面积分的应用(x 21y 2)dS + (x y 2)dS2 (x 2 2 y )、. 2dxdy (xD2y )dxdy(.2 1) (x 2y 2)dxdy (1D3d八2).例5计算 z 2dS ,其中 为 x 2 y 24介于z 0,z 6之间的部分•【分析】积分曲面 如图11-13所示,此积分为对面积的曲面积分,积分曲面关于xoz 面,yoz 面对称,被积函数是偶函数,则有z 2dS = 4 z 2dS , 1故可利用对称性解之•解 设1 : x 4 y 2,其在yoz 面的投影域为D yz :dS . 1 x y 2x z2dydzdydzz dS = 4 z ? dS =4Ddy 288 .1例6求物质曲面S: z (x2 y2)(0 z 1)的质量,其面密度z((x, y,z) S).2解S在xoy平面上的投影区域D : x2 y2(、‘2)2.解以球心为原点,铅锤直径为Z 轴建立直角坐标系,则球面方程为x 2y 2z 2R 2, 且任意点M (x,y, z)处的密度为x 2y 2.设球壳的质心坐标为(x,y,z),由对称性知,x y 0 .z dS于是球壳的质量为2 R43 R4R12 3 3,于是半球壳的质心坐标为-2R 3 324.4 教材习题解答1.有一个分布着质量的曲面,在点(X, y, z)处它的面密度u(x,y, z),用对面积的曲面积分表示这曲面对于 x 轴转动惯量。
培训学习资料-曲面积分_2022年学习资料

-2ads +2aas +a as--∫∫2ava2-y2-z2ds-=8m+2aj∬adydz-2a∬a dk=8m-或「-x+y+zs=2mas=2ars-=2a·a.4m2=8m-∬2aa+va2-y2-z2 s-va-z2-yi-2+∬2aa-va2-y2-z2ds-10
例5.计算1=乐x2+y2dS,其中∑是球面x2+y2-+z2=2x+y+z-解:显然球心为1,1,1,半 为3-利用对称性可知ds=月22ds=22ds-12-2+as-月a*as-乐、ds=1s=乐ds-利用重 公式--4d5=4ds-乐2ds-八ds-=4.1·4π 32=48π -11
〔小Pdyd称为P在有向曲面Σ 上对y,之的曲面积分;-小dzdx称为2在有向曲面Σ 上对x,x的曲面积分;dxdy称为R在有向曲面Σ 上对x,y的曲面积分。-引例中,流过有向曲面∑的流体的流量为-Φ =J八Pdydz -Qddx+-Rdxdy-若记∑正侧的单位法向量为n=cos,cosB,c0sy-叉-dS=ndS=d y
四、对坐标的曲面积分的计算法-定理:设光滑曲面∑:z=fx,y,x,∈Dy取上侧-Rx,y,z是∑上的连续 数,则-八Rx,,dxdy=∬o-Rx,y,fx,ydxdy-设积分曲面是由方程Z=x,y-所给出的曲面上 -在xOy面上的投影区域为D,y-函数z=fx,y在Dw上具有一阶-连续偏导数,被积函数Rx,y-z在上连 。-一代、二投、三定向-15
二、对面积的曲面积分的计算法-定理:设有光滑曲面-∑:z=zx,y,x,y∈Dxy-f化,yz在∑上连续, 曲面积分-小fx,八,zdS存在,且有-fv.2ds-=nfx.zx》1+z2x月+z,xad-一代、二换 三投影-化为二重积分计算-3
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
o
Bx
注意, 本题只在不含原点的单连通区域内积分与路径
三、平面上曲线积分与路径无关的等价条件
定理2. 定理 设D 是单连通域 , 函数 在D 内 具有一阶连续偏导数, 则以下四个条件等价: ∂P ∂Q = . (1) 在 D 内每一点都有 ∂y ∂x (2) 沿D 中任意光滑闭曲线 L , 有 ∫ Pdx + Qdy = 0.
证明 (4)
(1)
设存在函数 u ( x , y ) 使得
则
du = P dx + Qdy ∂u ∂u = P(x, y), = Q(x, y) ∂x ∂y
P, Q 在 D 内具有连续的偏导数, 从而在D内每一点都有 ∂P ∂Q = ∂y ∂x
说明: 说明
∂P ∂Q 若在某区域内 = , ∂y ∂x
第十章
第四节
对面积的曲面积分
一、对面积的曲面积分的概念与性质
引例: 曲面形构件具有连续面密度 引例 设曲面形构件 曲面形构件 量 M. z 类似求平面薄板质量的思想, 采用 “大化小 常代变 近似和 求极限 大化小, 常代变, 近似和, 求极限” 大化小 的方法, 可得 求质 质
(ξk ,ηk ,ζ k )
y0 x0 x0 y y0 x
( x0 , y0 ) x
P(x, y)dx + Q(x, y)dy
y
y
y0 x0
x
例5. 验证
是某个函数的全微分, 并求
2 2
出这个函数.
∂P ∂Q = 2xy = 证: 设P = xy , Q = x y, 则 ∂x ∂y
由定理2 可知, 存在函数 u (x , y) 使
∂Q ∂Q ∫L Pd x + Qd y = ∫∫D′ ( ∂x − ∂x )dxdy ∂P ∂Q 因此在D上 ≡ ∂y ∂x
D D′ L
∫L Pdx + Qdy = 0.
说明: 说明
根据定理2 , 若在某区域内 且满足定理条件(单连通 单连通、 单连通 D内一阶连续偏导 一阶连续偏导)则 一阶连续偏导
A
L Bx
可见, 在不含原点的单连通区域内积分与路径无关.
取圆弧 AB : x = cosθ , y = sinθ (θ : →0) 2 2 2 k y W =∫ ( y dx − x dy) 2 AB r A
π
π
π
L
= k 2 思考: 思考 积分路径是否可以取 AO∪OB ? 为什么?
无关 !
π
例3. 设 ∑: x2 + y2 + z2 = a2
z∑
o x
1
Dx y y
计算 I =
∫∫∑ f (x, y, z) d S .
2 2
解: 锥面 z = x + y 与上半球面 z = a2 − x2 − y2 的 交线为 投影域为 Dxy = { (x, y) x2 + y2 ≤ 1 a2 }, 则 2
1
Pdx + Qdy
2
L2
B
L1
A
=∫
L1+L− 2
Pdx + Qdy
L2
(根据条件(1))
= ∫ Pdx + Qdy
说明: 说明 积分与路径无关时, 曲线积分可记为
∫AB Pdx + Qdy = ∫A Pdx + Qdy
B
设L为D中任一分段光滑闭曲线, 所围区域为 D′ ⊂ D (如图) , 利用格林公式 , 得 格林公式
+ ∫ (3 x2 y − 3xy2 + y2 ) dy u (x, y) = ∫ 5 x dx 0
4 0 x
y
1 3 3 2 2 3 = x + x y − xy + y 3 2 因此方程的通解为 5 3 2 2 3 1 3 x + x y − xy + y = C 2 3
5
y
(x, y)
o (x,0) x
∂Q ∂P ∫∫ ∂x − ∂y dxdy = ∫ Pdx + Qdy D L
二、平面上曲线积分与路径无关的条件
定理2. 定理 设D 是单连通域 , 函数 单连通域 具有一阶连续偏导数 则: 一阶连续偏导数, 一阶连续偏导数 (1)沿D 中任意光滑闭曲线 L , 有 在D 内
∫L Pdx + Qdy = 0.
则
可用积分法求d u = P dx + Q dy在域 D 内的原函数: 取定点 ( x0, y0 ) ∈D及动点 ( x, y ) ∈D, 则原函数为
u ( x, y) = ∫
( x, y )
= ∫ P(x, y0 )dx +∫ Q(x, y)dy
或 u (x, y) = Q(x0 , y)dy + P(x, y)dx ∫ ∫
设∑1为上半球面夹于锥面间的部分,它在 xoy 面上的
I = ∫∫ (x2 + y2 ) d S
∑1
I = ∫∫ (x2 + y2 ) d S
∑1
= ∫∫
=∫
Dx y
(x + y )
2 2
1 2
a a2 − x2 − y2 2 ar r dr 2 2 a −r
d xd y
记作
∫∫ f (x, y, z)d S
∑
都存在, 则称此极限为函数 f (x, y, z) 在曲面 ∑ 上对面积 都存在 的曲面积分 或第一类曲面积分 其中 f (x, y, z) 叫做被积 第一类曲面积分. 函数, 叫做积分曲面. 函数 ∑ 叫做积分曲面 据此定义, 据此定义 曲面形构件的质量为 M = ∫∫ ρ(x, y, z) d S
定理: 定理 设有光滑曲面 f (x, y, z) 在 ∑ 上连续 则曲面积分 连续, 连续 存在, ∫∫∑ f (x, y, z)dS 存在 且有
= ∫∫
Dxy
f (x, y,
)
说明: 说明 1) 如果曲面方程为
或
x = x( y, z), ( y, z) ∈Dyz 可有类似的公式. y = y(x, z), (x, z) ∈Dxz
= −∫ 0⋅ dx + x∫0
1
x
y
dy x2 + y2
或
dy =∫ 0 1+ y2yx源自= − arctan 2 yπ
四、全微分方程
若 在u(x, y) 使 du(x, y) = P(x, y) dx + Q(x, y) dy 存 则称 P(x, y) dx + Q(x, y) dy = 0 ①
即(2)对D 中任一分段光滑曲线 L, 曲线积分 (2) D
∫L Pdx + Qdy 与路径无关, 只与起止点有关.
∂P ∂Q = . 在 D 内每一点都有 ∂y ∂x
(2) 证明 (1) 设 L , L2 为D 内任意两条由A 到B 的有向分段光滑曲 1
线, 则
∫L Pdx + Qdy − ∫L
思考: 思考
若 ∑ 是球面 出的上下两部分, 出的上下两部分 则
被平行平面 z =±h 截 ±
z
0
)
dS ∫∫ z = ( ∑
Σ
h
o
y
dS a ∫∫ z = ( 4π aln h ) ∑
x
−h Σ
例2. 计算
其中∑ 是由平面 其中∑
与
坐标面所围成的四面体的表面. 坐标面所围成的四面体的表面 解: 设 ∑1, ∑2, ∑3, ∑4分别表示∑ 在平面 上的部分, 则 原式 = ∫∫ +∫∫
du = xy2 dx + x2 ydy
。 (0,0)
(x, y) 。
= ∫ x⋅ 0 dx + ∫
0
x
y 2 x y dy 0
(x,0)
=∫
y 2 x y dy 0
xd y − y d x 例6. 验证 在右半平面 ( x > 0 ) 内存在原函 2 2 x +y 数 , 并求出它. (x, y) −y x , Q= 2 证: 令 P = 2 2 x +y x + y2 2 2 ∂P y −x ∂Q (1,0) ( x,0) 则 = 2 = ( x > 0) ∂x (x + y2 )2 ∂y 由定理 2 可知存在原函数 定理
L
(3) 对D 中任一分段光滑曲线 L, 曲线积分 ∫ Pdx + Qdy
L
与路径无关, 只与起止点有关. (4) 即 在 D 内是某一函数 的全微分,
d u(x, y) = P dx + Qdy
(4) 证明 (3) 在D内取定点 与路径无关, 有函数
和任一点B( x, y ), 因曲线积分
B(x, y )
面, 计算
x + y + z ≤1, x ≥ 0 , y ≥ 0 , z ≥ 0的 表 z 1
解: 在四面体的四个面上 平面方程
dS
投影域
1 x
o
1y
z =1− x − y =1 y =0
3dxdy Dxy : 0 ≤ x ≤1, 0 ≤ y ≤1− x
同上
dzdx Dz x : 0 ≤ z ≤1, 0 ≤ x ≤1− z
A(x0, y0 )
( x+∆x, y)
C(x + ∆x, y )
则
∆xu = u(x + ∆x, y) − u (x, y)
=∫
( x+∆x, y)
( x, y)
Pd x + Qdy = ∫
( x, y)
Pd x
= P(x +θ ∆x, y)∆x ∆xu ∂u = lim P(x +θ ∆x, y) = P(x , y) ∴ = lim ∂ x ∆x→0 ∆x ∆x→0 ∂u 同理可证 = Q(x , y), 因此有 du = P dx + Qdy ∂y
