最新高中数学苏教版必修一第2章2.1.1第二课时课堂同步练习题含答案(同步练习).doc
新苏教版高中数学必修二同步练习:2.1.1《直线的斜率》(含答案)

随堂练习:直线的斜率1.对于下列命题①若α是直线l的倾斜角,则0°≤α<180°;②若k是直线的斜率,则k∈R;③任一条直线都有倾斜角,但不一定有斜率;④任一条直线都有斜率,但不一定有倾斜角.其中正确的有________个.2.斜率为2的直线经过点A(3,5)、B(a,7)、C(-1,b)三点,则a、b的值分别为________和________.3.直线经过原点和点(-1,-1),它的倾斜角是__________.4.直线l过原点(0,0),且不过第三象限,那么l的倾斜角α的取值范围是______________.5.若图中直线l1、l2、l3的斜率分别为k1、k2、k3,则k1、k2、k3的大小关系为______________.6.若直线AB与y轴的夹角为60°,则直线AB的倾斜角为________,斜率为________.7.一条光线从点A(-1,3)射向x轴,经过x轴上的点P反射后通过点B(3,1),求P点的坐标.8.设直线l过坐标原点,它的倾斜角为α,如果将l绕坐标原点按逆时针方向旋转45°,得到直线l1,那么l1的倾斜角为________.9.△ABC为正三角形,顶点A在x轴上,A在边BC的右侧,∠BAC的平分线在x轴上,求边AB与AC所在直线的斜率.答案1.32.4 -33.45°4.90°≤α<180°或α=0°5.k 1<k 3<k 26.30°或150° 33或-337.解 设P(x,0),则k PA =3-0-1-x =-3x +1,k PB =1-03-x =13-x ,依题意, 由光的反射定律得k PA =-k PB ,即3x +1=13-x,解得x =2,即P(2,0). 8.当0°≤α<135°时,倾斜角为α+45°;当135°≤α<180°时,倾斜角为α-135°9.解 如右图,由题意知∠BAO =∠OAC =30°,∴直线AB 的倾斜角为180°-30°=150°,直线AC 的倾斜角为30°, ∴k AB =tan 150°=-33, k AC =tan 30°=33.。
苏教版必修1第二章学生版同步练习函数的概念与图象参考答案1

必修1第2章 函数的概念与图象 参考答案第1课 函数的概念与图象(1) 1.①②③④;2.①③④;3.0,0,14,2n -;4.R ; 5.{|,x x R ∈且2}x ≠±;6.(1){|2x x ≥,且3}x ≠;(2){|1x x ≤,且4}x ≠-; 7.(1){0,3,8};(2)(,1]-∞;(3)[3,0)-.8.()|23|f x x =-,0()f x x =等; 9.()32f x x =-,2()f x x =,6()7f x x=-等; 10.解:若0k =,则()f x =其定义域为R ;若0k ≠,则20(4)430k k k >⎧⎨∆=-⨯⨯≤⎩,解得304k <≤; 综上所述,实数k 的取值范围为3[0,]4.第2课 函数的概念与图象(2)1.B ;2.D ;3.A ;4.(1)2,(2)3,(3)0,(4)1()f x <2()f x ; 5.(1)定义域(,0)(0,)-∞+∞U ,值域(,0)(0,)-∞+∞U ; (2)定义域(,0)(0,)-∞+∞U ,值域(,1)(1,)-∞+∞U .拓展延伸:6.解:2,[2,3)1,[1,2)()0,[0,1)1[1,0)2[2,1)x x f x x x x ⎧⎪∈⎪⎪∈⎪=∈⎨⎪-∈-⎪-∈--⎪⎪⎩M M7.分析:一般地,称x a =为||x a -的零点.对于含绝对值的函数问题,可先根据零点将区间(,)-∞+∞分成若干个区间(成为零点分段法),将函数转化为不含绝对值的分段函数,画出函数的图象,利用图象解决问题.解:函数|1||2|2y x x =++--的零点是1x =-和2x =,所以21,1,1,12,23, 2.x x y x x x --<-⎧⎪=-≤<⎨⎪-≥⎩作出函数的图象(如图),从函数的图象可以看出,函数的值域为[1,)+∞第3课 函数的概念与图象(3)1.C ;2.C ;3.1852,[0,)y x x =∈+∞;4.215S x x =-+,(0,15);5.44.1m ;6.3-;7.(1)350,(2)4;8.4480320()y x x=++,(0,4)x ∈. 9.(1)设每个零件的实际出厂价恰好降为51元时,一次订购量为x 0个依题意:0600.02(100)51x --=,即0625150x -=,0550x =. ∴ 当一次订购量为550个时,每个零件的实际出厂价恰好降为51元;(2)依题意,并结合(1),我们需要分三种情况来列出函数P f x =()的表达式.当0100<≤x 时,P =60;当100550<<x 时,P x x=--=-600021006250.(); 当x ≥550时,P =51.所以600100,()62100550,5051550,x x N x P f x x x N x x N<≤∈⎧⎪⎪==-<<∈⎨⎪≥∈⎪⎩ ; (3)设销售商的一次订购量为x 个时,工厂获得的利润为L 元,则()2200100,4022100550,5011550,x x x N x L P x x x x N xx x N <≤∈⎧⎪⎪=-=-<<∈⎨⎪≥∈⎪⎩当x =500时,L =6000;当x =1000时,L =11000.因此,当销售商一次订购500个零件时,该厂获得的利润是6000元;如果订购1000个,利润是11000元. 第4课 函数表示方法(1)1.C ;2. A ;3.B ;4.30;5.[1,)+∞;6.[1,11];7.(1)设()(0)f x kx b k =+≠,则(())()()f f x kf x b k kx b b =+=++2k x kb b =++,由题意,293k x kb b x ++=+,∴2(9)30k x kb b -++-=恒成立,∴29030k kb b ⎧-=⎨+-=⎩,解得334k b =⎧⎪⎨=⎪⎩或332k b =-⎧⎪⎨=-⎪⎩,∴3()34f x x =+或3()32f x x =--.(2)设21()()25(0)2f x a x a =-+<,即21()254f x ax ax a =-++, 设方程()0f x =的两根为1x ,2x ,则121a x x a -+=-=,1212512544a x x a a+==+,由题意,221213x x +=,∴21212()213x x x x +-=,∴12512()134a-+=,∴4a =-,此时,方程()0f x =即260x x --=,其根的判别式2(1)4(6)250∆=--⨯-=>,∴2()4424f x x x =-++.8.解:由图象可知,抛物线开口向上,顶点为(1,1)-,当3x =时,1y =, 设2()(1)1(0)f x a x a =-->,则2(3)(31)11f a =--=,解得12a =, ∴21()(1)12f x x =--,令21()(1)102f x x =--=,解得11x =21x =,结合图象知函数的定义域为[1-, ∴21()(1)12f x x =--,[1x ∈-.9.解:,0,()0,0.x x f x x ≥⎧=⎨<⎩∴当0x ≥时,(())()f f x f x x ==,当0x <时,(())(0)0f f x f ==,选D .10.解:当04x <≤时,114222y AB BP x x =⨯⨯=⨯⨯=; 当48x <≤时,1144822y AB BC =⨯⨯=⨯⨯=;当812x <<时,11(12)24222y AB AP AB x x =⨯⨯=⨯⨯-=-.∴2,(0,4],()8,(4,8],242,(8,12).x x y f x x x x ∈⎧⎪==∈⎨⎪-∈⎩第5课 函数的表示方法(2)1.B ;2.D ;3.D ; 4.[1,)-+∞,3(,0)(0,)2-∞U ; 5.45x -,[2,4];6.15{2,,1,}22--;7.2x +,3x +,x n +; 8.2(202),(0,10)y x x x =-∈;9.由于题目问的是“只可能是”,故解决问题的方法是寻找各选项所给图形中是否存在矛盾,从而排除不正确的选项.如选项B ,由直线过原点知0b =,但由抛物线的对称轴不是y 轴知0b ≠,矛盾.类似地可以判断,选项A 、D 都有矛盾,故选C . 10.D .第6课 函数的单调性(1)1. ()C ;2.()C ;3.()B 4. ()D ; 5.()B ; 6.①②. 7.设,11)1)(1()]1)([(11)()(,1121222121122222112121<<<---+-=---=-<<<-x x x x x x x x a x ax x ax x f x f x x Θ)()(0.0)1)(1(01,02122212112x f x f a x x x x x x >>∴>--∴>+>-∴时当此时f (x )为减函数.当a>0时,f(x 1)<f(x 2),此时f(x)为增函数.8.由.32060<-⎩⎨⎧<+<a b b a a 得即抛物线顶点横坐标<3,又开口向下,所以二次函数f (x )在[)∞+3上递增.[))()3(.3,,3,3πππf f >∴<+∞∈且Θ。
高中数学(苏教版,必修一) 第二章函数 2.2.2(二) 课时作业(含答案)

2.2.2 指数函数(二) 课时目标 1.理解指数函数的单调性与底数a 的关系,能运用指数函数的单调性解决一些问题.2.理解指数函数的底数a 对函数图象的影响.1.下列一定是指数函数的是________.①y =-3x ;②y =x x (x >0,且x ≠1);③y =(a -2)x (a >3);④y =(1-2)x .2.指数函数y =a x 与y =b x 的图象如图,则0,a ,b,1的大小关系为________.3.函数y =πx 的值域是________.4.已知集合M ={-1,1},N ={x |12<2x +1<4,x ∈Z },则M ∩N =________. 5.若(12)2a +1<(12)3-2a ,则实数a 的取值范围是______________. 6.若指数函数f (x )=(a +1)x 是R 上的减函数,那么a 的取值范围为________.一、填空题1.设P ={y |y =x 2,x ∈R },Q ={y |y =2x ,x ∈R },则P 、Q 的关系为________.2.函数y =16-4x 的值域是________.3.函数y =a x 在[0,1]上的最大值与最小值的和为3,则函数y =2ax -1在[0,1]上的最大值是________.4.若函数f (x )=3x +3-x 与g (x )=3x -3-x 的定义域均为R ,则下列命题正确的是________.(填序号)①f (x )与g (x )均为偶函数;②f (x )为偶函数,g (x )为奇函数;③f (x )与g (x )均为奇函数;④f (x )为奇函数,g (x )为偶函数.5.函数y =f (x )的图象与函数g (x )=e x +2的图象关于原点对称,则f (x )的解析式为________.6.已知a =1335-⎛⎫ ⎪⎝⎭,b =1235-⎛⎫ ⎪⎝⎭,c =1243-⎛⎫ ⎪⎝⎭,则a ,b ,c 三个数的大小关系是________. 7.春天来了,某池塘中的荷花枝繁叶茂,已知每一天新长出荷叶覆盖水面面积是前一天的2倍,若荷叶20天可以完全长满池塘水面,当荷叶刚好覆盖水面面积一半时,荷叶已生长了________天.8.已知函数f (x )是定义在R 上的奇函数,当x >0时,f (x )=1-2-x ,则不等式f (x )<-12的解集是________.9.函数y =2212x x -+⎛⎫ ⎪⎝⎭的单调递增区间是________.二、解答题10.(1)设f (x )=2u ,u =g (x ),g (x )是R 上的单调增函数,试判断f (x )的单调性;(2)求函数y =2212x x --的单调区间.11.函数f (x )=4x -2x +1+3的定义域为[-12,12]. (1)设t =2x ,求t 的取值范围;(2)求函数f (x )的值域.能力提升12.函数y =2x -x 2的图象大致是________.(填序号)13.已知函数f (x )=2x -12x +1. (1)求f [f (0)+4]的值;(2)求证:f (x )在R 上是增函数;(3)解不等式:0<f (x -2)<1517.1.比较两个指数式值的大小主要有以下方法:(1)比较形如a m 与a n 的大小,可运用指数函数y =a x 的单调性.(2)比较形如a m 与b n 的大小,一般找一个“中间值c ”,若a m <c 且c <b n ,则a m <b n ;若a m >c 且c >b n ,则a m >b n .2.了解由y =f (u )及u =φ(x )的单调性探求y =f [φ(x )]的单调性的一般方法.2.2.2 指数函数(二)双基演练1.③ 2.0<a <1<b3.(0,+∞)4.{-1}解析 解指数不等式12<2x +1<4,得-1<x +1<2, 所以-2<x <1,故N ={-1,0},所以M ∩N ={-1,1}∩{-1,0}={-1}.5.(12,+∞) 解析 ∵函数y =(12)x 在R 上为减函数, ∴2a +1>3-2a ,∴a >12. 6.-1<a <0作业设计1.Q P解析 因为P ={y |y ≥0},Q ={y |y >0},所以Q P .2.[0,4)解析 ∵4x >0,∴0≤16-4x <16,∴16-4x ∈[0,4).3.3解析 函数y =a x 在[0,1]上是单调的,最大值与最小值都在端点处取到,故有a 0+a 1=3,解得a =2,因此函数y =2ax -1=4x -1在[0,1]上是单调递增函数,当x =1时,y max =3.4.②解析 f (-x )=3-x +3x =f (x ),g (-x )=3-x -3x =-g (x ).5.f (x )=-e -x -2解析 ∵y =f (x )的图象与g (x )=e x +2的图象关于原点对称,∴f (x )=-g (-x )=-(e -x +2)=-e -x -2.6.c <a <b解析 ∵y =(35)x 是减函数,-13>-12, ∴b >a >1.又0<c <1,∴c <a <b .7.19解析 假设第一天荷叶覆盖水面面积为1,则荷叶覆盖水面面积y 与生长时间的函数关系为y =2x -1,当x =20时,长满水面,所以生长19天时,荷叶布满水面一半.8.(-∞,-1)解析 ∵f (x )是定义在R 上的奇函数,∴f (0)=0.当x <0时,f (x )=-f (-x )=-(1-2x )=2x -1.当x >0时,由1-2-x <-12,(12)x >32,得x ∈∅; 当x =0时,f (0)=0<-12不成立; 当x <0时,由2x -1<-12,2x <2-1,得x <-1. 综上可知x ∈(-∞,-1).9.[1,+∞)解析 利用复合函数同增异减的判断方法去判断.令u =-x 2+2x ,则y =(12)u 在u ∈R 上为减函数,问题转化为求u =-x 2+2x 的单调递减区间,即为x ∈[1,+∞).10.解 (1)设x 1<x 2,则g (x 1)<g (x 2).又由y =2u 的增减性得()12g x <()22g x ,即f (x 1)<f (x 2),所以f (x )为R 上的增函数.(2)令u =x 2-2x -1=(x -1)2-2,则u 在区间[1,+∞)上为增函数.根据(1)可知y =2212x x --在[1,+∞)上为增函数.同理可得函数y 在(-∞,1]上为单调减函数.即函数y 的增区间为[1,+∞),减区间为(-∞,1].11.解 (1)∵t =2x 在x ∈[-12,12]上单调递增, ∴t ∈[22,2]. (2)函数可化为:f (x )=g (t )=t 2-2t +3,g (t )在[22,1]上递减,在[1,2]上递增, 比较得g (22)<g (2). ∴f (x )min =g (1)=2,f (x )max =g (2)=5-2 2.∴函数的值域为[2,5-22].12.①解析 当x →-∞时,2x →0,所以y =2x -x 2→-∞,所以排除③、④.当x =3时,y =-1,所以排除②.13.(1)解 ∵f (0)=20-120+1=0, ∴f [f (0)+4]=f (0+4)=f (4)=24-124+1=1517. (2)证明 设x 1,x 2∈R 且x 1<x 2,则22x >12x >0,22x -12x >0, ∴f (x 2)-f (x 1)=212121212121x x x x ---++ =()()()21212222121x x x x -++>0,即f (x 1)<f (x 2),所以f (x )在R 上是增函数.(3)解 由0<f (x -2)<1517得f (0)<f (x -2)<f (4), 又f (x )在R 上是增函数,∴0<x -2<4,即2<x <6,所以不等式的解集是{x |2<x <6}.。
2019—2020年最新高中数学苏教版必修一第2章2.2.2第一课时课堂同步练习题含答案.doc

1.下列函数中指数函数的个数为________.①y=(13)x;②y=(13)x-1;③y=2·3x;④y=1x;⑤y=(13)2x-1;⑥y=x 1 2.解析:只有①是指数函数.答案:12.函数f(x)=(13)1x的定义域,值域依次是____________.解析:由函数f(x)=(13)1x的表达式得x≠0为其有意义的取值范围,1x≠0.∴(13)1x≠1且(13)1x>0.于是函数定义域为{x|x≠0,x∈R},值域为{y|y>0且y≠1}.答案:{x|x≠0,x∈R},{y|y>0且y≠1}3.根据条件写出正数a的取值范围.(1)若a-0.3<a0.2,则a∈________;(2)若a7.5<a4.9,则a∈________;(3)若a 74<1,则a∈________;(4)若a 23<a,则a∈________.解析:(1)∵-0.3<0.2,a-0.3<a0.2,∴函数y=a x是增函数,故a∈(1,+∞).(2)∵7.5>4.9,a7.5<a4.9,∴函数y=a x是减函数,故a∈(0,1).(3)∵a 74<1=a0,74>0,∴函数y=a x是减函数,故a∈(0,1).(4)∵23<1,a23<a1,∴函数y=a x是增函数,故a∈(1,+∞).答案:(1,+∞) (0,1) (0,1) (1,+∞)4.函数y=a2x-1(a>0且a≠1)的图象必过定点________.解析:令2x-1=0,∴x=1 2 .∴定点为(12,1).答案:(12,1) 5.右图所示的曲线是指数函数y=a x的图象.已知a的值取5 4,4 3,310,15,则相应于曲线C1,C2,C3,C4的a值依次为______________.解析:作直线x=1分别交曲线C1,C2,C3,C4于(1,a1),(1,a2),(1,a3),(1,a4),则a1,a2,a3,a4分别为C1,C2,C3,C4的函数式中的底数a,结合图形可知a1<a2<a3<a4,而15<310<54<43,故a的值依次为15,310,54,43.答案:15,310,54,43[A级基础达标]1.某种细菌在培养过程中,每20分钟分裂一次(一个分裂为两个),经过3小时这种细菌由1个可繁殖为________个.解析:经过3小时这种细菌分裂9次,共有29=512(个).答案:5122.函数y=2x与y=2x+1的图象的交点个数是________.解析:作出y=2x与y=2x+1的图象(如图)即可得交点个数是2个.答案:23.将30.9,90.3,(13)-0.2,2-0.2用“<”连接起来为________.解析:2-0.2<1<30.2<30.6<30.9.答案:2-0.2<(13)-0.2<90.3<30.94.如图所示,在同一坐标系中画出指数函数y=2x,y=3x,y=(13)x的图象,则①是函数________的图象;②是函数________的图象;③是函数________的图象.解析:图象①对应的指数函数是减函数,底数小于1,故①是函数y=(13)x的图象;指数函数y=2x,y=3x都是增函数,且当x=1时,21<31,直线x=1与函数y=2x图象的交点在与函数y=3x图象的交点下方,所以②是函数y=3x的图象,③是函数y=2x的图象.答案:y=(13)x y=3x y=2x5.根据图象解得方程2x-x=1的解集是________.解析:由图象(图略)可知方程有两解,再由观察及赋值可得.答案:{0,1}6.比较下列各组数中两个值的大小:(1)0.2-1.5和0.2-1.7;(2)(14)13和(14)23;(3)2-1.5和30.2.解:(1)考察函数y=0.2x.因为0<0.2<1,所以函数y=0.2x 在实数集R上是单调减函数.又因为-1.5>-1.7,所以0.2-1.5<0.2-1.7.(2)考察函数y=(14)x.因为0<14<1,所以函数y=(14)x在实数集R上是单调减函数.又因为13<23,所以(14)13>(14)23.(3)2-1.5<20,即2-1.5<1;30<30.2,即1<30.2,所以2-1.5<30.2. 7.已知函数f(x)=a x 在x ∈[-2,2]上恒有f(x)<2,求实数a 的取值范围.解:当a>1时,f(x)=a x 在[-2,2]上为增函数, ∴f(x)max =f(2),又∵x ∈[-2,2]时,f(x)<2恒成立,∴⎩⎪⎨⎪⎧a>1f (2)<2,即⎩⎪⎨⎪⎧a>1a 2<2,解得1<a<2.同理,当0<a<1时,⎩⎪⎨⎪⎧0<a<1f (x )max =f (-2)<2, 解得22<a<1.综上所述,a 的取值范围为(22,1)∪(1,2).[B 级 能力提升]8.以下关于函数值域的结论,其中正确的个数是________.①函数y =35x -1的值域是(0,+∞);②函数y =(12)12x -1的值域是(0,1)∪(1,+∞);③函数y =2x 2-2x 的值域是⎣⎢⎡⎭⎪⎫12,+∞;④函数y =(13)x +2的值域是(0,+∞).解析:∵5x -1≥0,∴y ≥1,故①错,②③④正确.答案:39.设23-2x ≤(0.5)3x -4,则x 的取值范围为________. 解析:∵(0.5)3x -4=24-3x 且2>1, ∵23-2x ≤24-3x ,∴3-2x ≤4-3x ,∴x ≤1. 故x 的取值范围为(-∞,1]. 答案:(-∞,1]10.根据下列条件,求x 的值:(1)4×4x -5×2x -6=0; (2)9x +6x =22x +1.解:(1)令2x =t ,则t>0,原方程可化为4t 2-5t -6=0,解得t1=2,t2=-34(舍).由2x=2得x=1.(2)将方程两边同除以4x,得(32)2x+(32)x-2=0,即[(32)x-1][(32)x+2]=0.因为(32)x+2>0,所以(32)x=1,所以x=0.11.(创新题)已知函数f(x)=12(a x+a-x)(a>0,且a≠1)的图象经过点(2,419).(1)求f(x)的解析式;(2)证明:f(x)在[0,+∞)上是增函数.解:(1)∵函数f(x)的图象过点(2,419),∴12(a2+a-2)=419,整理得9a4-82a2+9=0,解得a 2=9或a 2=19.又a >0,且a ≠1,∴a =3或a =13.当a =3时,f(x)=12(3x +3-x );当a =13时,f(x)=12[(13)x +(13)-x ]=12(3x +3-x ).综上可知,所求解析式为f(x)=12(3x +3-x ).(2)证明:设x 1,x 2∈[0,+∞),且x 1<x 2, 则f(x 1)-f(x 2)=12(3x 1+3-x 1)-12(3x 2+3-x 2) =12(3x 1-3x 2+13x 1-13x 2) =12[(3x 1-3x 2)+3x 2-3x 13x 1·3x 2]=12(3x 1-3x 2)(1-13x 1+x 2) =12(3x 1-3x 2)·3x 1+x 2-13x 1+x 2. ∵0≤x 1<x 2,∴3x 1-3x 2<0,且3x 1+x 2>1. ∴f(x 1)-f(x 2)<0,即f(x 1)<f(x 2),∴f(x)在[0,+∞)上是增函数.。
2018-2019学年最新高中数学苏教版必修一第2章2.1.3第二课时课堂同步练习题含答案

1.已知函数y =(x -1)2,则x ∈(-1,5)上的最小值为________.解析:因为函数y =(x -1)2的对称轴为x =1,所以其最小值为f(1)=0.答案:02.函数y =ax +1(a <0)在区间[0,2]上的最大值与最小值分别为________,________.解析:因为a <0,∴y =ax +1在[0,2]上是减函数,当x =0时,y max =1;当x =2时,y min =2a +1.答案:1 2a +13.函数y =-x 2+2x -1在[0,3]上的最小值为________. 解析:y =-x 2+2x -1=-(x -1)2,函数图象对称轴为x =1,结合图象(图略)可知,当x =3时,y min =-4. 答案:-44.函数f(x)=⎩⎪⎨⎪⎧2x 2, 0≤x ≤12, 1<x<2,3, x ≥2的最大值是________. 解析:0≤x ≤1时,f(x)=2x 2≤2;1<x<2时,f(x)=2; x ≥2时,f(x)=3.因此f(x)的最大值是3.答案:3[A 级 基础达标]1.若y =-2x,x ∈[-4,-1],则函数y 的最大值为________. 解析:函数y =-2x在[-4,-1]上是单调增函数,故y max =-2-1=2. 答案:22.函数y =(a -1)x 在[1,3]上的最大值是2,则a =________. 解析:若a>1,当x =3时,y max =2,∴(a -1)×3=2,a =53. 若a<1,当x =1时y max =2,∴(a -1)×1=2,a =3,与a<1矛盾,故舍去.因此满足条件的a =53. 答案:533.定义域为R 的函数y =f(x)的最大值为M ,最小值为N ,则函数y =f(2x)+3的最大值为________,最小值为________.解析:y=f(2x)的最大值为M,最小值为N,故y=f(2x)+3的最大值为M+3,最小值为N+3.答案:M+3 N+34.已知函数f(x)=-x2+4x+a,x∈[0,1],若f(x)有最小值-2,则f(x)的最大值为________.解析:f(x)=-(x2-4x+4)+a+4=-(x-2)2+4+a.∴函数f(x)图象的对称轴为x=2,∴f(x)在[0,1]上单调递增.又∵f(x)min=-2,∴f(0)=-2,即a=-2.∴f(x)max=f(1)=-1+4-2=1.答案:15.函数f(x)=-2x2+mx+1,当x∈[-2,+∞)时是减函数,则m的取值范围是________.解析:由题意函数f(x)的单调减区间为[m4,+∞).故m4≤-2,得m≤-8.答案:(-∞,-8]6.函数y=-x2-4x+1在区间[a,b](b>a>-2)上的最大值为4,最小值为-4,求a与b的值.解:∵y=-(x+2)2+5,∴函数图象对称轴是x=-2.故在[-2,+∞)上是减函数.又∵b>a>-2,∴y=-x2-4x+1在[a,b]上单调递减.∴f(a)=4,f(b)=-4.由f(a)=4,得-a2-4a+1=4,∴a2+4a+3=0,即(a+1)(a+3)=0.∴a=-1或a=-3(舍去),∴a=-1.由f(b)=-4,得-b2-4b+1=-4,∴b=1或b=-5(舍),∴b=1.7.求函数f(x)=x2-2ax+2在区间[-1,1]上的最小值.解:函数f(x)的对称轴为x=a,且函数图象开口向上,如图所示:当a>1时,f(x)在[-1,1]上单调递减,故f(x)min=f(1)=3-2a;当-1≤a≤1时,f(x)在[-1,1]上先减后增,故f(x)min=f(a)=2-a2;当a<-1时,f(x)在[-1,1]上单调递增,故f(x)min=f(-1)=3+2a.综上可知,f(x)min =⎩⎪⎨⎪⎧3-2a (a >1)2-a 2 (-1≤a ≤1).3+2a (a <-1)[B 级 能力提升]8.如果函数f(x)=x 2+bx +c 对任意实数x ,都有f(2+x)=f(2-x),则f(1),f(2),f(4)的大小关系为________. 解析:由题意知,函数以x =2为对称轴,f(1)=f(3),且在(2,+∞)上单调递增,故f(2)<f(1)<f(4).答案:f(2)<f(1)<f(4)9.函数f(x)=|x -1|+|2-x|的最小值为________. 解析:法一:f(x)=|x -1|+|2-x|=⎩⎪⎨⎪⎧2x -3, x>2,1, 1≤x ≤2,3-2x , x<1,作出函数图象(如图)易得f(x)最小值为1.法二:在数轴上,设实数1,2,x 分别对应点A ,B ,P ,则|x -1|+|2-x|=AP +BP ,结合图象易得AP +BP ≥AB =1,当P 在A ,B 之间时取等号.答案:110.已知函数f(x)=x2+2ax+5,x∈[-5,5].(1)当a=-1时,求函数f(x)的最小值和最大值;(2)求实数a的取值范围,使y=f(x)在区间[-5,5]上是单调函数.解:(1)当a=-1时,f(x)=x2-2x+5=(x-1)2+4.∴当x=1时,y min=4;当x=-5时,y max=40.(2)f(x)=(x+a)2+5-a2.由条件,得-a≤-5或-a≥5,∴a≤-5或a≥5.∴a的取值范围是(-∞,-5]∪[5,+∞).11.(创新题)已知函数f(x)=x2+2ax+1在区间[-1,2]上的最大值为4,求a的值.解:f(x)=x2+2ax+1=(x+a)2+1-a2,区间[-1,2]的中点为12,对称轴为直线x=-a,结合二次函数的图象(图略)知:当-a≥12,即a≤-12时,f(x)max=f(-1)=1-2a+1=4,∴a=-1≤-1 2;当-a<12,即a>-12时,f(x)max=f(2)=4+4a+1=4,∴a=-14>-12.综上所述,a =-1或a =-14.。
【苏教版】高中数学必修一同步辅导与检测(含答案) 第2章 第2章2.3映射的概念
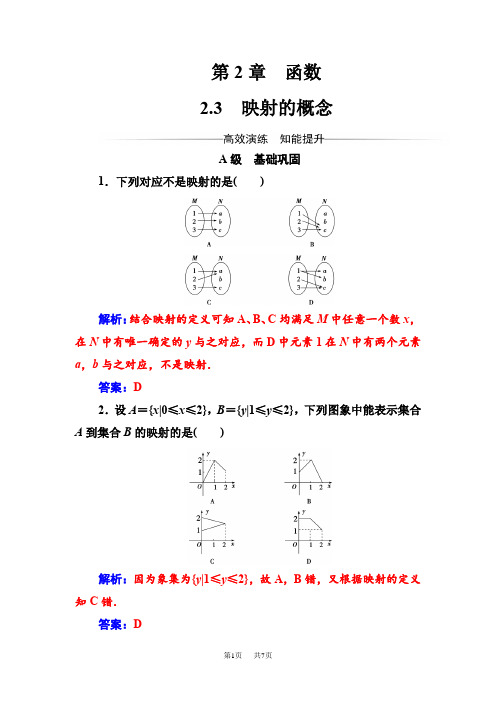
第2章函数2.3 映射的概念A级基础巩固1.下列对应不是映射的是()解析:结合映射的定义可知A、B、C均满足M中任意一个数x,在N中有唯一确定的y与之对应,而D中元素1在N中有两个元素a,b与之对应,不是映射.答案:D2.设A={x|0≤x≤2},B={y|1≤y≤2},下列图象中能表示集合A到集合B的映射的是()解析:因为象集为{y|1≤y≤2},故A,B错,又根据映射的定义知C错.答案:D3.已知集合A 中元素(x 、y )在映射f 下对应B 中元素(x +y ,x -y ),则B 中元素(4,-2)在A 中对应的元素为( )A .(1,3)B .(1,6)C .(2,4)D .(2,6)解析:由题意得⎩⎪⎨⎪⎧x +y =4,x -y =-2,解得⎩⎪⎨⎪⎧x =1,y =3.答案:A4.已知f :A →B 是集合A 到B 的映射,又A =B =R ,对应法则f :x →y =x 2+2x -3,k ∈B 且k 在A 中没有原象,则k 的取值范围是( )A .(-∞,-4)B .(-1,3)C .[-4,+∞)D .(-∞,-1)∪(3,+∞)解析:因为y =x 2+2x -3=(x +1)2-4≥-4,即象集为[-4,+∞),所以当k <-4时,k 就没有原象.答案:A5.设f :x →ax -1为从集合A 到B 的映射,若f (2)=3,则f (3)=________.解析:由f (2)=3,可知2a -1=3,所以a =2.所以f (3)=3a -1=3×2-1=5.答案:56.已知A ={a ,b },B ={0,1},则从A 到B 的映射共有________个.解析:由于A 中元素a 在B 中有两个元素与之对应,元素b 在B 中也有两个元素与之对应,所以从A 到B 的映射共有2×2=4(个).答案:47.已知M={正整数},P={正奇数},映射f:a(a∈M)→b=2a -1,则在映射f下,M中的元素11对应着P中的元素________,P 中的元素11对应着M中的元素________.解析:由题知a=11,b=21,即M中的元素11对应着P中的元素21;又b=11,代入b=2a-1,a=6,即P中的元素11对应着M中的元素6.答案:2168.集合A={a,b},B={-1,0.1},从A到B的映射f:A→B 满足f(a)+f(b)=0,那么这样的映射f:A→B的个数是________.解析:由f(a)=0,f(b)=0得f(a)+f(b)=0;f(a)=1,f(b)=-1得f(a)+f(b)=0;由f(a)=-1,f(b)=1得f(a)+f(b)=0.共3个.答案:39.若集合A={0,1,2},f:x→x2-2x是从A到B的映射,则集合B中至少有________个元素.解析:由A={0,1,2},f:x→x2-2x.令x=0,1,2,得x2-2x分别为0,-1,0.又由集合中元素的互异性,所以B中至少有元素0与-1.答案:210.观察数表:则f(g解析:由表中数据对应关系知g (3)=-4,f (-1)=-1,所以f (g (3)-f (-1))=f (-4+1)=f (-3)=4.答案:411.已知映射:f :A →B ,A =B ={(x ,y )|x ,y ∈R},f :A 中的元素(x ,y )对应B 中的元素为(3x -2y +1,4x +3y -1).(1)求A 中元素(1,2)在B 中对应的元素;(2)B 中元素(1,2)与A 中哪个元素对应?解:(1)A 中元素(1,2),即当x =1,y =2时,3x -2y +1=3×1-2×2+1=0,4x +3y -1=4×1+3×2-1=9,所以B 中对应的元素为(0,9).(2)当B 中元素为(1,2)时,则由⎩⎪⎨⎪⎧3x -2y +1=1,4x +3y -1=2.解得⎩⎪⎨⎪⎧x =617,y =917.所以B 中元素(1,2)与A 中的⎝ ⎛⎭⎪⎫617,917对应. 12.已知A ={a ,b ,c },B ={-1,0,1},映射f :A →B 满足f (a )+f (b )=f (c ),求映射f :A →B 的个数.解:(1)当A 中元素都对应一个元素时,由于f (a )+f (b )=f (c ),所以a ,b ,c 必须都对应元素0.(如图所示)共有1个映射.(2)当A 中元素对应两个元素时,根据f (a )+f (b )=f (c ),有下面4种情况.(3)当A 中元素对应三个元素时,由于f (a )+f (b )=f (c ),有下面两种情况.因此,满足题设条件的映射有7个.B 级 能力提升13.下列对应是从集合M 到集合N 的映射的是( )①M =N =R ;f :x →y =1x,x ∈M ,y ∈N .②M =N =R ;f :x →y =x 2,x ∈M ,y ∈N .③M =N =R ;f :x →y =1|x |+x,x ∈M ,y ∈N .④M =N =R ;f :x →y =x 3;x ∈M ,y ∈N .A .①②B .②③C .①④D .②④解析:对于①,集合M 中的元素0在N 中无元素与之对应,所以①不是映射.对于③,M 中的元素0及负实数在N 中没有元素与之对应,所以③不是映射.对于②④,M 中的元素在N 中都有唯一的元素与之对应,所以②④是映射.答案:D14.设M ={a ,b },N ={-2,0,2},则从M 到N 的映射中满足f (a )≥f (b )的映射f 的个数为________.解析:由f (a )≥f (b )知,f (a )>f (b )或f (a )=f (b ),当f (a )>f (b )时,有⎩⎪⎨⎪⎧f (a )=0,f (b )=-2或⎩⎪⎨⎪⎧f (a )=2,f (b )=0或⎩⎪⎨⎪⎧f (a )=2,f (b )=-2共三种可能; 当f (a )=f (b )时,也有f (a )=f (b )=0,2,-2三种可能.综上所述,满足条件f (a )≥f (b )的映射有6个.答案:6①函数f (x )=x 2(x ∈R)就是单函数;②若f (x )为单函数,x 1,x 2∈A 且x 1≠x 2,则f (x 1)≠f (x 2);③若f :A →B 为单函数,则对任意b ∈B ,它至多有一个原象. 答案:②③16.集合A ,B 是平面直角坐标系上的两个点集,给定从A →B 的映射f :(x ,y )→(x 2+y 2,xy ),求B 中的元素(5,2)所对应A 中的元素.解:依题意可得⎩⎪⎨⎪⎧x 2+y 2=5, ①xy =2. ②①+2×②,得(x +y )2=9,所以x +y =±3.于是,原方程组可化为如下的两个方程组:⎩⎪⎨⎪⎧x +y =3,xy =2或⎩⎪⎨⎪⎧x +y =-3,xy =2. 解得⎩⎪⎨⎪⎧x 1=1,y 1=2;⎩⎪⎨⎪⎧x 2=2,y 2=1;⎩⎪⎨⎪⎧x 3=-1,y 3=-2;⎩⎪⎨⎪⎧x 4=-2,y 4=-1, 所以B 中的元素(5,2)对应A 中的元素是(1,2),(2,1),(-1,-2),(-2,-1).17.已知集合A 为实数集R ,集合B ={y |y ≥2},x ∈A ,y ∈B ,对应法则f :x →y =x 2-2x +2,那么f :A →B 是A 到B 的映射吗?如果不是,可以如何变换集合A 或B (f 不变)使之成为映射?解:由于x 2-2x +2=(x -1)2+1≥1,即在f 下,A 中的元素变换成集合{y |y ≥1}中的元素,现在已知的集合B ={y |y ≥2},所以A 中的部分元素x ∈(0,2)在B 中无对应元素.所以f :A →B 不是A 到B 的映射.将B 改为{y |y ≥1},A 与f 不变,则f :A →B 成为A 到B 的一个映射.18.已知:集合A ={x |-2≤x ≤2},B ={x |-1≤x ≤1}.对应关系f :x →y =ax .若在f 的作用下能够建立从A 到B 的映射f :A →B ,求实数a 的取值范围.解:①当a ≥0时,由-2≤x ≤2得-2a ≤ax ≤2a .若能够建立从A 到B 的映射.则[-2a ,2a ]⊆[-1,1],即⎩⎪⎨⎪⎧-2a ≥-1,2a ≤1,所以0≤a ≤12. ②当a <0时,集合A 中元素的象满足2a ≤ax ≤-2a ,若能建立从A 到B 的映射,则[2a ,-2a ]⊆[-1,1],即⎩⎪⎨⎪⎧2a ≥-1,-2a ≤1,所以0>a ≥-12. 综合①②可知-12≤a ≤12.。
【苏教版】高中数学同步辅导与检测:必修1 第2章2.2-2.2.1函数的单调性-附答案

第2章函数2.2 函数的简单性质2.2.1 函数的单调性A级基础巩固1.函数f(x)的图象如图所示,则()A.函数f(x)在[-1,2]上是增函数B.函数f(x)在[-1,2]上是减函数C.函数f(x)在[-1,4]上是减函数D.函数f(x)在[2,4]上是增函数解析:增函数具有“上升”趋势;减函数具有“下降”趋势,故A正确.答案:A2.已知函数f(x)是(-∞,+∞)上的增函数,若a∈R,则() A.f(a)>f(2a) B.f(a2)<f(a)C.f(a+3)>f(a-2) D.f(6)>f(a)解析:因为a+3>a-2,且f(x)在(-∞,+∞)上是增函数,所以f(a+3)>f(a-2).答案:C3.y=2x在区间[2,4]上的最大值、最小值分别是()A.1,12 B.12,1 C.12,14 D.14,12解析:因为函数y=2x在[2,4]上是单调递减函数,所以y max=22=1,y min=24=12.答案:A4.函数y=x2-6x的减区间是() A.(-∞.2] B.[2,+∞) C.[3,+∞) D.(-∞,3] 解析:y=x2-6x=(x-3)2-9,故函数的单调减区间是(-∞,3].答案:D5.下列说法中,正确的有()①若任意x1,x2∈I,当x1<x2时,f(x1)-f(x2)x1-x2>0,则y=f(x)在I上是增函数;②函数y=x2在R上是增函数;③函数y=-1x在定义域上是增函数;④函数y=1x的单调区间是(-∞,0)∪(0,+∞).A.0个B.1个C.2个D.3个解析:当x1<x2时,x1-x2<0,由f(x1)-f(x2)x1-x2>0知f(x1)-f(x2)<0,所以f(x1)<f(x2),①正确;②③④均不正确.答案:B6.已知函数f(x)=4x-3+x,则它的最小值是()A .0B .1 C.34 D .无最小值解析:因为函数f (x )=4x -3+x 的定义域是⎣⎢⎡⎭⎪⎫34,+∞,且是增函数,所以f (x )min =f ⎝ ⎛⎭⎪⎫34=34. 答案:C7.函数y =f (x )的图象如图所示,则函数f (x )的单调递增区间是________________.解析:由图象可知函数f (x )的单调递增区间是(-∞,1]和(1,+∞).答案:(-∞,1]和(1,+∞)8.已知f (x )是R 上的减函数,则满足f (2x -1)>f (1)的实数x 的取值范围是________.解析:因为f (x )在R 上是减函数,且f (2x -1)>f (1),所以2x -1<1,即x <1.答案:(-∞,1)9.已知函数f (x )=x 2-2x +3在闭区间[0,m ]上的最大值为3,最小值为2,则m 的取值范围是________.解析:因为f (x )=(x -1)2+2,其对称轴为直线x =1,所以当x =1时,f (x )min =2,故m ≥1.又因为f (0)=3,所以f (2)=3.所以m ≤2.故1≤m ≤2.答案:[1,2]10.某公司在甲乙两地同时销售一种品牌车,利润(单位:万元)分别为L 1=-x 2+21x 和L 2=2x (其中销售量单位:辆).若该公司在两地共销售15辆,则能获得的最大利润为________万元.解析:设公司在甲地销售x 台,则在乙地销售(15-x )台,公司获利为L =-x 2+21x +2(15-x )=-x 2+19x +30=-⎝ ⎛⎭⎪⎫x -1922+30+1924, 所以当x =9或10时,L 最大为120万元.答案:12011.讨论函数y =x 2-2(2a +1)x +3在[-2,2]上的单调性. 解:因为函数图象的对称轴x =2a +1,所以当2a +1≤-2,即a ≤-32时,函数在[-2.2]上为增函数. 当-2<2a +1<2,即-32<a <12时, 函数在[-2,2a +1]上是减函数,在[2a +1,2]上是增函数.当2a +1≥2,即a ≥12时,函数在[-2,2]上是减函数. 12.已知f (x )=x +12-x,x ∈[3,5]. (1)利用定义证明函数f (x )在[3,5]上是增函数;(2)求函数f (x )的最大值和最小值.解:(1)f (x )在区间[3,5]上是增函数,证明如下:设x 1,x 2是区间[3,5]上的两个任意实数,且x 1<x 2,则f(x1)-f(x2)=x1+12-x1-x2+12-x2=3(x1-x2)(2-x1)(2-x2).因为3≤x1<x2≤5,所以x1-x2<0,2-x1<0,2-x2<0.所以f(x1)<f(x2).所以f(x)在区间[3,5]上是增函数.(2)因为f(x)在区间[3,5]上是增函数,所以当x=3时,f(x)取得最小值为-4,当x=5时,f(x)取得最大值为-2.B级能力提升13.若函数f(x)=4x2-kx-8在[5,8]上是单调函数,则k的取值范围是()A.(-∞,40)B.[40,64]C.(-∞,40]∪[64,+∞)D.[64,+∞)解析:对称轴为x=k8,则k8≤5或k8≥8,解得k≤40或k≥64.答案:C14.若y=ax与y=-bx在区间(0,+∞)上都是减函数,则y=ax2+bx在区间(0,+∞)上是()A.增函数B.减函数C.先增后减D.先减后增解析:本题通过一次函数、反比例函数的单调性,判断出a,b的符号.因为y=ax与y=-bx在区间(0,+∞)上都是减函数,所以a<0,b<0,所以函数y=ax2+bx的对称轴方程为x=-b2a<0,故函数y =ax 2+bx 在区间(0,+∞)上是减函数.答案:B15.当0≤x ≤2时,a <-x 2+2x 恒成立,则实数a 的取值范围是________.解析:令f (x )=-x 2+2x (0≤x ≤2)=-(x 2-2x +1)+1=-(x -1)2+1,图象如下.所以f (x )最小值为f (0)=f (2)=0.而a <-x 2+2x 恒成立,所以a <0.答案:(-∞,0)16.画出函数f (x )=⎩⎨⎧-2x ,x ∈(-∞,0),x 2+2x -1,x ∈[0,+∞)的图象,并写出函数的单调区间及最小值.解:f (x )的图象如图所示,f (x )的单调递增区间是(-∞,0)和[0,+∞),函数的最小值为f (0)=-1.17.已知函数f (x )=x 2-2x +2.(1)求f (x )在区间⎣⎢⎡⎦⎥⎤12,3上的最大值和最小值; (2)若g (x )=f (x )-mx 在[2,4]上是单调函数,求m 的取值范围.解:(1)因为f (x )=x 2-2x +2=(x -1)2+1,x ∈⎣⎢⎡⎦⎥⎤12,3,对称轴是x =1.所以f (x )的最小值是f (1)=1.又f ⎝ ⎛⎭⎪⎫12=54,f (3)=5, 所以f (x )在区间⎝ ⎛⎭⎪⎫12,3上的最大值是5,最小值是1. (2)因为g (x )=f (x )-mx =x 2-(m +2)x +2,所以m +22≤2或m +22≥4,即m ≤2或m ≥6. 故m 的取值范围是(-∞,2]∪[6,+∞).18.若二次函数满足f (x +1)-f (x )=2x 且f (0)=1.(1)求f (x )的解析式;(2)若在区间[-1,1] 上不等式f (x )>2x +m 恒成立,求实数m 的取值范围.解:(1)设f (x )=ax 2+bx +c (a ≠0),因为f (0)=1,所以c =1.所以f (x )=ax 2+bx +1.因为f (x +1)-f (x )=2x ,所以2ax +a +b =2x .所以⎩⎪⎨⎪⎧2a =2,a +b =0.所以⎩⎪⎨⎪⎧a =1,b =-1. 所以f (x )=x 2-x +1.(2)由题意,得x 2-x +1>2x +m 在[-1,1]上恒成立, 即x 2-3x +1-m >0在[-1,1]上恒成立.令g (x )=x 2-3x +1-m =⎝ ⎛⎭⎪⎫x -322-54-m , 其对称轴为x =32, 所以g (x )在区间[-1,1]上是减函数.所以g(x)min=g(1)=1-3+1-m>0.所以m<-1.所以实数m的取值范围是(-∞,-1).。
高中数学(苏教版,必修一) 第二章函数 2.2.1 课时作业(含答案)

§2.2 指数函数 2.2.1 分数指数幂课时目标 1.了解指数函数模型的实际背景,体会引入有理数指数幂的必要性.2.理解有理数指数幂的含义,知道实数指数幂的意义,掌握幂的运算.1.如果一个实数x 满足________________,那么称x 为a 的n 次实数方根. 2.式子na 叫做______,这里n 叫做________,a 叫做__________. 3.(1)n ∈N *时,(na )n =____.(2)n 为正奇数时,n a n =____;n 为正偶数时,na n =______.4.分数指数幂的定义:(1)规定正数的正分数指数幂的意义是:m na =__________(a >0, m 、n ∈N *,且n >1);(2)规定正数的负分数指数幂的意义是:m na -=____________(a >0,m 、n ∈N *,且n >1); (3)0的正分数指数幂等于____,0的负分数指数幂__________. 5.有理数指数幂的运算性质: (1)a r a s =______(a >0,r 、s ∈Q ); (2)(a r )s =______(a >0,r 、s ∈Q ); (3)(ab )r =______(a >0,b >0,r ∈Q ).一、填空题1.下列说法中:①16的4次方根是2;②416的运算结果是±2;③当n 为大于1的奇数时,n a 对任意a ∈R 都有意义;④当n 为大于1的偶数时,n a 只有当a ≥0时才有意义.其中正确的是________(填序号).2.若2<a <3,化简(2-a )2+4(3-a )4的结果是________. 3.在(-12)-1、122-、1212-⎛⎫⎪⎝⎭、2-1中,最大的是______________________________. 4.化简3a a 的结果是________.5.下列各式成立的是________.(填序号)①3m 2+n 2=()23m n +;②(b a)2=12a 12b ;③6(-3)2=()133-;④34=132.6.下列结论中,正确的个数为________.①当a <0时,()322a=a 3;②na n =|a |(n >0);③函数y =()122x --(3x -7)0的定义域是(2,+∞);④若100a =5,10b =2,则2a +b =1. 7.614-3338+30.125的值为________. 8.若a >0,且a x=3,a y=5,则22y x a+=________.9.若x >0,则(214x +323)(214x -323)-412x -·(x -12x )=________.二、解答题10.(1)化简:3xy 2·xy -1·xy ·(xy )-1(xy ≠0); (2)计算:122-+(-4)02+12-1-(1-5)0·238.11.设-3<x <3,求x 2-2x +1-x 2+6x +9的值.能力提升12.化简:4133223384a a b b a-+÷(1-23b a)×3a .13.若x >0,y >0,且x -xy -2y =0,求2x -xyy +2xy的值.§2.2 指数函数 2.2.1 分数指数幂知识梳理1.x n =a (n >1,n ∈N *) 2.根式 根指数 被开方数 3.(1)a (2)a |a | 4.(1)na m (2)1m na(3)0 没有意义 5.(1)a r +s (2)a rs (3)a r b r作业设计 1.③④解析 ①错,∵(±2)4=16, ∴16的4次方根是±2; ②错,416=2,而±416=±2. 2.1解析 原式=|2-a |+|3-a |,∵2<a <3,∴原式=a -2+3-a =1. 3.1212-⎛⎫⎪⎝⎭解析 ∵(-12)-1=-2, 122-=22,1212-⎛⎫⎪⎝⎭=2,2-1=12,且2>22>12>-2, ∴1212-⎛⎫ ⎪⎝⎭>122->2-1>(-12)-1.4.12a解析 12a .5.④解析 ①被开方数是和的形式,运算错误;(b a )2=b 2a2,②错;6(-3)2>0,()133-<0,③错.6.1解析 ①中,当a <0时,()322a =[()122a ]3=(-a )3=-a 3,∴①不正确;②中,若a =-2,n =3,则3(-2)3=-2≠|-2|,∴②不正确;③中,有⎩⎪⎨⎪⎧x -2≥0,3x -7≠0,即x ≥2且x ≠73,故定义域为[2,73)∪(73,+∞),∴③不正确;④中,∵100a =5,10b =2,∴102a =5,10b =2,102a ×10b =10,即102a +b =10. ∴2a +b =1,④正确. 7.32解析 原式=(52)2-3(32)3+3(12)3 =52-32+12=32. 8.9 5 解析 22y x a +=(a x )2·()12y a=32·125=9 5. 9.-23解析 原式=412x -33-412x +4=-23.10.解 (1)原式=()113212xy xy-⎡⎤⎢⎥⎣⎦·()12xy ·(xy )-1 =13x ·23y 16x16y-·12x-·12y-=13x ·13x-=⎩⎪⎨⎪⎧1, x >0-1, x <0. (2)原式=12+12+2+1-22 =22-3.11.解 原式=(x -1)2-(x +3)2 =|x -1|-|x +3|,∵-3<x <3,∴当-3<x <1时,原式=-(x -1)-(x +3)=-2x -2; 当1≤x <3时,原式=(x -1)-(x +3)=-4.∴原式=⎩⎪⎨⎪⎧-2x -2 (-3<x <1)-4 (1≤x <3).12.解 原式=()1321123333842aa b b a b a-++÷1133132a b a-×13a=()1321123333842aa b b a b a -++·1311332aa b-·13a =()33113382a a b a b -⎛⎫⎛⎫- ⎪ ⎪⎝⎭⎝⎭=a (a -8b )a -8b=a .13.解 ∵x -xy -2y =0,x >0,y >0, ∴(x )2-xy -2(y )2=0, ∴(x +y )(x -2y )=0, 由x >0,y >0得x +y >0, ∴x -2y =0,∴x =4y , ∴2x -xy y +2xy =8y -2y y +4y =65.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.下列坐标系中的曲线或直线,能作为函数的y=f(x)的图象的有________(填序号).
解析:根据函数定义,对每一个自变量x,有且只有一个函数值与之对应,因而①,③不是函数的图象,故只有②,④是函数的图象.
答案:②④
2.函数y=f(x)的图象如图所示,填空:
(1)f(-1)=________;
(2)f(1)=________;
(3)f(2)=________.
解析:由图象过点(-1,0),(1,1),(2,0),可知f(-1)=0,f(1)=1,f(2)=0.
答案:0 1 0
3.函数f(x)=ax2+bx+c(a≠0)的图象如图所示,则f(2
5)与f(
5
2
)
的大小关系是________.
解析:f(x)对称轴为x=2,∵2-2
5
>
5
2
-2,∴f(
2
5
)>f(
5
2
).
答案:f(2
5)>f(
5
2
)
4.已知函数y=f(x)的图象如图所示,则f(x)的定义域为________,值域为________.
解析:观察图象中任一点(x,y)的取值情况.
答案:(-∞,-1]∪(1,+∞) (-∞,-1]∪(1,3)
5.函数y=f(x)的图象如图所示,则
(1)使f(x)=0成立的x的集合________;
(2)若1<x1<x2<2,则f(x1)与f(x2)的大小关系是________;
(3)若1<x0<3,则f(x0)的符号为________.(填正或负)
解析:观察函数图象可得.
答案:{-1,1,3} f(x1)>f(x2) 负
[A级基础达标]
1.若f(x)=x-1
x
,则方程f(4x)=x的根是________.
解析:f(4x)=4x-1
4x
,由
4x-1
4x
=x得x=
1
2
.
答案:x=1 2
2.如果一次函数图象如图所示,则该一次函数的解析式为________.
解析:设一次函数f(x)=ax +b ,其图象过点(1,0)与(0,1),
因此有⎩⎪⎨⎪⎧f (1)=0,f (0)=1,即⎩⎪⎨⎪⎧a +b =0,
a ·0+
b =1,
∴⎩⎪⎨⎪⎧a =-1,
b =1,
∴f(x)=-x +1. 答案:f(x)=-x +1
3.函数y =|x|
x
+x 的图象是________.(填序号)
解析:分x>0和x<0,得到解析式. 答案:④
4.函数y =f(x)图象如右图所示,则f(x)的值域为________.
解析:观察图象可得y的取值范围为[0,1].
答案:[0,1]
5.如图,函数f(x)的图象是曲线OAB,其中点O,A,B的
坐标分别为(0,0),(1,2),(3,1),则f(
1
f(3)
)的值等于
________.
解析:由题意,f(3)=1,∴f(1
f(3)
)=f(1)=2.
答案:2
6.画出下列函数的图象,并求值域:
(1)y=3x-1,x∈[1,2];(2)y=x2,x∈{0,1,2,3};
(3)y=|x-1|;(4)y=x2-x x-1
.
解:函数图象如下所示,由图象观察易得:(1)值域为[2,5];
(2)值域为{0,1,4,9};(3)值域为[0,+∞);(4)y=x(x≠1),值域为{y|y∈R且y≠1}.
7.已知函数f(x)=ax +b ,且f(-1)=-4,f(2)=5, 求:(1)a ,b 的值;(2)f(0)的值.
解:(1)由⎩⎪⎨⎪⎧f (-1)=-4f (2)=5⇒⎩⎪⎨⎪⎧-a +b =-4
2a +b =5
⇒a =3,b =-1.
(2)由(1)知f(x)=3x -1,∴f(0)=-1. [B 级 能力提升]
8.下面所给出的四个图象和三个事件:
①我离开家不久,发现自己把作业本忘在家里了,于是立刻返回家里取了作业本再上学;
②我骑着车一路以匀速行驶离开家,只是在途中遇到一次交通堵塞,耽搁了一些时间;
③我从家里出发后,心情轻松,缓缓行进,后来为了赶时间开始加速.
图象与这三个事件发生的顺序相吻合的分别为________.
解析:离家不久发现自己作业本忘在家里,回到家里,这时离家的距离为0,故①与图象d 相吻合;途中有一段时间交通堵塞,则这段时间与家的距离必为一定值,故②与图象a 相吻合;加速赶向学校,图象上升地就越来越快,故③与图象b 相吻合.
答案:①-d ,②-a ,③-b
9.若关于x 的方程2x 2-3x -k =0在(-1,1)内仅有一个实根,则k 的取值范围是________.
解析:本题可转化为函数y =2x 2-3x 与函数y =k 在区间(-
1,1)内交点个数问题,作出函数y =2x 2-3x =2(x -3
4)2-9
8在
(-1,1)上的图象,
如图所示.
由图象知当-1≤k<5或k=-9
8
时,y=k与y=2x2-3x仅有
一个交点.
答案:-1≤k<5或k=-9 8
10.画出f(x)=-x2+2x+3的图象,并根据图象回答下列问题.
(1)比较f(0)、f(1)、f(3)的大小;
(2)若x1<x2<1,比较f(x1)与f(x2)的大小.
(1)
解:利用描点法作出f(x)=-x2+2x+3的图象,结合其图象对称性及变化情况来比较大小.(1)函数图象如图(1)所示.可见f(0)=f(2),
f(1)>f(2)>f(3),
∴f(1)>f(0)>f(3).
(2)
(2)如图(2)所示,当x1<x2<1时,f(x1)<f(x2).
11.(创新题)若函数f(x)=1
2x2-x+
3
2
的定义域和值域都是[1,
b](b>1),求b的值.
解:f(x)=1
2
(x-1)2+1,作出y=
1
2
(x-1)2+1的图象(图略),
观察图象可知在[1,b]上,当x=1时,f(x)min=1;当x=b
时,f(x)max=1
2
b2-b+
3
2
,∴f(x)值域为[1,
1
2
b2-b+
3
2
].又∵f(x)
的值域是[1,b],∴1
2
b2-b+
3
2
=b,∴b=1(舍)或b=3.因此b
=3.。
