人教版八年级下数学一次函数压轴题研究(六)特殊平行四边形存在性(讲义及答案)

合集下载

(完整)一次函数特殊平行四边形存在性

特殊平行四边形存在性➢课前预习1.一般情况下我们如何处理存在性问题？(1)研究背景图形坐标系背景下研究____________、____________;几何图形研究____________、____________、____________．（2）根据不变特征，确定分类标准研究定点，动点,定线段，确定分类标准不变特征举例:①等腰三角形（两定一动）以定线段作为_________或者___________来分类，利用_______________确定点的位置．②等腰直角三角形(两定一动）以________________来分类，然后借助_________或者___________确定点的位置．(3)分析特殊状态的形成因素，画出符合题意的图形并求解（4）结果验证2.用铅笔做讲义第1，2题,并将计算、演草保留在讲义上，先看知识点睛，再做题,思路受阻时（某个点做了2～3分钟）重复上述动作，若仍无法解决，课堂重点听．➢知识点睛1.存在性问题处理框架：①研究背景图形．②根据不变特征,确定分类标准．③分析特殊状态的形成因素，画出符合题意的图形并求解．④结果验证．2.特殊平行四边形存在性问题不变特征举例：①菱形存在性问题（两定两动）转化为等腰三角形存在性问题;以定线段作为底边或者腰确定分类标准，利用两圆一线确定一动点的位置，然后通过平移确定另一动点坐标．②正方形存在性问题（两定两动）转化为等腰直角三角形存在性问题；根据直角顶点确定分类标准，利用两腰相等或者45°角确定一动点的位置,然后通过平移确定另一动点坐标．➢ 精讲精练1. 如图,在平面直角坐标系xOy 中,直线l ：24y x =-与x 轴交于点A ，与y 轴交于点B ．（1)求点A ,B 的坐标．（2）若P 是直线2x =-上的一动点，则在坐标平面内是否存在点Q ,使得以A ，B ，P ,Q 为顶点的四边形是菱形?若存在,求出点Q 的坐标；若不存在，请说明理由．2. 如图，在平面直角坐标系xOy 中，直角梯形OABC 的顶点A 在y 轴正半轴上，顶点C的坐标为（18-，0)，A B∥O C,∠OCB=45°，且BC=．（1）求点B的坐标．（2）直线BE与线段OA交于点E，且OE=6．若P是直线BE上的一动点,则在坐标平面内是否存在点Q,使得以O，E，P，Q为顶点的四边形是菱形？若存在,求出点Q的坐标；若不存在，请说明理由．3.如图，在平面直角坐标系xOy中,□ABCD的顶点A，B的坐标分别为A（0，3)，B（顶点C在x轴正半轴上，顶点D在第一象限，且AD=象限内是否存在点F，使得以A，C，F,M为顶点的四边形是正方形？若存在，求出点F的坐标；若不存在,请说明理由．4.如图，在平面直角坐标系中，已知点A，B，C的坐标分别为A（9 ，0），B（16，0),C(0，12），D是线段BC上的一动点(不与点B，C重合），过点D作直线DE⊥OB,垂足为点E．若M为坐标平面内一点，则在直线DE上是否存在点N,使得以C,B，M，N为顶点的四边形是正方形？若存在，求出点N的坐标；若不存在，请说明理由．(完整)一次函数特殊平行四边形存在性【参考答案】➢课前预习1．（1）坐标、表达式；边、角、形（2）①腰底两圆一线②直角顶点两腰相等 45°角(完整)一次函数特殊平行四边形存在性➢精讲精练1．（1）A（2，0)，B（0，-4)（2）存在，点Q的坐标为（0，4）,(-4,—2），（—4，—6)或（4，7-）22．（1)B（—6，12）（2）存在，点Q的坐标为(6，6），（-，（-或(3-,3)3．存在，点F的坐标为(3,3，(3或(4．存在，点N的坐标为（12，28），(4，16-），（14，14)或(2，2-）。

一次函数中四边形存在性问题 2022-2023学年八年级数学下学期期末复习专练(人教版)(解析版)

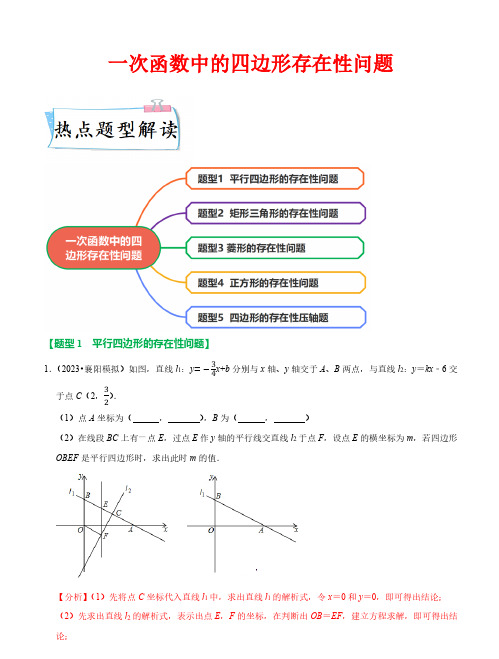
一次函数中的四边形存在性问题【题型1 平行四边形的存在性问题】1．（2023•襄阳模拟）如图，直线l 1：y =−34x +b 分别与x 轴、y 轴交于A 、B 两点，与直线l 2：y ＝kx ﹣6交于点C （2，32）．（1）点A 坐标为（，），B 为（，）（2）在线段BC 上有一点E ，过点E 作y 轴的平行线交直线l 2于点F ，设点E 的横坐标为m ，若四边形OBEF 是平行四边形时，求出此时m 的值．【分析】（1）先将点C 坐标代入直线l 1中，求出直线l 1的解析式，令x ＝0和y ＝0，即可得出结论；（2）先求出直线l 2的解析式，表示出点E ，F 的坐标，在判断出OB ＝EF ，建立方程求解，即可得出结论；【解答】解：∵点C（2，32）在直线l1：y=−34x+b上，∴−34×2+b=32，∴直线l1的解析式为y=−34x+3，令x＝0，∴y＝3，∴B（0，3），令y＝0，∴−34x+3＝0，∴x＝4，∴A（4，0），故答案为：4，0，0，3；（2）∵点C（2，32）在直线l2：y＝kx﹣6上，∴2k﹣6=32，∴k=154，∴直线l2的解析式为y=154x﹣6，∵EF∥y轴，点E的横坐标为m，∴点F的横坐标为m，∵点E l1上，∴E（m，−34m+3），∵点F在直线l2：y=154x﹣6上，∴F（m，154m﹣6），∵四边形OBEF是平行四边形，且BO∥EF，∴OB＝EF，EF=−34m+3﹣（154m﹣6）＝3，∴m=4 3；【点评】此题是一次函数综合题，主要考查了待定系数法，平行四边形的性质，三角形的面积公式，利用方程的思想解决问题是解本题的关键．2．（2022春•涟水县校级月考）如图，平行四边形ABCD 在直角坐标系中，点B 、点C 都在x 轴上，其中OA ＝8，OB ＝6，AD ＝12，E 是线段OD 的中点．（1）直接写出点C ，D 的坐标；（2）求直线AE 的关系式；（3）平面内是否存在一点F ，使以A 、D 、E 、F 为顶点的四边形是平行四边形？若存在，请直接写出点F 的坐标；若不存在，请说明理由．【分析】（1）根据平行四边形的性质得AD ＝BC ＝12，AD ∥BC ，根据题意可得OC ＝6，点A 的坐标为（0，8），点D 的坐标为（12，8），即可得点C 的坐标为（6，0）；（2）根据E 是线段OD 的中点得E （6，4），设直线AE 的关系式为：y ＝kx +b ，根据直线AE 经过点A ，点E ，即可得{b =86x +b =4，进行计算即可得；（3）分情况讨论：①当EF 为平行四边形的边时，根据对边相等即可得；②当EF 为平行四边形的对角线时，根据对角线互相平分即可得．BC【解答】解：（1）∵四边形ABCD 是平行四边形，∴AD ＝BC ＝12，AD ∥BC ，∵点B 、C 都在x 轴上，点A 在y 轴上，OA ＝8，OB ＝6，∴OC ＝BC ﹣OB ＝12﹣6＝6，点A 的坐标为（0，8），点D 的坐标为（12，8），∴点C 的坐标为（6，0）；（2）∵E 是线段OD 的中点，∴E （6，4），设直线AE 的关系式为：y ＝kx +b ，∵直线AE 经过点A ，点E ，∴{b =86x +b =4，解得{b =8k =−23， ∴直线AE 的关系式：y =−23x +8；（3）存在，F坐标为（﹣6，4）或（18，4）或（6，12），①如图所示，当EF为平行四边形的边时，EF＝AD＝12，∴点F的坐标为：（﹣6，4）或（18，4），②如图所示，当EF为平行四边形的对角线时，则DG＝AG＝6，FG＝GE＝4，即点F的坐标为：（6，12），综上，点F的坐标为：（﹣6，4）或（18，4）或（6，12）．【点评】本题考查了平行四边形的判定与性质，一次函数的性质，解题的关键是掌握并灵活运用这些知识点．3．（2022春•昌江县期末）如图，直线y＝﹣x+4分别交x轴、y轴于A、B两点，直线BC与x轴交于点C （﹣2，0），P是线段AB上的一个动点（点P与A、B不重合）．（1）求直线BC所对应的函数表达式；（2）设动点P的横坐标为t，△POA的面积为S．①求出S与t的函数关系式，并写出自变量t的取值范围；②在线段BC上存在点Q，使得四边形COPQ是平行四边形，求此时点Q的坐标．【分析】（1）根据直线y ＝﹣x +4分别交x 轴、y 轴于A 、B 两点，直线BC 与x 轴交于点C （﹣2，0），可以得到点B 的坐标，从而可以得到直线BC 的函数表达式；（2）①根据题意，可以用含t 的代数式表示出点P 的坐标，从而可以得到S 与t 的函数关系式，并写出自变量t 的取值范围；②根据题意和平行四边形的性质，可以用含t 的代数式表示出点Q 的坐标，再根据OC ＝PQ ，即可得到点Q 的坐标．【解答】解：（1）∵直线y ＝﹣x +4分别交x 轴、y 轴于A 、B 两点，∴点A 的坐标为（4，0），点B 的坐标为（0，4），设直线BC 所对应的函数表达式为y ＝kx +b ，{b =4−2k +b =0，解得，{k =2b =4，即直线BC 所对应的函数表达式是y ＝2x +4；（2）①∵点O （0，0），点A （4，0），∴OA ＝4，∵动点P 的横坐标为t ，△POA 的面积为S ，P 是线段AB 上的一个动点（点P 与A 、B 不重合）， ∴动点P 的纵坐标为﹣t +4，∴S =4×(−t+4)2=−2t +8，即S 与t 的函数关系式是S ＝﹣2t +8（0＜t ＜4）；②过点P 作PQ ∥x 轴，交BC 于点Q ，∵点P 的坐标为（t ，﹣t +4），∴点Q 的纵坐标为﹣t +4，∵点Q 在直线y ＝2x +4上，∴﹣t +4＝2x +4，得x ＝﹣0.5t ，∵四边形COPQ是平行四边形，OC＝2，∴OC＝PQ，∴2＝t﹣（﹣0.5t），解得，t=4 3，∴点Q的坐标为（−23，83）．【点评】本题是一道一次函数综合题，主要考查一次函数的性质、平行四边形的性质、待定系数法求一次函数解析式，三角形的面积，解答本题的关键是明确题意，找出所求问题需要的条件，利用数形结合的思想解答．4．（2023春•鲤城区校级期中）如图1，在平面直角坐标系中，直角梯形OABC的顶点A的坐标为（4，0），直线y=−14x+3经过顶点B，与y轴交于顶点C，AB∥OC．（1）求顶点B的坐标；（2）如图2，直线l经过点C，与直线AB交于点M，点O'与点O关于直线l对称，连接CO′并延长交直线AB于第一象限的点D，当CD＝5时，求直线l的解析式；（3）在（2）条件下，点P在直线l上运动，点Q在直线OD上运动，当四边形PBCQ是平行四边形时，求点P的坐标．【分析】（1）根据AB∥OC，可得点B的横坐标为4，再代入y=−14x+3，即可求解；（2）过C点作CN⊥AB于N，可得到∠DCM＝∠DMC，从而得到CD＝MD＝5，再求出OC＝3，DN＝3，从而得到NM＝5﹣3＝2，继而得到AM＝1，可得到点M（4，1），即可求解；（3）连接OD，先求出D点坐标为（4，6），可得直线OD解析式为y=32x，设P点坐标为(a，−12a+3)，Q点坐标为(b，32b)，然后根据平行四边形对角线互相平分，即可求解．【解答】解：（1）∵A（4，0），AB∥OC，∴点B的横坐标为4，把x＝4代入y=−14x+3中，得y＝2，∴B（4，2）；（2）如图，过C点作CN⊥AB于N，∵AB∥OC，∴∠OCM＝∠DMC，∵点O'为点O关于直线l的对称点，∴∠DCM＝∠OCM，∴∠DCM＝∠DMC，∴CD＝MD＝5，∵y=−14x+3，当x＝0时，y＝3，∴点C（0，3），∴OC＝3，∵CN＝OA＝4，∴DN=√CD2−CN2=√52−42=3，∴NM＝5﹣3＝2，∴AM＝AN﹣NM＝3﹣2＝1，∴M（4，1），设直线l解析式y＝kx+b把C（0，3），M（4，1）代入得：{3=b 1=4k +b，解得：{k =−12b =3，∴直线l 的解析式为：y =−12x +3；（3）如图，连接OD ，∵AD ＝AM +MD ＝1+5＝6，AD ∥OC ，A 点坐标为（4，0），∴D 点坐标为（4，6），设OD 直线解析式为y ＝kx ，将（4，6）代入可得4k ＝6，解得k =32，∴直线OD 解析式为y =32x ，∵点P 在直线l 上运动，点Q 在直线OD 上运动，∴设P 点坐标为(a ，−12a +3)，Q 点坐标为(b ，32b)，∵四边形PBCQ 是平行四边形，∴平行四边形对角线互相平分，{4+b 2=a+022+32b 2=−12a+3+32，解得：{a =5b =1，当a ＝5时，−12a +3=−12×5+3=12，∴P 点坐标为(5，12)．【点评】本题主要考查了一次函数与四边形的综合题，熟练掌握一次函数的图象和性质，平行四边形的性质是解题的关键．【题型2 矩形的存在性问题】1．如图，在平面直角坐标系xOy中，已知直线l与直线y＝2x平行，且直线l与x、y轴分别交于点A（﹣1，0）、点B，点C（1，a）在直线l上．（1）求直线l的表达式以及点C的坐标；（2）点P在y轴正半轴上，点Q是坐标平面内一点，如果四边形P AQC为矩形，求点P、Q的坐标．【分析】（1）根据题意设直线l的解析式为y＝2x+b，代入A（﹣1，0）求得b，即可求得直线l的解析式，然后代入C（1，a），就可求得a的值；（2）先证得Q在y轴上，根据勾股定理求得AB，然后根据矩形的性质即可求得P、Q的坐标．【解答】解：（1）∵直线l与直线y＝2x平行，∴直线l的斜率为2，设直线l的解析式为y＝2x+b，∵直线l经过A（﹣1，0），∴2×（﹣1）+b＝0，解得b＝2，∴直线l的表达式为y＝2x+2，∵点C（1，a）在直线l上，∴a＝2×1+2＝4；（2）∵y＝2x+2，∴B（0，2），∵A（﹣1，0），C（1，4），∴AB＝BC，∵四边形P AQC为矩形，点P在y轴正半轴上，∴Q点在y轴负半轴上，∵A（﹣1，0），∴AB=√12+22=√5，∴PB＝QB=√5，∴P（0，2+√5），Q（0，2−√5）．【点评】本题考查了两条直线相交或平行问题，待定系数法求一次函数的解析式，矩形的性质，熟练掌握矩形的对角线相等且互相平分是解题的关键．2．（2023•阜阳三模）如图，四边形OABC是矩形，点A、C分别在x轴、y轴上，△ODE是△OCB绕点O 顺时针旋转90°得到的，点D在x轴上，直线BD交y轴于点F，交OE于点H，点B的坐标为（﹣2，4）．（1）求直线BD的表达式；（2）求△DEH的面积；（3）点M在x轴上，平面内是否存在点N，使以点D、F、M、N为顶点的四边形是矩形？若存在，请直接写出点N的坐标；若不存在，请说明理由．【分析】（1）根据矩形的性质和旋转的性质可得点D坐标，再利用待定系数法求直线BD的表达式即可；（2）先利用待定系数法求出直线OE 的解析式，再联立{y =12x y =−23x +83，求出点H 坐标，再根据△DEH 的面积=12DE ⋅HG 求解即可；（3）先求出点F 坐标，以点D 、F 、M 、N 为顶点的四边形是矩形，分情况讨论：①当FD 是矩形的对角线时，②当FD 为矩形的边时，分别求出点M 的坐标，根据平移的性质即可确定点N 坐标．【解答】解：（1）在矩形ABCO 中，∠OCB ＝90°，∵点B 坐标为（﹣2，4），∴OC ＝4，BC ＝2，根据旋转的性质可得，OD ＝OC ＝4，DE ＝BC ＝2，∠ODE ＝∠OCB ＝90°，∴点D 坐标为（4，0），点E 坐标为（4，2），设直线BD 的解析式为y ＝kx +b （k ≠0，k ，b 为常数），代入点B （﹣2，4），点D （4，0），得{−2k +b =44k +b =0，解得{k =−23b =83， ∴直线BD 的解析式为y =−23x +83；（2）过点H 作HG ⊥DE 于点G ，如图所示：设直线OE 的解析式为y ＝mx （m ≠0，m 为常数），代入点E （4，2），得4m ＝2，解得m =12， ∴直线OE 的解析式为y =12x ，联立{y =12x y =−23x +83，解得{x =167y =87， ∴点H 坐标为（167，87）， ∴HG ＝4−167=127， ∵DE ＝2，∴△DEH 的面积=12DE ⋅HG =12×2×127=127；（3）存在点N ，点N 坐标为（4，83）或（209，−83），理由如下：当x ＝0时，y =−23x +83=83，∴点F 坐标为（0，83），以点D 、F 、M 、N 为顶点的四边形是矩形，分情况讨论：①当FD 是矩形的对角线时，如图所示：此时M 点与点O 重合，∴N 点坐标为（4，83）； ②当FD 为矩形的边时，如图所示：设OM ＝m ，在Rt △OMF 中，根据勾股定理，得MF 2=m 2+(83)2，∵DF 2=42+(83)2，MF ＝4+m ，在Rt △MDF 中，根据勾股定理，得MF 2+DF 2＝DM 2，∴m 2+(83)2+42+(83)2=(m +4)2，解得m =169， ∴点M 坐标为（−169，0），根据平移的性质，可得点N 坐标为（209，−83），综上所述，点N 坐标为（4，83）或（209，−83）．【点评】本题考查了一次函数的综合题，涉及待定系数法求解析式，旋转的性质，矩形的性质，三角形的面积，存在性问题等，本题综合性较强，难度较大．3．（2020春•香坊区校级月考）如图，在平面直角坐标系中，矩形OABC 的顶点A 、C 分别落在x 轴、y 轴正半轴上，点E 在边OA 上，点F 在边OC 上，且AE ＝EF ，已知B （6，8），F （0，2√3 ）．（1）求点E 的坐标；（2）点E 关于点A 的对称点为点D ，点P 从C 点出发，以每秒1个单位的速度沿射线CB 运动，设P 点的运动时间为t 秒，△PBD 的面积为S ，用含t 的代数式表示S ；（3）在（2）的条件下，点M 为平面内一点，点P 在线段BC 上运动时，作∠PDO 的平分线交y 轴于点N ，t 为何值时，四边形DPNM 为矩形？并求此时点M 的坐标．【分析】（1）先确定出点A 的坐标，进而得出OA ，最后在Rt △OEF 中，利用勾股定理求出OE 即可得出点E 的坐标；（2）分两种情况，用三角形的面积公式即可解决问题；（3）先利用对称求出点D 的坐标，进而得出OD ，由角平分线的性质定理得出DP ＝OD 求出点P 的坐标，进而求出直线PD ，MD 的解析式，再利用勾股定理求出点N 的坐标，进而得出直线MN 的解析式，联立直线DM和MN的解析式即可得结论．【解答】解：（1）在矩形OABC中，BC∥OA，B（6，8），∴A（6，0），∴OA＝6，设OE＝a，∴EF＝AE＝OA﹣OE＝6﹣a，∵F（0，2√3），∴OF＝2√3，在Rt△AEF中，根据勾股定理得，OE2+OF2＝EF2，∴a2+12＝（6﹣a）2，∴a＝2，∴E（2，0）；（2）由（1）知，E（2，0），∴AE＝4，∵点D是点E关于点A的对称点，∴D（10，0），∵BC∥OA，B（6，8），OC＝AB＝8，∴P（t，8），PB＝|t﹣6|①当点P在边BC上时，如图1，∴0≤t＜6，∴PB＝6﹣t，∴S＝S△PBD=12PB•OC=12×（6﹣t）×8＝﹣4t+24，②当点P在CB的延长时，如图2，∴t＞6，∴PB＝t﹣6，∴S＝S△PBD=12PB•OC=12×（t﹣6）×8＝4t﹣24，即：S={−4t+24(0＜t＜6) 4t−24(t＞6)，（3）如图3，由（2）知，D（10，0），∴OD ＝10，∵四边形DPNM 是矩形，∴∠DPN ＝90°＝∠DON ，∴NP ⊥DP ，NO ⊥OD ，∵DN 是∠PDO 的平分线，∴NO ＝NP ，在Rt △NDO 和Rt △NDP 中，{DN =DN NO =NP， ∴Rt △NDO 和Rt △NDP （HL ），∴DP ＝OD ＝10，∵P （t ，8），D （10，0），∴DP 2＝（t ﹣10）2+64＝100，∴t ＝16（由于点P 在线段BC 上，所以舍去）或t ＝4，∴P （4，8），∵D （10，0），∴DP 的解析式为y =−43x +403，∵DM ⊥DP ，∴直线DM 的解析式为y =34x 152①，设N （0，n ），∴ON ＝n ，∴PN ＝n ，CN ＝OC ﹣ON ＝8﹣n ，∵P （4，8），∴CP ＝4，在Rt △CNP 中，根据勾股定理得，CN 2+CP 2＝PN 2，∴（8﹣n ）2+16＝n 2，∴n ＝5，∴N （0，5），∵PD ∥NM ，∴直线NM 的解析式为y =−43x +5②，联立①②解得，x＝6，y＝﹣3，∴M（6，﹣3）．【点评】此题是四边形综合题，主要考查了矩形的性质，角平分线的性质定理，待定系数法，勾股定理，解（1）的关键是利用勾股定理求出OE，解（2）的关键是分两种情况讨论计算，解（3）的关键是求出点P的坐标．【题型3 菱形的存在性问题】1．（2023春•江阴市期中）将矩形OABC如图所示放置在第一象限，点B的坐标为（3，4），一次函数y=−23x+b的图象与边OC、AB分别交于点D、E，并且满足OD＝BE，点M是线段DE上的一个动点．（1）填空：b＝；（2）设点N是x轴上方平面内的一点，以O、D、M、N为顶点的四边形是菱形，求点M的坐标．【分析】（1）分别表示出D和E点的坐标，根据OD＝BE列出等式即可求出b的值；（2）分当OD为菱形一边时和当OD为菱形一条对角线时两种情况，根据菱形邻边相等或对角线的对称性等特点找到等量列出等式即可求出M点坐标．【解答】解：（1）∵点B的坐标为（3，4），矩形OABC放置在第一象限，∴A（3，0），C（0，4），D（0，b），E（3，b﹣2），∵OD＝BE，∴b＝4﹣（b﹣2），∴b＝3；（2）①当OD 为菱形一边时，OD ＝OM ，如图所示：设M(m ，3−23m)， ∴m 2+(3−23m)2=32，解得，m =3613＜3或m ＝0（不合题意，舍去），∴M(3613，1513)；②当OD 为菱形一条对角线时，过OD 中点P 作PM ⊥OD 交直线CE 于点M ，∴点M 的纵坐标为32， ∴32=−23c +3， ∴c =94＜3，∴点M(94，32)，综上，符合条件的点M 有两个，其坐标分别为(94，32)或(3613，1513)．【点评】本题属于一次函数综合题，考查了一次函数基本性质以及菱形的基本性质等知识，熟练掌握好一次函数的基本性质以及平面直角坐标系中点的综合变化，并能将菱形特点与平面直角坐标系坐标变化相互结合，灵活运用是解决本题的关键．2．（2023•赫山区校级一模）如图，在平面直角坐标系中，直线y =12x +3分别与x 轴、y 轴交于点B ，C ，且与直线y =−12x 交于A ．（1）分别求出A ，B ，C 的坐标；（2）若D 是线段OA 上的点，且△COD 的面积为3，求直线CD 的函数解析式；（3）在（2）的条件下，设P 是射线CD 上的点，在平面内是否存在点Q ，使以O ，C ，P ，Q 为顶点的四边形是菱形？若存在，直接写出点Q 的坐标；若不存在，请说明理由．【分析】（1）由函数图象上点的坐标特征直接求解即可；（2）求出D 点坐标，再由待定系数法求解即可；（3）设P （t ，t +3），Q （x ，y ），根据对角线的情况，再分三种情况讨论即可．【解答】解：（1）令x ＝0，y ＝3，∴C （0，3），令y ＝0，x ＝﹣6，∴B （﹣6，0），联立方程组{y =12x +3y =−12x ，解得{x =−3y =32， ∴A （﹣3，32）；（2）由 S △COD =12OC ⋅ℎOC =12×3ℎOC =3，∴h OC ＝2，∴当x ＝﹣2时，y ＝1，∴D （﹣2，1），设直线CD 的函数解析式为y ＝kx +b （k ≠0），∴{b =3−2k +b =1，解得{k =1b =3， ∴直线CD 的函数解析式为y ＝x +3；（3）存在点Q ，使以O ，C ，P ，Q 为顶点的四边形是菱形，理由如下：设P （t ，t +3），Q （x ，y ），①当PQ 为菱形对角线时，OP ＝PC ，∴{t +x =0t +3+y =3t 2+(t +3)2=t 2+t 2，解得{ t =−32x =32y =32， ∴Q （32，32）； ②当PO 为菱形对角线时，CO ＝PC ，∴{t =xt +3=y +39=t 2+t 2，解得{ t =32√2x =32√2y =32√2（舍）{ t =−32√2x =−32√2y =−32√2， ∴Q （−32√2，−32√2）；③当PC 为菱形对角线时，OP ＝OC ，∴{t =xt +6=y t 2+(t +3)2=9，解得{t =0x =0y =6（舍）或{t =−3x =−3y =3，∴Q （﹣3，3）；综上所述：满足条件的点Q 的坐标是（32，32）或（−32√2，−32√2）或（﹣3，3）．【点评】本题考查一次函数的图象及性质，熟练掌握一次函数的图象及性质，菱形的判定及性质，分类讨论是解题的关键．3．（2023春•新吴区期中）如图矩形OABC 的顶点A 、C 分别在x 轴、y 轴的正半轴上，点B 的坐标为（5，7），一次函数y =−13x +5的图象与边OC 、AB 分别交于D 、E 两点，点M 是线段DE 上的一个动点．（1）则BE 的长为；（2）连接OM ，若△ODM 的面积为152，求点M 的坐标；（3）在（2）的条件下，设点P 是x 轴上一动点，点Q 是平面内的一点，以O 、M 、P 、Q 为顶点的四边形是菱形，直接写出点Q 的坐标．【分析】（1）把点E 的横坐标代入一次函数解析式求出纵坐标得到AE 的长度，进而得到BE ＝AB ﹣AE 的长度；（2）根据△ODM 的面积为152列方程求解即可；（3）画出菱形，找到点Q 的位置，根据菱形的性质分情况分别计算即可．【解答】解：（1）∵四边形OABC 是矩形，∴AB ⊥x 轴，∵B （5，7），AB ＝7，∴E 点的横坐标为5，∵一次函数y =−13x +5的图象过点E ，∴当x ＝5时，y =−53+5=103，∴AE =103，∴BE ＝AB ﹣AE ＝7−103=113，故答案为：113；（2）∵一次函数y =−13x +5的图象交y 轴于点D ，∴当x ＝0时，y ＝5，∴D （0，5），∴OD ＝5，∵△ODM的面积为15 2，∴12×5×x M=152，∴x M＝3，当x＝3时，y=−13×3+5＝4，∴M（3，4）；（3）∵M（3，4），∴OM=√32+42=5，如图，当OM为菱形的边长时，QM∥x轴，QM＝OM＝5，∴Q（﹣2，4）或（8，4）；如图，当OP是菱形的对角线时，MQ⊥x轴于点F，FQ＝FM＝4，∴Q（3，﹣4）；如图，当OM是菱形对角线时，QM∥x轴，QM＝OQ，设Q（q，4），∵QM2＝OQ2，∴（3﹣q）2＝q2+42，解得：q=−7 6，∴Q （−76，4）；综上所述，点Q 的坐标为：（﹣2，4）或（8，4）或（3，﹣4）或（−76，4）．【点评】本题考查一次函数综合题，考查分类讨论的思想，画出菱形，找到点Q 的位置，根据菱形的性质分情况分别计算是解题的关键．4．（2022春•荔湾区校级期中）如图1，在平面直角坐标系中，直线L 2：y =−12x +6与L 1：y =12x 交于点A ，分别与x 轴、y 轴交于点B 、C ．（1）分别求出点A 、B 、C 的坐标；（2）若D 是线段OA 上的点，且△COD 的面积为12，求直线CD 的函数表达式；（3）在（2）的条件下，设P 是直线CD 上的点，在平面内是否存在其它点Q ，使以O 、C 、P 、Q 为顶点的四边形是菱形？若存在，求出点Q 的坐标；若不存在，请说明理由．【分析】（1）构建方程组确定交点A 的坐标，利用待定系数法确定B ，C 两点坐标即可．（2）设D （m ，12m ），利用三角形的面积公式，构建方程求出m 的值，再利用待定系数法即可解决问题．（3）分三种情形：根据OC ＝PC ，设P （m ，12m ），利用两点间距离公式，构建方程求出m 即可．如图2﹣1中，当OC 为菱形的对角线时，OC 垂直平分线段P ′Q ′，利用对称性解决问题即可．当OC ＝OP 时，P ″（6，0），Q ″（6，6）．【解答】解：（1）由{y =−12x +6y =12x，解得{x =6y =3， ∴A （6，3）．∵y =−12x +6与分别与x 轴、y 轴交于点B 、C ， ∴C （0，6），B （12，0）；（2）设D （m ，12m ），由题意：OC ＝6，△COD 的面积为12，∴12×6×m ＝12， ∴m ＝4，∴D （4，2），∵C （0，6），设直线CD 的解析式为y ＝kx +b ，则有{4k +b =2b =6，解得{k =−1b =6， ∴直线CD 的解析式为y ＝﹣x +6；（3）当四边形OCPQ ∴OC ＝PC ＝6，设P （m ，﹣m +6），∴m 2+m 2＝36，∴m ＝3√2或﹣3√2，∴P （3√2，﹣3√2+6），∵PQ ∥OC ，PQ ＝OC ，∴Q （3√2，﹣3√2），如图2﹣1中，当OC 为菱形的对角线时，OC 垂直平分线段P ′Q ′，易知P ′（3，3），Q ′（﹣3，3），∴满足条件的点Q ′的坐标为（﹣3，3）．当OC ＝OP 时，P ″（6，0），Q ″（6，6）．综上所述，满足条件的点Q 的坐标为（3√2，﹣3√2）或（﹣3，3）或（6，6）．【点评】本题属于一次函数综合题，考查了待定系数法，三角形的面积，菱形的判定和性质等知识，解题的关键是学会利用参数构建方程解决问题，属于中考常考题型．【题型4 正方形的存在性问题】1．（2022•前进区二模）△P AC在平面直角坐标系中的位置如图所示，AP与y轴交于点B（0，2），点P的坐标为（﹣1，3），线段OA，OC的长分别是方程x2﹣9x+14＝0的两根，OC＞OA．（1）求线段AC的长；（2）动点D从点O出发，以每秒1个单位长度的速度沿x轴负半轴向终点C运动，过点D作直线l与x轴垂直，设点D运动的时间为t秒，直线l扫过四边形OBPC的面积为S，求S与t的关系式；（3）M为直线l上一点，在平面内是否存在点N，使以A，P，M，N为顶点的四边形为正方形？若存在，请直接写出点的坐标；若不存在，请说明理由．【分析】（1）解方程可求得OA，OC的长，则可求得A、C的坐标，利用两点之间的距离公式即可求解；（2）分两种情况：①当0＜t≤1时；②当1＜t≤7时，利用梯形的面积公式即可求解；（3）分两种情况：①AP为正方形的对角线时，②AP为正方形的边时，根据正方形以及等腰直角三角形的性质，可求得N点坐标．【解答】解：（1）解方程x2﹣9x+14＝0可得x＝2或x＝7，∵线段OA，OC的长分别是方程x2﹣9x+14＝0的两根，且OC＞OA，∴OA＝2，OC＝7，∴AC＝2+7＝9，∴线段AC的长为：7；（2）①如图，当0＜t≤1时，点E（﹣t，t+2），∴S=S梯形OBDE =12t(2+t+2)=12t2+2t（0＜t≤1）；②如图，当1＜t≤7时，设直线CP解析式为：y＝mx+n，∵C（﹣7，0），点P的坐标为（﹣1，3），代入得{−7m+n=0−m+n=3，解得：{m=12n=72，∴直线CP解析式为：y=12x+72；设E（﹣t，−12t+72），∴DE=−12t+72，∴S＝S梯形OBPH+S梯形HPED=12×（2+3）×1+12（t﹣1）（−12t+72+3）=−14t2+72t−34（1＜t≤7），∴S=12t2+2t(0＜t≤1)或S=−14t2+72t−34(1＜t≤7)；（3）存在，分两种情况：①AP为正方形的对角线时，如图，∵A（2，0），B（0，2），∴∠OAB＝45°，∵四边形AMPN是正方形，∴∠P AN＝45°，∠NAM＝90°，∴∠OAB+∠P AN＝90°，∴点M在x轴上，NA⊥x轴，NP∥c轴，∴N（2，3）；②AP为正方形的边时，如图，∵∠OAB＝45°，四边形AMPN是正方形，∴∠NAO＝∠OAB＝45°，AP＝AN，∴HN＝PH＝3，∴N（﹣1，﹣3），∵MH＝AH＝3，∴M（﹣4，0），∴N（﹣4，0）或（﹣1，﹣3），综上可知，存在满足条件的N点，其坐标为（2，3）或（﹣4，0）或（﹣1，﹣3）．【点评】本题考查了一次函数的性质、一元二次方程、勾股定理、待定系数法、正方形的性质等知识．在（1）中求得OA、OC的长是解题的关键，在（2）中求得P点坐标是解题的关键，在（3）中分类思想的运用是解题的关键．2．如图，在平面直角坐标系中，OB和OC的长是方程x2﹣15x+36＝0的两个根，且OB＜OC．∠BAC＝90°，D是x轴上一点，且将△ADC沿AD翻折，AC恰好落在y轴上的AE处．（1）求点A的坐标；（2）求直线CE的解析式；（3）M是直线AC上一点，在平面上是否存在一点N，使以A，B，M，N为顶点的四边形为正方形？若存在，请直接写出点N的坐标；若不存在，请说明理由．【分析】（1）解方程得出OB和OC的值，证△AOB∽△COA，根据线段比例关系求出OB即可确定B 点的坐标；（2）由（1）得出C点和E点的坐标，用待定系数法求出直线CE的解析式即可；（3）用待定系数法求出直线AC的解析式，平移AC过B点，设出N点坐标，根据BN＝AB确定N点坐标即可．【解答】解：（1）解方程x2﹣15x+36＝0，得x＝3或x＝12，∵OB＜OC，∴OB＝3，OC＝12，∵∠BAO+∠ABO＝90°，∠BAO+∠CAO＝90°，∴∠ABO ＝∠CAO ，又∵∠AOB ＝∠COA ＝90°，∴△AOB ∽△COA ，∴OB OA =OA OC ，∴OA =√OB ⋅OC =√3×12=6，∴A （0，6）；（2）由（1）知A （0，6），C （12，0），∴AC =√62+122=6√5，∴OE ＝AC ﹣OA ＝6√5−6，∴E （0，6﹣6√5），设直线CE 的解析式为y ＝kx +b ，代入C 点和E 点坐标得{12k +b =0b =6−6√5，解得{k =12√5−12b =6−6√5， ∴直线CE 的解析式为y ＝（12√5−12）x +6﹣6√5；（3）存在点N ，使以A ，B ，M ，N 为顶点的四边形为正方形，理由如下：①若M 点在线段AC 上，∵∠BAM ＝90°，∴存在四边形ABNM 为正方形，设直线AC 的解析式为y ＝sx +t ，代入A 点和C 点的坐标得{t =612s +t =0，解得{s =−12t =6，∴直线AC 的解析式为y =−12x +6，平移直线AC与直线BN重合，则直线BN得解析式为y=−12x+m，∵B（﹣3，0），∴m=−3 2，即直线BN得解析式为y=−12x−32，设N（n，−n2−32），∵四边形ABNM是正方形，∴BN2＝AB2，即（n+3）2+（−n2−32）2＝32+62，解得n＝3或n＝﹣9（舍去），故N点得坐标为（3，﹣3），②若M点在CA延长线上，由①知，此时N点也在直线y=−12x−32上，设N（p，−p2−32），∵四边形ABNM是正方形，∴BN2＝AB2，即（p+3）2+（−p2−32）2＝32+62，解得p＝3（舍去）或p＝﹣9，故N点得坐标为（﹣9，3），∴点N的坐标为（3，﹣3）或（﹣9，3）时四边形ABNM是正方形．【点评】本题主要考查一次函数的综合题型，熟练掌握待定系数法求函数解析式及一次函数的性质是解题的关键．3．（2021春•柳南区校级期末）如图，直线L 1：y ＝x +1与直线L 2：y ＝﹣x +5相交于点C 直线L 1与x 轴相交于点A ，直线L 2与x 轴相交于点B ．（1）求三角形ABC 的面积；（2）若经过点C 的一条直线交x 轴于D ，直线CD 把三角形ABC 分成两个三角形，且这两个三角形面积的比为1：2，请直接写出点D 的坐标；（3）假设G 是直线y ＝x +1上的点，在坐标平面上是否存在一点Q ，使以A ，B ，Q ，G 为顶点的四边形是正方形，若存在求出点Q 的坐标，若不存在请说明理由．【分析】（1）利用待定系数法求出A 、B 、C 三点坐标即可解决问题；（2）分两种情形分别求解即可；（3）分两种情形讨论①在L 1上取点G （G 异于A ），且CG ＝CA ，在L 2上取点Q （Q 异于B ），且CQ ＝CB ，可以证明四边形ABGQ ②当G 与C 重合时，以AB 为对称轴作G 的对称点Q ，于是四边形AQBG 为正方形．【解答】解：（1）在y ＝x +1中，当y ＝0时，则x ＝﹣1∴A （﹣1，0）在y ＝﹣x +5中当y ＝0时，则x ＝5B （5，0）∴AB ＝OA +OB ＝6，由{y =x +1y =−x +5解得{x =2y =3， ∴C （2，3）∴作CE⊥x轴于E．∴E（2，0）∴CE＝3∴S△ABC=12•AB•CE=12×6×3＝9，（2）由题意A（﹣1，0），B（5，0），AD＝2BD或BD＝2AD，可得D（1，0）或D（3，0）．（3）设y＝x+1交y轴于F，则F（0，1）．∴OF＝OA∴∠OAF＝45°同理∠ABC＝45°∴∠ACB＝90°∴CA＝CB，在L1上取点G（G异于A），且CG＝CA，在L2上取点Q（Q异于B），且CQ＝CB∴CG＝CA＝CQ＝CB，又∵AG⊥BQ，∴四边形ABGQ为正方形，又∵A（﹣1，0）AB＝AQ＝6当G与C重合时，以AB为对称轴作G的对称点Q，于是四边形AQBG为正方形．又∵G（2，3），∴Q（2，﹣3）综合上述：Q（﹣1，6）或Q（2，﹣3）．【点评】本题考查一次函数综合题、三角形的面积、正方形的性质等知识，解题的关键是熟练掌握基本知识，学会用分类讨论的思想思考问题，属于中考压轴题．【题型5 四边形存在性的压轴题】1．（2023春•宜兴市期中）如图，在平面直角坐标系中，已知A（0，4），点B、C都在x轴上，BC＝12，AD∥BC，CD所在直线的函数表达式为y＝﹣x+9，E是BC的中点，点P是BC边上一个动点．（1）当PB＝时，以点P、A、D、E为顶点的四边形为平行四边形；（2）点P在BC边上运动过程中，以点P、A、D、E为顶点的四边形能否构成菱形？试说明理由．【分析】（1）若以点P、A、D、E为顶点的四边形为平行四边形，则AD＝PE，有两种情况：①当P在E的左边，利用已知条件可以求出BP的长度；②当P在E的右边，利用已知条件也可求出BP的长度；（2）以点P、A、D、E为顶点的四边形能构成菱形．由（1）知，当BP＝11时，以点P、A、D、E为顶点的四边形是平行四边形，根据已知条件分别计算一组邻边，证明它们相等即可证明是菱形．【解答】解：（1）∵AD∥BC，点A坐标是（0，4），CD所在直线的函数关系式为y＝﹣x+9，∴D点的纵坐标为4，y＝4时，4＝﹣x+9，x＝5，∴D点的横坐标为5，∵CD所在直线的函数关系式为y＝﹣x+9，y＝0时，0＝﹣x+9，x＝9，∴C（9，0），∴OC＝9，作DN⊥BC交于N，如图1所示，则四边形OADN为矩形，∴CN＝OC﹣ON＝OC﹣AD＝9﹣5＝4，DN＝4，∴△DNC为等腰直角三角形，∴CD=√42+42=4√2，若以点P、A、D、E为顶点的四边形为平行四边形，则AD＝PE＝5，有两种情况：①当P在E的左边，∵E是BC的中点，∴BE＝6，∴PB＝BE﹣PE＝6﹣5＝1；②当P在E的右边，PB＝BE+PE＝6+5＝11；故当PB＝1或11时，以点P、A、D、E为顶点的四边形为平行四边形，故答案为：1或11；（2）点P在BC边上运动过程中，以点P、A、D、E为顶点的四边形能构成菱形，理由如下：①当BP＝1时，此时CN＝DN＝4，NE＝5﹣3＝2，∴DE=√DN2+NE2=√42+22=2√5≠AD，故不能构成菱形．②当BP＝11时，以点P、A、D、E为顶点的四边形是平行四边形，∴EP＝AD＝5，过D作DN⊥BC于N，如图2所示：由（1）得：DN＝CN＝4，∴NP＝BP﹣BN＝BP﹣（BC﹣CN）＝11﹣（12﹣4）＝3．∴DP=√DN2+NP2=√42+32=5，∴EP＝DP＝AD＝5，故此时平行四边形PDAE是菱形，即以点P、A、D、E为顶点的四边形能构成菱形．【点评】本题是一次函数综合题，考查了等腰直角三角形的判定与性质、勾股定理、平行四边形的判定、矩形的判定、菱形的判定等知识，解题的关键是学会用分类讨论的思想思考问题，灵活运用所学知识解决问题，属于中考压轴题．2．如图，已知直线y=−1x+3与x轴，y轴分别交于点A，B，以AB为直角边，∠B为直角作等腰直角三2角形ABC（点C在第一象限）．（1）求点A，B，C坐标；（2）点D A，B，C，D四点围成的四边形为正方形时，求点D坐标；（3）点P为x轴上一动点，点Q为线段AC上一动点，是否存在四边形BP AQ为平行四边形？若存在，求出P，Q点的坐标，若不存在，说明理由．【分析】（1）利用待定系数法求出A，B的坐标，过点C作CH⊥y轴于点H．构造全等三角形求出点C 的坐标；（2）利用正方形的性质，平移变换的性质求解即可；（3）求出直线AC 的解析式，再利用平行四边形的性质求解即可．【解答】解：（1）对于直线y =−12x +3，令y ＝0，得到x ＝6，∴A （6，0），令x ＝0，得到y ＝3，∴B （0，3），∴OA ＝6，OB ＝3，过点C 作CH ⊥y 轴于点H ．∵∠BHC ＝∠CBA ＝∠AOB ＝90°，∴∠CBH +∠ABO ＝90°，∠ABO +∠BAO ＝90°，∴∠CBH ＝∠BAO ，在△BHC 和△AOB 中，{∠BHC =∠AOB∠CBH =∠BAO BC =AB，∴△BHC ≌△AOB （AAS ），∴CH ＝OB ＝3，BH ＝AO ＝6，∴OH ＝9，∴C （3，9）；（2）∵四边形ABCD 是正方形，∴BC ＝AD ，BC ∥AD ，∵点B 向右平移3个单位，向上平移6个单位得到点C ，∴点A 向右平移3个单位，向上平移6个单位得到点D ，∴D （9，6）；（3）∵A （6，0），C （3，9），设直线AC 的解析式为y ＝kx +b ，则有{6k +b =03k +b =9，解得{k =−3b =18， ∴直线AC 的解析式为y ＝﹣3x +18，∵四边形APBQ 是平行四边形，∴BQ ∥AP ，BQ ＝AP ，∴Q（5，3），∴BQ＝AP＝5，∴P（1，0）．【点评】本题属于一次函数综合题，考查了一次函数的性质，正方形的性质，平行四边形的性质等知识，解题的关键是学会添加常用辅助线，构造全等三角形解决问题．3．（2023•武陵区一模）如图，在平面直角坐标系中，直线AB交x轴于点A（﹣2，0），交y轴于点B（0，4），直线y＝kx+b经过点B且交x轴正半轴于点C，已知△ABC面积为10．（1）点C的坐标是（，），直线BC的表达式是；（2）如图1，点E为线段AB中点，点D为y轴上一动点，连接DE，以DE为直角边作等腰直角三角形△EDF，且DE＝DF，在点的运动过程中，当点F落在直线BC上时，求点D的坐标；（3）如图2，若G为线段BC上一点，且满足S△ABG＝S△ABO，点M为直线AG上一动点，在x轴上是否存在点N，使以点B，C，M，N为顶点的四边形为平行四边形？若存在，请直接写出点N的坐标；若不存在，请说明理由．【分析】（1）由△ABC 面积为10，可得AC ＝5，即可求C 点坐标，再将点B 与C 代入y ＝kx +b ，解二元一次方程组可求y =−43x +4；（2）当D 点在E 上方时，过点D 作MN ⊥y 轴，过E 、F 分别作ME 、FN 垂直与x 轴，与MN 交于点M 、N ，由△EDF 是等腰直角三角形，可证得△MED ≌△NDF （AAS ），设D （0，y ），F （m ，−43m +4），E （﹣1，2），由ME ＝y ﹣2，MD ＝1，DN ＝y ﹣2，NF ＝1，得到m ＝y ﹣2，y ＝1+（−43m +4）＝5−43m ，求出D （0，237）；当点D 在点E 下方时，过点D 作PQ ⊥y 轴，过P 、Q 分别作PE 、FQ 垂直与x 轴，与PQ 交于点P 、Q ，同理可证△PED ≌△QDF （AAS ），设D （0，y ），F （m ，−43m +4），得到PE ＝2﹣y ，PD ＝1，DQ ＝2﹣y ，QF ＝1，所以m ＝2﹣y ，1=−43m +4﹣y ，求得D （0，﹣1）；（3）连接OG ，由S △ABG ＝S △ABO ，可得OG ∥AB ，求出AB 的解析式为y ＝2x +4，所以OG 的解析式为y＝2x ，可求出G （65，125），进而能求出AG 的解析式为y =34x +32，设M （t ，34t +32），N （n ，0）， ①当BC 、MN 分别为对角线时，BC 的中点为（32，2），MN 的中点为（t+n 2，38t +34），求得N （−13，0）；②当BM 、CN 分别为对角线时，BM 的中点为（t 2，38t +114），CN 的中点为（3+n 2，0），求得N （−313，0）；③当BN 、CM 分别为对角线时，BN 的中点为（n 2，2），CM 的中点为（t+32，38t +34），求得N （193，0）．【解答】解：（1）∵△ABC 10，∴12×AC ×OB =12×AC ×4＝10， ∴AC ＝5，∵A （﹣2，0），∴C （3，0），将点B 与C 的坐标代入y ＝kx +b ，可得{b =43k +b =0， ∴{k =−43b =4，∴y =−43x +4，故答案为（3，0），y =−43x +4；（2）当D 点在E 上方时，过点D 作MN ⊥y 轴，过E 、F 分别作ME 、FN 垂直于x 轴，与MN 交于点M 、N ，。

八年级下册数学重难点题型(人教版)专题动点与平行四边形存在性问题大视野(原卷版)

专题动点与平行四边形存在性问题大视野【例题精讲】题型一、平行四边形存在性问题例1.【2019·长沙市天心区期中】如图，在平面直角坐标系中，点A和点B分别在x轴和y轴的正半轴上，OA=3，OB=2OA，C为直线y=2x与直线AB的交点，点D在线段OC上，OD= ．（1）求点C的坐标；（2）若P为线段AD上一动点（不与A、D重合）．P的横坐标为x，△POD的面积为S，请求出S与x的函数关系式；（3）若F为直线AB上一动点，E为x轴上一点，是否存在以O、D、E、F为顶点的四边形是平行四边形？若存在，写出点F的坐标；若不存在，请说明理由．题型二、特殊平行四边形（矩形）存在性问题例1.【2019·武汉市期中】如图，在平行四边形ABCD中，对角线BD=12cm，AC=16cm，AC，BD相交于点O，若E，F是AC上两动点，分别从A，C两点以相同的速度向C、A运动，其速度为0.5cm/s．（1）证明：当E在AO上运动，F在CO上运动，且E与F不重合时，四边形DEBF是平行四边形；（2）点E，F在AC上运动过程中，以D、E、B、F为顶点的四边形是否可能为矩形？如能，求出此时的运动时间t的值；如不能，请说明理由．例2.【2019·禹城市期末】如图，在△ABC中，点O是AC边上一动点，过点O作BC的平行线交∠ACB 的角平分线于点E，交∠ACB的外角平分线于点F（1）求证：EO＝FO；（2）当点O运动到何处时，四边形CEAF是矩形？请证明你的结论．（3）在第（2）问的结论下，若AE＝3，EC＝4，AB＝12，BC＝13，请直接写出凹四边形ABCE的面积为．题型三、特殊平行四边形（菱形）存在性问题例1.【2019·福州市晋安区期末】如图，在平面直角坐标系中，矩形ABCD的顶点A、B、D的坐标分别为（0，5）、（0，2）、（4，5），直线l的解析式为y＝kx+2﹣4k（k＞0）．（1）当直线l经过原点O时，求一次函数的解析式；（2）通过计算说明：不论k为何值，直线l总经过点C；（3）在（1）的条件下，点M为直线l上的点，平面内是否存在x轴上方的点N，使以点O、A、M、N为顶点的四边形是菱形？若存在，请直接写出点M的坐标：若不存在，请说明理由．题型四、特殊平行四边形（正方形形）存在性问题例1.【2019·华蓥市期末】如图，已知一次函数y=12-x+b的图象过点A（0，3），点p是该直线上的一个动点，过点P分别作PM垂直x轴于点M，PN垂直y轴于点N，在四边形PMON上分别截取：PC=13 MP，MB=13OM，OE=13ON，ND=13NP．（1）b=______；（2）求证：四边形BCDE是平行四边形；（3）在直线y=12-x+b上是否存在这样的点P，使四边形BCDE为正方形？若存在，请求出所有符合的点P的坐标；若不存在，请说明理由．【刻意练习】1.【2019·阳江市期中】如图，直角坐标系中的网格由单位正方形构成，△ABC中，A点坐标为（2，3），B 点坐标为（-2，0），C点坐标为（0，-1）（1）AC的长为______；（2）求证：AC⊥BC；（3）若以A、B、C及点D为顶点的四边形组成平行四边形，画出符合条件的所有平行四边形，并写出D 点的坐标______．2.【2018·莆田市期中】已知：在△ABC中，AD是BC边上的中线，点E是AD的中点；过点A作AF∥BC，交BE的延长线于F，连接CF．（1）求证：四边形ADCF是平行四边形；（2）填空：①当AB=AC时，四边形ADCF是______形；②当∠BAC=90°时，四边形ADCF是______形．3.【2018·琼中县期中】如图在Rt△ABC中，∠ACB＝90°，AC＝4，BC＝3，D为斜边AB上一点，以CD、CB为边作平行四边形CDEB，当AD＝，平行四边形CDEB为菱形．4.【2019·宿迁市期末】如图，平行四边形ABCD中，AB=8cm，AD=12cm，点P在AD边上以每秒1cm的速度从点A向点D运动，点Q在BC边上，以每秒4cm的速度从点C出发，在CB间往返运动，两个点同时出发，当点P到达点D时停止（同时点Q也停止），在运动以后，以P、D、Q、B四点组成平行四边形的次数有______次．5.【2019·惠州市期末】如图所示，在梯形ABCD中，AD∥BC，∠B=90°，AD=24cm，BC=26cm，动点P 从点A出发沿AD方向向点D以1cm/s的速度运动，动点Q从点C开始沿着CB方向向点B以3cm/s的速度运动．点P、Q分别从点A和点C同时出发，当其中一点到达端点时，另一点随之停止运动．（1）经过多长时间，四边形PQCD是平行四边形？（2）经过多长时间，四边形PQBA是矩形？6.【2019·武昌期末】如图，在平面直角坐标系中，OA=OB,△OAB的面积是2.（1）求线段OB的中点C的坐标.（2）连结AC，过点O作OE⊥AC于E，交AB于点D，①直接写出点E的坐标.②连结CD，求证：∠ECO=∠DCB.（3）点P为x轴上一动点，点Q为平面内一点，以点A、C、P、Q为顶点作菱形，直接写出点Q的坐标.7.【2018·襄阳市期中】如图,矩形OABC的边OA,OC分别与坐标轴重合,并且点B的坐标为（8，）.将该矩形沿OB折叠,使得点A落在点E处,OE与BC的交点为D.（1）求证:△OBD为等腰三角形;（2）求点E的坐标;（3）坐标平面内是否存在一点F,使得以点B,E,F,O为顶点的四边形是平行四边形,若存在,请直接写出点F 的坐标;若不存在,请说明理由.8.【2019·天津蓟县期中】如图，在△ABC中，点F是BC的中点，点E是线段AB的延长线上的一动点，连接EF，过点C作AB的平行线CD，与线段EF的延长线交于点D，连接CE、BD．（1）求证：四边形DBEC是平行四边形．（2）若∠ABC=120°，AB=BC=4，则在点E的运动过程中：①当BE=时，四边形BECD是矩形，试说明理由；②当BE=时，四边形BECD是菱形．。

(人教版)八年级数学下册19.2特殊的平行四边形含答案

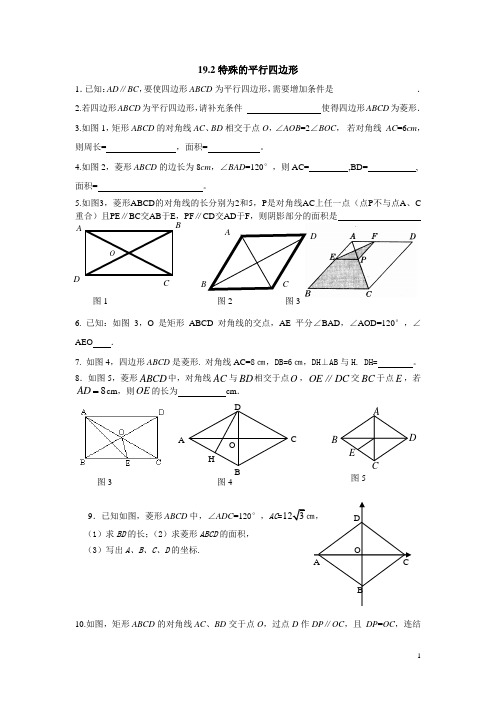
19.2特殊的平行四边形1．已知：AD ∥BC ，要使四边形ABCD 为平行四边形，需要增加条件是___________________． 2.若四边形ABCD 为平行四边形，请补充条件使得四边形ABCD 为菱形． 3.如图1，矩形ABCD 的对角线AC 、BD 相交于点O ，∠AOB =2∠BOC ，若对角线 AC =6cm ，则周长= ，面积= 。

4.如图2，菱形ABCD 的边长为8cm ，∠BAD =120°，则AC= ,BD= , 面积= 。

5.如图3，菱形ABCD 的对角线的长分别为2和5，P 是对角线AC 上任一点（点P 不与点A 、C重合）且PE ∥BC 交AB 于E ，PF ∥CD 交AD 于F ，则阴影部分的面积是图1 图2 图36. 已知：如图3，O 是矩形ABCD 对角线的交点，AE 平分∠BAD ，∠AOD=120°，∠AEO ．7. 如图4，四边形ABCD 是菱形. 对角线AC=8㎝，DB=6㎝，DH ⊥AB 与H. DH= 。

8．如图5，菱形ABCD 中，对角线AC 与BD 相交于点O ，OE DC ∥交BC 于点E ，若8AD cm ，则OE 的长为 cm ．图3 图49．已知如图，菱形ABCD 中，∠ADC =120°，AC =123㎝，（1）求BD 的长；（2）求菱形ABCD 的面积，（3）写出A 、B 、C 、D 的坐标.10.如图，矩形ABCD 的对角线AC 、BD 交于点O ，过点D 作DP ∥OC ，且 DP =OC ，连结B A DCOA BCDABDCOH图5ABDCEABCODCP ，试判断四边形CODP 的形状．并证明。

如果题目中的矩形变为菱形(图一)，结论应变为什么？如果题目中的矩形变为正方形(图二)，结论又应变为什么？10.以△ABC 的边AB 、AC 为边作等边△ABD 和等边△ ACE ，四边形ADFE 是平行四边形．① 当∠BAC 等于时，四边形ADFE 是矩形；② 当∠BAC 等于时，平行四边形ADFE 不存在；③ 当△ABC 分别满足什么条件时，平行四边形ADFE 是菱形、正方形．11.如图1：正方形ABCD 的对角线AC 、BD 相交于点O ，E 是AC 上的一点，连接EB ，过点A 作AM ⊥BE ，垂足M ，AM 交BD 于点F ． ①求证OE =OF ；②如图2所示，若点E 在AC 的延长线上，AM ⊥EB 的延长线于点M ，交DB 的延长线于AODPB CPCDOBA图二B CAEF DA BD C OP 图一点F ，其他条件都不变，则结论“OE=OF”还成立吗？如果成立，请给出证明；如果不成立，请说明理由ABC D O F EM图1ABC DFEM O图2。

探究平行四边形的存在性问题——以2016_年安顺市中考的一道抛物线题为例

探究平行四边形的存在性问题以２０１６年安顺市中考的一道抛物线题为例刘利果(河北省邢台市沙河市第三中学ꎬ河北邢台０５４１００)摘㊀要:抛物线中的动点问题ꎬ尤其是与存在性有关的动点问题ꎬ是中考的一个难点.文章以２０１６年贵州省安顺市的一道中考题为例ꎬ借助网络画板ꎬ从试验探究㊁思路分析㊁一题多解的角度来进行深度探究.关键词:抛物线ꎻ动点ꎻ平行四边形ꎻ存在性ꎻ探究中图分类号:Ｇ６３２㊀㊀㊀文献标识码:Ａ㊀㊀㊀文章编号:１００８－０３３３(２０２３)３５－００９２－０３收稿日期:２０２３－０９－１５作者简介:刘利果(１９８１.１０－)ꎬ女ꎬ河北省邢台人ꎬ本科ꎬ中小学高级教师ꎬ从事初中数学教学研究.㊀㊀抛物线中平行四边形的存在性问题ꎬ是中考的一个难点ꎬ也是热点ꎬ常常以压轴题的形式出现.如何突破这一类试题呢?笔者以２０１６年安顺市一道中考题为例进行探究.１试题呈现抛物线经过Ａ(－１ꎬ０)ꎬＢ(５ꎬ０)ꎬＣ０ꎬ－５２æèçöø÷三点.(１)求抛物线的解析式.(２)在抛物线的对称轴上有一点Ｐꎬ使ＰＡ＋ＰＣ的值最小ꎬ求点Ｐ的坐标.(３)若Ｍ为ｘ轴上一动点ꎬ在抛物线上是否存在一点Ｎꎬ使ＡꎬＣꎬＭꎬＮ四点构成的四边形为平行四边形?若存在ꎬ求点Ｎ的坐标ꎻ若不存在ꎬ请说明理由[１].２思路分析第(１)(２)问略.第(３)问:①如图１所示ꎬＡＣ为对角线时ꎬ取ＡＣ中点Ｏᶄꎬ连接Ｍ４Ｏᶄꎬ交抛物线于点Ｎ４ꎻ如图２所示ꎬ若ＡＣ为边ꎬ平移ＡＣ得到另外三种情况.过四边形顶点作横平坚直线(平行于坐标轴)构造全等三角形解决问题.图１㊀ＡＣ为对角线②设Ｍ(ｘꎬ０)ꎬ分别以ＡＣꎬＡＭꎬＡＮ为对角线ꎬ分三种情况根据平行四边形两组相对顶点横坐标之和相等ꎬ纵坐标之和也相等ꎬ表示出点Ｎ的坐标ꎬ代入抛物线解析式求解即可.③如图３所示ꎬ从路径(轨迹)角度分析.假设以ＡꎬＣꎬＭꎬＮ为顶点的平行四边形存在.在ｘ轴上任取一动点Ｍꎬ把Ｍ看作定点ꎬ然后分别以ＡＭꎬＡＣꎬＣＭ为对角线作出三个平行四边形ꎬ设第四个顶点分别为Ｎ１ꎬＮ２ꎬＮ３.若拖动动点Ｍ可以发现ꎬ动点Ｎ１ꎬＮ２ꎬＮ３运动的路径均为与ｘ轴平行的直线.易得Ｎ１ꎬＮ３到ｘ轴的距离等于ＯＣ＝５２ꎬ到ｘ轴的距离为２９５２的直线有两条.易知ꎬ点Ｎ１的路径为直线ｙ＝５２ꎬ点Ｎ２ꎬＮ３的路径为直线ｙ＝－５２.所以求点Ｎ的坐标就可以转化为由抛物线的解析式与点Ｎ的路径解析式组成的方程组的解的问题.图２㊀ＡＣ为边３一题多解解㊀(１)ｙ＝１２ｘ２－２ｘ－５２.(２)点Ｐ的坐标是２ꎬ－３２æèçöø÷.过程略.(３)解法１㊀存在点Ｎꎬ使ＡꎬＣꎬＭꎬＮ四点为顶点构成的四边形为平行四边形.①当ＡＣ为边时ꎬ如图２所示ꎬ若点Ｎ在ｘ轴下方.图３㊀让Ｍ运动又对称轴为直线ｘ＝２ꎬＣ０ꎬ－５２æèçöø÷ꎬ所以点Ｎ１４ꎬ－５２æèçöø÷.当点Ｎ在ｘ轴上方时ꎬ过点Ｎ２作Ｎ２Ｄʅｘ轴于点Ｄ.ȵＡＣ＝Ｍ２Ｎ２ꎬøＣＡＯ＝øＮ２Ｍ２ＤꎬøＣＯＡ＝øＮ２ＤＭ２ꎬʑәＡＯＣ≅әＭ２ＤＮ２ꎬʑＮ２Ｄ＝ＯＣ＝５２ꎬ即Ｎ２点的纵坐标为５２.ʑ１２ｘ２－２ｘ－５２＝５２ꎬ解得ｘ＝２＋１４或ｘ＝２－１４ꎬʑＮ２２＋１４ꎬ５２æèçöø÷ꎬＮ３２－１４ꎬ５２æèçöø÷.②如图１所示ꎬ当ＡＣ为对角线时ꎬ由四边形ＡＭ４ＣＮ４为平行四边形ꎬ知ＣＮ４ʊＡＭ４ꎬ所以点Ｎ４的纵坐标为－５２ꎬʑＮ４４ꎬ－５２æèçöø÷.综上所述ꎬ符合条件的点Ｎ的坐标为４ꎬ－５２æèçöø÷或２＋１４ꎬ５２æèçöø÷或２－１４ꎬ５２æèçöø÷.解法２㊀设Ｍ(ｘꎬ０)ꎬＮｘＮꎬｙＮ().①若ＡＣ为对角线ꎬ则有－１＋０＝ｘ＋ｘＮꎬ０－５２＝０＋ｙＮꎬìîíïïï即ｘＮ＝－１－ｘꎬｙＮ＝－５２.ìîíïïï将Ｎ－１－ｘꎬ－５２æèçöø÷代入抛物线表达式ꎬ得１２(－１－ｘ)２－２(－１－ｘ)－５２＝－５２ꎬ解得ｘ＝－１或－５ꎬ即ｘＮ＝０或ｘＮ＝４ꎬ所以Ｎ０ꎬ－５２æèçöø÷(与Ｃ重合ꎬ舍去)或Ｎ４ꎬ－５２æèçöø÷.②若ＡＮ为对角线ꎬ则有－１＋ｘＮ＝ｘ＋０ꎬ０＋ｙＮ＝０－５２ꎬìîíïïï即ｘＮ＝ｘ＋１ꎬｙＮ＝－５２.ìîíïïïꎬ将Ｎｘ＋１ꎬ－５２æèçöø÷代入抛物线表达式ꎬ即１２(ｘ＋１)２－２(ｘ＋１)－５２＝－５２ꎬ解得ｘ＝－１或３ꎬ即ｘＮ＝０或ｘＮ＝４ꎬ所以Ｎ０ꎬ－５２æèçöø÷(与Ｃ重合ꎬ舍去)或Ｎ４ꎬ－５２æèçöø÷.③若ＡＭ为对角线ꎬ则有－１＋ｘ＝ｘＮ＋０ꎬ０＋０＝ｙＮ－５２ꎬìîíïïï即ｘＮ＝ｘ－１ꎬｙＮ＝５２.ìîíïïï将Ｎｘ－１ꎬ５２æèçöø÷代入抛物线表达式ꎬ即１２(ｘ－１)２－２(ｘ－１)－５２＝５２ꎬ解得ｘ１＝３＋１４３９或ｘ２＝３－１４ꎬ即ｘＮ＝２＋１４或ｘＮ＝２－１４ꎬ所以Ｎ２＋１４ꎬ５２æèçöø÷或Ｎ２－１４ꎬ５２æèçöø÷.综上所述ꎬ符合条件的点Ｎ的坐标为４ꎬ－５２æèçöø÷或２＋１４ꎬ５２æèçöø÷或２－１４ꎬ５２æèçöø÷.解法３㊀如图４所示ꎬ在ｘ轴上任取一点Ｍꎬ连接ＣＭꎬ分别过点ＡꎬＣꎬＭ作ＣＭꎬＡＭꎬＡＣ的平行线ꎬ得平行四边形ＡＣＭＮ１ꎬ四边形ＣＭＡＮ２ꎬ四边形ＡＣＮ３Ｍꎬ分别过Ｎ１ꎬＮ２ꎬＮ３作ｘ轴的垂线ꎬ垂足分别为ＦꎬＧꎬＥ.过点Ｍ作ＭＨʅＮ２Ｎ３于点Ｈ.易证明Ｎ１Ｆ＝Ｎ２Ｇ＝Ｎ３Ｅ＝ＯＣ＝５２.图４㊀探究点Ｎ的路径所以Ｎ１运动的路径为直线ｙ＝５２ꎬＮ２ꎬＮ３运动的路径为直线ｙ＝－５２.因为Ｎ１ꎬＮ２ꎬＮ３在抛物线ｙ＝１２ｘ２－２ｘ－５２上ꎬ所以Ｎ的坐标满足ｙ＝５２ꎬｙ＝１２ｘ２－２ｘ－５２ìîíïïïï或ｙ＝－５２ꎬｙ＝１２ｘ２－２ｘ－５２ꎬìîíïïïï解得ｘ１＝２＋１４ꎬｙ１＝５２ꎬìîíïïïｘ２＝２－１４ꎬｙ２＝５２ꎬìîíïïïｘ３＝０ꎬｙ３＝－５２ìîíïïï(舍去)ꎬｘ４＝４ꎬｙ３＝－５２.ìîíïïï综上所述ꎬ符合条件的点Ｎ的坐标为４ꎬ－５２æèçöø÷ꎬ２＋１４ꎬ５２æèçöø÷或２－１４ꎬ５２æèçöø÷.解法４㊀如图３所示ꎬ因为Ａ(－１ꎬ０)ꎬＣ０ꎬ－５２æèçöø÷ꎬ所以ＡꎬＣ两点间的水平距离为１ꎬ坚直距离为５２.设点Ｍ的坐标为(ｍꎬ０)ꎬ将点Ｍ按ＣңＡ方向平移ꎬ得到点Ｎ１ｍ－１ꎬ５２æèçöø÷ꎬ将点Ｃ按ＭңＡ方向平移ꎬ得到点Ｎ２－ｍ－１ꎬ－５２æèçöø÷ꎬ将点Ｍ按ＡңＣ方向平移ꎬ得到点Ｎ３ｍ＋１ꎬ－５２æèçöø÷.将点Ｎ１ｍ－１ꎬ５２æèçöø÷ꎬＮ２－ｍ－１ꎬ－５２æèçöø÷ꎬＮ３ｍ＋１ꎬ－５２æèçöø÷分别代代入抛物线的解析式ｙ＝１２ｘ２－２ｘ－５２得①１２(ｍ－１)２－２(ｍ－１)－５２＝５２ꎬ解得ｍ＝３－１４或ｍ＝１４＋３ꎬʑＮ１２＋１４ꎬ５２æèçöø÷或Ｎ１２－１４ꎬ５２æèçöø÷.②１２(－ｍ－１)２－２(－ｍ－１)－５２＝－５２ꎬ解得ｍ＝－１或ｍ＝－５ꎬʑＮ２０ꎬ－５２æèçöø÷(与Ｃ重合ꎬ舍去)或Ｎ２４ꎬ－５２æèçöø÷.③１２(ｍ＋１)２－２(ｍ＋１)－５２＝－５２ꎬ解得ｍ＝－１或ｍ＝３ꎬʑＮ３０ꎬ－５２æèçöø÷(与Ｃ重合ꎬ舍去)或Ｎ３４ꎬ－５２æèçöø÷.综上所述ꎬ符合条件的点Ｎ的坐标为４ꎬ－５２æèçöø÷ꎬ２＋１４ꎬ５２æèçöø÷或２－１４ꎬ５２æèçöø÷.对于平行四边形的存在性问题中已知两个定点ꎬ先虚拟一个动点ꎬ围成一个三角形ꎬ过三角形的每一个顶点画对边的平行线ꎬ三条直线两两相交ꎬ就可以确定平行四边形的第四个顶点.按照虚拟的第三个点ꎬ第四个顶点存在三种情况.但是第四个点到底有几个ꎬ要具体问题具体分析.参考文献:[１]董红凤.有效解决函数中动点型综合题教学探究[Ｊ].数学学习ꎬ２０１６(０１):２５－３０.[责任编辑:李㊀璟]４９。

2020年人教版八年级数学下册培优复习一次函数压轴题(含答案)

第 6 页共 12 页
参考答案 1.解：（1）∵一次函数 y=﹣2x+8 的图象与 x 轴，y 轴分别交于点 A，点 C， ∴A（4，0），C（0，8），∴OA=4，OC=8， ∵AB⊥x 轴，CB⊥y 轴，∠AOC=90°，∴四边形 OABC 是矩形， ∴AB=OC=8，BC=OA=4，
（3）将正方形 OBDE 沿 x 轴正方向平移得到正方形 O1B1D1E1，其中点 O,B,D,E 的对应点分别为点 O1，B1，D1，E1，连接 CD,CE,设点 E 的坐标为（a，0）,其中 a≠2,△CD1E1 的面积为 S． ①当 1＜a＜2 时,请直接写出 S 与 a 之间的函数表达式；
②在平移过程中,当 S= 时,请直接写出 a 的值．
5.如图,在平面直角坐标系 xOy 中,矩形 ABCD 的 AB 边在 x 轴上,AB=3,AD=2,经过点 C 的直线 y=x ﹣2 与 x 轴、y 轴分别交于点 E、F．（1）求：①点 D 的坐标；②经过点 D,且与直线 FC 平行的直线的函数表达式；（2）直线 y=x﹣2 上是否存在点 P,使得△PDC 为等腰直角三角形？若存在,求出点 P 的坐标；若不存在,请说明理由．（3）在平面直角坐标系内确定点 M,使得以点 M、D、C、E 为顶点的四边形是平行四边形，请直接写出点 M 的坐标．
线段AC、AB上(点P不与点A、C重合)，满足∠BPQ=∠BAO.
(1))当点P在什么位置时，△APQ≌△CBP，说明理由。
(3)当△PQB为等腰三角形时，求点P的坐标.
3.如图，直线 y=2x+m(m>0)与 x 轴交于点 A(-2,0)直线 y=-x+n(n>0)与 x 轴、y 轴分别交于 B、C 两点，并与直线 y=2x+m(m>0)相交于点 D，若 AB=4．（1）求点 D 的坐标；（2）求出四边形 AOCD 的面积；（3）若 E 为 x 轴上一点，且△ACE 为等腰三角形，直接写出点 E 的坐标．

人教版八年级数学下册《特殊平行四边形》专题训练习题(含答案)

人教版八年级数学下册《特殊平行四边形》专题训练习题（含答案）一、选择题1.如图,在菱形ABCD中,AB=5,∠BCD=120°,则△ABC的周长等于( )A.20B.15C.10D.5答案 B ∵四边形ABCD是菱形,∴AB=BC,AB∥CD,∴∠B+∠BCD=180°,∴∠B=180°-∠BCD=180°-120°=60°,∴△ABC是等边三角形,故△ABC的周长=3AB=15.2.如图,四边形ABCD的对角线互相平分,要使它变为矩形,需要添加的条件是( )A.AB=CDB.AD=BCC.AC=BDD.AB=BC答案 C 可添加AC=BD,∵四边形ABCD的对角线互相平分,∴四边形ABCD是平行四边形,∵AC=BD,∴平行四边形ABCD是矩形,故选C.3.已知:如图,菱形ABCD中,对角线AC与BD相交于点O,OE∥DC交BC于点E,AD=6cm,则OE 的长为( )12A.6 cmB.4 cmC.3 cmD.2 cm答案 C 因为菱形的四条边相等且对角线互相垂直平分,所以可以由OE ∥DC 证得点E 是BC 的中点,此时利用三角形的中位线或直角三角形斜边上中线的性质都可以求得OE 的长为3 cm.4.如图,在菱形ABCD 中,AB=8,点E 、F 分别在AB 、AD 上,且AE=AF,过点E 作EG ∥AD 交CD 于点G,过点F 作FH ∥AB 交BC 于点H,EG 与FH 交于点O.当四边形AEOF 与四边形CGOH 的周长之差为12时,AE 的值为( )A.6.5B.6C.5.5D.5 答案 C 设AE=x,则EB=8-x,∵四边形ABCD 是菱形,AE=AF,EG ∥AD,FH ∥AB, ∴四边形AEOF 和四边形OHCG 都是菱形. ∵四边形AEOF 与四边形CGOH 的周长之差为12, ∴4x -4(8-x)=12,解得x=5.5.故选C.5.如图,将一个长为10 cm,宽为8 cm 的矩形纸片先按照从左向右对折,再按照从下向上的方向对折两次后,沿所得矩形两邻边中点的连线(虚线)剪下(如图1-4-5①),再打开,得到如图1-4-5②所示的小菱形的面积为( )A.10 cm 2B.20 cm 2C.40 cm 2D.80 cm 2答案 A 由题意可得AC=5 cm, BD=4 cm,故小菱形的面积为×4×5=10(cm 2).故选A. 6.如图,正方形ABCD 中,E 、F 是对角线AC 上两点,连接BE 、BF 、DE 、DF,则添加下列条3件:①∠ABE=∠CBF;②AE=CF;③AB=AF;④BE=BF.可以判定四边形BEDF 是菱形的条件有( )A.1个B.2个C.3个D.4个答案 C 连接BD,交AC 于点O,在正方形ABCD 中,AB=BC,∠BAC=∠ACB,AC ⊥BD,OB=OD,① 在△ABE 与△CBF 中, ∠ ∠∠ ∠∴△ABE ≌△CBF(ASA),∴AE=CF,∵OA=OC,∴OE=OF,又∵AC⊥BD,∴四边形BEDF 是菱形,故①正确.②正方形ABCD 中,OA=OB=OC=OD,∵AE=CF,∴OE=OF,又EF ⊥BD,BO=OD,∴四边形BEDF 是菱形,故②正确.③由AB=AF 不能推出四边形BEDF 其他边的关系,故不能判定它是菱形,故③错误.④在正方形ABCD 中,OA=OC=OB=OD,AC ⊥BD,∵BE=BF,EF⊥BD,∴OE=OF,∴四边形BEDF 是菱形,故④正确.故选C.7.如图所示,在菱形ABCD 中,BE ⊥AD,BF ⊥CD,E 、F 为垂足,AE=ED,则∠EBF 等于( )A.75°B.60°C.50°D.45°答案 B 连接BD.因为BE ⊥AD,AE=ED,所以AB=BD.又因为AB=AD,所以△ABD 是等边三角形,所以∠A=60°,所以∠ADC=120°.在四边形BEDF中,∠EBF=360°-∠BED-∠BFD-∠ADC=360°-90°-90°-120°=60°,故选B.8.如图所示,矩形纸片ABCD 中,AB=6 cm, BC=8 cm,现将其沿EF 对折,使得点C 与点A 重合,则AF 长为( )A .cm B.cm C.cm D.8cm答案 B 设AF=x cm,则D'F=DF=(8-x)cm,在Rt△AFD'中,(8-x)2+62=x2,解得x=.9.如图所示,把一个长方形的纸片对折两次,然后剪下一个角,为了得到一个钝角为120°的菱形,剪口与第二次折痕所成角的度数应为( )A.15°或30°B.30°或45°C.45°或60°D.30°或60°答案 D 画出所剪的图形示意图如图.∵四边形ABCD是菱形,∴∠ABD=∠ABC,∠BAC=∠BAD,AD∥BC,∵∠BAD=120°,∴∠ABC=180°-∠BAD=180°-120°=60°,∴∠ABD=30°,∠BAC=60°.∴剪口与第二次折痕所成的角的度数应为30°或60°.故选D.10.如图,E、F分别是正方形ABCD的边CD、AD上的点,且CE=DF,AE、BF相交于点O,下列结论:(1)AE=BF;(2)AE⊥BF;(3)AO=OE;(4)S△AOB=S四边形DEOF,其中正确的有( )4A.4个B.3个C.2个D.1个答案 B ∵四边形ABCD为正方形,∴AB=AD=DC,∠D=∠BAD=90°,∵CE=DF,∴DE=AF,∴△DEA≌△AFB,∴AE=BF,∠DEA=∠AFB,又∠DEA+∠DAE=90°,∴∠AFB+∠DAE=90°,∴∠AOF=90°,即AE⊥BF.由△DEA≌△AFB得S△DEA=S△AFB,∴S△DEA-S△AOF=S△AFB-S△AOF,∴S△AOB=S四边形DEOF,所以正确的是(1)(2)(4),共3个,故选B.二、填空题11.如图,菱形ABCD中,对角线AC、BD相交于点O,不添加任何辅助线,请添加一个条件,使四边形ABCD是正方形(填一个即可).答案AC=BD(答案不唯一)12.如图,O是矩形ABCD的对角线AC的中点,M是AD的中点,若AB=5,AD=12,则四边形ABOM 的周长为.答案20解析在Rt△ABC中,由勾股定理易得AC=13,由矩形的性质得AO=BO=AC=,而OM是△ACD 的中位线,所以OM=CD=,所以四边形ABOM的周长为AB+BO+OM+AM=5+++6=20.513.如图,已知矩形ABCD的对角线AC与BD相交于点O,若AO=1,那么BD= .答案2解析∵在矩形ABCD中,AC与BD相交于点O,AO=1,∴AO=CO=BO=DO=1,∴BD=2.14.如图,在矩形ABCD中,AB=3,对角线AC,BD相交于点O,AE垂直平分OB于点E,则AD的长为.答案3解析∵AE垂直平分OB,AB=3,∴AB=AO=3,∵四边形ABCD是矩形,∴BO=AO=3,∴BD=2BO=6,∴AD=-=-=3.15.如图,两个完全相同的三角尺ABC和DEF在直线l上滑动.要使四边形CBFE为菱形,还需添加的一个条件是(写出一个即可).答案CB=BF(或BE⊥CF或∠EBF=60°或BD=BF等,答案不唯一)解析由已知得CB∥EF,CB=EF,∴四边形CBFE是平行四边形.因此可以添加CB=BF;BE⊥CF;∠EBF=60°;BD=BF等,都能说明四边形CBFE是菱形.16.如图,正方形ABCO的顶点C,A分别在x轴,y轴上,BC是菱形BDCE的对角线,若∠D=60°,BC=2,则点D的坐标是.67答案 (2+ ,1)解析过点D 作DF ⊥x 轴,垂足为F,在正方形ABCO 中,∠BCO=90°,所以∠BCF=90°,在菱形BDCE 中,BD=DC,又因为∠D=60°,所以△BCD 是等边三角形,因为BC=2,所以CD=2,又∠BCD=60°,所以∠DCF=30°,在Rt △DCF 中,因为∠DCF=30°,CD=2,所以DF=CD=1,由勾股定理得CF= ,所以OF=OC+CF=2+ ,所以点D 的坐标为(2+ ,1).17.如图，菱形ABCD 的面积为120 cm 2,正方形AECF 的面积为50 cm 2,则菱形的边长为 cm.答案 13解析连接BE,EF,FD,AC,∵菱形、正方形为轴对称图形,对角线所在直线是其对称轴,∴B,E,F,D 在同一条直线上, ∵S 正方形AECF = AC ·EF=AC 2=50 cm 2, ∴AC=10 cm,∵S 菱形ABCD =AC ·BD=120 cm 2, ∴BD=24 cm. 设AC,BD的交点为O,由菱形的性质可得AC ⊥BD,AO=5 cm,OB=12cm,∴AB= = =13 cm.18.如图,在菱形ABCD 中,∠BAD=120°,点E 、F 分别在边AB 、BC 上,△BEF 与△GEF关于直线EF对称,点B的对称点是点G,且点G在边AD上.若EG⊥AC,AB=6,则FG的长为.答案3解析设AC与EG相交于点O,∵四边形ABCD是菱形,∠BAD=120°,∴∠EAC=∠DAC=60°,∠B=60°,AB=BC.∴△ABC是等边三角形.又∵AB=6,∴△ABC的面积为18.∴菱形ABCD的面积为36,∵EG⊥AC,∴∠AOE=∠AOG=90°.∴∠AGE=90°-60°=30°.∵△BEF与△GEF关于直线EF对称,点B的对称点是点G,∴∠EGF=∠B=60°,∴∠AGF=∠EGF+∠AGE=90°.∴FG⊥AD,∴FG=菱形==3.三、解答题19.如图,在菱形ABCD中,对角线AC、BD相交于点O,过点D作对角线BD的垂线交BA的延长线于点E.(1)证明:四边形ACDE是平行四边形;(2)若AC=8,BD=6,求△ADE的周长.8答案(1)证明:∵四边形ABCD是菱形,∴AB∥CD,AC⊥BD,∴AE∥CD,∠AOB=90°,又∵DE⊥BD,即∠EDB=90°,∴∠AOB=∠EDB.∴DE∥AC.∴四边形ACDE是平行四边形.(2)∵四边形ABCD是菱形,AC=8,BD=6,∴AO=4,DO=3,∴AD=CD==5.又∵四边形ACDE是平行四边形,∴AE=CD=5,DE=AC=8.∴△ADE的周长为AD+AE+DE=5+5+8=18.20.如图,在△ABC中,∠BAC=90°,AD是中线,E是AD的中点,过点A作AF∥BC交BE的延长线于F,连接CF.(1)求证:AD=AF;(2)如果AB=AC,试判断四边形ADCF的形状,并证明你的结论.答案(1)证明:∵AF∥BC,∴∠EAF=∠EDB,∵E是AD的中点,∴AE=DE,在△AEF和△DEB中,9∴△AEF≌△DEB(ASA),∴AF=BD,∵在△ABC中,∠BAC=90°,AD是中线,∴AD=BD=DC=BC,∴AD=AF.(2)四边形ADCF是正方形.∵AF=BD=DC,AF∥BC,∴四边形ADCF是平行四边形,∵AB=AC,AD是中线,∴AD⊥BC,∵AD=AF,∴四边形ADCF是正方形.21.如图,在正方形ABCD中,点E、F分别在边AB、BC上,∠ADE=∠CDF.(1)求证:AE=CF;(2)连接DB交EF于点O,延长OB至点G,使OG=OD,连接EG、FG,判断四边形DEGF是否为菱形,并说明理由.答案(1)证明:在正方形ABCD中,AD=CD,∠A=∠C=90°,在△ADE和△CDF中,∴△ADE≌△CDF(ASA),∴AE=CF.(2)四边形DEGF是菱形.理由如下:在正方形ABCD中,AB=BC,∵AE=CF,10∴AB-AE=BC-CF,即BE=BF,∴BD垂直平分EF,∴OE=OF,又∵OG=OD,∴四边形DEGF为平行四边形,∵△ADE≌△CDF,∴DE=DF,∴四边形DEGF是菱形.22.如图,AB∥CD,点E、F分别在AB、CD上,连接EF.∠AEF、∠CFE的平分线交于点G,∠BEF、∠DFE的平分线交于点H.(1)求证:四边形EGFH是矩形;(2)小明在完成(1)的证明后继续进行了探索.过G作MN∥EF,分别交AB、CD于点M、N,过H 作PQ∥EF,分别交AB、CD于点P、Q,得到四边形MNQP.此时,他猜想四边形MNQP是菱形.请在下列框图中补全他的证明思路.答案(1)证明:∵EH平分∠BEF,∴∠FEH=∠BEF.∵FH平分∠DFE,∴∠EFH=∠DFE.11∵AB∥CD,∴∠BEF+∠DFE=180°,∴∠FEH+∠EFH=(∠BEF+∠DFE)=×180°=90°,又∠FEH+∠EFH+∠EHF=180°,∴∠EHF=180°-(∠FEH+∠EFH)=180°-90°=90°.同理可证,∠EGF=90°.∵EG平分∠AEF,∴∠FEG=∠AEF.∵EH平分∠BEF,∴∠FEH=∠BEF.∵点A、E、B在同一条直线上,∴∠AEB=180°,即∠AEF+∠BEF=180°.∴∠FEG+∠FEH=(∠AEF+∠BEF)=×180°=90°,即∠GEH=90°.∴四边形EGFH是矩形.(2)本题答案不唯一,下面答案供参考.例如,FG平分∠CFE;GE=FH;∠GME=∠FQH;∠GEF=∠EFH.23.已知E,F分别为正方形ABCD的边BC,CD上的点,AF,DE相交于点G,当E,F分别为边BC,CD 的中点时,有:①AF=DE;②AF⊥DE成立.试探究下列问题:(1)如图①,若点E不是边BC的中点,F不是边CD的中点,且CE=DF,上述结论①,②是否仍然成立?(请直接回答“成立”或“不成立”,不需要证明)(2)如图②,若点E,F分别在CB的延长线和DC的延长线上,且CE=DF,此时,上述结论①,②是否仍然成立?若成立,请写出证明过程,若不成立,请说明理由;(3)如图③,在(2)的基础上,连接AE和EF,若点M,N,P,Q分别为AE,EF,FD,AD的中点,请判断四边形MNPQ是“矩形、菱形、正方形”中的哪一种,并证明你的结论.12答案(1)成立.(2)仍然成立.证明:∵四边形ABCD为正方形,∴AD=DC,∠BCD=∠ADC=90°.在△ADF和△DCE中,∴△ADF≌△DCE(SAS),∴AF=DE,∠FAD=∠EDC,∵∠ADG+∠EDC=90°,∴∠ADG+∠DAF=90°,∴∠AGD=90°,即AF⊥DE.(3)四边形MNPQ是正方形.证明:如图,设MQ,DE分别交AF于点G,O,PQ交DE于点H,∵点M,N,P,Q分别为AE,EF,FD,AD的中点,∴MQ=PN=DE,PQ=MN=AF,MQ∥DE,PQ∥AF,13∴四边形OHQG是平行四边形,∵AF=DE,∴MQ=PQ=PN=MN,∴四边形MNPQ是菱形,∵AF⊥DE,∴∠AOD=90°,∴∠HQG=∠AOD=90°,∴四边形MNPQ是正方形.14。

一次函数压轴题专题突破8：一次函数与平行四边形(含解析)

（1）若点P的横坐标为m，则PD的长度为（用含m的式子表示）；
（2）如图1，已知点Q是直线y＝ x+n上的一个动点，点E是x轴上的一个动点，是否存在以A，B，E，Q为顶点的平行四边形，若存在，求出E的坐标；若不存在，说明理由；
（3）如图2，将△BPD绕点B旋转，得到△BD′P′，且旋转角∠PBP′＝∠OCA，当点P的对应点P′落在坐标轴上时，请直接写出点P的坐标．
3．已知：如图，在平面直角坐标系中，O为坐标原点．直线AB：y＝mx+8m（m≠0）交x轴负半轴于A，交y轴正半轴于B，直线BC：y＝nx+2n（n≠0）交x轴负半轴于C，且∠OAB＝2∠OBC．
（1）求m、n的值；
（2）点P（t，0）是x轴上一动点，过P作y轴的平行线，交AB于Q，交BC于R，设QR＝d，求d与t的函数关系式，并写出自变量t的取值范围；
（1）求直线l2的解析式；
（2）若在第二象限中有一点P（m，5）使得S△AOP＝S△AOB，请求出点P的坐标；
（3）已知直线y＝2x﹣2分别交x轴、y轴于E、F两点，M、N分别是直线l1、l2上的动点，请直接写出能使E、F、M、N四点构成平行四边形的点M的坐标．
8．如图，直线l1的解析表达式为：y＝3x﹣3，且l1与x轴交于点D，直线l2经过点A，B，直线l1，l2交于点C．
（3）如图2，若M为线段BC上一点，且满足S△AMB＝S△AOB，点E为直线AM上一动点，在x轴上是存在点D，使以点D，E，B，C为顶点的四边形为平行四边形？若存在，请直接写出点D的坐标；若不存在，请说明理由．
2．如图，直线y＝ x+n交x轴于点A（﹣8，0），直线y＝﹣ x﹣4经过点A，交y轴于点B，点P是直线y＝﹣ x﹣4上的一个动点，过点P作x轴的垂线，过点B作y轴的垂线，两条垂线交于点D，连接PB，设点P的横坐标为m．

中考数学压轴题专项汇编专题特殊平行四边形的存在性

专题24 特殊平行四边形的存在性破解策略在平行四边形的基础上增加一些条件，即可得到特殊的平行四边形因而可以结合”等腰三角形的存在性”，”直角三角形的存在性”和”平行四边形的存在性”来解决这类问题．例题讲解例1：如图，在平面直角坐标系xOy 中，抛物线y ＝ax 2－2ax －3a （a ＜0）与x 轴交于A ，B 两点（点A 在点B 的左侧）．经过点A 的直线l ：y ＝ax ＋a 与抛物线的另一交点为C ，设P 是抛物线的对称轴上的一点，点Q 在抛物线上，那么以点A ，C ，P ，Q 为顶点是四边形能否成为矩形?若能，求出点P 的坐标;若不能，请说明理由．解：以点A ，C ，P ，Q 为都顶点的四边形能成为矩形．令ax 2－2a －3a ＝ax ＋a ．解得x 1＝－1，x 2＝4，所以点A 的坐标为（－1，0），C 的坐标为（4，5a ）．因为y ＝ax 2－2ax －3a ，所以抛物线的对称轴为x ＝1．则x P ＝1． ①若AC 是矩形的一条边，如图，则x A ＋x P ＝x C ＋x Q ，可得x Q ＝－4，从而点Q 坐标为（－4，21a ）．同样y A ＋y P ＝y C ＋y Q ，可得y P ＝26a ，从而点P 坐标为（1，26a ）．因为AC ＝PQ ，所以有22＋（26a ）2＝82＋（16a ）2，解得)(77,7721舍去=-=a a ，此时点P 的坐标为（1，7726-）②若AC 是矩形的一条对角线，如图．则x A ＋x C ＝x P ＋x Q ，可得x Q ＝2，从而点Q 坐标为（2，－3a ）．同样y A ＋y C ＝y P ＋y Q ，可得y P ＝8a ，从而点P 坐标为（1，8a ）．因为AC ＝PQ ，所以有52＋（5a ）2＝12＋（11a ）2，算得)(21,2143舍=-=a a ，所以此时点P 的坐标为（1，－4）综上可得，以点A ，C ，P ，Q 为顶点的四边形能成为矩形，点P 的坐标为（1，7726-）或（1，－4）．例2：如图，在平面直角坐标系xOy 中，菱形ABCD 的中心与原点重合，C ，D 两点的坐标分别为（4，0），（0，3）．现有两动点P ，Q 分别从A ，C 同时出发，点P 沿线段AD 向终点D 运动，点Q 沿折线CBA 向终点A 运动，设运动时间为t 秒．（1）菱形ABCD 的边长是_____，面积是_____，高BE 的长是_____;（2）若点P 的速度为每秒1个单位．点Q 的速度为每秒k 个单位．在运动过程中，任何时刻都有对应的k 值，使得△APQ 沿它的一边翻折，翻折前后两个三角形组成的四边形为菱形．请探究当t ＝4秒时的情形，并求出k 的值．解：（1）5，24，4．8．（2）要使△APQ 沿它的一边翻折，翻折前后的两个三角形组成的四边形为菱形，根据轴对称的性质，翻折前后两个图形是全等的，所以要满足四边形是菱形只需△APQ 为等腰三角形即可．当t ＝4时，AP ＝4．①如图，当点Q 在线段BC 上时，PQ ≥BE ＞AP ，同理，AQ ＞AP ，所以只存在QA ＝QP 的等腰三角形．过点Q 作QH ⊥AP 于点H ，交AC 于点F ，则AH ＝PH ＝21AP ＝2 易证：△AFH ∽△CFQ ∽△ADO ，所以43===AODO CQFQ AHFH可得522,1033,23===CQ FQ FH从而k ＝10114=CQ ②当Q 在BA 上时，有两种情况的等腰三角形存在：（i ）如图1，当AP ＝AQ 时，此时点P ，Q 关于x 轴对称，BQ ＝PD ＝1 所以，k ＝234=+BQ CB （ⅱ）如图3，当PA ＝PQ 时，过点P 作PH ⊥AB 于点H ．易证△AHP ∽△AEB ，所以AH AP AE AB=，其中AE ＝227.5AB BE -= 所以AH ＝2825，AQ ＝2AH ＝5625，所以k ＝97450CB BQ +=．（ⅲ）由①可得，AP 的垂直平分线与BC 相交，所以点Q 在线段AB 上时，不存在AQ ＝PQ 这种情况．综上所得，满足条件的k 值为32，1110，9750．y xP QHE A CB DO例3 如图，二次函数212y x x c =-+的图象与x 轴分别交于A ，B 两点，顶点M 关于x 轴的对称点是M ′．问：是否存在抛物线212y x x c =-+使得四边形AMBM ′为正方形？若存在，请求出抛物线的表达式；若不存在，请说明理由．xyBM′MAO解：存在易得AMBM ’是菱彤，所以当AB ＝MM ′时，四边彤AMBM ′是正方形设点A 的坐标为（x 1，0），B 的坐标为（x 2，0）．令2102x x c -+=所以x 1＋x 2＝2，x 1·x 2＝2c 所以AB ＝()212124x x x x +-＝48.c -点M 的纵坐标为2421.42ac b c a --=若四边形AMBM ’为正方形，则有214822c c --=⨯．解得1213,.22c c ==-又因为已知抛物线与x 轴有两个交点，所以()2214140.2b ac c ∆=-=--⨯>解得c ＜12，所以c 的值为3.2-．所以存在抛物线21322y x x =--，使得四边彤AMBM '为正方形．进阶训练1．已知抛物线C 1： y ＝－2x 2＋8x －6与抛物线C 关于原点对称，抛物线C 2与x 轴分别交于点A ，B 两点（点A 在点B 的左侧），顶点为M ，抛物线C 2与x 轴分别交于C ，D 两点（点C 在点D 的左侧）顶点为N ．（1）求抛物线C 2的表达式；（2）若抛物线C 1与抛物线C 2同时以每秒1 个单位的速度沿x 轴方向分别向左、向右运动，此时记A ，B ，C ，D ，M ，N 在某一时刻的新位置分别为A'，B'，C'，D'，M'，N'，当点A'与点D'重合时运动停止，在运动过程中，四边形B'，M'，C'，N'能否形成矩形？若能，求出此时运动时间t （秒）的值；若不能，请说明理由．解：（1）抛物线C 2的表达式为2286y x x =++ （2）能．1＝[提示]（2）如图，由轴对称的性质可得四边形C 'N 'B 'M '为平行四边形．所以当∠B 'M 'C '＝90 或B 'C '＝M 'N '时．四边形为矩形，由此可列方程，从面求得t ．2．如图，抛物线22725()326y x =--与x 轴的右交点为A ，与y 轴的交点为B ，设E （x ，y ）是抛物线上一动点，且位于第四象限，若四边形OEAF 是以OA 为对角线的平行四边形．（1）该四边形的面积为24时，判断平行四边形OEAF 是否为菱形；（2）是否存在点E ，使平行四边形OEAF 为正方形？若存在，求出点E 的坐标；若不存在，请说明理由．xyAFEBO解：（1）当点E 的坐标为（3，－4）时，平行四边形OAEF 是菱形;（2）不存在，理由：若平行四边形OEAF 是正方形，则OA ⊥EF 且OA ＝EF ．此时的点E 不在抛物线上．3．如图，抛物线经过原点O 与x 轴上一点A （4，0），抛物线的顶点为E ，它的对称轴x 轴交于点D ，直线y ＝－2x －1经过抛物线上一点B （－2，m ），与抛物线的对称轴交于点F ．（1）求抛物线的表达式；（2）Q 是平面内任意一点，点M 从点F 出发，沿对称轴向上以每秒1个单位长度的速度均速运动，设点M 的运动时间为t 秒，是否能使以Q ，A ，E ， M 四点顶点的四边形是菱形？若能，请直接写出点M 的运动时间；若不能，请说明理由．xyDFBE A O解：（1）抛物线的表达式为214y x x =-；（2）能，t 的值为45-，6，45+或132． [提示]（2）如图，点M 的运动过程中，以Q ，A ，E ，M 为顶点的四边形是菱形有以下四种情况，根据菱形的性质即可求得对应的t 的值． xyQ 1DFBEA OxQ 2A E BFDOxy Q 3A E BFDOxyQ 4A E BFDO4．如图，抛物线y ＝－x 2＋bx ＋c 经过A （－1，0）两点，且与y 轴交于点C ，D 是抛物线的顶点，抛物线的对称轴DE 交x 轴于点E ，连结B D ．（1）P 是线段BD 上一点，当PE ＝PC 时，请求出点P 的坐标；（2）在（1）的条件下，过点P 作PF ⊥x 轴于点F ，G 为抛物线上一动点，M 为x 轴上一动点，N 为直线PF 上一动点，当以F ，M ，N ，G 为顶点的四边形是正方形时，请求出点M 的坐标．xyCPDBEAO解：（1）点P 的坐标为（2，2），（2）点M 的坐标为1211213133130000.22⎛⎫⎛⎫⎫⎫-+ ⎪ ⎪⎪⎪ ⎪ ⎪⎪⎪⎝⎭⎝⎭⎝⎭⎝⎭，，，[提示]（1）易求得抛物线的l 表达式为223y x x =-++．所以C （0，3），D （1，4），E （1，0），从而直线BD 的表达式为y ＝－2x ＋6．设点P 的坐标为（t ，－2t ＋6）．若PE ＝P C ．则有t 2＋（－2t ＋6－3）()()22126t t =-+-+，解得t ＝2，从而得到点P 的坐标为（2．2）．（2）可设点M 的坐标为（m ，0），则点G 的坐标为（m ，223m m -++）．而以F ，M ，N ，G为顶点的四边形是正方形．所以MF ＝MG ，从而2223m m m -=-++，解得m =，或m =M 的坐标．。

人教版八年级下数学一次函数压轴题研究(五)平行四边形存在性(讲义及答案)精选全文完整版

可编辑修改精选全文完整版一次函数压轴题研究（五）平行四边形存在性（讲义及答案）➢课前预习1.如图，点A，B，C是平面内不在同一直线上的三点，点D是平面内任意一点，若以点A，B，C，D为顶点的四边形是平行四边形，则在平面内符合该条件的点D有________个．CBA➢知识点睛1.存在性问题处理框架：①研究背景图形．②根据不变特征，确定分类标准．③分析特殊状态的形成因素，画出符合题意的图形并求解．④结果验证．2.平行四边形存在性问题特征举例：①三定一动，连接定点出现三条定线段．定线段分别作为平行四边形的________，利用________确定点的坐标．②两定两动，连接定点出现一条定线段．若定线段作为平行四边形的________，则通过________确定点的坐标；若定线段作为平行四边形的________，则定线段绕________旋转，利用________________确定点的坐标．➢精讲精练1.如图，在平面直角坐标系中，点A的坐标为(1，0)，点B的坐标为(4，0)，点C在y轴正半轴上，且OB=2OC．若M是坐标平面内一点，且以点M，A，B，C为顶点的四边形是平行四边形，则点M的坐标为_____________________．2.如图，在平面直角坐标0)，B(0，1)，C(2，2)，若D是坐标平面内一点，且以点A，B，C，D为顶点的四边形是平行四边形，则点D的坐标为______________．3.如图，在平面直角坐标系中，直线2y x=+与坐标轴分别交于点A，B，点C在y轴正半轴上，且12OAAC=，直线CD⊥AB于点P，交x轴于点D．在坐标平面内是否存在点M，使得以点B，P，D，M为顶点的四边形是平行四边形？若存在，求出点M的坐标；若不存在，请说明理由．4.如图，在平面直角坐标系中，直线334y x=-+与x轴、y轴分别交于点A，B，点C的坐标为(0，2-)．若点D在直线AB上运动，点E在直线AC上运动，当以点O，A，D，E为顶点的四边形是平行四边形时，求点D的坐标．5.1经过点A ，且与y 轴交于点D ．若M 是直O ，B ，M ，N 为顶点的四边形是平行四边6.【参考答案】➢课前预习1. 3➢知识点睛2.①对角线平移②边平移对角线其中点中点坐标公式➢精讲精练1.(3,2)，(-3,2)，(5，-2)2.(5,1)，(-1,3)，(1，-1)3.存在(，3)，(-，3)，(-3)4.(125，65)，(285，-65)5.存在(-3，0)，(7,0)，(3,0)6.存在(3，(1-，)，(1+，8)。

人教版八年级数学下册一次函数的图象和性质(基础)典型例题讲解+练习及答案.doc

【若缺失公式、图片现象属于系统读取不成功，文档内容齐全完整，请放心下载。

】一次函数的图象与性质（基础）责编：杜少波【学习目标】1. 理解一次函数的概念，理解一次函数y kx b =+的图象与正比例函数y kx =的图象之间的关系；2. 能正确画出一次函数y kx b =+的图象．掌握一次函数的性质．利用函数的图象解决与一次函数有关的问题，还能运用所学的函数知识解决简单的实际问题．3. 对分段函数有初步认识，能运用所学的函数知识解决实际问题．【要点梳理】要点一、一次函数的定义一般地，形如y kx b =+（k ，b 是常数，k ≠0）的函数，叫做一次函数.要点诠释：当b ＝0时，y kx b =+即y kx =，所以说正比例函数是一种特殊的一次函数.一次函数的定义是根据它的解析式的形式特征给出的，要注意其中对常数k ，b 的要求，一次函数也被称为线性函数.要点二、一次函数的图象与性质1.函数y kx b =+（k 、b 为常数，且k ≠0）的图象是一条直线；当b ＞0时，直线y kx b =+是由直线y kx =向上平移b 个单位长度得到的；当b ＜0时，直线y kx b =+是由直线y kx =向下平移|b |个单位长度得到的.2.一次函数y kx b =+（k 、b 为常数，且k ≠0）的图象与性质：3. k 、b 对一次函数y kx b =+的图象和性质的影响：k 决定直线y kx b =+从左向右的趋势，b 决定它与y 轴交点的位置，k 、b 一起决定直线y kx b =+经过的象限．4. 两条直线1l ：11y k x b =+和2l ：22y k x b =+的位置关系可由其系数确定：（1）12k k ≠⇔1l 与2l 相交；（2）12k k =，且12b b ≠⇔1l 与2l 平行；【：391659 一次函数的图象和性质，待定系数法求函数的解析式】要点三、待定系数法求一次函数解析式一次函数y kx b =+（k ，b 是常数，k ≠0）中有两个待定系数k ，b ，需要两个独立条件确定两个关于k ，b 的方程，这两个条件通常为两个点或两对x ，y 的值.要点诠释：先设出函数解析式，再根据条件确定解析式中未知数的系数，从而具体写出这个式子的方法，叫做待定系数法.由于一次函数y kx b =+中有k 和b 两个待定系数，所以用待定系数法时需要根据两个条件列二元一次方程组（以k 和b 为未知数），解方程组后就能具体写出一次函数的解析式.要点四、分段函数对于某些量不能用一个解析式表示，而需要分情况（自变量的不同取值范围）用不同的解析式表示，因此得到的函数是形式比较复杂的分段函数.解题中要注意解析式对应的自变量的取值范围，分段考虑问题.要点诠释：对于分段函数的问题，特别要注意相应的自变量变化范围.在解析式和图象上都要反映出自变量的相应取值范围.【典型例题】类型一、待定系数法求函数的解析式1、根据函数的图象，求函数的解析式．【思路点拨】由于此函数的图象过（0，2），因此b ＝2，可以设函数的解析式为2y kx =+，再利用过点（1.5，0），求出相应k 的值.【答案与解析】利用待定系数法求函数的解析式.解：设函数的解析式为y kx b =+.Q 它的图象过点（1.5，0），（0，2）41.50322k b k b b ⎧+==-⎧⎪⎨⎨=⎩⎪=⎩∴∴ ∴该函数的解析式为423y x =-+. 【总结升华】用待定系数法时需要根据两个条件列二元一次方程组（以k 和b 为未知数），解方程组后就能具体写出一次函数的解析式.举一反三：【变式1】已知一次函数的图象与正比例函数2y x =的图象平行且经过(2，1)点，则一次函数的解析式为________．【答案】 23y x =-；提示：设一次函数的解析式为y kx b =+，它的图象与2y x =的图象平行，则2k =，又因为一次函数的图象经过(2，1)点，代入得1＝2×2＋b ．解得3b =-． ∴ 一次函数解析式为23y x =-．【变式2】（2015春•广安校级月考）已知函数y1=2x﹣3，y2=﹣x+3．（1）在同一坐标系中画出这两个函数的图象．（2）求出函数图象与x轴围成三角形的面积．【答案】解：（1）函数y1=2x﹣3与x轴和y轴的交点是（1.5，0）和（0，﹣3），y2=﹣x+3与x轴和y轴的交点是（3，0）和（0，3），其图象如图：（2）设y1=2x﹣3，y2=﹣x+3的交点为点A，可得：，可得：，S△ABC=BC•1=×（3﹣1.5）×1=．类型二、一次函数图象的应用2、（2016春•南昌期末）电力公司为鼓励市民节约用电，采取按月用电量分段收费的办法，已知某户居民每月应缴电费y（元）与用电量x（度）的函数图象是一条折线（如图所示），根据图象解答下列问题．（1）分别写出当0≤x≤100和x＞100时，y与x之间的函数关系式；（2）若该用户某月用电80度，则应缴费多少元？若该用户某月缴费105元，则该用户该月用了多少度电？【思路点拨】（1）对0≤x≤100段，列出正比例函数y=kx，对x≥100段，列出一次函数y=kx+b；将坐标点代入即可求出．（2）根据（1）的函数解析式以及图标即可解答即可．【答案与解析】解：（1）当0≤x≤100时，设y=kx，则有65=100k，解得k=0.65．∴y=0.65x ．当x ＞100时，设y=ax +b ，则有，解得 ∴y=0.8x ﹣15．（2）当用户用电80度时，该月应缴电费0.65×80=52（元）．当用户缴费105元时，由105=0.8x ﹣15，解得x=150．∴该用户该月用电150度．【总结升华】本题主要考查一次函数的应用，关键考查从一次函数的图象上获取信息的能力．举一反三：【变式】小高从家骑自行车去学校上学，先走上坡路到达点A ，再走下坡路到达点B ，最后走平路到达学校C ，所用的时间与路程的关系如图所示.放学后，如果他沿原路返回，且走平路、上坡路、下坡路的速度分别保持和去上学时一致，那么他从学校到家需要的时间是( )A.14分钟B.17分钟C.18分钟D.20分钟【答案】D ；提示：由图象可知，上坡速度为80米/分；下坡速度为200米/分；走平路速度为100米/分.原路返回，走平路需要8分钟，上坡路需要10分钟，下坡路需要2分钟，一共20分钟.类型三、一次函数的性质3、已知一次函数()()243y m x n =++-．（1）当m 、n 是什么数时，y 随x 的增大而增大；（2）当m 、n 是什么数时，函数图象经过原点；（3）若图象经过一、二、三象限，求m 、n 的取值范围.【答案与解析】解：（1）240m +>，即m ＞－2，n 为任何实数时，y 随x 的增大而增大；（2）当m 、n 是满足24030m n +≠⎧⎨-=⎩即23m n ≠-⎧⎨=⎩时，函数图象经过原点；（3）若图象经过一、二、三象限，则24030mn+>⎧⎨->⎩，即23mn>-⎧⎨<⎩．【总结升华】一次函数y kx b=+的图象有四种情况：①当k＞0，b＞0时，函数y kx b=+的图象经过第一、二、三象限，y的值随x 的值增大而增大；②当k＞0，b＜0时，函数y kx b=+的图象经过第一、三、四象限，y的值随x 的值增大而增大；③当k＜0，b＞0时，函数y kx b=+的图象经过第一、二、四象限，y的值随x 的值增大而减小；④当k＜0，b＜0时，函数y kx b=+的图象经过第二、三、四象限，y的值随x 的值增大而减小．4、（2015春•咸丰县期末）已知点A（4，0）及在第一象限的动点P（x，y），且x+y=5，0为坐标原点，设△OPA的面积为S．（1）求S关于x的函数解析式；（2）求x的取值范围；（3）当S=4时，求P点的坐标．【思路点拨】（1）根据题意画出图形，由x+y=5可知y=5﹣x，再由三角形的面积公式即可得出结论；（2）由点P（x，y）在第一象限，且x+y=5得出x的取值范围即可；（3）把S=4代入（1）中的关系式求出x的值，进而可得出y的值．【答案与解析】解：（1）如图所示，∵x+y=5，∴y=5﹣x，∴S=×4×（5﹣x）=10﹣2x；（2）∵点P（x，y）在第一象限，且x+y=5，∴0＜x＜5；（3）∵由（1）知，S=10﹣2x，∴10﹣2x=4，解得x=3，∴y=2，∴P（3，2）．【总结升华】本题考查的是一次函数的性质，根据题意画出图形，利用数形结合求解是解答此题的关键．举一反三：【变式】函数(0)y kx k k =+≠在直角坐标系中的图象可能是（）．【答案】B ；提示：不论k 为正还是为负，k 都大于0，图象应该交于x 轴上方,故选B.。

部编数学八年级下册专题06特殊平行四边形的两种考法全攻略(解析版)含答案

专题06 特殊平行四边形的两种考法全攻略类型一、最值问题例1．（将军饮马）如图，在菱形ABCD 中，120ABC Ð=°，E 是AB 边的中点，P 是AC 边上一动点，PB PE +PE 的最小值为（）A ．2B C ．1D ．0.5由菱形的对角线互相垂直平分，可得B 、∴1602ABD ABC Ð=Ð=°，PE PB PE +=即DE 就是PB PE +的最小值，例2．（中点模型）如图，矩形,2,4ABCD AB BC ==，点A 在x 轴正半轴上，点D 在y 轴正半轴上，当点A 在x 轴上运动时，点D 也随之在y 轴上运动，在这个运动过程中，点C 到原点O 的最大距离为（）A ．2B ．2C 1D ．【答案】A 【详解】如图，取AD 的中点H ，连接CH ，OH ，Q 矩形ABCD ，2AB =，4BC =，2CD AB \==，4AD BC ==，例3．（截补模型）如图，在Rt ABC △中，90C =o ∠，2AC BC ==，点D 、E 分别是边BC 、AC 上的动点．且BD CE =，连接AD 、BE ，则AD BE +的最小值为______．∵90ACB Ð=°，AC =∴90FBD ACB Ð=Ð=∵BD CE =，∴(SAS BDF CEB ≌△△AC=，以BC为对角线作正方形BDCE，连例4．（瓜豆模型）如图，平面内三点A，B，C，4AB=，3接AD，则AD的最大值是______．【变式训练1】如图，矩形ABCD 中，84AB AD ==，，E 为AB 的中点，F 为EC 上一动点，P 为DF 中点，连接PB ，则PB 的最小值是___________．当点F 与点C 重合时，点P 在1P 当点F 与点E 重合时，点P 在2P ∴PP EC ∥且1PP CE =．【变式训练2】如图，已知线段12AB =，点C 在线段AB 上，且ACD V 是边长为4的等边三角形，以CD 为边的右侧作矩形CDEF ，连接DF ，点M 是DF 的中点，连接MB ，则线段MB 的最小值为_______________．【答案】6【详解】∵ACD V 为等边三角形，∴AC AD =，60DAC Ð=°，∵四边形DCFE 是矩形，点M 是DF 的中点，∴DM ＝CM ，【变式训练3】如图，在正方形ABCD 中，边长2AB =，点Q 是边CD 的中点，点P 是线段AC 上的动点，则DP PQ +的最小值为 _____．【变式训练4】如图，在菱形ABCD 中，10AB =，16AC =，点M ，N 在AC 上，且2MN =，连接BM ，DN ，则BM DN +的最小值为 ______【变式训练5】如图，在Rt ABC △中，90BAC Ð=°，且3BA =，4AC =，点D 是斜边BC 上的一个动点，过点D 分别作DM AB ^于点M ，DN AC ^于点N ，连接MN ，则线段MN 的最小值为_____．类型二、动点问题例1．如图，在正方形ABCD中，E为AB的中点，以A为原点，AB、AD所在直线为x轴、y轴，建立平－向点D运动，面直角坐标系．正方形ABCD的边长是方程28160-+=的根．点P从点B出发，沿BC CDx x-向点C运动，点P的速度是每秒2个单位长度，点Q的速度是每秒1个同时点Q从点E出发，沿EB BC△的面积为单位长度．当点P运动到点D时，P、Q两点同时停止运动，设点P运动的时间为t秒，AQPS．(1)求点C的坐标；(2)求S关于t的函数关系式；△是以AP为底边的等腰三角形时，直接写出点P的坐标．(3)当AQP由题意得：EQ t =，2BP t =，∴2AQ AE EQ t =+=+，2BQ t =-，2222222(2)44,(2)(2)AQ t t t PQ BP t t \=+=+++=-+2544t t =-+当AQ PQ =时，22AQ PQ =，∴2244544t t t t ++=-+，解得0=t (舍去)或2，∴4BP =，∴当0t 2££，AQP △是以AP 为底边的等腰三角形时，()44P ，；②24t <£时，如图：由题意得：EB BQ t +=，2BC CP t +=，∴2BQ t BE t =-=-，6CQ BC BE t t =+-=-，224CP t BC t =-=-，282PD BC CD t t =+-=-，22224(2)AQ AB BQ t \=+=+-2420t t =-+2222(6)PQ CQ CP t =+=-22(24)52852t t t +-=-+当AQ PQ =时，22AQ PQ =，∴2242052852t t t t -+=-+，解得2t =(舍去)或4，∴0DP =，∴()04P ，；∴当24t <£，AQP △是以AP 为底边的等腰三角形时，()04P ，，综上所述，当AQP △是以AP 为底边的等腰三角形时，点P 的坐标为()44，或()04，例2.如图，在长方形ABCD 中，4AB =，3BC =，点E 为AD 延长线上一点，且6AE =，点P 从点A 出发，沿A —B —C —D 向终点D 运动．同时点Q 从点B 出发，沿B —C —D —E 向终点E 运动，它们的速度均为每秒1个单位长度．设APQ △的面积为S ，点P 运动的时间为t 秒．(1)当2t =时，S = ；当72t =时，S = ．(2)当07t <£时，用含t 的代数式表示S ．直接写出结果并化简．(3)当点P 在CD 边上，且APQ △为等腰三角形时，直接写出t 的取值或者范围．【变式训练1】如图，在ABCD Y 中，ABC Ð为锐角，5AB =，9BC =，36ABCD S =Y ．动点P 从点A 出发，以每秒2个单位的速度沿A B C D A ®®®®运动．同时，动点Q 从点A 出发，以每秒3个单位的速度沿A D C B A ®®®®运动．当其中一个点到达终点时，另一个点也随之停止运动．设点P 的运动时间为t 秒．(1)点P 在BC 上运动时，CP =_____________；点P 在CD 上运动时，CP =_____________．（用含t 的代数式表示）(2)点P 在CD 上，PQ BC ∥时，求t 的值．(3)当直线PQ 平分ABCD Y 的面积时，求t 的值．(4)若点Q 的运动速度改变为每秒a 个单位．当972t << ，ABCD Y 的某两个顶点与P 、Q 所围成的四边形为菱形时，直接写出a 的值．【变式训练2】如图，长方形ABCD 中，AD BC ∥，90B Ð=°，104AD BC cm AB cm ===，，动点P 从点B 出发，以每秒1cm 的速度沿B A D ®®的方向，向终点D 运动；动点Q 从点B 出发以每秒1cm 的速度沿B C ®的方向向终点C 运动．以PQ 为边向右上方作正方形PQMN ，其中一个动点到达终点时，另一个动点也随之停止运动，设点P Q 、同时出发，运动时间为t 秒0t （＞）．(1)当04t ＜＜时，AP ＝______（用含t 的代数式表示）；(2)当点N 落在AD 边上时，求t 的值；(3)当正方形PQMN 与长方形ABCD 的重叠部分为四边形时，求重叠部分的面积S （用含t 的代数式表示）；(4)请直接写出当t满足什么条件时，正方形PQMN与长方形ABCD的重叠部分为三角形．如图3，当M 点运动到D 点处时，∵10214CQ t CQ PM PM t ===-﹣，，，∴2014t t -=-（1），解得6t =，∴当6t =时，正方形PQMN 与长方形ABCD 的重叠部分为三角形，∴46t ££时，正方形PQMN 与长方形ABCD 的重叠部分为三角形；如图4，当Q 点运动与C 点时，10t =，此时正方形PQMN 与长方形ABCD 的重叠部分为三角形；∴610t ＜＜时，正方形PQMN 与长方形ABCD 的重叠部分为四边形，如图5，【变式训练3】已知在矩形ABCD中，AB＝4，AD＝9，点M在AD上，且AM＝4，动点P从点B出发，以每秒1个单位长度的速度，沿B﹣C﹣D﹣A向终点A运动，运动时间为t秒．(1)当点P在BC边上时，BP＝，CP＝．（用含t的代数式表示）(2)点P在运动过程中，△ABP是直角三角形时，t的取值范围为．(3)点P在运动过程中，△DMP是等腰三角形时，t的值为．(4)连接CM，当点P在线段CM的垂直平分线上时，t的值为．【答案】(1)t，9﹣t(2)0＜t≤9或13≤t＜22(3)1或7或6.5当点P 在线段BC 上时，CP =MP =9-t ，PH =t -4，MH =4，∵△MPH 是直角三角形，∴2222MH PH PM CP +=＝即()()222449t t -=+-，∴t ＝4.9，当点P 在线段AD 上时，同法可得PM ＝CPCP =MP =18-t ，DP =t -13，CD =4∵△CDP 是直角三角形，∴2222CD DP PM CP +=＝即()()22241318t t =+--，∴t ＝13.9．综上所述，满足条件的t 的值为4.9或13.9．故答案为：4.9或13.9．。

2023八年级数学下册平行四边形压轴题人教版

第一部分：引言在2023年的八年级数学下册中，平行四边形压轴题成为了人教版教材中的一个重要内容。

平行四边形作为几何学中的重要概念，对于学生的数学思维能力和几何直觉的培养起着至关重要的作用。

在本文中，我们将深入探讨2023年八年级数学下册中关于平行四边形的压轴题，并从简单到复杂逐步展开，帮助读者全面理解这一重要概念。

第二部分：基本概念1. 什么是平行四边形？在几何学中，平行四边形是指具有两组对边分别平行的四边形。

它具有一些特殊的性质和定理，是几何学中一个重要且基础的概念。

2. 平行四边形的性质平行四边形有多项重要性质，例如对边平行、对角线相等、对角线互相平分等。

这些性质是我们学习和应用平行四边形时的重要依据。

第三部分：2023年八年级数学下册平行四边形压轴题在本部分，我们将结合具体的题目，深入探讨2023年八年级数学下册中的平行四边形压轴题。

通过逐一分析题目，我们将帮助读者更好地理解平行四边形的相关知识。

1. 题目一：已知ABCD是平行四边形，AC的中点为E，连接BE，证明BE是平行四边形AD的一条对角线。

这道题目要求我们运用平行四边形的基本性质和定理，结合中点定理和平行线的性质来进行证明。

通过对角线的平行性质的理解和运用，我们可以得出BE是平行四边形AD的一条对角线的结论。

2. 题目二：如图，在平行四边形ABCD中，E,F,G,H分别是AB,BC,CD,AD的中点，连接EG，FH，证明EG=FH。

这道题目要求我们利用中点定理和平行四边形的性质来进行证明。

通过对平行四边形中点连线的性质的理解和应用，我们可以得出EG=FH 的结论。

第四部分：总结与回顾平行四边形作为数学中的一个重要概念，其性质和定理对于我们理解几何学和数学的其他分支起着重要的作用。

在2023年的八年级数学下册中，关于平行四边形的压轴题也进一步考察了学生对于这一概念的理解和运用能力。

通过本文的深入探讨，相信读者对于平行四边形的相关知识已经有了更深入的了解与掌握。

《特殊平行四边形》初中八年级下册数学教案教学设计课后反思人教版

附件2:柳江区2018年中考复习备考赛教活动教学设计学校：执教教师：教学过程教学环节教师活动学生活动设计意图环节一：（8分钟）一、展示学习目标二、复习特殊平行四边形的定义：三、复习特殊平行四边形的性质：四、复习特殊平行四边形的判定方法全体齐读学生在老师引导下口答并理解，学生在老师引导下口答并理解，学生在老师引导下口答并理解，让学生知道这节课要达到的目标让学生能系统地复习特殊平行四边形定义，了解平行四边形与矩形、菱形、正方形的关系，让学生能系统地复习特殊平行四边形性质，了解平行四边形与矩形、菱形、正方形的关系，让学生能系统地复习特殊平行四边形判定方法，了解平行四边形与矩形、菱形、正方形的关系，环节二：（7分钟）一、课堂自主练习，师巡视指导有困难的学生。

1. 矩形具有而一般的平行四边形不具有的性质是 ( )A.对角相等B.对边相等C.对角线相等D.对角线互相平分2.如图，要使平行四边形ABCD成为菱形，需要添加的条件是( )A．AC＝BD B．AD＝BCC．AB＝CD D．AB＝BC3．如图，已知正方形的边长为4㎝，则其对角线长是（）A．8cm B．16 cmC．32 cm D．4 cm4．[2017·衡阳]如图，菱形的两条对角线分别是12和16，则此菱形的边长是( )A．10 B．8C．6 D．55．（2017甘肃兰州）如图，矩形ABCD的对角线AC与BD交于点O, ∠ADB＝30°,AB＝4,则OC的长为（）A．2 B．4C．4 D．6学生结合矩形知识，独立做题学生结合正方形知识，独立做题学生结合菱形知识，独立做题学生结合菱形知识，独立做题学生结合矩形知识，独立做题检测学生是否掌握柜形的性质检测学生是否掌握正方形的性质检测学生是否掌握菱形的判定方法检测学生是否掌握菱形的性质检测学生是否能用柜形的性质来解决计算方面的问题环节三（15分钟）一、例题：1、[2017·百色] 如图，在矩形ABCD中，E，F分别是AD，BC的中点，CE，AF分别交DB于G，H两点．求证：(1)四边形AFCE是平行四边形；(2)EG＝HF.小组合作交流经历分析、推理、验证等过程，让学生掌握研究解决几何证明题的一般思路二、知识巩固：1：如图，在▱ABCD中，E，F分别是AB，DC边上的点，且AE＝CF，∠DEB＝90°，求证：四边形DEBF是矩形．做练习训练学生的分析、推理思维的能力环节四（2分钟）一、归纳小结让学生谈谈自己在这堂课上的收获或是说学到了什么。

八年级(下)数学同步讲义四边形的存在性(解析版)

本节包含两部分，平行四边形的存在性及梯形的存在性，常见题型是存在菱形和正方形，根据题目中的条件及特殊的平行四边形的性质构造等量关系，求出相应的点的坐标；常见的梯形的问题中，经常需要添加辅助线．考察学生的分类讨论思想及逻辑思维能力．平行四边形的问题是近几年来考试的热点，考察学生的分类讨论的思想．常见的题型是在平面直角坐标系中已知三点和第四点构成平行四边形，求第四点；或者已知两点，另外两点在某函数图像上，四点构成平行四边形；利用两点间的距离公式和平移的思想，结合题目中的条件构造等量关系．四边形的存在性内容分析知识结构模块一：平行四边形的存在性知识精讲2 / 28【例1】如图所示，在梯形ABCD 中，AD ∥BC ，∠B =90°，AD =24 cm ，BC =26 cm ，动点P 从点A 出发沿AD 方向向点D 以1cm /s 的速度运动，动点Q 从点C 开始沿着CB 方向向点B 以3cm /s 的速度运动．点P 、Q 分别从点A 和点C 同时出发，当其中一点到达端点时，另一点随之停止运动．（1）经过多长时间，四边形PQCD 是平行四边形；（2）经过多长时间，四边形PQBA 是矩形．【解析】（1）,x PQCD 设经过秒后，四边形为平行四边形,243,66.PD CQ x x x PQCD ∴=∴-=∴=∴，经过秒后四边形是平行四边形（2）y PQBA 设经过秒后,四边形为矩形, ,263,13,2132AP BQ y y y PQBA ∴=∴=-∴=∴设经过秒后,四边形为矩形.【总结】本题主要考查了平行四边形和矩形的判定．例题解析【例2】如图，在平面直角坐标系中，点A 的坐标为A (3， 0)，点B 的坐标为A (0， 4)．（1）求直线AB 的解析式；（2）点C 是线段AB 上一点，点O 为坐标原点，点D 在第二象限，且四边形BCOD 为菱形，求点D 坐标；（3）在（2）的条件下，点E 在x 轴上，点P 在直线AB 上，且以B 、D 、E 、P 为顶点的四边形是平行四边形，请写出所有满足条件的点P 的坐标．【解析】（1）,AB y kx b =+设直线的解析式为3044344- 4.3k b b k b AB y x +=⎧∴⎨=⎩⎧=-⎪∴⎨⎪=⎩∴=+直线的解析式为（2）,BCOD 四边形是菱形 ,,(0,2),2,4324,,323(,2),23(-,2).2OB CD OB CD OB C y y x x C D ∴⊥∴==-+=∴∴且与互相平分的中点坐标为点的纵坐标是把代入得点坐标为点坐标为（3）339(6)(,2)(,2).222P --点的坐标为，或或【总结】本题主要考查了用待定系数法求一次函数解析式，菱形的性质及平行四边形的判定和性质．ABOxy4 / 28【例3】如图已知点A (m ，6)和点B (6，2)（点B 在点A 的右侧）在反比例函数的图像上，直线BC //x 轴，与y 轴交于点C ．（1）求m 的值及直线AC 的解析式；（2）如果点D 在x 轴的正半轴上，点E 在反比例函数的图像上，当四边形ACDE 是平行四边形时，求CD 的长．【解析】（1）,ky x=设反比例函数解析式为12(6,2),12,,6,2,,(0,2),,(2,6),(0,2)2222;B k y xy m BC x C AC y kx b A C k b AC y x =∴===∴=+=⎧⎨=⎩∴=+将代入解析式得当时得∥轴点坐标为设直线的解析式为将代入得：直线的解析式为（2）,,,AC x G EH x H ⊥延长交轴于作轴垂足为 ,,,,,,,,,,,90,,90,,,(),A AN x x N BC M ACDE AC DE AGO EDH BC x AGO ACM ACM EDH AN x AN BC AMC EH x EHD AMC EHD AMC EDH AMC EHD ACM EDH AC ED AMC EDH AAS ⊥∴∴∠=∠∴∠=∠∴∠=∠⊥∴⊥∴∠=︒⊥∴∠=︒∴∠=∠∆∆∠=∠⎧⎪∠=∠⎨⎪=⎩∴∆≅∆过点作轴交轴于点交于点四边形为平行四边形∥∥轴轴轴在和中2224,2,412,3,(3,4),3,1,21 5.AM EH CM DH E E y xx E OH OD OH DH CD OC OD ∴====∴=∴=∴∴==-=∴=+=+=点纵坐标为，在反比例函数图像上点坐标为【总结】本题主要考查了用待定系数法求反比例函数和一次函数解析式，全等三角形的判定和性质及平行四边形的性质．【例4】如图，在平面直角坐标系中，过点(2，3)的直线y ＝kx ＋2与x 轴交于点A ，与y 轴AB C D EOxyG HN M交于点B ，将此直线向下平移3个单位，所得到的直线l 与x 轴交于点C ．（1）求直线l 的表达式；（2）点D 为该平面直角坐标系内的点，如果以点A 、B 、C 、D 为顶点的四边形是平行四边形，求点D 的坐标．【解析】（1）1(2,3)2,,2y kx k =+=将代入得12,2(4,0),(0,2),131,211;2y x A B y x l y x ∴=+∴-=-∴=-向下平移个单位，得直线的表达式为（2）11,2y x =- (2,0),,(6,2),,(2,2),,(6,2).C ABD AC D BC D ∴---点坐标为当为对角线时点坐标为当为对角线时点坐标为当为对角线时点坐标为【总结】本题主要考查了一次函数图像的平移及平行四边形的性质和判定．【例5】如图，已知直线l 1经过点A (－5，－6)且与直线l 2：362y x =-+平行，直线l 2与x轴、y 轴分别交于点B 、C ．（1）求直线l 1的表达式及其与x 轴的交点D 的坐标；（2）判断四边形ABCD 是什么四边形．并证明你的结论；（3）若点E 是直线AB 上一点，平面内存在一点F ，使得四边形CBEF 是正方形，求点E 的坐标，请直接写出答案．xABOyC6 / 28【解析】（1）1,l y kx b =+设直线解析式为（2）236,2l y x =-+为22222222220,6,(0,6),0,4,(4,0),22,,33,,,69117,6452,169,,90,;DC AB x y C y x B k k AB DC AD BC ABCD DC BC BD BD DC BC BCD ABCD ==∴==∴∴==∴∴=+==+==∴=+∴∠=︒∴当时点坐标为当时点坐标为∥∥四边形为平行四边形四边形是矩形（3）,E EG x x G ⊥过点作轴交轴于点 90,,90,,90,90,,,90,(),,,(10,4),(2,4).BGE CBEF CBE CB BE OCB OBC OBC EBG OCB EBG CB BE COB BGE COB BGE AAS OB EG CO BG E B E E B E ∴∠=︒∴∠=︒=∠+∠=︒∠+∠=︒∴∠=∠=∠==︒∴∆≅∆∴==--正方形当点在点右侧时，点坐标为当点在点左侧时，点坐标为【总结】本题主要考查了用待定系数法求一次函数解析式，矩形的判定及正方形的判定和性质．G E BADxO yC F1136,23,2(56),36(5),227,2327,220,9,(9,0);l y x k l A b b y x y x D =-+∴=---∴-=-⨯-+∴=-∴=--==-∴-与平行经过点，当时点坐标为【例6】直线364y x =-+与坐标轴分别交与点A 、B 两点，点P 、Q 同时从O 点出发，同时到达A 点，运动停止．点Q 沿线段OA 运动，速度为每秒1个单位长度，点P 沿O B A →→运动．（1）直接写出A 、B 两点的坐标；（2）设点Q 的运动时间为t 秒，△OPQ 的面积为S ，求出S 与t 之间的函数关系式．（3）当485S =时，求出点P 的坐标，并直接写出以点O 、P 、Q 为顶点的平行四边形的第四个顶点M 的坐标．【解析】（1）(8,0),(0,6);A B（2）8,6,OA OB == 2210,88,16102(/),803,,2,38,,6102162,,,11244868(162),,22551324,.255AB Q O A P P OB t OQ t OP t S t P BA t OQ t AP t t P PD OA D t PD t PD S OQ PD t t ∴==+∴=≤≤===≤==+-=-⊥-⨯⨯=⨯⨯-∴=∴=⋅=-+点由到的时间是（秒）点的速度是单位长度秒当在线段上运动（即）时当在线段上运动（即＜）时如图过点作于点（3）48,5S =当时 22248136,,5232448,4,5554864242432,16248,8(),55553288248,(,),5555282412241224(,),(,),(,).555555P AB t t t PD AP AD OD P M >⨯⨯∴∴-+=∴=-⨯∴===-⨯==-=∴=-=∴∴--点在上点坐标为点坐标为【总结】本题主要考查了一次函数的图像和性质及平行四边形的判定和性质．8 / 28【例7】已知：如图，四边形ABCD 是菱形，∠B 是锐角，AF ⊥BC 于点F ， CH ⊥AD 于点H ，在AB 边上取点E ，使得AE ＝AH ，在CD 边上取点G ，使得CG ＝CF ．联结EF 、FG 、GH 、HE ．（1）求证：四边形EFGH 是矩形；（2）当∠B 为多少度时，四边形EFGH 是正方形．并证明．【答案】见解析．【解析】（1）,,BD FH 如图，连结,,,,,,,,,(),,,,,,,,ABCD AD BC BAD BCD ABC ADC AF BC CH AD AF AD CH BC AFCH AH CF AE CG AEH FCG SAS EH FG EF HG EFGH BE BF AE AH AEH AHE BEF BFE AEH AHE BEF BFE ABC ∴∠=∠∠=∠⊥⊥∴⊥⊥∴∴===∴∆≅∆∴==∴==∴∠=∠∠=∠∠+∠+∠+∠+∠+∠四边形是菱形∥四边形为矩形，同理可证：四边形是平行四边形360,BAD =︒,180,90,90,AD BC ABC BAD BEF AEH FEH EFGH ∴∠+∠=︒∴∠+∠=︒∴∠=︒∴∥四边形是平行四边形.（2）45,;B EFGH ∠当等于度时四边形是正方形 ,,,,,,180,180,,,,,45,,,180451352AC ABCD AB BC BAC ACB AE CF BE BF BEF BFE BAC ACB ABC BEF BFE ABC BAC BEF EF AC EFH FOC EFGH EFH FOC AFCH OF OC OFC OCF ∴=∴∠=∠=∴=∴∠=∠∠+∠+∠=︒∠+∠+∠=︒∴∠=∠∴∴∠=∠∴∠=︒=∠∴=︒-︒∴∠=∠==连接与FH 相交于Ｏ点菱形∥正方形四边形是矩形2135,,135,2,180,45,45ABCD AB CD OCF OCD BCD AB CD ABC BCD ABC B EFGH ︒︒∴∠==∴∠=︒∴∠+∠=︒∴∠=︒∴∠，菱形∥，∥等于度时，四边形是正方形．【总结】本题主要考查了菱形的性质，矩形的判定和性质及正方形的性质．A BCDEFGH O【例8】如图所示，平面直角坐标系中，O 是坐标原点，正比例函数y =kx （x 为自变量）的图像与双曲线2y x=-交于点A ，且点A 的横坐标为2-．（1）求k 的值；（2）将直线y =kx （x 为自变量）向上平移4个单位得到直线BC ，直线BC 分别交x 轴、y 轴于B 、C ，如点D 在直线BC 上，在平面直角坐标系中求一点P ，使以O 、B 、D 、P 为顶点的四边形是菱形．【解析】（1）2,A -点的横坐标为 2,2 2(2,2)22,1;y y A k k =--∴=∴-∴=-∴=-由题意得：，，（2）4,BC y x =-+直线的解析式： 1 1122 33444,45,,, 4(422,22),(2222),:(422)(22,22)(04),(44), (22),(22)(2222)(22,22)(44)(22).OB OC OBC OBDP OB BD DP PO BD D P D P D P D P P ∴==∴∠=︒∴===∴=-∴-+-----四边形是菱形，由勾股定理可以求出，同理可得，，，，，，，综上所述点坐标为，或或，或，【总结】本题主要考查了一次函数与反比例函数的交点坐标等关系及菱形的判定和性质．ABC Oxy10 / 28【例9】在直角△ABC 中，∠C =90°，∠A =30°，AB =4，将一个30°角的顶点P 放在AB边上滑动，保持30°角的一边平行于BC ，且交边AC 于点E ，30°的另一边交射线BC 于点D ，连ED ．（1）如图，当四边形PBDE 为等腰梯形时，求AP 长；（2）四边形PBDE 有可能为平行四边形吗．若可能，求出PBDE 为平行四边形时，AP 的长，若不可能，说明理由；（3）若点D 在BC 边上（不与B 、C 重合），试写出线段AP 的取值范围．【解析】（1）90,30,C A ∠=︒∠=︒ ,60,30,603030,,30,22,28.36,30PBDE ED PB BDE B PE BC BDP DPE EDP DPE PE ED PB A AP PE PB AP AB B ∴=∠=∠=︒∴∠=∠=︒∴∠=︒-︒=︒=∠∴∠∴===︒∠=︒∴==∴==若是等腰梯形,，∥ （2）D BC PBDE 当点位于线段上时，有可能为平行四边形, 180603090,224,416.55PDE DPB AP PE BD PB AP AB ∠=∠=︒-︒-︒=︒∴===∴==这时（3）D C 当与重合时，24,33,4,4,3 4.AB BC PB AP AB D B AP AP ==∴==∴<<当点趋于点时趋于【总结】本题主要考查了等腰梯形和平行四边形的判定和性质．ABC DEP梯形的分类讨论题多见于各类压轴题中，由于这类题目都与图形的运动有关，需要学生有一定的想象力、分析力和运算力．梯形的主要特征是两底平行，特殊梯形又可分为等腰梯形和直角梯形两大类．常见题型为在直角坐标平面内已知三点求第四点，抓住梯形两底平行的特征，对应的一次函数的解析式的k 相等而b 不相等．若是等腰梯形，常需添设辅助线，过上底的两个顶点作下底的垂线，构造两个全等的直角三角形．若是直角梯形，则需连接对角线或过上底的一顶点作下底的高构造直角三角形．【例10】在梯形ABCD 中，AD ∥BC ，AD =12cm ，DC =8cm ，且∠C =60°，动点P 以1cm/s的速度从点A 出发，沿AD 方向向点D 移动，同时，动点Q 以2cm /s 的速度从点C 出发，沿CB 方向向点B 移动，连接PQ ，（1）得四边形ABQP 和四边形PQCD ．若设移动的时间为t 秒（0＜t ＜7），四边形PQCD 的面积为ycm ²，求y 与t 的函数关系式；（2）当t 为何值时，四边形PQCD 是等腰梯形．说明理由；（3）当t 为何值时，四边形PQCD 是直角梯形．【解析】（1）,D DE BC BC E ⊥过点作交于点860,434,2,12,1(122)432324 3.2PQCD DC C DE EC t AP t CQ t PD t S t t t =∠=︒∴====∴=-∴=-+⋅=+，，，时间为时，（2）,PQCD 当四边形为等腰梯形时2,CQ CE PD =+202812,.3t t t ∴=+-∴=（3）,PQCD 当四边形是直角梯形时CQ CE PD =+162412-,.3t t t ∴=+∴=【总结】本题主要考查了等腰梯形和直角梯形的性质和判定．模块二：梯形的存在性知识精讲例题解析Q PB CDAE12 / 28【例11】如图，已知(1)A m -，与(233)B m +，是反比例函数ky x=图像上的两个点．（1）求k 的值；（2）若点(10)C -，，则在反比例函数ky x=图像上是否存在点D ，使得以A 、B 、C 、D 为顶点的四边形是梯形．若存在，请直接写出点D 的坐标；若不存在，请说明理由．【解析】（1）,A B 在反比例函数上,3322323m kk m m k =-⎧⎪∴⎨+=⎪⎩⎧=-⎪∴⎨=⎪⎩ （2）3(6,)(1,23)(-2,-3).3D 点坐标为或或【总结】本题主要考查了反比例函数的图像和性质与四边形性质的结合运用．A BC ．O xy【例12】如图，一次函数33y x b =+的图像与x 轴相交于点A (53，0)、与y 轴相交于点B ．（1）求点B 的坐标及∠ABO 的度数；（2）如果点C 的坐标为（0，3），四边形ABCD 是直角梯形，求点D 的坐标【解析】（1）3(53,0),5,3A y x b b =+=-将点带入得 35,3(0,-5),5,10,60.y x B OB AB ABO ∴=-∴∴==∴∠=︒点坐标为（2）ABCD 四边形是直角梯形， ,,-3,015,15,-315,33,3333-315336(33,6),,(53,3),(33,6)(53,3).D CD AD AB A AB y x c c c y x C AB y x y x y x x y D BC AD BC D D ∴∴⊥=+∴=-+∴=∴=+=+⎧=+⎪∴⎨⎪=+⎩⎧=⎪∴⎨=⎪⎩∴∴是直角顶点，当为底边时设过点且与垂直的直线解析式为过与平行的直线解析式为点坐标为当为底边时，∥点坐标为综上所述点坐标为或【总结】本题主要考查了用待定系数法求一次函数解析式及直角梯形的性质的判定．ABCO xy14 / 28【例13】如图，在平行四边形ABCD 中，O 为对角线的交点，点G 为BC 的中点，点E 为线段BC 延长线上的一点，且CE ＝12BC ，过点E 作EF //CA ，交CD 于点F ，联结OF ．（1）求证：OF //BC ；（2）如果四边形OBEF 是等腰梯形，判断四边形ABCD 的形状，并给出证明．【解析】（1）,EF AD M 延长交于,,,,1,21122,ABCD AD BC AD BC EF CA ACEM AM CE CE BC AD BC AM CE BC AD MD AD BC ADC ECF CEF DMF CFE DFM ADC ECF CE MD CEF DMF AAS CF DF ABCD OB OD OF BC ∴=∴∴===∴====∴∠=∠∆∆∠=∠⎧⎪∠=∠⎨⎪=⎩∴∆≅∆∴=∴=∴在平行四边形中，∥∥四边形是平行四边形，，，∥，，在和中，（）,，四边形是平行四边形，∥．（2）;OBEF ABCD 如果四边形是等腰梯形，那么四边形是矩形 ,,2,2,,.OF CE EF CO OCEF EF OC OBEF BO EF OB OC ABCD AC OC BD BO AC BD ABCD ∴∴=∴=∴=∴==∴=∴∥∥四边形是平行四边形，，四边形是等腰梯形，，，四边形是平行四边形，四边形是矩形【总结】本题主要考查了平行四边形的判定和性质及等腰梯形的判定和性质．ABC DEFG OM【例14】如图，在平面直角坐标系中，直线l 1经过O 、A (1，2)两点，将直线l 1向下平移6个单位得到直线l 2，交x 轴于点C ，B 是直线l 2上一点，且四边形ABCO 是平行四边形．（1）求直线l 2的表达式及点B 的坐标；（2）若D 是平面直角坐标系内的一点，且以O 、A 、C 、D 四个点为顶点的四边形是等腰梯形，求点D 的坐标．【解析】（1）1,l y kx =设直线解析式为2(12),2,2,2-6,(3,0),,2,22-6,4,(4,2).A k y x l y x C ABCOB x x B ∴=∴=∴=∴∴∴=∴=∴过点，解析式为点坐标为四边形是平行四边形点纵坐标为点坐标（2）AD OC 当∥时， 1112222,,2,(2,2),-3,,(,),,1,(1,1),(,26),,14,5142(,),55142(2,2)(1,1)(,).55D A A O C D D y y x x x x x D OD AC AC y x OD y x D a a AO CD a D OD AC D a a AC OD a D D ==-=-∴=∴=+∴=--=∴=∴--=∴=∴---点坐标为当时，解析为解析式为设点坐标为点坐标为当时，设点坐标为点坐标为综上所述点坐标为或或【总结】本题主要考查了用待定系数法求一次函数解析式及等腰梯形的性质．A OCxy16 / 28【例15】已知一次函数142y x =-+的图像与x 轴、y 轴分别相交于点A 、B ，梯形AOBC 的边AC =5．（1）求点C 的坐标；（2）如果点A 、C 在一次函数y =kx +b （k 、b 为常数，且k <0）的图像上，求这个一次函数的解析式【解析】（1）14,,2y x x y A B -+一次函数＝的图象与轴、轴分别相交于点222128,08,4,5,8,5,45,84055,11,5,411,48,55,411,4A B AOBC OA OB AC AC OB C BC OA C x AC x x x C C ∴====∴-+-=∴==∴（）,（0,4）,在梯形中，当∥时（如图1），点的坐标为（）,当∥时（如图2），设点（）,（）（），这时点的坐标为（）或（）,点的坐标为（）或（）或（）；（2）,0A C y kx b k =+点在一次函数（＜）的图象上, 8,511,45,40,084543323432.33C k k b k bk b y x ∴=+⎧∴⎨=+⎩⎧=-⎪⎪∴⎨⎪=⎪⎩∴=-+点（）与（）都不符合题意，只有当为（）时，＜这个一次函数的解析式为【总结】本题主要考查了一次函数的综合运用及梯形的判定和性质．【例16】如图1，在平面直角坐标系中，已知点A (0，2)，点P 是x 轴上一动点，以线段AP为一边，在其一侧作等边三角形APQ ．当点P 运动到原点O 处时，记Q 的位置为B ．（1）求点B 的坐标；（2）当点P 在x 轴上运动（P 不与O 重合）时，求证：∠ABQ ＝90°；（3）是否存在点P ，使得以A 、O 、Q 、B 为顶点的四边形是梯形．若存在，请求出点P 的坐标；若不存在，请说明理由．【解析】（1）B BC x C ⊥过点作轴于点，0,2,,2,60301,3,3,1A AOB AB OB BOA BOC BC OC B ∆∴==∠=︒∴∠=︒∴==∴（）为等边三角形，，（）；（2）P x P O 当点在轴上运动（不与重合）时， 60,(),90,90PAQ OAB PAO QAB APO AQB AP AQPAO QAB AO AB APO AQB SAS ABQ AOP P x P O ABQ ∠=∠=︒∴∠=∠∆∆=⎧⎪∠=∠⎨⎪=⎩∴∆≅∆∴∠=∠=︒∴∠=︒，在和中，当点在轴上运动（不与重合）时，；ABOPQxy ABO xy图1备用图C18 / 28（3）2,Q B AB 由（）可知点总在过点且与垂直的直线上， ,, 90,60,23,2,3,-3,0;, AO BQ P x Q B AB OQ AOQB AB OQ BQO BOQ ABO OB OA BQ APO AQB OP BQ P P x Q B AQ OB AOBQ AQ OB ∠=︒∠=∠=︒===∆≅∆∴==∴∠可见与不平行①当点在轴负半轴上时，点在点的下方，此时，若∥四边形即是梯形，当∥时，，可求得由（）可知，此时的坐标为（）②当点在轴正半轴上时，点在的上方，此时，若∥四边形即是梯形，当∥时，9060?2,23,2,23,23,0;-3,023,0ABQ QAB ABO AB BQ APO AQB OP BQ P P =︒∠=∠=︒==∆≅∆∴==∴，．又可求得由（）可知，此时的坐标为（）综上，的坐标为（）或（）．【总结】本题主要考查了等边三角形的性质，全等三角形的判定和性质及梯形的性质．【例17】在直角平面内，O 为原点，点A 的坐标为（1，0），点C 的坐标为（0，4），直线CM ∥x 轴（如图所示）．点B 与点A 关于原点对称，直线y =x +b （b 为常数）经过点B ，且与直线CM 相交于点D ，连接OD ．（1）求b 的值和点D 的坐标；（2）设点P 在x 轴的正半轴上，若△POD 是等腰三角形，求点P 的坐标；（3）若动点P 在x 轴的正半轴上，以每秒2个单位长的速度向右运动；动点Q 在射线CM 上，且以每秒1个单位长的速度向右运动，若P 、Q 分别由O 点、C 点同时出发，问几秒后，以P 、Q 、O 、D 为顶点的四边形可以成为平行四边形；以P 、Q 、O 、D 为顶点的四边形是否可以成为等腰梯形．写出理由．【解析】（1）1,0B A 与（）关于原点对称，1,010,1,1,414,3,3,4B y x b B b b y x y x x D ∴-=+∴-+==∴=+=+==∴（）,过点，当时，（）；（2）,DE x E ⊥作轴于点 1112222223,4,5,5,5,0,5,3,6,6,0,,,,OE DE OD POD O OD x P OP OD P D DO x P DP DO DE OP P E OE OP P ==∴===∴==⊥∴==∴=∴则若△为等腰三角形，则有以下三种情况，①以为圆心，为半径作弧交轴的正半轴于点则（）②以为圆心，为半径作弧轴的正半轴于点则（）AOxMy CD20 / 28331233334,33,43(,2),233252,,428325,48250,625,0,6255,06,0,06,,OD K K OD x P OP DP OD y x KP y x b K b b y x y x P P P P P ===-+∴=-⨯+∴=∴=-+==∴∴③取的中点，过作的垂线交轴的正半轴于点则可求解析式为设解析式为过点当时，（）符合条件的点有三个,分别是（）,（）,（）;（3）,QD PO ∥,,,,,32,1,1,,,,,,,232,3(),232,3(),,,,P Q O D QD PO t t t P Q O D P Q O D OQ PD t t t t OD PQ t t t t P Q O D ∴-=∴=∴=+-=∴==+-=∴=∴当以为顶点的四边形是平行四边形时则∥秒后，以为顶点的四边形为平行四边形,当以为顶点的四边形为等腰梯形时当腰时，舍当腰时,舍以为顶点的四边形不能构成等腰梯形.【总结】本题主要考查了用待定系数法求一次函数解析式，等腰三角形、平行四边形和等腰梯形的性质．【习题1】如图，在平面直角坐标系中，函数y ＝2x ＋12的图像分别交x 轴、y 轴于A 、B两点．过点A 的直线交y 轴正半轴于点C ，且点C 为线段OB 的中点．（1）求直线AC 的表达式；（2）如果四边形ACPB 是平行四边形，求点P 的坐标．【拓展】如果以A 、C 、P 、B 为顶点的四边形是平行四边形，求点P 的坐标．【解析】（1）212,y x =+函数的解析式为6,00,120,6,6061,6,6;A B OB C AC y kx b b k b k b AM y x ∴-∴=+=⎧∴⎨=-+⎩∴==∴=+（）,（）,点C 为线段的中点,（）,设直线的解析式为：直线的解析式为：（2）,ACPB 四边形是平行四边形 ,,,,,6,6,18,6,18;PC AB PC AB PB AC PB AC P y Q PQB AOC PQ AO BQ CO QO QB OB P ∴==∆≅∆∴====∴=+=∴且∥且∥如图过点作轴的垂线，垂足为可证（）（3）,BC 当为对角线时(6,18),,(6,6),,(0,6),(6,18)(6,6)(6,6).P AB P AC P P --∴---点坐标为当为对角线时点坐标为当为对角线时点坐标为点坐标为或或【总结】本题主要考查了用待定系数法求一次函数解析式以及平行四边形的性质的判定．随堂检测AB COxy22 / 28【习题2】如图，在平面直角坐标系中，直线162y x =-+与y 轴交于点A ，与直线12y x =相交于点B ，点C 是线段OB 上的点，且△AOC 的面积为12．（1）求直线AC 的表达式；（2）设点P 为直线AC 上的一点，在平面内是否存在点Q ，使四边形OAPQ 为菱形，若存在，求点Q 的坐标，若不存在，请说明理由．【解析】（1）,AC y kx b =+设解析式为16,(0,6),216621321(6,3),,2112,612,4,24,2,(4,2),612466;AOC c c y x A y x x y y xB OB y x S x x x yC b k k b b y x ∆=-+∴⎧=-+⎪=⎧⎪∴⎨⎨=⎩⎪=⎪⎩∴∴==∴⨯⨯=∴===∴==-⎧⎧∴∴⎨⎨=+=⎩⎩∴=-+点坐标为，点坐标为解析式为当时点坐标为，（2）存在；6,(6,0),,45,62,626,(32,66,,2,32),(32,32),y x E AO OE AEO OAPQ OA AP PQ QO P A AC OA AP P P E OAE AE Q =-+∴∴=∠=======∠=︒∴=∴=-∴-∴-当四边形为菱形时，若在点右侧为45,6,(32,3.,2),OAP OQ P A OQ AP AO Q Q ∠=︒=-=∴∴∠若在点左侧∥ 当AO 时对角线时，P （3,3）Q （-3,3），综上当四边形OAPQ 是菱形时， (32,32)(32,32)3,3)Q --点坐标为或或（【总结】本题主要考查了用待定系数法求一次函数解析式以及菱形的性质．AB OxyC E【习题3】如图，已知在梯形ABCD 中，AD//BC ，∠B ＝90°，AD ＝24cm ，AB ＝8cm ，BC ＝26cm ，动点P 从A 点开始沿AD 边以1cm /s 的速度向D 运动，动点Q 从C 点开始沿CB 边以3 cm /s 的速度向B 运动，P 、Q 分别从A 、C 同时出发，当其中一点到端点时，另一点也随之停止运动．设运动时间为t 秒，当t 为何值时，线段PQ ＝CD ．【答案】见解析．【解析】,t PQ CD =设时间为秒，1243,6226242,432447,67,.DP CQ PQCD t t t DE CB E CE CB DA CQ DP PQCD PD QC t t t t PQ CD =-==⊥=-=-=∴-=≠--==∴=（）当时，四边形是平行四边形，此时解得：（秒）；（）作，为垂足，则当时，四边形为等腰梯形，且，此时（），解得：（秒）为秒或秒线段【总结】本题主要考查了平行四边形和等腰梯形的判定．【习题4】如图所示，正比例函数y =k 1x 和一次函数y =k 2x +b 的图像相交于点A （-3，4），且OB =35OA ．（1）求正比例函数和一次函数的解析式；（2）求△AOB 的面积和周长；（3）在平面直角坐标系中是否存在点P 、O 、A 、B 成为直角梯形的四个顶点．若存在，请直接写出P 点的坐标；若不存在，请说明理由．ABCDQ PABCDE24 / 28【解析】（1）1(3,4)A y k x -=把代入，122224,343(3,4),5,3,53,(3,0),(3,4),(3,0),034322322;3k y x A OA OB OA OB B A B y k x b k b k b b k y x =-∴=--∴==∴=∴-=+=+⎧⎨=-+⎩=⎧⎪∴⎨=-⎪⎩∴=-+得，把代入得（2）1436,2AOB S ∆=⨯⨯=213,5,3,8213.AOB AB AO OB C ∆===∴=+（3）2718513427136131313132525P 点坐标为（3,4）或（,-）或（-,）或（-,）. 【总结】本题主要考查了用待定系数法求函数解析式和一次函数图像的性质以及直角梯形的性质．【作业1】如图，在平面直角坐标系中，一次函数的图像与反比例函数的图像相交于A 、B两点，点A 的坐标为(2，3)，点B 的横坐标为6．（1）求反比例函数与一次函数的解析式；（2）如果点C 、D 分别在x 轴、y 轴上，四边形ABCD 是平行四边形，求直线CD 的表达式．【解析】（1）12,,k y y k x b x==+设反比例函数解析式为一次函数解析式为 11222(2,3),3,6,26,6,1,(6,1),163212414;2A kk y xx y B k b k b k b y x ∴=∴=∴===∴=+⎧∴⎨=+⎩⎧=-⎪∴⎨⎪=⎩∴=-+反比例函数解析式为当时一次函数解析式为（2）(23),(61),A B ，，2222225,,,25,1,2(0,),(2,0),(2)20,22,112 2.22AB ABCD ABp CD AB CD CD y x n D n C n Rt ODC OD OC DC n n n CD y x y x ∴=∴===-+∴∆+=∴+=∴=-∴=-+=--四边形是平行四边形∥设直线的解析式为在中，，或直线的解析式为或【总结】本题考查了一次函数在直角坐标系中的综合应用及平行四边形的判定和性质．ABOxy课后作业26 / 28【作业2】已知一条直线y =kx +b 在y 轴上的截距为2，它与x 轴、y 轴的交点分别为A 、B ，且△ABO 的面积为4．（1）求点A 的坐标；（2）若k <0，在直角坐标平面内有一点D ，使四边形ABOD 是一个梯形，且AD ∥BO ，其面积又等于20，试求点D 的坐标．【解析】（1）(,0),A x 设点坐标为2,(0,2),1124,224,(4,0)(-4,0);ABO b B S OA OB x x A ∆=∴=⨯⨯=⨯⨯=∴=±∴由题意得：点坐标为点坐标为或（2）0,k < (4,0),4,,,11()(2)420228(4,-8)48.ABOD A OA AD OB OB OA S OB AD OA AD AD D ∴∴=⊥∴=⨯+⨯=⨯+⨯=∴=∴梯形点坐标为∥，，点坐标为或（，）【总结】本题考查了一次函数在直角坐标系中的综合应用及梯形的判定问题．【作业3】定义[p ，q ]为一次函数y ＝px ＋q 的特征数．（1）若特征数为[3，k －1]的一次函数为正比例函数，求k 的值；（2）一次函数y ＝kx ＋b 的图像与x 轴交于点A (3-，0)，与y 轴交于点B ，且与正比例函数43y x =的图像的交点为C (m ，4)．求过A 、B 两点的一次函数的特征数；（3）在（2）的条件下，若点D 与A 、O 、C 构成的四边形为平行四边形，直接．．写出所有符合条件的点D 的坐标．【解析】（1）10,k -=由题意得：1;k ∴=（2）(3,0),A y kx b -=+把代入 :0-3,4(,4),3,3(3,4),(3,4),:43,0-34323222,32,2;3k b C m y x m C C y kx b k b k b k bk b y x =+==∴=+=+=+⎧∴⎨=+⎩⎧=⎪∴⎨⎪=⎩∴=+⎡⎤∴⎢⎥⎣⎦得把代入得：把代入得一次函数特征数为（3）(0,4)(6,4)(-6,-4).D 点坐标为或或【总结】本题主要考查的是学生的归纳总结及创新能力．AB COxy28 / 28【作业4】如图所示，直线y =-2x +12，分别与x 轴、y 轴交于点A 、B ，点C 是线段AB 的中点，点D 在线段OC 上，点D 的纵坐标是4．（1）求点C 的坐标和直线AD 的解析式；（2） P 是直线AD 上的点，请你找出一点Q ，使得以O 、A 、P 、Q 这四个点为顶点的四边形是菱形，写出所有满足条件的Q 的坐标．【解析】（1）212,y x =-+(6,0),(0,12),,(3,6),2,42,(2,4),,0642166;A B C AB C OC y x y x D AD y kx b k b k b k b y x ∴∴∴===∴=+=+⎧∴⎨=+⎩=-⎧∴⎨=⎩∴=-+是的中点坐标为解析式为当时，点坐标为设解析式为（2）,如图所示 111222333,(3,3),,(32,32),,(-32,32).OP AQ Q OAP Q Q AP Q O Q --当为菱形时当为菱形时当为菱形时【总结】本题主要考查了待定系数法求一次函数解析及菱形的性质．A BCD xy O。

2020—2021年人教版初中数学八年级下册中考试题汇编含精讲解析特殊的平行四边形3及答案(精品试题).docx

特殊的平行四边形3一．解答题（共10小题）1．（2015•酒泉）如图，平行四边形ABCD中，AB=3cm，BC=5cm，∠B=60°，G是CD的中点，E是边AD上的动点，EG的延长线与BC的延长线交于点F，连结CE，DF．（1）求证：四边形CEDF是平行四边形；（2）①当AE= cm时，四边形CEDF是矩形；②当AE= cm时，四边形CEDF是菱形．（直接写出答案，不需要说明理由）2．（2015•哈尔滨）如图1，▱ABCD中，点O是对角线AC的中点，EF过点O，与AD，BC分别相交于点E，F，GH过点O，与AB，CD 分别相交于点G，H，连接EG，FG，FH，EH．（1）求证：四边形EGFH是平行四边形；（2）如图2，若EF∥AB，GH∥BC，在不添加任何辅助线的情况下，请直接写出图2中与四边形AGHD面积相等的所有平行四边形（四边形AGHD除外）．3．（2015•扬州）如图，将▱ABCD沿过点A的直线l折叠，使点D落到AB边上的点D′处，折痕l交CD边于点E，连接BE．（1）求证：四边形BCED′是平行四边形；（2）若BE平分∠ABC，求证：AB2=AE2+BE2．4．（2015•桂林）如图，在▱ABCD中，E、F分别是AB、CD的中点．（1）求证：四边形EBFD为平行四边形；（2）对角线AC分别与DE、BF交于点M、N，求证：△ABN≌△CDM．5．（2015•乌鲁木齐）如图，▱ABCD中，点E，F在直线AC上（点E 在F左侧），BE∥DF．（1）求证：四边形BEDF是平行四边形；（2）若AB⊥AC，AB=4，BC=2，当四边形BEDF为矩形时，求线段AE的长．6．（2015•宿迁）如图，四边形ABCD中，∠A=∠ABC=90°，AD=1，BC=3，E是边CD的中点，连接BE并延长与AD的延长线相交于点F．（1）求证：四边形BDFC是平行四边形；（2）若△BCD是等腰三角形，求四边形BDFC的面积．7．（2015•遂宁）如图，▱ABCD中，点E，F在对角线BD上，且BE=DF，求证：（1）AE=CF；（2）四边形AECF是平行四边形．8．（2015•毕节市）如图，将▱ABCD的AD边延长至点E，使DE=AD，连接CE，F是BC边的中点，连接FD．（1）求证：四边形CEDF是平行四边形；（2）若AB=3，AD=4，∠A=60°，求CE的长．9．（2015•柳州）如图，在四边形ABCD中，AD∥BC，∠B=90°，AB=8cm，AD=12cm，BC=18cm，点P从点A出发以2cm/s的速度沿A→D→C 运动，点P从点A出发的同时点Q从点C出发，以1cm/s的速度向点B运动，当点P到达点C时，点Q也停止运动．设点P，Q运动的时间为t秒．（1）从运动开始，当t取何值时，PQ∥CD？（2）从运动开始，当t取何值时，△PQC为直角三角形？10．（2015•南通）如图，在▱ABCD中，点E，F分别在AB，DC上，且ED⊥DB，FB⊥BD．（1）求证：△AED≌△CFB；（2）若∠A=30°，∠DEB=45°，求证：DA=DF．18.2 特殊的平行四边形3参考答案与试题解析一．解答题（共10小题）1．（2015•酒泉）如图，平行四边形ABCD中，AB=3cm，BC=5cm，∠B=60°，G是CD的中点，E是边AD上的动点，EG的延长线与BC的延长线交于点F，连结CE，DF．（1）求证：四边形CEDF是平行四边形；（2）①当AE= 3.5 cm时，四边形CEDF是矩形；②当AE= 2 cm时，四边形CEDF是菱形．（直接写出答案，不需要说明理由）考点：平行四边形的判定与性质；菱形的判定；矩形的判定．专题：动点型．分析：（1）证△CFG≌△EDG，推出FG=EG，根据平行四边形的判定推出即可；（2）①求出△MBA≌△EDC，推出∠CED=∠AMB=90°，根据矩形的判定推出即可；②求出△CDE是等边三角形，推出CE=DE，根据菱形的判定推出即可．解答：（1）证明：∵四边形ABCD是平行四边形，∴CF∥ED，∴∠FCG=∠EDG，∵G是CD的中点，∴CG=DG，在△FCG和△EDG中，，∴△FCG≌△EDG（ASA）∴FG=EG，∵CG=DG，∴四边形CEDF是平行四边形；（2）①解：当AE=3.5时，平行四边形CEDF是矩形，理由是：过A作AM⊥BC于M，∵∠B=60°，AB=3，∴BM=1.5，∵四边形ABCD是平行四边形，∴∠CDA=∠B=60°，DC=AB=3，BC=AD=5，∵AE=3.5，∴DE=1.5=BM，在△MBA和△EDC中，，∴△MBA≌△EDC（SAS），∴∠CED=∠AMB=90°，∵四边形CEDF是平行四边形，∴四边形CEDF是矩形，故答案为：3.5；②当AE=2时，四边形CEDF是菱形，理由是：∵AD=5，AE=2，∴DE=3，∵CD=3，∠CDE=60°，∴△CDE是等边三角形，∴CE=DE，∵四边形CEDF是平行四边形，∴四边形CEDF是菱形，故答案为：2．点评：本题考查了平行四边形的性质和判定，菱形的判定，矩形的判定，等边三角形的性质和判定，全等三角形的性质和判定的应用，注意：有一组邻边相等的平行四边形是菱形，有一个角是直角的平行四边形是矩形．2．（2015•哈尔滨）如图1，▱ABCD中，点O是对角线AC的中点，EF过点O，与AD，BC分别相交于点E，F，GH过点O，与AB，CD 分别相交于点G，H，连接EG，FG，FH，EH．（1）求证：四边形EGFH是平行四边形；（2）如图2，若EF∥AB，GH∥BC，在不添加任何辅助线的情况下，请直接写出图2中与四边形AGHD面积相等的所有平行四边形（四边形AGHD除外）．考点：平行四边形的判定与性质；全等三角形的判定与性质．分析：（1）由四边形ABCD是平行四边形，得到AD∥BC，根据平行四边形的性质得到∠EAO=∠FCO，证出△OAE≌△OCF，得到OE=OF，同理OG=OH，根据对角线互相平分的四边形是平行四边形得到结论；（2）根据两组对边分别平行的四边形是平行四边形即可得到结论．解答：（1）证明：∵四边形ABCD是平行四边形，∴AD∥BC，∴∠EAO=∠FCO，在△OAE与△OCF中，∴△OAE≌△OCF，∴OE=OF，同理OG=OH，∴四边形EGFH是平行四边形；（2）解：与四边形AGHD面积相等的所有平行四边形有▱GBCH，▱ABFE，▱EFCD，▱EGFH；∵四边形ABCD是平行四边形，∴AD∥BC，AB∥CD，∵EF∥AB，GH∥BC，∴四边形GBCH，ABFE，EFCD，EGFH为平行四边形，∵EF过点O，GH过点O，∵OE=OF，OG=OH，∴▱GBCH，▱ABFE，▱EFCD，▱EGFH，▱ACHD它们面积=▱ABCDA 的面积，∴与四边形AGHD面积相等的所有平行四边形有▱GBCH，▱ABFE，▱EFCD，▱EGFH．点评：本题考查了平行四边形的判定和性质，全等三角形的判定和性质，熟练掌握平行四边形的判定定理是解题的关键．3．（2015•扬州）如图，将▱ABCD沿过点A的直线l折叠，使点D落到AB边上的点D′处，折痕l交CD边于点E，连接BE．（1）求证：四边形BCED′是平行四边形；（2）若BE平分∠ABC，求证：AB2=AE2+BE2．考点：平行四边形的判定与性质；勾股定理；翻折变换（折叠问题）．专题：证明题．分析：（1）利用翻折变换的性质以及平行线的性质得出∠DAE=∠EAD′=∠DEA=∠D′EA，进而利用平行四边形的判定方法得出四边形DAD′E 是平行四边形，进而求出四边形BCED′是平行四边形；（2）利用平行线的性质结合勾股定理得出答案．解答：证明：（1）∵将▱ABCD沿过点A的直线l折叠，使点D落到AB边上的点D′处，∴∠DAE=∠D′AE，∠DEA=∠D′EA，∠D=∠AD′E，∵DE∥AD′，∴∠DEA=∠EAD′，∴∠DAE=∠EAD′=∠DEA=∠D′EA，∴∠DAD′=∠DED′，∴四边形DAD′E是平行四边形，∴DE=AD′，∵四边形ABCD是平行四边形，∴AB DC，∴CE D′B，∴四边形BCED′是平行四边形；（2）∵BE平分∠ABC，∴∠CBE=∠EBA，∵AD∥BC，∴∠DAB+∠CBA=180°，∵∠DAE=∠BAE，∴∠EAB+∠EBA=90°，∴∠AEB=90°，∴AB2=AE2+BE2．点评：此题主要考查了平行四边形的判定与性质以及勾股定理等知识，得出四边形DAD′E是平行四边形是解题关键．4．（2015•桂林）如图，在▱ABCD中，E、F分别是AB、CD的中点．（1）求证：四边形EBFD为平行四边形；（2）对角线AC分别与DE、BF交于点M、N，求证：△ABN≌△CDM．考点：平行四边形的判定与性质；全等三角形的判定．专题：证明题．分析：（1）根据平行四边形的性质：平行四边的对边相等，可得AB ∥CD，AB=CD；根据一组对边平行且相等的四边形是平行四边形，可得答案；（2）根据平行四边的性质：平行四边形的对边相等，可得AB∥CD，AB=CD，∠CDM=∠CFN；根据全等三角形的判定，可得答案．解答：（1）证明：∵四边形ABCD是平行四边形，∴AB∥CD，AB=CD．∵E、F分别是AB、CD的中点，∴BE=DF，∵BE∥DF，∴四边形EBFD为平行四边形；（2）证明：∵四边形EBFD为平行四边形，∴DE∥BF，∴∠CDM=∠CFN．∵四边形ABCD是平行四边形，∴AB∥CD，AB=CD．∴∠BAC=∠DCA，∠ABN=∠CFN，∴∠ABN=∠CDM，在△ABN与△CDM中，，∴△ABN≌△CDM （ASA）．点评：本题考查了平行四边形的判定与性质，利用了平行四边形的判定与性质，全等三角形的判定，根据条件选择适当的判定方法是解题关键．5．（2015•乌鲁木齐）如图，▱ABCD中，点E，F在直线AC上（点E 在F左侧），BE∥DF．（1）求证：四边形BEDF是平行四边形；（2）若AB⊥AC，AB=4，BC=2，当四边形BEDF为矩形时，求线段AE的长．考点：平行四边形的判定与性质；全等三角形的判定与性质；矩形的性质．分析：（1）通过全等三角形△BEC≌△DFA的对应边相等推知BE=DF，则结合已知条件证得结论；（2）根据矩形的性质计算即可．解答：（1）证明：∵四边形ABCD是平行四边形，∴AD∥BC，AD=BC，∴∠DAF=∠BCE．又∵BE∥DF，∴∠BEC=∠DFA．在△BEC与△DFA中，，∴△BEC≌△DFA（AAS），∴BE=DF．又∵BE∥DF，∴四边形BEDF为平行四边形；（2）连接BD，BD与AC相交于点O，如图：∵AB⊥AC，AB=4，BC=2，∴AC=6，∴AO=3，∴Rt△BAO中，BO=5，∵四边形BEDF是矩形，∴OE=OB=5，∴点E在OA的延长线上，且AE=2．点评：本题考查了全等三角形的判定与性质、平行四边形的判定与性质．平行四边形的判定方法共有五种，应用时要认真领会它们之间的联系与区别，同时要根据条件合理、灵活地选择方法．6．（2015•宿迁）如图，四边形ABCD中，∠A=∠ABC=90°，AD=1，BC=3，E是边CD的中点，连接BE并延长与AD的延长线相交于点F．（1）求证：四边形BDFC是平行四边形；（2）若△BCD是等腰三角形，求四边形BDFC的面积．考点：平行四边形的判定与性质；等腰三角形的性质．分析：（1）根据同旁内角互补两直线平行求出BC∥AD，再根据两直线平行，内错角相等可得∠CBE=∠DFE，然后利用“角角边”证明△BEC 和△FCD全等，根据全等三角形对应边相等可得BE=EF，然后利用对角线互相平分的四边形是平行四边形证明即可；（2）分①BC=BD时，利用勾股定理列式求出AB，然后利用平行四边形的面积公式列式计算即可得解；②BC=CD时，过点C作CG⊥AF于G，判断出四边形AGCB是矩形，再根据矩形的对边相等可得AG=BC=3，然后求出DG=2，利用勾股定理列式求出CG，然后利用平行四边形的面积列式计算即可得解；③BD=CD时，BC边上的中线应该与BC垂直，从而得到BC=2AD=2，矛盾．解答：（1）证明：∵∠A=∠ABC=90°，∴BC∥AD，∴∠CBE=∠DFE，在△BEC与△FED中，，∴△BEC≌△FED，∴BE=FE，又∵E是边CD的中点，∴CE=DE，∴四边形BDFC是平行四边形；（2）①BC=BD=3时，由勾股定理得，AB===2，所以，四边形BDFC的面积=3×2=6；②BC=CD=3时，过点C作CG⊥AF于G，则四边形AGCB是矩形，所以，AG=BC=3，所以，DG=AG﹣AD=3﹣1=2，由勾股定理得，CG===，所以，四边形BDFC的面积=3×=3；③BD=CD时，BC边上的中线应该与BC垂直，从而得到BC=2AD=2，矛盾，此时不成了；综上所述，四边形BDFC的面积是6或3．点评：本题考查了平行四边形的判定与性质，等腰三角形的性质，全等三角形的判定与性质，（1）确定出全等三角形是解题的关键，（2）难点在于分情况讨论．7．（2015•遂宁）如图，▱ABCD中，点E，F在对角线BD上，且BE=DF，求证：（1）AE=CF；（2）四边形AECF是平行四边形．考点：平行四边形的判定与性质；全等三角形的判定与性质．专题：证明题．分析：（1）根据平行四边形的性质可得AB=CD，AB∥CD，然后可证明∠ABE=∠CDF，再利用SAS来判定△ABE≌△DCF，从而得出AE=CF．（2）首先根据全等三角形的性质可得∠AEB=∠CFD，根据等角的补角相等可得∠AEF=∠CFE，然后证明AE∥CF，从而可得四边形AECF是平行四边形．解答：证明：（1）∵四边形ABCD是平行四边形，∴AB=CD，AB∥CD．∴∠ABE=∠CDF．在△ABE和△CDF中，，∴△ABE≌△DCF（SAS）．∴AE=CF．（2）∵△ABE≌△DCF，∴∠AEB=∠CFD，∴∠AEF=∠CFE，∴AE∥CF，∵AE=CF，∴四边形AECF是平行四边形．点评：此题主要考查了平行四边形的性质和判定，关键是掌握平行四边形对边平行且相等，一组对边平行且相等的四边形是平行四边形．8．（2015•毕节市）如图，将▱ABCD的AD边延长至点E，使DE=AD，连接CE，F是BC边的中点，连接FD．（1）求证：四边形CEDF是平行四边形；（2）若AB=3，AD=4，∠A=60°，求CE的长．考点：平行四边形的判定与性质．分析：（1）利用平行四边形的性质得出AD=BC，AD∥BC，进而利用已知得出DE=FC，DE∥FC，进而得出答案；（2）首先过点D作DN⊥BC于点N，再利用平行四边形的性质结合勾股定理得出DF的长，进而得出答案．解答：（1）证明：∵四边形ABCD是平行四边形，∴AD=BC，AD∥BC，∵DE=AD，F是BC边的中点，∴DE=FC，DE∥FC，∴四边形CEDF是平行四边形；（2）解：过点D作DN⊥BC于点N，∵四边形ABCD是平行四边形，∠A=60°，∴∠BCD=∠A=60°，∵AB=3，AD=4，∴FC=2，NC=DC=，DN=，∴FN=，则DF=EC==．点评：此题主要考查了平行四边形的判定与性质以及勾股定理等知识，熟练应用平行四边形的判定方法是解题关键．9．（2015•柳州）如图，在四边形ABCD中，AD∥BC，∠B=90°，AB=8cm，AD=12cm，BC=18cm，点P从点A出发以2cm/s的速度沿A→D→C 运动，点P从点A出发的同时点Q从点C出发，以1cm/s的速度向点B运动，当点P到达点C时，点Q也停止运动．设点P，Q运动的时间为t秒．（1）从运动开始，当t取何值时，PQ∥CD？（2）从运动开始，当t取何值时，△PQC为直角三角形？考点：平行四边形的判定与性质；勾股定理的逆定理；直角梯形．专题：动点型．分析：（1）已知AD∥BC，添加PD=CQ即可判断以PQDC为顶点的四边形是平行四边形．（2）点P处可能为直角，点Q处也可能是直角，而后求解即可．解答：解：（1）当PQ∥CD时，四边形PDCB是平行四边形，此时PD=QC，∴12﹣2t=t，∴t=4．∴当t=4时，四边形PQDC是平行四边形．（2）过P点，作PE⊥BC于E，DF⊥BC，∴DF=AB=8．FC=BC﹣AD=18﹣12=6．①当PQ⊥BC，则BE+CE=18．即：2t+t=18，∴t=6；②当QP⊥PC，∴PE=4，CE=3+t，QE=12﹣2t﹣（3+t）=9﹣3t，∴16=（3+t）（9﹣3t），解得：t=，③情形：当PC⊥BC时，因∠DCB＜90°，此种情形不存在．∴当t=3或时，△PQC是直角三角形．点评：此题主要考查了一组对边平行且相等的四边形是平行四边形以及圆与圆的位置关系等知识，注意分情况讨论和常见知识的应用．10．（2015•南通）如图，在▱ABCD中，点E，F分别在AB，DC上，且ED⊥DB，FB⊥BD．（1）求证：△AED≌△CFB；（2）若∠A=30°，∠DEB=45°，求证：DA=DF．考点：平行四边形的判定与性质；全等三角形的判定与性质；含30度角的直角三角形．专题：证明题．分析：（1）由四边形ABCD为平行四边形，利用平行四边形的性质得到对边平行且相等，对角相等，再由垂直的定义得到一对直角相等，利用等式的性质得到一对角相等，利用ASA即可得证；（2）过D作DH垂直于AB，在直角三角形ADH中，利用30度所对的直角边等于斜边的一半得到AD=2DH，在直角三角形DEB中，利用斜边上的中线等于斜边的一半得到EB=2DH，易得四边形EBFD为平行四边形，利用平行四边形的对边相等得到EB=DF，等量代换即可得证．解答：证明：（1）∵平行四边形ABCD，∴AD=CB，∠A=∠C，AD∥CB，∴∠ADB=∠CBD，∵ED⊥DB，FB⊥BD，∴∠EDB=∠FBD=90°，∴∠ADE=∠CBF，在△AED和△CFB中，，∴△AED≌△CFB（ASA）；（2）作DH⊥AB，垂足为H，在Rt△ADH中，∠A=30°，∴AD=2DH，在Rt△DEB中，∠DEB=45°，∴EB=2DH，∴四边形EBFD为平行四边形，∴FD=EB，∴DA=DF．点评：此题考查了平行四边形的判定与性质，全等三角形的判定与性质，以及含30度直角三角形的性质，熟练掌握平行四边形的判定与性质是解本题的关键．。

2020—2021年人教版初中数学八年级下册中考试题汇编含精讲解析特殊的平行四边形1及答案(精品试题).docx

特殊的平行四边形1一．选择题（共19小题）1．（2015•河北）如图，点A，B为定点，定直线l∥AB，P是l上一动点，点M，N分别为PA，PB的中点，对下列各值：①线段MN的长；②△PAB的周长；③△PMN的面积；④直线MN，AB之间的距离；⑤∠APB的大小．其中会随点P的移动而变化的是（）A．②③B．②⑤C．①③④D．④⑤2．（2015•山西）如图，在△ABC中，点D、E分别是边AB，BC的中点．若△DBE的周长是6，则△ABC的周长是（）A．8 B．10 C．12 D．143．（2015•铁岭）如图，点D、E、F分别为△ABC各边中点，下列说法正确的是（）A．DE=DF B．EF=AB C．S△ABD=S△ACD D．AD平分∠BAC4．（2015•安顺）如图，在▱ABCD中，点E是边AD的中点，EC交对角线BD于点F，则EF：FC等于（）A．3：2 B．3：1 C．1：1 D．1：25．（2015•衢州）如图，在▱ABCD中，已知AD=12cm，AB=8cm，AE 平分∠BAD交BC边于点E，则CE的长等于（）A．8cm B．6cm C．4cm D．2cm6．（2015•玉林）如图，在▱ABCD中，BM是∠ABC的平分线交CD于点M，且MC=2，▱ABCD的周长是在14，则DM等于（）A．1 B．2 C．3 D．47．（2015•绥化）如图，▱ABCD的对角线AC、BD交于点O，AE平分∠BAD交BC于点E，且∠ADC=60°，AB=BC，连接OE．下列结论：①∠CAD=30°；②S▱ABCD=AB•AC；③OB=AB；④OE=BC，成立的个数有（）A．1个B．2个C．3个D．4个8．（2015•河南）如图，在▱ABCD中，用直尺和圆规作∠BAD的平分线AG交BC于点E．若BF=6，AB=5，则AE的长为（）A．4 B．6 C．8 D．109．（2015•本溪）如图，▱ABCD的周长为20cm，AE平分∠BAD，若CE=2cm，则AB的长度是（）A．10cm B．8cm C．6cm D．4cm10．（2015•福建）如图，在▱ABCD中，O是对角线AC，BD的交点，下列结论错误的是（）A．AB∥CD B．AB=CD C．AC=BD D．OA=OC11．（2015•陕西）在▱ABCD中，AB=10，BC=14，E，F分别为边BC，AD上的点，若四边形AECF为正方形，则AE的长为（）A．7 B．4或10 C．5或9 D．6或812．（2015•营口）▱ABCD中，对角线AC与BD交于点O，∠DAC=42°，∠CBD=23°，则∠COD是（）A．61°B．63°C．65°D．67°13．（2015•巴彦淖尔）如图，P为平行四边形ABCD的边AD上的一点，E，F分别为PB，PC的中点，△PEF，△PDC，△PAB的面积分别为S，S1，S2．若S=3，则S1+S2的值为（）A．24 B．12 C．6 D．314．（2015•常州）如图，▱ABCD的对角线AC、BD相交于点O，则下列说法一定正确的是（）A．AO=OD B．AO⊥OD C．AO=OC D．AO⊥AB15．（2015•淄博）如图，在平行四边形ABCD中，∠B=60°，将△ABC 沿对角线AC折叠，点B的对应点落在点E处，且点B，A，E在一条直线上，CE交AD于点F，则图中等边三角形共有（）A．4个B．3个C．2个D．1个16．（2015•连云港）已知四边形ABCD，下列说法正确的是（）A．当AD=BC，AB∥DC时，四边形ABCD是平行四边形B．当AD=BC，AB=DC时，四边形ABCD是平行四边形C．当AC=BD，AC平分BD时，四边形ABCD是矩形D．当AC=BD，AC⊥BD时，四边形ABCD是正方形17．（2015•台湾）坐标平面上，二次函数y=﹣x2+6x﹣9的图形的顶点为A，且此函数图形与y轴交于B点．若在此函数图形上取一点C，在x轴上取一点D，使得四边形ABCD为平行四边形，则D点坐标为何？（）A．（6，0）B．（9，0）C．（﹣6，0）D．（﹣9，0）18．（2015•绵阳）如图，在四边形ABCD中，对角线AC，BD相交于点E，∠CBD=90°，BC=4，BE=ED=3，AC=10，则四边形ABCD的面积为（）A．6 B．12 C．20 D．2419．（2014•泰安）如图，∠ACB=90°，D为AB的中点，连接DC并延长到E，使CE=CD，过点B作BF∥DE，与AE的延长线交于点F．若AB=6，则BF的长为（）A．6 B．7 C．8 D．10二．填空题（共11小题）20．（2015•泰安）如图，在矩形ABCD中，M、N分别是边AD、BC 的中点，E、F分别是线段BM、CM的中点．若AB=8，AD=12，则四边形ENFM的周长为．21．（2015•巴中）如图，在△ABC中，AB=5，AC=3，AD、AE分别为△ABC的中线和角平分线，过点C作CH⊥AE于点H，并延长交AB 于点F，连结DH，则线段DH的长为．22．（2015•盐城）如图，点D、E、F分别是△ABC各边的中点，连接DE、EF、DF．若△ABC的周长为10，则△DEF的周长为．23．（2015•无锡）已知：如图，AD、BE分别是△ABC的中线和角平分线，AD⊥BE，AD=BE=6，则AC的长等于．24．（2015•宿迁）如图，在Rt△ABC中，∠ACB=90°，点D，E，F分别为AB，AC，BC的中点．若CD=5，则EF的长为．25．（2015•广州）如图，四边形ABCD中，∠A=90°，AB=3，AD=3，点M，N分别为线段BC，AB上的动点（含端点，但点M不与点B重合），点E，F分别为DM，MN的中点，则EF长度的最大值为．26．（2015•云南）如图，在△ABC中，BC=1，点P1，M1分别是AB，AC边的中点，点P2，M2分别是AP1，AM1的中点，点P3，M3分别是AP2，AM2的中点，按这样的规律下去，P n M n的长为（n 为正整数）．27．（2015•珠海）如图，在△A1B1C1中，已知A1B1=7，B1C1=4，A1C1=5，依次连接△A1B1C1三边中点，得△A2B2C2，再依次连接△A2B2C2的三边中点得△A3B3C3，…，则△A5B5C5的周长为．28．（2015•衢州）如图，小聪与小慧玩跷跷板，跷跷板支架高EF为0.6米，E是AB的中点，那么小聪能将小慧翘起的最大高度BC等于米．29．（2015•昆明）如图，在△ABC中，AB=8，点D、E分别是BC、CA 的中点，连接DE，则DE= ．30．（2015•陕西）如图，AB是⊙O的弦，AB=6，点C是⊙O上的一个动点，且∠ACB=45°．若点M，N分别是AB，BC的中点，则MN 长的最大值是．18.2 特殊的平行四边形1参考答案与试题解析一．选择题（共19小题）1．（2015•河北）如图，点A，B为定点，定直线l∥AB，P是l上一动点，点M，N分别为PA，PB的中点，对下列各值：①线段MN的长；②△PAB的周长；③△PMN的面积；④直线MN，AB之间的距离；⑤∠APB的大小．其中会随点P的移动而变化的是（）A．②③B．②⑤C．①③④D．④⑤考点：三角形中位线定理；平行线之间的距离．分析：根据三角形的中位线平行于第三边并且等于第三边的一半可得MN=AB，从而判断出①不变；再根据三角形的周长的定义判断出②是变化的；确定出点P到MN的距离不变，然后根据等底等高的三角形的面积相等确定出③不变；根据平行线间的距离相等判断出④不变；根据角的定义判断出⑤变化．解答：解：∵点A，B为定点，点M，N分别为PA，PB的中点，∴MN是△PAB的中位线，∴MN=AB，即线段MN的长度不变，故①错误；PA、PB的长度随点P的移动而变化，所以，△PAB的周长会随点P的移动而变化，故②正确；∵MN的长度不变，点P到MN的距离等于l与AB的距离的一半，∴△PMN的面积不变，故③错误；直线MN，AB之间的距离不随点P的移动而变化，故④错误；∠APB的大小点P的移动而变化，故⑤正确．综上所述，会随点P的移动而变化的是②⑤．故选B．点评：本题考查了三角形的中位线平行于第三边并且等于第三边的一半，等底等高的三角形的面积相等，平行线间的距离的定义，熟记定理是解题的关键．2．（2015•山西）如图，在△ABC中，点D、E分别是边AB，BC的中点．若△DBE的周长是6，则△ABC的周长是（）A．8 B．10 C．12 D．14考点：三角形中位线定理．分析：首先根据点D、E分别是边AB，BC的中点，可得DE是三角形BC的中位线，然后根据三角形中位线定理，可得DE=AC，最后根据三角形周长的含义，判断出△ABC的周长和△DBE的周长的关系，再结合△DBE的周长是6，即可求出△ABC的周长是多少．解答：解：∵点D、E分别是边AB，BC的中点，∴DE是三角形BC的中位线，AB=2BD，BC=2BE，∴DE∥BC且DE=AC，又∵AB=2BD，BC=2BE，∴AB+BC+AC=2（BD+BE+DE），即△ABC的周长是△DBE的周长的2倍，∵△DBE的周长是6，∴△ABC的周长是：6×2=12．故选：C．点评：（1）此题主要考查了三角形中位线定理的应用，要熟练掌握，解答此题的关键是要明确：三角形的中位线平行于第三边，并且等于第三边的一半．（2）此题还考查了三角形的周长和含义的求法，要熟练掌握．3．（2015•铁岭）如图，点D、E、F分别为△ABC各边中点，下列说法正确的是（）A．DE=DF B．EF=AB C．S△ABD=S△ACD D．AD平分∠BAC考点：三角形中位线定理．分析：根据三角形中位线定理逐项分析即可．解答：解：A、∵点D、E、F分别为△ABC各边中点，∴DE=AC，DF=AB，∵AC≠AB，∴DE≠DF，故该选项错误；B、由A选项的思路可知，B选项错误、C、∵S△ABD=BD•h，S△ACD=CD•h，BD=CD，∴S△ABD=S△ACD，故该选项正确；D、∵BD=CD，AB≠AC，∴AD不平分∠BAC，故选C．点评：本题考查了三角形中位线定理的运用，解题的根据是熟记其定理：三角形的中位线平行于第三边，并且等于第三边的一半．4．（2015•安顺）如图，在▱ABCD中，点E是边AD的中点，EC交对角线BD于点F，则EF：FC等于（）A．3：2 B．3：1 C．1：1 D．1：2考点：平行四边形的性质；相似三角形的判定与性质．专题：几何图形问题．分析：根据题意得出△DEF∽△BCF，进而得出=，利用点E是边AD的中点得出答案即可．解答：解：∵▱ABCD，故AD∥BC，∴△DEF∽△BCF，∴=，∵点E是边AD的中点，∴AE=DE=AD，∴=．故选：D．点评：此题主要考查了平行四边形的性质以及相似三角形的判定与性质等知识，得出△DEF∽△BCF是解题关键．5．（2015•衢州）如图，在▱ABCD中，已知AD=12cm，AB=8cm，AE 平分∠BAD交BC边于点E，则CE的长等于（）A．8cm B．6cm C．4cm D．2cm考点：平行四边形的性质．分析：由平行四边形的性质得出BC=AD=12cm，AD∥BC，得出∠DAE=∠BEA，证出∠BEA=∠BAE，得出BE=AB，即可得出CE的长．解答：解：∵四边形ABCD是平行四边形，∴BC=AD=12cm，AD∥BC，∴∠DAE=∠BEA，∵AE平分∠BAD，∴∠BAE=∠DAE，∴∠BEA=∠BAE，∴BE=AB=8cm，∴CE=BC﹣BE=4cm；故答案为：C．点评：本题考查了平行四边形的性质、等腰三角形的判定；熟练掌握平行四边形的性质，并能进行推理计算是解决问题的关键．6．（2015•玉林）如图，在▱ABCD中，BM是∠ABC的平分线交CD于点M，且MC=2，▱ABCD的周长是在14，则DM等于（）A．1 B．2 C．3 D．4考点：平行四边形的性质．分析：根据BM是∠ABC的平分线和AB∥CD，求出BC=MC=2，根据▱ABCD的周长是14，求出CD=5，得到DM的长．解答：解：∵BM是∠ABC的平分线，∴∠ABM=∠CBM，∵AB∥CD，∴∠ABM=∠BMC，∴∠BMC=∠CBM，∴BC=MC=2，∵▱ABCD的周长是14，∴BC+CD=7，∴CD=5，则DM=CD﹣MC=3，故选：C．点评：本题考查的是平行四边形的性质和角平分线的定义，根据平行四边形的对边相等求出BC+CD是解题的关键，注意等腰三角形的性质的正确运用．7．（2015•绥化）如图，▱ABCD的对角线AC、BD交于点O，AE平分∠BAD交BC于点E，且∠ADC=60°，AB=BC，连接OE．下列结论：①∠CAD=30°；②S▱ABCD=AB•AC；③OB=AB；④OE=BC，成立的个数有（）A．1个B．2个C．3个D．4个考点：平行四边形的性质；等腰三角形的判定与性质；等边三角形的判定与性质；含30度角的直角三角形．分析：由四边形ABCD是平行四边形，得到∠ABC=∠ADC=60°，∠BAD=120°，根据AE平分∠BAD，得到∠BAE=∠EAD=60°推出△ABE 是等边三角形，由于AB=BC，得到AE=BC，得到△ABC是直角三角形，于是得到∠CAD=30°，故①正确；由于AC⊥AB，得到S▱ABCD=AB•AC，故②正确，根据AB=BC，OB=BD，且BD＞BC，得到AB≠OB，故③错误；根据三角形的中位线定理得到OE=AB，于是得到OE=BC，故④正确．解答：解：∵四边形ABCD是平行四边形，∴∠ABC=∠ADC=60°，∠BAD=120°，∵AE平分∠BAD，∴∠BAE=∠EAD=60°∴△ABE是等边三角形，∴AE=AB=BE，∵AB=BC，∴AE=BC，∴∠BAC=90°，∴∠CAD=30°，故①正确；∵AC⊥AB，∴S▱ABCD=AB•AC，故②正确，∵AB=BC，OB=BD，∵BD＞BC，∴AB≠OB，故③错误；∵CE=BE，CO=OA，∴OE=AB，∴OE=BC，故④正确．故选C．点评：本题考查了平行四边形的性质，等边三角形的判定和性质，直角三角形的性质，平行四边形的面积公式，熟练掌握性质定理和判定定理是解题的关键．8．（2015•河南）如图，在▱ABCD中，用直尺和圆规作∠BAD的平分线AG交BC于点E．若BF=6，AB=5，则AE的长为（）A．4 B．6 C．8 D．10考点：平行四边形的性质；等腰三角形的判定与性质；勾股定理；作图—基本作图．专题：计算题．分析：由基本作图得到AB=AF，加上AO平分∠BAD，则根据等腰三角形的性质得到AO⊥BF，BO=FO=BF=3，再根据平行四边形的性质得AF∥BE，所以∠1=∠3，于是得到∠2=∠3，根据等腰三角形的判定得AB=EB，然后再根据等腰三角形的性质得到AO=OE，最后利用勾股定理计算出AO，从而得到AE的长．解答：解：连结EF，AE与BF交于点O，如图，∵AB=AF，AO平分∠BAD，∴AO⊥BF，BO=FO=BF=3，∵四边形ABCD为平行四边形，∴AF∥BE，∴∠1=∠3，∴∠2=∠3，∴AB=EB，而BO⊥AE，∴AO=OE，在Rt△AOB中，AO===4，∴AE=2AO=8．故选C．点评：本题考查了平行四边形的性质：平行四边形的对边相等；平行四边形的对角相等；平行四边形的对角线互相平分．也考查了等腰三角形的判定与性质和基本作图．9．（2015•本溪）如图，▱ABCD的周长为20cm，AE平分∠BAD，若CE=2cm，则AB的长度是（）A．10cm B．8cm C．6cm D．4cm考点：平行四边形的性质．分析：根据平行四边形的性质得出AB=CD，AD=BC，AD∥BC，推出∠DAE=∠BAE，求出∠BAE=∠AEB，推出AB=BE，设AB=CD=xcm，则AD=BC=（x+2）cm，得出方程x+x+2=10，求出方程的解即可．解答：解：∵四边形ABCD是平行四边形，∴AB=CD，AD=BC，AD∥BC，∴∠DAE=∠BAE，∵AE平分∠BAD，∴∠DAE=∠BAE，∴∠BAE=∠AEB，∴AB=BE，设AB=CD=xcm，则AD=BC=（x+2）cm，∵▱ABCD的周长为20cm，∴x+x+2=10，解得：x=4，即AB=4cm，故选D．点评：本题考查了平行四边形的在，平行线的性质，等腰三角形的判定的应用，解此题的关键是能推出AB=BE，题目比较好，难度适中．10．（2015•福建）如图，在▱ABCD中，O是对角线AC，BD的交点，下列结论错误的是（）A．AB∥CD B．AB=CD C．AC=BD D．OA=OC考点：平行四边形的性质．分析：根据平行四边形的性质推出即可．解答：解：∵四边形ABCD是平行四边形，∴AB∥CD，AB=CD，OA=OC，但是AC和BD不一定相等，故选C．点评：本题考查了平行四边形的性质的应用，能熟记平行四边形的性质是解此题的关键，注意：平行四边形的对边相等且平行，平行四边形的对角线互相平分．11．（2015•陕西）在▱ABCD中，AB=10，BC=14，E，F分别为边BC，AD上的点，若四边形AECF为正方形，则AE的长为（）A．7 B．4或10 C．5或9 D．6或8考点：平行四边形的性质；勾股定理；正方形的性质．专题：分类讨论．分析：设AE的长为x，根据正方形的性质可得BE=14﹣x，根据勾股定理得到关于x的方程，解方程即可得到AE的长．解答：解：如图：设AE的长为x，根据正方形的性质可得BE=14﹣x，在△ABE中，根据勾股定理可得x2+（14﹣x）2=102，解得x1=6，x2=8．故AE的长为6或8．故选：D．点评：考查了平行四边形的性质，正方形的性质，勾股定理，关键是根据勾股定理得到关于AE的方程．12．（2015•营口）▱ABCD中，对角线AC与BD交于点O，∠DAC=42°，∠CBD=23°，则∠COD是（）A．61°B．63°C．65°D．67°考点：平行四边形的性质．分析：由平行四边形的性质可知：AD∥BC，进而可得∠DAC=∠BCA，再根据三角形外角和定理即可求出∠COD的度数．解答：解：∵四边形ABCD是平行四边形，∴AD∥BC，∴∠DAC=∠BCA=42°，∴∠COD=∠CBD+∠BCA=65°，故选C．点评：本题考查了平行四边形的性质以及三角形的外角和定理，题目比较简单，解题的关键是灵活运用平行四边形的性质，将四边形的问题转化为三角形问题．13．（2015•巴彦淖尔）如图，P为平行四边形ABCD的边AD上的一点，E，F分别为PB，PC的中点，△PEF，△PDC，△PAB的面积分别为S，S1，S2．若S=3，则S1+S2的值为（）A．24 B．12 C．6 D．3考点：平行四边形的性质；三角形中位线定理．分析：过P作PQ平行于DC，由DC与AB平行，得到PQ平行于AB，可得出四边形PQCD与ABQP都为平行四边形，进而确定出△PDC与△PCQ面积相等，△PQB与△ABP面积相等，再由EF为△BPC的中位线，利用中位线定理得到EF为BC的一半，且EF平行于BC，得出△PEF与△PBC相似，相似比为1：2，面积之比为1：4，求出△PBC的面积，而△PBC面积=△CPQ面积+△PBQ面积，即为△PDC面积+△PAB面积，即为平行四边形面积的一半，即可求出所求的面积．解答：解：过P作PQ∥DC交BC于点Q，由DC∥AB，得到PQ∥AB，∴四边形PQCD与四边形APQB都为平行四边形，∴△PDC≌△CQP，△ABP≌△QPB，∴S△PDC=S△CQP，S△ABP=S△QPB，∵EF为△PCB的中位线，∴EF∥BC，EF=BC，∴△PEF∽△PBC，且相似比为1：2，∴S△PEF：S△PBC=1：4，S△PEF=3，∴S△PBC=S△CQP+S△QPB=S△PDC+S△ABP=S1+S2=12．故选：B．点评：此题考查了平行四边形的性质，相似三角形的判定与性质，熟练掌握平行四边形的判定与性质是解本题的关键．14．（2015•常州）如图，▱ABCD的对角线AC、BD相交于点O，则下列说法一定正确的是（）A．AO=OD B．AO⊥OD C．AO=OC D．AO⊥AB考点：平行四边形的性质．分析：根据平行四边形的性质：对边平行且相等，对角线互相平分进行判断即可．解答：解：对角线不一定相等，A错误；对角线不一定互相垂直，B错误；对角线互相平分，C正确；对角线与边不一定垂直，D错误．故选：C．点评：本题考查度数平行四边形的性质，掌握平行四边形的对边平行且相等，对角线互相平分是解题的关键．15．（2015•淄博）如图，在平行四边形ABCD中，∠B=60°，将△ABC 沿对角线AC折叠，点B的对应点落在点E处，且点B，A，E在一条直线上，CE交AD于点F，则图中等边三角形共有（）A．4个B．3个C．2个D．1个考点：平行四边形的性质；等边三角形的判定；翻折变换（折叠问题）．分析：根据折叠的性质可得∠E=∠B=60°，进而可证明△BEC是等边三角形，再根据平行四边形的性质可得：AD∥BC，所以可得∠EAF=60°，进而可证明△EFA是等边三角形，由等边三角形的性质可得∠EFA=∠DFC=60°，又因为∠D=∠B=60°，进而可证明△DFC是等边三角形，问题得解．解答：解：∵将△ABC沿对角线AC折叠，点B的对应点落在点E处，∴∠E=∠B=60°，∴△BEC是等边三角形，∵四边形ABCD是平行四边形，∴AD∥BC，∠D=∠B=60°，∴∠B=∠EAF=60°，∴△EFA是等边三角形，∵∠EFA=∠DFC=60°，∠D=∠B=60°，∴△DFC是等边三角形，∴图中等边三角形共有3个，故选B．点评：本题考查了平行四边形的性质、折叠的性质以及等边三角形的判定和性质，解题的关键是熟记等边三角形的各种判定方法特别是经常用到的判定方法：三个角都相等的三角形是等边三角形．16．（2015•连云港）已知四边形ABCD，下列说法正确的是（）A．当AD=BC，AB∥DC时，四边形ABCD是平行四边形B．当AD=BC，AB=DC时，四边形ABCD是平行四边形C．当AC=BD，AC平分BD时，四边形ABCD是矩形D．当AC=BD，AC⊥BD时，四边形ABCD是正方形考点：平行四边形的判定；矩形的判定；正方形的判定．分析：由平行四边形的判定方法得出A不正确、B正确；由矩形和正方形的判定方法得出C、D不正确．解答：解：∵一组对边平行且相等的四边形是平行四边形，∴A不正确；∵两组对边分别相等的四边形是平行四边形，∴B正确；∵对角线互相平分且相等的四边形是矩形，∴C不正确；∵对角线互相垂直平分且相等的四边形是正方形，∴D不正确；故选：B．点评：本题考查了平行四边形的判定、矩形的判定、正方形的判定；熟练掌握平行四边形、矩形、正方形的判定方法是解决问题的关键．17．（2015•台湾）坐标平面上，二次函数y=﹣x2+6x﹣9的图形的顶点为A，且此函数图形与y轴交于B点．若在此函数图形上取一点C，在x轴上取一点D，使得四边形ABCD为平行四边形，则D点坐标为何？（）A．（6，0）B．（9，0）C．（﹣6，0）D．（﹣9，0）考点：平行四边形的判定；二次函数的性质．分析：首先将二次函数配方求得顶点A的坐标，然后求得抛物线与y 轴的交点坐标，根据电C和点B的纵坐标相同求得点C的坐标，从而求得线段BC的长，根据平行四边形的性质求得AD的长即可求得点D 的坐标．解答：解：∵y=﹣x2+6x﹣9=﹣（x﹣3）2，∴顶点A的坐标为（3，0），令x=0得到y=﹣9，∴点B的坐标为（0，﹣9），令y=﹣x2+6x﹣9=﹣9，解得：x=0或x=6，∴点C的坐标为（6，﹣9），∴BC=AD=6，∴OD=OA+AD=3+6=9，∴点D的坐标为（9，0），故选B．点评：本题考查了平行四边形的判定、二次函数的性质等知识，主要利用了抛物线与坐标轴交点的求法，平行四边形的对边平行且相等的性质，综合题，但难度不大．18．（2015•绵阳）如图，在四边形ABCD中，对角线AC，BD相交于点E，∠CBD=90°，BC=4，BE=ED=3，AC=10，则四边形ABCD的面积为（）A．6 B．12 C．20 D．24考点：平行四边形的判定与性质；全等三角形的判定与性质；勾股定理．分析：根据勾股定理，可得EC的长，根据平行四边形的判定，可得四边形ABCD的形状，根据平行四边形的面积公式，可得答案．解答：解：在Rt△BCE中，由勾股定理，得CE===5．∵BE=DE=3，AE=CE=5，∴四边形ABCD是平行四边形．四边形ABCD的面积为BC•BD=4×（3+3）=24，故选：D．点评：本题考查了平行四边形的判定与性质，利用了勾股定理得出CE的长，又利用对角线互相平分的四边形是平行四边形，最后利用了平行四边形的面积公式．19．（2014•泰安）如图，∠ACB=90°，D为AB的中点，连接DC并延长到E，使CE=CD，过点B作BF∥DE，与AE的延长线交于点F．若AB=6，则BF的长为（）A．6 B．7 C．8 D．10考点：三角形中位线定理；直角三角形斜边上的中线．分析：根据直角三角形斜边上的中线等于斜边的一半得到CD=AB=3，则结合已知条件CE=CD可以求得ED=4．然后由三角形中位线定理可以求得BF=2ED=8．解答：解：如图，∵∠ACB=90°，D为AB的中点，AB=6，∴CD=AB=3．又CE=CD，∴CE=1，∴ED=CE+CD=4．又∵BF∥DE，点D是AB的中点，∴ED是△AFB的中位线，∴BF=2ED=8．故选：C．点评：本题考查了三角形中位线定理和直角三角形斜边上的中线．根据已知条件求得ED的长度是解题的关键与难点．二．填空题（共11小题）20．（2015•泰安）如图，在矩形ABCD中，M、N分别是边AD、BC 的中点，E、F分别是线段BM、CM的中点．若AB=8，AD=12，则四边形ENFM的周长为20 ．考点：三角形中位线定理；勾股定理；矩形的性质．分析：根据M是边AD的中点，得AM=DM=6，根据勾股定理得出BM=CM=10，再根据E、F分别是线段BM、CM的中点，即可得出EM=FM=5，再根据N是边BC的中点，得出EM=FN，EN=FM，从而得出四边形EN，FM的周长．解答：解：∵M、N分别是边AD、BC的中点，AB=8，AD=12，∴AM=DM=6，∵四边形ABCD为矩形，∴∠A=∠D=90°，∴BM=CM=10，∵E、F分别是线段BM、CM的中点，∴EM=FM=5，∴EN，FN都是△BCM的中位线，∴EN=FN=5，∴四边形ENFM的周长为5+5+5+5=20，故答案为20．点评：本题考查了三角形的中位线，勾股定理以及矩形的性质，是2015年中考常见的题型，难度不大，比较容易理解．21．（2015•巴中）如图，在△ABC中，AB=5，AC=3，AD、AE分别为△ABC的中线和角平分线，过点C作CH⊥AE于点H，并延长交AB 于点F，连结DH，则线段DH的长为 1 ．考点：三角形中位线定理；等腰三角形的判定与性质．分析：首先证明△ACF是等腰三角形，则AF=AC=3，HF=CH，则DH 是△BCF的中位线，利用三角形的中位线定理即可求解．解答：解：∵AE为△ABC的角平分线，CH⊥AE，∴△ACF是等腰三角形，∴AF=AC，∵AC=3，∴AF=AC=3，HF=CH，∵AD为△ABC的中线，∴DH是△BCF的中位线，∴DH=BF，∵AB=5，∴BF=AB﹣AF=5﹣3=2．∴DH=1，故答案为：1．点评：本题考查了等腰三角形的判定以及三角形的中位线定理，正确证明HF=CH是关键．22．（2015•盐城）如图，点D、E、F分别是△ABC各边的中点，连接DE、EF、DF．若△ABC的周长为10，则△DEF的周长为 5 ．考点：三角形中位线定理．分析：由于D、E分别是AB、BC的中点，则DE是△ABC的中位线，那么DE=AC，同理有EF=AB，DF=BC，于是易求△DEF的周长．解答：解：如上图所示，∵D、E分别是AB、BC的中点，∴DE是△ABC的中位线，∴DE=AC，同理有EF=AB，DF=BC，∴△DEF的周长=（AC+BC+AB）=×10=5．故答案为5．点评：本题考查了三角形中位线定理．解题的关键是根据中位线定理得出边之间的数量关系．23．（2015•无锡）已知：如图，AD、BE分别是△ABC的中线和角平分线，AD⊥BE，AD=BE=6，则AC的长等于．考点：三角形中位线定理；勾股定理．专题：计算题．分析：延长AD至F，使DF=AD，过点F作平行BE与AC延长线交于点G，过点C作CH∥BE，交AF于点H，连接BF，如图所示，在直角三角形AGF中，利用勾股定理求出AG的长，利用SAS证得△BDF≌△CDA，利用全等三角形对应角相等得到∠ACD=∠BFD，证得AG∥BF，从而证得四边形EBFG是平行四边形，得到FG=BE=6，利用AAS 得到三角形BOD与三角形CHD全等，利用全等三角形对应边相等得到OD=DH=3，得出AH=9，然后根据△AHC∽△AFG，对应边成比例即可求得AC．解答：解：延长AD至F，使DF=AD，过点F作FG∥BE与AC延长线交于点G，过点C作CH∥BE，交AF于点H，连接BF，如图所示，在Rt△AFG中，AF=2AD=12，FG=BE=6，根据勾股定理得：AG==6，在△BDF和△CDA中，∴△BDF≌△CDA（SAS），∴∠ACD=∠BFD，∴AG∥BF，∴四边形EBFG是平行四边形，∴FG=BE=6，在△BOD和△CHD中，，∴△BOD≌△CHD（AAS），∴OD=DH=3，∵CH∥FG，∴△AHC∽△AFG，∴=，即=，解得：AC=，故答案为：点评：本题考查了三角形全等的判定和性质，三角形相似的判定和性质，平行四边形的判定和性质以及勾股定理的应用，作出辅助线构建直角三角形和平行四边形是解题的关键．24．（2015•宿迁）如图，在Rt△ABC中，∠ACB=90°，点D，E，F分别为AB，AC，BC的中点．若CD=5，则EF的长为 5 ．考点：三角形中位线定理；直角三角形斜边上的中线．分析：已知CD是Rt△ABC斜边AB的中线，那么AB=2CD；EF是△ABC的中位线，则EF应等于AB的一半．解答：解：∵△ABC是直角三角形，CD是斜边的中线，∴CD=AB，又∵EF是△ABC的中位线，∴AB=2CD=2×5=10cm，∴EF=×10=5cm．故答案为：5．点评：此题主要考查了三角形中位线定理以及直角三角形斜边上的中线等知识，用到的知识点为：（1）直角三角形斜边的中线等于斜边的一半；（2）三角形的中位线等于对应边的一半．25．（2015•广州）如图，四边形ABCD中，∠A=90°，AB=3，AD=3，点M，N分别为线段BC，AB上的动点（含端点，但点M不与点B重合），点E，F分别为DM，MN的中点，则EF长度的最大值为 3 ．考点：三角形中位线定理；勾股定理．专题：动点型．分析：根据三角形的中位线定理得出EF=DN，从而可知DN最大时，EF最大，因为N与B重合时DN最大，此时根据勾股定理求得DN=DB=6，从而求得EF的最大值为3．解答：解：∵ED=EM，MF=FN，∴EF=DN，∴DN最大时，EF最大，∵N与B重合时DN最大，此时DN=DB==6，∴EF的最大值为3．故答案为3．点评：本题考查了三角形中位线定理，勾股定理的应用，熟练掌握定理是解题的关键．26．（2015•云南）如图，在△ABC中，BC=1，点P1，M1分别是AB，AC边的中点，点P2，M2分别是AP1，AM1的中点，点P3，M3分别是AP2，AM2的中点，按这样的规律下去，P n M n的长为（n为正整数）．考点：三角形中位线定理．专题：规律型．分析：根据中位线的定理得出规律解答即可．解答：解：在△ABC中，BC=1，点P1，M1分别是AB，AC边的中点，点P2，M2分别是AP1，AM1的中点，点P3，M3分别是AP2，AM2的中点，可得：P1M1=，P2M2=，故P n M n=，故答案为：点评：此题考查三角形中位线定理，关键是根据中位线得出规律进行解答．27．（2015•珠海）如图，在△A1B1C1中，已知A1B1=7，B1C1=4，A1C1=5，依次连接△A1B1C1三边中点，得△A2B2C2，再依次连接△A2B2C2的三边中点得△A3B3C3，…，则△A5B5C5的周长为 1 ．考点：三角形中位线定理．专题：规律型．分析：由三角形的中位线定理得：A2B2、B2C2、C2A2分别等于A1B1、B1C1、C1A1的一半，所以△A2B2C2的周长等于△A1B1C1的周长的一半，以此类推可求出△A5B5C5的周长为△A1B1C1的周长的．解答：解：∵A2B2、B2C2、C2A2分别等于A1B1、B1C1、C1A1的一半，∴以此类推：△A5B5C5的周长为△A1B1C1的周长的，∴则△A5B5C5的周长为（7+4+5）÷16=1．故答案为：1点评：本题主要考查了三角形的中位线定理，关键是根据三角形的中位线定理得：A2B2、B2C2、C2A2分别等于A1B1、B1C1、C1A1的一半，所以△A2B2C2的周长等于△A1B1C1的周长的一半．28．（2015•衢州）如图，小聪与小慧玩跷跷板，跷跷板支架高EF为0.6米，E是AB的中点，那么小聪能将小慧翘起的最大高度BC等于 1.2 米．考点：三角形中位线定理．专题：应用题．分析：先求出F为AC的中点，根据三角形的中位线求出BC=2EF，代入求出即可．解答：解：∵EF⊥AC，BC⊥AC，∴EF∥BC，∵E是AB的中点，∴F为AC的中点，∴BC=2EF，∵EF=0.6米，∴BC=1.2米，故答案为：1.2．点评：本题考查了三角形的中位线性质，平行线的性质和判定的应用，解此题的关键是求出BC=2EF，注意：垂直于同一直线的两直线平行．29．（2015•昆明）如图，在△ABC中，AB=8，点D、E分别是BC、CA 的中点，连接DE，则DE= 4 ．考点：三角形中位线定理．分析：根据三角形的中位线等于第三边的一半即可得出DE=AB=4．解答：解：∵在△ABC中，点D、E分别是BC、CA的中点，AB=8，∴DE是△ABC的中位线，∴DE=AB=×8=4．故答案为4．点评：本题考查了三角形中位线定理，掌握三角形的中位线平行于第三边，并且等于第三边的一半是解题的关键．。

【常考压轴题】专题04 一次函数中的特殊平行四边形存在性问题(原卷版)九年级数学上册压轴题攻略

专题04一次函数中的特殊平行四边形存在性问题类型一、菱形问题(1)如图1，请直接写出点A 的坐标，并求出直线AB 的解析式．(2)如图2，直线2y x b =+是线段AB 的垂直平分线，垂足为点D ，且交线CD 上的一动点，当点P 使得32ACP ACD S S =△△时，请求出符合条件的点(3)在（2）的条件下，若点P 在直线CD 上且在第三象限内，在平面内是否存在其它点P 、Q 为顶点的四边形是菱形？若存在，直接写出点Q 的坐标；若不存在，请说明理由．(1)求A C 、两点坐标；(2)若点M 是直线CB 上一点，且(3)点P 是y 轴上的点，在坐标平面内是否存在点直接写出点Q 坐标，若不存在，请说明理由．【变式训练】将一个矩形纸片OABC 放置于平面直角坐标系中，点O ()0,0，点B ()10,6，点A 在x 轴，点C 在y 轴．在AB 边上取一点D ，将CBD △沿CD 翻折，点B 恰好落在边OA 上的点E 处．(1)如图1，求点E 坐标和直线CE 的解析式；(2)点P 为x 轴正半轴上的动点，设OP t =．①如图2，当点P 在线段OA （不包含端点A ，O ）上运动时，过点P 作直线l ∥y 轴，直线l 被CED △截得的线段长为d ．求d 关于t 的函数关系式，并直接写出自变量t 的取值范围；②在该坐标系所在平面内找一点G ，使以点C ，E ，P ，G 为顶点的四边形为菱形，请直接写出点G 的坐标．类型二、矩形存在性问题例．（两个动点）如图，四边形OABC 是矩形，点A 、C 在坐标轴上，ODE 是由OCB 绕点O 顺时针旋转90︒得到的，点D 在x 轴上，直线BD 交y 轴于点F ，交OE 于点H ，线段BC OC 、的长是2和4；(1)求直线BD 的表达式；(2)求OFH 的面积；(3)点M 在坐标轴上，平面内是否存在点N ，使以点D 、F 、M 、N 为顶点的四边形是矩形？若存在，请直接写出点N 的坐标；若不存在，请说明理由．【变式训练1】如图，A ，B 是直线6y x =-+与两坐标轴的交点，直线2y x m =+过点A ，与x 轴交于点C ．(1)求A ，B ，C 三点的坐标；(2)点D 是折线B A C --上一动点．①如图（1），当点D 是线段AB 的中点时，在y 轴上找一点E ，使ED EB +最小；用直尺和圆规画出点E 的位置（保留作图痕迹，不要求写作法和证明），并求出点E 的坐标；②是否存在点D ，使BCD △为直角三角形，若存在，直接写出点D 的坐标；若不存在，请说明理由．类型三、正方形存在性问题(1)求点A ，点B 的坐标；(2)若AOC BCP S S =△△，求点P 的坐标；(3)若点E 是直线54y x =上的一个动点，在平面内是否存在点F ，使四边形APEF 点E 的坐标；若不存在，请说明理由．(1)求直线CD 的解析式；(2)连接OP 、BC ，若直线AB 上存在一点Q ，使得(3)将直线CD 向下平移1个单位长度得到直线，直线角坐标系中，是否存在点M ，使以点O ，E ，N ，M 标；若不存在，请说明理由．(1)求直线l 的解析式；(2)求证：ABC 是等腰直角三角形；(3)将直线l 沿y 轴负方向平移，当平移恰当的距离时，直线与存在点P ，使得A B P ''△是等腰直角三角形，请直接写出所有符合条件的点(1)求直线1l 的解析式；(2)设2P m （，），求ABP 的面积S (3)当ABP 的面积为3时，则以点2．如图1，在平面直角坐标系中，△3．如图，在平面直角坐标系中，直线6y x =-+与x 轴、y 轴分别交于点D 、C ，直线AB 与y 轴交于点()0,3B -，与直线CD 交于点(),3A m ．(1)求直线AB 的解析式；(2)点E 是射线CD 上一动点，过点E 作EF y ∥轴，交直线AB 于点F ．若以O 、C 、E 、F 为顶点的四边形是平行四边形，请求出点E 的坐标；(3)设P 是射线CD 上一点，在平面内是否存在点Q ，使以B 、C 、P 、Q 为顶点的四边形是菱形？若存在，请直接写出点Q 的坐标；若不存在，请说明理由．（2）迁移应用：如图2，将一块等腰直角的三角板（3）拓展应用：如图3，在平面直角坐标系内，已知直线轴上方，点C 在x 轴正半轴上，且5OC OA =，连接，BC CD ，已知2ADC ABC S S =△△．(1)求直线AB 的表达式；(2)求点D 的坐标；(3)在线段AD CD ，上分别取点M ，N ，使得MN x ∥轴，在x 轴上取一点P ，连接MN NP MP ，，，是否存在点M ，使得MNP △为等腰直角三角形？若存在，求出点M 的坐标；若不存在，请说明理由．6．如图，在平面直角坐标系中，直线1l ：()0y kx b k =+≠与直线2l ：y x =交于点()2,A a ，与y 轴交于点()0,6B ，与x 轴交于点C ．(1)求直线1l 的函数表达式；(2)在平面直角坐标系中有一点()5,P m ，使得AOP AOC S S = ，请求出点P 的坐标；(3)点M 为直线1l 上的动点，过点M 作y 轴的平行线，交2l 于点N ，点Q 为y 轴上一动点，且MNQ △为等腰直角三角形，请直接写出满足条件的点M 的坐标．。