探索梯形面积计算公式_梯形的面积
梯形的面积公式

梯形的面积公式梯形是我们在数学学习中经常会遇到的一种几何图形。
那什么是梯形呢?梯形就是只有一组对边平行的四边形。
而要计算梯形的面积,就需要用到特定的公式。
梯形的面积公式是:(上底+下底)×高 ÷ 2 。
为了更好地理解这个公式,我们先来看看梯形的各个部分。
梯形有上底、下底和高。
上底和下底是平行的两条边,其中较短的那条边称为上底,较长的那条边称为下底。
高则是指上底和下底之间的垂直距离。
想象一下,我们有两个完全一样的梯形。
把这两个梯形拼在一起,会得到一个什么样的图形呢?没错,会得到一个平行四边形。
这个平行四边形的底就是梯形的上底与下底之和,高则与梯形的高相等。
因为平行四边形的面积等于底乘以高,所以这个由两个梯形拼成的平行四边形的面积就是(上底+下底)×高。
但这是两个梯形拼成的图形的面积呀,那一个梯形的面积不就得除以 2 嘛,所以梯形的面积就是(上底+下底)×高 ÷ 2 。
让我们通过几个具体的例子来实际运用一下这个公式。
假设我们有一个梯形,上底是 3 厘米,下底是 5 厘米,高是 4 厘米。
那么根据梯形的面积公式,这个梯形的面积就是(3 + 5)× 4 ÷ 2 =16 平方厘米。
再比如,有一个梯形的上底是 2 厘米,下底是 8 厘米,高是 6 厘米。
它的面积就是(2 + 8)× 6 ÷ 2 = 30 平方厘米。
在实际生活中,梯形的面积公式也有很多的应用。
比如,在建筑工地上,工人师傅要计算梯形的地基面积;在农业生产中,农民伯伯要计算梯形的农田面积以便合理种植农作物;在制作家具时,木匠师傅也可能需要计算梯形部件的面积来确定所需的材料。
总之,梯形的面积公式是一个非常实用的数学工具,它帮助我们解决了很多与梯形面积相关的问题。
只要我们牢记这个公式,并且能够正确地找到梯形的上底、下底和高,就能够轻松地计算出梯形的面积。
无论是在学习中还是在生活中,数学知识都无处不在,而梯形的面积公式就是其中一个小小的但却十分重要的部分。
梯形面积的概念

梯形面积的概念梯形是一种具有两对平行边的四边形,其中两对平行边被称为上底和下底,两条连接上底和下底的非平行边被称为腰。
梯形的面积是指该梯形所包围的平面区域的大小,通常用平方单位表示。
计算梯形面积的公式是将上底和下底长度相加,再乘以高,最后除以2,即:面积= (上底+ 下底) ×高÷2。
以下详细介绍了梯形面积的概念及其相关内容。
一、梯形的基本定义梯形是由两对平行边和一对非平行边组成的四边形。
梯形的两对平行边分别被称为上底和下底,两条连接上底和下底的非平行边被称为腰。
梯形的两条腰的长度可以相等,也可以不相等。
二、梯形面积的计算公式梯形的面积计算需要用到上底、下底和高的长度。
假设梯形的上底长度为a,下底长度为b,高的长度为h,则梯形的面积S可以使用以下公式进行计算:S = (a + b) ×h ÷2。
这个公式的推导可以通过将梯形划分成两个三角形并分别计算其面积来得到。
三、梯形面积计算的实例假设有一个梯形,其上底长度为5cm,下底长度为10cm,高为8cm。
根据梯形面积的计算公式,可以得到该梯形的面积S = (5 + 10) ×8 ÷2 = 15 ×8÷2 = 120cm²。
因此,该梯形的面积为120平方厘米。
四、梯形面积的特点1. 面积公式中的上底和下底长度是梯形面积计算的关键因素。
当上底和下底的长度增加或减少时,梯形的面积也会相应地增加或减少。
2. 面积公式中的高度是梯形面积计算的另一个重要因素。
当高度增加或减少时,梯形的面积也会相应地增加或减少。
3. 如果梯形的两个底边相等,则该梯形被称为等腰梯形。
在等腰梯形中,两个底边之间的距离(高度)是最短的,因此等腰梯形的面积相对较小。
4. 如果梯形的两个底边平行且且腰的长度相等,则该梯形被称为矩形。
矩形的面积可以使用矩形的边长乘积来计算,因为矩形的两条腰边垂直于底边,所以可以看作是高度。
如何计算梯形的面积

如何计算梯形的面积梯形是几何学中一种常见的平面图形,它由两条平行的边和连接这两条边的两条斜边组成。
计算梯形的面积是数学中的基本技能之一,本文将介绍如何准确计算梯形的面积。
在计算梯形的面积之前,我们需要了解几何图形的基本术语。
对于一个梯形而言,我们将两条平行的边称为上底和下底,两条斜边分别称为上斜边和下斜边。
此外,我们还需要知道两条平行边之间的距离,通常称为高。
根据梯形的定义和几何原理,我们可以得出计算梯形面积的公式。
梯形的面积等于上底和下底之和的一半,再乘以高。
因此,梯形的面积公式可以表示为:面积 = (上底 + 下底) * 高 / 2接下来,我们将通过示例来演示如何使用这个公式计算梯形的面积。
假设我们有一个梯形,其上底长度为10 cm,下底长度为16 cm,高为6 cm。
我们可以按照以下步骤来计算它的面积:1. 首先,将上底和下底相加:10 cm + 16 cm = 26 cm。
2. 将上一步得到的结果乘以高,即26 cm * 6 cm = 156 cm^2。
3. 最后,将上一步得到的结果除以2,即156 cm^2 / 2 = 78 cm^2。
因此,这个梯形的面积为78平方厘米。
除了上述公式,还有其他方法可以计算梯形的面积。
如果我们知道梯形的高和两个底边的长度,我们可以使用以下公式计算面积:面积 = 高 * (上底 + 下底) / 2该公式与前面介绍的公式类似,只是乘法和除法的顺序不同。
使用该公式也可以得到相同的结果。
当然,如果我们只知道梯形的斜边长度,而不知道上底、下底和高,那么计算面积将会比较复杂。
在这种情况下,我们可以利用梯形的性质和三角形的相关知识,将梯形分为两个三角形和一个矩形,然后计算每个部分的面积,并将它们相加得到最终的结果。
总之,计算梯形的面积是一个基本的几何计算技能。
我们可以使用梯形的面积公式来计算,根据已知的参数,包括上底、下底、高等。
同时,我们还可以根据斜边长度和三角形的相关知识来计算梯形的面积。
梯形的公式面积
梯形的公式面积
梯形面积公式
1、梯形的面积公式:(上底+下底)×高÷2
梯形的面积等于上下两底之和与高的乘积的一半。
如果梯形的上下两底分别用 a和 b表示,高用 h表示,梯形的面积s=(a+b)×h÷2 。
2、梯形的面积公式:中位线×高
根据梯形中位线的长度等于上下两底和的一半,梯形的面积也等于中位线与高的乘积。
如果梯形的中位线用 m表示,高用 h表示,梯形的面积s=mh 。
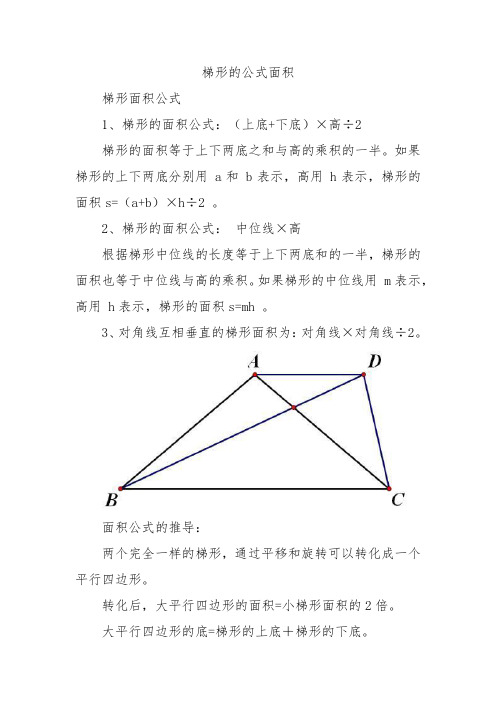
3、对角线互相垂直的梯形面积为:对角线×对角线÷2。
面积公式的推导:
两个完全一样的梯形,通过平移和旋转可以转化成一个平行四边形。
转化后,大平行四边形的面积=小梯形面积的2倍。
大平行四边形的底=梯形的上底+梯形的下底。
大平行四边形的高=梯形的高。
因为,平行四边形的面积=底×高,
所以,梯形的面积=(上底+下底)×高÷2。
梯形面积测量的计算公式和实用技巧

梯形面积测量的计算公式和实用技巧梯形是我们在数学中经常遇到的图形,它有两个并行的底边和两个不一样长的斜边。
我们经常需要计算梯形的面积,在这篇文章中,我将介绍一些梯形面积测量的计算公式和一些实用技巧。
首先,我们需要知道梯形的面积计算公式。
梯形的面积等于两底边长度之和的一半乘以高。
用数学符号表示就是:面积 = (上底 + 下底) ×高 / 2其中,上底和下底分别表示梯形的两个底边的长度,高表示梯形的高度。
那么,如何测量梯形的底边长度呢?我们可以使用直尺或者测量仪器来测量底边的长度。
将直尺或者测量仪器平放在梯形的底边上,然后读取其长度。
如果底边不直,可以选择测量仪器,如卷尺,可以沿着底边的曲线测量,然后找到底边的平均长度。
接下来,我们需要测量梯形的高度。
高度是从一条底边到另一条底边的垂直距离。
我们可以使用直尺或者测量仪器来测量高度。
将直尺或者测量仪器垂直放置在两条底边之间,然后读取其长度。
在测量完成后,我们可以使用梯形的面积计算公式来计算其面积。
将底边的长度和高度代入公式中,进行计算即可得到梯形的面积。
除了直接使用梯形面积计算公式之外,我们还可以利用一些实用技巧来简化计算过程。
下面我将介绍一些常见的实用技巧。
首先是利用相似三角形的性质。
如果我们知道梯形的两个斜边的长度和高度,可以通过相似三角形的比例关系来计算底边的长度。
设斜边的长度分别为a和b,高度为h,底边的长度为x,则有以下关系式:a/x = h/(h+b)通过解这个方程,我们可以得到底边的长度x,从而计算出梯形的面积。
其次是将梯形分解为两个三角形和一个矩形。
我们可以将梯形划分为上底、下底和高度所围成的两个三角形,以及两条底边之间的矩形。
分别计算出两个三角形和一个矩形的面积,然后将它们相加即可得到梯形的面积。
此外,我们还可以利用圆的面积公式来计算梯形的面积。
将梯形和一个扇形组合在一起,形成一个扇形和一个三角形。
我们可以计算扇形的面积,然后减去三角形的面积,就可以得到梯形的面积。
关于梯形的全部公式

关于梯形的全部公式梯形是一个四边形,其中两边是平行的,而另外两边则不平行。
梯形也可以被定义为一个几何图形,在顶部是矩形,而底部是一个直角三角形。
在本文中,我们将详细介绍关于梯形的全部公式。
1. 周长(Perimeter):梯形的周长是指所有边的长度之和。
对于一个梯形来说,周长的计算方法如下:周长=a+b+c+d2. 面积(Area):梯形的面积是指由其两边和夹角所围成的区域的大小。
梯形的面积计算方法如下:面积=(a+b)×h÷2其中,a和b分别为梯形的上底和下底的长度,h为梯形两底之间的高。
3. 高(Height):梯形的高是指两底之间的垂直距离。
高可以通过以下公式计算:h=(面积×2)÷(a+b)4. 上底(Upper Base):梯形的上底是指梯形的一边,且与下底平行。
上底的长度可以通过以下公式计算:上底=2×面积÷(b+h)5. 下底(Lower Base):梯形的下底是指梯形的一边,且与上底平行。
下底的长度可以通过以下公式计算:下底=2×面积÷(a+h)6. 对角线 (Diagonal):对角线是指梯形内部两个非平行边之间的线段。
梯形的对角线可以通过以下公式计算:对角线=√((a-b)²+h²)其中,a和b分别为梯形的上底和下底的长度,h为梯形两底之间的高。
7. 中线(Midline):梯形的中线是指连接梯形的两个非平行边中点的直线。
梯形的中线可以通过以下公式计算:中线=(a+b)÷2其中,a和b分别为梯形的上底和下底的长度。
8. 内角(Interior Angles):梯形的内角指的是由其边界形成的角度。
对于一个梯形来说,其内角有四个,分别可以通过以下公式计算:C₁ = C₃ = arctan(h ÷ (b - a))C₂ = C₄ = arctan(h ÷ (a - b))其中,a和b分别为梯形的上底和下底的长度,h为梯形两底之间的高。
梯形的面积计算方法

梯形的面积计算方法梯形是一种具有特定形状的四边形,它的两边平行,而另两边不平行。
计算梯形的面积是一项基本的几何运算,下面将介绍一种常用的方法来计算梯形的面积。
我们需要知道梯形的两个底边的长度,分别记为a和b,以及梯形的高h。
底边a和底边b可以是任意长度,而高h则是连接两个底边的垂直距离。
我们可以将梯形分成两个三角形和一个矩形。
其中,两个三角形的面积分别为1/2 * a * h 和 1/2 * b * h,而矩形的面积为 a * h。
因此,梯形的面积可以通过以下公式计算:梯形面积 = 1/2 * a * h + 1/2 * b * h + a * h为了更好地理解这个公式,我们可以通过一个具体的例子来进行计算。
假设梯形的底边a为5,底边b为8,高h为4。
那么根据上述公式,梯形的面积可以计算如下:梯形面积 = 1/2 * 5 * 4 + 1/2 * 8 * 4 + 5 * 4= 10 + 16 + 20= 46因此,当底边a为5,底边b为8,高h为4时,这个梯形的面积为46平方单位。
除了使用上述公式计算梯形的面积之外,还有一个更简单的方法。
我们可以将梯形看作是一个大矩形减去一个小矩形的面积。
我们计算出大矩形的面积,即底边a和底边b之和乘以高h的一半。
然后,计算出小矩形的面积,即底边a和底边b之差乘以高h的一半。
最后,将大矩形的面积减去小矩形的面积,即可得到梯形的面积。
通过这种方法,我们可以用以下公式来计算梯形的面积:梯形面积 = (a + b) * h / 2 - |a - b| * h / 2其中,|a - b|表示a和b之差的绝对值。
以上就是计算梯形面积的两种常用方法。
无论是使用公式还是将梯形看作是一个大矩形减去一个小矩形,只要掌握了计算的原理,我们就可以轻松地计算出梯形的面积。
在实际应用中,计算梯形的面积是非常常见的。
比如,在建筑设计中,我们经常需要计算梯形地板的面积;在土地测量中,我们也需要计算梯形地块的面积。
梯形的面积计算知识点总结

梯形的面积计算知识点总结梯形是一种常见的几何图形,它由两条平行的底边和连接两底边的两条斜边组成。
计算梯形的面积是数学中的基本问题之一,本文将总结梯形的面积计算知识点,帮助读者更好地理解和应用梯形的面积公式。
1. 梯形的定义梯形是一个四边形,它有两边是平行线段,这两条平行线段被称为梯形的底边,而连接两底边的两条线段被称为梯形的斜边。
梯形的两个底边可以是不等长的,但它们平行。
2. 梯形的面积公式梯形的面积可以通过以下公式计算:面积 = (上底 + 下底) ×高 ÷ 2其中,上底和下底分别表示梯形上下两条平行线段的长度,高表示连接上底和下底的垂直线段的长度。
3. 梯形面积计算示例为了更好地理解梯形的面积计算方法,下面通过一个示例来演示。
假设梯形的上底长为6cm,下底长为10cm,高为4cm。
根据上述公式,可以计算出该梯形的面积:面积 = (6 + 10) × 4 ÷ 2 = 16cm²因此,该梯形的面积为16平方厘米。
4. 梯形面积计算的重点在计算梯形的面积时,需要注意以下几点:- 底边必须是平行的。
如果底边不平行,则不能使用梯形的面积计算公式。
- 高必须是连接上底和下底的垂直线段。
只有垂直于底边的线段才能作为梯形的高进行计算。
- 单位必须一致。
在进行梯形面积计算时,底边和高的单位必须相同,否则计算结果将无意义。
5. 应用举例梯形的面积计算可以应用于各种实际问题中,例如计算梯形形状的地板面积、屋顶面积等。
通过计算梯形的面积,可以帮助我们更好地规划和设计建筑物或进行土地测量。
6. 总结梯形的面积计算是数学中的基本知识点,通过本文的总结,我们了解了梯形的定义、面积计算公式和注意事项。
掌握了这些知识,我们可以准确地计算梯形的面积,并将其应用于实际问题中。
希望本文对读者在学习和应用梯形面积计算方面有所帮助。
梯形的周长和面积常用公式

梯形的周长和面积常用公式1. 周长公式梯形的周长是指围绕梯形的边的总长度。
我们可以使用以下公式来计算梯形的周长:周长 = 上底长度 + 下底长度 + 左斜边长度 + 右斜边长度2. 面积公式梯形的面积是指梯形内部的填充区域的大小。
我们可以使用以下公式来计算梯形的面积:面积 = (上底长度 + 下底长度) ×高度 ÷ 2其中,高度是梯形的两个底之间的垂直距离。
3. 例子让我们通过一个例子来说明如何使用这些公式计算梯形的周长和面积。
假设有一个梯形,上底长度为 5 cm,下底长度为 8 cm,高度为 4 cm。
现在我们来计算它的周长和面积。
根据公式,周长 = 5 cm + 8 cm + 左斜边长度 + 右斜边长度。
要计算左斜边长度和右斜边长度,我们需要知道更多的信息,比如梯形的角度或其他边长。
但由于没有提供这些信息,我们无法准确计算它们的长度。
对于面积,根据公式,面积 = (5 cm + 8 cm) × 4 cm ÷ 2 = 26 cm²。
所以,这个梯形的周长无法准确计算,但面积为 26 cm²。
请记住,在实际问题中,我们通常需要更多的信息才能准确计算梯形的周长和面积。
这些公式只适用于特定的情况,请确保在使用时考虑到额外的条件。
4. 总结梯形的周长和面积计算可以使用相应的公式进行。
周长公式包括上底长度、下底长度、左斜边长度和右斜边长度的总和。
面积公式则是根据上底长度、下底长度和高度来计算。
请注意,这些公式只在给定足够信息的情况下才能进行准确计算。
梯形的面积计算

梯形的面积计算梯形是一种四边形,其两边平行且两边长度不相等。
计算梯形的面积是一个基本的几何问题,涉及到梯形的底和高的长度。
下面将介绍如何计算梯形的面积。
首先,需要明确梯形的底和高的定义。
梯形的底是指两个平行边中的任意一个边,通常用字母a和b表示。
梯形的高是指两个平行边的距离,通常用字母h表示。
梯形的面积公式为:面积 = (底1 + 底2) * 高 / 2这个公式的推导过程可以通过将梯形拆分为一个矩形和两个三角形来理解。
具体计算步骤如下:1. 确定梯形的底和高的长度:根据题目中的给定条件,得到梯形的底1、底2和高的数值。
假设底1的长度为a,底2的长度为b,高的长度为h。
2. 应用面积公式计算:将底1、底2和高的数值代入梯形的面积公式。
计算过程如下:面积 = (a + b) * h / 23. 按照计算器的指令计算:将底1、底2和高的数值代入公式,并通过计算器进行计算。
4. 得出结果:根据计算结果,得出梯形的面积。
注意在结果中保留合适的小数位数,根据题目要求决定结果的精度。
例如,假设梯形的底1长度为5 cm,底2长度为10 cm,高度为8 cm。
按照上述计算步骤,可以得出梯形的面积。
面积 = (5 + 10) * 8 / 2 = 15 * 8 / 2 = 120 / 2 = 60 平方厘米因此,该梯形的面积为60平方厘米。
在实际应用中,可以通过测量梯形的底和高的长度来计算面积。
如果只给出梯形的周长或其他相关信息,则需要根据提供的信息使用相关的几何定理来计算梯形的面积。
总之,计算梯形的面积是一个简单又常见的几何计算问题。
通过应用梯形的面积公式,并按照给定的底和高的长度,可以准确计算出梯形的面积。
通过掌握这个计算方法,可以更好地理解和应用几何学的相关知识。
梯形面积计算公式
.
.
试一试
❖ 下图是一个梯形,我们用a、b、h分别表示梯 形的上底、下底和高,求面积S。
a
梯形面积=(上底+下底) × 高÷2
h
S=( a + b ) h ÷ 2
b
看图填表。(每个方格的边长是1cm)
2
4
2
4
2
4
4
12
4
12
5
15
答:它的面积是10530平方米。
这堆圆木有几根?你能列式计算吗?
下底
平行四边形面积=2×梯形的面积
梯形面积=平行四边行面积÷2
梯形面积=平行四边形的底×高÷2 梯形面积=(上底&#——平行四边形
高÷2
下底+上底
平行四边形面积=
底
×高
‖
‖
‖
梯形面积=(上底+下底) ×(高÷2)
即: 梯形面积=(上底+下底) × 高÷2
了. 解 其 它 割 补 方 法
复习
h a
S=ah
平
行 四
a= S ÷h
边
形
h=S÷a
h a
S = a h ÷2
三
角
a= 2S ÷h
形
h = 2S ÷a
梯形的面积初探
上底 高
下底
重看
梯形的面积初探
上底 高
下底
上底
上底
高
高
下底
下底+上底
梯形的面积计算

梯形的面积计算梯形是一种具有特殊形状的四边形,它拥有两个平行的底边和两个不平行的斜边。
计算梯形的面积可以使用公式:面积 = (底边之和)×高 ÷ 2。
在本文中,我们将详细介绍如何通过给定的梯形尺寸计算其面积。
梯形的定义可以简单地表述为:两个底边之和乘以高再除以2。
为了更好地理解这个公式,让我们以具体的梯形为例来进行计算。
假设我们有一个梯形,其底边1的长度为a,底边2的长度为b,高为h。
我们可以使用以下公式计算梯形的面积:面积 = (a + b) × h ÷ 2现在,让我们通过一个实际的例子来演示如何计算梯形的面积。
假设我们有一个梯形,其底边1的长度为6cm,底边2的长度为10cm,高为4cm。
我们可以使用上述公式,将这些值代入计算梯形的面积。
面积 = (6 + 10) × 4 ÷ 2= 16 × 4 ÷ 2= 64 ÷ 2= 32因此,这个梯形的面积为32平方厘米。
通过这个简单的例子,我们可以看出,计算梯形的面积并不复杂。
只需将底边1和底边2的长度相加,再乘以高,最后除以2,就可以得到梯形的面积。
需要注意的是,计算梯形面积时,确保使用相同的长度单位,以保持计算的准确性。
如果底边和高的单位不一致,我们需要先将其统一转换为相同单位再进行计算。
在实际应用中,计算梯形面积的知识可以用于建筑、工程、地理和数学等领域。
无论是计算房屋屋顶的面积还是测量地图上的梯形区域,掌握计算梯形面积的方法都是非常有用的。
总结起来,计算梯形面积需要使用梯形面积计算公式:面积 = (底边之和)×高 ÷ 2。
确保底边和高的单位一致,代入数值后进行计算即可。
这项技能在实际生活和工作中都非常实用,帮助我们理解和解决与梯形相关的问题。
梯形的面积计算公式推导过程

梯形的面积计算公式推导过程
推导一:甲、乙两个梯形全等,且上底为a,下底为b,高为h。
将这两个梯形拼接成一个平行四边形,则平行四边形的一条底边长为a+b,此底边上的高与梯形的高h相等,那么一个梯形的面积是平行四边形面积的一半。
梯形的面积=(a+b)h÷2=1/2(a+b)h 。
推导二:一个梯形上底为a,下底为b,高为h。
在梯形内连接一组对角的顶点作一虚线,将三角形沿中点旋转,拼成一个大三角形。
则有:
梯形的面积=(b+a)h÷2=1/2(a+b)h 。
推导三:一个梯形上底为a,下底为b,高为h。
在梯形内连接顶点到一腰中点作一虚线,将梯形分为两个等高不同底的三角形。
则有:
第一个三角形的面积=1/2ah。
第二个三角形的面积=1/2bh。
梯形的面积=1/2ah+1/2bh=1/2(a+b)h 。
推导四:一个梯形上底为a,下底为b,高为h。
在梯形内作一虚线,将梯形分为一个平行四边形和一个三角形。
则有:平行四边形的面积=ah 。
三角形的面积=(b-a)h÷2=1/2bh-1/2ah 。
梯形的面积= ah+1/2bh-1/2ah=1/2ah+1/2bh=1/2(a+b)h。
梯形基础的计算公式

梯形基础的计算公式
梯形是一种四边形,它有两条平行的边。
梯形的面积计算公式为,面积 = (上底 + 下底)× 高÷ 2。
其中,上底和下底分别代表梯形的两条平行边的长度,高代表梯形两平行边之间的垂直距离。
这个公式可以帮助我们计算梯形的面积。
另外,梯形的周长计算公式为,周长 = 上底 + 下底 + 左斜边 + 右斜边。
其中,左斜边和右斜边分别代表梯形的两条非平行边的长度。
这些公式可以帮助我们在实际问题中计算梯形的面积和周长,从而更好地理解和运用梯形的基础知识。
梯形的面积计算公式用母线

梯形的面积计算公式用母线梯形是一种四边形,其两条平行边被称为上底和下底,而连接这两条平行边的两条非平行边被称为斜边。
梯形的面积计算公式是基于梯形的高和上底、下底的长度来计算的。
在本文中,我们将以梯形的面积计算公式为基础,以母线为标题,探讨梯形的性质、应用以及相关的数学概念。
首先,让我们来看一下梯形的面积计算公式。
梯形的面积计算公式为:\[ A = \frac{1}{2} \times h \times (a + b) \]其中,A代表梯形的面积,h代表梯形的高,a代表梯形的上底的长度,b代表梯形的下底的长度。
这个公式告诉我们,要计算梯形的面积,我们需要知道梯形的高和上底、下底的长度。
母线是梯形的两条非平行边之一,它连接梯形的两个顶点,并且平分梯形的高。
母线的长度等于上底和下底的平均值,即 \( c = \frac{a + b}{2} \)。
因此,我们可以将梯形的面积计算公式改写为:\[ A = h \times c \]这个公式告诉我们,梯形的面积可以用梯形的高和母线的长度来计算。
这个公式的推导过程可以帮助我们更好地理解梯形的性质和特点。
梯形是几何形状中常见的一种,它的性质和特点也是我们在数学学习中经常接触到的内容。
梯形的对角线互相垂直,且相交于对角线的交点将梯形分成两个全等的三角形。
这个性质可以帮助我们在解题过程中更好地理解梯形的结构,从而更好地应用梯形的面积计算公式。
梯形的面积计算公式也有着广泛的应用。
在日常生活和工作中,我们经常会遇到需要计算梯形面积的情况。
比如,在建筑施工中,我们需要计算梯形形状的屋顶的面积;在制造业中,我们需要计算梯形形状的零件的表面积。
梯形的面积计算公式可以帮助我们快速准确地计算出梯形的面积,从而更好地应用到实际工作中。
除了梯形的面积计算公式,梯形还有一些其他的数学概念和性质。
比如,梯形的中位线是连接梯形的两个非平行边中点的线段,它的长度等于上底和下底长度的平均值。
梯形的中位线将梯形分成两个全等的三角形,且中位线的长度等于梯形的高。
梯形的体积计算公式和面积计算公式

梯形的体积计算公式和面积计算公式
梯形是一个平面图形,由两组平行线和它们之间的四个边组成。
梯形
的体积计算公式和面积计算公式是根据其特点和属性推导出来的数学公式。
一、梯形的体积计算公式:
要计算梯形的体积,首先需要知道梯形的底的长度、上底的长度和梯
形的高。
假设梯形的底的长度为a,上底的长度为b,梯形的高为h。
梯形的
体积(V)可以通过以下公式计算:
V=(1/2)*(a+b)*h
公式中,(1/2)*(a+b)表示梯形的平均宽度,而h表示梯形的高度。
通过将平均宽度与高度相乘,再乘以1/2,可得到梯形的体积。
值得注意的是,梯形的体积通常用立方单位(如立方米、立方厘米)
表示。
二、梯形的面积计算公式:
要计算梯形的面积,需要知道梯形的上底长度、下底长度和梯形的高。
假设梯形的上底长度为a,下底长度为b,梯形的高为h。
可以使用
以下公式计算梯形的面积(A):
A=(1/2)*(a+b)*h
公式中,(1/2)*(a+b)表示梯形的平均宽度,而h表示梯形的高度。
通过将平均宽度与高度相乘,再乘以1/2,可得到梯形的面积。
梯形的面积也可以通过其他方法计算,比如分解成两个三角形的面积之和。
将梯形分解成一个上底和下底相等的两个三角形,每个三角形的底边为(a+b)/2,高为h,那么梯形的面积可以表示为:
A=面积1+面积2
=1/2*[(a+b)/2]*h+1/2*[(a+b)/2]*h
=1/2*(a+b)*h
与之前的公式一致。
梯形的面积通常用平方单位(如平方米、平方厘米)表示。
梯形面积公式四种推导方法

梯形面积公式四种推导方法梯形是一个四边形,它的两边是平行线段,而另外两边分别连接这两条平行线段的两个非相邻顶点。
梯形的面积可以通过四种不同的方法推导出来。
方法一:使用高和底边长度推导梯形面积设梯形的上底长为a,下底长为b,高为h。
可以将梯形分为两个三角形和一个矩形。
矩形的面积为a×h,两个三角形的面积之和为1/2×a×h+1/2×b×h=1/2×(a+b)×h。
将矩形的面积与两个三角形的面积相加,得到整个梯形的面积为(a+b)×h。
方法二:使用对角线和非平行边的长度推导梯形面积设梯形的对角线之和为d,非平行边的长度分别为a和b,其中a > b。
可以将梯形分为两个直角三角形和一个矩形。
两个直角三角形的面积之和为1/2×a×b + 1/2×(a-b)×b = 1/2×(a+b)×b,矩形的面积为a×(d-b)。
将两个直角三角形的面积与矩形的面积相加,得到整个梯形的面积为(a+b)×b + a×(d-b) = (a+b)×b + ad - ab = ab + bd - ab + ad = ad + bd。
方法三:使用两个非平行边和夹角的正弦推导梯形面积设梯形的两个非平行边的长度为a和b,夹角为θ。
可以将梯形分为两个直角三角形和一个矩形。
两个直角三角形的面积之和为1/2×a×b×sinθ + 1/2×(a+b)×h = 1/2×(a+b)×h,其中h为夹角θ的高。
矩形的面积为b×h。
将两个直角三角形的面积与矩形的面积相加,得到整个梯形的面积为1/2×(a+b)×h + b×h = 1/2×(a+b)×h + 1/2×(a+b)×h = (a+b)×h。
探索活动(三)梯形的面积
探索活动(三)梯形的面积
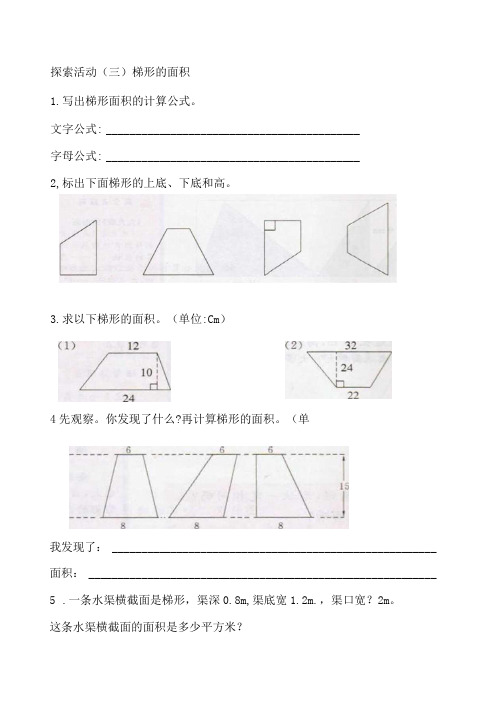
1.写出梯形面积的计算公式。
文字公式: ___________________________________________
字母公式: ___________________________________________
2,标出下面梯形的上底、下底和高。
3.求以下梯形的面积。
(单位:Cm)
4先观察。
你发现了什么?再计算梯形的面积。
(单
我发现了:_______________________________________________________ 面积:___________________________________________________________ 5.一条水渠横截面是梯形,渠深0.8m,渠底宽1.2m.,渠口宽?2m。
这条水渠横截面的面积是多少平方米?
6.有两张面积相等的纸板,一张是梯形,上底是20cm,下底是6cm,
高是IoCm;另一张是三角形,底是25cm
少厘米?
7.在两块直角三角形草坪中间,有一个长4m、宽Irn的通道。
算一算这两块草坪共有多少平方米。
