【人教版】数学(理)一轮复习:第5章《数列》(第4节)ppt课件
2015届高考数学(人教,理科)大一轮配套练透:第5章 数列 第4节

[课堂练通考点]1.数列112,314,518,7116,…,(2n -1)+12n ,…的前n 项和S n 的值等于( )A .n 2+1-12nB .2n 2-n +1-12nC .n 2+1-12n -1D .n 2-n +1-12n解析:选A 该数列的通项公式为a n =(2n -1)+12n ,则S n =[1+3+5+…+(2n -1)]+⎝⎛⎭⎫12+122+…+12n =n 2+1-12n .2.(2014·济南模拟)数列{a n }中,a n +1+(-1)n a n =2n -1,则数列{a n }前12项和等于( ) A .76 B .78 C .80D .82解析:选B 由已知a n +1+(-1)n a n =2n -1,得a n +2+(-1)n +1a n +1=2n +1,得a n +2+a n =(-1)n (2n -1)+(2n +1),取n =1,5,9及n =2,6,10,结果相加可得S 12=a 1+a 2+a 3+a 4+…+a 11+a 12=78.故选B.3.若数列{a n }的通项公式是a n =(-1)n ·(3n -2),则a 1+a 2+…+a 10=( ) A .15 B .12 C .-12D .-15解析:选A 记b n =3n -2,则数列{b n }是以1为首项,3为公差的等差数列,所以a 1+a 2+…+a 9+a 10=(-b 1)+b 2+…+(-b 9)+b 10=(b 2-b 1)+(b 4-b 3)+…+(b 10-b 9)=5×3=15.4.已知等比数列{a n }中,a 1=3,a 4=81,若数列{b n }满足b n =log 3a n ,则数列⎩⎨⎧⎭⎬⎫1b n b n +1的前n 项和S n =________.解析:设等比数列{a n }的公比为q ,则a 4a 1=q 3=27,解得q =3.所以a n =a 1q n -1=3×3n -1=3n ,故b n =log 3a n =n ,所以1b n b n +1=1n (n +1)=1n -1n +1.则数列⎩⎨⎧⎭⎬⎫1b n b n +1的前n 项和为1-12+12-13+…+1n -1n +1=1-1n +1=n n +1.答案:nn +15.(2014·惠州调研)已知向量p =(a n,2n ),向量q =(2n +1,-a n +1),n ∈N *,向量p 与q垂直,且a 1=1.(1)求数列{a n }的通项公式;(2)若数列{b n }满足b n =log 2a n +1,求数列{a n ·b n }的前n 项和S n . 解:(1)∵向量p 与q 垂直,∴2n +1a n -2n a n +1=0,即2n a n +1=2n +1a n ,∴a n +1a n=2,∴{a n }是以1为首项,2为公比的等比数列, ∴a n =2n -1.(2)∵b n =log 2a n +1=n -1+1=n , ∴a n ·b n =n ·2n -1,∴S n =1+2·2+3·22+4·23+…+n ·2n -1,① ∴2S n =1·2+2·22+3·23+…+(n -1)·2n -1+n ·2n ,②①-②得,-S n =1+2+22+23+24+…+2n -1-n ·2n=1-2n1-2-n ·2n =(1-n )2n -1,∴S n =1+(n -1)2n .[课下提升考能]第Ⅰ卷:夯基保分卷1.数列{1+2n -1}的前n 项和为( )A .1+2nB .2+2nC .n +2n -1D .n +2+2n解析:选C 由题意得a n =1+2n -1,所以S n =n +1-2n1-2=n +2n -1,故选C.2.已知等差数列{a n }的前n 项和为S n ,a 5=5,S 5=15,则数列⎩⎨⎧⎭⎬⎫1a n a n +1的前100项和为( )A.100101B.99101C.99100D.101100解析:选A 设等差数列{a n }的首项为a 1,公差为d . ∵a 5=5,S 5=15,∴⎩⎪⎨⎪⎧a 1+4d =5,5a 1+5×(5-1)2d =15,∴⎩⎪⎨⎪⎧a 1=1,d =1,∴a n =a 1+(n -1)d =n . ∴1a n a n +1=1n (n +1)=1n -1n +1, ∴数列⎩⎨⎧⎭⎬⎫1a n a n +1的前100项和为1-12+12-13+…+1100-1101=1-1101=100101. 3.(2013·北京东城一模)已知函数f (n )=n 2cos n π,且a n =f (n )+f (n +1),则a 1+a 2+a 3+…+a 100=( )A .0B .-100C .100D .10 200解析:选B f (n )=n 2cos n π=⎩⎪⎨⎪⎧-n 2 (n 为奇数)n 2 (n 为偶数)=(-1)n ·n 2, 由a n =f (n )+f (n +1)=(-1)n ·n 2+(-1)n +1·(n +1)2=(-1)n [n 2-(n +1)2]=(-1)n +1·(2n +1),得a 1+a 2+a 3+…+a 100=3+(-5)+7+(-9)+…+199+(-201)=50×(-2)=-100. 4.已知数列{a n }的前n 项和S n =n 2-6n ,则{|a n |}的前n 项和T n =( ) A .6n -n 2B .n 2-6n +18C.⎩⎪⎨⎪⎧ 6n -n 2(1≤n ≤3)n 2-6n +18(n >3) D.⎩⎪⎨⎪⎧6n -n 2(1≤n ≤3)n 2-6n (n >3)解析:选C ∵由S n =n 2-6n 得{a n }是等差数列, 且首项为-5,公差为2. ∴a n =-5+(n -1)×2=2n -7, ∴n ≤3时,a n <0,n >3时,a n >0,∴T n =⎩⎪⎨⎪⎧6n -n 2(1≤n ≤3),n 2-6n +18(n >3).5.已知数列{a n }满足a n +a n +1=(-1)n +12(n ∈N *),a 1=-12,S n 是数列{a n }的前n 项和,则S 2 013=________.解析:由题意知,a 1=-12,a 2=1,a 3=-32,a 4=2,a 5=-52,a 6=3,…,所以数列{a n }的奇数项构成了首项为-12,公差为-1的等差数列,偶数项构成了首项为1,公差为1的等差数列,通过分组求和可得S 2 013=⎣⎡⎦⎤⎝⎛⎭⎫-12×1 007+1 007×1 0062×(-1)+⎝⎛⎭⎫1×1 006+1 006×1 0052×1=-1 0072. 答案:-1 00726.(创新题)对于数列{a n },定义数列{a n +1-a n }为数列{a n }的“差数列”,若a 1=2,{a n }的“差数列”的通项公式为2n ,则数列{a n }的前n 项和S n =________.解析:∵a n +1-a n =2n ,∴a n =(a n -a n -1)+(a n -1-a n -2)+…+(a 2-a 1)+a 1 =2n -1+2n -2+…+22+2+2=2-2n1-2+2=2n -2+2=2n .∴S n =2-2n +11-2=2n +1-2.答案:2n +1-27.(2013·江西高考)正项数列{a n }满足:a 2n -(2n -1)a n -2n =0. (1)求数列{a n }的通项公式a n ;(2)令b n =1(n +1)a n,求数列{b n }的前n 项和T n .解:(1)由a 2n -(2n -1)a n -2n =0,得(a n -2n )(a n +1)=0. 由于{a n }是正项数列,所以a n =2n . (2)由a n =2n ,b n =1(n +1)a n ,得b n =12n (n +1)=12⎝⎛⎭⎫1n -1n +1.T n =12⎝⎛⎭⎫1-12+12-13+…+1n -1-1n +1n -1n +1=12⎝⎛⎭⎫1-1n +1=n 2(n +1). 8.(2014·襄阳调研)已知数列{a n },如果数列{b n }满足b 1=a 1,b n =a n +a n -1,n ≥2,n ∈N *,则称数列{b n }是数列{a n }的“生成数列”.(1)若数列{a n }的通项为a n =n ,写出数列{a n }的“生成数列”{b n }的通项公式; (2)若数列{c n }的通项为c n =2n +b (其中b 是常数),试问数列{c n }的“生成数列”{q n }是否是等差数列,请说明理由;(3)已知数列{d n }的通项为d n =2n +n ,求数列{d n }的“生成数列”{p n }的前n 项和T n . 解:(1)当n ≥2时,b n =a n +a n -1=2n -1, 当n =1时,b 1=a 1=1适合上式, ∴b n =2n -1(n ∈N *).(2)q n =⎩⎪⎨⎪⎧2+b ,n =1,4n +2b -2,n ≥2,当b =0时,q n =4n -2,由于q n +1-q n =4, 所以此时数列{c n }的“生成数列”{q n }是等差数列. 当b ≠0时,由于q 1=c 1=2+b ,q 2=6+2b ,q 3=10+2b , 此时q 2-q 1≠q 3-q 2,所以此时数列{c n }的“生成数列”{q n }不是等差数列.(3)p n =⎩⎪⎨⎪⎧3,n =1,3·2n -1+2n -1,n ≥2,当n >1时,T n =3+(3·2+3)+(3·22+5)+…+(3·2n -1+2n -1),∴T n =3+3(2+22+23+…+2n -1)+(3+5+7+…+2n -1)=3·2n +n 2-4.又n =1时,T 1=3,适合上式,∴T n =3·2n +n 2-4. 第Ⅱ卷:提能增分卷1.(2014·浙江协作体三模)在直角坐标平面上有一点列P 1(x 1,y 1),P 2(x 2,y 2),…,P n (x n ,y n ),…,对一切正整数n ,点P n 在函数y =3x +134的图像上,且P n 的横坐标构成以-52为首项,-1为公差的等差数列{x n }.(1)求点P n 的坐标;(2)设抛物线列C 1,C 2,C 3,…,C n ,…中的每一条的对称轴都垂直于x 轴,抛物线C n的顶点为P n ,且过点D n (0,n 2+1).记与抛物线C n 相切于点D n 的直线的斜率为k n ,求1k 1k 2+1k 2k 3+…+1k n -1k n. 解:(1)∵x n =-52+(n -1)×(-1)=-n -32,∴y n =3x n +134=-3n -54.∴P n ⎝⎛⎭⎫-n -32,-3n -54. (2)∵C n 的对称轴垂直于x 轴,且顶点为P n , ∴设C n 的方程为y =a ⎝⎛⎭⎫x +2n +322-12n +54.把D n (0,n 2+1)代入上式,得a =1, ∴C n 的方程为y =x 2+(2n +3)x +n 2+1. ∴k n =y ′|x =0=2n +3, ∴1k n -1k n =1(2n +1)(2n +3)=12⎝⎛⎭⎫12n +1-12n +3, ∴1k 1k 2+1k 2k 3+…+1k n -1k n=12⎣⎡⎦⎤⎝⎛⎭⎫15-17+⎝⎛⎭⎫17-19+…+⎝⎛⎭⎫12n +1-12n +3 =12⎝⎛⎭⎫15-12n +3=110-14n +6.2.已知数列{a n }的前n 项和为S n =3n ,数列{b n }满足b 1=-1,b n +1=b n +(2n -1)(n ∈N *).(1)求数列{a n }的通项公式a n ; (2)求数列{b n }的通项公式b n ;(3)若c n =a n ·b n n ,求数列{c n }的前n 项和T n .解:(1)∵S n =3n , ∴S n -1=3n -1(n ≥2),∴a n =S n -S n -1=3n -3n -1=2×3n -1(n ≥2).当n =1时,2×31-1=2≠S 1=a 1=3,∴a n =⎩⎪⎨⎪⎧3,n =1,2×3n -1,n ≥2. (2)∵b n +1=b n +(2n -1),∴b 2-b 1=1,b 3-b 2=3,b 4-b 3=5,…,b n -b n -1=2n -3. 以上各式相加得b n -b 1=1+3+5+…+(2n -3)=(n -1)(1+2n -3)2=(n -1)2.∵b 1=-1,∴b n =n 2-2n .(3)由题意得c n =⎩⎪⎨⎪⎧-3,n =1,2(n -2)×3n -1,n ≥2. 当n ≥2时,T n =-3+2×0×31+2×1×32+2×2×33+…+2(n -2)×3n -1,∴3T n =-9+2×0×32+2×1×33+2×2×34+…+2(n -2)×3n , ∴相减得-2T n =6+2×32+2×33+…+2×3n -1-2(n -2)×3n .∴T n =(n -2)×3n -(3+32+33+…+3n -1) =(n -2)×3n-3n -32=(2n -5)3n +32.∴T n =⎩⎪⎨⎪⎧-3,n =1,(2n -5)3n +32,n ≥2.∴T n =(2n -5)3n +32(n ∈N *).3.已知正项数列{a n },{b n }满足a 1=3,a 2=6,{b n }是等差数列,且对任意正整数n ,都有b n ,a n ,b n +1成等比数列.(1)求数列{b n }的通项公式;(2)设S n =1a 1+1a 2+…+1a n ,试比较2S n 与2-b 2n +1a n +1的大小.解:(1)∵对任意正整数n ,都有b n ,a n ,b n +1成等比数列, 且{a n },{b n }都为正项数列, ∴a n =b n b n +1(n ∈N *).可得a 1=b 1b 2=3,a 2=b 2b 3=6, 又{b n }是等差数列,∴b 1+b 3=2b 2, 解得b 1=2,b 2=322.∴b n =22(n +1). (2)由(1)可得a n =b n b n +1=(n +1)(n +2)2,则1a n =2(n +1)(n +2)=2⎝⎛⎭⎫1n +1-1n +2, ∴S n =2⎣⎡⎦⎤⎝⎛⎭⎫12-13+⎝⎛⎭⎫13-14+…+⎝⎛⎭⎫1n +1-1n +2 =1-2n +2,∴2S n =2-4n +2,又2-b 2n +1a n +1=2-n +2n +3,∴2S n -⎝ ⎛⎭⎪⎫2-b 2n +1a n +1=n +2n +3-4n +2=n 2-8(n +2)(n +3). ∴当n =1,2时,2S n <2-b 2n +1a n +1;当n ≥3时,2S n >2-b 2n +1a n +1.。
2015年高考数学一轮总复习精品课件:第五章+数列 5.1 数列的概念与简单表示法(共28张PPT)

(1)已知 a1 且 an-an-1=f(n)(n≥2),可以用“累加法”,即
an-an-1=f(n),an-1-an-2=f(n-1),…,a3-a2=f(3),a2-a1=f(2).
所有等式左右两边分别相加,代入 a1 得 an.
(2)已知 a1 且
=f(n)(n≥2),可以用“累乘法”,
1 024
1
2
1
2
( -1)
2
·
1 -2
2
关闭
·…·
1 2
2
·
1 1
2
=
.
( -1)
2
≥
1
64
,当 n≥5
.∴从第 5 项开始各项均小于
1
1 000
.
答案
考点一
考点二
考点三
第十七页,编辑于星期五:十一点 十一分。
探究突破
方法提炼
由 a1 和递推关系求通项公式,可观察其特点,一般常利用“累加法”“累
2.在数列{an}中,已知 a1=a,a2=b,an+1+an-1=an(n≥2),则 a6 等于(D)
A.a
B.b
C.b-a
D.a-b
第十页,编辑于星期五:十一点 十一分。
梳理自测
(a,b,c
+
3.已知数列{an}的通项 an=
是(
都是正实数),则 an 与 an+1 的大小关系
)
A.an>an+1
如果已知数列{an}的
的递推公式.它是数列的一种表示法.
6.数列与函数的内在联系
从映射、函数的观点看,数列可以看作是一个定义域为
人教版高中数学高考一轮复习--数列的概念(课件)

故Sn=2×3n-1.
2×3n-1
.
能力形成点3
由数列的递推关系式求通项公式
表示,那么这个式子叫做这个数列的通项公式,常用an=f(n)(n∈N*)表示.
问题思考
数列的通项公式an=3n+5与函数y=3x+5有何区分与联系?
数列的通项公式an=3n+5是特殊的函数,其定义域为N*,而函数y=3x+5的
定义域是R,an=3n+5的图象是离散的点,且在y=3x+5的图象上.
6.数列的递推公式
得到正确的选项.
对点训练 1
2 4 6
(1)数列 0, , , ,…的一个通项公式为( C )
3 5 7
-1
-1
2(-1)
A.an=
B.an=
C.an=
+2
2+1
2-1
2
D.an=
2+1
(方法一:直接法)由第2,3,4项的分母可知,通项公式的分母为奇数1,3,5,7,…,
故a1的分母为1,an的分母为2n-1.
第二环节
关键能力形成
能力形成点1
由数列的前几项求数列的通项公式
例 1 根据下面各数列前几项的值,写出数列的一个通项公式:
(1)-1,7,-13,19,…;
1
1
1
1
(2),
,,
,…;
1×2 2×3 3×4 4×5
2 4 6 8 10
(3)3 , 15 , 35 , 63 , 99,…;
1 9 25
1 4 9 16 25
2
察,即2 , 2 , 2 , 2 , 2 ,…,从而可得该数列的一个通项公式 an= 2 .
高考数学一轮总复习 第5章 数列 第4节 数列求和课件 理 新人教版
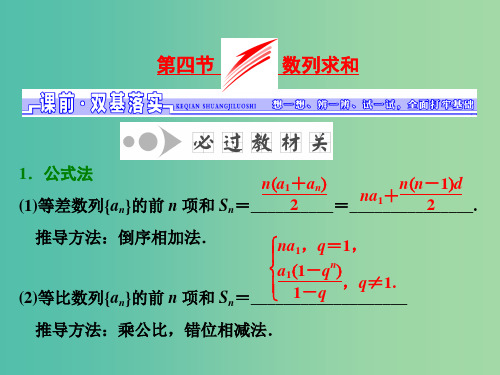
2.若等比数列{an}满足 a1+a4=10,a2+a5=20,则{an}的前 n 项和 Sn=________.
解析:由题意 a2+a5=q(a1+a4),得 20=q×10,故 q=2, 代入 a1+a4=a1+a1q3=10,得 9a1=10,即 a1=190. 故 Sn=19011--22n=190(2n-1). 答案:190(2n-1)
(2015·湖北高考)设等差数列{an}的公差为 d,前 n 项和为 Sn,等 比数列{bn}的公比为 q.已知 b1=a1,b2=2,q=d,S10=100. (1)求数列{an},{bn}的通项公式; (2)当 d>1 时,记 cn=abnn,求数列{cn}的前 n 项和 Tn.
解析
[由题悟法]
bn=3
an+1 2
,求数列an+2 1·bn的前
n
项和
Sn.
an+1
解:由(1)可得 bn=3 2 =3n,
所以an+2 1·bn=n·3n,
[即时应用]
已知等比数列{an}中,首项 a1=3,公比 q>1,且 3(an+2 +an)-10an+1=0(n∈N*). (1)求数列{an}的通项公式; (2)设bn+13an是首项为 1,公差为 2 的等差数列,求数列 {bn}的通项公式和前 n 项和 Sn.
解析
考点三 错位相减法求和 重点保分型考点——师生共研 [典例引领]
(3)错位相减法:如果一个数列的各项是由一个等差数列和 一个等比数列的对应项之积构成的,那么求这个数列 的前 n 项和即可用错位相减法求解.
(4)倒序相加法:如果一个数列{an}与首末两端等“距离” 的两项的和相等或等于同一个常数,那么求这个数列 的前 n 项和即可用倒序相加法求解.
高考数学一轮总复习第五章数列5数列的热点问题课件高三全册数学课件

考点四 数列中的新定义问题 【例 4】 若数列{an}满足an1+1-a1n=d(n∈N*,d 为常数),则称数 列{an}为“调和数列”,已知正项数列b1n为“调和数列”,且 b1+b2
+…+b2 019=20 190,则 b2b2 018 的最大值是___1_0_0___.
第十五页,共二十七页。
考点三 数列中的数阵问题 【例 3】 观察如图所示的数表:
2 46 8 10 12 14 16 18 20 22 24 26 28 30 ……
设 2 018 是该数表第 m 行第 n 列的数,则 mn=__4__9_8_0__.
第十六页,共二十七页。
【解析】 第 1 行有 1 个偶数,第 2 行有 2 个偶数,第 3 行 有 22 个偶数,以此类推,第 n 行有 2n-1 个偶数,∴前 n 行共有 1 +2+22+…+2n-1=11--22n=2n-1(个)偶数,第 n 行最后一个偶数 是(2n-1)×2=2n+1-2,令 2n+1-2≥2 018,得 2n+1≥2 020,∴ 2n≥1 010,∴n≥10,∴第 10 行最后一个数是 2 046,第 10 行有 512 个偶数,∴2 018 是第 10 行第 498 列的数,∴m=10,n=498, ∴mn=4 980.
第二十七页,共二十七页。
第四页,共二十七页。
(2)∵(3n-5)·2n·m≥6n2-31n+35(n≥2,n∈N*)恒成立, ∴m≥6n23-n-315n+·2n35=3n-3n5-52n·2-n 7=2n2-n 7,即 m≥2n2-n 7对 任意 n≥2,n∈N*恒成立.
设 kn=2n2-n 7,则 kn+1-kn=22nn-+15-2n2-n 7=92-n+21n, 当 n≤4 时,kn+1>kn; 当 n≥5 时,kn+1<kn. ∴(kn)max=k5=235=332,∴m≥332.
高考数学一轮复习 第五章 数列 5.4 数列求和与数列的综合应用课件 理 高三全册数学课件

2021/12/8
第二十三页,共五十七页。
解析:(1)令数列{an}的前 n 项和为 Sn,则 S20=a1+a2+a3 +…+a20=2(1+2+3+…+20)-12+212+213+…+2120=420- 1-2120=419+2120.
(2)an=2+22+23+…+2n=2-1-2n2+1=2n+1-2, 所以 Sn=(22+23+24+…+2n+1)-(2+2+2+…+2)= 221--22n+2-2n=2n+2-4-2n.
2021/12/8
第十八页,共五十七页。
课堂探究·深度剖析
课堂升华 强技提能
2021/12/8
第十九页,共五十七页。
考向一 分组求和法
【例 1】 (1)若数列{an}的通项公式为 an=2n+2n-1,则数列{an}
的前 n 项和为( C )
A.2n+n2-1
B.2n+1+n2-1
C.2n+1+n2-2 D.2n+n-2
2021/12/8
第十三页,共五十七页。
4.(2019·武汉市调研考试)对任一实数序列 A=(a1,a2,a3,…), 定义新序列 ΔA=(a2-a1,a3-a2,a4-a3,…),它的第 n 项为 an+1-an.
假定序列 Δ(ΔA)的所有项都是 1,且 a12=a22=0,则 a2= 100 .
第五章
数列(shùliè)
2021/12/8
第一页,共五十七页。
第四节 数列求和(qiúhé)与数列的综合应用
2021/12/8
第二页,共五十七页。
2021/12/8
第三页,共五十七页。
知识(zhī shi)梳理·自主学
习
课堂(kètáng)探究·深度剖 析
高考数学一轮复习 第五章 数列 5.3 等比数列及其前n项和课件

(4)如果数列{an}为等比数列,则数列{ln an}是等差数列.( × )
(5)数列{an}的通项公式是
an=an,则其前
n
项和为
a1-an Sn= 1-a .(
×
)
(6)数列{an}为等比数列,则 S4,S8-S4,S12-S8 成等比数列.( × )
答案
2
考点自测
1.(2015·课标全国Ⅱ)已知等比数列{an}满足a1=3,a1+a3+a5=21,则 a3+a5+a7等于( B )
A.6
B.5
C.4
D.3
解析 数列{lg an}的前8项和S8=lg a1+lg a2+…+lg a8=lg(a1·a2·…·a8) =lg(a1·a8)4 =lg(a4·a5)4=lg(2×5)4=4.
1 2345
解析答案
4.(2015·安徽)已知数列{an}是递增的等比数列,a1+a4=9,a2a3=8,则 数列{an}的前n项和等于 2n-1 . 解析 由等比数列性质知a2a3=a1a4,又a2a3=8,a1+a4=9,
A.21
B.42
C.63
D.84
解析 设等比数列{an}的公比为q, 则由a1=3,a1+a3+a5=21得3(1+q2+q4)=21, 解得q2=-3(舍去)或q2=2,
于是a3+a5+a7=q2(a1+a3+a5)=2×21=42,故选B.
1 2345
解析答案
2.设等比数列{an}的前n项和为Sn.若S2=3,S4=15,则S6等于( C )
第五章 数 列
§5.3 等比数列及其前n项和
内容 索引
基础知识 自主学习 题型分类 深度剖析 思想与方法系列 思想方法 感悟提高 练出高分
2022届高考数学一轮复习第五章数列第四节数列求和课件新人教版

1.在数列{an}中,an=
1 nn+1
,若{an}的前n项和为
2 2
019 020
,则项数n为
(D )
A.2 016
B.2 017
C.2 018
D.2 019
2.已知数列:1
1 2
,2
1 4
,3
1 8
,…,
n+21n
,…,则其前n项和关于n的表
达式为________.
答案:nn2+1+1-21n
B.22
019 020
2 019 C.2 018
D.12
019 010
2.(2021·张掖期末测试)我国古代数学名著《九章算术》中,有已知长
方形面积求一边的算法,其方法的前两步为:
第一步:构造数列1,21,31,41,…,1n.①
第二步:将数列①的各项乘以n,得到一个新数列a1,a2,a3,…,an,
a2-5=3(a1-3). 因为a1=3,所以an=2n+1. (2)由(1)得2nan=(2n+1)2n, 所以Sn=3×2+5×22+7×23+…+(2n+1)×2n.① 从而2Sn=3×22+5×23+7×24+…+(2n+1)×2n+1.② ①-②得-Sn=3×2+2×22+2×23+…+2×2n-(2n+1)×2n+1,所以 Sn=(2n-1)2n+1+2.
2n-1,
故数列{bn}的前n项和Tn=b1+b2+…+bn=( 3 -1)+( 5 - 3 )+…+
( 2n+1- 2n-1)= 2n+1-1.
裂项相消法求和的实质和解题关键 裂项相消法求和的实质是将数列中的通项分解,然后重新组合, 使之能消去一些项,最终达到求和的目的,其解题的关键就是准 确裂项和消项. (1)裂项原则:一般是前边裂几项,后边就裂几项,直到发现被消 去项的规律为止. (2) 消 项 规 律 : 消 项 后 前 边 剩 几 项 , 后 边 就 剩 几 项 , 前 边 剩 第 几 项,后边就剩倒数第几项.
高三数学一轮复习 5.1数列的概念与简单表示法课件

a3=2sin3 2 =-2≠2,其他选项都适合,故选B.
完整版ppt
10
3.把1,3,6,10,15,21,…这些数叫做三角形数,这是因为以这些 数目的点可以排成一个正三角形(如图).
则第7个三角形数是( )
A.27
B.28
C.29
D.30
【解析】选B.由图可知,第7个三角形数是
1+2+3+4+5+6+7=28完. 整版ppt
2n
(3)奇数项为负,偶数项为正,故通项公式的符号为(-1)n;各项绝
对值的分母组成数列1,2,3,4,…;而各项绝对值的分子组成的数
列中,奇数项为1,偶数项为3,即奇数项为2-1,偶数项为2+1,
所以an=1n •2,也1可n 写完为整版ppt
18
n
an=
3 n
1 ,n为 正 奇 数 n ,n为 正 偶 数 .
A.①②
B.③④
C.①③
完整版ppt
D.②④
8
【解析】选D.①错误.不是所有的数列的第n项都能使用公式表 达. ②正确.根据数列的前几项归纳出的数列的通项公式可以有多个. ③错误.如已知an+2=an+1+2an,则只要知道任意连续两项都可 以确定这个数列. ④正确.根据数列的前n项和的定义可知.
完整版ppt
13
6.在数列{an}中,a1=1,an+2=an+1-an(n∈N*),则a100等
于
.
【解析】因为an+2=an+1-an, 所以an+3=an+2-an+1. 两式相加得an+3=-an, 则an+6=-an+3=an, 即数列{an}的周期为6,
人教版高中总复习一轮数学精品课件 第5章 数列 5.5 数学归纳法

(5)用数学归纳法证明等式“1+2+22+…+2n+2=2n+3-1”,验证当n=1结论成立
时,左边式子应为1+2+22+23.( √ )
2.用数学归纳法证明:首项是 a1,公差是 d 的等差数列{an}的前 n 项和公式是
(-1)
Sn=na1+
d 时,假设当 n=k 时,公式成立,则 Sk 等于( C )
2
(1 + )
A.a1+(k-1)d
B.
2
(-1)
(+1)
C.ka1+
d
D.(k+1)a1+
d
2
2
假设当 n=k 时,公式成立,只需把公式中的 n 换成 k 即可,即
3.已知数列{an}满足an+1=2 -nan+1,n∈N*,且a1=2,则a2=a3=源自4,a4=5
,猜想an=
n+1
当n=k+1时,待证等式左边=1+2+3+…+(2k+1)+(2k+2)+(2k+3),
所以从n=k到n=k+1,左边需增添的代数式是(2k+2)+(2k+3).
第二环节
关键能力形成
能力形成点1
例1
用数学归纳法证明等式
1
1
1
1
用数学归纳法证明:
+
+
+…+
=
(n∈N*).
2×4 4×6 6×8
2(2+2) 4(+1)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
• 3.错位相减法 • 如果一个数列的各项是由一个等差数列 和一个等比数列的对应项之积构成的,那 么这个数列的前n项和即可用此法来求,等 比数列的前n项和就是用此法推导的. • 4.裂项相消法 • 把数列的通项拆成两项之差,在求和时 中间的一些项可以相互抵消,从而求得其 和.
[基础自测自评] 1.设数列{(-1)n}的前 n 项和为 Sn,则对任意正整数 n,Sn= ( n[(-1)n-1] A. 2 (-1)n+1 C. 2 (-1)n-1+1 B. 2 (-1)n-1 D. 2 )
D [因为数列{(-1)n}是首项与公比均为-1 的等比数列,所 -1-(-1)n×(-1) (-1)n-1 以 Sn= = .] 2 1-(-1)
2.(教材习题改编)等差数列{an}的通项公式为 an=2n+1,其前 n 项的和为
Sn 的前 Sn,则数列 n
10 项的和为 ( )
15 5 n+1 =- +2-n · 3 . 2
• •
•
•
• [规律方法] 用错位相减法求和应注意: (1)要善于识别题目类型,特别是等比数列 公比为负数的情形; (2)在写出“Sn”与“qSn”的表达式时应特别 注意将两式“错项对齐”以便下一步准确 写出“Sn-qSn”的表达式. (3)在应用错位相减法求和时,若等比数列 的公比为参数,应分公比等于1和不等于1 两种情况求解.
C [a1+„+ak+„+a10=240-(2+„+2k+„+20)= (2+20)×10 240- =240-110=130.] 2
4.若数列{an}的通项公式为 an=2n+2n-1,则数列{an}的前 n 项和为________. 2(1-2n) n(1+2n-1) n+1 解析 Sn= + =2 -2+n2. 2 1-2 答案 2n+1+n2-2
• •
•
•
Hale Waihona Puke • [关键要点点拨] 数列求和的方法 (1)一般的数列求和,应从通项入手,若无 通项,先求通项,然后通过对通项变形, 转化为与特殊数列有关或具备某种方法适 用特点的形式,从而选择合适的方法求 和. (2)解决非等差、等比数列的求和,主要有 两种思路: ①转化的思想,即将一般数列设法转化为 等差或等比数列,这一思想方法往往通过 通项分解或错位相减来完成.
②
由①-②得
1 1 1 2 1 2 13 n Tn=5×3 +43 +3 +„+ 3 - 3 1n+1 (4n+1)× 3 1n 1n+1 1 11 12 13 = +43 +3 +3 +„+3 -(4n+1)× 3 3
1 1 ·1-3n 1n+1 3 1 = +4· -(4n+1)× 3 3 1 1- 3
1 1 1 n+1 = +21-3n-(4n+1)× . 3 3 1n ∴2Tn=7-(4n+7)× 3 , 1n 7 7 1 ∴Tn= - (4n+7)× 3 <2. 2 2
[规律方法] 分组转化法求和的常见类型 (1)若 an=bn±cn,且{bn},{cn}为等差或等比数列,可采用分组求 和法求{an}的前 n 项和. (2)通项公式为
bn,n为奇数, an= 的数列,其中数列{bn},{cn}是 cn,n为偶数
等比数列或等差数列,可采用分组求和法求和.
• [跟踪训练] • 1.已知数列{xn}的首项x1=3,通项xn= 2np+nq(n∈N*,p,q为常数),且x1,x4, x5成等差数列.求: • (1)p,q的值; • (2)数列{xn}前n项和Sn的公式.
解析
(1)由 x1=3,得 2p+q=3,
又因为 x4=24p+4q, x5=25p+5q,且 x1+x5=2x4, 得 3+25p+5q=25p+8q, 解得 p=1,q=1. (2)由(1),知 xn=2n+n, 所以 Sn=(2+2 +„+2 )+(1+2+„+n)=2
• 二、非等差、等比数列求和的常用方法 • 1.倒序相加法 • 如果一个数列{an},首末两端等“距离” 的两项的和相等或等于同一常数,那么求 这个数列的前n项和即可用倒序相加法, 等差数列的前n项和即是用此法推导的. • 2.分组转化求和法 • 若一个数列的通项公式是由若干个等差 数列或等比数列或可求和的数列组成,则 求和时可用分组转化法,分别求和而后相 加减.
2 n n +1
n(n+1) -2+ . 2
错位相减法求和
[典题导入] (理)(2013· 东北三省四市联考)数列{an}的前 n 项和为 Sn, 3 1 3 且 Sn= (an-1),数列{bn}满足 bn= bn-1- (n≥2),且 b1=3. 2 4 4 (1)求数列{an}与{bn}的通项公式; (2)设数列{cn}满足 cn=an·log2(bn+1),其前 n 项和为 Tn,求 Tn.
15 5 n+1 =- +2-n · 3 . 2
(文)(2014· 东北三省四市联考)数列{an}的前 n 项和为 Sn, 3 1 且 Sn= (an-1),数列{bn}满足 bn+1= bn,且 b1=4. 2 4 (1)求数列{an}与{bn}的通项公式; (2)设数列{cn}满足 cn=am·log2bn,其前 n 项和为 Tn,求 Tn.
[听课记录]
3 (1)对于数列{an}有 Sn= (an-1), ① 2
3 Sn-1= (an-1-1)(n≥2), ② 2 3 由①-②得 an= (an-an-1),即 an=3an-1, 2 3 n=1 时,S1= (a1-1)得 a1=3, 2 则 an=a1· qn-1=3· 3n-1=3n.
(2)由(1)得
n-1 ,n为奇数, 2 bn= 2n-3,n为偶数,
∴T2n=1+2× 2-3+22+2× 4-3+24+…+22n-2+2× 2n-3 =1+22+24+…+22n-2+4(1+2+…+n)-3n 1-4n n(n+1) 4n 1 = +4· -3n= - +2n2-n. 2 3 3 1-4
(2)由(1)可知 cn=an·log2(bn+1)=3n·log242-n =3n·log224-2n=3n(4-2n). Tn=2· 31+0· 32+(-2)· 33+„+(4-2n)· 3n,③ 3Tn=2· 32+0· 33+„+(6-2n)· 3n+(4-2n)· 3n+1, ④
由③-④得 -2Tn=2· 3+(-2)· 32+(-2)· 33+„+(-2)· 3n-(4-2n)· 3n+1 =6+(-2)(32+33+„+3n)-(4-2n)· 3n+1. 9(1-3n-1) 则 Tn=-3+ +(2-n)· 3n+1 1-3
1 3 对于数列{bn}有 bn= bn-1- (n≥2), 4 4 bn+1 1 1 1 可得 bn+1= bn-1+ ,即 = . 4 4 bn-1+1 4
1 1 n-1 n-1 2 -n bn+1=(b1+1)4 =4 = 4 , 4
即 bn=42-n-1.
• 第四节
数列求和
• [主干知识梳理] • 一、公式法 • 1.如果一个数列是等差数列或等比数列, 则求和时直接利用等差、等比数列的前n 项和公式,注意等比数列公比q的取值情 况要分q=1或q≠1.
2.一些常见数列的前 n 项和公式: n(n+1) (1)1+2+3+4+„+n= ; 2 (2)1+3+5+7+„+2n-1= n2 (3)2+4+6+8+„+2n= n2+n ; .
分组转化法求和
[典题导入] (2014· 潍坊模拟)已知数列{an}是各项均不为 0 的等差数 1 2 列,Sn 为其前 n 项和,且满足 S2n-1= an,n∈N*. 2 (1)求 an;
n-1 2 ,n为奇数, (2)数列{bn}满足 bn=1 Tn 为数列{bn}的前 n 项和, a - ,n为偶数, 2 n 1
[跟踪训练] 2.(理)(2014· 合肥一模)已知数列{an}的前 n 项和为 Sn,且 2Sn+3 =3an(n∈N*). (1)求数列{an}的通项公式; 4n+1 7 (2)设 bn= ,Tn=b1+b2+„+bn,求证:Tn< (n∈N*) an 2
解析:(1)当 n=1 时,2S1+3=3a1⇒a1=3;
[听课记录]
3 (1)对于数列{an}有 Sn= (an-1), ① 2
3 Sn-1= (an-1-1)(n≥2), ② 2 3 由①-②得 an= (an-an-1),即 an=3an-1, 2 3 n=1 时,S1= (a1-1)得 a1=3, 2 则 an=a1· qn-1=3· 3n-1=3n. 1 对于数列{bn}有 bn+1= bn, 4 可得
A.120 C.75
B.70 D.100
n(a1+an) C [∵Sn= =n(n+2), 2 Sn S1 S2 S10 ∴ =n+2.故 + +„+ =75.] n 1 2 10
3. 数列 a1+2, „, ak+2k, „, a10+20 共有十项, 且其和为 240, 则 a1+„+ak+„+a10 的值为 ( A.31 C.130 B.120 D.185 )
当 n≥2 时,2Sn+3=3an,2Sn-1+3=3an-1,
∴当 n≥2 时,2Sn-2Sn-1=3an-3an-1⇒an=3an-1.
∴数列{an}是以 3 为首项,公比为 3 的等比数列, ∴数列{an}的通项公式为 an=3n.
1 4n+1 n (2)证明:由(1)得 bn= =(4n+1) 3 , an
1n-1 2-n bn=4× = 4 . 4
(2)由(1)可知 cn=an·log2bn=3n·log242-n =3n·log224-2n=3n(4-2n). Tn=2· 31+0· 32+(-2)· 33+„+(4-2n)· 3n, 3Tn=2· 32+0· 33+„+(6-2n)· 3n+(4-2n)· 3n+1, -2Tn=2· 3+(-2)· 32+(-2)· 33+„+(-2)· 3n-(4-2n)· 3 n +1 =6+(-2)(32+33+„+3n)-(4-2n)· 3n+1, 9(1-3n-1) 则 Tn=-3+ +(2-n)· 3n+1 1-3
