化学计量在实验中的应用——相关公式的推导
化学计量在实验中的应用阿伏伽德罗定律

首先检查装置的气密性瓶中除去杂质,最 后通过量气管测量气体的体积。
注意事项
在操作过程中要保持温度不变,且要控制反应速率以免产 生过大误差。同时,要选择合适的药品和洗气液以确保实 验的准确性和安全性。
04 阿伏伽德罗定律在实验中 的应用
化学计量在实验中的应用阿伏伽德 罗定律
目录
• 引言 • 化学计量基础知识 • 阿伏伽德罗定律实验原理 • 阿伏伽德罗定律在实验中的应用 • 数据处理与结果分析 • 实验注意事项与拓展思考
01 引言
目的和背景
01
探讨化学计量在实验中的应用, 特别是在气体反应和化学平衡研 究中的重要性。
02
介绍阿伏伽德罗定律的基本原理 和应用,以及其在化学和相关领 域中的意义。
02 化学计量基础知识
化学计量定义及意义
化学计量是研究物质的量及其变化的 一门科学,它涉及到化学实验中各种 物理量和化学量的测量和计算。
化学计量的意义在于为化学研究和应 用提供准确、可靠的数据支持,有助 于揭示化学反应的本质和规律,推动 化学学科的发展。
常用化学计量单位
物质的量的单位:摩尔(mol)
运用数学方法对实验数据进行处理,如计算平均值、 标准差等,以揭示数据间的内在联系和规律。
结果表示与讨论
文字描述
用简洁、准确的语言描述实验结 果,包括观察到的现象、测量得 到的数据等。
图表展示
通过图表展示实验结果,如数据 分布图、趋势图等,使结果更加 直观、易于理解。
结果讨论
对实验结果进行分析和讨论,解 释实验现象的原因,探讨实验结 果的意义和价值。
在指定区域进行实验
确保实验在通风良好的指定实验室区域进行,以减少有害气体的 积聚。
化学计量在实验中的应用-

一、物质的量及其单位:1、物质的量:与质量、长度等一样,是一个新的物理量。
表示含有一定数目粒子的集体的物理量。
1) 物质的量符号用“n”表示。
2) “物质的量”专有名词,不可分割、不能增减。
3) 物质的量研究的对象是微观粒子。
如原子、分子、离子、电子等。
4) 使用mol时应用化学式指明粒子的种类。
5) 物质的量的单位是摩尔。
2、摩尔:摩尔是表示物质的量的单位。
(mol)1) 摩尔与物质的量的关系就是质量与千克的关系。
2) 1摩尔:科学上以12克所含的原子数作为摩尔的基准。
即每摩尔物质含有阿伏加德罗常数个微粒,近似值为6.02×1023。
二、阿伏加德罗常数1) 1摩尔任何粒子的粒子数叫做阿伏加德罗常数。
2) 符号为N A3) 通常使用近似值为6.02×1023 近似值。
三、物质的量(n)与微粒个数(N)和阿佛加德罗常数(N A)的关系n(mol)=N/N A注:不能说1摩氢、1摩氧,因这样说指哪种微粒不明确。
231mol物质中,微粒数是确定的,因而其总质量也随之确定。
1、定义:1mol物质的质量叫该物质的摩尔质量。
2、符号:M3、单位:g/mol Kg/mol4、数学表达式、 n = m / M【练习】:1、含有6.02×1023个Na+的NaCl的物质的量为--------------------------------()A.1molB.6.02×1023molC.6.02×1023gD.0.1mol2、某物质1个分子的质量为ag,它的相对分子质量为M,则阿伏加德罗常数可表示为-------------------------------------------------------------------------()A.aB.aMC.M/aD.a/M3、与0.3molH2O中含有相同氢原子数的是下列哪种物质------------------------()A.0.3molHNO3B.3.612×1023个HNO3分子C.0.1molH3PO4D.0.2molCH44、质量相等的下列物质中分子数目最多的是------------------------()A. H2B. N2C. H2SO4D. CH4二、填空1、1.2molO2和0.8molO3,它们所含的分子数,所含的氧原子数。
1.2化学计量在实验中的应用(第2课时)

如:在同温同压下,A、B两种气体 = =
【板书】4.阿伏加德罗定律推论:
在同温、同压下,任何气体的体积之比与气体的分子数(或物质的量)之比成正比。即: = =
【教师点拨】
阿伏加德罗定律还有很多推论,请同学们结合气体状态方程PV=nRT(P代表压强;V代表体积;n代表物质的量;R是常数;T代表温度)课后推导下列关系式:
22.4
O2
1
32
1.429
22.4
CO2
1
44
1.977
22.3
结论:在标准状况下,1mol任何气体的体积都约是22.4L。
【学生活动】思考并计算。
【教师总结】
【过渡】以上我们讨论了气体的体积与物质的量的关系,那么对于固体或液体来讲是否有相同的关系呢?
【问题5】下表列出了20℃时几种固体和液体的密度,请计算出1 mol这几种物质的体积,从中你会得到什么结论?
【教师强调】本节课的课标是:初步了解气体摩尔体积的概念及其在化学计算中的简单应用。
【板书】二、气体摩尔体积
(二)合作探究(师生共用)
【复习回顾】通过上一节课的学习,我们知道,1 mol任何物质的粒子个数都相等,都约为6.02×1023个,1 mol任何物质的质量都是以g为单位,在数值上等于构成该物质的粒 子(分子,原子,离子等)的式量。那么,1 mol任何物质的体积又该如何 确定呢?请同学们先考虑下面的问题。
2.对于固态或液态物质来讲,粒子之间的距离是非常小的,这使的固态或液态的粒子本身的“直径”远远大于粒子之间的距离,所以决定固体或液体的体积大小的主要因素是:
化学计量在化学实验中的应用

2.一定物质的量浓度的计算公式 (1)溶质的质量、溶液的体积和物质的量浓度之间的计 算:n=Mm=c·V。 (2)气体溶质溶于水中制得的溶液的 c 的求算: 标准状况下,1 L 水中溶解某气体 V′ L,所得溶液密度 为 ρ g·cm-3,则 c 和 w 的表达式分别为
V′ c=Vn=1000×12+2.42V2.′4×M=221400000+ρVM′V′;
达式分别为
S c=Vn=100M+S=M(1010000ρ+SS),S=100100ρ0c-McM。
1000ρ
第三单元 化学计量在化学实验中的应用
知识归纳
3.以“守恒”的观点计算溶液的浓度 (1)溶液的稀释规律: 在稀释或混合前后,溶液中:①溶质的物质的量总量不变, 即有:c1·V1=c2·V2、c1V1+c2V2=c 混 V 混。 ②溶质的质量不变:ρ1·V1·w1+ρ2·V2·w2=(ρ1·V1+ρ2·V2)·w 混。 (2)电解质溶液中的电荷守恒,如 Na2SO4 溶液中存在:c(Na+) =2c(SO24-)。
第三单元 化学计量在化学实验中的应用
• (3)向饱和Na2CO3溶液中加入Na2CO3固体后冷却至室温,其 物质的量浓度变大( )
• × [解析] 饱和溶液的浓度不发生变化,Na2CO3固体加入 后会析出Na2CO3·10H2O晶体,但溶液仍为饱和溶液。
• (4)欲配制1.00 L 1.00 mol·L-1的NaCl溶液,可将58.5 g NaCl 溶于1.00 L水中( )
知识归纳
(6)将标准状况下 44.8 L HCl 溶于 100 mL 水中,所得溶液的 密度为 1.384 g/mL,则其物质的量浓度为 1.5 mol/L( ) × [解析] m(溶液)=224.44.L8/mL ol×36.5 g/mol+100 g=173 g, V(溶液)=1.318743gg/mL=125 mL,c(HCl)=02.1m25olL=16 mol/L。
化学计量在实验中的应用
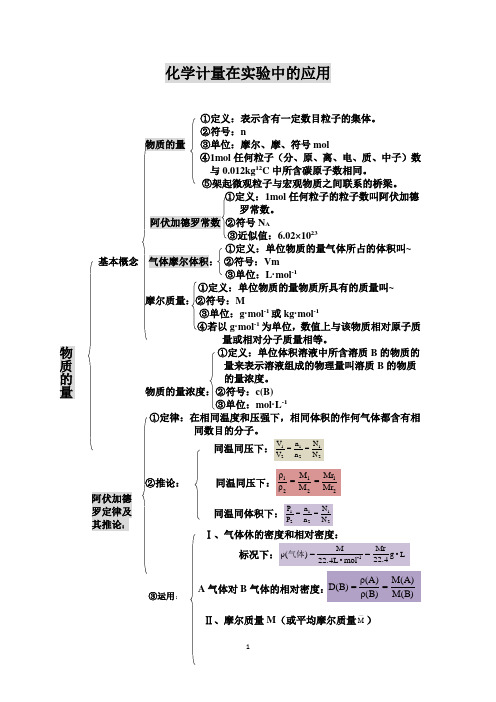
化学计量在实验中的应用nmol任何粒子(分、原、离、电、质、中子)数12C中所含碳原子数相同。
1mol 任何粒子的粒子数叫阿伏加德罗常数。
N A6.02×1023~基本概念VmL·mol -1~Mg·mol -1或kg·mol -1g·mol -1为单位,数值上与该物质相对原子质①定义:单位体积溶液中所含溶质B 的物质的量来表示溶液组成的物理量叫溶质B 的物质的量浓度。
物质的量浓度:②符号:c(B)③单位:mol·L -1①定律:在相同温度和压强下,相同体积的作何气体都含有相同数目的分子。
②推论: Ⅰ、气体休的密度和相对密度: A 气体对B Ⅱ、摩尔质量M (或平均摩尔质量M —) ③运用: 阿伏加德 罗定律及 其推论:M=22.4L·mol-1×ρ,•••+)B(n+)A(n•••+ )B(M•)B(n+)A(M•)A(n=M—M—=M(A)ф(A)+M(B)ф(B)+··· ф为体积分数。
相对密度D=M1/M2(M1是未知气体的摩尔质量,M2是已知气体的摩尔质量) 一、物质的量及其应用1、物质的量(1)定义:科学上用来研究一定数目微粒集体的一个物理量。
符号:n. 单位:摩尔(mol)。
(2)基准:以0.012kg 126C中所含的碳原子数为基准,即阿伏加德罗常数。
2、阿伏加德罗常数(1)符号:N A。
单位:mol-1.(2)阿伏加德罗常数是一个可以用实验测出的准确值,只是目前的科学手段有限,只测出6.0221367×1023mol-1,在应用中用6.02×1023 mol-1作为它的最大近似值用于计算。
(3)阿伏加德罗常数是一个非常大的数,只适用于表示微观粒子。
(4)阿伏加德罗常数(NA)与物质的量(n)的关系:(N:微粒数)注意:(1)用物质的量来表示微粒时,要用化学式注明微粒的名称;(2)物质的量只适用于微观粒子3、摩尔质量定义:单位物质的量的物质所具有的质量。
1.3化学计量在化学实验中的应用(一)—物质的量

第27页 共 112 页
难点探究
以物质的量为中心的各物理量的相互换算 1.以物质的量为中心的各物理量的相互换算
第28页 共 112 页
第29页 共 112 页
第30页 共 112 页
2.抓住气体摩尔体积的“四要素” (1)状态:即气体摩尔体积是对于气态物质而言;“气态物 质”可以是纯净物,也可以是混合物。 (2)状况:因为一定量气体的体积是随温度、压强等外界条 件的改变而改变的。因此应用气体摩尔体积时应指明某一特 定状况。如标准状况(0 ℃、101 kPa);同温、同压等。
D.甲的相对分子质量比乙的相对分子质量小 答案:B
第35页 共 112 页
解析:由 V=
m
同,且气体的物质的量与体积成正比,A项错误,B项正确。 同温同压下,气体的摩尔体积相等,C项错误。由 M m n 知,m甲=m乙,n甲<n乙,则M甲>M乙,D项错误。
N n NA 系为:__________。
第3页 共 112 页
3.摩尔质量 (1)概念:单位物质的量的物质所具有的质量。 (2)符号:M。 (3)单位:g/mol或kg/mol。 (4)当摩尔质量以g/mol为单位时,在数值上与物质相对原子 质量或相对分子质量相等。
N n NA (5)物质的量、物质的质量和摩尔质量间的关系为:_______。
(Vm),但数值并不一定为22.4 L/mol。故要确定物质的体积, 必须确定物质自身的状态、所处状况和物质所含有的粒子数 目(或物质的物质的量)。
第32页 共 112 页
3.阿伏加德罗定律:同温同压下,相同体积的任何气体都含 有相同数目的分子。 阿伏加德罗定律的推论:
第33页 共 112 页
第34页 共 112 页
1-2 化学计量在实验中的应用

1-2 物质的量在实验中的应用引言:化学反应既是原子、分子或离子之间按一定的数目关系进行的,又是可用器具称量的物质按一定质量关系进行的。
所以需要将反应物质在微观粒子数目与可称质量关系上联系起来,而反应粒子极小,稍有一定质量就数目极多,不利于直接计算,需用一定数目粒子的集合体来计量。
一、物质的量1、定义——从组成基本粒子数目角度表示物质多少的物理量。
但并不是直接运用微粒个数,而是指含有一定数目粒子的集合体。
2、符号——;3、表征对象——组成宏观物质微观的基本单元,包括基本微粒(原子、分子、离子、原子团、电子、质子和中子)和基本微粒的特定组合如NaCl。
4、单位——摩尔,简称摩,符号;(1)规定以(0.012kg即12g)12C所含碳原子数为标准,称为阿伏加德罗常数,符号NA,是一个经过精密计算得到的一个较为精确的实验值,通常用近似值(6.02*1023mol-1)表示。
(2)每摩尔任何物质均含有阿伏伽德罗常数个基本微粒或单元。
(3)特定称谓“物质的量”是表示物质所含多少阿伏伽德罗常数个微粒的物理量。
5、公式—— (n=N/NA)6、推论——在任何情况下,相同或不同物质的微粒个数比都等于其物质的量的比。
*回顾:表示物质多少的物理量·质量1、定义——从可称量角度表示物质多少的物理量。
2、符号——3、表征对象——可称量的宏观物质4、单位——(克或千克,符号g或kg)5、公式——m=dV或m=ρV二、摩尔质量1、定义——单位物质的量的物质所具有的质量。
2、符号——;3、单位——;(g/mol或g·mol-1)4、公式——M=m/n或M=NA·m05、数值关系——等于式量(相对原子或分子质量)推导:NA个C——1molC——12gC微粒个体微粒集体可称物质结合性对原子质量定义(该原子的质量与12C原子质量的1/12的比值)···6、推论——物质的量相等时,两物质的质量比等于其摩尔质量比或式量比。
化学计量在实验中的应用物质的量

THANK YOU
感谢聆听
1摩尔的任何物质所含有的微粒数目 等于阿伏伽德罗常数,约为 6.022×10^23个/mol。
根据质量计算
根据气体摩尔体积计算
在标准状况下(0°C,101kPa),1 摩尔任何气体所占的体积约为22.4L, 这个体积叫做该气体的摩尔体积。
根据物质的质量和摩尔质量计算物质 的量,公式为n=m/M。
03
05
化学计量在实验中的实际应用案例
酸碱滴定实验中物质的量的应用
酸碱滴定实验是化学实验中常见的一种,通过滴定操作, 可以确定溶液中待测物的含量。在实验过程中,物质的量 起到了关键作用。通过滴定操作,可以计算出待测物与标 准溶液之间的反应量,从而确定待测物的浓度或含量。
在酸碱滴定实验中,物质的量还可以帮助我们了解反应的 完全程度。通过计算反应所需的体积和浓度,可以判断反 应是否达到终点,从而确保实验结果的准确性。
溶液浓度的标定实验中物质的量的应用
溶液浓度的标定实验是化学实验中的 基础实验之一,通过该实验可以了解 溶液中溶质的含量。在实验过程中, 物质的量同样发挥了重要作用。通过 滴定操作,结合物质的量的计算,可 以确定溶液中溶质的浓度。
VS
物质的量在溶液浓度标定实验中的应 用,不仅可以帮助我们了解溶液的性 质,还可以为其他相关领域的研究提 供数据支持。例如,在药物分析、环 境监测等领域中,溶液浓度的标定可 以为相关分析方法的建立提供依据。
化学平衡的计算
确定平衡常数
通过化学计量,可以计算出化 学平衡常数,从而了解反应在 平衡状态下的性质和过程。
预测反应方向
基于化学计量,可以预测反应 方向,例如正向或逆向进行, 从而了解反应的进行方式和过 程。
优化平衡条件
高中化学 化学计量知识点总结

高一化学计量在实验中的应用期末复习知识点总结化学计量在实验中的应用1 物质的量物质的量实际上表示含有一定数目粒子的集体2 摩尔物质的量的单位3 标准状况STP 0℃和1标准大气压下4 阿伏加德罗常数NA 1mol任何物质含的微粒数目都是6.021023个5 摩尔质量M 1mol任何物质质量是在数值上相对质量相等6 气体摩尔体积Vm 1mol任何气体的标准状况下的体积都约为22.4l7 阿伏加德罗定律(由PV=nRT推导出) 同温同压下同体积的任何气体有同分子数n1 N1 V1n2 N2 V28 物质的量浓度CB 1L溶液中所含溶质B的物质的量所表示的浓度CB=nB/V nB=CBV V=nB/CB9 物质的质量m m=Mn n=m/M M=m/n10 标准状况气体体积V V=nVm n=V/Vm Vm=V/n11 物质的粒子数N N=NAn n =N/NA NA=N/n12 物质的量浓度CB与溶质的质量分数=1000 M13 溶液稀释规律C(浓)V(浓)=C(稀)V(稀)以物质的量为中心考点一:物质的量、阿伏伽德罗常数1、重要概念(1)物质的量及其单位:物质的量是国际单位制中的七个基本物理量之一,符号为“n”,单位是“mol”(2)阿伏加德罗常数与6.02×1023 阿伏加德罗常数:符号为NA。
定义为:0.012Kg12C所含碳原子的准确数目,是一个精确值。
在现有条件下,测得其数值约为 6.02×1023注意:6.02×1023 只是其近似值。
(3) 摩尔质量与相对分子质量的关系:摩尔质量是单位物质的量的物质所具有的质量,摩尔质量在数值上等于相对分子质量,单位是g/mol。
(4)气体摩尔体积与22.4L/mol. 气体摩尔体积是单位物质的量的气体所占的体积,单位是L/mol,符号为Vm。
由于气体体积与温度、压强有关,故Vm也随温度压强的变化而变化,在标况下(0℃,101千帕):Vm=22.4L/mol2、阿伏加德罗定律及其推论:(1)阿伏加德罗定律:同温同压下,相同体积的任何气体都具有相同的分子数(物质的量)。
化学计量在实验中的应用——物质的量

化学计量在实验中的应用——物质的量一、知识网络: 物质的质量/g 物质的量浓度/m o l L ·物质含有的粒子数物质的量/m o l ×22.4 ÷22.4 L ·m o l L ·m o l ÷g ·m o l M /×N A ×溶液体积/L×g ·m o l M /÷N A ÷溶液体积/L 标准状况下气体的体积/L-1-1-1-1-1二、基本公式:(1) 物质的量与微粒个数的关系: n =A N N (2) 物质的量与质量的关系: n =M m M =n m m =M ·n (3) 气体物质的量与体积的关系:n =m V V n =1molL 22.4-⋅V (标准状况) V m = n V V =ρm (4) 物质的量浓度:c =Vn n =c ·V (5) 溶液物质的量浓度与质量分数的关系: c =M ρω⋅⋅1000 (密度的单位:g/cm 3 ) n =MρV ω⋅⋅(6) 溶液稀释: c 1V 1=c 2V 2 三、物质的量的相关知识和概念:1、物质的量:是表示大量粒子集体的一个物理量,符号为n ,单位是摩尔(mol )。
2、摩尔:是物质的量的单位;国际上规定, 1摩尔粒子集体所含的粒子数与0.012 kg C 中所含的碳原子数相同,约为6.02×10233、阿伏加德罗常数:1摩尔的任何粒子的粒子数,即1摩尔粒子数的准确值,用符号N A 表示,N A 的近似值为6.02×1023mol -1。
计算公式:n =AN N 4、使用摩尔这个单位时要注意:①使用范围,只能用于微观(原子、离子等),不适用于宏观②使用时应该用化学式指明粒子的种类,而不使用该粒子的中文名称。
5、物质的量与物质质量的关系:1任何粒子或物质的质量以克为单位,其数值都与该粒子的相对原子质量或相对分子质量相等。
化学计量在实验中的应用_21

化学计量在实 验中的应用
三、物质的量在化学实验 中的应用
1、物质的量浓度
定义:表示单位体积(1L)溶液里所含溶质B 的物质的量,叫做B的物质的量浓度。
nB
v 公式四:CB=
溶液的体积
单位:
nB: mol V: L
CB: mol/L
物质的量浓度(CB)
CBV
粒子数(N)
N/NA
物质的量 (nB)
加水 倒立 瓶塞旋转180o
观察 倒立
观察
如何检漏?
Байду номын сангаас
③不能在其中溶解(有吸热或放热现象),不能将热的溶 液倒入,会影响体积的准确性。
④读数时 ,应平视,使溶液的凹液面正好与刻度相切;不能 作反应容器,不能长期存放溶液,只能用作配制的量具。移 动容量瓶,应手握刻度线以上部分。
100ml 20℃
容量瓶使用前应查是否检漏水,其方法是:
往瓶内加水,塞好瓶塞(瓶口和瓶塞要干, 且不涂任何油脂等),用食指顶住瓶塞,另 一只手托住瓶底把瓶倒立过来,观察瓶塞周 围是否有水漏出,如不漏水,把瓶塞旋转 180°塞紧,仍把瓶倒立过来,再检查是否 漏水,经检查不漏水的容量瓶才能使用。
②配制物质的量浓度溶液的主要 仪器
烧杯、容量瓶、玻璃棒、胶头滴管、托盘 天平、药匙(固体溶质使用)、量筒 (液体溶质使用)
1、步骤:
计算、称量、溶解、移液、洗涤、 定容、摇匀、装瓶贴标签。
2.仪器:
托盘天平或量筒、烧杯、玻璃棒、 容量瓶、胶头滴管、试剂瓶、药匙
作业:课本P18 2、3、 4、 6 题
谢谢观赏
质 量(m) m /M
气体在标准状况 下的体积(V)
V/Vm
第二节化学计量在实验中的应用

第二节化学计量在实验中的应用物质的量和摩尔质量教学目的 知识与技能1、认识摩尔是物质的是的差不多单位,了解物质的量与微观粒子之间的关系,了解 摩尔质量的概念,了解提出摩尔这一概念的重要性和必要性,明白得阿伏加德罗常数的涵义2、了解物质的量、摩尔质量、物质的质量之间的关系,能用于进行简单的化学运算。
过程与方法1、初步培养学生演绎推理、归纳推理、逻辑推理和运用化学知识进行运算的能力2、通过物质的量这一联系微观粒子与宏观质量的物理量的学习,引导学生以化学的眼光、从微观的角度地认识丰富多彩的物质世界,认识到宏观和微观的相互转化是研究化学的科学方法之一。
情感态度与价值观1、通过对概念的透彻明白得,培养学生严谨、认确实学习态度,体会定量研究的方法对研究和学习化学的重要作用。
重点物质的量及单位;摩尔质量的概念和有关摩尔质量的运算难点物质的量及单位------摩尔知识结构与板书设计第二节 化学计量在实验中的应用一、物质的量(amount of substance)的单位---摩尔(mole) 1.是一个物理量,符号为 n ,单位为摩尔(mol)。
2、阿伏加德罗常数:表示1mol 任何粒子的粒子数,符号为N A ,单位为mol -1,数值约为6.02*1023 mol -13、注意:使用mol 时,必须指明粒子的种类,能够是分子、原子、离子、电子等。
4.N 、N A 与n 的关系:n N NA= A 1=C 1C m m 1212m 1m =1 mol 任何粒子或物质的质量是以克为单位,在数值上就等于该粒子的相对原子(分子、离子)质量。
5、摩尔质量:(1)定义:单位物质的量的物质所具有的质量,符号为M (2)、公式:M =nm单位 g ·mol -1 6、有关摩尔质量的相关运算例1:24.5 g H 2SO 4 的物质的量是_________解:H 2SO 4 的相对分子质量为98,则M (H 2SO 4 )=98 g ·mol-1。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
化学计量在实验中的应用——相关公式的推导
1.物质的量浓度和质量分数的关系
如图所示,体积为V L ,密度为ρ g·cm -3的溶液,含有摩尔质量为M g·mol -1的溶质m g ,溶质的质量分数为w 。
则物质的量浓度c 与质量分数w 的关系是:c =n V =m /M V =m MV =1 000ρw V MV =
1 000ρw M ,w =cM 1 000ρ。
2.物质的量浓度与溶解度的换算
若某饱和溶液的密度为ρ g·cm -3,溶质的摩尔质量为M g·mol -1,溶解度为S g ,
则溶解度S 与物质的量浓度的关系是:c =n V =S /M 100+S 1 000ρ
= 1 000ρS M (100+S )
;S =100cM 1 000ρ-cM。
3.同溶质不同物质的量浓度溶液的混合计算
(1)混合后溶液体积保持不变时,c 1V 1+c 2V 2=c 混×(V 1+V 2)。
(2)混合后溶液体积发生改变时,c 1V 1+c 2V 2=c 混V 混,其中V 混=m 混ρ混。
4.溶质相同、质量分数不同的两溶液混合定律
同一溶质、质量分数分别为a %、b %的两溶液混合。
(1)等体积混合
①当溶液密度大于1 g·cm -3时,必然是溶液浓度越大,密度越大(如H 2SO 4、
HNO 3、HCl 、NaOH 等多数溶液),等体积混合后质量分数w >12(a %+b %)。
②当溶液密度小于1 g·cm -3时,必然是溶液浓度越大,密度越小(如酒精、
氨水溶液),等体积混合后,质量分数w <12(a %+b %)。
(2)等质量混合
两溶液等质量混合时(无论ρ>1 g·cm -3还是ρ<1 g·cm -3),混合后溶液中溶质
的质量分数w =12(a %+b %)。
5. 求算气体摩尔质量的五种常用方法
(1)根据标准状况下气体的密度:M =ρ标×22.4 g·mol -1。
(2)根据气体的相对密度⎝ ⎛⎭⎪⎫D =ρ1ρ2:M 1M 2
=D 。
(3)根据物质的质量(m )和物质的量(n ):M =m n 。
(4)根据一定质量(m )的物质中微粒数目(N )和阿伏加德罗常数(N A ):M =N A ·m N 。
(5)对于混合气体,求其平均摩尔质量,上述计算式仍然成立;还可以用下式计算:M =M 1×a %+M 2×b %+M 3×c %+…,a %、b %、c %指混合物中各成分的物质的量分数(或体积分数)。
