大学物理第三章_刚体的转动
合集下载
大学物理.第三章.刚体的转动

动 .试计算细杆转动到与竖直线成 角时的角加速度
和角速度 .
解 细杆受重力和
铰链对细杆的约束力
FN
作用 3g sin
2l
3g (1 cos )
l
§3-4 力矩的功 定轴转动的动能定理
一、力矩的功
z
O
d r
速度ω 绕端点转动,摩擦系数为μ 求M摩擦力。
ω
解: 质量线密度:
m L
dm
r dr
质量元:
r dm dr
所受摩擦力为:
dF gdm gdr
例3-5 现有一圆盘在平面内以角速度ω 转动,求 摩擦力产生的力矩(μ 、m、R)。
dr
ωr
解:
dm ds rdrd dF gdm grdrd dM1 rdF r2gdrd
I mi ri2 -质量不连续分布
i
r 2dm -质量连续分布
d -线分布λ=m/ι 质量元: dm ds -面分布σ=m/S
dV -体分布ρ=m/V
二、决定转动惯量的三因素
1)刚体的质量; 2)刚体的质量分布; (如圆 环与圆盘的不同);
3)刚体转轴的位置。 (如细棒绕中心、绕一端)
运动。 一、何谓刚体
在任何情况下形状和大小都不发生变化的
物体。即每个质元之间的距离无论运动或
受外力时都保持不变。
理想模型
ri j c mj
二、刚体运动的两种基本形式 mi
平动----刚体运动时,刚体内任一直线恒保 持平行的运动(即该直线方向保持不变)
刚体的平动过程
c a b
刚体的平动过程
能运用以上规律分析和解决包括 质点和刚体的简单系统的力学问题.
和角速度 .
解 细杆受重力和
铰链对细杆的约束力
FN
作用 3g sin
2l
3g (1 cos )
l
§3-4 力矩的功 定轴转动的动能定理
一、力矩的功
z
O
d r
速度ω 绕端点转动,摩擦系数为μ 求M摩擦力。
ω
解: 质量线密度:
m L
dm
r dr
质量元:
r dm dr
所受摩擦力为:
dF gdm gdr
例3-5 现有一圆盘在平面内以角速度ω 转动,求 摩擦力产生的力矩(μ 、m、R)。
dr
ωr
解:
dm ds rdrd dF gdm grdrd dM1 rdF r2gdrd
I mi ri2 -质量不连续分布
i
r 2dm -质量连续分布
d -线分布λ=m/ι 质量元: dm ds -面分布σ=m/S
dV -体分布ρ=m/V
二、决定转动惯量的三因素
1)刚体的质量; 2)刚体的质量分布; (如圆 环与圆盘的不同);
3)刚体转轴的位置。 (如细棒绕中心、绕一端)
运动。 一、何谓刚体
在任何情况下形状和大小都不发生变化的
物体。即每个质元之间的距离无论运动或
受外力时都保持不变。
理想模型
ri j c mj
二、刚体运动的两种基本形式 mi
平动----刚体运动时,刚体内任一直线恒保 持平行的运动(即该直线方向保持不变)
刚体的平动过程
c a b
刚体的平动过程
能运用以上规律分析和解决包括 质点和刚体的简单系统的力学问题.
大学物理 刚体的定轴转动

⑶ t =6 ·0 s 时转过的角度为
6s
0
6s
d t 0
0(1et)dt
0 [te t]6 0 s 9 [6 ( 2 0 0) 5 (0 2 )]369rad
则 t =6 ·0 s
时电动机转过的圈数
N 587圈 2
5.2 5.4 刚体的转动定律及应用
5.2.1力对转轴的力矩
转轴
§5.1 刚体的运动的描述 §5.2 刚体定轴转动 §5.3 转动惯量的计算 §5.4 转动定律应用 §5.5 角动量守恒 §5.6 定轴转动中的功和能
5.1 刚体的运动的描述
•刚体(rigid body)
任何情况下形状和体积都不改变的物体(理想化模型)。 刚体是特殊的质点系。 刚体可以看作是由许多质点组成,每一个质点叫做 刚体的一个质元,刚体这个质点系的特点是,在外 力作用下各质元之间的相对位置保持不变。
2、刚体定轴转动的转动定律
M d(J )dL J
dt dt
刚体绕定轴转动时,它的角加速度与作用于刚体上的 合外力矩成正比,与刚体对转轴的转动惯量成反比。
刚体定轴转动的转动定律
M=J 与 F ma地位相当 m反映质点的平动惯性,J 反映刚体的转动惯性
力矩是使刚体转动状态发生改变而产生角加速度的原因。力
ri
即 F itfitΔ m iri
则刚体转动定律为
变形有 F ir tifir tiΔm iri2
M J
对所有质元求和:
F ir ti fir ti (m ir i2 ) 上式表明:
这里 FitriM i M外
刚体绕定轴转动时,刚
fitri 0 定义 JΔmiri2 叫转动惯量
体的角加速度与它所 受的合外力矩成正比.
大学物理 第3章-1刚体

定轴转动:
转轴固定不动的转动。
显然,刚体是个理想化的模型,但是它有 实际的意义。 刚体是特殊的质点系, 其上各质点间的相对 位置保持不变。 质点系的规律都可用于刚体, 而且考虑到刚体的特点,规律的表示还可较一 般的质点系有所简化。
刚体的一般运动可看作: 随质心的平动
+
绕质心的转动
的合成
一般运动
2
I1
1 3
m2r
4 3
mr 2
r
摆锤转动惯量:
I 2 I C md
2
1 2
mr 2
2
I I1 I 2
4 3
mr
2
19 2
mr
2
65 6
mr
3-1-4
刚体对定轴的角动量定理 和转动定律
由质点系对轴的角动量定理,可得
dm 2π rdr
2
I r dm 2π r 3dr
o R
r
dr
I 2π r dr
3 0
R
π R 2
4
1 2
mR
2
转动惯量的大小取决于刚体的质量、形 状及转轴的位置 . a) 平行轴定理 质量为 m 的刚体,如果对 其质心轴的转动惯量为 I C ,则 对任一与该轴平行,相距为 d 的转轴的转动惯量
d
d
3g 2l
π 2 0
cos d
3g 2l cos d
A
π 2 0
0
d
C O
B
1 2
2
3g 2l
l
sin
3g 2l
大学物理第三章知识点

dt dt
t2 Mdt
t1
2 d(J) J
1
2 1
d
J2
J1
冲量矩
---角动量定理(积分式)
X. J. Feng
作用于刚体上冲量矩等于刚体角动量的增量
3.角动量守恒定律
t2
t1
Mdt
J2
J1
M 0时,J2 J1
若转动物体的合外力矩为零,则系统的角动量守恒
转动系统由两个或两个以上物体组成时:
X. J. Feng
M合 0时 Jii 常数
若系统的合外力矩为零,则系统的角动量守恒
讨论:1. J、ω均不变, J ω=常数 2. J、ω都改变, 但 J ω不变
注意: 1).运用角动量守恒时,系统中各物体均绕同一转轴转动
2).角动量定理、角动量守恒定律中各角速度或速度均需 相对同一惯性参照系。
花样滑冰运动员通过改变 身体姿态即改变转动惯量 来改变转速
ω
X. J. Feng
猫的下落
例: 杆( m,l ),可扰固定端O在竖直平面内自由转动, X. J. Feng
一子弹( m,v0 )射入杆的下端,求杆上摆的最大角度?
O 判断:
m,l
mv0 (m m)V
1 2
mv 0 2
刚体定轴转动定律: 功能关系:
M 合 J
刚体转动动能定理:
A
1 2
J2 2
1 2
J12
刚体重力势能: EP mghc
机械能守恒定律:
若W外+ W内非=0 则Ek +Ep =常量
X. J. Feng
t2 Mdt
t1
2 d(J) J
1
2 1
d
J2
J1
冲量矩
---角动量定理(积分式)
X. J. Feng
作用于刚体上冲量矩等于刚体角动量的增量
3.角动量守恒定律
t2
t1
Mdt
J2
J1
M 0时,J2 J1
若转动物体的合外力矩为零,则系统的角动量守恒
转动系统由两个或两个以上物体组成时:
X. J. Feng
M合 0时 Jii 常数
若系统的合外力矩为零,则系统的角动量守恒
讨论:1. J、ω均不变, J ω=常数 2. J、ω都改变, 但 J ω不变
注意: 1).运用角动量守恒时,系统中各物体均绕同一转轴转动
2).角动量定理、角动量守恒定律中各角速度或速度均需 相对同一惯性参照系。
花样滑冰运动员通过改变 身体姿态即改变转动惯量 来改变转速
ω
X. J. Feng
猫的下落
例: 杆( m,l ),可扰固定端O在竖直平面内自由转动, X. J. Feng
一子弹( m,v0 )射入杆的下端,求杆上摆的最大角度?
O 判断:
m,l
mv0 (m m)V
1 2
mv 0 2
刚体定轴转动定律: 功能关系:
M 合 J
刚体转动动能定理:
A
1 2
J2 2
1 2
J12
刚体重力势能: EP mghc
机械能守恒定律:
若W外+ W内非=0 则Ek +Ep =常量
X. J. Feng
大学物理第三章刚体力学

薄板的正交轴定理:
Jz Jx J y
o x
y
X,Y 轴在薄板面上,Z轴与薄板垂直。
例3、质量m,长为l 的四根均匀细棒, O 组成一正方形框架,绕过其一顶点O 并与框架垂直的轴转动,求转动惯量。 解:由平行轴定理,先求出一根棒 对框架质心C的转动惯量:
C
m, l
1 l 2 1 2 2 J ml m( ) ml 12 2 3
M F2 d F2 r sin
若F位于转动平面内,则上式简化为
M Fd Fr sin
力矩是矢量,在定轴转动中, 力矩的方向沿着转轴,其指向 可按右手螺旋法则确定:右手 四指由矢径r的方向经小于的 角度转向力F方向时,大拇指的 指向就是力矩的方向。根据矢 量的矢积定义,力矩可表示为:
例9 行星运动的开普勒第二运动定律:行星对太阳 的位矢在相等的时间内扫过相等的面积。 解:行星在太阳引力(有心 力)作用下沿椭圆轨道运动, 因而行星在运行过程中,它 对太阳的角动量守恒不变。
L rmvsin 常量
因而掠面速度:
dS dt
r dr sin 2dt
1 rv sin 常量 2
Fi fi Δmi ai
切向的分量式为
Fi sin i f i sin i mi ri
Fi sin i f i sin i mi ri
两边同乘ri,得
Fi ri sin i fi ri sin i mi ri2
上式左边第一项为外力Fi对转轴的力矩,而第二项是 内力fi 对转轴的力矩。对刚体的所有质点都可写出类 似上式的方程,求和得
质点的角动量一质量为m的质点以速度v运动相对于坐标原点o的位置矢量为r定义质点对坐标原点o的角动量为sinrmv282质点的角动量定理质点所受的合外力对某一参考点的力矩等于质点对该点的角动量对时间的变化率角动量定理
大学物理-刚体的转动
O
L
C
Jo m(
3L)23m2L 3
可见,同一刚体对不同转轴的转动惯量是不同的,只 有指出刚体对某一转轴的转动惯量才有明确的意义。
例题 均匀杆质量m,长l,求杆对O轴和C轴的转动惯量。
解: dmdx
l
O x dx
JO
x2dm l x2dx 0
l3 1 ml2
J2
3、刚体的转动惯量 rotational inertia (moment of inertia)
J miri2
单位: kg m2
质量连续分布时
体分布 dmdv 体密度
J r2dm 面分布 dmds 面密度 线分布 dmdl 线密度
转动惯量与下列三个因素有关: ⑴形状、大小相同的均匀刚体总质量越大,转动惯量越大。 ⑵总质量相同的刚体,质量分布离轴越远,转动惯量越大。 ⑶同一刚体,转轴不同,质量对轴的分布就不同,因而转
刚体定轴转动定律的应用
例题:一轻绳跨过一定滑轮,滑轮视为圆盘,绳的两
端分别悬有质量为m 1 和m 2 的物体,m 1 < m 2 ,如图所 示,设滑轮的质量为m,半径为r,所受的摩擦阻力
矩为 M r ,绳与轮之间无相对滑动。试求物体的加速
度和绳的张力。
T2
解: 受力分析如图
a
按牛顿运动定律和转动定律 m2g 可列出下列方程
刚体定轴转动的特点
z
⑴刚体上各个质点都在做圆周运动,但 各质点圆周运动的半径不一定相同; ⑵各质点圆周运动的平面垂直于轴,圆 心在轴线上; ⑶各质点的矢径,在相同的时间内转过 的角度是相同.
4、刚体的一般运动
A r1
o1
A'
大学物理刚体的定轴转动
2l
l
17
例 一匀质细杆,长为 l 质量为 m ,在摩擦系数为
的水平桌面上转动,求摩擦力的力矩 M阻。 解: 建立如图坐标,取质元
dm dx
质元受阻力矩:
dM 阻 dmgx
o
xl dm m dx
x
细杆受的阻力矩
M阻
dM
阻
0l
gxdx
1 mgl
2
18
例 一半径为R,质量为m的均匀圆盘平放在粗糙的
令 J miri2
刚体绕Z轴转动的转动惯量
即
M z J ----刚体的定轴转动定律
说明
1. 上式是矢量式(力矩只有两个方向)。
2. M、J、是对同一轴而言的。
3. 具有瞬时性,是力矩的瞬时效应。
4. 转动惯量J是刚体转动惯性大小的量度。
8 8
3、转动惯量的计算
转动惯量: J miri2
l
r
dr
d
dm g
M
dM
l
0
mg l
r
cosdr
mg
l 2
cos
16
M J 1 ml2
3
3g cos
2l
(2) d d d d 3g cos dt d dt d 2l
分离变量积分 g cos d l d
02
03
(3g sin ) l
300 , 3g 900 , 3g
i
质量连续分布的刚体: J r2dm
质量为线分布: dm dl
面分布: dm ds
体分布: dm dV
1)总质量
转动惯量与下列因素有关: 2)质量分布 3)转轴位置
9
✓ J与质量分布有关:
大学物理上第3章 刚体的定轴转动

z
(ω, β )
r fi
F 两边乘以r 两边乘以ri ,有: it ri + f it ri = ∆mi ait ri
对所有质元的同样的式子求和, 对所有质元的同样的式子求和,有:
fit
∆mi
Fit
r Fi
Fir
o
Fit ri + ∑ f it r i = ∑ ∆mi ait ri = β ∑ ( ∆mi ri 2 ) ∑
表示合外力矩,记作M ∑ F r 表示合外力矩,记作 表示内力矩之和, ∑ f r 表示内力矩之和,其值等于零
it i
it i
(∆mi ri 2 ) 称为刚体对轴的转动惯量,记作J 称为刚体对轴的转动惯量,记作 ∑
则上式可简写成: 则上式可简写成:M = Jβ
11
M = Jβ
刚体定轴转动定律: 刚体定轴转动定律:刚体所受的对于某一固定转动 轴的合外力矩等于刚体对此转轴的转动惯量与刚体 在此合外力矩作用下所获得的角加速度的乘积。 在此合外力矩作用下所获得的角加速度的乘积。 说明: 说明: 1. 上式是矢量式(在定轴转动中力矩只有两个方向)。 上式是矢量式(在定轴转动中力矩只有两个方向)。 2. M、J、β是对同一轴而言的。 是对同一轴而言的。 3. 上式反映了力矩的瞬时效应。M = Jβ = J dω 上式反映了力矩的瞬时效应。 dt 4. 刚体转动定律的地位与牛顿第二定律相当。 刚体转动定律的地位与牛顿第二定律相当。 5. 转动惯量 是刚体转动惯性大小的量度。 转动惯量J是刚体转动惯性大小的量度 是刚体转动惯性大小的量度。
2
§3.1
3.1.1 刚体的运动
刚体定轴转动的描述
刚体的平动:刚体在运动过程中, 刚体的平动:刚体在运动过程中,其 上任意两点的连线始终保持平行。 上任意两点的连线始终保持平行。 可以用质点动力学的方法 来处理刚体的平动问题。 来处理刚体的平动问题。 刚体的定轴转动: 刚体的定轴转动:刚体上各点都绕同 一直线作圆周运动, 一直线作圆周运动,而直线本身在空 间的位置保持不动的一种转动。 间的位置保持不动的一种转动。这条 直线称为转轴 转轴。 直线称为转轴。
大学物理 第3章 刚体力学基础

2 1
Jd
1 2
J22
1 2
J12
2 Md (1 J2 )
1
2
力矩对刚体所做的功,等于刚体转动动能的增量。
例 如图所示,一根质量为m,长为l的均匀细棒OA,可绕固定点O在竖直平 面内转动.今使棒从水平位置开始自由下摆,求棒摆到与水平位置成30°角 时中心点C和端点A的速度.
F
·
F
式中为力F到轴的距离
F
若力的作用线不在转动在平面内,
则只需将力分解为与轴垂直、平行
r
的两个分力即可。
力对固定点的力矩为零的情况:
1、力F等于零, 2、力F的作用线与矢径r共线
(有心力对力心的力矩恒为零)。
力对固定轴的力矩为零的情况:
若力的作用线与轴平行 若力的作用线与轴相交
则力对该轴无力矩作用。
dJ R2dm
考虑到所有质元到转轴的距离均为R,所以细圆环对中心轴的转动惯量为
J dJ R2dm R2 dm mR2
m
m
(2)求质量为m,半径为R的圆盘对中心轴的转动惯量.整个圆盘可以看成许
多半径不同的同心圆环构成.为此,在离转轴的距离为r处取一小圆环,如
图2.36(b)所示,其面积为dS=2πrdr,设圆盘的面密度(单位面积上的质量)
力矩在x,y,z轴的分量式,称力对轴的矩。例如上面所列
Mx , My , Mz , 即为力对X轴、Y轴、Z轴的矩。 设力F 的作用线就在Z轴
的转动平面内,作用点到Z
轴的位矢为r,则力对Z轴
的力矩为
M z rF sin
r sin F F rF sin rF
大学物理课件第3章-刚体

F
T
m
o
x
例4. 质量为M =16 kg的实心滑轮,半径为R = 0.15 m。 一根细绳绕在滑轮上,一端挂一质量为m的物体。
求(1)由静止开始1秒钟后,物体下降的距离。(2) 绳子的张力。
解: TR
a
1 2
MR
2
a R
T
1 2
Ma
2
mg T ma
M
T
mg mM 2
注: 可以用质点动力学 的方法来处理刚体 的平动问题。
转动:
刚体上所有质点都绕同一直线作圆 周运动。这种运动称为刚体的转动。这 条直线称为转轴。
定轴转动:
转轴固定不动的转动。
刚体的转动动能
mn
rn
o
r1
m1
r2
m2
令
I mi ri
i
2
kg m
2
I 为刚体对 z 轴的转动惯量。
结论: 刚体的转动惯量与刚体的形状、大小、质量 的分布以及转轴的位置有关。 对于质量连续分布的刚体:
2
2
( mi ri )
Ek
1 2
J
2
设在外力矩 M 的作用下,刚体绕定轴发生角位移d 元功:
dA Md
A I
d dt
A
由转动定律 有
d dt
d I d
1 2 1 2
dA I
2
1
I d
I 2 -
2
I 1
2
刚体绕定轴转动的动能定理 :合外力矩对刚体所 做的功等于刚体转动动能的增量。
l a v
o
30°
机械能守恒:
11 l 2 2 2 Ml ma mga1 cos 30 Mg 1 cos 30 23 2
T
m
o
x
例4. 质量为M =16 kg的实心滑轮,半径为R = 0.15 m。 一根细绳绕在滑轮上,一端挂一质量为m的物体。
求(1)由静止开始1秒钟后,物体下降的距离。(2) 绳子的张力。
解: TR
a
1 2
MR
2
a R
T
1 2
Ma
2
mg T ma
M
T
mg mM 2
注: 可以用质点动力学 的方法来处理刚体 的平动问题。
转动:
刚体上所有质点都绕同一直线作圆 周运动。这种运动称为刚体的转动。这 条直线称为转轴。
定轴转动:
转轴固定不动的转动。
刚体的转动动能
mn
rn
o
r1
m1
r2
m2
令
I mi ri
i
2
kg m
2
I 为刚体对 z 轴的转动惯量。
结论: 刚体的转动惯量与刚体的形状、大小、质量 的分布以及转轴的位置有关。 对于质量连续分布的刚体:
2
2
( mi ri )
Ek
1 2
J
2
设在外力矩 M 的作用下,刚体绕定轴发生角位移d 元功:
dA Md
A I
d dt
A
由转动定律 有
d dt
d I d
1 2 1 2
dA I
2
1
I d
I 2 -
2
I 1
2
刚体绕定轴转动的动能定理 :合外力矩对刚体所 做的功等于刚体转动动能的增量。
l a v
o
30°
机械能守恒:
11 l 2 2 2 Ml ma mga1 cos 30 Mg 1 cos 30 23 2
大学物理3_2 刚体定轴转动的动力学描述

显然
Fij Fji
两力对转轴的力矩:
M ij Fij ri sin i
M ji Fji rj sin j
由于 ri sin i rj sin j d 所以
Mij M ji
整个刚体
M M ij 0
第三章 刚体的转动 3 – 2 刚体定轴转动的动力学描述 例1 如图所示,有一半径为 R 、质量为 m的均匀圆盘, 可绕通过圆盘中心 O 并与盘面垂直的轴的转动.转轴与圆 盘之间的摩擦略去不计.圆盘上绕有轻而细的绳索,绳的一 端固定在圆盘上,另一端系一质量为m 的物体.试求作用在 圆盘上的力矩.
J A mi ri 2 0 2m l2 m(l 2 l 2 ) 4m l2 (1)
i 1
4
4
l2 l2 2 (2) J 0 mi ri 2 4m( ) 2ml2 2 i 1
(3)
J AD
l2 l2 2 mi ri 2 2m( ) ml2 2 i 1
第三章 刚体的转动
例3-4 质量分别为 m1和 m2 的两个物体A、B分别悬挂 在图所示的组合轮两端。设两轮的半径分别为 R和 r,两 轮的转动惯量分别为 J1和 J 2,轮与轴承间、绳索与轮间的 摩擦力均略去不计,绳的质量也略去不计。试求两物体的 加速度和绳的张力。 解 作受力图,如图所示
3 – 2 刚体定轴转动的动力学描述
dJ r dm 2π r dr R 3 4 J 2π r dr π R 0
2
而
m π R
2
所以
1 2 J mR 2
3 – 2 刚体定轴转动的动力学描述 注意
第三章 刚体的转动
Fij Fji
两力对转轴的力矩:
M ij Fij ri sin i
M ji Fji rj sin j
由于 ri sin i rj sin j d 所以
Mij M ji
整个刚体
M M ij 0
第三章 刚体的转动 3 – 2 刚体定轴转动的动力学描述 例1 如图所示,有一半径为 R 、质量为 m的均匀圆盘, 可绕通过圆盘中心 O 并与盘面垂直的轴的转动.转轴与圆 盘之间的摩擦略去不计.圆盘上绕有轻而细的绳索,绳的一 端固定在圆盘上,另一端系一质量为m 的物体.试求作用在 圆盘上的力矩.
J A mi ri 2 0 2m l2 m(l 2 l 2 ) 4m l2 (1)
i 1
4
4
l2 l2 2 (2) J 0 mi ri 2 4m( ) 2ml2 2 i 1
(3)
J AD
l2 l2 2 mi ri 2 2m( ) ml2 2 i 1
第三章 刚体的转动
例3-4 质量分别为 m1和 m2 的两个物体A、B分别悬挂 在图所示的组合轮两端。设两轮的半径分别为 R和 r,两 轮的转动惯量分别为 J1和 J 2,轮与轴承间、绳索与轮间的 摩擦力均略去不计,绳的质量也略去不计。试求两物体的 加速度和绳的张力。 解 作受力图,如图所示
3 – 2 刚体定轴转动的动力学描述
dJ r dm 2π r dr R 3 4 J 2π r dr π R 0
2
而
m π R
2
所以
1 2 J mR 2
3 – 2 刚体定轴转动的动力学描述 注意
第三章 刚体的转动
大学物理课课件第3章_刚体的定轴转动

G2 G1
(m1-m2)g R(m1+ m2+ m 2) (m1-m2)g R(m1+ m2+ m 2)
a
gt 2
(rad)
两匀直细杆
两者瞬时角加速度之比 转动定律例题五
θ
θ
根据
1 2 1 2
θ θ
1 3 1 3
地面 从等倾角 处静止释放
短杆的角加速度大 且与匀质直杆的质量无关
第3节 机械能守恒定律
用两个对 转的顶浆
(支奴干 CH47)
A、B两轮共轴 A以ωΑ作惯性转动
守恒例题一
两轮啮合后 一起作惯性转动的角速度
ωΑΒ
以A、B为系统,忽略轴摩擦,脱离驱动力矩后,系 统受合外力矩为零,角动量守恒。
初态角动量 末态角动量
得
守恒例题二
木棒 弹
以弹、棒为系统 击入阶段 子弹击入木棒瞬间,系统在
铅直位置,受合外力矩为零,角动量守恒。 该瞬间之始 该瞬间之末 棒 弹 棒
对 质点运动和刚体转动定律
m 1 m 2 和 m 分别应用
及
β
R
T2 T2
m
T1 T1 m1
m1 g – T1 = m1a T2 – m2 g = m2a ( T1 – T2 ) R = Iβ
得 故
a = Rβ
1 I = 2 mR2 常量
β
(m1-m2)g = R(m1+ m2+ m 2) 由
m2
a
定轴转动物理量
1. 角位置
描述刚体(上某点)的位置 刚体定轴转动 的运动方程 刚体
刚体中任 一点
(t+△t) (t) 参考 方向
2. 角位移
(m1-m2)g R(m1+ m2+ m 2) (m1-m2)g R(m1+ m2+ m 2)
a
gt 2
(rad)
两匀直细杆
两者瞬时角加速度之比 转动定律例题五
θ
θ
根据
1 2 1 2
θ θ
1 3 1 3
地面 从等倾角 处静止释放
短杆的角加速度大 且与匀质直杆的质量无关
第3节 机械能守恒定律
用两个对 转的顶浆
(支奴干 CH47)
A、B两轮共轴 A以ωΑ作惯性转动
守恒例题一
两轮啮合后 一起作惯性转动的角速度
ωΑΒ
以A、B为系统,忽略轴摩擦,脱离驱动力矩后,系 统受合外力矩为零,角动量守恒。
初态角动量 末态角动量
得
守恒例题二
木棒 弹
以弹、棒为系统 击入阶段 子弹击入木棒瞬间,系统在
铅直位置,受合外力矩为零,角动量守恒。 该瞬间之始 该瞬间之末 棒 弹 棒
对 质点运动和刚体转动定律
m 1 m 2 和 m 分别应用
及
β
R
T2 T2
m
T1 T1 m1
m1 g – T1 = m1a T2 – m2 g = m2a ( T1 – T2 ) R = Iβ
得 故
a = Rβ
1 I = 2 mR2 常量
β
(m1-m2)g = R(m1+ m2+ m 2) 由
m2
a
定轴转动物理量
1. 角位置
描述刚体(上某点)的位置 刚体定轴转动 的运动方程 刚体
刚体中任 一点
(t+△t) (t) 参考 方向
2. 角位移
大学物理3_4 刚体绕定轴转动的动能定理

t 3 3 3 5 3 2
3–4
刚体绕定轴转动的动能定理
第三章 刚体的转动
例3 留声机的转盘绕通过盘心垂直盘面的轴以角速度 作匀速转动.放上唱片后,唱片将在摩擦力作用下随转盘一 起转动.设唱片的半径为 R 、质量为 m ,它与转盘间的摩 擦系数为 .求(1)唱片与转盘间的摩擦力矩;(2)唱片达到 角速度 需要多长时间;(3)在这段时间内,转盘的驱动力 矩作了多少功? 解 (1)如图所示,在唱片上取长为 dl 宽为 dr 的面积元 dS dldr ,该面 积元所受的摩擦力为:
1 2 1 2 1 1 1 2 2 2 2 W J J0 mR 0 mR 2 2 2 2 4
3–4
第三章 刚体的转动 刚体绕定轴转动的动能定理 例3-11 一长为 l , 质量为 m0 的均质细竿可绕支点O自 由转动 . 一质量为 m、速率为 v0 的子弹射入竿内一端, 使竿的偏转角为30º 问子弹的初速率为多少 ? .
加速度
力 质量
dr v dt dv a dt
F
d 角速度 dt d 角加速度 dt
力矩
M
m
转动惯量 J
动量
P mv
角动量
L J
r
dm
2
3–4
刚体绕定轴转动的动能定理
第三章 刚体的转动
质点运动规律与刚体定轴转动的规律对照 质点的平动 刚体的定轴转动
EPB EkB EPA EkA
3–4
第三章 刚体的转动 刚体绕定轴转动的动能定理 1 2 4 2 2 J J1 J 2 ml ml ml 3 3
取A点的重力势能为零,即 则有 而
EPA 0
3–4
刚体绕定轴转动的动能定理
第三章 刚体的转动
例3 留声机的转盘绕通过盘心垂直盘面的轴以角速度 作匀速转动.放上唱片后,唱片将在摩擦力作用下随转盘一 起转动.设唱片的半径为 R 、质量为 m ,它与转盘间的摩 擦系数为 .求(1)唱片与转盘间的摩擦力矩;(2)唱片达到 角速度 需要多长时间;(3)在这段时间内,转盘的驱动力 矩作了多少功? 解 (1)如图所示,在唱片上取长为 dl 宽为 dr 的面积元 dS dldr ,该面 积元所受的摩擦力为:
1 2 1 2 1 1 1 2 2 2 2 W J J0 mR 0 mR 2 2 2 2 4
3–4
第三章 刚体的转动 刚体绕定轴转动的动能定理 例3-11 一长为 l , 质量为 m0 的均质细竿可绕支点O自 由转动 . 一质量为 m、速率为 v0 的子弹射入竿内一端, 使竿的偏转角为30º 问子弹的初速率为多少 ? .
加速度
力 质量
dr v dt dv a dt
F
d 角速度 dt d 角加速度 dt
力矩
M
m
转动惯量 J
动量
P mv
角动量
L J
r
dm
2
3–4
刚体绕定轴转动的动能定理
第三章 刚体的转动
质点运动规律与刚体定轴转动的规律对照 质点的平动 刚体的定轴转动
EPB EkB EPA EkA
3–4
第三章 刚体的转动 刚体绕定轴转动的动能定理 1 2 4 2 2 J J1 J 2 ml ml ml 3 3
取A点的重力势能为零,即 则有 而
EPA 0
大学物理03-刚体力学基础

15
J
r
m
2
dm
• 刚体的形状(质量分布)
16
J
注 意
r
m
2
dm
只有对于几何形状规则、质量连续且均匀分布 的刚体,才能用积分计算出刚体的转动惯量
例3-2 一均匀细棒,质量为 m ,长为 l 。求该棒对下列转轴 的转动惯量:(1)通过棒中心且与棒垂直的轴;(2)通过 棒的一端且与棒垂直的轴。 解:取如图坐标,在棒上任取质元,到转轴的垂直距离为x, 长度为 d x,该质元的质量为 dm = (m/l )dx (质量为线分布)。 A L/2 C
S
O
Mz r d
P
F
M r F
O r
F
P
F
F //
大小: M rF sin Fd 方向: 由右手螺旋法则确定
转动平面
F 应该理解为外力在转动平面内的 分力F//
转动平面
在定轴转动中,M 的方向只有两种可能指向。若先选 定了转轴的正方向,则 M 与转轴方向一致时取正 值,反之为负值
11
(3) 如果有几个外力矩作用在刚体上,则合力矩等 于各个力矩的代数和
M
i i i
ri Fi
12
2
二 刚体绕定轴的转动定律
刚体可视为由许多质点组成的,而每一个质点都遵从质点力学 的规律。刚体转动定律可由牛顿第二定律直接导出。
Fi f i mi ai mi ri
一、力对转轴的力矩
力是引起质点运动状态变化的原因,而力 矩是引起转动物体运动状态变化的原因
(2) 外力F 不在转动平面内(任意力) 可将 F 分解为转动平面内的分力 F// 和垂直于转动平面的分力F F不能引起刚体转动状态的变化 力矩:
J
r
m
2
dm
• 刚体的形状(质量分布)
16
J
注 意
r
m
2
dm
只有对于几何形状规则、质量连续且均匀分布 的刚体,才能用积分计算出刚体的转动惯量
例3-2 一均匀细棒,质量为 m ,长为 l 。求该棒对下列转轴 的转动惯量:(1)通过棒中心且与棒垂直的轴;(2)通过 棒的一端且与棒垂直的轴。 解:取如图坐标,在棒上任取质元,到转轴的垂直距离为x, 长度为 d x,该质元的质量为 dm = (m/l )dx (质量为线分布)。 A L/2 C
S
O
Mz r d
P
F
M r F
O r
F
P
F
F //
大小: M rF sin Fd 方向: 由右手螺旋法则确定
转动平面
F 应该理解为外力在转动平面内的 分力F//
转动平面
在定轴转动中,M 的方向只有两种可能指向。若先选 定了转轴的正方向,则 M 与转轴方向一致时取正 值,反之为负值
11
(3) 如果有几个外力矩作用在刚体上,则合力矩等 于各个力矩的代数和
M
i i i
ri Fi
12
2
二 刚体绕定轴的转动定律
刚体可视为由许多质点组成的,而每一个质点都遵从质点力学 的规律。刚体转动定律可由牛顿第二定律直接导出。
Fi f i mi ai mi ri
一、力对转轴的力矩
力是引起质点运动状态变化的原因,而力 矩是引起转动物体运动状态变化的原因
(2) 外力F 不在转动平面内(任意力) 可将 F 分解为转动平面内的分力 F// 和垂直于转动平面的分力F F不能引起刚体转动状态的变化 力矩:
大学物理学-刚体的转动定律

1 1 ∆mi vi 2 = ∆mi (riω ) 2 则i质元的动能为 质元的动能为 2 2 则整个刚体的转动动能
ω
v ri
vi
∆mi
v
Ek =
∑
i =1
n
1 1 n 1 2 2 2 2 ∆ m i ri ω = ( ∑ ∆ m i ri )ω = J ω 2 2 2 i =1 2
刚体绕定轴转动时的转动动能等于刚体的转动惯量 与角速度平方乘积的一半. 与角速度平方乘积的一半.
第2章 运动定律与力学中的守恒定律
支架S 支架S
外环 陀螺G 陀螺G 内环
2–6 刚体的定轴转动 6 直升机螺旋桨的设置
尾桨的设置: 尾桨的设置:直升机发动后机身要在旋翼旋转相反方向旋 产生一个向下的角动量。 转,产生一个向下的角动量。为了不让机身作这样的反向 旋转,在机身尾部安装一个尾桨, 旋转,在机身尾部安装一个尾桨,尾桨的旋转在水平面内 产生了一个推力,以平衡单旋翼所产生的机身扭转作用。 产生了一个推力,以平衡单旋翼所产生的机身扭转作用。 对转螺旋桨的设置:双旋翼直升机则无需尾桨, 对转螺旋桨的设置:双旋翼直升机则无需尾桨,它在直立 轴上安装了一对对转螺旋桨, 轴上安装了一对对转螺旋桨,即在同轴心的内外两轴上安 装了一对转向相反的螺旋桨。工作时它们转向相反, 装了一对转向相反的螺旋桨。工作时它们转向相反,保持 系统的总角动量仍然为零。 系统的总角动量仍然为零。
力矩的功
A=
∫θ
θ2
1
M dθ
力矩的功率 力矩的功率
dA dθ P= =M = Mω dt dt
第2章 运动定律与力学中的守恒定律
2–6 刚体的定轴转动 6
9
3、刚体定轴转动的动能定理 、
ω
v ri
vi
∆mi
v
Ek =
∑
i =1
n
1 1 n 1 2 2 2 2 ∆ m i ri ω = ( ∑ ∆ m i ri )ω = J ω 2 2 2 i =1 2
刚体绕定轴转动时的转动动能等于刚体的转动惯量 与角速度平方乘积的一半. 与角速度平方乘积的一半.
第2章 运动定律与力学中的守恒定律
支架S 支架S
外环 陀螺G 陀螺G 内环
2–6 刚体的定轴转动 6 直升机螺旋桨的设置
尾桨的设置: 尾桨的设置:直升机发动后机身要在旋翼旋转相反方向旋 产生一个向下的角动量。 转,产生一个向下的角动量。为了不让机身作这样的反向 旋转,在机身尾部安装一个尾桨, 旋转,在机身尾部安装一个尾桨,尾桨的旋转在水平面内 产生了一个推力,以平衡单旋翼所产生的机身扭转作用。 产生了一个推力,以平衡单旋翼所产生的机身扭转作用。 对转螺旋桨的设置:双旋翼直升机则无需尾桨, 对转螺旋桨的设置:双旋翼直升机则无需尾桨,它在直立 轴上安装了一对对转螺旋桨, 轴上安装了一对对转螺旋桨,即在同轴心的内外两轴上安 装了一对转向相反的螺旋桨。工作时它们转向相反, 装了一对转向相反的螺旋桨。工作时它们转向相反,保持 系统的总角动量仍然为零。 系统的总角动量仍然为零。
力矩的功
A=
∫θ
θ2
1
M dθ
力矩的功率 力矩的功率
dA dθ P= =M = Mω dt dt
第2章 运动定律与力学中的守恒定律
2–6 刚体的定轴转动 6
9
3、刚体定轴转动的动能定理 、
刚体的平动转动和定轴转动

状态特一点样:,各如点:v运、动a
等都相同.
刚体平动 质点运动
第三章 刚体的转动
2
大学物理
3-1 刚体的平动 转动和定轴转动
ቤተ መጻሕፍቲ ባይዱ
转动:分定轴转动和非定轴转动
刚体的平面运动
第三章 刚体的转动
3
大学物理
3-1 刚体的平动 转动和定轴转动
刚体的一般运动可看作:
随质心的平动 + 绕质心的转动 的合成
第三章 刚体的转动
结合匀加速圆周运动中角加速度的关系式,有
2 1 100 40 15.7(rad/s2 )
t t
12
第三章 刚体的转动
大学物理
3-1 刚体的平动 转动和定轴转动
又因 (2 02) / 2
22 12 (100 )2 (40 )2 840 (rad)
2
2 15.7
所以在这12s内,转子转过的转数为
解 (1)结合题意有
d d ( At Bt3 Ct4 ) A 3Bt2 4Ct3
dt
dt
第三章 刚体的转动
13
大学物理
3-1 刚体的平动 转动和定轴转动
结合角速度与角加速度的关系,有
d d ( A 3Bt2 4Ct3) 6Bt 12Ct2
dt
dt
(2)根据线速度与角速度之间的关系式(3-2)
v R R( A 3Bt2 4Ct3)
at R R(6Bt 12Ct2 ) an R2 R( A 3Bt 2 4Ct3)2
第三章 刚体的转动
v02 2a(x x0 )
2
2 0
2 (
0
)
第三章 刚体的转动
8
大学物理
《大学物理》第三章 刚体的定轴转动

P
t
=
1 2
ω J 2 自
t
=
ω J 2 自 2P
=
2×105× (30π)
2×736×103
2
=
1.21×103s
(2) ω进 = 1度 秒 = 0.0175rad/s
ω进 =
M
Jω自
M = Jω进ω自
M = 2×105×0.0175×30π= 3.3×105 N返回.m退出
3-14 在如图所示的回转仪中,转盘的 质量为 0.15kg , 绕其轴线的转动惯量为: 1.50×10-4 kg.m2 ,架子的质量为 0.03kg, 由转盘与架子组成的系统被支持在一个支柱 的尖端O,尖端O到转盘中心的距离为0.04 m , 当转盘以一定角速度ω 绕其轴旋转时, 它便在水平面内以1/6 rev/s的转速进动。
为25cm,轴的一端 A用一根链条挂起,如
果原来轴在水平位置,并使轮子以ω自=12 rad/s的角速度旋转,方向如图所示,求:
(1)该轮自转的角动量;
(2)作用于轴上的外力矩;
(3)系统的进动角速度, ω
并判断进动方向。
AO
B
R
l 返回 退出
解:
(1)
J
=
m
R
2
回
=
5×(0.25 )2
ω
= 0.313 kg.m2
a
=
m
1+
m m
1g 2+
J
r2
T1 =
m 1g (m 2+ J m 1+m 2 + J
r 2) r2
T2 =
m 1m 2g m 1+m 2 + J
大学物理(上)课件-第03章刚体的定轴转动3-2

解 : (1) 棒在任意位置时的重力矩 l M = mg cos θ 2 1 3g M = Jβ = ml 2 β β= cos θ 3 2l
N
o
c
⋅
θ
dθ
⋅
1 1 dω (2) mg cos θ = ml 2 2 3 dt 1 dω dθ 1 2 dω = ml 2 = ml ω 3 dθ dt 3 dθ
ω
o
r1
r2 v1
∆m1
E
27
K
1 2 = J ω ——刚体定轴转动的动能 2
3. 刚体定轴转动的动能定理
设在外力矩 M 的作用下,刚体绕定轴发生角位移 dθ 元功:
dA = Mdθ
dω 由转动定律 M = J β = J dt dω 有 dA = J dθ = Jω dω dt
A=
∫ω
ω2
1
1 1 2 2 = J ω - J ω Jω d ω 2 1 2 2
28
刚体绕定轴转动的动能定理 :合外力矩对刚体所做的 功等于刚体转动动能的增量。
ω = (2 β h r )1 2 = 9.08 rad ⋅ s −1
§3.3 定轴转动刚体的功与能
1.力矩的功 � 刚体在力 F 作用绕轴转过一微小角位移 dθ � � � � 力 F 作功为dA = F ⋅ dr = F cos(π − ϕ ) dr
2 = F sin ϕ dr = F sin ϕds = Fr sin ϕdθ � 力F使刚体由θ 0转到θ 时, 力矩的功为
2
4 2 19 2 65 2 J = J1 + J 2 = mr + mr = mr 3 2 6
22
例1 一个质量为M、半径为R的定滑 轮(当作均匀圆盘)上面绕有细绳, 绳的一端固定在滑轮边上,另一端挂 一质量为m的物体而下垂。忽略轴处 摩擦,求物体m由静止下落高度h时 的速度和此时滑轮的角速度。 解:
N
o
c
⋅
θ
dθ
⋅
1 1 dω (2) mg cos θ = ml 2 2 3 dt 1 dω dθ 1 2 dω = ml 2 = ml ω 3 dθ dt 3 dθ
ω
o
r1
r2 v1
∆m1
E
27
K
1 2 = J ω ——刚体定轴转动的动能 2
3. 刚体定轴转动的动能定理
设在外力矩 M 的作用下,刚体绕定轴发生角位移 dθ 元功:
dA = Mdθ
dω 由转动定律 M = J β = J dt dω 有 dA = J dθ = Jω dω dt
A=
∫ω
ω2
1
1 1 2 2 = J ω - J ω Jω d ω 2 1 2 2
28
刚体绕定轴转动的动能定理 :合外力矩对刚体所做的 功等于刚体转动动能的增量。
ω = (2 β h r )1 2 = 9.08 rad ⋅ s −1
§3.3 定轴转动刚体的功与能
1.力矩的功 � 刚体在力 F 作用绕轴转过一微小角位移 dθ � � � � 力 F 作功为dA = F ⋅ dr = F cos(π − ϕ ) dr
2 = F sin ϕ dr = F sin ϕds = Fr sin ϕdθ � 力F使刚体由θ 0转到θ 时, 力矩的功为
2
4 2 19 2 65 2 J = J1 + J 2 = mr + mr = mr 3 2 6
22
例1 一个质量为M、半径为R的定滑 轮(当作均匀圆盘)上面绕有细绳, 绳的一端固定在滑轮边上,另一端挂 一质量为m的物体而下垂。忽略轴处 摩擦,求物体m由静止下落高度h时 的速度和此时滑轮的角速度。 解:
大学物理——第3章-角动量定理和刚体的转动
M
α
I
有何联系?
13
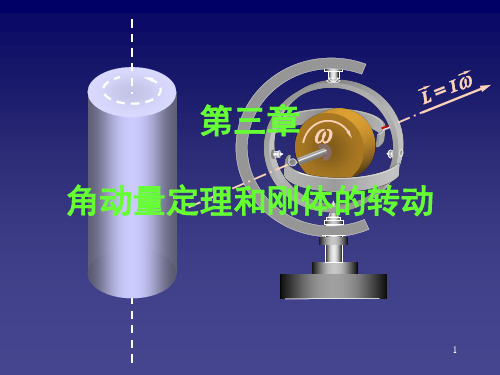
实验指出,定轴转动的刚体的角加速度 α与刚体所受的合外 力矩 M 成正比,与刚体的转动惯量 I 成反比.
v dω v M = Iα = I dt
v
定轴转动定理
v v F = ma
定轴转动定律在转动问题中的地 位相当于平动时的牛顿第二定律
应用转动定理解题步骤与牛顿第二定律时完全相同.
1 1 2 2 2 Eki = miυi = mi ri ω 2 2
质点质量 整个刚体的动能:
N
圆周运动的速率和半径
1 N 2 2 Ek = ∑Eki = (∑mi ri )ω 2 i=1 i=1
刚体对转轴的转动惯量:I
7
刚体定轴转动动能公式
物体的平动动能(质点动能)
1 2 Ek = Iω 2
角速度 ω 转动惯量 I 物体绕轴的转动惯性
λ :质量线密度 σ :质量面密度 ρ :质量体密度
10
I = ∫ r 2dm
单位: kg m2
转动惯量的大小取决于刚体的质量,质量分布及转轴的位置.
O
O l/2 O′
1 I= ml2 12
O
O O′
1 2 I = ml 3
r
O′
1 I = mr2 4
O′
1 I = mr2 2
11
平行轴
垂直轴
平行轴定理 质量为 m 的刚体,如果对其质心轴的转动惯量为 IC,则对任 一与该轴平行,相距为 d 的转轴的转动惯量:
2 θ 3Rω0 n= = 2π 16π g
26
讨论
用定轴转动的动能定理较之用转动定律求解, 省去了求角加速度,而直接求得,更为简捷.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
l/2 2
(2).绕过棒端与棒⊥轴的转动惯量
1 λx 3 1 3 1 2 2 J A = ∫ λx dx = = λl = ml 0 3 3 0 3
l
l
A
x o dm=λdx
d
x
l O轴与A轴间距d = ,且二轴平行 2 1 2 1 l 2 2 J A J O = ml ml = m( ) = md 2 3 12 2
微积分
华理生活网
§3-1 刚体的定轴转动 刚体的定轴转动
定轴转动:刚体上各质元均做圆周运动, 定轴转动:刚体上各质元均做圆周运动,
dm
ω
r O
各圆的圆心都在转轴上,是最简单的转动. 各圆的圆心都在转轴上,是最简单的转动.
一,特征: 特征:
1.各点都有相同的θ,ω,α
EP = ∑ mi gzi =
i
∑m z
i
C m × i
i i
m
(mg ) = mgzc
zc
zi
二, 定轴转动的功能原理 质点系功能原理对刚体仍成立: 质点系功能原理对刚体仍成立:
ω
O
ri mi i
v
E k = ∑ E ki = 1 ∑ (miri 2 )ω2 = 1 Jω2 华理生活网 2i 2 i
1 1 2 合 力矩对定轴转动刚体所作的 A = Jω2 Jω12 ——合外力矩 2 2 功等于刚体转动动能的增量 转动动能的增量
刚体的重力势能: 刚体的重力势能:
t h
N
α
a
m mg
G
T
对轮: 对轮: TR= Jα (1): 对m = 华理生活网
mg T = ma (2)
TR= Jα (1) =
mg T = ma (2)
运动学关系: 运动学关系: a α= (3) R 1 2 h = at (4) 2
定轴O 定轴 m t R 绳 v0=0 h
当M=0时,刚体匀速转动或静止 时 华理生活网
2. 力不在转动平面内
F1
M =r
×
F
F
转动 平面
= r × ( F1 + F2 ) =r r
× ×
F1 + r × F2
r
F2
F 1 只能引起轴的
变形,对转动无贡献. 变形,对转动无贡献.
在定轴转动问题中,若不讨论轴上受力, 在定轴转动问题中,若不讨论轴上受力,则所考虑的力 矩是指力在转动平面内的分力对转轴的力矩. 矩是指力在转动平面内的分力对转轴的力矩.
华理生活网
第三章 刚体的转动
两种基本形式 平动: 连结体内两点的直线在空间指向保持平行. 平动 连结体内两点的直线在空间指向保持平行. 通常用物体质心的运动来代表. 通常用物体质心的运动来代表. 质心的运动来代表 转动:连结刚体内两点的直线方向在运动过程中 转动: 改变. 改变.
T1
α1
α2
A
B
R1 T2
R2
{A 解: ,B}
M = J1α1 + J 2α 2
R1α1 = R2α 2 1 J1 = m1 R12 2 1 2 J 2 = m2 R2 2
α1 α2
正确解:
{A}: M + T1R1 T2 R1 = J1α1 (1) {B}: T2 R2 T1R2 = J 2α 2 (2)
华理生活网
§3-2 刚体的转动定律 刚体的转动定律
一,力矩是改变刚体转动状态的原因 1. 力在转动平面内 M = r × F M = F r sin = F d
M
r d
F
※定轴转动:M 定轴转动:
+:刚体逆时针转 +:刚体逆时针转 -:刚体顺时针转 刚体顺时针转
dθ ds F O α r
ห้องสมุดไป่ตู้
θ1 → θ 2 : A = ∫ dA = ∫ Mdθ
θ1
θ2
=
∫
θ2
θ1
Jαdθ =
∫
θ2
θ1
dω J dθ = dt
∫
ω2
ω1
1 1 2 2 Jωdω = Jω2 Jω1 2 2
的动能: 质元 mi 的动能: 1 m v 2 = 1 m (ωr )2 = 1 m r 2ω2 Eki = i i i i i i 2 2 2 刚体的转动动能: 刚体的转动动能:
3 J2O = m R2 24
JO = J1O J2O
3 J2O = m R2 24
2 2 J1O = mR 3
4 m1 = m 3
13 JO = mR2 24
m o
R
R 2
O′
华理生活网
[例题 已知:M=2Kg,m=5Kg,R=0.1m,ω0=10rad/s, 例题]已知 例题 已知: (1)求α,T, (2)ω=0时,m上升h. 解:(1) M,m受力如图所示 mg T = ma 2 ω0 α = 81.7(rad / s ) 1 2 TR = ( MR )α R 2 T = 9.15( N ) a =α R M (2) h = Rθ
R1α1 = R2α 2 (3)
1 J1 = m1 R12 (4) 2 1 2 J 2 = m2 R2 (5) 2 (1) 关键点:两轮的α不同 关键点:两轮的 不同 华理生活网 (2)
α1 α2
§3-3 刚体转动中的功能关系 刚体转动中的功能关系
一,定轴转动中动能定理 dA = Fds cos α = Frdθ cos(900 ) = Fr sin dθ = Mdθ z
+:刚体逆时针转 +:刚体逆时针转 -:刚体顺时针转 刚体顺时针转 3.角量与线量
ω
v
O
θ
2. ω
ω
x
S = rθ v = rω at = rα an = rω 2 华理生活网
二,匀变速转动 (α为常量) 1 2 θ = θ 0 + ω0 t + α t 2 2 ω 2 ω 0 = 2α ( θ θ 0 ) ω = ω0 + α t
平行轴定理: 平行轴定理 JO′ = JO + md
2
其中: 其中 JO:刚体对过质心轴的转动惯量 JO':刚体对平行于过质心轴的轴的转动惯量
华理生活网 d:两平行轴间的距离
2.均匀园环 2.均匀园环m,R 均匀园环 (1)绕过中心与环面⊥ (1)绕过中心与环面⊥轴的转动惯量 绕过中心与环面 解: dJ = R dm = R
华理生活网
二,转动定律
对 m i 质点 Fi 外力 fi 内力
刚体
z ω,α , fi φ Fi ri θ
Δmi
应用牛顿第二定律: 应用牛顿第二定律:
F + fin = mi ain F + fi = mai in i i it F + fit = mi ait
三个基本物理量: 三个基本物理量:
机械能(Ek + E p ), 动量(mv ), 角动量(L = r × mv )
三个定理: 三个定理:
A外=∫ F ds = Ek I = ∫ F dt = P dt = L ∫M
三条守恒定理的条件: 三条守恒定理的条件:
A外+A非保守=0 机械能守恒 F外=0动量守恒 M 外=0 角动量守恒
3 2
2
华理生活网
3.均匀盘m,R绕过中心与环面⊥轴转动惯量
dJ = r 2 dm = r 2σds = r 2σ 2πrdr
1 J = ∫ 2πσr 3 dr = πσr 4 0 2
R R 0
=
1 mR 2 2
dr dm=σ2πrdr
r
物体的质量 J的大小与 质量的分布 的大小与 转轴的位置
i i
M外
0
Jα
转动定律: 转动定律:M外 = Jα 三,转动惯量(J) 转动惯量( )
平动: F = ma 转动: M = Jα
刚体
z ω,α , fi φ Fi θ ri
Δmi
是转动惯性 大小的量度
定轴
华理生活网
1.定义式 定义式: 定义式
∑ ri 2 mi 质量非连续分布 i r为质元到转轴距离 J = ∫m r 2 dm 质量连续分布 线分布:dm = λdx 面分布:dm = σds 质量元dm
def
体分布:dm = ρdV
2.转动惯量的计算示例 转动惯量的计算示例 1.均匀细棒m,l (1).绕过中心与棒⊥轴的转动惯量 解: dJ0= x2dm = x2λdx
l /2
o
x x dm=λdx
1 3 J O = ∫ dJ 0 = ∫ λx 华理生活网 λx 3 dx = = λl = 1 ml 2 l / 2 3 12 l / 2 12
gt 2 2 联立解得: 联立解得: J = ( 1)mR 2h 9.8× 3 1)×1× 0.22 = 1.14(kg m2 ) =( 2×1.5
2
华理生活网
已知:A轮:R1,m1, 受恒力矩M. B轮:R2,m2 M 轮与皮带间无滑动. 求:两轮的角加速度.
m o
R
R 2
O ′
1 1 4 2 2 2 J1O = m1 R = ( m) R = mR 2 2 2 3 3 m 4 πR 2 = m) (m1 = σ πR 2 = R 2 3 2 πR π ( ) 2 华理生活网
J 2O
1 R 2 R 2 3 = m2 ( ) + m2 ( ) = m2 R 2 2 2 2 8 1 1 J2O′ m2 = m1 = m 4 3
2 2
R
λdl
2
dm=λdl
dl
J=∫
2πR
(2).绕过棒端与棒⊥轴的转动惯量
1 λx 3 1 3 1 2 2 J A = ∫ λx dx = = λl = ml 0 3 3 0 3
l
l
A
x o dm=λdx
d
x
l O轴与A轴间距d = ,且二轴平行 2 1 2 1 l 2 2 J A J O = ml ml = m( ) = md 2 3 12 2
微积分
华理生活网
§3-1 刚体的定轴转动 刚体的定轴转动
定轴转动:刚体上各质元均做圆周运动, 定轴转动:刚体上各质元均做圆周运动,
dm
ω
r O
各圆的圆心都在转轴上,是最简单的转动. 各圆的圆心都在转轴上,是最简单的转动.
一,特征: 特征:
1.各点都有相同的θ,ω,α
EP = ∑ mi gzi =
i
∑m z
i
C m × i
i i
m
(mg ) = mgzc
zc
zi
二, 定轴转动的功能原理 质点系功能原理对刚体仍成立: 质点系功能原理对刚体仍成立:
ω
O
ri mi i
v
E k = ∑ E ki = 1 ∑ (miri 2 )ω2 = 1 Jω2 华理生活网 2i 2 i
1 1 2 合 力矩对定轴转动刚体所作的 A = Jω2 Jω12 ——合外力矩 2 2 功等于刚体转动动能的增量 转动动能的增量
刚体的重力势能: 刚体的重力势能:
t h
N
α
a
m mg
G
T
对轮: 对轮: TR= Jα (1): 对m = 华理生活网
mg T = ma (2)
TR= Jα (1) =
mg T = ma (2)
运动学关系: 运动学关系: a α= (3) R 1 2 h = at (4) 2
定轴O 定轴 m t R 绳 v0=0 h
当M=0时,刚体匀速转动或静止 时 华理生活网
2. 力不在转动平面内
F1
M =r
×
F
F
转动 平面
= r × ( F1 + F2 ) =r r
× ×
F1 + r × F2
r
F2
F 1 只能引起轴的
变形,对转动无贡献. 变形,对转动无贡献.
在定轴转动问题中,若不讨论轴上受力, 在定轴转动问题中,若不讨论轴上受力,则所考虑的力 矩是指力在转动平面内的分力对转轴的力矩. 矩是指力在转动平面内的分力对转轴的力矩.
华理生活网
第三章 刚体的转动
两种基本形式 平动: 连结体内两点的直线在空间指向保持平行. 平动 连结体内两点的直线在空间指向保持平行. 通常用物体质心的运动来代表. 通常用物体质心的运动来代表. 质心的运动来代表 转动:连结刚体内两点的直线方向在运动过程中 转动: 改变. 改变.
T1
α1
α2
A
B
R1 T2
R2
{A 解: ,B}
M = J1α1 + J 2α 2
R1α1 = R2α 2 1 J1 = m1 R12 2 1 2 J 2 = m2 R2 2
α1 α2
正确解:
{A}: M + T1R1 T2 R1 = J1α1 (1) {B}: T2 R2 T1R2 = J 2α 2 (2)
华理生活网
§3-2 刚体的转动定律 刚体的转动定律
一,力矩是改变刚体转动状态的原因 1. 力在转动平面内 M = r × F M = F r sin = F d
M
r d
F
※定轴转动:M 定轴转动:
+:刚体逆时针转 +:刚体逆时针转 -:刚体顺时针转 刚体顺时针转
dθ ds F O α r
ห้องสมุดไป่ตู้
θ1 → θ 2 : A = ∫ dA = ∫ Mdθ
θ1
θ2
=
∫
θ2
θ1
Jαdθ =
∫
θ2
θ1
dω J dθ = dt
∫
ω2
ω1
1 1 2 2 Jωdω = Jω2 Jω1 2 2
的动能: 质元 mi 的动能: 1 m v 2 = 1 m (ωr )2 = 1 m r 2ω2 Eki = i i i i i i 2 2 2 刚体的转动动能: 刚体的转动动能:
3 J2O = m R2 24
JO = J1O J2O
3 J2O = m R2 24
2 2 J1O = mR 3
4 m1 = m 3
13 JO = mR2 24
m o
R
R 2
O′
华理生活网
[例题 已知:M=2Kg,m=5Kg,R=0.1m,ω0=10rad/s, 例题]已知 例题 已知: (1)求α,T, (2)ω=0时,m上升h. 解:(1) M,m受力如图所示 mg T = ma 2 ω0 α = 81.7(rad / s ) 1 2 TR = ( MR )α R 2 T = 9.15( N ) a =α R M (2) h = Rθ
R1α1 = R2α 2 (3)
1 J1 = m1 R12 (4) 2 1 2 J 2 = m2 R2 (5) 2 (1) 关键点:两轮的α不同 关键点:两轮的 不同 华理生活网 (2)
α1 α2
§3-3 刚体转动中的功能关系 刚体转动中的功能关系
一,定轴转动中动能定理 dA = Fds cos α = Frdθ cos(900 ) = Fr sin dθ = Mdθ z
+:刚体逆时针转 +:刚体逆时针转 -:刚体顺时针转 刚体顺时针转 3.角量与线量
ω
v
O
θ
2. ω
ω
x
S = rθ v = rω at = rα an = rω 2 华理生活网
二,匀变速转动 (α为常量) 1 2 θ = θ 0 + ω0 t + α t 2 2 ω 2 ω 0 = 2α ( θ θ 0 ) ω = ω0 + α t
平行轴定理: 平行轴定理 JO′ = JO + md
2
其中: 其中 JO:刚体对过质心轴的转动惯量 JO':刚体对平行于过质心轴的轴的转动惯量
华理生活网 d:两平行轴间的距离
2.均匀园环 2.均匀园环m,R 均匀园环 (1)绕过中心与环面⊥ (1)绕过中心与环面⊥轴的转动惯量 绕过中心与环面 解: dJ = R dm = R
华理生活网
二,转动定律
对 m i 质点 Fi 外力 fi 内力
刚体
z ω,α , fi φ Fi ri θ
Δmi
应用牛顿第二定律: 应用牛顿第二定律:
F + fin = mi ain F + fi = mai in i i it F + fit = mi ait
三个基本物理量: 三个基本物理量:
机械能(Ek + E p ), 动量(mv ), 角动量(L = r × mv )
三个定理: 三个定理:
A外=∫ F ds = Ek I = ∫ F dt = P dt = L ∫M
三条守恒定理的条件: 三条守恒定理的条件:
A外+A非保守=0 机械能守恒 F外=0动量守恒 M 外=0 角动量守恒
3 2
2
华理生活网
3.均匀盘m,R绕过中心与环面⊥轴转动惯量
dJ = r 2 dm = r 2σds = r 2σ 2πrdr
1 J = ∫ 2πσr 3 dr = πσr 4 0 2
R R 0
=
1 mR 2 2
dr dm=σ2πrdr
r
物体的质量 J的大小与 质量的分布 的大小与 转轴的位置
i i
M外
0
Jα
转动定律: 转动定律:M外 = Jα 三,转动惯量(J) 转动惯量( )
平动: F = ma 转动: M = Jα
刚体
z ω,α , fi φ Fi θ ri
Δmi
是转动惯性 大小的量度
定轴
华理生活网
1.定义式 定义式: 定义式
∑ ri 2 mi 质量非连续分布 i r为质元到转轴距离 J = ∫m r 2 dm 质量连续分布 线分布:dm = λdx 面分布:dm = σds 质量元dm
def
体分布:dm = ρdV
2.转动惯量的计算示例 转动惯量的计算示例 1.均匀细棒m,l (1).绕过中心与棒⊥轴的转动惯量 解: dJ0= x2dm = x2λdx
l /2
o
x x dm=λdx
1 3 J O = ∫ dJ 0 = ∫ λx 华理生活网 λx 3 dx = = λl = 1 ml 2 l / 2 3 12 l / 2 12
gt 2 2 联立解得: 联立解得: J = ( 1)mR 2h 9.8× 3 1)×1× 0.22 = 1.14(kg m2 ) =( 2×1.5
2
华理生活网
已知:A轮:R1,m1, 受恒力矩M. B轮:R2,m2 M 轮与皮带间无滑动. 求:两轮的角加速度.
m o
R
R 2
O ′
1 1 4 2 2 2 J1O = m1 R = ( m) R = mR 2 2 2 3 3 m 4 πR 2 = m) (m1 = σ πR 2 = R 2 3 2 πR π ( ) 2 华理生活网
J 2O
1 R 2 R 2 3 = m2 ( ) + m2 ( ) = m2 R 2 2 2 2 8 1 1 J2O′ m2 = m1 = m 4 3
2 2
R
λdl
2
dm=λdl
dl
J=∫
2πR
