高中数学苏教必修三规范训练 第1章 算法初步23 含答案
苏教版高中数学必修三算法初步检测试卷答案.docx

高中数学学习材料马鸣风萧萧*整理制作高二单元测试试卷(参考答案)一、选择题(每题5分,共60分)题号 1 2 3 4 5 6 7 8 9 10 11 12 答案 C B B B C B D D D B A D二、填空题(每题5分,共20分)0 3713、------------------------------------ 14、-----------------------------------2/5 ④⑤⑥15、------------------------------------ 16、-----------------------------------三、解答题(本大题共5小题,共80分,解答应写出文字说明、证明过程或演算步骤)17、(10分)Read x 流程图:略----------5分If x < 0, Then f(x):= x+3Else If x = 0,Then f(x):=0;Else f(x):= ∙x-5.End IfEnd IfPrint f(x) ------------------------5分18.(16分)解:(1)流程图如图所示:或者:开始S=0i=1 开始S=0 i=1是是 否 否8分(2)①最上方添Read 10分②Print n+1 应改为Print n ; 12分③S=1应改为S=0 16分19.(16分)解:Read a, b, cIf a>b thent ←aa ←bb ←aElse ----------------------------------------4分If a>c thent ←aa ←cc ←tElse ----------------------------------------8分If b>c thent ←bb ←cc ←t ----------------------------------------12分End IfEnd IfEnd IfPrint a,b,c -----------------------------------------16分20、(18分)解:依编号顺序平均分成的10个小组分别为0~9, 10~19, 20~29, 30~39, 40~49,50~59,60~69,70~79,80~89,90~99. ----------6分输出i -1 结束结束因第7组抽取的号码个位数字应是3,所以抽取的号码是63. ----------14分这个样本的号码依次是6,18,29,30,41,52,63,74,85,96这10个号.---------18分21.(20分)解:用c (单位:元)表示通话费用t (单位:分钟)表示通话时间,则依题意必有⎪⎩⎪⎨⎧∉>+-+∈>-+≤<=),3()1]3([1.02.0),3()3(1.02.0)30(2.0Z t t t Z t t t t c[t-3]表示取不大于t-3的整数部分。
高中数学必修3第一章课后习题解答

新课程标准数学必修3第一章课后习题解答第一章 算法初步 1.1算法与程序框图练习(P5) 1、算法步骤:第一步,给定一个正实数r .第二步,计算以r 为半径的圆的面积2S r π=.第三步,得到圆的面积S .2、算法步骤:第一步,给定一个大于1的正整数n .第二步,令1i =.第三步,用i 除n ,等到余数r .第四步,判断“0r =”是否成立. 若是,则i 是n 的因数;否则,i 不是n 的因数.第五步,使i 的值增加1,仍用i 表示.第六步,判断“i n >”是否成立. 若是,则结束算法;否则,返回第三步.练习(P19)算法步骤:第一步,给定精确度d ,令1i =.的到小数点后第i 位的不足近似值,赋给a 的到小数点后第i 位的过剩近似值,赋给b . 第三步,计算55b am =-.第四步,若m d <,则得到5a;否则,将i 的值增加1,仍用i 表示.返回第二步. 第五步,输出5a.程序框图:习题1.1 A 组(P20)1、下面是关于城市居民生活用水收费的问题.为了加强居民的节水意识,某市制订了以下生活用水收费标准:每户每月用水未超过7 m3时,每立方米收费1.0元,并加收0.2元的城市污水处理费;超过7m 3的部分,每立方收费1.5元,并加收0.4元的城市污水处理费.设某户每月用水量为x m 3,应交纳水费y 元,那么y 与x 之间的函数关系为 1.2,071.9 4.9,7x x y x x ≤≤⎧=⎨->⎩我们设计一个算法来求上述分段函数的值.算法步骤:第一步:输入用户每月用水量x .第二步:判断输入的x 是否不超过7. 若是,则计算 1.2y x =;若不是,则计算 1.9 4.9y x =-.第三步:输出用户应交纳的水费y .程序框图:2、算法步骤:第一步,令i =1,S=0.第二步:若i ≤100成立,则执行第三步;否则输出S.第三步:计算S=S+i 2.第四步:i = i +1,返回第二步.程序框图:3、算法步骤:第一步,输入人数x ,设收取的卫生费为m 元.第二步:判断x 与3的大小. 若x >3,则费用为5(3) 1.2m x =+-⨯;若x ≤3,则费用为5m =.第三步:输出m .程序框图:B 组 1、算法步骤:第一步,输入111222,,,,,a b c a b c ..第二步:计算21121221b c b c x a b a b -=-.第三步:计算12211221a c a c y ab a b -=-.第四步:输出,x y .程序框图:INPUT “a ,b=”;a ,bsum=a+b diff=a -b pro=a*b quo=a/bPRINT sum ,diff ,pro ,quoEND2、算法步骤:第一步,令n =1第二步:输入一个成绩r ,判断r 与6.8的大小. 若r ≥6.8,则执行下一步;若r<6.8,则输出r ,并执行下一步.第三步:使n 的值增加1,仍用n 表示.第四步:判断n 与成绩个数9的大小. 若n ≤9,则返回第二步;若n >9,则结束算法.程序框图:说明:本题在循环结构的循环体中包含了一个条件结构.1.2基本算法语句 练习(P24)1、程序:、程序:3、程序: 练习(P29)1、程序:INPUT “a ,b ,c=”;a ,b ,cIF a+b>c AND a+c>b AND b+c>a THEN PRINT “Yes.” ELSEPRINT “No.” END IF ENDINPUT “a ,b ,c=”;a ,b ,cp=(a+b+c)/2 s=SQR(p*(p -a) *(p -b) *(p -c))PRINT “s=”;sENDINPUT “F=”;F C=(F -32)*5/9 PRINT “C=”;C END4、程序: INPUT “a ,b ,c=”;a ,b ,c sum=10.4*a+15.6*b+25.2*cPRINT “sum =”;sumEND2、本程序的运行过程为:输入整数x . 若x 是满足9<x <100的两位整数,则先取出x 的十位,记作a ,再取出x 的个位,记作b ,把a ,b 调换位置,分别作两位数的个位数与十位数,然后输出新的两位数. 如输入25,则输出52.34练习(P321习题1.2 A 组(P33)1、1(0)0(0)1(0)x x y x x x -+<⎧⎪==⎨⎪+>⎩2、程序:习题1.2 B 组(P33)1、程序:31.3算法案例 练习(P45) 1、(1)45; (2)98; (3)24; (4)17.2、2881.75.3、2200811111011000=() ,820083730=() 习题1.3 A 组(P48) 1、(1)57; (2)55. 2、21324.4、习题1.3 B 组(P48)1、算法步骤:第一步,令45n =,1i =,0a =,0b =,0c =.第二步,输入()a i .第三步,判断是否0()60a i ≤<. 若是,则1a a =+,并执行第六步. 第四步,判断是否60()80a i ≤<. 若是,则1b b =+,并执行第六步. 第五步,判断是否80()100a i ≤≤. 若是,则1c c =+,并执行第六步. 第六步,1i i =+. 判断是否45i ≤. 若是,则返回第二步.第七步,输出成绩分别在区间[0,60),[60,80),[80,100]的人数,,a b c .2、如“出入相补”——计算面积的方法,“垛积术”——高阶等差数列的求和方法,等等.1、(1)程序框图:程序:1、(2)程序框图:程序:2、见习题1.2 B组第1题解答.INPUT “x=”;x IF x<0 THENy=0ELSEIF x<1 THENy=1ELSEy=xEND IFEND IFPRINT “y=”;y ENDINPUT “x=”;x IF x<0 THENy=(x+2)^2 ELSEIF x=0 THENy=4ELSEy=(x-2)^2 END IFEND IFPRINT “y=”;y END34、程序框图:程序:INPUT “t=0”;t IF t<0 THENPRINT “Please input again.” ELSEIF t>0 AND t<=180 THEN y=0.2 ELSEIF (t -180) MOD 60=0 THEN y=0.2+0.1*(t-180)/60 ELSEy=0.2+0.1*((t-180)\60+1) END IF END IFPRINT “y=”;y END IF ENDINPUT “n=”;n i=1 S=0WHILE i<=n S=S+1/i i=i+1 WENDPRINT “S=”;S END5、 (1)向下的运动共经过约199.805 m (2)第10次着地后反弹约0.098 m (3)全程共经过约299.609 m 第二章 复习参考题B 组(P35)1、 2、3、算法步骤:第一步,输入一个正整数x 和它的位数n .第二步,判断n 是不是偶数,如果n 是偶数,令2n m =;如果n 是奇数,令12n m -=. 第三步,令1i =第四步,判断x 的第i 位与第(1)n i +-位上的数字是否相等. 若是,则使i 的值增加1,仍用i 表示;否则,x 不是回文数,结束算法.第五步,判断“i m >”是否成立. 若是,则n 是回文数,结束算法;否则,返回第四步. i=100 sum=0 k=1 WHILE k<=10 sum=sum+i i=i /2 k=k+1 WEND PRINT “(1)”;sum PRINT “(2)”;i PRINT “(3)”;2*sum -100 ENDINPUT “n=”;n IF n MOD 7=0 THEN PRINT “Sunday ” END IF IF n MOD 7=1 THEN PRINT “Monday ” END IF IF n MOD 7=2 THEN PRINT “Tuesday ” END IF IF n MOD 7=3 THEN PRINT “Wednesday ” END IF IF n MOD 7=4 THEN PRINT “Thursday ” END IF IF n MOD 7=5 THEN PRINT “Friday ” END IF IF n MOD 7=6 THEN PRINT “Saturday ” END IF END。
高中数学苏教必修三规范训练 第章 算法初步 含答案

1.3.4循环语句双基达标(限时15分钟)1.下面的程序段中,语句Print I*J执行的次数是________次.For I From1To 3For J From5To1Step-1Print I*JEnd ForEnd For解析对于每个I,内循环都执行5次,而I有3个取值,所以共执行15次.答案152.已知:S←0I←5While I≤20S←S+II←I+5End WhilePrint S上述伪代码运行的结果是________.解析此程序为循环结构I=5S=5I=10S=15I=15S=30I=20S=50 I=25输出:S=50答案503.某程序的伪代码如下:S←0For I From 2 To 10 Step 2.S←S+IEnd ForPrint S则程序运行后输出的结果是________.解析由题意可知:S=2+4+6+8+10=30.答案304.已知下列算法语句:I←12S←IDoS←S×II←I-2Until I<8End DoPrint S则语句执行后输出结果为________.解析①S=12,②S=12×10,③S=12×10×8=960.答案9605.下列算法输出的结果是________.x←0While x<20x←x+1x←x2End WhilePrint x解析∵①x=1,②x=4,③x=25>20,∴输出25.答案256.根据下列伪代码画出流程图.s←1n←1While s<5 000s←s×nn←n+1End WhilePrint n解从上面的伪代码可以看出,这一个用循环语句写出的伪代码,从s←1,n←1开始,第一次循环为求1×1,第二次循环为求1×2,第三次循环为求1×2×3……第n次循环为求1×2×3×…×n.因此,此伪代码就是输出使1×2×3×…×n<5 000的最大整数.故流程图为:综合提高(限时30分钟)7.计算1×3×5×7×9×11×13的算法,图中给出了程序的一部分,则横线上应补充的是________.解析将S乘上I后再赋给S,则S最终为1×3×5× (13)答案S←S×I8.该伪代码表示算法的功能是________.解析循环语句中的循环体是逐个判断x i是否小于0,若x i<0,则变量n增加1,最终n的值就是10个数中负数的个数.答案统计10个数中负数的个数9.如果在程序中运行后输出的结果为132,那么在While后面的条件应为________.解析由输出值为132,而132=12×11,∴循环体执行2次,又While语句是条件成立时执行循环体,∴循环条件应为I>10.另外也可以是I≥11或S<132.答案I>1010.把求1×2×3×…×n的程序补充完整,则横线处应填入________.解析由于求1×2×3×…×n,所以需用累积运算.答案S←S×i11.设计一个计算2+4+6+8+…+80的算法,并分别用For语句与While语句表示.解For语句:S←0For i From 2 To 80 Step 2S←S+iEnd ForPrint SWhile语句:S←0i←2While i≤80S←S+ii←i+2End WhilePrint S12.下列伪代码是求1+3+5+…+99的伪代码,读伪代码完成问题:i←1p←0While i≤99p←p+ii←i+2End WhilePrint p(1)伪代码中的循环语句是________型的循环语句;(2)将伪代码用另一类型的循环语句来实现.解(1)当(2)改成直到型循环语句如下:i←1p←0Dop←p+ii←i+2Until i>99End DoPrint p13.(创新拓展)某城市现有人口总数为100万人,如果年自然增长率为1.2%,试解答下面的问题:(1)写出该城市人口数y(万人)与年份x(年)的函数关系式;(2)用伪代码写出计算10年以后该城市人口总数的算法;(3)用伪代码写出计算大约多少年以后该城市人口将达到120万人的算法.解(1)y=100×(1+0.012)x.(2)10年后该城市人口总数为y=100×(1+0.012)10.伪代码如下:y←100t←1.012For I From1To10y←y×tI←I+1End ForPrint y(3)设x年后该城市人口将达到120万人,即100×(1+0.012)x=120.伪代码如下:S←100I←1.012T←0While S<120S←S×IT←T+1End WhilePrint T。
高中数学必修三第一章《算法初步》章节练习题(含答案)

《算法初步》章节练习题(30分钟50分)一、选择题(每小题3分,共18分)1.如图是某程序框图的一部分,其算法的逻辑结构为( )A.顺序结构B.判断结构C.条件结构D.循环结构2.下列各进位制数中,最大的数是( )A.11111(2)B.1221(3)C.312(4)D.56(8)3.如图所示,当输入x为2 006时,输出的y= ( )A.28B.10C.4D.2【补偿训练】执行如图所示的程序框图,若输出的结果是9,则判断框内m的取值范围是( )A.(42,56]B.(56,72]C.(72,90]D.(42,90]4.168,54,264的最大公约数是( )A.4B.6C.8D.95.下列程序的功能是( )S=1i=3WHILE S<=10000S=S ii=i+2WENDPRINT iENDA.求1×2×3×4×…×10 000的值B.求2×4×6×8×…×10 000的值C.求3×5×7×9×…×10 001的值D.求满足1×3×5×…×n>10 000的最小正整数n【补偿训练】如图程序框图中,语句“S=S×n”将被执行的次数是( )A.4B.5C.6D.76.执行如图所示程序框图,输出的k值为( )A.3B.4C.5D.6【补偿训练】如图是计算函数y=的值的程序框图,则在①、②和③处应分别填入的是( )A.y=-x,y=0,y=x2B.y=-x,y=x2,y=0C.y=0,y=x2,y=-xD.y=0,y=-x,y=x2二、填空题(每小题4分,共12分)7.执行如图所示的程序框图,若输入n的值为8,则输出s的值为.【补偿训练】某程序框图如图所示,若使输出的结果不大于37,则输入的整数i的最大值为.8.对任意非零实数a,b,若a⊗b的运算原理如图所示,则log8⊗= .29.阅读如图所示的程序框图,运行相应的程序,输出的结果s= .【补偿训练】阅读如图所示的程序框图,运行相应的程序,输出的S值等于.三、解答题(每小题10分,共20分)10.已知一个5次多项式为f(x)=5x5+2x4+3.5x3-2.6x2+1.7x-0.8,用秦九韶算法求这个多项式当x=5时的值.11.为了节约用水,学校改革澡堂收费制度,实行计时收费,洗澡时间在30分钟以内(含30分钟),每分钟收费0.1元,30分钟以上超出的部分每分钟0.2元,请设计程序,使用基本语句完成澡堂计费工作,要求输入时间,输出费用.【补偿训练】陈老师购买安居工程集资房62m2,单价为3 000元/m2.一次性国家财政补贴27 900元,学校补贴18 600元,余款由个人负担.房地产开发公司对教师实行分期付款(注①),每期为一年,等额付款.签订购房合同后一年付款一次,再经过一年又付款一次,共付10次,10年后付清.如果按年利率5.6%,每年按复利计算(注②),那么每年应付款多少元?画出程序框图,并写出计算所需的程序.注:①各期所付款的本息和的总和,应等于个人负担的购房余款的本息和.②每年按复利计算,即本年利息计入次年的本金中生息.《算法初步》章节练习题参考答案(30分钟50分)一、选择题(每小题3分,共18分)1.如图是某程序框图的一部分,其算法的逻辑结构为( )A.顺序结构B.判断结构C.条件结构D.循环结构【解析】选C.条件结构是处理逻辑判断并根据判断结果进行不同处理的结构,由算法流程图知,该算法的逻辑结构为条件结构.2.下列各进位制数中,最大的数是( )A.11111(2)B.1221(3)C.312(4)D.56(8)【解析】选C.11111(2)=1+1×2+1×22+1×23+1×24=1+2+4+8+16=31.1221(3)=1+2×3+2×32=1+6+18+27=52.312(4)=2+1×4+3×42=2+4+48=54.56(8)=6+5×8=6+40=46.3.(2015·陕西高考改编)如图所示,当输入x为2 006时,输出的y= ( )A.28B.10C.4D.2【解题指南】模拟执行程序框图,依次写出每次循环得到的x的值,当x=-2时不满足条件x ≥0,计算并输出y的值为10.【解析】选B.模拟执行程序框图,可得x=2 006,x=2 004满足条件x≥0,x=2 002满足条件x≥0,x=2 000…满足条件x≥0,x=0满足条件x≥0,x=-2不满足条件x≥0,y=10输出y的值为10.【补偿训练】执行如图所示的程序框图,若输出的结果是9,则判断框内m的取值范围是( )A.(42,56]B.(56,72]C.(72,90]D.(42,90]【解析】选B.第一次运行:S=2,k=2;第二次运行:S=6,k=3;…;第七次运行:S=56,k=8;第八次运行:S=2+4+6+…+16=72,k=9,输出结果.故判断框中m的取值范围是(56,72].4.(2015·襄阳高一检测)168,54,264的最大公约数是( )A.4B.6C.8D.9【解析】选B.168-54=114,114-54=60,60-54=6,54-6=48,48-6=42,42-6=36,36-6=30,30-6=24,24-6=18,18-6=12,12-6=6,故168和54的最大公约数为6.又因为264=44×6+0,所以6是264和6的最大公约数.所以这三个数的最大公约数为6.5.下列程序的功能是( )S=1i=3WHILE S<=10000S=S ii=i+2WENDPRINT iENDA.求1×2×3×4×…×10 000的值B.求2×4×6×8×…×10 000的值C.求3×5×7×9×…×10 001的值D.求满足1×3×5×…×n>10 000的最小正整数n【解析】选D.法一:S是累乘变量,i是计数变量,每循环一次,S乘以i一次且i增加2.当S>10 000时停止循环,输出的i值是使1×3×5×…×n>10 000成立的最小正整数n.法二:最后输出的是计数变量i,而不是累乘变量S.【补偿训练】如图程序框图中,语句“S=S×n”将被执行的次数是( )A.4B.5C.6D.7【解析】选B.由程序框图知:S=1×2×3×…×n.又1×2×3×4×5=120<200,1×2×3×4×5×6=720>200.故语句“S=S×n”被执行了5次,选B.6.(2015·北京高考改编)执行如图所示程序框图,输出的k值为( )A.3B.4C.5D.6【解题指南】按照程序框图顺序执行.【解析】选B.k=0,a=3,q=;a=,k=1;a=,k=2;a=,k=3;a=,k=4.【补偿训练】如图是计算函数y=的值的程序框图,则在①、②和③处应分别填入的是( )A.y=-x,y=0,y=x2B.y=-x,y=x2,y=0C.y=0,y=x2,y=-xD.y=0,y=-x,y=x2【解析】选B.当x> -1不成立时,y=-x,故①处应填“y=-x”;当x>-1成立时,若x>2,则y=x2,即②处应填“y=x2”,否则y=0,即③处应填“y=0”.二、填空题(每小题4分,共12分)7.(2015·苏州高一检测)执行如图所示的程序框图,若输入n的值为8,则输出s的值为.【解析】第一次循环,s=×(1×2)=2,i=4,k=2;第二次循环,s=×(2×4)=4,i=6,k=3;第三次循环,s=×(4×6)=8,i=8,k=4.此时退出循环,输出s的值为8.答案:8【补偿训练】某程序框图如图所示,若使输出的结果不大于37,则输入的整数i的最大值为.【解析】S=(20+1)+(21+1)+(22+1)+…+(2i-1+1).当i=1时,S=2;当i=2时,S=2+3=5;当i=3时,S=2+3+5=10;当i=4时,S=2+3+5+9=19;当i=5时,S=2+3+5+9+17=36;当i=6时,S=2+3+5+9+17+33>37.所以i的最大值为5.答案:58⊗= .8.对任意非零实数a,b,若a⊗b的运算原理如图所示,则log2【解析】log28<,则题意知,log28⊗=3⊗4==1.答案:19.(2015·大同高一检测)阅读如图所示的程序框图,运行相应的程序,输出的结果s= .【解析】程序在运行过程中各变量的值如下表示:第一次循环:当n=1时,得s=1,a=3.第二次循环:当n=2时,得s=4,a=5.第三次循环:当n=3时,得s=9,a=7,此时n=3,不再循环,所以输出s=9.答案:9【补偿训练】阅读如图所示的程序框图,运行相应的程序,输出的S值等于.【解析】第一次循环:S=1,k=1<4,S=2×1-1=1,k=1+1=2.第二次循环:k=2<4,S=2×1-2=0,k=2+1=3.第三次循环:k=3<4,S=2×0-3=-3,k=3+1=4,当k=4时,k<4不成立,循环结束,此时S=-3.答案:-3三、解答题(每小题10分,共20分)10.已知一个5次多项式为f(x)=5x5+2x4+3.5x3-2.6x2+1.7x-0.8,用秦九韶算法求这个多项式当x=5时的值.【解析】根据秦九韶算法,把多项式改写成如下形式:f(x)=((((5x+2)x+3.5)x-2.6)x+1.7)x-0.8,按照从内到外的顺序,依次计算一次多项式当x=5时的值;v0=5;v1=5×5+2=27;v2=27×5+3.5=138.5;v3=138.5×5-2.6=689.9;v4=689.9×5+1.7=3 451.2;v5=3 451.2×5-0.8=17 255.2;所以,当x=5时,多项式的值等于17 255.2.的值.”【延伸探究】若本题中已知条件不变,求“当x=2时v3【解析】v0=5;v1=5×2+2=12;v2=12×2+3.5=27.5;v3=27.5×2-2.6=52.4.故x=2时,v3=52.4.11.(2015·武汉高一检测)为了节约用水,学校改革澡堂收费制度,实行计时收费,洗澡时间在30分钟以内(含30分钟),每分钟收费0.1元,30分钟以上超出的部分每分钟0.2元,请设计程序,使用基本语句完成澡堂计费工作,要求输入时间,输出费用.【解题指南】题目为分段函数,用条件结构求解.【解析】设时间为t分钟,则费用y为y=程序框图如图所示.这里应用的是条件结构,应该用条件语句来表述,INPUT tIF t<=30 THENy=0.1tELSEy=3+(t-30)0.2END IFPRINT yEND【补偿训练】陈老师购买安居工程集资房62m2,单价为3 000元/m2.一次性国家财政补贴27 900元,学校补贴18 600元,余款由个人负担.房地产开发公司对教师实行分期付款(注①),每期为一年,等额付款.签订购房合同后一年付款一次,再经过一年又付款一次,共付10次,10年后付清.如果按年利率5.6%,每年按复利计算(注②),那么每年应付款多少元?画出程序框图,并写出计算所需的程序.注:①各期所付款的本息和的总和,应等于个人负担的购房余款的本息和.②每年按复利计算,即本年利息计入次年的本金中生息.【解析】设每年应付款x元,那么第一年付款的本息和为x×1.0569元,第二年付款的本息和为x×1.0568元,…第九年付款的本息和为x×1.056元,第十年付款为x元.所以各期所付款的本息和的总和为x(1+1.056+1.0562+…+1.0569).所购房余款的本息和为[3 000×62-(27 900+18 600)]×1.05610=139 500×1.05610,故有x(1+1.056+1.0562+…+1.0569)=139 500×1.05610,即x=.程序框图如下图所示:。
新高中数学苏教版必修三同步练习:1.4_算法案例(含答案解析)

数学·必修3( 苏教版 )第1章算法初步1.4算法事例基础稳固1.高二年级两个班的学生一同排队出操,假如9 人排一行,多出一个人;假如10 人排一行,相同多出一个人.已知每个班人数不超出50,这两个班共有 ________人.分析:假如将两个班的人数减少 1 人,则 9 人一排或10 人一排都正好排完没有节余,所以两班人数减 1 是 9 和 10 的公倍数,又由于每个班人数不超出50,能够求出9 和 10 的最小公倍数,而后再加上 1.所以,这两个班共有9×10+1= 91(人 ).答案: 912.把几十个苹果均匀分红若干份,每份9 个余 8 个,每份 8 个余 7 个,每份 4 个余 3个.这堆苹果起码有________个.分析:依题意知,这堆苹果总个数添进 1 个苹果后,正好是9,8, 4 的倍数.由于9,8, 4 的最小公倍数是9×8=72,所以这堆苹果起码有9×8- 1= 71(个 ).答案: 713. 294 和 84 的最大条约数为________.分析: 294= 84×3+ 42, 84= 42×2+ 0.答案: 424.两个整数490 和 910 的最小公倍数是________.分析: 910= 490×1+420, 490= 420×1+ 70, 420= 70× 6+0.∴490 与 910 的最大条约数是 70.∴ 490 与 910 的最小公倍数是:(490 ×910) ÷70= 6 370.答案: 6 3705.求方程 x3- 2x= 0 的近似解,要先将它近似地放在某两个连续整数之间,最好应放在 ________之间.答案: 1和26.用展转相除法和更相减损术求80 和 36 的最大条约数.分析:用展转相除法:80= 36×2+ 8, 36= 8×4+ 4,8= 4×2+0.故 80 和 36 的最大条约数是 4.用更相减损术:80- 36=44, 44- 36= 8,36- 8= 28, 28- 8=2020- 8= 12, 12- 8=4,8- 4= 4.∴80 和 36 的最大条约数是 4.7.写出用二分法求方程 x3- 2x -3= 0 在区间 [1,2]内的一个近似根 (偏差不超出 0.001) 的一个算法伪代码.分析:算法伪代码以下:a← 1b← 2c← 0.001Doa+ bx0←23f(a) ←a- 2a- 3f(x 0) ←x03- 2x0- 3If f(x 0)= 0 Then Exit DoIf f(a)f(x 0 )<0 Thenb← x0Elsea← x0End IfUntil |a -b|<cEnd DoPrint x0能力升级8.现有长度为 2.4 m 和 5.6 m 两种规格的钢筋若干,要焊接一批正方体模型,问如何设计,才能保证正方体体积最大,且不浪费资料?分析:要焊接正方体,就是将两种规格的钢筋裁成长度相等的钢筋条,为了保证不浪费资料,应使每一种规格的钢筋裁剪后无节余,所以裁剪的长度应是 2.4 和 5.6 的条约数,要使正方体的体积最大,亦即棱长最长,就要使正方体的棱长为 2.4 和 5.6 的最大条约数.用欧几里得展转相除法求得 2.4 和 5.6 的最大条约数: 5.6= 2.4× 2+ 0.8,2.4= 0.8 ×3+ 0,即 2.4和 5.6 的最大条约数为0.8.所以将正方体的棱长设为0.8 m时,体积最大且不浪费资料.9. (2014·汉调考武)分别用展转相除法和更相减损术求(1)98和63; (2)8 251 和 6 105的最大条约数,从中你有什么发现?分析:展转相除法是做两个数的带余除法,更相减损术是做两个数的减法.(1)用展转相除法:S1 98=63×1+ 35,S2 63=35×1+ 28,S3 35=28×1+ 7,S4 28=4×7.∴ 98 和 63 的最大条约数是7.用更相减损术:S1 98-63= 35,S2 63-35= 28,S3 35-28= 7,S4 28-7= 21,S5 21-7= 14,S6 14-7= 7,∴ 98 和 63 的最大条约数为7.(2)用展转相除法:S1 8 251= 6 105 ×1+ 2 146,S2 6 105= 2 146 ×2+ 1 813,S3 2 146= 1 813 ×1+ 333,S4 1 813= 333 ×5+ 148,S5 333= 148 ×2+37,S6 148= 37×4.∴ 8 251 和 6 105 的最大条约数为37.用更相减损术:S1 8 251- 6 105= 2 146,S2 6 105- 2 146= 3 959,S3 3 959- 2 146= 1 813,S4 2 146- 1 813= 333,S5 1 813- 333=1 480,S6 1 480- 333=1 147,S7 1 147- 333=814,S8 814- 333= 481,S9 481- 333= 148,S10 333- 148=185,S11 185-148= 37,S12 148- 37= 111,S13 111- 37=74,S14 74- 37= 37,∴ 8 251 和 6 105 的最大条约数为37.发现:展转相除法和更相减损术在实质上是一致的,但在实质操作中,用展转相除法比用更相减损术的计算步骤要少,但计算量相对较大,因此两者平分秋色.10.用展转相除法或更相减损术求三个数135, 243, 324 的最大条约数.分析:方法一(展转相除法 ):∵ 324=243×1+81, 243= 81×3+ 0,∴ 324 与 243 的最大条约数为81.又∵ 135=81×1+ 54, 81= 54×1+ 27,54= 27×2+ 0,∴ 81与135 的最大条约数为27.∴三个数135, 243, 324 的最大条约数为27.方法二(更相减损术):∵ 324- 243=81,243- 81= 162,162- 81= 81;135- 81=54,81- 54= 27, 54- 27= 27.∴三个数135, 243, 324 的最大条约数为27.11.有甲、乙、丙三种溶液,分别重13246 kg、 34 kg、29 kg.现要将它们分别所有装入小瓶中,每个小瓶装入液体的重量相同.问每瓶最多装多少?分析: 416=256=15036;334=154=13536;229=209=8036;15036-13536=1536;13536-1536=12036;12036-15= 105; 105- 15= 90;90- 15= 75;75- 15=60; 60- 15= 45;45- 15= 30;30- 15=36 3636 36 36 36 36 36 36 36 36 36 36 36 36 36 36 36 36 1536;即 41、 33的最大条约数是15 6 436.8036-1536=6536;6536-3615=5036;3650-1536=3536;3536-1536=2036;2036-3615=365;1536-365=1036;1036-5=5.36 36即 41、 33、 22的最大条约数是5.649365所以每瓶最多装36 kg.12.甲、乙、丙三种溶液分别重147 g、343 g、133 g,现要将它们分别所有装入小瓶中,每个小瓶装入液体的重量相同,问每瓶最多装多少?分析:由题意,每个小瓶应装的溶液的重量是三种溶液重量的最大条约数.先求147与 343 的最大条约数: 343= 147× 2+ 49,147= 49×3+ 0.所以 147 与 343 的最大条约数是49.再求 49 与 133 的最大条约数:133= 49×2+ 35, 49= 35×1+14, 35=14× 2+7, 14= 7×2+0.所以 147, 343,133 的最大条约数是 7.所以每瓶最多装 7 g.13.相传一片太古丛林栖息着凤凰,麒麟和九头鸟,凤凰有 1 个头,1 个头, 4 只脚,九头鸟有9 个头, 2 只脚,它们这 3 种动物的头共有100只.问丛林中 3 种动物各有多少只?试设计一个算法并写出伪代码.2 只脚,麒麟有个,脚共有100分析:设丛林中有凤凰x 只,麒麟y 只,九头鸟z 只.此题的重点是如何考虑x、 y、z三个变量之间的关系.由题意可知算法以下:S1 当凤凰 x= 1 时,变量麒麟y 的取值能够从 1 到 24;S2 让变量 y 从 1 开始取值 (比如: y 的值为 1);S3 经过表达式 (100-x- y)/9 ,计算 z 的值;S4 达成上述步骤后,x、y、z 三个变量都取到了自己相应的值,但是这三个值是不是正确的呢?我们一定经过以下的两个条件来判断:x+ y+ 9z= 100 且2x+ 4y+ 2z= 100;S5假如两个条件所有知足,就输出x、y、z 的值,假如不知足,就让y 值加1,而后重复S2 到S4,直至y 的取值超出24.而后让x 的取值加 1 后,重复S1 到S5 的操作,直至x 的取值超出50 为止,此时退出算法.伪代码以下:For x From 1To 50For y From 1 To 24z← (100- x- y)/9If 2x+ 4y+2z= 100 Andx+ y+ 9z= 100ThenPrint x, y, zEnd IfEnd ForEnd For14.古希腊优秀的数学家丢番图的墓碑上有这样一首诗:这里是一座古墓,里面埋葬着丢番图.“请你告诉我,丢番图寿数几何?”“他的童年占去一世的六分之一,接着十二分之一是少年期间,又过了七分之一的光阴,他找到了终生伴侣.五年以后,婚姻之神赏给他一个儿子.但是儿子命运不济,只活到父亲寿数的一半,就急忙而去.这对父亲是一个深重的打击.整整四年,为失掉爱子而伤心,终于辞别数学,走开人间.”试写出其算法剖析及流程图与伪代码.分析:可设丢番图的寿数为x,则x 为正整数,而且依题意可有11116x+ 12x+7x+ 5+ 2x+ 4= x.其算法为:S1x←1.1111S2 判断6x+12x+7x+ 5+2x+ 4= x 能否建立.假如建立,则输出x,转至 S3;假如不建立,则x←x+ 1,转 S2.S3结束.其流程图与相应的伪代码以下.x←1If x/6 +x/12 + x/7 + 5+ x/2+ 4=x ThenPrint xElsex← x+ 1End If。
必修3第一章《算法初步》训练题(含答案)

必修③第一章《算法初步》练习题一、选择题:1.下面对算法描述正确的一项是:( )A .算法只能用自然语言来描述B .算法只能用图形方式来表示C .同一问题可以有不同的算法D .同一问题的算法不同,结果必然不同 2. 算法的三种基本结构是 ( )A. 顺序结构、模块结构、条件结构B. 顺序结构、循环结构、模块结构C. 顺序结构、条件结构、循环结构D. 模块结构、条件结构、循环结构 3.用二分法求方程022=-x 的近似根的算法中要用哪种算法结构( ) A .顺序结构 B .条件结构 C .循环结构 D .以上都用 4.对赋值语句的描述正确的是 ( )①可以给变量提供初值 ②将表达式的值赋给变量 ③可以给一个变量重复赋值 ④不能给同一变量重复赋值 A .①②③ B .①② C .②③④ D .①②④5. 将两个数a=8,b=17交换,使a=17,b=8,下面语句正确一组是 ( ) A. B. C. D.6、下列程序语句不正确...的是( ) A 、INPUT “MATH=”;a+b+c B 、PRINT “MATH=”;a+b+c C 、c b a += D 、1a =c b - 7.下列给变量赋值的语句正确的是( )A. 5=aB.a +2=aC. a =b =4D. a =2*a8. 给出以下四个问题,①输入一个数x ,输出它的相反数.②求面积为6的正方形的周长.③求三个数a,b,c 中的最大数. ④求函数1,0()2,0x x f x x x -≥⎧=⎨+<⎩的函数值.其中不需要用条件语句来描述其算法的有 ( )A. 1个B. 2个C. 3个D. 4个 9.给出以下四个问题: ①解不等式32-x a>23-x a(0>a 且1≠a ) .②求边长为6的正三角形的面积.③求函数21,0()43,0x x f x x x -≥⎧=⎨+<⎩的函数值 ④若集合}1,1{-=A ,}1|{==mx x B ,且A B A =⋃,求m 的值。
苏教版必修3全套练习第一章 算法初步.docx

第一章算法初步1.1算法的含义【新知导读】1.什么是算法?试从日常生活中找3个例了,描述它们的算法.2.我们从小学到初中再到高中所学过的许多数学公式是算法吗?【范例点睛】例].早上从起床到出门需要洗脸刷牙(5min)、刷水壶(2min)、烧水(8min)、泡面(3min)、吃饭(lOmin)、听广播(8min)几个步骤.从下列选项中选出较好的一种算法A.第一步洗脸刷牙、第二步刷水壶、第三步烧水、第四步泡面、第五步吃饭、第六步听广播.B.第一步刷水壶、第二步烧水同时洗脸刷牙、第三步泡面、第四步吃饭、第五步听广播C第一步刷水壶、第二步烧水同时洗脸刷牙、第三步泡面、第四步吃饭同时听广播.D.第一步吃饭同时听广播、第二步泡面、第三步烧水同时洗脸刷牙、第四步刷水壶. 思路点拨:从四个答案所给出的步骤是否合理、最少需要花费多少时间入手,进行判断.易错辨析:选择A很大程度上是受人们的通常的习惯所影响,即起床后首先应该洗脸刷牙再做其他的事情.方法点评:作为完成过程的算法来说,要讲究一个优劣之分,也即完成这个过程用时最少的是一个好算法,所以.应选C.例2. —位商人有9枚银元,其中有1枚略轻的是假银元.你能用天平(不用舷码)将假银元找出来吗?思路点拨:最容易想到的解决这个问题的一种方法是:把9枚银元按顺序排成一列,先称前2枚,若不平衡,则可找出假银元;若平衡,则2枚银元是真的,再依次与剩下的银元比较,就能找出假银元. 这种算法最少要称1次,最多要称7次,是不是还有更好的办法,使得称量次数少一些?我们可以采用下面的方法:1.把银元分成3组,每组3枚.2.先将两组分别放在天平的两边.如果天平不平衡,那么假银元就在轻的那一组;如果天平平衡,则假银元就在未称的第3组里.3.取出含假银元的那一组,从中任取两枚银元放在天平的两边,如果左右不平衡,则轻的那一边就是假银元;如果天平两边平衡,则未称的那一枚就是假银元.方法点评:经分析发现,这种算法只需称量2次,这种做法要明显好于前一种做法.从以上两个问题中可以看出,同一个问题可能存在着多种算法,其中一些可能要比另一些好. 在实际问题和算法理论中,找出好的算法是一项重要的工作.【课外链接】1.设计一个算法,求840与1764的最大公因数.思路点拨:该算法是在对自然数进行素因数分解的基础上设计的•解答这个问题需要按以下思路进行.首先,对两个数分别进行素因数分解:其次,确定两数的公共素因数:2,3,7.接着,确定公共素因数的指数:对于公共素因数2,2?是1764的因数,2彳是840的因数,因此22是这两个数的公因数,这样就确定了公共素因数2的指数为2.同样,可以确定出公因 数3和7的指数均为1.这样,就确定了 840与1764的最大公因数为22X 3X 7 = 84【随堂演练】1.算法是指()A.为解决问题而编写的计算机程序B.为解决问题而采取的方法和步骤C.为解决问题而需要采用的计算机程序C.为解决问题而采用的计算方法 2.看下面的四段话,其中不是解决问题的算法的是()(A )从济南到北京旅游,先坐火车,再坐飞机抵达(B )解一元一次方程的步骤是去分母、去括号、移项、 合并同类项、系数化为1(C ) 方程/-1=0有两个实根(D ) 求 1+2+3+4+5 的值,先计算 1+2=3,再求 3+3=6, 6+4=10, 10+5=15,最终结果为 15 4. 买一个茶杯1. 5元,现要写出计算买n 个茶杯所需要的钱数的一个算法,则这个算法中必须要用到的一个表达式为 ___________________5. 设计算法,判断97是否为素数.6. 设计算法,求1356和2400的最小公倍数.7. 有两个瓶子A 和B,分别盛放醋和酱油,要求将它们互换(即A 瓶原来盛醋,现改盛酱 油;B 瓶则相反)[2x + 3y = 7 [3x +4y = 10的 解 集 是 ________________________________&设计算法,将三个数按从大到小的顺序排列.9.有13个球看上去一模一样,但其中一个质量不同(它比其他12个略重),现在有一个天平(没有確码),要求给出一种操作方法,把这个球找出来.1.2.1顺序结构【新知导读】1.什么是流程图,它有哪些常用符号?2.顺序结构的流程图是什么?【范例点睛】例1.尺规作图,确定线段AB的一个5等分点.思路点拨:确定线段AB的5等分点,是指在线段AB上确定-点M,使得AM因此解决这个问题的方法是:第一,从A点出发作一条与原直线不重合的射线;第二,任取射线上一点C,并在射线上作线段AD,使AD =5AC;第二,连接并过C点作的平行线交AB于M,M就是要找的5等分点.这个实现过程用流程图表不:易错辨析:有些同学想直接从已的。
最新高一数学题库 必修3算法初步练习题及答案

第一章算法初步1.1算法与程序框图1.1.1算法的概念1.下面的结论正确的是【】A.一个程序的算法步骤是可逆的B.一个算法可以无止境地运算下去的C.完成一件事情的算法有且只有一种D.设计算法要本着简单方便的原则2.下面对算法描述正确的一项是【】A.算法只能用自然语言来描述B.算法只能用图形方式来表示C.同一问题可以有不同的算法D.同一问题的算法不同,结果必然不同3.下面哪个不是算法的特征【】A.抽象性B.精确性C.有穷性D.唯一性4.算法的有穷性是指【】A.算法必须包含输出B.算法中每个操作步骤都是可执行的C.算法的步骤必须有限D.以上说法均不正确5.早上从起床到出门需要洗脸刷牙(5min)、刷水壶(2min)、烧水(8min)、泡面(3min)、吃饭(10min)、听广播(8min)几个步骤,从下列选项中选最好的一种算法【】A.S1洗脸刷牙、S2刷水壶、S3烧水、S4泡面、S5吃饭、S6听广播B.S1刷水壶、S2烧水同时洗脸刷牙、S3泡面、S4吃饭、S5听广播C. S1刷水壶、S2烧水同时洗脸刷牙、S3泡面、S4吃饭同时听广播D.S1吃饭同时听广播、S2泡面;S3烧水同时洗脸刷牙;S4刷水壶6.看下面的四段话,其中不是解决问题的算法是【】A.从济南到北京旅游,先坐火车,再坐飞机抵达B.解一元一次方程的步骤是去分母、去括号、移项、合并同类项、系数化为1C.方程210x-=有两个实根D.求1+2+3+4+5的值,先计算1+2=3,再计算3+3=6,6+4=10,10+5=15,最终结果为157.写出求1+2+3+4+5+6+…+100的一个算法.可运用公式1+2+3+…+n=(1)2n n+直接计算.第一步______①_______;第二步_______②________;第三步输出计算的结果.8.写出1×2×3×4×5×6的一个算法.1.1.2 程序框图1.算法的三种基本结构是【】A. 顺序结构、模块结构、条件结构 B. 顺序结构、循环结构、模块结构C. 顺序结构、条件结构、循环结构D. 模块结构、条件结构、循环结构2.给出以下四个问题,①输入x, 输出它的相反数;②求面积为6的正方形的周长;③在三个不等实数,,a b c中,求一个数的最大数;④求函数1,0()2,0x xf xx x-≥⎧=⎨+<⎩的函数值。
苏教版必修三第1章算法初步作业题及答案解析:第1章算法初步章末复习课

章末复习课课时目标 1.进一步巩固和理解本章重要知识点.2.学会用算法的思想处理问题.1.下列关于算法的说法正确的有________.(填序号)①求解某一类问题的算法是唯一的;②算法必须在有限步操作之后停止;③算法的每一步操作必须是明确的,不能有歧义;④算法执行后一定产生明确的结果.2.下图的程序语句输出的结果S为________.I←1 While I<8S←2I+3I←I+2 End While Print S3.下列关于选择结构的说法中正确的是________.(填序号)①选择结构的流程图有一个入口和两个出口;②无论选择结构中的条件是否满足,都只能执行两条路径之一;③选择结构中的两条路径可以同时执行;④对于一个算法程序来说,菱形框中的条件是唯一的.4.下边是一个算法的流程图,当输入的x值为3时,输出y的结果恰好是13,则处的关系式是____________.(填上一个你认为正确的算式即可)5.要使以下For循环执行20次,循环变量的初值应当是________.For k From________To -5 Step -16.三个数72、120、168的最大公约数是________.一、填空题1.如果执行下面的流程图,那么输出的S等于____________.2.完善下面的伪代码所表示的算法.Read xIf x≥0 Theny←6Elsey←5Print y3.若“x←3×5”与“x←x+1”是某一个程序中先后相邻的两个语句,那么下列说法正确的是________.(填序号)①x←3×5的意思是x=3×5=15,此式与数学中的算术式是一样的;②“x←3×5”是将数值15赋给x;③“x←3×5”可以写成“3×5=x”;④“x←x+1”在执行时赋值号右边x的值是15,执行后左边x的值是16.4.下列伪代码的运行结果是________.A←5B←4If B≥AThenB←A+BElseB←A-BEnd IfPrint B5.程序:(\用来取商)上述伪代码如果输入的值是51,则运行结果是________________________________.6.如图所示,伪代码的输出结果为132,则判断框中应填________.7.执行下面的伪代码,输出的结果是________.N ←0I ←0While I <30I ←(I +1)2N ←N +1End WhilePrint N8.下边伪代码运行后,输出的值为________.S ←1i ←1While i ≤5S ←S ×i i ←i +1End WhilePrint S9.用辗转相除法求333与24的最大公约数时的循环次数为________.二、解答题10.画出求12-22+32-42+…+992-1002的值的流程图.11.已知函数y =⎩⎪⎨⎪⎧ 2x 2-1 (x >0)2x +1 (x =0)-2x 2+4 (x <0),试写出伪代码,输入x 的值后输出y 的值.能力提升12.设计一个算法,计算两个正整数a ,b 的最小公倍数,并将此算法用流程图表示.13.某电信部门规定,拨打市内电话时,如果通话时间不超过3分钟,则收取通话费0.2元;如果通话时间超过3分钟,则超过部分按每分钟0.1元收取通话费(通话不足1分钟时按1分钟计).试设计一个计算通话费用的算法,画出流程图,并写出伪代码.1.算法是对一类问题一般解法的抽象与概括,是把问题的解法划分为若干个可执行的步骤,有时需重复多次,但最终都必须在有限个步骤之内完成,所以在设计算法解决问题时要注意:(1)与解决问题的一般方法相联系,从中提炼出算法.(2)可引入有关的参数和变量对算法步骤加以表达.(3)解决问题的过程可分解为若干个步骤,并能用简洁实用的语言表达.(4)算法过程要便于在计算机上执行.2.流程图是用规定的图形和流程线来形象、直观、准确的表示算法的图形.设计流程图时,要先进行算法分析,确定算法的逻辑结构和各步的功能再画流程图,同时要考虑到编写程序的要求.读、画流程图是高考在本章中考查的重点.3.基本算法语句有输入语句、输出语句、赋值语句、条件语句和循环语句五种,主要对应顺序结构、选择结构和循环结构.明确各语句的功能和格式,是执行程序的关键,掌握常用的算法对理解程序也很有帮助,用算法语句编写程序时,一般先画流程图.答案双基演练1.②③④解析根据算法的定义有②③④三种说法正确.2.17解析当I为7的时候I<8,即S=17.3.②4.y←3x(答案不唯一)解析当x=3时,因为x>0,所以x=3-2=1;又x=1>0,所以x=1-2=-1;x=,-1时,y=13∴内可填y=3x(答案不唯一).5.14解析每循环一次,k值减少1,而最后一次循环时k的值为-5,注意到要循环20次,故初始的k值应为14(14-(-5)+1=20).这是因为当I∈[-5,14]时,就执行循环.6.24解析三个数中任意两个数的最大公约数与第三个数,求其最大公约数就是这三个数的最大公约数.这三个数的最大公约数为24.作业设计1.2 550解析本流程图含有循环结构.第1次循环为1≤50;S=0+2×1;k=1+1=2;第2次循环为2≤50;S=2+2×2;k=2+1=3;……第50次循环为50≤50;S=2+4+…+100=2 550.k=51>50,退出循环,输出S. 2.End If3.②④解析赋值语句有固定的格式,与数学中算术式是不一样的,故①是错误,③也是错误的,根据赋值语句的功能知②④是正确的.4.15.15解析∵x=51,∴9<x<100,∴a=51\10=5,b=51 Mod 10=1.∴10×b+a=10×1+5=15.即输出结果为15.6.i≥11(或i>10)7.4解析I=1,N=1→I=4,N=2→I=25,N=3→I=262,N=4.故N的取值为4,实际上它表示循环的次数.8.120解析i=1时,S=1;i=2,S=2;i=3时,S=6;i=4时,S=6×4=24,i=5时,S=24×5=120;i=6时不满足i≤5,执行“Print S”,所以S=120.9.3次解析333=13×24+21,24=21+3,21=7×3,共操作3次.10.解11.解Read xIf x>0Theny←2x2-1ElseIf x=0Theny←2x+1Elsey←-2x2+4End IfEnd IfPrint y12.解算法:S1输入a,b;S2n←1;S3如果Mod(n,a)≠0或Mod(n,b)≠0,那么转S4,否则转S5;S4n←n+1,转S3;S5输出n.流程图:13.解 我们用C(单位:元)表示通话费,t(单位:分钟)表示通话时间,则依题意有C =⎩⎪⎨⎪⎧0.2 (t ∈N *,0<t ≤3),0.2+0.1(t -3) (t ∈N *,t >3).算法步骤如下:S1 输入通话时间t .S2 如果t ≤3,那么C ←0.2;否则,C ←0.2+0.1×(t -3).S3 输出通话费用C .流程图如图所示: 伪代码如下:。
苏教版高中数学必修三算法初步检测试卷答案

高二单元测试试卷(参考答案)0 3713、------------------------------------ 14、-----------------------------------2/5 ④⑤⑥15、------------------------------------ 16、-----------------------------------三、解答题(本大题共5小题,共80分,解答应写出文字说明、证明过程或演算步骤)17、(10分) Read x流程图:略 ----------5分If x < 0, Then f(x):= x+3Else If x = 0,Then f(x):=0;Else f(x):= ∙x-5.End IfEnd IfPrint f(x) ------------------------5分18.(16分)解:(1)流程图如图所示:(2)①最上方添Read 10分②Print n+1 应改为Print n; 12分③S=1应改为S=0 16分19.(16分)解:Read a, b, cIf a>b thent←aa←bb←aElse ----------------------------------------4分 If a>c thent←aa←cc←tElse ----------------------------------------8分If b>c thent←bb←cc←t ----------------------------------------12分End If End If End IfPrint a,b,c -----------------------------------------16分20、(18分)解:依编号顺序平均分成的10个小组分别为0~9, 10~19, 20~29, 30~39, 40~49,50~59,60~69,70~79,80~89,90~99. ----------6分因第7组抽取的号码个位数字应是3,所以抽取的号码是63. ----------14分这个样本的号码依次是6,18,29,30,41,52,63,74,85,96这10个号.---------18分 21.(20分)解:用c (单位:元)表示通话费用t (单位:分钟)表示通话时间,则依题意必有⎪⎩⎪⎨⎧∉>+-+∈>-+≤<=),3()1]3([1.02.0),3()3(1.02.0)30(2.0Z t t t Z t t t t c[t-3]表示取不大于t-3的整数部分。
高中数学苏教必修三规范训练 第章 算法初步+ 含答案

1.3.1赋值语句1.3.2输入、输出语句双基达标(限时15分钟)1.下列给出的赋值语句中正确的是________.①3←A②m←-m③B←A←2④x+y←0解析赋值语句只能把常数或表达式的值赋给变量,并且一个赋值语句只能给一个变量赋值,故①、③、④都不正确,②正确.答案②2.写出下列用伪代码描述的算法执行后的结果a←2a←4a←a+aPrint a执行结果:________.解析根据赋值语句的意义,输出结果为8.答案83.将两个数a=8,b=17交换,使a=17,b=8,下面语句正确的一组是________(填写相应的序号).①a←b b←a;②c←b b←a a←c;③b←a a←b;④a←c c←b b←a解析两个变量值的互换应引进第三个变量,每个变量都有各自的“门牌号”.答案②4.伪代码M←1M←M+1M←M+2Print M的输出结果为________.解析本题表示的算法为1+1+2=4.答案 45.下面伪代码运行的结果是________.a←1b←2c←a-bb←a+c-bPrint a、b、c解析由输出及赋值语句的特点知,输出结果为1,-2,-1.答案1、-2、-16.如图是利用赋值语句和输入、输出语句i←10j←2i+5k←2j+5Print k+j写出的算法,请画出该算法的流程图.解流程图如下图所示:综合提高(限时30分钟)7.如下图所示的伪代码中依次输入128,130,109,141,则输出的结果为________.Read M1,M2,M3,M4M←(M1+M2+M3+M4)/4Print M解析图中伪代码表示的是求这四个数的平均数.答案1278.在如图所示的伪代码中输入x=1,则输出的结果x是________.解析该算法表示计算1×2×3×4×5×6Read xx←2xx←3xx←4xx←5xx←6xPrint x的值,再把720赋值给x.答案7209.读伪代码,完成下列题目:Read xY←x2+2xPrint Y(1)若输入“3”则执行结果为________.(2)若执行结果为3,则输入的值可能为________.解析(1)若输入3,则:Y=3×3+2×3=15.(2)若执行结果为3,即输出3.即:x2+2x=3,解之得x=-3或x=1即输入的值为-3或1.答案(1)15(2)1或-310.下面的算法的功能是求所输入的两个正数的平方和,已知最后输出的结果为3.46,试据此将算法补充完整.Read x1,x2x1←1.1x2←________S←________Print S解析由于算法的功能是求所输入的两个正数的平方和,所以,S=x12+x22;又由于最后输出的结果是3.46,所以3.46=1.12+x22,解得x22=2.25,又x2是正数,所以x2=1.5.答案 1.5x12+x2211.读下列两个伪代码,回答问题:①②x←3 x←3y←4 y←4x←y y←xPrint x,y Print x,y(1)上述两个伪代码的运行结果分别是________、________.(2)上述两个伪代码的第三行有什么区别?答案(1)4,43,3(2)伪代码①中的x←y是将y的值4赋给x,赋值后x的值变为4,y的值不变;②中y←x是将x的值3赋给y,赋值后y的值变为3,x的值不变.12.随着人的年龄的增加,成人的肺活量会逐渐减少,假如我们用V表示人的肺活量(单位:L),用h表示人的身高(单位:英寸),a表示年龄,则这几个量近似地满足关系式:V =0.104h-0.018a-2.69.请写出伪代码.解Read a,hV←0.104h-0.018a-2.69Print V13.(创新拓展)设中国的通货膨胀率保持在3%左右,所谓通货膨胀率为3%,指的是每年消费品的价格增长率为3%.在这种情形下,某种品牌的钢琴2010年的价格是10 000元,请用算法描述这种钢琴今后4年的价格变化情况,并输出4年后钢琴的价格.画出流程图,写出伪代码.解算法流程图如图所示:伪代码如下:p←10 000p←p(1+3%) p←p(1+3%) p←p(1+3%) p←p(1+3%) Print p。
高中数学苏教必修三规范训练 第1章 算法初步33 含答案

1.3.3 条件语句双基达标 (限时15分钟)1.条件语句的一般形式是“If A Then B Else C ”,其中B 表示的是________.(填序号)①满足条件时执行的内容;②条件语句;③条件;④不满足条件时执行的内容.解析 由条件语句的结构及功能知B 表示的是满足条件时执行的内容.答案 ①2.下面是一个算法的伪代码,如果输入的x 值是10,则输出的y 值是________. Read xIf x ≤5 Theny ←10xElse y ←8.5xEnd IfPrint y解析 由输入x 的值为10,得y =8.5×10=85.答案 853.在如图所示的算法过程中,当分别输入x =-2,x =3时,则输出的函数值分别为________. Read xIf x ≤0 Theny ←x 2Else y ←2xEnd IfPrint y解析 表示求函数:y =⎩⎪⎨⎪⎧x 2,x ≤02x ,x >0,当x =-2,x =3时求y 的值. 答案 4和64.通过下面伪代码,输出的y 的值为________.x ←3If x >3 Theny ←x 2Else y ←2xEnd IfPrint y解析 由3不大于3,得y =2x =6.答案 65.写出如图所示的伪代码表示的函数:________. Read xIf x ≤6 Theny ←3x +2Else y ←x +2 012End IfPrint y解析 由条件语句的功能知本题伪代码表示的函数是分段函数.答案 y =⎩⎪⎨⎪⎧3x +2, x ≤6,x +2 012, x >6. 6.下面是某一问题算法的伪代码.Read xIf x <2 Theny ←x 2-1Elsey ←-x 2+1End IfPrint y(1)此伪代码是哪个问题的伪代码?(2)当输入的x 值为3时,求输出的结果.解 (1)求函数y =⎩⎪⎨⎪⎧x 2-1, x <2,-x 2+1, x ≥2的函数值的伪代码. (2)-8.综合提高 (限时30分钟)7.下面由伪代码运行的结果是________. a ←2b ←3If a <b Thent ←a a ←bb ←tEnd IfPrint a ,b解析 其表示的算法为a 、b 按从大到小的顺序排列.答案 3,28.为了在运行下面的程序之后得到输出的y 值为16,键盘输入的x 可以是________.解析 本题中伪代码是求函数y =⎩⎪⎨⎪⎧(x +1)2, x <0,(x -1)2 x ≥0的函数值,由输出的y 值为16,从而有(x +1)2=16(x <0)或(x -1)2=16(x ≥0),∴x =-5或x =5.答案 -5或59.以下给出的是用条件语句编写的一个程序,根据该程序回答:(1)若输入4,则输出结果是________.(2)该程序的功能是求函数________的函数值.Read xIf x <3 Then y ←2xElseIf x >3 Theny ←x 2-1Else y ←2End IfEnd IfPrint y解析 由条件语句的功能可知:x =4>3则y =42-1=15,此程序的功能为:求函数f (x )=⎩⎪⎨⎪⎧ 2x x <32 x =3的函数值.x 2-1 x >3答案 (1)15 (2)f (x )=⎩⎪⎨⎪⎧ 2x x <32 x =3x 2-1 x >310.将下列程序补充完整. (1)输入两个数,输出其中较小的数,则①应为________.Read a ,bIf a <b ThenPrint aElse①____End If(2)求函数y=|x-4|+1的函数值,则②应为________.Read xIf x≥4Theny←x-3Else____②____End IfPrint y解析(1)Else后面是否满足条件“a<b”时执行的内容,应该是输出较小的数b.故填Print b.(2)Else后面是否满足条件“x≥4”时执行的内容,应该是y=|x-4|+1=4-x+1=5-x,故填:y←5-x.答案(1)Print b(2)y←5-x11.给定三个函数y1=x2-1,y2=2x-3,y3=x2+6x.给出一个x的值,分别计算它们的函数值,并输出它们中最小的一个.试用伪代码写出根据输入的x的值计算y值的一个算法并画出算法流程图.解伪代码如下.Read xy1←x2-1y2←2x-3y3←x2+6x;If y1≤y2,y1≤y3ThenPrint y1Else If y2≤y3ThenPrint y2ElsePrint y3End IfEnd If算法流程图如图所示.12.某商场为了促销,采用购物打折的优惠办法.每位顾客一次购物:①1 000元以上打九五折;②2 000元以上打九折;③3 000元以上打八五折;④5 000元以上打八折.试编写伪代码程序求优惠价.解 设购物款数原为x 元,优惠后价格为y 元,则优惠付款方式可用分段函数表示为:y =⎩⎪⎨⎪⎧ x , x <1 000,0.95x , 1 000≤x <2 000,0.9x , 2 000≤x <3 000,0.85x , 3 000≤x <5 000,0.8x , x ≥5 000.伪代码如下:Read xIf x <1 000 Theny ←xElse If x <2 000 Theny ←0.95xElse If x <3 000 Theny ←0.9xElse If x <5 000 Theny ←0.85xElsey ←0.8xEnd IfEnd IfEnd IfEnd IfPrint y 13.(创新拓展)写出求一元二次方程ax 2+bx +c =0的解的算法,并画出流程图.解伪代码如下:Read a,b,cΔ←b2-4acp←-b2aq←|Δ| 2aIfΔ≥0Thenx1←p+qx2→p-qIf x1=x2ThenPrint原方程有两个相等实数根x1,x2ElsePrint原方程有两个不等实数根x1,x2End IfElsePrint原方程无实数根End If。
高中数学苏教必修三规范训练 第1章 算法初步1 含答案

1.1 算法的含义双基达标 (限时15分钟)1.下面的结论正确的是________.①一个程序的算法步骤是可逆的②一个算法可以无止境地运算下去③完成一件事情的算法有且只有一种④设计算法要本着简单方便的原则解析 由算法的含义及特点可得:④正确.答案 ④2.下面对算法描述正确的一项是________.①算法只能用自然语言来描述;②算法只能用图形方式来表示;③同一问题可以有不同的算法;④同一问题的算法不同,结果必然不同.解析 根据算法的概念即可得知.答案 ③3.以下不是算法的特征的是________.①确定性;②唯一性;③有限性.解析 根据算法的主要特点知,算法不是唯一的.答案 ②4.我们学习的算法不同于求解一个具体问题的方法,下列说法中正确的是________.(填序号)①写出的算法,必须能解决一类问题,并且能重复使用;②求解某个问题的算法是唯一的;③算法过程要一步一步执行,每一步执行的操作,必须确切,不能含糊不清,而且经过有限步或无限步后能得出结果;④算法要求按部就班地做,最终可以有不同的结果.解析 算法并不是唯一的,且有限步得出结果,故②③④错.答案 ①5.下列语句表达中是算法的有________个.①从济南去巴黎可以先乘火车到北京,再乘飞机抵达;②利用公式S =12ah 计算底为1,高为2的三角形的面积; ③12x >2x +4; ④求M (1,2)与N (-3,-5)两点连线的方程可先求直线MN 的斜率再利用点斜式方程求得.解析 ③不是,只提出问题,没有给出解决方法.答案 36.下面给出一个问题的算法:S1 输入x ;S2 若x ≥4,执行S3,否则执行S4;S3 输出2x -1;S4 输出x 2-2x +3.(1)这个算法解决的问题是什么?(2)当输入的x 为何值时,输出的数值最小?解 (1)这个算法解决的问题是求分段函数f (x )=⎩⎪⎨⎪⎧2x -1, x ≥4,x 2-2x +3, x <4,的函数值的问题. (2)当x ≥4时,f (x )=2x -1≥7;当x <4时,f (x )=x 2-2x +3=(x -1)2+2≥2,∴当输入x =1时,f (x )min =2.综合提高 (限时30分钟)7.写出求2+4+6+…+200的一个算法.可以运用公式2+4+6+…+2n =n (n +1)直接计算.S1 _____________________________________________________________________; S2 _____________________________________________________________________; S3 输出运算结果.解析 本题考查算法步骤.解此题应首先求出算式中n 的值,然后将n 的值代入公式n (n +1)进行计算,即可得此题的一个算法.答案 取n =100 计算n (n +1)8.已知一个三角形的三边边长分别为2,3,4,将求其面积的一个算法补充完整:1.取a =2,b =3,c =4;2.计算p =________;3.计算S =p (p -a )(p -b )(p -c )4.输出S 的值等于________.解析 由计算三角形的面积的海伦公式,得p =a +b +c 2, S =p (p -a )(p -b )(p -c )=3154. 答案 a +b +c 2 3154 9.家中配电盒至冰箱的电路断了,检测故障的算法中,第一步检测________最快(填写相应的序号).①靠近配电盒的一小段;②电路中点处检测;③靠近冰箱的一小段;④随意挑一段检测.解析利用二分法的思想,应取中点,每次减半,这样从理论上是最快的,故选②.答案②10.有9颗形状大小相同的珠子,其中只有一粒重量比其他的轻,某同学利用天平找出了这颗最轻的珠子,则最少需称量的次数为________.解析先分三组,每组三个,一次可以测出这个珠子在哪一组,同理,第二次可测出是哪一个,故最少需称量2次.答案 211.某城市在法定工作时间内,每小时的工资为8元,加班工资每小时是10元,某人一周内工作60 h,其中加班20 h,税金是10%,写出这个人净得的工资额的算法.解S1计算加班工资a=10×20=200(元);S2计算法定工作时间内的工资b=8×(60-20)=320(元);S3计算这个人一周的工资总额c=a+b=200+320=520(元);S4计算这个人净得的工资额d=c×(1-10%)=520×(1-10%)=468(元);S5输出d.12.三个士兵来到一条有鳄鱼的深河的左岸,只有一条小船可供使用,船上有两个儿童,这条船一次只能承载两个儿童或一个士兵,这三个士兵怎样渡到右岸.请设计过河的算法.解算法步骤如下:第一步两个儿童把船划到右岸;第二步他们之中一个上岸,另一个划回来;第三步儿童上岸,一个士兵把船划过去;第四步士兵上岸,让儿童划回来;第五步如果左岸还有士兵,那么转第一步,否则结束.13.(创新拓展)写出交换两个大小相同的杯子中的液体(A水,B酒)的两个算法.解算法一:S1再找一个大小与A相同的空杯子C;S2将A中的水倒入C中;S3将B中的酒倒入A中;S4将C中的水倒入B中,结束.算法二:S1再找两个空杯子C和D;S2将A中的水倒入C中,将B中的酒倒入D中;S3将C中的水倒入B中,将D中的酒倒入A中,结束.。
高中数学必修三习题:第一章1.3算法案例含答案

第一章算法初步1.3算法事例A 级基础稳固一、选择题1.以下说法中正确的个数为()①展转相除法也叫欧几里得算法;②展转相除法的基本步骤是用较大的数除以较小的数;③求最大条约数的方法除展转相除法以外,没有其余方法;④编写展转相除法的程序时,要用到循环语句.A.1B.2C.3D.4分析:依照展转相除法可知,①②④正确,③错误.答案: C2.用更相减损术求48 和 132 的最大条约数时,需做减法的次数是() A.2B.3C.4D.5分析: 132- 48= 84, 84-48= 36, 48-36= 12, 36- 12= 24, 24- 12= 12.答案: D3.若用秦九韶算法求多项式f (x) = 45-x2+2 当x= 3 时的值,则需要做乘法运算和x加减法运算的次数分别为 ()A.4,2 B . 5,3 C .5,2 D .6, 2分析: f ( x)=4x5- x2+2=((((4x) x) x-1)x) x+2,因此需要做5次乘法运算和 2 次加减运算.答案: C4.已知一个k进制的数123 与十进制的数38 相等,那么k等于 ()A.7或 5B.- 7C. 5D.都不对分析: (123)( k ) =1×k2+2×k+3=k2+2k+3,因此 k2+2k+3=38,即 k2+2k-35=0.解得 k=5或 k=-7(舍去).答案: C5.已知 44= 36,把 67( k)转变为十进制数为 ()( k)A. 8B. 55 C. 56D. 62分析:当题意得,36=4×k1+4×k0,因此k= 8.则 67( k)= 67(8)=6×81+7×80= 55.答案: B二、填空题6.用秦九韶算法求 f ( x)=2x3+ x-3当 x=3时的值 v2=________.分析: f ( x)=((2 x+0) x+1) x-3,v0=2;v1=2×3+0=6;v2=6×3+1=19.答案: 197.已知函数 f ( x)= x3-2x2-5x+6,用秦九韶算法,则 f (10)=________.分析: f ( x)= x3-2x2-5x+6=( x2-2x-5) x+6=[( x-2) x-5] x+6.当 x=10时, f (10)=[(10-2)×10-5]×10+6=(8×10-5)×10+6=75×10+6=756.答案: 7568.已知 1 0 b1(2)=a02(3),则 ( a,b) = ________.分析:由于 1 0 b1(2)=1×23+b×2+ 1= 2b+ 9,2a02(3)=a×3+2=9a+2,因此 2b+ 9= 9a+ 2,即 9a- 2b= 7.由于 a∈{1,2}, b∈{0,1},因此当 a=1时, b=1切合题意,11当 a=2时, b=2不合题意,因此 a=1,b=1.因此( a,b)=(1,1).答案: (1 ,1)三、解答题9.分别用展转相除法和更相减损术求261, 319 的最大条约数.解:展转相除法:319=261×1+ 58,261=58×4+ 29,58=29×2.因此 319 与 261 的最大条约数是29.更相减损术:319- 261=58,261- 58=203,203- 58=145,145- 58=87,87- 58= 29,58- 29= 29,因此 319 与 261 的最大条约数是29.10.已知函数f ( x) =x3- 3x2-4x+ 5,试用秦九韶算法求 f (2)的值.解:依据秦九韶算法,把多项式改写成以下形式:f (x) =x3- 3x2-4 +5=(x2- 3x- 4)x+ 5=x(( x- 3) x-4) x+ 5.把 x=2代入函数式得f (2)=((2-3)×2-4)×2+5=-7.B 级能力提高1.m是一个正整数,关于两个正整数a, b,假如 a- b 是 m的倍数,则称a, b 对模 m 同余,用符号ab(MOD m)表示,则以下各式中不正确的为()A. 127(MOD 5)B. 2110(MOD 3)C. 3420(MOD 2)D. 477(MOD 40)分析:逐个考证,关于A, 12- 7=5 是 5 的倍数;关于B, 21- 10= 11 不是 3 的倍数;关于 C, 34- 20= 14 是 2 的倍数;关于D, 47- 7= 40 是 40 的倍数.答案: B2. 324, 243, 135 三个数的最大条约数是________.分析: 324=243×1+ 81,243=81×3,因此 243 与 324 的最大条约数是81.又 135=81×1+ 54,81=54×1+ 27,54=27×2+ 0,因此 135 与 81 的最大条约数是27.答案: 273.已知三个数12(16),25(7),33(4),将它们按由小到大的次序摆列为________________ .分析:将三个数都化为十进制数.12(16)=1×16+ 2= 18, 25(7)=2×7+ 5= 19,33(4)=3×4+ 3= 15,因此 33(4)< 12(16)<25(7).答案: 33(4)< 12(16)< 25(7)。
高中数学苏教版必修三阶段质量检测(一)算法初步含答案
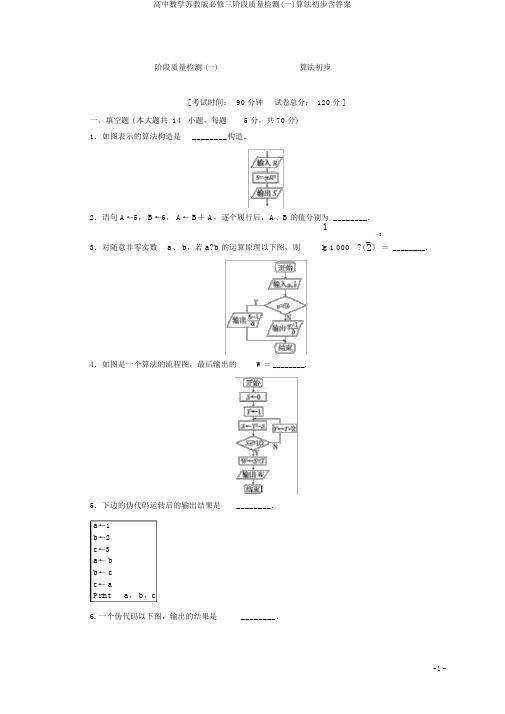
阶段质量检测 (一)算法初步[ 考试时间:90 分钟试卷总分: 120 分 ]一、填空题 ( 本大题共 14小题,每题 5 分,共 70 分)1.如图表示的算法构造是________构造.2.语句A←5,B←6,A←B+A,逐个履行后,A、B 的值分别为________.1-23.对随意非零实数a、 b,若 a?b 的运算原理以下图,则lg 1 000 ?( 2)=________. 4.如图是一个算法的流程图,最后输出的W=________.5.下边的伪代码运转后的输出结果是________.a←1b←2c←3a← bb← cc← aPrint a, b,c6. 一个伪代码以下图,输出的结果是________.S←1For I From 1 to 10S←S+3× IEnd ForPrint S7.下边的伪代码输出的结果是________.i←1s←1While i≤4s←s× ii← i +1End WhilePrint s8.459 与 357 的最大条约数是________.9.以下算法,当输入数值26 时,输出结果是________.Read xIf9<x<100Thena←x\10b←Mod(x, 10)x←10b+aPrint xEnd If10. ( 广东高考 ) 履行以下图的程序框图,若输入n 的值为4,则输出 s 的值为________.(10 题图 )(11 题图 )11.以下图的流程图输出的结果为________.12.履行以下图的程序框图,假如输出s=3,那么判断框内应填入的条件是________.13.以下代运转后出的果________.a←0j←1While j ≤5a←mod a+j ,5j← j +1End WhilePrint a14.行如所示的流程,若出的果是8,判断框内m的取范是________.二、解答 ( 本大共 4 小,共50 分 )15. ( 本小分12 分 ) 写出求最小的奇数I ,使1×3×5×7×⋯× I >2 012的代.16.( 本小分12 分 ) 高中会考等定:成在85~100“ A”,70~84“ B”,60~ 69 “ C”, 60 分以下“ D”.制代算法,入50 名学生的考成( 百分制,且均整数 ) ,出其相的等.17. ( 本小分12 分 ) 下边是算个人所得税的算法程,其算法以下:S1入工x( x≤8 000);S2假如x≤3 500,那么y=0;假如 3 500< x≤5 000 ,那么y=0.03( x-3 500);否 y=45+0.1( x-5 000)S3出税款y,束.写出算法的代及流程.18. ( 本小分14 分 ) 某城市有人口数100 万人,假如年自然增率 1.2%,解答以下:(1)写出城市人口数 y(万人)与年份 x(年)的函数关系式;(2)用代表示算 10 年此后城市人口数的算法;(3) 用流程表示算大多少年此后城市人口将达到120 万人的算法.答案1.分析:由流程知序构.答案:序2.分析:∵A= 5,B= 6,∴A=6+ 5= 11,B= 6.答案: 11、61 -2b-14- 13.分析:令a=lg 1 000=3,b=(2)=4,∴ a<b,故出a=3=1.答案: 14.分析:第一次循后知S=1.第二次循后知T=3, S=9-1=8.第三次循后知T=5,S=25-8=17.因此出 W=17+5=22.答案: 225.分析:第4行开始交,a=2, b=3, c 后的a,∴ c=2.答案: 2,3,26.分析:由代可知S=1+3×1+3×2+⋯+3×10=1+3×(1+2+⋯+10)=166.答案: 1667.分析:由算法句知s=1×1×2×3×4=24.答案: 248.分析: 459=357×1+ 102,357 =102×3+ 51,102 =51×2,因此459 与 357 的最大公数是 51.答案: 519.分析:是一个由条件句主体的一个算法,注意算法言的与理解.此算法的目的是交十位、个位数字获得一个新的二位数.( x\10 是取x除以 10 的商的整数部分) .答案: 6210.分析:本第1次循:s=1+(1-1)=1,i=1+1=2;第2次循:s=1+(2-1)= 2,i= 2+ 1= 3;第 3 次循:s=2+ (3 - 1) = 4,i= 3+ 1=4;第 4 次循:s= 4+ (4 - 1) =7,i=4+ 1= 5. 循止,出s 的7.答案: 711.分析:由意知,出的b24= 16.答案: 1612.分析:依照循构运算并合出果确立条件.k=2, s=1, s=1×log23=log23, k=3,s=log23·log34=log24,k=4, s=log24·log45=log25, k=5, s=log25·log56=log26, k=6, s=log26·lo g67=log 27,k=7, s=log27·log78=log28=3.停止,明判断框内填k≤7或 k<8.答案:k≤7(或 k<8)13.分析:第一步:a=mod(1,5)=1,j=2;第二步:a=mod(1+2,5)=3,j=3;第三步:a=mod(3+3,5)=1, j =4;第四步: a=mod(1+4,5)=0, j =5; a=mod(0+5,5)=0,j =6,此出,∴ a=0.答案: 014.分析:由知,k= 1,S= 0,第一次循,S= 2,k=2;第二次循,S= 2+2×2= 6,k=3;⋯⋯;第六次循, S=30+2×6=42, k=6+1=7;第七次循, S=42+2×7=56,k= 7+ 1= 8,此出k的,进而易知m的取范是 (42,56] .答案: (42,56]15.解:t←1I ←1While t ≤2 012t←t × II←I+2End WhilePrint I -216.解:伪代码如图:I←1While I ≤50Read a I学生成绩If a I< 60ThenPrint“D”Else If a I<70 ThenPrint“C”Else If a I<85 ThenPrint“B”ElsePrint“A”End IfI←I +1End While17.解:伪代码:Read x( x≤8 000)If x≤3 500 Theny←0ElseIf x≤5 000 Theny←0.03( x-3 500)Elsey←45+0.1( x -5 000)End IfEnd IfPrint y流程图18.解: (1) y=100×1.012 x(2)伪代码以下:S←100I←1.012For x From 1 To 10S←S×IEnd ForPrint S(3) 即求知足100×1.012 x≥120 的最小正整数x,其算法流程图如图.。
高中数学苏教版必修三教学案:第1章 1.1 算法的含义含答案

第1章 算 法 初 步1.2013年全运会在沈阳举行,运动员A 报名参赛100米短跑并通过预赛、半决赛、决赛最后获得了银牌.问题1:请简要写出该运动员参赛并获银牌的过程. 提示:报名参赛→预赛→半决赛→决赛. 问题2:上述参赛过程有何特征? 提示:参赛过程是明确的.问题3:假若你家住南京,想去沈阳观看A 的决赛,你如何设计你的旅程?提示:首先预约定票,然后选择合适的交通工具到沈阳,按时到场,检票入场,进入比赛场地,观看比赛.2.给出方程组⎩⎪⎨⎪⎧x +y =2, ①x -y =1, ②问题1:利用代入法求解此方程组. 提示:由①得y =2-x ,③把③代入②得x -(2-x )=1, 即x =32.④把④代入③得y =12.得到方程组的解⎩⎪⎨⎪⎧x =32,y =12.问题2:利用消元法求解此方程组. 提示:①+②得x =32.③将③代入①得y =12,得方程组的解⎩⎪⎨⎪⎧x =32,y =12.问题3:从问题1、2可以看出,解决一类问题的方法唯一吗? 提示:不唯一.1.算法的概念对一类问题的机械的、统一的求解方法称为算法. 2.算法的特征(1)算法是指用一系列运算规则能在有限步骤内求解某类问题,其中的每条规则必须是明确定义的、可行的.(2)算法从初始步骤开始,每一个步骤只能有一个确定的后继步骤,从而组成一个步骤序列,序列的终止表示问题得到解答或指出问题没有解答.1.算法的基本思想就是探求解决问题的一般性方法,并将解决问题的步骤用具体化、程序化的语言加以表述.2.算法是机械的,有时要进行大量重复计算,只要按部就班地去做,总能算出结果,通常把算法过程称为“数学机械化”,其最大优点是可以让计算机来完成.3.求解某一个问题的算法不一定只有唯一的一个,可能有不同的算法.[例1] 下列关于算法的说法: ①求解某一类问题的算法是唯一的 ②算法必须在有限步操作后停止③算法的每一步操作必须是明确的,不能存在歧义 ④算法执行后一定能产生确定的结果 其中,不正确的有________.[思路点拨] 利用算法特征对各个表述逐一判断,然后解答.[精解详析] 由算法的不唯一性,知①不正确; 由算法的有穷性,知②正确; 由算法的确定性,知③和④正确. [答案] ① [一点通]1.针对这个类型的问题,正确理解算法的概念及其特点是解决此类问题的关键. 2.注意算法的特征:有限性、确定性、可行性.1.下列语句表达中是算法的有________.①从济南到巴黎可以先乘火车到北京,再坐飞机抵达 ②利用公式S =12ah 计算底为1,高为2的三角形的面积③12x >2x +4 ④求M (1,2)与N (-3,-5)两点连线的方程,可先求MN 的斜率,再利用点斜式方程求得 解析:算法是解决问题的步骤与过程,这个问题并不仅仅限于数学问题.①②④都表达了一种算法.答案:①②④2.计算下列各式中的S 值,能设计算法求解的是________. ①S =1+2+3+…+100 ②S =1+2+3+…+100+… ③S =1+2+3+…+n (n ≥1且n ∈N)解析:算法的设计要求步骤是可行的,并且在有限步之内能完成任务.故①、③可设计算法求解.答案:①③[例2] 已知直线l 1:3x -y +12=0和l 2:3x +2y -6=0,求l 1,l 2,y 轴围成的三角形的面积.写出解决本题的一个算法.[思路点拨] 先求出l 1,l 2的交点坐标,再求l 1,l 2与y 轴的交点的纵坐标,即得到三角形的底;最后求三角形的高,根据面积公式求面积.[精解详析] 第一步 解方程组⎩⎪⎨⎪⎧3x -y +12=0,3x +2y -6=0得l 1,l 2的交点P (-2,6);第二步 在方程3x -y +12=0中令x =0得y =12,从而得到A (0,12);第三步 在方程3x +2y -6=0中令x =0得y =3,得到B (0,3); 第四步 求出△ABP 底边AB 的长|AB |=12-3=9; 第五步 求出△ABP 的底边AB 上的高h =2; 第六步 代入三角形的面积公式计算S =12|AB |·h ;第七步 输出结果. [一点通]设计一个具体问题的算法,通常按以下步骤: (1)认真分析问题,找出解决此题的一般数学方法; (2)借助有关变量或参数对算法加以表述; (3)将解决问题的过程划分为若干步骤; (4)用简练的语言将这个步骤表示出来.3.写出求两底半径分别为1和4,高也为4的圆台的侧面积、表面积及体积的算法.解:算法步骤如下:第一步 取r 1=1,r 2=4,h =4; 第二步 计算l =r 2-r 12+h 2;第三步 计算S 1=πr 21,S 2=πr 22;S 侧=π(r 1+r 2)l ; 第四步 计算S 表=S 1+S 2+S 侧; 第五步 计算V =13(S 1+S 1S 2+S 2)h .4.已知球的表面积为16π,求球的体积.写出解决该问题的两个算法. 解:算法1: 第一步 S =16π; 第二步 计算R =S4π(由于S =4πR 2);第三步 计算V =43πR 3;第四步 输出运算结果V . 算法2:第一步 S =16π; 第二步 计算V =43π(S4π)3;第三步 输出运算结果V .[例3] (12分)某居民区的物业部门每月向居民收取卫生费,计算方法是:3人或3人以下的住房,每月收取5元;超过3人的住户,每超出1人加收1.2元.设计一个算法,根据输入的人数,计算应收取的卫生费.[精解详析] 设某户有x 人,根据题意,应收取的卫生费y 是x 的分段函数,即y =⎩⎪⎨⎪⎧5, x ≤3,1.2x +1.4,x >3.(4分)算法如下:第一步 输入人数x ;(6分)第二步 如果x ≤3,则y =5, 如果x >3,则y =1.2x +1.4; (10分)第三步 输出应收卫生费y .(12分)[一点通]对于此类算法设计应用问题,应当首先建立过程模型,根据模型,完成算法.注意每步设计时要用简炼的语言表述.5.如下算法: 第一步 输入x 的值;第二步 若x ≥0成立,则y =2x,否则执行第三步; 第三步 y =log 2(-x ); 第四步 输出y 的值.若输出结果y 的值为4,则输入的x 的值为________. 解析:算法执行的功能是给定x ,求分段函数y =⎩⎪⎨⎪⎧2x,x ≥0,log 2-x ,x <0对应的函数值.由y =4知2x=4或log 2(-x )=4. ∴x =2或-16. 答案:2或-166.已知直角三角形的两条直角边分别为a ,b ,设计一个求该三角形周长的算法. 解:算法如下:第一步 计算斜边c =a 2+b 2; 第二步 计算周长l =a +b +c ;第三步 输出l .1.算法的特点:有限性、确定性、逻辑性、不唯一性、普遍性. 2.在具体设计算法时,要明确以下要求:(1)算法设计是一类问题的一般解法的抽象与概括,它要借助一般问题的解决方法,又要包含这类问题的所有可能情形.设计算法时往往要把问题的解法划分为若干个可执行的步骤,有些步骤是重复执行的,但最终却必须在有限个步骤之内完成.(2)借助有关的变量或参数对算法加以表述. (3)要使算法尽量简单,步骤尽量少.课下能力提升(一)一、填空题1.写出解方程2x +3=0的一个算法过程.第一步__________________________________________________________________; 第二步__________________________________________________________________. 答案:第一步 将常数项3移到方程右边得2x =-3; 第二步 在方程两边同时除以2,得x =-32.2.已知一个学生的语文成绩为89,数学成绩为96,外语成绩为99.求他的总分和平均分的一个算法为:第一步 令A =89,B =96,C =99; 第二步 计算总分S =________; 第三步 计算平均分M =________; 第四步 输出S 和M .解析:总分S 为三个成绩数之和, 平均数M =A +B +C 3=S3. 答案:A +B +C S33.给出下列算法:第一步 输入x 的值;第二步 当x >4时,计算y =x +2;否则执行下一步; 第三步 计算y =4-x ; 第四步 输出y .当输入x =0时,输出y =__________. 解析:由于x =0>4不成立,故y =4-x =2. 答案:24.已知点P 0(x 0,y 0)和直线l :Ax +By +C =0,求点到直线距离的一个算法有如下几步: ①输入点的坐标x 0,y 0; ②计算z 1=Ax 0+By 0+C ; ③计算z 2=A 2+B 2;④输入直线方程的系数A ,B 和常数C ; ⑤计算d =|z 1|z 2;⑥输出d 的值.其正确的顺序为________. 解析:利用点到直线的距离公式:d =|Ax 0+By 0+C |A 2+B2. 答案:①④②③⑤⑥5.已知数字序列:2,5,7,8,15,32,18,12,52,8.写出从该序列搜索18的一个算法. 第一步 输入实数a .第二步 __________________________________________________________________. 第三步 输出a =18.解析:从序列数字中搜索18,必须依次输入各数字才可以找到. 答案:若a =18,则执行第三步,否则返回第一步 二、解答题6.写出求a ,b ,c 中最小值的算法. 解:算法如下:第一步 比较a ,b 的大小,当a >b 时,令“最小值”为b ;否则,令“最小值”为a ; 第二步 比较第一步中的“最小值”与c 的大小,当“最小值”大于c 时,令“最小值”为c ;否则,“最小值”不变;第三步 “最小值”就是a ,b ,c 中的最小值,输出“最小值”. 7.某铁路部门规定甲、乙两地之间旅客托运行李的费用为c =⎩⎪⎨⎪⎧0.53ω, ω≤50,50×0.53+ω-50×0.85, ω>50.其中ω(单位:kg)为行李的重量,如何设计计算费用c (单位:元)的算法. 解:算法步骤如下:第一步 输入行李的重量ω;第二步 如果ω≤50,那么c =0.53ω;如果ω>50,那么c =50×0.53+(ω-50)×0.85; 第三步 输出运费c .8.下面给出一个问题的算法: 第一步 输入a ;第二步 若a ≥4,则执行第三步,否则执行第四步; 第三步 输出2a -1; 第四步 输出a 2-2a +3.问题:(1)这个算法解决的是什么问题? (2)当输入a 等于多少时,输出的值最小? 解:(1)这个算法解决的问题是求分段函数f (x )=⎩⎪⎨⎪⎧2x -1,x ≥4,x 2-2x +3,x <4的函数值问题.(2)当x ≥4时,f (x )=2x -1≥7,当x <4时,f (x )=x 2-2x +3=(x -1)2+2≥2. ∴当x =1时,f (x )min =2.即当输入a 的值为1时,输出的值最小.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.2.3 循环结构
双基达标 (限时15分钟)
1.已知下列说法
①选择结构中,根据条件是否成立有不同的流向; ②循环结构中循环体根据条件是否成立会被反复执行; ③循环结构的形式只有一种. 其中正确的是________.
解析 循环结构有“当型”和“直到型”两种,∴③不正确,由选择结构和循环结构的条件知①②正确.
答案 ①②
2.如图给出的是计算12+14+16+…+1
100值的一个程序框图,其中判断框中应该填的条
件是________.
解析 本题是当型循环,条件成立则继续相加,最后一次I =98,经过I ←I +2后I 为100,注意也可以是I ≤98,I <99,但不能是I ≤100.
答案 I <100 3.
如图,表示的是输出所有立方小于1 000的正整数的程序框图,那么判断框中应补充的条件为________.
解析根据条件,n3应满足n3<1 000,则输出n.
答案n3<1 000
4.若按如图所示的流程图运算,输出k=2,则输入x的取值范围是________.
解析由题意,循环体执行两次,从而2x+1≤115得x≤57,第2次运行后2(2x+1)+1>115,得x>28,∴28<x≤57.
答案28<x≤57
5.下列程序框图的运算结果为________.
解析由流程图知S=5×4=20,结束时a=3.
答案20
6.某位同学为了求1×2×3×4×…×30的值,画出了一个流程图,如图所示.请你指出其中的错误,并画出正确的流程图.
解第一处错误是第二个处理框中应是“P←1”,而不是“P←0”;第二处错误是判断框中应是“i>29”,而不是“i>30”,正确的流程图如图所示.
综合提高(限时30分钟)
7.如图所示程序为求:S=1+2+4+7+11+…的前20项和的流程图,①处应填________.
解析由程序运行的过程可知P←P+i.
答案P←P+i
8.(2011·新课标全国卷)执行上面的程序框图(即算法流程图),如果输入的N是6,那么输出的p是________.
解析由框图可知,最终输出的p=1×2×3×4×5×6=720.
答案720
9.(2011·江西高考)下图是某算法的程序框图(算法流程图),则程序运行后输出的结果是________.
解析第一次循环:S=(0+1)×1=1,n=2;第二次循环:S=(1+2)×2=6,n=3;第三次循环:S=(6+3)×3=27,n=4,符合要求,循环终止,此时输出最新S的值为27.
答案27
10.给出30个数:1,2,4,7,…,其规律是:第1个数是1,第2个数比第1个数大1,第3个数比第2个数大2,第4个数比第3个数大3,…,依此类推.要计算这30个数的和,现已给出了该问题算法的流程图,则在图中判断框①处和处理框②处的语句分别为________和________.
解析根据题意,i是计数变量,用于确定30个数,p是相应的数,由给定条件知第i +1个数比第i个数大i,从而p←p+i.
答案i≤30p←p+i
11.如图是两个流程图中的一部分,其余部分完全相同,试问它们表示的算法相同吗?
解 题图①中,当x =1时,输出x ,然后用x +1=2代替x ,此时输出x =2,...,当输出x =9时,x +1变为10,但不满足大于10的条件,从而再输出x 时,x 的值是10,从而输出值依次为x =1,2,3, (10)
题图②中,当x =1时,输出值x =1,然后用x +1=2代替x ,输出x =2,…,当x 的输出值是10时,x +1变为11,此时不再满足x ≤10,因而结束循环,故x 的输出值依次是x =1,2,3,…,10.所以两个流程图表示的算法相同.
12.根据下面的算法画出相应的流程图. 算法: S1 T ←0; S2 I ←2; S3 T ←T +I ; S4 I ←I +2;
S5 如果I 不大于200,转S3; S6 输出T ,结束.
解 这是计算2+4+6+…+200的一个算法. 流程图如下:
13.(创新拓展)设计算法求满足1+14+17+110+…+1
n >2的最大正整数n ,用流程图表
示出来.
解 流程图如图所示.
法一 法二。
