苏教版高中数学必修五模块综合检测卷
苏教版高中数学必修5试卷必修5综合检测
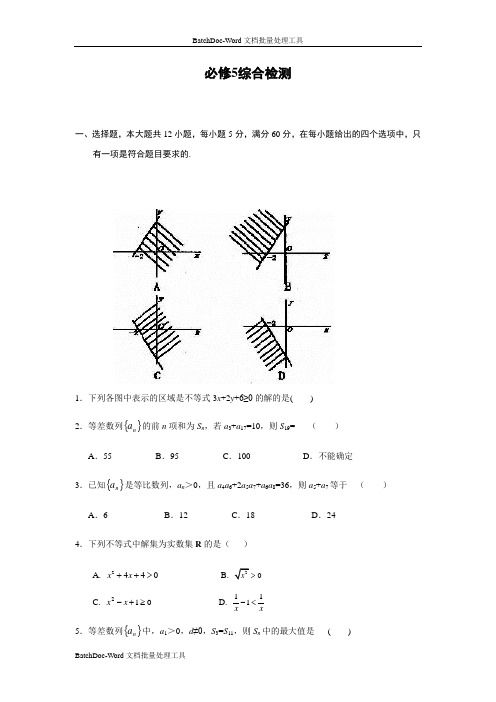
必修5综合检测一、选择题,本大题共12小题,每小题5分,满分60分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.下列各图中表示的区域是不等式3x +2y +6≥0的解的是( )2.等差数列{}n a 的前n 项和为S n ,若a 3+a 17=10,则S 19= ( )A .55B .95C .100D .不能确定3.已知{}n a 是等比数列,a n >0,且a 4a 6+2a 5a 7+a 6a 8=36,则a 5+a 7等于() A .6 B .12 C .18 D .244.下列不等式中解集为实数集R 的是( )A. 2440x x ++>B. 0C. 012≥+-x xD. x x 111<-5.等差数列{}n a 中,a 1>0,d ≠0,S 3=S 11,则S n 中的最大值是 ( )A .S 7B .S 7或S 8C .S 14D .S 86. 不等式0)1)(1(>-+x x 的解集是( )A .{}10<≤x x B. {}1,0-≠<x x x C. {}11<<-x x D. {}1,1-≠<x x x7. 已知12=+y x ,则y x 42+的最小值为( )A .8B .6C .22D .238.设{}n a 是正数等差数列,{}n b 是正数等比数列,且a 1=b 1,a 2n +1=b 2n +1,则 ( )A .a n +1=b n +1B .a n +1>b n +1C .a n +1<b n +1D .a n +1≥b n +19. 不等式2(2)2(2)40a x a x -+--<对一切x ∈R 恒成立,则实数a 的取值范围是A. )2,(-∞B. []2,2-C. ]2,2(-D.)2,(--∞10.已知A 、B 、C 是△ABC 的三个内角,且sin 2cos sin A B C =,则------------------( )(A) B =C (B) B >C (C) B <C (D) B ,C 的大小与A 的值有关11.在△ABC 中,如果sin :sin :sin 2:3:4A B C =,那么cos C 等于 ( )2A.3 2B.-3 1C .-3 1D.-412.给出下列三个命题(1)若tan A tan B >1,则△ABC 一定是钝角三角形;(2)若sin 2A +sin 2B =sin 2C ,则△ABC 一定是直角三角形;(3)若cos(A -B )cos(B -C )cos(C -A )=1,则△ABC 一定是等边三角形以上正确命题的个数有 ( )A .0个B .1个C .2个D .3个二、填空题,本大题共6小题,每小题4分,满分24分,把正确的答案写在题中横线上.13.在等差数列{a n }中,已知公差d =21,且a 1+a 3+a 5+…+a 99=60,则a 1+a 2+a 3+…+a 99+a 100=______________14.已知平面平域D 由下列约束条件确定:2x -3y +5≥0,x +2y -8≤0,x -5y +6≥0,当点(x ,y )在D 上时,(1) 若y =3x -4y,则y 的最大值是______________,最小值是_______________(2) 当y =x 2+y 2时,则y 的最大值是_____________,最小值是_________________ 15.设等比数列{a n }共有3n 项,它的前2n 项的和为100,后2n 项之和为200,则该等比数列中间n 项的和等于___________________16. 设1≥x ,则函数1)3)(2(+++=x x x y 的最小值是 .17.在△ABC 2sin b A =,则B 等于_____________18.等差数列{a n }中,S n 是它的前n 项之和,且S 6<S 7,S 7>S 8,则①比数列的公差d <0 ②S 9一定小于S 6③a 7是各项中最大的一项 ④S 7一定是S n 中的最大值其中正确的是_______________________(填入你认为正确的所有序号)三、解答题, 本大题共5小题,共66分,解答应写出必要的文字说明、证明过程和演算步骤.19.(本题满分12分)若不等式0252>-+x ax 的解集是⎭⎬⎫⎩⎨⎧<<221x x ,求不等式01522>-+-a x ax 的解集.已知f (x +1)=x 2-4,等差数列{a n }中,a 1=f (x -1),a 2=-23,a 3=f (x ) (1)求x 的值;(2)求通项a n ;(3)求a 2+a 5+a 8+…+a 26的值.△ABC 的三个内角A 、B 、C 对边分别是a , b , c ,且t a n t a n 3t a n t a n A B A B +=-72c =,又△ABC 的面积为ABC S ∆=. 求(1)角C ;(2)a +b 的值.某工厂要制造A种电子装置45台,B种电子装置55台,需用薄钢板给每台装置配一个外壳,已知薄钢板的面积有两种规格:甲种薄钢板每张面积2㎡,可做A、B的外壳分别为3个和5个,乙种薄钢板每张面积3㎡,可做A、B的外壳分别为5个和6个,求两种薄钢板各用多少张,才能使总的用料面积最小?试判断,能否构造一个等比数列{a n},使其满足下列三个条件:①a1+a6=11 ②a3a4=329③至少存在一个自然数m,使23a m-1、a m2、a m+1+49依次组成等差数列,若能,写出这个数列的通项公式;若不能,请说明理由.。
苏教版高中数学必修五模块考试.docx

高中2005~2006级模块考试(必修5)一、选择题:(每小题5分,共60分)1、ΔABC 中,a =1,b =3, A =30°,则B 等于 A .60° B .60°或120° C .30°或150° D .120°2、两灯塔A,B 与海洋观察站C 的距离都等于a (km), 灯塔A 在C 北偏东30°,B 在C 南偏东60°,则A,B 之间相距A .a (km)B .3a (km)C .2a (km)D .2a (km)3、等差数列{a n }中,已知a 1=13,a 2+a 5=4,a n =33,则n 为A .50B .49C .48D .474、已知等比数列{a n }的公比为2, 前4项的和是1, 则前8项的和为 A .15. B .17. C .19. D .215、等差数列{a n }中,a 1+a 2+…+a 50=200,a 51+a 52+…+a 100=2700,则a 1等于 A .-1221 B .-21.5 C .-20.5 D .-206、设集合y x y x y x A --=1,,|),{(是三角形的三边长},则A 所表示的平面区域(不含边界的阴影部分)是Aoy x0.50.5oy x0.50.5oyx0.50.5oyx0.50.5. A B . C . D .7、已知-9,a 1,a 2,-1四个实数成等差数列,-9,b 1,b 2,b 3,-1五个实数成等比数列,则b 2(a 2-a 1)= ()A.8B.-8C.±8D.8、目标函数y x z +=2,变量y x ,满足43035251x y x y x -+<⎧⎪+≤⎨⎪≥⎩,则有A .3,12min max ==z zB .,12max =z z 无最小值C .z z ,3min =无最大值D .z 既无最大值,也无最小值9、在三角形ABC 中,如果()()3a b c b c a bc +++-=,那么A 等于A .030B .060C .0120D .0150 10、已知数列{}n a 的前n 项和()21n S n n =+则5a 的值为A .80B .40C .20D .1011、f x ax ax ()=+-21在R 上满足f x ()<0,则a 的取值范围是 A .a ≤0 B .a <-4 C .-<<40a D .-<≤40a 12.若实数a 、b 满足a +b =2,则3a +3b 的最小值是A .18B .6C .23D .243 二、填空题:(每小题4分,共16分,答案写在第二卷上) 13、在△ABC 中,sin A =2cos B sin C ,则三角形为 三角形14、不等式21131x x ->+的解集是 .15、已知数列{ a n }满足条件a 1 = –2 , a n + 1 =2 +nna 1a 2-, 则a 5 = . 16、若关于x 的不等式m x x ≥-42对任意]1,0[∈x 恒成立,则实数m 的取值范围是 .日照实验高中2004级模块考试(必修5)一、填空题答案:1 3、 14、15、 16、 三、解答题: 17、(12分)三个数成等比数列,其积为512,如果第一个数与第三个数各减2,则89成等差数列,求这三个数.18、(12分)解关于x 的不等式ax 2-(a +1)x +1<0.19、(12分)如图,在四边形ABCD 中,已知AD ⊥CD, AD=10, AB=14, ∠BDA=60︒,∠BCD=135︒ 求BC 的长.20、(12分)在某海滨城市附近海面有一台风,据测,当前台风中心位于城市O (如图)的东偏南)102(cos =θθ方向300km 的O θ东北东海面P处,并以20km/h的速度向西偏北45°方向移动,台风侵袭的范围为圆形区域,当前半径为60km,并以10km/h的速度不断增大,问几小时后该城市开始受到台风的侵袭?受到台风的侵袭的时间有多少小时?21、(12分)某工厂用两种原料A、B配成甲、乙两种药品,每生产一箱甲药品使用4kg的A原料,耗时1小时,每生产一箱乙药品使用4kg的B原料,耗时2小时,该厂每天最多可从原料厂获取16kg的A原料和12kg的B原料,每天只能有8小时的合成生产时间,该厂生产一箱甲药品获得3万元,生产一箱乙药品获得1万元,怎样安排生产才能获利最大?最大利润是多少?22、(14分)设,4,221==a a 数列}{n b 满足:,1n n n a a b -=+ 122n n b b +=+,(1)求证:数列}2{+n b 是等比数列(要指出首项与公比), (2)求数列}{n a 的通项公式.参考答案:一、选择题1-5BCABC 6-10ABDBC 11-12DB 二、填空题13、等腰14、 1|23x x ⎧⎫-<<-⎨⎬⎩⎭ 15、107 16、(,3]-∞-三、解答题17、解:设三数为.,,aq a q a ⎪⎩⎪⎨⎧⎩⎨⎧==⇒=-+⎪⎪⎭⎫ ⎝⎛-=∴282)2(25123q a a aq q a a 或⎪⎩⎪⎨⎧==.218q a 则三数为,4,816或,168,.418、解: 16.解:当a =0时,不等式的解为x >1;当a ≠0时,分解因式a (x-a1)(x -1)<0当a <0时,原不等式等价于(x -a1)(x -1)>0,不等式的解为x >1或x <a1;当0<a <1时,1<a1,不等式的解为1<x <a1;当a >1时,a1<1,不等式的解为a1<x <1;当a =1时,不等式的解为 。
数学·必修5(苏教版)练习模块综合检测卷(二) Word版含解析

模块综合检测卷(二)(测试时间:分钟评价分值:分)一、选择题(每小题共个小题,每小题共分,共分,在每小题给出的四个选项中,只有一项符合题目要求).对于任意实数,,,命题:①若>,≠,则>;②若<,则>;③若>,则>.其中真命题的个数是( )....解析:当<时,①不正确;当=时,②不正确;只有③正确.答案:.历届现代奥运会召开时间表如下:)....解析:由题意得,历届现代奥运会召开时间构成以为首项,为公差的等差数列,所以=+(-)·,解得=.答案:.若点(,)位于曲线=与=所围成的封闭区域,则-的最小值为( ).-.-..解析:=与=的图象围成一个三角形区域,如图所示,个顶点的坐标分别是(,),(-,),(,).在封闭区域内平移直线=,在点(-,)时,-=-取最小值.答案:.如图所示,设,两点在河的两岸,一测量者在所在的同侧河岸边选定一点,测出的长为,∠=°,∠=°后,就可以计算出,两点的距离为( )...解析:由正弦定理得∠)=∠),又因为∠=°-°-°=°,所以=∠∠)==().答案:.等比数列{}前项的积为,若是一个确定的常数,那么数列,,,中也是常数的项是( )....解析:因为··=···=是一个确定常数,所以为确定的常数.=··…·=(),所以选.答案:.以原点为圆心的圆全部都在平面区域内,则圆面积的最大值为( ).π.π解析:作出不等式组表示的平面区域如图所示,。
2022-2021学年高二数学苏教版必修5 综合检测卷

综合检测卷(时间:120分钟 满分:160分)一、填空题(本大题共14小题,每小题5分,共70分)1.已知集合A ={x |x 2-16<0},B ={x |x 2-4x +3>0},则A ∪B =________. 答案 R解析 A ={x |-4<x <4},B ={x |x <1,或x >3},所以A ∪B =R .2.△ABC 的内角A 、B 、C 的对边分别为a 、b 、c .若a 、b 、c 成等比数列,且c =2a ,则cos B =________.答案 34解析 由题意,得b 2=ac , 又c =2a ,由余弦定理,得cos B =a 2+c 2-b 22ac =a 2+4a 2-a ×2a 2a ×2a=34.3.若S n 是等差数列{a n }的前n 项和,a 2+a 10=4,则S 11的值为________. 答案 22解析 S 11=(a 1+a 11)×112=11×(a 2+a 10)2=22.4.当x >1时,不等式x +1x -1≥a 恒成立,则实数a 的取值范围是________.答案 (-∞,3]解析 ∵x >1,∴x +1x -1=(x -1)+1x -1+1≥2(x -1)·1x -1+1=3.∴a ≤3.5.等差数列{a n }满足a 24+a 27+2a 4a 7=9,则其前10项之和为________.答案 ±15解析 a 24+a 27+2a 4a 7=(a 4+a 7)2=9,∴a 4+a 7=±3,∴a 1+a 10=±3, ∴S 10=10(a 1+a 10)2=±15.6.在△ABC 中,BC =2,B =π3,当△ABC 的面积等于32时,sin C =________.答案 12解析 由三角形的面积公式,得S =12AB ·BC sin π3=32,易求得AB =1,由余弦定理,得AC 2=AB 2+BC 2-2AB ·BC ·cos π3,得AC =3,再由三角形的面积公式,得S =12AC ·BC sin C =32,即可得出sin C =12.7.函数y = x 2+mx +m2对一切x ∈R 恒成立,则实数m 的取值范围是________.答案 0≤m ≤2解析 Δ=m 2-4×m2=m 2-2m ≤0,∴0≤m ≤2.8.已知数列{a n }的通项公式为a n =2×3n -1,则由此数列的偶数项所组成的新数列的前n 项的和为________.答案 34(9n -1)解析 新数列是首项为a 2=6,公比为q =9的等比数列,所以S n =6(9n -1)9-1=34(9n -1).9.若变量x ,y 满足⎩⎪⎨⎪⎧2x +y ≤40,x +2y ≤50,x ≥0,y ≥0.则z =3x +2y 的最大值是________.答案 70解析 作出可行域如图所示.由于2x +y =40、x +2y =50的斜率分别为-2、-12,而3x +2y =0的斜率为-32,故线性目标函数的倾斜角大于2x +y =40的倾斜角而小于x +2y =50的倾斜角,由图知,3x +2y =z 经过点A (10,20)时,z 有最大值,z 的最大值为70.10.国家为了加强对烟酒生产的宏观管理,实行征收附加税政策.现知某种酒每瓶70元,不加附加税时,每年大约产销100万瓶,若政府征收附加税,每销售100元要征税k 元(叫做税率k %),则每年的产销量将削减10k 万瓶.要使每年在此项经营中所收取附加税金不少于112万元,则k 的取值范围为________.答案 [2,8]解析 设产销量为每年x 万瓶,则销售收入每年70x 万元,从中征收的税金为70x ·k %万元,其中x =100-10k .由题意,得70(100-10k )k %≥112,整理得k 2-10k +16≤0,解得2≤k ≤8.因此,当2≤k ≤8(单位:元)时,每年在此项经营中所收附加税金不少于112万元. 11.设正实数x ,y ,z 满足x 2-3xy +4y 2-z =0.则当zxy 取得最小值时,x +2y -z 的最大值为________.答案 2解析 由题意知:z =x 2-3xy +4y 2,则z xy =x 2-3xy +4y 2xy =x y +4y x-3≥1,当且仅当x =2y 时取等号,此时z =xy =2y 2. 所以x +2y -z =2y +2y -2y 2=-2y 2+4y =-2(y -1)2+2≤2. 12.观看下列等式 12=1 12-22=-312-22+32=6 12-22+32-42=-10 ……照此规律,第n 个等式可为12-22+32-…+(-1)n +1n 2=________.答案 (-1)n +1·n (n +1)2解析 观看等式左边的式子,每次增加一项,故第n 个等式左边有n 项,指数都是2,且正、负相间,所以等式左边的通项为(-1)n +1n 2.等式右边的值的符号也是正、负相间,其确定值分别为1,3,6,10,15,21,….设此数列为{a n },则a 2-a 1=2,a 3-a 2=3,a 4-a 3=4,a 5-a 4=5,…,a n -a n -1=n ,各式相加得a n -a 1=2+3+4+…+n ,即a n =1+2+3+…+n =n (n +1)2.所以第n 个等式为12-22+32-42+…+(-1)n +1n 2=(-1)n +1n (n +1)2. 13.如图,在坡度为15°的观礼台上,某一列座位所在直线AB 与旗杆所在直线MN 共面,在该列的第一个座位A 和最终一个座位B 测得旗杆顶端N 的仰角分别为60°和30°,且座位A 、B 的距离为106米,则旗杆的高度为____米.答案 30解析 由题意,可知∠BAN =105°,∠BNA =30°, 由正弦定理,得AN sin 45°=106sin 30°,解得AN =203米,在Rt △AMN 中,MN =203sin 60°=30米. 故旗杆的高度为30米.14.设z =kx +y ,其中实数x ,y 满足⎩⎪⎨⎪⎧x +y -2≥0,x -2y +4≥0,2x -y -4≤0.若z 的最大值为12,则实数k =________.答案 2解析 作出可行域如图阴影部分所示:由图可知当0≤-k <12时,直线y =-kx +z 经过点A (4,4)时z 最大,所以4k +4=12,解得k =2(舍去);当-k ≥12时,直线y =-kx +z 经过点B (0,2)时z 最大,此时z 的最大值为2,不合题意;当-k <0时,直线y =-kx +z 经过点A (4,4)时z 最大,所以4k +4=12,解得k =2,符合题意. 综上可知,k =2.二、解答题(本大题共6小题,共90分)15.(14分)设S n 是等差数列{a n }的前n 项和,已知13S 3,14S 4的等比中项为15S 5;13S 3,14S 4的等差中项为1,求数列{a n }的通项公式.解 设等差数列{a n }的首项a 1=a ,公差为d ,则S n =na +n (n -1)2d ,依题意,有⎩⎨⎧13⎝⎛⎭⎫3a +3×22d ×14⎝⎛⎭⎫4a +4×32d =125⎝⎛⎭⎫5a +5×42d 2,13⎝⎛⎭⎫3a +3×22d +14⎝⎛⎭⎫4a +4×32d =1×2.整理得⎩⎪⎨⎪⎧3ad +5d 2=0,2a +52d =2.∴a =1,d =0或a =4,d =-125.∴a n =1或a n =325-125n ,经检验,a n =1和a n =325-125n 均合题意.∴所求等差数列的通项公式为a n =1或a n =325-125n .16.(14分)已知a ,b ,c 分别为△ABC 三个内角A ,B ,C 的对边,a cos C +3a sin C -b -c =0. (1)求A ;(2)若a =2,△ABC 的面积为3,求b ,c .解 (1)由a cos C +3a sin C -b -c =0及正弦定理得sin A cos C +3sin A sin C -sin B -sin C =0. 由于B =π-A -C ,所以3sin A sin C -cos A sin C -sin C =0.由于sin C ≠0,所以sin ⎝⎛⎭⎫A -π6=12. 又0<A <π,故A =π3.(2)△ABC 的面积S =12bc sin A =3,故bc =4.而a 2=b 2+c 2-2bc cos A ,故b 2+c 2=8. 解得b =c =2.17.(14分)某渔业公司今年年初用98万元购进一艘渔船用于捕捞,第一年需要各种费用12万元.从其次年起包括修理费在内每年所需费用比上一年增加4万元.该船每年捕捞总收入50万元. (1)问捕捞几年后总盈利最大,最大是多少? (2)问捕捞几年后的平均利润最大,最大是多少? 解 (1)设该船捕捞n 年后的总盈利y 万元.则 y =50n -98-[12×n +n (n -1)2×4]=-2n 2+40n -98 =-2(n -10)2+102∴当捕捞10年后总盈利最大,最大是102万元.(2)年平均利润为y n =-2(n +49n -20)≤-2(2 n ·49n -20)=12,当且仅当n =49n ,即n =7时上式取等号.所以,当捕捞7年后年平均利润最大,最大是12万元. 18.(16分)已知函数f (x )=x 2-2x -8,g (x )=2x 2-4x -16,(1)求不等式g (x )<0的解集;(2)若对一切x >2,均有f (x )≥(m +2)x -m -15成立,求实数m 的取值范围. 解 (1)g (x )=2x 2-4x -16<0, ∴(2x +4)(x -4)<0,∴-2<x <4, ∴不等式g (x )<0的解集为{x |-2<x <4}. (2)∵f (x )=x 2-2x -8.当x >2时,f (x )≥(m +2)x -m -15恒成立, ∴x 2-2x -8≥(m +2)x -m -15, 即x 2-4x +7≥m (x -1). ∴对一切x >2,均有不等式x 2-4x +7x -1≥m 成立.而x 2-4x +7x -1=(x -1)+4x -1-2≥2(x -1)×4x -1-2=2(当x =3时等号成立).∴实数m 的取值范围是(-∞,2].19.(16分)如图,某校有一块形如直角三角形ABC 的空地,其中∠B 为直角,AB 长为40米,BC 长为50米,现欲在此空地上建筑一间健身房,其占地外形为矩形,且B 为矩形的一个顶点,求该健身房的最大占地面积.解 如图,设矩形为EBFP ,FP 长为x 米,其中0<x <40,健身房占地面积为y 平方米. 由于△CFP ∽△CBA ,所以FP BA =CF CB ,x 40=50-BF 50,求得BF =50-54x ,从而y =BF ·FP =(50-54x )x =-54x 2+50x=-54(x -20)2+500≤500,当且仅当x =20时,等号成立.答 该健身房的最大占地面积为500平方米.20.(16分)已知数列{a n }的前n 项和为S n ,a 1=1,a n +1=2S n +1(n ∈N *),等差数列{b n }中,b n >0(n ∈N *),且b 1+b 2+b 3=15,又a 1+b 1、a 2+b 2、a 3+b 3成等比数列. (1)求数列{a n }、{b n }的通项公式; (2)求数列{a n ·b n }的前n 项和T n , 解 (1)∵a 1=1,a n +1=2S n +1(n ∈N *), ∴a n =2S n -1+1(n ∈N *,n >1), ∴a n +1-a n =2(S n -S n -1),即a n +1-a n =2a n ,∴a n +1=3a n (n ∈N *,n >1). 而a 2=2a 1+1=3,∴a 2=3a 1.∴数列{a n }是以1为首项,3为公比的等比数列, ∴a n =3n -1(n ∈N *).∴a 1=1,a 2=3,a 3=9, 在等差数列{b n }中,∵b 1+b 2+b 3=15,∴b 2=5.又∵a 1+b 1、a 2+b 2、a 3+b 3成等比数列,设等差数列{b n }的公差为d ,则有(a 1+b 1)(a 3+b 3)=(a 2+b 2)2. ∴(1+5-d )(9+5+d )=64,解得d =-10或d =2, ∵b n >0(n ∈N *),∴舍去d =-10,取d =2,∴b 1=3,∴b n =2n +1(n ∈N *).(2)由(1)知T n =3×1+5×3+7×32+…+(2n -1)·3n -2+(2n +1)3n -1,① ∴3T n =3×3+5×32+7×33+…+(2n -1)3n -1+(2n +1)3n ,② ∴①-②得-2T n =3×1+2×3+2×32+2×33+…+2×3n -1-(2n +1)3n =3+2(3+32+33+…+3n -1)-(2n +1)3n =3+2×3-3n1-3-(2n +1)3n=3n -(2n +1)3n =-2n ·3n . ∴T n =n ·3n .。
高中数学 模块综合检测 苏教版必修5

模块综合检测(时间120分钟,满分160分)一、填空题(本大题共14小题,每小题5分,共70分.将答案填在题中的横线上) 1.函数f (x )=lg(x 2-2x -3)的定义域为________. 解析:由x 2-2x -3>0得x <-1或x >3. 答案:(-∞,-1)∪(3,+∞)2.在△ABC 中,a ,b ,c 所对的角分别为A ,B ,C ,若a =2,A =π4,B =5π12,则b =________.解析:由正弦定理a sin A =bsin B得,b =a sin B sin A=2×6+2422=3+1.答案:3+13.已知等比数列{a n },a 4=7,a 6=21,则a 10=________. 解析:∵a 4=a 1q 3,a 6=a 1q 5, ∴q 2=a 6a 4=3. ∴a 10=a 6q 4=189. 答案:1894.已知不等式x 2-2x +k 2-1>0对一切实数x 恒成立,则实数k 的取值范围是________. 解析:由题意知Δ=(-2)2-4(k 2-1)<0,即k 2-2>0,所以k ∈(-∞,-2)∪(2,+∞).答案:(-∞,-2)∪(2,+∞) 5.函数y =log 2⎝⎛⎭⎪⎫x +1x -1+5(x >1)的最小值为________. 解析:∵x >1,∴x +1x -1+5=x -1+1x -1+6≥2x -1x -1+6=8. 当且仅当x -1=1x -1即x =2时取等号. ∴y =log 2⎝ ⎛⎭⎪⎫x +1x -1+5≥log 28=3. ∴y =log 2⎝⎛⎭⎪⎫x +1x -1+5(x >1)的最小值为3.答案:36.等差数列{a n }的前n 项和为S n ,若S 10=0,S 15=25,则S n =________.解析:由题意知⎩⎪⎨⎪⎧10a 1+10×9d 2=0,15a 1+15×14d2=25,解得d =23,a 1=-3,所以S n =-3n +n n -2×23=n 2-10n 3. 答案:n 2-10n37.在平面直角坐标系xOy 中,M 为不等式组⎩⎪⎨⎪⎧2x -y -2≥0,x +2y -1≥0,3x +y -8≤0所表示的区域上一动点,则直线OM 斜率的最小值为________.解析:已知的不等式组表示的平面区域如图中阴影所示,显然当点M 与点A 重合时直线OM 的斜率最小,由直线方程x +2y -1=0和3x +y -8=0,解得A (3,-1),故OM 斜率的最小值为-13.答案:-138.已知各项不为0的等差数列{a n }满足a 4-2a 27+3a 8=0,数列{b n }是等比数列,且b 7=a 7,则b 2b 8b 11=________.解析:设等差数列的公差为d ,由a 4-2a 27+3a 8=0,得a 7-3d -2a 27+3(a 7+d )=0,从而有a 7=2或a 7=0(a 7=b 7,而{b n }是等比数列,故舍去).设{b n }的公比为q ,则b 7=a 7=2,所以b 2b 8b 11=b 7q5·b 7q ·b 7q 4=(b 7)3=23=8.答案:89.在数列{a n }中,已知a 1=2,a 2=7,a n +2等于a n a n +1(n ∈N *)的个位数,则a 2 016的值是________.解析:a 1a 2=2×7=14,所以a 3=4,7×4=28,所以a 4=8,4×8=32,所以a 5=2,8×2=16,所以a 6=6,a 7=2,a 8=2,a 9=4,a 10=8,a 11=2,所以从第三项起,{a n }成周期数列,周期数为6,2 016=336×6,所以a 2 016=a 6=6.答案:610.若△ABC 的内角A ,B ,C 满足6sin A =4sin B =3sin C ,则cos B =________. 解析:依题意,结合正弦定理得6a =4b =3c ,设3c =12k (k >0),则有a =2k ,b =3k ,c =4k ;由余弦定理得cos B =a 2+c 2-b 22ac=k2+k 2-k22×2k ×4k=1116. 答案:111611.张晓华同学骑电动自行车以24 km/h 的速度沿着正北方向的公路行驶,在点A 处望见电视塔S 在电动车的北偏东30°方向上,15 min 后到点B 处望见电视塔在电动车的北偏东75°方向上,则电动车在点B 时与电视塔S 的距离是________ km.解析:如图,由条件知AB =24×1560=6.在△ABS 中,∠BAS =30°,AB =6,∠ABS =180°-75°=105°,所以∠ASB =45°.由正弦定理知BS sin 30°=ABsin 45°,所以BS =ABsin 45°sin 30°=3 2.即电动车在点B 时与电视塔S 的距离是3 2 km. 答案:3 212.若正数x ,y 满足x 2+3xy -1=0,则x +y 的最小值是________. 解析:对于x 2+3xy -1=0可得y =13⎝ ⎛⎭⎪⎫1x -x ,即x +y =2x 3+13x ≥22x 3·13x =223,当且仅当x =22时取等号. 答案:22313.已知二次函数f (x )=ax 2-x +c (x ∈R)的值域为[0,+∞),则c +2a +a +2c的最小值为________.解析:∵二次函数f (x )=ax 2-x +c (x ∈R)的值域[0,+∞), ∴a >0,且4ac -14a =0.∴ac =14,∴c >0.∴c +2a +a +2c =c a +a c +2a +2c≥2c a ·ac+24ac=2+8=10,当且仅当a =c 时取等号. 答案:1014.已知{a n }是首项为1的等比数列,S n 是{a n }的前n 项和,且9S 3=S 6,则数列⎩⎨⎧⎭⎬⎫1a n 的前5项和为________.解析:设等比数列{a n }的公比为q ,∴9S 3=S 6. ∴8(a 1+a 2+a 3)=a 4+a 5+a 6. ∴a 4+a 5+a 6a 1+a 2+a 3=q 3=8.∴q =2,∴a n =2n -1.∴1a n =⎝ ⎛⎭⎪⎫12n -1. ∴数列⎩⎨⎧⎭⎬⎫1a n 是首项为1,公比为12的等比数列,故数列⎩⎨⎧⎭⎬⎫1a n 的前5项和为1×⎣⎢⎡⎦⎥⎤1-⎝ ⎛⎭⎪⎫1251-12=3116.答案:3116二、解答题(本大题共6小题,共90分,解答应写出文字说明、证明过程或演算步骤) 15.(本小题满分14分)求不等式12x 2-ax >a 2(a ∈R)的解集. 解:原不等式可化为(3x -a )(4x +a )>0.当a >0时,不等式的解集为⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪ x <-a 4或x >a3; 当a =0时,不等式的解集为{x |x ∈R 且x ≠0};当a <0时,不等式的解集为⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪x <a 3或x >-a4. 16.(本小题满分14分)△ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,已知a =b cos C +c sin B .(1)求B ;(2)若b =2,求△ABC 面积的最大值.解:(1)由已知及正弦定理得sin A =sin B cos C +sin C sin B . ① 又A =π-(B +C ),故sin A =sin(B +C )=sin B cos C +cos B sin C . ② 由①②和C ∈(0,π)得sin B =cos B . 又B ∈(0,π),所以B =π4.(2)△ABC 的面积S =12ac sin B =24ac .由已知及余弦定理得4=a 2+c 2-2ac cos π4.又a 2+c 2≥2ac ,故ac ≤42-2,当且仅当a =c 时,等号成立.因此△ABC 面积的最大值为2+1.17.(本小题满分14分)某企业准备投入适当的广告费对产品进行促销,在一年内预计销售量Q (万件)与广告费x (万元)之间的函数关系为Q =3x +1x +1(x ≥0).已知生产此产品的年固定投入为3万元,每生产1万元此产品仍需再投入32万元,若每件销售价为“年平均每件生产成本的150%”与“年平均每件所占广告费的50%”之和.(1)试将年利润W (万元)表示为年广告费x (万元)的函数;(2)当年广告费投入多少万元时,企业年利润最大?最大利润为多少?解:(1)由题意可得,产品的生产成本为(32Q +3)万元,每万件销售价为32Q +3Q×150%+x Q×50%万元,所以年销售收入为⎝⎛⎭⎪⎫32Q +3Q ×150%+x Q ×50%·Q =32(32Q +3)+12x 万元,所以年利润W =32(32Q +3)+12x -(32Q +3)-x =12(32Q +3-x )=-x 2+98x +35x +(x ≥0).(2)令x +1=t (t ≥1), 则W =-t -2+t -+352t=50-⎝ ⎛⎭⎪⎫t 2+32t .因为t ≥1,所以t 2+32t ≥2t 2·32t=8,即W ≤42, 当且仅当t 2=32t,即t =8时,W 有最大值42,此时x =7.答:当年广告费为7万元时,企业年利润最大,最大值为42万元.18.(本小题满分16分)已知公差不为0的等差数列{a n }的首项a 1为a (a ∈R),且1a 1,1a 2,1a 4成等比数列.(1)求数列{a n }的通项公式;(2)对n ∈N *,试比较1a 2+1a 22+1a 23+…+1a 2n 与1a 1的大小.解:(1)设等差数列{a n }的公差为d ,由题意可知⎝ ⎛⎭⎪⎫1a22=1a 1·1a 4,即(a 1+d )2=a 1(a 1+3d ),从而a 1d =d 2. 因为d ≠0.所以d =a 1=a . 故通项公式a n =na .(2)记T n =1a 2+1a 22+…+1a 2n ,因为a 2n =2na ,所以T n =1a ⎝ ⎛⎭⎪⎫12+122+ (12)=1a ·12⎣⎢⎡⎦⎥⎤1-⎝ ⎛⎭⎪⎫12n 1-12=1a ⎣⎢⎡⎦⎥⎤1-⎝ ⎛⎭⎪⎫12n . 从而,当a >0时,T n <1a 1;当a <0时,T n >1a 1.19.(本小题满分16分)在△ABC 中,内角A ,B ,C 所对的边分别为a ,b ,c ,且满足a =2sin A ,cos B cos C +2a c +bc=0.(1)求c 的值;(2)求△ABC 面积的最大值. 解:(1)∵cos B cos C +2a c +bc =0,∴c cos B +2a cos C +b cos C =0,∴sin C cos B +sin B cos C +2sin A cos C =0, ∴sin A +2sin A cos C =0.又∵sin A ≠0, ∴cos C =-12,∴C =2π3,∴c =a sin A·sin C = 3.(2)∵cos C =-12=a 2+b 2-32ab ,∴a 2+b 2+ab =3,∴3ab ≤3,即ab ≤1,当且仅当a =b =1时取等号, ∴S △ABC =12ab sin C ≤34,即△ABC 面积的最大值为34. 20.(本小题满分16分)在△ABC 中,a ,b ,c 分别为角A ,B ,C 的对边,a 2-c 2=b 2-8bc5,a =3,△ABC 的面积为6,D 为△ABC 内(不包括三角形的边)任一点,点D 到三边距离之和为d .(1)求角A 的正弦值; (2)求边b ,c; (3)求d 的取值范围.解:(1)a 2-c 2=b 2-8bc 5⇒b 2+c 2-a 22bc =45⇒cos A =45⇒sin A =35.(2)∵S △ABC =12bc sin A =6.∴bc =20.由b 2+c 2-a 22bc =45及bc =20与a =3解得b =4,c =5或b =5,c =4.(3)设点D 到三边的距离分别为x ,y ,z , 则S △ABC =12(3x +4y +5z )=6,d =x +y +z=125+15(2x +y ), 又x ,y 满足⎩⎪⎨⎪⎧3x +4y <12,x >0,y >0,画出不等式表示的平面区域得125<d <4.。
苏教版高中数学必修五 章末综合测评(一).docx

高中数学学习材料马鸣风萧萧*整理制作章末综合测评(一)(时间120分钟,满分160分)一、填空题(本大题共14小题,每小题5分,共70分.请把答案填在题中的横线上)1.在△ABC 中,AB =6,A =75°,B =45°,则AC = .【导学号:92862026】【解析】 C =180°-75°-45°=60°,由正弦定理得AB sin C =AC sin B ,即6sin 60°=AC sin 45°,解得AC =2.【答案】 22.在△ABC 中,已知c =6,a =4,B =120°,则b = . 【解析】 由b 2=16+36-2×4×6cos 120°, 得b =219. 【答案】 2193.在△ABC 中,a =4,b =43,A =30°,则B = . 【解析】 sin B =b sin A a =43sin 30°4=32.又a <b ,故B >A ,∴B =60°或120°. 【答案】 60°或120°4.在△ABC 中,化简b cos C +c cos B = .【解析】 利用余弦定理,得b cos C +c cos B =b ·a 2+b 2-c 22ab +c ·a 2+c 2-b 22ac =a .【答案】 a5.在△ABC 中,若sin A ∶sin B ∶sin C =2∶3∶4,则cos C = . 【解析】 ∵sin A ∶sin B ∶sin C =a ∶b ∶c , ∴a ∶b ∶c =2∶3∶4. 设a =2k ,b =3k ,c =4k ,则 cos C =4k 2+9k 2-16k 22×2k ×3k =-14.【答案】 -146.在△ABC 中,若A =60°,b =16,S △ABC =2203,则a = . 【解析】 由12bc sin A =2203,可知c =55.又a 2=b 2+c 2-2bc cos A =2 401, ∴a =49. 【答案】 497.在△ABC 中,若sin A =34,a =10,则边长c 的取值范围是 . 【解析】 ∵c sin C =a sin A =403, ∴c =403sin C ,∴0<c ≤403. 【答案】 ⎝ ⎛⎦⎥⎤0,4038.根据下列情况,判断三角形解的情况,其中正确的是 .(填序号)【导学号:92862027】(1)a =8,b =16,A =30°,有两解; (2)b =18,c =20,B =60°,有一解; (3)a =5,c =2,A =90°,无解; (4)a =30,b =25,A =150°,有一解. 【解析】 (1)中,∵a sin A =bsin B , ∴sin B =16×sin 30°8=1,∴B =90°,即只有一解; (2)中,sin C =20sin 60°18=539,且c >b ,∴C >B ,故有两解;(3)中,∵A =90°,a =5,c =2,∴b =a 2-c 2=25-4=21,即有解,故(1)(2)(3)都不正确.所以答案为(4).【答案】 (4)9.已知锐角△ABC 的内角A ,B ,C 的对边分别为a ,b ,c,23cos 2A +cos 2A =0,a =7,c =6,则b = .【解析】 化简23cos 2A +cos 2A =0,得23cos 2A +2cos 2A -1=0,解得cos A =15.由余弦定理,知a 2=b 2+c 2-2bc cos A ,代入数据解方程,得b =5.【答案】 5 10.在△ABC 中,若acos A 2=b cos B 2=c cos C 2,那么△ABC 是 三角形. 【解析】 由正弦定理得,sin A cos A 2=sin B cos B 2=sin Ccos C 2, ∴sin A 2=sin B 2=sin C 2.∵0<A 2,B 2,C 2<π2,∴A 2=B 2=C2,即A =B =C ,∴△ABC 是等边三角形. 【答案】 等边11.如图1所示,在△ABC 中,∠ACB 的平分线CD 交AB 于D ,AC →的模为2,BC →的模为3,AD →的模为1,那么DB →的模为.图1【解析】 由三角形内角平分线的性质得|AC →|∶|BC →|=|AD →|∶|DB →|, 故|DB →|=32. 【答案】 3212.如图2所示,在山底测得山顶仰角∠CAB =45°,沿倾斜角为30°的斜坡走1 000 m 至S 点,又测得山顶仰角∠DSB =75°,则山高BC 为m.图2【解析】 由题可知,∠SAB =45°-30°=15°,又∠SBD =15°,∴∠ABS =45°-15°=30°,AS =1 000.由正弦定理可知BS sin 15°=1 000sin 30°,∴BS =2 000sin 15°,∴BD =BS ·sin 75°=2 000sin 15°cos 15°=1 000sin 30°=500,且DC =1 000sin 30°=500,∴BC =DC +BD =1 000 m.【答案】 1 00013.已知角A ,B ,C 是三角形ABC 的内角,a ,b ,c 分别是其对边长,向量m =⎝ ⎛⎭⎪⎫23sin A 2,cos 2A 2,n =⎝ ⎛⎭⎪⎫cos A 2,-2,m ⊥n ,且a =2,cos B =33,则b = .【解析】 ∵m·n =0,∴23sin A 2cos A 2-2cos 2A 2=0,∵cos A2≠0, ∴tan A 2=33,∴A2=30°,∴A =60°, ∵a sin A =bsin B ,sin B =1-⎝ ⎛⎭⎪⎫332=63, ∴b =a sin B sin A =2×6332=43 2.【答案】 43 214.在锐角△ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,若b a +ab =6cos C ,则tan C tan A +tan Ctan B 的值是 .【解析】 ∵b a +ab =6cos C , ∴a 2+b 2ab =6·a 2+b 2-c 22ab , 即a 2+b 2=32c 2, ∴tan C tan A +tan C tan B =tan C ⎝ ⎛⎭⎪⎫cos A sin A +cos B sin B=sin 2Ccos C sin A sin B =2c 2a 2+b 2-c 2=4. 【答案】 4二、解答题(本大题共6小题,共90分.解答时应写出文字说明、证明过程或演算步骤)15.(本小题满分14分)在△ABC 中,a ,b ,c 分别是角A ,B ,C 所对的边,已知b 2=ac ,且a 2-c 2=ac -bc ,求角A 的大小及b sin Bc .【解】 由b 2=ac 及a 2-c 2=ac -bc ,得b 2+c 2-a 2=bc . 在△ABC 中,cos A =b 2+c 2-a 22bc =12. ∵0°<A <180°,∴A =60°. 在△ABC 中,由正弦定理得sin B =b sin Aa .又∵b 2=ac ,A =60°, ∴b sin B c =b 2sin A ac =sin 60°=32.16.(本小题满分14分)已知△ABC 的内角A ,B ,C 所对的边分别为a ,b ,c ,且a =2,cos B =35.(1)若b =4,求sin A 的值;(2)若△ABC 的面积S △ABC =4,求b ,c 的值. 【解】 (1)∵cos B =35>0,且0<B <π, ∴sin B =1-cos 2B =45. 由正弦定理得a sin A =bsin B , sin A =a sin B b =2×454=25. (2)∵S △ABC =12ac sin B =4, ∴12×2×c ×45=4,∴c =5.由余弦定理得b 2=a 2+c 2-2ac cos B =22+52-2×2×5×35=17,∴b =17. 17.(本小题满分14分)在△ABC 中,内角A ,B ,C 的对边分别为a ,b ,c .已知cos A -2cos C cos B=2c -a b .(1)求sin Csin A 的值;(2)若cos B =14,△ABC 的周长为5,求b 的长. 【解】 (1)由正弦定理,设a sin A =b sin B =csin C =k , 则2c -a b =2k sin C -k sin A k sin B=2sin C -sin A sin B ,所以cos A -2cos C cos B =2sin C -sin Asin B,即(cos A -2cos C )sin B =(2sin C -sin A )cos B ,化简可得sin(A +B )=2sin(B +C ). 又A +B +C =π,所以sin C =2sin A . 因此sin Csin A =2.(2)由sin Csin A =2,得c =2a ,由余弦定理及cos B =14得b 2=a 2+c 2-2ac cos B =a 2+4a 2-4a 2×14=4a 2, 所以b =2a .又a +b +c =5,从而a =1, 因此b =2.18.(本小题满分16分)在△ABC 中a ,b ,c 分别为内角A ,B ,C 的对边,且2a sin A =(2b +c )sin B +(2c +b )sin C .(1)求A 的大小;(2)若sin B +sin C =1,试判断△ABC 的形状.【导学号:92862028】【解】 (1)由2a sin A =(2b +c )sin B +(2c +b )sin C ,得2a 2=(2b +c )b +(2c +b )c ,即a 2=b 2+c 2+bc , ∴b 2+c 2-a 2=-bc , ∴2bc cos A =-bc ,∴cos A =-12,又A ∈(0,π), ∴A =2π3.(2)由(1)得sin 2A =sin 2B +sin 2C +sin B sin C , 又sin B +sin C =1,得sin B =sin C =12. 又B ,C ∈⎝ ⎛⎭⎪⎫0,π2,故B =C . 所以△ABC 是等腰三角形.19.(本小题满分16分)在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,且cos(A -B )cos B -sin(A -B )sin(A +C )=-35.(1)求sin A 的值;(2)若a =42,b =5,求向量BA→在BC →方向上的投影.【解】 (1)由cos(A -B )cos B -sin(A -B )sin(A +C )=-35,得cos(A -B )cos B -sin(A -B )sin B =-35,则cos(A -B +B )=-35,即cos A =-35. 又0<A <π,则sin A =45.(2)由正弦定理,有a sin A =bsin B , 所以sin B =b sin A a =22.由题知a >b ,则A >B ,故B =π4.根据余弦定理,有(42)2=52+c 2-2×5c ×⎝ ⎛⎭⎪⎫-35,解得c =1或c =-7(负值舍去).故向量BA →在BC →方向上的投影为|BA →|cos B =22.20.(本小题满分16分)如图3,游客从某旅游景区的景点A 处下山至C 处有两种路径.一种是从A 沿直线步行到C ,另一种是先从A 沿索道乘缆车到B ,然后从B 沿直线步行到C .现有甲、乙两位游客从A 处下山,甲沿AC 匀速步行,速度为50 m/min.在甲出发2 min 后,乙从A 乘缆车到B ,在B 处停留1 min 后,再从B 匀速步行到C .假设缆车匀速直线运行的速度为130 m/min ,山路AC 长为1 260 m ,经测量,cos A =1213,cos C =35.图3(1)求索道AB的长;(2)问乙出发多少min后,乙在缆车上与甲的距离最短?(3)为使两位游客在C处互相等待的时间不超过3 min,乙步行的速度应控制在什么范围内?【解】(1)在△ABC中,因为cos A=1213,cos C=35,所以sin A=513,sin C=45.从而sin B=sin[]π-(A+C)=sin(A+C)=sin A cos C+cos A sin C=513×35+1213×45=6365.由ABsin C=ACsin B,得AB=ACsin B×sin C=1 2606365×45=1 040(m).所以索道AB的长为1 040 m.(2)设乙出发t min后,甲、乙两游客距离为d m,此时,甲行走了(100+50t)m,乙距离A处130t m,所以由余弦定理得d2=(100+50t)2+(130t)2-2×130t×(100+50t)×12 13=200(37t2-70t+50),因0≤t≤1 040130,即0≤t≤8,故当t=3537min时,甲、乙两游客距离最短.(3)由BCsin A=ACsin B,得BC=ACsin B×sin A=1 2606365×513=500(m).乙从B出发时,甲已走了50×(2+8+1)=550(m),还需走710 m才能到达C.设乙步行的速度为v m/min,由题意得-3≤500v-71050≤3,解得1 25043≤v ≤62514,所以为使两位游客在C 处互相等待的时间不超过3 min ,乙步行的速度应控制在⎣⎢⎡⎦⎥⎤1 25043,62514(单位:m/min)范围内.。
【苏教版】高中数学必修5同步辅导与检测:模块综合检测卷(二)(含答案)

模块综合检测卷(二)(测试时间:120分钟评价分值:150分)一、选择题(每小题共12个小题,每小题共5分,共60分,在每小题给出的四个选项中,只有一项符合题目要求)1.对于任意实数a,b,c,d命题:①若a>b,c≠0,则ac>bc;②若a<b,则ac2>bc2;③若ac2>bc2,则a>b.其中真命题的个数是()A.0B.1C.2D.3解析:当c<0时,①不正确;当c=0时,②不正确;只有③正确.答案:B2.历届现代奥运会召开时间表如下:A.29 B.30 C.31 D.32解析:由题意得,历届现代奥运会召开时间构成以1 896为首项,4为公差的等差数列,所以2 016=1 896+(n-1)·4,解得n=31.答案:C3.若点(x,y)位于曲线y=|x|与y=2所围成的封闭区域,则2x -y的最小值为()A .-6B .-2C .0D .2解析:y =|x |与y =2的图象围成一个三角形区域,如图所示,3个顶点的坐标分别是(0,0),(-2,2),(2,2).在封闭区域内平移直线y =2x ,在点(-2,2)时,2x -y =-6取最小值.答案:A4.如图所示,设A ,B 两点在河的两岸,一测量者在A 所在的同侧河岸边选定一点C ,测出AC 的长为50 m ,∠ACB =45°,∠CAB =105°后,就可以计算出A ,B 两点的距离为()A .50 2 mB .50 3 mC .25 2 mD.2522m解析:由正弦定理得AB sin ∠ACB =ACsin ∠ABC ,又因为∠ABC =180°-45°-105°=30°, 所以AB =AC sin ∠ACB sin ∠ABC=50×2212=502(m).答案:A5.等比数列{a n }前n 项的积为T n ,若a 3a 6a 18是一个确定的常数,那么数列T 10,T 13,T 17,T 25中也是常数的项是( )A .T 10B .T 13C .T 17D .T 25解析:因为a 3·a 6·a 18=a 9q 6·a 9q 3·a 9·q 9=a 39是一个确定常数,所以a 9为确定的常数.T 17=a 1·a 2·…·a 17=(a 9)17,所以选C. 答案:C6.以原点为圆心的圆全部都在平面区域⎩⎪⎨⎪⎧x -3y +6≥0,x -y +2≥0内,则圆面积的最大值为( )A.18π5B.9π5C .2πD .π 解析:作出不等式组表示的平面区域如图所示,由图可知,最大圆的半径为点(0,0)到直线x -y +2=0的距离, 即|0-0+2|12+(-1)2=2,所以圆面积的最大值为π·(2)2=2π. 答案:C7.已知三角形的两边长分别为4,5,它们夹角的余弦值是方程2x 2+3x -2=0的根,则第三边长是( )A.20B.21C.22D.61解析:设长为4,5的两边的夹角为θ,由2x 2+3x -2=0得x =12或x =-2(舍),所以cos θ=12,所以第三边长为 42+52-2×4×5×12=21.答案:B8.已知数列{a n }的前n 项和S n =n 2-9n ,第k 项满足5<a k <8,则k 等于( )A .6B .7C .8D .9解析:a n =⎩⎨⎧S 1,n =1,S n -S n -1,n ≥2=⎩⎨⎧-8,n =1,-10+2n ,n ≥2.因为n =1时适合a n =2n -10, 所以a n =2n -10(n ∈N *). 因为5<a k <8,所以5<2k -10<8. 所以152<k <9.又因为k ∈N *,所以k =8.答案:C9.函数f (x )=1x ln(x 2-3x +2+-x 2-3x +4)的定义域为( )A .(-∞,-4)∪[2,+∞)B .(-4,0)∪(0,1)C .[-4,0)∪(0,1]D .[-4,0)∪(0,1)解析:函数f (x )有定义等价于⎩⎪⎨⎪⎧x ≠0,x 2-3x +2≥0,-x 2-3x +4>0或⎩⎪⎨⎪⎧x ≠0,x 2-3x +2>0,-x 2-3x +4≥0,解得-4≤x <0或0<x <1.答案:D10.设△ABC 的内角A ,B ,C 所对的边分别为a ,b ,c ,若b cos C +c cos B =a sin A ,则△ABC 的形状为( )A .锐角三角形B .直角三角形C .钝角三角形D .不确定解析:因为b cos C +c cos B =b ·b 2+a 2-c 22ab +c ·c 2+a 2-b 22ac=b 2+a 2-c 2+c 2+a 2-b 22a=2a 22a =a =a sin A , 所以sin A =1.因为A ∈(0,π),所以A =π2,即△ABC 是直角三角形.答案:B11.在数列{x n }中,2x n =1x n -1+1x n +1(n ≥2),且x 2=23,x 4=25,则x 10等于( )A.211B.16C.112D.15解析:由已知可得⎩⎨⎧⎭⎬⎫1x n 成等差数列,而1x 2=32,1x 4=52,所以2d =52-32=1,即d =12.故1x 10=1x 1+(10-1)d =⎝ ⎛⎭⎪⎫32-12+9×12=112.所以x 10=211. 答案:A12.已知x >0,y >0,且2x +1y =1,若x +2y >m 2+2m 恒成立,则实数m 的取值范围是( )A .(-∞,-2]∪[4,+∞)B .(-∞,-4]∪[2,+∞)C .(-2,4)D .(-4,2)解析:因为x >0,y >0且2x +1y =1,所以x +2y =(x +2y )⎝ ⎛⎭⎪⎫2x +1y =4+4y x +xy ≥4+24y x ·x y =8,当且仅当4y x =x y,即x =4,y =2时取等号, 所以(x +2y )min =8.要使x +2y >m 2+2m 恒成立, 只需(x +2y )min >m 2+2m 恒成立, 即8>m 2+2m ,解得-4<m <2. 答案:D二、填空题(本大题共4小题,每小题5分,共20分.把答案填在题中横线上)13.若函数f (x )=⎩⎪⎨⎪⎧x 2+1,x >0,-x ,x ≤0.则不等式f (x )<4的解集是________.解析:不等式f (x )<4等价于⎩⎨⎧x >0,x 2+1<4或⎩⎨⎧x ≤0,-x <4,即0<x <3或-4<x ≤0.因此,不等式f (x )<4的解集是(-4,3). 答案:(-4,3)14.已知数列{a n }的通项公式为a n =2n -2004,则这个数列的前________项和最小.解析:设a n =2n -2 004的对应函数为y =2x -2 004.易知函数y =2x -2 004在R 上是增函数,且当y =0时,x =1 002. 因此,数列{a n }是单调递增数列,且当1≤n ≤1 002时,a n ≤0;当n >1 002时,a n >0. 所以数列{a n }的前1 001项或前1 002项的和最小. 答案:1 001或1 002.15.在△ABC 中,内角A ,B ,C 的对边分别是a ,b ,c ,若a 2-b 2=3bc ,sin C =23sin B ,则A 等于________.解析:由正弦定理,且sin C =23sin B ⇒c =23b .又a 2-b 2=3bc ,故由余弦定理得cos A =b 2+c 2-a 22bc =b 2+c 2-(b 2+3bc )2bc =c 2-3bc 2bc =(23b )2-3b ·23b 2b ·23b=32,所以A =30°. 答案:30°16.(2015·山东卷)定义运算“⊗”:x ⊗y =x 2-y 2xy (x ,y ∈R ,xy ≠0).当x >0,y >0时,x ⊗y +(2y )⊗x 的最小值为________.解析:因为x ⊗y =x 2-y 2xy ,所以(2y )⊗x =4y 2-x 22xy .又x >0,y >0,故x ⊗y +(2y )⊗x =x 2-y 2xy +4y 2-x 22xy =x 2+2y 22xy ≥22xy2xy =2,当且仅当x =2y 时,等号成立. 答案: 2三、解答题(本大题共6小题,共70分.解答题应写出文字说明、证明过程或推演步骤)17.(本小题满分10分)(2015·江苏卷)在△ABC 中,已知AB =2,AC =3,A =60°.(1)求BC 的长; (2)求sin 2C 的值.解:(1)由余弦定理知,BC 2=AB 2+AC 2-2AB ·AC ·cos A =4+9-2×2×3×12=7,所以BC =7.(2)由正弦定理知,AB sin C =BCsin A ,所以sin C =ABBC ·sin A =2sin 60°7=217.因为AB <BC ,所以C 为锐角, 则cos C =1-sin 2C =1-37=277. 因此sin 2C =2sin C ·cos C =2·217·277=437.18.(本小题满分12分)设{a n }是公比为正数的等比数列,a 1=2,a 3=a 2+4.(1)求{a n }的通项公式;(2)设{b n }是首项为1,公差为2的等差数列,求数列{a n +b n }的前n 项和S n .解:(1)设q 为等比数列{a n }的公比,则由a 1=2,a 3=a 2+4得2q 2=2q +4,即q 2-q -2=0,解得q =2或q =-1(舍去),因此q =2,所以{a n }的通项为a n =2·2n -1=2n (n ∈N +).(2)S n =2(1-2n )1-2+n ·1+n (n -1)2·2=2n +1+n 2-2.19.(本小题满分12分)在△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c .已知△ABC 的周长为2+1,且sin A +sin B =2sin C .(1)求边c 的长;(2)若△ABC 的面积为16sin C ,求C 的大小.解:(1)由sin A +sin B =2sin C 及正弦定理可知: a +b =2c .又因为a +b +c =2+1,所以2c +c =2+1,从而c =1. (2)三角形面积S =12ab sin C =16sin C ,所以ab =13,a +b = 2.因为cos C =a 2+b 2-c 22ab =(a +b )2-2ab -12ab =12,又因为0<C <π,所以C =π3.20.(本小题满分12分)如图所示,公园有一块边长为2的等边三角形ABC 的边角地,现修成草坪,图中DE 把草坪分成面积相等的两部分,点D 在AB 上,点E 在AC 上.(1)设AD =x (x ≥0),ED =y ,求用x 表示y 的函数关系式; (2)如果DE 是灌溉水管,为节约成本,希望它最短,DE 的位置应在哪里?如果DE 是参观线路,则希望它最长,DE 的位置又在哪里?解:S △ABC =34×4=3,所以S △ADE =12·x ·AE · sin 60°=32,所以x ·AE =2,所以AE =2x≤2,所以x ≥1.(1)在△ADE 中,y 2=x 2+⎝ ⎛⎭⎪⎫2x 2-2·x ·2x ·cos 60°=x 2+4x 2-2,所以y =x 2+4x2-2(1≤x ≤2).(2)令t =x 2,则1≤t ≤4,所以y =t +4t-2(1≤t ≤4). 当t =2,即x =2时,即当AD =2,AE =2时,DE 最短为2;当t =1或4,即AD =2,AE =1或AD =1,AE =2时,DE 最长为 3.21.(本小题满分12分)已知函数f (x )=x 2-ax (a ∈R), (1)若不等式f (x )>a -3的解集为R ,求实数a 的取值范围; (2)设x >y >0,且xy =2,若不等式f (x )+f (y )+2ay ≥0恒成立,求实数a 的取值范围.解:(1)不等式f (x )>a -3的解集为R ,即不等式x 2-ax -a +3>0的解集为R ,所以Δ=a 2+4(a -3)<0恒成立,即a 2+4a -12<0恒成立,所以-6<a <2.(2)不等式f (x )+f (y )+2ay ≥0恒成立,即不等式x 2-ax +y 2-ay +2ay ≥0恒成立,所以x 2+y 2≥a (x -y )恒成立.所以实数a 的取值范围为(-∞,4].22.(本小题满分12分)已知公差大于0的等差数列{a n }的前n 项和为S n ,且满足:a 3a 4=117,a 2+a 5=22.(1)求数列{a n }的通项公式a n ;(2)若数列{b n }是等差数列,且b n =S n n +c,求非零常数c ; (3)若(2)中的{b n }的前n 项和为T n ,求证:2T n -3b n -1>64b n (n +9)b n +1. (1)解:{a n }为等差数列,因为a 3+a 4=a 2+a 5=22, 又因为a 3·a 4=117,所以a 3,a 4是方程n 2-22x +117=0的两个根. 又因为公差d >0,所以a 3<a 4,所以a 3=9,a 4=13.所以⎩⎨⎧a 1+2d =9,a 1+3d =13即⎩⎨⎧a 1=1,d =4,所以a n =4n -3.(2)解:由(1)知,S n =n ·1+n (n -1)2·4=2n 2-n , 所以b n =S n n +c =2n 2-n n +c ,所以b 1=11+c ,b 2=62+c, b 3=153+c. 因为{b n }是等差数列,所以2b 2=b 1+b 3,所以2c 2+c =0,所以c =-12或c =0(舍去). (3)证明:由(2)得b n =2n 2-n n -12=2n ,T n =2n +n (n -1)·22=n 2+n ,2T n -3b n -1=2(n 2+n )-3(2n -2)=2(n -1)2+4≥4,当n =1时取“=”,又n >1,所以取不到“=”,即2T n -3b n -1>4.64b n (n +9)b n +1=64×2n (n +9)·2(n +1)=64n n 2+10n +9=64n +9n+10≤4,当n =3时取“=”.上述两式中“=”不可能同时取到,所以2T n -3b n -1>64b n (n +9)b n +1.。
苏教版高中数学必修五模块综合检测

模块综合检测(时间120分钟 满分150分)一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.若f (x )=3x 2-x +1,g (x )=2x 2+x -1,则f (x )与g (x )的大小关系为( ) A .f (x )>g (x ) B .f (x )=g (x ) C .f (x )<g (x )D .随x 值变化而变化解析:选A 因为f (x )-g (x )=(3x 2-x +1)-(2x 2+x -1)=x 2-2x +2=(x -1)2+1>0,所以f (x )>g (x ).2.在△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,若a =2,b =3,B =60°,那么角A 等于( )A .135°B .90°C .45°D .30°解析:选C 由正弦定理知a sin A =bsin B, ∴sin A =a sin Bb =2sin 60°3=22. 又a <b ,B =60°,∴A <60°,∴A =45°. 3.若a 1=1,a n +1=a n3a n +1,则给出的数列{a n }的第4项是( ) A.116 B.117 C.110D.125解析:选C a 2=a 13a 1+1=13+1=14, a 3=a 23a 2+1=1434+1=17,a 4=a 33a 3+1=1737+1=110.4.若关于x 的不等式x 2-3ax +2>0的解集为(-∞,1)∪(m ,+∞),则a +m =( ) A .-1 B .1 C .2D .3解析:选D 由题意,知1,m 是方程x 2-3ax +2=0的两个根,则由根与系数的关系,得⎩⎪⎨⎪⎧ 1+m =3a ,1×m =2,解得⎩⎪⎨⎪⎧a =1,m =2,所以a +m =3,故选D. 5.已知x >0,y >0,且x +y =8,则(1+x )(1+y )的最大值为( )A .16B .25C .9D .36解析:选B (1+x )(1+y )≤⎣⎡⎦⎤(1+x )+(1+y )22=⎣⎡⎦⎤2+(x +y )22=⎝⎛⎭⎫2+822=25,因此当且仅当1+x =1+y 即x =y =4时,(1+x )(1+y )取最大值25,故选B.6.已知数列{a n }为等差数列,且a 1=2,a 2+a 3=13,则a 4+a 5+a 6等于( ) A .40 B .42 C .43D .45解析:选B 设等差数列{a n }的公差为d ,则2a 1+3d =13, ∴d =3,故a 4+a 5+a 6=3a 1+12d =3×2+12×3=42.7.在△ABC 中,内角A ,B ,C 的对边分别为a ,b ,c .若2cos 2A +B 2-cos 2C =1,4sin B=3sin A ,a -b =1,则c 的值为( )A.13B.7C.37D .6解析:选A 由已知可得cos 2C =2cos 2A +B2-1=cos(A +B )=cos(π-C )=-cos C ,则2cos 2C +cos C -1=0.∵C ∈(0,π),解得cos C =12,根据余弦定理得12=a 2+b 2-c 22ab.∵4sin B =3sin A ,由正弦定理可得4b =3a .又∵a -b =1,∴b =3,a =4,代入余弦公式得到c 的值为13.故选A.8.已知S n 为正项等比数列{a n }的前n 项和,S 3=3a 1+2a 2,且a 2-12,a 4,a 5成等差数列,则a 1=( )A .2 B.12 C.14D .4解析:选C 设数列{a n }的公比为q (q >0),则由S 3=3a 1+2a 2可得q 2-q -2=0,解得q =2或q =-1(舍去),又a 2-12,a 4,a 5成等差数列,所以2a 4=a 2-12+a 5,即a 2=12,所以a 1=14. 9.在△ABC 中,a ,b ,c 分别为内角A ,B ,C 的对边.若2sin C =sin A +sin B ,cos C =35,且S △ABC =4,则c =( ) A.463B .4C.263D .5解析:选A 在△ABC 中,2sin C =sin A +sin B , 由正弦定理可得2c =a +b .∵cos C =35,∴sin C =1-cos 2C =45.∵S △ABC =4,即12ab sin C =4,∴ab =10.由余弦定理,得a 2+b 2-c 22ab =35,∴(a +b )2-2ab -c 22ab =35,即4c 2-20-c 220=35,解得c =463(负值舍去).故选A.10.设函数f (x )=mx 2-mx -1,若对任意的x ∈[1,3],f (x )<-m +4恒成立,则实数m 的取值范围为( )A .(-∞,0] B.⎣⎡⎭⎫0,57 C .(-∞,0)∪⎝⎛⎭⎫0,57 D.⎝⎛⎭⎫-∞,57 解析:选D 函数f (x )=mx 2-mx -1, 若对任意的x ∈[1,3],f (x )<-m +4恒成立, 即mx 2-mx +m -5<0对于x ∈[1,3]恒成立.令g (x )=mx 2-mx +m -5,当m =0时,-5<0恒成立. 当m <0时,g (x )max =g (1)=m -5<0,解得m <5, ∴m <0.当m >0时,g (x )max =g (3)=7m -5<0,解得m <57,∴0<m <57.综上所述,实数m 的取值范围为⎝⎛⎭⎫-∞,57. 11.已知△ABC 的内角A ,B ,C 所对的边分别为a ,b ,c ,sin A +2sin B =2sin C ,b =3,当内角C 最大时,△ABC 的面积等于( )A.9+334B.6+324C.326-24D.36-324解析:选A 根据正弦定理及sin A +2sin B =2sin C 得a +2b =2c ,∴c =a +322,cosC =a 2+b 2-c 22ab =a 2+9-a 2+62a +1846a =a 8+34a -24≥2a 8·34a -24=6-24,当且仅当a 8=34a ,即a =6时,等号成立.此时sin C =6+24,S △ABC =12ab sin C =12×6×3×6+24=9+334. 12.已知数列{a n }的通项公式为a n =5-n ,其前n 项和为S n ,将数列{a n }的前4项抽去其中一项后,剩下三项按原来顺序恰为等比数列{b n }的前3项,记{b n }的前n 项和为T n .若存在m ∈N *,使对任意n ∈N *,总有S n <T m +λ成立,则实数λ的取值范围是( )A .[2,+∞)B .(3,+∞)C .[3,+∞)D .(2,+∞)解析:选D 由已知得S n =-12n 2+92n ,(S n )max =S 4=S 5=10.等比数列{b n }的前3项为4,2,1,所以T n =8⎝⎛⎭⎫1-12n ,显然{T n }是递增数列,且4≤T n <8.因为存在m ∈N *,使对任意n ∈N *,总有S n <T m +λ成立,则10<8+λ,所以λ>2.故选D.二、填空题(本大题共4小题,每小题5分,共20分.请把正确答案填在题中的横线上) 13.若实数x ,y 满足xy =1,则x 2+2y 2的最小值为________.解析:因为实数x ,y 满足xy =1,所以x 2+2y 2≥2x 2·2y 2=22(xy )2=22,并且仅当x 2=2y 2且xy =1,即x 2=2y 2=2时等号成立,故x 2+2y 2的最小值为2 2.答案:2 214.已知△ABC 的一个内角为120°,并且三边长构成公差为4的等差数列,则△ABC 的面积为________.解析:由于三边长构成公差为4的等差数列, 故可设三边长分别为x -4,x ,x +4.由一个内角为120°,知其必是最长边x +4所对的角.由余弦定理得,(x +4)2=x 2+(x -4)2-2x (x -4)·cos 120°,∴2x 2-20x =0,∴x =0(舍去)或x =10,∴S △ABC =12×(10-4)×10×sin 120°=15 3.答案:15 315.设S n 是数列{a n }的前n 项和,且a 1=-1,a n +1=S n S n +1,则S n =________. 解析:∵a n +1=S n +1-S n ,a n +1=S n S n +1,∴S n +1-S n =S n S n +1. ∵S n ≠0,∴1S n -1S n +1=1,即1S n +1-1S n =-1. 又1S 1=-1, ∴⎩⎨⎧⎭⎬⎫1S n 是首项为-1,公差为-1的等差数列. ∴1S n =-1+(n -1)×(-1)=-n , ∴S n =-1n . 答案:-1n16.设a 为实常数,y =f (x )是定义在R 上的奇函数,且当x <0时,f (x )=9x +a 2x +7.若f (x )≥a+1对一切x ≥0成立,则a 的取值范围是________.解析:当x <0时,-9x -a 2x ≥6|a |, ∴f (x )≤7-6|a |.∵f (x )是定义在R 上的奇函数, ∴当x >0时,f (x )≥6|a |-7. ∵a +1≤f (x )对一切x >0成立, ∴a +1≤f (x )min ,即a +1≤6|a |-7,∴⎩⎪⎨⎪⎧a +1≤6a -7,a ≥0,a +1≤-6a -7,a <0.解得a ≤-87或a ≥85.当x =0时,f (0)=0≥a +1,∴a ≤-1. 综上可知a ≤-87.答案:⎝⎛⎦⎤-∞,-87 三、解答题(本大题共6小题,共70分,解答时写出必要的文字说明、证明过程或演算步骤)17.(本小题满分10分)(2018·全国卷Ⅰ)在平面四边形ABCD 中,∠ADC =90°,∠A =45°,AB =2,BD =5.(1)求cos ∠ADB ;(2)若DC =22,求BC .解:(1)在△ABD 中,由正弦定理得BD sin ∠A =AB sin ∠ADB,即5sin 45°=2sin ∠ADB ,所以sin ∠ADB =25. 由题设知,∠ADB <90°, 所以cos ∠ADB =1-225=235. (2)由题设及(1)知,cos ∠BDC =sin ∠ADB =25. 在△BCD 中,由余弦定理得BC 2=BD 2+DC 2-2BD ·DC ·cos ∠BDC =25+8-2×5×22×25=25, 所以BC =5.18.(本小题满分12分)已知f (x )=2x 2+bx +c ,不等式f (x )<0的解集是(0,5). (1)求f (x )的解析式;(2)若对于任意的x ∈[-1,1],不等式f (x )+t ≤2恒成立,求t 的取值范围.解:(1)因为f (x )=2x 2+bx +c ,不等式f (x )<0的解集是(0,5),所以2x 2+bx +c <0的解集是(0,5),所以0和5是方程2x 2+bx +c =0的两个根, 由根与系数的关系,知-b 2=5,c2=0,所以b =-10,c =0, 所以f (x )=2x 2-10x .(2)对任意的x ∈[-1,1],f (x )+t ≤2恒成立等价于对任意的x ∈[-1,1],2x 2-10x +t -2≤0恒成立.设g (x )=2x 2-10x +t -2,则由二次函数的图象可知g (x )=2x 2-10x +t -2在区间[-1,1]上为减函数, 所以g (x )max =g (-1)=10+t , 所以10+t ≤0,即t ≤-10, 所以t 的取值范围为(-∞,-10].19.(本小题满分12分)(2018·全国卷Ⅰ)已知数列{a n }满足a 1=1,na n +1=2(n +1)a n .设b n=a nn .(1)求b 1,b 2,b 3;(2)判断数列{b n }是否为等比数列,并说明理由; (3)求{a n }的通项公式.解:(1)由条件可得a n +1=2(n +1)n a n .将n =1代入得,a 2=4a 1,而a 1=1,所以a 2=4. 将n =2代入得,a 3=3a 2,所以a 3=12. 从而b 1=1,b 2=2,b 3=4.(2)数列{b n }是首项为1,公比为2的等比数列. 由条件可得a n +1n +1=2a nn ,即b n +1=2b n ,又b 1=1,所以数列{b n }是首项为1,公比为2的等比数列. (3)由(2)可得a n n =2n -1,所以a n =n ·2n -1.20.(本小题满分12分)十九大指出中国的电动汽车革命早已展开,通过以新能源汽车替代汽、柴油车,中国正在大力实施一项将重塑全球汽车行业的计划.2018年某企业计划引进新能源汽车生产设备,通过市场分析,全年需投入固定成本2 500万元,每生产汽车x (百辆),需另投入成本C (x )(万元),且C (x )=⎩⎪⎨⎪⎧10x 2+100x ,0<x <40,501x +10 000x -4 500,x ≥40.由市场调研知,每辆车售价5万元,且全年内生产的车辆当年能全部销售完.(1)求出2018年的利润L (x )(万元)关于年产量x (百辆)的函数关系式;(利润=销售额-成本)(2)2018年产量为多少百辆时,企业所获利润最大,并求出最大利润.解:(1)当0<x <40时,L (x )=5×100x -10x 2-100x -2 500=-10x 2+400x -2 500; 当x ≥40时,L (x )=5×100x -501x -10 000x+4 500-2 500=2 000-⎝⎛⎭⎫x +10 000x . ∴L (x )=⎩⎪⎨⎪⎧-10x 2+400x -2 500,0<x <40,2 000-⎝⎛⎭⎫x +10 000x ,x ≥40. (2)当0<x <40时,L (x )=-10(x -20)2+1 500, ∴当x =20时,L (x )max =L (20)=1 500;当x ≥40时,L (x )=2 000-⎝⎛⎭⎫x +10 000x ≤2 000-2 x ·10 000x =2 000-200=1 800,当且仅当x =10 000x ,即x =100时,L (x )max =L (100)=1 800>1 500.∴当x =100时,即2018年生产100百辆时,该企业获得利润最大,且最大利润为1 800万元.21.(本小题满分12分)在△ABC 中,BC =6,点D 在BC 边上,且(2AC -AB )cos A =BC cos C .(1)求角A 的大小;(2)若AD 为△ABC 的中线,且AC =23,求AD 的长;(3)若AD 为△ABC 的高,且AD =33,求证:△ABC 为等边三角形.解:(1)由(2AC -AB )cos A =BC cos C 及正弦定理,有(2sin B -sin C )cos A =sin A cos C , 得2sin B cos A =sin C cos A +sin A cos C =sin(A +C )=sin B ,所以cos A =12.因为0°<A <180°,所以A =60°.(2)由正弦定理BC sin A =AC sin B ,得sin B =AC sin A BC =12.因为A +B <180°,所以B =30°,所以C =90°. 因为D 是BC 的中点,所以DC =3, 由勾股定理,得AD =AC 2+DC 2=21. (3)证明:因为12AD ·BC =12AB ·AC sin A ,且AD =33,BC =6,sin A =32, 所以AB ·AC =36.因为BC 2=AB 2+AC 2-2AB ·AC cos A , 所以AB 2+AC 2=72, 所以AB =AC =6=BC , 所以△ABC 为等边三角形.22.(本小题满分12分)已知数列{a n }的前n 项和S n 和通项a n 满足2S n +a n =1,数列{b n }中,b 1=1,b 2=12,2b n +1=1b n +1b n +2(n ∈N *).(1)求数列{a n },{b n }的通项公式;(2)数列{c n }满足c n =a n b n ,求证:c 1+c 2+c 3+…+c n <34.解:(1)由2S n +a n =1,得S n =12(1-a n ).当n ≥2时,a n =S n -S n -1=12(1-a n )-12(1-a n -1)=-12a n +12a n -1,即2a n =-a n +a n -1,∴a n a n -1=13(由题意可知a n -1≠0). ∴{a n }是公比为13的等比数列,而S 1=a 1=12(1-a 1),∴a 1=13,∴a n =13×⎝⎛⎭⎫13n -1=⎝⎛⎭⎫13n.由2b n +1=1b n +1b n +2,1b 1=1,1b 2=2,得d =1b 2-1b 1=1⎝⎛⎭⎫d 为等差数列⎩⎨⎧⎭⎬⎫1b n 的公差, ∴1b n =n ,∴b n =1n. (2)证明:c n =a nb n=n ⎝⎛⎭⎫13n ,设T n =c 1+c 2+…+c n ,则T n =1×⎝⎛⎭⎫131+2×⎝⎛⎭⎫132+3×⎝⎛⎭⎫133+…+n ×⎝⎛⎭⎫13n ,13T n =1×⎝⎛⎭⎫132+2×⎝⎛⎭⎫133+…+(n -1)×⎝⎛⎭⎫13n +n ×⎝⎛⎭⎫13n +1,由错位相减,得23T n =13+⎝⎛⎭⎫132+…+⎝⎛⎭⎫13n -n ×⎝⎛⎭⎫13n +1=13⎣⎡⎦⎤1-⎝⎛⎭⎫13n 1-13-n ×⎝⎛⎭⎫13n +1=12-12×⎝⎛⎭⎫13n -n ×⎝⎛⎭⎫13n +1, 所以T n =34-34×⎝⎛⎭⎫13n -12n ×⎝⎛⎭⎫13n =34-2n +34×13n <34.由Ruize收集整理。
2019-2020年苏教版高中数学必修5 期末模块综合检测卷(含答案)

模块综合检测卷(测试时间:120分钟 评价分值:150分)一、选择题(每小题共10个小题,每小题共5分,共50分,在每小题给出的四个选项中,只有一项符合题目要求)1.已知{a n }为等比数列,a 4+a 7=2,a 5a 6=-8,则a 1+a 10=(D ) A .7 B .5 C .-5 D .-7解析:∵{a n }为等比数列,∴a 4a 7=a 5a 6=-8.又a 4+a 7=2,∴⎩⎪⎨⎪⎧a 4=4,a 7=-2或⎩⎪⎨⎪⎧a 4=-2,a 7=4.当a 4=4,a 7=-2时,a 1=-8,a 10=1,∴a 1+a 10=-7; 当a 4=-2,a 7=4时,a 10=-8,a 1=1,∴a 1+a 10=-7. 综上,a 1+a 10=-7.2.某人投资10 000万元,如果年收益利率是5%,按复利计算,5年后能收回本利和为(B )A .10 000×(1+5×5%)B .10 000×(1+5%)5C .10 000×1.05×(1-1.054)1-1.05 D .10 000×1.05×(1-1.055)1-1.05解析:注意与每年投入10 000万元区别开来.3.在△ABC 中,已知cos A =513,sin B =35,则cos C 的值为(A )A.1665B.5665 C.1665或5665 D .-1665解析:∵cos A =513>0,∴sin A =1213>sin B =35.∴B 为锐角,故cos B =45.从而cos C =-cos(A +B )=-cos A cos B +sin A sin B =1665.4.若a <b <0,d >c >0,则不等式①ad >bc ;②c a >cb;③a 2>b 2;④a -d <b -c 中正确的个数是(C )A .1个B .2个C .3个D .4个解析:①错,②③④正确.将a <b <0转化为-a >-b >0,可得(-ad )>(-bc ),即ad <bc ,故知①错;由a <b <0⇒1a >1b,c >0,故②正确;因为函数y =x 2在(-∞,0)上单调递减,故③正确;由d >c >0,得-d <-c <0,故知a -d <b -c ,故④正确.5.设x ,y ∈R +,且xy -(x +y )=1,下列结论中正确的是(A ) A .x +y ≥22+2 B .xy ≤2+1 C .x +y ≤(2+1)2D .xy ≥22+2解析:∵1+x +y =xy ≤⎝ ⎛⎭⎪⎫x +y 22,∴(x +y )2-4(x +y )-4≥0.即x +y ≥2(1+2)(当x=y =1+2时等号成立),x +y 的最小值为2(1+2).6.数列{a n }的通项公式为a n =n cos n π2,其前n 项和为S n ,则S 2 015等于(D )A .1 006B .1 008C .-1 006D .-1 008 解析:由a n =n cosn π2可得S 2 015=1×0-2×1+3×0+4×1+…-2 014×1+2 015×0=-2+4-6+…-2 010+2 012-2 014=2×503-2 014=-1 008.7.已知方程x 2+(m +2)x +m +5=0有两个正实根,则实数m 的取值范围是(D ) A .(-∞,-2) B .(-∞,-4] C .(-5,+∞) D .(-5,-4] 解析:方程两根为正,则 ⎩⎪⎨⎪⎧Δ≥0,-(m +2)>0,⇒-5<m ≤-4m +5>0. 8.已知-1<a +b <3且2<a -b <4,则2a +3b 的取值范围是(D)A.⎝ ⎛⎭⎪⎫-132,172B.⎝ ⎛⎭⎪⎫-72,112C.⎝ ⎛⎭⎪⎫-72,132D.⎝ ⎛⎭⎪⎫-92,132 解析:用待定系数法可得 2a +3b =52(a +b )-12(a -b ),由⎩⎪⎨⎪⎧-1<a +b <3,2<a -b <4⇒⎩⎪⎨⎪⎧-52<52(a +b )<152,-2<-12(a -b )<-1. 两式相加即得-92<2a +3b <132.9.已知锐角三角形的边长分别是2,3,x ,则x 的取值范围是(B ) A .(1,3) B .(5,13) C .(0,5) D .(13,5)解析:由三角形的三个角为锐角,结合余弦定理的推论可知,⎩⎪⎨⎪⎧22+32-x 2>0,22+x 2-32>0,32+x 2-22>0,解得5<x 2<13,即5<x < 13.10.已知函数f (x )=ax 2+2ax +4(a >0),若x 1<x 2,x 1+x 2=0,则(A ) A .f (x 1)<f (x 2) B .f (x 1)=f (x 2)C .f (x 1)>f (x 2)D .f (x 1)与f (x 2)的大小不能确定解析:函数f (x )=ax 2+2ax +4(a >0),二次函数的图象开口向上,对称轴为x =-1,a >0,又∵x 1+x 2=0,x 1与x 2的中点为0,x 1<x 2,∴x 2到对称轴的距离大于x 1到对称轴的距离.∴f (x 1)<f (x 2),故选A.二、填空题(本大题共4小题,每小题5分,共20分,把答案填在题中横线上) 11.(2013·新课标全国卷Ⅰ)已知锐角△ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,23cos 2A +cos 2A =0,a =7,c =6,则b =________.解析:先求出角A 的余弦值,再利用余弦定理求解. 由23cos 2A +cos 2A =0得23cos 2A +2cos 2A -1=0, 解得cos A =±15.∵A 是锐角,∴cos A =15.又a 2=b 2+c 2-2bc cos A , ∴49=b 2+36-2×b ×6×15.∴b =5或b =-135.又∵b >0,∴b =5. 答案:512.(2013·陕西卷)观察下列等式:12=1,12-22=-3,12-22+32=6,12-22+32-42=-10,…,照此规律,第n 个等式可为____________.解析:当n 为偶数时,(12-22)+(32-42)+…+[(n -1)2-n 2]=-n (n +1)2;当n 为奇数时,(12-22)+(32-42)+…+[(n -2)2-(n -1)2]+n 2=-(n -1)n 2+n 2=n (n +1)2.答案:12-22+32-42+…+(-1)n +1n 2=(-1)n +1n (n +1)213.若变量x ,y 满足约束条件⎩⎪⎨⎪⎧y ≤1,x +y ≥0,x -y -2≤0,则z =x -2y 的最大值为________.解析:作出可行域(如图),由z =x -2y 得y =12x -z2,则当目标函数过C (1,-1)时z取得最大值,所以z max =1-2×(-1)=3.答案:314.若a >b >0,m >0,n >0,则b a ,a b ,b +m a +m ,a +nb +n由大到小的顺序是__________________________.解析:用特殊值法或作差比较法都很容易得出答案. 答案:a b >a +nb +n >b +m a +m >ba三、解答题(本题共6小题,共80分.解答题应写出文字说明、证明过程或推演步骤) 15.(本小题满分12分)等差数列{}a n 不是常数列,a 5=10,且a 5,a 7,a 10是某一等比数列{}b n 的第1,3,5项.(1)求数列{}a n 的第20项; (2)求数列{}b n 的通项公式.解析:(1)设数列{}a n 的公差为d ,则a 5=10,a 7=10+2d ,a 10=10+5d . 因为等比数列{}b n 的第1、3、5项成等比数列, 所以a 27=a 5a 10,即(10+2d )2=10(10+5d ). 解得d =2.5,d =0(舍去). 所以a 20=47.5.(2)由(1)知{}a n 为各项非负的数列,所以q 2=b 3b 1=a 7a 5=32.∴q =±32.又b 1=a 5=10, ∴b n =b 1q n -1=±10·⎝ ⎛⎭⎪⎫32n -12,n ∈N *.16.(本小题满分12分)(2013·北京卷)在△ABC 中,a =3,b =26,∠B =2∠A . (1)求cos A 的值; (2)求c 的值.解析:(1)由正弦定理得: 3sin A =26sin 2A ,解得cos A =63. (2)由cos A =63⇒sin A =33,又∠B =2∠A , ∴cos B =2cos 2A -1=13.∴sinB =223,sin C =sin(A +B )=sin A cos B +cos A sin B =33×13+63×223=539. ∴c =a sin Csin A=5. 17.(本小题满分14分)已知关于x 的不等式ax 2+2x +c >0的解集为⎝ ⎛⎭⎪⎫-13,12,求-cx 2+2x -a >0的解集.解析:由ax 2+2x +c >0的解集为⎝ ⎛⎭⎪⎫-13,12知a <0,-13和12是方程ax 2+2x +c =0的两个根,由韦达定理-13+12=-2a ,-13×12=c a ,解得a =-12,c =2,∴-cx 2+2x -a >0,即-2x 2+2x +12>0亦即x 2-x -6<0.其解集为(-2,3).18.(本小题满分14分)某营养师要为某个儿童预订午餐和晚餐.已知一个单位的午餐含12个单位的碳水化合物、6个单位的蛋白质和6个单位的维生素C ;一个单位的晚餐含8个单位的碳水化合物、6个单位的蛋白质和10个单位的维生素C.另外,该儿童这两餐需要的营养中至少含64个单位的碳水化合物、42个单位的蛋白质和54个单位的维生素C.如果一个单位的午餐、晚餐的费用分别是2.5元和4元,那么要满足上述的营养要求,并且花费最少,应当为该儿童分别预订多少个单位的午餐和晚餐?解析:方法一 设需要预订满足要求的午餐和晚餐分别为x 个单位和y 个单位,所花的费用为z 元,则依题意得:z =2.5x +4y ,且x ,y 满足⎩⎪⎨⎪⎧x ≥0,y ≥0,12x +8y ≥64,6x +6y ≥42,6x +10y ≥54, 即⎩⎪⎨⎪⎧x ≥0,y ≥0,3x +2y ≥16,x +y ≥7,3x +5y ≥27.z 在可行域的四个顶点A (9,0),B (4,3),C (2,5),D (0,8)处的值分别是 z A =2.5×9+4×0=22.5, z B =2.5×4+4×3=22, z C =2.5×2+4×5=25, z D =2.5×0+4×8=32.比较之,z B 最小,因此,应当为该儿童预订4个单位的午餐和3个单位的晚餐,就可满足要求.方法二 设需要预订满足要求的午餐和晚餐分别为x 个单位和y 个单位,所花的费用为z 元,则依题意得z =2.5x +4y ,且x ,y 满足⎩⎪⎨⎪⎧x ≥0,y ≥0,12x +8y ≥64,6x +6y ≥42,6x +10y ≥54,即⎩⎪⎨⎪⎧x ≥0,y ≥0,3x +2y ≥16,x +y ≥7,3x +5y ≥27.作出平行域如下图所示.让目标函数表示的直线2.5x+4y=z在可行域上平移,由此可知z=2.5x+4y在B(4,3)处取得最小值.因此,应当为该儿童预订4个单位的午餐和3个单位的晚餐,就可满足要求.19.(本小题满分14分)如右图,某观测站C在城A南偏西20°的方向上,由A城出发有一条公路,走向是南偏东40°,在C处测得距C为31千米的公路上B处有一人正沿公路向A城走去,走了20千米后,到达D处,此时C、D间距离为21千米,问这人还需走多少千米到达A城?解析:根据题意,可得下图,其中BC =31千米,BD =20千米,CD =21千米,∠CAD =60°.设∠ACD =α,∠CDB =β. 在△CDB 中,由余弦定理得:cos β=CD 2+BD 2-BC 22CD ·BD =212+202-3122×21×20=-17,sin β=1-cos 2β=437. sin α=sin(180°-∠CAD -∠CDA ) =sin(180°-60°-180°+β) =sin(β-60°)=sin βcos 60°-cos βsin 60° =437×12+17×32=5314.在△ACD 中,由正弦定理得:AD =CDsin A ·sin α=21sin 60°×5314=15. 此人还得走15千米到达A 城.20.(本小题满分14分)数列{a n }中,a 1=8,a 4=2且满足a n +2=2a n +1-a n ,n ∈N *. (1)求数列{a n }的通项公式;(2)设S n =|a 1|+|a 2|+…+|a n |,求S n ; (3)设b n =1n (12-a n )(n ∈N *),T n =b 1+b 2+…+b n (n ∈N *),是否存在最大的整数m ,使得对任意n ∈N *,均有T n >m32成立?若存在,求出m 的值;若不存在,请说明理由.解析:(1)由a n +2=2a n +1-a n ⇒a n +2-a n +1=a n +1-a n , 可知{a n }成等差数列,d =a 4-a 14-1=-2,∴a n =8+(n -1)·(-2)=10-2n (n ∈N). (2)由a n =10-2n ≥0得n ≤5,∴当n ≤5时,S n =-n 2+9n .当n >5时,S n =|a 1|+|a 2|+…+|a n |=a 1+a 2+…+a 5-a 6-a 7-…-a n =2(a 1+a 2+…+a 5)-(a 1+a 2+…+a n ) =n 2-9n +40.故S n =⎩⎪⎨⎪⎧-n 2+9n ,1≤n ≤5,n 2-9n +40,n ≥5.(3)b n =1n (12-a n )=1n (2n +2)=12⎝ ⎛⎭⎪⎫1n -1n +1.∴T n =b 1+b 2+…+b n=12⎣⎢⎡⎝ ⎛⎭⎪⎫1-12+⎝ ⎛⎭⎪⎫12-13+⎝ ⎛⎭⎪⎫13-14+…+⎦⎥⎤⎝ ⎛⎭⎪⎫1n -1-1n +⎝ ⎛⎭⎪⎫1n -1n +1 =12⎝ ⎛⎭⎪⎫1-1n +1=n 2(n +1)>n -12n =T n -1>T n -2>…T 1.∴要使T n >m 32总成立,需m 32<T 1=14恒成立,即m <8(m ∈Z).故适合条件的m 的最大值为。
高中数学苏教版必修5模块综合测评含解析

模块综合测评(时间120分钟,满分160分)一、填空题(本大题共14小题,每小题5分,共70分.请把答案填在题中的横线上)1.在△ABC 中,a ,b ,c 所对的角分别为A ,B ,C ,若a =2,A =π4,B =π6,则b 等于________.【解析】 由正弦定理得b =asin Bsin A=2×1222= 2.【答案】 22.已知等比数列{a n }的公比q 为正数,且a 5·a 7=4a 24,a 2=1,则a 1=________. 【解析】 ∵{a n }成等比数列,∴a 5·a 7=a 26,∴a 26=4a 24,∴q 2=4,∴q =±2. 又q>0,∴q =2. ∴a 1=a 2q =12.【答案】123.设x>0,y>0,下列不等式中等号不成立的是________. ①x +y +2xy≥4;②(x +y)⎝ ⎛⎭⎪⎫1x +1y ≥4;③⎝ ⎛⎭⎪⎫x +1x ⎝ ⎛⎭⎪⎫y +1y ≥4;④x 2+3x 2+2≥2.【解析】 ④中,x 2+3x 2+2=x 2+2+1x 2+2.因为x 2+2≥2,故应用不等式时,等号不成立. 【答案】 ④4.等差数列{a n }满足a 24+a 27+2a 4a 7=9,则其前10项之和为________.【解析】由a24+a27+2a4a7=9,可知a4+a7=±3.∴S10=10(a1+a10)2=10(a4+a7)2=±15.【答案】±155.已知点A(3,-1),B(-1,2)在直线ax+2y-1=0的同侧,则实数a的取值范围为________.【解析】由题意可知,(3a-3)(-a+3)>0,即(a-1)(a-3)<0,∴1<a<3.【答案】(1,3)6.已知2a+1<0,关于x的不等式x2-4ax-5a2>0的解集是________.【解析】x2-4ax-5a2>0,即(x-5a)(x+a)>0,而方程(x-5a)(x+a)=0的根为x1=-a,x2=5a.∵2a+1<0,则a<-12,∴-a>5a,∴原不等式的解集为{x|x<5a或x>-a}.【答案】{x|x<5a或x>-a}7.在△ABC中,内角A,B,C的对边分别为a,b,c,若a,b,c,成等比数列,且c=2a,则cos B=________.【解析】由已知可知b2=ac.又c=2a,∴cos B=a2+c2-b22ac=a2+4a2-b22ac=a2+4a2-2a24a2=34.【答案】3 48.(2016·南通高二检测)已知数列1,a1,a2,4等差数列,且实数列1,b1,b 2,b3,4成等比数列,则a1+a2b2的值为________.【91730077】【解析】∵a1+a2=1+4=5,b22=1×4=4,但b2=1×q2>0,∴b 2=2,故a 1+a 2b 2=52. 【答案】529.台风中心从A 地以20 km/h 的速度向东北方向移动,离台风中心30 km 内的地区为危险区,城市B 在A 的正东40 km 处,B 城市处于危险区内持续的时间为________小时.【解析】 设t 小时后,B 市处于危险区内,则由余弦定理得(20t)2+402-2×20t ×40cos 45°≤302.化简得4t 2-82t +7≤0,∴t 1+t 2=22,t 1·t 2=74.从而|t 1-t 2|=(t 1+t 2)2-4t 1t 2=1. 【答案】 110.设x ,y 满足约束条件⎩⎨⎧x +2y ≤4,x -y ≤1,x +2≥0,则目标函数z =3x -y 的最大值为________.【解析】 首先画出线性约束条件⎩⎨⎧x +2y ≤4,x -y ≤1,x +2≥0的可行域(如图阴影部分),是一个三角形,然后在可行域内平行移动目标函数z =3x -y ,当经过x +2y =4与x -y =1的交点(2,1)时,目标函数取得最大值z =3×2-1=5.【答案】 511.已知数列{a n }:12,13+23,14+24+34,15+25+35+45,…,那么数列⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫1a n a n +1的前n 项和为________.。
苏教版高中数学必修五测试题全套带答案.docx

最新苏教版高中数学必修五测试题全套带答案模块综合测评(时间120分钟,满分160分)一、填空题(本大题共14小题,每小题5分,共70分•请把答案填在题中的横线上)TT 7T1.在£\ABC 中,a,b,c 所对的角分别为C,若则b 等于 ______________________________.2X 丄【解析】 由正弦定理得b =豊晋=话 =©2【答案】^22. ________________________________________________________ 已知等比数列{a”}的公比g 为正数,且05应7 = 4必 血=1,贝Uai= _______________ • 【解析】T {a”}成等比数列, ・•.血5二尿, ••- dg 二 4^4 !• •孑=4 ]:・ q = ±2.又 q>0 ,:・q 二 2. ・ °2 1 ・・©二严. 【答案】I3. ________________________________________ 设兀>0,尹>0,下列不等式中等号不成立的是 __________________________________________②(*+叨1+册4;因为毎刁上2 ,故应用不等式时,等号不成立. 【答案】④4. ___________________________________________________ 等差数列仪”}满足a ;+t^+2<24Q7 = 9,则其前10项之和为 ___________________________【解析】 由 «4 + «7 + 2fl4«7 = 9,可知 04 + ^7 = ±3. . 10(如 + <710) 10(血 + 07)丄仁 • •510 — r\ 一 ° 一 ±13.x 2+ 3 【解析】④中,主壬=归花+:7^眉®x+y24;【答案】±155. __ 已知点A (3, -1), 5(-1,2)在直线ax+2y~1^0的同侧,则实数a 的取值范围 为__________ •【解析】由题意可知, (3。
高中数学苏教版必修5模块综合检测B

模块综合检测(B)(时间:120分钟 满分:160分)一、填空题(本大题共14小题,每小题5分,共70分)1.已知等比数列{a n }的前n 项和S n =x ·3n -1-16,则x =________.2.已知等比数列{a n }的公比为正数,且a 3·a 9=2a 25,a 2=1,则a 1=________.3.在△ABC 中,已知sin 2B -sin 2C -sin 2A =3sin A sin C ,则角B 的大小为________.4.关于x 的不等式ax -b >0的解集是(1,+∞),则关于x 的不等式ax +bx -2≤0的解集是________.5.设x ,y 满足约束条件⎩⎪⎨⎪⎧x +2y ≤4,x -y ≤1,x +2≥0,则目标函数z =3x -y 的最大值为________.6.不等式2x -3x +1≤12(x >0)的解为______________.7.已知等差数列{a n }的前n 项和为S n ,且S 21=42,记A =2a 211-a 9-a 13,则A 的值为________.8.设a >0,b >0,若3是3a 与3b的等比中项,则1a +1b的最小值为________.9.在△ABC 中,A =60°,b =1,其面积为3,则a +b +csin A +sin B +sin C=________.10.已知等比数列{a n }的各项均为正数,公比q ≠1,设P =12(log 0.5a 5+log 0.5a 7),Q =log 0.5a 3+a 92,P 与Q 的大小关系是________.11.已知f (x )=32x -k ·3x+2,当x ∈R 时,f (x )恒为正值,则k 的取值范围为________.12.已知数列{a n }满足a 1=33,a n +1-a n =2n ,则a nn的最小值为________.13.设实数x ,y 满足⎩⎪⎨⎪⎧x -y -2≤0,x +2y -5≥0,y -2≤0,则u =x 2+y 2xy的取值范围是________.14.在△ABC 中,A 、B 、C 分别为a 、b 、c 边所对的角.若a 、b 、c 成等差数列,则B 的取值范围是________. 二、解答题15.(14分)记等差数列{}a n 的前n 项和为S n ,设S 3=12,且2a 1,a 2,a 3+1成等比数列,求S n .16.(14分)在△ABC 中,a 、b 、c 分别为∠A 、∠B 、∠C 的对边,若2b =a +c ,∠B =30°,△ABC 的面积为32,求b .17.(14分)已知a 、b 、c 都是实数,求证:a 2+b 2+c 2≥a +b +c 23.。
苏教版高中数学必修五模块综合检测卷

高中数学学习资料金戈铁骑整理制作模块综合检测卷(测试时间: 120 分钟评论分值:150分)一、选择题 (每题共 10 个小题,每题共 5 分,共 50 分,在每题给出的四个选项中,只有一项切合题目要求 )1.已知 {a n}为等比数列, a4+a7= 2,a5a6=- 8,则 a1+a10= (D) A.7 B.5 C.- 5D.- 7分析:∵{a n}为等比数列,∴ a4a7=a5a6=- 8.又a4+a7= 2,∴a4=4,a4=- 2,或a7= 4.a7=- 2当 a4=4,a7=- 2 时, a1=- 8, a10=1,∴ a1+a10=- 7;当 a4=- 2,a7= 4 时, a10=- 8,a1=1,∴ a1+a10=- 7.综上, a1+a10=- 7.2.某人投资 10 000 万元,假如年利润利率是5% ,按复利计算,5 年后能回收本利和为 (B)A .10 000×(1+5×5%)B . 10 000× (1+5%)5C .10 000××( 1-4)D .10 000××( 1-5)1-1-分析:注意与每年投入 10 000 万元差别开来.533.在△ ABC 中,已知 cosA =13,sin B =5,则 cosC 的值为 (A)1656A.65B.6516 56 16C.65或65D .- 65512 3分析: ∵cosA =13>0,∴ sin A =13>sin B =5.∴B 为锐角,故 cosB =4进而 =- + =-5.cosC cos(A B) cos Acos16B + sin Asin B = 65.4.若 a<b<0,d>c>0,则不等式① ad>bc ;②a c >cb ;③ a 2>b 2;④ a-d<b -c 中正确的个数是 (C)A .1 个B .2 个C .3 个D .4 个分析:①错,②③④正确. 将 a<b<0 转变为- a>-b>0,可得 (-1 1ad)>(-bc),即 ad<bc ,故知 ①错;由 a<b<0? a >b ,c>0,故 ②正确;由于函数 y =x 2 在(-∞,0)上单一递减,故 ③正确;由 d>c>0,得-d<-c<0,故知 a -d<b -c ,故 ④正确.+5.设 x ,y ∈R ,且 xy -(x +y)=1,以下结论中正确的选项是 (A)C.x+y≤( 2+1)2D.xy≥2 2+2分析:∵1+x+y=xy≤x+y 2,∴ (x+ y)2-4(x+ y)-4≥0.即 x 2+y≥2(1+2)(当 x=y=1+ 2等号建立 ),x+ y 的最小 2(1+2).nπ6.数列 {a n}的通公式a n=ncos 2,其前n和S n,S2 015等于 (D)A.1 006 B.1 008C.- 1 006 D.- 1 008nπ分析:由 a n= ncos 2 可得S2 015=1×0-2×1+3×0+ 4×1+⋯-2 014×1+2 015×0=-2+4-6+⋯-2 010+2 012-2 014=2×503-2 014=- 1 008.7.已知方程 x2+(m+2)x+m+5=0 有两个正根,数m 的取范是 (D)A.(-∞,- 2) B.(-∞,- 4]C.(-5,+∞ ) D.(-5,- 4]分析:方程两根正,Δ≥0,-( m+2)>0,?-5<m≤-4.m+5>08.已知- 1<a+b<3 且 2<a-b<4, 2a+3b 的取范是(D)A. -13,17B. -7,11 2222C. -7,13D. -9,132222分析:用待定系数法可得512a+3b=2(a+b)-2(a-b),-1<a+b< 3,-5<5(a+b)<15,2 22由<-<?12 a b 4-2<-2(a- b)<- 1.913两式相加即得-2<2a+3b<2 .9.已知锐角三角形的边长分别是2,3,x,则 x 的取值范围是(B)A.(1,3) B.( 5,13) C.(0, 5) D.( 13,5)分析:由三角形的三个角为锐角,联合余弦定理的推论可知,22+32- x2>0,22+x2- 32>0,解得 5< x2<13,即 5<x<13.32+x2- 22>0,10.已知函数 f(x)=ax2+2ax+ 4(a>0),若 x1<x2,x1+x2= 0,则(A)A.f(x1)<f(x2) B.f(x1)=f(x2)C.f(x1)>f(x2) D.f(x1)与 f(x2)的大小不可以确立分析:函数 f(x)=ax2+2ax+4(a>0),二次函数的图象张口向上,对称轴为 x=- 1,a>0,又∵ x1+ x2=0,x1与 x2的中点为 0,x1<x2,∴x2到称的距离大于 x1到称的距离.∴ f(x1)<f(x2),故 A. 二、填空(本大共 4 小,每小 5 分,共 20 分,把答案填在中横上 )11.(2013 ·新全国卷Ⅰ)已知角△ ABC 的内角 A,B,C 的2分 a,b,c,23cosA+cos 2A=0,a=7,c=6, b=________.分析:先求出角 A 的余弦,再利用余弦定理求解.2+=得2+2-=,由 23cosA cos 2A 023cosA2cosA 101解得 cosA=±.51∵A 是角,∴ cosA=5.又 a2=b2+c2-2bccosA,∴49=b2+36- 2×b×6×1 5.13∴b=5 或 b=-5 .又∵b> 0,∴ b=5.答案:512. (2013 · 西卷 )察以下等式: 12= 1,12-22=- 3,12-22+32= 6,12-22+32- 42=- 10,⋯,照此律,第n 个等式可____________.分析:当 n 偶数, (12-22)+(32-42+⋯+-2-n2]=)[(n1)-n(n+1);2当 n 奇数, (12-22)+(32-42)+⋯+[(n-2)2-(n-1)2]+n2(n -1)n2n (+ )=-n1.2+n =2答案: 12-22+ 32-42+⋯+ (-1)n +1n 2=(-1)n +1n ( n +1)2y ≤1,.若 量 x , y 足 束条件x +y ≥0,= - 2y 的最13z xx -y -2≤0,大 ________.分析:作出可行域 (如 ),由 z =x - 2y 得 y =12x -2z, 当目函数 C(1,- 1)z 获得最大 ,所以z max =1-2×(-1)=3.答案:314.若b a b +m a + na >b >0,m >0,n >0, a ,b ,a +m ,b + n 由大到小的 序是.分析:用特别 法或作差比 法都很简单得出答案.a a +nb +m b答案: b>b +n>a +m>a三、解答 (本 共 6 小 ,共 80 分.解答 写出文字 明、证明过程或推演步骤 )15.(本小题满分 12 分)等差数列{a n}不是常数列, a5= 10,且 a5,a7,a10是某一等比数列{b n}的第 1,3, 5 项.(1)求数列{a n}的第 20 项;(2)求数列{b n}的通项公式.分析:(1)设数列{a n}的公差为 d,则 a5=10,a7=10+2d,a10=10+5d.由于等比数列 {b n}的第1、3、5项成等比数列,所以 a72= a5a10,即 (10+2d)2=10(10+5d).解得 d=,d= 0(舍去 ).所以 a20=47.5.(2)由 (1)知{a n}为各项非负的数列,所以2b3a73q=b1=a5=2.∴q=±3.又 b1=a5= 10,2-3 n-1∴b n=b1q n 1=±10·2,n∈ N* .216.(本小题满分12 分)(2013 北·京卷 )在△ ABC 中,a=3,b=26,∠B=2∠A.(1)求 cosA 的值;(2)求 c 的值.分析: (1)由正弦定理得:3266sin A =sin 2A,解得cosA=3.(2)由=6? sin A =3,又 ∠B =2∠ A ,cosA33212 2∴cosB =2cosA - 1=3.∴ sin B = 3 ,sin C =sin(A +B)=sin Acos B +cos Asin B = 3 1 6 2 23 ×3+3 × 3=59 3.asin C∴c = sin A =5.17.(本小题满分 14 分)已知对于 x 的不等式 ax 2+2x +c >0 的解集为 -31,12 ,求- cx 2+2x -a >0 的解集.21 11 1分析:由 ax +2x +c > 0 的解集为 -3,2 知 a <0,-3和2是方21 1 21 1 c程 ax +2x +c =0 的两个根,由韦达定理- 3+2=-a ,- 3×2=a ,解得 a =- 12,c =2,∴- cx 2+2x -a >0,即- 2x 2+2x +12>0 亦即x 2-x -6<0.其解集为 (-2,3).18. (本小题满分 14 分 )某营养师要为某个小孩预定午饭和晚餐.已知一个单位的午饭含12 个单位的碳水化合物、 6 个单位的蛋白质和 6 个单位的维生素 C ;一个单位的晚饭含 8 个单位的碳水化合物、 6 个单位的蛋白质和 10 个单位的维生素 C.此外,该小孩这两餐需要的营养中起码含64 个单位的碳水化合物、42 个单位的蛋白质和54 个单位的维生素C.假如一个单位的午饭、晚饭的花费分别是元和 4 元,那么要知足上述的营养要求,而且花销最少,应该为该小孩分别预定多少个单位的午饭和晚饭?分析:方法一设需要预定知足要求的午饭和晚饭分别为 x 个单位和y 个单位,所花的花费为 z 元,则依题意得: z=+4y,且 x,y知足x≥0,y≥0,x≥ 0,y≥0,12x+8y≥64,3x+2y≥16,即6x+6y≥42,x+y≥7,6x+10y≥54,3x+5y≥27.z在可行域的四个极点 A(9, 0),B(4, 3),C(2,5),D(0,8)处的值分别是z A=×9+4×0=,z B=×4+4×3=22,z C=×2+4×5=25,z D=×0+ 4×8=32.比较之, z B最小,所以,应该为该小孩预定 4 个单位的午饭和3个单位的晚饭,便可知足要求.方法二设需要预定知足要求的午饭和晚饭分别为x 个单位和 y 个单位,所花的花费为 z 元,则依题意得 z=+4y,且 x,y 知足x≥0,y≥0,x≥ 0,y≥0,12x+8y≥64,3x+2y≥16,即6x+6y≥42,x+y≥7,6x+10y≥54,3x+5y≥27.作出平行域以以下图所示.让目标函数表示的直线+4y=z 在可行域上平移,由此可知z=+4y 在 B(4,3)处获得最小值.所以,应该为该小孩预定 4 个单位的午饭和 3 个单位的晚饭,就可知足要求.19.(本小题满分 14 分)如右图,某观察站 C 在城 A 南偏西 20°的方向上,由 A 城出发有一条公路,走向是南偏东40°,在C 处测得距 C 为31 千米的公路上 B 处有一人正沿公路向 A 城走去,走了20 千米后,抵达 D 处,此时 C、D 间距离为 21 千米,问这人还需走多少千米抵达 A 城?分析:依据题意,可得以下图,此中 BC = 31 千米, BD = 20 千米, CD =21 千米,∠CAD =60 ° .设∠ACD =α,∠ CDB =β.在△CDB 中,由余弦定理得:cos β= CD 2+BD 2-BC 2 212+202-312 12CD · = × × =- 7,BD 2 21 202 4 3sin β= 1-cos β= 7 .sin α=sin(180°- ∠CAD -∠CDA)=sin(180°- 60°- 180°+ β)= s in(β-60°)=sin βcos 60°- cos βsin 60°4 3 1 1 3= 7 ×2+7×25 3= 14 .在△ACD 中,由正弦定理得:CD 215 3AD =sin A ·sin α= °× 14 = 15.sin 60这人得走 15 千米抵达 A 城.20.(本小分 14 分)数列 {a n}中, a1=8,a4=2 且足 a n+2=2a n+1-a n, n∈N *.(1)求数列 {a n}的通公式;(2)S n =|a1+ 2 +⋯+n,求S n;||a ||a |(3)b n =1∈ *,T n=b1+b2+⋯+ b n∈*,是n(12-a n)(n N )(n N )否存在最大的整数m,使得随意 n∈N*,均有 T n>m建立?若存32在,求出 m 的;若不存在,明原因.分析:(1)由 a n+2=2a n+1-a n? a n+2- a n+1=a n+1-a n,a4-a1可知 {a n}成等差数列, d==-2,∴a n=8+ (n-1) ·(-2)= 10- 2n(n∈N).(2)由 a n=10-2n≥0 得 n≤5,∴当 n≤5 , S n=- n2+9n.当 n>5 ,S n=|a1|+ |a2|+⋯+|a n|=a1+a2+⋯+a5-a6-a7-⋯-a n=2(a1+a2+⋯+a5)-(a1+a2+⋯+ a n)=n2-9n+40.-n2+9n,1≤n≤5,故 S n=n2- 9n+40,n≥5.11 1 11(3)b n=n(12-a n)=n(2n+2)=2 n-n+1.∴T n=b1+ b2+⋯+b n1 1 1 1 1 1=2 1-2 + 2-3 + 3- 4 +⋯+1 1 1 1- -n + n - + 1 n 1n 1 1=2 1-n +1n )> n -1 = ( + 2n =T n -1>T n - 2>⋯T 1. 2 n 1∴要使 m T n >32 建立,需 m 1 32< T 1=4恒建立,即 m < 8(m ∈ Z).故合适条件的 m 的最大。
2019-2020学年高中数学新同步苏教版必修5模块测评

模块综合测评(满分:150分 时间:120分钟)一、选择题(本大题共12小题,每小题5分,满分60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.已知不等式ax 2+bx +2>0的解集是(-1,2),则a +b 的值为( ) A .1 B .-1 C .0D .-2C [由已知得-b a =-1+2,2a =-1×2,a <0,解得a =-1,b =1,故a +b =0,故选C.]2.已知一个等差数列{a n }的第8,9,10项分别为b -1,b +1,2b +3,则通项a n 等于( )A .2n -5B .2n -9C .2n -13D .2n -17D [依题意得2(b +1)=b -1+2b +3,解得b =0,∴d =2,a 8=-1,a n =a 8+(n -8)d =-1+(n -8)×2=2n -17.]3.在△ABC 中,已知sin A cos B =sin C =cos C ,那么△ABC 一定是( ) A .直角三角形 B .等腰三角形 C .等腰直角三角形D .正三角形C [由sin A cos B =sin C 及正、余弦定理得a ·a 2+c 2-b 22ac =c ,可得b 2+c 2=a 2,即A =90°,由sin C =cos C 得C =45°.故△ABC 为等腰直角三角形.]4.在等差数列{a n }中,若a 4+a 5+a 6+a 7+a 8=450,则a 4+a 8的值为( ) A .45 B .75 C .180D .300C [a 4+a 5+a 6+a 7+a 8=(a 4+a 8)+(a 5+a 7)+a 6=5a 6=450,∴a 6=90. ∴a 4+a 8=2a 6=2×90=180.]5.下列不等式中,恒成立的是( ) A .x +1x ≥2(x ≠0) B .x 2-2x -3>0 C.2x 2-x +2x 2-x +1>1 D .log 12(x 2+1)≥0C [当x <0时,x +1x ≥2不成立;当-1≤x ≤3时,不等式x 2-2x -3>0不成立;因为x 2+1≥1,则log 12(x 2+1)≤log 121=0,故D 项不成立;由于x 2-x +1>0,不等式等价于2x 2-x +2>x 2-x +1,即x 2+1>0,故C 项正确.]6.已知a >0,b >0,a +b =2,则y =1a +4b 的最小值是( ) A.72 B .4 C.92D .5C [∵2y =2⎝ ⎛⎭⎪⎫1a +4b =(a +b )⎝ ⎛⎭⎪⎫1a +4b =5+4a b +b a ,又∵a >0,b >0,∴2y ≥5+24a b ·ba =9,∴y min =92,当且仅当b =2a 时“=”成立.]7.已知△ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,且c -b c -a =sin Asin C +sin B ,则B =( )A.π6B.π4C.π3D.3π4C [因为c -bc -a =sin A sin C +sin B ,所以c -b c -a =ac +b ,即(c -b )·(c +b )=a (c -a ),所以a 2+c 2-b 2=ac ,所以cos B =12,又B ∈(0,π),所以B =π3.]8.如果数列{a n }满足a 1=2,a 2=1,且a n -1-a n a n -1=a n -a n +1a n +1(n ≥2),则这个数列的第10项等于( )A.1210B.129C.110D.15D [当n ≥2时,由已知得1-a n a n -1=a na n +1-1,∴2=a na n -1+a n a n +1,∴2a n =1a n -1+1a n +1,∴数列⎩⎨⎧⎭⎬⎫1a n 是等差数列,又∵a 1=2,a 2=1,∴1a 1=12,1a 2=1,d =1a 2-1a 1=12,∴1a n=n 2,∴a n =2n ,∴a 10=210=15.]9.若关于x 的不等式x 2+ax -a -2>0和2x 2+2(2a +1)x +4a 2+1>0的解集依次为A 和B ,那么,使得A =R 和B =R 至少有一个成立的实常数a ( )A .可以是R 中的任何一个数B .有无穷多个,但并不是R 中所有的实数都能满足要求C .有且仅有一个D .不存在B [若A =R ,则Δ1=a 2+4(a +2)<0成立,显然是不可能的,即这样的a ∈∅;若B =R ,则Δ2=4(2a +1)2-8(4a 2+1)<0成立,即(2a -1)2>0,因而存在无穷多个实常数a ,当a =12时,上述不等式不成立,从而选B.]10.已知不等式x 2-ax +a -2>0的解集为(-∞,x 1)∪(x 2,+∞),其中x 1<0<x 2,则x 1+x 2+2x 1+2x 2的最大值为( )A.32 B .0 C .2D .-32B [不等式x 2-ax +a -2>0的解集为(-∞,x 1)∪(x 2,+∞),其中x 1<0<x 2,所以x 1+x 2=a ,x 1x 2=a -2<0,所以x 1+x 2+2x 1+2x 2=(x 1+x 2)+2(x 1+x 2)x 1x 2=a +2a a -2=a +2a -4+4a -2=a +2+4a -2=(a -2)+4a -2+4;又a -2<0,所以-(a -2)>0, 所以-(a -2)-4a -2≥2-(a -2)×⎝ ⎛⎭⎪⎫-4a -2=4, 当且仅当-(a -2)=-4a -2,即a =0时,取“=”.所以(a -2)+4a -2+4≤-4+4=0, 即x 1+x 2+2x 1+2x 2的最大值为0.]11.若直线ax +2by -2=0(a ,b ∈R +)始终平分圆x 2+y 2-4x -2y -8=0的周长,则1a +2b 的最小值为( )A .1B .5C .4 2D .3+2 2D [∵直线平分圆, ∴直线过圆心(2,1),即2a +2b -2=0,a +b =1,1a +2b =a +b a +2a +2b b =3+b a +2ab ≥3+2 2.] 12.如图所示,一货轮航行到M 处,测得灯塔S 在货轮的北偏东15°,且货轮与灯塔S 相距20海里,货轮按北偏西30°的方向航行30分钟后,又测得灯塔在货轮的东北方向,则货轮的速度为( )A .20(2+6)海里/小时B .20(6-2)海里 /小时C .20(3+6)海里/小时D .20(6-3)海里/小时B [设货轮的速度为v 海里/小时,∠NMS =45°,∠MNS =105°,则∠MSN =30°,由MS =20,MN =v 2,则v2sin 30°=20sin 105°,v =20sin 105°=20(6-2).]二、填空题(每小题5分,共20分,把答案填在题中横线上)13.已知x >1,y >1,且ln x,1,ln y 成等差数列,则x +y 的最小值为________. 2e [由已知ln x +ln y =2, ∴xy =e 2,x +y ≥2xy =2e.当且仅当x =y =e 时取“=”,∴x +y 的最小值为2e.]14.已知{a n }是等差数列,S n 为其前n 项和,n ∈N +,若a 3=16,S 20=20,则S 10的值为________.110 [设等差数列{a n }的首项为a 1,公差为d ,则a 3=a 1+2d =16,S 20=20a 1+20×192d =20,∴⎩⎪⎨⎪⎧a 1+2d =162a 1+19d =2,解得d =-2,a 1=20.∴S 10=10a 1+10×92d =200-90=110.]15.在△ABC 中,已知|AB →|=4,|AC →|=1,S △ABC =3,则AB →·AC →的值为________. 2或-2 [∵S △ABC =12|AB →||AC →|·sin A =12×4×1×sin A =3,∴sin A =32.∴cos A =12或-12. ∵AB →·AC →=|AB →|·|AC →|·cos A , ∴AB →·AC →=2或-2.]16.某公司一年购买某种货物400吨,每次都购买x 吨,运费为4万元/次,一年的总存储费用为4x 万元,要使一年的总运费与总存储费用之和最小,则x =________吨.20 [设一年的总费用为y 万元,则y =4×400x +4x =1 600x +4x ≥2 1 600x ·4x =160.当且仅当1 600x =4x ,即x =20时,等号成立.]三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤)17.(本小题满分10分)在△ABC 中,cos A =-513,cos B =35. (1)求sin C 的值;(2)设BC =5,求△ABC 的面积.[解] (1)由cos A =-513,得sin A =1213,由cos B =35,得sin B =45. ∴sin C =sin(A +B )=sin A cos B +cos A sin B =1213×35+⎝ ⎛⎭⎪⎫-513×45=1665.(2)由正弦定理得AC =BC ·sin B sin A =5×451213=133.∴△ABC 的面积S =12·BC ·AC ·sin C =12×5×133×1665=83.18.(本小题满分12分)已知等差数列{a n }的前n 项和为S n ,等比数列{b n }的前n 项和为T n ,a 1=-1,b 1=1,a 2+b 2=2.(1)若a 3+b 3=5,求{b n }的通项公式; (2)若T 3=21,求S 3.[解] 设{a n }的公差为d ,{b n }的公比为q ,则a n =-1+(n -1)d ,b n =q n -1. 由a 2+b 2=2得d +q =3.① (1)由a 3+b 3=5得2d +q 2=6.②联立①和②解得⎩⎪⎨⎪⎧ d =3,q =0,(舍去)或⎩⎪⎨⎪⎧d =1,q =2.所以b n =2n -1.(2)∵b 1=1,T 3=21,∴1+q +q 2=21. 解得q =4或q =-5.当q =4时,由①得d =-1,则S 3=-6; 当q =-5时,由①得d =8,则S 3=21.19.(本小题满分12分)已知f (x )=-3x 2+a (6-a )x +6. (1)解关于a 的不等式f (1)>0;(2)若不等式f (x )>b 的解集为(-1,3),求实数a ,b 的值. [解] (1)∵f (x )=-3x 2+a (6-a )x +6, ∴f (1)=-3+a (6-a )+6=-a 2+6a +3, ∴原不等式可化为a 2-6a -3<0, 解得3-23<a <3+2 3.∴原不等式的解集为{a |3-23<a <3+23}.(2)f (x )>b 的解集为(-1,3)等价于方程-3x 2+a (6-a )x +6-b =0的两根为-1,3,等价于⎩⎨⎧-1+3=a (6-a )3,-1×3=-6-b3,解得⎩⎪⎨⎪⎧a =3±3,b =-3.20.(本小题满分12分)△ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,已知2cos C (a cos B +b cos A )=c .(1)求C ;(2)若c =7,△ABC 的面积为332,求△ABC 的周长. [解] (1)由已知及正弦定理得, 2cos C (sin A cos B +sin B cos A )=sin C , 2cos C sin(A +B )=sin C . 故2sin C cos C =sin C . 可得cos C =12,所以C =π3. (2)由已知,得12ab sin C =332. 又C =π3,所以ab =6.由已知及余弦定理得,a 2+b 2-2ab cos C =7. 故a 2+b 2=13,从而(a +b )2=25.∴a +b =5. 所以△ABC 的周长为5+7.21.(本小题满分12分)已知数列{a n }满足a 1=5,a 2=5,a n +1=a n +6a n -1(n ≥2). (1)求证:{a n +1+2a n }是等比数列; (2)求数列{a n }的通项公式.[解] (1)证明:∵a n +1=a n +6a n -1(n ≥2), ∴a n +1+2a n =3a n +6a n -1=3(a n +2a n -1)(n ≥2). 又a 1=5,a 2=5,∴a 2+2a 1=15,∴a n +2a n -1≠0(n ≥2),∴a n +1+2a na n +2a n -1=3(n ≥2),∴数列{a n +1+2a n }是以15为首项,3为公比的等比数列. (2)由(1)得a n +1+2a n =15×3n -1=5×3n , 则a n +1=-2a n +5×3n , ∴a n +1-3n +1=-2(a n -3n ). 又∵a 1-3=2,∴a n -3n ≠0,∴{a n -3n }是以2为首项,-2为公比的等比数列, ∴a n -3n =2×(-2)n -1, 即a n =2×(-2)n -1+3n (n ∈N *).22.(本小题满分12分)某学校为了解决教职工的住房问题,计划征用一块土地盖一幢总建筑面积为A (m 2)的宿舍楼.已知土地的征用费为2 388元/m 2,且每层的建筑面积相同,土地的征用面积为第一层的2.5倍.经工程技术人员核算,第一、二层的建筑费用相同都为445元/m 2,以后每增高一层,其建筑费用就增加30元/m 2.试设计这幢宿舍楼的楼高层数,使总费用最少,并求出其最少费用.(总费用为建筑费用和征地费用之和)[解] 设楼高为n 层,总费用为y 元,则征地面积为2.5A n m 2,征地费用为5 970An 元,楼层建筑费用为[445+445+(445+30)+(445+30×2)+…+445+30×(n -2)]·A n =⎝ ⎛⎭⎪⎫15n +30n +400A 元,从而y =5 970A n +15nA +30A n +400A =(15n +6 000n +400)A ≥1 000A (元).当且仅当15n =6 000n ,即n =20(层)时,总费用y 最少.故当这幢宿舍楼的楼高层数为20层时,费用最少,最少总费用为1 000A 元.。
苏教版高中数学必修五综合测试(一)

高中数学学习材料 (灿若寒星 精心整理制作)高中新课标数学必修(5)综合测试(一)一、选择题:(本大题共10小题,每小题5分,共50分)1.下列四个数中,哪一个是数列{(1)n n +}中的一项 ( A )A .380B . 39C . 35D . 232.已知数列{}n a 满足12a =,110n n a a +-+=()n N *∈ ,则此数列的通项n a 等于 ( D )A .21n + B .1n + C .1n - D .3n -3.等差数列{}n a 的前m 项和为30,前2m 项和为100,则它的前3m 项和为 ( C ) A .170 B 。
190C 。
210D 。
2304.在等差数列{}n a 中,公差为d ,且1054S S =,则1a d等于 ( C ) A.14B. 8C. 12D. 4 5.在ΔABC 中,BAba tan tan 22=,则ΔABC 是( D )A .等腰三角形B .直角三角形C .等腰三角形D .等腰或直角三角形6.若数列{}n a 满足,11=a nn a a n n 11+=+,则此数列是 ( A ) A . 等差数列 B . 等比数列C . 既是等差数列又是等比数列D . 既非等差数列又非等比数列7.设S n 是等差数列{}n a 的前n 项和,若5359a a =,则95SS 的值为 ( A ) A .1 B .-1 C .2 D .218.各项为正数的等比数列{}n a 的公比1q ≠,且2311,,2a a a 成等差数列,则3445a a a a ++的值是 ( B ) A.512+ B. 512- C. 152- D. 512+或512-9.将棱长相等的正方体按右图所示的形状摆放,从上往下依次为第1层,第2层,第3 层,…,则第6层正方体的个数是 ( B ) A .28 B .21 C .15 D .1110.某人坚持早晨在一条弃用的旧公路上步行锻炼身体,同时数数训练头脑,他先从某地向前走2步后后退1步,再向前走4步后后退2步,··· ,再向前走2n步后后退n 步,··· 。
高中数学 第三章模块综合检测 苏教版必修5

科学就医安全用药知识讲座小结科学就医安全用药知识讲座小结一、科学就医科学就医是保障人们健康的基本保障,科学的就医方式包括对疾病的科学诊断、合理的治疗方案和科学的用药。
在就医过程中,要选择正规的医院和有资质的医生进行诊断和治疗,不要盲目相信一些偏方或者没有医学依据的治疗方法。
二、安全用药安全用药是保障治疗效果和减少药物不良反应的关键环节。
在医生的指导下使用药物,按照医嘱来服药,严格控制用药的剂量和频次。
对于药物的储存和保存也要做好相应的工作,避免药品受潮或者过期。
药物治疗过程中要定期复诊,及时向医生反馈用药效果以及药物可能出现的不良反应。
三、知识讲座小结在此次就医安全用药知识讲座中,医生强调了科学就医的重要性,同时提出了安全用药的注意事项。
医生对于常见疾病的早期症状、就医途径等方面进行了全面的介绍,强调了对疾病的早期预防和及时治疗的重要性。
医生重点讲解了药物的正确使用方法和常见不良反应,提醒听众在用药过程中要严格按照医嘱进行用药,并定期复诊。
医生还针对一些常见的误区和不良用药行为进行了详细讲解,提醒大家不要盲目听信一些不科学、不合理的用药观念。
四、个人观点和理解通过此次知识讲座,我深刻地意识到了科学就医和安全用药的重要性。
在日常生活中,我们要提高预防意识,注意身体健康,一旦出现异常症状要及时就医。
在用药过程中,要严格按照医生的指导进行用药,避免盲目自行更改用药方案或者减少用药剂量。
也要养成良好的药品储存习惯,避免药品受潮或者过期。
科学的就医和安全的用药是保障我们身体健康的基础,我们要时刻关注自己的身体健康,保持科学的生活方式和用药态度。
总结通过本次知识讲座,我深刻认识到了科学就医和安全用药对于保障人们健康的重要性。
科学就医包括对疾病的科学诊断、合理的治疗方案和科学的用药,要选择正规的医院和有资质的医生进行诊断和治疗。
安全用药是保障治疗效果和减少药物不良反应的重要环节,要在医生的指导下使用药物,严格控制用药的剂量和频次。
苏教版高中数学必修五 章末综合测评(一).docx

高中数学学习材料鼎尚图文*整理制作章末综合测评(一)(时间120分钟,满分160分)一、填空题(本大题共14小题,每小题5分,共70分.请把答案填在题中的横线上)1.在△ABC 中,AB =6,A =75°,B =45°,则AC = .【导学号:92862026】【解析】 C =180°-75°-45°=60°,由正弦定理得AB sin C =AC sin B ,即6sin 60°=AC sin 45°,解得AC =2.【答案】 22.在△ABC 中,已知c =6,a =4,B =120°,则b = . 【解析】 由b 2=16+36-2×4×6cos 120°, 得b =219. 【答案】 2193.在△ABC 中,a =4,b =43,A =30°,则B = . 【解析】 sin B =b sin A a =43sin 30°4=32.又a <b ,故B >A ,∴B =60°或120°. 【答案】 60°或120°4.在△ABC 中,化简b cos C +c cos B = .【解析】 利用余弦定理,得b cos C +c cos B =b ·a 2+b 2-c 22ab +c ·a 2+c 2-b 22ac =a .【答案】 a5.在△ABC 中,若sin A ∶sin B ∶sin C =2∶3∶4,则cos C = . 【解析】 ∵sin A ∶sin B ∶sin C =a ∶b ∶c , ∴a ∶b ∶c =2∶3∶4. 设a =2k ,b =3k ,c =4k ,则 cos C =4k 2+9k 2-16k 22×2k ×3k =-14.【答案】 -146.在△ABC 中,若A =60°,b =16,S △ABC =2203,则a = . 【解析】 由12bc sin A =2203,可知c =55.又a 2=b 2+c 2-2bc cos A =2 401, ∴a =49. 【答案】 497.在△ABC 中,若sin A =34,a =10,则边长c 的取值范围是 . 【解析】 ∵c sin C =a sin A =403, ∴c =403sin C ,∴0<c ≤403. 【答案】 ⎝ ⎛⎦⎥⎤0,4038.根据下列情况,判断三角形解的情况,其中正确的是 .(填序号)【导学号:92862027】(1)a =8,b =16,A =30°,有两解; (2)b =18,c =20,B =60°,有一解; (3)a =5,c =2,A =90°,无解; (4)a =30,b =25,A =150°,有一解. 【解析】 (1)中,∵a sin A =bsin B , ∴sin B =16×sin 30°8=1,∴B =90°,即只有一解; (2)中,sin C =20sin 60°18=539,且c >b ,∴C >B ,故有两解;(3)中,∵A =90°,a =5,c =2,∴b =a 2-c 2=25-4=21,即有解,故(1)(2)(3)都不正确.所以答案为(4).【答案】 (4)9.已知锐角△ABC 的内角A ,B ,C 的对边分别为a ,b ,c,23cos 2A +cos 2A =0,a =7,c =6,则b = .【解析】 化简23cos 2A +cos 2A =0,得23cos 2A +2cos 2A -1=0,解得cos A =15.由余弦定理,知a 2=b 2+c 2-2bc cos A ,代入数据解方程,得b =5.【答案】 5 10.在△ABC 中,若acos A 2=b cos B 2=c cos C 2,那么△ABC 是 三角形. 【解析】 由正弦定理得,sin A cos A 2=sin B cos B 2=sin Ccos C 2, ∴sin A 2=sin B 2=sin C 2.∵0<A 2,B 2,C 2<π2,∴A 2=B 2=C2,即A =B =C ,∴△ABC 是等边三角形. 【答案】 等边11.如图1所示,在△ABC 中,∠ACB 的平分线CD 交AB 于D ,AC →的模为2,BC →的模为3,AD →的模为1,那么DB →的模为.图1【解析】 由三角形内角平分线的性质得|AC →|∶|BC →|=|AD →|∶|DB →|, 故|DB →|=32. 【答案】 3212.如图2所示,在山底测得山顶仰角∠CAB =45°,沿倾斜角为30°的斜坡走1 000 m 至S 点,又测得山顶仰角∠DSB =75°,则山高BC 为m.图2【解析】 由题可知,∠SAB =45°-30°=15°,又∠SBD =15°,∴∠ABS =45°-15°=30°,AS =1 000.由正弦定理可知BS sin 15°=1 000sin 30°,∴BS =2 000sin 15°,∴BD =BS ·sin 75°=2 000sin 15°cos 15°=1 000sin 30°=500,且DC =1 000sin 30°=500,∴BC =DC +BD =1 000 m.【答案】 1 00013.已知角A ,B ,C 是三角形ABC 的内角,a ,b ,c 分别是其对边长,向量m =⎝ ⎛⎭⎪⎫23sin A 2,cos 2A 2,n =⎝ ⎛⎭⎪⎫cos A 2,-2,m ⊥n ,且a =2,cos B =33,则b = .【解析】 ∵m·n =0,∴23sin A 2cos A 2-2cos 2A 2=0,∵cos A2≠0, ∴tan A 2=33,∴A2=30°,∴A =60°, ∵a sin A =bsin B ,sin B =1-⎝ ⎛⎭⎪⎫332=63, ∴b =a sin B sin A =2×6332=43 2.【答案】 43 214.在锐角△ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,若b a +ab =6cos C ,则tan C tan A +tan Ctan B 的值是 .【解析】 ∵b a +ab =6cos C , ∴a 2+b 2ab =6·a 2+b 2-c 22ab , 即a 2+b 2=32c 2, ∴tan C tan A +tan C tan B =tan C ⎝ ⎛⎭⎪⎫cos A sin A +cos B sin B=sin 2Ccos C sin A sin B =2c 2a 2+b 2-c 2=4. 【答案】 4二、解答题(本大题共6小题,共90分.解答时应写出文字说明、证明过程或演算步骤)15.(本小题满分14分)在△ABC 中,a ,b ,c 分别是角A ,B ,C 所对的边,已知b 2=ac ,且a 2-c 2=ac -bc ,求角A 的大小及b sin Bc .【解】 由b 2=ac 及a 2-c 2=ac -bc ,得b 2+c 2-a 2=bc . 在△ABC 中,cos A =b 2+c 2-a 22bc =12. ∵0°<A <180°,∴A =60°. 在△ABC 中,由正弦定理得sin B =b sin Aa .又∵b 2=ac ,A =60°, ∴b sin B c =b 2sin A ac =sin 60°=32.16.(本小题满分14分)已知△ABC 的内角A ,B ,C 所对的边分别为a ,b ,c ,且a =2,cos B =35.(1)若b =4,求sin A 的值;(2)若△ABC 的面积S △ABC =4,求b ,c 的值. 【解】 (1)∵cos B =35>0,且0<B <π, ∴sin B =1-cos 2B =45. 由正弦定理得a sin A =bsin B , sin A =a sin B b =2×454=25. (2)∵S △ABC =12ac sin B =4, ∴12×2×c ×45=4,∴c =5.由余弦定理得b 2=a 2+c 2-2ac cos B =22+52-2×2×5×35=17,∴b =17. 17.(本小题满分14分)在△ABC 中,内角A ,B ,C 的对边分别为a ,b ,c .已知cos A -2cos C cos B=2c -a b .(1)求sin Csin A 的值;(2)若cos B =14,△ABC 的周长为5,求b 的长. 【解】 (1)由正弦定理,设a sin A =b sin B =csin C =k , 则2c -a b =2k sin C -k sin A k sin B=2sin C -sin A sin B ,所以cos A -2cos C cos B =2sin C -sin Asin B,即(cos A -2cos C )sin B =(2sin C -sin A )cos B ,化简可得sin(A +B )=2sin(B +C ). 又A +B +C =π,所以sin C =2sin A . 因此sin Csin A =2.(2)由sin Csin A =2,得c =2a ,由余弦定理及cos B =14得b 2=a 2+c 2-2ac cos B =a 2+4a 2-4a 2×14=4a 2, 所以b =2a .又a +b +c =5,从而a =1, 因此b =2.18.(本小题满分16分)在△ABC 中a ,b ,c 分别为内角A ,B ,C 的对边,且2a sin A =(2b +c )sin B +(2c +b )sin C .(1)求A 的大小;(2)若sin B +sin C =1,试判断△ABC 的形状.【导学号:92862028】【解】 (1)由2a sin A =(2b +c )sin B +(2c +b )sin C ,得2a 2=(2b +c )b +(2c +b )c ,即a 2=b 2+c 2+bc , ∴b 2+c 2-a 2=-bc , ∴2bc cos A =-bc ,∴cos A =-12,又A ∈(0,π), ∴A =2π3.(2)由(1)得sin 2A =sin 2B +sin 2C +sin B sin C , 又sin B +sin C =1,得sin B =sin C =12. 又B ,C ∈⎝ ⎛⎭⎪⎫0,π2,故B =C . 所以△ABC 是等腰三角形.19.(本小题满分16分)在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,且cos(A -B )cos B -sin(A -B )sin(A +C )=-35.(1)求sin A 的值;(2)若a =42,b =5,求向量BA→在BC →方向上的投影.【解】 (1)由cos(A -B )cos B -sin(A -B )sin(A +C )=-35,得cos(A -B )cos B -sin(A -B )sin B =-35,则cos(A -B +B )=-35,即cos A =-35. 又0<A <π,则sin A =45.(2)由正弦定理,有a sin A =bsin B , 所以sin B =b sin A a =22.由题知a >b ,则A >B ,故B =π4.根据余弦定理,有(42)2=52+c 2-2×5c ×⎝ ⎛⎭⎪⎫-35,解得c =1或c =-7(负值舍去).故向量BA →在BC →方向上的投影为|BA →|cos B =22.20.(本小题满分16分)如图3,游客从某旅游景区的景点A 处下山至C 处有两种路径.一种是从A 沿直线步行到C ,另一种是先从A 沿索道乘缆车到B ,然后从B 沿直线步行到C .现有甲、乙两位游客从A 处下山,甲沿AC 匀速步行,速度为50 m/min.在甲出发2 min 后,乙从A 乘缆车到B ,在B 处停留1 min 后,再从B 匀速步行到C .假设缆车匀速直线运行的速度为130 m/min ,山路AC 长为1 260 m ,经测量,cos A =1213,cos C =35.图3(1)求索道AB的长;(2)问乙出发多少min后,乙在缆车上与甲的距离最短?(3)为使两位游客在C处互相等待的时间不超过3 min,乙步行的速度应控制在什么范围内?【解】(1)在△ABC中,因为cos A=1213,cos C=35,所以sin A=513,sin C=45.从而sin B=sin[]π-(A+C)=sin(A+C)=sin A cos C+cos A sin C=513×35+1213×45=6365.由ABsin C=ACsin B,得AB=ACsin B×sin C=1 2606365×45=1 040(m).所以索道AB的长为1 040 m.(2)设乙出发t min后,甲、乙两游客距离为d m,此时,甲行走了(100+50t)m,乙距离A处130t m,所以由余弦定理得d2=(100+50t)2+(130t)2-2×130t×(100+50t)×12 13=200(37t2-70t+50),因0≤t≤1 040130,即0≤t≤8,故当t=3537min时,甲、乙两游客距离最短.(3)由BCsin A=ACsin B,得BC=ACsin B×sin A=1 2606365×513=500(m).乙从B出发时,甲已走了50×(2+8+1)=550(m),还需走710 m才能到达C.设乙步行的速度为v m/min,由题意得-3≤500v-71050≤3,解得1 25043≤v ≤62514,所以为使两位游客在C 处互相等待的时间不超过3 min ,乙步行的速度应控制在⎣⎢⎡⎦⎥⎤1 25043,62514(单位:m/min)范围内.。
苏教版高中数学必修五 章末综合测评(三)

高中数学学习材料(灿若寒星精心整理制作)章末综合测评(三)(时间120分钟,满分160分)一、填空题(本大题共14小题,每小题5分,共70分.请把答案填在题中的横线上)1.若不等式x2-2x-3<0的解集为A,不等式x2+x-6<0的解集为B,不等式x2+ax+b<0的解集为A∩B,那么a+b=.【解析】因为x2-2x-3<0的解集为A={x|-1<x<3},不等式x2+x-6<0的解集为B={x|-3<x<2},不等式x2+ax+b<0的解集为A∩B={x|-1<x<2},所以x2+ax+b=0的解为x1=-1,x2=2.由根与系数的关系,得a=-1,b=-2,则a+b=-3.【答案】-32.某高科技企业生产产品A和产品B需要甲、乙两种新型材料.生产一件产品A需要甲材料1.5 kg,乙材料1 kg,用5个工时;生产一件产品B需要甲材料0.5 kg,乙材料0.3 kg,用3个工时.生产一件产品A的利润为2 100元,生产一件产品B的利润为900元.该企业现有甲材料150 kg,乙材料90 kg,则在不超过600个工时的条件下,生产产品A、产品B的利润之和的最大值为元.【解析】设生产产品A x件,产品B y件,则⎩⎪⎨⎪⎧1.5x +0.5y ≤150,x +0.3y ≤90,5x +3y ≤600,x ≥0,x ∈N *,y ≥0,y ∈N *.目标函数z =2 100x +900y .作出可行域为图中的阴影部分(包括边界)内的整数点,图中阴影四边形的顶点坐标分别为(60,100),(0,200),(0,0),(90,0).当直线z =2 100x +900y 经过点(60,100)时,z 取得最大值,z max =2 100×60+900×100=216 000(元).【答案】 216 0003.利用基本不等式求最值,下列运用正确的是 . ①y =|x |2+4|x |≥2|x |2·4|x |=4|x |≥0;②y =sin x +4sin x ≥2sin x ·4sin x =4(x 为锐角);③已知ab ≠0,a b +ba ≥2a b ·ba=2; ④y =3x +43x ≥23x ·43x =4.【解析】 ①错,右侧不为定值;②错,sin x =4sin x ,则sin x =2>1;③错,a b 与ba 为负时不成立.【答案】 ④4.某工厂第一年的产量为A ,第二年的增长率为a ,第三年的增长率为b .这两年的平均增长率为x ,则x 与a +b2的大小关系为 .【导学号:92862106】【解析】 由题意可知A (1+x )2=A (1+a )(1+b )≤A ⎝⎛⎭⎪⎫2+a +b 22,∴x ≤a +b 2. 【答案】 x ≤a +b25.若0≤x ≤1,0≤y ≤2,且2y -x ≥1,则z =2y -2x +4的最小值为 . 【解析】 由已知作出可行域(如图),由z =2y -2x +4,得y =x -2+z 2, 当x =1,y =1时,z min =4. 【答案】 46.设M =a +1a -2(2<a <3),N =,x ∈R ,则M ,N 的大小关系为 .【解析】 M =a -2+1a -2+2≥2+2=4, 此时a -2=1,a =3, 而2<a <3,则M >4,∴M >N . 【答案】 M >N7.在如图1所示的可行域内(阴影部分且包括边界),目标函数z =x +ay 取得最小值的最优解有无数个,则a 的一个可能值是 .图1【解析】 若最优解有无数个,则y =-1a x +za 与其中一条边平行,而三边的斜率分别为13,-1,0,与-1a 对照可知a =-3或1,又因z =x +ay 取得最小值,则a =-3.【答案】 -38.将一根铁丝切割成三段做一个面积为2 m 2,形状为直角三角形的框架,在下列四种长度的铁丝中,选用最合理(够用且浪费最少)的是 .(1)6.5 m ;(2)6.8 m ;(3)7 m ;(4)7.2 m.【解析】 设两直角边分别为a ,b ,直角三角形的框架的周长为l ,则12ab =2,∴ab =4,l =a +b +a 2+b 2≥2ab +2ab =4+22≈6.828(m).因为要求够用且浪费最少,故答案为(3).【答案】 (3)9.方程x 2+(m -2)x +5-m =0的两根都大于2,则m 的取值范围是 .【解析】 令f (x )=x 2+(m -2)x +5-m , 要使f (x )=0的两根都大于2,则⎩⎪⎨⎪⎧Δ=(m -2)2-4(5-m )≥0,f (2)>0,-m -22>2,解得⎩⎨⎧m 2≥16,m >-5,⇒-5<m ≤-4,m <-2故答案为(-5,-4]. 【答案】 (-5,-4]10.已知等比数列{a n }各项均为正数,公比q ≠1,设P =a 2+a 92,Q =a 4a 7,则P 与Q 的大小关系是 .【解析】 ∵{a n }是等比数列, ∴a 2·a 9=a 4·a 7, ∴a 2+a 92≥a 2a 9=a 4a 7.又q ≠1,∴a 2≠a 9, ∴a 2+a 92>a 4a 7,∴P >Q . 【答案】 P >Q11.已知函数f (x )=⎩⎨⎧x 2+2ax ,x ≥2,2x +1,x <2,若f (f (1))>3a 2,则a 的取值范围是 .【解析】 f (1)=2+1=3,f (f (1))=f (3)=32+6a ,若f (f (1))>3a 2,则9+6a >3a 2,即a 2-2a -3<0,解得-1<a <3.【答案】 (-1,3)12.已知x ,y ,z ∈(0,+∞),且满足x -2y +3z =0,则y 2xz 的最小值为 .【解析】 由题意知y =x +3z 2,所以y 2xz =x 2+9z 2+6xz 4xz=x 2+9z 24xz +32≥29x 2z 24xz+32=32+32=3,当且仅当x 2=9z 2时等号成立, 所以y 2xz 的最小值为3. 【答案】 313.已知f (x )是定义域为R 的偶函数,当x ≥0时,f (x )=x 2-4x ,那么不等式f (x +2)<5的解集是 .【导学号:92862107】【解析】 因为f (x )为偶函数,所以f (|x +2|)=f (x +2), 则f (x +2)<5可化为f (|x +2|)<5, 即|x +2|2-4|x +2|<5, (|x +2|+1)(|x +2|-5)<0,所以|x +2|<5,解得-7<x <3,所以不等式f (x +2)<5的解集是(-7,3). 【答案】 (-7,3)14.设m >1,在约束条件⎩⎨⎧y ≥x ,y ≤mx ,x +y ≤1下,目标函数z =x +5y 的最大值为4,则m 的值为 .【解析】 不等式组表示的平面区域如图中阴影所示,把目标函数化为y =-15x +z 5,显然当y =-15x +z5过点A 时取到最大值.此时z =4,即y =-15x +45.由⎩⎨⎧x +5y =4,y =x ,得A ⎝ ⎛⎭⎪⎫23,23.把A ⎝ ⎛⎭⎪⎫23,23代入y =mx 得,23m =23,∴m =1. 【答案】 1二、解答题(本大题共6小题,共90分.解答时应写出文字说明、证明过程或演算步骤)15.(本小题满分14分)解关于x 的不等式:x -ax -a 2<0(a ∈R ). 【解】 原不等式等价于(x -a )(x -a 2)<0. (1)当a =0时,原不等式为x 2<0, ∴x ∈∅.(2)当a =1时,原不等式为(x -1)2<0, ∴x ∈∅.(3)当0<a <1时,a >a 2,∴原不等式的解集为{x |a 2<x <a }. (4)当a <0或a >1时,a 2>a , ∴原不等式的解集为{x |a <x <a 2}.综上,当a =0或a =1时,不等式解集为∅; 当0<a <1时,不等式解集为{x |a 2<x <a }; 当a <0或a >1时,不等式解集为{x |a <x <a 2}.16.(本小题满分14分)已知关于x 的不等式kx 2-2x +6k <0(k ≠0). (1)若不等式的解集是{x |x <-3或x >-2},求k 的值; (2)若不等式的解集是R ,求k 的取值范围.【解】 (1)因为不等式的解集为{x |x <-3或x >-2},所以-3,-2是方程kx 2-2x +6k =0的两根且k <0.由根与系数的关系得⎩⎪⎨⎪⎧(-3)×(-2)=6,(-3)+(-2)=2k ,解得k =-25.(2)因为不等式的解集为R ,所以⎩⎨⎧k <0,Δ=4-4k ·6k <0,即⎩⎨⎧k <0,k >66或k <-66,所以k <-66.即k 的取值范围是⎝⎛⎭⎪⎫-∞,-66.17.(本小题满分14分)画出不等式组⎩⎨⎧x -y +5≥0,x +y ≥0,x ≤3表示的平面区域,并回答下列问题:(1)指出x ,y 的取值范围; (2)平面区域内有多少个整点? (3)求z =x -2y 的最大值.【解】 (1)不等式x -y +5≥0表示直线x -y +5=0上及其右下方的点的集点,x +y ≥0表示直线x +y =0上及其右上方的点的集合,x ≤3表示直线x =3上及其左方的点的集合.所以,不等式组⎩⎨⎧x -y +5≥0,x +y ≥0,x ≤3表示的平面区域如图所示.结合图中可行域得x ∈⎣⎢⎡⎦⎥⎤-52,3,y ∈[-3,8].(2)由图形及不等式组知⎩⎪⎨⎪⎧-x ≤y ≤x +5,-52≤x ≤3,且x ∈Z ,当x =3时,-3≤y ≤8,有12个整点;当x =2时,-2≤y ≤7,有10个整点;当x =1时,-1≤y ≤6,有8个整点;当x =0时,0≤y ≤5,有6个整点;当x =-1时,1≤y ≤4,有4个整点;当x =-2时,2≤y ≤3,有2个整点.所以平面区域内的整点共有2+4+6+8+10+12=42(个).(3)平移直线y=12x-z2,所以当直线过点()3,-3时z值最大.所以zmax=3-2×(-3)=9.18.(本小题满分16分)在锐角三角形ABC中,若sin A=2sin B sin C,求tan A tan B tan C的最小值.【导学号:92862108】【解】在锐角三角形ABC中,∵sin A=2sin B sin C,∴sin(B+C)=2sin B sin C,∴sin B cos C+cos B sin C=2sin B sin C,等号两边同除以cos B cos C,得tan B+tan C=2tan B tan C.∴tan A=tan[π-(B+C)]=-tan(B+C)=tan B+tan Ctan B tan C-1=2tan B tan C tan B tan C-1.①∵A,B,C均为锐角,∴tan B tan C-1>0,∴tan B tan C>1.由①得tan B tan C=tan A tan A-2.又由tan B tan C>1得tan Atan A-2>1,∴tan A>2.∴tan A tan B tan C=tan2A tan A-2=(tan A-2)2+4(tan A-2)+4tan A-2=(tan A-2)+4tan A-2+4≥24+4=8,当且仅当tan A-2=4tan A-2,即tan A=4时取得等号.故tan A tan B tan C的最小值为8.19.(本小题满分16分)规定:max(a,b,c)与min(a,b,c)分别表示a,b,c中的最大数与最小数,若正系数二次函数f(x)=ax2+bx+c的图象与x轴有公共点,试证:(1)max(a,b,c)≥49f(1);(2)min(a ,b ,c )≤14f (1).【证明】 由题意知a ,b ,c >0,f (1)=a +b +c ,Δ=b 2-4ac ≥0. (1)若b ≥49f (1),结论显然成立; 下面证明当b <49f (1)时,结论也成立.记f (1)=a +b +c =d .,由b 2-4ac ≥0,可知ac ≤b 24<481d 2,而a +c =d -b >59d ,所以a 2+481d 2≥a 2+ac =a (a +c )>59ad ,即⎝ ⎛⎭⎪⎫a -19d ⎝ ⎛⎭⎪⎫a -49d >0,解得a <19d 或 a >49d .若a <19d ,则a +c >59d ,c >49d . 因此,必有a >49f (1)或b ≥49f (1)或 c >49f (1),于是max(a ,b ,c )≥49f (1). (2)若a ≤14f (1),结论显然成立;下面证明当a >14f (1)时,结论也成立. 因为b +c =d -a <34d 且b 2≥4ac >cd , 所以c +cd <c +b <34d , 整理为⎝ ⎛⎭⎪⎫c +32d ⎝ ⎛⎭⎪⎫c -12d <0,解得c <14d .因此,必有a ≤14f (1)或c <14f (1),于是min(a ,b ,c )≤14f (1).20.(本小题满分16分)某个集团公司下属的甲、乙两个企业在2016年1月的产值都为a 万元,甲企业每个月的产值与前一个月相比增加的产值相等,乙企业每个月的产值与前一个月相比增加的百分数相等,到2017年1月两个企业的产值再次相等.(1)试比较2016年7月甲、乙两个企业产值的大小,并说明理由. (2)甲企业为了提高产能,决定投入3.2万元买台仪器,并且从2017年2月1日起投入使用.从启用的第一天起连续使用,第n 天的维修保养费为n +4910元,(n ∈N *),求前n 天这台仪器的日平均耗资(含仪器的购置费),并求日平均耗资最少时使用的天数?【解】 (1)设从2016年1月到2017年1月甲企业每个月的产值分别为a 1,a 2,a 3,…,a 13,乙企业每个月的产值分别为b 1,b 2,…,b 13,由题意{a n }成等差数列,{b n }成等比数列,所以a 7=12(a 1+a 13),b 7=b 1·b 13,因为a 1=b 1,a 13=b 13,从而a 7=12(a 1+a 13)>a 1·a 13=b 1·b 13=b 7,所以到7月份甲企业的产值比乙企业的产值要大. (2)设一共使用了n天,n天的平均耗资P (n )=32 000+⎝ ⎛⎭⎪⎫1+4910+2+4910+3+4910+…+n +4910n=32 000+49n 10+n (n +1)20n=32 000n +n 20+9920≥232 000n ×n 20+9920=1 69920(元),当且仅当32 000n =n20时,取得最小值,此时n =800,即日平均耗资最少时使用了800天.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高中数学学习材料金戈铁骑整理制作模块综合检测卷(测试时间:120分钟 评价分值:150分)一、选择题(每小题共10个小题,每小题共5分,共50分,在每小题给出的四个选项中,只有一项符合题目要求)1.已知{a n }为等比数列,a 4+a 7=2,a 5a 6=-8,则a 1+a 10=(D )A .7B .5C .-5D .-7解析:∵{a n }为等比数列,∴a 4a 7=a 5a 6=-8.又a 4+a 7=2,∴⎩⎪⎨⎪⎧a 4=4,a 7=-2或⎩⎪⎨⎪⎧a 4=-2,a 7=4.当a 4=4,a 7=-2时,a 1=-8,a 10=1,∴a 1+a 10=-7; 当a 4=-2,a 7=4时,a 10=-8,a 1=1,∴a 1+a 10=-7. 综上,a 1+a 10=-7.2.某人投资10 000万元,如果年收益利率是5%,按复利计算,5年后能收回本利和为(B )A .10 000×(1+5×5%)B .10 000×(1+5%)5C .10 000×1.05×(1-1.054)1-1.05D .10 000×1.05×(1-1.055)1-1.05解析:注意与每年投入10 000万元区别开来.3.在△ABC 中,已知cos A =513,sin B =35,则cos C 的值为(A ) A.1665 B.5665C.1665或5665 D .-1665解析:∵cos A =513>0,∴sin A =1213>sin B =35. ∴B 为锐角,故cos B =45.从而cos C =-cos(A +B )=-cos A cos B +sin A sin B =1665. 4.若a <b <0,d >c >0,则不等式①ad >bc ;②c a >c b;③a 2>b 2;④a -d <b -c 中正确的个数是(C )A .1个B .2个C .3个D .4个解析:①错,②③④正确.将a <b <0转化为-a >-b >0,可得(-ad )>(-bc ),即ad <bc ,故知①错;由a <b <0⇒1a >1b,c >0,故②正确;因为函数y =x 2在(-∞,0)上单调递减,故③正确;由d >c >0,得-d <-c <0,故知a -d <b -c ,故④正确.5.设x ,y ∈R +,且xy -(x +y )=1,下列结论中正确的是(A )A .x +y ≥22+2B .xy ≤2+1C .x +y ≤(2+1)2D .xy ≥22+2解析:∵1+x +y =xy ≤⎝ ⎛⎭⎪⎫x +y 22,∴(x +y )2-4(x +y )-4≥0.即x +y ≥2(1+2)(当x =y =1+2时等号成立),x +y 的最小值为2(1+2).6.数列{a n }的通项公式为a n =n cosn π2,其前n 项和为S n ,则S 2 015等于(D )A .1 006B .1 008C .-1 006D .-1 008解析:由a n =n cos n π2可得 S 2 015=1×0-2×1+3×0+4×1+…-2 014×1+2 015×0=-2+4-6+…-2 010+2 012-2 014=2×503-2 014=-1 008.7.已知方程x 2+(m +2)x +m +5=0有两个正实根,则实数m 的取值范围是(D )A .(-∞,-2)B .(-∞,-4]C .(-5,+∞)D .(-5,-4]解析:方程两根为正,则⎩⎪⎨⎪⎧Δ≥0,-(m +2)>0,⇒-5<m ≤-4m +5>0. 8.已知-1<a +b <3且2<a -b <4,则2a +3b 的取值范围是(D)A.⎝ ⎛⎭⎪⎫-132,172 B.⎝ ⎛⎭⎪⎫-72,112 C.⎝ ⎛⎭⎪⎫-72,132 D.⎝ ⎛⎭⎪⎫-92,132 解析:用待定系数法可得2a +3b =52(a +b )-12(a -b ), 由⎩⎪⎨⎪⎧-1<a +b <3,2<a -b <4⇒⎩⎪⎨⎪⎧-52<52(a +b )<152,-2<-12(a -b )<-1.两式相加即得-92<2a +3b <132. 9.已知锐角三角形的边长分别是2,3,x ,则x 的取值范围是(B )A .(1,3)B .(5,13)C .(0,5)D .(13,5)解析:由三角形的三个角为锐角,结合余弦定理的推论可知,⎩⎪⎨⎪⎧22+32-x 2>0,22+x 2-32>0,32+x 2-22>0,解得5<x 2<13,即5<x < 13.10.已知函数f (x )=ax 2+2ax +4(a >0),若x 1<x 2,x 1+x 2=0,则(A )A .f (x 1)<f (x 2)B .f (x 1)=f (x 2)C .f (x 1)>f (x 2)D .f (x 1)与f (x 2)的大小不能确定解析:函数f (x )=ax 2+2ax +4(a >0),二次函数的图象开口向上,对称轴为x =-1,a >0,又∵x 1+x 2=0,x 1与x 2的中点为0,x 1<x 2,∴x 2到对称轴的距离大于x 1到对称轴的距离.∴f (x 1)<f (x 2),故选A.二、填空题(本大题共4小题,每小题5分,共20分,把答案填在题中横线上)11.(2013·新课标全国卷Ⅰ)已知锐角△ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,23cos 2A +cos 2A =0,a =7,c =6,则b =________.解析:先求出角A 的余弦值,再利用余弦定理求解.由23cos 2A +cos 2A =0得23cos 2A +2cos 2A -1=0,解得cos A =±15. ∵A 是锐角,∴cos A =15. 又a 2=b 2+c 2-2bc cos A ,∴49=b 2+36-2×b ×6×15. ∴b =5或b =-135. 又∵b >0,∴b =5.答案:512.(2013·陕西卷)观察下列等式:12=1,12-22=-3,12-22+32=6,12-22+32-42=-10,…,照此规律,第n 个等式可为____________.解析:当n 为偶数时,(12-22)+(32-42)+…+[(n -1)2-n 2]=-n (n +1)2; 当n 为奇数时,(12-22)+(32-42)+…+[(n -2)2-(n -1)2]+n 2=-(n -1)n 2+n 2=n (n +1)2. 答案:12-22+32-42+…+(-1)n +1n 2=(-1)n +1n (n +1)213.若变量x ,y 满足约束条件⎩⎪⎨⎪⎧y ≤1,x +y ≥0,x -y -2≤0,则z =x -2y 的最大值为________.解析:作出可行域(如图),由z =x -2y 得y =12x -z 2,则当目标函数过C (1,-1)时z 取得最大值,所以z max =1-2×(-1)=3.答案:314.若a >b >0,m >0,n >0,则b a ,a b ,b +m a +m ,a +n b +n由大到小的顺序是__________________________.解析:用特殊值法或作差比较法都很容易得出答案.答案:a b >a +n b +n >b +m a +m >b a三、解答题(本题共6小题,共80分.解答题应写出文字说明、证明过程或推演步骤)15.(本小题满分12分)等差数列{}a n 不是常数列,a 5=10,且a 5,a 7,a 10是某一等比数列{}b n 的第1,3,5项.(1)求数列{}a n 的第20项;(2)求数列{}b n 的通项公式.解析:(1)设数列{}a n 的公差为d ,则a 5=10,a 7=10+2d ,a 10=10+5d .因为等比数列{}b n 的第1、3、5项成等比数列,所以a 27=a 5a 10,即(10+2d )2=10(10+5d ).解得d =2.5,d =0(舍去).所以a 20=47.5.(2)由(1)知{}a n 为各项非负的数列,所以q 2=b 3b 1=a 7a 5=32.∴q =±32.又b 1=a 5=10, ∴b n =b 1q n -1=±10·⎝ ⎛⎭⎪⎫32n -12,n ∈N *. 16.(本小题满分12分)(2013·北京卷)在△ABC 中,a =3,b =26,∠B =2∠A .(1)求cos A 的值;(2)求c 的值.解析:(1)由正弦定理得: 3sin A =26sin 2A ,解得cos A =63.(2)由cos A =63⇒sin A =33,又∠B =2∠A , ∴cos B =2cos 2A -1=13.∴sin B =223, sin C =sin(A +B )=sin A cos B +cos A sin B =33×13+63×223=539. ∴c =a sin C sin A=5. 17.(本小题满分14分)已知关于x 的不等式ax 2+2x +c >0的解集为⎝ ⎛⎭⎪⎫-13,12,求-cx 2+2x -a >0的解集. 解析:由ax 2+2x +c >0的解集为⎝ ⎛⎭⎪⎫-13,12知a <0,-13和12是方程ax 2+2x +c =0的两个根,由韦达定理-13+12=-2a ,-13×12=c a,解得a =-12,c =2,∴-cx 2+2x -a >0,即-2x 2+2x +12>0亦即x 2-x -6<0.其解集为(-2,3).18.(本小题满分14分)某营养师要为某个儿童预订午餐和晚餐.已知一个单位的午餐含12个单位的碳水化合物、6个单位的蛋白质和6个单位的维生素C ;一个单位的晚餐含8个单位的碳水化合物、6个单位的蛋白质和10个单位的维生素C.另外,该儿童这两餐需要的营养中至少含64个单位的碳水化合物、42个单位的蛋白质和54个单位的维生素C.如果一个单位的午餐、晚餐的费用分别是2.5元和4元,那么要满足上述的营养要求,并且花费最少,应当为该儿童分别预订多少个单位的午餐和晚餐?解析:方法一 设需要预订满足要求的午餐和晚餐分别为x 个单位和y 个单位,所花的费用为z 元,则依题意得:z =2.5x +4y ,且x ,y 满足⎩⎪⎨⎪⎧x ≥0,y ≥0,12x +8y ≥64,6x +6y ≥42,6x +10y ≥54,即⎩⎪⎨⎪⎧x ≥0,y ≥0,3x +2y ≥16,x +y ≥7,3x +5y ≥27.z 在可行域的四个顶点A (9,0),B (4,3),C (2,5),D (0,8)处的值分别是z A =2.5×9+4×0=22.5,z B =2.5×4+4×3=22,z C =2.5×2+4×5=25,z D =2.5×0+4×8=32.比较之,z B 最小,因此,应当为该儿童预订4个单位的午餐和3个单位的晚餐,就可满足要求.方法二 设需要预订满足要求的午餐和晚餐分别为x 个单位和y 个单位,所花的费用为z 元,则依题意得z =2.5x +4y ,且x ,y 满足 ⎩⎪⎨⎪⎧x ≥0,y ≥0,12x +8y ≥64,6x +6y ≥42,6x +10y ≥54,即⎩⎪⎨⎪⎧x ≥0,y ≥0,3x +2y ≥16,x +y ≥7,3x +5y ≥27.作出平行域如下图所示.让目标函数表示的直线2.5x+4y=z在可行域上平移,由此可知z=2.5x+4y在B(4,3)处取得最小值.因此,应当为该儿童预订4个单位的午餐和3个单位的晚餐,就可满足要求.19.(本小题满分14分)如右图,某观测站C在城A南偏西20°的方向上,由A城出发有一条公路,走向是南偏东40°,在C处测得距C为31千米的公路上B处有一人正沿公路向A城走去,走了20千米后,到达D处,此时C、D间距离为21千米,问这人还需走多少千米到达A城?解析:根据题意,可得下图,其中BC=31千米,BD=20千米,CD=21千米,∠CAD=60°.设∠ACD=α,∠CDB=β.在△CDB中,由余弦定理得:cos β=CD2+BD2-BC22CD·BD=212+202-3122×21×20=-17,sin β=1-cos2β=43 7.sin α=sin(180°-∠CAD-∠CDA)=sin(180°-60°-180°+β)=sin(β-60°)=sin βcos 60°-cos βsin 60°=437×12+17×32=53 14.在△ACD中,由正弦定理得:AD=CDsin A·sinα=21sin 60°×5314=15.此人还得走15千米到达A 城.20.(本小题满分14分)数列{a n }中,a 1=8,a 4=2且满足a n +2=2a n +1-a n ,n ∈N *.(1)求数列{a n }的通项公式;(2)设S n =|a 1|+|a 2|+…+|a n |,求S n ;(3)设b n =1n (12-a n )(n ∈N *),T n =b 1+b 2+…+b n (n ∈N *),是否存在最大的整数m ,使得对任意n ∈N *,均有T n >m 32成立?若存在,求出m 的值;若不存在,请说明理由.解析:(1)由a n +2=2a n +1-a n ⇒a n +2-a n +1=a n +1-a n ,可知{a n }成等差数列,d =a 4-a 14-1=-2, ∴a n =8+(n -1)·(-2)=10-2n (n ∈N).(2)由a n =10-2n ≥0得n ≤5,∴当n ≤5时,S n =-n 2+9n .当n >5时, S n =|a 1|+|a 2|+…+|a n |=a 1+a 2+…+a 5-a 6-a 7-…-a n=2(a 1+a 2+…+a 5)-(a 1+a 2+…+a n ) =n 2-9n +40.故S n =⎩⎪⎨⎪⎧-n 2+9n ,1≤n ≤5,n 2-9n +40,n ≥5. (3)b n =1n (12-a n )=1n (2n +2)=12⎝ ⎛⎭⎪⎫1n -1n +1. ∴T n =b 1+b 2+…+b n=12⎣⎢⎡⎝⎛⎭⎪⎫1-12+⎝⎛⎭⎪⎫12-13+⎝⎛⎭⎪⎫13-14+…+⎦⎥⎤⎝⎛⎭⎪⎫1n-1-1n+⎝⎛⎭⎪⎫1n-1n+1=12⎝⎛⎭⎪⎫1-1n+1=n2(n+1)>n-12n=T n-1>T n-2> (1)∴要使T n>m32总成立,需m32<T1=14恒成立,即m<8(m∈Z).故适合条件的m的最大值为。
