【精品】三角形角平分线专题讲解
三角形的角平分线定理解析

三角形的角平分线定理解析三角形的角平分线定理是指:三角形内任意一条角的角平分线,都能将该角分成两个相等的角。
这个定理在解决三角形相关问题时非常有用,可以帮助我们推导出一些重要的结论和性质。
接下来,我们将对三角形的角平分线定理进行详细的解析。
一、角平分线的定义在三角形ABC中,假设角A的角平分线与边BC相交于点D,那么我们可以称线段AD为角A的角平分线。
角平分线的作用是将角A 分成两个相等的角BAD和CAD。
二、角平分线定理的几何解析根据角平分线的定义,我们可以得出以下几何结论:1. 任意角的角平分线两端的线段长度相等。
即AD = CD。
证明:作BD与AC的延长线交于点E。
由于△ABD和△CAD中有AD = AD(公共边)、∠BAD = ∠CAD(角平分线的定义)和∠BDA = ∠CDA(共同内角),所以根据ASA(边角边)的性质可以得出△ABD ≌△CAD。
因此,AD = CD。
2. 角平分线将对边分成两个与角平分线所在边等长的线段。
即BD = CD。
证明:由于△ABD和△ACD中有∠BDA = ∠CDA(共同的内角),∠ABD = ∠ACD(角平分线的定义)和AD = AD(公共边),根据ASA(角边角)的性质可以得出△ABD ≌△ACD。
因此,BD = CD。
三、角平分线定理的应用角平分线定理不仅可以帮助我们推导出一些证明,还可以在解题过程中起到积极的作用。
下面我们通过一些例子来说明角平分线定理的应用。
例子1:给定三角形ABC,角BAD是角A的角平分线,若∠BAD = 60°,求∠ACB的度数。
解:由角平分线定理可知BD = CD,且∠BAD = ∠CAD = 60°。
由于∠BAD + ∠CAD + ∠ACB = 180°(三角形内角和定理),代入已知信息可得60° + 60° + ∠ACB = 180°,解得∠ACB = 60°。
专题 角平分线四大模型在三角形中的应用(知识解读)-中考数学(全国通用)

N M O A B PPO N M B A专题01 角平分线四大模型在三角形中的应用(知识解读)【专题说明】角平分线在几何中占有重要地位,是解决许多问题的桥梁和纽带,角平分线把一个角分成相等的两个部分,其“轴承对称功能”衍生出“角平分线上的点到角两边的距离相等”以及“等腰三角形三线合一”、“三角形的内心到三边的距离相等”等性质,而角平分线与平行线相结合构造出等腰三角形,也常在解题中给我们带来帮助,本专题介绍四种常考解题方法。
【方法技巧】模型1 角平分线上的点向两边作垂线如图,P 是∠MON 的平分线上一点,过点P 作PA ⊥OM 于点A ,PB ⊥ON 于点B 。
结论:PB=PA 。
【模型分析】利用角平分线的性质:角平分线上的点到角两边的距离相等,构造模型,为边相等、角相等、三角形全等创造更多的条件,进而可以快速找到解题的突破口。
模型2 截取构造对称全等如图,P 是∠MON 的平分线上一点,点A 是射线OM 上任意一点,在ON 上截取OB=OA ,连接PB 。
结论:△OPB ≌△OPA 。
P O N M B AQP O N M 【模型分析】利用角平分线图形的对称性,在角的两边构造对称全等三角形,可以得到对应边、对应角相等。
利用对称性把一些线段或角进行转移,这是经常使用的一种解题技巧。
模型3 角平分线+垂线构造等腰三角形如图,P 是∠MO 的平分线上一点,AP⊥OP 于P 点,延长AP 于点B 。
结论:△AOB 是等腰三角形。
【模型分析】构造此模型可以利用等腰三角形的“三线合一”,也可以得到两个全等的直角三角形,进而得到对应边、对应角相等。
这个模型巧妙地把角平分线和三线合一联系了起来。
模型4 角平分线+平行线如图,P 是∠MO 的平分线上一点,过点P 作PQ ∥ON ,交OM 于点Q 。
结论:△POQ 是等腰三角形。
【模型分析】有角平分线时,常过角平分线上一点作角的一边的平行线,构造等腰三角形,为证明结论提供更多的条件,体现了角平分线与等腰三角形之间的密切关系。
解三角形的角平分线问题(最新版)

解三角形专题------角平分线与三角形4心秒杀秘籍一:张角定理在△ABC 中,D 为BC 边上的一点,连接AD ,设βα=∠=∠CAD BAD ,,则一定有ABAC AD βαβαsin sin )sin(+=+,(证明:等积法) 【例1】在△ABC 中,角A 、B 、C 所对的边分别为a 、b 、c ,△ABC=120°,BD△BC 交AC 于点D ,且BD=1,则2a +c 的最小值为 .【例2】在在△ABC 中,角A 、B 、C 所对的边分别为a 、b 、c ,已知点D 在BC 边上,AD△AC ,sin△BAC=322,AB=23,AD=3,则CD 的长为【例3】(2015年全国课标卷II )在△ABC 中,D 是BC 上的点,AD 平分△BAC ,△ABD 的面积是△ACD 面积的2倍.(1)求CBsin sin 的值;(2)若22,1==DC AD ,求BD 和AC 的长.秒杀秘籍二:角平分线张角定理,当βα=时, ①)(21cos c AD b AD +=α(角平分线张角定理) ②ααtan sin )(212AD c b AD S ABC ≥+=∆(角平分线面积) 证明:αααααααtan sin 2sin 2sin sin )(21sin )11(212sin 21∆∆==≥+=+⋅==S AD S AD bc AD c b AD AD c b bc bc S 【例4】在△ABC 中,角A 、B 、C 所对的边分别为a 、b 、c ,b cosC=a ,点M 在线段AB 上,且△ACM=△BCM ,若b=6CM=6,则cos△BCM=( )46.47.43.410.D C B A 【例5】在△ABC 中,角A 、B 、C 所对的边分别为a 、b 、c ,32π=∠ABC ,△ABC 的平分线交AC 于点D ,BD=1,则a +c 的最小值为 .【例6】在△ABC 中,角A 、B 、C 所对的边分别为a 、b 、c ,32π=∠ABC ,BD 平分△ABC 交AC 于点D ,BD=2,则△ABC 的面积的最小值为( )36.35.34.33.D C B A秒杀秘籍3:角平分线之斯库顿定理如图,AD 是△ABC 的角平分线,则DC BD AC AB AD ⋅-⋅=2.就其位置关系而言:中方=上积-下积 求证:AC AB DC BD AD ⋅=⋅+2,,~ACAEAD AB ADC ABE =∴∆∆ 即,)(,AC AB DE AD AD AC AB AE AD ⋅=+⋅∴⋅=⋅证毕注意:角平分线张角定理强调的是角度,斯库顿定理强调的是长度,斯库顿定理可以绕过求张角而直接求出三角形的各边长,通常和内角平分线定理合在一起出考题.【例7】在△ABC 中,AB=5,AC=7,BC=6,△A 的平分线AD 交BC 于点D ,则AD= . 【例8】在△ABC 中,△C=2△B ,AC=3,BC=5,求AB 之长. 秒杀秘籍4:角平分线之倍角定理)(2);(2);(2222b c c a C A a b b c B C c a a b A B +=⇔=+=⇔=+=⇔=,这样的三角形称为“倍角三角形”【例9】在△ABC 中,内角A 、B 、C 所对的边分别是a 、b 、c ,已知8b=5c ,C=2B ,则cosC=( )2524.257.257.257.D C B A ±-【例10】设锐角△ABC 的内角A 、B 、C 所对的边分别是a 、b 、c ,且c=1,A=2C ,则△ABC 周长的取值范围为( )]33,22.()33,22.()33,0.()22,0.(++++++D C B A【例11】在△ABC 中,内角A 、B 、C 所对的边分别是a 、b 、c ,若bc b a +=22且)2,3(ππ∈A ,则ba的取值范围是 .【12】如图,四边形ABCD 中,CE 平分△ACD ,AE=CE=32,DE=3,若△ABC=△ACD ,则四边形ABCD 周长的最大值为( )3315.318.3312.24.++D C B A例1、设G 是ABC ∆的重心,且0)sin 35()sin 40()sin 56(=++GC C GB B GA A ,则角B 的大小为_______例2、若点O 在ABC ∆的内部,且053=++OB OC OA ,则ABC ∆的面积与AOC ∆的面积之比是________. 例3、若点O 在ABC ∆的内部,且02 =++OC m OB OA ,74=∆∆ABC AOB S S ,则实数m =_________. 例4、(2016清华大学自主招生)若点O 在ABC ∆的内部,2:3:4::=∆∆∆AOC BOC AOB S S S ,设AC AB AO μλ+=,则实数λ=_____,μ=_____.例5、已知ABC Δ的外接圆的圆心为O ,且60∠=A ,若)∈β,α(βαR AC AB AO +=,则βα+的最大值是 能力提升1、已知ABC ∆中,I 为内心,,4,3,2===AB BC AC 且AC y AB x AI +=,则,则y x +的值为______ .2、设P 是ABC ∆所在平面上一点,且满足)0(,43>=+m AB m PC PA ,若ABP ∆的面积为8,则ABC ∆的面积是_______.3、在ABC ∆中,H BC AC AB ,2,3,4===为ABC ∆的垂心,AC y AB x AH +=,则xy=______. 4、已知G 是ABC ∆的重心,点N M ,分别在边AC AB ,上,满足AN y AM x AG +=,1=+y x ,若,43AB AM =则ABC ∆和AMN ∆的面积之比是____________.5、正三角形ABC 内一点M ,满足CB n CA m CM +=,45=∠MCA ,则nm=______________. 6、已知ABC ∆的外接圆O 的半径为1,且BC BA BO μλ+=,若60=∠ABC ,则μλ+的最大值是________. 7、已知点O 是锐角ABC ∆的外心,3π=∠A ,且OC y OB x OA +=,则y x -2的取值范围是_______________.三角形的四“心”,四“线”① 已知G 是ABC △所在平面上的一点,若0GA GB GC ++=,则G 是ABC △的重心.已知O 是平面上一定点,A B C ,,是平面上不共线的三个点,动点P 满足()OP OA AB AC λ=++,(0)λ∈+∞,,则P 的轨迹一定通过ABC △的重心.② P 是ABC △所在平面上一点,若PA PC PC PB PB PA ⋅=⋅=⋅,则P 是ABC △的垂心.已知O 是平面上一定点,AB C ,,是平面上不共线的三个点,动点P 满足cos cos AB AC OP OA AB B AC C λ⎛⎫ ⎪=++ ⎪⎝⎭,(0)λ∈+∞,,则动点P 的轨迹一定通过ABC △的垂心.③ 已知I 为ABC △所在平面上的一点,且AB c =,AC b =,BC a = .若0aIA bIB cIC ++=,则I 是ABC △的内心.已知O 是平面上一定点,AB C ,,是平面上不共线的三个点,动点P 满足AB AC OP OA AB AC λ⎛⎫⎪=++ ⎪⎝⎭,(0)λ∈+∞,,则动点P 的轨迹一定通过ABC △的内心.④ 已知O 是ABC △所在平面上一点,若222OA OB OC ==,则O 是ABC △的外心.已知O 是平面上的一定点,AB C ,,是平面上不共线的三个点,动点P 满足2cos cos OB OC AB AC OP AB B AC C λ⎛⎫+ ⎪=++ ⎪⎝⎭,(0)λ∈+∞,,则动点P 的轨迹一定通过ABC △的外心。
角平分线三个定理-概述说明以及解释

角平分线三个定理-概述说明以及解释1.引言1.1 概述角平分线三个定理是解决与角度相关的几何问题时,非常重要且常用的定理。
它们分别应用于角的平分线问题,帮助我们更深入地理解角的性质与构造。
这三个定理不仅在数学学科中有广泛的应用,而且在实际生活中也具有重要的意义。
在解释这三个定理之前,我们先回顾一下角的基本概念。
在几何学中,角是由两条线段或射线共享一个公共端点而形成的图形。
以公共端点为中心,可以将角分为两个部分,分别称为角的两个腿。
角的大小通常用度或弧度来表示,这取决于所用的单位。
第一个定理是角的平分线定理,它指出:如果一条直线将一个角平分成两个相等的角,那么这条直线称为这个角的平分线。
换句话说,平分线将角分为两个相等的部分。
这个定理有广泛的应用,例如在三角形中,利用角平分线定理可以证明角的大小相等,从而推导出三角形的一些特殊性质。
第二个定理是外角平分线定理,它指出:如果一条直线通过一个三角形的外角的顶点,并将外角的两个邻角平分成两个相等的角,那么这条直线称为该三角形的外角平分线。
这个定理在解决外角问题时非常有用,它保证了外角平分线的存在性,并简化了我们分析与推导相关问题的步骤。
第三个定理是内角平分线定理,它指出:如果一条直线通过一个三角形的内角的顶点,并将内角的两个邻角平分成两个相等的角,那么这条直线称为该三角形的内角平分线。
这个定理与外角平分线定理类似,但是涉及的是三角形的内角。
利用内角平分线定理,我们可以简化三角形内角相关问题的分析过程。
角平分线三个定理在几何学中占据着重要的地位,是研究角度关系和解决几何问题的基础。
它们不仅具有理论意义,还具有广泛的应用价值。
通过深入理解和熟练运用这三个定理,我们能够提高问题解决的效率,并在实际生活中更好地应用几何知识。
1.2文章结构文章结构:本文主要介绍了角平分线的三个定理,分为引言、正文和结论三个部分。
引言部分首先概述了角平分线的意义和应用,以及本文的目的。
三角形角平分线专题讲解(精选.)

由角平分线想到的辅助线口诀:图中有角平分线,可向两边作垂线。
也可将图对折看,对称以后关系现。
角平分线平行线,等腰三角形来添。
角平分线加垂线,三线合一试试看。
角平分线具有两条性质:a、对称性;b、角平分线上的点到角两边的距离相等。
对于有角平分线的辅助线的作法,一般有两种。
①从角平分线上一点向两边作垂线;②利用角平分线,构造对称图形(如作法是在一侧的长边上截取短边)。
通常情况下,出现了直角或是垂直等条件时,一般考虑作垂线;其它情况下考虑构造对称图形。
至于选取哪种方法,要结合题目图形和已知条件。
与角有关的辅助线一)、截取构全等几何的证明在于猜想与尝试,种尝试与猜想是在一定的规律基本之上的,希望同学们能掌握相关的几何规律, 在解决几何问题中大 胆地去猜想, 按一定的规律去尝试。
下面就几何中常见的定理所 涉及到的辅助线作以介绍。
如图 1-1 ,∠∠,如取,并连接、 ,则有△≌△,从而为我们 证明线段、角相等创造了条件。
例1. 如图 1-2 ,,平分∠,平分∠, 点 E 在上,求证:。
分析:此题中就涉及到角平分线, 可以利用角平分线来构造全等三角形, 对称图形, 同时此题也是证明线段的和差倍分问题, 在证明线段 的和差倍分问题中常用到的方法是延长法或截取法来证明, 延长 短的线段或在长的线段长截取一部分使之等于短的线段。
但无论 延长还是截取都要证明线段的相等, 延长要证明延长后的线段与某条线段相等,截取要证明截取后剩下的线段与某条线段相等, 进而达到所证明的目的。
简证:在此题中可在长线段上截取,再证明,从而达到证明 的目的。
这里面用到了角平分线来构造全等三角形。
另外一个全 等自已证明。
此题的证明也可以延长与的延长线交于一点来证 明。
自已试一试。
例2. 已知:如图 1-3 ,2,∠∠,,求证⊥即利用解平分线来构造轴 图1-2分析:此题还是利用角平分线来构造全等三角形。
构造的方法还是截取线段相等。
其它问题自已证明。
(完整)全等三角形和角平分线专题讲解和练习题

C EODBA21C EDB A21OA全等三角形专题讲解专题一 全等三角形判别方法的应用专题概说:判定两个三角形全等的方法一般有以下4种: 1.三边对应相等的两个三角形全等(简写成“SSS ”)2.两边和它们的夹角对应相等的两个三角形全等(简写成“SAS") 3.两角和它们的夹边对应相等的两个三角形全等(简写成“ASA ”)4.两个角和其中一个角的对边对应相等的两个三角形全等(简写成“AAS")而在判别两个直角三角形全等时,除了可以应用以上4种判别方法外,还可以应用“斜边、直角边”,即斜边和一条直角边对应相等的两个直角三角形全等(简写成“HL ”).也就是说“斜边、直角边”是判别两个直角三角形全等的特有的方法,它仅适用于判别两个直角三角形全等.三角形全等是证明线段相等,角相等最基本、最常用的方法,这不仅因为全等三角形有很多重要的角相等、线段相等的特征,还在于全等三角形能把已知的线段相等、角相等与未知的结论联系起来.那么我们应该怎样应用三角形全等的判别方法呢?(1)条件充足时直接应用在证明与线段或角相等的有关问题时,常常需要先证明线段或角所在的两个三角形全等,而从近年的中考题来看,这类试题难度不大,证明两个三角形的条件比较充分.只要同学们认真观察图形,结合已知条件分析寻找两个三角形全等的条件即可证明两个三角形全等.例1 已知:如图1,CE ⊥AB 于点E ,BD ⊥AC 于点D ,BD 、CE 交于点O,且AO 平分∠BAC .那么图中全等的三角形有___对.图1(2)条件不足,会增加条件用判别方法此类问题实际是指条件开放题,即指题中没有确定的已知条件或已知条件不充分,需要补充使三角形全等的条件.解这类问题的基本思路是:执果索因,逆向思维,逐步分析,探索结论成立的条件,从而得出答案.例2 如图2,已知AB=AD ,∠1=∠2,要使△ABC ≌△ADE,还需添加的条件是(只需填一个)_____. 图2(3)条件比较隐蔽时,可通过添加辅助线用判别方法在证明两个三角形全等时,当边或角的关系不明显时,可通过添加辅助线作为桥梁,沟通边或角的关系,使条件由隐变显,从而顺利运用全等三角形的判别方法证明两个三角形全等.例3 已知:如图3,AB=AC,∠1=∠2. 求证:AO 平分∠BAC .分析:要证AO 平分∠BAC ,即证∠BAO=∠BCO,要证∠BAO=∠BCO,只需证∠BAO 和∠BCO 所在的两个三角形全等.而由已知条件知,只需再证明BO=CO 即可.图3GABF DEC ODA CBFCEDBA(4)条件中没有现成的全等三角形时,会通过构造全等三角形用判别方法有些几何问题中,往往不能直接证明一对三角形全等,一般需要作辅助线来构造全等三角形.例4 已知:如图4,在Rt △ABC 中,∠ACB=90º,AC=BC ,D 为BC 的中点,CE ⊥AD 于E ,交AB 于F ,连接DF .求证:∠ADC=∠BDF .说明:常见的构造三角形全等的方法有如下三种:①涉及三角形的中线问题时,常采用延长中线一倍的方法,构造出一对全等三角形;②涉及角平分线问题时,经过角平分线上一点向两边作垂线,可以得到一对全等三角形;③证明两条线段的和等于第三条线段时,用“截长补短”法可以构造一对全等三角形.(5)会在实际问题中用全等三角形的判别方法新课标强调了数学的应用价值,注意培养同学们应用数学的意识,形成解决简单实际问题的能力﹒在近年中考出现的与全等三角形有关的实际问题,体现了这一数学理念,应当引起同学们的重视.例5 要在湖的两岸A 、B 间建一座观赏桥,由于条件 限制,无法直接度量A ,B 两点间的距离﹒请你用学过的数 学知识按以下要求设计一测量方案﹒(1)画出测量图案﹒(2)写出测量步骤(测量数据用字母表示)﹒ 图5 (3)计算A 、B 的距离(写出求解或推理过程,结果用字母表示)﹒分析:可把此题转化为证两个三角形全等.第(1)题,测量图案如图5所示.第(2)题,测量步骤:先在陆地上找到一点O ,在AO 的延长线上取一点C ,并测得OC=OA ,在BO 的延长线上取一点D ,并测得OD=OB,这时测得CD 的长为a ,则AB 的长就是a .第(3)题易证△AOB ≌△COD ,所以AB=CD ,测得CD 的长即可得AB 的长.解:(1)如图6示.(2)在陆地上找到可以直接到达A 、B 的一点O,在AO 的延长线上取一点C ,并测得OC =OA ,在BO 的延长线上取一点D ,并测得OD =OB,这时测出CD 的长为a ,则AB 的长就是a .(3)理由:由测法可得OC=OA ,OD=OB . 又∠COD=∠AOB ,∴△COD ≌△AOB .∴CD=AB=a . 图6评注:本题的背景是学生熟悉的,提供了一个学生动手操作的机会,重点考查了学生的操作能力,培养了 学生用数学的意识﹒练习:1.已知:如图7,D 是△ABC 的边AB 上一点,AB ∥FC ,DF 交AC 于点E ,DE=FE . 求证:AE=CE .C ED B AAO Q M CPBN A D C PBHF EGAD CBADCFBEA2.如图8,在△ABC 中,点E 在BC 上,点D 在AE 上,已知∠ABD=∠ACD ,∠BDE=∠CDE .求证:BD=CD .3.用有刻度的直尺能平分任意角吗?下面是一种方法:如图9所示,先在∠AOB 的两边上取OP=OQ ,再取PM=QN,连接PN 、QM,得交点C ,则射线OC 平分∠AOB .你能说明道理吗?4.如图10,△ABC 中,AB=AC,过点A 作GE ∥BC ,角平分线BD 、CF 相交于点H ,它们的延长线分别交GE 于点E 、G .试在图10中找出3对全等三角形,并对其中一对全等三角形给出证明.5.已知:如图11,点C 、D 在线段AB 上,PC=PD .请你添加一个条件,使图中存在全等三角形,并给予证明.所添条件为__________,你得到的一对全等三角形是△_____≌△_____.6.如图12,∠1=∠2,BC=EF ,那么需要补充一个直接条件_____(写出一个即可),才能使△ABC ≌△DEF .7图13,在△ABD 和△ACD 中,AB=AC,∠B=∠C .求证:△ABD ≌△ACD .AODCBAFCGBEAF DCB EOED218.如图14,直线AD与BC相交于点O,且AC=BD,AD=BC.求证:CO=DO.9.已知△ABC,AB=AC,E、F分别为AB和AC延长线上的点,且BE=CF,EF交BC于G.求证:EG=GF.10.已知:如图16,AB=AE,BC=ED,点F是CD的中点,AF⊥CD.求证:∠B=∠E.11.如图17,某同学把一把三角形的玻璃打碎成了三块,现在要到玻璃店去配一块大小形状完全一样的玻璃,那么最省事的办法是()﹒(A)带①和②去 (B)带①去(C)带②去(D)带③去12.有一专用三角形模具,损坏后,只剩下如图18中的阴影部分,你对图中做哪些数据度量后,就可以重新制作一块与原模具完全一样的模具,并说明其中的道理.13.如图19,将两根钢条AA’、BB’的中点O连在一起,使AA’、BB’可以绕着点O自由转动,就做成了一个测量工件,则A' B'的长等于内槽宽AB,那么判定△OAB≌△OAB的理由是( )(A)边角边(B)角边角(C)边边边(D)角角边专题二角的平分线从一个角的顶点出发,把一个角分成相等的两个角的射线,叫做这个角的平分线.角的平分线有着重要的作用,它不仅把角分成相等的两部分,而且角的平分线上的点到角两边的距离相等,到一个角的两边距离相等的点在这个角的平分线上,再加上角的平分线所在的直线是角的对称轴.因此当题目中有角的平分线时,可根据角的平分线性质证明线段或角相等,或利用角的平分线构造全等三角形或等腰三角形来寻找解题思路.(1)利用角的平分线的性质证明线段或角相等F ED CB A 21A FH DCGBEADCBE AF DC BE C E D例6 如图20,∠1=∠2,AE ⊥OB 于E , BD ⊥OA 于D ,交点为C .求证:AC=BC .说明:本题若用全等方法证明点C 到OA 、OB 距离相等,浪费时间和笔墨,不如直接应用角平分线性质证明,原因在于同学们已经习惯了用全等的方法,不善于直接应用定理,仍去找全等三角形,结果相当于重新证明了一次定理,以后再学新定理,应用时要注意全等定势的干扰,注意采用简捷证法. 例7 已知:如图21,△ABC 中, BD=CD ,∠1=∠2.求证:AD 平分∠BAC .说明:遇到有关角平分线的问题时,可引角的两边的垂线,先证明三角形全等,然后根据全等三角形的性质得出垂线段相等,再利用角的平分线性质得出两角相等.(2)利用角的平分线构造全等三角形 ①过角平分线上一点作两边的垂线段例8 如图22,AB ∥CD ,E 为AD 上一点,且BE 、CE 分别平分∠ABC 、∠BCD . 求证:AE=ED .分析:由于角平分线上一点到角的两边的距离相等,而点E 是两条角平分线的交点,因此我们自然想到过点E 分别作AB 、BC 、CD 的垂线段.②以角的平分线为对称轴构造对称图形例9 如图23,在△ABC 中,AD 平分∠BAC,∠C=2∠B .求证:AB=AC+CD .分析:由于角平分线所在的直线是这个角的对称轴,因此在AB 上截取AE=AC,连接DE ,我们就能构造出一对全等三角形,从而将线段AB 分成AE 和BE 两段,只需证明BE=CD 就可以了.③延长角平分线的垂线段,使角平分线成为垂直平分线 例10 如图24,在△ABC 中,AD 平分∠BAC ,CE ⊥AD 于E . 求证:∠ACE=∠B+∠ECD .分析:注意到AD 平分∠BAC ,CE ⊥AD ,于是可延长CE 交AB 于点F,即可构造全等三角形..(3)利用角的平分线构造等腰三角形如图25,在△ABC 中,AD 平分∠BAC ,过点D 作DE ∥AB ,DE 交AC 于点E .易证△AED 是等腰三角形. 因此,我们可以过角平分线上一点作角的一边的平行线,构造等腰三角形.CF E BADQPCBACB AD EA例11 如图26,在△ABC 中,AB=AC,BD 平分∠ABC ,DE ⊥BD 于D ,交BC 于点E .求证:CD=21BE .分析:要证CD=21BE ,可将BE 分成两条线段,然后再证明CD 与这两条线段都相等.练习:1.如图27,在△ABC 中,∠B=90º,AD 为∠BAC 的平分线,DF ⊥AC 于F,DE=DC .求证:BE=CF .2.已知:如图28,AD 是△ABC 的中线,DE ⊥AB 于E ,DF ⊥AC 于F ,且BE=CF .求证:(1)AD 是∠BAC 的平分线;(2)AB=AC .3.在△ABC 中,∠BAC=60º,∠C=40º,AP 平分∠BAC 交BC 于P,BQ 平分∠ABC 交AC 于Q . 求证:AB+BP=BQ+AQ .4.如图30,在△ABC 中,AD 平分∠BAC ,AB=AC+CD . 求证:∠C=2∠B .5.如图31,E 为△ABC 的∠A 的平分线AD 上一点,AB >AC . 求证:AB —AC >EB-EC .CB AD 4321C E BADF CE BAD CEBADCBADACBD6.如图32,在四边形ABCD 中,BC >BA ,AD=CD ,BD 平分∠ABC . 求证:∠A+∠C=180º.7.如图33所示,已知AD ∥BC ,∠1=∠2,∠3=∠4,直线DC 过点E 作交AD 于点D ,交BC 于点C .求证:AD+BC=AB .8.已知,如图34,△ABC 中,∠ABC=90º,AB=BC,AE 是∠A 的平分线,CD ⊥AE 于D .求证:CD=21AE .9.△ABC 中,AB=AC,∠A=100º,BD 是∠B 的平分线.求证:AD+BD=BC .10.如图36,∠B 和∠C 的平分线相交于点F ,过点F 作DE ∥BC 交AB 于点D ,交AC 于点E ,若BD+CE=9,则线段DE 的长为( )A .9B .8C .7D .611.如图37,△ABC 中,AD 平分∠BAC ,AD 交BC 于点D ,且D 是BC 的中点.求证:AB=AC .A CF E B M D12.已知:如图38,△ABC 中,AD 是∠BAC 的平分线,E 是BC 的中点,EF ∥AD ,交AB 于M ,交CA 的延长线于F .求证:BM=CF .。
三角形角平分线的定理

三角形角平分线的定理角平分线是指将一个角分成两个相等角的直线。
在三角形中,角平分线起着重要的作用。
本文将介绍三角形角平分线的定理以及其相关性质。
一、三角形角平分线的定理三角形角平分线的定理是指:在一个三角形中,如果一条直线从一个顶点平分对角的两个角,那么这条直线将平分对角的对边。
具体而言,设△ABC为一个三角形,AD是∠BAC的角平分线,交BC于点D。
那么有以下结论:1.∠BAD = ∠DAC,即∠BAD和∠DAC是相等的。
2.∠ABD = ∠CAD,即∠ABD和∠CAD是相等的。
3.BD/CD = AB/AC,即BD与CD的比值等于AB与AC的比值。
二、三角形角平分线的证明要证明三角形角平分线的定理,首先我们可以通过角平分线的定义得出∠BAD = ∠DAC和∠ABD = ∠CAD。
接下来,我们需要证明BD/CD = AB/AC。
根据正弦定理,我们可以得到以下等式:AB/AC = sin∠BAC/sin∠ABCBD/CD = sin∠BAC/sin∠CBD由于∠ABC = ∠CBD,所以sin∠ABC = sin∠CBD。
因此,我们可以得出BD/CD = AB/AC。
三、三角形角平分线的应用三角形角平分线的定理在几何学中有广泛的应用。
以下是一些常见的应用场景:1.角平分线定理可以用来解决三角形内角的问题。
通过已知条件,我们可以利用角平分线的性质来求解未知角度的大小。
2.角平分线定理可以用来证明三角形的相似性。
当两个三角形的角平分线相交于同一点时,我们可以利用角平分线的性质证明这两个三角形是相似的。
3.角平分线定理可以用来证明三角形的内心存在。
内心是三角形内切圆的圆心,它同时也是三条角平分线的交点。
4.角平分线定理可以用来证明三角形的垂心存在。
垂心是三角形三条高的交点,其中两条高与第三条高的交点恰好是角平分线的交点。
四、总结三角形角平分线的定理是几何学中的重要定理之一。
通过角平分线的性质,我们可以解决三角形内角的问题,证明三角形的相似性以及存在性等问题。
专题04 三角形的角平分线及其规律

专题04三角形的角平分线及其规律【专题解读】无论是中考,或者是竞赛中,常常有与三角形的角平分线(包括内、外角的平分线)相关的问题.这类题目形式多样,变化方向非常广泛。
如果我们能够善于对这类有关三角形的角平分线的基本图形进行归类,并对角平分线的性质和结论做好总结,那么必将对我们的学习产生很大的帮助,也将更有利于我们有效地找寻到解决有关的较难几何证明题的思路与方法.思维索引例1.(1)如图(1),在△ABC中,AD、AE分别是△ABC的高和角平分线,已知:∠B=30°,∠C=50°,求∠DAE的度数;(2)如图(2),∠BAC的角平分线AF交BC于点E,过点F作FD⊥BC于点D,若∠C-∠B=30°,求∠F的度数.EDAEDA BBF图(1)图(2)例2.已知:∠MON=40°,OE平分∠MON,点A、B、C分别是射线OM、OE、ON上的动点(A、B、C不与点O重合),连接AC交射线OE于点D.设OAC x∠=︒图1 图2(1)如图1,若AB/∥ON,则①∠ABO的度数是____________②当∠BAD=∠ABD时,x=__________;当∠BAD=∠BDA时,x=____________(2)如图2,若AB⊥OM,则是否存在这样的x的值,使得△ADB中有两个相等的角?若存在,求出x的值;若不存在,说明理由.例3.已知:△ABC 中,记,BAC ACB αβ∠=∠=.(1)如图1,若AF 平分∠BAC ,BF 、CF 分别平分△ABC 的外角∠CBD 和∠BCE ,BG ⊥AF 于点G . ①用α的代数式表示∠BFC 的度数;②用β的代数式表示∠FBG 的度数;(2)如图2,若点F 为△ABC 的三条内角平分线的交点,且BG ⊥AF 于点G . ①请补全图形;②猜想(1)中的两个结论是否发生变化?如果不变,请说明理由;如果变化,请直接写出正确的结论.EB图1 图2素养提升1.△ABC 中,∠ABC 和∠ACB 的角平分线相交于点D ,连接AD ,若∠BDC =130°,则∠BAD 为( ) A.65° B.60° C.40° D.35°2.如图,在△ABC 中,∠B=42°,△ABC 的外角∠EAC 和∠FCA 的平分线交于点D ,则∠ADC 为( ) A.75° B.69° C.63° D.45°3.如图,∠ABC 、∠ACB 的三等分线交于点F 、D ,若∠BEC=132°,∠BGC=118°,则∠A 为( ) A.65° B.66° C.70°D.78°BBEB第1题图 第2题图 第3题图4.如图,在△ABC 中,∠A=52°,∠ABC 与∠ACB 的角平分线交于1D ,∠AB 1D 与∠AC 1D 的角平分线于点2D ,依次类推,∠AB 5D 与∠AC 5D 的角平分线交于点6D ,则∠B 6D C 的度数是( ) A.56° B.60° C.68° D.54°5.如图,∠ABC =∠ACB ,AD 、BD 、CD 分别平分△ABC 的外角∠EAC 、内角∠ABC 、外角∠ACF .以下结论:①AD //BC ;②∠ACB=2∠ADB ;③90ADC ABD ∠=︒-∠;④BD 平分∠ADC ;⑤∠BDC =12∠BAC .其中正确的结论有( )A.2个B.3个C.4个D.5个BBB第4题图 第5题图 第6题图6.△ABC 的外角平分线CD 与∠ABC 平分线BD 交于点D ,若∠BDC =40°,则∠CAD =________. 7.如图,在△ABC 中,∠A =m °,∠ABC 的平分线与∠ACD 的平分线交于点1A ,∠1A BC 的平分线与1ACD ∠的平分线交于点21,,n A A BC -∠的平分线与1n A CD -∠的平分线交于点n A ,则n A ∠=__________°.(用含m 的代数式表示) 8.如图,在四边形ABCD 中,∠ABC 的角平分线与∠DCB 的外角平分线相交于点F ,且∠A +∠D=210°,则∠F =_____________°.9.如图,若AB //CD ,BF 平分∠ABE ,CF 平分∠DCE ,∠BEC=86°,则∠BFC =__________°.2BB第7题图 第8题图 第9题图10.如图,在△ABC 中,∠A=60°,HI 、FI 分别平分∠ABC 、∠ACB ,BD 、CD 分别平分∠HBC 、∠BCF ,BE 、CE 分别平分∠DBC 、∠DCG ,则∠E =_________°.11.(1)如图甲,在凹四边形ABCD 中,∠ABD 与∠ACD 的角平分线交于点E ,∠A=60°,∠BDC=140°,则∠E =__________°(2)如图乙,∠ABD ,∠BAC 的角平分线交于点E ,∠C=40°,∠BDC=140°,求∠AEB 的度数; (3)如图丙,∠ABD ,∠ACD 的10等分线相交于点1F 、2F 、…、9F ,若∠BDC =120°,∠B 3F C =64°,则∠A 的度数为___________.B图甲 图乙 图丙12.如图,已知点A 、B 分别在∠ECF 的两边上(不与点C 重合),AD 、BD 平分∠EAB 和∠ABF 相交于点D .(1)如图1,若∠ECF =90,试猜想∠ADB =________________°; (2)在(1)的基础上,若∠ECF 每秒钟变小10°,经过了1秒(09t <<), ①试用含t 的代数式表示∠ADB 的度数;②并求出当t 取何值时,∠ECF 与∠ADB 的度数相等;(3)如图3,在(2)的条件下,若BG 平分∠ABC ,其它条件不改变,是否存在t ,使得23BGD ADB ∠=∠,若存在直接写出t 的值,若不存在,请说明理由.CA图(1) 图(2)13.(1)如图1,BD 、BC 分别平分∠ABC 、∠ACB ,∠A =70°,则∠BDC = .(2)如图2,将△ABC 沿BC 向右平移后可得△FCE ,BD 、DE 分别平分∠ABC 、∠FE C .∠A =n °,求∠BDE 的度数;(3)如图3,将△ABC 绕点C 旋转180°得△EFC ,DA 平分∠BAC ,DB 平分∠ABC ,GF 平分∠CFE 、GE 平分∠CEF 的外角,试探究∠ADB 与∠FGE 有何确定的数量关系,并说明理由.BCD A BCDEFAAH GFEDCB图1 图2 图314.直线EF 与直线MN 垂直相交于O ,点A 在直线EF 上运动,点B 在直线MN 上运动.(1)如图1,已知AG 、BG 分别是∠BAO 和∠ABO 角的平分线,点A 、B 在运动的过程中,∠AGB 的大小是否会发生变化?若发生变化,请说明变化的情况;若不发生变化,试求出∠AGB 的大小;(2)如图2,已知AB 不平行CD ,AD 、BC 分别是∠EAB 和∠ABM 的角平分线,又DG 、CG 分别是∠ADC 和∠BCD 的角平分线,点A 、B 在运动的过程中,∠CGD 的大小是否会发生变化?若发生变化,请说明理由;若不发生变化,试求出其值;(3)如图3,延长AB ,已知∠BAO 和它的外角平分线分别与∠AON 的角平分线及其延长线相交于G 、C ,在△BCG 中,如果有一个角是另一个角的4倍,试求∠BAO 的度数.AOMGF E BNAONM GFED CB A ONMG FECB图1 图2 图3专题04三角形的角平分线及其规律【思维索引】例1.(1)∠DAE =10° (2)∠F =15°例2.(1)①∠ABO =20° ②120;60 (2)20;35;50;125例3.(1)①∠BFC =90°-12α; ②.∠FBG =90°-12β (2)①∠BFC =90°+12α; ②∠FBG =12β.【素养提升】1.C ; 2.B ; 3.C ; 4.D ; 5.C ; 6.50°; 7.2nm; 8.15°; 9.43°; 10.30°; 11.(1)100°; (2)130°; (3)40°;12.(1)45°; (2)①45°+5t ; ②t =3秒; (3)t =1.8. 13.(1)125°; (2) 90°+12n ; (3)∠ADB =90°+∠FGE .14.(1)45°; (2)67.5°; (3)45°或36°.。
角的平分线的性质知识讲解

角的平分线的性质(提高)【学习目标】1掌握角平分线的性质,理解三角形的三条角平分线的性质.2•掌握角平分线的判定及角平分线的画法.3.熟练运用角的平分线的性质解决问题.【要点梳理】要点一、角的平分线的性质角的平分线的性质:角的平分线上的点到角两边的距离相等要点诠释:用符号语言表示角的平分线的性质定理:若CD平分/ ADB点P是CD±一点,且/KAD于点E, PF丄BD于点F,则PE二PF.要点二、角的平分线的判定角平分线的判定:角的内部到角两边距离相等的点在角的平分线上要点诠释: 用符号语言表示角的平分线的判定:若PEL AD 于点E, PFL BD 于点F, PE二PF,贝U PD 平分/ ADB要点三、角的平分线的尺规作图角平分线的尺规作图(1) 以0为圆心,适当长为半径画弧,交0A于D, 交0B于E.1(2) 分别以D E为圆心,大于DE的长为半径画弧,两弧在/ AOB内部交于点C.2(3) 画射线0C.射线0C即为所求.要点四、三角形角平分线的性质三角形三条角平分线交于三角形内部一点,此点叫做三角形的内心且这一点到三角形三边的距离相等•三角形的一内角平分线和另外两顶点处的外角平分线交于一点•这点叫做三角形的旁心三角形有三个旁心•所以到三角形三边所在直线距离相等的点共有4个.如图所示:△ ABC的内心为R '旁心为Fa, F S,P4‘这四个点到△ ABC三边所在直线距离相等・P4【典型例题】类型一、角的平分线的性质及判定1、如图,在厶ABC中,/ ABC的平分线与/ ACB的外角的平分线相交于点P,连接AP.(1) 求证:PA平分/ BAC的外角/ CAM(2) 过点C作CELAP, E是垂足,并延长CE交BM于点D.求证:CE=EDB c N【思路点拨】C )过P作PTL BC于T, PSL AC于S, PCL BA于Q根据角平分线性质求出PQ=PS=PT根据角平分线性质得出即可;(2)根据ASA求出△ AED^AAEC即可.【答案与解析】证明:C)过p作PTLBC于T, PSI AC于S,PQLBA于Q如图,・••在△ ABC中,/ ABC的平分线与/ ACB的外角的平分线相交于点P,••• PQ=PT PS=PT••• PQ=PS・AP平分/ DAC即PA平分/ BAC的外角/ CAMR c r jV(2)T PA平分/ BAC的外角/ CAM•••/ DAE=/ CAE •••CEL AP, •••/ AEDM AEC=90 ,在厶AED 和厶AEC 中r ZDAE=ZCAE*AE 二AEL ZDEA=ZCEA•••A AED A A AEC・CE=ED【总结升华】本题考查了角平分线性质和全等三角形的性质和判定的应用,解此题的矢键是能正确作出辅助线并进一步求出PQ=PS A AAED^AAEC注意:角平分线上的点到角两边的距离相等.举一反三:【变式】如图,AD是/ BAC的平分线,DEIAB,交AB的延长线于点E, DF丄AC于点F,且DB二DC.求证:BE二CF.【答案】证明:・DELAE, DF丄AC,AD是/ BAC的平分线,• DE= DF,/ BED=Z DFC= 90°一- 出:DB=DC在RtA BDE 与Rt △ CDF 中,、DE = DF・R tA BDE A RtA CDF( HL)・B E= CF2、如图,久。
三角形角平分线经典例题讲解

三角形角平分线经典例题讲解今天咱们聊聊三角形的角平分线,这个东西可真有趣。
大家都知道,三角形有三个角,对吧?而角平分线就是把其中一个角分成两个相等的角。
想象一下,一个小朋友在划分他的糖果,想让每一部分都一样,生怕一边多一颗,一边少一颗。
角平分线就是这么一个公正的“糖果分配者”。
说到这,大家有没有想过,三角形的角平分线跟其他线段有什么不同呢?它不仅仅是个直线,它还有许多有趣的性质。
角平分线的定义可不是随便说说的。
它是从一个顶点出发,直达对边,确保两个角完全相等。
想想看,如果你在画图,随便一条线怎么能做到这点呢?得用心!在我们生活中,很多地方都能看到角平分线的影子,想象一下,那些精致的甜品店,做蛋糕时的对称美,都是在追求这种“公平”的理念。
真是妙不可言。
大家知道吗?角平分线还有个酷炫的性质,就是它把对边分成的两部分,有个奇妙的比例关系。
这可不是开玩笑,跟数学中的“比”有关系哦,具体说就是:角平分线把对边分成的两段长度,跟这条线的两条边的长度成比例。
听起来可能有点复杂,咱们举个简单的例子吧。
假设有一个三角形ABC,角A是个大角,咱们把它的角平分线叫做AD。
AD把BC分成了两部分,BD和DC。
这个时候,AD的长度和AB、AC的长度之间就有了某种美丽的平衡。
就像一位和蔼可亲的老师在课堂上把学生分成了两组,确保每组都有足够的成员,让每个孩子都能参与进来。
真是温馨的一幕呢。
角平分线的性质不仅让人觉得公平,还能在一些复杂的问题中帮我们解决难题。
数学题目就像过家家的游戏,难免会有点混乱。
这时,找到角平分线,就好比找到了一根指路明灯,让我们能顺利地走出迷雾。
大家都想过,怎么利用角平分线解决实际问题吗?比如在地理上,角平分线可以帮助我们划分区域,确保每个区域都被合理地利用。
说到这,我就想到了一个经典的应用题。
有一天,小明跟小红在讨论一个三角形的面积,争论得不可开交。
小明说,他觉得从一个顶点画条角平分线,把对边分成两段,面积也分成两个比例,结果小红立刻不服气,开始反驳。
三角形的角平分线

三角形的角平分线引言三角形是几何学中最基本的图形之一,它由三条边和三个顶点组成。
在三角形中,角平分线是指从一个角的顶点出发,将该角分为两个相等的角的线段。
本文将介绍三角形的角平分线的性质和相关定理。
角平分线的定义在三角形ABC中,假设角A的顶点是顶点A,其角平分线是指从顶点A出发,将角A分为两个相等的角。
角平分线的性质在三角形ABC中,角平分线有以下性质:1.角平分线将角分为两个相等的角。
证明:假设角A的角平分线为AD,可以通过角A的两边与角平分线的交点D分别连接线段CD和BD,得到三个小三角形ACD、BCD和ABD。
根据直角三角形的性质,我们知道ACD ≌ BCD 和ABD ≌ BCD,因此角ACD和角ABD是相等的。
2.角平分线上的点到三角形的两边距离相等。
证明:假设角A的角平分线为AD,可以通过点D分别作垂线DE和DF分别与边AC和边BC相交。
根据直角三角形的性质,我们可以得知三角形AED ≌三角形BED和三角形AFD ≌ 三角形BFD。
因此,DE = DF。
3.三角形的三条角平分线交于一点。
证明:假设角A的角平分线为AD,角B的角平分线为BE,角C的角平分线为CF。
我们可以通过两条角平分线相交的性质,得到∠CAD = ∠BAD 和∠BAE =∠CAE。
由于∠CAD = ∠BAE,所以角DAB = ∠CAB。
同理,可以证明角BAC = ∠BAC。
因此,三个角平分线交于点D。
角平分线的相关定理角平分线定理在三角形ABC中,角A的角平分线和边BC的关系为:angle_bisector_theoremangle_bisector_theorem其中,BD为角平分线,根据角平分线的性质可得:AB/AC = BD/CD。
角平分线的外角定理在三角形ABC中,如果角平分线BD将边AC分成了线段AE和EC,那么∠BAD = ∠BCE。
角平分线的内角定理在三角形ABC中,如果角平分线BD将角BAC分成了角BAD和角CAD,那么∠BAD = ∠CAD。
三角形中的角平分线问题解法

三角形中的角平分线问题解法三角形是几何学中的重要概念,其中角平分线问题是解题中经常遇到的一类问题。
本文将介绍三角形中的角平分线问题以及其解法。
一、问题描述在三角形中,角平分线是指从一个角的顶点出发,将该角分成两个相等的角的线段。
角平分线经过三角形内部的一点,称为角平分线的内心。
现在,我们来解决如下问题:如何找到三角形的角平分线及其内心。
二、解法一:角平分线的性质在解决问题之前,我们先来了解一下角平分线的性质。
在任意三角形ABC中,如果AD是∠BAC的角平分线,那么AD与BC的交点E 将BC平分成两个相等的线段。
同时,BD/DC=AB/AC(即角平分线将对边按比例分割)。
基于上述性质,我们可以用以下步骤得到角平分线及其内心:1.画出三角形ABC。
2.画出角BAC的角平分线AD。
3.延长AD与BC交于点E,连接AE。
4.利用角平分线的性质,得到BD/DC=AB/AC。
5.将角平分线按比例分割BC,即可得到角平分线的内心。
三、解法二:角平分线的几何构造上述解法通过角平分线的性质找到了角平分线及内心,但有时候,我们可能需要通过几何构造来找到角平分线。
我们来介绍解法二。
1.画出三角形ABC。
2.以点A为圆心,以AB为半径画弧,交BC于点D。
3.以点B为圆心,以BA为半径画弧,交AC于点E。
4.连接DE。
5.延长DE至AB(交于F),连接FC。
6.连接AF,交BC于点G。
7.则CG即为角BAC的角平分线,点G即为角平分线的内心。
四、解法三:角平分线的角度计算除了通过角平分线的性质和几何构造找到角平分线,我们还可以通过角度计算的方式来解决问题。
下面是解法三:1.已知三角形ABC的三边长a、b、c。
2.根据余弦定理计算∠BAC的角度A:cos(A) = (b²+c²-a²)/(2bc)。
3.计算出∠BAC的角度A后,将其除以2即可得到角平分线的角度。
通过上述解法,我们可以找到三角形中的角平分线及其内心,解决相关问题。
三角形中的角平分线

三角形中的角平分线三角形是中学数学中常见的一个几何图形,它由三条线段组成,每条线段连接两个角,并形成三个角。
在三角形中,角平分线是指从一个角的顶点出发,将该角分成两个相等的角,并与对边相交的线段。
角的平分线在三角形中具有重要的几何性质和应用。
本文将详细介绍三角形中角平分线的特点和应用。
一、定义角平分线是指从一个角的顶点出发,将该角分成两个相等的角,并与对边相交的线段。
对于任意三角形ABC,若AD为角BAC的角平分线,则∠BAD≅∠CAD。
二、三角形角平分线的性质1. 角平分线将角分成两个相等的角。
若AD为角BAC的角平分线,则∠BAD≅∠CAD。
2. 角平分线与对边相交于三角形的内心。
三角形的内心是角平分线三条的交点,记为I。
即角平分线BE、CF和AD的交点为内心I。
3. 角平分线与对边的比例关系。
根据内切角的性质,有以下比例关系:AB/AC = BD/DC = c/bBC/BA = CE/EA = a/cCA/CB = AF/FB = b/a4. 角平分线长度的性质。
设角BAC的角平分线AD与对边BC相交于点D,则有以下关系: BD/DC = AB/AC (根据角平分线与对边的比例关系)AD/DC = AB/BC (根据角平分线定理)根据以上性质,可以推导出角平分线长度的计算公式。
三、三角形角平分线的应用1. 寻找三角形的内心。
通过求解角平分线的交点,可以确定三角形的内心。
内心是三角形的一个重要特征点,在几何学和三角学中有广泛的应用。
2. 解决三角形的相关问题。
通过应用角平分线的性质,可以解决各种与角平分线相关的三角形问题,如角平分线的长度、角平分线与周长的关系等。
这些问题是解决几何学和三角学中经典问题的重要方法之一。
3. 构造等分角。
如果需要将某个角等分为多个角,可以通过绘制角平分线来实现。
通过绘制角平分线,可以将原角等分为任意个相等的角。
四、结语三角形中的角平分线在数学中具有重要的地位和应用。
三角形的角平分线

三角形的角平分线角平分线是指从一个三角形的顶点出发,将该角分成两个相等的角的线段。
在三角形中,每个角都有三条平分线,它们相交于一个点,称为内心。
角平分线的性质有很多,下面我们来逐一介绍。
1. 内心:三角形的角平分线相交于一个点,这个点被称为三角形的内心。
内心到三角形的三条边的距离相等,这个距离被称为内心到三边的距离,也是内心半径。
2. 角平分线长度:三角形的角平分线将对边分成两个段,这两个段的长度与角平分线所在边的长度的比相等。
也就是说,如果一条角平分线将对边分成长度为a和b的两段,那么 a:b等于边所占对边的比。
3. 角平分线的垂直性:三角形的角平分线与对边垂直。
即在一个三角形ABC中,角A的平分线与边BC垂直,角B的平分线与边AC垂直,角C的平分线与边AB垂直。
4. 角平分线的外角平分性:三角形的外角是指一个三角形内部的一个角的补角。
角平分线同时也是外角的平分线,也就是说,如果一条角平分线平分了某个外角,那么这个外角被平分成两个相等的角。
5. 角平分线的交点:三角形的三条角平分线相交于一个点,称为内心。
内心是三角形内心圆的圆心,内心到三角形的三条边的距离相等,即内心到三边的距离相等。
此外,内心到三角形三个顶点的距离相等,即内心到顶点的距离也是相等的。
角平分线在三角形的研究中具有广泛的应用。
它不仅可以用于求解三角形的各个参数,还可以应用到三角形的几何性质证明中。
最后,角平分线也是解决三角形相关题目中的一个有效的思路和方法。
通过运用角平分线的性质,可以使问题的求解更加简单和方便。
总结起来,角平分线是一个具有重要性质的几何概念,它不仅能够划分和研究三角形内部的角度,还可以应用到解决三角形问题的过程中。
对于了解三角形的角平分线性质以及灵活运用角平分线的方法,对于解决相关问题和提升几何推理能力都具有重要作用。
第03讲 三角形与角平分线
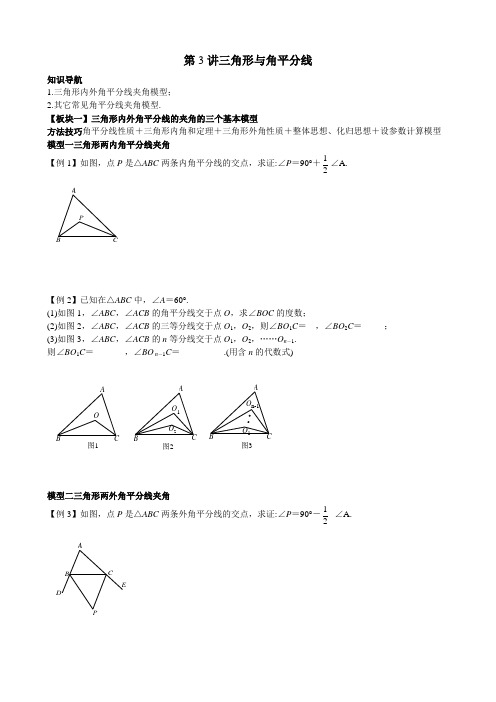
第3讲三角形与角平分线知识导航1.三角形内外角平分线夹角模型;2.其它常见角平分线夹角模型.【板块一】三角形内外角平分线的夹角的三个基本模型方法技巧角平分线性质+三角形内角和定理+三角形外角性质+整体思想、化归思想+设参数计算模型 模型一三角形两内角平分线夹角【例1】如图,点P 是△ABC 两条内角平分线的交点,求证:∠P =90°+12∠A. PCBA【例2】已知在△ABC 中,∠A =60°.(1)如图1,∠ABC ,∠ACB 的角平分线交于点O ,求∠BOC 的度数;(2)如图2,∠ABC ,∠ACB 的三等分线交于点O 1,O 2,则∠BO 1C =__,∠BO 2C =_____; (3)如图3,∠ABC ,∠ACB 的n 等分线交于点O 1,O 2,……O n -1. 则∠BO 1C =_______,∠BO n -1C =__________.(用含n 的代数式)图1图2图3O 2O 1A CA BCO模型二三角形两外角平分线夹角【例3】如图,点P 是△ABC 两条外角平分线的交点,求证:∠P =90°-12∠A. ABCDE模型三三角形一内角平分线与一外角平分线的夹角【例4】如图,点D是BC延长线上一点,PB平分∠ABC,PC平分∠AC D.求证:∠P=12∠A.AB C DE针对练习11.如图,在△ABC中,∠A=60°,BP,BE把∠ABC三等分,线段CP,CE把∠ACB三等分,求∠BPE的度数.PACE2.如图,在平面直角坐标系中,点A为x轴上的一点,点B为y轴上的一点,AC平分∠BAx,BC平分∠ABy,求∠C的度数.3.如图,在平面直角坐标系中,点A为x轴上的一点,点B为y轴上的一点,AD平分∠BAx,BP平分∠OBA,BP与DA的延长线交于点P,求∠P的度数.【板块二】与三角形有关的其它角平分线模型 ◆方法技巧◆角平分长性质+三角形内角和定理十三角形外角性质+整体思想,化归思想+设参数计算 模型四◆角平分线+高线夹角模型(设参计算+整体思想)【例5】(1)已知△ABC 中,∠B >∠C ,AD ⊥BC 于D ,AE 平分∠BAC ,如图1,设∠B =x ,∠C =y ,试用x ,y 表示∠DAE ,并说明理由;(2)在图2中,其他条件不变,若把“AD ⊥BC 于D ”改为“F 是AE 上一点,FD ⊥BC 于D ",试用x ,y 表示∠DFE =_________;(3)在图3中,若把(2)中的“点F 在AE 上”改为“点F 是AE 延长线上一点”,其余条件不变,试用x ,y 表示∠DFE =_______;(4)在图3中,分别作出∠BAE 和∠EDF 的角平分线,交于点P ,如图4,试用x ,y 表示∠P =_____.图4图1图2图3PF DBE AFDBE CEBD AABCDEF模型五燕尾形双角平分(设参计算+整体思想)【例6】如图,BP ,CP 分别平分∠ABD ,∠ACD ,它们交于点P .求证:∠P =12(∠A +∠D ). P DCBA模型六蝶形(8字形)双角平分(设参计算+整体思想)【例7】(1)模型:如图1,AD ,BC 交于O 点.求证:∠D +∠C =∠A +∠B. (2)模型应用:如图2,∠BAD 和∠BCD 的平分线交于点E . ①若∠D =30°,∠B =40°,则∠E 的度数是______;②直接写出∠E 与∠D ,∠B 之间的数量关系是:__________;(3)类比应用:如图3,∠BAD 的平分线AE 与∠BCD 的平分线CE 交于点E .若∠D =m °,∠B =n °,(m <n ).求∠E 的度数.(用含有m ,n 的式子表示)图1图2图3EABCDBCDOEDC A针对练习21.如图,∠ABD ,∠ACD 的角平分线交于点P ,若∠P =20°,∠D =10°,求∠A 的度数.ABCDP2.如图,∠ABD 的平分线与∠ACD 的邻补角∠ACE 的平分线所在的直线交于点I . (1)写出∠I 与∠A ,∠D 之间的数量关系式并证明;(2)直接写出∠I 与∠A ,∠D 之间的数量关系式为___________.图1图2I ABDCE AB CD EI。
三角形的角平分线

三角形的角平分线三角形是几何学中研究的重要图形之一,它由三条边和三个角组成。
在三角形的内部,存在着一种特殊的线段,被称为角平分线。
本文将介绍三角形的角平分线及其性质。
一、角平分线的定义在一个三角形ABC中,如果有一条线段AD从顶点A出发,且将角BAC分成两个相等的角BAM和MAC,那么线段AD被称为角BAC的平分线,点D被称为角BAC的平分点。
二、角平分线的性质1. 角平分线的存在性:对于任意一个三角形ABC的内角BAC,都存在一条唯一的角平分线。
2. 角平分线的角度相等性:如果一条线段AD是三角形ABC的角BAC的平分线,那么角BAM和角MAC的度数相等。
3. 角平分线的内切性质:角平分线上的点D到三角形的两边AB和AC的距离相等,即AD=BD=CD。
4. 角平分线的外切性质:如果一条线段AD是三角形ABC的角BAC的平分线,那么AD与边BC的比值等于边AB与边AC的比值,即AB/AC=BD/CD。
5. 角平分线的唯一性:在三角形ABC中,如果角分线AD和AE相交于点A,并且AB≠AC,那么AD必定与AE重合,即D和E重合。
三、角平分线的应用1. 角平分线定理:如果在一个三角形内,一条平行于边AC的直线通过角BAM的平分点D,与边AB和角BAC分别交于点E和F,那么AE/EB=AF/FC。
2. 角平分线的几何构造:可以利用尺规作图的方式来构造三角形的角平分线。
例如,已知一条边和另外两个角,可以通过作等角的方式找到对应的平分线。
3. 角平分线的性质在三角形的证明中经常被使用,可以用来求解三角形的各种长度、角度关系等。
四、实际应用角平分线的概念和性质在现实生活中有广泛的应用。
例如,在地理测量中,可以利用三角形的角平分线来进行方位角的测量;在建筑设计中,可以利用角平分线来确定墙壁的垂直度等。
总结:本文介绍了三角形的角平分线及其性质。
角平分线是三角形内部的一条特殊线段,它具有唯一性和一些重要的性质。
了解角平分线的定义和性质有助于深入理解三角形的几何性质,并能应用于解决实际问题。
专题02 三角形角平分线模型的应用(解析版)

专题02 三角形角平分线模型的应用参考答案与解析【考点1 双内角平分线】【条件】BP 、CP 分别为∠ABC 、∠ACB 的角平分线.【结论】∠P=90°+∠A.【例1】(2019春•东阿县期末)已知任意一个三角形的三个内角的和是180°.如图1,在△ABC 中,∠ABC 的角平分线BO 与∠ACB 的角平分线CO 的交点为O(1)若∠A =70°,求∠BOC 的度数;(2)若∠A =a ,求∠BOC 的度数;【答案】(1)∴∠BOC =125°(2)∴∠BOC =90°+21【直击考点】 【典例分析】【解答】解:(1)∵∠A=70°,∴∠ABC+∠ACB=180°﹣∠A=110°,∵在△ABC中,∠ABC的角平分线BO与∠ACB的角平分线CO的交点为O,∴∠OBC=∠ABC,∠OCB=ACB,∴∠OBC+∠OCB=(∠ABC+∠ACB)=55°,∴∠BOC=180°﹣(∠OBC+∠OCB)=125°;(2)∵∠A=α,∴∠ABC+∠ACB=180°﹣∠A=180°﹣α,∵在△ABC中,∠ABC的角平分线BO与∠ACB的角平分线CO的交点为O,∴∠OBC=∠ABC,∠OCB=ACB,∴∠OBC+∠OCB=(∠ABC+∠ACB)=(180°﹣α)=90°﹣,∴∠BOC=180°﹣(∠OBC+∠OCB)=180°﹣(90°﹣)=90°+【变式1】(2021秋•四川)如图,△ABC中,(1)若∠B=70°,点P是△ABC的∠BAC和∠ACB的平分线的交点,求∠APC的度数.(2)如果把(1)中∠B=70°这个条件去掉,试探索∠APC和∠B之间有怎样的数量关系.【答案】(1)∴∠P=180°﹣55°=125°(2)∠APC==90°+∠B【解答】解:(1)∵∠B=70°,∴∠BAC+∠BCA=110°,∵点P是△ABC的∠BAC和∠ACB的平分线的交点,∴∠P AC=∠BAC,∠PCA=∠BCA,∴∠P AC+∠PCA=(∠P AC+∠PCA)=×110°=55°,∴∠P=180°﹣55°=125°;(2)∵点P是△ABC的∠BAC和∠ACB的平分线的交点,∴∠P AC=∠BAC,∠PCA=∠BCA,∴∠P AC+∠PCA=(∠P AC+∠PCA),∴∠P=180°﹣(∠P AC+∠PCA)=180°﹣(∠BAC+∠BCA)=180°﹣(180°﹣∠B)=90°+∠B.【变式2】(2021春•松北区期末)如图,∠ABD=15°,∠ACD=30°,∠A=45°,则∠BDC的度数为°.【答案】90【解答】解:延长BD交AC于点E,∵∠CEB=∠A+∠ABD,∠BDC=∠CEB+∠ACD,∴∠BDC=∠A+∠ABD+∠ACD,∵∠ABD=15°,∠ACD=30°,∠A=45°,∴∠BDC=45°+30°+15°=90°,故答案为90.【考点2 双外角平分线】【条件】BP 、CP 分别为∠EBC 、∠BCD 的角平分线.【结论】∠P=90°-∠A.【例2】(2021春•沈丘县期末)如图,已知∠ABC 、∠ACB 的外角平分线交于D 点.∠A=40°,那么∠D = .【答案】70°【解答】解:∵∠A =40°,∠ABC +∠A +∠ACB =180°,∴∠ABC +∠ACB =180°﹣40°=140°,∵∠ABC +∠CBF =180°,∠ACB +∠BCE =180°,∴∠ABC +∠CBF +∠ACB +∠BCE =360°,∴∠CBF +∠BCE =360°﹣140°=220°,∵BD 平分∠CBF ,CD 平分∠BCE ,∴∠DBC +∠DCB =(∠CBF +∠BCE )=110°,∵∠DBC +∠DCB +∠D =180°,∴∠D =180°﹣110°=70°,故答案为70°.【变式1】(2020秋•讷河市期末)在△ABC 中,∠B =58°,三角形的外角∠DAC 和∠ACF的平分线交于点E ,则∠AEC = .21【答案】61°【解答】解:∵三角形的外角∠DAC和∠ACF的平分线交于点E,∴∠EAC=∠DAC,∠ECA=∠ACF,∵∠DAC=∠B+∠2,∠ACF=∠B+∠1∴∠DAC+∠ACF=(∠B+∠2)+(∠B+∠1)=(∠B+∠B+∠1+∠2),∵∠B=58°(已知),∠B+∠1+∠2=180°(三角形内角和定理),∴∠DAC+∠ACF=119°∴∠AEC=180°﹣(∠DAC+∠ACF)=61°.故答案是:61°.【变式2】(2020秋•前郭县期末)如图所示,在△ABC中,BO,CO分别平分∠ABC和∠ACB;BD、CD分别平分∠ABC和∠ACB的外角.(1)若∠BAC=70°,求:∠BOC的度数;(2)探究∠BDC与∠A的数量关系.(直接写出结论,无需说明理由)【答案】(1)∠A=70°(2)∠BDC=90°﹣∠A【解答】解:(1)∵OB、OC分别是∠ABC和∠ACB的角平分线,∴∠OBC+∠OCB=∠ABC+∠ACB=(∠ABC+∠ACB),∵∠A=70°,∴∠OBC+∠OCB=(180°﹣70°)=55°,∴∠BOC=180°﹣(∠OBC+∠OCB)=180°﹣55°=125°;(2)∠BDC=90°﹣∠A.理由如下:∵BD、CD为△ABC两外角∠ABC、∠ACB的平分线,∴∠BCD=(∠A+∠ABC)、∠DBC=(∠A+∠ACB),由三角形内角和定理得,∠BDC=180°﹣∠BCD﹣∠DBC,=180°﹣[∠A+(∠A+∠ABC+∠ACB)],=180°﹣(∠A+180°),=90°﹣∠A;【考点3内外角平分线】【条件】BP、CP分别为∠ABC、∠ACD的角平分线.【结论】∠A=2∠P.【例3】(2021春•莲湖区期末)如图,BP是△ABC中∠ABC的平分线,CP是∠ACB的外角的平分线,若∠ABP=20°,∠ACP=60°,则∠A﹣∠P=()A.70°B.60°C.50°D.40°【答案】B【解答】解:∵BP是△ABC中∠ABC的平分线,CP是∠ACB的外角的平分线,∠ABP =20°,∠ACP=60°,∴∠ABC=2∠ABP=40°,∠ACM=2∠ACP=120°,∠MCP=∠ACP=60°,∠CBP =∠ACP=20°,∴∠A=∠ACM﹣∠ABC=120°﹣40°=80°,∠P=∠PCM﹣∠CBP=60°﹣20°=40°,∴∠A﹣∠P=80°﹣40°=40°,故选:D.【变式1】(2020秋•莲湖区期末)如图,已知在△ABC中,CE是外角∠ACD的平分线,BE是∠ABC的平分线.(1)求证:∠A=2∠E;(2)若∠A=∠ABC,求证:AB∥CE.【答案】(1)略(2)略【解答】证明:(1)∵∠ACD是△ABC的一个外角,∠2是△BCE的一个外角,(已知),∴∠ACD=∠ABC+∠A,∠2=∠1+∠E(三角形外角的性质),∴∠A=∠ACD﹣∠ABC,∠E=∠2﹣∠1(等式的性质),∵CE是外角∠ACD的平分线,BE是∠ABC的平分线(已知),∴∠ACD=2∠2,∠ABC=2∠1(角平分线的性质),∴∠A=2∠2﹣2∠1(等量代换),=2(∠2﹣∠1)(提取公因数),=2∠E(等量代换);(2)由(1)可知:∠A=2∠E∵∠A=∠ABC,∠ABC=2∠ABE,∴2∠E=2∠ABE,即∠E=∠ABE,∴AB∥CE.【变式2】(2021春•宽城县期末)如图,△ABC中,∠A=100°,BI、CI分别平分∠ABC,∠ACB,则∠BIC=,若BM、CM分别是∠ABC,∠ACB的外角平分线,则∠M=.【答案】140°;40°【解答】解:∵∠A =100°,∵∠ABC +∠ACB =180°﹣100°=80°,∵BI 、CI 分别平分∠ABC ,∠ACB ,∴∠IBC =∠ABC ,∠ICB =∠ACB ,∴∠IBC +∠ICB =∠ABC +∠ACB =(∠ABC +∠ACB )=×80°=40°,∴∠I =180°﹣(∠IBC +∠ICB )=180°﹣40°=140°;∵∠ABC +∠ACB =80°,∴∠DBC +∠ECB =180°﹣∠ABC +180°﹣∠ACB =360°﹣(∠ABC +∠ACB )=360°﹣80°=280°,∵BM 、CM 分别是∠ABC ,∠ACB 的外角平分线,∴∠1=∠DBC ,∠2=ECB ,∴∠1+∠2=×280°=140°,∴∠M =180°﹣∠1﹣∠2=40°.故答案为:140°;40°.1.(2020秋•薛城区期末)如图,CD 、BD 分别平分∠ACE 、∠ABC ,∠A =80°,则∠BDC 【跟踪训练】=()A.35°B.40°C.30°D.45°【答案】B【解答】解:∵∠ACE是△ABC的外角,∴∠A=∠ACE﹣∠ABC,∵CD、BD分别平分∠ACE、∠ABC,∴∠DCE=∠ACE,∠DBE=∠ABC,∵∠DCE是△BCD的外角,∴∠D=∠DCE﹣∠DBC=∠ACE﹣∠ABC=(∠ACE﹣∠ABC)===40°,故选:B.2.(2020春•江阴市期中)AD是∠CAE的平分线,∠B=35°,∠DAE=60°,则∠ACD =()A.25°B.60°C.85°D.95°【答案】D【解答】解:∵AD是∠CAE的平分线,∴∠EAC=2∠DAE=120°,∴∠ACB=∠EAC﹣∠B=85°,∴∠ACD=180°﹣85°=95°,故选:D.3.(2019秋•保山期末)如图,若∠A=27°,∠B=45°,∠C=38°,则∠DFE等于()A.110°B.115°C.120°D.125°【答案】A【解答】解:∵∠A=27°,∠C=38°,∴∠AEB=∠A+∠C=65°,∵∠B=45°,∴∠DFE=65°+45°=110°,故选:A.4.(2021春•淮阳区期末)如图,在△ABC中,BP平分∠ABC,AP平分∠NAC,CP平分△ABC的外角∠ACM,连接AP,若∠BPC=40°,则∠NAP的度数是()A.30°B.40°C.50°D.60°【答案】C【解答】解:∵BP平分∠ABC,CP平分△ABC的外角∠ACM,∴∠PCM=ACM,∠PBC=ABC,∵∠ACM=∠ABC+∠BAC,∠PCM=∠PBC+∠BPC,∴∠PCM=ABC+BAC=+∠BPC,∴∠BPC=∠BAC=40°,∴∠BAC=80°,∴∠NAC=100°,∴∠NAP=50°,故选:C.5.(2021春•茌平区期末)如图,在△ABC中,∠ABC,∠ACB的平分线交于点O,D是∠ACF与∠ABC平分线的交点,E是△ABC的两外角平分线的交点,若∠BOC=130°,则∠D的度数为()A.25°B.30°C.40°D.50°【答案】C【解答】解:由题意得:CO,CD分别平分∠ACB,∠ACF,∴∠ACO=∠ACB,∠ACD=∠ACF,∵∠ACB+∠ACF=180°,∴∠OCD=∠ACO+∠ACD=90°,∵∠BOC=130°,且∠BOC是△OCD的外角,∴∠D=∠BOC﹣∠OCD=130°﹣90°=40°.故选:C.6.(2020秋•费县期末)如图,BA1和CA1分别是△ABC的内角平分线和外角平分线,BA2是∠A1BD的角平分线,CA2是∠A1CD的角平分线,BA3是∠A2BD的角平分线,CA3是∠A2CD的角平分线,…,若∠A=α,则∠A2021为.【答案】【解答】解:∵A1B是∠ABC的平分线,A1C是∠ACD的平分线,∴∠A1BC=∠ABC,∠A1CD=∠ACD,又∵∠ACD=∠A+∠ABC,∠A1CD=∠A1BC+∠A1,∴(∠A+∠ABC)=∠ABC+∠A1,∴∠A1=∠A,同理可得∠A2=∠A1,∠A3=∠A2,……则∠A2021=∠A=.故答案为:.8.(2021春•衡阳县期末)如图①,在△ABC中,∠ABC与∠ACB的平分线相交于点P.(1)如果∠A=80°,求∠BPC的度数;(2)如图②,作△ABC外角∠MBC,∠NCB的角平分线交于点Q,试探索∠Q、∠A之间的数量关系.(3)如图③,延长线段BP、QC交于点E,△BQE中,存在一个内角等于另一个内角的2倍,求∠A的度数.【解答】(1)解:∵∠A=80°.∴∠ABC+∠ACB=100°,∵点P是∠ABC和∠ACB的平分线的交点,∴∠P=180°﹣(∠ABC+∠ACB)=180°﹣×100°=130°,(2)∵外角∠MBC,∠NCB的角平分线交于点Q,∴∠QBC+∠QCB=(∠MBC+∠NCB)=(360°﹣∠ABC﹣∠ACB)=(180°+∠A)=90°+∠A∴∠Q=180°﹣(90°+∠A)=90°﹣∠A;(3)延长BC至F,∵CQ为△ABC的外角∠NCB的角平分线,∴CE是△ABC的外角∠ACF的平分线,∴∠ACF=2∠ECF,∵BE平分∠ABC,∴∠ABC=2∠EBC,∵∠ECF=∠EBC+∠E,∴2∠ECF=2∠EBC+2∠E,即∠ACF=∠ABC+2∠E,又∵∠ACF=∠ABC+∠A,∴∠A=2∠E,即∠E=∠A;∵∠EBQ=∠EBC+∠CBQ=∠ABC+∠MBC=(∠ABC+∠A+∠ACB)=90°.如果△BQE中,存在一个内角等于另一个内角的2倍,那么分四种情况:①∠EBQ=2∠E=90°,则∠E=45°,∠A=2∠E=90°;②∠EBQ=2∠Q=90°,则∠Q=45°,∠E=45°,∠A=2∠E=90°;③∠Q=2∠E,则90°﹣∠A=∠A,解得∠A=60°;④∠E=2∠Q,则∠A=2(90°﹣∠A),解得∠A=120°.综上所述,∠A的度数是90°或60°或120°.15。
解析三角形的角平分线关系

解析三角形的角平分线关系三角形是几何学中的基本形状之一,在解析三角形的性质和关系时,角平分线是一个重要的概念。
本文将对三角形的角平分线关系进行解析,并探讨相关性质。
一、角平分线的定义和性质角平分线是指从一个角的顶点出发,将该角分成两个相等角的线段。
三角形中,每个内角都有两条角平分线,分别与对边的延长线相交于三角形外部。
角平分线有以下性质:1. 角平分线互相垂直在三角形中,角平分线互相垂直于对边。
即若一条角平分线与对边相交于某点,那么从该点出发,绘制另一条角平分线与对边相交,两条角平分线的交点与顶点构成的两个角相等,而与对边构成的两个内角互为补角。
2. 角平分线平分对角内的弧若以三角形的外接圆为准,角平分线平分对角内的弧。
这是因为角平分线同时是弧的法线,弧和角互为补角,故角平分线与弧相等。
3. 角平分线的内外角性质对于任意一条角平分线,它把外部角分成两等分,同时也把内角的对应的外部角分成两等分。
二、角平分线的应用角平分线在三角形中有广泛的应用。
下面介绍其中几个常见的应用。
1. 角平分线的相交点三角形的三条角平分线互相交于一个点,称为内心。
内心是三角形内切圆的圆心,距离三边的距离相等。
2. 角平分线与垂直性质三角形的一条角平分线与对边垂直,当且仅当该三角形是等边三角形。
3. 角平分线与三角形相似性质三角形的两条角平分线分别平分两个相邻外角,则这两条角平分线与这两个外角所对的内角分别相等,从而可得到相似三角形。
4. 角平分线分割边长若一条角平分线从顶点分割对边,根据角平分线定理可知,该条角平分线所在的边上的两个线段之比等于顶角两个内角的正弦值比。
这一性质在解析三角形的问题中经常用到。
三、解析三角形中的角平分线关系实例分析以三角形ABC为例,其中∠BAC的角平分线交BC于点D,∠ABC的角平分线交AC于点E,我们可以利用角平分线关系解析该三角形。
题目要求证明 AD/DC = AB/BC。
解法如下:由角平分线的定义可知,∠BAD ≅∠DAC,∠ABD ≅∠DAB,∠ADC ≅∠ACD。
解三角形角平分线处理方法

解三角形角平分线处理方法三角形角平分线是指从三角形内角的顶点出发,将该角分成两个相等角的线段。
角平分线有许多性质和应用,可以用来解决一些实际问题和几何推理。
在这篇文章中,我们将探讨三角形角平分线的性质和处理方法。
首先,我们来讨论三角形角平分线的性质。
设三角形ABC的内角A有一个平分线AD,其中D位于BC上。
根据平分线的定义,∠BAD=∠DAC。
由于∠DAB和∠CAB是同一直线上的两个补角,所以它们的和为180度。
同样地,∠DAC和∠BAC的和也为180度。
因此,我们可以得出结论:角平分线将角分成两个相等角。
接下来,我们讨论三角形角平分线的处理方法。
角平分线的处理方法主要包括角平分线的性质应用、角平分线的长度计算以及角平分线的交点等。
首先,我们研究角平分线的性质应用。
由于角平分线将角分成两个相等角,所以我们可以利用这个性质解决一些实际问题和几何推理。
例如,当我们需要证明两条边相等时,可以通过找到这两条边的角平分线,再利用角平分线的性质得出结论。
另外,角平分线的性质还可以用来判断是否有直角三角形。
如果一个三角形的一些角的角平分线与对边重合,那么这个三角形就是直角三角形。
其次,我们探讨角平分线的长度计算。
对于一个已知的三角形,我们可以通过角平分线的长度计算来确定它的形状和大小。
根据角平分线的定义,可以得出角平分线的长度与三角形的两边的比例关系。
假设角平分线AD将边BC平分为两段,分别为BD和CD,那么根据角平分线定理,AD/BD=AC/AB,并且AD/CD=AB/AC。
通过这个比例关系,我们可以通过已知边的长度来计算角平分线的长度。
最后,我们讨论角平分线的交点。
在三角形的内部,三条角平分线会相交于一个点,称为内心。
内心是三角形的一个重要特点,有许多与内心相关的性质。
例如,内心到三角形三边的距离相等,内心是三角形垂心的外接圆圆心等。
通过角平分线的性质和计算,我们可以确定内心的位置,进而研究与内心相关的性质和定理。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
【关键字】精品二由角平分线想到的辅助线口诀:图中有角平分线,可向两边作垂线。
也可将图对折看,对称以后关系现。
角平分线平行线,等腰三角形来添。
角平分线加垂线,三线合一试试看。
角平分线具有两条性质:a、对称性;b、角平分线上的点到角两边的距离相等。
对于有角平分线的辅助线的作法,一般有两种。
①从角平分线上一点向两边作垂线;②利用角平分线,构造对称图形(如作法是在一侧的长边上截取短边)。
通常情况下,出现了直角或是笔直等条件时,一般考虑作垂线;其它情况下考虑构造对称图形。
至于选取哪种方法,要结合题目图形和已知条件。
与角有关的辅助线(一)、截取构全等几何的证明在于猜想与尝试,但这种尝试与猜想是在一定的规律基本之上的,希望同学们能掌握相关的几何规律,在解决几何问题中大胆地去猜想,按一定的规律去尝试。
下面就几何中常见的定理所涉及到的辅助线作以介绍。
如图1-1,∠AOC=∠BOC,如取OE=OF,并连接DE、DF,则有△OED≌△OFD,从而为我们证明线段、角相等创造了条件。
例1.如图1-2,AB//CD,BE平分∠BCD,CE平分∠BCD,点E在AD上,求证:BC=AB+CD。
分析:此题中就涉及到角平分线,可以利用角平分线来构造全等三角形,即利用解平分线来构造轴对称图形,同时此题也是证明线段的和差倍分问题,在证明线段的和差倍分问题中常用到的方法是延长法或截取法来证明,延长短的线段或在长的线段长截取一部分使之等于短的线段。
但无论延长还是截取都要证明线段的相等,延长要证明延长后的线段与某条线段相等,截取要证明截取后剩下的线段与某条线段相等,进而达到所证明的目的。
简证:在此题中可在长线段BC上截取BF=AB,再证明CF=CD,从而达到证明的目的。
这里面用到了角平分线来构造全等三角形。
另外一个全等自已证明。
此题的证明也可以延长BE与CD的延长线交于一点来证明。
自已试一试。
例2.已知:如图1-3,AB=2AC,∠BAD=∠CAD,DA=DB,求证DC⊥AC分析:此题还是利用角平分线来构造全等三角形。
构造的方法还是截取线段相等。
其它问题自已证明。
例3.已知:如图1-4,在△ABC中,∠C=2∠B,AD平分∠BAC,求证:AB-AC=C D分析:此题的条件中还有角的平分线,在证明中还要用到构造全等三角形,此题还是证明线段的和差倍分问题。
用到的是截取法来证明的,在长的线段上截取短的线段,来证明。
试试看可否把短的延长来证明呢?练习1.已知在△ABC中,AD平分∠BAC,∠B=2∠C,求证:AB+BD=AC2.已知:在△ABC中,∠CAB=2∠B,AE平分∠CAB交BC于E,AB=2AC,求证:AE=2CE3.已知:在△ABC中,AB>AC,AD为∠BAC的平分线,M为AD上任一点。
求证:BM-CM>AB-AC4.已知:D是△ABC的∠BAC的外角的平分线AD上的任一点,连接DB、DC。
求证:BD+CD>AB+AC。
(二)、角分线上点向角两边作垂线构全等过角平分线上一点向角两边作垂线,利用角平分线上的点到两边距离相等的性质来证明问题。
例1.如图2-1,已知AB>AD, ∠BAC=∠FAC,CD=BC。
求证:∠ADC+∠B=180分析:可由C 向∠BAD 的两边作垂线。
近而证∠ADC 与∠B 之和为平角。
例2. 如图2-2,在△ABC 中,∠A=90 ,AB=AC ,∠ABD=∠CBD 。
求证:BC=AB+AD分析:过D 作DE ⊥BC 于E ,则AD=DE=CE ,则构造出全等三角形,从而得证。
此题是证明线段的和差倍分问题,从中利用了相当于截取的方法。
例3. 已知如图2-3,△ABC 的角平分线BM 、CN 相交于点P 。
求证:∠BAC 的平分线也经过点P 。
分析:连接AP ,证AP 平分∠BAC 即可,也就是证P 到AB 、AC 的距离相等。
练习:1.如图2-4∠AOP=∠BOP=15 ,PC//OA ,PD ⊥OA , 如果PC=4,则PD=( )A 4B 3C 2D 12.已知在△ABC 中,∠C=90 ,AD 平分∠CAB ,CD=1.5,DB=2.5.求AC 。
3.已知:如图2-5, ∠BAC=∠CAD,AB>AD ,CE ⊥AB , AE=(AB+AD ).求证:∠D+∠B=180 。
4.已知:如图2-6,在正方形ABCD 中,E 为CD 的中点,F 为BC 上的点,∠FAE=∠DAE 。
求证:AF=AD+CF 。
5.已知:如图2-7,在Rt △ABC 中,∠ACB=90 ,CD ⊥AB ,垂足为D ,AE 平分∠CAB 交CD 于F ,过F 作FH//AB 交BC 于H 。
求证CF=BH 。
图2-6ECD图2-7DBA(三):作角平分线的垂线构造等腰三角形从角的一边上的一点作角平分线的垂线,使之与角的两边相交,则截得一个等腰三角形,垂足为底边上的中点,该角平分线又成为底边上的中线和高,以利用中位线的性质与等腰三角形的三线合一的性质。
(如果题目中有垂直于角平分线的线段,则延长该线段与角的另一边相交)。
例1. 已知:如图3-1,∠BAD=∠DAC ,AB>AC,CD ⊥AD 于D ,H 是BC 中点。
求证:DH=21(AB-AC ) 分析:延长CD 交AB 于点E ,则可得全等三角形。
问题可证。
例2. 已知:如图3-2,AB=AC ,∠BAC=90 ,AD 为∠A BC 的平分线,CE ⊥BE.求证:BD=2CE 。
分析:给出了角平分线给出了边上的一点作角平分线的垂线,可延长此垂线与另外一边相交,近而构造出等腰三角形。
例3.已知:如图3-3在△ABC 中,AD 、AE 分别∠BAC 的内、外角平分线,过顶点B 作BFAD ,交AD 的延长线于F ,连结FC 并延长交AE 于M 。
求证:AM=ME 。
分析:由AD 、AE 是∠BAC 内外角平分线,可得EA ⊥AF ,从而有BF//AE ,所以想到利用比例线段证相等。
例4. 已知:如图3-4,在△ABC 中,AD 平分∠BAC ,AD=AB ,CM ⊥AD 交AD 延长线于M 。
求证:AM=21(AB+AC ) 分析:题设中给出了角平分线AD ,自然想到以AD 为轴作对称变换,作△AB D 关于AD 的对称△AED ,然后只需证DM=21EC ,另外由求证的结果AM=21(AB+AC ),即2AM=AB+AC ,也可B图3-2BC图3-3E尝试作△ACM 关于CM 的对称△FCM ,然后只需证DF=CF 即可。
练习: 1.已知:在△ABC 中,AB=5,AC=3,D 是BC 中点,AE 是∠BAC 的平分线,且CE ⊥AE 于E ,连接DE ,求DE 。
2.已知BE 、BF 分别是△ABC 的∠ABC 的内角与外角的平分线,AF ⊥BF于F ,AE ⊥BE 于E ,连接EF 分别交AB 、AC 于M 、N ,求证MN=21BC (四)、以角分线上一点做角的另一边的平行线有角平分线时,常过角平分线上的一点作角的一边的平行线,从而构造等腰三角形。
或通过一边上的点作角平分线的平行线与另外一边的反向延长线相交,从而也构造等腰三角形。
如图4-1和图4-2所示。
图4-2图4-1ABC BIG例4 如图,AB>AC, ∠1=∠2,求证:AB -AC>BD -CD 。
例5 如图,BC>BA ,BD 平分∠ABC ,且AD=CD ,求证:∠A+∠C=180。
1 2ACDBBDA例6 如图,AB ∥CD ,AE 、DE 分别平分∠BAD 各∠ADE ,求证:AD=AB+CD 。
练习:1. 已知,如图,∠C=2∠A ,AC=2BC 。
求证:△ABC 是直角三角形。
2.已知:如图,AB=2AC ,∠1=∠2,DA=DB ,求证:DC ⊥AC3.已知CE 、AD 是△ABC 的角平分线,∠B=60°,求证:AC=AE+CDAB ECDCAB AEBD CABDC1 24.已知:如图在△ABC 中,∠A=90°,AB=AC ,BD 是∠ABC 的平分线,求证:BC=AB+AD三 由线段和差想到的辅助线口诀:线段和差及倍半,延长缩短可试验。
线段和差不等式,移到同一三角去。
遇到求证一条线段等于另两条线段之和时,一般方法是截长补短法: 1、截长:在长线段中截取一段等于另两条中的一条,然后证明剩下部分等于另一条;2、补短:将一条短线段延长,延长部分等于另一条短线段,然后证明新线段等于长线段。
对于证明有关线段和差的不等式,通常会联系到三角形中两线段之和大于第三边、之差小于第三边,故可想办法放在一个三角形中证明。
一、 在利用三角形三边关系证明线段不等关系时,如直接证不出来,可连接两点或廷长某边构成三角形,使结论中出现的线段在一个或几个三角形中,再运用三角形三边的不等关系证明,如:例1、 已知如图1-1:D 、E 为△ABC 内两点,求证:AB+AC>BD+DE+CE. 证明:(法一)将DE 两边延长分别交AB 、AC 于M 、N , 在△AMN 中,AM+AN>MD+DE+NE;(1) 在△BDM 中,MB+MD>BD ;(2) 在△CEN 中,CN+NE>CE ;(3) 由(1)+(2)+(3)得:AM+AN+MB+MD+CN+NE>MD+DE+NE+BD+CEABCDABCDEN M 11 图∴AB+AC>BD+DE+EC (法二:图1-2)延长BD 交AC 于F ,廷长CE 交BF 于G ,在△ABF 和△GFC 和△GDE 中有:AB+AF>BD+DG+GF (三角形两边之和大于第三边) (1)GF+FC>GE+CE (同上)(2) DG+GE>DE (同上)(3) 由(1)+(2)+(3)得:AB+AF+GF+FC+DG+GE>BD+DG+GF+GE+CE+DE ∴AB+AC>BD+DE+EC 。
二、 在利用三角形的外角大于任何和它不相邻的内角时如直接证不出来时,可连接两点或延长某边,构造三角形,使求证的大角在某个三角形的外角的位置上,小角处于这个三角形的内角位置上,再利用外角定理:例如:如图2-1:已知D 为△ABC 内的任一点,求证:∠BDC>∠BAC 。
因为∠BDC 与∠BAC 不在同个三角形中,没有直接的联系,可适当添加辅助线构造新的三角形,使∠BDC 处于在外角的位置,∠BAC 处于在内角的位置;证法一:延长BD 交AC 于点E ,这时∠BDC 是△EDC 的外角, ∴∠BDC>∠DEC ,同理∠DEC>∠BAC ,∴∠BDC>∠BAC 证法二:连接AD ,并廷长交BC 于F ,这时∠BDF 是△ABD 的 外角,∴∠BDF>∠BAD ,同理,∠CDF>∠CAD ,∴∠BDF+ ∠CDF>∠BAD+∠CAD ,即:∠BDC>∠BAC 。
