2017春八年级数学下册 20.3 一次函数的性质(2)教案沪教版五四制

合集下载

八年级数学下册20.3一次函数的性质1教学设计沪教版五四制

八年级数学下册20.3一次函数的性质1教学设计沪教版五四制一. 教材分析《沪教版八年级数学下册20.3一次函数的性质1》这一节主要让学生掌握一次函数的性质，包括斜率、截距等概念，并能够运用这些性质解决一些实际问题。

教材通过例题和练习题的形式，帮助学生理解和掌握一次函数的性质。

二. 学情分析八年级的学生已经学习了函数的基本概念，对函数有一定的理解，但一次函数的性质可能还没有完全掌握。

因此，在教学过程中，需要通过具体例题和练习题，让学生加深对一次函数性质的理解。

三. 教学目标1.了解一次函数的斜率和截距的概念。

2.能够运用一次函数的性质解决实际问题。

3.培养学生的数学思维能力和解决问题的能力。

四. 教学重难点1.一次函数斜率和截距的定义。

2.一次函数性质的应用。

五. 教学方法采用问题驱动法，通过设置问题，引导学生思考和探索一次函数的性质。

同时，运用例题和练习题，让学生在实践中掌握一次函数的性质。

六. 教学准备1.准备相关的教学PPT。

2.准备一些一次函数的实际问题。

3.准备一次函数的性质的练习题。

七. 教学过程1.导入（5分钟）通过一个实际问题，引导学生思考一次函数的性质。

例如：假设有一辆汽车以每小时60公里的速度行驶，问它在行驶3小时后的位置。

这个问题可以引导学生思考一次函数的斜率和截距。

2.呈现（10分钟）通过PPT呈现一次函数的性质，包括斜率和截距的定义，以及一次函数的图像。

同时，给出一些一次函数的实际例子，让学生理解一次函数的性质。

3.操练（10分钟）让学生通过PPT上的例题，练习一次函数的性质。

教师可以设置一些问题，引导学生思考和探索。

例如：给定一个一次函数，如何求它的斜率和截距？如何通过斜率和截距来确定一次函数的图像？4.巩固（10分钟）通过PPT上的练习题，让学生巩固一次函数的性质。

教师可以设置一些问题，引导学生思考和探索。

例如：给定两个一次函数，如何比较它们的斜率和截距？如何判断两个一次函数是否平行？5.拓展（10分钟）让学生通过PPT上的拓展题，进一步探索一次函数的性质。

沪教版数学八年级下册20.2《一次函数的图象与性质》教学设计1

沪教版数学八年级下册20.2《一次函数的图象与性质》教学设计1一. 教材分析沪教版数学八年级下册20.2《一次函数的图象与性质》是学生在学习了函数概念、一次函数表达式的基础上，进一步研究一次函数的图象与性质。

本节内容主要包括一次函数的图象、一次函数的性质、一次函数的应用等。

通过本节的学习，使学生进一步理解函数与方程的关系，提高解决实际问题的能力。

二. 学情分析学生在之前的学习中已经掌握了函数概念、一次函数表达式，对于一次函数的图象与性质有一定的了解。

但部分学生对于一次函数的性质理解不够深入，对于一次函数在实际问题中的应用还不够熟练。

因此，在教学过程中，要注意引导学生通过观察、操作、思考、交流等活动，深入理解一次函数的性质，提高解决实际问题的能力。

三. 教学目标1.理解一次函数的图象与性质；2.学会如何运用一次函数解决实际问题；3.提高学生的数学思维能力、合作交流能力和动手操作能力。

四. 教学重难点1.一次函数的图象与性质；2.一次函数在实际问题中的应用。

五. 教学方法采用问题驱动法、案例教学法、合作学习法等多种教学方法，引导学生通过观察、操作、思考、交流等活动，深入理解一次函数的图象与性质，提高解决实际问题的能力。

六. 教学准备1.准备相关的一次函数图象与性质的PPT；2.准备一些实际问题，用于引导学生运用一次函数解决；3.准备一些练习题，用于巩固所学知识。

七. 教学过程1.导入（5分钟）通过一个实际问题，引导学生回顾一次函数表达式，为新课的学习做好铺垫。

2.呈现（15分钟）利用PPT展示一次函数的图象与性质，引导学生观察、思考，理解一次函数的图象与性质。

3.操练（15分钟）让学生通过动手操作，绘制一次函数的图象，进一步理解一次函数的性质。

4.巩固（10分钟）通过一些练习题，让学生巩固所学的一次函数的图象与性质知识。

5.拓展（10分钟）引导学生运用一次函数解决实际问题，提高学生的应用能力。

6.小结（5分钟）对本节课的主要内容进行小结，加深学生对一次函数图象与性质的理解。

沪教版(五四学制)八年级数学下册教案：20一次函数复习二

直线截距为________；点P 的坐标为_________；直线上所有位于点P 上方的点的横坐标的取值范围是______；这些点的纵坐标的取值范围是_________；答案：3，（-1，415），x ＜-1，y ＞415 如果直线 I 的表达式为y kx b =+，那么关于x 的不等式0kx b +>的解集是； 0kx b +<解集是__ ______．答案：x ＜4，x ＞4例1-2、直线11:l y k x b =+与直线22:l y k x =在同一平面直角坐标系中的图象如图所示，则关于x 的不等式21k x k x b >+的解集为．答案：x ＜-1练习：1、如图，已知一次函数y =kx +b 的图像经过点A （5,0）与B （0,-4），那么关于x 的不等式kx +b <0的解集是………………（）答案：A （A ）x <5；（B ）x >5；（C ）x <-4；（D ）x >-4．2、如图14，已知(4)A n -，，(24)B -，是一次函数y kx b =+的图象和反比例函数my x=的图象的两个交点． (1)求方程0=-+xmb kx 的解（请直接写出答案）； (2)求不等式0<-+xmb kx 的解集（请直接写出答案）. 答案：（1）x=-4或2（2）-4＜x ＜2例2-1、如图所示一艘轮船和一艘快艇沿相同路线从甲港出发到乙港行使过程随时间变化的图象，根据图像下列结论错误的是（）答案：DA 、轮船的速度为20千米/时B 、快艇的速度为40千米/时C 、轮船的比快艇先出发2小时D 、快艇不能赶上轮船xyBAO（第1题图）Oy （千米）x 小时快艇轮船816080642x O-1y l 2l 13，两种台湾水例2-2、随着大陆惠及台胞政策措施的落实，台湾水果进入了大陆市场．一水果经销商购进了A B果各10箱，分配给他的甲、乙两个零售店（分别简称甲店、乙店）销售．预计每箱水果的盈利情况如下表：A种水果/箱B种水果/箱甲店11元17元乙店9元13元有两种配货方案（整箱配货）：方案一：甲、乙两店各配货10箱，其中A种水果两店各5箱，B种水果两店各5箱；方案二：按照甲、乙两店盈利相同配货，其中A种水果甲店箱，乙店箱；B种水果甲店箱，乙店箱．（1）如果按照方案一配货，请你计算出经销商能盈利多少元；（2）请你将方案二填写完整（只填写一种情况即可），并根据你填写的方案二与方案一作比较，哪种方案盈利较多？答案：（1）按照方案一配货，经销商盈利：5×11+5×9+5×17+5×13=250（元）（2）设A种水果给甲x箱，B种水果给甲y箱，则给乙店分别是（10-x）箱，（10-y）箱，根据题意得：11x+17y=9（10-x）+13（10-y），即2x+3y=22，则非负整数解是：第一种x=2,y=6，第二种x=5,y=4 ，第三种x=8，y=,2则第一种情况：2，8，6，4；第二种情况：5，5，4，6；第三种情况：8，2，2，8．按第一种情况计算：（2×11+17×6）×2=248（元）；按第二种情况计算：（5×11+4×17）×2=246（元）；按第三种情况计算：（8×11+2×17）×2=244（元）．答：方案一比方案二盈利较多．练习：1、小文家与学校相距1000米．某天小文上学时忘了带一本书，走了一段时间才想起，于是返回家拿书，然后加快速度赶到学校．下图是小文与家的距离y（米）关于时间x（分钟）的函数图象．请你根据图象中给出的信息，解答下列问题：（1）小文走了多远才返回家拿书？（2）求线段AB所在直线的函数解析式；x 分钟时，求小文与家的距离。

2017春八年级数学下册20.1一次函数的概念教案沪教版五四制2017093011

一次函数的概念课题20.1 一次函数的概念设计教材章节分析：依据学生学情分析：（注：只在开始新章节教学课必填）课型新授课教1．理解一次函数、常值函数的概念；学2．理解一次函数与正比例函数的关系；目3. 会利用待定系数法求一次函数的解析式标重点一次函数与正比例函数概念的关系；难点用待定系数法求一次函数的解析式.教学正比例函数与反正比例函数准备学生活交流，操作，讨论动形式教学过程设计意图课题引入：一次函数的概一、创设情境，复习导入念.问题1：汽车油箱里原有汽油120升，已知每行驶10千米耗油2升，如果汽车油箱的剩余是y（升）汽车行驶的路程为x（千米），试用解析式表示y•与x的关系．学生独立完成.分析：每行驶10千米耗油2升，那么每行驶1千米耗油0.2升，因此有的放矢的讲y与x的函数关系式为：评y=120－0.2x （0≤x≤600）当然，这个函数也可表示为：y=－0.2x+120 （0≤x≤600）说明当一个函数以解析式表示时,如果对函数的定义域未加说明,那么定义域由这个函数的解析式确定；否则,应指明函数的定义域.这个函数是不是我们所学的正比例函数？它与正比例函数有何不同？它的图像又具备什么特征？从今天开始我们将讨论这些问题．知识呈现：1．概念辨析问题2：某人驾车从甲地出发前往乙地，汽车行驶到离甲地80千米的A处发生故障，修好后以60千米／小时的速度继续行驶.以汽车从A处驶出的时刻开始计时，设行驶的时间为t（小时），某人离开甲地所走的路程完成后教师再为s（千米），那么s与t的函数解析式是什么？让学生写出定类似问题1：这个函数解析式是义域,S=60t+801思考：这个解析式和y=-0.2x+120有什么共同特点？说明为什么0 说明通过讨论使学生能够从它们的函数表达式得出表示函数的式子≤x＜10都是自变量的一次整式.如果我们用k表示自变量的系数，b表示常数．•这些函数就可以写成：y=kx+b（k≠0）的形式.一般地，形如y=kx+b（k、b是常数，且k≠0•）的函数，•叫做一次函数（•linear function）．一次函数的定义域是一切实数.当b=0时，y=kx+b即y=kx（k是常数，且k≠0•）．所以说正比例函数是一种特殊的一次函数. 教师强调都是关于自变量的一次整式当k=0时，y等于一个常数，这个常数用c来表示，一般地，我们把函数y=c（c是常数）叫做常值函数（constant function）它的定义域由所讨论的问题确定．2．例题分析例题1 根据变量x、y的关系式, 判断y是否是x的一次函数.揭示正比例函（1）y 2 x；（2）y 1 1 x；（3） 1 2 ；（4）x y数与一次函数2 3 的关系.3.例题2 已知变量x、y之间的关系式是y=（a+1）x+a(其中a是常数),那么y是x的一次函数吗?例题3 已知一个一次函数,当自变量x=2时，函数值y=-1；当x=5时，y=8.求这个函数的解析式.分析：求一次函数解析式，关键是求出k、b值．由此可列出关于k、b的二元一次方程组，解之可得. 提示学生题中解设所求一次函数的解析式为y=kx+b；y关于x的函数由x=2时y=-1,得-1=2k+b；式是否已写成由x=5时y=8,得8=5k+b. y=kx+b的一般12k b解二元一次方程组8 5k b形式了k=3, b=-7.所以,这个一次函数的解析式是y 3x 7 .说明这里求一次函数解析式的方法是待定系数法.解析式中k,b是待定系数,利用两个已知条件列出关于k、b的方程组再求解,可确定它们的值. 揭示常值函数.3．巩固练习：1．下列函数中哪些是一次函数，哪些又是正比例函数？（1）y 8x．（2）y 3 ．x 让学生思考.方法一观察法;方法二先把它写2（3）y5x2 6．（3）y3x1．成一般形式,然后根据定义解2．一个小球从斜坡由静止开始向下滚动，其速度每秒增加2米．这个小答.球的速度v随时间t变化的函数关系是一次函数吗？3．汽车油箱中原有油50升，如果行驶中每小时用油5升，求油箱中的油量y（升）随行驶时间x（小时）变化的函数关系式，并写出自变量x的取值范围．y是x的一次函数吗？用待定系数法4．已知一次函数图象过点（3，5）与（-4，-9），求这个一次函数的解设出所求的解析式．析式为y=kx+b.课堂小结：一般地，形如y=kx+b（k、b是常数，且k≠0•）的函数，•叫做一次函数．一次函数的定义域是一切实数.当b=0时，y=kx+b即y=kx（k是常数，且k≠0•）．所以说正比例函数是一种特殊的一次函数.当k=0时，y等于一个常数，这个常数用c来表示，一般地，我们把函数y=c（c是常数）叫做常值函数它的定义域由所讨论的问题确定．课外练习册作业预习一次函数的图像要求教学后记与反思1、课堂时间消耗：教师活动20 分钟；学生活动20 分钟）2、本课时实际教学效果自评（满分10分）：分3、本课成功与不足及其改进措施：3。

八年级数学下册20.2一次函数的图象2教学设计沪教版五四制

八年级数学下册20.2一次函数的图象2教学设计沪教版五四制一. 教材分析《沪教版五四制》八年级数学下册20.2一次函数的图象2，主要介绍了如何通过一次函数的图象来判断一次函数的性质。

本节内容是在学生已经掌握了函数的概念、一次函数的定义和性质的基础上进行学习的，旨在让学生通过图象来更深入地理解一次函数的性质，培养学生观察、分析、解决问题的能力。

二. 学情分析八年级的学生已经具备了一定的函数基础，对一次函数的概念和性质有一定的了解。

但学生在学习过程中，可能对如何通过图象来判断一次函数的性质还不够清晰，需要教师在教学过程中进行引导和讲解。

三. 教学目标1.理解一次函数的图象与一次函数的性质之间的关系。

2.学会通过一次函数的图象来判断一次函数的性质。

3.培养学生的观察能力、分析能力和解决问题的能力。

四. 教学重难点1.教学重点：一次函数的图象与一次函数的性质之间的关系。

2.教学难点：如何通过一次函数的图象来判断一次函数的性质。

五. 教学方法1.讲授法：教师通过讲解一次函数的图象与性质之间的关系，引导学生理解并掌握知识点。

2.案例分析法：教师通过展示一次函数的图象，让学生分析并判断一次函数的性质，培养学生的观察和分析能力。

3.小组讨论法：教师学生进行小组讨论，分享各自的判断方法和心得，培养学生的合作意识。

六. 教学准备1.教学课件：教师准备一次函数图象的相关课件，用于讲解和展示。

2.练习题：教师准备一些相关的练习题，用于巩固所学知识。

七. 教学过程1.导入（5分钟）教师通过提问方式引导学生回顾一次函数的性质，激发学生的学习兴趣。

2.呈现（10分钟）教师利用课件展示一次函数的图象，让学生观察并分析一次函数的性质。

3.操练（10分钟）教师给出一些一次函数的图象，让学生判断一次函数的性质，并解释判断的依据。

4.巩固（10分钟）教师学生进行小组讨论，分享各自的判断方法和心得，让学生在讨论中巩固知识。

5.拓展（10分钟）教师提出一些拓展问题，引导学生运用所学知识进行解决，提高学生的解决问题的能力。

八年级数学下册 20.3 一次函数的应用教案2 沪教版五四

一次函数的应用教学目标1、熟练掌握一次函数的图像与性质；2、掌握一次函数的应用；重点、难点1、熟练掌握一次函数的图像与性质；2、掌握一次函数的应用；考点及考试要求1、熟练掌握一次函数的图像与性质；2、掌握一次函数的应用；教学内容一、课堂检测1、某年“国际攀岩比赛”在重庆举行．小丽从家出发开车前去观看，途中发现忘了带门票，于是打电话让妈妈马上从家里送来，同时小丽也往回开，遇到妈妈后聊了一会儿，接着继续开车前往比赛现场．设小丽从家出发后所用时间为t，小丽与比赛现场的距离为S．下面能反映S与t的函数关系的大致图象是( )2、在一个标准大气压下，能反映水在均匀加热过程中，水的温度（T）随加热时间（t）变化的函数图象大致是（）A、 B、 C、 D、二、讲练结合例1：如果一个定值电阻R两端所加电压为5伏时，通过它的电流为1安培，那么通过这一电阻的电流I随它的两端电压U变化的图像是（）A B C D练习1：如图所示的球形容器上连接着两根导管，容器中盛满了不溶于水的比空气重的某种气体，现在要用向容器中注水的方法来排净里面的气体．水从左导管匀速地注入，气体从右导管排出，那么，容器内剩余气体的体积与注水时间的函数关系的大致图象是（）例2：已知A 、B 两地的路程为240千米．某经销商每天都要用汽车或火车将x 吨保鲜品一次性由A 地运往B 地．受各种因素限制，下一周只能采用汽车和火车中的一种进行运输，且须提前预订．现有货运收费项目及收费标准表、行驶路程s （千米）与行驶时间t （时）的函数图象（如图1）、上周货运量折线统计图（如图2）等信息如下：货运收费项目及收费标准表：运输工具运输费单价：元/（吨•千米）冷藏费单价：元/（吨•时）固定费用：元/次汽车 2 5 200 火车1.652280（1）汽车的速度为_________千米/时，火车的速度为_________千米/时；（2）设每天用汽车和火车运输的总费用分别为y 汽（元）和y 火（元），分别求y 汽、y 火与 x 的函数关系式（不必写出x 的取值范围），及x 为何值时y 汽＞y 火（总费用=运输费+冷藏费+固定费用）（3）请你从平均数、折线图走势两个角度分析，建议该经销商应提前为下周预定哪种运输工具，才能使每天的运输总费用较省？练习2：甲、乙两列火车分别从A 、B 两城同时匀速驶出，甲车开往B 城，乙车开往A 城．由于墨迹遮盖，图中提供的只是两车距B 城的路程s 甲(千米)、s 乙(千米)与行驶时间t(时)的函数图象的一部分．（1）乙车的速度为________千米/时；（2）分别求出s 甲、s 乙与t 的函数关系式(不必写出t 的取值范围)；（3）求出两城之间的路程，及t 为何值时两车相遇；（4）当两车相距300千米时，求t 的值．A B D C体积时间体积时间体积时间体积时间三、课堂检测1、如图1，某容器由A、B、C三个长方体组成，其中A、B、C的底面积分别为25cm2、10cm2、5cm2，C的容积是容器容积的14（容器各面的厚度忽略不计）．现以速度v（单位：cm3/s）均匀地向容器注水，直至注满为止．图1是注水全过程中容器的水面高度h（单位：cm）与注水时间t（单位：s）的函数图象．（1）在注水过程中，注满A所用时间为______s，再注满B又用了_____s；（2）求A的高度h A及注水的速度v；（3）求注满容器所需时间及容器的高度．四、课堂总结____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________五、家庭作业1、小明家今年种植的“红灯”樱桃喜获丰收，采摘上市20天全部销售完，小明对销售情况进行了跟踪记录，并将记录情况绘成图象，日销售量y（单位：千克）与上市时间x（单位：天）的函数关系如图1所示，樱桃价格z （单位：元/千克）与上市时间x（单位：天）的函数关系如图2所示。

2024春八年级数学下册20.3一次函数的性质2教学设计沪教版五四制

2024春八年级数学下册20.3一次函数的性质2教学设计沪教版五四制一. 教材分析20.3一次函数的性质2是沪教版五四制八年级数学下册中的一节内容。

本节课的主要内容是让学生掌握一次函数的性质，能够运用一次函数的性质解决实际问题。

教材通过例题和练习题的形式，帮助学生理解和掌握一次函数的性质。

二. 学情分析学生在学习本节课之前，已经学习了平面直角坐标系、函数的概念和一次函数的定义。

他们对一次函数有一定的了解，但可能对一次函数的性质的理解不够深入。

因此，在教学过程中，需要注重引导学生理解和掌握一次函数的性质。

三. 教学目标1.知识与技能：学生能够理解和掌握一次函数的性质，能够运用一次函数的性质解决实际问题。

2.过程与方法：通过观察、分析和归纳，学生能够发现一次函数的性质，培养学生的逻辑思维能力。

3.情感态度与价值观：学生能够体验到数学与生活的紧密联系，增强对数学的兴趣和信心。

四. 教学重难点1.教学重点：学生能够理解和掌握一次函数的性质。

2.教学难点：学生能够运用一次函数的性质解决实际问题。

五. 教学方法1.引导发现法：通过观察、分析和归纳，引导学生发现一次函数的性质。

2.实例讲解法：通过例题和练习题，讲解一次函数的性质，并引导学生运用一次函数的性质解决实际问题。

六. 教学准备1.教学PPT：制作教学PPT，包括教材中的例题和练习题。

2.教学素材：准备一些实际问题，用于引导学生运用一次函数的性质解决实际问题。

七. 教学过程1.导入（5分钟）教师通过提问方式引导学生回顾一次函数的定义和一次函数的图像，为新课的学习做好铺垫。

2.呈现（15分钟）教师通过PPT展示教材中的例题，引导学生观察和分析一次函数的性质。

教师讲解一次函数的性质，并解释一次函数的性质在实际问题中的应用。

3.操练（15分钟）教师给出一些练习题，让学生独立完成。

教师选取部分学生的作业进行讲解和分析，巩固学生对一次函数性质的理解。

4.巩固（10分钟）教师给出一些实际问题，让学生运用一次函数的性质进行解决。

2017春八年级数学下册20.2一次函数的图像2教案沪教版五四制2017093013

一次函数的图像课题20.2（2）一次函数的图像设计教材章节分析：依据（注：只学生学情分析：在开始新章节教学课必填）课型新授课教 1.通过操作、观察、探究直线相对于x轴的倾斜程度、直线上下左右平行移动，学k和b的变化关系，领会用运动变化观点处理问题的方法.2.知道两条平行直线表达式之间的关系.目标重点研究直线相对于x轴的倾斜程度及两条平行直线表达式之间的关系.难点研究直线相对于x轴的倾斜程度及两条平行直线表达式之间的关系.教学准备学生活交流，操作，讨论动形式教学过程设计意图课题引入：1．操作在同一直角坐标系中画出下列直线1（1）直线y= x+2；（2）直线y=3x+2；3揭示数与形之1（3）直线y=-2x+2；（4）直线y=- x+2.32．观察间的关系.(1)观察上述四条直线，发现截距相同时，直线都过什么样的点?(2)观察上述四条直线相对于x轴的倾斜程度，即直线与x轴正方向1夹角的大小3．思考直线相对于x轴的倾斜程度，即直线与x轴正方向夹角的大小与k的大小有何关系？知识呈现：1．b的作用在坐标平面上画直线y=kx+b (k≠0)，截距b相同的直线经过同一点k为互为相反(0,b).数2．k的作用k值不同，则直线相对于x轴正方向的倾斜程度不同.(1)k>0时，K值越大，倾斜角越大(2)k<0时，K值越大，倾斜角越大说明（1）倾斜角是指直线与x轴正方向的夹角；（2）常数k称为直线的斜率.关于斜率的确切定义和几何意义，将在高中数学中讨论.3．例题分析设法把学生的11例4 在同一直角坐标系中画出直线y=- x+2与直线y=- x，并判断这22两条直线之间的位置关系.思考问题的方分析描出直线上的两点,再过这两点画直线即可，问题在于如何判断这向引到k的符两条直线之间的位置关系.可以通过特殊点和任意点的坐标变化规律，进行号上来.判断.1解直线y=- x+2与x轴的交点是A(4,0),与y轴的交点是B(0,2).画2出直线AB.1直线y=- x过原点O(0,0)和点C(2,-1).画出直线OC.211则直线AB、直线OC分别就是直线y=- x+2与直线y=- x22（图略）在图中，观察点B相对于点O的位置，可知点O向上平移2个单位就与点B重合.1 1对于直线y=- x上的任意一点P，设它的坐标为(x1,y1),则y1=- x1.221过点P作垂直于x轴的直线，与直线y=- x+2的交点记为Q，可知点Q与21点P有相同的横坐标，设点Q的坐标为(x1,y2),则y2=- x1+2.211由y2-y1=(- x1+2)-( - x1)=2,可知点Q在点P上方且相距2个单位，22即点P向上平移2个单位就与点Q重合.11因为P是直线y=- x上的任意一点，所以把直线y=- x“向上平移222111个单位”，就与直线y=- x+2重合.因此，直线y=- x+2与直线y=- x222平行.（可借助几何画板展示图形的动态变化过程）4．直线平移一般地，一次函数y=kx+b(b0)的图像可由正比例函数y=kx的图像平移得到.当b>0时，向上平移b个单位；当b<0时，向下平移|b|个单位. 5．直线平行如果k1=k2 ,b1b2，那么直线y=k1x+b1与直线y=k2x+b2平行.如果直线y=k1x+b1与直线y=k2x+b2平行，那么k1=k2 ,b1b2 .6．例题分析1例5 已知一次函数的图像经过点A(2,-1),且与直线y= x+1平行，2求这个函数的解析式.解设一次函数解析式为y=kx+b(k≠0).11因为直线y=kx+b与直线y= x+1平行，所以k= .22311因为直线y=kx+b经过点A(2,-1),又k= ，所以×2+b=-1.221解得b=-2 所以这个函数的解析式为y= x-2.23．问题拓展已知直线y=2x-3，把这条直线沿y轴向上平移5个单位，再沿x轴向右平移3个单位，求两次平移后的直线解析式.分析无论是上下平移，还是左右平移，直线的斜率k不变，所以要求出直线解析式y=kx+b，只要求出b就可以了.问题是如何求出b,解决问题的突破口:不妨取直线y=2x-3上的一个点A(0,-3),经过两次平移后,得点A1(3,2).然后把点A1(3,2)的坐标代入y=2x+b就可求出b,从而使问题得解.三、巩固练习1.指出下列直线中互相平行的直线：(1)直线y=5x+1；(2)直线y=-5x+1；(3)直线y=x+5；(4)直线y=5x-3；(5)直线y=x-3；(6)直线y=-5x+5.2.已知直线y=(m-1)x+m与直线y=2x+1平行.(1)求m的值；(2)求直线y=(m-1)x+m与x轴的交点坐标.3.已知一次函数的图像经过点M(-3,2),且平行于直线y=4x-1.(1)求这个函数的解析式；(2)求这个函数图像与坐标轴围成的三角形面积.要求学生画出草图再求三角形的面积,并规范书写.课堂小结：1.直线相对于x轴的倾斜程度与k的大小有何关系?2.两条直线平行需要满足什么条件?3.求直线与坐标轴围成的三角形面积时,需要注意什么?练习册习题20.2(2)课外作业20.2(3)能借助一次函数，进一步认识一元一次方程、一元一次不等式的解的情预习况，并理解一次函数与一元一次方程、一元一次不等式之间的关系.要求教学后记与反思1、课堂时间消耗：教师活动20 分钟；学生活动20 分钟）2、本课时实际教学效果自评（满分10分）：分3、本课成功与不足及其改进措施：。

八年级数学下册20.3一次函数的应用教案2沪教版五四制

第（1）课时课题：书法---写字基本知识课型：新授课教学目标：1、初步掌握书写的姿势，了解钢笔书写的特点。

2、了解我国书法发展的历史。

3、掌握基本笔画的书写特点。

重点：基本笔画的书写。

难点：运笔的技法。

教学过程：一、了解书法的发展史及字体的分类：1、介绍我国书法的发展的历史。

2、介绍基本书体：颜、柳、赵、欧体，分类出示范本，边欣赏边讲解。

二、讲解书写的基本知识和要求：1、书写姿势：做到“三个一”：一拳、一尺、一寸（师及时指正）2、了解钢笔的性能：笔头富有弹性；选择出水顺畅的钢笔；及时地清洗钢笔；选择易溶解的钢笔墨水，一般要固定使用，不能参合使用。

换用墨水时，要清洗干净；不能将钢笔摔到地上，以免笔头折断。

三、基本笔画书写1、基本笔画包括：横、撇、竖、捺、点等。

2、教师边书写边讲解。

3、学生练习，教师指导。

（姿势正确）4、运笔的技法：起笔按，后稍提笔，在运笔的过程中要求做到平稳、流畅，末尾处回锋收笔或轻轻提笔，一个笔画的书写要求一气呵成。

在运笔中靠指力的轻重达到笔画粗细变化的效果，以求字的美观、大气。

5、学生练习，教师指导。

（发现问题及时指正）四、作业：完成一张基本笔画的练习。

板书设计：写字基本知识、一拳、一尺、一寸我的思考：通过导入让学生了解我国悠久的历史文化，激发学生学习兴趣。

这是书写的起步，让学生了解书写工具及保养的基本常识。

基本笔画书写是整个字书写的基础，必须认真书写。

课后反思：学生书写的姿势还有待进一步提高，要加强训练，基本笔画也要加强训练。

总第（2）课时课题：书写练习1课型：新授课教学目标：1、教会学生正确书写“杏花春雨江南”6个字。

2、使学生理解“杏花春雨江南”的意思，并用钢笔写出符合要求的的字。

重点：正确书写6个字。

难点：注意字的结构和笔画的书写。

教学过程：一、小结课堂内容，评价上次作业。

二、讲解新课：1、检查学生书写姿势和执笔动作（要求做到“三个一”）。

2、书写方法是：写一个字看一眼黑板。

八年级数学下册20.4一次函数的应用(2)教案沪教版五四制(2021学年)

2０１７春八年级数学下册20．4 一次函数的应用（2)教案沪教版五四制编辑整理：尊敬的读者朋友们:这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方，但是任然希望（２0１7春八年级数学下册 2０.4 一次函数的应用（2)教案沪教版五四制)的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。

本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步,以下为201７春八年级数学下册２０.4 一次函数的应用(２)教案沪教版五四制的全部内容。

一次函数的应用以上就是本文的全部内容,可以编辑修改。

高尔基说过:“书是人类进步的阶梯。

”我希望各位朋友能借助这个阶梯不断进步。

物质生活极大丰富，科学技术飞速发展，这一切逐渐改变了人们的学习和休闲的方式。

很多人已经不再如饥似渴地追逐一篇文档了,但只要你依然有着这样一份小小的坚持，你就会不断成长进步,当纷繁复杂的世界牵引着我们疲于向外追逐的时候,阅读一文或者做一道题却让我们静下心来,回归自我。

用学习来激活我们的想象力和思维，建立我们的信仰,从而保有我们纯粹的精神世界，抵御外部世界的袭扰。

Ｔhe aｂove iｓｔhｅ whole ｃonteｎt of ｔhis arｔｉcle, Gｏrky sai ｄ: "the ｂｏoｋｉｓ the laｄdｅｒｏf hｕmａn pｒｏｇress." I ｈope you caｎｍａke progress wiｔh the help ｏf this laｄdeｒ. Material liｆe iｓ eｘtｒemｅly rich, sｃienｃe and ｔｅchnoｌoｇy are deveｌoping ｒapｉdｌy, aｌl of ｗｈｉch gｒaｄｕally cｈange thｅway ｏf pｅoｐlｅ's studｙand leisure. Manｙ pｅople are no longer eageｒ to ｐuｒsue a dｏcument, but ａｓ lｏng as ｙou sｔilｌ have sｕch a sｍalｌpersistence, ｙou ｗiｌｌ cｏｎｔinue to grｏｗand proｇrｅss. When t ｈe complex wｏrld leads us ｔo chase oｕt, ｒｅaｄing an artｉｃle or doi ｎg ａ prｏｂｌeｍｍakes us cａlm dｏｗn aｎｄｒeｔｕrn to ourselvｅs. Witｈ lｅａrning, we ｃan actiｖate our imagiｎaｔｉon ａnd thinking, estabｌish our belief, ｋeep oｕr ｐure spiｒitual world and resiｓt ｔhe attacｋ oｆｔhe ｅxternal ｗoｒld.。

八年级数学下册20.3一次函数的性质2教案沪教版五四制

一次函数的性质课题引入：课前练习一课前练习二3.已知P1(x1,y1),P2(x2,y2)是直线y=-21x+1上的两点,且x1<x2,则y1 ___y2.一般地,一次函数y=kx+b(k 、b 为常数,k 0),当k >0时,函数值y 随自变量x 的值增大而______. 当k<0时,函数值y 随自变量x 的值增大而______.直线y=kx+b 经过点(-1,2),且函数值y 随自变量x 的值增大而减小,请写出一个符合条件的直线表达式:_______. 知识呈现：新课探索一（1）观察一次函数①y=4x;②y=4x+2;③y=4x-2.(1)它们在性质上有什么共同之处？(2)它们的图像在位置上有什么关系？因为k=4 0,所以这三个函数有共同的性质,即函数值y随自变量x 的值增大而增大.这三条直线平行,将直线y=4x向上平移2个单位可得直线y=4x+2;将直线y=4x向下平移2个单位可得直线y=4x-2.猜想直线y=4x+2经过哪几个象限?直线y=4x-2呢?直线y=4x+2经过一、二、三象限;直线y=4x-2经过一、三、四象限.说说你是怎么想的？议一议直y=kx+b(k=0,b=0),经过哪几个象限与什么有关?请归纳出一般的规律.新课探索一（2）直线y=kx+b 过点(0,b)且与直线y=kx平行.由直线y=kx在直角坐标平面内的位置情况,可知:当k 0,且b 0时,直线y=kx+b经过第_______象限;当k 0,且b 0时,直线y=kx+b经过第________象限.把上述判断反过来叙述,也是正确的.友情提示:不要强记,借助数形结合来帮助自己理解、记忆新课探索二例题已知一次函数y=(2-a)x-3的函数值y随着自变量x的值增大而增大.(1)求实数a的取值范围;(2)指出图像所经过的象限.课内练习一1.由下列函数图像,确定一次函数y=kx+b中,k,b的符号:2.直线y=2x+1的截距等于___,这条直线不经过第_______象限.3.若直线y=kx+b 不经过第二象限,则k___0,b____0. 课内练习二4.已知直线y=(1-3m)x+(2m-1).分别根据下列条件求m 的值或m 的取值范围: (1)这条直线过原点;(2)这条直线与已知直线y=-3x+5平行; (3)这条直线经过第二、三、四象限.课内练习三5.当m=________时,函数y=(1-2m)x3m-2+m-4是一次函数,这个函数的图像经过第____象限,函数值y 随自变量x 的值增大而_______.课内练习四6.已知直线y=kx+b 与直线y=-34x 交于A(m,4),与y 轴交于点B,且OB=2OA,又知直线y=kx+b 经过二、三、四象限,求k 和b.课堂小结：。

沪教版数学八年级下册20.2《一次函数的图象与性质》教学设计3

沪教版数学八年级下册20.2《一次函数的图象与性质》教学设计3一. 教材分析沪教版数学八年级下册20.2《一次函数的图象与性质》是学生在学习了《一次函数》的基础上，进一步研究一次函数的图象与性质。

本节内容主要让学生掌握一次函数的图象特点，了解一次函数的增减性、对称性和最值问题。

教材通过实例和活动，引导学生探索一次函数的图象与性质，培养学生的观察能力、操作能力和解决问题的能力。

二. 学情分析学生在之前的学习中已经掌握了二次函数的图象与性质，对函数的概念和性质有一定的了解。

但学生在解决实际问题时，还缺乏对函数性质的灵活运用。

因此，在教学过程中，教师需要关注学生的认知基础，通过引导和激励，激发学生的学习兴趣，帮助学生建立函数性质的知识体系。

三. 教学目标1.知识与技能：让学生掌握一次函数的图象特点，了解一次函数的增减性、对称性和最值问题。

2.过程与方法：通过观察、操作、探究等活动，培养学生解决问题的能力。

3.情感态度与价值观：激发学生学习数学的兴趣，培养学生的团队协作能力和自主学习能力。

四. 教学重难点1.重点：一次函数的图象特点，一次函数的增减性、对称性和最值问题。

2.难点：一次函数性质在实际问题中的应用。

五. 教学方法1.引导发现法：教师通过提出问题，引导学生观察、思考，发现一次函数的图象与性质。

2.案例分析法：教师通过列举实例，让学生了解一次函数的性质在实际问题中的应用。

3.小组合作学习：学生分组讨论，共同完成任务，培养学生的团队协作能力。

六. 教学准备1.教学课件：制作一次函数的图象与性质的相关课件。

2.实例素材：收集一些与一次函数性质相关的生活实例。

3.练习题：准备一些一次函数性质的练习题，用于巩固所学知识。

七. 教学过程导入（5分钟）教师通过提问方式复习一次函数的概念，引导学生回忆已学过的知识。

然后，教师提出本节课的学习目标，激发学生的学习兴趣。

呈现（10分钟）1.教师通过课件展示一次函数的图象，引导学生观察并发现一次函数的图象特点。

沪教版(上海)八年级数学第二学期-20.3 一次函数的性质-教案设计

一般来说，一次函数y=kx+b（k、b为常数，k≠0）具有以下性质：
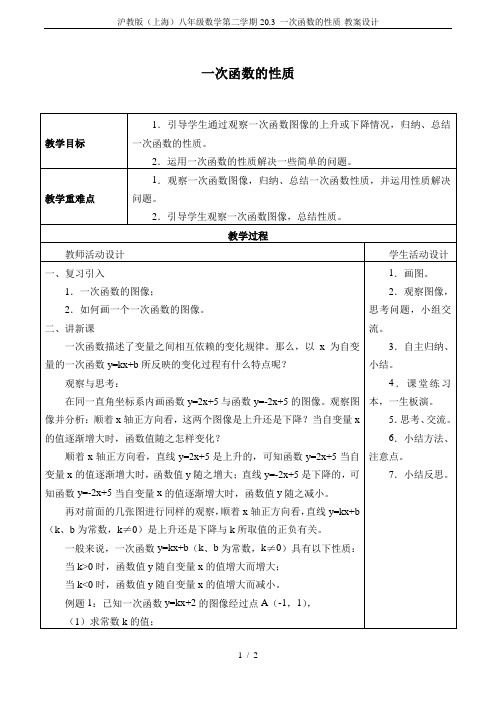
当k>0时，函数值y随自变量x的值增大而增大；
当k<0时，函数值y随自变量x的值增大而减小。
例题1：已知一次函数y=kx+2的图像经过点A（-1，1），
（1）求常数k的值；
（2）当自变量x的值逐渐增大时，函数值y随之增大还是减小？
解：
（1）因为一次函数y=kx+2的图像经过点A（-1，1），所以1=-k+2，解得k=1．
（2）因为k>0，所以函数值y随自变量x的值增大而增大。
例题2：已知一次函数y=（1-2m）x+m+1，函数值y随自变量x的值增大而减小，
（1）求m的取值范围；
（2）在平面直角坐标系xoy中，这个函数的图像与y轴的交点M位于y轴的正半轴还是负半轴？
顺着x轴正方向看，直线y=2x+5是上升的，可知函数y=2x+5当自变量x的值逐渐增大时，函数值y随之增大；直线y=-2x+5是下降的，可知函数y=-2x+5当自变量x的值逐渐增大时，函数值y随之减小。
再对前面的几张图进行同样的观察，顺着x轴正方向看，直线y=kx+b（k、b为常数，k≠0）是上升还是下降与k所取值的正负有关。
解：在函数解析式y= x+m中，k= ，可知函数值y随x的值增大而减小。
因为点A（-1，a）和B（1，b）在这个函数的图像上，所以当x分别取-1，1时，对应的函数值分别为A、B．由-1<1，得a>B．
想一想：在例题3中，还有其他方法比较a与b的大小吗？
三、课堂小结
1．一次函数的性质？
2．怎样运用性质解题？
解：

沪教版数学八年级下册20.2《一次函数的图象与性质》教学设计2

沪教版数学八年级下册20.2《一次函数的图象与性质》教学设计2一. 教材分析《一次函数的图象与性质》是沪教版数学八年级下册第20.2节的内容。

本节内容是在学生已经掌握一次函数的定义、表达式的基础上，进一步研究一次函数的图象与性质。

教材通过实例引入一次函数的图象，引导学生观察、分析、归纳一次函数的性质，从而加深学生对一次函数的理解和应用。

二. 学情分析学生在八年级上册已经学习了直线、射线、线段的性质，对图象有一定的认识。

同时，学生已经掌握了了一次函数的定义、表达式，为本节内容的学习奠定了基础。

但是，对于一次函数图象与性质的深入理解，学生还需通过实例进行分析、归纳。

三. 教学目标1.理解一次函数的图象特征，掌握一次函数图象的性质。

2.能够运用一次函数的图象与性质解决实际问题。

3.培养学生的观察能力、分析能力、归纳能力。

四. 教学重难点1.一次函数的图象特征2.一次函数图象的性质3.一次函数图象与实际问题的结合五. 教学方法采用问题驱动法、案例分析法、小组合作法、引导发现法等，引导学生观察、分析、归纳一次函数的图象与性质。

六. 教学准备1.教学PPT2.实例图片七. 教学过程1. 导入（5分钟）通过复习一次函数的定义、表达式，引导学生回忆一次函数的相关知识。

然后，提出问题：“你们认为一次函数的图象会是什么样子呢？”让学生思考，激发学生的学习兴趣。

2. 呈现（10分钟）展示一次函数的图象实例，如y=2x+1。

引导学生观察图象，观察图象与x轴、y轴的交点，以及图象的斜率。

通过实例，让学生直观地感受一次函数的图象特征。

3. 操练（15分钟）让学生分组讨论，每组选取一个实例，分析一次函数的图象特征。

学生通过自主探究，总结一次函数图象的性质。

教师巡回指导，解答学生的疑问。

4. 巩固（10分钟）出示练习题，让学生运用一次函数的图象与性质解决问题。

教师及时批改，给予反馈，巩固学生对知识的理解。

5. 拓展（10分钟）出示一些实际问题，如线性方程的解、线性函数的最值等，让学生运用一次函数的图象与性质解决实际问题。

2017届八年级数学下册20.3的性质1教案沪教版五四制

课内练习一
1、如果一次函数y=(k+2)x+1的函数值随x的值增大而减小，那么k的取值范围是（）
2、已知函数：
在这些函数中，函数值y随自变量x的值增大而增大的函数有__________
课内练习二
3.已知函数y=(m-2)x+m(m是常数).
(1)当m取何值时,函数值y随x的值增大而增大?
(2)当m取何值时,函数值y随x的值增大而减小?
(2)正比例函数y=- x的图象经过第________象限,函数值y随x的增大而_______.
正比例函数图像性质表述的科学性.
判断图像的增减性，有必要计算出比例系数k.
解不等式时，注意不等号方向的变化.
强调：两种方法都是非常有效的方法.
知识呈现：
新课探索一（1）
观察与思考函数y=2x+5与函数y=-2x+5的图像如图.观察图像并分析:顺着x轴的正方向看,这两个图像是上升还是下降?当自变量x的值逐渐增大时,函数值随之怎样变化?
课外
作业
练习册
预习
要求
掌握一次函数的增减性以及函数图像经过的象限，会利用增减性、图像的位置，确定字母系数的值.
教学后记与反思
1、课堂时间消耗：教师活动15分钟；学生活动25分钟）
2、本课时实际教学效果自评（满分10分）：分
3、本课成功与不足及其改进措施：
新课探索一（2）
一般地,一次函数y=kx+b(k、b为常数,k=0)具有以下性质:
当k >0时,函数值y随自变量x的值增大而增大;
当k< 0时,函数值y随自变量x的值增大而减小;
正比例函数是特殊的一次函数,它的性质与一次函数的性质是一致的.

沪教版(上海)数学八年级第二学期20.3 一次函数的性质(2) 教案

如果别人思考数学的真理像我一样深入持久，他也会找到我的发现。

——高斯20.3一次函数的性质（2）执教：教学目标：1．通过类比的方法，形成一次函数图像所在象限的性质．2．理解直线()0≠+=k b kx y 中的常数k 、b 的符号与直线所在象限的联系． 3．在形成一次函数的性质过程中，体会类比和数形结合的数学思想． 4．在一次函数运用的过程中，感受化归的数学思想．教学重点：一次函数的性质．教学难点：直线()0≠+=k b kx y 中的常数k 、b 的符号与直线所在象限的联系．教学过程：教师活动学生活动设计意图一、复习引入：正比例函数的性质：正比例函数)0(≠=k kx y 的性质0>ky 随x 的增大而增大图像经过第一、三象限0<ky 随x 的增大而减小图像经过第二、四象限二、新课探究：例题4：已知一次函数)0(≠+=k b kx y 的图像是与直线x y 4=平行的直线.（1）随着自变量x 的值的增大，函数值y 增大还是学生口答.解：（1）因为直线)0(≠+=k b kx y 与直线x y 4=平行，所以本节课的知识是建立在正比例函数图像的性质以及上节课一次函数的性质（1）的基础上，所以先复习旧知．本题承前启后，在复习了两条平行线表达式之间的关系和一次符号之间的关系：上述结论反过来叙述，也是正确的．练习：1．学生互动练习，以达到对新知识的熟练．（1）直线52+=x y 经过第象限；（2）直线3-=x y 经过第象限；（3）直线82+-=x y 经过第象限；（4）直线54--=x y 经过第象限；（5）如果一次函数b kx y +=的图像如图所示：那么k ，b（6）直线b kx y +=经过第二、三、四象限，则k 、b 的取值范围是什么？（7）直线b kx y +=经过第一、三、四象限，则k 、b 的取值范围是什么？（8）直线b kx y +=经过第一、二、四象限，则k 、b 的取值范围是什么？（9）直线b kx y +=经过第一、二、三象限，则k 、b 的取值范围是什么？（10）直线b kx y +=不经过第四象限，则k 、b 的（1）一、二、三（2）一、三、四（3）一、二、四（4）二、三、四（5）k >0，b <0（6）k <0，b <0（7）k >0，b <0（8）k <0，b >0（9）k >0，b >0出，渗透数形结合的数学思想．巩固一次函数的性质的正用和逆用．取值范围是什么？（11）直线b kx y +=不经过第一象限，则k 、b 的取值范围是什么？二、性质的运用例题5 已知一次函数()32--=x a y 的函数值y 随着自变量x 的值增大而增大．（1）求实数a 的取值范围；（2）指出这个函数的图像所经过的象限．学生口述，教师板书．三、课堂练习1、课本P14/练习20.3（2）第3题2、补充练习：已知一次函数()173-+-=m x m y 的图像经过第一、二、四象限，求整数m 的值．变式练习：已知一次函数()173-+-=m x m y 的图像不经过第三象限，求m 的取值范围．四、课堂小结谈谈这节课你有什么收获、体会或想法?教师补充：类比、数形结合、化归的数学思想．五、布置作业练习册：习题20.3（2）（10）k >0，b ≥0（11）k <0，b ≤0 解：（1）函数值y 随着自变量x 的值增大而增大，2202<∴->-∴>-∴a a a(2) 02>-=a k ，03<-=b∴这个函数的图像经过一、三、四象限． 2、解略，m =2.帮助学生理解和巩固一次函数的性质．把函数问题转化为解一元一次不等式的问题，感受化归的数学思想．进一步巩固一次函数性质的运用．梳理知识点，培养学生归纳反思的能力．一天，毕达哥拉斯应邀到朋友家做客。