高中数学两个向量的数量积课件新人教B版选修2

合集下载

2020版高中数学人教B版选修2-1课件：3.1.3 两个向量的数量积

第三章空间向量与立体几何3.1.3两个向量的数量积高中数学选修2-1·精品课件引入课题空间中任意两个向量均为共面向量，平面向量的概念及运算在空间中仍然成立，将平面向量的数量积推广到空间向量.基础梳理1.两个向量的夹角AOB BB①定义：∠AOB 有共同起点②表示：< a ,b >ab ③范围：[0，π]2.数量积的定义 a ∙b =| a||b|cos< a ,b >3.数量积的几何意义θab b 在 a 方向上的投影| a |与b 在 a 方向上的投影的积4.数量积的运算律(1)(λa )·b ＝____________；(2)a ·b ＝____________；(3)a ·(b ＋ c )=_____________.λ(a ·b )b ·a a ·b ＋a · c 5.一个非常重要的性质|a |2=a 2=a ·a求模即为求数量积解：例1 已知正四面体P ABC 的棱长为2，E 、F 分别为AB 和PC 的中点，求PE 与BF 夹角的余弦值.CPABEF 设PA = a ，PB =b ，PC = c ，则 a ，b ， c 长度都为2，两两夹角为60°，∴ a ∙b =b ∙ c = c ∙ a =2，又PE =12(a +b)，BF =12c −b ，四个面均为全等的正三角形∴PE∙BF=12a+b∙12c−b=1 2(12a∙c+12b∙c−a∙b−b2)=12(1+1-2-4)=-2，又|PE|=|BF|=3，∴cos<PE,BF>=−23×3=−23.跟踪训练1.在空间四边形OABC 中，OA ＝8，AB ＝6，AC ＝4，BC ＝5，∠OAC ＝45°，∠OAB ＝60°，求OA 与BC 夹角的余弦值．【答案】3−225C OABC OAB几何条件向量化例2 在正四面体ABCD 中，棱长为a ，M ，N 分别是棱AB ，CD 上的点，且|MB |＝2|AM |，|CN |＝12|ND |，求|MN |.C D ABMN|MN |设AB = a ，AC =b ，AD = c ，则 a ，b ， c 长度都为a ，两两夹角为60°，∴ a ∙b = b ∙ c = c ∙ a =a 22，MN =MB +BC +CN=23AB +(AC -AB )+13(AD -AC )=−13AB +23AC +13AD = −13a+23b +13c .解：∴|MN|2=MN2=(−13a+23b+13c)2=1 9a2+49b2+19c2-49a∙b+49b∙c-29a∙c=1 9a2+49a2+19a2-19a2=59a2，∴|MN|= |MN|=53a.且BE 与FD 的夹角为120°，∴BD 2=(BE +EF +FD )2=BE 2+EF 2+FD 2+2BE ·EF +2EF ·FD +2BE ·FD=3+3+4-3=7，∴|BD |=7.跟踪训练2.把长AB 和宽AD 分别为23和2的长方形ABCD 沿对角线AC 折成60°的二面角，求B 、D 间的距离．DABCEF解：在△ABC 内作BE ⊥AC ，垂足为E ，则BE =3，在△ACD 内作DF ⊥AC ，垂足为F ，则DF =3，则BD =BE +EF +FD ，由条件可知|EF |=2,典例分析例3 已知空间四边形OABC中，∠AOB＝∠BOC＝∠AOC，且OA＝OB＝OC，M、N分别是OA、BC的中点，G是MN的中点．求证：OG⊥BC.设∠AOB＝∠BOC＝∠AOC＝θ，OA＝OB＝OC=a，OA＝a, OB＝b, OC=c，则OG=12(OM+ON)=12[12a+12(b+c)]=1 4(a+b+c)，abc解：几何条件向量化典例分析BC=c−b，(a+b+c)·( c−b)∴OG·BC=14=a·c-a·b+b·c-b2+ c2-c·b=0，∴OG⊥BC，即OG⊥BC.跟踪训练3.已知在空间四边形OABC中，OB＝OC，AB＝AC，求证：OA⊥BC.证明:∵OB＝OC，AB＝AC，OA＝OA，∴△OAC≌△OAB.∴∠AOC＝∠AOB.∵OA·BC＝OA·(OC－OB)＝OA·OC－OA·OB＝|OA||OC|cos∠AOC－|OA||OB|·cos∠AOB＝0，∴OA⊥BC.归纳小结1．注意向量乘法的结合律是不成立的，即a·(b·c)＝(a·b)·c不成立．事实上a·(b·c)表示与a平行的向量，而(a·b)·c表示与c平行的向量．2．两个非零向量共线时，如果同向，夹角为0，如果异向，夹角为π，特别的<a，a>＝0，<a，－a>＝π.3．注意二个向量夹角的范围：[0，π]，当夹角为锐角时其余弦值为正，当夹角为钝角时其余弦值为负．反之当两向量不共线时亦成立.当堂训练1．下列式子正确的是()A ．a ·|a |＝aB ．(a ·b )2＝a ·bC ．(a ·b ) c ＝a ·(b · c )D ．|a ·b |≤|a ||b |2．若向量m 同时垂直两个向量a 和b ，向量n ＝λa ＋μb (λ，μ∈R ，λ，μ≠0)则()A ．m ∥nB ．m ⊥nC ．m 与n 既不平行也不垂直D ．以上三种情况均有可能D B再见。

人教B版高中数学选择性必修第一册精品课件第1章空间向量与立体几何第2课时空间向量的数量积

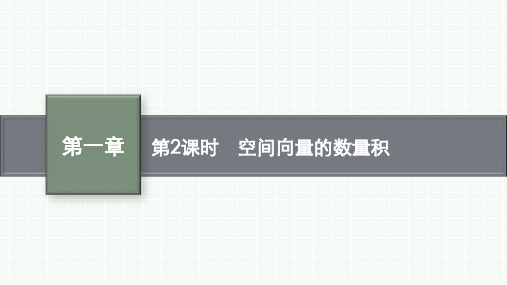
【变式训练】如图,在四面体O-ABC中,OA=8,AB=6,AC=4,BC=5,
∠OAC=45°,∠OAB=60°,求与
夹角的余弦值.
解:∵ = − ,
∴ · = ·( − )= · − ·
=||| |cos<, >-||||·cos<, >
π
事实上,两向量夹角的取值范围是[0,π],异面直线所成的角的范围是 0, 2 .设
π
异面直线 l1,l2 所成的角为 θ,方向向量分别为 a,b,当 0<<a,b>≤ 时,θ=<a,b>,
2
即 cos
π
θ=cos<a,b>;当2 <<a,b><π 时,θ=π-<a,b>,即
cos θ=|cos<a,b>|.
第一章
第2课时空间向量的数量积
内
容
索
引
01
自主预习新知导学
02
合作探究释疑解惑
03
随堂练习
课标定位素养阐释
1.了解两个向量的夹角的概念.
2.掌握空间中两个向量的数量积定义及运算律和性质.
3.重点提升数学抽象、数学运算、直观想象和逻辑推理素养.
自主预习新知导学
一、空间向量的夹角
1.空间中任意两个向量是否一定共面?
又 BC=√2,所以△BCA1 是正三角形,
π
故异面直线 A1C 与 B1C1 所成的角为3.
π
故答案为 .
3
π
答案:
3
探究三
求向量的模
【例3】如图所示,在平行六面体ABCD-A1B1C1D1中,从同一顶点出发的三

人教B版高中数学选择性必修第一册精品课件第一章空间向量与立体几何第2课时空间向量的数量积

2 2
2
2
2
2
2
1
=2(|b|2-|a|2)=0,所以1
⊥ ,即 A1O⊥BD.
同理可证1 ⊥ ,即 A1O⊥OG.
又OG∩BD=O,OG⊂平面GBD,BD⊂平面GBD,
∴A1O⊥平面GBD.
成果验收·课堂达标检测
1.已知四面体 ABCD 的所有棱长都是 2,点 E 是 AD 的中点,则 · =( A )
作直线l(或平面α)的垂线,假设垂足为A,B,则向量称为a在直线l(或平面
α)上的投影.
(3)空间向量的数量积
两个非零向量a与b的数量积(也称为内积)定义为a·b=|a||b|cos<a,b>.规定
零向量与任意向量的数量积为0.
名师点睛
1.空间向量的数量积是一个实数而不是一个向量.
2.数量积的正负取决于向量的夹角,注意两向量反向时夹角为π.
(λa)·b=λ(a·b),λ∈R
交换律
a·b=b·a
分配律
(a+b)·c=a·c+b·c
名师点睛
1.a⊥b的充要条件是a·b=0,这是用向量证明空间中垂直关系的根本方法,
同时也说明由a·b=0不能得到a=0或b=0.
2.向量的数量积不满足结合律.
过关自诊
1.判断正误.(正确的画√,错误的画×)
(1)对于非零向量b,由a·b=b·c,可得a=c.( × )
1
C.
4
解析由题意得 = + = +
· = ·(
2
1
|
|
2
=
1
.故选
2
D.
1
+ 2

高中数学第三章空间向量与立体几何3.1.3两个向量的数量积学案新人教B版选修21

高中数学第三章空间向量与立体几何3.1.3两个向量的数量积学案新人教B 版选修211．掌握空间向量的夹角与长度的概念．2．掌握空间向量的数量积的定义、性质、运算律及计算方法．(重点) 3．能用向量的数量积解决立体几何问题．(难点)[基础·初探]教材整理1 空间向量的夹角阅读教材P 85～P 86“两个向量的数量积”上面内容，完成下列问题． 1．夹角的定义已知两个非零向量a ，b ，在空间中任取一点O ，作OA →＝a ，OB →＝b ，则角∠AOB 叫做向量a 与b 的夹角，记作〈a ，b 〉．图31202．夹角的范围空间任意两个向量的夹角θ的取值范围是[0，π]．特别地，当θ＝0时，两向量同向共线；当θ＝________时，两向量反向共线，所以若a ∥b ，则〈a ，b 〉＝0或π；当〈a ，b 〉＝π2时，两向量________，记作________．【答案】 π 垂直 a ⊥b判断(正确的打“√”，错误的打“×”)(1)〈a ，b 〉与(a ，b )都表示直角坐标系下的点．( ) (2)在△ABC 中，〈AB →，BC →〉＝∠B .( )(3)在正方体ABCD A ′B ′C ′D ′中，AB →与A ′C ′→的夹角为45°.( )【答案】(1)×(2)×(3)√教材整理2 空间向量的数量积及其性质阅读教材P86“两个向量的数量积”～P87“例2”，以上部分内容，完成下列问题．1．已知空间中两个非零向量a，b，则________叫做a，b的数量积，记作________．规定：零向量与任何向量的数量积为________，即0·a＝________.【答案】|a||b|cos〈a，b〉a·b0 02．空间向量数量积满足下列运算律(1)(λa)·b＝λ(a·b)；(2)交换律：a·b＝b·a；(3)分配律：(a＋b)·c＝________.【答案】a·b＋b·c3．空间向量数量积的性质若a，b是非零向量，e是与b方向相同的单位向量，θ是a与e的夹角，则(1)e·a＝a·e＝|a| cos θ；(2)a⊥b⇔a·b＝0；(3)a·a＝|a|2或|a|＝________；(4)若θ为a，b的夹角，则cos θ＝a·b|a||b|；(5)|a·b|≤|a|·|b|.【答案】a·a下列式子中正确的是( )A．|a|a＝a2B．(a·b)2＝a2b2C．a(a·b)＝b·a2D．|a·b|≤|a||b|【解析】根据数量积的定义知，A，B，C均不正确．故选D.【答案】 D[质疑·手记]预习完成后，请将你的疑问记录，并与“小伙伴们”探讨交流：疑问1：________________________________________________________ 解惑：________________________________________________________ 疑问2：________________________________________________________ 解惑：________________________________________________________ 疑问3：________________________________________________________ 解惑：________________________________________________________[小组合作型]空间向量数量积的运算(1)如图3121，三棱锥P ABC 中，PA ⊥平面ABC ，∠ABC ＝90°，PA ＝AC ，则在向量AB →，BC →，CA →，PA →，PB →，PC →中，夹角为90°的共有( )图3121A ．6对B ．5对C ．4对D ．3对(2)已知空间四边形ABCD 的每条边和对角线的长都等于a ，点E ，F 分别是BC ，AD 的中点，则AE →·AF →＝________.图3122(3)如图3122所示，正方体ABCD A 1B 1C 1D 1的棱长为1，求下列数量积： ①AB →·BA 1→＝________； ②AB →·BC 1→＝________.【自主解答】 (1)AB →与BC →，PA →与AB →，PA →与BC →，PA →与CA →，PB →与BC →夹角为90°. (2)AE →·AF →＝⎝⎛⎭⎪⎫AB →＋12BC →·12AD →＝12AB →·AD →＋14BC →·AD →＝12a 2cos 60°＝14a 2. (3)①AB →·BA 1→＝1×2cos 135° ＝－1；②AB →·BC 1→＝AB →·(BC →＋CC 1→)＝AB →·BC →＋AB →·CC 1→ ＝0.【答案】 (1)B (2)14a 2(3)①－1 ②01．求两向量数量积的解题思路 (1)解模：解出两向量的模．(2)求夹角：根据向量的方向求出两向量的夹角． (3)求结果：使用公式a ·b ＝|a ||b |cos 〈a ，b 〉得结果． 2．数量积的运算结果是一个数量，正、负、零皆有可能．[再练一题]1．已知空间向量a ，b 满足|a |＝4，|b |＝8，a 与b 的夹角为150°，求下列各式的值． (1)a ·b ；(2)(a ＋2b )·(2a －3b )．【解】 (1)a ·b ＝|a ||b |cos 〈a ，b 〉＝4×8×cos 150°＝4×8×⎝ ⎛⎭⎪⎫－32＝－16 3. (2)(a ＋2b )·(2a －3b )＝2a 2＋a ·b －6b 2＝2|a |2＋|a ||b |cos 150°－6|b |2＝2×42－163－6×82＝－352－16 3.求两个空间向量的夹角如图3123，在正方体ABCD A 1B 1C 1D 1中，求BC →1与AC →夹角的大小．图3123【精彩点拨】 (1)怎样用向量AB →，AD →，AA →1表示向量BC →1与AC →？ (2)求两向量的夹角公式是怎样的？【自主解答】不妨设正方体的棱长为1， BC →1·AC →＝(BC →＋CC →1)·(AB →＋BC →)＝(AD →＋AA →1)·(AB →＋AD →)＝AD →·AB →＋AD →2＋AA →1·AB →＋AA →1·AD →＝0＋AD →2＋0＋0＝AD →2＝1，又∵|BC →1|＝2，|AC →|＝2，∴cos 〈BC 1→，AC →〉＝BC →1·AC →|BC →1||AC →|＝12×2＝12.∵0°≤〈BC →1，AC →〉≤180°， ∴〈BC →1，AC →〉＝60°. ∴BC →1与AC →夹角的大小为60 °.1．由于向量的夹角的取值范围为[0，π]，而异面直线所成的角的取值范围为⎝ ⎛⎦⎥⎤0，π2，因此利用向量数量积求异面直线所成的角时，要注意角度之间的关系．当〈a ，b 〉∈ ⎝ ⎛⎦⎥⎤0，π2时，它们相等；而当〈a ，b 〉∈ ⎝ ⎛⎦⎥⎤π2，π时，它们互补．2．利用数量积求异面直线所成角θ的余弦值的步骤 (1)取向量；(2)求向量夹角余弦cos 〈a ，b 〉； (3)定结果cos θ＝|cos 〈a ，b 〉|.[再练一题]2.如图3124，已知直三棱柱ABC A ′B ′C ′中，AC ＝BC ＝AA ′，∠ACB ＝90°，D ，E 分别为AB ，BB ′的中点．图3124(1)求证：CE ⊥A ′D ；(2)求异面直线CE 与AC ′所成角的余弦值．【解】 (1)证明：设CA →＝a ，CB →＝b ，CC ′→＝c ，根据题意，|a |＝|b |＝|c |且a ·b ＝b ·c ＝c ·a ＝0. ∴CE →＝b ＋12c ，A ′D →＝－c ＋12b －12a .∴CE →·A ′D →＝－12c 2＋12b 2＝0，∴CE →⊥A ′D →，即CE ⊥A ′D . (2)∵AC ′→＝－a ＋c ，∴|AC ′→|＝2|a |，|CE →|＝52|a |，∵AC ′→·CE →＝(－a ＋c )·⎝ ⎛⎭⎪⎫b ＋12c ＝12c 2＝12|a |2，∴cos 〈AC ′→，CE →〉＝12|a |22·52|a |2＝1010. ∴异面直线CE 与AC ′所成角的余弦值为1010. [探究共研型]利用数量积求距离探究1 已知A (1,2,1)，B (2,0,2)，求|AB →|的值．【提示】 AB →＝(1，－2,1)，∴|AB →|＝12＋－22＋12＝ 6.探究2 求两点间距离或线段的长度的方法．【提示】利用向量的数量积求两点间的距离，可以转化为求向量的模的问题，其基本思路是先选择以两点为端点的向量，将此向量表示为几个已知向量的和的形式，求出这几个已知向量的两两之间的夹角以及它们的模，利用公式|a |＝a ·a 求解即可．平行四边形ABCD 中，AB ＝2AC ＝2且∠ACD ＝90°，将它沿对角线AC 折起，使AB 与CD 成60°角，求点B ，D 间的距离．图3125【精彩点拨】 (1)由已知可以得出AC 与CD ，AC 与AB 垂直吗？ (2)根据AB 与CD 成60°角可建立什么方程？能直接求出|BD →|吗？【自主解答】由已知得AC ⊥CD ，AC ⊥AB ，折叠后AB 与CD 所成角为60°，于是，AC →·CD →＝0，BA →·AC →＝0，且〈BA →，CD →〉＝60°或120°.|BD →|2＝(BA →＋AC →＋CD →)2＝BA →2＋AC →2＋CD →2＋2BA →·AC →＋2AC →·CD →＋2BA →·CD →＝22＋12＋22＋2×2×2cos〈BA →，CD →〉，故|BD →|2＝13或5，解得|BD →|＝13或5，即B ，D 间的距离为13或 5.1．利用空间向量的数量积与空间向量模的关系，常把空间两点距离问题转化为空间向量模的大小问题加以计算．2．用数量积求两点间距离的步骤 (1)用向量表示此距离； (2)用其他向量表示此向量； (3)用公式a ·a ＝|a |2，求|a |； (4)|a |即为所求距离．[再练一题]3.如图3126所示，在空间四边形OABC 中，OA ，OB ，OC 两两成60°角，且OA ＝OB ＝OC ＝2，E 为OA 的中点，F 为BC 的中点，试求E ，F 间的距离．图3126【解】 EF →＝EA →＋AF →＝12OA →＋12(AB →＋AC →)＝12OA →＋12[(OB →－OA →)＋(OC →－OA →)]＝－12OA →＋12OB →＋12OC →，所以EF 2→＝14OA →2＋14OB →2＋14OC →2＋2×⎝ ⎛⎭⎪⎫－12×12OA →·OB →＋2×⎝ ⎛⎭⎪⎫－12×12OA →·OC →＋2×12×12OB →·OC →＝2.∴|EF →|＝2，即E ，F 间的距离为 2.[构建·体系]1．已知e 1，e 2为单位向量，且e 1⊥e 2，若a ＝2e 1＋3e 2，b ＝k e 1－4e 2，a ⊥b ，则实数k 的值为( )A ．－6B ．6C ．3D ．－3【解析】由题意可得a ·b ＝0，e 1·e 2＝0， |e 1|＝|e 2|＝1，∴(2e 1＋3e 2)·(k e 1－4e 2)＝0， ∴2k －12＝0，∴k ＝6. 【答案】 B2．在空间四边形OABC 中，OB ＝OC ，∠AOB ＝∠AOC ＝π3，则cos 〈OA →，BC →〉的值为( )A.12 B ．22C ．－12D ．0【解析】 OA →·BC →＝OA →·(OC →－OB →)＝OA →·OC →－OA →·OB →＝|OA →||OC →|cos ∠AOC －|OA →|·|OB →|cos ∠AOB ＝12|OA →||OC →|－12|OA →||OB →|＝0，∴OA →⊥BC →.∴cos 〈OA →，BC →〉＝0. 【答案】 D3．在空间四边形ABCD 中，AB →·CD →＋BC →·AD →＋CA →·BD →＝________.【导学号：15460065】【解析】原式＝AB →·CD →＋BC →·AD →＋CA →·(AD →－AB →)＝AB →·(CD →－CA →)＋AD →·(BC →＋CA →) ＝AB →·AD →＋AD →·BA →＝0. 【答案】 04.如图3127，四面体ABCD 的每条棱长都等于2，点E ，F 分别为棱AB ，AD 的中点，则|AB →＋BC →|＝________，|BC →－EF →|＝________，EF →与AC →所成的角为________．图3127【解析】 |AB →＋BC →|＝|AC →|＝2； EF →＝12BD →，BD →·BC →＝2×2×cos 60°＝2，故|BC →－EF →|2＝⎪⎪⎪⎪⎪⎪BC →－12BD →2＝BC →2－BC →·BD →＋14BD →2＝4－2＋14×4＝3.故|BC →－EF →|＝ 3.又因为EF →＝12BD →＝12(AD →－AB →)，故AC →·EF →＝12AC →·(AD →－AB →)＝12(AC →·AD →－AC →·AB →)＝0，因为〈EF →，AC →〉∈[0°，180°]，所以〈EF →，AC →〉＝90°. 【答案】 23 90°5.如图3128，三棱柱ABC A 1B 1C 1中，M ，N 分别是A 1B ，B 1C 1上的点，且BM ＝2A 1M ，C 1N＝2B 1N .设AB →＝a ，AC →＝b ，AA 1→＝c .图3128(1)试用a ，b ，c 表示向量MN →；(2)若∠BAC ＝90°，∠BAA 1＝∠CAA 1＝60°，AB ＝AC ＝AA 1＝1，求MN 的长．【解】 (1)MN →＝MA 1→＋A 1B 1→＋B 1N →＝13BA 1→＋AB →＋13B 1C 1→ ＝13(c －a )＋a ＋13(b －a ) ＝13a ＋13b ＋13c . (2)∵(a ＋b ＋c )2＝a 2＋b 2＋c 2＋2a ·b ＋2b ·c ＋2a ·c ＝1＋1＋1＋0＋2×1×1×12＋2×1×1×12＝5，∴|a ＋b ＋c |＝5， ∴|MN →|＝13|a ＋b ＋c |＝53，即MN ＝53.我还有这些不足：(1)________________________________________________________ (2)________________________________________________________ 我的课下提升方案：(1)________________________________________________________ (2)________________________________________________________学业分层测评 (建议用时：45分钟)[学业达标]一、选择题1．设a ，b ，c 是任意的非零平面向量，且它们相互不共线，下列命题：①(a ·b )c －(c ·a )b ＝0；②|a |＝a ·a ；③a 2b ＝b 2a ；④(3a ＋2b )·(3a －2b )＝9|a |2－4|b |2.其中正确的有( )A ．①②B ．②③C ．③④D ．②④【解析】由于数量积不满足结合律，故①不正确，由数量积的性质知②正确，③中，|a |2·b ＝|b |2·a 不一定成立，④运算正确．【答案】 D2．已知a ＋b ＋c ＝0，|a |＝2，|b |＝3，|c |＝4，则a 与b 的夹角〈a ，b 〉＝( ) A ．30° B ．45° C ．60°D ．以上都不对【解析】 ∵a ＋b ＋c ＝0，∴a ＋b ＝－c ，∴(a ＋b )2＝|a |2＋|b |2＋2a ·b ＝|c |2，∴a ·b ＝32，∴cos 〈a ，b 〉＝a ·b |a ||b |＝14. 【答案】 D3．已知四边形ABCD 为矩形，PA ⊥平面ABCD ，连接AC ，BD ，PB ，PC ，PD ，则下列各组向量中，数量积不为零的是( )A.PC →与BD → B ．DA →与PB → C.PD →与AB →D ．PA →与CD →【解析】用排除法，因为PA ⊥平面ABCD ，所以PA ⊥CD ，故PA →·CD →＝0，排除D ；因为AD ⊥AB ，PA ⊥AD ，又PA ∩AB ＝A ，所以AD ⊥平面PAB ，所以AD ⊥PB ，故DA →·PB →＝0，排除B ，同理PD →·AB →＝0，排除C.【答案】 A4.如图3129，已知空间四边形每条边和对角线都等于a ，点E ，F ，G 分别是AB ，AD ，DC 的中点，则下列向量的数量积等于a 2的是( )图3129A ．2BA →·AC →B ．2AD →·DB →C ．2FG →·AC →D ．2EF →·CB →【解析】 2BA →·AC →＝－a 2，故A 错；2AD →·DB →＝－a 2，故B 错；2EF →·CB →＝－12a 2，故D错；2FG →·AC →＝AC →2＝a 2，故只有C 正确．【答案】 C5．在正方体ABCD A 1B 1C 1D 1中，有下列命题： ①(AA 1→＋AD →＋AB →)2＝3AB →2； ②A 1C →·(A 1B 1→－A 1A →)＝0； ③AD 1→与A 1B →的夹角为60°. 其中正确命题的个数是( ) A ．1个 B ．2个 C ．3个D ．0个【解析】由题意知①②都正确，③不正确，AD 1→与A 1B →的夹角为120°. 【答案】 B 二、填空题6．已知|a |＝2，|b |＝3，〈a ，b 〉＝60°，则|2a －3b |＝_________________.【导学号：15460066】【解析】 |2a －3b |2＝(2a －3b )2＝4a 2－12a ·b ＋9b 2＝4×|a |2＋9×|b |2－12×|a |·|b |·cos 60°＝61， ∴|2a －3b |＝61. 【答案】617．已知|a |＝2，|b |＝1，〈a ，b 〉＝60°，则使向量a ＋λb 与λa －2b 的夹角为钝角的实数λ的取值范围是________．【解析】由题意知⎩⎪⎨⎪⎧a ＋λb ·λa －2b <0，cos 〈a ＋λb ，λa －2b 〉≠－1.即⎩⎪⎨⎪⎧a ＋λb ·λa －2b <0，a ＋λb ·λa －2b ≠－|a ＋λb ||λa －2b |得λ2＋2λ－2<0. ∴－1－3<λ<－1＋ 3. 【答案】 (－1－3，－1＋3)8.如图3130，已知正三棱柱ABC A 1B 1C 1的各条棱长都相等，M 是侧棱CC 1的中点，则异面直线AB 1和BM 所成的角的大小是________．图3130【解析】不妨设棱长为2，则AB →1＝BB 1→－BA →，BM →＝BC →＋12BB 1→，cos 〈AB 1→，BM →〉＝BB 1→－BA →·⎝⎛⎭⎪⎫BC →＋12BB 1→22×5＝0－2＋2－022×5＝0，故填90°.【答案】 90° 三、解答题9．如图3131，在正方体ABCD A 1B 1C 1D 1中，O 为AC 与BD 的交点，G 为CC 1的中点．求证：A 1O ⊥平面BDG .图3131【证明】设A 1B 1→＝a ，A 1D 1→＝b ，A 1A →＝c . 则a ·b ＝0，a ·c ＝0，b ·c ＝0.而A 1O →＝A 1A →＋AO →＝A 1A →＋12(AB →＋AD →)＝c ＋12(a ＋b )，BD →＝AD →－AB →＝b －a ，OG →＝OC →＋CG →＝12(AB →＋AD →)＋12CC 1→＝12(a ＋b )＋12c .∴A 1O →·BD →＝⎝ ⎛⎭⎪⎫c ＋12a ＋12b ·(b －a )＝c ·(b －a )＋12(a ＋b )·(b －a )＝c ·b －c ·a ＋12(b 2－a 2)＝12(|b |2－|a |2)＝0. ∴A 1O →⊥BD →. ∴A 1O ⊥BD . 同理可证A 1O →⊥OG →. ∴A 1O ⊥OG .又OG ∩BD ＝O 且A 1O ⊄平面BDG ， ∴A 1O ⊥平面BDG .10．已知长方体ABCD A 1B 1C 1D 1中，AB ＝AA 1＝2，AD ＝4，E 为侧面AB 1的中心，F 为A 1D 1的中点，试计算：(1)BC →·ED 1→；(2)BF →·AB 1→；(3)EF →·FC 1→.【解】如图所示，设AB →＝a ，AD →＝b ，AA 1→＝c ，则|a |＝|c |＝2，|b |＝4，a·b ＝b·c ＝c·a ＝0.(1)BC →·ED 1→＝AD →·(EA 1→＋A 1D 1→)＝AD →·⎣⎢⎡⎦⎥⎤12AA 1→－AB →＋AD →＝b ·⎣⎢⎡⎦⎥⎤12c －a ＋b ＝|b |2＝42＝16.(2)BF →·AB 1→＝(BA 1→＋A 1F →)·(AB →＋BB 1→)＝⎝⎛⎭⎪⎫AA 1→－AB →＋12AD →·(AB →＋AA 1→)＝⎝⎛⎭⎪⎫c －a ＋12b ·(a ＋c )＝|c |2－|a |2＝22－22＝0.(3)EF →·FC 1→＝(EA 1→＋A 1F →)·(FD 1→＋D 1C 1→) ＝⎣⎢⎡⎦⎥⎤12AA 1→－AB →＋12AD →·⎝ ⎛⎭⎪⎫12AD →＋AB → ＝⎣⎢⎡⎦⎥⎤12c －a ＋12b ·⎝ ⎛⎭⎪⎫12b ＋a ＝12(－a ＋b ＋c )·⎝ ⎛⎭⎪⎫12b ＋a＝－12|a |2＋14|b |2＝2.[能力提升]1．已知边长为1的正方体ABCD A 1B 1C 1D 1的上底面A 1B 1C 1D 1的中心为O 1，则AO 1→·AC →的值为( )A ．－1B ．0C ．1D ．2【解析】 AO 1→＝AA 1→＋A 1O 1→＝AA 1→＋12(A 1B 1→＋A 1D 1→)＝AA 1→＋12(AB →＋AD →)，而AC →＝AB →＋AD →，则AO 1→·AC →＝12(AB →2＋AD →2)＝1，故选C.【答案】 C2．已知a ，b 是两异面直线，A ，B ∈a ，C ，D ∈b ，AC ⊥b ，BD ⊥b 且AB ＝2，CD ＝1，则直线a ，b 所成的角为( )A ．30°B ．60°C ．90°D ．45°【解析】由于AB →＝AC →＋CD →＋DB →，则AB →·CD →＝(AC →＋CD →＋DB →)·CD →＝CD →2＝1. cos 〈AB →，CD →〉＝AB →·CD →|AB →|·|CD →|＝12，得〈AB →，CD →〉＝60°.【答案】 B3．已知正三棱柱ABC DEF 的侧棱长为2，底面边长为1，M 是BC 的中点，若直线CF 上有一点N ，使MN ⊥AE ，则CN CF＝________.【导学号：15460067】【解析】设CN CF＝m ，由于AE →＝AB →＋BE →， MN →＝12BC →＋mAD →，又AE →·MN →＝0，得12×1×1×⎝ ⎛⎭⎪⎫－12＋4m ＝0，解得m ＝116. 【答案】1164.如图3132，平行六面体ABCD A 1B 1C 1D 1中，AB ＝1，AD ＝2，AA 1＝3，∠BAD ＝90°，∠BAA 1＝∠DAA 1＝60°，求AC 1的长．图3132【解】 ∵AC 1→＝AB →＋AD →＋AA 1→， ∴|AC 1→|＝AB →＋AD →＋AA 1→2＝ AB →2＋AD →2＋AA 1→2＋2AB →·AD →＋AB →·AA 1→＋AD →·AA 1→.∵AB ＝1，AD ＝2，AA 1＝3，∠BAD ＝90°，∠BAA 1＝∠DAA 1＝60°， ∴〈AB →，AD →〉＝90°，〈AB →，AA 1→〉＝〈AD →，AA 1→〉＝60°， ∴|AC 1→|＝1＋4＋9＋21×3×cos 60°＋2×3×cos 60° ＝23.。

高中数学(人教B版)教材《向量的数量积》完美课件1

向量的数量积满足模的性质，即 $|vec{a}| = sqrt{vec{a} cdot vec{a}}$。
03
CATALOGUE
向量的数量积的应用
在物理中的应用
力的合成与分解
通过向量的数量积，可以计算出合力的大小和方向，也可以计算
出分力的大小和方向。
速度和加速度
在物理中，速度和加速度都是向量，通过向量的数量积可以计算出物体在某段时间内的位移和速度变化。
01
分配律是数量积的一个基本性质，可以用来简化计算。
结合几何意义理解
02
通过结合向量的几何意义，可以更直观地理解数量积的计算过
程。
掌握特殊情况的处理方法
03
对于一些特殊情况，如两个向量垂直或平行，需要掌握相应的
处理方法。
易错点解析
理解概念不准确
对于数量积的概念理解不准确，导致在计算中出现错误。
运算错误
性质
01
02
总结词：向量的数量积的性质
详细描述
03
04
05
1. 向量的数量积满足交换律，即$mathbf{A} cdot mathbf{B} = mathbf{B} cdot mathbf{A}$。
2. 向量的数量积满足分配律，即$(mathbf{A} + mathbf{B}) cdot mathbf{C} = mathbf{A} cdot mathbf{C} + mathbf{B} cdot mathbf{C}$。
向量与自身的数量积为该向量的模的平方，即$vec{a} cdot vec{a} = |vec{a}|^2$。
运算性质
向量的数量积满足非负性，即 $vec{a} cdot vec{b} geq 0$，当且仅当$vec{a}$与$vec{b}$同

新教材人教B版高中数学必修3精品课件：第八章向量数量积的概念向量数量积的运算律

如图（1 ）, 当〈 a， b 〉 <π2 时，��′��′的方向与b的方向相同，而且
| ��′��′|＝|a|cos〈a，b〉；
图（1）
如
图（2）
,当〈a
，b〉
＝π时
2
，
��′��′为零向量，即| ��′��′|＝0；
如
图
（
3
）
另外，我们还能得到数量积的如下性质. （3）a，b垂直的充要条件是它们的数量积为0，即
�� ⊥ �� ⇔ �� · ��＝0.
（4）如果a，b都是非零向量，则
cos〈a，b〉＝
��∙��
.
点拨 1.性质（1）中，当且仅当�� ∥ ��时，等号成立，此性质可用来解决不等式的相关问题. 2.性质（2）用数量积来求向量的模.实现了实数运算与向量运算的相互转化. 3.性质（3）可用来证明向量垂直或由向量垂直推出等量关系. 4.性质（4）是数量积定义的变形，又称为夹角公式，建立了向量与三角函数的联系.
π
例如，下图中向量a与b的夹角为π4，即〈a，b〉＝ 4 .
类似地，上图中，向量a与c的夹角为π2，即〈a，c〉＝π2；向量a与d的夹角为0，即〈a，d〉＝0；向量a与e的夹角为π，即〈a，e〉＝ π .
根据向量夹角的定义可知，两个非零向量的夹角是唯一确定的，而且
0≤〈a，b〉≤π，〈a，b〉＝〈b，a〉. 当〈a，b〉＝π2时，称向量a与向量b垂直，记作a⊥b. 由于零向量方向是不确定的，在讨论垂直问题时，规定零向量与任意向量垂直.

高中数学2-3-3向量数量积的坐标运算与度量公式课件新人教B版必修

[答案] B
[解析] 3x＋1×(－3)＝0，∴x＝1.
3．已知A、B、C是坐标平面上的三点，其坐标分别为
A(1,2)，B(4,1)，C(0，－1)，则△ABC的形状为( A．直角三角形 C．等腰直角三角形 [答案] C
→ ＝(3，－1)，AC → ＝(－1，－3) [解析] AB →· → ＝3×(－1)＋(－1)×(－3)＝0 AB AC → |＝|AC → |＝ 10∴△ABC 为等腰直角三角形．且|AB
[点评] 处理有关垂直总是要注意利用a⊥b⇔a·b＝
0(a，b是非零向量)，或者利用a⊥b⇔a1b1＋a2b2＝0(a＝(a1， a2)，b＝(b1，b2))．
[例2] 设a＝(4，－3)，b＝(2,1)，若a＋tb与b的夹角为 45°，求实数t的值． [分析] 利用公式a·b＝|a||b|cosθ建立方程，解t的值．
a－b＝(cosα－cosβ，sinα－sinβ)．又∵(a＋b)·(a－b) ＝ (cosα ＋ cosβ)(cosα － cosβ) ＋ (sinα ＋ sinβ)(sinα － sinβ) ＝cos2α－cos2β＋sin2α－sin2β＝0，
∴(a＋b)⊥(a－b)．
解法二：∵a＝(cosα，sinα)，b＝(cosβ，sinβ)， ∴(a＋b)·(a－b)＝a2－b2＝|a|2－|b|2 ＝(cos2α＋sin2α)－(cos2β＋sin2β)＝1－1＝0， ∴(a＋b)⊥(a－b)．
二、填空题
5 ．已知 a ＝ (x － 2 ， x ＋ 3) ， b ＝ (2x － 3 ，－ 2) ，若 a⊥b，则x＝________.
[答案]
[解析]
2
9 0 或2
∵a⊥b，∴a· b＝(x－2)(2x－3)－2(x＋3)＝0

高二数学选修课件：3-1-3两个向量的数量积

通常规定0°≤<a，b>≤180° 且<a，b>＝<b，a>
人教 B 版数学
如果 <a ， b> ＝ 90° ，则称 ________________ ，记作
________．
第三章
空间向量与立体几何
2．两个向量一定共面．但在作向量a，b时，它们的基
线可能不同在任一平面内，我们把不同在任一平面内的两条直线叫做________．把异面直线平移到一个平面内，这时两条直线的夹角(锐角或直角)叫做________，如果所成的角是直角，则称两条异面直线________．
(2)∵(3a － 2b)·(a ＋ 2b) ＝ 3|a|2 ＋ 4a·b － 4|b|2 ＝ 3|a|2 ＋ 4|a||b|cos120°－4|b|2，
1 ∴(3a－2b)· (a＋2b)＝3×9＋4×3×4×(－2)－4×16 ＝27－24－64＝－61.
第三章
空间向量与立体几何
向量a、b之间的夹角为30°，且|a|＝3，|b|＝4，求a·b， a2，b2，(a＋2b)·(a－b)．
人教 B 版数学
第三章
空间向量与立体几何
空间两个向量的数量积的性质．
与平面上两个向量的数量积一样，空间两个向量的数量积也具有如下性质． a．a·e＝|a|cos<a，e> b．a⊥b⇔a·b＝0
人教 B 版数学
c．|a|2＝a·a
d．|a·b|≤|a||b|
第三章
空间向量与立体几何
人教 B 版数学
3．把平面向量的数量积
a·b＝|a||b|cos<a，b> 也叫做两个空间向量a，b的________________．

新教材人教B版高中数学必修第三册第八章向量的数量积与三角恒等变换精品教学课件(共305页)

[变式训练 1] 设 a，b，c 是任意的非零向量，且它们相互不共线，给出下列结论：
①a·c－b·c＝(a－b)·c； ②(b·c)·a－(c·a)·b 不与 c 垂直； ③|a|－|b|<|a－b|； ④(3a＋2b)·(3a－2b)＝9|a|2－4|b|2. 其中正确的序号是__①__③__④___.
[答一答] 1．如何理解平面向量的数量积？
提示：(1)此定义式同时也是两向量数量积的计算式． (2)向量的数量积 a·b，不能表示为 a×b 或 ab. (3)两个向量的数量积是一个数量，而不是向量． (4)a·b 的几何意义是：a 的长度与 b 在 a 方向上的射影的数量的乘积或 b 的长度与 a 在 b 方向上的射影的数量的乘积．
2．向量的数量积(内积) (1)当 a 与 b 都是非零向量时，称__|_a_||b_|_c_o_s〈__a_，__b_〉__为向量 a 与 b 的数量积(也称为内积)，记作 a·b，即 a·b＝__|a_||_b_|c_o_s_〈__a_，__b_〉． (2)两向量的数量积不是向量而是__实__数__，它可以为正数、
第八章向量的数量积与三角恒等变换
8.1.1 向量数量积的概念 8.1.2 向量数量积的运算律 P24 8.1.3 向量数量积的坐标运算 P51 8.2.1 两角和与差的余弦 P80 8.2.2 两角和与差的正弦、正切第1课时两角和与差的正弦 P112 第2课时两角和与差的正切 P148 8.2.3 倍角公式 P186 8.2.4 三角恒等变换的应用
求平面向量数量积的步骤是：(1)求 a 与 b 的夹角 θ，θ∈[0， π]；(2)分别求|a|和|b|；(3)求数量积，即 a·b＝|a||b|cosθ，要特别注意书写时 a 与 b 之间用实心圆点“·”连接，而不能用“×” 连接，也不能省去．

2019-2020学年高中数学人教B版选修2-1课件： 3.1.3 两个向量的数量积

()
A.1
B.2
C.4
D.8
2.已知正四面体O-ABC的棱长为1. 求:(1) OA OB. (2) (OA＋OB) (CA＋CB).
【解题探究】 1.典例1中向量 APi (i=1,2,…)在向量 AB 方向上的投影是多少? 提示:向量 A(Pi=i 1,2,…)在向量方A向B上的投影就是AB的长,|AB|=1.
3.已知|a|=3,|b|=2,a·b=-3,则<a,b>=
.
【解析】因为|a|=3,|b|=2,a·b=-3,
所以cos<a,b>= a b 3 1 ,
| a || b | 3 2 2
又因为<a,b>∈[0,π],所以<a,b>= 2 .
3的夹角为60°,那么|3a
(3)注意点:①数量积的符号由夹角的余弦值决定. ②当a≠0时由a·b=0可得a⊥b或b=0. ③空间向量没有除法运算:即若a·b=k,则没有a= k .
b
(4)a·b的几何意义数量积a·b等于a的长度|a|与b在a方向上的投影 |b|cos θ的乘积.
4.对空间向量数量积性质的三点说明 (1)向量模的应用:式子|a|= a a 可以解决有关空间长度问题. (2)向量夹角的应用:空间中两条直线(特别是两条异面直线)的夹角,可以通过求出这两个向量的夹角而求得.
【思考】判断: (1)对于非零向量a,b,<a,b>与<a,-b>相等. ( ) (2)对于任意向量a,b,c,,都有(a·b)c=a(b·c).
() (3)若a·b=b·c,且b≠0,则a=c. ( ) (4)(3a+2b)·(3a-2b)=9|a|2-4|b|2. ( )

1.1.2 空间向量的数量积运算课件(人教版)

同理,AO⊥CO,BO⊥CO.
所以AO,BO,CO两两垂直.
2.两个非零向量a,b的夹角〈a,b〉的范围是③ [0,π] ;若〈a,b〉=0,则向量a,b方向④相同;若〈a,b〉=π,则向量a,b方向⑤ 相反 ;若〈a,b〉=π ,则向量a,b⑥ 互相垂直 .
2
空间向量的数量积
1.定义已知两个非零向量a,b,则⑦ |a||b|cos〈a,b〉叫做a,b的数量积,记作⑧ a·b . 即a·b=|a||b|cos〈a,b〉. 规定:零向量与任意向量的数量积为⑨ 0 . 2.运算律 (1)(λa)·b=⑩ λ(a·b) ,λ∈R; (2)交换律:a·b= b·a ; (3)分配律:a·(b+c)= a·b+a·c .
3.由于向量的夹角的取值范围为[0,π],而异面直线所成的角的取值范围为
0,
π 2
,因此利用向
量的数量积求异面直线所成的角时,要注意角度之间的关系,当〈a,b〉∈
0,
π 2
时,它们相等;
当〈a,b〉∈
π 2
,π
时,它们互补.
利用空间向量的数量积求距离(或线段长)
1.用数量积求两点间距离的步骤 (1)用向量的模表示此距离; (2)用已知模和夹角的向量表示此向量; (3)用公式a·a=|a|2求|a|; (4)|a|即为所求距离. 2.求模公式的推广由公式|a|= a a 可以推广为|a±b|= （a b）= a2 2abb2.
(1)已知空间四边形ABCD的每条边和对角线的长都等于a,点E,F分别是BC,AD的中点,则 AE
·AF =
;
(2)在四面体OABC中,棱OA,OB,OC两两垂直,且OA=1,OB=2,OC=3,G为△ABC的重心,则OG ·

6.2.4向量的数量积课件(人教版)

记作a b ，即a b a b cos.
A
规定:零向量与任一向量的数量积为0.
O
B
四、小试牛刀，巩固落实
课本P17例9 已知 a 5, b 4, a与b 的夹角 2 ，求a b.
3
变式：已知 a 5, b 4, a b 10，求a与b 的夹角.
解：a b a b cos 分析：由a b a b cos
为锐角
为钝角
五、几何角度，深化理解
3、投影及投影向量的定义：
A
CA
1
B
a
b
B1
设a,b是两个非零向量，AB a,CD b,过 AB 的终点A, B，分别作CD所在的直线的垂线，垂足为A1, B1 ，得到A1B1 ，我们称上述变换为向量a 向向量b 的投影， A1B1叫做向量a在b上的投影向量.
向量的数量积
册别：必修第二册学科：高中数学（人教A版）
一、温故知新，提出问题
问题1：前面我们学习了向量的加、减运算，类比数的运算，向量之间还可以
建立哪些运算？
二、借助物理，创设情境
问题2：类比研究向量运算中加法运算的基本路径，怎样来研究向量的乘法？
物理
力
力的合成
数学
向量
向量的加法
则AOB （0 ）叫a与b 的夹角.
A
O
B
三、抽象概念，建构新知
特殊的夹角
0
O
B
2
A
O
B
A
O
a与b 方向相同
a与b垂直记作a b
B a与b 方向相反
三、抽象概念，建构新知
2、向量数量积的定义：
已知两个非零向量a与b ，它们的夹角为，

高中数学 3.1.3 两个向量的数量积课件新人教B版选修2

RB ·数学选修2-1
教
学
易
教
错
法
易
分析
3.1.3 两个向量的数量积
误辨析
教学
教师用书独具演示
当
方
堂

案
双
设
基
计
●三维目标
达标
课
前自
1.知识与技能
课
主
时
导学
掌握空间向量夹角和模的概念及表示方法；掌握空间向作业
课量的数量积及其运算律．
堂互动探究
教师备课资源
菜单
RB ·数学选修2-1
教师备课资源
菜单
教
学
教
●教学流程
法
分
析
教学方案设计
课前自主导学
课堂互动探究
菜单
RB ·数学选修2-1
易错易误辨析
当堂双基达标
课时作业
教师备课资源
教学教法分析
教学方案设计
课前自主导学
课堂互动探究
菜单
RB ·数学选修2-1
易错易误辨析
当堂双基达标
课时作业
教师备课资源
教学教法分析
教学方案设计
课前自主导学
课堂互动探究
菜单
RB ·数学选修2-1
易错易误辨析
当堂双基达标
课时作业
教师备课资源
析
辨
教
为了突破重点、化解难点，使学生能达到本节课设定的析

高二数学选修2 两个向量的数量积课件

9.5 空间向量及其运算
两个向量的数量积
教学过程
一、几个概念
1）两个向量的夹角的定义
a b
O
A
a
B
b
注意：（ 1 ）范围： 0 a, b
(2)a, b b, a
夹角的顶点为两个向量的起点
(3)OA, OB AO, OB
注意：（ 1 ）范围： 0 a, b
D
C
A B
例３、如图所示，已知线段AB在平面α内，线段 AC⊥α，线段BD⊥AB，线段DD' 交于 D',DBD’=30.如果AB＝a，AC＝BD＝b，（1）求C、D间的距离; （2）求异面直线DC,BD' 所成的角．
C
D
E
F
D'

A
B
2 2 2
( ) ( ) ( )
( ) ( )
5) p q p q p 2 q 2
例4
已知在平行六面体 ABCD ABC D中，AB 4 ,
AD 3 , AA 5 , BAD 90 , BAA DAA 60,
求对角线 AC 的长。
注意： ①两个向量的数量积是数量，而不是向量. ②零向量与任意向量的数量积等于零。
（3）公式变形： cos a, b
a b ab
3）射影
A1 B1叫做向量AB在轴l上的或在e方向上的正射影，简称射影。 A1 B1 AB cos a, e a e
e
A1
A
B
B1
l
注意： AB 在轴L上的正射影A1B1是一个可正可负的实数，它的符号代表向量 AB 与L的方向的相对关系，大小代表在Ｌ上射 b, a (3)OA, OB AO, OB

2018年秋人教B版数学选修2-1课件：3.1.3 两个向量的数量积

(5)若 a· b=k,不能得出 a= ;
(6)a⊥b的充要条件是a· b=0,这是用向量证明空间中垂直关系的根本方法.
��
题型一
题型二
题型三
求空间向量的夹角【例1】如图,在正方体ABCD - A'B'C'D'中,求下列各向量的夹角:
(1)�� 与��'; (2)�� 与��. 分析: 结合图形,利用空间向量的夹角的定义求解.
题型一
题型二
题型三
求空间向量的数量积
【例 2】已知长方体 ABCD - A'B'C'D',AB=AA'=2,AD=4,E 为侧面 AB'的中心,F 为 A'D'的中点,计算下列数量积:(1)�� ·��'; (2)�� · ��'; (3)�� ·��'.
5.两个空间向量的数量积满足的运算律 (1)(λa)· b=λ(a· b); (2)a· b=b· a(交换律); (3)(a+b)· c=a· c+b· c(分配律). 【做一做4】下列各式不正确的是 .(填序号)
① ��· �� = ��;
②a· b=0⇒a=0或b=0; ③|a· b|=|a||b|; ④a· (b+c)=(b+c)· a. 解析:①∵ ��· �� = |��|, ∴ 命题错误; ②∵a· b=0⇒a⊥b,∴命题错误; ③∵|a· b|=|a||b||cos<a,b>|,∴命题错误; ④正确. 答案:①②③

人教B版高中数学选修(2-1)-3.1《两个向量的数量积》拔高练习

3.1.3两个向量的数量积1．已知在平行六面体ABCD －A 1B 1C 1D 1中，同一顶点为端点的三条棱长都等于1，且彼此的夹角都是60°，则此平行六面体的对角线AC 1的长为( )． A. 3 B ．2 C. 5 D. 62．已知a ，b 是异面直线，A 、B ∈a ，C 、D ∈b ，AC ⊥b ，BD ⊥b ，且AB ＝2，CD ＝1，则a 与b 所成的角是( )．A ．30°B ．45°C ．60°D ．90°3．已知|a |＝32，|b |＝4，m ＝a ＋b ，n ＝a ＋λb ，〈a ，b 〉＝135°，m ⊥n ，则λ＝________．4．如图，已知正三棱柱ABC －A 1B 1C 1的各条棱长都相等，M 是侧棱CC 1的中点，则异面直线AB 1和BM 所成的角的大小是______．5．如图所示，已知△ADB 和△ADC 都是以D 为直角顶点的直角三角形，且AD ＝BD ＝CD ，∠BAC ＝60°.求证：BD ⊥平面ADC .6．(创新拓展)如图，正三棱柱ABC －A 1B 1C 1中，底面边长为2.(1)设侧棱长为1，求证：AB 1⊥BC 1；(2)设AB 1与BC 1的夹角为π3，求侧棱的长．参考答案1. 解析：∵AC 1→＝AB →＋AD →＋AA 1→ ∴AC 1→2＝(AB →＋AD →＋AA 1→)2＝AB →2＋AD →2＋AA 1→2＋2AB →·AD →＋2AB →·AA 1→＋2AD →·AA 1→＝1＋1＋1＋2(cos 60°＋cos 60°＋cos 60°)＝6，∴|AC 1→|＝ 6. 答案：D2. 解析 ∵AB →·CD →＝(AC →＋CD →＋DB →)·CD →＝AC →·CD →＋|CD →|2＋DB →·CD→＝|CD →|2＝1， ∴cos 〈AB →，CD →〉＝AB →·CD →|AB →||CD →|＝12， ∴a 与b 的夹角为60°.答案 C3. 解析由m ⊥n ，得(a ＋b )·(a ＋λb )＝0，∴a 2＋(1＋λ)a ·b ＋λb 2＝0，∴18＋(λ＋1)×32×4cos 135°＋16λ＝0，即4λ＋6＝0，∴λ＝－32.答案－324. 解析不妨设棱长为2，则AB 1→＝BB 1→－BA →，BM →＝BC →＋12BB 1→，cos 〈AB 1→，BM →〉＝（BB 1→－BA →）·（BC →＋12BB 1→）22×5＝0－2＋2－022×5＝ 0，故填90°.答案 90°5. 证明不妨设AD ＝BD ＝CD ＝1，则AB ＝AC ＝ 2.BD →·AC →＝(AD →－AB →)·AC →＝AD →·AC →－AB →·AC→，由于AD →·AC →＝AD →·(AD →＋DC →)＝AD →·AD →＝1，AB →·AC →＝|AB →|·|AC →|cos 60°＝2×2×。