四边形辅助线练习(含答案)

合集下载

(易错题精选)初中数学四边形专项训练解析含答案(1)

（易错题精选）初中数学四边形专项训练解析含答案(1)一、选择题1．一个多边形切去一个角后，形成的另一个多边形的内角和为1080°，那么原多边形的边数为（）A ．7B ．7或8C ．8或9D ．7或8或9【答案】D【解析】试题分析：设内角和为1080°的多边形的边数是n ，则（n ﹣2）•180°=1080°，解得：n=8．则原多边形的边数为7或8或9．故选D ．考点：多边形内角与外角．2．如图，足球图片正中的黑色正五边形的内角和是( )．A ．180°B ．360°C ．540°D ．720°【答案】C【解析】【分析】根据多边形内角和公式2180()n -⨯︒即可求出结果．【详解】解：黑色正五边形的内角和为：5218540(0)-⨯︒=︒，故选：C ．【点睛】本题考查了多边形的内角和公式，解题关键是牢记多边形的内角和公式．3．如图，在菱形ABCD 中，60ABC ∠=︒，1AB =，点P 是这个菱形内部或边上的一点，若以点P ，B ，C 为顶点的三角形是等腰三角形，则P ，D （P ，D 两点不重合）两点间的最短距离为（）A ．12B ．1C 3D 31【答案】D【解析】【分析】分三种情形讨论①若以边BC为底．②若以边PC为底．③若以边PB为底．分别求出PD 的最小值，即可判断．【详解】解：在菱形ABCD中，∵∠ABC=60°，AB=1，∴△ABC，△ACD都是等边三角形，①若以边BC为底，则BC垂直平分线上（在菱形的边及其内部）的点满足题意，此时就转化为了“直线外一点与直线上所有点连线的线段中垂线段最短“，即当点P与点A重合时，PD值最小，最小值为1；②若以边PC为底，∠PBC为顶角时，以点B为圆心，BC长为半径作圆，与BD相交于一点，则弧AC（除点C外）上的所有点都满足△PBC是等腰三角形，当点P在BD上时，PD1③若以边PB为底，∠PCB为顶角，以点C为圆心，BC为半径作圆，则弧BD上的点A与点D均满足△PBC为等腰三角形，当点P与点D重合时，PD最小，显然不满足题意，故此种情况不存在；上所述，PD的最小值为1故选D．【点睛】本题考查菱形的性质、等边三角形的性质、等腰三角形的判定和性质等知识，解题的关键是学会用分类讨论的思想思考问题，属于中考常考题型．4．在平面直角坐标系中，A，B，C三点坐标分别是（0，0），（4，0），（3，2），以A，B，C三点为顶点画平行四边形，则第四个顶点不可能在（）.A．第一象限B．第二象限C．第三象限D．第四象限【答案】C【解析】A点在原点上，B点在横轴上，C点在第一象限，根据平行四边形的性质：两组对边分别平行，可知第四个顶点可能在第一、二、四象限，不可能在第三象限，故选C5．一个多边形的每一个外角都是72°，那么这个多边形的内角和为( )A．540°B．720°C．900°D．1080°【答案】A【解析】【详解】解：∵多边形的每一个外角都是72°，∴多边形的边数为：360572=，∴该多边形的内角和为：（5-2）×180°=540°．故选A．【点睛】外角和是360°，除以一个外角度数即为多边形的边数．根据多边形的内角和公式可求得该多边形的内角和．6．如图，正方形ABCD的边长为4，点E、F分别在AB、BC上，且AE=BF=1，CE、DF交于点O，下列结论：①∠DOC=90°，②OC=OE，③CE=DF，④tan∠OCD=43，⑤S△DOC=S四边形EOFB中，正确的有（）A．1个B．2个C．3个D．4个【答案】D【解析】分析：由正方形ABCD的边长为4，AE=BF=1，利用SAS易证得△EBC≌△FCD，然后全等三角形的对应角相等，易证得①∠DOC=90°正确，③CE=D F正确；②由线段垂直平分线的性质与正方形的性质，可得②错误；易证得∠OCD=∠DFC，即可求得④正确；由①易证得⑤正确．详解：∵正方形ABCD的边长为4，∴BC=CD=4，∠B=∠DCF=90°．∵AE=BF=1，∴BE=CF=4﹣1=3．在△EBC和△FCD中，BC CDB DCFBE CF=⎧⎪∠=∠⎨⎪=⎩，∴△EBC≌△FCD（SAS），∴∠CFD=∠BEC，CE=DF，故③正确，∴∠BCE+∠BEC=∠BCE+∠CFD=90°，∴∠DOC=90°；故①正确；连接DE，如图所示，若OC=OE．∵DF⊥EC，∴CD=DE．∵CD=AD＜DE（矛盾），故②错误；∵∠OCD+∠CDF=90°，∠CDF+∠DFC=90°，∴∠OCD=∠DFC，∴tan∠OCD=tan∠DFC=DCFC=43，故④正确；∵△EBC≌△FCD，∴S△EBC=S△FCD，∴S△EBC﹣S△FOC=S△FCD﹣S△FOC，即S△ODC=S四边形BEOF．故⑤正确；故正确的有：①③④⑤．点睛：本题考查了正方形的性质、全等三角形的判定与性质、直角三角形的性质以及三角函数等知识．此题综合性较强，难度适中，注意掌握数形结合思想与转化思想的应用．7．如图，在平行四边形ABCD中，用直尺和圆规作∠BAD的平分线AG交BC于点E，若BF=6，AB=5，则AE的长为()A．4 B．8 C．6 D．10【答案】B【解析】【分析】【详解】解：设AG与BF交点为O，∵AB=AF，AG平分∠BAD，AO=AO，∴可证△ABO≌△AFO，∴BO=FO=3，∠AOB=∠AOF=90º，AB=5，∴AO=4，∵AF∥BE，∴可证△AOF≌△EOB，AO=EO，∴AE=2AO=8，故选B．【点睛】本题考查角平分线的作图原理和平行四边形的性质．8．下列说法中正确的是（）A．有一个角是直角的四边形是矩形B．两条对角线互相垂直的四边形是菱形C．两条对角线互相垂直平分的四边形是正方形D．两条对角线相等的菱形是正方形【答案】D【解析】【分析】本题考查了菱形，矩形，正方形的判定方法，熟练掌握菱形，矩形，正方形的判定方法是解题的关键.A. 有一个角是直角的四边形是矩形,错误；B. 两条对角线互相垂直的四边形是菱形，错误；C. 两条对角线互相垂直平分的四边形是正方形，错误；D. 两条对角线相等的菱形是正方形，正确.故选D.【点睛】本题考查了菱形，矩形，正方形的判定方法，熟练掌握菱形，矩形，正方形的判定方法是解题的关键，考查了学生熟练运用知识解决问题的能力.9．如图，11,,33AB EF ABP ABC EFP EFC ∠=∠∠=∠∥，已知60FCD ∠=︒，则P ∠的度数为（）A ．60︒B ．80︒C ．90︒D ．100︒【答案】B【解析】【分析】延长BC 、EF 交于点G ，根据平行线的性质得180ABG BGE +=︒∠∠，再根据三角形外角的性质和平角的性质得60180120EFC FCD BGE BGE BCF FCD =+=︒+=︒-=︒∠∠∠∠，∠∠，最后根据四边形内角和定理求解即可．【详解】延长BC 、EF 交于点G∵//AB EF∴180ABG BGE +=︒∠∠∵60FCD ∠=︒∴60180120EFC FCD BGE BGE BCF FCD =+=︒+=︒-=︒∠∠∠∠，∠∠ ∵11,33ABP ABC EFP EFC ∠=∠∠=∠ ∴360P PBC BCF PFC =︒---∠∠∠∠2236012033ABG EFC =︒---︒∠∠ ()223606012033ABG BGE =︒--︒+-︒∠∠223604012033ABG BGE =︒--︒--︒∠∠ ()22003ABG BGE =︒-+∠∠ 22001803=︒-⨯︒ 80=︒故答案为：B ．【点睛】本题考查了平行线的角度问题，掌握平行线的性质、三角形外角的性质、平角的性质、四边形内角和定理是解题的关键．10．如图，ABCD Y 的对角线AC 与BD 相交于点O ，AD BD ⊥，30ABD ∠=︒，若23AD =．则OC 的长为（）A ．3B ．3C 21D ．6【答案】C【解析】【分析】先根据勾股定理解Rt ABD △求得6BD =，再根据平行四边形的性质求得3OD =，然后根据勾股定理解Rt AOD △、平行四边形的性质即可求得21OC OA ==【详解】解：∵AD BD ⊥∴90ADB ∠=︒∵在Rt ABD △中，30ABD ∠=︒，23AD =∴243AB AD ==∴226BD AB AD =-=∵四边形ABCD 是平行四边形∴132OB OD BD ===，12OA OC AC ==∴在Rt AOD △中，AD =3OD =∴OA =∴OC OA ==故选：C【点睛】本题考查了含30°角的直角三角形的性质、勾股定理、平行四边形的性质等知识点，熟练掌握相关知识点是解决问题的关键．11．在四边形ABCD 中，AD ∥BC ，要使四边形ABCD 是平行四边形，可添加的条件不正确的是（）A ．AB ∥CDB ．∠B ＝∠DC ．AD ＝BC D ．AB ＝CD【答案】D【解析】【分析】根据平行四边形的判定解答即可．【详解】∵AD ∥BC ，AB ∥CD ，∴四边形ABCD 是平行四边形，故A 正确；∵AD ∥BC ，AD=BC ，∴四边形ABCD 是平行四边形，故C 正确；∵AD ∥BC ，∴∠D+∠C=180°，∵∠B=∠D ，∴∠B+C=180°，∴AB ∥CD ，∴四边形ABCD 是平行四边形，故B 正确；故选：D ．【点睛】此题考查平行四边形的判定，解题关键是根据平行四边形的判定解答．12．如图，菱形OBCD 在平面直角坐标系中的位置如图所示，顶点B （0，DOB =60°，点P 是对角线OC 上的一个动点，已知A （﹣1，0），则AP +BP 的最小值为（）A．4 B．5 C．33D．19【答案】D【解析】【分析】点B的对称点是点D，连接AD，则AD即为AP+BP的最小值，求出点D坐标解答即可．【详解】解：连接AD，如图，∵点B的对称点是点D，∴AD即为AP+BP的最小值，∵四边形OBCD是菱形，顶点B（0，23），∠DOB=60°，∴点D的坐标为（3，3），∵点A的坐标为（﹣1，0），∴AD=22+=，(3)419故选：D．【点睛】此题考查菱形的性质，关键是根据两点坐标得出距离．13．如图，四边形ABCD的对角线为AC、BD，且AC=BD，则下列条件能判定四边形ABCD 为矩形的是（）A．BA=BCB．AC、BD互相平分C．AC⊥BDD．AB∥CD【答案】B【解析】试题分析：根据矩形的判定方法解答．解：能判定四边形ABCD是矩形的条件为AC、BD互相平分．理由如下：∵AC、BD互相平分，∴四边形ABCD是平行四边形，∵AC=BD，∴▱ABCD是矩形．其它三个条件再加上AC=BD均不能判定四边形ABCD是矩形．故选B．考点：矩形的判定．14．如图，在矩形ABCD中，AD=2AB，点M、N分别在边AD、BC上，连接BM、DN．若四边形MBND是菱形，则AMMD等于（）A．35B．23C．38D．45【答案】A【解析】试题分析：设AB=a,根据题意知AD=2a，由四边形BMDN是菱形知BM=MD，设AM=b,则BM=MD=2a-b.在Rt△ABM中，由勾股定理即可求值.试题解析：∵四边形MBND是菱形，∴MD=MB．∵四边形ABCD是矩形，∴∠A=90°．设AB=a，AM=b，则MB=2a-b，（a、b均为正数）．在Rt△ABM中，AB2+AM2=BM2，即a2+b2=（2a-b）2，解得a=4b3，∴MD=MB=2a-b=53 b，∴3553AM bMD b==.故选A.考点：1.矩形的性质；2.勾股定理；3.菱形的性质．15．如图，在菱形ABCD 中，60BCD ∠=︒，BC 的垂直平分线交对角线AC 于点F ，垂足为E ，连接BF 、DF ，则DFC ∠的度数是（）A ．130︒B ．120︒C ．110︒D ．100︒【答案】A【解析】【分析】首先求出∠CFB=130°，再根据对称性可知∠CFD=∠CFB 即可解决问题；【详解】∵四边形ABCD 是菱形，∴∠ACD ＝∠ACB ＝12∠BCD=25°， ∵EF 垂直平分线段BC ，∴FB=FC ，∴∠FBC=∠FCB=25°，∴∠CFB=180°-25°-25°=130°，根据对称性可知：∠CFD=∠CFB=130°，故选：A ．【点睛】此题考查菱形的性质、线段的垂直平分线的性质，解题的关键是熟练掌握基本知识，属于中考常考题型．16．如图，在 ABCD 中，CD=2AD ，BE ⊥AD 于点E ，F 为DC 的中点，连结EF 、BF ，下列结论：①∠ABC=2∠ABF ；②EF=BF ；③S 四边形DEBC =2S △EFB ；④∠CFE=3∠DEF,其中正确结论的个数共有（）.A ．1个B ．2个C ．3个D ．4个【答案】D【解析】分析：如图延长EF 交BC 的延长线于G ，取AB 的中点H 连接FH ．证明△DFE ≌△FCG 得EF=FG ，BE ⊥BG ，四边形BCFH 是菱形即可解决问题；详解：如图延长EF 交BC 的延长线于G ，取AB 的中点H 连接FH ．∵CD=2AD，DF=FC，∴CF=CB，∴∠CFB=∠CBF，∵CD∥AB，∴∠CFB=∠FBH，∴∠CBF=∠FBH，∴∠ABC=2∠ABF．故①正确，∵DE∥CG，∴∠D=∠FCG，∵DF=FC，∠DFE=∠CFG，∴△DFE≌△FCG，∴FE=FG，∵BE⊥AD，∴∠AEB=90°，∵AD∥BC，∴∠AEB=∠EBG=90°，∴BF=EF=FG，故②正确，∵S△DFE=S△CFG，∴S四边形DEBC=S△EBG=2S△BEF，故③正确，∵AH=HB，DF=CF，AB=CD，∴CF=BH，∵CF∥BH，∴四边形BCFH是平行四边形，∵CF=BC，∴四边形BCFH是菱形，∴∠BFC=∠BFH，∵FE=FB，FH∥AD，BE⊥AD，∴FH⊥BE，∴∠BFH=∠EFH=∠DEF，∴∠EFC=3∠DEF，故④正确，故选D．点睛：本题考查平行四边形的性质和判定、菱形的判定和性质、直角三角形斜边中线的性质、全等三角形的判定和性质等知识，解题的关键是学会添加常用辅助线，构造全等三角形解决问题，属于中考选择题中的压轴题．17．如图，矩形纸片ABCD中，AB=6cm，BC=8cm．现将其沿AE对折，使得点B落在边AD上的点B1处，折痕与边BC交于点E，则CE的长为（）A．6cm B．4cm C．3cm D．2cm【答案】D【解析】分析：根据翻折的性质可得∠B=∠AB1E=90°，AB=AB1，然后求出四边形ABEB1是正方形，再根据正方形的性质可得BE=AB，然后根据CE=BC-BE，代入数据进行计算即可得解．详解：∵沿AE对折点B落在边AD上的点B1处，∴∠B=∠AB1E=90°，AB=AB1，又∵∠BAD=90°，∴四边形ABEB1是正方形，∴BE=AB=6cm，∴CE=BC-BE=8-6=2cm．故选：D．点睛：本题考查了矩形的性质，正方形的判定与性质，翻折变换的性质，判断出四边形ABEB1是正方形是解题的关键．18．如图a是长方形纸带，∠DEF=20°，将纸带沿EF折叠成图b，再沿BF折叠成图c，则图c中的∠CFE的度数是（）A．110°B．120°C．140°D．150°【答案】B【解析】【详解】解：∵AD∥BC，∴∠DEF=∠EFB=20°，图b中∠GFC=180°-2∠EFG=140°，在图c中∠CFE=∠GFC-∠EFG=120°，故选B．19．下列说法正确的是（）A．对角线相等的四边形一定是矩形B．任意掷一枚质地均匀的硬币10次，一定有5次正面向上C．如果有一组数据为5，3，6，4，2，那么它的中位数是6D．“用长分别为5cm、12cm、6cm的三条线段可以围成三角形”这一事件是不可能事件【答案】D【解析】【分析】根据矩形的判定定理，数据出现的可能性的大小，中位数的计算方法，不可能事件的定义依次判断即可.【详解】A.对角线相等的平行四边形是矩形，故该项错误；B. 任意掷一枚质地均匀的硬币10次，不一定有5次正面向上，故该项错误；C. 一组数据为5，3，6，4，2，它的中位数是4，故该项错误；D. “用长分别为5cm、12cm、6cm的三条线段可以围成三角形” 这一事件是不可能事件，正确，故选：D.【点睛】此题矩形的判定定理，数据出现的可能性的大小，中位数的计算方法，不可能事件的定义，综合掌握各知识点是解题的关键.20．如图，△ABC中，AB＝AC＝10，BC＝12，D是BC的中点，DE⊥AB于点E，则DE的长为（）A．65B．85C．125D．245【答案】D【解析】【分析】连接AD，根据已知等腰三角形的性质得出AD⊥BC和BD=6，根据勾股定理求出AD，根据三角形的面积公式求出即可．【详解】解：连接AD∵AB=AC，D为BC的中点，BC=12，∴AD⊥BC，BD=DC=6，在Rt△ADB中，由勾股定理得：22221068AB BD=+=，∵S△ADB=12×AD×BD＝12×AB×DE，∴DE=8624105 AD BDAB⨯⨯==，故选D．【点睛】本题考查了等腰三角形的性质（等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合）、勾股定理和三角形的面积，能求出AD的长是解此题的关键．。

人教版初二数学8年级下册第18章(平行四边形)含辅助线证明题训练(含答案)

人教版数学八年级下期第十八章平行四边形含辅助线证明题训练1.已知边长为2的正方形ABCD中，P是对角线AC上的一个动点（与点A，C不重合），过点P作PE⊥PB，PE交DC于点E，过点E作EF⊥AC，垂足为点F．（1）求证：PB＝PE；（2）在点P的运动过程中，PF的长度是否发生变化？若不变，求出这个不变的值；若变化，试说明理由．2.在▱ABCD中，BE平分∠ABC交AD于点E．（1）如图1，若∠D=30°，AB=6，求△ABE的面积；（2）如图2，过点A作AF⊥DC，交DC的延长线于点F，分别交BE，BC于点G，H，且AB=AF．求证：ED-AG=FC．3.如图，在平行四边形ABCD中，AC，BD交于点O，且AO＝BO，∠ADB的平分线DE交AB于点E．（1）求证：四边形ABCD是矩形．（2）若AB＝8，OC＝5，求AE的长．4.如图，在正方形ABCD中，E是边AB上一动点（不与点A，B重合），连接DE，点A关于直线DE的对称点为F，连接EF并延长交BC于点G，连接DG，过点E 作EH⊥DE交DG的延长线于点H，连接BH．（1）求证：GF＝GC；（2）用等式表示线段BH与AE的数量关系，并证明．5.如图，在平行四边形ABCD中，∠BAD的平分线交BC于点E，交DC的延长线于F，以EC，CF为邻边作平行四边形ECFG．（1）证明平行四边形ECFG是菱形；（2）若∠ABC=120°，连接BG，CG，DG，①求证：△DGC≌△BGE；②求∠BDG的度数；（3）若∠ABC=90°，AB=8，AD=14，M是EF的中点，求DM的长．6.已知正方形ABCD如图所示，连接其对角线AC，∠BCA的平分线CF交AB于点F，过点B作BM⊥CF于点N，交AC于点M，过点C作CP⊥CF，交AD延长线于点P．(1)求证：DP＝BF；(2)若正方形ABCD的边长为4，求DP的长；(3)求证：CP＝BM＋2FN．7.如图，四边形ABCD是菱形，E是AB的中点，AC的垂线EF交AD于点M，交CD的延长线于点F．（1）求证：AM=AE；（2）连接CM，DF=2．①求菱形ABCD的周长；②若∠ADC=2∠MCF，求ME的长．8.在菱形ABCD中，AB＝4，∠ABC＝60°，E是对角线AC上一点，F是线段BC延长线上一点．且CF＝AE，连接BE、EF．（1）如图1，若E是线段AC的中点，求EF的长；（2）如图2．若E是线段AC延长线上的任意一点，求证：BE＝EF．AC，将菱形ABCD绕着点B （3）如图3，若E是线段AC延长线上的一点，CE＝12顺时针旋转α°（0≤α≤360），请直接写出在旋转过程中DE的最大值．9.如图所示，在边长为1的菱形ABCD中，∠DAB=60°，M是AD上不同于A，D两点的一动点，N是CD上一动点，且AM+CN=1.（1）证明：无论M，N怎样移动，△BMN总是等边三角形；（2）求△BMN面积的最小值.10.如图，正方形ABCD中，F在CD上，AE平分∠BAF，E为BC的中点．求证：AF=BC+CF．11.已知：如图（1），点E、F分别为正方形ABCD的边BC、DC上的点，线段AE和AF分别交BD于点M和点N，连接MF，MF⊥AE于点M．（1）求证：∠EAF＝45°；（2）如图（2），连接EF，当AD＝5，DF＝1时，求线段EF的长度；BD．（3）如图（3），作FR⊥BD于R．求证：RM=12BC，CE⊥AB于点E，F是AD的中点，连接12.如图，在平行四边形ABCD中，AB=12EF，CF．求证：（1）EF=CF；（2）∠EFD=3∠AEF．13.如图1，点E为正方形ABCD的边AB上一点，EF⊥EC，且EF=EC，连接AF．（1）求∠EAF的度数；（2）如图2，连接FC交BD于M，交AD于N．求证：BD=AF+2DM．14.已知：如图，G为平行四边形ABCD中BC边的中点，点E在AD边上，且∠1＝∠2．（1）求证：E是AD的中点；（2）若F为CD延长线上一点，连接BF，得∠3＝∠2，求证：CD＝BF+DF．15.如图，四边形ABCD是平行四边形，AD=AC，AD⊥AC，E是AB的中点，F是AC延长线上一点．(1)若ED⊥EF，求证：ED=EF：(2)在(1)的条件下，若DC的延长线与FB交于点P，试判断四边形ACPE是否为平行四边形．并证明你的结论(请先补全图形，再解答)：(3)若ED=EF，则ED与EF垂直吗?若垂直给出证明，若不垂直说明理由．16.在▱ABCD中，∠BAD的平分线交直线BC于点E，交直线DC于点F。

中考数学考点系统复习第五章四边形方法技巧突破(五) 四边形中常见辅助线的作法

证明：(1)∵四边形 ABCD 为菱形， ∴AB＝CD，且∠BAE＝∠DCF，又∵AE＝CF，∴△ABE≌△CDF(SAS)．
(2)连接 BD 交 AC 于点 O，如解图． ∵四边形 ABCD 为菱形， ∴AC⊥BD，且 O 为 AC，BD 中点，又∵ AE＝CF，∴EO＝FO， ∴BD 与 EF 互相垂直且平分，故四边形 BEDF 是菱形．
在 Rt△BCE 中，由勾股定理可得 BC＝8，
由矩形性质易知 OB＝OD，∴OF 为△BCD 的中位线，∴OF＝12BC＝4.
1
1
∴△ODE 的面积为2DE·OF＝2××4＝24.
4．如图，在梯形 ABCD 中，AD∥BC，若 E 为 AB 的中点，若梯形 ABCD 的面积为 34 个平方单位，则△ECD(阴影部分)的面积为 1 177 个平方单位．
5．如图，矩形 ABCD 的对角线 AC，BD 相交于点 O，过点 B 作 AC 的平行线交 DC 的延长线于点 E. (1)求证：BD＝BE； (2)若 BE＝10，CE＝6，连接 OE，求△ODE 的面积．
2．(2021 春·靖江期末)如图，在▱ABCD 中，BE 垂直平分 CD 于点 E，∠
BAD＝45°，AD＝6，则▱ABCD 的对角线 AC 的长为
( A)
A．6 5 B．4 5 C．10 3 D．10 2
3．(2021·随州)如图，在菱形 ABCD 中，E，F 是对角线 AC 上的两点，且 AE＝CF. (1)求证：△ABE≌△CDF； (2)证明四边形 BEDF 是菱形．
方法技巧突破(五) 四边形中常见辅助线的作法
1．(2021 春·铜官区期末)如图，在△ABC 中，∠C＝90°，AC＝8，BC＝
6，点 P 为斜边 AB 上一动点，过点 P 作 PE⊥AC 于点 E，PF⊥BC 于点 F，

初中数学四边形专项训练解析附答案

初中数学四边形专项训练解析附答案一、选择题1．如图，在菱形ABCD 中，AB ＝10，两条对角线相交于点O ，若OB ＝6，则菱形面积是（）A ．60B ．48C ．24D ．96【答案】D【解析】【分析】由菱形的性质可得AC ⊥BD ，AO ＝CO ，BO ＝DO ＝6，由勾股定理可求AO 的长，即可求解．【详解】解：∵四边形ABCD 是菱形，∴AC ⊥BD ，AO ＝CO ，BO ＝DO ＝6，∴AO ＝22100368AB OB -=-=，∴AC ＝16，BD ＝12， ∴菱形面积＝12162⨯＝96，故选：D ．【点睛】本题考查了菱形的性质，勾股定理，掌握菱形的对角线互相垂直平分是本题的关键．2．如图，在四边形ABCD 中，90,150,BAD BCD ADC ∠=∠=︒∠=o 连接对角线BD ，过点D 作//DE BC 交AB 于点,E 若23,AB AD CD =+=，则CD =（）A ．2B ．1C ．13+D 3【答案】B【解析】【分析】先根据四边形的内角和求得∠ABC 30︒=，再根据平行线的性质得到∠AED 30︒=，∠EDB=∠DBC ，然后根据三角形全等得到∠ABD=∠DBC ，进而得到EB=ED ，最后在Rt ADE V 中，利用勾股定理即可求解．【详解】解：在四边形ABCD 中∵90,150,BAD BCD ADC ∠=∠=︒∠=o∴∠ABC 30︒=∵//DE BC∴∠AED 30︒=，∠EDB=∠DBC在Rt ABD V 和Rt BCD △中 ∵AD CD BD BD =⎧⎨=⎩∴Rt ABD Rt BCD ≅V V∴∠ABD=∠DBC∴∠EDB=∠ABD∴EB=ED ∵23AB =+在Rt ADE △中，设AD=x,那么DE=2x,AE=232x +-()2222322x x x ++-=解得：121;73x x ==+（舍去）故选：B ．【点睛】此题主要考查四边形的内角和、全等三角形的判断、平行线的性质和勾股定理的应用，熟练进行逻辑推理是解题关键．3．如图，在矩形ABCD 中，6AB =，8BC =，若P 是BD 上的一个动点，则PB PC PD ++的最小值是（）A ．16B ．15.2C ．15D ．14.8【答案】D【解析】【分析】根据题意，当PC ⊥BD 时，PB PC PD ++有最小值，由勾股定理求出BD 的长度，由三角形的面积公式求出PC 的长度，即可求出最小值.【详解】解：如图，当PC ⊥BD 时，PB PC PD BD PC ++=+有最小值，在矩形ABCD 中，∠A=∠BCD=90°，AB=CD=6，AD=BC=8，由勾股定理，得 226810BD =+=，∴=10PB PD BD +=，在△BCD 中，由三角形的面积公式，得11=22BD PC BC CD ••，即1110=8622PC ⨯⨯⨯⨯，解得： 4.8PC =， ∴PB PC PD ++的最小值是：10 4.814.8PB PC PD BD PC ++=+=+=；故选：D.【点睛】本题考查了勾股定理解直角三角形，最短路径问题，垂线段最短，以及三角形的面积公式，解题的关键是熟练掌握勾股定理，正确确定点P 的位置，得到PC 最短.4．如图，□ABCD 的对角线AC 与BD 相交于点O ，AB ⊥AC .若4AB =,6AC =，则BD 的长为（）A ．11B ．10C ．9D ．8 【答案】B【解析】【分析】根据勾股定理先求出BO 的长，再根据平行四边形的性质即可求解.【详解】∵6AC =，∴AO=3，∵AB ⊥AC ，∴BO=2234+=5∴BD=2BO=10，故选B.【点睛】此题主要考查平行四边形的性质，解题的关键是熟知勾股定理的应用.5．如图，在菱形ABCD 中，点E 在边AD 上，30BE ADBCE ⊥∠=︒，.若2AE =，则边BC 的长为( )A 5B 6C 7D ．22【答案】B【解析】【分析】由菱形的性质得出AD ∥BC ，BC=AB=AD ，由直角三角形的性质得出3，在Rt △ABE 中，由勾股定理得：BE 2+22=3）2，解得：2，即可得出结果．【详解】∵四边形ABCD 是菱形，∴AD BC BC AB =，∥.∵BE AD ⊥.∴BE BC ⊥.∴30BCE ∠=︒，∴2EC BE =， ∴223AB BC EC BE BE ==-=.在Rt ABE △中，由勾股定理得)22223BE BE +=，解得2BE =，∴36BC BE ==故选B.【点睛】此题考查菱形的性质，含30°角的直角三角形的性质，勾股定理，熟练掌握菱形的性质，由勾股定理得出方程是解题的关键．6．如图，点M 是正方形ABCD 边CD 上一点，连接AM ，作DE ⊥AM 于点E ，BF ⊥AM 于点F ，连接BE ，若AF ＝1，四边形ABED 的面积为6，则∠EBF 的余弦值是（）A ．21313B ．31313C ．23D ．1313【答案】B【解析】【分析】首先证明△ABF ≌△DEA 得到BF=AE ；设AE=x ，则BF=x ，DE=AF=1，利用四边形ABED 的面积等于△ABE 的面积与△ADE 的面积之和得到12•x•x+•x×1=6，解方程求出x 得到AE=BF=3，则EF=x-1=2，然后利用勾股定理计算出BE ，最后利用余弦的定义求解．【详解】∵四边形ABCD 为正方形，∴BA ＝AD ，∠BAD ＝90°，∵DE ⊥AM 于点E ，BF ⊥AM 于点F ，∴∠AFB ＝90°，∠DEA ＝90°，∵∠ABF+∠BAF ＝90°，∠EAD+∠BAF ＝90°，∴∠ABF ＝∠EAD ，在△ABF 和△DEA 中 BFA DEA ABF EAD AB DA ∠=∠⎧⎪∠=⎨⎪=⎩∴△ABF ≌△DEA （AAS ），∴BF ＝AE ；设AE ＝x ，则BF ＝x ，DE ＝AF ＝1，∵四边形ABED 的面积为6， ∴111622x x x ⋅⋅+⋅⨯=，解得x 1＝3，x 2＝﹣4（舍去）， ∴EF ＝x ﹣1＝2，在Rt △BEF 中，222313BE + ∴313cos 13BF EBF BE ∠=== 故选B ．【点睛】本题考查了正方形的性质：正方形的四条边都相等，四个角都是直角；正方形具有四边形、平行四边形、矩形、菱形的一切性质．会运用全等三角形的知识解决线段相等的问题．也考查了解直角三角形．7．如图，在矩形ABCD 中， 4,6,AB BC ==点E 是AD 的中点，点F 在DC 上，且1,CF =若在此矩形上存在一点P ，使得PEF V 是等腰三角形，则点P 的个数是（）A ．3B ．4C ．5D ．6【答案】D【解析】【分析】根据等腰三角形的定义，分三种情况讨论：①当EF 为腰，E 为顶角顶点时，②当EF 为腰，F 为顶角顶点时，③当EF 为底，P 为顶角顶点时，分别确定点P 的位置，即可得到答案．【详解】∵在矩形ABCD 中，461AB BC CF ===，，，点E 是AD 的中点，32184EF ∴==>．∴PEF V 是等腰三角形，存在三种情况：①当EF 为腰，E 为顶角顶点时，根据矩形的轴对称性，可知：在BC 上存在两个点P ，在AB 上存在一个点P ，共3个，使PEF V 是等腰三角形；②当EF 为腰，F 为顶角顶点时，186,Q∴在BC 上存在一个点P ，使PEF V 是等腰三角形；③当EF 为底，P 为顶角顶点时，点P 一定在EF 的垂直平分线上，∴EF 的垂直平分线与矩形的交点，即为点P ，存在两个点．综上所述，满足题意的点P 的个数是6．故选D ．【点睛】本题主要考查等腰三角形的定义，矩形的性质，熟练掌握等腰三角形的定义和矩形的性质，学会分类讨论思想，是解题的关键．8．如图，在边长为8的菱形ABCD 中，∠DAB =60°，以点D 为圆心，菱形的高DF 为半径画弧，交AD 于点E ，交CD 于点G ，则图中阴影部分的面积是（）A ．183π-B ．183-πC ．32316π-D ．1839π-【答案】C【解析】【分析】由菱形的性质得出AD=AB=8，∠ADC=120°，由三角函数求出菱形的高DF ，图中阴影部分的面积=菱形ABCD 的面积-扇形DEFG 的面积，根据面积公式计算即可．【详解】解：∵四边形ABCD 是菱形，∠DAB=60°，∴AD=AB=8，∠ADC=180°-60°=120°，∵DF 是菱形的高，∴DF ⊥AB ，∴DF=AD •sin60°=3843⨯=， ∴图中阴影部分的面积=菱形ABCD 的面积-扇形DEFG 的面积=2120(43)84332316360ππ⨯⨯-=-．故选：C.【点睛】本题考查了菱形的性质、三角函数、菱形和扇形面积的计算；由三角函数求出菱形的高是解决问题的关键．9．已知，如图，在ABC V 中，90ACB ∠=︒，30A ∠=︒，求证：12BC AB =．在证明该结论时，需添加辅助线，则作法不正确的是（）A ．延长BC 至点D ，使CD BC =，连接ADB ．在ACB ∠中作BCE B ∠=∠，CE 交AB 于点EC ．取AB 的中点P ，连接CPD ．作ACB ∠的平分线CM ，交AB 于点M【答案】D【解析】【分析】分别根据各选项的要求进行证明，推出正确结论，则问题可解.【详解】解：选项A ：如图，由辅助线可知，ABC ADC ≅V ;，则有AB=AD ，再由90ACB ∠=︒，由30BAC ∠=︒，则60B ∠=︒，∴ABD △是等边三角形 ∴1122BC DB AB == 故选项A 正确；选项B:如图，由辅助线可知，EBD △是等边三角形则60BEC EAC ECA ∠=∠+∠=︒,BE=EC∵30A ∠=︒∴30ECA A ∠=∠=︒∴AE=EC∴12BC AB =故选项B 正确选项C 如图，有辅助线可知，CP 为直角三角形斜边上的中线∴AP=CP=BP∵30A ∠=︒∴60B ∠=︒∴PBC V 是等边三角形 ∴12BC BP AB ==综上可知选项D 错误故应选D【点睛】此题主要考查了全等三角形的判定，等边三角形的判定与性质的综合应用，根据条件选择正确的证明方法是解题的关键．10．如图，在▱ABCD 中，E 为边AD 上的一点，将△DEC 沿CE 折叠至△D ′EC 处，若∠B ＝48°，∠ECD ＝25°，则∠D ′EA 的度数为（）A ．33°B ．34°C ．35°D ．36°【答案】B【解析】【分析】由平行四边形的性质可得∠D ＝∠B ，由折叠的性质可得∠D '＝∠D ，根据三角形的内角和定理可得∠DEC ，即为∠D 'EC ，而∠AEC 易求，进而可得∠D 'EA 的度数．【详解】解：∵四边形ABCD 是平行四边形，∴∠D ＝∠B ＝48°，由折叠的性质得：∠D '＝∠D ＝48°，∠D 'EC ＝∠DEC ＝180°﹣∠D ﹣∠ECD ＝107°， ∴∠AEC =180°﹣∠DEC =180°﹣107°＝73°，∴∠D 'EA ＝∠D 'EC ﹣∠AEC ＝107°﹣73°=34°.故选：B ．【点睛】本题考查了平行四边形的性质、折叠的性质、三角形的内角和定理等知识，属于常考题型，熟练掌握上述基本知识是解题关键．11．下列结论正确的是（）A．平行四边形是轴对称图形B．平行四边形的对角线相等C．平行四边形的对边平行且相等D．平行四边形的对角互补，邻角相等【答案】C【解析】【分析】分别利用平行四边形的性质和判定逐项判断即可．【详解】A、平行四边形不一定是轴对称图形，故A错误；B、平行四边形的对角线不相等，故B错误；C、平行四边形的对边平行且相等，故C正确；D、平行四边形的对角相等，邻角互补，故D错误．故选：C．【点睛】此题考查平行四边形的性质，掌握特殊平行四边形与一般平行四边形的区别是解题的关键．12．如图，点P是矩形ABCD的对角线AC上一点，过点P作EF∥BC，分别交AB，CD于E、F，连接PB、PD．若AE=2，PF=8．则图中阴影部分的面积为（）A．10 B．12 C．16 D．18【答案】C【解析】【分析】首先根据矩形的特点，可以得到S△ADC=S△ABC，S△AMP=S△AEP，S△PFC=S△PCN，最终得到S矩形EBNP= S ,即可得S△PEB=S△PFD，从而得到阴影的面积．矩形MPFD【详解】作PM⊥AD于M，交BC于N．则有四边形AEPM，四边形DFPM，四边形CFPN，四边形BEPN都是矩形，∴S△ADC=S△ABC，S△AMP=S△AEP，S△PFC=S△PCN∴S矩形EBNP= S矩形MPFD ,又∵S△PBE= 12S矩形EBNP，S△PFD=12S矩形MPFD，∴S△DFP=S△PBE=12×2×8=8，∴S阴=8+8=16，故选C．【点睛】本题考查矩形的性质、三角形的面积等知识，解题的关键是证明S△PEB=S△PFD．13．如图1，在△ABC中，∠B＝90°，∠C＝30°，动点P从点B开始沿边BA、AC向点C以恒定的速度移动，动点Q从点B开始沿边BC向点C以恒定的速度移动，两点同时到达点C，设△BPQ的面积为y（cm2）．运动时间为x（s），y与x之间关系如图2所示，当点P 恰好为AC的中点时，PQ的长为（）A．2 B．4 C．3D．3【答案】C【解析】【分析】点P、Q的速度比为33x＝2，y＝3P、Q运动的速度，即可求解．【详解】解：设AB＝a，∠C＝30°，则AC＝2a，BC3a，设P、Q同时到达的时间为T，则点P的速度为3aT，点Q3a，故点P、Q的速度比为33故设点P、Q的速度分别为：3v3，由图2知，当x＝2时，y＝3P到达点A的位置，即AB＝2×3v＝6v，BQ＝3＝3，y＝12⨯AB×BQ＝12⨯6v3v＝3v＝1，故点P、Q的速度分别为：3，3，AB＝6v＝6＝a，则AC＝12，BC＝63，如图当点P在AC的中点时，PC＝6，此时点P运动的距离为AB+AP＝12，需要的时间为12÷3＝4，则BQ＝3x＝43，CQ＝BC﹣BQ＝63﹣43＝23，过点P作PH⊥BC于点H，PC＝6，则PH＝PC sin C＝6×12＝3，同理CH＝33，则HQ＝CH﹣CQ＝33﹣23＝3，PQ＝22PH HQ+＝39+＝23，故选：C．【点睛】本题考查的是动点图象问题，此类问题关键是：弄清楚不同时间段，图象和图形的对应关系，进而求解．14．如图，张明同学设计了四种正多边形的瓷砖图案，在这四种瓷砖图案不能铺满地面的是（）A．B．C．D．【答案】D【解析】【分析】分别计算各正多边形每个内角的度数，看是否能整除360°，即可判断．【详解】解：A．正六边形每个内角为120°，能够整除360°，不合题意；B．正三角形每个内角为60°，能够整除360°，不合题意；C．正方形每个内角为90°，能够整除360°，不合题意；D．正五边形每个内角为108°，不能整除360°，符合题意．故选：D．【点睛】能够铺满地面的图形是看拼在同一顶点的几个角是否构成周角．15．如图，在□ABCD 中，E 、F 分别是边BC 、CD 的中点，AE 、AF 分别交BD 于点G 、H ，则图中阴影部分图形的面积与□ABCD 的面积之比为（）A ．7 : 12B ．7 : 24C ．13 : 36D ．13 : 72【答案】B【解析】【分析】根据已知条件想办法证明BG=GH=DH ，即可解决问题；【详解】解：∵四边形ABCD 是平行四边形，∴AB ∥CD ，AD ∥BC ，AB=CD ，AD=BC ，∵DF=CF ，BE=CE ， ∴12DH DF HB AB ==，12BG BE DG AD ==， ∴13DH BG BD BD ==， ∴BG=GH=DH ，∴S △ABG =S △AGH =S △ADH ，∴S 平行四边形ABCD =6 S △AGH ，∴S △AGH ：ABCD S 平行四边形=1：6，∵E 、F 分别是边BC 、CD 的中点, ∴12EF BD =, ∴14EFC BCDD S S =V V , ∴18EFCABCD S S =V 四边形, ∴1176824AGH EFC ABCD S S S +=+=V V 四边形=7∶24, 故选B.【点睛】本题考查了平行四边形的性质、平行线分线段成比例定理、等底同高的三角形面积性质，题目的综合性很强，难度中等．16．如图，在矩形ABCD中，AD=2AB，∠BAD的平分线交BC于点E，DH⊥AE于点H，连接BH并延长交CD于点F，连接DE交BF于点O，下列结论：①∠AED=∠CED；②OE=OD；③BH=HF；④BC﹣CF=2HE；⑤AB=HF，其中正确的有（）A．2个B．3个C．4个D．5个【答案】C【解析】【分析】【详解】试题分析：∵在矩形ABCD中，AE平分∠BAD，∴∠BAE=∠DAE=45°，∴△ABE是等腰直角三角形，∴2AB，∵2AB，∴AE=AD，又∠ABE=∠AHD=90°∴△ABE≌△AHD（AAS），∴BE=DH，∴AB=BE=AH=HD，∴∠ADE=∠AED=12（180°﹣45°）=67.5°，∴∠CED=180°﹣45°﹣67.5°=67.5°，∴∠AED=∠CED，故①正确；∵∠AHB=12（180°﹣45°）=67.5°，∠OHE=∠AHB（对顶角相等），∴∠OHE=∠AED，∴OE=OH，∵∠OHD=90°﹣67.5°=22.5°，∠ODH=67.5°﹣45°=22.5°，∴∠OHD=∠ODH，∴OH=OD，∴OE=OD=OH，故②正确；∵∠EBH=90°﹣67.5°=22.5°，∴∠EBH=∠OHD，又BE=DH，∠AEB=∠HDF=45°∴△BEH≌△HDF（ASA），∴BH=HF，HE=DF，故③正确；由上述①、②、③可得CD=BE、DF=EH=CE，CF=CD-DF，∴BC-CF=（CD+HE）-（CD-HE）=2HE，所以④正确；∵AB=AH，∠BAE=45°，∴△ABH不是等边三角形，∴AB≠BH，∴即AB≠HF，故⑤错误；综上所述，结论正确的是①②③④共4个．故选C．【点睛】考点：1、矩形的性质；2、全等三角形的判定与性质；3、角平分线的性质；4、等腰三角形的判定与性质17．如图，四边形ABCD的对角线为AC、BD，且AC=BD，则下列条件能判定四边形ABCD 为矩形的是（）A．BA=BCB．AC、BD互相平分C．AC⊥BDD．AB∥CD【答案】B【解析】试题分析：根据矩形的判定方法解答．解：能判定四边形ABCD是矩形的条件为AC、BD互相平分．理由如下：∵AC、BD互相平分，∴四边形ABCD是平行四边形，∵AC=BD，∴▱ABCD是矩形．其它三个条件再加上AC=BD均不能判定四边形ABCD是矩形．故选B．考点：矩形的判定．18．如图，□ABCD的对角线AC、BD交于点O，AE平分BAD交BC于点E，且∠ADC＝60°，AB＝12BC，连接OE．下列结论：①AE＝CE；②S△ABC＝AB•AC；③S△ABE＝2S△AOE；④OE＝14BC,成立的个数有（）A．1个B．2个C．3个D．4【答案】C【解析】【分析】利用平行四边形的性质可得∠ABC=∠ADC=60°，∠BAD=120°，利用角平分线的性质证明△ABE是等边三角形，然后推出AE=BE=12BC，再结合等腰三角形的性质：等边对等角、三线合一进行推理即可．【详解】∵四边形ABCD是平行四边形，∴∠ABC=∠ADC=60°，∠BAD=120°，∵AE平分∠BAD，∴∠BAE=∠EAD=60°∴△ABE是等边三角形，∴AE=AB=BE，∠AEB=60°，∵AB=12 BC，∴AE=BE=12 BC，∴AE=CE，故①正确；∴∠EAC=∠ACE=30°∴∠BAC=90°，∴S△ABC=12AB•AC，故②错误；∵BE=EC，∴E为BC中点，O为AC中点，∴S △ABE =S △ACE=2 S △AOE ，故③正确；∵四边形ABCD 是平行四边形，∴AC=CO ，∵AE=CE ，∴EO ⊥AC ，∵∠ACE=30°，∴EO=12EC ， ∵EC=12AB ， ∴OE=14BC ，故④正确；故正确的个数为3个，故选：C ．【点睛】此题考查平行四边形的性质，等边三角形的判定与性质．注意证得△ABE 是等边三角形是解题关键．19．如图，在ABC V 中，D E ，是AB AC ，中点，连接DE 并延长至F ，使EF DE =，连接AF CD ，，CF ．添加下列条件，可使四边形ADCF 为菱形的是( )A ．AB AC =B ．AC BC = C ．CD AB ⊥ D ．AC BC ⊥【答案】D【解析】【分析】根据AE ＝CE ，EF ＝DE 可证得四边形ADCF 为平行四边形，再利用中位线定理可得DE ∥BC 结合AC ⊥BC 可证得AC ⊥DF ，进而利用对角线互相垂直的平行四边形是菱形即可得证．【详解】解：∵点E 是AC 中点，∴AE ＝CE ，∵AE ＝CE ，EF ＝DE ，∴四边形ADCF 为平行四边形，∵点D 、E 是AB 、AC 中点，∴DE 是△ABC 的中位线，∴DE ∥BC ，∴∠AED ＝∠ACB ，∴∠ACB＝90°，∴∠AED＝90°，∴AC⊥DF，∴平行四边形ADCF为菱形故选：D．【点睛】本题考查了菱形的判定，三角形的中位线性质，熟练掌握相关图形的性质及判定是解决本题的关键．20．如图，△ABC中，AB＝AC＝10，BC＝12，D是BC的中点，DE⊥AB于点E，则DE的长为（）A．65B．85C．125D．245【答案】D【解析】【分析】连接AD，根据已知等腰三角形的性质得出AD⊥BC和BD=6，根据勾股定理求出AD，根据三角形的面积公式求出即可．【详解】解：连接AD∵AB=AC，D为BC的中点，BC=12，∴AD⊥BC，BD=DC=6，在Rt△ADB中，由勾股定理得：22221068AB BD=+=，∵S△ADB=12×AD×BD＝12×AB×DE，∴DE=8624105 AD BDAB⨯⨯==，故选D．本题考查了等腰三角形的性质（等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合）、勾股定理和三角形的面积，能求出AD的长是解此题的关键．。

平行四边形几何辅助线专题详解

平行四边形几何辅助线专题详解1 平行四边形知识框架{分类讨论思想{动态讨论{1个点的移动2个点的移动高的位置的讨论{过点作下(上)侧边的高过点作右(左)侧边的高求平行四边形第4个点的坐标平行四边形的面积{利用面积解决问题方程思想构造中位线{连接法{连接两中点知一中点，取另一中点知两中点，构双中位线倍长法{倍长垂直于角平分线的线段倍长线段方法1 分类讨论思想分类讨论思想{动态讨论{1个点的移动2个点的移动高的位置的讨论{过点作下(上)侧边的高过点作右(左)侧边的高求平行四边形第4点坐标一、动态讨论解题技巧：点在线段的不同位置，也会造成不同的结果（1）1个点的移动如下图，1个点C 在直线AB 上移动，会出现3种情况：①在线段AB 左侧；②在线段AB 当中；③在线段AB 右侧，具体见例1.（2）2个点的移动如下图，2个点C、D在线段AB上移动（C、D两点在AB中），会出现2种情况：①点C在点D的左侧；②点C在点D的右侧，具体见例2.例1.▱ABCD的内角∠BCD的平分线CE交射线DA于点E，若AE=3，DE=4，求▱ABCD的周长。

例2.在▱ABCD中，AD=8，AE平分∠BAD交BC于点E，DF平分∠ADC交BC于点F，且EF=2，求AB的长。

二、高的位置的讨论解题技巧：在平行四边形中作高，会出现2种情况：①在图形内；②在图形外。

（1）过点作下（上）侧边的高如下图，过点A作▱ABCD下侧的边CD上的高AE。

因▱ABCD倾斜方向的变化，高会存在两种情况，具体见例1（2）过点右（左）侧边的高如下图，过点B作▱ABCD的右侧边AD上的高AE。

因▱ABCD倾斜大小的变化，高会存在两种情况，具体见例2上述两种情况实质是同一种情况经过翻折后得到的，为同一种情况。

例1.在面积为15的平行四边形ABCD中，过点A作AE垂直于直线BC于点E，若AB=5，BC=6，求CE的值。

例2.在▱ABCD中，AD=BD=4，BE是AD边上的高，∠EBD=30°，求△ABD的面积。

人教版八年级数学下册18.2：特殊四边形辅助线构讲义(pdf版,含答案)

教师辅导讲义
C专题——辅助线添加
添加中位线：
一、三角形中点：遇中点，想中位线
1.如图，△ABC中，是中线，是角平分线，CF⊥AE于，，，则的长为
2、如图,AD 是△ABC 的中线,E 是AD 的中点,F 是BE 延长线与AC 的交点,求证:AF=2
1CF 3、已知:如图,在▱ABCD 中,E 是CD 的中点,F 是AE 的中点,FC 与BE 交于G.
求证:GF=GC .
、如图,,M、N
.
2、如图,点P是四边形ABCD的对角线BD的中点,E,F分别是AB,CD的中点,AD=BC,∠CBD=45°，∠ADB=105°，试探
3、如图，已知四边形ABCD中，AD＝BC，E、F分别是DC、AB边的中点，FE的延长线分别与AD、BC的延长线交于点
H、G，求证：∠AHF＝∠BGF.
2、已知：△ABD和△(1)说明：MB=MC；
5、如图，在矩形ABCD
．
2、.已知菱形ABCD的边长为6，∠A=60°，如果点P是菱形内一点，且PB=PD=2，那么AP的长为_________．。

北师大版八年级下册数学第六章平行四边形含辅助线证明题—截长补短类训练

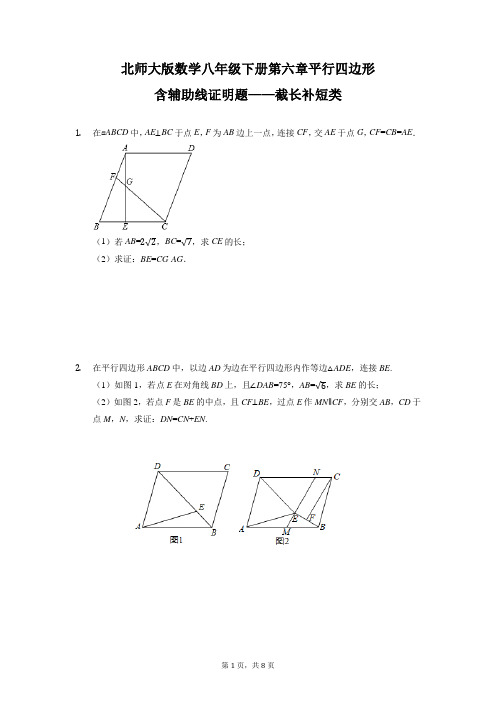
北师大版数学八年级下册第六章平行四边形含辅助线证明题——截长补短类1.在▱ABCD中，AE⊥BC于点E，F为AB边上一点，连接CF，交AE于点G，CF=CB=AE．（1）若AB=2√2，BC=√7，求CE的长；（2）求证：BE=CG-AG．2.在平行四边形ABCD中，以边AD为边在平行四边形内作等边△ADE，连接BE.（1）如图1，若点E在对角线BD上，且∠DAB=75°，AB=√6，求BE的长；（2）如图2，若点F是BE的中点，且CF⊥BE，过点E作MN∥CF，分别交AB，CD于点M，N，求证：DN=CN+EN.3.如图，在▱ABCD中，AE⊥BC，垂足为E，AE=CE.BF⊥AC，垂足为F，分别与AE，AD交于点G，H.（1）若AG=GE=BE=1，求▱ABCD的面积；（2）若CH平分∠BCD，求证：BC=AG+CH.4.已知在▱ABCD中，AE⊥CD，且AB=AE，F为AE上一点，且BF平分∠ABC，（1）若∠ABC=60°，AB=√3，求EF的长；（2）求证：AF+DE=BC.5.在平行四边形ABCD中，E为对角线AC上任意一点，连接BE（1）如图①所示，若AB=BE，AC=BC，∠BAC=75°，AB=2√2，求平行四边形ABCD的面积；（2）如图②所示，延长BE至F，使得EF=EB，连接CF，FD，求证：CE=AE+FD．6.在平行四边形ABCD中，连接BD，过点B作BE⊥BD于点B交DA的延长线于点E，过点B作BG⊥CD于点G．（1）如图1，若∠C=60°，∠BDC=75°，BD=6√2，求AE的长度；（2）如图2，点F为AB边上一点，连接EF，过点F作FH⊥FE于点F交GB的延长线于点H，在△ABE的异侧，以BE为斜边作Rt△BEQ，其中∠Q=90°，若∠QEB=∠BDC，EF=FH，求证：BF+BH=BQ．7.在平行四边形ABCD中，以AB为边作等边△ABE，点E在CD上，以BC为边作等边△BCF，点F在AE上，点G在BA延长线上且FG=FB．（1）若CD=6，AF=3，求△ABF的面积；（2）求证：BE=AG+CE．8.如图，在▱ABCD中，点F是对角线BD上一点，且满足AB=AF，过点F作EG交AD于E，交BC于G，作AH⊥BC于点H，交BD于M．（1）若F为MD中点，AF=2，AM=√3，求BC的长度；（2）若∠ABH=∠AFE，求证：BH+FG=HG．9.如图，平行四边形ABCD中，AB∥CD，AD∥BC，点G是线段BC的中点，点E是线段AD上的一点，点F是线段AB延长线上一点，连接DF，且∠ABE=∠CDG=∠FDG.（1）∠A=45°，∠ADF=75°，CD=3+√3，求线段BC的长；（2）求证：AB=BF+DF.10.如图，△ABC的高AD与中线BE相交于点F，过点C作BE的平行线，过点F作AB的平行线，两平行线相交于点G，连接BG，FG．（1）若AE＝2.5，CD＝3，BD＝2，求AB的长；（2）若∠CBE＝30°，求证：CG＝AD+EF．11.如图，在□ABCD中，E为BC边的中点，连接AE，F为CD边上一点，且满足∠DFA=2∠BAE.（1）若∠D=100°，∠DAF=30°，求∠FAE的大小；（2）求证：AF=CD+CF.12.已知在平行四边形ABCD中，过点D作DE⊥BC于点E，且AD=DE．连接AC交DE于点F，作DG⊥AC于点G．（1）如图1，若EFDF =12，AF=√13，求DG的长；（2）如图2，作EM⊥AC于点M，连接DM，求证：AM-EM=2DG．13.如图，在平行四边形ABCD中，AE⊥BC于点E，AE=AD，EG⊥AB于点G，延长GE、DC交于点F，连接AF.（1）若BE=2EC，AB=√13，求AD的长；（2）请猜想线段EG、BG、FC之间的等量关系并证明.14.如图，已知平行四边形ABCD中，DE⊥BC于点E，DH⊥AB于点H，AF平分∠BAD，分别交DC、DE、DH于点F、G、M，且DE=AD，CE=3，AB=5．(1)求线段CF的长度；(2)求证：AB=DG+CE．15.如图所示，在平行四边形ABCD中，∠DAC=60°，点E是BC边上一点，连接AE，AE=AB，点F是对角线AC边上一动点，连接EF.（1）如图1，若点F与对角线交点O重合，已知BE=4，OC：EC=5：3，求AC的长度；（2）如图2，若EC=FC，点G是AC边上一点，连接BG、EG，已知∠AEG=60°，∠AGB+∠BCD=180°，求证：BG+EG=DC.16.如图所示，平行四边形ABCD和平行四边形CDEF有公共边CD，边AB和EF在同一条直线上，AC⊥CD且AC=AF，过点A作AH⊥BC交CF于点G，交BC于点H，连接EG．（1）若AE=2，CD=5，求△BCF的周长；（2）求证：BC=AG+EG．。

2020初中数学中考专题复习——四边形中的线段最值问题专项训练2(附答案详解)

【详解】
解：∵在△ABC中，AB=6，AC=8，BC=10，
∴AB2+AC2=BC2，
即∠BAC=90°．
又PE⊥AB于E，PF⊥AC于F，
∴四边形AEPF是矩形，
∴EF=AP．
∵M是EF的中点，
∴AM= EF= AP,
因为AP的最小值即为直角三角形ABC斜边上的高
AP= ,
∴AM的最小值是．
故选C．
②根据对称性：连接ED交BC于点P，此时AP+EP＝AD，最小，再过点D作DF垂直AC的延长线于点F，根据勾股定理即可求解．
【详解】
如图所示：
（1）∵BD∥CE，CD∥BE，
∴四边形BDCE是平行四边形，
∵CE⊥AB，
∴∠BEC＝90°，
∴四边形BECD是矩形；
（2）①当BE的长为时，四边形BECD是菱形．理由如下：
6．C
【解析】
【分析】
根据勾股定理的逆定理可以证明∠BAC=90°，根据直角三角形斜边上的中线等于斜边的一半，则AM= EF，要求AM的最小值，即求EF的最小值；根据三个角都是直角的四边形是矩形得四边形AEPF是矩形，根据矩形的对角线相等，得EF=AP，则EF的最小值即为AP的最小值，根据垂线段最短知：AP的最小值即等于直角三角形ABC斜边上的高．
【详解】
设与AC交于点O，作 ⊥ 于，如图所示：
在Rt△ABC中，∠BAC=90 ，∠ACB=45 ，
∴ ，
∵四边形PAQC是平行四边形，
∴ ，
∵ ⊥ ，∠ACB=45 ，
∴ ，
当与重合时，OP的值最小，则PQ的值最小，
∴PQ的最小值
故选：A．
【点睛】
本题考查了勾股定理的运用、平行四边形的性质以及垂线段最短的性质，利用垂线段最短求线段的最小值是解题的关键．

2024成都中考数学第一轮专题复习微专题遇到中点如何添加辅助线知识精练(含答案)

2024成都中考数学第一轮专题复习微专题遇到中点如何添加辅助线知识精练1. 如图，在Rt △ABC 中，∠BAC ＝90°，BC ＝4，E ，F 分别是BC ，AC 的中点，延长BA 到点D ，使AD ＝12AB ，则DF 的长为________．第1题图2. 如图，在△ABC 中，AB ＝AC ＝5，BC ＝6，点M 为BC 的中点，MN ⊥AC 于点N ，则MN 的长为________．第2题图3.如图，AD 是△ABC 的中线，点E 是AB 上一点，且BE ＝2AE ，连接CE 交AD 于点F ，若CF ＝3，则EF 的长为________．第3题图4. 如图，在Rt △ABC 中，∠ACB ＝90°，AD 为△ABC 的中线，点E 为AD 的中点，点F 为BE 的中点，连接DF .若DF ⊥BE ，则tan ∠DBE 的值为________．第4题图5. 如图，在▱ABCD 中，BC ＝2AB ，过点A 作AE ⊥CD 于点E ，F 为BC 的中点，连接EF ，若∠B ＝70°，则∠BFE 的度数为________．第5题图6. 如图，在四边形ABCD 中，∠BAD ＝90°，AD ＝2BA ＝6，M ，N 分别是BC ，CD 的中点，连接AM ，AN ，MN .若△CMN 的面积为32，则△AMN 的面积为________．第6题图7. 如图，在▱ABCD 中，E 为AD 的中点，F 是CD 边上一点，连接EF 交BD 于点G ，若DF ＝2，CF ＝4，DG ＝3，则BG 的长为________．第7题图8. 如图，已知△ABC 和△CEF 是等腰直角三角形，其中∠ABC ＝∠CEF ＝90°，且E 是中线AD 的中点，连接BF ，若AB ＝4，则线段BF 的长度为________．第8题图9. 如图，在矩形ABCD 中，点E 为AB 上一点，连接DE ，CE ，且EC 平分∠DEB ，点F 为CE 的中点，连接AF ，BF .求证：AF ⊥BF .第9题图参考答案与解析1. 2 【解析】如解图，连接EF ，AE .∵E ，F 分别为BC ，AC 的中点，∴BE ＝EC ，AF ＝CF ，∴EF ∥AB ，EF ＝12 AB .∵AD ＝12 AB ，∴AD ＝EF ，∴四边形ADFE 是平行四边形，∴DF ＝AE ，∵∠BAC ＝90°，∴AE ＝12BC ＝2，∴DF ＝AE ＝2.第1题解图2.125【解析】如解图，连接AM ，∵AB ＝AC ，点M 为BC 的中点，∴AM ⊥CM (三线合一)，BM ＝CM .∵AB ＝AC ＝5，BC ＝6，∴BM ＝CM ＝3，在Rt △ABM 中，AB ＝5，BM ＝3，∴根据勾股定理得AM ＝AB 2－BM 2 ＝52－32 ＝4.∵S △AMC ＝12 MN ·AC ＝12 AM ·CM ，∴MN ＝AM ·CM AC ＝4×35 ＝125.第2题解图一题多解3. 1 【解析】解法一：如解图①，过点D 作DG ∥AB 交CE 于点G ，则∠EAF ＝∠GDF .∵AD 是△ABC 的中线，∴点D 是BC 的中点，∴DG 是△BCE 的中位线，∴BE ＝2DG ，CG ＝EG .∵BE ＝2AE ，∴AE ＝DG .∵∠AFE ＝∠DFG ，∴△AEF ≌△DGF ，∴EF ＝GF ，∴EF ＝13 CF ＝13 ×3＝1.解法二：如解图②，过点D 作DH ∥CE 交AB 于点H ，∵AD 是△ABC 的中线，∴DH 是△BCE 的中位线，∴DH ＝12 CE ，BH ＝EH .∵BE ＝2AE ，∴AE ＝EH ，∴EF 是△ADH 的中位线，∴EF＝12 DH ，∴EF ＝14 CE ，∴EF ＝13 CF ＝13×3＝1.图①图② 第3题解图4.33【解析】如解图，连接CE ，设CD ＝a ，∵AD 是BC 边上的中线，∴CD ＝BD ＝a .∵点F 为BE 的中点，∴EF ＝BF .∵DF ⊥BE ，∴BD ＝ED ＝a .∵E 为AD 的中点，∠ACB ＝90°，∴CE ＝ED ＝CD ＝a ，∴△CED 为等边三角形，即∠CDE ＝60°.又∵BD ＝ED ，∴∠DEF ＝∠DBF ＝12 ∠CDE ＝30°，∴tan ∠DBE ＝33.第4题解图5. 165° 【解析】如解图，延长EF 交AB 的延长线于点M ，连接AF ，∵四边形ABCD 是平行四边形，∴AB ∥CD ，∴∠C ＝∠MBF .∵F 为BC 的中点，∴BF ＝CF .在△BFM 和△CFE 中，⎩⎪⎨⎪⎧∠MBF ＝∠C ，BF ＝CF ，∠BFM ＝∠CFE ， ∴△BFM ≌△CFE (ASA)，∴MF ＝EF ，∠CEF ＝∠M .∵AE ⊥CD ，∴∠AEC ＝90°，∴∠EAB ＝90°.∵MF ＝EF ，∴AF ＝EF ＝MF ，∴∠M ＝∠MAF .∵四边形ABCD 是平行四边形，∴∠D ＝∠ABC ＝70°，∠BCD ＝110°.∵BC ＝2AB ，∴AB ＝BF ，∴∠MAF ＝(180°－70°)÷2＝55°，∴∠M ＝55°，∴∠CEF ＝55°，∴∠CFE ＝180°－110°－55°＝15°，∴∠BFE ＝180°－15°＝165°.第5题解图6. 6 【解析】如解图，连接AC ，BD .∵M ，N 分别是BC ，CD 的中点，∴MN ＝12 BD ，MN ∥BD ，S △ACN ＝S △DAN ，S △ABM ＝S △AMC ，S △CMN ＝14 ·S △DBC .∵S △CMN ＝32 ，∴S △DBC ＝6.∵∠BAD ＝90°，AD ＝2BA ＝6，∴S △ABD ＝12AD ·AB ＝9，∴S四边形ABCD ＝S △BCD ＋S △ABD ＝15，∴S △ACN ＋S △ACM＝12 S 四边形ABCD ＝152，∴S △AMN ＝S △ACN ＋S △ACM －S △CMN ＝6.第6题解图7. 12 【解析】如解图，延长FE 交BA 的延长线于点H ，∵四边形ABCD 是平行四边形，∴AB ∥CD ，AB ＝CD ，∴∠H ＝∠DFE ，∠HAE ＝∠FDE .∵E 为AD 的中点，∴AE ＝DE ，∴△AEH ≌△DEF ，∴AH ＝DF ＝2，∴BH ＝AB ＋AH ＝CD ＋AH ＝4＋2＋2＝8.又∵AB ∥CD ，∴△BGH ∽△DGF ，∴BG DG ＝BH DF ，即BG 3 ＝82，解得BG ＝12.第7题解图8. 2 【解析】如解图，过点E 作EG ∥BC 交AC 于点G ，连接BG ，∵点E 是AD 的中点，∴点G 是AC 的中点．∵△ABC 和△CEF 是等腰直角三角形，∠ABC ＝∠CEF ＝90°，∴AB ＝BC ，CE ＝EF ，∴∠ACB ＝∠ECF ＝45°，CB ＝2 CG ，CF ＝2 CE ，∴∠GCE ＝∠BCF ，CG CB ＝CE CF ＝22 ，∴△GCE ∽△BCF ，∴GE BF ＝22 .∵BC ＝AB ＝4，AD 是中线，∴BD ＝CD ＝2.∵点E ，G 分别是AD ，AC 的中点，∴EG 是△ADC 的中位线，∴GE ＝12 CD ＝1，∴BF ＝2 .第8题解图9. 证明：∵四边形ABCD 是矩形， ∴AB ∥CD ，∴∠DCE ＝∠CEB . ∵EC 平分∠DEB ， ∴∠DEC ＝∠CEB ， ∴∠DCE ＝∠DEC ， ∴DE ＝DC . 如解图，连接DF ，∵DE ＝DC ，F 为CE 的中点， ∴DF ⊥EC ，∴∠DFC ＝90°.在矩形ABCD 中，AB ＝DC ，∠ABC ＝90°， ∴BF ＝CF ＝EF ＝12 EC ，∴∠ABF ＝∠CEB . ∵∠DCE ＝∠CEB ， ∴∠ABF ＝∠DCF . 在△ABF 和△DCF 中， ⎩⎪⎨⎪⎧BF ＝CF ，∠ABF ＝∠DCF ，AB ＝DC ，∴△ABF ≌△DCF (SAS)， ∴∠AFB ＝∠DFC ＝90°， ∴AF ⊥BF .第9题解图。

2020春浙教版八年级数学下册课件：四边形中常用辅助线专题训练(共43张PPT)

(2)作 AH⊥BD 于点 H，由题意知∠AGB＝60°，
∠ABG＝45°，∴△ABH 为等腰直角三角形，
△AGH 为含 30°角的直角三角形，∵AB＝1，
∴AH＝BH＝
2 2
，HG＝
6 6
，∴BG＝
2 2
＋
6 6
.
14．在正方形ABCD中，对角线BD所在的直线上有两点E，F满足BE＝DF，连接AE，AF， CE，CF，如图所示． (1)求证：△ABE≌△ADF； (2)试判断四边形AECF的形状，并说明理由．
8．如图，点E，F，G，H分别在矩形ABCD的边AB，BC，CD，DA(不包括端点)上运动，且满足AE＝CG，AH＝CF. (1)求证：△AEH≌△CGF； (2)试判断四边形EFGH的形状，并说明理由．
(3)请探究四边形EFGH的周长一半与矩形 ABCD一条对角线长的大小关系，并说明理由．
14．证明：(1)∵正方形ABCD，∴AB＝AD， ∴∠ABD＝∠ADB，∴∠ABE＝∠ADF，可证 △ABE≌△ADF(SAS)；
(2)连接AC，四边形AECF是菱形．理由：∵正方形ABCD，∴OA＝OC， OB＝OD，AC⊥EF，∴OB＋BE＝OD＋DF，即OE＝OF，∵OA＝OC，OE＝OF， ∴四边形AECF是平行四边形，∵AC⊥EF， ∴四边形AECF是菱形．
八年级数学(下)——测试卷(二十四)
四边形中常用辅助线专题训练
一、平行四边形有关的辅助线作法 1．如图，已知点O是平行四边形ABCD的对角线AC的中点，四边形OCDE是平行四边形．求证：OE与AD互相平分．
1．证明：连结AE、OD，因为四边形OCDE是平行四边形，所以OC∥DE，OC＝DE，因为O是AC的中点，所以AO∥ED，AO＝ED，所以四边形 AODE是平行四边形，所以AD与OE互相平分．

难点解析京改版八年级数学下册第十五章四边形专题测试试题(含答案解析)

京改版八年级数学下册第十五章四边形专题测试考试时间：90分钟；命题人：数学教研组考生注意：1、本卷分第I 卷（选择题）和第Ⅱ卷（非选择题）两部分，满分100分，考试时间90分钟2、答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上3、答案必须写在试卷各个题目指定区域内相应的位置，如需改动，先划掉原来的答案，然后再写上新的答案；不准使用涂改液、胶带纸、修正带，不按以上要求作答的答案无效。

第I 卷（选择题 30分）一、单选题（10小题，每小题3分，共计30分）1、如图，在正方形有ABCD 中，E 是AB 上的动点，（不与A 、B 重合），连结DE ，点A 关于DE 的对称点为F ，连结EF 并延长交BC 于点G ，连接DG ，过点E 作EH ⊥DE 交DG 的延长线于点H ，连接BH ，那么BHAE 的值为（）A ．1BCD ．22、在平面直角坐标系中，点()4,1A -关于原点对称的点的坐标是（）A ．()41-,B ．()4,1C ．()4,1-D ．()4,1--3、下列图形中，既是轴对称图形，又是中心对称图形的是（）A．B．C．D．4、如图，菱形OABC在平面直角坐标系中的位置如图所示，∠AOC＝45°，OA C的坐标为（）A．1）B．（1，1）C．（1D．，1）5、如图，∠A+∠B+∠C+∠D+∠E+∠F的度数为（）A．180°B．360°C．540°D．不能确定6、如图，四边形ABCD为平行四边形，延长AD到E，使DE=AD，连接EB，EC，DB，添加一个条件，不能使四边形DBCE成为矩形的是（）A ．AB =BE B ．DE ⊥DC C ．∠ADB =90°D ．CE ⊥DE7、如图，在六边形ABCDEF 中，若1290∠+∠=︒，则3456∠+∠+∠+∠=（）A ．180°B ．240°C ．270°D ．360°8、如图，四边形ABCD 中，∠A =60°，AD =2，AB =3，点M ，N 分别为线段BC ，AB 上的动点（含端点，但点M 不与点B 重合），点E ，F 分别为DM ，MN 的中点，则EF 长度的最大值为（）A B C D 9、平面直角坐标系内与点P ()2,3-关于原点对称的点的坐标是（）A ．()3,2-B ．()2,3C ．()2,3-D ．()2,3--10、如图，菱形ABCD 中，60C ∠=°，2AB =．以A 为圆心，AB 长为半径画BD ，点P 为菱形内一点，连PA ，PB ，PD ．若PA PB =，且120APB ∠=︒，则图中阴影部分的面积为（）A ．23y π= B ．23y π= C ．23y π= D ．23y π=第Ⅱ卷（非选择题 70分）二、填空题（5小题，每小题4分，共计20分）1、如图，四边形ABCD 和四边形OMNP 都是边长为4的正方形，点O 是正方形ABCD 对角线的交点，正方形OMNP 绕点O 旋转过程中分别交AB ，BC 于点E ，F ，则四边形OEBF 的面积为______．2、如图，在矩形ABCD 中，=8AB ，=5AD ，点E 是线段CD 上的一点（不与点D ，C 重合），将△BCE 沿BE 折叠，使得点C 落在'C 处，当△'C CD 为等腰三角形时，CE 的长为___________．3、一个正多边形的每个外角都等于45°，那么这个正多边形的内角和为______度．4、如图，△ABC 中，D 、E 分别是AB 、AC 的中点，若DE ＝4cm ，则BC ＝_____cm ．5、如图，在平面直角坐标系内，矩形OABC的顶点A（3，0），C（0，9），点D和点E分别位于线段AC，AB上，将△ABC沿DE对折，恰好能使点A和点C重合．若x轴上有一点P，使△AEP为等腰三角形，则点P的坐标为________．三、解答题（5小题，每小题10分，共计50分）1、（教材重现）如图是数学教材第135页的部分截图．在多边形中，三角形是最基本的图形．如图4.4.5所示，每一个多边形都可以分割成若干个三角形．数一数每个多边形中三角形的个数，你能发现什么规律？在多边形中，连接不相邻的两个顶点，所得到的线段称为多边形的对角线．（问题思考）结合如图思考，从多边形的一个顶点出发，可以得到的对角线的数量，并填写表：（问题探究）n边形有n个顶点，每个顶点分别连接对角线后，每条对角线重复连接了一次，由此可推导出，n边形共有对角线（用含有n的代数式表示）．（问题拓展）（1）已知平面上4个点，任意三点不在同一直线上，一共可以连接条线段．（2）已知平面上共有15个点，任意三点不在同一直线上，一共可以连接条线段．（3）已知平面上共有x个点，任意三点不在同一直线上，一共可以连接条线段（用含有x 的代数式表示，不必化简）．2、如图，将矩形1111DCBA沿EF折叠，使1B点落在11A D边上的B点处；再将矩形1111DCBA沿BG折叠，使1D点落在D点处且BD过F点．（1）求证：四边形BEFG是平行四边形；（2）当1B FE∠是多少度时，四边形BEFG为菱形?试说明理由．3、如图1，在平面直角坐标系中，直线y＝2x＋8与x轴交于点A，与y轴交于点B，过点B的另一条直线483y x=-+交x轴正半轴于点C．（1）写出C点坐标；（2）若M为线段BC上一点，且满足S△AMB＝S△AOB，请求出点M的坐标；（3）如图2，设点F为线段AB中点，点G为y轴正半轴上一动点，连接FG，以FG为边向FG右侧作正方形FGQP，在G点的运动过程中，当顶点Q落在直线BC上时，求出点G的坐标．4、如图，在长方形ABCD中，AB＝3，BC＝4，点E是BC边上一点，连接AE，将∠B沿直线AE折叠，使点B落在点B'处．（1）如图1，当点E与点C重合时，CB'与AD交于点F，求证：FA＝FC；（2）如图2，当点E不与点C重合，且点B'在对角线AC上时，求CE的长．5、在菱形ABCD中，∠ABC＝60°，P是直线BD上一动点，以AP为边向右侧作等边APE（A，P，E 按逆时针排列），点E的位置随点P的位置变化而变化．（1）如图1，当点P在线段BD上，且点E在菱形ABCD内部或边上时，连接CE，则BP与CE的数量关系是，BC与CE的位置关系是；（2）如图2，当点P在线段BD上，且点E在菱形ABCD外部时，（1）中的结论是否还成立？若成立，请予以证明；若不成立，请说明理由；（3）当点P在直线BD上时，其他条件不变，连接BE．若AB＝BE＝APE的面积．-参考答案-一、单选题1、B【分析】作辅助线，构建全等三角形，证明△DAE≌△ENH，得AE=HN，AD=EN，再说明△BNH是等腰直角三角形，可得结论．【详解】解：如图，在线段AD上截取AM，使AM=AE，，∵AD=AB，∴DM=BE，∵点A关于直线DE的对称点为F，∴△ADE≌△FDE，∴DA=DF=DC，∠DFE=∠A=90°，∠1=∠2，∴∠DFG=90°，在Rt△DFG和Rt△DCG中，∵DF DC DG DG=⎧⎨=⎩，∴Rt△DFG≌Rt△DCG（HL），∴∠3=∠4，∵∠ADC=90°，∴∠1+∠2+∠3+∠4=90°，∴2∠2+2∠3=90°，∴∠2+∠3=45°，即∠EDG=45°，∵EH⊥DE，∴∠DEH=90°，△DEH是等腰直角三角形，∴∠AED +∠BEH =∠AED +∠1=90°，DE =EH ，∴∠1=∠BEH ，在△DME 和△EBH 中，∵1DM BE BEHDE EH =⎧⎪∠=∠⎨⎪=⎩，∴△DME ≌△EBH （SAS ），∴EM =BH ，Rt △AEM 中，∠A =90°，AM =AE ，∴EM ，∴BH ，即BHAE．故选：B ．【点睛】本题考查了正方形的性质，全等三角形的判定定理和性质定理，等知识，解决本题的关键是作出辅助线，利用正方形的性质得到相等的边和相等的角，证明三角形全等．2、A【分析】关于原点成中心对称的两个点的坐标规律：横坐标与纵坐标都互为相反数，根据原理直接作答即可.【详解】解：点()4,1A -关于原点对称的点的坐标是：4,1,故选A【点睛】本题考查的是关于原点成中心对称的两个点的坐标规律，掌握“关于原点成中心对称的两个点的坐标规律：横坐标与纵坐标都互为相反数”是解题的关键.3、B【详解】解：A、是轴对称图形，不是中心对称图形，故本选项不符合题意；B、既是轴对称图形，又是中心对称图形，故本选项符合题意；C、不是轴对称图形，是中心对称图形，故本选项不符合题意；D、不是轴对称图形，是中心对称图形，故本选项不符合题意；故选：B．【点睛】本题考查了轴对称图形和中心对称图形，熟记中心对称图形的定义（在平面内，把一个图形绕某点旋转180 ，如果旋转后的图形与另一个图形重合，那么这两个图形互为中心对称图形）和轴对称图形的定义（如果一个图形沿一条直线折叠，直线两旁的部分能够完全重合，那么这个图形叫做轴对称图形）是解题关键．4、B【分析】作CD⊥x轴，根据菱形的性质得到OC=OA Rt△OCD中，根据勾股定理求出OD的值，即可得到C点的坐标．【详解】：作CD⊥x轴于点D，则∠CDO=90°，∵四边形OABC是菱形，OA∴OC=OA又∵∠AOC=45°，∴∠OCD=90°-∠AOC=90°-45°=45°，∴∠DOC=∠OCD，∴CD=OD，在Rt△OCD中，OC CD2+OD2=OC2，∴2OD2=OC2=2，∴OD2=1，∴OD=CD=1（负值舍去），则点C的坐标为（1，1），故选：B．【点睛】此题考查了菱形的性质、等腰直角三角形的性质以及勾股定理，根据勾股定理和等腰直角三角形的性质求出OD=CD=1是解决问题的关键．5、B【分析】设BE与DF交于点M，BE与AC交于点N，根据三角形的外角性质，可得∠=∠+∠∠=∠+∠，再根据四边形的内角和等于360°，即可求解．BMD B F CNE A E,【详解】解：设BE与DF交于点M，BE与AC交于点N，∵,BMD B F CNE A E ∠=∠+∠∠=∠+∠ ，∴A B C D E F BMD CNE C D ∠+∠+∠+∠+∠+∠=∠+∠+∠+∠ ，∵360BMD CNE C D ∠+∠+∠+∠=︒，∴360A B C D E F ∠+∠+∠+∠+∠+∠=︒ ．故选：B【点睛】本题主要考查了三角形的外角性质，多边形的内角和，熟练掌握三角形的一个外角等于与它不相邻的两个内角的和；四边形的内角和等于360°是解题的关键．6、B【分析】先证明四边形BCED 为平行四边形，再根据矩形的判定进行解答．【详解】解：∵四边形ABCD 为平行四边形，∴AD ∥BC ，且AD =BC ，又∵AD =DE ，∴DE ∥BC ，且DE =BC ，∴四边形BCED 为平行四边形，A 、∵AB =BE ，DE =AD ，∴BD ⊥AE ，∴□DBCE 为矩形，故本选项不符合题意；B 、∵DE ⊥DC ，∴∠EDB =90°+∠CDB ＞90°，∴四边形DBCE 不能为矩形，故本选项符合题意；C 、∵∠ADB =90°，∴∠EDB =90°，∴□DBCE 为矩形，故本选项不符合题意；D 、∵CE ⊥DE ，∴∠CED =90°，∴□DBCE 为矩形，故本选项不符合题意．故选：B ．【点睛】本题考查了平行四边形的判定和性质、矩形的判定等知识，判定四边形BCED 为平行四边形是解题的关键．7、C【分析】根据多边形外角和360︒求解即可．【详解】解：123456360∠+∠+∠+∠+∠+∠=︒ ，1290∠+∠=︒()345636012270∴∠+∠+∠+∠=︒-∠+∠=︒，故选：C【点睛】本题考查了多边形的外角和定理，掌握多边形外角和360︒是解题的关键．【分析】DN，从而可知DN最大时，EF最大，因为N与B重合时DN最大，根据三角形的中位线定理得出EF=12此时根据勾股定理求得DN，从而求得EF的最大值．连接DB，过点D作DH⊥AB交AB于点H，再利用直角三角形的性质和勾股定理求解即可；【详解】解：∵ED=EM，MF=FN，DN，∴EF=12∴DN最大时，EF最大，∴N与B重合时DN=DB最大，在R t△ADH中，∵∠A=60°ADH∴∠=︒30=1，DH=∴AH=2×12∴BH=AB﹣AH=3﹣1=2，∴DBDB，∴EF max=12∴EF【点睛】本题考查了三角形的中位线定理，勾股定理，含30度角的直角三角形的性质，利用中位线求得EF =12DN 是解题的关键．9、C【分析】根据关于原点对称的点，横坐标与纵坐标都互为相反数求解即可．【详解】解：由题意，得点P （-2，3）关于原点对称的点的坐标是（2，-3），故选：C ．【点睛】本题考查了关于原点对称的点的坐标，解决本题的关键是掌握好对称点的坐标规律：关于x 轴对称的点，横坐标相同，纵坐标互为相反数；关于y 轴对称的点，纵坐标相同，横坐标互为相反数；关于原点对称的点，横坐标与纵坐标都互为相反数．10、C【分析】过点P 作PM AB ⊥交于点M ，由菱形ABCD 得60DAB C ∠=∠=︒，2AB AD ==，由PA PB =，120APB ∠=︒得112AM AB ==，1602APM APB ∠=∠=︒，故可得30PAM ∠=︒，603030PAD DAB PAM ∠=∠-∠=︒-︒=︒，根据SAS 证明ABP ADP ≅，求出PM =ABP ADP ABD S S S S =--阴扇形．【详解】如图，过点P 作PM AB ⊥交于点M ，∵四边形ABCD 是菱形，∴60DAB C ∠=∠=︒，2AB AD ==，∵PA PB =，120APB ∠=︒， ∴112AM AB ==，1602APM APB ∠=∠=︒， ∴30PAM ∠=︒，603030PAD DAB PAM ∠=∠-∠=︒-︒=︒，在ABP △与ADP △中，AB AD PAB PAD AP AP =⎧⎪∠=∠⎨⎪=⎩， ∴()ABP ADP SAS ≅，∴ABP ADP S S =△△，在Rt AMP △中，30PAM ∠=︒，∴2AP PM =，222AP PM AM =+，即2241PM PM =+，解得：PM =∴260211222360223ABP ADPABD S S S S ππ⋅=--=-⨯⨯=阴扇形故选：C ．【点睛】此题主要考查了菱形的性质以及求不规则图形的面积等知识，掌握扇形的面积公式是解答此题的关键．二、填空题1、4【分析】过点O 作OG ⊥AB ，垂足为G ，过点O 作OH ⊥BC ，垂足为H ，把四边形OEBF 的面积转化为正方形OGBH的面积，等于正方形ABCD 面积的14．【详解】如图，过点O 作OG ⊥AB ，垂足为G ，过点O 作OH ⊥BC ，垂足为H ，∵四边形ABCD 的对角线交点为O ，∴OA =OC ，∠ABC =90°，AB =BC ，∴OG ∥BC ，OH ∥AB ，∴四边形OGBH 是矩形，OG =OH =1122AB CB =，∠GOH =90°， ∴22211==()(4)22OGBH S OG AB =⨯四边形=4，∵∠FOH +∠FOG =90°，∠EOG +∠FOG =90°，∴∠FOH =∠EOG ，∵∠OGE =∠OHF =90°，OG =OH ，∴△OGE ≌△OHF ，∴=OGE OHF S S △△，∴=OGBH OEBF S S 四边形四边形，∴OEBF S 四边形=4，故答案为：4．【点睛】本题考查了正方形的性质，三角形的全等与性质，补形法计算面积，熟练掌握正方形的性质，灵活运用补形法计算面积是解题的关键．2、52或203【分析】根据题意分C D C C ''=，CC CD '=，DC DC '=三种情况讨论，构造直角三角形，利用勾股定理解决问题．【详解】解：∵四边形ABCD 是矩形∴90C ∠=︒，8,5CD AB BC AD ====∵将△BCE 沿BE 折叠，使得点C 落在'C 处，∴BCE BC E '≌,90C E CE BC E BCE ''∴=∠=∠=︒，BC BC '=，设CE x =，则8DE CD x x =-=-①当C D C C ''=时，如图过点C '作,C F CD C G BC ''⊥⊥，则四边形C GCF '为矩形 C D C C ''=142C G DF FC CD '∴====，4EF x =- 在Rt BC G '中3BG =532C F CG '∴==-=在Rt C FE '中222C E C F EF ''=+即()22224x x =+- 解得52x = 52CE ∴= ②当CC CD '=时，如图，设,CC BE '交于点O ，设OE y =,BC BC EC EC ''==BE ∴垂直平分CC '11422OC OC CC CD ''∴====3OB在Rt OCE 中222OE OC CE +=即2224y x +=在Rt BCE 中，222BE BC CE =+即()2223+5y x =+联立()22222243+5y x y x ⎧+=⎪⎨=+⎪⎩，解得203163x y ⎧=⎪⎪⎨⎪=⎪⎩ 203EC ∴= ③当DC DC '=时，如图，又BC BC '=DB ∴垂直平分CC ',BC BC EC EC ''==BE ∴垂直平分CC '此时,D E 重合，不符合题意综上所述，203=EC 或52 故答案为：52或203【点睛】本题考查了矩形的性质，勾股定理，等腰三角形的性质与判定，垂直平分线的性质，分类讨论是解题的关键．3、1080【分析】利用多边形的外角和为360°计算出这个正多边形的边数，然后再根据内角和公式进行求解即可．【详解】解：∵正多边形的每一个外角都等于45︒，∴正多边形的边数为360°÷45°=8，所有这个正多边形的内角和为（8-2）×180°=1080°．故答案为：1080．【点睛】本题考查了多边形内角与外角等知识，熟知多边形内角和定理（n﹣2）•180 °（n≥3）和多边形的外角和等于360°是解题关键．4、8【分析】运用三角形的中位线的知识解答即可．【详解】解：∵△ABC中，D、E分别是AB、AC的中点∴DE是△ABC的中位线，∴BC=2DE=8cm．故答案是8．【点睛】本题主要考查了三角形的中位线，掌握三角形的中位线等于底边的一半成为解答本题的关键．5、（8，0）或（-2，0）-2，0）或（8，0）【分析】由矩形的性质可得BC=OA =3，AB=OC=9，∠B=90°=∠OAE，由折叠的性质可得AE=CE，由勾股定理可求AE的长，由等腰三角形的性质可求解．【详解】解：∵四边形OABC矩形，且点A（3，0），点C（0，9），∴BC=OA =3，AB=OC=9，∠B=90°=∠OAE，∵将△ABC沿DE对折，恰好能使点A与点C重合．∴AE =CE ，∵CE 2=BC 2+BE 2，∴CE 2=9+（9-CE ）2，∴CE =5，∴AE =5，∵△AEP 为等腰三角形，且∠EAP =90°，∴AE =AP =5，∴点E 坐标（8，0）或（-2，0）故答案为：（8，0）或（-2，0）【点睛】本题考查了翻折变换，等腰三角形的性质，矩形的性质，勾股定理，坐标与图形变化-对称，求出AE 的长是本题的关键．三、解答题1、规律为：多边形的边数减去2，就是多边形中的三角形的个数； 2条，3条，9条，3n -条；(3)2n n -条；（1）6；（2）105；（3）()12x x - 【分析】通过观察多边形边数与其分割的三角形个数，即可发现规律利用规律，多边形的边数3-=一个顶点出发的对角线数，直接填写表格即可先求出所有顶点得到的对角线之和，最后除以2即可得到n 边形的对角线条数（1）根据题意，四边形一个顶点可以得到一条，四个点共4条，再去除一半，加上四个点单独连接的4条线段，即可得到答案．（2）根据规律可以发现：十五边形的每个点可以得到12条，15点有180条，去掉一半，加上15个点组成的十五边形的的15条边，即可得到答案．（3）通过上述两小题，即可以找到对应的规律，利用规律进行求解即可．【详解】由图可以直接发现：多边形的边数与其分割的三角形个数相差2，故规律为：多边形的边数减去2，就是多边形中的三角形的个数．利用上图规律，便可以知道从五边形的一个顶点出发，得到2条对角线；六边形的一个顶点出发，得到3条对角线；十二边形的一个顶点出发，得到9条对角线；n边形的一个顶点出发，得到3n-条对角线．n边形的一个顶点可以得到3n-条对角线，故n个顶点共有(3)n n-，由于每条对角线重复连接了一次，故n边形共有(3)2n n-条对角线（1）解：有四个点可以组成四边形，每个点可以得到1条对角线，四个点共4条，每条对角线重复连接了一次，∴对角线条数为2，四边形的边数为4，∴一共可以连接2+4=6条线段．（2）解：有15个点可以组成十五边形，每个点可以得到12条对角线，四个点共180条，每条对角线重复连接了一次，∴对角线条数为90，四边形的边数为15，∴一共可以连接90+15=105条线段．（3）解：由前面题的规律可知：有x个点可以组成x边形，每个点可以得到3x-条对角线，四个点共(3)x x-条，每条对角线重复连接了一次，∴对角线条数为(3)2x x-，四边形的边数为x ，∴一共可以连接()()3122x x x x x --+=条线段．【点睛】本题主要是考察了图形类的规律问题以及列代数式，根据题意，找到对角线与多边形的边数关系是解决本题的关键，另外，注意本题是问的点与点之间可连接的线段数，不要只算对角线的条数．2、（1）见解析；（2）当∠B 1FE =60°时，四边形EFGB 为菱形，理由见解析【分析】（1）由题意，1B FE FEB ∠=∠，结合1B FE BFE ∠=∠，得BE BF =，同理可得FG BF =，即BE FG =，结合BE FG ∥，依据平行四边形的判定定理即可证明四边形BEFG 是平行四边形；（2）根据菱形的性质可得BE EF =，结合（1）中结论得出BEF 为等边三角形，依据等边三角形的性质及（1）中结论即可求出角的大小．【详解】证明：（1）∵1111A D B C ∥，∴1B FE FEB ∠=∠．又∵1B FE BFE ∠=∠，∴FEB BFE ∠=∠．∴BE BF =．同理可得：FG BF =．∴BE FG =，又∵BE FG ∥，∴四边形BEFG 是平行四边形；（2）当160B FE ∠=︒时，四边形EFGB 为菱形．理由如下：∵四边形BEFG 是菱形，∴BE EF =，由（1）得：BE BF =，∴BE EF BF ==，∴BEF 为等边三角形，∴60BFE BEF ∠=∠=︒，∴160B FE ∠=︒．【点睛】题目主要考查平行四边形和菱形的判定定理和性质，矩形的折叠问题，等边三角形的性质，熟练掌握特殊四边形的判定和性质是解题关键．3、（1）点C （6，0）；（2）点1224(,)55M ；（3）满足条件的点G 坐标为34(0,)7或(0,-2)．【分析】（1）直接利用直线483y x =-+，令y=0，解方程即可；（2）结合图形，由S △AMB ＝S △AOB 分析出直线OM 平行于直线AB ，再利用两直线相交建立方程组2483y x y x =⎧⎪⎨=-+⎪⎩，解方程组求得交点M 的坐标；（3）分两种情形：①当n ＞4时，如图2-1中，点Q 落在BC 上时，点Q 落在BC 上时，过G 作MN 平行于x 轴，过点F ，Q 作该直线的垂线，分别交于M ，N ．求出Q （n-4，n-2）．②当n ＜4时，如图2-2中，同法可得Q （4-n ，n +2），代入直线BC 的解析式解方程即可解决问题．【详解】解：（1）∵直线483y x =-+交x 轴正半轴于点C ． ∴当y =0时，48=03x -+，解得x =6∴点C （6，0）故答案为（6，0）；（2）连接OM 并双向延长，∵S △AMB ＝S △AOB ，∴点O 到AB 与点M 到AB 的距离相等，∴直线OM 平行于直线AB ，∵AB 解析式为y ＝2x ＋8，故设直线OM 解析式为：2y x =，将直线OM 的解析式与直线BC 的解析式联立得方程组得：2483y x y x =⎧⎪⎨=-+⎪⎩，解得：125245x y ⎧=⎪⎪⎨⎪=⎪⎩故点1224(,)55M ；（3）∵直线y ＝2x ＋8与x 轴交于点A ，与y 轴交于点B ，∴令y=0，2x ＋8=0，解得x =-4，∴A （-4，0），令x =0，则y ＝8∴B （0，8），∵点F 为AB 中点，点F 横坐标为()1-4+0=-22，纵坐标为()10+8=42∴F （-2，4），设G （0，n ），①当n ＞4时，如图2-1中，点Q 落在BC 上时，过G 作MN 平行于x 轴，过点F ，Q 作该直线的垂线，分别交于M ，N ．∵四边形FGQP 是正方形，∴FG =QG ，∠FGQ =90°，∴∠MGF +∠NGQ =180°-∠FGQ=180°-90°=90°，∵FM ⊥MN ，QN ⊥MN ，∴∠M =∠N =90°，∴∠MFG +∠MGF =90°，∴∠MFG =∠NGQ ，在△FMG 和△GNQ 中，M N MFG NGQ FG GQ ∠=∠⎧⎪∠=∠⎨⎪=⎩， ∴△FMG ≌△GNQ ，∴MG =NQ =2，FM =GN =n -4，∴Q （n -4，n -2），∵点Q 在直线483y x =-+上， ∴42(4)43n n -=--+， ∴34=7n , ∴34(0,)7G ． ②当n ＜4时，如图2-2中，点Q 落在BC 上时，过G 作MN 平行于x 轴，过点F ，Q 作该直线的垂线，分别交于M ，N ． ∵四边形FGQP 是正方形，∴FG =QG ，∠FGQ =90°，∴∠MGF +∠NGQ =180°-∠FGQ=180°-90°=90°，∵FM ⊥MN ，QN ⊥MN ，∴∠M =∠N =90°，∴∠MFG +∠MGF =90°，∴∠MFG =∠NGQ ，在△FMG 和△GNQ 中，M N MFG NGQ FG GQ ∠=∠⎧⎪∠=∠⎨⎪=⎩， ∴△FMG ≌△GNQ ，∴MG =NQ =2，FM =GN = 4-n ，∴Q （4- n ， n +2），∵点Q 在直线483y x =-+上， ∴42(4)83n n +=--+，∴n =-2，∴(0,-2)G ．综上所述，满足条件的点G 坐标为34(0,)7或(0,-2)．【点睛】本题属于一次函数综合题，考查了一次函数与坐标轴的交点，平行线性质，两直线联立解方程组，全等三角形的判定和性质，正方形的性质等知识，解题的关键是学会用分类讨论的思想思考问题，学会添加常用辅助线，构造全等三角形解决问题，属于中考压轴题．4、（1）见解析；（2）CE=52．【分析】（1）根据平行线的性质及折叠性质证明∠FAC=∠FCA即可．（2）由题意可得90EB C'∠=，根据勾股定理求出AC=5，进而求出B'C=2，设CE= x．然后在Rt△CEB'中，根据勾股定理EC2=EB'2+B C'2列方程求解即可；【详解】解：（1）如图1，∵四边形ABCD是矩形，∴AD BC，∴∠FAC=∠ACB，∵∠ACB=∠ACF，∴∠FAC=∠FCA，∴FA=FC．（2）∵90EB C'∠=，如图2，设CE= x，∵四边形ABCD 是矩形，∴∠B =90°，∴AC 2=AB 2+BC 2= 32+42=25，∴AC =5，由折叠可知：90AB E B '∠=∠=，AB AB 3'==，4EB EB x '==-，∴B C '=5-3=2，在Rt △CEB '中，EC 2=EB '2+B C '2∴x 2=（4-x ）2+22，∴x =52，∴CE =52．【点睛】本题属于矩形折叠问题，考查了矩形的性质，勾股定理，直角三角形的判定和性质，等腰三角形的判定和性质等知识，解题的关键是学会利用参数构建方程解决问题，属于中考常考题型．5、（1）BP ＝CE ，CE ⊥BC ；（2）仍然成立，见解析；（3）【分析】（1）连接AC ，根据菱形的性质和等边三角形的性质证明△BAP ≌△CAE 即可证得结论；（2）（1）中的结论成立，用（1）中的方法证明△BAP≌△CAE即可；（3）分两种情形：当点P在BD的延长线上时或点P在线段DB的延长线上时，连接AC交BD于点O，由∠BCE＝90°，根据勾股定理求出CE的长即得到BP的长，再求AO、PO、PD的长及等边三角形APE的边长可得结论．【详解】解：（1）如图1，连接AC，延长CE交AD于点H，∵四边形ABCD是菱形，∴AB＝BC，∵∠ABC＝60°，∴△ABC是等边三角形，∴AB＝AC，∠BAC＝60°；∵△APE是等边三角形，∴AP＝AE，∠PAE＝60°，∴∠BAP＝∠CAE＝60°﹣∠PAC，∴△BAP≌△CAE（SAS），∴BP＝CE；∵四边形ABCD是菱形，∴∠ABP＝1∠ABC＝30°，2∴∠ABP＝∠ACE＝30°，∴∠BCE＝60°+30°＝90°，∴CE⊥BC；故答案为：BP＝CE，CE⊥BC；（2）（1）中的结论：BP＝CE，CE⊥AD仍然成立，理由如下：如图2中，连接AC，设CE与AD交于H，∵菱形ABCD，∠ABC＝60°，∴△ABC和△ACD都是等边三角形，∴AB＝AC，∠BAD＝120°，∠BAP＝120°+∠DAP，∵△APE是等边三角形，∴AP＝AE，∠PAE＝60°，∴∠CAE＝60°+60°+∠DAP＝120°+∠DAP，∴∠BAP＝∠CAE，∴△ABP≌△ACE（SAS），∴BP＝CE，∠ACE＝∠ABD＝30°，∴∠DCE＝30°，∵∠ADC＝60°，∴∠DCE+∠ADC＝90°，∴CE⊥AD；∴（1）中的结论：BP＝CE，CE⊥AD仍然成立；（3）如图3中，当点P在BD的延长线上时，连接AC交BD于点O，连接CE，BE，作EF⊥AP于F，∵四边形ABCD是菱形，∴AC⊥BD BD平分∠ABC，∵∠ABC＝60°，AB＝∴∠ABO＝30°，AB OB＝3，∴AO＝12∴BD＝6，由（2）知CE⊥AD，∵AD∥BC，∴CE⊥BC，∵BE＝BC＝AB＝∴CE＝8，由（2）知BP＝CE＝8，∴DP＝2，∴OP＝5，∴AP∵△APE是等边三角形，∴S△AEP）2＝如图4中，当点P在DB的延长线上时，同法可得AP∴S△AEP2＝【点睛】此题是四边形的综合题，重点考查菱形的性质、等边三角形的性质、全等三角形的判定与性质、勾股定理等知识点，解题的关键是正确地作出解题所需要的辅助线，将菱形的性质与三角形全等的条件联系起来，此题难度较大，属于考试压轴题．。

四边形的几何变换-练习与解答

走进四边形的几何变换在近几年的各地中考中，几何变换作为一种数学思想与方法，不断地被命题者青睐与关注，在现行的初中数学课本中，主要存在平移、旋转和轴对称(即翻折)三种几何变换. 它们最大的特征都是不改变图形的形状和大小，只改变图形位置的变换。

而四边形作为初中阶段最核心最重要的内容，越来越被作为呈现知识和能力的载体。

为此，让我们结合年各地中考试题，一同走进四边形中的变换世界，感受它的魅力与亮点。

一、在平移中构造与发现例：(年咸宁市)如图，将矩形ABCD 沿对角线AC 剪开，再把ACD △沿CA 方向平移得到A C D '''△．（）证明A AD CC B '''△≌△；（）若30ACB ∠=°，试问当点C '在线段AC 上的什么位置时，四边形ABC D ''是菱形，并请说明理由．思路点拨：在平移过程中对应的边与角的大小不变，仅仅是位置发生改变，借助边角边可证出两个三角形全等；同时与′′始终平行且相等，可知四边形′′平行四边形，要使其为菱形，需满足′，而∠°，∠°，可得21，即点′是线段的中点。

解析：()矩形ABCD 沿对角线AC 剪开，再把ACD △沿CA 方向平移得到A C D '''△ 得A D ''，A D ''∥∥，′′，∴∠′′′∠，∴⊿′′≌⊿′。

（）当点′是线段的中点时，四边形′′是菱形，理由如下：∵四边形是矩形， A C D '''△由ACD △平移得到，′′，由（）知′′，∴四边形是平行四边形。

在⊿中，点′是线段的中点，∴′21，而∠°，∴21，∴′，∴四边形′′是菱形。

点评：决定平移后图形位置的两个基本因素是平移的方向和距离，本题通过“平移不改变图形的形状和大小”的性质，再结合平移前后图形的相应位置进行分析、综合、探究与解答。

人教版初二数学8年级下册第18章(平行四边形)含辅助线证明专项训练(含答案)

人教版数学八年级下册第十八章平行四边形含辅助线证明训练一1.如图，□ABCD中，AC⊥AB，点E在线段AC上，AE=AB，BE的延长线交边AD于点F，AG⊥BC，且AG=AF，AG交BF于点O．（1）若AD=13，AC=12，求BE的长；（2）若点O恰好是线段AG的中点，连接GE，求证：AF=GE．2.已知正方形ABCD如图所示，连接其对角线AC，∠DAC的平分线AE交CD于点E，过点D作DM⊥AE于F，交AC于点M，共过点A作AN⊥AE交CB延长线于点N．(1)若AD=3，求△CAN的面积；(2)求证：AN=DM+2EF．3.如图1，已知正方形ABCD中，点E在BC上，连接AE，过点B作BF⊥AE于点G，交CD于点F.图1 图2（1）如图1，连接AF，若AB＝4，BE＝1，求AF的长；（2）如图2，连接BD，交AE于点N，连接AC，分别交BD、BF于点O、M，连接GO,求证：AG-BG=2GO4.如图，平行四边形ABCD中，BF⊥DC交DC于点F，且BF=AB，E点是BC边上一点，连接AE交BF于G；（1）若AE平分∠DAB，∠C=60∘，BE=3，求BG的长；（2）若AD=BG+FC，求证：AE平分∠DAB．5.如图，在□ABCD中，AD上有一点E，连接BE,AH⊥BC于H,AH、BE交于点G,连接CG并延长交AB于F,且GC=CD,∠GCD=90∘.(1) 若GC＝6，∠BAG＝30∘，求四边形AGCD的面积；(2) 求证：DE=2BG．6.如图，▱ABCD中，点E为BC边上一点，过点E作EF⊥AB于F，已知∠D=2∠AEF．（1）若∠BAE=70°，求∠BEA的度数；（2）连接AC，过点E作EG⊥AC于G，延长EG交AD于点H，若∠ACB=45°，求AC．证：AH=AF+227.如图，▱ABCD中，DF平分∠ADC交AC于点H，G为DH的中点．（1）如图①，若M为AD的中点，AB⊥AC，AC=9，CF=8，CG=25，求GM；（2）如图②，M为线段AB上一点，连接MF，满足∠MCD=∠BCG，∠MFB=∠BAC．求证：MC=2CG．8.如图，在▱ABCD中，连结BD，点E在BD上，且DE=DC，连结CE并延长它与AD交于点F，过点C作CG⊥BD垂足为G，交AD于点H．（1）若DG=3，CG=23，求△CDE的面积；（2）若∠DFC=45°，求证：EF+2FH=CF．9.如图所示，在正方形ABCD的边CB的延长线上取点F，连结AF，在AF上取点G，使得AG=AD，连结DG，过点A作AE⊥AF，交DG于点E．（1）若正方形ABCD的边长为4，且AB=2FB，求FG的长；（2）求证：AE+BF=AF．10.如图，▱ABCD中，E为平行四边形内部一点，连接AE，BE，CE．（1）如图1，AE⊥BC交BC于点F，已知∠EBC=45°，∠BAF=∠ECF，AB=5，EF=1，求AD的长；（2）如图2，AE⊥CD交CD于点F，AE=CF且∠BEC=90°，G为AB上一点，作GP⊥BE 且GP=CE，并以BG为斜边作等腰Rt△BGH，连接EP、EH．求证：EP=2EH．11.如图1，在等腰△ABO中，AB=AO，分别延长AO、BO至点C、点D，使得CO=AO、BO=BO，连接AD、BC．（1）如图1，求证：AD=BC；（2）如图2，分别取边AD、CO、BO的中点E、F、H，猜想△EFH的形状，并说明理由．12.已知，如图，▱ABCD的对角线AC、BD相交于点O，（1）如图1，若AC=AD过点A作AE⊥BC于点E，若AE=3,BC=5，求AB边的长；（2）如图2，过点A作BD的垂线，垂足为F，且AF=BF，过点B作BC的垂线，两条垂线相交于点G，若∠BAG=∠BFC，连接DG.求证：GF=4FO13.已知，在平行四边形ABCD中，AB⊥BD,E为射线BC上一点，连接AE交BD于点F，AB=BD.（1）如图1，若点E与点C重合，且AF=25，求AD的长；（2）如图2，若点E在BC边上时，过点D作DG⊥AE于G,延长DG交BC于H，连接FH.求证：AF=DH+FH;（3）如图3，当点E在射线BC上运动时，过点D作DG⊥AE于G,M为AG的中点，点N在BC边上且BN=1，已知AB=42，请直接写出MN的最小值。

初中数学四边形专题训练50题含答案

中考数学四边形专题训练50题含答案(单选、填空、解答题)一、单选题1．平行四边形不一定具有的性质是（）A ．对角线互相垂直B ．对边平行且相等C ．对角线互相平分D ．对角相等 2．如图，在MON ∠的两边．上分别截取,OA OB ，使OA OB =；分别以点A ，B 为圆心，OA 长为半径作弧，两弧交于点C ；连接,,,AC BC AB OC ．若2AB =，四边形OACB 的面积为4．则OC 的长为（）A ．2B ．3C ．4D ．5 3．在ABCD 中，下列结论错误的是（）A ．//AB CD B ．B D ∠=∠C ．AC BD =D ．180C D ∠+∠=︒ 4．如图，在平行四边形ABCD 中，E 是AB 延长线上的一点，若∠A=60°，则∠1的度数为（）A ．120°B ．60°C ．45°D ．30° 5．若平行四边形中两个内角的度数比为1∠2，则其中较大的内角是（） A ．100° B ．60° C ．120° D ．90° 6．如图，正方形OABC 与正方形ODEF 是位似图形，点O 为位似中心，位似比为2:3，点B 、E 在第一象限．若点A 的坐标为()1,0，则点E 的坐标是（）A ．0)B ．33,22⎛⎫ ⎪⎝⎭C ．D ．(2,2) 7．四边形ABCD 中，对角线AC ，BD 交于点O ，AD//BC ，为了判定四边形是平行四边形，还需一个条件，其中错误．．的是（） A ．AB//CD B ．∠A=∠C C ．AB=CD D ．AO=CO 8．一个多边形的内角和等于外角和，则这个多边形的边数为（）A ．10B ．8C ．6D ．49．顺次连接等腰梯形各边中点所围成的四边形是（）A ．平行四边形B ．矩形C ．菱形D ．正方形 10．已知平行四边形ABCD 的周长为32，AB ＝4，则BC 的长为（）A ．4B ．12C ．24D ．48 11．如图,四边形ABCD 是矩形,,把矩形沿直线AC 折叠,点B 落在点E处,连结DE,则的值是（）A ．B ．C ．8D ．7：25 12．如图，在平行四边形ABCD 中，AB=4，CE 平分∠BCD 交AD 边于点E ，且AE=3，则BC 的长为（）A ．4B ．6C ．7D ．813．如图，在矩形ABCD ，对角线AC 与BD 相交于点O ，EO AC ⊥于点O ，交BC 于点E ，若ABE ∆的周长为8，3AB =，则AD 的长为（）A ．2B ．5.5C ．5D ．414．如图，矩形ABCD 中，4AB =，2BC =．点E 在边AB 上，点F 在边CD 上，点G 、H 在对角线AC 上．若四边形EGFH 是菱形，则BE 的长是（）A ．B C ．2.5 D ．1.5 15．如图，在平行四边形ABCD 中，过点P 作直线EF 、GH 分别平行于AB 、BC ，那么图中共有（）平行四边形．A ．4个B ．5个C ．8个D ．9个 16．如图，已知直线PQ CD ⊥于点P ，B 是CPQ ∠内部一点，过点B 作BA PQ ⊥于点A ，BC CD ⊥于点C ，四边形PABC 是边长为8cm 的正方形，N 是AB 的中点，动点M 从点P 出发，以2cm/s 的速度，沿P A B C →→→方向运动，到达点C 停止运动，设运动时间为()s t ，当CM PN =时，t 等于（）A ．2B ．4C ．2或4D ．2或617．如图，在菱形中，，，是的中点．过点作，垂足为．将沿点到点的方向平移，得到．设、分别是、的中点，当点与点重合时，四边形的面积为A ．B ．C ．D ． 18．如图，点EF 、分别是菱形ABCD 的边AD 、DC 的中点，如果阴影部分的面积和是10，则菱形对角线AC 与BD 的乘积AC BD ⋅等于（）A ．10B ．32C ．20D ．1619．如图，在正方形1ABCB 中，AB =AB 与直线l 所夹锐角为60，延长1CB 交直线l 于点1A ，作正方形1112A B C B ，延长12C B 交直线l 于点2A ，作正方形2223A B C B ，延长23C B 交直线l 于点3A ，作正方形3334A B C B ⋯，依次规律，则线段20212022A A =（）A ．20192⨯⎝⎭B ．20202⨯⎝⎭C ．20212⨯⎝⎭D ．20222⨯⎝⎭20．如图，平行四边形ABCD 的对角线AC 与BD 相交于点O ，添加一个条件使平行四边形ABCD 为矩形的是（）A ．AD AB = B ．AB AD ⊥C ．AB AC =D ．CA BD ⊥二、填空题21．如图，这个图案是用形状、大小完全相同的等腰梯形密铺而成的，则这个图案中的等腰梯形的底角(指锐角)是_________度．22．如图，点E 在矩形ABCD 的对角线BD 上，EF BC ⊥于点F ，连接AF ，若5BC =，2EF =，则ABF △的面积为_________．23．已知菱形的两条对角线长分别为3和4，则菱形的面积为______．24．有一个边长为50cm 的正方形洞口，要用一个圆盖去盖住这个洞口，那么圆盖的直径至少应为_____．25．如图，Rt ABC 中，90C BC AC ∠=︒>，，以AB BC AC ，，三边为边长的三个正方形面积分别为1S ，2S ，3S ．若ABC 的面积为7，140S =，则32S S －的值等于______．26．如图，将长方形ABCD沿AE折叠，已知50∠=︒，则BADCED'∠'的大小是_____27．如图，在菱形ABCD中，AB=1，∠DAB=60°，把菱形ABCD绕点A顺时针旋转30°得到菱形AB′C′D′，其中点C的运动路径为CC'，则图中阴影部分的面积为__．28．用直角边分别为3和4的两个直角三角形拼成一个平行四边形（非矩形），所得的平行四边形的周长是______．29．如图，菱形ABCD中，点O为对角线AC的三等分点且AO＝2OC，连接OB，OD，OB＝OC＝OD，已知AC＝3，那么菱形的边长为_____．30．如图，将四边形ABCD沿BD、AC剪开，得到四个全等的直角三角形，已知，OA ＝4，OB＝3，AB＝5将这四个直角三角形拼为一个没有重叠和缝隙的四边形，则重新拼成的四边形的周长为_____．31．在长方形ABCD中，10AB=，将长方形ABCD折叠，折痕为EF．AD=，8（1）如图1，当A'与B重合时，EF=_______；（2）如图1，当直线EF过点D时，点A的对应点A'落在线段BC上，则线段EF的长为______．32．如图，P 是▱ABCD 内的任意一点，连接P A 、PB 、PC 、PD ，得到△P AB 、△PBC 、△PCD 、△PDA ，设它们的面积分别是S 1、S 2、S 3、S 4，给出如下结论：∠S 1+S 3＝S 2+S 4，∠若S 3＝2S 1，则S 2＝2S 4，∠若S 1+S 3＝5，则ABCD 的面积为10；∠S 1+S 2＝S 3+S 4．其中正确的结论的序号是____________（把所有正确结论的序号都填在横线上）．33．如图，直线l 是四边形ABCD 的对称轴，若AB CD =，有下面的结论：∠AB BC ⊥；∠AC BD ⊥；∠//AB CD ；∠AO OC =．其中正确的结论有__．34．如图1是三国时期的数学家赵爽创制的一幅“勾股圆方图”．将图2的矩形分割成四个全等三角形和一个正方形，恰好能拼成这样一个“勾股圆方图”，则该矩形与拼成的正方形的周长之比为________．35．如图，平行四边形ABCD 中，45B ∠=︒，7BC =，CD =E ，F 分别是边AB ，BC 的中点，连接CE ，DF ，取CE ，DF 的中点G ，H ，连接GH ，则GH 的长度为__________．36．如图，正方形ABCD的边长为1，AC，BD是对角线，将∠DCB绕着点D顺时针旋转45°得到∠DGH，HG交AB于点E，连接DE交AC于点F，连接FG，则下列结论：∠DE平分∠ADB；∠BE∠四边形AEGF是菱形；∠BC+FG=1.5．其中结论正确的序号是_______．37．如图，点E、F是平行四边形ABCD的边AB、DC上的点，F与DE相交于点P，BF与CE相交于点Q若S△APD=14cm2，S△BCQ=16cm2，四边形PEQF的面积为______．38．如图，在正方形ABCD中，AB＝4，G是BC的中点，点E是正方形内一个动点，且EG＝2，连接DE，将线段DE绕点D逆时针旋转90°得到线段DF，连接CF，则线段CF长的最小值为_____．39．如图，四边形ABCD是菱形，O是两条对角线的交点，过O点的三条直线将菱形分成阴影和空白部分．当菱形的两条对角线的长分别为6和8时，则阴影部分的面积为__________．三、解答题40．□ABCD 的对角线AC 的垂直平分线与边AD 、BC 分别交于E 、F ，四边形AFCE 是否是菱形？为什么？41．如图，平行四边形ABCD 的对角线AC ，BD 相交于点O ，延长CD 到E ，使DE CD =，连接AE ．(1)求证：四边形ABDE 是平行四边形；(2)连接OE ，若60ABC ∠=︒，且8AD DE ==，求OE 的长．42．如图，点E 、F 分别在ABCD 的边AB 、CD 的延长线上，且BE ＝DF ，连接AC 、EF 、AF 、CE ，AC 与EF 交于点O ．（1）求证：AC 、EF 互相平分；（2）若EF 平分∠AEC ，判断四边形AECF 的形状并证明．43．正方形ABCD 的对角线交点为O ，连AE 交BC 于E ，交OB 于F ，2EC FO =，求证：AE 平分BAC ∠.44．如图，在三角形ABC 中，90C ∠=︒，四边形DEFC 是边长为4的正方形，且D 、E 、F 分别在边AC AB BC 、、上．把三角形ADE 绕点E 逆时针旋转一定的角度．(1)当点D 与点F 重合时，点A 的对应点G 落在边BC 上，此时四边形ACGE 的面积为___________；(2)当点D 的对应点1D 落在线段BE 上时，点A 的对应点为点1A ，在旋转过程中点A 经过的路程为1l ，点D 经过的路程为2l ，且12:3:2l l =，求线段1AD 的长． 45．如图所示，已知四边形ABCD 是平行四边形，在AB 的延长线上截取BE=AB ，BF=BD ，连接CE ，DF ，相交于点M ．求证：CD=CM ．46．如图，在直角梯形ABCD 中，AD ∠BC ，AD ∠CD ，M 为腰AB 上一动点，联结MC 、MD ，AD ＝10，BC ＝15，cot B 512=．（1）求线段CD 的长．（2）设线段BM 的长为x ，∠CDM 的面积为y ，求y 关于x 的函数解析式，并写出它的定义域．47．在Rt ABC 与Rt BDE 中，90ABC DBE ∠=∠=︒，AB BC =，BD BE =．(1)如图1，若点D ，B ，C 在同一直线上，连接AD ，CE ，则AD 与CE 的关系为_________；(2)如果将图1中的BDE △绕点B 在平面内顺时针旋转到如图2的位置，那么请你判断AD 与CE 的关系，并说明理由；(3)如图3，若6AB =，2BD =，连接AE ，分别取DE ，AE ，AC 的中点M ，P ，N ，连接MP ，NP ，MN ，将BDE △绕点B 在平面内顺时针旋转一周，请直接写出旋转过程中MPN△面积的最小值和最大值．48．如图，在矩形ABCD中，AD=4，CD=3，点E为AD的中点．连接CE，将∠CDE 沿CE折叠得∠CFE，CE交BD于点G，交BA的延长线于点M，延长CF交AB于点N．(1)求DG的长；(2)求MN的长．49．如图，抛物线顶点P(1，4)，与y轴交于点C(0，3)，与x轴交于点A，B．（1）求抛物线的解析式．（2）Q是抛物线上除点P外一点，△BCQ与△BCP的面积相等，求点Q的坐标．（3）若M，N为抛物线上两个动点，分别过点M，N作直线BC的垂线段，垂足分别为D，E．是否存在点M，N使四边形MNED为正方形？如果存在，求正方形MNED 的边长；如果不存在，请说明理由．参考答案：1．A【分析】结合平行四边形的性质即可判定．【详解】结合平行四边形的性质可知选项B、C、D均正确，但平行四边形的对角线不垂直，则A不正确.故选A．【点睛】本题考查了平行四边形的性质，熟练掌握平行四边形的性质是正确解题的关键．2．C【分析】根据作法判定出四边形OACB是菱形，再根据菱形的面积等于对角线乘积的一半列式计算即可得解．【详解】解：根据作图，AC＝BC＝OA，∠OA＝OB，∠OA＝OB＝BC＝AC，∠四边形OACB是菱形，∠AB＝2，四边形OACB的面积为4，∠12AB•OC＝12×2×OC＝4，解得OC＝4．故选：C．【点睛】本题主要考查菱形的性质与判定，熟练掌握菱形的性质与判定是解题的关键．3．C【分析】根据平行四边形的性质逐项判断即可．【详解】解：A、由平行四边形行两组对边分别平行可得//AB CD，故A正确；B、由平行四边形对角相等可得B D∠=∠，故B正确；C、AC、BD为平行四边形对角线，平行四边形对角线互相平分，但不一定相等，故C错误；D、由平行四边形行两组对边分别平行可得//AD BC，两直线平行同旁内角互补，可得180C D∠+∠=︒，故D正确．故选：C．【点睛】本题主要考查平行四边形的性质及其推论，熟练掌握平行四边形的性质是解题关键．4．B【详解】解：∠四边形ABCD 是平行四边形，∠AD∠BC ，∠∠1=∠A=60°．故选B ．5．C【分析】据平行四边形的性质得出AB //CD ，推出∠B ＋∠C ＝180°，根据∠B ：∠C ＝1：2，求出∠C 即可．【详解】解：∠四边形ABCD 是平行四边形∠AB //CD ，∠∠B ＋∠C ＝180°，∠∠B ：∠C ＝1：2，∠∠C ＝23×180°＝120°，故选：C ．【点睛】本题考查了平行线的性质和平行四边形的性质的应用，能熟练地运用性质进行计算是解此题的关键，题目比较典型，难度不大．6．B【分析】由题意可得:2:3OA OD =，又由点A 的坐标为()1,0，即可求得OD 的长，又由正方形的性质，即可求得E 点的坐标．【详解】解：∠正方形OABC 与正方形ODEF 是位似图形，O 为位似中心，相似比为2:3， ∠:2:3OA OD =，∠点A 的坐标为()1,0，即1OA =， ∠32OD =， ∠四边形ODEF 是正方形，∠32 DE OD==．∠E点的坐标为：33,22⎛⎫ ⎪⎝⎭．故选：B．【点睛】此题考查了位似变换的性质与正方形的性质．此题比较简单，注意理解位似变换与相似比的定义是解此题的关键．7．C【分析】根据平行四边形的判定定理逐项判断即可．【详解】解：A.根据两组对边分别平行可判定是平行四边形，不符合题意；B.根据平行线性质可得另一对内角相等，根据两组对角分别相等可判定是平行四边形，不符合题意；C.不能判定是平行四边形，可能是等腰梯形，符合题意；D.可通过全等证对角线互相平分，能判定是平行四边形，不符合题意；故选：C．【点睛】本题考查了平行四边形的判定，解题关键是熟知平行四边形的判定定理，准确进行判断．8．D【分析】设这个多边形的边数为n，根据内角和等于外角和列方程解答即可．【详解】解：设这个多边形的边数为n，则()2180360n-⨯︒=︒，解得4n=，故选：D．【点睛】此题考查了多边形内角和与外角和的计算，熟练掌握多边形内角和公式及外角和是解题的关键．9．C【分析】由E、F、G、H分别为AB、BC、CD、DA的中点，得出EF，HG，FG，EH是中位线，再得出四条边相等，根据“四条边都相等的四边形是菱形”进行证明．【详解】解：如图所示，因为E、F、G、H分别为AB、BC、CD、DA的中点，连接AC、BD，因为E、F分别是AB、BC的中点，所以EF=12AC ，且EF∠AC同理可得HG=12AC ，且HG∠AC ， FG=12BD ，且FG∠BD ， EH=12BD ，且EH∠BD ， ∠EF∠HG ，HE ∠FG ，∠四边形EFGH 是平行四边形，又因为等腰梯形的对角线相等，即AC=BD ，因此有EF=FG=GH=HE ，所以连接等腰梯形各中点所得四边形为菱形．故选：C【点睛】此题考查三角形中位线的性质，解题的关键是掌握三角形的中位线定理及菱形的判定．10．B【详解】由题意得：2()32,4,12AB BC AB BC +===得： .故选B.11．D【详解】试题分析：从D,E 处向AC 作高DF,EH ．设AB=4k,AD=3k,则AC=5k ．由∠AEC的面积=4k×3k=5k×EH,得EH=95k k；根据勾股定理得CH=,∠四边形ACED是等腰梯形,∠CH=AF=95 k,所以DE=5k﹣95k×2=75k．所以DE：AC=75k：5k=7：25．故选D．考点：翻折变换．12．C【分析】由平行四边形的性质可得AD∠BC，且AD=BC，结合角平分线的性质可求得DE=DC=AB=4，则可求得AD的长，可求得答案．【详解】解：∠四边形ABCD为平行四边形，∠AB=CD=4，AD∠BC，AD=BC，∠∠DEC=∠BCE．∠CE平分∠BCD，∠∠DCE=∠BCE，∠∠DEC=∠DCE，∠DE=DC=4．∠AE=3，∠AD=BC=3+4=7．故选C．【点睛】本题主要考查平行四边形的性质，利用平行线的性质及角平分线的性质求得DE=DC是解题的关键．13．C【分析】由矩形的性质可得AO＝CO，由线段垂直平分线的性质可得AE＝EC，即可求解．【详解】解：∵四边形ABCD是矩形，∴AO＝CO，BC＝AD，∵EO⊥AC，∴AE＝EC，∵△ABE的周长为8，∴AB+AE+BE＝8，∴3+BC＝8，∴AD ＝BC ＝5，故选：C ．【点睛】本题考查了矩形的性质，线段垂直平分线的性质，掌握矩形的性质是本题的关键．14．D【分析】由矩形ABCD 中，四边形EGFH 是菱形，易证得()COF AOE AAS ≌，即可得OA OC =，然后由勾股定理求得AC 的长，继而求得OA 的长，又由AOE ABC ∽△△，利用相似三角形的对应边成比例，即可求得答案．【详解】解：如图，连接EF ，交AC 于O ，∠四边形EHFG 是菱形，EF AC OE OF ∴⊥=，，∠四边形ABCD 是矩形，90B D ∴∠=∠=︒，AB CD ∥，ACD CAB ∴∠=∠，在COF 与AOE △中，FCO OAE FOC AOE OF OE ∠=∠⎧⎪∠=∠⎨⎪=⎩，()COF AOE AAS ∴≌，AO CO ∴=，AC AB ==12AO AC ∴==， 90CAB CAB AOE B ∠=∠∠=∠=︒，，AOE ABC ∴∽，∠AO AE AB AC=，=， 2.5AE ∴=，1.5BE ∴=，故选：D ．【点睛】本题考查了菱形的性质、矩形的性质、全等三角形的判定与性质以及相似三角形的判定与性质，准确作出辅助线是解此题的关键．15．D【详解】∠AD∠BC 、AB∠CD ，EF∠AB ，GH∠BC ，∠AB∠EF∠DC ，AD∠GH∠BC ，∠共有9个平行四边形，如平行四边形AGPE ，平行四边形BGPF ，平行四边形PEDH ，平行四边形PFCH ，平行四边形ABFE ，平行四边形EFCD ，平行四边形AGHD ，平行四边形BGHC ，平行四边形ABCD ，故选D.16．D【分析】分点M 是AP 的中点和点M 与点N 重合两种情况讨论，由全等三角形的性质和正方形的性质即可求解．【详解】解：当点M 是AP 的中点时，∵四边形P ABC 是正方形，∴PC ＝P A ＝AB ，∠CP A ＝∠P AN ＝90°，∵N 是AB 的中点，点M 是AP 的中点，∴PM ＝AN ＝4，在△CPM 和△P AN 中，PA CP CPA PAN PM AN =⎧⎪∠=∠⎨⎪=⎩∴△CPM ≌△P AN （SAS ），∴PN ＝CM ，∴t 42==2，当点M 与点N 重合时，由正方形的对称性可得PN ＝CM ，∴t842+==6，故选：D【点睛】本题考查了正方形的性质，全等三角形的性质，利用分类讨论思想解决问题是解题的关键．17．A【详解】试题分析：作在菱形中，，,是的中点是的中点，故答案选A.考点：平行四边形的面积，三角函数.18．B【分析】设EF交BD于G，AC交BD于O，由三角形中位线的性质可得EF=12AC，EF//AC，可得EG为∠AOD的中位线，可得DG=12OD，根据菱形的性质可得BG=34BD，根据菱形的面积公式列方程即可得答案．【详解】设EF交BD于G，AC交BD于O，∠点E F 、分别是菱形ABCD 的边AD 、DC 的中点， ∠EF=12AC ，EF//AC ，∠EG 为∠AOD 的中位线， ∠OG=12OD ，∠四边形ABCD 是菱形， ∠OD=OB=12BD ，BD∠AC ， ∠BG=34BD ，BG∠EF ， ∠S 菱形ABCD =S 阴影+S △BEF ，阴影部分的面积和是10， ∠12AC·BD=10+12EF·BG=10+12·12AC·34BD ，解得：AC·BD=32．故选：B【点睛】本题考查菱形的性质、三角形中位线的性质及菱形的面积公式，菱形的对角线互相垂直且平分；菱形的面积等于两条对角线乘积的一半；三角形的中位线平行于第三边且等于第三边的一半；熟练掌握相关性质及公式是解题关键．19．C【分析】利用特殊角的三角函数值分别求出11A B 、22A B 、33A B ，以此类推找到规律求出20222022A B ，最后根据202120222022Rt A A B 中20212022202290A B A ∠=︒，20222021202230A A B ∠=︒，即可求解．【详解】解：∠AB 与直线l 所夹锐角为60︒，且1BAB ∠是正方形1ABCB 的一个顶角， ∠11180609030B AA ∠=︒-︒-︒=︒，又∠1190AB A ∠=︒，∠在11Rt AB A △中，11111tan A B AB A AB =⨯∠，∠正方形1ABCB 的边长AB∠11111tan A B AB A AB =⨯∠同理可求得： 222A B =⎝⎭，333A B =⎝⎭，以此类推可知： 20222021202120222022A B ===⎝⎭⎝⎭⎝⎭，∠202120222022Rt A A B 中20212022202290A B A ∠=︒，20222021202230A A B ∠=︒，∠2021202120222022202222A A A B ==⨯⎝⎭，故C 正确．故选：C ．【点睛】本题主要考查了正方形的性质、含特殊角的锐角三角函数等知识，含30°的直角三角形的性质．利用从特殊到一般寻找规律是解题的关键．20．B【分析】根据矩形的判定和平行四边形的性质分别对各个选项进行判断即可．【详解】解： A 、AD AB =时，平行四边形ABCD 是菱形，故选项A 不符合题意； B 、AB AD ⊥时，∠BAD ＝90°，则平行四边形ABCD 是矩形，故选项B 符合题意； C 、AB AC =时，平行四边形ABCD 不一定是矩形，故选项C 不符合题意；D 、CA BD ⊥时，平行四边形ABCD 是菱形，故选项D 不符合题意；故选：B ．【点睛】此题考查的是平行四边形的性质、矩形的判定以及等腰三角形的判定等知识；熟练掌握矩形的判定和平行四边形的性质是解答此题的关键．21．60°【分析】根据图案的特点，可知密铺的一个顶点处的周角，由3个完全相同的等腰梯形的较大内角组成，即可求出等腰梯形的较大内角的度数，进而即可得到答案.【详解】由图案可知：密铺的一个顶点处的周角，由3个完全相同的等腰梯形的较大内角组成，∠等腰梯形的较大内角为360°÷3=120°，∠等腰梯形的两底平行，∠等腰梯形的底角（指锐角）是：180°-120°=60°．故答案是：60°．【点睛】本题主要考查等腰梯形的性质以及平面镶嵌，掌握平面镶嵌的性质是解题的关键．22．5【分析】证明∠BEF∠∠BCD，由相似三角形的性质求得BF•CD，即求得BF•AB，进而由三角形的面积公式求得结果．【详解】解：∠四边形ABCD是矩形，∠AB=CD，∠ABC=∠BCD=90°，∠EF∠BC，∠EF∠CD，∠∠BEF∠∠BDC，∠BF EF BC CD=，∠BC=5，EF=2，∠BF•CD=BC•EF=5×2=10，∠BF•AB=10，∠∠ABF的面积=12BF•AB=5，故答案为：5．【点睛】本题主要考查了矩形的性质，相似三角形的判定与性质，三角形的面积计算，关键是由相似三角形求得BF•AB的值．23．6【分析】根据菱形的面积等于对角线乘积的一半列式进行计算即可得解．【详解】解：∠菱形的两条对角线长分别为3和4，∠菱形的面积为134=6 2⨯⨯故答案为：6【点睛】本题考查了菱形的性质，菱形的面积通常有两种求法，可以用底乘以高，也可以用对角线乘积的一半求解，计算时要根据具体情况灵活运用．24．【分析】根据圆与其内切正方形的关系，易得圆盖的直径至少应为正方形的对角线的长，已知正方形边长为50cm，进而由勾股定理可得答案．【详解】解：根据题意，知圆盖的直径至少应为正方形的对角线的长；再根据勾股定理，50故答案为：．【点睛】题主要考查正多边形和圆的相关知识；注意：熟记等腰直角三角形的斜边是直角边的倍，可以给解决此题带来方便．25．【分析】结合正方形面积公式，平方差公式，勾股定理，三角形面积公式，可知()()2223S S BC AC BC AC BC AC -=-=+-，2240BC AC +=，14BC AC ⋅=，然后运用完全平方公式()2222a b a b ab ±=+±求解即可．【详解】解：根据题意，2140S AB ==，22S BC =，23S AC = ∠()()2223S S BC AC BC AC BC AC -=-=+-在Rt ABC 中，根据勾股定理，222BC AC AB +=∠2240BC AC +=∠7Rt ABC S = ∠172BC AC ⋅⋅= ∠14BC AC ⋅=∠BC AC +==BC AC -====∠()()BC AC BC AC +-==即23S S -=故答案为：【点睛】本题考查勾股定理与三角形、正方形的面积，完全平方公式与平方差公式的灵活应用，掌握并熟练应用勾股定理和各类公式是解题的关键．26．40【详解】试题分析：先根据折叠的性质求得、的度数，即可求得、的度数，再根据长方形的性质求解即可.∠50CED ∠='︒，AE 为折痕∠∠∠BAD ∠'. 考点：折叠的性质点评：折叠的性质是初中数学的重点，贯穿于整个初中数学的学习，是中考中比较常见的知识点，一般难度不大，需熟练掌握.27．342π+【分析】根据菱形的性质以及旋转角为30°，连接CD ′和BC '，可得A 、D′、C 及A 、B 、C′分别共线，求出扇形的面积，再根据AAS 证得两个小三角形全等，求得面积，最后根据扇形ACC '的面积-两个小的三角形的面积即可．【详解】解：连接CD ′和BC '∠∠DAB =60°∠30DAC CAB ∠=∠=︒∠30C AB ∠''=︒∠A 、D′、C 及A 、B 、C′分别共线∠AC =∠扇形ACC′的面积为：2303604ππ⨯=∠AC =AC ′，AD′=AB在OCD OC B ''和中CD BC ACD AC D COD C OB '='⎧⎪∠=∠''⎨⎪∠'=∠'⎩∠()OCD OC B AAS ''≌∠OB =OD′，CO =C′O又∠60,30CBC BC O ︒∠'∠=='︒∠90BOC ∠'=︒在Rt BOC '中，())22211BO BO +-=解得13,22BO C O ='=∠S △OCB=12BO C O '⨯⨯=，∠322442C B AC OC S S Sππ''=-=-=+阴影扇形故答案为:342π+ 【点睛】本题考查了旋转的性质，菱形的性质，扇形的面积公式，熟练掌握旋转变换只改变图形的位置不改变图形的形状与大小是解题的关键．28．18或16【分析】首先由直角边分别为3和4，求得其斜边，然后分别从以边长为3，4，5的边为对角线拼成一个平行四边形（非矩形），去分析求解即可求得答案．【详解】解：直角边分别为3和4，∴5=，若以边长为3的边为对角线，则所得的平行四边形的周长是：2(54)18⨯+=；若以边长为4的边为对角线，则所得的平行四边形的周长是：2(53)16⨯+=；若以边长为5的边为对角线，则所得的平行四边形的周长是：2(34)14⨯+=（此时是矩形，舍去）；综上可得：所得的平行四边形的周长是：16或18．故答案为：16或18．【点睛】此题考查了平行四边形的性质以及勾股定理．注意掌握分类讨论思想的应用是解此题的关键．29【分析】如图，连接BD交AC于E，由四边形ABCD是菱形，推出AC∠BD，AE=EC，在Rt△EOD中，利用勾股定理求出DE，在Rt△ADE中利用勾股定理求出AD即可．【详解】如图，连接BD交AC于E．∠四边形ABCD是菱形，∠AC∠BD，AE＝EC，∠OA＝2OC，AC＝3，∠CO＝DO＝2EO＝1，AE＝32，∠EO＝12，DE＝EB==，∠AD=【点睛】本题考查菱形的性质、勾股定理等知识，解题的关键是灵活应用勾股定理解决问题.30．20，22，26，28【分析】以直角三角形边长相等的边为公共边，拼接四边形，再计算周长；【详解】解：∠如图周长=20；∠如图周长=22；∠如图周长=26；∠如图周长=28；∠如图周长=22；∠四边形的周长为：20，22，26，28；故答案为：20，22，26，28．【点睛】本题考查了图形的拼接，四边形的周长；作出拼接图形是解题关键．31．10【分析】（1）根据题意结合图形直接写出答案即可解决问题；（2）根据勾股定理首先求出A C'的长度；再次利用勾股定理求出AE的长度，即可解决问题．【详解】解：（1）如图1，当A'与B重合时，EF=10；（2）如图2，设AE=x，则BE=8-x；∠四边形ABCD为矩形，∠BC=AD=10，DC=AB=8；∠B=∠C=90°；由题意得：=A D AD '=10；由勾股定理得：222A C A D DC 1006436''=-=-=∠A C 6BA 1064''==-=，，在Rt∠A BE '中，由勾股定理得：222(8)4x x =-+解得：x=5，由勾股定理得：222EF =10+5=125∠EF =【点睛】该命题主要考查了翻折变换及其应用问题；能根据翻折变换的性质准确找出命题图形中隐含的等量关系是解题的关键．32．∠∠【分析】根据平行四边形的的性质可以得到AB ＝CD ，AD ＝BC ，设点P 到AB 、BC 、CD 、DA 的距离分别为h 1、h 2、h 3、h 4，然后利用三角形的面积公式列式整理判断即可得到答案．【详解】解：∠四边形ABCD 是平行四边形，∠AB ＝CD ，AD ＝BC ，设点P 到AB 、BC 、CD 、DA 的距离分别为h 1、h 2、h 3、h 4，hAB 、hBC 分别为平行四边形的AB 边和BC 边的高则S 1＝12AB •h 1，S 2＝12BC •h 2，S 3＝12CD •h 3，S 4＝12AD •h 4，hAB = h 1+h 3，hBC =h 2+h 4 ∠12AB •h 1+12CD •h 3＝12AB •hAB ，12BC •h 2+12AD •h 4＝12BC •hBC ，又∠S 平行四边形ABCD ＝AB •hAB ＝BC •hBC ，∠S 2+S 4＝S 1+S 3，故∠正确；根据S 3=2S 1只能判断h 3=2h 1，不能判断h 2=2h 4，即不能得出S 2=2S 4，故∠错误；根据S 1+S 3＝S 2+S 4，S 1+S 3＝5，能得出ABCD 的面积为5×2＝10，故∠正确；由题意只能得到S 2+S 4＝S 1+S 3无法得到S 1+S 2＝S 3+S 4，故∠错误；故答案为：∠∠．【点睛】本题主要考查了平行四边形的性质，三角形的面积，用平行四边形的面积表示出相对的两个三角形的面积是解题的关键．33．∠∠∠【分析】根据轴对称的性质得到直线l 垂直平分BD ，则根据线段垂直平分线的性质得AB AD =，CD CB =，由于AB=CD ，则AB BC CD BC ===，于是可判断四边形ABCD 为菱形，然后根据菱形的性质对4个结论进行判断．【详解】证明：∠直线l 是四边形ABCD 的对称轴，∴直线l 垂直平分BD ，AB AD ∴=，CD CB =，AB CD =，AB BC CD BC ∴===，∴四边形ABCD 为菱形，AC BD ∴⊥，//AB CD ，OA OC =，所以∠∠∠正确．故答案为∠∠∠．【点睛】本题考查了轴对称的性质：如果两个图形关于某直线对称，那么对称轴是任何一对对应点所连线段的垂直平分线．也考查了菱形的判定与性质．34．35）【分析】设图2的矩形分割成四个全等三角形的两直角边为a 、b （a ＞b ），由图1与图2的两个小正方形相同，得出a 与b 的关系，再求出矩形的边长和大正方形的边长，应用周长公式求得其周长，最后便可求得其比值．【详解】解：设图2的矩形分割成四个全等三角形的两直角边为a 、b （a ＞b ），小正方形的边长为a-b ，矩形的长为2a+a-b=3a-b ，宽为b ，∠矩形的周长为：2（3a-b+b ）=6a ，由图2知，中间小正方形的边长为b ，∠a-b=b ，∠a=2b ，∠大正方形的周长为,==∠该矩形与拼成的正方形的周长之比：=故答案为：3：5）．【点睛】本题主要考查了勾股定理，矩形的性质，正方形的性质，关键是根据图形求得全等直角三角形的两直角边与矩形和大正方形的边长的关系．35．134【分析】连接DG 并延长，交于AB 延长线于点M ，过点M 作MN ∠CB ，交于CB 延长线于点N ，首先根据平行四边形的性质证明(),CGD EGM AAS ≅得出,DG GM =即可得出1,2HG FM =再利用勾股定理求出FM ，即可求得答案．【详解】连接DG 并延长，交于AB 延长线于点M ，过点M 作MN ∠CB ，交于CB 延长线于点N ，如图，∠四边形ABCD 为平行四边形，∠CD ∠AB，AB CD ==∠CDG EMG ∠=∠又∠G 为CE 中点，∠,CG GE =在CGD △和EGM 中∠CDG EMG DGC MGE CG GE ∠=∠⎧⎪∠=∠⎨⎪=⎩∠(),CGD EGM AAS ≅∠,DG GM = ,CD EM = ∠1,2HG FM = AB EM =， ∠,AE BM =∠点E 为AB 的中点，∠1,2AE EB AB ==∠12EB BM AB ===，又∠45,B ∠=︒∠45,MBN ∠=︒∠,BN MN =设,BN MN x ==在Rt BMN 中，∠222,BN MN BM +=∠222x x +=，解得，5,2x = 即5,2BN MN == ∠点F 为BC 的中点， ∠17,22BF BC == ∠75622FN BF BN =+=+=, 在Rt MNF △中，∠222,NF MN MF +=∠13,2MF = ∠113,24HG FM == 故填：134．【点睛】本题考查平行四边形的性质，全等三角形的判定与性质，三角形中位线定理，勾股定理，解题关键是熟练掌握平行四边形的性质和三角形中位线定理．36．∠∠∠【分析】根据旋转的性质可知，∠DGH ∠∠DCB ，进而得知DH =DB ，∠H =∠CBD =45°，∠DGH =∠DCB =90°，DG =DC =AD ，之后可证∠ADF ∠∠GDF ，四边形AEGF 是菱形，再根据勾股定理可知AE 的长度，进而可以一一判断选出答案．【详解】解：根据旋转的性质可知，∠DGH ∠∠DCB ，∠DH =DB ，∠H =∠CBD =45°，∠DGH =∠DCB =90°，DG =DC =AD ，在Rt ∠AED 与Rt ∠GED 中，AD =DG ，ED =ED∠Rt ∠AED ∠Rt ∠GED （HL ）∠∠ADE =∠GDE ，即DE 平分∠ADB ，故∠正确；在∠ADF 和∠GDF 中，AD =DG ，∠ADF =∠GDF ，DF =DF ，∠∠ADF ∠∠GDF （SAS ）∠AF =GF ，∠DAF =∠DGF =45°又∠∠ABD =45°∠FG ∠AE∠∠DAC =45°，∠∠DAC =∠H ，∠AF ∠EG∠四边形AEGF 是平行四边形，又∠AF =GF∠平行四边形AEGF 是菱形，故∠正确；∠∠H =45°，∠HAE =90°∠AE =AH∠AE =AF =HD -AD =BD -AD∠正方形ABCD 的边长为1，根据勾股定理可知BD ==即HD∠AE 1∠BE =)11=2-∠正确； ∠四边形AEGF 是菱形∠FG =AE 1∠BC +FG =1∠错误；综上答案为：∠∠∠．【点睛】本题考查的是正方形的性质，菱形的判定与性质，勾股定理和直角三角形的性质，是一道综合性较强的题，能够充分调动所学知识是解题的关键．37．30cm 2。

初中数学四边形专题训练50题含参考答案

初中数学四边形专题训练50题含答案(单选、填空、解答题)一、单选题1．如果从某个多边形的一个顶点出发，可以作2条对角线，则这个多边形的边数是（）A ．4B ．5C ．6D ．7 2．如图，用一根绳子检查一平行四边形书架的侧边是否和上、下底都垂直，只需要用绳子分别测量比较书架的两条对角线AC ，BD 就可以判断，其推理依据是（）A ．矩形的对角线相等B ．矩形的四个角是直角C ．对角线相等的四边形是矩形D ．对角线相等的平行四边形是矩形3．在Rt ABC 中，90,30,4,C A BC D E ∠=︒∠=︒=、分别为AC AB 、边上的中点，连接DE 到F ，使得2EF ED =，连接BF ，则BF 长为（）A ．2B ．C ．4D ．4．一个多边形的内角和是外角和的5倍，这个多边形边数为（） A ．14 B ．12 C ．10 D ．8 5．在平面直角坐标系中，矩形ABCD 的位置如图所示，其中(1,1)B --，点A 在第二象限，//AB y 轴，3,4AB BC ==，则顶点D 的坐标为( )A．(3,2)B．(2,2)C．(3,3)D．(2,3)6．下列选项中，能判定四边形ABCD是平行四边形的是（）A．AB//CD，AD＝BC B．∠A＝∠D，∠B＝∠CC．AB//CD，∠A＋∠B＝180°D．∠A＝∠C，∠B＋∠D＝180°7．下列命题正确的是（）A．同一边上两个角相等的梯形是等腰梯形B．一组对边平行，一组对边相等的四边形是平行四边形C．如果顺次连接一个四边形各边中点得到的是一个正方形，那么原四边形一定是正方形D．对角线互相垂直的四边形面积等于对角线乘积的一半8．下列命题中，正确的是（）A．梯形的对角线相等B．菱形的对角线不相等C．矩形的对角线不能互相垂直D．平行四边形的对角线可以互相垂直9．如图，已知点D、E分别是△ABC的边AB、CB的中点，若AB＝8，CE＝6，AC＝10，则△BDE的周长为()A．12B．15C．19D．2410．一个正多边形的每个外角都等于36°，那么它是（）A．正五边形B．正六边形C．正八边形D．正十边形11．如图，将一边长AB为4的矩形纸片折叠，使点D与点B重合，折痕为EF，若EF＝）A ．32B ．28C ．30D ．36 12．将如图甲所示的长方形沿着虚线剪开得到两个全等三角形，现拼成如图乙所示的图形，取BC 的中点O ，连接OA ，OD ，AD ，若22.5ACB ∠=︒，4BC =，则AOD △的周长是（）A ．4B ．C ．4D ．4+13．如图，ABD △是等边三角形，CBD △是等腰三角形，且BC DC =，点E 是边AD 上的一点，满足//CE AB ，如果8AB =，6CE =，那么BC 的长是（）A ．6B ．CD ．14．如图，在矩形ABCD 中，3AB =，6BC =，点O 为对角线AC 和BD 的交点，延长BA 至E ，使AE AB =，以AE 为边向右侧作矩形AEFG ，点G 在AD 上，若4AG =，过点O 的一条直线平分该组合图形的面积，并分别交EF 、BC 于点P 、Q ，则2PQ 的值为（）A ．39B ．40C ．41D ．42 15．凸n 边形恰好只有三个内角是钝角，这样的多边形边数n 的最大值是（） A ．7 B ．6 C ．5 D ．4 16．如图，点E 为菱形ABCD 边上的一个动点，并沿A →B →C →D 的路径移动，设点E 经过的路径长为x ，∠ADE 的面积为y ，则下列图象能大致反映y 与x 的函数关系的是（）A ．B ．C ．D ．17．如图，AB CD =，AD BC =，4=AD ，6BE =，DCE △的面积为3，则四边形ABCD 的面积为（）A ．10B ．12C ．15D ．2018．如图，在矩形纸片ABCD 中，5AB =，3BC =，将BCD △沿BD 折叠到BED 位置，DE 交AB 于点F ，则cos ADF ∠的值为（）A ．817B ．715C ．1517D ．815 19．如图，矩形ABCD 中，2AB =，4BC =．点E ，G 分别在边BC ，AD 上，点F ，H 在对角线AC 上．若四边形EFGH 是菱形，则AG 的长是（）A ．2BC ．52D 20．如图，矩形ABCD 中，6,8AB BC ==．点E 、F 分别为边BC 、AD 上一点，连接EF ，将矩形ABCD 沿着EF 折叠，使得点A 落到边CD 上的点A '处，且2DA A C '='，则折痕EF 的长度为（）A ．B ．C D二、填空题21．▱ABCD 中，AC 、BD 交于点O ，已知6AB =，8AC =，10BD =，则DOC 的周长为______．22．如图，平行四边形OABC 的边OA 在x 轴上，顶点C 在反比例函数y ＝k x的图象上，BC 与y 轴相交于点D ，且D 为BC 的中点，若平行四边形OABC 的面积为6，则k ＝_____．23．四边形具有不稳定性．如图，矩形ABCD 按箭头方向变形成平行四边形A B C D ''''，当变形后图形面积是原图形面积的一半时，则A '∠=________．24．如图，ABCD 的对角线交于点O ．点M ，N ，P ，Q 分别是ABCD 四条边上不重合的点．下列条件能判定四边形MNPQ 是平行四边形的有_____（填序号）． ∠,AQ CN AM CP ==；∠,MP NQ 均经过点O ：∠NQ 经过点O ，AQ CN =．25．如图，DE 为ABC ∆的中位线，点F 在DE 上，且AFC ∠为直角，若6AC cm =，8BC cm =，则DF 的长为__________cm ．26．在ABCD 中，3AD =，2AB =，则ABCD 的周长是______．27．如图，在▱ABCD 中，对角线 AC 、BD 相交于 O ，E 为 DC 边的中点，如果▱ABCD 的周长为 24，且12AB BC =，则 OE 的长为_______．28．矩形纸片ABCD ，长8cm AD =，宽4cm AB =，折叠纸片，使折痕经过点B ，交AD 边于点E ，点A 落在点A '处，展平后得到折痕BE ，同时得到线段BA '，EA '，不再添加其它线段，当图中存在30角时，AE 的长为__________厘米．29．如图，将边长为4的正方形ABCD 沿着折痕EF 折叠，使点B 落在边AD 的中点G 处，则BE 的长为________．30．各角都相等的十五边形的每个内角的度数是_____度．31．如图，在Rt ABC 中，90ACB ∠=︒，以斜边AB 为边向下作正方形ADEB ，过点E 作EF BC ∥交AC 于点F ，过点C 作CG BE ∥交EF 于点G ，连接DG ，若3AF =，15DE =，则四边形CGEB 的面积为______．32．如图，矩形ABCD的两条对角线相交于点O，CD＝A为圆心，AD长为半径画弧，此弧恰好经过点O，并与AB交于点E，则图中阴影部分的面积为_____．33．如图，在平行四边形ABCD中，AD=5，AB=3，BE平分∠ABC，则DE=_____．34．在平面直角坐标系中，直线y=﹣x+3与x轴、y轴分别交于A、B，在AOB内部作正方形，使正方形的四个顶点都落在该三角形的边上，则此正方形落在x轴正半轴的顶点坐标为_____．35．如图，在矩形ABCD中，点E在BC上，连接AE、DE，若2==，AD DE∠=︒，则CE的长为______________．BAE15AE=，四边形ABCD是平行四边形，且顶点A、B、36．如图，在半圆O中，直径10C在半圆上，点D在直径AE上，连接CE，若8AD=，则CE长为________．37．如图，正方形ABCD内接于圆O，点E为BC上一点，连接BE，若15∠=，CBE5BE =，则正方形ABCD 的边长为________，BE 的长为________．38．如图，ABCD 的顶点A 、B 的坐标分别是()1,0-、()0,2-，顶点C 、D 均在函数(0,0)k y k x x =>>的图象上，AD 交y 轴于点E ，若612ABE ABCD S S ==四边形，则k 的值为_____________．39．如图,将边长为4的正方形ABCD 纸片沿EF 折叠,点C 落在AB 边上的点G 处,点D 与点H 重合, CG 与EF 交于点P ,取GH 的中点Q ，连接PQ ,则GPQ 的周长最小值是__________．40．在ABC 中，已知45ABC ∠=，BD AC ⊥于D ，2CD =，3AD =，则BD 的长为________．三、解答题41．如图，二次函数2y x bx c =-++的图像经过()0A 1，，()03B -，两点．(1)求这个抛物线的解析式及顶点坐标；(2)在抛物线的对称轴上是否存在一点P ，使得O 、B 、C 、P 四点为顶点的四边形是平行四边形？若存在，请直接写出P 点坐标；若不存在，请说明理由．42．如图，点A 在双曲线y=（x ＞0）上，点B 在双曲线y=﹣（x ＜0）上，且AB 平行于x 轴，BC∠AO 交x 轴于点C ，交双曲线y=﹣（x ＜0）于点D ，连接AD ．（1）设点A 的纵坐标为n ，用n 表示AB 的长为_________；（2）当OC=3时，求点D 的坐标．43．已知：如图，四边形DEBF 是平行四边形，且AE CF =．求证：四边形ABCD 是平行四边形．44．已知：点D 是ABC ∆的边BC 的中点，DE AB ⊥，DF AC ⊥，垂足分别为E 、F ，且BE CF =．（1）如图1，求证：AE AF =；（2）如图2，若90BAC ︒∠=，连接AD 交EF 于M ，连接BM 、CM ，在不添加任何辅助线的情况下，直接写出图中所有与AEF ∆面积相等的等腰三角形．45．已知：如图，已知∠O 的半径为1，菱形ABCD 的三个顶点A 、B 、D 在∠O 上，且CD 与∠O 相切．（1）求证：BC 与∠O 相切；（2）求阴影部分面积．46．在综合与实践课上，老师组织同学们以“矩形的折叠”为主题开展数学活动．【动手操作】某数学小组对图1的矩形纸片ABCD 进行如下折叠操作：第一步：如图2，把矩形纸片ABCD 对折，使AD 与BC 重合，得到折痕MN ，然后把纸片展开；第二步：如图3，将图2中的矩形纸片沿过点B 的直线折叠，使得点A 落在MN 上的点A '处，折痕与AD 交于点E ，然后展开纸片，连接AA '，BA '，EA ．【问题解决】(1)观察猜想：A BC '∠=______度(2)请判断图3中ABA '△的形状，并说明理由；(3)如图4，折痕BE 与MN 交于点F ，BA '的延长线交直线CD 于点P ，若1MF =，7BC =，请求出PD 的长．47．如图，在矩形ABCD 中，E 是对角线AC 上一点（不与A 、C 重合），过点E 作EF //CD ，且EF =DC ，连接DE 、BF 、CF ．(1)如图1，若AE=AB，求证：四边形ABFE是菱形．DE∠AC时，求线段BF的长．(2)如图2，若AB=2，BC48．已知：ABCD的对角线AC、BD相交于点O，E，F分别是OA，OC的中点．(1)如图∠，求证：DF＝BE；(2)如图∠，连接DE、BF，求证：四边形DEBF是平行四边形．49．如图，在菱形ABCD中，M，N分别是边AB，BC的中点，MP∠AB交边CD于点P，连接NM，NP．（1）若∠B=60°，这时点P与点C重合，则∠NMP= 度；（2）求证：NM=NP；（3）当∠NPC为等腰三角形时，求∠B的度数．参考答案：1．B【分析】根据n 边形从一个顶点出发可引出()3n -条对角线，得出32n -=，求出n 即可．【详解】解：设这个多边形的边数是n ，由题意得32n -=，解得5n =．故选：B ．【点睛】本题考查了多边形的对角线：连接多边形不相邻的两个顶点的线段，叫做多边形的对角线．掌握n 边形从一个顶点出发可引出()3n -条对角线是解题的关键．2．D【分析】根据矩形的判定定理：对角线相等的平行四边形是矩形即可判定．【详解】解：这种做法的依据是对角线相等的平行四边形为矩形，故选D ．【点睛】本题主要考查对矩形的性质和判定的理解和掌握，能熟练地运用矩形的性质解决实际问题是解此题的关键．3．C【分析】根据直角三角形的性质求出AB ，进而求出AE 、EB ，根据三角形中位线定理得到DE ∠BC ，得到∠AED =∠AED =60°，根据等边三角形的判定定理和性质定理解答即可．【详解】解：在Rt ∠ABC 中，∠C =90°，∠A =30°，BC =4，∠AB =2BC =8，∠ABC =60°，∠E 为AB 边上的中点，∠AE =EB =4，∠D 、E 分别为A C 、AB 边上的中点，∠DE ∠BC ，∠∠AED =∠AED =60°，∠∠BEF =∠ABC =60°，在Rt ∠AED 中，∠A =30°，∠AE =2DE ，∠EF =2DE ，∠AE =EF ，∠∠BEF 为等边三角形，∠BF =BE =4，故选：C ．【点睛】本题考查的是三角形中位线定理、等边三角形的判定和性质、直角三角形的性质，掌握三角形的中位线平行于第三边，并且等于第三边的一半是解题的关键． 4．B【分析】设这个多边形有n 条边，根据内角和是它的外角和的5倍，列出方程，然后解方程即可．【详解】解：设这个多边形有n 条边．由题意得：(2)1803605n -⨯︒=︒⨯，解得n =12．故这个多边形的边数是12．故选B【点睛】此题主要考查了多边形的外角和，内角和公式，做题的关键是正确把握多边形的内角和公式为：2180()n -⨯︒，外角和为360°．5．A【分析】由矩形的性质可得3AB CD ==，4CB AD ==，////AD BC x 轴，////AB CD y 轴，则可求点D 坐标．【详解】解：四边形ABCD 是矩形3AB CD ∴==，4CB AD ==，//AD BC ，//AB CD ，且//AB y 轴，////AD BC x ∴轴，////AB CD y 轴，(1,1)B --，3AB =，4BC =，∴点C 横坐标为3，点A 纵坐标为2，∴点D 坐标为(3,2)，故选：A ．【点睛】本题考查了矩形的性质，坐标与图形性质，熟练运用矩形的性质是本题的关键． 6．C【分析】平行四边形的判定定理：（1）两组对边分别平行的四边形是平行四边形（2）两组对边分别相等的四边形是平行四边形（3）一组对边平行且相等的四边形是平行四边形（4）两组对角分别相等的四边形是平行四边形（5）对角线互相平分的四边形是平行四边形．根据平行四边形的判定定理逐个分析即可解答．【详解】解：A、AB//CD，AD＝BC不能判定四边形ABCD是平行四边形，故此选项错误；B、∠A＝∠D，∠B＝∠C不能判定四边形ABCD是平行四边形，故此选项错误；C、因为∠A＋∠B＝180°，所以AD//BC，又因为AB//CD，所以四边形ABCD是平行四边形，故此选项正确；D、∠A＝∠C，∠B＋∠D＝180°不能判定四边形ABCD是平行四边形，故此选项错误；故选C．【点睛】本题主要考查平行四边形的判定定理，解决本题的关键是要熟练掌握平行四边形的判定定理.7．D【详解】试题分析：A、同一底上两个角相等的梯形可能是等腰梯形也可能是直角梯形，故A选项错误；B、一组对边平行且相等的四边形不一定是平行四边形，故B选项错误；C、如果顺次连接一个四边形各边中点得到的是一个正方形，那么原四边形对角线相等且互相垂直，不是任意的四边形，故C选项错误；D、对角线互相垂直的四边形面积等于对角线乘积的一半，故D选项正确．故选D．考点：1.等腰梯形的判定；2.平行四边形的判定；3.正方形的判定．8．D【详解】试题分析：根据特殊四边形的性质逐一作出判断：A .梯形的对角线不一定相等，命题错误；B.当菱形满足一个角是直角，即为正方形时，菱形的对角线相等，命题错误；C.当矩形满足一组邻边相等，即为正方形时，矩形的对角线互相垂直，命题错误；D.当平行四边形满足一组邻边相等，即为菱形时，平行四边形的对角线可以互相垂直，命题正确.故选D.考点：特殊四边形的性质.9．B【分析】根据三角形中位线定理得到DE=12AC=5，根据中点定义可得BE=CE=6，BD=12AB=4，再根据三角形的周长公式得到BD+BE+DE，计算即可．【详解】解：∠点D、E分别是△ABC的边AB、CB的中点，∠DE=12AC=5，BE=CE=6，BD=12AB=4，∠△BDE的周长=BD+BE+DE=4+6+5=15，故选：B．【点睛】本题考查三角形中位线性质，熟练掌握三角形中位线性质是解题的关键．10．D【详解】试题分析：正多边形的边数=外角和÷每个外角的度数.考点：多边形的外角11．A【分析】连接BD交EF于O，由折叠的性质可推出BD∠EF，BO＝DO，然后证明∠EDO∠∠FBO，得到OE＝OF，设BC＝x，利用勾股定理求BO，再根据∠BOF∠∠BCD，列出比例式求出x，即可求矩形面积．【详解】解：连接BD交EF于O，如图所示：∠折叠纸片使点D与点B重合，折痕为EF，∠BD∠EF，BO＝DO，∠四边形ABCD是矩形，∠AD∠BC∠∠EDO=∠FBO在∠EDO和∠FBO中，∠∠EDO=∠FBO，DO=BO，∠EOD=∠FOB=90°∠∠EDO∠∠FBO（ASA）∠OE ＝OF ＝12EF ∠四边形ABCD 是矩形，∠AB ＝CD ＝4，∠BCD ＝90°，设BC ＝x ，BD∠BO ， ∠∠BOF ＝∠C ＝90°，∠CBD ＝∠OBF ，∠∠BOF ∠∠BCD ， ∠OB BC ＝OF CD，即：2x 解得：x ＝8，∠BC ＝8，∠S 矩形ABCD ＝AB •BC ＝4×8＝32，故选：A ．【点睛】本题考查矩形的折叠问题，熟练掌握折叠的性质，全等三角形的判定，以及相似三角形的判定与性质是解题的关键．12．D【分析】根据直角三角形斜边的中线等于斜边的一半可得AOC 和BOD 均为等腰三角形，由22.5ACB ∠=︒，可得：45AOB DOC ∠=∠=︒，证得AOD △为等腰直角三角形，根据勾股定理求得AD =【详解】解：由题意可知ABC 与DBC △全等，且都为直角三角形，∠点O 是BC 的中点， ∠122OA OD BC BO CO =====， ∠AOC 和BOD 均为等腰三角形，∠22.5ACB ∠=︒，∠22.5OAC ∠=︒，∠45AOB OAC ACB ∠=∠+∠=︒，同理可得：45DOC ∠=︒，∠18090AOD AOB COD ∠=︒-∠-∠=︒，在Rt AOD 中，AD∠AOD △的周长是224AD OA OD ++=+=+故选：D ．【点睛】本题考查了矩形的性质，全等三角形的性质，直角三角形斜边的中线，勾股定理等知识，根据题意证出AOD △为等腰直角三角形是解题的关键．13．B【分析】连结AC ，过E 作EF ∠AB 于F ，过C 作CG ∠AB 于G ，先确定AC 为对称轴，得到∠BAC =∠DAC ，∠ACB =∠ACD ，由CE∥AB ，可得∠ECA =∠BAC =∠EAC ，得等腰三角形AE =CE =6，求出AF =AE cos60°=3，EF =AE sin60°=EFGC 为矩形，求出GB = AF +FG -AB =1，在Rt △BCG 中，由勾股定理BC【详解】解：连结AC ，过E 作EF ∠AB 于F ，过C 作CG ∠AB 于G ，∠△ABC 为等边三角形，△BCD 为等腰三角形，AC 为对称轴，∠∠BAC =∠DAC ，∠ACB =∠ACD ，∠CE∥AB ，∠∠ECA =∠BAC =∠EAC ，∠AE =CE =6，∠AF =AE cos60°=61=32⨯，∠EF =AE sin60°=6 ∠CE∥AB ，EF ∠AB ， CG ∠AB ，∠FE ∠EC ，CG ∠EC ，∠∠EFG =∠FEC =∠CGF =90°∠四边形EFGC 为矩形，∠EF =CG CE =FG =6，∠GB = AF +FG -AB =3+6-8=1，在Rt ∠BCG 中，由勾股定理BC =故选择：B ．【点睛】本题考查等边三角形性质，等腰三角形判定与性质，锐角三角函数，矩形判定与性质，勾股定理，掌握等边三角形性质，等腰三角形判定与性质，锐角三角函数，矩形判定与性质，勾股定理是解题关键．14．B【分析】根据题意可得PQ 必过矩形EFGA 的对角线交点，连接AF ，EG 交于点H ，取AE 的中点M ，AB 的中点N ，连接HM ，ON ，过点H 作HT ∠ON 于T ，设PQ 与AD 的交点为S ，根据三角形中位线定理可得133,22ON BC AN ===，∠ANO =∠ABC =90°，32,2NH AM ==，∠AMH =90°，再由勾股定理可得OH 的长，再证明∠ASO ∠∠CQO ，可得SO =OQ ，即可求解．【详解】解：∠过点O 的一条直线平分该组合图形的面积，∠PQ 必过矩形EFGA 的对角线交点，连接AF ，EG 交于点H ，取AE 的中点M ，AB 的中点N ，连接HM ，ON ，过点H 作HT ∠ON 于T ，设PQ 与AD 的交点为S ，∠四边形ABCD 是矩形，∠AO =CO ，又∠点N 是AB 的中点，∠133,22ON BC AN ===，ON ∠BC ， ∠∠ANO =∠ABC =90°，同理：32,2NH AM ==，∠AMH =90°，∠HT∠NO，∠四边形MHTN为矩形，∠MH=NT=2，MT=MN=3，∠TO=1，∠HO=∠AD∠BC，∠∠DAC=∠BCA，∠ASO=∠CQO，在∠ASO和∠CQO中，∠DAC ACBASO CQOAO CO∠=∠⎧⎪∠=∠⎨⎪=⎩，∠∠ASO∠∠CQO（AAS），∠SO=OQ，同理PH=SH，∠2PQ HO==∠240PQ=．故选：B【点睛】本题考查了矩形的性质，三角形中位线定理，全等三角形的判定和性质，勾股定理，灵活运用这些性质解决问题是本题的关键．15．B【分析】由题意知在n边形的外角中恰好有3个锐角，则其余（n－3）个外角是直角或钝角，而n个外角中最多只能有4个直角或3个钝角，而4个直角已不可能，所以n－3≤3，由此即得答案.【详解】解：因为n 边形恰好只有三个内角是钝角，所以在n 边形的外角中恰好有3个锐角，所以其余（n －3）个外角是直角或钝角，又由于n 边形的外角和是360°，其n 个外角中最多只能有4个直角或3个钝角，而4个直角显然已不可能，所以n －3≤3，解得n ≤6，即n 的最大值为6.故选B.【点睛】本题考查了多边形的内角、外角的概念与外角和，从多边形的外角的角度入手分析是解题的关键.16．D【分析】分三段来考虑点E 沿A→B 运动，∠ADE 的面积逐渐变大；点E 沿B→C 移动，∠ADE 的面积不变；点E 沿C→D 的路径移动，∠ADE 的面积逐渐减小，据此选择即可．【详解】解：点E 沿A →B 运动，∠ADE 的面积逐渐变大，设菱形的边长为a ，∠A ＝β， ∠AE 边上的高为AB sinβ＝a •sinβ，∠y ＝12•a •sinβ，点E 沿B →C 移动，∠ADE 的面积不变；点E 沿C →D 的路径移动，y ＝12(3a ﹣x )•sinβ，∠ADE 的面积逐渐减小．故选：D ．【点睛】本题考查了动点问题的函数图像，分析判断几何动点问题的函数图象的题目一般有两种类型：（1）观察型（函数的图象有明显的增减性差异）：根据题目描述，只需确定函数值在每段函数图象上随自变量的增减情况或变化的快慢即可得解．（2）计算型：先根据自变量的取值范围对函数进行分段，再求出每段函数的解析式，最后由每段函数的解析式确定每段函数的图象．17．B【分析】根据两组对边分别相等的四边形是平行四边形证明四边形ABCD 是平行四边形，再根据DCE △的面积为3计算出DH ，最后根据平行四边形的面积公式即可得到答案．【详解】解：过点D 作DH CE ⊥，垂足为H ，∠AB CD =，AD BC =，∠四边形ABCD 是平行四边形，∠2CE BE BC BE AD =-=-=， ∠112322DCE S CE DH DH =⨯=⨯⨯=， ∠3DH =，∠4312ABCD S BC DH =⨯=⨯=，故选：B ．【点睛】本题考查平行四边形的判断，解题的关键是熟知两组对边分别相等的四边形是平行四边形．18．C【分析】先根据矩形的性质和折叠的性质，利用“AAS”证明AFD EFB ∆∆≌，得出AF EF =，DF BF =，设AF EF x ==，则5BF x =-，根据勾股定理列出关于x 的方程，解方程得出x 的值，最后根据余弦函数的定义求出结果即可．【详解】解：∠四边形ABCD 为矩形，∠CD =AB =5，AB =BC =3，90A C ∠=∠=︒，根据折叠可知，3BE BC ==，5DE DE ==，90∠=∠=︒E C ，∠在∠AFD 和∠EFB 中903A E AFD EFB AD BE ∠=∠=︒⎧⎪∠=∠⎨⎪==⎩，∠AFD EFB ∆∆≌（AAS ），∠AF EF =，DF BF =，设AF EF x ==，则5BF x =-，在Rt BEF ∆中，222BF EF BE =+，即()22253x x -=+，解得：85x =，则817555DF BF ==-=， ∠315cos 17175AD ADF DF ∠===，故C 正确．故选：C ．【点睛】本题主要考查了矩形的折叠问题，三角形全等的判定和性质，勾股定理，三角函数的定义，根据题意证明AFD EFB ∆∆≌，是解题的关键．【分析】连接EG 交AC 于O ，根据菱形和矩形的性质证明∠CEO ∠∠AGO ，推出AO=CO ，由勾股定理求出AC 得到AO ，再证明∠AOG ∠∠ADC ，得到AG AO AC AD=，代入数值即可求出AG ．【详解】解：连接EG 交AC 于O ，∠四边形EFGH 是菱形，∠EG ∠FH ，OE=OG ，∠四边形ABCD 是矩形，∠∠B =∠D =90°，AD BC ∥，∠∠ACB =∠CAD ，∠∠CEO ∠∠AGO ，∠AO=CO ，∠AC ==∠12AO AC == ∠∠AOG =∠D =90°，∠OAG =∠CAD ，∠∠AOG ∠∠ADC ， ∠AG AO AC AD=，=， ∠AG =52故选：C ．【点睛】此题考查了菱形的性质，矩形的性质，勾股定理，全等三角形的判定及性质，相似三角形的判定及性质，是图形类的综合题，熟练掌握各知识点是解题的关键．【分析】由2DA A C '='，6DC =，可求出DA '，A C '的长，再根据折叠和勾股定理可求出DF 和FA '，依据三角形相似可求出NC 、NA '，进而求出MF ，最后根据勾股定理求出EF ．【详解】解：如图，过点E 作EM AD ⊥，垂足为M ，2DA A C ''=，6DC =， 243DA DC '==，123A C DC '==，由折叠得，AF FA ='，6AB A B =''=，设DF x =，则8FA FA x ='=-，在Rt DFA ∆'中，由勾股定理得，2224(8)x x +=-，解得3x =，即3DF =，835FA FA ∴='=-=，1809090NAC DA F ∠'+∠'=︒-︒=︒，90NAC A NC ∠'+∠'=︒，DA F A NC ∴∠'=∠'，90C D ∴∠=∠=︒，∴∠A NC '∽∠FA D '，∴A C NC A N FD A D FA ''==''，即2345NC A N '==，解得83NC =，103A N '=， 108633B N A B A N NC ∴'=''-'=-==， ∴∠()A CN ENB AAS '≅∆'，103EN A N ∴='=， 108633EC EN NC MD ∴=+=+==， 633MF ∴=-=，在Rt EFM ∆中，EF故选：A ．【点睛】本题考查矩形的性质、折叠轴对称、相似三角形、全等三角形以及勾股定理等知识，掌握折叠的性质和直角三角形的边角关系是得出答案的前提，建立图形中线段之间的关系是解决问题的关键．21．15【分析】根据平行四边形的对角线互相平分，求得OC 与OD 的长，继而可求得答案．【详解】解：四边形ABCD 是平行四边形，142OC AC ∴==，152OD BD ==，6CD AB ==， OCD ∴△的周长为：64515CD OC OD ++=++=．故答案为：15．【点睛】本题重点考查了平行四边形的性质，并利用性质解题．平行四边形基本性质：∠平行四边形两组对边分别平行；∠平行四边形的两组对边分别相等；∠平行四边形的两组对角分别相等；∠平行四边形的对角线互相平分．22．3-【分析】由D 为BC 的中点，平行四边形OABC 的面积为6，可得∠OCD 的面积为平行四边形OABC 的面积的14，再根据反比例函数系数k 的几何意义即可求出答案．【详解】解：∠D 为BC 的中点，平行四边形OABC 的面积为6，∠∠OCD 的面积为6×14＝1.5， ∠12|k |＝1.5， ∠k ＜0，∠3k =-．故答案为：3-．【点睛】本题考查了反比例函数k 的几何意义，平行四边形的性质，求得∠OCD 的面积是解题的关键．23．30︒【分析】根据矩形和平行四边形的面积公式可知，平行四边形A 'B 'C 'D '的底边A D ''边上的高等于A B ''的一半，据此可得∠A '为30°．【详解】解：如图，过点B '作B E A D '⊥''于点E ．设矩形ABCD 的边AD 长为a ，AB 长为b ，B E '长为c ，则ABCD S ab =矩形，A B C D Sac ''''=． ∠12A B C D ABCDS S ''''=矩形， ∠12ac ab =， ∠12c b =， ∠sin A '12c b ==， ∠30A ∠'=︒．【点睛】本题主要考查了四边形的不稳定性、矩形与平行四边形的面积公式、解直角三角形等相关知识，熟记特殊角的三角函数值是解答本题的关键．24．∠∠##∠∠【分析】∠根据平行四边形的性质结合已知条件，证明AMQ CPN ≌，DQP BNM ≌，可得MQ NP =，MN PQ =，根据两组对边相等的四边形是平行四边形，即可判断∠，∠根据平行四边形是中心对称图形，即可判断∠，根据已知条件不能判断∠．【详解】解：∠四边形ABCD 是平行四边形A C ∴∠=∠，B D ∠=∠,,AD BC AB CD == ∠,AQ CN AM CP ==∠AMQ CPN ≌∠MQ NP =,AQ CN AM CP ==∴,DQ BN DP BM ==又B D ∠=∠DQP BNM ∴≌MN PQ ∴=∴四边形MNPQ 是平行四边形故∠正确 ∠四边形ABCD 的对角线交于点O ,,MP NQ 均经过点O ：,OQ ON OM OP ∴==∴四边形MNPQ 是平行四边形故∠正确∠NQ 经过点O ，AQ CN =，,M P 的位置未知，不能判断四边形MNPQ 是平行四边形故∠不正确故答案为：∠∠【点睛】本题考查了平行四边形的性质与判定，掌握平行四边形的性质与判定是解题的关键．25．1【分析】根据三角形中位线定理求出DE ，根据直角三角形的性质求出EF ，结合图形计算即可．【详解】∠DE 为△ABC 的中位线， ∠DE=12BC=4(cm)， ∠∠AFC 为直角，E 为AC 的中点， ∠FE=12AC=3(cm)，∠DF=DE−FE=1(cm)，故答案为1cm.【点睛】此题考查三角形中位线定理，解题关键在于掌握其性质定义.26．10【分析】平行四边形的两组对边相等，以此便可求解．【详解】解：如图：平行四边形ABCD 的周长为：2()2(32)10AD AB +=⨯+=．故答案是：10．【点睛】本题考查平行四边形两组对边相等的性质，解题的关键是掌握其性质． 27．4【分析】直接利用三角形中位线的性质，证明EO ＝AB ，然后根据平行四边形的性质列方程得出答案．【详解】解：∠四边形ABCD 是平行四边形，∠AB ＝DC ，BO ＝DO ，又∠E 为DC 边的中点，∠EO 是△DBC 的中位线，∠EO ＝12BC ， ∠EO ＝AB∠▱ABCD 的周长为24，∠设AB ＝x ，则BC ＝2x ，则2（x ＋2x ）＝24，解得：x ＝4，故EO ＝4．故答案为4．【点睛】此题主要考查了平行四边形的性质、三角形中位线的性质等，正确得出EO 是△DBC 的中位线是解题关键．28 8-【分析】分∠ABE=30°或∠AEB=30°或∠ABA′=30°时三种情况，利用锐角三角函数进行求解即可．【详解】解：当∠ABE=30°时，∠AB=4cm ，∠A=90°，；当∠AEB=30°时，则∠ABE=60°，∠AB=4cm ，∠A=90°，∠AE=AB·tan60°=；当∠ABE=15°时，∠ABA′=30°，延长BA′交AD 于F ，如下图所示，设AE=x ，则EA′=x ，sin 60x EF ==︒∠x +=∠8x =-∠8AE =-cm ．8- 【点睛】本题考查了矩形与折叠，以及分类讨论的数学思想，分类讨论是解答本题的关键．29．2.5【分析】由折叠的性质可得CF=HF ，BE=GE ，设BE=GE=x ，则AE=4-x ，在Rt △AEG 中利用勾股定理求出x 的值．【详解】解：由题意，点C 与点H ，点B 与点G 分别关于直线EF 对称，∠CF=HF ，BE=GE ，设BE=GE=x ，则AE=4-x ，∠四边形ABCD 是正方形，∠∠A=90°，∠AE 2+AG 2=EG 2，∠B 落在边AD 的中点G 处，∠AG=2，∠（4-x ）2+22=x 2，解得：x=2.5，∠BE=2.5．故答案为：2.5．【点睛】本题考查了折叠问题与勾股定理以及正方形的性质，掌握翻折的性质是解题的关键．30．156【分析】根据多边形的内角和公式即可得出结果．【详解】解：∠十五边形的内角和＝（15﹣2）•180°＝2340°，又∠十五边形的每个内角都相等，∠每个内角的度数＝2340°÷15＝156°．故答案为156．【点睛】本题考查了多边形的内角和计算公式．多边形内角和定理：多边形内角和等于（n ﹣2）•180°．31．81【分析】先证明四边形CGBE 是平行四边形，然后证明CGF BAC ≌，再解直角三角形即可求得BH 的长度，进而根据BE BH ⨯即可求得答案．【详解】如图，设,AB CG 交于点H ，四边形ADEB 是正方形，15AB BE ∴==，EF BC ∥,CG BE ∥，∴四边形CGBE 是平行四边形，15CG BE AB ∴===，BE AB ⊥，CG AB ∴⊥，90ABC HCB ∴∠+∠=︒，90ACB ∠=︒，∴90ABC CAB ∠+∠=︒，HCB CAB ∴∠=∠，EF BC ∥，HCB CGF ∴∠=∠，90GFC ACB ∠=∠=︒，CGF BAC ∴∠=∠，∴CGF BAC ≌，CB FC ∴=，设CB x =，则3AC AF FC x =+=+，Rt ABC 中，222AB AC BC =+，即()222153x x =++，解得9x =或12x =-（舍）， 9312,9AC BC ∴=+==，93cos 155BC CBA AB ∴∠===， 327cos 955HB BC CBA ∴=⋅∠=⨯=， ∴平行四边形CGEB 的面积为BE BH ⨯2715815BE BH =⨯=⨯=，故答案为：81．【点睛】本题考查了正方形的性质，平行四边形的判定，全等三角形的性质与判定，勾股定理，解直角三角形等知识，熟练掌握知识间的联系，是解答本题的关键.32．43π 【分析】根据题意得到ADO ∆是等边三角形，从而得到角度，再结合特殊角的直角三角形三边关系得到4=AD ，8AC =，分别求出ACD S ∆=83AOD S π=扇形，43AOE S π=扇形，最后根据图形得到=ACD AOD AOE S S S S ∆-+阴影扇形扇形，代值求解即可．【详解】解：矩形ABCD 的两条对角线相交于点O ，OA OB OC OD ∴===，以点A 为圆心，AD 长为半径画弧，此弧恰好经过点O ，AO AD OD ∴==，即ADO ∆是等边三角形，60DAO ∴∠=︒，30OAE ∠=︒，在Rt ACD ∆中，30ACD OAE ∠=∠=︒，90ADC ∠=︒，CD =4=AD ，8AC =， 11422ACD S AD CD ∆∴==⨯⨯ 260843603AOD S ππ︒=⨯⨯=︒扇形， 230443603AOE S ππ︒=⨯⨯=︒扇形， 844=333ACD AOD AOE S S S S πππ∆∴-+=+=阴影扇形扇形，故答案为：43π 【点睛】本题考查阴影图形面积，对于不规则图形面积求解，我们要根据题中图形转化为规则图形面积间接表示出来，在求解此题过程中涉及到矩形的性质、等边三角形的判定与性质、特殊角度的直角三角形三边关系、三角形面积公式和扇形面积公式，将阴影部分面积转化为常见图形面积来间接求解是解决问题的关键．33．2【分析】根据平行四边形性质求出AD∠BC ，由平行线的性质可得∠AEB=∠CBE ，然后由角平分线的定义知∠ABE=∠AEB ，所以∠ABE=∠AEB ，即可得AB=AE ，由此即可求出DE 的长．【详解】∠四边形ABCD 是平行四边形，∠AD∠BC ，∠∠AEB=∠CBE ．∠BE 平分∠ABC ，∠∠ABE=∠CBE ，∠∠ABE=∠AEB ，∠AB=AE=3，∠DE=AD-AE=5-3=2．故答案是：2．【点睛】本题考查了平行四边形性质、三角形的角平分线的定义，平行线的性质的应用，证得AB=AE 是解题的关键．34．（1.5，0）或（1，0）．。

初中几何辅助线——四边形辅助线大全

初中几何辅助线——四边形辅助线大全题型1.平行四边形的两邻边之和等于平行四边形周长的一半.例1已知,□ABCD的周长为60cm，对角线AC、BD相交于点O，△AOB的周长比△BOC的周长多8cm，求这个四边形各边长.解：∵四边形ABCD为平行四边形∴AB = CD，AD = CB，AO = CO∵AB＋CD＋DA＋CB = 60AO＋AB＋OB－(OB＋BC＋OC) = 8∴AB＋BC = 30，AB－BC =8∴AB = CD = 19，BC = AD = 11答：这个四边形各边长分别为19cm、11cm、19cm、11cm.题型 2.平行四边形被对角线分成四个小三角形，相邻两个三角形周长之差等于邻边之差.（例题如上）题型3.有平行线时常作平行线构造平行四边形.例2已知，如图，Rt△ABC，∠ACB = 90o，CD⊥AB于D，AE平分∠CAB交CD于F，过F 作FH∥AB交BC于H求证：CE = BH证明：过F作FP∥BC交AB于P，则四边形FPBH 为平行四边形∴∠B =∠FP A，BH = FP∵∠ACB = 90o，CD⊥AB∴∠5＋∠CAB = 45o，∠B＋∠CAB = 90o∴∠5 =∠B∴∠5 =∠FP A又∵∠1 =∠2，AF = AF∴△CAF≌△P AF∴CF = FP∵∠4 =∠1＋∠5，∠3 =∠2＋∠B∴∠3 =∠4∴CF = CE∴CE = BH练习：已知，如图，AB∥EF∥GH，BE = GC求证：AB = EF＋GH54321PHFEDCB AGHFEB AC题型4.有以平行四边形一边中点为端点的线段时常延长此线段.例3已知，如图，在□ABCD中，AB = 2BC，M为AB中点求证：CM⊥DM证明：延长DM、CB交于N∵四边形ABCD为平行四边形∴AD = BC，AD∥BC∴∠A = ∠NBA∠ADN=∠N又∵AM = BM∴△AMD≌△BMN∴AD = BN∴BN = BC∵AB = 2BC，AM = BM∴BM = BC = BN∴∠1 =∠2，∠3 =∠N∵∠1＋∠2＋∠3＋∠N = 180o，∴∠1＋∠3 = 90o∴CM⊥DM题型5.平行四边形对角线的交点到一组对边距离相等.例4如图：OE=OF题型 6.平行四边形一边（或这边所在的直线）上的任意一点与对边的两个端点的连线所构成的三角形的面积等于平行四边形面积的一半.例5如图：S△BEC= 12S□ABCD题型7.平行四边形内任意一点与四个顶点的连线所构成的四个三角形中，不相邻的两个三角形的面积之和等于平行四边形面积的一半.例6如图：S△AOB＋S△DOC= S△BOC＋S△AOD = 12S□ABCDEDCBAODCBA321NM BAD CFEODCBA题型8.任意一点与同一平面内的矩形各点的连线中，不相邻的两条线段的平方和相等. 例7如图：AO 2＋OC 2 = BO 2 ＋DO 2题型9.平行四边形四个内角平分线所围成的四边形为矩形.例8如图：四边形GHMN 是矩形（题型5～题型9请自己证明）题型10.有垂直时可作垂线构造矩形或平行线.例9已知，如图，E 为矩形ABCD 的边AD 上一点，且BE = ED ，P 为对角线BD 上一点，PF ⊥BE 于F ，PG ⊥AD 于G 求证：PF ＋PG = AB证明：证法一：过P 作PH ⊥AB 于H ，则四边形AHPG 为矩形∴AH = GP PH ∥AD ∴∠ADB =∠HPB∵BE = DE ∴∠EBD = ∠ADB ∴∠HPB =∠EBD 又∵∠PFB =∠BHP = 90o∴△PFB ≌△BHP∴HB = FP∴AH ＋HB = PG ＋PF 即AB = PG ＋PF证法二：延长GP 交BC 于N ，则四边形ABNG 为矩形，（证明略）NP H G FE D C B AN M HG DCBAA DC B OO B CD A题型11.直角三角形常用辅助线方法⑴作斜边上的高例10已知，如图,若从矩形ABCD的顶点C作对角线BD的垂线与∠BAD的平分线交于点E 求证：AC = CE证明：过A作AF⊥BD，垂足为F，则AF∥EG∴∠F AE = ∠AEG∵四边形ABCD为矩形∴∠BAD = 90o OA = OD∴∠BDA =∠CAD∵AF⊥BD∴∠ABD＋∠ADB= ∠ABD＋∠BAF= 90o∴∠BAF =∠ADB =∠CAD∵AE为∠BAD的平分线∴∠BAE =∠DAE∴∠BAE－∠BAF =∠DAE－∠DAC即∠F AE =∠CAE∴∠CAE =∠AEG∴AC = EC⑵作斜边中线，当有下列情况时常作斜边中线①有斜边中点时例11已知，如图，AD、BE是△ABC的高，F是DE的中点，G是AB的中点求证：GF⊥DE证明：连结GE、GD∵AD、BE是△ABC的高，G是AB的中点∴GE = 12AB，GD =12AB∴GE = GD∵F是DE的中点∴GF⊥DE②有和斜边倍分关系的线段时例12已知，如图，在△ABC中，D是BC延长线上一点，且DA⊥BA于A，AC = 12 BD求证：∠ACB = 2∠B证明：取BD中点E，连结AE，则AE = BE = 12 BD∴∠1 =∠BGOFEDCBAFEDCBA∵AC =12BD ∴AC = AE∴∠ACB =∠2 ∵∠2 =∠1＋∠B ∴∠2 = 2∠B ∴∠ACB = 2∠B题型12.正方形一条对角线上一点到另一条对角线上的两端距离相等.例13已知，如图，过正方形ABCD 对角线BD 上一点P ，作PE ⊥BC 于E ，作PF ⊥CD 于F 求证：AP = EF证明:连结AC 、PC∵四边形ABCD 为正方形∴BD 垂直平分AC ，∠BCD = 90o∴AP = CP∵PE ⊥BC ，PF ⊥CD ，∠BCD = 90o ∴四边形PECF 为矩形 ∴PC = EF ∴AP = EF 题型13.有正方形一边中点时常取另一边中点.例14已知,如图，正方形ABCD 中，M 为AB 的中点，MN ⊥MD ，BN 平分∠CBE 并交MN 于N求证：MD = MN证明：取AD 的中点P ，连结PM ，则DP = P A =12AD ∵四边形ABCD 为正方形 ∴AD = AB , ∠A =∠ABC = 90o∴∠1＋∠AMD = 90o ，又DM ⊥MN ∴∠2＋∠AMD = 90o ∴∠1 =∠2 ∵M 为AB 中点∴AM = MB = 12AB∴DP = MB AP = AM ∴∠APM =∠AMP = 45o ∴∠DPM =135o ∵BN 平分∠CBE ∴∠CBN = 45o∴∠MBN =∠MBC ＋∠CBN = 90o ＋45o = 135o 即∠DPM =∠MBN ∴△DPM ≌△MBN21EDCBAP F ED CB A21P NEDCA∴DM = MN注意：把M 改为AB 上任一点，其它条件不变，结论仍然成立。

辅助线练习题

一、由角平分线想到的辅助线口诀：图中有角平分线，可向两边作垂线。

也可将图对折看，对称以后关系现。

角平分线平行线，等腰三角形来添。

角平分线加垂线，三线合一试试看。

（一）、截取构全等例1．如图1-2，AB//CD ，BE 平分∠ABC ，CE 平分∠BCD ，点E 在AD 上，求证：BC=AB+CD 。

例2．已知：如图1-3，AB=2AC ，∠BAD=∠CAD ，DA=DB ，求证DC ⊥AC例3．已知：如图1-4，在△ABC 中，∠C=2∠B,AD 平分∠BAC ，求证：AB-AC=CD图1-2ADBCEF图1-3ABCDE图1-4A BCDE（二）、角分线上点向角两边作垂线构全等例1．如图2-1，已知AB>AD, ∠BAC=∠FAC,CD=BC 。

求证：∠ADC+∠B=180例2．如图2-2，在△ABC 中，∠A=90 ，AB=AC ，∠ABD=∠CBD 。

求证：BC=AB+AD例3．已知如图2-3，△ABC 的角平分线BM 、CN 相交于点P 。

求证：∠BAC 的平分线也经过点P 。

（三）：作角平分线的垂线构造等腰三角形例1．已知：如图3-1，∠BAD=∠DAC ，AB>AC,CD ⊥AD 于D ，H 是BC 中点。

求证：DH=21（AB-AC ）图2-1ABCDEF图2-2ABCDE图2-3PABC M NDF 图示3-1ABCDHE例2．已知：如图3-2，AB=AC ，∠BAC=90 ，AD 为∠A BC 的平分线，CE ⊥BE.求证：BD=2CE 。

例3．已知：如图3-3在△ABC 中，AD 、AE 分别∠BAC 的内、外角平分线，过顶点B 作BFAD ，交AD 的延长线于F ，连结FC 并延长交AE 于M 。

求证：AM=ME 。

例4．已知：如图3-4，在△ABC 中，AD 平分∠BAC ，AD=AB ，CM ⊥AD 交AD 延长线于M 。

求证：AM=21（AB+AC ）图3-2DABEFC图3-3DBEFN ACM图3-4nEBAD CMF（四）、以角分线上一点做角的另一边的平行线图4-2图4-1CABC BA FIEDHG例4 如图，AB>AC, ∠1=∠2，求证：AB －AC>BD －CD 。

2022年冀教版八年级数学下册第二十二章四边形章节训练试题(含答案解析)

八年级数学下册第二十二章四边形章节训练考试时间：90分钟；命题人：数学教研组考生注意：1、本卷分第I卷（选择题）和第Ⅱ卷（非选择题）两部分，满分100分，考试时间90分钟2、答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上3、答案必须写在试卷各个题目指定区域内相应的位置，如需改动，先划掉原来的答案，然后再写上新的答案；不准使用涂改液、胶带纸、修正带，不按以上要求作答的答案无效。

第I卷（选择题 30分）一、单选题（10小题，每小题3分，共计30分）1、若一个多边形截去一个角后变成了六边形，则原来多边形的边数可能是（）A．5或6 B．6或7 C．5或6或7 D．6或7或82、如图，已知长方形ABCD，R，P分别是DC，BC上的点，E，F分别是AP，RP的中点，当点P在BC上从点B向点C移动，而点R不动时，那么下列结论成立的是（）A．线段EF的长逐渐增大B．线段EF的长逐渐减少C．线段EF的长不变D．线段EF的长先增大后变小3、下列命题中是真命题的是（）．A．有一组邻边相等的平行四边形是菱形B．对角线互相垂直且相等的四边形是菱形C．对角线相等的四边形是矩形D．有一个角为直角的四边形是矩形4、如图，为了测量一块不规则绿地B，C两点间的距离，可以在绿地的一侧选定一点A，然后测量出AB，AC的中点D，E，如果测量出D，E两点间的距离是8m，那么绿地B，C两点间的距离是（）A ．4mB ．8mC ．16mD ．20m5、如图，在▱ABCD 中，点E 在边BC 上，连接AE ，EM ⊥AE ，垂足为E ，交CD 于点M ．AF ⊥BC ，垂足为F ．BH ⊥AE ，垂足为H ，交AF 于点N ，连接AC 、NE .若AE =BN ，AN =CE ，则下列结论中正确的有（）个．①ANB CEA ≌△△；②ABC 是等腰直角三角形；③NFE 是等腰直角三角形；④ANE ECM ≌△△；⑤AD EC =+．A ．1B ．3C ．4D ．56、如图，四边形ABCD 的对角线交于点O ，下列哪组条件不能判断四边形ABCD 是平行四边形（）A ．OA ＝OC ，OB ＝ODB ．AB ＝CD ，AO ＝COC ．AB ＝CD ，AD ＝BC D ．∠BAD ＝∠BCD ，AB ∥CD7、如图，任意四边形ABCD 中，E ，F ，G ，H 分别是各边上的点，对于四边形E ，F ，G ，H 的形状，小聪进行了探索，下列结论错误的是（）A．E，F，G，H是各边中点．且AC=BD时，四边形EFGH是菱形B．E，F，G，H是各边中点．且AC⊥BD时，四边形EFGH是矩形C．E，F，G，H不是各边中点．四边形EFGH可以是平行四边形D．E，F，G，H不是各边中点．四边形EFGH不可能是菱形8、如图，已知菱形ABCD的边长为2，∠DAB＝60°，则对角线BD的长是（）A．1 B．4 C．2 D．69、将一张长方形纸片按如图所示的方式折叠，BD、BE为折痕，则∠EBD的度数（）A．80°B．90°C．100°D．110°10、下列多边形中，内角和与外角和相等的是（）A．B．C．D．第Ⅱ卷（非选择题 70分）二、填空题（5小题，每小题4分，共计20分）1、如图，90,ACB AC BC ∠=︒=，D 为ABC 外一点，且,AD BD DE AC =⊥交CA 的延长线于E 点，若1,3AE ED ==，则BC =_______．2、如图，四边形ABCD 是平行四边形，BE 平分∠ABC ，与AD 交于点E ，BC ＝5，DE ＝2，则AB 的长为 ___．3、如图，正方形ABCD 的边长为4，E 是BC 的中点，在对角线BD 上有一点P ，则PC +PE 的最小值是_______．4、如图，在平行四边形ABCD 中，对角线AC ，BD 交于点O ，AC ⊥AB ，AB AC ：BD ＝2：3，那么AC 的长为___．5、如图，已知在△ABC中，D，E分别是AB，AC的中点，F，G分别是AD，AE的中点，且FG＝2 cm，则BC的长度是_______ cm．三、解答题（5小题，每小题10分，共计50分）1、尺规作图并回答问题：（保留作图痕迹）已知：如图，四边形ABCD是平行四边形．求作：菱形AECF，使点E，F分别在BC，AD上．请回答：在你的作法中，判定四边形AECF是菱形的依据是．2、如图所示，在四边形ABCD中，∠A＝80°，∠C=75°，∠ADE为四边形ABCD的一个外角，且∠ADE＝125°,试求出∠B的度数.3、已知：在平行四边形ABCD中，分别延长BA，DC到点E，H，使得BE＝2AB，DH＝2CD．连接EH，分别交AD，BC于点F，G．(1)求证：AF ＝CG ；(2)连接BD 交EH 于点O ，若EH ⊥BD ，则当线段AB 与线段AD 满足什么数量关系时，四边形BEDH 是正方形？4、如图，在平行四边形ABCD 中，E 、F 分别是边AB 、DC 上的点，且AE CF =，90DEB ∠=︒，求证：四边形DEBF 是矩形5、如图，直线12l l ∥，线段AD 分别与直线1l 、2l 交于点C 、点B ，满足AB CD =．(1)使用尺规完成基本作图：作线段BC 的垂直平分线交1l 于点E ，交2l 于点F ，交线段BC 于点O ，连接ED 、DF 、FA 、AE ．（保留作图痕迹，不写做法，不下结论）(2)求证：四边形AEDF 为菱形．（请补全下面的证明过程）证明：12l l ∥1∴∠=____①____EF 垂直平分BCOB OC ∴=，90EOC FOB ︒∠=∠=∴____②____FOB ∆≌OE ∴=____③____AB CD =OB AB OC DC +=+∴OA OD ∴=∴四边形AEDF 是___④_____EF AD ⊥∴四边形AEDF 是菱形（______⑤__________）（填推理的依据）．-参考答案-一、单选题1、C【解析】【分析】实际画图，动手操作一下，可知六边形可以是五边形、六边形、七边形截去一个角后得到．【详解】解：如图，原来多边形的边数可能是5，6，7．【点睛】本题考查的是截去一个多边形的一个角，解此类问题的关键是要从多方面考虑，注意不能漏掉其中的任何一种情况．2、C【解析】【分析】因为R 不动，所以AR 不变．根据三角形中位线定理可得EF ＝12AR ，因此线段EF 的长不变．【详解】解：连接AR ．E 、F 分别是AP 、RP 的中点，EF ∴为ΔAPR 的中位线，12EF AR ∴=，为定值． ∴线段EF 的长不改变．故选：C ．【点睛】本题考查了三角形的中位线定理，只要三角形的边AR 不变，则对应的中位线的长度就不变．3、A【解析】根据平行线四边形的性质得到对边相等，加上一组邻边相等，可得到四边都相等，根据菱形的定义对A 、B 进行判断；根据矩形的判定方法对C 、D 进行判断．【详解】解：A 、平行四边形的对边相等，若有一组邻边相等，则四边都相等，所以该选项正确；B 、对角线互相平分且垂直的四边形是菱形，所以该选项不正确；C 、对角线互相平分且相等的四边形为矩形，所以该选项不正确；D 、有三个角是直角的四边形是矩形，所以该选项不正确．故选：A ．【点睛】本题考查了命题与定理：判断事情的语句叫命题；正确的命题叫真命题；经过证明其正确性的命题称为定理．也考查了平行四边形、矩形和菱形的判定与性质．4、C【解析】【分析】根据三角形中位线定理即可求出BC ．【详解】解：ABC ∆中，D 、E 分别是AB 、AC 的中点，DE ∴为三角形ABC 的中位线，12DE BC ∴=， 22816m BC DE ∴==⨯=，故选：C ．【点睛】本题考查的是三角形中位线定理的应用，解题的关键是掌握三角形的中位线等于第三边的一半．5、C【解析】【分析】证出∠NBF=∠EAF=∠MEC，再证明△NBF≌△EAF（AAS），得出BF=AF，NF=EF，证明△ANB≌△CEA得出∠CAE=∠ABN，推出∠ABF=∠FAC=45°；再证明△ANE≌△ECM得出CM=NE，由NF，得出AF+EC，即可得出结论．【详解】解：∵BH⊥AE，AF⊥BC，AE⊥EM，∴∠AEB+∠NBF=∠AEB+∠EAF=∠AEB+∠MEC=90°，∴∠NBF=∠EAF=∠MEC，在△NBF和△EAF中，NBF EAFBFN EFAAE BN∠=∠⎧⎪∠=∠⎨⎪=⎩，∴△NBF≌△EAF（AAS）；∴BF=AF，NF=EF，∴∠ABC=45°，∠ENF=45°，∴△NFE是等腰直角三角形，故③正确；∵∠ANB=90°+∠EAF，∠CEA=90°+∠MEC，∴∠ANB=∠CEA，在△ANB和△CEA中，AN CEANB CEABN AE=⎧⎪∠=∠⎨⎪=⎩，∴△ANB≌△CEA（SAS），故①正确；∵AN=CE，NF=EF，∴BF=AF=FC，又∵AF⊥BC，∠ABC=45°，∴△ABC是等腰直角三角形，故②正确；在▱ABCD中，CD∥AB，且△ABC、△NFE都是等腰直角三角形，∴∠ACD=∠BAC=90°，∠ACB=∠FNE=45°，∴∠ANE=∠BCD=135°，在△ANE和△ECM中，MEC EAFAN ECANE ECM∠=∠⎧⎪=⎨⎪∠=∠⎩，∴△ANE≌△ECM（ASA），故④正确；∴CM=NE，又∵NF，∴AF+EC，∴AD=BC=2AF+2EC，故⑤错误．综上，①②③④正确，共4个，故选：C．【点睛】本题考查了平行四边形的性质、全等三角形的判定与性质、等腰直角三角形的判定和性质等知识；熟练掌握平行四边形的性质，证明三角形全等是解题的关键．6、B【解析】略7、D【解析】【分析】当E F G H ，，，为各边中点，EH BD FG EF AC GH ∥∥，∥∥，11====22EH BD FG EF AC GH ，，四边形EFGH 是平行四边形；A 中AC =BD ，则=EF FG ，平行四边形EFGH 为菱形，进而可判断正误；B 中AC ⊥BD ，则EF FG ⊥，平行四边形EFGH 为矩形，进而可判断正误；E ，F ，G ，H 不是各边中点，C 中若四点位置满足==EH FG EF GH EH FG EF GH ∥，∥，，，则可知四边形EFGH 可以是平行四边形，进而可判断正误；D 中若四点位置满足===EH FG EF GH EH FG EF GH ∥，∥，，则可知四边形EFGH 可以是菱形，进而可判断正误．【详解】解：如图，连接AC BD 、当E F G H ，，，为各边中点时，可知EH EF FG GH 、、、分别为ABD ABC BCD ACD 、、、的中位线∴11====22EH BD FG EF AC GH EH BD FG EF AC GH ∥∥，∥∥，， ∴四边形EFGH 是平行四边形A 中AC =BD ，则=EF FG ，平行四边形EFGH 为菱形；正确，不符合题意；B 中AC ⊥BD ，则EF FG ⊥，平行四边形EFGH 为矩形；正确，不符合题意；C 中E ，F ，G ，H 不是各边中点，若四点位置满足==EH FG EF GH EH FG EF GH ∥，∥，，，则可知四边形EFGH 可以是平行四边形；正确，不符合题意；D中若四点位置满足===∥，∥，，则可知四边形EFGH可以是菱形；错误，EH FG EF GH EH FG EF GH符合题意；故选D．【点睛】本题考查了平行四边形、菱形、矩形的判定，中位线等知识．解题的关键在于熟练掌握特殊平行四边形的判定．8、C【解析】略9、B【解析】【分析】根据翻折的性质可知，∠ABE=∠A′BE，∠DBC=∠DBC′，又∠ABE+∠A′BE+∠DBC+∠DBC′=180°，且∠EBD=∠A′BE+∠DBC′，继而即可求出答案．【详解】解：根据翻折的性质可知，∠ABE=∠A′BE，∠DBC=∠DBC′，又∵∠ABE+∠A′BE+∠DBC+∠DBC′=180°，=90°．∴∠EBD=∠A′BE+∠DBC′=180°×12故选B．【点睛】此题考查翻折变换的性质，三角形折叠以后的图形和原图形全等，对应的角相等，得出∠ABE=∠A′BE，∠DBC=∠DBC′是解题的关键．10、B【分析】根据多边形的内角和公式（n-2）•180°与多边形的外角和定理列式进行计算即可得解．【详解】解：设所求多边形的边数为n，根据题意得：（n-2）•180°=360°，解得n=4．故选：B．【点睛】本题考查了多边形的内角和公式与外角和定理，熟记公式与定理是解题的关键．二、填空题1、2【解析】【分析】过点D作DM⊥CB于M，证出∠DAE=∠DBM，判定△ADE≌△BDM，得到DM=DE=3，证明四边形CEDM是矩形，得到CE=DM=3，由A E=1，求出BC=AC=2．【详解】解：∵DE⊥AC，∴∠E=∠C=90°，∥，∴CB ED过点D作DM⊥CB于M，则∠M=90°=∠E，∵AD=BD，∴∠BAD=∠ABD，∴∠CAB=∠CBA ，∴∠DAE=∠DBM ，∴△ADE ≌△BDM ，∴DM=DE =3，∵∠E=∠C=∠M =90°，∴四边形CEDM 是矩形，∴CE=DM =3，∵A E =1，∴BC=AC =2，故答案为：2．【点睛】此题考查了全等三角形的判定及性质，矩形的判定及性质，等边对等角证明角度相等，正确引出辅助线证明△ADE ≌△BDM 是解题的关键．2、3【解析】【分析】根据平行四边形的性质可得5AD BC ==，AD BC ∥，结合图形，利用线段间的数量关系可得3AE =，由平行线及角平分线可得AEB EBC ∠=∠，ABE EBC ∠=∠，得出AEB ABE ∠=∠，根据等角对等边即可得出结果．【详解】解：∵四边形ABCD 为平行四边形，∴5AD BC ==，AD BC ∥，∵2DE =，∴3AE AD DE =-=，∵AD BC ∥，BE 平分ABC ∠，∴AEB EBC ∠=∠，ABE EBC ∠=∠，∴AEB ABE ∠=∠，∴3AB AE ==，故答案为：3．【点睛】题目主要考查平行四边形的性质，利用角平分线计算及平行线的性质，等角对等边求边长等，理解题意，结合图形，综合运用这些知识点是解题关键．3、【解析】【分析】要求PE +PC 的最小值，PE ，PC 不能直接求，可考虑通过作辅助线转化PE ，PC 的值，从而找出其最小值求解．【详解】解：如图，连接AE ，PA ，∵四边形ABCD是正方形，BD为对角线，∴点C关于BD的对称点为点A，∴PE+PC=PE+AP，根据两点之间线段最短可得AE就是AP+PE的最小值，∵正方形ABCD的边长为4，E是BC边的中点，∴BE=2，∴AE=√AA2+AA2=√42+22=2√5，故答案为：【点睛】本题主要考查了正方形的性质和轴对称及勾股定理等知识的综合应用．根据已知得出两点之间线段最短可得AE就是AP+PE的最小值是解题关键．4、4【解析】【分析】四边形ABCD是平行四边形，可得1122AO CO AC BO DO BD==＝，＝，由:2:3AC BD＝，可知:2:3AO BO＝，由AC AB⊥可知在Rt ABO中勾股定理求解AO的值，进而求解AC的值．【详解】解：∵四边形ABCD 是平行四边形 ∴1122AO CO AC BO DO BD ==＝，＝ ∵:2:3AC BD ＝∴:2:3AO BO ＝∵AC AB ⊥∴222AO AB BO +＝∴设23AO x BO x ＝，＝则()()22223x x += 解得：1x ＝则2AO ＝故4AC ＝故答案为：4．【点睛】本题考查了勾股定理，平行四边形的性质等知识．解题的关键在于正确的求解．5、8【解析】略三、解答题1、证明见解析；邻边相等的平行四边形是菱形，对角线垂直的平行四边形是菱形．【解析】【分析】根据邻边相等的平行四边形是菱形或对角线垂直的平行四边形是菱形证明即可．【详解】解：如图，四边形AECF 即为所求作．理由：四边形ABCD 是平行四边形，∴AE ∥CF ，∴∠EAO =∠FCO ，∵EF 垂直平分线段AC ，∴OA =OC ，在△AEO 和△CFO 中，EAO FCO AO OCAOE COF ∠∠⎧⎪⎨⎪∠∠⎩＝＝＝， ∴△AEO ≌△CFO （ASA ），∴AE =CF ，∴四边形AECF 是平行四边形，∵EA =EC 或AC ⊥EF ，∴四边形AECF 是菱形．故答案为：邻边相等的平行四边形是菱形，对角线垂直的平行四边形是菱形．【点睛】本题考查作图-复杂作图，平行四边形的性质，菱形的判定等知识，解题的关键是熟练掌握基本知识，属于中考常考题型．2、150°【解析】【分析】先根据邻补角的定义求出∠ADC的度数，再根据四边形的内角和求出∠B的度数．【详解】解：∵∠ADE为四边形ABCD的一个外角，且∠ADE＝125°，∴∠ADC=180°-∠ADE＝55°，∵∠A+∠B+∠C+∠ADE＝360°，∴∠B=360°-∠A-∠C-∠ADE＝360°-80°-75°-55°=150°．【点睛】此题考查了多边形外角定义，多边形的内角和，熟记多边形的内角和进行计算是解题的关键．3、 (1)见解析(2)当AD时，四边形BEDH是正方形【解析】【分析】（1）要证明AF=CG，只要证明△EAF≌△HCG即可；（2）利用已知可得四边形BEDH是菱形，所以当AE2+DE2=AD2时，∠BED=90°，四边形BEDH是正方形．(1)证明：∵四边形ABCD是平行四边形，∴AB∥CD，AB=CD，∠BAD=∠BCD，∴∠AEF=∠CHG，∵BE=2AB，DH=2CD，∴BE=DH，∴BE-AB=DH-DC，∴AE=CH，∴∠BAD+∠EAF=180°，∠BCD+∠GCH=180°，∴∠EAF=∠GCH，∴△EAF≌△HCG(ASA)，∴AF=CG；(2)解：当AD时，四边形BEDH是正方形；理由：∵BE∥DH，BE=DH，∴四边形EBHD是平行四边形，∵EH⊥BD，∴四边形EBHD是菱形，∴ED=EB=2AB，当AE2+DE2=AD2时，则∠BED=90°，∴四边形BEDH是正方形，即AB2+(2AB)2=AD2，∴AD，∴当AD时，四边形BEDH是正方形．．【点睛】本题考查了正方形的判定，菱形的判定，平行四边形的性质，全等三角形的判定与性质，结合图形分析并熟练掌握正方形的判定，平行四边形的性质，是解题的关键．4、证明见解析【解析】【分析】平行四边形ABCD ，可知AB CD AB CD =，；由于AE CF = ，可得BE DF =，BE DF ，知四边形DEBF 为平行四边形，由90DEB ∠=︒可知四边形DEBF 是矩形．【详解】证明：∵四边形 ABCD 是平行四边形∴AB CD AB CD =，∵AE CF BE AB AE DF DC CF ==-=-，，∴BE DF =∵BE DF BE DF =，∴四边形DEBF 为平行四边形又∵90DEB ∠=︒∴四边形DEBF 是矩形．【点睛】本题考查了平行四边形的性质与判定，矩形的判定等知识．解题的关键在于灵活掌握矩形的判定．5、 (1)见解析(2)①2∠；②EOC ∆；③OF ；④平行四边形；⑤对角线互相垂直的平行四边形是菱形【解析】【分析】（1）分别以A 、D 为圆心，大于AD 的一半长为半径，画弧，两弧交于两点，然后过这两点作直线交l 1于E ，交l 2于F ，直线EF 为线段AD 的垂直平分线，连接ED 、DF 、FA 、AE 即可；（2）：根据12l l ∥，内错角相等得出1∠=∠2①，根据EF 垂直平分BC ，得出OB OC =，90EOC FOB ︒∠=∠=，可证②△EOC FOB ∆≌，根据全等三角形性质得出OE =OF ③，再证OA OD =，根据对角线互相平分的四边形是平行四边形判定四边形AEDF 是平行四边形④，根据对角线互相垂直EF AD ⊥即可得出四边形AEDF 是菱形（对角线互相垂直的平行四边形是菱形⑤）． (1)解：分别以A 、D 为圆心，大于AD 的一半长为半径，画弧，两弧交于两点，然后过这两点作直线交l 1于E ，交l 2于F ，直线EF 为线段AD 的垂直平分线，连接ED 、DF 、FA 、AE 即可；如图所示(2)证明：12l l ∥，1∴∠=∠2①， EF 垂直平分BC ，OB OC ∴=，90EOC FOB ︒∠=∠=，∴②△EOC FOB ∆≌，OE ∴=OF ③，AB CD =，OB AB OC DC +=+∴，OA OD ∴=，∴四边形AEDF 是平行四边形④，EF AD ⊥，∴四边形AEDF 是菱形（对角线互相垂直的平行四边形是菱形⑤），故答案为：①2∠；②EOC ∆；③OF ；④平行四边形；⑤对角线互相垂直的平行四边形是菱形．【点睛】本题考查尺规作图，垂直平分线性质，三角形全等判定与性质，菱形的判定，掌握尺规作图，垂直平分线性质，三角形全等判定与性质，菱形的判定是解题关键．。