弹性力学ansys分析

图1为一个承受内压的薄板，在其中心位置有一个小圆孔，相关的结构尺寸参考图1所示。

材料属性：弹性模量E=2e11Pa，泊松比为0.3。

拉伸载荷为：q=3000Pa。

平板的厚度为：t=0.01mm。

通过简单力学分析，该问题属于平面应力问题，又因为平板结构的对称性，所以只要分析其中的1/4即可，如图2所示。

图1 板的结构示意图图2 有限元分析见图一、前处理（1）定义工作文件名：Utility Menu>File>Change Jobname，弹出如图3所示的Change Jobname对话框，在Enter new Jobname后面的输入栏中输入Plate，并将New Log and error files复选框选为yes，单击OK。

图3 定义工作文件名对话框（2）定义工作标题：Utility Menu>File>Change Title，在出现的对话框中输入The Analysis of Plate Stress with small Circle，单击OK。

图4 定义工作标题对话框（3）重新显示：Utility Menu>Plot>Replot。

（4）关闭三角坐标符号：Utility Menu>PlotCtrls>Window Controls>Window options，弹出一个对话框，在Location of triad 后面的下拉式选择框中，选择Not Shown，单击OK。

（5）选择单元类型：Main Menu>Preprocessor>Element Type>Add/Edit/Delete，弹出Element Type对话框，单击Add按钮，又弹出如图5所示的Library of Element Types对话框，在选择框中分别选择Structural Solid和Quad 8node 82，单击OK，然后单击Close。

ANSYS 入门教程 - 结构的弹性稳定性分析

ANSYS 入门教程- 结构的弹性稳定性分析2011-01-09 15:06:42| 分类：默认分类| 标签：|字号大中小订阅第7 章结构弹性稳定分析7.1 特征值屈曲分析的步骤7.2 构件的特征值屈曲分析7.3 结构的特征值屈曲分析一、结构失稳或结构屈曲：当结构所受载荷达到某一值时，若增加一微小的增量，则结构的平衡位形将发生很大的改变，这种现象叫做结构失稳或结构屈曲。

结构稳定问题一般分为两类:★第一类失稳：又称平衡分岔失稳、分枝点失稳、特征值屈曲分析。

结构失稳时相应的载荷可称为屈曲载荷、临界载荷、压屈载荷或平衡分枝载荷。

★第二类失稳：结构失稳时，平衡状态不发生质变，也称极值点失稳。

结构失稳时相应的载荷称为极限载荷或压溃载荷。

●跳跃失稳：当载荷达到某值时，结构平衡状态发生一明显的跳跃，突然过渡到非邻近的另一具有较大位移的平衡状态。

可归入第二类失稳。

★结构弹性稳定分析= 第一类稳定问题ANSYS 特征值屈曲分析（Buckling Analysis）。

★第二类稳定问题ANSYS 结构静力非线性分析，无论前屈曲平衡状态或后屈曲平衡状态均可一次求得，即“全过程分析”。

这里介绍ANSYS 特征值屈曲分析的相关技术。

在本章中如无特殊说明，单独使用的“屈曲分析”均指“特征值屈曲分析”。

7.1 特征值屈曲分析的步骤①创建模型②获得静力解③获得特征值屈曲解④查看结果一、创建模型注意三点：⑴仅考虑线性行为。

若定义了非线性单元将按线性单元处理。

刚度计算基于初始状态（静力分析后的刚度），并在后续计算中保持不变。

⑵必须定义材料的弹性模量或某种形式的刚度。

非线性性质即便定义了也将被忽略。

⑶单元网格密度对屈曲载荷系数影响很大。

例如采用结构自然节点划分时（一个构件仅划分一个单元）可能产生100% 的误差甚至出现错误结果，尤其对高阶屈曲模态的误差可能更大，其原因与形成单元应力刚度矩阵有关。

经验表明，仅关注第1 阶屈曲模态及其屈曲载荷系数时，每个自然杆应不少于 3 个单元。

弹性力学ansys求解实例详解

弹性力学a n s y s求解实例详解Revised on November 25, 2020ANSYS 上机实验报告一、题目描述如图1所示，一简支梁横截面是矩形，其面积202.0m A =，对弯曲中性轴的惯性矩451067.6m I zz -⨯=，高m h 2.0=，材料的pa E 11101.2⨯=，横向变形系数3.0=μ。

该梁的自重就是均布载荷N q 4000=和梁中点处的集中力N F 2000=，试讨论在均布荷载作用下，简支梁的最大挠度。

二、问题的材料力学解答由叠加法可知：梁上同时作用几个载荷时，可分别求出每一载荷单独作用时的变形，把各个形变叠加即为这些载荷共同作用时的变形。

在只有均布载荷q 作用时，计算简支梁的支座约束力，写出弯矩方程，利用EI M dxw d =22积分两次，最后得出：铰支座上的挠度等于零，故有0=x 时，0=w ，因为梁上的外力和边界条件都对跨度中点对称，挠曲线也应对该点对称。

因此，在跨度中点，挠曲线切线的斜率等于零，即：2l x =时，0=dx dw ，把以上两个边界条件分别代入w 和0=dxdw 的表达式，可以求出243ql C -=，0=D ，于是得转角方程及挠曲线方程为： x ql x q x ql EIw ql x q x ql EI dx dw EI 2424122464343332--=--==θ （1）在跨度中点，挠曲线切线的斜率等于零，挠度为极值，由（1）中式子可得：即EIql w q c 3845)(4-=。

在集中力F 单独作用时，查材料力学中梁在简单载荷作用下的变形表可得EIFl w F c 48)(3-=。

叠加以上结果，求得在均布载荷和集中力共同作用下，梁中点处的挠度是EIFl EI ql w w w F c q c c 483845)()(34--=+=，将各参数代入得m w c 410769.0-⨯=三、问题的ansys 解答建立几何模型此问题为可采用Beam 分析，所以该几何模型可用线表示。

ANSYS分析报告

ANSYS分析报告引言：1.问题描述：在这个分析中，我们将研究一个承重结构的稳定性。

该结构由一根钢杆和两个支撑点组成，其中一端支撑固定，另一端加有外部力。

我们的目标是确定结构在受力情况下的位移和应力分布，并评估结构的稳定性。

2.建模与加载条件：我们使用ANSYS软件对该结构进行三维建模，并为其设置了适当的边界条件和加载条件。

钢杆的材料参数和几何尺寸通过实验测定获得。

加载条件设为一端受到垂直向下的力，同时另一端固定。

我们采用静态结构分析模块进行分析。

3.结果与分析：经过ANSYS分析，我们获得了结构的位移和应力分布情况。

在受力情况下，钢杆的位移主要集中在受力一侧，而另一侧的位移较小。

应力分布也呈现相似的趋势，受力一侧的应力较大，而另一侧的应力较小。

这是由于外部力对结构的影响导致结构发生变形。

4.结构稳定性评估：在评估结构的稳定性时，我们对结构进行了稳定性分析。

通过计算结构的临界载荷，我们可以确定结构在受力情况下的稳定性。

根据计算结果，结构的临界载荷大于所施加的外部力，说明结构是稳定的，不会发生失稳现象。

5.敏感性分析：为了进一步评估结构的性能，我们进行了敏感性分析。

通过改变结构的材料参数和几何尺寸，我们得到了不同条件下结构的位移和应力分布。

根据敏感性分析结果，我们发现结构的位移和应力对材料的弹性模量和截面尺寸非常敏感。

较高的弹性模量和更大的截面尺寸会使结构更加稳定。

结论：通过ANSYS软件进行的分析，我们得到了结构在受力情况下的位移和应力分布，并评估了结构的稳定性。

我们发现外部力对结构的位移和应力分布有明显的影响，但结构仍然保持稳定。

此外，结构的性能对材料参数和几何尺寸非常敏感。

综合分析结果，我们可以优化结构设计，以提高结构的稳定性和性能。

以上是对ANSYS分析报告的一个简单写作示例，可以根据实际情况进行适当调整和修改。

弹性力学及有限元法 ANSYS实例演示课件

有限元法是一种数值分析方法，通过将连续的物理系统离散化为有限数量的单元，利用这些单元的组合来逼近真实系统的行为。
它广泛应用于工程领域，用于解决各种复杂的力学、热学、电磁学等问题。
有限元法的实现过程
01
离散化
将连续的物理系统划分为有限数量的离散单元。
整体分析
将所有单元的数学模型组合起来，形成整个系统的数学模型。
使用ANSYS的几何建模功能，创建一个矩形薄板模型。
选择适当的单位制，如国际单位制（SI）。
为薄板指定弹性模量、泊松比和密度等材料属性。
通过与已知解进行比较，验证模型的正确性和准确性。
材料属性设置与网格划分
01
02
03
材料属性
根据问题描述，为薄板设置弹性模量、泊松比和密度等材料属性。
局限性
ANSYS软件的学习曲线较陡峭，需要用户具备一定的专业背景和经验；同时，对于某些特殊问题，可能需要结合其他软件或方法进行求解。
未来研究与发展的方向
多物理场耦合
进一步发展多物理场耦合的有限元分析方法，以模拟更复杂的工程问题。
智能化与自动化
研究有限元分析的智能化和自动化技术，提高分析效率和精度。
网格划分
对薄板进行网格划分，选择合适的网格密度以提高求解精度。
网格质量检查
检查网格质量，确保网格划分满足求解精度要求。
边界条件与载荷设置
边界条件
载荷与边界条件验证
根据实际情况，为薄板的边界设置约束条件，如固定约束或简支约束。
通过有限元分析理论，验证所设置的载荷和边界条件的正确性。
载荷设置
结构分析
有限元法能够模拟复杂结构的力学行为，为工程设计和优化提供依据。

ANSYS弹性及塑性分析报告(非常经典)

目录什么是塑性 (1)路径相关性 (1)率相关性 (1)工程应力、应变与真实应力、应变 (1)什么是激活塑性 (2)塑性理论介绍 (2)屈服准则 (2)流动准则 (3)强化准则 (3)塑性选项 (5)怎样使用塑性 (6)ANSYS输入 (7)输出量 (7)程序使用中的一些基本原则 (8)加强收敛性的方法 (8)查看结果 (9)塑性分析实例（GUI方法） (9)塑性分析实例（命令流方法） (14)弹塑性分析在这一册中,我们将详细地介绍由于塑性变性引起的非线性问题--弹塑性分析,我们的介绍人为以下几个方面:•什么是塑性•塑性理论简介•ANSYS程序中所用的性选项•怎样使用塑性•塑性分析练习题什么是塑性塑性是一种在某种给定载荷下,材料产生永久变形的材料特性,对大多的工程材料来说,当其应力低于比例极限时,应力一应变关系是线性的。

另外,大多数材料在其应力低于屈服点时，表现为弹性行为，也就是说，当移走载荷时，其应变也完全消失。

由于屈服点和比例极限相差很小，因此在ANSYS程序中，假定它们相同。

在应力一应变的曲线中，低于屈服点的叫作弹性部分，超过屈服点的叫作塑性部分，也叫作应变强化部分。

塑性分析中考虑了塑性区域的材料特性。

路径相关性：即然塑性是不可恢复的，那么这种问题的就与加载历史有关，这类非线性问题叫作与路径相关的或非保守的非线性。

路径相关性是指对一种给定的边界条件，可能有多个正确的解—内部的应力，应变分布—存在，为了得到真正正确的结果，我们必须按照系统真正经历的加载过程加载。

率相关性：塑性应变的大小可能是加载速度快慢的函数，如果塑性应变的大小与时间有关，这种塑性叫作率无关性塑性，相反，与应变率有关的性叫作率相关的塑性。

大多的材料都有某种程度上的率相关性，但在大多数静力分析所经历的应变率范围，两者的应力－应变曲线差别不大，所以在一般的分析中，我们变为是与率无关的。

工程应力，应变与真实的应力、应变：塑性材料的数据一般以拉伸的应力—应变曲线形式给出。

12-ansys弹性力学与有限元法实验报告

弹性力学与有限元法实验报告学院班级姓名学号实验一一已知条件板孔问题：(其中板厚，,，泊松比)，绘出其变形图和在圆心所在的横截面内MISES应力的分布情况。

二实验目的和要求（1）掌握用ANSYS建立开孔平板几何模型的方法。

（2）掌握用ANSYS划分立开孔平板网格的方法。

（3）掌握用ANSYS对开孔平板加载与求解的方法。

（4）掌握用ANSYS对开孔平板计算结果后处理及分析的方法。

三实验过程概述首先做出一个长2000，宽200的长方形，然后在长方形的中央挖出一个直径为10的孔。

将长方形网格化，把固定点设在中心，在两侧分别设一个向外的力P（60KN）。

最后进行运算，结果用云图表示。

四实验内容分析由云图可以看出沿X轴的应力呈线性分布，大小由中间向外递增，其中四个角处的应力也为最小值。

最大应力值在施力点，为0.237406MPa。

形变只发生在施力点处。

由应力图可知，圆心横截面处的应力从外向内递增，但孔处没有应力。

五实验小结和体会对于网格划分，矩形单元比三角形单元更加接近理论求解结果。

而网格加密会使求解结果收敛于理论值，但是这也会加大计算机的计算量。

因此，对于比较复杂的模型，在进行有限元仿真模拟时既要考虑到计算结果的精确度，又要考虑到经济成本的合理性，这时选择一个合理的网格划分就显得十分重要了。

因此，在进行有限元仿真模拟时要选择合适的网格划分方法，划分合理的网格数量。

有限元法是一种求解连续介质、连续场力学和物理问题的数值方法，是工程分析和科学研究的重要工具；必须是对连续地介质等，因而也存在局限性。

实验二一已知条件如图所示支架中的三根杆件材料相同，弹性模量E=200GPa, 泊松比 =0.3，杆1的横截面面积为200mm2,杆2的横截面面积为300mm2,长为1m，杆3的横截面面积为400mm2。

若P=30kN，试求各杆的应力及铰支点的反力。

二实验目的和要求（1）掌握用ANSYS建立杆件系统几何模型的方法。

（2）掌握用ANSYS划分杆件系统网格的方法。

ANSYS弹性及塑性分析非常经典

目录什么是塑性 (1)路径相关性 (1)率相关性 (1)工程应力、应变与真实应力、应变 (1)什么是激活塑性 (2)塑性理论介绍 (2)屈服准则 (2)流动准则 (3)强化准则 (3)塑性选项 (5)怎样使用塑性 (6)ANSYS输入 (7)输出量 (7)程序使用中的一些基本原则 (8)加强收敛性的方法 (8)查看结果 (9)塑性分析实例（GUI方法） (9)塑性分析实例（命令流方法） (14)弹塑性分析在这一册中,我们将详细地介绍由于塑性变性引起的非线性问题--弹塑性分析,我们的介绍人为以下几个方面:•什么是塑性•塑性理论简介•ANSYS程序中所用的性选项•怎样使用塑性•塑性分析练习题什么是塑性塑性是一种在某种给定载荷下,材料产生永久变形的材料特性,对大多的工程材料来说,当其应力低于比例极限时,应力一应变关系是线性的。

另外,大多数材料在其应力低于屈服点时，表现为弹性行为，也就是说，当移走载荷时，其应变也完全消失。

由于屈服点和比例极限相差很小，因此在ANSYS程序中，假定它们相同。

在应力一应变的曲线中，低于屈服点的叫作弹性部分，超过屈服点的叫作塑性部分，也叫作应变强化部分。

塑性分析中考虑了塑性区域的材料特性。

路径相关性：即然塑性是不可恢复的，那么这种问题的就与加载历史有关，这类非线性问题叫作与路径相关的或非保守的非线性。

路径相关性是指对一种给定的边界条件，可能有多个正确的解—内部的应力，应变分布—存在，为了得到真正正确的结果，我们必须按照系统真正经历的加载过程加载。

率相关性：塑性应变的大小可能是加载速度快慢的函数，如果塑性应变的大小与时间有关，这种塑性叫作率无关性塑性，相反，与应变率有关的性叫作率相关的塑性。

大多的材料都有某种程度上的率相关性，但在大多数静力分析所经历的应变率范围，两者的应力－应变曲线差别不大，所以在一般的分析中，我们变为是与率无关的。

工程应力，应变与真实的应力、应变：塑性材料的数据一般以拉伸的应力—应变曲线形式给出。

弹性力学与有限元ANSYS建模教程

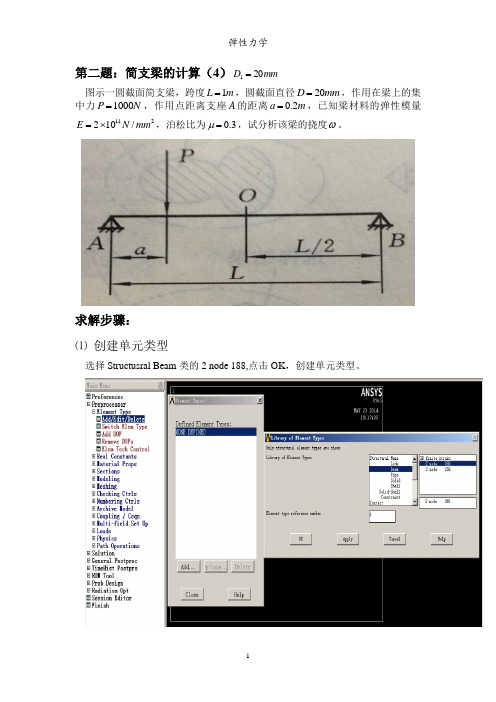
第二题：简支梁的计算（4）mm D 201=图示一圆截面简支梁，跨度m L 1=，圆截面直径mm D 20=，作用在梁上的集中力N P 1000=，作用点距离支座A 的距离m a 2.0=，已知梁材料的弹性模量211/102mm N E ⨯=，泊松比为3.0=μ，试分析该梁的挠度ω。

求解步骤： ⑴ 创建单元类型选择Structusral Beam 类的2 node 188,点击OK ，创建单元类型。

（2）定义材料特性Material Props→Material Models→Material Model Number1→Structural→Linear →Elastic→Isotropic。

输入（泊松比）=PE⨯rxy（弹性模量），3.010211=x（3）创建关键点MainMenu→Proprocessor→Modeling→Creat→Keypoints→In Active CS在弹出对话框的NPT文本框中输入1，在“X、Y、Z”文本框中分别输入0，0，0。

单击Apply按钮，在NPT文本框中输入2。

在“X、Y、Z”文本框中分别输入1，0，0。

单击OK按钮，关键点1、2创建如图所示：（4）显示关键点号Utility Menu→PlotCtrls→Numbering。

在弹出的对话框中，将关键点号打开，单击ok按钮。

（5）创建杆件截面MainMenu→Preprocessor→Sections→Beam→Common Sections弹出来一个对话框，在Sub-Type中选择圆形截面，m，点击OK。

.0R01（6）创建直线MainMenu→Preprocessor→Modeling→Create→Lines→ Lines→Straight Line。

弹出拾取窗口，拾取关键点1和2，单击OK按钮。

（7）划分单元MainMenu→Preprocessor→Meshing→MeshTool。

弹出MeshTool对话框，单击“Size Controls”区域中的“Line”中的Set 按钮，弹出拾取框口，拾取直线，单击OK按钮，在NDIV文本框中输入50。

ANSYS有限元分析——弹性力学基础知识二

15
弹性力学待求的物理量
空间问题
15个
[ ] { }σ = σ x
σy
σz
τ xy
τ yz
τT zx
[ ] { }ε = ε x
εy
εz
γ xy
γ yz
γT zx
{δ }= [u v w]T
平面问题
8个
[ ] {σ }= σ x
σy
τT xy
[ ] {ε}= ε x
εy
γT xy
{δ }= [u v]T 16
(3) y = +h, X = 0,Y = 0
( ) (σ
x
) s
⋅
0
+
τ xy
⋅ (+1) = 0
s
( ) ( ) σ y
⋅ (+1) +
s
τ xy
⋅0 = 0
s
( ) ( ) σ y s = 0, τ xy s = 0 σ y τ yx
σx
σx
τ xy
τ yx τ xy 29
σy
2-6 几何方程
平面应力问题
平面应变问题
非平面问题
思考：黑板和甲板力学模型各属于弹性力学那类问题?
21
2-4 平衡微分方程
取微元体PABC（P点附近），
PA = dx PB = dy
Z 方向取单位长度。
AC面：
σx
+
∂σ x
∂x
dx
+
1 ∂2σ x
2! ∂x2
≈σx
(dx)2 + L
+ ∂σ x dx
∂x
τ
O
y yx +

ANSYS弹性及塑性分析(非常经典)

目录什么是塑性 (1)路径相关性 (1)率相关性 (1)工程应力、应变与真实应力、应变 (1)什么是激活塑性 (2)塑性理论介绍 (2)屈服准则 (2)流动准则 (3)强化准则 (3)塑性选项 (5)怎样使用塑性 (6)ANSYS输入 (7)输出量 (7)程序使用中的一些基本原则 (8)加强收敛性的方法 (8)查看结果 (9)塑性分析实例（GUI方法） (9)塑性分析实例（命令流方法） (14)弹塑性分析在这一册中,我们将详细地介绍由于塑性变性引起的非线性问题--弹塑性分析,我们的介绍人为以下几个方面:什么是塑性塑性理论简介ANSYS程序中所用的性选项怎样使用塑性塑性分析练习题什么是塑性塑性是一种在某种给定载荷下,材料产生永久变形的材料特性,对大多的工程材料来说,当其应力低于比例极限时,应力一应变关系是线性的。

另外,大多数材料在其应力低于屈服点时，表现为弹性行为，也就是说，当移走载荷时，其应变也完全消失。

由于屈服点和比例极限相差很小，因此在ANSYS程序中，假定它们相同。

在应力一应变的曲线中，低于屈服点的叫作弹性部分，超过屈服点的叫作塑性部分，也叫作应变强化部分。

塑性分析中考虑了塑性区域的材料特性。

路径相关性：即然塑性是不可恢复的，那么这种问题的就与加载历史有关，这类非线性问题叫作与路径相关的或非保守的非线性。

路径相关性是指对一种给定的边界条件，可能有多个正确的解—内部的应力，应变分布—存在，为了得到真正正确的结果，我们必须按照系统真正经历的加载过程加载。

率相关性：塑性应变的大小可能是加载速度快慢的函数，如果塑性应变的大小与时间有关，这种塑性叫作率无关性塑性，相反，与应变率有关的性叫作率相关的塑性。

大多的材料都有某种程度上的率相关性，但在大多数静力分析所经历的应变率范围，两者的应力－应变曲线差别不大，所以在一般的分析中，我们变为是与率无关的。

工程应力，应变与真实的应力、应变：塑性材料的数据一般以拉伸的应力—应变曲线形式给出。

ANSYS弹性及塑性分析非常经典

目录什么是塑性 (1)路径相关性 (1)率相关性 (1)工程应力、应变与真实应力、应变 (1)什么是激活塑性 (2)塑性理论介绍 (2)屈服准则 (2)流动准则 (3)强化准则 (3)塑性选项 (5)怎样使用塑性 (6)ANSYS输入 (7)输出量 (7)程序使用中的一些基本原则 (8)加强收敛性的方法 (8)查看结果 (9)塑性分析实例（GUI方法） (9)塑性分析实例（命令流方法） (14)弹塑性分析在这一册中,我们将详细地介绍由于塑性变性引起的非线性问题--弹塑性分析,我们的介绍人为以下几个方面:•什么是塑性•塑性理论简介•ANSYS程序中所用的性选项•怎样使用塑性•塑性分析练习题什么是塑性塑性是一种在某种给定载荷下,材料产生永久变形的材料特性,对大多的工程材料来说,当其应力低于比例极限时,应力一应变关系是线性的。

另外,大多数材料在其应力低于屈服点时，表现为弹性行为，也就是说，当移走载荷时，其应变也完全消失。

由于屈服点和比例极限相差很小，因此在ANSYS程序中，假定它们相同。

在应力一应变的曲线中，低于屈服点的叫作弹性部分，超过屈服点的叫作塑性部分，也叫作应变强化部分。

塑性分析中考虑了塑性区域的材料特性。

路径相关性：即然塑性是不可恢复的，那么这种问题的就与加载历史有关，这类非线性问题叫作与路径相关的或非保守的非线性。

路径相关性是指对一种给定的边界条件，可能有多个正确的解—内部的应力，应变分布—存在，为了得到真正正确的结果，我们必须按照系统真正经历的加载过程加载。

率相关性：塑性应变的大小可能是加载速度快慢的函数，如果塑性应变的大小与时间有关，这种塑性叫作率无关性塑性，相反，与应变率有关的性叫作率相关的塑性。

大多的材料都有某种程度上的率相关性，但在大多数静力分析所经历的应变率范围，两者的应力－应变曲线差别不大，所以在一般的分析中，我们变为是与率无关的。

工程应力，应变与真实的应力、应变：塑性材料的数据一般以拉伸的应力—应变曲线形式给出。

利用ANSYS对木梁进行弹性分析

利用ANSYS对木梁进行弹性分析1 引言木材是一种非常有效的建筑材料。

然而一直以来,木材材性因不同树种和产地,其差别和离散性很大,对木材的研究多以试验为主。

也正因为木材的特殊材性,这种材料的延性也很少被了解,理论分析及利用ANSYS有限元模拟的研究也很少见。

本文以木梁为研究对象,利用通用有限元软件ANSYS对木梁进行了弹性分析,对木梁的设计有一定的指导作用。

2 模型的建立本文的木梁模型如图1所示，截面为40mm×80mm,长度是1520mm。

加载位置及支座处用40mm×40mm×8mm钢片做垫块。

图1 模型示意图3 有限元计算模型的建立木材和垫块均采用SOLID45单元。

因为SOLID45单元是八节点三维实体单元,每一个节点具有三个自由度:x、y和z方向平移。

单元的几何形状、结点位置和单元坐标系如图2所示。

该单元具有塑性、蠕变、膨胀、应力强化以及大变形大应变和模拟各向异性等功能,所以本文木材单元采用SOLID45各向异性塑性材料实体单元。

计算中,考虑垫块是为了防止应力集中。

为防止应力集中和附加变形，如图2所示在支座处只约束垫块中线处y方向的位移,让垫块可以自由绕z轴旋转,减少垫块对木纤维多余的约束作用,模拟铰支座。

图2 木材梁底座的约束模型以及材料、单元定义完成后,开始进行网格划分。

在木梁和垫块不同单元交界的地方,必须保证不同单元间有共同节点以达到两者的节点变形协调,采用先划分体单元,然后将节点合并。

用边界长度为20mm的单元来划分网格。

划分单元后,每个单元都有自己的单元坐标系。

由于木材属于正交异性材料,材性的确定与单元坐标系有关,只能通过局部坐标系定义单元坐标系的方向。

先要定义一局部坐标系,然后通过局部坐标系来定义单元坐标系的方向。

建成后的模型如图3所示。

图3 木材梁的有限元模型图4 木梁顶部的载荷4 木梁的线弹性分析图4给出了模型的载荷施加方式，其木材弹性特性见表1所示。

ANSYS弹性及塑性分析(非常经典)

目录什么是塑性 (1)路径相关性 (1)率相关性 (1)工程应力、应变与真实应力、应变 (1)什么是激活塑性 (2)塑性理论介绍 (2)屈服准则 (2)流动准则 (3)强化准则 (3)塑性选项 (5)怎样使用塑性 (6)ANSYS输入 (7)输出量 (7)程序使用中的一些基本原则 (8)加强收敛性的方法 (8)查看结果 (9)塑性分析实例（GUI方法） (9)塑性分析实例（命令流方法） (14)弹塑性分析在这一册中,我们将详细地介绍由于塑性变性引起的非线性问题--弹塑性分析,我们的介绍人为以下几个方面:•什么是塑性•塑性理论简介•ANSYS程序中所用的性选项•怎样使用塑性•塑性分析练习题什么是塑性塑性是一种在某种给定载荷下,材料产生永久变形的材料特性,对大多的工程材料来说,当其应力低于比例极限时,应力一应变关系是线性的。

另外,大多数材料在其应力低于屈服点时，表现为弹性行为，也就是说，当移走载荷时，其应变也完全消失。

由于屈服点和比例极限相差很小，因此在ANSYS程序中，假定它们相同。

在应力一应变的曲线中，低于屈服点的叫作弹性部分，超过屈服点的叫作塑性部分，也叫作应变强化部分。

塑性分析中考虑了塑性区域的材料特性。

路径相关性：即然塑性是不可恢复的，那么这种问题的就与加载历史有关，这类非线性问题叫作与路径相关的或非保守的非线性。

路径相关性是指对一种给定的边界条件，可能有多个正确的解—内部的应力，应变分布—存在，为了得到真正正确的结果，我们必须按照系统真正经历的加载过程加载。

率相关性：塑性应变的大小可能是加载速度快慢的函数，如果塑性应变的大小与时间有关，这种塑性叫作率无关性塑性，相反，与应变率有关的性叫作率相关的塑性。

大多的材料都有某种程度上的率相关性，但在大多数静力分析所经历的应变率范围，两者的应力－应变曲线差别不大，所以在一般的分析中，我们变为是与率无关的。

工程应力，应变与真实的应力、应变：塑性材料的数据一般以拉伸的应力—应变曲线形式给出。

ANSYS弹性及塑性分析(详细、全面分析)1

目录什么是塑性 (1)路径相关性 (1)率相关性 (1)工程应力、应变与真实应力、应变 (1)什么是激活塑性 (2)塑性理论介绍 (2)屈服准则 (2)流动准则 (3)强化准则 (3)塑性选项 (5)怎样使用塑性 (6)ANSYS输入 (7)输出量 (7)程序使用中的一些基本原则 (8)加强收敛性的方法 (8)查看结果 (9)塑性分析实例（GUI方法） (9)塑性分析实例（命令流方法） (14)弹塑性分析在这一册中,我们将详细地介绍由于塑性变性引起的非线性问题--弹塑性分析,我们的介绍人为以下几个方面:∙什么是塑性∙塑性理论简介∙ANSYS程序中所用的性选项∙怎样使用塑性∙塑性分析练习题什么是塑性塑性是一种在某种给定载荷下,材料产生永久变形的材料特性,对大多的工程材料来说,当其应力低于比例极限时,应力一应变关系是线性的。

另外,大多数材料在其应力低于屈服点时，表现为弹性行为，也就是说，当移走载荷时，其应变也完全消失。

由于屈服点和比例极限相差很小，因此在ANSYS程序中，假定它们相同。

在应力一应变的曲线中，低于屈服点的叫作弹性部分，超过屈服点的叫作塑性部分，也叫作应变强化部分。

塑性分析中考虑了塑性区域的材料特性。

路径相关性：即然塑性是不可恢复的，那么这种问题的就与加载历史有关，这类非线性问题叫作与路径相关的或非保守的非线性。

路径相关性是指对一种给定的边界条件，可能有多个正确的解—内部的应力，应变分布—存在，为了得到真正正确的结果，我们必须按照系统真正经历的加载过程加载。

率相关性：塑性应变的大小可能是加载速度快慢的函数，如果塑性应变的大小与时间有关，这种塑性叫作率无关性塑性，相反，与应变率有关的性叫作率相关的塑性。

大多的材料都有某种程度上的率相关性，但在大多数静力分析所经历的应变率范围，两者的应力－应变曲线差别不大，所以在一般的分析中，我们变为是与率无关的。

工程应力，应变与真实的应力、应变：塑性材料的数据一般以拉伸的应力—应变曲线形式给出。

ansys教程(超详细)

1.1弹性力学平面问题的分析——带孔平板的有限元分析1、分析的物理模型分析结构如下图1-1所示。

图1-1 平面问题的计算分析模型2、ANSYS分析单元设置单元设置如下图1-2和图1-3所示。

图1-2 单元设置图1-3 单元行为选项设置3、实常数设置设置平面问题的厚度为1，过程如下图1-4所示。

图1-4 实常数设置4、材料属性设置材料的弹性模量和泊淞比设定如下图1-5所示。

图1-5 材料模型5、几何建模先创建一个矩形如下图1-6所示，然后再创建一个圆如图1-7所示。

图1-6 矩形创建图1-7 创建圆进行布尔运算，先选取大的矩形，然后再选取小圆，之后完成布尔减运算，其过程如下图1-8所示。

选取矩形选取小圆运算后结果图1-8 执行布尔减运算6、网格划分按如下图1-9所示完成单元尺寸设置，设置每个边划分4个单元。

之后，按图1-10所示完成单元划分。

图1-9 单元尺寸设置图1-10 单元划分7、模型施加约束和外载约束施加：先施加X方向固定约束如图1-11所示，再施加Y向位移约束如图1-12所示。

图1-11 施加X方向位移约束图1-12 施加Y方向位移约束施加外载图1-13 施加外载荷图1-14 求解8、结果后处理查看受力后工件所受X方向应力和等效应力分布情况。

图1-15 后处理节点结果应力提取图1-16 X方向应力Mpa图1-17 米塞斯等效应力Mpa1.2弹性力学平面问题的分析——无限长厚壁圆筒问题描述：一无限长厚壁圆筒,如图1所示，内外壁分别承受压力p1=p2=10N/mm2。

受载前R1=100mm，R2=150mm，E=210Gpa，μ=0.3 。

取横截面八分之一进行计算，支撑条件及网格划分如下图2所示。

求圆筒内外半径的变化量及节点8处的支撑力大小及方向，给出节点位移云图和等效应力云图。

图1 图2此问题是弹性力学中的平面应变问题。

一、选择图形界面方式ANSYS main menu>preferences>structural可以不选择图形界面方式。

弹性力学ansys求解实例详解

弹性力学a n s y s求解实例详解Company number：【WTUT-WT88Y-W8BBGB-BWYTT-19998】ANSYS 上机实验报告一、题目描述如图1所示，一简支梁横截面是矩形，其面积202.0m A =，对弯曲中性轴的惯性矩451067.6m I zz -⨯=，高m h 2.0=，材料的pa E 11101.2⨯=，横向变形系数3.0=μ。

该梁的自重就是均布载荷N q 4000=和梁中点处的集中力N F 2000=，试讨论在均布荷载作用下，简支梁的最大挠度。

二、问题的材料力学解答由叠加法可知：梁上同时作用几个载荷时，可分别求出每一载荷单独作用时的变形，把各个形变叠加即为这些载荷共同作用时的变形。

在只有均布载荷q 作用时，计算简支梁的支座约束力，写出弯矩方程，利用EI M dxw d =22积分两次，最后得出：铰支座上的挠度等于零，故有0=x 时，0=w ，因为梁上的外力和边界条件都对跨度中点对称，挠曲线也应对该点对称。

因此，在跨度中点，挠曲线切线的斜率等于零，即：2l x =时，0=dx dw ，把以上两个边界条件分别代入w 和0=dxdw 的表达式，可以求出243ql C -=，0=D ，于是得转角方程及挠曲线方程为： x ql x q x ql EIw ql x q x ql EI dx dw EI 2424122464343332--=--==θ （1）在跨度中点，挠曲线切线的斜率等于零，挠度为极值，由（1）中式子可得：即EIql w q c 3845)(4-=。

在集中力F 单独作用时，查材料力学中梁在简单载荷作用下的变形表可得EIFl w F c 48)(3-=。

叠加以上结果，求得在均布载荷和集中力共同作用下，梁中点处的挠度是EIFl EI ql w w w F c q c c 483845)()(34--=+=，将各参数代入得m w c 410769.0-⨯=三、问题的ansys 解答建立几何模型此问题为可采用Beam 分析，所以该几何模型可用线表示。

弹性力学及有限元法ANSYS实例演示

图5.1
图5.2
实例——静力学分析位移变形图
X方向位移
Y方向位移
Z方向位移
整体位移
实例——静力学分析受力图
X方向受力
Z方向受力
Y方向受力整体受力
Mises应力图
实例——动力学分析
动力学分析单元的选择
由于实体建模单元数多，计算慢，效率低，所以，这种轴对称模型我们一般用梁单元(beam)和壳单元 (shell)来模拟。这种简化单元具有精度高，运算速度快，效率高的优点。
ANSYS界面介绍
图2 信息输出窗口
APDL简介
ANSYS参数化设计语言(APDL)是一门可用来自动完成有限元常规分析操作或通过参数化变量方式建立分析模型的脚本语言，用建立职能化分析的手段为用户提供自动完成有限元分析过程，即程序的输入可设定为根据制定的函数、变量以及选用的分析类型来做决定，是完成优化设计和自适应网格的最主要的基础。APDL允许复杂的数据输入，使用户实际上对任何设计或分析属性有控制权，如分析模型的尺寸、材料的性能、载荷、边界条件施加的位置和网格的密度等。APDL扩展了传统有限元分析的范围，并扩展了更高级运算包括灵敏度研究、零件库参数化建模、设计修改和设计优化等。
ANSYS界面介绍
(6) 图形窗口：是ANSYS的图形输出区域，一般的交互式图形操作也在此区域进行。
(7) 状态栏：显示当前操作的有关提示。 (8) 输出窗口：如图2所示。输出窗口接受ANSYS软件运
行时所有的文本输出，比如命令的响应、注释、警告、错误以及其他的各种信息。一般情况下，这个窗口隐藏在主窗口后面。
下面我们先简单介绍一下Beam188单元
实例——动力学分析
Beam188单元适合于分析从细长到中等粗短的梁结构，该单元基于铁木辛哥梁结构理论，并考虑了剪切变形的影响。

ANSYS命令流学习笔记17-超弹性材料分析和WB-ABAQUS分析对比

! ANSYS 命令流学习笔记17-超弹性材料分析及WB-ABAQUS 分析对比 !学习重点：非线性材料建立在线性材料的基础上，理解好线性才行，在概念上就能理解好非线性材料。

但是非线性的计算又是另外一个概念，先学习材料部分知识吧。

理解应力应变的张量形式、应变能函数、高度非线性下应变能函数形式。

!1、应变张量张量最初是用来表示弹性介质中各点应力状态的，在三维坐标下，应力和应变的状态可以用9个分量来表示，超弹性材料主要使用应变张量及应变张量不变量这两个概念。

任意一点的应变状态可由矩阵表示：⎪⎪⎪⎭⎫ ⎝⎛z zy zxyz y yx xz xy x εγγγεγγγε存在三个相互垂直的方向。

在这三个方向上没有角度偏转，只有轴向的应变，该正应变称为主应变，此三方向成为主方向。

此时，该点应力状态由矩阵表示：但是应变张量表达中，某一点的应变状态矩阵，和坐标方向的选取有着很大关系。

为了表达坐标无关的某点应变状态，定义应变张量不变量I 1、I 2、I 3 ，分别为应变张量的第一，第二和第三不变量。

由下式表示：取= 1/3*I 1，将应变张量可以分解为应变球张量和应变偏张量，分别对应应变的形状改变部分和体积改变部分。

⎪⎪⎪⎭⎫ ⎝⎛+⎪⎪⎪⎭⎫⎝⎛---=m mm m z zyzx yzmy yxxzxy m x ijεεεεεγγγεεγγγεεε000000⎪⎪⎪⎭⎫ ⎝⎛=321000000εεεεij m ε!2、应变能函数一维应变能函数：U =F d ∆L = S ∙L ∙σx εx0∆Ld εx一维应变能密度函数：W = σx εxd εxW 或U 函数形式能够确定的话，应力与应变之间的关系也就完全确定了，反之应变应力关系确定可以反推应变能密度函数。

可以认为应变能密度函数是材料本构关系的一种表达形式。

!3、应变能函数形式（1）延伸率、不变量、体积比在确定应变能函数形式之前，首先要确定应变能函数的变量。