测试装置的基本特性概要
2测试装置的基本特性

第二节 测试装置的静态特性
测试装置的静态特性是指静态测量情况下描述实际测试 装置与理想定常线性系统的接近程度。 •线性度 •灵敏度 •分辨力 •回程误差 •漂移
一、线性度
定义:测量装置输出、输入之间的关系与理想比例关系 的偏离程度。 线性误差的两种表达形式: * 静态标定所得输入、输出数据点与理想直线的最大偏差Δmax * 百分数表达
2 n H ( s) 2 2 s 2n s n
二、一阶、二阶系统的特性 (1)一阶系统
+ u i(t ) - R + C u o(t ) -
dxo RC xo xi dt
dy t a0 y t b0 x t 一般形式的一阶微分方程式: a1 dt dy t 改写为: T y t Sx t dt
(4)脉冲响应函数
已知: 若装置的输入为单位脉冲函数 由于 ,则有 。
对上式两边取拉氏逆变换,且令 则有
上式表明,单位脉冲函数的响应同样可描述测量系统的动态特性,它同 传递函数是等效的,不同的是一个在复频域 ,一个是在时间域,通常称 h(t) 为脉冲响应函数。脉冲响应函数可视为系统特性的时域描述。
T=a1/a0-系统时间常数 ; S=b0/a0-系统静态灵敏度 ; 为了分析方便,令S=1,
dy t T y t x t dt
一阶系统的特性
•传递函数: H ( s ) •频响函数:H ( )
1 Ts 1
1 jT 1
1 1 (T ) 2
x(t) 0 t0 t
测量装置实现测量不失真的频率特性
时域条件
y(t)= A0 x(t- t0)
式中:A0、t0均为常数。
第三章 测试装置的基本特性

S=y/x
如果是线性理想系统,则
y
1——标定曲线
2——拟合直线
S y y b0 常数 x x a0
1. 一位移传感器,当位移变化为1mm时, 输出电压变化为300mV,则灵敏度
S=300/1 =300mV/mm
2.一机械式位移传感器,输入位移变化为 0.01mm时,输出位移变化为10mm,则 灵敏度(放大倍数) S=10/0.01=1000
无论你怎样地表示愤怒,都不要做出 任何无法挽回的事来。
——弗兰西斯·培根
Francis Bacon
英国 哲学家 1561-1626
第三章 测试装置的基本特性
§3.1 概述
▼
§3.2 测试装置的静态特性
▼
§3.3 测试装置的动态特性
▼
§3.4 实现不失真测量的条件
▼
§3.5 典型系统的频率响应特性
▼
输入和输出的各阶导数均等于零。
yy((tt))
静态输入
y b0 x Sx a0
➢ 理想测试装置的输入、输出之间呈单调、线性
线性段
比例关系。即输入、输出关系是一条理想的直
线,斜率为S= b0/a0 。
00
线性段
xx((tt))
理实想际线线性性
(1) 灵敏度
当测试装置的输入x有一增量x,引起输出 y 发生相应的 变化y时,则灵敏度定义:
实例
线性误差=Bmax/A×100%
y
1——)
Bi =2V
xi
y
1——标定曲线
2——拟合直线
2
1
yi
y(i)
Bi =2V
xi
10V 1000V
0
输入范围
4.测试装置的基本特性

20
测量装置基本特性
4. τ值的试验测定
对于一阶系统,其动态参数τ值可以经过试验测定。
① 时域法: 测试系统对于单位阶跃输入的响应y(t),令:
Z
ln(1
y(t ) )
t
ln(e
)
t
A
画出Z-t曲线,若该曲线为直线时,τ即直线斜率绝对值的倒
数。不然,该系统不是一阶系统。
② 频率法: 系统输入正弦波,依次求出输出与输入的幅值比及
100%
δi:线性度 △max:特性曲线与参考直线的最大偏差 △F.S:满量程输出的平均值
根据参考直线的定义方法,可将线性度分为:
① 理论线性度:参考直线由0点和满量程输出点确定 ② 独立线性度:参考直线由最小二乘法确定。 有时,系统的输出输入在局部范围内是直线,则取此段做为 标称输出范围。
2019/9/11
2019/9/11
测试技术基础
机械工程及自动化学院
1
测试技术基础
第性 4.3 动态特性 4.4 典型测试装置的动态特性
2019/9/11
2
测量装置基本特性
4.1 概述
系统是由若干相互作用,相互依赖的事物组合而成的具有特 定功能的整体;系统的特性是指系统的输出和输入的关系。
2019/9/11
14
测量装置基本特性
4.4 典型测试装置的动态特性
一个大的系统往往可以分解成一些小系统的组合,这些 小系统可分为零阶系统,一阶系统,二阶系统。其他高阶系 统可由这三个理想化的小系统组合而成。因此只需要对这三 个环节的动态特性有所了解,对高阶系统的性能分析也是可 能的。
N阶系统
H (s)
测试装置的基本特性

P 1
P
1
2
(2) Bode 图 ---- 对数频率特性图 a)对数频率特性
lg G j lg A e
j
lg A
j lg e
对数频率特性由对数幅频特性图、对数相频特性图描述; b)对数频率特性图(Bode图)坐标系
x (t ) y (t )
x1 ( t ) x 2 ( t ) y1 ( t ) y 2 ( t )
⑵ 比例性 ax ( t ) ay ( t )
dx ( t ) dt dy ( t ) dt
(3)微分性
系统对原输入信号的微分等于原输出信号的微
分,即 若 x(t) → y(t),则 x’(t) → y’(t)
⑷ 积分:初始状态为零:t=0时,
x (t ) dx ( t ) dt y (t ) 0
t0
x ( t ) dt
0
t0
y ( t ) dt
0
⑸ 频率保持性:输入为某一频率的信号 输出必为同一频率的信号
若 x(t)=Acos(ωt+φx)
则 y(t)=Bcos(ωt+φy)
A
L
对数 幅频 100 特性 10 图
1
60 dB 40 20
L 20 lg A Q arctg P
1
10
100
对数 相频 特性 图
20 0
1
10
100
20
Bode图介绍
Bode图介绍
dx ( t )
(完整版)测试装置的基本特性
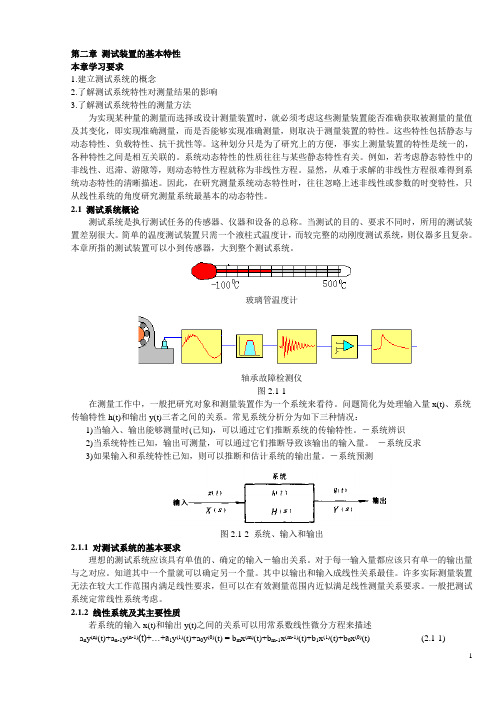
第二章测试装置的基本特性本章学习要求1.建立测试系统的概念2.了解测试系统特性对测量结果的影响3.了解测试系统特性的测量方法为实现某种量的测量而选择或设计测量装置时,就必须考虑这些测量装置能否准确获取被测量的量值及其变化,即实现准确测量,而是否能够实现准确测量,则取决于测量装置的特性。
这些特性包括静态与动态特性、负载特性、抗干扰性等。
这种划分只是为了研究上的方便,事实上测量装置的特性是统一的,各种特性之间是相互关联的。
系统动态特性的性质往往与某些静态特性有关。
例如,若考虑静态特性中的非线性、迟滞、游隙等,则动态特性方程就称为非线性方程。
显然,从难于求解的非线性方程很难得到系统动态特性的清晰描述。
因此,在研究测量系统动态特性时,往往忽略上述非线性或参数的时变特性,只从线性系统的角度研究测量系统最基本的动态特性。
2.1 测试系统概论测试系统是执行测试任务的传感器、仪器和设备的总称。
当测试的目的、要求不同时,所用的测试装置差别很大。
简单的温度测试装置只需一个液柱式温度计,而较完整的动刚度测试系统,则仪器多且复杂。
本章所指的测试装置可以小到传感器,大到整个测试系统。
玻璃管温度计轴承故障检测仪图2.1-1在测量工作中,一般把研究对象和测量装置作为一个系统来看待。
问题简化为处理输入量x(t)、系统传输特性h(t)和输出y(t)三者之间的关系。
常见系统分析分为如下三种情况:1)当输入、输出能够测量时(已知),可以通过它们推断系统的传输特性。
-系统辨识2)当系统特性已知,输出可测量,可以通过它们推断导致该输出的输入量。
-系统反求3)如果输入和系统特性已知,则可以推断和估计系统的输出量。
-系统预测图2.1-2 系统、输入和输出2.1.1 对测试系统的基本要求理想的测试系统应该具有单值的、确定的输入-输出关系。
对于每一输入量都应该只有单一的输出量与之对应。
知道其中一个量就可以确定另一个量。
其中以输出和输入成线性关系最佳。
第二章测试装置的基本特性(精)

输入输出(响应)系统第二章 测试装置的基本特性第一节 概述测试是具有试验性质的测量,是从客观事物取得有关信息的过程。
在此过程中须借助测试装置。
为实现某种量的测量而选择或设计测量装置时,就必须考虑这些测量装置能否准确获取被测量的量值及其变化,即实现准确测量,而能否实现准确测量,则取决于测量装置的特性。
这些特性包括动态特性、静态特性、负载特性、抗干扰性等。
测量装置的特性是统一的,各种特性之间是相互关联的。
1、测试装置的基本要求通常工程测试问题总是处理输入量)(t x 、装置(系统)的传输特性)(t h 和输出量)(t y 三者之间的关系。
图2-1系统、输入和输出1)当输入、输出是可测量的(已知),可以通过它们推断系统的传输特性。
(系统辨识)。
2)当系统特性已知,输出可测量,可以通过它们推断导致该输出的输入量。
(反求)。
3)如果输入和系统特性已知,则可以推断和估计系统的输出量。
(预测) 。
测试装置的基本特性主要讨论测试装置及其输入、输出的关系。
理想的测试装置应该具有单值的、确定的输入——输出关系。
即对应于某一输入量,都只有单一的输出量与之对应 。
知道其中的一个量就可以确定另一个量。
以输出和输入成线性关系为最佳。
一般测量装置只能在较小工作范围内和在一定误差允许范围内满足这项要求。
2、测量装置的静态特性测试系统的静态特性就是在静态测量情况下,描述实际测试装置与理想定常线性系统的接近程度。
测量装置的静态特性是通过某种意义的静态标定过程确定的。
静态标定是一个实验过程,这一过程是在只改变测量装置的一个输入量,而其他所有的可能输入严格保持为不变的情况下,测量对应得输出量,由此得到测量装置的输入输出关系。
3、测量装置的动态特性测量装置的动态特性是当被测量即输入量随时间快速变化时,测量输入与响应输出之间的动态关系得数学描述。
研究测量装置动态特性时,认为系统参数不变,并忽略迟滞、游隙等非线性因素,可用常系数线性微分方程描述测量装置输入与输出间的关系。
测试技术 第二章 测试装置的基本特性

四、分辨力
定义: 定义 引起测量装置输出值产生一个可察觉变化的 最小输入量(被测量) 最小输入量(被测量)变化值称为分辨力 表征测量系统的分辨能力 说明: 说明 1、分辨力 --- 是绝对数值,如 0.01mm,0.1g,10ms,…… 、 是绝对数值, , , , 2、分辨率 --- 是相对数值: 、 是相对数值: 能检测的最小被测量的 变换量相对于 满量程的 百分数, 百分数,如: 0.1%, 0.02%
y
(a) 端点连线法 端点连线法: 算法: 检测系统输入输出曲线的两端点连线 算法: 特点: 简单、方便,偏差大, 特点: 简单、方便,偏差大,与测量值有关 (b) 最小二乘法 最小二乘法: 算法: 计算: 算法: 计算:有n个测量数据 (x1,y1), (x2,y2), … , (xn,yn), (n>2) 个测量数据: 个测量数据 , 残差: 残差平方和最小: 残差:∆i = yi – (a + b xi) 残差平方和最小:∑∆2i=min
线性 y 线性 y 非线性y
x
x
x
非线性原因: 非线性原因
外界干扰 温 度 湿 度 压 力 冲 击 振 动 电 磁 场 场
输入 x
检测系统
输入 y = f(x)
摩 擦
间 隙
松 动
迟 蠕 滞 变
变 老 形 化
误差因素
严格的说,很多测试装置是时变的 因为不稳定因素的存 严格的说 很多测试装置是时变的(因为不稳定因素的存 很多测试装置是时变的 但在工程上认为大多数测试装置是时不变线性系统 在),但在工程上认为大多数测试装置是时不变线性系统 但在工程上认为大多数测试装置是 (定常线性系统 该类测试装置的输入与输出的关系可 定常线性系统).该类测试装置的输入与输出的关系可 定常线性系统 用常系数线性微分方程来描述. 用常系数线性微分方程来描述
二测试装置的基本特性概要PPT课件
10
第二节测试装置的静态特性
根据(2-1)式,线性定常系统的静态特性:
y b0 x Sx a0
本章主要讨论测试装置及其与输入、输出的关系。
图 2-0 典型的测试装置
22
第一节 概述
一、对测试装置的基本要求 1、解决的问题 通常的工程测试问题总是处理输入量x(t)、装置(系统)的传输特性h(t)和输 出量y(t)三者之间的关系(图2·1)。即: ① 如果输入、输出是可以观察(已知)的量,则可以推断系统的传输特性; ② 如果系统特性已知,输出可测,则可以推断导致该输出的输入量; ③ 如果输入和系统特性已知,则可以推断和估计与该输出对应的系统输
(三)量程和测量范围
量程:测量装置的示值范围的上、下限之差的模。 测量范围:是指使该装置的误差处于允许极限内它所能测量的被测量值的 范围。对于用于动态测量的装置还标明在允许误差极限内所能测量的频率 (范四围)信。噪比
信噪比:信号功率与干扰(噪声)功率之比,记为SNR,单位为分贝(dB)。
SNR 10 lg Ns
测量装置的准确度反映测量装置的总误差。该总误差包括系统误差和 随机误差两部分。测量装置的随机误差分量可用对同一被测量在同一行程 方向连续进行多次测量,其示值的分散性来表述。通常这也称为测量装置 的重复性误差。
在实际工作中,往往使用到测量装置的引用误差一词。它是指测量装 置的示值绝对误差与引用值之比,并以百分数表示。引用值往往是指测量 装置的量程或示值范围的最高值。
。
静态测量:是指测量期间被测量值可认为是恒定的测量。
动态测量:是为确定量的瞬时值及(或)其随时间变化的量所进行的测量。 (二)测量装置的误差和准确度 装置的示值误差:测量装置的示值和被测量的真值之间的差值。若不会引 起混淆,可简称为测量装置的误差。
第2章 测试装置的基本特性

• 传递函数的特点 • 1)H(s)与输入x(t)及系统的初始状态无关,它 只表达系统的传输特性。 • 对具体系统而言,它的H(s)不因输入x(t)变化 而不同,却对任一具体输入x(t)都确定地给出 相应的、不同的输出y(t)。 • • •
• 2)H(s)是对物理系统的微分方程,即式(2—1)取拉 普拉斯变换而求得的,它只反映系统传输特性而 不拘泥于系统的物理结构。同一形式的传递函数 可以表征具有相同传输特性的不同物理系统。 • • • 例如 液柱温度计和RC低通滤波器同是一阶系统, 具有形式相似的传递函数,而其中一个是热学系 统,另一个却是电学系统,两者的物理性质完全 不同。 • •
• 一些实际测量装置无法在较大工作范围内满足 这种要求,而只能在较小工作范围内和在一定 误差范围内满足这项要求。
• 二、线性系统及其主要性质 • 常系数线性微分方程来进行描述
• 主要性质 • 1)符合叠加原理:几个输入所产生的总输 出是各个输入所产生的输出叠加的结果。
• 2)比例特性:
• 3)系统对输入导数的响应等于对原输入响 应的导数
• 因此,频率响应函数就成为实验研究系统 的重要工具。
(1)幅频特性、相频特性和频率响应函数 根据定常线性系统的频率保持性,系统在简谐信号 x(t)=X0sinωt的激励下,所产生的稳态输出也是简谐信 号y(t)=Y0sin(ωt+φ)。这一结论可从微分方程解的理 论得出。此时输入和输出虽为同频率的简谐信号,但两 者的幅值并不一样。其幅值比A=Yo/Xo和相位差φ都随 频率ω而变,是ω的函数。
• 一、对测量装置的基本要求 • 对于测量系统我们希望系统的输入输出之间具有一一 对应的直线关系,具有这样关系的系统被称为线性系 统。 • • 理想的测量装置应该具有单值的、确定的输入一输出 关系。 • 对于每一输入量都应只有单一的输出量与之对应。知 道其中的一个量就可以确定另一个量。
第二章测试装置的基本特性

输入输出(响应)系统第二章 测试装置的基本特性第一节 概述测试是具有试验性质的测量,是从客观事物取得有关信息的过程。
在此过程中须借助测试装置。
为实现某种量的测量而选择或设计测量装置时,就必须考虑这些测量装置能否准确获取被测量的量值及其变化,即实现准确测量,而能否实现准确测量,则取决于测量装置的特性。
这些特性包括动态特性、静态特性、负载特性、抗干扰性等。
测量装置的特性是统一的,各种特性之间是相互关联的。
1、测试装置的基本要求通常工程测试问题总是处理输入量)(t x 、装置(系统)的传输特性)(t h 和输出量)(t y 三者之间的关系。
图2-1系统、输入和输出1)当输入、输出是可测量的(已知),可以通过它们推断系统的传输特性。
(系统辨识)。
2)当系统特性已知,输出可测量,可以通过它们推断导致该输出的输入量。
(反求)。
3)如果输入和系统特性已知,则可以推断和估计系统的输出量。
(预测) 。
测试装置的基本特性主要讨论测试装置及其输入、输出的关系。
理想的测试装置应该具有单值的、确定的输入——输出关系。
即对应于某一输入量,都只有单一的输出量与之对应 。
知道其中的一个量就可以确定另一个量。
以输出和输入成线性关系为最佳。
一般测量装置只能在较小工作范围内和在一定误差允许范围内满足这项要求。
2、测量装置的静态特性测试系统的静态特性就是在静态测量情况下,描述实际测试装置与理想定常线性系统的接近程度。
测量装置的静态特性是通过某种意义的静态标定过程确定的。
静态标定是一个实验过程,这一过程是在只改变测量装置的一个输入量,而其他所有的可能输入严格保持为不变的情况下,测量对应得输出量,由此得到测量装置的输入输出关系。
3、测量装置的动态特性测量装置的动态特性是当被测量即输入量随时间快速变化时,测量输入与响应输出之间的动态关系得数学描述。
研究测量装置动态特性时,认为系统参数不变,并忽略迟滞、游隙等非线性因素,可用常系数线性微分方程描述测量装置输入与输出间的关系。
测试装置的基本特性

第二章 测试装置的基本特性一、 知识要点及要求1、掌握线性系统及其主要特性。
2、掌握测试装置的动态特性及静态特性。
3、掌握一、二阶测试装置的频率响应特性。
4、掌握测试装置的不失真测试条件。
二、 重点内容1、测试装置的基本要求测试装置的基本特性主要讨论测试装置及其输入、输出的关系。
理想的测试装置应该具有单值的、确定的输入——输出关系。
即,对应于某一输入量,都只有单一的输出量与之对应 。
知道其中的一个量就可以确定另一个量。
2、线性系统及其主要性质线性系统的输入)(t x 与输出)(t y 之间的关系可用下面的常系数线性微分方程)()()()()()()()(0111101111t x b dt t dx b dtt x d b dt t x d b t y a dt t dy a dtt y d a dt t y d a m m m m m m n n n n n n ++++=++++------ 来描述时,则称该系统为时不变线性系统,也称定常线性系统。
式中t 为时间自变量,n a 、1-n a 、…、1a 、0a 和n b 、1-n b 、…、1b 、0b 均为常数。
时不变线性系统的主要性质:1)叠加原理特性 2)比例特性3)系统对输入导数的响应等于对原输入响应的导数 4) 如系统的初始状态均为零,则系统对输入积分的响应等同于对原输入响应的积分。
5)频率保持性3、测试装置的静态特性测试装置的静态特性就是在静态测量情况下描述实际测试装置与理想定常线性系统的接近程度。
描述测试装置静特性的主要指标有:1) 线性度是指测量装置输出、输入之间保持常值比例关系的程度。
作为技术指标则采用线性误差来表示,即用在装置标称输出范围A 内,校准曲线与拟合直线的最大偏差B 来表示。
也可用相对误差来表示,如线性误差=%100⨯AB2)灵敏度S 当装置的输入x 有一个变化量x ∆,引起输出y 发生相应的变化为y ∆,则定义灵敏度为:dxdyx y S =∆∆=3)回程误差 当输入量由小增大和由大减小时,对于同一输入量所得到的两个输出量却往往存在着差值,把在全测量范围内,最大的差值h 称为回程误差。
02测试装置的基本特性

※测试装置的静态特性: 就是在静态测量情况下描述实际测试装置 与理想时不变线性系统的接近程度。 (主要讨论在静态测量情况下,描述输入 与输出之间的关系)
测量装置的静态特性由通过某种意义的静态标定过程所确定。 静态标定:是一个实验过程。这一过程是在只改变测量装置的 一个输入量,而其他所有的可能输入严格保持不变 的情况下,测量对应的输出量,由此得到测量装置 输入与输出间的关系。
x(t ) x0 e jt,则
y(t ) y 0 e
j (t )
三、测试和测试装置的若干术语 ※静态测量:测量期间被测量值可认为是恒定的测量量, 即被测量不随时间变化,则称为静态测量。
5
2.1 概述
※动态测量:是为确定值的瞬时值及其随时间变化的量所 进行的测量。 ※信噪比:信号功率与干扰噪声功率之比,记作 SNR 用分贝(dB)来表示,即 Ns SNR 10 lg Nn N s —信号功率
2.3 测试装置的动态特性(dynamic characteristics)
b频率响应函数的求法 方法二:通过实验测定 方法三:H()=Y()/X()(初始条件全为零的条件下) 说明:尽管频率响应函数对简谐信号而言,但是,任何信 号都可以分解为简谐信号的叠加。因而,在任何复杂信号 输入下,系统频率响应特性都适用。
x1 (t ) x2 (t ) y1 (t ) y2 (t )
※作用在定常系统的各个输入所产生的输出互不影响。 n个激励同时作用一个测试系统,其响应等于这n个激励单独 作用的响应和。复杂信号→系列谐波信号(付氏级数展开)
②比例特性/均匀性:对于任意常数
ax(t ) ay(t )
※灵敏度
单位输入引起输出的变化,即S=△y/△x。 通常用理想直线的斜率作为灵敏度值。(量纲) y △y △x
测试技术第二章测试装置的基本特性

第二章测试装置的基本特性第一节概述一、对测试装置的基本要求1.工程测试问题通常的工程测试问题总是处理输入量x(t)、装置(系统)的传输特性h(t)和输出量y(t)三者之间的关系如图2-1,即:系统(响应)1)如果x(t)、y(t)可以观察(已知)的量,则可推断h(t)。
2)如果h(t)已知,y(t)可测,则可推断x(t)。
3)如果x(t)和h(t)已知,则可推断和估计y(t)。
2.理想的测试装置①输出和输入成线性关系。
即具有单值的、确定的输入-输出关系。
②系统为时不变线性系统。
3.实际的测试装置①只能在较小工作范围内和在一定误差允许范围内满足线性要求。
②很多物理系统是时变的。
在工程上,常可以以足够的精确度认为系统中的参数是时不变的常数。
二、线性系统及其主要性质1.线性方程方程中的所有变量的幂次不大于1的方程称为线性方程。
注意导数的阶次与幂次的区别,以及经过拉氏变换后所得到的相函数中,阶次与幂次的表现形式。
2.线性系统用线性方程来描述的系统就是线性系统。
线性系统符合叠加性和均匀性(齐次性)。
3.时不变线性系统当系统的输入x(t)和输出y(t)之间的关系可以用常系数线性微分方程)()(0)(1)(1)(0)(1)(1)(1111t x b bb b t y a a a a dtt dx dt t x d m dt t x d mdtt dy dtt y d n dtt y d n m m mm n n nn ++⋅⋅⋅++=++⋅⋅⋅++------ (2-1)来描述时,该系统称为时不变线性系统,也称定常线性系统。
式中t 为时间自变量。
系统的系数a n , a n-1, …,a 1, a 0和 b m , b m-1, …, b 1, b 0均为常数,既不随时间而变化,也不是自变量x 、因变量y 及它们各阶导数的函数。
4.时不变线性系统的性质如以x (t )→ y (t )表示上述系统的输入、输出的对应关系,则时不变线性系统具有以下一些主要性质。
