七年级上1.2.3绝对值课件
合集下载
七年级数学上册(湘教版)课件:1.2.3 绝对值

A.2 015
B.-2 015
C.±2 015
1 D.2 015
4.(2分)如图,数轴上有A,B,C,D四个点,其中绝对值相 等的点是( C )
A.点A与点D B.点A与点C C.点B与点C D.点B与点D 5.(3分)下列各式中,不成立的是( D ) A.|-2|=2 B.-|-2|=-2 C.|-2|=|2| D.-|-2|=2
1.2 数轴、相反数与绝对值 1.2.3 绝对值
1.正数的绝对值是它_本__身___;负数的绝对值是它的__相__反__数__;0的 绝对值是_0___;互为相反数的两个数的绝对值__相__等___. 2.一个数的绝对值等于数轴上表示这个数的点与____原__点_____的 ___距__离___. 3.一般地,如果a表示一个数,则(1)当a是正数时,|a|=__a__;(2) 当a=0时,|a|=__0__;(3)当a是负数时,|a|=__-__a__.即|a|是指a和 -a中___非__负__数____的那一个.
解:(1)第3,4,5件零件的质量相对好一些;质量越好的零件, 其误差的绝对值越小,越接近标准尺寸;(2)有3件优等品,2件 合格品,1件次品
Байду номын сангаас
19.(8分)已知|a-2|+|b-3|+|c-4|=0. (1)求a,b,c的值; (2)计算:2|a|+3|-b|+4|c|. 解:(1)根据题意,得|a-2|=0,|b-3|=0,|c-4|=0,则a =2,b=3,c=4;(2)原式=29.
10.(4分)下列说法正确的有( B ) ①绝对值等于它本身的数是0和1; ②一个有理数的绝对值必是正数; ③任何有理数的绝对值都不是负数; ④绝对值等于它的相反数的数是负数; ⑤绝对值等于同一个正数的数有两个. A.1个 B.2个 C.3个 D.4个
2022年秋七年级数学上册 第1章 有理数 1.2 数轴、相反数与绝对值 1.2.3 绝对值课件 (

•
9、 人的价值,在招收诱惑的一瞬间被决定 。2022/3/12022/3/1Tuesday, March 01, 2022
•
10、低头要有勇气,抬头要有低气。2022/3/12022/3/12022/3/13/1/2022 8:39:43 AM
•
11、人总是珍惜为得到。2022/3/12022/3/12022/3/1M ar-221- Mar-22
B.原点或原点左侧
C.原点右侧
D.原点或原点右侧
2. 已知在数轴上,O为原点,A,B两点所表示的数 分别为a,b,利用下列A,B,O三点在数轴上的位置关 系,可以判断|a|<|b|的选项是( B )
A
B
C
D
3. 下列说法中正确的是( C ) A.任何一个有理数的绝对值都是正数 B.负数的绝对值是负数 C.若|a|+|b|=0,则|a|=0且|b|=0 D.若a≠b,则|a|≠|b| 4. 化简:|π-3.14|= π-3.14 , -|-25|= -25 .
【解析】当 a=0 时,A、B、C 说法均不正确,而|a| +1≥1,一定是正数,故 D 项正确.
6. 若|x-3|+|y-2|=0,则|x+y|的值为 5 . 7. a,b 在数轴上位置如图,化简|a|-|b|=-a-b .
1.若|a|=-a,则实数 a 在数轴上的对应点一定在
(B) A.原点左侧
②|-6|= 6 ;|-3.1|= 3.1 ;|-2.7|= 2.7 ; ③|0|= 0 . (2)根据(1)中的规律发现,不论正数、负数和0,它 们的绝对值一定是 非负数 ,即|a|≥0.
(3)根据(2)解决下列问题: ①当x= 0 时,|x|+5有最小值,此时的最小值 是 5; ②当x= 1 时,7-|x-1|有最大值,此时的最大值 是7.
新沪科版七年级上册数学教学课件 第1章 有理数 1.2 数轴、相反数和绝对值 第3课时 绝对值

(A)|﹣5|= 5 (B)﹣|5|= ﹣|﹣5| (C)|﹣5|=|5|(D)﹣|﹣5|= 5
【教材P12 练习 第4题】
4. 计算
(1)|﹣8|+|9|=17
(2)|﹣12|÷|12|=1
(3)|0.6|-|
3|=0 5
(4)|﹣3|×|﹣2|=6
拓展延伸
a
a
(1)若a>0,则 a = 1,若 a =___1__,
则a是__正__数___.
(2)若|x| = 3,则x =__±__3__;若|﹣x| = 4,
则 x =__±__4__.
1.通过这节课的学习,你有哪些收获? 2.你还存在哪些疑问,与同伴交流。
1.从教材习题中选取, 2.完成练习册本课时的习题.
同学们,通过这节课的学习 ,你有什么收获呢?
谢谢 大家
判断:
a=0
Ⅰ.若 a = ﹣a,则a<0. (× ) 还有 0
Ⅱ.绝对值等于它本身的数一定是正数. (× )
Ⅲ.绝对值最小的数是 1. ( ×)
Ⅳ.任何有理数的绝对值都是正数. ( ×)
0 的绝对值是 0,但 0 不是正数
互为相反数的两个数的绝对值有什么关系? 分析:一对相反数虽然分别在原点两边, 但它们到原点的距离是相等的. 结论:互为相反数的两个数的绝对值相等.
22 是多少?
在数轴上,表示数 a 的点与原点的距离叫作
数 a 的绝对值,记作|a|.
这里的数a可以是
正数、负数和0.
|-4|
|4|
﹣5 ﹣4 ﹣3 ﹣2 ﹣1 0 1 2 3 4 5
+4和-4符号相反,表示它们的点位于原点的两 侧,但与原点的距离都等于4,即它们的绝对值都是 4,记作|+4|=4,|-4|=4.
【教材P12 练习 第4题】
4. 计算
(1)|﹣8|+|9|=17
(2)|﹣12|÷|12|=1
(3)|0.6|-|
3|=0 5
(4)|﹣3|×|﹣2|=6
拓展延伸
a
a
(1)若a>0,则 a = 1,若 a =___1__,
则a是__正__数___.
(2)若|x| = 3,则x =__±__3__;若|﹣x| = 4,
则 x =__±__4__.
1.通过这节课的学习,你有哪些收获? 2.你还存在哪些疑问,与同伴交流。
1.从教材习题中选取, 2.完成练习册本课时的习题.
同学们,通过这节课的学习 ,你有什么收获呢?
谢谢 大家
判断:
a=0
Ⅰ.若 a = ﹣a,则a<0. (× ) 还有 0
Ⅱ.绝对值等于它本身的数一定是正数. (× )
Ⅲ.绝对值最小的数是 1. ( ×)
Ⅳ.任何有理数的绝对值都是正数. ( ×)
0 的绝对值是 0,但 0 不是正数
互为相反数的两个数的绝对值有什么关系? 分析:一对相反数虽然分别在原点两边, 但它们到原点的距离是相等的. 结论:互为相反数的两个数的绝对值相等.
22 是多少?
在数轴上,表示数 a 的点与原点的距离叫作
数 a 的绝对值,记作|a|.
这里的数a可以是
正数、负数和0.
|-4|
|4|
﹣5 ﹣4 ﹣3 ﹣2 ﹣1 0 1 2 3 4 5
+4和-4符号相反,表示它们的点位于原点的两 侧,但与原点的距离都等于4,即它们的绝对值都是 4,记作|+4|=4,|-4|=4.
新版人教版七年级数学上册《绝对值》课件(17张)
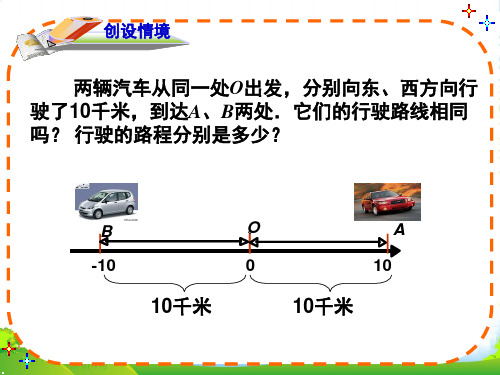
创设情境
两辆汽车从同一处O出发,分别向东、西方向行 驶了10千米,到达A、B两处.它们的行驶路线相同 吗? 行驶的路程分别是多少?
B
O
A
-10
0
10
10千米
10千米
做游戏
请两位同学分别站在老师的左右两边,两位同学 同时向东、西相反的方向走1米,把这两位同学所 站位置用数轴上的点表示出来.
距
距
离
离
是1
学生活动 2.互为相反数的两个数的绝对值有什么关系?
一对相反数虽然分别在原点两边,但它们 到原点的距离是相等的.所以互为相反数的两 个数的绝对值相等.
7 图1.2-7
学生活动
你能把14个气温从低到高排列吗?能把这14个数 用数轴上的点表示出来吗?观察这些点在数轴上的位 置,思考它们与温度的高低之间的关系,你觉得两个 有理数可以比较大小吗?
(B )
A.可以是负数 B.不可能是负数
C.必是正数
D.可以是正数也可以是负数
温馨提示: 认真完成作业是巩固知识的有效方法!!
12、首先是教师品格的陶冶,行为的教育,然后才是专门知识和技能的训练。 13、在教师手里操着幼年人的命运,便操着民族和人类的命运。2022/5/52022/5/5May 5, 2022 14、孩子在快乐的时候,他学习任何东西都比较容易。 15、人自身有一种力量,用许多方式按照本人意愿控制和影响这种力量,一旦他这样做,就会影响到对他的教育和对他发生作用的环境。
练习2:|-13 |的相反数是 ;若|a|=2,则a=±2 .
练习3:绝对值小于3.5的整数是-3,-2,-1,0,1,2,3 . 练习4:已知:x342y0,则x= -3 ,y= 2 .
课堂练习
两辆汽车从同一处O出发,分别向东、西方向行 驶了10千米,到达A、B两处.它们的行驶路线相同 吗? 行驶的路程分别是多少?
B
O
A
-10
0
10
10千米
10千米
做游戏
请两位同学分别站在老师的左右两边,两位同学 同时向东、西相反的方向走1米,把这两位同学所 站位置用数轴上的点表示出来.
距
距
离
离
是1
学生活动 2.互为相反数的两个数的绝对值有什么关系?
一对相反数虽然分别在原点两边,但它们 到原点的距离是相等的.所以互为相反数的两 个数的绝对值相等.
7 图1.2-7
学生活动
你能把14个气温从低到高排列吗?能把这14个数 用数轴上的点表示出来吗?观察这些点在数轴上的位 置,思考它们与温度的高低之间的关系,你觉得两个 有理数可以比较大小吗?
(B )
A.可以是负数 B.不可能是负数
C.必是正数
D.可以是正数也可以是负数
温馨提示: 认真完成作业是巩固知识的有效方法!!
12、首先是教师品格的陶冶,行为的教育,然后才是专门知识和技能的训练。 13、在教师手里操着幼年人的命运,便操着民族和人类的命运。2022/5/52022/5/5May 5, 2022 14、孩子在快乐的时候,他学习任何东西都比较容易。 15、人自身有一种力量,用许多方式按照本人意愿控制和影响这种力量,一旦他这样做,就会影响到对他的教育和对他发生作用的环境。
练习2:|-13 |的相反数是 ;若|a|=2,则a=±2 .
练习3:绝对值小于3.5的整数是-3,-2,-1,0,1,2,3 . 练习4:已知:x342y0,则x= -3 ,y= 2 .
课堂练习
七年级数学上册第1章有理数1.2数轴相反数与绝对值1.2.3绝对值习题课件新版湘教版

全的人,主要是担心漏掉重要内容,影响以后的复习与思考.,这样不仅失去了做笔记的意义,也将课堂“听”与“记”的关系本末倒置了﹙太忙于记录, 便无暇紧跟老师的思路﹚。 如果只是零星记下一些突出的短语或使你感兴趣的内容,那你的笔记就可能显得有些凌乱。 做提纲式笔记因不是自始至终全都埋头做笔记,故可在听课时把时间更多地用于理解所听到的内容.事实上,理解正是做好提纲式笔记的关键。 课堂笔记要注意这五种方法:一是简明扼要,纲目清楚,首先要记下所讲章节的标题、副标题,按要点进行分段;二是要选择笔记语句,利用短语、数 字、图表、缩写或符号进行速记;三是英语、语文课的重点词汇、句型可直接记在书页边,这样便于复习时查找﹙当然也可以记在笔记本上,前提是你 能听懂﹚;四是数理化生等,主要记老师解题的新思路、补充的定义、定理、公式及例题;五是政治、历史等,着重记下老师对问题的综合阐述。
编后语
做笔记不是要将所有东西都写下,我们需要的只是“详略得当“的笔记。做笔记究竟应该完整到什么程度,才能算详略得当呢?对此很难作出简单回答。 课堂笔记,最祥可逐字逐句,有言必录;最略则廖廖数笔,提纲挈领。做笔记的详略要依下面这些条件而定。
讲课内容——对实际材料的讲解课可能需要做大量的笔记。 最讲授的主题是否熟悉——越不熟悉的学科,笔记就越需要完整。 所讲授的知识材料在教科书或别的书刊上是否能够很容易看到——如果很难从别的来源得到这些知识,那么就必须做完整的笔记。 有的同学一味追求课堂笔记做得“漂亮”,把主要精力放在做笔记上,常常为看不清黑板上一个字或一句话,不断向四周同学询问。特意把笔记做得很
2019/5/25
最新中小学教学课件
23
谢谢欣赏!
2019/5/25
最新中小学教学课件
24
ቤተ መጻሕፍቲ ባይዱ
编后语
做笔记不是要将所有东西都写下,我们需要的只是“详略得当“的笔记。做笔记究竟应该完整到什么程度,才能算详略得当呢?对此很难作出简单回答。 课堂笔记,最祥可逐字逐句,有言必录;最略则廖廖数笔,提纲挈领。做笔记的详略要依下面这些条件而定。
讲课内容——对实际材料的讲解课可能需要做大量的笔记。 最讲授的主题是否熟悉——越不熟悉的学科,笔记就越需要完整。 所讲授的知识材料在教科书或别的书刊上是否能够很容易看到——如果很难从别的来源得到这些知识,那么就必须做完整的笔记。 有的同学一味追求课堂笔记做得“漂亮”,把主要精力放在做笔记上,常常为看不清黑板上一个字或一句话,不断向四周同学询问。特意把笔记做得很
2019/5/25
最新中小学教学课件
23
谢谢欣赏!
2019/5/25
最新中小学教学课件
24
ቤተ መጻሕፍቲ ባይዱ
2024秋季新教材湘教版七年级上册数学1.2.3 绝对值 课件

七年级上册数学(湘教版)
第1章 有理数
1.2 数轴、相反数与绝对值
1.2.3 绝对值
÷
教学目标
1. 初步理解绝对值的概念,通过应用绝对值解决实际 问题,体会绝对值的意义和作用.
2. 会求一个已知数的绝对值,会用分类讨论的思想在 已知一个数的绝对值的条件下求这个数.
3. 会用数形结合的思想体会绝对值的几何意义和作用. 重点:从数、形两方面理解绝对值的意义,并会求一
练一练
1.写出下列各数的绝对值:
6,8,3.9, 5 , 2 ,100,0 2 11
解:6 6, 8 8, 3.9 3.9, 5 5, 22
2 2 , 100 100, 0 0 11 11
议一议
a 的正负性未知,需要分类讨论.
探究二 如果 a 表示一个数,则 | a | 等于多少?
a = b 或 a = -b
典例精析
例2 若 | a | = 8.7,求 a. 解: 因为绝对值等于 8.7 的有理数有 8.7 和 -8.7 两个, 所以 a = 8.7 或 a = -8.7.
练一练 3. 已知 | x |=2,| y |=3,且 x<y,求 x,y. 解析: 由绝对值的定义知 x=±2,y=±3,再 由 x<y 决定 x,y 的值.
个数的绝对值. 难点:利用分类讨论的方法解决问题.
情境导入
甲、乙两辆汽车从同一处 O 出发,分别向东西方向行 驶 10 km,达到 A,B 两处,请在数轴上表示出来并回答 问题(规定向东为正方向).
B
O
-10
0
(1) 它们行驶的路线相同吗?
(2) 它们行驶的路程相等吗?
A 10
为什么呢?
探究新知
求一个数的绝对值 由绝对值求数
第1章 有理数
1.2 数轴、相反数与绝对值
1.2.3 绝对值
÷
教学目标
1. 初步理解绝对值的概念,通过应用绝对值解决实际 问题,体会绝对值的意义和作用.
2. 会求一个已知数的绝对值,会用分类讨论的思想在 已知一个数的绝对值的条件下求这个数.
3. 会用数形结合的思想体会绝对值的几何意义和作用. 重点:从数、形两方面理解绝对值的意义,并会求一
练一练
1.写出下列各数的绝对值:
6,8,3.9, 5 , 2 ,100,0 2 11
解:6 6, 8 8, 3.9 3.9, 5 5, 22
2 2 , 100 100, 0 0 11 11
议一议
a 的正负性未知,需要分类讨论.
探究二 如果 a 表示一个数,则 | a | 等于多少?
a = b 或 a = -b
典例精析
例2 若 | a | = 8.7,求 a. 解: 因为绝对值等于 8.7 的有理数有 8.7 和 -8.7 两个, 所以 a = 8.7 或 a = -8.7.
练一练 3. 已知 | x |=2,| y |=3,且 x<y,求 x,y. 解析: 由绝对值的定义知 x=±2,y=±3,再 由 x<y 决定 x,y 的值.
个数的绝对值. 难点:利用分类讨论的方法解决问题.
情境导入
甲、乙两辆汽车从同一处 O 出发,分别向东西方向行 驶 10 km,达到 A,B 两处,请在数轴上表示出来并回答 问题(规定向东为正方向).
B
O
-10
0
(1) 它们行驶的路线相同吗?
(2) 它们行驶的路程相等吗?
A 10
为什么呢?
探究新知
求一个数的绝对值 由绝对值求数
绝对值ppt课件

M
4个单位长度
4个单位长度
P
-5 -4 -3 -2 -1 0 1 2 3 4 5 6
课内练习
1.填表:
数 21 0
3 −4
相反数 -21
0 3 4
绝对值 21 0 3 4
求一个数的绝对值时,一个正数的绝对值是它本身,一个负数的绝 对值是它的相反数,零的绝对值是零。互为相反数的两个数的绝对 值相等。
6.计算:
(1)-7+-54--12. -7+-54--12=7+54-12=734.
(2)-45-1-25. -45-1-25=45-35=15. (3)6÷-3+-17×49.
6÷-3+-17×49=6÷3+17×49=2+7=9.
分层练习-巩固
7.已知a=5, |a|=|b|,则b的值是( D )
A,B两点与原
我们以O为原点取适当的单位长度画数点轴的 是,距多并离少标分?出别AB的位置.
6
6
A
O
B
西 -6 -5 -4 -3
2.数轴上表示-5和5的点到原点的距离分别是多少?
表示−
3和3的点呢?
44
5
5 你发现了什
么规律吗?
-5 -4 -3 -2 -1 0 1 2 3 4 5 6
课本例题
▶例 1 求下列各数的绝对值: 85, +10, 3, 0 ,-1.6, -10, -4.
解:
8 5
= 85, |+10|=10,
|3|=3,|0|=0 ,|-1.6|=1.6,
|-10|=10, |-4|=4.
求得的绝对值 与原数之间有 什么关系呢?
概念归纳
求一个数的绝对值时, 一个正数的绝对值是它本身, 一个负数的绝对值是它的相反数, 零的绝对值是零。 互为相反数的两个数的绝对值相等。
绝对值 ppt课件

导入新课
探究新知
习题巩固
课堂小结
课后作业
作业一:导学案上的复习巩固和拓广探索 作业二:对下一节课进行预习
好好学习,天天向上
祝贺你,在学习中获得了新知识!
研究过程
好好学习,天天向上
导入新课
探究新知
习题巩固
课堂小结
课后作业
讲授新知
由绝对值的定义可知: 一个正数的绝对值是它本身;一个负数的绝对值是它的
相(1)反如数分果; 析a0>的0,绝那对么值|是a| 0=.a即;
(2) 如研果究a过=0程,那么|a| =0; (3) 如果a<0,那么|a| =-a.
习题巩固
课堂小结
课后作业
在数轴上表示的两个数,右边的数总比左边的数大.
小
大
–6–5–4–3–2–1 0 1 2 3 4 5 6
好好学习,天天向上
导入新课
探究新知
习题巩固
课堂小结
运用法则比较有理数的大小
1.正数大于0,负数小于0,正数大于负数; 2.两个负数,绝对值大的反而小.
课后作业
思考
有没有最大的有理数?有没有最小的有理数?
为什么?
好好学习,天天向上
导入新课
探究新知
习题巩固
课堂小结
课后作业
课堂练习
1.画数轴并在数轴上画出表示下列各数的点,并用“<”号把这 些数连接起来.
3,-5,|-(-2)|,32 ,-1.5
好好学习,天天向上
导入新课
探究新知
习题巩固
课堂练习
2. 比较下列各组数的大小: (1)π和3.14; (2)-4和-7; (3) -1和-2 ;
导入新课
绝对值ppt课件

(1)试指出哪件样品的大小更符合要求;
分析:判断哪个产品更符合标准的问题,关键是求各数据的绝对值,绝
对值越小的越接近标准.
解:(1)因为|-0.05|<|+0.1|<|-0.15|<|-0.2|<|+0.25|,
所以第4件样品的大小更符合要求.
三、典例精析
(2)如果规定误差的绝对值在0.18 mm之内是正品,误差的绝对
跟踪练习:
比较下列每组数的大小:(1) –1和 –5; (2)– 5 和 – 2.7
6
分析:可以利用绝对值比较两个负数的大小。
还有其他
方法吗?
还可以利用数轴比较两个负数的大小。
三、典例精析
例 1:求下列各数的相反数和绝对值.
1
1
2,- ,3 ,0,-0.4.
2
5
1 1
1
1
解:2,- ,3 ,0,-0.4 的相反数分别是-2,,-3 ,0,0.4,
二、新知探究
跟踪练习:
判断题,看谁回答的又对又快!
√)
(2)30是30的相反数( × )
(1)-6是6的相反数(
√)
( ×)
(3)1.2与-1.2互为相反数(
(4)-3是相反数
注意:相反数
是成对出现的
二、新知探究
思考:如何求一个数的相反数呢?
求一个数的相反数,就是在这个数的前面添上“-”号。
一般地,a的相反数是
−
对应的点在数轴上的位置有什么关系?与同伴进行交流。
-5
-3
-6 -5 -4
-3
3
-2
-1
0
1
2
3
5
1.3绝对值课件(14张PPT)

+4和-4
问:为什么绝对值等于4的数有两个?
-4
4
三、辨别应用,巩固新知
(1)填表
课本21-22面课内练习
数
相反数
绝对值210Fra bibliotek-(2)画一条数轴,在数轴上分别标出绝对值是6,1.2,0的数.
再次播放动画,观察几个数的绝对值大小和对应点离原点的位置远近,你有什么发现?
一个数的绝对值越大,数轴上的对应点离原点越远;
2.互为相反数的两个数有什么相同点和不同点?
五、目标检测
课本22面作业题
同学们再见!
授课老师:
时间:2024年9月15日
是它本身
是0
是它的相反数
如果a>0,那么|a|=a
如果a=0,那么|a|=0
如果a<0,那么|a|=-a
问题5 (口答)说出下列各数的绝对值:
7
-7
-2.05
0
1000
观察绝对值的大小,你有什么发现?
任何数的绝对值都大于或等于0
问题6 求绝对值等于4的数.
答:数轴上到原点的距离等于4个单位长度的点总共有两个, 左右各一个。
|+5|=5
问题3:借助数轴,请你说出数轴上30,-1.6,-10,-4对应的点到原点的距离分别是多少?并求出它们的绝对值.
3对应的点到原点的距离是3,则3的绝对值是3,即|3|=3
+10对应的点到原点的距离是10,则+10的绝对值是10,即|+10|=10
对应的点到原点的距离是,则的绝对值是,即=
一个数的绝对值越小,数轴上的对应点离原点越近;
(3)举一个生活中的例子,说明解决某些问题只需考虑数的绝对值.
问:为什么绝对值等于4的数有两个?
-4
4
三、辨别应用,巩固新知
(1)填表
课本21-22面课内练习
数
相反数
绝对值210Fra bibliotek-(2)画一条数轴,在数轴上分别标出绝对值是6,1.2,0的数.
再次播放动画,观察几个数的绝对值大小和对应点离原点的位置远近,你有什么发现?
一个数的绝对值越大,数轴上的对应点离原点越远;
2.互为相反数的两个数有什么相同点和不同点?
五、目标检测
课本22面作业题
同学们再见!
授课老师:
时间:2024年9月15日
是它本身
是0
是它的相反数
如果a>0,那么|a|=a
如果a=0,那么|a|=0
如果a<0,那么|a|=-a
问题5 (口答)说出下列各数的绝对值:
7
-7
-2.05
0
1000
观察绝对值的大小,你有什么发现?
任何数的绝对值都大于或等于0
问题6 求绝对值等于4的数.
答:数轴上到原点的距离等于4个单位长度的点总共有两个, 左右各一个。
|+5|=5
问题3:借助数轴,请你说出数轴上30,-1.6,-10,-4对应的点到原点的距离分别是多少?并求出它们的绝对值.
3对应的点到原点的距离是3,则3的绝对值是3,即|3|=3
+10对应的点到原点的距离是10,则+10的绝对值是10,即|+10|=10
对应的点到原点的距离是,则的绝对值是,即=
一个数的绝对值越小,数轴上的对应点离原点越近;
(3)举一个生活中的例子,说明解决某些问题只需考虑数的绝对值.
上海沪科版初中数学七年级上册1.2 第3课时 绝对值ppt课件

中考 试题
例2
点A为数轴上表示-2的动点,当点A沿数轴移动4个单位长度到
点B时,点B所表示的实数为( C ).
A.2
B. -6 C.2或-6
D.不同于以上答案
分析 利用数轴,可以直观地看到问题的答案.
解 如果点A是向左移动,则点B表示-6,如果点A是向右移动, 则点B表示2,故选C.
中考 试题
例3
动脑筋
学校位于数轴的原点处,小光、小明、小亮家 分别位于点A,B,C处,单位长度表示1km,小光、 小明、小亮的家分别距学校多远?
小光家到学校4km远.
小亮家到学校2km远.
小明家到学校2km远.
结论
在数轴上,表示一个数的点与原点的 距离叫作这个数的绝对值.
结论
一个正数的绝对值等于它本身.
一个负数的绝对值等于它的相反数. 0 的绝对值等于 0.
1.在数轴上表示出四家公共场所的位置. 2.列式计算青少年宫与商场之间的距离.
分析
画数轴要注意数轴的三要素,选择适当的点(学校)为坐标原点,求数轴
上两点的距离时要利用数形结合思想.
解 (1)
-200 -100 0 100 200 300 400 500
商场
学校
青少年宫 医院
(2) 青少年宫与商场之间的距离为300-(-200)=500米.
9
3
0
5
-3 5
-9
2.73
-2.73
0
2.求下列各数的绝对值:3,3.14,
1 5
,-2.8.
解:
| 3 |=3;
| 3.14 |=3.14;
-ቤተ መጻሕፍቲ ባይዱ 5
=
1 5
;
相关主题
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
绝 对 值
导
上图中,单位长度为1米,那么 小黄狗、大白兔、小灰狗分别距 离原点多远?
赶快思考 啊!!!
3
-3
-2
-1
0
1
2
3
聪明的同学们一眼就可以看 出来了吧。
小黄狗距离原点3米 大白兔距离原点2米
小灰狗距离原点3米
学习目标:
• 1、从几何和代数两个角度理解绝对值的意 义; • 2、给出一个数,求出它的绝对值(重点) • 3、理解绝对值的非负性,并能够运用绝对 值的非负性解决问题。(难点)
(2)如果a<0,那么|a|=-a (3)如果a=0,那么|a|=0
绝 若用a表示任一有理数, 对 值 则用式子来表示为 的 a + _____ a 0 代 数 -a a 0 + a _____ 意 0 _____ 义 a 0 0
评
因此可以得到: 非负数 。 一个数的绝对值是一个_________
a
a a a
-a
3.在数轴上表示的有理数,它们从左到右的顺序,就是 从小到大 的顺序,即左边的数 小于 右边的数. _______
二、深入学习 4、-5的绝对值是(B 1) A.-5 B.5 C. 5 D.5 A) 5、 - 2 的相反数是( 1 1 A.-2 B.- C. D.2 2 2 6.在数轴上表示-2的点与原点的距离等于(A ) A.2 B.-2 C. 2 D.4 7.下列说法错误的是( B ) A.若 a b ,则 a b 或 a b B.若 a b ,则 a b ; 0 a 0 且 b 0 C.若a b ,则 D.若 a a ,则 a 0 ;若 b b ,则b 0 8.若 x 2 ,则 x 2 ;若 - x 2 ,则 x 2 . ,-3,3,-4,4 9.绝对值小于5的整数有0,-1,1,-2,2.
检 判断(对的打“√”,错的打“×”
)1 : ( )一个有理数的绝对值一定是正数。
(2)-1.4<0,则│-1.4│<0。 (3) │-32︱的相反数是32 ( ( ( ) ) )
(4) 如果两个数的绝对值相等,那么这两个数 相等 ( (5) 互为相反数的两个数的绝对值相等 (
) )
一般地,数轴上表示数a的点与原点
的距离叫ቤተ መጻሕፍቲ ባይዱ数a的绝对值(absolute value)。记作|a|。
你能明白吗?
由绝对值的定义可知:
它本身 一个正数的绝对值是__________; 相反数 一个负数的绝对值是它的__________; 0 0的绝对值是_______.
• 互为相反数的两个数的绝对值有什么关系? •一对相反数虽然分别在原点两边, 但它们到原 点的距离是相等的.
评
一个数a的绝对值就是数轴上表示数a的点与原点的距离.
一个数的绝对值就是在这个数的两旁各画一条 竖线,如+2的绝对值等于2,记作|+2|=2。 数a的绝对值记作|a|. 如图,在数轴上表示-5的点与原点的距离是5, 即-5的绝对值是5,记作|-5|=5.
评
因为正数可用a>0表示,负数可用 a<0表示,所以上述三条可表述成: (1)如果a>0,那么|a|=a
思
认真独立完成导学提纲。
议(5分钟)
对议:找出个人有异议的问题, 讨论解决。 组议:找出组内共同有疑问的问题, 并讨论解决。(组长负责)
一、了解感知
原点的距离 叫做数 a 的绝对值, 1.一般地,数轴上表示 的点与 a . 记作 ;一个负数的绝对值是 2.一个正数的绝对值是 它本身 它的相反数;0的绝对值是 0 ________ . a = a ; (1)当 是正数时, (2)当 是负数时, ; a = (3)当 =0时, a = 0 .
• 13.一辆出租车从A站出发,先向东行驶12km,接着向西行 驶8km,然后又向东行驶4km. • (1)画一条数轴,以A站为原点,向东为正方向,在数 轴上表示出租车行驶的终点位置B; • (2)求各次路程的绝对值的和,并说明这个数据的实际 意义是什么? • (3)若出租车每行驶1km耗油0.06升,求出租车由起点A 到终点B共耗油多少升?
三、迁移应用 10.若a 1 b 2 0 ,求 a , b 的值. 解:由题意可知 a 1 0 ,
b20
由此可知
a 1
b2
11.分类讨论:已知 a 3 , b 2,且a b , 求 a b 的值.
解:因为丨a丨=3 所以解得a=±3 因为丨b丨=2 所以解得b=±2 又因为a<b 则①当a=﹣3时,b=﹣2 ②当a=﹣3时,b=2 解得a+b等于﹣5或﹣1
导
上图中,单位长度为1米,那么 小黄狗、大白兔、小灰狗分别距 离原点多远?
赶快思考 啊!!!
3
-3
-2
-1
0
1
2
3
聪明的同学们一眼就可以看 出来了吧。
小黄狗距离原点3米 大白兔距离原点2米
小灰狗距离原点3米
学习目标:
• 1、从几何和代数两个角度理解绝对值的意 义; • 2、给出一个数,求出它的绝对值(重点) • 3、理解绝对值的非负性,并能够运用绝对 值的非负性解决问题。(难点)
(2)如果a<0,那么|a|=-a (3)如果a=0,那么|a|=0
绝 若用a表示任一有理数, 对 值 则用式子来表示为 的 a + _____ a 0 代 数 -a a 0 + a _____ 意 0 _____ 义 a 0 0
评
因此可以得到: 非负数 。 一个数的绝对值是一个_________
a
a a a
-a
3.在数轴上表示的有理数,它们从左到右的顺序,就是 从小到大 的顺序,即左边的数 小于 右边的数. _______
二、深入学习 4、-5的绝对值是(B 1) A.-5 B.5 C. 5 D.5 A) 5、 - 2 的相反数是( 1 1 A.-2 B.- C. D.2 2 2 6.在数轴上表示-2的点与原点的距离等于(A ) A.2 B.-2 C. 2 D.4 7.下列说法错误的是( B ) A.若 a b ,则 a b 或 a b B.若 a b ,则 a b ; 0 a 0 且 b 0 C.若a b ,则 D.若 a a ,则 a 0 ;若 b b ,则b 0 8.若 x 2 ,则 x 2 ;若 - x 2 ,则 x 2 . ,-3,3,-4,4 9.绝对值小于5的整数有0,-1,1,-2,2.
检 判断(对的打“√”,错的打“×”
)1 : ( )一个有理数的绝对值一定是正数。
(2)-1.4<0,则│-1.4│<0。 (3) │-32︱的相反数是32 ( ( ( ) ) )
(4) 如果两个数的绝对值相等,那么这两个数 相等 ( (5) 互为相反数的两个数的绝对值相等 (
) )
一般地,数轴上表示数a的点与原点
的距离叫ቤተ መጻሕፍቲ ባይዱ数a的绝对值(absolute value)。记作|a|。
你能明白吗?
由绝对值的定义可知:
它本身 一个正数的绝对值是__________; 相反数 一个负数的绝对值是它的__________; 0 0的绝对值是_______.
• 互为相反数的两个数的绝对值有什么关系? •一对相反数虽然分别在原点两边, 但它们到原 点的距离是相等的.
评
一个数a的绝对值就是数轴上表示数a的点与原点的距离.
一个数的绝对值就是在这个数的两旁各画一条 竖线,如+2的绝对值等于2,记作|+2|=2。 数a的绝对值记作|a|. 如图,在数轴上表示-5的点与原点的距离是5, 即-5的绝对值是5,记作|-5|=5.
评
因为正数可用a>0表示,负数可用 a<0表示,所以上述三条可表述成: (1)如果a>0,那么|a|=a
思
认真独立完成导学提纲。
议(5分钟)
对议:找出个人有异议的问题, 讨论解决。 组议:找出组内共同有疑问的问题, 并讨论解决。(组长负责)
一、了解感知
原点的距离 叫做数 a 的绝对值, 1.一般地,数轴上表示 的点与 a . 记作 ;一个负数的绝对值是 2.一个正数的绝对值是 它本身 它的相反数;0的绝对值是 0 ________ . a = a ; (1)当 是正数时, (2)当 是负数时, ; a = (3)当 =0时, a = 0 .
• 13.一辆出租车从A站出发,先向东行驶12km,接着向西行 驶8km,然后又向东行驶4km. • (1)画一条数轴,以A站为原点,向东为正方向,在数 轴上表示出租车行驶的终点位置B; • (2)求各次路程的绝对值的和,并说明这个数据的实际 意义是什么? • (3)若出租车每行驶1km耗油0.06升,求出租车由起点A 到终点B共耗油多少升?
三、迁移应用 10.若a 1 b 2 0 ,求 a , b 的值. 解:由题意可知 a 1 0 ,
b20
由此可知
a 1
b2
11.分类讨论:已知 a 3 , b 2,且a b , 求 a b 的值.
解:因为丨a丨=3 所以解得a=±3 因为丨b丨=2 所以解得b=±2 又因为a<b 则①当a=﹣3时,b=﹣2 ②当a=﹣3时,b=2 解得a+b等于﹣5或﹣1
