最新人教版七年级数学绝对值PPT课件
合集下载
1.2.4《绝对值》课件-2024-2025学年人教版(2024)数学 七年级上册

-5.25
(3)绝对值等于5.25的负数是______;
2或-2
(4)绝对值等于2的数是_______。
【点睛】注意绝对值等于某个正数的数有两个,他们互为相反数,解题时不要遗
漏负值。
课堂练习
3. 如果| a |+| b-1 |=0,那么a = 0 ,b = 1
。
4. 已知x =30,y =-4,则| x | - 3 | y |= 18 。
B
-10
10
O
0
10
A
10
-10与10在数轴上所表示的点到原点的距离是 10个单位长度 ,它们
的 符号 不同。我们把这个距离10叫做+10和-10的 绝对值 。
新知探究
定义
距离不能是负数,所以任何
数的绝对值一定是非负数
( |a| ≥ 0)
一般地,数轴上表示数a的点与原点的距离叫做数a的绝对值,
记作|a|.
1. 求下列各数的绝对值.
12, - 3 , -7.5 , 0
5
解: | 12 | =12;
|- 3 |= 3
5
5
正数的绝对值等于它本身
负数的绝对值等于它的相反数
| -7.5 | = 7.5;
| 0 | = 0。
0的绝对值是0
随堂检测
2. 填一填:
0
(1)绝对值等于0的数是___;
5.25
(2)绝对值等于5.25的正数是_____;
(5) 绝对值等于同一个正数的数有两个,且这两个数互为相反数.(
√
)
新知探究
我们知道,互为相反数的两
个数(除0之外)只有符号不同,
这两个数的相同部分在数轴上表
示什么?
(3)绝对值等于5.25的负数是______;
2或-2
(4)绝对值等于2的数是_______。
【点睛】注意绝对值等于某个正数的数有两个,他们互为相反数,解题时不要遗
漏负值。
课堂练习
3. 如果| a |+| b-1 |=0,那么a = 0 ,b = 1
。
4. 已知x =30,y =-4,则| x | - 3 | y |= 18 。
B
-10
10
O
0
10
A
10
-10与10在数轴上所表示的点到原点的距离是 10个单位长度 ,它们
的 符号 不同。我们把这个距离10叫做+10和-10的 绝对值 。
新知探究
定义
距离不能是负数,所以任何
数的绝对值一定是非负数
( |a| ≥ 0)
一般地,数轴上表示数a的点与原点的距离叫做数a的绝对值,
记作|a|.
1. 求下列各数的绝对值.
12, - 3 , -7.5 , 0
5
解: | 12 | =12;
|- 3 |= 3
5
5
正数的绝对值等于它本身
负数的绝对值等于它的相反数
| -7.5 | = 7.5;
| 0 | = 0。
0的绝对值是0
随堂检测
2. 填一填:
0
(1)绝对值等于0的数是___;
5.25
(2)绝对值等于5.25的正数是_____;
(5) 绝对值等于同一个正数的数有两个,且这两个数互为相反数.(
√
)
新知探究
我们知道,互为相反数的两
个数(除0之外)只有符号不同,
这两个数的相同部分在数轴上表
示什么?
人教版七年级数学上册1.2.4《绝对值》课件 (13张PPT)

人民教育出版社七年级上册
1.2.4(1) 绝对值
1、数轴三要素
2、什么是互为相反数
谁离乒乓球网架远呢?
20 20
-20 -15 -10 -5 5 10 0 15 20 -20与+20在数轴上所表示的点到原点的距离都是 20个单位,距离20是-20和20的绝对值.
-20的绝对值表示-20的点到原点的距离,它的绝对值是20. -3的绝对值表示什么呢?它的绝对值是多少呢?
数轴原点表示的是0,0绝对值是0
绝对值性质:对于任意一个有理数a都有, 1、当a>0 时, |a|= _____ a ;
0 ; 2、当a=0 时, |a|= _____
3、当a<0 时, |a|= _____. -a
绝对值的代 数意义
1.填空:
1.7 |-1.7|_____ ; -4 ; -|-4|=____
-7 7
绝 对 值 发 生 器
7 7
、数轴原点右边表示的是什么数?该数的绝对值与这个数有什 么关系?
数轴原点右边表示的是正数,正数的绝对值是它本身
、数轴原点左边表示的是什么数?该数的绝对值与这个数有 什么关系?
数轴原点左边表示的是负数,负数的绝对值是它的相反数
、数轴原点表示的是什么数?该数的绝对值是多少?
1、绝对值的几何意义及表示方法 2、绝对值的代数意义 (1)一个正数的绝对值是它本身;
(2)零的绝对值是零;
(3)一个负数的绝对值是它的相反数;
1、必做题:习题1.2 第5、8题 2、选做题:绝对值评测训练
2的绝对值表示什么呢?它的绝对值是多少呢? 2 3 的绝对值表示什么呢?它的绝对值是多少呢?
2 3
-3 -2 -1
0
1.2.4(1) 绝对值
1、数轴三要素
2、什么是互为相反数
谁离乒乓球网架远呢?
20 20
-20 -15 -10 -5 5 10 0 15 20 -20与+20在数轴上所表示的点到原点的距离都是 20个单位,距离20是-20和20的绝对值.
-20的绝对值表示-20的点到原点的距离,它的绝对值是20. -3的绝对值表示什么呢?它的绝对值是多少呢?
数轴原点表示的是0,0绝对值是0
绝对值性质:对于任意一个有理数a都有, 1、当a>0 时, |a|= _____ a ;
0 ; 2、当a=0 时, |a|= _____
3、当a<0 时, |a|= _____. -a
绝对值的代 数意义
1.填空:
1.7 |-1.7|_____ ; -4 ; -|-4|=____
-7 7
绝 对 值 发 生 器
7 7
、数轴原点右边表示的是什么数?该数的绝对值与这个数有什 么关系?
数轴原点右边表示的是正数,正数的绝对值是它本身
、数轴原点左边表示的是什么数?该数的绝对值与这个数有 什么关系?
数轴原点左边表示的是负数,负数的绝对值是它的相反数
、数轴原点表示的是什么数?该数的绝对值是多少?
1、绝对值的几何意义及表示方法 2、绝对值的代数意义 (1)一个正数的绝对值是它本身;
(2)零的绝对值是零;
(3)一个负数的绝对值是它的相反数;
1、必做题:习题1.2 第5、8题 2、选做题:绝对值评测训练
2的绝对值表示什么呢?它的绝对值是多少呢? 2 3 的绝对值表示什么呢?它的绝对值是多少呢?
2 3
-3 -2 -1
0
绝对值PPT教学课件

│-5│=5 A
│4│=4 B
-6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6
-5的绝对值应该记作│-5︱=?
4的绝对值应该记作 │4︱ =?
0的绝对值应该如何表示呢?
│0︱ =?
练习:
-6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6
1.表示+7的点与原点的距离是 7 , 即+7的绝对值是 7 ,记作 7 7 ;
催化剂
△
2SO3
SO2 +Cl2 +2H2O = H2SO4+2HCl (氯水褪色) SO2 +Br2+2H2O = H2SO4+2HBr (溴水褪色)
4. SO2的氧化性 SO2+2H2S = 3S + 2H2O
5. SO2的漂白性
实验
现象: 品红溶液褪色,
ห้องสมุดไป่ตู้
向试管中加
加热后溶液变回红色
入5ml SO2 水溶液,滴
测试时间 0小时 1小 2小 4小 5小 后 时后 时后 时后 时后
雨水的pH值 4.74 4.63 4.57 4.53 4.53
1.请你写出酸雨开始呈酸性的化学方程式.
SO2+H2O H2SO3 2SO2+O2=2SO3 O2+2H2SO3=2 H2SO4 SO3+H2O=H2SO4
2.这种雨水的pH值逐渐减小,其原因何在? (提示:从硫元素的化合价和酸性强弱方面考虑)
练习:
6.绝对值小于3的负整数有_-_2_、_-1__;
7.
2.3
-__2_.__3,
2 15
2 __1__5_,
9
人教版七年级数学上册 1.2.4.1 绝对值的定义及性质 教学课件(共28张PPT)

练习1:判断并改错: (1)一个数的绝对值等于本身,则这个数一定是正数; (2)一个数的绝对值等于它的相反数,则这个数一定是负数; (3)如果两个数的绝对值相等,那么这两个数一定相等; (4)如果两个数不相等,那么这两个数的绝对值一定不相等; (5)有理数的绝对值一定是非负数;
课堂精练
练习2:写出下列各数的绝对值:
人教版七年级数学上册
第一章 有理数 1.2.4.1 绝对值的定义及性质
新课导入
1. 什么是数轴?数轴定义包含哪几层含义? 2. 数轴上的点与有理数间的关系是怎样的? 3. 什么是相反数? 4. 相反数的代数意义和几何意义分别是什么?
合作探究
问题1 看图回答问题: 两辆汽车从同一处O出发,分别向东、西方向行驶10 km,到达A,B两处, 它们的行驶路线相同吗?它们的行驶路程相同吗?
6,8,3.9, 5 , 2 ,100,0 2 11
3.口答:
6 = 0=
2 = 7
-3 =
8.2 =
-1 = 3
合作探究
问题1 结合上面口答题结果,一个数的绝对值与这个数有什么 关系?你能从中发现什么规律?
(1)一个正数的绝对值是它本身; (1)若a 0,则 a a;
(2)一个负数的绝对值是它的相反数;(2)若a 0,则 a -a;
(3)0的绝对值是0.
例如:上面的问题中在数轴上表示-3的点和表示3的点到原 点的距离都是3,所以3和-3的绝对值都是3,即|-3|=|3|=3. 你能说说-2和2吗?
合作探究
-3 -2 -1 0 1 2 3 4
大象离原点4个单位长度:|4|=4. 那么两只小狗呢?
合作探究
1.-2的绝对值是____,说明数轴上表示-2的点到____的距离是 ____个长度单位. 2.-0.8的绝对值是____ .
课堂精练
练习2:写出下列各数的绝对值:
人教版七年级数学上册
第一章 有理数 1.2.4.1 绝对值的定义及性质
新课导入
1. 什么是数轴?数轴定义包含哪几层含义? 2. 数轴上的点与有理数间的关系是怎样的? 3. 什么是相反数? 4. 相反数的代数意义和几何意义分别是什么?
合作探究
问题1 看图回答问题: 两辆汽车从同一处O出发,分别向东、西方向行驶10 km,到达A,B两处, 它们的行驶路线相同吗?它们的行驶路程相同吗?
6,8,3.9, 5 , 2 ,100,0 2 11
3.口答:
6 = 0=
2 = 7
-3 =
8.2 =
-1 = 3
合作探究
问题1 结合上面口答题结果,一个数的绝对值与这个数有什么 关系?你能从中发现什么规律?
(1)一个正数的绝对值是它本身; (1)若a 0,则 a a;
(2)一个负数的绝对值是它的相反数;(2)若a 0,则 a -a;
(3)0的绝对值是0.
例如:上面的问题中在数轴上表示-3的点和表示3的点到原 点的距离都是3,所以3和-3的绝对值都是3,即|-3|=|3|=3. 你能说说-2和2吗?
合作探究
-3 -2 -1 0 1 2 3 4
大象离原点4个单位长度:|4|=4. 那么两只小狗呢?
合作探究
1.-2的绝对值是____,说明数轴上表示-2的点到____的距离是 ____个长度单位. 2.-0.8的绝对值是____ .
新版人教版七年级数学上册《绝对值》课件(17张)
创设情境
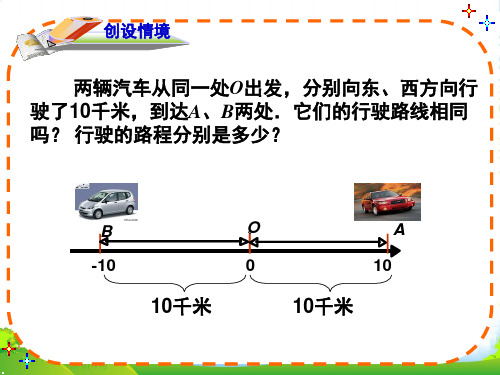
两辆汽车从同一处O出发,分别向东、西方向行 驶了10千米,到达A、B两处.它们的行驶路线相同 吗? 行驶的路程分别是多少?
B
O
A
-10
0
10
10千米
10千米
做游戏
请两位同学分别站在老师的左右两边,两位同学 同时向东、西相反的方向走1米,把这两位同学所 站位置用数轴上的点表示出来.
距
距
离
离
是1
学生活动 2.互为相反数的两个数的绝对值有什么关系?
一对相反数虽然分别在原点两边,但它们 到原点的距离是相等的.所以互为相反数的两 个数的绝对值相等.
7 图1.2-7
学生活动
你能把14个气温从低到高排列吗?能把这14个数 用数轴上的点表示出来吗?观察这些点在数轴上的位 置,思考它们与温度的高低之间的关系,你觉得两个 有理数可以比较大小吗?
(B )
A.可以是负数 B.不可能是负数
C.必是正数
D.可以是正数也可以是负数
温馨提示: 认真完成作业是巩固知识的有效方法!!
12、首先是教师品格的陶冶,行为的教育,然后才是专门知识和技能的训练。 13、在教师手里操着幼年人的命运,便操着民族和人类的命运。2022/5/52022/5/5May 5, 2022 14、孩子在快乐的时候,他学习任何东西都比较容易。 15、人自身有一种力量,用许多方式按照本人意愿控制和影响这种力量,一旦他这样做,就会影响到对他的教育和对他发生作用的环境。
练习2:|-13 |的相反数是 ;若|a|=2,则a=±2 .
练习3:绝对值小于3.5的整数是-3,-2,-1,0,1,2,3 . 练习4:已知:x342y0,则x= -3 ,y= 2 .
课堂练习
两辆汽车从同一处O出发,分别向东、西方向行 驶了10千米,到达A、B两处.它们的行驶路线相同 吗? 行驶的路程分别是多少?
B
O
A
-10
0
10
10千米
10千米
做游戏
请两位同学分别站在老师的左右两边,两位同学 同时向东、西相反的方向走1米,把这两位同学所 站位置用数轴上的点表示出来.
距
距
离
离
是1
学生活动 2.互为相反数的两个数的绝对值有什么关系?
一对相反数虽然分别在原点两边,但它们 到原点的距离是相等的.所以互为相反数的两 个数的绝对值相等.
7 图1.2-7
学生活动
你能把14个气温从低到高排列吗?能把这14个数 用数轴上的点表示出来吗?观察这些点在数轴上的位 置,思考它们与温度的高低之间的关系,你觉得两个 有理数可以比较大小吗?
(B )
A.可以是负数 B.不可能是负数
C.必是正数
D.可以是正数也可以是负数
温馨提示: 认真完成作业是巩固知识的有效方法!!
12、首先是教师品格的陶冶,行为的教育,然后才是专门知识和技能的训练。 13、在教师手里操着幼年人的命运,便操着民族和人类的命运。2022/5/52022/5/5May 5, 2022 14、孩子在快乐的时候,他学习任何东西都比较容易。 15、人自身有一种力量,用许多方式按照本人意愿控制和影响这种力量,一旦他这样做,就会影响到对他的教育和对他发生作用的环境。
练习2:|-13 |的相反数是 ;若|a|=2,则a=±2 .
练习3:绝对值小于3.5的整数是-3,-2,-1,0,1,2,3 . 练习4:已知:x342y0,则x= -3 ,y= 2 .
课堂练习
人教版七年级数学上册1.2.4《绝对值》 课件(共23张ppt)

课堂小结
3.不论有理数a取何值,它的绝对值总是正数或0(非负数), 即对任意有理数a,总有|a|≥0.
4.互为相反数的两个数的绝对值相等. 5.数轴上的数的排列规律是: 在数轴上表示有理数,它们从左到右的顺序,就是从 小到大的顺序,即左边的数小于右边的数.
课件PPT部编版课件统编版部编版人 教版七 年级数 学上册1.2.4《 绝对值 》 课件(共23张ppt)课件优质课课件免 费课件PPT
课件PPT部编版课件统编版部编版人 教版七 年级数 学上册1.2.4《 绝对值 》 课件(共23张ppt)课件优质课课件免 费课件PPT
课堂小结
6.有理数大小比较法则: (1)正数大于0,0大于负数,正数大于负数; (2)两个负数,绝对值大的反而小.
课件PPT部编版课件统编版部编版人 教版七 年级数 学上册1.2.4《 绝对值 》 课件(共23张ppt)课件优质课课件免 费课件PPT
21 21
77
又∵
8 <3 21 7
,即
- 8 <-3
21
7
,
∴
- 8 >- 3
21
7
.
(3)化简,得:-(-0.3)=0.3,-
1 3
=
1 3
.
1 ∵0.3< 3 ,
∴-(-0.3)<
-1 3
.
课堂练习
1.比较大小:
(1)-2_<__5,
-7 2
_>__
+
3 8
,
-0.01_>__-1;
4 (2)- 5
合作探究
一个正数的绝对值是什么?0的绝对值是什么?负数呢?
归纳:一个正数的绝对值是它本身;一个负数的绝对值是它的相反 数;0的绝对值是0.
绝对值PPT课件

-6 -5 -4 -3 -2
│4│=4
0 1 2 3 4
B
5 6
-1
-5的绝对值应该记作│-5︱=? 4的绝对值应该记作 │4︱ =? 0的绝对值应该如何表示呢? │0︱ =?
练习:
-6 -5 -4 -3 -2
-1
0
1
2
3
4
5
6
1.表示+7的点与原点的距离是 7 , 即+7的绝对值是 7 ,记作 7 7 ; 表示2.8的点与原点的距离是 2.8 , 即2.8的绝对值是 2.8 ,记作 2.8 2.8 ; 2.表示0的点与原点的距离是 0 , 即0的绝对值是 0 ,记作 0 0 ;
0 0
7 7
1、(1)正数的绝对值是它的本身;
(2)0的绝对值是0;
(3)负数的绝对值是它的相反数。
2、非负性 由绝对值的定义可知绝对值 具有非负性,即|a|≥0。
练习:
1、判断下列各题: (1)负数没有绝对值。 × (2)有些数的绝对值有两个。× (3)正数和零的绝对值是它的本身。√ (4)负数和零的绝对值是它的相反数。√ √ (5)任何有理数的绝对值一定不是负数。
答:记为-8的足球质量好一些。
因为 │-20│= 20, │-8│ = 8, │+10│=10, │+12│=12, │-11│=11;
所以│-8│ < │+10│ < │-11│ < │+12│ < │-20│
也就是说记为-8的足球与规定的质量相差比较小, 因此其质量比较好。
思考:
1.计算:|–(+3.6)| + |–(–1.2)| – |–[+(–4)]| 2.已知 |x–2| + |y–3| + |z–4| = 0, 求x+y–z的值。
│4│=4
0 1 2 3 4
B
5 6
-1
-5的绝对值应该记作│-5︱=? 4的绝对值应该记作 │4︱ =? 0的绝对值应该如何表示呢? │0︱ =?
练习:
-6 -5 -4 -3 -2
-1
0
1
2
3
4
5
6
1.表示+7的点与原点的距离是 7 , 即+7的绝对值是 7 ,记作 7 7 ; 表示2.8的点与原点的距离是 2.8 , 即2.8的绝对值是 2.8 ,记作 2.8 2.8 ; 2.表示0的点与原点的距离是 0 , 即0的绝对值是 0 ,记作 0 0 ;
0 0
7 7
1、(1)正数的绝对值是它的本身;
(2)0的绝对值是0;
(3)负数的绝对值是它的相反数。
2、非负性 由绝对值的定义可知绝对值 具有非负性,即|a|≥0。
练习:
1、判断下列各题: (1)负数没有绝对值。 × (2)有些数的绝对值有两个。× (3)正数和零的绝对值是它的本身。√ (4)负数和零的绝对值是它的相反数。√ √ (5)任何有理数的绝对值一定不是负数。
答:记为-8的足球质量好一些。
因为 │-20│= 20, │-8│ = 8, │+10│=10, │+12│=12, │-11│=11;
所以│-8│ < │+10│ < │-11│ < │+12│ < │-20│
也就是说记为-8的足球与规定的质量相差比较小, 因此其质量比较好。
思考:
1.计算:|–(+3.6)| + |–(–1.2)| – |–[+(–4)]| 2.已知 |x–2| + |y–3| + |z–4| = 0, 求x+y–z的值。
人教版七年级数学上册课件:.4绝对值

做一做:
(1)在数轴上表示下列各数,并比较它 们的大小;
- 1.5 , - 3 , - 1 , - 5 ;
(2)求出(1)中各数的绝对值,并比 较它们的大小;
(3)你发现了什么?
解:(1)如图 -5 -4 -3 -2 -1 0 1 2 3
∴ - 5 < - 3 <- 1.5 < - 1 (2)| -1.5 | = 1.5 ; | - 3 | = 3;
试一试: 若பைடு நூலகம்母a表示一个有理数,
你知道a的绝对值等于什么吗?
正数的绝对值是它本身
(1)当a是正数时,|a|=_a___;
a
(2)当a是负数时,|a|=_-a_; | a | a
(3)当a=0时,|a|=_0__负是. 数它的的相绝反对数值 0
(a 0) (a 0) (a 0)
0的绝对值是0
因为- 2.7在 -
5 6
的左边,所以-
2.7﹤ -
5 6
例2 比较 7 和 6 的大小.
8
7
分析: 比较两个负数的大小,应先比较它们绝
对值的大小,再根据“两个负数,绝对值大的
反而小”来判断它们的大小.
解:∵ | 6 | 6 48
7 7 56
| 7 | 7 49 8 8 56
49 48 56 56
1、正数都大于零,负数都小于零,
正数大于一切负数.
2、两个正数比较大小,绝对值大的数大; 两个负数比较大小,绝对值大的数反而小.
填一填
(1)绝对值小于 3 的整数有 __________________.
(2)绝对值不大于 3 的负整数是 ________________.
(3)绝对值大于 2/3 而小于 8/3 的整数 是_________.
人教版初一数学 1.2.4 绝对值PPT课件

-1 5
= 1; 5
|-2.8|=2.8.
当堂训练
能力提升题
化简: | 0.2 |=__0_.2___;
-2 3 7
=__2_73___;
| b |=__-_b___ (b<0); | a – b | =__a_-_b__(a>b).
当堂训练
拓广探索题 正答式:排第五球个比排赛球对的所质用量的好一排些球,重因量为是它有的严绝对格值规最定小的,,也现就检是离查标5个准排重 球量的的重克数量最,近超.过规定重量的克数记作正数,不足规定重量的克数 记作负数,检查结果如下:
第一章 有理数
1.2 有理数及其大小比较 1.2.4 绝对值
学习目标
1.理解绝对值的概念及其几何意义. 2.会求一个数(不涉及字母)的绝对值. 3.会求绝对值已知的数. 4.了解绝对值的非负性,并能用其非负性解决相关问题.
导入新课
两辆汽车从同一处O出发分别向东、西方向行驶10km,到 达A、B两处.
|5|= 5 |3.5|= 3.5 |-3|= 3 |-4.5|= 4.5 |0|= 0
-3 -4.5
0
5
0 3.5 0
0
01
探究新知
知识点 2 绝对值的性质 观察这些表示绝对值的数,它们有什么共同点?
|5|=5 |100|=100 |-4.5|=4.5
|-10|=10 |-3|=3 |-5000|=5000
探究新知
例如,下图所示:
-5到原点的距离是5, 所以-5的绝对值是5, 记作|-5|=5.
-6
-5
-4
-3
-2
0 1
|-5| = 5
-1
0到原点的距离是0,所以 0的绝对值是0,记作
人教版数学七年级上124绝对值(第1课时)(14张PPT)

B
1
0
-10
O
1
A
0
0
10
思考: 1.两车的行驶路线相同吗?它们的行驶路程相等吗?
、B两点与原点距离分别是多少?
知识讲解
1.绝对值的定义
一般地,数轴上表示数 a 的点与原点的距离叫做数a的绝对值,记作|a|.
上面例子中,A、B两点分别表示10和 -10,它们与原点的距离都是10,所以10和 -10的绝对值都是10.即|10|=10,|-10|=10
归纳总结 1.绝对值相等的两个数相等或互为相反数, 2.互为相反数的两个数的绝对值相等.
知识讲解
例3 已知|x-3|+|y-2|=0,求x+y的值 分析:
一个数的绝对值总是大于或等于0,即为非负数,若两个非负数 的和为0,则这两个数同时为0. 解:根据题意可知x-3=0,y-2=0,所以x=3,y=2,故x+y=5.
|-10|=10 |-3|=3
|-1.5|=1.5 |-2000|=2000
|0|=0
思考:一个正数的绝对值是什么? 一个负数的绝对值是什么? 0的绝对值是什么?结论: 一个正数的绝对值 Nhomakorabea是它本身.
一个负数的绝对值 是它的相反数.
0的绝对值是0.
知识讲解
思考
字母a表示一个有理数,你知道a的绝对值等于什么吗
(1)当a是正数时,|a|=__a_;
(2)当a是负数时,|a|=_-a;
正数的绝对值是它本身 负数的绝对值是它的相反数
(3)当a=0时,|a|=_0 .
0的绝对值是0
a | a | a
0
(a 0) (a 0) (a 0)
|a|≥0 任何一个有理数的绝对值都是非负数.
1.2.4 有理数 绝对值 课件(共13张PPT)2024—2025学年七年级上学期数学人教版

满足条件的所有x的值为
0,1,-1,2,-2,-3
.
同学们,再见!
的距离叫做a的绝对值,记
知识点1 绝对值的概念及符号的理解
【例1】(1)6的绝对值是
是
0
,-8的绝对值是
6
,0的绝对值
8
;
-4.5的绝对值
(2)(多维原创)|-4.5|读作
上表示-4.5的点与原点的距离
5
【变式1】(1)2的绝对值是
绝对值是
,其结果等于
,它表示
4.5
.
,-3.9的绝对值是
3.9
点之间的距离,那么|5+2|可以看作|5-(-2)|,表示5与-2
这两个数在数轴上所对应的两点之间的距离.
(1)数轴上,有理数4与-1所对应的点之间的距离为
5
;
(2)结合数轴找出符合条件的整数x,使|x+1|=3,则x=
2或
-4 ;
(3)利用数轴分析,若x是整数,且满足|x+3|+|x-2|=5,则
,反之,绝对值相等的两个
.
1.-3的绝对值是(
1
A.
3
C )
1
B.-
3
C.3
D.-3
2.(2023·深圳一模)下列各数中,绝对值最小的是(
A.-2
B.3
3.若|x|=9,则x的值是(
A.9
B.-9
C.0
C
D.-3
)
C.±9
D.0
C
)
4.(人教7上P11T2改编)判断下列说法,正确的是
③④
.
①符号相反的数互为相反数;
C
A.x=y
B.x与y互为相反数
0,1,-1,2,-2,-3
.
同学们,再见!
的距离叫做a的绝对值,记
知识点1 绝对值的概念及符号的理解
【例1】(1)6的绝对值是
是
0
,-8的绝对值是
6
,0的绝对值
8
;
-4.5的绝对值
(2)(多维原创)|-4.5|读作
上表示-4.5的点与原点的距离
5
【变式1】(1)2的绝对值是
绝对值是
,其结果等于
,它表示
4.5
.
,-3.9的绝对值是
3.9
点之间的距离,那么|5+2|可以看作|5-(-2)|,表示5与-2
这两个数在数轴上所对应的两点之间的距离.
(1)数轴上,有理数4与-1所对应的点之间的距离为
5
;
(2)结合数轴找出符合条件的整数x,使|x+1|=3,则x=
2或
-4 ;
(3)利用数轴分析,若x是整数,且满足|x+3|+|x-2|=5,则
,反之,绝对值相等的两个
.
1.-3的绝对值是(
1
A.
3
C )
1
B.-
3
C.3
D.-3
2.(2023·深圳一模)下列各数中,绝对值最小的是(
A.-2
B.3
3.若|x|=9,则x的值是(
A.9
B.-9
C.0
C
D.-3
)
C.±9
D.0
C
)
4.(人教7上P11T2改编)判断下列说法,正确的是
③④
.
①符号相反的数互为相反数;
C
A.x=y
B.x与y互为相反数
1.2.4 绝对值 课件-人教版(2024)数学七年级上册

应 记作 |a| . (这里的数a可以是正数、负数和0). 用
0到原点的距
-5到原点的距 离是5,所以-5的 绝对值是5,记 做|-5|=5
离是0,所以0 的绝对值是0, 记做|0|=0
4到原点的距离是4, 所以4的绝对值是4, 记做|4|=4
│-5│=5 │4│=4 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6
第一章 有理数 1.2.4 绝对值
回顾
知 1、什么是数轴? 识
数轴的三 要素
关 数轴是规定了原点、正方向、单位长度的直线
联
-2 -1 0 1 2
2、什么是相反数? 只有符号不同的两个数叫做互为相反数. 规定:0的相反数是0.探情究来自1 导绝入对值的概念探
究
甲、乙两辆出租车在一条东西走向的街道上行驶,
(2)原式=4.2-4.2=0
拓展
探 例4 下列关系一定成立的是
()
究 A.若|m|=|n|,则m=n
B.若|m|=n,则m=n
与 应 C.若|m|=-n,则m=n
D.若m=-n,则|m|=|n|
用 例5 如图 数轴上有四个点M,P,N,Q,若点M,N表示的数互为相反数,则图中四
个点表示的数的绝对值最大的是 ( )
;绝对值最小的数是 .
5.绝对值小于2的整数有 个,它们分别是
.
检测
课
堂 1.直接填写结果:︱+6︱= 6
,︱-1.5︱= 1.5
,|-
小 |= 结
32,︱0︱=32 0
, -︱-12︱= -12 .
与 2.如果一个数的绝对值等于10,那么这个数等于 10或-10.
检 3.如果一个数的绝对值是它本身,那么这个数一定是 非负数 测
1.2.4 绝对值 课件 人教版七年级数学上册 (25)

3.下列说法正确的是
A.一个数的绝对值的相反数一定不是负数
B.一个数的绝对值一定不是负数
C.一个数的绝对值一定是正数
D.一个数的绝对值一定是非正数
.
(
)
(
)
(
)
随堂练习
4.若|x-3|+|y-2|=0,则x= 5.判断正误 (1)绝对值是它本身的数是正数;……………(
,y= )
(2)当a≠0时,|a|总是大于0;………………(
)
(3)绝对值小于2的整数是1和-1;……………(
)
6.如果|a|=|-2|,那么a=_________;如果m是负数,且|m|=10,那么m= ________.
随堂练习
7.化简下列各数: +|-3.5|, -|-11|, |+(-15)|, |-(-7)|, |-(+9)|.
课堂小结
课堂小结1.本节课你有哪些收获? 一个正数的绝对值是它本身,一个负数的绝对值是它的相 反数,0的绝对值是0. 即 (1)如果 a>0,那么|a|= a ; (2)如果 a=0,那么|a|= 0 ; (3)如果 a<0,那么|a|=- a .
旧知回顾
1.数轴三要素:
、
和
2. -(-3)是
的相反数
是+(-6)的相反数
3.相反数的定义:
。 。
情景导入
(1)两只小狗相向而行,速度都相同,吃到骨头后停止在数轴上表示出这一情景.
情景导入
(2)它们所要跑的路线相同吗? 解:路线不同. (3)它们所要跑的路程(线段OA、OB的长度)一样吗?
解:路程一样,到原点的距离相等(不管方向),OA=OB. 我们知道,互为相反数的两个数(除0以外)只有符号不同,这两个数的相同 部分在数轴上表示什么?
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
|8|=8, |-8|=8.
.
4
活动3:练一练,想一想
完成下列表格
数a 4 3 1.5 0
—1.5 —3 —4
数a的绝对值|a| |4|= 4 |3|= 3 |1.5|= 1.5 |0|= 0
|—1.5|= 1.5 |—3|= 3
|—4|=4
—1.5 O 1.5
-4 -3 -2 -1 0 1 2 3 4
练习1 化简 (1)|-0.1|=____; (2) |-101|=____; (3)| 3 |=______; (4) |-8|=_____;
100
(5) |+6|=____ ; (6) |0| ______;
(7) -|-7.5|=_____; (8 -|+8|=_____;
(9)如果|x|=2,则x=______
.
5
1、一个正数的绝对值是它本身;一个负数的绝对值是 它的相反数;0的绝对值是0.
(1)当a是正数时,|a|=__a__; (2)当a是负数时,|a|=__-a; (3)当a=0时,|a|=___0。
a (a 0) | a| a (a 0)
0 (a 0)
2.互为相反数的两个数的绝对值相等
.
6
.
9
回顾与小结
本节课里你学到了什么???
(1)绝对值的几何意义及代数意义。 (2)如何求一个数的绝对值。
:教材P15第4、10题。
.
10
1.2.4
.
1
活动1:想一想
问题1:小明的家与两个商店在同一直线上, 其中商店A在小明家东边1km处,商店B在小 明家西边2km。
(1)怎样用数轴表示两个商店与小明家的位置关系?
(2)如果小明要 买笔记本,你认为小明应该选择去哪个商 店呢?
B
2km
O 1km A
-2
-1
0
ห้องสมุดไป่ตู้
1
2
活动2:绝对值概念的学习和理解
一般地,数轴上表示数a的点与原点 的距离叫做数a的绝对值,记作|a|。
B
O
A
-2
0
1
想一想:
根据上面的数轴表示,你能求出-2和1的绝对值吗?
.
3
思考:-8与8是相反数,把它们在数轴 上表示出来,那么它们的方向又有什么 关系?到原点的距离又有什么关系?
8
-8
8
0
8
-8与8虽然符号不同,但它们在数轴上所表示 的点到原点的距离都是是8个单位长度,我们把这 个距离8叫做+8和-8的绝对值。记为:
.
7
练习2
(1)绝对值是3的数有几个?各是什 么?
(2)绝对值是0的数有几个?各是什 么?
(3)绝对值是-2的数是否存在?若 存在,请说出来?
.
8
练习3 判断
( 1 ) |-1.4|>0 ( 2 ) |-0.3|=|0.3| ( 3 ) 有理数的绝对值一定是正数。 ( 4 ) 绝对值最小的数是0。 ( 5 ) 如果数a的绝对值等于a,那么a一定为正数。 ( 6 ) 一个数的绝对值越大,表示它的点在数轴上越 靠 右。 ( 7) 一个数的绝对值越大,表示它的点在数轴上离原 点越远 ( 8 ) 若a=b,则|a|=|b| ( 9 ) 若|a|=|b|,则a=b。
