4抛物线下的直角三角形
直角三角形存在性问题解决方法汇总

【问题描述】如图,在平面直角坐标系中,点A 坐标为(1,1),点B 坐标为(5,3),在x 轴上找一点C 使得△ABC 是直角三角形,求点C 坐标.【几何法】两线一圆得坐标(1)若∠A 为直角,过点A 作AB 的垂线,与x 轴的交点即为所求点C ;(2)若∠B 为直角,过点B 作AB 的垂线,与x 轴的交点即为所求点C ;(3)若∠C 为直角,以AB 为直径作圆,与x 轴的交点即为所求点C .(直径所对的圆周角为直角)重点还是如何求得点坐标,C1、C2求法相同,以C2为例:【构造三垂直】01问题与方法C3、C4求法相同,以C3为例:构造三垂直步骤:第一步:过直角顶点作一条水平或竖直的直线;第二步:过另外两端点向该直线作垂线,即可得三垂直相似.【代数法】表示线段构勾股还剩下C1待求,不妨来求下C1:【解析法】还有个需要用到一个教材上并没有出现但是大家都知道的算法:互相垂直的两直线斜率之积为-1.考虑到直线AC1与AB互相垂直,k1k2=-1,可得:kAC=-2,又直线AC1过点A(1,1),可得解析式为:y=-2x+3,所以与x轴交点坐标为(1.5,0),即C1坐标为(1.5,0).确实很简便,但问题是这个公式出现在高中的教材上方法小结几何法:(1)两线一圆作出点;(2)构造三垂直相似,利用对应边成比例求线段,必要时可设未知数.代数法:(1)表示点A、B、C坐标;(2)表示线段AB、AC、BC;(3)分类讨论①AB²+AC²=BC²、②AB²+BC²=AC²、③AC²+BC²=AB²;(4)代入列方程,求解.02从等腰直角说起再特殊一些,如果问题变为等腰直角三角形存在性,则同样可采取上述方法,只不过三垂直得到的不是相似,而是全等.2019兰州中考删减【等腰直角存在性——三垂直构造全等】通过对下面数学模型的研究学习,解决问题.【模型呈现】如图,在Rt△ABC,∠ACB=90°,将斜边AB绕点A顺时针旋转90°得到AD,过点D作DE⊥AC于点E,可以推理得到△ABC≌△DAE,进而得到AC=DE,BC=AE.我们把这个数学模型成为“K型”.推理过程如下:【模型迁移】二次函数y=ax²+bx+2的图像交x轴于点A(-1,0),B(4,0)两点,交y轴于点C.动点M从点A出发,以每秒2个单位长度的速度沿AB方向运动,过点M作MN⊥x轴交直线BC于点N,交抛物线于点D,连接AC,设运动的时间为t秒.(1)求二次函数y=ax²+bx+2的表达式;(2)在直线MN上存在一点P,当△PBC是以∠BPC为直角的等腰直角三角形时,求此时点D的坐标.2017本溪中考【直角顶点已知or未知】如图,在平面直角坐标系中,抛物线y=1/2x²+bx+c与x轴交于A、B两点,点B (3,0),经过点A的直线AC与抛物线的另一交点为C(4,5/2),与y轴交点为D,点P是直线AC下方的抛物线上的一个动点(不与点A、C重合).(1)求该抛物线的解析式.(2)点Q在抛物线的对称轴上运动,当△OPQ是以OP为直角边的等腰直角三角形时,请直接写出符合条件的点P的坐标.【小结】对于构造三垂直来说,直角顶点已知的和直角顶点的未知的完全就是两个题目!也许能画出大概位置,但如何能画出所有情况,才是问题的关键.其实只要再明确一点,构造出三垂直后,表示出一组对应边,根据相等关系列方程求解即可.2019阜新中考【对未知直角顶点的分析】如图,抛物线y=ax²+bx+2交x轴于点A(-3,0)和点B(1,0),交y轴于点C.(1)求这个抛物线的函数表达式.(2)点D的坐标为(-1,0),点P为第二象限内抛物线上的一个动点,求四边形ADCP面积的最大值.(3)点M为抛物线对称轴上的点,问:在抛物线上是否存在点N,使△MNO为等腰直角三角形,且∠MNO为直角?若存在,请直接写出点N的坐标;若不存在,请说明理由.【小结】无论直角顶点确定与否,事实上,所有的情况都可以归结为同一个方程:NE=FM.故只需在用点坐标表示线段时加上绝对值,便可计算出可能存在的其他情况.03一般直角三角形的处理一般直角三角形存在性,同样构造三垂直,区别于等腰直角构造的三垂直全等,没了等腰的条件只能得到三垂直相似.而题型的变化在于动点或许在某条直线上,也可能在抛物线上等.2018安顺中考【对称轴上寻动点】如图,已知抛物线y=ax²+bx+c(a≠0)的对称轴为直线x=-1,且抛物线与x轴交于A、B两点,与y轴交于C点,其中A(1,0),C(0,3).(1)若直线y=mx+n经过B、C两点,求直线BC和抛物线的解析式;(2)在抛物线的对称轴x=-1上找一点M,使点M到点A的距离与到点C的距离之和最小,求出点M的坐标;(3)设点P为抛物线的对称轴x=-1上的一个动点,求使△BPC为直角三角形的点P的坐标.2018怀化中考【抛物线上寻动点】如图,在平面直角坐标系中,抛物线y=ax²+2x+c与x轴交于A(-1,0),B(3,0)两点,与y轴交于点C,点D是该抛物线的顶点.(1)求抛物线的解析式和直线AC的解析式;(2)请在y轴上找一点M,使△BDM的周长最小,求出点M的坐标;(3)试探究:在拋物线上是否存在点P,使以点A,P,C为顶点,AC为直角边的三角形是直角三角形?若存在,请求出符合条件的点P的坐标;若不存在,请说明理由.2019鄂尔多斯中考【动点还可能在……】如图,抛物线y=ax²+bx-2(a≠0)与x轴交于A(-3,0),B(1,0)两点,与y轴交于点C,直线y=-x与该抛物线交于E,F两点.(1)求抛物线的解析式.(2)P是直线EF下方抛物线上的一个动点,作PH⊥EF于点H,求PH的最大值.(3)以点C为圆心,1为半径作圆,圆C上是否存在点M,使得△BCM是以CM为直角边的直角三角形?若存在,直接写出M点坐标;若不存在,说明理由.。
抛物线与直线形由动点生成的特殊三角形问题

抛物线与直线形(1)——由动点生成的特殊三角形问题知识纵横抛物线与直线形的结合表现形式之一是,以抛物线为载体,探讨是否存在一些点,使其能够成某些特殊三角形,有以下常见的基本形式:(1)抛物线上的点能否构成等腰三角形;(2)抛物线上的点能否构成直角三角形;(3)抛物线上的点能否构成相似三角形;解这类问题的基本思路:假设存在,数形结合,分类归纳,逐一考察。
例题求解【例1】如图,抛物线y =ax2 -5ax - 4经过.'ABC的三个顶点,已知BC // x轴,点A在x轴上,点C在y轴上,且AC =BC •(1)求抛物线的对称轴;(2)写出代B,C三点的坐标并求抛物线的解析式;(3)探究:若点P是抛物线对称轴上且在x轴下方的动点,是否存在■ PAB是等腰三角形?(龙岩市中考题)思路点拨对于(3)只需求出P点纵坐标,将问题转化为相关线段长。
解题的关键是分情况讨论并正确画图。
【例2】已知抛物线y = kx2 - 2kx _ 3k ,交x轴于A, B两点(A在B的左边),交y轴于C点,且y有最大值4.(1)求抛物线的解析式;(2)在抛物线上是否存在点P ,使PBC是直角三角形?若存在,求出P点坐标;若不存在,说明理由.(包头市中考题)思路点拨对于(2),设P点坐标为(a,b ),寻找相似三角形,建立a、b的另一关系式,解联立而得到的方程组,可求出a、b的值。
【例3】抛物线y = —l(x-i f十3与y轴交于点A,顶点为B,对称轴BC与x轴交于点4C .(1)如图1 .求点A的坐标及线段0C的长;(2 )点P在抛物线上,直线PQ // BC交x轴于点Q,连接BQ .①若含45角的直角三角板如图2所示放置.其中,一个顶点与点C重合,直角顶点D在BQ上,另一个顶点E在PQ上•求直线BQ的函数解析式;②若含30角的直角三角板一个顶点与点C重合,直角顶点D在直线BQ上,另一个顶点E在PQ上,求点P的坐标.S 1 2 2(2011年绍兴市中考题) 思路点拨对于(2),解题的关键是求出CQ的长。
抛物线及其性质知识点大全
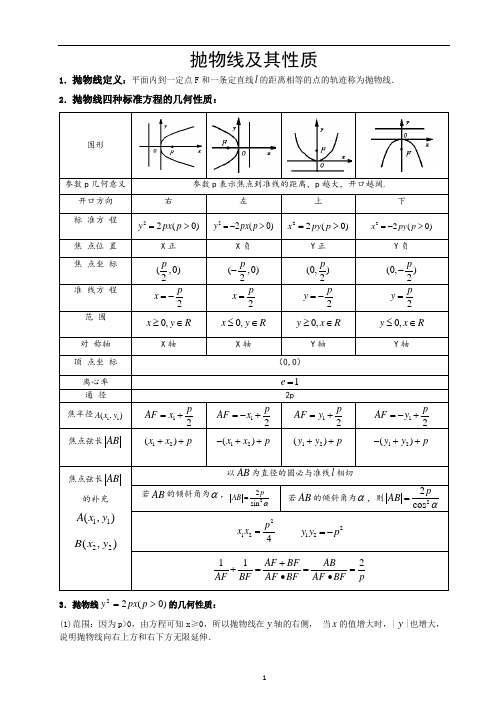
抛物线及其性质1.抛物线定义:平面内到一定点F 和一条定直线l 的距离相等的点的轨迹称为抛物线. 2.抛物线四种标准方程的几何性质:图形参数p 几何意义 参数p 表示焦点到准线的距离,p 越大,开口越阔.开口方向 右左上下 标 准方 程 22(0)y px p => 22(0)y px p =-> 22(0)x py p =>22(0)x py p =->焦 点位 置 X 正X 负Y 正Y 负焦 点坐 标 (,0)2p (,0)2p -(0,)2p(0,)2p -准 线方 程 2p x =-2p x =2p y =-2p y =范 围 0,x y R ≥∈0,x y R ≤∈0,y x R ≥∈0,y x R ≤∈对 称轴 X 轴X 轴Y 轴Y 轴顶 点坐 标 (0,0)离心率 1e =通 径 2p焦半径11(,)A x y 12p AF x =+12p AF x =-+12p AF y =+12p AF y =-+焦点弦长AB12()x x p ++ 12()x x p -++ 12()y y p ++ 12()y y p -++焦点弦长AB 的补充11(,)A x y22(,)B x y以AB 为直径的圆必与准线l 相切若AB 的倾斜角为α,22sin p AB α=若AB 的倾斜角为α,则22cos pAB α=2124p x x = 212y y p =-112AF BF AB AF BF AF BF AF BF p++===•• 3.抛物线)0(22>=p px y 的几何性质:(1)范围:因为p>0,由方程可知x ≥0,所以抛物线在y 轴的右侧, 当x 的值增大时,|y |也增大,说明抛物线向右上方和右下方无限延伸.(2)对称性:对称轴要看一次项,符号决定开口方向. (3)顶点(0,0),离心率:1=e ,焦点(,0)2p F ,准线2px -=,焦准距p . (4) 焦点弦:抛物线)0(22>=p px y 的焦点弦AB ,),(11y x A ,),(22y x B ,则p x x AB ++=21||. 弦长|AB|=x 1+x 2+p,当x 1=x 2时,通径最短为2p 。
抛物线的焦点弦经典性质及其证明过程

抛物线的焦点弦经典性质及其证明过程抛物线所示的是具有经典性质的几何图形,其定义为一个特别的二次函数:当其焦点在原点上时,抛物线形式为y = ax2;当其焦点在非原点处时,抛物线形式为 y = a(x - h)\pt2 + k,其中h是抛物线的焦点的横坐标位置,k是焦点的纵坐标位置,a是抛物线的斜率系数。
抛物线具有许多经典性质,最为重要的是焦点弦性质,它是抛物线的几何和数学基础。
焦点弦的定义是连接抛物线上任意两点的直线都与焦点构成直角,或者说从焦点连接到抛物线上任意点都构成直角三角形。
证明抛物线经典性质焦点弦证明:抛物线具有经典性质焦点弦可以应用三角函数定理证明。
设点P(x,y)位于抛物线上,则有 y = a(x - h)² + k;设F为抛物线的焦点,则有 F (h,k) ;∠FPQ 为钝角,则有:tan∠FPQ = /FP/ \cos∠FPQ/PQ/即 /FP/\ G(x-h, y-k)/PQ/由已知:FP:((h - x), (k - y))PQ:((x' - x), (y' - y))可得:/(h-x)(y'-y)-(k-y)(x'-x)\tan∠FPQ = ----------------------/(x'-x)²+(y'-y)²\\式子两边同乘以(x'-x)²+(y’-y)²即 /(h-x)(y'-y)-(k-y)(x'-x)(x'-x)²+(y'-y)²\t an∠FPQ = ------------------------------------/ (x'-x)²+(y'-y)²)²\\即/(h-x)y'+(k-y)x'-(h-x)y-(k-y)x\tan∠FPQ = -----------------------------------/ (x'-x)²+(y'-y)²\\将已知带入即可得tan∠FPQ = 0即点F、P、Q三点构成的三角形为钝角,即证明了抛物线具有经典性质的焦点弦性质。
与抛物线有关的两个重要三角形

与抛物线有关的两个重要三角形刘伟 重庆市北碚区江北中学(400714)二次函数是初等函数中最为重要的一个函数,其图象抛物线,进一步加强了代数与几何的联系,其中蕴含的数学思想和方法,对学生观察问题、研究问题、解决问题是十分有益的。
二次函数的图象抛物线与坐标轴交点构成的有关线段、三角形面积等代数与几何综合问题,是历年中考数学压轴题的重点和热点。
抛物线c bx ax y ++=2,当△=b 2-4ac >0时,抛物线与x 轴必有两个交点为)0,(1x A 、)0,(2x B ;当0=x 时,抛物线与y 轴相交于点C (0,c )。
设抛物线的顶点为P ,此时我们得到与抛物线有关的两个重要三角形:△ABC 与△ABP 。
那么这两个三角形的面积、形状与抛物线的系数a,b,c, 有怎样的内在联系呢?下面就此问题作如下探讨:一、关于△ABC∵抛物线与x 轴的两个交点为)0,(1x A 、)0,(2x B ,则02=++c bx ax 。
根据一元二次方程根与系数的关系有:ac x x a b x x =-=+2121, 所以A 、B 两点间的距离.4444)()(22222121221212aa acb a ac b a c a b x x x x x x x x AB ∆=-=-=⨯-⎪⎭⎫ ⎝⎛-=-+=-=-= 即 aAB ∆= …………………………………………(1) 这就是抛物线与x 轴的两个交点之间的距离公式。
而|OC|=|y c |=|c|, 所以S △ABC =.212121∆⋅=⋅∆⋅=⋅a c c a OC AB 即 S △ABC =.2∆⋅ac ……………………………………(2) 这就是抛物线与两坐标轴交点构成三角形的面积公式。
二、关于△ABP由抛物线的对称性可知,它的形状、大小由P ,A ,B 三点坐标确定。
由(1)知:aAB ∆=. 设D 是抛物线对称轴与x 轴的交点,则|PD|=|y p |=.4442aa b ac ∆=- 设∠PAB=α,在Rt △PAD 中,..4:,21242ααtg a a AD PD tg =∆∆=∆⋅∆==平方整理得 于是我们得到:①当α=600时,△ABP 为等边三角形,此时α24tg =∆02604tg ==12;②当α=450时,△ABP 为等腰直角三角形,此时α24tg =∆02454tg ==4。
抛物线内接直角三角形的一个性质及应用

抛物线内接直角三角形的一个性质及应用抛物线内接直角三角形是几何学中一个重要的定理,它告诉我们:如果一个直角三角形的一个顶点在抛物线上,那么其它两个顶点的坐标也会在这个抛物线上。
本文将简要介绍抛物线内接直角三角形的定义、性质及其应用。
首先,抛物线内接直角三角形定义为:一个直角三角形,其中一个顶点在抛物线上,另外两个顶点也在抛物线上,且抛物线的准线和直角三角形的两条腰都相交。
因此,抛物线内接直角三角形的性质有以下三点:
1)直角三角形的一个顶点在抛物线上,另外两个顶点也在同一
条抛物线上;
2)抛物线的准线与直角三角形的腰相交;
3)抛物线内接直角三角形的面积小于等于抛物线面积的一半。
此外,抛物线内接直角三角形还有一些其它特性:抛物线内接直角三角形的高度等于抛物线的端点之间的距离;两点定理说明了任何一点到抛物线上的点的距离等于直角三角形的斜边的长度。
抛物线内接直角三角形有许多实际应用,其中最为重要的是在机械设计中,抛物线被用来设计螺旋形线路,使得机械运动更加均匀,减少了摩擦力,减少了损耗。
在建筑过程中,抛物线也被用来设计电梯的曲线,使其运行曲线十分柔和,降低了电梯的震动,减少了乘客的不适感受。
另外,抛物线内接直角三角形也被用于医学领域中的X 射线成像技术,使得X射线的扫描更加准确,精确诊断病症。
综上所述,抛物线内接直角三角形是几何学中一个重要的定理,它描述了三角形和抛物线之间的关系,它的定义、性质和应用在许多不同的领域中有广泛的应用,它能够减少摩擦力、降低震动,使X射线扫描更准确,为人类带来科学和技术上的进步。
高考数学 专题13 抛物线解答题解法荟萃(解析版)

专题13 抛物线解答题解法荟萃一.【学习目标】1.掌握抛物线的定义;2.掌握焦点三角形的应用和几何意义;3.掌握抛物线方程的求法;4.掌握直线与抛物线的位置关系;5.熟练掌握定点、定值、最值和范围问题。
二.【知识点】 1.抛物线的定义平面内与一定点F 和一条定直线l 的距离______的点的轨迹叫做抛物线,定点F 叫做抛物线的焦点,直线l 叫做抛物线的准线.2.抛物线的标准方程、图形及几何性质 标准y 2=2px (p >0) y 2=-2px (p >0) x 2=2py (p >0) x 2=-2py (p >0)方程图 形焦点 )0,2(p F 准线x =p 2范围 ① x ≥0,y ∈R ② x ≤0,y ∈R③ x ∈R ,y ≥0 ④ x ∈R ,y ≤0对称轴 ⑤________ ⑥_________ 顶点 O (0,0) O (0,0) 离心率 e =1e =1开口⑦____ ⑧____⑨____ ⑩____3.抛物线y 2=2px (p >0)上一点P (x 0,y 0)到焦点)0,2(pF 的距离|PF |=x 0+p 2.三.【方法总结】1.求抛物线标准方程的实质是求p 值,常用的方法是待定系数法,若开口不定时,可以设抛物线方程为y 2=mx(m≠0)或x 2=ny(n≠0).2.利用抛物线定义可知,抛物线的焦半径与焦点弦有许多特殊的性质,应用起来非常方便.如:已知AB 是抛物线y 2=2px(p>0)的焦点弦,且A(x 1,y 1),B(x 2,y 2),点F 是抛物线的焦点(如图),可以证明:(1)y 1y 2=-p 2,x 1x 2=p 24. (2)|AB|=x 1+x 2+p.(3)1|AF|+1|BF|为定值2p .(4)以AB 为直径的圆与抛物线的准线相切. (5)以AF(或BF)为直径的圆与y 轴相切. (6)∠CFD =90°. 四.【题型方法】(一)抛物线的轨迹方程 (二)定点问题(三)直线与抛物线涉及的面积问题 (四)直线与抛物线中涉及的角的问题 (五)定值问题 (六)范围问题(七)抛物线与向量的综合 (八)最值问题 五.【题型举例】(一)抛物线的轨迹方程例1. 已知曲线()2C:2y x =+上有一点A ,定点()B 2,0,求线段AB 中点P 的轨迹方程。
2020届中考数学二轮复习专题训练:二次函数与几何(含答案)

2020届中考数学二轮复习专题训练:二次函数与几何1. 如图,抛物线1C :y =ax 2+bx+1的顶点坐标为D (1,0),(1)求抛物线1C 的解析式;(2)如图1,将抛物线1C 向右平移1个单位,向下平移1个单位得到抛物线2C ,直线y x c =+,经过点D 交y 轴于点A ,交抛物线2C 于点B ,抛物线2C 的顶点为P,求△DBP 的面积(3)如图2,连结AP,过点B 作BC ⊥AP 于C,设点Q 为抛物线上点P 至点B 之间的一动点,连结PQ 并延长交BC 于点E ,连结 BQ 并延长交AC 于点F ,试证明:()FC AC EC +为定值.图1yxO P DBA图2QyxO P F E CDB A【解答】(1)∵抛物线顶点为(1,0)P ,经过点(0,1)∴可设抛物线的解析式为:2(1)y a x =-,得: 1a = ∴抛物线的解析式为221y x x =-+(2)根据题意的p (2,-1)∴抛物线的解析式为:2(2)1y x =--,∴A(0,-1),B(4,3)∴△DBP 的面积 =3(3)过点Q 作QM AC ⊥于点M ,过点Q 作QN BC ⊥于点N ,设点Q 的坐标是2(,43)t t t -+,则2(2)QM CN t ==-,4MC QN t ==-.∵//QM CE ∴PQM ∆∽PEC ∆ ∴QM PM EC PC = 即2(2)12t t EC --=,得2(2)EC t =- ∵//QN FC ∴BQN ∆∽BFC ∆ ∴QN BN FC BC = 即243(43)4t t t FC ---+=,得4FC t = 又∵4AC =∴4()[42(2)]8FC AC EC t t+=+-==,即()FC AC EC +为定值8.2. 如图,已知抛物线C 1:()522-+=x a y 的顶点为P ,与x 轴相交于A 、B 两点(点A 在点B 的左边),点B 的横坐标是1.(1)求P 点坐标及a 的值;(3分)(2)如图1,抛物线C 2与抛物线C 1关于x 轴对称,将抛物线C 2向右平移,平移后的抛物线记为C 3,C 3的顶点为M ,当点P 、M 关于点B 成中心对称时,求C 3的解析式;(4分) (3)如图2,点Q 是x 轴正半轴上一点,将抛物线C 1绕点Q 旋转180°后得到抛物线C 4.抛物线C 4的顶点为N ,与x 轴相交于E 、F 两点(点E 在点F 的左边),当以点P 、N 、F 为顶点的三角形是直角三角形时,求点Q 的坐标.(5分)(1)由抛物线C 1:()522-+=x a y 得顶点P 的为(-2,-5)∵点B (1,0)在抛物线C 1上∴()52102-+=a ,∴a =59 (2)连接PM ,作PH ⊥x 轴于H ,作MG ⊥x 轴于G∵点P 、M 关于点B 成中心对称,∴PM 过点B ,且PB =MB ∴△PBH ≌△MBG ,∴MG =PH =5,BG =BH =3∴顶点M 的坐标为(4,5),抛物线C 2由C 1关于x 轴对称得到,抛物线C 3由C 2平移得到∴抛物线C 3的表达式为()54952+--=x y (3)∵抛物线C 4由C 1绕点x 轴上的点Q 旋转180°得到∴顶点N 、P 关于点Q 成中心对称由(2)得点N 的纵坐标为5设点N 坐标为(m ,5) 作PH ⊥x 轴于H ,作NG ⊥x 轴于G ,作PK ⊥NG 于K ∵旋转中心Q 在x 轴上 ∴EF =AB =2BH =6 ∴FG =3,点F 坐标为(m +3,0)H 坐标为(2,0),K 坐标为(m ,-5), 根据勾股定理得 PN 2=NK 2+PK 2=m 2+4m +104PF 2=PH 2+HF 2=m 2+10m +50 NF 2=52+32=34①当∠PNF =90º时,PN 2+ NF 2=PF 2,解得m =443,∴Q 点坐标为(193,0)②当∠PFN =90º时,PF 2+ NF 2=PN 2,解得m =103,∴Q 点坐标为(23,0) ③∵PN >NK =10>NF ,∴∠NPF ≠90º综上所得,当Q 点坐标为(193,0)或(23,0)时,以点P 、N 、F 为顶点的三角形是直角三角形.3. 已知: 如图1, 二次函数y =a (x -1)2-4的图象交x 轴负半轴于点A , 交x 轴正半轴于点B , 交y 轴负半轴于点C , 且OB =3OA . (1) 求二次函数的解析式;(2) 如图2, M 是抛物线的顶点, P 是抛物线在B 点右侧上一点, Q 是对称轴上一点, 并且AQ ⊥PQ , 是否存在这样的点P , 使得∠P AQ =∠AMQ ? 若存在, 请求出P 点坐标; 若不存在, 请说明理由.(3)如图3, 设(1)中抛物线的顶点为M ,R 为x 轴正半轴上一点,将(1)中抛物线绕R 旋转1800得到抛物线C 1: y =-a (x -h)2+k 交x 轴于D,E 两点,.若tan ∠BME=1,求R 点的坐标。
抛物线中角的存在性问题

• 18 .理科考试研究•数学版2021年2月10日抛物线中角的存在性沔题罗峻1段利芳2(1•阳新县白沙中学湖北黄石435241; 2.汉南区纱帽中学湖北武汉430090)摘要:本文通过一道典型习题的“一题五问”来设置问题,破解抛物线中角的存在性问题,让学生了解抛物线存在性问题的题目设置特点及解答策略,培养学生逻辑思维能力和综合运用几何知识构造基本图形,运用函数、方程思想 解决问题的能力,从而领悟解题方法,提高解题效益.关键词:二次函数;角的存在性;一题多问;求解策略函数与几何是初中数学的重点知识和核心内容, 将这两方面的内容结合在同一题目中,难度及综合性 有所增大,这类题目可以考查学生灵活运用知识的能 力,创新意识和数学素养.下面通过一个问题的五问 来破解函数与几何相结合的角的存在性问题,供大家 参考[1].题目如图1,二次函数y =-2* -6与坐标轴交于点4,B ,C ,点为顶点.1 75°角存在问题问题1如图2,P 是B C 下方抛物线上一动点,若乙PCB =75°,求点/1的坐标.图2 图3分析由= 易发现zOCfi =45。
,构造平行线,将75°分成45。
和30。
角之和,出现30。
的特殊 角,利用30°的条件,构造直角三角形并运用含30°角 的直角三角形的三边之比,用某一字母表示点P 坐 标,代人函数解析式则问题获解.解析易求/1(-2,0),5(6,0),(:(0,-6),如图 3,过点C 作C £ //4B 交抛物线于点£,过点P 作C £的垂线,垂足为点F .易求乙 B C F = Z 0BC =45。
,则乙 ECP = 30。
.设= m ■,贝ij C F =,P (爪,一6 - m ) •J E P (V 3m , - 6 - m )jt ;A y = y "*2 ~2x -6,^%爪=¥,所以二1^).2 45°角存在问题问题2对称轴上有一动点M ,使乙CMB =45。
2023年中考数学压轴题专题02 二次函数与直角三角形问题【含答案】

专题2二次函数与直角三角形问题解直角三角形的存在性问题,一般分三步走,第一步寻找分类标准,第二步列方程,第三步解方程并验根.一般情况下,按照直角顶点或者斜边分类,然后按照三角比或勾股定理列方程.有时根据直角三角形斜边上的中线等于斜边的一半列方程更简便.解直角三角形的问题,常常和相似三角形、三角比的问题联系在一起.如果直角边与坐标轴不平行,那么过三个顶点作与坐标轴平行的直线,可以构造两个新的相似直角三角形,这样列比例方程比较简便.我们先看三个问题:1.已知线段AB,以线段AB为直角边的直角三角形ABC有多少个?顶点C的轨迹是什么?2.已知线段AB,以线段AB为斜边的直角三角形ABC有多少个?顶点C的轨迹是什么?3.已知点A(4,0),如果△OAB是等腰直角三角形,求符合条件的点B的坐标.图1图2图3如图1,点C在垂线上,垂足除外.如图2,点C在以AB为直径的圆上,A、B两点除外.如图3,以OA为边画两个正方形,除了O、A两点以外的顶点和正方形对角线的交点,都是符合题意的点B,共6个.如图4,已知A(3,0),B(1,-4),如果直角三角形ABC的顶点C在y轴上,求点C的坐标.我们可以用几何的方法,作AB为直径的圆,快速找到两个符合条件的点C.如果作BD⊥y轴于D,那么△AOC∽△CDB.设OC=m,那么341m m-=.这个方程有两个解,分别对应图中圆与y轴的两个交点.对于代数法,可以采用两条直线的斜率之积来解决.【例1】(2022•滨州)如图,在平面直角坐标系中,抛物线y=x2﹣2x﹣3与x轴相交于点A、B(点A在点B的左侧),与y轴相交于点C,连接AC、BC.(1)求线段AC的长;(2)若点P为该抛物线对称轴上的一个动点,当PA=PC时,求点P的坐标;(3)若点M为该抛物线上的一个动点,当△BCM为直角三角形时,求点M的坐标.【例2】.(2022•辽宁)如图,抛物线y=ax2﹣3x+c与x轴交于A(﹣4,0),B两点,与y轴交于点C(0,4),点D为x轴上方抛物线上的动点,射线OD交直线AC于点E,将射线OD绕点O逆时针旋转45°得到射线OP,OP交直线AC于点F,连接DF.(1)求抛物线的解析式;(2)当点D在第二象限且=时,求点D的坐标;(3)当△ODF为直角三角形时,请直接写出点D的坐标.【例3】.(2022•广安)如图,在平面直角坐标系中,抛物线y=ax2+x+m(a≠0)的图象与x轴交于A、C 两点,与y轴交于点B,其中点B坐标为(0,﹣4),点C坐标为(2,0).(1)求此抛物线的函数解析式.(2)点D是直线AB下方抛物线上一个动点,连接AD、BD,探究是否存在点D,使得△ABD的面积最大?若存在,请求出点D的坐标;若不存在,请说明理由.(3)点P为该抛物线对称轴上的动点,使得△PAB为直角三角形,请求出点P的坐标.【例4】.(2022•柳州)已知抛物线y=﹣x2+bx+c与x轴交于A(﹣1,0),B(m,0)两点,与y轴交于点C(0,5).(1)求b,c,m的值;(2)如图1,点D是抛物线上位于对称轴右侧的一个动点,且点D在第一象限内,过点D作x轴的平行线交抛物线于点E,作y轴的平行线交x轴于点G,过点E作EF⊥x轴,垂足为点F,当四边形DEFG的周长最大时,求点D的坐标;(3)如图2,点M是抛物线的顶点,将△MBC沿BC翻折得到△NBC,NB与y轴交于点Q,在对称轴上找一点P,使得△PQB是以QB为直角边的直角三角形,求出所有符合条件的点P的坐标.1.(2022•公安县模拟)如图,已知二次函数y=﹣x2+bx+c经过A,B两点,BC⊥x轴于点C,且点A(﹣1,0),C(2,0),AC=BC.(1)求抛物线的解析式;的最大值以及此时E点的坐标;(2)点E是抛物线AB之间的一个动点(不与A,B重合),求S△ABE(3)根据问题(2)的条件,判断是否存在点E使得△ABE为直角三角形,如果存在,求出E点的坐标,如果不存在,说明理由.2.(2022•高邮市模拟)如图,抛物线y=ax2+bx﹣3经过A(﹣1,0),与y轴交于点C,过点C作BC∥x 轴,交抛物线于点B,连接AC、AB,AB交y轴于点D,若.(1)求点B的坐标;(2)点P为抛物线对称轴上一点,且位于x轴上方,连接PA、PC,若△PAC是以AC为直角边的直角三角形,求点P的坐标.3.(2022•碑林区校级模拟)如图,已知抛物线y=﹣x2+bx+c与x轴交于A(﹣2,0),B(4,0)两点.(1)求b,c的值;(2)点E为抛物线y=﹣x2+bx+c上一点,且点E在x轴上方,连接BE,以点E为直角顶点,BE为直角边,作等直角△BED,使得点D恰好落在直线y=x上,求出满足条件的所有点E的坐标.4.(2022•雁峰区校级模拟)如图,抛物线y=﹣x2+bx+c经过A(﹣1,0),B(3,0)两点,与y轴交于点C,直线y=x+1与x轴交于点E,与y轴交于点D.(1)求抛物线的解析式;(2)P为抛物线上的点,连接OP交直线DE于Q,当Q是OP中点时,求点P的坐标;(3)M在直线DE上,当△CDM为直角三角形时,求出点M的坐标.5.(2022•平南县二模)如图,二次函数y=x2+bx+c的图象与x轴交于A、B两点,与y轴交于点C,且A (﹣1,0),对称轴为直线x=2.(1)求该抛物线的表达式;(2)直线l过点A与抛物线交于点P,当∠PAB=45°时,求点P的坐标;(3)在抛物线的对称轴上是否存在一点Q,使得△BCQ是直角三角形?若存在,请直接写出点Q的坐标;若不存在,请说明理由.6.(2022•太原一模)综合与实践如图,抛物线y=x2+2x﹣8与x轴交于A,B两点(点A在点B左侧),与y轴交于点C.点D在直线AC 下方的抛物线上运动,过点D作y轴的平行线交AC于点E.(1)求直线AC的函数表达式;(2)求线段DE的最大值;(3)当点F在抛物线的对称轴上运动,以点A,C,F为顶点的三角形是直角三角形时,直接写出点F的坐标.7.(2022•桐梓县模拟)在平面直角坐标系xOy中,已知抛物线y=﹣与x轴交于A,B两点(点B在点A的右侧),与y轴交于点C,它的对称轴与x轴交于点D,直线L经过C,D两点,连接AC.(1)求A,B两点的坐标及直线L的函数表达式;(2)探索直线L上是否存在点E,使△ACE为直角三角形,若存在,求出点E的坐标;若不存在,说明理由.8.(2022•沈阳模拟)如图1,在平面直角坐标系中,抛物线y=ax2+bx+c与x轴交于A(﹣1,0),B(3,0),与y轴交于点C(0,﹣3).(1)求抛物线的解析式.(2)若点M是抛物线上B,C之间的一个动点,线段MA绕点M逆时针旋转90°得到MN,当点N恰好落在y轴上时,求点M,点N的坐标.(3)如图2,若点E坐标为(2,0),EF⊥x轴交直线BC于点F,将△BEF沿直线BC平移得到△B'E'F',在△B'E'F'移动过程中,是否存在使△ACE'为直角三角形的情况?若存在,请直接写出所有符合条件的点E′的坐标;若不存在,请说明理由.9.(2022•东坡区校级模拟)如图,抛物线y=x2﹣(m+2)x+4的顶点C在x轴的正半轴上,直线y=x+2与抛物线交于A,B两点,且点A在点B的左侧.(1)求m的值;(2)点P是抛物线y=x2﹣(m+2)x+4上一点,当△PAB的面积是△ABC面积的2倍时,求点P的坐标;(3)将直线AB向下平移k(k>0)个单位长度,平移后的直线与抛物线交于D,E两点(点D在点E的左侧),当△DEC为直角三角形时,求k的值.10.(2022•海沧区二模)抛物线y1=ax2﹣2ax+c(a<2且a≠0)与x轴交于A(﹣1,0),B两点,抛物线的对称轴与x轴交于点D,点M(m,n)在该抛物线上,点P是抛物线的最低点.(1)若m=2,n=﹣3,求a的值;(2)记△PMB面积为S,证明:当1<m<3时,S<2;(3)将直线BP向上平移t个单位长度得直线y2=kx+b(k≠0),与y轴交于点C,与抛物线交于点E,当x <﹣1时,总有y1>y2.当﹣1<x<1时,总有y1<y2.是否存在t≥4,使得△CDE是直角三角形,若存在,求t的值;若不存在,请说明理由.11.(2021•葫芦岛模拟)如图,在平面直角坐标系中,矩形OABC,点A在y轴上,点C在x轴上,其中B(﹣2,3),已知抛物线y=﹣x2+bx+c经过点A和点B.(1)求抛物线解析式;(2)如图1,点D(﹣2,﹣1)在直线BC上,点E为y轴右侧抛物线上一点,连接BE、AE,DE,若S△BDE=4S△ABE,求E点坐标;(3)如图2,在(2)的条件下,P为射线DB上一点,作PQ⊥直线DE于点Q,连接AP,AQ,PQ,若△APQ为直角三角形,请直接写出P点坐标.12.(2021•和平区一模)如图,抛物线y=ax2+bx﹣,交y轴于点A,交x轴于B(﹣1,0),C(5,0)两点,抛物线的顶点为D,连接AC,CD.(1)求直线AC的函数表达式;(2)求抛物线的函数表达式及顶点D的坐标;(3)过点D作x轴的垂线交AC于点G,点H为线段CD上一动点,连接GH,将△DGH沿GH翻折到△GHR(点R,点G分别位于直线CD的两侧),GR交CD于点K,当△GHK为直角三角形时.①请直接写出线段HK的长为;②将此Rt△GHK绕点H逆时针旋转,旋转角为α(0°<α<180°),得到△MHN,若直线MN分别与直线CD,直线DG交于点P,Q,当△DPQ是以PQ为腰的等腰三角形时,请直接写出点P的纵坐标为﹣或﹣.13.(2021•莱芜区三模)二次函数y=ax2+bx+c交x轴于点A(﹣1,0)和点B(﹣3,0),交y轴于点C (0,﹣3).(1)求二次函数的解析式;(2)如图1,点E为抛物线的顶点,点T(0,t)为y轴负半轴上的一点,将抛物线绕点T旋转180°,得到新的抛物线,其中B,E旋转后的对应点分别记为B′,E′,当四边形BEB'E'的面积为12时,求t的值;(3)如图2,过点C作CD∥x轴,交抛物线于另一点D.点M是直线CD上的一个动点,过点M作x轴的垂线,交抛物线于点P.当以点B、C、P为顶点的三角形是直角三角形时,求所有满足条件的点M的坐标.14.(2021•雁塔区校级模拟)已知二次函数y=x2+bx+c经过A、B两点,BC垂直x轴于点C,且A(﹣1,0),C(4,0),AC=BC.(1)求抛物线的解析式;(2)请画出抛物线的图象;(3)点P是抛物线对称轴上一个动点,是否存在这样的点P,使三角形ABP为直角三角形?若存在,求出P点坐标;若不存在,请说明理由.15.(2021•武汉模拟)如图,抛物线y=x2+bx+12(b<0)与x轴交于A,B两点(A点在B点左侧),且OB=3OA.(1)请直接写出b=﹣8,A点的坐标是(2,0),B点的坐标是(6,0);(2)如图(1),D点从原点出发,向y轴正方向运动,速度为2个单位长度/秒,直线BD交抛物线于点E,若BE=5DE,求D点运动时间;(3)如图(2),F点是抛物线顶点,过点F作x轴平行线MN,点C是对称轴右侧的抛物线上的一定点,P点在直线MN上运动.若恰好存在3个P点使得△PAC为直角三角形,请求出C点坐标,并直接写出P 点的坐标.16.(2021•北碚区校级模拟)如图1,在平面直角坐标系中,抛物线y=﹣x+2与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,点P为直线BC上方抛物线上一动点.(1)求直线BC的解析式;(2)过点A作AD∥BC交抛物线于D,连接CA,CD,PC,PB,记四边形ACPB的面积为S1,△BCD的面积为S2,当S1﹣S2的值最大时,求P点的坐标和S1﹣S2的最大值;(3)如图2,将抛物线水平向右平移,使得平移后的抛物线经过点O,G为平移后的抛物线的对称轴直线l上一动点,将线段AC沿直线BC平移,平移过程中的线段记为A'C'(线段A'C'始终在直线l左侧),是否存在以A',C',G为顶点的等腰直角△A'C'G?若存在,请写出满足要求的所有点G的坐标并写出其中一种结果的求解过程,若不存在,请说明理由.17(2021•广东模拟)如图,直线y=x﹣3与x轴,y轴分别交于B、C两点.抛物线y=x2+bx+c经过点B、C,与x轴另一交点为A,顶点为D.(1)求抛物线的解析式;(2)设点P从点D出发,沿对称轴向上以每秒1个单位长度的速度匀速运动.设运动的时间为t秒.①点P在运动过程中,若∠CBP=15°,求t的值;②当t为何值时,以P,A,C为顶点的三角形是直角三角形?求出所有符合条件的t值.18.(2021•巴中)已知抛物线y=ax2+bx+c与x轴交于A(﹣2,0)、B(6,0)两点,与y轴交于点C(0,﹣3).(1)求抛物线的表达式;(2)点P在直线BC下方的抛物线上,连接AP交BC于点M,当最大时,求点P的坐标及的最大值;(3)在(2)的条件下,过点P作x轴的垂线l,在l上是否存在点D,使△BCD是直角三角形,若存在,请直接写出点D的坐标;若不存在,请说明理由.19.(2021•毕节市)如图,抛物线y=x2+bx+c与x轴相交于A,B两点,与y轴相交于点C,对称轴为直线x=2,顶点为D,点B的坐标为(3,0).(1)填空:点A的坐标为(1,0),点D的坐标为(2,﹣1),抛物线的解析式为y=x2﹣4x+3;(2)当二次函数y=x2+bx+c的自变量x满足m≤x≤m+2时,函数y的最小值为,求m的值;(3)P是抛物线对称轴上一动点,是否存在点P,使△PAC是以AC为斜边的直角三角形?若存在,请求出点P的坐标;若不存在,请说明理由.20.(2021•兰溪市模拟)如图,在平面直角坐标系中,已知二次函数y=a(x﹣m)2﹣m+4图象的顶点为C,其中m>0,与x轴相交于点A、B(点A在点B的左侧),与y轴相交于点D,点M的坐标为(0,4).(1)当m=2时,抛物线y=a(x﹣m)2﹣m+4(m>0)经过原点,求a的值;(2)当a=﹣1时,①若点M,点D,点C三点组成的三角形是直角三角形,求此时点D的坐标.②设反比例函数y=﹣(x>0)与抛物线y=a(x﹣m)2﹣m+4(m>0)相交于点E(p,q).当2<p <4时,求m的取值范围.【例1】.(2022•滨州)如图,在平面直角坐标系中,抛物线y=x2﹣2x﹣3与x轴相交于点A、B(点A在点B的左侧),与y轴相交于点C,连接AC、BC.(1)求线段AC的长;(2)若点P为该抛物线对称轴上的一个动点,当PA=PC时,求点P的坐标;(3)若点M为该抛物线上的一个动点,当△BCM为直角三角形时,求点M的坐标.【分析】(1)根据坐标轴上点的特点求出点A,C的坐标,即可求出答案;(2)设出点P的坐标,利用PA=PC建立方程求解,即可求出答案;(3)分三种情况,利用等腰直角三角形的性质求出前两种情况,利用三垂线构造出相似三角形,得出比例式,建立方程求解,即可求出答案.【解析】(1)针对于抛物线y=x2﹣2x﹣3,令x=0,则y=﹣3,∴C(0,﹣3);令y=0,则x2﹣2x﹣3=0,∴x=3或x=﹣1,∵点A在点B的左侧,∴A(﹣1,0),B(3,0),∴AC==;(2)∵抛物线y=x2﹣2x﹣3的对称轴为直线x=﹣=1,∵点P为该抛物线对称轴上,∴设P(1,p),∴PA==,PC==,∵PA=PC,∴=,∴p=﹣1,∴P(1,﹣1);(3)由(1)知,B(3,0),C(0,﹣3),∴OB=OC=3,设M(m,m2﹣2m﹣3),∵△BCM为直角三角形,∴①当∠BCM=90°时,如图1,过点M作MH⊥y轴于H,则HM=m,∵OB=OC,∴∠OCB=∠OBC=45°,∴∠HCM=90°﹣∠OCB=45°,∴∠HMC=45°=∠HCM,∴CH=MH,∵CH=﹣3﹣(m2﹣2m﹣3)=﹣m2+2m,∴﹣m2+2m=m,∴m=0(不符合题意,舍去)或m=1,∴M(1,﹣4);②当∠CBM=90°时,过点M作M'H'⊥x轴,同①的方法得,M'(﹣2,5);③当∠BMC=90°时,如图2,Ⅰ、当点M在第四象限时,过点M作MD⊥y轴于D,过点B作BE⊥DM,交DM的延长线于E,∴∠CDM=∠E=90°,∴∠DCM+∠DMC=90°,∵∠DMC+∠EMB=90°,∴∠DCM=∠EMB,∴△CDM∽△MEB,∴,∵M(m,m2﹣2m﹣3),B(3,0),C(0,﹣3),∴DM=m,CD=﹣3﹣(m2﹣2m﹣3)=﹣m2+2m,ME=3﹣m,BE=﹣(m2﹣2m﹣3)=﹣m2+2m+3,∴,∴m=0(舍去)或m=3(点B的横坐标,不符合题意,舍去)或m=(不符合题意,舍去)或m =,∴M(,﹣),Ⅱ、当点M在第三象限时,M(,﹣),即满足条件的M的坐标为(1,﹣4)或(﹣2,5)或(,﹣),或(,﹣).【例2】.(2022•辽宁)如图,抛物线y=ax2﹣3x+c与x轴交于A(﹣4,0),B两点,与y轴交于点C(0,4),点D为x轴上方抛物线上的动点,射线OD交直线AC于点E,将射线OD绕点O逆时针旋转45°得到射线OP,OP交直线AC于点F,连接DF.(1)求抛物线的解析式;(2)当点D在第二象限且=时,求点D的坐标;(3)当△ODF为直角三角形时,请直接写出点D的坐标.【分析】(1)将点A(﹣4,0),C(0,4)代入y=ax2﹣3x+c,即可求解;(2)过点D作DG⊥AB交于G,交AC于点H,设D(n,﹣n2﹣3n+4),H(n,n+4),由DH∥OC,可得==,求出D(﹣1,6)或(﹣3,4);(3)设F(t,t+4),当∠FDO=45°时,过点D作MN⊥y轴交于点N,过点F作FM⊥MN交于点M,证明△MDF≌△NOD(AAS),可得D点纵坐标为2,求出D点坐标为(,2)或(,2);当∠DFO=90°时,过点F作KL⊥x轴交于L点,过点D作DK⊥KL交于点K,证明△KDF≌△LFO(AAS),得到D点纵坐标为4,求得D(0,4)或(﹣3,4).【解析】(1)将点A(﹣4,0),C(0,4)代入y=ax2﹣3x+c,∴,解得,∴y=﹣x2﹣3x+4;(2)过点D作DG⊥AB交于G,交AC于点H,设直线AC的解析式为y=kx+b,∴,解得,∴y=x+4,设D(n,﹣n2﹣3n+4),H(n,n+4),∴DH=﹣n2﹣4n,∵DH∥OC,∴==,∵OC=4,∴DH=3,∴﹣n2﹣4n=3,解得n=﹣1或n=﹣3,∴D(﹣1,6)或(﹣3,4);(3)设F(t,t+4),当∠FDO=45°时,过点D作MN⊥y轴交于点N,过点F作FM⊥MN交于点M,∵∠DOF=45°,∴DF=DO,∵∠MDF+∠NDO=90°,∠MDF+∠MFD=90°,∴∠NDO=∠MFD,∴△MDF≌△NOD(AAS),∴DM=ON,MF=DN,∴DN+ON=﹣t,DN=ON+(﹣t﹣4),∴DN=﹣t﹣2,ON=2,∴D点纵坐标为2,∴﹣x2﹣3x+4=2,解得x=或x=,∴D点坐标为(,2)或(,2);当∠DFO=90°时,过点F作KL⊥x轴交于L点,过点D作DK⊥KL交于点K,∵∠KFD+∠LFO=90°,∠KFD+∠KDF=90°,∴∠LFO=∠KDF,∵DF=FO,∴△KDF≌△LFO(AAS),∴KD=FL,KF=LO,∴KL=t+4﹣t=4,∴D点纵坐标为4,∴﹣x2﹣3x+4=4,解得x=0或x=﹣3,∴D(0,4)或(﹣3,4);综上所述:D点坐标为(,2)或(,2)或(0,4)或(﹣3,4).【例3】(2022•广安)如图,在平面直角坐标系中,抛物线y=ax2+x+m(a≠0)的图象与x轴交于A、C两点,与y轴交于点B,其中点B坐标为(0,﹣4),点C坐标为(2,0).(1)求此抛物线的函数解析式.(2)点D是直线AB下方抛物线上一个动点,连接AD、BD,探究是否存在点D,使得△ABD的面积最大?若存在,请求出点D的坐标;若不存在,请说明理由.(3)点P为该抛物线对称轴上的动点,使得△PAB为直角三角形,请求出点P的坐标.【分析】(1)把点B,C两点坐标代入抛物线的解析式,解方程组,可得结论;(2)存在.如图1中,设D(t,t2+t﹣4),连接OD.构建二次函数,利用二次函数的性质,解决问题;(3)如图2中,设抛物线的对称轴交x轴于点N,过点B作BM⊥抛物线的对称轴于点M.则N(﹣1.0).M (﹣1,﹣4),分三种情形:∠PAB=90°,∠PBA=90°,∠APB=90°,分别求解可得结论.【解析】(1)∵抛物线y=ax2+x+m(a≠0)的图象经过点B(0,﹣4),点C(2,0),∴,解得,∴抛物线的解析式为y=x2+x﹣4;(2)存在.理由:如图1中,设D(t,t2+t﹣4),连接OD.令y=0,则x2+x﹣4=0,解得x=﹣4或2,∴A(﹣4,0),C(2,0),∵B(0,﹣4),∴OA=OB=4,=S△AOD+S△OBD﹣S△AOB=×4×(﹣﹣t+4)+×4×(﹣t)﹣×4×4=﹣t2﹣4t=﹣(t+2)∵S△ABD2+4,∵﹣1<0,∴t=﹣2时,△ABD的面积最大,最大值为4,此时D(﹣2,﹣4);(3)如图2中,设抛物线的对称轴交x轴于点N,过点B作BM⊥抛物线的对称轴于点M.则N(﹣1.0).M (﹣1,﹣4);∵OA=OB=4,∠AOB=90°,∴∠OAB=∠OBA=45°,当∠P1AB=90°时,△ANP1是等腰直角三角形,∴AN=NP1=3,∴P1(﹣1,3),当∠ABP2=90°时,△BMP2是等腰直角三角形,可得P2(﹣1,﹣5),当∠APB=90°时,设P(﹣1,n),设AB的中点为J,连接PJ,则J(﹣2,﹣2),∴PJ=AB=2,∴12+(n+2)2=(2)2,解得n=﹣2或﹣﹣2,∴P3(﹣1,﹣2),P4(﹣1,﹣﹣2),综上所述,满足条件的点P的坐标为(﹣1,3)或(﹣1,﹣5)或(﹣1,﹣2)或(﹣1,﹣﹣2).【例4】.(2022•柳州)已知抛物线y=﹣x2+bx+c与x轴交于A(﹣1,0),B(m,0)两点,与y轴交于点C(0,5).(1)求b,c,m的值;(2)如图1,点D是抛物线上位于对称轴右侧的一个动点,且点D在第一象限内,过点D作x轴的平行线交抛物线于点E,作y轴的平行线交x轴于点G,过点E作EF⊥x轴,垂足为点F,当四边形DEFG的周长最大时,求点D的坐标;(3)如图2,点M是抛物线的顶点,将△MBC沿BC翻折得到△NBC,NB与y轴交于点Q,在对称轴上找一点P,使得△PQB是以QB为直角边的直角三角形,求出所有符合条件的点P的坐标.【分析】(1)把A(﹣1,0),C(0,5)代入y=﹣x2+bx+c,解二元一次方程组即可得b,c的值,令y=0即可得m的值;(2)设D(x,﹣x2+4x+5),则E(4﹣x,﹣x2+4x+5),表示出四边形DEFG的周长,根据二次函数的最值即可求解;(3)过点C作CH⊥对称轴于H,过点N作NK⊥y轴于K,证明△MCH≌△NCK,根据全等三角形的性质得NK=MH=4,CK=CH=2,则N(﹣4,3),利用待定系数法可得直线BN的解析式为y=﹣x+,可得Q(0,),设P(2,p),利用勾股定理表示出PQ2、BP2、BQ2,分两种情况:①当∠BQP=90°时,②当∠QBP=90°时,利用勾股定理即可求解.【解析】(1)把A(﹣1,0),C(0,5)代入y=﹣x2+bx+c,得,解得.∴这个抛物线的解析式为:y=﹣x2+4x+5,令y=0,则﹣x2+4x+5=0,解得x1=5,x2=﹣1,∴B(5,0),∴m=5;(2)∵抛物线的解析式为:y=﹣x2+4x+5=﹣(x﹣2)2+9,∴对称轴为x=2,设D(x,﹣x2+4x+5),∵DE∥x轴,∴E(4﹣x,﹣x2+4x+5),∵过点D作x轴的平行线交抛物线于点E,作y轴的平行线交x轴于点G,过点E作EF⊥x轴,∴四边形DEFG是矩形,∴四边形DEFG的周长=2(﹣x2+4x+5)+2(x﹣4+x)=﹣2x2+12x+2=﹣2(x﹣3)2+20,∴当x=3时,四边形DEFG的周长最大,∴当四边形DEFG的周长最大时,点D的坐标为(3,8);(3)过点C作CH⊥对称轴于H,过点N作NK⊥y轴于K,∴∠NKC=∠MHC=90°,由翻折得CN=CM,∠BCN=∠BCM,∵B(5,0),C(0,5).∴OB=OC,∴∠OCB=∠OBC=45°,∵CH⊥对称轴于H,∴CH∥x轴,∴∠BCH=45°,∴∠BCH=∠OCB,∴∠NCK=∠MCH,∴△MCH≌△NCK(AAS),∴NK=MH,CK=CH,∵抛物线的解析式为:y=﹣x2+4x+5=﹣(x﹣2)2+9,∴对称轴为x=2,M(2,9),∴MH=9﹣5=4,CH=2,∴NK=MH=4,CK=CH=2,∴N(﹣4,3),设直线BN的解析式为y=mx+n,∴,解得,∴直线BN的解析式为y=﹣x+,∴Q(0,),设P(2,p),∴PQ2=22+(p﹣)2=p2﹣p+,BP2=(5﹣2)2p2=9+p2,BQ2=52+()2=25+,分两种情况:①当∠BQP=90°时,BP2=PQ2+BQ2,∴9+p2=p2﹣p++25+,解得p=,∴点P的坐标为(2,);②当∠QBP=90°时,P′Q2=BP′2+BQ2,∴p2﹣p+=9+p2+25+,解得p=﹣9,∴点P′的坐标为(2,﹣9).综上,所有符合条件的点P的坐标为(2,),(2,﹣9).1.(2022•公安县模拟)如图,已知二次函数y=﹣x2+bx+c经过A,B两点,BC⊥x轴于点C,且点A(﹣1,0),C(2,0),AC=BC.(1)求抛物线的解析式;的最大值以及此时E点的坐标;(2)点E是抛物线AB之间的一个动点(不与A,B重合),求S△ABE(3)根据问题(2)的条件,判断是否存在点E使得△ABE为直角三角形,如果存在,求出E点的坐标,如果不存在,说明理由.【分析】(1)先求得点B的坐标,然后将点A和点B的坐标代入抛物线的解析式可得到关于b、c的方程组,从而可求得b、c的值;(2)过点E作EF∥y轴交线段AB于点F,设点E(t,﹣t2+2t+3),则F(t,t+1),则可得到EF与x的函数关系式,利用配方法可求得EF的最大值以及点E的坐标,最后根据EF的最大值可得△ABE的面积;(3)存在,设E(m,﹣m2+2m+3),分三种情况:分别以A,B,E为直角顶点,作出辅助线,构造相似列出方程,解方程即可.【解析】(1)∵点A(﹣1,0),C(2,0),∴AC=3,OC=2,∵AC=BC=3,∴B(2,3),把A(﹣1,0)和B(2,3)代入二次函数y=x2+bx+c中得:,解得:,∴二次函数的解析式为:y=﹣x2+2x+3;(2)∵直线AB经过点A(﹣1,0),B(2,3),设直线AB的解析式为y=kx+b′,∴,解得:,∴直线AB的解析式为:y=x+1,如图,过点E作EF∥y轴交线段AB于点F,∴设点E(t,﹣t2+2t+3),则F(t,t+1),∴EF=﹣t2+2t+3﹣(t+1)=﹣(t﹣)2+,∴当t=时,EF的最大值为,∴点E的坐标为(,),最大,S△ABE=•EF•(x B−x A)=××(2+1)=.∴此时S△ABE(3)在问题(2)的条件下,存在点E使得△ABE为直角三角形;设E(m,﹣m2+2m+3),①当点A为直角顶点,过点A作AB的垂线,与AB之间的抛物线无交点,故不可能存在点E使得△ABE为以点A为直角顶点的直角三角形,②当点B为直角顶点,如下图,此时∠EBA=90°,过点E作EG⊥CB,交CB延长线于点G,∵BC⊥x轴于点C,且AC=BC,∴△ABC是等腰直角三角形,∠ABC=45°,∴∠EBG=45°,∴△BEG是等腰直角三角形,EG=BG,∵EG的长为点E与直线BC的距离,即2﹣m,且BG=CG﹣BC=﹣m2+2m+3﹣3=﹣m2+2m,∴2﹣m==﹣m2+2m,解得m=1或m=2(舍),∴E(1,4);③如下图,此时∠AEB=90°,作EM∥x轴,交CB的延长线于点M,过点A作AN⊥x轴交ME的延长线于点N,∴∠BEM+∠AEN=90°,∵在Rt△AEN中,∠EAN+∠AEN=90°,∴∠BEM=∠EAN,∴△AEN∽△BEM,∴BM:EN=EM:AN,∴(﹣m2+2m):(m+1)=(2﹣m):(﹣m2+2m+3),即﹣m(2﹣m)(m+1)(m﹣3)=(2﹣m)(m+1),∵2﹣m≠0,m+1≠0,∴m2﹣3m+1=0,解得m=或m=(舍).∴E(,)综上,根据问题(2)的条件,存在点E(1,4)或(,)使得△ABE为直角三角形.2.(2022•高邮市模拟)如图,抛物线y=ax2+bx﹣3经过A(﹣1,0),与y轴交于点C,过点C作BC∥x 轴,交抛物线于点B,连接AC、AB,AB交y轴于点D,若.(1)求点B的坐标;(2)点P为抛物线对称轴上一点,且位于x轴上方,连接PA、PC,若△PAC是以AC为直角边的直角三角形,求点P的坐标.【分析】(1)根据A(﹣1,0),得到OA=l,对于y=ax2+bx﹣3,令x=0,则y=﹣3,得到C(0,﹣3),OC=3,根据BC∥x轴,得到△AOD∽△BCD,推出,得到BC=2,即可得B(2,﹣3);(2)把A(﹣1,0),B(2,﹣3)代入y=ax2+bx﹣3,求得a=1,b=﹣2,得到抛物线解析式并配方为y =x2﹣2x﹣3=(x﹣1)2﹣4,得到抛物线的对称轴是直线x=1,设P(1,m),写出PA2=m2+22=m2+4.PC2=(m+3)2+12=(m+3)2+1.AC2=12+32=10.根据△PAC是以AC为直角边的直角三角形,当∠PAC=90°时,PA2+AC2=PC2.得到m2+4+10=(m+3)2+1,求得m=;当∠PCA=90°时,PC2+AC2=AP2,得到(m+3)2+1+10=m2+4,求出m=﹣;即可得点P的坐标.【解析】∵A(﹣1,0),∴OA=l,在y=ax2+bx﹣3中,令x=0,则y=﹣3,∴C(0,﹣3),∴OC=3,∵BC∥x轴,∴△AOD∽△BCD,∴,∴BC=2,∴B(2,﹣3);(2)把A(﹣1,0),B(2,﹣3)代入y=ax2+bx﹣3,∴,解得,∴抛物线解析式为y=x2﹣2x﹣3=(x﹣1)2﹣4,∴抛物线的对称轴是直线x=1,设P(1,m),∴PA2=m2+22=m2+4.PC2=(m+3)2+12=(m+3)2+1.AC2=12+32=10.∵△PAC是以AC为直角边的直角三角形,当∠PAC=90°时,PA2+AC2=PC2.∴m2+4+10=(m+3)2+1,解得m=;当∠PCA=90°时,PC2+AC2=AP2,∴(m+3)2+1+10=m2+4,解得m=﹣(不符合题意,舍去).∴P(1,).3.(2022•碑林区校级模拟)如图,已知抛物线y=﹣x2+bx+c与x轴交于A(﹣2,0),B(4,0)两点.(1)求b,c的值;(2)点E为抛物线y=﹣x2+bx+c上一点,且点E在x轴上方,连接BE,以点E为直角顶点,BE为直角边,作等直角△BED,使得点D恰好落在直线y=x上,求出满足条件的所有点E的坐标.【分析】(1)运用待定系数法即可求得答案;(2)设D(m,m),E(n,﹣n2+2n+8),分两种情况:当点E1在点D左侧,∠DE1B=90°,BE1=D1E1时,当点E2在点D2右侧,∠D2E2B=90°,BE2=D2E2时,利用等腰直角三角形性质,添加辅助线构造全等三角形,再利用全等三角形的性质建立方程求解即可得出答案.【解析】(1)∵抛物线y=﹣x2+bx+c与x轴交于A(﹣2,0),B(4,0)两点,∴,解得:,∴b=2,c=8;(2)∵点D在直线y=x上,点E在抛物线解析式为y=﹣x2+2x+8上,∴设D(m,m),E(n,﹣n2+2n+8),当点E1在点D左侧,∠DE1B=90°,BE1=D1E1时,如图,过点E1作E1G∥x轴,过点B作BF⊥EG于点F,过点D1作D1G⊥E1G于点G,则∠BFE1=∠E1GD1=90°,BF=﹣n2+2n+8,E1F=4﹣n,E1G=m﹣n,D1G=m﹣(﹣n2+2n+8)=n2﹣2n﹣8+m,∴∠E1BF+∠BE1F=90°,∵∠D1E1G+∠BE1F=90°,∴∠E1BF=∠D1E1G,在△BE1F和△E1D1G中,,∴△BE1F≌△E1D1G(AAS),∴E1F=D1G,BF=E1G,∴,解得:,当n=2时,﹣n2+2n+8=﹣22+2×2+8=8,∴E1(2,8);当点E2在点D2右侧,∠D2E2B=90°,BE2=D2E2时,如图,过点E2作E2H⊥x轴于点H,过点D2作D2K ⊥E2H于点K,则∠BHE2=∠E2KD2=90°,BH=4﹣n,E2H=﹣n2+2n+8,E2K=﹣n2+2n+8﹣m,D2K=n﹣m,同理可得△BE2H≌△E2D2K(AAS),∴E2H=D2K,BH=E2K,∴,解得:或,∴E(1+,2)或(1﹣,2);综上所述,满足条件的所有点E的坐标为(2,8)或(1+,2)或(1﹣,2).4.(2022•雁峰区校级模拟)如图,抛物线y=﹣x2+bx+c经过A(﹣1,0),B(3,0)两点,与y轴交于点C,直线y=x+1与x轴交于点E,与y轴交于点D.(1)求抛物线的解析式;(2)P为抛物线上的点,连接OP交直线DE于Q,当Q是OP中点时,求点P的坐标;(3)M在直线DE上,当△CDM为直角三角形时,求出点M的坐标.【分析】(1)根据抛物线y=﹣x2+bx+c经过A(﹣1,0),B(3,0)两点,列方程组,于是得到答案;(2)令x=0,则y=x+1=1,求得OD=1,作PH⊥OB,垂足为H,得到∠COA=∠PHO=90°,根据平行线的性质得到∠P=∠DOQ,∠PFQ=∠ODQ,根据全等三角形的性质得到PF=OD=1,设P点横坐标为x,得到方程﹣x2+2x+3﹣(x+1)=1,求得x1=2,x2=﹣,当x=2时,y=3,当x=﹣时,y =,于是得到答案;(3)求得CD=OC﹣OD=2,设M(a,a+1),分两种情况①当∠CMD=90°时,②当∠DCM=90°时,根据勾股定理即可得到结论.【解析】(1)∵抛物线y=﹣x2+bx+c经过A(﹣1,0),B(3,0)两点,∴,解得:,∴抛物线的解析式是y=﹣x2+2x+3;(2)令x=0,则y=x+1=1,∴OD=1,如图,作PH⊥OB,垂足为H,交ED于F,则∠COA=∠PHO=90°,∴PH∥OC,∴∠OPF=∠DOQ,∠PFQ=∠ODQ,又Q是OP中点,∴PQ=OQ,∴△PFQ≌△ODQ(AAS),∴PF=OD=1设P点横坐标为x,则﹣x2+2x+3﹣(x+1)=1,解得:x1=2,x2=﹣,当x=2时,y=3,当x=﹣时,y=,∴点P的坐标是(2,3)或(﹣,);(3)令x=0,则y=﹣x2+2x+3=3,∴OC=3,∴CD=OC﹣OD=2,设M(a,a+1),∴CM2=a2+(3﹣a﹣1)2=a2﹣2a+4,DM2=a2+(a+1﹣1)2=a2,①当∠CMD=90°时,∴CD2=CM2+DM2,∴22=a2﹣2a+4+a2,解得:a1=,a2=0(舍去),当a=时,a+1=,∴M(,);②当∠DCM=90°时,∴CD2+CM2=DM2,∴22+a2﹣2a+4=a2,解得:a=4,当a=4时,a+1=3,∴M(4,3);解法二:∵∠DCM=90°,∴CM∥x轴,∴a+1=3,解得a=4,∴M(4,3);综上所述:点M的坐标为(,)或(4,3).5.(2022•平南县二模)如图,二次函数y=x2+bx+c的图象与x轴交于A、B两点,与y轴交于点C,且A (﹣1,0),对称轴为直线x=2.(1)求该抛物线的表达式;(2)直线l过点A与抛物线交于点P,当∠PAB=45°时,求点P的坐标;(3)在抛物线的对称轴上是否存在一点Q,使得△BCQ是直角三角形?若存在,请直接写出点Q的坐标;若不存在,请说明理由.【分析】(1)设y=(x﹣2)2+k,用待定系数法可得抛物线的解析式为y=x2﹣4x﹣5;(2)过点P作PM⊥x轴于点M,设P(m,m2﹣4m﹣5),根据∠PAB=45°知AM=PM,即|m2﹣4m﹣5|=m+1,解得m的值,即可得P的坐标是(6,7)或P(4,﹣5);(3)由y=x2﹣4x﹣5求出B(5,0),C(0,﹣5),设Q(2,t),有BC2=50,BQ2=9+t2,CQ2=4+(t+5)2,分三种情况:当BC为斜边时,9+t2+4+(t+5)2=50,当BQ为斜边时,50+4+(t+5)2=9+t2,当CQ 为斜边时,50+9+t2=4+(t+5)2,分别解得t的值,即可求出相应Q的坐标.【解析】(1)设y=(x﹣2)2+k,把A(﹣1,0)代入得:(﹣1﹣2)2+k=0,解得:k=﹣9,∴y=(x﹣2)2﹣9=x2﹣4x﹣5,答:抛物线的解析式为y=x2﹣4x﹣5;(2)过点P作PM⊥x轴于点M,如图:设P(m,m2﹣4m﹣5),则PM=|m2﹣4m﹣5|,∵A(﹣1,0),∴AM=m+1∵∠PAB=45°∴AM=PM,∴|m2﹣4m﹣5|=m+1,即m2﹣4m﹣5=m+1或m2﹣4m﹣5=﹣(m+1),当m2﹣4m﹣5=m+1时,解得:m1=6,m2=﹣1(不合题意,舍去),当m2﹣4m﹣5=﹣(m+1),解得m3=4,m4=﹣1(不合题意,舍去),∴P的坐标是(6,7)或P(4,﹣5);(3)在抛物线的对称轴上存在一点Q,使得△BCQ是直角三角形,理由如下:在y=x2﹣4x﹣5中,令x=0得y=﹣5,令y=0得x=﹣1或x=5,∴B(5,0),C(0,﹣5),由抛物线y=x2﹣4x﹣5的对称轴为直线x=2,设Q(2,t),∴BC2=50,BQ2=9+t2,CQ2=4+(t+5)2,当BC为斜边时,BQ2+CQ2=BC2,∴9+t2+4+(t+5)2=50,解得t=﹣6或t=1,∴此时Q坐标为(2,﹣6)或(2,1);当BQ为斜边时,BC2+CQ2=BQ2,∴50+4+(t+5)2=9+t2,解得t=﹣7,∴此时Q坐标为(2,﹣7);当CQ为斜边时,BC2+BQ2=CQ2,∴50+9+t2=4+(t+5)2,解得t=3,∴此时Q坐标为(2,3);综上所述,Q的坐标为(2,3)或(2,﹣7)或(2,1)或(2,﹣6).6.(2022•太原一模)综合与实践如图,抛物线y=x2+2x﹣8与x轴交于A,B两点(点A在点B左侧),与y轴交于点C.点D在直线AC 下方的抛物线上运动,过点D作y轴的平行线交AC于点E.(1)求直线AC的函数表达式;(2)求线段DE的最大值;(3)当点F在抛物线的对称轴上运动,以点A,C,F为顶点的三角形是直角三角形时,直接写出点F的坐标.【分析】(1)分别令x=0,y=0,求得点C、A的坐标,再运用待定系数法即可求得答案;(2)设D(m,m2+2m﹣8),则E(m,﹣2m﹣8),可得DE=﹣2m﹣8﹣(m2+2m﹣8)=﹣m2﹣4m=﹣(m+2)2+4,运用二次函数的性质即可求得线段DE的最大值;(3)设F(﹣1,n),根据两点间距离公式可得:AF2=32+n2=n2+9,AC2=42+82=80,CF2=12+(n+8)2=n2+16n+65,分三种情况:①当∠AFC=90°时,②当∠CAF=90°时,③当∠ACF=90°时,分别建立方程求解即可.【解析】(1)在y=x2+2x﹣8中,令x=0,得y=﹣8,∴C(0,﹣8),令y=0,得x2+2x﹣8=0,解得:x1=﹣4,x2=2,∴A(﹣4,0),B(2,0),设直线AC的解析式为y=kx+b,则,解得:,∴直线AC的解析式为y=﹣2x﹣8;(2)设D(m,m2+2m﹣8),则E(m,﹣2m﹣8),∵点D在点E的下方,∴DE=﹣2m﹣8﹣(m2+2m﹣8)=﹣m2﹣4m=﹣(m+2)2+4,∵﹣1<0,∴当m=﹣2时,线段DE最大值为4;(3)∵y=x2+2x﹣8=(x+1)2﹣9,∴抛物线的对称轴为直线x=﹣1,设F(﹣1,n),又A(﹣4,0),C(0,﹣8),∴AF2=32+n2=n2+9,AC2=42+82=80,CF2=12+(n+8)2=n2+16n+65,①当∠AFC=90°时,∵AF2+CF2=AC2,∴n2+9+n2+16n+65=80,解得:n1=﹣4﹣,n2=﹣4+,∴F(﹣1,﹣4﹣)或(﹣1,﹣4+);②当∠CAF=90°时,∵AF2+AC2=CF2,∴n2+9+80=n2+16n+65,解得:n=,∴F(﹣1,);③当∠ACF=90°时,∵CF2+AC2=AF2,∴n2+16n+65+80=n2+9,解得:n=﹣,∴F(﹣1,﹣);综上所述,点F的坐标为(﹣1,﹣4﹣)或(﹣1,﹣4+)或(﹣1,)或(﹣1,﹣).7.(2022•桐梓县模拟)在平面直角坐标系xOy中,已知抛物线y=﹣与x轴交于A,B两点(点B在点A的右侧),与y轴交于点C,它的对称轴与x轴交于点D,直线L经过C,D两点,连接AC.(1)求A,B两点的坐标及直线L的函数表达式;(2)探索直线L上是否存在点E,使△ACE为直角三角形,若存在,求出点E的坐标;若不存在,说明理由.【分析】(1)令x=0,y=0,可分别求出A、B、C三点坐标,在求出函数的对称轴即可求D点坐标,利用待定系数法求直线解析式即可;(2)设E(t,﹣t+2),分三种情况讨论:①当∠CAE=90°时,AC2+AE2=CE2,②当∠ACE=90°时,AC2+CE2=AE2,③当∠AEC=90°时,AE2+CE2=AC2,分别利用勾股定理求解即可.【解析】(1)令y=0,则﹣=0,解得x=﹣2或x=6,∴A(﹣2,0),B(6,0),令x=0,则y=2,∴C(0,2),∵y=﹣=﹣(x﹣2)2+,∴抛物线的对称轴为直线x=2,∴D(2,0),设直线CD的解析式为y=kx+b,。
2023年九年级数学中考专题:二次函数综合压轴题(特殊三角形问题)(含简略答案)

(1)求直线 的解析式;
(2)如图1,点 是直线 下方抛物线上的一点,连接 ,当 的面积最大时,连接 ,设 分别是线段 上的点,且 ,求四边形 的面积;
(3)如图2,点 是线段 的中点,将抛物线 沿 轴正方向平移得到新抛物线 , 经过点 , 的顶点为 ,在新抛物线 的对称轴上,是否存在点 ,使得 为等腰三角形?若存在,写出点 的坐标;若不存在,请说明理由.
(3)若点Q是上述抛物线上一点,且满足∠ABQ=2∠ABC,求满足条件的点Q的坐标.
11.如图,在平面直角坐标系中,已知抛物线 与直线 相交于 , 两点,其中 , .
(1)求该抛物线的函数表达式;
(2)点 为直线 下方抛物线上的任意一点,连接 , ,求 面积的最大值;
(3)在抛物线对称轴上找一点 ,使点 , , 三点构成的图形是直角三角形,求点 的坐标.
(2)当△PBC的面积最大时,求P点的坐标.
(3)在X轴上是否存在点N,使△NBC是等腰三角形,若存在直接写出所有符合条件的点N的坐标,若不存在说明理由
8.如图,直线 交 轴于点 ,交 轴于点B,抛物线 的顶点为 ,且经过点 .
(1)求该抛物线所对应的函数表达式;
(2)点 是抛物线上的点, 是以 为直角边的直角三角形,请直接写出点 的坐标.
13.如图,抛物线 经过 , 两点,且与 轴交于点 ,点 是抛物线的顶点,抛物线的对称轴 交 轴于点 ,连接 .
(1)求经过 三点的抛物线的函数表达式;
(2)点 在该抛物线的对称轴上,若 是以 为直角边的直角三角形,求点 的坐标;
(3)若 为 的中点,过点 作 轴于点 , 为抛物线上一动点, 为 轴上一动点, 为直线 上一动点,当以 、 、 、 为顶点的四边形是正方形时,请求出点 的坐标.
抛物线与直角三角形

7 , 4
解出 P2 (
9 105 7 9 105 7 , ) , P3 ( , )。 4 4 4 4
复习要点 激活问题图式,拓展延伸
效能分析:由等腰三角形变化为等腰直角三角形,数学思维训练如抽丝剥茧,层层 深入,通过以上问题变式,打破了学生思维的封闭性,训练学生类比推理的能力,
通过“再建模型”培养了学生的求异思维,深化了对分类讨论、建模转化等方法的
解法探究:
如图,设直线 PC 的解析式为 y kx 1 ,设 P(t , kt 1) ,类比上述方法,过点 P 作 PE x 轴于 点 E , PE OE EB , (kt 1)2 t (4 t ) , k 2t 2 2(k 2)t 1 0 ,有且只有一个点 P ,意涵
串联融通,丰富了学生解题经验。
复习要点 激活问题图式,拓展延伸
拓展 1 如图,已知抛物线 y
1 2 1 b x (b 1) x 4 4 4
( b 是实数且 b 2) 与 x 轴的正半轴分别交于点 A 、 B (点 A 位于点 B 的左侧) ,与 y 轴的正半 轴交于点 C 。 (1)点 B 的坐标为______,点 C 的坐标为_______(用含 b 的代数式表示) ; (2)请 你探索在第一象限内是否存在点 P ,使得四边形 PCOB 的面积等于 2b ,且 PBC 是以点 P 为 直角顶点的等腰直角三角形?如果存在,求出点 P 的坐标;如果不存在,请说明理由。
复习要点 激活问题图式,拓展延伸
问题图式是与问题解决有关的知识组块,是已有问题解决成功样例的概 括和抽象。它可被当前问题情境的某些线索激活,进而预测或猜测某些未知 觉到的线索,有助于问题表征的形成。这里,从典型问题出发,通过变式进 行纵向拓展,逐渐演化成代表一类问题的概括性内部表征,是形成灵活应用
抛物线与直角三角形结合的解题方法

抛物线与直角三角形结合的解题方法【最新版3篇】篇1 目录1.引言:抛物线与直角三角形的结合问题在数学题目中十分常见,本文将探讨如何利用抛物线的性质和直角三角形的特征来解题。
2.抛物线的基本性质:介绍抛物线的定义、标准方程和顶点坐标等基本概念。
3.直角三角形的特征:介绍直角三角形的定义、直角边和斜边的关系等特征。
4.抛物线与直角三角形结合的解题方法:通过实例分析,讲解如何利用抛物线和直角三角形的性质求解相关问题。
5.结论:总结抛物线与直角三角形结合的解题方法,并鼓励读者在实际解题中灵活运用。
篇1正文一、引言在数学题目中,抛物线与直角三角形的结合问题常常出现,这类问题不仅考验了学生的计算能力,还考验了他们的几何直观和逻辑思维能力。
为了更好地解决这类问题,本文将从抛物线的基本性质和直角三角形的特征出发,探讨如何利用它们来解题。
二、抛物线的基本性质抛物线是平面上到定点距离与到定直线距离相等的点的轨迹。
它有以下基本性质:1.抛物线的定义:设焦点 F 和直线 l,满足到定点 F 的距离与到定直线 l 的距离相等的点的轨迹称为抛物线。
2.标准方程:抛物线的标准方程为 y^2=2px,其中 p 为焦点到准线的距离。
3.顶点坐标:抛物线的顶点坐标为 (0, p)。
三、直角三角形的特征直角三角形是指有一个内角为 90 度的三角形,它有以下特征:1.定义:有一个内角为 90 度的三角形称为直角三角形。
2.直角边和斜边的关系:直角三角形的两条直角边的长度满足勾股定理,即 a^2 + b^2 = c^2,其中 a、b 为直角边,c 为斜边。
四、抛物线与直角三角形结合的解题方法在解决抛物线与直角三角形结合的问题时,我们可以利用抛物线的性质和直角三角形的特征,通过以下几个步骤来求解:1.画图:首先画出抛物线和直角三角形,标出已知条件。
2.寻找关键点:观察图形,找到可能对解题有帮助的关键点,如抛物线的顶点、直角三角形的直角顶点等。
抛物线的基本知识点

抛物线的基本知识点(经典版)编制人:__________________审核人:__________________审批人:__________________编制单位:__________________编制时间:____年____月____日序言下载提示:该文档是本店铺精心编制而成的,希望大家下载后,能够帮助大家解决实际问题。
文档下载后可定制修改,请根据实际需要进行调整和使用,谢谢!并且,本店铺为大家提供各种类型的经典范文,如工作报告、工作计划、活动方案、规章制度、演讲致辞、合同协议、条据文书、教学资料、作文大全、其他范文等等,想了解不同范文格式和写法,敬请关注!Download tips: This document is carefully compiled by this editor. I hope that after you download it, it can help you solve practical problems. The document can be customized and modified after downloading, please adjust and use it according to actual needs, thank you!Moreover, our store provides various types of classic sample essays, such as work reports, work plans, activity plans, rules and regulations, speeches, contract agreements, documentary evidence, teaching materials, complete essays, and other sample essays. If you would like to learn about different sample formats and writing methods, please pay attention!抛物线的基本知识点抛物线的基本知识点整理朋友们知道吗?初中抛物线的基本知识点公式平面内,到一个定点F和一条定直线l距离相等的点的轨迹(或集合)称之为抛物线。
专题12 抛物线及其性质(知识梳理+专题过关)(解析版)

专题12抛物线及其性质【考点预测】知识点一、抛物线的定义平面内与一个定点F 和一条定直线()l F l ∉的距离相等的点的轨迹叫做抛物线,定点F 叫抛物线的焦点,定直线l 叫做抛物线的准线.注:若在定义中有F l ∈,则动点的轨迹为l 的垂线,垂足为点F .知识点二、抛物线的方程、图形及性质抛物线的标准方程有4种形式:22y px =,22y px =-,22x py =,22(0)x py p =->,其中一次项与对称轴一致,一次项系数的符号决定开口方向图形标准方程22(0)y px p =>22(0)y px p =->22(0)x py p =>22(0)x py p =->顶点(00)O ,范围0x ≥,y R ∈0x ≤,y R∈0y ≥,x R ∈0y ≤,x R∈对称轴x 轴y 轴焦点(0)2pF ,(0)2p F -,(0)2p F ,(0)2pF -,离心率1e =准线方程2p x =-2p x =2p y =-2p y =焦半径11()A x y ,12pAF x =+12p AF x =-+12p AF y =+12p AF y =-+【方法技巧与总结】1、点00(,)P x y 与抛物线22(0)y px p =>的关系(1)P 在抛物线内(含焦点)2002y px ⇔<.(2)P 在抛物线上2002y px ⇔=.(3)P 在抛物线外2002y px ⇔>.2、焦半径抛物线上的点00(,)P x y 与焦点F 的距离称为焦半径,若22(0)y px p =>,则焦半径02pPF x =+,max2p PF =.3、(0)p p >的几何意义p 为焦点F 到准线l 的距离,即焦准距,p 越大,抛物线开口越大.4、焦点弦若AB 为抛物线22(0)y px p =>的焦点弦,11(,)A x y ,22(,)B x y ,则有以下结论:(1)2124p x x =.(2)212y y p =-.(3)焦点弦长公式1:12AB x x p =++,12x x p +≥=,当12x x =时,焦点弦取最小值2p ,即所有焦点弦中通径最短,其长度为2p .焦点弦长公式2:22sin pAB α=(α为直线AB 与对称轴的夹角).(4)AOB ∆的面积公式:22sin AOB p S α∆=(α为直线AB 与对称轴的夹角).5、抛物线的弦若AB 为抛物线22(p 0)y px =>的任意一条弦,1122(,),(,)A x y B x y ,弦的中点为000(,)(0)M x y y ≠,则(1)弦长公式:1212(0)AB AB x y k k =-=-=≠(2)0AB p k y =(3)直线AB 的方程为000()py y x x y -=-(4)线段AB 的垂直平分线方程为000()y y y x x p-=--6、求抛物线标准方程的焦点和准线的快速方法(4A法)(1)2(0)y Ax A =≠焦点为(,0)4A ,准线为4Ax =-(2)2(0)x Ay A =≠焦点为(0,)4A ,准线为4Ay =-如24y x =,即24y x =,焦点为1(0,)16,准线方程为116y =-7、参数方程22(0)y px p =>的参数方程为222x pt y pt ⎧=⎨=⎩(参数t R ∈)8、切线方程和切点弦方程抛物线22(0)y px p =>的切线方程为00()y y p x x =+,00(,)x y 为切点切点弦方程为00()y y p x x =+,点00(,)x y 在抛物线外与中点弦平行的直线为00()y y p x x =+,此直线与抛物线相离,点00(,)x y (含焦点)是弦AB 的中点,中点弦AB 的斜率与这条直线的斜率相等,用点差法也可以得到同样的结果.9、抛物线的通径过焦点且垂直于抛物线对称轴的弦叫做抛物线的通径.对于抛物线22(0)y px p =>,由()2p A p ,,()2p B p -,,可得||2AB p =,故抛物线的通径长为2p .10、弦的中点坐标与弦所在直线的斜率的关系:0py k=11、焦点弦的常考性质已知11()A x y ,、22()B x y ,是过抛物线22(0)y px p =>焦点F 的弦,M 是AB 的中点,l 是抛物线的准线,MN l ⊥,N 为垂足.(1)以AB 为直径的圆必与准线l 相切,以AF (或BF )为直径的圆与y 轴相切;(2)FN AB ⊥,FC FD⊥(3)2124p x x =;212y y p =-(4)设BD l ⊥,D 为垂足,则A 、O 、D 三点在一条直线上【专题过关】【考点目录】考点一:抛物线的定义与方程考点二:抛物线的轨迹方程考点三:与抛物线有关的距离和最值问题考点四:抛物线中三角形,四边形的面积问题考点五:焦半径问题考点六:抛物线的性质【典型考题】考点一:抛物线的定义与方程1.(2022·江苏·高二)已知抛物线的顶点在原点,对称轴为y 轴,其上一点(),4A m -到焦点F 的距离为6.求抛物线的方程及点A 的坐标.【解析】由题意,设抛物线方程为()220x py p =->,则其准线方程为2p y =,∴462p+=,得p =4,故抛物线方程为28x y =-;又∵点(),4A m -在抛物线上,∴232m =,∴m =±即点A 的坐标为()4-或()4--.2.(多选题)(2022·全国·高二单元测试)下列方程的图形为抛物线的是()A .10x +=B .2y -=C D .2230x x y --+=【答案】ACD【解析】对于A ,方程10x +=化为1x +=(,)x y 到定点(0,0)的距离与到定直线1x =-的距离相等,且定点(0,0)不在定直线1x =-上,原方程表示的图形是抛物线,A 是;对于B ,方程2y -=(,)x y 到定点(1,2)-的距离与到定直线2y =的距离相等,而定点(1,2)-在定直线2y =上,原方程表示的图形不是抛物线,B 不是;对于C (,)x y 到定点(2,3)的距离与到定直线3410x y +-=的距离相等,且定点(2,3)不在定直线3410x y +-=上,原方程表示的图形是抛物线,C 是;对于D ,方程2230x x y --+=化为223y x x =-+,方程表示的图形是抛物线,D 是.故选:ACD3.(多选题)(2022·广东清远·高二期末)已知0mn ≠,则方程221mx ny +=与2ny mx =在同一坐标系内对应的图形可能是()A .B .C .D .【答案】BC【解析】将对应方程化为标准方程得22111x ym n+=,2m y x n=,所以抛物线2my x n=的焦点在x 轴上,故排除D 选项,对于A 选项,由图可知0mn>,0m <,0n >,矛盾,故A 错误;对于B 选项,由图可知0mn<,0m <,0n >,满足,故B 正确;对于C 选项,由图可知,0mn>,0m >,0n >,满足,故C 正确;故选:BC.4.(2022·江西吉安·高二期末(理))已知抛物线C :()220y px p =>的焦点为F ,准线l 上有两点A ,B ,若FAB 为等腰直角三角形且面积为8,则抛物线C 的标准方程是()A .2y =B .28y x =C .2y =或28y x =D .24y x=【答案】C【解析】由题意得,当2AFB π∠=时,1282AFB S p p =⨯⨯=△,解得p =;当2FAB π∠=或2FBA π∠=时,2182AFB S p ==△,解得4p =,所以抛物线的方程是2y =或28y x =.故选:C.5.(2022·全国·高二课时练习)下列条件中,一定能得到抛物线的标准方程为28y x =的是______(填序号)(写出一个正确答案即可).①焦点在x 轴上;②焦点在y 轴上;③抛物线上横坐标为1的点到焦点的距离为3;④焦点到准线的距离为4;⑤由原点向过焦点的某直线作垂线,垂足坐标为()1,1-.【答案】①③(答案不唯一)【解析】若要得到抛物线的方程为28y x =,则焦点一定在x 轴上,故①必选,②不选.若选①③,由抛物线的定义可知132p+=,得4p =,则抛物线的方程为28y x =.若选①⑤,设焦点,02p F ⎛⎫⎪⎝⎭()0p >,()1,1A -,112AF k p =-,1OA k =-,由1AF OA k k ⋅=-,得1112p =-,解得4p =,故抛物线的方程为28y x =.由④可知4p =,故还可选择①④.故答案可为①③或①⑤或①④.故答案为:①③(答案不唯一)6.(2022·全国·高二课时练习)位于德国东部萨克森州的莱科勃克桥(如图所示)有“仙境之桥”之称,它的桥形可以近似地看成抛物线,该桥的高度为5m ,跨径为12m ,则桥形对应的抛物线的焦点到准线的距离为______m .【答案】185【解析】以抛物线的最高点O 为坐标原点,建立如图所示的平面直角坐标系,设抛物线的解析式为22x py =-,0p >,因为抛物线过点()6,5-,所以3610p =,可得185p =,所以抛物线的焦点到准线的距离为18m 5.故答案为:1857.(2022·全国·高二课时练习)设抛物线C 的顶点在坐标原点,焦点F 在坐标轴上,点P 在抛物线C 上,52PF =,若以线段PF 为直径的圆过坐标轴上距离原点为1的点,试写出一个满足题意的抛物线C 的方程为______.【答案】22x y =(答案不唯一)【解析】由题意,若抛物线的焦点F 在y 轴正半轴上,则可设抛物线方程为22x py =(0p >),()00,P x y ,0,2p F ⎛⎫ ⎪⎝⎭,由焦半径公式可知0522p y +=,圆的半径为54,得052p y -=,并且线段PF 中点的纵坐标是05224py +=,所以以线段PF 为直径的圆与x 轴相切,切点坐标为()1,0-或()1,0,所以02x =±,即点P 的坐标为52,2p -⎛⎫± ⎝⎭,代入抛物线方程22x py =(0p >)得5422p p -=⋅,解得1p =或4p =,即当点F 在y 轴正半轴上时,抛物线方程是22x y =或28x y =.同理,当点F 在y 轴负半轴时,抛物线方程为22x x =-或28x y =-,当点F 在x 轴正半轴时,抛物线方程为22y x =或28y x =,当点F 在x 轴负半轴时,抛物线方程为22y x =-或28y x =-.故答案为:22x y =(答案不唯一).8.(2022·山西·怀仁市第一中学校高二期中(理))设抛物线2:2(0)C y px p =>的焦点为F ,准线为l ,A 为C 上一点,以F 为圆心,FA 为半径的圆交l 于B ,D 两点.若90ABD ∠=︒,且ABF的面积为C 的方程为()A .22y x =B .24y x =C .28y x =D .216y =【答案】B【解析】∵以F 为圆心,FA 为半径的圆交l 于B ,D 两点,90ABD ∠=︒,结合抛物线的定义可得:AB AF BF==ABF ∴是等边三角形,30FBD ∴∠=︒.ABF2=4BF ∴=.又点F 到准线的距离为sin 302BF p ︒==,则该抛物线的方程为24y x =.故选:B .9.(2022·全国·高二课时练习)如图,过抛物线()220y px p =>的焦点F 的直线交抛物线于点,A B ,交其准线l 于点C ,若2BC BF =,且3AF =,则此抛物线的方程为()A .29y x =B .26y x =C .23y x =D .212y x=【答案】C【解析】作AD l ⊥,BE l ⊥,垂足分别为,D E ,设l 与x 轴交于点G ,由抛物线定义知:BE BF =,3AD AF ==,设BF a =,则BE a =,2BC a =,1sin 22a BCE a ∴∠==,则6BCE π∠=,26AC AD ∴==,又33AC AF BF BC a =++=+,1a \=,1BE ∴=,23BE BC FGCF==,32FG ∴=,即32p =,∴抛物线方程为:23y x =.故选:C.10.(2022·全国·高二课时练习)已知抛物线y 2=2px (p >0)经过点M (x 0,),若点M 到准线l 的距离为3,则该抛物线的方程为()A .y 2=4xB .y 2=2x 或y 2=4xC .y 2=8xD .y 2=4x 或y 2=8x【答案】D【解析】∵抛物线y 2=2px (p >0)经过点M (x 0,),∴202px =,可得04x p=.又点M 到准线l 的距离为3,∴432pp +=,解得p =2或p =4.则该抛物线的方程为y 2=4x 或y 2=8x .故选:D.11.(2022·全国·高二课时练习)苏州市“东方之门”是由两栋超高层建筑组成的双塔连体建筑(如图1所示),“门”的内侧曲线呈抛物线形.图2是“东方之门”的示意图,已知30m CD =,60m AB =,点D 到直线AB 的距离为150m ,则此抛物线顶端O 到AB 的距离为()A .180mB .200mC .220mD .240m【答案】B【解析】以O 为坐标原点,建立如图所示的平面直角坐标系,设抛物线的方程为()220x py p =->,由题意设()15,D h ,0h <,()30,150B h -,则()22152302150php h ⎧=-⎪⎨=--⎪⎩,解得502.25h p =-⎧⎨=⎩,所以此抛物线顶端O 到AB 的距离为()50150200m +=.故选:B .考点二:抛物线的轨迹方程12.(2022·全国·高二课时练习)点()1,0A ,点B 是x 轴上的动点,线段PB 的中点E 在y 轴上,且AE 垂直PB ,则点P 的轨迹方程为______.【答案】24y x =()0x ≠【解析】设(),P x y ,(),0B m ,则,22x m y E +⎛⎫⎪⎝⎭.由点E 在y 轴上,得02x m +=,则m x =-,即0,2y E ⎛⎫⎪⎝⎭.又AE PB ⊥,若0x ≠,则21012AE PB yy k k x⋅=⨯=--,即24y x =.若0x =,则0m =,此时点P ,B 重合,直线PB 不存在.所以点P 的轨迹方程是24y x =()0x ≠.故答案为:24y x =()0x ≠.13.(2022·全国·高二课时练习)若动点(,)M x y 满足()()225123412x y x y -+-=-+,则点M 的轨迹是()A .圆B .椭圆C .双曲线D .抛物线【答案】D【解析】由题意,动点(,)M x y 满足()()225123412x y x y -+-=-+,()()223412125x y x y -+-+-=,即动点(,)M x y 到定点(1,2)的距离等于动点(,)M x y 到定直线34120x y -+=的距离,又由点(1,2)不在直线34120x y -+=上,根据抛物线的定义,可得动点M 的轨迹为以(1,2)为焦点,以34120x y -+=的抛物线.故选:D.14.(2022·江西·赣州市赣县第三中学高二开学考试(理))已知动圆⊙M 经过定点(1,0)A ,且和直线1x =-相切,则点M 的轨迹方程为()A .22y x=B .24y x=C .22y x=-D .24y x=-【答案】B【解析】因为动圆⊙M 经过定点(1,0)A ,且和直线1x =-相切,所以点M 到点(1,0)A 的距离等于它到直线1x =-的距离,即M 的轨迹为以点(1,0)A 为焦点,直线1x =-为准线的抛物线,所以12p=,解得2p =,轨迹方程为24y x =.故选:B .15.(2022·全国·高二课时练习)若动圆M 经过双曲线2213y x -=的左焦点且与直线x =2相切,则圆心M 的坐标满足的方程是______.【答案】28y x=-【解析】双曲线2213y x -=的左焦点为F (-2,0),动圆M 经过F 且与直线x =2相切,则圆心M 到点F 的距离和到直线x =2的距离相等,由抛物线的定义知圆心的轨迹是焦点为F ,准线为x =2的抛物线,其方程为28y x =-.故答案为:28y x =-.16.(2022·全国·高二课时练习)若点(),P x y 满足方程3412x y =++,则点P 的轨迹是______.【答案】抛物线【解析】由|3412|x y =++|3412|5x y ++=,等式左边表示点(),x y 和点()1,2的距离,等式的右边表示点(),x y 到直线34120x y ++=的距离.整个等式表示的意义是点(),x y 到点()1,2的距离和到直线34120x y ++=的距离相等,其轨迹为抛物线.故答案为:抛物线17.(2022·全国·高二课时练习)与点()0,3F -和直线30y -=的距离相等的点的轨迹方程是______.【答案】212x y=-【解析】由抛物线的定义可得平面内与点()0,3F -和直线30y -=的距离相等的点的轨迹为抛物线,且()0,3F -为焦点,直线3y =为准线,设抛物线的方程为22(0)x py p =->,可知32p=,解得6p =,所以该抛物线方程是212x y =-,故答案为:212x y=-18.(2022·河北唐山·高二期中(理))已知动点(,)P x y 满足341x y =+-,则点P 的轨迹为()A .直线B .抛物线C .双曲线D .椭圆【答案】B【解析】把341x y =+-3415x y +-,3415x y +-可看做(,)x y 与(1,2)的距离等于(,)x y 到直线3410x y +-=的距离,由于点(1,2)不在直线3410x y +-=上,满足抛物线的定义,则点P 的轨迹为抛物线,故选:B19.(2022·全国·高二课时练习)平面上动点M 到定点()3,0F 的距离比M 到直线l :10x +=的距离大2,求动点M 满足的方程.【解析】因为动点M 到定点()3,0F 的距离比M 到直线l :10x +=的距离大2,所以动点M 到定点()3,0F 的距离与M 到直线l :30x +=的距离相等,所以M 的轨迹是以()3,0F 为焦点,直线l :3x =-为准线的抛物线,此时6p =,故所求的点M 满足的方程是212y x =.20.(2022·全国·高二课时练习)已知点M 与点(4,0)F 的距离比它到直线:60l x +=的距离小2,求点M 的轨迹方程.【解析】由题意知动点M 到(4,0)的距离比它到直线:6l x =-的距离小2,即动点M 到(4,0)的距离与它到直线4x =-的距离相等,由抛物线定义可知动点M 的轨迹为以(4,0)为焦点的抛物线,则点M 的轨迹方程为216y x =.21.(2022·全国·高二课时练习)已知圆A :(x +2)2+y 2=1与定直线l :x =1,且动圆P 和圆A 外切并与直线l 相切,求动圆的圆心P 的轨迹方程.【解析】由题意知:点P 到圆心A (-2,0)的距离和到定直线x =2的距离相等,所以点P 的轨迹为抛物线,且焦点为A ,准线为x =2,故点P 的轨迹方程为y 2=-8x .22.(2022·全国·高二课时练习)已知点()1,0A ,直线:1l x =-,两个动圆均过A 且与l 相切,若圆心分别为1C 、2C ,则1C 的轨迹方程为___________;若动点M 满足22122C M C C C A =+,则M 的轨迹方程为___________.【答案】24y x =221y x =-【解析】由抛物线的定义得动圆的圆心轨迹是以()1,0A 为焦点,直线l :1x =-为准线的抛物线,所以1C 的轨迹方程为24y x =,设()1,C a b ,()2,C m n ,(),M x y ,因为动点M 满足22122C M C C C A =+,所以()()()2,,1,x m y n a m b n m n --=--+--,即21x a =+,2y b =,所以21a x =-,2b y =,因为24b a =,所以()()22421y x =-,所以221y x =-,即M 的轨迹方程为221y x =-.故答案为:24y x =;221y x =-.考点三:与抛物线有关的距离和最值问题23.(2022·全国·高二课时练习)已知点()2,0P ,点Q 在曲线2:2C y x =上.(1)若点Q 在第一象限内,且2PQ =,求点Q 的坐标;(2)求PQ 的最小值.【解析】(1)设()(),0,0Q x y x y >>,则22y x =,由已知条件得2PQ ==,将22y x =代入上式,并变形得,220,x x -=解得x=0(舍去)或x =2.当x =2时,2y =±,只有x =2,y =2满足条件,所以()2,2Q ;(2)PQ ,其中22y x =,所以()()()22222224130PQ x x x x x x =-+=-+=-+≥,所以当x =1时,min PQ =24.(2022·全国·高二课时练习)若M 是抛物线22y x =上一动点,点103,3P ⎛⎫⎪⎝⎭,设d 是点M 到准线的距离,要使d MP +最小,求点M 的坐标.【解析】由题意,可知抛物线的焦点1(,0)2F ,由抛物线的定义有||||d MP MF MP PF +=+≥,所以d MP +最小值为||PF ,此时点M 为直线PF 与抛物线的交点,而直线PF 的方程求得为:4233y x =-,所以有242332y x y x ⎧=-⎪⎨⎪=⎩,解得4143x y =⎧⎪⎨=⎪⎩或1413x y ⎧=⎪⎪⎨⎪=-⎪⎩(舍),所以14(4,)3M 25.(2022·全国·高二课时练习)已知抛物线22y x =的焦点是F ,点P 是抛物线上的动点,若()3,2A ,则PA PF +的最小值为______,此时点P 的坐标为______.【答案】72【解析】易知点A 在抛物线内部,设抛物线的准线为l ,则l 的方程为12x =-,过点P 作PQ l ⊥于点Q ,则PA PF PA PQ +=+,当PA l ⊥,即A ,P ,Q 三点共线时,PA PF +最小,最小值为17322+=,此时点P 的纵坐标为2,代入22y x =,得2x =,所以此时点P 的坐标为()2,2.故答案为:72;()2,2.26.(2022·全国·高二课时练习)设P 是抛物线24y x =上的一个动点,点F 是焦点.(1)求点P 到点()1,1A -的距离与点P 到直线1x =-的距离之和的最小值;(2)若()3,2B ,求PB PF +的最小值.【解析】(1)抛物线24y x =的焦点为()1,0F ,准线是1x =-.由抛物线的定义,知点P 到直线1x =-的距离等于点P 到焦点F 的距离,所以问题转化为求抛物线上一点P 到点()1,1A -的距离与其到点()1,0F 的距离之和的最小值,如图,当A ,P ,F 共线时上述距离之和最小,连接AF 交抛物线于点P ,此时所求的最小值为||AF =(2)由题意()3,2B ,可知2243<⨯,故点B 在抛物线内部(焦点所在一侧),如图,作BQ 垂直准线于点Q ,交抛物线于点1P ,连接1PF ,此时11PQ PF =,当点P 与点1P 重合时,PB PF +的值最小,此时3(1)4PB PF BQ +==--=,即PB PF +的最小值为4.27.(多选题)(2022·全国·高二单元测试)已知F 是抛物线24y x =的焦点,P 是抛物线24y x =上一动点,Q 是()()22:411C x y -+-=上一动点,则下列说法正确的有()A .PF 的最小值为1B .QFC .PF PQ +的最小值为4D .PF PQ +1+【答案】AC【解析】抛物线焦点为()1,0F ,准线为1x =-,作出图象,对选项A :由抛物线的性质可知:PF 的最小值为1OF =,选项A 正确;对选项B :注意到F 是定点,由圆的性质可知:QF 的最小值为1CF r -=,选项B 错误;对选项CD :过点P 作抛物线准线的垂线,垂足为M ,由抛物线定义可知PF PM =,故PF PQ PM PQ +=+,PM PQ +的最小值为点Q 到准线1x =-的距离,故最小值为4,从而选项C 正确,选项D 错误.故选:AC.28.(2022·河南·襄城县实验高级中学高二阶段练习(文))已知P 为抛物线()2:20C y px p =>上的动点,C 的准线l 与x 轴的交点为A ,当点P 的横坐标为1时,2PF =,则PF PA的取值范围是()A .⎤⎥⎣⎦B .⎤⎥⎣⎦C .⎣⎦D .22⎡⎢⎣⎦【答案】B【解析】因为抛物线C 的方程为()22 0y px p =>,所以其准线方程为2p x =-.因为当点P 的横坐标为1时,2PF =,所以122p+=,所以 2p =,故拋物线C 的方程为24y x =.设直线PA 的倾斜角为θ,PP l '⊥垂足为P ',()1,0A -,由抛物线的性质可得PP PF '=,所以cos PF PP PAPAθ'==,所以当直线PA 与抛物线C 相切时,cos θ最小.设直线PA 的方程为1x my =-,联立方程组214x my y x=-⎧⎨=⎩,得2440y my -+=,由216160m ∆=-=,得1m =±,2tan 1,cos 2θθ==,所以cos 12θ≤≤,故PF PA ⎤∈⎥⎣⎦.故选:B29.(2022·四川·阆中中学高二阶段练习(理))已知抛物线21:8C y x =的焦点为F ,P 为C 上的动点,直线PF 与C 的另一交点为Q ,P 关于点(4,12)N 的对称点为M .当PQ QM +的值最小时,直线PQ 的方程为________.【答案】20x y -+=【解析】设A 为PQ 的中点,连接NA ,设抛物线C 的准线为l ,作QD l ⊥,AG l ⊥,PE l ⊥,垂足分别为D ,G ,E .则2MQ NA =,2PQ PF QF PE QD AG =+=+=,()2PQ QM AG NA ∴+=+,又点N 到直线l 的距离为13,13AG NA ∴+≥,当G ,N ,A 三点共线且A 在G ,N 之间时,13AN AG NG +==,此时,点A 的横坐标为4A x =.PQ ∵过点()0,2F ,故设PQ 方程为2y kx =+,代入218y x =,得28160x kx --=()11,P x y ,()22,Q x y ,则128x x k +=.当G ,N ,A 三点共线时,12288A x x x k +===,解得1k =,直线AM 的方程为2y x =+,此时()4,6A 点A 在G ,N 之间,13AN AG NG +==成立.所以当PQ QM +的值最小时,直线PQ 的方程为20x y -+=故答案为:20x y -+=30.(2022·天津一中高二期中)已知抛物线C :22y px =的准线为1x =-,若M 为C 上的一个动点,设点N 的坐标为()3,0,则MN 的最小值为___________.【答案】【解析】由题意知,2p =,∴抛物线C :24y x =.设()()000,0M x y x ≥,由题意知2004y x =,则()()()2222200000334188x y x x MN x =-+=-+=-+≥,当01x =时,2MN 取得最小值8,∴MN 的最小值为.故答案为:31.(2022·河南·濮阳一高高二期中(文))抛物线y 2=4x 的焦点为F ,点A (2,1),M 为抛物线上一点,且M 不在直线AF 上,则△MAF 周长的最小值为____.【答案】3【解析】如图所示,过M 作MN 垂直于抛物线的准线l ,垂足为N .易知F (1,0),因为△MAF 的周长为|AF |+|MF |+|AM |,|AF ||MF |+|AM |=|AM |+|MN |,所以当A 、M 、N 三点共线时,△MAF 的周长最小,最小值为2+13=.故答案为:332.(2022·上海市长征中学高二期中)抛物线2y x =,其上一点P 到A (3,-1)与到焦点距离之和为最小,则P 点坐标为________【答案】(1,1)-【解析】因为点(3,1)A -在抛物线内部,如图所示,设抛物线的准线为l ,过抛物线上一点P ,作PQ l ⊥于Q ,过A 作AB l ⊥于B .||||||||||PA PF PA PQ AB +=+≥,故当且仅当,,P A B 共线时,||||PA PF +的值最小.此时点P 坐标为0(,1)P x -,代入2y x =,得01x =.故点P 的坐标为(1,1)-.故答案为:(1,1)-33.(2022·河南·高二期中(文))如图所示,已知P 为抛物线()2:20C y px p =>上的一个动点,点()1,1Q ,F 为抛物线C 的焦点,若PF PQ +的最小值为3,则抛物线C 的标准方程为______.【答案】28y x=【解析】过点P 、Q 分别作准线的垂线,垂直分别为M 、N ,由抛物线定义可知PF PQ PM PQ NQ +=+≥,当P ,M ,Q 三点共线时等号成立所以132pNQ =+=,解得4p =所以抛物线C 的标准方程为28y x =.故答案为:28y x=34.(2022·上海·华东师范大学附属东昌中学高二期中)已知点()6,0A ,点P 在抛物线216y x=上运动,点B 在曲线()2241x y -+=上运动,则2PAPB的最小值是___________.【答案】6【解析】抛物线216y x =的焦点为(4,0)F ,设P 点坐标(,)x y ,则||4PF x =+22222||(6)(6)16436PA x y x x x x =-+=-+=++,由题意当||||15PB PF x =+=+时,225436P P x B x Ax +=++,令5x t +=,则5x t =-,222(5)4(5)36466141PAt t t PB t t t tt -++=+=+--=-,由基本不等式知41t t+≥t =时等号成立故2PA PB的最小值为6.故答案为:635.(多选题)(2022·福建泉州·高二期中)在平面直角坐标系xOy 中,(3,2)M -,F 为抛物线2:2(0)C x py p =->的焦点,点P 在C 上,PA x ⊥轴于A ,则()A .当2p =时,||||PF PM +的最小值为3B .当4p =时,||||PF PM +的最小值为4C .当4p =时,||||PA PM -的最大值为1D .当PF x ∥轴时,cos OPF ∠为定值【答案】BCD【解析】对于A :2p =时抛物线2:4C x y =-,焦点()0,1F -,点(3,2)M -在抛物线外,所以||||PF PM FM +≥当且仅当M 、P 、F 三点共线且P 在MF 之间时取等号(如下图所示),故A 错误;对于B 、C :当4p =时抛物线2:8C x y =-,焦点()0,2F -,准线方程为2y =,点(3,2)M -在抛物线内,设PA 与准线交于点N ,则||||PF PN =,所以()||||||||224PF PM PN PM MN +=+≥=--=,当且仅当M 、P 、N 三点共线且P 在MN 之间时取等号(如下图所示),故B 正确;||||||2||||||2||21PA PM PN PM PF PM FM -=--=--≤-=,当且仅当M 、P 、F 三点共线且F 在MP 之间时取等号(如下图所示),故C 正确;对于D :抛物线2:2C x py =-,焦点0,2p F ⎛⎫- ⎪⎝⎭,准线方程为2p y =,当//PF x ,此时2P p y =-,则222p x p ⎛⎫=-⨯- ⎪⎝⎭,解得p x p =±,即,2p P p ⎛⎫-- ⎪⎝⎭或,2p P p ⎛⎫- ⎪⎝⎭,如图取,2p P p ⎛⎫-- ⎪⎝⎭,则PF p =,()2252p OP p ⎛⎫=-+- ⎪⎝⎭,所以25cos 552PFp OPF OPp ∠==D 正确;故选:BCD36.(2022·江西赣州·高二期中(理))已知抛物线216y x =的焦点为F ,P 点在抛物线上,Q 点在圆()()22:624C x y -+-=上,则PQ PF +的最小值为()A .4B .6C .8D .10【答案】C【解析】如图,过点P 向准线作垂线,垂足为A ,则PF PA =,当CP 垂直于抛物线的准线时,CP PA +最小,此时线段CP 与圆C 的交点为Q ,因为准线方程为4x =-,()6,2C ,半径为2,所以PQ PF +的最小值为21028AQ CA =-=-=.故选:C37.(2022·新疆维吾尔自治区喀什第二中学高二期中(理))已知A ()4,2-,F 为抛物线28y x =的焦点,点M 在抛物线上移动,当MA MF +取最小值时,点M 的坐标为()A .()0,0B .(1,-C .()2,2-D .1,22⎛⎫- ⎪⎝⎭【答案】D【解析】如图所示,过M 点作准线l 的垂线,垂足为E ,由抛物线定义,知MF .ME =当M 在抛物线上移动时,ME MA +的值在变化,显然M 移动到M '时,,,A M E 三点共线,ME MA +最小,此时//AM Ox ',把2y =-代入28y x =,得12x =,所以当MA MF +取最小值时,点M 的坐标为1,22⎛⎫- ⎪⎝⎭.故选:D.38.(2022·黑龙江·哈师大附中高二期中(文))若点P 为抛物线2:2C y x =上的动点,F 为抛物线C 的焦点,则PF 的最小值为()A .1B .12C .14D .18【答案】D【解析】由22y x =,得212x y =,∴122p =,则128p =,所以焦点10,8F ⎛⎫⎪⎝⎭,由抛物线上所有点中,顶点到焦点的距离最小,得PF 的最小值为18.故选:D .39.(2022·黑龙江·大兴安岭实验中学高二期中)已知抛物线28y x =,定点A (4,2),F 为焦点,P 为抛物线上的动点,则PF PA +的最小值为()A .5B .6C .7D .8【答案】B【解析】如图,作,PQ AN 与准线2x =-垂直,垂足分别为,Q N ,则PQ PF =,6PF PA PQ PA AN +=+≥=,当且仅当,,Q P A 三点共线即P 到M 重合时等号成立.故选:B .40.(2022·四川省资阳中学高二开学考试(理))已知点P 是抛物线2:8C y x =上的动点,过点P 作圆()22:21M x y -+=的切线,切点为Q ,则PQ 的最小值为()A .1B 2C 3D .32【答案】C【解析】设点P 的坐标为(),m n ,有28n m =,由圆M 的圆心坐标为()2,0,是抛物线C 的焦点坐标,有22PM m =+≥,由圆的几何性质可得PQ QM ⊥,又由22221213PM P P M Q QM=-=-≥-=PQ 3故选:C.41.(2022·全国·高二期中)已知抛物线的方程为24y x =,焦点为F ,点A 的坐标为()3,4,若点P 在此抛物线上移动,记P 到其准线的距离为d ,则d PA +的最小值为______,此时P 的坐标为______.【答案】5355+⎝【解析】过点P 作抛物线准线的垂线,垂足为H ,连接PF ,作图如下:根据抛物线的定义,d PH PF ==,数形结合可知,当且仅当,,A P F 三点共线,且P 在,A F 之间时取得最小值;即d PA +的最小值为AF ,又()()3,4,1,0A F ,故()2231425AF =-+=此时直线AF 的方程为:()21y x =-,联立抛物线方程24y x =,可得:2310x x -+=,解得35x -=35x +=15y =即此时点P 的坐标为355+⎝.故答案为:253552⎛ ⎝.考点四:抛物线中三角形,四边形的面积问题42.(2022·河南洛阳·高二期末(理))已知点()1,0A ,点B 为直线1x =-上的动点,过B 作直线1x =-的垂线1l ,线段AB 的中垂线与1l 交于点P .(1)求点P 的轨迹C 的方程;(2)若过点()2,0E 的直线l 与曲线C 交于M ,N 两点,求MOE △与NAE 面积之和的最小值.(O 为坐标原点)【解析】(1)如图所示,由已知得点P 为线段AB 中垂线上一点,即PA PB =,即动点P 到点()1,0A 的距离与点P 到直线1x =-的距离相等,所以点P 的轨迹为抛物线,其焦点为()1,0A ,准线为直线1x =-,所以点P 的轨迹方程为24y x =,(2)如图所示:设2x ty =+,点()11,M x y ,()11N x y ,,联立直线与抛物线方程242y x x ty ⎧=⎨=+⎩,得2480y ty --=,()()2244816320t t ∆=--⨯-=+>,124y y t +=,128y y ⋅=-,1112MOE S OE y y =×=V ,21122NAE N S AE y y =×=V ,所以1212112422MOE ANE S S y y y y +=+³=V V ,当且仅当1212y y =,即12y =,24y =-时取等号,此时1224y y t +=-=,即12t =-,所以当直线直线1:22l x y =-+,时MOE ANE S S +V V 取得最小值为4.43.(2022·陕西西安·高二期末(文))已知抛物线C :()220y px p =>上的点()()4,0A m m >到其准线的距离为5.(1)求抛物线C 的方程;(2)已知O 为原点,点B 在抛物线C 上,若AOB 的面积为6,求点B 的坐标.【解析】(1)由抛物线C 的方程可得其准线方程2p x =-,依抛物线的性质得452p+=,解得2p =.∴抛物线C 的方程为24y x =.(2)将()4,A m 代入24y x =,得4m =.所以()4,4A ,直线OA 的方程为y x =,即0x y -=.设()2,2B t t ,则点B 到直线OA 的距离222t t d -=,又42OA =由题意得22142622t t -⨯=,解得1t =-或3t =.∴点B 的坐标是()1,2-或()9,6.44.(2022·新疆石河子一中高二阶段练习(理))已知抛物线()2:20C y px p =>的焦点为F ,点M 为C 上一点,点N 为x 轴上一点,若FMN 是边长为2的正三角形,则抛物线的方程为___________.【答案】22y x =或26y x=【解析】抛物线()2:20C y px p =>的焦点为,02p F ⎛⎫ ⎪⎝⎭,由抛物线的对称性,不妨设点M 为第一象限的点,因为点M 为C 上一点,点N 为x 轴上一点,FMN 是边长为2的正三角形,所以当N 在,02p F ⎛⎫ ⎪⎝⎭的右边时,点M 的坐标为2p M ⎛+ ⎝,所以2212p p ⎛⎫=+ ⎪⎝⎭,化简得2230p p +-=,解得1p =或3p =-(舍去),所以抛物线的方程为22y x =,当N 在,02p F ⎛⎫ ⎪⎝⎭的左边时,点M 的坐标为2p M ⎛- ⎝,所以2212p p ⎛⎫=- ⎪⎝⎭,化简得2230p p --=,解得1p =-或3p =,所以抛物线的方程为26y x =,综上,所求的抛物线方程为22y x =或26y x =故答案为:22y x =或26y x=45.(2022·全国·高二单元测试)抛物线()220y px p =>的焦点为F ,过抛物线上一点P 作x轴的平行线交y 轴于M 点,抛物线的准线交x 轴于点N ,四边形PMNF 为平行四边形,则点P 到x 轴的距离为___________.(用含P 的代数式表示)【解析】由題意可知,,02p F ⎛⎫⎪⎝⎭,准线方程为2p x =-,,02p N ⎛⎫- ⎪⎝⎭,不妨设(P x ,四边形PMNF 为平行四边形,||||,PM NF ∴=∴,x p =∴点P 到x .46.(2022·陕西咸阳·高二期末(理))已知双曲线2222:1(0,0)x y C a b a b -=>>的离心率54e =,且双曲线C 的两条渐近线与抛物线22(0)y px p =>的准线围成的三角形的面积为3,则p 的值为()A .1B .2C .22D .4【答案】D【解析】根据题意,2514c b e a a ⎛⎫==+= ⎪⎝⎭,可得2916b a ⎛⎫= ⎪⎝⎭,所以双曲线的渐近线方程为34y x =±,抛物线的准线方程为2p x =-,设准线与抛物线的交点分别为M ,N ,则,23,4p x y x ⎧=-⎪⎪⎨⎪=-⎪⎩,可解得3,28p p M ⎛⎫- ⎪⎝⎭,同理3,28p p N ⎛⎫-- ⎪⎝⎭,所以2133322416OMNp p Sp =⨯-⨯==,解得4p =.故选:D .47.(2022·四川师范大学附属中学高二阶段练习(理))已知双曲线22221(0,0)x y a b a b-=>>的两条渐近线与抛物线22(0)y px p =>的准线分别交于点A 、B ,O 为坐标原点,若双曲线的离心率为2,三角形AOB 3p =()A .1B .32C .2D .3【答案】C【解析】由双曲线的离心率为2知,3ba=3y x =,又抛物线的准线方程为2p x =-,则设渐近线与准线的交点为3(,22p A --,3(,)22p B -,三角形AOB 的面积为133(322p p p⨯⨯=(0p >)解得2p =,故选:C48.(2022·湖北咸宁·高二期末)已知O 是坐标原点,F 是抛物线C :()220y px p =>的焦点,()0,4P x 是C 上一点,且4=PF ,则POF 的面积为()A .8B .6C .4D .2【答案】C【解析】由题可知0042162p x px ⎧+=⎪⎨⎪=⎩,解得024x p =⎧⎨=⎩,所以POF 的面积为12442⨯⨯=,故选:C49.(2022·黑龙江·哈师大附中高二开学考试)已知点()0,1F ,点()(),0A x y y ≥为曲线C 上的动点,过A 作x 轴的垂线,垂足为B ,满足1AF AB +=.(1)曲线C 的方程(2)若,G H 为曲线C 上异于原点的两点,且满足0FG FH ⋅=,延长,GF HF 分别交曲线C 于点,M N ,求四边形GHMN 面积的最小值.【解析】(1)1AF AB +=,∴点A 到直线1y =-的距离等于其到点()0,1F 的距离,∴点A 轨迹是以F 为焦点的抛物线,∴曲线C 方程为:24x y =.(2)由题意知:直线,GM HN 斜率都存在,不妨设直线:1GM y kx =+,()11,G x y ,()22,M x y ,由214y kx x y =+⎧⎨=⎩得:2440x kx --=,则121244x x k x x +=⎧⎨=-⎩,()241GM k ∴==+;设直线1:1HN y x k =-+,同理可得:2141HN k ⎛⎫=+ ⎪⎝⎭,∴四边形GHMN 面积()2222111811822S GM HN k k k k ⎛⎫⎛⎫=⋅=++=++ ⎪ ⎪⎝⎭⎝⎭,又2212k k +≥(当且仅当221k k =,即1k =±时取等号),()82232S ∴≥⨯+=,即四边形GHMN 面积的最小值为32.50.(2022·黑龙江·大庆实验中学高二期中(理))设点30,2F ⎛⎫⎪⎝⎭,动圆P 经过点F 且和直线32y =-相切,记动圆的圆心P 的轨迹为曲线w .(1)求曲线w 的方程;(2)过点F 作互相垂直的直线1l 、2l ,分别交曲线w 于A 、C 和B 、D 两个点,求四边形ABCD 面积的最小值.【解析】(1)由抛物线的定义知点P 的轨迹为以F 为焦点的抛物线,322p =,即3p =,∴2:6w x y =.(2)设3:2AC y kx =+,由223,069026y kx k x kx x y⎧=+≠⎪⇒--=⎨⎪=⎩.设()11,A x y ,()22,C x y ,236360k ∆=+>121269x x kx x +=⎧⎨=-⎩()261AC k ==+,∵1l 与2l 互相垂直,∴以1k -换k 得2161BD k ⎛⎫=+ ⎪⎝⎭,()22111616122ABCD S AC BD k k ⎛⎫==⨯+⨯+ ⎪⎝⎭()221182182272k k ⎛⎫=++⨯+= ⎪⎝⎭≥,当1k =±时取等号,∴四边形ABCD 面积的最小值为72.51.(2022·全国·高二期中)已知曲线C :y =22x ,D 为直线y =12-上的动点,过D 作C 的两条切线,切点分别为A ,B .(1)证明:直线AB 过定点:(2)若以E (0,52)为圆心的圆与直线AB 相切,且切点为线段AB 的中点,求四边形ADBE的面积.【解析】(1)证明:设1(,2D t -,11(,)A x y ,则21112y x =.又因为212y x =,所以y'x =.则切线DA 的斜率为1x ,故1111()2y x x t +=-,整理得112210tx y -+=.设22(,)B x y ,同理得222210tx y -+=.11(,)A x y ,22(,)B x y 都满足直线方程2210tx y -+=.于是直线2210tx y -+=过点,A B ,而两个不同的点确定一条直线,所以直线AB 方程为2210tx y -+=.即2(21)0tx y +-+=,当20,210x y =-+=时等式恒成立.所以直线AB 恒过定点1(0,)2.(2)由(1)得直线AB 的方程为12y tx =+.。
抛物线中由动点产生的特殊三角形的存在性问题

抛物线中由动点产生的特殊三角形的存在性问题解析二次函数的图像与三角形的结合是代数与平面几何生成的综合性问题的一种重要形式.其呈现方式多以抛物线为载体、探索满足某种条件的三角形的存在性.这类试题旨在全面考查学生分析问题、解决问题的能力和创新思维能力.由于其涉及的知识面广,内容丰富,综合性和灵活性以及解题技巧性都较强,因而对大多数考生来说常感到束手无策.解决这类问题的关键是,弄清函数与几何图形之间的关系,在解题过程中将函数问题几何化,几何问题数量化,数形统一.一般步骤是:先假设其存在,再画出相应的图形,然后根据所画的图形进行解答,得出某些结论;最后,如果结论符合题目要求或定义、定理,则假设成立;如果出现与题目要求或定义、定理相悖的情况,则假设错误,所设不存在.一.由抛物线上的动点产生的等腰三角形用代数方法探求等腰三角形问题一般分三步:按腰相等分三种情况,再根据两点间距离列方程,解之并检验.有些等腰三角形当角度特殊时,三种情况下的动点可能会重合在一起.例1.如图1,在平面直角坐标系中,直线y=﹣2x+10与x 轴,y 轴相交于A,B 两点,点C 的坐标是(8,4),连接AC,BC .(1)求过O,A,C 三点的抛物线的解析式,并判断△ABC的形状;(2)动点P 从点O 出发,沿OB 以每秒2个单位长度的速度向点B 运动;同时,动点Q 从点B 出发,沿BC 以每秒1个单位长度的速度向点C 运动.规定其中一个动点到达端点时,另一个动点也随之停止运动.设运动时间为t 秒,当t 为何值时,PA=QA ?(3)在抛物线的对称轴上,是否存在点M,使以A,B,M 为顶点的三角形是等腰三角形?若存在,求出点M 的坐标;若不存在,请说明理由.【分析】(1)先确定出点A,B 坐标,再用待定系数法求出抛物线解析式;用勾股定理逆定理判断出△ABC 是直角三角形;(2)根据运动表示出OP=2t,CQ=10﹣t,判断出Rt△AOP ≌Rt△ACQ ,得到OP=CQ 即可;(3)分三种情况用平面坐标系内,两点间的距离公式计算即可.【解答】(1)∵直线y=﹣2x+10与x 轴,y 轴分别交于A,B 两点,∴A(5,0),B(0,10).∵抛物线过原点, ∴设抛物线解析式为y=ax 2+bx,∵抛物线过点B(0,10),C(8,4),∴2550,6484a b a b +=⎧⎨+=⎩ ∴16,56a b ⎧=⎪⎪⎨⎪=-⎪⎩图1∴抛物线解析式为y=16x 2﹣56x, ∵A(5,0),B(0,10),C(8,4),∴AB 2=52+102=125,BC 2=82+(8﹣5)2=100,AC 2=42+(8﹣5)2=25, ∴AC 2+BC 2=AB 2, ∴△ABC 是直角三角形.(2)如图2,当P,Q 运动t 秒,即OP=2t,CQ=10﹣t 时,由(1)得,AC=OA,∠ACQ=∠AOP=90°,在Rt△AOP 和Rt△ACQ 中,,AC OA PA QA=⎧⎨=⎩ ∴Rt△AOP ≌Rt△ACQ , ∴OP=CQ, ∴2t=10﹣t, ∴t=103, ∴当运动时间为103时,PA=QA ; (3)存在,∵y=16x 2﹣56x, ∴抛物线的对称轴为x=52, ∵A(5,0),B(0,10), ∴AB=55 如图3,设点M(52,m), 按边相等分为三种情况: ①当BM=BA 时, ∴(52)2+(m ﹣10)2=125, ∴m 1=205192+,m 2=205192-, ∴M 1(52,205192+),M 2(52,205192-). ②当AM=AB 时, ∴(52)2+m 2=125, ∴m 3=5192, m 4=﹣5192, ∴M 3(52,5192),M 4(52,﹣5192). ③当MA=MB 时,∴(52﹣5)2+m 2=(52)2+(10﹣m)2, ∴m=5, ∴M 5(52,5),此时点M 恰为线段AB 的中点,构不成三角形,舍去. x OA 2M 1M C3M 4M B y 图3 图2∴综合上所述点M 的坐标为:M 1(52,205192+),M 2(52,205192-),M 3(52,5192),M 4(52,﹣5192) 【点评】本题作为压轴题,立意新颖,具有较强的综合性.试题主要考查一次函数、二次函数的性质,待定系数法求函数解析式,三角形全等的性质和判定,等腰三角形、直角三角形的性质.解本题第三问的关键是分情况讨论,这也是本题的难点.二.由抛物线上的动点产生的直角三角形对于直角三角形问题,若用代数方法探求,也需先按直角分三种情况,再根据两点间的距离列方程,然后解方程并检验.但下面例题中已指明斜边,故不需讨论.例2.如图4,在平面直角坐标系中,点O 为坐标原点,直线l 与抛物线y=mx 2+nx 相交于A(1,33),B(4,0)两点.(1)求出抛物线的解析式;(2)在坐标轴上是否存在点D,使得△ABD 是以线段AB 为斜边的直角三角形?若存在,求出点D 的坐标;若不存在,说明理由;(3)点P 是线段AB 上一动点,(点P 不与点A 、B重合),过点P 作PM ∥OA,交第一象限内的抛物线于点M,过点M 作MC ⊥x 轴于点C,交AB 于点N,若△BCN 、△PMN 的面积S △BC N 、S △P MN 满足S △B C N =2S △PMN ,求出MN NC的值,并求出此时点M 的坐标. 【分析】(1)由A 、B 两点的坐标,利用待定系数法可求得抛物线解析式;(2)分D 在x 轴上和y 轴上,分别向不同的坐标轴坐垂线段.用点D 的坐标表示出AD 、BD ,列出关于d 的方程,即可求得D 点的坐标;(3)过P 作PF ⊥CM 于点F,利用Rt △ADO ∽Rt △MFP 以及三角函数,可用PF 分别表示出MF 和NF,从而可表示出MN,设BC=a,则可用a 表示出CN,再利用S △BC N =2S △PMN ,可用PF 表示出a 的值,从而可用PF 表示出CN,可求得MN NC的值;借助a 可表示出M 点的坐标,代入抛物线解析式可求得a 的值,从而可求出M 点的坐标.【解答】(1)∵A(1,33),B(4,0)在抛物线y=mx 2+nx 的图象上,∴33,1640m n m n ⎧+=⎪⎨+=⎪⎩ 解得3,43m n ⎧=-⎪⎨=⎪⎩ ∴抛物线解析式为y=﹣3x 2+43x ;图4(2)存在三个点满足题意,理由如下:①当点D 在x 轴上时,如图4,过点A 作AD ⊥x 轴于点D,∵A(1,33), ∴D 坐标为(1,0);②当点D 在y 轴上时(图略),设D(0,d),则AD 2=1+(33﹣d)2,BD 2=42+d 2,且AB 2=(4﹣1)2+(33)2=36,∵△ABD 是以AB 为斜边的直角三角形,∴AD 2+BD 2=AB 2, 即1+(33﹣d)2+42+d 2=36,解得d=33112±, ∴D 点坐标为(0, 33112+)或(0, 33112-); 综上可知存在满足条件的D 点,其坐标为(1,0)或(0,33112+) 或(0,33112-); (3)如图5,过P 作PF ⊥CM 于点F,∵PM ∥OA, ∴Rt △ADO ∽Rt △MFP,∴MF AD PF OA==33, ∴MF=33PF, 在Rt △ABD 中,BD=3,AD=33,∴tan ∠ABD=3,∴∠ABD=60°,设BC=a,则CN=3a,在Rt △PFN 中,∠PNF=∠BNC=30°,∴tan ∠PNF=33PF FN =, ∴FN=3PF, ∴MN=MF+FN=43PF,∵S △BC N =2S △P MN , ∴32a 2=2××43PF 2, 图5∴a=22PF,∴NC=3a=26PF,∴4326MN PF NC PF==2, ∴MN=2NC=2×3a=6a, ∴MC=MN+NC=(6+3)a, ∴M 点坐标为(4﹣a,(6+3)a),又M 点在抛物线上,代入可得﹣3(4﹣a)2+43(4﹣a)=(6+3)a, 解得a=3﹣2或a=0(舍去), OC=4﹣a=2+1,MC=26+3, ∴点M 的坐标为(2+1, 26+3).【点评】本题是二次函数综合题,主要考查待定系数法求函数解析式,相似三角形、全等三角形以及直角三角形的性质.本题已指明了直角三角形的斜边是线段AB,不需要讨论;但需按点D 的位置分类讨论,这是解本题(2)的关键,也是本题之难点所在.三.由抛物线上的动点产生的等腰直角三角形此类问题可仿问题一、二的方法讨论.例3.如图6,已知点A 的坐标为(﹣2,0),直线y=﹣x+3与x 轴、y 轴分别交于点B 和点C,连接AC,顶点为D 的抛物线y=ax 2+bx+c 过A 、B 、C 三点.(1)请直接写出B 、C 两点的坐标,抛物线的解析式及顶点D 的坐标;(2),设抛物线的对称轴DE 交线段BC 于点E,P 是第一象限内抛物线上一点,过点P 作x 轴的垂线,交线段BC 于点F,若四边形DEFP 为平行四边形,求点P 的坐标;(3)设点M 是线段BC 上的一动点,过点M 作MN ∥AB,交AC 于点N,点Q 从点B 出发,以每秒1个单位长度的速度沿线段BA 向点A 运动,运动时间为t(秒),当t(秒)为何值时,存在△QMN 为等腰直角三角形?【分析】(1)由 y=﹣34x+3易得B 和C 的坐标,然后设抛物线的交点式为y=a(x+2)(x ﹣4),把C 的坐标代入抛物线解析式即可求出a 的值和顶点D 的坐标;(2)若四边形DEFP 为平行四边形,则DP ∥BC,设直线DP 的解析式为y=mx+n,则m=﹣34,求出直线DP 的解析式后,联立抛物线解析式和直线DP 的解析式即可求出P 的坐标;(3)由题意可知,0≤t≤6,若△QMN 为等腰直角三角形,则共有三种情况,①∠NMQ=90°;②∠MNQ=90°;③∠NQM=90°.【解答】(1)B(4,O),C(0,3).抛物线的解析式为233 3.84y x x =++顶点D 的坐标为)827,1( .(2)如图6,把x=1代入,49343=+-=y x y 得, 9(1,),4E ∴,8949827=-=∴DE 因点P 为第一象限内抛物线上一点,所以可设点P 坐标为),34383,(2++-x x m 点F 的坐标为(m,-43m+3). 若四边形DEFP 为平行四边形,则PF=DE. 即-83m 2+43m+3-(-43m+3)=89. 解之,得m 1=3,m 2=1(不合题意,舍去).∴当点P 坐标为(3,815)时,四边形DEFP 为平行四边形. (3)设点M 的坐标为(m,-343+m ),MN 交y 轴于点G . ,//AB MN ∴∆MNC ∽∆BAC, COCG AB MN =∴ ①如图图7-①,当∠QMN=90°,MN=MQ=OG 时,,336MN MN -=解之,MN=2. ,2343=+-∴m 解之,⋅=)2,34(,34M m ⋅=-=∴38344),0.34(t Q 即 ②如图7-②,当∠QNM=90°,MN=NQ=OG 时∵,336MN MN -=解之,MN=2. ,2343=+-∴m 解之,⋅=)2,34(,34M m ∴GM=43,NG=23, ⋅-)0,32(Q ⋅=--=∴314)32(4t ③如图7-③当∠MQN=90°,QM=QN 时,OG= QK= 21NM, ,32136MN MN -=∴解之,得MN=3.⋅=∴23OG ,23343=+-∴x 解之,得x=2,即).23.1(),23,2(-N M MN 的中点K 的坐标为⋅⋅)2321().0,21(Q ∴即.27214=-=t ∴当t 为38或314或27时,存在△QMN 为等腰直角三角形. 图7-① G 图7-② G 图7-③ K G【点评】本题考查待定系数法求函数的解析式,及一次函数中k 值和点的坐标的求法,抛物线的对称性,相似三角形、等腰直角三角形等知识. 是一道综合性较强的试题.要会利用数形结合的思想把代数和几何图形结合起来,利用点的坐标的意义表示线段的长度,从而求出线段之间的关系.由于本题未指明三角形的直角,故需按直角分类讨论.例4.如图8,抛物线y=﹣53[(x﹣2)2+n]与x轴交于点A(m﹣2,0)和B(2m+3,0)(点A在点B的左侧),与y轴交于点C,连结BC.(1)求m、n的值;(2)如图9,点N为抛物线上的一动点,且位于直线BC上方,连接CN、BN.求△NBC面积的最大值;(3)如图10,点M、P分别为线段BC和线段OB上的动点,连接PM、PC,是否存在这样的点P,使△PCM为等腰三角形,△PMB为直角三角形同时成立?若存在,求出点P的坐标;若不存在,请说明理由.【分析】(1)易知抛物线的对称轴为直线x=2,由对称性得2﹣(m﹣2)=2m+3﹣2,解得m的值,即得A(﹣1,0),B(5,0),然后把A点坐标代入y=﹣35 [(x﹣2)2+n]可求n的值;(2)作ND∥y轴交BC于D,如图9,由抛物线解析式确定C(0,3),再利用待定系数法求出BC的解析式为y=﹣35x+3,设N(x,﹣35x2+125x+3),则D(x,﹣35x+3),根据三角形面积公式,利用S△NBC=S△NDC+S△NDB可得S△BCN=﹣32x2+152x,然后利用二次函数的性质求解;(3)先由勾股定理求出BC=34,再分类讨论:当∠PMB=90°,则∠PMC=90°,△PMC为等腰直角三角形,MP=MC,设PM=t,则CM=t,MB=34﹣t,证明△BMP∽△BOC,利用相似比可求出BP的长,再计算OP后可得到P点坐标;当∠MPB=90°,则MP=MC,设PM=t,则CM=t,MB=34﹣t,证明△BMP∽△BCO,利用相似比求出BP的长,再计算OP后可得P点坐标.【解答】解:(1)∵抛物线的解析式为y=﹣35[(x﹣2)2+n]=﹣35(x﹣2)2﹣35n,∴抛物线的对称轴为直线x=2,∵点A和点B为对称点, ∴2﹣(m﹣2)=2m+3﹣2,解得m=1, ∴A(﹣1,0),B(5,0),把A(﹣1,0)代入y=﹣35[(x﹣2)2+n]得9+n=0,解得n=﹣9;图8(2)作ND ∥y 轴交BC 于D,如图9,抛物线解析式为y=﹣35[(x ﹣2)2﹣9]=﹣35x 2+125x+3, 当x=0时,y=3,则C(0,3),设直线BC 的解析式为y=kx+b,把B(5,0),C(0,3)代入得 50,3k b b +=⎧⎨=⎩ 解得3,53k b ⎧=-⎪⎨⎪=⎩ ∴直线BC 的解析式为y=﹣35x+3, 设N(x,﹣35x 2+125x+3),则D(x,﹣35x+3), ∴ND=﹣35x 2+125x+3﹣(﹣35x+3)=﹣35x 2+3x, ∴S △NBC =S △NDC +S △NDB =12•5•ND=﹣32x 2+152x=﹣(x ﹣52)2+758, 当x=52时,△NBC 面积最大,最大值为758; (3)存在.∵B(5,0),C(0,3),∴BC=223534,+=①如图10,当∠PMB=90°时,亦有∠PMC=90°,而MP=M,故△PMC 为等腰三角形,∴△PMC 为等腰直角三角形,MP=MC,设PM=t,则CM=t,MB=34﹣t,∵∠MBP=∠OBC, ∴△BMP ∽△BOC ,∴,PM BM BP OC OB BC == 即 34,3534t t BP -== 解得 334,8t =17,4BP = ∴OP=OB ﹣BP=5﹣174=34, 此时P 点坐标为(34,0); ②如图11,当∠MPB=90°时,则MP=MC,设PM=t,则CM=t,MB=34﹣t,∵∠MBP=∠CBO, ∴△BMP ∽△BCO ,∴ ,MP BM BP OC BC BO == 即34,3534t t BP -== 图10 M 图11M解得10225t -= 345BP -=∴OP=OB ﹣BP=5 , 此时P 点坐标为,0). 综上所述,P 点坐标为(34,0)或 (34,0). 评析:本题中虽然有“△PCM 为等腰三角形”, 但结合”△PCM 为等腰三角形,△PMB 为直角三角形同时成立”进行分析, 故不需对“等腰”分类,只需对“直角”讨论,解题过程迅速得以简化.通过对以上例题的分析与解答,我们对这类问题有了新的认识与了解,对解决抛物线中的等腰三角形及直角三角形问题寻求到了有效的解题途径,为今后九年级师生解决同类问题起到了抛砖引玉的作用.。
抛物线与三角形知识点

抛物线与三角形知识点引言在数学中,抛物线和三角形是两个重要的几何概念。
抛物线是一种特殊的曲线,具有许多有趣的特性和应用。
三角形则是由三条线段组成的多边形,是几何学中最基本的形状之一。
本文将以“抛物线与三角形知识点”为主题,分步骤介绍这两个概念。
抛物线抛物线是由平面上到定点的距离与到定直线的距离相等的点的轨迹。
它有一个对称轴和一个焦点。
下面是抛物线的一些重要概念和性质: 1. 焦点和直线:抛物线上的每个点到焦点的距离等于该点到直线的距离。
这是抛物线定义的基本特性。
2. 对称轴:抛物线的对称轴是通过焦点和垂直于直线的一条直线。
抛物线上的任意两个点关于对称轴对称。
3. 标准方程:抛物线的标准方程是y = ax^2 + bx + c,其中a、b、c是常数。
通过调整这些常数的值,可以改变抛物线的形状和位置。
4.抛物线的焦距:焦距是焦点到对称轴的距离。
焦距与抛物线的形状相关,可以用来描述抛物线的“胖瘦”程度。
三角形三角形是由三条线段组成的多边形。
它有三个顶点、三条边和三个内角。
下面是三角形的一些重要概念和性质: 1. 内角和:三角形的三个内角之和是180度。
这是三角形的基本性质。
2. 三边关系:三角形的三边之间有一些特殊的关系。
例如,三边关系定理中的余弦定理和正弦定理可以用来计算三角形的边长和角度。
3. 直角三角形:一个角为90度的三角形被称为直角三角形。
直角三角形有一些特殊的性质,例如勾股定理,它描述了直角三角形的边长之间的关系。
4. 等边三角形:三个边长相等的三角形被称为等边三角形。
等边三角形的三个内角均为60度。
抛物线与三角形的关系抛物线与三角形之间存在一些有趣的关系。
以下是其中两个重要的关系: 1. 贝塞尔曲线:贝塞尔曲线是由一组控制点和插值点定义的曲线,其中控制点位于抛物线上。
贝塞尔曲线在计算机图形学和设计等领域有广泛的应用。
2. 斜抛运动:当我们以一定的初速度和角度将物体抛出时,它的运动轨迹将是一个抛物线。
抛物线与直角三角形

抛物线与直角三角形关键信息项:1、抛物线的方程及相关参数2、直角三角形的边长和角度3、抛物线与直角三角形的位置关系4、相关计算方法和公式5、约束条件和假设6、协议的有效范围和适用场景1、引言11 本协议旨在探讨抛物线与直角三角形之间的关系,以及在特定条件下的相关分析和计算方法。
2、抛物线的定义与性质21 抛物线的标准方程为 y = ax²+ bx + c,其中 a、b、c 为常数,且a ≠ 0。
22 抛物线的对称轴为 x = b /(2a) 。
23 抛物线的顶点坐标为(b /(2a),(4ac b²) /(4a))。
3、直角三角形的定义与性质31 直角三角形的两条直角边的平方和等于斜边的平方。
32 直角三角形的内角和为 180°,其中一个角为 90°。
33 直角三角形的面积为两条直角边乘积的一半。
4、抛物线与直角三角形的位置关系41 直角三角形的一个顶点在抛物线上。
42 直角三角形的一条边与抛物线相切。
43 直角三角形的三条边所在直线与抛物线相交。
5、相关计算方法和公式51 当直角三角形的一个顶点在抛物线上时,可将该顶点的坐标代入抛物线方程,求解相关参数。
52 若直角三角形的一条边与抛物线相切,可通过求导得出切线的斜率,进而计算相关边长和角度。
53 当三条边所在直线与抛物线相交时,联立方程求解交点坐标,从而计算三角形的边长和面积。
6、约束条件和假设61 假设所讨论的抛物线和直角三角形均在同一平面内。
62 边长和角度的计算基于欧几里得几何原理。
63 忽略其他可能的干扰因素,如摩擦力、空气阻力等。
7、协议的有效范围和适用场景71 本协议适用于数学研究、教学以及相关工程计算中涉及抛物线与直角三角形关系的问题。
72 对于复杂的实际问题,需在本协议的基础上结合具体情况进行进一步的分析和处理。
8、结论81 本协议为研究抛物线与直角三角形之间的关系提供了基本的框架和方法。
抛物线中的直角三角形

中考压轴题分类专题四——抛物线中的直角三角形基本题型:已知AB ,抛物线()02≠++=a c bx ax y ,点P 在抛物线上(或坐标轴上,或抛物线的对称轴上),AB 为直角边时,分两类讨论: ①以A ∠为直角时(即AP AB ⊥): ②以B ∠为直角时(即BP BA ⊥):例3、在平面直角坐标系中,现将一块等腰直角三角板ABC 放在第二象限,斜靠在两坐标轴上,且点A (0,2),点C (-1,0),如图所示,抛物线22y ax ax =+-经过点B 。
(1)求点B 的坐标; (2)求抛物线的解析式; (3)在抛物线上是否还存在点P (点B 除外),使△ACP 仍然是以AC 为直角边的等腰直角三角形?若存在,求所有点P 的坐标;若不存在,请说明理由。
同步训练:1、如图所示,在平面直角坐标系中.二次函数()221y a x =--图象的顶点为P ,与x 轴交点为 A 、B ,与y 轴交点为C .连结BP 并延长交y 轴于点D 。
(1)写出点P 的坐标;(2)连结AP ,如果△APB 为等腰直角三角形,求a 的值及点C 、D 的坐标;(3)在(2)的条件下,连结BC 、AC 、AD ,点E (0,b )在线段CD (端点C 、D 除外)上,将△BCD 绕点E 逆时针方向旋转90°,得到一个新三角形.设该三角形与△ACD 重叠部分的面积为S ,根据不同情况,分别用含b 的代数式表示S .选择其中一种情况给出解答过程,其它情况直接写出结果;判断当b 为何值时,重叠部分的面积最大?写出最大值.2(福建2009年宁德市)、如图,已知抛物线C 1:()522-+=x a y 的顶点为P ,与x 轴相交于A 、B 两点(点A 在点B 的左边),点B 的横坐标是1.(1)求P 点坐标及a 的值;(4分)(2)如图(1),抛物线C 2与抛物线C 1关于x 轴对称,将抛物线C 2向右平移,平移后的抛物线记为C 3,C 3的顶点为M ,当点P 、M 关于点B 成中心对称时,求C 3的解析式;(4分)(3)如图(2),点Q 是x 轴正半轴上一点,将抛物线C 1绕点Q 旋转180°后得到抛物线C 4.抛物线C 4的顶点为N ,与x 轴相交于E 、F 两点(点E 在点F 的左边),当以点P 、N 、F 为顶点的三角形是直角三角形时,求点Q 的坐标.(5分)3、如图14(1),抛物线22y x x k =-+与x 轴交于A 、B 两点,与y 轴交于点C (0,3-).[图14(2)、图14(3)为解答备用图](1)k =,点A 的坐标为 ,点B 的坐标为 ; (2)设抛物线22y x x k =-+的顶点为M ,求四边形ABMC 的面积;(3)在x 轴下方的抛物线上是否存在一点D ,使四边形ABDC 的面积最大?若存在,请求出点D 的坐标;若不存在,请说明理由;(4)在抛物线22y x x k =-+上求点Q ,使△BCQ 是以BC 为直角边的直角三角形.图14(1) 图14(2) 图14(3)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
【例1】如图,抛物线y=-x2+mx+n与线的解析式; (2)在抛物线的对称轴上是否存在这样的点P,使得 △PAC为直角三角形?若存在,请求出所有可能点P的 坐标;若不存在,请说明理由.
·
P
【练】如图,已知抛物线y=-x2+4x-3与x轴相 交于A、B两点,与y轴交与点C。在抛物线的 对称轴上是否存在点P,使得△PAC为直角三 角形?若存在,请求出所有符合条件的点P的 坐标;若不存在,请说明理由.
【例2】如图,已知抛物线
y
3 8
x2
3 4
x
3与x轴交于A和
B两点,与y轴相交于点C,顶点为D.
(1)求出点A、B、D的坐标;
(2)若点M是抛物线上一点,点N在y轴上,连接CM、
MN. 当△CMN是以MN为直角边的等腰直角三角形时,
直接写出点N的坐标.
