离散数学第16章

合集下载

离散数学sec16-17 群

整数加群<Z,+>，由 2 生成的子群是 <2> = { 2k | k∈Z } = 2Z
模 6 加群 <Z6, >中由 2 生成的子群 <2> = { 0, 2, 4 }
21
特殊子群2
例设G为群，令C是与G中所有的可交换的元素构成的集合，即 C＝{a|a∈G∧x∈G(ax＝xa)} 则C是G的子群，称为G的中心。
限群。群G的基数称为群G的阶，有限群G的阶记作|G|。
(2)只含单位元的群称为平凡群。
(3)若群G中的二元运算是可交换的，则称G为交换群或阿贝尔(Abel)群。
11
群论中常用的概念－元素的n次幂
定义设G是群，a∈G，n∈Z，则a的n次幂 P250 定义17.4
e a n a n1a
(a 1 )n
换 σ∈Sn，逆置换σ1是σ 的逆元. 这就证明了Sn关于置换的乘法构成一个群，称为 n
元对称群. n元对称群的子群称为 n元置换群.
31
例设 S = {1, 2, 3}，3元对称群
S3的对称群是？运算表？ S3的子群？
32
n元置换的分解式
• k阶轮换与轮换分解方法定义11.11 P258
定义设<G,>是代数系统，为二元运算。如果运算是可结合的，存在单位元e∈G，并且对G中的任何元素x都有x-1∈G,则称G为群（group）。 (P249定义17.1)
例 <Z,+>,<Q,+>,<R,+>,<Z+,+>,<N,+>是不是群？
<Zn,>是群?
8

离散数学图论-树

中序遍历（次序：左－根－右) 前序遍历（次序：根－左－右) 后序遍历（次序：左－右－根) b 中序遍历: c b e d g f a I k h j 前序遍历: a b c d e f g h i k j 后序遍历: c e g f d b k i j h a
例：给定二叉树，写出三种访问结点的序列
是否为根树
(a) (no)
(b) (no)
(c) (yes)
从树根到T的任意顶点v的通路(路径)长度称为v的层数。 v5的层数为层。
层数最大顶点的层数称为树高．将平凡树也称为根树。右图中树高为（）。
v1
v2 v3
v4 v8v5Fra bibliotekv6v7 v10
v9
在根树中，由于各有向边的方向是一致的，所以画根树时可以省去各边上的所有箭头，并将树根画在最上方．
等长码：0-000；1-001；2-010；3-011；4-100； 5-101；6-110；7-111. 总权值: W2=3*100=300
4、二叉树的周游（遍历）
二叉树的周游：对于一棵二叉树的每一个结点都访问一次且仅一次的操作 1）做一条绕行整个二叉树的行走路线（不能穿过树枝） 2）按行走路线经过结点的位臵（左边、下边、右边）得到周游的方法有三种：中序遍历（路线经过结点下边时访问结点）访问的次序：左子树－根－右子树前序遍历（路线经过结点左边时访问结点）访问的次序：根－左子树－右子树后序遍历（路线经过结点右边时访问结点）访问的次序：左子树－右子树－根
2、根树中顶点的关系
定义：设T为一棵非平凡的根树， v2 ∀vi,vj∈V(T),若vi可达vj,则称vi为 vj的祖先,vj为vi的后代； v4 v5 若vi邻接到vj(即<vi,vj>∈E(T)，称 vi为vj的父亲,而vj为vi的儿子 v8 若vj,vk的父亲相同，则称vj与vk是兄弟

离散数学第3版习题答案

离散数学第3版习题答案离散数学是一门重要的数学学科，它研究的是离散对象和离散结构的数学理论。

离散数学的应用广泛，涉及到计算机科学、信息技术、通信工程等领域。

在学习离散数学的过程中，习题是不可或缺的一部分，通过解答习题可以加深对知识的理解和掌握。

本文将为大家提供《离散数学第3版》习题的答案，希望能对学习者有所帮助。

第一章：命题逻辑1.1 习题答案：1. (a) 真值表如下：p | q | p ∧ qT | T | TT | F | FF | T | FF | F | F(b) 命题“p ∧ q”的真值表如下：p | q | p ∧ qT | T | TT | F | FF | T | FF | F | F(c) 命题“p ∨ q”的真值表如下：p | q | p ∨ qT | T | TT | F | TF | T | TF | F | F(d) 命题“p → q”的真值表如下：p | q | p → qT | T | TT | F | FF | T | TF | F | T1.2 习题答案：1. (a) 命题“¬(p ∧ q)”等价于“¬p ∨ ¬q”。

(b) 命题“¬(p ∨ q)”等价于“¬p ∧ ¬q”。

(d) 命题“¬(p ↔ q)”等价于“(p ∧ ¬q) ∨ (¬p ∧ q)”。

1.3 习题答案：1. (a) 命题“p → q”的否定是“p ∧ ¬q”。

(b) 命题“p ∧ q”的否定是“¬p ∨ ¬q”。

(d) 命题“p ∨ q”的否定是“¬p ∧ ¬q”。

1.4 习题答案：1. (a) 命题“p → q”与命题“¬p ∨ q”等价。

离散数学(第16-17章)陈瑜

2019/1/16 计算机学院 8/128
定理16.1(移项法则)设<R,+, *>是一个环， θ是加法幺元，对任意a，b，c R有: a+b=c a+b-c=θ
2019/1/16
计算机学院
9/128
定理16.2设<R,+, *>是一个环，θ是加法幺元，对任意a，b，c R有: ① a*θ=θ*a=θ(加法幺元是乘法零元) ② (-a)*b=a*(-b)=-(a*b) ③ (-a) *(-b)=a*b ④ (b-c) *a=b*a-c*a ⑤ a* (b-c）=a*b-a*c
2019/1/16 计算机学院 7/128
例 16.2 设 Zk 表示整数集 Z 上的模 k 剩余类集合，即: Zk={[0]，[1]，[2]，…，[k-1]} <Zk ，>是群（剩余类加群）， <Zk ，>是半群（剩余类乘半群）， ∵ 对 [i]，[j]，[k] Zk 有[i]（[j][k]）=[i(j+k)]=[ij+ik] =[ij][ik] =([i][j])([i][k]） ∴ <Zk ，，>是环，称为（模k）剩余类环。特别， k=2时，称为布尔环。
2019/1/16 计算机学院 6/128
例 16.2 设 Zk 表示整数集 Z 上的模 k 剩余类集合，即: Zk={[0]，[1]，[2]，…，[k-1]} <Zk ，>是群（剩余类加群）， <Zk ，>是半群（剩余类乘半群）， ∵ 对 [i]，[j]，[k] Zk 有[i]（[j][k]）=[i(j+k)]=[ij+ik] =[ij][ik] =([i][j])([i][k]） ∴ <Zk ，，>是环，称为（模k）剩余类环。特别， k=2时，称为布尔环。

《离散数学》课件-第16章树

解：易见所求为该图的一棵最小生成树，如图所示总造价为57
18
16.3 根树及其应用
19
定义（有向树）设D是有向图，如果D的基图是无向树，则称D为有向树。
在有向树中最重要的是根树。定义16.6（根树）一棵非平凡的有向树，如果恰有一个顶点的入度为O，其余所有顶点的入度均为1,则称该树为根树。入度为0的顶点称为树根，入度为1出度为0的顶点称为树叶，入度为1出度不为0的点称为内点，内点和树根统称为分支点。树根到一个顶点的有向通路的长度称为该顶点的层数。层数最大顶点的层数称为树高。平凡树也称为根树。
2
16.1 树及其性质
3
定义16.1（树和森林）连通且无回路的无向图称为无向树，简称为树，常用
T表示树。平凡图为树，称为平凡树。非连通且每个连通分支是树的无向图称为森林。 T中度数为1的顶点（悬挂顶点）称为树叶，度数大于
1的顶点称为分支点。称只有一个分支点，且分支点的度数为n-1的n（n≥3）
定义16.8（子树）设T为一棵根树，则其任一顶点v 及其后代导若将层数相同的顶点都标定次序，则称T为有序树。
根据每个分支点的儿子数以及是否有序，可将根树分成如下若干类：
定义（跟树分类）设T为一棵根树（1）若T的每个分支点至多有r个儿子，则称T为r叉树。又若r叉树是有序的，则称它为r叉有序树。（2）若T的每个分支点恰好有r个儿子，则称T为r叉正则树。又若r叉正则树是有序的，则称它为r叉正则有序树。（3）若T为r叉正则树，且每个树叶的层数均为树高，则称T为r叉完全正则树。又若r叉完全正则树是有序的，则称它为r叉完全正则有序树。
8
平均编码长度为：L = ∑ P( i )× l( i ) = 2.53bit i=1

离散数学答案-屈婉玲版-第二版-高等教育出版社课后答案

离散数学答案屈婉玲版第二版高等教育出版社课后答案第一章部分课后习题参考答案16 设p、q的真值为0；r、s的真值为1，求下列各命题公式的真值。

（1）p∨(q∧r)⇔0∨(0∧1) ⇔0（2）（p↔r）∧(﹁q∨s) ⇔（0↔1）∧(1∨1) ⇔0∧1⇔0.（3）（⌝p∧⌝q∧r）↔(p∧q∧﹁r) ⇔（1∧1∧1）↔ (0∧0∧0)⇔0(4)（⌝r∧s）→(p∧⌝q) ⇔（0∧1）→(1∧0) ⇔0→0⇔117．判断下面一段论述是否为真：“π是无理数。

并且，如果3是无理数，则2也是无理数。

另外6能被2整除，6才能被4整除。

”答：p: π是无理数 1q: 3是无理数0r: 2是无理数 1s:6能被2整除 1t: 6能被4整除0命题符号化为：p∧(q→r)∧(t→s)的真值为1，所以这一段的论述为真。

19．用真值表判断下列公式的类型：（4）(p→q) →(⌝q→⌝p)（5）(p∧r) ↔(⌝p∧⌝q)（6）((p→q) ∧(q→r)) →(p→r)答：（4）p q p→q ⌝q ⌝p ⌝q→⌝p (p→q)→(⌝q→⌝p)0 0 1 1 1 1 10 1 1 0 1 1 11 0 0 1 0 0 11 1 1 0 0 1 1所以公式类型为永真式（5）公式类型为可满足式（方法如上例）（6）公式类型为永真式（方法如上例）第二章部分课后习题参考答案3.用等值演算法判断下列公式的类型，对不是重言式的可满足式，再用真值表法求出成真赋值.(1) ⌝(p∧q→q)(2)(p→(p∨q))∨(p→r)(3)(p∨q)→(p∧r)答：(2)（p→(p∨q)）∨(p→r)⇔(⌝p∨(p∨q))∨(⌝p∨r)⇔⌝p∨p∨q∨r⇔1所以公式类型为永真式(3)P q r p∨q p∧r （p∨q）→(p∧r)0 0 0 0 0 10 0 1 0 0 10 1 0 1 0 00 1 1 1 0 01 0 0 1 0 01 0 1 1 1 11 1 0 1 0 01 1 1 1 1 1所以公式类型为可满足式4.用等值演算法证明下面等值式：(2)(p→q)∧(p→r)⇔(p→(q∧r))(4)(p∧⌝q)∨(⌝p∧q)⇔(p∨q) ∧⌝(p∧q)证明（2）(p→q)∧(p→r)⇔ (⌝p∨q)∧(⌝p∨r)⌝p∨(q∧r))p→(q∧r)（4）(p∧⌝q)∨(⌝p∧q)⇔(p∨(⌝p∧q)) ∧(⌝q∨(⌝p∧q)(p∨⌝p)∧(p∨q)∧(⌝q∨⌝p) ∧(⌝q∨q)1∧(p∨q)∧⌝(p∧q)∧1(p∨q)∧⌝(p∧q)5.求下列公式的主析取范式与主合取范式，并求成真赋值(1)(⌝p→q)→(⌝q∨p)(2)⌝(p→q)∧q∧r(3)(p∨(q∧r))→(p∨q∨r)解：（1）主析取范式(⌝p →q)→(⌝q ∨p)⌝(p ∨q)∨(⌝q ∨p)(⌝p ∧⌝q)∨(⌝q ∨p)⇔ (⌝p ∧⌝q)∨(⌝q ∧p)∨(⌝q ∧⌝p)∨(p ∧q)∨(p ∧⌝q)(⌝p ∧⌝q)∨(p ∧⌝q)∨(p ∧q)⇔320m m m ∨∨⇔∑(0,2,3)主合取范式：(⌝p →q)→(⌝q ∨p)⌝(p ∨q)∨(⌝q ∨p)(⌝p ∧⌝q)∨(⌝q ∨p)⇔(⌝p ∨(⌝q ∨p))∧(⌝q ∨(⌝q ∨p))⇔1∧(p ∨⌝q)⇔(p ∨⌝q) ⇔ M 1⇔∏(1)(2) 主合取范式为：⌝(p →q)∧q ∧r ⇔⌝(⌝p ∨q)∧q ∧r⇔(p ∧⌝q)∧q ∧r ⇔0所以该式为矛盾式.主合取范式为∏(0,1,2,3,4,5,6,7)矛盾式的主析取范式为 0(3)主合取范式为：(p ∨(q ∧r))→(p ∨q ∨r)⌝(p ∨(q ∧r))→(p ∨q ∨r)(⌝p ∧(⌝q ∨⌝r))∨(p ∨q ∨r)(⌝p ∨(p ∨q ∨r))∧((⌝q ∨⌝r))∨(p ∨q ∨r))⇔1∧1⇔1所以该式为永真式.永真式的主合取范式为 1主析取范式为∑(0,1,2,3,4,5,6,7)第三章部分课后习题参考答案14. 在自然推理系统P中构造下面推理的证明：(2)前提：p→q,⌝(q∧r),r结论：⌝p(4)前提：q→p,q↔s,s↔t,t∧r结论：p∧q证明：（2）①⌝(q∧r) 前提引入②⌝q∨⌝r ①置换③q→⌝r ②蕴含等值式④r 前提引入⑤⌝q ③④拒取式⑥p→q 前提引入⑦￢p（3）⑤⑥拒取式证明（4）：①t∧r 前提引入②t ①化简律③q↔s 前提引入④s↔t 前提引入⑤q↔t ③④等价三段论⑥（q→t）∧(t→q) ⑤置换⑦（q→t）⑥化简⑧q ②⑥假言推理⑨q→p 前提引入⑩p ⑧⑨假言推理(11)p∧q ⑧⑩合取15在自然推理系统P中用附加前提法证明下面各推理：(1)前提：p→(q→r),s→p,q结论：s→r证明①s 附加前提引入②s→p 前提引入③p ①②假言推理④p→(q→r) 前提引入⑤q→r ③④假言推理⑥q 前提引入⑦r ⑤⑥假言推理16在自然推理系统P中用归谬法证明下面各推理：(1)前提：p→⌝q,⌝r∨q,r∧⌝s结论：⌝p证明：①p 结论的否定引入②p→﹁q 前提引入③﹁q ①②假言推理④￢r∨q 前提引入⑤￢r ④化简律⑥r∧￢s 前提引入⑦r ⑥化简律⑧r∧﹁r ⑤⑦合取由于最后一步r∧﹁r 是矛盾式,所以推理正确.第四章部分课后习题参考答案3. 在一阶逻辑中将下面将下面命题符号化,并分别讨论个体域限制为(a),(b)条件时命题的真值:(1) 对于任意x,均有2=(x+)(x).(2) 存在x,使得x+5=9.其中(a)个体域为自然数集合.(b)个体域为实数集合.解：F(x): 2=(x+)(x).G(x): x+5=9.(1)在两个个体域中都解释为)∀，在（a）中为假命题，在(b)中为真命题。

离散数学——树ppt课件

11
无向树的性质
定理16.2 设T是n阶非平凡的无向树，则T中至少有两片树叶。
证明
设T有x片树叶，由握手定理及定理16.1可知，
2(n 1) d(vi ) x 2(n x)
由上式解出x≥2。
12
例16.1
例16.1 画出6阶所有非同构的无向树。
解答设Ti是6阶无向树。由定理16.1可知，Ti的边数mi＝5，由握手定理可知，∑dTi(vj)＝10，且δ(Ti)≥1，△(Ti)≤5。于是Ti的度数列必为以下情况之一。
(1) 1，1，1，1，1，5 (2) 1，1，1，1，2，4 (3) 1，1，1，1，3，3 (4) 1，1，1，2，2，3 (5) 1，1，2，2，2，2
(4)对应两棵非同构的树，在一棵树中两个2度顶点相邻，在另一棵树中不相邻，其他情况均能画出一棵非同构的树。
13
例16.1
人们常称只有一个分支点，且分支点的度数为n-1的 n(n≥3)阶无向树为星形图，称唯一的分支点为星心。
知，G-e已不是连通图，所以，e为桥。
9
(5)(6)
如果G是连通的且G中任何边均为桥，则G中没有回路，但在任何两个不同的顶点之间加一条新边，在所得图中得到唯一的一个含新边的圈。
因为G中每条边均为桥，删掉任何边，将使G变成不连通图，所以，G中没有回路，也即G中无圈。
又由于G连通，所以G为树，由(1) (2)可知，
u,v∈V，且u≠v，则u与v之间存在唯一的路径Г，
则Г∪(u,v)（(u,v)为加的新边）为G中的圈，显然圈是唯一的。
10
(6)(1)
如果G中没有回路，但在任何两个不同的顶点之间加一条新边，在所得图中得到唯一的一个含新边的圈，则G是树。

离散数学答案屈婉玲版第二版高等教育出版社课后答案

离散数学答案屈婉玲版第二版高等教育出版社课后答案第一章部分课后习题参考答案16 设p、q的真值为0；r、s的真值为1,求下列各命题公式的真值;1p∨q∧r⇔0∨0∧1 ⇔02pr∧﹁q∨s ⇔01∧1∨1 ⇔0∧1⇔0.3⌝p∧⌝q∧rp∧q∧﹁r ⇔1∧1∧1 0∧0∧0⇔04⌝r∧s→p∧⌝q ⇔0∧1→1∧0 ⇔0→0⇔117．判断下面一段论述是否为真：“π是无理数;并且,如果3是无理数,则2也是无理数;另外6能被2整除,6才能被4整除;”答：p: π是无理数 1q: 3是无理数0r: 2是无理数 1s:6能被2整除 1t: 6能被4整除0命题符号化为：p∧q→r∧t→s的真值为1,所以这一段的论述为真;19．用真值表判断下列公式的类型：4p→q →⌝q→⌝p5p∧r ↔⌝p∧⌝q6p→q ∧q→r →p→r答： 4p q p→q ⌝q ⌝p ⌝q→⌝p p→q→⌝q→⌝p0 0 1 1 1 1 10 1 1 0 1 1 11 0 0 1 0 0 11 1 1 0 0 1 1所以公式类型为永真式5公式类型为可满足式方法如上例6公式类型为永真式方法如上例第二章部分课后习题参考答案3.用等值演算法判断下列公式的类型,对不是重言式的可满足式,再用真值表法求出成真赋值.1 ⌝p∧q→q2p→p∨q∨p→r3p∨q→p∧r答：2p→p∨q∨p→r⇔⌝p∨p∨q∨⌝p∨r⇔⌝p∨p∨q∨r⇔1所以公式类型为永真式3P q r p∨q p∧r p∨q→p∧r0 0 0 0 0 10 0 1 0 0 10 1 0 1 0 00 1 1 1 0 01 0 0 1 0 01 0 1 1 1 11 1 0 1 0 01 1 1 1 1 1所以公式类型为可满足式4.用等值演算法证明下面等值式：2p→q∧p→r⇔p→q∧r4p∧⌝q∨⌝p∧q⇔p∨q ∧⌝p∧q证明2p→q∧p→r⇔⌝p∨q∧⌝p∨r⇔⌝p∨q∧r⇔p→q∧r4p∧⌝q∨⌝p∧q⇔p∨⌝p∧q ∧⌝q∨⌝p∧q⇔p∨⌝p∧p∨q∧⌝q∨⌝p ∧⌝q∨q⇔1∧p∨q∧⌝p∧q∧1⇔p∨q∧⌝p∧q5.求下列公式的主析取范式与主合取范式,并求成真赋值1⌝p→q→⌝q∨p2⌝p→q∧q∧r3p∨q∧r→p∨q∨r解：1主析取范式⌝p→q→⌝q∨p⇔⌝p∨∨⌝∨p⇔⌝p∧⌝∨⌝∨p⇔⌝p∧⌝∨⌝∧p∨⌝q∧⌝p∨p∧q∨p∧⌝q⇔⌝p∧⌝q∨p∧⌝q∨p∧q⇔∑0,2,3主合取范式：⌝p→q→⌝q∨p⇔⌝p∨∨⌝∨p⇔⌝p∧⌝∨⌝∨p⇔⌝p∨⌝q∨p∧⌝∨⌝∨p⇔1∧p∨⌝q⇔p∨⌝q ⇔ M1⇔∏12 主合取范式为：⌝p→∧∧r⇔⌝⌝p∨∧∧r⇔p∧⌝∧∧r⇔0所以该式为矛盾式.主合取范式为∏0,1,2,3,4,5,6,7矛盾式的主析取范式为 03主合取范式为：p∨q∧r→p∨q∨r⇔⌝p∨q∧r→p∨q∨r⇔⌝p∧⌝q∨⌝r∨p∨q∨r⇔⌝p∨p∨q∨r∧⌝q∨⌝r∨p∨q∨r⇔1∧1⇔1所以该式为永真式.永真式的主合取范式为 1主析取范式为∑0,1,2,3,4,5,6,7第三章部分课后习题参考答案14. 在自然推理系统P中构造下面推理的证明：2前提：p→q,⌝q∧r,r结论：⌝p4前提：q→p,q↔s,s↔t,t∧r结论：p∧q证明：2①⌝q∧r 前提引入②⌝q∨⌝r ①置换③q→⌝r ②蕴含等值式④r 前提引入⑤⌝q ③④拒取式⑥p→q 前提引入⑦￢p3 ⑤⑥拒取式证明4：①t∧r 前提引入②t ①化简律③q↔s 前提引入④s↔t 前提引入⑤q↔t ③④等价三段论⑥q→t∧t→q ⑤置换⑦q→t ⑥化简⑧q ②⑥假言推理⑨q→p 前提引入⑩p ⑧⑨假言推理11p∧q ⑧⑩合取15在自然推理系统P中用附加前提法证明下面各推理：(1)前提：p→q→r,s→p,q结论：s→r证明①s 附加前提引入②s→p 前提引入③p ①②假言推理④p→q→r 前提引入⑤q→r ③④假言推理⑥q 前提引入⑦r ⑤⑥假言推理16在自然推理系统P中用归谬法证明下面各推理：1前提：p→⌝q,⌝r∨q,r∧⌝s结论：⌝p证明：①p 结论的否定引入②p→﹁q 前提引入③﹁q ①②假言推理④￢r∨q 前提引入⑤￢r ④化简律⑥r∧￢s 前提引入⑦r ⑥化简律⑧r∧﹁r ⑤⑦合取由于最后一步r∧﹁r 是矛盾式,所以推理正确.第四章部分课后习题参考答案3. 在一阶逻辑中将下面将下面命题符号化,并分别讨论个体域限制为a,b条件时命题的真值:1 对于任意x,均有x2−2=x+√2x−√2.2 存在x,使得x+5=9.其中a个体域为自然数集合.b个体域为实数集合.解：Fx: x2−2=x+√2x−√2.Gx: x+5=9.1在两个个体域中都解释为)∀,在a中为假命题,在b中为真命题;(xxF2在两个个体域中都解释为)(x∃,在ab中均为真命题;xG4. 在一阶逻辑中将下列命题符号化:1 没有不能表示成分数的有理数.2 在北京卖菜的人不全是外地人.解:1Fx: x能表示成分数Hx: x是有理数命题符号化为: ))x∧F⌝∃x⌝(x()(H2Fx: x是北京卖菜的人Hx: x是外地人命题符号化为: ))F⌝∀xx→(x(H)(5. 在一阶逻辑将下列命题符号化:1 火车都比轮船快.3 不存在比所有火车都快的汽车.解:1Fx: x是火车; Gx: x是轮船; Hx,y: x比y快命题符号化为: ))FyxGy∀∀∧x→))((,H)x((y(2 1Fx: x是火车; Gx: x是汽车; Hx,y: x比y快命题符号化为: )))xFxyG∧∀y→⌝∃H)(,(((y()x9.给定解释I如下:a 个体域D为实数集合R.b D中特定元素a ̅=0.c 特定函数f x,y=x−y,x,y D∈.d 特定谓词F̅x,y:x=y,G̅x,y:x<y,x,y D∈.说明下列公式在I下的含义,并指出各公式的真值:答:1 对于任意两个实数x,y,如果x<y, 那么x≠y. 真值1.2 对于任意两个实数x,y,如果x-y=0, 那么x<y. 真值0.10. 给定解释I如下：a 个体域D=NN为自然数集合.b D中特定元素a̅=2.c D上函数f(x,y)=x+y,g̅x,y=xy.d D上谓词F̅x,y:x=y.说明下列各式在I下的含义,并讨论其真值.(1)xFgx,a,x(2)xyFfx,a,y→Ffy,a,x答:1 对于任意自然数x, 都有2x=x, 真值0.2 对于任意两个自然数x,y,使得如果x+2=y, 那么y+2=x. 真值0.11. 判断下列各式的类型:1 F(x,y)→(G(x,y)→F(x,y)).3 xyF(x,y)→x yFx,y.解:1因为1→pq⇔qp为永真式；pp→⌝()(⇔)∨⌝∨所以F(x,y)→(G(x,y)→F(x,y)).为永真式；3取解释I个体域为全体实数Fx,y：x+y=5所以,前件为任意实数x存在实数y使x+y=5,前件真；后件为存在实数x对任意实数y都有x+y=5,后件假,此时为假命题再取解释I个体域为自然数N,Fx,y：:x+y=5所以,前件为任意自然数x存在自然数y使x+y=5,前件假;此时为假命题;此公式为非永真式的可满足式;13. 给定下列各公式一个成真的解释,一个成假的解释;1 x Fx∨G(x))2 xFx∧Gx∧Hx解:1个体域:本班同学Fx：x会吃饭, Gx：x会睡觉.成真解释Fx：x是泰安人,Gx：x是济南人.2成假解释2个体域:泰山学院的学生Fx ：x 出生在山东,Gx:x 出生在北京,Hx:x 出生在江苏,成假解释. Fx ：x 会吃饭,Gx ：x 会睡觉,Hx ：x 会呼吸. 成真解释.第五章部分课后习题参考答案5.给定解释Ｉ如下:a 个体域D={3,4};b )(x f f 为3)4(,4)3(==f f c 1)3,4()4,3(,0)4,4()3,3(),(====F F F F y x F 为. 试求下列公式在Ｉ下的真值. 1),(y x yF x ∃∀3)))(),((),((y f x f F y x F y x →∀∀ 解:1 ))4,()3,((),(x F x F x y x yF x ∨∀⇔∃∀2 )))(),((),((y f x f F y x F y x →∀∀ 12.求下列各式的前束范式;1),()(y x yG x xF ∀→∀5)),()((),(2121211x x G x x H x x F x ⌝∃→→∃ 本题课本上有错误解:1 ),()(y x yG x xF ∀→∀),()(y t yG x xF ∀→∀⇔)),()((y t G x F y x →∀∃⇔ 5 )),()((),(2121211x x G x x H x x F x ⌝∃→→∃ 15.在自然数推理系统F 中,构造下面推理的证明:(1) 前提: ))())()((()(y R y G y F y x xF →∨∀→∃,)(x xF ∃结论: ∃xRx(2) 前提: ∀xFx →Ga ∧Rx, xFx结论:xFx ∧Rx 证明1①)(x xF ∃ 前提引入 ②Fc ①EI③))())()((()(y R y G y F y x xF →∨∀→∃ 前提引入 ④))())()(((y R y G y F y →∨∀ ①③假言推理 ⑤Fc ∨Gc →Rc ④UI⑥Fc ∨Gc ②附加 ⑦Rc ⑤⑥假言推理 ⑧∃xRx ⑦EG 2①∃xFx 前提引入 ②Fc ①EI③∀xFx →Ga ∧Rx 前提引入 ④Fc →Ga ∧Rc ③UI⑤Ga ∧Rc ②④假言推理 ⑥Rc ⑤化简 ⑦Fc ∧Rc ②⑥合取引入 ⑧∃xFx ∧Rx ⑦EG第六章部分课后习题参考答案5.确定下列命题是否为真： 1∅⊆∅ 真 2∅∈∅ 假 3}{∅⊆∅ 真 4}{∅∈∅ 真 5｛a,b ｝⊆｛a,b,c,｛a,b,c ｝｝真 6｛a,b ｝∈｛a,b,c,｛a,b ｝｝真 7｛a,b ｝⊆｛a,b,｛｛a,b ｝｝｝真 8｛a,b ｝∈｛a,b,｛｛a,b ｝｝｝假6．设a,b,c 各不相同,判断下述等式中哪个等式为真: 1｛｛a,b ｝,c,∅｝=｛｛a,b ｝,c ｝假2｛a ,b,a ｝=｛a,b ｝真 3｛｛a ｝,{b}｝=｛｛a,b ｝｝假 4｛∅,｛∅｝,a,b ｝=｛｛∅,｛∅｝｝,a,b ｝假 8．求下列集合的幂集：1｛a,b,c ｝ PA={ ∅,{a},{b},{c},{a,b},{a,c},{b,c},{a,b,c}}2｛1,｛2,3｝｝PA={ ∅, {1}, {{2,3}}, {1,{2,3}} }3｛∅｝PA={ ∅, ｛∅｝ }4｛∅,｛∅｝｝PA={ ∅, {1}, {{2,3}}, {1,{2,3}} }14．化简下列集合表达式：1A B B -A B2A B C-B C A解:1A B B -A B=A B B ～A B=A B ～A B B=∅ B=∅2A B C-B C A=A B C ～B C A=A ～B C B C ～B C A=A ～B C ∅ A=A ～B C A=A18．某班有25个学生,其中14人会打篮球,12人会打排球,6人会打篮球和排球,5人会打篮球和网球,还有2人会打这三种球;已知6个会打网球的人都会打篮球或排球;求不会打球的人数;解: 阿A={会打篮球的人},B={会打排球的人},C={会打网球的人}|A|=14, |B|=12, |A B|=6,|A C|=5,| A B C|=2,|C|=6,C⊆A B如图所示;25-5+4+2+3-5-1=25-14-5-1=5不会打球的人共5人21.设集合A＝{{1,2},{2,3},{1,3},{∅}},计算下列表达式：1 A2 A3 A4 A解:1 A={1,2} {2,3} {1,3} {∅}={1,2,3,∅}2 A={1,2} {2,3} {1,3} {∅}=∅3 A=1 2 3 ∅=∅4 A=∅27、设A,B,C是任意集合,证明1A-B-C=A- B⋃C2A-B-C=A-C-B-C证明1 A-B-C=A ～B ～C= A ～B ～C= A ～B⋃C =A- B⋃C2 A-C-B-C=A ～C ～B ～C= A ～C ～B C=A ～C ～B A ～C C= A ～C ～B ∅= A ～B⋃C =A- B⋃C 由1得证;第七章部分课后习题参考答案7.列出集合A={2,3,4}上的恒等关系I A,全域关系E A,小于或等于关系L A,整除关系D A. 解：I={<2,2>,<3,3>,<4,4>}A={<2,2>,<2,3>,<2,4>,<3,4>,<4,4>,<3,2>,<3,3>,<4,2>,<4,3>}EA={<2,2>,<2,3>,<2,4>,<3,3>,<3,4>,<4,4>}LAD={<2,4>}A13.设A={<1,2>,<2,4>,<3,3>}B={<1,3>,<2,4>,<4,2>}求A⋃B,A⋂B, domA, domB, domA⋃B, ranA, ranB, ranA⋂B , fldA-B.解：A⋃B={<1,2>,<2,4>,<3,3>,<1,3>,<4,2>}A⋂B={<2,4>}domA={1,2,3}domB={1,2,4}domA∨B={1,2,3,4}ranA={2,3,4}ranB={2,3,4}ranA⋂B={4}A-B={<1,2>,<3,3>},fldA-B={1,2,3}14.设R={<0,1><0,2>,<0,3>,<1,2>,<1,3>,<2,3>}求R R, R-1, R↑{0,1,}, R{1,2}解：R R={<0,2>,<0,3>,<1,3>}R -1,={<1,0>,<2,0>,<3,0>,<2,1>,<3,1>,<3,2>}R ↑{0,1}={<0,1>,<0,2>,<0,3>,<1,2>,<1,3>}R{1,2}=ranR|{1,2}={2,3}16．设A={a,b,c,d},1R ,2R 为A 上的关系,其中1R ={},,,,,a a a b b d求23122112,,,R R R R R R ;解: R 1 R 2={<a,d>,<a,c>,<a,d>}R 2 R 1={<c,d>}R 12=R 1 R 1={<a,a>,<a,b>,<a,d>}R 22=R 2 R 2={<b,b>,<c,c>,<c,d>}R 23=R 2 R 22={<b,c>,<c,b>,<b,d>}36．设A={1,2,3,4},在A ⨯A 上定义二元关系R,∀<u,v>,<x,y>∈A ⨯A ,〈u,v> R <x,y>⇔u + y = x + v.(1)证明R 是A ⨯A 上的等价关系.2确定由R 引起的对A ⨯A 的划分.1证明：∵<u,v>R<x,y> ⇔u+y=x-y∴<u,v>R<x,y>⇔u-v=x-y∀<u,v>∈A ⨯A∵u-v=u-v∴<u,v>R<u,v>∴R 是自反的任意的<u,v>,<x,y>∈A ×A如果<u,v>R<x,y> ,那么u-v=x-y∴x-y=u-v ∴<x,y>R<u,v>∴R 是对称的任意的<u,v>,<x,y>,<a,b>∈A ×A若<u,v>R<x,y>,<x,y>R<a,b>则u-v=x-y,x-y=a-b∴u-v=a-b ∴<u,v>R<a,b>∴R是传递的∴R是A×A上的等价关系2 ∏={{<1,1>,<2,2>,<3,3>,<4,4>}, {<2,1>,<3,2>,<4,3>}, {<3,1>,<4,2>},{<4,1>}, {<1,2>,<2,3>,<3,4>}, {<1,3>,<2,4>}, {<1,4>} }41.设A={1,2,3,4},R为A⨯A上的二元关系, ∀〈a,b〉,〈c,d〉∈A⨯A ,〈a,b〉R〈c,d〉⇔a + b = c + d(1)证明R为等价关系.(2)求R导出的划分.1证明：∀<a,b〉∈A⨯Aa+b=a+b∴<a,b>R<a,b>∴R是自反的任意的<a,b>,<c,d>∈A×A设<a,b>R<c,d>,则a+b=c+d∴c+d=a+b ∴<c,d>R<a,b>∴R是对称的任意的<a,b>,<c,d>,<x,y>∈A×A若<a,b>R<c,d>,<c,d>R<x,y>则a+b=c+d,c+d=x+y∴a+b=x+y ∴<a,b>R<x,y>∴R是传递的∴R是 A×A上的等价关系2∏={{<1,1>}, {<1,2>,<2,1>}, {<1,3>,<2,2>,<3,1>}, {<1,4>,<4,1>,<2,3>,<3,2>}, {<2,4>,<4,2>,<3,3>}, {<3,4>,<4,3>}, {<4,4>}}43. 对于下列集合与整除关系画出哈斯图:1 {1,2,3,4,6,8,12,24}2 {1,2,3,4,5,6,7,8,9,10,11,12}解:1 245.下图是两个偏序集<A,R >的哈斯图.分别写出集合A 和偏序关系R 的集合表达式.a b解: aA={a,b,c,d,e,f,g}R ={<a,b>,<a,c>,<a,d>,<a,e>,<a,f>,<a,g>,<b,d>,<b,e>,<c,f>,<c,g>}A I ⋃ b A={a,b,c,d,e,f,g} R ={<a,b>,<a,c>,<a,d>,<a,e>,<a,f>,<d,f>,<e,f>}A I ⋃46.分别画出下列各偏序集<A,R >的哈斯图,并找出A 的极大元`极小元`最大元和最小元.1A={a,b,c,d,e} R ={<a,d>,<a,c>,<a,b>,<a,e>,<b,e>,<c,e>,<d,e>}⋃I A . 2A={a,b,c,d,e}, R ={<c,d>}⋃IA.解:1 2项目 1 2极大元: e a,b,d,e极小元: a a,b,c,e最大元: e 无最小元: a 无第八章部分课后习题参考答案1．设f :N →N,且f x=12x x x ⎧⎪⎨⎪⎩，若为奇数若为偶数，求f 0, f {0}, f 1, f {1}, f {0,2,4,6,…},f {4,6,8}, f -1{3,5,7}.解：f 0=0, f {0}={0}, f 1=1, f {1}={1},f {0,2,4,6,…}=N,f {4,6,8}={2,3,4}, f -1 {3,5,7}={6,10,14}.4. 判断下列函数中哪些是满射的哪些是单射的哪些是双射的1 f:N →N, fx=x 2+2 不是满射,不是单射2 f:N →N,fx=xmod 3,x 除以3的余数不是满射,不是单射3 f:N →N,fx=10x x ⎧⎨⎩，若为奇数，若为偶数不是满射,不是单射 4 f:N →{0,1},fx=01x x ⎧⎨⎩，若为奇数，若为偶数是满射,不是单射 5 f:N-{0}→R,fx=lgx 不是满射,是单射6 f:R →R,fx=x 2-2x-15 不是满射,不是单射5. 设X={a,b,c,d},Y={1,2,3},f={<a,1>,<b,2>,<c,3>,}判断以下命题的真假:1f 是从X 到Y 的二元关系,但不是从X 到Y 的函数; 对2f 是从X 到Y 的函数,但不是满射,也不是单射的; 错3f 是从X 到Y 的满射,但不是单射; 错4f 是从X 到Y 的双射. 错第十章部分课后习题参考答案4．判断下列集合对所给的二元运算是否封闭：（1）整数集合Z 和普通的减法运算;封闭,不满足交换律和结合律,无零元和单位元（2）非零整数集合Z ∗和普通的除法运算;不封闭（3）全体n n ⨯实矩阵集合M n R 和矩阵加法及乘法运算,其中n ≥2;封闭均满足交换律,结合律,乘法对加法满足分配律；加法单位元是零矩阵,无零元；乘法单位元是单位矩阵,零元是零矩阵；4全体n n ⨯实可逆矩阵集合关于矩阵加法及乘法运算,其中n ≥2;不封闭5正实数集合R +和 ° 运算,其中 ° 运算定义为：a ，b ∈R +，a ° b = ab −a −b不封闭因为 +∉-=--⨯=R 11111116n ∈Z +,nZ ={nz | z ∈ Z }.nZ 关于普通的加法和乘法运算;封闭,均满足交换律,结合律,乘法对加法满足分配律加法单位元是0,无零元；乘法无单位元1>n ,零元是0；1=n 单位元是17A = {},,,21n a a a n ≥2.° 运算定义如下：a ，b ∈ A ，a ° b = b封闭不满足交换律,满足结合律,8S = {2x −1|x ∈Z +}关于普通的加法和乘法运算;封闭均满足交换律,结合律,乘法对加法满足分配律9S = {0,1},S 是关于普通的加法和乘法运算;加法不封闭,乘法封闭；乘法满足交换律,结合律10S = {x | x =2n ,n ∈Z +} ,S 关于普通的加法和乘法运算;加法不封闭,乘法封闭,乘法满足交换律,结合律5．对于上题中封闭的二元运算判断是否适合交换律,结合律,分配律;见上题7．设为+Z 上的二元运算+∈∀Z y x ,,X Y = min x,y ,即x 和y 之中较小的数.(1)求4 6,7 3;4, 32 在+Z 上是否适合交换律,结合律,和幂等律满足交换律,结合律,和幂等律3求运算的单位元,零元及+Z 中所有可逆元素的逆元;单位元无,零元1, 所有元素无逆元8．Q Q S ⨯= Q 为有理数集,为S 上的二元运算,<a,b>,<x,y > ∈ S 有< a,b ><x,y> = <ax,ay + b>1运算在S 上是否可交换,可结合是否为幂等的不可交换：<x,y><a,b >= <xa,xb +y>≠< a,b ><x,y>可结合：<a,b ><x,y><c,d>=<ax,ay + b><c,d>=<axc,axd +ay+b ><a,b ><x,y><c,d>=<a, b><xc,xd+y>=<axc,axd +y+b ><a,b ><x,y><c,d>=<a,b ><x,y><c,d>不是幂等的2运算是否有单位元,零元如果有请指出,并求S 中所有可逆元素的逆元;设<a,b>是单位元,<x,y > ∈ S ,<a,b ><x,y>= <x,y><a,b >=<x,y>则<ax,ay+b>=<xa,xb+y>=<x,y>,解的<a,b>=<1,0>,即为单位;设<a,b>是零元,<x,y > ∈ S ,<a,b ><x,y>= <x,y><a,b >=<a,b>则<ax,ay+b>=<xa,xb+y>=<a,b>,无解;即无零元;<x,y > ∈ S,设<a,b>是它的逆元<a,b ><x,y>= <x,y><a,b >=<1,0><ax,ay+b>=<xa,xb+y>=<1,0>a=1/x,b=-y/x所以当x ≠0时,x y x y x -=><-,1,1 10．令S={a,b},S 上有四个运算：,°，和□分别有表确定; a b c d1这4个运算中哪些运算满足交换律,结合律,幂等律a 交换律,结合律,幂等律都满足, 零元为a,没有单位元；b 满足交换律和结合律,不满足幂等律,单位元为a,没有零元c 满足交换律,不满足幂等律,不满足结合律没有单位元, 没有零元d 不满足交换律,满足结合律和幂等律没有单位元, 没有零元(2)求每个运算的单位元,零元以及每一个可逆元素的逆元;见上16．设V=〈 N,+ , 〉,其中+ ,分别代表普通加法与乘法,对下面给定的每个集合确定它是否构成V 的子代数,为什么1S 1={2n | n ∈Z } 是2S 2={2n +1 | n ∈Z } 不是加法不封闭3S 3 = {-1,0,1} 不是,加法不封闭第十一章部分课后习题参考答案8.设S={0,1,2,3},为模4乘法,即"∀x,y ∈S, xy=xymod 4 问〈S,〉是否构成群为什么解：1 ∀x,y ∈S, xy=xymod 4S ∈,是S 上的代数运算; 2 ∀x,y,z ∈S,设xy=4k+r 30≤≤rx y z =xymod 4z=r z=rzmod 4=4kz+rzmod 4=4k+rzmod 4 =xyzmod 4同理x y z =xyzmod 4所以,x y z = x y z,结合律成立; 3 ∀x ∈S, x 1=1x=x,,所以1是单位元;4,33,1111==-- 0和2没有逆元所以,〈S,〉不构成群9.设Z 为整数集合,在Z 上定义二元运算;如下：" ∀x,y ∈Z,xoy= x+y-2问Z 关于o 运算能否构成群为什么解：1 ∀x,y ∈Z, xoy= x+y-2Z ∈,o 是Z 上的代数运算;2 ∀x,y,z ∈Z,xoy oz =x+y-2oz=x+y-2+z-2=x+y+z-4同理xoyoz= xoyoz,结合律成立;3设e 是单位元,∀x ∈Z, xo e = e ox=x,即x+e -2= e +x-2=x, e=24 ∀x ∈Z , 设x 的逆元是y, xoy= yox=e , 即x+y-2=y+x-2=2,所以,x y x -==-41所以〈Z,o 〉构成群11.设G=⎭⎬⎫⎩⎨⎧⎪⎪⎭⎫ ⎝⎛--⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛1001,1001,1001,1001,证明G 关于矩阵乘法构成一个群．解：1 ∀x,y ∈G, 易知xy ∈G,乘法是Z 上的代数运算;2 矩阵乘法满足结合律3设⎪⎪⎭⎫ ⎝⎛1001是单位元,4每个矩阵的逆元都是自己;所以G 关于矩阵乘法构成一个群．14.设G 为群,且存在a∈G,使得G={a k ∣k∈Z}证明：G 是交换群;证明:∀x,y ∈G,设l k a y a x ==,,则所以,G 是交换群17.设G 为群,证明e 为G 中唯一的幂等元;证明:设G e ∈0也是幂等元,则020e e =,即e e e 020=,由消去律知e e =018.设G 为群,a,b,c∈G,证明∣abc∣=∣bca∣=∣cab∣证明：先证设e bca e abc k k =⇔=)()(设,)(e abc k =则e abc abc abc abc =)())()(( ,即 e a bca bca bca bca a =-1)())()((左边同乘1-a ,右边同乘a 得反过来,设,)(e bac k =则.)(e abc k= 由元素阶的定义知,∣abc∣=∣bca∣,同理∣bca∣=∣cab∣19.证明：偶数阶群G 必含2阶元;证明：设群G 不含2阶元,G a ∈∀,当e a =时,a 是一阶元,当e a ≠时,a 至少是3阶元,因为群G 时有限阶的,所以a 是有限阶的,设a 是k 阶的,则1-a 也是k 阶的,所以高于3阶的元成对出现的,G 不含2阶元,G 含唯一的1阶元e ,这与群G 是偶数阶的矛盾;所以,偶数阶群G 必含2阶元20.设G 为非Abel 群,证明G 中存在非单位元a 和b,a≠b,且ab=ba.证明：先证明G 含至少含3阶元;若G 只含1阶元,则G={e},G 为Abel 群矛盾；若G 除了1阶元e 外,其余元a 均为2阶元,则e a =2,a a =-1ba ba b a ab ab ab b b a a G b a ======∈∀------111111)(,)(,,,,所以,与G 为Abel 群矛盾；所以,G 含至少含一个3阶元,设为a ,则≠a 2a ,且22aa a a =;令2a b =的证;21.设G 是M n R 上的加法群,n≥2,判断下述子集是否构成子群;1全体对称矩阵是子群2全体对角矩阵是子群3全体行列式大于等于0的矩阵. 不是子群4全体上下三角矩阵; 是子群22.设G 为群,a 是G 中给定元素,a 的正规化子Na 表示G 中与a 可交换的元素构成的集合,即Na={x ∣x ∈G ∧xa=ax}证明Na 构成G 的子群;证明：ea=ae,φ≠∈)(a N ea xy ya x ay x y xa y ax xy a )()()()()()(=====,所以)(a N xy ∈由xa ax =,得111111,------==eax ae x xax x axx x ,即11--=ax a x ,所以)(1a N x ∈- 所以Na 构成G 的子群31.设ϕ1是群G 1到G 2的同态,ϕ2是G 2到G 3的同态,证明ϕ1ϕ 2是G 1到G 3的同态;证明：有已知ϕ1是G 1到G 2的函数,ϕ2是G 2到G 3的函数,则ϕ1·ϕ2是G 1到G 3的函数;所以:ϕ1·ϕ2是G 1到G 3的同态;33.证明循环群一定是阿贝尔群,说明阿贝尔群是否一定为循环群,并证明你的结论; 证明：设G 是循环群,令G=<a>,G y x ∈∀,,令l k a y a x ==,,那么yx a a a a a a xy k l k l l k l k =====++,G 是阿贝尔群克莱因四元群,},,,{c b a e G =是交换群,但不是循环群,因为e 是一阶元,a,b,c 是二阶元;36.设τσ,是5元置换,且⎪⎪⎭⎫ ⎝⎛=3541254321σ,⎪⎪⎭⎫⎝⎛=2154354321τ 1计算τσσσττσστ111,,,,---；2将τσσττσ11,,--表成不交的轮换之积;3将2中的置换表示成对换之积,并说明哪些为奇置换,哪些为偶置换; 解：1 ⎪⎪⎭⎫ ⎝⎛=1235454321τσ ⎪⎪⎭⎫ ⎝⎛=5213454321στ ⎪⎪⎭⎫ ⎝⎛=-32154543211τ 2 )1425(=τσ )14253(1=-τ )25)(143(1=-τσσ3 )15)(12)(14(=τσ 奇置换,)13)(15)(12)(14(1=-τ 偶置换)25)(13)(14(1=-τσσ 奇置换第十四章部分课后习题参考答案5、设无向图G 有10条边,3度与4度顶点各2个,其余顶点的度数均小于3,问G 至少有多少个顶点在最少顶点的情况下,写出度数列、)()(G G δ、∆;解：由握手定理图G 的度数之和为：20102=⨯3度与4度顶点各2个,这4个顶点的度数之和为14度;其余顶点的度数共有6度;其余顶点的度数均小于3,欲使G 的顶点最少,其余顶点的度数应都取2, 所以,G 至少有7个顶点, 出度数列为3,3,4,4,2,2,2,2)(,4)(==∆G G δ.7、设有向图D 的度数列为2,3,2,3,出度列为1,2,1,1,求D 的入度列,并求)(),(D D δ∆, )(),(D D ++∆δ,)(),(D D --∆δ.解：D 的度数列为2,3,2,3,出度列为1,2,1,1,D 的入度列为1,1,1,2.2)(,3)(==∆D D δ,1)(,2)(==∆++D D δ,1)(,2)(==∆--D D δ8、设无向图中有6条边,3度与5度顶点各1个,其余顶点都是2度点,问该图有多少个顶点解：由握手定理图G 的度数之和为：1262=⨯设2度点x 个,则1221513=+⨯+⨯x ,2=x ,该图有4个顶点.14、下面给出的两个正整数数列中哪个是可图化的对可图化的数列,试给出3种非同构的无向图,其中至少有两个时简单图;1 2,2,3,3,4,4,52 2,2,2,2,3,3,4,4解：1 2+2+3+3+4+4+5=23 是奇数,不可图化；2 2＋2+2+2+3+3+4+4=16, 是偶数,可图化；18、设有3个4阶4条边的无向简单图G 1、G 2、G 3,证明它们至少有两个是同构的;证明：4阶4条边的无向简单图的顶点的最大度数为3,度数之和为8,因而度数列为2,2,2,2；3,2,2,1；3,3,1,1;但3,3,1,1对应的图不是简单图;所以从同构的观点看,4阶4条边的无向简单图只有两个：所以,G 1、G 2、G 3至少有两个是同构的;20、已知n 阶无向简单图G 有m 条边,试求G 的补图G 的边数m '; 解：m n n m --='2)1( 21、无向图G 如下图1求G 的全部点割集与边割集,指出其中的割点和桥；2 求G 的点连通度)(G k 与边连通度)(G λ;解：点割集: {a,b},d边割集{e2,e3},{e3,e4},{e1,e2},{e1,e4}{e1,e3},{e2,e4},{e5})(G k =)(G λ=123、求G 的点连通度)(G k 、边连通度)(G λ与最小度数)(G δ;解：2)(=G k 、3)(=G λ 、4)(=G δ28、设n 阶无向简单图为3-正则图,且边数m 与n 满足2n-3=m 问这样的无向图有几种非同构的情况解：⎩⎨⎧=-=mn m n 3223 得n=6,m=9.31、设图G 和它的部图G 的边数分别为m 和m ,试确定G 的阶数; 解：2)1(+=+n n m m 得2)(811m m n +++-= 45、有向图D 如图1求2v 到5v 长度为1,2,3,4的通路数；2求5v 到5v 长度为1,2,3,4的回路数；3求D 中长度为4的通路数；4求D 中长度小于或等于4的回路数；5写出D 的可达矩阵;解：有向图D 的邻接矩阵为：⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=0101000101100000010110000A ,⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=00202200000101020000010102A ⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=40000020200020202020002023A 12v 到5v 长度为1,2,3,4的通路数为0,2,0,0；25v 到5v 长度为1,2,3,4的回路数为0,0,4,0；3D 中长度为4的通路数为32；4D 中长度小于或等于4的回路数10；4出D 的可达矩阵⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=1111111111111111111111111P 第十六章部分课后习题参考答案1、画出所有5阶和7阶非同构的无向树.2、一棵无向树T 有5片树叶,3个2度分支点,其余的分支点都是3度顶点,问T 有几个顶点解：设3度分支点x 个,则)135(232315-++⨯=+⨯+⨯x x ,解得3=xT 有11个顶点3、无向树T 有8个树叶,2个3度分支点,其余的分支点都是4度顶点,问T 有几个4度分支点根据T 的度数列,请至少画出4棵非同构的无向树;解：设4度分支点x 个,则)128(243218-++⨯=+⨯+⨯x x ,解得2=x4、棵无向树T 有i n i=2,3,…,k 个i 度分支点,其余顶点都是树叶,问T 应该有几片树叶解：设树叶x 片,则)1(21-+⨯=⨯+⨯x n x i n i i ,解得2)2(+-=i n i x评论：2,3,4题都是用了两个结论,一是握手定理,二是1-=n m5、nn≥3阶无向树T 的最大度(T)至少为几最多为几解：2,n-16、若nn ≥3阶无向树T 的最大度(T) =2,问T 中最长的路径长度为几解：n-17、证明：nn ≥2 阶无向树不是欧拉图.证明：无向树没有回路,因而不是欧拉图;8、证明：nn ≥2 阶无向树不是哈密顿图.证明：无向树没有回路,因而不是哈密顿图;9、证明：任何无向树T 都是二部图.证明：无向树没有回路,因而不存在技术长度的圈,是二部图;10、什么样的无向树T 既是欧拉图,又是哈密顿图解：一阶无向树14、设e 为无向连通图G 中的一条边, e 在G 的任何生成树中,问e 应有什么性质解：e 是桥15、设e为无向连通图G中的一条边, e不在G的任何生成树中, 问e应有什么性质解：e是环23、已知n阶m条的无向图G是kk≥2棵树组成的森林,证明：m = n-k.；证明：数学归纳法;k=1时, m = n-1,结论成立；时,结论成立,当k=t时,无向图G是t棵树组成的森林,任取两棵树,每棵树任取一个设k=t-1t-11顶点,这两个顶点连线;则所得新图有t-1棵树,所以m = n-k-1.所以原图中m = n-k得证;24、在图所示2图中,实边所示的生成子图T是该图的生成树.1指出T的弦,及每条弦对应的基本回路和对应T的基本回路系统.2 指出T的所有树枝, 及每条树枝对应的基本割集和对应T的基本割集系统.a b图解：aT的弦：c,d,g,hT的基本回路系统: S={{a,c,b},{a,b,f,d},{e,a,b,h},{e,a,b,f,g}}T的所有树枝: e,a,b,fT的基本割集系统: S={{e,g,h},{a,c,d,g,h},{b,c,d,g,h},{f,d,g}}b有关问题仿照给出25、求图所示带权图中的最小生成树.a b图解：注：答案不唯一;37、画一棵权为3,4,5,6,7,8,9的最优2叉树,并计算出它的权.38.下面给出的各符号串集合哪些是前缀码A1={0,10,110,1111} 是前缀码A2={1,01,001,000} 是前缀码A3={1,11,101,001,0011} 不是前缀码A4={b,c,aa,ac,aba,abb,abc} 是前缀码A5={ b,c,a,aa,ac,abc,abb,aba} 不是前缀码41.设7个字母在通信中出现的频率如下:a: 35% b: 20%c: 15% d: 10%e: 10% f: 5%g: 5%用Huffman算法求传输它们的前缀码.要求画出最优树,指出每个字母对应的编码.并指出传输10n n ≥2个按上述频率出现的字母,需要多少个二进制数字.解：a:01 b:10 c:000 d:110 e:001 f:1111 g:1110WT=54+54+103+103+153+202+352=255传输10n n≥2个按上述频率出现的字母,需要25510n-2个二进制数字.。

（完整版）洪帆《离散数学基础》（第三版）课后习题答案

（完整版）洪帆《离散数学基础》（第三版）课后习题答案第1章集合1、列举下列集合的元素 (1) ⼩于20的素数的集合 (2) ⼩于5的⾮负整数的集合 (3) 2{|,10240515}i i I i i i ∈--<≤≤且答：(1) {1,3,5,7,11,13,17,19}(2) {0,1,2,3,4} (3) {5,6,7,8,9,10,11}2、⽤描述法表⽰下列集合 (1) 12345{,,,,}a a a a a 答：{|,15}i a i I i ∈≤≤ (2) {2,4,8,}L 答：{2|}i i N ∈ (3) {0,2,4,100}L答：{2|,050}i i Z i ∈≤≤3、下⾯哪些式⼦是错误的？ (1) {}{{}}a a ∈答：正确 (2) {}{{}}a a ? 答：错误 (3) {}{{},}a a a ∈答：正确 (4) {}{{},}a a a ? 答：正确4、已给{2,,{3},4}S a =和{{},3,4,1}R a =，指出下⾯哪些论断是正确的？哪些是错误的？ (1) {}a S ∈错误(2) {}a R ∈正确 (3) {,4,{3}}a S ? 正确 (4) {{},1,3,4}a R ? 正确 (5)R S = 错误 (6) {}a S ? 正确 (7) {}a R ?错误 (8) R φ?正确 (9) {{}}a R φ?? 正确 (10) {}S φ?错误 (11) R φ∈错误 (12) {{3},4}φ?正确5、列举出集合,,A B C 的例⼦，使其满⾜A B ∈，B C ∈且A C ?答：{}A a =，{{}}B a =，显然A B ∈，{{{}}}C a =，显然B C ∈，但是A C ?。

6、给出下列集合的幂集 (1) {,{}}a b答：幂集{,{},{{}},{,{}}a b a b φ (2) {,,{}}a a φ答：幂集{,{},{},{{}},{,},{,{}},{,{}},{,,{}}}a a a a a a a a φφφφφ 7、设{}A a =，给出A 和2A 的幂集答：2{,{}}A a φ= 22{,{{}},{{}},{,{}}}Aa a φφφ=8、设128{,,,}A a a a =L 由17B 和31B 所表⽰的A 的⼦集各是什么？应如何表⽰⼦集2,67{,}a a a 和13{,}a a 答：170001000148{,}B B a a ==310001111145678{,,,,}B B a a a a a ==2,670100011070{,}a a a B B ==，1310100000160{,}a a B B ==9、设{1,2,3,4,5}U =，{1,4}A =，{1,2,5}B =，{2,4}C =，确定集合： (1) A B '? (2) ()A B C '?? (3) ()A B C ?? (4)()()A B A C (5) ()A B '? (6) A B ''? (7) ()B C '? (8)B C ''? (9) 22A C - (10)22A C ? 答：(1) {3,4}B '=，{4}A B '?=(2) {1}A B ?=，{1,3,5}C '=，(){1,3,5}A B C '??= (3) {2}B C ?=，(){1,2,4}A B C ??=(4) {1,2,4,5}A B ?=，{1,2,4}A C ?=，()(){1,2,4}A B A C = (5) (){2,3,4,5}A B '?= (6) {2,3,5}A '=，{2,3,4,5}A B ''?= (7){1,2,4,5}B C ?=，(){3}B C '?= (8) {3,4}B '=，{1,3,5}C '=，{3}B C ''?=(9) 2{,{1},{4},{1,4}}A φ=，2{,{2},{4}{24}}C φ=，，，22{{1},{1,4}}A C -= (10) 22{,{4}}A C φ?=10、给定⾃然数集N 的下列⼦集：{1,2,7,8}A =，2{|50}B i i =<，{|330}C i i i =≤≤可被整数，0{|2,,06}k D i i k Z k ==∈≤≤求下列集合： (1) (())A B C D 答：{1,2,3,4,5,6,7}B =，{0,3,6,9,12,15,18,21,24,27,30}C =，{1,2,4,8,16,32,64}D =(()){0,1,2,3,4,5,6,7,8,9,12,15,16,18,21,24,27,30,32,64}A B C D = (2) (())A B C D φ=(3) ()B A C -?解：{0,1,2,3,6,7,8,9,12,15,18,21,24,27,30}A C ?=，(){4,5}B A C -?= (4) ()A B D '??解：{3,4,5,6}A B B A '?=-=，(){1,2,3,4,5,6,8,16,32,64}A B D '??=11、给定⾃然数集N 的下列⼦集{|12}A n n =<，{|8}B n n =≤，{|2,}C n n k k N ==∈，{|3,}D n n k k N ==∈ {|21,}E n n k k N ==-∈将下列集合表⽰为由,,,,A B C D E 产⽣的集合：(1) {2,4,6,8} (2){3,6,9} (3){10} (4){|369}n n n n ==≥或或 (5) {|109}n n n n n ≤>是偶数且或是奇数且 (6) {|6}n n 是的倍数答：{1,2,3,4,5,6,7,8,9,10,11}A =，{1,2,3,4,5,6,7,8}B ={2,4,6,8,}C =L ，{3,6,9,12,}D =L ，{1,3,5,7,}E =L {2,4,6,8}B C =? {3,6,9}=A D ? {10}=(())A B D E ---(4){|369}n n n n ==≥=或或{3}{6}{9,10,11,12,}??L{3,6,9,10,11,12,}()A D B '==??L(5) {2,4,6,8,10,11,13,15,}(()())(())A E E B A D B =-?--?-L (6) {|6}{6,12,18,24,30}n n ==L 是的倍数C D ?12、判断以下哪些论断是正确的，哪些论断是错误的，并说明理由。

《离散数学》讲义(胡盛)

小结
合式公式（命题公式）及其判定自然语言的翻译（符号化形式）
列出原子命题，并符号化不同的原子命题使用不同的符号，符号使用最少选择合适的联结词，根据命题表达的真实含义，而不拘泥于形式
离散数学
30
1-3 命题公式与翻译
P12(3)(5)ad(7)
离散数学
31
第一章数理逻辑 1-4 真值表与等价公式
(PQ) (PQ) T F F T
35
1、真值表
例题4 给出(PQ)(PQ)的真值表公式不论命题变元做何种指派，其真值永为真，我们把这类公式记为T。
P Q PQ (PQ) P Q PQ T T T F F T F F T F F F F T T T F F T T F T F T F T T T (PQ)( PQ) T T T T
定义1-5.1
给定一命题公式，若无论对分量作怎样的指派，其对应的真值永为T，则称该命题公式为重言式或永真公式。例如：表1-4.4
明天下雨
2. 我们去看电影
房间里有十张凳子
二元运算
离散数学 17
1-2 联结词
析取(),其定义可用如下真值表表示
P T T F Q T F T PQ T T T 今天我在家看电视或去剧场看戏
她可能是100米或400米赛跑的冠军
他昨天作了二十或三十道习题可兼或
F
F
F
排斥或
二元运算
离散数学 18
它可以是有意义的一般论证，也可以是科学理论中的数学证明或结论。建立逻辑学的主要目的在于探索出一套完整的规则，按照这些规则，就可以确定任何特定论证是否有效。这些规则，通常称为推理规则。
离散数学
6

离散数学 16章

3/7/2011 8:48 AM Discrete Math. , huang liujia 4
CHAPTER Fourteen
先证G中无回路中无回路。中存在某个结点v上的环 ②⇒③ 先证中无回路。若G中存在某个结点上的环，中存在某个结点上的环，存在一条路L ∀u∈V，由条件知到v存在一条路 1：u…v， ∈ ，由条件知u到存在一条路，有另一条路L 则u到v有另一条路 2：u…vv，矛盾。到有另一条路，矛盾。中存在长度大于等于2的一条回路若G中存在长度大于等于的一条回路，则回路上两个结点之间存中存在长度大于等于的一条回路，在不同的路, 矛盾。所以G中无回路中无回路。在不同的路矛盾。所以中无回路。以下用归纳法证明m=n–1。。以下用归纳法证明为平凡图，当n=1时，G为平凡图，m=0=1–1=n–1。结论成立。时为平凡图。结论成立。设n≤k时，结论成立。下证时结论成立。下证n=k+1时，结论也成立。时结论也成立。中的一条边，中无回路，设e=(u,v)是G中的一条边，由于中无回路，所以 e有两个连是中的一条边由于G中无回路所以G- 通分支G 设它们的结点数和边数分别为：通分支 1和G2，设它们的结点数和边数分别为：n1，m1和n2，m2。于是有n 和于是有 1≤k和n2≤k，由归纳假设知：m1=n1–1和m2=n2-1，，由归纳假设知：和， m=m1＋m2＋1=n1-1＋n2-1＋1=n-1。＋＋。
3/7/2011 8:48 AM
Discrete Math. , huang liujia
8
例题
CHAPTER Fourteen
已知无向树T有片树叶度与度顶点各1个片树叶, 度与3度顶点各例2 已知无向树有5片树叶 2度与度顶点各个, 其余顶点的度数均为4. 求T的阶数并画出满足要求的所有非同构的无向树. 数均为的阶数n, 并画出满足要求的所有非同构的无向树的阶数的阶数为n, 度顶点的个数为n− 解设T的阶数为则边数为 −1, 4度顶点的个数为 −7. 由握手定的阶数为则边数为n− 度顶点的个数为理得 2m=2(n−1)=5×1+2×1+3×1+4(n−7) − × × × − 解出n=8, 4度顶点为个. 度顶点为1个解出度顶点为 T的度数列为的度数列为1,1,1,1,1,2,3,4 的度数列为有3棵非同构的无向树棵非同构的无向树

《离散数学》教学大纲

《离散数学》教学大纲（Discrete Mathematics）适用专业：电子信息类课程类别：学科基础课课程学时：48课程学分：3.0先修课程：高等数学、线性代数等一、课程简介离散数学是研究离散量的结构及其相互关系的数学学科，是现代数学的一个重要分支，是计算机科学中基础理论的核心课程，是计算机科学与技术的支撑学科。

它在计算机科学与技术领域有着广泛的应用，同时离散数学也是计算机专业的许多专业课程，如程序设计语言、数据结构、操作系统、编译技术、人工智能与机器人、数据库、网络、计算机图形学、算法设计与分析、理论计算机科学基础等必不可少的先行课程。

通过离散数学的学习，不但可以掌握离散结构的描述工具和处理方法，为后续课程的学习创造条件，而且可以提高抽象思维和严格的逻辑推理能力，为将来参与创新性的研究和开发工作打下坚实的基础。

二、教学目的与任务离散数学是一门培养学生缜密思维、严格推理，具有综合归纳分析能力的课程。

通过本课程的学习，使学生有一定的严格逻辑推理与抽象思维能力，掌握离散量的处理及运算技能，能够将离散数学应用到解决计算机技术中的实际问题中。

不仅能为学生奠定计算机科学的专业基础，并且能为将后续课程的学习及将来开发软、硬件技术及研究、应用提供有力的工具。

三、课程内容第1章命题逻辑的基本概念1.1命题与联结词1.2命题公式及其赋值第2章命题逻辑等值演算2.1等值式2.2析取范式与合取范式* 2.3联结词的完备集* 2.4可满足性问题与消解法第3章命题逻辑的推理理论3.1推理的形式结构3.2自然推理系统P3.3消解证明法第4章一阶逻辑基本概念4.1一阶逻辑命题符号化4.2一阶逻辑公式及其解释第5章一阶逻辑等值演算与推理5.1一阶逻辑等值式与置换规则5.2一阶逻辑前束范式* 5.3一阶逻辑的推理理论第6章集合代数6.1集合的基本概念6.2集合的运算6.3有穷集的计数6.4集合恒等式第7章二元关系7.1有序对与笛卡儿积7.2二元关系7.3关系的运算7.4关系的性质7.5关系的闭包7.6等价关系与划分7.7偏序关系第8章函数8.1函数的定义与性质8.2函数的复合与反函数* 8.3双射函数与集合的基数* 8.4一个电话系统的描述实例第14章图的基本概念14.1图14.2通路与回路14.3图的连通性14.4图的矩阵表示* 14.5图的运算第15章欧拉图与哈密顿图15.1欧拉图15.2哈密顿图15.3最短路问题、中国邮递员问题与货郎担问题第16章树16.1无向树及其性质16.2生成树16.3根树及其应用三、课程学时分配、教学内容与教学基本要求四、教学方法与教学手段说明该课程教学方式主要有：课堂教学、交互学习、课后作业。

离散数学16教案讲稿

旅行售货商问题与线性规划的指派问题相关但不等价，因此，当问题很大时，应使用整数规划技术．在此，我们仅讨论与图有关方面的问题．
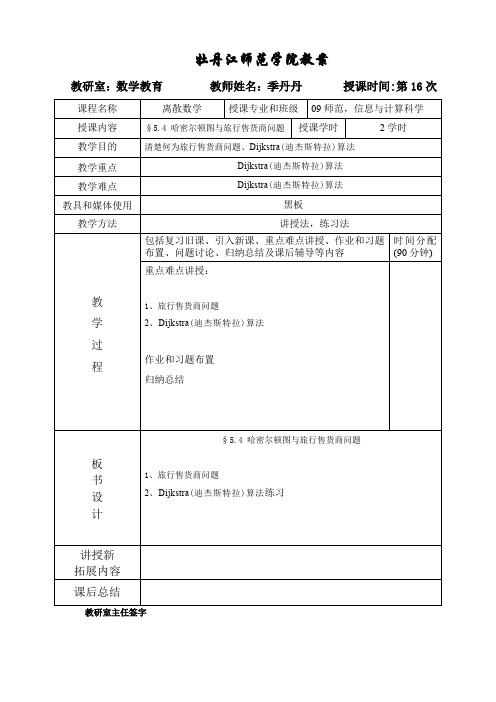
Dijkstra(迪杰斯特拉)算法：
Dijkstra(迪杰斯特拉)算法是典型的单源最短路径算法，用于计算一个节点到其他所有节点的最短路径．主要特点是以起始点为中心向外层层扩展，直到扩展到终点为止．Dijkstra算法是很有代表性的最短路径算法，在很多专业课程中都作为基本内容有详细的介绍，如数据结构，运筹学等等．Dijkstra一般的表述通常有两种方式，一种用永久和临时标号方式，一种是用OPEN,CLOSE表的方式，这里均采用永久和临时标号的方式．注意该算法要求图中不存在负权边．
1．设置，，，（，是永久标号，其余标号均为临时标号）
2．循环所有与关联的临时标号的顶点
1）如果（是与两顶点间边的权值）
那么设置
2）计算且有临时标号
置为永久标号
3）如果
那么设置，
3．对每一个顶点，，利用从开始回溯找到到的最短路径
4．算法结束．
如果用本算法求一个图中全部的最短路，则要以每个点为源点调用一次Dijkstra算法．至今还没有找到解决货郎担问题的更有效算法，它是众多NP难解问题中的一个．
例4在带权图5-4-7中，求从到其余各点的最短路径和距离．
解，
，
，
， .
例5现有一电脑代理商要从她所在城市出发，乘飞机去5个城市，然后回到出发点．如图5-4-8所示，顶点代表城市．是她所在的城市．边代表城市间的直达航线．她怎么才能访问每个城市恰巧一次，最后回到出发点呢？
解从图中我们可以看出，销售代表要到达城市，只能经由或，因此她的飞行路线必须包括和．这就使得她必须走路线，否则她就得走路线，但这样一来就提早的形成了一个圈．同理，她也不能走路线．再通过简单的分析，找到两条可行的路线： , , 和 , , ．从而得到她的这个行程应为：或者．当然，她还可以将顺序颠倒，得到4条不同的巡回路线．

离散数学答案版(全)

第一章命题逻辑内容：命题及命题联结词、命题公式的基本概念，真值表、基本等价式及永真蕴涵式，命题演算的推理理论中常用的直接证明、条件证明、反证法等证明方法。

教学目的：1. 熟练掌握命题、联结词、复合命题、命题公式及其解释的概念。

2. 熟练掌握常用的基本等价式及其应用。

3. 熟练掌握（主）析/合取范式的求法及其应用。

4. 熟练掌握常用的永真蕴涵式及其在逻辑推理中的应用。

5. 熟练掌握形式演绎的方法。

教学重点：1 .命题的概念及判断2 .联结词，命题的翻译3. 主析（合）取范式的求法4. 逻辑推理教学难点：1. 主析（合）取范式的求法2. 逻辑推理1.1命题及其表示法1.1.1 命题的概念数理逻辑将能够判断真假的陈述句称作命题。

1.1.2 命题的表示命题通常使用大写字母 A , B,…，Z或带下标的大写字母或数字表示,如A i, [10], R等，例如A1：我是一名大学生。

A1：我是一名大学生.[10]:我是一名大学生。

R：我是一名大学生。

1.2命题联结词1.2.1否定联结词「P1.2.2合取联结词A1.2.3 析取联结词V1.2.4 条件联结词—125126 与非联结词T性质：(1)P T P=「( PAP)二「P；(2)(P T Q)T( P T Q) -「( P T Q) - PAQ；(3)( P T P)T( Q TQ) -「P T「Q= P V Q。

127 或非联结词J性质:(1) P J P=「( P V Q) =「P;(2)( P J Q )；( P J Q) =「( P J Q) = P V Q;(3)( P J P)J( Q J Q) =「P Q=P V-Q) = PAQ1.3 命题公式、翻译与解释1.3.1 命题公式定义命题公式，简称公式，定义为：（1）单个命题变元是公式；（2 ）如果P是公式，则「P是公式；（3）如果P、Q是公式,则PAQ、PVQ、P > Q、P Q都是公式；（4）当且仅当能够有限次的应用（1）、（2）、（3）所得到的包括命题变元、联结词和括号的符号串是公式。

离散数学第2版课后答案

5)?x?1(mod 5)????x?1(mod 3)
?x?3(mod8)??x?1(mod 3) ：求解同余方程组 ?x?1(mod 5)?
m1=8 ， m2=3 ，m3=5 ，m=120 ，m1=15 ， m2=40 ， m3=24
15x≡1(mod 8),40x ≡1(mod 3),24x ≡1(mod 5的) 特解：
所以， p=3
11 计算 2400 mod 319 。
解：
14(2) 解同余方程： 56x≡88(mod 96) 。
解：
（1） (a,m)=(56,96)=8 ， 8|96 ，方程有解
（2） a?=56/8=7 ， b?=88/8=11 ，m?=96/8=12
（3）由辗转相除法可求得 p 和 q 满足 pa?+qm?=1 ， p=-5 ， q=3
?5x?7(mod 12)16(2) 解同余方程组 ? 7x?1(mod 10)?
解：
5x≡7(mod 12) ? 12?(5x -7) ? 4?(5x-7) 且 3?(5x- 7) ? 5x ≡7(mod 4)
且 5x≡7(mod 3) ∴同余方程 5x≡7(mod 12) 与同余方程
组??5x?7(mod 4) 同解
c1=7,c2=1,c3=4
19 ． *设 m1 和 m2 是正整数， b1 和 b2 是整数。证明一次同余方程
5 ．设 a、b、 c、 d 是正整数，满足 ab=cd 。证明： a4+b4+c4+d4 不是素数。证明：设 11)(n-1)! ∴ n 整除 (1++?+2n-1adp?? ，其中 p 和 q 是互素的正整数 cbq aq=cp ? p?aq ? p?a （∵ p 和 q 互素）于是， ?u?n ，使 a=pu ? c=qu

14.4+16离散数学

13
有向图关联矩阵的性质：有向图关联矩阵的性质：
14
有向图关联矩阵的性质：有向图关联矩阵的性质：
（1）∑ m ij = 0( j = 1,2,⋯, m ) ，从而 ∑ ∑ m ij = 0 ，这说明 j=1 i =1 i =1 有向图关联矩阵中所有元素之和为0。
n
m
n
0 0 0 − 1 1 1 −1 1 0 0 0 0 0 1 1 0 0 − 1 − 1 − 1
(1 ) i = 1 j= 1
n
n
长度为1的通路的总数。长度为1的通路的总数。而中环的个数，中长度为1的回路总数。 ∑ a ii 为D中环的个数，即D中长度为1的回路总数。
(1 ) i =1 n
24
问下图中有多少条长度为2、3、4…. 的通路？
25
0 0 0 ' A = 0 0 0 0
0 0 0 0
2 1 0 0 1 0 0 0 1 0 1 1
∑a
j= 1
n
(1 ) ij
，于是 n n a (1) = n d + ( v ) = m = d ( v i )(i = 1,2,⋯, n ) ∑ ∑ ij ∑ i
+
i =1 j=1 i =1
∑a
i =1
4
强连通图和单向连通图的判别定理定理14 14. 定理14.8 有向图D是强连通图当且仅当D中存在经过每个顶点至少一次的回路。定理14.9 有向图D是单向连通图当且仅当D 定理14.9 中存在经过每个顶点至少一次的通路。
5
例
（1）
（2）
（3）
（1）是强连通图（2）是单向连通图（3）是弱连通图

离散数学主范式习题

主范式习题
一、本章的主要内容及要求 1．基本内容等值式与等值演算基本的等值式（16 组，24 个公式）主析取与主合取范式联结词完备集
2. 要求深刻理解等值式的概念牢记基本等值式的名称及它们的内容了解简单析取式、简单合取式、析取范式、合取范式的概念深刻理解极小项、极大项的概念、名称及下角标与成真、成假赋值的关系，并理解简单合取式与极小项的关系熟练掌握求主范式的方法（等值演算、真值表等）会用公式的主范式求公式的成真、成假赋值及判断公式的类型、简单应用会将任何公式化成任何联结词完备集中的公式
④ A (pqrsu)(pqrsu) 结论：由④可知，A 的成真赋值为 00110 与 11001，因而
派孙、李去（赵、钱、周不去）或派赵、钱、周去（孙、李不去）
A 的演算过程
A (pq)((qr)(qr))
(su)(u(pq))
（1）若赵去，钱也去. （2）李、周两人中必至少有一人去（3）钱、孙两人中去仅去一人. （4）孙、李两人同去或同不去. （5）若周去，则赵、钱也去.
用等值演算法分析该公司如何选派他们出国？解此类问题的步骤应为：
○1 将简单命题符号化 ○2 写出各复合命题 ○3 写出由②中复合命题组成的合取式 ○4 将③中公式化成析取式（最好是主析取范式）
解（1）为真，这是显然的
（2）为假. 注意, 任何公式与它的主范式是等值的，显然重言式不能与 0 等值。重言式的主合取范式不含极大项，因而主合取范式为 1.
（3）的分析类似于（2），矛盾式的主析取范式为 0. （4）为假，因为{, }不是完备集，比如矛盾式(pq)q
不能化成{, }中的公式. （5）为真，注意{, , }的子集{, }为完备集.