01 质点运动学答案
1.质点运动学答案

质点运动学1一、选择题1、 分别以r 、s 、υ和a 表示质点运动的位矢、路程、速度和加速度,下列表述中正确的是A 、r r ∆=∆B 、υ==dt ds dt r dC 、dt d a υ=D 、υ=dt dr [ B ] 2、 一质点沿Y 轴运动,其运动学方程为324t t y -=, 0=t 时质点位于坐标原点,当质点返回原点时,其速度和加速度分别为 A 、116-⋅s m ,216-⋅s mB 、116-⋅-s m ,216-⋅s mC 、116-⋅-s m ,216-⋅-s mD 、116-⋅s m ,216-⋅-s m [ C ]3、已知质点的运动方程为:θθcos cos 2Bt At x +=,θθsin sin 2Bt At y +=,式中θ、、B A 均为恒量,且0>A ,0>B ,则质点的运动为:A .一般曲线运动;B .圆周运动;C .椭圆运动;D .直线运动;( D )[分析] 质点的运动方程为 22cos cos sin sin x At Bt y At Bt θθθθ⎧=+⎨=+⎩由此可知θtan =xy, 即 ()x y θtan = 由于=θ恒量,所以上述轨道方程为直线方程。
又 ()()⎩⎨⎧+=+=θθsin cos Bt A v Bt A v y x 22⎩⎨⎧====恒量恒量θθsin cos B a B a yx 22由于0>A ,0>B ,显然v 与a 同号,故质点作匀加速直线运动。
4、质点在平面内运动,位矢为)(t r,若保持0=dtdr,则质点的运动是A 、匀速直线运动B 、 变速直线运动C 、圆周运动D 、匀速曲线运动 [ C ]二、填空题5、一质点沿直线运动,其运动学方程为26t t x -=,则t 由0至4s 的时间间隔内,质点的位移大小为 8 m ,在t 由0到4s 的时间间隔内质点走过的路程为 10 m 。
6、质点的运动方程为j t t i t t r)3121()21(32+++-=,当s t 2=时,其加速度=a4r i j =-+。
大学物理第1章习题参考答案

习 题 解 答第一章 质点运动学1-1 (1) 质点t 时刻位矢为:j t t i t r⎪⎭⎫ ⎝⎛-+++=4321)53(2(m)(2) 第一秒内位移j y y i x x r)()(01011-+-=∆)101(3)01(21)01(32ji ⎥⎦⎤⎢⎣⎡-+--=(3) (4) (5) (6) 1-2 =v c t t t c t v x x +++=+==⎰⎰241d d 34当t =2时x =4代入求证 c =-12 即1224134-++=t t t xtt tv a t t v 63d d 23223+==++=将t =3s 代入证)sm (45)sm (56)(414123133--⋅=⋅==a v m x1-3 (1) 由运动方程⎩⎨⎧+==ty t x 2342消去t 得轨迹方程0)3(2=--y x(2) 1秒时间坐标和位矢方向为 m y m x 5411==[4,5]m: ︒===3.51,25.1ααx y tg(3) 第1秒内的位移和平均速度分别为)m (24)35()04(1j i j i r+=-+-=∆(4) 1-41-5 g)(25m/s1047.280.13600101600223≈⨯=⨯⨯==t v a基本上未超过25g.1.80s 内实验车跑的距离为)(m 40080.13600210160023=⨯⨯⨯==t v s1-6 (1)设第一块石头扔出后t 秒未被第二块击中,则2021gt t v h -=代入已知数得28.9211511t t ⨯-=解此方程,可得二解为s 22.1s,84.111='=t t第一块石头上升到顶点所用的时间为s 53.18.9/15/10===g v t m由于m t t >1,这对应于第一块石头回落时与第二块相碰;又由于m t t <'1这对应于第一块石头上升时被第二块赶上击中.以20v 和'20v 分别对应于在t 1和'1t 时刻两石块相碰时第二石块的初速度,则由于2111120)(21)(t t g t t v h ∆∆---=(2) .对应于t 13.184.122212120-=-="t t v ∆m /s )(0.23=1-7 以l 表示从船到定滑轮的绳长,则t l v d /d 0-=.由图可知22h l s -=于是得船的速度为02222d d d d v sh s tl hl l ts v +-=-==负号表示船在水面上向岸靠近. 船的加速度为3202022d d d dd d s v h t l v hl l lt va -=⎥⎥⎦⎤⎢⎢⎣⎡⎪⎪⎭⎫ ⎝⎛--== 负号表示a 的方向指向岸边,因而船向岸边加速运动. 1-8 所求位数为522422221048.9601.0)106(44⨯=⨯⨯⨯==ππωgr n gr1-9 物体A 下降的加速度(如图所示)为222m/s 2.04.022=⨯==h a在1-10 2m /s 2.1=a ,s 5.00=t ,m 5.10=h .如图所示,相对南面,小球开始下落时,它和电梯的速度为m/s)(6.05.02.100=⨯==at v以t 表示此后小球落至底板所需时间,则在这段时间内,小球下落的距离为2021gt t v h +=电梯下降的距离为习题1-9图 习题1-10图2021at t v h +='又20)(21t a g h h h -='-=由此得s 59.02.18.95.1220=-⨯=-=ag h t而小球相对地面下落的距离为2021gt t v h +=259.08.92159.06.0⨯⨯+⨯=m 06.2= 1-11风地vb )两图中风地v应是同一矢量.1-12 (1) vLv L t 22==(2) 22212uv vL uv L uv L t t t -=++-=+=1212-⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛-=v u v L(3) v L v L t t t '+'=+=21,如图所示风速u 由东向西,由速度合成可得飞机对地速度v u v+=',则22uv V -='.习题1-12图习题1-11图2221222⎪⎭⎫ ⎝⎛-=--='=v u v L uv L v L t 证毕1-13 (1)设船相对岸的速度为V '(如图所示),由速度合成得V u V +='V 的大小由图1.7示可得αβcos cos u V V +'=即332323cos cos -=⨯-=-='αβu V V而1212sin sin =⨯=='αβu V船达到BD OB AB 将式(1) (2) 由t =即 c o s α故船头应与岸垂直,航时最短.将α值代入(3)式得最短航时为s)(500105.021012/sin 101333min =⨯=⨯=⨯=s u t π(3) 设l OB =,则ααββsin cos 2sin sin 22u uV Vu D V D V D l -+=''==欲使l 最短,应满足极值条件.习题1-13图a a uV Vu u D l'⎢⎢⎣⎡''-+-='cos sin cos 2d d 22αα0c o s 2s i n s i n 2222=⎥⎦⎤'-+''+αuV Vu a a uV简化后可得01cos cos 222=+'+-'αuVV u a即 01c o s 613c o s 2=+'-'αa解此方程得32cos ='α︒=='-2.4832cos1α将α'AB。
(完整版)大学物理01质点运动学习题解答

第一章质点运动学一选择题1.以下说法中,正确的选项是:()A.一物体若拥有恒定的速率,则没有变化的速度;B.一物体拥有恒定的速度,但仍有变化的速率;C.一物体拥有恒定的加快度,则其速度不行能为零;D. 一物体拥有沿x 轴正方向的加快度而有沿x 轴负方向的速度。
解:答案是 D。
2.长度不变的杆 AB,其端点 A 以 v0匀速沿 y 轴向下滑动, B 点沿 x 轴挪动,则 B 点的速率为:()A . v0 sinB .v0 cos C.v0 tan D.v0 / cos解:答案是 C。
简要提示:设 B 点的坐标为 x, A 点的坐标为 y,杆的长度为l,则x2y2l 2对上式两边关于时间求导:dx dy0,因dxv,dyv0,所以2 x 2 ydtdt dt dt2xv2yv0 = 0即v=v0 y/x =v0tan所以答案是 C。
3.如图示,路灯距地面高为 H,行人身高为 h,若人以匀速 v 背向路灯行走,灯y人头A H vv0hθvx影sB选择题 3图选择题 2图则人头影子挪动的速度u 为()H h Hv h HA.vB.H H h H h 解:答案是 B 。
简要提示:设人头影子到灯杆的距离为 x ,则x s h , x Hs , x H H hdx H ds HvuH h dt Hdt h所以答案是 B 。
4. 某质点作直线运动的运动学方程为x = 3t-5t 3 + 6 (SI),则该质点作A. 匀加快直线运动,加快度沿 x 轴正方向.B. 匀加快直线运动,加快度沿 x 轴负方向.C. 变加快直线运动,加快度沿 x 轴正方向.D. 变加快直线运动,加快度沿x 轴负方向.()解: 答案是 D5. 一物体从某一确立高度以v 0 的初速度水平抛出,已知它落地时的速度为v t ,那么它的运动时间是: ()v t - v 0v t v 0v t2 22v v 0 v t A.B.C.gD.2 gg2 g解:答案是 C 。
大学物理第一章 质点运动学-习题及答案

第一章 质点运动学1-1 一质点在平面上运动,已知质点位置矢量的表示式为j i r 22bt at += (其中b a ,为常量) 则该质点作(A )匀速直线运动 (B )变速直线运动(C )抛物线运动 (D )一般曲线运动 [B]解:由j i rv bt at t 22d d +==知 v 随t 变化,质点作变速运动。
又由x aby bt y at x =⎪⎭⎪⎬⎫==22 知质点轨迹为一直线。
故该质点作变速直线运动。
1-2 质点作曲线运动,r 表示位置矢量,s 表示路程,t a 表示切向加速度,下列表达式中,① a t v =d ② v t r =d ③ v t s =d d ④ t a t =d d v (A )只有(1)、(4)是对的。
(B )只有(2)、(4)是对的。
(C )只有(2)是对的。
(D )只有(3)是对的。
[D]解:由定义:t vt a d d d d ≠=v ; t r t s t v d d d d d d ≠==r ; t t v a d d d d v ≠=τ只有③正确。
1-3 在相对地面静止的坐标系内,A 、B 二船都以21s m -⋅的速率匀速行驶,A 船沿x 轴正向,B 船沿y 轴正向。
今在A 船上设置与静止坐标系方向相同的坐标系(x ,y 方向单位矢用j i ,表示),那么在A 船上的坐标系中,B 船的速度(以1s m -⋅为单位)为(A )j i 22+ (B )j i 22+-(C )j i 22-- (D )j i 22- [B]解:由i v 2=对地A ,j v 2=对地B 可得 A B A B 地对对地对v v v +=⎰对地对地A B v v -=i j 22-=j i 22+-= (1s m -⋅)1-4 一质点沿x 方向运动,其加速度随时间变化关系为)SI (23t a +=如果初始时质点的速度0v 为51s m -⋅,则当t 为3s 时,质点的速度1s m 23-⋅=v解:⎰+=tta v v 00d13s m 23d )23(5-⋅=++=⎰tt1-5 一质点的运动方程为SI)(62t t x -=,则在t 由0至4s 的时间间隔内,质点的位移大小为 8m ,在t 由0到4s 的时间间隔内质点走过的路程为 10m 。
大学物理第一章 质点运动学-习题及答案

第一章 质点运动学1-1 一质点在平面上运动,已知质点位置矢量的表示式为j i r 22bt at += (其中b a ,为常量) 则该质点作(A )匀速直线运动 (B )变速直线运动(C )抛物线运动 (D )一般曲线运动 [B]解:由j i rv bt at t 22d d +==知 v 随t 变化,质点作变速运动。
又由x aby bt y at x =⎪⎭⎪⎬⎫==22 知质点轨迹为一直线。
故该质点作变速直线运动。
1-2 质点作曲线运动,r 表示位置矢量,s 表示路程,t a 表示切向加速度,下列表达式中,① a t v =d ② v t r =d ③ v t s =d d ④ t a t =d d v (A )只有(1)、(4)是对的。
(B )只有(2)、(4)是对的。
(C )只有(2)是对的。
(D )只有(3)是对的。
[D]解:由定义:t vt a d d d d ≠=v ; t r t s t v d d d d d d ≠==r ; t t v a d d d d v ≠=τ只有③正确。
1-3 在相对地面静止的坐标系内,A 、B 二船都以21s m -⋅的速率匀速行驶,A 船沿x 轴正向,B 船沿y 轴正向。
今在A 船上设置与静止坐标系方向相同的坐标系(x ,y 方向单位矢用j i ,表示),那么在A 船上的坐标系中,B 船的速度(以1s m -⋅为单位)为(A )j i 22+ (B )j i 22+-(C )j i 22-- (D )j i 22- [B]解:由i v 2=对地A ,j v 2=对地B 可得 A B A B 地对对地对v v v +=⎰对地对地A B v v -=i j 22-=j i 22+-= (1s m -⋅)1-4 一质点沿x 方向运动,其加速度随时间变化关系为)SI (23t a +=如果初始时质点的速度0v 为51s m -⋅,则当t 为3s 时,质点的速度1s m 23-⋅=v解:⎰+=tta v v 00d13s m 23d )23(5-⋅=++=⎰tt1-5 一质点的运动方程为SI)(62t t x -=,则在t 由0至4s 的时间间隔内,质点的位移大小为 8m ,在t 由0到4s 的时间间隔内质点走过的路程为 10m 。
第一章质点运动学习题答案

第一章质点运动学习题答案1-1 质点做直线运动,运动方程为其中以s为单位,以m为单位,求:(1)=4s时,质点的位置、速度和加速度;(2)质点通过原点时的速度;(3)质点速度为零时的位置;(4) 做出-t图、-t图、-t图.解:(1) 根据直线运动情况下的定义,可得质点的位置、速度和加速度分别为(1)(2)(3)当=4s时,代入数字得:mm/sm/s(2)当质点通过原点时,=0,代入运动方程得:=0解得:,代入(2)式得:m/s=-12m/s(3) 将代入(2)式,得解得:s代入(1)式得:12m-6m=6m1.2一质点在平面上运动,运动方程为=3+5,=2+3-4.式中以 s计,,以m计.(1)以时间为变量,写出质点位置矢量的表示式;(2)求出=1 s 时刻和=2s 时刻的位置矢量,计算这1秒内质点的位移;(3)计算=0s时刻到=4s时刻内的平均速度;(4)求出质点速度矢量表示式,计算=4s 时质点的速度;(5)计算=0s 到=4s 内质点的平均加速度;(6)求出质点加速度矢量的表示式,计算=4s 时质点的加速度.解:(1)(2)将,代入上式即有(3)∵∴(4)则(5)∵(6)这说明该点只有方向的加速度,且为恒量.1-4 一质点沿一直线运动,其加速度为,式中的单位为m,的单位为m/s,试求该质点的速度与位置坐标之间的关系.设时,=4m/s解:依题意积分得1-5质点沿直线运动,加速度,如果当=3时,,,求质点的运动方程. (其中以m/s为单位,以s为单位,以m为单位,以m/s为单位)解:加速度表示式对积分,得将=3s,=9m,m/s代入以上二式,得积分常数m/s,=0.75m,则1-6 当物体以非常高的速度穿过空气时,由空气阻力产生的反向加速度大小与物体速度的平方成反比,即,其中为常量. 若物体不受其他力作用沿方向运动,通过原点时的速度为,试证明在此后的任意位置处其速度为.解:根据加速度定义得:,因,代入上式,分离变量,整理后得:,应用初始条件,两边积分得得即有:1-7试写出以矢量形式表示的质点做匀速圆周运动的运动学方程,并证明做匀速圆周运动质点的速度矢量和加速度矢量的标积等于零,即解:以直角坐标表示的质点运动学方程为以矢量形式表示的指点运动学方程为速度和加速度分别为所以1-8一质点在平面内运动,其运动方程为,其中均为大于零的常量.(1)试求质点在任意时刻的速度;(2)证明质点运动的轨道为椭圆;(3)证明质点的加速度恒指向椭圆的中心.解:(1)质点在任意时刻的速度(2)由消去,可得轨道方程可见是椭圆方程,表明质点作椭圆运动(3)加速度因为>0,所以的方向恒与反向,即恒指向椭圆中心.1-9路灯离地面高度为,一个身高为的人,在灯下水平路面上以匀速度步行. 如图所示,求当人与灯的水平距离为时,他的头顶在地面上的影子移动的速度的大小.解:建立如图所示的坐标,时刻头顶影子的坐标为,设头顶影子的移动速度为,则由图中可看出有,则有所以有1-10 1.10质点沿半径为的圆周按=的规律运动,式中为质点离圆周上某点的弧长,,都是常量,求:(1)时刻质点的加速度;(2)为何值时,加速度在数值上等于.解:(1)则加速度与半径的夹角为(2)由题意应有即∴当时,1-11质点做半径为20cm的圆周运动,其切向加速度恒为5cm/s,若该质点由静止开始运动,需要多少时间:(1)它的法向加速度等于切向加速度;(2)法向加速度等于切向加速度的二倍.解:质点圆周运动半径=20cm,切向加速度=5cm/s,时刻速度为,法向加速度为,因此有(1)当时,s(2)当时,s1-12 (1)地球的半径为6.37m,求地球赤道表面上一点相对于地球中心的向心加速度. (2)地球绕太阳运行的轨道半径为1.5m,求地球相对于太阳的向心加速度. (3)天文测量表明,太阳系以近似圆形的轨道绕银河系中心运动,半径为2.8m,速率为2.5m/s,求太阳系相对于银河系的向心加速度.解:(1)地球赤道表面一点相对于地球中心的向心角速度为m/s(2)地球相对太阳的向心加速度为m/s(3)太阳系相对银河系的向心加速度m/s1-13 以初速度=20抛出一小球,抛出方向与水平面成60°的夹角,求:(1)球轨道最高点的曲率半径;(2)落地处的曲率半径.解:设小球所作抛物线轨道如题1-13图所示.题1-13图(1)在最高点,又∵∴(2)在落地点,,而∴1-14一架飞机在水平地面的上方,以174m/s的速率垂直俯冲,假定飞机以圆形路径脱离俯冲,而飞机可以承受的最大加速度为78.4m/s,为了避免飞机撞到地面,求飞机开始脱离俯冲的最低高度. 假定整个运动中速率恒定.解:设飞机以半径为圆形路径俯冲,其加速度为当为飞机所能承受的最大加速度时,即为最小,所以m1-15一飞轮以速度rev/min转动,受制动而均匀减速,经s 静止,求(1) 角加速度和从制动开始到静止飞轮转过的转数;(2) 求制动开始后,s时飞轮的角速度;(3) 设飞轮半径=1m,求s时,飞轮边缘上一点的速度和加速度.解:(1)飞轮的初角速度,当s时,;代入得从开始到静止,飞轮转过的角度及其转数为:radrev(2)s 时,飞轮的角速度为rad/s(3)s 时,飞轮边缘上一点的速度为m/s相应的切线和法线加速度为m/sm/s1-16一质点沿半径为1m的圆周运动,运动方程为,式中以弧度计,以秒计,求:(1)=2s时,质点的切向和法向加速度;(2)当加速度的方向和半径成角时,其角位移是多少?解:(1)时,(2)当加速度方向与半径成角时,有即亦即则解得于是角位移为1-17一圆盘半径为3m,它的角速度在=0时为3.33rad/s,以后均匀地减小,到=4s时角速度变为零. 试计算圆盘边缘上一点在=2s时的切向加速度和法向加速度的大小.解:角速度均匀减小,因此,角加速度为rad/s圆盘做匀角加速度,故有当s时,rad/s法向和切向加速度分别为m/s=-7.8 m/s1-18某雷达站对一个飞行中的炮弹进行观测,发现炮弹达最高点时,正好位于雷达站的上方,且速率为,高度为,求在炮弹此后的飞行过程中,在(以s为单位)时刻雷达的观测方向与铅垂直方向之间的夹角及其变化率(雷达的转动角速度)解:以雷达位置为坐标原点,取坐标系如图所示,根据题意,炮弹的运动方程为可解得:(1)则将(1)式两边对求导数,得则有1-19 汽车在大雨中行驶,车速为80km/h,车中乘客看见侧面的玻璃上雨滴和铅垂线成角,当车停下来时,他发现雨滴是垂直下落的,求雨滴下落的速度.解:取车为运动参考系,雨滴相对于车的速度为,雨滴对地速度为,车对地的速度为,相对运动速度合成定理为见如图所示的速度合成图,则有m/s1-20一升降机以加速度1.22m/s上升,当上升速度为2.44 m/s时,有一螺帽自升降机的天花板松落,天花板与升降机底面相距 2.74m,计算:(1)螺帽从天花板落到底面所需的时间;(2)螺帽相对于升降机外固定柱子的下降距离.解:以升降机外固定柱子为参考系,竖直向上为坐标轴正向,螺帽松落时升降机底面位置为原点. 螺帽从=2.74m处松落,以初速度=2.44m/s做竖直上抛运动,升降机底面则从原点以同样的初速度做向上的加速运动,加速度=1.22m/s,它们的运动方程分别为螺帽:底面:螺帽落到底面上时,,由以上两式得=0.705s(2)螺帽相对于升降机外固定柱子的下降距离为m1-21某人骑自行车以速率向西行使,北风以速率吹来(对地面),问骑车者遇到风速及风向如何?解:地为静系E,人为动系M。
普通物理学 01运动学习题 答案

解: x = v t
L cos q = v t
y
=
1 2
gt2
L sinq =
1 2
gt2
2
L=
2 v 2sinq g cos 2q
=
2 ×30.6 sin 450 9.8×cos2450
= 270m
Lq
目录
1-15一个人扔石头的最大出手速率为 v=25m/s, 他能击中一个与他的手水平 距离为L = 50m而高h =13m的一个目标 吗在?这个距离上他能击中的最大高度是多少?
1-8 在质点运动中, 已知 x = aekt
dy/,dx = -bke-kt, 当 t = 0, y=y0=b
求: 质点的速度和轨道方程。
结束 目录
1-9一质点的运动方程为r = i + 4 j + tk
t2式中r、t分别以m、s为单位.试求:
它的速度与加速度;
它的轨迹方程。
解: v = d r = 8 tj +
(4)3s末的瞬时速度。?
结束 目录
解: x = 4t -
(1)2Δt3x = x 0 = 4t - 2t=3 4×2 2×23 = 8 m
v=
Δ Δ
x t
=
8 2=
4m
s
v=
dx dt
=
4
6 t2 = 4
6 ×22 =
20 m
s
(2) Δx = x3 x2
= (4×3 2×33 ) (4×1 2×13 )
k
dt
a
=
d d
v t
=
8j
x = 1 y =4 t2 z = t
轨迹方程: y = x = 1
(完整版)大学物理01质点运动学习题解答

第一章 质点运动学一 选择题1. 下列说法中,正确的是:( )A. 一物体若具有恒定的速率,则没有变化的速度;B. 一物体具有恒定的速度,但仍有变化的速率;C. 一物体具有恒定的加速度,则其速度不可能为零;D. 一物体具有沿x 轴正方向的加速度而有沿x 轴负方向的速度。
解:答案是D 。
2. 长度不变的杆AB ,其端点A 以v 0匀速沿y 轴向下滑动,B 点沿x 轴移动,则B 点的速率为:( )A . v 0 sin θB . v 0 cos θC . v 0 tan θD . v 0 / cos θ 解:答案是C 。
简要提示:设B 点的坐标为x ,A 点的坐标为y ,杆的长度为l ,则222l y x =+ 对上式两边关于时间求导:0d d 2d d 2=+t y y t x x ,因v =tx d d ,0d d v -=t y ,所以 2x v -2y v 0 = 0 即 v =v 0 y /x =v 0tan θ所以答案是C 。
3. 如图示,路灯距地面高为H ,行人身高为h ,若人以匀速v 背向路灯行走,则人头影子移动的速度u 为( ) A.v H h H - B. v h H H - C. v H h D. v hH 解:答案是B 。
v x选择题2图灯s选择题3图简要提示:设人头影子到灯杆的距离为x ,则H h x s x =-,s hH H x -=, v hH H t s h H H t x u -=-==d d d d 所以答案是B 。
4. 某质点作直线运动的运动学方程为x =3t -5t 3 + 6 (SI),则该质点作A. 匀加速直线运动,加速度沿x 轴正方向.B. 匀加速直线运动,加速度沿x 轴负方向.C. 变加速直线运动,加速度沿x 轴正方向.D. 变加速直线运动,加速度沿x 轴负方向. ( )解:答案是D5. 一物体从某一确定高度以v 0的初速度水平抛出,已知它落地时的速度为v t ,那么它的运动时间是:( ) A. g 0v v -t B. g 20v v -t C. g 202v v -t D. g2202v v -t 解:答案是C 。
(完整版)01质点运动学习题解答汇总,推荐文档

第一章 质点运动学一 选择题1. 下列说法中,正确的是 ()A. 一物体若具有恒定的速率,则没有变化的速度B. 一物体具有恒定的速度,但仍有变化的速率C. 一物体具有恒定的加速度,则其速度不可能为零D. 一物体具有沿x 轴正方向的加速度,其速度有可能沿x 轴的负方向解:答案是D 。
2. 某质点作直线运动的运动方程为x =3t -5t 3 + 6 (SI),则该质点作 ( )A. 匀加速直线运动,加速度沿x 轴正方向B. 匀加速直线运动,加速度沿x 轴负方向C. 变加速直线运动,加速度沿x 轴正方向D. 变加速直线运动,加速度沿x 轴负方向解:答案是D3. 如图示,路灯距地面高为H ,行人身高为h ,若人以匀速v 背向路灯行走,则人头影子移动的速度u 为( )A.B.C.D. v HhH -v hH H-v Hhv hH 解:答案是B 。
设人头影子到灯杆的距离为x ,则,,H h x s x =-s h H Hx -=v hH Ht s h H H t x u -=-==d d d d 所以答案是B 。
4. 一质点的运动方程为,其中t 1时刻的位矢为。
j i r )()(t y t x +=j i r )()(111t y t x +=问质点在t 1时刻的速率是()A.B.C.D. d d 1t r d d 1tr 1d dt t t=r 122)d d ()d d (t t ty t x =+解 根据速率的概念,它等于速度矢量的模。
本题答案为D 。
5. 一物体从某一确定高度以v 0的初速度水平抛出,已知它落地时的速度为v t ,那么它的运动时间是 ( )s选择题3图A.B.C.D.g 0v v -t g20v v -t g202v v -t g2202v v -t 解:答案是C 。
,,所以答案是C 。
gt t ty =-=202v v v g t t /202v v -=6. 质点作圆周运动时,下列说表述中正确的是 ()A. 速度方向一定指向切向,加速度方向一定指向圆心B. 速度方向一定指向切向,加速度方向也一般指向切向C. 由于法向分速度为零,所以法向加速度也一定为零D. 切向加速度仅由速率的变化引起解 答案是D 。
第1章 质点运动学——习题解答

第1章 质点运动学1-1 一运动质点某一瞬时位于径矢()r x y ,的端点处,关于其速度的大小有4种不同的看法,即 (1)d d tr; (2)d d t r; (3)d d sr;(4下列判断正确的是( ). (A) 只有(1)和(2)正确 (B) 只有(2)正确 (C) 只有(3)和(4)正确 (D) (1)(2)(3)(4)都正确 答案:(C )解析:瞬时速度的大小等于瞬时速率,故(3)正确;速度可由各分量合成,故(4)正确。
1-2 一质点的运动方程为22cos cos sin sin x At Bt y At Bt θθθθ⎧⎪⎨⎪⎩=+,=+,式中A ,B ,θ均为常量,且A >0,B >0,则该质点的运动为( ). (A) 一般曲线运动(B) 匀速直线运动 (C) 匀减速直线运动(D) 匀加速直线运动答案:(D )解析:由tan yxθ=可知,质点做直线运动.a x =2B cos θa y =2B sin θa =2B加速度a 为定值,故质点做匀加速直线运动.1-3 一质点沿半径为R 的圆周运动,其角速度随时间的变化规律为ω=2bt ,式中b 为正常量.如果t =0时,θ0=0,那么当质点的加速度与半径成45°角时,θ角的大小为( ) rad.(A) 12(B) 1 (C) b (D) 2b答案:(A )解析: a t =R β=2bRa n =R 2ω=4Rb 2t 2a t =a n t 2=b21θ=20tω⎰d t =bt 2=211-4 一人沿停靠的台阶式电梯走上楼需时90 s ,当他站在开动的电梯上上楼,需时60 s .如果此人沿开动的电梯走上楼,所需时间为( ).(A) 24 s (B) 30 s (C) 36 s (D) 40 s答案:(C )解析:设电梯长度为s ,则=+9060s s st , 解得t =36 s.1-5 已知质点的加速度与位移的关系式为32a x =+,当t =0时,v 0=0,x 0=0,则速度v 与位移x 的关系式为________. 答案:v 2=3x 2+4x 解析: d d d d d d d d v v x v a v t x t x ===, d d v v a x =,d =(3+2)d vxv v x x ⎰⎰,v 2=3x 2+4x .1-6 在地面上以相同的初速v 0,不同的抛射角θ斜向上抛出一物体,不计空气阻力.当θ=________时,水平射程最远,最远水平射程为________. 答案:45°20v g解析:对于斜抛运动:0cos x v t θ⋅=201sin 2y v t gt θ⋅=-当y =0时,解得02sin v t gθ=物体的水平射程20sin 2v x gθ=当θ=45°时有最远水平射程,其大小为20max v x g=1-7 某人骑摩托车以115m s -⋅的速度向东行驶,感觉到风以115m s -⋅的速度从正南吹来,则风速的大小为________ m·s -1,方向沿________.答案:m/s 东偏北45° 解析:如答案1-7图所示,由图可知=+v v v 风地风人人地故风速大小m/s v 风地=方向为东偏北45°.v 地风v 人地15v 人风15答案1-7图1-8 一质点作直线运动,加速度2sin a A t ωω=,已知t =0时,x 0=0,v 0=-ωA ,则该质点的运动方程为_______________. 答案:sin x A t ω=-,解析: d d v a t =20d sin d vtAv A t t ωωω-=⎰⎰解得,该质点的速度为cos v A t ωω=-d d x v t =d cos d xtx A t t ωω=-⎰⎰解得,该质点的运动方程为sin x A t ω=-1-9 一质点在xOy 平面上运动,运动方程为x =3t +5,y =12t 2+3t -4式中,t 以s 计,x ,y 以m 计.(1) 以时间t 为变量,写出质点位置矢量的表示式; (2) 计算第1 s 内质点的位移;(3) 计算t =0 s 时刻到t =4 s 时刻内的平均速度;(4) 求出质点速度矢量表示式,计算t =4 s 时质点的速度; (5) 计算t =0 s 到t =4 s 内质点的平均加速度;(6) 求出质点加速度矢量的表示式,计算t =4 s 时质点的加速度. (位置矢量、位移、平均速度、瞬时速度、平均加速度、瞬时加速度都表示成直角坐标系中的矢量式) 解:(1) 质点t 时刻位矢为21(35)342r t i t t j ⎛⎫=+++- ⎪⎝⎭(m)(2) 第1 s 内位移为11010()()r x x i y y j ∆=-+-2213(10)(10)3(10)23 3.5()i ji j m ⎡⎤=-+-+-⎢⎥⎣⎦=+(3) 前4 s 内平均速度为11(1220)35(m s )4r v i j i j t -∆==⨯+=+⋅∆ (4) 质点速度矢量表示式为1d 3(3)(m s )d rv i t j t-==++⋅ t =4 s 时质点的速度为143(43)37(m s )v i j i j -=++=+⋅(5) 前4 s 内平均加速度为240731(m s )4s 4v v v a j j t -∆--====⋅∆(6) 质点加速度矢量的表示式为2d 1(m s )d va j t-==⋅t =4 s 时质点的加速度为241(m s )a j -=⋅1-10 质点沿直线运动,速度v =(t 3+3t 2+2) m·s -1,如果当t = 2 s 时,x =4 m ,求:t =3 s 时,质点的位置、速度和加速度. 解: 32d 32d x v t t t==++ 431d d 24x x v t t t t c ===+++⎰⎰当t =2时,x =4,代入可得c =-12.则质点的位置、速度和加速度的表达式分别为4312124x t t t =++-32232d 36d v t t v a t tt=++==+ 将t =3 s 分别代入得上述各式,解得1233341.25m 56m s 45m s x v a --==⋅=⋅,,1-11 质点的运动方程为2[4(32)] m r t i t j =++,t 以s 计.求: (1) 质点的轨迹方程;(2) t =1 s 时质点的坐标和位矢方向; (3) 第1 s 内质点的位移和平均速度; (4) t =1 s 时质点的速度和加速度.解:(1) 由运动方程2432x t y t⎧=⎨=+⎩消去t 得轨迹方程2(3)0x y --=(2) t =1 s 时,114m 5m x y ==,,故质点的坐标为(4,5). 由11tan 1.25y x α==得51.3α=︒,即位矢与x 轴夹角为53.0°. (3) 第1 s 内质点的位移和平均速度分别为1(40)(53)42(m)r i j i j ∆=-+-=+1142(m s )r v i j t-∆==+⋅∆ (4) 质点的速度与加速度分别为d 82d r v ti j t ==+d 8d va i t==故t =1 s 时的速度和加速度分别为1182m s v i j -=+⋅() 218m s a i -=⋅()1-12 以速度v 0平抛一球,不计空气阻力,求:t 时刻小球的切向加速度a t 和法向加速度a n 的量值. 解:小球下落过程中速度为v故切向加速度为2t d d v a t =由222n t a g a =-得,法向加速度为n a =1-13 一种喷气推进的实验车,从静止开始可在1.80 s 内加速到1 600 km·h -1的速率.按匀加速运动计算,它的加速度是否超过了人可以忍受的加速度25g ?这1.80 s 内该车跑了多少距离?解:实验车的加速度为3222160010m /s 2.4710m/s 3600 1.80v a t ⨯===⨯⨯故它的加速度略超过25g . 1.80 s 内实验车跑的距离为3160010 1.80m 400m 223600v s t ⨯==⨯=⨯ 1-14 在以初速率-1015.0 m s v ⋅=竖直向上扔一块石头后,(1) 在1.0 s 末又竖直向上扔出第二块石头,后者在h =11.0 m 高度处击中前者,求第二块石头扔出时的速率;(2) 若在1.3 s 末竖直向上扔出第二块石头,它仍在h =11.0 m 高度处击中前者,求这一次第二块石头扔出时的速率.解:(1) 设第一块石头扔出后经过时间t 被第二块击中,则2012h v t gt =-代入已知数据得2111159.82t t =-⨯解此方程,可得二解为111.84s 1.22s t t ==,′第一块石头上升到顶点所用的时间为10m 15.0s 1.53s 9.8v t g ===1m t t >,这对应于第一块石头回落时与第二块相碰;1m t t <′,这对应于第一块石头上升时被第二块赶上击中.设20v 和20v ′分别为在t 1和1t ′时刻两石块相碰时第二石块的初速度,则由于22011111()()2h v t t g t t =--- 所以2211201111()119.8(1.841)22m/s 17.2m/s 1.841h g t t v t t +-∆+⨯⨯-===-∆- 同理,2211201111()119.8(1.221)22m/s 51.1m/s 1.221h g t t v t t +-∆+⨯⨯-===-∆-′′′ (2) 由于211.3s t t ∆=>′,所以第二块石头不可能在第一块上升时与第一块相碰。
01 质点运动学和动力学习题答案

质点运动学和动力学习题参考答案一、选择题1、D ;解析:题目只说明质点作直线运动,没有确定是匀加速还是变加速直线运动,故任意时刻的速度都不确定。
2、D 。
3、B ;解析:由题意知质点的运动轨迹为y =ax /b ,加速度a =d 2r /dt 2=ai +bj ,是一个常量,故质点作匀加速直线运动。
4、C ;解析:有题目可知人与风运动速度可用下图表示,由速度合成得到可知人感受到的风高手刀锋来自西北方向。
5、B ;解析:由题意知M 水=0.04M 地,R 水=0.4R 地;则由万有引力f =GMm /R 2≈mg 可得 G M 地m / R 地2=m 地g 地和G M 水m / R 水2=m 水g 水,由此推得g 水=0.25g 。
6、A ;解析:物体收尾时作匀速运动,则其加速度为零,即mg =kv 2,即得收尾速度为v =(mg /k )1/2。
7、D ;8、A ;解析:设绳中张力为T ,则弹簧秤的读数为2T ,因为A 、B 两物体的加速度大小相等,方向相反,可设加速度大小为a ,对A 、B 两物体应用牛顿运动定律m 1g -T =m 1a ,T -m 2g =m 2a ,可得。
二、填空题1、j 50cos50t i 50sin5t - v+=,a τ=0,x 2+y 2=100;解析:有运动方程可知x =10cos5t 与y =10sin5t ,则其运动轨迹为x 2+y 2=1,j 50cos50t i 50sin5t - /dt r d v +==,圆周运动的a τ=0。
2、变速曲线运动,变速直线运动;解析:a τ≠0与a n ≠0时在切向与法向上都具有位移,因此为变速曲线运动,而a τ≠0与a n =0时只表示在切向上有位移,故为变速直线运动。
3、V =V 0+Ct 3/3,x=x 0+V 0t +Ct 4/12; 解析:3002310Ct V V dt Ct dV adt dV dtdV a tVV +=⇒=⇒=⇒=⎰⎰;400030121310Ct t V x x dt Ct V dx Vdt dx dtdx V tx x ++=⇒⎪⎭⎫⎝⎛+=⇒=⇒=⎰⎰。
第1章质点运动学(部分答案)

一、选择题:1. 某质点沿半径为R 的圆周运动一周,它的位移和路程分别为(B) A. πR ,0; B. 0,2πR ;C. 0,0;D. 2πR ,2πR 。
2. 质点作直线运动,运动方程为242x t t =--(SI 制),则质点在最初2秒内的位移为(C)A. -6 m ;B. 4 m ;C. -4 m ;D. 6 m 。
3.一质点在平面上作一般曲线运动,其瞬时速度为v ,瞬时速率为v ,某一时间内的平均速度为v ,平均速率为v ,它们之间的关系必定有( D ) A. v v =,v v =;B. v v ≠,v v =;C. v v ≠,v v ≠;D. v v =,v v ≠。
4.质点作曲线运动,r 表示位置矢量,v 表示速度,a表示加速度,S 表示路程,a t 表示切向加速度,下列表达式中( D ) (1) a t = d /d v , (2) v =t r d /d ,(3) v =t S d /d , (4) t a t =d /d v。
A. 只有(1)、(4)是对的; B. 只有(2)、(4)是对的; C. 只有(2)是对的;D.只有(3)是对的。
5. 一运动质点在某瞬时位于矢径()y x r ,的端点处,其速度大小为( D )A.d d rt ; B.d d r t ;C.d d r t;6. 一质点作直线运动,某时刻的瞬时速度v =2m/s ,瞬时加速度a =-2m/s 2,则一秒钟后质点的速度(D)A.等于零;B.等于-2 m/s ;C.等于2 m/s ;D.不能确定。
7. 沿直线运动的物体,其速度大小与时间成反比,则其加速度的大小与速度大小有如下关系( B )A.与速度大小成正比;B.与速度大小的平方成正比;C.与速度大小成反比;D.与速度大小的平方成反比。
8. 下列说法中,正确的是( D )A. 物体走过的路程越长,它的位移也越大;B. 质点在时刻t 和t +Δt 的速度分别为1v 和2v ,则在时间Δt 内的平均速度为()122v v +;C. 如物体的加速度为常量,则它一定做匀变速直线运动;D. 在质点的曲线运动中,加速度的方向与速度的方向总是不一致的。
第01章(质点运动学)习题答案

思 考 题1-1 什么是矢径?矢径和对初始位置的位移矢量之间有何关系?怎样选取坐标原点才能够 使两者一致?答:矢径即位置矢量,是从坐标原点O 指向质点所在处P 的有向线段。
位移 r vD 和矢径r v不同,矢径确定某一时刻质点的位置,位移则描述某段时间内始未质点位置的变化。
矢径是相对坐标原点的,位移矢量是相对初始位置的。
对于相对静止的不同坐标系来说,位矢依 赖于坐标系的选择,而位移则与所选取的坐标系无关。
若取初始位置为坐标原点才能够使两 者一致。
1-2 在下列各图中质点 M 作曲线运动,指出哪些运动是不可能的?答:(A) 质点只要作曲线运动,肯定有法向加速度,不可能加速度为零。
(C) 在质点作曲线运动时,加速度的方向总是指向轨迹曲线凹的一侧。
(D) 质点只要作曲线运动,肯定有法向加速度,不可能只有切向加速度。
1-3 下列说法哪一条是正确的?(A) 加速度恒定不变时,物体运动方向也不变. (B) 平均速率等于平均速度的大小.(C) 不管加速度如何,平均速率表达式总可以写成 ( ) 2 / 2 1 v v v += ,其中 v 1、v 2 分 别为初、末速率.(D) 运动物体速率不变时,速度可以变化.答:加速度恒定不变时,意味着速度的大小和方向的变化是恒定的。
不是物体运动方向 不变。
平均速率不等于平均速度的大小。
若速率的变化是线性的(加速度恒定)平均速率表 达式才可以写成 ( ) 2 / 2 1 v v v + = , 否则不可以。
只有运动物体速率不变时, 速度可以变化. 才 是正确的。
1-4 如图所示,质点作曲线运动,质点的加速度 a 是恒矢量(a 1=a 2=a 3=a ).试问质点是否能作匀变速率运动? 答:质点作匀变速率运动要求切向加速度是恒量,如图 所示, 质点作曲线运动, 质点的加速度 a 是恒矢量(a 1=a 2=a 3=a) 则切向分量不一样,质点不能作匀变速率运动。
1-5 以下五种运动形式中,加速度 a 保持不变的运动是哪一a 3M 1M 2M 3a 3a 3思考题 1-4图aMMMvva =0 (A)(B)(C)(D)a vM av思考题 1-2图种或哪几种?(A) 单摆的运动. (B) 匀速率圆周运动.(C) 行星的椭圆轨道运动. (D) 抛体运动. (E) 圆锥摆运动.答:加速度a 保持不变(意味加速度 a 的大小和方向都保持不变)的运动是抛体运动。
(完整版)大学物理学(课后答案)第1章.doc

第 1 章质点运动学习题一选择题1-1 对质点的运动,有以下几种表述,正确的是[](A)在直线运动中,质点的加速度和速度的方向相同(B)在某一过程中平均加速度不为零,则平均速度也不可能为零(C)若某质点加速度的大小和方向不变,其速度的大小和方向可不断变化(D)在直线运动中,加速度不断减小,则速度也不断减小解析:速度是描述质点运动的方向和快慢的物理量,加速度是描述质点运动速度变化的物理量,两者没有确定的对应关系,故答案选C。
1-2 某质点的运动方程为x 2t 3t 312(m) ,则该质点作[](A)匀加速直线运动,加速度沿 ox 轴正向(B)匀加速直线运动,加速度沿ox 轴负向(C)变加速直线运动,加速度沿ox 轴正向(D)变加速直线运动,加速度沿ox 轴负向dx 2 dv解析:vdt 2 9t ,adt18t,故答案选 D。
1-3 一质点在平面上作一般曲线运动,其瞬时速度为v ,瞬时速率为 v ,某一段时间内的平均速率为 v ,平均速度为 v ,他们之间的关系必定有 [](A) v v , v v (B) v v , v v(C) v v , v v (D) v v , v v解析:瞬时速度的大小即瞬时速率,故v v ;平均速率 vs ,而平均速r,故 v v 。
答案选 D。
t度 v =t1-4 质点作圆周运动时,下列表述中正确的是[](A) 速度方向一定指向切向,所以法向加速度也一定为零(B)法向分速度为零,所以法向加速度也一定为零(C)必有加速度,但法向加速度可以为零(D)法向加速度一定不为零解析:质点作圆周运动时,v 2dva a n e n a t e te ndte t,所以法向加速度一定不为零,答案选 D 。
1-5 某物体的运动规律为dvkv 2t ,式中, k 为大于零的常量。
当 t 0 时,dt初速为 v 0 ,则速率 v 与时间 t 的函数关系为 [](A) v 1 kt 2 v 0(B)1 kt2 12v 2 v 0(C) v1 kt2 v 0 (D)1 kt2 12v2v 0解析:由于dvvt( kv 2t) dt ,得到1kt 21,故答案kv 2t ,所以 dvdtv 0v 2 v 0选 B 。
第一章质点运动学 作业答案
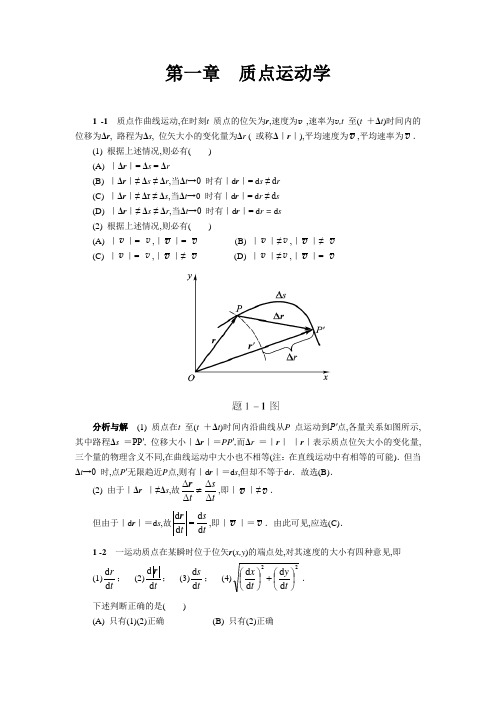
第一章 质点运动学1 -1 质点作曲线运动,在时刻t 质点的位矢为r ,速度为v ,速率为v ,t 至(t +Δt )时间内的位移为Δr , 路程为Δs , 位矢大小的变化量为Δr ( 或称Δ|r |),平均速度为v ,平均速率为v .(1) 根据上述情况,则必有( ) (A) |Δr |= Δs = Δr(B) |Δr |≠ Δs ≠ Δr ,当Δt →0 时有|d r |= d s ≠ d r (C) |Δr |≠ Δr ≠ Δs ,当Δt →0 时有|d r |= d r ≠ d s (D) |Δr |≠ Δs ≠ Δr ,当Δt →0 时有|d r |= d r = d s (2) 根据上述情况,则必有( )(A) |v |= v ,|v |= v (B) |v |≠v ,|v |≠ v (C) |v |= v ,|v |≠ v (D) |v |≠v ,|v |= v分析与解 (1) 质点在t 至(t +Δt )时间内沿曲线从P 点运动到P′点,各量关系如图所示, 其中路程Δs =PP′, 位移大小|Δr |=PP ′,而Δr =|r |-|r |表示质点位矢大小的变化量,三个量的物理含义不同,在曲线运动中大小也不相等(注:在直线运动中有相等的可能).但当Δt →0 时,点P ′无限趋近P 点,则有|d r |=d s ,但却不等于d r .故选(B).(2) 由于|Δr |≠Δs ,故ts tΔΔΔΔ≠r ,即|v |≠v .但由于|d r |=d s ,故ts td d d d =r ,即|v |=v .由此可见,应选(C).1 -2 一运动质点在某瞬时位于位矢r (x,y )的端点处,对其速度的大小有四种意见,即(1)t rd d ; (2)t d d r; (3)t sd d ; (4)22d d d d ⎪⎭⎫⎝⎛+⎪⎭⎫ ⎝⎛t y t x . 下述判断正确的是( )(A) 只有(1)(2)正确 (B) 只有(2)正确(C) 只有(2)(3)正确 (D) 只有(3)(4)正确 分析与解tr d d 表示质点到坐标原点的距离随时间的变化率,在极坐标系中叫径向速率.通常用符号v r 表示,这是速度矢量在位矢方向上的一个分量;td d r 表示速度矢量;在自然坐标系中速度大小可用公式ts d d =v 计算,在直角坐标系中则可由公式22d d d d ⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛=t y t x v 求解.故选(D).1 -3 质点作曲线运动,r 表示位置矢量, v 表示速度,a 表示加速度,s 表示路程, a t表示切向加速度.对下列表达式,即(1)d v /d t =a ;(2)d r /d t =v ;(3)d s /d t =v ;(4)d v /d t |=a t. 下述判断正确的是( )(A) 只有(1)、(4)是对的 (B) 只有(2)、(4)是对的 (C) 只有(2)是对的 (D) 只有(3)是对的 分析与解td d v 表示切向加速度a t,它表示速度大小随时间的变化率,是加速度矢量沿速度方向的一个分量,起改变速度大小的作用;tr d d 在极坐标系中表示径向速率v r (如题1 -2 所述);ts d d 在自然坐标系中表示质点的速率v ;而td d v 表示加速度的大小而不是切向加速度at.因此只有(3) 式表达是正确的.故选(D).1 -4 一个质点在做圆周运动时,则有( ) (A) 切向加速度一定改变,法向加速度也改变 (B) 切向加速度可能不变,法向加速度一定改变 (C) 切向加速度可能不变,法向加速度不变 (D) 切向加速度一定改变,法向加速度不变分析与解 加速度的切向分量a t起改变速度大小的作用,而法向分量a n 起改变速度方向的作用.质点作圆周运动时,由于速度方向不断改变,相应法向加速度的方向也在不断改变,因而法向加速度是一定改变的.至于a t是否改变,则要视质点的速率情况而定.质点作匀速率圆周运动时, a t恒为零;质点作匀变速率圆周运动时, a t为一不为零的恒量,当a t改变时,质点则作一般的变速率圆周运动.由此可见,应选(B).1 -5 已知质点沿x 轴作直线运动,其运动方程为32262t t x -+=,式中x 的单位为m,t 的单位为 s .求:(1) 质点在运动开始后4.0 s 内的位移的大小; (2) 质点在该时间内所通过的路程;(3) t =4 s 时质点的速度和加速度.分析 位移和路程是两个完全不同的概念.只有当质点作直线运动且运动方向不改变时,位移的大小才会与路程相等.质点在t 时间内的位移Δx 的大小可直接由运动方程得到:0Δx x x t -=,而在求路程时,就必须注意到质点在运动过程中可能改变运动方向,此时,位移的大小和路程就不同了.为此,需根据0d d =tx 来确定其运动方向改变的时刻t p ,求出0~t p 和t p ~t 内的位移大小Δx 1 、Δx 2 ,则t 时间内的路程21x x s ∆+∆=,如图所示,至于t =4.0 s 时质点速度和加速度可用tx d d 和22d d tx 两式计算.题 1-5 图解 (1) 质点在4.0 s 内位移的大小m 32Δ04-=-=x x x (2) 由 0d d =tx得知质点的换向时刻为s 2=p t (t =0不合题意)则m 0.8Δ021=-=x x xm 40Δ242-=-=x x x所以,质点在4.0 s 时间间隔内的路程为m 48ΔΔ21=+=x x s(3) t =4.0 s 时1s0.4sm 48d d -=⋅-==t tx v2s0.422m.s36d d -=-==t tx a1 -6 已知质点的运动方程为j i r )2(22t t -+=,式中r 的单位为m,t 的单位为s.求: (1) 质点的运动轨迹;(2) t =0 及t =2s时,质点的位矢;(3) 由t =0 到t =2s内质点的位移Δr 和径向增量Δr ;分析 质点的轨迹方程为y =f (x ),可由运动方程的两个分量式x (t )和y (t )中消去t 即可得到.对于r 、Δr 、Δr 、Δs 来说,物理含义不同,(详见题1-1分析).解 (1) 由x (t )和y (t )中消去t 后得质点轨迹方程为2412x y -=这是一个抛物线方程,轨迹如图(a)所示.(2) 将t =0s和t =2s分别代入运动方程,可得相应位矢分别为j r 20= , j i r 242-=图(a)中的P 、Q 两点,即为t =0s和t =2s时质点所在位置. (3) 由位移表达式,得j i j i r r r 24)()(Δ020212-=-+-=-=y y x x其中位移大小m 66.5)(Δ)(ΔΔ22=+=y x r而径向增量m 47.2ΔΔ2020222202=+-+=-==y x y x r r r r题 1-6 图1 -16 一质点沿半径为R 的圆周按规律2021bt t s -=v 运动,v 0 、b 都是常量.(1) 求t时刻质点的总加速度;(2) t 为何值时总加速度在数值上等于b ?(3) 当加速度达到b 时,质点已沿圆周运行了多少圈?分析 在自然坐标中,s 表示圆周上从某一点开始的曲线坐标.由给定的运动方程s =s (t ),对时间t 求一阶、二阶导数,即是沿曲线运动的速度v 和加速度的切向分量a t,而加速度的法向分量为a n =v 2 /R .这样,总加速度为a =a te t+a n e n .至于质点在t 时间内通过的路程,即为曲线坐标的改变量Δs =s t -s 0.因圆周长为2πR,质点所转过的圈数自然可求得.解 (1) 质点作圆周运动的速率为bt ts -==0d d v v其加速度的切向分量和法向分量分别为b ts a t -==22d d , Rbt Ra n 202)(-==v v故加速度的大小为R)(402222bt b a aa a t tn-+=+=v其方向与切线之间的夹角为⎥⎦⎤⎢⎣⎡--==Rb bt a a θt n20)(arctan arctan v(2) 要使|a |=b ,由b bt b R R=-+4022)(1v 可得 bt 0v =(3) 从t =0 开始到t =v 0 /b 时,质点经过的路程为bs s s t 220v =-=因此质点运行的圈数为bRRs n π4π22v ==1 -19 一无风的下雨天,一列火车以v 1=20.0 m·s-1 的速度匀速前进,在车内的旅客看见玻璃窗外的雨滴和垂线成75°角下降.求雨滴下落的速度v2 .(设下降的雨滴作匀速运动)题 1-19 图分析 这是一个相对运动的问题.设雨滴为研究对象,地面为静止参考系S,火车为动参考系S′.v 1 为S′相对S 的速度,v 2 为雨滴相对S的速度,利用相对运动速度的关系即可解.解 以地面为参考系,火车相对地面运动的速度为v 1 ,雨滴相对地面竖直下落的速度为v 2 ,旅客看到雨滴下落的速度v 2′为相对速度,它们之间的关系为1'22v v v += (如图所示),于是可得1o12sm 36.575tan -⋅==v v。
01章 质点运动学 习题解答

x(m)
b
30° 120° 20 10 30
c
45°
t(s)
t图像中为曲线斜率。由于三种图像都是直线,因此三种运动都是匀速直线运动,设直线 与x轴正向夹角为α,则速度 v tg x / t 对于a种运动:
v tg120 3m / s, x |t 0 20m, t | x 0 20tg 30 11.55s
S 2 | x 2 (30) x 2 (0) | x 2 (0) x 2 (30) 195 60 135m
1-17 电梯以1.0m/s的匀速率下降,小孩在电梯中跳离地板0.50m高,问当小孩再次落到地板上 时,电梯下降了多长距离? 解:以电梯为参考系,小孩相对电梯做竖直上抛运动,他从起跳到再次落到地板所需
1-14质点从坐标原点出发时开始计时,沿x轴运动,其加速度ax
=
2t
(cms-
2),求在下列两种情况下质点的运动学方程,出发后6s时质点的位置、在此期间所走过的
位移及路程。⑴初速度v0=0;⑵初速度v0的大小为9cm/s,方向与加速度方向相反。 解: dv x a x dt 2tdt ,
x
vx
3 2
3g
2
2
120列车在圆弧形轨道上自东转向北行驶,在我们所讨论的时
北
间范围内,其运动学方程为S=80tv O
S
东 an α a
τ
aτ
t2(m,s),t=0时,列车在图中O点,此圆弧形轨道的半径r=1500m,求列车驶过O点以后 前进至1200m处的速率及加速度。 解:S=80t-t2 ① v=dS/dt=80-2t ② 令S=1200,由①可求得对应时间:
a x a, a v x a, a a x a
