中科院考研06、07、08 信号与系统试题与答案
信号与线性系统分析试题及答案(10套)

标准答案(一)一、填空题(每空1分,共30分)1、无线电通信中,信号是以电磁波形式发射出去的。
它的调制方式有调幅、调频、调相。
2、针对不同的调制方式有三种解调方式,分别是检波、鉴频、和鉴相。
3、在单调谐放大器中,矩形系数越接近于1、其选择性越好;在单调谐的多级放大器中,级数越多,通频带越窄、(宽或窄),其矩形系数越(大或小)小。
4、调幅波的表达式为:uAM(t)= 20(1 +0.2COS100πt)COS107πt(V);调幅波的振幅最大值为24V,调幅度Ma为20℅,带宽fBW为100Hz,载波fc为5*106Hz。
5、在无线电技术中,一个信号的表示方法有三种,分别是数学表达式、波形、频谱。
6、调频电路有直接调频、间接调频两种方式。
7、检波有同步、和非同步检波两种形式。
8、反馈式正弦波振荡器按照选频网络的不同,可分为LC、RC、石英晶振等三种。
9、变频器可由混频器、和带通滤波器两部分组成。
10、列出三个常见的频谱搬移电路调幅、检波、变频。
11、用模拟乘法器非线性器件实现调幅最为理想。
二、选择题(每小题2分、共20分)将一个正确选项前的字母填在括号内1、下列哪种信号携带有调制信号的信息(C )A、载波信号B、本振信号C、已调波信号2、小信号谐振放大器的主要技术指标不包含(B )A、谐振电压增益B、失真系数C、通频带D、选择性3、丙类谐振功放其谐振回路调谐于( A )分量A、基波B、二次谐波C、其它高次谐波D、直流分量4、并联型石英晶振中,石英谐振器相当于(C )元件A、电容B、电阻C、电感D、短路线5、反馈式正弦波振荡器的起振条件为( B )A、|AF|=1,φA+φF= 2nπB、|AF| >1,φA+φF = 2nπC、|AF|>1,φA+φF ≠2nπD、|AF| =1,φA+φF ≠2nπ6、要实现集电极调制特性应使功放工作在(B )状态A、欠压状态B、过压状态C、临界状态D、任意状态7、自动增益控制可简称为( B )A、MGCB、AGCC、AFCD、PLL8、利用非线性器件相乘作用来实现频率变换其有用项为( B )A、一次方项B、二次方项C、高次方项D、全部项9、如右图所示的电路是(D )A、普通调幅电路B、双边带调幅电路C、混频器D、同步检波器10、在大信号包络检波器中,由于检波电容放电时间过长而引起的失真是(B)A、频率失真B、惰性失真C、负峰切割失真D、截止失真三、判断题,对的打“√”,错的打“×”(每空1分,共10分)1、谐振放大器是采用谐振回路作负载的放大器。
(完整word版)信号与系统考试试题及答案,推荐文档

长沙理工大学拟题纸课程编号 1拟题教研室(或老师)签名 教研室主任签名 符号说明:)sgn(t 为符号函数,)(t δ为单位冲击信号,)(k δ为单位脉冲序列,)(t ε为单位阶跃信号,)(k ε为单位阶跃序列。
一、填空(共30分,每小题3分)1. 已知)()4()(2t t t f ε+=,求_______)("=t f 。
)('4)(2)("t t t f δε+2. 已知}4,2,4,3{)(},1,2,2,1{)(=-=k h k f ,求______)()(=*k h k f 。
}4,6,8,3,4,10,3{)()(-=*k h k f3. 信号通过系统不失真的条件为系统函数_______)(=ωj H 。
0)(t j Kej H ωω-=4. 若)(t f 最高角频率为m ω,则对)4(t f 取样的最大间隔是______。
m T ωπωπ4max max ==5. 信号t t t f ππ30cos 220cos 4)(+=的平均功率为______。
101122222=+++==∑∞-∞=n n F P6. 已知一系统的输入输出关系为)3()(t f t y =,试判断该系统是否为线性时不变系统______。
故系统为线性时变系统。
7. 已知信号的拉式变换为)1)(1(1)(2-+=s s s F ,求该信号的傅立叶变换)(ωj F =______。
故傅立叶变换)(ωj F 不存在。
8. 已知一离散时间系统的系统函数2121)(---+=z z z H ,判断该系统是否稳定______。
故系统不稳定。
9. =+-+⎰∞∞-dt t t t )1()2(2δ______。
310. 已知一信号频谱可写为)(,)()(3ωωωωA e A j F j -=是一实偶函数,试问)(t f 有何种对称性______。
关于t=3的偶对称的实信号。
二、计算题(共50分,每小题10分)1. 已知连续时间系统的单位冲激响应)(t h 与激励信号)(t f 的波形如图A-1所示,试由时域求解该系 统的零状态响应)(t y ,画出)(t y 的波形。
信号与系统复习题含答案完整版

信号与系统复习题含答案HEN system office room 【HEN16H-HENS2AHENS8Q8-HENH1688】(C ))(t δ+(-6e -t +8e -2t)u(t) (D )3)(t δ +(-9e -t +12e -2t)u(t)6、 连续周期信号的频谱具有(A ) 连续性、周期性 (B )连续性、收敛性 (C )离散性、周期性 (D )离散性、收敛性7、 周期序列2)455.1(0+k COS π的 周期N 等于(A) 1 (B )2 (C )3 (D ) 48、序列和()∑∞-∞=-k k 1δ等于(A )1 (B) ∞ (C) ()1-k u (D) ()1-k ku9、单边拉普拉斯变换()se s s s F 2212-+=的愿函数等于10、信号()()23-=-t u te t f t的单边拉氏变换()s F 等于二、填空题(共9小题,每空3分,共30分) 1、 卷积和[()k+1u(k+1)]*)1(k -δ=________________________2、 单边z 变换F(z)= 12-z z的原序列f(k)=______________________ 3、 已知函数f(t)的单边拉普拉斯变换F(s)=1+s s,则函数y(t)=3e -2t·f(3t)的单边拉普拉斯变换Y(s)=_________________________4、 频谱函数F(j ω)=2u(1-ω)的傅里叶逆变换f(t)=__________________5、 单边拉普拉斯变换s s s s s F +++=2213)(的原函数 f(t)=__________________________6、 已知某离散系统的差分方程为)1(2)()2()1()(2-+=----kf k f k y k y k y ,则系统的单位序列响应h(k)=_______________________7、 已知信号f(t)的单边拉氏变换是F(s),则信号⎰-=2)()(t dxx f t y 的单边拉氏变换Y(s)=______________________________ 8、描述某连续系统方程为 该系统的冲激响应h(t)=9、写出拉氏变换的结果()=t u 66 ,=k t 22三(8分)已知信号()()()⎪⎩⎪⎨⎧><==↔./1,0,/1,1s rad s rad jw F j F t f ωωω设有函数()(),dtt df t s =求⎪⎭⎫ ⎝⎛2ωs 的傅里叶逆变换。
信号与系统复习题与答案

1.系统的激励是 e( t ) ,响应为 r( t ) ,若满足 r( t ) de( t ) ,则该系统为线性、dt时不变、因果。
(是否线性、时不变、因果?)2.求积分( t21) ( t 2 )dt 的值为 5 。
3.当信号是脉冲信号f(t) 时,其低频分量主要影响脉冲的顶部,其高频分量主要影响脉冲的跳变沿。
4.若信号 f(t) 的最高频率是 2kHz,则 f( 2t) 的乃奎斯特抽样频率为8kHz 。
5.信号在通过线性系统不产生失真,必须在信号的全部频带内,要求系统幅频特性为一常数相频特性为 _一过原点的直线(群时延)。
6.系统阶跃响应的上升时间和系统的截止频率成反比。
7.若信号的 F(s)=3s,求该信号的 F ( j )j3。
(s+4)(s+2) +4)(j +2)(j8.为使 LTI 连续系统是稳定的,其系统函数 H ( s ) 的极点必须在 S 平面的左半平面。
9.已知信号的频谱函数是F ( j ) ( )()0 0,则其时间信号 f(t)为1 sin(t ) 。
j10.若信号 f(t) 的 F( s ) s 1 2,则其初始值 f ( 0 ) 1 。
( s 1)二、判断下列说法的正误,正确请在括号里打“√”,错误请得分打“×”。
(每小题 2 分,共 10 分)1. 单位冲激函数总是满足( t )( t ) (√ )2. 满足绝对可积条件 f ( t )dt的信号一定存在傅立叶变换,不满足这一条件的信号一定不存在傅立叶变换。
(× )3. 非周期信号的脉冲宽度越小,其频带宽度越宽。
(√ )4.连续 LTI 系统的冲激响应的形式取决于系统的特征根,于系统的零点无关。
( √ )5. 所有周期信号的频谱都是离散谱,并且随频率的增高,幅度谱总是渐小的。
( × )三、计算分析题( 1、 3、 4、 5 题每题 10 分, 2 题 5 分, 得分6 题 15 分,共 60分), 0 t 11. 信号 f ( t )e tu( t ) ,信号 1分) f 2( t ) ,试求 f 1( t ) * f 2 ( t ) 。
完整版信号与系统试题附答案.doc
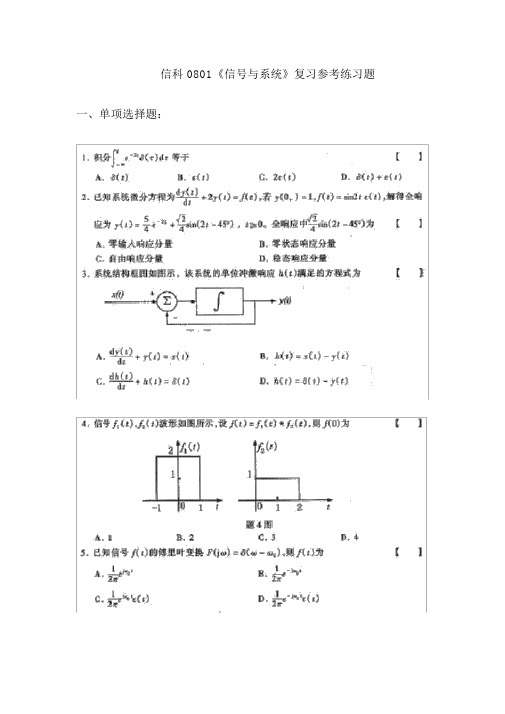
信科 0801《信号与系统》复习参考练习题一、单项选择题:14 、已知连续时间信号 f (t )sin 50(t2) ,则信号 f (t)·cos104t所占有的频带宽度(C)100(t 2)A .400rad / sB 。
200 rad / s C。
100 rad / s D。
50 rad / s15 、已知信号 f (t) 如下图(a)所示,其反转右移的信号f1(t) 是(D)16 、已知信号f1 (t ) 如下图所示,其表达式是( B )A 、ε( t)+ 2ε (t- 2) -ε (t- 3)B 、ε (t- 1) +ε (t-2) - 2ε (t-3)C 、ε (t)+ε (t- 2) -ε (t- 3)D、ε (t- 1) +ε -(t 2) -ε -(t 3)17 、如图所示: f( t)为原始信号, f 1(t)为变换信号,则f1(t) 的表达式是(D)A、 f(- t+1)B、 f(t+1)C、 f(- 2t+1)D、 f( -t/2+1)18 、若系统的冲激响应为h(t), 输入信号为f(t), 系统的零状态响应是(C)19 。
信号f (t) 2 cos (t 2) 3sin (t 2) 与冲激函数(t 2) 之积为( B )4 4A、2B、 2 (t 2)C、 3 (t 2) D 、 5 (t 2)20.已知 LTI 系统的系统函数H( s )s 12 , Re[s ]>- 2,则该系统是()s 5s 6因果不稳定系统非因果稳定系统C、因果稳定系统非因果不稳定系统21 、线性时不变系统的冲激响应曲线如图所示,该系统微分方程的特征根是( B )A、常数B、实数 C 、复数D、实数 +复数22 、线性时不变系统零状态响应曲线如图所示,则系统的输入应当是( A )A、阶跃信号B、正弦信号 C 、冲激信号 D 、斜升信号23. 积分 f (t ) (t )dt 的结果为( A )A f (0)B f (t ) C. f (t )(t) D. f ( 0)(t )24. 卷积(t) f (t ) (t ) 的结果为( C )A.(t)B.(2t )C.f (t)D. f ( 2t )25.零输入响应是 ( B )A. 全部自由响应B. 部分自由响应C.部分零状态响应D. 全响应与强迫响应之差2A 、e1e3、e3、127.信号〔ε (t)-ε -(t 2)〕的拉氏的收域( C )A.Re[s]>0B.Re[s]>2C.全S 平面D.不存在28.已知系二微分方程的零入响y zi (t ) 的形式Ae t Be 2t ,其 2 个特征根 ( A )A 。
《中山大学911信号与系统2007-2018年考研真题及答案解析》

《中山大学信号与系统历年考研真题及答案解析》
3 / 169
七、(18 分)
图
4
所示的抽头滤波器,如果要求其传输系数在
w=0
时为
1,在
w1
=
2
*103
rad
/s
及
w2 = *103 rad /s 时为 0.求图中各标量乘法器的传输值,并绘出幅频特性曲线(注:输入信
号的抽样间隔为 1ms)
《中山大学信号与系统历年考研真题及答案解析》
《中山大学信号与系统历年考研真题及答案解析》
5 / 169
四、(35 分)
计算
(1)求象函数
F (z)
(z
z2 z 1)( z 2
z
1)
,|
z
| 1的逆z变换
(2)利用 z 变换的性质求序列 (k-1)2u(k-1) 的 z 变换,并注明收敛域。
1 (3)求象函数 s(s+1)2 的拉普拉斯逆变换 f(t)。
5 系统 y(t) x(2t) 是线性因果系统。
6、在仅知线性时不变(LTI)系统的系统函数和系统的初始状态的条件下,可以获得该 系统的零输入响应。
7、离散时间系统的频率响应 H (e jw ) 为 H (z) 在单位圆的 z 变换。
三、(20 分) 已知 LTI 系统的冲激响应 h(t) e2tu(t) (1)若激励信号为 f (t) et[u(t) u(t 2) a (t 2)] 式中 a 为常数,确定该系统的
零状态响应。
(2)若激励信号表示为 f (t) x(t)[u(t) u(t 2) a (t 2)] ,式中 x(t) 为任意 t 的 函数,若要求系统在 t>2 的响应为 0,试确定 a 值应等于多少?
级信号与系统(A类)答案

第 1 页/共 4 页2023年年级信号与系统(A 类)答案及评分标准(A 卷)一 基础题1. sin '()A t t dt A δ∞-∞=-⎰ (8分)2.()()(2)(2)h t tu t t u t =--- (8分) 3、()x t 周期信号,T =4, 02πω=(8分)()x t 奇半波偶对称函数,所以只含奇次余弦次,即只含0,003,5ωωω±±±⋅⋅⋅频率成分;但通过截止频率为/c rad s ωπ=的()H ω时,有0k ωπ≤,即2k ≤,且k 为奇数, 所以输出频率中含有2π±频率成分。
4、()()()()33sin sin sin sin 8888111n j n n n n n x n e n n n n πππππππππ⎛⎫⎛⎫ ⎪ ⎪=++=+-+ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭(8 5. 5.0)5.0(141)(][>-⋅=←→z z z z X n x (4分)2221)1(][2<-⋅-=←→-z z z z X n x(4分)6. 00)(2233≥⎥⎦⎤⎢⎣⎡-=--t e e e e t t t t tϕ(8分)二 计算题 1. (17分)(1)∵12()()()()df t du t f t t dt dtδ=== ∴2()f t 的零状态响应部分应为1()f t 零状态响应部分的导数,即:12()()s s df t f t dt=(5分) (2)当1()f t 作用时02()t e u t y t t -=1s 入()+y () (a )当2f t ()作用时 12200()()()()s s dy t t y t y t y t dtδ=+=+入入() (b ) 两式相减得:11()()()2()t s s dy t y t t e u t dtδ--=- 两边L 变换121(1)()111s s Y s s s --=-=++ ∴11()1Y s s =+1()()t s y t e u t -= 零状态响应 (5分)(3)1110()()()2()()()t t t s y t y t y t e u t e u t e u t ---=-=-=入零输入响应 (4分) (4)系统的单位冲激响应为:202()()()()()t h t y t y t t e u t δ-=-=- (3分) 2 (18分)(1):m ω=8, ()()()111222x t x t X X ωω⎛⎫=↔=⎪⎝⎭,频带宽度216/m rad s ω=,2232/s m rad s ωω==,16s f Hz π=,116s T s f π==; ()()()22222t x t x X X ωω⎛⎫=↔= ⎪⎝⎭,频带宽度4/2m rad s ω=,28/2m s rad s ωω==14s T s f π== (9分) (2)22816/8s m T s rad s πωω=∴==⨯=○1()()()1816s s k k X X k X k T ωωωωπ+∞+∞=-∞=-∞=-=-∑∑ (3分) ○2()2x t 的抽样信号()2s x t 的频谱为 (3分) ()()()1111816s s k k X X k X k T ωωωωπ+∞+∞=-∞=-∞=-=-∑∑○3()()()2221816s s k k X X k X k T ωωωωπ+∞+∞=-∞=-∞=-=-∑∑ (3第 3 页/共 4 页分)3.(17分)-+)(1s UV u u u 2)0()0(0)0(321===---(2分)8 -161643131134)34()1(4)(1+⋅-⋅=++=s s s s s s U)()3134()(431t u e t u t--=(8分)43141134)1(4)()(+⋅+=++==s s s s sU s I)(41)()(43t u e t t i t-+=δ(7分)。
中科院信号与系统课程硕士研究生入学考试试题与答案

中科院2005年招收攻读硕士学位研究生入学考试试题试题名称:信号与系统 一、已知当输入信号为)(t x 时,某连续时间LTI 因果系统的输出信号为)(t y ,)(t x 和)(t y 的波形如图A-1所示。
试用时域方法求:(共26分)1. 该系统的单位阶跃响应)(t s ,并概画出)(t s 的波形;(12分)2. 在系统输入为图A-2所示的)(1t x 时的输出信号)(1t y ,并概画出)(1t y 的波形。
(14分)1t1)(1t x图A-1 图A-2二、由差分方程∑=----=--4])1[2][(]1[5.0][k k n x k n x n y n y 和非零起始条件1]1[=-y 表示的离散时间因果系统,当系统输入][][n n x δ=时,试用递推算法求:(共16分)1. 该系统的零状态响应][n y ZS (至少计算出前6个序列值);(10分)2. 该系统的零输入响应][n y Zi (至少计算出前4个序列值);(6分)三、已知连续时间信号)102cos()10(2)]110(2sin[)(633t t t t x ⨯--=-πππ毫安,若它是能量信号,试求其能谱密度和它在单位电阻上消耗的能量;若它是功率信号,则求其功率谱密度函数和它在单位电阻上消耗的平均功率。
(共14分)四、已知][~n x 是周期为4的周期序列,且已知8点序列][~][n x n x =,70≤≤n ,的8点DFT 系数为: ,0)(,1)6()4()2()0(=====k X X X X X 其他k 。
试求:(共24分) 1. 周期序列][~n x ,并概画出它的序列图形;(12分)2. 该周期序列][~n x 通过单位冲激响应为2222)2/(sin )1(][n n n h ππ-=的数字滤波器后的输出][n y ,并概画出它的序列图形;(12分)五、已知)(t x 是最高频率为4KHz 的连续时间带限信号,(共24分) 1. 若对)(t x 进行平顶抽样获得的已抽样信号)(t x p 如图A-3所示,试由)(t x p 恢复出)(t x 的重构滤波器的频率响应)(ωL H ,并概画出其幅频响应和相频响应;(16分)图A-32. 你在1小题求得的重构滤波器为什么不可实现?为实现无失真恢复原信号,需对抽样频率和重构滤波器频率响应)(ωL H 作怎样的修改?(8分) 六、如图A-4的信号流图所示的数字滤波器,试求:(共22分)1. 它的系统函数)(z H 及其收敛域,并画出它用一个一阶全通滤波器和一个4阶FIR 滤波器的级联实现的方框图或信号流图;(12分)2. 概画出该数字滤波器的幅频响应)(~ΩH (或)(Ωj e H )。
中科院信号与系统课程硕士研究生入学考试试题与答案

中科院2005年招收攻读硕士学位研究生入学考试试题试题名称:信号与系统 一、已知当输入信号为)(t x 时,某连续时间LTI 因果系统的输出信号为)(t y ,)(t x 和)(t y 的波形如图A-1所示。
试用时域方法求:(共26分)1. 该系统的单位阶跃响应)(t s ,并概画出)(t s 的波形;(12分)2. 在系统输入为图A-2所示的)(1t x 时的输出信号)(1t y ,并概画出)(1t y 的波形。
(14分)图A-1 图A-2 二、由差分方程∑=----=--4])1[2][(]1[5.0][k k n x k n x n y n y 和非零起始条件1]1[=-y 表示的离散时间因果系统,当系统输入][][n n x δ=时,试用递推算法求:(共16分)1. 该系统的零状态响应][n y ZS (至少计算出前6个序列值);(10分)2. 该系统的零输入响应][n y Zi (至少计算出前4个序列值);(6分)三、已知连续时间信号)102cos()10(2)]110(2sin[)(633t t t t x ⨯--=-πππ毫安,若它是能量信号,试求其能谱密度和它在单位电阻上消耗的能量;若它是功率信号,则求其功率谱密度函数和它在单位电阻上消耗的平均功率。
(共14分)四、已知][~n x 是周期为4的周期序列,且已知8点序列][~][n x n x =,70≤≤n ,的8点DFT 系数为: ,0)(,1)6()4()2()0(=====k X X X X X 其他k 。
试求:(共24分) 1. 周期序列][~n x ,并概画出它的序列图形;(12分)2. 该周期序列][~n x 通过单位冲激响应为2222)2/(sin )1(][n n n h ππ-=的数字滤波器后的输出][n y ,并概画出它的序列图形;(12分)五、已知)(t x 是最高频率为4KHz 的连续时间带限信号,(共24分) 1. 若对)(t x 进行平顶抽样获得的已抽样信号)(t x p 如图A-3所示,试由)(t x p 恢复出)(t x 的重构滤波器的频率响应)(ωL H ,并概画出其幅频响应和相频响应;(16分)图A-32. 你在1小题求得的重构滤波器为什么不可实现?为实现无失真恢复原信号,需对抽样频率和重构滤波器频率响应)(ωL H 作怎样的修改?(8分) 六、如图A-4的信号流图所示的数字滤波器,试求:(共22分)1. 它的系统函数)(z H 及其收敛域,并画出它用一个一阶全通滤波器和一个4阶FIR 滤波器的级联实现的方框图或信号流图;(12分)2. 概画出该数字滤波器的幅频响应)(~ΩH (或)(Ωj e H )。
07硕士信号与系统答案

中国民航大学2007年硕士研究生入学考试试卷答案科目名称:信号与系统 (A 卷)一、某LTI 因果系统,已知当激励为e 1(t )=u (t )时, 其零状态响应为r 1(t )=(3e -t +4 e -2t ) u (t )。
求当激 励为e 2(t )时(如图1所示),该系统的零状态响应 r 2(t )。
(10分)解: e 2(t )=3[u (t )- u (t -4)]∴ r 2(t )=3(3e -t +4 e -2t ) u (t ) -3[3e -(t -4)+4 e -2(t -4)] u (t -4) =(9e -t +12 e -2t ) u (t ) -[9e -(t -4)+12 e -2(t -4)] u (t -4)二、某LTI 因果系统的单位样值响应是h (n )=a n u (n ),其中0<a <1。
若激励信号为x (n ) =u (n )- u (n -3),求系统的零状态响应y (n )。
(11分) 解: x (n )= u (n )- u (n -3) =δ(n )+ δ(n -1)+ δ(n -2)∴ y (n )= x (n )* h (n )=[δ(n )+ δ(n -1)+ δ(n -2)] * h (n ) = h (n ) + h (n -1)+ h (n -2) =a n u (n )+ a n -1u (n -1)+ a n -2u (n -2)三、已知某LTI 因果系统的激励e (t )=sin t ●u (t ),其零状态响应r zs (t )=t [u (t )-u (t -4)]/4,求该系统的单位冲激响应h (t )。
(14分) 解: r zs (t )= e (t )* h (t )= sin t ●u (t ) * h (t )r ’zs (t )= e ’(t )* h (t )= cos t ●u (t ) * h (t ) r ’ ’zs (t )= e ’ ’(t )* h (t )= [δ(t )-sin t ●u (t )] * h (t )= h (t )- e (t )* h (t )= h (t ) - r zs (t ) ∴ h (t )= r ’ ’zs (t )+ r zs (t )=)]4()([4)4()4(41)(41'--+----t u t u tt t t δδδ图1四、已知周期信号f (t )的傅里叶级数表示式为f (t )=1+sin (ω1t )+2cos (ω1t )+cos (2ω1t +π/4),其中ω1为基波的角频率。
信号与线性系统分析复习题及答案

信号与线性系统复习题单项选择题。
1. 已知序列3()cos()5f k k π=为周期序列,其周期为 ( C ) A . 2 B. 5 C. 10 D. 122. 题2图所示()f t 的数学表达式为 ( B )图题2A .()10sin()[()(1)]f t t t t πεε=+- B. ()10sin()[()(1)]f t t t t πεε=-- C. ()10sin()[()(2)]f t t t t πεε=-- D. ()10sin()[()(2)]f t t t t πεε=+-3.已知sin()()()t f t t dt t πδ∞-∞=⎰,其值是 ( A )A .π B. 2π C. 3π D. 4π4.冲激函数()t δ的拉普拉斯变换为 ( A )A . 1 B. 2 C. 3 D. 45.为了使信号无失真传输,系统的频率响应函数应为 ( D ) A . ()djwt H jw e= B. ()djwt H jw e-= C. ()djwt H jw Ke= D. ()djwt H jw Ke-=6.已知序列1()()()3kf k k ε=,其z 变换为 ( B )A .13z z + B.13z z - C.14z z + D.14z z -7.离散因果系统的充分必要条件是 ( A ) A .0,0)(<=k k h B. 0,0)(>=k k h C. 0,0)(<<k k h D. 0,0)(>>k k h8.已知()f t 的傅里叶变换为()F jw ,则(3)f t +的傅里叶变换为 ( C ) A .()jwF jw e B. 2()j wF jw eC. 3()j wF jw eD. 4()j wF jw e9.已知)()(k k f kεα=,)2()(-=k k h δ,则()()f k h k *的值为( B ) A .)1(1--k k εαB. )2(2--k k εαC. )3(3--k k εαD. )4(4--k k εα10.连续时间系统的零输入响应的“零”是指( A ) A. 激励为零 B. 系统的初始状态为零 C. 系统的冲激响应为零 D. 系统的阶跃响应为零 11. 已知序列kjek f 3)(π=为周期序列,其周期为 ( )A . 2 B. 4 C. 6 D. 812. 题2图所示()f t 的数学表达式为 ( )A .)1()1()(--+=t t t f εε B.)1()1()(-++=t t t f εε C. )1()()(--=t t t f εε D. )1()()(-+=t t t f εε13.已知)2()(),1()(21-=-=t t f t t f εδ,则 12()()f t f t *的值是 ( ) A .)(t ε B. )1(-t ε C. )2(-t ε D. )3(-t ε14.已知ωωj j F =)(,则其对应的原函数为 ( ) A .)(t δ B. )('t δ C. )(''t δ D. )('''t δ15.连续因果系统的充分必要条件是 ( ) A . 0,0)(==t t h B. 0,0)(<=t t h C. 0,0)(>=t t h D. 0,0)(≠=t t h16.单位阶跃序列)(k ε的z 变换为 ( )A .1,1<+z z z B. 1,1>+z z z C. 1,1<-z z z D. 1,1>-z z z 17.已知系统函数ss H 1)(=,则其单位冲激响应()h t 为 ( )A .)(t ε B. )(t t ε C. )(2t t ε D. )(3t t ε18.已知()f t 的拉普拉斯变换为()F s ,则)5(t f 的拉普拉斯变换为 ( )tA .)5(s F B. )5(31s F C. )5(51s F D. )5(71s F 19.已知)2()(2-=-k k f k εα,)2()(-=k k h δ,则()()f k h k *的值为( )A .)1(1--k k εα B. )2(2--k k εαC. )3(3--k k εαD. )4(4--k k εα20.已知)(t f 的傅里叶变换为)(ωj F ,则)(jt F 的傅里叶变换为( ) A. )(ωπ-fB. )(ωπfC. )(2ωπ-fD. )(2ωπf21. 下列微分或差分方程所描述的系统是时变系统的是 ( ) A . )(2)()(2)(''t f t f t y t y -=+ B. )()(sin )('t f t ty t y =+ C. )()]([)(2't f t y t y =+ D. )()2()1()(k f k y k y k y =--+22. 已知)()(),()(21t t f t t t f εε==,则)()(21t f t f *的值是 ( ) A .)(1.02t t ε B. )(3.02t t ε C. )(5.02t t ε D. )(7.02t t ε23.符号函数)sgn(t 的频谱函数为 ( )A .ωj 1 B. ωj 2 C. ωj 3 D. ωj 424.连续系统是稳定系统的充分必要条件是 ( ) A . M dt t h ≤⎰∞∞-)( B. M dt t h ≥⎰∞∞-)(C.M dt t h ≤⎰∞∞-)( D.M dt t h ≥⎰∞∞-)(25.已知函数)(t f 的象函数)5)(2()6()(+++=s s s s F ,则原函数)(t f 的初值为 ( )A . 0 B. 1 C. 2 D. 3 26.已知系统函数13)(+=s s H ,则该系统的单位冲激响应为 ( ) A .)(t e tε- B.)(2t e tε- C.)(3t e tε- D. )(4t e tε- 27.已知)2()(),1()(1-=-=-k k h k k f k δεα,则)()(k h k f *的值为 ( )A .)(k kεα B.)1(1--k k εα C.)2(2--k k εα D. )3(3--k k εα28. 系统的零输入响应是指( ) A.系统无激励信号 B. 系统的初始状态为零C. 系统的激励为零,仅由系统的初始状态引起的响应D. 系统的初始状态为零,仅由系统的激励引起的响应 29.偶函数的傅里叶级数展开式中 ( )A .只有正弦项 B.只有余弦项 C. 只有偶次谐波 D. 只有奇次谐波 10. 已知信号()f t 的波形,则)2(t f 的波形为 ( ) A .将()f t 以原点为基准,沿横轴压缩到原来的12B. 将()f t 以原点为基准,沿横轴展宽到原来的2倍C. 将()f t 以原点为基准,沿横轴压缩到原来的14D. 将()f t 以原点为基准,沿横轴展宽到原来的4倍 填空题1. 已知象函数223()(1)s F s s +=+,其原函数的初值(0)f +为___________________。
