信号与线性系统 答案
信号与线性系统分析_(吴大正_第四版)习题答案12264精编版
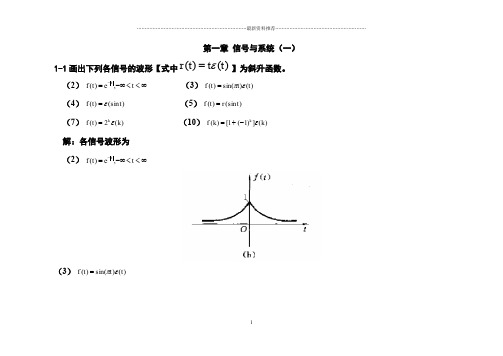
第一章 信号与系统(一)1-1画出下列各信号的波形【式中)()(t t t r ε=】为斜升函数。
(2)∞<<-∞=-t e t f t ,)( (3))()sin()(t t t f επ= (4))(sin )(t t f ε= (5))(sin )(t r t f = (7))(2)(k t f k ε= (10))(])1(1[)(k k f k ε-+= 解:各信号波形为 (2)∞<<-∞=-t e t f t ,)((3))()sin()(t t t f επ=(4))fεt=(sin)(t(5))trf=(sin)(t(7))t(kf kε=)(2(10))f kεk-=(k+(])1(1[)1-2 画出下列各信号的波形[式中)()(t t t r ε=为斜升函数]。
(1))2()1(3)1(2)(-+--+=t t t t f εεε (2))2()1(2)()(-+--=t r t r t r t f(5))2()2()(t t r t f -=ε (8))]5()([)(--=k k k k f εε(11))]7()()[6sin()(--=k k k k f εεπ (12))]()3([2)(k k k f k---=εε 解:各信号波形为 (1))2()1(3)1(2)(-+--+=t t t t f εεε(2))2()1(2)()(-+--=t rt rt rtf(5))2()2()(ttrtf-=ε(8))]5()([)(--=k k k k f εε(11))]7()()[6sin()(--=k k k k f εεπ(12))]()3([2)(kkkf k---=εε1-3 写出图1-3所示各波形的表达式。
1-4 写出图1-4所示各序列的闭合形式表达式。
1-5 判别下列各序列是否为周期性的。
如果是,确定其周期。
(2))63cos()443cos()(2ππππ+++=k k k f (5))sin(2cos 3)(5t t t f π+=解:1-6 已知信号)(t f 的波形如图1-5所示,画出下列各函数的波形。
专升本《信号与线性系统》-试卷-答案

专升本《信号与线性系统》一、(共60题,共156分)1. 能量有限信号是指总能量为有限值而平均功率为____的信号。
(2分).标准答案:1. 零;2. 系统响应中随时间增长而趋于稳定的部分称为________________分量。
(2分).标准答案:1. 稳态响应;3. 单位函数响应h(k)是指离散时间系统对____________________________________________的零状态响应。
(2分).标准答案:1. 单位函数(或δ(k));4. 若周期函数f (t)满足,则称其为________函数。
(2分).标准答案:1. 奇谐;5. h(t)是连续因果LTI系统的冲激响应,则系统稳定的充要条件是________________________________________________________________________ ________________________________________________________________________ ________________________________________________________________________ ________________________________________________________________________ ____________________。
(2分).标准答案:1. ;6. ____。
(2分).标准答案:1. 0;7. 时间函数中变化较____的信号必定具有较宽的频带。
(2分).标准答案:1. 快;8. 信号的最小抽样频率为________________________________________________________________________ ________________________________________________________________________ ________________________________________________________________________ ________________________________________________________________________ ____________________ Hz。
信号与线性系统课后习题答案4

即: 1 =
(3) 平均功率 p =
∴ 电压有效值 =
(4) Q Fn =
2
1 T2 1 1 − jn π t 1 − e − jn π − jn π t f(t)e dt = e dt = , n = ±1, ±2..... T ∫− T 2 2 ∫0 j2nπ
∴ Fn F0 =
=
1 − e − jn π j2nπ
1
1 ⎡1 − e − j(n −1) π 1 − e − j(n +1) π ⎤ 1 + (−1) n ∴ Fn = ⎢ − ⎥= 4 j ⎣ j(n − 1) π j(n + 1) π ⎦ 2 π(1 − n 2 )
题 4.11 某 1 Ω 电阻两端的电压 u(t) 如图 4-2 所示
u/V
1
−2t FT ⎡ ⎣ e ε ( t + 1) ⎤ ⎦ =
∫
∞ −∞
e − 2 t ε ( t + 1) e − j ω t d t =
∫
∞ −1
e − ( jω + 2 ) t d t =
e jω + 2 jω + 2
(5) Q ε(t) ↔ πδ(ω) +
⎡ 1 1⎤ e − jω , ∴ ε(t − 1) ↔ e − jω ⎢ πδ(ω) + ⎥ = πδ(ω) + jω jω ⎦ jω ⎣
∴ u(t) =
令 n = 2k + 1, k = 0,1,2...... ,则
u(t) = = 1 ∞ 2 sin [ (2k + 1) πt ] +∑ 2 k =0 (2k + 1) π 1 2 ∞ 1 sin [ (2k + 1) πt ] + ∑ 2 π k =0 (2k + 1) π 1 1 , 而 u( ) = 1 2 2
信号与线性系统分析_(第四版)习题答案

专业课习题解析课程xxxxxx大学844信号与系统专业课习题解析课程第1讲第一章信号与系统(一)专业课习题解析课程第2讲第一章 信号与系统(二)1-1画出下列各信号的波形【式中)()(t t t r ε=】为斜升函数。
(2)∞<<-∞=-t e t f t ,)( (3))()sin()(t t t f επ=(4))(sin )(t t f ε= (5))(sin )(t r t f =(7))(2)(k t f kε= (10))(])1(1[)(k k f kε-+=解:各信号波形为(2)∞<<-∞=-t e t f t ,)((3))()sin()(t t t f επ=(4))(sin )(t t f ε=(5))tf=r)(sin(t(7))f kε=t)(2(k(10))(])1(1[)(k k f k ε-+=1-2 画出下列各信号的波形[式中)()(t t t r ε=为斜升函数]。
(1))2()1(3)1(2)(-+--+=t t t t f εεε (2))2()1(2)()(-+--=t r t r t r t f(5))2()2()(t t r t f -=ε (8))]5()([)(--=k k k k f εε(11))]7()()[6sin()(--=k k k k f εεπ(12))]()3([2)(k k k f k ---=εε解:各信号波形为(1))2()1(3)1(2)(-+--+=t t t t f εεε(2))2()1(2)()(-+--=t r t r t r t f(5))2()2()(t t r t f -=ε(8))]5()([)(--=k k k k f εε(11))]7()()[6sin()(--=kkkkfεεπ(12))]()3([2)(kkkf k---=εε1-3 写出图1-3所示各波形的辯达式。
1-4 写出图1-4所示各序列的闭合形式辯达式。
信号与线性系统_习题答案(有错版)

2.1 (1) 已知连续时间信号 x(t ) 如图 P2.1(a)所示。试画出下列各信号的波形图,并加以标 注。 (a) x(t − 2) (b) x(1 − t ) (c) x(2t + 2) (2) 根据图 P2.1(b)所示的信号 h(t ) ,试画出下列各信号的波形图,并加以标注。 (a) h(t + 3) (b) h( − 2) (c) h(1 − 2t ) (3) 根据图 P2.1(a)和(b)所示的 x(t ) 和 h(t ) ,画出下列各信号的波形图,并加以标注。 (a) x(t )h(−t ) (b) x(1 − t )h(t − 1) (c) x(2 − ) h(t + 4)
其基波周期 T0 是 T1 , T2 的最小公倍数。 (b) x(n) 和 y ( n) 是周期的, x(n + = N1 ) x(n), y (n + N = y ( n) 2) 令 f= (n) x(n) + y (n) ,欲使 f (n) 是周期的,必须有
= N 0 kN = mN 2 1
πn
4
,对所有 n ,
7
1 n , n奇 显然 x(n) 是非周期的,但 y1 (n) 是周期的。 h(n) = 3 0, n偶
(c) 正确。若 x(n) 的周期为 N ,则 y2 (n) 的周期为 2 N 。 (d) 正确。若 y2 (n) 的周期为 N ,则 N 只能是偶数。 x(n) 的周期为 N / 2 。 2.7 判断下列各信号是否是周期信号,如果是周期信号,求出它的基波周期。 (a) = x(t ) 2 cos(3t + π / 4) (c) x(t ) = e (e) = x ( n)
1
信号与线性系统-白恩健书答案

第1章基本概念K第1章习题k1.1解:(1)x(t)为周期信号,周期为T=10。
(2)x(t)为非周期信号。
(3)x[n]为非周期信号。
(4)x[n]为周期信号,周期为N=2。
(5)x(t)为非周期信号。
(6)x[n]为周期信号,周期为N=2。
1.2解:(1)x(t)为功率信号。
(2)x(t)既不是能量信号也不是功率信号。
(3)x[n]为能量信号。
(4)x(t)为能量信号。
(5)x(t)为能量信号。
(6)x[n]为能量信号。
1.3略。
1.4略。
1.5(原题有误)一个离散时间系统的激励与响应的关系为y[n]=M∑i=0b i x[n−i]。
用算符S−k代表将信号x[n]平移k个单位时间得到输出信号x[n−k]的系统,即x[n−k]=S−k(x[n])。
写出联系y[n]与x[n]的系统算符T及其可逆系统的算符T inv。
解:提示:可逆系统为y[n]−M∑i=1b i x[n−i]=b0x[n]。
1.6解:(1)因果、无记忆、非线性、时不变、BIBO稳定系统。
(2)因果、无记忆、线性、时变和BIBO稳定系统。
(3)因果、无记忆、线性、时变和非稳定系统。
(4)因果、记忆、线性、时不变和BIBO稳定系统。
(5)因果、无记忆、线性、时变和BIBO稳定系统。
(6)因果、记忆、时不变、非稳定系统。
–2/48–第1章基本概念(7)因果、无记忆、线性、时不变和BIBO稳定系统。
(8)非因果系统、无记忆、线性、时不变、BIBO稳定系统。
1.7证明略。
1.8解:(1)x[n]的响应为{1,1,−1,2,n=0,1,2,3}。
(2)x[n]的响应为{1,1,−3,1,3,−5,2,n=−3∼3}。
(3)x[n]的响应为{1,0,−1,4,−3,2,n=−2∼3}。
1.9证明提示:根据微积分的极限定义证明。
1.10解:(1)x(t)的响应为4(1−e−t)u(t)−6(1−e−t+1)u(t−1)。
(2)x(t)的响应为[2(t+e−t)−2]u(t)。
信号与线性系统课后答案

(c)
p
图题 2 - 9
g(t)
t
0_
hτ( )dτ
[e 2τ
e τ ]
t 0
ε(t
)
(e t
e 2 t
)ε(t)
.
2 -10 如图题 2-10 所示系统,已知两个子系统的冲激响应分别为 h1(t) (t1),
h2(t) (t),试求整个系统的冲激响应 h(t)。
f (t)
h2(t)
y (t)
h1(t) 图题 2 - 10
f1(t) 1
t -2 0 2
(a)
解:
f2(t)
(1)
(1)
f3(t) (1) (1)
t -2 0 2
(b)
3 02 4
t
(-1)
(c)
图题 2 - 11
f4(t) 1
t -1 0 1
(d)
f1 (t )
1 2
(t
2) (t
2)
t (t)
1 2
(t
2) (t
2)
1 f1(t)*f2(t)
(1) f1(t) * f2 (t) f1(t 2) f1(t 2)
(a) 已知 i(0-) = 0,u(0-) = 5V,求 ux(t); (b) 已知 u(0-) = 4V,i(0-) = 0,求 ix(t); (c) 已知 i(0-) = 0,u(0-) = 3V,求 ux(t) .
解: (a) Z( p) 0 5 p 6 0 p2 5p 6 0 p
(3) f1(t) et (t) , f2 (t) e 2t (t) ;
(4) f1(t) et (t) , f2 (t) sin t (t) ;
(完整版)信号与线性系统分析_(吴大正_第四版)习题答案

1-1画出下列各信号的波形【式中)()(t t t r ε=】为斜升函数。
(2)∞<<-∞=-t et f t,)( (3))()sin()(t t t f επ=(4))(sin )(t t f ε= (5))(sin )(t r t f = (7))(2)(k t f kε= (10))(])1(1[)(k k f kε-+=解:各信号波形为 (2)∞<<-∞=-t et f t,)((3))()sin()(t t t f επ=(4))(sin )(t t f ε=(5))f=rt)(sin(t (7))t(k=f kε)(2(10))f kεk=(k+-((])11[)1-2 画出下列各信号的波形[式中)()(t t t r ε=为斜升函数]。
(1))2()1(3)1(2)(-+--+=t t t t f εεε (2))2()1(2)()(-+--=t r t r t r t f(5))2()2()(t t r t f -=ε (8))]5()([)(--=k k k k f εε(11))]7()()[6sin()(--=k k k k f εεπ(12))]()3([2)(k k k f k ---=εε解:各信号波形为(1))2()1(3)1(2)(-+--+=t t t t f εεε(2))2()1(2)()(-+--=t r t r t r t f(5))2()2()(t t r t f -=ε(8))]5()([)(--=k k k k f εε(11))]7()()[6sin()(--=k k k k f εεπ(12))]()3([2)(k k k f k---=εε1-3 写出图1-3所示各波形的表达式。
1-4 写出图1-4所示各序列的闭合形式表达式。
1-5 判别下列各序列是否为周期性的。
如果是,确定其周期。
(2))63cos()443cos()(2ππππ+++=k k k f (5))sin(2cos 3)(5t t t f π+=解:1-6 已知信号)(t f 的波形如图1-5所示,画出下列各函数的波形。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验一 信号的MATLAB 表示三、 实验内容:1. 用MA TLAB 表示连续信号:t Ae α,)cos(0ϕω+t A ,)sin(0ϕω+t A 。
t Ae αt=0:001:10; A=1; a=-0.4;ft=A*exp(a*t); plot(t,ft))cos(0ϕω+t At=0:0.1:10; A=1; a=1; b=pi/4;ft=A*sin(a*t+b); plot(t,ft))sin(0ϕω+t At=0:0.1:10; A=1; a=1; b=pi/4;ft=A*cos(a*t+b); plot(t,ft)2. 用信号处理工具箱提供的函数表示抽样信号、矩形脉冲信号及三角脉冲信号。
y=sinc(t)y=sinc(t);plot(t,y)y=rectpuls(t, width)t=0:0.01:4;T=1;y=rectpuls(t-2*T, 2*T);plot(t,y)y=tripuls(t , width, skew) t=-5:0.01:5;width=2;skew=0.6;y=tripuls(t, width, skew); plot(t,y)3. 编写如图所示的MA TLAB 函数,并画出)5.0(t f ,)5.02(t f 的图形。
-11-112)(t ft=-2:0.01:3;ft=rectpuls(t+0.5, 1)+(1-t).*rectpuls(t-0.5,1)-rectpuls(t-1.5, 1); plot(t,ft)f5.0(t)function ft=f(t)ft=rectpuls(t+0.5, 1)+(1-t).*rectpuls(t-0.5,1)-rectpuls(t-1.5, 1); plot(t,ft)t=-5:0.01:5;y=f(0.5*t);plot(t,y))5.02(t ft=-2:0.01:8; y=f(2-0.5*t); plot(t,y)4. 用MA TLAB 表示离散信号:k a ,)sin(k A 。
k ak=0:0.2:10; a=2; y=a.^k; stem(k,y)Asin(k)k=0:0.2:10; A=2;y=A*sin(k); stem(k,y)实验二 连续时间系统的时域分析三、实验内容:1. 分别用函数lsim 和卷积积分两种方法求如图所示系统的零状态响应。
其中L=1,R=2,)()(t e t e t ε-=,2)0(=-i 。
-+e (t ) i (t )RL用函数lsimL=1;R=2;sys=tf([1],[L R]); t=0:0.1:10; f=exp(-t);y=lsim(sys,f,t); plot(t,y);xlabel('Time(sec)') ylabel('y(t)')用卷积积分L=1;R=2;sys=tf([1],[L R]);t=0:0.001:10;f=exp(-t);y=impulse(sys,t);z=conv(y,f);plot(z)2. 求上述系统的冲激响应与阶跃响应。
冲激响应L=1;R=2;sys=tf([1],[L R]);t=0:0.1:10;f=exp(-t);y=impulse(sys,t);plot(t,y)xlabel('Time(sec)')ylabel('y(t)')阶跃响应L=1;R=2;sys=tf([1],[L R]); t=0:0.1:10;f=exp(-t);y=step(sys,t);plot(t,y)xlabel('Time(sec)') ylabel('y(t)')实验三信号的Fourier分析三、实验内容:1. 求如图所示周期矩形脉冲信号的Fourier级数表达式,画出频谱图,并用前N次谐波合成的信号近似。
画出周期矩形脉冲信号的频谱图N=8;n1=-N:-1;c1=-2*j*sin(n1*pi/2)/pi./n1;c0=0;n2=1:N;c2=-2*j*sin(n2*pi/2)/pi./n2;cn=[c1 c0 c2];n=-N:N;subplot(1,2,1);stem(n,abs(cn));ylabel('Cn的幅度');xlabel('\Omega');subplot(1,2,2);stem(n,angle(cn));ylabel('Cn的相位');xlabel('\Omega');用前N次谐波合成的信号近似建立M函数f.mfunction s=f(m)s=0;p=0;t=0:0.01:10;for n=1:2:mp=p+1/n*(sin(n*t));ends=(4/pi)*p;plot(t,s)f(20);xlabel('Time(sec)')ylabel('f(t)')2. 求信号)(2t te t ε-的幅度谱。
w=-2*pi:0.2:2*pi; c=(2+j*w).^(-2); plot(w,abs(c)); ylabel('C 的幅度'); xlabel('\Omega');实验四连续系统的频域分析三、实验内容:如图所示系统:+-(1) 对不同的RC值,用freqs函数画出系统的幅频曲线。
for rc=0:200:1000b=[1];a=[rc,1];[Hz,w]=freqs(b,a);w=w./pi;magh=abs(Hz);zeroslndx=find(magh==0);magh(zeroslndx)=1;magh=20*log10(magh);magh(zeroslndx)=-inf;subplot(3,2,(rc+200)/200);plot(w,magh);grid onxlabel('特征角频率(\times\pi rads/sample)')title('幅频特性曲线|H(w)|(dB)');end(2) 信号)3000cos()100cos()(t t t f +=包含了一个低频分量和一个高频分量。
确定适当的RC 值,滤除信号中的高频分量并画出信号)(t f 和)(t y 在2.0~0=t s 范围内的波形。
确定RC 的值 Hz(1)=0; RC=1;while abs(Hz(1))<0.9 b=[1]; a=[RC,1];Hz=freqs(b,a,[100,3000]); RC=RC-0.001; end RCRC =0.0030滤除信号中的高频分量并画出信号)(t f 和)(t y 在2.0~0 t s 范围内的波形 t=0:0.001:0.2;fun1=cos(100*t)+cos(3000*t); sys=tf([1/RC],[1,1/RC]); y=lsim(sys,fun1,t); subplot(2,1,1); plot(t,fun1); xlabel('f(t)'); subplot(2,1,2); plot(t,y,'r'); xlabel('y(t)'); hold off;实验五调制与解调三、实验内容:调制信号为一取样信号,利用MA TLAB分析幅度调制(AM)产生的信号频谱,比较信号调制前后的频谱并解调已调信号。
设载波信号的频率为100Hz。
调制信号syms t;a=20;et=sin(a*t)/(a*t);ezplot(et,[-2,2]);axis([-2 2 -0.5 1.5])对et进行傅立叶变换fourier(et)ans =1/20*pi*(heaviside(w+20)-heaviside(w-20))et 幅普图N=40;w=-N:N;cn=1/20*pi*(heaviside(w+20)-heaviside(w-20)); stem(w,abs(cn));ylabel('幅度');xlabel('\Omega');对信号进行调制并傅立叶变换A0=1;fourier((A0+et)*cos(100*t),'w')ans =1/40*pi*(-heaviside(-w-120)+heaviside(w-80)+heaviside(-w-80)-heaviside(w-120)+40*dirac(w+10 0)+40*dirac(w-100))调制信号的幅度普N=140;w=-N:N;cn=1/40*pi*(-heaviside(-w-120)+heaviside(w-80)+heaviside(-w-80)-heaviside(w-120)+40*dirac(w +100)+40*dirac(w-100));stem(w,abs(cn));ylabel('幅度');xlabel('\Omega');解调clear,syms w;>>ifourier(1/40*pi*(-heaviside(-w-120)+heaviside(w-80)+heaviside(-w-80)-heaviside(w-120)+40*dir ac(w+100)+40*dirac(w-100)),'t')ans =cos(100*t)+1/80*(-i*exp(-80*i*t)+i*exp(80*i*t)+i*exp(-120*i*t)-i*exp(120*i*t))/tclear,syms t;et2=(cos(100*t)+1/80*(-i*exp(-80*i*t)+i*exp(80*i*t)+i*exp(-120*i*t)-i*exp(120*i*t))/t)/cos(100* t)-1;ezplot(et2,[-2 2]);axis([-2 2 -0.5 1.5])实验六无失真传输与滤波三、实验内容:1. 信号任选,分析以下几种情况下信号的频谱和波形变化:(1)系统满足线性不失真条件时;t0=-3*pi;ts=3*pi;dt=0.01;t=t0:dt:ts;T=2*pi;Et=0.5*tripuls(t,2,0);plot(t,Et)(2)系统只满足恒定幅值条件时;t0=-3*pi-1000;ts=3*pi-1000;dt=0.01;t=t0:dt:ts;T=2*pi;E1t=0.5.*(0.5*tripuls(t+1000,2*T,0)+0.5*tripuls(t-1000,2*T,0)); subplot(1,2,1);plot(t,E1t)t0=-3*pi+1000;ts=3*pi+1000;dt=0.01;t=t0:dt:ts;T=2*pi;E1t=0.5.*(0.5*tripuls(t+1000,2*T,0)+0.5*tripuls(t-1000,2*T,0)); subplot(1,2,2);plot(t,E1t)(3)系统只满足相位条件时;clear;t0=-3*pi-1000;ts=3*pi-1000;dt=0.01;t=t0:dt:ts;figure(1);T=2*pi;T1=2;Rt=0.5*(0.5.*tripuls(t+1000,2*T,0)+0.5.*tripuls(t+1000,2*T,0)).*(tripuls(t-1000,2*T1,0)+tripuls(t+ 1000,2*T1,0));subplot(1,2,1);plot(t,Rt)t0=-3*pi+1000;ts=3*pi+1000;dt=0.01;t=t0:dt:ts;Rt=0.5*(0.5.*tripuls(t-1000,2*T,0)+0.5.*tripuls(t-1000,2*T,0)).*(tripuls(t-1000,2*T1,0)+tripuls(t+1 000,2*T1,0));subplot(1,2,2);plot(t,Rt)(4)系统两个条件均不满足时。
