瞬时速度矢量与瞬时加速度矢量
牛顿第二定律的应用(瞬时性、矢量性)

m a2 g2
设弹力与水平方向的夹角为,则:
tan α mg g ma a
【解题回顾】 (一)硬杆对小球的弹力的方向并不一定 沿杆的方向,这可借助于牛顿运动定律来 进行受力分析:
1、物体处于平衡状态时,合外力应为0; 2、物体处于变速运动状态时,满足:
F合=ma, F合方向与加速度方向一致. (二)应用牛顿定律解题时要注意a与F合方向 一致性的关系.有时可根据已知合力方向确定加
明确“轻绳”和“轻弹簧” 两个理想物理模型的 区别.
如图所示,质量均为m的木块A和B用一轻弹簧相连,竖直 放在光滑的水平面上,木块A上放有质量为2m的木块C,三 者均处于静止状态。现将木块C迅速移开,若重力加速度 为g,则在木块C移开的瞬间( C )
A.木块B对水平面的压力迅速变为2mg
B.弹簧的弹力大小为mg
T1
θ T2
m
F合
mg
T2
F合 TG
F合=mg tan a=g tan
T
T
G2
G1
G
F合=mg sin a=g sin
如图质量为 m 的小球用水平弹簧系住,并用倾角为 30°的光
滑木板 AB 托住,小球恰好处于静止状态.当木板 AB 突然
向下撤离的瞬间,小球的加速度为 A.
( C)
B.大小为2 3 3g,方向竖直向下
【例1】小车上固定着光滑的斜面, 斜面的倾 角为θ.小车以恒定的加速度向前运动,有一物 体放于斜面上, 相对斜面静止, 此时这个物体 相对地面的加速度是多大?
F合=G tan a =g tan
N
F合 a
θ
G
例 2:如图所示,动力小车上有一竖杆,杆顶端
速度与加速度的矢径表示法

二、点的加速度
在一般情况下,动点的速度的大小和方向都可能随时间变化。为了表 明点的速度的变化情况,用加速度来表示每一瞬时点的速度对于时间 的变化率。加速度既包括速度大小的变化,也包括速度方向的变化。
设动点 M 在瞬时t 的速度是 v ,在瞬时 t t 的速度是 v ,
如图4-10所示,则速度的变化是 v v v ,故动点的平均加 速度为
线的切线方向,如图4-11所示。加速度的单位是 m/s2。
图4-11
理论力学
r dr
v lim v* lim r
t 0
t0 t dt
所以,动点的速度等于动点的矢径对于时间的一阶导数。 注意:函数对时间的导数用在函数上方加 “ ”表示。
速度 v 描述点在瞬时 t 运动的快慢与方向。点的速度是矢量,
它的方向就是 r 或MM 在极限情况下的方向,也就是轨迹曲 线上 M 点的切线方向。一般地说,点的运动方向指的是速度 的方向。 速度的单位是m/s。
图4-9
r
t 描述点在时间间隔 t 内运动的平均快慢程度,称为动点在 时间间隔 t 内的平均速度矢量,以 v * 表示,即
v* r MM t t
因为时间是标量,故知 v * 的方向与 r 的方向相同。t 越小,MM 与 的 MM 差别就越小,平均速度就越趋近于动点的真实速度。因此当 t 趋近于零时,即得动点的瞬时速度,即 v 表示,即
a* v t
图4-10
当 t 趋近于零时,即得动点在瞬时 t 的加速度为
a
lim
t 2
动点的加速度等于动点的速度对于时间的一阶导数,或等于动点的矢
径对于时间的二阶导数。
如由任一定点 O 作相当于各瞬时 t1,t2 ,t3, 的速度矢 量 v1 ,v2 ,v3 , ,连接速度矢量端点的曲线称为速度矢端曲线。 由瞬时加速度的概念,可知瞬时加速度的方向是沿着动点速度矢端曲
瞬时速度与瞬时加速度

3、物体运动曲线 度是 A.6
s = 2t
3,
则在t=3秒时的瞬时速 则在t=3秒时的瞬时速 C.54 D.81
……( ……( C ) B.18
4、物体运动曲线 s = 3t − t 2,则物体的初速度 是
3
.
5、作直线运动的物体,位移s(m)与时间t(s)的函 作直线运动的物体,位移s(m)与时间t(s)的函 数关系 s = 5t -2t2 (1) 求物体在第5秒和第6秒时的瞬时速度; 求物体在第5秒和第6 (2) 求物体在t时刻的瞬时速度; 求物体在t (3) 求物体t时刻运动的加速度,并判断物体 求物体t 作什么运动?
v= — △t
△S
例1、在高台跳水运动中,运动员相对于水面的高度 在高台跳水运动中, h(单位 单位: 与起跳后的时间t 单位: h(单位:米)与起跳后的时间t(单位:s)存在函数关 系:h(t)= - 4.9 t2+ 6.5t +10. (2)求运动员在t∈[2,2+△t]内的平均速度; )求运动员在t [2, t]内的平均速度; v= ————————
(2+△t) -2 2+△ h( 2+△t )- h(2) 2+△
= -13.1-4.9△t 13.1-
(m/s) m/s)
思考:当△t→0时, v表示什么? t→0时 表示什么? 思考:
--表示在 --表示在 t=2 时刻处的瞬时速度. 时刻处的瞬时速度.
小结 在t时刻处的瞬时速度怎么求? 1、先求[t,t+△t]段的平均速度; 、先求[t, t]段的平均速度;
课堂检测
1、曲线 A.2 在点(1 y = 2x 在点(1,2)处的瞬时变化率为
2
第二章 质点运动学

第二章 质点运动学运动学的任务是描述随时间的推移物体位置变化(运动)的规律,不涉及物体间相互作用与运动的关系。
§2.1 质点的运动学方程一、质点的位置矢量和运动学方程 要描述某质点在空间的位置,可以在参考系上先建立一个空间直角坐标系xyz o -,从坐标原点向该质点引一条有向线段,用r表示。
1、 位置矢量定义:自参考点(原点o )引向质点P 所在位置的矢量。
质点位矢在直角坐标系中的表示:k z j y i x r++=ˆˆk j i,ˆ,ˆ分别为沿x 轴,y 轴,z 轴正方向的单位矢量,z y x ,,称为质点的位置坐标,质点的一组位置坐标就对应于一个位置矢量,也就对应质点一空间位置。
位矢的大小: 222z y x r r ++==位矢的方向(用方向余弦表示):rzr y r x ===γβαcos ,cos ,cos 1cos cos cos 222=++γβα γβα,,分别为位矢与x 轴,y 轴,z 轴正方向的夹角。
2、质点的运动学方程由于质点的运动的不同时刻,位矢不同,则有:)(t r r= 即为质点的运动学方程,它给出了任意时刻质点的位置。
方程在直角坐标系中的正交分解式:k t z j t y i t x t r)()()()(++=质点运动学方程的标量形式为: )(),(),(t z z t y y t x x === 3、质点的运动轨迹质点运动时位矢端点描出的曲线,称质点运动轨迹。
由运动学方程消去t 得: 0),,(=z y x f[例] 一质点的运动学方程为:j t r i t R rsin cos +=,求其轨迹。
解:由已知,tR y t R x sin cos == ,则轨迹方程:222R y x =+,圆心在原点。
二、质点的位移和路程1、位移:描述质点在一定时间间隔内位置变动的物理量,用r∆表示。
)()(t r t t r r-∆+=∆位移在直角坐标中的正交分解式: k t z j t y i t x t r t t r r)()()()()(∆+∆+∆=-∆+=∆注意:质点的位移是矢量,其大小 12r r r r -=∆≠∆2、路程:描述质点在一定时间间隔内在其轨迹上经过路径的长度,用l ∆表示。
《力学》教学大纲

《力学》课程教学大纲一、课程基本信息英文名称 Mechanics 课程代码 PHYS1001课程性质 大类基础课程 授课对象 物理学学 分 4学分 学 时 72学时主讲教师 修订日期 2021年9月指定教材 张汉壮. 力学(第四版)高等教育出版社, 2019.二、课程目标(一)总体目标:通过力学课程的学习,使学生能够系统的掌握力学的基础知识,掌握力学基础的研究方法;在获取知识的同时,对简化模型的选取、量纲分析、数量级估计与定量计算的能力、提出问题和分析问题的能力、理论联系实际的能力等都应有所提高和发展。
适当的为物理学的前沿打开窗口,开阔学生的眼界、启迪并激发学生的探索和创新精神,更深层次地提升其科学素质。
(二)课程目标:课程目标1:使学生理解物理学的思想和研究问题的方法,培养其独立思考问题的能力和创新能力;使学生理解力与运动之间的关系,掌握力学的基本概念,基本定律和基本原理,能较为灵活地加以运用;为学生后继专业基础课程,例如光学、电磁学、理论力学等课程的学习及进一步获取有关知识奠定必要的物理基础。
课程目标2:系统的掌握力学的基础知识和研究方法,获取知识的同时,对简化模型的选取、量纲分析、数量级估计与定量计算的能力、提出问题和分析问题的能力、理论联系实际的能力等都应有所提高和发展,并进一步根据实际的物理运动过程构建模型,解决实际问题,综合提高学生的科学素养。
课程目标3:回顾力学发展史,了解一门学科发展过程中科学家所做贡献和其展现的科学精神;介绍物理学的前沿知识,适当引入新中国在工程建设、航天航空等方面取得的一系列成就,开阔学生的眼界、启迪并激发学生的探索和创新精神,更深层次地提升其科学素质的同时培养学生的爱国情怀。
使学生了解人类文明发展的现状是人才素质培养的一个重要方面。
(三)课程目标与毕业要求、课程内容的对应关系表1:课程目标与课程内容、毕业要求的对应关系表课程目标对应课程内容对应毕业要求(及对应关系说明)课程目标1 第O章 绪论第一章 质点运动学第二章 惯性系下质点动力学第三章 非惯性系下质点动力学第四章 动量定理与动量守恒定律第五章 功能原理与机械能守恒定律第六章 角动量定理与角动量守恒定律第七章 刚体第八章 流体第九章 振动第十章 波动2-2 掌握物理知识和物理方法,能应用物理知识和方法描述自然现象和规律2-3 掌握物理学理论知识,能解释或理解自然现象和自然规律,具有初步解决科学问题的能力7-1 能够运用各类搜索工具搜索网络信息和文献资料能规范撰写物理相关领域或课题进展调研报告系统掌握力学的基础知识,掌握力学基础的研究方法。
3.求瞬时速度和加速度
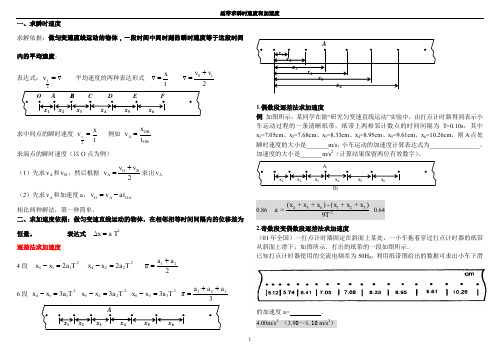
1一、求瞬时速度求解依据:做匀变速直线运动的物体,一段时间中间时刻的瞬时速度等于这段时间内的平均速度。
表达式:v v t =2平均速度的两种表达形式 t xv = 20t v v v +=求中间点的瞬时速度 t xv t =2例如 OBOB A t x v = 求端点的瞬时速度(以O 点为例) (1)先求A v 和B v ,然后根据 2BO A v v v +=求出A v (2)先求A v 和加速度a ,OA A O at v v -=相比两种解法,第一种简单。
二、求加速度依据:做匀变速直线运动的物体,在相邻相等时间间隔内的位移差为恒量。
表达式 2a T x =∆ 逐差法求加速度4段 21132T a x x =- 22242T a x x =- 221a a a +=6段 21143T a x x =- 22253T a x x =- 23363T a x x =- 3321a a a a ++=1.偶数段逐差法求加速度例 如图所示,某同学在做“研究匀变速直线运动”实验中,由打点计时器得到表示小车运动过程的一条清晰纸带,纸带上两相邻计数点的时间间隔为T =0.10s ,其中x 1=7.05cm 、x 2=7.68cm 、x 3=8.33cm 、x 4=8.95cm 、x 5=9.61cm 、x 6=10.26cm ,则A 点处瞬时速度的大小是_______m/s ,小车运动的加速度计算表达式为________________,加速度的大小是_______m/s 2(计算结果保留两位有效数字)。
2.奇数段变偶数段逐差法求加速度(01年全国)一打点计时器固定在斜面上某处,一小车拖着穿过打点计时器的纸带从斜面上滑下,如图所示.打出的纸带的一段如图所示.已知打点计时器使用的交流电频率为50H Z ,利用纸带图给出的数据可求出小车下滑的加速度a = . 4.00m/s 2 (3.90~4.10 m/s 2)23.已知不相邻的两段相等时间内的位移求加速度一条残缺的纸带如图所示,打点计时器所用交流电频率为50 Hz 。
大学物理1.2 质点的位移、速度和加速度

vxi v y j vzk
vx
dx dt
vy
dy dt
速度的大小为 v
v2 x
v
2 y
v
2 z
速度的方向用方向余弦表示为
vz
dz dt
( dx )2 ( dy )2 ( dz )2 dt dt dt
cos α vx , cos β vy , cos γ vz
v
v
v
讨论 v v 吗?
周期内质点位移的大小 r 2R ,位矢大小的增量为
r R R 0
二、 速度Байду номын сангаас
1. 平均速度
v
r (t
t)
r (t)
r
t
t
2. 瞬时速度
r
(1) 匀速直线运动
瞬时速度
v
=
_
v
Δr
t
(2)变速曲线运动
瞬时速度
v lim
r
dr
t0 t dt
瞬时速度 = 平均速度
v2
Δ r2 t2
v v(t t) v(t) v v(t t) v(t)
a v b
c
v(t) v(t t)
在Ob上截取 oc oa
有
v cb
O
vvvtn
ac ac cb
cb
vn vt
速度方向变化 速度大小变化
1.3.a3加dd速2tr2度
d2 dt 2
(xi
yj
zk )
d2x d2y d2z
r1 xAi yA j r2 xBi yB j 位移 r r2 r1
y
yB A r
r y A 1
r2
高一第一学期物理-2-平均速度、瞬时速度和加速度

辅导讲义加速度的方向同我们规定的正方向相同,也和初速度的方向相同。
分析方法二:△v 与a 同向,与v 0方向相同。
物体在做加速直线运动时,加速度的方向与初速度的方向相同3. 减速运动分析方法一:速度是矢量,我们规定汽车的初始方向为正方向,经过2s 后,那么△v=﹣3m/s,a=﹣1.5m/s.加速度为负值,说明加速度的方向同我们规定的正方向相反,也和初速度的方向相反。
分析方法二:△v 与a 同向,与v 0方向相反。
物体在做减速直线运动时,加速度的方向与初速度的方向相反结论:在直线运动的过程中,物体加速运动时,物体的加速度的方向与初速度相同,物体减速运动时,物体加速度的方向与初速度的方向相反。
【课堂练习】一、平均速度与瞬时速度1、某次列车20:00准点从A站发车,至次日18:00到达B站,行程1150Km 。
该列车在A.B站间行驶的平均速度约为 Km/h 。
2、物体先以11m/s 的速度行驶了10s,再以5m/s 的速度行驶了2s,那么该物体在全程中的平均速度是 。
3、某物体在一条直线上运动,它在前10s 中通过的路程是15m,在接下去的第二个10s 钟通过的路程是17m,那么,物体在第一个10s 钟内的平均速度为 ,在第二个10s 钟内的平均速度为 ,它在前20s 钟的平均速度为 。
4、某物体运动速度为4m/s,最有可能属于下列哪个物体的平均速度( )A.飞机B.火车C.小汽车D.跑步的人5、两辆汽车同时从甲地开出沿同一公路驶往乙地,4h 后,两车同时开到相距100Km 的乙地,则下列说法中错误的是v ∆ 0v t vv ∆5m/s 0v 2m/st v( )A.在这4h 中两车的平均速度相等 B.在这100Km 路程上两车的平均速度相等C.前60Km 路程上两车平均速度可能相等也可能不等D.在前2h 内两车的平均速度一定相等6、下列关于平均速度的说法正确的是( )A.平均速度是反映物体位置变化的物理量B.平均速度只能大体上反映物体运动的快慢程度C.平均速度可以精确地反映物体在某一位置的快慢程度D.平均速度可以精确的反映物体在某一时刻的快慢程度7、运动员百米赛跑时,起跑的速度为8m/s,中途的速度是9m/s,最后冲刺的速度是10m/s,如果他的成绩是12.5s, 则他跑完全程的平均速度是( )A.9.67m/sB.12m/sC.8m/sD.9m/s8、用刻度尺和表可测出小车从斜面滚下的平均速度。
速度、加速度

运动学的两类基本问题
第一类:已知运动方程求速度加速度 第一类:已知运动方程求速度加速度——微分法 微分法
dr v= dt
dv d r a= = 2 dt dt
2
第二类:已知速度或加速度求运动方程或速度 第二类:已知速度或加速度求运动方程或速度——积分法 积分法 此类问题必须已知初始条件! 此类问题必须已知初始条件!
j = vxi + vy + vzk Y X dx 其中: 其中: v = dr r x v= = lim dt t 0 dt t dy x y z vy = j + k) = lim ( i + t 0 t dt t t
dx dy dz i+ j+ k = dt dt dt
r
dz vz = dt
�
2
v ⊥r
v r = 0
4t ( 6 t 2 ) 2t = 0 t1 = 0 t2 = 2 s
( 2 ) r = x 2 + y 2 = 4t 2 + ( 6 t 2 ) 2 t1 = 0, r1 = 6m
t 2 = 2 s, r2 = 4.47m ∴ rmin = 4.47m
一质点沿x轴作直线运动 轴作直线运动, 例题,一质点沿 轴作直线运动,其v-t曲线如 曲线如 图所示, 图所示,如t=0时,质点位于坐标原点,求: 时 质点位于坐标原点, t=4.5秒时,质点在 轴上的位置. 秒时, 轴上的位置. 秒时 质点在x轴上的位置 解:实际上可以
∫ dv = ∫ adt ∫ dr = ∫ v dt
一质点由静止开始作直线运动, 例题 一质点由静止开始作直线运动, 初始加速度为a0,以后加速度均匀增 每经过τ秒增加a 加,每经过τ秒增加a0,求经过t秒后 质点的速度和运动的距离.
瞬时速度的三种公式

瞬时速度的三种公式
瞬时速度是衡量物体在某一方向上运动速度的量。
它与传统的速度有所不同,
通常涉及一段时间的运动情况,而瞬时速度更多地涉及物体在特定时刻的瞬时运动状态。
平常我们提到的速度有可能只是某一段时间内物体的运动速度,而以“瞬时”去使用它,暗示着对物体短时间段内的瞬时运动状况进行测量。
计算瞬时速度有三种公式,第一种是瞬时加速度公式,它的计算公式是v = v₀+ at,即瞬时速度等于初速加上加速度乘以时间。
另外两种分别是“位移法”和“相似三角形法”,位移法计算公式是v=Δd/Δt,即以两个时刻物体的位移差除
以时间跨度来求得瞬时速度;而相似三角形法计算公式是v= V₀ / (1 + at/V₀),
即特定时刻物体瞬时速度等于初始速度除以1加上加速度与初始速度的乘积。
瞬时速度是科学家精确测量物体运动状态的指标,但它也很容易在日常生活中
被观察到。
比如在追赶飞机的时候,正前方的飞机在比自己原来更快的速度前行,我们就可以对它计算出瞬时加速度;比如在上山时,有个人正快步爬行,从它面前瞬息的距离可以一眼看出瞬时速度的大致方向和数值,根据位移法进行计算。
究其原因,由于瞬时速度的定义便容易被理解,因此可以使用普通的直观原理
来对它进行大致的观察与计算。
虽然它的数值不能满足严格的精确测量,但已足够满足我们生活中的测量需求。
质点的瞬时速度和瞬时加速度计算方法研究

质点的瞬时速度和瞬时加速度计算方法研究质点的瞬时速度和瞬时加速度是描述物体运动状态的重要物理量。
在研究物体的运动规律和动力学性质时,准确计算质点的瞬时速度和瞬时加速度是必不可少的。
本文将探讨质点瞬时速度和瞬时加速度的计算方法。
一、质点的瞬时速度计算方法瞬时速度是指物体在某一瞬间的瞬时位移与瞬时时间的比值。
在一段时间内,如果物体的位移随时间的变化率保持不变,那么该物体的运动是匀速直线运动。
在这种情况下,质点的瞬时速度等于平均速度,即位移与时间的比值。
但是,在大多数情况下,物体的运动是变速运动,因此需要使用微积分的方法来计算质点的瞬时速度。
对于一维运动,质点的瞬时速度可以通过求导数来计算。
设质点的位移函数为s(t),其中t表示时间。
则质点的瞬时速度v(t)等于位移函数对时间的导数,即v(t)= ds(t)/dt。
这个导数表示了位移随时间的变化率,也可以理解为质点在某一瞬间的瞬时速度。
对于二维或三维运动,质点的瞬时速度的计算稍微复杂一些。
在这种情况下,需要将质点的运动分解为各个方向上的运动,并对每个方向上的位移函数分别求导数。
例如,在平面直角坐标系中,设质点的位移函数为s(t) = (x(t), y(t)),其中x(t)和y(t)分别表示质点在x轴和y轴上的位移。
则质点的瞬时速度v(t)等于(x'(t), y'(t)),其中x'(t)和y'(t)分别表示x(t)和y(t)对时间的导数。
二、质点的瞬时加速度计算方法瞬时加速度是指物体在某一瞬间的瞬时速度与瞬时时间的比值。
与瞬时速度类似,质点的瞬时加速度也可以通过求导数来计算。
对于一维运动,设质点的速度函数为v(t),则质点的瞬时加速度a(t)等于速度函数对时间的导数,即a(t) = dv(t)/dt。
对于二维或三维运动,质点的瞬时加速度的计算也需要将运动分解为各个方向上的运动,并对每个方向上的速度函数分别求导数。
例如,在平面直角坐标系中,设质点的速度函数为v(t) = (v_x(t), v_y(t)),其中v_x(t)和v_y(t)分别表示质点在x轴和y轴上的速度。
《普通物理学教程 力学(第二版》电子教案目录精编版

第八章 弹性体的应力和应变
§8.1 弹性体的拉伸和压缩 §8.2 弹性体的剪切形变 §8.3 弯曲和扭转
第九章 振 动
§9.1简谐振动的动力学特征 §9.2简谐振动的运动学 §9.3简谐振动的能量转换 §9.4简谐振动的合成 §9.5 振动的分解 §9.6 阻尼振动 §9.7 受迫振动 §9.8“不守规矩”的摆 混沌行为 §9.9 参数振动自激振动
漆安慎 杜婵英 著
普通物理学教程 力学(第二版)
电子教案
何丽珠 研制
高 等 教 育 出版社 高等教育电子音像出版社
第一章 物理学和力学
§1.1 发展着的物理学 §1.2 物理学研究的方法 §1.3 时间和长度的测量 §1.4 单位制和量纲 §1.5 数量级估计 §1.6 参考系·坐标系与时间坐标轴 §1.7 力学——学习物理学的开始
第十章 波动和声
§10.1 波的基本概念 §10.2 平面简谐波方程 §10.3 波动方程与波速 §10.4 平均能流密度·声强与声压 §10.5 波的叠加和干涉·驻波 §10.6 多普勒效应
第十一章 流体力学
§11.1 理想流体 §11.2 静止流体内的压强 §11.3 流体运动学的基本概念 §11.4 伯努利方程 §11.5 流体的动量和角动量 §11.6 黏性流体的运动 §11.7 固体在流体中受到的阻力 §11.8 机翼的升力
第二章 质点运动学
§ 2.1 质点的运动学方程 §2.2 瞬时速度矢量与瞬时加速度矢量 §2.3 质点直线运动——从坐标到速度和加速度 §2.4质点直线运动——从加速度到速度和坐标 §2.5 平面直角坐标系·抛体运动 §2.6 自然坐标·切向和法向加速度 §2.7 极坐标系·径向速度与横向速度 §2.8 伽利略变换
大学物理-1-3-速度-加速度

1-3 速度 加速度
第一章 质点运动学
2 瞬时加速度:
当 t 0 时,求得平均加速度的极限,表示质点
通过A 点的瞬时加速度,简称加速度。表示为
d d d r d2 r
a lim ( ) t0 t d t d t d t d t2
加速度等于速度对时间的一阶导数,或位矢对时间的二阶导数。
方向:总是指向位置曲线凹的一侧。
上页 下页 返回 帮助
1-3 速度 加速度
2 平均速率(标量)
第一章 质点运动学
质点在 t 内所经过的路程 s 与所用时间的比值,即
y
s
t
平均速率是标量,数值上等于质点
A r (t)
s
B
r
r(t t)
在单位时间内所通过的路程。
o
x
国际单位制中,速度和速率的单位都是 m s1
平均速度和平均速率都是粗略描述质点的运动情况。
1-3 速度 加速度
第一章 质点运动学
一、平均速度矢量
1 平均速度矢量
时刻
t : A, r(t)
时刻 t t : B, r (t t) 质点在 t 内的位移为 r
y
A r (t)
s
B
r
r(t t)
定义:
v r
o
x
表示在
t
t
时间内,质点位置矢量
r(t)
的平均变化率
v 平均速度是矢量,平均速度
与 r 同方向。
矢量和加速度矢量。
解 由于 x 10 为常量, 所以质点在 x 轴上距原点10cm
处的 Oyz 平面上运动。运动方程为
x 10
y
15t
z
5t 2
力学 第二章 质点运动学

v
arccos vz 5618'
v
二、平均加速度与瞬时加速度
1、平均加速度:速度矢量对时间的平均变化率。
a v v(t t) v(t)
t
t
v(t )
v
速度矢端曲线
v( t t )
§2.3 质点的直线运动(x vx ax )
一、运动学方程
x xt
二、速度和加速度
1、速度(瞬时速度)
vx
dx dt
大小表示质点在t时刻运动的快慢;
正负分别对应于质点沿Ox正向和负向运动。
2、加速度
ax
dvx dt
d2x dt 2
ax与vx同号,则加速;ax与vx反号,则减速。
4、质点的运动学轨迹方程
质点运动时描出的轨迹称为质点的轨迹。 也就是位置矢量的矢端曲线。
质点在平面Oxy上运动,
轨迹方程: y y(x) 或者:f (x, y, z) 0
例题:r R cos tiˆ R sin tˆj, 求:轨迹方程。
y R
解: x2 y2 R2.
x
二、位移
v
v
v
4、注意:
(1)平均速度的大小不等于平均速率。 (2)瞬时速度的大小等于瞬时速率。 (3)即使位置矢量的大小不变,也可以有速度。
ΔS
r(t )
r
S
r(
t
t
)
o
dr / dt
r(t )
ΔS
S
r
r( t t )
大学物理知到章节答案智慧树2023年仲恺农业工程学院

大学物理知到章节测试答案智慧树2023年最新仲恺农业工程学院第一章测试1.某质点的运动学方程x=6+3t-5t3,则该质点作()。
参考答案:变加速直线运动,加速度为负值2.质点以速度作直线运动,沿质点运动直线作Ox轴,并已知t=3s时,质点位于x=9m处,则该质点的运动学方程为()。
参考答案:3.半径的飞轮缘上一点A的运动学方程为(t以s为单位,S以m为单位),则当A点的速度大小时,A点的切向加速度和法向加速度大小为()。
参考答案:6;15004.根据瞬时加速度矢量的定义,其用直角坐标和自然坐标的表示形式,它的大小可表示为()。
参考答案:5.一运动质点在某瞬时位于矢径的端点处,其速度大小为()。
参考答案:6.一质点作直线运动,某时刻的瞬时速度,瞬时加速度,则一秒钟后质点的速度()。
参考答案:不能确定。
7.质点作曲线运动,表示位置矢量,表示速度,表示加速度,S表示路程,表示切向加速度,下列表达式中,()。
① ,② ,③ ,④ .()参考答案:只有③是对的.8.()。
参考答案:9.某质点沿直线运动,其加速度是,那么下述结论正确者为()。
参考答案:因为导数有无穷多个原函数,按题给条件,无法确定此质点的速度公式10.质点沿半径为R的圆周作匀速率运动,经过时间T转动一圈,那么在2T的时间内,其平均速度的大小和平均速率分别为()。
参考答案:第二章测试1.质点作曲线运动时,其法向加速度一般并不为零,但也有可能在某时刻法向加速度为零。
()参考答案:对2.一质量为M的斜面原来静止于水平光滑平面上,将一质量为m的木块轻轻放于斜面上,如图.如果此后木块能静止于斜面上,则斜面将()参考答案:保持静止.3.质量分别为m1和m2的两滑块A和B通过一轻弹簧水平连结后置于水平桌面上,滑块与桌面间的摩擦系数均为,系统在水平拉力F作用下匀速运动,如图所示.如突然撤消拉力,则刚撤消后瞬间,二者的加速度a A和a B分别为()。
参考答案:a A<0 , a B=0.4.把一质量为m,各边长均为2a的均质货箱,由位置(I)翻转到位置(II),则人力所做的功为()。
平面向量的速度与加速度

平面向量的速度与加速度在物理学中,平面向量是指具有大小和方向的向量,可以用来描述物体在平面上的运动。
在研究物体运动的过程中,我们经常需要计算平面向量的速度和加速度,以了解物体的运动特征和变化趋势。
速度是描述物体在单位时间内位移变化的大小和方向的物理量,即物体在单位时间内沿着某个方向移动的距离。
在平面运动中,我们可以用矢量来表示速度,即速度矢量。
速度矢量的大小表示物体在单位时间内的位移大小,而方向则表示物体运动的方向。
以平面上的直线运动为例,我们可以根据位移的定义来计算速度矢量。
假设物体在时间t1处于位置A,在时间t2处于位置B,位移矢量为AB。
我们可以利用以下公式来计算平均速度矢量v:v = AB / (t2 - t1)其中,v代表平均速度矢量,AB代表位移矢量,t2和t1分别表示时间t2和时间t1。
该公式表示平均速度矢量的定义为位移矢量与时间间隔的比值。
当我们希望得到物体在某一特定时刻的瞬时速度矢量时,可以通过将时间间隔t2 - t1无限缩小,使其趋近于零,从而得到物体在该时刻的瞬时速度矢量。
该矢量可以用微分形式表示为:v = dS / dt其中,v表示瞬时速度矢量,dS表示位移矢量的微元,dt表示时间的微元。
这个公式表示物体在某一时刻的速度矢量等于物体的位移矢量微元与时间微元之比。
除了速度,加速度也是描述物体运动的重要物理量。
加速度是指物体在单位时间内速度变化的大小和方向。
在平面运动中,加速度矢量的方向始终与速度矢量的方向相同或相反,而大小则表示速度变化的快慢。
给定速度矢量v1和速度矢量v2,位移矢量为AB,时间间隔为t2 - t1,我们可以通过以下公式来计算平均加速度矢量a:a = (v2 - v1) / (t2 - t1)其中,a代表平均加速度矢量,v2和v1分别表示时间t2和时间t1时的速度矢量,t2和t1表示时间间隔。
该公式表示平均加速度矢量的定义为速度矢量变化与时间间隔的比值。
与速度类似,我们也可以通过缩小时间间隔t2 - t1的幅度,使其趋近于零,从而得到物体在某一特定时刻的瞬时加速度矢量。
瞬时速度与瞬时加速度

△t 0.1 0.01 0.001 0.0001 0.00001 0.000001
平均速度 -13.59
-13.149 -13.1049 -13.10049 -13.100049 -13.1000049
当△可作为运动员在2s时的瞬时速度。
即t=2s时,高度对于时间的瞬时变化率。
PT。此时割线PQ的斜率趋向于切线PT的斜率,
y
y=f(x)
当△x→0时,割线PQ的斜率 f(x0+x)
Q
的极限,就是曲线在点P处的
Q
切线的斜率,即
Q
T
f ( x + x) f ( x)
k lim
x0
x
f(x0) O
P
)a)))
x0
M
x x0+x
练习:曲线的方程为y=x2+1 ,求曲线在点P(1,2) 处的切线方程。
a v vs f (t0 + t) f (t0 ) 。
t t
t
a 可作为物体在t0时刻的加速度的近似值, t 越小,
近似的程度就越好。所以当t0时,极限
lim v
t0 t
就是物体在t0时刻的瞬时加速度,即
lim v
a tt0 to t
lim f (t0 + t) f (t0 ) 。
解:曲线在点P(1,2) 处的切线斜率为:
k lim f (x0 + x) f (x0 )
x0
x
lim (1+ x)2 +1 (1+1)
x0
x
lim 2x + (x)2
x0
x
2
8
加速度a的公式

加速度a的公式
加速度a的公式:a=(v2-v1)/t,a平=△v/△t,瞬时加速度a=dv/dt。
加速度表征
单位时间内速度改变程度的矢量。
加速度公式
在最简单的匀加速直线运动中,加速度的大小等于单位时间内速度的增量。
若动点的
速度v1经t秒后变成v2,则其加速度可表示为:a=(v2-v1)/t
动点Q做一般空间运动时,速度矢量的变化和所经时间△t的比,称为△t时间内的
平均加速度,记为a平:a平=[v(t+△t)-vt]/△t=△v/△t
当时间间隔△t趋于零时,平均加速度的极限称为瞬时加速度,简称加速度,记为a:a=dv/dt
因而加速度的严格定义为:加速度矢量等于速度矢量对时向的导数,其方向沿着速端
图的切线方向并指向轨迹的凹侧。
加速度相关公式
1、平均速度:V平=s/t(定义式),有用推论Vt2-Vo2=2as
2、中间时刻速度:Vt/2=V平=Vt+Vo/2
3、末速度:Vt=Vo+at
4、位移:s=V平t=Vot+at2/2=Vt/2t
6、加速度:a=Vt-Vo/t{以Vo为正方向,a与Vo同向加速a>0;反向则a<0}
7、实验用推论:Δs=aT2{Δs为连续相邻相等时间T内位移之差}
感谢您的阅读,祝您生活愉快。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
v
vb(t t)
①说到平均加速度,一定要明确是哪一段时间或
哪一段位移中的平均加速度.
②一般 v与v方向不同.
上页 下页 返回 结束
第二章 质点运动学
2. 瞬时加速度(简称加速度)
定义
a
lim v
dv
t 0 dt
dt
d dt
( dr) dt
d 2 r dt 2
a是矢量, 一般a与v方向不同.
v
r4
dt
dr
Q
Q
r3
r2
Q
r1
P
瞬时速度反映质点在某时或某位置的运动状态.
上页 下页 返回 结束
第二章 质点运动学
在直角坐标系中的分解式
v
vxi
vy
j
vzk
dx dt
i
dy dt
j
dz dt
k
v | v|
v
2 x
v
2 y
v
2 z
cos v
vx v
cos
v
vy v
cos
v
第二章 质点运动学
§2.2 瞬时速度矢量与瞬时加速度矢量
§2.2.1 平均速度与瞬时速度 §2.2.2 平均加速度与瞬时加速度
上页 下页 返回 结束
第二章 质点运动学
§2.2 瞬时速度矢量与瞬时加速度矢量
§2.2.1 平均速度与瞬时速度
1.平均速度
定义
v
r
t
__ v
是
矢
量,
方 向 与r相 同
大小为
[解]
(1)
v
dr
15 j
10tk
(单位m/s , s)
z
v( )
dt
大小 v v 152 (10t )2
225 100t 2
v(0)
y
O
上页 下页 返回 结束
第二章 质点运动学
方向 cos vx 0 0
vv
cos v y 15
vv
cos vz 10t
vv
t =0时, v 15 m/s cos 0,cos 1,cos 0
dt t0 t
d ( 102 (15t)2 (5t)2 dt
t =0 时, v =0
t =1 s时, v 550 m/s 16 m/s
250
5
上页 下页 返回 结束
第二章 质点运动学
§2.2.2 平均加速度与瞬时加速度
1.平均加速度
定义
a
v
t
方 向 同v
注意:
vb(t t)
va (t)
r
10i
15tj
5t
2
k
(单位m,s)
求质点的加速度矢量.
[解]
a
dv dt
d
2
r
dt 2 10k
a =10 m/s2
方向沿 z 轴.
上页 下页 返回 结束
t =1s时, v 5 13 m/s
cos 0,cos 3 0.832,cos 2 0.555
13
13
(2)
v
r1 r0
(10i 15 j 5k ) (10i )
t1 t0
10
15 j 5k (m/s)
上页 下页 返回 结束
第二章 质点运动学
(3) v dr lim r
直角坐标中
a
dv x dt
i
dv
y
dt
j
dvt
dt
k
d2x d2 y dt 2 i dt 2
d2z j dt 2 k
axi ay j azk
a | a|
a
2 x
a
2 y
az2
cos a
ax a
cos
a
ay a
cos
a
az a
上页 下页 返回 结束
第二章 质点运动学
[例题2]某质点的运动学方程为
__
r
v
t
P
r(t)
r
Q
r(t
t )
O
平均速率 v s 0 s为路程 t
v不能反映位移变化相对于时间的不均匀性.
上页 下页 返回 结束
第二章 质点运动学
2. 瞬时速度(简称速度)
定义
v
lim
v
lim
r
dr
t 0
t0 t dt
v是 矢 量 ,
方向:质点运动路径的切向. Q
大小:v
v
dr
vz v
瞬时速率(简称速率)
v lim t 0
r t
lim s ds t0 t dt
s是 路 程
上页 下页 返回 结束
第二章 质点运动学
[例题1]某r 质点10的i运 1动5t学j 方5t程2k为 (单位m,s)
求:(1)t = 0,1s时质点的速度矢量; (2)t =0到t =1s质点的平均速度; (3)t =0,t =1s时的瞬时速率.
