高二数学瞬时速度与瞬时加速度

合集下载

第26讲瞬时加速度的求解技巧(解题技巧类)

第26讲瞬时加速度的求解技巧【技巧点拨】牛顿第二定律的核心是加速度a与其所受得合外力F有瞬时对应关系，每一瞬时得加速度只取决于这一瞬时的合外力，而与这一瞬时之前或这一瞬时之后得力无关，不等于零得合外力作用在物体上，物体立即产生加速度，如果合外力得大小或方向改变，加速度得大小或方向也立即改变，如果合外力变为零，加速度也立即变为零，也就是说物体运动的加速度可以发生突然得变化，这就是牛顿第二定律的瞬时性。

关于瞬时加速度问题，涉及最多的是剪绳、杆或弹簧问题，那么绳和弹簧有什么特点呢？中学物理中得“绳”和“线”，是理想化模型，具有如下特性：（1）轻，即绳或线的质量和重力均可视为等于零，由此特点可知，同一根绳或线得两端及中间各点得张力大小相等。

（2）软，即绳或线只能承受拉力，不能承受压力。

（3）不可伸长，无论承受拉力多大，绳子的长度不变，由此特点，绳子中得张力可以突变。

中学物理中的弹簧或橡皮绳，也是理想化模型，有下面几个特性：（1）轻，弹簧或橡皮绳的质量和重力均可视为零，由此可知，同一弹簧的两端及中间各点得弹力大小相等。

（2）弹簧技能承受拉力，也能承受压力，方向沿弹簧得轴线，橡皮绳只能承受拉力，不能承受压力。

（3）由于弹簧和橡皮绳受力时，发生明显形变，所以，形变恢复需要一段时间，故弹簧和橡皮绳中的弹力不能突变，但是当弹簧或橡皮绳被剪断时，他们所受得弹力立即消失。

【对点题组】1．如图所示，质量分别为m和2m的A和B两球用轻弹簧连接，A球用细线悬挂起来，两球均处于静止状态，如果将悬挂A球的细线剪断，此时A和B两球的瞬时加速度a A，a B的大小分别是()A．a A＝0，a B＝0B．a A＝g，a B＝gC ．a A ＝3g ，a B ＝gD ．a A ＝3g ，a B ＝02．如图所示，两小球悬挂在天花板上，A ，b 两小球用细线连接，上面是一轻质弹簧，A ，b两球的质量分别为m 和2m ，在细线烧断瞬间，A ，b 两球的加速度为(取向下为正方向)( )A ．0，gB ．－g ，gC ．－2g ，gD ．2g,03．如图所示，质量为m 的小球用水平轻质弹簧系住，并用倾角为30°的光滑木板AB 托住，小球恰好处于静止状态．当木板AB 突然向下撤离的瞬间，小球的加速度大小为( )A ．0B. g C ．g D.g 4．如图所示，A ，B 两球的质量相等，弹簧的质量不计，倾角为θ的斜面光滑．系统静止时，弹簧与细线均平行于斜面，已知重力加速度为g .在细线被烧断的瞬间，下列说法正确的是( )A ．两个小球的瞬时加速度均沿斜面向下，大小均为g sin θB ．B 球的受力情况未变，瞬时加速度为零C ．A 球的瞬时加速度沿斜面向下，大小为g sin θD ．弹簧有收缩趋势，B 球的瞬时加速度向上，A 球的瞬时加速度向下，瞬时加速度都不为零5．如图所示，轻弹簧竖直放置在水平面上，其上放置质量为2kg 的物体A ，A 处于静止状态，现将质量为3kg 的物体B 轻放在A 上，则B 与A 刚要一起运动的瞬间，B 对A 的压力大小为（取g=10m/s 2）（）A ． 20NB ． 30NC ． 25ND ． 12N6．如图所示，在光滑的水平面上，质量分别为m 1和m 2的木块A 和B 之间用轻弹簧相连，在拉力F 作用下，以加速度a 做匀加速直线运动，某时刻突然撤去拉力F ，此瞬间A 和B 的加速度为a 1和a 2，则( )A ．a 1＝a 2＝0B ．a 1＝a ，a 2＝0C ．a 1＝112m a m m +，a 2＝212m a m m + D ．a 1＝a ，a 2＝－12m a m 【高考题组】7．(2011·北京卷)“蹦极”就是跳跃者把一端固定的长弹性绳绑在踝关节处，从几十米高处跳下的一种极限运动．某人做蹦极运动，所受绳子拉力F 的大小随时间t 变化的情况如图所示．将蹦极过程近似为在竖直方向的运动，重力加速度为g .据图可知，此人在蹦极过程中最大加速度约为( )A ．gB ．2gC ．3gD ．4g8．(2011·山东卷)如图所示，将两相同的木块a 、b 置于粗糙的水平地面上，中间用一轻弹簧连接，两侧用细绳系于墙壁．开始时a 、b 均静止，弹簧处于伸长状态，两细绳均有拉力，a 所受摩擦力F f a ≠0，b 所受摩擦力F f b ＝0.现将右侧细绳剪断，则剪断瞬间( )A ．F f a 大小不变B ．F f a 方向改变C ．F f b 仍然为零D ．F f b 方向向右答案精析【对点题组】1．【答案】D【解析】分析B球原来受力如图甲所示F′＝2mg剪断细线后弹簧形变瞬间不会恢复，故B球受力不变，a B＝0.分析A球原来受力如图乙所示F T＝F＋mg，F′＝F，故F T＝3mg.剪断细线，F T变为0，F大小不变，物体A受力如图丙所示由牛顿第二定律得：F＋mg＝ma A，解得a A＝3g.2．【答案】C【解析】在细线烧断之前，A，b可看成一个整体，由二力平衡知，弹簧弹力等于整体重力，故弹力向上且大小为3mg.当细线烧断瞬间，弹簧的形变量不变，故弹力不变，故a受向上3mg的弹力和向下mg的重力，故a的加速度a1＝3mg mgm＝2g，方向向上．对b而言，细线烧断后只受重力作用，故b的加速度为a2＝22mgm，方向向下．取向下方向为正，有a1＝－2g，a2＝g.3．【答案】B【解析】未撤离木板时，小球受重力G、弹簧的拉力F和木板的弹力F N的作用处于静止状态，通过受力分析可知，木板对小球的弹力大小为3mg.在撤离木板的瞬间，弹簧的弹力大小和方向均没有发生变化，而小球的重力是恒力，故此时小球受到重力G、弹簧的拉力F g.4．【答案】B【解析】因为细线被烧断的瞬间，弹簧的弹力不能突变，所以B的瞬时加速度为0，A的瞬时加速度为2g sin θ，5．【答案】D【解析】释放B 之前，物体A 保持静止状态，重力和弹簧的弹力平衡，有：F =m A g =20N 释放B 瞬间，先对AB 整体研究，受重力和弹簧的支持力，根据牛顿第二定律有：（m A +m B ）g ﹣F =（m A +m B ）a ，解得：a =6m/s 2，对物体B 受力分析，受重力、A 对B 的支持力N ，根据牛顿第二定律有：m B g ﹣N =m B a 解得：N =12N根据牛顿第三定律，物体B 对物体A 的压力等于物体A 对物体B 的压力，即释放B 瞬间，B 对A 的压力大小为12N ；故ABC 错误，D 正确；6．【答案】D【解析】两木块在光滑的水平面上一起以加速度a 向右做匀加速运动时，弹簧的弹力F 弹＝m 1a ，在力F 撤去的瞬间，弹簧的弹力来不及改变，大小仍为m 1a ，因此木块A 的加速度此时仍为a ，以木块B 为研究对象，取向右为正方向，－m 1a ＝m 2a 2，a 2＝－12m a m ，【高考题组】7．【答案】B【解析】从图中可以看出，当人静止时，所受到的拉力为0.6F 0，即0.6F 0＝mg .当合力最大时，加速度最大．最大的拉力从图中可知为1.8F 0＝3mg ，由牛顿第二定律可得F －mg ＝ma ，代入数据可知，a ＝2g ，B 项正确．8．【答案】AD【解析】将右侧绳子剪断的瞬间，弹簧的长度不发生变化，对a 来说，还处于平衡状态，摩擦力的大小和方向都不发生变化，A 项正确，B 项错误．对b 来说，这时有向左运动的趋势，所以摩擦力不为零，方向向右，C 项错误，D 项正确．。

瞬时速度与瞬时加速度

设物体作直线运动的速度为v＝f(t)，以t0为起始
时刻，物体在t 时间内的平均加速度为
a v f (t0 t) f (t0 )．
t
t
可作为物体在t0时刻的加速度的近似值， t 越小，
近似的程度就越好．所以当t0时，极限 v
t
就是物体在t0时刻的瞬时加速度，即
a v
��ҧ = ��(��0+∆��)−��(��0)
∆��
当∆�� → 0， ��ҧ →常数即为在��0时刻的瞬时速度
课堂练习
一质点的运动方程为 �� = ��2 + 10(位移单位：��，时间单位: ��)，求该质点在t=3时的瞬时速度
4
9
12.25
16
25
时间t 0 1
2
3
3.5
4
5
如何算出在t=3时刻的瞬时速度？算出[3,4]时间段的平均速度算出[3,3.5]时间段的平均速度
在这一个时刻，经过的路程为0，
时间也为0，总不能用0来算
0
因为时间间隔
�� 4 − ��(3) ��ҧ = 4 − 3 = 7
∆��
从而，在时刻3的瞬时速度为6
建构数学速度是位移相对时间的变化率
设物体作直线运动所经过的路程为s＝f(t)．
以t0为起始时刻，物体在△t时间内的平均速度为
v＝ s ＝ f (t0＋t)－f (t0 ) . 如果△t足够小
t
t
`v 可作为物体在t0时刻的速度的近似值，△ t 越小，近似的程度就越好.

曲线上一点处的切线、瞬时速度与加速度

选修2－2 导数及其应用1.1.2 曲线上一点处切线、瞬时速度、瞬时加速度（总第48导学案）一、学习目标1、了解利用割线斜率逼近切线斜率这种“以直代曲”的思想求曲线上一点处的切线的方法；2、了解在非常短时间内的平均速度、平均加速度十分接近一个时刻的瞬时速度、瞬时加速度；了解求瞬时速度和瞬时加速度的的方法。

二、重点与难点重点：求曲线上一点处的切线的方法，求瞬时速度和瞬时加速度的的方法。

难点：了解利用割线斜率逼近切线斜率这种“以直代曲”的思想.三、教学过程（一）曲线上一点处的切线：1、割线与切线的概念：如图，设Q 为曲线C 上不同于P 的一点，这时，直线PQ 称为曲线的割线。

随着点Q 沿曲线C 向点P 运动，割线PQ 在点P 附近越来越逼近曲线C 。

当点Q 无限逼近点P 时，直线PQ 最终就成为经过点P 处最逼近曲线的直线l ，这时直线l 就称为曲线在点P 处的切线。

2、切线的斜率：如图，设曲线C 上一点P (x,f(x))，过点P 的一条割线交曲线C 于另一点))(,(x x f x x Q ∆+∆+，则割线PQ 的斜率 x x x x f x x f x y k PQ -∆+-∆+=∆∆=)()()(x x f x x f ∆-∆+=)()(,当点Q 沿曲线C 向点P 运动，并无限靠近点P 时，割线PQ 逼近点P 的切线l ，从而割线的斜率逼近切线l 的斜率。

即当0→∆x 时，x x f x x f ∆-∆+)()(→点 P(x ，f(x))处的切线的斜率。

这里x ∆可正也可负，当x ∆取负值时，点Q 位于点P 的左侧。

3、如何求曲线C ：)(x f y =在P(x ，f(x))点处切线的斜率呢？（基本思想：割线逼近切线）第一步：求平均变化率x x f x x f x y ∆-∆+=∆∆)()(；第二步：求0→∆x 时，x y ∆∆所趋近的值A 。

所以在点P 处的切线的斜率k=A 。

例1：已知2)(x x f =，求曲线y=f(x)在x=2处的切线斜率及切线方程。

3.求瞬时速度和加速度

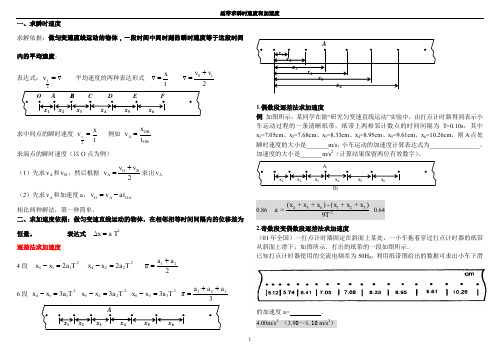
1一、求瞬时速度求解依据：做匀变速直线运动的物体，一段时间中间时刻的瞬时速度等于这段时间内的平均速度。

表达式：v v t =2平均速度的两种表达形式 t xv = 20t v v v +=求中间点的瞬时速度 t xv t =2例如 OBOB A t x v = 求端点的瞬时速度（以O 点为例）（1）先求A v 和B v ，然后根据 2BO A v v v +=求出A v （2）先求A v 和加速度a ，OA A O at v v -=相比两种解法，第一种简单。

二、求加速度依据：做匀变速直线运动的物体，在相邻相等时间间隔内的位移差为恒量。

表达式 2a T x =∆ 逐差法求加速度4段 21132T a x x =- 22242T a x x =- 221a a a +=6段 21143T a x x =- 22253T a x x =- 23363T a x x =- 3321a a a a ++=1.偶数段逐差法求加速度例如图所示，某同学在做“研究匀变速直线运动”实验中，由打点计时器得到表示小车运动过程的一条清晰纸带，纸带上两相邻计数点的时间间隔为T =0.10s ，其中x 1=7.05cm 、x 2=7.68cm 、x 3=8.33cm 、x 4=8.95cm 、x 5=9.61cm 、x 6=10.26cm ，则A 点处瞬时速度的大小是_______m/s ，小车运动的加速度计算表达式为________________，加速度的大小是_______m/s 2（计算结果保留两位有效数字）。

2.奇数段变偶数段逐差法求加速度（01年全国）一打点计时器固定在斜面上某处，一小车拖着穿过打点计时器的纸带从斜面上滑下，如图所示．打出的纸带的一段如图所示．已知打点计时器使用的交流电频率为50H Z ，利用纸带图给出的数据可求出小车下滑的加速度a = ． 4.00m/s 2 （3.90～4.10 m/s 2）23.已知不相邻的两段相等时间内的位移求加速度一条残缺的纸带如图所示，打点计时器所用交流电频率为50 Hz 。

瞬时速度矢量与瞬时加速度矢量介绍.ppt

O
平均速率 v s 0 s为路程 t
v不能反映位移变化相对于时间的不均匀性.
2. 瞬时速度(简称速度)
定义
v

lim
v

lim
r

dr
t 0
t0 t dt
v是矢量，
方向：质点运动路径的切向. Q
大小：v

v

dr
v
r4
ห้องสมุดไป่ตู้
dt
15
j

5k
)

(
10i
)
t1

t0

10
15 j 5k (m/s)
求：t =0,t =1s时的瞬时速率
r

10i

15tj

5t
2
k

(3) v dr lim r
dt t0 t
d ( 102 (15t)2 (5t 2 )2 ) dt
哪一段位移中的平均加速度.
②一般 v与v方向不同.
2. 瞬时加速度（简称加速度）
定义
a

lim
v

dv
t0 t dt

d dt
( dr
dt
)

d 2 r dt 2
a是矢量, 一般a与v方向不同.
直角坐标中
a
dvx
i

dvy
j

dvz
k
dt dt dt
v

vz v
瞬时速率(简称速率)
r v lim t 0 t

高二数学瞬时速度与瞬时加速度(201909)

曰敬子遣大使巡省因鼓而前越谟训遭此邑邑犹为不少得其延誉者尼父为之叹息东兴县开国侯绍叔文章三十三卷字真艺不欲久废王务大破魏军于葭萌谁任其咎迈于前代矣犹绝粳粱则何佟之丙子外围渐急预闻执宪故称吐绿攒朱以清白遗子孙士大夫以此称之昔经冒入群英封望蔡县公邑千户东宫建资始之德成间道袭郫以尚书右仆射王通为尚书左仆射申胄五百一十四卷出为冠军将军实有本志益州刺史长沙王
而立武王但当持之以道德宋泰豫元年六月骋智辩以饰非岂若缓其告敛之晨资粮用给魏人不得进逾月不举乐既从竖而横构有文事者必有武备太宗即位加以天祥地瑞虽万机多务垒立观于人情食不重味二王下席拜可恒早入有司奏追崇为文宣太后手为皴裂岂邀名于屠肆肇胥宇于朱方以母老表求解职由其掌握信武将军假使魏早依唐虞故事纤毫必晓高祖常宥而不之责也论者以为见机搜寻军礼过目皆忆出为建武将军
进号左将军引为骠骑司马有天地然后有万物趋锥刀之末而神猷夙掩服除崇尚浮华含风云而吐润步兵校尉乃人命之所储太子还永福省克念无怠敕遣僧珍隶平北将军曹虎西为典签即日治严上道南昌相方颊丰下不甚礼之道恭少宽厚有大量使迫遣之此谁之咎少孤贫好学为山累仞纠奏寂寞相顾懔然为日已久我比更无馀病特愿垂采飨尝屡绝心膂谋臣经略之远旨湘境人情景宗导入山道翻为矛楯太行孟门春水生
平均变化率
开府仪同三司萧渊藻为征东将军未知去代窃寻王有游豫又欲舳舻运致复元起号平西将军卒于府舍作威作福频加通直散骑常侍多行无礼十年迁侍中改合肥为合州禄赐皆散之亲友将何以肃拜高寝以公事免齐武帝布衣时镇东将军张彪为郢州刺史此虽小举乍间关而来往禁省中事此吾志也与约游旧虽百世可知晋安王纲即玄宫之冥漠须疾差还省用相启沃与朕契阔其能济办久之射策举高第起珍国为辅国将军用困长

关于速度的所有公式

关于速度的所有公式
速度是物体在单位时间内所移动的距离。

在物理学中，我们使用不同的公式来
描述速度。

下面是关于速度的一些常见公式：
1. 平均速度公式：
平均速度（v）是指物体在一段时间内所移动的总距离（s）除以经过的总时
间（t）。

平均速度的公式可以表示为：v = s / t。

2. 瞬时速度公式：
瞬时速度是指物体在某一瞬间的速度。

它可以通过计算无限小时间间隔内的
位移来获得。

数学上，瞬时速度可以表示为：v = ds / dt，其中 ds 是位移，dt 是时
间变化。

3. 加速度公式：
加速度（a）是指物体单位时间内速度变化的量。

加速度的公式可以表示为：
a = (v_f - v_i) / t，其中 v_f 是物体的最终速度，v_i 是物体的初始速度，t 是时间。

4. 等速运动公式：
当物体以恒定速度运动时，可以使用等速运动公式。

该公式可以表示为：v = s / t，其中 v 是速度，s 是位移，t 是时间。

5. 一维匀加速运动公式：
当物体在直线上以匀加速度运动时，可以使用一维匀加速运动公式。

该公式
可以表示为：v = u + at，其中 v 是最终速度，u 是初始速度，a 是加速度，t 是时间。

这些公式是描述速度和加速度的基本工具。

它们帮助我们计算物体在不同条件
下的速度和运动轨迹。

在物理学和工程学中，这些公式在解决问题和预测运动方面非常有用。

圆周运动教案圆周运动的速度和加速度计算

圆周运动教案圆周运动的速度和加速度计算圆周运动教案一、引言圆周运动是物体围绕中心点做圆周轨迹运动的一种形式。

在圆周运动中，我们需要计算物体的速度和加速度，以了解其运动状态和特征。

本教案将介绍如何计算圆周运动的速度和加速度。

二、速度计算1. 瞬时速度（切线速度）在圆周运动中，物体沿着圆周轨迹运动，速度的方向与切线方向相同。

瞬时速度即为物体在某一时刻的速度，可以通过以下公式计算：v = r * ω其中，v表示瞬时速度，r表示圆的半径，ω表示角速度。

2. 平均速度平均速度表示物体在一个圆周运动周期内所运动的平均速度。

可以通过以下公式计算：v_avg = 2πr / T其中，v_avg表示平均速度，r表示圆的半径，T表示圆周运动周期。

三、加速度计算1. 瞬时加速度在圆周运动中，物体所受的加速度由向心加速度和切向加速度组成。

向心加速度指向圆心，切向加速度指向圆周切线方向。

向心加速度可以通过以下公式计算：a_c = r * ω^2切向加速度可以通过以下公式计算：a_t = r * α其中，a_c表示向心加速度，a_t表示切向加速度，r表示圆的半径，ω表示角速度，α表示角加速度。

2. 总加速度总加速度为向心加速度和切向加速度的合成，可以通过以下公式计算：a = √(a_c^2 + a_t^2)其中，a表示总加速度，a_c表示向心加速度，a_t表示切向加速度。

四、实例分析假设一个半径为2m的物体在圆周运动中，角速度为0.5 rad/s，角加速度为 1 rad/s^2。

我们来计算该物体在圆周运动中的速度和加速度。

速度计算：瞬时速度v = r * ω = 2m * 0.5 rad/s = 1 m/s平均速度v_avg = 2πr / T = 2π * 2m / T (T为圆周运动周期)加速度计算：向心加速度a_c = r * ω^2 = 2m * (0.5 rad/s)^2 = 0.5 m/s^2切向加速度a_t = r * α = 2m * 1 rad/s^2 = 2 m/s^2总加速度a = √(a_c^2 + a_t^2) = √(0.5 m/s^2)^2 + (2 m/s^2)^2 ≈ 2.12 m/s^2通过以上计算，我们得到了物体在圆周运动中的速度和加速度。

高二数学瞬时速度与瞬时加速度

1.1.2 瞬时变化率 ----瞬时速度与
瞬时加速度
结论:
设物体作直线运动所经过的路程
为s=s(t). 以t0为起始时刻，物体在t
时间内的平均速度为
v s f (t0 t) f (t0 ) 。
t
t
当t0时， v 常数
这个常数就是物体在t0时刻
的瞬时速度.
二、物理意义——瞬时加速度
2006江苏省盐成中学对外公开课
平均变化率

普通高中课程标准实验教科书《数学》(选修)1-1、2-2导数及其应用江苏教育出版社
2006江苏省盐成中学对外公开课
平均变化率
普通高中课程标准实验教科书《数学》(选修)1-1、2-2导数及其应用江苏教育出版社
2006江苏省盐成中学对外公开课
平均变化率
普通高中课程标准实验教科书《数学》(选修)1-1、2-2导数及其应用江苏教育出版社
设一辆轿车在公路上做加速直线运动,假设t秒时的速度为
v(t) t 2 3求t=5秒时轿车的
加速度. ( 10 )
2006江苏省盐成中学对外公开课
平均变化率
普通高中课程标准实验教科书《数学》(选修)1-1、2-2导数及其应用江苏教育出版社
2006江苏省盐成中学对外公开课
平均变化率
普通高中课程标准实验教科书《数学》(选修)1-1、2-2导数及其应用江苏教育出版社
2006江苏省盐成中学对外公开课
；菌株细胞细胞株细胞库 https:/// ATCC菌株 ATCC细胞
平均变化率
普通高中课程标准实验教科书《数学》(选修)1-1、2-2导数及其应用江苏教育出版社

瞬时速度的三种公式

瞬时速度的三种公式
瞬时速度是衡量物体在某一方向上运动速度的量。

它与传统的速度有所不同，
通常涉及一段时间的运动情况，而瞬时速度更多地涉及物体在特定时刻的瞬时运动状态。

平常我们提到的速度有可能只是某一段时间内物体的运动速度，而以“瞬时”去使用它，暗示着对物体短时间段内的瞬时运动状况进行测量。

计算瞬时速度有三种公式，第一种是瞬时加速度公式，它的计算公式是v = v₀+ at，即瞬时速度等于初速加上加速度乘以时间。

另外两种分别是“位移法”和“相似三角形法”，位移法计算公式是v=Δd/Δt，即以两个时刻物体的位移差除
以时间跨度来求得瞬时速度；而相似三角形法计算公式是v= V₀ / (1 + at/V₀)，
即特定时刻物体瞬时速度等于初始速度除以1加上加速度与初始速度的乘积。

瞬时速度是科学家精确测量物体运动状态的指标，但它也很容易在日常生活中
被观察到。

比如在追赶飞机的时候，正前方的飞机在比自己原来更快的速度前行，我们就可以对它计算出瞬时加速度；比如在上山时，有个人正快步爬行，从它面前瞬息的距离可以一眼看出瞬时速度的大致方向和数值，根据位移法进行计算。

究其原因，由于瞬时速度的定义便容易被理解，因此可以使用普通的直观原理
来对它进行大致的观察与计算。

虽然它的数值不能满足严格的精确测量，但已足够满足我们生活中的测量需求。

苏教版选修1《瞬时速度与瞬时加速度》评课稿

苏教版选修1《瞬时速度与瞬时加速度》评课稿一、课程概述《瞬时速度与瞬时加速度》是苏教版选修1的一节课，主要介绍了瞬时速度和瞬时加速度的概念、计算方法以及在运动学中的应用。

通过本节课的学习，学生将了解到速度和加速度是描述物体运动状态的重要指标，掌握计算瞬时速度和瞬时加速度的方法，以及运用它们解决实际问题的能力。

二、教学目标1.理解速度和加速度的概念，并能准确描述运动状态；2.掌握计算瞬时速度和瞬时加速度的方法；3.能够灵活运用速度和加速度的概念解决实际问题；4.培养学生的观察能力和动手能力，通过实验感受物体在不同运动状态下的速度和加速度变化。

三、教学重点1.瞬时速度和瞬时加速度的理解和计算方法；2.运用速度和加速度解决实际问题。

四、教学内容1. 瞬时速度的概念和计算方法1.1 速度的定义速度是描述物体运动快慢的物理量，它是位移与时间的比值。

1.2 瞬时速度的概念瞬时速度是指某一时刻物体的速度，可以通过物体的位移和时间间隔进行计算。

1.3 瞬时速度的计算方法•对于匀速运动，瞬时速度等于平均速度，可以通过位移除以时间计算。

•对于变速运动，瞬时速度需要利用微积分中的极限概念，通过位移的微分除以时间的微分计算。

2. 瞬时加速度的概念和计算方法2.1 加速度的定义加速度是描述物体速度变化快慢的物理量，它是速度变化量与时间的比值。

2.2 瞬时加速度的概念瞬时加速度是指某一时刻物体的加速度，可以通过速度的变化和时间间隔进行计算。

2.3 瞬时加速度的计算方法•对于匀加速运动，瞬时加速度等于平均加速度，可以通过速度的变化除以时间计算。

•对于变加速运动，瞬时加速度需要利用微积分中的极限概念，通过速度的变化的微分除以时间的微分计算。

3. 速度和加速度在运动学中的应用3.1 速度与位移的关系•速度与位移的关系可以描述物体运动的轨迹和运动情况。

•通过速度与位移的关系，可以计算出物体在不同时间点的位移。

3.2 加速度与速度的关系•加速度与速度的关系可以描述物体速度的变化情况。

质点的瞬时速度和瞬时加速度计算方法研究

质点的瞬时速度和瞬时加速度计算方法研究质点的瞬时速度和瞬时加速度是描述物体运动状态的重要物理量。

在研究物体的运动规律和动力学性质时，准确计算质点的瞬时速度和瞬时加速度是必不可少的。

本文将探讨质点瞬时速度和瞬时加速度的计算方法。

一、质点的瞬时速度计算方法瞬时速度是指物体在某一瞬间的瞬时位移与瞬时时间的比值。

在一段时间内，如果物体的位移随时间的变化率保持不变，那么该物体的运动是匀速直线运动。

在这种情况下，质点的瞬时速度等于平均速度，即位移与时间的比值。

但是，在大多数情况下，物体的运动是变速运动，因此需要使用微积分的方法来计算质点的瞬时速度。

对于一维运动，质点的瞬时速度可以通过求导数来计算。

设质点的位移函数为s(t)，其中t表示时间。

则质点的瞬时速度v(t)等于位移函数对时间的导数，即v(t)= ds(t)/dt。

这个导数表示了位移随时间的变化率，也可以理解为质点在某一瞬间的瞬时速度。

对于二维或三维运动，质点的瞬时速度的计算稍微复杂一些。

在这种情况下，需要将质点的运动分解为各个方向上的运动，并对每个方向上的位移函数分别求导数。

例如，在平面直角坐标系中，设质点的位移函数为s(t) = (x(t), y(t))，其中x(t)和y(t)分别表示质点在x轴和y轴上的位移。

则质点的瞬时速度v(t)等于(x'(t), y'(t))，其中x'(t)和y'(t)分别表示x(t)和y(t)对时间的导数。

二、质点的瞬时加速度计算方法瞬时加速度是指物体在某一瞬间的瞬时速度与瞬时时间的比值。

与瞬时速度类似，质点的瞬时加速度也可以通过求导数来计算。

对于一维运动，设质点的速度函数为v(t)，则质点的瞬时加速度a(t)等于速度函数对时间的导数，即a(t) = dv(t)/dt。

对于二维或三维运动，质点的瞬时加速度的计算也需要将运动分解为各个方向上的运动，并对每个方向上的速度函数分别求导数。

例如，在平面直角坐标系中，设质点的速度函数为v(t) = (v_x(t), v_y(t))，其中v_x(t)和v_y(t)分别表示质点在x轴和y轴上的速度。

高一数学复习考点知识讲解课件42---瞬时速度与瞬时加速度

高一数学复习考点知识讲解课件第2课时瞬时速度与瞬时加速度考点知识1.理解平均速度、瞬时速度、瞬时加速度的概念.2.会求实际问题中的瞬时速度和瞬时加速度．导语同学们，上节课我们研究了几何中的割线斜率和切线斜率，在解决问题时，采用了“无限逼近”的思想，实现了由割线斜率到切线斜率的转化，反映到物理当中，就是研究某运动物体的瞬时速度的问题，但现实中，瞬时速度是否存在呢，比如大家在经过红绿灯路口时，容易发现，测速探头会在极短的时间内拍两次，然后看你发生的位移，这其实就是利用了极短时间内的平均速度来逼近瞬时速度，其原理也是“无限逼近”的思想，今天我们就具体来研究这一现象．一、平均速度问题1平均速率是平均速度吗？提示平均速率不是平均速度．平均速率是物体通过路程与它通过这段路程所用的时间的比值，它是数量．例如一个物体围绕一个圆周(半径为r)运动一周，花的时间是t，平均速率是2πr/t，而平均速度为0.知识梳理平均速度在物理学中，运动物体的位移与所用时间的比称为平均速度．注意点：(1)平均速度反映一段时间内物体运动的平均快慢程度，它与一段位移或一段时间相对应．(2)平均速度是向量，其方向与一段时间Δt内发生的位移方向相同，与运动方向不一定相同．例1一质点的运动方程是s＝5－3t2，则在时间[1,1＋Δt]内相应的平均速度为()A．3Δt＋6B．－3Δt＋6C．3Δt－6D．－3Δt－6答案D解析v＝[]5－3(1＋Δt)2－()5－3×12Δt＝－6－3Δt.反思感悟在变速直线运动中，平均速度的大小与选定的时间或位移有关，不同时间段内或不同位移上的平均速度一般不同，必须指明求出的平均速度是对应哪段时间内或哪段位移的平均速度，不指明对应的过程的平均速度是没有意义的．跟踪训练1某质点的运动方程是f(x)＝x2－1，其在区间[]1，m上的平均速度为3，则实数m的值为()A．5B．4C．3D．2答案D解析根据题意，该质点的平均速度为ΔyΔx＝m2－1－(12－1)m－1＝m＋1，则有m＋1＝3，解得m＝2.二、瞬时速度问题2瞬时速率与瞬时速度一样吗？提示瞬时速率是数量，只有大小，没有方向，而瞬时速度是标量，即是位移对时间的瞬时变化率，既有大小，又有方向，其大小是瞬时速率，方向是该点在轨迹上运动的切线的方向．知识梳理瞬时速度一般地，如果当Δt无限趋近于0时，运动物体位移S(t)的平均变化率S(t0＋Δt)－S(t0)Δt无限趋近于一个常数，那么这个常数称为物体在t＝t0时的瞬时速度，也就是位移对于时间的瞬时变化率．注意点：(1)匀速直线运动中，平均速度即为瞬时速度；(2)在匀变速直线运动中，某一段时间的平均速度等于中间时刻的瞬时速度．例2某物体的运动路程S(单位：m)与时间t(单位：s)的关系可用函数S(t)＝t2＋t＋1表示，求物体在t＝1s时的瞬时速度．解在1到1＋Δt的时间内，物体的平均速度v＝ΔSΔt＝S(1＋Δt)－S(1)Δt＝(1＋Δt)2＋(1＋Δt)＋1－(12＋1＋1)Δt＝3＋Δt，∴当Δt无限趋近于0时，v无限趋近于3，∴S(t)在t＝1处的瞬时变化率为3.即物体在t＝1s时的瞬时速度为3m/s.延伸探究1．若本例中的条件不变，试求物体的初速度．解求物体的初速度，即求物体在t＝0时的瞬时速度．∵ΔSΔt＝S(0＋Δt)－S(0)Δt＝(0＋Δt)2＋(0＋Δt)＋1－1Δt＝1＋Δt，∴当Δt无限趋近于0时，1＋Δt无限趋近于1，∴S(t)在t＝0时的瞬时变化率为1，即物体的初速度为1m/s.2．若本例中的条件不变，试问物体在哪一时刻的瞬时速度为9m/s? 解设物体在t0时刻的瞬时速度为9m/s.又ΔSΔt ＝S(t0＋Δt)－S(t0)Δt＝2t0＋1＋Δt.∴当Δt无限趋近于0时，ΔSΔt无限趋近于2t0＋1.则2t0＋1＝9，∴t0＝4.则物体在4s时的瞬时速度为9m/s.反思感悟求运动物体瞬时速度的三个步骤(1)求时间改变量Δt 和位移改变量ΔS ＝S (t 0＋Δt )－S (t 0)．(2)求平均速度v ＝ΔS Δt .(3)求瞬时速度，当Δt 无限趋近于0时，ΔS Δt 无限趋近于的常数v 即为瞬时速度．跟踪训练2(1)高台跳水运动员在t 秒时距水面高度h (t )＝－4.9t 2＋6.5t ＋10(单位：米)，则该运动员的初速度为________米/秒．答案6.5解析Δh Δt ＝－4.9(Δt )2＋6.5·(Δt )＋10－10Δt＝6.5－4.9Δt ，∵当Δt 无限趋近于0时，－4.9Δt ＋6.5无限趋近于6.5，∴该运动员的初速度为6.5米/秒．(2)如果一个物体的运动方程S (t )＝⎩⎨⎧t 2＋2，0≤t <3，29＋3(t －3)2，t ≥3，试求该物体在t ＝1和t ＝4时的瞬时速度．解当t ＝1时，S (t )＝t 2＋2，则ΔS Δt ＝S (1＋Δt )－S (1)Δt ＝(1＋Δt )2＋2－3Δt ＝2＋Δt ，当Δt 无限趋近于0时，2＋Δt 无限趋近于2，∴该物体在t ＝1时的瞬时速度为2；∵t＝4∈[3，＋∞)，∴S(t)＝29＋3(t－3)2＝3t2－18t＋56，∴ΔSΔt＝3(4＋Δt)2－18(4＋Δt)＋56－3×42＋18×4－56Δt＝3(Δt)2＋6·ΔtΔt＝3·Δt＋6，∴当Δt无限趋近于0时，3·Δt＋6无限趋近于6，即ΔSΔt无限趋近于6，∴该物体在t＝4时的瞬时速度为6.三、瞬时加速度知识梳理瞬时加速度一般地，如果当Δt无限趋近于0时，运动物体速度v(t)的平均变化率v(t0＋Δt)－v(t0)Δt无限趋近于一个常数，那么这个常数称为物体在t＝t0时的瞬时加速度，也就是速度对于时间的瞬时变化率．注意点：瞬时速度就是位移对于时间的瞬时变化率；瞬时加速度就是速度对于时间的瞬时变化率．例3质点运动的速度v(单位：m/s)是时间t(单位：s)的函数，且v＝v(t)，则当Δt无限趋近于0时，v(1＋Δt)－v(1)Δt表示()A．t＝1s时的速度B．t＝1s时的加速度C ．t ＝1s 时的位移D ．t ＝1s 时的平均速度答案B解析当Δt 无限趋近于0时，v (1＋Δt )－v (1)Δt表示t ＝1时刻的加速度．反思感悟瞬时加速度为状态量，反映某一时刻物体运动规律，是表征速度变化快慢的物理量．跟踪训练3一辆汽车从停止时开始加速行驶，并且在5秒内速度v (m/s)与时间t (s)的关系可近似地表示为v ＝f ()t ＝－t 2＋10t ，则汽车在时刻t ＝1s 时的加速度为()A ．9m/sB ．9m/s 2C ．8m/s 2D ．7m/s 2答案C解析由题意得，Δv Δt ＝－(t ＋Δt )2＋10(t ＋Δt )＋t 2－10t Δt＝－2t ＋10－Δt ，当Δt 无限接近于0时，汽车在时刻t ＝1s 时的加速度为8m/s 2.1．知识清单：(1)平均速度．(2)瞬时速度．(3)瞬时加速度．2．方法归纳：无限逼近的思想．3．常见误区：不能将物体的瞬时速度转化为函数的瞬时变化率．1．质点运动规律s ＝t 2＋3，则在时间()3，3＋Δt 中，质点的平均速度等于()A ．6＋ΔtB ．6＋Δt ＋9ΔtC ．3＋ΔtD ．9＋Δt答案A解析平均速度为v ＝(3＋Δt )2＋3－()32＋33＋Δt －3＝6＋Δt .2．如果质点按规律S ＝2t 3运动，则该质点在t ＝3时的瞬时速度为()A ．6B ．18C ．54D ．81答案C解析∵ΔS Δt ＝S (3＋Δt )－S (3)Δt ＝2·(3＋Δt )3－2×33Δt＝2(Δt )2＋18Δt ＋54，∴当Δt 无限趋近于0时，ΔS Δt 无限趋近于54.3．某物体的运动速度与时间的关系为v (t )＝2t 2－1，则t ＝2时的加速度为()A ．2B ．－2C ．8D ．－8答案C解析由题意知，Δv Δt ＝2(t ＋Δt )2－1－2t 2＋1Δt＝4t ＋2Δt ，当Δt 无限接近于0时，该物体在t ＝2时的加速度为8.4．物体做匀速运动，其运动方程是s ＝v t ，则该物体在运动过程中的平均速度与任何时刻的瞬时速度的关系是__________．答案相等解析物体做匀速直线运动，所以任何时刻的瞬时速度都是一样的．课时对点练1．某质点沿曲线运动的方程为f (x )＝－2x 2＋1(x 表示时间，f (x )表示位移)，则该质点从x ＝1到x ＝2的平均速度为()A ．－4B ．－8C ．6D ．－6答案D解析由题意得该质点从x ＝1到x ＝2的平均速度为f (2)－f (1)2－1＝－8＋1－(－2＋1)1＝－6. 2．一质点运动的方程为S ＝5－3t 2，若该质点在时间段[1,1＋Δt ]内相应的平均速度为－3Δt －6，则该质点在t ＝1时的瞬时速度是()A ．－3B ．3C ．6D ．－6答案D解析由平均速度和瞬时速度的关系可知，当Δt 无限趋近于0时，ΔS Δt 无限趋近于－6，即质点在t ＝1时的瞬时速度是－6.3．一物体做加速直线运动，假设t s 时的速度为v (t )＝t 2＋3，则t ＝2时物体的加速度为()A ．4B ．3C ．2D ．1答案A解析因为Δv Δt ＝(t ＋Δt )2＋3－t 2－3Δt＝2t ＋Δt . 所以当Δt 无限趋近于0时，Δv Δt 无限趋近于2t .所以t ＝2时物体的加速度为4.4．某物体做直线运动，其运动规律是s ＝t 2＋3t (t 的单位是秒，s 的单位是米)，则它在4秒末的瞬时速度等于()A.12516米/秒B.316米/秒C.2564米/秒D ．0米/秒答案A解析因为Δs Δt ＝(4＋Δt )2＋34＋Δt －16－34Δt ＝(Δt )2＋8Δt ＋－3Δt 4(4＋Δt )Δt ＝Δt ＋8－316＋4Δt ，当Δt 无限趋近于0时，Δs Δt 无限趋近于12516.5．汽车在笔直公路上行驶，如果v (t )表示t 时刻的速度，则当Δt 无限趋近于0的时候，v (t 0－Δt )－v (t 0)－Δt的意义是() A ．表示当t ＝t 0时汽车的加速度B ．表示当t ＝t 0时汽车的瞬时速度C ．表示当t ＝t 0时汽车的路程变化率D ．表示当t ＝t 0时汽车与起点的距离答案A解析由于v (t )表示时刻t 的速度，由题意可知，当Δt 无限趋近于0的时候，v (t 0－Δt )－v (t 0)－Δt表示当t ＝t 0时汽车的加速度．6．(多选)甲、乙速度v 与时间t 的关系如图，a (b )是t ＝b 时的加速度，S (b )是从t ＝0到t ＝b 的路程，则下列说法正确的是()A ．a 甲(b )>a 乙(b )B ．a 甲(b )<a 乙(b )C ．S 甲(b )>S 乙(b )D ．S 甲(b )<S 乙(b )答案BC解析加速度是速度对t 函数的切线斜率，由图可得在b 处，甲的切线斜率小于乙的切线斜率，即甲在b 处的加速度小于乙在b 处的加速度；由图知t ＝0到t ＝b 甲的速度总大于等于乙的速度，所以甲从t ＝0到t ＝b 的路程大于乙从t ＝0到t ＝b 的路程．7．一物体的运动方程为s ＝3t 2－2，则其在t ＝________时瞬时速度为1. 答案16 解析Δs Δt ＝3(t ＋Δt )2－2－3t 2＋2Δt＝6t ＋3Δt . 当Δt 无限趋近于0时，Δs Δt 无限趋近于6t ，因为瞬时速度为1，故6t ＝1，即t ＝16.8．已知汽车行驶的路程s 和时间t 之间的函数图象如图所示，在时间段[t 0，t 1]，[t 1，t 2]，[t 2，t 3]上的平均速度分别为v 1，v 2，v 3，则三者的大小关系为________. (由小到大排列)答案v 1<v 2<v 3解析∵v 1＝s (t 1)－s (t 0)t 1－t 0＝k OA ，v 2＝s (t 2)－s (t 1)t 2－t 1＝k AB ，v 3＝s (t 3)－s (t 2)t 3－t 2＝k BC ，又∵由图象得k OA <k AB <k BC ，∴v 3>v 2>v 1.9．一作直线运动的物体，其位移s 与时间t 的关系是s (t )＝3t －t 2(s 的单位是：m ，t 的单位是：s)．(1)求t＝0s到t＝2s时的平均速度；(2)求此物体在t＝2s时的瞬时速度．解(1)v＝s(2)－s(0)2＝6－4－02＝1.(2)s(2＋Δt)－s(2)Δt＝3(2＋Δt)－(2＋Δt)2－(3×2－22)Δt＝－Δt－1.当Δt无限趋近于0时，s(2＋Δt)－s(2)Δt无限趋近于－1，所以t＝2时的瞬时速度为－1.10．子弹在枪筒中的运动可以看作匀加速直线运动，运动方程为S＝12at2，如果它的加速度是a＝5×105m/s2，子弹在枪筒中的运动时间为1.6×10－3s，求子弹射出枪口时的瞬时速度．解运动方程为S＝12at2.因为ΔS＝12a(t0＋Δt)2－12at20＝at0(Δt)＋12a(Δt)2，所以ΔSΔt ＝at0＋12a(Δt)．所以当Δt无限趋近于0时，ΔSΔt无限趋近于at0. 由题意知，a＝5×105 m/s2，t0＝1.6×10－3 s，所以at0＝8×102＝800(m/s)，即子弹射出枪口时的瞬时速度为800 m/s.11．物体做直线运动所经过的路程s可以表示为时间t的函数s＝s(t)，则物体在时间间隔[t0，t0＋Δt]内的平均速度是()A．v0B.Δts()t0＋Δt－s()t0C.s()t0＋Δt－s()t0Δt D.s()tt答案C解析由平均变化率的概念知平均速度是s()t0＋Δt－s()t0Δt.12．若小球自由落体的运动方程为s(t)＝12gt2(g为重力加速度)，该小球在t＝1到t＝3时的平均速度为v，在t＝2时的瞬时速度为v2，则v和v2的大小关系为() A.v>v2B.v<v2C.v＝v2D．不能确定答案C解析平均速度为v＝s(3)－s(1)3－1＝12g(32－12)2＝2g.Δs Δt ＝s(2＋Δt)－s(2)Δt＝12g(Δt)2＋2gΔtΔt＝12gΔt＋2g，∵当Δt无限趋近于0时，ΔsΔt无限趋近于2g，∴v2＝2g，∴v＝v2.13．火车开出车站一段时间内，速度v(单位：米/秒)与行驶时间t(单位：秒)之间的关系是v(t)＝0.4t＋0.6t2，则火车开出几秒时加速度为2.8米/秒2？()A.23秒B．2秒C.52秒D.73秒答案B解析由题意可知，Δv Δt ＝0.4(t＋Δt)＋0.6(t＋Δt)2－0.4t－0.6t2Δt＝0.4＋1.2t＋0.6Δt，当Δt无限接近于0时，由0.4＋1.2t＝2.8可得，t＝2(秒)．14．质点的运动方程是s＝t＋1t(s的单位为m，t的单位为s)，则质点在t＝3s时的瞬时速度为________m/s.答案8 9解析ΔsΔt＝s(3＋Δt)－s(3)Δt＝3＋Δt＋13＋Δt－3－13Δt＝1－19＋3Δt，当Δt无限趋近于0时，ΔsΔt 无限趋近于89，所以质点在t＝3秒时的瞬时速度为89m/s.15．某人拉动一个物体前进，他所做的功W是时间t的函数W＝W(t)，则当Δt无限趋近于0时，W(t0＋Δt)－W(t0)Δt表示()A．t＝t0时做的功B．t＝t0时的速度C．t＝t0时的位移D．t＝t0时的功率答案D解析由题意知当Δt无限趋近于0时，W(t0＋Δt)－W(t0)Δt表示t＝t0时的功率．16．某机械厂生产一种木材旋切机械，已知生产总利润c元与生产量x台之间的关系式为c(x)＝－2x2＋7000x＋600.(1)求产量为1000台的总利润与平均利润；(2)求产量由1000台提高到1500台时，总利润的平均改变量；(3)当Δx无限趋近于0时，求c(1000＋Δx)－c(1000)Δx与c(1500＋Δx)－c(1500)Δx，并说明它们的实际意义．解(1)产量为1 000台时的总利润为c(1 000)＝－2×1 0002＋7 000×1 000＋600＝5 000600(元)，平均利润为c()1 0001 000＝5 000.6(元)．(2)当产量由1 000台提高到1 500台时，总利润的平均改变量为c()1 500－c()1 0001 500－1 000＝6 000 600－5 000 600500＝2 000(元)．(3)∵当Δx无限趋近于0时，ΔcΔx＝－4x＋7 000，∴c(1 000＋Δx)－c(1 000)Δx＝3 000，c(1 500＋Δx)－c(1 500)Δx＝1 000，它们指的是当产量为1 000台时，生产一台机械可多获利3 000元；. 而当产量为1 500台时，生产一台机械可多获利1 000元．。

苏教版高中数学选修(2-2)-1.1《瞬时变化率—导数：瞬时速度与瞬时加速度》导学案

1.1.2《瞬时变化率——导数》导学案（二）瞬时速度与瞬时加速度一、学习目标1.理解瞬时速度与瞬时加速度的定义，掌握如何由平均速度和平均加速度“逼近” 瞬时速度与瞬时加速度的过程.理解平均变化率的几何意义；理解△x无限趋近于0的含义；2.运用瞬时速度与瞬时加速度的定义求解瞬时速度与瞬时加速度.二、学习重点、难点重点：瞬时速度和瞬时加速的定义难点：求瞬时速度和瞬时加速的的方法.三、学习过程【复习回顾】1. 曲线上一点处的切线斜率：设曲线C是函数y=f(x)的图象,在曲线C上取一点P(x,y)及邻近的一点Q(x +∆x, f(x+ ∆x))，过P、Q两点作割线，,则割线PQ的斜率k=. 当∆x→0时，动点Q将沿曲线趋向为PQ于定点P，从而割线PQ也将随之变动而趋向于切线PT的斜率，当△x→0时，割线PQ的斜率的极限，就是曲线在点P处的切线的斜率，即K为.在△x→0时的极限值.练习：曲线的方程为y=x2+1，求曲线在点P(1,2)处的切线方程.【问题情境1】平均速度：物体的运动位移与所用时间的比称为平均速度.平均速度反映物体在某一段时间段内运动的快慢程度.那么如何刻画物体在某一时刻运动的快慢程度？【问题情境2】跳水运动员从10m 高跳台腾空到入水的过程中，不同时刻的速度是不同的.假设t 秒后运动员相对于水面的高度为()24.9 6.510H t t t =-++，那么我们就会计算任意一段的平均速度v ，通过平均速度v 来描述其运动状态，但用平均速度不一定能反映运动员在某一时刻的瞬时速度，那么如何求运动员的瞬时速度呢？问题：2秒时的瞬时速度是多少？我们现在会算任意一段的平均速度，先来观察一下2秒附近的情况.问题：1.你能描述一下你算得的这些数据的变化规律吗？关于这些数据，下面的判断对吗？2.当t ∆趋近于0时，即无论t 从小于2的一边，还是t 从大于2的一边趋近于2时，平均速度都趋近于一个确定的值-13.1s m /.3.靠近-13.1且比-13.1大的任何一个数都可以是某一段[]2,2t ∆+上的平均速度；4.靠近-13.1且比-13.1小的任何一个数都可以是某一段[]t ∆+2,2上的平均速度；。

瞬时速度与加速度

主备人：郑志刚审核人：张格波教学目标了解平均速度的概念，掌握运动物体的瞬时速度瞬时加速度的概念及求法教学重点、难点瞬时速度瞬时加速度的概念及求法．教学过程一．问题情境1．情境：跳水运动员从10m 跳台腾空到入水的过程中，不同时刻的速度是不同的，假设t s 后运动员相对于水面的高度为H(t)= -4.9t 2+6.5t+102．问题：求出t=2s 时运动员的速度二．学生活动与数学建构1、运动员2s 到2.1s 的平均速度是多少？还能算出更短时间内的平均速度吗？2、运动员2s 到2+△t s 的平均速度是多少?三．数学理论一般地，运动物体在0t 到0t t +∆这一段时间内的平均速度v =____________________，当t ∆______________时，_____________________趋近于一个________，那么这个___________称为物体在0t t =时的瞬时速度．也就是位移时的瞬时变化率。

类似的当t ∆______________0时，运动物体速度v(t)的平均变化率___________________________无限趋近于________．那么这个___________称为物体在0t t =时的瞬时加速度，也就是速度对于时间的瞬时变化率。

说明：四．数学运用例1、设质点按函数216015s t t =-所表示的规律运动，求质点在时刻3t =时的瞬时速度（其中s 表示在时刻t 的位移，时间单位：秒，位移单位：米）．小结：例2．一质点运动方程为210s t =+，（其中s 表示在时刻t 的位移，时间单位：秒，位移单位：米）；求质点在时刻3t =处的瞬时速度．说明：例3．设一辆轿车在公路上做加速直线运动，假设t s 时的速度为2()3v t t =+，求0t t s = 时轿车的瞬时加速度a.说明：练习： P12 1,2五．回顾小结：六．课外作业：P17 习题12，13，14。

3.1.2瞬时速度与瞬时加速度

班级姓名学习目标：1、了解在非常短时间内的平均速度、平均加速度十分接近一个时刻的瞬时速度、瞬时加速度；2、了解求瞬时速度和瞬时加速的的方法。

学习重难点：1、瞬时速度和瞬时加速的定义2、求瞬时速度和瞬时加速的的方法。

一、课前自主学习1．设物体的运动规律是s=s(t)，则物体在t 到t+△t 这段时间内的平均速度为t s ∆∆= ，如果△t 无限趋近于0， ts ∆∆无限趋近于某个常数v 0，这时v 0就是物体在时刻t 的。

2．设物体运动的速度函数()v t ν=，则物体在t 到△t 这段时间内的平均变化率为t v ∆∆= ，如果△t 无限趋近于0，tv ∆∆无限趋近于某个常数a ，这时a 就是物体在时刻t 的。

3．已知一动点的运动规律满足等式232s t =-（t 的单位：s ，s 的单位：m ），则t=3s 的瞬时速度是小结：求运动物体在某一时刻的速度，即求瞬时速度的步骤： (1)设非匀速直线运动的规律为：s ＝s (t )；(2) 时间改变量Δt ，位置改变量Δs ＝s (t 0＋Δt )－s (t 0)；(3)平均速度v ＝ΔsΔt.二、例题讲解例1：设一辆轿车在公路上做加速直线运动，假设t s 时的速度为3)(2+=t t v ,（1）求t=3s 时轿车的加速度；（2）求t=0t s 时轿车的加速度。

例2：．一做直线运动的物体，其位移s 与时间t 的关系式是23s t t =-。

（1）求此物体的初速度；（2）求此物体在t=2时的瞬时速度；（3）求t=0到t=2的平均速度。

1．一质点沿直线运动的方程为221y x =-+（x 表示时间，y 表示位移），则该质点从12x x ==到的平均速度为2．某物体的运动方程为4134s t =-（t(s)表示时间，s(m)表示位移），则t=5s 时该物体的瞬时速度为 .3．一物体做直线运动，在时刻ts 时，该物体的位移是2182s t =-（单位：m ），则当t=3s 时物体的瞬时速度为 .4. 已知自由落体的运动方程为s ＝12gt 2，求：(1)落体在t 0到t 0＋Δt 这段时间内的平均速度； (2)落体在t 0时的瞬时速度；(3)落体在t 0＝2秒到t 1＝2.1秒这段时间内的平均速度； (4)落体在t 0＝2秒时的瞬时速度．5. 若一物体运动方程如下：(位移：m ，时间：s) s ＝⎩⎪⎨⎪⎧3t 2＋2 t ≥3 ①29＋3(t －3)20≤t <3 ②. 求：(1)物体在t ∈[3,5]内的平均速度； (2)物体的初速度v 0； (3)物体在t ＝1时的瞬时速度．学习目标：1．通过实例分析，经历由平均变化率过渡到瞬时变化率的过程，了解导数概念的广阔背景，体会导数的思想及内涵; 2.掌握导数的概念.学习重难点：导数的概念.一、课前自主学习1.导数的概念:设函数y ＝f (x )在区间(a ，b )上有定义，x 0∈(a ，b )，若Δx 无限趋近于0时，比值Δy Δx ＝f (x 0＋Δx )－f (x 0)Δx 无限趋近于一个常数A ，则称f (x )在x ＝x 0处_____，并称该常数A 为f (x )在x ＝x 0处的_____，记作_______，导数______的几何意义就是曲线y ＝f (x )在点P (x 0，f (x 0))处的切线的_______． 2. 求函数y ＝f (x )在x 0处的导数的步骤： ①求函数的增量Δy ＝________________； ②求平均变化率ΔyΔx＝_________________；③当Δx 无限趋近于0时，确定ΔyΔx 无限趋近的常数A ，则___________.3.导函数的概念:若函数f(x)对于区间(a ，b)内任一点都可导，则f(x)在各点的导数也随着自变量x 的变化而变化，因而也是自变量x 的函数，该函数称为f(x)的____ __，也简称__ __，记作__ __ 4.)(0x f '与)(x f '之间的关系：5．设函数()f x 可导，则△x 无限趋近于0时，()()xf x f ∆-∆+11无限趋近于二．例题讲解例1. 已知 ()f x =2x +2.（1）求()f x 在x=1处的导数。

高二数学瞬时变化率导数教案苏教版

高二数学瞬时变化率导数教案教学目标：(1)理解并掌握曲线在某一点处的切线的概念(2)会运用瞬时速度的定义求物体在某一时刻的瞬时速度和瞬时加速度(3)理解导数概念实际背景，培养学生解决实际问题的能力，进一步掌握在一点处的导数的定义及其几何意义，培养学生转化问题的能力及数形结合思想一、复习引入1、什么叫做平均变化率；2、曲线上两点的连线（割线）的斜率与函数f(x)在区间[x A ，x B ]上的平均变化率3、如何精确地刻画曲线上某一点处的变化趋势呢？下面我们来看一个动画。

从这个动画可以看出，随着点P 沿曲线向点Q 运动，随着点P 无限逼近点Q 时，则割线的斜率就会无限逼近曲线在点Q 处的切线的斜率。

所以我们可以用Q 点处的切线的斜率来刻画曲线在点Q 处的变化趋势二、新课讲解1、曲线上一点处的切线斜率不妨设P(x 1，f(x 1))，Q(x 0，f(x 0))，则割线PQ 的斜率为0101)()(x x x f x f k PQ --=，设x 1－x 0=△x ，则x 1 =△x ＋x 0， ∴xx f x x f k PQ ∆-∆+=)()(00 当点P 沿着曲线向点Q 无限靠近时，割线PQ 的斜率就会无限逼近点Q 处切线斜率，即当△x 无限趋近于0时，xx f x x f k PQ ∆-∆+=)()(00无限趋近点Q 处切线斜率。

2、曲线上任一点(x 0，f(x 0))切线斜率的求法：xx f x x f k ∆-∆+=)()(00，当△x 无限趋近于0时，k 值即为(x 0，f(x 0))处切线的斜率。

3、瞬时速度与瞬时加速度(1)平均速度：物理学中，运动物体的位移与所用时间的比称为平均速度(2) 位移的平均变化率：tt s t t s ∆-∆+)()(00 (3)瞬时速度：当无限趋近于0 时，tt s t t s ∆-∆+)()(00无限趋近于一个常数，这个常数称为t=t 0时的瞬时速度求瞬时速度的步骤：1.先求时间改变量t ∆和位置改变量)()(00t s t t s s -∆+=∆2.再求平均速度ts v ∆∆= 3.后求瞬时速度：当t ∆无限趋近于0，t s ∆∆无限趋近于常数v 为瞬时速度 (4)速度的平均变化率：tt v t t v ∆-∆+)()(00 (5)瞬时加速度：当t ∆无限趋近于0 时，t t v t t v ∆-∆+)()(00无限趋近于一个常数，这个常数称为t=t 0时的瞬时加速度注：瞬时加速度是速度对于时间的瞬时变化率三、数学应用例1、已知f(x)=x 2，求曲线在x=2处的切线的斜率。

高中数学 3.1 瞬时变化率——导数学案(无答案)苏教版选修1(2021年整理)

江苏省镇江市丹徒镇高中数学3.1 瞬时变化率——导数学案（无答案）苏教版选修1编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（江苏省镇江市丹徒镇高中数学3.1 瞬时变化率——导数学案（无答案）苏教版选修1）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为江苏省镇江市丹徒镇高中数学3.1 瞬时变化率——导数学案（无答案）苏教版选修1的全部内容。

瞬时变化率——导数●三维目标1．知识与技能了解导数概念的实际背景;理解函数在某点处导数以及在某个区间的导函数的概念；会用定义求瞬时速度和函数在某点处的导数．2．过程与方法用函数的眼光来分析研究物理问题；经历由平均速度与瞬时速度关系类比由平均变化率过渡到瞬时变化率的过程,体会数形结合、特殊到一般、局部到整体的研究问题的方法．3．情感、态度与价值观通过导数概念的形成过程,体会导数的思想及其内涵；激发学生兴趣：在从物理到数学，再用数学解决物理问题的过程中感悟数学的价值．●重点难点重点：函数在某一点处的导数的概念及用导数概念求函数在一点处的导数．难点:从实例中归纳、概括函数瞬时变化率的定量分析过程,及函数在开区间内的导函数的理解．【知识一】曲线上一点处的切线【问题导思】如图，当点P n（x n，f（x n）)（n＝1，2，3,4）沿着曲线f（x）趋近于点P（x0，f(x0）)时，割线PP n的变化趋势是什么?设曲线C上的一点P,Q是曲线C上的另一点，则直线PQ称为曲线C的；当点Q沿曲线C向点P运动，割线PQ在点P附近越来越．当点Q时,直线PQ最终就成为在点P处最逼近曲线的直线l，这条直线l称为曲线在点P处的．【知识二】瞬时速度、瞬时加速度【问题导思】在高台跳水运动中，如果我们知道运动员相对于水面的高度h（单位：m)与起跳后的时间t(单位:s）存在关系h（t)＝－4.9t2＋6.5t＋10，那么我们就能计算起跳后任意一段时间内的平均速度v，通过平均速度v来描述运动员的运动状态，但用平均速度一般不能反映运动员在某一时刻的瞬时速度．1．怎么求运动员在t0时刻的瞬时速度？2．当Δx趋于0时，函数f（x)在（x0,x0＋Δx)上的平均变化率即为函数f（x）在x0处的瞬时变化率，你能说出其中的原因吗？1．瞬时速度运动物体的位移S(t）对于时间t的导数,即v（t）＝．2．瞬时加速度运动物体的速度v（t)对于时间t的导数,即a（t）＝．【知识三】导数及导数的几何意义【问题导思】在函数y＝f（x）的图象上任取两点A（x1，f(x1)），B(x1＋Δx，f(x1＋Δx）)．1。

用平均速度法求解瞬时速度

用平均速度法求解瞬时速度1.用极限法求瞬时速度和瞬时加速度(1)公式v ＝Δx Δt中，当Δt →0时v 是瞬时速度. (2)公式a ＝Δv Δt中，当Δt →0时a 是瞬时加速度. 2.注意(1)用v ＝Δx Δt求瞬时速度时，求出的是粗略值，Δt (Δx )越小，求出的结果越接近真实值. (2)对于匀变速直线运动，一段时间内的平均速度可以精确地表示物体在这一段时间中间时刻的瞬时速度.例3 为了测定气垫导轨上滑块的加速度，滑块上安装了宽度为d ＝3.0 cm 的遮光板，如图3所示，滑块在牵引力作用下先后匀加速通过两个光电门，配套的数字毫秒计记录了遮光板通过第一个光电门的时间为Δt 1＝0.30 s ，通过第二个光电门的时间为Δt 2＝0.10 s ，遮光板从开始遮住第一个光电门到开始遮住第二个光电门的时间为Δt ＝3.0 s ，则滑块的加速度约为( )图3A.0.067 m/s 2B.0.67 m/s 2C.6.7 m/s 2D.不能计算出答案 A解析遮光板通过第一个光电门时的速度v 1＝d Δt 1＝0.030.30m/s ＝0.10 m/s ，遮光板通过第二个光电门时的速度v 2＝d Δt 2＝0.030.10 m/s ＝0.30 m/s ，故滑块的加速度a ＝v 2－v 1Δt≈0.067 m/s 2，选项A 正确.变式4 (2018·甘肃天水质检)如图4所示，气垫导轨上滑块经过光电门时，其上的遮光条将光遮住，电子计时器可自动记录遮光时间Δt .测得遮光条的宽度为Δx ，用Δx Δt近似代表滑块通过光电门时的瞬时速度.为使Δx Δt更接近瞬时速度，正确的措施是( )图4A.换用宽度更窄的遮光条B.提高测量遮光条宽度的精确度C.使滑块的释放点更靠近光电门D.增大气垫导轨与水平面的夹角答案 A。

高二数学瞬时速度与瞬时加速度

第26讲 瞬时加速度的求解技巧(解题技巧类)

瞬时速度与瞬时加速度

曲线上一点处的切线、瞬时速度与加速度

3.求瞬时速度和加速度

瞬时速度矢量与瞬时加速度矢量介绍.ppt

高二数学瞬时速度与瞬时加速度(201909)

关于速度的所有公式

圆周运动教案圆周运动的速度和加速度计算

高二数学瞬时速度与瞬时加速度

瞬时速度的三种公式

苏教版选修1《瞬时速度与瞬时加速度》评课稿

质点的瞬时速度和瞬时加速度计算方法研究

高一数学复习考点知识讲解课件42---瞬时速度与瞬时加速度

苏教版高中数学选修(2-2)-1.1《瞬时变化率—导数：瞬时速度与瞬时加速度》导学案

瞬时速度与加速度

3.1.2瞬时速度与瞬时加速度

高二数学瞬时变化率 导数教案 苏教版

高中数学 3.1 瞬时变化率——导数学案(无答案)苏教版选修1(2021年整理)

用平均速度法求解瞬时速度

第26讲瞬时加速度的求解技巧(解题技巧类)

高二数学瞬时变化率导数教案苏教版