圆柱和圆锥的易错题整理
人教版六年级数学圆柱与圆锥易错题专项练习

人教版六年级数学圆柱与圆锥易错题专项练习一、圆柱与圆锥1.有一个底面直径为20厘米的装有一些水的圆柱形玻璃杯,已知杯中水面距杯口2.24厘米.若将一个半径为9厘米的圆锥形铅锤完全浸入水中,水会溢出314立方厘米.求铅锤的高.【答案】解:3.14×(20÷2)2×2.24+314=3.14×100×2.24+314=703.36+314=1017.36(立方厘米),1017.36 ÷(3.14×92)=1017.36×3÷254.34=3052.08÷254.34=12(厘米),答:铅锤的高是12厘米。
【解析】【分析】根据题意可知,先求出圆锥形铅锥的体积,用圆柱形玻璃杯上面的空白部分的体积+溢出的水的体积=圆锥形铅锥的体积,然后用圆锥形铅锥的体积÷÷铅锥的底面积=铅锥的高,据此列式解答.2.计算下面圆柱的表面积和体积,圆锥的体积。
(1)(2)【答案】(1)解:表面积:3.14×52×2+3.14×5×2×13=157+408.2=565.2(cm2)体积:3.14×52×13=1020.5(dm3)(2) ×3.14×82×15= ×3.14×64×15=1004.8(cm3)【解析】【分析】(1)圆柱的表面积=底面积×2+侧面积,侧面积=底面周长×高,圆柱的体积=底面积×高,根据公式计算即可;(2)圆锥的体积=底面积×高×,根据公式计算体积即可。
3.一个圆锥形沙堆,高是1.8米,底面半径是5米,每立方米沙重1.7吨,这堆沙约重多少吨?【答案】解:沙堆的体积: ×3.14×52×1.8= ×3.14×25×1.8=47.1(立方米)沙堆的重量:1.7×47.1≈80.07(吨)答:这堆沙约重80.07吨。
小学数学圆柱圆锥易错题练习题

小学数学圆柱圆锥易错题练习题问题一:已知一个圆柱的高度为10 cm,底面直径为6 cm。
求这个圆柱的体积和表面积。
解答:首先计算底面的半径,由于底面直径为6 cm,所以半径为3 cm。
接下来,我们可以使用下面的公式来计算圆柱的体积和表面积:体积公式:V = 底面积 ×高度表面积公式:A = 2πr² + 2πrh (其中π取3.14)将已知数据代入公式我们可以得到:底面积= πr² = 3.14 × 3² ≈ 28.26 cm²体积 = 底面积 ×高度 = 28.26 cm² × 10 cm = 282.6 cm³表面积= 2πr² + 2πrh = 2 × 3.14 × 3² + 2 × 3.14 × 3 × 10 ≈ 188.4 cm²因此,这个圆柱的体积约为282.6 cm³,表面积约为188.4 cm²。
问题二:已知一个圆锥的高度为8 cm,底面半径为4 cm。
求这个圆锥的体积和母线长度。
解答:首先我们可以使用下面的公式来计算圆锥的体积和母线长度:体积公式:V = 1/3 ×底面积 ×高度母线公式:l = √(高度² + 底面半径²) (其中√表示平方根)将已知数据代入公式我们可以得到:底面积= πr² = 3.14 × 4² = 50.24 cm²体积 = 1/3 ×底面积 ×高度= 1/3 × 50.24 cm² × 8 cm ≈ 133.18 cm³母线长度= √(高度² + 底面半径²) = √(8² + 4²) ≈ √80 ≈ 8.94 cm因此,这个圆锥的体积约为133.18 cm³,母线长度约为8.94 cm。
2023-2024学年人教版六年级数学下册圆柱与圆锥常考易错应用题训练(附参考答案)

2023-2024学年六年级下册数学圆柱与圆锥常考易错应用题训练1.一个圆柱体,如果把它的高截短4dm,它的表面积减少125.6dm²。
这个圆柱体积减少多少立方分米?2.一个正方体包装箱,从里面量棱长是4.1dm。
用它装一件底面周长是12.56dm,体积是62.8dm3的圆柱形玻璃器皿,能否装得下?3.乐乐将一个铁皮油桶在地上滚动一圈,量得其痕迹长12.56分米、宽6分米。
制作这个油桶至少需要铁皮多少平方分米?(桶口和盖忽略不计)4.把一块长10厘米、宽8厘米、高3.14厘米的长方体铁块完全浸没在一个盛有水的圆柱形玻璃容器内,容器的底面直径为20厘米,容器内的水面会上升多少?(已知水不会溢出)5.工地有一堆圆锥形沙土,底面周长是31.4m,高1.5m,把这堆沙土用渣土车运出工地,每辆渣土车每次运8m3,用一辆渣土车运出这些沙土,大约需运多少次?6.一个圆柱形水池,水池内壁和底面都要镶上瓷砖,水池底面直径6米7.节约用水是我们每个人的义务,学校的自来水管内直径为0.2分米,自来水的流速是每秒5分米,若忘记关上水龙头,一分钟将浪费多少升水?8.下图中,以红色线为轴,快速旋转后会形成一个立体图形,请求出这个立体图形的体积。
9.下面是一个圆柱的展开图,制作这样的一个圆柱至少需要铁皮多少平方分米?10.一个无盖的圆柱形铁皮水桶,底面直径是30厘米,高是50厘米。
(得数保留整数) (1)做这样一个水桶,至少需用铁皮多少平方厘米?(2)这个水桶最多能盛水多少升?11.一个圆锥形沙堆,底面周长是12.56米,高是1.8米,把这些沙铺在6米宽的公路上,如果沙后2厘米,可以铺多长?12.一个圆锥形沙堆,底面周长是37.68m,高是5m,用这堆沙在10m宽的公路上铺5cm 厚的路面,能铺多长?,做这个水桶至少13.一个无盖的圆柱形铁皮水桶,高为10分米,底面直径是高的25用铁皮多少平方分米?(得数保留整数)14.把一个高是64厘米的圆柱按照5:3的比截成了两个圆柱,截后的表面积比原来增加了484平方厘米。
圆柱、圆锥易错点

(3)圆柱体的体积与长方体的体积相等。
(×)
(4)圆柱体的底面直径和高可以相等。
(√ )
判断:
1.体积一般比表面积大。
(×)
2.底面积相等的两个圆柱体积相等。 (×) 3.圆锥体的体积总是圆柱体体积的3倍 (×)
4.求圆柱形容积,就是1 求这个圆柱形容器的
3
体积。
(×)
5.把一个圆柱平均切割成3个小圆柱,那么每个
小圆柱的表面积一定是原来圆柱表面积的
三分之一。
(×)
1、一个圆柱体状的杯子的体积就是它的容积。 (×)
2等、。若两个圆柱体的侧面积相等,则它们的体积也(相×)
3体、积圆扩柱大体9倍的。高不变,底面半径如果扩大3倍,则(它√ 的)
4、如果一个物体上下两个底是相同的圆,侧面是曲面,
则56、、这圆以个锥三物的 角体体 形一积 的定等 一是于 条圆圆边柱柱为体体轴。积旋的转三一分周一之定一可。以得((到××一))个
3. 正方体、长方体、圆锥体的体积都等于底面
积×高。
(× )
4. 等底等高的圆柱和圆锥,如果圆柱体的体积 是27立方米,那么圆锥的体积是9立方米。(√ )
二、填空。
1.一个圆柱削成一个与它等底等高的圆锥,削去部分的 体积是圆锥体积的(2倍),是圆柱体积的( 2 )。
2.把一个棱长为6厘米的正方体,削成一个最大的3 圆柱体, 这个圆柱体的体积是( )立方厘米。
• A、31.4 B、125.6 C、31400
• 3. 一个圆柱的体积是一个等底圆锥体积的6倍,这个圆柱 的高是圆锥高的。( )
• A、6倍 B、3倍 C、2倍
• 4. 把一个圆柱形的材料切削成和它等底等高的圆锥,削去 部分的体积是原材料的。( )
圆柱和圆锥易错题专项练习

圆柱和圆锥易错题专项练习第四讲:圆柱和圆锥易错题专项练姓名:得分:一、认真审题,再填空(19×2=38分)1、等底等高的圆柱和圆锥,体积之比为():()2、一个圆柱与一个圆锥等底等高,它们的体积之和是48dm²,圆柱的体积是()dm³,圆锥的体积是()dm³。
3、一个圆柱形与一个圆锥形的底面直径都是10cm,高都是12cm,先在圆锥形里注满水,再把圆锥形的水倒入圆柱形中,圆柱形里的水深()厘米。
4、把一个棱长10dm的正方体切削成一个最大的圆柱,圆柱的体积是()5、把一个高24cm的圆柱形铁块熔铸成一个和它等底的圆锥,圆锥高()cm.6、一个圆锥,底面半径5cm,高3cm,这个圆锥的体积是()cm³。
7、一个圆锥形沙堆,占地面积15㎡,高4m,这个沙堆的体积是()m³。
8、把一个棱长6cm的正方体木块切削成一个最大的圆锥,得到的圆锥的体积是()cm³。
9、在一个底面半径4dm,高6dm的圆柱形中装满水,再把一个与这个圆柱等底等高的圆锥放入圆柱形中,水会溢出()立方分米。
10、把一个圆柱切削成一个最大的圆锥,削掉了60 cm³,原来这个圆柱的体积是()。
11、一个圆锥的体积是12立方厘米,底面积是4平方厘米,高是()。
12、一个圆锥形的,从内里量高9厘米,先装满水,然后把水所有倒入和它等底的圆柱描述器里,水面高()厘米。
13、直角三角形ABC的AB边长为3厘米,BC边长为4厘米,AC边长为5厘米。
以AB边为轴旋转一周后,形成一个立体图形。
它的体积是()。
14、一个圆柱与一个圆锥体积相等,高也相等。
圆柱的底面积是60平方厘米,圆锥的底面积是(。
)。
15、一个圆柱形水桶里装有一块与水桶(从里面量)等底等高的圆锥形铁锭,加入24升水,正好盛满一桶。
圆锥形铁锭的体积是()立方分米,如果圆锥形铁锭的底面积是4平方分米,水桶的高是()分米。
小升初必备:圆柱与圆锥典型及易错题型分析

小升初必备:圆柱与圆锥典型及易错题型分析圆柱与圆锥典型及易错题型(一)关于圆锥与圆柱相互之间的关系:1.若圆锥与圆柱等底等高,则它们的体积不等(圆锥的体积是圆柱的三分之一);2.若圆锥与圆柱等底等体积,则它们的高不等(圆锥的高是圆柱的3倍);3.若圆锥与圆柱等高等体积,则它们的底不等(圆锥的底面积是圆柱的3倍)。
练:1、一个圆柱和一个圆锥等底等高,它们的体积和是24立方分米,那么圆柱的体积是_________立方分米.2、一个圆柱和一个圆锥的底面直径相等,圆锥的高是圆柱的3倍,圆锥的体积是12立方分米,圆柱的体积是()立方分米。
A12B36C4D8(二)、关于圆柱、圆锥的典型实际问题:1.实质求圆柱的侧面积:通风管(如圆柱形烟囱)压路机1、做一根长1米,底面周长是2分米的圆柱形通风管,需要铁皮多少平方分米?(管壁厚度忽略不计)2.求的滚轮转动一周所压过的路面面积就是求圆柱(滚轮)的侧面积;(所压过的路面面积=圆柱(滚轮)的侧面积×转动速度×时间)1、压路机的滚筒是个圆柱,它的宽是3米,滚筒横截面半径是1米,那么滚筒转一周可压路面多少平方米?如果压路机的滚筒每分钟转10周,那么5分钟可以行驶多少米?3.求无盖的圆柱形表面积。
1、求圆柱形水桶能装水多少升,是求它的();做一节圆柱形通风管要多少铁皮,是求它的()A.侧面积B.表面积C.体积D.容积2、一个圆柱形儿童游泳池底面半径是4米,深0.5米.在它的四周和池底抹上水泥,每平方米需要水泥10千克,一共用水泥多少千克?3、一个无盖的圆柱形铁皮水桶,高50厘米,底面直径30厘米,做这个水桶约莫需用几何铁皮? (得数保留整数)4、做一个无盖的圆柱形鱼缸,底面半径3dm,高5dm。
(1)做这个鱼缸至少要几何平方分米?(得数保留整十平方分米)(2)这个鱼缸能装几何千克水?(1升水重1千克)5、圆柱的体积求底面积或高时,要用体积除以底面积或高,圆锥的体积求底面积或高时,要先乘以3再除以底面积或高。
圆柱与圆锥易错题

圆柱与圆锥易错题一、圆柱与圆锥1.一个圆锥沙堆,底面半径是2米,高1.5米,每立方米的黄沙重2吨,这堆沙重多少吨? 【答案】解: ×3.14×22×1.5×2= ×3.14×4×1.5×2=6.26×2=12.56(吨)答:这堆沙重12.56吨。
【解析】【分析】圆锥的体积=底面积×高×,根据体积公式计算出沙子的体积,再乘每立方米黄沙的重量即可求出总重量。
2.一个圆柱形的汽油桶,底面半径是2分米,高是5分米,做这个桶至少要用多少平方分米的铁皮?它的容积是多少升?【答案】解:3.14×22×2+3.14×2×2×5=3.14×4×2+3.14×4×5=25.12+62.8=87.92(dm2)3.14×22×5=62.8(dm3)62.8dm3=62.8L答:做这个桶至少要用87.92平方分米的铁皮。
它的容积是62.8升。
【解析】【分析】需要铁皮的面积就是油桶的表面积,用底面积的2倍加上侧面积就是表面积,圆柱的侧面积=底面周长×高;圆柱的容积=底面积×高,根据公式计算即可。
3.一个圆柱形钢管,内直径是20cm,水在钢管内的流速是每秒40cm,每秒流过的水是多少cm3?【答案】解:3.14×(20÷2)2×40=314×40=12560(cm3)答:每秒流过的水是12560cm3。
【解析】【分析】钢管是圆柱形,流出的水也是圆柱形。
用钢管的横截面面积乘每秒流出水的长度即可求出流过水的体积。
4.一个酒瓶里面深30cm,底面内直径是10cm,瓶里酒深15cm。
把瓶口塞紧后使其瓶口向下倒立,这时酒深25cm。
求酒瓶的容积。
【答案】解:3.14×(10÷2)2×[15+(30-25)]=1570(cm3)答:酒瓶的容积是1570 cm3。
六年级数学下册《圆柱和圆锥》易错题精选

1500立方厘米=(1500 )毫升=( 1.5 )升
圆锥的侧面展开图是一个(扇形),圆锥有(1)条高。
二、易错判断题
长方体中最多有4个面可能是正方形。
(×)
一个圆柱,如果底面直径和高相等,则圆柱的侧面展开是正方形。
(×)
如果一个物体上、下底面是面积相等的两个圆,那么这个物体一定是圆柱。
(×)
如果两个圆柱的侧面积相等,那么他们的底面周长也相等。
(×)
把一个圆柱的底面直径扩大2倍,高不变,那么它的侧面积也扩大2倍。
(√)
圆柱体的高越大,它的侧面积就越大。
( ×)
三、易错应用题
1.画出下面圆柱的展开图,并求出它的表面积。
(单位:厘米)。
圆柱与圆锥易错题目(1)

圆柱与圆锥易错题目(1)一、圆柱与圆锥1.看图计算.(1)求圆柱的表面积(单位:dm)(2)求零件的体积(单位:cm)【答案】(1)解:3.14×10×20+3.14×(10÷2)2×2=628+3.14×25×2=628+157=785(平方分米)答:圆柱的表面积是785平方分米。
(2)解: ×3.14×(2÷2)2×3+3.14×(2÷2)2×4= ×3.14×1×3+3.14×1×4=3.14+12.56=15.7(立方厘米)答:零件的体积是15.7立方厘米。
【解析】【分析】(1)圆柱的表面积是两个底面积加上一个侧面积,根据圆面积公式计算出底面积,用底面周长乘高求出侧面积;(2)圆柱的体积=底面积×高,圆锥的体积=底面积×高×,根据公式计算,用圆柱的体积加上圆锥的体积就是总体积。
2.计算圆锥的体积。
【答案】解:3.14×2²×15×=3.14×4×5=62.8(dm³)【解析】【分析】圆锥的体积=底面积×高×,根据圆锥的体积公式计算体积即可。
3.一根圆柱形木材长20分米,把它截成3段,表面积增加了12.56平方分米。
这根木材体积是多少立方米?【答案】解:12.56÷4×20=62.8(立方分米)=0.0628(立方米)答:这根木材体积是0.0628立方米。
【解析】【分析】将圆柱形木材截成3段,增加了4个底面积,用增加的表面积除以4即可求出圆柱的底面积,然后用底面积乘高即可求出这根圆柱形木材的体积。
4.将一根底面直径是20厘米,长1米的圆木沿着直径劈成相等的两半。
每半块木头的表面积和体积是多少?【答案】解:1米=100厘米,表面积:3.14×(20÷2)2+[3.14×20×100]÷2+20×100=5454(平方厘米)体积:3.14×(20÷2)2×100÷2=15700(立方厘米)答:每半块木头的表面积是5454平方厘米,体积是15700立方厘米。
北师大版数学六年级(下册)圆柱与圆锥经典易错题型
北师大版数学六年级(下册)圆柱与圆锥经典易错题型一、圆柱与圆锥1.看图计算.1〕求圆柱的表面积〔单位:dm〕2〕求部件的体积〔单位:cm〕【答案】〔1〕解:×10×〔×10÷2〕2×2×25×2628+157785〔平方分米〕答:圆柱的表面积是785平方分米。
〔2〕解:×〔×2÷2〕2×〔×2÷2〕2×4=××1××1×4〔立方厘米〕答:部件的体积是立方厘米。
【分析】【剖析】〔1〕圆柱的表面积是两个底面积加上一个侧面积,依据圆面积公式计算出底面积,用底面周长乘高求出侧面积;2〕圆柱的体积=底面积×高,圆锥的体积=底面积×高×,依据公式计算,用圆柱的体积加上圆锥的体积就是整体积。
2.如图,一个内直径是 20cm的贞洁水水桶里装有贞洁水,水的高度是22cm.将水桶倒放时,空余局部的高度是3cm,无水局部是圆柱形.这个贞洁水水桶的容积是多少升?【答案】解:×〔20÷2〕2×〔×20÷2〕2×3×100×〔22+3〕×100×257850〔立方厘米〕7850立方厘米=升答:这个贞洁水水桶的容积是升。
【分析】【剖析】水桶的容积包含水的体积和空余局部的体积,依据圆柱的体积公式分别计算后再相加即可求出水桶的容积。
3.有一个底面直径为20厘米的装有一些水的圆柱形玻璃杯,杯中水面距杯口厘9厘米的圆锥形铅锤完整浸入水中,水会溢出314立方厘米.求铅锤米.假定将一个半径为的高.【答案】解:×〔20÷2〕2×2.24+314×100×2.24+314703.36+314〔立方厘米〕,2〕÷〔×9×3÷÷12〔厘米〕,答:铅锤的高是12厘米。
六年级圆柱与圆锥易错题

六年级圆柱与圆锥易错题
以下是一些六年级圆柱与圆锥的易错题:
1. 一个圆柱体和一个圆锥体的底面积相等、体积也相等,圆锥的高是27厘米,圆柱的高是多少厘米.
2. 一个圆柱体和一个圆锥体的底面积和体积都相等,圆锥的高是18厘米,圆柱的高是多少厘米.
3. 一个圆柱体和一个圆锥体的底面积相等、体积不相等,圆锥的体积是圆柱的(1/3),圆锥的高是27厘米,圆柱的高是多少厘米.
4. 一个圆柱体和一个圆锥体的底面积相等、高相等,它们的体积之和是144立方厘米,圆锥的体积是多少立方厘米.
5. 圆锥体的底面积不变,高增加(1/5),则体积增加多少
6. 圆柱体与一个圆锥体的底面积相等、高也相等,圆柱的体积是3立方分米,圆锥的体积是多少立方分米.
7. 圆柱体与一个圆锥体的底面积和体积都相等,圆锥的高是9分米,圆柱的高是多少分米.
8. 一个圆柱体和一个圆锥体的底面积和体积都相等,圆锥的高是24厘米,圆柱的高是多少厘米.
9. 一个圆柱体和一个圆锥体的底面积相等、高不相等,圆柱的体积是圆锥的(3/5),圆锥的高是27厘米,圆柱的高是多少厘米.
10. 一个圆柱体和一个圆锥体的底面积和体积都相等,已知圆锥的高是18
厘米,则圆柱的高是多少厘米.
这些题目需要学生仔细理解并应用圆柱和圆锥的体积公式(V=πr^2h)以
及相关的数学知识。
如果他们在这方面有困难,可能需要更多的练习和解释。
人教版数学6年级下册 第3单元(圆柱和圆锥)易错题拔高训练(含答案)
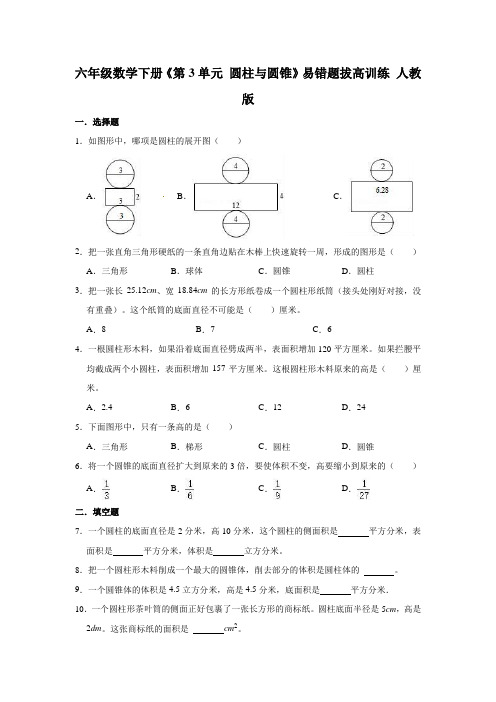
六年级数学下册《第3单元圆柱与圆锥》易错题拔高训练人教版一.选择题1.如图形中,哪项是圆柱的展开图()A.B.C.2.把一张直角三角形硬纸的一条直角边贴在木棒上快速旋转一周,形成的图形是()A.三角形B.球体C.圆锥D.圆柱3.把一张长25.12cm、宽18.84cm的长方形纸卷成一个圆柱形纸筒(接头处刚好对接,没有重叠)。
这个纸筒的底面直径不可能是()厘米。
A.8B.7C.64.一根圆柱形木料,如果沿着底面直径劈成两半,表面积增加120平方厘米。
如果拦腰平均截成两个小圆柱,表面积增加157平方厘米。
这根圆柱形木料原来的高是()厘米。
A.2.4B.6C.12D.245.下面图形中,只有一条高的是()A.三角形B.梯形C.圆柱D.圆锥6.将一个圆锥的底面直径扩大到原来的3倍,要使体积不变,高要缩小到原来的()A.B.C.D.二.填空题7.一个圆柱的底面直径是2分米,高10分米,这个圆柱的侧面积是平方分米,表面积是平方分米,体积是立方分米。
8.把一个圆柱形木料削成一个最大的圆锥体,削去部分的体积是圆柱体的。
9.一个圆锥体的体积是4.5立方分米,高是4.5分米,底面积是平方分米.10.一个圆柱形茶叶筒的侧面正好包裹了一张长方形的商标纸。
圆柱底面半径是5cm,高是2dm。
这张商标纸的面积是cm2。
11.一个圆锥的底面直径是8厘米,高12厘米,沿底面直径将它切成两个完全相等的部分,表面积增加平方厘米.12.一个圆锥的底面半径是4厘米,高是6厘米,沿着顶点到圆心切开,表面积增加平方厘米.三.判断题13.把一个圆柱体拼成一个近似的长方体,体积不变,表面积变了..14.一个圆柱形的玻璃杯可盛水1立方分米,我们就说玻璃杯容积是1升..15.圆锥的高有无数条..16.把一个圆柱体削成一个最大的圆锥体,削去的部分的体积与原来的体积之比是2:3.17.圆柱的侧面展开后是正方形,说明底面直径和高的比是1:1..四.计算题18.计算下面立体图形的体积19.计算下面图形的表面积和体积.五.应用题20.把一个底面直径12厘米的圆锥形金属铸件浸没在棱长1.5分米的正方体容器中,水面比原来升高1.2厘米,求这个圆锥的体积.21.一个无盖的圆柱形铁桶,底面周长是6.28dm,桶深4dm.做这个铁桶至少需要多大面积的铁皮?这个铁桶最多能装多少升水(铁皮厚度忽略不计)?22.一张长方形的铁皮(如下图),剪下图中的阴影部分恰好可以做成一个油桶(接头处不计)。
六年级圆柱圆锥易错题精选

六年级圆柱圆锥易错题精选圆柱圆锥易错题1.用一张长30厘米,宽18厘米的长方形纸,围成一个圆柱,这个圆柱体的侧面积是()平方厘米。
解:首先,我们需要知道圆柱的侧面积公式为2πrh,其中r为底面半径,h为圆柱的高。
由于题目没有给出高,我们需要先求出底面半径。
根据长方形纸的长度和宽度,可以得到圆柱的底面周长为2(30+18)=96厘米,即2πr=96,解得r=48/π。
再根据圆柱的高为18厘米,代入公式2πrh,即可得到圆柱体的侧面积为2π×48/π×18=1728平方厘米。
2.一个圆柱的侧面展开是正方形,当圆柱的高是15分米时,圆柱的底面周长是()分米。
解:根据题意,圆柱的侧面展开是正方形,说明圆柱的高等于底面周长。
因此,底面周长为15分米。
3.等底等高的圆柱和圆锥。
圆柱的体积是36立方厘米,圆锥的体积是()立方厘米;圆锥的体积是36立方厘米圆柱体积比圆锥大()立方厘米。
解:由于圆柱和圆锥等底等高,它们的底面积相等。
设它们的底面积为S,圆柱的高为h,圆锥的高为H,则圆柱的体积为V1=S×h=36,圆锥的体积为V2=1/3×S×H。
将V1代入可得S×h=36,带入V2可得V2=1/3×S×(3h)=1/3×36×3h=36h。
因此,圆锥的体积为36h立方厘米,圆柱的体积比圆锥大36-36h立方厘米。
如果圆锥的体积是36立方厘米,则圆柱的体积比圆锥大0立方厘米,圆锥的体积为1立方厘米。
4.把一个底面直径和高都是6分米的圆柱的,底面分成若干等份,再切开拼成一个长方体。
这个长方体的长是()分米,宽是()分米,高是()分米,体积是()立方分米。
解:首先,我们需要知道圆柱的底面积为πr²,其中r为底面半径。
由于底面直径为6分米,即r=3分米。
将底面分成n等份,则每份的弧长为2πr/n,每份的面积为πr²/n。
人教版数学6年级下册 第3单元(圆柱和圆锥)易错题特训(含解析)

人教版数学6年级下册第3单元(圆柱和圆锥)易错题特训一.选择题(共10小题)1.甲圆柱体的底面直径是8厘米,高是10厘米;乙圆柱体的底面直径是10厘米,高是8厘米.它们的表面积相比较()A.甲>乙B.甲=乙C.甲<乙D.无法确定2.将一张长10厘米、宽8厘米的长方形纸卷成一个圆柱,这个圆柱的侧面积是()A.25.12平方厘米B.18.84平方厘米C.9.42平方厘米D.80平方厘米3.修一个底面半径为2m、深3m的圆柱形蓄水池,这个蓄水池的占地面积是()A.12.56m2B.50.24m2C.37.68m24.做一个圆柱形的厨师帽,至少需要布料的面积是求圆柱()A.侧面积B.侧面积+一个底面面积C.表面积5.用一张长6.28cm,宽1dm的长方形铁皮,围成一个圆柱体,这个圆柱的侧面积是()A.31.4cm2B.3.14 m2C.12.56cm2 D.62.8cm26.一个圆柱的底面直径扩大到原来的2倍,高缩小到原来的,圆柱的侧面积()A.扩大到原来的2倍B.缩小到原来的C.不变D.扩大到原来的3倍7.一个圆柱形物体的底面直径4分米,高是5分米,求它的表面积,列式是()A.3.14×5+3.14×()2×2B.3.14×4×5+3.14×()2×2C.52+3.14×()2×2D.3.14×2×5+3.14×()3×28.一个圆柱体纸盒,侧面展开是正方形.这个纸盒的底面半径是5厘米,它的高是()厘米.A.10B.15.7C.31.4D.78.59.两块同样的长方形纸板,卷成形状不同的圆柱(接头处不重叠),并装上两个底面,那么制成的两个圆柱体的()相等.A.底面积B.侧面积C.表面积10.有一个圆柱,底面直径是10厘米,若高增加4厘米,则侧面积增加()平方厘米.A.31.4B.62.8C.125.6二.填空题(共6小题)11.一个圆柱的侧面展开是正方形,这个圆柱的底面半径是5厘米,那么圆柱的高是厘米。
人教版数学6年级下册 第3单元(圆柱和圆锥)易错题三(含答案)

第3单元圆柱与圆锥-易错题-人教版易错点大集合易错点一:圆柱的表面积典例把一个圆柱体的侧面展开得到一个正方形,这个圆柱体的底面周长是10厘米,高是多少厘米,侧面积是多少平方厘米.跟踪训练1.将一个边长为5分米的正方形纸片卷成圆柱筒,这个圆柱的侧面积是多少平方分米.2.用铁皮制成一个高是5分米,底面周长是12.56分米的圆柱形水桶(没有盖),至少需要多少平方米铁皮?答:至少需要多0.7536平方米铁皮.3.一个圆柱底面半径是4分米,圆柱侧面积是62.8平方分米,这个圆柱的表面积是多少?4.一个圆柱体,底面半径是7厘米,表面积是1406.72平方厘米.这个圆柱的高是多少?5.圆柱侧面展开是一个正方形,已知圆柱的底面积是10平方厘米,则圆柱的侧面积是多少平方厘米?易错点二:圆柱的体积典例将一根长4米的圆柱形木料锯成3段,表面积增加了60平方分米。
这根木料的体积多少立方分米。
跟踪训练1.把一个棱长是6分米的正方体木块,削成一个最大的圆柱体,这个圆柱体的体积是多少立方分米。
2.把一个底面直径是20厘米的圆柱沿直径竖直切成两半,表面积比原来增加了400平方厘米,原来这个圆柱的底面积是多少,体积是多少。
3.一个长5cm、宽4cm的长方形纸,以这个长方形的长边为轴旋转一周,得到的立体图形是什么图形,它的体积是多少cm3。
4.一个圆柱底面半径是5cm,高是8cm,这个圆柱的侧面积是多少cm2,表面积是多少cm2,体积是多少cm3。
5.一个圆柱体油桶的体积是192dm3,底面积是16dm2,它的高是多少dm。
易错点三:圆锥的体积典例直角三角形的两条直角边分别是3厘米,4厘米。
若以其中一条直角边所在的直线为轴旋转一周,得到一个体积最大的圆锥,这个圆锥的体积是多少立方厘米。
跟踪训练1.一个圆锥形沙堆,高1.2m,底面直径是6m,这堆沙子的体积是多少m3。
2.一个圆锥的底面半径是3cm,高是4cm,它的体积是多少cm3。
圆柱与圆锥易错题总结

圆柱与圆锥易错题总结一、圆柱与圆锥1.如图,一个内直径是20cm的纯净水水桶里装有纯净水,水的高度是22cm.将水桶倒放时,空余部分的高度是3cm,无水部分是圆柱形.这个纯净水水桶的容积是多少升?【答案】解:3.14×(20÷2)2×22+3.14×(20÷2)2×3=3.14×100×(22+3)=3.14×100×25=7850(立方厘米)7850立方厘米=7.85升答:这个纯净水水桶的容积是7.85升。
【解析】【分析】水桶的容积包括水的体积和空余部分的体积,根据圆柱的体积公式分别计算后再相加即可求出水桶的容积。
2.一个圆锥体形的沙堆,底面周长是25.12米,高1.8米,用这堆沙在8米宽的公路上铺5厘米厚的路面,能铺多少米?【答案】解:5厘米=0.05米沙堆的底面半径:25.12÷(2×3.14)=25.12÷6.28=4(米)沙堆的体积: ×3.14×42×1.8=3.14×16×0.6=3.14×9.6=30.144(立方米)所铺沙子的长度:30.144÷(8×0.05)=30.144÷0.4=75.36(米).答:能铺75.36米。
【解析】【分析】根据1米=100厘米,先将厘米化成米,除以进率100,然后求出沙堆的底面半径,用公式:C÷2π=r,要求沙堆的体积,用公式:V=πr2h,最后用沙堆的体积÷(公路的宽×铺沙的厚度)=铺沙的长度,据此列式解答.3.一个圆锥形沙堆,占地面积是30平方米,高2.7米,每立方米沙重1.7吨。
如果用一辆载重8吨的汽车把这些沙子运走,至少需要运多少次?【答案】解:30×2.7× ×1.7÷8≈6(次)答:至少需要运6次。
圆柱与圆锥典型及易错题型

圆柱与圆锥典型及易错题型一、圆柱与圆锥1.一个底面半径为12厘米的圆柱形杯中装有水,手里浸泡了一个底面直径是12厘米,高是18厘米的圆锥体铁块,当铁块从杯中取山来时,杯中的水面会下降多少厘米??【答案】解: ×3.14×(12÷2)2×18÷(3.14×122)= ×3.14×36×18÷(3.14×144)=1.5(厘米)答:桶内的水将下降1.5厘米。
【解析】【分析】水面下降部分水的体积就是圆锥的体积,根据圆锥的体积公式先计算出圆锥体铁块的体积,也就是水面下降部分水的体积。
用水面下降部分水的体积除以杯子的底面积即可求出水面下降的高度。
2.将一根底面直径是20厘米,长1米的圆木沿着直径劈成相等的两半。
每半块木头的表面积和体积是多少?【答案】解:1米=100厘米,表面积:3.14×(20÷2)2+[3.14×20×100]÷2+20×100=5454(平方厘米)体积:3.14×(20÷2)2×100÷2=15700(立方厘米)答:每半块木头的表面积是5454平方厘米,体积是15700立方厘米。
【解析】【分析】根据题意,劈开的每半块木头的表面积是原来木头的表面积的一半增加了一个切面的面积,据此代入公式解答即可;劈开的每半块木头的体积是原来木头的体积的一半,据此代入公式解答即可;圆柱表面积S=2×底面积+侧面积=2×3.14×r2+3.14×d×h;截面面积S=dh;体积V=3.14×r2×h。
3.计算下面圆柱的表面积。
(单位:厘米)【答案】解:3.14×(4÷2)²×2+3.14×4×6=100.48(平方厘米)【解析】【分析】圆柱体的表面积是两个底面积加上一个侧面积,底面积根据圆面积公式计算,用底面周长乘高求出侧面积。
六下数学 圆柱与圆锥 易错题专项训练50题 带答案

六年级下学期圆柱与圆锥易错题专项训练50题1、圆柱的侧面展开是一个长方形,长方形的长等于圆柱的(底面周长),长方形的宽等于圆柱的(高)2、一个圆柱的底面半径扩大2倍,高不变,它的底面积扩大(4)倍,侧面积扩大(2)倍,体积扩大(4)倍;一个圆柱的底面半径扩大2倍,高也扩大2倍,它的底面积扩大( 4 )倍,侧面积扩大(4)倍,体积扩大( 8)倍;一个圆柱的底面半径扩大2倍,高扩大3倍,它的底面积扩大(4)倍,侧面积扩大( 6 )倍,体积扩大(12 )倍。
3、一个圆柱的底面半径为2厘米,侧面展开后正好是一个正方形,这个圆柱的体积是(157.7536立方厘米)4、等底等高的圆柱和圆锥的体积的和是96立方分米,这个圆柱的体积是(72 )立方分米,这个圆锥的体积是(24)立方分米。
5、把一个圆锥体浸没在底面积是30平方厘米的圆柱形盛有水的容器里,水面升高4厘米,这个圆锥体的体积是(120 )立方厘米。
6、用一个高36厘米的圆锥形容器盛满水,倒入和它等底等高的圆柱形容器中,水的高度是( 12 )厘米。
7、一个棱长是3分米的正方形容器装满水后,倒入一个底面积是3平方分米的圆锥形容器里正好装满,这个圆锥的高是(27)分米。
8、一个圆柱和一个圆锥的体积相等,底面积相等。
圆锥的高是6分米,圆柱的高是( 2 )分米。
9、一个圆锥的体积是126立方厘米,底面积是42平方厘米,高是(9)厘米。
10将一个边长为5分米的正方形纸片卷成圆柱筒,这个圆柱的侧面积是(25 )平方分米。
11、一段圆钢长4米,底面半径是5厘米,把他平均分成3段后,表面积增加了(117.75)平方厘米。
12、一个圆柱的底面面积是25平方厘米,高是10分米,它的体积是( 2500 )立方厘米。
13、有一块正方体木料,棱长是6分米,把它削成为一个最大的圆柱体,这个圆柱体的体积是(169.56)立方分米。
14、一个圆柱体,把它削成一个与圆柱等底等高的圆锥体,圆锥体的体积是削去部分的(1/2)。
圆柱圆锥12种易错题型

圆柱圆锥12种易错题型
以下是一些与圆柱和圆锥相关的易错题型:
1. 计算圆柱或圆锥的体积时,忘记将高度和半径或直径的单位统一换算。
2. 混淆圆柱的体积公式和表面积公式,或者混淆圆锥的体积公式和表面积公式。
3. 在计算圆柱或圆锥的体积时,未正确平方或立方半径或直径的值。
4. 错误地将圆柱的底面面积与圆柱的侧面积相加来求圆柱的表面积。
5. 错误地将圆柱的表面积与圆柱的体积相加来求圆柱的总表面积。
6. 忽略圆锥的底面积,在计算圆锥的表面积时只考虑侧面积。
7. 错误地将圆锥的表面积与圆锥的体积相加来求圆锥的总表面积。
8. 混淆圆柱和圆锥的形状,例如将一个圆锥误认为是圆柱。
9. 在解决与圆锥相关的问题时,未将斜高或母线的长度考虑在内。
10. 未正确使用三角函数来计算圆锥的斜高或母线的长度。
11. 在计算圆锥的体积时,未正确将半径或直径的平方乘以高度再乘以π。
12. 忽略圆柱或圆锥的单位问题,在计算结果中缺少单位。
请注意,这只是一些常见的易错题型,根据具体的问题和知识点可能会有其他的易错点。
在解答题目时,请仔细阅读题目要求,理清思路,避免粗心导致的错误。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第二单元《圆柱、圆锥》试卷错题
1、正方体内有一个最大的圆柱,圆柱的侧面积是75.36平方厘米,圆柱的直径=(),圆柱的半径=()的一半。
圆柱的高=()。
这个正方体的表面积是()。
圆柱的底面积是正方体底面积的()%,圆柱的4个侧面之和是正方体侧面积的()%,圆柱的体积是正方体体积的()%。
2、正方体内有一个最大的圆锥,圆锥的直径=(),圆锥的半径=()的一半。
圆锥的高=()。
圆锥的体积是正方体内挖出的最大的圆柱的体积的()。
3、有一个密封的容器,它是由一个圆柱和一个圆锥组成的。
圆锥和圆柱等底等高,高都是6厘米,圆柱朝下,圆锥在上,容器内有一部分水,水的高度是4厘米,把容器倒过来圆锥朝下,圆柱在上,现在水面的高度是()。
4、把一个高100厘米的圆柱沿着直径切拼成一个近似的长方体,这时它的表面积增加200平方厘米,这个圆柱的体积是()。
5、一个圆柱高100厘米,如果把他它的高减少20厘米,表面积将减少251.2平方厘米,原来圆柱的体积是()。
6、一根2米长的圆柱形木料,横截面的直径是20厘米,沿着横截面的直径锯开,分成相等的两部分,每一部分的体积和表面积各是()()。
7、一根圆柱形木材长2米,把它截成相等的4段后,表面积增加18.84平方厘米,原来这根圆木的体积是()。
8、一个圆柱的体积是72立方厘米,与它等底等高的圆锥的体积是()。
如果圆锥的底面积是18平方厘米,那么圆锥的高是()。
如果圆锥的高是2厘米,圆锥的底面积是()。
9、一个圆锥和圆柱的底面积之比是3:1,如果高相等,则圆锥和圆柱的体积比是()。
如果高的比是2:1,则圆锥和圆柱的体积比是()。
10、一个圆锥和圆柱的高的比是3:1,如果底面积相等,则圆锥和圆柱的体积比是()。
圆锥的体积是12立方分米,则圆柱的体积是()。
如果底面积的比是2:1,则圆锥和圆柱的体积比是()。
圆锥的体积是12立方分米,则圆柱的体积是()。
11、一个圆锥和圆柱的体积比是3:1,如果底面积相等,则圆锥和圆柱的高的比是()。
如果底面积的比是2:1,则圆锥和圆柱的高比是()。
12、一个长方体、正方体、圆柱、圆锥等底等高,则体积比是()。
如果一个长方体、正方体、圆柱、圆锥体积和高都相等,则长方体的高是()。
圆锥的高是()。
13、圆柱的高不变,底面半径扩大2倍,直径扩大()。
底面积扩大(),侧面积扩大(),表面积扩大(),体积扩大()。
14、圆锥的高不变,底面半径扩大2倍,直径扩大()。
底面积扩大(),体积扩大()。
15、一个圆柱形汽油桶的容积是45立方分米,底面积是7.5平方分米,桶内装的汽油占油桶容积的十二分之七,桶内汽油高是()。
16、一个圆锥形沙堆的底面直径是4米,高4.2米,用这对沙在10米宽的公路上铺2厘米厚,能铺()米长。
17、有2张5元、4张2元、8张1元的人民币。
要拿出12元钱有()种拿法。
18、将相同的小长方形拼成一个大长方形,大长方形的周长是13.2厘米,大长方形的面积是()。
19、学校原有篮球和足球共630个,其中乒乓球占五分之三,后来又买进一些乒乓
球,这时乒乓球占现有两种球的十分之七,又买进乒乓球()。
20、甲地有89吨货物要送往乙地,大卡车载重量是7吨,小卡车载重量是4吨,大卡车一次耗油14升,小卡车一次耗油9升,运完这批货物至少要耗油()升。
21、自来水水管的内直径是2厘米,水管内的水的流速是每秒8厘米,一位同学去洗手,走时忘记关水龙头,5分钟浪费()升水。
22、食堂原来一些大米,第一周吃掉总数的35%,第二周吃掉180千克,这时吃掉的大米和剩下的大米一样多,食堂原来有大米()千克,
23、某市供电公司将原来的每度电0.52元,调整为峰时(8:00-21:00)每度电0.55元,谷时每度电(21:00-第二天8:00)每度电0.30元,张老师家这个月用电421度,用新方法计费比原来少付37.87元,这个月张老师家峰时用电()度。
24、将圆柱的底面平均分成若干份,拼成一个近似的长方体,表面积比原来增加400平方厘米,圆柱的高是20厘米,圆柱的体积是()立方厘米。
25、将一个圆锥形的零件浸没在底面周长是12.56分米的圆柱形玻璃容器中,容器水面上升了0.4分米,这个零件的体积是()。
26、圆锥形沙滩的底面周长是12.56米,高1.2米,用这堆沙铺在一条长是20米、宽5米的长方形路上,能铺多厚?
27、将一个长10分米、宽8分米、高6分米的长方体加工成一个最大的圆柱,所得圆柱的体积是()。
28、圆柱的侧面展开是正方形,底面半径是10厘米,高是()厘米。
底面直径和高的比是()。
29、将棱长2分米的正方体木块,削成一个最大的圆锥,所得圆锥的体积是()。
削去部分的体积是()。
30、将体积为282.6立方厘米的长方体熔铸成一个底面半径是6厘米的圆锥形机器零件,圆锥形零件的高是()。
31、圆柱的高是8厘米,将它的高增加2厘米,表面积就增加25.12平方厘米,原来圆柱的体积是()。
32、圆柱的侧面积是50.24平方厘米,高和底面半径相等,它的表面积是()。
33、一个半径是10米地圆柱形水池,能蓄水1570立方米,如果再挖深2.5米,这个蓄水池能蓄水()立方米。
34、压路机滚筒的半径是0.8米,宽是1.5米,如果滚筒每分钟转动5周,那么每分钟压路得面积是()平方米。
35、圆锥形容器(顶点朝下)内装有0.2升水,水面高度正好是圆锥高度的一半,这个容器还能装水()升。
36、一个直角三角形三条边分别是4厘米、3厘米、5厘米,以斜边为轴旋转一周得到的立体图形的体积是()。
37、一个钝角三角形,最短边上的高是6厘米,以最短边(6厘米)为轴旋转一周,旋转后的大圆锥的高是10厘米,得到的立体图形的体积是()。
