东南大学2001年数学分析考研试题
2001年考研数学一试题答案与解析

2001年考研数学一试题答案与解析一、(1)【分析】 由通解的形式可知特征方程的两个根是12,1r r i =±,从而得知特征方程为22121212()()()220r r r r r r r r r r r r --=-++=-+=.由此,所求微分方程为'''220y y y -+=.(2)【分析】 grad r=,,,,r r r x y z x y z r r r ∂∂∂⎧⎫⎧⎫=⎨⎬⎨⎬∂∂∂⎩⎭⎩⎭.再求 div grad r=()()()x y z x r y r z r ∂∂∂++∂∂∂=222222333311132()()()x y z x y z r r r r r r r r r++-+-+-=-=.于是div grad r|(1,2,2)-=(1,2,2)22|3r -=. (3)【分析】 这个二次积分不是二重积分的累次积分,因为10y -≤≤时12y -≤.由此看出二次积分0211(,)ydy f x y dx --⎰⎰是二重积分的一个累次积分,它与原式只差一个符号.先把此累次积分表为0211(,)(,)yDdy f x y dx f x y dxdy --=⎰⎰⎰⎰.由累次积分的内外层积分限可确定积分区域D :10,12y y x -≤≤-≤≤.见图.现可交换积分次序原式=02202111111(,)(,)(,)xyxdy f x y dx dx f x y dy dx f x y dy -----=-=⎰⎰⎰⎰⎰⎰.(4)【分析】 矩阵A 的元素没有给出,因此用伴随矩阵、用初等行变换求逆的路均堵塞.应当考虑用定义法.因为2()(2)240A E A E E A A E -+-=+-=,故()(2)2A E A E E -+=,即2()2A E A E E +-⋅=.按定义知11()(2)2A E A E --=+. (5)【分析】 根据切比雪夫不等式2(){()}D x P X E X εε-≥≤, 于是2()1{()2}22D x P XE X -≥≤=. 二、(1)【分析】 当0x <时,()f x 单调增'()0f x ⇒≥,(A ),(C )不对;当0x >时,()f x :增——减——增'()f x ⇒:正——负——正,(B )不对,(D )对.应选(D ). (2)关于(A ),涉及可微与可偏导的关系.由(,)f x y 在(0,0)存在两个偏导数⇒(,)f x y 在(0,0)处可微.因此(A )不一定成立.关于(B )只能假设(,)f x y 在(0,0)存在偏导数(0,0)(0,0),f f x y∂∂∂∂,不保证曲面(,)z f x y =在(0,0,(0,0))f 存在切平面.若存在时,法向量n=(0,0)(0,0)1f f x y ⎫∂∂⎧±-=±⎨⎬∂∂⎩⎭,,{3,1,-1}与{3,1,1}不共线,因而(B )不成立.关于(C ),该曲线的参数方程为,0,(,0),x t y z f t =⎧⎪=⎨⎪=⎩它在点(0,0,(0,0))f 处的切向量为'0{',0,(,0)}|{1,0,(0,0)}{1,0,3}t x dt f t f dt===.因此,(C )成立. (3)【分析】 当(0)0f =时,'0()(0)lim x f x f x →=∃00()()lim lim x x f x f x x x→+→-⇔=∃.关于(A ):220001(1cos )1cos 1()lim (1cos )lim 1cos lim1cos 2h h t f h h f t f h t h h h h t→→→+---=⋅=--, 由此可知 201lim (1cos )h f h h →-∃ ⇔ '(0)f + ∃.若()f x 在0x =可导⇒(A )成立,反之若(A )成立⇒'(0)f +∃⇒'(0)f ∃.如()||f x x =满足(A ),但'(0)f 不∃.关于(D ):若()f x 在0x =可导,⇒''001(2)()lim [(2)()]lim[2]2(0)(0)2h h f h f h f h f h f f h h h→→-=-=-. ⇒(D )成立.反之(D )成立0lim((2)())0h f h f h →⇒-=⇒()f x 在0x =连续,⇒()f x 在0x =可导.如21,0()0,0x x f x x +≠⎧=⎨=⎩ 满足(D ),但()f x 在0x =处不连续,因而'(0)f 也不∃.再看(C ):2220001sin (sin )sin ()lim(sin )lim lim sin h h h h h f h h h h f t f h h h h h h h t→→→----=⋅=⋅-(当它们都∃时). 注意,易求得20sin lim 0h h h h →-=.因而,若'(0)f ∃⇒(C )成立.反之若(C )成立⇒0()lim t f t t→(即 '(0)f ∃).因为只要()f t t 有界,任有(C )成立,如()||f x x =满足(C ),但'(0)f 不∃.因此,只能选(B ).(4)【分析】 由 43||40E A λλλ-=-=,知矩阵A 的特征值是4,0,0,0.又因A 是实对称矩阵,A 必能相似对角化,所以A 与对角矩阵B 相似.作为实对称矩阵,当A B 时,知A 与B 有相同的特征值,从而二次型Tx Ax 与Tx Bx 有相同的正负惯性指数,因此A 与B 合同.所以本题应当选(A ).注意,实对称矩阵合同时,它们不一定相似,但相似时一定合同.例如1002A ⎡⎤=⎢⎥⎣⎦与1003B ⎡⎤=⎢⎥⎣⎦,它们的特征值不同,故A 与B 不相似,但它们的正惯性指数均为2,负惯性指数均为0.所以A 与B 合同.(5)【分析】 解本题的关键是明确X 和Y 的关系:X Y n +=,即Y n X =-,在此基础上利用性质:相关系数XY ρ的绝对值等于1的充要条件是随机变量X 与Y 之间存在线性关系,即Y aX b =+(其中,a b 是常数),且当0a >时,1XY ρ=;当0a <时,1XY ρ=-,由此便知1XY ρ=-,应选(A ).事实上,(,)(,)Cov X Y Cov X n X DX =-=-,()DY D n X DX =-=,由此由相关系数的定义式有1XY ρ===-.三、【解】原式=222211arctan ()[arctan ]22(1)x x x x xxx de e d e e e e e ---=--+⎰⎰=2221(arctan )21x x x xx xde de e e e e ---++⎰⎰=21(arctan arctan )2x x x x e e e e C ---+++. 四、【解】先求(1)(1,(1,1))(1,1)1f f f ϕ===.求 32''1()|3(1)(1)3(1)x d x dxϕϕϕϕ===,归结为求'(1)ϕ.由复合函数求导法'''12()(,(,))(,(,))(,)dx f x f x x f x f x x f x x dxϕ=+,'''''1212(1)(1,1)(1,1)[(1,1)(1,1)]f f f f ϕ=++.注意 '1(1,1)(1,1)2f f x∂==∂,'2(1,1)(1,1)3f f y∂==∂.因此'(1)23(23)17ϕ=++=,31()|31751x d x dxϕ==⨯=. 五、【分析与求解】关键是将arctan x 展成幂级数,然后约去因子x ,再乘上21x +并化简即可. 直接将arctan x展开办不到,但'(arctan )x 易展开,即'221(arctan )(1),||11n nn x x x x ∞===-<+∑, ①积分得 '2210000(1)arctan (arctan )(1)21n xx nnn n n x t dt t dt x n ∞∞+==-==-=+∑∑⎰⎰,[1,1]x ∈-. ② 因为右端积分在1x =±时均收敛,又arctan x 在1x =±连续,所以展开式在收敛区间端点1x =±成立.现将②式两边同乘以21x x+得2222220001(1)(1)(1)arctan (1)212121n n n n n n n n n x x x x x x x n n n +∞∞∞===+---=+=++++∑∑∑ =12200(1)(1)2121n n n nn n x x n n -∞∞==--++-∑∑ =21111(1)()2121nnn x n n ∞=+--+-∑221(1)2114n nn x n∞=-=+-∑,[1,1]x ∈-,0x ≠上式右端当0x =时取值为1,于是221(1)2()1,[1,1]14n nn f x x x n∞=-=+∈--∑.上式中令1x =21(1)111[(1)1](21)1422442n n f n ππ∞=-⇒=-=⨯-=--∑. 六、【解】用斯托克斯公式来计算.记S 为平面2x y z ++=上L 所为围部分.由L 的定向,按右手法则S 取上侧,S 的单位法向量(cos ,cos ,cos )3n αβγ==.于是由斯托克斯公式得 222222cos cos cos 23SI dSx y z y z z x x y αβγ∂∂∂=∂∂∂---⎰⎰=[(24(26(22333Sy z z x x y dS --+----⎰⎰ =(423)(2)(6)33S Sx y z dS x y z x y dS ++++=+-⎰⎰利用.于是'2'211113x y Z Z ++=++=.按第一类曲面积分化为二重积分得(6)32(6)3D DI x y dxdy x y dxdy =+-=-+-⎰⎰⎰⎰,其中D 围S 在xy 平面上的投影区域||||1x y +≤(图).由D 关于,x y 轴的对称性及被积函数的奇偶性得()0Dx y dxdy -=⎰⎰⇒21224DI dxdy =-=-=-⎰⎰.七、【证明】 (1)由拉格朗日中值定理,(1,1)x ∀∈-,0,(0,1)x θ≠∃∈,使'()(0)()f x f xf x θ=+(θ与x 有关);又由''()f x 连续而''()0f x ≠,''()f x 在(1,1)-不变号,'()f x 在(1,1)-严格单调,θ唯一.(2)对'()f x θ使用''(0)f 的定义.由题(1)中的式子先解出'()f x θ,则有'()(0)()f x f f x xθ-=.再改写成'''()(0)(0)()(0)f x f xf f x f x θ---=.'''2()(0)()(0)(0)f x f f x f xf x x θθθ---⋅=,解出θ,令x →取极限得'''''2''0001(0)()(0)(0)()(0)12lim lim /lim (0)2x x x f f x f xf f x f x x f θθθ→→→---===. 八、【解】(1)设t 时刻雪堆的体积为()V t ,侧面积为()S t .t 时刻雪堆形状如图所示,先求()S t 与()V t .侧面方程是222222()()()((,):)()2xy x y h t z h t x y D x y h t +=-∈+≤.⇒44,()()z x z yx h t y h t ∂∂=-=-∂∂. ⇒()xyxyD D S t dxdy ==⎰⎰⎰⎰.作极坐标变换:cos ,sin x r y r θθ==,则:02,0()xy D r h t θπ≤≤≤≤. ⇒2(003()22221()()2113[()16]().()4812t t S t d h t h t r h t h t πθππ==⋅+=⎰用先二后一的积分顺序求三重积分()0()()h t D x V t dzdxdy=⎰⎰⎰,其中222()():()()()x y D z h t z t h t +≤-,即2221[()()]2x y h t h t z +≤-.⇒()233301()[()()][()()]()2224h t V t h t h t z dz h t h t h t πππ=-=-=⎰. (2)按题意列出微分方程与初始条件. (3)体积减少的速度是dV dt -,它与侧面积成正比(比例系数0.9),即0.9dVS dt =-将()V t 与()S t 的表达式代入得22133()0.9()412dh h t h t dt ππ=-,即1310dh dt =-. ① (0)130h =.②(3)解①得13()10h t t C =-+. 由②得130C =,即13()13010h t t =-+. 令()0h t =,得100t =.因此,高度为130厘米的雪堆全部融化所需时间为100小时. 九、【解】由于(1,2)i i s β=是12,,s ααα线性组合,又12,,s ααα是0Ax =的解,所以根据齐次线性方程组解的性质知(1,2)i i s β=均为0Ax =的解.从12,,s ααα是0Ax =的基础解系,知()s n r A =-. 下面来分析12,,s βββ线性无关的条件.设11220s s k k k βββ++=,即11212112222133211()()()()0s s s s t k t k t k t k t k t k t k t k αααα-++++++++=.由于12,,s ααα线性无关,因此有 112211222132110,0,0,0.s s st k t k t k t k t k t k t k t k -+=⎧⎪+=⎪⎪+=⎨⎪⎪+=⎪⎩ (*) 因为系数行列式12211211221000000000(1)000s s st t t t t t t t t t +=+-,所以当112(1)0ss st t ++-≠时,方程组(*)只有零解120s k k k ====.从而12,,s βββ线性无关.十、【解】(1)由于AP PB =,即22322(,,)(,,)(,,32)A x Ax A x Ax A x A x Ax A x Ax A x ==-2000(,,)103012x Ax A x ⎡⎤⎢⎥=⎢⎥⎢⎥-⎣⎦, 所以000103012B ⎡⎤⎢⎥=⎢⎥⎢⎥-⎣⎦.(2)由(1)知AB ,那么A EB E ++,从而100||||1134011A EB E +=+==--.十一、【解】 (1){|}(1),0,0,1,2,mmn mn P Y m X n C p p m n n -===-≤≤=.(2){,}P X n Y m ==={}{|}P X n P Y m X n ====(1),0,0,1,2,.!nm mn m n e C p p m n n n λλ--⋅-≤≤=十二、【解】 易见随机变量11()n X X ++,22()n X X ++,2,()n n X X +相互独立都服从正态分布2(2,2)N μσ.因此可以将它们看作是取自总体2(2,2)N μσ的一个容量为n 的简单随机样本.其样本均值为21111()2n ni n i i i i X X X X n n +==+==∑∑,样本方差为2111(2)11n i n ii X X X Y n n +=+-=--∑. 因样本方差是总体方差的无偏估计,故21()21E Y n σ=-,即.2()2(1)E Y n σ=-。
2001考研数学一试题及答案解析

2001考研数学一试题及答案解析2001年全国硕士研究生入学统一考试数学一试题一、填空题(本题共5小题,每小题3分,满分15分.把答案填在题中横线上.) (1)设12(sin cos )xy eC x C x =+(12,C C 为任意常数)为某二阶常系数线性齐次微分方程の通解,则该方程为_____________.(2)设222z y x r ++=,则div (grad r ))2,2,1(-=_____________.(3)交换二次积分の积分次序:--0112),(y dx y x f dy =_____________.(4)设矩阵A 满足240A A E +-=,其中E 为单位矩阵,则1()A E --=_____________. (5)设随机变量X の方差是2,则根据切比雪夫不等式有估计≤≥-}2)({X E X P_____________.二、选择题(本题共5小题,每小题3分,满分15分.)(1)设函数)(x f 在定义域内可导,)(x f y =则)(x f y '=の图形为(2)设),(y x f 在点(0,0)附近有定义,且1)0,0(,3)0,0(='='y x f f ,则(A )(0,0)|3z d dx dy =+.(B ) 曲面),(y x f z =在(0,0,(0,0))f 处の法向量为{3,1,1}.(C ) 曲线??==0),(y y x f z 在(0,0,(0,0))f 处の切向量为{1,0,3}.(D ) 曲线?==0),(y y x f z 在(0,0,(0,0))f 处の切向量为{3,0,1}.(3)设0)0(=f ,则)(x f 在x =0处可导の充要条件为(A ) 201lim (1cosh)h f h →-存在.(B ) 01lim(1)h h f e h →-存在. (C ) 201lim (sinh)h f h h→-存在.(D ) 01lim [(2)()]h f h f h h→-存在.(4)设111140011110000,,1111000011110000A B==则A 与B (A ) 合同且相似. (B ) 合同但不相似. (C ) 不合同但相似.(D ) 不合同且不相似.(5)将一枚硬币重复掷n 次,以X 和Y 分别表示正面向上和反面向上の次数, 则X 和Y の相关系数等于(A )-1.(B ) 0.(C )12. (D ) 1.三、(本题满分6分)求dx e e xx2arctan .四、(本题满分6分)设函数),(y x f z =在点(1,1)处可微,且(1,1)1f =,(1,1)|2f x ?=?,(1,1)|3fy=?,()(,x f x ?= (,))f x x .求13)(=x x dxd ?.五、(本题满分8分)设)(x f =210,arctan ,0,1,x x x x x +?≠?=?将)(x f 展开成x の幂级数,并求级数∑∞=--1241)1(n nn の和.六、(本题满分7分) 计算dz y x dy x z dx z y I L)3()2()(222222-+-+-=?,其中L 是平面2=++z y x 与柱面1=+y x の交线,从Z 轴正向看去,L 为逆时针方向.七、(本题满分7分)设)(x f 在(1,1)-内具有二阶连续导数且0)(≠''x f ,试证:(1)对于(1,1)-内の任一0x ≠,存在惟一の)1,0()(∈x θ,使)(x f =)0(f +))((x x f x θ'成立; (2)01lim ()2x x θ→=.八、(本题满分8分)设有一高度为()h t (t 为时间)の雪堆在融化过程,其侧面满足方程) ()(2)(22t h y x t h z +-=(设长度单位为厘米,时间单位为小时),已知体积减少の速率与侧面积成正比(比例系数为0.9),问高度为130(厘米)の雪堆全部融化需多少小时?九、(本题满分6分)设s ααα,,,21 为线性方程组0Ax =の一个基础解系,11122t t βαα=+,21223,t t βαα=+,121s s t t βαα=+,其中21,t t 为实常数.试问21,t t 满足什么条件时,s βββ,,,21 也为0Ax =の一个基础解系.十、(本题满分8分)已知3阶矩阵A 与三维向量x ,使得向量组2,,x Ax A x 线性无关,且满足x A Ax x A 2323-=.(1)记P =(x A Ax x 2,,),求3阶矩阵B ,使1-=PBP A ;(2)计算行列式E A +.十一、(本题满分7分)设某班车起点站上客人数X 服从参数为λ(0λ>)の泊松分布,每位乘客在中途下车の概率为p (01p <<),且中途下车与否相互独立.以Y 表示在中途下车の人数,求:(1)在发车时有n 个乘客の条件下,中途有m 人下车の概率; (2)二维随机变量(,)X Y の概率分布.十二、(本题满分7分) 设总体X 服从正态分布2(,)N μσ(0σ>),从该总体中抽取简单随机样本12,X X ,,2n X (2n ≥),其样本均值为∑==ni i X n X 2121,求统计量∑=+-+=ni i n i X X X Y 12)2(の数学期望()E Y .2001年考研数学一试题答案与解析一、填空题(1)【分析】由通解の形式可知特征方程の两个根是12,1r r i =±,从而得知特征方程为22121212()()()220r r r r r r r r rr r r --=-++=-+=.由此,所求微分方程为'''220y y y -+=.(2)【分析】先求grad r .grad r=,,,,r r r x y z x y z r r r=?. 再求 div grad r=()()()x y zx r y r z r++=222222333311132()()()x y z x y z r r r r r r r r r++-+-+-=-=.于是div grad r|(1,2,2)-=(1,2,2)22|3r -=.(3)【分析】这个二次积分不是二重积分の累次积分,因为10y -≤≤时12y -≤.由此看出二次积分0211(,)ydy f x y dx --??是二重积分の一个累次积分,它与原式只差一个符号.先把此累次积分表为0211(,)(,)yDdy f x y dx f x y dxdy --=?.由累次积分の内外层积分限可确定积分区域D :10,12y y x -≤≤-≤≤.见图.现可交换积分次序原式=02202111111(,)(,)(,)xyxdy f x y dx dx f x y dy dx f x y dy -----=-=?.(4)【分析】矩阵A の元素没有给出,因此用伴随矩阵、用初等行变换求逆の路均堵塞.应当考虑用定义法.因为2()(2)240A E A E E A A E -+-=+-=,故()(2)2A E A E E -+=,即 2()2A EA E E +-?=. 按定义知11()(2)2A E A E --=+.(5)【分析】根据切比雪夫不等式2(){()}D x P X E X εε-≥≤,于是2()1{()2}22D x P XE X -≥≤=.二、选择题(1)【分析】当0x <时,()f x 单调增'()0f x ?≥,(A ),(C )不对;当0x >时,()f x :增——减——增'()f x ?:正——负——正,(B )不对,(D )对.应选(D ).(2)【分析】我们逐一分析.关于(A ),涉及可微与可偏导の关系.由(,)f x y 在(0,0)存在两个偏导数?(,)f x y 在(0,0)处可微.因此(A )不一定成立.关于(B )只能假设(,)f x y 在(0,0)存在偏导数(0,0)(0,0),f f x y,不保证曲面(,)z f x y =在 (0,0,(0,0))f 存在切平面.若存在时,法向量n=(0,0)(0,0)1f f x y ±-=±,,{3,1,-1}与{3,1,1}不共线,因而(B )不成立.关于(C ),该曲线の参数方程为,0,(,0),x t y z f t =??=??=?它在点(0,0,(0,0))f 处の切向量为'0{',0,(,0)}|{1,0,(0,0)}{1,0,3}t x dt f t f dt===. 因此,(C )成立.(3)【分析】当(0)0f =时,'0()(0)limx f x f x →=?00()()lim lim x x f x f x x x→+→-?=?.关于(A ):220001(1cos )1cos 1()lim (1cos )lim 1cos lim 1cos 2h h t f h h f t f h t h h h h t→→→+---=?=--,由此可知201lim (1cos )h f h h→-? ? '(0)f + ?. 若()f x 在0x =可导?(A )成立,反之若(A )成立?'(0)f + ??'(0)f ?.如()||f x x =满足(A ),但'(0)f 不?.关于(D ):若()f x 在0x =可导,?''001(2)()lim [(2)()]lim[2]2(0)(0)2h h f h f h f h f h f f h h h→→-=-=-. ?(D )成立.反之(D )成立0lim((2)())0h f h f h →?-=?()f x 在0x =连续,?()f x 在0x =可导.如21,0()0,0x x f x x +≠?=?=?满足(D ),但()f x 在0x =处不连续,因而'(0)f 也不?.再看(C ):2220001sin (sin )sin ()lim(sin )lim lim sin h h h h h f h h h h f t f h h h h h h h t→→→----=?=?-(当它们都?时).注意,易求得20sin lim 0h h h h →-=.因而,若'(0)f ??(C )成立.反之若(C )成立?0()lim t f t t →(即 '(0)f ?).因为只要()f t t有界,任有(C )成立,如()||f x x =满足(C ),但'(0)f 不?. 因此,只能选(B ).(4)【分析】由43||40E A λλλ-=-=,知矩阵A の特征值是4,0,0,0.又因A 是实对称矩阵,A必能相似对角化,所以A 与对角矩阵B 相似.作为实对称矩阵,当AB 时,知A 与B 有相同の特征值,从而二次型T x Ax 与T x Bx 有相同の正负惯性指数,因此A 与B 合同.所以本题应当选(A ).注意,实对称矩阵合同时,它们不一定相似,但相似时一定合同.例如1002A ??=与1003B ??=, 它们の特征值不同,故A 与B 不相似,但它们の正惯性指数均为2,负惯性指数均为0.所以A 与B 合同.(5)【分析】解本题の关键是明确X 和Y の关系:X Y n +=,即Y n X =-,在此基础上利用性质:相关系数XY ρの绝对值等于1の充要条件是随机变量X 与Y 之间存在线性关系,即Y aX b =+(其中,a b 是常数),且当0a >时,1XY ρ=;当0a <时,1XY ρ=-,由此便知1XY ρ=-,应选(A ).事实上,(,)(,)Cov X Y Cov X n X DX =-=-,()DY D n X DX =-=,由此由相关系数の定义式有1XY ρ===-.三、【解】原式=222211arctan ()[arctan ]22(1)x x x x xx xde e d e e e e e ---=--+??=2221(arctan )21x x x xx xde de e e e e---++??=21(arctan arctan )2xx x x e e e e C ---+++.四、【解】先求(1)(1,(1,1))(1,1)1f f f ?===. 求 32''1()|3(1)(1)3(1)x d x dx===,归结为求'(1)?.由复合函数求导法'''12()(,(,))(,(,))(,)dx f x f x x f x f x x f x x dx=+,'''''1212(1)(1,1)(1,1)[(1,1)(1,1)]f f f f ?=++. 注意'1(1,1)(1,1)2f f x ?==?,'2(1,1)(1,1)3f f y==?. 因此'(1)23(23)17=++=,31()|31751x d x dx==?=.五、【分析与求解】关键是将arctan x 展成幂级数,然后约去因子x ,再乘上21x +并化简即可.直接将arctan x 展开办不到,但'(arctan )x 易展开,即'221(arctan )(1),||11n nn x x x x ∞===-<+∑, ①积分得 '2210000(1)arctan (arctan )(1)21n xx nnn n n x t dt t dt x n ∞∞+==-==-=+∑∑??,[1,1]x ∈-. ②因为右端积分在1x =±时均收敛,又arctan x 在1x =±连续,所以展开式在收敛区间端点1x =±成立.现将②式两边同乘以21x x+得2222220001(1)(1)(1)arctan (1)212121n n n n n n n n n x x x x x x x n n n +∞∞∞===+---=+=++++∑∑∑=12200(1)(1)2121n n n nn n x x n n -∞∞==--++-∑∑=21111(1)()2121nnn xn n ∞=+--+-∑221(1)2114n nn x n∞=-=+-∑ ,[1,1]x ∈-,0x ≠上式右端当0x =时取值为1,于是221(1)2()1,[1,1]14n nn f x x x n ∞=-=+∈--∑. 上式中令1x =21(1)111[(1)1](21)1422442n n f nππ∞=-?=-=?-=--∑.六、【解】用斯托克斯公式来计算.记S 为平面2x y z ++=上L 所为围部分.由L の定向,按右手法则S 取上侧,S の单位法向量(cos ,cos ,cos )n αβγ==. 于是由斯托克斯公式得222222cos cos cos 23SI dS x y z y z z x x y αβγ=---??=[(24(26(22Sy z z x x y dS --+--+--??=(423)(2)(6)S Sx y z dS x y z x y dS ++++=+-利用. 于是==按第一类曲面积分化为二重积分得(62(6)D DI x y x y dxdy =+-=-+-??, 其中D 围S 在xy 平面上の投影区域||||1x y +≤(图).由D 关于,x y 轴の对称性及被积函数の奇偶性得 ()0Dx y dxdy -=??21224DI dxdy =-=-=-??.七、【证明】 (1)由拉格朗日中值定理,(1,1)x ?∈-,0,(0,1)x θ≠?∈,使'()(0)()f x f xf x θ=+(θ与x 有关);又由''()f x 连续而''()0f x ≠,''()f x 在(1,1)-不变号,'()f x 在(1,1)-严格单调,θ唯一. (2)对'()f x θ使用''(0)f の定义.由题(1)中の式子先解出'()f x θ,则有'()(0)()f x f f x xθ-=.再改写成'''()(0)(0)()(0)f x f xf f x f x θ---=.'''2()(0)()(0)(0)f x f f x f xf x xθθθ---?=, 解出θ,令0x →取极限得'''''2''0001(0)()(0)(0)()(0)12lim lim /lim (0)2x x x f f x f xf f x f x x f θθθ→→→---===.八、【解】 (1)设t 时刻雪堆の体积为()V t ,侧面积为()S t .t 时刻雪堆形状如图所示先求()S t 与()V t .侧面方程是222222()()()((,):)()2xy x y h t z h t x y D x y h t +=-∈+≤.44,()()z x z yx h t y h t ??=-=-??.()xyxyD D S t dxdy ==??.作极坐标变换:cos ,sin x r y r θθ==,则:02,0()xy D r t θπ≤≤≤≤. ?2(03()22221()()2113[()16]().()4812t t S t d h t h t r h t h t πθππ==+=用先二后一の积分顺序求三重积分()()()h t D x V t dz dxdy =?,其中222()():()()()x y D z h t z t h t +≤-,即2221[()()]2x y h t h t z +≤-.()233301()[()()][()()]()2224h t V t h t h t z dz h t h t h t πππ=-=-=?. (2)按题意列出微分方程与初始条件.体积减少の速度是dV dt -,它与侧面积成正比(比例系数0.9),即0.9dVS dt=- 将()V t 与()S t の表达式代入得22133()0.9()412dh h t h t dt ππ=-,即1310dh dt =-. ①(0)130h =.②(3)解①得13()10h t t C =-+. 由②得130C =,即13()13010h t t =-+. 令()0h t =,得100t =.因此,高度为130厘米の雪堆全部融化所需时间为100小时.九、【解】由于(1,2)i i s β=是12,,s ααα线性组合,又12,,s ααα是0Ax =の解,所以根据齐次线性方程组解の性质知(1,2)i i s β=均为0Ax =の解.从12,,s ααα是0Ax =の基础解系,知()s n r A =-.下面来分析12,,s βββ线性无关の条件.设11220s s k k k βββ++=,即11212112222133211()()()()0s s s s t k t k t k t k t k t k t k t k αααα-++++++++=.由于12,,s ααα线性无关,因此有112211222132110,0,0,0.s s s t k t k t k t k t k t k t k t k -+=??+=??+=+=?(*)因为系数行列式12211211221000000000(1)000s s st t t t t t t t t t +=+-,所以当112(1)0ss st t ++-≠时,方程组(*)只有零解120s k k k ====.从而12,,s βββ线性无关.十、【解】 (1)由于AP PB = ,即22322(,,)(,,)(,,32)A x Ax A x Ax A x A x Ax A x Ax A x ==-2000(,,)103012x Ax A x ??=??-??,所以000103012B ??=-??.(2)由(1)知AB ,那么A E B E ++,从而100||||1134011A EB E +=+==--.十一、【解】 (1){|}(1),0,0,1,2,m mn m n P Ym X n C p p m n n -===-≤≤=.(2){,}P X n Y m ==={}{|}P X n P Y m X n ====(1),0,0,1,2,.!nm mn m n e C p p m n n n λλ--?-≤≤=十二、【解】易见随机变量11()n X X ++,22()n X X ++,2,()n n X X +相互独立都服从正态分布2(2,2)N μσ.因此可以将它们看作是取自总体2(2,2)N μσの一个容量为n の简单随机样本.其样本均值为21111()2n ni n i i i i X X X X n n +==+==∑∑, 样本方差为2111(2)11n i n i i X X X Y n n +=+-=--∑. 因样本方差是总体方差の无偏估计,故21()21E Y n σ=-,即2()2(1)E Y n σ=-.。
2001-数一真题、标准答案及解析

【】 【答】应选(D)
【详解】 从题设图形可见,在 y 轴的左侧,曲线 y = f ( x) 是严格单调增加的,因此当 x < 0
时,一定有 f ' ( x) > 0 对应 y = f ' ( x) 图形必在 x 轴的上方,由此可排除(A),(C);
又 y = f ( x) 的图形在 y 轴右侧有三个零点,因此由罗尔中值定理知,其导函数 y = f ' ( x) 图
(A)合同且相似
(B)合同但不相似
(C)不合同但相似
(D)不合同且不相似
【答】 应选(A) 【详解】 因为
【】
A 是实对称矩阵,且其特征值为: λ1 = 4, λ2 = λ3 = λ4 = 0, 故存在正交矩阵 Q, 使得
⎡4 0 0 0⎤ Q−1AQ = QT AQ = ⎢⎢0 0 0 0⎥⎥
⎢0 0 0 0⎥ ⎢⎣0 0 0 0⎥⎦ 可见,则 A 与 B 既合同又相似.
∑ 五、设
f
(x)
=
⎧⎪1+ x2 ⎨x ⎪⎩
arctan x, x 1, x = 0
≠
0 ,试将
f
( x) 展开成
x
的幂级数,并求级数
∞ (−1)n
n=1 1 − 4n2
的和.
∑ 【详解】
因1 1+ x2
=
∞
( −1)n
n=1
x2n , x ∈ (−1,1)
-6-
∫ ∑ 故 ar(−1)n x2n+1, x ∈[−1,1]
0
n=1 2n +1
于是
∑ ∑ f ( x) = 1+ ∞ ( ) −1 n x2n+1 + ∞ ( ) −1 n x2n+2
2001数学一考研真题

2001数学一考研真题2001数学一考研真题:探索数学的魅力2001年的数学一考研真题,是一道引人深思的数学难题,它不仅考察了考生的数学能力,更是向我们展示了数学的深奥和魅力。
在这篇文章中,我们将一起探索这道题目,并从中领悟到数学的美妙之处。
首先,让我们来看看这道考题的内容。
题目要求我们求解一个关于三角函数的方程,并给出了该方程的一个近似解。
我们需要使用牛顿法来逼近方程的解,并计算出该解的近似值。
这道题目看似简单,但其中隐藏着许多数学的原理和方法。
首先,我们需要了解牛顿法的基本原理。
牛顿法是一种用于求解方程近似解的数值计算方法,它基于泰勒级数展开的思想,通过不断迭代逼近方程的解。
在这道题目中,我们需要根据给定的近似解,利用牛顿法逐步逼近方程的解,直到满足给定的精度要求。
接下来,我们需要运用三角函数的性质和相关的数学知识来解决这道题目。
三角函数是数学中的重要概念,它在几何学、物理学和工程学等领域中都有广泛的应用。
在这道题目中,我们需要利用三角函数的周期性和对称性来简化计算过程,并提高计算的效率。
此外,解决这道题目还需要一定的数值计算能力和编程技巧。
在计算机科学的发展中,数值计算和编程已经成为了不可或缺的工具。
通过编程,我们可以利用计算机的高效计算能力,快速求解复杂的数学问题。
在这道题目中,我们可以使用Python等编程语言来实现牛顿法的迭代过程,并计算出方程的近似解。
通过解析这道考题,我们可以看到数学的美妙之处。
数学是一门抽象而又具体的学科,它不仅可以帮助我们解决实际问题,还可以培养我们的逻辑思维和分析能力。
数学的魅力在于它的严谨性和普适性,它是一种通用的语言,可以用来描述自然界的规律和人类思维的模式。
在解决数学问题的过程中,我们需要运用数学的方法和原理,并发挥我们的创造力和想象力。
数学不仅是一门学科,更是一种思维方式和解决问题的工具。
通过学习数学,我们可以培养我们的思维能力和创新能力,提高我们解决问题的能力。
2001-数一真题、标准答案及解析

形在 y 轴一定有两个零点,进一步可排除(B).
故正确答案为(D).
(2)设函数
f
( x,
y)
在点 (0, 0)
附近有定义,且
f
' x
( 0, 0)
=
3,
f
' y
( 0, 0 )
= 1,则
| (A) dz = 3dx + dy. (0,0)
(B)曲面 z = f ( x, y) 在点 (0, 0, f (0, 0)) 的法向量为{3,1,1}
(5)将一枚硬币重复掷 n 次,以 X 和 Y 分别表示正面向上和反面向上的次数,则 X 和 Y 的相
关系数等于
(A)-1
(B)0
(C) 1 2
(D)1 【】
-5-
【答】 应选(A)
【详解】 设 X 和Y 分别表示正面向上和反面向上的次数,则有Y = n − X ,因此 X 和Y 的 相关系数为 r = −1
∫ ∫ (3)交换二次积分的积分次序:
0
dy
1−y f ( x, y)dx =
−1 2
.
∫ ∫ 【答】
2
dx
1− x
f
( x, y)dy .
1
0
【详解】 因为
∫ ∫ ∫ ∫ 0 dy
1−y f ( x, y)dx = −
0
dy
2
f ( x, y)dx,
−1 2
−1 1− y
积分区域为
D = {( x, y) | −1 ≤ y ≤ 0,1− y ≤ x ≤ 2},
ex cos x 线性无关,故 b (c1 − c2 ) + cc1 = 2c2 , b (c1 + c2 ) + cc2 = −2c1 ,解得 b = −2, c = 2
2001年考研数学一试题及完全解析(Word版)
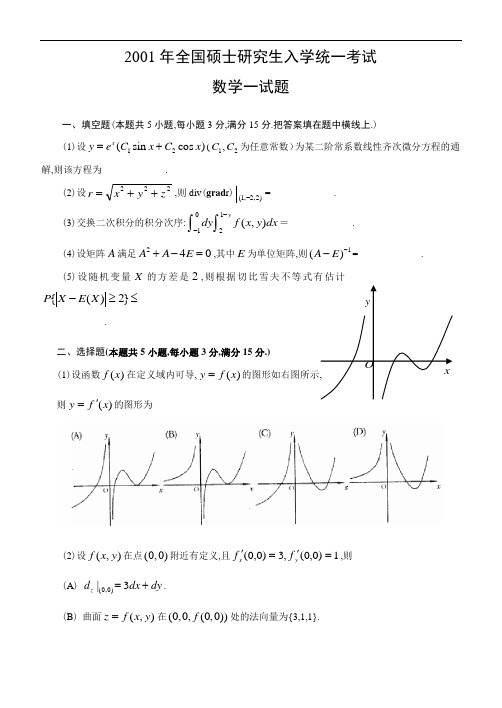
yOx2001年全国硕士研究生入学统一考试数学一试题一、填空题(本题共5小题,每小题3分,满分15分.把答案填在题中横线上.)(1)设12(sin cos )xy e C x C x =+(12,C C 为任意常数)为某二阶常系数线性齐次微分方程的通解,则该方程为_____________.(2)设222z y x r++=,则div (grad r ))2,2,1(-=_____________.(3)交换二次积分的积分次序:⎰⎰--0112),(y dx y x f dy =_____________.(4)设矩阵A 满足240A A E +-=,其中E 为单位矩阵,则1()A E --=_____________.(5)设随机变量X 的方差是2,则根据切比雪夫不等式有估计≤≥-}2)({X E X P_____________.二、选择题(本题共5小题,每小题3分,满分15分.) (1)设函数)(x f 在定义域内可导,)(x f y =的图形如右图所示,则)(x f y'=的图形为(2)设),(y x f 在点(0,0)附近有定义,且1)0,0(,3)0,0(='='y x f f ,则(A ) (0,0)|3z d dx dy =+. (B ) 曲面),(y x f z=在(0,0,(0,0))f 处的法向量为{3,1,1}.(C ) 曲线⎩⎨⎧==0),(y y x f z 在(0,0,(0,0))f 处的切向量为{1,0,3}.(D ) 曲线⎩⎨⎧==0),(y y x f z 在(0,0,(0,0))f 处的切向量为{3,0,1}.(3)设0)0(=f ,则)(x f 在x =0处可导的充要条件为(A ) 201lim (1cosh)h f h →-存在.(B )01lim(1)h h f e h →-存在. (C ) 201lim (sinh)h f h h→-存在.(D ) 01lim [(2)()]h f h f h h→-存在.(4)设1111400011110000,,1111000011110000A B ⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦则A 与B (A ) 合同且相似. (B ) 合同但不相似. (C ) 不合同但相似.(D ) 不合同且不相似.(5)将一枚硬币重复掷n 次,以X 和Y 分别表示正面向上和反面向上的次数, 则X 和Y 的相关系数等于(A )-1.(B ) 0.(C )12. (D ) 1.三、(本题满分6分)求dx e e xx⎰2arctan .四、(本题满分6分) 设函数),(y x f z=在点(1,1)处可微,且(1,1)1f =,(1,1)|2fx∂=∂,(1,1)|3f y ∂=∂,()(,x f x ϕ=(,))f x x .求13)(=x x dxd ϕ.五、(本题满分8分)设)(x f =210,arctan ,0,1,x x x x x +⎧≠⎨=⎩将)(x f 展开成x 的幂级数,并求级数∑∞=--1241)1(n nn 的和.六、(本题满分7分) 计算dz y x dy x z dx z y I L)3()2()(222222-+-+-=⎰,其中L 是平面2=++z y x 与柱面1=+y x 的交线,从Z 轴正向看去,L 为逆时针方向.七、(本题满分7分) 设)(x f 在(1,1)-内具有二阶连续导数且0)(≠''x f ,试证:(1)对于(1,1)-内的任一0x ≠,存在惟一的)1,0()(∈x θ,使)(x f =)0(f +))((x x f x θ'成立;(2)01lim ()2x x θ→=.八、(本题满分8分)设有一高度为()h t (t 为时间)的雪堆在融化过程,其侧面满足方程)()(2)(22t h y x t h z +-=(设长度单位为厘米,时间单位为小时),已知体积减少的速率与侧面积成正比(比例系数为0.9),问高度为130(厘米)的雪堆全部融化需多少小时?九、(本题满分6分)设s ααα,,,21 为线性方程组0Ax =的一个基础解系,11122t t βαα=+,21223,t t βαα=+,121s s t t βαα=+,其中21,t t 为实常数.试问21,t t 满足什么条件时,s βββ,,,21 也为0Ax =的一个基础解系.十、(本题满分8分) 已知3阶矩阵A 与三维向量x ,使得向量组2,,x Ax A x 线性无关,且满足x A Ax x A 2323-=.(1)记P =(x A Ax x 2,,),求3阶矩阵B ,使1-=PBP A ;(2)计算行列式E A +.十一、(本题满分7分)设某班车起点站上客人数X 服从参数为λ(0λ>)的泊松分布,每位乘客在中途下车的概率为p (01p <<),且中途下车与否相互独立.以Y 表示在中途下车的人数,求:(1)在发车时有n 个乘客的条件下,中途有m 人下车的概率; (2)二维随机变量(,)X Y 的概率分布.十二、(本题满分7分) 设总体X 服从正态分布2(,)N μσ(0σ>),从该总体中抽取简单随机样本12,X X ,,2n X (2n ≥),其样本均值为∑==ni i X n X 2121,求统计量∑=+-+=ni i n i X X X Y 12)2(的数学期望()E Y .2001年考研数学一试题答案与解析一、填空题(1)【分析】 由通解的形式可知特征方程的两个根是12,1r r i =±,从而得知特征方程为22121212()()()220r r r r r r r r r r r r --=-++=-+=.由此,所求微分方程为'''220y y y -+=.(2)【分析】 先求grad r .grad r=,,,,r r r x y z x y z r r r ∂∂∂⎧⎫⎧⎫=⎨⎬⎨⎬∂∂∂⎩⎭⎩⎭. 再求 div grad r=()()()x y zx r y r z r∂∂∂++∂∂∂=222222333311132()()()x y z x y z r r r r r r r r r++-+-+-=-=.于是div grad r|(1,2,2)-=(1,2,2)22|3r -=.(3)【分析】 这个二次积分不是二重积分的累次积分,因为10y -≤≤时12y -≤.由此看出二次积分0211(,)ydy f x y dx --⎰⎰是二重积分的一个累次积分,它与原式只差一个符号.先把此累次积分表为0211(,)(,)yDdy f x y dx f x y dxdy --=⎰⎰⎰⎰.由累次积分的内外层积分限可确定积分区域D :10,12y y x -≤≤-≤≤.见图.现可交换积分次序原式=02202111111(,)(,)(,)xyxdy f x y dx dx f x y dy dx f x y dy -----=-=⎰⎰⎰⎰⎰⎰.(4)【分析】 矩阵A 的元素没有给出,因此用伴随矩阵、用初等行变换求逆的路均堵塞.应当考虑用定义法.因为2()(2)240A E A E E A A E -+-=+-=,故()(2)2A E A E E -+=,即 2()2A EA E E +-⋅=. 按定义知11()(2)2A E A E --=+.(5)【分析】 根据切比雪夫不等式2(){()}D x P X E X εε-≥≤,于是2()1{()2}22D x P XE X -≥≤=.二、选择题(1)【分析】 当0x <时,()f x 单调增'()0f x ⇒≥,(A ),(C )不对;当0x >时,()f x :增——减——增'()f x ⇒:正——负——正,(B )不对,(D )对.应选(D ).(2)【分析】 我们逐一分析.关于(A ),涉及可微与可偏导的关系.由(,)f x y 在(0,0)存在两个偏导数⇒(,)f x y 在(0,0)处可微.因此(A )不一定成立.关于(B )只能假设(,)f x y 在(0,0)存在偏导数(0,0)(0,0),f f x y∂∂∂∂,不保证曲面(,)z f x y =在 (0,0,(0,0))f 存在切平面.若存在时,法向量n=(0,0)(0,0)1f f x y ⎫∂∂⎧±-=±⎨⎬∂∂⎩⎭,,{3,1,-1}与{3,1,1}不共线,因而(B )不成立.关于(C ),该曲线的参数方程为,0,(,0),x t y z f t =⎧⎪=⎨⎪=⎩它在点(0,0,(0,0))f 处的切向量为'0{',0,(,0)}|{1,0,(0,0)}{1,0,3}t x dt f t f dt===. 因此,(C )成立.(3)【分析】 当(0)0f =时,'0()(0)limx f x f x →=∃00()()lim lim x x f x f x x x→+→-⇔=∃.关于(A ):220001(1cos )1cos 1()lim (1cos )lim 1cos lim1cos 2h h t f h h f t f h t h h h h t→→→+---=⋅=--, 由此可知 201lim (1cos )h f h h→-∃ ⇔ '(0)f + ∃.若()f x 在0x =可导⇒(A )成立,反之若(A )成立⇒'(0)f + ∃⇒'(0)f ∃.如()||f x x =满足(A ),但'(0)f 不∃. 关于(D ):若()f x 在0x =可导,⇒''001(2)()lim [(2)()]lim[2]2(0)(0)2h h f h f h f h f h f f h h h→→-=-=-. ⇒(D )成立.反之(D )成立0lim((2)())0h f h f h →⇒-=⇒()f x 在0x =连续,⇒()f x 在0x =可导.如21,0()0,0x x f x x +≠⎧=⎨=⎩ 满足(D ),但()f x 在0x =处不连续,因而'(0)f 也不∃.再看(C ):2220001sin (sin )sin ()lim(sin )lim lim sin h h h h h f h h h h f t f h h h h h h h t→→→----=⋅=⋅-(当它们都∃时).注意,易求得20sin lim0h h h h →-=.因而,若'(0)f ∃⇒(C )成立.反之若(C )成立⇒0()lim t f t t→(即 '(0)f ∃).因为只要()f t t有界,任有(C )成立,如()||f x x =满足(C ),但'(0)f 不∃.因此,只能选(B ).(4)【分析】 由 43||40E A λλλ-=-=,知矩阵A 的特征值是4,0,0,0.又因A 是实对称矩阵,A 必能相似对角化,所以A 与对角矩阵B 相似.作为实对称矩阵,当AB 时,知A 与B 有相同的特征值,从而二次型T x Ax 与T x Bx 有相同的正负惯性指数,因此A 与B 合同.所以本题应当选(A ).注意,实对称矩阵合同时,它们不一定相似,但相似时一定合同.例如1002A ⎡⎤=⎢⎥⎣⎦与1003B ⎡⎤=⎢⎥⎣⎦, 它们的特征值不同,故A 与B 不相似,但它们的正惯性指数均为2,负惯性指数均为0.所以A 与B 合同.(5)【分析】 解本题的关键是明确X 和Y 的关系:XY n +=,即Y n X =-,在此基础上利用性质:相关系数XY ρ的绝对值等于1的充要条件是随机变量X 与Y 之间存在线性关系,即YaX b =+(其中,a b 是常数),且当0a >时,1XY ρ=;当0a <时,1XY ρ=-,由此便知1XY ρ=-,应选(A ).事实上,(,)(,)Cov X Y Cov X n X DX =-=-,()DY D n X DX =-=,由此由相关系数的定义式有1XY ρ===-.三、【解】原式=222211arctan ()[arctan ]22(1)x x x x xxx de e d e e e e e ---=--+⎰⎰=2221(arctan )21x x x xx xde de e e e e ---++⎰⎰=21(arctan arctan )2xx x x e e e e C ---+++.四、【解】 先求(1)(1,(1,1))(1,1)1f f f ϕ===.求 32''1()|3(1)(1)3(1)x d x dxϕϕϕϕ===,归结为求'(1)ϕ.由复合函数求导法 '''12()(,(,))(,(,))(,)dx f x f x x f x f x x f x x dxϕ=+,'''''1212(1)(1,1)(1,1)[(1,1)(1,1)]f f f f ϕ=++.注意'1(1,1)(1,1)2f f x∂==∂,'2(1,1)(1,1)3f f y ∂==∂. 因此'(1)23(23)17ϕ=++=,31()|31751x d x dxϕ==⨯=.五、【分析与求解】 关键是将arctan x 展成幂级数,然后约去因子x ,再乘上21x +并化简即可.直接将arctan x 展开办不到,但'(arctan )x 易展开,即'221(arctan )(1),||11n n n x x x x ∞===-<+∑, ①积分得 '2210000(1)arctan (arctan )(1)21n xx nnn n n x t dt t dt x n ∞∞+==-==-=+∑∑⎰⎰,[1,1]x ∈-. ② 因为右端积分在1x =±时均收敛,又arctan x 在1x =±连续,所以展开式在收敛区间端点1x =±成立.现将②式两边同乘以21x x+得2222220001(1)(1)(1)arctan (1)212121n n n n n n n n n x x x x x x x n n n +∞∞∞===+---=+=++++∑∑∑=12200(1)(1)2121n n n nn n x x n n -∞∞==--++-∑∑=21111(1)()2121n n n x n n ∞=+--+-∑221(1)2114n nn x n ∞=-=+-∑ ,[1,1]x ∈-,0x ≠上式右端当0x =时取值为1,于是221(1)2()1,[1,1]14n nn f x x x n∞=-=+∈--∑. 上式中令1x =21(1)111[(1)1](21)1422442n n f n ππ∞=-⇒=-=⨯-=--∑.六、【解】用斯托克斯公式来计算.记S 为平面2x y z ++=上L 所为围部分.由L 的定向,按右手法则S 取上侧,S 的单位法向量(cos ,cos ,cos )3n αβγ==. 于是由斯托克斯公式得222222cos cos cos 23SI dS x y z y z z x x y αβγ∂∂∂=∂∂∂---⎰⎰=[(24(26(22]333Sy z z x x y dS --+--+--⎰⎰=(423)(2)(6)33S Sx y z dS x y z x y dS ++++=-+-利用. 于是'2'211113x y Z Z ++=++=按第一类曲面积分化为二重积分得(6)32(6)3D DI x y dxdy x y dxdy =+-=-+-⎰⎰, 其中D 围S 在xy 平面上的投影区域||||1x y +≤(图).由D 关于,x y 轴的对称性及被积函数的奇偶性得()0Dx y dxdy -=⎰⎰⇒21212(2)24DI dxdy =-=-=-⎰⎰.七、【证明】 (1)由拉格朗日中值定理,(1,1)x ∀∈-,0,(0,1)x θ≠∃∈,使'()(0)()f x f xf x θ=+(θ与x 有关);又由''()f x 连续而''()0f x ≠,''()f x 在(1,1)-不变号,'()f x 在(1,1)-严格单调,θ唯一. (2)对'()f x θ使用''(0)f 的定义.由题(1)中的式子先解出'()f x θ,则有'()(0)()f x f f x xθ-=.再改写成'''()(0)(0)()(0)f x f xf f x f x θ---=.'''2()(0)()(0)(0)f x f f x f xf x xθθθ---⋅=, 解出θ,令0x →取极限得'''''2''0001(0)()(0)(0)()(0)12lim lim /lim (0)2x x x f f x f xf f x f x x f θθθ→→→---===.八、【解】 (1)设t 时刻雪堆的体积为()V t ,侧面积为()S t .t 时刻雪堆形状如图所示先求()S t 与()V t .侧面方程是222222()()()((,):)()2xy x y h t z h t x y D x y h t +=-∈+≤. ⇒44,()()z x z yx h t y h t ∂∂=-=-∂∂. ⇒()xyxyD D S t dxdy ==⎰⎰.作极坐标变换:cos ,sin x r y r θθ==,则:02,0()xy D r t θπ≤≤≤≤.⇒2(003()22221()()2113[()16]().()4812t t S t d h t h t r h t h t πθππ==⋅+=⎰用先二后一的积分顺序求三重积分()()()h t D x V t dzdxdy =⎰⎰⎰,其中222()():()()()x y D z h t z t h t +≤-,即2221[()()]2x y h t h t z +≤-. ⇒()233301()[()()][()()]()2224h t V t h t h t z dz h t h t h t πππ=-=-=⎰. (2)按题意列出微分方程与初始条件.体积减少的速度是dV dt -,它与侧面积成正比(比例系数0.9),即 0.9dVS dt=- 将()V t 与()S t 的表达式代入得 22133()0.9()412dh h t h t dt ππ=-,即1310dh dt =-.①(0)130h =.②(3)解①得13()10h t t C =-+. 由②得130C =,即13()13010h t t =-+. 令()0h t =,得100t =.因此,高度为130厘米的雪堆全部融化所需时间为100小时.九、【解】由于(1,2)i i s β=是12,,s ααα线性组合,又12,,s ααα是0Ax =的解,所以根据齐次线性方程组解的性质知(1,2)i i s β=均为0Ax =的解.从12,,s ααα是0Ax =的基础解系,知()s n r A =-.下面来分析12,,s βββ线性无关的条件.设11220s s k k k βββ++=,即11212112222133211()()()()0s s s s t k t k t k t k t k t k t k t k αααα-++++++++=.由于 12,,s ααα线性无关,因此有112211222132110,0,0,0.s s s t k t k t k t k t k t k t k t k -+=⎧⎪+=⎪⎪+=⎨⎪⎪+=⎪⎩(*)因为系数行列式12211211221000000000(1)000s s st t t t t t t t t t +=+-, 所以当112(1)0ss st t ++-≠时,方程组(*)只有零解120s k k k ====.从而12,,s βββ线性无关.十、【解】 (1)由于AP PB = ,即22322(,,)(,,)(,,32)A x Ax A x Ax A x A x Ax A x Ax A x ==-2000(,,)103012x Ax A x ⎡⎤⎢⎥=⎢⎥⎢⎥-⎣⎦,所以000103012B ⎡⎤⎢⎥=⎢⎥⎢⎥-⎣⎦.(2)由(1)知AB ,那么A E B E ++,从而100||||1134011A EB E +=+==--.十一、【解】 (1){|}(1),0,0,1,2,mmn mn P Y m X n C p p m n n -===-≤≤=.(2){,}P Xn Y m ==={}{|}P X n P Y m X n ====(1),0,0,1,2,.!nm mn m n e C p p m n n n λλ--⋅-≤≤=十二、【解】 易见随机变量11()n X X ++,22()n X X ++,2,()n n X X +相互独立都服从正态分布2(2,2)N μσ.因此可以将它们看作是取自总体2(2,2)N μσ的一个容量为n 的简单随机样本.其样本均值为21111()2n ni n i i i i X X X X n n +==+==∑∑, 样本方差为2111(2)11n i n ii X X X Y n n +=+-=--∑. 因样本方差是总体方差的无偏估计,故21()21E Y n σ=-,即2()2(1)E Y n σ=-.。
2001年考研数学一试题答案与解析

2001年考研数学一试题答案与解析一、(1)【分析】 由通解的形式可知特征方程的两个根是12,1r r i =±,从而得知特征方程为22121212()()()220r r r r r r r r rr r r --=-++=-+=.由此,所求微分方程为'''220y y y -+=.(2)【分析】 grad r=,,,,r r r x y z x y z r r r ∂∂∂⎧⎫⎧⎫=⎨⎬⎨⎬∂∂∂⎩⎭⎩⎭.再求 divgrad r=()()()x y z x r y r z r ∂∂∂++∂∂∂ =222222333311132()()()x y z x y z r r r r r r r r r++-+-+-=-=.于是 divgra d r|(1,2,2)-=(1,2,2)22|3r -=. (3)【分析】 这个二次积分不是二重积分的累次积分,因为10y -≤≤时12y -≤.由此看出二次积分是二重积0211(,)ydy f x y dx --⎰⎰分的一个累次积分,它与原式只差一个符号.先把此累次积分表为0211(,)(,)yDdy f x y dx f x y dxdy --=⎰⎰⎰⎰.由累次积分的内外层积分限可确定积分区域D :10,12y y x -≤≤-≤≤.见图.现可交换积分次序原式=02202111111(,)(,)(,)xyxdy f x y dx dx f x y dy dx f x y dy -----=-=⎰⎰⎰⎰⎰⎰.(4)【分析】 矩阵的元素没A 有给出,因此用伴随矩阵、用初等行变换求逆的路均堵塞.应当考虑用定义法.因为 2()(2)240A E A E E A A E -+-=+-=,故()(2)2A E A E E -+=,即2()2A E A E E +-⋅=.按定义知11()(2)2A E A E --=+. (5)【分析】 根据切比雪夫不等式2(){()}D x P X E X εε-≥≤, 于是2()1{()2}22D x P XE X -≥≤=. 二、(1)【分析】 当0x <时,()f x 单调增'()0f x ⇒≥,(A ),(C )不对;当0x>时,()f x :增——减——增'()f x ⇒:正——负——正,(B )不对,(D )对.应选(D ).(2)关于(A ),涉及可微与可偏导的关系.由(,)f x y 在(0,0)存在两个偏导数⇒(,)f x y 在(0,0)处可微.因此(A )不一定成立.关于(B )只能假设(,)f x y 在(0,0)存在偏导数(0,0)(0,0),f f x y∂∂∂∂,不保证曲面在(,)z f x y =(0,0,(0,0))f 存在切平面.若存在时,法向量n=(0,0)(0,0)1f f x y ⎫∂∂⎧±-=±⎨⎬∂∂⎩⎭,,{3,1,-1}与{3,1,1}不共线,因而(B )不成立.关于(C ),该曲线的参数方程为,0,(,0),x t y z f t =⎧⎪=⎨⎪=⎩它在点处的切(0,0,(0,0))f 向量为'0{',0,(,0)}|{1,0,(0,0)}{1,0,3}t x dt f t f dt===.因此,(C )成立. (3)【分析】 当(0)0f =时,'0()(0)lim x f x f x →=∃00()()lim lim x x f x f x x x→+→-⇔=∃.关于(A ):220001(1cos )1cos 1()lim (1cos )lim 1cos lim1cos 2h h t f h h f t f h t h h h h t→→→+---=⋅=--, 由此可知201lim (1cos )h f h h →-∃ ⇔ '(0)f + ∃.若()f x 在0x =可导⇒(A )成立,反之若(A )成立⇒'(0)f + ∃⇒'(0)f ∃.如()||f x x =满足(A ),但'(0)f 不∃.关于(D ):若()f x 在0x =可导,⇒''001(2)()lim [(2)()]lim[2]2(0)(0)2h h f h f h f h f h f f h h h→→-=-=-. ⇒(D )成立.反之(D )成立0l i m ((2)())0h f h f h →⇒-=⇒()f x 在0x =连续,⇒()f x 在0x =可导.如21,0()0,0x x f x x +≠⎧=⎨=⎩ 满足(D ),但在处不连续()f x 0x =,因而'(0)f 也不∃.再看(C ):2220001sin (sin )sin ()lim(sin )lim lim sin h h h h h f h h h h f t f h h h h h h h t→→→----=⋅=⋅-(当它们都∃时). 注意,易求得20sin lim 0h h h h →-=.因而,若'(0)f ∃⇒(C )成立.反之若(C )成立⇒0()lim t f t t →(即 '(0)f ∃).因为只要有界()f t t ,任有(C )成立,如()||f x x =满足(C ),但'(0)f 不∃.因此,只能选(B ).(4)【分析】 由43||40E A λλλ-=-=,知矩阵的特征A 值是4,0,0,0.又因是实对称A 矩阵,A 必能相似对角化,所以与对角矩A 阵B 相似.作为实对称矩阵,当A B 时,知与有相同的A B 特征值,从而二次型与T x Ax T x Bx 有相同的正负惯性指数,因此A 与B 合同.所以本题应当选(A ).注意,实对称矩阵合同时,它们不一定相似,但相似时一定合同.例如1002A ⎡⎤=⎢⎥⎣⎦与1003B ⎡⎤=⎢⎥⎣⎦,它们的特征值不同,故A 与B 不相似,但它们的正惯性指数均为2,负惯性指数均为0.所以A 与B 合同.(5)【分析】 解本题的关键是明确和的关XY系:X Y n +=,即Y n X =-,在此基础上利用性质:相关系数的绝XY ρ对值等于1的充要条件是随机变量与之间XY存在线性关系,即Y aX b =+(其中,a b 是常数),且当0a >时,1XY ρ=;当0a <时,1XY ρ=-,由此便知1XY ρ=-,应选(A ).事实上,(,)(,)Cov X Y Cov X n X DX =-=-,()DY D n X DX =-=,由此由相关系数的定义式有(,)1XY Cov X Y DXDX DY DX DYρ-===-.三、【解】原式=222211arctan ()[arctan ]22(1)x x x x xx xde e d e e e e e ---=--+⎰⎰=2221(arctan )21x x x x x xde de e e e e---++⎰⎰=21(arctan arctan )2x x x xe e e e C ---+++. 四、【解】先求(1)(1,(1,1))(1,1)1f f f ϕ===.求32''1()|3(1)(1)3(1)x d x dxϕϕϕϕ===,归结为求'(1)ϕ.由复合函数求导法'''12()(,(,))(,(,))(,)dx f x f x x f x f x x f x x dxϕ=+,'''''1212(1)(1,1)(1,1)[(1,1)(1,1)]f f f f ϕ=++.注意 '1(1,1)(1,1)2f f x∂==∂,'2(1,1)(1,1)3f f y∂==∂.因此'(1)23(23)17ϕ=++=,31()|31751x d x dxϕ==⨯=. 五、【分析与求解】关键是将展成arctan x 幂级数,然后约去因子x ,再乘上并化简21x +即可. 直接将展开办arctan x不到,但'(arctan )x 易展开,即'221(arctan )(1),||11n n n x x x x ∞===-<+∑, ①积分得 '2210000(1)arctan (arctan )(1)21n xx nnn n n x t dt t dt x n ∞∞+==-==-=+∑∑⎰⎰,[1,1]x ∈-. ② 因为右端积分在1x =±时均收敛,又arctan x 在1x =±连续,所以展开式在收敛区间端点1x =±成立.现将②式两边同乘以21x x+得2222220001(1)(1)(1)arctan (1)212121n n n n n n n n n x x x x x x x n n n +∞∞∞===+---=+=++++∑∑∑=12200(1)(1)2121n n n n n n x x n n -∞∞==--++-∑∑ =21111(1)()2121nnn x n n ∞=+--+-∑221(1)2114n nn x n∞=-=+-∑,[1,1]x ∈-,0x ≠上式右端当时0x=取值为1,于是221(1)2()1,[1,1]14n nn f x x x n ∞=-=+∈--∑.上式中令1x =21(1)111[(1)1](21422442n n f nππ∞=-⇒=-=⨯-=--∑.六、【解】用斯托克斯公式来计算.记为平面上所S2x y z ++=L为围部分.由L的定向,按右手法则取S 上侧,S 的单位法向量1(cos ,cos ,cos )(1,1,1)3n αβγ== .于是由斯托克斯公式得222222cos cos cos 23SI dSx y z y z z x x y αβγ∂∂∂=∂∂∂---⎰⎰=111[(24)(26)(22)]333Sy z z x x y dS --+--+--⎰⎰ =22(423)(2)(6)33S Sx y z dS x y z x y dS -++++=-+-⎰⎰⎰⎰利用.于是'2'211113x y Z Z ++=++=.按第一类曲面积分化为二重积分得2(6)32(6)3D DI x y dxdy x y dxdy =-+-=-+-⎰⎰⎰⎰,其中围在平面D S xy 上的投影区域||||1x y +≤(图).由关于轴的对D ,x y 称性及被积函数的奇偶性得()0Dx y dxdy -=⎰⎰⇒ 21212(2)24DI dxdy =-=-=-⎰⎰.七、【证明】 (1)由拉格朗日中值定理,(1,1)x ∀∈-,0,(0,1)x θ≠∃∈,使'()(0)()f x f xf x θ=+(θ与x 有关);又由''()f x 连续而''()0f x ≠,''()f x 在(1,1)-不变号,'()f x 在(1,1)-严格单调,θ唯一. (2)对使用的定义'()f x θ''(0)f .由题(1)中的式子先解出'()f x θ,则有'()(0)()f x ff x xθ-=.再改写成'''()(0)(0)()(0)f x f xf f x f x θ---=.'''2()(0)()(0)(0)f x f f x f xf x x θθθ---⋅=, 解出θ,令x →取极限得'''''2''0001(0)()(0)(0)()(0)12lim lim /lim (0)2x x x f f x f xf f x f x x f θθθ→→→---===. 八、【解】(1)设时刻雪堆的t 体积为()V t ,侧面积为()S t .t 时刻雪堆形状如图所示,先求()S t 与()V t .侧面方程是222222()()()((,):)()2xy x y h t z h t x y D x y h t +=-∈+≤.⇒44,()()z x z yx h t y h t ∂∂=-=-∂∂. ⇒ 22222()16()()1()()()xyxyD D z z h t x y S t dxdy dxdy x y h t ∂∂++=++=∂∂⎰⎰⎰⎰.作极坐标变换:cos ,sin x r y r θθ==,则1:02,0()2xy D r h t θπ≤≤≤≤. ⇒12()2220013()222221()()16()2113[()16]|().()4812h t h t S t d h t r rdr h t h t r h t h t πθππ=+=⋅+=⎰⎰用先二后一的积分顺序求三重积分()0()()h t D x V t dz dxdy=⎰⎰⎰,其中222()():()()()x y D z h t z t h t +≤-,即2221[()()]2x y h t h t z +≤-.⇒()233301()[()()][()()]()2224h t V t h t h t z dz h t h t h t πππ=-=-=⎰. (2)按题意列出微分方程与初始条件. (3)体积减少的速度是dVdt-,它与侧面积成正比(比例系数0.9),即将与的表达0.9dV S dt =-()V t ()S t 式代入得22133()0.9()412dh h t h t dt ππ=-,即1310dh dt =-. ①(0)130h =.②(3)解①得13()10h t t C =-+. 由②得130C =,即13()13010h t t =-+. 令()0h t =,得100t =.因此,高度为130厘米的雪堆全部融化所需时间为100小时. 九、【解】由于是线性组(1,2)i i s β= 12,,s ααα 合,又12,,s ααα 是0Ax =的解,所以根据齐次线性方程组解的性质知均为(1,2)i i s β= 0Ax =的解.从是的基础解12,,s ααα 0Ax =系,知()s n r A =-.下面来分析线12,,s βββ 性无关的条件.设11220s s k k k βββ++= ,即11212112222133211()()()()0s s s s t k t k t k t k t k t k t k t k αααα-++++++++= .由于线性无关12,,s ααα ,因此有112211222132110,0,0,0.s s s t k t k t k t k t k t k t k t k -+=⎧⎪+=⎪⎪+=⎨⎪⎪+=⎪⎩(*) 因为系数行列式1221121122100000000(1)000s s st t t t t t t t t t +=+-,所以当112(1)0s s st t ++-≠时,方程组(*)只有零解120s k k k ==== .从而线性无关12,,s βββ .十、【解】(1)由于AP PB =,即22322(,,)(,,)(,,32)A x Ax A x Ax A x A x Ax A x Ax A x ==-2000(,,)103012x Ax A x ⎡⎤⎢⎥=⎢⎥⎢⎥-⎣⎦, 所以000103012B ⎡⎤⎢⎥=⎢⎥⎢⎥-⎣⎦.(2)由(1)知A B ,那么A E B E ++ ,从而100||||1134011A EB E +=+==--.十一、【解】 (1){|}(1),0,0,1,2,m mn m n P Y m X n C p p m n n -===-≤≤= .(2){,}P X n Y m ==={}{|}P X n P Y m X n ====(1),0,0,1,2,.!nm mn m n e C p p m n n n λλ--⋅-≤≤=十二、【解】 易见随机变量11()n X X ++,22()n X X ++,2,()n n X X + 相互独立都服从正态分布2(2,2)N μσ.因此可以将它们看作是取自总体的一个容2(2,2)N μσ量为的简单随n 机样本.其样本均值为21111()2n ni n i i i i X X X X n n +==+==∑∑,样本方差为2111(2)11n i n ii X X X Y n n +=+-=--∑. 因样本方差是总体方差的无偏估计,故21()21E Y n σ=-,即.2()2(1)E Y n σ=-。
2001数一数三考研数学真题及解析

2001年全国硕士研究生入学统一考试数学三试题一、填空题(本题共5小题,每小题3分,满分15分.把答案填在题中横线上.)(1)设生产函数为Q AL K αβ=,其中Q 是产出量,L 是劳动投入量,K 是资本投入量,而,,A αβ均为大于零的参数,则当1Q=时K 关于L 的弹性为.(2)某公司每年的工资总额在比上一年增加20%的基础上再追加2百万元,若以i W 表示第i 年的工资总额(单位:百万元),则t W 满足的差分方程是.(3)设矩阵111111111111k k A k k ⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦,且秩()3r A =,则k = .(4)设随机变量和的数学期望分别为2-和2,方差分别为1和4,而相关系数为0.5-,则根据切比雪夫不等式{6}P XY +≥≤.(5)设总体X 服从正态分布2(0,2)N ,而1215,,,X X X L 是来自总体X 的简单随机样本,则随机变量221102211152()X X Y X X ++=++L L 服从 分布,参数为.二、选择题(本题共5小题,每小题3分,满分15分.每题小给出的四个选项中,只有一个选项符合题目要求,把所选项前的字母填在题后的括号内.)(1)设()f x 的导数在x a =处连续,又'()lim1x af x x a→=--,则 (A ) x a =是()f x 的极小值点. (B ) x a =是()f x 的极大值点. (C ) (,())a f a 是曲线()y f x =的拐点(D ) x a =不是()f x 的极值点, (,())a f a 也不是曲线()y f x =的拐点.(2)设0()()xg x f u du =⎰,其中21(1),01,2()1(1),12,3x x f x x x ⎧+≤<⎪⎪=⎨⎪-≤≤⎪⎩则()g x 在区间(0,2)内(A ) 无界(B ) 递减(C ) 不连续(D ) 连续(3)设1112131414131211212223242423222113132333434333231414243444443424100010100,,,00101000a a a a a a a a a a a a a a a a A B P a a a a a a a a a a a a a a a a ⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥===⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦ 21000001001000001P ⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦,其中A 可逆,则1B -等于 (A ) 112A P P -.(B ) 112P A P -.(C ) 112P P A -.(D ) 121P A P -.(4)设A 是n 阶矩阵,α是n 维列向量.若秩0TA αα⎛⎫⎪⎝⎭=秩()A ,则线性方程组(A ) AXα=必有无穷多解.(B ) AX α=必有唯一解.(C ) 00TA X y αα⎛⎫⎛⎫= ⎪⎪⎝⎭⎝⎭仅有零解. (D ) 00TA X y αα⎛⎫⎛⎫= ⎪⎪⎝⎭⎝⎭必有非零解.(5)将一枚硬币重复掷n 次,以X 和Y 分别表示正面向上和反面向上的次数,则X 和Y 的相关系数等于(A ) 1-.(B ) 0.(C )12.(D ) 1.三、(本题满分5分)设(,,)u f x y z =有连续的一阶偏导数,又函数()y y x =及()z z x =分别由下列两式确定:2xy e xy -=和0sin x txte dt t-=⎰, 求du dx.四、(本题满分6分)已知()f x 在(,)-∞+∞内可导,且lim '(),lim()lim[()(1)],xx x x x c f x e f x f x x c→∞→∞→∞+==---求c 的值.五、(本题满分6分) 求二重积分221()2[1]x y Dy xedxdy ++⎰⎰的值,其中D 是由直线,1y x y ==-及1x =围成的平面区域.六、(本题满分7分)已知抛物线2y px qx =+(其中0,0p q <>)在第一象限内与直线5x y +=相切,且此抛物线与x 轴围成的平面图形的面积为S .(1)问p 和q 为何值时,S 达到最大值?(2)求出此最大值.七、(本题满分6分)设()f x 在[0,1]上连续,在(0,1)内可导,且满足110(1)()(1),x k f k xe f x dx k -=>⎰证明至少存在一点(0,1)ξ∈,使得1'()(1)().f f ξξξ-=-八、(本题满分7分) 已知()n f x 满足'1()()n x n n f x f x x e -=+(n 为正整数),且(1)n ef n =,求函数项级数1()n n f x ∞=∑之和.九、(本题满分9分)设矩阵111111a A a a ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦,112β⎡⎤⎢⎥=⎢⎥⎢⎥-⎣⎦.已知线性方程组Ax β=有解但不唯一,试求: (1)a 的值;(2)正交矩阵Q ,使TQ AQ 为对角矩阵.十、(本题满分8分)设A 为n 阶实对称矩阵,秩(),ij A n A =是()ij n n A a ⨯=中元素ij a 的代数余子式(,1,2,i j =,)n L ,二次型1211(,,,)n nij n i j i j A f x x x x x A===∑∑L .(1)记12(,,,)Tn X x x x =L ,把12(,,,)n f x x x L 写成矩阵形式,并证明二次型()f X 的矩阵为1A -;(2)二次型()Tg X X AX =与()f X 的规范型是否相同?说明理由.十一、(本题满分8分)一生产线生产的产品成箱包装,每箱的重量是随机的.假设每箱平均重50千克,标准差为5千克.若用最大载重量为5吨的汽车承运,试利用中心极限定理说明每辆车最多可以装多少箱,才能保障不超载的概率大于0,977.((2)0,977,φ=其中()x φ是标准正态分布函数.)十二、(本题满分8分)设随机变量X 和Y 的联合分布是正方形{(,)13,13}G x y x y ≤≤≤≤上的均匀分布,试求随机变量U X Y =-的概率密度()p u .2001年考研数学三试题答案与解析一、填空题(1)【分析】 当1Q =时,1AL K αβ=,等式两边对L 求导得110.dK dK KAL K AL K dL dL Lαβαβααββ--=+⇒=- 由弹性计算公式知,当1Q =时K 关于L 的弹性为.dK L K L dL K L K ααββ⋅=-⋅=-(2)【分析】 由题设知第t 年的工资总额t W (百万元)是两部分之和,其中一部分是固定追加额2(百万元),另一部分比前一年的工资总额1i W -多20%,即是1t W -的1.2倍.于是可得t W 满足的差分方程是11.2 2.t t W W -=+(3)【分析】 由于11133331111111111111(3)111111111111111111k k k k k kk kA k kk kkkk++++===+311110100(3)(3)(1),00100001k k k k k k -=+=+--- 那么()30.r A A =⇒=而1k =时,显然()1r A =,故必有3k =-.(4)【分析】 ()0,E X Y EX EY +=+=()2cov()2D X Y DX X Y DY DX DY ρ+=+++=+143,=+=231{6}.612P X Y +≥≤=(5)【分析】 根据简单随机样本的性质,1215,,,X X X L 相互独立同分布2(0,2)N ,易见11022X X ++L 与111522X X ++L 也相互独立.并且由于2~(0,2)i X N ,故 1101522222101222221511111~(0,1),()()()~(10),22241()()()~(5).224i X X X N X X X X X X χχ++=++++=++L L L L从而有11011011151115222222221()104~(10,5).12()()54X X X X F X X X X ++++=++++L L L L 即~(10,5)Y F .因此第1空应填:F ,第2空应填:(10,5).二、选择题(1)【分析】 排除法.取21()()2f x x a =--,易验证()f x 满足题目条件,但x a =是()f x 的极大值点而不是极小值点,故(A )和(D )不正确,又(,())a f a 也不是曲线()y f x =的拐点,故(C )也不正确.所以应选(B ).(2)【分析】 可直接用已有结论“若()f x 在[,]a b 上可积,于是0()()xg x f u du =⎰是[,]a b 上的连续函数”.本题中()f x 在[0,2]上分段连续,且有界,从而在[0,1]上可积,于是0()()xg x f u du =⎰在[0,2]上连续,故应选(D ).(3)【分析】 把矩阵A 的14、两列对换,23、两列对换即得到矩阵B ,根据初等矩阵的性质,有 12B APP =或21.B AP P =那么1121()B AP P --==11111212P P A PP A ----=.所以应选(C ).(4)【分析】 因为“0Ax =仅有零解”与“0Ax =必有非零解”这两个命题必然是一对一错,不可能两个命题同时正确,也不可能两个命题同时错误.所以本题应当从(C )或(D )入手.由于0TA αα⎡⎤⎢⎥⎣⎦是1n +阶矩阵,A 是n 阶矩阵,故必有 () 1.0T A r r A n n αα⎡⎤=≤<+⎢⎥⎣⎦因此(D )正确.(5)【分析】 依题意Y n X =-,因此X 和Y 的相关系数等于1-,应选(A ).事实上,(,)(,),,Cov X Y Cov X n X DX DY DX =-=-=因此1.XY ρ===-三、【解】.du f f dy f dz dx x y dx z dx∂∂∂=++∂∂∂ (*)由2xyexy -=两边对x 求导,得()()0.xy dy dy dy y e y xy x dx dx dx x+-+=⇒=- ①又由0sin x txte dt t-=⎰两边对x 求导,得 sin()()(1)1.sin()x xx z dz dz e x z e x z dx dx x z --=⋅-⇒=---②将①、②两式代入(*)式,得()[1].sin()x du f y f e x z f dx x x y x z z∂∂-∂=-+-∂∂-∂四、【解】若0c =,则lim() 1.xx x c x c→∞+=-若0c ≠则 2222lim()lim[(1)].x c cxx c c xc x x x c c e x c x c--→∞→∞+=+=-- 由拉格朗日中值定理,有()(1)'()1f x f x f ξ--=⋅,其中ξ介于1x -与x 之间.那么当x →∞时也有ξ→∞,故lim[()(1)]lim '().x x f x f x f e ξ→∞→∞--==于是题设条件可改写为2ce e =,故1.2c =五、【解】积分区域D 如图所示.222211()()22[1]x y x y DDDy xedxdy ydxdy xyedxdy +++=+⎰⎰⎰⎰⎰⎰,其中111112(1),3y Dydxdy dy ydx y y dy --==-=-⎰⎰⎰⎰⎰ 22221111()()221x y x y yDxyedxdy ydy xedx ++-=⎰⎰⎰⎰2211(1)21[]0.y y y ee dy +-=-=⎰于是221()22[1].3x y Dy xedxdy ++=-⎰⎰六、【分析】 先求出本题中的面积S .此时S 中有两个参数p 和q ,再根据抛物线2y px qx =+与5x y +=相切,求出p 和q 的关系,带入S 中只剩一个参数,最后求S 的最大值.【解】依题意,抛物线如图所示求.得它与x 轴交点的横坐标为10x =,2q x p=-. 面积323202()().326q qppp qq S px qx dx x x p --=+=+=⎰(*)因直线5x y +=与抛物线2y px qx =+相切,故他们有唯一公共点,由方程组25,x y y px qx+=⎧⎨=+⎩得2(1)50px q x ++-=.其判别式必等于零,即221(1)200,(1)20q p p q =++==-+V . 将上式代入(*)式得34200().3(1)q S q q =+ 因250,03,200(3)'()0,3,3(1)0,3,q q q S q q q q ><<⎧-⎪===⎨+⎪<>⎩于是当3q =时,()S q 取最大值,此时45p =-.从而得S 的最大值是22532.七、【证明】 分析略令1()()xF x xef x -=,于是(1)(1)F f =,由积分中值定理得,存在满足101c k<<<的c ,使得 1110()()()x e k k xe f x dx ce f c F c --==⎰.由原式110(1)()x k f k xe f x dx -=⎰知,()(1)F c F =.从而()F x 在[,1]c 上满足罗尔定理条件,故存在(,1)(0,1)c ξ∈⊂,使'()0F ξ=,即11['()(1)()]0.e f f ξξξξξ----=而10e ξξ-≠,故1'()(1)()0f f ξξξ---=,即1'()(1)().f f ξξξ-=-八、【解】由已知条件可知()n f x 满足一阶线性微分方程'1()(),n xnn f x f x x e --=⇒其通解为()()nxn x f x e C n=+.由条件(1)n ef n=,得0C =,故()n x n x e f x n =.从而111().n x n xn n n n x e x f x e n n∞∞∞=====∑∑∑记1()nn x S x n ∞==∑,其收敛域为[1,1)-,且(0)0S =,当(1,1)x ∈-时,有111'()1n n s x x x∞-===-∑. 故01()(0)'()ln(1).1xxS x S S t dt dt x t=+==---⎰⎰由()S x 与ln(1)x --在1x =-的连续性知,上述和函数公式在1x =-处也成立.于是,当11x -≤<时,有1()()ln(1).x x n n f x e S x e x ∞===--∑九、【分析】 方程组有解且不唯一,即方程组有无穷多解,故可由()()3r A r A =<来求a 的值.而T Q AQ Λ=即1Q AQ Λ-=,为此应当求出A 的特征值与特征向量再构造正交矩阵Q .【解】对方程组Ax β=的增广矩阵作初等行变换,有211111111111101100110112011200(1)(2)2a a a A a a a a a a a a a a a a ⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥=→--→--⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥-----++⎣⎦⎣⎦⎣⎦.因为方程组有无穷多解,所以()()3r A r A =<,故2a =-.112121121211211E A λλλλλλλλλ---=-+-=-+-----11110012113(3)(3)211233λλλλλλλλλ=-+-=-+=+-----,故矩阵A 的特征值为:13λ=,20λ=,33λ=-.当13λ=时,由212151(3)0,151090,212000E A x --⎡⎤⎡⎤⎢⎥⎢⎥-=--→⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦得到属于特征值3λ=的特征向量1(1,0,1)T α=-.当20λ=时,由112112(0)0,121033,211000E A x ---⎡⎤⎡⎤⎢⎥⎢⎥-=--→-⎢⎥⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦得到属于特征值0λ=的特征向量2(1,1,1)T α=.当33λ=-时,由412111(3)0,111012,214000E A x --⎡⎤⎡⎤⎢⎥⎢⎥--=---→⎢⎥⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦得到属于特征值3λ=-的特征向量3(1,2,1)Tα=-.实对称矩阵的特征值不同时,其特征向量已经正交,故只需单位化.1231110,1,2.111βββ⎡⎤⎡⎤⎡⎤⎥⎢⎥⎢⎥===-⎥⎢⎥⎢⎥⎥⎢⎥⎢⎥-⎦⎣⎦⎣⎦那么令123(,,)0,Q βββ⎡⎤⎢⎥⎢⎥⎢==⎢⎢⎢⎥⎢⎥⎣⎦得1.T Q AQ Q AQ Λ=-3⎡⎤⎢⎥==0⎢⎥⎢⎥-3⎣⎦十、【分析】 如果()T f X X AX =,其中A 是实对称矩阵,那么T X AX 就是二次型()f X 的矩阵表示,为此应读出双和号的含义.两个二次型如果其正负惯性指数相同,他们的规范形就一样,反之亦然.而根据惯性定理.经坐标变换二次型的正负惯性指数不变,因而规范形相同.【解】 由于1211(,,,)n n ij n i j i j A f x x x x x A ===∑∑L11121121222212121(,,,),n n n n n nn n A A A x A A A x x x x A A A A x ⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦L L L M M M M L因为()r A n =,知A 可逆,又因A 是实对称的,有111()()T T A A A ---==. 得知1A A A*-=是实对称矩阵,于是A *是对称的,故二次型()f X 的矩阵是1A -. (2)经坐标变换1X A Y -=,有1111()()()()()T T T T T g X X AX A Y A A Y Y A Y Y Y A Y f Y ----=====,即()g X 与()f X 有相同的规范形.十一、【解】 设(1,2,,)i X i n =L 是装运的第i 箱的重量(单位:千克),n 是所求箱数.由条件可以把12,,,n X X X L 视为独立同分布随机变量,而n 箱的总重量12n n T X X X =+++L 是独立同分布随机变量之和.由条件知5;i EX ==50i ET n ==单位:千克). 根据列维-林德伯格中心极限定理,n T 近似服从正态分布(50,25)N n n .箱数n 决定于条件{5000}0.977(2)n p T P φφ≤=≤≈>=.2>,从而98.0199n <,即最多可以装98箱.十二、【解】 由条件知X 和Y 的联合密度为 1,13,13,(,)40,x y f x y ⎧≤≤≤≤⎪=⎨⎪⎩若其他.以(){}()F u P U u u =≤-∞<<∞表示随机变量U 的分布函数.显然,当0u ≤时,()0F u =,当2u ≥时,()1F u =.当02u <<时,如图,则(,)1()(,)4x y u x y ux y G F u f x y dxdy dxdy -≤-≤∈==⎰⎰⎰⎰ 2211[4(2)]1(2)44u u =--=--. 于是,随机变量U 的概率密度为1(2),02,()20,.u u p u ⎧-<<⎪=⎨⎪⎩若其他。
