用一个平面去截正方体截面形状总结

合集下载

2021年七上数学期中复习-图形的性质_图形认识初步_截一个几何体-单选题专训及答案

2021年七上数学期中复习-图形的性质_图形认识初步_截一个几何体-单选题专训及答案截一个几何体单选题-专训1、(2021峡江.七上期末) 用一个平面去截正方体（如图），下列关于截面（截出的面）的形状的结论：①可能是锐角三角形；②可能是直角三角形；③可能是钝角三角形；④可能是平行四边形.其中所有正确结论的序号是（）A . ①②B . ①④C . ①②④D . ①②③④2、(2017红山.七上期末) 一个物体的外形是长方体，其内部构造不详．用5个水平的平面纵向平均截这个物体时，得到了一组（自下而上）截面，截面形状如图所示，这个长方体的内部构造可能是（）A . 球体B . 圆柱C . 圆锥D . 球体或圆锥3、(2020达州.七上期中) 如图，是一个正方体，用一个平面去截这个正方体，截面形状不可能为下图中的（）A .B .C .D .4、(2016连城.七上期末) 指出图中几何体截面的形状（）A .B .C .D .5、(2016深圳.七上期末) 下列说法正确的是（）A . 经过一点可以作两条直线B . 棱柱侧面的形状可能是一个三角形C . 长方体的截面形状一定是长方形D . 棱柱的每条棱长都相等6、(2016深圳.七上期末) 用一个平面去截一个正方体，截面的形状不可能是（）A . 梯形B . 五边形C . 六边形D . 七边形7、(2019贵阳.七上期末) 用一个平面去截一个几何体，如果截面的形状是圆，则原来的几何体可能是（）A . 正方体B . 三棱柱C . 四棱锥D . 球8、(2020银川.七上期末) 下列说法错误的是（）A . 单项式－ab2c3的系数为－1B . 多项式ab2+b5的次数为5C . 过七边形一个顶点与其他顶点连线可以分成5个三角形D . 用平面截一个正方体，截面的形状不可能是六边形9、(2019北京.七上期中) 如图，用水平的平面截几何体，所得几何体的截面图形标号是（）A .B .C .D .10、(2021酒泉.七上期中) 用平面截一个正方体，可能截出的边数最多的多边形是（）A . 七边形B . 六边形C . 五边形D . 四边形11、(2021.七上期中) 用一个平面去截正方体，截面不可能是（）A . 长方形B . 五边形C . 六边形D . 七边形12、(2018丹东.七上期中) 用一个平面去截一个几何体，如果截面是三角形，那么这个几何体不可能是( )A . 圆锥B . 长方体C . 圆柱D . 三棱柱13、(2018北票.七上期中) 用一个平面截一个正方体，截面可能是下列图形中的（）①三角形②正方形③长方形④梯形⑤圆A . ①②③④B . ①②③C . ②③⑤D . ③④14、(2018宿州.七上期中) 下面几何体截面一定是圆的是（）A . 圆柱B . 圆锥C . 球D . 圆台15、(2020宁德.七上期中) 用一个平面去截一个正方体，则截面不可能是（）A .B .C .D .16、(2018和平.七上期中) 下面几何体的截面图可能是圆的是（）A . 圆锥B . 正方体C . 长方体D . 棱柱17、(2019深圳.七上期中) 如图所示，用一个平面分别去截下列水平放置的几何体，所截得的截面不可能是三角形的是（）A .B .C .D .18、(2019深圳.七上期中) (2018七上·深圳期末) 用一个平面截下列几何体,截面可能是三角形的是（）①正方体②球体③圆柱④圆锥A . ①B . ①②C . ①④D . ①③④19、(2021济南.七上期中) 用一个平面去截下列几何体，截得的平面图形不可能是三角形的是（）A .B .C .D .20、(2020兰州.七上期末) 正方体的截面中，边数最多的多边形是（）A . 四边形B . 五边形C . 六边形D . 七边形21、(2017张掖.七上期中) 用一个平面截一个几何体，得到的截面是四边形，这个几何体可能是（）A . 圆锥B . 圆柱C . 球体D . 以上都有可能22、(2020丹东.七上期末) 下列叙述：①最小的正整数是；②若是一个负数，则一定是负数；③用一个平面去截正方体，截面不可能是六边形；④三角形是多边形；⑤绝对值等于本身的数是正整数.其中正确的个数有（）A .B .C .D .23、(2020青羊.七上期中) 用一个平面去截一个正方体，截面不可能是（）A . 梯形B . 五边形C . 六边形D . 七边形24、(2020吉州.七上期末) 用一个平面去截圆柱体，则截面形状不可能是（）A . 正方形B . 三角形C . 长方形D . 圆25、(2021丹东.七上期中) 用平面去截一个几何体，如果截面的形状是长方形，则原来的几何体不可能是（）A . 正方体B . 棱柱体C . 圆柱D . 圆锥26、(2021渠.七上期中) 有下列说法：①两个有理数比较大小，绝对值大的反而小：②用一个平面去截正方体，面的形状可能是五边形；③数轴上表示两个有理数的点，较大的数表示的点离原点较远；④若a是3的相反数，则a的倒数是；⑤一个数的绝对值等于它的相反数，这个数一定是负数．其中正确的说法有（）A . 5个B . 4个C . 3个D . 2个27、(2021沈阳.七上月试) 用一个平面去截正方体，截面的形状不可能是（）A . 四边形B . 五边形C . 六边形D . 七边形28、(2021青白江.七上期中) 下面几何体的截面图不可能是圆的是（）A . 圆柱B . 圆锥C . 球D . 棱柱29、(2020大田.七上期末) 圆锥的截面不可能是（）A . 三角形B . 圆C . 长方形D . 椭圆30、(2020吉安.七上期末) 用平面去截下列几何体，能截得长方形、三角形、等腰梯形三种形状的截面，这个几何体是( )A .B .C .D .截一个几何体单选题-答案1.答案：B2.答案：C3.答案：C4.答案：B5.答案：B6.答案：D7.答案：D8.答案：D9.答案：A10.答案：B11.答案：D12.答案：C13.答案：A14.答案：C15.答案：D16.答案：A17.答案：B18.答案：C19.答案：C20.答案：C21.答案：B22.答案：B23.答案：24.答案：25.答案：26.答案：27.答案：28.答案：29.答案：30.答案：。

用一个平面去截一个正方体PPT课件

You Know, The More Powerful You Will Be
15
结束语
当你尽了自己的最大努力时，失败也是伟大的，所以不要放弃，坚持就是正确的。
When You Do Your Best, Failure Is Great, So Don'T Give Up, Stick To The End 演讲人：XXXXXX 时间：XX年XX月XX日
用平面裁正方体
1
截一截：用一个平面去截一个正方体，
截面(section)会是什么形状？
截一截
2
返回
3
返回
4
返回
5
返回
6
返回
7
返回8返回Fra bibliotek9三边形四边形
五边形六边形
10
三边形
用平面截去正方形的一个角即可
11
四边形
用平面水平（或斜着）裁开正方形即可
12
五边形
一条棱的中点（和该棱平行的两条棱上的点）还有该棱垂直的面上的与之不相交的棱的两条棱的中点沿平面截过即可
16
13
六边形
取六条连折闭合(注意是一个平面切)的棱的中点即可
详细：1.先取一个顶点引出的三条棱除了竖棱外的另外两条棱的中点
2.加上与其分别相交的两条棱的中点 3.再取1.的两条棱的平行的面但上与它没有棱
连接的那两条棱的中点 4.用平面沿着画好的6条棱截开
14
学习总结
经常不断地学习,你就什么都知道。你知道得越多,你就越有力量 Study Constantly, And You Will Know Everything. The More

平面截正方体典例解析

正方体截面问题
用平面去截一个几何体，截面的情况可以帮助我们更好地认识几何体，对于一个几何体不同切截方式，所以得截面可能出现不同的情况.下面让我们来探索用平面截正方体所得截面的形状.
我们知道正方体有六个面，用一个平面去解正方体至少要经过三个面，最多经过六个面.所以出现的截面只可能是三角形、四边形、五边形和六边形.
一、截面是三角形
用一平面截正方体，当平面经过正方体的三个面时，所得的截面的形状为三角形.所得的三角形可能是锐角三角形（如图1）；等腰三角形（如图2）；等边三角形（如图3）.其中等边三角形三个顶点是正方形的顶点.
图1 图2 图3
二、截面是四边形
用一个平面截正方体，当平面经过正方体的四个面时，所得截面可能是正方形、长方形、梯形.
①用平行于底面的一个平面去截正方体时，按图4方式得到的截面是正方形.
图4
②按图5或图6或图7的方式切截，得到的截面是长方形
图5 图6 图7
③按图8的方式所得截面为梯形.
图8
三、截面是五边形
用平面截正方体，当平面经过正方体的五个面时，所得截面是五边形.如图9.
图9
四、截面是六边形
用平面截正方体，当平面经过正方体的六个面时，所得截面是六
边形，如图10.
图10
总结：用一个平面截正方体，截面可以是三角形，四边形，五边形，六边形。

但是由于正方体共有六个面，所以截面不可能是七边形.。

北师大版数学七年级上册第一章丰富的图形世界截一个几何体

图形编号
①
②
③
截面形状
图形编号
⑤
⑥
⑦
截面形状
答案 ①圆 ②三角形(等腰三角形) ③圆 ④长方形 ⑤三角形 ⑥梯形 ⑦三角形 ⑧长方形
栏目索引 ④ ⑧
3 截一个几何体
栏目索引
1.用一个平面去截①圆锥;②圆柱;③球;④五棱柱,能得到截面是圆面的是 ( ) A.①②③ B.①②④ C.②③④ D.①③④
答案 D 几何体共有几个面,截面最多是几边形.四棱柱共六个面,五棱柱共七个面,圆柱共三个面,它们都截不出八边形,七棱柱共九个面,能截出八边形.
3 截一个几何体
栏目索引
4.如图1-3-3,观察下列几何体,用平面分别截这些几何体,请在表中填写各图形截面(阴影部分)的形状.
图1-3-3
3 截一个几何体
答案 B 经过圆锥顶点且垂直于底面的截面是等腰三角形.
3 截一个几何体
栏目索引
2.用一个平面去截一个几何体,截面形状为三角形,则这个几何体可能为 ①正方体;②圆柱;③圆锥;④正三棱柱.
.(写出所有正确结果的序号)
答案 ①③④
解析 ①截去一角,截面形状为三角形;②用任何平面截圆柱都不能截出三角形;③沿竖截面截,截面形状为三角形;④用与底面平行的面截,截面形状为三角形.
3 截一个几何体
栏目索引
图1-3-4①是一个正六面体,把它按图1-3-4②中所示方法切割,可以得到一个正六边形的截面,则下列展开图中正确画出所有的切割线的是 ()
图1-3-4
3 截一个几何体
栏目索引
答案 C 截面没有过立方体的任何一个顶点,只有C选项符合.故选C.
3 截一个几何体
栏目索引

正方体截面的形状

返回
2、四边形
1）若截面与两两平行的四个面相交，则截面至少是平行四边形。（定理5.4）也可以是特殊的平行四边形，例如：矩形、正方形、菱形
2）若截面与共定点的三个平面和另一与其中之一平行的平面相交，则截面为梯形，可以是等腰梯形，但不会是直角梯形。可以用垂边形呢？
正方体截面的形状
按边分：1）三角形 2）四边形 3）五边形 4）六边形
前进
1、当截面为三角形时
按边分： 1）等边三角形 2）等腰三角形 3）一般三角形
反思：
问题：三角形按角分：锐角三角形、直角三角形、钝角三角形，它们都可能是正方体截面的形状吗？
截面只可能是锐角三角形，以后等我们学习了解三角形，可以用余弦定理加以证明。
不可以。因为正方体有六个面，一个平面去截正方体，最多可以和六个表面都相交。所以截面最多可以是六边形。

细说正方体的截面图形

细说正方体的截面图形在实际生活中时常出现实物几何体的切面所形成的截面图形形状，在中学数学中也学习了几何体的截面图形，截面是一个平面去截一个几何体得到的平面图形或一个平面与几何体表面交线围成的封闭图形，。

截面图形更好的将平面几何与立体几何联系起来，探究具体几何体的截面图形有助于更深入的认识几何体，发展正确的空间观念。

对于一个几何体不同的切截方式所得到的截面图形可能出现不同的情况。

现具体以正方体为例来探究正方体的截面图形形状。

一个平面截正方体与各面的交线都是线段，因此正方体的截面图形都是平面图形。

正方体有六个面，用一个平面去截正方体至少要经过正方体的三个面而最多要经过六个面，所有出现的截面图形边数至少是三条而最多是六条，则只可能出现三角形、四边形、五边形、六边形。

一、截面图形是三角形用一平面去截正方体经过正方体三个面时得到的截面图形是三角形1.截面图形是锐角三角形如下图，一个平面截正方体任意三个面得到截面△EFG ，BE=a,BF=b,BG=c.可得EF=22b a +,EG=22c a +,FG=22c b +.（1）如图①，当a ≠b ≠c 时，则EG ≠FG ≠EF,即截面△EFG 是一般三角形。

（2）如图②，当a=b ≠c 时，则EG=FG ≠EF 即截面△EFG 是等腰三角形。

同理可得a=c ≠b 或b=c ≠a 时截面△EFG 是等腰三角形。

（3）如图③,当a=b=c 时EF=FG=EG 即截面△EFG 是等边三角形2.截面图形不能是直角三角形如图①，2EF =22b a +，2FG =22c b +,2EG =22c a +,则222EG FG EF +<,222EG EF FG +<,222EG FG EF +<,所以截面三角形不可能是直角三角形。

3.截面图形不可能是钝角三角形如图①，cos ∠FEG=EG EF FG EG EF ⋅-+2222=22222222222ca b a c b c a b a +⋅+--+++ =22222c a b a a +⋅+>0,则0<∠FEG< 90.同理可得0<∠EFG< 90.0<∠EGF< 90. 所有截面图形不可能是钝角三角形。

北师大版-数学-七年级上册-《截一个几何体》知识全解

1.3截一个几何体新知概览：知识要点课标要求中考考点用平面去截几何体所得截面的形状探索并理解几何体的截面形状。

截面的定义（掌握）几种常见几何体的截面掌握几种常见几何体的截面。

判断一个几何体的截面(应用)本节重、难点1.重点：截面的定义和形状．2.难点：利用截面解决实际问题．知识全解知识点1截面（1）截面的概念：用一个平面去截几何体，截出的面叫做截面．（2）正方体的截面：根据面与面相交可以得到线可知用一个平面去截正方体的三个面，得到的截面是三角形.如果用一个平面去截正方体的四个面，就能得到四边形，除能得到正方形、长方形这样的四边形外，还能得到其他的四边形，如梯形、平行四边形等.知识警示：（1）正方体总共有六个面，用一个平面去截最多只能得到六条交线，从而截面的边数最多只能是六，还可以得到五，但不可能截得七边形.（2）一般地，截面与几何体的几个面相交就得到几条交线，截面就是几边形.因此，若一个几何体有n个面，则截面最多的边数是n．知识拓展正方体的截面主要有三角形、四边形、五边形和六边形，如图1-3-1所示.【试练例题1 】如图1-3-2所示的一块长方体木头，想象沿虚线所示位置截下去所得到的截面图形是（）思路导引：首先根据两组对边平行，可确定为平行四边形；又有一角为直角，故截面图形是长方形．答案：B.长方体的截面，经过长方体四个侧面，长方体中，对边平行，故可确定为平行四边形，交点垂直于底边，故为长方形．知识方法：截面的形状既与被截的几何体有关，还与截面的角度和方向有关．对于这类题，最好是动手动脑相结合，亲自动手做一做，从中学会分析和归纳的思想方法．知识点2几种常见几何体的截面（1）如图1-3-3所示，用平面截圆柱体，可能出现以下的几种情况．（2）如图1-3-4所示，用平面去截一个圆锥，能截出圆和三角形两种截面．图1-3-1A图1-3-2B C D（3）如图1-3-5所示,用平面去截球体，只能出现一种形状的截面---圆.知识警示： (1) 用一个平面去截一个圆柱所得到的截面有圆、长方形、椭圆、拱形形状和梯形.(2) 用一个平面去截圆锥，可得到圆、三角形、拱形形状和椭圆.【试练例题2】如图1-3-6中几何体的斜截面形状是（）思路导引：几何体是一个圆柱体，用一个平面斜截它，得到的截面应该是类似拱形的图形．答案C 用一个平面去截一个圆柱体，过平行于上下底面的面去截可得到圆；圆柱体的轴截面是矩形；过侧面且不平行于上下底面的面去截可得到椭圆；过一底面不平行于另一底面的面去截可得到类似拱形的截面．方法：平面与平面相交得直线，平面与曲面相交可能得到直线，也可能得到曲线．图1-3-5图1-3-4 图1-3-6。

正方体截面总结

结论如下：1、可能出现的：锐角三角型、等边、等腰三角形，正方形、矩形、非矩形的平行四边形、梯形、等腰梯形、五边形、六边形、正六边形2、不可能出现：钝角三角形、直角三角形、直角梯形、正五边形、七边形或更多边形正方体的截面形状一：问题背景在家做饭时，切菜尤其是切豆腐时，发现截面有很多形状。

若用不同的截面去截一个正方体，得到的截面会有哪几种不同的形状？二：研究方法先进行猜想，再利用土豆和萝卜通过切割实验研究。

三：猜想及其他可能的证明：1.正方形：因为该立体几何图形是正方体，所以用从任意位置与该正方体上下底面平行的平面进行截取可以得到，或者和侧面平行进行截取，由下列图示证明：====》》》由图示可知，水平方向截取正方体，得到的截面为正方形。

====》》》由图示可知，竖直方向截取正方体，得到的截面为正方形。

2.矩形：因为正方形也属于矩形，所以对正方形的证明同适用于矩形。

其次，当长宽不等的矩形截面的图示如下：由上图所示可知，按不同角度截取正方体可以得到矩形。

例如，正方体的六个对角面都是矩形。

3.平行四边形：当平面与正方体的各面都不平行时，所得截面为平行四边形，图示如下：==》由上图所示可知，当截面不与正方体的各面平行时，所得截面可能为平行四边形。

4.三角形：根据一定角度过正方体的三条棱进行截取可以得到三角形的截面，图示如下:==》》》由上图可知，正方体可以截得三角形截面。

但一定是锐角三角形，包括等腰和等边三角形特别的，当截面刚好经过三个面的对角线时，所得的三角形截面为正三角形，图示如下：==》得到：正三棱锥5.猜想之外的截面形状：（1）菱形：如下图所示，当A,B为所在棱的中点时，该截面为菱形：（2）梯形：如图所示，当按一定角度使截面在正方体的上下底面上所存在的线段长短有异时，所得截面可能是梯形：==》》》（3）五边形：如图所示，可以截得五边形截面：=》通过实践及资料查询可知，无法得到正五边形。

（4）六边形：如图所示，可以截得六边形截面：=》特别的，当平面与正方体各棱的交点为中点时，截面为正六边形，如图所示：拓展探究：1.正方体最大面积的截面三角形 2.正方体最大面积的截面四边形3.最大面积的截面形状4.截面五边形、六边形性质1.正方体最大面积的截面三角形：如该图所示可证明，由三角面对角线构成的三角形。

立体几何中截面问题重难考点归纳总结

高三二轮专题复习立体几何中截面问题重难考点归纳总结作空间几何体截面的常见方法：（1）直接连接法：有两点在几何体的同一个面上，连接该两点即为几何体与截面的交线，找截面就是找交线的过程；（2）作平行线法：过直线与直线外一点作截面，若直线所在的平面与点所在的平面平行，可以通过过点找直线的平行线找到几何体与截面的交线；（3）作延长线找交点法：若直线相交但是立体图形中未体现，可通过作延长线的方法先找到交点，然后借助交点找到截面形成的交线；（4）辅助平面法：若三个点两两都不在一个侧面或者底面中，则在作截面时需要作一个辅助平面.考点一：截面形状的判断1．在立体几何中，用一个平面去截一个几何体得到的平面图形叫截面．平面以任意角度截正方体，所截得的截面图形不可能为（） A ．等腰梯形B ．非矩形的平行四边形C ．正五边形D ．正六边形2．在立体几何中，用一个平面去截一个几何体得到的平面图形叫截面，如图，在正方体ABCD ﹣A 1B 1C 1D 1中，点E 、F 分别是棱B 1B 、B 1C 中点，点G 是棱CC 1的中点，则过线段AG 且平行于平面A 1EF 的截面图形为（）A ．矩形B ．三角形C ．正方形D ．等腰梯形3．如图所示的几何体是由一个圆柱挖去一个以圆柱的上底面为底面，下底面圆心为顶点的圆锥而得到的组合体，现用一个垂直于圆柱底面的平面去截这个组合体﹐则截面图形可能是______（填序号）．4．（多选题）一个正方体内有一个内切球，用一个平面去截，所得截面图形可能是图中的（）A ．AB ．BC ．CD ．D5．在正方体中，M ，N ，Q 分别为棱AB ，的中点，过点M ，N ，Q 作该正方体的截面，则所得截面的形状是（） A ．三角形B ．四边形C ．五边形D ．六边形考点二：求截面面积6．已知圆柱的上、下底面的中心分别为，，过直线的平面截该圆柱所得的截面是面积为16的正方形，则该圆柱的表面积为（） A ． B ． C ． D ． 7．已知球O 的表面积为，则过球Q 一条半径的中点，且与该半径垂直的截面圆的面积为___________. 8．已知圆锥的侧面积为，若其过轴的截面为正三角形，则该圆锥的母线的长为___________. 9．已知正四棱柱中、的交点为，AC 、BD 的交点为，连接，点为的中点.过点且与直线AB 平行的平面截这个正四棱柱所得截面面积的最小值和最大值分别为1，则正四棱柱的体积为______________.111-ABCD A B CD 111,B B C D 1O 2O 12O O 24π20π8π29π11A C 11B D 1O 2O 12O O O 12O O O 1111ABCD A B C D -10．已知正四棱柱中，，，则该四棱柱被过点，C ，E 的平面截得的截面面积为______. 11．已知圆锥的侧面积为20π，底面圆O 的直径为8，当过圆锥顶点的平面截该圆锥所得的截面面积最大时，则点O 到截面的距离为______________.12．在立体几何中，用一个平面去截一个几何体得到的平面图形叫截面. 如图，在棱长为1的正方体中，点分别是棱的中点，点是棱的中点，则过线段且平行于平面的截面的面积为A ． B． C ． D13．已知棱长为的正四面体，，，分别是棱，，的中点，则正四面体的外接球被三角形所在的平面截得的截面面积是（）A ．B ．C ．D ． 14．已知三棱锥的所有棱长均相等，四个顶点在球的球面上，平面经过棱，，的中点，若平面截三棱锥和球所得的截面面积分别为，，则（） ABC ．D ． 15．已知正方体的长为2，直线平面，下列有关平面截此正方体所得截面的结论中，说法正确的序号为______．①截面形状一定是等边三角形：②截面形状可能为五边形；③截面面积的最大值为④存在唯一截面，使得正方体的体积被分成相等的两部分．16．已知某圆锥轴截面的顶角为，过圆锥顶点的平面截此圆锥所得截面面积的最大值为，则该圆锥的1111ABCD A B C D -1124BE BB ==143AB AA =1A 1111ABCD A B C D -,E F 111,B B B C G 1CC AG 1A EF 198894ABCD E F N AB AC AD ABCD EFN 73π83π103π163πA BCD -O αAB AC AD αA BCD -O 1S 2S 12S S =38π364π1111ABCD A B C D -1AC ⊥αα120 2底面半径为（） ABC ．D ．17．在长方体中，已知，，分别为，的中点，则平面被三棱锥外接球截得的截面圆面积为___________.考点三：求截面周长18．如图，在正方体中，，为棱的中点，为棱的四等分点（靠近点），过点作该正方体的截面，则该截面的周长是___________.19．已知在棱长为6的正方体ABCD -A 1B 1C 1D 1中，点E ，F 分别是棱C 1D 1，B 1C 1的中点，过A ，E ，F 三点作该正方体的截面，则截面的周长为________．20．正三棱柱ABC ﹣A 1B 1C 1中，所有棱长均为2，点E ，F 分别为棱BB 1，A 1C 1的中点，若过点A ，E ，F 作一截面，则截面的周长为（）1111ABCD A B C D -122AA AB AD ===E F 1BB 11D C 11A BCD 1C CEF -1111ABCD A B C D -4AB =E BC F 11A D 1D ,,A E FA ．B ．C ．D ．21．在三棱锥中，，截面与，都平行，则截面的周长等于（）A ．B ．C ．D ．无法确定考点四：截面最值问题22．已知三棱锥的四个顶点在球的球面上，，的正三角形，三棱锥的体积为，为的中点，则过点的平面截球所得截面面积的取值范围是（） A ． B ． C ． D ． 23．正四面体ABCD 的棱长为4，E 为棱AB 的中点，过E 作此正四面体的外接球的截面，则该截面面积的取值范围是（） A ． B ． C ． D ． 24．已知球O 是正三棱锥A -BCD （底面是正三角形，顶点在底面的射影为底面中心）的外接球，BC =3，AB =E 在线段BD 上，且BD =3BE ．过点E 作球O 的截面，则所得截面面积的最小值是（） A ． B． C ． D ．25．如图，四边形为四面体的一个截面，若四边形为平行四边形，，，则四边形的周长的取值范围是___________.26．如图，设正三棱锥的侧棱长为，，分别是上的点，过作三棱锥的截面，则截面周长的最小值为________.+A BCD -AB CD a ==MNPQ AB CD MNPQ 2a 4a a P ABC -O PA PB PC ==ABC ∆P ABC -16Q BC Q O 13,24ππ⎡⎤⎢⎥⎣⎦12,23ππ⎡⎤⎢⎥⎣⎦13,44ππ⎡⎤⎢⎥⎣⎦12,43ππ⎡⎤⎢⎥⎣⎦[]46ππ，[]412ππ，[]4ππ，[]6ππ，2π3π4π5πEFGH ABCD EFGH 4AB =6CD =EFGH P ABC -240APB ∠=︒,E F ,BP CP ,,A E F AEF27．正三棱锥，点在棱上，且，已知点都在球的表面上，过点作球的截面，则截球所得截面面积的最小值为___________.考点五：有关截面的综合问题28．如图，在正方体中，点P 为线段上的动点（点与，不重合），则下列说法不正确的是（）A ．B ．三棱锥的体积为定值C ．过，，三点作正方体的截面，截面图形为三角形或梯形D ．DP 与平面所成角的正弦值最大为 29．（多选题）在棱长为2的正方体中，以下结论正确的有（）A ．三棱锥外接球的体积是B ．当点在直线上运动时，的最小值是P ABC -AB ==E PA 3PE EA =P A B C 、、、O E O ααO 1111ABCD A B C D -11A C P 1A 1C BD CP ⊥C BPD -P C 1D 1111D C B A 131111ABCD A B C D -11B A DC -Q 1BC 1A Q QC +8+C ．若棱，，的中点分别是，，，过，，三点作正方体的截面，则所得截面面积为D ．若点是平面上到点和距离相等的点，则点的轨迹是直线30．（多选题）如图，正方体的棱长为1，P 为的中点，Q 为线段上的动点，过点A ，P ，Q 的平面截该正方体所得的截面多边形记为S ，则下列命题正确的是（）A ．当时，S 为等腰梯形B ．当时，S 与的交点R 满足C ．当时，S 为六边形D ．当时，S31．（多选题）在正方体中，，点E ，F 分别为，中点，点P 满足，，则（）A ．当时，平面截正方体的截面面积为B ．三棱锥体积为定值 AB 1AA 11CDEFG E F G M 1111D C B A D 1C M 11A D 1111ABCD A B C D -BC 1CC 12CQ =34CQ =11C D 113C R =314CQ <<1CQ =1111ABCD A B C D -2AB =AB BC 1AP AA λ= [0,1]λ∈1λ=PEF 941P ECC -C ．当时，平面截正方体的截面形状为五边形D ．存在点P ，二面角为45°10,3λ⎛⎤∈ ⎥⎝⎦PEF P EF A --Word 版见：高考高中资料无水印无广告word 群559164877详细解析1．C 【详解】画出截面图形如图：可以画出等腰梯形，故A 正确；在正方体中，作截面（如图所示）交，，，分别于点，，，，根据平面平行的性质定理可得四边形中，，且，故四边形是平行四边形，此四边形不一定是矩形，故B 正确；经过正方体的一个顶点去切就可得到五边形．但此时不可能是正五边形，故C 错误；正方体有六个面，用平面去截正方体时最多与六个面相交得六边形，且可以画出正六边形，故D 正确．故选：C1111ABCD A B C D EFGH 11C D 11A B AB CD E F G H EFGH //EF HG //EH FGEFGH高中数学教研群 QQ 群号929518278 精品资料每天更新2．D 【详解】取的中点，如图连接、、、，由题意得：，，不在平面内，平面内，∴平面.不在平面内，平面内，∴平面.，平面，平面平面，过线段且平行于平面的截面图形为等腰梯形．故选：．3．①⑤【详解】由题意，当截面过旋转轴时，圆锥的轴截面为等腰三角形，此时①符合条件；当截面不过旋转轴时，圆锥的轴截面为双曲线的一支，此时⑤符合条件，综上可知截面的图形可能是①⑤.故答案为：①⑤4．AB 【详解】由组合体的结构特征可知：当截面过球与正方体切点时可知A 正确、C 错误；当截面过正方体的对角面时可知B 正确；此题是正方体的内切球，可知D 错误.故选：AB5．D 【详解】如图所示：分别为中点，M ，N ，Q 确定平面，且，故，，故，同理可得，，，故截面为六边形.故选：D. BC H AH GH 1D G 1AD //GH EF 1//AH A F GH 1A EF EF ⊆1A EF ||GH 1A EF AH 1A EF 1A F ⊆1A EF ||AH 1A EF GH AH H = ,GH AH ⊆1AHGD ∴1//AHGD 1A EF AG AEF 1AHGDD ,,EF H 111,,AD DD B C αNH MQ ∥N α∈NH α⊂,Q H αα∈∈QH α⊂FQ α⊂EF α⊂EM α⊂6．B 【详解】根据题意，所得截面是边长为4的正方形，结合圆柱的特征，可知该圆柱的底面是半径为的圆，且高为4，所以其表面积.故选：B. 7．【详解】设球的半径为，则，解得.设截面圆的半径为，由题知：，所以截面圆的面积.故答案为： 8．【详解】设圆锥的底面半径为r ，圆锥的母线为l ,又圆锥过轴的截面为正三角形，圆锥的侧面积为， ∴， ∴.故答案为：. 9．3【详解】设正四棱柱的底面边长为a ，高为h ，由题知当截面平行于平面时，截面面积最小；当截面为平面时，截面面积最大，2()22222424S =⨯+⨯⨯=πππ32ππR 248R ππ=R =r r ==232S ππ==32π2329π22,9l r rl ππ==23l =23ABCD 11A B CD因为过点且与直线AB 平行的平面截这个正四棱柱所得截面面积的最小值和最大值分别为1，所以，于是正四棱柱的体积为.故答案为：3.10．由题意，正四棱柱中，，，可得，在上取点，使得，连接，则有，所以四边形是平行四边形，由勾股定理可得，所以所以，所以四边形是平行四边形的面积为，故答案为：O 21a ⎧=⎪⎨=⎪⎩13a h =⎧⎨=⎩1111ABCD A B C D -23a h =1111ABCD A B C D -1124BE BB ==143AB AA =1118,2AA BB CC BE ====1DD F 12D F =1,A F CF 11,//A F CE A F CE =1A ECF 11A E CE A C ====2221111cos 2A E CE A C A EC A E CE +-∠===⨯1sin A EC ∠=1A ECF 11sin A E EC A EC ⨯⨯∠==11设圆锥的底面圆的半径为r ，高为h ,母线长为l ,则，∴，h =3,由于h<r ,所以圆锥的轴截面为钝角三角形，所以过圆锥顶点的平面截该圆锥所得的截面为直角三角形时面积最大，如图，△SAB 为截面三角形，SO 为圆锥的高，设点O 到截面的距离为d ，则∴，即， ∴，即点O. 12．B 【详解】取BC 的中点H ，连接，4,20r rl ππ==5l =25,2SAB AB S == 14,2AOB OA OB S ===⨯= 1133SAB AOB S d S h ⋅=⋅ 12513323d ⨯⋅=d =,AH GH因为面AHGD1，面AHGD1，面AHGD1，同理，面AHGD1，又，则平面AHGD1∥平面A1EF，等腰梯形AHGD1，，故选B．13．D【详解】过点作平面的垂线，垂足为，交平面于点，设该四面体外接球球心为，连接，作图如下所示：因为四面体为正四面体，且面，故点为△的外心，则该四面体的球心一定在上，不妨设外接球球心为；因为分别为的中点，则//，//，又，且面，面，故平面//平面，故面，又为中点，故也为中点.因为正四面体的所有棱长为，故1,EF BC GH EF⊄GH⊂EF∴∥1A E∥1A E EF E⋂=98A BCD H EFN'O O,OB BHABCD AH⊥BCDH BCD AH O,,E F N,,AB AC AD EF BC FN CD,EF FN F BC CD C⋂=⋂= ,EF FN⊂EFN,BC CD⊂BCD EFN BCDAO'⊥EFN E AB'O AHABCD4243BH==则设该四面体的外接球半径为，即，则，在△中，，即，解得即外接球球心到平面，设平面截外接球所得圆的半径为，则，解得，故截面圆的面积为.故选：D. 14．B 【详解】设平面截三棱锥所得正三角边长为a ，截面圆的半径为r ，则，由正弦定理可得，，故选：B15．④【详解】如图可知，截面形状可以是等边三角形、六边形、正六边形，∴①②明显错误；截面面积的最小值可以趋向于零，故③错误；当截面为正六边形时，截面过正方体的中心，此时正方体的体积被分成相等的两部分．故④正确.故答案为：④AH ===12O H AH ='=R OA OB R ==OH AH R R =-=Rt OHB 222OH BH OB +=222R R ⎫+=⎪⎪⎭R =OO R AO =-==''O EFN EFN r 222r +=2163r =163παA BCD -21S =sin 60a r ==︒22243πa S πr ∴==12S S =∴16．A 【详解】如图，由题可知，，又过圆锥顶点的平面截此圆锥所得截面面积的最大值为，∴，即，在中，.故选：A. 17．【详解】以点为原点建立空间直角坐标系如图所示：120APB ∠= 30ABP ∠= 22122l =2l =Rt POB cos302r l === 98πD依题意得：，，，则，，所以，则；设为中点，因为则，所以点为三棱锥外接球的球心，则设球心到平面的距离为，又因为为中点，所以点到平面的距离为，由于，所以故截面圆的半径为，所以截面圆面积为. 故答案为：18如图，取的中点，取上靠近点的三等分点，()0,2,0C ()1,2,1E ()0,1,2F ()1,0,1EC =-- ()111EF ,,=-- 1010EC EF ⋅=+-= EF EC ⊥O CF EF EC ⊥1EO OC FO C O ===O 1C CEF -12R CF ==O 11A BCD h O CF F 11A BCD 2h 111244h C D ==⨯=h =r ==98π98π11C D H 1CC 1C G连接，易证，则五边形为所求截面.因为，所以，则，故该截面的周长是.19．如图，延长EF ，A 1B 1，相交于点M ，连接AM ，交BB 1于点H ，延长FE ，A 1D1，相交于点N ，连接AN，交DD 1于点G ，连接FH，EG，可得截面为五边形AHFEG .因为ABCD-A 1B 1C 1D1是棱长为6的正方体，且E ，F 分别是棱C 1D 1，B 1C 1的中点，由中位线定理易得：EF ＝：AG ＝AH ＝EG ＝FH AH ＋HF ＋EF ＋EG ＋AG ＝故答案为：20．B 【详解】如图，在正三棱柱中，延长AF 与CC 1的延长线交于M ，连接EM 交B 1C 1于P ，连接FP ，则四边形AEPF 为所求截面.,,,,AE EG GH HF FA //,//AE HF AF EG AEGHF 4AB =111182,3,1,3BE CE C H D H A F D F CG =======143C G =103AE EG ==5,GH HF AF ===AE EG GH HF AF ++++=+111ABC A B C -过E 作EN 平行于BC 交CC 1于N ，则N 为线段CC 1的中点，由相似于可得MC 1=2，由相似于可得：，在中，，则，在中，，则在中，，则在中，，由余弦定理：，则故选：B.21．A 【详解】设，因为平面，平面平面，平面，所以，同理可得，，，故四边形为平行四边形，所以，. 因为，所以，， 1MFC MAC △1MPC △MEN 111242,2333PC PC B P =⇒==1Rt AA F 112,1AA A F ==AF ==Rt ABE △2,1AB BE ==AE ==1Rt B EP 1121,3B E B P ==PE ==1C FP 11141,,603C F C P FC P ==∠=︒2224413121cos 60339PF ⎛⎫=+-⨯⨯⨯︒= ⎪⎝⎭PF ==AM k CM=//AB MNPQ ABC MNPQ MN =AB ÌABC //MN AB //PQ AB //MQ CD //NP CD MNPQ 11MN PQ AB AB k ==+1MQ NP k CD CD k==+AB CD a ==1a MN PQ k ==+1ak MQ NP k==+所以四边形的周长为. 故选：A.22．A 【详解】设在底面上的射影为，因为，所以为的中心，由题可知，，由，解得在正中，可得.从而直角在中解得. 进而可得，，，因此正三棱锥可看作正方体的一角，正方体的外接球与三棱锥的外接球相同，正方体对角线的中点为球心. 记外接球半径为，则所以过的平面截球所得截面的面积最大为；又为中点，由正方体结构特征可得由球的结构特征可知，当垂直于过的截面时， MNPQ 2211a ak MN PQ MQ NP a k k ⎛⎫+++=+= ⎪++⎝⎭P ABC M PA PB PC ==M ABC ∆ABC S ∆1136P ABC ABC V PM S -∆=⨯⨯=PM =ABC ∆AM =ABC 1PA =PA PB ⊥PB PC ⊥PC PA ⊥P ABC -P ABC -O R R Q O 2max 34S R ππ==Q BC 1122OQ PA ==OQ Q截面圆半径最小为. 因此，过的平面截球所得截面的面积范围为. 故选：A.23．A 【详解】如图，将正四面体补为边长是ABCD 的外接球为正方体的外接球，球心O在体对角线的中点，且球的半径；当OE 垂直于截面时，截面面积最小，截面圆的半径为面积为；当截面过球心O 时，截面面积最大，截面圆的半径为，面积为故选:A24．A【详解】解：如图，O 1是A 在底面的射影，由正弦定理得，△BCD 的外接圆半径r ==2min 12S r ππ==Q O 13,24ππ⎡⎤⎢⎥⎣⎦R =12r ==4π1r R =6π1031sin 602r =⨯=由勾股定理得棱锥的高AO 1；设球O 的半径为R ，则，解得，所以OO 1=1；在△BO 1E 中，由余弦定理得所以O 1E =1；所以在△OEO 1中，OE；当截面垂直于OE. 故选：A25．【详解】解：四边形为平行四边形，；平面，平面，平面；又平面，平面平面，，同理可得；设，，，，；又，，，，且；四边形的周长为，；四边形周长的取值范围是．故答案为：26．将正三棱锥的三个侧面展开如图，由图可知，为使的周长最小，只需让四点共线即可，则当为与交点时，的周长最小，由题意，，∴，得的周长3==()223R R =-2R =2113211,O E =+-⨯==2π(8,12) EFGH //EH FG ∴EH ⊂/ ABD FG ⊂ABD //EH ∴ABD EH ⊂ ABC ABC ABD AB =//EH AB ∴//EF CD EH x =EF y =∴EH CE AB CA =EF AE CD AC =∴1EH EF CE AE AC AB CD CA AC AC+=+==4AB =Q 6CD =∴146x y +=614x y ⎛⎫∴=- ⎪⎝⎭04x <<∴EFGH 2()2[6(1)]4xl x y x =+=+-12x =-81212x ∴<-<∴EFGH (8,12)(8,12)AEF 1,,,A E F A ,E F 1AA ,BP CP AEF 140BPC CPA APB ∠=∠=∠=︒1120APA ∠=︒1AA ===AEF的最小值为故答案为：27．【详解】，，，同理，故可把正三棱锥补成正方体（如图所示），其外接球即为球，直径为正方体的体对角线，故，设的中点为，连接，则.所以，当平面时，平面截球O 的截面面积最小，，故截面的面积为.故答案为：28．D 【详解】由题可知平面，所以，故A 正确；由等体积法得为定值，故B 正确；设的中点为，当时，如下图所示：3π4PA PC PB === AB AC BC ===222PA PC AC ∴+=2CPA π∴∠=2CPB BPA π∠=∠=O 2R =PA F OF OF =OF PA ⊥3OE ==OE ⊥αα=3π3πBD ⊥11ACC A BD CP ⊥113C BPD P BCD BCD V V S AA --==⋅⋅ 11A C M 1P MC ∈此时截面是三角形，当时，如下图所示：此时截面是梯形，故C 正确；选项D ，在正方体中，连接，则为在平面上的射影，则为与平面所成的角，设正方体的棱长为1，，则当取得最小值时，的值最大，即时，，所以D 不正确. 故选：D.29．ACD 【详解】对于A ：三棱锥的外接球即为正方体的外接球，因为正方体的外接球的直径即为正方体的体对角线，即所以外接球的体积是，故选项A 正确；1D QC 1PMA ∈1D QRC 1D P 1D P DP 1111D C B A 1D PD ∠DP 1111D C B A 1PD x =DP =1sin D PD ∠x 1sin D PD ∠111D P A C ⊥x 1sin D PD ∠11B A DC -1111ABCD A B C D -2R =R 34π3V =´=对于B ：把沿翻折到与在同一个平面（如图所示），连接，则是的最小值，其中是边长为的等边三角形，是直角边为的等腰直角三角形，所以，即故选项B 错误；对于C ：分别取棱，，的中点，，，连接，，，，，，则易知过，，三点的截面是正六边形，1BCC 1BC 11A C B △1A C 1A C 1A Q QC +11A C B △1BCC 211A C A Q QC =+==1A Q QC +11A D 1CC BC H M N EF FH HG GM MN NE E F G EFHGMN所以截面面积为故选项C 正确；对于D ：因为是平面上到点和距离相等的点，所以点的轨迹是平面与线段的垂直平分平面的交线，即点的轨迹是平面与平面的交线，所以点的轨迹是直线，即选项D 正确．故选：ACD.30．ABD 【详解】解：过点A ，P ，Q 的平面截正方体，当时，其截面形状为梯形如图1，特别地当时，截面形状为等腰梯形，当时，其截面形状为五边形如图2．若，则，所以．当时，与重合，其截面形状为四边形如图3，此时，因为P 为的中点，且，所以为的中点，所以，同理，所以四边形为平行四边形，所以四边形为菱形，其面积为ABD 正确．故选：ABD.31．BCD 【详解】A 选项中，当时，与重合，则截面为等腰梯形，其面积为，故A 选项错误； 1(62⨯=M 1111D C B A D 1C M 1111D C B A 1DC 11A BCD M 1111D C B A 11A BCD 11A D M 11A D 102CQ <≤12CQ =112CQ <<34CQ =1113C Q C R QC CM ==113C R =1CQ =Q 1C PQ AP =BC CP AD ∕∕Q MN PC AE ∕∕QE AP ∕∕APQE APQE 112AC PE ⋅==1λ=P 1A 92B 选项中，因为平面，故P 到平面的距离不变，故三棱锥体积为定值．故B 选项正确：C 选项中，当时，其截面刚好为五边形，时，截面为五边形；故C 选项正确；D 选项中，当点P 与重合时，其二面角正切值为，此时二面角大于45°，所以存在点P ，二面角为45°，D 选项正确；故选：BCD ．1//AA 1ECC 1ECC 1P ECC -13λ=103λ<<1A P EF A --。

截一个几何体知识点归纳

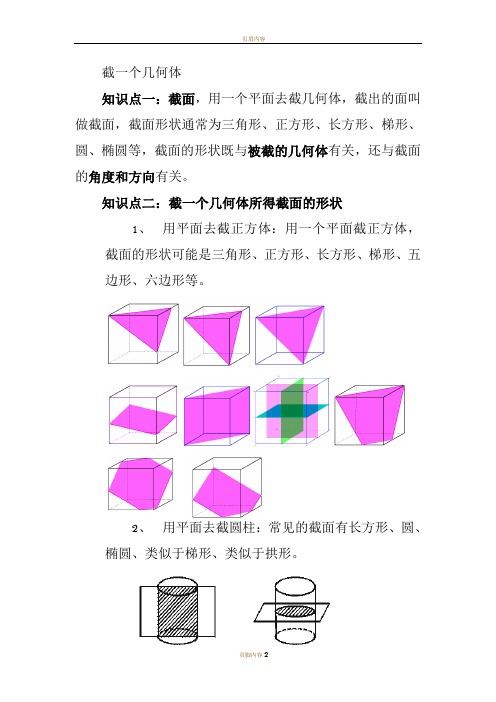
截一个几何体
知识点一：截面，用一个平面去截几何体，截出的面叫做截面，截面形状通常为三角形、正方形、长方形、梯形、圆、椭圆等，截面的形状既与被截的几何体有关，还与截面的角度和方向有关。

知识点二：截一个几何体所得截面的形状
1、用平面去截正方体：用一个平面截正方体，
截面的形状可能是三角形、正方形、长方形、梯形、五
边形、六边形等。

2、用平面去截圆柱：常见的截面有长方形、圆、
椭圆、类似于梯形、类似于拱形。

3、用平面去截圆锥：截面的形状可能是三角形、圆、椭圆、类似于拱形。

4、用平面去截球：截面的形状都是圆。

截一个几何体从三个方向看物体的形状

教学内容【重点知识归纳及讲解】1、截面用一个平面去截一个几何体，截出的面叫做截面用一个平面从不同的方向去截同一个几何体，所得到的截面形状可能是不同的．充分想像截面可能的形状，可以先找出平面和几何体的面相交而成的线，然后再判断这些线围成的截面形状.2、从不同方向观察物体从不同方向观察同一物体时，可能看到不一样的结果．当观察画在纸上面的立体图形时，只能通过想像，推出从其他方向观察这个物体所可能得到的结果.3、物体的主视图、左视图、俯视图从不同的方向观察同一物体时，可能看到不同的图形，其中，把正面看到的图叫做主视图，从左面看到的图叫做左视图，从上面看到的图叫做俯视图，合称三视图.这里所说的主视图、俯视图、左视图是相对于观察者而言的，位于物体不同方向的观察者，他们所画出的主视图、俯视图、左视图可能是不同的.4、多边形多边形是由一些线段首尾顺次相连围成的封闭图形，多边形根据它的边数可以分为三角形（即三边形）、四边形、五边形等，多边形的边数为n（n≥3）的叫做n边形．在多边形中，三角形是最基本的图形.从一个多边形的某个顶点出发，分别连接这个顶点与其余各顶点，可以把这个多边形分割成若干个三角形，n边形可以分割成(n－2)个三角形，这样，多边形可以化归为三角形来研究．【难点知识剖析】1、物体三视图的画法及识别对于简单物体的三视图，要能识别观察方向，能够想像出物体的原形.2、平面图形的组合和分割再复杂的平面图形都是由若干简单的基本图形组合而成的，就是由三角形、正方形、长方形、多边形、圆、扇形等基本图形组成．对于平面图形能进行简单的分割和组合.【典型例题解析】【例1】（1）如果用一个平面去截一个几何体，如果截面是圆，那么原来的几何体可能是什么？（2）如果用一个平面去截一个几何体，如果截面是三角形，那么原来的几何体可能是是什么？解：（1）如图所示，用平面去截球体，圆锥、圆柱等一些几何体，都可能使截面是圆。

（2）如图所示，用平面去截三棱锥、四棱锥、三棱柱，四棱柱、圆锥等一些几何体，都可能使截面是一个三角形。

初中数学教学课例《截一个几何体》教学设计及总结反思

数学活动过程，发展学生的动手操作、自主探究、合作
交流和分析归纳能力。
3、情感目标：通过以教师为主导，引导学生观察
发现、大胆猜想、动手操作、自主探究、合作交流，使
学生在合作学习中体验到：数学活动充满着探索和创
造。使学生获得成功的体验，增强自信心，提高学习数
学的兴趣。
（分析学生在本课中所需学习方法的掌握情况、学
用一个平面去截一个几何体，截出的面叫做截面。从不同的角度去截一个几何体，所得到的截面就有可能不同。
并由此引出课题-----今天我们就来研究用平面《截一个几何体》。
2、自主探究，获取新知。 <活动二>设置问题：用一个平面去截一个立方体，所得到的截面可能是什么形状？让学生猜想可能截出的截面形状，想象怎样能截出这样的截面。让学生独立思考后，小组合作讨论交流，以此来促进学生间的交流合作，提高学生的空间想象力。然后让学生动手切截课前准备的立方体模型。通过动手实践来验证自己的猜想。并找学生到前面演示不同的截面和切截的方法。从而提高学生的动手操作能力和语言表达能力。在上述过程中，学生比较容易想到截面是三角形，四边形（包括正方形，长方形，梯形）的情况，并能够比较容易的截出这几种形状的截面。但截面是五边形，六边形的情况却不容易想到和截出。所以后面我设计了动画演示的内容，让学生更系统直观的看到每一种截面的切截方法，发现没有猜想到的
初中数学教学课例《截一个几何体》教学设计及总结反思
学科
初中数学
教学课例名
《截一个几何体》
称
（简单说明本课的学习内容，说明课题教学的重点
和难点）
1、教材的地位和作用：
本节课位于初中数学六年级上册第一章第三节，截
一个几何体是本章的一个重点，教材在安排上通过学生

2024秋季北师大版新教材七年级上册1.2-课时3-截一个几何体

北师大版七年级(上册) 2024新版教材
1.2 课时3 截一个几何体
学习目标
1.经历用一个平面切截几何体的活动过程，体会几何体在被截过程中的变化，在面与体的转换中积累数学活动经验.
2.通过用一个平面截一个几何体的活动，认识圆柱、圆锥、棱柱、球等几何体截面的一些特征，发展几何直观.
新知导入
在生活中我们常常需要将一个物体截开，如切西瓜、锯木头等.
探究新知
思考4：用一个平面去截一个圆锥，截面的形状可能是什么样?
探究新知
思考4：用一个平面去截一个圆锥，截面的形状可能是什么样?
等腰三角形圆形
椭去截一个球体，截面的形状可能是什么样?
用一个平面无论如何截球，截面的形状总是圆，只是大小可能不同.
圆形
课堂练习
2. 如图，往一个密封的正方体容器持续注入一些水，注水的过程中，可将容器任意放置，水平面形状不可能是( D )
A.三角形 B.正方形 C.六边形 D.七边形
课堂练习
3. 用一个平面去截一个三棱柱,截面的形状不可能是( C )
A
B
C
D
课堂练习
4.如图，用一个平面去截下列各几何体，所得截面可能是三角形的是( D )
探究新知
思考2：用一个平面去截一个棱柱（以三棱柱为例），截面可能是什么形状?
三角形长方形(正方形) 梯形
五边形
归纳：
棱柱的面数与其截面的边数的关系用一个平面去截棱柱时，一个棱柱有几个面，截面最多就有几条边，n 棱柱(有(n +2)个面)的截面形状是多边形，其边数 m 满足3≤ m ≤n +2.
A
B
C
D
课堂练习
5. 下列几何体中，截面可能是圆形的有( B ) (1)圆柱;(2)正方体;(3)棱柱;(4)球;(5)圆锥;(6)长方体

正方体截面总结(最全,适用于公务员图形推理)

M / * B结论如下：1可能出现的：锐角三角型、等边、等腰三角形，正方形、矩形、边形、梯形、等腰梯形、五边形、六边形、正六边形2、不可能出现：钝角三角形、直角三角形、直角梯形、正五边形、非矩形的平行四七边形或更多边正方体的截面形状一：问题背景在家做饭时，切菜尤其是切豆腐时，发现截面有很多形状。

若用不同的截面去截一个正方体，得到的截面会有哪几种不同的形状？二：研究方法先进行猜想，再利用土豆和萝卜通过切割实验研究。

三：猜想及其他可能的证明：1•正方形：因为该立体几何图形是正方体，所以用从任意位置与该正方体上下底面平行的平面进行截取可以得到，或者和侧面平行进行截取，由下列图示证明：由图示可知，水平方向截取正方体，得到的截面为正方形。

由图示可知，竖直方向截取正方体，得到的截面为正方形。

2矩形：因为正方形也属于矩形，所以对正方形的证明同适用于矩形。

其次，当长宽不等的矩形截面的图示如下: 由上图所示可知，按不同角度截取正方体可以得到矩形。

例如，正方体的六个对角面都是矩形。

3. 平行四边形：当平面与正方体的各面都不平行时，所得截面为平行四边形，图示如下:==》》》 ==》》》由上图所示可知，当截面不与正方体的各面平行时，所得截面可能为平行四边形。

4. 三角形：根据一定角度过正方体的三条棱进行截取可以得到三角形的截面，图示如下==》由上图可知，正方体可以截得三角形截面。

但一定是锐角三角形，包括等腰和等边三角形特别的，当截面刚好经过三个面的对角线时，所得的三角形截面为正三角形，图示如下:==》得到: 正三棱锥5. 猜想之外的截面形状：（1）菱形：如下图所示，当A,B 为所在棱的中点时，该截面为菱形:(2)梯形：如图所示，当按一定角度使截面在正方体的上下底面上所存在的线段长短有异时，所得截面可能是梯形：(3 )五边形:(4 )六边形：如图所示，可以截得六边形截面:==》》》如图所示，可以截得五边形截面:通过实践及资料查询可知，无法得到正五边形。

正方体截面总结(最全,适用于公务员图形推理)

正方体截面的形状可能出现锐角三角型、等边、等腰三角形，但不可能出现直角和钝角三角形Λ/ Y 月/L/F■■1IZ/:⅛/ 电曲四边形：可能出现正方形、矩形、非矩形的平行四边形、菱形、梯形、等腰梯形不可能出现直角梯形结论如下：1可能出现的：锐角三角型、等边、等腰三角形，正方形、矩形、非矩形的平行四边形、梯形、等腰梯形、五边形、六边形、正六边形2、不可能出现：钝角三角形、直角三角形、直角梯形、正五边形、七边形或更多边正方体的截面形状一：问题背景在家做饭时，切菜尤其是切豆腐时，发现截面有很多形状。

若用不同的截面去截一个正方体，得到的截面会有哪几种不同的形状？二：研究方法先进行猜想，再利用土豆和萝卜通过切割实验研究。

三：猜想及其他可能的证明：1.正方形：因为该立体几何图形是正方体，所以用从任意位置与该正方体上下底面平行的平面进行截取可以得到，或者和侧面平行进行截取，由下列图示证明：由图示可知，竖直方向截取正方体，得到的截面为正方形。

2矩形：因为正方形也属于矩形，所以对正方形的证明同适用于矩形。

其次，当长宽不等的矩形截面的图示如下:====》》》由图示可知，水平方向截取正方体，得到的截面为正方形。

》》》由上图所示可知，按不同角度截取正方体可以得到矩形。

例如，正方体的六个对角面都是矩形3. 平行四边形：当平面与正方体的各面都不平行时，所得截面为平行四边形，图示如下:由上图所示可知，当截面不与正方体的各面平行时，所得截面可能为平行四边形。

4.三角形：根据一定角度过正方体的三条棱进行截取可以得到三角形的截面，图示如下由上图可知，正方体可以截得三角形截面。

但一定是锐角三角形，包括等腰和等边三角形特别的，当截面刚好经过三个面的对角线时，所得的三角形截面为正三角形，图示如下:==》得到: 正三棱锥5. 猜想之外的截面形状：（1 ）菱形：如下图所示，当A,B为所在棱的中点时，该截面为菱形:（2）梯形：如图所示，当按一定角度使截面在正方体的上下底面上所存在的线段长短有异时，所得截面可能是梯形:==》》》（3）五边形：如图所示，可以截得五边形截面:通过实践及资料查询可知，无法得到正五边形。