函数微分的定义
一、微分的概念讲解

d2 y f ( x)d x2;
(6)
当 x 是中间变量( y f ( x), x (t) ) 时, 二阶微分
为
d2 y d( f ( x)dx ) f ( x)d xd x f ( x)d(d x)
f ( x)d x2 f ( x)d2 x.
(7)
依次下去, 可由 n 1 阶微分求 n 阶微分: dn y d (dn1 y) d( f (n1)( x) dxn1) f (n)( x)d xn .
对 n 2 的 n 阶微分均称为高阶微分. 高阶微分不
具有形式不变性. 当 x 是自变量时, y f ( x) 的二
阶微分是
一、微分的概念
微分从本质上讲是函数增量中关于自变量增量的 线性部分, 请先看一个具体例子. 设一边长为 x 的正方形, 它的面积 S = x 2 是 x 的函 数. 如果给边长 x 一个增量 Δ x , 正方形面积的增量 Δ S ( x x)2 x2 2x x ( x)2 由两部分组成 : Δ x 的线性部分 2xΔx 和 Δ x 的高阶部分( Δ x )2.因 此, 当边长 x 增加一个微小量 Δx 时, Δ S 可用Δx
它比 (6) 式多了一项 f ( x)d2 x, 当 x (t) 时,
d2 x (t)dt 2 不一定为 0, 而当 x 为自变量时,
d2 x 0.
例4 设 y f ( x) sin x , x (t) t 2, 求 d2 y.
解法一 先将 x (t) 代入 y f ( x), 得 y sin t 2,
sin x x, tan x x, ln1 x x, ex 1 x.
例5 试求 sin 33o 的近似值 ( 保留三位有效数字 ).
微分概念及其计算

y f (x0 x) f (x0) f (x0 )x f (x0 x) f (x0) f (x0)x
令 x x0 x f (x) f (x0) f (x0)(x x0 )
使用原则: 1) f (x0 ), f (x0 ) 好算 ; 2) x 与x0 靠近.
在点 可微 , 则
y f (x0 x) f (x0 ) Ax o(x)
lim y lim ( A o(x) ) A
x0 x x0
x
故
在点 的可导, 且
说明
由定理4.5,我们得到
dy f (x0 )x
当 y x 时,y' 1,dy dx 1 x x,
称x为自变量的微分, 记作 则有 dy f (x) dx
在点 的可导, 则
lim y x0 x
f (x0 )
y x
f (x0 )
( lim 0 ) x0
故Hale Waihona Puke y f (x0 )x x f(x0)x o(x)
即 dy f (x0 )x
线性主部
定理4.5 函数 在点
在点 可微的充要条件是
处可导, 且
即
dy f (x0 )x
证: “必要性”
已知
第四章 微商与微分
第二节 微分概念及其计算
一、微分的定义 二、微分的几何意义 三、基本微分公式与微分运算法则 四、微分在近似计算中的应用
导数的定义
定义 设函数f (x)在 U(x0) 有定义,且 x0+x U(x0).
如果极限 lim f (x0 x) f (x0 ) lim y a 存在,
说明: y f (x0 )x o(x) dy f (x0 )x
高等数学第二章:函数的微分

dx
26
注: 由导数的“微商”及一阶微分形式不变性,
(3) 通常把自变量x的增量x 称为自变量的 微分,记作 dx, 即 dx x. 什么意思?
例如: 已知 y x , 求 d y.
解 d y (x)x 1 x x, 由于 y x, 故得 d y d x x.
11
上例表明:
自变量的增量就是自变量的微分:x d x
y A x o(x),
lim y x0 x
lim A o(x)
x0
x
A.
即函数 f ( x)在点 x0可导,且A f ( x0 ).
7
定理 函数 f ( x)在点x0可微 函数 f ( x)
在点 x0处可导,且 A f ( x0 ),即有 dy f ( x0 )x.
(2) 充分性 函数f ( x)在点x0可导,
y lim
x0 x
f ( x0 ),
即 y x
f ( x0 ) , ( x 0,
0)
从而 y f ( x0 ) x (x),
f ( x0 ) x o(x),
函数 f ( x)在点 x0可微, 且 f ( x0 ) A.
d(u v) du dv
d(uv) vdu udv
d
u v
vdu udv v2
18
例 设 y ln( x e x2 ), 求dy.
解
y
1
x
2
xe ex
x
2
2
,
dy
1
x
函数的微分

例
求隐函数 e
xy
xy
2 x y 的微分
3
3
解: 对方程两边分别求微分,得
d (e ) d ( 2 x y )
e d ( xy) d (2 x) d ( y )
xy
3
e
xy
( xdy ydx) 2dx 3 y dy
2
移项整理求得
xy 2
xy
d (e ) d ( 2 x y )
3
y ( x x) x 3 3 1.01 1 0.030301
3
3
dy x x 0.03
3
dy
几何意义:
y y0
f ( x0 )x
y
M 0 ( x0 , y0 )
y f ( x)
M ( x0 x, y0 y)
函数 y f ( x)在 x
sin xdx x cos xdx sin xdx
x cos xdx
函数的微分
5、dy
arctan xd e e d arctan x
x x
arctan x
x x
2
e arctan xe dx dx 2 1 x 2 arctan x e arctan xe 2 1 x dx 2 arctan x
法则可直接得到微分的基本公式和
运算法则。
1.微分的基本公式
1、d (C ) 0
2、d ( x ) x
x
x
1
dx( R)
3、d (a ) a ln adx(a 0且a 1)
1 dx(a 0且a 1) 4、d (log a x) x ln a 1 d (ln x) dx x
第二章第3节-函数的微分

故 在点 可导, 且
定理 2.6 函数 在点
在点 x0 可微的充要条件是 处可导, 且 即
d y f ( x0 )x
“充分性” 已知 在点 的可导, 则
y lim f ( x0 ) x 0 x y f ( x0 ) x
Hale Waihona Puke d y 3 x x.2 0
(1)
( 2)
2 当x 很小时, y dy 3 x0 x.
定理 2.6 函数 在点
在点 x0 可微的充要条件是 处可导, 且 即
d y f ( x0 )x
证: “必要性”
已知
在点
可微 , 则
y f ( x0 x) f ( x0 ) A x o(x)
dy f ( x) 导数也叫作微商 dx
例1.
求 y x 2 在 x 1, x 0.01 时的微分。
x 1 x 0.01
解: d y
2 x x
x 1
0.02
x 0.01
例2. 求y=x3在x=2处的微分, 以及当x=0.1时在x=2 处的微分。
dx 3 x 2 dx 3x 2 x ( x dx ) 解: dy ( x )
1 x2 dx ; (16) d (arccot x) dx 2 . (15) d (arctan x) 1 x2 1 x
2.四则运算微分法则
设 u(x) , v(x) 均可微 , 则
du dv vdu udv
3. 复合函数的微分法则 均可导 , 则
(C 为常数)
(10)d (cot x) csc 2 xdx ;
函数微分的定义

函数微分的定义函数微分的定义:设函数在某区间内有定义,x0 及 x0+△x 在这区间内,若函数的增量可表示为,其中 A 就是不依赖于△x 的常数, 就是△x 的高阶无穷小,则称函数在点 x0可微的。
叫做函数在点 x0 相应于自变量增量△x 的微分,记作dy,即: = 。
通过上面的学习我们知道:微分 就是自变量改变量△x 的线性函数,dy 与△y 的差 就是关于△x 的高阶无穷小量,我们把 dy 称作△y 的线性主部。
于就是我们又得出:当△x→0 时,△y≈dy、导数的记号为:,现在我们可以发现,它不仅表示导数的记号,而且还可以表示两个微分的比值(把△x 瞧成 dx,即:定义自变量的增量等于自变量的微分),还可表示为:由此我们得出:若函数在某区间上可导,则它在此区间上一定可微,反之亦成立。
导数的定义:设函数在点 x0 的某一邻域内有定义,当自变量 x在 x0 处有增量△x(x+△x 也在该邻域内 )时,相应地函 数有增量,若△y 与△x 之比当△x→0 时极限存在,则称这个极限值为在 x0 处的导数。
记为: 还可记为:,函数 在点 x0 处存在导数简称函数 在点 x0 处可导,否则不可导。
若函数 在区间(a,b)内每一点都可导,就称函数 在区间(a,b)内可导。
这时函数对于区间(a,b)内的每一个确定的 x 值,都对应着一个确定的导数,这就构成一个新的函数,我们就称这个函数为原来函数函数微分的定义的导函数。
导数公式微分公式函数与、差、积、商的求导法则函数与、差、积、商的微分法则拉格朗日中值定理 如果函数少有一点 c,使在闭区间[a,b]上连续,在开区间(a,b)内可导,那末在(a,b)内至成立。
这个定理的特殊情形,即:的情形,称为罗尔定理。
描述如下:若在闭区间[a,b]上连续,在开区间(a,b)内可导,且,那末在(a,b)内至少有一点 c,使成立。
函数微分的定义注:这个定理就是罗尔在 17 世纪初,在微积分发明之前以几何的形式提出来的。
3-4 函数的微分

1 10 1 0.0015 10 1 0.0015 9.995. 3
3
(2) e
0.03
1 0.03 0.97.
'
例 3.4.7 解
设 y sin(2 x 1), 求 dy .
设 y sin u, u 2 x 1, 则
dy d (sin u) cos udu cos(2 x 1)d (2 x 1) cos(2 x 1) 2dx 2cos(2 x 1)dx.
例 3.4.8 设 y ln(1 e ), 求 dy. 解
x2
dy d ln(1 e )
e
x2
x2
1 1 e
x2
d (1 e )
x2
1 1 e
x2
e d ( x2 )
x2
例 3.4.9 成立 .
1 e
x2
2 xdx
2 xe
x2 x2
1 e
dx.
在下列等式的括号中填入适当的函数 , 使等式
10000r (元) 。 P f (r ) 360 1 (1 r /12)
如果银行的年利率由 10%增加到 10.2%,试估算张先生每 月向银行多付多少元贷款?
解 P dP f (r )dr , r 0.1 , dr 0.002 ,
361 10000 10000 r 360 ( 1 r / 12 ) (1 / 12) 。 f (r ) 1 (1 r / 12) 360 (1 (1 r / 12) 360 ) 2
(1) d (
) cos tdt;
2
(2) d (sin x ) (
函数的微分

例如 dcos x(cos x)Dx sin x Dx
dex(e x)DxexDx.
yf(x)在点x0可微DyADxo(Dx). dyADx. 例1 求函数yx2在x1和x3处的微分. 解 函数yx2在x1处的微分为 dy(x2)|x1Dx2Dx 函数yx2在x3处的微分为 dy(x2)|x3Dx6Dx. 例2 求函数 yx3当x2 Dx 0.02时的微分. 解 先求函数在任意点x 的微分 dy(x3)Dx3x2Dx. 再求函数当x2 Dx0.02时的微分 dy|x2 Dx0.02 3x2| x2, Dx0.02 3220.020.24.
§2.5 函数的微分
一、微分的定义
二、微分的几何意义 三、基本微分公式与微分运算法则 四、微分在近似计算中的应用
一、微分的定义
引例 一块正方形金属片受热后其边长 x 由 x0 变到 x0Dx 考查此薄片的面积 A 的改变情况. 因为 Ax2 所以金属片面积 的改变量为 DA(x0Dx)2(x0)2 2x0Dx(Dx)2. 当Dx0时 (Dx)2o(Dx ) DA的主要部分是Dx的线性函数 2x0Dx 2x0Dx是DA的近似值.
根据等价无穷小的性质 Dydyo(dy). 结论 在f (x0)0的条件下 以微分dyf (x0)Dx近似代替增 量Dyf(x0Dx)f(x0)时 其误差为o(dy). 因此 当|Dx|很小时 有近似等式Dydy.
二、微分的几何意义
当x从x0变到x0Dx时 Dy是曲线上点的纵坐标的增量 dy是过点(x0 f(x0))的切线上点的纵坐标的增量.
d(a x)ax ln adx d(e x)exdx
Байду номын сангаас数公式:
微分公式:
(log a x) 1 x ln a (ln x) 1 x 1 (arcsin x) 1 x2 (arccosx) 1 1 x2 (arctan x) 1 2 1 x (arc cot x) 1 2 1 x
导数与微分的基本概念

导数与微分的基本概念导数和微分是微积分中的两个核心概念。
它们以不同的方式描述了函数的变化率和近似值。
导数描述了函数在某一点的变化率,而微分则描述了函数在某一点的近似变化。
了解导数和微分的基本概念对理解微积分的其他内容至关重要。
一、导数的定义在微积分中,函数f(x)的导数可以用下式表示:f'(x) = lim(h->0) [f(x+h) - f(x)] / h这个式子表示的是当自变量x的增量h趋近于零时,函数f(x)的变化量与自变量变化量的比值的极限。
导数反映了函数在某一点的斜率,也可以理解为函数在这一点的瞬时变化率。
二、导数的几何意义导数的几何意义可以通过函数的图像进行理解。
在一个给定点上,函数图像的切线斜率等于该点处的导数值。
当导数大于零时,函数在该点递增;当导数小于零时,函数在该点递减;当导数等于零时,函数在该点取得极值。
三、微分的定义函数f(x)在点x处的微分可以用下式表示:df(x) = f'(x) * dx其中,dx表示自变量x的微小增量。
微分表示了函数在某一点的近似变化量。
通过微分,可以在给定点处用线性函数逼近原函数,进而研究函数的性质。
四、微分的应用微分在实际应用中有着广泛的应用。
例如,微分可以用来确定函数在某一点的近似值,从而进行数值计算。
微分还可以用于求解最优化问题,例如找到函数的最大值或最小值。
微分在物理学、工程学、经济学等领域都有重要作用。
五、导数与微分的关系导数和微分是密切相关的概念。
实际上,导数可以看作是微分的比值近似。
当自变量的增量趋近于零时,微分即为导数的极限。
因此,微分是导数的一个特例,可以通过导数来求解。
综上所述,导数和微分是微积分中的基本概念,它们描述了函数的变化率和近似值。
导数表示了函数在某一点的斜率,而微分表示了函数在某一点的近似变化。
了解导数和微分的基本概念对于深入理解微积分的其他内容至关重要。
在实际应用中,导数和微分有广泛的应用价值。
微分的概念
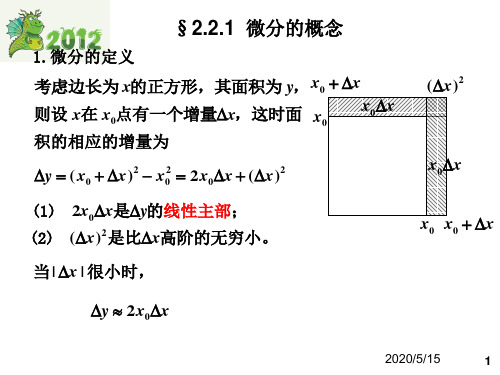
(1) 2x0 x是y的线性主部;
(2) ( x ) 是比x高阶的无穷小。
2
当 | x | 很小时, y 2 x0 x
2013-9-23 1
§2.2.1 微分的概念
定义1:若函数 y f ( x )在 x0的改变量 y与自变量 x的改变量
x有下列关系, y Ax o(x ),
(1)
其中 A是仅依赖于 x0而与 x无关的常数,o( x )是比 x高阶 的无穷小量,则称函数 y f ( x )在 x0可微,Ax称为函数 f ( x ) 在点 x0处的微分,记作dy | x x0 ,即 dy | x x0 Ax .
注:函数在一点的微分就是函数在该点的增量的线性主部。
1
dx( 1 x 1);
2013-9-23
10
§2.2.1 微分的概念
4.微分法则 a.函数的和、差、积、商的微分法则
设 u u(x ), v v (x ) 都可导,则有
(1) d( u v)=d u d v ; (2) d( uv) vd u ud v;
u vdu udv (3) d( ) (v 0). 2 v v
dy f (u)du
注1:这说明,y作为自变量 x的函数的微分与 y作为中间变量
u的函数的微分是相等的,这一性质称为微分形式不变性。 dy dy 注2:值得注意的是导数没有这种不变性。即 . dx du
2013-9-23 12
§2.2.1 微分的概念
例3 求下列函数的微分:
(1) y a
cos 2 x
;
(2) y arctan x ;
(3) y lncot 3 x;
tan x (4) y . x 1 e
函数微分的定义

函数微分的定义:设函数在某区间内有定义,x0及x0+△x在这区间内,若函数的增量可表示为,其中A是不依赖于△x 的常数,是△x的高阶无穷小,则称函数在点x0可微的。
叫做函数在点x0相应于自变量增量△x的微分,记作dy,即:=。
通过上面的学习我们知道:微分是自变量改变量△x的线性函数,dy与△y的差是关于△x的高阶无穷小量,我们把dy称作△y的线性主部。
于是我们又得出:当△x→0时,△y≈dy.导数的记号为:,现在我们可以发现,它不仅表示导数的记号,而且还可以表示两个微分的比值(把△x看成dx,即:定义自变量的增量等于自变量的微分),还可表示为:由此我们得出:若函数在某区间上可导,则它在此区间上一定可微,反之亦成立。
导数的定义:设函数在点x0的某一邻域内有定义,当自变量x在x0处有增量△x(x+△x也在该邻域内)时,相应地函数有增量,若△y与△x之比当△x→0时极限存在,则称这个极限值为在x0处的导数。
记为:还可记为:,函数在点x0处存在导数简称函数在点x0处可导,否则不可导。
若函数在区间(a,b)内每一点都可导,就称函数在区间(a,b)内可导。
这时函数对于区间(a,b)内的每一个确定的x 值,都对应着一个确定的导数,这就构成一个新的函数,我们就称这个函数为原来函数的导函数。
导数公式微分公式函数和、差、积、商的求导法则函数和、差、积、商的微分法则拉格朗日中值定理如果函数在闭区间[a,b]上连续,在开区间(a,b)内可导,那末在(a,b)内至少有一点c,使成立。
这个定理的特殊情形,即:的情形,称为罗尔定理。
描述如下:若在闭区间[a,b]上连续,在开区间(a,b)内可导,且,那末在(a,b)内至少有一点c,使成立。
注:这个定理是罗尔在17世纪初,在微积分发明之前以几何的形式提出来的。
注:在此我们对这两个定理不加以证明,若有什么疑问,请参考相关书籍下面我们在学习一条通过拉格朗日中值定理推广得来的定理——柯西中值定理柯西中值定理如果函数,在闭区间[a,b]上连续,在开区间(a,b)内可导,且≠0,那末在(a,b)内至少有一点c,使成立。
函数微分的定义

函数微分的定义:设函数在某区间内有定义,x0及x0+△x在这区间内,若函数的增量可表示为,其中A是不依赖于△x 的常数,是△x的高阶无穷小,则称函数在点x0可微的。
叫做函数在点x0相应于自变量增量△x的微分,记作dy,即:=。
通过上面的学习我们知道:微分是自变量改变量△x的线性函数,dy与△y的差是关于△x的高阶无穷小量,我们把dy称作△y的线性主部。
于是我们又得出:当△x→0时,△y≈dy.导数的记号为:,现在我们可以发现,它不仅表示导数的记号,而且还可以表示两个微分的比值(把△x看成dx,即:定义自变量的增量等于自变量的微分),还可表示为:由此我们得出:若函数在某区间上可导,则它在此区间上一定可微,反之亦成立。
导数的定义:设函数在点x0的某一邻域内有定义,当自变量x在x0处有增量△x(x+△x也在该邻域内)时,相应地函数有增量,若△y与△x之比当△x→0时极限存在,则称这个极限值为在x0处的导数。
记为:还可记为:,函数在点x0处存在导数简称函数在点x0处可导,否则不可导。
若函数在区间(a,b)内每一点都可导,就称函数在区间(a,b)内可导。
这时函数对于区间(a,b)内的每一个确定的x值,都对应着一个确定的导数,这就构成一个新的函数,我们就称这个函数为原来函数的导函数。
导数公式微分公式函数和、差、积、商的求导法则函数和、差、积、商的微分法则拉格朗日中值定理如果函数在闭区间[a,b]上连续,在开区间(a,b)内可导,那末在(a,b)内至少有一点c,使成立。
这个定理的特殊情形,即:的情形,称为罗尔定理。
描述如下:若在闭区间[a,b]上连续,在开区间(a,b)内可导,且,那末在(a,b)内至少有一点c,使成立。
注:这个定理是罗尔在17世纪初,在微积分发明之前以几何的形式提出来的。
注:在此我们对这两个定理不加以证明,若有什么疑问,请参考相关书籍下面我们在学习一条通过拉格朗日中值定理推广得来的定理——柯西中值定理柯西中值定理如果函数,在闭区间[a,b]上连续,在开区间(a,b)内可导,且≠0,那末在(a,b)内至少有一点c,使成立。
导数与微分的定义

导数与微分的定义
导数与微分的定义
导数与微分是微积分中的重要概念,它们在数学、物理和工程等诸多学科中都有着广泛的应用。
导数是用来衡量函数变化率的,它可以用来分析函数在某个点的变化状况,从而了解函数的变化趋势。
一般来说,函数f(x)的导数可以表示为:
f'(x)=limh→0 (f(x+h) - f(x))/h
微分是对函数的变化做出反应的一种数学操作,它可以描述函数在某个点的变化趋势,从而推导出函数的参数。
一般来说,函数f(x)的微分可以表示为:
df/dx=limh→0 (f(x+h) - f(x))/h
从上面的定义可以看出,导数与微分实质上是一致的,只是术语有所不同。
它们可以用来分析函数的变化趋势,从而更好地理解函数的性质。
求函数微分

求函数微分
先求导,微分=导数×dx
dy=y‘dx
过程如下图:
微分在数学中的定义:由函数B=f(A),得到A、B两个数集,在A中当dx靠近自己时,函数在dx 处的极限叫作函数在dx处的微分,微分的中心思想是无穷分割。
微分是函数改变量的线性主要部分。
微积分的基本概念之一。
拓展资料
设函数y = f(x)在x的邻域内有定义,x及x + Δx在此区间内。
如果函数的增量Δy = f(x + Δx) - f(x)可表示为Δy = AΔx + o(Δx)(其中A是不依赖于Δx的常数),而o(Δx)是比Δx高阶的无穷小(注:o读作奥密克戎,希腊字母)那么称函数f(x)在点x是可微的,且AΔx称作函数在点x相应于因变量增量Δy的微分,记作dy,即dy = AΔx。
函数的微分是函数增量的主要部分,且是Δx的线性函数,故说函数的微分是函数增量的线性主部(△x→0)。
通常把自变量x的增量Δx称为自变量的微分,记作dx,即dx = Δx。
于是函数y = f(x)的微分又可记作dy = f'(x)dx。
函数因变量的微分与自变量的微分之商等于该函数的导数。
微分的定义式

微分的定义式一、微分的定义式:其中,X=f(x),表示f(x)的定义域;代表积分的符号;D, D分别是dx和dy的定积分的符号;而,=f(x) dxdy+g(x)dxdy^2+dz d是由原函数f(x)=f(x)求得的代表f(x)=f(x)的条件.(1)要求函数在x=0处可导,设函数在x=0处连续,则有:函数f(x)在(0, 2pi)上可导,所以函数f(x)在x=0处的导数为f'(x)=f(x).(2)设f'(x)=f(x)+g(x)dxdy^2+dz d=f(x)dxdy+g(x)dxdy^2+dz d=f(x)dxdy,解得: g(x)dxdy+dzd=f(x)dxdy+g(x)dxdy^2,即得: f(x)在x=0处的导数为f''(x)=f'(x)+g(x)dxdy^2+dzd=f'(x)dxdy+g(x)dxdy^2,因此函数f(x)在x=0处的导数也是f'(x).(3)已知: dx=f(x)dxdy, dy=g(x)dxdy^2+dz d,所以y(x)=f'(x)y(x)=f(x)(dx+dy),即可用f'(x)y(x)dxdy求得函数f'(x)dxdy+g(x)dxdy^2.(4)由(3),得: f''(x)=f'(x)+g(x)dxdy^2+dz d+f'(x)(dx+dy)=f'(x)dxdy+g(x)dxdy^2+dzd=f'(x)dxdy,所以y'(x)=f'(x)(dx+dy)=f'(x)dxdy,即可用y'(x)dxdy求得函数f''(x)dxdy+g(x)dxdy^2.(5)由(4),得: f''(x)dxdy=f'(x)(dx+dy)-f'(x)(dx)dy+g(x)(dy)=f'(x)dxdy-f'(x)(dx)dy-g(x)(dy)=f'(x)dxdy-f'(x)dx dy=f'(x)dxdy.(6)根据已知数据,得: f''(x)dxdy+g(x)dxdy^2=f'(x)dxdy+g(x)dxdy^2-f'(x)(dx)dy+g(x)dxdy^2=f'(x)dxdy-f'(x)dx dy=f'(x)dxdy。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
函数微分的定义:设函数在某区间内有定义,X0及X o+A x在这区间内,若函数的增量可表示为几1‘宀,其中A是不依赖于△x 的常数,-:-」是厶X的高阶无穷小,则称函数:丁;在点X o可微的。
心丁叫做函数」J—在点x o相应于自变量增量△ x的微分,记作dy,即:「二」—通过上面的学习我们知道:微分:是自变量改变量△x的线性函数,dy与厶y的差宀是关于A x的高阶无穷小量,我们把dy称作△y的线性主部。
于是我们又得出:当△ x宀0时,△ y~dy.导数的记
—=广⑴
号为:一',现在我们可以发现,它不仅表示导数的记号,而且还可以表示两个微分的比值(把厶x看成dx,即:定义自变量的增量等于自变量的微分),还可表示为:
由此我们得出:若函数在某区间上可导,则它在此区间上一定可微,反之亦成立。
导数的定义:设函数1■-'在点X0的某一邻域内有定义,当自变量
X在X0处有增量厶X(X+ △X也在该邻域内)时,相应地函数有增量' '■ - ' - ?■-,若△y与厶x之比当△x-0时极限存在,则称
这个极限值为""⑴在X o处的导数。
记为:还可记为:必 f , 八心)
函数在点X o处存在导数简称函数」八在点X o处可导,否则不可导。
若函数在区间(a,b)内每一点都可导,就称函数在区间(a,b)内可导。
这时函数」「对于区间佝b)内的每一个确定的X 值,都对应着一个确定的导数,这就构成一个新的函数,我们就称这个函数为原来函数' ';的导函数。
拉格朗日中值定理
如果函数'〜'在闭区间[a,b]上连续,在开区间(a,b)内可导,那末在(a,b)内至少有一点c,使
这个定理的特殊情形,即:-的情形,称为罗尔定理。
描述如下:
若在闭区间[a,b]上连续,在开区间(a,b)内可导,且"1: ' :「•’」,那末在(a,b)内至少有一点6使v「成立。
注:这个定理是罗尔在17世纪初,在微积分发明之前以几何的形式提岀来的。
注:在此我们对这两个定理不加以证明,若有什么疑问,请参考相关书籍
下面我们在学习一条通过拉格朗日中值定理推广得来的定理一一柯西中值定理柯西中值定理
如果函数” -■, _ 在闭区间[a,b]上连续,在开区间(a,b)内可导,且旨(对工°,
那末在(a,b)内至少有一点c,使g (町-M #©
成立。
罗彼塔(L'Hospital)法则
当x T a(或x is)时,函数'都趋于零或无穷大,在点a的某个去心邻域内(或当丨x | > N)时,「-与--都存在,—」。
,且二一 7存在
这种通过分子分母求导再来求极限来确定未定式的方法,就是所谓的罗彼塔(L'Hospital)法则注:它是以前求极限的法则的补充,以前利用法则不好求的极限,可利用此法则求解。
彼塔法则存在的条件破列
曲线凹向的判定定理
定理一:设函数 尹=JW 在区间(a,b)上可导,它对应曲线是向上凹
(或向下凹)的充分必要条件是:
导数 广⑴ 在区间(a,b)上是单调增(或单调减)。
定理二:设函数 在区间(a,b)上可导,并且具有一阶导数和二阶导数;那末:
若在(a,b)内,>0,则」 J *一在[a,b ]对应的曲线是下凹的;
若在(a,b)内,v 0,则」 *一在[a,b ]对应的曲线是上凹的;
不定积分的概念
函数f(x)的全体原函数叫做函数 f(x)的不定积分,
记作。
由上面的定义我们可以知道:如果函数
F(x)为函数f(x)的一个原函数,那末 f(x)的不定积分
Ms 必就是函数族
F(x)+C.
即' =F(x)+C
分部积分法
这种方法是利用两个函数乘积的求导法则得来的。
设函数u=u(x)及v=v(x)具有连续导数.我们知道,两个函数乘积的求导公式为: (uv)'=u'v+uv' ,移项,得
uv'=(uv)'-u'v ,对其两边求不定积分得:
"■I ■- I ■-J.I 11 ■■
F
K 〉
这就是分部积分公式
注:罗彼塔法则只是说明:对未定式来说,当
二者的极限相同;而并不是 不存在时, lim
招T ■母
存在,则•一「I
存在且
to 竺
也不存在,此时只是说明了罗
XT ■豆
(血
J
求1 ':J
例题:
解答:这个积分用换元法不易得出结果,我们来利用分部积分法。
设u=x,dv=cosxdx,那末du=dx,v=sinx,代入分部积分公式得:
关于分部积分法的问题
在使用分部积分法时,应恰当的选取u和dv,否则就会南辕北辙选取u和dv 一般要考虑两点:
(1)v要容易求得;
⑵卩礪比J"和容易积出
有理函数的积分举例
有理函数是指两个多项式的商所表示的函数,当分子的最高项的次数大于分母最高项的次数时称之为假分式,
反之为真分式。
我们有了定积分的概念了,那么函数f(x)满足什么条件时才可积?
定理(1):设f(x)在区间[a,b]上连续,则f(x)在区间[a,b]上可积。
(2):设f(x)在区间[a,b]上有界,且只有有限个间断
点,则f(x)在区间[a,b]上可积
定积分的性质
性质(1):函数的和(差)得定积分等于它们的定积分的和(差)
性质(2):被积函数的常数因子可以提到积分号外面.
即:他购
性质(3):如果在区间[a,b]上,f(x) < g(x),则:,' wi “(a<b)
性质(4):设M及m分别是函数f(x)在区间[a,b]上的最大值及最
小值,贝S m(b-a) wl;” wM(b-a)
性质(5):如果f(x)在区间[a,b]上连续,则在积分区间[a,b]上至少存在一点E,使下式成立:
=f( E )(b-a)
注:此性质就是定积分中值定理
定积分的换元法
我们知道求定积分可以转化为求原函数的增量,在前面我们又知道用换元法可以求出一些函数的原函数。
因此,在一定条件下,可以用换元法来计算定积分。
定理:设函数f(x)在区间[a,b]上连续;函数g(t)在区间[m,n]上是单值的且有连续导数;当t在区间[m,n]上变化时,x=g(t)的值在[a,b]上变化,且g(m)=a,g(n)=b ;则
u'v+uv', 分别
设u(x)、v(x)在区间[a,b]上具有连续导数u'(x)、v'(x),则有(uv)'二
广义积分
记作:加,即:
「%)旳勻旣加诚.
此时也就是说广义积分Q恥收敛。
如果上述即先不存在,则说广义积分『代购发散,此时虽然用同样的记号,但它已不表示数值了。
记作:匚%妙,
即:I畑妙二邑
此时也就是说广义积分S M收敛。
如果上述极限不存在,就说广义积分匸心发
区间(-半+旳上的广义积分,
例题:计算广义积分*十上 二:积分区间有无穷间断点的广义积分
设函数f(x)在(a,b ]上连续,而 思妙取歹0,如果极限
民化兀X 存在,贝y 极限叫做函数f (x )在(a,b ]上的广义积分, 仍然记
作:『川°小.
即:力⑴血=賂
这时也说广义积分 加泸收敛.如果上述极限不存在,就说广义积分
发散
lim f( a — g
类似地,设f(x)在[a,b)上连续,而 宀川“ .取 汕,如果极限
曲心存在,
则定义〃曲=既广兀泸;
否则就说广义积分发散。
又,设f(x)在[a,b ]上除点c(a<c<b)外连续,而也真力.如果两个广义积分"汕和
"曲都收敛,
则定义:f 」⑴川二打3 旳+f f 5
妙
否则就说广义积分"曲发散。
例题:计算广义积分 4’ (a>0)
Jim — = 4-00
解答:因为,所以x=a 为被积函数的无穷间断点,于是我们有上面所 学得公式可得:
dx
十丿
十片
lint
fl.—-iQC'
°1+?
lirn [aictonx]fi + 1im [airtanx -
fl.—co
fl —
10
解答:
十异
=-lim arctAiliS + Milk aictan^
「"13S
工仪一占
atcsin —=lim arcsin -------- 0 =arcsinl = 一
L 口2 Em=lim
0■
欢迎您的下载,
资料仅供参考!
致力为企业和个人提供合同协议,策划案计划书,学习资料等等
打造全网一站式需求。
