高中数学 第二章 圆锥曲线 抛物线第二课时教案 北师大版选修1-1

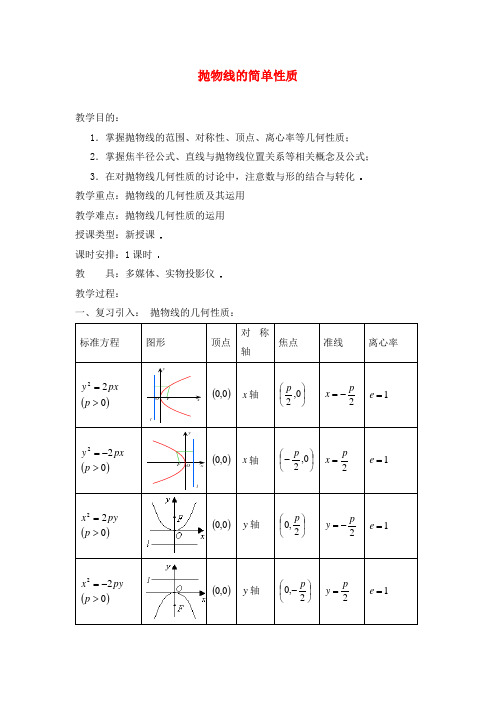
抛物线的简单性质教学目的：1．掌握抛物线的范围、对称性、顶点、离心率等几何性质；2．掌握焦半径公式、直线与抛物线位置关系等相关概念及公式；3．在对抛物线几何性质的讨论中，注意数与形的结合与转化教学重点：抛物线的几何性质及其运用教学难点：抛物线几何性质的运用授课类型：新授课课时安排：1课时教具：多媒体、实物投影仪教学过程：一、复习引入：抛物线的几何性质：()022>=p pyx()0,0y 轴⎪⎭⎫ ⎝⎛2,0p 2p y -=1=e()022>-=p pyx()0,0y 轴⎪⎭⎫ ⎝⎛-2,0p2py =1=e注意强调p 的几何意义：是焦点到准线的距离抛物线不是双曲线的一支，抛物线不存在渐近线二、讲解新课：1.抛物线的焦半径及其应用：定义：抛物线上任意一点M 与抛物线焦点F 的连线段，叫做抛物线的焦半径焦半径公式：抛物线)0(22>=p px y ，0022x pp x PF +=+= 抛物线)0(22>-=p px y ，0022x pp x PF -=-= 抛物线)0(22>=p py x ，0022y pp y PF +=+= 抛物线)0(22>-=p py x ，0022y pp y PF -=-= 2．直线与抛物线： （1）位置关系：相交（两个公共点或一个公共点）；相离（无公共点）；相切（一个公共点）下面分别就公共点的个数进行讨论：对于)0(22>=p px y当直线为0y y =，即0=k ，直线平行于对称轴时，与抛物线只有唯一的交点当0≠k ，设b kx y l +=:将b kx y l +=:代入0:22=++++F Ey Dx Cy Ax C ，消去y ，得到 关于x 的二次方程2=++c bx ax （*）若0>∆，相交；0=∆，相切；0<∆，相离综上，得： 联立⎩⎨⎧=+=pxy b kx y 22，得关于x 的方程02=++c bx ax 当0=a （二次项系数为零），唯一一个公共点（交点） 当0≠a ，则若0>∆，两个公共点（交点）0=∆，一个公共点（切点）0<∆，无公共点 （相离）（2）相交弦长： 弦长公式：21k ad +∆=，其中a 和∆分别是02=++c bx ax （*）中二次项系数和判别式，k 为直线b kx y l +=:的斜率当代入消元消掉的是y 时，得到02=++c by ay ，此时弦长公式相应的变为：d =（3）焦点弦：定义：过焦点的直线割抛物线所成的相交弦。

焦点弦公式：设两交点),(),(2211y x B y x A ，可以通过两次焦半径公式得到： 当抛物线焦点在x 轴上时，焦点弦只和两焦点的横坐标有关： 抛物线)0(22>=p px y ， )(21x x p AB ++=抛物线)0(22>-=p px y ， (21x x p AB +-=当抛物线焦点在y 轴上时，焦点弦只和两焦点的纵坐标有关： 抛物线)0(22>=p py x ， (21y y p AB ++=抛物线)0(22>-=p py x ，(21y y p AB +-=（4）通径：定义：过焦点且垂直于对称轴的相交弦直接应用抛物线定义，得到通径：p d 2=（5）若已知过焦点的直线倾斜角θ则⎪⎩⎪⎨⎧=-=px y p x k y 2)2(20222=--⇒p y k p y ⎪⎩⎪⎨⎧-==+⇒221212py y k p y y θsin 24422221p p k p y y =+=-⇒θθ221sin 2sin 1p y y AB =-=⇒ （6）常用结论：⎪⎩⎪⎨⎧=-=pxy p x k y 2)2(20222=--⇒p y k p y 和04)2(22222=++-p k x p p k x k 221p y y -=⇒和421x x =3．抛物线的法线：过抛物线上一点可以作一条切线，过切点所作垂直于切线的直线叫做抛物线在这点的法线，抛物线的法线有一条重要性质：经过抛物线上一点作一直线平行于抛物线的轴，那么经过这一点的法线平分这条直线和这点与焦点连线的夹角如图．抛物线的这一性质在技术上有着广泛的应用．例如，在光学上，如果把光源放在抛物镜的焦点F 处，射出的光线经过抛物镜的反射，变成了平行光线，汽车前灯、探照灯、手电筒就是利用这个光学性质设计的．反过来，也可以把射来的平行光线集中于焦点处，太阳灶就是利用这个原理设计的4．抛物线)0(22>=p px y 的参数方程：⎩⎨⎧== 222pt y pt x （t 为参数）三、讲解范例：例 正三角形的一个顶点位于坐标原点，另外两个顶点在抛物线)0(22>=p px y 上，求这个正三角形的边长．分析：观察图，正三角形及抛物线都是轴对称图形，如果能证明x 轴是它们公共的对称轴，则容易求出三角形边长．解：如图，设正三角形OAB 的顶点A 、B 在抛物线上，且坐标分别为),(11y x 、),(22y x ，则 1212px y =，2222px y =又|OA|＝|OB|，所以 22222121y x y x +=+ 即 22212122px x px x +=+0)(2)(212221=-+-x x p x x0)](2)[(2121=-++x x p x x∵ 02,0,021>>>p x x ，∴ 21x x =．由此可得||||21y y =，即线段AB 关于x 轴对称． 因为x 轴垂直于AB ，且∠AOx＝30°，所以3330tan 011==x y 所以p y px y 3212111=⋅=， p y AB 342||1== 四、课堂练习：1．正三角形的一个顶点位于坐标原点，另外两个顶点在抛物线()022>=p px y 上，求这个正三角形的边长（答案：边长为p 34）2．正三角形的一个顶点位于坐标原点，另外两个顶点在抛物线()022>=p px y 上，求正三角形外接圆的方程分析：依题意可知圆心在x 轴上，且过原点，故可设圆的方程为：022=++Dx y x ，又∵ 圆过点()32,6p A ， ∴ 所求圆的方程为0822=-+px y x3．已知ABC ∆的三个顶点是圆0922=-+x y x 与抛物线()022>=p px y 的交点，且ABC ∆的垂心恰好是抛物线的焦点，求抛物线的方程（答案：x y 42=）4．已知直角OAB ∆的直角顶点O 为原点，A 、B 在抛物线()022>=p px y 上，（1）分别求A 、B 两点的横坐标之积，纵坐标之积；（2）直线AB 是否经过一个定点，若经过，求出该定点坐标，若不经过，说明理由；（3）求O 点在线段AB 上的射影M 的轨迹方程答案：（1）2214p y y -=； 2214p x x = ；（2）直线AB 过定点()0,2p（3）点M 的轨迹方程为()()0222≠=+-x py p x5．已知直角OAB ∆的直角顶点O 为原点，A 、B 在抛物线()022>=p px y 上，原点在直线AB 上的射影为()1,2D ，求抛物线的方程（答案：x y 252=） 6．已知抛物线()022>=p px y 与直线1+-=x y 相交于A 、B 两点，以弦长AB为直径的圆恰好过原点，求此抛物线的方程（答案：x y =2）7．已知直线b x y +=与抛物线px y 22=()0>p 相交于A 、B 两点，若OB OA ⊥，（O 为坐标原点）且52=∆AOB S ，求抛物线的方程（答案：x y 22=）8．顶点在坐标原点，焦点在x 轴上的抛物线被直线12+=x y 截得的弦长为15，求抛物线的方程（答案：x y 122=或x y 42-=）五、小结 ：焦半径公式、直线与抛物线位置关系等相关概念及公式六、课后作业：七、板书设计（略）八、测 试 题：1．顶点在原点，焦点在y 轴上，且过点P （4，2）的抛物线方程是（ ） (A) x 2＝8y (B) x 2＝4y (C) x 2＝2y (D) y x 212=2．抛物线y 2＝8x 上一点P 到顶点的距离等于它们到准线的距离，这点坐标是(A) （2，4） (B) （2，±4） (C) （1，22） (D) （1，±22）3．抛物线顶点在原点，以坐标轴为对称轴，过焦点且与y 轴垂直的弦长等于8，则抛物线方程为4．抛物线y 2＝－6x ，以此抛物线的焦点为圆心，且与抛物线的准线相切的圆的方程是5．以双曲线191622=-y x 的右准线为准线，以坐标原点O 为顶点的抛物线截双曲线的左准线得弦AB ，求△OAB 的面积．测试题答案： 1．A 2．D 3．x 2＝±8y 4．9)23(22=++y x 525。