同轴线谐振腔资料
谐振腔的原理与应用

谐振腔的原理与应用简介谐振腔是一种用来存储电磁能量的装置,它可以通过提供一个特定的频率和模式来放大电磁波。
在物理学和工程学中,谐振腔被广泛应用于多个领域。
本文将介绍谐振腔的原理和常见的应用。
原理谐振腔的工作原理基于电磁场的相互作用。
谐振腔通常由金属或介电材料制成,形状多样,最常见的是圆筒形或长方形。
在谐振腔内部,电磁波在壁反射,并在腔内来回传播。
当电磁波的频率等于腔内的固有频率时,会出现谐振现象。
谐振频率谐振腔的谐振频率取决于腔体的几何形状和尺寸以及腔内的介质。
常见的谐振频率计算公式为:f = (n * c) / (2 * L)其中,f是谐振频率,n是模式数,c是光速,L是腔体的长度。
谐振模式谐振腔支持多种谐振模式,包括基本模式(也称为TEM模式)和高阶模式。
基本模式是最简单且最常见的模式,电场和磁场分布均沿腔体的传播方向保持不变。
高阶模式的电场和磁场分布更为复杂,通常在高频率应用中使用。
应用谐振腔在科学研究和技术应用中有广泛的应用。
以下是几个常见的应用领域:微波加热谐振腔被广泛应用于微波加热领域。
通过选择合适的谐振频率和模式,可以高效地将微波能量传送到加热目标。
微波加热被用于食品加热、工业材料处理和纳米材料制备等。
光学谐振腔在光学领域有着广泛的应用。
例如,在激光系统中,谐振腔用于放大激光光束。
通过调整谐振腔的参数,可以控制激光的频率和输出功率。
量子力学在量子力学领域,谐振腔被用作量子信息处理和量子计算的基础。
谐振腔可以用来储存和操控量子比特,以实现量子计算和通信。
无线通信谐振腔可以用来增强无线通信系统的性能。
例如,在微波通信中,谐振腔可以用作微波滤波器和放大器,以提高通信质量和传输距离。
总结谐振腔是一种重要的装置,通过谐振现象可以将电磁能量存储和放大。
谐振腔的原理和应用涉及多个学科领域,广泛应用于微波加热、光学、量子力学和无线通信等领域。
对谐振腔的深入理解和应用研究有助于推动科学技术的发展和创新。
第五章 谐振腔

微波谐振器又称作微波谐振腔,它广泛应用于微波信号源、微波 滤波器及波长计中。它相当于低频集中参数的LC谐振回路,是一 种基本的微波元件。谐振腔是速调管、磁控管等微波电子管的重 要组成部分。 微波谐振器可由一段两端短路或两端开路的传输线段组成,电 磁波在其上呈驻波分布,即电磁能量不能传输,只能来回振荡。 因此,微波谐振器是具有储能与选频特性的微波元件。 微波谐振器可以定性地看作是由集中参数LC谐振回路过渡而来 的,如图所示。
微波谐振器中电磁能量关系和集中参数LC谐振回路中能量关系有许 多相似之处,如图。
但微波谐振器和LC谐振回路也有许多不同之处。
1、LC谐振回路的电场能量集中在电容器中,磁场能量集中在电感器,
而微波谐振器是分布参数回路,电场能量和磁场能量是空间分布的;
2、LC谐振回路只有一个谐振频率,而微波谐振器一般有无限多个谐 振频率;微波谐振器可以集中较多的能量,且损耗较小,因此它的 品质因数远大于LC集中参数回路的品质因数,另外,微波谐振器有 不同的谐振模式(即谐振波型)。
即使同一个腔长,对于不同的模式 都会同时谐振于同一个频率上,这就 是圆柱腔存在的干扰模问题。
f 2 23.4GHz
调谐范围: 15.8GHz~23.4GHz
五、微带谐振器 由微带线构成的具有谐振特性的元件,总有一部分未被导体包 围,未能构成腔体,所示称为微带谐振器。微带谐振器有微带线 段谐振器、微带环形谐振器和微带盘形谐振器等形式。 (一)、/2和/4微带谐振器 微带线是一种准TEM波传输线,因此和同轴谐c cp D mn 2 l
2
2
2
对于圆柱腔TMmnp谐振模,有
f 0 D
2
cv cp D mn 2 l
第5章光学谐振腔的基本理论

B sin n
sin
D sin n sin (n 1)
sin
arccos
1 2
(A
D)
1、值是实数(-1<cos<1)时, Tn各元素有界谐
振腔为稳定腔。 2、值有虚部时(-1>cos或者cos>1),旁轴 光线往返有限次后便会逸出谐振腔,谐振腔为非
稳腔。
3、值等于0或者π(cos=±1),Tn各项元素的值
38
§3 谐振腔的衍射理论基础
激光器中所使用的谐振腔是一种开腔, 在这种没有侧面边界的区域内是否存在电磁 场的本征态,即不随时间而变化的稳态场分 布?如何求出这种场分布?这些问题需要用谐 振腔的衍射理论来解决。本节首先给出理想 开腔的模型——孔阑传输线,在此基础上引 入稳态场分布——自再现模的概念。
T
2 R1
10
1 0
L 1
1 2
R2
10
1 0
L 1
1 L 1 L
2 R1
1
2L R1
2 R2
1
2L R2
2L
1 R2
2 R1
2 R2
4L R1R2
2L2
2L R1
2L R2
(1 2L )(1 R1
2L R2
)
=
A C
B
D
15
A
1
2L R2
2(1
L R2
)
1
2g2
1
2L2
L
B 2L R2 2L(1 R2 ) 2Lg2
4L 2 2 2 L L 2L2
C
( )
R1R2 R1 R2
L R1 R2 R1R2
4.5 同轴线谐振腔
l
于是切向电场Er可写成
2 E m a p Er j sin z r l
(4-72)
其中
Em E0 E0
第四章 微波谐振器
§4.5 同轴线谐振腔
因为
E jH
(4-72)
2 Em a p cos z 得到腔内磁场分量Hφ为 H r l
A
Zc
C l
A'
在参考面AA’处,总电纳为零
B | f fr 0
等效电路
第四章 微波谐振器
§4.5 同轴线谐振腔
对于短路的平行双线 对于电容 则
jBl jYc ctgl
jBc j0C
B | f fr Bl Bc f fr 0
2f r C 1 2f r l ctg Zc v
b l ln 2 a Q0 l 1 1 2 ln b a b a
(4-77)
当ι=λr/4时,
b ln 2 a Q0 1 1 8 ln b a b r a
两个传播方向相反的行波叠加时,场的表达式为
E0 a jz E0 a jz Er e e r r
第四章 微波谐振器
§4.5 同轴线谐振腔
在z=0与z=ι处的边界条件:短路板上切向电场Er=0 所以
E0 E0 p l p 或 ( p 1,2,3)
lp
r
2
(4-71)
2a
r
2
2b
lp
即,当ι等于λr/2 或其整数倍,则腔产生谐振.
第四章 微波谐振器
谐振腔的原理及应用

谐振腔的原理及应用1. 什么是谐振腔?谐振腔(Resonant cavity)是一种由金属或其他导电材料制成的封闭空间,用于储存和放大电磁波。
谐振腔可以将特定频率的电磁波在内部反复反射,增强波的能量,从而形成驻波,并将能量传输到相应的装置中。
谐振腔通常由两个或更多的反射面组成,例如金属板、球体或者其他形状。
2. 谐振腔的工作原理谐振腔的工作原理基于在反射面之间来回反射的电磁波。
当电磁波进入谐振腔时,它们会与反射面发生反射,并在腔内形成驻波。
驻波通过波的干涉效果增强了波的幅度,形成高强度的电磁场。
谐振腔中的电磁场可以分为不同的模式,每种模式对应于谐振腔中特定的频率。
这些模式由谐振腔的几何形状和尺寸决定。
例如,对于一个球形谐振腔,最低频率的模式为球壳模式,而对于一个长方体谐振腔,最低频率的模式为长方体模式。
3. 谐振腔的应用谐振腔在许多科学和工程领域中都有广泛的应用。
以下是谐振腔的几个主要应用:3.1 激光器谐振腔是激光器中的重要组成部分。
激光器通过在谐振腔内产生和放大光的驻波,来产生高质量、相干性高的激光光束。
谐振腔可以选择性地增强特定频率的光,并抑制其他频率的光的产生,从而使激光器输出单一波长、窄线宽的光。
3.2 加速器谐振腔在粒子加速器中起着关键作用。
在加速器中,电磁波通过谐振腔与粒子相互作用,给粒子提供加速的能量。
通过调节谐振腔的频率和腔内的电场分布,可以实现对粒子的加速和聚焦。
3.3 通信系统谐振腔在通信系统中也有一定的应用。
例如,在微波通信系统中,谐振腔可以用作滤波器,选择特定频率的信号进行放大和传输,同时抑制其他不需要的频率。
谐振腔还可以用于无线电频率的选择性放大和合成。
3.4 传感器谐振腔还广泛应用于传感器领域,用于检测和测量各种物理量和化学量。
通过改变谐振腔的结构和尺寸,可以实现对不同物理量和化学量的敏感度和选择性。
4. 总结谐振腔是一种能够储存和放大电磁波的封闭空间,通过在反射面之间来回反射的电磁波形成驻波,并将能量传输到相应的装置中。
谐振腔的原理和应用

谐振腔的原理和应用1. 谐振腔的概述谐振腔是一种具有特定谐振频率的封闭空腔,可以通过输入适当的能量来产生共振现象。
它是典型的储存和处理电磁能量的装置。
谐振腔通常由两个或多个导体构成,可以是球体、圆柱体或其他形状。
谐振腔中的电磁波在腔内来回传播,当波长与谐振腔的尺寸相匹配时,波的幅度会增强,形成共振现象。
2. 谐振腔的工作原理谐振腔的工作原理基于波在腔内来回传播的特性。
当波的波长与腔的尺寸相匹配时,波将在腔内形成驻波,从而引起共振现象。
驻波是指波的前进波和反射波在空间中叠加形成的特定波形。
谐振腔的尺寸会对共振频率产生影响,通常使用特定的尺寸使腔内波的特定频率产生共振。
3. 谐振腔的种类谐振腔可分为几种主要类型,包括: - 矩形谐振腔:由矩形金属盒构成,通常用于微波和毫米波领域中的应用。
- 圆柱形谐振腔:由圆柱形导体构成,广泛应用于激光器、微波器件和电子设备中。
- 球形谐振腔:由金属球壳构成,常用于高频电路和粒子加速器中。
- 其他形状:还有其他形状的谐振腔,如椭圆形、方形等,根据具体要求来设计制造。
4. 谐振腔的应用领域谐振腔在许多领域中有广泛的应用,包括但不限于: - 无线通信:谐振腔被用于构建无线电发射器和接收器中的振荡器和滤波器。
- 激光器:谐振腔是激光器中的关键组件,通过谐振腔可实现激光的输出和放大。
- 科学研究:谐振腔在物理学、天文学等科学研究中扮演着重要的角色,用于研究波的行为、光的性质等。
- 医学成像:MRI(磁共振成像)中的谐振腔用于产生和检测磁共振信号。
- 粒子加速器:谐振腔在粒子加速器中起到重要的作用,用于加速并聚焦激发粒子。
5. 谐振腔的优缺点谐振腔作为一种装置有其优点和缺点: ### 优点 - 高效率:谐振腔可以储存和处理电磁能量,具有较高的能量传递效率。
- 精确控制:通过设计和改变谐振腔的尺寸和形状,可以实现对特定频率的精确控制。
- 宽频带:一些谐振腔可以工作在宽频带范围内,适用于多种应用场景。
4-1.2同轴线谐振腔解析

而
ˆ H Js n
2
s
s
s
(4-15)
J s H
第四章 微波谐振器
§4.2 谐振腔的主要特性参数
2 1 故 P Rs H dS 2 s 所以固有品质因数可写为
Q0 2
V
H H
2
dV
S
2
(4-16)
dS
这里δ为趋肤深度:
1 f
腔本身的损耗功率
外界负载上损耗的功率
第四章 微波谐振器
§4.2 谐振腔的主要特性参数
有载品质因数还可以写成
1 Pi Pc Pi Pc 1 1 QL rW rW rW Q0 Qc
(4-21)
固有品质因数
耦合品质因数
Qc
若腔体和外界负载之间的耦合程度定义一个量 k Q0 (4-22)
1.场解法 分析规则波导时,用场解法. 求解波动方程,中间过程 得到关于K的特征方程.
求谐振腔的谐振频率方法类似
边界 条件 ˆE 0 n ˆH 0 n
2 H K 2 H 0
特征值Kc (无穷多个)
截止波长 截止频率 不同之处:特 征值Kr,不仅 与横向参量有 关,也与纵向 参量有关。
e e,max
反之,当磁场最大时,电场为零,且此时总储能为 2 * H H dV H dV (4-13) W Wm Wm ,max 2Βιβλιοθήκη 2v
2
v
v
2
v
谐振腔的耗能包括导体和介质损耗,假定介质是无耗的, 2 则腔内损耗功率为 1 (4-14) P R J dS
同轴谐振腔

和 C 一定时,存在有许多个谐振频率 01, 02,。
另一方面,如果给定 0 和
C,则由上式可求得谐振腔的长
度
l
=
0
2
arctan
1 0CZ
0
p
0
2
上式中,p = 0,1,2, 。
图 5.5-5 电容加载同轴腔的
边缘电场线
1
Z0 C1
cot(l) = a2
d
0C
=
0 C2
=
C = C1 C2
频率 下降 。 注意,如果腔的上
下底整个地向内或向外变化,其谐
图 5-6-1
圆柱形谐振腔 E010 模场分布
振频率 将不变化。 因为圆柱形谐 振腔 E010 模的谐振波长 0 = 2.62R,
与柱体的高度 l 无关。
2.介质微扰
若在谐振腔中一小区域 v 内介质参数由 , 改变为 和 ,则有
振频率,从而实现谐振腔的磁调谐。
图 5.6-4 脊形波导
二、谐振腔的激励与耦合
微波谐振腔必须与外电路相连接组成微波系统才能工 作,而且还必须由外电路中的微波信号激励才能在腔体中 建立振荡;而腔体中的电磁振荡又必须通过耦合才能输出 到外界负载上去。 由于微波元件电磁能量传输的可逆特性, 谐振腔的激励元件和耦合元件的结构和工作特性是完全相 同的。 也就是说,一个元件用作激励和用作耦合时所具 有的特性完全相同,它们两者的差别仅在于波在其中的传 输方向相反。
边缘电场线为 1/4 圆弧。
图 5.5-5 电容加载同轴腔的
边缘电场线
图 5.5-4 电容加载同轴腔的等效电路
1 Z0
cot(l)
0C
=
0
内导体端面与端壁之间平板电容可按下式来计算:
《电磁场与微波技术教学课件》4.5同轴线谐振腔

03
同轴线谐振腔的工作模式
同轴线谐振腔的主模
定义
01
同轴线谐振腔的主模是指在该谐振腔中,电磁场分布最简单且
能量主要集中在腔体内部的一种工作模式。
特点
02
主模的电场和磁场分布具有旋转对称性,且在主模下,同轴线
谐振腔的谐振频率由腔体的几何尺寸决定。
应用
03
同轴线谐振腔的主模常用于微波信号的选频、滤波和放大等应
它利用同轴线内导体和外导体之间的电容效应,以及高介电常数 介质对电场的影响,实现微波信号的谐振。
同轴线谐振腔的原理
同轴线谐振腔的原理基于微波谐振理论,当特定频率的微波 信号输入时,会在同轴线谐振腔内产生谐振,能量被限制在 腔内,从而实现信号的选频和放大。
同轴线谐振腔的谐振频率由其几何尺寸和高介电常数介质的 性质决定。
关键环节。
04
同轴线谐振腔的设计与优化
同轴线谐振腔的设计原则
结构简单
同轴线谐振腔的结构应尽可能简单,以降低制造成本 和复杂度。
高Q值
为了获得更好的性能,同轴线谐振腔应具有高Q值, 这意味着较低的能量损耗。
易于调整
设计时应考虑未来可能需要的调整,以便在必要时对 同轴线谐振腔进行优化。
同轴线谐振腔的优化方法
80%
介质常数
填充介质的介电常数会影响同轴 线谐振腔的谐振频率和品质因数 。
同轴线谐振腔的特性
谐振频率
同轴线谐振腔具有特定的谐振 频率,由其长度和填充介质的 介电常数决定。
品质因数
同轴线谐振腔的品质因数表示 其能量储存和放出的能力,是 评估其性能的重要参数。
阻抗特性
同轴线谐振腔的阻抗特性对其 应用具有重要影响,阻抗匹配 是实际应用中需要考虑的问题 。
同轴谐振腔2

) 。
因此, /4 同轴线谐振腔的谐振波长为 4l 0 = 2p 1
/4 同轴线谐振腔的品质因数为 0 1 Q0 = 4 l 1 (D d)
D ln( D d )
/4 同轴线谐振腔与 /2
同轴线谐振腔的差别仅在于它 图 5.5-2 /4 同轴线谐振腔 少一个端面的导体损耗。
图 5.5-3
电容加载同轴腔
图 5.5-4
电容加载同轴腔的等效电路
1 cot( l ) 0C = 0 Z0 等效电路中集中参数的电容 C 由两部分组成:一部分 是由内导体端面与端壁构成的平板电容,另一部分是由内 导体侧面与端壁构成的边缘电容。 图 5.5-5 给出了内导体端面与端壁之间电容的示意图。 作为定性分析,假设图 5.5-5 中 边缘电场线为 1/4 圆弧。
/2 和 /4 同轴线谐振腔的横向尺寸的选择应由下列条
件确定: (1)为保证同轴线谐振腔工作于 TEM 模而不出现高次 模要求
(d D)/2 < 0min 即 (a b) < 0min (2)为保证同轴线谐振腔有较高的 Q0 值,应取
2 (D/d) 6
即
2 (b/a) 6
一段两端短路的同轴线构成 的,如图 5.5-1 所示。 图中 D = 2b 为同轴腔的外导体的 内直径,d = 2a 为同轴腔的 内导体直径。
图 5.5-1
/2 同轴线谐振腔
为了满足腔的两端面为纯驻波电压波节点的边界条件,
在谐振时其腔长应等于 0 /2 的整数倍,即 l = p 0/2(p = 1, 因此, /2 同轴线谐振腔的谐振波长为 2,3,)。 2l 0 = p 1) 当腔长 l 一定时,相应于 不同的 p 值存在许多个谐 振波长 0, 这种特性称为 多谐性;
第5章谐振腔资料.

r22
1
1 F
0 1
r1 0
r1 r1
F
平行于光轴的光线过焦点
(3)若 r1 F1
r22
1
1 F
0 1
F1 1
F1
0
过焦点的光线平行于光轴
过光心的 2 光线不改
变方向
r1,r2
-2 2
F
F 1
r1,r2
例1 入射光线的坐标为r1=5cm,1=0.02弧度,求 通过曲率半径分别为R=0.4m、R=2.5m的凹面反射
g
2
2
g
2
1
R1、R2:两反射镜面曲率半径 L:谐振腔长度
证
①
②
R1
R2
④
③
L
r22 T1r11 r33 T2 r22 T2T1r11 r44 T3r33 T3T2T1r11 r55 T4 r44 T4T3T2T1r11
T T4T3T2T1
1 L
T1 T3 0 1
非稳 非稳 稳定
3、平凹腔: L<R时稳定
非稳 非稳
稳定
4、双凸腔、双平腔、平凸腔为非稳腔
§4 谐振腔衍射理论
推导思路:
出发点:菲涅尔基尔霍夫积分公式
应用
于谐振腔 利用自再现模概念,引进复常数
因子
衍射积分方程(一般表达式)
§4 谐振腔衍射理论
一、谐振腔模型——孔阑传输线 二、自再现模
1、概念光在腔内往返传播后,可以再现的一种稳定横向光场分布
ik
4
M
'
uq
(x'
,
y'
)
e
ik
(1 cos )ds'
微波技术同轴谐振腔

同轴谐振腔的市场发展前景
01
通信领域的应用
同轴谐振腔在通信领域具有广泛的应用,如卫星通信、移动通信等,其
高性能和高稳定性能够满足通信设备的需求,未来市场前景广阔。
同轴谐振腔具有高品质因数、高稳定性、易于集成等优点,广泛应用于微波通信、 雷达、电子对抗等领域。
同轴谐振腔的工作原理
01
当电磁波在同轴谐振腔中传播时,会在腔内形成驻波,即电场 和磁场在空间上呈现周期性分布。
02
在特定频率下,电磁波在腔内形成稳定的共振,能量被限制在
腔内并不断循环。
同轴谐振腔的谐振频率由腔体尺寸、介质材料和电磁波的传播
低。
机械加工法
通过车削、铣削、钻孔等机械加工 方法,将金属块加工成同轴谐振腔 的形状。该方法精度较高,适用于 对精度要求较高的应用。
焊接法
将多个金属部件焊接在一起,形成 同轴谐振腔。该方法适用于复杂结 构的同轴谐振腔制造。
04
同轴谐振腔的微波技术 应用
在雷达系统中的应用
雷达发射机
同轴谐振腔可以作为雷达发射机的微 波功率放大器,将低功率的微波信号 放大到足够的功率,以实现远距离的 探测和目标识别。
微波技术同轴谐振腔
目录
• 同轴谐振腔简介 • 同轴谐振腔的特性 • 同轴谐振腔的设计与制造 • 同轴谐振腔的微波技术应用 • 同轴谐振腔的发展趋势与展望
01
同轴谐振腔简介
同轴谐振腔的定义
同轴谐振腔是一种微波谐振器件,由同轴传输线围成环形空间,并填充介质材料。
它由内外导体构成,内导体位于中心,外导体围绕内导体,形成一个封闭的空腔。
第五章微波谐振腔1

) 。
因此, /4 同轴线谐振腔的谐振波长为 4l 0 2p 1
/4 同轴线谐振腔的品质因数为 0 1 Q0 4 l 1 (D d)
D ln( D d )
/4 同轴线谐振腔与 /2
同轴线谐振腔的差别仅在于它 图 5.2-2 /4 同轴线谐振腔 少一个端面的导体损耗。
Q0
上式中,
2 V H dv
2
S H t ds
2
0 c 性材料,c 0,|H | 为腔中磁场,|Ht| 为腔壁导体
为腔壁导体的趋肤深度。 对于非磁
表面的切向磁场。 上式适用于各种型式的谐振腔,只要能 够求出腔中的磁场分布就能够用它来计算 Q0 值。
图 5.2-1
谐振腔的并联等效电路
第5章
§5.2
微波谐振腔
同轴谐振腔和微带谐振腔
一、同轴线谐振腔
二、微带谐振器
同轴线和微带线分别工作于 TEM 模和准 TEM 模,因 此由它们所构成的谐振腔具有工作频带宽、振荡模式简单 和场结构稳定等优点。
一、同轴线谐振腔(Coaxial Cavity)
同轴线谐振腔共有三种形式:/2 同轴腔,/4 同轴腔 和电容加载同轴腔。
时间上有 /2 的相位差,即在电场为最大时磁场为零,而在 电场为零时,磁场为最大。 纯驻波电场和磁场虽然交织在一起, 谐振腔中的振荡过程与在 LC 谐振回路中相似,也是 电磁场能量以电能和磁能两种形式相互转换的过程。
但是在电场波腹处,磁场为零;在磁场波腹处,电场为零。
谐振腔和 LC 回路的比较: 共性: 1. 都是谐振元件,都具有储能和选频的特性; 2.具有相同的振荡过程。 不同之处: 1. 谐振腔是分布参数电路,而 LC 回路是集中参数电路; 2. 谐振腔具有多谐性,即相应于腔中不同的驻波场分布, 可以存在有许多个不同的谐振频率,而 LC 回路只能有单个 谐振频率; 3.谐振腔的品质因数 Q 值要比 LC 回路高得多。
第三谐振腔

3. 矩形谐振腔Q值的求解
(2)介质损耗。
j " r 0 (1 j tan )
对于导电媒质
" tan
tan
(1 j ) r 0 (1 j tan )
1 2 W 2 V E dV P 1 E 2 dV L 2 0 V 0W 1 Q0 d PL tg
2. 矩形谐振腔谐振波长和谐振频率
0
c
2 m n p a b l
2 2 2
r r
f0
1
1 m n p 2 a b l
2
2
2
下标m,n,p为自然数,分别表示场沿X,Y,Z方向变化的 半个驻波数的个数。对于TEmnp来说,p不能为零。 谐振波长r最大的振荡模式为谐振腔的最低振荡模式或主振荡 模式 。
kmnp 2
1 p r r c 2l c
2
2
谐振波长 λr
举例:对于(a*b)=7.112mm *3.556 mm矩形波导腔l=8.57mm。
2 c kc
2 m n a b
2 2
离散值
谐振腔光学谐振腔激光谐振腔汽车谐振腔微腔的谐振原理谐振腔的作用进气谐振腔矩形谐振腔串联谐振谐振频率
第三章 微波谐振器 本章重点:
1. 谐振腔的基本参数及计算公式
2. 各类谐振器的特性,包括矩形波导谐 振器、圆波导谐振腔,同轴线谐振腔
历 史
1938年,美国斯坦福大学(University of Stanford)的W.W.Hansen教授发表了关于 谐振腔(当时叫Rumbatron)的想法。并且, 他指导Varian兄弟(R.Varian和S.Varian) 利用谐振腔对电子束进行速度调制,从而发明 了双腔速调管(Klystron),解决了在厘米波 段产生小功率振荡的问题。
4-1.2同轴线谐振腔解析

(4-17) (4-18)
δ和表面电阻率的关系为
f
第四章 微波谐振器
§4.2 谐振腔的主要特性参数
为大致看出Q0与腔容积、表面面积之间的关系, 将Q0的表达式变形.
令
H
2
V
H dV V
2 H V
2
2
H
2
S
H dS S
2
则
Q0
H S
2
A
V S
2
构成谐振器 的相应传输 线或者波导 的截至频率.
(4-8)
(4-9)
一个p对应一个β,对应一个谐振频率。 所以微波谐振器具有多谐性,与低频的LC谐振器不同。
第四章 微波谐振器
§4.2 谐振腔的主要特性参数
4.2.2 品质因数 表征谐振器选择性的优劣和能量损耗程度.
分为固有品质因数Q0和有载品质因数QL 1.固有品质因数
而
ˆ H Js n
2
s
s
s
(4-15)
J s H
第四章 微波谐振器
§4.2 谐振腔的主要特性参数
2 1 故 P Rs H dS 2 s 所以固有品质因数可写为
Q0 2
V
H H
2
dV
S
2
(4-16)
dS
这里δ为趋肤深度:
1 f
第四章 微波谐振器
§4.2 谐振腔的主要特性参数
主要参数:谐振频率、品质因数和谐振电导
4.2.1谐振频率 低频的谐振回路,谐振频率
fr
1 2 LC
取决于电感、电容 微波谐振器可以在一系列频率下产生电磁振荡 谐振频率、谐振波长 本节介绍求谐振频率的四种方法
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(4-73) 二端面上的损耗 (4-74)
侧壁上的损耗 当ι=λr/2时,
1 Q0 1 1 a b 8 b r ln a
2
在谐振频率一定时,Q0与同轴线谐振腔的横截面尺寸a、b有关.
用求极值的方法可以得到,当b/a≈3.6时,Q0有极大值。
第四章 微波谐振器
§4.5 同轴线谐振腔
b l ln 2 a Q0 l 1 1 2 ln b a b a
(4-77)
当ι=λr/4时,
b ln 2 a Q0 1 1 8 ln b a b r a
故
l 2 p 1
2 ( p 1,2,3)
l 2 p 1
r
4
( p 1,2,3)
(4-75)
可见,当ι等于λr/4或它的奇数倍时,腔产生谐振. 故称:四分之一波长型同轴线谐振腔,多谐性.
第四章 微波谐振器
§4.5 同轴线谐振腔
2.固有品质因数 (1)可用公式计算,参考二分之一波长型同轴线谐振腔的计 算方法; (2)直接利用二分之一波长型同轴线谐振腔的结论 由于缺少一块短路板,则短路板上的损耗是二分之一波 长型同轴线谐振腔的一半,于是,Q0可写为
(4-78)
第四章 微波谐振器
§4.5 同轴线谐振腔
4.5.3 电容加载同轴线谐振腔
内导体端面与短路板间平板电容为 a 2
C t
2a
A
2b l
t
考虑边缘电容后的修正式
4a 2 36.8t b a 12 C 6.94 1 lg 10 t 4a t F
谐振腔构造
A
Zc
C l
A'
在参考面AA’处,总电纳为零
B | f fr 0
等效电路
第四章 微波谐振器
§4.5 同轴线谐振腔
对于短路的平行双线 对于电容 则
jBl jYc ctgl
jBc j0C
B | f fr Bl Bc f fr 0
2f r C 1 2f r l ctg Zc v
即
(4-79)
当已知 Z c , v, l , C 利用上式可求出谐振频率fr
第四章 微波谐振器
§4.5 同轴线谐振腔
也可以用图4-13(a)所示的图解法来确定fr
(1)以角频率ωr为横坐标,做函数ωrC的曲线。 该曲线是一条斜率为C的直线,且经过原点。
1 l ctg 的曲线,是一系列余切曲线。 (2)做函数 Zc v
lp
r
2
(4-71)
2a
r
2
2b
lp
即,当ι等于λr/2 或其整数倍,则腔产生谐振.
第四章 微波谐振器
§4.5 同轴线谐振腔
2.固有品质因数
一般表达式
Q0 2V
S
2 H dV
2 H dS
求磁场
同轴线中为TEM波,电场只有Er分量,即
E0a jz Er e r
第四章 微波谐振器
§4.5 同轴线谐振腔
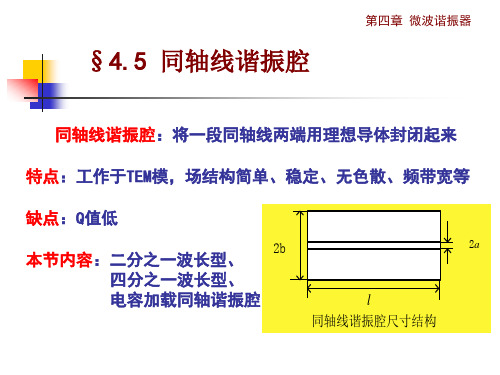
同轴线谐振腔:将一段同轴线两端用理想导体封闭起来 特点:工作于TEM模,场结构简单、稳定、无色散、频带宽等 缺点:Q值低
本节内容:二分之一波长型、 四分之一波长型、 电容加载同轴谐振腔
2b
2a
l 同轴线谐振腔尺寸结构
第四章 微波谐振器
§4.5 同轴线谐振腔
4.5.1 二分之一波长型同轴线谐振腔 1.谐振波长 利用电纳法可以求出
l
于是切向电场Er可写成
2 E m a p Er j sin z r l
(4-72)
其中
Em E0 E0
第四章 微波谐振器
§4.5 同轴线谐振腔
因为
E jH
(4-72)
2 Em a p cos z 得到腔内磁场分量Hφ为 H r l
4.5.2
1.谐振波长 电纳法:从开路端向短路 端看去的输入阻抗为 Zin (l ) jZctgl
四分之一波长型同轴线谐振腔开路l 2 p 1r4
2b
2a
谐振时,开路处
或者电纳
Zin (l )
Bin (l ) 1 0 Zin (l )
短路
第四章 微波谐振器
§4.5 同轴线谐振腔
两个传播方向相反的行波叠加时,场的表达式为
E0 a jz E0 a j z Er e e r r
第四章 微波谐振器
§4.5 同轴线谐振腔
在z=0与z=ι处的边界条件:短路板上切向电场Er=0 所以
E0 E0 p l p 或 ( p 1,2,3)
则固有品质因数表达式可写为
Q0
2 H dS
S
2V
H dV
2
(4-16)
将Hφ在腔体内进行体积分 将Hτ在腔体的内、外表面上进行面积分
第四章 微波谐振器
§4.5 同轴线谐振腔
积分结果代入上面固有品质因数计算公式,得
b l ln 2 a Q0 b 1 1 l 4 ln a b a
(3)取两组曲线的交点就是谐振频率,无穷多个 . 当已知 Z c , v, f r , C 时,可用下式可求出腔长度ι
r 1 r l arctg p 2 2f r CZc 2 由p,可看出,有无穷多个ι
§4.5 同轴线谐振腔
例题
