特殊平行四边形的性质和判定总结
平行四边形性质总结

平行四边形性质总结平行四边形是高中数学中一个重要的几何概念,它具有一系列特殊的性质。
本文将对平行四边形的性质进行总结,并展示其在几何证明和问题求解中的应用。
一、平行四边形的定义和特征平行四边形是指有四个边两两平行的四边形。
其特征包括:1. 两对对边分别相等(对边)。
2. 两对对角线互相平分(对角线)。
3. 对角线互相等长(对角线)。
4. 具有相对的顶点角和内角互补(角)。
二、平行四边形的性质和定理1. 对边性质:平行四边形的两对对边相等。
证明方法:利用平行线之间的性质,应用等腰三角形的性质进行证明。
2. 对角线性质:平行四边形的两对对角线互相平分且等长。
证明方法:利用平行线之间的性质,应用垂直线的性质进行证明。
3. 顶点角性质:平行四边形的相对的顶点角互补。
证明方法:利用平行线之间的性质,应用同位角的性质进行证明。
4. 内角性质:平行四边形的内角以及相对的补角相等。
证明方法:利用平行线之间的性质,应用同位角和内错角的性质进行证明。
5. 边性质:平行四边形的对边平行且相等。
证明方法:利用平行线之间的性质进行证明。
三、平行四边形的证明方法和例题1. 判断平行四边形:通过观察边的性质,判断是否为平行四边形。
如果边平行并且长度相等,则可判断为平行四边形。
2. 证明平行四边形:根据给定条件,利用平行线的性质和等腰三角形的性质进行推导和证明。
例题1:已知ABCD为平行四边形,证明对角线AC和BD相等。
证明:首先,根据平行四边形的性质,可以得出AB∥CD且AB=CD,以及AD∥BC且AD=BC。
然后,根据平行四边形的对角线性质,可以得出对角线AC和BD 互相平分且相等。
因此,根据等分线的性质,AC=BD。
例题2:已知ABCD为平行四边形,证明∠A=∠C。
证明:首先,根据平行四边形的性质,可以得出AB∥CD且AD∥BC。
然后,根据平行线的性质,∠A和∠C是同位角,同位角相等。
因此,∠A=∠C。
四、平行四边形的应用1. 几何证明:平行四边形常用于几何定理的证明过程中,通过利用平行四边形的特性和性质,简化证明过程,提高证明的效率。
平行四边形的性质与判定

平行四边形的性质与判定平行四边形是几何学中常见的一个概念,具有一些特殊的性质和判定条件。
本文将介绍平行四边形的性质,并通过实例展示如何判定一组线段或角度是否构成平行四边形。
一、平行四边形的定义平行四边形是指具有两对对边分别平行的四边形。
根据定义,我们可以得出平行四边形的性质和判定条件。
二、平行四边形的性质1. 相对边相等:平行四边形的对边长度相等。
即AB=CD,AD=BC。
2. 相对角相等:平行四边形的对角角度相等。
即∠A=∠C,∠B=∠D。
3. 对角线互相平分:平行四边形的对角线互相平分。
即AC平分BD,BD平分AC。
4. 对角线相等:平行四边形的对角线相等。
即AC=BD。
5. 内角和为360度:平行四边形的内角和等于360度。
三、判定平行四边形的条件要判定一组线段或角度构成平行四边形,需要满足以下条件之一。
1. 对边相等:如果四边形的对边长度相等,即AB=CD,AD=BC,则这个四边形是平行四边形。
2. 对角线互相平分:如果四边形的对角线互相平分,即AC平分BD,BD平分AC,则这个四边形是平行四边形。
3. 相对角相等:如果四边形的相对角度相等,即∠A=∠C,∠B=∠D,则这个四边形是平行四边形。
在实际问题中,我们可以通过测量边长、角度或线段平分关系来判定是否为平行四边形。
下面举例说明。
例题一:已知线段AB与线段CD互相平分,且∠A=∠C,∠B=∠D,判断ABCD是否为平行四边形。
解析:根据给定条件得知,线段AB与线段CD互相平分,且相对角度相等。
根据判定平行四边形的条件,我们可以得出这个四边形是平行四边形。
例题二:在平面直角坐标系中,顶点坐标分别为A(2, 3),B(7, 3),C(9, -2),D(4, -2)的四边形ABCD,判断是否为平行四边形。
解析:根据给定坐标可以计算出AB的斜率为0,CD的斜率也为0。
根据斜率的性质,我们可以得出AB与CD是平行的。
另外,根据对边长度可以计算出AB=CD,AD=BC。
平行四边形的特征与性质

平行四边形的特征与性质平行四边形是一种特殊的四边形,具有一些独特的特征和性质。
了解这些特征和性质有助于我们更好地理解和应用平行四边形的知识。
本文将介绍平行四边形的定义、特征以及与其他几何形状的关系。
一、平行四边形的定义平行四边形是指具有两对对边分别平行的四边形。
这意味着平行四边形的相邻边线是平行的,而且对角线之间也是平行的。
二、平行四边形的特征与性质1. 对边性质:平行四边形的对边长度相等。
这意味着它的两对对边分别相等。
2. 对角线性质:平行四边形的对角线互相平分。
也就是说,平行四边形的对角线相交于一点,并且把对角线分成相等的两段。
3. 内角性质:平行四边形的内角之和是180度。
由于相邻边是平行的,所以对应的内角互补,即相加等于180度。
4. 外角性质:平行四边形的外角等于其不相邻的内角。
也就是说,平行四边形的外角是其相邻内角的补角。
5. 高度性质:平行四边形的任意一条边都可以看做是它的底边,并且这条底边上的高度是固定的。
三、平行四边形与其他几何形状的关系1. 矩形:矩形是一种特殊的平行四边形,它的所有内角都是直角(90度)。
也就是说,矩形具备平行四边形的所有性质,并且还具有所有角度相等的特征。
2. 菱形:菱形是一种特殊的平行四边形,它的所有边长都相等。
虽然菱形的对边平行,但不一定是直角。
因此,菱形在某些性质上与矩形和普通平行四边形有所不同。
3. 正方形:正方形是一种特殊的矩形和菱形,它既具有所有内角都是直角的特点,也具有所有边长相等的特点。
因此,正方形不仅是一个平行四边形,同时也是一个矩形和菱形。
总结:平行四边形具有对边相等、对角线互相平分、内角之和为180度等特征与性质。
通过了解这些特征和性质,我们可以更好地理解和应用平行四边形的知识。
此外,平行四边形还与矩形、菱形和正方形等几何形状存在一定的关联。
通过比较和分析这些形状之间的关系,我们可以更全面地认识几何学中不同形状的特征和性质。
让我们深入学习平行四边形的特征与性质,为我们的几何学知识打下坚实的基础。
平行四边形的定义及特殊四边形的性质及判定

平行四边形之马矢奏春创作二、平行四边形1.平行四边形界说:两组对边分别平行的四边形是平行四边形.2.平行四边形的判定定理:(1)判定界说:两组对边分别平行的四边形是平行四边形.(2)判定定理1:一组对边平行且相等的四边形是平行四边形.(3)判定定理2:两组对边分别相等的四边形是平行四边形.(4)判定定理3:两组对角分别相等的四边形是平行四边形.(5)判定定理4:对角线互相平分的四边形是平行四边形.3.平行四边形的性质:(6)平行四边形的邻角互补, 对角相等.(7)平行四边形的对边平行且相等.(8)夹在两条平行线间的平行线段相等.(9)平行四边形的对角线互相平分.(10)平行四边形是中心对称图形.4.平行四边形的面积:面积=底边长×高= ah(a是平行四边形任何一边长, h必需是a边与其对边的距离.)三、矩形1.矩形的界说:有一个角是直角的平行四边形是是矩形.2.矩形的判定定理:(1)判定界说:有一个角是直角的平行四边形是是矩形.(2)判定定理1:有三个角是直角的四边形是矩形.(3)判定定理2:对角线相等的平行四边形是矩形.3.矩形的性质:(1)具有平行四边形的一切性质.(2)矩形的四个角都是直角.(3)矩形的对角线相等.(4)矩形既是轴对称图形又是中心对称图形.4.矩形的面积:矩形的面积=长×宽四、菱形1.菱形的界说:有一组邻边相等的平行四边形是菱形.2.菱形的判定定理:(1)判定界说:有一组邻边相等的平行四边形是菱形.(2)判定定理(1):四边都相等的四边形是菱形.(3)判定定理(2):对角线互相垂直的平行四边形是菱形. 3.菱形的性质:(1)具有平行四边形的一切性质.(2)菱形的四条边都相等.(3)菱形的对角线互相垂直, 而且每一条对角线平分一组对角.(4)菱形既是轴对称图形又是中心对称图形.4.菱形的面积:菱形的面积=底×高=对角线乘积的一半五、正方形1.正方形的界说:四边都相等且有一个角是直角的四边形是正方形.2.正方形的判定定理:(1)判定界说:四边都相等且有一个角是直角的四边形是正方形.(2)有一组邻边相等而且由一个角是直角的平行四边形是正方形.(3)有一组邻边相等的矩形是正方形.(4)有一个角是直角的菱形是正方形.(5)既是矩形又是菱形的四边形是正方形.3.正方形的性质:(1)正方形具有平行四边形、矩形、菱形的一切性质.(2)边——四边相等, 邻边垂直, 对边平行且相等.(3)角——四个角都是直角.(4)对角线——相等, 互相垂直平分, 每一条对角线平分一组对角.(5)正方形既是轴对称图形又是中心对称图形.(6)正方形一条对角线上一点到另一条对角线上的两端距离相等.(7)正方形既是轴对称图形又是中心对称图形.4.正方形的面积:正方形的面积=边长的平方=两条对角线乘积的一半六、平行四边形、矩形、菱形和正方形的边、角、对角线之间的关系:。
平行四边形及特殊的平行四边形的性质和判定

平行四边形及特殊的平行四边形一、性质:1.平行四边形的对角;邻角;对边;对角线;是中心对称图形。
2.矩形的四个角为;对边;对角线;是中心对称图形,也是轴对称图形,对称轴有条。
3.菱形的对角;邻角;四条边都;对角线;是中心对称图形,也是轴对称图形,对称轴有条。
4.正方形的四个角为;四条边都;对角线;是中心对称图形,也是轴对称图形,对称轴有条。
二、判定:1.平行四边形的判定:(1)叫做平行四边形。
(定义)(2)的四边形是平行四边形。
(3)的四边形是平行四边形。
(4)的四边形是平行四边形。
2.矩形的判定:(1)的平行四边形叫做矩形。
(定义)(2)的四边形是矩形。
(3)的平行四边形是矩形。
3.菱形的判定:(1)的平行四边形叫做菱形。
(定义)(2)的四边形是菱形。
(3)的平行四边形是菱形。
4.正方形的判定:(1)的平行四边形叫做正方形。
(定义)(2)的矩形是正方形。
(3)的菱形是正方形。
三、其它:1.n边形的内角和为(n≥3),外角和为。
2.平行线的性质定理:夹在两条平行线间的相等。
推论:夹在两条平行线间的相等。
3.对称中心平分连结两个的线段。
4.连结三角形两边中点的线段叫做。
5.中位线定理:三角形的中位线平行于,并且等于第三边的。
6.平行线的传递性:在同一平面内,如果两条直线都和第三条直线平行,那么这两条直线也互相。
7.在证明一个命题时,人们有时先假设命题,从这样的假设出发,经过推理得出和已知条件矛盾,或者与、基本事实、等矛盾,从而得出假设命题不成立是错误的,即所求证的命题正确。
这种证明方法叫做。
1。
平行四边形的定义及特殊四边形的性质及判定

平行四边形的定义及特殊四边形的性质及判定在我们的数学世界中,四边形家族有着各种各样的成员,其中平行四边形是非常重要的一类。
接下来,让我们一起深入了解平行四边形的定义,以及几种特殊四边形的性质和判定方法。
首先,平行四边形的定义很简单:两组对边分别平行的四边形叫做平行四边形。
这就像是给平行四边形打上了一个独特的标签,让我们能够轻易地识别它。
那平行四边形都有哪些性质呢?其一,平行四边形的两组对边分别相等。
想象一下,平行四边形的左右两条边和上下两条边就像是双胞胎,长度是一样的。
其二,平行四边形的两组对角分别相等。
也就是说,相对的两个角大小是相同的。
其三,平行四边形的对角线互相平分。
这就好像两条对角线在平行四边形的内部进行了一场平分的游戏。
其四,平行四边形是中心对称图形,对称中心是两条对角线的交点。
把平行四边形绕着这个交点旋转180 度,它能和原来的图形完全重合。
了解了平行四边形的性质,那怎么判定一个四边形是不是平行四边形呢?方法一,如果两组对边分别相等,那么这个四边形就是平行四边形。
就好像我们通过比较四边形的四条边,发现两两相等,那就可以确定它是平行四边形啦。
方法二,如果两组对边分别平行,那也能判定是平行四边形。
这是从定义出发的判定方法,边的平行关系直接决定了四边形的类型。
方法三,一组对边平行且相等的四边形是平行四边形。
想象一下,有一组边既平行又长度相等,那这个四边形自然就具备了平行四边形的特征。
方法四,两组对角分别相等的四边形是平行四边形。
从角的角度来判断,只要相对的角大小一样,那它就是平行四边形。
方法五,对角线互相平分的四边形是平行四边形。
当两条对角线友好地把对方平分时,这个四边形也就成了平行四边形。
在平行四边形这个大家庭中,还有一些特殊的成员,比如矩形、菱形和正方形。
矩形,也叫长方形,它不仅具有平行四边形的所有性质,还有自己独特的地方。
矩形的四个角都是直角。
那怎么判定一个平行四边形是矩形呢?首先,如果一个平行四边形有一个角是直角,那么它就是矩形。
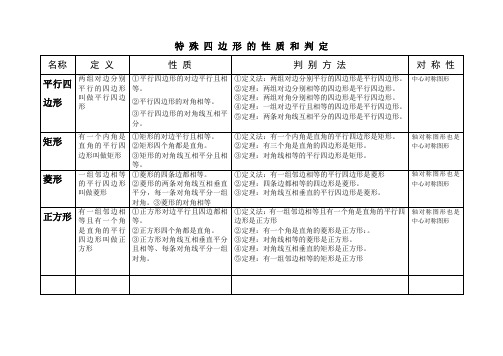
特殊平行四边形性质与判定归纳
特殊四边形的性质和判定
名称定义性质判别方法对称性
直角三角形有一个角是直角
的三角形是直角
三角形
①两个锐角互余
②勾股定理:如果直角三角形的两
直角边为a、b,斜边为c。
那么
2
2
2c
b
a=
+
③直角三角形中,30°的角所对的
直角边是斜边的一半,反之也成立
④直角三角形斜边的中线等于斜边
的一半
①有一个角是直角的三角形是直角三角形
②两个内角互余的三角形是直角三角形
③勾股定理逆定理:如果三角形的三边长a、b、c满足
2
2
2c
b
a=
+,那么这个三角形是直角三角形
④一边中线是这边一半的三角形是直角三角形
特殊四边形的关系。
小学五年级数学重要知识总结平行四边形的性质与判断

小学五年级数学重要知识总结平行四边形的性质与判断小学五年级数学重要知识总结:平行四边形的性质与判断在小学五年级的数学学习中,平行四边形是一个非常重要的概念。
本文将以此为重点,总结平行四边形的性质与判断方法。
一、平行四边形的定义平行四边形是一个特殊的四边形,它的对边是平行的。
我们知道,平行的线段具有相同的斜率,因此平行四边形的对边斜率相等。
二、平行四边形的性质1. 对边性质:平行四边形的对边相等。
即如果ABCD是一个平行四边形,那么AB与CD的长度相等,AD与BC的长度也相等。
2. 同位角性质:平行四边形的同位角相等。
同位角是指位于平行四边形相邻的两边之间且在同一侧的角。
3. 内角性质:平行四边形的内角和为180度。
即平行四边形的任意两个内角之和等于180度。
4. 对角性质:平行四边形的对角线相等且平分。
即平行四边形的对角线AC和BD相等且平分,即点O为AC和BD的交点,AO=OC=BO=OD。
三、根据性质判断平行四边形1. 判断对边是否相等:如果已知一个四边形的对边相等,那么可以判断它是平行四边形。
2. 判断同位角是否相等:如果已知一个四边形的同位角相等,那么可以判断它是平行四边形。
3. 判断内角之和是否为180度:如果已知一个四边形的内角之和为180度,那么可以判断它是平行四边形。
4. 判断对角线是否相等且平分:如果已知一个四边形的对角线相等且平分,那么可以判断它是平行四边形。
通过以上的性质和判断方法,我们可以判断一个四边形是否是平行四边形。
在实际问题中,平行四边形的特性也常常被用到,例如在绘制图形、计算面积等方面。
总结:平行四边形是小学五年级数学学习中的重要知识点。
了解平行四边形的定义、性质以及判断方法,有助于我们更好地理解和运用它们。
通过积极的练习和实践,我们能够在数学学习中轻松应对相关问题,并提高自己的数学素养。
以上就是小学五年级数学重要知识总结的文章内容。
希望对你有所帮助!。
平行四边形的定义及特殊四边形的性质及判定

平行四边形的定义及特殊四边形的性质及判定平行四边形是指四边形的对边两两平行,且对边相等的四边形。
其特殊性质有以下几点:1. 对边平行:平行四边形的定义中已经提到,其对边两两平行。
这意味着它有两对平行的边,且它的对边相等。
2. 对角线平分:平行四边形的两条对角线互相平分。
这意味着从顶点到顶点的线段长相等。
且对角线长度之和等于两倍的中线长度。
3. 内角和为360度:平行四边形的内部角度之和为360度。
这是由于它可以看作是一个由两个相反的等腰三角形组成的四边形。
4. 相邻角互补:平行四边形相邻两个角互补。
即相邻的两个内角之和为180度。
5. 对角线重心:平行四边形的对角线的交点是平行四边形的重心。
这意味着,从平行四边形的任意一个顶点出发,连接对角线交点的线段长度均相等。
如何判定是否是平行四边形?为了判定一个四边形是否为平行四边形,我们需要注意以下几点:1. 同位角是否相等:如果四边形的对边相等,且同位角相等,则它是一个平行四边形。
2. 对角线是否互相平分:如果四边形的对角线互相平分,则它是一个平行四边形。
3. 内角是否和为360度:如果四边形的内角和为360度,则它是一个平行四边形。
4. 相邻角是否补角:如果四边形的相邻两个角互补,则它是一个平行四边形。
总之,平行四边形不仅有着独特的特性,而且在日常生活中随处可见。
我们可以通过了解它的性质和判定方法,来更好地理解和应用它在实际问题中的作用。
平行四边形在几何中的重要性不言而喻。
它具有许多基本的性质,在解决几何问题时能够发挥重要的作用。
因此,对于学习者来说,理解和掌握平行四边形及其相关性质是非常重要的。
首先,平行四边形经常用于测量和设计。
例如,平面中的平行线和平行四边形常常被用来构建建筑和道路。
在测量中,以平行四边形为基础可以利用三角函数法求其面积。
当然,求解时需要知道两个相邻的边长和它们之间夹角的大小。
这也是平行四边形的另一个重要性质,它的相邻角互补。
其次,平行四边形经常用于计算图形的重心及其他几何量。
平行四边形的性质与特征

平行四边形的性质与特征平行四边形是一种特殊的四边形,它具有一些独特的性质和特征。
理解和掌握这些性质和特征对于几何学的学习至关重要。
本文将介绍平行四边形的定义、性质以及与其他几何形状的关系。
一、平行四边形的定义平行四边形是指具有两对对边分别平行的四边形。
简单来说,平行四边形的两对对边是平行的。
在平行四边形中,相邻的两个内角之和为180度,即相邻角互补。
二、平行四边形的性质1. 对边性质:平行四边形的对边长度相等。
这是因为平行四边形的定义中要求两对对边平行,所以对边之间的距离相等。
2. 对角线性质:平行四边形的对角线互相等长,且二分之一对角线相互垂直。
这是因为平行四边形可以看作是一个长方形被一条对角线切分而成,而长方形的对角线是相等的且相互垂直。
3. 内角性质:平行四边形的内角相等。
具体来说,两对相对的内角分别相等。
4. 外角性质:平行四边形的外角相等。
具体来说,平行四边形的内角与其相邻的外角互补,即内角和外角的和为180度。
5. 底角性质:平行四边形的底角相等。
底角是指与底边相邻的内角,它们相等是因为平行四边形中对边之间的距离相等。
6. 对边角性质:平行四边形的对边角互补。
具体来说,平行四边形中相对的对边之间的内角和为180度。
三、平行四边形与其他几何形状的关系1. 矩形:平行四边形的特殊情况之一是矩形。
矩形拥有平行四边形的所有性质,同时它的内角都是直角,即90度。
2. 正方形:正方形是矩形的特殊情况,也是平行四边形的特殊情况。
正方形的四条边相等且垂直,也可以看作是一个特殊的平行四边形。
3. 菱形:菱形是另一种特殊的平行四边形,它拥有平行四边形的部分性质。
菱形的对角线相等且互相垂直,但它的内角并不一定相等。
总结:平行四边形具有两对对边平行的性质,其内角和为180度。
平行四边形的对边相等,对角线互相等长且垂直。
平行四边形可以是矩形、正方形和菱形的特例。
掌握平行四边形的性质与特征,有助于我们更好地理解几何学中的各种形状关系和计算。
平行四边形的性质与判定条件

平行四边形的性质与判定条件平行四边形是几何学中一种重要的四边形,它具有一些独特的性质和判定条件。
在本文中,我们将介绍平行四边形的定义,性质和判定条件,并通过实例进行说明。
一、平行四边形的定义平行四边形是指具有两组对边分别平行的四边形。
简单来说,就是四边形的两组相对边是平行的。
二、平行四边形的性质1. 对边性质:平行四边形的对边长度相等。
证明:设平行四边形ABCD的对边AB和CD平行,我们可以利用平行线的性质来证明其对边长度相等。
首先,我们连接AC和BD,并延长线段AD和BC相交于点E。
由于AB和CD平行,根据同位角的性质,我们可以得到∠AEC = ∠CED 和∠BED = ∠CEB。
又由于三角形AEC和BCD的对应边相等(共边AC和BC相等,BE = CE),以及共边CED,所以可以得出三角形AEC和BCD全等,即AE = BD。
同理,可以证明BC = AD。
因此,平行四边形的对边长度相等。
2. 对角性质:平行四边形的对角线互相平分,并且长度相等。
证明:仍设平行四边形ABCD的对边AB和CD平行,连接AC和BD。
利用同位角的性质,可以证明∠ACD = ∠BAC和∠CBD =∠CBA。
根据直角三角形的性质,我们可以得到AC平方 = AD平方 +CD平方和BC平方 = CD平方 + BD平方。
由于AD = BC(平行四边形的对边长度相等),所以AC平方 = BC平方 + CD平方。
同理,可以证明BD平方 = AC平方 + AB平方。
由于AC平方 = BD平方,所以AC = BD。
因此,平行四边形的对角线互相平分,并且长度相等。
3. 同位角性质:平行四边形的同位角相等。
证明:设平行四边形ABCD的对边AB和CD平行,我们可以利用同位角的性质来证明其同位角相等。
根据同位角的定义,对于平行线AB和CD,若用割线EF与它们相交于点E和F, 分别连接AE,BF,CE,DF,可以得出∠AED = ∠BFE和∠DEC = ∠CFD。
平行四边形的性质与判定

平行四边形的性质与判定平行四边形是一种特殊的四边形,具有一些独特的性质和判定方法。
在本文中,我们将详细介绍平行四边形的性质以及如何通过这些性质来判定一个四边形是否为平行四边形。
一、平行四边形的性质1. 对角线互相平分平行四边形的两条对角线相交于一点,且互相平分。
这意味着通过对角线的交点,可以将平行四边形分成四个相等的三角形。
2. 对边互相平行平行四边形的对边互相平行。
也就是说,平行四边形的任意两条边都是平行的,其对边长度相等。
3. 同位角相等平行四边形中,同位角是指位于平行四边形相邻和同位的两个内角。
这些同位角是相等的。
4. 对角线长度关系平行四边形的对角线之间存在特殊的长度关系。
具体而言,平行四边形的对角线互相等于对角线之和的一半。
二、平行四边形的判定方法1. 对边平行判定法当一个四边形的对边分别平行时,可以判定该四边形为平行四边形。
通过观察四边形的边是否平行,可以快速判断是否为平行四边形。
2. 对角线等长判定法如果一个四边形的对角线相等,那么这个四边形是平行四边形。
这是因为平行四边形的对角线之间存在特殊的长度关系。
3. 同位角相等判定法观察四边形的内角,如果发现四个同位角相等,那么这个四边形就是平行四边形。
4. 边长和角度判定法通过测量四边形的边长和角度,可以利用数学公式来判断一个四边形是否为平行四边形。
例如,如果一个四边形的对边长度相等,且相邻内角之和为180度,那么它就是平行四边形。
三、实例分析举个例子来说明平行四边形的性质和判定方法。
假设有一个四边形ABCD,我们需要判断是否为平行四边形。
首先,我们观察四边形的边,发现AB和CD平行,同时BC和AD也平行。
因此,根据对边平行判定法,我们可以确定这是一个平行四边形。
接下来,我们可以测量四边形的角度。
假设∠A=120度,∠B=60度,∠C=120度,∠D=60度。
通过计算可以发现,相邻内角∠A和∠B的和为180度,∠C和∠D的和也为180度。
平行四边形的性质与判定方法

平行四边形的性质与判定方法在几何学中,平行四边形是四边形的一种特殊形式,具有独特的性质和判定方法。
本文将介绍平行四边形的性质以及常用的判定方法。
一、平行四边形的性质1. 对边平行性质:平行四边形的对边是平行的。
也就是说,如果一条线段与一边平行,并且与另一边平行,则该线段与其他两条边也是平行的。
2. 对角线性质:平行四边形的对角线相互平分。
也就是说,平行四边形的对角线相交于一点,并且该交点将对角线分成相等的两段。
3. 对边长度性质:平行四边形的对边长度相等。
也就是说,对边AB与CD长度相等,对边BC与AD长度相等。
4. 内角性质:平行四边形的内角是180度的。
也就是说,平行四边形的相邻内角和为180度。
二、平行四边形的判定方法1. 对边平行判定方法:如果两组对边分别平行,则该四边形是平行四边形。
常用的判定方法有以下几种:a. 使用角度关系:如果四边形的内角满足相邻内角和为180度,且任意一组对边上的对应角相等,则该四边形是平行四边形。
b. 使用边长关系:如果四边形的两组对边长度相等,则该四边形是平行四边形。
2. 对角线等分判定方法:如果一组对角线互相等分,则该四边形是平行四边形。
常用的判定方法有以下几种:a. 使用距离关系:如果四边形的两组对角线上的中点相互连接后,相交的线段等长,则该四边形是平行四边形。
b. 使用角度关系:如果四边形的一组对角线与另一组对角线的交点将两组对边等分,则该四边形是平行四边形。
三、示例应用假设我们有一个四边形ABCD,其中AB与CD平行,AD与BC平行。
我们可以通过以下步骤来判定该四边形是否为平行四边形:1. 计算角度关系:测量四边形的内角,如果相邻内角和为180度,且两组对边上的对应角相等,那么我们可以初步判断该四边形可能是平行四边形。
2. 计算边长关系:测量四边形的对边长度,如果对边AB与CD长度相等,对边AD与BC长度相等,那么我们可以确认该四边形是平行四边形。
3. 进一步验证:我们可以通过判断对角线等分关系来进一步验证。
平行四边形的性质与判断方法

平行四边形的性质与判断方法平行四边形是几何学中的一种特殊四边形,它具有一些独特的性质和判断方法。
本文将介绍平行四边形的性质,并提供相关判断方法。
性质一:对边平行性平行四边形的定义是具有两组对边分别平行的四边形。
所谓对边,是指四边形的相对边。
如果一组对边平行,则另一组对边也平行。
这是平行四边形的基本性质之一。
性质二:对角线性质平行四边形的对角线互相平分,并且平分线交点的连线等于对角线的一半。
具体来说,平行四边形的两条对角线交于一点,将对角线分成两段。
这两段是相等的,并且平行四边形的两对角线上的点在平分线交点处连成的线段等于对角线的一半。
性质三:同位角性质同位角是指两条平行线被一条横切直线所切割时,所形成的对应角。
平行四边形的同位角相等。
这是由平行四边形的定义和同位角的性质可推导出来的。
判断方法一:边平行判断要判断一个四边形是否为平行四边形,可以通过判断其对边是否平行来确定。
如果一个四边形的两组对边都平行,则可以判定为平行四边形。
判断方法二:对角线性质判断另一种判断平行四边形的方法是通过对角线的性质来判断。
如果一个四边形的对角线互相平分,并且平分线交点的连线等于对角线的一半,则可以确定为平行四边形。
判断方法三:同位角性质判断同位角的性质也可以用来判断平行四边形。
如果一个四边形的同位角相等,则可以确定为平行四边形。
举例说明:假设有一个四边形ABCD,我们要判断它是否为平行四边形。
首先,我们可以通过观察四边形的边来判断。
如果AB∥CD且BC∥AD,即对边平行,则可以确定为平行四边形。
其次,我们可以连接对角线AC和BD,通过观察它们的性质来判断。
如果AC和BD互相平分,并且平分线交点的连线等于对角线的一半,则可以确定为平行四边形。
最后,我们可以通过观察同位角来判断。
如果∠A=∠C且∠B=∠D,则可以确定为平行四边形。
总结:平行四边形具有对边平行性、对角线性质和同位角性质。
可以通过判断对边是否平行,对角线是否互相平分以及同位角是否相等来确定一个四边形是否为平行四边形。
几种特殊平行四边形的性质和判定

3.一组对边平行且相等
4.两组对角分别相等
5.两条对角线互相平分
1.有三个角是直角的四边形
2.有一个角是直角的平行四边形
3.对角线相等的平行四边形
1.四边相等的四边形
2.每条对角线平分一组对角的四边形
3.对角线互相垂直的平行四边形
4.有一组邻边相等的平行四边形
1.有一个角是直角的菱形
2.对角线相等的菱形
3.有一组邻边相等的矩形
4.对角线互相垂直的矩形
对称性
只是中心对称图形
既是轴对称图形,又是中心对称图形
面积
S=底×高
S=底×高
S=底×高=对角线乘积的一半
S=边长×边长
几种特殊平行四边形的性质和判定
平行四边形
矩形
菱形
正方形
性质
边
对边平行且相等
对边平行且相等
对边平行,四边相等
对边平行,四边相等
角对角相等对角相等并且个角都是直角对角相等四个角都是直角
对角线
互相平分
互相平分且相等
互相垂直平分,且每条对角线平分一组对角
互相垂直平分且相等,每条对角线平分一组对角
判
定
1.两组对边分别平行
特殊平行四边形的性质和判定总结

判定:
平行四边形的对边平行且相等
边
两组对边分别平行的四边形是平行四边形
平行四边形的对角相等
两组对边分别相等的四边形是平行四边形
平行四边形的对角线互相平分
一组对边平行且相等的四边形是平行四边形
平行四边形的邻角互补
角
两组对角分别相等的四边形是平行四边形
对角线
对角线互相平分的四边形是平行四边形
一.平行四边形的性质及判定:
对角线互相垂直平分且相等的四边形是正方形
二.面积公式
1.平行四边形=底✖️高
2.矩形=长✖️宽
3.菱形=对角线✖️对角线➗2
=底✖️高
4.正方形=边长✖️边长
=对角线✖️对角线➗2
平行四边形___________________菱形
性质:
判定
菱形具有平行四边形的所有性质
边
四条边相等的四边形是菱形
菱形的四条边都相等
菱形的两条对角线互相垂直,并且每一条对角线平分一组对角
对角线
对角线互相垂直的平行四边形是菱形
对角线互相垂直且平分的四边形是菱形
3.正方形:
平行四边形____________________________________正方形
特殊的平行四边形:
1.矩形:
平行四边形___________________矩形
性质:
判定
矩形具有平行四的平行四边形是矩形
矩形的四个角都是直角
有三个角是直角的四边形是矩形
矩形的对角线相等
对角线
对角线相等的平行四边形是矩形
对角线互相平分且相等的四边形是矩形
2.菱形(重点):
性质:
判定:
正方形具有平行四边形、矩形、菱形的所有性质
平行四边形的性质与判定

平行四边形的性质与判定平行四边形是几何学中的一种特殊形状,它具备一系列独特的性质和特点。
本文将探讨平行四边形的性质和如何进行判定。
一、平行四边形的定义与性质平行四边形是指具有两对对边分别平行的四边形。
根据定义,我们可以得出以下性质:1. 对边性质:平行四边形的对边相等。
也就是说,相对的两边长度相等,例如AB=CD,BC=AD。
2. 对角线性质:平行四边形的对角线互相平分。
直线AC与BD互相平分,即AC=BD。
3. 同位角性质:对位的内角相等,对位的外角相等。
例如∠A=∠C,∠B=∠D,∠E=∠G,∠F=∠H。
4. 内角和性质:平行四边形的内角和为360度。
也就是说∠A+∠B+∠C+∠D=360°。
5. 任意一组内角互补:相邻内角互补,即∠A+∠B=180°,∠C+∠D=180°。
二、判定平行四边形的方法判定一个四边形是否为平行四边形,我们可以依据以下方法:1. 对边判定法:如果四边形的对边相等,则为平行四边形。
例如AB=CD且BC=AD,则四边形ABCD为平行四边形。
2. 对角线判定法:如果四边形的对角线互相平分,则为平行四边形。
例如AC=BD,则四边形ABCD为平行四边形。
3. 内角判定法:如果四边形的对位内角相等,则为平行四边形。
例如∠A=∠C且∠B=∠D,则四边形ABCD为平行四边形。
需要注意的是,判定平行四边形时需要满足以上多个条件,只满足其中一个条件是不够的。
三、平行四边形的应用平行四边形是几何学中重要且常见的概念,具有广泛的应用。
以下列举其中几个常见的应用场景:1. 工程设计:在建筑设计中,平行四边形的性质可以用于确定墙面、地板、天花板等部分的平行性,确保设计符合美学和结构要求。
2. 制图与测量:在制图与测量中,利用平行四边形的性质可以进行定位和测量,提高精度和准确性。
3. 数学证明:平行四边形是许多几何证明的基础,通过运用平行四边形的性质可以推导出其他更复杂的几何关系和定理。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
平行四边形有一组领边相等_菱形
性质:
判定
周长
面积
菱形具有平行四边形的所有性质
边
四条边相等的四边形是菱形
边长×4
对角线积的一半或底×高
菱形的四条边都相等
菱形的两条对角线互相垂直,并且每一条对角线平分一组对角
对角线
对角线互相垂直的平行四边形是菱形
对角线互相垂直且平分的四边形是菱形
3.正方形:
对角线互相垂直的矩形是正方形
对角线相等的菱形是正方形
对角线互相垂直且相等的平行四边形是正方形
对角线互相垂直平分且相等的四边形是正方形
一.平行四边形的性质及判定:
特殊的平行四边形:1.矩形:
平行四边形_有一个角是直角_矩形
性质:
判定
周长
面积
矩形具有平行四边形的所有性质
角
有一个角是直角的平行四边形是矩形
邻边之和的二倍
底×高
矩形的四个角都是直角
有三个角是直角的四边形是矩形
矩形的对角线相等
对角线
对角线相等的平行四边形是矩形
对角线互相平分且相等的四边形是矩形
性质:
判定:
周长
面积
平行四边形的对边平行且相等
边
两组对边分别平行的四边形是平行四边形
邻边之和的二倍
底×高
平行四边形的对角相等
两组对边分别相等
一组对边平行且相等的四边形是平行四边形
平行四边形的邻角互补
角
两组对角分别相等的四边形是平行四边形
对角线
对角线互相平分的四边形是平行四边形
平行四边形有一组邻边相等且有一个角是直角___正方形
性质:
判定:
周长
面积
正方形具有平行四边形、矩形、菱形的所有性质
边
一组邻边相等的矩形是正方形
边长×4
边长的平方或对角线积的一半
四个角都是直角,四条边都相等
角
有一角是直角的菱形是正方形
正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角
对角线
