浙教版初中数学几何计算型综合问题(含答案)

合集下载

浙教版九年级数学下学期综合练习及答案

浙教版九年级数学下学期综合练习及答案一、单选题（共10题）1. 由5个相同的正方体组成的几何体如图所示，则它的主视图是（）A ．B ．C ．D ．(第1题) (第2题) (第3题)2. 两个大小不同的球在水平面上靠在一起，组成如图所示的几何体，则该几何体的左视图是（）A．两个外离的圆B．两个外切的圆C．两个相交的圆D．两个内切的圆3. 如图所示的是某几何体的三视图，则该几何体的形状是（）A．三棱锥B．正方体C．三棱柱D．长方体4. 下列立体图形中，左视图是圆的是（）A ．B ．C ．D ．5. 如图是几何体的三视图，该几何体是A．圆锥B．圆柱C．正三棱柱D．正三棱锥(第5题) (第6题) (第7题)6. 如图，AP、BP分别切⊙O于点A、B，∠P=60°，点C是圆上一动点，则∠C度数为（）A.60° C.40° D.72°D、60°或120°7. 如图，△ABC的边AC与⊙O相交于C、D两点，且经过圆心O，边AB与⊙O相切，切点为B．已知∠A=30°，则∠C的大小是（）A．30°B．45°C．60°D．40°8. 如图，Rt△ABC中，∠ACB=90°，AC=4，BC=6，以斜边AB上的一点O为圆心所作的半圆分别与AC、BC相切于点D、E，则AD为（）A．2.5 B．1.6 C．1.5 D．1(第8题) (第9题) (第10题)9. 已知：如图，PA切⊙O于点A，PB切⊙O于点B，如果∠APB=60°，⊙O半径是3，则劣弧AB的长为（）A．πB ．C．2πD．3π10. 如图，点O是△ABC的内切圆的圆心，若∠BAC=80°，则∠BOC=（）A．130°B．100°C．50°D．65°二、填空题（共10题）11. 如图所示，一半径为1的圆内切于一个圆心角为60°的扇形，则扇形的周长为．(第11题) (第12题) (第13题)12. 如图，Rt△ABC中，∠C=90°，AC=6，BC=8．则△ABC的内切圆半径r =13. 如图，方格纸中的每个小方格都是边长为1个单位长度的正方形，每个小正方形的顶点叫格点．△ABC的顶点都在方格的格点上，则cosA=．14. 如图，在小山的东侧A点处有一个热气球，由于受风向的影响，该热气球以每分钟30米的速度沿与地面成75°角的方向飞行，25分钟后到达C处，此时热气球上的人测得小山西侧B点的俯角为30°，则A，B两点间的距离为米．(第14题) (第15题) (第17题)15. 如图，在四边形ABCD中，E、F分别是AB、AD的中点。

初中数学几何综合-含答案

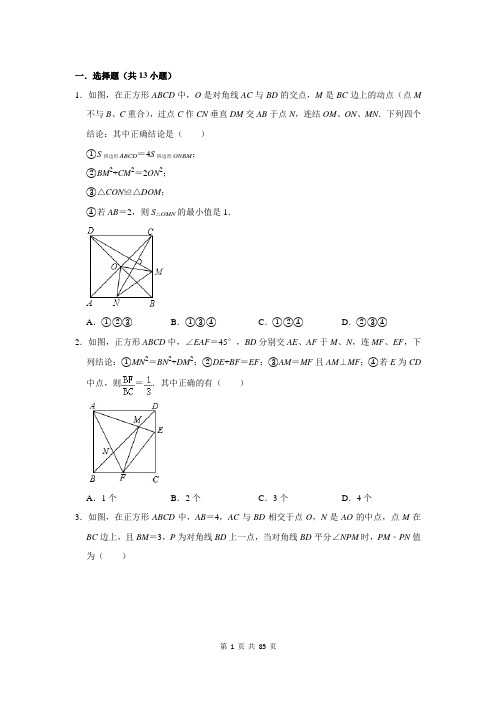
一．选择题（共13小题）1．如图，在正方形ABCD中，O是对角线AC与BD的交点，M是BC边上的动点（点M 不与B、C重合），过点C作CN垂直DM交AB于点N，连结OM、ON、MN．下列四个结论：其中正确结论是（）①S四边形ABCD＝4S四边形ONBM；②BM2+CM2＝2ON2；③△CON≌△DOM；④若AB＝2，则S△OMN的最小值是1．A．①②③B．①③④C．①②④D．②③④2．如图，正方形ABCD中，∠EAF＝45°，BD分别交AE、AF于M、N，连MF、EF，下列结论：①MN2＝BN2+DM2；②DE+BF＝EF；③AM＝MF且AM⊥MF；④若E为CD 中点，则＝．其中正确的有（）A．1个B．2个C．3个D．4个3．如图，在正方形ABCD中，AB＝4，AC与BD相交于点O，N是AO的中点，点M在BC边上，且BM＝3，P为对角线BD上一点，当对角线BD平分∠NPM时，PM﹣PN值为（）A．1B．C．2D．4．如图，在正方形ABCD内一点E连接BE、CE，过C作CF⊥CE与BE延长线交于点F，连接DF、DE．CE＝CF＝1，DE＝，下列结论中：①△CBE≌△CDF；②BF⊥DF；③点D到CF的距离为2；④S四边形DECF＝+1．其中正确结论的个数是（）A．1B．2C．3D．45．如图，已知E，F分别为正方形ABCD的边AB，BC的中点，AF与DE交于点M．则下列结论：①∠AME＝90°，②∠BAF＝∠EDB，③AM＝MF，④ME+MF＝MB．其中正确结论的有（）A．4个B．3个C．2个D．1个6．如图，正方形ABCD和正方形CEFG中，点D在CG上，BC＝1，CE＝3，H是AF的中点，EH与CF交于点O．则HE的长为（）A．2B．C．2D．或27．如图，在正方形ABCD中，E为BC上一点，过点E作EF∥CD，交AD于F，交对角线BD于G，取DG的中点H，连结AH，EH，FH．下列结论：①FH∥AE；②AH＝EH且AH⊥EH；③∠BAH＝∠HEC；④△EHF≌△AHD；⑤若，则．其中哪些结论是正确（）A．①②④⑤B．②③④C．①②③D．②③④⑤8．如图，在正方形ABCD中，AC、BD相交于点O，E、F分别为BC、CD上的两点，BE ＝CF，AE、BF分别交BD、AC于M、N两点，连OE、OF．下列结论：①AE＝BF；②AE⊥BF；③CE+CF＝BD；④S四边形OECF＝S正方形ABCD，其中正确的是（）A．①②B．①④C．①②④D．①②③④9．如图，在正方形ABCD中，M是对角线BD上的一点，点E在AD的延长线上，连接AM、EM、CM，延长EM交AB于点F，若AM＝EM，∠E＝30°，则下列结论：①FM＝ME；②BF＝DE；③CM⊥EF；④BF+MD＝BC，其中正确的结论序号是（）A．①②③B．①②④C．②③④D．①②③④10．如图，在正方形ABCD中，对角线AC，BD交于点O，AG平分∠BAC交BD于G，DE ⊥AG于点H．下列结论：①AD＝2AE：②FD＝AG；③CF＝CD：④四边形FGEA是菱形；⑤OF＝BE，正确的有（）A．2个B．3个C．4个D．5个11．如图，以正方形ABCD的顶点A为圆心，以AD的长为半径画弧，交对角线AC于点E，再分别以D，E为圆心，以大于DE的长为半径画弧，两弧交于图中的点F处，连接AF并延长，与BC的延长线交于点P，则∠P＝（）A．90°B．45°C．30°D．22.5°12．如图，正方形ABCD中，点E在边CD上，连接AE，过点A作AF⊥AE交CB的延长线于点F，连接EF，AG平分∠F AE，AG分别交BC，EF于点G，H，连接EG，DH．则下列结论中：①AF＝AE；②∠EGC＝2∠BAG；③DE+BG＝EG；④AD+DE＝DH；⑤若DE＝CE，则CE：CG：EG＝3：4：5，其中正确的结论有（）A．2个B．3个C．4个D．5个13．如图，矩形ABCD中，O为AC的中点，过点O的直线分别与AB、CD交于点E、F，连接BF交AC于点M，连接DE、BO．若∠COB＝60°，FO＝FC＝2，则下列结论：①FB⊥OC；②△EOB≌△CMB；③四边形EBFD是菱形；④MB＝2．其中正确结论的个数是（）A．1个B．2个C．3个D．4个二．填空题（共3小题）14．如图，点E为正方形ABCD外一点，且ED＝CD，连接AE，交BD于点F．若∠CDE ＝40°，则∠DFC的度数为．15．如图，正方形ABCD中，在AD的延长线上取点E，F，使DE＝AD，DF＝BD，连接BF分别交CD，CE于H，G，下列结论：①EC＝2DG；②∠GDH＝∠GHD；③S△CDG＝S四边形DHGE；④图中只有8个等腰三角形．其中正确的有（填番号）．16．如图，在正方形ABCD中，P为AB的中点，BE⊥PD的延长线于点E，连接AE、BE、F A⊥AE交DP于点F，连接BF，FC．若AE＝2，则FC＝．三．解答题（共24小题）17．如图，在直线l上将正方形ABCD和正方形ECGF的边CD和边CE靠在一起，连接DG，过点A作AH∥DG，交BG于点H．连接HF，AF，其中FH交DG于点M．（1）求证：△AHF为等腰直角三角形．（2）若AB＝3，EC＝4，求DM的长．18．如图，已知正方形ABCD的面积是8，连接AC、BD交于点O，CM平分∠ACD交BD 于点M，MN⊥CM，交AB于点N，（1）求∠BMN的度数；（2）求BN的长．19．如图示，正方形ABCD的对角线交于点O，点E、F分别在AB，BC的延长线上，且∠EOF＝90°，OE与BC交于点M，连接EF，G是EF的中点，连接OG．（1）求证：OE＝OF（2）若∠BOG＝65°，求∠BOE的度数；（3）是否存在点M是BC中点，且使（1）的结论成立，若存在，请给予证明；若不存在，请说明理由．20．如图，正方形ABCD中，AB＝，在边CD的右侧作等腰三角形DCE，使DC＝DE，记∠CDE为α（0°＜α＜90°），连接AE，过点D作DG⊥AE，垂足为G，交EC的延长线于点F，连接AF．（1）求∠DEA的大小（用α的代数式表示）；（2）求证：△AEF为等腰直角三角形；（3）当CF＝时，求点E到CD的距离．21．如图1，在正方形ABCD中，点E在边CD上（不与点C，D重合），AE交对角线BD 于点G，GF⊥AE交BC于点F．（1）求证：AG＝FG．（2）若AB＝10，BF＝4，求BG的长．（3）如图2，连接AF，EF，若AF＝AE，求正方形ABCD与△CEF的面积之比．22．在正方形ABCD中，点E是DC上一点，连结AC，AE．（1）如图1，若AC＝8，AE＝10，求△ACE的面积．（2）如图2，EF⊥AC于点F，连结BF．求证：AE＝BF．23．如图1，正方形ABCD中，点E是边BC延长线上一点，连接DE，过点B作BF⊥DE，垂足为点F，BF与CD相交于点G．（1）求证：△BCG≌△DCE；（2）如图2，连接BD，若，求BG的长．24．如图，在正方形ABCD中，对角线AC、BD相交于点O，E为OC上动点（不与O、C 重合），作AF⊥BE，垂足为G，分别交BC、OB于F、H，连接OG、CG．（1）求证：△AOH≌△BOE；（2）求∠AGO的度数；（3）若∠OGC＝90°，BG＝，求△OGC的面积．25．如图，O为正方形ABCD对角线的交点，E为AB边上一点，F为BC边上一点，△EBF 的周长等于BC的长．（1）若AB＝24，BE＝6，求EF的长；（2）求∠EOF的度数；（3）若OE＝OF，求的值．26．如图，正方形ABCD中，E为BC上一点，过B作BG⊥AE于G，延长BG至点F使∠CFB＝45°（1）求证：∠BAG＝∠CBF；（2）求证：AG＝FG；（3）若GF＝2BG，CF＝，求AB的长．27．如图1，在正方形ABCD中，点P是对角线BD上的一点，点E在AD的延长线上，且P A＝PE，PE交CD于点F，（1）证明：PC＝PE；（2）求∠CPE的度数；（3）如图2，把正方形ABCD改为菱形ABCD，其他条件不变，当∠ABC＝120°，连接CE，试探究线段AP与线段CE的数量关系，并说明理由．28．如图，△ABC中，点O为AC边上的一个动点，过点O作直线MN∥BC，设MN交∠BCA的外角平分线CF于点F，交∠ACB内角平分线CE于E．（1）试说明EO＝FO；（2）当点O运动到何处时，四边形AECF是矩形并证明你的结论；（3）若AC边上存在点O，使四边形AECF是正方形，猜想△ABC的形状并证明你的结论．29．如图，已知平行四边形ABCD中，对角线AC、BD交于点O，E是DB延长线上一点，且△ACE是等边三角形．（1）求证：四边形ABCD是菱形；（2）若∠AEB＝2∠EAB，求证：四边形ABCD是正方形．30．如图1，在正方形ABCD中，G为线段BD上一点，连接AG，过G作AG⊥GE交BC 于E，连接AE．（1）求证：BG＝DG+BE；（2）如图2，AB＝4，E为BC中点，P，Q分别为线段AB，AE上的动点，满足QE＝AP，则在P，Q运动过程中，当以PQ为对角线的正方形PRQS的一边恰好落在△ABE的某一边上时，直接写出正方形PRQS的面积．31．如图，在平行四边形ABCD中，AC⊥AD，延长DA于点E，使得DA＝AE，连接BE．（1）求证：四边形AEBC是矩形；（2）过点E作AB的垂线分别交AB，AC于点F，G，连接CE交AB于点O，连接OG，若AB＝6，∠CAB＝30°，求△OGC的面积．32．如图，在四边形ABCD中，AD∥BC，AB＝BC，对角线AC、BD交于点O，BD平分∠ABC，过点D作DE⊥BC，交BC的延长线于点E，连接OE．（1）求证：四边形ABCD是菱形；（2）若DC＝2，AC＝4，求OE的长．33．如图，在菱形ABCD中，对角线AC、BD交于点O，过点A作AE⊥BC于点E，延长BC至F，使CF＝BE，连接DF．（1）求证：四边形AEFD是矩形；（2）若BF＝8，DF＝4，求CD的长．34．已知：如图，点E为▱ABCD对角线AC上的一点，点F在线段BE的延长线上，且EF ＝BE，线段EF与边CD相交于点G．（1）求证：DF∥AC；（2）如果AB＝BE，DG＝CG，联结DE、CF，求证：四边形DECF是矩形．35．如图，▱ABCD的对角线AC，BD交于点O，过点D作DE⊥BC于E，延长CB到点F，使BF＝CE，连接AF，OF．（1）求证：四边形AFED是矩形．（2）若AD＝7，BE＝2，∠ABF＝45°，试求OF的长．36．如图，平行四边形ABCD中，AC⊥BC，过点D作DE∥AC交BC的延长线于点E，点M为AB的中点，连接CM．（1）求证：四边形ADEC是矩形；（2）若CM＝5，且AC＝8，求四边形ADEC的周长．37．如图，已知△OAB中，OA＝OB，分别延长AO、BO到点C、D．使得OC＝AO，OD ＝BO，连接AD、DC、CB．（1）求证：四边形ABCD是矩形；（2）以OA、OB为一组邻边作▱AOBE，连接CE，若CE⊥BD，求∠AOB的度数．38．如图，在菱形ABCD中，对角线AC，BD交于点O，过点A作AE⊥BC于点E，延长BC到点F，使CF＝BE，连接DF．（1）求证：四边形AEFD是矩形；（2）连接OE，若AD＝10，EC＝4，求OE的长度．39．如图，在平行四边形BPCD中，点O为BD中点，连接CO并延长交PB延长线于点A，连接AD、BC，若AC＝CP，（1）求证：四边形ABCD为矩形；（2）在BA的延长线上取一点E，连接OE交AD于点F，若AB＝9，BC＝12，AE＝3，则AF的长为．40．如图，菱形ABCD中，AC与BD交于点O，DE∥AC，DE＝AC．（1）求证：四边形OCED是矩形；（2）连结AE，交OD于点F，连结CF，若CF＝CE＝1，求AC长．2021年01月06日杨莲莲的初中数学组卷参考答案与试题解析一．选择题（共13小题）1．如图，在正方形ABCD中，O是对角线AC与BD的交点，M是BC边上的动点（点M 不与B、C重合），过点C作CN垂直DM交AB于点N，连结OM、ON、MN．下列四个结论：其中正确结论是（）①S四边形ABCD＝4S四边形ONBM；②BM2+CM2＝2ON2；③△CON≌△DOM；④若AB＝2，则S△OMN的最小值是1．A．①②③B．①③④C．①②④D．②③④【分析】根据正方形的性质，依次判定△CNB≌△DMC，△AON≌△BOM，根据全等三角形的性质以及勾股定理进行计算即可得出结论．【解答】解：∵四边形ABCD是正方形，∴AC⊥BD，AO＝AC，BO＝BD，AC＝BD，∴AO＝BO，∠OAN＝∠OBM＝45°，∠AOB＝90°，∵CN⊥DM，∴∠MCN+∠CMD＝∠CMD+∠CDM＝90°，∴∠CDM＝∠BCN，∵CD＝BC，∠DCM＝∠CBN，∴△CDM≌△BCN（AAS），∴CM＝BN，∴AN＝BM，∴△AON≌△BOM（SAS），∴S△AON＝S△BOM，∴S四边形ONBM＝S△AOB＝S正方形ABCD，∴S四边形ABCD＝4S四边形ONBM；故①正确；∵△AON≌△BOM，∴ON＝OM，∠AON＝∠BOM，∴∠NOM＝∠AOB＝90°，∴△NOM是等腰直角三角形，∴MN2＝2ON2，∵BN2+BM2＝MN2，∴CM2+BM2＝2ON2，故②正确；∵∠MON＝∠COD＝90°，∴∠NOC＝∠MOD，∵OD＝OC，ON＝OM，∴△CON≌△DOM（SAS），故③正确；∵AB＝2，∴S正方形ABCD＝4，∵△AON≌△BOM，∴四边形BMON的面积＝△AOB的面积＝1，即四边形BMON的面积是定值1，∴当△MNB的面积最大时，△MNO的面积最小，设BN＝x＝CM，则BM＝2﹣x，∴△MNB的面积＝x（2﹣x）＝﹣x2+x＝﹣（x﹣1）2+，∴当x＝1时，△MNB的面积有最大值，此时S△OMN的最小值是1﹣＝，故④不正确，故选：A．【点评】本题主要考查了正方形的性质、全等三角形的判定与性质，二次函数的最值以及勾股定理的综合应用，解题时注意二次函数的最值的运用．2．如图，正方形ABCD中，∠EAF＝45°，BD分别交AE、AF于M、N，连MF、EF，下列结论：①MN2＝BN2+DM2；②DE+BF＝EF；③AM＝MF且AM⊥MF；④若E为CD 中点，则＝．其中正确的有（）A．1个B．2个C．3个D．4个【分析】①过B作BD的垂线，截取BH＝MD，连接AH，HN，如图，易证△ADM≌△ABH，△AHN≌△AMN，得MN＝HN，最后根据勾股定理可作判断；②延长CB，截取BI＝DE，连接AI，如图，易证△ADE≌△ABI，△AIF≌△AEF，得IF＝EF，即DE+BF＝EF，成立．③作辅助线，则可证△AFJ为等腰直角三角形，CK＝BF＝KJ，证明∠JCK＝45°，推出四边形BCJK为平行四边形，所以GJ＝BC＝AD，可证△GJM≌△DAM，则M为AJ的中点，又∠AFJ＝90°，故AM＝MF且AM⊥MF，成立．④延长CB，截取BL＝DE，连接AL，可设DE＝a，BF＝x，则EF＝LF＝a+x，CF＝2a﹣x，CE＝a，由勾股定理可知：3x＝2a，则＝＝，成立．【解答】解：①过B作BD的垂线，截取BH＝MD，连接AH，HN，如图，∵四边形ABCD是正方形，∴AD＝AB，∠ADB＝∠ABD＝45°，∠BAD＝90°，∴∠ABH＝45°＝∠ADM，在△ADM和△ABM中，∵，∴△ADM≌△ABH（SAS），∴∠DAM＝∠BAH，AM＝AH，∵∠EAF＝45°，∠BAD＝90°，∴∠DAM+∠BAN＝∠BAH+∠BAN＝45°，∴∠MAN＝∠HAN＝45°，在△AHN和△AMN中，∵，∴△AHN≌△AMN（SAS），∴MN＝HN，Rt△BHN中，HN2＝BH2+BN2，∴MN2＝BN2+DM2，成立．②延长CB，截取BI＝DE，连接AI，如图，在△ADE和△ABI中，∵∴△ADE≌△ABI（SAS），同理得△AIF≌△AEF（SAS），∴IF＝EF，即DE+BF＝EF，成立；③如图，过F作FJ⊥AF交AE的延长线于J，过J作JK⊥BC于K，连接CJ，过J作JG ∥BC交BD于G，∴∠AFJ＝∠AFB+∠JFK＝90°，∵∠AFB+∠BAF＝90°，∴∠BAF＝∠JFK，∵∠EAF＝45°，∠AFJ＝90°，∴△AFJ是等腰直角三角形，在△ABF和△FKJ中，∵，∴△ABF≌△FKJ（SAS），∴AB＝FK＝BC，BF＝KJ，∴CK＝BF＝KJ，∴∠JCK＝45°，∴∠DBC＝∠JCK，∴BG∥CJ，∵JG∥BC，∴四边形BCJK为平行四边形，∴GJ＝BC＝AD，∵AD∥BC∥GJ，∴∠DAM＝∠MJK，在△GJM和△DAM中，∵，∴△GJM≌△DAM（AAS），∴AM＝MJ，则M为AJ的中点，又∠AFJ＝90°，故AM＝MF且AM⊥MF，成立．④延长CB，截取BL＝DE，连接AL，可设DE＝a，BF＝x，则EF＝LF＝a+x，∵E为CD中点，∴CD＝BC＝2a，∴CF＝2a﹣x，CE＝a，在Rt△EFC中，由勾股定理得：EF2＝CE2+CF2∴（a+x）2＝a2+（2a﹣x）2解得：3x＝2a，则＝＝，成立．故选：D．【点评】本题考查了正方形的性质，全等三角形的判定和性质，勾股定理，正确的作出辅助线是解题的关键．3．如图，在正方形ABCD中，AB＝4，AC与BD相交于点O，N是AO的中点，点M在BC边上，且BM＝3，P为对角线BD上一点，当对角线BD平分∠NPM时，PM﹣PN值为（）A．1B．C．2D．【分析】作以BD为对称轴作N的对称点N'，连接MN'，PN'，根据PM﹣PN＝PM﹣PN'≤MN'，当P，M，N'三点共线时，取“＝”，再证得△MCN'∽△BCA，从而推得△MCN'为等腰直角三角形，结合BM＝3．正方形的边长为4，求得CM，即为MN'，问题可解．【解答】解：如图所示，∵对角线BD平分∠NPM，∴作以BD为对称轴N的对称点N'，连接MN'，PN'，根据轴对称性质可知，PN＝PN'，∠NPO＝N′PO，NO＝N′O∵在正方形ABCD中，AB＝4∴AC＝AB＝4，∵O为AC中点∴OA＝OC＝2∵N为OA的中点∴ON＝∴ON'＝CN'＝∴AN'＝3∵BM＝3∴CM＝4﹣3＝1∴＝＝∵∠MCN'＝∠BCA∴△MCN'∽△BCA∴∠CMN'＝∠ABC＝90°∵∠MCN'＝45°∴△MCN'为等腰直角三角形∴MN'＝CM＝1∴PM﹣PN的值为1．故选：A．【点评】本题主要考查了正方形的性质，明确正方形的相关性质及相似三角形的判定、勾股定理等知识点，是解题的关键．4．如图，在正方形ABCD内一点E连接BE、CE，过C作CF⊥CE与BE延长线交于点F，连接DF、DE．CE＝CF＝1，DE＝，下列结论中：①△CBE≌△CDF；②BF⊥DF；③点D到CF的距离为2；④S四边形DECF＝+1．其中正确结论的个数是（）A．1B．2C．3D．4【分析】根据正方形的性质、全等三角形的判定和性质、勾股定理等知识逐项判断即可．【解答】解：∵四边形ABCD是正方形，∴BC＝CD，∠BCD＝90°，∵CF⊥CE，∴∠ECF＝∠BCD＝90°，∴∠BCE＝∠DCF，在△BCE与△DCF中，，∴△BCE≌△DCF（SAS），故①正确；∵△BCE≌△DCF，∴∠CBE＝∠CDF，∴∠DFB＝∠BCD＝90°，∴BF⊥DF，故②正确，过点D作DM⊥CF，交CF的延长线于点M，∵∠ECF＝90°，FC＝EC＝1，∴∠CFE＝45°，∵∠DFM+∠CFB＝90°，∴∠DFM＝∠FDM＝45°，∴FM＝DM，∴由勾股定理可求得：EF＝，∵DE＝，∴由勾股定理可得：DF＝2，∵EF2+BE2＝2BE2＝BF2，∴DM＝FM＝，故③错误，∵△BCE≌△DCF，∴S△BCE＝S△DCF，∴S四边形DECF＝S△DCF+S△DCE＝S△ECF+S△DEF＝+，故④错误，故选：B．【点评】本题考查四边形的综合问题，涉及正方形的性质、全等三角形的性质与判定、勾股定理、三角形面积公式等知识内容，综合程度高，需要学生灵活运用知识解答．5．如图，已知E，F分别为正方形ABCD的边AB，BC的中点，AF与DE交于点M．则下列结论：①∠AME＝90°，②∠BAF＝∠EDB，③AM＝MF，④ME+MF＝MB．其中正确结论的有（）A．4个B．3个C．2个D．1个【分析】根据正方形的性质可得AB＝BC＝AD，∠ABC＝∠BAD＝90°，再根据中点定义求出AE＝BF，然后利用“边角边”证明△ABF和△DAE全等，根据全等三角形对应角相等可得∠BAF＝∠ADE，然后求出∠ADE+∠DAF＝∠BAD＝90°，从而求出∠AMD ＝90°，再根据邻补角的定义可得∠AME＝90°，得出①正确；根据中线的定义判断出∠ADE≠∠EDB，然后求出∠BAF≠∠EDB，判断出②错误；设正方形ABCD的边长为2a，利用勾股定理列式求出AF，再根据似三角形对应边成比例求出AM，然后求出MF，消掉a即可得到AM＝MF，判断出③正确；过点M作MN⊥AB于N，由相似三角形的性质得出＝＝，解得MN＝a，AN＝a，得出NB＝AB﹣AN＝2a﹣a＝a，根据勾股定理得BM＝a，求出ME+MF＝+a＝a，MB＝a，得出ME+MF＝MB，故④正确．于是得到结论．【解答】解：在正方形ABCD中，AB＝BC＝AD，∠ABC＝∠BAD＝90°，∵E、F分别为边AB，BC的中点，∴AE＝BF＝BC，在△ABF和△DAE中，，∴△ABF≌△DAE（SAS），∴∠BAF＝∠ADE，∵∠BAF+∠DAF＝∠BAD＝90°，∴∠ADE+∠DAF＝∠BAD＝90°，∴∠AMD＝180°﹣（∠ADE+∠DAF）＝180°﹣90°＝90°，∴∠AME＝180°﹣∠AMD＝180°﹣90°＝90°，故①正确；∵DE是△ABD的中线，∴∠ADE≠∠EDB，∴∠BAF≠∠EDB，故②错误；设正方形ABCD的边长为2a，则BF＝a，在Rt△ABF中，AF＝＝＝a，∵∠BAF＝∠MAE，∠ABC＝∠AME＝90°，∴△AME∽△ABF，∴＝，即＝，解得：AM＝a，∴MF＝AF﹣AM＝a﹣a＝a，∴AM＝MF，故③正确；如图，过点M作MN⊥AB于N，则MN∥BC，∴△AMN∽△AFB，∴＝＝，即＝＝，解得MN＝a，AN＝a，∴NB＝AB﹣AN＝2a﹣a＝a，根据勾股定理得：BM＝＝＝a，∵ME+MF＝+a＝a，MB＝a，∴ME+MF＝MB，故④正确．综上所述，正确的结论有①③④共3个．故选：B．【点评】本题考查了正方形的性质，全等三角形的判定与性质，相似三角形的判定与性质，勾股定理等知识；仔细分析图形并作出辅助线构造出直角三角形与相似三角形是解题的关键．6．如图，正方形ABCD和正方形CEFG中，点D在CG上，BC＝1，CE＝3，H是AF的中点，EH与CF交于点O．则HE的长为（）A．2B．C．2D．或2【分析】利用直角三角形斜边上的中线等于斜边的一半，分别求得HO和OE的长后即可求得HE的长．【解答】解：∵AC、CF分别是正方形ABCD和正方形CGFE的对角线，∴∠ACD＝∠GCF＝45°，∴∠ACF＝90°，又∵H是AF的中点，∴CH＝HF，∵EC＝EF，∴点H和点E都在线段CF的中垂线上，∴HE是CF的中垂线，∴点H和点O是线段AF和CF的中点，∴OH＝AC，在Rt△ACD和Rt△CEF中，AD＝DC＝1，CE＝EF＝3，∴AC＝，∴CF＝3，又OE是等腰直角△CEF斜边上的高，∴OE＝，∴HE＝HO+OE＝2．故选：C．【点评】本题考查了正方形的性质、直角三角形的性质及勾股定理的知识，综合性较强，难度较大．7．如图，在正方形ABCD中，E为BC上一点，过点E作EF∥CD，交AD于F，交对角线BD于G，取DG的中点H，连结AH，EH，FH．下列结论：①FH∥AE；②AH＝EH且AH⊥EH；③∠BAH＝∠HEC；④△EHF≌△AHD；⑤若，则．其中哪些结论是正确（）A．①②④⑤B．②③④C．①②③D．②③④⑤【分析】①根据正方形对角线互相垂直、过一点有且只有一条直线与已知直线垂直即可得结论；②根据矩形的判定和性质、直角三角形的性质，证明三角形全等即可得结论；③根据全等三角形性质、矩形的性质进行角的计算即可得结论；④根据边边边证明三角形全等即可得结论；⑤根据割补法求四边形的面积，再求等腰直角三角形的面积，即可得结论．【解答】证明：①在正方形ABCD中，∠ADC＝∠C＝90°，∠ADB＝45°，∵EF∥CD∴∠EFD＝90°，得矩形EFDC．在Rt△FDG中，∠FDG＝45°，∴FD＝FG，∵H是DG中点，∴FH⊥BD∵正方形对角线互相垂直，过A点只能有一条垂直于BD的直线，∴AE不垂直于BD，∴FH与AE不平行．所以①不正确．②∵四边形ABEF是矩形，∴AF＝EB，∠BEF＝90°，∵BD平分∠ABC，∴∠EBG＝∠EGB＝45°，∴BE＝GE，∴AF＝EG．在Rt△FGD中，H是DG的中点，∴FH＝GH，FH⊥BD，∴∠AFH＝∠AFE+∠GFH＝90°+45°＝135°，∠EGH＝180°﹣∠EGB＝180°﹣45°＝135°，∴∠AFH＝∠EGH，∴△AFH≌△EGH，∴AH＝EH，∠AHF＝∠EHG，∴∠AHF+AHG＝∠EHG+∠AHG，即∠FHG＝∠AHE＝90°，∴AH⊥EH．所以②正确．③∵△AFH≌△EGH，∴∠F AH＝∠GEH，∵∠BAF＝CEG＝90°，∴∠BAH＝∠HEC．所以③正确．④∵EF＝AD，FH＝DH，EH＝AH，∴△EHF≌△AHD所以④正确．⑤如图，过点H作HM⊥AD于点M，设EC＝FD＝FG＝x，则BE＝AF＝EG＝2x，∴BC＝DC＝AB＝AD＝3x，HM＝x，AM＝x，∴AH2＝（x）2+（x）2＝x2，S四边形DHEC＝S梯形EGDC﹣S△EGH＝（2x+3x）•x﹣×＝2x2S△AHE＝AH•EH＝AH2＝x2∴＝＝．所以⑤不正确．故选：B．【点评】本题考查了正方形的性质、矩形的判定和性质、全等三角形的判定和性质、直角三角形的性质、三角形和梯形的面积等内容，解题关键是综合利用以上知识解决问题．8．如图，在正方形ABCD中，AC、BD相交于点O，E、F分别为BC、CD上的两点，BE ＝CF，AE、BF分别交BD、AC于M、N两点，连OE、OF．下列结论：①AE＝BF；②AE⊥BF；③CE+CF＝BD；④S四边形OECF＝S正方形ABCD，其中正确的是（）A．①②B．①④C．①②④D．①②③④【分析】①易证得△ABE≌△BCF（ASA），则可证得结论①正确；②由△ABE≌△BCF，可得∠FBC＝∠BAE，证得AE⊥BF，选项②正确；③证明△BCD是等腰直角三角形，求得选项③错误；④证明△OBE≌△OCF，根据正方形被对角线将面积四等分，即可得出选项④正确．【解答】解：①∵四边形ABCD是正方形，∴AB＝BC，∠ABE＝∠BCF＝90°，在△ABE和△BCF中，∵，∴△ABE≌△BCF（SAS），∴AE＝BF，故①正确；②由①知：△ABE≌△BCF，∴∠FBC＝∠BAE，∴∠FBC+∠ABF＝∠BAE+∠ABF＝90°，∴AE⊥BF，故②正确；③∵四边形ABCD是正方形，∴BC＝CD，∠BCD＝90°，∴△BCD是等腰直角三角形，∴BD＝BC，∴CE+CF＝CE+BE＝＝BC，故③错误；④∵四边形ABCD是正方形，∴OB＝OC，∠OBE＝∠OCF＝45°，在△OBE和△OCF中，∵，∴△OBE≌△OCF（SAS），∴S△OBE＝S△OCF，∴S四边形OECF＝S△COE+S△OCF＝S△COE+S△OBE＝S△OBC＝S正方形ABCD，故④正确；故选：C．【点评】此题属于四边形的综合题．考查了正方形的性质，全等三角形的判定与性质、勾股定理以及等腰直角三角形的性质．注意掌握全等三角形的判定与性质是解此题的关键．9．如图，在正方形ABCD中，M是对角线BD上的一点，点E在AD的延长线上，连接AM、EM、CM，延长EM交AB于点F，若AM＝EM，∠E＝30°，则下列结论：①FM＝ME；②BF＝DE；③CM⊥EF；④BF+MD＝BC，其中正确的结论序号是（）A．①②③B．①②④C．②③④D．①②③④【分析】①证明△AFM是等边三角形，可判断；②③证明△CBF≌△CDE（ASA），可作判断；④设MN＝x，分别表示BF、MD、BC的长，可作判断．【解答】解：①∵AM＝EM，∠AEM＝30°，∴∠MAE＝∠AEM＝30°，∴∠AMF＝∠MAE+∠AEM＝60°，∵四边形ABCD是正方形，∴∠F AD＝90°，∴∠F AM＝90°﹣30°＝60°，∴△AFM是等边三角形，∴FM＝AM＝EM，故①正确；②连接CE、CF，∵四边形ABCD是正方形，∴∠ADB＝∠CDM，AD＝CD，在△ADM和△CDM中，∵，∴△ADM≌△CDM（SAS），∴AM＝CM，∴FM＝EM＝CM，∴∠MFC＝∠MCF，∠MEC＝∠ECM，∵∠ECF+∠CFE+∠FEC＝180°，∴∠ECF＝90°，∵∠BCD＝90°，∴∠DCE＝∠BCF，在△CBF和△CDE中，∵，∴△CBF≌△CDE（ASA），∴BF＝DE；故②正确；③∵△CBF≌△CDE，∴CF＝CE，∵FM＝EM，∴CM⊥EF，故③正确；④过M作MN⊥AD于N，设MN＝x，则AM＝AF＝2x，AN＝x，DN＝MN＝x，∴AD＝AB＝x+x，∴DE＝BF＝AB﹣AF＝x+x﹣2x＝x﹣x，∴BF+MD＝（x﹣x）+x＝x，∵BC＝AD＝x+x x，故④错误；所以本题正确的有①②③；故选：A．【点评】本题考查了正方形的性质，全等三角形的判定与性质，等腰三角形的性质和判定，熟记正方形的性质确定出△AFM是等边三角形是解题的关键．【点评】此题考查的是正方形的性质，等腰直角三角形的性质和判定以及菱10．如图，在正方形ABCD中，对角线AC，BD交于点O，AG平分∠BAC交BD于G，DE⊥AG于点H．下列结论：①AD＝2AE：②FD＝AG；③CF＝CD：④四边形FGEA是菱形；⑤OF ＝BE，正确的有（）A．2个B．3个C．4个D．5个【分析】①根据正方形的性质和角平分线的定义得：∠BAG＝∠CAG＝22.5°，由垂直的定义计算∠AED＝90°﹣22.5°＝67.5°，∠EAD＝∠EAD＝22.5°，得ED是AG的垂直平分线，则AE＝EG，△BEG是等腰直角三角形，则AD＝AB＞2AE，可作判断；②证明△DAF≌△ABG（ASA），可作判断；③分别计算∠CDF＝∠CFD＝67.5°，可作判断；④根据对角线互相平分且垂直的四边形是菱形可作判断；⑤设BG＝x，则AF＝AE＝x，表示OF和BE的长，可作判断．【解答】解：①∵四边形ABCD是正方形，∴∠BAD＝90°，∠BAC＝45°，∵AG平分∠BAC，∴∠BAG＝∠CAG＝22.5°，∵AG⊥ED，∴∠AHE＝∠EHG＝90°，∴∠AED＝90°﹣22.5°＝67.5°，∴∠ADE＝22.5°，∵∠ADB＝45°，∴∠EDG＝22.5°＝∠ADE，∵∠AHD＝∠GHD＝90°，∴∠DAG＝∠DGA，∴AD＝DG，AH＝GH，∴ED是AG的垂直平分线，∴AE＝EG，∴∠EAG＝∠AGE＝22.5°，∴∠BEG＝45°＝∠ABG，∴∠BGE＝90°，∴AE＝EG＜BE，∴AD＝AB＞2AE，故①不正确；②∵四边形ABCD是正方形，∴AD＝AB，∠DAF＝∠ABG＝45°，∵∠ADF＝∠BAG＝22.5°，∴△DAF≌△ABG（ASA），∴DF＝AG，故②正确；③∵∠CDF＝45°+22.5°＝67.5°，∠CFD＝∠AFE＝90°﹣22.5°＝67.5°，∴∠CDF＝∠CFD，∴CF＝CD，故③正确；④∵∠EAH＝∠F AH，∠AHE＝∠AHF，∴∠AEF＝∠AFE，∴AE＝AF，∴EH＝FH，∵AH＝GH，AG⊥EF，∴四边形FGEA是菱形；故④正确；⑤设BG＝x，则AF＝AE＝x，由①知△BEG是等腰直角三角形，∴BE＝x，∴AB＝AE+BE＝x+x＝（+1）x，∴AO＝＝，∴OF＝AO﹣AF＝﹣x＝，∴＝＝，∴OF＝BE；故⑤正确；本题正确的结论有：②③④⑤；故选：C．形的判定与性质等知识．此题综合性较强，难度较大，注意掌握正方形的性质，注意数形结合思想的应用．11．如图，以正方形ABCD的顶点A为圆心，以AD的长为半径画弧，交对角线AC于点E，再分别以D，E为圆心，以大于DE的长为半径画弧，两弧交于图中的点F处，连接AF并延长，与BC的延长线交于点P，则∠P＝（）A．90°B．45°C．30°D．22.5°【分析】根据正方形的性质得到∠DAC＝∠ACD＝45°，由作图知，∠CAP＝∠DAC ＝22.5°，根据三角形的内角和即可得到结论．【解答】解：∵四边形ABCD是正方形，∴∠DAC＝∠ACD＝45°，由作图知，∠CAP＝∠DAC＝22.5°，∴∠P＝180°﹣∠ACP﹣∠CAP＝22.5°，故选：D．【点评】本题考查了正方形的性质，角平分线定义，正确的理解题意是解题的关键．12．如图，正方形ABCD中，点E在边CD上，连接AE，过点A作AF⊥AE交CB的延长线于点F，连接EF，AG平分∠F AE，AG分别交BC，EF于点G，H，连接EG，DH．则下列结论中：①AF＝AE；②∠EGC＝2∠BAG；③DE+BG＝EG；④AD+DE＝DH；⑤若DE＝CE，则CE：CG：EG＝3：4：5，其中正确的结论有（）A．2个B．3个C．4个D．5个【分析】①正确．证明△ADE≌△ABF（ASA）可得结论．②正确．证明△AGF≌△AGE（SAS），推出∠AGF＝∠AGE＝90°﹣∠BAG，推出∠EGF ＝180°﹣2∠BAG可得结论．③正确．证明△GAF≌△GAE，推出GF＝GE可得结论．④正确．过点H作HM⊥AD于M，HN⊥CD于N，证明△HMA≌△HNE（AAS），推出AM＝EN，HM＝HN，再证明四边形HMDN是正方形可得结论．⑤正确．当DE＝EC时，设DE＝EC＝a，BG＝x，则EG＝a+x，GC＝2a﹣x，利用勾股定理构建方程求出x即可解决问题．【解答】解：∵四边形ABCD是正方形，∴AB＝AD，∠ABC＝∠ABF＝∠ADE＝∠BAD＝90°，∵AE⊥AF，∴∠EAF＝∠BAD＝90°，∴∠BAF＝∠DAE，∴△ADE≌△ABF（ASA），∴AE＝AF，故①正确，∵AG平分∠EAF，∴∠GAF＝∠GAE，∵AF＝AE，AG＝AG，∴△AGF≌△AGE（SAS），∴∠AGF＝∠AGE＝90°﹣∠BAG，∴∠EGF＝180°﹣2∠BAG，∵∠EGF＝180°﹣∠EGC，∴∠EGC＝2∠BAG，故②正确，∵△ADE≌△ABF，∴DE＝BF，∵△GAF≌△GAE，∴GF＝GE，∵FG＝BF+BG＝DE+BG，∴EG＝BG+DE，故③正确，过点H作HM⊥AD于M，HN⊥CD于N，∵AE＝AF，∠EAF＝90°，AH平分∠EAF，∴AH⊥EF，HF＝HE，∴HA＝HE＝HF，∵∠ADE+∠AHE＝180°，∴∠HAD+∠DEH＝180°，∵∠DEH+∠HEN＝180°，∴∠HAM＝∠HEN，∵∠AMH＝∠ENH＝90°，∴△HMA≌△HNE（AAS），∴AM＝EN，HM＝HN，∵∠HMD＝∠HND＝∠MDN＝90°，∴四边形HMDN是矩形，∵HM＝HN，∴四边形HMDN是正方形，∴DM＝DN＝HM＝HN，DH＝DM，∴DA+DE＝DM+AM+DN﹣EN＝2DM＝DH，故④正确，当DE＝EC时，设DE＝EC＝a，BG＝x，则EG＝a+x，GC＝2a﹣x，在Rt△ECG中，∵EG2＝EC2+CG2，∴（x+a）2＝a2+（2a﹣x）2，解得x＝a，∴CG＝a，EG＝a，∴CE：CG：EG＝a：a：＝3：4：5，故⑤正确，故选：D．【点评】本题考查正方形的性质，全等三角形的判定和性质，勾股定理等知识，解题的关键是正确寻找全等三角形解决问题，学会利用参数构建方程解决问题，属于中考选择题中的压轴题．13．如图，矩形ABCD中，O为AC的中点，过点O的直线分别与AB、CD交于点E、F，连接BF交AC于点M，连接DE、BO．若∠COB＝60°，FO＝FC＝2，则下列结论：①FB⊥OC；②△EOB≌△CMB；③四边形EBFD是菱形；④MB＝2．其中正确结论的个数是（）A．1个B．2个C．3个D．4个【分析】连接BD，先证明△BOC是等边三角形，得FO＝FC，BO＝BC，故①正确；因为△EOB≌△FOB≌△FCB，故△EOB不会全等于△CBM，故②错误；再证明四边形EBFD是平行四边形，由OB⊥EF推出四边形EBFD是菱形故③正确，先判断出CM＝，再由∠CBM＝30°，判断出BC＝2，进而判断出④，由此不难得到答案．【解答】解：连接BD，∵四边形ABCD是矩形，∴AC＝BD，AC、BD互相平分，∵O为AC中点，∴BD也过O点，∴OB＝OC，∵∠COB＝60°，OB＝OC，∴△OBC是等边三角形，∴OB＝BC＝OC，∠OBC＝60°，在△OBF与△CBF中，，∴△OBF≌△CBF（SSS），∴△OBF与△CBF关于直线BF对称，∴FB⊥OC，OM＝CM；∴①正确，∵∠OBC＝60°，∴∠ABO＝30°，∵△OBF≌△CBF，∴∠OBM＝∠CBM＝30°，∴∠ABO＝∠OBF，∵AB∥CD，∴∠OCF＝∠OAE，∵OA＝OC，∠AOE＝∠FOC∴△AOE≌△COF（ASA），∴OE＝OF，∴OB⊥EF，∴四边形EBFD是菱形，∴③正确，∵△EOB≌△FOB≌△FCB，∴△EOB≌△CMB错误．∴②错误；∵FO＝FC＝2，FM⊥OC，∠FCM＝30°，∴CM＝，∵∠CBM＝30°，∴BC＝2，∴BM＝3，∴④错误．综上可知其中正确结论的个数是2个，故选：B．【点评】本题属于四边形的综合题，考查矩形的性质、等边三角形的判定和性质．全等三角形的判定和性质、菱形的判定、勾股定理等知识，解题的关键是灵活运用这些知识解决问题，属于中考常考题型．二．填空题（共3小题）14．如图，点E为正方形ABCD外一点，且ED＝CD，连接AE，交BD于点F．若∠CDE ＝40°，则∠DFC的度数为110°．【分析】根据正方形性质和已知得：AD＝DE，利用等腰三角形性质计算∠DAE＝25°，由三角形的内角和定理得：∠AFD＝110°，证明△ADF≌△CDF（SAS），∠DFC＝∠AFD ＝110°．【解答】解：∵四边形ABCD是正方形，∴AD＝DC，∠ADC＝90°，∴∠ADB＝∠BDC＝45°，∵DC＝DE，∴AD＝DE，∴∠DAE＝∠DEA，∵∠ADE＝90°+40°＝130°，∴∠DAE＝＝25°，∴∠AFD＝180°﹣25°﹣45°＝110°，在△ADF和△CDF中，∵，∴△ADF≌△CDF（SAS），∴∠DFC＝∠AFD＝110°，故答案为：110°．【点评】本题考查了正方形的性质、三角形全等的性质和判定、等腰三角形的性质、三角形内角和定理，属于基础题，熟练掌握正方形的性质是关键．15．如图，正方形ABCD中，在AD的延长线上取点E，F，使DE＝AD，DF＝BD，连接BF分别交CD，CE于H，G，下列结论：①EC＝2DG；②∠GDH＝∠GHD；③S△CDG＝S四边形DHGE；④图中只有8个等腰三角形．其中正确的有②③（填番号）．【分析】根据正方形的性质和已知推出四边形DECB是平行四边形，得到BD＝CE，BD ∥CE，无法证出G为CE的中点；得到BD∥CE，推出∠DCG＝∠BDC＝45°，求出∠BGC＝∠GBC，得到BC＝CG＝CD，求出∠CDG＝∠DHG即可；根据三角形的面积公式推出△CDG和四边形DHGE的面积相等；可得有9个等腰三角形．【解答】解：∵正方形ABCD，DE＝AD，∴AD∥BC，DE＝BC，∠EDC＝90°，∴四边形DECB是平行四边形，∴BD＝CE，BD∥CE，∵DE＝BC＝AD，∴∠DCE＝∠DEC＝45°，要使CE＝2DG，只要G为CE的中点即可，但DE＝DC，DF＝BD，∴EF≠BC，即△EFG和△BCG不全等，∴G不是CE中点，∴①错误；∵∠ADB＝45°，DF＝BD，∴∠F＝∠DBH＝∠ADB＝22.5°，∴∠DHG＝180°﹣90°﹣22.5°＝67.5°，∵BD∥CE，∴∠DCG＝∠BDC＝45°，∵∠DHG＝67.5°，∴∠HGC＝22.5°，∠DEC＝45°，∵∠BGC＝180°﹣22.5°﹣135°＝22.5°＝∠GBC，∴BC＝CG＝CD，∴∠CDG＝∠CGD＝（180°﹣45°）＝67.5°＝∠DHG，∴②正确；∵CG＝DE＝CD，∠DCE＝∠DEC＝45，∠HGC＝22.5°，∠GDE＝90﹣∠CDG＝90﹣67.5＝22.5°，∴△DEG≌△CHG，要使△CDG和四边形DHGE的面积相等，只要△DEG和△CHG的面积相等即可，根据已知条件△DEG≌△CHG，∴③S△CDG＝S四边形DHGE；正确，等腰三角形有△ABD，△CDB，△BDF，△CDE，△BCG，△DGH，△EGF，△CDG，△DGF；∴④错误；故答案为：②③．【点评】本题主要考查对三角形的内角和定理，等腰三角形的性质和判定，正方形的性质，平行四边形的性质和判定等知识．综合运用这些性质进行推理是解此题的关键．16．如图，在正方形ABCD中，P为AB的中点，BE⊥PD的延长线于点E，连接AE、BE、F A⊥AE交DP于点F，连接BF，FC．若AE＝2，则FC＝2．【分析】根据正方形的性质可得AB＝AD，再求出∠BAE＝∠DAF，∠ABE＝∠ADF，然后利用“角边角”证明△ABE和△ADF全等，根据全等三角形对应边相等可得AE＝AF，从而判断出△AEF是等腰直角三角形，根据AE的长度求出EF，过点A作AH⊥EF于H，连接BH，根据等腰直角三角形的性质可得AH＝EH＝FH，利用“角边角”证明△APH 和△BPE全等，根据全等三角形对应边相等可得BE＝AH，然后求出△BEH是等腰直角三角形，根据等腰直角三角形的性质可得∠EHB＝45°，然后求出∠AHB＝∠FHB，再利用“边角边”证明△ABH和△FBH全等，根据全等三角形对应边相等可得AB＝BF，再根据全等三角形对应边相等求出BE＝DF，全等三角形对应角相等求出∠BAH＝∠BFE，然后求出∠BFE＝∠ADF，根据等角的余角相等求出∠EBF＝∠FDC，再利用“边角边”证明△BEF和△DFC全等，根据全等三角形对应边相等可得FC＝EF．【解答】解：在正方形ABCD中，AB＝AD，∠BAD＝90°，∵F A⊥AE，∴∠EAF＝90°，∴∠BAE＝∠DAF，∵∠ABE+∠BPE＝∠ADF+∠APD＝90°，∴∠ABE＝∠ADF，在△ABE和△ADF中，，∴△ABE≌△ADF（ASA），∴AE＝AF，BE＝DF，∵F A⊥AE，∴△AEF是等腰直角三角形，∴EF＝AE＝2，过点A作AH⊥EF于H，连接BH，。

几何复习专题卷(含答案)初中数学浙教版八年级上册

几何复习专题卷题号一二三总分得分一、选择题(每题3分，共30分)1．[母题·教材P41目标与评定T1 2024·温州期末]用三根木棒首尾相接围成△ABC，其中AC＝6 cm，BC＝9 cm，则AB的长可能是( )A．2 cm B．3 cm C．14 cm D．15 cm2．[新考向知识情境化]如图，在平分角的仪器中，AB＝AD，BC＝DC，将点A放在一个角的顶点，AB和AD分别与这个角的两边重合，能说明AC就是这个角的平分线的数学依据是( )(第2题)A．SSS B．ASA C．SAS D．AAS3．如图，已知O是△ABC中∠ABC，∠ACB的平分线的交点，OD∥AB交BC于点D，OE∥AC交BC于点E．若BC＝10 cm，则△ODE 的周长为( )(第3题)A．10 cm B．8 cmC．12 cm D．20 cm4．[2024·宁波奉化区期末]下列命题的逆命题是假命题的是( ) A．直角三角形的两个锐角互余B．两直线平行，内错角相等C．三条边对应相等的两个三角形是全等三角形D．同角的余角相等5．过直线l外一点P作直线l的垂线PQ，下列尺规作图错误的是( )A B C D 6．[2024·杭州西湖区期末]如图，阴影部分表示以直角三角形各边为直径的三个半圆所组成的两个新月形，已知S1＋S2＝9，且AC＋BC＝10，则AB的长为( )(第6题)A．6B．7C．8D．627．如图，AB＝AD，AC＝AE，∠DAB＝∠CAE＝50°，以下结论：①△ADC≌△ABE；②CD＝BE；③∠DOB＝50°；④CD平分∠ACB．其中正确的有( )(第7题)A．1个B．2个C．3个D．4个8．如图，在△ABC中，∠BAC＝90°，点D在边BC上，AD＝AB，则有( )(第8题)A．若AC＝2AB，则∠C＝30°B．若3AC＝4AB，则7BD＝18CDC．若∠B＝2∠C，则AC＝2ABD．若∠B＝2∠C，则S△ABD＝2S△ACD9．[2024·宁波奉化区期末]如图，在△ABC中，AB＝23，∠B＝60°，∠A＝45°，D为BC上一点，点P，Q分别是点D关于AB，AC的对称点，则PQ的最小值是( )(第9题)A．6B．8C．32D．310．[2023·金华]如图，在Rt△ABC中，∠ACB＝90°，以其三边为边在AB的同侧作三个正方形，点F在GH上，CG与EF交于点P，CM与BE交于点Q．若HF＝FG，则S四边形PCQE的值是( )S正方形ABEF(第10题)A．14B．15C．312D．625二、填空题(每题4分，共24分)11．如图，在△ABC中，∠ACB＝90°，D为AB的中点，AC＝6，BC ＝8，则CD＝．(第11题)12．如图，在△ABC的边AB上取点D，以D为圆心，DA长为半径画圆弧，交AC于点E；以E为圆心，ED长为半径画圆弧，交AB 于点F．若∠CEF＝∠BFE，则∠A＝ °．(第12题)13．[2024·温州期末]如图，在等腰三角形ABC中，AD是底边BC 上的高线，CE⊥AB于点E，交AD于点F．若∠BAC＝45°，AF ＝6，则BD的长为．(第13题)14．如图，D为等边三角形ABC的AB边的中点，P是BC上的一个动点，连结DP，将△DBP沿DP翻折，得到△DEP，连结AE，若∠BAE＝40°，则∠BDP的度数为．(第14题)15．如图，在长方形ABCD中，AB＝4，AD＝3，长方形内有一个点P，连结AP，BP，CP，已知∠APB＝90°，CP＝CB，延长CP交AD于点E，则AE等于．(第15题)16．[新考法分类讨论法]如图①是一副直角三角板，已知在△ABC和△DEF中，∠BAC＝∠EDF＝90°，∠B＝45°，∠F＝30°，点B，D，C，F在同一直线上，点A在DE上．如图②，△ABC固定不动，将△EDF绕点D逆时针旋转α(0°＜α＜135°)，得到△E'DF'，当直线E'F'与直线AC，BC所围成的三角形为等腰三角形时，α的大小为．(第16题)三、解答题(共66分)17．(6分) [新视角·动手操作题2024·金华月考]如图，在正方形网格中，每个小正方形的边长都为1，△ABC的三个顶点均在格点上，请按要求完成下列问题(仅用无刻度的直尺作图，且保留必要的作图痕迹)：(1)在AB上找一点D，使CD⊥AB；(2)在AC上找一点E，使BE平分∠ABC．18．(6分)如图，BD是△ABC的角平分线，DE∥BC，交AB于点E．(1)求证：∠EBD＝∠EDB；(2)当AB＝AC时，请判断CD与ED的大小关系，并说明理由．19．(6分)“儿童散学归来早，忙趁东风放纸鸢”．又到了放风筝的最佳时节，某实践探究小组在放风筝时想测量风筝离地面的垂直高度，通过勘测，得到如下记录表：测量示意图的全部数据就可以计算出风筝离地面的垂直高度AD．请完成以下任务．(1)如图，在Rt△ABC中，∠ACB＝90°，BC＝15 m，AB＝17 m，求线段AD的长．(2)如果小明想要风筝沿DA方向再上升12 m，BC长度不变，则他应该再放出多少米线？20．(8分) [新考法构造全等三角形法]如图，在四边形ABCD中，∠B＝∠D＝90°，点E，F分别在AB，AD上，且AE＝AF，CE＝CF．(1)求证：CB＝CD；(2)若AE＝CE＝5，AB＝AD＝8，求线段EF的长．21．(8分)[2024·杭州西湖区期中]如图，在△ABC中，点D，E分别在边AB，AC上，连结CD，BE，BD＝BC＝BE．(1)若∠A＝30°，∠ACB＝70°，求∠BDC，∠ACD的度数；(2)设∠ACD＝α，∠ABE＝β，求α与β之间的数量关系，并说明理由．22．(10分)[2023·宁波七中期中]如图，在△ABC中，AB＝AC＝2，∠A＝90°．D为BC边的中点，E，F分别在边AB，AC上，DE⊥DF．(1)求证：△DEF是等腰三角形；(2)求EF的最小值．23．(10分)[2024·衢州月考]如图①，在等腰三角形ABC中，AD是BC边上的中线，延长BC至点E，使AD＝DE，连结AE．(1)求证：△ADE是等腰直角三角形；(2)如图②，过点B作AC的垂线交AE于点P，试判断△ABP的形状，并说明理由；(3)如图③，在(2)的条件下，AD＝4，连结CP，若△CPE是直角三角形，求CE的长．24．(12分)如果两个顶角相等的等腰三角形具有公共的顶角顶点，并将它们的底角顶点分别对应连结起来得到两个全等三角形，那么我们把这样的图形称为“手拉手”图形．如图①，在“手拉手”图形中，AB＝AC，AD＝AE，∠BAC＝∠DAE，连结BD，CE，则△ABD ≌△ACE．(1)请证明图①的结论成立；(2)如图②，△ABC和△ADE是等边三角形，连结BD，EC交于点O，求∠BOC的度数；(3)如图③，AB＝BC，∠ABC＝∠BDC＝60°，试探究∠A与∠BCD的数量关系．答案一、1．C 2．A 3．A 4．D 5．C 6．C7．C 【点拨】∵∠DAB ＝∠CAE ，∴∠DAB ＋∠BAC ＝∠CAE ＋∠BAC ．∴∠DAC ＝∠BAE ．在△ADC 和△ABE 中，{AD ＝AB ，∠DAC ＝∠BAE ，AC ＝AE ，∴△ADC ≌△ABE (SAS )．∴CD ＝BE ，∠ADC ＝∠ABE ．又∵∠AFD ＝∠BFO ，∴∠DOB ＝∠DAB ＝50°，故①②③正确．现有条件无法得到CD 平分∠ACB ．8．B 【点拨】A ．若AC ＝2AB ，则BC ＝AB 2＋AC 2＝5AB ，若∠C ＝30°，则易得BC ＝2AB ，故A 选项错误．B ．若3AC ＝4AB ，则AC ＝43AB ，∴BC ＝AB 2＋AC 2＝53AB ．作AE ⊥BC ，则S △ABC ＝12AB ·AC ＝12BC ·AE ，可得AE ＝AB ·AC BC ＝45AB ．∵AD ＝AB ，∴BE ＝DE ＝AB 2－AE 2＝35AB ．∴BD ＝65AB ．∴DC ＝BC －BD ＝715AB ．∴7BD ＝18CD ，故B 选项正确．C ．若∠B ＝2∠C ，∵∠BAC ＝90°，∴∠B ＋∠C ＝90°．∴∠C ＝30°，∠B ＝60°．∴易得BC ＝2AB ．∴AC ＜2AB ，故C 选项错误．D ．若∠B ＝2∠C ，由选项C 可得∠C ＝30°，∠B ＝60°．∵AD ＝AB ，∴△ABD 为等边三角形．∴∠ADB＝60°．∴∠DAC＝∠ADB－∠C＝30°＝∠C．∴AD＝DC＝BD，即AD为△ABC的中线．∴S△ABD＝S△ACD，故D选项错误．9．C　【点拨】连结AD，AP，AQ．∵点P，Q分别是点D关于AB，AC的对称点，∴AD＝AP，AD＝AQ，∠PAD＝2∠DAB，∠QAD＝2∠DAC．∴AD＝AP＝AQ，∠PAQ＝2(∠BAD＋∠CAD)＝2∠BAC＝90°．∴△PAQ是等腰直角三角形．∴易知PQ＝2AP＝2AD．∵D为BC上一点，∴当AD⊥BC时，AD取得最小值，此时PQ取得最小值．当AD⊥BC时，∠ADB＝90°．∵∠ABD＝60°，∴∠BAD＝180°－∠ABD－∠ADB＝30°．AB＝3．∴AD＝AB2－BD2＝3．∴易得BD＝12∴PQ＝2AD＝32．∴PQ的最小值为32．10．B　【点拨】设AC＝b，AB＝c，BC＝a，HF＝FG＝x，则a2＋b2＝c2．∵四边形ACGH，四边形BCMN，四边形ABEF都是正方形，∴AC＝AH＝HG＝b，AB＝AF，∠H＝∠G＝∠EBA＝∠AFE＝∠BCM＝90°．∴b＝2x．在Rt△AHF与Rt△ACB中，∵AH＝AC，AF＝AB，∴Rt△AHF≌Rt△ACB(HL)．∴HF＝BC＝FG＝a＝x，∠HFA＝∠ABC，S△AHF＝S△ACB．∵∠HFA＋∠GFP＝180°－90°＝90°＝∠ABC＋∠CBQ，∴∠GFP ＝∠CBQ．在△GFP与△CBQ中，∵∠G＝∠BCQ＝90°，FG＝BC，∠GFP＝∠CBQ，∴△GFP≌△CBQ(ASA)．∴S△GFP＝S△CBQ．∵S正方形ACGH＝S△AHF＋S△PFG＋S四边形ACPF＝b2，∴S正方形ACGH＝S△ABC＋S△BCQ＋S四边形ACPF＝b2．∴S四边形PCQE＝S正方形ABEF－(S△ABC＋S△BCQ＋S四边形ACPF)＝S正方形ABEF－S正方形ACGH＝c2－b2＝a2．在Rt△ABC中，由勾股定理得c2＝b2＋a2＝(2x)2＋x2＝5x2．∴S四边形PCQE S正方形ABEF ＝a2c2＝x25x2＝15．二、11．5　12．3613．3　【点拨】在等腰三角形ABC中，AD是底边BC上的高线，∴AD⊥BC，BD＝CD．∴∠ADC＝90°．∵CE⊥AB，∴∠AEF＝∠CEB＝90°．又∵∠BAC＝45°，∴∠ACE＝45°＝∠BAC．∴AE＝CE．∵∠ADC＝∠AEF＝90°，∠AFE＝∠CFD，∴∠BAD＝∠BCE．∴△AEF≌△CEB(ASA)．∴AF＝BC＝6．∴BD＝3．14．40°　【点拨】∵D为等边三角形ABC的AB边的中点，∴AD＝BD，将△DBP沿DP翻折，得到△DEP，∴BD＝DE＝AD，∠BDP＝∠PDE．∴∠BAE＝∠AED＝40°．∴∠BDE＝40°＋40°＝80°．∠BDE＝40°．∴∠BDP＝12　【点拨】延长AP交CD于点F．15．43∵∠APB＝90°，∴∠FPB＝90°，∠OAB＋∠ABP＝90°．∴∠CPF＋∠CPB＝90°．∵四边形ABCD是长方形，∴∠D＝∠DAB＝∠ABC＝90°，CD＝AB＝4，BC＝AD＝3．∴∠EAP＋∠BAP＝∠ABP＋∠BAP＝∠ABP＋∠CBP＝90°．∴∠EAP＝∠ABP．∵CP＝CB＝3，∴∠CPB＝∠CBP．∴∠CPF＝∠ABP＝∠EAP．又∵∠EPA＝∠CPF，∴∠EAP＝∠APE．∴AE＝PE．在Rt△CDE中，CD2＋DE2＝CE2，．∴42＋(3－AE)2＝(3＋AE)2，解得AE＝4316．7．5°或75°或97．5°或120°【点拨】设直线E'F'与直线AC，BC分别交于点P，Q，∵△CPQ为等腰三角形，∴∠PCQ为顶角或∠CPQ为顶角或∠CQP为顶角．①当∠PCQ为顶角时，∠CPQ＝∠CQP，若∠PCQ为钝角，如图①，∵∠BAC＝90°，∠B＝45°，∴∠ACB＝45°．∴∠CPQ＋∠CQP＝∠ACB＝45°．∴∠CQP＝22．5°．∵∠E'F'D＝30°，∴∠F'DQ＝∠E'F'D－∠CQP＝30°－22．5°＝7．5°，即α＝7．5°．若∠PCQ为锐角，如图②，则∠CPQ＝∠CQP＝67．5°．∵∠E'DF'＝90°，∠F'＝30°，∴∠E'＝60°．∴∠E'DQ＝∠CQP－∠E'＝67．5°－60°＝7．5°．∴α＝90°＋7．5°＝97．5°．②当∠CPQ为顶角时，∠CQP＝∠PCQ＝45°，如图③．∵∠DE'F'＝∠CQP＋∠QDE'，∴∠QDE'＝∠DE'F'－∠CQP＝60°－45°＝15°．∴α＝90°－15°＝75°．③当∠CQP为顶角时，∠CPQ＝∠PCQ＝45°，如图④，∴∠CQP＝90°．∴∠QDF'＝90°－∠DF'E'＝60°．∴∠QDE'＝∠E'DF'－∠QDF'＝30°，∴α＝90°＋30°＝120°．综上所述，α的大小为7．5°或75°或97．5°或120°．三、17．【解】(1)如图，点D即为所求．(2)如图，点E即为所求．18．(1)【证明】∵BD是△ABC的角平分线，∴∠CBD＝∠EBD．∵DE∥BC，∴∠CBD＝∠EDB．∴∠EBD＝∠EDB．(2)【解】CD＝ED，理由如下：∵AB＝AC，∴∠C＝∠ABC．∵DE∥BC，∴∠ADE＝∠C，∠AED＝∠ABC．∴∠ADE＝∠AED．∴AD＝AE．∴CD＝BE．由(1)得∠EBD＝∠EDB，∴BE＝DE．∴CD＝ED．19．【解】(1)由题易知CD＝1．7 m．∵在△ABC中，∠ACB＝90°，BC＝15 m，AB＝17 m，∴AC＝AB2－BC2＝172－152＝8(m)．∴AD＝AC＋CD＝8＋1．7＝9．7(m)．(2)∵风筝沿DA方向再上升12 m后，AC＝8＋12＝20(m)，∴此时风筝线的长为202＋152＝25(m)．25－17＝8(m)．答：他应该再放出8 m线．20．(1)【证明】如图，连结AC．在△AEC与△AFC中，{AC＝AC，CE＝CF，AE＝AF，∴△AEC≌△AFC(SSS)．∴∠CAE＝∠CAF．又∵∠B＝∠D＝90°，∴CB＝CD．(2)【解】如图，过F作FG⊥AB，垂足为G．∵AE＝CE＝5，AB＝8，∴EB＝3，AF＝5，∠ACE＝∠CAE．由勾股定理得BC＝4．由(1)知△AEC≌△AFC，∴∠ECA＝∠FCA．∴∠FCA＝∠CAE．∴AE∥CF．∴FG＝BC＝4．易知AG＝3，∴EG＝2．在Rt△EFG中，易知EF＝20．21．【解】(1)∵∠A＋∠ACB＋∠ABC＝180°，∠A＝30°，∠ACB＝70°，∴∠ABC＝80°．＝50°．在△BDC中，BD＝BC，∴∠BDC＝∠BCD＝180°－80°2∴∠ACD＝∠BDC－∠A＝20°．(2)2α＝β．理由：设∠BCD＝x，则∠BDC＝x，∴∠DBC＝180°－2x．∵BE＝BC，∴∠BEC＝∠BCE＝α＋x．∴∠EBC＝180°－2(α＋x)．∴∠DBC－∠EBC＝180°－2x°－[180°－2(α＋x)]＝2α．又∵∠DBC－∠EBC＝∠ABE＝β，∴2α＝β．22．(1)【证明】如图，连结AD．∵AB＝AC，∠BAC＝90°，∴∠B＝45°．∵D 为BC 边的中点，∴AD ⊥BC ，∠BAD ＝∠CAD ＝12∠BAC ＝45°＝∠B ．∴AD ＝BD ＝12BC ，∠ADB ＝90°．∵DE ⊥DF ，∴∠EDF ＝90°．∴∠ADF ＝90°－∠ADE ＝∠BDE ．在△ADF 和△BDE 中，{∠DAF ＝∠B ，AD ＝BD ，∠ADF ＝∠BDE ，∴△ADF ≌△BDE (ASA )．∴DF ＝DE ．∴△DEF 是等腰三角形．(2)【解】∵AB ＝AC ＝2，∠BAC ＝90°，∴BC ＝AB 2＋AC 2＝22＋22＝8．∴AD ＝12BC ＝12×8＝82．如图，取EF 的中点G ，连结AG ，DG ．∵∠EAF ＝∠EDF ＝90°，∴AG ＝DG ＝12EF ．∴EF ＝2AG ＝AG ＋DG ．又∵AG ＋DG ≥AD ，∴EF ≥82．∴EF 的最小值为82．23．(1)【证明】∵AB ＝AC ，AD 是BC 边上的中线，∴AD ⊥BC ．∴∠ADC ＝90°．又∵AD ＝DE ，∴△ADE 是等腰直角三角形．(2)【解】△ABP 是等腰三角形．理由如下：∵∠ADC ＝90°，∴∠CAD ＋∠DCA ＝90°．∵BP ⊥AC ，∴易得∠PBE ＋∠DCA ＝90°．∴∠CAD＝∠PBE．∵AB＝AC，AD是BC边上的中线，∴∠BAD＝∠CAD．∴∠BAD＝∠PBE．∵△ADE是等腰直角三角形∴∠DAE＝∠E．∴∠BAD＋∠DAE＝∠PBE＋∠E，即∠BAP＝∠BPA．∴BA＝BP．∴△ABP是等腰三角形．(3)【解】①如图①，若∠PCE＝90°．在△ABD和△BPC中，{∠BDA＝∠BCP=90°，∠BAD＝∠PBC，AB＝BP，∴△ABD≌△BPC(AAS)(证△ACD≌△BPC亦可)．∴BC＝AD＝DE ＝4．∵AD是BC边上的中线，∴BD＝CD．设CE＝x，则CD＝4－x，∴BD＝4－x．∴BC＝8－2x．∴8－2x＝4，解得x＝2，即CE＝2．②如图②，若∠CPE＝90°．作PF⊥CE于点F，同理可证△ABD≌△BPF，∴BF＝AD＝4．设EF＝x，易知∠E＝45°，∴易得CF＝EF＝x．∴CD＝4－2x．∴BD＝4－2x．∴BC＝8－4x．∴BF＝8－3x．∴8－3x ＝4，解得x ＝43．∴CE ＝2x ＝83．综上，CE 的长为2或83．24．(1)【证明】∵∠BAC ＝∠DAE ，∴∠BAC ＋∠CAD ＝∠DAE ＋∠CAD ，即∠BAD ＝∠CAE ．在△ABD 和△ACE 中，{AB ＝AC ，∠BAD ＝∠CAE ，AD ＝AE ，∴△ABD ≌△ACE (SAS )．(2)【解】由题意可知△ABD ≌△ACE ．∴∠ADB ＝∠AEC ．在等边三角形ADE 中，∠DAE ＝60°．记AD 与CE 的交点为G ．∵∠AGE ＝∠DGO ，∴∠DOE ＝∠DAE ＝60°．∴∠BOC ＝∠DOE ＝60°．(3)【解】如图，延长DC 至点P ，使DP ＝DB ．∵∠BDC ＝60°，∴△BDP 是等边三角形．∴BD ＝BP ，∠DBP ＝60°．∵∠ABC ＝60°＝∠DBP ，∴∠ABD ＝∠CBP ．∵AB ＝CB ，∴△ABD ≌△CBP (SAS )．∴∠BCP ＝∠A ．又∵∠BCD＋∠BCP＝180°，∴∠A＋∠BCD＝180°．21。

浙教版数学七年级上册专项突破二与几何相关的代数式问题(含答案)

专项突破二与几何相关的代数式问题
训练内容
①与长方形、正方形有关的代数式问题(第2，4，5，6， 7，9，10题)； ②与数轴、线段或角有关的代数式问题(第1，3，8， 11题).
一、选择题
1．(2021秋·金华市婺城区期末)如图，已知线段AB＝a，线段CD
＝b，当线段CD在线段AB上运动(点C，D始终在线段AB上)时，
【答案】
m－n 2
抓重点
8．如图，线段AB表示某两地之间的一条东西走向的道路．在点A 的东面5 km处设置第一个广告牌，之后往东每12 km就设置一个广告牌．一辆汽车从点A的东面3km处出发，沿此道路向东行驶．当经过第n个广告牌时，此车所行驶的路程为________km.
【解析】由题意，得(5－3)＋12(n－1)＝(12n－10)km. 【答案】 (12n－10)
三、解答题
抓重点
10．(2020秋·舟山市定海区期末)如图，用大小不完全相同的5个正方形和1个长方形(阴影部分)拼成长方形ABCD，其中EF＝2 cm，最小的正方形的边长为x(cm). (1)用含x的代数式表示FG＝________cm，DG＝________cm. (2)若长方形ABCD的周长为52 cm，求x的值． (3)若FG∶DG＝2∶3，求四边形FGDH(阴影部分)的面积．
D. ab－3π2b2
【解析】由题意，得装饰物所占的面积为 πb42＝1π6b2，
∴窗户中能射进阳光的面积是 ab－1π6b2.故选 C.
【答案】 C
抓重点
3．(2020秋·金华市金东区期末)如图，三角尺MON的
直角顶点O在直线AB 上，OC是∠MOB的平分线．若
∠AOM的度数为y，∠NOC的度数为x，则y用含x的代

解直角三角形与几何综合(压轴题专项)—2023-2024学年九年级数学下册(浙教版)(解析版)

解直角三角形与几何综合【典例1】如图，在Rt△AEB中，∠AEB=90°，点C在线段BE的延长线上，过点C作CD∥AB，连接AD，再过点A作AF⊥CD于点F；（1）如图1，连接EF，若∠BAE=30°，∠D=45°，DF=6，AE=4，求线段EF的长；（2）如图2，在线段CE上取一点H，连接AH、DH，当AH平分∠BHD，∠ABH=∠DAH时，求证：DH=HC+ 2HE．（3）如图3，在（2）的条件下，连接ED，若AE=12，BE=4，当(ED+DF)取得最小值时，请直接写出线段AH的长．（1）过点E作EM⊥AF于M，利用勾股定理可得EM=√AE2−AM2=2√3，EF=√EM2+MF2=2√7；（2）连接AC，过A作AW⊥HD于，则有∠AWH=∠AWD=90°，可证Rt△AHE≌Rt△AHW(HL)，则HE=HW，然后可得A、H、C、D四点共圆，则可证△AEC≌△AWD(AAS)，进而问题可求证；（3）在线段EB上截取EG=EH，延长AF交BC的延长线于M，连接AG，AC，DM，可证得△AEG≌△AEH(SAS)，，利用解直角三角形可得EM=36，再由勾股定理可得AM=△AGC≌△AHD(SAS)，设∠BAE=α，则tanα=13√AE2+EM2=12√10，作点E关于DM的对称点E′，连接EE′，DE′，EE′交DM于P，则DE=DE′，由于ED+ DF=DE′+DF≥EF，故当且仅当E′、D、F三点共线时，ED+DF=EF为最小值，过点E′作E′N⊥BC于N，过点D作DK⊥CM于K，应用解直角三角形即可求得答案．（1）解：过点E作EM⊥AF于M，如图1，则∠AME=∠EMF=90°，∵AF⊥CD，CD∥AB，∴∠BAF=∠AFD=90°，∵∠BAE=30°，∴∠EAM=60°，∴∠AEM=30°，∵AE=4，AE=2，∴AM=12在Rt△AEM中，EM=√AE2−AM2=√42−22=2√3，在Rt△ADF中，∠D=45°，DF=6，∴AF=DF=6，∴MF=AF−AM=6−2=4，在Rt△EMF中，EF=√EM2+MF2=√(2√3)2+42=2√7，∴线段EF的长为2√7；（2）证明：连接AC，过A作AW⊥HD于W，如图2，则∠AWH=∠AWD=90°，∵∠AEB=90°，∴∠AEH=90°，∵AH平分∠BHD，AE⊥HB，AW⊥HD，∴AE=AW，在Rt△AHE和Rt△AHW中，{AH=AHAE=AW，∴Rt△AHE≌Rt△AHW(HL)，∴HE=HW，∵CD∥AB，∴∠ABH+∠BCD=180°，∵∠ABH=∠DAH，∴∠DAH+∠BCD=180°，∵∠DAH与∠BCD在DH异侧，∴A、H、C、D四点共圆，∴∠ACH=∠ADW，∵AE=AW，∠AEC=∠AWD=90°，∴△AEC≌△AWD(AAS)，∴EC=WD，∴DH=HW+WD=HE+EC=HE+HE+HC，即DH=HC+2HE；（3）解：如图3，在线段EB上截取EG=EH，延长AF交BC的延长线于M，连接AG，AC，DM，则CG=HC+2HE，由（2）得DH=HC+2HE，∴CG=DH，在△AEG和△AEH中，{EG=EH∠AEG=∠AEH=90°AE=AE，∴△AEG≌△AEH(SAS)，∴AG=AH，∠AGC=∠AHE，∵AH平分∠BHD，∴∠AHE=∠AHD，∴∠AGC=∠AHD，∴△AGC≌△AHD(SAS)，∴AC=AD，∵AF⊥CD，∴DF=CF，∴DM=CM，设∠BAE=α，则tanα=BEAE =412=13，∵∠BAE+∠MAE=∠AME+∠MAE=90°，∴∠AME=∠BAE=α，∴AEEM =tanM=13，∴EM=3AE=3×12=36，∴AM=√AE2+EM2=√122+362=12√10，如图4，作点E关于DM的对称点E，连接EE′，DE′，EE′交DM于P，则DE=DE′，∴ED+DF=DE′+DF≥E′F，当且仅当E′、D、F三点共线时，ED+DF=EF为最小值，过点E′作E′N⊥BC于N，过点D作DK⊥CM于K，则∠AMD=∠CE′E=∠CE′N=∠CDK=∠AME=α，设CF=DF=x，则FM=CFtanα=3x，∴CM=√CF2+FM2=√x2+(3x)2=√10x，∵sin∠DCK=DKCD =FMCM，即DK2x=√10x，∴DK=3√105x，∵cos∠DCK=CKCD =CFCM，即CK2x=√10x，∴CK=√105x，∴MK=CM−CK=√10x−√105x=4√105x，∴tan2α=DKMK =3√105x4√105x=34，∴PEPM =tan2α=34，设PE=3y，则PM=4y，∵PE2+PM2=EM2，∴(3y)2+(4y)2=362，∴y=365（负值舍去），∴PE=3×365=1085，PM=4×365=1445，∴EE′=2PE=2165，∵sin2α=ENEE′=PEEM，即EN2165=108536，∴EN=64825，∴MN=EM−EN=36−64825=25225，∴E′N=ENtan2α=6482534=86425，∴CN=E′N⋅tanα=86425×13=28825，∴CM=CN+MN=28825+25225=1085，∴FM=CM⋅cosα=1085×3√1010=162√1025，CF=13FM=54√1025，∴AF=AM−FM=12√10−162√1025=138√1025，在Rt△ADF中，AD=√AF2+DF2=(138√1025)+(54√1025)=12√615，∵∠DAH=∠ABH=∠MAE，∴∠DAH−∠MAH=∠MAE−∠MAH，即∠DAF=∠HAE，∴cos∠DAF=cos∠HAE，∴AFAD =AEAH，即138√102512√615=12AH，∴AH=12√61023．1．（2023·辽宁·中考真题）△ABC是等边三角形，点E是射线BC上的一点（不与点B，C重合），连接AE，在AE的左侧作等边三角形AED，将线段EC绕点E逆时针旋转120°，得到线段EF,连接BF．交DE于点M．（1）如图1，当点E为BC中点时，请直接写出线段DM与EM的数量关系；（2）如图2．当点E在线段BC的延长线上时，请判断（1）中的结论是否成立？若成立，请写出证明过程；若不成立，请说明理由；（3）当BC=6，CE=2时，请直接写出AM的长．【思路点拨】（1）可证得∠BAD=∠BAE=30°，进一步利用等腰三角形的三线合一得出结果；（2）连接BD、DF，可证明△BAD≌△CAE，从而∠ABD=∠ACE=120°，BD=CE，进而得出∠DBE=60°，从而得出∠DBE+∠BEF=60°+120°=180°，从而BD∥EF，结合BD=EF得出四边形BDFE是平行四边形，从而得出DM=EM；（3）分为两种情形∶当点E在BC的延长线上时，作AG⊥BC于G，可得出CG=3，AG=3√3，从而EG=CG+ CE=3+2=5，进而得出AE=2√13，进一步得出结果；当点E在BC上时，作AG⊥BC于G，可得出EG=1，AE=2√7，进一步得出结果．【解题过程】（1）解∶∵△ABC是等边三角形，点E是BC的中点，∠BAC，∴∠BAC=60°，∠BAE=12∴∠BAE=30°，∵△ADE是等边三角形，∴∠DAE=60°，AD=AE，∴∠BAD=∠DAE−∠BAE=60°−30°=30°，∴∠DAE=∠BAE，∴DM=EM；（2）解：如图l，DM=EM仍然成立，理由如下∶连接BD、DF，∵△ABC和△ADE是等边三角形，∴∠ABC=∠BAC=∠DAE=∠ACB=60°，AB=AC，AD=AE，∴∠BAC−∠DAC=∠DAE−∠DAC，∴∠BAD=∠CAE，∴△BAD≌△CAE(SAS)，∴∠ABD=∠ACE=180°−∠ACB=120°，BD=CE，∴∠DBE=∠ABD−∠ABC=120°−60°=60°，∴∠DBE+∠BEF=60°+120°=180°，∴BD∥EF，∵CE=EF，∴BD =EF ，∴四边形BDFE 是平行四边形，∴DM =EM ；（3）解：如图2，当点E 在BC 的延长线上时，作AG⟂BC 于G ，∵∠ACB =60°，∴CG =AC ⋅cos60°=12AC =3，AG =AC ⋅sin60°=√32AC =3√3，∴EG =CG +CE =3+2=5，∴AE =√AC 2+EC 2=√(3√3)2+52=2√13．由（2）知∶DM =EM ，∴AM ⊥DE ，∴∠AME =90°，∴∠AED =60°，∴AM =AE ⋅sin60°=2√13×√32=√39，如图3，当点E 在BC 上时，作AG ⊥BC 于G ，由上知∶AG =3√3，CG =3，∴EG =CG −CE =3−2=1，∴AE=√AG2+EG2=√(3√3)2+12=2√7，∴AM=2√7×√32=√21，综上所述∶AM=√39或√21．2．（22·23下·安徽·专题练习）在△ABC中，∠ACB=90°，ACBC=m，D是边BC上一点，将△ABD沿AD折叠得到△AED，连接BE．（1）特例发现：如图1，当m=1，AE落在直线AC上时．①求证：∠DAC=∠EBC；②填空：CDCE的值为；（2）类比探究：如图2，当m≠1，AE与边BC相交时，在AD上取一点G，使∠ACG=∠BCE，CG交AE于点H．探究CGCE的值（用含m的式子表示），并写出探究过程；（3）拓展运用：在（2）的条件下，当m=√22，D是BC的中点时，若EB⋅EH=6，求CG的长．【思路点拨】（1）①由折叠知，∠AFB=90°=∠ACB，再由等角的余角相等，即可得出结论；②由①知，∠DAC=∠EBC，再判断出AC=BC，进而用ASA判断出，△ACD≌△BCE，即可得出结论；（2）同（1）①的方法，即可得出结论；（3）先判断出DF是△BCE的中位线，得出DF∥CE，进而得出∠BEC=∠BFD=90°，∠AGC=∠ECG，∠GAH=∠CEA，再判断出AG=CE，设CG=x，则AG=√2x，BE=2x，得出AG=CE进而用AAS判断出△AGH≌△ECH，得出GH=12x，再用勾股定理求出AH=32x，即可得出结论．【解题过程】（1）如图1，延长AD交BE于F，由折叠知，∠AFB=90°=∠ACB，∴∠DAC+∠ADC=∠BDF+∠EBC=90°，∵∠ADC=∠BDF，∴∠DAC=∠EBC；②由①知，∠DAC=∠EBC，∵m=1，∴AC=BC，∵∠ACD=∠BCE，∴△ACD≌△BCE(ASA)，∴CD=CE，=1，∴CDCE故答案为1．（2）如图2，延长AD交BE于F，由（1）①知，∠DAC=∠EBC，∵∠ACG=∠BCE，∴△ACG∽△BCE，∴CGCE =ACBC=m；（3）由折叠知，∠AFB=90°，BF=FE，∵点D是BC的中点，∴BD=CD，∴DF是△BCE的中位线，∴DF∥CE，∴∠BEC=∠BFD=90°，∠AGC=∠ECG，∠GAH=∠CEA，由（2）知，△ACG∽△BCE，∴∠AGC=∠BEC=90°，ACCD =AC12BC=2m=√2，∴CGAG =tan∠GAC=DCAC=1√2，设CG=x，则AG=√2x，BE=2x，∴AG=CE，∴△AGH≌△ECH(AAS)，∴AH=EH，GH=CH，∴GH=12x，在Rt△AGH中，根据勾股定理得，AH=√AG2+GH2=32x，∵EB⋅EH=6，∴2x⋅32x=6，∴x=√2或x=−√2（舍)，即CG=√2．3．（22·23·濮阳·一模）数学活动课上，老师组织数学小组的同学们以“正方形折叠”为主题开展数学活动．【动手实践】（1）如图（1），已知正方形纸片ABCD，数学小组将正方形纸片沿过点A的直线折叠，使点B落在正方形ABCD的内部，点B的对应点为点M，折痕为AE，再将纸片沿过点A的直线折叠使AD与AM重合，折痕为AF，易知点E、M、F共线，则∠EAF=°，EF、BE、DF三条线段的关系为；【拓展应用】（2）解决下面问题：①如图（2）作FN⊥AE于点N，交AM于点P，求证：△ANP≌△FNE；②如图（3），数学小组在图（1）的基础上进行如下操作：将正方形纸片沿EF继续折叠，点C的对应点为点N，他们发现，当点E的位置不同时，点N的位置也不同，若点N恰好落在△AEF边上，AB=3，请直接写出此时BE的长度．【思路点拨】∠BAD=45°．由∠AME=（1）根据折叠的性质可得∠EAM=∠EAB,∠FAM=∠FAD，由此可得∠EAF=12∠B=90°,∠AMF=∠D=90°可得E、M、F三点共线．又由ME=BE,MF=DF可得EF=BE+DF．（2）①由∠ANF=90°，∠EAF=45°可得∠AFN=45°，于是可得AN=FN，由“同角的余角相等”可得∠EAM=∠NFE，最后根据角边角即可证明△ANP≌△FNE．②分两种情况：当点N落在AE上时，当点N落在AF上时，分别利用三角函数解直角三角形即可求得BE的长．【解题过程】（1）∵四边形ABCD是正方形，∴∠BAD=∠B=∠D=90°,AB=AD．∵△ABE沿AE折叠后得△AME，△ADF沿AF折叠后得△AMF，∴△AME≌△ABE,△AMF≌△ADF，∴∠EAM=∠EAB,∠FAM=∠FAD，∠BAD=45°，∴∠EAM+∠FAM=∠EAB+∠FAB=12即∠EAF=45°．∵∠AME=∠B=90°,∠AMF=∠D=90°，∴∠AME+∠AMF=180°．∴E、M、F三点共线．∵ME=BE,MF=DF，∴ME+MF=BE+DF，∴EF=BE+DF．故答案为：45，EF=BE+DF．（2）①∵FN⊥AE，∴∠ANF=∠FNE=90°．∵∠EAF=45°，∴∠AFN=45°，∴AN=FN．∵△AEM中，∠AME=90°，∴∠EAM+∠AEM=90°．∵△FNE中，∠FNE=90°，∴∠NFE+∠AEM=90°，∴∠EAM=∠NFE．在△ANP和△FNE中，{∠NAP=∠NFEAN=FN∠ANP=∠FNE，∴△ANP≌△FNE(ASA)．②如图，当点N落在AE上时，∵四边形ABCD是正方形，∴∠C=∠B=∠D=∠BAD=90°．由折叠的性质可得∠AEB=∠AEM=∠CEF，∵∠AEB+∠AEM+∠CEF=180°，∴∠AEB=∠AEM=∠CEF=60°．∵AB=3，∴BE=ABtan∠AEB =ABtan60°=√3=√3；如图，当N落在AF上时，∵四边形ABCD是正方形，∴∠C=∠B=∠D=∠BAD=90°，由折叠的性质可得∠AFE=∠CFE=∠AFD，又∵∠AFE+∠CFE+∠AFD=180°，∴∠AFE=∠CFE=∠AFD=60°，∴DF=ADtan∠AFD =ADtan60°=3√3=√3，∴CF=CD−DF=3−√3，∴EC=CF⋅tan∠CFE=(3−√3)×√3=3√3−3，∴BE=BC−EC=3−(3√3−3)6−3√3，综上，BE的长为√3或6−3√3．4．（22·23下·泉州·模拟预测）已知：如图1，在矩形ABCD中，AB=4，AD=6，点P是AD的中点，点F是AB上的动点，连接FP并延长交CD的延长线于点M，过点P作PE⊥FM，交直线BC于点E，连接EF．（1）求tan∠PEF的值；（2）如图2，连接EM，点Q是EM的中点．①当∠AFP=2∠BEF时，求PQ的长；②点F从A点运动到B点的过程中，求点Q经过的路径长．【思路点拨】（1）作PG⊥BC于点G，由四边形ABCD是矩形，点P是AD的中点，得∠A=∠B=∠PGB=90°，PA=PD=1 2AD=3，可证明△APF∽△GPE，则tan∠PEF=PFPE=PAPG=34；（2）①作EF的垂直平分线KN交BE于点N，连接FN，则∠BEF=∠NFE，所以∠BNF=2∠BEF，则∠AFP=∠BNF，可证明∠NFP=∠EPM=90°，则FN∥PE，所以∠BEF=∠NFE=∠PEF，则BF=PF，由勾股定理得32+(4−PF)2=PF2，求得PF=258，则FE=12524，再证明PF=PM，则PQ=12FE=12548；②作PG⊥BC于点G，连接AG、PC，取PC的中点I，连接IQ，可证明PC∥AG，则∠DPI=∠PAG，再证明△PFE∽△PAG，得∠PFE=∠PAG，可推导出∠DPI=∠MPQ，则∠IPQ=∠DPM=∠APF，再证明△PIQ∽△PAF，则∠PIQ=∠PAF=90°，可知点Q在线段PC的垂直平分线上运动，延长IQ、PD交于点L，当点F从点A运动到点B，则点Q从点I运动到点L，由ILPI =tan∠DPI=tan∠PAG=PGPA=43，求得IL=43PI=103，则点Q经过的路径长是103．【解题过程】（1）解：作PG⊥BC于点G∵四边形ABCD是矩形，AB=4，AD=6，点P是AD的中点，∴∠A=∠B=∠PGB=90°，PA=PD=12AD=3，∴四边形ABGP是矩形，∴PG=AB=4，∠APG=90°，∵PE⊥FM，交直线BC于点E，∴∠FPE=90°，∴∠APF=∠GPE=90°−∠FPE，∵∠A=∠PGE=90°，∴△APF∽△GPE，∴tan∠PEF=PFPE =PAPG=34，∴tan∠PEF的值是34；（2）解：①作EF的垂直平分线KN交BE于点N，连接FN，则EN=FN，如图2所示：∴∠BEF=∠NFE，∴∠BNF=∠BEF+∠NFE=2∠BEF，∵∠AFP=2∠BEF，∴∠AFP=∠BNF，∴∠AFP+∠BFN=∠BNF+∠BFN=90°，∴∠NFP=∠EPM=90°，∴FN∥PE，∴∠BEF=∠NFE=∠PEF，∵BF⊥EB，PF⊥EP，∴BF=PF，∵AP2+AF2=PF2，AF=4−BF=4−PF，∴32+(4−PF)2=PF2，解得PF=258，设PF=3m，则PE=4m，由3m=258得m=2524，∴FE=√PF2+PE2=√(3m)2+(4m)2=5m=5×2524=12524，∵AF∥DM，∴PFPM =PAPD=1，∴PF=PM，∵点P是FM的中点，点Q是EM的中点，∴PQ=12FE=12×12524=12548，∴PQ的长是12548；②作PG⊥BC于点G，连接AG、PC，取PC的中点I，连接IQ，如图3所示：∵BC=AD=6，GB=PA=3，∴CG=BC−GB=6−3=3=∵CG∥AP，∴四边形APCG是平行四边形，∴PC∥AG，∴∠DPI=∠PAG，∵PFPE =PAPG，∴PFPA =PEPG，∴△PFE∽△PAG，∴∠PFE=∠PAG，∴∠DPI=∠PFE，∵∠MPQ=∠PFE，∴∠DPI=∠MPQ，∴∠DPI−∠DPQ=∠MPQ−∠DPQ，∴∠IPQ=∠DPM=∠APF，∵PC=AG=√PA2+PG2=√32+42=5，∴PI=12PC=12×5=52，∴PIPA =523=56，∵FEPF =53，FE=2PQ，∴2PQPF =53，∴PQPF =56=PIPA，∴△PIQ∽△PAF，∴∠PIQ=∠PAF=90°，∴点Q在线段PC的垂直平分线点上运动，延长IQ、PD交于点L，当点F从点A运动到点B，则点Q从点I运动到点L，∵ILPI =tan∠DPI=tan∠PAG=PGPA=43，∴IL=43PI=43×52=103，∴点Q经过的路径长是103．5．（2023·江苏镇江·中考真题）【发现】如图1，有一张三角形纸片ABC，小宏做如下操作：（1）取AB，AC的中点D，E，在边BC上作MN=DE；（2）连接EM，分别过点D，N作DG⊥EM，NH⊥EM，垂足为G，H；（3）将四边形BDGM剪下，绕点D旋转180°至四边形ADPQ的位置，将四边形CEHN剪下，绕点E旋转180°至四边形AEST的位置；（4）延长PQ ，ST 交于点F ．小宏发现并证明了以下几个结论是正确的： ①点Q ，A ，T 在一条直线上； ②四边形FPGS 是矩形； ③△FQT≌△HMN ；④四边形FPGS 与△ABC 的面积相等．【任务1】请你对结论①进行证明．【任务2】如图2，在四边形ABCD 中，AD∥BC ，P ，Q 分别是AB ，CD 的中点，连接PQ ．求证：PQ =12(AD +BC )．【任务3】如图3，有一张四边形纸ABCD ，AD∥BC ，AD =2，BC =8，CD =9，sin∠DCB =45，小丽分别取AB ，CD 的中点P ，Q ，在边BC 上作MN =PQ ，连接MQ ，她仿照小宏的操作，将四边形ABCD 分割、拼成了矩形．若她拼成的矩形恰好是正方形，求BM 的长．【思路点拨】（1）由旋转的性质得对应角相等，即∠ABC =∠QAD ，∠ACB =∠TAE ，由三角形内角和定理得∠ABC ＋∠BAC ＋∠ACB =180°，从而得∠QAD ＋∠BAC ＋∠TAE =180°，即Q ，A ，T 三点共线；（2）梯形中位线的证明问题常转化为三角形的中位线问题解决，连接AQ 并延长，交BC 的延长线于点E ，证明△ADQ≌△ECQ ，可得AQ =EQ ，AD =CE ，由三角形中位线定理得PQ =12BE =12(AD +BC )；（3）过点D 作DR ⊥BC 于点R ，由DC =9，sin∠DCB =45得DR =365，从而得S 梯形ABCD =12×(2+8)×365=36，由【发现】得S 正方形GEST =S 梯形ABCD ，则GE =6，PE =3，由【任务2】的结论得PQ =5，由勾股定理得EQ =4．过点Q 作QH ⊥BC ，垂足为H ．由CQ=92及sin∠DCB =45得QH =185，从而得CH =2710，证明△PEQ∽△QHM ，得HM =245，从而得BM =BC −HM −CH =12．【解题过程】 [任务1]证法1：由旋转得，∠QAD =∠ABC ，∠TAE =∠ACB ．在△ABC 中，∠ABC ＋∠BAC ＋∠ACB =180°， ∴∠QAD ＋∠BAC ＋∠TAE =180°， ∴点Q ，A ，T 在一条直线上．证法2：由旋转得，∠QAD =∠ABC ，∠TAE =∠ACB ．∴AQ∥BC，AT∥BC．∴点Q，A，T在一条直线上．[任务2]证明：如图1，连接AQ并延长，交BC的延长线于点E．∵AD∥BC，∴∠DAQ=∠E．∵Q是CD的中点，∴DQ=CQ．在△ADQ和△ECQ中，{∠DAQ=∠E,∠AQD=∠EQC, DQ=CQ,∴△ADQ≌△ECQ(AAS)．∴AQ=EQ，AD=CE．又∵P是AB的中点，∴AP=BP，∴PQ是△ABE的中位线，∴PQ=12BE=12(CE+BC)，∴PQ=12(AD+BC)．[任务3]的方法画出示意图如图2所示．由【任务2】可得PQ ∥BC ，PQ =12(AD +BC )=12×(2+8)=5．过点D 作DR ⊥BC ，垂足为R ．在Rt △DCR 中，sin∠DCB =DR CD ，∴DR =CD ⋅sin∠DCB =9×45=365．∴S 正方形GEST =S 梯形ABCD =12×(2+8)×365=36，∴GE =6，PE =3．在Rt △PEQ 中，由勾股定理得EQ =√PQ 2−PE 2= √52−32=4．过点Q 作QH ⊥BC ，垂足为H ． ∵Q 是CD 的中点， ∴CQ =12CD =12×9=92．在Rt △QHC 中，sin∠DCB =QH CQ，∴QH =CQ ⋅sin∠DCB =92×45=185．又由勾股定理得CH =√CQ 2−QH 2=√(92)2−(185)2=2710．由PQ ∥BC ，得∠PQE =∠QMH ．又∵∠PEQ =∠QHM =90°， ∴△PEQ∽△QHM ． ∴PE QH =EQ HM ，即3185=4HM ，∴HM =245．∴BM =BC −HM −CH =8−245−2710=12．6．（23·24九年级上·江苏无锡·阶段练习）【基本图形】（1）如图1，在矩形ABCD 中，CE ⊥BD 于点H ，交AD于点E．求证：CEBD =CDBC；【类比探究】（2）如图2，在四边形ABCD中，∠A=∠B=90°,AD=4，BC=9，CD=7．E是边AB上的一动点，过点C作CG⊥ED，交ED的延长线于点G，交AD的延长线于点F．试探究CFDE是否为定值?若是，请求出CFDE的值；若不是，请说明理由；【拓展延伸】（3）如图3，在Rt△ABD中，∠BAD=90°，将△ABD沿BD翻折得到△CBD，点E,F分别在边AB,AD上，连接CF,DE．若∠AED=∠AFC，且CFDE =35，则ADAB的值为______（直接写出结果）．【思路点拨】（1）证明△CED∽△BDC，利用相似三角形的性质即可证明CEBD =CDBC；（2）过点C作CH⊥AF交AF延长线于点H，首先证明四边形ABCH为矩形，易得AB=CH，BC=AH，再证明△DEA∽△CFH，由相似三角形的性质可得CFDE =CHAD，然好由勾股定理解得CH=2√6，即可证明CFDE=CHAD=√62，即可获得答案；（3）过点C作CG⊥AD于点G，交BD于点H，作HM⊥CD于点M，证明CG∥AB，易得∠ABD=∠GHD，再证明△AED∽△GFC，由相似三角形的性质可得CFDE =CGAD=35，由折叠的性质可得AD=CD，∠ADB=∠CDB，设GC=3x，则AD=CD=5x，由勾股定理可得DG=√CD2−CG2=4x，然后由角平分线的性质定理可得HG=HM，结合S△HDG+S△CHD=S△CDG，可求得HG=4x3，然后可推导tan∠ABD=tan∠DHG=DGHG=3，即可获得ADAB得值．【解题过程】解：（1）∵四边形ABCD为矩形，∴∠ADC=∠DCB=90°，∵CE⊥BD，∴∠DBC+∠BCH=∠BCH+∠ECD=90°，∴∠DBC=∠ECD，∴△CED∽△BDC，∴CE BD =CDBC；（2）CFDE是否为定值，如下图，过点C作CH⊥AF交AF延长线于点H，∴∠A=∠B=∠H=90°，∴四边形ABCH为矩形，∴AB=CH，BC=AH，∵∠GFD=∠HFC，∠GDF=∠ADE，又∵∠GFD+∠GDF=∠HFC+∠HCF，∴∠ADE=∠HCF，∵∠A=∠H，∴△DEA∽△CFH，∴CF DE =CHAD，∵BC=9，CD=7，AD=4，∴DH=AH−AD=BC−AD=5，∴CH=√CD2−DH2=2√6，∴CF DE =CHAD=2√64=√62，∴CF DE 为定值√62；（3）如下图，过点C作CG⊥AD于点G，交BD于点H，作HM⊥CD于点M，∴∠CGF=∠A=90°，∴CG∥AB，∴∠ABD=∠GHD，∵∠AED=∠AFC，∠CGF=∠A，∴△AED∽△GFC，∴CF DE =CGAD=35，∵将△ABD沿BD翻折得到△CBD，∴AD=CD，∠ADB=∠CDB，设GC=3x，则AD=CD=5x，∴DG=√CD2−CG2=4x，∵HG⊥AD，HM⊥CD，∠ADB=∠CDB，∴HG=HM，∵S△HDG+S△CHD=S△CDG，即12×4x×HG+12×5x×HM=12×3x×4x，∴HG=4x3，∴tan∠ABD=tan∠DHG=DGHG =4x43x=3，∴ADAB=3．7．（21·22九年级下·辽宁盘锦·期中）如图，在矩形ABCD中，AB=3,BC=5，BE平分∠ABC交AD于点E．连接CE，点F是BE上一动点，过点F作FG∥CE交BC于点G．将△BFG绕点B旋转得到△BF′G′，（1）如图1，连接CG′,EF′，求证：△BEF′∽△BCG′；（2）当点G′恰好落在直线AE上时，若BF=3，求EG′的值；（3）如图3，连接GG′，当GG′与BE交于点F时，猜想FG与FG′的数量关系，并证明．【思路点拨】（1）平行得到△BFG∽△BEC，得到BFBE =BGBC，旋转得到BF=BF′,BG=BG′,∠GBF=∠G′BF′，进而得到BF′BE =BG′BC，∠FBF′=∠GBG′，即可得证；（2）分点G′在线段AE和在线段EA的延长线上，两种情况进行讨论求解；（3）过点F作FH⊥BG于点H，过点B作BP⊥GG′于点P，易得BH=FH，根据矩形的性质，平行线的性质，得到∠FGB=∠ECB=∠CED，进而得到tan∠FGB=tan∠CED=CDDE =32，cos∠FGB=cos∠CED=EDCE=2√1313，推出tan∠FGB=FHGH =32，cos∠FGB=PGBG=2√1313，设FH=3a,HG=2a，分别求出FG,FG′，即可得解．【解题过程】（1）证明：∵FG∥CE，∴△BFG∽△BEC，∴BF BE =BGBC，∵将△BFG绕点B旋转得到△BF′G′，∴BF=BF′,BG=BG′,∠GBF=∠G′BF′，∴BF′BE =BG′BC，∠FBF′=∠GBG′，∴BF′BG′=BEBC，∴△BEF′∽△BCG′；（2）解：∵矩形ABCD中，AB=3,BC=5，∴AD∥BC，∠A=∠ABC=90°，∴∠AEB=∠EBC，∵BE 平分∠ABC ， ∴∠ABE =∠EBC =45°， ∴∠ABE =∠AEB =45°， ∴AE =AB =3，BE =3√2，由（1）知：BFBE =BGBC ，即：3√2=BG 5，∴BG =5√22， ∴BG ′=BG =5√22， ①当点G ′在线段AE 上时，在Rt △BAG ′中，AG ′=√G ′B 2−AB 2=√142， ∴EG ′=AE −AG ′=3−√142； ②当点G ′在线段EA 的延长线上时，在Rt △BAG ′中，AG ′=√G ′B 2−AB 2=√142， ∴EG ′=AE +AG ′=3+√142；综上：EG ′=3−√142或3+√142；（3）FGFG ′=137；证明如下：过点F 作FH ⊥BG 于点H ，过点B 作BP ⊥GG ′于点P ，由（2）知，∠FBC =45°，AE =3， ∴BH =FH ， ∵矩形ABCD ，∴AD ∥BC,AD =BC =5,CD =AB =3,∠D =90°， ∴DE =5−3=2，∠CED =∠ECB ，∴CE=√DE2+CD2=√13，∵FG∥CE，∴∠FGB=∠ECB=∠CED，∴tan∠FGB=tan∠CED=CDDE =32，cos∠FGB=cos∠CED=EDCE=2√1313，∴tan∠FGB=FHGH =32，cos∠FGB=PGBG=2√1313，设FH=3a,HG=2a，则：FG=√FH2+HG2=√13a，BH=FH=3a，∴BG=BH+HG=5a，∴PG=10√1313a，∵旋转，∴BG=BG′，∴GG′=2PG=20√1313a，∴FG′=GG′−FG=7√1313a，∴FG FG′=√13a7√13a13=137．8．（21·22下·沧州·二模）如图1，在一平面内，线段AB=20，M，N是线段AB上两点，且AM=BN=2，点C从点M开始向终点N AC，BC为边在线段AB同侧作等边△ACD和等边△BCE，设AC=x．（1）直接写出CD和BE位置关系：______；（2）如图2，连接AE，BD，求证：AE=BD；（3）如图3，点G，点H分别是CD，BE的中点，①求当x为何值时，线段GH取得最小值？最小值是多少？②当线段GH取得最小值此时，求△ACE的面积；（4）如图4，设DE的中点为P，则点P移动路径的长为______．【思路点拨】（1）根据平行线的判定即可；（2）证明△ACE≌△DCB(SAS)即可；（3）①连接AG并延长交直线BE于F，连接CH、CF，先证明四边形CGFH是矩形，得FC=GH，当FC⊥AB 时GH最小即可，②过E作EK⊥AB于K，∠ECB=60°，再根据三角函数及三角形的面积公式即可；（4）以点A为原点，直线AB为x轴，过点A垂直于直线AB的直线为y轴，建立平面直角坐标系，过点D作DG⊥AC于点G，过点E作EH⊥AC于点H，再表示出点P的坐标即可．【解题过程】（1）解：在等边△ACD和等边△BCE中，∴∠ACD=∠B=60°，∴CD∥BE．故答案为：平行．（2）解：∵△ACD和△BCE是等边三角形，∴AC=CD，CE=CB，∠ACD=∠BCE=60°，∴∠ACD+∠DCE=∠BCE+∠DCE，即：∠ACE=∠DCB，∴△ACE≌△DCB(SAS)，∴AE=BD；（3）解：①连接AG并延长交直线BE于F，连接CH、CF，∵△ACD和△BCE是等边三角形，∴∠ACD=∠B=60°，∴CD∥BE，∴∠DCH=∠CHB，∵点G，点H分别是CD，BE的中点，∴∠AGC=∠CHE=∠CHB=90°，∠BAF=30°∴∠CGF=∠AGC=∠DCH=90°，∴∠CGF=∠CHE=∠DCH=90°，∴四边形CGFH是矩形，∴FC=GH，∴当FC⊥AB时GH最小，在△ABF中，AF=ABsin60°=在△AFC中，AC=AFcos30°=15，FC=AF⋅sin30°=5√3，∵2≤AC≤18，∴当x=15时，线段GH取得最小值，最小值是5√3；②过E作EK⊥AB于K，∠ECB=60°，在△CEK中，∠ECB=60°，CB=AB−AC=5，EK=CE⋅sin60°=5√3，2∴S △ACE =12⋅AC ⋅EK =754√3；（4）解：如图，以点A 为原点，直线AB 为x 轴，过点A 垂直于直线AB 的直线为y 轴，建立平面直角坐标系，过点D 作DG ⊥AC 于点G ，过点E 作EH ⊥AC 于点H ，则M(2,0),B(20,0),N(18,0),C(x,0)， AC =x,BC =20−x ，∵△ACD,△BCE 均为等边三角形，∴∠DAC =∠ECH =60°，AG =12AC =x2,CH =12BC =20−x 2，∴AH =AC +CH =x +20−x 2=x2+10，∴DG =OG ⋅tan60°=x 2×√3=√3x2，EH =CH ⋅tan60°=(10−x2)×√3=−√3x2+10√3，∴D(x 2,√3x 2)，E(x2+10,−√3x 2+10√3)，则DE 的中点为P 的坐标为P(x2+5,5√3)(2≤x ≤18)， ∵P 的纵坐标为定值，即点P 在平行于x 轴的直线上运动， x =2时，P 1(6,5√3)， x =18时，P 2(14,5√3)，点P 移动路径的长为P 1P 2=14−6=8，故答案为：8．9．（23·24九年级上·吉林长春·阶段练习）如图①，在▱ABCD 中，∠A =60°，AB =4，AD =6，点E 在边BC 上，且BE =2，动点P 从点E 出发，沿折线EB −BA −AD 以每秒2个单位长度的速度运动．作∠PEQ =60°，EQ 交边AD 或边DC 于点Q ，连接PQ ．当点Q 与点C 重合时，点P 停止运动．设点P 的运动时间为t 秒．（t >0）（1）当点P和点B重合时，线段PQ的长为______；（2）当点Q和点D重合时，求tan∠PQE．（3）如图②，当点Q在边DC上运动时，证明：PD=CQ．（4）作点E关于直线PQ的对称点F，连接PF、QF，当四边形EPFQ和▱ABCD重叠部分图形为轴对称四边形时，直接写出t的值．【思路点拨】（1）首先证明四边形ABEQ是平行四边形，取QE中点M,连接BM，则△AQP是直角三角形，利用勾股定理解题即可；（2），过点D作DN⊥BC于点N,在Rt△QNC中,CN=2，EN=2，在Rt△QCN中,利用勾股定理求出QN= 2√3，然后根据tan∠PQE=tan∠QEC=DN解题即可；EN（3）连接DE,过点D作DG⊥BC于点G,利用ASA证明△PED≌△QEC解题即可；（4）当Q点位于CD中点时.四边形EPFQ与ABCD重叠部分四边形为轴对称四边形，根据题意求出t的值．【解题过程】（1）)解: ∵四边形ABCD是平行四边形，∴AQ∥BE，∴∠A+∠ABC=180°，∵∠A=60°，∴∠ABC=120°，又∵∠PEQ=60°，∴∠ABE+∠PEQ=180°，∴AB∥QE，∴四边形ABEQ是平行四边形.∴QE=AB=4,AQ=BE=2，取QE中点M,连接BM，∴QM=ME=2，又∵∠PEQ=60°，∴△BME是等边三角形，∴QM=BM=ME，∴∠MBE=60°，∴∠MQP=∠QPM=30°,∴∠QPE=90°，∵AQ∥BE，∴∠AQP=90°，∴△AQP是直角三角形，∴在Rt△AQP中QP=√AB²−AQ²=√42−22=2√3，∴当P点和B点重合时,PQ的长为2故答案为：2√3；（2）)解:∴四边形ABCD是平行四边形. ∴AD∥BC,∠A=∠C=60°∴∠PQE=∠QEC∵BC=AD=6,BE=2.∴CE=4如图2，过点D作DN⊥BC于点N,在Rt△QNC中,∠QNC=90°,∠C=60°∴∠NQC=30°∴CN=12CD=12×4=2，∴EN=EC−CN=4−2=2∴在Rt△QCN中,∴QN=√CQ²−CN²=√42−22=2√3，∴tan∠PQE=tan∠QEC=DNEN =2√32=√3，∴当Q点和D点重合时,tan∠PQE=√3；（3）证明:连接DE,过点D作DG⊥BC于点G,如图3由(2)知EC=CD=4,∠C=60°，∴△CDE是等边三角形∴DE=EC=CD=4又∵四边形ABCD是平行四边形.∴∠ADC=120°又∵∠PEQ=60°，∠DEC=∠C=∠EDC=60°，∴∠PED+∠DEQ=∠QEC+∠DEQ，∴∠PDE=∠QCE=60°，∠PED=∠QEC，∴△PED≌△QEC(ASA)，∴PD=QC，（4）解:由题意得，当Q点位于CD中点时.四边形EPFQ与ABCD重叠部分四边形为轴对称四边形.理由如下：如图4，连接DE，由(3)知△CDE是等边三角形,∵Q点为CD的中点，∴QD=QC=1CD=22∴QE⊥CD，∴∠CQE=90°，又∵∠C=60°∴∠CEQ=30°∴∠PEQ=60°∴∠PEC=90°∴PE⊥BC，又∵AD∥BC，∴PE⊥AD∴DE=4,PE=2√3，PD=2，∴PD=QD，∴Rt△PDE≌Pt△QDE(HL).∴四边形EPFQ与ABCD的重叠部分为EPDQ为轴对称四边形，∴P点的运动轨迹为EB+BA+AP=2+4+4=10，∵P点的速度为2个单位长度每秒，∴2t=10∴t=5∴t的值为5．10．（21·22·武汉·模拟预测）问题背景：如图（1），在四边形ABCD中，P是BC上一点，∠ABC=∠BCD=∠APD，求证：△ABP∽△PCD；尝试运用：如图（2），D,E,F三点分别在等边△ABC边BC,AB,AC上，∠ABC=∠EDF,BD=CD．已知BC=4，设EF=x,△DEF的面积为y，求y关于x的函数关系式（不求自变量x的取值范围）；拓展创新：如图（3），D是等边△ABC边BC上一点，连接AD,E是AD上一点，CD=2BD,∠BEC=120°，请用一个等式直接写出BE与CE的数量关系．【思路点拨】问题背景：如图（1），根据三角形相似的判定定理：两角对应相等的两个三角形相似证明即可；尝试运用：过点D分别作DG⊥AB,DH⊥AC，垂足分别为G,H，如图所示，D，E，F三点分别在等边ΔABC边BC，AB，AC上，∠ABC=∠EDF，BD=CD．已知BC=4，设EF=x，ΔDEF的面积为y，根据相似三角形判定与性质，再结合解直角三角形即可得到答案；拓展创新：将ΔBCE绕点C顺时针旋转60°，作DF∥CE，如图所示，可得DF∥CE∥AE′，证得△BDF∽△BCE，设BE=m，EC=x，可得EF的长，由△DFE∽△AE′E，利用相似三角形的性质可得结果．【解题过程】问题背景：证明：如图所示：∵∠ABC=∠APD，∴∠BAP+∠BPA=∠CPD+∠BPA，∴∠BAP=∠CPD，又∵∠ABP=∠PCD，∴△ABP∽△PCD；尝试运用：解：过点D分别作DG⊥AB,DH⊥AC，垂足分别为G,H，如图所示：∵△ABC是等边三角形，∠ABC=∠EDF，∴∠ABC=∠EDF=∠C=60°，由（1）知△BDE∽△CFD，∴BECD =DEFD，∵BD=CD，∴BEBD =DEFD，又∵∠ABC=∠EDF，∴△BDE∽△DFE，∴∠BED=∠DEF，∴DG=DH，在Rt△BDG中，∠ABC=60°，BD=2，则sinB=DGBD =DG2，即DG=2×√32=√3，∴DH=√3，∴y=√32x；拓展创新：解：CE=√2BE．将△BCE绕点C顺时针旋转60°，作DF∥CE，如图所示：∵将△BCE绕点C顺时针旋转60°得到△ACE′，∴BE=AE′，∠AE′C=120°，CE=CE′，∵DF∥CE，∠BEC=120°，∴∠CEE′=60°，∴△CEE′为等边三角形，∴∠CE′E=60°，EE′=CE，∴∠AE′B=60°，∴CE∥AE′，∵DF∥CE，∴DF∥AE′，∴△BDF∽△BCE，∴BFBE =DFCE=BDBC=13，设BE=m，∴BF=13m，EF=23m，设CE=x，∴DF=x3，∵△DFE∽△AE′E，∴EFEE′=DFAE′，∴23mx=13xm，∴x2=2m2，∵x>0，m>0，∴x=√2m，∴EC=√2BE．11．（22·23·信阳·三模）综合与实践【问题情境】在△ABC中，AB=AC，∠BAC=α，点D为BC边上一动点（不与B，C重合），连接AD，以AD为始边顺时针作∠ADE=β(α+β=180°)，DF平分∠ADE．【初步探究】（1）如图1，DE与AC的延长线交于点E，若α=60°，β=120°，CD=2BD，则BDCF的值为_____，∠CDF与∠E的数量关系是_________．【类比探究】（2）如图2，DE与AC的延长线交于点E，若α=β=90°，CD=2BD，求出BDCF的值及∠CDF与∠E的数量关系．【拓展应用】（3）如图3，DE与AC交于点E，α=β=90°，∠CAD=15°，AB=6√2，将△ADF绕点在平面内自由旋转，当B，A，F三点共线时，直接写出AFBD的值．【思路点拨】（1）可证得△ABD∽△DCF，从而BDCF =ABCD，进而得出BDCF=32，由∠BAD+∠DAE=60°可得出∠CDF=∠E；（2）可证得△ABD∽△DCF，从而得出BDCF =ABCD，进而得出BDCF=3√24，根据∠BAD+∠DAE=90°可推出∠CDF=∠E；（3）作AH⊥BC于H，作AR⊥DF，交DF的延长线于R，解直角三角形ABH求得AH=6，解Rt△ADH求得AD的值，解Rt△ADR求得AR和BR的值，解Rt△ARF求得AF和RF，进而求得AF，当F在BA的延长线上时，解Rt△DFX求得FX和DX的值，解Rt△ADX求得BD，进一步得出结果；当F在AB上时，作DV⊥AB于V，同样的方法得出结果．【解题过程】解：（1）∵AB=AC，∠BAC=60°，∴△ABC是等边三角形，∴∠B=∠C=60°，∴∠BAD+∠ADB=120°，∵∠ADF=12∠ADE=60°，∴∠DB+∠CDE=120°，∴∠BAD=∠CDF，∴△ABD∽△DCF，∴BDCF =ABCD，∵CD=2BD，∴AB=BC=32CD，∴BDCF =32，∵∠BAD+∠DAE=60°，∴∠CDF+60°−∠E=60°，∴∠CDF=∠E，故答案为：32，相等；（2）∵AB=AC，∠BAC=90°，∴∠B=∠C=45°，∴∠BAD+∠ADB=135°，∵∠ADF=12∠ADE=45°，∴∠DB+∠CDE=135°，∴∠BAD=∠CDF，∴△ABD∽△DCF，∴BDCF =ABCD，∵CD=2BD，∴BC=32CD，∵AB=√22BC，∴BDCF =3√24，∵∠BAD+∠DAE=90°，∴∠CDF+90°−∠E=90°，∴∠CDF=∠E；（3）如图1，作AH⊥BC于H，作AR⊥DF，交DF的延长线于R，∵AB=AC，∠BAC=90°，∴∠B=∠C=45°，BH=CH，∴AH=√22AB=6，在Rt△ADH中，∠ADH=∠DAC+∠C=60°，AH=6，∴AD=6 sin60°=4√3，在Rt△ADR中，AD=4√3，∠ADF=45°，∴AR=DR=√22AD=2√6，在Rt△ARF中，AR=2√6，∠AFR=∠DAC+∠ADF=15°+45°=60°，∴AF=2√6 sin60°=√6√32=4√2，RF=2√6=√6√3=2√2，∴AF=2FR=DF=DR−RF=2√6−2√2，如图2，当F在BA的延长线上时，作DX⊥AF于X，在Rt△DFX中，DF=2√6−2√2，∠DFX=60°，∴FX=12DF=√6−√2，DX=DF⋅sin60°=3√2−√6，在Rt△ADX中，BX=AB+AF+FX=6√2+4√2+√6−√2=9√2+√6，DX=3√2−√6，∴BD=√(9√2+√6)2+(3√2−√6)2=2√48+6√3，∴ AFBD =√22√48+6√3=√24+3√324+3√3，如图3，当F在AB上时，作DV⊥AB于V，由上知：FV=√6−√2，DV=3√2−√6，∴BV=AB−AF−FV=6√2−4√2−(√6−√2)=3√2−√6，∴BD=√2BV=√2(3√2−√6)，∴AFBD =√2√2(3√2−√6)=3√2+√63，综上所述： AFBD =√24+3√324+3√3或3√2+√63．12．（23·24九年级上·辽宁沈阳·阶段练习）在平面直角坐标系中，已知点A(0，6)，点B在线段AO上，且AB=2BO，若点P在x轴的正半轴上，连接BP，过点P作PQ⊥PB．（1）如图1，点E是射线PQ上一点，过点E作EC⊥x轴，垂足为点C．①点B的坐标__________．②求证：△BOP∼△PCE；（2）在（1）的条件下，如图2，若点C坐标为(8，0)．过点A作DA⊥y轴，且和CE的延长线交于点D．若点C关于直线PQ的对称点C′正好落在线段AD上．连接PC，则点P的坐标__________．（3）如图3，若∠BPO=60°，点E在直线PQ上，EC⊥x轴，垂足为点C．若以点E，P，C为顶点的三角形和△BPE相似，请直接写出点E的坐标__________．【思路点拨】（1）①根据OA=6,AB=2OB求解即可.②根据两角对应相等，两三角形相似证明即可.（2）如图2中, 过点C′作C′G⊥OC于G, 延长PB交DA的延长线于F.设OP=x,则PC=4−x.在Rt△EBC′中，根据C′P2=PG2+C′G2,构建方程求解即可.（3）如图3中, 由题意∠PBQ=∠ECP=90°, 分四种情形, 当∠PE1B=30°时, 以点E,P,C为顶点的三角形和△BPE相似, 当∠PBE2=30°时, 以点E,P,C为顶点的三角形和△BPE相似, 当∠PE3B=30°时, 以点E,P,C 为顶点的三角形和△BPE相似，当∠PBE4=30°时, 以点E,P,C为顶点的三角形和△BPE相似, 分别求解即可.【解题过程】（1）①∵A(0,6)，∴OA=6,∵AB=2BO,∴AB=4, OB=2,∴B(0,1)；故答案为：(0,1)②证明: 如图1中,∵PQ⊥PB,EC⊥OC,∴∠ECP=∠BPE=∠POB=90°,∴∠OPB+∠EPC=90°,∠EPC+∠CEP=90°,∴∠OPB=∠PEC,∴△BOP∽△PCE.（2）如图2中, 过点C′作C′G⊥OC于G, 延长PB交DA的延长线于F.设OP=x, 则PC=4−x.∵AF∥OP,∴∠F=∠BPO，∠FAB=∠BOP，∴△FBA∽△PBO,∴FAOP =ABOB=2，∴AF=2x,∵∠EPC+∠OPB=90°,∠EPC′+∠C′PF=90°∵∠EPC=∠EPC′，∴∠C′PF=∠OPB，∵∠OPB=∠F,∴∠F=∠C′PF，∴C′F=C′P=PC=8−x,∴AC′=8−3x，∴C′D=3x，∴PG=PC−CG=8−4x,在Rt△EBC′中,∵C′P2=PG2+C′G2，∴(8−x)2=(8−4x)2+62,解得x=65或x=2,∴P(65，0) 或(2,0).故答案为：(65，0) 或(2,0)；（3）如图3中,∵OB=2,∠POB=90°,∠OPB=60°,∴∠PBO=30°,∴OP=OB⋅tan30°=2√33，PB=2OP=4√33，∵∠BPQ=90°,∴∠QPC=30°,∵∠PBQ=∠ECP=90°,∴当∠PE1B=30°时, 以点E,P,C为顶点的三角形和△BPE相似,∴PE1=√3PB=4,∴E1C=12PE1=2,PC=2√3∴OC=8√33,∴E1(8√33，2)，当∠PBE2=30°时, 以点E,P,C为顶点的三角形和△BPE相似,，同法可得E2(4√33，23).当∠PE3B=30°时, 以点E,P,C为顶点的三角形和△BPE相似,同法可得E3(−4√33，−2).当∠PBE4=30°时, 以点E,P,C为顶点的三角形和△BPE相似,同法可得E4(0，−23).综上所述，满足条件的点E的坐标为(8√33，2)或(4√33，23)或(−4√33，−2)或(0，−23).13．（23·24·全国·专题练习）（1）如图①，在矩形ABCD的AB边上取一点E，将△ADE沿DE翻折，使点A落在BC上A′处，若AB=6,BC=10，求AEEB的值；（2）如图②，在矩形ABCD的BC边上取一点E，将四边形ABED沿DE翻折，使点B落在DC的延长线上B′处，若BC⋅CE=24,AB=6，求BE的值；（3）如图③，在△ABC中，∠BAC=45°，AD⊥BC，垂足为点D，AD=10,AE=6，过点E作EF⊥AD交AC于点F，连接DF，且满足∠DFE=2∠DAC，直接写出BD+53EF的值．【思路点拨】（1）由矩形性质和翻折性质、结合勾股定理求得A′B=2，设AE=A′E=x则BE=AB−AE=6−x，Rt△A′BE中利用勾股定理求得x=103，则AE=103，BE=6−103=83，进而求解即可；（2）由矩形的性质和翻折性质得到∠EBC=∠BDA，证明△EBC∽△BDA，利用相似三角形的性质求得BC= 4，则BD=10，在Rt△ABD中，利用勾股定理求得AD=8，进而求得BC=8,CE=3可求解；（3）证明△AEF∽△ADC得到CD=53EF，则BD+53EF=BD+CD=BC；设EF=3k，CD=5k，过点D作DH⊥AC于H，证明△CHD≌△FHD(ASA)得到DF=CD=5k，在Rt△EFD中，由勾股定理解得k=1，进而可求得AC=5√5．过B作BG⊥AC于G，证明∠CBG=∠CDH=∠DAC，则sin∠CBG=sin∠DAC=√55，cos∠CBG=cos∠DAC=2√55，再证明AG=BG，在Rt△BCG中利用锐角三角函数和AG+CG=BG+CG= AC，求得BC，即可求解．【解题过程】解：（1）∵四边形ABCD是矩形，∴AD=BC=10,CD=AB=6,∠A=∠B=∠C=90°，由翻折性质得AD=A′D=10,AE=A′E，在Rt△A′CD中，A′C=√A′D2−CD2=√102−62=8，∴A′B=BC−AC=2，。

浙教版数学七年级上册第六章综合测试卷图形的初步知识(含答案)

第六章综合测试卷图形的初步知识班级学号得分姓名一、选择题(本大题有10小题，每小题3分，共30分)1.如图的平面图形绕虚线旋转一周得到的实物图是( )2.下列各图形中，有交点的是( )3. 已知点 M是线段AB 的中点，那么(①AB=2AM;②BM₂AB;③AM=BM;④AM+BM=AB上面四个式子中，正确的有( )A. 1个B. 2 个C. 3个D. 4个4. 如图,点 C 是线段AB 上一点,点M是AC 的中点,点 N 是 BC 的中点,如果 MC 比 NC 长2cm,AC比 BC长( )A. 2cmB. 4cmC. 1cmD. 6cm5.若∠α与∠β互为补角,且∠α>∠β,则∠β的余角是( )6.下列关于余角、补角的说法，正确的是( )A. 若∠1+∠2+∠3=90°,则∠1,∠2,∠3互余B. 若∠α+∠β+∠γ=180°,则∠α,∠β,∠γ互补C. 若∠1+∠2=90°,则∠1与∠2互补D. 若∠α+∠β=90°,则∠α与∠β互余7.以下给出的四个语句中，正确的有( )①如果线段AB=BC,则点 B是线段AC 的中点;②线段和射线都可看作直线上的一部分；③大于直角的角是钝角；④如图,∠ABD也可用∠B表示.A. 1个B. 2 个C. 3 个D. 4 个8.如图，长度为18cm的线段AB的中点为M，点C是线段MB的一个三等分点，则线段AC的长为( )A. 12 cmB. 6 cmC. 9 cmD. 3 cm9. 已知B是线段AC上的一点，M是线段AB 的中点，N 是线段AC 的中点，P 是线段NA 的中点，Q是线段MA的中点,则MN:PQ等于( )A. 1: 1B. 2 : 1C. 3 : 2D. 4 : 310. 如图,点 A,O,B 在同一条直线上,∠COE和∠BOE互余,射线 OF 和OD 分别平分∠COE和∠BOE,则∠AOF+∠BOD与∠DOF的关系是( )A. ∠AOF+∠BOD=∠DOFB. ∠AOF+∠BOD=2∠DOFC. ∠AOF+∠BOD=3∠DOFD. ∠AOF+∠BOD=4∠DOF二、填空题(本大题有6小题，每小题4分，共24分)11. 把一段弯曲的河流改直，可以缩短航程，其理由是 .12. 如果∠1与∠2互余,∠2与∠3互余,且∠1=25°,则∠3= .13. 早上6点 20分时，时针与分针所夹的小于平角的角为度.14. 如图,将长方形纸片 ABCD 沿直线EN,EM进行折叠后(点 E 在AB 边上),B'点刚好落在A'E上，若折叠角,则另一个折叠角∠BEM=.15. 画一个∠AOB,使∠AOB=50°,再作OC⊥OA,OD⊥OB,则∠COD的度数是 .16. 如图,直线AB,CD 相交于点O,OE平分∠AOD,OF⊥OC,∠1与∠3的度数之比为3:4,则∠EOC=°,∠2= °.三、解答题(本大题有8小题，共66分)17.(6分)如图,已知平面内两点A,B.(1)用尺规按下列要求作图，并保留作图痕迹：①连结 AB;②在线段AB的延长线上取点C，使BC=AB；③在线段 BA的延长线上取点D,使 AD=AC.(2)图中,若AB=6,则AC的长度为 ,BD的长度为 .18. (6分)已知m,n满足等式(1)求 m,n的值;(2)已知线段AB=m,在直线AB上取一点 P,恰好使AP=nPB,Q为PB 的中点.求线段 AQ的长.19. (6分)数轴上点 A，B，C所表示的数分别是，线段AB的中点为D.(1)求线段 AB 的长;(2)求点 D所表示的数；(3)若求 x的值.20.(8分)如图,已知OA,OB,OC,OD是射线,,OD 平分.求的度数.21. (8分)如图，已知OB的方向是南偏东OA 平分OC平分(1)请直接写出OA 的方向是，OC的方向是；(2)求的度数.22.(10分)如图,点 A,O,B在同一条直线上,射线OD平分(1)当求的度数；(2)射线 OE 是.的平分线吗? 为什么?23.(10分)如图所示,B 是线段AD 上一动点,沿A→D→A以2cm/s的速度往返运动1次,C是线段BD的中点，,设点 B的运动时间为ts(0≤t≤10).(1) 当时，②求线段CD的长度；(2) 用含 t 的代数式表示运动过程中AB 的长.24. (12分)将一副三角板叠放在一起：(1)如图①，在此种图案的情形下，已知.求∠CAE的度数;(2)如图②，在此种图案的情形下，能否成立? 若能成立，请求出.的度数；若不能成立，请说明理由.第六章综合测试卷图形的初步知识1. D2. B3. D4. B5. A6. D7. A8. A9. B10. C11. 两点之间,线段最短 12. 25° 13. 70 14. 59°45'15. 50°或 130° 16. 153 5417. 解:(1)如图所示.(2)∵AB=BC,∴AC=2AB=2×6=12.∵AD=AC=12,∴BD=AD+AB=12+6=18.故答案为12;18.18. 解:(1)由题意得:m-8=0,n--m+5=0,解得m=8,n=3. (2)7 或1019. (1)AB=10 (2)D所表示的数为÷1 (3)x=12或-420. 解:∵∠BOC=2∠AOB,∴∠AOC=∠BOC+∠AOB=3∠AOB.∵OD平分∠AOB₂∠AOB.∵∠BOD=16°,∴∠AOB=32°21.解:(1)北偏东 62.5° 东北方向(2)由题意可知:,所以∠BON=∠BOE+∠NOE=,因为 OA 平分∠NOB,所以∠NOA=又因为OC平分∠NOE,所以所以∠AOC=22. 解:(1)∵OD平分∠AOC,∴∠AOD=∠DOC,∵∠AOC=80°,∴∠AOD=40°,∵∠DOE=90°,(2)OE是∠BOC的平分线.理由如下:∵OD平分∠AOC,∴∠AOD=∠DOC,又∠DOE=90°,∴∠COD+∠COE=90°,则. 即 OE是∠BOC的平分线.23. 解:(1)①4②∵AD=10cm,AB=4cm,∴BD=10-4=6(cm).∵C是线段BD 的中点,(2)当0≤t≤5时,AB=2tcm;当5<t≤10时,AB=(20-2t) cm.24. 解:(1)∵∠α=3∠β,∠α+∠β=90°,∴3∠β+∠β=90°,∴∠β=22.5°,又∠CAE+∠α=90°,∴∠CAE=∠β=22.5°.(2)能,设∠BCE的度数为x,则∠ACE=90°-x,∠BCD=60°-x.列方程,得θ(对快对快对2(60°-x),解得x=30°.∴怏∠ACD=∠ACE+∠ECD=60°+60°=120°.。

【期末复习】浙教版2022年七年级上册：“几何类题型大全”一卷过关(40道题)(含解析)

【期末复习】浙教版2022年七年级上册：“几何类题型大全”一卷过关（40道题）一．选择题1．如图，建筑工人在砌墙时，经常用细绳在墙的两端之间拉一条直的参照线，这样做蕴含的数学原理是（）A．两点之间线段最短B．两点确定一条直线C．经过一点有无数条直线D．垂线段最短2．下列说法中，正确的是（）A．相等的角是对顶角B．若AB＝BC，则点B是线段AC的中点C．过一点有一条而且仅有一条直线垂直于已知直线D．若一个角的余角和补角都存在，则这个角的补角一定比这个角的余角大90度3．平面上有三点A，B，C，如果AB＝8，AC＝5，BC＝3，下列说法正确的是（）A．点C在线段AB上B．点C在线段AB的延长线上C．点C在直线AB外D．点C可能在直线AB上，也可能在直线AB外4．如图，AC⊥BC，CD⊥AB，AC＝4，BC＝3，AB＝5，CD＝2.4，那么点C到AB的距离是（）A．3B．5C．4D．2.45．如图，三角形ABC中，AC⊥BC，CD⊥AB于点D，则下列线段关系成立的是（）A．AD+BC＜AB B．BD+AC＜AB C．BC+AC＞2CD D．AC+BC＜AB6．下列四个图中，能表示线段x＝a+c﹣b的是（）A．B．C．D．7．将一副尺子中的两个三角板按如图方式摆放，其中∠1＝∠2的有几个（）A．1B．2C．3D．48．如图，射线OA表示北偏西36°方向，OB平分∠AOC，则∠BOC的度数为（）A．54°B．63°C．64°D．68°9．已知数轴上的三点A、B、C所对应的数a、b、c满足a＜b＜c、abc＜0和a+b+c＝0．那么线段AB与BC的大小关系是（）A．AB＞BC B．AB＝BC C．AB＜BC D．不确定的10．如图，将一个三角板60°角的顶点与另一个三角板的直角顶点重合，∠1＝26°18'，则∠2的度数是（）A．26°18'B．52°20'C．56°23'D．56°18'11．如图，已知线段AB＝12．点C在线段AB上，BC＝AB，点D是AB的中点，则CD的长度为（）A．2B．4C．6D．812．如图，将两块三角尺AOB与COD的直角顶点O重合在一起，若∠AOD＝4∠BOC，OE为∠BOC的平分线，则∠DOE的度数为（）A．36°B．45°C．60°D．72°13．如图，OA⊥OC，OB⊥OD，四位同学观察图形后分别说了自己的观点．甲：∠AOB＝∠COD；乙：∠BOC+∠AOD＝180°；丙：∠AOB+∠COD＝90°；丁：图中小于平角的角有6个．其中观点正确的有（）A．甲、乙、丙B．甲、丙、丁C．乙、丙、丁D．甲、乙、丁14．已知∠α与∠β满足2∠α+3∠β＝180°（∠α≠0°，∠β≠0°），下列式子表示的角：①90°﹣∠β；②30°+∠α；③∠α+∠β；④2∠α+∠β中，其中是∠β的余角的是（）A．①②B．①③C．②④D．③④二．填空题15．54°30'角的补角等于．16．∠a的余角＝﹣∠a．17．若∠α＝42°24′，∠β＝15.3°，则∠α与∠β的和等于．18．如图，∠COD是Rt∠，∠BOD＝35°，则∠AOC＝．19．如图AO⊥BO，∠BOC＝20°，OD平分∠AOC，则∠BOD的度数为．20．如图，P是线段MN上一点，Q是线段PN的中点．若MN＝10，MP＝6，则MQ的长是．21．如图放置一副三角板，若∠BOC＝∠COD，则∠AOD的度数是．22．已知线段AB＝24cm，点D是线段AB的中点，直线AB上有一点C，且CD＝3BC，则线段CD＝cm．23．已知线段AB＝1cm，延长线段AB至点C，使BC＝4AB，M是线段AC的中点，N是线段AM的中点，则BN ＝cm．24．如图1，两条直线相交，以交点为端点的射线有4条；如图2，三条直线相交，以交点为端点的射线最多有12条；如图3，四条直线相交，以交点为端点的射线最多有24条．那么六条直线相交，以交点为端点的射线最多有条．25．将一根绳子对折1次后从中间剪一刀（如图），绳子变成3段；将一根绳子对折3次后从中间剪一刀，绳子变成段．将一根绳子对折（2n﹣1）次后从中间剪一刀，绳子变成段．26．如图，将量角器的中心与∠AOB的顶点重合，读出射线OA，OB分别经过刻度18和140，把∠AOB绕点O顺时针方向旋转到∠A'OB'，读出∠AOA'的平分线OC经过刻度32，则∠AOB'的平分线经过的刻度是．三．解答题27．如图，已知点A，B，C，按下列要求画出图形．（1）作射线BA，直线AC；（2）过点B画直线AC的垂线段BH28．为了落实“村村通管道煤气”工程，煤气公司准备向村庄C铺设煤气管线，三个村庄A，B，C的位置如图所示（假设煤气管线铺设线路上无任何障碍）．（1）若准备自村庄A向村庄C修建煤气管线，怎样铺设最节省？请你画出示意图；（2）若线段AB表示的是村庄A，B之间铺设的煤气管线，准备从线段AB上取一个点D，向村庄C修建一条煤气管线，怎样铺设最节省？请你画出示意图．29．如图，已知平面上三点A，B，C，按下列要求完成作图和解答；（1）画射线AC，线段BC．（2）连结AB，并用圆规在线段AB的延长线上截取BD＝BC（保留画图痕迹）．（3）过点C作CE⊥AB于点E；点C到AB的距离是的长；线段AC，CE，BC这三条线段大小关系是（用“＜”号连接）．30．如图，直线AB，CD交于点O，射线OE，OF都在直线AB的上方，且OE⊥OF．（1）若∠AOC＝28°，∠BOF＝30°，求∠DOE的度数．（2）若OB平分∠DOF，请写出图中与∠AOE互余的角．（直接写出所有答案）31．如图，直线AE与CD相交于点B，BF⊥AE．（1）若∠DBE＝60°，求∠FBD的度数；（2）猜想∠CBE与∠DBF的数量关系，并说明理由．32．如图，直线AB，CD相交于点O，OE平分∠BOC，OF⊥OE．（1）写出与∠BOF互余的角．（2）若∠BOF＝57°，求∠AOD的度数．33．如图，已知OB，OC，OD是∠AOE内三条射线，OB平分∠AOE，OD平分∠COE．（1）若∠AOB＝70°，∠DOE＝20°，求∠BOC的度数．（2）若∠AOE＝136°，AO⊥CO，求∠BOD的度数．（3）若∠DOE＝20°，∠AOE+∠BOD＝220°，求∠BOD的度数．34．将直角三角板OMN的直角顶点O放在直线AB上，射线OC平分∠AON．（1）如图，若∠BON＝60°，求∠COM的度数；（2）将直角三角板OMN绕顶点O按逆时针方向旋转，在旋转过程中：①当∠BON＝140°时，求∠COM的度数；②直接写出∠BON和∠COM之间的数量关系．35．如图，数轴上C，D两点把线段AB分成2：5：3三部分，E为AB的中点．（1）若点A，B，D所表示的数分别是﹣10，+20，x，求x的值．（2）若ED＝3cm，求线段AB的长．36．已知点C在线段AB上，AC＝2BC，点D、E在直线AB上，点D在点E的左侧，（1）若AB＝18，DE＝8，线段DE在线段AB上移动，①如图1，当E为BC中点时，求AD的长；②当点C是线段DE的三等分点时，求AD的长；（2）若AB＝2DE，线段DE在直线上移动，且满足关系式，则＝．37．如图，数轴上A，B两点对应的数分别为﹣4，﹣1．（1）求线段AB的长度．（2）若点D在数轴上，且DA＝3DB，求点D对应的数．（3）若点A的速度为7个单位长度/秒，点B的速度为2个单位长度/秒，点O的速度为1个单位长度/秒，点A，B，O同时向右运动，几秒后，OA＝3OB？38．如图，已知数轴上点A表示的数为10，点B位于点A左侧，AB＝15．动点P从点A出发，以每秒2个单位长度的速度沿数轴向左匀速运动，设运动时间为t秒．（1）当点P在A、B两点之间运动时，①用含t的代数式表示PB的长度；②若PB＝2P A，求点P所表示的数；（2）动点Q从点B出发，以每秒5个单位长度的速度沿数轴向右匀速运动，当点Q到达点A后立即原速返回．若P，Q两点同时出发，其中一点运动到点B时，两点停止运动．求在这个运动过程中，P，Q两点相遇时t的值．39．阅读理解：在钟面上，把一周分成12个大格，每个大格分成5个小格，所以每个大格对应的是30°角，每个小格对应的是6°角，时针每分钟转过的角度是0.5度，分针每分针转过的角度是6度．解决问题：（1）当时钟的时刻是8：30时，求此时分针与时针所夹的锐角的度数；（2）8：00开始几分钟后分针第一次追上时针；（3）设在8：00时，分针的位置为OA，时针的位置为OB，运动后的分针为OP，时针为OQ．问：在8：00～9：00之间，从8：00开始运动几分钟，OB，OP，OQ这三条射线，其中一条射线是另外两条射线所夹的角的平分线？40．如图，已知实数a（a＞0）表示在数轴上对应的位置为点P．现对点P进行如下操作：先把点P沿数轴以每秒1个单位的速度向左移动t秒，再把所得到的点沿数轴以每秒2个单位的速度向右移动a秒，得到点P'．我们把这样的操作称为点P的“回移”，点P'为点P的“回移点”．（1）当t＝2时，①若a＝4，求点P的回移点P'表示的实数；②若回移点P'与点P恰好重合，求a的值；（2）是否存在这样的情况：原点O，点P及其回移点P'中，一个点是以另外两点的端点的线段的三等分点？若存在，请用含a的代数式表示t；若不存在，请说明理由．参考答案一．选择题1．【解答】解：建筑工人砌墙时，经常用细绳在墙的两端之间拉一条参照线，这样做蕴含的数学原理是：两点确定一条直线．故选：B．2．【解答】解：A、对顶角相等，但是相等的角不一定是对顶角，故本选项不符合题意；B、三点不在一条直线上，AB＝BC，但是B不是线段AC的中点，故本选项不符合题意；C、平面内，过一点有且只有一条直线与已知直线垂直，正确，故此选项不符合题意；D、若一个角的余角和补角都存在，则这个角的补角一定比这个角的余角大90度，故此选项符合题意；故选：D．3．【解答】解：从图中我们可以发现AC+BC＝AB，所以点C在线段AB上．故选：A．4．【解答】解：∵CD⊥AB，CD＝2.4，∴CD＝2.4，故选：D．5．【解答】解：在Rt△CDB中，∠CDB＝90°，∴BD＜BC，∴AD+BC＞AD+BD＝AB，故选项A结论不成立；同理，BD+AC＞AB，AC+BC＞AB，故选项A、D结论不成立；∵BC＞CD，AC＞CD，∴BC+AC＞2CD，故选项C结论正确，符合题意；故选：C．6．【解答】解：根据线段的和差可得，能表示线段x＝a+c﹣b的是B，故选：B．7．【解答】解：图一：∠1＝∠2＝135°；图二：∠1＝∠2；图三：∠1+∠2＝90°；图四：∠1≠∠2；故选：B．8．【解答】解：由题意得：∠AOC＝90°+36°＝126°，∵OB平分∠AOC，∴∠BOC＝∠AOC＝63°，故选：B．9．【解答】解：∵a＜b＜c，abc＜0，a+b+c＝0，∴a＜0，b＞0，c＞0，|a|＝b+c，∴AB＝|a﹣b|＝b﹣a＞|a|，BC＝|b﹣c|＝c﹣b＜|a|，∴AB＞BC．故选：A．10．【解答】解：∵∠1+∠EAC＝60°，∠1＝26°18'，∴∠EAC＝60°﹣∠1＝60°﹣26°18'＝33°42'，∵∠EAC+∠2＝90°，∴∠2＝90°﹣∠EAC＝90°﹣33°42'＝56°18'．故选：D．11．【解答】解：∵BC＝AB，AB＝12，∴BC＝4，∵D是线段AB的中点，∴BD＝AB＝6，∴CD＝BD﹣BC＝2．故选：A．12．【解答】解：∵∠AOB＝90°，∠COD＝90°，∴∠AOB+∠COD＝180°，∵∠AOB＝∠AOC+∠BOC，∠COD＝∠BOC+∠BOD，∴∠AOC+∠BOC+∠BOC+∠BOD＝180°，∴∠AOD+∠BOC＝180°，∵∠AOD＝4∠BOC，∴4∠BOC+∠BOC＝180°，∴∠BOC＝36°，∵OE为∠BOC的平分线，∴∠COE＝∠BOC＝18°，∴∠DOE＝∠COD﹣∠COE＝90°﹣18°＝72°，故选：D．13．【解答】解：∵OA⊥OC，OB⊥OD，∴∠AOC＝∠BOD＝90°．∴∠AOC﹣∠BOC＝∠BOD﹣∠BOC．∴∠AOB＝∠COD．∴甲同学说的正确；∵∠BOC+∠AOD＝∠AOC+∠COD+∠BOC＝∠AOC+∠BOD＝90°+90°＝180°，∴乙同学说的正确；∵∠AOB+∠BOC＝∠AOB＝90°，∠BOC和∠COD不一定相等，∴丙同学说的错误；∵图中小于平角的角有∠AOB、∠AOC、∠AOD、∠BOC、∠BOD、∠COD，共6个，∴丁同学说的正确．故选：D．14．【解答】解：∠β的余角是90°﹣∠β，故①正确；∵∠α与∠β满足2∠α+3∠β＝180°，∴3∠β＝180°﹣2∠α，∴∠β＝60°﹣∠α，∴∠β的余角是90°﹣（60∠α）＝30°+∠α，故②错误；∵∠α+β＝∠α+（60°﹣∠α）＝∠α+30°﹣＝30°+∠α，∴∠α+∠β是∠β的余角，故③正确；∵2∠α+∠β＝2∠α+60°﹣∠α＝60°+∠α≠30°+∠α，故④错误；即正确的是①③，故选：B．二．填空题15．【解答】解：180°﹣54°30′＝125°30′，故答案为：125°30′．16．【解答】解：∠a的余角＝90°﹣∠a．故答案为：90°．17．【解答】解：∵∠β＝15.3°＝15°+0.3×60′＝15°18′，∴∠α+∠β＝42°24′+15°18′＝57°42′．故答案为：57°42′．18．【解答】解：∵∠AOC+∠COD+∠BOD＝180°，∠COD＝90°，∠BOD＝35°，∴∠AOC＝180°﹣90°﹣35°＝55°，故答案为：55°．19．【解答】解：因为OA⊥OB，所以∠AOB＝90°，因为∠BOC＝20°，所以∠AOC＝∠AOB+∠BOC＝90°+20°＝110°，因为OD平分∠AOC，所以∠COD＝∠AOC＝55°，所以∠BOD＝∠COD﹣∠COB＝55°﹣20°＝35°，故答案为：35°．20．【解答】解：∵MN＝10，MP＝6，∴NP＝MN﹣MP＝10﹣6＝4．∵点Q为线段PN的中点，∴PQ＝NP＝2，∴MQ＝MP+PQ＝6+2＝8．故答案为：8．21．【解答】解：∠BOC＝∠COD＝20°，∠BOD＝∠COD﹣∠BOC＝60°﹣20°＝40°，∴∠AOD＝∠AOB+∠BOD＝90°+40°＝130°．故填130°22．【解答】解：∵AB＝24cm，点D是线段AB的中点，∴BD＝12cm，设BC＝xcm，则CD＝3BC＝3xcm，当C点在B、D之间时，DC＝BD﹣BC，即3x＝12﹣x，解得x＝3，∴CD＝9（cm）；当C点在DB的延长线上时，DC＝DB+BC，即3x＝12+x，解得x＝6，∴CD＝18（cm）；故答案为：9或18．23．【解答】解：∵BC＝4AB，AB＝1cm，∴BC＝4×1＝4cm，∴AC＝AB+BC＝1+4＝5cm，∵M是线段AC的中点，∴AM＝＝＝2.5cm，∵N是线段AM的中点，∴AN＝AM＝＝1.25cm，∴BN＝AN﹣AB＝1.25﹣1＝0.25cm，故答案为：0.25．24．【解答】解：两条直线相交，以交点为端点的射线有4条，4＝2×（2×1），三条直线相交，以交点为端点的射线最多有12条，12＝3×（2×2），四条直线相交，以交点为端点的射线最多有24条，24＝4×（2×3），那么，六条直线相交，以交点为端点的射线最多有：6×（2×5）＝60条，故答案为：60．25．【解答】解：∵对折1次从中间剪断，有21+1＝3；对折2次，从中间剪断，有22+1＝5．∴对折3次，从中间剪断，有23+1＝9，∴对折（2n﹣1）次，从中间剪一刀全部剪断后，绳子变成（22n﹣1+1）段．故答案为：9；（22n﹣1+1）．26．【解答】解：如图，设∠AOB′的角平分线是OD，∵射线OA，OB分别经过刻度18和140，∴∠AOB＝140﹣18＝122°，∴∠C＝∠AOB＝122°，∵∠AOA'的平分线OC经过刻度32，∴∠AOC＝32﹣18＝14°，∠AOA′＝2∠AOC＝28°，∴∠AOB′＝∠AOA′+∠A′OB′＝28°+122°＝150°，∴∠AOD＝AOB′＝75°，∴射线OD经过的刻度是18+75＝93．故答案为：93．三．解答题27．【解答】解：（1）如图，射线BA，直线AC为所作；（2）如图，线段BH为所作．28．【解答】解：（1）如图，线段AC即为所求．（2）如图，线段CD即为所求．29．【解答】解：（1）如图，射线AC，线段BC即为所求；（2）如图，BD即为所求；（3）点C到AB的距离是CE的长；线段AC，CE，BC这三条线段大小关系是CE＜BC＜AC．故答案为：CE，CE＜BC＜AC．30．【解答】解：（1）∵∠BOD＝∠AOC＝28°，∠BOF＝30°，∴∠DOF＝∠BOD+∠BOF＝28°+30°＝58°，∵OE⊥OF，∴∠EOF＝90°，∴∠DOE＝∠DOF+∠EOF＝58°+90°＝148°；（2）∵∠EOF＝90°，∠AOE+∠BOF+∠EOF＝180°，∴∠AOE+∠BOF＝90°，∵OB平分∠DOF，∴∠BOF＝∠BOD，∴∠AOE+∠BOD＝90°，∵∠AOC＝∠BOD，∴∠AOC+∠AOE＝90°，∴图中与∠AOE互余的角∠BOF，∠BOD，∠AOC，故答案为：∠BOF，∠BOD，∠AOC．31．【解答】（1）解：∵BF⊥AE，∴∠EBF＝∠ABF＝90°，∵∠FBD＝∠EBF﹣∠DBE，∴∠FBD＝90°﹣60°＝30°；（2）∠CBE﹣∠DBF＝90°．证明：∵∠ABD﹣∠FBD＝∠ABF，∴∠ABD﹣∠FBD＝90°，∵∠CBE＝∠ABD，∴∠CBE﹣∠DBF＝90°．32．【解答】解：（1）∵OF⊥OE，∴∠BOF+∠BOE＝90°，∵OE平分∠BOC，∴∠BOE＝∠COE，∴∠BOF+∠COE＝90°，∴与∠BOF互余的角为∠BOE，∠COE；（2）∵∠BOF＝57°，∠BOF+∠BOE＝90°，∴∠BOE＝90°﹣57°＝33°，∵OE平分∠BOC，∴∠BOC＝2∠BOE＝66°，∴∠AOD＝∠BOC＝66°．33．【解答】解：（1）∵OB平分∠AOE，OD平分∠COE，∴∠BOE＝∠AOB＝70°，∠COE＝2∠DOE＝40°，∵∠BOC＝﹣∠BOE﹣∠COE，∴∠BOC＝70°﹣40°＝30°．（2）∵OB平分∠AOE，OD平分∠COE，∴∠BOE＝∠AOE，∠DOE＝∠COE，∵∠BOD＝∠BOE﹣∠DOE，∴∠BOD＝（∠AOE﹣∠COE）＝∠AOC，∵AO⊥CO，∴∠AOC＝90°，∴∠BOD＝45°．（3）∵OB平分∠AOE，∴∠AOE＝2∠BOE，∵∠AOE+∠BOD＝220°，∴2∠BOE+∠BOD＝220°，∵∠BOE﹣∠BOD＝∠DOE，∴∠BOE﹣∠BOD＝20°，∴2∠BOE﹣2∠BOD＝40°，∴3∠BOD＝180°，∴∠BOD＝60°．34．【解答】解：∵∠BON＝60°，∴∠AON＝120°，∵OC平分∠AON，∴∠CON＝60°，∵∠MON＝90°，∴∠COM＝90°﹣60°＝30°；（2）①当ON在直线AB上方时，如图1，∵∠BON＝140°，∴∠AON＝40°，∵OC平分∠AON，∴∠CON＝20°，∵∠MON＝90°，∴∠COM＝70°，当ON在直线AB下方时，如图2，∵∠BON＝140°，∴∠AON＝40°，∵OC平分∠AON，∴∠CON＝20°，∵∠MON＝90°，∴∠COM＝110°，综上所述，∠COM的度数为70°或110°．②∠BON＝2∠COM或∠BON+2∠COM＝360°．35．【解答】解：（1）∵点A，B所表示的数分别是﹣10，+20，∴AB＝30，∵C，D两点把线段AB分成2：5：3三部分，∴DB＝AB＝9，∴D所表示的数x＝20﹣9＝11，∴x的值为11．（2）∵C，D两点把线段AB分成2：5：3三部分，∴设AC＝2y，CD＝5y，DB＝3y，∵E为AB的中点，∴EB＝12AB＝5y，∵ED＝3cm，∴ED＝EB﹣DB＝5y﹣3y＝3cm，∴y＝32，∴AB＝10y＝15（cm），∴线段AB的长为15cm．36．【解答】解：（1）∵AC＝2BC，AB＝18，∴BC＝6，AC＝12，①∵E为BC中点，∴CE＝3，∵DE＝8，∴CD＝5，∴AD＝AC﹣CD＝12﹣5＝7；②∵点C是线段DE的三等分点，DE＝8，∴当点C靠近E点时，CE＝DE＝，∴CD＝，∴AD＝AC﹣CD＝12﹣＝；当点C靠近点D时，DC＝DE＝，∴AD＝AC﹣CD＝12﹣＝；（2）当点E在线段BC之间时，如图，设BC＝x，则AC＝2BC＝2x，∴AB＝3x，∵AB＝2DE，∴DE＝1.5x，设CE＝y，∴AE＝2x+y，BE＝x﹣y，∴AD＝AE﹣DE＝2x+y﹣1.5x＝0.5x+y，∵，∴，∴y＝x，∴CD＝1.5x﹣x＝x，∴；当点E在点A的左侧，如图，设BC＝x，则DE＝1.5x，设CE＝y，∴DC＝EC+DE＝y+1.5x，∴AD＝DC﹣AC＝y+1.5x﹣2x＝y﹣0.5x，∵，BE＝EC+BC＝x+y，∴，∴y＝4x，∴CD＝y+1.5x＝4x+1.5x＝5.5x，BD＝DC+BC＝y+1.5x+x＝6.5x，∴AB＝BD﹣AD＝6.5x﹣y+0.5x＝6.5x﹣4x+0.5x＝3x，∴，当点E在线段AC上及点E在点B右侧时，无解，综上所述的值为或．另一解法：可设AB＝6，则AC＝4，CB＝2，DE＝3，以A为原点，以AB的方向为正方向建立数轴，则A表示0，C表示4，B表示6，如图，设D表示的数为x，则E表示x+3，可得AD＝|x|，EC＝|x+3﹣4|＝|x﹣1|，BE＝|x+3﹣6|＝|x﹣3|，CD＝|x﹣4|，，①当x＜0或x≥3时，上式可化为：，解得x＝﹣7，则；②1≤x＜3时，上式化为：，解得：x＝，则；③0≤x＜1时，上式化为：，解得：x＝（舍去）．综上所述的值为或．故答案为：或．37．【解答】解：（1）∵A，B两点对应的数分别为﹣4，﹣1，∴AB＝﹣1﹣（﹣4）＝3；（2）①当点D在AB之间时，有：DA+DB＝AB，∵DA＝3DB，∴3DB+DB＝3，解得：DB＝，∴点D表示的数是：﹣1﹣＝﹣；②当点D是B的右侧，有：DA＝AB+DB，∵DA＝3DB，∴3DB＝3+DB，解得：DB＝，∴点D表示的数是：；综上所述：D对应的数为﹣或；（3）设经过t秒后，OA＝3OB，由题意得：OA＝|﹣4+7t﹣t|＝|﹣4+6t|，OB＝|﹣1+2t﹣t|＝|﹣1+t|，∵OA＝3OB，∴|﹣4+6t|＝3|﹣1+t|，解得：t＝或，答：秒或秒后，OA＝3OB．38．【解答】解：（1）①∵点A表示的数为10，点B位于点A左侧，AB＝15，∴点B表示的数为10﹣15＝﹣5，∴点P在A、B两点之间运动时PB＝15﹣2t；②∵PB＝2P A，∴15﹣2t＝2×2t，∴t＝2.5，∴P A＝2×2.5＝5，∴10﹣5＝5，∴点P所表示的数为5；（2）在这个运动过程中，P，Q两点有两次相遇，设P，Q两点第一次相遇的时间为t秒，根据题意得（2+5）t＝15，∴t＝；设P，Q两点第二次相遇的时间为t秒，根据题意得2t+15＝5t，∴t＝5，∴在这个运动过程中，P，Q两点相遇时t的值为秒或5秒．39．【解答】解：（1）∵8：30时，时针与分针的夹角是2.5个大格，∴夹角是30°×2.5＝75°，∴分针与时针所夹的锐角的度数是75°；（2）设x分钟后分针第一次追上时针，6x﹣0.5x＝240，解得x＝，答：8：00开始分钟后分针第一次追上时针；（3）设运动m分钟后，OB，OP，OQ这三条射线，其中一条射线是另外两条射线所夹的角的平分线，分三种情况：如图①，当OB平分∠QOP时，∠QOB＝∠POB，∴0.5m＝240﹣6m，解得m＝；如图②，当OP平分∠QOB时，∠QOB＝2∠POB，∴0.5m＝2（6m﹣240），解得m＝；如图③，当OQ平分∠BOP时，∠POB＝2∠QOB，∴6m﹣240＝2×0.5m，解得m＝48．综上，运动分钟或分钟或48分钟后，OB，OP，OQ这三条射线，其中一条射线是另外两条射线所夹的角的平分线．40．【解答】解：（1）①t＝2，a＝4时，回移点P'表示的实数是4﹣2×1+2×4＝10；②t＝2时，回移点P'表示的实数是a﹣2×1+2a＝3a﹣2，∵回移点P'与点P恰好重合，∴3a﹣2＝a，解得a＝1，答：a的值是1；（2）存在原点O，点P及其回移点P'中，一个点是以另外两点的端点的线段的三等分点，根据题意，P表示的数是a，O表示的数是0，P'表示的数是a﹣t+2a＝3a﹣t，∴OP＝a，OP'＝|3a﹣t|，PP'＝|2a﹣t|，当O为PP'三等分点时，OP'＝2OP或OP'＝OP，∴|3a﹣t|＝2a或|3a﹣t|＝a，解得t＝a（不符合题意，舍去）或t＝5a或t＝a（不符合题意，舍去）或t＝a；当P'是OP的三等分点时，OP'＝2PP'或OP'＝PP'，∴|3a﹣t|＝2|2a﹣t|或|3a﹣t|＝|2a﹣t|，解得t＝a（不符合题意，舍去）或t＝a或t＝4a（不符合题意，舍去）或t＝a，当P为OP'的三等分点时，OP＝2PP'或OP＝PP'，∴a＝2|2a﹣t|或a＝|2a﹣t|，解得t＝a或t＝a（不符合题意，舍去）或t＝4a（不符合题意，舍去）或t＝0（不符合题意，舍去），综上所述，t＝5a或t＝a或t＝a或t＝a或t＝a．。

5.4.2 几何图形问题浙教版七年级数学上册素养提升卷(含解析)

第5章　一元一次方程5.4　一元一次方程的应用第2课时　几何图形问题基础过关全练知识点1　图形面积问题1.某校即将举行运动会,要做两直角边长分别为0.4 m、0.3 m的直角三角形小旗共64面,则需用长1.6 m、宽1.2 m的长方形红彩纸至少( ) A.1张 B.2张 C.3张D.4张2.如图,将两个边长为14 cm的正方形的一部分重合在一起,此时整个图形的面积为360 cm2,已知重合部分是一个长为8 cm的长方形,则它的宽为()( )A.2 cmB.3 cmC.4 cmD.5 cm3.小颖用44根木棒拼成一个睡倒的“目”字图形(如图),已知“目”字图形的长∶宽=5∶3,每根木棒的长度为3 cm,则这个图形的面积为( )A.150 cm2B.420 cm2C.480 cm2D.540 cm24.如图,小玲将一个正方形纸片剪去一个宽为2 cm的长条后,再从剩下的长方形纸片上剪去一个宽为3 cm的长条,如果两次剪下的长条面积正好相等,那么原正方形的边长为 cm.()知识点2　图形体积问题5.如图,在水平桌面上有甲、乙两个内部呈圆柱形的容器,内部底面积分别为80 cm2、100 cm2,且甲容器装满水,乙容器是空的.若将甲中的水全部倒入乙中,则乙中的水位高度比原先甲中的水位高度低了8 cm,则甲的容积是()( )A.1 280 cm3B.2 560 cm3C.3 200 cm3D.4 000 cm36.【教材变式·P129例4】用橡皮泥捏制成一个大圆柱体,它的底面积为10 cm2,高为20 cm,现将这个圆柱体改成大小完全相同的20个高为4 cm的小圆柱体,则小圆柱体的底面积为多少?()能力提升全练7.如图所示,一个长方形的周长为30 cm,若这个长方形的长减少4 cm,宽增加3 cm,就可以围成一个正方形,那么这个长方形的长和宽分别为()( )A.8 cm,7 cmB.9 cm,6 cmC.10 cm,5 cmD.11 cm,4 cm8.【教材变式·P128例3】(2023浙江宁波北仑期中,11,★★☆)用四个完全相同的长方形和一个小正方形(如图)拼成了一个大正方形.大正方形的面积是100平方米,小正方形的面积是16平方米,则长方形的宽为( )A.1米B.2米C.3米D.4米9.(2023浙江绍兴柯桥联盟期中,9,★★★)一张长为a,宽为b的长方形纸片(a>3b),分成两个正方形和一个长方形共三部分(如图所示),现将前两部分图形对折,折痕为AB,再将后两部分图形对折,折痕为CD,则长方形ABCD的周长为( )A.4bB.2(a-b)C.2aD.a+b10.(2023浙江绍兴建功中学期中,10,★★★)如图,长方形ABCD被分成六个小的正方形,已知中间一个小正方形的边长为2,其他正方形的边长分别为a,b,c,d,则a的值为()( )A.10B.8C.11D.911.如图,把一块长为40 cm的长方形硬纸板的四角各剪去一个边长为5 cm的小正方形,然后把纸板沿虚线折起,做成一个无盖长方体纸盒.若纸盒的体积是1 500 cm3,则长方形硬纸板的宽为 cm.()12.(2022黑龙江绥化中考,22,★★★)在长为2,宽为x(1<x<2)的长方形纸片上,从它的一侧,剪去一个以长方形纸片的宽为边长的正方形(第一次操作);从剩下的长方形纸片一侧再剪去一个以宽为边长的正方形(第二次操作);按此方式,如果第三次操作后,剩下的纸片恰为正方形,则x的值为 .()13.学校礼堂舞台正上方有一个长为1 800 cm的长方形电子显示屏,如图所示,每次搞活动都会在电子显示屏播出主题活动的标题,由于各次活动的主题不同,标题字数也就不等,为了制作及显示时方便美观,负责播出的工作人员对有关数据作出了如下规定:边空宽∶字宽∶字距=3∶4∶1.若某次主题活动的标题字数为17个字,求字距是多少.14.如图所示,有一圆柱形的实心铁柱直立于一个内部装有水的圆柱形水桶内,水桶内的水面高度为12 cm,且水桶与铁柱的底面半径之比为2∶1.现将铁柱移至水桶外部,过程中水桶内的水量未改变,若不计水桶的厚度,则水桶内的水面高度变为多少厘米?素养探究全练15.【模型观念】一根竹竿插入水池底部的淤泥中,竹竿的入泥部分占全长的15,淤泥以上的入水部分比入泥部分长12米,露出水面的部分为1310米.问:竹竿有多长?()(1)某同学解得正确答案:竹竿的长为3米.现在他将题目改编,如果将题中的“比入泥部分长12米”改为“比入泥部分短12米”,最后答案要求不变,那么题中“露出水面的部分为1310米”应改为露出水面的部分为多少米?(2)将原题改编为一根竹竿插入水池底部的淤泥中,竹竿的入泥部分占全长的15,露出水面的部分为1310米.若此时将竹竿向上拔高15米,则淤泥以上的入水部分比入泥部分长25米,问竹竿有多长.答案全解全析基础过关全练1.B　设需要长方形红彩纸x张.×0.3×0.4×64,解得x=2.根据题意得1.6×1.2×x=12∴需要长方形红彩纸至少2张.2.C　设它的宽为x cm,依题意得8x+360=14×14×2,解得x=4.所以它的宽为4 cm.3.D　设“目”字图形的长=5x cm,则其宽=3x cm,依题意有2×5x+4×3x=3×44,解得x=6,则5x=5×6=30,3x=3×6=18,30×18=540(cm2).所以这个图形的面积为540 cm2.4.6解析　设原正方形的边长为x cm,则2x=3(x-2),解得x=6.所以原正方形的边长是6 cm.5.C　设甲的容积为x cm3,根据题意得x80―x100=8,解得x=3 200,所以甲的容积为3 200 cm3.故选C.6.解析　设小圆柱体的底面积为x cm2,根据题意可得20×10=20×4x,解得x=2.5.答:小圆柱体的底面积为2.5 cm2.能力提升全练7.D　设长方形的长为x cm,则长方形的宽为(15-x)cm,根据题意,得x-4=(15-x)+3,解得x=11,∴15-x=15-11=4,即长方形的长为11 cm,宽为4 cm.8.C　∵大正方形的面积是100平方米,小正方形的面积是16平方米,∴大正方形的边长为100=10米,小正方形的边长为16=4米,设长方形的宽为x米,则长方形的长为(x+4)米,根据题意得x+4+x=10,解得x=3,∴长方形的宽为3米.故选C.9.A　如图,由题意得EF=GH=b,设BF=CG=x.则2(b+x)+b=a,.解得x=a―3b2∴BC=a-2b-(a-3b)=b,∴四边形ABCD的周长为4b.故选A.10.B　由题意得b=a+2,∴c=b+2=a+4,∴d=c+2=a+6,∵c+d=b+2a,∴a+4+a+6=a+2+2a,解得a=8.11.20解析　设长方形硬纸板的宽为x cm,则做成的无盖长方体纸盒的宽为(x-2×5)cm,易知长方体纸盒的底面的长为(40-2×5)cm,根据题意得(40-2×5)(x-2×5)×5=1 500,解得x=20,∴长方形硬纸板的宽为20 cm.12.1.2或1.5解析　第一次操作后剩余长方形相邻两边的长分别是x和(2-x),第二次操作后剩余长方形相邻两边的长分别是(2x-2)和(2-x).当2x-2>2-x时,有2x-2=2(2-x),解得x=1.5,当2x-2<2-x时,有2(2x-2)=2-x,解得x=1.2.13.解析　设字距是x cm,∵边空宽∶字宽∶字距=3∶4∶1,∴边空宽为3x cm,字宽为4x cm,根据题意得2×3x+17×4x+(17-1)x=1 800,解得x=20.答:字距是20 cm.14.解析　设铁柱的底面半径为x cm ,将铁柱移至水桶外部后,水桶内的水面高度为h cm ,根据题意得,12[π(2x )2-πx 2]=π(2x )2h ,解得h =9.答:水桶内的水面高度变为9 cm .素养探究全练15.解析　(1)设竹竿的长为x 米,当x =3时,x -15x ―x ―=35x +12=35×3+12=2310,所以应改为露出水面的部分为2310米.(2)设竹竿的长为m 米,则m -15m ―1310=m ―+25,解得m =52.答:竹竿的长为52米.。

浙教版七年级上册数学第6章图形的初步知识含答案(综合题)

浙教版七年级上册数学第6章图形的初步知识含答案一、单选题(共15题，共计45分)1、下列说法错误的是（）A.因为M是线段AB的中点，所以AM=MB= ABB.在线段AM延长线上取一点B，如果AB=2AM，那么点M是线段AB的中点 C.因为A，M，B在同一直线上，且AM=MB，所以M是线段AB的中点 D.因为AM=MB，所以点M是AB的中点2、按组成面的平或曲划分，与其它三个几何体不同类的是（）A.正方体B.长方体C.球D.棱柱3、有一圆形纸片，要用折叠的方法找出其圆心，至少要折叠（）A.1次B.2次C.3次D.4次4、如图，P为边长为2的正方形ABCD的对角线BD上任一点，过点P作PE⊥BC 于点E，PF⊥CD于点F，连接EF.给出以下4个结论：①AP=EF；②AP⊥EF；③EF最短长度为；④若∠BAP=30°时，则EF的长度为2.其中结论正确的有（）A.①②③B.①②④C.②③④D.①③④5、以下说法正确的是（）A.两点之间直线最短B.延长直线到点，使C.相等的角是对顶角D.连结两点的线段的长度就是这两点间的距离6、45°的余角是A.45°B.90°C.135°D.180°7、下列说法错误的是（）A.同角或等角的余角相等B.同角或等角的补角相等C.两个锐角的余角相等D.两个直角的补角相等8、如图，∠AOB是直角，∠AOC=38°，OD平分∠BOC，则∠AOD的度数为（）A.52°B.38°C.64°D.26°9、如图，直线AB、CD交于点O，射线OM平分∠AOC，若∠BOD=76°，则∠BOM 等于（）A.38°B.104°C.142°D.144°10、下面四个图形中，与是对顶角的是（）A. B. C.D.11、若点为直线外一定点，点为直线上一定点，且，点到直线的距离为，则的取值范围为（）A. B. 或 C. 或 D.或12、下列说法：①在同一平面内过一点有且只有一条直线和已知直线垂直；②垂线段最短；③在同一平面内平行于同一条直线的两条直线也互相平行；④同位角相等.其中正确的个数有（）A.1个B.2个C.3个D.4个13、如图，和的位置关系是( )A.同位角B.内错角C.同旁内角D.对顶角14、下列说法正确的是（）.A.两点之间，直线最短B.连接两点间的线段，叫做这两点的距离C.两条射线组成的图形叫做角D.经过两点有一条直线，并且只有一条直线15、下列语句中正确的是( )A.延长直线AB到C，使BC= ABB.延长线段AB到C，使C为AB的中点 C.延长线段AB到C，使BC= AB D.反向延长线段AB到C，使BC= AC二、填空题(共10题，共计30分)16、已知∠A=47°，则∠A的余角等于________度．17、如图，直线、相交于点，将量角器的中心与点重合，发现表示的点在直线上，表示的点在直线上，则________ ．18、如图，点O是△ABC的两条角平分线的交点，若∠BOC＝110°，则∠A＝________°．19、已知，它的余角的三分之一是________.（用度、分、秒表示）20、夜晚的流星划过天空时留下一道明亮的光线，由此说明了________ 的数学事实．21、 ________.22、如图所示，点P到l的垂线段为________，P到l的距离为________ cm．23、如图，O是直线AB上一点，OD是∠BOC的平分线，若∠AOC＝70°，则∠BOD＝________．24、在看中央电视台“动物世界”节目时，我们可以看到这样的画面：非洲雄狮在广阔的草原上捕食鹿时，总是沿直线狂奔，其中蕴含的数学知识是________25、如图，AB∥CD，直线MN分别交AB、CD于点E，F，EG平分∠AEF，EG⊥FG 于点G，若∠BEM=60°，则∠CFG=________．三、解答题(共5题，共计25分)26、已知如图，点O在直线AB上，射线OC平分∠DOB．若∠COB=35°，求∠AOD的度数．27、如图所示，已知∠ADE=∠B，∠1=∠2，GF⊥AB，求证：CD⊥AB．28、如图，点B和点C为线段AD上两点，点B、C将AD分成三部分，M是AD 的中点，若AB：BC：CD=2：3：4，MC=2，求AD的长.29、如图，线段AB被点C、D分成2：3：4三部分，M为AC的中点，N为BD的中点，且MN=2.4，求AB的长．30、如图，在中，是的角平分线，，交于点，，，求的度数参考答案一、单选题(共15题，共计45分)1、D2、3、4、A5、D6、A7、C8、C9、C10、C11、D12、C13、B14、D15、C二、填空题(共10题，共计30分)17、18、19、20、21、22、23、24、三、解答题(共5题，共计25分)26、28、30、。

浙教版初中数学几何计算型综合问题(含答案)

几何计算型综合问题【考点透视】几何计算型综合问题，是以计算为主线的综合各种几何知识的问题.在近年全国各地中考试卷中占有相当的分量.这类问题的主要特点是包含知识点多、覆盖面广、逻辑关系复杂、解法灵活.考查方式偏重于考查考生分析问题、探究问题、综合应用数学知识解决实际问题的能力，要求学生熟练掌握三角形、四边形、三角函数、圆等几何知识，较熟练地应用转化思想、方程思想、分类讨论思想、数形结合思想等常见的数学思想. 解题时必须在充分利用几何图形的性质及题设的基础上挖掘几何图形中隐含的数量关系和位置关系，在复杂的“背景”下辨认、分解基本图形，或通过添加辅助线补全或构造基本图形，并善于联想所学知识，突破思维障碍，合理运用方程等各种数学思想才能解决.值得注意的是近年中考几何综合计算的呈现形式多样，如折叠类型、探究型、开放型、运动型、情境型等，背景鲜活，具有实用性和创造性，在考查考生计算能力的同时，考查考生的阅读理解能力、动手操作能力、抽象思维能力、建模能力……力求引导考生将数学知识运用到实际生活中去.【典型例题】例1 在生活中需要测量一些球（如足球、篮球…）的直径，某学校研究性学习小组，通过实验发现下面的测量方法：如图，将球放在水平的桌面上，在阳光的斜射下，得到球的影子AB，设光线AD、CB分别与球相切于点E、F，则E、F即为球的直径．若测得AB的长为41.5cm，∠ABC=37°.请你计算出球的直径（精确到1cm）分析：本题实际上是解直角梯形ABFE中的问题，作AG⊥CB于G，在Rt△ABG中，求出AG即可．解：作AG⊥CB于G，∵AD、CB分别与圆相切于E、F，∴EF⊥FG，EF⊥EA，∴四边形AGFE是矩形，∴AG=EF在Rt△ABG中，AB=41.5，∠ABG=37°，∴AG=AB·sin∠ABG=41.5×sin37°≈25.∴球的直径约为25cm.说明：将几何计算题与研究性学习问题和方案设计问题有机的结合起来，是近年中考题的又一热点．这类题一般难度不太大，关键是考查建模能力.例2．在边长为2的菱形ABCD中，∠B=45°，AE为BC边上的高，将△ABE沿AE所在DABCQ P直线翻折得△AB ’E ，那么△AB ’E 与四边形AECD 重叠部分的面积是 .分析：解答本题首先要根据题意，画出图形（如图11-2）然后根据对称性和相关几何知识进行求解．解：在Rt △ABE 中，∵∠B=45°，AB=2，∴AE=BE=2 ，∴S △ABE =1．由翻折知：△AB ’E ≌△ABE ，∴EB ’=EB=2 ∴B ’C=BB ’－BC=22－2， ∵四边形ABCD 是菱形，∴CF ∥BA ．∴∠ B ’FC=∠B ’AB=90°, ∠B ’CF=∠B=45° ∴CF=2222-=BC ∴S △B’FC =221CF =32－2∴S 阴=S △AB’E －S △CFB’=22－2．说明：图形折叠问题的本质是全等变换, 也是近年中考题中的一个亮点．这类问题的解决方法是要抓住因折叠而形成的等线段和等角，这些相等关系是解决问题的关键.常用代数方程求解．例3．如图，在矩形ABCD 中，AB=12cm ，BC=6cm ，点P 沿AB 边从点A 开始向点B 以2cm/s 的速度移动；点Q 沿DA 边从点D 开始向点A 以1cm/s 的速度移动.如果P 、Q 同时出发，用t(s)表示移动的时间（0≤t ≤6），那么： ⑴当t 为何值时，△QAP 为等腰直角三角形？⑵求四边形QAPC 的面积；提出一个与计算结果有关的结论； ⑶当t 为何值时，以点Q 、A 、P 为顶点的三角形与△ABC 相似？分析：⑴中应由△QAP 为等腰直角三角形这一结论，需补充条件AQ=AP，由AQ=6－t ，AP=2t ，可求出t 的值；⑵中四边形QAPC 是一个不规图形，其面积可由矩形面积减去△DQC 与△PBC 的面积求出；⑶中由于题目中未给出三角形的相似对应方式，因此须分类讨论.解：⑴AP=2t ，DQ=t ，QA=6－t ，当QA=AP ，即6－t=2t ，t=2（s ）时，△QAP 为等腰直角三角形；⑵S △DQC =21·12·t=6t, S △PBC =21·6·(12－2t)=36－6t, ∴S 四边形QAPC =12·6－6t －（36－6t ）=36（cm 2），由计算结果可见：在P 、Q 两点移动的过程中，四边形QAPC 的面积始终保持不变； ⑶∵∠QAP=∠ABC=90°，①当BC AP AB QA =时，△QAP ∽△ABC ，∴62126tt =-，解之得t=1.2（s ）； ②当AB AP BC QA =时，△PAQ ∽△ABC ，∴12266tt =-，解之得t=3（s ）. 故当t=1.2s 或3s 时，以点Q 、A 、P 为顶点的三角形与△ABC 相似.说明：本例是动态几何题，同时也是一道探究题．要求学生具有一定的发现、归纳和表达能力，这就要求我们通过计算分析，抓其本质，揭示出变中不变的规律．其结论也可提出：“P 、Q 两点到对角线AC 的距离之和保持不变”，四边形QAPC 的面积也可由△QAC 与△CAP 的面积求出，；⑶中考察了分类讨论的数学思想，结论具有一定的开放性.例4. 当你进入博物馆的展览厅时，你知道站何处观赏最理想？如图，设墙壁上的展品最高处点P 距离场面a 米，最低处点Q 距离场面b 米，观赏者的眼睛点E 距离地面m 米．当过点P 、Q 、E 三点的圆与过点E 的水平线相切于点E 时，视角∠PEQ 最大，站在此处观赏最理想．(1)设点E 到墙壁的距离为x ，求a 、b 、m 、x 的关系式； (2)当a=2.5，b=2，m=1.6时，求：○1和墙壁的距离为x 米；○2视角∠PEQ 的度数（精确到1度）解：(1)∵水平直线HE 切⊙O 于点E. ∴HE 2=QH ·HP又HE=x ，QH=b －m ，PH=a －m ， ∴x 2=（a －m ）（b －m ）.(2)○1当a=2.5，b=2，m=1.6时，由(1)中所得： x 2=（2.5－1.6）（2－1.6）∴x=0.6 ∴点E 与墙壁距离x 的值为0.6米.○2作OD ⊥PR 于D ，则∠POQ=2∠POD ，∵∠POQ=2∠PEQ ， ∴∠PEQ=∠POD.在Rt △POD 中，tan ∠POD=125=OD PD ∴∠PEQ=23°说明：将几何计算题富于一个实际情境是中考中的一个新视点，符合新课程标准的精神，在今后的中考命题将会有很强的生命力，解这类题时，要能从实际中抽象出纯数学问题，然后利用相关知识解决问题.复习中应注意对常规题进行演变，有对针性训练.例5.如图,方形ABCD 的AB 边为直径，在正方形内部作半圆，圆心为O ，DF 切半圆于F点E ，交AB 的延长线于点F ，BF=4．求：(1)cos ∠F 的值；(2)BE 的长.分析：(1)要求cos ∠F 的值，就要把∠F “放”到直角三角形中，由于DF 是半圆切线，只要连结OF 即可，然后利用相似三角形与切割线定理，求出OF 、EF ；(2)利用勾股定理和相似三角形即可求得．解：(1)连结OE.∵DF 切半圆于E ， ∴∠OEF=90°，在正方形ABCD 中，AB=AD ，∠DAF=90°， ∴∠OEF=∠DAF.又∵∠F 为公共角，∴△OEF ∽△DAF. ∴21===AB OE DA OE AF EF .即AF=2EF. ∵DF 切半圆O 于E ，∴EF 2=FB ·FA=BF ·2EF ， ∴EF=2BF=8，AF=2EF=16.∴AB=AF －BF=12，FO=21AB+BF=21×12+4=10. 在Rt △OEF 中，cos ∠F=54108==FO EF . (2)连结AE ，∵DF 切半圆于E ，∴∠EAF=∠BEF. ∵∠F=∠F ，∴△BEF ∽△EAF. ∴21168===AF EF EA BE .设BE=k(k ＞0)，则AE=2k ， ∵AB 为半圆O 的直径， ∴∠AEB=90°.在Rt △AEB 中，AE 2+BE 2=AB 2，（2k ）2+k 2=122, ∴BE=k=5512. 说明：在相似形、圆等问题中渗透三角形函数知识、方程知识，围绕有关相似比、面积之比来命题是近年中考题命题又一新特点．解这类题要善于把三角函数的值与线段比相互转化，并能设参数来表示有关线段，运用勾股定理或相似三角形的有关比例式来解决．例6．已知：如图与⊙O 2相交于A 、B 两点，O 1在⊙O 2上，⊙O 2的弦BC 切⊙O 1与B ，延长BO 1、CA 交于点P ，PB 与⊙O 1交于点D ．O 2O 1图①图②⑴求证：AC 是⊙O 1的切线；⑵如果PD=1，⊙O 1的半径为2，求BC 的长．分析：⑴由于AC 与⊙O 1有共公点A ，只要证AC ⊥AO 1即可． ⑵欲证AD ∥O 1C ，借公共弦这一“桥梁”．证∠ACO 1=∠PAD ， ⑶根据图形借助切割线及其推论或三角形相似，通过线段比来解决.解：⑴连结AO 1，∵BC 是⊙O 1的切线，∴∠O 1BC=90°, ∵四边形AO 1BC 是⊙O 2的内接四边形，∴∠O 1BC+∠O 1AC=180°.∴∠O 1AC=90°，∴AC 是⊙O 1的切线 ⑵连结AB,∵PC 切⊙O 1于点A, ∴∠PAD=∠ABP, 又∠ACO 1=∠ABO 1 ,∴∠PAD=∠ACO 1 ∴AD ∥O 1C⑶∵PC 是⊙O 1的切线，PB 是⊙O 1的割线，∴PA 2=PD·PB ∵PD=1，PB=5，∴PA=5∵AC 、BC 分别切⊙O 1于A 、B ∴O 1B ⊥BC ，O 1A ⊥PC ∴∠PBC=∠PAO 1=90° 又∠P=∠P ∴△PBC ∽△PAO 1 ∴552,1==BC PA PB AO BC 即 ∴BC=52 说明：解几何计算综合题要善于把复杂的几何图形“分解”为若干个基本图形，并综合这些基本图形的性质及图形中元素的内在联系去思考，则能快速找到解题途径．如本题若把原图分解为下列①②两个图形，则⑶的解题思路一目了然．例7.有一长方形的餐厅，长10m ，宽7m ，现只摆放两套同样大小的圆桌和椅子，一套圆桌和椅子占据的地面部分可看成半径为1.5m 的圆形（如图1所示）.在保证通道最狭窄处的宽度不小于0.5m 的前提下，问此餐厅内能否摆下三套或四套同样大小的圆桌和椅子呢？请在摆放三套或四套的两种方案中选取一种，在右下方14×20方格纸内画出设计示图1图2图3图4意图.（提示：①画出的圆应符合比例要求；②为了保证示意图的清晰，请你在有把握后才将设计方案正式画在方格纸上）分析：这是一道方案设计问题，图2中每一正方形小格宽度均表示0.5m ，餐厅内能否摆下三套或四套同样大小的圆桌和椅子，就看能否在图2中画出三个或四个半径为三格宽的圆，并使圆与圆之间、圆与方格纸外边框之间的间距不少于一格，我们可以按画三个圆、画四个圆分别计算.解：此餐厅内能摆下三套和四套同样大小的圆桌和椅子.摆放三套与四套的设计方案参考图3、图4，只要满足如下条件：① 每个圆的半径为1.5cm ；② 每个圆的圆心到方格纸外边框的距离不小于2cm ； ③ 任意两圆的圆心距不小于3.5cm.说明：对于一道运用几何计算进行探索的综合型问题，要注意相关的条件,可以先假设结论成立，然后通过计算求相应的值，再作存在性的判断.该试题是在考生容易想象的情境中考查学生用数学的能力，源于生活，打破常规，重视学生探究问题的能力的培养和动手操作意识的形成，这是今后中考试题的一个方向.ABCPQABC习题11⒈如图，在△ABC 中,已知BC=6,∠C=600,sinA=0.8,求AB 和AC 的长.(结果保留根号)⒉如图，挂着“庆祝凤凰广场竣工”条幅的氢气球升在广场上空，已知气球的直径为4m ，在地面A 点测得气球中心O 的仰角∠OAD=60°，测得气球的视角∠BAC=2°（AB 、AC 为⊙O 的切线，B 、C 为切点）则气球中心O 离地面的高度OD 为（）。

浙教版八年级下册数学2019年几何压轴题培优专题(含答案)

浙教版八年级下册数学2019年浙江省杭州市几何培优卷1、在矩形ABCD中，AB=4，BC=8，对角线AC、BD相交于点O，过点O作OE垂直AC交AD于点E，则AE的长是（ B ）（第1题图）A．3 B．5 C．2.4 D．2.52、在平面直角坐标系xOy中，已知直线y=kx+b（k≠0）与双曲线y=m（m≠0）交于点A（2，-3）和点B（n，2）；x（1）求直线与双曲线的表达式；（2）点P是双曲线y=m（m≠0）上的点，其横、纵坐标都是整数，过点P作x轴的垂线，交直线AB于点Q，当点xP位于点Q下方时，请直接写出点P的坐标．解：（1）双曲线y=m（m≠0）经过点A（2，-3），x∴m=-6，∴反比例函数的解析式为y=-6，x∵B（n，2）在y=-6上，x∴n=-3，∴B（-3，2），2k+b=−3，则有：{−3k+b=2k=−1，解得：{b=−1∴一次函数的解析式为y=-x-1．（2）由题意点P在点B的左侧或在y轴的右侧点A的左侧，∵点P的横坐标与纵坐标为整数，∴满足条件点点P坐标为（-6，1）或（1，-6）．l321S 4S 3S 2S 13、四边形ABCD 中，∠A=90°，AB=3，AD=3，点M ，N 分别为线段BC ，AB 上的动点（含端点，但点M 不与点B 重合），点E ，F 分别为DM ，MN 的中点，则EF 长度的最大值为 3 ．4、在平面直角坐标系中，O 为坐标原点，矩形OABC 中，A （10，0），C （0，4），D 为OA 的中点，P 为BC边上一点．若△POD 为等腰三角形，则所有满足条件的点P 的坐标为（2.5，4），或（3，4），或（2，4），或（8，4）．5、正方形ABCD 的边长为4，线段GH=AB ，将GH 的两端放在正方形的相邻的两边上同时滑动，如果G 点从A 点出发，沿图中所示方向按A →B →C →D →A 滑动到A 止，同时点H 从点B 出发，沿图中所示方向按B →C →D →A →B 滑动到B 止，在这个过程中，线段GH 的中点P 所经过的路线围成的图形的面积为 16﹣4π .6、在直线l 上依次摆放着七个正方形(如图所示)．已知斜放置的三个正方形的面积分别是1、2、3，正放置的四个正方形的面积依次是S 1、S 2、S 3、S 4，则S 1＋S 2＋S 3＋S 4＝ 4 ．第6题图7、正方形ABCD 的边长为4，点E 、F 分别从点A 、点D 以相同速度同时出发，点E 从点A 向点D 运动，点F 从点D 向点C 运动，点E 运动到D 点时，E 、F 停止运动．连接BE 、AF 相交于点G ，连接CG ．有下列结论：①AF ⊥BE ；②点G 随着点E 、F 的运动而运动，且点G 的运动路径的长度为π；③线段DG 的最小值为252-；④当线段DG 最小时，△BCG 的面积8855S =+.其中正确的命题有 ① ② ③ ．（填序号）第3题图第4题图第5题图（第7题图）8、菱形纸片ABCD的边长为2，∠ABC=60°，翻折∠B，∠D，使点B，D两点重合于对角线BD上一点P，EF，GH分别是折痕（如图2）．设AE=x（0<x<2），给出下列判断：①当x=1时，点P是菱形ABCD的中心；②当x=12时，EF+GH>AC；③当0<x<2时，六边形AEFCHG面积的最大；④当0<x<2时，六边形AEFCHG周长的值不变．其中正确结论是①④．（填序号）9、学校植物园的护栏是由两种大小不等的正方形间隔排列组成，将护栏的图案放在平面直角坐标系中，已知小正方形的边长为1米，则A1的坐标为（2，2）、A2的坐标为（5，2）（1）A3的坐标为（8，2），A n的坐标（用n的代数式表示）为（3n﹣1，2）．（2）2020米长的护栏，需要两种正方形各多少个？解：（1）∵A1的坐标为（2，2）、A2的坐标为（5，2），∴A1，A2，A3，…，A n各点的纵坐标均为2，∵小正方形的边长为1，∴A1，A2，A3，…，A n各点的横坐标依次大3，∴A3（5+3，2），A n（，2），即A3（8，2），A n（3n﹣1，2），故答案为（8，2）；（3n﹣1，2）；（2）∵2020÷3＝673…1，∴需要小正方形674个，大正方形673个．10、（如图1，在正方形ABCD中，BD是对角线，点E在BD上，△BEG是等腰直角三角形，且∠BEG=90°，点F是DG的中点，连结EF与CF．（1）求证：EF=CF；（2）求证：EF⊥CF；（3）如图2，若等腰直角三角形△BEG绕点B按顺时针旋转45°，其他条件不变，请判断△CEF的形状，并证明你的结论．P F EDCBAP DCB APF E D CBA 解析：（1）证明：∵∠BEG=90°，点F 是DG 的中点，∴EF=DF=DG ，∵正方形ABCD 中，∠BCD=90°，点F 是DG 的中点，∴CF=DF=DG ， ∴EF=CF ；（2）证明：∵EF=DF ，CF=DF ，∴∠FDE=∠FED ，∠FCD=∠FDC ，∴∠EFC=∠EFG+∠CFG=∠FDE+∠FED+∠FCD+∠FDC=2∠FDE+2∠FDC=2∠BDC ，在正方形ABCD 中，∠BDC=45°，∴∠EFC=2×45°=90°，∴EF ⊥CF ；（3）解：△CEF 是等腰直角三角形．理由如下：如图，延长EF 交CD 于H ， ∵∠BEG=90°，∠BCD=90°，∴∠BEG=∠BCD ，∴EG ∥CD ，∴∠EGF=∠HDF ， ∵点F 是DG 的中点，∴DF=GF ，在△EFG 和△HFD 中，，∴△EFG ≌△HFD （ASA ），∴EG=DH ，EF=FH ，∵BE=EG ，BC=CD ，∴BC ﹣EB=CD ﹣DH ，即CE=CH ，∴EF ⊥CF （等腰三角形三线合一），CF=EF=EH ，∴△CEF 是等腰直角三角形．11、四边形ABCD 是长方形．（1）Ｐ为矩形内一点（如图a ），求证: 2222PD PB PC PA +=+;（2）探索若点P 在AD 边上(如图b ）、矩形ABCD 外(如图c ）时，结论是否仍然成立．解析：（1）过P 作AB EF ⊥于E 点交CD 于F 点，如图a ：222222222222)()()()(PD PB AE PF BE PE CF PF PE AE PC PA +=+++=+++=+(2) 如图b ：2222PD PB PC PA +=+仍然成立．（证明略）过P 作BA EF ⊥的延长线于E 点交CD 的延长线于F 点，如图c ： 2222PD PB PC PA +=+仍然成立．（证明略）12、在△ABC 中，AB ＝AC ，AD ⊥BC 于D ，分别延长AC 至E ，BC 至F ，且CE ＝EF ，延长FE 交AD 的延长线于G ．（1）求证：AE ＝EG ；（2）如图2，分别连接BG ，BE ，若BG ＝BF ，求证：BE ＝EG ；（3）如图3，取GF 的中点M ，若AB ＝5，求EM 的长．【分析】（1）根据平行线的性质和等腰三角形的三线合一的性质得：∠CAD ＝∠G ，可得AE ＝EG ；（2）作辅助线，证明△BEF ≌△GEC （SAS ），可得结论；（3）如图3，作辅助线，构建平行线，证明四边形DMEN 是平行四边形，得EM ＝DN ＝AC ，计算可得结论．【解答】证明：（1）如图1，过E 作EH ⊥CF 于H ，∵AD⊥BC，∴EH∥AD，∴∠CEH＝∠CAD，∠HEF＝∠G，∵CE＝EF，∴∠CEH＝∠HEF，∴∠CAD＝∠G，∴AE＝EG；（2）如图2，连接GC，∵AC＝BC，AD⊥BC，∴BD＝CD，∴AG是BC的垂直平分线，∴GC＝GB，∴∠GBF＝∠BCG，∵BG＝BF，∴GC＝BE，∵CE＝EF，∴∠CEF＝180°﹣2∠F，∵BG＝BF，∴∠GBF＝180°﹣2∠F，∴∠GBF＝∠CEF，∴∠CEF＝∠BCG，∵∠BCE＝∠CEF+∠F，∠BCE＝∠BCG+∠GCE，∴∠GCE＝∠F，在△BEF和△GCE中，∵，∴△BEF≌△GEC（SAS），∴BE＝EG；（3）如图3，连接DM，取AC的中点N，连接DN，由（1）得AE＝EG，∴∠GAE＝∠AGE，在Rt△ACD中，N为AC的中点，∴DN＝AC＝AN，∠DAN＝∠ADN，∴∠ADN＝∠AGE，∴DN∥GF，在Rt△GDF中，M是FG的中点，∴DM＝FG＝GM，∠GDM＝∠AGE，∴∠GDM＝∠DAN，∴DM∥AE，∴四边形DMEN是平行四边形，∴EM＝DN＝AC，∵AC＝AB＝5，∴EM＝．【点评】本题是三角形的综合题，主要考查了全等三角形的判定与性质，直角三角形斜边中线的性质，等腰三角形的性质和判定，平行四边形的性质和判定等知识，解题的关键是作辅助线，并熟练掌握全等三角形的判定方法，特别是第三问，辅助线的作法是关键．13、已知正方形ABCD。

浙教版初中数学九年级下册专题50题(含答案)

浙教版初中数学九年级下册专题50题含答案一、单选题1．下列几何体中，主视图为三角形的是（）A．B．C．D．250 ，下列按键顺序正确的是（）A．B．C．D．3．下列四个几何体中，主视图与其它三个不同的是（）A．B．C．D．4．在Rt△ABC中，∠C＝90°，tanA＝125，则cosB的值为（）A．1213B．512C．125D．5135．这是由5个小正方体搭成的几何体，从以下方向看这个几何体看到的图形形状相同的是（）A．正面和上面B．正面和左面C．左面和上面D．正面、左面和上面6．如图，在Rt ABC中，斜边AB m=，A32∠=，则直角边BC的长为()A．msin32B．ncos32C．msin32D．mcos327．已知圆锥的母线长为3，底面圆半径为1，则圆锥侧面展开图的圆心角为（）A．30°B．60°C．120°D．150°8．在直角坐标平面内，点的坐标为，点的坐标为，圆的半径为2．下列说法中不正确的是（）A．当时，点在圆上B．当时，点在圆内；C．当时，点在圆外D．当时，点在圆内．9）A．B．C．D．10．在Rt ABC∆中，90︒∠=C，若三角形各边同时扩大三倍，则tan A的值（）A．扩大为原来的3倍B．不变C．缩小为原来的13D．不确定11．一个几何体的三视图如图所示，该几何体是（）A．正方体B．圆锥C．三棱柱D．四棱柱12．下列几何体的主视图与其他三个不同的是（）A．B．C．D．13．两圆的半径分别为3和5，圆心距为7，则两圆的位置关系是（）.A．内切B．相交C．外切D．外离14．如图，圆锥的底面半径r＝6，高h＝8，则圆锥的侧面积是（）A．15πB．30πC．45πD．60π15．如图，在平面直角坐标系中，Rt∠OAB的顶点A在x轴的正半轴上．顶点B的坐标为（3，点C的坐标为（12，0），点P为斜边OB上的一个动点，则P A+PC的最小值为（）A B C D．16．如图，AB是∠O的直径，AB=10，P是半径OA上的一动点，PC∠AB交∠O于点C，在半径OB上取点Q，使得OQ=CP，DQ∠AB交∠O于点D，点C，D位于AB 两侧，连结CD交AB于点E，点P从点A出发沿AO向终点O运动，在整个运动过程中，△CEP与△DEQ的面积和的变化情况是（）A．一直减小B．一直不变C．先变大后变小D．先变小后变大17．如图的几何体的俯视图是（）A．B．C．D．18．如图，点D、E分别是O的内接正三角形ABC的AB、AC边上的中点，若O 的半径为2，则DE的长等于()B C．1DA19．如图，在锐角∠ABC中，∠B＝60°，AD∠BC，AD＝3，AC＝5，则BC的长为()B．7C．5.5D．4＋A．4∠∠DFP∠∠BPH；∠DP2=PH·PC；∠若AB=2，则S△BPD1；其中正确的是（）A ．∠∠∠∠B ．∠∠C ．∠∠∠D ．∠∠∠二、填空题21．圆锥的底面半径为2，母线长为4，则它的侧面积为（）A ．8πB ．16πC ．D ．4π22．ABC 中，若sin A ，tan B ∠C =_______．23．小明喜欢构建几何图形，利用“数形结合”的思想解决代数问题．在计算tan 22.5︒时，如图，在Rt ACB 中，9045C ABC ∠=︒∠=︒，，延长CB 使BD AB =，连接AD ，得22.5D ∠=︒，所以tan 22.51AC CD ︒====，类比小明的方法，计算tan15︒的值为________．24．某商场准备改善原有楼梯的安全性能，把坡角由37︒减至30︒，已知原楼梯长为5米，则调整后的楼梯会加长________________米．（参考数据：3sin 375︒≈，4cos375≈︒，3tan 374︒≈）25．一般地，用光线照射物体，在某个平面（地面、墙壁等）上得到的影子叫做物体的________．照射光线叫做________，投影所在的平面叫做________．26．在Rt ACB △中，斜边13cm AB =，直角边5cm AC =，以直线AB 为轴旋转1周形成纺锤形，则这个纺锤形的表面积为____________．27．如图所示是若干个大小相同的小正方体搭成的几何体从不同方向看到的图形，则搭成这个几何体的小正方体的个数最多是______．28．如图1，是由一些棱长为单位1的相同的小正方体组合成的简单几何体，右侧方格中分别画出了几何体的视图．按所画的视图，最多还能在图1中添加__________个小正方体．29．如图，某传送带与地面所成斜坡的坡度为1:2.4i=，它把物品从地面A送到离地面5米高的B处，则物体从A到B所经过的路程为______．30．如图,AB是∠O的直径,C、D是圆上的两点.若BC=8,2cos3D=,则AB的长为________.31．如图，∠ABC中，AB＝AC＝2，∠BAC＝120°，D、E分别是BC、AC边上的动点，且∠ADE＝∠ABC，连接BE，则∠AEB的面积的最小值为_______．32．如图，在正方形ABCD中，AD=BC绕点B逆时针旋转30︒得到线段BP，连接AP并延长交CD于点E，连接PC，则CE的长为______．33．如图，圆锥的母线长为10，侧面展开图的面积为60π，则圆锥主视图的面积为__________．34．如图，在菱形ABCD 中，DE AB ⊥，2BE =，3cos 5A =，则菱形的周长为 _____．35．半径为4cm 的圆内正六边形的边心距是______cm ． 36．如图，在矩形纸片ABCD 中，24==AD AB ，点M ，N 分别是AD ，BC 的中点，点E ，F 分别在AB ，CD 上，且AE CF =.将AEM ∆沿EM 折叠，点A 的对应点为点P ，将NCF ∆沿NF 折叠，点C 的对应点为点Q ，当四边形PMQN 为菱形时，则AE =_______．37．某数学课外活动小组想利用树影测量树高,他们在同一时刻测得一身高为1.5 m 的同学的影长为1.35 m,由于大树靠近一幢建筑物,因此树影的一部分落在建筑物上,如图所示,他们测得地面部分的影长为3.6 m,建筑物上的影长为1.8 m,则树的高度为________.38．如图，在平面直角坐标系中，130,MOA ︒∠=1122233341,,A n n n A B B A B B A B B B B +△△△……△都是等边三角形，点123,,?··n A A A A 在轴上，点1231,,n B B B B +……在OM 上，1223341//////n n A B A B A B A B y +……轴，1OA =n 个等边1n n n A B B +△的面积是__________．39．如图，在矩形ABCD 中，AB =4，BC =P 在线段BC 上运动（含B 、C 两点），连接AP ，以点A 为中心，将线段AP 逆时针旋转60°到AQ ，连接DQ ，则线段DQ 的最小值为____．40．如图，半径为2的∠O 与直线l 相切于点A ，P 是∠O 上的一个动点（不与点A 重合），过点P 作PB ∠l ，垂足为B ，连接P A ．设P A =x ，PB =y ，则（x -y ）的最大值是________．三、解答题41．(1)计算：6sin60°+(π0﹣|﹣2|；(2)化简：(2x﹣3y)2﹣(2x+y)(2x﹣y).42．如图，在平面直角坐标系中，已知点A、点B的坐标分别为（﹣1，0）和（5，0），点C在y轴的正半轴上，且CO＝4OA，CM是∠ABC的中线．（1）求直线CM的表达式；（2）点Q是射线CM上的一个动点，当∠QMB与∠COM相似时，求点Q的坐标．43．如图，小明同学在东西方向的环海路A处，测得海中灯塔P在北偏东60°方向上，在A处正东500米的B处，测得海中灯塔P在北偏东30°方向上，则灯塔P到环海路的距离PC等于多少米？44．如图，如图，△ABC中，点O是边AB上任意一点，以O为圆心，OB为半径的圆交AC于E，交AB交于D，给出下列信息：∠∠C＝90°；∠∠BDF＝∠F；∠AC是∠O 的切线；（1）请在上述3条信息中选择其中两条作为条件，其余的一条作为结论组成一个命题．试判断这个命题是否正确，并说明理由．你选择的条件是，结论是（只要填写序号）．（2）如果CF＝1，sin A=35，求∠O的半径．45．（1）计算：（π﹣2）0﹣2cos30°|1（2）解方程：x2﹣5x+4＝0．46．如图，已知ABC 是等边三角形，以AB 为直径作O ，交BC 边于点D ，交AC 边于点F ，作DE AC ⊥于点E ．(1)求证：DE 是O 的切线；(2)若ABC 的边长为4，求EF 的长度． 47．计算：48．已知二次函数21342y x x =-+.（1）求它的对称轴与x 轴交点D 的坐标；（2）将该抛物线沿它的对称轴向上平移，如图所示，设平移后的抛物线的顶点为M ，与x 轴、y 轴的交点分别为A 、B 、C 三点，连结AC 、BC,若∠ACB =90°. ∠求此时抛物线的解析式；∠以AB 为直径作圆，试判断直线CM 与此圆的位置关系，并说明理由.49．如图，正方形ABCD 中，G 是BC 中点，DE∠AG 于E ，BF∠AG 于F ，GN∠DE ，M 是BC 延长线上一点．（1）求证：∠ABF∠∠DAE（2）尺规作图：作∠DCM 的平分线，交GN 于点H （保留作图痕迹，不写作法和证明），试证明GH=AG ．50．如图在矩形ABCD中，AB＝6，AD＝8，E为对角线AC上的动点，EF∠DE交BC 边于点F，以DE，EF为邻边作矩形DEFG．（1）当AE＝2时，求EDEF_______；（2）点H在AD上且HD＝3，连接HG，则HG的取值范围是_______．参考答案：1．B【分析】根据主视图是从正面看看到的图形进行逐一判断即可．【详解】解：A、正方体从正面看看到的图形是正方形，不是三角形，不符合题意；B、圆锥从正面看看到的图形是三角形，符合题意；C、圆柱从正面看看到的图形是长方形，不是三角形，不符合题意；D、长方体从正面看看到的图形是长方形，不是三角形，不符合题意；故选B．【点睛】本题主要考查了简单几何图的三视图，熟知三视图的定义是解题的关键．2．A【分析】简单的电子计算器工作顺序是先输入者先算，其中R-CM表示存储、读出键，M+为存储加键，M-为存储减键，根据按键顺序写出式子，再根据开方运算即可求出显示的结果．【详解】解：利用该型号计算器计算2sin50°，按键顺序正确的是．故选：A．【点睛】本题主要考查了利用计算器求数的开方，要求学生对计算器上的各个功能键熟练掌握，会根据按键顺序列出所要计算的式子．借助计算器这样的工具做题既锻炼了学生动手能力，又提高了学生学习的兴趣．3．D【分析】找到从正面看所得到的图形即可，注意所有的看到的棱都应表现在主视图中．【详解】解：A、B、C三种几何体的主视图是D几何体的主视图是故选：D．【点睛】本题考查了三视图的知识，主视图是从物体的正面看得到的视图．4．A【分析】根据正切的定义有tan A125BCAC==，可设BC=12x，则AC=5x，根据勾股定理可计算出AB=12x，然后根据余弦的定义得到cos BBCAB=，代入可得结论．【详解】如图，∠∠C=90°，tan A125 =，∠tan A125 BCAC==．设BC=12x，则AC=5x，∠AB===13x，∠cos B12121313 BC xAB x===．故选：A．【点睛】本题考查了锐角三角函数的定义：在直角三角形中，一个锐角的余弦等于这个角的邻边与斜边的比值，一个锐角的正切等于这个角的对边与邻边的比值．也考查了勾股定理．5．B【分析】先确定三视图的形状，再根据图形的形状确定是否相同即可．【详解】解：从正面看得到的图形是两列，左边列3个正方形，右边列1个正方形，从左面看得到的图形是两列，左边列3个正方形，右边列1个正方形，从上面看得到的图形是两列，左边列2个正方形，右边列1个正方形，∠三视图中主视图与左视图得到的图形形状相同．故选B．【点睛】本题考查组合体的三视图，掌握三视图的定义是解题关键．6．A【分析】根据正弦的定义解答．【详解】在Rt ABC中，BC sinAAB=，则BC AB sinA msin32=⋅=，故选A．【点睛】本题考查的是锐角三角函数的定义，掌握锐角A的对边a与斜边c的比叫做A∠的正弦是解题的关键．7．C【分析】根据圆锥的底面周长等于圆锥的侧面展开图的弧长，首先求得展开图的弧长，然后根据弧长公式即可求解．【详解】解：圆锥侧面展开图的弧长是：2π×1=2π，设圆心角的度数是n度，则3180nπ⨯=2π，解得：n=120．故选：C．【点睛】本题主要考查了圆锥的有关计算，正确理解圆锥的侧面展开图与原来的扇形之间的关系是解决本题的关键，理解圆锥的母线长是扇形的半径，圆锥的底面圆周长是扇形的弧长．8．B【详解】如图：∠A （1，0），∠A 的半径是2，∠AC=AE=2，∠OE=1，OC=3，A 、当a=-1时，点B 在E 上，即B 在∠A 上，故本选项错误；B 、当a=-3时，B 在∠A 外，即说当a ＜1时，点B 在圆A 内错误，故本选项正确；C 、当a ＜-1时，AB ＞2，即说点B 在圆A 外正确，故本选项错误；D 、当-1＜a ＜3时，B 在∠A 内正确，故本选项错误；故选B ．9．B【分析】根据正六边形的特点，通过中心作边的垂线，连接半径，结合解直角三角形的有关知识解决．【详解】解：如图，连接O A 、OB ；过点O 作OG ∠AB 于点G ．在Rt △AOG 中，OG∠AOG =30°，∠OA=2，∠这个正六边形的面积=6S △OAB =1622⨯⨯= 故选：B ．【点睛】此题主要考查正多边形和圆，根据题意画出图形，再根据正多边形的性质及锐角三角函数的定义解答即可．10．B【分析】三角函数值的大小只跟角的大小有关,，当角度一定时，其三角函数值不变.【详解】解：根据锐角三角函数的概念，可知若各边长都扩大三倍，则tan A 的值不变．故选B ．【点睛】本题主要考查了锐角三角函数的定义.根据锐角A 的各个三角函数值等于直角三角形的边的比值可直接得到答案.11．C【分析】根据三棱柱的三视图解题．【详解】直三棱柱的主视图是三角形，左视图是矩形，俯视图是一个矩形，且矩形的中间有一条实线，故C 选项符合题意，选项A 、B 、D 均不符合题意，故选：C ．【点睛】本题考查简单几何体的三视图，是基础考点，掌握相关知识是解题关键． 12．C【详解】试题分析：根据几何体的三视图可知，A 、B 、D 的主视图都是下面有3个小正方形，上面中间有1个小正方形，而C 图的主视图上面有2个小正方形，与其他三个不同．故选C ．考点：几何体的三视图．13．B【分析】本题直接告诉了两圆的半径及圆心距，根据数量关系与两圆位置关系的对应情况便可直接得出答案．外离，则d ＞R ＋r ；外切，则d ＝R ＋r ；相交，则R−r ＜d ＜R ＋r ；内切，则d ＝R−r ；内含，则d ＜R−r ．（d 表示圆心距，R ，r 分别表示两圆的半径）．【详解】根据题意，得R ＋r ＝5＋3＝8，R−r ＝5−3＝2，圆心距＝7，∠2＜7＜8，∠两圆相交．故选：B ．【点睛】本题考查了由数量关系来判断两圆位置关系的方法．14．D 【分析】圆锥的侧面积：122S r l rl ππ=⋅⋅=，求出圆锥的母线l 即可解决问题．【详解】解：圆锥的母线10l =，∠圆锥的侧面积10660ππ=⨯⨯=，故选D ．【点睛】本题考查圆锥的侧面积，勾股定理等知识，解题的关键是记住圆锥的侧面积公式．15．B【分析】作A 关于OB 的对称点D ，连接CD 交OB 于P ，连接AP ，过D 作DN ∠OA 于N ，则此时P A +PC 的值最小，根据锐角三角函数可得∠B =60°，再由勾股定理可求出AM =32，再根据直角三角形的性质可得AN =12AD =32，从而得到DN CN =1，即可求解，求出AD ，求出DN 、CN ，根据勾股定理求出CD ，即可得出答案．【详解】解：作A 关于OB 的对称点D ，连接CD 交OB 于P ，连接AP ，过D 作DN ∠OA 于N ，则此时P A +PC 的值最小，根据题意得：DP =P A ，AD ∠OB ，∠P A +PC =PD +PC =CD ，∠B （3，∠OAB =90°，∠ABOA =3，∠tan AB AOB OA ∠==， ∠∠B =60°，由勾股定理得：OB∠12×OA ×AB =12×OB ×AM ，∠AM =32， ∠AD =2×32=3， ∠∠AMB =90°，∠B =60°，∠∠BAM =30°，∠∠BAO =90°，∠∠OAM=60°，∠DN∠OA，∠∠NDA=30°，∠AN=12AD=32，由勾股定理得：DN∠C（12，0），∠CN=3﹣12﹣32=1，在Rt∠DNC中，由勾股定理得：DC=即P A+PC故选：B【点睛】本题主要考查了坐标与图形，直角三角形的性质，锐角三角函数，勾股定理等知识，熟练掌握相关知识点是解题的关键．16．B【分析】连接OC，OD，PD，CQ.设PC=x，OP=y.延长CP与圆交于点F，证∠FOD为直角，得到∠PCE=45°，可得△CEP与△DEQ的面积和为S=（x2+y2）÷2=0D2÷2=12.5，即可判断，【详解】解：连接OC，OD，PD，CQ.设PC=x，OP=y.延长CP与圆交于点F，∠PC∠AB，QD∠AB，∠∠CPO=∠OQD=90°，∠PC=OQ，OC=OD，∠Rt△OPC∠Rt△DQO，∠Rt△OPC∠Rt△DQ0，∠∠FOD=90°，∠∠PCE=45°，∠OP=DQ=y，∠△CEP与△DEQ的面积和为S=（x2+y2）÷2=0D2÷2=12.5.故选B.【点睛】本题考查勾股定理、全等三角形的判定和性质、三角形的面积等知识，解题的关键是学会添加常用辅助线，构造全等三角形解决问题，属于中考选择题中的压轴题. 17．C【分析】安装几何体三视图进行判断即可；【详解】解：本几何体的俯视图是后排有三个，前排有两个，即答案为C.【点睛】本题主要考查了简单几何体的三视图，掌握是从物体正面、左面和上面看物体以及较好的空间思维能力是解答本题的关键.18．A【分析】连接BO 并延长交∠O 于F ，连接CF ，则BF 为∠O 的直径，证∠BCF =90°，∠F =∠A =60°，求出BF =4，BC =DE =12BC 【详解】解：连接BO 并延长交∠O 于F ，连接CF ，则BF 为∠O 的直径，∠∠BCF =90°，∠∠ABC 是等边三角形，∠∠A =60°，∠∠F =∠A =60°，∠∠O 的半径为2，∠BF =4，∠BC =∠点D 、E 分别是AB 、AC 边上的中点，∠DE =12BC故选A【点睛】本题考核知识点：1．三角形的外接圆与外心；2．等边三角形的性质;3．三角形中位线定理．解题关键点：理解相关知识点.19．A【详解】∠AD∠BC 于点D ，∠∠ADB=∠ADC=90°，∠∠B=60°，AD=3，AC=5，∠tanB=AD BD=4，∠BD=3=∠BC=BD+CD=4故选A.20．A【分析】由等边三角形的性质和正方形的性质，得到∠ABE=∠DCF=30°，即可判断∠；利用角的和差关系，根据两角对应相等，得到∠DFP∠∠BPH ，可以判断∠；由相似三角形的性质，得到DP PH PC DP=，即可判断∠；先得到PM 和PN 的长度，由面积的割补法，即可求出面积，可对∠进行判断；即可得到答案.【详解】解：∠∠BPC 是等边三角形，∠BP=PC=BC ，∠PBC=∠PCB=∠BPC=60°，在正方形ABCD 中，∠AB=BC=CD ，∠A=∠ADC=∠BCD=90°∠∠ABE=∠DCF=30°，∠BE=2AE ；故∠正确；∠PC=CD ，∠PCD=30°，∠∠PDC=75°，∠∠FDP=15°，∠∠DBA=45°，∠∠PBD=15°，∠∠FDP=∠PBD ，∠∠DFP=∠BPC=60°，∠∠DFP∠∠BPH ；故∠正确；∠∠PDH=∠PCD=30°，∠DPH=∠DPC ，∠∠DPH∠∠CPD ， ∠DP PH PC DP=， ∠DP 2=PH•PC ，故∠正确；如图，过P 作PM∠CD ，PN∠BC ，∠正方形的边长AB=2，∠BPC 为正三角形，∠∠PBC=∠PCB=60°，PB=PC=BC=CD=2，∠∠PCD=30°，PM=PC•sin30°=1， ∠S △BPD =S 四边形PBCD -S △BCD =S △PBC +S △PDC -S △BCD∠11122122121222BPD S ∆=⨯⨯⨯-⨯⨯=-=；故∠正确； ∠正确的结论有：∠∠∠∠；故选：A.【点睛】本题考查的解直角三角形，特殊角的三角函数，正方形的性质，等边三角形的性质以及相似三角形的判定和性质，解答此题的关键是熟练掌握性质和定理．21．A【详解】解：圆锥的侧面积=底面周长×母线长故选A ．22．105°【分析】根据特殊角的三角函数值分别求出∠A 、∠B 的度数，然后根据三角形的内角和定理求出∠C 的度数．【详解】解：∠sin A =tan B =，∠45A ∠=︒，30B ∠=︒，∠180A B C ∠+∠+∠=︒，∠1801804530105C A B ∠=︒-∠-∠=︒-︒-︒=︒．故答案为105︒．【点睛】本题考查了特殊角的三角函数值和三角形内角和定理，掌握几个特殊角的三角函数值是解题的关键．23．2【分析】仿照题意构造含15度角的直角三角形进行求解即可．【详解】解：如图，在Rt ACB 中，9030C ABC ∠=︒∠=︒，，延长CB 使BD AB =，连接AD ，∠∠BAD =∠D ，2AB BD AC ==，∠cos BC AC ABC =⋅∠，∠(2CD BC BD AC =+=，∠∠ABC =∠BAD +∠D ，∠=15D ︒∠，∠tan =tan15=AC D CD ︒∠故答案为：2．【点睛】本题主要考查了解直角三角形，三角形外角的性质，等腰三角形的性质，正确理解题意构造出含15度角的直角三角形是解题的关键．24．1【分析】根据正弦三角函数的定义先求出楼梯的高度，然后因为楼梯的高度不变，再根据正弦三角函数的定义求出调整后楼梯的长度，则可调整后的楼梯的长度变化．【详解】解：由题意得：sin 375h ︒=，∠3535h =⨯=， ∠调整后的楼梯长36sin 30==︒， ∠调整后的楼梯会加长：651m -=．故答案为：1．【点睛】本题考查的是解直角三角形的应用，坡度坡角问题，掌握坡角的概念，熟记三角函数的定义是解题的关键．25．投影投影线投影面【解析】略26．21020cm 13π 【分析】根据勾股定理求出BC 的长，利用等积法求出斜边AB 上的高，即圆锥底面圆的半径，进而根据纺锤形的表面积是两个圆锥的侧面积之和求出答案即可．【详解】解：∠Rt ACB △中，斜边13cm AB =，直角边5cm AC =，∠12(cm)BC =，∠Rt ACB △斜边AB 上的高为51260=(cm)1313⨯，以直线AB 为轴旋转1周形成纺锤形是由两个同底的圆锥组成的几何体，底面圆周长为601202=π(cm)1313π⨯， ∠纺锤形的表面积为()()211201020ππ512cm 21313=⨯⨯+=，故答案为：21020πcm 13【点睛】此题考查了圆锥的侧面积，勾股定理等知识，熟练掌握圆锥侧面积公式是解题的关键．27．8【分析】在俯视图上摆小立方体，确定每个位置上最多可摆小立方体的个数，即可得出答案．【详解】解：在俯视图标出相应位置上最多可摆小立方体的个数，如图：∠搭成这个几何体的小正方体的个数最多是8．【点睛】本题考查了由简单的组合图形的三视图推测小立方体的个数，解题关键是根据三视图的特点，在俯视图上摆小立方体，确定每个位置上最多可摆小立方体的个数．28．5【分析】根据几何体的三视图进行判断即可．【详解】根据几何体的三视图可得第一层最多可以添加4个小正方体第二层最多可以添加1个小正方体第三层最多可以添加0个小正方体故最多还能在图1中添加5个小正方体故答案为：5．【点睛】本题考查了几何体三视图的问题，掌握几何体三视图的性质是解题的关键．29．13m##13米【分析】根据坡度的概念求出AF，然后根据勾股定理计算即可．【详解】解：如图，过B作BF∠AF于F，由题意得，BF＝5米，∠斜坡的坡度i＝1∠2.4，∠BFAF＝12.4，即512.4AF=，解得：AF＝12（米），由勾股定理得，AB13（米）．故答案是：13米．【点睛】本题主要考查了解直角三角形、坡比的计算、勾股定理等知识点，将坡度问题转化为解直角三角形的问题成为解答本题的关键．30．12【分析】连接AC，先根据圆周角定理得到∠B=∠D，然后根据锐角三角函数求出AB的长度．【详解】连接AC，根据圆周角定理可知：∠B=∠D，∠AB是直径，∠∠ACB是直角，∠cos∠B=BCAB=cos∠D=23，∠BC=8，∠AB=12，故答案为：12.【点睛】本题考查了圆周角定理，解直角三角形，正确添加辅助线，熟练掌握和灵活运用相关知识是解题的关键.31【分析】过点A作AH∠BC于H，过点E作EK∠BA交BA的延长线于K．设AE=y，BD=x．利用相似三角形的性质求出y的最小值，可得结论．【详解】解：过点A作AH∠BC于H，过点E作EK∠BA交BA的延长线于K．设AE=y，BD=x．∠AB=AC=2，AH∠BC，∠BAC=120°，∠BH=CH，∠BAH=∠CAH=60°，∠BH=CH=AB∠BC =2BH∠CDx ，EC =2-y ，在Rt △AEK 中，EK =AE ，∠S △ABE =12AB •EK =12， ∠∠ADC =∠ADE +∠EDC =∠ABC +∠DAB ，∠ADE =∠ABD ，∠∠EDC =∠DAB ，∠∠C =∠ABD ，∠∠ADB ∠∠DEC ， ∠AB DB DC EC=，2x y=-，整理得y =12x 2+2=12（x 2+12， ∠12＞0， ∠xy 的值最小，最小值为12，∠∠ABE 的面积的最小值【点睛】本题考查相似三角形的判定和性质，二次函数的性质，解直角三角形等知识，解题的关键是正确寻找相似三角形解决问题，学会构建二次函数解决最值问题，属于中考填空题中的压轴题．32．2【分析】由旋转的旋转得到30,,CBP BC BP ∠=︒=结合正方形的性质证明ABP 为等边三角形，求解30,DAE ∠=︒ 利用锐角三角函数求解,DE 从而可得答案．【详解】解：由旋转得：30,,CBP BC BP ∠=︒=正方形ABCD ，90,AB BC AD CD ABC BAD ADC ∴====∠=∠=∠=︒,60,AB BP ABP ∴=∠=︒ABP ∴为等边三角形，60,BAP ∴∠=︒30,DAE ∴∠=︒tan ,DE DAE AD∠== 2,DE ∴=2.CE DC DE ∴=-=故答案为： 2.【点睛】本题考查的是旋转的性质，等边三角形的判定与性质，正方形的性质，解直角三角形，掌握以上知识是解题的关键．33．48【分析】圆锥的主视图是等腰三角形，根据圆锥侧面积公式S=πrl 代入数据求出圆锥的底面半径长，再由勾股定理求出圆锥的高即可．【详解】根据圆锥侧面积公式：S=πrl ，圆锥的母线长为10，侧面展开图的面积为60π，故60π=π×10×r ，解得：r=6．由勾股定理可得圆锥的高∠圆锥的主视图是一个底边为12，高为8的等腰三角形，∠它的面积=1128=482⨯⨯，故答案为：48【点睛】本题考查了三视图的知识，圆锥侧面积公式的应用，正确记忆圆锥侧面积公式是解题关键．34．20【分析】根据菱形的性质可得AB BC CD AD ===，结合3cos 5AE A AD ==，设3AE k =，则5AD k =，再建立方程求解k 的值，从而可得答案．【详解】解：∠四边形ABCD 是菱形，∠AB BC CD AD ===，∠DE AB ⊥，∠90DEA ∠=︒， ∠3cos 5AE A AD ==，设3AE k =，则5AD k =，∠5322BE k k k =-==，∠1k =，∠5AD =，∠菱形的周长44520AD ==⨯=，故答案为：20．【点睛】本题考查的是菱形的性质，锐角三角函数的应用，熟记锐角的余弦的定义，并灵活应用是解本题的关键．35．【分析】求出正六边形的中心角，连接两个顶点，可得等边三角形，于是可得到正六边形的边长，再根据等边三角形的性质和锐角三角函数的定义解答即可．【详解】如图所示，连接OA ，OB ，∠多边形为正六边形， ∠∠AOB=3606=60°，又∠OA=OB ，∠∠AOB 是等边三角形，∠AB=OA=4．过O 作OE∠AB 于E ；∠∠AOB 是等边三角形， ∠12,302AE AB AOE ==∠=，tan 3203AE OE ∴===故答案为：【点睛】本题考查了正多边形和圆的知识；求得正六边形的中心角为60°，得到等边三角形是正确解答本题的关键．36．4【分析】连接MN，PQ交于点O，延长PQ交CD于H，延长QP交AB于G．解直角三角形求出AG，EG即可解决问题．【详解】如图，连接MN，PQ交于点O，延长PQ交CD于H，延长QP交AB于G．∠四边形PNQM是菱形，∠MN∠PQ，∠点M、N分别是AD、BC的中点，∠AM=BN，又∠矩形ABCD中，AM∠BN，∠A=90°，∠四边形AMNB是矩形，∠∠AMN=90°∠PQ∠AD∠BC，∠AG=DK=OM=12AB=14AD=1，∠PM=AM=2，∠sin∠MPO=12，∠∠MPO=30°，∠∠EPM=90°，∠∠EPG=90°-30°=60°∠OG=2，，∠AE=AG-EG=1-（）故答案为：【点睛】本题考查了矩形的性质，翻折变换，菱形的性质，解直角三角形等知识，解题的关键是熟练掌握折叠的性质．37．5.8m【分析】根据同一时刻影长与物长的比值相等即可解题.【详解】解：如下图,延长光线交地面与点C, 由题可知：AB BC =1.51.35,∠AB=1.8, ∠BC=1.62,∠如果没有建筑物遮挡,树的影长为3.6+1.62=5.22米,∠树高：5.22=1.5:1.35,∠树高=5.8米【点睛】本题考查了平行投影的实际应用,属于简单题,熟练应用平行投影的概念是解题关键.38．4n -【分析】利用三角函数求出12A B =2，得到112A B B S △=21211s 60422A B in ⨯⋅=22322311=s 601622A B B in S A B =⋅⨯=△33423411=s 6064422A B B i S A B n ⋅=⨯=△. 【详解】∠12A B ∠y 轴，∠∠O 12A B =90°，∠130,MOA ︒∠=1OA =∠12A B =2，∠112A B B S △=21211s 60422A B in ⨯⋅==， ∠∠22OA B =90°-∠223B A B =30°=1MOA ∠，∠22223OB A B B B ==，121A A OA =∠ 2OA 23A B =4，∠ 22322311=s 601622A B B in S A B =⋅⨯=△同理：3348OA A B =，∠33423411=s 6064422A B B i S A B n ⋅=⨯=△ ，第n 个等边1n n n A B B +△的面积是4n -故答案为：4n -【点睛】此题考查图形类规律的探究，等边三角形的性质，锐角三角函数，三角形面积公式，等腰三角形的等角对等边证明边相等，根据图形求出面积得到规律是解题的关键. 39．2【分析】以AB 为边向右作等边ABF △，作射线FQ 交AD 于点E ，过点D 作DH ∠QE 于点H ，证明△BAP△△F AQ ，由全等性质可以得到∠ABP =∠AFQ ，进一步解三角形求得AE 的值，判断出点Q 的运动轨迹是射线FE ，在∠DHE 中，当点Q 与点H 重合时，DH 的值最小，利用特殊角的锐角三角函数值求解即可．【详解】解：以AB 为边向右作等边ABF △，作射线FQ 交AD 于点E ，过点D 作DH ∠QE 于点H ，如下图：∠四边形ABCD 是矩形∠∠ABP =∠BAE =90∠∠ABF 和∠APQ 是等边三角形∠∠BAF =∠P AQ =60，BA =F A ，P A =QA∠∠BAP +∠P AF =∠P AF +∠F AQ∠∠BAP =∠F AQ在∠BAP 和∠F AQ 中，BA FA BAP FAQ PA QA =⎧⎪∠=∠⎨⎪=⎩∠BAP FAQ ≅∠∠ABP =∠AFQ =90∠∠F AE =906030-=∠∠AEF =903060-=∠AB =AF =4∠4=cos303AF AE = ∠点Q 的运动轨迹是射线FE∠AD =BC =∠DE =AD -AE ∠DH ∠EF ，∠DEH =∠AEF =60∠43sin 6023DH DE ===由垂线段最短可知，当点Q 与点H 重合时，DH 的值最小，最小值为2故答案为：2【点睛】本题考查三角形全等的性质和证明，等边三角形的性质，特殊角的三角函数值计算等相关知识点，能够根据已知条件作出相关的辅助线是解题重点．40．1【分析】作直径AC ，连接CP ，得到∠APC ∠∠PBA ，得到AP AC PB PA =，得到214y x =，所以22211121444()x y x x x x x -=-=-+=--+，得到当2x =时，x y -有最大值是1．【详解】解：如图，作直径AC ，连接CP ，∠AC 为直径，∠∠CP A =90°，∠AB 为切线，∠CA ∠AB ，又∠PB ∠l ，∠AC ∠PB ，∠△APC ∠△PBA ， ∠AP AC PB PA=， ∠P A =x ，PB =y ，r =2， ∠4x y x=， ∠214y x =， ∠22211121444()x y x x x x x -=-=-+=--+， ∠当2x =时，x y -有最大值是1，故答案为：1．【点睛】此题考查了切线的性质，平行线的性质，相似三角形的判定与性质，以及二次函数的性质，熟练掌握性质及定理是解本题的关键．41．(1)-1；(2)10y 2﹣12xy ．【分析】（1）本题需根据零指数幂、二次根式化简、绝对值、特殊角的三角函数值分别进行计算，然后根据实数的运算法则求得计算结果；（2）先根据完全平方公式、平方差公式计算，再去括号合并同类项即可求解．【详解】(1) 6sin60°+(π0﹣|﹣2|＝612+- ＝﹣1；(2)(2x ﹣3y )2﹣(2x +y )(2x ﹣y )＝4x 2﹣12xy +9y 2﹣4x 2+y 2＝10y 2﹣12xy ．【点睛】本题考查实数的综合运算能力，是各地中考题中常见的计算题型．解决此类题目的关键是熟记特殊角的三角函数值，熟练掌握零指数幂、二次根式、绝对值、完全平方公式、平方差公式、特殊角的三角函数值等考点的运算．42．（1）y ＝−2x ＋4；（2）（135，−65）或（5，−6）【分析】（1）根据点A 、B 的坐标和CO ＝4OA 可以推知点C 的坐标，结合CM 是∠ABC 的中线求得点M 的坐标，利用待定系数法确定函数关系式；（2）求出OM 的长，再利用勾股定理列式求出CM ，令y ＝0，解关于x 的一元二次方程求出点B 的坐标，得到OB 的长度，再求出BM ，然后分：∠∠BQM ＝90°时，∠COM ∽∠BQM 相似，利用相似三角形对应边成比例列式求出BQ ，过点Q 作QD ∠x 轴于D ，解直角三角形求出BD 、QD ，然后求出OD ，从而写出点Q 的坐标；∠∠MBQ ＝90°时，∠COM ∽ ∠QBM 相似，利用相似三角形对应边成比例列式求出BQ ，再写出点Q 的坐标．【详解】解：（1）∠点A 的坐标分别为（−1，0），∠OA ＝1．又∠CO ＝4OA ，∠CO ＝4，则C （0，4）．又∠点B 的坐标为（5，0），CM 是∠ABC 的中线，∠M （2，0）．设直线CM 的表达式为y ＝kx ＋b （k ≠0），则420b k b =⎧⎨+=⎩，解得24k b =-⎧⎨=⎩，。

专题2.3 勾股定理与几何综合(压轴题专项讲练)(浙教版)(解析版)

专题2.3 勾股定理与几何综合【典例1】如图，△ABC中，∠C=90°，AB=10cm，BC=6cm，若动点P从点C开始，按C→A→B→C 的路径运动，且速度为每秒1cm，设出发的时间为t秒．（1）出发2s后，求△ABP的周长；（2）求出t为何值时，△BCP为等腰三角形；（3）当点P运动到△ABC任意一条角平分线上时（不与顶点A、B、C重合），直接写出t的值．（1）利用勾股定理得出AC=8cm，进而表示出AP的长，由勾股定理求出PB，进而得出答案；（2）利用分类讨论的思想和等腰三角形的特点及三角形的面积求出答案；（3）分三种情况讨论，当点P恰好在∠ABC的角平分线上时，利用角平分线的性质以及勾股定理得出方程，解方程即可；当点P恰好在∠ACB的角平分线上时，利用面积法求得PBPA =34，据此可求解；当点P恰好在∠BAC的角平分线上，同理利用角平分线的性质以及勾股定理得出方程，解方程即可．（1）解：∵∠C=90°，AB=10cm，BC=6cm，∴由勾股定理得AC=8(cm)，由题意得，出发2秒后，则CP=2cm，那么AP=6cm．∵∠C=90°，∴由勾股定理得PB=．∴△ABP的周长为：AP+PB+AB=6+10+=(16+(cm)；（2）解：若P在边AC上时，BC=CP=6cm，此时用的时间为6s，故t=6s时△BCP为等腰三角形；若P在AB边上时，有三种情况：①BP=CB=6cm，此时AP=4cm，P运动的路程为12cm，所以用的时间为12s，故t=12s时△BCP为等腰三角形；②若CP=BC=6cm，过C作斜边AB的高CD，根据面积法，12×6×8=12×10×CD，∴CD=4.8cm，根据勾股定理求得BD 3.6(cm)，所以P运动的路程为18−2×3.6=10.8(cm)，∴所以用的时间为10.8s，故t=10.8s时△BCP为等腰三角形；③若BP=CP时，则∠PCB=∠PBC，∵∠ACP+∠BCP=90°，∠PBC+∠CAP=90°，∴∠ACP=∠CAP，∴PA=PC，∴PA=PB=5cm，∴P的路程为13cm，所以时间为13s，故t=13s时△BCP为等腰三角形．∴t为6s或10.8s或12s或13s时△BCP为等腰三角形；（3）解：点P恰好在∠ABC的角平分线上时，如图所示，过点P作PG⊥AB于点G，∴PG=PC．在Rt△BPC与Rt△BPG中，PG=PC BP=BP，∴Rt△BPC≌Rt△BPG(HL)，∴BG=BC=6cm，∴AG=10−6=4cm．设PC =x ，则PA =(8−x)，在RtΔAPG 中，PG 2+AG 2=PA 2，即x 2+42=(8−x)2，解得：x =3，∴当t =3s 时，点P 恰好在∠ABC 的角平分线上；当点P 恰好在∠ACB 的角平分线上时，作PE ⊥AC 于E ，PF ⊥BC 于F ．∵PC 平分∠ACB ，∴PE =PF ，∴S ΔBCP S ΔAPC =PB PA =12⋅BC⋅PF 12⋅AC⋅PE =BC AC =68=34，∴PA =47AB =407，∴P 的路程为967cm ，∴当t =967s 时，点P 恰好在∠ABC 的角平分线上；当点P 恰好在∠BAC 的角平分线上，过P 作PH ⊥AB ，∵点P 恰好在∠BAC 的角平分线上，且∠C =90°，AB =10cm ，BC =6cm ，AC =8cm ，∴CP =HP ，∴△ACP≌△AHP ，∴AH =AC =8cm ，BH =10−8=2(cm)．设CP =a ，则BP =6−a ，PH =a ，∴RtΔBHP 中，BH 2+PH 2=BP 2，即22+a 2=(6−a)2，解得a =83，∴P 的路程为24−83=643(cm)，∴当t =643s 时，点P 恰好在∠BAC 的角平分线上；综上所述，满足条件的t 的值为3s 或967s 或643s ．1．（2023春·浙江·九年级专题练习）已知△ABC 与△ABD 在同一平面内，点C ，D 不关于AB 对称，∠ABC =∠ABD =30°，AB =2，AC =AD =CD 长为（）A ．2B ．2C D ．2【思路点拨】分类讨论，①当点D 和点C 在直线AB 同侧时，过点A 作AE ⊥BD 于点E ．②当点D 和点C 在直线AB 异侧时，过点A 作AM ⊥BD 于点M ，AF ⊥BC 交BC 延长线于点F ，过点C 作CN ⊥BD 于点N ．分别根据含30度角的直角三角形的性质和勾股定理即可求解．【解题过程】解：分类讨论，①当点D 和点C 在直线AB 同侧时，如图，过点A 作AE ⊥BD 于点E ．∵∠ABC =30°，∠AEB =90°，AB=1．∴AE=12∵在Rt△AEC中，AC∴EC=1．同理在Rt△AED中，可求DE=1，∴CD=EC+DE=2；②当点D和点C在直线AB异侧时，如图，过点A作AM⊥BD于点M，AF⊥BC交BC延长线于点F，过点C作CN⊥BD于点N，由作图可知∠AFB=∠AMB=90°，∠ABC=∠ABD=30°，AB=1，BF=BM==∴AF=AM=12∵在Rt△ADM中，AD=∴DM=1，∴BD=DM+BM=1同理可求CF=1，∴BC=BF−CF．∵∠CBA+∠ABD=60°，即∠CBN=60°，∠CNB=90°BC=CN∴BN=12∴DN=BD−BN=1+在Rt△CDN中，CD=综上可知CD长为2故选B．2．（2023春·八年级课时练习）如图，在△ABC中，AB＝AC＝6，∠BAC＝120°，过点A作AD⊥BA交BC 于点D，过点D作DE⊥BC交AC于点E，则AE的长为（）A．1B．2C．3D．4【思路点拨】根据等腰三角形的性质可得∠B=∠C，根据含30°角的直角三角形的性质可得AD的长，再求出EC的长，即可确定AE的长．【解题过程】解：∵AB=AC=6，∠BAC=120°，∴∠B=∠C=30°，∵AD⊥BA，∴∠BAD=90°，设AD=x，则BD=2x，根据勾股定理，可得62+x2=(2x)2，解得x=x=∴AD=∵∠DAC=120°−90°=30°，∴∠C=∠DAC，∴DC=AD=∵DE⊥BC，∴∠EDC=90°，设ED=m，则EC=2m，根据勾股定理，得m2+2=(2m)2，∴m=2或m=−2（舍去），∴EC=2m=4，∴AE=6−4=2，故选：B ．3．（2023春·全国·八年级专题练习）如图，三角形纸片ABC 中，点D 是BC 边上一点，连接AD ，把△ABD 沿着直线AD 翻折，得到△AED ，DE 交AC 于点G ，连接BE 交AD 于点F ．若DG ＝EG ，AF ＝4，AB ＝5，△AEG 的面积为92，则BD 2的值为（）A ．13B ．12C ．11D ．10【思路点拨】首先根据SAS 证明△BAF ≌△EAF 可得AF ⊥BE ，根据三角形的面积公式求出AD ，根据勾股定理求出BD 即可．【解题过程】解：由折叠得，AB =AE ，∠BAF =∠EAF ，在△BAF 和△EAF 中，AB =AE ∠BAF =∠EAF AF =AF，∴△BAF ≌△EAF (SAS )，∴BF =EF ，∴AF ⊥BE ，又∵AF ＝4，AB ＝5，∴BF=3，在△ADE 中，EF ⊥AD ，DG ＝EG ，设DE 边上的高线长为h ，∴S △ADE =12AD ⋅EF =12DG ⋅ℎ+12EG ⋅ℎ，即S △ADG +S △AEG =12AD ⋅EF ，∵S △AEG =12⋅GE ⋅ℎ=92，S △ADG =S △AEG ，∴S △ADG +S △AEG =92+92=9，AD⋅3，∴9=12∴AD=6，∴FD=AD−AF=6−4=2，在Rt△BDF中，BF=3，FD=2，∴BD2=BF2+FD2=32+22=13，故选：A．4．（2023春·八年级单元测试）如图，在等腰Rt△ABC中，∠A=90°，BD平分∠ABC，BE平分∠DBC，M、N分别为射线BE、BC上的动点，若BD=8，则CM+MN的最小值为（）A．4B．6C．8D．10【思路点拨】如图，作N关于BE的对称点N′，则MN=MN′，当C,M,N′三点共线时最短即CN′，当CN′⊥BF时最短，过点C 作CF⊥BD，交BD的延长线于点F，即N′与F点重合时最短，过点D作DG⊥BC于点G，根据等面积法求得CF，即可求解．【解题过程】解：如图，作N关于BE的对称点N′，过点C作CF⊥BD，交BD的延长线于点F，过点D作DG⊥BC于点G，∴MN=MN′，当C,M,N′三点共线时CM+MN最小即CN′，当CN′⊥BF时最短，CF即为所求，∵DG⊥BC，Rt△ABC是等腰直角三角形，∴△DGC是等腰直角三角形，∴DC=∵BD 平分∠ABC ，∴DA =DG∵AC =AB ，设AD =a ，则AB =AC =(1+a在Rt △ABD 中，BD =8,AD =a,AB =(1+a∵BD 2=AD 2+AB 2∴82=a 2+(1+a2解得a 2=∴BC ==+2)a∵S △BDC =12BC ×DG =12BD ×CF∴CF =BC ×DG BD=2)(=+=4故选A ．5．（2023春·八年级课时练习）如图，在等腰RtΔABC 中，∠C =90°，AB =8，点D 和E 分别是BC 和AB 上两点，连接DE ，将△BDE 沿DE 折叠，得到△B ′DE ，点B ′恰好落在AC 的中点处，DE 与BB ′交于点F ，则折痕DE 的长度为（）A ．BCD 【思路点拨】在 Rt △BCB ′ 中，求出 BB ′= 设 BD =x ，则 CD =，B ′D =x ，在 Rt △CDB ′ 中，由勾股定理得 x 2=2 +2，求得 BD = 在 Rt △BDF 中，求出 DF 过点B ′怍 B ′G ⊥AB 于点 G ，则 AG =B ′G =2，设 BE =y ，则 G E =6−y ，B ′E =y ，在 Rt △B ′GE 中， GE2+B′G2=B′E2，可求BE=10，在Rt△BEF中，EF2=BE2−BF2，可求EF则3ED=DF+EF【解题过程】解∶由折叠可知，BD=B′D，BF=B′F，DF⊥BF，∵等腰Rt△ABC中，∠C=90∘，AB=8，∴BC=AC=∵B′是AC的中点，∴CB′=在Rt△BCB′中，BB′===∴BF=设BD=x，则CD=，B′D=x，在Rt△CDB′中，B′D=∴x2=2+2∴x∴BD在Rt△BDF中，DF过点B′作B′G⊥AB于点G，∵∠A=45∘，∴AG=B′G∵AB′=∴AG=B′G=2，设BE=y，则GE=6−y，B′E=y，在Rt△B′GE中，GE2+B′G2=B′E2，∴(6−x)2+4=x2∴x=103∴BE=10 3在Rt△BEF中，EF2=BE2−BF2，∴EF2=−2=109，∴EF∴ED=DF+EF+故选∶ C．6．（2023春·八年级课时练习）如图，在纸片ΔABC中，AB=AC=12，∠B=30°，折叠纸片，使点B落在AC 的中点D处，折痕为EF，则ΔDEF的面积为（）A B．C．D【思路点拨】过点D作AB的垂线，垂足为G，过D作CF的垂线，垂足为H，过A作BC的垂线，垂足为N，分别求出△DEA和△DFC的面积，利用S△DEF＝12×（S△ABC－S△DEA－S△DFC）可得结果．【解题过程】解：过点D作AB的垂线，垂足为G，∵∠BAC＝120°，∴∠GAC ＝60°，∠GDA ＝30°，∴AG ＝12AD =14AC =3，DG 设AE ＝x ，则BE ＝12－x ＝DE ，在Rt △DGE 中，DE 2=GE 2+GD 2，即(12−x )2=(x +3)2+27，解得：x ＝185，∴S △ADE ＝12DG ×AE ＝12×185×过D 作CF 的垂线，垂足为H ，过A 作BC 的垂线，垂足为N ，∵∠B =30°，∴AN ＝12AB ＝6，BN =，∴BC ＝设DF ＝y ，则CF ＝，DH ＝12CD =3，CH =则有DH 2+FH 2=DF 2，即32+12=y 2，解得：y则S △DFC ＝12DH ⋅CF =12×3×12=∴S △DEF ＝12 ×（S △ABC －S △DEA －S △DFC ）＝12×BC ⋅AN−S △DEA −S △DFC＝12×＝故选A ．7．（2023秋·浙江宁波·八年级统考期末）如图，在平面直角坐标系中，A 点坐标为0，2，B 是x 轴上一点．以AB 为腰，作等腰直角三角形ABC ，∠ABC =90°，连接OC ，则AC +OC 的最小值为_________________．【思路点拨】如图所示，过点C作CD⊥x轴于D，设点B的坐标为m，0(m≥0)，证明△AOB≌△BDC，得到BD=OA=2，CD=OB=m，进而求出点C的坐标为m+2，m，利用勾股定理得到OC+AC=AC+OC的最小值即为点−1，1到点0，−2由此求解即可．【解题过程】解：如图所示，过点C作CD⊥x轴于D，设点B的坐标为m，0(m≥0)，∴∠AOB=∠BDC=90°，∵点A的坐标为0，2，∴OA=2，∵△ABC是等腰直角三角形，∠ABC=90°，∴∠OBA+∠OAB=90°=∠DBC+∠OBA，AB=BC，∴∠OAB=∠DBC，∴△AOB≌△BDC(AAS)，∴BD=OA=2，CD=OB=m，∴OD=OB+BD=m+2，∴点C的坐标为m+2，m，∴OC AC=∴OC+AC∴AC+OC的最小值可以看做在x轴上的一点到点−1，1和到点0，−2∴AC+OC的最小值×由对称性可知，当m<0，同理可证AC+OC的最小值=故答案为：8．（2023春·八年级课时练习）如图，长方形ABCD中，AB=5,AD=6，点P是射线AD上一点，将△ABP 沿BP折叠得到△A′BP，点A′恰好落在BC的垂直平分线l上（直线l也是AD的垂直平分线），线段AP的长为___________．【思路点拨】设直线l与AD、BC交于点E、F，分两种情况讨论：当点P在线段AE上时，设，设AP=A′P=x,PE=3−x；当点P在射线AD上时，设AP=A′P=y,PE=y−3，分别利用勾股定理求解即可．【解题过程】解：根据题意，四边形ABCD为长方形，直线l是BC、AD的垂直平分线，AD=3，则AB=CD=5,AD=BC=6,BC⊥l,AD⊥l，AE=12设直线l与AD、BC交于点E、F，可分两种情况讨论：①如下图，当点P在线段AE上时，设AP=A′P=x,PE=3−x，在Rt△BFA′中，BC=3，BA′=BA=5，∠BFA′=90°，∵BF=12∴FA′4，∵EF=AB=5，∴A′E=5−4=1，∴在Rt△A′PE中，可有A′P2=PE2+A′E2，，即有x2=(3−x)2+12，解得x=53即AP=5；3②如下图，当点P在射线AD上时，设AP=A′P=y,PE=y−3，在Rt△BFA′中，BC=3，BA′=BA=5，∠BFA′=90°，∵BF=12∴FA′4，∵EF =AB =5，∴A ′E =5+4=9，∴在Rt △A ′PE 中，可有A ′P 2=PE 2+A ′E 2，即有y 2=(y−3)2+92，解得 y =15，即AP =15．综上所述，线段AP 的长为53或15．故答案为：53或15．9．（2023春·八年级课时练习）如图，在ΔABC 中，BD 平分∠ABC ，∠A =3∠C ，AB =6，BC =10，则AD =______．【思路点拨】作出如图的辅助线，证明ΔABD≌ΔEBD(SAS)，推出∠EAC =∠C ，AE =EC ，再证明BD 是AE 垂直平分线，利用勾股定理和面积法求得BG 和AF ，再求得AC 的长，再利用面积法求得AD AC =38，据此求解即可．【解题过程】解：在BC 上取点E ，使BE =AB ，作AF ⊥BC 于点F ，连接AE 交BD 于点G ，如图，∵BD 平分∠ABC ，∴∠ABD =∠EBD又∵BE =AB ，BD =BD ，∴ΔABD≌ΔEBD(SAS)，∴AD =ED ，∠BAD =∠BED =3∠C ，∠BAE =∠BEA =∠EAC +∠C ，∴∠BAC =∠BAE +∠EAC =∠EAC +∠C +∠EAC =2∠EAC +∠C ，∴3∠C =2∠EAC +∠C ，即∠EAC =∠C ，∴AE =EC ，∵AB =6，BC =10，∴AE =EC =10−6=4，∵BD 平分∠ABC ，BE =AB ，∴BD 是AE 的垂直平分线，∴AG =EG =2，∴BG =∵12AE ×BG =12BE ×AF ，∴AF =EF =43，∴CF =CE +EF =163，∴AC =∵BD 平分∠ABC ，∴点D 到AB 和BC 边上的距离相等，∴S ΔABD S ΔCBD =AB BC =610=35=AD CD ，即AD AC =38，∴AD =38×10．（2023春·八年级课时练习）如图，长方形ABCD 中，AD =3，AB =5，点E 为射线DC 上一动点(不与D 重合)，将△ADE 沿AE 折叠得到△D ′AE ，连接D ′B ，若△ABD ′为直角三角形，则AE = ________【思路点拨】分两种情况讨论：①当点E 在线段CD 上时，B,D ′,E 三点共线，根据S △ABE =12AB ⋅AD =12BE ⋅AD ′可求得BE =5，再由勾股定理可得BD ′4，进而可计算DE =D ′E =1，在Rt △ADE 中，由勾股定理计算AE 的值；②当点E 在射线CD 上时，设CE =x ，则D ′E =DE =x +5，BE =x +1，由勾股定理可解得x =4，进而可计算DE =9，在Rt △ADE 中，由勾股定理计算AE 的值即可．【解题过程】解：根据题意，四边形ABCD 为长方形，AD =3，AB =5，将△ADE 沿AE 折叠得到△D ′AE ，则∠D =∠ED ′A =90°，AD =BC =AD ′=3，AB =CD =5，①如图1，当点E 在线段CD 上时，∵∠ED ′A =∠D =∠AD ′B =90°，∴B,D ′,E 三点共线，∵S △ABE =12AB ⋅AD =12BE ⋅AD ′，∴BE =AB =5，∵BD ′===4，∴DE =D ′E =BE−BD ′=5−4=1；∴在Rt △ADE 中，AE ②如图2，当点E 在射线CD 上时，∵∠AD ′B =∠BCE =90°，AD =BC =AD ′=3，AB =CD =5，∴BD ′==4，设CE =x ，则D ′E =DE =x +5，∴BE =D ′E−BD ′=x +1，∵CE 2+BC 2=BE 2，即x 2+32=(x +1)2，解得x =4，∴DE =CD +CE =5+4=9，∴在Rt △ADE 中，AE综上所述，AE11．（2023秋·浙江杭州·八年级校联考期末）如图，△ABC 中，AB =AC ，AD ⊥BC 于点D ，DE 平分∠ADC ，交AC 与点E ，EF ⊥AB 于点F ，且交AD −于点G ，若AG =2,BC =12，则AF =_____．【思路点拨】过点B 作BH ⊥AC 于H ，过点D 作DK ⊥AC 于K ，过点E 作EM ⊥CD 于M ，EN ⊥AD 于N ，连接BE ，先证得△DEG≌△DEC ，运用勾股定理可得AB =10，利用面积法可求得：DK =245，BH =485，EM =EN =247，AE =407，EF =19235，再运用勾股定理即可求得答案．【解题过程】解：如图，点B 作BH ⊥AC 于H ，过点D 作DK ⊥AC 于K ，过点E 作EM ⊥CD 于M ，EN ⊥AD 于N ，连接BE∵AB =AC,AD ⊥BC ，∴BD =CD =12BC =12×12=6，∠BAD +∠ABC =90°，∠ABC =∠C ，∵EF ⊥AB ，∴∠BAD +∠AGF =90°，∴∠ABC =∠AGF =∠C ，∵∠AGF =∠DGE ，∴∠DGE =∠C ，∵DE 平分∠ADC ，EM ⊥CD,EN ⊥AD ，∴EM =EN,∠EDG =∠EDC ，在△DEG 和△DEC 中，∠DGE =∠C ∠EDG =∠EDC DE =DE，∴△DEG≌△DEC(AAS)，∴DG =CD =6，∵AG =2，∴AD =AG +DG =2+6=8，在Rt △ABD 中，AB=10，∴AC =AB =10，∵AC ⋅DK =AD ⋅CD ，∴10DK =8×6，∴DK =245，∵AC ⋅BH =BC ⋅AD，∴10BH =12×8，∴BH =485，∵S △ADE +S △CDE =S △ACD ，∴12AD ⋅EN +12CD ⋅EM =12AD ⋅CD ，∴4EN +3EM =24，∵EN =EM ，∴7EN =24，∴EN =247，∴EM =EN =247，∵DK ⋅AE =AD ⋅EN ，∴245AE =8×247，∴AE =407，∵AB ⋅EF =AE ⋅BH ，∴10EF =407×485，∴EF ＝19235，在Rt △AEF 中，AF =85．故答案为：85．12．（2023秋·吉林长春·八年级统考期末）如图，在△ABC 中，AB ＝50cm ，BC ＝30cm ，AC ＝40cm ．（1）求证：∠ACB ＝90°（2）求AB 边上的高．（3）点D 从点B 出发在线段AB 上以2cm /s 的速度向终点A 运动，设点D 的运动时间为t （s ）．①BD 的长用含t 的代数式表示为．②当△BCD为等腰三角形时，直接写出t的值．【思路点拨】（1）运用勾股定理的逆定理即可证得∠ACB=90°；（2）运用等面积法列式求解即可；（3）①由路程=速度x时间，可得BD=2t；②分三种情况进行求解，即可完成解答.【解题过程】证明：（1）∵BC2+AC2＝900+1600＝2500cm2，AB2＝2500cm2，∴BC2+AC2＝AB2，∴∠ACB＝90°，∴△ABC是直角三角形；（2）设AB边上的高为hcm，由题意得S△ABC＝50⋅ℎ2=30×402，解得h＝24．∴AB边上的高为24cm；（3）①∵点D从点B出发在线段AB上以2cm/s的速度向终点A运动，∴BD＝2t；故答案为：2t；②如图1，若BC＝BD＝30cm，则t＝302＝15s，如图2，若CD＝BC，过点C作CE⊥AB，由（2）可知：CE＝24cm，∴BE18cm，∵CD＝BC，且CE⊥BA，∴DE＝BE＝18cm，∴BD＝36cm，∴t＝36＝18s，2若CD＝DB，如图2，∵CD2＝CE2+DE2，∴CD2＝（CD﹣18）2+576，∴CD＝25，s，∴t＝252s时，△BCD为等腰三角形．综上所述：当t＝15s或18s或25213．（2023春·八年级课时练习）如图，ΔABC中，∠ACB=90°，AB=10cm，BC=8cm，若点P从点A出发，以每秒2cm的速度沿折线A−B−C−A运动，设运动时间为t秒(t>0)．（1）点P运动结束，运动时间t=______；（2）当点P到边AB、AC的距离相等时，求此时t的值；（3）在点P运动过程中，是否存在t的值，使得△ACP为等腰三角形，若存在，求出t的值，若不存在，请说明理由．【思路点拨】（1）根据勾股定理定理求出AC长，从而根据时间=路程÷速度计算即可得到答案；（2）当点P恰好在∠ABC的角平分线上，点P到边AB、AC的距离相等时，设PD=PC=y，则AP=3−y，在RtΔADP中，依据AD2+PD2=AP2，列方程求解即可得到t的值；（3）分四种情况：当P在AB上且AP=CP时，当P在AB上且AP=CA=3时，当P在AB上且AC=PC时，当P 在BC上且AC=PC=3时，分别依据等腰三角形的性质即可得到t的值．【解题过程】（1）解：∵ΔABC中，∠ACB=90°，AB=10cm，BC=8cm，∴AC==6cm，∴C△ABC=AB+BC+AC=6+8+10=24cm，∵点P从点A出发，以每秒2cm的速度沿折线A−B−C−A运动，∴点P运动结束，运动时间t=242=12（秒），故答案为：12；（2）解：如图，过P作PD⊥AB于D，∵BP平分∠ABC，∠C=90°，∴PD=PC，BC=BD=8，∴AD=10−8=2，设PD=PC=y，则AP=6−y，在RtΔADP中，AD2+PD2=AP2，∴22+y2=(6−y)2，解得y=83，∴CP=83，∴t=AB BC CP2=108832313s；当点P与点B重合时，点P也在∠ABC的角平分线上，此时，t=AB2=5；综上所述，点P恰好在∠ABC的角平分线上，t的值为313或5；（3）解：根据题意，可分四种情况：①如图，当P在AB上且AP=CP时，∠A =∠ACP ，而∠A +∠B =90°，∠ACP +∠BCP =90°，∴∠B =∠BCP ，∴CP =BP ，∴P 是AB 的中点，即AP =12AB =5，∴t =AP 2=52；②如图，当P 在AB 上且AP =CA =6时，t =AP 2=3；③如图，当P 在AB 上且AC =PC 时，过C 作CD ⊥AB 于D ，则CD =AC·BC AB =245，∴RtΔACD 中，AD =185，∴AP =2AD =365，∴t =AP 2=185；④如图，当P 在BC 上且AC =PC =6时，BP =8−6=2，∴t =AB PB 2=6．综上所述，当t =52或3或185或6s 时，ΔACP 为等腰三角形．14．（2023·全国·八年级专题练习）如图，在△ABC 中，AB=AC =5，BC =6，动点P 从点C 出发，按C-A-B-C 的路径运动（回到C 点停止），且速度为每秒3个单位，设出发时间为t 秒．（1）求BC 边上的高线AE 的长与AC 边上的高线BD 的长；（2）当CP ⊥AB 时, 求t 的值；（3）若△ACP 是等腰三角形，直接写出所有满足条件的t 的值．【思路点拨】（1）如图，根据等腰三角形的性质可得BE ，然后再运用勾股定理可求得AE ，然后再根据S △ABC =12BC ⋅AH =12AC ⋅BD 即可求得BD ；（2）如图：过C 作CF ⊥AB 于F ，先求得CF =245，进而求得AC +AF ，最后根据速度、路程和时间的关系即可解答；（2）分①CA =CP .②CA =AP ，③AP =PC 三种情形，分由等腰三角形的性质和勾股定理分别求解即可．【解题过程】（1）解：∵AB=AC =5，BC =6，BC 边上的高线AE∴BE =EC =12BC =3在Rt △ABE 中，AE ===4∵12BC ×AE =12AC ×BD∴6×4=5BD ,解得：BD =245 ．（2）解：如图：过C 作CF ⊥AB 于F同（1）的方法可得CF =245在Rt △AFC 中，AF 75∴当CP ⊥AB 时，点P 走过的路程为75+5=6.4∴t =6.43=3215．（3）解：①当AC =CP =5时且在AB 上，如图：过点C 作CE ⊥AP 于点E ，∵AC =CP =5∴AE =PE ，∵CE ⊥AB ，BD ⊥AC ，∴由（2）可得，CF =245由勾股定理可得：AF =75∴AC +AP =AC +2AF =5+2.8=7.8∴t =7.83=2.6；当AC =CP =5时且在BC 上，则有AC +AB +BP =11∴t =113；②如图，当PA =AC 时，即点P 与点B 重合，∴AC +AP =AC +AB =5+5=10∴t =103；③如图，当AP =PC 时，点P 在BC 上，过点A 作AH ⊥BC 于H∵AB =AC ，∴AH ⊥BC∴BH =CH =3 ，由（1）可知：AH =4，∵点P 在BC 上∴PC =16−3t ，PH =13−3t ，∴(13−3t)2+42=(16−3t)2，解得t =7118．综上所述，满足条件的的值为2.6或113或103或7118．15．（2023秋·湖南衡阳·八年级校考期末）如图1，在△ABC 中，∠ACB =90°,AB =5,BC =3，点P 从点A 出发，以每秒1个单位长度的速度沿路线A→C→B→A 运动．设点P 的运动时间为t 秒．（1）AC=_________；当点P在AC上时，CP=_________（用含t的代数式表示）；（2）如图2，若点P在∠ABC的角平分线上，求t的值；（3）在整个运动过程中，当△BCP是等腰三角形时，求t的值．【思路点拨】（1）利用勾股定理求出AC，利用CP=AC−AP，求出CP；（2）过点P作PD⊥AB，交AB于点D，利用勾股定理列式求解即可；（3）分BC=CP,BP=CP,BC=BP，三种情况进行讨论求解即可．【解题过程】（1）解：∵∠ACB=90°,AB=5,BC=3，∴AC==4；∵点P从点A出发，以每秒1个单位长度的速度沿路线A→C→B→A运动，∴当点P在AC上时，AP=t，∴CP=AC−AP=4−t；故答案为：4,4−t；（2）解：点P作PD⊥AB，交AB于点D，则：∠PDA=∠PDB=90°，∵点P在∠ABC的角平分线上，∠ACB=90°，∴∠ACB=∠PDB=90°，PD=PC，又∵BP=BP，∴△PBD≌△PBC(HL)，∴BD=BC=3，∴AD=AB−BD=2，由（1）知AP=t,CP=4−t，∴PD=PC=4−t，在Rt△ADP中，AP2=PD2+AD2，即：t2=(4−t)2+22，解得：t=5；2（3）解：P 点运动的总时间为：(5+4+3)÷1=12秒，当△BCP 是等腰三角形时：①当BC =CP ，点P 在AC 上时：如图，此时：4−t =3，解得：t =1；当BC =CP ，点P 在AB 上时：如图，过点C 作CE ⊥AB ，交AB 于点E ，则：BP =t−AC−BC =t−7=2BE ，∵S △ABC =12AC ⋅BC =12AB ⋅CE ，即：4×3=5CE ，∴CE =125，∴BE =95，∴BP =t−7=185，∴t =535；②当BP =CP 时，如图：由①可知：BE =95,BP =t−7,CE =125，∴PE =t−7−95,CP =t−7，在Rt△PEC中，CP2=PE2+CE2，即：(t−7)2=t−+，解得：t=9.5；③当BC=BP时，如图：此时：BP=t−7=3，解得t=10；综上：当△BCP是等腰三角形时，t的值为：1或53或9.5或10．516．（2023秋·山东烟台·七年级统考期末）在Rt△ABC中，∠ACB=90°，CB=CA=D是射线AB 上一点，连接CD，在CD右侧作∠DCE=90°，且CE=CD，连接AE，已知AE=1．（1）如图1，当点D在线段AB上时，①求∠CAE的度数；②求线段CD的长；（2）当点D在线段AB的延长线上时，其他条件不变，请在图2中画出图形，并直接写出∠CAE的度数和CD的长．【思路点拨】（1）①先证明△BCD≌△ACE(SAS)，得到∠B＝∠CAE即可求解；②先利用勾股定理求出AB=4，再证明∠DAE＝∠BAC+∠CAE=90°，最后利用勾股定理即可求解；（2）先证明△BCD≌△ACE(SAS)，再得到∠CBD＝135°，即可求出∠CAE=135°，利用勾股定理即可求出CD的长．【解题过程】（1）①∵∠ACB =90°，∠DCE =90°，∴∠ACB−∠ACD ＝∠DCE−∠ACD ，∴∠BCD ＝∠ACE ，在△BCD 和△ACE 中，BC =AC ∠BCD =∠ACE CD =CE，∴△BCD≌△ACE (SAS)，∴∠B ＝∠CAE ，∵∠ACB ＝90°，AC ＝BC ，∴∠B ＝45°，∴∠CAE ＝45°；②连接DE ，如图1，∵∠ACB ＝90°， CB =CA =∴∠B ＝∠BAC ＝45°，在Rt △ABC 中，由勾股定理得：AC 2+BC 2=AB 2∴AB==4，∵△BCD≌△ACE ，∴∠B ＝∠CAE ＝45°，BD ＝AE ＝1，∴∠DAE ＝∠BAC +∠CAE =90°，AD ＝AB−BD ＝4−1＝3，由勾股定理得：DA 2+AE 2=DE 2∵∠DCE ＝90°，由勾股定理得：DC 2+CE 2=DE 2∴DA 2+AE 2=DC 2+CE 2∵CE ＝CD，∴32+1=2CD2∴CD（2）画图见图2，∠CAE＝135°，CD=∵∠ACB=90°，∠DCE=90°，∴∠ACB−∠BCE＝∠DCE−∠BCE，∴∠BCD＝∠ACE，在△BCD和△ACE中，BC=AC∠BCD=∠ACECD=CE，∴△BCD≌△ACE(SAS)，∴∠CBD＝∠CAE，∵∠ACB＝90°，AC＝BC，∴∠CBA＝45°，∴∠CBD＝135°∴∠CAE＝135°；连接DE，∵∠CBD＝∠CAE＝135°，BD＝AE＝1，∴∠DAE＝∠CAE−∠BAC=90°，AD＝AB+BD＝4+1＝5，由勾股定理得：DA2+AE2=DE2∵∠DCE＝90°，由勾股定理得：DC2+CE2=DE2∴DA2+AE2=DC2+CE2∵CE＝CD，∴52+1=2CD2∴CD17．（2023秋·福建莆田·八年级期末）如图，在平面直角坐标系中，点A在y轴上，点B、C在x轴上，∠ABO=30°，AB=2，OB=OC．（1）如图1，求点A、B、C的坐标；（2）如图2，若点D在第一象限且满足AD=AC，∠DAC=90°，线段BD交y轴于点G，求线段BG的长；（3）如图3，在（2）的条件下，若在第四象限有一点E，满足∠BEC=∠BDC．请探究BE、CE、AE之间的数量关系．【思路点拨】AB=1，进而有BO（1）根据∠ABO=30°，AB=2，在Rt△ABO中，有：AO=12（2）求出AC2，即AB=AC，可得∠ABD=∠ADB，接着求出∠BAG=120°，证明△BAO≌△CAO，即有∠BAO=60°=∠CAO，可得∠GAD=180°−∠DAC−∠OAC=30°，得出∠BAD=∠BAG+∠GAD=150°，进而有∠ABD=∠ADB=15°，可得∠GBO=∠ABD+∠ABO=45°，即有∠GBO=∠BGO=45°，问题随之得解；（3）由（2）可知：∠ADB=15°，可得∠BDC=∠ADB+∠ADC=60°，进而有∠BEC=∠BDC=60°，延长EB 至F，使BF=CE，连接AF，过A点作AM⊥EF于M点，根据∠OAB=∠OAC=60°，即有∠BAC=120°，进一步有∠BAC+∠BEC=180°，即可证明∠ABF=∠ACE，接着证明△ABF≌△ACE(SAS)，问题随之得解．【解题过程】（1）∵∠ABO=30°，AB=2，AB=1，∴在Rt△ABO中，有：AO=12∴BO∵OB=OC，∴OB=OC=∴A(0,1)，B(，C；（2）∵OC=AO=1，∴在Rt△ACO中，AC==2，即AB=AC，∵AD=AC，∴AD=2，∴AD=2=AB，∴∠ABD=∠ADB，∵∠ABO=30°，∠AOB=90°，∴∠BAO=60°，即∠BAG=120°，∵OB=OC，AB=AC=2，AO=AO，∴△BAO≌△CAO，∴∠BAO=60°=∠CAO，∵∠DAC=90°，∴∠GAD=180°−∠DAC−∠OAC=30°，∵∠BAG=120°，∴∠BAD=∠BAG+∠GAD=150°，∴∠ABD=∠ADB=15°，∵∠ABO=30°，∠AOB=90°，∴∠GBO=∠ABD+∠ABO=45°，∴∠GBO=∠BGO=45°，∴BO=OG，∵BO∴BO=OG∴在△BOG中，BG=（3）BE+CE=，理由如下：由（2）可知：∠ADB=15°，∵AD=AC，∠DAC=90°，∴∠ADC=∠ACD=45°，∴∠BDC=∠ADB+∠ADC=60°，∴∠BEC =∠BDC =60°，延长EB 至F ，使BF =CE ，连接AF ，过A 点作AM ⊥EF 于M 点，如图，∵∠OAB =∠OAC =60°，∴∠BAC =120°，∴∠BAC +∠BEC =180°，∴∠ACE +∠ABE =180°，∵∠ABF +∠ABE =180°，∴∠ABF =∠ACE ，又∵AB =AC ，BF =CE ，∴△ABF≌△ACE (SAS)，∴AF =AE ，∠BAF =∠CAE ，∴∠FAE =∠BAC =120°，∴∠F =∠AEF =30°，∵AM ⊥EF ，AF =AE ，∴AM =12AE ，ME =12EF ，∴ME∴FE =，∴BE +CE =BE +BF =FE =，即BE +CE =．18．（2023秋·山东济南·八年级统考期末）已知∠AOB =∠COD =90°，OA =OB =10，OC =OD =8（1）如图1，连接AC 、BD ，问AC 与BD 相等吗？并说明理由．（2）若将△COD 绕点O 逆时针旋转，如图2，当点C 恰好在AB 边上时，请写出AC 、BC 、OC 之间关系，并说明理由．（3）若△COD 绕点O 旋转，当∠AOC =15°时，直线CD 与直线AO 交于点F ，求AF 的长．【思路点拨】（1）根据题意可证得△AOC≌△BOD (SAS)，据此即可解答；（2）连接BD ，可证得∠AOC =∠BOD ，据此即可证得△AOC≌BOD (SAS)，AC =BD ，∠CAO =∠DBO ，根据勾股定理可得CD 2=2OC 2，再根据等腰直角三角形的性质可证得∠CBD =90°，根据勾股定理即可证得结论；（3）过点O 作OE ⊥CD 于点E ，利用勾股定理可求得CD =OE =情况，分别计算即可求得．【解题过程】（1）解：AC 与BD 相等；理由如下：∵∠AOB =∠COD =90°，∴∠AOB +∠BOC =∠COD +∠BOC ，即∠AOC =∠BOD ，在△AOC 和△BOD 中OA =OB ∠AOC =∠BOD OC =OD∴△AOC≌BOD (SAS)，∴AC =BD ；（2）解：结论：BC 2+AC 2=2OC 2理由如下：如图：连接BD，∵∠AOB =∠COD =90°，∴∠AOB−∠BOC =∠COD−∠BOC ，即∠AOC =∠BOD在△AOC 和△BOD 中OA =OB ∠AOC =∠BOD OC =OD∴△AOC≌BOD (SAS)，∴AC =BD ，∠CAO =∠DBO ，∵∠AOB =∠COD =90°，OA =OB ，OC =OD ，∴∠BAO =∠ABO =45°，CD 2=OC 2+OD 2=2OC 2，∴∠CAO =∠DBO =45°，∴∠CBD =∠ABO +∠DBO =45°+45°=90°，∴BC 2+BD 2=CD 2，∴BC 2+AC 2=2OC 2；（3）解：如图：过点O 作OE ⊥CD 于点E ，∵∠COD =90°，OC =OD =8，∴CD∵S △OCD =12OC ⋅OD =12CD ⋅OE ，∴OE =OC⋅OD CD=如图：当点F 在OA 的延长线上时，∵∠DCO =45°，∠AOC =15°，∴∠F =∠DCO−∠AOC =45°−15°=30°，∴OF =2OE =∴AF =OF−OA =；如图：当点F 在线段OA 上时，∵∠DCO =45°，∠AOC =15°，∴∠DFO =∠DCO +∠AOC =45°+15°=60°，∴∠FOE =90°−60°=30°，∴EF =12OF ，∵OF 2=EF 2+OE 2，∴OF 2=OF 2+2，解得OF =∴AF =OA−OF =综上，AF 的长为或19．（2023秋·浙江宁波·八年级统考期末）定义：在任意△ABC 中，如果一个内角度数的2倍与另一个内角度数的和为90°，那么称此三角形为“倍角互余三角形”．（1）【基础巩固】若△ABC 是“倍角互余三角形”，∠C >90°，∠A =60°，则∠B =________°；（2）【尝试应用】如图1，在Rt △ABC 中，∠ACB =90°，点D 为线段BC 上一点，若∠CAD 与∠CAB 互余．求证：△ABD 是“倍角互余三角形”；（3）【拓展提高】如图2，在Rt △ABC 中，∠ACB =90°，AC =3，BC =4，试问在边BC 上是否存在点E ，使得△ABE 是“倍角互余三角形”？若存在，请求出BE 的长；若不存在，请说明理由．【思路点拨】（1）根据“倍角互余三角形”的概念结合∠C >90°，∠A =60°，即可求解；（2）根据∠ACB =90°，得出∠B +∠CAB =90°，又根据∠CAB +∠CAD =90°，得出∠B =∠CAD ，即可证明；（3）①当AE 平分∠CAB 时，则2∠EAB +∠B =90°，证明出△ACE≌△AFE ，得出BF =2，设CE =a ，则EF =a ，BE =4−a ，利用勾股定理求解得a =32，所以BE =4−a =52．②当∠CAE =∠B 时，作点A 关于BC 的对称点H ，连接AE 、HE ，并延长HE 交AB 于点F ．设∠CAE =x ，则∠ABC =x ，根据点A 、点H 关于BC 对称，进一步得出∠BEF +∠ABC =90°，即HF ⊥AB ，利用等积法求得：HF =245，在利用勾股定理求解即可．【解题过程】（1）解：∵△ABC 是“倍角互余三角形”，∠C >90°，∠A =60°，∴∠A +2∠B =90°，∴∠B =12(90°−60°)=15°，故答案为：15；（2）解：∵∠ACB =90°，∴∠B +∠CAB =90°，又∵∠CAB +∠CAD =90°，∴∠B =∠CAD ，∴∠B +∠CAD +∠BAD =2∠B +∠BAD =90°∴△ABD 是倍角互余三角形．（3）解：①当AE 平分∠CAB 时，则2∠EAB +∠B =90°，∠CAE =∠FAE,∠ACE =∠AFE,AE =AE∴△ACE≌△AFE ，∴AE =AC =3，则BF =2，设CE =a ，则EF =a ，BE =4−a ，在Rt △BEF 中，(4−a)2=a 2+22，解得a =32，所以BE =4−a =52．②当∠CAE =∠B 时，作点A 关于BC 的对称点H ，连接AE 、HE ，并延长HE 交AB 于点F ．设∠CAE =x ，则∠ABC =x ，∵点A 、点H 关于BC 对称，∴∠AHE =∠CAE =x ，∴∠CEH =90°−x =∠BEF ，∴∠BEF +∠ABC =90°，即HF ⊥AB ，利用等积法求得：S △ABH =AH ×BC ×12=AB ×HF ×12，∴HF =245，在Rt △AHF 中，AF 185设AE =HE =a ，在Rt △AEF 中，a 2=−a 2+，∴a =154，在Rt △ACE 中，CE =94，∴BE =4−94=74，综上所述，BE =52或74时，△ABE 为倍角互余三角形．20．（2023秋·浙江宁波·八年级统考期末）定义：若三角形满足：两边的平方和与这两边乘积的差等于第三边的平方，则称这个三角形为“类勾股三角形”．如图1在△ABC 中，AB 2+AC 2−AB ⋅AC =BC 2，则△ABC 是“类勾股三角形”．（1）等边三角形一定是“类勾股三角形”，是___________________命题（填真或假）．（2）若Rt △ABC 中，∠C =90°,AB =c,AC =b,BC =a ，且b >a ，若△ABC 是“类勾股三角形”，求∠B 的度数．（3）如图2，在等边三角形ABC 的边AC,BC 上各取一点D ，E ，且AD <CD,AE,BD 相交于点F ，BG 是△BEF 的高，若△BGF 是“类勾股三角形”，且BG >FG ．①求证：AD =CE ．②连结CG ，若∠GCB =∠ABD ，那么线段AG,EF,CD 能否构成一个“类勾股三角形”？若能，请证明；若不能，请说明理由．【思路点拨】（1）根据等边三角形的性质，“类勾股三角形”的定义判断；（2）根据勾股定理得到a 2+b 2=c 2，分三种情况，根据“类勾股三角形”的定义解答；（3）①根据“类勾股三角形”的定义得到∠BFG =60°，证明△ABD≅△CAE ，根据全等三角形的性质证明结论；②证明△ABF≅△CAG ，得到AG =BF ，设FG =x ，EG =y ，分别用x 、y 表示出 AG 2、EF 2、CD 2，根据“类勾股三角形”的定义判断即可．【解题过程】（1）当△ABC为等边三角形时，AB=AC=BC，∴AB2+AC2−AB⋅AC=BC2+BC2−BC⋅BC=BC2，∴等边三角形一定是“类勾股三角形”故答案为：真（2）∵∠C=90°,AB=c,AC=b,BC=a，∴a2+b2=c2，当a2+b2−ab=c2时，则−ab=0（舍去），当a2+c2−ac=b2时，则，a2+c2−ac=c2−a2，∴ac=2a2，∴c=2a，∴a:b:c=，∴∠B=60°当b2+c2−bc=a2时，则，b2+c2−bc=c2−b2，∴bc=2b2，∴c=2b，∴a:b:c=（舍去），综上所述：△ABC是“类勾股三角形”时，∠B=60°（3）①∵△ABC是等边三角形，∴AB=AC=BC，∠ABC=∠ACB=∠BAC=60°，∵BG是△BEF的高，△BGF是“类勾股三角形”，∴由（2）可得FG:BG:BF=，∠BFG=60°，∴∠FAB+∠FBA=∠BFG=60°，∵∠FAB+∠EAC=∠BAC=60°，∴∠FBA=∠EAC，在△ABD和△CAE中，∠BAD =∠ACE BA =AC ∠DBA =∠EAC，∴△ABD≅△CAE(ASA)，∴AD =CE②∵∠GCB =∠ABD ，AB =AC ，∴∠FAB =60°−∠ABD =60°−∠GCB =∠ACG ，在△ABF 和△CAG 中，∠FAB =∠GCA BA =AC ∠ABF =∠CAG，∴△ABF≅△CAG ，∴AG =BF ，∵AB =BC,AD =CE ，∴BE =CD ，设FG =x ，EG =y ，则BG，BF =2x ，∴AG 2=BF 2=4x 2，EF 2=(x +y)2=x 2+2xy +y 2，CD 2=2+y 2=3x 2+y 2，∴AG 2+EF 2−AG ⋅EF =4x 2+x 2+2xy +y 2−2x(x +y)=3x 2+y 2，∴AG 2+EF 2−AG ⋅EF =CD 2，∴线段AG,EF,CD 能构成一个“类勾股三角形”．21．（2023春·全国·八年级专题练习）问题背景：如图1，某车间生产了一个竖直放在地面上的零件AB ，过点A 搭了一个支架AC ，测得支架AC 与地面成60°角，即∠ACB =60°；在AC 的中点D 处固定了一个激光扫描仪，需要对零件AB 进行扫描，已知扫描光线的张角恒为60°，即∠EDF =60°．问题提出：数学兴趣小组针对这个装置进行探究，研究零件AB 边上的被扫描部分（即线段EF ），和未扫到的部分（即线段AE 和线段BF）之间的数量关系．问题解决：（1）先考虑特殊情况：①如果点E刚好和点A重合，或者点B刚好和点F重合时，AE+BF________EF（填“>”，“<”或“=”）；②当点E位于特殊位置，比如当∠ADE=30°时，AE+BF________EF（填“>”或“<”）；（2）特殊到一般：猜想：如图2，当0°<∠ADE<60°时，AE+BF________EF，证明你所得到的结论：（3）研究特殊关系：如果BF2+EF2=AE2，求出EF的值．AE【思路点拨】（1）①连接BD，先证明△CDB是等边三角形，即∠ACB=60°=∠CBD=∠BDC，当F点与B点重合时，即BF=0，根据“三线合一”可得AE=EF，即有AE+BF=EF，同理：如果点E刚好和点A重合，同样有AE+BF=EF；问题得解；②先证明△DEF是等边三角形，根据等腰三角形的性质可得AE=EF，再结合含30°角的直角三角形的性质可以求出BF=，即问题得解；（2）将DF绕D点逆时针旋转120°至DM，连接AM，ME，先证明△DEM≌△DEF，再证明△ADM≌△BDF，问题即可得解；（3）将DF绕D点逆时针旋转120°至DN，连接AN，NE，根据（2）中的方法，同理可证明：△DEN≌△DEF，△ADN≌△BDF，再证明△ANE是直角三角形，∠ANE=90°，结合含30°角的直角三角形的性质即可求解．【解题过程】（1）①如图，连接BD，根据题意有∠ABC=90°，∠ACB=60°，即∠CAB=30°，∵点D为AC中点，AC，∴AD=DC=BD=12∴△CDB是等边三角形，（此结论也适用于第（2）和（3）问）∴∠ACB=60°=∠CBD=∠BDC，∵∠CAB=30°，AC，∴在Rt△ABC中，BC=12∴AB=，当F点与B点重合时，如上图左图，即BF=0，∵∠EDF=60°=∠DBC，∴DE∥BC，∴∠AED=∠ABC=90°，∴DE⊥AF，∵AD=BD，∴AE=EF，∵BF=0，∴AE+BF=EF，同理：如果点E刚好和点A重合，同样有AE+BF=EF，故答案为：=；②当∠ADE=30°时，如图，∵∠ADE=30°，∠DAE=30°，∴∠DEF=60°，AE=DE，∵∠EDF=60°，∴△DEF是等边三角形，∠ADF=90°，∴DE=EF，∴AE=EF，∵∠ADF=90°，∠DAE=30°，AF，∴在Rt△ADF中，DF=12∴AF=AB=，∴AF=，∴BF=AB−AF，∵AE=EF，BF=，∴AE+BF＞EF，故答案为：＞；（2）AE+BF＞EF，理由如下：将DF绕D点逆时针旋转120°至DM，连接AM，ME，如图，根据旋转的性质有：∠MDF=120°，DF=DM，∵∠FDE=60°，∴∠MDE=60°，∵DE=DE，∴△DEM≌△DEF，∴EM=EF，∵∠CDB=60°，∴∠ADB=120°，即：∠ADB=∠MDF，∵∠ADB=∠ADF+∠FDB，∠MDF=∠ADF+∠ADM，∴∠BDF=∠ADM，∵AD =BD ，MD =DF ，∴△ADM≌△BDF ，∴AM =BF ，∴在△AME 中，AM +AE ＞ME ，∴BF +AE ＞EF ，故答案为：＞；（3）将DF 绕D 点逆时针旋转120°至DN ，连接AN ，NE ，如图，根据（2）中的方法，同理可证明：△DEN≌△DEF ，△ADN≌△BDF ，∴AN =BF ，NE =EF ，∠DBF =∠DAN ，∵BF 2+EF 2=AE 2，∴AN 2+NE 2=AE 2，∴△ANE 是直角三角形，∠ANE =90°，∵在（1）中已证明∠CBD =60°，∴∠DAN =∠DBF =30°，∴∠NAE =∠DAN +∠CAB =60°，∴∠AEN =30°，∴AN =12AE ，∴NE =，∴EF AE =NE AE 22．（2023春·八年级单元测试）【问题探究】如图1，锐角△ABC 中，分别以AB 、AC 为边向外作等腰直角△ABE 和等腰直角△ACD ，使AE ＝AB ，AD ＝AC ，∠BAE ＝∠CAD ＝90°，连接BD ，CE 交于点F ，试猜想BD 与CE 的大小关系及位置关系，并说明理由；【拓展应用】（1）在【问题探究】的条件下，连接DE，若AE=5，AD=3，则BC2+DE2=______；（2）如图2，在△ABC中，∠ACB＝45°，以AB为直角边，A为直角顶点向外作等腰直角△ABD，连接CD，若AC BC＝3，则CD长为_______；（3）如图3，已知在平面直角坐标系xOy中，O为坐标原点，A（0，P（3，0），过点P作直线l⊥x轴，点B是直线l上的一个动点，线段AB绕点A按逆时针方向旋转30°得到线段AC，则AC+PC的最小值为_______．【思路点拨】【问题探究】首先根据等式的性质证明∠EAC=∠BAD，则根据SAS即可证明△EAC≌△BAD，根据全等三角形的性质即可证明BD＝CE．再由直角三角形中两锐角和等于90度，结合∠AEF=∠ABD通过等量代换得出BD⊥CE．【拓展应用】（1）图中一共有6个直角三角形，多次通过勾股定理找出两直角边的平方和等于斜边的平方．通过等量代换得出BC2+DE2=BE2+CD2=AE2+AB2+AC2+AD2，把AE=5，AD=3代入计算即可．（2）构造如[问题探究]的图形，得出CD=BE，再在Rt△BCE中求出BE即可．（3）如图，在射线AO上截取AD=AP，连接BD，作点D关于直线l的对称点D′，连接BD′先证△CAP≌△BDA，再通过等量代换得AC+CP的最小值为AD′，然后通过勾股定理求出AD′的值即可．【解题过程】【问题探究】解：结论：BD＝CE，BD⊥CE理由如下：如图1中，。

浙教版数学综合试题及答案

浙教版数学综合试题及答案一、选择题（每题3分，共30分）1. 下列哪个选项是最小的正整数？A. 0B. 1C. -1D. 22. 如果一个数的平方等于该数本身，那么这个数是：A. 0B. 1C. -1D. 0和13. 一个长方体的长、宽、高分别是10cm、8cm和6cm，其体积是：A. 480cm³B. 400cm³C. 600cm³D. 800cm³4. 下列哪个分数是最简分数？A. 4/8B. 5/6C. 6/9D. 3/45. 一个数除以3的商是7，余数是1，这个数是：A. 22B. 23C. 24D. 256. 一个数的75%是30，那么这个数是：A. 40B. 33.33C. 60D. 1007. 一个班级有40名学生，其中2/5是男生，那么女生的人数是：A. 16B. 24C. 32D. 288. 下列哪个选项不是质数？A. 2B. 3C. 9D. 59. 一个数的1/3加上它的1/4等于这个数的1/2，这个数是：A. 6B. 12C. 24D. 3610. 一个圆的直径是14cm，那么它的半径是：A. 7cmB. 14cmC. 28cmD. 21cm二、填空题（每题4分，共20分）11. 一个数的1/5加上它的2/5等于______。

12. 一本书的价格是35元，打8折后的价格是______元。

13. 一个长方体的体积是120cm³，长是10cm，宽是6cm，高是_______cm。

14. 一个数的3/4加上它的1/4等于______。

15. 一个数的20%是10，那么这个数是______。

三、解答题（共50分）16. （10分）小明和小红合作完成一项工作，小明单独完成需要4小时，小红单独完成需要6小时。

现在他们合作，共同完成这项工作需要多少时间？17. （15分）一辆汽车以每小时60公里的速度从甲地开往乙地，2小时后，一辆摩托车以每小时80公里的速度从甲地出发追赶汽车。

浙教版八年级上专题1.5 角度计算的综合大题专项训练(含解析)

角度计算的综合大题专项训练（30道）1．（2021春•平顶山期末）如图，已知△ABC，AD平分∠BAC交BC于点D，AE⊥BC于点E，∠B ＜∠C．（1）若∠B＝44°，∠C＝72°，求∠DAE的度数；（2）若∠B＝27°，当∠DAE＝度时，∠ADC＝∠C．2．（2021春•长春期末）如图，点A、B分别在射线OM、ON上运动（不与点O重合），AC、BC 分别是∠BAO和∠ABO的角平分线，BC延长线交OM于点G．解决问题：（1）若∠OBA＝80°，∠OAB＝40°，则∠ACG＝；（直接写出答案）（2）若∠MON＝100°，求出∠ACG的度数．3．（2021春•兴化市期末）如图，在△ABC中，∠ACB＝90°，AE平分∠CAB，CD⊥AB，AE、CD 相交于点F．（1）若∠DCB＝50°，求∠CEF的度数；（2）求证：∠CEF＝∠CFE．4．（2021春•海陵区期末）如图，CD是△ABC的角平分线，DE∥BC，交AB于点E．（1）若∠A＝45°，∠BDC＝70°，求∠CED的度数；（2）若∠A﹣∠ACD＝34°，∠EDB＝97°，求∠A的度数．5．（2021春•宽城区期末）如图，在△ABC中，点E是边AC上一点，∠AEB＝∠ABC．（1）如图1，作∠BAC的平分线交CB、BE于D、F两点．求证：∠EFD＝∠ADC．（2）如图2，作△ABC的外角∠BAG的平分线，交CB的延长线于点D，延长BE、DA交于点F，试探究（1）中的结论是否成立？请说明理由．6．（2021春•镇江期中）如图，将一张三角形纸片ABC的一角折叠，使得点A落在四边形BCDE的外部A'的位置，且A'与点C在直线AB的异侧，折痕为DE，已知∠C＝90°，∠A＝30°．（1）求∠1﹣∠2的度数；（2）若保持△A′DE的一边与BC平行，求∠ADE的度数．7．（2021春•常熟市期中）已知△ABC中，AD⊥BC于点D，AE平分∠BAC，过点A作直线GH∥BC，且∠GAB＝60°，∠C＝40°．（1）求△ABC的外角∠CAF的度数；（2）求∠DAE的度数．8．（2020秋•红桥区期末）如图，在△ABC中，AD是高，角平分线AE，BF相交于点O，∠BAC＝50°，∠C＝70°，求∠DAC和∠BOA的大小．9．（2020秋•涪城区期末）如图，在△ABC中，∠1＝∠2＝∠3．（1）证明：∠BAC＝∠DEF；（2）∠BAC＝70°，∠DFE＝50°，求∠ABC的度数．10．（2021春•苏州期末）如图，△ABC中，D为BC上一点，∠C＝∠BAD，△ABC的角平分线BE 交AD于点F．（1）求证：∠AEF＝∠AFE；（2）G为BC上一点，当FE平分∠AFG且∠C＝30°时，求∠CGF的度数．11．（2020秋•恩施市期末）已知：如图，△ABC中，∠BAD＝∠EBC，AD交BE于F．（1）试说明：∠ABC＝∠BFD；（2）若∠ABC＝35°，EG∥AD，EH⊥BE，求∠HEG的度数．12．（2020秋•白银期末）（1）探究：如图1，求证：∠BOC＝∠A+∠B+∠C．（2）应用：如图2，∠ABC＝100°，∠DEF＝130°，求∠A+∠C+∠D+∠F的度数．13．（2021春•新蔡县期末）如图，△ABC中，AD是高，AE、BF是角平分线，它们相交于点O，∠CAB＝50°，∠C＝60°，求∠DAE和∠BOA的度数．14．（2020春•香坊区校级月考）如图，在△ABC中，∠C＝40°，AE、BF分别为△ABC的角平分线，它们相交于点O．（1）求∠EOF的度数．（2）AD是△ABC的高，∠AFB＝80°时，求∠DAE的度数．15．（2021春•海陵区校级月考）如图1，△ABC中，AD平分∠BAC交BC于点D，AE⊥BC，垂足为E，CF∥AD．（1）如图1，∠B＝30°，∠ACB＝70°，求∠CFE的度数；（2）若（1）中的∠B＝α，∠ACB＝β（α＜β），则∠CFE＝；（用α、β表示）（3）如图2，（2）中的结论还成立么？请说明理由．16．（2021春•市北区期末）阅读并填空将三角尺（△MPN，∠MPN＝90°）放置在△ABC上（点P在△ABC内），如图1所示，三角尺的两边PM、PN恰好经过点B和点C．我们来探究：∠ABP 与∠ACP是否存在某种数量关系．（1）特例探索：若∠A＝50°，则∠PBC+∠PCB＝度；∠ABP+∠ACP＝度；（2）类比探索：∠ABP、∠ACP、∠A的关系是；（3）变式探索：如图2所示，改变三角尺的位置，使点P在△ABC外，三角尺的两边PM、PN仍恰好经过点B和点C，则∠ABP、∠ACP、∠A的关系是．17．（2021春•东海县期末）如图1．△ABC的外角平分线BF、CF交于点F．（1）若∠A＝50°．则∠F的度数为；（2）如图2，过点F作直线MN∥BC，交AB，AC延长线于点M、N．若设∠MFB＝α，∠NFC＝β，则∠A与a+β满足的数量关系是；（3）在（2）的条件下，将直线MN绕点F转动．①如图3，当直线MN与线段BC没有交点时，试探索∠A与α，β之间满足的数量关系，并说明理由；②当直线MN与线段BC有交点时，试问①中∠A与α，β之间的数量关系是否仍然成立？若成立，请说明理由；若不成立，请直接写出三者之间满足的数量关系．18．（2021春•宽城区期末）在△ABC中，∠ACB＝90°，点D、E分别是边AC、BC上的点，点P 是一动点．令∠PDA＝∠1，∠PEB＝∠2，∠DPE＝∠α．（1）如图1，点P在斜边AB上运动．①若∠α＝70°，则∠1+∠2＝度．②写出∠α、∠1、∠2之间的关系，并说明理由．（2）如图2，点P在斜边AB的延长线上运动（CE＜CD），BE、PD交于点F，试说明∠1﹣∠2＝90°+∠α．（3）如图3，点P在△ABC外运动（只需研究图③的情形），直接写出∠α、∠1、∠2之间的关系．19．（2021春•延庆区期末）在三角形ABC中，点D在线段AC上，ED∥BC交AB于点E，点F在线段AB上（点F不与点A，E，B重合），连接DF，过点F作FG⊥FD交射线CB于点G．（1）如图1，点F在线段BE上，用等式表示∠EDF与∠BGF的数量关系，并证明；（2）如图2，点F在线段BE上，求证：∠ABC+∠BFG﹣∠EDF＝90°；（3）当点F在线段AE上时，依题意，在图3中补全图形，请直接用等式表示∠EDF与∠BGF的数量关系，不需证明．20．（2021春•中山市期末）同学们以“一块直角三角板和一把直尺”开展数学活动，提出了很多数学问题，请你解答：（1）如图1，∠α和∠β具有怎样的数量关系？请说明理由；（2）如图2，∠DFC的平分线与∠EGC的平分线相交于点Q，求∠FQG的大小；（3）如图3，点P是线段AD上的动点（不与A，D重合），连接PF、PG，的值是否变化？如果不变，请求出比值；如果变化，请说明理由．21．（2021春•禅城区期末）△ABC中，AD是∠BAC的角平分线，AE是△ABC的高．（1）如图1，若∠B＝40°，∠C＝60°，求∠DAE的度数；（2）如图2（∠B＜∠C），试说明∠DAE与∠B、∠C的数量关系；（3）拓展：如图3，四边形ABDC中，AE是∠BAC的角平分线，DA是∠BDC的角平分线，猜想：∠DAE与∠B、∠C的数量关系是否改变．说明理由．22．（2021春•侯马市期末）（1）已知：如图①的图形我们把它称为“8字形”，试说明：∠A+∠B ＝∠C+∠D．（2）如图②，AP，CP分别平分∠BAD，∠BCD，若∠ABC＝36°，∠ADC＝16°，求∠P的度数．（3）如图（3），直线AP平分∠BAD，CP平分∠BCD的外角∠BCE，猜想∠P与∠B、∠D的数量关系是；（4）如图（4），直线AP平分∠BAD的外角∠FAD，CP平分∠BCD的外角∠BCE，猜想∠P与∠B、∠D的数量关系是．23．（2020春•西城区校级期末）在△ABC中，BD，CE是它的两条角平分线，且BD，CE相交于点M，MN⊥BC于点N．将∠MBN记为∠1，∠MCN记为∠2，∠CMN记为∠3．（1）如图1，若∠A＝110°，∠BEC＝130°，则∠2＝ °，∠3﹣∠1＝ °；（2）如图2，猜想∠3﹣∠1与∠A的数量关系，并证明你的结论；（3）若∠BEC＝α，∠BDC＝β，用含α和β的代数式表示∠3﹣∠1的度数．（直接写出结果即可）24．（2020春•福山区期中）直线在同一平面内有平行和相交两种位置关系，线段首尾连接可以变换出很多不同的图形，这些不同的角又有很多不同关系，今天我们就来探究一下这些奇妙的图形吧！【问题探究】（1）如图1，请直接写出∠A+∠B+∠C+∠D+∠E＝；（2）将图1变形为图2，∠A+∠DBE+∠C+∠D+∠E的结果如何？请写出证明过程；（3）将图1变形为图3，则∠A+∠B+∠C+∠D+∠E的结果如何？请写出证明过程．【变式拓展】（4）将图3变形为图4，已知∠BGF＝160°，那么∠A+∠B+∠C+∠D+∠E+∠F的度数是．25．（2020春•蓬溪县期末）某校七年级数学兴趣小组对“三角形内角或外角平分线的夹角与第三个内角的数量关系”进行了探究．（1）如图1，在△ABC中，∠ABC与∠ACB的平分线交于点P，∠A＝64°，则∠BPC＝；（2）如图2，△ABC的内角∠ACB的平分线与△ABC的外角∠ABD的平分线交于点E．其中∠A＝α，求∠BEC．（用α表示∠BEC）；（3）如图3，∠CBM、∠BCN为△ABC的外角，∠CBM、∠BCN的平分线交于点Q，请你写出∠BQC与∠A的数量关系，并说明理由．（4）如图4，△ABC外角∠CBM、∠BCN的平分线交于点Q，∠A＝64°，∠CBQ，∠BCQ的平分线交于点P，则∠BPC＝ °，延长BC至点E，∠ECQ的平分线与BP的延长线相交于点R，则∠R＝ °．26．（2021春•鄂州期末）探究知：任何一个三角形都满足三角形三内角和等于180°，我们把这个结论称之为三角形三内角和定理．如图1，AB∥CD，且∠BED+∠CDE＝120°，请根据题目条件，结合三角形三内角和定理，探究下列问题：（1）如图2，在图1基础上作：∠BEF∠DEF，∠CDE＝3∠CDF，EF与DF交于点F，求∠EFD 的度数；（2）如图3，在图1基础上作：过B作BG⊥AB，交CD于点F，且∠CDG∠CDE，求的值．27．（2020秋•南昌期中）【问题探究】将三角形ABC纸片沿DE折叠，使点A落在点A′处（1）如图1，当点A落在四边形BCDE的边CD上时，直接写出∠A与∠1之间的数量关系；（2）如图2，当点A落在四边形BCDE的内部时，求证：∠1+∠2＝2∠A；（3）如图3，当点A落在四边形BCDE的外部时，探索∠1，∠2，∠A之间的数量关系，并加以证明；【拓展延伸】（4）如图4，若把四边形ABCD纸片沿EF折叠，使点A、D落在四边形BCFE的内部点A′、D ′的位置，请你探索此时∠1，∠2，∠A，∠D之间的数量关系，写出你发现的结论，并说明理由．28．（2021春•桥西区期末）请认真思考，完成下面的探究过程．已知在△ABC中，AE是∠BAC的角平分线，∠B＝60°，∠C＝40°．【解决问题】如图1，若AD⊥BC于点D，求∠DAE的度数；【变式探究】如图2，若F为AE上一个动点（F不与E重合），且FD⊥BC于点D时，则∠DFE＝ °；【拓展延伸】如图2，△ABC中，∠B＝x°，∠C＝y°，（且∠B＞∠C），若F为线段AE上一个动点（F不与E重合），且FD⊥BC于点D时，试用x，y表示∠DFE的度数，并说明理由．29．（2021春•庐江县期末）如图1，AB⊥BC于点B，CD⊥BC于点C，点E在线段BC上，且AE⊥DE．（1）求证：∠EAB＝∠CED；（2）如图2，AF、DF分别平分∠BAE和∠CDE，则∠F的度数是（直接写出答案即可）；（3）如图3，EH平分∠CED，EH的反向延长线交∠BAE的平分线AF于点G．求证：EG⊥AF．（提示：三角形内角和等于180°）30．（2021春•崇川区期末）在△ABC中，BD是△ABC的角平分线，E为边AC上一点，EF⊥BC，垂足为F，EG平分∠AEF交BC于点G．（1）如图1，若∠BAC＝90°，延长AB、EG交于点M，∠M＝α．①用含α的式子表示∠AEF为；②求证：BD∥ME；（2）如图2，∠BAC＜90°，延长DB，EG交于点N，请用等式表示∠A与∠N的数量关系，并证明．角度计算的综合大题专项训练（30道）1．（2021春•平顶山期末）如图，已知△ABC，AD平分∠BAC交BC于点D，AE⊥BC于点E，∠B ＜∠C．（1）若∠B＝44°，∠C＝72°，求∠DAE的度数；（2）若∠B＝27°，当∠DAE＝　21　度时，∠ADC＝∠C．【解题思路】（1）利用三角形的内角和求出∠BAC，再利用内角与外角的关系先求出∠ADC，再求出∠DAE；（2）利用三角形的内角和定理及推论，用含∠C的代数式表示出∠BAC、∠ADC，根据∠C＝∠ADC 得到关于∠C的方程，先求出∠C，再求出∠DAE的度数．【解答过程】解：∵AD平分∠BAC交BC于点D，AE⊥BC于点E，∴∠BAD＝∠CAD∠BAC，∠AED＝90°．（1）∵∠B＝44°，∠C＝72°，∴∠BAC＝180°﹣∠B﹣∠C＝180°﹣44°﹣72°＝64°．∴∠BAD64°＝32°．∵∠ADC＝∠B+∠BAD＝44°+32°＝76°，∴∠DAE＝90°﹣∠ADC＝90°﹣76°＝24°．（2））∵∠B＝27°，∠C＝∠ADC，∴∠BAC＝180°﹣∠B﹣∠C＝180°﹣27°﹣∠C＝153°﹣∠C．∴∠BAD（153°﹣∠C）＝76.5°．∴∠ADC＝∠B+∠BAD＝27°+76.5°∠C＝103.5°∠C．∵∠ADC＝∠C，∴103.5°∠C＝∠C．∴∠ADC＝∠C＝69°．∴∠DAE＝∠AED﹣∠ADC＝90°﹣69°＝21°．故答案为：21．2．（2021春•长春期末）如图，点A、B分别在射线OM、ON上运动（不与点O重合），AC、BC 分别是∠BAO和∠ABO的角平分线，BC延长线交OM于点G．解决问题：（1）若∠OBA＝80°，∠OAB＝40°，则∠ACG＝　60°　；（直接写出答案）（2）若∠MON＝100°，求出∠ACG的度数．【解题思路】（1）由角平分线的定义可求出∠CBA和∠CAB的度数，再根据三角形外角的性质求出∠ACG的度数即可；（2）先根据三角形内角和定理求出∠OBA+∠OAB的度数，然后再根据角平分线的定义求出∠CBA+∠CAB的度数，最后根据三角形外角的性质求出结果即可．【解答过程】解：（1）∵AC、BC分别是∠BAO和∠ABO的角平分线，∴∠CBA∠ABO，∠CAB∠BAO，∵∠OBA＝80°，∠OAB＝40°，∴∠CBA＝40°，∠CAB＝20°，∴∠ACG＝∠CBA+∠CAB＝60°．故答案为：60°．（2）∵∠MON＝100°，∴∠BAO+∠ABO＝180°﹣100°＝80°，∵AC、BC分别是∠BAO和∠ABO的角平分线，∴∠CBA∠ABO，∠CAB∠BAO，∴∠CBA+∠CAB（∠ABO+∠BAO）80°＝40°，∴∠ACG＝∠CBA+∠CAB＝40°．3．（2021春•兴化市期末）如图，在△ABC中，∠ACB＝90°，AE平分∠CAB，CD⊥AB，AE、CD 相交于点F．（1）若∠DCB＝50°，求∠CEF的度数；（2）求证：∠CEF＝∠CFE．【解题思路】（1）根据直角三角形的性质得到∠DCB+∠B＝90°，∠CAB+∠B＝90°，进而得到∠CAB＝∠DCB，根据角平分线的定义计算即可；（2）根据角平分线的定义得到∠BAE＝∠CAE，根据直角三角形的性质得到∠CEF＝∠AFD，根据对顶角相等证明结论．【解答过程】（1）解：∵CD⊥AB，∴∠DCB+∠B＝90°，∵∠ACB＝90°，∴∠CAB+∠B＝90°，∴∠CAB＝∠DCB＝50°，∵AE平分∠CAB，∴∠CAE∠CAB＝25°，∴∠CEF＝90°﹣∠CAE＝65°；（2）证明：∵AE平分∠CAB，∴∠BAE＝∠CAE，∵∠CAE+∠CEF＝90°，∠BAE+∠AFD＝90°，∴∠CEF＝∠AFD，∵∠CFE＝∠AFD，∴∠CEF＝∠CFE．4．（2021春•海陵区期末）如图，CD是△ABC的角平分线，DE∥BC，交AB于点E．（1）若∠A＝45°，∠BDC＝70°，求∠CED的度数；（2）若∠A﹣∠ACD＝34°，∠EDB＝97°，求∠A的度数．【解题思路】（1）利用三角形内角和定理求出∠ACB，再求出∠ECD，∠EDC，可得结论．（2）设∠A＝x，则∠ACD＝x﹣34°，根据∠EDB＝∠A+∠AED，构建方程求解即可．【解答过程】解：（1）∵∠CDB＝∠A+∠ACD，∴∠ACD＝70°﹣45°＝25°，∵CD平分∠ACB，∴∠DCB＝∠ACB＝25°，∵DE∥CB，∴∠EDC＝∠BCD＝25°，∴∠DEC＝180°﹣25°﹣25°＝130°．（2）设∠A＝x，则∠ACD＝x﹣34°，∵CD平分∠ACB，∴∠ACB＝2x﹣68°，∵DE∥CB，∴∠AED＝∠ACB＝2x+68°，∵∠EDB＝∠A+∠AED，∴97°＝x+2x﹣68°，∴x＝55°，∴∠A＝55°．5．（2021春•宽城区期末）如图，在△ABC中，点E是边AC上一点，∠AEB＝∠ABC．（1）如图1，作∠BAC的平分线交CB、BE于D、F两点．求证：∠EFD＝∠ADC．（2）如图2，作△ABC的外角∠BAG的平分线，交CB的延长线于点D，延长BE、DA交于点F，试探究（1）中的结论是否成立？请说明理由．【解题思路】（1）首先根据角平分线的性质可得∠BAD＝∠DAC，再根据内角与外角的性质可得∠EFD＝∠DAC+∠AEB，∠ADC＝∠ABC+∠BAD，进而得到∠EFD＝∠ADC；（2）首先根据角平分线的性质可得∠BAD＝∠DAG，再根据等量代换可得∠FAE＝∠BAD，然后再根据内角与外角的性质可得∠EFD＝∠AEB﹣∠FAE，∠ADC＝∠ABC﹣∠BAD，进而得∠EFD ＝∠ADC．【解答过程】解：（1）∵AD平分∠BAC，∴∠BAD＝∠DAC，∵∠EFD＝∠DAC+∠AEB，∠ADC＝∠ABC+∠BAD，又∵∠AEB＝∠ABC，∴∠EFD＝∠ADC；（2）探究（1）中结论仍成立；理由：∵AD平分∠BAG，∴∠BAD＝∠GAD，∵∠FAE＝∠GAD，∴∠FAE＝∠BAD，∵∠EFD＝∠AEB﹣∠FAE，∠ADC＝∠ABC﹣∠BAD，又∵∠AEB＝∠ABC，∴∠EFD＝∠ADC．6．（2021春•镇江期中）如图，将一张三角形纸片ABC的一角折叠，使得点A落在四边形BCDE的外部A'的位置，且A'与点C在直线AB的异侧，折痕为DE，已知∠C＝90°，∠A＝30°．（1）求∠1﹣∠2的度数；（2）若保持△A′DE的一边与BC平行，求∠ADE的度数．【解题思路】（1）先求出∠B的度数，在根据四边形内角和求出∠1+∠BFD的度数，由∠BFD＝∠A′FE和∠A’的度数可求出答案．（2）分EA'∥BC和DA'∥BC两种情况讨论．当DA'∥BC时，先求出∠A′DA＝90°，再根据折叠可得出∠ADE＝45°；当EA'∥BC时，根据平行线的性质求出∠2＝∠ABC＝60°，由（1）得出∠1＝120°，再根据折叠可求出∠ADE的度数．【解答过程】解：（1）由折叠可知，∠A′＝∠A＝30°，在△A′EF中，∠A′+∠2+∠A′FE＝180°，∴∠2＝180°﹣∠A′﹣∠A′FE＝150°﹣∠A′FE，在△ABC中，∠B＝180°﹣∠C﹣∠A＝60°，在四边形BCDF中，∠1+∠C+∠B+∠BFD＝360°，∴∠1＝360°﹣∠C﹣∠B﹣∠BFD＝210°﹣∠BFD，∵∠BFD＝∠A′FE，∴∠1﹣∠2＝210°﹣150°＝60°；（2）当DA'∥BC时，如图，∠A′DA＝∠ACB＝90°，∵△ADE沿DE折叠到△A′DE，∴∠ADE＝∠A′DE∠ADA′＝45°，当EA'∥BC时，如图，∠2＝∠ABC＝60°．由（1）知，∠1﹣∠2＝60°，∴∠1＝∠2+60°＝120°，∵△ADE沿DE折叠到△A′DE，∴∠ADE＝∠A′DE∠ADA′＝（180°﹣∠1）＝30°．综上所述∠ADE的度数为：45°或30°．7．（2021春•常熟市期中）已知△ABC中，AD⊥BC于点D，AE平分∠BAC，过点A作直线GH∥BC，且∠GAB＝60°，∠C＝40°．（1）求△ABC的外角∠CAF的度数；（2）求∠DAE的度数．【解题思路】（1）根据平行线的性质、对顶角相等计算即可；（2）根据角平分线的定义得到∠BAE＝40°，根据平行线的性质求出∠GAD＝90°，结合图形计算，得到答案．【解答过程】解：（1）∵GH∥BC，∠C＝40°，∴∠HAC＝∠C＝40°，∵∠FAH＝∠GAB＝60°，∴∠CAF＝∠HAC+∠FAH＝100°；（2）∵∠HAC＝40°，∠GAB＝60°，∴∠BAC＝80°，∵AE平分∠BAC，∴∠BAE＝40°，∵GH∥BC，AD⊥BC，∴∠GAD＝90°，∴∠BAD＝90°﹣60°＝30°，∴∠DAE＝∠BAE﹣∠BAD＝10°．8．（2020秋•红桥区期末）如图，在△ABC中，AD是高，角平分线AE，BF相交于点O，∠BAC＝50°，∠C＝70°，求∠DAC和∠BOA的大小．【解题思路】根据三角形高线可得∠ADC＝90°，利用三角形的内角和定理可求解∠DAC的度数；由三角形的内角和可求解∠B的度数，再根据角平分线的定义可求出∠BAO和∠ABO的度数，再利用三角形的内角和定理可求解．【解答过程】解：∵AD是△ABC的高线，∴∠ADC＝90°，∵∠ADC+∠C+∠CAD＝180°，∠C＝70°，∴∠CAD＝180°﹣90°﹣70°＝20°；∵∠ABC+∠C+∠CAB＝180°，∠C＝70°，∠BAC＝50°，∴∠ABC＝180°﹣70°﹣50°＝60°，∵AE，BF分别平分∠BAC，∠ABC，AE，BF相交于点O，∴∠BAO∠BAC＝25°，∠ABO∠ABC＝30°，∵∠ABO+∠BAO+∠AOB＝180°，∴∠AOB＝180°﹣25°﹣30°＝125°．9．（2020秋•涪城区期末）如图，在△ABC中，∠1＝∠2＝∠3．（1）证明：∠BAC＝∠DEF；（2）∠BAC＝70°，∠DFE＝50°，求∠ABC的度数．【解题思路】（1）利用三角形的外角的性质解决问题即可．（2）利用三角形的外角的性质解决问题即可．【解答过程】（1）证明：∵∠BAC＝∠1+∠CAE，∠DEF＝∠3+∠CAE，∠1＝∠3，∴∠BAC＝∠DEF．（2）∵∠ABC＝∠2+∠ABD，∠1＝∠2，∴∠ABC＝∠1+∠ABD＝∠EDF，由（1）可知∠DEF＝∠BAC＝70°，∴∠ABC＝∠1+∠ABD＝∠EDF＝180°﹣∠DEF﹣∠DFE＝180°﹣70°﹣50°＝60°，∴∠ABC＝60°．10．（2021春•苏州期末）如图，△ABC中，D为BC上一点，∠C＝∠BAD，△ABC的角平分线BE 交AD于点F．（1）求证：∠AEF＝∠AFE；（2）G为BC上一点，当FE平分∠AFG且∠C＝30°时，求∠CGF的度数．【解题思路】（1）由角平分线定义得∠ABE＝∠CBE，再根据三角形的外角性质得∠AEF＝∠AFE；（2）由角平分线定义得∠AFE＝∠GFE，进而得∠AEF＝∠GFE，由平行线的判定得FG∥AC，再根据平行线的性质求得结果．【解答过程】解：（1）证明：∵BE平分∠ABC，∴∠ABE＝∠CBE，∴∠ABF+∠BAD＝∠CBE+∠C，∵∠AFE＝∠ABF+∠BAD，∠AEF＝∠CBE+∠C，∴∠AEF＝∠AFE；（2）∵FE平分∠AFG，∴∠AFE＝∠GFE，∵∠AEF＝∠AFE，∴∠AEF＝∠GFE，∴FG∥AC，∵∠C＝30°，∴∠CGF＝180°﹣∠C＝150°．11．（2020秋•恩施市期末）已知：如图，△ABC中，∠BAD＝∠EBC，AD交BE于F．（1）试说明：∠ABC＝∠BFD；（2）若∠ABC＝35°，EG∥AD，EH⊥BE，求∠HEG的度数．【解题思路】（1）根据三角形的外角性质即可得出结论；（2）根据三角形内角和和互余进行分析解答即可．【解答过程】解：（1）∵∠BFD＝∠ABF+∠BAD，∠ABC＝∠ABF+∠FBC，∵∠BAD＝∠EBC，∴∠ABC＝∠BFD；（2）∵∠BFD＝∠ABC＝35°，∵EG∥AD，∴∠BEG＝∠BFD＝35°，∵EH⊥BE，∴∠BEH＝90°，∴∠HEG＝∠BEH﹣∠BEG＝55°．12．（2020秋•白银期末）（1）探究：如图1，求证：∠BOC＝∠A+∠B+∠C．（2）应用：如图2，∠ABC＝100°，∠DEF＝130°，求∠A+∠C+∠D+∠F的度数．【解题思路】（1）作射线OA，由三角形外角的性质可知∠1+∠B＝∠3，∠2+∠C＝∠4，两式相加即可得出结论；（2）连接AD，由（1）的结论可知∠F+∠2+∠3＝∠DEF，∠1+∠4+∠C＝∠ABC，两式相加即可得出结论．【解答过程】解：（1）作射线OA，∵∠3是△ABO的外角，∴∠1+∠B＝∠3，①∵∠4是△AOC的外角，∴∠2+∠C＝∠4，②①+②得，∠1+∠B+∠2+∠C＝∠3+∠4，即∠BOC＝∠A+∠B+∠C；（2）连接AD，同（1）可得，∠F+∠2+∠3＝∠DEF③，∠1+∠4+∠C＝∠ABC④，③+④得，∠F+∠2+∠3+∠1+∠4+∠C＝∠DEF+∠ABC＝130°+100°＝230°，即∠A+∠C+∠D+∠F＝230°．13．（2021春•新蔡县期末）如图，△ABC中，AD是高，AE、BF是角平分线，它们相交于点O，∠CAB＝50°，∠C＝60°，求∠DAE和∠BOA的度数．【解题思路】先利用三角形内角和定理可求∠ABC，在直角三角形ACD中，易求∠DAC；再根据角平分线定义可求∠CBF、∠EAF，可得∠DAE的度数；然后利用三角形外角性质，可先求∠AFB，再次利用三角形外角性质，容易求出∠BOA．【解答过程】解：∵∠CAB＝50°，∠C＝60°∴∠ABC＝180°﹣50°﹣60°＝70°，又∵AD是高，∴∠ADC＝90°，∴∠DAC＝180°﹣90°﹣∠C＝30°，∵AE、BF是角平分线，∴∠CBF＝∠ABF＝35°，∠EAF＝25°，∴∠DAE＝∠DAC﹣∠EAF＝5°，∠AFB＝∠C+∠CBF＝60°+35°＝95°，∴∠BOA＝∠EAF+∠AFB＝25°+95°＝120°，∴∠DAC＝30°，∠BOA＝120°．故∠DAE＝5°，∠BOA＝120°．14．（2020春•香坊区校级月考）如图，在△ABC中，∠C＝40°，AE、BF分别为△ABC的角平分线，它们相交于点O．（1）求∠EOF的度数．（2）AD是△ABC的高，∠AFB＝80°时，求∠DAE的度数．【解题思路】（1）先根据三角形内角和定理得∠C＝180°﹣（∠BAC+∠ABC）的度数，由角平分线的定义和三角形内角和定理可得结论；（2）先根据垂直的定义及三角形内角和可得到∠CAD的度数，再求出∠1的度数，最后根据三角形内角和即可求解．【解答过程】解：（1）∵∠CAB+∠ABC＝180°﹣∠C，∵AE、BF是角平分线，∴∠EAB∠BAC，∠FBA∠ABC，∴∠EAB+∠FBA（∠BAC+∠ABC）（180°﹣∠C）＝90°∠C，∴∠AOB＝180°﹣（90°∠C）＝90°∠C，∵∠C＝40°，∴∠AOB＝110°，∴∠EOF＝∠AOB＝110°．（2）∵AD⊥BC，∠C＝40°，∴∠CAD＝50°，∵∠AFB＝80°，∴∠1＝180°﹣50°﹣80°＝50°，∴∠DAE＝180°﹣∠1﹣∠AOB＝180°﹣50°﹣110°＝20°．15．（2021春•海陵区校级月考）如图1，△ABC中，AD平分∠BAC交BC于点D，AE⊥BC，垂足为E，CF∥AD．（1）如图1，∠B＝30°，∠ACB＝70°，求∠CFE的度数；（2）若（1）中的∠B＝α，∠ACB＝β（α＜β），则∠CFE＝　βα　；（用α、β表示）（3）如图2，（2）中的结论还成立么？请说明理由．【解题思路】（1）求∠CFE的度数，求出∠DAE的度数即可，只要求出∠BAE﹣∠BAD的度数，由平分和垂直易得∠BAE和∠BAD的度数即可；（2）由（1）类推得出答案即可；（3）类比以上思路，把问题转换为∠CFE＝90°﹣∠ECF即可解决问题．【解答过程】解：（1）∵∠B＝30°，∠ACB＝70°，∴∠BAC＝180°﹣∠B﹣∠ACB＝80°，∵AD平分∠BAC，∴∠BAD＝40°，∵AE⊥BC，∴∠AEB＝90°∴∠BAE＝60°∴∠DAE＝∠BAE﹣∠BAD＝60°﹣40°＝20°，∵CF∥AD，∠B＝α，∠ACB＝β，∴∠CFE＝∠DAE＝20°；（2）∵∠BAE＝90°﹣∠B，∠BAD∠BAC（180°﹣∠B﹣∠ACB），∵CF∥AD，∴∠CFE＝∠DAE＝∠BAE﹣∠BAD＝90°﹣∠B（180°﹣∠B﹣∠BCA）（∠ACB﹣∠B）βα，故答案为：βα；（3）（2）中的结论成立．∵∠B＝α，∠ACB＝β，∴∠BAC＝180°﹣α﹣β，∵AD平分∠BAC，∴∠DAC∠BAC＝90°αβ，∵CF∥AD，∴∠ACF＝∠DAC＝90°αβ，∴∠BCF＝β+90°αβ＝90°αβ，∴∠ECF＝180°﹣∠BCF＝90°αβ，∵AE⊥BC，∴∠FEC＝90°，∴∠CFE＝90°﹣∠ECFβα．16．（2021春•市北区期末）阅读并填空将三角尺（△MPN，∠MPN＝90°）放置在△ABC上（点P 在△ABC内），如图1所示，三角尺的两边PM、PN恰好经过点B和点C．我们来探究：∠ABP 与∠ACP是否存在某种数量关系．（1）特例探索：若∠A＝50°，则∠PBC+∠PCB＝　90　度；∠ABP+∠ACP＝　40　度；（2）类比探索：∠ABP、∠ACP、∠A的关系是　∠ABP+∠ACP＝90°﹣∠A　；（3）变式探索：如图2所示，改变三角尺的位置，使点P在△ABC外，三角尺的两边PM、PN仍恰好经过点B和点C，则∠ABP、∠ACP、∠A的关系是　∠ACP﹣∠ABP＝90°﹣∠A　．【解题思路】（1）利用三角形内角和定理即可解决问题．（2）结论：∠ABP+∠ACP＝90°﹣∠A．利用三角形内角和定理即可证明．（3）不成立；存在结论：∠ACP﹣∠ABP＝90°﹣∠A．利用三角形内角和定理即可解决问题．【解答过程】解：（1）∵∠A＝50°，∴∠ABC+∠ACB＝130°，∵∠P＝90°，∴∠PBC+∠PCB＝90°，∴∠ABP+∠ACP＝130°﹣90°＝40°，故答案为：90，40；（2）结论：∠ABP+∠ACP＝90°﹣∠A．证明：∵（∠PBC+∠PCB）+（∠ABP+∠ACP）+∠A＝180°，∴90°+（∠ABP+∠ACP）+∠A＝180°，∴∠ABP+∠ACP+∠A＝90°，∴∠ABP+∠ACP＝90°﹣∠A．故答案为：∠ABP+∠ACP＝90°﹣∠A；（3）结论：∠ACP﹣∠ABP＝90°﹣∠A，理由是：设AB交PC于O，如图2：∵∠AOC＝∠POB，∴∠ACO+∠A＝∠P+∠PBO，即∠ACP+∠A＝90°+∠ABP，∴∠ACP﹣∠ABP＝90°﹣∠A，故答案为：∠ACP﹣∠ABP＝90°﹣∠A．17．（2021春•东海县期末）如图1．△ABC的外角平分线BF、CF交于点F．（1）若∠A＝50°．则∠F的度数为　65°　；（2）如图2，过点F作直线MN∥BC，交AB，AC延长线于点M、N．若设∠MFB＝α，∠NFC＝β，则∠A与a+β满足的数量关系是　α+β∠A＝90°　；（3）在（2）的条件下，将直线MN绕点F转动．①如图3，当直线MN与线段BC没有交点时，试探索∠A与α，β之间满足的数量关系，并说明理由；②当直线MN与线段BC有交点时，试问①中∠A与α，β之间的数量关系是否仍然成立？若成立，请说明理由；若不成立，请直接写出三者之间满足的数量关系．【解题思路】（1）根据三角形内角和定理以及角平分线的定义，即可得到∠F的度数；（2）根据三角形内角和定理以及角平分线的定义，即可得到∠BFC的度数，再根据平行线的性质，即可得到∠A与α+β的数量关系；（3）①根据（2）中的结论∠BFC＝90°﹣∠A，以及平角的定义，即可得到∠A与α，β之间的数量关系；②分两种情况进行讨论，根据（2）中的结论∠BFC＝90°﹣∠A，以及平角的定义，即可得到∠A 与α，β之间的数量关系．【解答过程】解：（1）如图1，∵∠A＝50°，∴∠ABC+∠ACB＝130°，∴∠DBC﹣∠ECB＝360°﹣130°＝230°，又∵△ABC的外角平分线交于点F，∴∠FBC+∠FCB（∠DBC+∠ECD）230°＝115°，∴△BCF中∠F＝180°﹣115°＝65°，故答案为65°；（2）如图2，∵∠ABC+∠ACB＝180°﹣∠A，∴∠DBC+∠ECB＝360°﹣（180°﹣∠A）＝180°+∠A，又∵△ABC的外角平分线交于点F，∴∠FBC+∠FCB（∠DBC+∠ECB）（180°+∠A）＝90°∠A，∴△BCF中，∠BFC＝180°﹣（90°∠A）＝90°∠A，又∵∠MFB＝α，∠NFC＝β，MN∥BC，∴∠FBC＝α，∠FCB＝β，∵△BCF中，∠FBC+∠FCB+∠BFC＝180°，∴α+β+90°∠A＝180°，即α+β∠A＝90°，故答案为：α+β∠A＝90°；（3）①α+β∠A＝90°，理由如下：如图3，由（2）可得，∠BFC＝90°∠A，∵∠MFB+∠NFC+∠BFC＝180°，∴α+β+90°∠A＝180°，即α+β∠A＝90°，②当直线MN与线段BC有交点时，①中∠A与α，β之间的数量关系不成立，分两种情况：如图4，当M在线段AB上，N在AC延长线上时，由（2）可得，∠BFC＝90°∠A，∵∠BFC﹣∠MFB+∠NFC＝180°，∴90°∠A﹣α+β＝180°，即β﹣α∠A＝90°；如图5，当M在AB的延长线上，N在线段AC上时，由（2）可得，∠BFC＝90°∠A，∴∠BFC﹣∠NFC+∠MFB＝180°，∴90°∠A﹣β+α＝180°，即α﹣β∠A＝90°；综上所述，∠A与α，β之间的数量关系为β﹣α∠A＝90°或α﹣β∠A＝90°．18．（2021春•宽城区期末）在△ABC中，∠ACB＝90°，点D、E分别是边AC、BC上的点，点P 是一动点．令∠PDA＝∠1，∠PEB＝∠2，∠DPE＝∠α．（1）如图1，点P在斜边AB上运动．①若∠α＝70°，则∠1+∠2＝　160　度．②写出∠α、∠1、∠2之间的关系，并说明理由．（2）如图2，点P在斜边AB的延长线上运动（CE＜CD），BE、PD交于点F，试说明∠1﹣∠2＝90°+∠α．（3）如图3，点P在△ABC外运动（只需研究图③的情形），直接写出∠α、∠1、∠2之间的关系．【解题思路】（1）①求出∠CEP+∠CDP，可得结论．②结论：∠1+∠2＝90°+∠α．连接PC，利用三角形的外角的性质解决问题即可．（2）利用三角形的外角的性质以及三角形内角和定理证明即可．（3）利用基本结论∠C+∠3＝∠P+∠4，构建关系式，可得结论．【解答过程】解：（1）①∵∠C＝90°，α＝70°，∴∠CEP+∠CDP＝360°﹣（90°+70°）＝200°，∴∠1+∠2＝360°﹣200°＝160°，故答案为：160．②结论：∠1+∠2＝90°+∠α．理由：如图1中，连结CP．∵∠1＝∠DCP+∠CPD，∠2＝∠ECP+∠CPE，∴∠1+∠2＝∠DCP+∠CPD+∠ECP+∠CPE，∵∠DCP+∠ECP＝∠ACB＝90°，∠CPD+∠CPE＝∠DPE＝∠α，∴∠1+∠2＝90°+∠α．（2）如图2中，∵∠1＝∠ACB+∠CFD，∠CFD＝∠2+∠α，∴∠1＝∠ACB+∠2+∠α．∵∠ACB＝90°，∴∠1＝90°+∠2+∠α．∴∠1﹣∠2＝90°+∠α．（3）结论：∠2﹣∠1＝90°﹣∠α．理由：如图3中，∵∠C+∠3＝∠P+∠4，∠C＝90°，∠P＝α，∴90°+（180°﹣∠2）＝α+（180°﹣∠1），∴∠2﹣∠1＝90°﹣∠α．19．（2021春•延庆区期末）在三角形ABC中，点D在线段AC上，ED∥BC交AB于点E，点F在线段AB上（点F不与点A，E，B重合），连接DF，过点F作FG⊥FD交射线CB于点G．（1）如图1，点F在线段BE上，用等式表示∠EDF与∠BGF的数量关系，并证明；（2）如图2，点F在线段BE上，求证：∠ABC+∠BFG﹣∠EDF＝90°；（3）当点F在线段AE上时，依题意，在图3中补全图形，请直接用等式表示∠EDF与∠BGF的数量关系，不需证明．【解题思路】（1）结论：∠EDF+∠BGF＝90°．如图1中，过点F作FH∥BC交AC于点H．利用平行线的性质求解即可．（2）如图2中，过点F作FH∥BC交AC于点H．利用平行线的性质求解即可．（3）作出图形，利用平行线的性质求解即可．【解答过程】（1）解：结论：∠EDF+∠BGF＝90°．理由：如图1中，过点F作FH∥BC交AC于点H．∵ED∥BC，∴ED∥FH．∴∠EDF＝∠1．∵FH∥BC，∴∠BGF＝∠2．∵FG⊥FD，∴∠DFG＝90°．∴∠1+∠2＝90°．∴∠EDF+∠BGF＝90°．（2）证明：如图2中，过点F作FH∥BC交AC于点H．∴∠ABC＝∠AFH．∴∠ABC＝∠1+∠3．∴∠3＝∠ABC﹣∠1．∵∠EDF＝∠1，∴∠3＝∠ABC﹣∠EDF．∵FG⊥FD，∴∠DFG＝90°．∴∠BFG+∠3＝90°．∴∠3＝90°﹣∠BFG．∴90°﹣∠BFG＝∠ABC﹣∠EDF．∴∠ABC+∠BFG﹣∠EDF＝90°．（3）解：结论：∠BGF﹣∠EDF＝90°．理由：设DE交FG于J．∵DE∥BC，∴∠BGF＝∠FJE，∵∠FJE＝∠DEJ+∠EDF，∠DEJ＝90°，∴∠BGF﹣∠EDF＝90°20．（2021春•中山市期末）同学们以“一块直角三角板和一把直尺”开展数学活动，提出了很多数学问题，请你解答：（1）如图1，∠α和∠β具有怎样的数量关系？请说明理由；（2）如图2，∠DFC的平分线与∠EGC的平分线相交于点Q，求∠FQG的大小；（3）如图3，点P是线段AD上的动点（不与A，D重合），连接PF、PG，的值是否变化？如果不变，请求出比值；如果变化，请说明理由．【解题思路】（1）如图1，延长AM交EG于M．由题意知：DF∥EG，∠ACB＝90°，故∠α＝∠GMC，∠ACB＝∠GMC+∠CGM＝90°．进而推断出∠β+∠α＝90°．（2）如图2，延长AC交EG于N．由题意知：DF∥EN，∠ACB＝90°，得∠1＝∠GNC，∠CGN+∠GNC＝90°，故∠1+∠CGN＝90°．因为∠DFC的平分线与∠EGC的平分线相交于点Q，所以∠QFC，∠GQC＝90°．那么，∠FQG＝360°﹣∠QFC﹣∠QGC﹣∠ACB＝135°．（3）由题意知：DF∥EG，得∠FOG＝∠EGO，故1．【解答过程】解：（1）如图1，延长AM交EG于M．∠β+∠α＝90°，理由如下：由题意知：DF∥EG，∠ACB＝90°．∴∠α＝∠GMC，∠ACB＝∠GMC+∠CGM＝90°．∵∠EGB和∠CGM是对顶角，∴∠β＝∠CGM．∴∠β+∠α＝90°．（2）如图2，延长AC交EG于N．由题意知：DF∥EN，∠ACB＝90°．∴∠1＝∠GNC，∠CGN+∠GNC＝90°．∴∠1+∠CGN＝90°．∵QF平分∠DFC，∴∠QFC．同理可得：∠GQC＝90°．∵四边形QFCG的内角和等于360°．∴∠FQG＝360°﹣∠QFC﹣∠QGC﹣∠ACB＝360°﹣（90°）﹣（90°）﹣90°．（3）如图3，由题意知：DF∥EG．∴∠FOG＝∠EGO．∴1．∴的值不变．21．（2021春•禅城区期末）△ABC中，AD是∠BAC的角平分线，AE是△ABC的高．（1）如图1，若∠B＝40°，∠C＝60°，求∠DAE的度数；（2）如图2（∠B＜∠C），试说明∠DAE与∠B、∠C的数量关系；（3）拓展：如图3，四边形ABDC中，AE是∠BAC的角平分线，DA是∠BDC的角平分线，猜想：∠DAE与∠B、∠C的数量关系是否改变．说明理由．【解题思路】（1）根据三角形的内角和定理可求得∠BAC＝80°，由角平分线的定义可得∠CAD 的度数，利用三角形的高线可求∠CAE得度数，进而求解即可得出结论；（2）根据（1）的推理方法可求解∠DAE、∠B、∠C的数量关系；（3）连接BC交AD于F，过点A作AM⊥BC于M，过点D作DN⊥BC于N，根据角平分线的定义得到∠EAM（∠ACB﹣∠ABC），同理，∠ADN（∠BCD﹣∠CBD），求得∠MAD＝∠ADN，根据角的和差即可得到结论．【解答过程】解：（1）∵∠B＝40°，∠C＝60°，∠BAC+∠B+∠C＝180°，∵AD是∠BAC的角平分线，∴∠CAD＝∠BAD∠BAC＝40°，∵AE是△ABC的高，∴∠AEC＝90°，∵∠C＝60°，∴∠CAE＝90°﹣60°＝30°，∴∠DAE＝∠CAD﹣∠CAE＝10°；（2）∵∠BAC+∠B+∠C＝180°，∴∠BAC＝180°﹣∠B﹣∠C，∵AD是∠BAC的角平分线，∴∠CAD＝∠BAD∠BAC，∵AE是△ABC的高，∴∠AEC＝90°，∴∠CAE＝90°﹣∠C，∴∠DAE＝∠CAD﹣∠CAE∠BAC﹣（90°﹣∠C）（180°﹣∠B﹣∠C）﹣90°+∠C ∠C∠B，即∠DAE∠C∠B；（3）不变，理由：连接BC交AD于F，过点A作AM⊥BC于M，过点D作DN⊥BC于N，∵AE是∠BAC的角平分线，AM是高，∴∠EAM（∠ACB﹣∠ABC），同理，∠ADN（∠BCD﹣∠CBD），∵∠AFM＝∠DFN，∠AMF＝∠DNF＝90°，∴∠MAD＝∠ADN，∴∠DAE＝∠EAM+∠MAD＝∠EAM+∠ADN（∠ACB﹣∠ABC）（∠BCD﹣∠CBD）（∠ACD﹣∠ABD）．22．（2021春•侯马市期末）（1）已知：如图①的图形我们把它称为“8字形”，试说明：∠A+∠B ＝∠C+∠D．（2）如图②，AP，CP分别平分∠BAD，∠BCD，若∠ABC＝36°，∠ADC＝16°，求∠P的度数．（3）如图（3），直线AP平分∠BAD，CP平分∠BCD的外角∠BCE，猜想∠P与∠B、∠D的数量关系是　∠P＝90°（∠B+∠D）　；（4）如图（4），直线AP平分∠BAD的外角∠FAD，CP平分∠BCD的外角∠BCE，猜想∠P与∠B、∠D的数量关系是　∠P＝180°（∠B+∠D）　．【解题思路】（1）根据三角形的内角和等于180°列式整理即可得证；（2）根据角平分线的定义可得∠1＝∠2，∠3＝∠4，再根据（1）的结论列出整理即可得解；（3）表示出∠PAD和∠PCD，再根据（1）的结论列出等式并整理即可得解；（4）根据四边形的内角和等于360°可得（180°﹣∠1）+∠P+∠4+∠B＝360°，∠2+∠P+（180°﹣∠3）+∠D＝360°，然后整理即可得解．【解答过程】解：（1）∵∠A+∠B+∠AOB＝180°，∠C+∠D+∠COD＝180°，∴∠A+∠B+∠AOB＝∠C+∠D+∠COD．∵∠AOB＝∠COD，∴∠A+∠B＝∠C+∠D．（2）∵AP，CP分别平分∠BAD，∠BCD，∴∠BAP＝∠PAD，∠BCP＝∠PCD，由（1）的结论得，∠P+∠BCP＝∠ABC+∠BAP，①，∠P+∠PAD＝∠ADC+∠PCD②，①+②得，2∠P+∠BCP+∠PAD＝∠BAP+∠PCD+∠ABC+∠ADC，∴2∠P＝∠ABC+∠ADC，∵∠ABC＝36°，∠ADC＝16°，∴∠P＝26°．（3）∵直线AP平分∠BAD，CP平分∠BCD的外角∠BCE，∴∠PAB＝∠PAD，∠PCB＝∠PCE，∴2∠PAB+∠B＝180°﹣2∠PCB+∠D，∴180°﹣2（∠PAB+∠PCB）+∠D＝∠B，∵∠P+∠PAD＝∠PCB+∠AOC＝∠PCB+∠B+2∠PAD，∴∠P＝∠PAD+∠B+∠PCB＝∠PAB+∠B+∠PCB，∴∠PAB+∠PCB＝∠P﹣∠B，∴180°﹣2（∠P﹣∠B）+∠D＝∠B，即∠P＝90°（∠B+∠D）．故答案为：∠P＝90°（∠B+∠D）．（4）∵直线AP平分∠BAD的外角∠FAD，CP平分∠BCD的外角∠BCE，∴∠FAP＝∠PAO，∠PCE＝∠PCB，在四边形APCB中，（180°﹣∠FAP）+∠P+∠PCB+∠B＝360°①，在四边形APCD中，∠PAD+∠P+（180°﹣∠PCE）+∠D＝360°②，①+②得：2∠P+∠B+∠D＝360°，∴∠P＝180°（∠B+∠D）．故答案为：∠P＝180°（∠B+∠D）．23．（2020春•西城区校级期末）在△ABC中，BD，CE是它的两条角平分线，且BD，CE相交于点M，MN⊥BC于点N．将∠MBN记为∠1，∠MCN记为∠2，∠CMN记为∠3．（1）如图1，若∠A＝110°，∠BEC＝130°，则∠2＝　20　°，∠3﹣∠1＝　55　°；（2）如图2，猜想∠3﹣∠1与∠A的数量关系，并证明你的结论；（3）若∠BEC＝α，∠BDC＝β，用含α和β的代数式表示∠3﹣∠1的度数．（直接写出结果即可）解：（2）∠3﹣∠1与∠A的数量关系是：　∠3﹣∠1∠A　．（3）∠3﹣∠1＝　30°　．【解题思路】（1）根据三角形的一个外角等于与它不相邻的两个内角的和可得∠ACE＝∠BEC﹣∠A，再根据角平分线的定义可得∠2＝∠ACE；根据角平分线的定义求出∠ACB，再根据三角形的内角和定理求出∠ABC，然后求出∠1，根据直角三角形两锐角互余求出∠3，然后相减即可得解；（2）根据角平分线的定义可得∠1∠ABC，∠2∠ACB，再根据直角三角形两锐角互余表示出∠3，然后表示出∠3﹣∠1＝90°∠ACB∠ABC，再根据三角形的内角和定理可得∠ACB+∠ABC＝180°﹣∠A，然后代入整理即可得解；（3）在△BCE和△BCD中，根据三角形内角和定理列式整理得到∠1+∠2，再根据三角形的内角和定理和角平分线的定义用∠A表示出∠1+∠2，然后根据∠3﹣∠1∠A整理即可得解．【解答过程】（1）解：在△ACE中，∠ACE＝∠BEC﹣∠A＝130°﹣110°＝20°，∵CE平分∠ACE，∴∠2＝∠ACE＝20°，∴∠ACB＝2∠2＝2×20°＝40°，在△ABC中，∠ABC＝180°﹣∠A﹣∠ACB＝180°﹣110°﹣40°＝30°，∵BD平分∠ABC，∴∠1∠ABC30°＝15°，∵MN⊥BC，∴∠3＝90°﹣∠2＝90°﹣20°＝70°，∴∠3﹣∠1＝70°﹣15°＝55°，故答案为：20，55；（2）∠3﹣∠1与∠A的数量关系是：∠3﹣∠1∠A．证明：在△ABC中，BD，CE是它的两条角平分线，∴∠1∠ABC，∠2∠ACB，∵MN⊥BC于点N，∴∠MNC＝90°，在△MNC中，∠3＝90°﹣∠2，∴∠3﹣∠1＝90°﹣∠2﹣∠1，＝90°∠ACB∠ABC，＝90°（∠ACB+∠ABC），∵在△ABC中，∠ACB+∠ABC＝180°﹣∠A，∴∠3﹣∠1＝90°（180°﹣∠A）∠A；故答案为：∠3﹣∠1∠A；（3）∵BD，CE是△ABC的两条角平分线，∴∠ABC＝2∠1，∠ACB＝2∠2，在△BCE和△BCD中，∠1+2∠2+β＝180°，∠2+2∠1+α＝180°，∴∠1+∠2＝120°，∵∠1+∠2（∠ACB+∠ABC）（180°﹣∠A），∴120°（180°﹣∠A），整理得，∠A30°，∴∠3﹣∠130°．故答案为：30°．24．（2020春•福山区期中）直线在同一平面内有平行和相交两种位置关系，线段首尾连接可以变换出很多不同的图形，这些不同的角又有很多不同关系，今天我们就来探究一下这些奇妙的图形吧！【问题探究】（1）如图1，请直接写出∠A+∠B+∠C+∠D+∠E＝　180°　；（2）将图1变形为图2，∠A+∠DBE+∠C+∠D+∠E的结果如何？请写出证明过程；（3）将图1变形为图3，则∠A+∠B+∠C+∠D+∠E的结果如何？请写出证明过程．【变式拓展】（4）将图3变形为图4，已知∠BGF＝160°，那么∠A+∠B+∠C+∠D+∠E+∠F的度数是　320°　．【解题思路】（1）根据三角形外角的性质，得到∠2＝∠C+∠E，∠1＝∠A+∠2，根据三角形内角和等于180°即可求解．（2）根据三角形外角的性质，得到∠ABE＝∠C+∠E，∠DBC＝∠A+∠D，即可证明此结论．（3）根据三角形外角的性质，得到∠DFG＝∠B+∠E，∠FGD＝∠A+∠C，即可证明此结论；（4）根据三角形外角的性质，得到∠BGF＝∠B+∠2＝160°，∠2＝∠D+∠F，∠BGF＝∠1+∠E ＝160°，∠1＝∠A+∠C，即可得到结论．【解答过程】（1）解：如图1，∵∠2＝∠C+∠E，∠1＝∠A+∠2，∴∠A+∠B+∠C+∠D+∠E＝∠1+∠B+∠D＝180°，故答案为：180°；（2）证明：∵∠ABE＝∠C+∠E，∠DBC＝∠A+∠D，∠ABE+∠DBE+∠DBC＝180°，∴∠A+∠DBE+∠C+∠D+∠E＝180°∴将图①变形成图②∠A+∠DBE+∠C+∠D+∠E仍然为180°；。

浙江省绍兴县杨汛桥镇中学九年级数学上册《几何综合》试题浙教版

∵AB=AC AC=CD，
CF.
∵ AB=AC AC=CD ∴ AE⊥ BC， CF⊥ AD
∴AE⊥ BC， CF ⊥ AD．
∴ A、 F、E、 C 四点共圆
∴A、 F、 E、 C四点共圆．
设∠ B=∠ ACB=2 ∠ ACF=∠ DCF=2
设∠ B=∠ ACB=2 ∴∠ ACF=∠BCF= ∴∠ AEF=∠ACF =
4
1
x2
2x 5
1
x
5 x
2
1
5 2x
x
2
1
25
2
3
=
5 ，从而， MA
2
MB
35 2
5 1 ，当 x
2
5 时，上式等号成立．故 MA 的最 MB
大值为 5 1 ． 2
6
16. 证明：由点 K 分别向边 AB， AC作垂线，垂足为 S， T，延长 AK 与圆 O交于点 P．
因为 SK AB, PB AB , 所以， SK / / BP ．
几何
3. 下列命题：如图，正方形 ABCD中， E、 F 分别为 AB、 AD上的点， AF＝ BE， CE、 BF交于 H，
BF交 AC于 M， O为 AC的中点， OB交 CE于 N，连 OH. 下列结论中：① BF⊥ CE；② OM＝ ON；
③ OH 1 CN ；④ 2OH BH CH . 其中正确的命题有 2
PQ
=
．
AB
三、解答题 ( 共 72 分)
13．已知⊿ ABC，以 AC 为边在⊿ ABC外作等腰⊿ ACD，且 AC=AD，作 AH⊥ BC交 BC于 H，当 BD2 =4AH2+BC2 时，试探究∠ DAC与∠ ABC之间的关系，并加以证明．（本题 10 分）

2019年浙教版七年级数学上册《几何图形初步》课后练习(有答案)

几何图形初步课后练习题一：下列哪个正方体的展开图不可能，如图所示( )A ．B ．C ．D ．题二：如图，它是一个正方体的表面展开图，也就是说，如图形状的方格式纸片可以折成一个正方体，所折成的正方体应是( )A ．B ．C ．D ．题三： (1)M ，N 是线段AB 的三等分点，P 是NB 的中点，若AB =12，求线段PA 的长度；(2)已知∠AOC =60°，∠AOB ：∠BOC =1：2，求∠BOC 的度数．题四： (1)已知线段AB 和BC 在同一条直线上，如果AC =6.4，BC =3.6，求线段AC 和BC 的中点间的距离．(2)已知OA ⊥OC ，且∠AOB ：∠AOC =2：3，求∠BOC 的度数．题五： (1)223224'''︒=____︒；78.26°=_________'''︒．(2)如图是一个时钟的钟面，下午1点30分，时钟的分针与时针所夹的角等于________．题六： (1)1061424'''︒=____︒；56.32°=_________'''︒．(2)从下午3点45分到晚上8点21分，时针转过了多少度？题七：如图是正方体的表面展开图，标注了字母a 的面是正方体的正面．若正方体相对的两个面上的数字相等，求和y的值．题八：如图是一个正方体的表面展开图，请回答下列问题：(1)与面B、C相对的面分别是____、____；(2)若A=a3+15a2b+3，B=12a2b－3，C=a3－1，D=－12(a2b－6)，且相对两个面所表示的代数式的和都相等，求E、F分别代表的代数式．期中期末串讲--几何图形初步课后练习参考答案题一： B．详解：根据图示可知与空心圆相邻的是白色的三角形，和实心圆相邻的是白色的三角形和白色的正方形．故不可能的是B．故选B．题二： D．详解：根据展开图可得出正方体有两底面是两阴影小正方体相连接组成的图案，符合要求的只有A、D，但对角线相连部分，不可能与正方形再次相连，则A错误．故选D．题三： 10或8；40°或120°．详解：(1)因为M，N是线段AB的三等分点，所以NB=13AB=4，①如图1，当N在靠近B的一端时，∵P是NB的中点，∴PB=12NB=2，∴PA=12－2=10；②如图2，当N在靠近A的一端时，∵P是NB的中点，∴P与M重合，∴PA=12－4=8．故PA=10或8．(2)①如图1，当OB在∠AOC内时，∵∠AOC=60°，∠AOB：∠BOC=1：2，∴∠BOC=23×60°= 40°；②如图2，当OB在∠AOC外时，∵∠AOC=60°，∠AOB：∠BOC=1：2，∴∠BOC=2∠AOC=2×60°=120°．故∠BOC的度数是40°或120°．题四： 1.4或5；30°或150°．详解：(1)∵M为AC的中点，AC=6.4，∴CM=12AC=3.2，∵N为BC的中点，BC=3.6，∴CN=12BC=1.8，分为以下两种情况：①如图1，当B在线段AC上时，MN=CM－CN=3.2－1.8=1.4；②如图2，当B 在AC 的延长线时，MN =CM +CN =3.2+1.8=5．故线段AC 和BC 的中点间的距离是1.4或5．(2)∵OA ⊥OC ，∴∠AOC =90°，∵∠AOB ：∠AOC =2：3，∴∠AOB =60°．因为∠AOB 的位置有两种：一种是在∠AOC 内，一种是在∠AOC 外． ①如图1，当在∠AOC 内时，∠BOC =90°－60°=30°；②如图2，当在∠AOC 外时，∠BOC =90°+60°=150°．故∠BOC 的度数是30°或150°．题五： 22.54°，781536'''︒；135°．详解：(1)24''÷60=0.4'，32.4'÷60=0.54°，则223224'''︒=22.54°； 0.26×60=15.6，0.6×60=36，则78.26°=781536'''︒．(2)由钟面平均分成12份，得每份30°，于是30°×(4+12)=30°×92=135°．答：时钟的分针与时针所夹的角等于135°．题六： 106.24°，561912'''︒；138°．详解：(1)24''÷60=0.4'，14.4'÷60=0.24°，1061424'''︒=106.24°； 0.32°×60=19.2'，0.2'×60=12''，则56.32°=561912'''︒．(2)8时21分=8.35时，3时45分=3.75时，则8.35－3.75= 4.6(时)，由钟面平均分成12份，得每份30°，于是30°×4.6=138°．答：时针转过了138°．题七： 1，－1．详解：正方体的表面展开图，相对的面之间一定相隔一个正方形，所以，y +2与2－1是相对面，2y 与－3是相对面．∵正方体相对的两个面上的数字相等，∴22123y x y x +=-⎧⎨=-⎩，整理，得2323x y x y -=⎧⎨-=⎩①②， ①×2－②，得3=3，解得=1，把=1代入①，得y =－1，所以，方程组的解是11x y =⎧⎨=-⎩．题八：F、E；－310a2b+7，a3－45a2b+9．详解：(1)由图可得：面A和面D相对，面B和面F，相对面C和面E相对，(2)由题意得，A+D=B+F=C+E，代入可得a3+15a2b+3+[－12(a2b－6)]=12a2b－3+F，a3+15a2b+3+[－12(a2b－6)]=a3－1+E，解得F=a3－45a2b+9，E=－310a2b+7．。

浙教版七年级数学上《几何图形初步》专题复习讲义(含答案)

期中期末串讲--几何图形初步
易考点、易考题型梳理
正方体的展开图
题一：把正方体的表面沿某些棱展开后成一个平面图形，请判断这个平面图形可以围成的正方体是（）
数形结合、分类讨论题二：(1)线段AB 的中点也是线段AC 的三等分点，如果AB =1cm ，那么BC =______cm ；
(2)已知∠BOC =12∠AOC ，∠BOC =15°，则∠AOB=______．
角的运算
时钟问题
题三：(1)61836____'''︒=︒；33.33_________'''︒=︒．
(2)从2点30分到2点45分，时针和分针各走了多少度？
满分冲刺
题一：正方体六个面展开如图所示，六个面分别用字母A 、B 、C 、D 、E 、F 表示，已知：
2243A x xy y =-+，1()2
B C A =-，2232C x xy y =--，2E B C =-，若正方体相对的两个面上的多项式的和相等，求D 、F ．(用含x ，y 的多项式表示)
期中期末串讲--几何图形初步讲义参考答案
易考点、易考题型梳理题一：C ．题二：12或14
；45°或15°．题三：6.31，33，19，48；7.5°，90°．满分冲刺题一：2
2374x xy y -+；229112x xy y -+．。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

浙教版初中数学几何计算型综合问题(含答案)

浙教版九年级数学下学期综合练习及答案

初中数学几何综合-含答案

几何复习专题卷(含答案)初中数学浙教版八年级上册

浙教版数学七年级上册专项突破二 与几何相关的代数式问题(含答案)

解直角三角形与几何综合(压轴题专项)—2023-2024学年九年级数学下册(浙教版)(解析版)

浙教版数学七年级上册 第六章综合测试卷 图形的初步知识(含答案)

【期末复习】浙教版2022年七年级上册：“几何类题型大全”一卷过关(40道题)(含解析)

5.4.2 几何图形问题 浙教版七年级数学上册素养提升卷(含解析)

浙教版七年级上册数学第6章 图形的初步知识含答案(综合题)

浙教版初中数学几何计算型综合问题(含答案)

浙教版八年级下册数学2019年几何压轴题培优专题(含答案)

浙教版初中数学九年级下册专题50题(含答案)

专题2.3 勾股定理与几何综合(压轴题专项讲练)(浙教版)(解析版)

浙教版数学综合试题及答案

浙教版八年级上专题1.5 角度计算的综合大题专项训练(含解析)

浙江省绍兴县杨汛桥镇中学九年级数学上册《几何综合》试题浙教版

2019年浙教版七年级数学上册《几何图形初步》课后练习(有答案)

浙教版七年级数学上《几何图形初步》专题复习讲义(含答案)

浙教版数学七年级上册专项突破二与几何相关的代数式问题(含答案)

浙教版数学七年级上册第六章综合测试卷图形的初步知识(含答案)

5.4.2 几何图形问题浙教版七年级数学上册素养提升卷(含解析)

浙教版七年级上册数学第6章图形的初步知识含答案(综合题)