罗尔定理教学设计
罗尔定理的几种类型及其应用

罗尔定理的几种类型及其应用1 引言最原始的罗尔定理是由法国数学家罗尔于 1691 年在题为 《任意次方程的一个解法的证明》 的论 文中给出的 (罗尔 1652 年 4 月 21 日生于昂贝尔特, 1719 年 11月 8 日卒于巴黎 ) ,主要内容是 : 在多项式方程 f x =0 的两个相邻的实根之间,方程 f x 0 至少有一个根.在一百多年后, 1846 年尤斯托( Giusto Bellavitis )将这一定理推广到可微函数,尤斯托还 把此定理命名为罗尔定理,这就是现在我们常用的罗尔定理 .2 微分中值定理2.1 罗尔定理1 (P若函数 f x 满足以下条件:( 1)在闭区间 a,b 上连续;( 2)在开区间 a,b 上可导;( 3) fa fb . 则至少存在一个数 a,b ,使得 f 0.罗尔定理的几何意义是:在每一点都可导的一段连续曲线上,如果曲线的两端点高度相同,那 么曲线至少存在一条水平切线 . 罗尔定理是大学微分学中很重要的中值定理, 它演绎了拉格朗日中值 定理与柯西中值定理,这三个定理构成了微分学中值基本理论,在高等数学中占有十分重要的地 位.下面给出拉格朗日中值定理和柯西中值定理的内容和几何意义 .2.2 拉格朗日中值定理x 满足:( 1) 在闭区间 a,b 连续;( 2) 在开区间 a,b 上可导;则至少存在拉格朗日中值定理的几何意义是:在每一点都可导的的连续曲线上,如果两端点也连续,那么 至少存在一个点,该点的切线平行于两端点的连线 .2.3 柯西中值定理 1若函数 f x 和 g x 满足:( 1)在闭区间 a,b 连续;( 2)在开区间 a,b 上可导;( 3) f x 和 g x 不同时为 0;( 4) g a g b 则存在 a,b ;使得fa。
若函数个数 a,b ,使得 ff a f b ab柯西中值定理的几何意义与前两个定理的几何意义类似,只是要把f x 和g x 这两个函数写成以x 为参量的参量方程u g xv f x于是两函数联系在平面uOv 上一段连续曲线上了,若曲线的两端点也连续,则在曲线上至少存在一点,该点的切线与两端点的连线平行。
罗尔定理教学设计

(一)新课导入回顾以前学习的内容、对罗尔做下简单介绍,引入本节所要研究的课题。
(二)新课讲解1、教师给出罗尔定理的条件和结论。
教师写出C x f ∈)(],[b a ,D x f ∈)(),(b a 让学生说出这两种符号代表的含义,引导学生回顾以前学过的知识。
定理1(Rolle ):设函数)(x f 满足条件:⑴ C x f ∈)(],[b a ;⑵ D x f ∈)(),(b a ;⑶ )()(b f a f =,则在),(b a 内至少存在一点ξ,使得0)(='ξf 。
2、通过罗尔定理的条件和结论,引导学生发现罗尔定理的几何意义。
教师画图,让学生思考交流得出罗尔定理的几何意义。
提问:⑴C x f ∈)(],[b a 在几何上表示什么?⑵D x f ∈)(),(b a 在几何上表示什么含义?⑶ )()(b f a f =表明曲线的什么几何意义?⑷ 罗尔定理的结论的直观意义是什么?即:在),(b a 内至少存在一点ξ,使0)(='ξf ,表明什么?3、教师指出定理要注意的要点及罗尔定理的作用,举出例题。
让 学生思考解决问题,教师补充。
※罗尔定理的三个条件必须同时满足定理才成立。
例1、函数,)(x x f =]1,0[∈x 满足罗尔定理吗?※ 罗尔定理可用于讨论方程的根。
例2、对于函数)1)(1()(-+=x x x f ,证明方程()0f x '=有一个实数 根。
※ 用罗尔定理怎样来求出点ξ。
例3、对于函数x x x f 2)(2-=,求出点ξ使得0)(='ξf 。
4、小结:本节课我们学习了罗尔定理。
重点是罗尔定理的条件、结论和几何意义,要求同学们务必掌握,并学会用罗尔定理解决问题。
5、作业:(1)阅读教科书,了解罗尔定理证明的推导过程。
(2)完成课后练习第一题。
罗尔定理的证明与应用案例

罗尔定理的证明与应用案例罗尔定理是微积分中的重要概念之一,它是由法国数学家米歇尔·罗尔于1691年提出的。
罗尔定理是微积分中的一个基本定理,它与导数和函数的零点有关。
在本文中,我们将会介绍罗尔定理的证明以及一些应用案例。
一、罗尔定理的证明罗尔定理是微积分中的一个重要定理,它为函数在闭区间上的导数与函数在该闭区间的边界上的函数值之间建立了关系。
下面是罗尔定理的数学表述:设函数f(x)在闭区间[a, b]上连续,在开区间(a, b)上可导,且满足f(a) = f(b),则在开区间(a, b)上至少存在一点ξ,使得f'(ξ) = 0。
证明罗尔定理的关键是使用了导数的连续性和介值定理。
首先,由于f(x)在闭区间[a, b]上连续且在开区间(a, b)上可导,根据导数的连续性定理,f'(x)在闭区间[a, b]上也连续。
然后,我们考虑函数g(x) = f(x) - f(a),它在闭区间[a, b]上连续,在开区间(a, b)上可导。
根据罗尔定理的条件,g(a) = g(b) = 0。
由于g(x)在闭区间[a, b]上连续且在开区间(a, b)上可导,根据介值定理,存在一个点ξ,使得g'(ξ) = 0。
而g'(ξ) = f'(ξ) - f'(a) = f'(ξ),因此,我们得到了罗尔定理的结论:在开区间(a, b)上至少存在一点ξ,使得f'(ξ) = 0。
二、罗尔定理的应用案例罗尔定理在实际问题中有着广泛的应用。
下面我们将介绍一些罗尔定理的应用案例。
1. 寻找函数的极值点根据罗尔定理,如果函数f(x)在闭区间[a, b]上连续,在开区间(a, b)上可导,并且满足f(a) = f(b),则在开区间(a, b)上至少存在一点ξ,使得f'(ξ) = 0。
因此,我们可以利用罗尔定理来寻找函数的极值点。
通过求函数的导数,并找到导数为零的点,即可得到函数的极值点。
教案微分中值定理

微分中值定理教案章节一:引言与预备知识【教学目标】1. 理解微分中值定理的概念和意义。
2. 掌握基本函数的求导法则。
【教学内容】1. 介绍微分中值定理的背景和应用。
2. 复习基本函数的求导法则,包括幂函数、指数函数、对数函数和三角函数的求导。
【教学活动】1. 教师讲解微分中值定理的概念和意义,引导学生理解其重要性。
2. 学生自主学习基本函数的求导法则,并进行练习。
教案章节二:罗尔定理【教学目标】1. 理解罗尔定理的表述和证明。
2. 掌握罗尔定理在实际问题中的应用。
【教学内容】1. 介绍罗尔定理的表述和证明方法。
2. 通过例题讲解罗尔定理在实际问题中的应用。
【教学活动】1. 教师讲解罗尔定理的表述和证明,引导学生理解其原理。
2. 学生跟随例题学习罗尔定理的应用,并进行练习。
教案章节三:拉格朗日中值定理【教学目标】1. 理解拉格朗日中值定理的表述和证明。
2. 掌握拉格朗日中值定理在实际问题中的应用。
【教学内容】1. 介绍拉格朗日中值定理的表述和证明方法。
2. 通过例题讲解拉格朗日中值定理在实际问题中的应用。
【教学活动】1. 教师讲解拉格朗日中值定理的表述和证明,引导学生理解其原理。
2. 学生跟随例题学习拉格朗日中值定理的应用,并进行练习。
教案章节四:柯西中值定理【教学目标】1. 理解柯西中值定理的表述和证明。
2. 掌握柯西中值定理在实际问题中的应用。
【教学内容】1. 介绍柯西中值定理的表述和证明方法。
2. 通过例题讲解柯西中值定理在实际问题中的应用。
【教学活动】1. 教师讲解柯西中值定理的表述和证明,引导学生理解其原理。
2. 学生跟随例题学习柯西中值定理的应用,并进行练习。
教案章节五:微分中值定理的应用【教学目标】1. 理解微分中值定理在实际问题中的应用。
2. 掌握利用微分中值定理解决实际问题的方法。
【教学内容】1. 介绍微分中值定理在实际问题中的应用,如求函数的单调区间、极值和最值等。
2. 通过例题讲解如何利用微分中值定理解决实际问题。
教案微分中值定理

微分中值定理教案章节一:预备知识1.1 函数的极限教学目标:理解函数极限的概念,掌握极限的计算方法。
教学内容:引入函数极限的概念,探讨极限的性质和计算方法,如夹逼定理、单调有界定理等。
教学方法:通过具体例子和问题引导学生理解极限的概念,利用图形和数学分析软件演示极限过程,让学生体会极限的意义。
1.2 连续函数教学目标:理解连续函数的概念,掌握连续函数的性质和判断方法。
教学内容:介绍连续函数的定义,探讨连续函数的性质,如保号性、保界性等,学习连续函数的判断方法。
教学方法:通过具体例子和问题引导学生理解连续函数的概念,利用图形和数学分析软件演示连续函数的性质,让学生掌握判断连续函数的方法。
教案章节二:微分中值定理2.1 罗尔定理教学目标:理解罗尔定理的内容和意义,学会运用罗尔定理解决问题。
教学内容:介绍罗尔定理的定义,探讨罗尔定理的条件和结论,学习如何应用罗尔定理解决问题。
教学方法:通过具体例子和问题引导学生理解罗尔定理的内容,利用图形和数学分析软件演示罗尔定理的应用,让学生学会运用罗尔定理解决问题。
2.2 拉格朗日中值定理教学目标:理解拉格朗日中值定理的内容和意义,学会运用拉格朗日中值定理解决问题。
教学内容:介绍拉格朗日中值定理的定义,探讨拉格朗日中值定理的条件和结论,学习如何应用拉格朗日中值定理解决问题。
教学方法:通过具体例子和问题引导学生理解拉格朗日中值定理的内容,利用图形和数学分析软件演示拉格朗日中值定理的应用,让学生学会运用拉格朗日中值定理解决问题。
教案章节三:微分中值定理的应用3.1 导数的应用教学目标:理解导数的概念,掌握导数的计算方法。
教学内容:引入导数的概念,探讨导数的性质和计算方法,如求导法则、高阶导数等。
教学方法:通过具体例子和问题引导学生理解导数的概念,利用图形和数学分析软件演示导数过程,让学生体会导数的意义。
3.2 函数的单调性教学目标:理解函数单调性的概念,掌握函数单调性的判断方法。
高等数学教学设计——中值定理
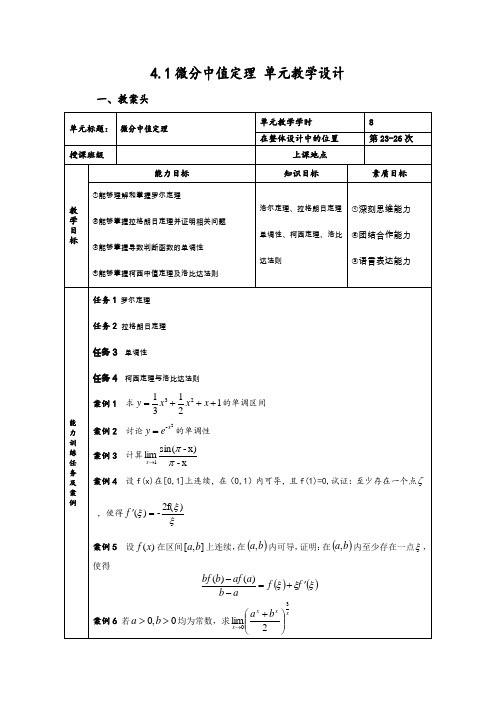
4.1微分中值定理单元教学设计一、教案头二、教学设计4.2函数的极值和最值单元教学设计一、教案头二、教学设计案例应用 案例1 求1213123+++=x x x y 的极值案例2 讨论2-x e y =的极值案例3 有一块宽为2a 的长方形铁皮,将宽的两个边缘向上折起,做成一个开口水槽,其横截面积为矩形,高为x,问高x 取和值时水槽的流量最大?案例4 铁路线AB 距离为100公里,工厂C 距A 为20公里,AC 垂直于AB ,今要在AB 上选定一个点D 向工厂修筑一条公路,已知铁路与公路每公里货运费之比是3:5,问D 点选在何处才能使从B 到C 的运费最少? 案例5 现在用一张铝合金材料加工一个日字型窗框,问它的长和宽分别为多少时,才能是窗户的面积最大,最大面积是多少?如下图4.3函数图像的描绘 单元教学设计一、教案头任务1 函数的凸凹性和拐点 任务2 函数的渐近线. 任务3 按步骤描绘函数图像案例1(注水曲线凸凹) 设水以常数0,/3>a s am 注入下图的容器中,请做出水上升的高度关于时间t 的函数)(t f y =,并阐明此函数的拐点和凸凹性。
案例2 描绘函数2-)1(42xx y +=的图像。
案例3(最值问题) 要用铁皮造一个容积为V 的圆柱形闭合油罐,问底半径r 和高h 等于多少时,能使所使用的铁皮最省?这时候的半径r 和高h 的比值是多少?案例4(最值问题) 要建造一个上面是半球形,下面是圆柱形的粮仓,其容积是V ,问当圆柱体的高h 和底半径r 为何值时,粮仓所使用的建筑材料最省?二、教学设计渐近线(1)斜渐近线 若)(x f 满足:k xx f x =∞→)(lim,且b kx]-[f(x)lim =∞→x则曲线)(x f y =有渐近线b kx y += 如下图:例 求曲线3-223x x x y +=的斜渐近线例 求曲线22-123xx y +=的斜渐近线 (2)垂直渐近线如果C x →(或者+→C x 或者-C x →)时,∞→)(x f 。
罗尔定理.

y f (a) y f (x) f 0 b
xy
f (b)
两端点的函数值不相等
f (a)
y
y f (x)
f (a)
f (b)
0a b
x
区间内有不连续的点
0a
x0 b
x
图3-2
例1 设函数f (x) = (x +1) (x1) (x2) (x3), 证明方程f (x)=0有三个实根,并指出它们所在的区间。 证:显然, f (x)分别在闭区间[1, 1], [1, 2], [2, 3]上连续,
第1节 微分中值定理
一、罗尔定理 二、拉格朗日中值定理 三、柯西定理
一、罗尔定理
若函数 f (x)满足下列条件: (i)在闭区间[a, b]上连续; (ii)在开区间(a, b)内可导; (iii)f (a)= f (b).
则至少存在一点 (a, b) 使 f ( ) 0
罗尔定理的几何意义:
C
如果连续曲线除端点 y
外处处都具有不垂直ox 轴
的切线,且两端点处的纵
A
y f (x) B
坐标相等,那么其上至少
x
O
有一条平等于ox 轴的切线.
a
b
图3-1
值得注意的是,该定理要求函数y=f(x)应同时满
足三个条件.若定理的三个条件不完全满足的话,则
定理的结论可能成立,也可能不立.(如图3-2)
在(1,2)内可导 且 x (1,2)时,F(x) 0.
又f (1) 1, f (2) 8, F(1) 2, F(2) 5, f (x) 3x2, F(x) 2x
设 f (2) f (1) 3 2 ,解得=14 (1,2)
罗尔定理的条件和结论精选全文完整版

可编辑修改精选全文完整版罗尔定理的条件和结论罗尔定理是三角形的数学定理,它可以说明三条内角的和等于180度。
它是17月由埃里克罗尔发现的,它被认为是很难被发现的,并且在三角形中被广泛使用。
罗尔定理有许多应用,如几何、工程学、统计学、计算机图形和电子计算机等,它也被用来证明更多的数学定理。
罗尔定理的基本条件是:任何三条内角和等于180度,并且三条内角都必须小于180度。
罗尔定理的第一部分是任何三角形的三条内角和(也就是角平分线)等于180度,而第二部分是任何三角形的三条内角均小于180度,这表明任何三角形的边长都必须小于等于它的周长。
这个定理在三角形学中发挥了重要作用,它为几何形状设定了基本条件,它还可以用来解决各种复杂的几何问题。
它最重要的优势或功效是可以用一种简单而有效的方法来解决很多复杂的几何问题。
此外,它还可以识别几何图形的结构,如三角形的形状,内角的大小等。
因此,罗尔定理是能够解决复杂几何问题的有效方法。
它不仅能够对三角形的构成进行描述,而且还能够解决多边形的构成。
罗尔定理在电子计算机、统计学、工程学和数学几何中也被广泛应用,它还可以被用来证明一些数学定理,如四边形的和等于360度、六边形的和等于720度等。
由于罗尔定理的广泛应用,它仍然被认为是很重要的定理,它的研究或应用也使得许多几何图案的实际应用更加容易。
罗尔定理可以说是理论几何学中最重要的定理,它可以用于解决许多复杂问题,并且也可以用来证明许多数学定理。
综上所述,罗尔定理是一个重要的定理,它可以用来解决许多复杂几何问题,它也可以用来证明许多数学定理,如四边形、六边形的和等于360度和720度等。
罗尔定理的条件是任何三条内角和等于180度,并且三条内角都必须小于180度,这个定理的研究和应用可以使许多几何图案的实际应用更加容易。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《罗尔定理》教学设计
一、 教学目的
理解罗尔定理的推导,掌握罗尔定理,灵活运用罗尔定理.
二、 教学重难点
重点:罗尔定理及其应用
难点:罗尔定理的条件的讨论
三、 教学过程
(一) 复习回顾
1、闭区间上连续函数的性质
1f x a b ,f x a b 2f x a b f a f b 0f =0ξξ()(最大值和最小值定理)设()在[,]连续则()在[,]上可以取到最大值和最小值。
()(零点定理)设()在[,]连续,且()()〈,
则至少存在一点使得() 2、费马定理:若函数()x f 在(a,b)内一点x 0 取得最值,且()x f 在x 0 可导,则()0='x f .
(二)、新课讲授
1、罗尔定理:设函数()x f 满足:
(1) 闭区间[]b a ,上连续;
(2) 开区间()b a ,内可导;
(3) 端点函数值相等()()b f a f =,
则至少存在一个()b a ,∈ξ,使得()0='ξf .
注:(1)罗尔定理的几何意义:在满足条件时,曲线()x f y =上的点))(,(ξξf 处一
定有水平切线,即斜率()0='=ξf k ;
(2)罗尔定理研究的是导函数方程()0='x f 的根的存在性问题
;
(3)罗尔定理的条件是充分的
2、罗尔定理的条件的讨论
3、罗尔定理的简单应用
例4:证明方程0=1+52
x x 有且今有一个小于1的正实根。
4、小结:
A 、罗尔定理的三个条件
(1)()x f 在 [a ,b]上连续;
(2)()x f 在(a ,b)内可导;
(3)f (a )=f(b),
B 、罗尔定理的结论: 至少存在一个()b a ,∈ξ,使得()0='ξf . 几何解释:曲线有水平切线.
C 、罗尔定理研究的是导函数方程()0='x f 的根的存在性问题;
D 、罗尔定理的条件是充分非必要条件.
]
1,1[,)( 2-∈=x x x f 例)( ];1,0[,)( 3略例∈=x x x f ⎩⎨⎧=<≤= 1 010 )( 1时时例x x x x f。
