晶体学基础(第三章)
合集下载
X射线晶体学(第三章)

Ee 0
kr
f是k的函数,而 k 4 sin ,所以是 sin
的函数
右图是f与 sin 的
关系曲线,各元素的原 子散射因子可从书后附 录中查出。
.
§3-5 晶胞对X射线的散射
一、系统消光 假设一束单色X射线以θ
角投射到简单立方晶胞的 (001)面上产生衍射时,11′ 和22′之间的光程差为一个 波长的整数倍(假设为1倍), 所以1′和2′是同位相的, 为干涉加强,如图(a)。
.
二、厄瓦尔德图解 1、衍射矢量三角形
由 衍s射、矢量s 0 方和程的s图解s表0达形g式是三
个矢量构成的等腰矢量三角形, 它表明了入射线方向、衍射线方 向和倒易矢量之间的几何关系。
.
2、厄瓦尔德图解法的依据
当一束X射线以一定的角度投射到晶体上时,可 能会有若干个晶面族满足衍射条件,在若干个方向
第三章 X射线衍射理论
.
当X射线光子投射到试样上,对于被原子核束缚 得较紧的电子而言,将在入射波的电磁场作用下 作受迫振动,并成为新的电磁波源,向四周发射 出与入射线相同频率的电磁波,而且这些电磁波 互相干涉,被称之为相干散射波。
晶体中每个原子都是这样的相干散射波波源。 这些相干波相互干涉的结果,在空间的某些方向 上各波始终是互相加强的,而在另一些方向上各 波互相抵消。这样,一束X射线照射到试样上,不 仅在直射方向有X射线,而在某些特定方向(始终 加强的方向)也可能有X射线,把这种现象称为X 射线在晶体上的衍射现象,特定方向的X射线称为 衍射X射线,简称为衍射线。
si2n4a22 H2K2L2
而四方晶系为 sin242H2a2K2 cL22
可见。对不同晶系,或同一晶系而晶胞大小不同 的晶体,其衍射花样是不同的,所以说,布拉格方 程可以反映出晶体结构中晶胞大小及形状的变化。
晶体学基础第三章-晶体的定向和晶体学符号

晶体定向的几个基本概念:
(1)结晶轴:晶体坐标系中的坐标轴,需满足晶体对称性 特征。用x轴、y轴、z轴或X轴、Y轴、Z轴表示。 (2)轴角:两个结晶轴正向之夹角。用a,b,g 表示。
(3)轴单位:晶体坐标系中结晶轴的长度单位。是相应 晶体点阵中平行于晶轴的行列上相邻节点间距。用a, b, c分 别表示x轴位之连比。用a:b:c 表示。
(5)晶体几何常数:轴率a:b:c和轴角a,b,g的合称。表 示晶体坐标系特征的一组参数,用以区分不同的晶系。
第三章 晶体的定向和晶体学符号
➢ 晶体学坐标系 ➢ 各晶系的定向方法 ➢ 晶胞与原子坐标 ➢ 晶面指数 ➢ 晶向指数 ➢ 晶带指数
3.1 晶体学坐标系
晶体定向的目的:
建立坐标系,简单明确地描述晶体中晶面、晶列的 空间方位。为研究晶体的结构特性提供定量标记。
晶体的定向:
在晶体中设置符合晶体对称特征或与晶体点阵参数 一致的坐标系,并将晶体按相应的空间取向关系进行安 置。
(完整版)1《材料科学基础》第一章晶体学基础

一、晶向指数 二、晶面指数 三、六方晶系的晶向指数和晶面指数 四、晶带 五、晶面间距
晶向、晶
钯的PDF卡片-----Pd 89-4897
crystal system,space
图 2 CdS纳米棒的TEM照片(左)和 HRTEM照片(右)
图2 选区电子衍射图
图1. La(Sr)3SrMnO7的低 温电子衍射图
晶向、晶面、晶面间距
晶向:空间点阵中行列的方向代表晶体中原子排 列的方向,称为晶向。
晶面:通过空间点阵中任意一组结点的平面代表 晶体中的原子平面,称为晶面。
L M
P点坐标?
(2,2,2)或222
N
一、晶向指数
1、晶向指数:表示晶体中点阵方向的指数,由晶向上结点的 坐标值决定。
2、求法 1)建立坐标系。 以晶胞中待定晶向上的某一阵点O为原点,
联系:一般情况下,晶胞的几何形状、大小与对应的单胞是 一致的,可由同一组晶格常数来表示。
不区分 图示
晶 胞
空间点阵
单
胞
•NaCl晶体的晶胞,对应的是立方面心格子 •晶格常数a=b=c=0.5628nm,α=β=γ=90°
大晶胞
大晶胞:是相对 于单位晶胞而言 的
例:六方原始格子形式的晶胞就是常见的大晶胞
① 所选取的平行六面体应能反映整个空间点阵的对称性; ② 在上述前提下,平行六面体棱与棱之间的直角应最多; ③ 在遵循上两个条件的前提下,平行六面体的体积应最小。
具有L44P的平面点阵
单胞表
3、单胞的表征
原点:单胞角上的某一阵点 坐标轴:单胞上过原点的三个棱边 x,y,z 点阵参数:a,b,c,α,β,γ
准晶
是一种介于晶体和非晶体之间的固体。准晶具有长程定向有 序,然而又不具有晶体所应有的平移对称性,因而可以具有 晶体所不允许的宏观对称性。
晶向、晶
钯的PDF卡片-----Pd 89-4897
crystal system,space
图 2 CdS纳米棒的TEM照片(左)和 HRTEM照片(右)
图2 选区电子衍射图
图1. La(Sr)3SrMnO7的低 温电子衍射图
晶向、晶面、晶面间距
晶向:空间点阵中行列的方向代表晶体中原子排 列的方向,称为晶向。
晶面:通过空间点阵中任意一组结点的平面代表 晶体中的原子平面,称为晶面。
L M
P点坐标?
(2,2,2)或222
N
一、晶向指数
1、晶向指数:表示晶体中点阵方向的指数,由晶向上结点的 坐标值决定。
2、求法 1)建立坐标系。 以晶胞中待定晶向上的某一阵点O为原点,
联系:一般情况下,晶胞的几何形状、大小与对应的单胞是 一致的,可由同一组晶格常数来表示。
不区分 图示
晶 胞
空间点阵
单
胞
•NaCl晶体的晶胞,对应的是立方面心格子 •晶格常数a=b=c=0.5628nm,α=β=γ=90°
大晶胞
大晶胞:是相对 于单位晶胞而言 的
例:六方原始格子形式的晶胞就是常见的大晶胞
① 所选取的平行六面体应能反映整个空间点阵的对称性; ② 在上述前提下,平行六面体棱与棱之间的直角应最多; ③ 在遵循上两个条件的前提下,平行六面体的体积应最小。
具有L44P的平面点阵
单胞表
3、单胞的表征
原点:单胞角上的某一阵点 坐标轴:单胞上过原点的三个棱边 x,y,z 点阵参数:a,b,c,α,β,γ
准晶
是一种介于晶体和非晶体之间的固体。准晶具有长程定向有 序,然而又不具有晶体所应有的平移对称性,因而可以具有 晶体所不允许的宏观对称性。
晶体制备 第三章

相图的作用: 相图的作用:
• 预示不同条件下可能出现的各种组态以及条件 改变时,各种组态可能发生转变的方向和限度; 改变时,各种组态可能发生转变的方向和限度; • 了解体系在不同条件下的相转变及相平衡存在 的状态; 的状态; • 为提高已有材料的性能及设计、 为提高已有材料的性能及设计、开发和研制新 材料提供重要依据; 材料提供重要依据; • 预测材料的性能,为制定材料的制备、 预测材料的性能,为制定材料的制备、合成和 加工工艺提供参考依据。 加工工艺提供参考依据。
相平衡三要素: 相平衡三要素: 三要素
力学平衡 热平衡 化学平衡 合力为零 ∆T = 0 任一组元在各相 相等, 中的 µ 相等,
四个普适定律( 四个普适定律(理):
相律: 相律: 对于一个达到相平衡的系统而言,定有: 对于一个达到相平衡的系统而言,定有:
F =C−P+n
杠杆定理: 杠杆定理: 计算两相区内平衡存在的两个相的相 对质量。 对质量。 相平衡定律: 相平衡定律: 体系中各相的数量并不影响这些相 的平衡组成和性质。 的平衡组成和性质。 质量作用定律: 单位时间从相( 转化到相( 质量作用定律: 单位时间从相(1)转化到相(2) 的分子数应当与该组分在相( 的分子数应当与该组分在相(1)中的有效浓度 成正比;反向转化的分子数应当与它在相( 成正比;反向转化的分子数应当与它在相(2) 中的有效浓度成正比。 中的有效浓度成正比。
1865
G : 3Y2O3 • 5Al2O3 (YAG) M : 2Y2O3 • Al2O3
P : Y2O3 • Al2O3 (YAP)
M +G
Y2O3
M
P
摩尔分数
G
Al2O3
Y2O3 − Al2O3 二元系相图(部分) 二元系相图(部分)
晶体的定向和晶面符号

不要弄混淆.
•
每个晶系的国际符号写法见表4-2(此表很重要, 要熟记!).
整理课件
21
表4-3各晶系对称型的国际符号中各序位所代表的方向: 、U
整理课件
22
晶系
选轴原则
等轴晶系 四方晶系
三方晶系 及六方晶系
斜方晶系 单斜晶系
以互相垂直的L4或Li4或相互垂直的L2 分别作为X、Y、Z轴
L4或Li4为Z轴,以垂直Z轴,并互相垂直的 L2或P的法线为X、Y轴,在Li42L22P对称 型中,以两个L2为X、Y轴。
整理课件
12
三斜晶系的定向:
晶体几何常数:
a < > b < > g < > 90 °
a<>b<>c 适当的晶棱为 x, y, z 轴。 大致上 z 轴直立, y 轴 左右, x 轴前后。
整理课件
13
三方和六方晶系的四轴定向:
– 选择唯一的高次轴作为直立结晶轴Z轴,在垂直Z 轴的平面内选择三个相同的、即互成60°交角的L2 或P的法线,或适当的显著晶棱方向作为水平结晶 轴,即x 轴、 y 轴以及 d 轴(U轴)
OA1= ma,OB1= pb,OC1= sc OA2 = na,OB2 = qb,OC2 =tc m, n, p, q, s, t都为整数,故m/n:p/q:s/t可化为整数比。
整理课件
39
z unknown face (A2B2C2) 2 reference face (A1B1C1) 1
2
2
整理课件
44
四轴定向时的晶棱符号
[1- 20
• 以[u v m w]的形式表达
• 也有三指数形式: [u v w] • 四指数和三指数
材料科学导论-第一章 晶体学基础3
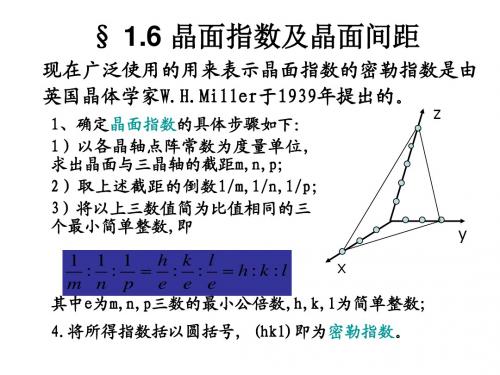
3、六方晶系晶面指数标定
根据六方晶系的对称特点,对六方晶系采用a1,a2,a3 及c四个晶轴,a1,a2,a3之间的夹角均为120度,这样, 其晶面指数就以(h k i l)四个指数来表示。 根据几何学可知,三维空间独立的坐标轴最多不超过三 个。前三个指数中只有两个是独立的,它们之间存在以 下关系:i =- ( h + k ) 。
三轴晶面指数(h k l) 四轴晶面指数(h k i l) i=- ( h + k )
立方晶系:
d hkl
a h k l
2 2 2
§ 1.6 晶面指数及晶面间距 范例:
m/l
c
a
m/k
b
m/h
画出晶面 (100),(110),(111),(201),(211),(321)
பைடு நூலகம்
c a
(100)
b
画出晶面 (100),(110),(111),(201),(211),(321)
d V [h b c sin k a c sin l a b sin
2 2 2 2 2 2 2 2 2 2 2 2
2hkabc (cos cos cos )
2
2kla bc(cos cos cos )
2
2hlab c(cos cos cos )]
2
2 2 2
1
2
1 2
V abc(1 cos cos cos 2cos cos cos )
单斜晶系:d=sinβ(h2/a2+k2sin2β/b2+l2/c2-2hlcosβ/ac)-1/2 正交晶系:d=[h2/a2+k2/b2+l2/c2]-1/2 四方晶系:d=[(h2+k2)/a2+l2/c2]-1/2 六方晶系:d=[4(h2+hk+k2)/3a2+l2/c2]-1/2
材料科学基础第三章

注意: 阵点可以是原子或分子的中心, 也可以是彼此等同 阵点可以是原子或分子的中心,
的原子群或分子群的中心, 的原子群或分子群的中心 ,但 各个阵点的周围环境必须相 同。
4
空间点阵: 空间点阵:阵点在三维空间呈周期性规则排列所组成 的阵列。(阵点是构成空间点阵的基本要素) 的阵列。 阵点是构成空间点阵的基本要素) 晶格(空间格子) 为了便于描述空间点阵的图形, 晶格(空间格子):为了便于描述空间点阵的图形, 可用许多平行的直线把所有阵点连接起来, 可用许多平行的直线把所有阵点连接起来 , 构成一个 三维的几何格架, 称为晶格或空间格子 。 ( 可以形象 三维的几何格架 , 称为晶格或空间格子。 描述空间点阵的几何形状,实质仍是空间点阵) 描述空间点阵的几何形状,实质仍是空间点阵) 晶胞:能够代表晶格中原子排列特征的最小单元体。 晶胞:能够代表晶格中原子排列特征的最小单元体。 (将晶胞作三维的重复堆砌就构成了空间点阵) 将晶胞作三维的重复堆砌就构成了空间点阵)
c/a值的范围:1.568(铍, 值的范围: 值的范围 ( Be)~ 1.886(镉,Cd) )~ ( )
21
22
3.3.3 晶胞中的原子数 fcc: n = 8 × 1 (顶角) 6 × 1 2 : 8 + (面心)= 4 bcc: n = 8 × 1 8 : (顶角) 1(体心) = 2 + hcp: hcp:n = 12 × 1 6 (顶角) 2 × 1 2 + (面心) (中心)=6 +3
5
c
β
a γ
α b
空间点阵、 空间点阵、晶胞
6
3.2.2 晶
胞
晶胞通常是平行六面体。 晶胞通常是平行六面体。 选取晶胞的原则: 选取晶胞的原则: a. 几何形状与晶体具有同样的对称性; 几何形状与晶体具有同样的对称性; b. 平行六面体内相等的棱和角的数目最多; 平行六面体内相等的棱和角的数目最多; c. 当平行六面体棱间夹角存在直角时,直角数目 当平行六面体棱间夹角存在直角时, 应最多; 应最多; d. 在满足上述条件下,晶胞应具有最小的体积。 在满足上述条件下,晶胞应具有最小的体积。
第三章_晶体学基础

简单格子 底心格子 体心格子 面心格子
十四种空间格子(布拉菲格子)
综合考虑单位平行六面体的划分和附加结点的类型,七个晶系空间格 子的基本类型共有十四种。
三斜晶系:三斜简单格子; 单斜晶系:单斜简单格子,单斜底心格子; 斜方晶系:斜方简单格子,斜方底心格子, (正交) 斜方体心格子,斜方面心格子; 四方晶系:四方简单格子,四方体心格子; 三方晶系:三方简单格子(三方菱面体格子); 六方晶系:六方简单格子; 立方晶系:立方简单格子,立方体心格子, 立方面心格子。
简单P
立方I
立方F
立方晶系:a = b=c
α=β=γ=90°
四方P 四方晶系: a = b≠c
四方I α=β=γ=90°
正交P
正交C 正交晶系:a≠b ≠ c
正交I α=β=γ=90°
正交F
单斜P 单斜晶系:a≠b ≠ c
单斜C α=γ=90° β> 90°
六方H
三方R
三斜P
六方晶系: a = b≠c 三方晶系: a = b=c 三斜晶系:a≠b≠c
故确定的步骤为:
● 选定晶轴X、Y、Z和a、b、c为轴单位;
● 平移晶向(棱)直线过原点;
● 在该直线上任取一结点M,将其投影至X、
。
Y、Z轴得截距OX、OY、OZ;
● 作OX/a:OY/b:OZ/c = u:v:w(最小
整数比);
● 去掉比号,加中括号,[u v w]即为晶
向符号。
某一晶向指数代表一组在
结构基元:组成晶体的离 子、原子或分子。基元内 的原子数等于晶体中原子 的种类数。
晶体结构=空间点阵+结构基元
实际晶体——质点体积忽略——空间点阵——阵点连线——晶格(空间格子)
十四种空间格子(布拉菲格子)
综合考虑单位平行六面体的划分和附加结点的类型,七个晶系空间格 子的基本类型共有十四种。
三斜晶系:三斜简单格子; 单斜晶系:单斜简单格子,单斜底心格子; 斜方晶系:斜方简单格子,斜方底心格子, (正交) 斜方体心格子,斜方面心格子; 四方晶系:四方简单格子,四方体心格子; 三方晶系:三方简单格子(三方菱面体格子); 六方晶系:六方简单格子; 立方晶系:立方简单格子,立方体心格子, 立方面心格子。
简单P
立方I
立方F
立方晶系:a = b=c
α=β=γ=90°
四方P 四方晶系: a = b≠c
四方I α=β=γ=90°
正交P
正交C 正交晶系:a≠b ≠ c
正交I α=β=γ=90°
正交F
单斜P 单斜晶系:a≠b ≠ c
单斜C α=γ=90° β> 90°
六方H
三方R
三斜P
六方晶系: a = b≠c 三方晶系: a = b=c 三斜晶系:a≠b≠c
故确定的步骤为:
● 选定晶轴X、Y、Z和a、b、c为轴单位;
● 平移晶向(棱)直线过原点;
● 在该直线上任取一结点M,将其投影至X、
。
Y、Z轴得截距OX、OY、OZ;
● 作OX/a:OY/b:OZ/c = u:v:w(最小
整数比);
● 去掉比号,加中括号,[u v w]即为晶
向符号。
某一晶向指数代表一组在
结构基元:组成晶体的离 子、原子或分子。基元内 的原子数等于晶体中原子 的种类数。
晶体结构=空间点阵+结构基元
实际晶体——质点体积忽略——空间点阵——阵点连线——晶格(空间格子)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
对称面可以是垂直等分某些晶面的平面, 或是包含某些晶棱的平面。
3.3.ห้องสมุดไป่ตู้ 对称轴 对称轴为一假想的直线,对应的对称变换为围绕此 直线的旋转,每转过一定角度,各等同部分就发生 一次重复。旋转一周重合的次数叫轴次,用n表示; 整个物体复原需要的最小转角则称为基转角。
n
360
n=1,为一次轴,国际符号为1。
3.3.2 对称面 对称面为假想的平面,相 应的对称操作为对此平面 的反映。习惯符号为P,国 际符号为m。 如果m和xy平面一致,那么 对称变化矩阵为:
1 0 0 0 1 0 0 0 1
3.3.2 对称面
如果m和xz以及yz平面一致,那么相应的对 称转换矩阵则可分别表示为:
3.3.4 倒转轴
3.3.4 倒转轴
3.3.4 倒转轴 我们可以得出各次倒转轴与其它对称要素(或 对称要素的联合)间的等效关系如下: Li1=L1+C=C Li2=L2+P=P (P Li2)
Li3=L3+C
Li6=L3+P
(L3 Li3)
(L3 Li6, P L3)
只有Li4是一个独立的对称要素,不能由其 他简单或它们的联合来等效代替。
二、三、四、六次轴,国际符号分别记为2,3, 4,6。对称轴的习惯符号用Ln表示。
3.3.3 对称轴
晶体对称定律(law of crystal
symmetry):在晶体中,只可能出现轴
次为一次、二次、三次、四次和六次的
对称轴,而不存在五次及高于六次的对 称轴。
3.3.3 对称轴
a 2a cos ma cos ( m 1) / 2
1 0 0 4[001]2 0 1 0 0 0 1
4
3
[001]
0 1 0 1 0 0 0 0 1
3.3.3 对称轴
六次轴的变换矩阵:
6[001] 1 2 3 2 0 3 2 1 2 0 0 0 1 1 2 3 2 6[001] 2 0
3.3.3 对称轴 因此,r到r'变换的解析式是∶
又可写成r'=Rr ,式中R是变换矩阵
cos sin 0
sin cos 0
0 0 1
教材P.26
3.3.3 对称轴
更一般的情况,r绕任意方向的单位矢量 S=uX1+vX2+wX3(把S记作[uvw])转动角到达r 的变换矩阵是:
1 0 0 0 1 0 0 0 1
3.3.1 对称心
如果通过对称中心作任意一直线,则此直 线上距对称直线等距离的两端,必为可找 到的对应点。 一个具有对称心的图形,其相对应的面、 棱、角都体现为反向平行。 可以推论出,晶体中若存在对称心,其晶 面必然两两平行而且相等。这一点可以用 作判别晶体或晶体模型有无对称心的依据。
3.3.4 倒转轴
对于倒转轴,通常只考虑其中的Li4和Li6两者, Li4作为一种独立的对称要素,自然是必须考虑 的。Li6虽与L3+P的联合等效,但它在对称分类中 有特定的意义(属六方晶系),所以我们采用 Li6代替L3+P的联合。
在晶体中,独立的Li4和Li6出现的可能情况是:一 个晶体,如没有C,但有一L3,且垂直此L3还有一 个P时,则在此L3的方向上肯定有一个Li6存在; 一个晶体,如没有C,但有L2时,则此L2可能就是 一个Li4,但并非必定就是一个Li4;若确为Li4时, 则此L2将被包含在Li4之间而不再独立存在。
a11 a21 a 31
a12 a22 a32
a13 a23 a33
称为对称变换矩阵。对任一对称操作,都有惟 一的对称变换矩阵与之对应。
3.3.1 对称心 对称心为一假想的几何 点,相应的对称操作是 对于这个点的反伸。这 个对称操作的习惯符号 为C,国际符号记为 1
3.3.3 对称轴
二次轴的变换矩阵:
1 0 0 2[001] 0 1 0 0 0 1
3.3.3 对称轴
三次轴的变换矩阵:
3.3.3 对称轴 因为三次旋转轴也常选用 仿射坐标系:a1、a2轴的 单位矢量长度相同夹角为 120o,a1、a2轴都垂直于c 轴。
3.1 对称的概念
3.1 对称的概念
对称(symmetry):物体(或图形)中相同部分之 间有规律的重复。对称的定义说明,对称的物体或 图形,至少由两个或两个以上的等同部分组成,对 称的物体通过一定的对称操作(即所谓的“有规 律”)后,各等同部分调换位置,整个物体恢复原 状,分辨不出操作前后的差别。例如建筑物的左右 两边可以通过中平面反映彼此重合。
3.3.4 倒转轴 倒转轴同样遵守晶体对称定律,只有一次、 二次、三次、四次和六次,国际符号分别 记为 1 , 2 , 3 , 和 6 。习惯符 4 号为Lin,n为轴次。 变换矩阵
cos sin 0
sin cos 0
0 0 1
早春寒谷寒春早 林木香茶香木林 叠叠青山青叠叠 森森暮竹暮森森 美兰雨舍雨兰美 金果田中田果金 燕喜天霄天喜燕 音回一曲一回音
3.2 晶体的对称 晶体的对称具有如下特点: 晶体的对称不仅仅体现在外形上,同时也体现在其物 理性质上(如光学、力学和电学性质等)。其对称不 仅包含几何意义,也包含了物理意义。 晶体的对称性主要特征在于,晶体是由在三维空间规 则排列的原子或原子基团组成的。通过平移,可使之 重复。这种规则的重复就是平移对称的一种形式。所 以说,从微观角度,所有的晶体都是对称的。 晶体的对称性同时受到格子构造的限制,只有符合格 子构造规律的对称才能在晶体上出现,因此,晶体的 对称是有一定限制的。
1 2 3 5 6[001] 2 0
3 2 1 2 0
0 0 1
3.3.3 对称轴 选用仿射坐标系
1 1 0 6[001] 1 0 0 0 0 1 0 1 0 6[001]2 1 1 0 0 0 1 1 0 0 6[001]3 0 1 0 0 0 1
3.3 晶体的宏观对称元素和对称操作
晶体的宏观对称主要表现在外部形态上,如晶体的 晶面、晶棱和角顶作有规律的重复。 要使对称图形中等同部分重复,就必须通过一定的 操作,这种操作就称为对称操作(symmetry operation),或者说对称操作使能够使对称物体 (或图形)中等同部分作有规律重复的变换动作。 在进行对称操作中所凭借的辅助几何要素(点、线、 面)称为对称元素(symmetry element)。
0 1 0 1 1 0 3[001] 0 0 1
1 1 0 1 0 0 2 3[001] 0 0 1
3.3.3 对称轴 四次轴的变换矩阵:
0 1 0 4[001] 1 0 0 0 0 1
3.3 晶体的宏观对称元素和对称操作 对称操作和对称元素共五类:
反伸操作和对称心(center of symmetry)
反映操作和对称面(symmetry plane)
旋转操作和对称轴(symmetry axis) 旋转反伸操作和倒转轴(rotoinversion axis) 旋转反映操作和映转轴(rotoreflection axis)
1 1 0 4 6[001] 1 0 0 0 0 1
0 1 0 5 6[001] 1 1 0 0 0 1
3.3.3 对称轴
一个晶体可以没有对称轴,也可以有一个和若 干个对称轴,且对称轴的数目也可以不同。如 果在对称轴的方向上有不同轴次的对称轴,那 么只取轴次最高的那一个。
3.3.3 对称轴
3.3.3 对称轴 物体绕某个轴转动的变换 在X坐标系有一点r(x1, x2, x3),它也是从原点到此 点的矢量。 如果这一矢量绕X3轴转动 角,点到达的新位置为 r(x'1, x'2,, x'3)。 新位置的坐标为: x'1 = -r sin( -) = -r(sincos-cos sin) x'2 = rcos( -) = r(coscos +sin sin ) cos = x2/r 及sin = x1/r ,即 x'1=x1cos -x2sin x'2=x1sin+x2cos
在晶体中如有对称轴存在,其可能的位置是, 通过晶体的几何中心,并且为某两顶角的连线, 或两平行晶面中心的连线,或某两晶棱中心的 连线;如晶体无对称中心时,则还可能是某一 晶面的中心、晶棱的中点及顶角三者任意两者 之间的连线。
3.3.3 对称轴
3.3.4 倒转轴 倒转轴亦称旋转反伸轴,又称反轴或反演轴。 辅助的几何要素有两个:一根假想的直线和此直线 上的一个定点。相应的对称操作就是围绕此直线旋 转一定的角度及对于此定点的倒反(反伸)。 倒转轴的两个变换动作是构成整个对称变换的不 可分割的两个组成部分,无论是先旋转后倒反, 或是先倒反后旋转,两者的效果完全相同,但都 是在两个变换动作连续完成以后而使晶体复原。
上述对称概念只是朴素的定义。实际上,对称不仅 是自然科学最普遍和最基本的概念之一,它也是建 造大自然的一种神秘的密码,同时也是人类文明史 上永恒的审美要素。
3.1 对称的概念
形象对称
七律-早春〔对称回文〕
m1 m2 F G r0 2 r
q1q2 F K 2 r0 r
万有引力公式 库伦公式
1 0 0 0 1 0 0 0 1
1 0 0 0 1 0 0 0 1
