晶体学基础第二章-晶体的对称分类与布拉菲点阵
第二部分晶体的结构

第⼆部分晶体的结构第⼆部分晶体结构2.1 晶体学基础概述根据结合键类型不同,晶体可分为⾦属晶体、离⼦晶体、共价晶体和分⼦晶体。
晶体结构:晶体中原⼦(离⼦或分⼦)在三维空间的具体排列⽅式。
空间点阵与晶胞1.相关概念空间点阵(lattice)晶格(space lattice)阵点(结点)晶胞(cell)选取晶胞应遵循⼀定的原则晶胞⼤⼩和形状表⽰⽅法⼆、晶系和布拉菲点阵根据晶体的对称性和每个阵点周围具有相同的环境,布拉菲运⽤数学⽅法推算,将花样繁多的晶体结构归纳为14种空间点阵(称为布拉菲点阵)。
根据晶格常数a、b、c及α、β、γ是否相等,⼜将14中空间点阵归属于七⼤晶系。
晶体结构和空间点阵之间的区别空间点阵(space lattice):晶体中质点排列的⼏何学抽象,⽤以描述和分析晶体结构的周期性和对称性。
由于各阵点的周围环境相同,只有14种类型。
晶体结构(crystal structure):晶体中原⼦(离⼦或分⼦)在三维空间的具体排列⽅式。
由于组成晶体的物质质点及其排列⽅式不同,晶体结构是⽆限的,但总能按其原⼦(分⼦或离⼦)排列的同期性和对称性,归属于14种空间点阵中的⼀种。
七⼤晶系:1.三斜晶系(triclinic system):a≠b≠c,α≠β≠γ≠ 90°2.单斜晶系(monoclinic system ):a≠b≠c,α=γ=90°≠β2.正交(斜⽅)晶系(orthogonal system ):a≠b≠c,α=β=γ= 90°4.四(正)⽅晶系(tetragonal system ):a=b ≠ c,α=β=γ=90°5.⽴⽅晶系(cubic system ):a=b=c,α=β=γ=90°6.六⽅晶系(hexagonal system ):a=b ≠ c,α=β=90°,γ=120°7.菱形晶系(rhombohedral system):a=b=c,α=β=γ≠90°⼗四种空间点阵:1 简单⽴⽅点阵:a=b=c,α=β=γ =90°2 体⼼⽴⽅点阵:a=b=c,α=β=γ =90°3 ⾯⼼⽴⽅点阵:a=b=c,α=β=γ =90°4 简单四⽅点阵:a=b ≠ c,α=β=γ =90°5体⼼四⽅点阵:a=b ≠ c,α=β=γ =90°6 简单菱⽅点阵:a=b=c,α=β=γ≠ 90°7 简单六⽅点阵:a=b ≠ c,α=β=90°,γ =120°8 简单正交点阵:a≠b≠c,α= β= γ = 90°9 底⼼正交点阵:a≠b≠c,α= β= γ = 90°10 体⼼正交点阵:a≠b≠c,α= β= γ = 90°11 ⾯⼼正交点阵:a≠b≠c,α= β= γ = 90°12 简单单斜点阵:a≠b ≠c α= β =90°≠γ12 底⼼单斜点阵:a≠b ≠c α= β =90°≠γ14 简单三斜点阵:a≠b≠c α≠β≠γ≠90°⾦属晶体的结构主要为:FCC、BCC、HCP三、晶向指数和晶⾯指数1.⽴⽅晶系中的晶向指数晶向指数的确定⽅法晶向指数规律2.⽴⽅晶系中的晶⾯指数晶⾯指数的确定⽅法晶⾯指数规律2.六⽅晶系的晶向和晶⾯指数4.晶带晶带(zone)——相交或平⾏于某⼀直线的所有晶⾯的组合晶带轴:此直线为晶带轴。
晶体对称性
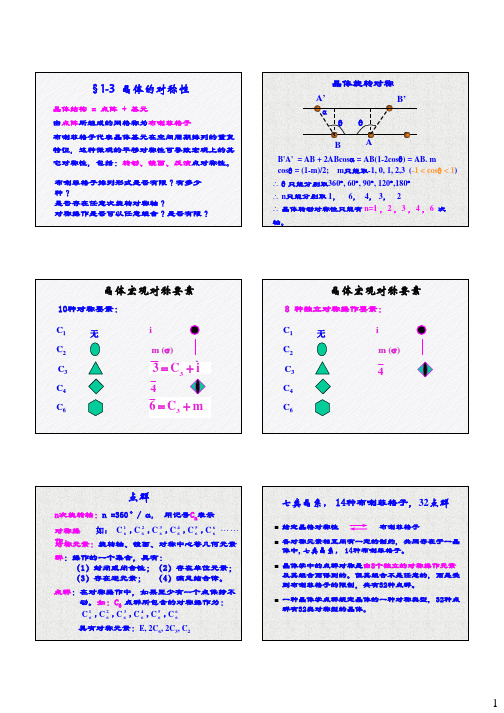
D2h D3h
Dnd群
D2d D3d
C4 C4v C4h D4 D4h
Sn群 S2 (Ci)
S4
Td群 T
Th
Td
Oh群 O
Oh
C6 C6v C6h D6 D6h
S6 (C3i)
下一页
32种点群
11种纯旋转点群:C11,,2C,2,3,C3,4,C46,,C6, 2D22,2,D33,2,D4,42D26,,6T2,2,O 23,432
轴。
晶体宏观对称要素
10种对称要素:
C1
无
C2
C3
C4
C6
i
m (σ)
33 = C3 + i
4
66= C3 + m
晶体宏观对称要素
8 种独立对称操作要素:
C1
无
C2
C3
C4
C6
i m (σ)
4
点群
n次旋转轴:n =360°/ α, 用记号Cn表示
对称操
如:
C
1 6
,C
2 6
,C
3 6
,C
4 6
,C
5 6
43m
Td
E, 8C3, 3C2, 6σd , 6S4 24
m3m (m3m)
Oh E, 8C3, 3C2, 6C2, 6C4, i, 48 8S6, 3σh, 6σd , 6S4
晶体点群的种类
点群
典型类型
Cn群 C1
C2
C3
Cnv群
C2v
C3v
Cnh群 C1h (m) C2h
C3h
Dn群
D2
D3
Dnh群
6
固体物理第二章第二节 对称性和布拉维格子的分类

晶体的对称性定律的证明
B
A
如图,A为格点,B为离A最近 a a 的格点之一,则与 AB 平行的 格点之间的距离一定是 AB A a B 的整数倍。 如果绕A转角,晶格保持不变(对称操作).则 该操作将使B 格点转到 B位臵,则由于转动对称 操作不改变格子,在 B 处必定原来就有一个格点。 因为B 和A 完全等价,所有旋转同样可以绕B 进行. 由此可设想绕B 转角,这将使A 格点转到 A的 位臵。同样 A处原来也必定有一个格点
A B H E
D
D
C G
F
C
正四面体既无四 度轴也无对称心
参考方俊鑫书 P37-39
A
G
B F E H
旋转反演对称操作中只有4度 旋转反演对称操作是独立的 独立的对称操作有8种, 即1,2,3,4,6,i, m, 4 。 或C1,C2,C3, C4,C6 ,Ci,Cs,S4。
3
4
1830年,赫塞耳(Johann Friedrich Christian Hessel)首先导出了32种点群,由32种点群出发, 可以对布拉维点阵进行分类,这正是1850年布 拉维所作的工作,他证明了只有7个晶系。(点 群不含平移对称操作,因为平移导致任何格点 都要动,而点群必须至少有一个格点不动) 熊夫利(Schoenflies1891)和费奥多罗夫 (Fedorove 1892) 为了研究复式晶格(几套简单 格子的平移)的分类,考虑了平移对称操作, 提出了空间群的概念,并证明只有230种独立 的空间群。 可由此证明只有14种三维布拉维 点阵
nm
n2 n2
nm
第二章 晶体结构

晶胞
• 有实在的具体质点所 组成
平行六面体
• 由不具有任何物理、化学 特性的几何点构成。
是指能够充分反映整个晶体结构特征的最小结构单位, 其形状大小与对应的单位平行六面体完全一致,并可用 晶胞参数来表征,其数值等同于对应的单位平行六面体 参数。
晶胞棱边长度a、b、c,其单位为nm ,棱间夹角α、β、 γ。这六个参数叫做点阵常数或晶格常数。
面网密度:面网上单位面积内结点的数目; 面网间距:任意两个相邻面网的垂直距离。
相互平行的面网的面网密度
和面网间距相等; 面网密度大的面网其面网间 距越大。
空间格子―――连接分布在三维空间的结点构成空 间格子。由三个不共面的行列就决定一个空间格子。
空间格子由一系列 平行叠放的平行六 面体构成
2-1 结晶学基础
一、空间点阵
1.晶体的基本概念 人们对晶体的认识,是从石英开始的。 人们把外形上具有规则的几何多面体形态的 固体称为晶体。 1912年劳厄(德国的物理学家)第一次成功 获得晶体对X射线的衍射线的图案,才使研究 深入到晶体的内部结构,才从本质上认识了 晶体,证实了晶体内部质点空间是按一定方 式有规律地周期性排列的。
第二章 晶体结构
第二章 晶体结构
1
结晶学基础 晶体化学基本原理 非金属单质晶体结构
2
3 4 5
无机化合物晶体结构
硅酸盐晶体结构
重点:重点为结晶学指数,晶体中质点的堆 积,氯化钠型结构,闪锌矿型结构,萤石型 (反萤石型)结构,钙钛矿型结构,鲍林规 则,硅酸盐晶体结构分类方法。 难点:晶体中质点的堆积,典型的晶体结构 分析。
• 结点分布在平行六面
体的顶角; •平行六面体的三组棱长 就是相应三组行列的结 点间距。
晶体学第二章-6

平移轴(translation axis ):一条直线,沿此直线平移一定距离可使晶体的等同部分重合,即整个晶体复原。
¾平移轴:布拉菲点阵中的任意行列¾平移轴的移距:使晶体复原的最小平移距离,即行列上相邻两点间距对称操作:平移t晶格平移矢量——原胞基矢的线性组合平移群{}332211a l a l a l v v v ++螺旋轴n s2131、3241、42、436l 、62、63、64、65•0<s <n/2;采用右手系(右螺旋轴),螺距为τ=(s /n )t 。
•若n/2<s <n ;采用左手系(左螺旋轴),螺距为τ=(1-s /n )t 。
•若s =n/2;中性螺旋轴,左右手系等效。
螺旋轴21,31,3241意为按左旋方向旋转90度后移距1/4 t 。
43意为按右旋方向旋转90度后移距1/4 t;6462螺旋轴61,62,63,64,65滑移面(glide plane):一假想平面,对此平面反映后平行于该平面平移一定距离可使晶体中每一个质点与其等同的质点重合,即整个晶体复原。
国际符号a,b,c,n,d¾滑移面(像移面):一种复合的对称要素¾辅助几何要素有两个:一个假想的平面和平行此平面的某一直线方向¾平移的距离(移距):该方向行列结点间距的一半对称操作:反映+ 平移(联合操作)¾沿晶轴方向移距为轴单位的1/2¾滑移矢量为a/2,b/2,c/2d ——金刚石型滑移面¾沿面对角线或体对角线滑移¾滑移矢量:(a+b)/4, (b+c)/4, (a+c)/4,(a+b+c)/4nn ——对角线滑移面¾沿面对角线或体对角线滑移¾滑移矢量:(a+b)/2, (b+c)/2, (a+c)/2,(a+b+c)/2滑移面a,b,c,n,dA:各种滑移面在3个轴方向上滑移矢量分布B:滑移面平行于投影面的投影C:滑移面垂直于投影面的投影晶体中可能存在的对称元素类型及符号:二、二维空间群1. 二维晶体的宏观对称元素:6个对称轴(1,2,3,4,6)、对称面(m)2. 二维晶系、布拉菲点阵与点群:¾晶轴只能取a和b,只剩下一个角度。
固体物理第二章第二节对称性和布拉维格子的分类

P28-29表2.1给出了32个晶体学点群,为了 便于大家看懂,下面给出符号的说明
Cn C1, C2 , C3, C4 , C6
900 1200
900
7个晶系(crystal system)相应的点群 S1, C2h , D2h , D4h , D3d , D6h , Oh
即:Ai G,i 1, 2,3 ,G {Ai}
必须满足下列条件: 1). 封闭性(closure property) 按照给定的乘法规则,群G中任何两个元素 相乘,得到的还是该群的一个元素。
Ai Aj Ak ,i j or i j
2). 群中一定包含一个不变元素(单位元素) E
E G, EAi Ai E Ai
我们这里要讨论的主要是晶格(或点阵)的对 称性(symmetry of lattice).
在晶格这个物理系统中,一种对称性是指某些 要素互相等价,而用来描述晶格的要素,无非就 是:点、线、面。而保持这些要素等价的操作---对称操作有三种:平移、旋转、镜反射。假设 在某一个操作过后,点阵保持不变,也就是每个 格点的位置都得到重复,那么这个相应的平移、 旋转或镜反射操作就叫作一个点阵对称操作。其 中的点、线、面分别叫做对称中心、对称轴、对 称面----称为对称元素
比如:绕x轴的旋转,设转角为θ,则有:
x x
y
y
cos
z sin
z
y
sin
z
cos
a11 a12 a13 1 0
0
布拉菲点阵

关于奥古斯特·布拉菲及布拉菲点阵浅析奥古斯特·布拉菲(August Bravais,1811—1863),法国物理学家,于1845年推导出了三维晶体原子排列的所有14种点阵结构,首次将群的概念应用到物理学,为固体物理学做出了重大贡献。
这是非常有意义的结论,为了纪念他,后人称这14种点阵为布拉菲点阵。
除此之外,布拉菲还对磁性、极光、气象、植物地理学、天文学和水文学等方面进行过研究。
图1 奥古斯特·布拉菲在几何学以及晶体学中,布拉菲晶格(又译布拉菲点阵)是为了纪念奥古斯特·布拉维在固态物理学的贡献命名的。
法国晶体学家布拉菲(A.Bravais)于1850年用数学群论的方法推导出空间点阵只能有十四种: 简单三斜、简单单斜、底心单斜、简单正交、底心正交、体心正交、面心正交、简单六方、简单菱方、简单四方、体心四方、简单立方、体心立方、面心立方。
根据其对称特点,它们分别属于七个晶系。
空间点阵到底有多少种排列形式?按照“每个阵点的周围环境相同”的要求,在这样一个限定条件下,法国晶体学家布拉菲(A. Bravais)曾在1848年首先用数学方法证明,空间点阵只有14种类型。
这14种空间点阵以后就被称为布拉菲点阵。
空间点阵是一个三维空间的无限图形,为了研究方便,可以在空间点阵中取一个具有代表性的基本小单元,这个基本小单元通常是一个平行六面体,整个点阵可以看作是由这样一个平行六面体在空间堆砌而成,我们称此平行六面体为单胞。
当要研究某一类型的空间点阵时,只需选取其中一个单胞来研究即可。
在同一空间点阵中,可以选取多种不同形状和大小的平行六面体作为单胞,如下图所示:其选取方式有,1.固体物理选法:在固体物理学中,一般选取空间点阵中体积最小的平行六面体作为单胞,这样的单胞只能反映其空间点阵的周期性,但不能反映其对称性。
如面心立方点阵的固体物理单胞并不反映面心立方的特征。
2.晶体学选法:由于固体物理单胞只能反映晶体结构的周期性,不能反映其对称性,所以在晶体学中,规定了选取单胞要满足以下几点原则:①要能充分反映整个空间点阵的周期性和对称性;②在满足①的基础上,单胞要具有尽可能多的直角;③在满足①、②的基础上,所选取单胞的体积要最小。
晶体学基础PPT课件
14
2.1.2 晶向指数和晶面指数
晶向:空间点阵中节点列的方向。空间中任两节点的 连线的方向,代表了晶体中原子列的方向。
晶面:空间中不在一直线任三个阵点的构成的平面, 代表了晶体中原子列的方向。 c
阵点坐标 op ua vb wc
b
a
15
1. 晶向指数
c
求法:
1)确定坐标系
[101]
3! 4 4组,如{111} 3!
d)h k l 有一个为0,应除以2,则有
3! 4 12组,如{1 2 0} 2
有二个为0,应除以22,则有
3! 2!22
4
3组,如{1
0
0}
24
3.六方晶系指数
三坐标系 a1,a2,c
120°
四轴坐标系 a1,a2,a3,c
120°
120°
(h k i l ) [u v t w]
晶胞 原胞
差别:晶胞能完整反映晶体内部原 子或离子在三维空间分布;原胞一 般不能保持晶体结构的对称性
8
5.晶系与布拉菲点阵 七个晶系,14个布拉菲点阵
• 简单晶胞(初级晶胞):只有在平行六面体每个顶角上有一阵点 • 复杂晶胞: 除在顶角外,在体心、面心或底心上有阵点
9
5.晶系与布拉菲点阵 七个晶系,14个布拉菲点阵
第二章 固体结构 The structure of Solids
气态
物质
液态 固态
晶体:原子在空间呈有规则的周期性重复排列 非晶体: 原子在空间无规则排列
金的原子力 显微照片
1
高分辨率电镜直接观察晶体中原子的排列
2
※ 2.1 晶体学基础
晶体结构的基本特征:原子(或分子、离子)在三维空 间呈周期性重复排列,即存在长程有序
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
立方晶系(等轴晶系):有4个 3
3.晶类: 属于同一点群的晶体。32个晶类。
二、晶体的14种布拉菲点阵(布拉菲格子)
—— 32种点群描述的晶体对称性 —— 对应的只有14种布拉菲点阵 —— 分为7个晶系
—— 单胞的三个下,它们构成斜坐标系
三个晶轴之间的夹角
7大晶系的形成
2.4 晶体的对称分类与布拉菲点阵
一、晶体的对称分类
按晶体的对称性特征晶体分类
1.晶族(crystal category):3个晶族 低级晶族:无高次轴 中级晶族:只有一个高次轴 高级晶族:高次轴多于一个
2.晶系(crystal system):7个晶系
三斜晶系:只有 1 或 1
单斜晶系:2 和 m 均不多于一个 正交晶系(斜方晶系):2 和 m 的总数不少于3个
