特殊的四边形培优
北师大新版九年级数学上学期第一章:特殊的平行四边形 单元培优卷 含解析

第一章特殊的平行四边形一.选择题(共6小题)1.如图,矩形ABCD中,BC>AB,对角线AC、BD交于O点,且AC=10,过B点作BE⊥AC 于E点,若BE=4,则AD的长等于()A.8 B.10 C.3D.42.如图,矩形ABCD中,BH⊥AC,DE∥BH交CB的延长线于点E,交AB于点G,P是DE上一点,∠BPD=∠BCD,且G为PF的中点.则①AF=CH;②AC=3FH;③BE=BG;④若AE=,则FG=3,以上结论正确的个数是()A.1 B.2 C.3 D.43.如图,在矩形ABCD中,AB=6,BC=6,点E是边BC上一动点,B关于AE的对称点为B′,过B′作B′F⊥DC于F,连接DB′,若△DB′F为等腰直角三角形,则BE的长是()A.6 B.3 C.3D.6﹣64.如图,已知E,F分别为正方形ABCD的边AB,BC的中点,AF与DE交于点M,O为BD 的中点,则下列结论:①∠AME=90°,②∠BAF=∠EDB,③AM=MF,④ME+MF=MB.其中正确结论的有()A.4个B.3个C.2个D.1个5.如图,以△ABC的各边为边,在边BC的同侧分别作三个正方形ABDI,BCFE,ACHG,对于四边形ADEG的形状,某班学生在一次数学活动课中,通过动手实践,探索出如下结论,其中错误的是()A.若△ABC为任意三角形,则四边形ADEG是平行四边形B.若∠BAC=90°,则四边形ADEG是矩形C.若AC=AB,则四边形ADEG是菱形D.若∠BAC=135°且AC=AB,则四边形ADEG是正方形6.如图是以KL所在的直线为对称轴的轴对称图形,六边形EFGHLK的各个内角相等,记四边形HCH′L、四边形EKE′A、△BGF的周长分别为C1、C2、C3,且C1=2C2=4C3,已知FG=LK,EF=6,则AB的长是()A.9.5 B.10 C.10.5 D.11二.填空题(共7小题)7.已知菱形ABCD的周长为52cm,对角线AC=10cm,则BD=cm.8.如图,在菱形ABCD中,∠B=60°,对角线AC平分角∠BAD,点P是△ABC内一点,连接PA、PB、PC,若PA=6,PB=8,PC=10,则菱形ABCD的面积等于.9.如图,菱形ABCD和菱形BEFG的边长分别是5和2,∠A=60°,连结DF,则DF的长为.10.如果从一个四边形一边上的点到对边的视角是直角,那么称该点为直角点.例如,如图的四边形ABCD中,点M在CD边上,连结AM、BM,∠AMB=90°,则点M为直角点.若点E、F分别为矩形ABCD边AB、CD上的直角点,且AB=5,BC=,则线段EF的长为.11.在矩形ABCD中,AB=3,BC=4,点E、F分别在BC与CD上,且∠EAF=45°(1)如图甲,若EA=EF,则EF=;(2)如图乙,若CE=CF,则EF=.12.在矩形ABCD中,AB=2,BC=6,直线EF经过对角线BD的中点O分别交边AD、BC与点E、F,点G、H分别是OB、OD的中点,当四边形EGFH为矩形时,则BF的长.13.如图,已知矩形ABCD,AB=8,AD=4,E为CD边上一点,CE=5,点P从B点出发,以每秒1个单位的速度沿着BA边向终点A运动,连接PE,设点P运动的时间为t秒,则当t的值为时,△PAE是以PE为腰的等腰三角形.三.解答题(共9小题)14.四边形ABCD是菱形,AC=16,DB=12,DH⊥AB于点H,求DH的长.15.菱形ABCD中,点P为CD上一点,连接BP.(1)如图1,若BP⊥CD,菱形ABCD边长为10,PD=4,连接AP,求AP的长.(2)如图2,连接对角线AC、BD相交于点O,点N为BP的中点,过P作PM⊥AC于M,连接ON、MN.试判断△MON的形状,并说明理由.16.菱形ABCD中,对角线AC和BD相交于O,已知AC=8,BD=6,求AB边上的高.17.如图,在▱ABCD中,E、F分别为边AB、CD的中点,BD是对角线,过点A作AG∥DB交CB的延长线于点.(1)求证:△ADE≌△CBF;(2)若∠G=90°,求证:四边形DEBF是菱形.18.如图,在四边形ABCD中,对角线AC,BD相交于点O,AO=CO,BO=DO,且∠ABC+∠ADC=180°.(1)求证:四边形ABCD是矩形;(2)若∠ADF:∠FDC=3:2,DF⊥AC,求∠BDF的度数.19.在△ABC中,AD⊥BC于点D,点E为AC边的中点,过点A作AF∥BC,交DE的延长线于点F,连接CF.(1)如图1,求证:四边形ADCF是矩形;(2)如图2,当AB=AC时,取AB的中点G,连接DG、EG,在不添加任何辅助线和字母的条件下,请直接写出图中所有的平行四边形(不包括矩形ADCF).20.在四边形ABCD中,对角线AC、BD相交于点O,过点O的两条直线分别交边AB、CD、AD、BC于点E、F、G、H.【感知】如图①,若四边形ABCD是正方形,且AG=BE=CH=DF,则S四边形AEOG=S;正方形ABCD【拓展】如图②,若四边形ABCD是矩形,且S四边形AEOG=S矩形ABCD,设AB=a,AD=b,BE=m,求AG的长(用含a、b、m的代数式表示);【探究】如图③,若四边形ABCD是平行四边形,且AB=3,AD=5,BE=1,试确定F、G、H的位置,使直线EF、GH把四边形ABCD的面积四等分.21.如图,在▱ABCD中,∠BAD的平分线交BC于点E,交DC的延长线于F,以EC、EF为邻边作▱ECFG.(1)证明▱ECFG是菱形;(2)若∠ABC=120°,连结BC、CG,求∠BDG的度数;(3)若∠ABC=90°,AB=6,AD=8,M是EF的中点,求DM的长.22.已知,矩形ABCD中,AB=4cm,BC=8cm,AC的垂直平分线EF分别交AD、BC于点E、F,垂足为O.(1)如图1,连接AF、CE.求证:四边形AFCE为菱形.(2)如图1,求AF的长.(3)如图2,动点P、Q分别从A、C两点同时出发,沿△AFB和△CDE各边匀速运动一周.即点P自A→F→B→A停止,点Q自C→D→E→C停止.在运动过程中,点P的速度为每秒1cm,设运动时间为t秒.①问在运动的过程中,以A、P、C、Q四点为顶点的四边形有可能是矩形吗?若有可能,请求出运动时间t和点Q的速度;若不可能,请说明理由.②若点Q的速度为每秒0.8cm,当A、P、C、Q四点为顶点的四边形是平行四边形时,求t的值.参考答案与试题解析一.选择题(共6小题)1.如图,矩形ABCD中,BC>AB,对角线AC、BD交于O点,且AC=10,过B点作BE⊥AC 于E点,若BE=4,则AD的长等于()A.8 B.10 C.3D.4【分析】根据矩形的性质得出∠BAD=90°,设AD=BC=a,AB=DC=b,求出a2+b2=102,ab=40,解方程组求出a即可.【解答】解:∵四边形ABCD是矩形,∴∠BAD=90°,设AD=BC=a,AB=DC=b,∵AC=10,BE⊥AC,BE=4,∴a2+b2=102,又∵S矩形ABCD=2S△ABC∴ab=2××10×4=40,∵BC>AB,解得:a=4,b=2,即AD=4,故选:D.2.如图,矩形ABCD中,BH⊥AC,DE∥BH交CB的延长线于点E,交AB于点G,P是DE上一点,∠BPD=∠BCD,且G为PF的中点.则①AF=CH;②AC=3FH;③BE=BG;④若AE=,则FG=3,以上结论正确的个数是()A.1 B.2 C.3 D.4【分析】①利用矩形的性质,证明△AFD与△CHB全等,即可推出结论①正确;②先证明四边形PBHF为矩形,推出PB=FH,再证明△AFG与△BPG全等,推出AF=FH =CH,即可②正确;③假设结论成立,可推出∠BAC=45°,BA=BC,故矩形ABCD必为正方形,不符合题意,故③错误;④先证明△EPB与△BHC全等,推出EB=BC,AB垂直平分EC,求出AC的长度,再证△ABH与△BCH相似,求出BH的长度,最后证△AFG与△AHB相似,即可求出GF的长度为2,故④错误.【解答】解:①∵四边形ABCD为矩形,∴AD=BC,AD∥BC,∠BCD=∠ABC=90°,∴∠DAF=∠BCH,∵BH⊥AC,∴∠BHC=∠BHA=90°,∴△AFD≌△CHB(AAS),∴AF=CH.故①正确;②由①知,∠PFH=∠BHF=90°,∵∠BPD=∠BCD=90°,∴∠BPD=∠PFH=∠BHF=90°,∴四边形PBHF为矩形,∴PB=FH,PB∥FH,∵∠AFG=∠BPG=90°,FG=PG,∠AGF=∠BGP,∴△AFG≌△BPG(ASA),∴BP=AF,∴AF=FH,由①知,AF=CH,∴AF=FH=CH,∴AC=3FH,故②正确;③假设BE=BG,∵∠EBG=90°,∴∠E=∠BGE=45°,在Rt△EFC中,∠FCB=90°﹣45°=45°,∴∠BAC=45°,∴BA=BC,∴矩形ABCD必为正方形,不符合题意,故③错误;④∵DE∥BH,∴∠PEB=∠HBC,由②知,四边形PBFH为矩形,PB=FH=CH,∴∠EPB=∠BHC=90°,∴△EPB≌△BHC(AAS),∴EB=BC,∵∠ABC=90°,∴AB垂直平分EC,∴AC=AE=6,由②知,AF=FH=HC,∴AF=FH=HC=AC=2,∴AH=4,∵∠BHC=∠AHB=90°,∴∠BAH+∠ABH=90°,∠ABH+∠HBC=90°,∴∠BAH=∠HBC,∴△ABH∽△BCH,∴=,即=,∴BH=4,∵DE∥BH,∴△AFG∽△AHB,∴=,即=,∴CF=2,故④错误,故选:B.3.如图,在矩形ABCD中,AB=6,BC=6,点E是边BC上一动点,B关于AE的对称点为B′,过B′作B′F⊥DC于F,连接DB′,若△DB′F为等腰直角三角形,则BE的长是()A.6 B.3 C.3D.6﹣6【分析】如图作B′H⊥AD于H交BC于M.首先证明四边形DFB′H是正方形,设边长为x,则AH=6﹣x,HB′=x,在Rt△AHB′中,根据AB′2=AH2+HB′2,构建方程求出x,再利用相似三角形的性质解决问题即可;【解答】解:如图作B′H⊥AD于H交BC于M.∵∠B′HD=∠HDF=∠DFB′=90°,∴四边形DFB′H是矩形,∵FD=FB′,∴四边形DFB′H是正方形,设边长为x,则AH=6﹣x,HB′=x,在Rt△AHB′中,∵AB′2=AH2+HB′2,∴62=(6﹣x)2+x2,解得x=3,∴B′M=CF=6﹣3,∵△AHB′∽△B′ME,∴=,∴=,∴EB′=6﹣6,∴BE=B′E=6﹣6,故选:D.4.如图,已知E,F分别为正方形ABCD的边AB,BC的中点,AF与DE交于点M,O为BD 的中点,则下列结论:①∠AME=90°,②∠BAF=∠EDB,③AM=MF,④ME+MF=MB.其中正确结论的有()A.4个B.3个C.2个D.1个【分析】根据正方形的性质可得AB=BC=AD,∠ABC=∠BAD=90°,再根据中点定义求出AE=BF,然后利用“边角边”证明△ABF和△DAE全等,根据全等三角形对应角相等可得∠BAF=∠ADE,然后求出∠ADE+∠DAF=∠BAD=90°,从而求出∠AMD=90°,再根据邻补角的定义可得∠AME=90°,得出①正确;根据中线的定义判断出∠ADE≠∠EDB,然后求出∠BAF≠∠EDB,判断出②错误;设正方形ABCD的边长为2a,利用勾股定理列式求出AF,再根据似三角形对应边成比例求出AM,然后求出MF,消掉a即可得到AM=MF,判断出③正确;如图,过点M作MN⊥AB于N,于是得到==,得到NB =AB﹣AN=2a﹣a=a,根据勾股定理得到BM==a,于是得到结论.【解答】解:在正方形ABCD中,AB=BC=AD,∠ABC=∠BAD=90°,∵E、F分别为边AB,BC的中点,∴AE=BF=BC,在△ABF和△DAE中,,∴△ABF≌△DAE(SAS),∴∠BAF=∠ADE,∵∠BAF+∠DAF=∠BAD=90°,∴∠ADE+∠DAF=∠BAD=90°,∴∠AMD=180°﹣(∠ADE+∠DAF)=180°﹣90°=90°,∴∠AME=180°﹣∠AMD=180°﹣90°=90°,故①正确;∵DE是△ABD的中线,∴∠ADE≠∠EDB,∴∠BAF≠∠EDB,故②错误;设正方形ABCD的边长为2a,则BF=a,在Rt△ABF中,AF==a,∵∠BAF=∠MAE,∠ABC=∠AME=90°,∴△AME∽△ABF,∴=,即=,解得:AM=a,∴MF=AF﹣AM=a﹣a=a,∴AM=MF,故③正确;设正方形ABCD的边长为2a,则BF=a,在Rt△ABF中,AF==a,∵∠BAF=∠MAE,∠ABC=∠AME=90°,∴△AME∽△ABF,∴=,即=,解得:AM=a,∴MF=AF﹣AM=a﹣a=a,∴AM=MF,故③正确;如图,过点M作MN⊥AB于N,则==,即==,解得MN=a,AN=a,∴NB=AB﹣AN=2a﹣a=a,根据勾股定理,BM==a,∵ME+MF=a+a=a,MB=a=a,∴ME+MF=MB.综上所述,正确的结论有①③④共3个.故选:B.5.如图,以△ABC的各边为边,在边BC的同侧分别作三个正方形ABDI,BCFE,ACHG,对于四边形ADEG的形状,某班学生在一次数学活动课中,通过动手实践,探索出如下结论,其中错误的是()A.若△ABC为任意三角形,则四边形ADEG是平行四边形B.若∠BAC=90°,则四边形ADEG是矩形C.若AC=AB,则四边形ADEG是菱形D.若∠BAC=135°且AC=AB,则四边形ADEG是正方形【分析】根据全等三角形的判定定理SAS证得△BDE≌△BAC,由△BDE≌△BAC,可得全等三角形的对应边DE=AG.然后利用正方形对角线的性质、周角的定义推知∠EDA+∠DAG =180°,易证ED∥GA,即可判断A;求出∠DAG=135°,根据矩形的判定即可判断B;然后由周角的定义求得∠BAC=135°;根据AD=AC=和菱形的判定即可判断C;根据正方形的判定即可判断D.【解答】解:A、∵四边形ABDI、四边形BCFE、四边形ACHG都是正方形,∴AC=AG,AB=BD,BC=BE,∠GAC=∠EBC=∠DBA=90°.∴∠ABC=∠EBD(同为∠EBA的余角).在△BDE和△BAC中,,∴△BDE≌△BAC(SAS),∴DE=AC=AG,∠BAC=∠BDE.∵AD是正方形ABDI的对角线,∴∠BDA=∠BAD=45°.∵∠EDA=∠BDE﹣∠BDA=∠BDE﹣45°,∠DAG=360°﹣∠GAC﹣∠BAC﹣∠BAD=360°﹣90°﹣∠BAC﹣45°=225°﹣∠BAC,∴∠EDA+∠DAG=∠BDE﹣45°+225°﹣∠BAC=180°,∴DE∥AG,∴四边形ADEG是平行四边形(一组对边平行且相等),正确,故本选项不符合题意;B、∵四边形ABDI和四边形ACHG是正方形,∴∠DAI=45°,∠GAC=90°,∵∠BAC=90°,∴∠DAG=360°﹣45°﹣90°﹣90°=135°,∵四边形ADEG是平行四边形,∴四边形ADEG不是矩形,错误,故本选项符合题意;C、∵四边形ADEG是平行四边形,∴若要四边形ADEG是菱形,则需AD=AG,即AD=AC.∵AD=AB,∴当AB=AD,即AB=AC时,四边形ADEG是菱形,正确,故本选项不符合题意;D、∵当∠BAC=135°时,∠DAG=360°﹣45°﹣90°﹣135°=90°,即平行四边形ADEG是平行四边形,∵当AB=AD,即AB=AC时,四边形ADEG是菱形,∴四边形ADEG是正方形,即当∠BAC=135°且AC=AB时,四边形ADEG是正方形,正确,故本选项不符合题意;故选:B.6.如图是以KL所在的直线为对称轴的轴对称图形,六边形EFGHLK的各个内角相等,记四边形HCH′L、四边形EKE′A、△BGF的周长分别为C1、C2、C3,且C1=2C2=4C3,已知FG=LK,EF=6,则AB的长是()A.9.5 B.10 C.10.5 D.11【分析】根据六边形EFGHLK的各个内角相等,即可得出△BFG,△AEK,△CHL都是等边三角形,由轴对称可得,四边形HCH′L、四边形EKE′A都是菱形,再根据C1=2C2=4C3,FG=LK,EF=6,即可得到AB=BF+EF+AE=11.【解答】解:∵六边形EFGHLK的各个内角相等,∴该六边形的每个内角为120°,每个外角都是60°,∴△BFG,△AEK,△CHL都是等边三角形,∴∠B=∠BAC=∠ACB=60°,BF=FG,AE=AK,CL=HL,∴△ABC是等边三角形,∴AB=AC,即BF+FE+AE=AK+KL+CL,又∵BF=FG=KL,∴EF=CL=6=CH,由轴对称可得,四边形HCH′L、四边形EKE′A都是菱形,∵C1=2C2,∴AE=CH=3,又∵2C2=4C3,∴C3=C2=×12=6,∴BF=×6=2,∴AB=BF+EF+AE=2+6+3=11,故选:C.二.填空题(共7小题)7.已知菱形ABCD的周长为52cm,对角线AC=10cm,则BD=24 cm.【分析】根据菱形的性质得出AC⊥BD,BD=2DO,AO=OC=AC=5cm,AD=AB=BC=CD =13cm,根据勾股定理求出OD即可.【解答】解:∵四边形ABCD是菱形,∴AC⊥BD,BD=2DO,AO=OC=AC==5cm,∵菱形ABCD的周长为52cm,∴AD=AB=BC=CD=×52cm=13cm,在Rt△AOD中,由勾股定理得:AD2=AO2+0D2,即OD==12(cm),∴BD=2OD=24cm,故答案为:24.8.如图,在菱形ABCD中,∠B=60°,对角线AC平分角∠BAD,点P是△ABC内一点,连接PA、PB、PC,若PA=6,PB=8,PC=10,则菱形ABCD的面积等于50.【分析】将线段AP绕点A顺时针旋转60°得到线段AM,连接PM,想办法证明∠APH=30°,利用勾股定理求出AB的平方即可解决问题.【解答】解:将线段AP绕点A顺时针旋转60°得到线段AM,连接PM,作AH⊥BP于H.∵四边形ABCD是菱形,∴AB=BC,∵∠ABC=60°,∴△ABC是等边三角形,∵AM=AP,∠MAP=60°,∴△AMP是等边三角形,∵∠MAP=∠BAC,∴∠MAB=∠PAC,∴△MAB≌△PAC,∴BM=PC=10,∵PM2+PB2=100,BM2=100,∴PM2+PB2=BM2,∴∠MPB=90°,∵∠APM=60°,∴∠APB=150°,∠APH=30°,∴AH=PA=3,PH=3,BH=8+3,∴AB2=AH2+BH2=100+48,∴菱形ABCD的面积=2•△ABC的面积=2××AB2=50+72,故答案为50+72.9.如图,菱形ABCD和菱形BEFG的边长分别是5和2,∠A=60°,连结DF,则DF的长为.【分析】延长FG交AD于点M,过点D作DH⊥AB交AB于点H,交GF的延长线于点N,由菱形的性质和勾股定理再结合已知条件可求出NF,DN的长,在直角三角形DNF中,再利用勾股定理即可求出DF的长.【解答】解:延长FG交AD于点M,过点D作DH⊥AB交AB于点H,交GF的延长线于点N,∵四边形ABCD和四边形BEFG都是菱形,∴GF∥BE,EF∥AM,∴四边形AMFE是平行四边形,∴AM=EF=2,MF=AE=AB+BE=5+2=7,∴DM=AD﹣AM=5﹣2=3,∵∠A=60°,∴∠DAH=30°,∴MN=DM=,∴DN==,NF=MF﹣MN=,在Rt△DNF中,DF==,故答案为:.10.如果从一个四边形一边上的点到对边的视角是直角,那么称该点为直角点.例如,如图的四边形ABCD中,点M在CD边上,连结AM、BM,∠AMB=90°,则点M为直角点.若点E、F分别为矩形ABCD边AB、CD上的直角点,且AB=5,BC=,则线段EF的长为或.【分析】作FH⊥AB于点H,利用已知得出△ADF∽△FCB,进而得出=,求得构造的直角三角形的两条直角边即可得出答案.【解答】解:作FH⊥AB于点H,连接EF.∵∠AFB=90°,∴∠AFD+∠BFC=90°,∵∠AMD+∠DAM=90°,∴∠DAF=∠BFC又∵∠D=∠C,∴△ADF∽△FCB,∴=,即=,∴FC=2或3.∵点F,E分别为矩形ABCD边CD,AB上的直角点,∴AE=FC,∴当FC=2时,AE=2,EH=1,∴EF2=FH2+EH2=()2+12=7,∴EF=.当FC=3时,此时点E与点H重合,即EF=BC=,综上,EF=或.故答案为:或.11.在矩形ABCD中,AB=3,BC=4,点E、F分别在BC与CD上,且∠EAF=45°(1)如图甲,若EA=EF,则EF=;(2)如图乙,若CE=CF,则EF=7﹣4..【分析】(1)已知EA=EF,∠EAF=45°,由三角形的内角和得∠AEF=90°,∠AEB+∠FEC=90°,又因∠BAE+∠AEB=90°,等量代换得∠BAE=∠CEF,从而证明△ABE≌△ECF;EF的长可由勾股定理求出.(2)作辅助线FM和EN,已知△CEF,构建两个等腰△DEM,△BEN可求出线段DF,AM,FC,BE和AN的长;证明△ANE∽△FMA,再由两个三角形相似的性质求出相似比,解出x 的值,由勾股定理(或三角函数)求出EF的长.【解答】解:(1)如图甲所示:∵EA=EF,∴△AEF是等腰直角形,∠EAF=∠EFA,∵∠EAF=45°,∴∠EFA=45°,又∵在△AEF中,∠EAF+∠EFA+∠AEF=180°,∴∠AEF=180°﹣45°﹣45°=90°,又∵∠AEB+∠AEF+∠FEC=180°,∴∠AEB+∠FEC=90°,又∵△ABE中,∠B+∠BAE+∠AEB=180°,∠B=90°,∴∠BAE+∠AEB=90°,∴∠BAE=∠CEF,在△ABE和△ECF中,∴△ABE≌△ECF(AAS)∴AB=EC,BE=CF,又∵AB=3,BC=4,∴EC=3,CF=1,在Rt△CEF中,由勾股定理得:==故答案为.(2)如图乙所示:作DM=DF,BN=BE,分别交AD,AB于点M和点N,设MD=x,∵四边形ABCDA是矩形,∴∠B=∠D=90°,∴∠BNE=45°,∠DMF=90°,又∵∠BNE+∠ENA=180°,∠FMD+∠FMA=180°,∴∠ENA=135°,∠FMA=135°,又∵∠EAF=45°,∠BAD=∠BAE+∠EAF+∠FAD=90°,∴∠BAE+∠FAD=45°,∵∠BAE+∠NEA=45°,在△ANE和△FMA中,∴△ANE∽△FMA(AA)∴;又∵MD=x,∴DF=x,∵CE=CF,AB=3,BC=4,∴FC=EC=3﹣x,BE=AB=x+1,AN=2﹣x,∴,解得:2﹣4,或﹣2﹣4(舍去),∴FC=3﹣()=7﹣2,∴EF=FC=(7﹣2)=7﹣4.故答案为7﹣4.12.在矩形ABCD中,AB=2,BC=6,直线EF经过对角线BD的中点O分别交边AD、BC与点E、F,点G、H分别是OB、OD的中点,当四边形EGFH为矩形时,则BF的长或.【分析】根据矩形ABCD中,AB=2,BC=6,可求出对角线的长,再由点G、H分别是OB、OD的中点,可得GH=BD,从而求出GH的长,若四边形EGFH为矩形时,EF=GH,可求EF的长,通过作辅助线,构造直角三角形,由勾股定理可求出MF的长,最后通过设未知数,列方程求出BF的长.【解答】解:如图:过点E作EM⊥BC,垂直为M,矩形ABCD中,AB=2,BC=6,∴AB=EM=CD=2,AD=BC=6,∠A=90°,OB=OD,在Rt△ABD中,BD=,又∵点G、H分别是OB、OD的中点,∴GH=BD=,当四边形EGFH为矩形时,GH=EF=,在Rt△EMF中,FM==,易证△BOF≌△DOE(AAS),∴BF=DE,∴AE=FC,设BF=x,则FC=6﹣x,由题意得:x﹣(6﹣x)=,或(6﹣x)﹣x=,∴x=或x=,故答案为:或.13.如图,已知矩形ABCD,AB=8,AD=4,E为CD边上一点,CE=5,点P从B点出发,以每秒1个单位的速度沿着BA边向终点A运动,连接PE,设点P运动的时间为t秒,则当t的值为2或时,△PAE是以PE为腰的等腰三角形.【分析】根据矩形的性质得出CD=AB=8,BC=AD=4,求出AP=8﹣t,DE=3,由勾股定理求出AE=5,PE2=EF2+PF2=42+(5﹣t)2,分为两种情况:①当AE=PE时,②当AP =PE时,求出即可.【解答】解:根据题意得:BP=t,∵四边形ABCD是矩形,AB=8,AD=4,∴CD=AB=8,BC=AD=4,∴AP=8﹣t,DE=DC﹣CE=8﹣5=3,由勾股定理得:AE==5,过E作EF⊥AB于F,则∠EFA=∠EFB=90°,∵∠C=∠B=90°,∴四边形BCEF是矩形,∴BF=CE=5,BC=EF=4,∴PF=5﹣t,由勾股定理得:PE2=EF2+PF2=42+(5﹣t)2,①当AE=PE时,52=42+(5﹣t)2,解得:t=2,t=8,∵t=8不符合题意,舍去;②当AP=PE时,(8﹣t)2=42+(5﹣t)2,解得:t=,即当t的值为2或时,△PAE是以PE为腰的等腰三角形,故答案为:2或.三.解答题(共9小题)14.四边形ABCD是菱形,AC=16,DB=12,DH⊥AB于点H,求DH的长.【分析】先根据菱形的性质得OA=OC,OB=OD,AC⊥BD,再利用勾股定理计算出AB=10,然后根据菱形的面积公式得到•AC•BD=DH•AB,再解关于DH的方程即可.【解答】解:∵四边形ABCD是菱形,∴OA=OC=8,OB=OD=6,AC⊥BD,在Rt△AOB中,AB==10,∵S菱形ABCD=•AC•BD,S菱形ABCD=DH•AB,∴DH•10=×12×16,∴DH=.15.菱形ABCD中,点P为CD上一点,连接BP.(1)如图1,若BP⊥CD,菱形ABCD边长为10,PD=4,连接AP,求AP的长.(2)如图2,连接对角线AC、BD相交于点O,点N为BP的中点,过P作PM⊥AC于M,连接ON、MN.试判断△MON的形状,并说明理由.【分析】(1)在RT△BCP中利用勾股定理求出PB,在RT△ABP中利用勾股定理求出PA 即可.(2)如图2中,延长PM交BC于E.先证明PD=BE,再利用三角形中位线定理证明MN =BE,ON=PD即可.【解答】解:(1)如图1中,∵四边形ABCD是菱形,∴AB=BC=CD=AD=10,AB∥CD∵PD=4,∴PC=6,∵PB⊥CD,∴PB⊥AB,∴∠CPB=∠ABP=90°,在RT△PCB中,∵∠CPB=90°PC=6,BC=10,∴PB===8,在RT△ABP中,∵∠ABP=90°,AB=10,PB=8,∴PA===2.(2)△OMN是等腰三角形.理由:如图2中,延长PM交BC于E.∵四边形ABCD是菱形,∴AC⊥BD,CB=CD,∵PE⊥AC,∴PE∥BD,∴=,∴CP=CE,∴PD=BE,∵CP=CE,CM⊥PE,∴PM=ME,∵PN=NB,∴MN=BE,∵BO=OD,BN=NP,∴ON=PD,∴ON=MN,∴△OMN是等腰三角形.16.菱形ABCD中,对角线AC和BD相交于O,已知AC=8,BD=6,求AB边上的高.【分析】首先利用菱形的性质得出AB的长,再利用菱形面积求法得出DE的长.【解答】解:∵菱形ABCD中,对角线AC和BD相交于O,AC=8,BD=6,∴AO=4,BO=3,∠AOB=90°,∴AB=5,∴×6×8=DE×AB,解得:DE=,即AB边上的高为:.17.如图,在▱ABCD中,E、F分别为边AB、CD的中点,BD是对角线,过点A作AG∥DB交CB的延长线于点.(1)求证:△ADE≌△CBF;(2)若∠G=90°,求证:四边形DEBF是菱形.【分析】(1)根据已知条件证明AE=CF,从而根据SAS可证明两三角形全等;(2)先证明DE=BE,再根据邻边相等的平行四边形是菱形,从而得出结论.【解答】证明:(1)∵四边形ABCD是平行四边形,∴AB=CD,AD=BC,∠A=∠C,∵点E、F分别是AB、CD的中点,∴AE=AB,CF=CD,∴AE=CF,在△ADE和△CBF中,∵,∴△ADE≌△CBF(SAS);(2)∵∠G=90°,AG∥BD,AD∥BG,∴四边形AGBD是矩形,∴∠ADB=90°,在Rt△ADB中∵E为AB的中点,∴AE=BE=DE,∵DF∥BE,DF=BE,∴四边形DEBF是平行四边形,∴四边形DEBF是菱形.18.如图,在四边形ABCD中,对角线AC,BD相交于点O,AO=CO,BO=DO,且∠ABC+∠ADC =180°.(1)求证:四边形ABCD是矩形;(2)若∠ADF:∠FDC=3:2,DF⊥AC,求∠BDF的度数.【分析】(1)根据平行四边形的判定得出四边形ABCD是平行四边形,求出∠ABC=90°,根据矩形的判定得出即可;(2)求出∠FDC的度数,根据三角形内角和定理求出∠DCO,根据矩形的性质得出OD=OC,求出∠CDO,即可求出答案.【解答】(1)证明:∵AO=CO,BO=DO,∴四边形ABCD是平行四边形,∴∠ABC=∠ADC,∵∠ABC+∠ADC=180°,∴∠ABC=∠ADC=90°,∴四边形ABCD是矩形;(2)解:∵∠ADC=90°,∠ADF:∠FDC=3:2,∴∠FDC=36°,∵DF⊥AC,∴∠DCO=90°﹣36°=54°,∵四边形ABCD是矩形,∴CO=OD,∴∠ODC=∠DCO=54°,∴∠BDF=∠ODC﹣∠FDC=18°.19.在△ABC中,AD⊥BC于点D,点E为AC边的中点,过点A作AF∥BC,交DE的延长线于点F,连接CF.(1)如图1,求证:四边形ADCF是矩形;(2)如图2,当AB=AC时,取AB的中点G,连接DG、EG,在不添加任何辅助线和字母的条件下,请直接写出图中所有的平行四边形(不包括矩形ADCF).【分析】(1)由△AEF≌△CED,推出EF=DE,又AE=EC,推出四边形ADCF是平行四边形,只要证明∠ADC=90°,即可推出四边形ADCF是矩形.(2)四边形ABDF、四边形AGEF、四边形GBDE、四边形AGDE、四边形GDCE都是平行四边形.【解答】(1)证明:∵AF∥BC,∴∠AFE=∠EDC,∵E是AC中点,∴AE=EC,在△AEF和△CED中,,∴△AEF≌△CED,∴EF=DE,∵AE=EC,∴四边形ADCF是平行四边形,∵AD⊥BC,∴∠ADC=90°,∴四边形ADCF是矩形.(2)∵线段DG、线段GE、线段DE都是△ABC的中位线,又AF∥BC,∴AB∥DE,DG∥AC,EG∥BC,∴四边形ABDF、四边形AGEF、四边形GBDE、四边形AGDE、四边形GDCE都是平行四边形.20.在四边形ABCD中,对角线AC、BD相交于点O,过点O的两条直线分别交边AB、CD、AD、BC于点E、F、G、H.【感知】如图①,若四边形ABCD是正方形,且AG=BE=CH=DF,则S四边形AEOG=S;正方形ABCD【拓展】如图②,若四边形ABCD是矩形,且S四边形AEOG=S矩形ABCD,设AB=a,AD=b,BE=m,求AG的长(用含a、b、m的代数式表示);【探究】如图③,若四边形ABCD是平行四边形,且AB=3,AD=5,BE=1,试确定F、G、H的位置,使直线EF、GH把四边形ABCD的面积四等分.【分析】【感知】如图①,根据正方形的性质和全等三角形的性质即可得到结论;【拓展】如图②,过O作ON⊥AD于N,OM⊥AB于M,根据图形的面积得到mb=AG•a,于是得到结论;【探究】如图③,过O作KL⊥AB,PQ⊥AD,则KL=2OK,PQ=2OQ,根据平行四边形的面积公式得到=,根据三角形的面积公式列方程即可得到结论.【解答】解:【感知】如图①,∵四边形ABCD是正方形,∴∠OAG=∠OBE=45°,OA=OB,在△AOG与△BOE中,,∴△AOG≌△BOE,∴S四边形AEOG=S△AOB=S正方形ABCD;故答案为:;【拓展】如图②,过O作ON⊥AD于N,OM⊥AB于M,∵S△AOB=S矩形ABCD,S四边形AEOG=S矩形ABCD,∴S△AOB=S四边形AEOG,∵S△AOB=S△BOE+S△AOE,S四边形AEOG=S△AOG+S△AOE,∴S△BOE=S△AOG,∵S△BOE=BE•OM=m b=mb,S△AOG=AG•ON=AG•a=AG•a,∴mb=AG•a,∴AG=;【探究】如图③,过O作KL⊥AB,PQ⊥AD,则KL=2OK,PQ=2OQ,∵S平行四边形ABCD=AB•KL=AD•PQ,∴3×2OK=5×2OQ,∴=,∵S△AOB=S平行四边形ABCD,S四边形AEOG=S平行四边形ABCD,∴S△AOB=S四边形AEOG,∴S△BOE=S△AOG,∵S△BOE=BE•OK=×1×OK,S△AOG=AG•OQ,∴×1×OK=AG•OQ,∴=AG=,∴当AG=CH=,BE=DF=1时,直线EF、GH把四边形ABCD的面积四等分.21.如图,在▱ABCD中,∠BAD的平分线交BC于点E,交DC的延长线于F,以EC、EF为邻边作▱ECFG.(1)证明▱ECFG是菱形;(2)若∠ABC=120°,连结BC、CG,求∠BDG的度数;(3)若∠ABC=90°,AB=6,AD=8,M是EF的中点,求DM的长.【分析】(1)平行四边形的性质可得AD∥BC,AB∥CD,再根据平行线的性质证明∠CEF =∠CFE,根据等角对等边可得CE=CF,再有条件四边形ECFG是平行四边形,可得四边形ECFG为菱形,即可解决问题;(2)先判断出∠BEG=120°=∠DCG,再判断出AB=BE,进而得出BE=CD,即可判断出△BEG≌△DCG(SAS),再判断出∠CGE=60°,进而得出△BDG是等边三角形,即可得出结论;(3)首先证明四边形ECFG为正方形,再证明△BME≌△DMC可得DM=BM,∠DMC=∠BME,再根据∠BMD=∠BME+∠EMD=∠DMC+∠EMD=90°可得到△BDM是等腰直角三角形,由等腰直角三角形的性质即可得到结论.【解答】解:(1)证明:,∵AF平分∠BAD,∴∠BAF=∠DAF,∵四边形ABCD是平行四边形,∴AD∥BC,AB∥CD,∴∠DAF=∠CEF,∠BAF=∠CFE,∴∠CEF=∠CFE,∴CE=CF,又∵四边形ECFG是平行四边形,∴四边形ECFG为菱形;(2)∵四边形ABCD是平行四边形,∴AB∥DC,AB=DC,AD∥BC,∵∠ABC=120°,∴∠BCD=60°,∠BCF=120°由(1)知,四边形CEGF是菱形,∴CE=GE,∠BCG=∠BCF=60°,∴CG=GE=CE,∠DCG=120°,∵EG∥DF,∴∠BEG=120°=∠DCG,∵AE是∠BAD的平分线,∴∠DAE=∠BAE,∵AD∥BC,∴∠DAE=∠AEB,∴∠BAE=∠AEB,∴AB=BE,∴BE=CD,∴△BEG≌△DCG(SAS),∴BG=DG,∠BGE=∠DGC,∴∠BGD=∠CGE,∵CG=GE=CE,∴△CEG是等边三角形,∴∠CGE=60°,∴∠BGD=60°,∵BG=DG,∴△BDG是等边三角形,∴∠BDG=60°;(3)如图2中,连接BM,MC,∵∠ABC=90°,四边形ABCD是平行四边形,∴四边形ABCD是矩形,又由(1)可知四边形ECFG为菱形,∠ECF=90°,∴四边形ECFG为正方形.∵∠BAF=∠DAF,∴BE=AB=DC,∵M为EF中点,∴∠CEM=∠ECM=45°,∴∠BEM=∠DCM=135°,在△BME和△DMC中,∵,∴△BME≌△DMC(SAS),∴MB=MD,∠DMC=∠BME.∴∠BMD=∠BME+∠EMD=∠DMC+∠EMD=90°,∴△BMD是等腰直角三角形.∵AB=6,AD=8,∴BD=10,∴DM=BD=5.22.已知,矩形ABCD中,AB=4cm,BC=8cm,AC的垂直平分线EF分别交AD、BC于点E、F,垂足为O.(1)如图1,连接AF、CE.求证:四边形AFCE为菱形.(2)如图1,求AF的长.(3)如图2,动点P、Q分别从A、C两点同时出发,沿△AFB和△CDE各边匀速运动一周.即点P自A→F→B→A停止,点Q自C→D→E→C停止.在运动过程中,点P的速度为每秒1cm,设运动时间为t秒.①问在运动的过程中,以A、P、C、Q四点为顶点的四边形有可能是矩形吗?若有可能,请求出运动时间t和点Q的速度;若不可能,请说明理由.②若点Q的速度为每秒0.8cm,当A、P、C、Q四点为顶点的四边形是平行四边形时,求t的值.【分析】(1)证△AEO≌△CFO,推出OE=OF,根据平行四边形和菱形的判定推出即可;(2)设AF=CF=a,根据勾股定理得出关于a的方程,求出即可;(3)①只有当P运动到B点,Q运动到D点时,以A、P、C、Q四点为顶点的四边形有可能是矩形,求出时间t,即可求出答案;②分为三种情况,P在AF上,P在BF上,P 在AB上,根据平行四边形的性质求出即可.【解答】(1)证明:∵四边形ABCD是矩形,∴AD∥BC,∴∠AEO=∠CFO,∵AC的垂直平分线EF,∴AO=OC,AC⊥EF,在△AEO和△CFO中∵,∴△AEO≌△CFO(AAS),∴OE=OF,∵OA=OC,∴四边形AECF是平行四边形,∵AC⊥EF,∴平行四边形AECF是菱形;(2)解:设AF=acm,∵四边形AECF是菱形,∴AF=CF=acm,∵BC=8cm,∴BF=(8﹣a)cm,在Rt△ABF中,由勾股定理得:42+(8﹣a)2=a2,a=5,即AF=5cm;(3)解:①在运动过程中,以A、P、C、Q四点为顶点的四边形有可能是矩形,只有当P运动到B点,Q运动到D点时,以A、P、C、Q四点为顶点的四边形有可能是矩形,P点运动的时间是:(5+3)÷1=8,Q的速度是:4÷8=0.5,即Q的速度是0.5cm/s;②分为三种情况:第一、P在AF上,∵P的速度是1cm/s,而Q的速度是0.8cm/s,∴Q只能在CD上,此时当A、P、C、Q四点为顶点的四边形不是平行四边形;第二、当P在BF上时,Q在CD或DE上,只有当Q在DE上时,当A、P、C、Q四点为顶点的四边形才有可能是平行四边形,如图,∵AQ=8﹣(0.8t﹣4),CP=5+(t﹣5),∴8﹣(0.8t﹣4)=5+(t﹣5),t=,第三情况:当P在AB上时,Q在DE或CE上,此时当A、P、C、Q四点为顶点的四边形不是平行四边形;即t=.。
特殊四边形培优习题精选及答案
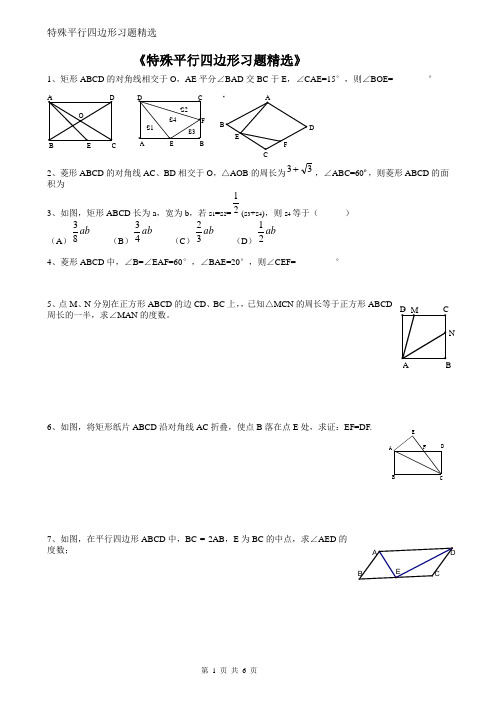
《特殊平行四边形习题精选》1、矩形ABCD 的对角线相交于O ,AE 平分∠BAD 交BC 于E ,∠CAE=15°,则∠BOE=________°2、菱形ABCD 的对角线AC 、BD 相交于O ,△AOB 的周长为33 ,∠ABC=60º,则菱形ABCD 的面积为__________3、如图,矩形ABCD 长为a ,宽为b ,若s 1=s 2=21(s 3+s 4),则s 4等于( )(A )ab 83 (B )ab 43 (C )ab 32 (D )ab214、菱形ABCD 中,∠B=∠EAF=60°,∠BAE=20°,则∠CEF=_________°5、点M 、N 分别在正方形ABCD 的边CD 、BC 上,,已知△MCN 的周长等于正方形ABCD周长的一半,求∠MAN 的度数。
6、如图,将矩形纸片ABCD 沿对角线AC 折叠,使点B 落在点E 处,求证:EF=DF.7、如图,在平行四边形ABCD 中,BC = 2AB ,E 为BC 的中点,求∠AED 的度数;D C BA MNA B CDOE A B C D E FS1S2S4S3A B C DEF FEDCB A8、如图,以正方形ABCD 的对角线AC 为一边,延长AB 到E ,使AE = AC ,以AE 为一边作菱形AEFC ,若菱形的面积为29,求正方形边长;9、如图AD 是⊿ABC 边BC 边上的高线,E 、F 、G 分别是AB 、BC 、AC 的中点,求证:四边形EDGF 是等腰梯形;10、如图1,正方形ABCD 边长为1,G 为CD 边上的一个动点(点G 与C 、D 不重合),以CG 为一边向正方形ABCD 外作正方形GCEF ,连接DE 交BG 的延长线于点H 。
(1)求证:①△BCG ≌△DCE ;②BH ⊥DE 。
(2)当点G 运动到什么位置时,BH 垂直平分DE ?请说明理由。
北师大版九年级数学上期末备考压轴题专项培优:特殊的平行四边形(解析版)

期末备考压轴题专项培优:特殊的平行四边形1.如图,四边形ABCD是正方形,△ABE是等边三角形,M为对角线BD(不含B点)上任意一点,将BM绕点B逆时针旋转60°得到BN,连接EN、AM、CM.设点N 的坐标为(m,n).(1)若建立平面直角坐标系,满足原点在线段BD上,点B(﹣1,0),A(0,1).且BM=t(0<t≤2),则点D的坐标为(1,0),点C的坐标为(0,﹣1);请直接写出点N纵坐标n的取值范围是0<n≤;(2)若正方形的边长为2,求EC的长,以及AM+BM+CM的最小值.(提示:连结MN:=+1,=﹣1)解:(1)如图1,以直线BD为x轴,直线AC为y轴,建立平面直角坐标系,∵四边形ABCD是正方形,∴OA=OB=OC=OD,∵点B(﹣1,0),A(0,1),∴D(1,0),C(0,﹣1);过N作NH⊥BD于h,∴∠NHB=90°,∵将BM绕点B逆时针旋转60°得到BN,∴∠NBH=60°,BM=BN,∴NH=BN=t,∵0<t≤2,∴点N纵坐标n的取值范围是0<n≤;故答案为:(1,0),(0,﹣1);0<n≤;(2)如图所示,连接MN,过E作EH⊥BC,交CB的延长线于H,由旋转可得,BM=BN,∠NBM=60°,∴△BMN是等边三角形,∴MN=BM,∵△ABE是等边三角形,∴BE=BA,∠ABE=60°,∴∠ABM=∠EBN,∴△ABM≌△EBN(SAS),∴AM=EN,∴AM+BM+CM=EN+MN+CM,∴当E,N,M,C在同一直线上时,AM+BM+CN的最小值是CE的长,又∵∠ABE=60°,∠ABH=90°,∴∠EBH=30°,∴Rt△EBH中,EH=EB=×2=1,∴BH===,∴CH=2+,∴Rt△CEH中,CE====;∴AM+BM+CM的最小值为+.2.如图,在▱ABCD中,∠BAD的平分线交BC于点E,交DC的延长线于F,以EC、CF为邻边作▱ECFG.(1)证明▱ECFG是菱形;(2)若∠ABC=120°,连结BD、CG,求∠BDG的度数;(3)若∠ABC=90°,AB=6,AD=8,M是EF的中点,求DM的长.解:(1)证明:,∵AF平分∠BAD,∴∠BAF=∠DAF,∵四边形ABCD是平行四边形,∴AD∥BC,AB∥CD,∴∠DAF=∠CEF,∠BAF=∠CFE,∴∠CEF=∠CFE,∴CE=CF,又∵四边形ECFG是平行四边形,∴四边形ECFG为菱形;(2)∵四边形ABCD是平行四边形,∴AB∥DC,AB=DC,AD∥BC,∵∠ABC=120°,∴∠BCD=60°,∠BCF=120°由(1)知,四边形CEGF是菱形,∴CE=GE,∠BCG=∠BCF=60°,∴CG=GE=CE,∠DCG=120°,∵EG∥DF,∴∠BEG=120°=∠DCG,∵AE是∠BAD的平分线,∴∠DAE=∠BAE,∵AD∥BC,∴∠DAE=∠AEB,∴∠BAE=∠AEB,∴AB=BE,∴BE=CD,∴△BEG≌△DCG(SAS),∴BG=DG,∠BGE=∠DGC,∴∠BGD=∠CGE,∵CG=GE=CE,∴△CEG是等边三角形,∴∠CGE=60°,∴∠BGD=60°,∵BG=DG,∴△BDG是等边三角形,∴∠BDG=60°;(3)如图2中,连接BM,MC,∵∠ABC=90°,四边形ABCD是平行四边形,∴四边形ABCD是矩形,又由(1)可知四边形ECFG为菱形,∠ECF=90°,∴四边形ECFG为正方形.∵∠BAF=∠DAF,∴BE=AB=DC,∵M为EF中点,∴∠CEM=∠ECM=45°,∴∠BEM=∠DCM=135°,在△BME和△DMC中,∵,∴△BME≌△DMC(SAS),∴MB=MD,∠DMC=∠BME.∴∠BMD=∠BME+∠EMD=∠DMC+∠EMD=90°,∴△BMD是等腰直角三角形.∵AB=6,AD=8,∴BD=10,∴DM=BD=5.3.如图,在正方形ABCD中,对角线AC、BD相交于点O,以AD为边向外作等边△ADE,连接CE,交BD于F.(1)如图1,若AE=,求DF的长;(2)如图2,点M为AB的延长线上一点,连接CM,连接FM且FM平分∠AMC,求证:CM=MF﹣AM.解:(1)如图1,连接OE,∵四边形ABCD是正方形,∴AD=CD,∠ADC=90°,OA=OD=OB=OC∵△ADE是等边三角形∴AD=DE=AE=,∠ADE=60°∴CD=AD=,OD=OB=∵AE=DE,OD=OA∴OE垂直平分AD即OE⊥AD,DH=AH∴OE=OH+EH=+=,∵∠ADC=∠DHE=90°∴CD∥OE∴△CDF∽△EOF∴=,即DF=OF∵DF+OF=OD=∴OF=﹣DF∴DF=(﹣DF),解得:DF=﹣1.(2)如图2,连接EO,过点F作PQ⊥CD交EO于N,在MA上截取MT=MC,连接FT,设正方形边长为a,∵四边形ABCD是正方形,△ADE是等边三角形∴AD=AB=CD=DE=a,∠ADC=∠DAB=90°∠ADE=60°易证OE⊥AD∴OE=a,OD=a,由(1)知△CDF∽△EOF∴=,即a•DF=a•OF∵DF+OF=a∴OF=a﹣DF∴a•DF=a(a﹣DF)∴DF=a,∵△DPF是等腰直角三角形∴DP=PF=DF=a,∴FQ=a﹣a=a=CP,∵FM平分∠AMC,∴∠CMF=∠AMF在△MCF和△MTF中∴△MCF≌△MTF(SAS)∴CF=FT∴Rt△CFP≌Rt△FTQ(HL)∴QT=PF=a,∵AQ=DP∴AQ=QT∵BM+AB﹣AT=MT=CM∴CM﹣BM=AB﹣AT=a﹣2×a=a,CM+BM=MT+BM=BT+2BM=a﹣2×a+2BM=a+2BM∴CM2﹣BM2=(CM﹣BM)(CM+BM)=a(a+2BM)∵CM2﹣BM2=BC2=a2,∴a(a+2BM)=a2,∴BM=a在Rt△BCM中,tan∠BMC===,∴∠BMC=60°∴∠AMF=30°∴=cos∠AMF=cos30°=∴2MQ=MF∵2MQ=2BM+2BQ=2BM+2BT+2QT=(BM+BT)+(BM+BT+AT)=CM+AM ∴CM+AM=MF即CM=MF﹣AM.4.在菱形ABCD中,∠ABC=60°,BD为菱形的一条对角线.(1)如图1,过A作AE⊥BC于点E,交BD于点F,若EF=2,求菱形ABCD的面积;(2)如图2,M为菱形ABCD外一点,过A作AN⊥BM交BM的延长线于点N,连接AM,DM,AG⊥DM于点G,且∠AMN=∠AMD,求证:DM=BM+AM.(1)解:如图1中,∵四边形ABC都是菱形,∠ABC=60°,∴∠ABD=∠DBC=30°,∵AE⊥BC,∴∠BEF=90°,∵EF=2,∴BF=2EF=4,∠BFE=60°,∵∠BFE=∠ABF+∠F AB,∴∠ABF=∠F AB=30°,∴BF=AF=4,∴AE=AF+EF=6,∴AB==4,∴BC=AB=4,∴S=BC•AE=24.菱形ABCD(2)证明:如图2中,∵∠AMN=∠AMG,AN⊥MN,AG⊥DM,∴AN=AG,∵∠MNA=∠MGA=90°,AM=AM,AN=AG,∴Rt△MAN≌Rt△MAG(HL),∴NM=MG,∵∠ANB=∠AGD=90°,AN=AG,AB=AD,∴Rt△ANB≌Rt△AGD(HL),∴∠ABN=∠ADG,BN=DG,∴∠BMD=△BAD=120°,∴∠NMG=60°,∴∠AMN=∠AMG=30°,∴DM﹣BM=MG+DG﹣(BN﹣MN)=2MN=AM,∴DM=BM+AM.5.如图,点A、B、C、D在同一条直线上,点E、F分别在直线AD的两侧,且AE=DF,∠A=∠D,AB=DC.(1)求证:四边形BFCE是平行四边形;(2)若AD=12,DC=3,∠EBD=60°,则BE=6时,四边形BFCE是菱形.(只需完成填空,不需写出具体过程.)(1)证明:∵在△ABE和△DCF中,∴△ABE≌△DCF(SAS),∴BE=FC,∠ABE=∠DCF,∴∠EBC=∠FCB,∴BE∥FC,∴四边形BFCE是平行四边形;(2)解:当四边形BFCE是菱形,则BE=EC,∵AD=12,DC=3,AB=DC,∴BC=6,∵∠EBD=60°,EB=EC,∴△EBC是等边三角形,∴BE=6.故答案为:6.6.已知:如图,在▱ABCD中,G、H分别是AD、BC的中点,E、O、F分别是对角线BD上的四等分点,顺次连接G、E、H、F.(1)求证:四边形GEHF是平行四边形;(2)当▱ABCD满足AB⊥BD条件时,四边形GEHF是菱形;(3)若BD=2AB,①探究四边形GEHF的形状,并说明理由;②当AB=2,∠ABD=120°时,直接写出四边形GEHF的面积.(1)证明:连接AC,如图1所示:∵四边形ABCD是平行四边形,∴OA=OC,OB=OD,∴BD的中点在AC上,∵E、O、F分别是对角线BD上的四等分点,∴E、F分别为OB、OD的中点,∵G是AD的中点,∴GF为△AOD的中位线,∴GF∥OA,GF=OA,同理:EH∥OC,EH=OC,∴EH=GF,EH∥GF,∴四边形GEHF是平行四边形;(2)解:当▱ABCD满足AB⊥BD条件时,四边形GEHF是菱形;理由如下:连接GH,如图2所示:则AG=BH,AG∥BH,∴四边形ABHG是平行四边形,∴AB∥GH,∵AB⊥BD,∴GH⊥BD,∴GH⊥EF,∴四边形GEHF是菱形;故答案为:AB⊥BD;(3)解:①四边形GEHF是矩形;理由如下:由(2)得:四边形GEHF是平行四边形,∴GH=AB,∵BD=2AB,∴AB=BD=EF,∴GH=EF,∴四边形GEHF是矩形;②作AM⊥BD于M,GN⊥BD于N,如图3所示:则AM∥GN,∵G是AD的中点,∴GN是△ADM的中位线,∴GN=AM,∵∠ABD=120°,∴∠ABM=60°,∴∠BAM=30°,∴BM=AB=1,AM=BM=,∴GN=,∵BD=2AB=4,∴EF=BD=2,∴△EFG的面积=EF×GN=×2×=,∴四边形GEHF的面积=2△EFG的面积=.7.如图,边长为6的正方形ABCD中,E,F分别是AD,AB上的点,AP⊥BE,P为垂足.(1)如图1,AF=BF,AE=2,点T是射线PF上的一个动点,当△ABT为直角三角形时,求AT的长;(2)如图2,若AE=AF,连接CP,求证:CP⊥FP.(1)解:在正方形ABCD中,可得∠DAB=90°.∵在Rt△BAE中,tan∠ABE===,∴∠ABE=30°.点T是射线PF上的一个动点,当△ABT为直角三角形时,分三种情况:①当点T在AB的上方,∠ATB=90°,显然此时点T和点P重合,即AT=AP=AB=3;②当点T在AB的下方,∠ATB =90°,如图①所示.在Rt△APB中,由AF=BF,可得:AF=BF=PF=3,∴∠BPF=∠FBP=30°,∴∠BFT=60°.在Rt△ATB中,TF=BF=AF=3,∴△FTB是等边三角形,∴TB=3,AT==3;③当点T在AB的下方,∠ABT=90°时,如图②所示.在Rt△FBT中,∠BFT=60°,BF=3,BT=BF•tan60°=3.在Rt△ATB中:AT==3.综上所述:当△ABT为直角三角形时,AT的长为3或3或3;(2)证明:如图③所示,∵四边形ABCD是正方形,∴AB=AD=BC,AD∥BC,∠DAB=90°,∴∠3=∠4.∵在Rt△EAB中,AP⊥BE,∴∠1+∠2=90°,∠3+∠2=90°,∴∠1=∠3,∴∠1=∠3=∠4,∵tan∠1=,tan∠3=,∴=,∵AE=AF,AB=BC,∴=,∴△PBC∽△P AF,∴∠5=∠6.∵∠6+∠7=90°,∴∠5+∠7=90°,即∠CPF=90°,∴CP⊥FP.8.已知:如图,在▱ABCD中,G、H分别是AD、BC的中点,AE⊥BD,CF⊥BD,垂足分别为E、F.(1)求证:四边形GEHF是平行四边形;(2)已知AB=5,AD=8.求四边形GEHF是矩形时BD的长.(1)证明:∵四边形ABCD是平行四边形,∴AD∥BC,AD=BC,∴∠GDE=∠FBH,∵G、H分别是AD、BC的中点,AE⊥BD,CF⊥BD,∴在Rt△AED和Rt△CFB中,EG=AD=GD,FH=BC=HB,∴EG=FH,∠GED=∠GDE,∠FBH=∠BFH,∴∠GED=∠BFH,∴EG∥FH,∴四边形GEHF是平行四边形;(2)解:连接GH,当四边形GEHF是矩形时,∠EHF=∠BFC=90°,∵∠FBH=∠BFH,∴△EFH∽△CBF,∴=,由(1)可得:GA∥HB,GA=HB,∴四边形GABH是平行四边形,∴GH=AB=5,∵在矩形GEHF中,EF=GH,且AB=5,AD=8,∴=,解得:BF=,∴BE=BF﹣EF=﹣5=,在△ABE和△CDF中∴△ABE≌△CDF(AAS),∴BE=DF=,∴BD=BF+DF=+=.9.如图,点M是正方形ABCD的边BC上一点,连接AM,点E是线段AM上一点,∠CDE的平分线交AM延长线于点F.(1)如图1,若点E为线段AM的中点,BM:CM=1:2,BE=,求AB的长;(2)如图2,若DA=DE,求证:BF+DF=AF.解:(1)设BM=x,则CM=2x,BC=3x,∵BA=BC,∴BA=3x.在Rt△ABM中,E为斜边AM中点,∴AM=2BE=2.由勾股定理可得AM2=MB2+AB2,即40=x2+9x2,解得x=2.∴AB=3x=6.(2)延长FD交过点A作垂直于AF的直线于H点,过点D作DP⊥AF于P点.∵DF平分∠CDE,∴∠1=∠2.∵DE=DA,DP⊥AF∴∠3=∠4.∵∠1+∠2+∠3+∠4=90°,∴∠2+∠3=45°.∴∠DFP=90°﹣45°=45°.∴AH=AF.∵∠BAF+∠DAF=90°,∠HAD+∠DAF=90°,∴∠BAF=∠DAH.又AB=AD,∴△ABF≌△ADH(SAS).∴AF=AH,BF=DH.∵Rt△F AH是等腰直角三角形,∴HF=AF.∵HF=DH+DF=BF+DF,∴BF+DF=AF.10.在四边形ABCD中,对角线AC、BD相交于点O,过点O的两条直线分别交边AB、CD、AD、BC于点E、F、G、H.【感知】如图①,若四边形ABCD是正方形,且AG=BE=CH=DF,则S四边形AEOG= S 正方形ABCD ;【拓展】如图②,若四边形ABCD 是矩形,且S 四边形AEOG =S 矩形ABCD ,设AB =a ,AD =b ,BE =m ,求AG 的长(用含a 、b 、m 的代数式表示);【探究】如图③,若四边形ABCD 是平行四边形,且AB =3,AD =5,BE =1,试确定F 、G 、H 的位置,使直线EF 、GH 把四边形ABCD 的面积四等分.解:【感知】如图①,∵四边形ABCD 是正方形,∴∠OAG =∠OBE =45°,OA =OB ,在△AOG 与△BOE 中,, ∴△AOG ≌△BOE ,∴S 四边形AEOG =S △AOB =S 正方形ABCD ;故答案为:;【拓展】如图②,过O 作ON ⊥AD 于N ,OM ⊥AB 于M ,∵S △AOB =S 矩形ABCD ,S 四边形AEOG =S 矩形ABCD ,∴S △AOB =S 四边形AEOG ,∵S △AOB =S △BOE +S △AOE ,S 四边形AEOG =S △AOG +S △AOE , ∴S △BOE =S △AOG , ∵S △BOE =BE •OM =mb =mb ,S △AOG =AG •ON =AG •a =AG •a , ∴mb =AG •a ,∴AG =;【探究】如图③,过O作KL⊥AB,PQ⊥AD,则KL=2OK,PQ=2OQ,∵S平行四边形ABCD=AB•KL=AD•PQ,∴3×2OK=5×2OQ,∴=,∵S△AOB =S平行四边形ABCD,S四边形AEOG=S平行四边形ABCD,∴S△AOB =S四边形AEOG,∴S△BOE =S△AOG,∵S△BOE =BE•OK=×1×OK,S△AOG=AG•OQ,∴×1×OK=AG•OQ,∴=AG=,∴当AG=CH=,BE=DF=1时,直线EF、GH把四边形ABCD的面积四等分.11.如图,在矩形ABCD中,AB=8cm,BC=16cm,点P从点D出发向点A运动,运动到点A停止,同时,点Q从点B出发向点C运动,运动到点C即停止,点P、Q 的速度都是1cm/s.连接PQ、AQ、CP.设点P、Q运动的时间为ts.(1)当t为何值时,四边形ABQP是矩形;(2)当t为何值时,四边形AQCP是菱形;(3)分别求出(2)中菱形AQCP的周长和面积.解:(1)∵在矩形ABCD中,AB=8cm,BC=16cm,∴BC=AD=16cm,AB=CD=8cm,由已知可得,BQ=DP=tcm,AP=CQ=(16﹣t)cm,在矩形ABCD中,∠B=90°,AD∥BC,当BQ=AP时,四边形ABQP为矩形,∴t=16﹣t,得t=8,故当t=8s时,四边形ABQP为矩形;(2)∵AP=CQ,AP∥CQ,∴四边形AQCP为平行四边形,∴当AQ=CQ时,四边形AQCP为菱形即=16﹣t时,四边形AQCP为菱形,解得t=6,故当t=6s时,四边形AQCP为菱形;(3)当t=6s时,AQ=CQ=CP=AP=16﹣6=10cm,则周长为4×10cm=40cm;面积为10cm×8cm=80cm2.12.如图,在四边形ABCD中,AB=AD,CB=CD,E是CD上的点,BE交AC于点F,连接DF.(1)求证:∠BAF=∠DAF,∠AFD=∠CFE;(2)若AB∥CD,试证明:四边形ABCD是菱形;(3)在(2)的条件下,试确定点E的位置,使得∠EFD=∠BCD,并说理由.证明:(1)在△ABC和△ADC中,,∴△ABC≌△ADC,∴∠BAC=∠DAC,在△ABF和△ADF中,∴△ABF≌△ADF,∴∠AFB=∠AFD,∵∠CFE=∠AFB,∴∠AFD=∠CFE,∴∠BAF=∠DAC,∠AFD=∠CFE;(2)∵AB∥CD,∴∠BAC=∠ACD,∵∠BAC=∠DAC,∴∠BAC=∠ACD,∴∠DAC=∠ACD,∴AD=CD,∵AB=AD,CB=CD,∴AB=CB=CD=AD,∴四边形ABCD是菱形;(3)∵四边形ABCD是菱形,∴BC=CD,∠BCF=∠DCF,∵CF=CF,∴△BCF≌△DCF,∴∠CBF=∠CDF,∵BE⊥CD,∴∠BEC=∠DEF=90°,∴∠EFD=∠BCD.13.如图,在△ABC中,点O是边AC上一个点,过点O作直线MN∥BC分别交∠ACB、外角∠ACD的平分线于点E、F.(1)若CE=8,CF=6,求OC的长;(2)连接AE、AF.问:当点O在边AC上运动到什么位置时,四边形AECF是矩形?证明你的结论.(1)证明:∵EF交∠ACB的平分线于点E,交∠ACB的外角平分线于点F,∴∠OCE=∠BCE,∠OCF=∠DCF,∵EF∥BC,∴∠OEC=∠BCE,∠OFC=∠DCF,∴∠OEC=∠OCE,∠OFC=∠OCF,∴OE=OC,OF=OC,∴OE=OF;∵∠OCE+∠BCE+∠OCF+∠DCF=180°,∴∠ECF=90°,在Rt△CEF中,由勾股定理得:EF==10,∴OC=OE=EF=5;(2)当点O在边AC上运动到AC中点时,四边形AECF是矩形.理由如下:当O为AC的中点时,AO=CO,∵EO=FO,∴四边形AECF是平行四边形,∵∠ECF=90°,∴平行四边形AECF是矩形.14.如图,菱形ABCD的对角线AC、BD相交于点O,过点D作DE∥AC且DE=AC,连接CE、OE,连接AE交OD于点F.(1)求证:OE=CD;(2)若菱形ABCD的边长为2,∠ABC=60°.求AE的长.(1)证明:在菱形ABCD中,OC=AC.∴DE=OC.∵DE∥AC,∴四边形OCED是平行四边形.∵AC⊥BD,∴平行四边形OCED是矩形.∴OE=CD.(2)在菱形ABCD中,∠ABC=60°,∴AC=AB=2.∴在矩形OCED中,CE=OD=.在Rt△ACE中,AE=.15.如图,以△ABC的各边,在边BC的同侧分别作三个正方形ABDI,BCFE,ACHG.(1)求证:△BDE≌△BAC;(2)求证:四边形ADEG是平行四边形.(3)直接回答下面两个问题,不必证明:①当△ABC满足什么条件时,四边形ADEG是矩形?②当△ABC满足什么条件时,四边形ADEG是正方形?(1)证明:∵四边形ABDI、四边形BCFE、四边形ACHG都是正方形,∴AC=AG,AB=BD,BC=BE,∠GAC=∠EBC=∠DBA=90°.∴∠ABC=∠EBD(同为∠EBA的余角).在△BDE和△BAC中,,∴△BDE≌△BAC(SAS),(2)∵△BDE≌△BAC,∴DE=AC=AG,∠BAC=∠BDE.∵AD是正方形ABDI的对角线,∴∠BDA=∠BAD=45°.∵∠EDA=∠BDE﹣∠BDA=∠BDE﹣45°,∠DAG=360°﹣∠GAC﹣∠BAC﹣∠BAD=360°﹣90°﹣∠BAC﹣45°=225°﹣∠BAC∴∠EDA+∠DAG=∠BDE﹣45°+225°﹣∠BAC=180°∴DE∥AG,∴四边形ADEG是平行四边形(一组对边平行且相等).(3)①当四边形ADEG是矩形时,∠DAG=90°.则∠BAC=360°﹣∠BAD﹣∠DAG﹣∠GAC=360°﹣45°﹣90°﹣90°=135°,即当∠BAC=135°时,平行四边形ADEG是矩形;②当四边形ADEG是正方形时,∠DAG=90°,且AG=AD.由①知,当∠DAG=90°时,∠BAC=135°.∵四边形ABDI是正方形,∴AD=AB.又∵四边形ACHG是正方形,∴AC=AG,∴AC=AB.∴当∠BAC=135°且AC=AB时,四边形ADEG是正方形.。
平行四边形和特殊四边形提高练习常考题和培优题(供参考)

平行四边形和特殊四边形提高练习常考题和培优题一.选择题(共5小题)1.如图,把大小相同的两个矩形拼成如下形状,则△FBD是()A.等边三角形B.等腰直角三角形C.一般三角形D.等腰三角形2.如图,正方形ABCD和正方形CEFG中,点D在CG上,BC=,CE=3,H 是AF的中点,那么CH的长是()A.3.5 B.C. D.23.如图,在矩形ABCD中,AB=4,BC=8,对角线AC、BD相交于点O,过点O 作OE垂直AC交AD于点E,则AE的长是()A.3 B.5 C.2.4 D.2.54.如图,在△ABC中,CF⊥AB于F,BE⊥AC于E,M为BC的中点,EF=7,BC=10,则△EFM的周长是()A.17 B.21 C.24 D.275.如图,在矩形ABCD中,AB=6,AD=8,P是AD上不与A和D重合的一个动点,过点P分别作AC和BD的垂线,垂足为E、F,则PE+PF的值为()A.10 B.4.8 C.6 D.5二.填空题(共4小题)6.如图,在矩形ABCD中,对角线AC与BD相交于点O,AE平分∠BAD交BC 于点E,若∠CAE=15°,则∠BOE的度数等于.7.如图,将平行四边形ABCD的边DC延长到E,使CE=CD,连接AE交BC于F,∠AFC=n∠D,当n=时,四边形ABEC是矩形.8.如图,在正五边形ABCDE中,连接AC、AD、CE,CE交AD于点F,连接BF,则线段AC、BF、CD之间的关系式是.9.如图,在平面直角坐标系中,O为原点,四边形OABC是矩形,A(﹣10,0),C(0,3),点D是OA的中点,点P在BC边上运动,当△ODP是腰长为5的等腰三角形时,点P的坐标是.三.解答题(共31小题)10.如图,正方形ABCD中,AE=AB,直线DE交BC于点F,求∠BEF的度数.11.如图,梯形ABCD中,AD∥BC,AB=CD,对角线AC、BD交于点O,AC⊥BD,E、F、G、H分别为AB、BC、CD、DA的中点.(1)求证:四边形EFGH为正方形;(2)若AD=1,BC=3,求正方形EFGH的边长.12.如图,点E、F分别是正方形ABCD的边CD和AD的中点,BE和CF交于点P.求证:AP=AB.13.如图,点P为正方形ABCD对角线BD上一点,PE⊥BC于E,PF⊥DC于F.(1)求证:PA=EF;(2)若正方形ABCD的边长为a,求四边形PFCE的周长.14.如图1,在正方形ABCD中,点E为BC上一点,连接DE,把△DEC沿DE折叠得到△DEF,延长EF交AB于G,连接DG.(1)求∠EDG的度数.(2)如图2,E为BC的中点,连接BF.①求证:BF∥DE;②若正方形边长为6,求线段AG的长.15.如图①,在正方形ABCD中,F是对角线AC上的一点,点E在BC的延长线上,且BF=EF.(1)求证:BF=DF;(2)求证:∠DFE=90°;(3)如果把正方形ABCD改为菱形,其他条件不变(如图②),当∠ABC=50°时,∠DFE=度.16.已知正方形ABCD中,对角线AC、BD相交于O.①如图1,若E是AC上的点,过A 作AG⊥BE于G,AG、BD交于F,求证:OE=OF②如图2,若点E在AC的延长线上,AG⊥EB交EB的延长线于G,AG延长DB 延长线于点F,其它条件不变,OE=OF还成立吗?17.如图,点P是菱形ABCD中对角线AC上的一点,且PE=PB.(1)求证:PE=PD;(2)求证:∠PDC=∠PEB;(3)若∠BAD=80°,连接DE,试求∠PDE的度数,并说明理由.18.如图,正方形ABCD中,AB=1,点P是BC边上的任意一点(异于端点B、C),连接AP,过B、D两点作BE⊥AP于点E,DF⊥AP于点F.(1)求证:EF=DF﹣BE;(2)若△ADF的周长为,求EF的长.19.如图,正方形ABCD的对角线AC、BD的交点为O,以O为端点引两条互相垂直的射线OM、ON,分别交边AB、BC于点E、F.(1)求证:0E=OF;(2)若正方形的边长为4,求EF的最小值.20.如图,在正方形ABCD中,点E是边AD上任意一点,BE的垂直平分线FG 交对角AC于点F.求证:(1)BF=DF;(2)BF⊥FE.21.已知:如图所示,四边形ABCD中,∠ABC=∠ADC=90°,M是AC上任一点,O是BD的中点,连接MO,并延长MO到N,使NO=MO,连接BN与ND.(1)判断四边形BNDM的形状,并证明;(2)若M是AC的中点,则四边形BNDM的形状又如何?说明理由.22.如图,在△ABC中,O是边AC上的一动点,过点O作直线MN∥BC,设MN 交∠BCA的平分线于点E,交∠BCA的外角平分线于点F.(1)求证:OE=OF;(2)当点O运动到何处时,四边形AECF是矩形?23.(1)如图矩形ABCD的对角线AC、BD交于点O,过点D作DP∥OC,且DP=OC,连接CP,判断四边形CODP的形状并说明理由.(2)如果题目中的矩形变为菱形,结论应变为什么?说明理由.(3)如果题目中的矩形变为正方形,结论又应变为什么?说明理由.24.如图1,已知AB∥CD,AB=CD,∠A=∠D.(1)求证:四边形ABCD为矩形;(2)E是AB边的中点,F为AD边上一点,∠DFC=2∠BCE.①如图2,若F为AD中点,DF=1.6,求CF的长度:②如图2,若CE=4,CF=5,则AF+BC=,AF=.25.如图,直线a、b相交于点A,C、E分别是直线b、a上两点且BC⊥a,DE ⊥b,点M、N是EC、DB的中点.求证:MN⊥BD.26.如图所示,在梯形ABCD中,AD∥BC,∠B=90°,AD=24cm,BC=26cm,动点P从点A出发沿AD方向向点D以1cm/s的速度运动,动点Q从点C开始沿着CB方向向点B以3cm/s的速度运动.点P、Q分别从点A和点C同时出发,当其中一点到达端点时,另一点随之停止运动.(1)经过多长时间,四边形PQCD是平行四边形?(2)经过多长时间,四边形PQBA是矩形?(3)经过多长时间,当PQ不平行于CD时,有PQ=CD.27.如图,E、F是正方形ABCD的边AD上的两个动点,满足AE=DF.连接CF 交BD于G,连接BE交AG于H.已知正方形ABCD的边长为4cm,解决下列问题:(1)求证:BE⊥AG;(2)求线段DH的长度的最小值.28.如图,点M是矩形ABCD的边AD的中点,点P是BC边上一动点,PE⊥MC,PF⊥BM,垂足为E、F.(1)当矩形ABCD的长与宽满足什么条件时,四边形PEMF为矩形?猜想并证明你的结论.(2)在(1)中,当点P运动到什么位置时,矩形PEMF变为正方形,为什么?29.某校数学兴趣小组开展了一次课外活动,过程如下:如图①,正方形ABCD 中,AB=4,将三角板放在正方形ABCD上,使三角板的直角顶点与D点重合.三角板的一边交AB于点P,另一边交BC的延长线于点Q.(1)求证:AP=CQ;(2)如图②,小明在图1的基础上作∠PDQ的平分线DE交BC于点E,连接PE,他发现PE和QE存在一定的数量关系,请猜测他的结论并予以证明;(3)在(2)的条件下,若AP=1,求PE的长.30.如图,在菱形ABCD中,AB=4cm,∠ADC=120°,点E、F同时由A、C两点出发,分别沿AB、CB方向向点B匀速移动(到点B为止),点E的速度为1cm/s,点F的速度为2cm/s,经过t秒△DEF为等边三角形,求t的值.31.如图,在Rt△ABC中,∠ABC=90°,点D是AC的中点,作∠ADB的角平分线DE交AB于点E,(1)求证:DE∥BC;(2)若AE=3,AD=5,点P为BC上的一动点,当BP为何值时,△DEP为等腰三角形.请直接写出所有BP的值.32.已知:如图,BF、BE分别是∠ABC及其邻补角的角平分线,AE⊥BE,垂足为点E,AF⊥BF,垂足为点F.EF分别交边AB、AC于点M、N.求证:(1)四边形AFBE是矩形;(2)BC=2MN.33.如图,在边长为5的菱形ABCD中,对角线BD=8,点O是直线BD上的动点,OE⊥AB于E,OF⊥AD于F.(1)对角线AC的长是,菱形ABCD的面积是;(2)如图1,当点O在对角线BD上运动时,OE+OF的值是否发生变化?请说明理由;(3)如图2,当点O在对角线BD的延长线上时,OE+OF的值是否发生变化?若不变请说明理由,若变化,请直接写出OE、OF之间的数量关系,不用明理由.34.如图,已知Rt△ABD≌Rt△FEC,且B、D、C、E在同一直线上,连接BF、AE.(1)求证:四边形ABFE是平行四边形.(2)若∠ABD=60°,AB=2cm,DC=4cm,将△ABD沿着BE方向以1cm/s的速度运动,设△ABD运动的时间为t,在△ABD运动过程中,试解决以下问题:(1)当四边形ABEF是菱形时,求t的值;(2)是否存在四边形ABFE是矩形的情形?如果存在,求出t的值,如果不存在,请说明理由.35.已知,矩形ABCD中,AB=4cm,BC=8cm,AC的垂直平分线EF分别交AD、BC于点E、F,垂足为O.(1)如图1,连接AF、CE.求证:四边形AFCE为菱形.(2)如图1,求AF的长.(3)如图2,动点P、Q分别从A、C两点同时出发,沿△AFB和△CDE各边匀速运动一周.即点P自A→F→B→A停止,点Q自C→D→E→C停止.在运动过程中,点P的速度为每秒1cm,设运动时间为t秒.①问在运动的过程中,以A、P、C、Q四点为顶点的四边形有可能是矩形吗?若有可能,请求出运动时间t和点Q的速度;若不可能,请说明理由.②若点Q的速度为每秒0.8cm,当A、P、C、Q四点为顶点的四边形是平行四边形时,求t的值.36.如图1,E,F是正方形ABCD的边上两个动点,满足AE=DF,连接CF交BD 于G,连接BE交AG于点H(1)求证:AG⊥BE;(2)如图2,连DH,若正方形的边长为4,则线段DH长度的最小值是.37.如图,在菱形ABCD中,AB=2,∠DAB=60°,点E时AD边的中点,点M时AB边上的一个动点(不与点A重合),延长ME交CD的延长线于点N,连接MD,AN.(1)求证:四边形AMDN是平行四边形.(2)填空:①当AM的值为时,四边形AMDN是矩形;②当AM的值为时,四边形AMDN是菱形.38.如图,已知正方形OABC的边长为4,顶点A、C分别在x、y轴的正半轴上,M是BC的中点,点P(0,m)是线段oc上的一动点9点P不与点O、C重合0,直线PM交AB的延长线于点D.(1)求点D的坐标;(用含m的代数式表示)(2)若△APD是以AP边为一腰的等腰三角形,求m的值.39.如图,在△ABC中,∠ABC=90°,点D为AC的中点,过点C作CE⊥BD于点E,过点A作BD的平行线,交CE的延长线于点F,在AF的延长线上截取FG=BD,连接BG、DF.(1)证明:四边形BDFG是菱形;(2)若AC=10,CF=6,求线段AG的长度.40.如图,在正方形ABCD中,点E在边AD上,点F在边BC的延长线上,连接EF与边CD相交于点G,连接BE与对角线AC相交于点H,AE=CF,BE=EG.(1)求证:EF∥AC;(2)求∠BEF大小;(3)若EB=4,则△BAE的面积为.初二数学平行四边形和特殊四边形提高练习常考题和培优题参考答案与试题解析一.选择题(共5小题)1.(2012春•炎陵县校级期中)如图,把大小相同的两个矩形拼成如下形状,则△FBD是()A.等边三角形B.等腰直角三角形C.一般三角形D.等腰三角形【分析】根据正方形性质得出FG=BC,∠G=∠C=90°,GB=CD,根据SAS证△FGB ≌△BCD,推出∠FBG=∠BDC,BF=BD,求出∠DBC+∠FBG=90°,求出∠FBD的度数即可.【解答】解:∵大小相同的两个矩形GFEB、ABCD,∴FG=BE=AD=BC,GB=EF=AB=CD,∠G=∠C=∠ABG=∠ABC=90°,∵在△FGB和△BCD中,∴△FGB≌△BCD,∴∠FBG=∠BDC,BF=BD,∵∠BDC+∠DBC=90°,∴∠DBC+∠FBG=90°,∴∠FBD=180°﹣90°=90°,即△FBD是等腰直角三角形,故选B.【点评】本题考查了等腰直角三角形,全等三角形的性质和判定,正方形性质的应用,关键是证出△FGB≌△BCD,主要考查学生运用性质进行推理的能力.2.(2015春•江阴市期中)如图,正方形ABCD和正方形CEFG中,点D在CG上,BC=,CE=3,H是AF的中点,那么CH的长是()A.3.5 B.C. D.2【分析】根据正方形的性质求出AB=BC=,CE=EF=3,∠E=90°,延长AD交EF于M,连接AC、CF,求出AM=4,FM=2,∠AMF=90°,根据正方形性质求出∠ACF=90°,根据直角三角形斜边上的中线性质求出CH=AF,根据勾股定理求出AF即可.【解答】解:∵正方形ABCD和正方形CEFG中,点D在CG上,BC=,CE=3,∴AB=BC=,CE=EF=3,∠E=90°,延长AD交EF于M,连接AC、CF,则AM=BC+CE=4,FM=EF﹣AB=2,∠AMF=90°,∵四边形ABCD和四边形GCEF是正方形,∴∠ACD=∠GCF=45°,∴∠ACF=90°,∵H为AF的中点,∴CH=AF,在Rt△AMF中,由勾股定理得:AF==2,∴CH=,故选:C.【点评】本题考查了勾股定理,正方形的性质,直角三角形斜边上的中线的应用,解此题的关键是能正确作出辅助线,并求出AF的长和得出CH=AF,有一定的难度.3.(2015春•泗洪县校级期中)如图,在矩形ABCD中,AB=4,BC=8,对角线AC、BD相交于点O,过点O作OE垂直AC交AD于点E,则AE的长是()A.3 B.5 C.2.4 D.2.5【分析】根据矩形的性质得出∠CDE=90°,AD=BC=8,AB=DC=4,AO=OC,根据线段垂直平分线性质得出AE=CE,在Rt△CDE中,由勾股定理得出CE2=CD2+DE2,代入求出即可.【解答】解:∵在矩形ABCD中,AB=4,BC=8,∴∠CDE=90°,AD=BC=8,AB=DC=4,AO=OC,∵OE⊥AC,∴AE=CE,在Rt△CDE中,由勾股定理得:CE2=CD2+DE2,即AE2=42+(8﹣AE)2,解得:AE=5,故选B.【点评】本题考查了矩形的性质,勾股定理,线段垂直平分线性质的应用,解此题的关键是得出关于AE的方程.4.(2015秋•无锡期中)如图,在△ABC中,CF⊥AB于F,BE⊥AC于E,M为BC的中点,EF=7,BC=10,则△EFM的周长是()A.17 B.21 C.24 D.27【分析】根据CF⊥AB于F,BE⊥AC于E,M为BC的中点,利用直角三角形斜边上的中线等于斜边的一半,求出FM和ME的长,即可求解.【解答】解:∵CF⊥AB,M为BC的中点,∴MF是Rt△BFC斜边上的中线,∴FM=BC=×10=5,同理可得,ME=BC=×10=5,又∵EF=7,∴△EFM 的周长=EF +ME +FM=7+5+5=17.故选A .【点评】此题主要考查学生对直角三角形斜边上的中线这个知识点的理解和掌握,解答此题的关键是利用直角三角形斜边上的中线等于斜边的一半,求出FM 和ME 的长.5.(2015春•乌兰察布校级期中)如图,在矩形ABCD 中,AB=6,AD=8,P 是AD 上不与A 和D 重合的一个动点,过点P 分别作AC 和BD 的垂线,垂足为E 、F ,则PE +PF 的值为( )A .10B .4.8C .6D .5【分析】连接OP ,利用勾股定理列式求出BD ,再根据矩形的对角线相等且互相平分求出OA 、OD ,然后根据S △AOD =S △AOP +S △DOP 列方程求解即可.【解答】解:如图,连接OP ,∵AB=6,AD=8,∴BD===10,∵四边形ABCD 是矩形,∴OA=OD=×10=5,∵S △AOD =S △AOP +S △DOP , ∴××6×8=×5•PE +×5•PF ,解得PE +PF=4.8.故选B .【点评】本题考查了矩形的性质,三角形的面积,熟记性质并利用三角形的面积列出方程是解题的关键.二.填空题(共4小题)6.(2016春•东平县期中)如图,在矩形ABCD 中,对角线AC 与BD 相交于点O ,AE 平分∠BAD 交BC 于点E ,若∠CAE=15°,则∠BOE 的度数等于 75° .【分析】由矩形ABCD ,得到OA=OB ,根据AE 平分∠BAD ,得到等边三角形OAB ,推出AB=OB ,求出∠OAB 、∠OBC 的度数,根据平行线的性质和等角对等边得到OB=BE ,根据三角形的内角和定理即可求出答案.【解答】解:∵四边形ABCD是矩形,∴AD∥BC,AC=BD,OA=OC,OB=OD,∠BAD=90°,∴OA=OB,∠DAE=∠AEB,∵AE平分∠BAD,∴∠BAE=∠DAE=45°=∠AEB,∴AB=BE,∵∠CAE=15°,∴∠DAC=45°﹣15°=30°,∠BAC=60°,∴△BAO是等边三角形,∴AB=OB,∠ABO=60°,∴∠OBC=90°﹣60°=30°,∵AB=OB=BE,∴∠BOE=∠BEO=(180°﹣30°)=75°.故答案为75°.【点评】本题主要考查了三角形的内角和定理,矩形的性质,等边三角形的性质和判定,平行线的性质,角平分线的性质,等腰三角形的判定等知识点,解此题的关键是求出∠OBC的度数和求OB=BE.7.(2014春•武昌区期中)如图,将平行四边形ABCD的边DC延长到E,使CE=CD,连接AE交BC于F,∠AFC=n∠D,当n=2时,四边形ABEC是矩形.【分析】首先根据四边形ABCD是平行四边形,得到四边形ABEC是平行四边形,然后证得FC=FE,利用对角线互相相等的四边形是矩形判定四边形ABEC是矩形.【解答】解:当∠AFC=2∠D时,四边形ABEC是矩形.∵四边形ABCD是平行四边形,∴BC∥AD,∠BCE=∠D,由题意易得AB∥EC,AB∥EC,∴四边形ABEC是平行四边形.∵∠AFC=∠FEC+∠BCE,∴当∠AFC=2∠D时,则有∠FEC=∠FCE,∴FC=FE,∴四边形ABEC是矩形,故答案为:2.【点评】此题考查了平行四边形的性质以及矩形的判定.此题难度适中,注意掌握数形结合思想的应用,解题的关键是了解矩形的判定定理.8.(2015春•南长区期中)如图,在正五边形ABCDE中,连接AC、AD、CE,CE 交AD于点F,连接BF,则线段AC、BF、CD之间的关系式是AC2+BF2=4CD2.【分析】首先根据菱形的判定方法,判断出四边形ABCF是菱形,再根据菱形的性质,即可判断出AC⊥BF;然后根据勾股定理,可得OB2+OC2=BC2,据此推得AC2+BF2=4CD2即可.【解答】解:∵五边形ABCDE是正五边形,∴AB∥CE,AD∥BC,∴四边形ABCF是平行四边形,又∵AB=BC=CD=DE=EA,∴四边形ABCF是菱形,∴AC⊥BF,∴OB2+OC2=BC2,∵AC=2OC,BF=2OB,∴AC2+BF2=(2OC)2+(2OB)2=4OC2+4OB2=4BC2,又∵BC=CD,∴AC2+BF2=4CD2.故答案为:AC2+BF2=4CD2.【点评】(1)此题主要考查了菱形的判定和性质的应用,要熟练掌握,解答此题的关键是要明确:菱形是在平行四边形的前提下定义的,首先它是平行四边形,但它是特殊的平行四边形,特殊之处就是“有一组邻边相等”,因而就增加了一些特殊的性质和不同于平行四边形的判定方法.(2)此题还考查了勾股定理的应用:在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方,要熟练掌握.9.(2015春•株洲校级期中)如图,在平面直角坐标系中,O为原点,四边形OABC是矩形,A(﹣10,0),C(0,3),点D是OA的中点,点P在BC边上运动,当△ODP是腰长为5的等腰三角形时,点P的坐标是(﹣4,3),或(﹣1,3),或(﹣9,3).【分析】先由矩形的性质求出OD=5,分情况讨论:(1)当OP=OD=5时;根据勾股定理求出PC,即可得出结果;(2)当PD=OD=5时;①作PE⊥OA于E,根据勾股定理求出DE,得出PC,即可得出结果;②作PF⊥OA于F,根据勾股定理求出DF,得出PC,即可得出结果.【解答】解:∵A(﹣10,0),C(0,3),∴OA=10,OC=3,∵四边形OABC是矩形,∴BC=OA=10,AB=OC=3,∵D是OA的中点,∴AD=OD=5,分情况讨论:(1)当OP=OD=5时,根据勾股定理得:PC==4,∴点P的坐标为:(﹣4,3);(2)当PD=OD=5时,分两种情况讨论:①如图1所示:作PE⊥OA于E,则∠PED=90°,DE==4,∴PC=OE=5﹣4=1,∴点P的坐标为:(﹣1,3);②如图2所示:作PF⊥OA于F,则DF==4,∴PC=OF=5+4=9,∴点P的坐标为:(﹣9,3);综上所述:点P的坐标为:(﹣4,3),或(﹣1,3),或(﹣9,3);故答案为:(﹣4,3),或(﹣1,3),或(﹣9,3).【点评】本题考查了矩形的性质、坐标与图形性质、等腰三角形的性质、勾股定理;熟练掌握矩形的性质,并能进行推理计算是解决问题的关键.三.解答题(共31小题)10.(2012春•西城区校级期中)如图,正方形ABCD中,AE=AB,直线DE交BC 于点F,求∠BEF的度数.【分析】设∠BAE=x°,根据正方形性质推出AB=AE=AD,根据等腰三角形性质和三角形的内角和定理求出∠AEB和∠AED的度数,根据平角定义求出即可.【解答】解:设∠BAE=x°,∵四边形ABCD是正方形,∴∠BAD=90°,AB=AD,∵AE=AB,∴AB=AE=AD,∴∠ABE=∠AEB=(180°﹣∠BAE)=90°﹣x°,∠DAE=90°﹣x°,∠AED=∠ADE=(180°﹣∠DAE)=[180°﹣(90°﹣x°)]=45°+x°,∴∠BEF=180°﹣∠AEB﹣∠AED,=180°﹣(90°﹣x°)﹣(45°+x°),=45°,答:∠BEF的度数是45°.【点评】本题考查了三角形的内角和定理,等腰三角形性质,正方形性质的应用,解此题的关键是如何把已知角的未知角结合起来,题目比较典型,但是有一定的难度.11.(2012秋•高淳县期中)如图,梯形ABCD中,AD∥BC,AB=CD,对角线AC、BD交于点O,AC⊥BD,E、F、G、H分别为AB、BC、CD、DA的中点.(1)求证:四边形EFGH为正方形;(2)若AD=1,BC=3,求正方形EFGH的边长.【分析】(1)先由三角形的中位线定理求出四边相等,然后由AC⊥BD入手,进行正方形的判断.(2)连接EG,利用梯形的中位线定理求出EG的长,然后结合(1)的结论求出EH2=2,也即得出了正方形EHGF的边长.【解答】(1)证明:在△ABC中,∵E、F分别是AB、BC的中点,∴EF=同理FG=,GH=,HE=在梯形ABCD中,∵AB=DC,∴AC=BD,∴EF=FG=GH=HE∴四边形EFGH为菱形.设AC与EH交于点M在△ABD中,∵E、H分别是AB、AD的中点,∴EH∥BD,同理GH∥AC又∵AC⊥BD,∴∠BOC=90°.∴∠EHG=∠EMC=∠BOC=90°∴四边形EFGH为正方形.(2)解:连接EG,在梯形ABCD中,∵E、G分别是AB、DC的中点,∴EG=(AD+BC)=(1+3)=2,在Rt△HEG中,EG2=EH2+HG2,4=2EH2,EH2=2,则EH=.即四边形EFGH的边长为.【点评】此题考查了等腰梯形的性质及三角形、梯形的中位线定理,解答本题的关键是根据三角形的中位线定理得出EH=HG=GF=FE,这是本题的突破口.12.(2013秋•青岛期中)如图,点E、F分别是正方形ABCD的边CD和AD的中点,BE和CF交于点P.求证:AP=AB.【分析】延长CF、BA交于点M,先证△BCE≌△CDF,再证△CDF≌△AMF得BA=MA 由直角三角形中斜边中线等于斜边的一半,可得Rt△MBP中AP=BM,即AP=AB.【解答】证明:延长CF、BA交于点M,∵点E、F分别是正方形ABCD的边CD和AD的中点,∴BC=CD,∠BCE=∠CDF,CE=DF,∴△BCE≌△CDF,∴∠CBE=∠DCF.∵∠DCF+∠BCP=90°,∴∠CBE+∠BCP=90°,∴∠BPM=∠CBE+∠BCP=90°.又∵FD=FA,∠CDF=∠MAF,∠CFD=∠MFA,∴△CDF≌△AMF,∴CD=AM.∵CD=AB,∴AB=AM.∴PA是直角△BPM斜边BM上的中线,∴AP=BM,即AP=AB.【点评】本题考查了正方形各边长相等、各内角为直角的性质,全等三角形的判定和对应边相等的性质,直角三角形斜边中线长为斜边长一半的性质,本题中求证△CDF≌△AMF是解题的关键.13.(2015春•禹州市期中)如图,点P为正方形ABCD对角线BD上一点,PE⊥BC于E,PF⊥DC于F.(1)求证:PA=EF;(2)若正方形ABCD的边长为a,求四边形PFCE的周长.【分析】(1)连接PC,证四边形PFCE是矩形,求出EF=PC,证△ABP≌△CBP,推出AP=PC即可;(2)证△CBD是等腰直角三角形,求出BF、PF,求出周长即可.【解答】解:证明:(1)连接PC,∵四边形ABCD是正方形,∴AB=CB,∠ABD=∠CBD=45°,∠C=90°,在△ABP与△CBP中,,∴△ABP≌△CBP(SAS),∴PA=PC,∵PE⊥BC,PF⊥CD,∴∠PFC=90°,∠PEC=90°.又∵∠C=90°,∴四边形PFCE是矩形,∴EF=PC,∴PA=EF.(2)由(1)知四边形PFCE是矩形,∴PE=CF,PF=CE,又∵∠CBD=45°,∠PEB=90°,∴BE=PE,又BC=a,∴矩形PFCE的周长为2(PE+EC)=2(BE+EC)=2BC=2a.【点评】本题主要考查正方形的性质,全等三角形的性质和判定等知识点的连接和掌握,能证出AP=PC是解此题的关键.14.(2015秋•福建校级期中)如图1,在正方形ABCD中,点E为BC上一点,连接DE,把△DEC沿DE折叠得到△DEF,延长EF交AB于G,连接DG.(1)求∠EDG的度数.(2)如图2,E为BC的中点,连接BF.①求证:BF∥DE;②若正方形边长为6,求线段AG的长.【分析】(1)由正方形的性质可得DC=DA.∠A=∠B=∠C=∠ADC=90°,由折叠的性质得出∠DFE=∠C,DC=DF,∠1=∠2,再求出∠DFG=∠A,DA=DF,然后由“HL”证明Rt△DGA≌Rt△DGF,由全等三角形对应角相等得出∠3=∠4,得出∠2+∠3=45°即可;(2)①由折叠的性质和线段中点的定义可得CE=EF=BE,∠DEF=∠DEC,再由三角形的外角性质得出∠5=∠DEC,然后利用同位角相等,两直线平行证明即可;②设AG=x,表示出GF、BG,根据点E是BC的中点求出BE、EF,从而得到GE 的长度,再利用勾股定理列出方程求解即可;【解答】(1)解:如图1所示:∵四边形ABCD是正方形,∴DC=DA.∠A=∠B=∠C=∠ADC=90°,∵△DEC沿DE折叠得到△DEF,∴∠DFE=∠C,DC=DF,∠1=∠2,∴∠DFG=∠A=90°,DA=DF,在Rt△DGA和Rt△DGF中,,∴Rt△DGA≌Rt△DGF(HL),∴∠3=∠4,∴∠EDG=∠3+∠2=∠ADF+∠FDC,=(∠ADF+∠FDC),=×90°,=45°;(2)①证明:如图2所示:∵△DEC沿DE折叠得到△DEF,E为BC的中点,∴CE=EF=BE,∠DEF=∠DEC,∴∠5=∠6,∵∠FEC=∠5+∠6,∴∠DEF+∠DEC=∠5+∠6,∴2∠5=2∠DEC,即∠5=∠DEC,∴BF∥DE;②解:设AG=x,则GF=x,BG=6﹣x,∵正方形边长为6,E为BC的中点,∴CE=EF=BE=×6=3,∴GE=EF+GF=3+x,在Rt△GBE中,根据勾股定理得:(6﹣x)2+32=(3+x)2,解得:x=2,即线段AG的长为2.【点评】本题考查了正方形的性质、全等三角形的判定与性质、等腰直角三角形的判定与性质、勾股定理、翻折变换的性质;熟练掌握正方形的性质,并能进行推理论证与计算是解决问题的关键.15.(2016春•召陵区期中)如图①,在正方形ABCD中,F是对角线AC上的一点,点E在BC的延长线上,且BF=EF.(1)求证:BF=DF;(2)求证:∠DFE=90°;(3)如果把正方形ABCD改为菱形,其他条件不变(如图②),当∠ABC=50°时,∠DFE=50度.【分析】(1)根据正方形的四条边都相等可得BC=DC,对角线平分一组对角可得∠BCF=∠DCF,然后利用“边角边”证明即可;(2)易证∠FBE=∠FEB,又因为∠FBE=∠FDC,所以可证明∠FEB=∠FDC,进而可证明∠DFE=90°;(3)根据全等三角形对应角相等可得∠CBF=∠CDF,根据等边对等角可得∠CBF=∠E,然后求出∠DFE=∠DCE,再根据两直线平行,同位角相等可得∠DCE=∠ABC,从而得解.【解答】(1)证明:在正方形ABCD中,BC=DC,∠BCF=∠DCF=45°,∵在△BCF和△DCF中,,∴△BCF≌△DCF(SAS);∴BF=DF;(2)证明:∵BF=EF,∴∠FBE=∠FEB,又∵∠FBE=∠FDC,∴∠FEB=∠FDC,又∵∠DGF=∠EGC,∴∠DFG=∠ECG=90°,即∠DFE=90°;(3)证明:由(1)知,△BCF≌△DCF,∴∠CBF=∠CDF,∵EE=FB,∴∠CBF=∠E,∵∠DGF=∠EGC(对顶角相等),∴180°﹣∠DGF﹣∠CDF=180°﹣∠EGC﹣∠E,即∠DFE=∠DCE,∵AB∥CD,∴∠DCE=∠ABC,∴∠DFE=∠ABC=50°,故答案为:50.【点评】本题考查了正方形的性质,全等三角形的判定与性质,菱形的性质,等边对等角的性质,熟记正方形的性质确定出∠BCF=∠DCF是解题的关键.16.(2015秋•泗县期中)已知正方形ABCD中,对角线AC、BD相交于O.①如图1,若E是AC上的点,过A 作AG⊥BE于G,AG、BD交于F,求证:OE=OF②如图2,若点E在AC的延长线上,AG⊥EB交EB的延长线于G,AG延长DB 延长线于点F,其它条件不变,OE=OF还成立吗?【分析】①由正方形的性质得出OA=OB,AC⊥BD,得出∠BOE=∠AOF=90°,由角的互余关系得出∠OBE=∠OAF,由ASA证明△BOE≌△AOF,得出对应边相等即可;②由正方形的性质得出OA=OB,AC⊥BD,得出∠BOE=∠AOF=90°,由角的互余关系得出∠OBE=∠OAF,由ASA证明△BOE≌△AOF,得出对应边相等即可.【解答】①证明:∵四边形ABCD是正方形,∴OA=OB,AC⊥BD,∴∠BOE=∠AOF=90°,∴∠OEB+∠OBE=90°,∵AG⊥BE,∴∠AGE=90°,∴∠OEB+∠OAF=90°,∴∠OBE=∠OAF,在△BOE和△AOF中,,∴△BOE≌△AOF(ASA),∴OE=OF;②解:OE=OF还成立;理由如下:∵四边形ABCD是正方形,∴OA=OB,AC⊥BD,∴∠BOE=∠AOF=90°,∴∠OEB+∠OBE=90°,∵AG⊥BE,∴∠AGE=90°,∴∠OEB+∠OAF=90°,∴∠OBE=∠OAF,在△BOE和△AOF中,,∴△BOE≌△AOF(ASA),∴OE=OF.【点评】本题考查了正方形的性质、全等三角形的判定与性质;熟练掌握正方形的性质,并能进行推理论证是解决问题的关键.17.(2016春•邳州市期中)如图,点P是菱形ABCD中对角线AC上的一点,且PE=PB.(1)求证:PE=PD;(2)求证:∠PDC=∠PEB;(3)若∠BAD=80°,连接DE,试求∠PDE的度数,并说明理由.【分析】(1)由菱形的性质得出AB=BC=CD=AD,AB∥CD,∠DCP=∠BCP,由SAS 证明△CDP≌△CBP,得出PB=PD,再由PE=PB,即可得出结论;(2)由等腰三角形的性质得出∠PBC=∠PEB,由全等三角形的性质得出∠PDC=∠PBC,即可得出∠PDC=∠PEB;(3)由四边形内角和定理得出∠DPE=100°,由等腰三角形的性质和三角形内角和定理即可得出结果.【解答】(1)解:∵四边形ABCD是菱形,∴AB=BC=CD=AD,AB∥CD,∠DCP=∠BCP,在△DCP和△BCP中,,∴△CDP≌△CBP(SAS),∴PB=PD,∵PE=PB,∴PE=PD;(2)证明:∵PE=PB,∴∠PBC=∠PEB,∵△CDP≌△CBP,∴∠PDC=∠PBC,∴∠PDC=∠PEB;(3)解:如图所示:∠PDE=40°;理由如下:在四边形DPEC中,∵∠DPE=360°﹣(∠PDC+∠PEC+∠DCB)=360°﹣(∠PEB+∠PEC+∠DCB)=360°﹣(180°+80°)=100°,∵PE=PD∴∠PDE=∠PED=40°.【点评】本题考查了菱形的性质、全等三角形的判定与性质、等腰三角形的性质;熟练掌握菱形的性质,证明三角形全等是解决问题的关键.18.(2016春•昆山市期中)如图,正方形ABCD中,AB=1,点P是BC边上的任意一点(异于端点B、C),连接AP,过B、D两点作BE⊥AP于点E,DF⊥AP于点F.(1)求证:EF=DF﹣BE;(2)若△ADF的周长为,求EF的长.【分析】(1)由正方形的性质得出AD=AB,证出∠DAF=∠ABE,由AAS证明△ADF ≌△BAE,得出AF=BE,DF=AE,即可得出结论;(2)设DF=a,AF=b,EF=DF﹣AF=a﹣b>0,由已知条件得出DF+AF=,即a+b=,由勾股定理得出a2+b2=1,再由完全平方公式得出a﹣b即可.【解答】(1)证明:∵BE⊥AP,DF⊥AP,∴∠DFA=∠AEB=90°,∠ABE+∠BAE=90°,∵四边形ABCD为正方形,∴AD=AB,∠DAB=90°=∠DAF+∠BAE,∴∠DAF=∠ABE,在△ADF和△BAE中,,∴△ADF≌△BAE(AAS),∴AF=BE,DF=AE,∴EF=AE﹣AF=DF﹣BE;(2)解:设DF=a,AF=b,EF=DF﹣AF=a﹣b>0,∵△ADF的周长为,AD=1,∴DF+AF=,即a+b=,由勾股定理得:DF2+AF2=AD2,即a2+b2=1,∴(a﹣b)2=2(a2+b2)﹣(a+b)2=2﹣=,∴a﹣b=,即EF=.【点评】本题考查了正方形的性质、全等三角形的判定与性质、勾股定理等知识;熟练掌握正方形的性质,由勾股定理得出a与b的关系式是解决问题(2)的关键.19.(2015春•繁昌县期中)如图,正方形ABCD的对角线AC、BD的交点为O,以O为端点引两条互相垂直的射线OM、ON,分别交边AB、BC于点E、F.(1)求证:0E=OF;(2)若正方形的边长为4,求EF的最小值.【分析】(1)根据正方形的性质可得∠EAO=∠FBO=45°,OA=OB,再根据同角的余角相等可得∠AOE=∠BOE,然后利用“角边角”证明△AOE和△BOF全等,根据全等三角形对应边相等即可得证;(2)根据等腰直角三角形△EOF,当OE最小时,再根据勾股定理得出EF的最小值.【解答】解:(1)∵四边形ABCD是正方形,∴OA=OB,∠AOB=90°,∠EAO=∠FBO=45°,∴∠AOE+∠BOE=90°,∵OE⊥OF,∴∠BOF+∠BOE=90°,∴∠AOE=∠BOF,在△AOE与△BOF中,,∴△AOE≌△BOF(ASA),∴OE=OF;(2)由(1)可知,△EOF是等腰直角三角形,∠EOF是直角,当OE最小时,EF的值最小,∵OA=OB,OE⊥AB,∴点E是AB的中点,∴OE=AB,∵AB=4,∴OE=2,∴EF=,即EF的最小值是2.【点评】本题考查了正方形的性质,解决此类问题的关键是正确的利用旋转不变量.正确作出辅助线是关键.20.(2016春•江宁区期中)如图,在正方形ABCD中,点E是边AD上任意一点,BE的垂直平分线FG交对角AC于点F.求证:(1)BF=DF;(2)BF⊥FE.【分析】(1)由正方形的性质得出AB=AD,∠BAF=∠DAF=45°,由SAS证明△BAF ≌△DAF,得出对应边相等即可;(2)由线段垂直平分线的性质得出BF=EF,证出EF=DF,得出∠FDE=∠FED,再由全等三角形的性质证出∠ABF=∠FED,由邻补角关系得出∠FED+∠FEA=180°,证出∠ABF+∠FEA=180°,由四边形内角和得出∠BAE+∠BFE=180°,求出∠BFE=90°即可.【解答】证明:如图所示:(1)∵四边形ABCD是正方形,∴AB=AD,∠BAF=∠DAF=45°,∠BAE=90°,在△BAF和△DAF中,,∴△BAF≌△DAF(SAS),∴BF=DF;(2)∵BE的垂直平分线FG交对角AC于点F,∴BF=EF,∵BF=DF,∴EF=DF,∴∠FDE=∠FED,∵△BAF≌△DAF,∴∠ABF=∠FDE,∴∠ABF=∠FED,∵∠FED+∠FEA=180°,∴∠ABF+∠FEA=180°,∴∠BAE+∠BFE=180°,∴∠BFE=90°,∴BF⊥FE.【点评】本题考查了正方形的性质、全等三角形的判定与性质、等腰三角形的判定与性质、四边形内角和定理等知识;熟练掌握正方形的性质,证明三角形全等是解决问题的关键.21.(2015春•台州校级期中)已知:如图所示,四边形ABCD中,∠ABC=∠ADC=90°,M是AC上任一点,O是BD的中点,连接MO,并延长MO到N,使NO=MO,连接BN与ND.(1)判断四边形BNDM的形状,并证明;(2)若M是AC的中点,则四边形BNDM的形状又如何?说明理由.【分析】(1)由对角线互相平分的四边形是平行四边形即可得出结论;(2)由直角三角形斜边上1的中线性质得出BM=AC,DM=AC,得出BM=DM,即可得出结论.【解答】(1)解:四边形BNDM是平行四边形,理由如下:。
2019年暑假北师大版九年级数学上册第一章特殊平行四边形提高培优讲义教案设计:中位线和斜边上的中线(

2019年暑假北师大版九年级数学上册第一章特殊平行四边形提高培优讲义教案:中位线和斜边上的中线一、三角形中位线4、例题讲解:例1、(1)如图1-1,在ABC△中,D,E,F分别是AB,BC,AC的中点,若ABC△的周长为20cm,则DEF△的周长为__________.(2)如图1-2,在Rt ABC△中,30A∠=︒,1BC=,点D,E分别是直角边BC,AC的中点,则DE的长为__________.图1-1 图1-2(3)如图1-3,ABC△中,6AB AC==,8BC=,AE平分BAC∠交BC于点E,点D为AB的中点,连接DE,则BDE△的周长是__________.(4)如图1-4,在四边形中,E 、F 分别为AB 、CD 的中点.求证:.图1-3 图1-4【解析】(1)10cm .(2)1. (3)10.(4)证明:取AD 的中点M ,连结EM 和FM . ∵E 、F 是AB 、CD 中点, ∴,.又∵EF EM FM <+,∴.例2、(1)如图2-1,在四边形ABCD 中,P 是对角线BD 的中点,E ,F 分别是AB ,CD 的中点,AD BC =,18PEF ∠=︒,则PFE ∠的度数是__________度.(2)如图2-2,已知四边形ABCD 的对角线AC BD =,E 、F 分别是AD 、BC 的中点,连结EF 分别交AC 、BD 于M 、N ,求证:AMN BNM =∠∠.(3)已知,如图2-3四边形ABCD 中,AD BC =,E 、F 分别是AB 和CD 的中点,AD 、EF 、BC 的延长线分别交于M 、N 两点.求证:AME BNE ∠=∠.ABCD 1()2EF AC BD <+F EDC BA 12EM BD =12FM AC =1()2EF AC BD <+MA BCD E FCM FE GNDBA图2-1 图2-2 图2-3【解析】(1)18.(2)设AB 的中点为G ,连结GE 、GF ,容易证得: GE //BD ,12EG BD =,GF //AC ,12EF AC =, 从而GF GE =,GEF GFE ∠=∠, ∴.(构造中位线来利用对角线相等的条件,也可以取或的中点.) (3)连接AC ,取AC 中点H ,连接FH 、EH . ∵DF CF =,AH CH =, ∴FH//AD ,12FH AD =, 同理,12EH BC =,EH//BC ,∵AD BC =,∴EH FH =, ∴HFE HEF ∠=∠, ∵FH//AM ,EH//BC ,∴AM E HFE ∠=∠,HEF BNE ∠=∠, ∴AME BNE ∠=∠.例3、如图,在ABC △中,D 、G 分别为AB 、AC 上的点,且BD CG =,M 、N 分别是BG 、CD 的中点,过MN 的直线交AB 于点P ,交AC 于点Q ,求证:AP AQ =.CM FE ND B AA CDM FE NBAMN BNM =∠∠AC BD AHC D M FE NB【解析】连DG ,找DG 的中点E ,连ME 、NE ,∵M 、N 分别是BG 与CD 的中点.∴ME//AB ,,NE//AC ,. ∴,.∵,∴, ∴,∴,∴. 二、直角三角形斜边中线3、例题讲解:例4、已知:在ABC △中,90ABC ∠=︒,点E 在直线AB 上,ED 与直线AC 垂直,垂足为D ,且点M 为EC 中点,连接BM 、DM .(1)如图4-1,若点E 在线段AB 上,探究线段BM 与DM 及BM D ∠与BCD ∠所满足的数量关系,并直接写出你得到的结论;(2)如图4-2,若点E 在BA 延长线上,你(1)中的结论是否发生变化?写出你的猜想并证明.NM PQG D C BAE ABC DG Q PM N12ME BD =12NE GC =APQ EMN ∠=∠AQP ENM ∠=∠BD GC =EM EN =EMN ENM ∠=∠APQ AQP ∠=∠AP AQ =图4-1 图4-2【解析】(1)BM DM =,2BMD BCD ∠=∠;(2)结论不变,由题意知,∴2BME BCM ∠=∠,2DME DCM ∠=∠,两式相减,得2BMD BCD ∠=∠.例5、如图,90MON ∠=︒,ABC △中,90BAC ∠=︒,2AB =,1AC =,AB 在MON ∠上滑动,求OC 的最大值.可得1OC ≤OC 的最大值为1+O 、D 、C 三点共线时). 三、中点辅助线综合例6、在Rt ABC △中,90BAC ∠=︒,AD BC ⊥,E 、F 、G 分别是AB 、AC 、BC 的中点,M 是DG 的中点,求证:ME MF =.【解析】连结DF 、EG ,可证DF GE =,MDF MGE ∠=∠,MD MG =,图2图1BEMCD AMEDCBAMB MC MD ==则MDF MGE △≌△,得证.例7、如图,在五边形ABCDE 中,90ABC AED ∠=∠=︒,BAC EAD ∠=∠,F 为CD 的中点.求证:BF EF =.【解析】方法一:如图1,取AC 中点M ,取AD 中点N ,连BM ,MF ,NF ,EN .∵90ABC AED ∠=∠=︒,1122BM AC FN EN AD MF ====,, ∴BMF FNE △≌△,∴BF EF =,方法二:如图2,延长CB 到M ,使得MB BC =, 延长DE 到N ,使得NE DE =, 连接AM ,AN ,MD ,CN . 由90ABC AED ∠=∠=°,AMC △,ADN △是等腰三角形,F 是CD 中点,则BF //MD ,12BF MD =,EF//CN ,12EF CN =,MAD CAN △≌△,MD CN =,∴BF EF =,此题的两种解法中综合了中点的三个基本用法:等腰三角形三线合一;直角三角形斜边中线;中位线,即以下三个模型:四、课后作业:1、(1)如图1-1,在ABC △中,点D 是BC 中点,AE 平分∠BAC ,BE ⊥AE 于E ,延长BE 交AC 于F .若AB =10厘米,AC =16厘米,则DE 的长度为__________.图2图1MNNMACBDEF F EDB CAFEDBCA(2)如图1-2,已知,在四边形ABCD 中,AD BC =,P 是对角线BD 的中点,N 是DC 的中点,M 是AB 的中点,30DBC ∠=︒,70ADB ∠=︒.求MNP ∠度数.图1-1 图1-2【解析】(1)3厘米;(2)∵在四边形ABCD 中,P 是对角线BD 的中点,M 、N 分别是AB 、CD 的中点,∴NP ,PM 分别是CDB △与DAB △的中位线, ∴12PN BC =,12PM AD =,PN//BC ,PM//AD , ∴30NPD DBC ∠=∠=︒,70MPB ADB ∠=∠=︒, ∴110DPM ∠=︒; ∴140NPM ∠=︒, ∵AD BC =;∴PN PM =,故NMP △是等腰三角形. ∵140NPM ∠=︒, ∴20PMN PNM ∠=∠=︒.2、(1)如图2-1,ABC △中,过点A 分别作ABC ∠、ACB ∠的外角平分线.....的垂线..AD 、AE ,垂足为D 、E .求证:①//ED BC ;②1()2ED AB AC BC =++.(2)(四川省中考题)如图2-2,已知:AD 是ABC △的中线,AE 是ABD △的中线,且AB BD =,求证:2AC AE =.图2-1 图2-2【解析】(1)①分别延长AD 、AE 与直线BC 交于点F 、G ,∵BD ⊥AD ,且BD 为ABF ∠的角平分线∴AD FD =,且AB BF =(等腰三角形的三线合一) 同理可得AE GE =,AC GC =, ∴DE 为AFG △的中位线, ∴ED //BC ,且12DE FG =. ②由(1)知12DE FG =, 且AB BF =,AC GC =, ∴111()()222ED FG=FB BC CG AB BC AC =++=++. (2)取AC 的中点F ,连结DF ,易得DF//AB ,12DF AB =,ADF BAD ∠=∠, 而1122DE BD AB ==,故DF DE =. 再证,∴,∴.3、(1)如图3-1,四边形ABCD 中,90ADC ∠=︒,取AC 中点O ,BC 中点E ,连接OD 、OE 、DE ,20CAD CAB ∠=∠=︒,则DOE ∠=__________.C E DBAADE ADF △≌△AE AF =2AC AE =CFEDBA(2)如图3-2所示,ABC △中,AH BC ⊥于H ,点E 、D 、F 分别是AB 、BC 、AC 的中点,10cm HF =,则ED 的长度是__________.图3-1 图3-2【解析】(1)60︒.(2)10cm .4、(1)如图4-1,在ABC △中,2B C ∠=∠,M 是BC 中点,AD BC ⊥于D .求证:12DM AB =.(2)如图4-2,已知:ABD △和ACE △都是直角三角形,且90ABD ACE ∠=∠=︒,BAD CAE ∠=∠.连接DE ,设M 为DE 的中点.求证:MB MC =.【解析】(1)法一:取AB 中点G ,连结GD 、GM ,则12GD AB =,GM AC ∥.则GMD C ∠=∠.而GD GB B GDB GMD DGM =⇒∠=∠=∠+∠ C DGM =∠+∠,由于2B C ∠=∠,所以DGM C GMD ∠=∠=∠.∴12MD GD AB ==. 法二:同理可以取AC 的中点N ,连接DN ,MN .(2)如图,分别取AD 、AE 的中点P 、Q ,连接PB 、PM 、QC 、QM , 由P 、M 、Q 分别是AD 、DE 、AE 的中点,OE DC BAMEDCBAAB GNMC ABD g∴PM//AE,12PM AE=,QM//AD,12QM AD=,∵ABD△、ACE△是直角三角形,∴12PB AD=,12CQ AE=,∴PB QM=,PM QC=,∵BAD CAE∠=∠,∴ADB AEC∠=∠,∴DPB CQE∠=∠,由AD//QM,AE//PM,∴APM AQM∠=∠,∴BPM MQC∠=∠,∴BPM MQC△≌△,∴MB MC=.QPAC D EM 图3。
2020-2021年度鲁教版八年级数学下册《第6章特殊的平行四边形》综合培优训练(附答案)
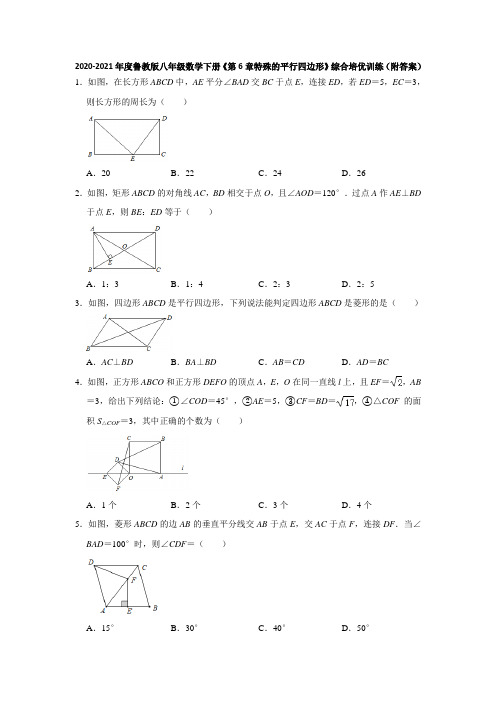
2020-2021年度鲁教版八年级数学下册《第6章特殊的平行四边形》综合培优训练(附答案)1.如图,在长方形ABCD中,AE平分∠BAD交BC于点E,连接ED,若ED=5,EC=3,则长方形的周长为()A.20B.22C.24D.262.如图,矩形ABCD的对角线AC,BD相交于点O,且∠AOD=120°.过点A作AE⊥BD 于点E,则BE:ED等于()A.1:3B.1:4C.2:3D.2:53.如图,四边形ABCD是平行四边形,下列说法能判定四边形ABCD是菱形的是()A.AC⊥BD B.BA⊥BD C.AB=CD D.AD=BC4.如图,正方形ABCO和正方形DEFO的顶点A,E,O在同一直线l上,且EF=,AB =3,给出下列结论:①∠COD=45°,②AE=5,③CF=BD=,④△COF的面积S△COF=3,其中正确的个数为()A.1个B.2个C.3个D.4个5.如图,菱形ABCD的边AB的垂直平分线交AB于点E,交AC于点F,连接DF.当∠BAD=100°时,则∠CDF=()A.15°B.30°C.40°D.50°6.如图,菱形ABCD中,∠D=135°,BE⊥CD于E,交AC于F,FG⊥BC于G.若△BFG的周长为4,则菱形ABCD的面积为()A.4B.8C.16D.167.如图,正方形ABCD中,点E是对角线AC上的一点,且AE=AB,连接BE,DE,则∠CDE的度数为()A.20°B.22.5°C.25°D.30°8.如图,矩形ABCD中,AD=5,AB=7,正方形MBND′的顶点M,N分别在矩形的边AB,BC上,点E为DC上一个动点,当点D与点D′关于AE对称时,DE的长为.9.把长方形ABCD沿着直线EF对折,折痕为EF,对折后的图形EB′GF的边FG恰好经过点C,若∠AFE=55°,则∠CEB'=.10.如图,在正方形ABCD中,E是对角线AC上的动点,以DE为边作正方形DEFG,H 是CD的中点.连接GH,若GH的最小值是1,则正方形ABCD的边长为.11.如图,正方形ABCD的边长为2,M是BC的中点,N是AM上的动点,过点N作EF ⊥AM分别交AB,CD于点E,F.(1)AM的长为;(2)EM+AF的最小值为.12.如图,以Rt△ABC的斜边AB为一边,在AB的右侧作正方形ABED,正方形对角线交于点O,连接CO,如果AC=4,CO=,那么BC=.13.如图,已知正方形ABCD的边长为2,对角线AC、BD相交于点O,AE平分∠BAC交BD于点E,则BE的长为.14.如图,已知正方形ABCD,E是AD上一点,过BE上一点O作BE的垂线,交AB于点G,交CD于点H.BE=6,则GH=.15.如图,菱形ABCD中,AC,BD相交于O,DE⊥BC于E,连接OE,∠BAD=40°,则∠OED的度数为.16.如图,正方形ABCD边长为2,F为BC上一动点,作DE⊥AF于E,连接CE.当△CDE是以CD为腰的等腰三角形时,DE的长为.17.如图正方形ABCD边长为2,E为CD边中点,P为射线BE上一点(P不与B重合),若△PDC为直角三角形,则BP=.18.如图,正方形ABCD的边长为6,E是边AB边一点,G是AD延长线上一点,BE=DG,连接EG,CF⊥EG交EG于点H,交AD于点F,连接CE,BH,若BH=4,则EG 的长等于.19.如图,在菱形ABCD中,E为对角线BD上一点,且AE=DE,连接CE.(1)求证:CE=DE.(2)当BE=2,CE=1时,求菱形的边长.20.菱形ABCD的边长为6,∠D=60°,点E在边AD上运动.(1)如图1,当点E为AD的中点时,求AO:CO的值;(2)如图2,F是AB上的动点,且满足BF+DE=6,求证:△CEF是等边三角形.21.如图,过△ABC边AC的中点O,作OE⊥AC,交AB于点E,过点A作AD∥BC,与BO的延长线交于点D,连接CD,CE,若CE平分∠ACB,CE⊥BO于点F.(1)求证:①OC=BC;②四边形ABCD是矩形;(2)若BC=3,求DE的长.22.如图,正方形ABCD中,点P是对角线AC上一点,连接PB,边作PE⊥PB交AD边于于点E,且点E不与点A,D重合,作PM⊥AD,PN⊥AB,垂足分别为点M和N.(1)求证:PM=PN;(2)求证:EM=BN.23.如图,在正方形ABCD中,E,F分别是AD,CD的中点,连接BE,AF交于点M,分别延长AF,BC交于点N.(1)求∠BMN的度数;(2)求证:CM=AD.24.如图,矩形ABCD的对角线相交于O,点E是CF的中点,DF∥AC交CE延长线于点F,连接AF.(1)求证:四边形AODF是菱形;(2)若∠AOB=60°,∠AFC=90°,AB=1,求CF的长.25.在正方形ABCD中,点E为CD中点,连接AE并延长交BC延长线于点G,点F在BC上,∠F AE=∠DAE,连接FE并延长交AD延长线于H,连接HG.(1)求证:四边形AFGH为菱形:(2)若DH=1.求四边形AFGH的面积.26.如图,在矩形ABCD中,AB=3cm,BC=6cm.点P从点D出发向点A运动,运动到点A即停止;同时,点Q从点B出发向点C运动,运动到点C即停止,点P、Q的速度都是1cm/s.连接PQ、AQ、CP.设点P、Q运动的时间为ts.(1)当t为何值时,四边形ABQP是矩形;(2)当t为何值时,四边形AQCP是菱形;(3)分别求出(2)中菱形AQCP的周长和面积.参考答案1.解:∵四边形ABCD是长方形,∴∠B=∠C=90°,AB=DC,∵ED=5,EC=3,∴DC===4,则AB=4,∵AE平分∠BAD交BC于点E,∴∠BAE=∠DAE,∵AD∥BC,∴∠DAE=∠AEB,∴∠BAE=∠BEA,∴AB=BE=4,∴长方形的周长为:2×(4+4+3)=22.故选:B.2.解:∵四边形ABCD是矩形,∴OA=OB=OD,∵∠AOD=120°,∴∠AOB=180°﹣120°=60°,∴△AOB为等边三角形,∵AE⊥BD,∴BE=OE=OB,∴ED=3BE,∴=,故选:A.3.解:能判定四边形ABCD是菱形的是AC⊥BD,理由如下:∵四边形ABCD是平行四边形,AC⊥BD,∴平行四边形ABCD是菱形,故选:A.4.解:①∵∠AOC=90°,∠DOE=45°,∴∠COD=180°﹣∠AOC﹣∠DOE=45°,故正确;②∵EF=,∴OE=2,∵AO=AB=3,∴AE=AO+OE=2+3=5,故正确;③作DH⊥AB于H,作FG⊥CO交CO的延长线于G,则FG=1,CF=,BH=3﹣1=2,DH=3+1=4,BD=,故错误;④△COF的面积S△COF=×3×1=,故错误;故选:B.5.解:如图,连接BF,∵四边形ABCD是菱形,∴CD=BC,∠DCF=∠BCF,在△BCF和△DCF中,∵,∴△BCF≌△DCF(SAS)∴∠CBF=∠CDF∵FE垂直平分AB,∠BAF=×100°=50°∴∠ABF=∠BAF=50°∵∠ABC=180°﹣100°=80°,∠CBF=80°﹣50°=30°∴∠CDF=30°.故选:B.6.解:∵菱形ABCD中,∠D=135°,∴∠BCD=45°,∵BE⊥CD于E,FG⊥BC于G,∴△BFG与△BEC是等腰直角三角形,∵∠GCF=∠ECF,∠CGF=∠CEF=90°,CF=CF,∴△CGF≌△CEF(AAS),∴FG=FE,CG=CE,设BG=FG=EF=x,∴BF=x,∵△BFG的周长为4,∴x+x+x=4,∴x=4﹣2,∴BE=2,∴BC=BE=4,∴菱形ABCD的面积=4×2=8,故选:B.7.解:∵四边形ABCD是正方形,∴AB=AD,∠ADC=90°,∠DAC=45°,∵AE=AB,∴AD=AE,∴∠ADE=∠AED=67.5°,∴∠CDE=90°﹣67.5°=22.5°,故选:B.8.解:如图,连接ED′,AD′,延长MD′交DC于点P,∵正方形MBND′的顶点M,N分别在矩形的边AB,BC上,点E为DC上一个动点,点D与点D′关于AE对称,∴设MD′=ND′=BM=x,∴AM=AB﹣BM=7﹣x,又折叠图形可得AD=AD′=5,∴x2+(7﹣x)2=25,解得x=3或4,即MD′=3或4.在Rt△EPD′中,设ED′=a,①当MD′=3时,AM=7﹣3=4,D′P=5﹣3=2,EP=4﹣a,∴a2=22+(4﹣a)2,解得a=,即DE=,②当MD′=4时,AM=7﹣4=3,D′P=5﹣4=1,EP=3﹣a,∴a2=12+(3﹣a)2,解得a=,即DE=.综上所述:DE的长为:或.故答案为:或.9.解:如图,在长方形ABCD中,AD∥BC,则∠FEC=∠AFE=55°.∴∠BEF=180°﹣55°=125°.根据折叠的性质知:∠B′EF=∠BEF=125°.∴∠CEB'=∠B′EF﹣∠FEC=125°﹣55°=70°.故答案是:70°.10.解:连接CG.∵四边形ABCD是正方形,四边形DECG是正方形,∴DA=DC,DE=DG,∠ADC=∠EDG=90°,∠DAC=45°,∴∠ADE=∠CDG,∴△ADE≌△CDG(SAS),∴∠DCG=∠DAE=45°,∴点G的运动轨迹是射线CG,根据垂线段最短可知,当GH⊥CG时,GH的值最小为1,∴CH=.∴CD=2CH=2,故答案为:2.11.解:(1)∵正方形ABCD的边长为2,∴AB=BC=2,∠ABC=90°,∵M是BC的中点,∴BM=,∴,故答案为:;(2)过F作FG⊥AB于G,则FG=BC=AB,∠ABM=∠FGE=90°,∵EF⊥AM,∴∠BAM+∠AEN=∠AEN+∠GFE=90°,∴∠BAM=∠GFE,∴△ABM≌△FGE(SAS),∴AM=EF,将EF沿EM方向平移至MH,连接FH,则EF=MH,∠AMH=90°,EM=FH,当A、F、H三点共线时,EM+AF=FH+AF=AH的值最小,此时EM+AF=AH=,∴EM+AF的最小值为,故答案为:.12.解:如图,延长CB到点G,使BG=AC=4,∵根据题意,四边形ABED为正方形,∴∠4=∠5=45°,∠EBA=90°,∴∠1+∠2=90°,又∵△ABC是直角三角形,AB为斜边,∴∠2+∠3=90°,∴∠1=∠3,∵∠1+∠5=∠3+∠4,∴∠CAO=∠GBO,在△CAO和△GBO中,,∴△CAO≌△GBO(SAS),∴CO=GO=,∠6=∠8,∵∠7+∠8=90°,∴∠6+∠7=90°,∴∠COG=90°,∴=,∴BC=CG﹣BG=12﹣4=8.故答案为:8.13.解:如图,过点E作EH⊥AB于H.∵四边形ABCD是正方形,∴AB=BC=CD=AD=2,BD=AC=2,OD=OB=,∵EA平分∠BAO,EH⊥AB,EO⊥AC,∴EH=EO,设EH=EO=a,则BE=a,∴a+a=,解得a=2﹣,∴BE=a=2﹣2.故答案为:2﹣2.14.解:过点A作GH的平行线,交DC于点H′,交BE于点O',如图所示:∵ABCD是正方形,∴AG∥H′H,BA=AD,∠BAE=∠D=90°,∴∠H′AD+∠AH′D=90°,∵GH⊥BE,AH′∥GH,∴AH′⊥BE,∴∠H′AD+∠BEA=90°,∴∠BEA=∠AH′D,在△BAE和△ADH′中,,∴△BAE≌△ADH′(AAS),∴BE=AH′,∵AG∥H′H,AH′∥GH,∴四边形AH′HG是平行四边形,∴GH=AH′,∴GH=BE=6,故答案为:6.15.解:∵四边形ABCD是菱形,∠BAD=40°,∴∠DAO=BAD=20°,AC⊥BD,DO=BO,AD∥BC,∴∠DOA=90°,∴∠ADO=90°﹣∠DAO=70°,∵AD∥BC,DE⊥BC,∴DE⊥AD,∴∠ADE=90°,∴∠ODE=∠AD∠E﹣∠ADO=20°,∵DE⊥BC,∴∠DEB=90°,∵DO=BO,∴OE=BD=OD,∴∠OED=∠ODE=20°,故答案为:20°.16.解:过C作CG⊥DE于G,∵四边形ABCD是正方形,∴AD=CD,∠ADC=90°,∵DE⊥AF,∴∠AED=90°,∴AD>DE,∴CD>DE,当△CDE是以CD为腰的等腰三角形时,此时只能CD=CE,∵CG⊥DE,∴EG=DG=DE,∵∠ADE+∠CDG=∠ADE+∠DAE=90°,∴∠CDG=∠DAE,∵∠AED=∠CGD=90°,∴△AED≌△DGC(AAS),∴AE=DG=DE,设AE=x,则DE=2x,在Rt△AED中,由勾股定理得:AE2+DE2=AD2,∵AD=2,∴x2+(2x)2=22,解得:x=,∵x>0,∴x=,∴DE=2x=,当F与B重合,则E与A重合,△CDE是以CD为腰的等腰三角形,此时DE=AD=2,故答案为:或2.17.解:分三种情况:①如图1,当∠DPC=90°时,∵E是CD的中点,且CD=2,∴PE=CD=1,∵四边形ABCD是正方形,∴BC=2,∠BCD=90°,∴BE==,∴BP=﹣1;②如图2,当∠DPC=90°时,同理可得BP=+1;③如图3,当∠CDP=90°时,∵∠BCE=∠EDP=90°,DE=CE,∠BEC=∠DEP,∴△BCE≌△PDE(ASA),∴PE=BE=,∴BP=2,综上,BP的长是﹣1或+1或2;故答案为:﹣1或+1或2.18.解:连接CG,∵四边形ABCD是正方形,∴CB=CD,∠CBE=∠ADC=90°,在△CGD与△CEB中,,∴△CGD≌△CEB(SAS),∴CG=CE,∠GCD=∠ECB,∴∠GCE=90°,即△GCE是等腰直角三角形.又∵CH⊥GE,∴CH=EH=GH.过点H作AB、BC的垂线,垂足分别为点M、N,则∠MHN=90°,又∵∠EHC=90°,∴∠1=∠2,在△HEM与△HCN中,,∴△HEM≌△HCN(AAS).∴HM=HN,∵∠HMB=∠ABC=∠BNH=90°,∴四边形MBNH为正方形,∵BH=4,∴BN=HN=4,∵HM∥AG,EH=GH,∴AG=2HM=2HN=8,∴DG=BE=AG﹣AD=8﹣6=2,∴AE=6﹣2=4,在Rt△AEG中,EG===4.故答案为:4.19.(1)证明:∵四边形ABCD是菱形,∴∠ABE=∠CBE,AB=CB,在△ABE和△CBE中,,∴△ABE≌△CBE(SAS),∴AE=CE,∵AE=DE,∴CE=DE;(2)解:如图,连接AC交BD于H,∵四边形ABCD是菱形,∴AH⊥BD,BH=DH,AH=CH,∵CE=DE=AE=1,∴BD=BE+DE=2+1=3,∴BH=BD=,EH=BE﹣BH=2﹣=,在Rt△AHE中,由勾股定理得:AH===,在Rt△AHB中,由勾股定理得:AB===,∴菱形的边长为.20.(1)解:∵四边形ABCD是菱形,∴BC=AD=6,AD∥BC,∵点E为AD的中点,∴AE=AD=3,∵AD∥BC,∴△AOE∽△COB,∴===;(2)证明:∵四边形ABCD是菱形,∴AB=BC,AD∥BC,∠B=∠D=60°,∴∠CAE=∠ACB,△ABC是等边三角形,∴AC=BC,∠ACB=60°,∴∠EAC=60°=∠B,∵AE+DE=AD=6,BF+DE=6,∴AE=BF,在△ACE和△BCF中,,∴△ACE≌△BCF(SAS),∴CE=CF,∠ACE=∠BCF,∴∠ACE+∠ACF=∠BCF+∠ACF=∠ACB=60°,即∠ECF=60°,∴△CEF是等边三角形.21.(1)证明:①∵CE平分∠ACB,∴∠OCE=∠BCE,∵BO⊥CE,∴∠CFO=∠CFB=90°,在△OCF与△BCF中,,∴△OCF≌△BCF(ASA),∴OC=BC;②∵点O是AC的中点,∴OA=OC,∵AD∥BC,∴∠DAO=∠BCO,∠ADO=∠CBO,在△OAD与△OCB中,,∴△OAD≌△OCB(ASA),∴AD=BC,∵AD∥BC,∴四边形ABCD是平行四边形,∵OE⊥AC,∴∠EOC=90°,在△OCE与△BCE中,,∴△OCE≌△BCE(SAS),∴四边形ABCD是矩形;(2)解:∵四边形ABCD是矩形,∴AD=BC=3,∠DAB=90°,AC=BD,∴OB=OC,∵OC=BC,∴OC=OB=BC,∴△OBC是等边三角形,∴∠OCB=60°,∴∠ECB=OCB=30°,∵∠EBC=90°,∴EB=EC,∵BE2+BC2=EC2,BC=3,∴EB=,EC=2,∵OE⊥AC,OA=OC,∴EC=EA=2,在Rt△ADE中,∠DAB=90°,∴DE===.22.证明:(1)∵四边形ABCD为正方形,∴AC平分∠BAD,又∵PM⊥AD,PN⊥AB,∴PM=PN.(2)∵PM⊥AD,PN⊥AB,∠MAN=90°,PM=PN,∴四边形PMAN为正方形,∴∠MPN=90°,即∠MPE+∠EPN=90°.∵PE⊥PB,∴∠EPN+∠NPB=90°,∴∠MPE=∠NPB.∵PM⊥AD,PN⊥AB,在△PME和△PNB中,,∴△PME≌△PNB(ASA),∴EM=BN.23.解:(1)∵四边形ABCD是正方形,∴AD=CD=AB,∠BAD=∠D=90°,∵E、F分别是AD、CD的中点,∴AE=AD,DF=CD,∴AE=DF,在△ABE和△DAF中,,∴△ABE≌△DAF(SAS),∴AF=BE,∠AEB=∠AFD,在直角△ADF中,∠DAF+∠AFD=90°,∴∠DAF+∠AEB=90°,∴∠AME=90°,∴AF⊥BE,∴∠BMN=90°;(2)证明:∵DF=CF,∠D=∠FCN=90°,∠AFD=∠NFC,在△ADF和△NCF中,,∴△ADF≌△NCF(ASA),∴AD=CN=CD=BC,在直角△BMN中,BC=CN,∴CM=BN=BC=AD.24.(1)证明:∵DF∥AC,∴∠DFC=∠OCF,∠EDF=∠EOC,∵点E是CF的中点,FE=CE,∴△DEF≌△OEC(AAS),∴DF=OC,∵四边形ABCD是矩形,∴OA=OC,OB=OD,AC=BD,∴OA=OD,∴DF=OA,且DF∥AO,∴四边形AODF是平行四边形,又∵OA=OD,∴平行四边形AODF是菱形;(2)解:由(1)得:OA=OB,∵∠AOB=60°,∴△AOB是等边三角形,∴OA=AB=1,∵四边形AODF是菱形,∴AF=OA=1,AF∥BD,∴∠F AC=∠AOB=60°,∵∠AFC=90°,∴∠ACF=30°,∴CF=AF=.25.(1)证明:∵四边形ABCD是正方形,∴AD∥BC,∴∠DAE=∠FGA,∵∠F AE=∠DAE,∴∠FGA=∠F AE,∴F A=FG,∵点E为CD中点,∴DE=CE,∵∠ADE=∠GCE=90°,在△ADE和△GCE中,,∴△ADE≌△GCE(AAS),∴AD=CG,同理:△DEH△CEF(AAS),∴DH=CF,∵AH=AD+DH,GF=CG+CF,∴AH∥FG,∵AH∥FG,∴四边形AFGH为平行四边形,∵F A=FG,∴四边形AFGH为菱形;(2)解:FC=DH=1,设AB=AD=x,由(1)知FC=DH=1,∴AF=AH=AD+DH=x+1,BF=BC﹣FC=x﹣1,在Rt△ABF中,根据勾股定理,得AF2=AB2+BF2,∴(x+1)2=x2+(x﹣1)2,解得x=4,x=0(舍去),∴AF=FG=x+1=5,∴菱形AFGH的面积为:FG•DC=5×4=20.26.解:(1)由已知可得,BQ=DP=t,AP=CQ=6﹣t 在矩形ABCD中,∠B=90°,AD∥BC,当BQ=AP时,四边形ABQP为矩形,∴t=6﹣t,得t=3故当t=3s时,四边形ABQP为矩形.(2)由(1)可知,四边形AQCP为平行四边形∴当AQ=CQ时,四边形AQCP为菱形即时,四边形AQCP为菱形,解得t=,故当t=s时,四边形AQCP为菱形.(3)当t=时,AQ=,CQ=,则周长为:4AQ=4×=15cm面积为:。
冲刺重点高中提前自主招生培优专题测试--特殊平行四边形(附答案详解)
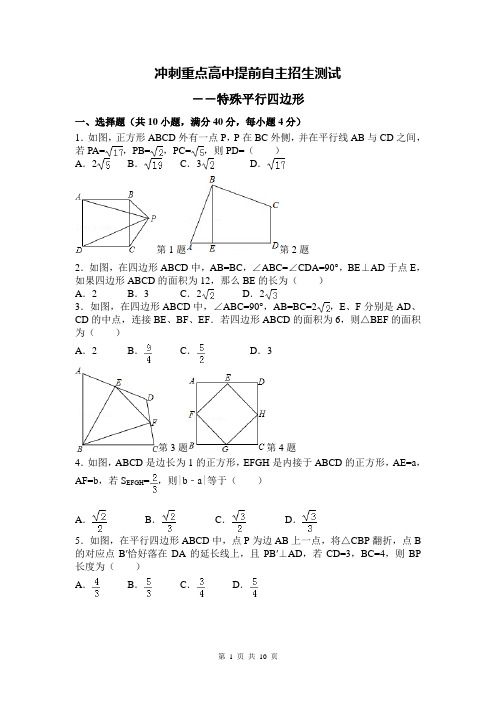
冲刺重点高中提前自主招生测试--特殊平行四边形一、选择题(共10小题,满分40分,每小题4分)1.如图,正方形ABCD外有一点P,P在BC外侧,并在平行线AB与CD之间,若PA=,PB=,PC=,则PD=()A.2B.C.3D.第1题第2题2.如图,在四边形ABCD中,AB=BC,∠ABC=∠CDA=90°,BE⊥AD于点E,如果四边形ABCD的面积为12,那么BE的长为()A.2 B.3 C.2D.23.如图,在四边形ABCD中,∠ABC=90°,AB=BC=2,E、F分别是AD、CD的中点,连接BE、BF、EF.若四边形ABCD的面积为6,则△BEF的面积为()A.2 B.C.D.3第3题第4题4.如图,ABCD是边长为1的正方形,EFGH是内接于ABCD的正方形,AE=a,AF=b,若S EFGH=,则|b﹣a|等于()A.B.C.D.5.如图,在平行四边形ABCD中,点P为边AB上一点,将△CBP翻折,点B 的对应点B′恰好落在DA的延长线上,且PB′⊥AD,若CD=3,BC=4,则BP 长度为()A.B.C.D.第5题第6题6.如图,在正方形ABCD 中,AD=5,点E 、F 是正方形ABCD 内的两点,且AE=FC=3,BE=DF=4,则EF 的长为( )A .B .C .D .7.如图,以正方形ABCD 的一边向形外作等边△ABE ,BD 与EC 交于点F ,且DF=EF ,则∠AFD 等于( )A .60°B .50°C .45°D .40°第7题第8题8.如图,正方形ABCD 的边长为1,点P 为BC 上任意一点(可与点B 或C 重合),分别过B 、C 、D 作射线AP 的垂线,垂足分别是B′、C′、D′,则BB′+CC′+DD′的最小值是( )A .1B .C .D .9.如图,正方形ABCD 的边长为8,∠DAC 的平分线交DC 于点E .若点P ,Q 分别是AD 和AE 上的动点,则DQ +PQ 的最小值是( )第9题A .4B .8C .4D .8第9题第10题10.如图,边长为1的正方形ABCD 的对角线AC ,BD 相交于点O ,∠MPN 为直角,使点P 与点O 重合,直角边PM ,PN 分别与OA ,OB 重合,然后逆时针旋转∠MPN ,旋转角为θ(0°<θ<90°),PM ,PN 分别交AB ,BC 于E ,F 两点,连接EF 交OB 于点G ,则下列结论:①EF=OE ;②S 四边形OEBF :S 正方形ABCD =1:4;③BE +BF=OA ;④在旋转过程中,当△BEF 与△COF 的面积之和最大时,AE=;⑤OG•BD=AE 2+CF 2.其中结论正确的个数是( )A.2个B.3个C.4个D.5个二、填空题(共10小题,满分40分,每小题4分)11.已知菱形ABCD的边长为6,∠A=60°,如果点P是菱形内一点,且PB=PD=2,那么AP的长为.12.如图,正方形ABCD中,点G为对角线AC上一点,AG=AB.∠CAE=16°且AE=AC,连接GE.将线段AE绕点A逆时针旋转得到线段AF,使DF=GE,则∠CAF的度数为.第12题第13题13.按如图所示,把一张边长超过10的正方形纸片剪成5个部分,则中间小正方形(阴影部分)的周长为.14.已知:如图,矩形ABCD的对角线相交于O,AE平分∠BAD交BC于E,∠CAE=15°,则∠BOE=°.第14题第15题15.如图,正方形ABCD的面积为256,点F在AD上,点E在AB的延长线上,直角△CEF的面积为200,则BE的值为.16.如图,四边形ABCD是菱形,E在AD上,F在AB延长线上,CE和DF 相交于点G,若CE=DF,∠CGF=30°,AB的长为6,则菱形ABCD的面积为.第16题第17题17.如图,ABCD是正方形,M是BC中点,将正方形折起,使点A与点M重合,设折痕为EF,若正方形面积是64,那么梯形AEFD的面积是.18.如图,将边长为4cm的正方形ABCD折叠,使点D落在BC边的中点E处,点A落在F处,折痕为MN交AB于M,交DC于N,则线段FM长为cm.第18题第19题19.如图,正方形ABCD中,点E、F分别是BC、CD边上的点,且∠EAF=45°,对角线BD交AE于点M,交AF于点N.若AB=2,BM=1,则MN的长为.20.一个矩形各边的长都是正整数,而且它的面积的数量等于其周长的数量的2倍,这样的矩形有个.三、解答题(共5小题,满分70分)21.(12分)(1)如图1,点P是正方形ABCD内的一点,把△ABP绕点B顺时针方向旋转,使点A与点C重合,点P的对应点是Q.若PA=3,PB=2,PC=5,求∠BQC的度数.(2)点P是等边三角形ABC内的一点,若PA=12,PB=5,PC=13,求∠BPA 的度数.第21题22.(12分)已知,如图,四边形ABCD中,AB=AD,∠BAD=∠BCD=90°,E为BC边上一点,作∠AEF=∠ACF=90°(1)试判断AE和EF的数量关系,并说明理由;(2)当四边形ABCD的面积为16,BC的长为6,求AD的长.第22题23.(14分)如图,在正方形ABCD中,点P是AD边上的一个动点,连接PB,过点B作一条射线与边DC的延长线交于点Q,使得∠QBE=∠PBC,其中E是边AB延长线上的点,连接PQ.(1)求证:△PBQ是等腰直角三角形;(2)若PQ2=PB2+PD2+1,求△PAB的面积.第23题24.(15分)已知:l1∥l2∥l3∥l4,平行线l1与l2、l2与l3、l3与l4之间的距离分别为d1、d2、d3,且d1=d3=1,d2=2.我们把四个顶点分别在l1、l2、l3、l4这四条平行线上的四边形称为“格线四边形”.(1)如图1,正方形ABCD为“格线四边形”,则正方形ABCD的边长为.(2)矩形ABCD为“格线四边形”,其长:宽=2:1,求矩形ABCD的宽.(3)如图1,EG过正方形ABCD的顶点D且垂直l1于点E,分别交l2,l4于点F,G.将∠AEG绕点A顺时针旋转30°得到∠AE′D′(如图2),点D′在直线l3上,以AD′为边在E′D′左侧作菱形AB′C′D′,使B′,C′分别在直线l2,l4上,求菱形AB′C′D′的边长.第24题25.(17分)如图一,已知点P是边长为a的等边△ABC内任意一点,点P到三边的距离PD、PE、PF的长分别记为h1,h2,h3,则h1,h2,h3之间有什么关系呢?分析:连接PA、PB、PC,则△ABC被分割成三个三角形,根据:S△PAB+S△PBC+S△PAC=S△ABC,即:,可得.问题1:若点P是边长为a的等边△ABC外一点(如图二所示位置),点P到三边的距离PD、PE、PF的长分别记为h1,h2,h3.探索h1,h2,h3之间有什么关系呢?并证明你的结论;问题2:如图三,正方形ABCD的边长为a,点P是BC边上任意一点(可与B、C重合),B、C、D三点到射线AP的距离分别是h1,h2,h3,设h1+h2+h3=y,线段AP=x,求y与x的函数关系式,并求y的最大值与最小值.第25题冲刺重点高中提前自主招生测试--特殊平行四边形参考答案与试题解析一、选择题(共10小题,满分40分,每小题4分)1.如图,正方形ABCD外有一点P,P在BC外侧,并在平行线AB与CD之间,若PA=,PB=,PC=,则PD=()A.2B.C.3D.【解析】延长AB,DC,过P分作PE⊥AE,PF⊥DF,则CF=BE,AP2=AE2+EP2,BP2=BE2+PE2,DP2=DF2+PF2,CP2=CF2+FP2,∴AP2+CP2=CF2+FP2+AE2+EP2,DP2+BP2=DF2+PF2+BE2+PE2,即AP2+CP2=DP2+BP2,代入AP,BP,CP得DP==2,故选A.2.如图,在四边形ABCD中,AB=BC,∠ABC=∠CDA=90°,BE⊥AD于点E,如果四边形ABCD的面积为12,那么BE的长为()A.2 B.3 C.2D.2【解析】过点B作BF⊥CD,于DC的延长线交于点F,如右图所示,∵BF⊥CD,BE⊥AD,∴∠BFC=∠BEA=90°,∵∠ABC=∠ADC=90°,∴∠ABE+∠EBC=90°,∠EBC+∠CBF=90°,∴∠ABE=∠CBF,∵AB=CB,∴△AEB≌△CFB(AAS)∴BE=BF,∵四边形ABCD的面积为12,∴四边形BEDF的面积为12,∴BE×BF=12,即BE2=12,∴BE=2,故选D.3.如图,在四边形ABCD中,∠ABC=90°,AB=BC=2,E、F分别是AD、CD的中点,连接BE、BF、EF.若四边形ABCD的面积为6,则△BEF的面积为()A.2 B.C.D.3【解析】连接AC,过B作EF的垂线交AC于点G,交EF于点H,∵∠ABC=90°,AB=BC=2,∴AC===4,∵△ABC为等腰三角形,BH⊥AC,∴△ABG,△BCG为等腰直角三角形,∴AG=BG=2=•AB•BC=×2×2=4,∵S△ABC∴S=2,△ADC∵=2,∵△DEF∽△DAC,∴GH=BG=,∴BH=,又∵EF=AC=2,∴S △BEF =•EF•BH=×2×=,故选C .方法二:S △BEF =S 四边形ABCD ﹣S △ABE ﹣S △BCF ﹣S △FED ,易知S △ABE +S △BCF =S 四边形ABCD =3,S △EDF =,∴S △BEF =S 四边形ABCD ﹣S △ABE ﹣S △BCF ﹣S △FED =6﹣3﹣=.故选C .4.如图,ABCD 是边长为1的正方形,EFGH 是内接于ABCD 的正方形,AE=a ,AF=b ,若S EFGH =,则|b ﹣a |等于( )A .B .C .D .【解析】在△AEF 和△DHE 中,,∴△AEF ≌△DHE ,∴AF=DE ,∵DE +AE=1,∴a +b=1,∵a 2+b 2=求解得:a=,b=,∴|b﹣a|=,故选D.5.如图,在平行四边形ABCD中,点P为边AB上一点,将△CBP翻折,点B 的对应点B′恰好落在DA的延长线上,且PB′⊥AD,若CD=3,BC=4,则BP 长度为()A.B.C.D.【解析】由折叠的性质可得:PB′=PB,∠PB′C=∠B,∵四边形ABCD是平行四边形,PB′⊥AD,∴∠B=∠D,∠PB′A=90°,∴∠D+∠CB′D=90°,∴∠DCB′=90°,∵CD=3,BC=4,∴AD=B′C=BC=4,∴DB′==5,∴AB′=DB′﹣AD=1,设BP=x,则PB′=x,PA=3﹣x,在Rt△AB′P中,PA2=AB′2+PB′2,∴x2+12=(3﹣x)2,解得:x=,∴BP=.故选A.6.如图,在正方形ABCD中,AD=5,点E、F是正方形ABCD内的两点,且AE=FC=3,BE=DF=4,则EF的长为()A.B.C.D.【解析】延长AE交DF于G,如图:∵AB=5,AE=3,BE=4,∴△ABE是直角三角形,∴同理可得△DFC是直角三角形,可得△AGD是直角三角形,∴∠ABE+∠BAE=∠DAE+∠BAE,∴∠GAD=∠EBA,同理可得:∠ADG=∠BAE,在△AGD和△BAE中,,∴△AGD≌△BAE(ASA),∴AG=BE=4,DG=AE=3,∴EG=4﹣3=1,同理可得:GF=1,∴EF=,故选D.7.如图,以正方形ABCD的一边向形外作等边△ABE,BD与EC交于点F,且DF=EF,则∠AFD等于()A.60°B.50°C.45°D.40°【解析】连接AC,∵BD为AC的垂直平分线,∴FA=FC,∵四边形ABCD是正方形,∴AD=DC=AB,在△DCF和△DAF中,,∴△DCF ≌△DAF ,∵三角形ABE 是等边三角形,∴AE=AB=AD ,在△DAF 和△EAF 中,,∴△DAF ≌△EAF ,∴△DCF ≌△DAF ≌△EAF ,得:∠DFC=∠AFD=∠AFE ,又∵∠DFC +∠AFD +∠AFE=180°∴∠DFC=∠AFD=∠AFE=60°故选 A .8.如图,正方形ABCD 的边长为1,点P 为BC 上任意一点(可与点B 或C 重合),分别过B 、C 、D 作射线AP 的垂线,垂足分别是B′、C′、D′,则BB′+CC′+DD′的最小值是( )A .1B .C .D .【解析】连接AC ,DP ,如图所示.∵四边形ABCD 是正方形,正方形ABCD 的边长为1,∴AB=CD ,S 正方形ABCD =1,∵S △ADP =S 正方形ABCD =,S △ABP +S △ACP =S △ABC =S 正方形ABCD =,∴S △ADP +S △ABP +S △ACP =1, ∴AP•BB′+AP•CC′+AP•DD′=AP•(BB′+CC′+DD′)=1,则BB′+CC′+DD′=,∵当点P与C重合时,PA的值最大,PA的最大值为,∴BB′+CC′+DD′的最小值是,故选B.9.如图,正方形ABCD的边长为8,∠DAC的平分线交DC于点E.若点P,Q分别是AD和AE上的动点,则DQ+PQ的最小值是()A.4 B.8 C.4D.8【解析】作D关于AE的对称点D′,再过D′作D′P′⊥AD于P′,∵DD′⊥AE,∴∠AFD=∠AFD′,∵AF=AF,∠DAE=∠CAE,∴△DAF≌△D′AF,∴D′是D关于AE的对称点,AD′=AD=8,∴D′P′即为DQ+PQ的最小值,∵四边形ABCD是正方形,∴∠DAD′=45°,∴AP′=P′D′,∴在Rt△AP′D′中,P′D′2+AP′2=AD′2,∵AP′=P′D',2P′D′2=AD′2=64,∴P′D′=4,即DQ+PQ的最小值为4.故选C.10.如图,边长为1的正方形ABCD 的对角线AC ,BD 相交于点O ,∠MPN 为直角,使点P 与点O 重合,直角边PM ,PN 分别与OA ,OB 重合,然后逆时针旋转∠MPN ,旋转角为θ(0°<θ<90°),PM ,PN 分别交AB ,BC 于E ,F 两点,连接EF 交OB 于点G ,则下列结论:①EF=OE ;②S 四边形OEBF :S 正方形ABCD =1:4;③BE +BF=OA ;④在旋转过程中,当△BEF 与△COF 的面积之和最大时,AE=;⑤OG•BD=AE 2+CF 2.其中结论正确的个数是( )A .2个B .3个C .4个D .5个【解析】①∵四边形ABCD 是正方形,∴OB=OC ,∠OBE=∠OCF=45°,∠BOC=90°,∴∠BOF +∠COF=90°,∵∠EOF=90°,∴∠BOF +∠COE=90°,∴∠BOE=∠COF ,在△BOE 和△COF 中,,∴△BOE ≌△COF (ASA ),∴OE=OF ,BE=CF ,∴EF=OE ;故正确;②∵S 四边形OEBF =S △BOE +S △BOE =S △BOE +S △COF =S △BOC =S 正方形ABCD ,∴S 四边形OEBF :S 正方形ABCD =1:4;故正确;③过点O 作OH ⊥BC ,∵BC=1,∴OH=BC=,设AE=x ,则BE=CF=1﹣x ,BF=x ,∴S △BEF +S △COF =BE•BF +CF•OH=x (1﹣x )+(1﹣x )×=﹣(x ﹣)2+,∵a=﹣<0,∴当x=时,S △BEF +S △COF 最大;即在旋转过程中,当△BEF 与△COF 的面积之和最大时,AE=;故错误;④∵∠EOG=∠BOE ,∠OEG=∠OBE=45°,∴△OEG ∽△OBE ,∴OE :OB=OG :OE ,∴OG•OB=OE 2,∵OB=BD ,OE=EF ,∴OG•BD=EF 2,∵在△BEF 中,EF 2=BE 2+BF 2,∴EF 2=AE 2+CF 2,∴OG•BD=AE 2+CF 2.故正确.故选B .二.填空题(共10小题,满分40分,每小题4分)11.已知菱形ABCD 的边长为6,∠A=60°,如果点P 是菱形内一点,且PB=PD=2,那么AP 的长为 或 .【解析】当P 与A 在BD 的异侧时:连接AP 交BD 于M ,∵AD=AB ,DP=BP ,∴AP ⊥BD (到线段两端距离相等的点在垂直平分线上),在直角△ABM 中,∠BAM=30°,∴AM=AB•cos30°=3,BM=AB•si n30°=3, ∴PM==,∴AP=AM +PM=4;当P 与A 在BD 的同侧时:连接AP 并延长AP 交BD 于点MAP=AM ﹣PM=2;当P 与M 重合时,PD=PB=3,与PB=PD=2矛盾,舍去.AP 的长为4或2.故答案为4或2.12.如图,正方形ABCD中,点G为对角线AC上一点,AG=AB.∠CAE=16°且AE=AC,连接GE.将线段AE绕点A逆时针旋转得到线段AF,使DF=GE,则∠CAF的度数为29°或61°.【解析】∵线段AE绕点A逆时针旋转得到线段AF,∴AE=AF,∵四边形ABCD是正方形,∴AB=AD,∵AG=AB,∴AD=AG,在△AGE和△ADF中,,∴△AGE≌△ADF(SSS),∴∠DAF=∠CAE=16°,∵AC为正方形ABCD的对角线,∴∠CAD=45°,点F在AD的下方时,∠CAF=∠CAD﹣∠DAF=45°﹣16°=29°,点F在AD的上方时,∠CAF=∠CAD+∠DAF=45°+16°=61°,综上所述,∠CAF的度数为29°或61°.故答案为:29°或61°.13.按如图所示,把一张边长超过10的正方形纸片剪成5个部分,则中间小正方形(阴影部分)的周长为20.【解析】延长BG,交AE与点C,∵∠ABC=45°∴△ABC是等腰直角三角形,∴AB=AC∴CE=5∵△CED是等腰直角三角形,∴CD=5∵CD=GF,∴中间的小正方形的边长是5,因而周长是20.故答案为2014.已知:如图,矩形ABCD的对角线相交于O,AE平分∠BAD交BC于E,∠CAE=15°,则∠BOE=75°.【解析】∵AE平分∠BAD交BC于E,∴∠AEB=45°,AB=BE,∵∠CAE=15°,∴∠ACB=∠AEB﹣∠CAE=45°﹣15°=30°,∴∠BAO=60°,又∵OA=OB,∴△BOA是等边三角形,∴OA=OB=AB,即OB=AB=BE,∴△BOE是等腰三角形,且∠OBE=∠OCB=30°,∴∠BOE=(180°﹣30°)=75°.故答案为:75.15.如图,正方形ABCD的面积为256,点F在AD上,点E在AB的延长线上,直角△CEF的面积为200,则BE的值为12.【解析】∵四边形ABCD是正方形,∴BC=CD,∠D=∠ABC=∠BCD=90°,∴∠CBE=90°,∵∠ECF=90°,∴BCE=∠DCF,在△BCE和△DCF中,,∴△BCE≌△DCF(ASA),∴CE=CF,∴△CEF是等腰直角三角形,∴△CEF的面积=CE•CF=CE2=200,∴CE=20,∵正方形ABCD的面积为256,∴BC==16,∴BE===12.故答案为:12.16.如图,四边形ABCD是菱形,E在AD上,F在AB延长线上,CE和DF 相交于点G,若CE=DF,∠CGF=30°,AB的长为6,则菱形ABCD的面积为18.【解析】连接AC、BD,交于点O,分别取AE、BF的中点M、N,连接OM、ON,在AB上截取AH=AM,连接OH,过C作CP⊥AF于P,∵四边形ABCD是菱形,∴O是BD的中点,也是AC的中点,∴OM=CE,ON=DF,∵CE=DF,∴OM=ON,∵AC平分∠DAB,∴∠DAC=∠BAC,∵AO=AO,∴△AMO≌△AHO,∴OM=OH,∠AMO=∠AHO,∴OM=OH=ON,∴∠OHN=∠ONH,∵∠AHO+∠OHN=180°,∴∠AMO+∠ONH=180,∵OM∥EC,ON∥DF,∴∠AMO=∠AEC,∠ONH=∠GFA,∴∠AEC+∠GFA=180°,∴∠DAB+∠EGF=180°,∵∠CGF=30°,∴∠EGF=150°,∴∠DAB=30°,∵AD∥BC,∴∠CBF=∠DAB=30°,∵AB=BC=6,∴CP=BC=3,∴菱形ABCD的面积=AB•CP=6×3=18,故答案为18.17.如图,ABCD是正方形,M是BC中点,将正方形折起,使点A与点M重合,设折痕为EF,若正方形面积是64,那么梯形AEFD的面积是24.【解析】依题意得,正方形的边长为8,设AE=x,由折叠可知EM=AE=x,BE=8﹣x,BM=8÷2=4,在Rt△BME中,BE2+BM2=EM2,即(8﹣x)2+42=x2,解得:x=5,再设DF=y,则CF=8﹣y,AD2+DF2=CF2+CM2,即82+y2=(8﹣y)2+42,解得:y=1,S梯形AEFD=×(AE+DF)×AD=×(5+1)×8=24.故答案为:24.18.如图,将边长为4cm的正方形ABCD折叠,使点D落在BC边的中点E处,点A落在F处,折痕为MN交AB于M,交DC于N,则线段FM长为cm.【解析】∵点E为BC的中点,∴CE=BC=2,由翻折的性质得,EN=DN,设CN=x,则EN=DN=4﹣x,在Rt△CEN中,CE2+CN2=EN2,即22+x2=(4﹣x)2,解得x=,过点M作MG⊥CD于G,连接DE,则MG=CD,由翻折的性质得,MN⊥DE,∴∠NMG=∠EDC,在△CDE和△GMN中,,∴△CDE≌△GMN(ASA),∴GN=CE=2cm,∴DG=4﹣﹣2=cm,∵MG⊥CD,四边形ABCD是正方形,∴四边形AMGD是矩形,∴AM=DG,由翻折的性质得,FM=AM=cm.故答案为:cm.19.如图,正方形ABCD中,点E、F分别是BC、CD边上的点,且∠EAF=45°,对角线BD交AE于点M,交AF于点N.若AB=2,BM=1,则MN的长为.【解析】如图,延长BC到G,使BG=DF连接AG,在AG截取AH=AN,连接MH、BH.∵四边形ABCD为正方形,∴AB=BC=CD=AD,∠4=∠5=45°,∠BAD=∠ADF=∠ABE=∠ABG=90°,在RT△ABG和RT△ADF中,,∴RT△ABG≌RT△ADF(SAS),∴∠1=∠2,∠7=∠G,AF=AG,∴∠GAE=∠2+∠3=∠1+∠3=∠BAD﹣∠EAF=90°﹣45°=45°=∠EAF,在△AMN和△AMH中,,∴△AMN≌△AMH(SAS),∴MN=MH,∵AF=AG,AN=AH,∴FN=AF﹣AN=AG﹣AH=GH,在△DFN和△BFH中,,∴△DFN≌△BGH(SAS),∴∠6=∠4=45°,DN=BH,∴∠MBH=∠ABH+∠5=∠ANG﹣∠6+∠5=90°﹣45°+45°=90°∴BM2+DN2=BM2+BH2=MH2=MN2,∵BD=AB=4,∴12+(4﹣1﹣MN)2=MN2,∴MN=,故答案为:.20.一个矩形各边的长都是正整数,而且它的面积的数量等于其周长的数量的2倍,这样的矩形有3个.【解析】设矩形的长和宽分别是y和x,∵矩形的面积(量数)是周长(量数)的2倍,∴xy=4(x+y),即xy﹣4x﹣4y=0.∴xy﹣4x﹣4y+16=16,即(x﹣4)(y﹣4)=16.不妨设x≤y,∴x﹣4=1,y﹣4=16 或者x﹣4=2,y﹣4=8 或者x﹣4=4,y﹣4=4,∴x=5时y=20;x=6时y=12;x=8时,y=8,∴(5,20)或者(6,12)或者(8,8).故答案为:3.三.解答题(共5小题,满分70分)21.(12分)(1)如图1,点P是正方形ABCD内的一点,把△ABP绕点B顺时针方向旋转,使点A与点C重合,点P的对应点是Q.若PA=3,PB=2,PC=5,求∠BQC的度数.(2)点P是等边三角形ABC内的一点,若PA=12,PB=5,PC=13,求∠BPA 的度数.【解析】(1)连接PQ.由旋转可知:,QC=PA=3.又∵ABCD是正方形,∴△ABP绕点B顺时针方向旋转了90°,才使点A与C重合,即∠PBQ=90°,∴∠PQB=45°,PQ=4.则在△PQC中,PQ=4,QC=3,PC=5,∴PC2=PQ2+QC2.即∠PQC=90°.故∠BQC=90°+45°=135°.(2)将此时点P的对应点是点P′.由旋转知,△APB≌△CP′B,即∠BPA=∠BP′C,P′B=PB=5,P′C=PA=12.又∵△ABC是正三角形,∴△ABP绕点B顺时针方向旋转60°,才使点A与C重合,得∠PBP′=60°,又∵P′B=PB=5,∴△PBP′也是正三角形,即∠PP′B=60°,PP′=5.因此,在△PP′C中,PC=13,PP′=5,P′C=12,∴PC2=PP′2+P′C2.即∠PP′C=90°.故∠BPA=∠BP′C=60°+90°=150°.22.(12分)已知,如图,四边形ABCD中,AB=AD,∠BAD=∠BCD=90°,E 为BC边上一点,作∠AEF=∠ACF=90°(1)试判断AE和EF的数量关系,并说明理由;(2)当四边形ABCD的面积为16,BC的长为6,求AD的长.【解析】(1)作AM⊥BC,AN⊥CD垂足分别为M、N,在线段AM上截取AH=CE,连接HE.∵∠AMC=∠MCN=∠=90°,∴四边形AMCN 是矩形,∴∠MAN=90°,∵∠BAD=90°,∴∠BAD=∠MAN ,∴∠BAM=∠DAN ,在△AMB 和△AND 中,,∴△AMB ≌△AND ,∴AM=AN ,∴四边形AMCN 是正方形,∴AM=CM ,∠ACM=45°,∵∠ACF=90°,∴∠ECF=135°,∵AH=EC ,∴MH=ME ,∴∠MHE=45°,∠AHE=135°=∠ECF ,∵∠FEC +∠AEM=90°,∠HAE +∠AEM=90°,∴∠FEC=∠HAE ,在△AHE 和△ECF 中,,∴△AHE ≌△ECF ,∴AE=EF .(2)由(1)可知:四边形AMCN 是正方形,△AMB ≌△AND ,∴S △AMB =S △AND ,∴S 四边形ABCD =S 正方形AMCN =16,∴AN=MC=4,∵BC=6,∴MB=ND=2,在RT△AND中,∵AN=4,ND=2,∴AD===2.23.(14分)如图,在正方形ABCD中,点P是AD边上的一个动点,连接PB,过点B作一条射线与边DC的延长线交于点Q,使得∠QBE=∠PBC,其中E是边AB延长线上的点,连接PQ.(1)求证:△PBQ是等腰直角三角形;(2)若PQ2=PB2+PD2+1,求△PAB的面积.【解析】(1)证明:∵∠QBE=∠PBC,∠QBE+∠QBC=90°,∴∠PBQ=∠PBC+∠QBC=90°,∵∠PBC+∠PBA=90°,∴∠PBA=∠QBC,在Rt△PAB和Rt△QCB中,,∴△PAB≌△QCB(ASA),∴PB=QB,∴△PBQ是等腰直角三角形;(2)设正方形的边长AB=a,PA=x,∵△PAB≌△QCB,∴QC=PA=x,∴DQ=DC+QC=a+x,PD=AD﹣PA=a﹣x,在Rt△PAB中,PB2=PA2+AB2=x2+a2,∵PQ2=PB2+PD2+1,∴(a﹣x)2+(a+x)2=x2+a2+(a﹣x)2+1,解得:2ax=1,∴ax=,∵△PAB的面积S=PA•PB=ax=.24.(15分)已知:l1∥l2∥l3∥l4,平行线l1与l2、l2与l3、l3与l4之间的距离分别为d1、d2、d3,且d1=d3=1,d2=2.我们把四个顶点分别在l1、l2、l3、l4这四条平行线上的四边形称为“格线四边形”.(1)如图1,正方形ABCD为“格线四边形”,则正方形ABCD的边长为.(2)矩形ABCD为“格线四边形”,其长:宽=2:1,求矩形ABCD的宽.(3)如图1,EG过正方形ABCD的顶点D且垂直l1于点E,分别交l2,l4于点F,G.将∠AEG绕点A顺时针旋转30°得到∠AE′D′(如图2),点D′在直线l3上,以AD′为边在E′D′左侧作菱形AB′C′D′,使B′,C′分别在直线l2,l4上,求菱形AB′C′D′的边长.【解析】(1)∵l1∥l2∥l3∥l4,∠AED=90°∴∠DGC=90°,∵四边形ABCD为正方形∴∠ADC=90°,AD=CD,∵∠ADE+∠2=90°,∴∠1+∠2=90°,∴∠1=∠ADE,∵l3∥l4∴∠1=∠DCG,∠ADE=∠DCG,在△AED与△DGC中,,∴△AED≌△GDC(AAS),∴AE=GD=1,ED=GC=3,∴AD==,故答案为:;(2)如图2过点B作BE⊥L1于点E,反向延长BE交L4于点F,则BE=1,BF=3,∵四边形ABCD是矩形,∴∠ABC=90°,∴∠ABE+∠FBC=90°,∵∠ABE+∠EAB=90°,∴∠FBC=∠EAB,当AB<BC时,AB=BC,∴AE=BF=,∴AB==;如图3当AB>BC时,同理可得:BC=,∴矩形的宽为:,;(3)如图4过点E′作ON垂直于l1分别交l1,l4于点O,N,∵∠OAE′=30°,则∠E′FN=60°∵AE′=AE=1,故E′O=,E′N=,E′D′=,由勾股定理可知菱形的边长为:==.25.(17分)如图一,已知点P是边长为a的等边△ABC内任意一点,点P到三边的距离PD、PE、PF的长分别记为h1,h2,h3,则h1,h2,h3之间有什么关系呢?分析:连接PA 、PB 、PC ,则△ABC 被分割成三个三角形,根据:S △PAB +S △PBC +S △PAC =S △ABC ,即:,可得.问题1:若点P 是边长为a 的等边△ABC 外一点(如图二所示位置),点P 到三边的距离PD 、PE 、PF 的长分别记为h 1,h 2,h 3.探索h 1,h 2,h 3之间有什么关系呢?并证明你的结论;问题2:如图三,正方形ABCD 的边长为a ,点P 是BC 边上任意一点(可与B 、C 重合),B 、C 、D 三点到射线AP 的距离分别是h 1,h 2,h 3,设h 1+h 2+h 3=y ,线段AP=x ,求y 与x 的函数关系式,并求y 的最大值与最小值.【解析】问题1:h 1+h 3﹣h 2=.理由:连接PA 、PB 、PC . ∵PE ⊥BC ,PD ⊥BA ,且△ABC 是边长为a 的等边三角形,∴S △PAB =,S △PBC =,∴S 四边形ABCP =S △PAB +S △PBC =+, 又∵S 四边形ABCP =S △APC +S △ABC =+a 2, ∴+=++a 2,即:h 1+h 3﹣h 2=;问题2:连接DP 、AC . 易求:S △APB +S △ADP +S △ACP =, 易证:S △DCP =S △ACP (同底等高), 而S 正方形ABCD =S △APB +S △ADP +S △DCP , ∴,∴y=(a ≤x ≤a ), ∵2a 2>0,∴y 随x 的增大而减少, ∴当x=a 时,y 最小=a ,当x=a 时,y 最大=2a .。
2019-2020北师大版九年级数学上册第一章特殊平行四边形单元培优试卷解析版(难度较大)

2019-2020北师大版九年级数学上册第一章特殊平行四边形单元培优试卷一.选择题(每小题3分,共24分)1.如图,在正方形ABCD的外侧,作等边三角形ADE,AC,BE相交于点F,则∠BFC为()A.45° B.55° C.60° D.75°2.将矩形ABCD按如图所示的方式折叠,BE,EG,FG为折痕,若顶点A,C,D都落在点O处,且点B,O,G在同一条直线上,同时点E,O,F在另一条直线上,则的值为()A.B.C.D.3.如图,正方形ABCD的边长为9,将正方形折叠,使顶点D落在BC边上的点E处,折痕为GH.若BE:EC=2:1,则线段CH的长是()A.3 B.4 C.5 D.64.如图,矩形ABCD的对角线AC、BD相交于点O,CE∥BD,DE∥AC,若AC=8,则四边形OCED的周长为()A.8 B.16 C.18 D.205.如图,在菱形ABCD和菱形BEFG中,点A、B、E在同一直线上,P是线段DF的中点,连接PG,PC.若∠ABC=∠BEF=60°,则=()A .B .C .D .6.如图,在正方形ABCD 中,点E ,F 将对角线AC 三等分,且AC =12,点P 在正方形的边上,则满足PE+PF =9的点P 的个数是( )A .0B .4C .6D .87.如图,在矩形ABCD 中,AB=4,BC=6,点E 为BC 的中点,将△ABE 沿AE 折叠,使点B 落在矩形内点F 处,连接CF ,则CF 的长为( )A .B .C .D .8.已知菱形ABCD ,E,F 是动点,边长为4,BE=AF ,∠BAD=120°,则下列结论正确的有几个( )①△BEC≌△AFC ; ②△ECF 为等边三角形③∠AGE=∠AFC ④若AF=1,则 A. 1 B. 2 C. 3 D. 431 GEGF二.填空题(每小题4分,共24分)9.如图,点P是矩形ABCD的对角线AC上一点,过点P作EF∥BC,分别交AB,CD于E、F,连接PB、PD.若AE=2,PF=8.则图中阴影部分的面积为.10.矩形ABCD与CEFG,如图放置,点B,C,E共线,点C,D,G共线,连接AF,取AF的中点H,连接GH.若BC=EF=2,CD=CE=1,则GH=.11.以正方形ABCD的边AD作等边△ADE,则∠BEC的度数是.12.如图,已知正方形ABCD的边长为5,点E、F分别在AD、DC上,AE=DF=2,BE与AF相交于点G,点H为BF的中点,连接GH,则GH的长为.13.如图,将正方形OEFG放在平面直角坐标系中,O是坐标原点,点E的坐标为(2,3),则点F的坐标为.14.如图,在平面直角坐标系xOy中,菱形OABC的边长为2,点A在第一象限,点C在x轴正半轴上,∠AOC=60°,若将菱形OABC绕点O顺时针旋转75°,得到四边形OA′B′C′,则点B的对应点B′的坐标为.三.解答题(共52分)15.(6分)如图,在四边形ABCD中,BC=CD,∠C=2∠BAD.O是四边形ABCD内一点,且OA=OB=OD.求证:(1)∠BOD=∠C;(2)四边形OBCD是菱形.16.(6分)在矩形ABCD中,点E在BC上,AE=AD,DF⊥AE,垂足为F.(1)求证.DF=AB;(2)若∠FDC=30°,且AB=4,求AD.17.(6分)在正方形ABCD中,对角线BD所在的直线上有两点E、F满足BE=DF,连接AE、AF、CE、CF,如图所示.(1)求证:△ABE≌△ADF;(2)试判断四边形AECF的形状,并说明理由.18.(6分)如图是一个长为a ,宽为b 的矩形,两个阴影图形都是一对底边长为1,且底边在矩形对边上的平行四边形.(1)用含字母a ,b 的代数式表示矩形中空白部分的面积;(2)当a =3,b =2时,求矩形中空白部分的面积.19.(9分)已知:在矩形ABCD 中,BD 是对角线,AE ⊥BD 于点E,CF ⊥BD 于点F ;(1)如图1,求证:AE=CF ;(2)如图2,当∠ADB=30°时,连接AF 、CE,在不添加任何辅助线的情况下,请直 接写出图2中四个三角形,使写出的每个三角形的面积都等于矩形ABCD面积的。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
特殊的四边形培优1.如图,已知在菱形ABCD中,DE⊥AB,DF⊥BC,垂足分别为E、F,且AE=BE,则∠EDF=______度.1.如图,四边形ABCD是正方形,△BDE是等边三角形,EF⊥DF,则∠BEF=________3.如图,正方形ABCD的面积为256,点F在AD上,点E在AB的延长线上,Rt△CEF的面积为200,则BE 的长为_______FB CA DE4. 如图,在菱形ABCD 中,AB=4a ,E 在BC 上,BE=2a ,∠BAD=120°,P 点在BD 上,则PE+PC 的最小值为( )5.如图,矩形AEFG 与矩形APQK 的周长都等于120cm,求△ABC 的周长6.如图,在矩形ABCD 中,M ,N 分别是AD ,DC 边的中点,AN 与MC 交于P 点,若∠MCB=∠NBC+33°,那么∠MPA 的大小是( )1. 边长为25cm 的正方形纸片,AD 上有一点P ,且AP=66cm,将这纸片折叠使B 落在P 上,则折痕的长是________2. 已知直角三角形ABCD 中,∠C=90°,AC=3,BC=5,以AB 为边向外作正方形ABEF 求此正方形KGP E BC中心O到C点的距离OC的长________3.如图,已知在矩形ABCD中,E为CB延长线上一点,CE=AC,F是AE的中点.(1)求证BF⊥DF(2)若AB=8,AD=6,求DF的长10.如图,已知三角形ABC中,AB=AC,点M为BC 的中点,MG⊥BA于G,MD⊥AC于D,GF⊥AC于点E,GF与DF相交于点F,(1)求证:四边形HGMD是菱形(2)若∠GMD=120°,求证:从M点向所对的HG 和HD边引出的两条垂线MK和MQ分别平分这两条线段.E FQKDG11.如图,将一矩形的每一内角三等分,连接靠近同一边上的两三等分线所交成4交点组成四边形EFGH,试判断四边形EFGH形状12.在正方形ABCD中,AK和AN是∠A内的两射线,BK⊥AK,BL⊥AN,DM⊥AK,DN⊥AN,试求KL=MN1.在锐角△ABC中,BE是高,CF是中线,若∠ACF=30°则BE:CF=________2.如图,D、E、F分别是△ABC三边的中点,G是AE的中点,BE与DF、DG分别交于P、Q两点,则PQ:BE=______.3.如图,△ABC中,∠BAC=120°,以AB,AC为边分别向形外作正三角形ABD和正三角形ACE,M为AD中点,N为AE中点,P为BC中点,求∠MPN的度数.4.凸五边形ABCDE中,∠ABC=∠AED=90°,∠CAD=30°,∠BAE=70°,F是CD中点,且FB=FE,则∠BAC=_________.5.已知:如图所示,在△ABC中,D、G分别为AB、AC上的点,且BD=CG,M、N分别是BG、CD的中点,过MN的直线交AB于点P,交AC于点Q,求证:AP=AQ。
6.如图,在等腰梯形ABCD中,AD平行BC,E,F,G,H,分别是AD ,BC,BE ,CE的中点.(1).求证:四边形EGFH是菱形(2).若BC=2AD.且梯形ABCD的面积为30平方厘米,求四边形EGFH的面积7.已知△ABC 中,∠B=2∠C,AD ⊥BC 于D,M 为BC 的中点,求证:DM=1/2AB8. 在△ABC 中,点D 在CA 的延长线上且AD=12 AC,E 为BC 的中点,DE 交AB 于F ,过F 引直线MN 垂直DE ,P 为MN 上一点,求证PD=PEFA BCDP910. 线段AB,CD 相交于点O,且AB=CD,E,F 分别为BC,AD 的中点,连接EF 分别交AB,CD 于P,H 如图,求证:OP=OHHP EF CDOA1.如图,在平行四边形ABCD 中,BC=2AB,M是AD的中点,CE⊥AB于点E.求证:∠DME=3∠AEM.2.如图,在平面直角坐标系xOy中,直线y=x+1与y=-34x+3交于点A,分别交x轴于点B和点C,点D 是直线AC上的一个动点.(1)求点A,B,C的坐标;(2)当△CBD为等腰三角形时,求点D的坐标;(3)在直线AB上是否存在点E,使得以点E,D,O,A为顶点的四边形是平行四边形?如果存在,直接写出的值;如果不存在,请说明理由.BECD3.如图,矩形纸片ABCD中,AD=9,AB=3,将其折叠,使点D与点B重合,折痕为EF,那么折痕EF的长为_____4.将一矩形纸片OABC放在直角坐标系中,O为原点,C在x轴上,OA=6,OC=10.(1)如图(1),在OA上取一点E,将△EOC沿EC 折叠,使O点落在AB边上的D点,求E点的坐标;(2)如图(2),在OA、OC边上选取适当的点E′、F,将△E′OF沿E′F折叠,使O点落在AB边上的D′点,过D′作D′G⊥C′O交E′F于T点,交OC′于G点,求证:TG=A′E′.(3)在(2)的条件下,设T(x,y)①探求:y与x 之间的函数关系式.②指出变量x的取值范围.(4)如图(3),如果将矩形OABC变为平行四边形OA″B″C″,使O C″=10,O C″边上的高等于6,其它条件均不变,探求:这时T(x,y)的坐标y与x之间是否仍然满足(3)中所得的函数关系,若满足,请说明理由;若不满足,写出你认为正确的函数关系式.5.在菱形ABCD中,∠ABC=60°,AB=1,E为边BC 的中点.则对角线BD上的动点P到E、C两点的距离之和的最小值为__________6. 如图,在矩形ABCD中,对角线长2,且∠1=∠2=∠3=∠4,则四边形EFGH的周长为()7.如图,在菱形ABCD中,已知AB=3,DF=1,∠DAB=60°,∠EFG=15°,FG⊥BC,求AE的长8.在矩形ABCD中,已知两邻边AD=12,AB=5,P是AD边上异于A和D的任意一点,且PE⊥BD,PF⊥AC,E、F分别是垂足,那么PE+PF=______.1. 如图,长方形ABCD的长为8,宽为5,E是AB的中点,点F在BC上,已知△DEF的面积为16,则点D到直线EF的距离为______.10.如图,直角三角形ABC中,AC=1,BC=2,P为斜边AB上一动点。
PE⊥BC,PF⊥CA,则线段EF长的最小值为()。
11. 如图,设ABCDE是正五边形,五角星ACEBD(阴影部分)的面积为1,设AC与BE的交点为P,BD与CE的交点为Q,则四边形APQD的面积等于______.12.已知:如图,菱形ABCD 的对角线AC与BD交于AB,点O,延长BA到E,使AE=12连接OE,延长DE交CA的延长线于F.求证:DF.OE=1213. 如图1,在△ABC中,点P为BC边中点,直线a绕顶点A旋转,若B、P在直线a的异侧,BM⊥直线a于点M,CN⊥直线a于点N,连接PM、PN;(1)延长MP交CN于点E(如图2)。
①求证:△BPM ≌△CPE;②求证:PM=PN;(2)若直线a绕点A旋转到图3的位置时,点B、P 在直线a的同侧,其它条件不变。
此时PM=PN还成立吗?若成立,请给予证明;若不成立,请说明理由;(3)若直线a绕点A旋转到与BC边平行的位置时,其它条件不变。
请直接判断四边形MBCN的形状及此时PM=PN还成立吗?不必说明理由。
14.如图,已知ABCD为正方形,△AEP为等腰直角三角形,∠EAP=90°,且D、P、E三点共线,若EA=AP=1,PB=5,则DP=_____.15.如图①,把正方形CGEF的对角线CE放在正方形ABCD的边BC的延长线上(CG>BC),⑴探究线段MD、MF的关系,加以证明(2)将正方形CGEF铙点C旋转任意角度后,其他条件不变,探究:MD、MF的关系,加以证明.16. 小杰和他的同学组成了“爱琢磨”学习小组,有一次,他们碰到这样一道题:“已知正方形ABCD ,点E、F、G、H分别在边AB、BC、CD、DA上,若EG ⊥FH,则EG = FH”经过思考,大家给出了以下两个方案:(甲)过点A作AM∥HF交BC于点M,过点B作BN∥EG交CD于点N ;(乙)过点A作AM∥HF 交BC于点M,作AN∥EG交CD的延长线于点N ;小杰和他的同学顺利地解决了该题后,大家琢磨着想改变问题的条件,作更多的探索。
……(1)对小杰遇到的问题,请在甲、乙两个方案中任选一个,加以证明(如图8);(2)如果把条件中的“正方形”改为“长方形”,并设AB =2,BC =3(如图9),试探究EG、FH之间有怎样的数量关系,并证明你的结论;(3)如果把条件中的“EG⊥FH”改为“EG与FH的夹角为45°”,并假设正方形ABCD的边长为1,FH的长为(如图10),试求EG的长度。
17.如图①所示,已知A、B为直线l上两点,点C为直线l上方一动点,连接AC、BC,分别以AC、BC为边向△ABC外作正方形CADF和正方形CBEG,过点D作DD1⊥l 于点D1,过点E作EE1⊥l于点E1.(1)如图②,当点E恰好在直线l上时(此时E1与E 重合),试说明DD1=AB;(2)在图①中,当D、E两点都在直线l的上方时,试探求三条线段DD1、EE1、AB之间的数量关系,并说明理由;(3)如图③,当点E在直线l的下方时,请直接写出三条线段DD1、EE1、AB之间的数量关系.(不需要证明)18.如图1,正方形ABCD中,点M在AB上,点N在CD上,点P在BC上,MN垂直AP于E .(1)求证:AP=MN.(2)如图2,点F在MN上,若EF=EA,连CF,点G为CF的中点,连DG,DE,求证:DE=2DG(3)在(2)的条件下,若DA=DE,且DN=32,BM=2,求DG的长19.如图,在正方形ABCD中,E是CD边的中点,点F 在BC上,∠EAF=∠DAE,则下列结论中正确的是()A.∠EAF=∠FAB B.BC=3FC C.AF=AE+FC D.AF=BC+FC20已知,如图,正方形ABCD的面积为25,菱形PQCB 的面积为20,求阴影部分的面积21.已知正方形ABCD的边长为1,E为BC边的延长线上一点,CE=1,连接AE,与CD交于点F,连接BF并延长与线段DE交于点G,则BG的长为_______22.在边长为2的正方形ABCD的四边上分别取点E、F、G、H、四边形EFGH四边的平方和EF 2+FG2+GH2+HE2最小时其面积为 .23.如图,已知:△AEC是以正方形ABCD的对角线为边的等边三角形,EF⊥AB,交AB延长线于F,则∠BEF度数为______°.24.如图,已知正方形ABCD,BE=BD,CE‖BD,BE与CD交于点F,证明:DE=DF.25.在平面直角坐标系xOy中,边长为a(a为大于0的常数)的正方形ABCD的对角线AC、BD相交于点P,顶点A在x轴正半轴上运动,顶点B在y轴正半轴上运动(x轴的正半轴、y轴的正半轴都不包含原点O),顶点C、D都在第一象限。
