网格中图形的分割

合集下载

网格化算法在三维模型构建中的应用

网格化算法在三维模型构建中的应用随着科技的不断发展，三维模型构建已经成为了极为普及的技术。

在这一领域中，网格化算法是一种非常重要的算法，它被广泛应用于三维模型的构建、分析和处理。

本文章将为您详细介绍网格化算法在三维模型构建中的应用。

一、网格化算法介绍网格化算法是一种将连续的物理空间离散化成有限数量的网格的算法。

这种算法可以将一个复杂的物理结构转换成一系列简单的网格单元。

网格化算法的实现涉及到以下几个过程：1. 空间分割：将三维图形分割成多个小三角形或小四面体。

可以有不同的分割方法，如球形分割、射线法分割等。

2. 网格单元定义：根据所采用的空间分割方法，定义出网格单元（三角形或四面体）。

3. 网格生成：按照不同的算法，以空间分割和网格单元定义为基础，生成网格。

二、网格化算法在三维模型构建中的应用1. 三维扫描的网格化处理当我们需要将一个物体转换成三维模型时，常常需要先进行三维扫描。

扫描完成后，我们需要进行网格化处理，得到三维网格模型。

这个过程需要使用到网格化算法。

2. CAD设计的网格化处理CAD设计软件中通常进行建模操作时，是将实体模型转化成集合模型（如B-Rep模型），而网格模型又是集合模型与体数据之间的重要接口。

在实现CAD建模过程中，经常需利用网格化算法将B-Rep模型转化为网络模型，这都需要采用网格化算法。

3. 游戏开发的网格化处理在游戏的开发过程中，需要使用三维模型作为游戏场景的背景，如角色模型、场景模型等。

这些模型通常需要进行网格化处理，用于在游戏引擎中呈现。

4. 建筑学的网格化处理建筑学中也常常使用三维模型构建出建筑物的形状。

在这个过程中，也需要使用到网格化算法，将实体模型转化为网格模型。

三、网格化算法的优势与挑战1. 优势a. 精度高：网格化算法可以将复杂的图形分割成相对简单的网格单元，精度较高。

b. 方便优化：网格化算法将三维图形转换成了网格单元，在优化数据时，可以针对单个网格单元进行操作，具有方便优化的特点。

三角形网格生成算法的研究与应用

三角形网格生成算法的研究与应用一、引言三角网格是计算机图形学领域中最常见的图形表示方式之一。

三角形网格生成算法的出现为图形学在各个领域的应用提供了强有力的支持，如计算机辅助设计、数字娱乐、医学图像处理等等。

然而目前三角形网格的生成算法依然存在许多难点，本文将针对这些难点进行研究和分析，探讨三角形网格生成算法的研究与应用。

二、先进的三角形网格生成算法三角形网格生成算法主要分为离散型和连续型两种。

离散型算法主要是针对离散数据点进行分析和处理，是传统算法的核心。

而连续型算法则主要考虑通过合理的数值方法对连续函数进行求解得到三角形网格。

2.1 离散型算法离散型算法主要方法包括 Delaunay 三角剖分、Voronoi 图、alpha 参数、最小生成树等等。

Delaunay 三角剖分是三角形网格分割中最常见的算法之一。

该算法的核心思想是保持尽量少的单纯形边长相交。

Voronoi 图是一种基于点的分割方法，可以将平面分割成一系列多边形。

Alpha 参数是控制 Delaunay 三角剖分质量的措施之一，通过调整 alpha 参数，可以在不同场景下获得合适的 Delaunay 三角剖分。

最小生成树算法则是对点集进行聚类的一种方法，通常用于优化 Delaunay三角剖分的质量。

2.2 连续型算法连续型算法主要包括渐近线、等值线、样条曲面拟合、卷积核方法等等。

渐近线的求解方法主要是对三角形网格表面进行采样后，通过函数空间中的拟合逼近来求解渐近线。

等值线方法则是在网格表面中寻找等值线，从而实现扫描三角形网格的目的。

样条曲面拟合是利用拟合优化方法，对离散的三角形网格点进行拟合，得到连续的三角形网格。

卷积核方法则通过对三角形表面求导以及在线性空间中构建卷积核，从而求得三角形网格表面的连续性信息。

三、三角形网格生成算法在计算机图形学领域的应用三角形网格生成算法在计算机图形学领域的应用十分广泛，主要包括三维重构、曲面拟合、形状建模、虚拟现实等等。

中考复习--网格、分割型作图剖析

9、正方形表示一张纸片,根据要求多次分割,把它分割成若干个直角三角形,操作过程如下:第一次分割,将正方形纸片分成4个全等的直角三角形,第二次分割上次得到的直角三角形中一个再分成4个全等的直角三角形;以后按第二次的作法进行下去: (1)请你设计出两种符合题意的分割方案图;
作直线交abab有什么样的关系时abc题意的两种图形使图形中的cd2cm启迪型有一块菱形的草地要在其上面修筑两条笔直的道路道路把这块草地分成面积相等的部分若路宽忽略不计请你设计三种不同的方案在下面给出的图形上分别作图示把它分割成若干个直角三角形个全等的直角三角形个全等的直角三角形请你就其中一种方案通过操作和观察将第二第三次分割后所得的最小的直角三角形的面积有什么关系
DA
D
B
C B
C B
C
变3：已知:矩形ABCD的边长为2和5,请设计二种不同的分法,将矩形ABCD分割成三个三角形,使每个三角形都相似.(要求画出分割线段,标出能说明分法所需的相等的角、边的长度，不标出有关数据扣分，两种分法是指第一种分法所成的图形与第二种分法所成的图形不全等） A
D
∽ ∽
．．．．．．
2、（2002年吉林省）正方形网格中的每个小正方形边长都是1，每个小格的顶点叫做格点，以格点为顶点分别按下列要求画三角形。（1）使三角形的三边长分别为3，（2）使三角形为钝角三角形且面积为4
2 2, 5
2 、此题是要利用勾股定理计算三角形各边的长度，画法有很多，图1、图2分别第（1）、（2）两题的其中一种画法。
四、网格与面积例4、
19．（7分）（2016•吉林）图1，图2都是8×8的正方形网格，每个小正方形的顶点成为格点，每个小正方形的边长均为1，在每个正方形网格中标注了6个格点，这6个格点简称为标注点（1）请在图1，图2中，以4个标注点为顶点，各画一个平行四边形（两个平行四边形不全等）；（2）图1中所画的平行四边形的面积为．

小学奥数习题版三年级几何图形的剪拼学生版

知识要点找对称【例 1】把一个33 的的网格分成形状、大小完全相同的四份。

【例 2】哥哥和弟弟一起做手工，想把一张红色的平行四边形蜡光纸沿着一条直线，把它剪成大小、形状完全相同的两部分。

想一想，你可以有多少种剪法？【例 3】要把一个正方形剪成形状相同、大小相等的4个图形，该怎样分？按照题目要求（形状和面积），根据图形与图形之间的内在联系，通过在纸上画图或者实际的剪拼，来掌握图形的变化，包括把一个几何图形分割成几个图形以及把几个几何图形拼成几个图形。

有兴趣的学生还可以自制“七巧板”或者“伤脑筋十二块”等中国传统益智拼板游戏，在闲暇时间尝试拼一下，说不定还能拼出自创的新颖有趣的图形。

图形的剪拼【例 4】你能把下面的图形分割成4个形状相同、大小相等的图形吗？【例 5】一个长6厘米，宽4厘米的长方形，从中间剪开，如图所示，得到2个大小、形状都相同的长方形，这两个新长方形的周长是多少？图形剪切【例 6】你能把一个正三角形分成形状相同，大小相等的2个、3个、4个、6个、9个三角形吗？分成【例 7】你能把一个正方形分成6个、7个、8个、9个小正方形吗？(不要求面积相等)【例 8】你能把下面的图形分割成4个形状相同、大小相等的图形吗？【例 9】把下图分成5个形状相同、大小相等的图形。

【例 10】下图是由18个小正方形组成的图形，请你把它分成6个完全相同的图形。

【例 11】你能把下面的图形分成7个大小相等的长方形吗？动手画一画。

【例 12】如右图所示是由三个正方形组成的图形，请把它分成大小、形状都相同的四个图形。

【例 13】阿凡提周游世界，有一天来到一个村庄。

一个地主对他说：“都传说你很聪明，我有一块地，你能把它分成大小相等、形状相同的2份，我就把地送给你。

”聪明的阿凡提不慌不忙，用木棍画了一道线，把这块地分成大小相等、形状相同的2份。

地主傻了眼，只好履行诺言。

后来，阿凡提把地分给了最穷的2户人家，你知道阿凡提是怎么分的吗？图形拼合【例 14】用下面的四块图形能拼成右边的正方形吗？怎样拼？1212124321【例 15】晚饭后，平平和妈妈玩拼木板游戏。

图形分割和格点问题

图形分割和格点问题
1.沿网格线把正方形分割成两个全等图形？试一试．
2．你能用四种不同的方法把一个长方形分成两个全等的图形吗？
3、把图形中的三角形网格图形用一条网格线分割成两个全等图形
4．如图，某地板砖厂要制作一批正六边形地板砖，为适应市场需求，要求在地板砖上设计的图案能够把正六边形六等分，请你帮他设计等分图案．（至少设计两种）
5．沿着图中的虚线，请将下面的图形分割成四个全等的图形.
6．如图中有12棵树，请你把这个正方形划分为四块，要求每块的形状、大小都相同，并且每块中恰好有3棵树．
7、如图，正方形ABCD的边长为a，正方形DEFG的边长为1/2a，将阴影部分划分为4个全等的部分
8、有一块长为4.8m、宽3m的长方形地毯,现在要把它铺到长4m、宽3.6m的房间里,请你把图①的地毯剪成两个全等图形,使其正好铺满图②的房间.
9、你能否将它们各分割成两个小三角形，使左边的两个小三角形分别与右边的两个小三角形全等？如果能，请画出分割线，写对两对全等三角形，再尝试说明理由
9、如图线段AB是一条格点线段(1) 画一条线段，使它与线段AB有一个公共端点。

且与线段AB相等，并证明这两条线段相等；
（2)在所给的网格中，你最多能画出几条满足（1）中要求的线段?。

CAD中图形切割和填充的技巧

CAD中图形切割和填充的技巧CAD软件是一种广泛应用于工程和设计领域的计算机辅助设计软件。

在CAD软件中，图形的切割和填充是常见的操作。

本篇文章将介绍一些CAD软件中关于图形切割和填充的技巧，帮助读者更加高效地使用CAD软件完成工作。

首先，我们来探讨图形的切割技巧。

在CAD软件中，图形切割是将一个图形的部分或整体分割成多个部分的操作。

有许多方法可以实现图形的切割，以下是其中几种常用的方法。

一种方法是使用trim命令。

在CAD软件中，trim命令可以将图形的不需要的部分切除。

首先，选择要切割的图形，然后选择要保留的部分。

CAD软件将自动将不需要的部分删除，只保留需要的部分。

这是一种简单而直观的图形切割方法。

另一种方法是使用split命令。

与trim命令类似，split命令也可以将图形分割成多个部分。

不同之处在于，split命令将图形分割为两个或多个部分，而trim命令只保留一个部分。

使用split命令时，选择要切割的图形和分割线，CAD软件将根据分割线的位置将图形分割成多个部分。

此外，还可以使用hatch命令实现图形的填充。

在CAD软件中，hatch命令可以填充一个封闭图形的内部空间。

选择要填充的图形并指定填充样式，CAD软件将自动填充图形的内部空间。

填充样式可以是线条、点状、网格等，根据需要进行选择。

除了上述方法，还有其他一些辅助工具可以帮助实现图形的切割和填充。

例如，使用插入点工具可以在需要的位置插入一个点，然后使用trim或split命令将图形分割成多个部分。

此外，使用辅助线或辅助圆等几何图形可以帮助我们更精确地进行图形切割和填充的操作。

在使用CAD软件进行图形切割和填充时，还需要注意一些技巧。

首先，要注意选择正确的图形进行切割和填充操作。

选择错误的图形可能导致意想不到的结果。

其次，选择合适的填充样式和比例，以使填充的效果符合设计要求。

此外，还应注意切割和填充操作的顺序以及分割线的位置，以确保图形被切割和填充的效果正确。

关于网格图形问题

关于网格图形问题我们知道，能够完全重合的两个图形，叫做全等形。

请你把下面4×4的正方形方格图形沿着虚线分割成两个全等的图形。

〖解〗：分割方法如下：〖反思〗：1、还有其它分割方法吗？2、从上面的分割方法中，你能发现分割的规律吗？题目：在△ABC中，AB=AC，CG⊥BA交BA的延长线与点G，一等腰三角尺按如图1所示的位置摆放，该三角尺的直角顶点为F，一直角边与AC边在一条直线上，另一条直角边恰好经过点B，（1）、在图1中，请你通过观察、测量BF与CG的长度，猜想并写出BF与CG满足的数量关系，然后证明你的猜想。

（图1）（2）、当三角尺沿AC方向平移到图2所示的位置时，一直角边仍与AC边在同一条直线上，另一条直角边交BC边于点D，过点D作DE⊥BA交BA于点E，此时，请你通过观察、测量DE、DF与CG 的长度，猜想并写出DE+DF与CG满足的数量关系，然后证明你的猜想。

（图2）（3）、当三角尺在（2）、的基础上沿AC方向继续平移到图3所示的位置（点F在线段AC上，且点F与点C不重合）时，（2）中的猜想是否仍然成立？（不用说明理由）（图3）〖点评〗：本题以图形的平移为素材，要求学生发现并证明自己所得的结论，将合情推理与逻辑推理融为一体，突出对数学思考的考察。

本题选自《2008年安徽省初中毕业学业考试纲要》数学试题样卷，仅题目文字就超过300字，又出现动点和平移问题，实在可以称之为一个“庞然大物”，如果你是一位初中生，千万不要被它吓到。

仔细审题，你会发现实际考察平时学习的两个小问题：1、等腰三角形两腰上的高相等（应用三角形的全等或三角形的面积公式证明）；2、等腰三角形底边上任意一点到两腰的距离和等于腰上的高（综合应用等腰三角形的性质、三角形的全等、矩形的判定和性质或三角形的面积公式证明）。

所以，在第一轮数学复习时，要注意概念复习和基础题的复习，不要脱离课本，注重数学思想和数学方法的复习。

对一些比较典型的题目，进行一题多思，一题多变，培养我们分析问题和解决问题的能力，以适应中考的需要。

fluent并行分割网格方法

1 网格分割的一般方法在用Fluent 的并行求解器时，需要将网格细分割为几组单元，以便在分离处理器上求解将未分割的网格读入并行求解器里，可用系统默认的分割原则(推荐使用）还可以在连续求解器里或将mesh 文件读入并行求解器后自己分割。

在建立问题(定义模型、边界条件等)之前或之后分割网格都可以，不过，由于某些模型的特点(象非等形接触面、滑移网格、shell-conduction encapsulation 的自适应)，最好是在建立问题后。

!!如果case 文件含有滑移网格或非等形接触面，要在计算过程中进行自适应，因此要用连续求解器分割。

值得注意的是计算节点间的相关单元的分布在网格自适应时要保持不变，除非是非等形接触面，这样在自适应后就不必重新分割了。

若在网格分割前用连续求解器建立问题，用于此项工作的计算机必须有足够大的内存来读入网格。

如果网格太大，不能读进连续求解器，可将未分割的网格直接读入并行求解器里(使用所有被定义主机的内存)，然后让并行机自动分割。

在这种情况下，你将在做一个初步网格分割后建立问题。

如果必要可以手工再重新分割一次。

2 自动分割网格在将case 文件读入并行求解器之前选用两分法或是其他网格分割方法来自动分割网格。

对一些方法，可预览来确定是否为最佳的网格分割，注意case 文件中含有滑移网格或非等形接触面，在计算过程中要自适应，则需要在连续求解器中分割此文件，然后再把它读入并行求解器，在Auto Partition Grid 控制面板上选择Case File 选项。

并行求解器上自动网格分割的步骤如下：1. (任选)在菜单栏上点Parallel Auto Partition...，弹出Auto Partition Grid 控制面板设置分割参数。

读入mesh 文件或case 文件时如果没有获取分割信息，那就保持Case File 选项开启，Fluent 会用Method 下拉菜单里的方法分割网格。

Gambit网格划分的一点技巧(二)---分块网格

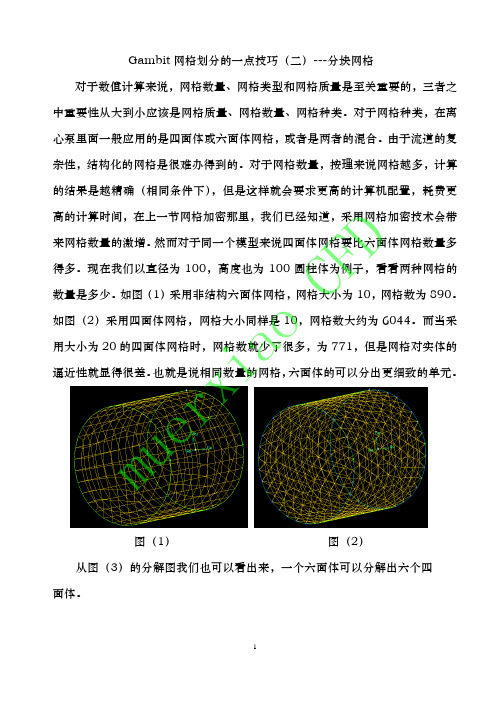
图（48）
图（49）
D 进水段边界条件设置要注意的问题：1）选择如图（50）所示两个面做 interface 。
CF 2）同时选择三块实体做流体域。
rxiao图（50） ue 2、叶轮 m 叶轮是离心泵的心脏，叶轮网格的质量、数量和分布对计算精度的影响是很
大的。虽然利用 Gambit 对整个叶轮划分六面体网格是困难的，但是我们可以通
图（66）
图（67）
CF 至此分块网格的一些技巧和命令的应用分享到这里。总结分块网格，有几个
问题是大家要注意的：第一，在划分网格之前要清楚知道想要怎样的分块，就是要在哪里把实体分割，分割成怎样的形状，这样的形状适合于什么形状的网格。
圆平面
点3
图（30）
图（31）
创建一个圆面 → 点击体命令 → 点击分割实体
图（32）
CFD→ 选择要分割的实体→
在 Split with 后面选择 Faces（real），如图（32）→ 选择前面创建的圆平面 → 点击 Apply，如图（33）。至此，圆柱段和锥段已经分开了。
ao 注意：用这种方法分割的两个实体是相互有联系的，在划分网格的时候，公共面 muerxi 上的节点是一一对齐的。
选择要分割的面
在 Split with 选择
选择直线 12
点击 Apply，如图（18）。
此时图形变成了蓝色，如图（19）。按此方法利用其他边分割平面，最后分割好
之后如图（20）。
5
图（18）
图（19）
CFD
iao图（20）
rx 点击划分网格 mue 四个面网格大小填 5
点击面网格
选择图（21）所示的
分割用的平面 4 分割用的平面 3

fluent并行分割网格方法

!!如果case 文件含有滑移网格或非等形接触面，要在计算过程中进行自适应，因此要用连续求解器分割。

值得注意的是计算节点间的相关单元的分布在网格自适应时要保持不变，除非是非等形接触面，这样在自适应后就不必重新分割了。

若在网格分割前用连续求解器建立问题，用于此项工作的计算机必须有足够大的内存来读入网格。

如果网格太大，不能读进连续求解器，可将未分割的网格直接读入并行求解器里(使用所有被定义主机的内存)，然后让并行机自动分割。

在这种情况下，你将在做一个初步网格分割后建立问题。

如果必要可以手工再重新分割一次。

2 自动分割网格在将case 文件读入并行求解器之前选用两分法或是其他网格分割方法来自动分割网格。

并行求解器上自动网格分割的步骤如下：1. (任选)在菜单栏上点Parallel Auto Partition...，弹出Auto Partition Grid 控制面板设置分割参数。

读入mesh 文件或case 文件时如果没有获取分割信息，那就保持Case File 选项开启，Fluent 会用Method 下拉菜单里的方法分割网格。

三年级几何图形的剪拼学生版

知识要点找对称【例 1】把一个33 的的网格分成形状、大小完全相同的四份。

【例 2】哥哥和弟弟一起做手工，想把一张红色的平行四边形蜡光纸沿着一条直线，把它剪成大小、形状完全相同的两部分。

【例 10】下图是由18个小正方形组成的图形，请你把它分成6个完全相同的图形。

【例 11】你能把下面的图形分成7个大小相等的长方形吗？动手画一画。

【例 12】如右图所示是由三个正方形组成的图形，请把它分成大小、形状都相同的四个图形。

【例 13】阿凡提周游世界，有一天来到一个村庄。

一个地主对他说：“都传说你很聪明，我有一块地，你能把它分成大小相等、形状相同的2份，我就把地送给你。

”聪明的阿凡提不慌不忙，用木棍画了一道线，把这块地分成大小相等、形状相同的2份。

地主傻了眼，只好履行诺言。

hypermesh网格划分技巧

其实各种CAE前处理的一个共同之处就是通过拆分把一个复杂体拆成简单体。

这个思路一定要记住，不要上来就想在原结构上分网，初学者往往是这个问题。

刚开始学，day1,day2,advanced training 和HELP先做一遍吧。

另外用熟24个快捷键。

做一下HELP里面的教程，多了解一些基本的概念和操作。

这样会快点入门。

划分的方法要灵活使用，再有就是耐心。

1、如何将.igs文件或.stl文件导入hypermesh进行分网？files\import\切换选项至iges格式，然后点击import...按钮去寻找你的iges文件吧。

划分网格前别忘了清理几何2、导入的为一整体，如何分成不同的comps？两物体相交，交线如何做？怎样从面的轮廓产生线（line）？都用surface editSurface edit的详细用法见HELP，点索引，输入surface edit3、老大，有没有划分3D实体的详细例子？打开hm,屏幕右下角help,帮助目录下hyperworks/tutorials/hyermesh tutorials/3D element,有4个例子。

4、如何在hypermesh里建实体？hm的几何建模能力不太强，而且其中没有体的概念，但它的曲面功能很强的.在2d面板中可以通过许多方式构建面或者曲面,在3D面板中也可以建造标准的3D 曲面,但是对于曲面间的操作,由于没有"体"的概念,布尔运算就少了,分割面作就可以了5、请问怎么在hypermesh中将两个相交平面到圆角啊？defeature/surf fillets6、使用reflect命令的话，得到了映射的另一半，原先的却不见了，怎么办呢？法1、在选择reflect后选择duplicate复制一个就可以法2、先把已建单元organize〉copy到一个辅助collector中，再对它进行reflect，将得到的新单元organize〉move到原collector中，最后将两部分equivalence，就ok拉。

几何第14讲_格点图形割补法(学生版)A4

随练1.1图中相邻格点围成的最小三角形的面积均为1平方厘米，下列图形的面积分别为多少？
随练1.2图中相邻两格点间的距离均为1厘米，下图图形的面积是多少？
随练1.3右图是一棵黄金树，其面积是26平方米，那么图中最小正方形面积是_______平方米．
随练1.4下图由16个面积为1平方厘米的小正方形组成
（1）写出A、B、C三点的坐标（2）求三角形ABC的面积
随练1.5图中相邻两格点间的距离均为1厘米，那么阴影图形的面积是多少平方厘米？
作业1如右图，已知每个小正方形格的面积是1平方厘米，则不规则图形的面积是多少？
作业2图中相邻格点围成的最小正方形的面积均为1平方厘米，下列图形的面积分别为多少？
作业3图中相邻格点围成的最小正方形的面积均为1平方厘米，下列图形的面积分别为多少？
格点面积计算方法
1．数格子法：格点图形为规则图形，像长方形、正方形、平行四边形、梯形、三角形等可以按照面积公式直接计算，也可以通过格点公式计算．
2．分割法：直接将格点图中的不规则图形分成若干个可求面积的规则图形，然后通过计算规则图形的面积来求原图形的面积．
3．扩展法：将原图形扩展成可直接计算面积的规则图形，同时扩展部分的图形面积也是可以直接计算的，那么原图形的面积就等于规则图形面积减去扩展部分的面积即可！
4．格点公式法：直接数出内点和边点数量，然后通过格点公式计算即可．
5．格点公式的逆用：通过格点数构造格点图形面积的大小．
重难点：分割与填补法求格点面积．注意最小三角形或正方形的面积是否为1．
题模一：分割法
例1.1.1图中相邻格点围成的最小三角形的面积均为1平方厘米，下列图形的面积分别为多少？
例1.1.2图中相邻两格点间的距离均为1厘米，下图图形的面积是多少？

三维网格模型的分割及应用技术综述

第17卷第8期2005年8月计算机辅助设计与图形学学报JOURNAL OF COMPU TER 2AIDED DESIGN &COMPU TER GRAPHICSVol 117,No 18Aug 1,2005　收稿日期:2004-03-09;修回日期:2004-07-08　基金项目:国家“八六三”高技术研究发展计划重点项目(2001AA231031,2002AA231021);国家重点基础研究发展规划项目(G1998030608);国家科技攻关计划课题(2001BA904B08);中国科学院知识创新工程前沿研究项目(20006160,20016190(C ))三维网格模型的分割及应用技术综述孙晓鹏1,2) 李　华1)1(中国科学院计算技术研究所智能信息处理重点实验室　北京　100080)2(中国科学院研究生院　北京　100039)(xpsun @ict 1ac 1cn )摘要　对三维网格模型分割的定义、分类和应用情况做了简要回顾,介绍并评价了几种典型的网格模型分割算法,如分水岭算法、基于拓扑和几何信息的分割算法等;同时,对网格分割在几种典型应用中的研究工作进行了分类介绍和评价1最后对三维分割技术今后的发展方向做出展望1关键词　分割Π分解;三维分割;形状特征;网格模型中图法分类号　TP391A Survey of 3D Mesh Model Segmentation and ApplicationSun Xiaopeng 1,2)　Li Hua 1)1(Key L aboratory of Intelligent Inf ormation Processi ng ,Instit ute of Com puti ng Technology ,Chi nese Academy of Sciences ,Beiji ng 100080)2(Graduate School of the Chi nese Academy of Sciences ,Beiji ng 100039)Abstract In this paper ,we present a brief summary to 3D mesh model segmentation techniques ,includ 2ing definition ,latest achievements ,classification and application in this field 1Then evaluations on some of typical methods ,such as Watershed ,topological and geometrical !method ,are introduced 1After some ap 2plications are presented ,problems and prospect of the techniques are also discussed 1K ey w ords segmentation Πdecomposition ;3D segmentation ;shape features ;mesh model1　引言基于三维激光扫描建模方法的数字几何处理技术,继数字声音、数字图像、数字视频之后,已经成为数字媒体技术的第四个浪潮,它需要几何空间内新的数学和算法,如多分辨率问题、子分问题、第二代小波等,而不仅仅是欧氏空间信号处理技术的直接延伸[1]1在三维网格模型已成为建模工作重要方式的今天,如何重用现有网格模型、如何根据新的设计目标修改现有模型,已成为一个重要问题1网格分割问题由此提出,并成为近年的热点研究课题[223]12　网格分割概述三维网格模型分割(简称网格分割),是指根据一定的几何及拓扑特征,将封闭的网格多面体或者可定向的二维流形,依据其表面几何、拓扑特征,分解为一组数目有限、各自具有简单形状意义的、且各自连通的子网格片的工作1该工作被广泛应用于由点云重建网格、网格简化、层次细节模型、几何压缩与传输、交互编辑、纹理映射、网格细分、几何变形、动画对应关系建立、局部区域参数化以及逆向工程中的样条曲面重建等数字几何处理研究工作中[223]1同时,三维网格模型的局部几何拓扑显著性也是对三维网格模型进行检索的一种有效的索引[4]1与网格曲面分割有关、并对其影响巨大的一个早期背景工作是计算几何的凸分割,其目的是把非凸的多面体分解为较小的凸多面体,以促进图形学的绘制和渲染效率1该工作已经有了广泛的研究,但多数算法难以实现和调试,实际应用往往不去分割多面体,而是分割它的边界———多边形网格1多面体网格边界的分割算法有容易实现、复杂形体输出的计算量往往是线性的等优势[5]1另外一个早期背景工作是计算机视觉中的深度图像分割,其处理的深度图像往往具有很简单的行列拓扑结构,而不是任意的,故其分割算法相对简单[6]1三维网格模型的分割算法一般是从上述两类算法推广而来1心理物理学认为:人类对形状进行识别时,部分地基于分割,复杂物体往往被看作简单的基本元素或组件的组合[728]1基于这个原理,Hoffman 等[9]于1984年提出人类对物体的认知过程中,倾向于把最小的负曲率线定义为组成要素的边界线,并据此将物体分割为几个组成要素,即视觉理论的“最小值规则”1由此得到的分割结果称为“有意义的”分割,它是指分割得到的子网格必须具有和其所在应用相关的相对尺寸和组织结构1由于曲率计算方法不同,很多算法给出的有意义的分割结果也存在差异1诸多应用研究[10214]证明,网格模型基于显著性特征的形状分割,是物体识别、分类、匹配和跟踪的基本问题1而有意义的分割对于网格模型显著占优特征的表示和提取、多尺度的存储和传输以及分布式局部处理都是十分有意义的1211　网格分割的发展较早的三维网格分割工作可以追溯到1991年,Vincent 等[15]将图像处理中的分水岭算法推广到任意拓扑连接的3D 曲面网格的分割问题上11992年,Falcidieno 等[16]按照曲率相近的原则,把网格曲面分割为凹面片、凸面片、马鞍面片和平面片11993年,Maillot 等[17]将三角片按法向分组,实现了自动分割;1995年,Hebert 等[18]给出了基于二次拟合曲面片的曲率估计方法,并把区域增长法修改推广应用到任意拓扑连接的网格曲面分割问题中;1995年,Pedersen [19]和1996年Krishnamurthy 等[20]在他们的动画的变形制作过程中,给出了用户交互的分割的方法11997年,Wu 等[3]模拟电场在曲面网格上的分布,给出了基于物理的分割方法;1998年Lee 等[21]和2000年Guskov 等[22]给出了几个对应于简化模型的多分辨率方法;1999年Mangan 等[2]使用分水岭算法实现网格分割,并较好地解决了过分割问题;2001年,Pulla 等[23224]改进了Mangan 的曲率估计工作;1999年,Gregory 等[25]提出一个动画设计中的交互应用,根据用户选择的特征点将网格曲面分割为变形对应片;1999年,Tan 等[26]基于顶点的简化模型建立了用于碰撞检测的、更紧致于网格曲面分割片的层次体包围盒12000年,Rossl 等[27]在逆向工程应用中,在网格曲面上定义了面向曲率信号的数学形态学开闭操作,从而得到去噪后的特征区域骨架,并实现了网格分割;2001年,Yu 等[28]的视觉系统自动将几何场景点云分割为独特的、用于纹理映射和绘制的网格曲面片二叉树;Li 等[29]为了碰撞检测,给出了基于边收缩得到描述几何和拓扑特征的骨架树,然后进行空间扫描自动分割;Sander 等[30]使用区域增长法,按照分割结果趋平、紧凑的原则分割、合并分割片1所有这些方法都是为了使分割的结果便于参数化,即只能产生凸的分割片1由此产生边界不连续的效果12002年,Werghi 等[31]识别三维人体扫描模型的姿态,根据人体局部形状索引进行网格模型的分割;Bischoff 等[32]和Alface 等[33]分别给出了网格分割片光谱在几何压缩和传输中的应用;Levy 等[34]在纹理生成工作中,以指定的法向量的夹角阈值对尖锐边滤波,对保留下来的边应用特征增长算法,最后使用多源Dijkstra 算法扩张分割片实现了网格模型的分割;2003年,Praun 等[35]将零亏格网格曲面投影到球面上,然后把球面投影到正多面体上得到与多面体各面对应的网格模型分割,最后将多面体平展为平面区域以进行参数化,但其结果不是有意义的分割1212　网格分割的分类早期的网格分割算法多为手工分割或者半自动分割,近两年出现了基于自动分割的应用工作1从网格模型的规则性来看,可将分割算法分为规则网格分割、半规则网格分割和任意结构的网格分割算法,根据分割结果可以分为有意义的分割和非有意义的分割1同时,面向不同的应用目标出现了不同的分割策略(见第4节)1目前,网格分割的质量指标主要有三个方面:边界光顺程度、是否有意义、过分割处理效果1多数分8461计算机辅助设计与图形学学报2005年割算法以边界光顺为目标,采用的方法有在三角网格上拟合B样条曲面然后采样[20],逼近边界角点(两个以上分割片的公共顶点)间的直线段[30]等1近年来多数分割算法都追求产生有意义的分割结果1对于过分割的处理方法目前主要有忽略、合并和删除三种方式1多数三维网格分割算法是从二维图像分割的思想出发,对图像分割算法作三维推广得到其三维网格空间的应用1如分水岭算法[2,15,23224,36239]、K2 means算法[40]、Mean2shift算法[41]以及区域增长算法[18,30]等1同样,与图像处理问题类似,光谱压缩[33,42243]、小波变换[31]等频谱信息处理方法在三维网格分割中也有算法1除此之外,同时考虑几何与拓扑信息的分割会产生较好的结果1这方面的工作主要有基于特征角和测地距离度量[44]、基于高斯曲率平均曲率[45247]、基于基本体元[32]、基于Reeb图[48250]、基于骨架提取和拓扑结构扫描[27,29,51252]等使用三维网格曲面形状特征的算法1作为网格模型的基础几何信息,曲率估计方法目前主要为曲面拟合、曲线拟合以及离散曲率等三种1其中曲面拟合法较为健壮,但是计算量大;离散曲率法计算量小,但是除个别算法外都不是很健壮,且无主方向主曲率信息;曲线拟合的曲率估计方法则集中了上述两种方法的优势[3],实际研究中使用较多13　典型三维网格分割算法311　分水岭算法1999年,Mangan等[2]的工作要求输入的是三角网格曲面,以及任何一种可以用来计算每个顶点曲率的附加信息(如曲面法向量等),并针对体数据和网格数据给出了两种曲率计算方法;但是分水岭算法本身和曲率的类型无关1首先,计算每个顶点的曲率(或者其他高度函数),寻找每个局部最小值,并赋予标志,每一个最小值都作为网格曲面的初始分割;然后,开始自下而上或者自上而下地合并分水岭高度低于指定阈值的区域,有时平坦的部分也会得到错误的分割,后处理解决过分割问题1分割为若干简单的、无明确意义的平面或柱面,属于非有意义的分割1Rettmann等[36237]结合测地距离,并针对分水岭算法的过分割给出一个后处理,实现了MRI脑皮层网格曲面的分割12002年,Marty[38]以曲率作为分水岭算法的高度函数,给出了有意义的分割结果1 2003年,Page等[39]的算法同样只分割三角网格,依据最小值规则,他们试图得到网格模型高层描述1其主要贡献为:创建了一个健壮的、对三角网格模型进行分割的贪婪分水岭法;使用局部主曲率定义了一个方向性的、遵循最小值规则的高度图;应用形态学操作,改进了分水岭算法的初始标识集1文献[39]在网格的每一个顶点计算主方向和主曲率,根据曲率阈值,使用贪婪的分水岭算法分割出由最小曲率等高线确定的区域1形态学的开闭操作应用于网格模型每个顶点的k2ring碟状邻域,闭操作会连接空洞,而开操作会消除峡部1创建了标识集后,依据某顶点与其邻接顶点之间的方向,由欧拉公式和已知主曲率计算该顶点在该方向上的法曲率从而得到在该方向上、该顶点与邻接顶点之间的方向曲率高度图,并将其作为方向梯度1对该顶点所在的标识区域使用分水岭算法得到分割片1上述工作表明,分水岭算法在改进高度函数的定义后,可以得到有意义的分割效果1312　基于拓扑信息的网格分割基于几何以及拓扑信息的形状分割方法可以归结为Reeb图[50]、中轴线[52]和Shock图[53254]等1基于拓扑信息的形状特征描述主要有水平集法[55]和基于拓扑持久性的方法[56]11999年,Lazarus等[51]提出从多面体顶点数据集提取轴线结构,在关键点处分割网格的水平集方法,如图1所示1这种轴线结构与定义在网格模型顶点集上的纯量函数关联,称之为水平集图,它能够为变形和动画制作提供整体外形和拓扑信息1图1　人体网格模型及其水平集图文献[51]针对三角剖分的多面体,使用与源点之间的最短路径距离作为水平集函数,基于Dijkstra 算法构造记录水平集图的结构树,其根结点、内部结点和叶子分别表示源点、水平集函数的鞍点和局部最大值点1该工作可以推广到非三角网格模型1 2001年,Li等[29]基于PM算法[57]的边收缩和94618期孙晓鹏等:三维网格模型的分割及应用技术综述空间扫掠,给出了一个有效的、自动的多边形网格分割框架1该工作基于视觉原理,试图将三维物体分割为有视觉意义和物理意义的组件1他们认为三维物体最显著的特征是几何特征和拓扑特征,由此,定义几何函数为扫掠面周长在扫掠结点之间的积分为骨架树中分支的面积;定义拓扑函数为相邻两个扫掠面拓扑差异的符号函数,并定义了基于微分几何和拓扑函数的关键点1文献[29]首先基于PM算法将每条边按照其删除误差函数排序,具有最小函数值的边收缩到边中点,删除其关联的三角形面片;如果某边没有关联任何三角片则指定为骨架边,保持其顶点不变;循环上述过程,得到一个新的、通过抽取给定多边形网格曲面骨架的方法1其次,加入虚拟边连接那些脱节的骨架边,称这些虚拟边以及原有的骨架边组成的树为骨架树,即为扫掠路径1扫掠路径为分段线条1然后,定义骨架树中分支面积(扫掠面周长函数在扫掠结点之间的积分),分支面积较小的首先扫掠,以保证小的、但是重要的分割片被首先抽取出来,以免被其他较大的分割片合并1最后,沿扫掠路径计算网格的几何、拓扑函数的函数值1一旦发现几何函数、拓扑函数的关键点,抽取两个关键点之间的网格曲面得到一个新的分割片1整个过程无需用户干涉12003年,Xiao等[48249]的工作基于人体三维扫描点云的离散Reeb图,给出了三维人体扫描模型的一个拓扑分割方法:通过探测离散Reeb图的关键点,抽取表示身体各部分的拓扑分支,进而进行分割1水平集法具有较高的计算速度和健壮的计算精度1基于拓扑持久性的方法结合代数学,能更准确地计算形状特征,但是没有解决分割问题[55256]1 313　基于实体表示的网格分割2002年,Bischoff等[32]把几何形状分割为表示其粗糙外形的若干椭球的集合,并附加一个独立的网格顶点的采样集合来表示物体的细节1生成的椭球完全填充了物体的内部,采样点就是原始的网格顶点1该方法的步骤如下:Step11首先,在物体原始网格的每一顶点上生成一个椭球,或者随机在物体原始网格上采样选择种子点;每个种子点作为球面上的一个顶点,沿该点的网格法向做球面扩展,直至与网格上另外一个顶点相交;然后沿此两点的垂直方向将球面扩张为最大椭球,直至与第三个网格顶点相交;最后沿此三点平面的法向(即该三点所在平面的柱向)扩张,直至与第四个网格顶点相近,由此得到一个椭球1Step21对生成的椭球进行优化选择,体积最大的椭球首先被选中,以后每一次都将选出对累计体积贡献最大的椭球1如果有若干体积累计贡献相近的椭球同时出现的情况发生,则最小半径最短的椭球被选出1为了简化体积累计贡献的计算,对椭球体素化后计算完全包含在椭球内的体素的数目进行堆排序1发送方传送选出的椭球集合;接收方得到包含基本几何和拓扑信息的椭球集合后,使用Marching Cubes算法或者Shrink2wrapping算法抽取0等值面1显然即使部分椭球丢失,工作依然可以继续:因为椭球是互相重叠的,抽取等值面不影响它们的拓扑关系,而且如果重叠充分,丢失少部分椭球不会影响重要形状信息的重构1如图2所示1图2　以不同数目椭球表示的网格分割Step31在生成很好地逼近原始物体的初始网格后,开始将采样点(即原始网格顶点)插入网格[58]1为了提高最终重构结果的质量,由Marching Cubes算法生成的临时网格顶点在网格原始顶点陆续到来后,最终被删除,因为它们不是物体的原始顶点1314　基于模糊聚类的层次分解2003年,Katz等[44]提出了模糊聚类的层次分解算法,算法处理由粗到精,得到分割片层次树1层次树的根表示整个网格模型S1在每个结点,首先确定需要进一步分割为更精细分割片的数目,然后执行一个k2way分割1如果输入的网格模型S由多个独立网格构成,则分别对每个网格进行同样的操作1分割过程中,算法不强调每个面片必须始终属于特定的分割片1大规模网格模型的分割在其简化模型上进行,然后将分割片投影到原始网格模型上,在不同的尺度下计算分割片之间的精确边界1文献[44]算法优点是:可以对任意拓扑连接的或无拓扑连接的、可定向的网格进行处理;避免了过分割和边界锯齿;考虑测地距离和凸性,使分割边界通过凹度最深的区域,从而得到有意义的分割结果1分割结果适用于压缩和纹理映射14　三维网格分割应用411　三维检索中的网格分割算法在三维VRML数据库中寻找一个与给定物体0561计算机辅助设计与图形学学报2005年相似的模型的应用需求,随着WWW的发展正变得越来越广泛,如计算生物学、CAD、电子商务等1形状描述子和基于特征的表示是实体造型领域中基本的研究问题,它们使对物体的识别和其他处理变得容易1因为相似的物体有着相似的分割,所以分割结构形状描述子可以用于匹配算法1中轴线、骨架等网格模型拓扑结构的形状描述子在三维模型检索中也得到研究,它可以从离散的体数据以及边界表示数据(网格模型)中抽取出来1对于后者,目前还没有精确、有效的结果[39]1但我们相信,依据拓扑信息进行分割得到的分布式形状描述子也是一种值得尝试的三维模型检索思路1 2002年,Bischoff等[32]提出从椭球集合中得到某种统计信息,如椭球半径的平均方差或者标准方差,以及它们的比率,由于这些统计信息在不同的形状修改中都保持不变,作为一种检索鉴别的标识的想法1但是没有严格的理论或者实验结果证明1 2002年,Zuckerberger等[59]在一个拥有388个VRML三维网格模型的数据库上,进行基于分割的变形、简化、检索等三个应用1首先将三维网格模型分割为数目不多的有意义的分割片,然后评价每一个分割片形状,确定它们之间的关系1为每个分割建立属性图,看作是与原模型关联的索引,当数据库中检索到与给定网格模型相似的物体时,只是去比较属性图相似的程度1属性图与其三维模型的关联过程分为三步:(1)分割网格曲面为有限数目的分割片;(2)每一个分割片拟合为基本二次曲面形状;(3)依据邻接分割片的相对尺寸关系进行过分割处理,最后构造网格曲面模型的属性图1对分割片作二次拟合,由此产生检索精确性较差的问题;分割片属性图的比较采用图同构的匹配方法,计算量较大,且是一个很困难的问题;从其实验结果看,有意义的分割显然还不够,出现飞机、灯座等模型被检索为与猫相似的结构;区分坐、立不同的人体模型效果显然也很差等12003年,Dey等[4]基于网格模型的拓扑信息,给出了名为“动力学系统”的形状特征描述方法,并模拟连续形状定义离散网格形状特征1实验表明该算法十分有效地分割二维及三维形状特征1他们还给出了基于此健壮特征分割方法的形状匹配算法1 412　几何压缩传输中的网格分割健壮的网格模型压缩传输方法必须保证即使部分几何信息丢失,剩下的部分至少能够得到一个逼近原始物体的重构,即逼近的质量下降梯度,要大大滞后于信息丢失梯度1无论是层次结构的还是过程表示的多边形网格模型,它们的缺陷是:严格的拓扑信息一致性要求1顶点和面片之间的交叉引用导致即使在传输中丢失了1%的网格数据,也将导致无法从99%的剩余信息里重建网格曲面的任何一部分1对此可以考虑引入高度的冗余信息,即使传输中丢失一定额度的数据,接收方依然可以重构大部分的几何信息1问题的关键是将几何体分割为相互独立的大块信息,如单个点,这样接收方可以在不依赖相关索引信息的情况下,重构流形的邻域关系1为了避免接收方从点云重构曲面的算法变得复杂,早期的健壮传输方法总假设至少整体拓扑信息可以无损地传送1一旦知道了粗糙的形状信息,接收方可以插入一些附加点生成逼近网格12002年,Bischoff等[32,58]在网格分割工作中将每个椭球互相独立地定义自己的几何信息1由于椭球的互相重叠,冗余信息由此产生,因此如果只有很少的椭球丢失,网格曲面的拓扑信息和整体形状不会产生变化1冗余信息不会使存储需求增加,因为每个椭球和三角网格中每个顶点一样,只需要9个存储纯量1其传送过程如下:种子点采样生成椭球集合;传送优化选择的椭球子集;接收方抽取等值面重构逼近网格;以陆续到来的原始网格顶点替换临时网格顶点11996年,Taubin等[42]首先在几何压缩处理中提出光谱压缩,其工作在三维网格模型按如下方式应用傅里叶变换:由任意拓扑结构的网络顶点邻接矩阵及其顶点价数,得到网格Laplacian矩阵的定义及由其特征向量构成的R n空间的正交基底,相对应的特征值即为频率1三维网格顶点的坐标向量在该空间的投影即为该网格模型的几何光谱1网格表面较为光顺的区域即为低频信号12000年,Karni等[43]将几何网格分割片光谱推广到传输问题上1光谱直接应用于定义几何网格的拓扑信息时,会产生伪频率信息1对于大规模的网格,由于在网格顶点数目多于1000时,Laplacian矩阵特征向量的计算几乎难以进行,因此该工作在最小交互前提下,将网格模型分割为有限数目的分割片1该方法有微小的压缩损失,且在分割片边界出现人工算法痕迹12003年,Alface等[33]提出了光谱表示交叠方法:扩张分割片,使分割片之间产生交叠1具体方法是把被分割在其他邻接分割片中的、但与该分割片15618期孙晓鹏等:三维网格模型的分割及应用技术综述邻接的三角片的顶点,按旋转方向加入到该分割片中,从而由于分割片重叠搭接产生冗余信息,并称这种分割片扩展冗余处理的光谱变换为交叠的正交变换1该工作在几何网格压缩和过程传输的应用中明显地改进了Karni等的工作1显然上述工作的基础是良好的网格分割1建立分片独立的基函数将使得分割效果更为理想1413　纹理贴图中的网格分割如果曲面网格的离散化是足够精细的,如细分网格,那么直接对顶点进行纹理绘制就足够了;否则就要把网格模型分割为一组与圆盘同胚的、便于进行参数化的分割片,再对每片非折叠的分割片参数化,最后分割片在纹理空间里拼接起来1网格模型的分割显然会因其局部性而降低纹理映射纹理贴图、网格参数化的扭曲效果1面向纹理的分割算法一般要求满足两个条件:(1)分割片的不连续边界不能出现人工算法痕迹;(2)分割片与圆盘同胚,而且不引入太大的变形就可以参数化1不要求有意义的分割结果12001年,Sander等[30]基于半边折叠的PM算法,使用贪婪的分割片合并方法(区域增长法)对网格模型进行分割1首先将网格模型的每一个面片都看作是独立的分割片,然后每个分割片与其邻接分割片组对、合并1在最小合并计算量的前提下,循环执行分割片对的合并操作,并更新其他待合并分割片的计算量1当计算量超出用户指定的阈值时,停止合并操作1分割片之间的边界为逼近角点间直线段的最短路径,从而减轻了锯齿情况12002年,Levy等[34]将网格模型分割为具有自然形状的分割片,但仍然没有得到有意义的分割结果1为了与圆盘同胚,该算法自动寻找位于网格模型高曲率区域的特征曲线,避免了在平展区域内产生分割片边界,并增长分割片使他们在特征曲线上相交,尽量获得尺寸较大的分割片1414　动画与几何变形中的网格分割影视动画制作中,多个对象间的几何变形特技使用基于网格分割的局部区域预处理1如建立动画区域对应关系,对多个模型进行一致分割,然后在多个模型的对应分割片之间做变形,将提高动画制作的精度和真实性;且每个“Polygon Soup”模型都可用来建立分割片对应;模型间的相似分割有利于保持模型的总体特征1目前,多数的自动对应算法精度较低,手工交互指定对应关系的效率又太低1 1996年,Krishnamurthy等[20]从高密度、非规则、任意拓扑结构的多边形网格出发,手工指定分割边界,构造张量积样条曲面片的动画模型1文献[20]首先在多边形网格的二维投影空间交互选择一个顶点序列,然后自动地将顶点序列关联到网格上最近的顶点上;对于序列中前后两个顶点计算在网格曲面上连接它们的最短路径;对该路径在面片内部进行双三次B样条曲面拟合、光顺、重新采样,得到分割片在两个顶点之间的边界曲线1但计算量的付出依然是非常昂贵的11999年,Gregory等[25]在两个输入的多面体曲面上交互选择多面体顶点,作为一个对应链的端点,对应链上其他顶点通过计算曲面上端点对之间的最短路径上的顶点确定,由此得到这些顶点和边构成的多面体表面网格的连通子图;然后将每一个多面体分割为相同数目的分割片,每个分割片都与圆盘同胚;在分割片之间建立映射、重构、局部加细,完成对应关系的建立;最后插值实现两个多面体之间的变形12002年,Shlafman等[40]的工作不再限制输入网格必须是零亏格或者是二维流形1该算法通过迭代,局部优化面片的归属来改进某些全局函数,因此与图像分割K2means方法相近,属于非层次聚类算法1最终分割片的数目可以由用户预先指定,从而避免了过分割,且适用于动画制作的需求1分割过程的关键在于确认给定的两个面片是否属于同一个分割片1其分割工作是非层次的,因为面片可能会在优化迭代中被调整到另外一个分割片去1该工作表明,基于分割的变形对于保持模型的特征有着重要的意义1局部投影算法能够产生精细的对应区域,且能自动产生有意义的分割片1415　模型简化中的网格分割网格简化是指把给定的一个有n个面片的网格模型处理为另一个保持原始模型特征的、具有较少面片、较大简化Π变形比的新模型1三维网格分割显然可以被看作是一种网格简化,其基本思想是在简化中增加一个预处理过程,先按模型显著特征将其分割为若干分割片,然后在每个分割片内应用简化算法,由此保持了模型的显著特征,如特征边、特征尖锐以及其他精细的细节1例如,把曲率变化剧烈的区域作为分割边界,将曲率变化平缓的区域各自分割开来,就是基于曲率阈值的网格简化方法1网格曲面分割结果的分割片数目在去除过分割后被限制在指定的范围内12561计算机辅助设计与图形学学报2005年。

第三章：划分网格——(第三节)面网格划分

GAMBIT 允许你指定下表提到的任何一个面网格“元素”选项
“元素”选项
描述
四边形（Quad）
划分的网格仅包括四边形网格元素
三角形（Tri）
划分的网格仅包括三角形网格元素
四边形/三角形
划分的网格主要由四边形网格元素组成，但在用户指定的地方采用三
（Quad/Tri）
角形网格元素
以上列出的每一个“元素”选项都对应着一个特定的“类型”选项
注二、如果你强制采用 Quad-Map 方案对某个面进行网格划分，GAMBIT 将根据面上顶点的指定类型进行评估，如果顶点类型不满足上述规则（逻辑矩形），GAMBIT 将试图改变顶点类型，以使该面可以采用 Quad-Map 方法划分网格。
本文由 wyxpuma 提供，不足之处欢迎指正
Email：wuyx02@ 本文仅作参考及学术讨论，拒绝一切商业行为
Email：wuyx02@ 本文仅作参考及学术讨论，拒绝一切商业行为
Quad-Map 面网格划分方案（scheme）主要适用于所要划分网格的面由四条或更多的边组成的情况，但并不是所有由四条或更多的边组成的面都适合用该种方案。为了能够用 Quad-Map 方案划分网格，面的组成不能违背以下参数的限制：
图 3－24：包含 5 条边的 Mappable 的平面
作为逻辑矩形边界的四个边定义如下表逻辑边 1 2 3 4
平面的边 Edge2 Edge3 Edge4
Edge1 和 edge5
为了采用 Map 方法对面进行网格划分，边 2 上的线段数（side 1）必须要等于边 4 上的
本文由 wyxpuma 提供，不足之处欢迎指正
Email：wuyx02@ 本文仅作参考及学术讨论，拒绝一切商业行为

HYPERMESH六面体网格划分小教程

ArmOOl 教程第一步：打开文件asmOOl.hm第二步：对几何实体进行切割分块操作。

1 进入Geom>Solid edit 面板，选择trim with plane/suf 子面板2激活with plane 下的solids黄色按钮，选择图形区中整个实体。

p pnpm Irrrirn-r3激活下面的绿色N1按钮，并如图依次选择N1、N2、N3、B这四个点-£ fij Xi Tnpi # :』i 中* -电卡岂创L艸4点击trim，将实体切割成为上下对称的两个体。

Model Irilo. E^ajfhtOI Jwf'r tin wth nQidffs广tin Hith Ines trlnwiTip Eme^sulr merge广dnechi『beolvHiisolkfe▼J詢血I W|!5Llff旨| |4 |厂凶郎W<un別t ln^…Il■TBjEb | r infflvuih nodes广Inm rtili luesFt Inn * 旳p sne/EU^ rfnei^er di^nu nr ti(Ki|凹「is Jflh輝・* G* •"名*>>C«np>J!?I応lidfe5激活with plane 下的solids黄色按钮，选择切割好的上半部分实体。

6激活线面的N1绿色按钮，如图依次选择N1、N2、N3这三个点。

7点击trim，将这上半部分实体切割成左右对称的两个实体。

第三步：删除多余实体和临时节点1点击F2快接键，进入Delete 面板。

2激活黄色的solids按钮，并勾选delete bounding surfs 。

在图形区中选择下半部分实体和上边的左半部分实体。

3点击delete entity ，删除掉多余的实体。

4进入Geom>temp node 面板，点击绿色的clear all按钮，删除掉多余的临时节点。

平面分割算法

平面分割算法
平面分割算法是计算机图形学中常用的算法，用于将三维空间中的物
体分割成多个平面进行处理。

以下是一些常见的平面分割算法：
1.基于网格的平面分割算法：将三维物体通过三角面片等网格结构进
行表示，然后对网格进行切割，生成多个平面。

2.基于距离场的平面分割算法：通过计算三维物体中每个点到最近平
面的距离，获得距离场，然后以距离场中的局部最小值作为平面的分割线。

3.基于约束优化的平面分割算法：将三维物体分割为多个部分，并对
不同的部分设置不同的约束条件，然后通过优化算法获得最优的平面分割
方案。

4.基于图论的平面分割算法：将三维物体转化为无向图，对图进行遍历，找到合适的平面分割方案。

5.基于点云的平面分割算法：通过激光扫描或者摄像头得到三维物体
的点云数据，并对点云进行聚类，找到平面点的集合，然后使用RANSAC
算法求解平面参数，从而实现平面分割。