一元二次不等式恒成立问题PPT课件
一元二次不等式PPT优秀课件

本节主要内容:一元二次不等式的解法, 一元二次不等式与相应的二次函数的图象、 方程之间的联系.要求能熟练、准确、迅速 地解一元二次不等式,会用分类讨论的方 法求解含参数的一元二次不等式,能够判 断一元二次不等式恒成立的条件.注意等价 转化的思想、函数与方程的思想、数形结 合的思想以及分类讨论的思想在解决问题 中的应用.
一元二次不等式与相应的二次函数的图象、 方程之间的关系如下
判别式 b2 4ac
二次函数 y ax2 bx c (a 0)的图象
△>0
y
x1 x2
x1
x2
O
x
△=0 y
x1 x2
O
x
方程ax2 bx c 0 (a 0)的根
有x1,2两不等实根 b b2 4ac
2
时
x
a
x
2
a
当 a 2 时,原不等式的解集是 x x 2 ;
a
2
时,原不等式的解集为
x
2 a
x
a ;
0a
2
时,原不等式的解集为
x
a
x
2 a
;
a 2 时,原不等式的解集是 R ;
2
a
0
时,不等式的解集为
85.每一年,我都更加相信生命的浪费是在于:我们没有献出爱,我们没有使用力量,我们表现出自私的谨慎,不去冒险,避开痛苦,也失去了快乐。――[约翰·B·塔布] 86.微笑,昂首阔步,作深呼吸,嘴里哼着歌儿。倘使你不会唱歌,吹吹口哨或用鼻子哼一哼也可。如此一来,你想让自己烦恼都不可能。――[戴尔·卡内基]
人教版高中数学必修一第二章一元二次函数方程和不等式全套PPT课件

【变式探究】
已知 且 ,求 的取值范围.
[解析] 令 , ,则 , .由 解得 ,又 , , , .
方法总结 不等式具有可加性(需同向)与可乘性(需同正),但不能相减或相除,应用时要充分利用所给条件进行适当变形来求范围,注意等价变形.
方法总结 应用基本不等式时,注意下列常见变形中等号成立的条件:
第二章 一元二次函数、方程和不等式
2.1 等式性质与不等式性质
学习目标
1.会用不等式(组)表示实际问题中的不等关系.(数学建模)
2.会运用作差法比较两个数或式子的大小.(数学运算)
3.梳理等式的性质,掌握不等式的性质,会用不等式的性质证明不等式或解决范围问题.(逻辑推理)
自主预习·悟新知
合作探究·提素养
(2)已知 , .求证: .
②
[解析] (1)对于①,若 , , , ,则 ,①错误;对于②,对于正数 , , ,若 ,则 ,所以 ,所以 ,又 ,所以 ,②正确.综上,正确结论的序号是②.(2)因为 ,所以 .所以 .又因为 ,所以 .所以 ,即 ,所以 .
探究2 重要不等式
设 , ,记 , , 分别为 , 的算术平均数、几何平均数、调和平均数.古希腊数学家帕波斯于公元4世纪在其名著《数学汇编》中研究过 时, , , 的大小关系.
问题1:.你能探究 , , 的大小关系吗?
[答案] 能,因为 , , ,所以 ,即 ; ,即 .所以 .所以 , , 中最大的为 ,最小的为 .
问题1:.小明的说法正确吗?用什么性质判断小明的说法是否正确?
[答案] 不正确,用等式的性质.当 时, 一定成立,反过来,当 时,不能推出 ,如当 时, 成立, 不成立.故“ 是 成立的充要条件”是错误的.
解决一元二次不等式的恒成立问题 高中数学课件

若f(x)=-x2+mx-1 的函数值没有正值,求m的取值范围。
解:f(x)= -x2+mx-1的函数值没有正值,意思是x取任何实数,都使f(x)≤ 0成立,
也就是关于x的不等式-x2+mx-1≤0 对一切实数x都成立。
因此,符合题意的二次函数f(x)= -x2+mx-1的图像为:
y
y
o
x
Байду номын сангаас
或
o
x
所以,Δ≤0,从而得到m的取值范围是:-2≤m≤2
y
解法三:画函数y=-x2+2x-3的图像
y o
x
o
x
根据图像,原不等式的解集为∅
根据图像,原不等式的 解集为∅
小结:这两种求不等式解集的方法都是用了数形结合的思想方法,但 是第三种是直接画不等式对应的二次函数图像,过程简洁明了,是非 常可取的办法。
知识讲解
例1:已知关于x的不等式x2-x+a>0的解 集是R,求a的取值范围。 分析:不等式的解集是R,意思是x取任 何实数,都能使不等式成立, 因此,二次函数y=x2-x+a的图像就要保 证x为任何实数时,都要使y>0,即:
3.2
解
决
一
人 教
元
A 版
二
高
次
中 数
不
学 必
等
修
式
五 第
的
三 章
恒
成
立
问
题
课题导入
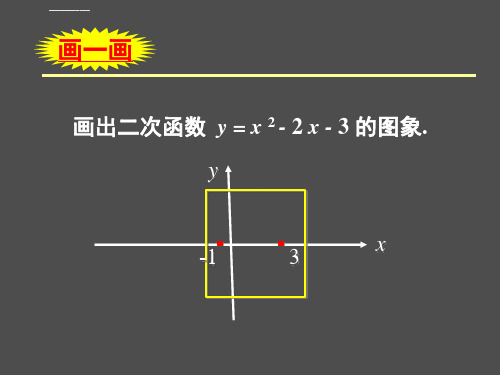
教材例2:求不等式-x2+2x-3>0的解集
:将不等式化为标准不等式 形式:x2-2x+3<0 因为y=x2-2x+3=(x-1)2+2>0
一元二次不等式恒成立问题

高校长组织写教育教学论文,对教师特别是我们青年教师,有很大的帮助.但说实在的,初上讲坛,理论与经验皆不足.说写学术论文,实则愧不敢当.“学术”二字,是经验丰富的特级高级教师、能力超群的青年骨干教师才担当得起的.如我刚步入教育行业之新手,实是不敢当.思忖良久,终觉胸内无文,只得将自己讲的一堂自我感觉还算良好的课,照搬了上来.文虽浅薄,但出自己手,虽不如他人,也算无愧了.一元二次不等式恒成立问题似曾相识燕归来(认真听讲,做好笔记,就不会似曾相识)无可奈何花落去(大而化之,步步紧逼,就不会无可奈何)大而化之,步步紧逼(化,分解讨论的意思)【师】好,我们今天来继续研究一元二次不等式问题.对于一元二次不等式,通过三四天的学习,想必大家已经非常熟悉了,对于一般的一元二次不等式,大家都能熟练的掌握.那么对于一元二次不等式的综合问题,大家可能还没有头绪,一拿到这种题,都可能头晕脑涨了.这不禁令我想起了古人的一句诗(师板书):似曾相识燕归来无可奈何花落去【生】(笑,课堂气氛活跃):老师,写反了!应该是:无可奈何花落去,似曾相识燕归来!【师】(故作严肃):我为什么写反啊?因为我们学数学需要逆向思维啊!…那么我们大家对于一元二次不等式的综合问题可能就是这个感觉.一接触到题就“似曾相识”,但一下笔就“无可奈何”了.(师在两句诗内相应的词下加下划线)这就要求我们平时听课的时候要认真听讲,做好笔记,这样一来我们做题的时候就不会似曾相似了,即使我们做不出来,我们也可以翻开笔记找到类似的题.(师在副标题相应的位置后面加认真听讲等语).(生思考,拿出笔记本)而即使做到记笔记了,认真听讲了,有些同学做这类综合题的时候也会觉得“无可奈何”,这是什么原因呢?这就要求我们多做多练,练熟了,遇到这类题时就不会是“无可奈何”了,而是“下笔千言”了.(生笑,认真听讲)那么对于这一类题,我们通常采用的是“大而化之,步步紧逼”的方法来解决.大家注意,这个“化”的意思是分解讨论的意思.(师在副标题下加上“大而化之,步步紧逼”8个字)它既然是个大难题,那么我们就把它化为几个容易的步骤,再依次的讨论,这类题就做出来了.好,我们今天就通过一个典型例题来研究不等式的恒成立问题.(师板书)一、典例例:关于x 的不等式()()042222<--+-x m x m 对一切实数x 恒成立,求实数m 的取值范围.【师】一拿到这类题,同学们可能都傻眼了,题目中好像什么都没给啊,这个题怎么做啊?大家不用怕,看上面(师示意学生看题目下的“大而化之”四个字),既然它是以大题的形式出现了,那么咱们就用做大题的方法去对付它,“大而化之”,咱们一步步的来分解它.那么大家看这个题它是个什么不等式啊?一元二次不等式吗?(师设下陷阱)【生】是!(大部分学生说是,只有一小部分说不一定,但声音小,底气不足)【师】(继续暗示)是吗?你敢肯定么?【生】(大部分反应过来)不一定!【师】为什么不一定啊?【生】因为)2(-m 的值不定!【师】(及时插入话)对!它的值不定,那么它的值不定我们该怎么做啊?【生】讨论!(因为前几节课都在培育学生具有讨论思想,所以学生能一口答出来)【师】对,它的值不定我们就要讨论它,这是我们学习数学必备的思想,大家一定要具备这个基本素质.下面我们来分类讨论这个不等式的系数()2-m ,看看它的庐山真面目到底是什么.(一)(准备工作):讨论系数(师边写边说:那么它的二次项系数分几种情况啊?生回答:两种.师问:是什么啊?生回答:等于零或不等于零两种.师板书并言语:那么我们来讨论这两种情况.)︒1当()02=-m 即2=m 时,那么原不等式变成了常数不等式︒2当()02≠-m 时,原不等式是一元二次不等式.【师】(板完后说)那么这是我们每个人脑海中都要具备最基本的东西,一遇到这类题,我们脑海中立马要想到讨论它的二次项系数,这一步你写出来了,高考时两分就拿到手了.(二)(具体步骤):分类讨论1当02=-m ,即2=m 时,原不等式可化为:04002<-⋅+⋅x x【师】那么这个不等式是不是最终成了04<-,它是不是无论x 取何值时不等式都恒成立成立啊?【生】是!∴ 2=m 时,不等式恒成立【师】那么我们来讨论第二步.2当02≠-m ,即2≠m 时,不等式()()042222<--+-x m x m 是一个一元二次不等式.【师】那么我们说解一元二次不等式分四个步骤.第一步是化为标准形式,也就是二次项系数大于零的形式.那么这个不等式好不好化啊?因为我们不知道()2-m 的正负,这样的话就需要讨论,而讨论起来又很麻烦,那么我们怎么做啊?那么大家回忆一下,学习数学最重要的两个思想是什么啊?【生】分类讨论和数形结合的思想!【师】对!那么这类题我们用数形结合的思想来做是很容易理解的.那么既然是数形结合,我们就先画出()()42222--+-=x m x m y 的图像.然后再在图像上找出0<y 时x 的取值是什么就可以了.那么它的图像有几种情况啊?无非就有两种.()02>-m 或()02<-m .那么我们就先画出()02>-m ,即开口向上时的情况.那么开口向上又分三种情况.那么这个图像又是经过),(40-的这个点的,那么我们先抛开这个条件,来根据与x 轴交点 是两个一个还是没有的情况做出开口向上时函数的图像.如下图:【师】那么当02>-m 时,图像就是这三种情况.那么大家看,不等式的对应方程()()042222=--+-x m x m 的根的情况对应图像上就分别是两个、一个或无.那么它的判别式依次是:0>∆、0=∆或0<∆.()1 0)2>-m (的图像)(102>-m 0>∆ )2( 02>-m 0=∆ )3( 02=-m 0<∆【师】好,那么我们把0)2(<-m 的情况也画出来,也是三个图像.)2( 0)2(<-m 的图像)(402<-m 0>∆ )5( 02<-m 0=∆ )6( 02<-m 0<∆【师】好,到此为止,体力活已经做完了,该做脑力活了.大家观察一下图像,再看一下题目,看哪个图像适合题目的条件啊?(念题目:不等式()()042222<--+-x m x m 对一切实数x 恒成立,求实数m 的取值范围).(到此,基本上所有的同学已经能顺利的指出第6个图像适合题目的要求,老师再逐个的分析,然后得出结论)(此时有一部分同学瞌睡,老师观察到这个现象后说道:同学们注意了,关键时刻到了.比如说我们看NBA 比赛,火箭队正和湖人队比赛,比赛已经到了第四节了,剩下十几秒的时 间了,科比或者姚明再投进去一个球,胜负都出来了,可不要错过精彩啊!生笑,注意力重新集中起来.课堂气氛活跃)【生】第6个图像满足!【师】对!第6个图像满足.那么不等式的对应方程()()042222=--+-x m x m应满足什么条件啊?。
一元二次函数方程和不等式课件ppt
y 3
= y
x
2-2x-
{ x | x﹤-1 或 x > 3 }
-1 3 x
(3)不等式 x 2 - 2 x - 3 < 0 的解集是
{ x | -1 < x < 3}
思考: 二次方程、二次不等式、二次函数, 三者之间有什么关系?
为 了 规 范 事 业单位 聘用关 系,建 立和完 善适应 社会主 义市场 经济体 制的事 业单位 工作人 员聘用 制度, 保障用 人单位 和职工 的合法 权益
只需 f (1)< 0, 即 4-2 a < 0,
所以 a > 2. x
y
1x
为 了 规 范 事 业单位 聘用关 系,建 立和完 善适应 社会主 义市场 经济体 制的事 业单位 工作人 员聘用 制度, 保障用 人单位 和职工 的合法 权益
例3. 若不等式 x 2 - 2 a x + 3 > 0 对任意 x ∈[ -1 , 3 ] 恒成立, 求实数 a 的取值范围.
看一看
为 了 规 范 事 业单位 聘用关 系,建 立和完 善适应 社会主 义市场 经济体 制的事 业单位 工作人 员聘用 制度, 保障用 人单位 和职工 的合法 权益
说一说
(1)方程 x 2 - 2 x - 3 = 0 的根是
x1 (2)不等式 x
= -1, 2- 2
x x
2
-
= 3
3 >
0
的解集是
解:依题意,-1 ,3 是方程
x2 +bx+c=0
x
的两根 , 所以
-1 + 3 = - b, -1×3 = c,
解得 b = -2 , c = -3.
2.3二次函数与一元二次方程、不等式(共49张PPT)

(
)
A.a=6,c=1
B.a=-6,c=-1
C.a=1,c=1
D.a=-1,c=-6
解析:选 B.由题意知,方程 ax2+5x+c=0 的两根为 x1=13,x2=12,由根与 系数的关系得 x1+x2=13+12=-5a,x1x2=13×12=ac,解得 a=-6,c=-1.
4.不等式(2x-5)(x+3)<0 的解集为________. 答案:x-3<x<25
解不等式应用题的步骤
1.若产品的总成本 y(万元)与产量 x(台)之间的函数关系式是 y=3 000+20x
-0.1x2(0<x<240),每台产品的售价为 25 万元,则生产者不亏本(销售收入不
小于总成本)时的最低产量是
()
A.100 台
B.120 台
C.150 台
D.180 台
解析:选 C.由题意知 y-25x=-0.1x2-5x+3 000≤0, 即 x2+50x-30 000≥0, 解得 x≥150 或 x≤-200(舍去).
6x+10=0 无实根,又二次函数 y=x2-6x+10 的图象开口向上,所以原不 等式的解集为∅.
解不含参数的一元二次不等式的方法 (1)若不等式对应的一元二次方程能够因式分解,即能够转化为几个代数式的 乘积形式,则可以直接由一元二次方程的根及不等号方向得到不等式的解 集. (2)若不等式对应的一元二次方程能够化为完全平方式,不论取何值,完全平 方式始终大于或等于零,则不等式的解集易得. (3)若上述两种方法均不能解决,则应采用求一元二次不等式的解集的通法, 即判别式法.
含参一元二次不a(a-1)>0,(a∈R). 解:因为关于 x 的不等式 x2+x-a(a-1)>0, 所以(x+a)(x+1-a)>0, 当-a>a-1, 即 a<12时,x<a-1 或 x>-a, 当 a-1>-a,
一元二次不等式恒成立问题

【解析】法一:当a>0时, ,由x∈(1,4),f(x)>0得
或 或
所以 或 或 ,所以 或 ,即 。
当a<0时, ,解得a∈ ;
当a=0时, , f(1)=0,f(4)=-6,∴不合题意.
综上可得,实数a的取值范围是 。.
法二:由f(x)>0,即 ,x∈(1,4),
则有 在(1,4)上恒成立.
令 , ,
所以要使f(x)>0在(1,4)上恒成立,只要 即可.故a的取值范围为 .
例3.已知不等式 -2x-m+1<0.
(1)若对所有的实数x不等式恒成立,求m的取值范围;
(2)设不等式对于满足|m|≤2的一切m的值都成立,求x的取值范围.
题型二.解高次不等式(方法:穿针引线法)
(1) (x+1)2(x-2)3<0(2) (x+2)3(x-2)2(x+2)>0 (3) (x+1)4(x-1)3(x2-1)<0
题型三.解分式不等式(方法:等价变换)
(1) (2) (3)
题型四.解含参数的一元二次不等式(分类讨论)
1.解关于 的不等式
数学分类讨论方法,就是将数学对象分成几类,分别进行讨论来解决问题的一种数学思想方法。有关分类讨论思想的数学问题具有明显的逻辑性、明显的综合性、明显的探索性,能训练人的思维条理性和概括性。分类讨论思想,贯穿于整个高中数学的全部内容。应用分类讨论,往往能够使复杂的问题简单化。分类的过程,可培养学生思考的周密性,条理性能力,而分类讨论,又促进学生研究问题,探索规律的能力,这是素质教育的本质所在。
(2)设f(m)=( -1)m+(1-2x),
《二次函数与一元二次方程、不等式》PPT课件高中数学人教版

• (1)若y在定义域内存在最大值m,则y<a(或y≤a)恒成立⇔a>m(或a≥m);
• (2)若y在定义域内存在最小值m,则y>a(或y≥a)恒成立⇔a<m(或 a≤m).
• 【对点练习】❶ 若关于x的不等式ax2+(a-2)x-2≤0恒成立,求实数 a的取值范围.
[解析] 若 a=0 时,原不等式为-2x-2≤0 不恒成立,所以 a≠0. 当 a≠0 时,则应有aΔ<≤0,0, 即aa<-0,22-4a-2≤0, 整理得aa<+0,22≤0, 解得 a=-2. 所以实数 a 的值为-2.
2.3 第2课时二次函数与一元二次方程、不等 式的应 用-【 新教材 】人教A 版(20 19)高 中数学 必修第 一册课 件(共2 6张PPT )
2.3 第2课时二次函数与一元二次方程、不等 式的应 用-【 新教材 】人教A 版(20 19)高 中数学 必修第 一册课 件(共2 6张PPT )
误区警示
2.3 第2课时二次函数与一元二次方程、不等 式的应 用-【 新教材 】人教A 版(20 19)高 中数学 必修第 一册课 件(共2 6张PPT )
[解析] 设桶的容积为 x 升,显然 x>8. 依题意,得(x-8)-4x-x 8≤28%·x. 由于 x>8,因而原不等式化简为 9x2-150x+400≤0, 即(3x-10)(3x-40)≤0. 因此130≤x≤430,从而 8<x≤430. 故桶的容积最大为430升.
当 m≠0 时,由二次函数的图象可知有mΔ=<04,-4mm-2<0, 解得 m<1- 2.
综上可知,m 的取值范围是{m|m<1- 2}.
[归纳提升] 求不等式恒成立问题中参数范围的常用方法
一元二次不等式恒成立问题

一元二次不等式恒成立问题一元二次不等式是指形式为ax^2 + bx + c > 0的不等式,其中a、b、c均为实数且a不等于0。
那么,如何判断一元二次不等式是否恒成立呢?首先,我们需要明确一元二次不等式的解集。
对于一元二次方程,我们可以先求解其对应的一元二次方程,然后将方程的解代入不等式中,判断不等式是否成立。
以一元二次不等式x^2 - 4x + 3 > 0为例,我们可以先求解对应的一元二次方程x^2 - 4x + 3=0。
通过求解方程,我们可以得到方程的根为x=1和x=3。
接下来,我们将方程的根代入不等式中,即将x分别取1和3,得到以下两个不等式:当x=1时,1^2 - 4*1 + 3 > 0,简化得0 > 0,不成立。
当x=3时,3^2 - 4*3 + 3 > 0,简化得3 > 0,成立。
由此可见,当x取3时,一元二次不等式恒成立。
也就是说,原不等式的解集为x>3。
那么,我们如何更一般地判断一元二次不等式是否恒成立呢?首先,我们需要找出一元二次不等式的判别式Δ=b^2-4ac。
判别式Δ可以帮助我们进一步判断不等式的解集。
根据判别式Δ的不同取值,我们可以有以下三种情况:1.当Δ>0时,即b^2-4ac>0。
这种情况下,一元二次方程有两个不相等的实根。
如果不等式左侧是正值,那么不等式恒成立;如果不等式左侧是负值,那么不等式不成立;如果不等式左侧等于0,则不等式没有解。
2.当Δ=0时,即b^2-4ac=0。
这种情况下,一元二次方程有两个相等的实根。
无论不等式左侧取什么值,不等式都不成立。
换句话说,一元二次不等式恒不成立。
3.当Δ<0时,即b^2-4ac<0。
这种情况下,一元二次方程没有实根。
不等式左侧可以取任意值,所以不等式恒成立。
通过以上分析,我们可以得到一元二次不等式恒成立的一般规律:-当a>0时,一元二次不等式恒成立的解集为xξ(负无穷,根据不等式的根)u(根,正无穷)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
. 2
3x
.
.
12
例2. 关于x的不等式 2x29xm≤ 0在区间[ 2, 3]
上恒成立,则实数m的取值范围是_m___≤__9_.
解:构造函数 f(x)2 x2 9 xm ,x [2 ,3 ],
则
f (2) ≤ 0
f
(3) ≤
0
y
10 m ≤ 0 9 m ≤ 0
m≤9.
o. 23x Nhomakorabea.
(3)数形结合思想
.
7
练习1:若不等式 x2-2x+m>0 对于x∈(0,3)恒 成立,则实数m的取值范围是_______.
练习2:若不等式 mx2-2x+1>0 对于x∈(0,3)恒 成立,则实数m的取值范围是_______.
练习3:若不等式 x2-mx+4>0 对于x∈(0,3)恒 成立,则实数m的取值范围是_______.
对任意实数x恒成立,求m取值范围。
分 析 : 函 数 f(x)x22xm 开 口 向 上 f(x)0恒 成 立 需 0
= ( - 2 ) 2 - 4 m 0 , 解 得 m 1
.
3
变式1:若函数 f(x) x22xm 的定义域为R, 则m的取值范围是__________。
变 式 2 .若 不 等 式 x 2 2 x m 0 的 解 集 为 空 集 ,则 实 数 m 的 取 值 范 围 是 _ _ _ _ .
.
8
变式:若对于任意 a [1,1] ,函数 f ( x) x2 ax 2 的值恒小
于 0,则 x 的取值范围是_______1____x____1_________.
g(a)xax22
g(1) g(1) 0
0
此题若把它看成关于x的二次函数,由于a, x都要 变,则函数的最小值很难求出,思路受阻.若视a为主元, 则给解题带来转机.
.
9
练习:若不等式 x2+ (a-4)x+4-2a>0 对于
a ∈[-1,1]恒成立,则实数x 的取值范围是_______.
x1或x3
g (a ) x 2 (a 4 )x 4 2 a
(x2)ax24x4
g g
(1) (1)
0
0
.
10
题型二方法小结
(1)与一元二次不等式有关的恒成立问题,可通过二次函数求最 值,也可通过分离参数,再求最值.
(2)解决恒成立问题一定要搞清谁是自变量,谁是参数,一般地, 知道谁的范围,谁就是变量,求谁的范围,谁就是参数.
(3)对于二次不等式恒成立问题,恒大于 0 就是相应的二次函数 的图象在给定的区间上全部在 x 轴上方,恒小于 0 就是相应的二 次函数的图象在给定的区间上全部在 x 轴下方.
.
11
例2. 关于x的不等式 2x29xm≤ 0在区间[ 2, 3]
变 式 3 若 关 于 x 的 不 等 式 : x 2 m x 1 0 的 解 集 为 R ,
求实数m的取值范围。
.
4
变式 4.设函数 f(x)=mx2-mx-1.
若对于一切实数 x,f(x)<0 恒成立,求 m 的取值范围;
规范解答 解 (1)要使 mx2-mx-1<0 恒成立,
若 m=0,显然-1<0;
上恒成立,则实数m的取值范围是_m___≤__9_.
解:构造函数 f(x ) 2 x 2 9 x m ,x [2 ,3 ],
问题等价于f(x)max≤0,
y
Q f(x)2 (x9)2m 8 1,x [2 ,3 ], 48
fm a x (x )f(3 ) m 9 ≤ 0 , o
m≤9.
(2)转换求函数的最值
m<0, 若 m≠0,则
Δ=m2+4m<0 所以-4<m≤0.
⇒-4<m<0.
练 习 : 若 关 于 x 的 不 等 式 : a x 2 2 a x + 2 0 的 解 集 为 R ,
求实数a的取值范围。
.
5
题型一方法小结
(1)二次不等式a x2 +bx +c > 0恒成立
a 0
b2
4ac
0
.
13
上恒成立,则实数m的取值范围是_m___≤__9_.
解:m≤-2x2+9x在区间[2,3]上恒成立,
记 g (x) 2 x2 9 x ,x [2 ,3 ],
则问题转化为 m≤g(x)min
Qgm in(x)g(3)9,m≤9.
分离参数法
【评注】对于一些含参数的不等式恒成立问题,如果能够将 不等式中的变量和参数进行剥离,即使变量和参数分别位于不 等式的左、右两边,然后通过求函数的值域的方法将问题化归 为解关于参数的不等式的问题.
(2)二次不等式a x2 +bx +c < 0恒成立
a 0 b2 4ac 0
(3)二次不等式a x2 +bx +c ≥ 0恒成立 a 0
b2 4ac 0
(4)二次不等式a x2 +bx +c ≤ 0恒成立 a0
b2 4ac0
.
6
题型二 定义域不为R时
例2. 关于x的不等式 2x29xm≤ 0在区间[ 2, 3]
一元二次不等式应用
恒成立问题
.
1
△>0
△=0
y
y
x1 O x2 x
O x1
x
有两相异实根 x1, x2 (x1<x2)
有两相等实根
x1=x2=
b 2a
{x|x<x1,或 x>x2}
{x|x≠
b
}
2a
{x|x1< x <x2 }
Φ
.
△<0 y
x O 没有实根
R Φ
2
题型一 定义域为R时
例1:若不等式 x22xm0
