初三-几何问题之角平分线题型
【中考数学必备专题】几何辅助线大揭秘 之角平分线问题(含答案)
【中考数学必备专题】几何辅助线大揭秘之角
平分线问题
一、证明题(共3道,每道40分)
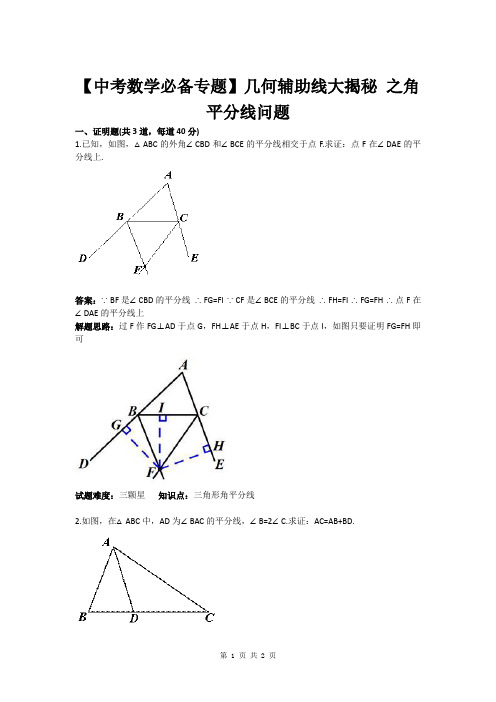
1.已知,如图,△ABC的外角∠CBD和∠BCE的平分线相交于点F.求证:点F在∠DAE的平分线上.
答案:∵BF是∠CBD的平分线∴FG=FI ∵CF是∠BCE的平分线∴FH=FI ∴FG=FH ∴点F在∠DAE的平分线上
解题思路:过F作FG⊥AD于点G,FH⊥AE于点H,FI⊥BC于点I,如图只要证明FG=FH即可
试题难度:三颗星知识点:三角形角平分线
2.如图,在△ABC中,AD为∠BAC的平分线,∠B=2∠C.求证:AC=AB+BD.
答案:∵AD是∠BAC的平分线∴∠BAD=∠EAD 在△ABD和△AED中AB=AE ∠BAD=∠EAD AD=AD ∴△ABD≌△AED(SAS)∴BD=ED,∠B=∠AED ∵∠AED=∠B=2∠C ∴∠CDE=∠AED ﹣∠C=∠C ∴DE=CE ∴BD=CE ∵AC=AE+CE ∴AC=AB+BD
解题思路:在AC上截取AE=AB,连接DE,如图只要证明BD=CE即可
试题难度:三颗星知识点:三角形角平分线
3.已知:如图,在△ABC中,BE平分∠ABC,AD⊥BE,垂足为点D.求证:∠BAD=∠DAE+∠C.
答案:∵BE平分∠ABC,AD⊥BE ∴△ABF为等腰三角形(三线合一)∴∠BAD=∠BFD ∵∠BFD 为△ACF的外角∴∠BFD=∠DAE+∠C ∴∠BAD=∠DAE+∠C
解题思路:延长AD与BC交于点F,如图只要证明∠BFD=∠BAD即可
试题难度:三颗星知识点:三角形角平分线。
全等三角形中角平分线问题的处理方法

全等三角形中角平分线问题的处理方法【全等三角形中角平分线问题的处理方法】1. 引言全等三角形中角平分线问题是几何学中的一个经典问题,旨在探讨如何将一个三角形的角平分线构造出来并求解相关问题。
这个问题在几何学中具有重要的应用价值和理论意义。
本文将从简单到复杂、由浅入深地介绍全等三角形中角平分线的处理方法,以帮助读者更全面、深刻和灵活地理解这一问题。
2. 基本定义与性质我们来回顾一下全等三角形的基本定义与性质。
全等三角形是指具有完全相同的大小和形状的三角形。
根据全等三角形的定义,对于两个全等三角形来说,它们的对应边长相等,对应角度相等。
这一性质是我们处理全等三角形中角平分线问题的基础。
3. 三角形角平分线的构造下面,我们开始介绍全等三角形中角平分线的构造方法。
考虑一个任意三角形ABC,我们的目标是构造出三角形ABC的角B的平分线。
(1)方法一:直接角平分线法我们可以借助直尺和圆规,以及平行线的性质来构造角平分线。
具体的步骤如下:a. 以顶点B为圆心,做一个与边AC相交于点D的圆;b. 以点D为圆心,与圆交于点E,连接BE;c. 连接线段BC和BA;根据圆周角的性质,角EBD是角ABC的一条平分线。
(2)方法二:割取角平分线法除了直接角平分线法之外,我们还可以使用割取角平分线的方法构造角平分线。
具体步骤如下:a. 过顶点B做一条与边AC相交于点F的直线;b. 以BF为半径,顶点B为圆心画一个圆;c. 连接圆与边BC、BA的交点分别为点D和点E,连接线段ED;根据圆内接四边形对角相等的性质,角BED是角ABC的一条平分线。
4. 角平分线的性质与应用了解了全等三角形中角平分线的构造方法之后,我们来探讨一些与角平分线相关的性质与应用。
(1)性质一:角平分线相交于三角形内心不仅在全等三角形中,对于任意三角形来说,角平分线的三条线段的交点恰好是三角形的内心。
这个性质是由角平分线与三角形内接圆的性质相关联的。
(2)性质二:角平分线的长度关系若一个角的平分线将另外两个角的平分线相交于点P,那么点P到三角形各边的距离满足以下关系:AP:BP:CP=AB:BC:CA。
几何辅助线之角平分线专题

几何辅助线之角平分线专题1、角平分线辅助线四种基本模型已知:AD是∠BOC的角平分线(1)(2)(3)(4)2、补充性质:如图,在△ABC中,AD平分∠BAC,则有AB:AC=BD:DC典型例题例1、已知:如图,在△ABC中,∠C=90°,AC=BC,AD平分∠CAB.求证:AC+CD=AB例2、已知:如图,在Rt△ABC中,∠C=90°,沿过B点的一条直线BE折叠这个三角形,使C点与AB边上的一点D重合,当∠A满足什么条件时,点D恰为AB中点?写出一个你认为适当的条件,并利用此条件证明D为AB中点.例3、如图,AB=2AC,∠BAD=∠DAC,DA=DB ,求证:DC⊥AC。
DEHA BC例4、如图所示,已知AD 是△ABC 的角平分线,DE AB ⊥,DF AC ⊥,垂足分别是E ,F .求证:AD 垂直平分EF .例5、 如图,在△ABC 中,∠A 等于60°,BE 平分∠ABC ,CD 平分∠ACB 求证:DH=EH例6、如图,已知等腰直角三角形ABC 中,∠A =90°,AB =AC ,BD 平分∠ABC ,CE ⊥BD ,垂足为E ,求证: BD =2CE 。
例7、如图,OP是∠MON的平分线,请你利用该图形画一对以OP所在直线为对称轴的全等三角形。
变式练习请你参考上图构造全等三角形的方法,解答下列问题:⑴如图,在△ABC中,∠ACB是直角,∠B=60°,AD、CE分别是∠BAC、∠BCA的平分线,AD、CE相交于点F。
请你判断写出FE与FD之间的数量关系;⑵如图,在△ABC中,如果∠ACB不是直角,而⑴中的其他条件不变,请问,你在⑴中所得结论是否依然成立?若成立请证明;若不成立,请说明理由。
课后练习1、已知:如图所示,∠C=2∠B,∠BAD=∠CAD,求证:AB=AC+CD。
2、已知,如图,BN 平分∠ABC,P为BN上一点,且PD⊥BC于D,AB+BC=2BD,求证:∠BAP+∠BCP=180°。
2022年九年级中考数学冲刺-几何模型讲义

2022年中考几何模型一、角平分线模型知识精讲1. 过角平分线上一点向角的两边作垂线段,利用角平分线上的点到角两边的距离相等的性质来解决问题2. 若题目中已经有了角平分线和角平分线上一点到一边的垂线段(距离),则作另一边的垂线段,例:已知:AD是的平分线,,过点D于点E,则.3. 在角的两边上取相等的线段,结合角平分线构造全等三角形(角边等,造全等),已知:点D是平分线上的一点,在OA、OB上分别取点E、F,且,连接DE、DF4. 过角平分线上一点作角的一边的平行线,构造等腰三角形,例:已知:点D是平分线上的一点,过点D作三角形,即.5. 有角平分线时,过角一边上的点作角平分线的平行线,交角的另一边所在直线于一点,也可构造等腰三角形,例:已知:OC平分,点D是OA上一点,过点D作交OB的反向延长线于点E,则.6. 从角的一边上的一点作角平分线的垂线,使之与角的另一边相交,则可得到一个等腰三角形,例:已知:OE平分∠AOB,点D在OA上,DE⊥OE,则可延长DE交OB于点F,则DE=EF,OD=OF,∠ODF=∠OFD.7. 有角平分线时,可将等角放到直角三角形中,构造相似三角形,也可以另加一对相等的角构造相似三角形,例:4321DA4231EFCB(1)已知:OC 平分,点E 、F 分别在OA 、OB 上,过点E M ,过点F N(2)已知:OC 平分,点E 、F 在OC 上,于点M ,于点N ,则(3)已知:OC 平分,点E 、F 在OC ,8. 利用“在同圆或等圆中,相等的圆周角(圆心角)所对的弦相等”可得相等线段,例:已知:∠BAC 是圆O 的圆周角,∠DOE 是圆O 的圆心角,AF 平分∠BAC ,OG 平分∠DOE ,连接BF 、CF 、DG 、EG ,则BF =CF ,DG =EG .9. 【内内模型】如图,两个内角平分线交于点D ,则.10. 【内外模型】如图,的一个内角平分线和一个外角平分线交于点D ,则.11. 【外外模型】如图,交于点D ,则.二、中点模型知识精讲1. 在等腰三角形中有底边中点或证明底边中点时,可以作底边的中线,利用等腰三角形的“三线合一”性质来解决问题.例:已知:在△ABC中,AB=AC,取BC的中点D,连接AD,则AD平分∠BAC,AD是边BC上的高,AD是BC边上的中线.【说明】应用等腰三角形“三线合一”的性质是证明两条直线垂直的重要方法.2. 在直角三角形中,有斜边中点或有斜边的倍分关系线段时,可以作斜边的中线解决问题,例:(1)如图,在Rt△ABC中,D为斜边AB的中点,连接CD,则CD=AD=BD.(2)如图,在Rt△ABC中,AB=2BC,作斜边AB上的中线CD,则AD=BD=CD=BC,△BCD是等边三角形.【总结】在直角三角形中,若遇到斜边的中点,则连接直角顶点与斜边的中点是解决问题的基本方法,作这条辅助线的目的是得到三条相等的线段及两对相等的角. 3. 将三角形的中线延长一倍,构造全等三角形或平行四边形(倍长中线),例:(1)如图,在△ABC中,AD为△ABC的中线,延长AD至点E,使得DE=AD,连接BE,则△ADC≌△EDB.(2)如图,在△ABC中,AD为△ABC的中线,延长AD至点E,使得DE=AD,连接BE,则四边形ABEC是平行四边形.4. 将三角形中线上的一部分延长一倍,构造全等三角形或平行四边形,例:如图,已知点E是△AD上的一点,延长AD至点F,使得DE=DF,连接BF、CF,则四边形BFCE为平行四边形或△BDF≌△CDE或△BED≌△CFD.【总结】证明两条线段相等常用的方法:①当要证明的两条线段是两个三角形的边时,一般通过证明这两条线段所在的两个三角形全等,通过三角形全等的对应边相等来证明两条线段相等;②当两条线段是同一个三角形的两条边时,一般证明这两条边所对的角相等,利用等角对等边证明两条线段相等.5. 有以线段中点为端点的线段时,可以倍长此线段,构造全等三角形或平行四边形,例:如图,已知点C边AE上一点,O为AB的中点,延长CO至点D,使得,连接AD、BD,四边形ADBC为平行四边形.6. 有三角形中线时,可过中点所在的边的两端点向中线作垂线,构造全等三角形,例:如图,AF为△ABC的中线,作BD⊥AF交AF延长线于点D,作CE⊥AF于点E,则△BDN≌△CEN.7. 在三角形中,有一边的中点时,过中点作三角形一边的平行线或把某条线段构造成中位线,利用已知的条件可求线段长,例:如图,D为AB的中点,过点D作DE∥BC,则DE为△ABC的中位线;过点B作BF∥DC 交AC的延长线于点F,则DC为△ABF的中位线.8. 有两个(或两个以上)中点时,连接任意两个中点可得三角形的中位线,例:如图,D、E、F分别为△ABC三边中点,连接DE、DF、EF,则.9. 有一边中点,并且在已知或求证中涉及线段的倍分关系时,可以取另一边的中点,构造三角形的中位线,例:如图,点E是△ABC边BC的中点,取AC的中点F,连接EF,则EF∥AB,10. 当圆心与弧(或弦)的中点,可以利用垂径定理解决问题,例:(1)如图,,连接AC、OB,则OB⊥AC,OB平分AC.(2)如图,点C为弦AB的中点,连接OC,则OC⊥AB.三、平行模型知识精讲在一些有平行线却没有截线的问题中,通常需要添加辅助线构造“三线八角”,再运用平行线的有关知识解题,常见的辅助线添加方式如下:如果遇到两条平行线之间夹折线,一般应过折点作出与已知平行线平行的直线.1. 如图,已知AB∥CD,点E为AB、CD间的一点,过点E作EF∥AB,则∠A+∠C=∠AEC.2. 如图,已知AB∥CD,则∠A+∠AEC+∠C=360°.3. 如图,AB∥CD,则∠B=∠D+∠E.4. 如图,AB∥CD,则∠BEG+∠D+∠F=180°.5. 如图,AB∥CD,则∠ABE=∠D+∠E.四、垂直模型1. 在三角形中,若题目中已经有一边的高了,常作另一边上的高,然后用同角的余角相等证明角相等.例:如图,在△ABC中,AD⊥BC于点D,过点B作BE⊥AC交AC于点E,交AD于点F,则∠CBE=∠CAD,∠AFE=∠C=∠BFD.除了能得到角度间的关系外,还可以通过构造相似三角形来证明线段成比例或者用于求线段的长度.2. 在四边形中,如果有高线,可以再作垂线,构造特殊的四边形或者直角三角形.例:如图,在四边形ABCD中,AB⊥BC,DC⊥BC,过点D作DE⊥BC,垂足为点E,则四边形BCDE为矩形,△ADE为直角三角形.3. 在直角三角形中,常作斜边上的高,利用同角(等角)的余角相等,可得到相似三角形.例:如图,在Rt△ABC中,∠ACB=90°,过点C作CD⊥AB于点D,则∠A=∠DCB,∠B=∠ACD,△ABC∽△CBD∽△ACD.4. 若题中已有直线的垂线时,可再作已知直线的垂线,得到两条平行线.例:如图,在△ABC中,AF⊥BC于点F,过AB上一点D作DE⊥BC于点E,则DE∥AF,∠BDE=∠BAF,∠ADE+∠BAF=180°,△BDE∽△BAF.5. 若存在过一条直线上两点同时向另一条直线作垂线,可以再作一条垂线,构造一组平行线,利用平行线等分线段定理解决问题.6. 当两条互相垂直的弦的交点恰好在圆上,构成90°的圆周角,可构造直径.例:如图,点A在圆O上,∠BAC=90°,连接BC,则BC就是圆O的直径.7. 当圆中有互相垂直的弦时,经常作直径所对的圆周角,可以得到垂直于同一条直线的两条直线,利用平行弦所夹的弧相等来解决问题.例:在圆O中,弦AB⊥CD于点E,连接CO并延长交圆O于点F,连接DF,则FD⊥CD,FD∥AB,.8. 当圆中有和弦垂直的线段时,作直径所对的圆周角,可以得到直角三角形,通过相似三角形来解决问题.例:如图,△ABC内接于圆O,CD⊥AB于点D,连接CO并延长交圆O于点E,连接AE,则△ACE∽△DCB.五、对角互补模型知识精讲1. 全等型—90º如图,已知∠AOB=∠DCE=90º,OC平分∠AOB.则可以得到如下几个结论:①CD=CE,②OD+OE=OC,③2. 如图,已知∠DCE的一边与AO的延长线交于点D,∠AOB=∠DCE=90º,OC 平分∠AOB.则可得到如下几个结论:①CD=CE,②OE-OD=OC,③.3. 全等型—60º和120º如图,已知∠AOB=2∠DCE=120º,OC平分∠AOB.则可得到如下几个结论:①CD=CE,②OD+OE=OC,③.4. 全等型—和如图,已知∠AOB=,∠DCE=,OC平分∠AOB.则可以得到以下结论:①CD=CE,②OD+OE=2OC·cos,③.5. 相似型—90º如图,已知∠AOB=∠DCE=90º,∠BOC=.结论:CE=CD·.六、半角模型知识精讲1. 如图,在正方形ABCD中,E、F分别是BC、CD上的点,且∠EAF=45º,则BE+DF=EF.2. 如图,在正方形ABCD中,E、F分别是BC、CD上的点,且∠EAF=45º,则AE平分∠BEF,AF平分∠DFE.3. 如图,在正方形ABCD中,E、F分别是BC、CD上的点,且∠EAF=45º,则4. 如图,在正方形ABCD中,E、F分别是BC、CD上的点,且∠EAF=45º,过点A作AH⊥EF交EF于点H,则AH=AB.简证:由上述结论可知AE平分∠BEF,又∵AB⊥BC,∴AH=AB.5. 如图,在正方形ABCD中,E、F分别是BC、CD上的点,且∠EAF=45º,. 简证:由结论1可得EF=BE+DF,CE+CF+EF=CE+CF+BE+DF=2AB.6. 如图,在正方形ABCD中,E、F分别是BC、CD上的点,且∠EAF=45º,AE、AF分别与BD相交于点M、N,则.简证:如图,将△AND绕点A顺时针旋90º得到△AGB,连接GM.通过证明△AMG≌△AMN得MN=MG,DN=BG,∠GBE=90º,即可证.7. 如图,在正方形ABCD中,E、F分别是BC、CD上的点,且∠EAF=45º,AE、AF分别与BD相交于点M、N,则△BME△DFN△AMN△BAN△DMA△AFE.简证:通过证明角相等得到三角形相似,要善于使用上述结论.8. 如图,在正方形ABCD中,E、F分别是BC、CD上的点,且∠EAF=45º,AE、AF分别与BD相交于点M、N,则简证:连接AC,∵∠DAF=∠EAC,∠ADB=∠ACB,∴△ECA△NDA,又∵△AMN△AFE,∴.【补充】通过面积比是相似比的平方比亦可得到9. 如图,在正方形ABCD中,E、F分别是BC、CD上的点,且∠EAF=45º,AE、AF分别与BD相交于点M、N,则.简证:由结论7可得△DAM△BNA,∴,即.10. 如图,在正方形ABCD中,E、F分别是BC、CD上的点,且∠EAF=45º,AE、AF分别与BD相交于点M、N,则.简证:设,在Rt△CEF中,,化简得,.11. 如图,在正方形ABCD中,E、F分别是BC、CD上的点,且∠EAF=45º,AE、AF分别与BD相交于点M、N,则当BE=DF时,EF.证明:如图,作△AEF的外接圆,点P为EF的中点,连接OA、OE、OF、PC,过点A作AH⊥EF.∵∠EAF=45º,∴∠EOF=90º,设,则,∴当点A、O、P、C四点共线时,即BE=DF,、EF大值.12. 如图,在正方形ABCD中,E、F分别是BC、CD上的点,且∠EAF=45º,AE、AF分别与BD相交于点M、N简证:由结论8可得△△ECA△NDA,同理可得补充:等腰直角三角形与“半角模型”如图所示,在等腰直角三角形ABC中,若∠DCE=45º,则.证明:如图,将△ACD绕着点C顺时针旋转90º得到△,连接.∵旋转,∴△ACD≌△,∴AD=,在△DCE与△中,ED=,∵∠BE=∠BC+∠EBC=∠DAC+∠EBC=90º,∴,.七、倍半角模型知识精讲一、二倍角模型处理方法1. 作二倍角的平分线,构成等腰三角形.例:如图,在△ABC中,∠ABC=2∠C,作∠ABC的平分线交AC于点D,则∠DBC=∠C,DB=DC,即△DBC是等腰三角形.2. 延长二倍角的一边,使其等于二倍角的另一边,构成两个等腰三角形.例:如图,在△ABC中,∠B=2∠C,延长CB到点D,使得BD=AB,连接AD,则△ABD、△ADC都是等腰三角形.二、倍半角综合1. 由“倍”造“半”已知倍角求半角,将倍角所在的直角三角形相应的直角边顺势延长即可.如图,若,则()2. 由“半”造“倍”已知半角求倍角,将半角所在的直角三角形相应的直角边截取线段即可.如图,在Rt△ABC(∠A<45º)的直角边AC上取点D,当BD=AD时,则∠BDC=2∠A,设,则,在Rt△BCD中,由勾股定理可得,解得,故有.三、一些特殊的角度1. 由特殊角30º求tan15º的值如图,先构造一个含有30º角的直角三角形,设BC=1,,AB=2,再延长CA至D,使得AD=AB=2,连接BD,构造等腰△ABD,则∠D=∠BAC=15º,.2. 由特殊角45º求tan22.5º的值由图可得,.3. “345”三角形(1)如图1,Rt△ABC三边比为3:4:5,Rt△BCD三边比为,,;(2)如图2,Rt△ABC三边比为3:4:5,Rt△BCD三边比为,,;(3)如图3,Rt△ABC三边比为3:4:5,Rt△BCD三边比为,,.八、全等模型知识精讲一、几何变换中的全等模型1. 平移全等模型,如下图:2. 对称(翻折)全等模型,如下图:3. 旋转全等模型,如下图:二、一线三等角全等模型4. 三垂直全等模型,如图:5. 一线三直角全等模型,如图:6. 一线三等角与一组对应边相等全等模型,如图:三、手拉手全等模型7. 等腰三角形中的手拉手全等模型如图,△ABC与△ADE均为等腰三角形,且∠BAC=∠DAE,连接BD、CE,则△ABD ≌△ACE.8. 等边三角形中的手拉手全等模型如图,△ABC与△CDE均为等边三角形,点B、C、E三点共线,连接AE、BD,则△BCD≌△ACE.9. 一般三角形中的手拉手全等模型如图,在任意△ABC中,以AB为边作等边△ADB,以AC为边作等边△ACE,连接DC、BE,则△ADC≌△ACE.10. 正方形中的手拉手全等模型如图,在任意△ABC中,以AB为边作正方形ABDE,以AC为边作正方形ACFG,连接EC、BG,则△AEC≌△ABG.九、相似模型知识精讲1. A字型与反A字型相似2. 8字型与反8字型相似3. 蝴蝶型相似4. 共角共边相似模型5. 一线三等角6. 旋转相似模型拓展讲解:1. 射影定理(1)双垂直,如图:结论①△ABD∽△ACB,AB2=AD·AC;②△ADC∽△ACB,AC2=AD·AB;③△CDB∽△ACB,CB2=BD·BA.(2)斜射影相似结论:△ABD∽△ACB,AB2=AD·AC.2. 对角互补相似如图,在Rt△ABC中,∠C=90º,点O是AB的中点,若∠EOF=90º,则.证明:过点O作OD⊥AC于点D,OH⊥BC于点H,如图所示:通过△ODE∽△OHF即可得到3. 三平行相似如图,AB∥EF∥CD,若,则.证明:∵EF∥AB,∴△DEF∽△DAB,∴,即①同理△BEF∽△BCD,∴,即②①+②,得,.4. 内接矩形相似如图,四边形DEFG是△ABC的内接矩形,EF在BC边上,D、G分别在AB、AC边上,则△ADG∽△ABC,△ADN∽△ABM,△AGN∽△ACM,.十、倍长中线模型知识精讲1. 如图,在矩形ABCD中,若BD=BE,DF=EF,则AF⊥CF.2. 如图,四边形ABCD是平行四边形,BC=2AB,M为AD的中点,CE⊥AB于点E,则∠DME=3∠AEM.3. 如图,△ADE与△ABC均为等腰直角三角形,且EF=CF,求证(1)DF=BF;(2)DF⊥BF.4. 如图,△OAB∽△ODC,∠OAB=∠ODC=90º,BE=EC,求证:(1)AE=DE;(2)∠AED=2∠ABO.十一、弦图模型知识精讲1. 证法一以a、b为直角边(b>a),以c为斜边作四个全等的直角三角形,则每个直角三角形的面积等于2. 证法二以a、b为直角边(b>a),以c为斜边作四个全等的直角三角形,则每个直角三角形的面积等于3. 证法三以a、b为直角边,以c为斜边作两个全等的直角三角形,则每个直角三角形的面积等于4. 证法四如图所示,分别以a、b为直角边,以c为斜边的四个直角三角形全等,图中3个正方形的边长分别为a、b、c,整个图形的面积为S5. 证法五分别以a、b为直角边,以c为斜边的四个直角三角形全等,将它们按如图所示拼成一个多边形,并延长AC交DF于点P.。
立足教材,追寻本质,发展思维——“角平分线”例题的教学与思考

-083-2021年第19期(总第271期)一、例题呈现北师大版教材八年级数学下册第一章《三角形的证明》第4节角 平分线例3:如图1,在∆ABC 中,AC =BC ,∠C =90°,AD 是∆ABC 的角平分线,DE ⊥AB ,垂足为E 。
(1)已知CD =4 cm,求AC 的长;(2)求证:AB =AC +CD 。
二、功能分析(一) 联系旧知,巩固新知本例题是在学生学习了角平分线的概念、角平分线的性质和全等三角形的基础上进行教学的,学生通过联系已有知识解答本例题,加深了对角平分线性质的理解,有效地巩固应用了新学知识。
解题回顾,本例题具备利用角平分线性质的条件,即∆ACD 和∆AED 以AD 所在直线为对称轴成轴对称图形,有过角平分线上一点向角两边作垂线,因此可得全等和等线段。
一般来说,我们可以把过角平分线上一点向角两边作垂线的方法叫作角分线边垂线法[1],基本图形如图2。
(二)通过变式,挖掘价值从知识的学习运用、挖掘例题的思想方法出发,可以使例题发挥更大的作用。
在教学设计中,笔者将例题里的一个条件隐藏,题目如下。
变式1:如图3,在∆ABC 中,AC =BC ,∠C =90°,AD是△ABC 的角平分线,DE ⊥AB ,垂足为E 。
(1)已知CD =4 cm,求AC 的长;(2)求证:AB =AC +CD 。
学生在解答时,需要分析题目中已知条件,联系以前学过的方法。
已知中含有构成三角形全等的部分条件,结合本节课学习的角平分线性质,辅助线添加顺理成章。
证法1:利用角平分线的性质,过点D 作DE ⊥AB ,垂足为E (见图4)。
不难看出,用原例题的解答方法即可完成证明。
帮助学生梳理与角平分线性质的相关内容,可以帮助学生进一步巩固全等三角形的性质和判定,培养学生合理联系已学知识,作辅助线的学习迁移能力。
从解题方法上看,这是间接利用截长补短的方法来解决线段的和差问题,即通过作垂线,将长线段AB 分割成两部分,利用全等得到线段AE =AC ,相当于在AB 上截取AE =AC ,再证明EB =CD ,问题迎刃而解。
初中数学复习几何模型专题讲解29--- 平行线中和角平分线有关的图形

初中数学复习几何模型专题讲解专题29 平行线中和角平分线有关的图形一、单选题1.在钝角△ABC中,延长BA到D,AE是∠DAC的平分线,AE//BC,则与∠B相等的角有()A.1个B.2个C.3个D.4个【答案】C【分析】依据角平分线的性质和平行线的性质即可求解.【详解】解析:依据角平分线的性质和平行线的性质,可知∠B =∠DAE=∠CAE=∠C故选C.【点睛】此题主要考查角平分线的性质与平行线的性质,解题的关键是熟知角平分线的性质.2.如图,点A、C为∠FBE边上的两点,AD∥BE,AC平分∠BAD,若∠F AD=45°,则∠ACE=()A.45°B.67.5°C.112.5°D.135°【答案】C【分析】先根据平角的定义求出∠BAD,根据角平分线的性质求出∠DAC,再利用平行线的性质,得到∠ACB的度数.最后通过平角求出∠ACE.【详解】解:∵∠F AD=45°,∴∠BAD=180°-45°=135°.∵AC平分∠BAD,∴∠DAC=12BAD∠=67.5°.∵AD∥BE,∴∠ACB=∠DAC=67.5°.∴∠ACE=180°-67.5°=112.5°.故选:C.【点睛】本题考查平行的性质和角平分线的性质,解题关键是运用题目中的条件去求解角的度数,能够从角平分线和平行这两个条件想到图中存在等腰三角形.3.如图,已知BM平分∠ABC,且BM//AD,若∠ABC=70°,则∠A的度数是()A.30°B.35°C.40°D.70°【答案】B【分析】先根据角平分线的性质,求出∠ABC的度数,再由平行线的性质得到∠A的度数.【详解】解:∵BM平分∠ABC,∴∠MBA=12∠ABC=35°.∵BM∥AD,∴∠A=∠MBA=35°.故选:B.【点睛】本题考查的是角平分线的性质,平行线的性质,掌握以上知识是解题的关键.二、解答题4.如图所示,直线AB∥CD,直线EF分别交AB、CD于E、F两点,∠BEF、∠DFE 的平分线相交于点K.(1)求∠EKF的度数;(2)如图(2)所示,作∠BEK、∠DFK的平分线相交于点K1,问∠K1与∠K的度数是否存在某种特定的等量关系?写出结论并证明.(3)在图(2)中作∠BEK1、∠DFK1的平分线相交于点K2,作∠BEK2、∠DFK2的平分线相交于点K3,依此类推,……,请直接写出∠K4的度数.【答案】(1)∠EKF=90°;(2)∠K=2∠K1,证明见解析;(3)∠K4=5.625°.【分析】(1)过K作KG∥AB,交EF于G,根据平行于同一条直线的两直线平行可得AB∥KG∥CD,从而得出∠BEK=∠EKG,∠GKF=∠KFD,∠BEK+∠FEK+∠EFK+∠DFK=180°,然后根据角平分线的定义即可求出∠BEK+∠DFK=90°,从而得出结论;(2)根据角平分线的定义可得∠BEK1=∠KEK1,∠KFK1=∠DFK1,结合(1)的结论可得∠BEK1+∠DFK1=45°,从而求出∠K1,即可得出结论;(3)根据(2)中的规律即可得出结论.【详解】(1)如图(1),过K作KG∥AB,交EF于G,∵AB∥CD,∴AB∥KG∥CD,∴∠BEK=∠EKG,∠GKF=∠KFD,∠BEK+∠FEK+∠EFK+∠DFK=180°,∵EK、FK分别为∠BEF与∠EFD的平分线,∴∠BEK=∠FEK,∠EFK=∠DFK,∴2(∠BEK+∠DFK)=180°,∴∠BEK+∠DFK=90°,则∠EKF=∠EKG+∠GKF=90°;(2)∠K=2∠K1,理由为:∵∠BEK、∠DFK的平分线相交于点K1,∴∠BEK1=∠KEK1,∠KFK1=∠DFK1,∵∠BEK+∠FEK+∠EFK+∠DFK=180°,即2(∠BEK+∠KFD)=180°,∴∠BEK+∠KFD=90°,即∠BEK1+∠DFK1=45°,同(1)得∠K1=∠BEK1+∠DFK1=45°,则∠K=2∠K1;(3)如图(3),根据(2)中的规律和推导方法可得:∠K2=12∠K1=22.5°,∠K3=12∠K2=11.25°,∠K4=12∠K3=5.625°.【点睛】此题考查的是平行线的性质及判定,掌握平行线的各个性质定理是解题关键.5.如图,已知AM∥BN,∠A=64°.点P是射线AM上一动点(与点A不重合),BC、BD分别平分∠ABP和∠PBN,分别交射线AM于点C,D.(1)①∠ABN的度数是;②∵AM∥BN,∴∠ACB=∠;(2)求∠CBD的度数;(3)当点P运动时,∠APB与∠ADB之间的数量关系是否随之发生变化?若不变化,请写出它们之间的关系,并说明理由:若变化,请写出变化规律;(4)当点P运动到使∠ACB=∠ABD时,∠ABC的度数是.【答案】(1)①116,︒②CBN;(2)58︒;(3)不变,:2:1APB ADB∠∠=,理由见解析;(4)29.︒【分析】(1)①由平行线的性质,两直线平行,同旁内角互补可直接求出;②由平行线的性质,两直线平行,内错角相等可直接写出;(2)由角平分线的定义可以证明∠CBD=12∠ABN,即可求出结果;(3)不变,∠APB:∠ADB=2:1,证∠APB=∠PBN,∠PBN=2∠DBN,即可推出结论;(4)可先证明∠ABC=∠DBN,由(1)∠ABN=116°,可推出∠CBD=58°,所以∠ABC+∠DBN=58°,则可求出∠ABC的度数.【详解】解:(1)①∵AM//BN,∠A=64°,∴∠ABN=180°﹣∠A=116°,故答案为:116°;②∵AM//BN,∴∠ACB=∠CBN,故答案为:CBN;(2)∵AM//BN,∴∠ABN+∠A=180°,∴∠ABN=180°﹣64°=116°,∴∠ABP+∠PBN=116°,∵BC平分∠ABP,BD平分∠PBN,∴∠ABP=2∠CBP,∠PBN=2∠DBP,∴2∠CBP+2∠DBP=116°,∴∠CBD=∠CBP+∠DBP=58°;(3)不变,∠APB:∠ADB=2:1,∵AM//BN,∴∠APB=∠PBN,∠ADB=∠DBN,∵BD平分∠PBN,∴∠PBN=2∠DBN,∴∠APB:∠ADB=2:1;(4)∵AM//BN,∴∠ACB=∠CBN,当∠ACB=∠ABD时,则有∠CBN=∠ABD,∴∠ABC+∠CBD =∠CBD+∠DBN∴∠ABC =∠DBN ,由(1)∠ABN =116°,∴∠CBD =58°,∴∠ABC+∠DBN =58°,∴∠ABC =29°,故答案为:29°.【点睛】本题考查了角平分线的定义,平行线的性质等,解题关键是能熟练运用平行线的性质并能灵活运用角平分线的定义等.6.如图1,在平面直角坐标系中,(,0),(,2)A a C b ,且满足2(2)20a b ++-=,过C 作CB x ⊥轴于B .(1)求ABC ∆的面积.(2)若过B 作//BD AC 交y 轴于D ,且,AE DE 分别平分,CAB ODB ∠∠,如图2,求AED ∠的度数.(3)在y 轴上存在点P 使得ABC ∆和ACP ∆的面积相等,请直接写出P 点坐标.【答案】(1)4;(2)45︒;(2)(0,3)P 或(0,1)-.【分析】(1)根据非负数的性质易得2a =-,2b =,然后根据三角形面积公式计算; (2)过E 作//EF AC ,根据平行线性质得////BD AC EF ,且1312CAB ∠=∠=∠,1422ODB ∠=∠=∠,所以112()2AED CAB ODB ∠=∠+∠=∠+∠;然后把90CAB ODB ∠+∠=︒ 代入计算即可;(3)分类讨论:设(0,)P t ,当P 在y 轴正半轴上时,过P 作//MN x 轴,//AN y 轴,//BM y 轴,利用4APC ANP CMP MNAC S S S S ∆∆∆=--=梯形可得到关于t 的方程,再解方程求出t ; 当P 在y 轴负半轴上时,运用同样方法可计算出t .【详解】解:(1)2(2)20a b ++-=,20a ∴+=,20b -=,2a ∴=-,2b =,CB AB ⊥(2,0)A ∴-,(2,0)B ,(2,2)C ,ABC ∆∴的面积12442=⨯⨯=; (2)解://CB y 轴,//BD AC ,5CAB ∴∠=∠,又∵590ODB ∠+∠=︒,∴90CAB ODB ∠+∠=︒,过E 作//EF AC ,如图①,//BD AC , ////BD AC EF ∴, 31∴∠=∠,42∠=∠ AE ∵,DE 分别平分CAB ∠,ODB ∠,即:132CAB ∠=∠,142ODB ∠=∠, 112()452AED CAB ODB ∴∠=∠+∠=∠+∠=︒;(3)(0,1)P -或(0,3). 解:①当P 在y 轴正半轴上时,如图②,设(0,)P t , 过P 作//MN x 轴,//AN y 轴,//BM y 轴,4APC ANP CMP MNAC S S S S ∆∆∆=--=梯形, ∴4(2)(2)42t t t t -+---=,解得3t =, ②当P 在y 轴负半轴上时,如图③4APC ANP CMP MNAC S S S S ∆∆∆=--=梯形 ∴4(2)(2)42t t t t -+-+--=,解得1t =-,综上所述:(0,3)P 或(0,1)-.【点睛】本题考查了平行线的判定与性质:两直线平行,内错角相等.也考查了非负数的性质、坐标与图形性质以及三角形面积公式.构造矩形求三角形面积是解题关键.7.阅读下面材料:彤彤遇到这样一个问题:已知:如图甲,AB //CD ,E 为AB ,CD 之间一点,连接BE ,DE ,得到∠BED . 求证:∠BED =∠B +∠D .彤彤是这样做的:过点E 作EF //AB ,则有∠BEF =∠B .∵AB //CD ,∴EF//CD.∴∠FED=∠D.∴∠BEF+∠FED=∠B+∠D.即∠BED=∠B+∠D.请你参考彤彤思考问题的方法,解决问题:如图乙.已知:直线a//b,点A,B在直线a上,点C,D在直线b上,连接AD,BC,BE平分∠ABC,DE平分∠ADC,且BE,DE所在的直线交于点E.(1)如图1,当点B在点A的左侧时,若∠ABC=60°,∠ADC=70°,求∠BED的度数;(2)如图2,当点B在点A的右侧时,设∠ABC=α,∠ADC=β,直接写出∠BED的度数(用含有α,β的式子表示).【答案】(1)65°;(2)11 18022αβ︒-+【分析】(1)如图1,过点E作EF∥AB,当点B在点A的左侧时,根据∠ABC=60°,∠ADC=70°,参考彤彤思考问题的方法即可求∠BED的度数;(2)如图2,过点E作EF∥AB,当点B在点A的右侧时,∠ABC=α,∠ADC=β,参考彤彤思考问题的方法即可求出∠BED的度数.【详解】(1)如图1,过点E作EF∥AB,有∠BEF=∠EBA.∵AB∥CD,∴EF∥CD.∴∠FED=∠EDC.∴∠BEF+∠FED=∠EBA+∠EDC.即∠BED=∠EBA+∠EDC,∵BE平分∠ABC,DE平分∠ADC,∴∠EBA=12∠ABC=30°,∠EDC=12∠ADC=35°,∴∠BED=∠EBA+∠EDC=65°.答:∠BED的度数为65°;(2)如图2,过点E作EF∥AB,有∠BEF+∠EBA=180°.∴∠BEF=180°﹣∠EBA,∵AB∥CD,∴EF∥CD,∴∠FED=∠EDC.∴∠BEF+∠FED=180°﹣∠EBA+∠EDC.即∠BED=180°﹣∠EBA+∠EDC,∵BE 平分∠ABC ,DE 平分∠ADC ,∴∠EBA =12∠ABC =12α,∠EDC =12∠ADC =12β, ∴∠BED =180°﹣∠EBA +∠EDC =180°﹣12α +12β. 答:∠BED 的度数为180°﹣12α +12β. 【点睛】本题考查了平行线的判定与性质以及角平分线的定义,解决本题的关键是熟练掌握平行线的判定与性质.8.如图,已知//AM BN ,60A ∠=︒,点P 是射线AM 上一动点(与点A 不重合),BC ,BD 分别平分ABP ∠和PBN ∠,分别交射线AM 于点C ,D .(1)求CBD ∠的度数(2)当点P 运动时,:APB ADB ∠∠的比值是否随之变化?若不变,请求出这个比值;若变化,请找出变化规律;(3)当点P 运动到某处时,ACB ABD =∠∠,求此时ABC ∠的度数.【答案】(1)60°;(2)不变,∠APB :∠ADB=2:1;(3)30°【分析】(1)根据角平分线的定义只要证明∠CBD=12∠ABN 即可; (2)不变.可以证明∠APB=∠PBN ,∠ADB=∠DBN=12∠PBN . (3)想办法证明∠ABC=∠CBP=∠DBP=∠DBN 即可解决问题;【详解】解:(1)∵AM∥BN,∴∠ABN=180°-∠A=120°,又∵BC,BD分别平分∠ABP和∠PBN,∴∠CBD=∠CBP+∠DBP=12(∠ABP+∠PBN)=12∠ABN=60°,(2)不变.理由如下:∵AM∥BN,∴∠APB=∠PBN,∠ADB=∠DBN,又∵BD平分∠PBN,∴∠ADB=∠DBN=12∠PBN=12∠APB,∴∠APB:∠ADB=2:1.(3)∵AM∥BN,∴∠ACB=∠CBN,又∵∠ACB=∠ABD,∴∠CBN=∠ABD,∴∠ABC=∠ABD-∠CBD=∠CBN-∠CBD=∠DBN,∴∠ABC=∠CBP=∠DBP=∠DBN,∴∠ABC=14∠ABN=30°,【点睛】本题考查平行线的性质、角平分线的定义等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.9.如图,已知AB∥CD,BE平分∠ABC,交CD于点D,∠CDE=160°,求∠C的度数【答案】140°【分析】先根据邻补角的定义求出∠CDB的度数,再根据平行线的性质及角平分线的定义得出∠ADB及∠ABC的度数,由平行线的性质可得出∠C的度数.【详解】解:∵∠CDE=160°,∴∠CDB=180°-∠CDE=180°-160°=20°,∵AB∥CD,∴∠ABD=∠CDB=20°,∵BE平分∠ABC,∴∠ABC=2∠ABD=2×20°=40°,∴∠C=180°-∠ABC=180°-40°=140°.【点睛】本题考查的是平行线的性质、角平分线的定义及邻补角的性质,熟知平行线的性质是解答此题的关键.10.如图,已知:AD⊥BC于D,EG⊥BC于G,AD平分∠BAC,求证:∠1=∠E.下面是部分推理过程,请你填空或填写理由证明:∵AD⊥BC,EG⊥BC (已知),∴∠ADC=∠EGC=90∘(),∴AD∥EG(),∴∠2=______,( )∠3=______(两直线平行,同位角相等) .又∵AD平分∠BAC(),∴∠2=∠3(),∴∠1=∠E()【答案】垂直的定义;同位角相等,两直线平行;∠1;两直线平行,内错角相等;∠E;已知;角平分线的定义;等量代换【分析】根据平行线的性质和判定以及角平分线的定义证明即可.【详解】证明:∵AD⊥BC,EG⊥BC (已知),∴∠ADC=∠EGC=90°(垂直的定义),∴AD//EG(同位角相等,两直线平行),∴∠2=1,(两直线平行,内错角相等)∠3=∠E(两直线平行,同位角相等) .又∵AD平分∠BAC(已知),∴∠2=∠3(角平分线的定义),∴∠1=∠E(等量代换).【点睛】本题主要考查平行线的性质及判定,角平分线的定义,掌握平行线的性质及判定是解题的关键.AB CD,直线EF分别交AB、CD于点A、C,CM是∠ACD的平分线,11.已知直线//CM交AB于点H,过点A作AG⊥AC交CM于点G.(1)如图1,点G在CH的延长线上时,若∠GAB =36°,求∠MCD的度数;(2)如图2,点G在CH上时,试说明:2∠MCD+∠GAB=90°.【答案】(1)63°;(2)见解析【分析】(1)依据AG⊥AC,∠GAB=36°,可得∠CAH的度数,依据角平分线的定义以及平行线的性质,即可得到∠MCD的度数;(2)结合(1)得ACD+∠CAH=180°,再依据角平分线的定义,即可得2∠MCD+∠GAB=90°.【详解】(1)∵AG⊥AC,∠GAB=36°,∴∠CAH=90°-36°=54°,∵AB∥CD,∴∠ACD+∠CAH=180°,∴∠ACD=126°,∵CM是∠ACD的平分线,∴∠ACH=∠DCM=63°;(2)∵∠ACH=∠DCM,∴∠ACD=2∠MCD,由(1)得ACD+∠CAH=180°,∵AG⊥AC,∴∠CAG=90°,∴2∠MCD+90°+∠GAB=180°,∴2∠MCD+∠GAB=90°.【点睛】本题主要考查了平行线的性质,垂直的定义,角平分线的定义,利用两直线平行,同旁内角互补是解决问题的关键.12.阅读理解:我们知道“三角形三个内角的和为180°”,在学习平行线的性质之后,可以对这一结论进行推理论证.请阅读下面的推理过程:如图①,过点A作DE//BC∴∠B=∠EAB,∠C=∠DAC又∵∠EAB+∠BAC+∠DAC=180°∴∠B+∠BAC+∠C=180°即:三角形三个内角的和为180°.阅读反思:从上面的推理过程中,我们发现平行线具有“等角转化”的功能,将∠BAC、∠B、∠C“凑”在一起,得出角之间的关系.方法运用:如图②,已知AB//DE,求∠B+∠BCD+∠D的度数.(提示:过点C作CF//AB)深化拓展:如图③,已知AB//CD,点C在点D的右侧,∠ADC=70°,点B在点A的左侧,∠ABC=60°,BE平分∠ABC,DE平分∠ADC,BE、DE所在的直线交于点E,且点E在AB与CD两条平行线之间,求∠BED的度数.【答案】方法运用:360°;深度拓展:65°【分析】方法运用:过C作CF∥AB,根据平行线的性质得到∠D=∠FCD,∠B=∠BCF,然后根据已知条件即可得到结论;深化拓展:过点E作EF∥AB,然后根据两直线平行内错角相等,再利用角平分线的定义和等量代换即可求∠BED的度数.【详解】方法运用:解:过点C作CF∥AB∴∠B=∠BCF∵CF∥AB且AB∥DE∴CF∥DE∴∠D=∠DCF∵∠BCD+∠BCF+∠DCF=360°∴∠B+∠BCD+∠D=360°深化拓展:过点E作EF∥AB∴∠BEF=∠ABE又∵BE平分∠ABC,∠ABC=60°∴∠BEF=∠ABE=12∠ABC=30°∵EF∥AB,AB∥CD∴EF∥CD∴∠DEF=∠EDC又∵DE平分∠ADC,∠ADC=70°∴∠DEF=∠EDC=12∠ADC=35°∴∠BED=∠BEF+∠DEF=30°+35°=65°【点睛】本题主要考查平行线的性质和角平分线的定义,能够作出平行线是解题的关键.13.在综合与实践课上,老师让同学们以“三条平行线m,n,l(即始终满足m∥n∥l)和一副直角三角尺ABC,DEF(∠BAC=∠EDF=90°,∠FED=60°,∠DFE=30°,∠ABC=∠ACB=45°)”为主题开展数学活动.操作发现(1)如图1,展翅组把三角尺ABC的边BC放在l上,三角尺DEF的顶点F与顶点B 重合,边EF经过AB,顶点E恰好落在m上,顶点D恰好落在n上,边ED与n相交所成的一个角记为∠1,求∠1的度数;(2)如图2,受到展翅组的启发,高远组把直线m向下平移后使得两个三角尺的两个直角顶点A、D分别落在m和l上,顶点C恰好落在n上,边AC与l相交所成的一个角记为∠2,边DF与m相交所成的一个角记为∠3,请你说明∠2﹣∠3=15°;结论应用(3)老师在点评高远组的探究操作时提出,在(2)的条件下,若点N是直线n上一点,CN恰好平分∠ACB时,∠2与∠3之间存在一个特殊的倍数关系,请你直接写出它们之间的倍数关系,不需要说明理由.【答案】(1)75°;(2)见解析;(3)∠2=3∠3【分析】(1)利用三角板的度数,求出∠DBC的度数,再利用平行线的性质得到∠BDN的度数,由此得到∠1的度数;(2)过B点作BG∥直线m,利用平行线的性质可得到∠3=DBG和∠LAB=∠ABG,再利用等量代换得到∠3+∠LAB=75°,利用余角性质得到∠LAB=90°-∠2,由此证明结论;(3)结论:∠2=3∠3.利用(2)中结论,结合平行线的性质得到∠2和∠3的度数由此证明结论.【详解】(1)∵直线n∥直线l,∴∠DBC=∠BDN,又∵∠DBC=∠ABC﹣∠ABD=45°﹣30°=15°,∴∠BDN=15°,∴∠1=90°﹣15°=75°.(2)如图所示,过B点作BG∥直线m,∵BG∥m,l∥m,∴BG∥l(平行于同一直线的两直线互相平行),∵BG∥m,∴∠3=DBG,又∵BG∥l,∴∠LAB=∠ABG,∴∠3+∠LAB=∠DBA=30°+45°=75°,又∵∠2和∠LAB互为余角,∴∠LAB =90°﹣∠2,∴∠3+90°﹣∠2=75°,∴∠2﹣∠3=15°.(3)结论:∠2=3∠3.理由:在(2)的条件下,∠2﹣∠3=15°,又∵CN 平分∠BCA ,∴∠BCN =∠CAN =22.5°,又∵直线n ∥直线l ,∴∠2=22.5°,∴∠3=7.5°,∴∠2=3∠3.【点睛】考查平行线的性质并结合了三角板中的特殊角度,学生需要作辅助线利用平行线的传递性将特殊的角的关系联系起来,熟悉掌握平行线之间角的关系是解题的关键. 14.如图,AB CD ∥,点E 、F 分别在直线AB 、CD 上,点O 在直线AB 、CD 之间,100EOF ∠=︒.(1)求BEO DFO ∠+∠的值;(2)如图2,直线MN 交BEO ∠、CFO ∠的角平分线分别于点M 、N ,求EMN FNM∠-∠的值;(3)如图3,EG 在AEO ∠内,AEG n OEG ∠=∠,FK 在DFO ∠内,DFK n OFK ∠=∠.直线MN 交FK 、EG 分别于点M 、N ,若50FMN ENM ∠-∠=︒,则n 的值是__________.【答案】(1)260° ;(2)40°;(3)53【分析】(1)如下图,过点O 作OG AB ,可得出AB OG CD ,然后利用平行的性质进行角度转换可得出答案;(2)如图,过点M 作MK AB ,过点N 作NH CD ∥,然后设BEM OEM x ∠=∠=,CFN OFN y ∠=∠=,利用方程思想进行角度推导,可得出答案;(3)如下图,过点O 作AB 的平行线OQ ,同样利用方程思想进行推导转化,可得出n 的值.【详解】(1)证明:过点O 作OG AB∵AB CD ∥∴AB OG CD∴180BEO EOG ∠+∠=︒,180DFO FOG ∠+∠=︒∴360BEO EOG DFO FOG ︒∠+∠+∠+∠=即360BEO EOF DFO ∠+∠+∠=︒∵100EOF ∠=︒∴260BEO DFO ︒∠+∠=(2)解:过点M 作MK AB ,过点N 作NH CD ∥,∵EM 平分BEO ∠,FN 平分CFO ∠设BEM OEM x ∠=∠=,CFN OFN y ∠=∠=∵260BEO DFO ︒∠+∠=∴21802260BEO DFO x y ︒︒∠+∠=+-=∴40x y -=︒∵MK AB ,NH CD ∥,AB CD ∥ ∴AB MK NH CD∴EMK BEM x ∠=∠=,HNF CFN y ∠=∠=,KMN HNM ∠=∠∴()EMN FNM EMK KMN HNM HNF ∠∠=∠+∠-∠+∠-x KMN HNM y =+∠-∠-40x y ︒=-=(3)如下图,过点O 作AB 的平行线OQ设∠NEO=x ,则∠AEN=nx设∠OFM=y,则∠MFD=ny∵AB∥CD,AB∥OQ∴AB∥OQ∥CD∴∠EOQ=∠AEO=(n+1)x,∠QOF=180°-(n+1)y∵∠EOF=100°∴∠EOQ+∠QOF=100°,化简得:(n+1)(y-x)=80°在△NPE中,∠ENP=180°-x-∠NPE在四边形POFM中,∠PMF=360°-y-100°-∠OPM∵∠PMF-∠ENP=50°∴∠PMF-∠ENP=50=360°-y-100°-∠OPM-(180°-x-∠NPE) ∵∠NPE=∠OPM∴∠PMF-∠ENP化简后得:150°+(y-x)=180°∴y-x=30°∵(n+1)(y-x)=80°∴解得:n=53.【点睛】本题考查平行线的综合应用,解题关键是构造平行线,然后利用方程思想进行角度转化求解.15.如图,已知∠AOB,作∠AOB的平分线OC,将直角尺DEMN如图所示摆放,使EM边与OB边重合,顶点D落在OA边上,DN边与OC交于点P.(1)猜想DOP是三角形;(2)补全下面证明过程:∵OC平分∠AOB∴=∵DN∥EM∴=∴=∴=【答案】等腰,∠DOP,∠BOP,∠DPO,∠BOP,∠DOP,∠DPO,OD,PD,见解析【分析】(1)三角形的种类有多种,从边和角的关系上看常见的有:等腰三角形、等边三角形、直角三角形、观察此三角形即可大体猜想出三角形的类型;(2)根据角平分线的性质和平行线的性质,求得∠DOP=∠DPO,即可判断三角形的形状.【详解】解:(1)我们猜想△DOP是等腰三角形;(2)补全下面证明过程:∵OC平分∠AOB,∴∠DOP =∠BOP ,∵DN ∥EM ,∴∠DPO =∠BOP ,∴∠DOP =∠DPO ,∴OD =PD .故答案为:等腰,∠DOP ,∠BOP ,∠DPO ,∠BOP ,∠DOP ,∠DPO ,OD ,PD .【点睛】本题考查了角平分线的性质和平行线的性质及等腰三角形,解决本题的关键是掌握平行线的性质定理,找到相等的角.16.在小学认识三角形的基础上我们来继续学习三角形.三角形可用符号“”表示. 例:如图1中的三角形可记作“ABC ”;在一个三角形中,如果有两个角相等,我们新定义这个三角形为等角三角形.(1)如图1,ABC ∠的角平分线交AC 于D ,//DE BC 交AB 于E ,①请在图1中依题意补全图形;②判断EBD △是不是等角三角形;(直接写出结论即可).(2)如图2,AF 是GAC ∠的角平分线,//BC AF .判断ABC 是不是等角三角形,并说明理由.(3)如图3,BM ,CM 分别是ABC ∠和ACB ∠的角平分线,请过图中某一点,作一条图中已有线段的平行线,使图中出现一个或两个等角三角形,标出字母,并就出现的一个三角形是等角三角形说明理由.【答案】(1)①见解析;②△EBD 是等角三角形;(2)△ABC 是等角三角形,理由见解析;(3)见解析【分析】(1)①根据题意画出图形即可;②根据角平分线定义可得∠ABD =∠DBC ,根据平行线的性质可得∠EDB =∠DBC ,进而可得∠EBD =∠EDB ,从而可得△EBD 是等角三角形;(2)根据平行线的性质可得∠1=∠B ,∠2=∠C ,再根据角平分线的性质可得∠1=∠2,进而可得结论;(3)过点M 作GH ∥BC ,交AB 于点G ,交AC 于点H ,利用平行线的性质和角平分线定义解答即可.【详解】解:(1)①补全图形如图4所示.②△EBD是等角三角形.理由:∵BD平分∠ABC,∴∠ABD=∠DBC,∵DE∥BC,∴∠EDB=∠DBC,∴∠EBD=∠EDB,∴△EBD是等角三角形;(2)△ABC是等角三角形.理由如下:如图5,∵AF∥BC,∴∠1=∠B,∠2=∠C,∵AF是∠GAC的角平分线,∴∠1=∠2,∴∠B=∠C,∴△ABC是等角三角形.(3)过点M作GH∥BC,交AB于点G,交AC于点H,如图6,出现两个等角三角形分别是:△GBM和△HMC.下面说明△GBM是等角三角形.理由:∵GH∥BC,∴∠1=∠2,∵BM是∠ABC角平分线,∴∠GBM=∠2,∴∠1=∠GBM,所以△GBM是等角三角形.【点睛】此题主要考查了平行线的性质以及角平分线的定义,正确理解题意、熟练掌握平行线的性质是解题的关键.17.如图,已知AB∥CD,CE、BE的交点为E,现作如下操作:第一次操作,分别作∠ABE和∠DCE的平分线,交点为E1,第二次操作,分别作∠ABE1和∠DCE1的平分线,交点为E 2,第三次操作,分别作∠ABE 2和∠DCE 2的平分线,交点为E 3,…,第n 次操作,分别作∠ABE n ﹣1和∠DCE n ﹣1的平分线,交点为E n .(1)如图①,已知∠ABE=50°,∠DCE=25°,则∠BEC = °;(2)如图②,若∠BEC=140°,求∠BE 1C 的度数;(3)猜想:若∠BEC =α度,则∠BE n C = °.【答案】(1)75;(2)70°;(3)2n α⎛⎫ ⎪⎝⎭【分析】(1)先过E 作EF ∥AB ,根据AB ∥CD ,得出AB ∥EF ∥CD ,再根据平行线的性质,得出∠B=∠1,∠C=∠2,进而得到∠BEC=∠ABE+∠DCE=75°;(2)先根据∠ABE 和∠DCE 的平分线交点为E 1,运用(1)中的结论,得出∠BE 1C=∠ABE 1+∠DCE 1=12∠ABE+12∠DCE=12∠BEC ; (3)根据∠ABE 1和∠DCE 1的平分线,交点为E 2,得出∠BE 2C=14∠BEC ;根据∠ABE 2和∠DCE 2的平分线,交点为E 3,得出∠BE 3C=18∠BEC ;…据此得到规律∠E n =12n ∠BEC ,最后求得∠BE n C 的度数.【详解】解:(1)如图①,过E 作EF ∥AB ,∵AB∥CD,∴AB∥EF∥CD,∴∠B=∠1,∠C=∠2,∵∠BEC=∠1+∠2,∴∠BEC=∠ABE+∠DCE=75°;故答案为:75;(2)如图2,∵∠ABE和∠DCE的平分线交点为E1,∴由(1)可得,∠BE1C=∠ABE1+∠DCE1=12∠ABE+12∠DCE=12∠BEC;∵∠BEC=140°,∴∠BE1C=70°;(3)如图2,∵∠ABE1和∠DCE1的平分线交点为E2,∴由(1)可得,∠BE 2C=∠ABE 2+∠DCE 2=12∠ABE 1+12∠DCE 1=12∠CE 1B=14∠BEC ; ∵∠ABE 2和∠DCE 2的平分线,交点为E 3,∴∠BE 3C=∠ABE 3+∠DCE 3=12∠ABE 2+12∠DCE 2=12∠CE 2B=18∠BEC ; …以此类推,∠E n =12n ∠BEC , ∴当∠BEC=α度时,∠BE n C 等于2n α⎛⎫ ⎪⎝⎭°. 故答案为:2n α⎛⎫ ⎪⎝⎭. 【点睛】本题主要考查了角平分线的定义以及平行线性质:两直线平行,内错角相等的运用.解决问题的关键是作平行线构造内错角,解题时注意:从一个角的顶点出发,把这个角分成相等的两个角的射线叫做这个角的平分线.18.完成下面的证明.如图:BAP ∠与APD ∠互补,BAE CPF ∠=∠,求证:E F ∠=∠.对于本题小明是这样证明的,请你将他的证明过程补充完整.证明:BAP ∠与APD ∠互补,(已知)//AB CD ∴.( )BAP ∴∠= .(两直线平行,内错角相等)BAE CPF ∠=∠,(已知)BAP BAE APC CPF ∴∠-∠=∠-∠,(等量代换)即EAP ∠= .∴ .(内错角相等,两直线平行)E F ∴∠=∠.( )19.如图,//AB CD ,点C 在点D 的右侧,ABC ∠,ADC ∠的平分线交于点E (不与B ,D 点重合),70ADC ∠=︒.设BED n ∠=︒.(1)若点B 在点A 的左侧,求ABC ∠的度数(用含n 的代数式表示)(2)将(1)中的线段BC 沿DC 方向平移,当点B 移动到点A 右侧时,请画出图形并判断ABC ∠的度数是否改变.若改变,请求出ABC ∠的度数(用含n 的代数式表示);若不变,请说明理由.【答案】同旁内角互补,两直线平行;APC ∠;APF ∠;//AE FP ;两直线平行,内错角相等.【分析】已知∠BAP 与∠APD 互补,根据同旁内角互补两直线平行,可得AB ∥CD ,再根据平行线的判定与性质及等式相等的性质即可得出答案.【详解】证明:BAP ∠与APD ∠互补,(已知)//AB CD ∴(同旁内角互补,两直线平行).BAP ∴∠=APC ∠(两直线平行,内错角相等), BAE CPF ∠=∠,(已知)BAP BAE APC CPF ∴∠-∠=∠-∠,即EAP ∠=APF ∠,//AE FP ∴(内错角相等,两直线平行),E F ∴∠=∠(两直线平行,内错角相等). 故答案为:同旁内角互补,两直线平行;APC ∠;APF ∠;//AE FP ;两直线平行,内错角相等.【点睛】本题考查了平行线的判定与性质和等式的性质,关键是正确理解与运用平行线的判定与性质.20.如图,AC ∥DE ,BD 平分∠ABC 交AC 于F ,∠ABC=70°,∠E=50°,求∠D ,∠A 的度数.【答案】95,60D A ∠=︒∠=︒【分析】根据BD 平分∠ABC ,∠ABC=70°得出1352ABF DBC ABC ∠=∠=∠=︒,再根据//,50AC CE E ∠=︒得出50∠=°ACB ,从而计算,D A ∠∠.【详解】∵根据BD 平分∠ABC 交AC 于F ,∠ABC=70° ∴1352ABF DBC ABC ∠=∠=∠=︒ 又∵//,50AC CE E ∠=︒∴50∠=°ACB∴180705060A ∠=︒-︒-︒=︒180355095BFC ∠=︒-︒-︒=︒∴95D BFC ∠=∠=︒综上所述:95,60D A ∠=︒∠=︒【点睛】本题考查了三角形的内角和定理以及平行线的性质,转化相关的角度是解题关键. 21.直线AB ∥CD ,直线EF 分别交AB 、CD 于点A 、C ,CM 是ACD ∠的平分线,CM 交AB 于点N .(1)如图①,过点A 作AC 的垂线交CM 于点M ,若55MCD ∠=,求MAN ∠的度数; (2)如图②,点G 是CD 上的一点,连接MA 、MG ,180MGD EAB ∠+∠=,MC 平分AMG ∠.①AMG ∠和EAB ∠满足怎么样的数量关系时EC AM ⊥?②若36AMG ∠=,求ACD ∠的度数.【答案】(1)20°;(2)①当AMG ∠+EAB ∠=180°时,EC AM ⊥;②108°【分析】(1)根据角平分线的定义求出∠ACD ,然后根据平行线的性质可得∠EAB=∠ACD=110°,然后根据垂直的定义求出∠MAE=90°,即可求出结论;(2)①当AMG ∠+EAB ∠=180°时,根据平行线的性质可推出∠AMG +∠ACD=180°,然后根据角平分线的定义可得出∠ACM +∠AMC=90°,利用三角形的内角和即可求出∠MAC=90°,从而得出EC AM ⊥;②设∠ACD=x ,根据角平分线的定义可得∠GCM=12ACD ∠=12x ,∠GMC=12∠AMG =18°,根据平行线的性质可得∠EAB=∠ACD=x ,从而得出∠MGD=180°-x ,然后根据三角形外角的性质列出方程即可求出结论.【详解】解:(1)∵CM 是ACD ∠的平分线,55∠=︒MCD∴∠ACD=2∠MCD=110°∵AB ∥CD ,∴∠EAB=∠ACD=110°∵MA ⊥AC∴∠MAE=90°∴∠MAN=∠EAB -∠MAE=20°(2)①当AMG ∠+EAB ∠=180°时,EC AM ⊥ ∵AB ∥CD ,∴∠EAB=∠ACD∴∠AMG +∠ACD=180°∵CM 是ACD ∠的平分线,MC 平分AMG ∠∴∠ACM=12ACD ∠,∠AMC=12∠AMG ∴∠ACM +∠AMC=12ACD ∠+12∠AMG =()12∠∠+ACD AMG =90° ∴∠MAC=180°-(∠ACM +∠AMC )=90° ∴EC AM ⊥;②设∠ACD=x∵CM 是ACD ∠的平分线,MC 平分AMG ∠,36∠=︒AMG∴∠GCM=12ACD ∠=12x ,∠GMC=12∠AMG =18° ∵AB ∥CD ,∴∠EAB=∠ACD=x∵180MGD EAB ∠+∠=∴∠MGD=180°-x∵∠MGD=∠GCM +∠GMC即180-x=12x +18 解得:x=108即∠ACD=108°【点睛】此题考查的是平行线的性质、垂直的定义、三角形内角和定理和三角形外角的性质,掌握平行线的性质、垂直的定义、三角形内角和定理和三角形外角的性质是解决此题的关键.22.已知AB//CD,点E是平行线之间一点.(测量发现)连结EA,EC,分别做∠EAB与ECD的角平分线交于点F,通过测量我们发现∠AEC=2∠AFC.(探索新知)如图,若∠EAF=14∠EAB,∠ECF=14∠ECD,试探索∠AFC与∠AEC之间的关系,请说明理由.(合理猜想)若∠EAF=1n∠EAB,∠ECF=1n∠ECD,请猜想∠AFC与∠AEC之间的关系,不必说明理由.【答案】∠AFC=34∠AEC,理由见解析;∠AFC=1nn∠AEC【分析】探索新知:过点F作FH//AB,先证∠BAE+∠DCE=∠AEC,再根据∠EAF=14∠EAB,∠ECF=14∠ECD即可证明;合理猜想:过点F作FH//AB,先证∠BAE+∠DCE=∠AEC,再根据∠EAF=1n∠EAB,∠ECF=1n∠ECD,即可证明.【详解】探索新知:过点F作FH//AB,∵AB//CD,∴FH//CD,∴∠AFH=∠FAB,∠CFH=∠FCD,∴∠BAC+∠DCA=180°,∵∠EAC+∠ECA+∠AEC=180°,∴∠BAE+∠DCE=∠AEC,∵∠EAF=14∠EAB,∠ECF=14∠ECD,∴∠FAB+∠FCD=34∠AEC,∴∠AFC=34∠AEC;合理猜想:过点F作FH//AB,∵AB//CD,∴FH//CD,∴∠AFH=∠FAB,∠CFH=∠FCD,∴∠BAC+∠DCA=180°,∵∠EAC+∠ECA+∠AEC=180°,∴∠BAE+∠DCE=∠AEC,∵∠EAF=1n∠EAB,∠ECF=1n∠ECD,∴∠FAB+∠FCD=1nn-∠AEC,∴∠AFC=1nn-∠AEC.【点睛】本题是对平行线性质的考查,熟练掌握平行线的性质定理是解决本题的关键.23.AB∥CD,C在D的右侧,BE平分∠ABC,DE平分∠ADC,BE、DE所在的直线交于点E.∠ADC=70°.(1)求∠EDC 的度数;(2)若∠ABC=30°,求∠BED 的度数;(3)将线段BC沿DC方向移动,使得点B在点A的右侧,其他条件不变,若∠ABC =n°,请直接写出∠BED 的度数(用含n的代数式表示).【答案】(1)35︒(2)50︒(3)12152n ︒-︒ 【分析】(1)根据角平分线定义即可得到答案;(2)过点E 作//EF AB ,然后根据角平分线的定义、平行线的判定和性质以及角的和差进行推导即可得解;(3)过点E 作//EF AB ,然后根据角平分线的定义、平行线的判定和性质以及角的和差进行推导即可得解.【详解】解:(1)∵DE 平分ADC ∠,70ADC ∠=︒ ∴1352EDC ADC ∠=∠=︒; (2)过点E 作//EF AB ,如图:∵DE 平分ADC ∠,70ADC ∠=︒;BE 平分ABC ∠,30ABC ∠=︒ ∴1352EDC ADC ∠=∠=︒,1152ABE ABC ∠=∠=︒ ∵//AB CD ,//EF AB∴////AB EF CD∴35FED CDE ∠=∠=︒,15FEB ABE ∠=∠=︒∴50BED FED FEB ∠=∠+∠=︒;(3)过点E 作//EF AB ,如图:∵DE 平分ADC ∠,70ADC ∠=︒;BE 平分ABC ∠,ABC n ∠=︒ ∴1352EDC ADC ∠=∠=︒,1122ABE ABC n ∠=∠=︒ ∵//AB CD ,//EF AB∴////AB EF CD∴35FED CDE ∠=∠=︒,11801802FEB ABE n ∠=︒-∠=︒-︒ ∴113518021522BED FED FEB n n ∠=∠+∠=︒+︒-︒=︒-︒. 故答案是:(1)35︒(2)50︒(3)12152n ︒-︒ 【点睛】本题考查了角平分线的定义、平行线的判定和性质以及角的和差,解答本题的关键是作出辅助线,要求同学们掌握平行线的性质,难度中等.24.如图①,BE 、DF 分别平分四边形ABCD 的外角MBC ∠和NDC ∠,设BAD ∠=α,BCD β∠=.(1)若110αβ+=︒,则MBC NDC ∠+∠= ︒;(2)若BE 与DF 相交于点G ,且25BGD ∠=︒,求α、β所满足的等量关系式,并说明理由;(3)如图②,若αβ=,试判断BE 、DF 的位置关系,并说明理由.【答案】(1)110;(2)50βα-=︒,理由见解析;(3)BE DF ∥,理由见解析【分析】(1)根据四边形的内角和与邻补角的性质即可求解;(2)连接BD ,先得到1()2CBG CDG αβ∠+∠=+,再根据三角形的内角和得到角度的关系即可求解;(3)由(1)有,∠MBC +∠NDC =αβ+,BE 、DF 分别平分四边形的外角∠MBC 和∠NDC ,则∠CBE +∠CDH =12(αβ+),∠CBE +β−∠DHB =12(αβ+),根据α=β,则有∠CBE +β−∠DHB =12(β+β)=β,得到∠CBE =∠DHB ,故可得到BE ∥DF .【详解】解:(1)∵∠ABC +∠ADC =360°−(αβ+)=250°,∴∠MBC +∠NDC =180°−∠ABC +180°−∠ADC =360°-(∠ABC +∠ADC )=αβ+=110°.故答案为:110;(2)50βα-=︒.理由如下:如解图①,连接BD ,由(1)知,MBC NDC αβ∠+∠=+, BE 、DF 分别平分四边形ABCD 的外角MBC ∠和NDC ∠, ∴12CBG MBC ∠=∠,12CDG NDC ∠= ()1111()2222CBG CDG MBC NDC MBC NDC αβ∴∠+∠=∠+=∠+=+. 在△BCD 中,∠BDC +∠CBD =180°−∠BCD =180°−β, 在△BDG 中,∠GBD +∠GDB +∠BGD =180°,∴∠CBG +∠CBD +∠CDG +∠BDC +∠BGD =180°,∴(∠CBG +∠CDG )+(∠BDC +∠CBD )+∠BGD =180°, ∴12(αβ+)+180°−β+25°=180°, 整理得50βα-=︒;(3)BE DF ∥.理由如下,如解图②所示,延长BC 交DF 于点H ,由(1)、(2)可知,MBC NDC αβ∠+∠=+,1()2CBE CDH αβ∠+∠=+.BCD CDH DHC ∠=∠+∠,CDH BCD DHC DHC β∴∠=∠-∠=-∠,1()2CBE DHC βαβ∴∠+-∠=+. αβ=,1()2CBE DHB ββββ∴∠+-∠=+=, CBE DHB ∴∠=∠,BE DF ∴∥.【点睛】此题考查了平行线的性质及其判定,多边形的内角和公式,利用多边形的内角和公式倒角为解题关键.25.已知AM ∥CN ,点B 为平面内一点,AB ⊥BC 于B(1)如图1,直接写出∠A 和∠C 之间的数量关系;(2)如图2,过点B 作BD ⊥AM 于点D ,求证:∠ABD=∠C ;(3)如图3,在(2)问的条件下,点E.F 在DM 上,连接BE.BF.CF ,BF 平分∠DBC ,BE 平分∠ABD ,若∠FCB+∠NCF=180°,∠ABF=2∠ABE ,求∠EBC 的度数.【答案】(1)90°;(2)详见解析;(3)105°【分析】(1)根据平行线的性质以及直角三角形的性质进行证明即可;(2)先过点B作BG∥DM,根据同角的余角相等,得出∠ABD=∠CBG,再根据平行线的性质,得出∠C=∠CBG,即可得到∠ABD=∠C;(3)先过点B作BG∥DM,根据角平分线的定义,得出∠ABF=∠GBF,再设∠DBE=α,∠ABF=β,根据∠CBF+∠BFC+∠BCF=180°,可得(2α+β)+3α+(3α+β)=180°,根据AB⊥BC,可得β+β+2α=90°,最后解方程组即可得到∠ABE=15°,进而得出∠EBC=∠ABE+∠ABC=15°+90°=105°.【详解】解:(1)如图1,AM与BC的交点记作点O,∵AM∥CN,∴∠C=∠AOB,∵AB⊥BC,∴∠A+∠AOB=90°,∴∠A+∠C=90°;(2)如图2,过点B作BG∥DM,∵BD⊥AM,∴DB⊥BG,即∠ABD+∠ABG=90°,又∵AB⊥BC,∴∠CBG+∠ABG=90°,∴∠ABD=∠CBG,∵AM∥CN,BG∥AM,∴CN∥BG,∴∠C=∠CBG,∴∠ABD=∠C;(3)如图3,过点B作BG∥DM,∵BF平分∠DBC,BE平分∠ABD,∴∠DBF=∠CBF,∠DBE=∠ABE,由(2)可得∠ABD=∠CBG,∴∠ABF=∠GBF,设∠DBE=α,∠ABF=β,则∠ABE=α,∠ABD=2α=∠CBG,∠GBF=β=∠AFB,∠BFC=3∠DBE=3α,∴∠AFC=3α+β,∵∠AFC+∠NCF=180°,∠FCB+∠NCF=180°,∴∠FCB=∠AFC=3α+β,△BCF中,由∠CBF+∠BFC+∠BCF=180°,可得(2α+β)+3α+(3α+β)=180°,①由AB⊥BC,可得β+β+2α=90°,②由①②联立方程组,解得α=15°,∴∠ABE=15°,∴∠EBC=∠ABE+∠ABC=15°+90°=105°.。
角平分线三个定理-概述说明以及解释

角平分线三个定理-概述说明以及解释1.引言1.1 概述角平分线三个定理是解决与角度相关的几何问题时,非常重要且常用的定理。
它们分别应用于角的平分线问题,帮助我们更深入地理解角的性质与构造。
这三个定理不仅在数学学科中有广泛的应用,而且在实际生活中也具有重要的意义。
在解释这三个定理之前,我们先回顾一下角的基本概念。
在几何学中,角是由两条线段或射线共享一个公共端点而形成的图形。
以公共端点为中心,可以将角分为两个部分,分别称为角的两个腿。
角的大小通常用度或弧度来表示,这取决于所用的单位。
第一个定理是角的平分线定理,它指出:如果一条直线将一个角平分成两个相等的角,那么这条直线称为这个角的平分线。
换句话说,平分线将角分为两个相等的部分。
这个定理有广泛的应用,例如在三角形中,利用角平分线定理可以证明角的大小相等,从而推导出三角形的一些特殊性质。
第二个定理是外角平分线定理,它指出:如果一条直线通过一个三角形的外角的顶点,并将外角的两个邻角平分成两个相等的角,那么这条直线称为该三角形的外角平分线。
这个定理在解决外角问题时非常有用,它保证了外角平分线的存在性,并简化了我们分析与推导相关问题的步骤。
第三个定理是内角平分线定理,它指出:如果一条直线通过一个三角形的内角的顶点,并将内角的两个邻角平分成两个相等的角,那么这条直线称为该三角形的内角平分线。
这个定理与外角平分线定理类似,但是涉及的是三角形的内角。
利用内角平分线定理,我们可以简化三角形内角相关问题的分析过程。
角平分线三个定理在几何学中占据着重要的地位,是研究角度关系和解决几何问题的基础。
它们不仅具有理论意义,还具有广泛的应用价值。
通过深入理解和熟练运用这三个定理,我们能够提高问题解决的效率,并在实际生活中更好地应用几何知识。
1.2文章结构文章结构:本文主要介绍了角平分线的三个定理,分为引言、正文和结论三个部分。
引言部分首先概述了角平分线的意义和应用,以及本文的目的。
有关三角形角平分线的有趣问题的讨论

有关三角形角平分线的有趣问题的讨论前言:角平分线这个词我们并不陌生,初中时,我们便知道等腰三角形两底角的平分线相等、全等三角形对应角平分线相等的一些有关三角形角平分线的定理,今天就让我们更加深入的探究角平分线的特性吧!正文:一.斯坦纳—雷米欧司定理尽然我们知道“等腰三角形两底角的平分线相等”是一个真命题,那么我们便可以猜想:它的逆命题是否也是真命题呢?也就是“有两条内角平分线相等的三角形是等腰三角形”是否成立?在两千多年前,欧几里得在他的经典巨著《几何原本》中便给出了上述第一个命题的证明,但是他却没有能够证明第二个命题也就是第一个命题的逆命题.直到十八世纪,雷米欧司重新提出这个题目,著名的德国几何学家斯坦纳才给出了这个逆命题的证明.所以,现在大家都把它叫“做斯坦纳—雷米欧司定理”既然连欧几里得也无法证明的命题,我们中学生该如何下手呢?自然地,我们便想到要不从最简单的方式入手吧?①反证法:我们先将命题化为几何语言:如图,已知BP、CQ分别是△ABC的内角∠ABC、∠ACB的平分线,且BP=CQ 求证:△ABC是等腰三角形证明:如上图,设∠ABP=∠PBC=½∠ABC=β,∠ACQ=∠QCB=½∠ACB=α设BP与CQ交点为O(这样要证明△ABC为等腰三角形便要转换为证明α=β)若α>β,于是在线段OP上可以取一点R使∠RCD=β且BR<BP在△BQC与△CRB中∵∠BQC=180°-(2β+α),∠CRB=180°-(2β+α)∴∠BQC=∠CRB又∵α>β∴∠QBC<∠RCB根据正弦定理 BR =Sin∠RCB > Sin∠QBC =CQBC Sin∠CRB Sin∠BQC BC∴BR>CQ=BP 这与BR<BP矛盾故α>β不成立同理可证α<β也不成立∴α只能与β相等∴∠ABC=∠ACB∴△ABC为等腰三角形同学们是否感觉到用反证法证明很容易呢?其实,斯坦纳一开始也是用反证法证明的,但他的方法比我们的方法更烦琐些,命题已经证完了,大家终于可以松一口气了,但是我们知道,反正法毕竟不能取代纯几何证法,纯几何证法才是能够使几何命题完善的.在斯坦纳证明该命题后,就陆续有数学爱好者提出了其他证明方法,海塞便是其中之一?②纯几何证法——海塞证法(在这里,已知、求证便不再写出)证明:在△BDC的外侧作∠BDF=∠ECB且使得DF=BC 连接BF在△BDF与△ECB{BD=EC ∠BDF=∠ECB DF=CB}∴△BDF≌△ECB ∴BF=EB ,∠FBD=∠BEC设∠ABD=α=∠DBC, ∠ACE=β=∠BCE则∠FBC=∠FBD+∠DBC=∠BEC+∠DBC=180°-(2α+β) +α=180°-(α+β)∠FDC=∠FDB+∠BDC=β+180°-(2β+α)=180°-(α+β)∴∠FBC=∠FDC∵2α+2β<180 ∴α+β<90°∴180°-(α+β) >90°即∠FBC=∠FDC>90°过点C作BF的垂线交FB延长线G,过点F作DC的垂线交CD 延长线于点H∴∠CBG=180°-∠FBC=180°-∠CDF=∠FDH又∵∠CGB=∠FHD=90°,BC=DF∴△CGB≌△FHD ∴FH=CG ,HD=GB连接CF ∵CF=FC ,FH=CG∴Rt△FCH≌Rt△CFG(HL)∴CH=FG∴CH-HD=FG-GB即CD=FB又∵BF=EB ∴CD=BE又∵EC=BD ,BC=BC∴△EBC≌△DCB∴∠EBC=∠DCB 即∠ABC=∠ACB ∴△ABC是等腰三角形二.角平分线定理说起角平分线,大家一定能想到:角平分线所联系的一些线段是否存在某种关系?比如:比例关系?下面我向大家介绍内角平分线定理与外角平分线定理【1】内角平分线定理已知:AD为△ABC的一条内角平分线求证:BD/CD=AB/AC①利用正弦定理证明AB= Sin∠ADB = Sin∠ADC =ACBD Sin∠BAD Sin∠CAD DC∴AB=BDAC DC②利用辅助线如图,过点C作CE∥DA交BA延长线于点E 则∠AEC=∠BAD , ∠ACE=∠DAC ∵∠BAD=∠DAC ∴∠AEC=∠ACE∴AE=AC∵AD∥EC ∴AB=BD ∴AB = BDAE DC AC DCPS:这个定理其实有很多种证法,这里只是列举了最简单的两种【2】外角平分线定理已知:如图,△ABC的外角∠ACE的平分线CD与BA的延长线交于点D求证:BC=BDAC AD证明:(面积法)在BC延长线上取点E使CE=AC在△ACD与△ECD中∵{AC=EC ∠ACD=∠ECD CD=CD }∴△ACD≌△ECD ∴S△ACD= S△ECD AC=CE∴BC = BC = S△BCD = S△BCD = BDAC CE S△DCE S△ACD AD(这里用了同高三角形的面积之比等于其对应底边之比)PS:这个定理也有很多证法,此证明为我原创竟然我们已经证明了角平分线所联系的一些线段存在比例关系,那么我们是否可以进一步完成角平分线的长度是否与这些线段有关呢?下面我们便来探索角平分线的长度定理三.Schooten定理Schooten定理是平面几何最著名定理之一,下面我们一起证明它的原命题:已知,如图,AD为△ABC的内角平分线求证:AD ²=AB·AC-BD·DC①辅助圆证法证明:延长AD交△ABC外交圆⊙O于点E连接BE由∠BAE=∠DAC, ∠E=∠C知△ABE∽△ADC∴AB = AE ∴AB·AC=AD·AEAD AC∵AE=AD+DE∴AB·AC=AD·AE=AD·(AD+DE)=AD²+AD·DE∵已知△BED∽△ACD∴AD =BD ∴AD·DE=DC·BDDC DE∴AB·AC=AD²+DC·BD即AD²=AB·AC-BD·DC②利用勾股定理证明过点A作AE⊥BC于点E,设点E在线段DC上设AD=t BD=m DC=n AC=b AB=c根据勾股定理:t²=AE²+DE²=b²-CE²+DE²=b²-(n-DE) ²+DE²=b²-n²+2Nde且t²=AE²+DE²=c²-BE²+DE²=c²-(m+DE) ²+DE ²=c²-m²-2m·DE∴DE= t²-b²+n²=c²-m²-t²2n 2m整理得:(m+n)t²=mb²+nc²-(m+n)mn根据内角平分线定理有: c = m ∴mb=ncb n而mb²=mb·b=nbc, nc²=nc·c=mbc∴(m+n)t²=(m+n)bc-(m+n)mn∴t²=bc-mn即AD²=AB·AC-BD·DCPS:其实,Schooten定理还可以用正弦定理以及和差化积推导出来,接下来我们一起尝试用正弦定理证明吧?③正弦定理证法证明:如图,设BD=m , DC=n, AD=t , AB=c,AC=b∠BAD=∠DAC=β, ∠ADC=α, ∠ADB=180°-α根据正弦定理:b =Sinα,c =Sin(180°-α)=Sinα, m =Sinβn =Sinβt SinC t SinB SinB t SinB t SinC∴b =Sinα·t , c =Sin(180°-α)=Sinα·t , m =Sinβ·t , n =Sinβ·t SinC SinB SinB SinB SinC∴bc-mn=Sinα·t·Sinα·t-Sinβ·t·Sinβ·tSinC SinB SinB SinC=Sin ²α-Sin ²β·t ²SinBSinC又∵Sin ²α-Sin ²β=(Sinα+Sinβ)(Sinα-Sinβ)=(2Sin(α+β)Cos(α-β)(2Cos(α+β)Sin(α-β) )2 2 2 2=Sin(α+β) ·Sin(α-β)由图,注意到α+β=180°-∠C, α-β=∠B∴Sin ²α-Sin ²β=Sin(180°-∠C) ·SinB=SinB·SinC∴bc-mn= SinB·SinC ·t ²=t ²SinB·SinC即AD ²=AB·AC-BD·DC补充说明:在①辅助圆证法中,我们得到了AD·DE=DC·BD这样的结论,这其实是一个普遍性的结论,也可以说是一个定理即“相交弦定理”如图,AB、CD是⊙O内的一对相交弦,交点为E则AE·BE=CE·DE另外,我们连接AC、BC、BD、AD,可得到一个圆内接四边形ABCD联系初中的几何知识, 我们知道∠CAD+∠CBD=180°, ∠ACB+∠ADB=180°反过来,在任意四边形中,只要存在一组对角互补,那么这个四边形就拥有一个外接圆,也就是存在一个圆使得这个四边形的四个顶点都在圆上,我们可称这个四个顶点共圆.如图,点A、C、B、D四点共圆(我们在二以及三的补充说明所作的努力,其实是为下面这个经典难题服务的)四.证明“三条角平分线对应相等的两个三角形全等”如图,设I是△A’B’C’的垂心,A、B、C是三条高的垂足,连接AB、BC、AC设AB与C’C交点于F,BC于AA’交于点E,AC与BB’交于点E设AD=Ta,BE=Tb,CF=Tc,ID=x,IE=y,IF=z易知点A、C’、B、I四点共圆,点A、B’、C、I四点共圆,点A’、B、I、C四点共圆∴∠ABI=∠AC’I , ∠IBC=∠IA’B’又∵∠AC’I=90°-∠C’B’C , ∠IA’B’=90°-∠C’B’C∴∠AC’I=∠IA’B’∴∠ABI=∠IBC ∴BE为△ABC的内角平分线同理可证AD、CF也为△ABC的角平分线∴点I为△ABC的内心∵BI是△ABD的内角平分线∴AB =AI =Ta-x =Ta -1 (内角平分线定理)BD ID x x∵BA’是△ABD的外角平分线∴AB =AA’ = AI+IA’= Ta-x+IA’= Ta +1 (外角平分线定理)BD DA’IA’-ID IA’-x IA’-X∴Ta +1= AB = Ta -1IA’-x BD x解这个方程(IA’为未知数)得IA’= 2x(Ta-x)²Ta-2x∴AI·A’I=(Ta-x) ·2x(Ta-x)= 2x(Ta-x) ²Ta-2x Ta-2x同理可证BI·IB’=2y(Tb-y)², CI·IC’= 2z(Tc-z)²Tb-2y Tc-2z∵A、B、A’、B’四点同圆∴AI·A’I=BI·B’I(相交弦定理)∵B、C、B’、C’四点共圆∴BI·IB’=CI·IC’∴2x(Ta-x)²= 2y(Tb-y)²= 2z(Tc-z)²Ta-2x Tb-2y Tc-2z∴设x =u , y =v , z =wTa Tb Tc代入上式得:Ta²·u(1-u)²=Tb²·v(1-v)²=Tc²·w(1-w)²(=k)1-2u 1-2v 1-2w单独对Ta²·u(1-u) ²=k分析1-2u设f(u)= u(1-2u)²= k1-2u Ta ²对f(u)的单调性进行判断,由于f(u )比较复杂,直接对其求导f’(u) = (1-u) (4u²-3u+1) = (1+u) [(2u-¾)²+7/16](1-2u)²(1-2u) ²∵u= x <1 ∴1-u>0 ∴f’(u) >0Ta可见f(u)是单调递增的函数,所以当Ta、k的值确定时,u的值是唯一确定的,而且当Ta的值确定时,u的值随k增大而增大同理,当Tb、k的值确定时,v的值是唯一确定的,而且当Tb的值确定时,v的值随k增大而增大当Tc、k的值确定时,w的值是唯一确定的,而且当Tc的值确定时,w的值随k增大而增大设BC=a ,AC=b, AB=c∵Ta -1= Ta-x = AB = AB+AC =AB+AC=c+bx x BD BD+DC BC a∴Ta = c+b +1= a+b+c 即有u= x = ax a a Ta a+b+c同理有v= y = b , w= z = cTb a+b+c Tc a+b+cu+v+w= a + b + c =1a+b+c a+b+c a+b+c由前面推导可知,当Ta、Tb、Tc的值确定时,u+v+w的值随k的增大而增大,现在又知道u+v+w=1,可见k的值不能任意改变,是唯一确定的但是又有u∶v∶w= a ∶ b ∶ c =a∶b∶ca+b+c a+b+c a+b+c可见当内角平分线的长度Ta、Tb、Tc确定时,△ABC三边的比值也是唯一确定的.这也就是,当两个三角形的内角平分线对应相等时,这两个三角形必定相似,不仅如此,如果这两个三角形的相似比不是1,它们的内角平分线不会对应相等,可见它们的相似比一定是1,所以这两个三角形一定相等.总结:从一到四,我们一共讨论了五个有关三角形角平分线的题,这些题目有些简单一看就懂;有的复杂,初看之后无从下手.我很喜欢张景中院士的一句话:“题目的难易取决于解题方法.”没错,有些“难题”一开始我们可能会无法解决,但只要我们在平常多积累有些巧妙的数学思想、解题方法,我们总有一天会解开,而且解题方法还可能简单的难以置信.一个个定理的相互联系也会让我们体会到数学的严密性、逻辑性.“数学是宇宙中最美得语言”我希望我能与大家一起热爱数学、探索数学,感受数学之美.注:参考文献《新概念几何》张景中P224《几何变换与几何证明》萧振刚P368、。
初中数学几何模型:双角平分线模型

双角平分线模型模型讲解【结论1】如图所示,在△ABC中,BD,CD分别是∠ABC和∠ACB的平分线,则∠BDC=90°+12∠A.【证明】设∠ABD=∠DBC= x,∠ACD=∠BCD = y.由△ABC的内角和为180°,得∠A+2x+2y=180°.①由△BDC的内角和为180°,得∠BDC+x+y=180°.②由②得x+y=180°-∠BDC.③把③代入①,得∠A+2(180°-∠BDC) =180°,即2∠BDC =180°+∠A,即∠BDC=90°+12∠A.【结论2】如图所示,△ABC的外角平分线BD和CD相交于点D,则∠BDC = 90°−12∠A.【证明】设∠EBD=∠CBD = x,BCD=∠FCD = y.由△BCD的内角和为180°,得x+y+∠BDC=180°,①易得2x+2y=180°+∠A.②由①得x+y=180°-∠BDC.③把③代入②,得2(180°―∠BDC) =180°+∠A,即2∠BDC = 180°-∠A,即∠BDC = 90°−12∠A.【结论3】如图所示,△ABC的内角平分线BD和外角平分线CD相交于点D,则∠D=12∠A.【证明】设∠ABD=∠DBC = x,∠ACD=∠ECD = y.由外角定理得2y=∠A+2x,①y=∠D+x.②把②代入①,得2(∠D+x)=∠A+2x,即∠D=12∠A.典型例题典例1如图,在△ABC中,∠ABC和∠ACB的平分线相交于点O,若∠BAC=80°,则∠BOC的度数是( ).A.130°B.120°C.100°D.90°典例2如图,BA1和CA1,分别是△ABC的内角平分线和外角平分线,BA2是∠A1BD的平分线,CA2是∠A1CD的平分线,BA3是∠A2BD的平分线,CA3是∠A2CD的平分线,……以此类推,若∠A=α,则A2020 =___________.典例3【问题】如图1,在△ABC中,BE平分∠ABC,CE平分∠ACB.若∠A=80°,则∠BEC=________;若∠A=n°,则∠BEC=______.【探究】(1)如图2,在△ABC中,BD,BE三等分∠ABC,CD,CE三等分∠ACB,若∠A=n°,则∠BEC=________;(2)如图3,O是∠ABC的平分线BO与∠ACD的平分线CO的交点,试分析∠BOC和∠A有怎样的关系,并说明理由;(3)如图4,O是三角形ABC的外角∠DBC与∠BCE的平分线BO和CO的交点,则∠BOC与∠A有怎样的关系? (只写结论,不需要证明)初露锋芒1.如图所示,在△ABC中,∠ABC,∠ACB的平分线BE,CD相交于点F,若∠A=60°,则∠BFC等于( ).A.121°B.120°C.119°D.118°2.如图,五边形ABCDE在∠BCD,∠EDC处的外角分别是∠FCD,∠GDC,CP,DP分别平分∠FCD和∠GDC且相交于点P.若∠A=160°,∠B=80°,∠E=90°,则∠CPD=_________.感受中考1.(2019黑龙江大庆中考真题)如图,在△ABC中,BE是∠ABC的平分线,CE是∠ACM的平分线,BE与CE相交于点E. 若∠A=60°,则∠BEC的度数为( ).A.15°B.30°C.45°D.60°参考答案典例1【答案】A【解析】∵BO,CO是△ABC的内角平分线,由“内内90°加一半”得,∠BOC=90°+12∠BAC,即∠BOC=90°+ 12×80°=130°.故选A.典例2【答案】(12)2020·α【解析】∵BA1为△ABC的内角平分线,CA1为△ABC的外角平分线,∴由“内外就一半”,得∠A1= 12∠A=12·α.同理,∠A2= 12∠A1=(12)2·α,∠A3= 12∠A2=(12)3·α,......∴∠A2020 = ( 12)2020·α.典例3【解析】【问题】130°;90°+ 12n°【探究】(1)由三角形内角和定理,得∠ABC+∠ACB=180°-∠A=180°- n°.∵BD,BE三等分∠ABC,CD,CE三等分∠ACB,∴∠EBC= 23∠ABC,∠ECB =23∠ACB,∴∠EBC+∠ECB= 23(∠ABC+∠ACB)=23×(180°- n°)=120°−23n°,∴∠BEC =180°- (∠EBC+∠ECB)=180°- (120°-23n°)= 60°+ 23n°.(2)∠BOC= 12∠A. 理由如下:由三角形的外角性质,得∠ACD=∠A+∠ABC,∠OCD=∠BOC+∠OBC.∵O是∠ABC的平分线BO与∠ACD的平分线CO的交点,∴∠ABC =2∠OBC, ∠ACD =2∠OCD,∴∠A+∠ABC=2 (∠BOC+∠OBC),∴∠A=2∠BOC,∴∠BOC = 12∠A.(3)∠BOC=90°−12∠A.初露锋芒1.【答案】B【解析】∵BE,CD均为△ABC的内角平分线,∴由“内内90°加一半”,得∠BFC=90°+12∠A = 90°+12×60°=120°.故选B.2.【答案】105°【解析】如图,延长BF,EG交于点H.在△CDH中,CP,DP分别平分∠HCD和∠HDC,∴由“内内90°加一半”,得∠CPD=90°+ 12∠H.又∠A+∠B+∠H+∠E =360°,∴∠H = 360°−160°−80°−90°= 30°,∴∠CPD = 90°+ 12×30°=105°.感受中考1.【答案】B【解析】∵BE为△ABC的内角平分线,CE为△ABC的外角平分线,∴由“内外就一半”,得∠BEC= 12∠A=12×60°=30°.故选B.11。
三角形角平分线专题讲解(精选.)

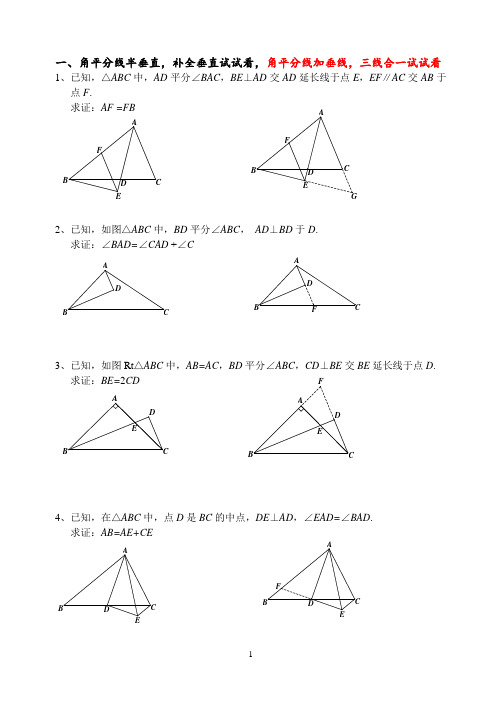
由角平分线想到的辅助线口诀:图中有角平分线,可向两边作垂线。
也可将图对折看,对称以后关系现。
角平分线平行线,等腰三角形来添。
角平分线加垂线,三线合一试试看。
角平分线具有两条性质:a、对称性;b、角平分线上的点到角两边的距离相等。
对于有角平分线的辅助线的作法,一般有两种。
①从角平分线上一点向两边作垂线;②利用角平分线,构造对称图形(如作法是在一侧的长边上截取短边)。
通常情况下,出现了直角或是垂直等条件时,一般考虑作垂线;其它情况下考虑构造对称图形。
至于选取哪种方法,要结合题目图形和已知条件。
与角有关的辅助线一)、截取构全等几何的证明在于猜想与尝试,种尝试与猜想是在一定的规律基本之上的,希望同学们能掌握相关的几何规律, 在解决几何问题中大 胆地去猜想, 按一定的规律去尝试。
下面就几何中常见的定理所 涉及到的辅助线作以介绍。
如图 1-1 ,∠∠,如取,并连接、 ,则有△≌△,从而为我们 证明线段、角相等创造了条件。
例1. 如图 1-2 ,,平分∠,平分∠, 点 E 在上,求证:。
分析:此题中就涉及到角平分线, 可以利用角平分线来构造全等三角形, 对称图形, 同时此题也是证明线段的和差倍分问题, 在证明线段 的和差倍分问题中常用到的方法是延长法或截取法来证明, 延长 短的线段或在长的线段长截取一部分使之等于短的线段。
但无论 延长还是截取都要证明线段的相等, 延长要证明延长后的线段与某条线段相等,截取要证明截取后剩下的线段与某条线段相等, 进而达到所证明的目的。
简证:在此题中可在长线段上截取,再证明,从而达到证明 的目的。
这里面用到了角平分线来构造全等三角形。
另外一个全 等自已证明。
此题的证明也可以延长与的延长线交于一点来证 明。
自已试一试。
例2. 已知:如图 1-3 ,2,∠∠,,求证⊥即利用解平分线来构造轴 图1-2分析:此题还是利用角平分线来构造全等三角形。
构造的方法还是截取线段相等。
其它问题自已证明。
专题05 三角形中的角平分线模型--2024年中考数学核心几何模型重点突破(解析版)

专题05三角形中的角平分线模型【模型1】如图,已知OP 平分AOB ∠,过点P 作OA PD ⊥,OB PE ⊥;可根据角平分线性质证得ODP ∆≌OEP ∆,从而可得OPE OPD ∠=∠,PE PD OE OD ==;。
【模型拓展】与角平分线有关的辅助线作法【辅助线作法一】如图,已知OP 平分AOB ∠,点C 是OA 上的一点,通常情况下,在OB 上取一点D,使得OC OD =,连接PD,结合OP OP =,POD POC ∠=∠,可证得OPC ∆≌OPD ∆。
从而可得PD PC =,PDO PCO ∠=∠,DPO CPO ∠=∠。
【辅助线作法二】如图,已知OP 平分AOB ∠,OP CP ⊥,通常情况下,延长CP 交OB 于点D,结合OP OP =,POD POC ∠=∠,︒=∠=∠90OPD OPC ,可证得OPC ∆≌OPD ∆。
从而可得PD PC =,PDO PCO ∠=∠,OD OC =。
【辅助线作法三】如图,已知OP 平分AOB ∠,通常情况下,过点P 作PC//OB,根据平行线性质:两直线平行内错角相等;结合POD POC ∠=∠,从而可得PC OC =,CPO COP ∠=∠。
【例1】如图,OC 为∠AOB 的角平分线,点P 是OC 上的一点,PD ⊥OA 于D ,PE ⊥OB 于E ,F 为OC 上另一点,连接DF ,EF ,则下列结论:①OD =OE ;②DF =FE ;③∠DFO =∠EFO ;④S △DFP =S △EFP ,正确的个数为()A .1个B .2个C .3个D .4个【答案】D 【分析】证明△ODP ≌△OEP (AAS ),由全等三角形的性质可推出OD =OE ,证明△DPF ≌△EPF (SAS ),由全等三角形的性质可推出DF =EF .∠DFP =∠EFP ,S △DFP =S △EFP ,则可得出答案.【解析】解:①∵OC 平分∠AOB ,∴∠DOP =∠EOP ,∵PD ⊥OA 于点D ,PE ⊥OB 于点E ,∴∠ODP =∠OEP =90°,∵OP =OP ,∴△ODP ≌△OEP (AAS ),∴OD =OE .故①正确;②∵△ODP ≌△OEP ,∴PD =PE ,∠OPD =∠OPE ,∴∠DPF =∠EPF ,∵PF =PF ,∴△DPF ≌△EPF (SAS ),∴DF =EF .故②正确;③∵△DPF ≌△EPF ,∴∠DFO =∠EFO ,故③正确;④∵△DPF ≌△EPF ,∴S △DFP =S △EFP ,故④正确.故选:D .【例2】如图,已知OC 平分∠MON ,点A 、B 分别在射线OM ,ON 上,且OA =OB .求证:△AOC ≌△BOC.【答案】见解析【分析】根据角平分线的性质和全等三角形的判定方法可以证明结论成立.【解析】证明:∵OC 平分∠MON ,∴∠AOC =∠BOC ,在△AOC 和△BOC 中,OA OB AOC BOC OC OC =⎧⎪∠=∠⎨⎪=⎩,∴△AOC ≌△BOC (SAS ).【例3】请阅读以下材料,并完成相应的问题:角平分线分线段成比例定理:如图1,在△ABC 中,AD 平分∠BAC ,则AB BD AC CD=,下面是这个定理的部分证明过程:证明:如图2,过C 作CE ∥DA ,交BA 的延长线于E .…任务:(1)请按照上面的证明思路,写出该证明的剩余部分;(2)如图3,已知Rt △ABC 中,AB =3,BC =4,∠ABC =90°,AD 平分∠BAC ,求BD 的长.(请按照本题题干的定理进行解决)【答案】(1)见解析;(2).【分析】(1)如图2:过C 作CE ∥DA .交BA 的延长线于E ,利用平行线分线段成比例定理得到BD CD =BA EA,利用平行线的性质得∠2=∠ACE ,∠1=∠E ,由∠1=∠2得∠ACE =∠E ,所以AE =AC 即可证明结论;(2)先利用勾股定理计算出AC =5,再利用(1)中的结论得到AC AB =CD BD ,即53=CD BD ,则可计算出BD =32,然后利用勾股定理计算出AD =2,从而可得到△ABD 的周长.【解析】(1)解:如图2:过C 作CE ∥DA .交BA 的延长线于E ,∵CE //AD ,∴BD CD =BA EA,∠2=∠ACE ,∠1=∠E ,∵AD 平分∠BAC∴∠1=∠2,∴∠ACE =∠E ,∴AE =AC ,∴AB AC =BD CD;(2)∵AB =3,BC =4,∠ABC =90°,∴AC =5,∵AD 平分∠BAC ,∴AC AB =CD BD ,即53=4BD BD -,∴BD =32,∴AD∴△ABD 的周长=32+3+2=92+.一、单选题1.如图,ABC 中,5AB =,6BC =,10CA =,点D ,E 分别在BC ,CA 上,DE AB ∥,F 为DE 中点,AF 平分BAC ∠,则BD 的长为()A .32B .65C .85D .2【答案】B【分析】根据角平分线和平行可得EA EF =,从而可得2DE AE =,然后证明EDC ABC △△∽,利用相似三角形的性质即可求出AE ,DE ,进而求出CD ,最后进行计算求出BD 即可解答.【解析】解:∵F 为DE 中点,∴2ED EF =,∵AF 平分BAC ∠,∴EAF FAB ∠=∠,∵DE AB ∥,∴FAB AFE ∠=∠,∴EAF AFE ∠=∠,∴EA EF =,∴2DE AE =,设AE x =,则2DE x =,∵DE AB ∥,∴EDC B ∠=∠,∵C C ∠=∠,∴EDC ABC △△∽,∴ED EC DC AB AC BC==,∵5AB =,6BC =,10CA =,∴210510x x -=,∴2x =,∴24DE x ==,∴456CD =,∴245CD =,∴246655BD BC CD =-=-=.故选:B .2.如图,平行四边形ABCD 中,∠A 的平分线AE 交CD 于E ,若AB =5,BC =3,则EC 的长为()A .1B .2C .2.5D .4【答案】B 【分析】根据平行四边形的性质可得AB =CD =5,AD =BC =3,AB ∥CD ,然后根据平行线的性质可得∠EAB =∠AED ,然后根据角平分线的定义可得∠EAB =∠EAD ,从而得出∠EAD =∠AED ,根据等角对等边可得DA =DE =3,即可求出EC 的长.【解析】解:∵四边形ABCD 是平行四边形,AB =5,BC =3,∴AB =CD =5,AD =BC =3,AB ∥CD∴∠EAB =∠AED∵AE 平分∠DAB∴∠EAB =∠EAD∴∠EAD =∠AED∴DA =DE =3∴EC =CD -DE =2故选B .3.如图,OP 平分MON ∠,PA ON ⊥于点A ,点Q 是射线OM 上的一个动点,则下列结论正确的是()A .PA PQ=B .PA PQ <C .PA PQ >D .PA PQ≤【答案】D 【分析】连接PQ ,当PQ ⊥OM 时,根据角平分线的性质得出PQ =PA ,利用直线外一点到直线的垂线段最短即可得出结论.【解析】解:连接PQ ,当PQ ⊥OM 时,∵OP 平分∠MON ,PQ ⊥OM ,PA ⊥ON ,∴PQ =PA ,此时点P 到OM 的距离PQ 最小,∴PA ≤PQ ,故选:D .4.如图,CD ,CE ,CF 分别是ABC 的高、角平分线、中线,则下列各式中错误的是()A.2AB BF=B.12ACE ACB∠=∠C.AE BE=D.CD BE⊥【答案】C【分析】从三角形的一个顶点向它的对边作垂线,垂足与顶点之间的线段叫做三角形的高.三角形一个内角的平分线与这个内角的对边交于一点,则这个内角的顶点与所交的点间的线段叫做三角形的角平分线.三角形一边的中点与此边所对顶点的连线叫做三角形的中线.依此即可求解.【解析】解:∵CD,CE,CF分别是△ABC的高、角平分线、中线,∴CD⊥AB,∠ACE=12∠ACB,AB=2BF,无法确定AE=BE.故选:C.5.如图,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于E,则下列结论:①AD平分∠CDE;②∠BAC=∠BDE;③DE平分∠ADB;④BE+AC=AB,其中正确的有()A.1个B.2个C.3个D.4个【答案】C【分析】根据题中条件,结合图形及角平分线的性质得到结论,与各选项进行比对,排除错误答案,选出正确的结果.【解析】解:∵AD平分∠BAC,∴∠DAC=∠DAE,∵∠C=90°,DE⊥AB,∴∠C=∠E=90°,∵AD=AD,∴△DAC≌△DAE,∴∠CDA=∠EDA,∴①AD平分∠CDE正确;无法证明∠BDE =60°,∴③DE 平分∠ADB 错误;∵BE +AE =AB ,AE =AC ,∴BE +AC =AB ,∴④BE +AC =AB 正确;∵∠BDE =90°-∠B ,∠BAC =90°-∠B ,∴∠BDE =∠BAC ,∴②∠BAC =∠BDE 正确.综上,正确的个数的3个,故选:C .6.如图,∠BAC =30°,AD 平分∠BAC ,DF ⊥AB 交AB 于F ,DE ⊥DF 交AC 于E ,若AE =8,则DF 等于()A .5B .4C .3D .2【答案】B 【分析】过点D 作DG AC ⊥,根据角平分线的性质可得DF DG =,根据角平分线的定义,平行线的性质以及等腰三角形的判定,可得AE ED =,进而根据含30度角的直角三角形的性质即可求解.【解析】如图,过点D 作DG AC ⊥ AD 平分∠BAC ,DF ⊥AB ,DG AC⊥∴DF DG =,CAD BAD∠=∠DE DF ⊥ ,DF ⊥AB ,AB DE∴∥BAD EDA∴∠=∠EAD EDA∴∠=∠EA ED∴=8AE = 8DE AE ∴== ∠BAC =30°,30DEG ∴∠=︒142DG DE ∴==4DF ∴=故选B二、填空题7.如图,已知AD 是△ABC 的角平分线,DE ∥AC 交AB 于点E ,请你添加一个条件________,使四边形AEDF 是菱形.【答案】DF ∥AB【分析】添加DF ∥AB ,根据DE ∥AC 交AB 于点E ,DF ∥AB 交AC 于点F ,可以判断四边形AEDF 是平行四边形,再根据角平分线的性质和平行线的性质即可证明结论成立.【解析】解:DF ∥AB ,理由如下:∵DE ∥AC 交AB 于点E ,DF ∥AB 交AC 于点F ,∴四边形AEDF 是平行四边形,∠EAD =∠ADF ,∵AD 是△ABC 的角平分线,∴∠EAD =∠FAD ,∴∠ADF =∠FAD ,∴FA =FD ,∴平行四边形AEDF 是菱形(有一组邻边相等的平行四边形是菱形).8.如图,在平行四边形ABCD 中,DE 平分∠ADC ,AD =8,BE =3,则AB 的长为________.【答案】5【分析】首先由在平行四边形ABCD 中,AD =8,BE =3,求得CE 的长,然后由DE 平分∠ADC ,可证CD =CE =5,即可求解.【解析】∵在平行四边ABCD 中,AD =8,∴BC =AD =8,AD //BC ,∴CE =BC -BE =8-3=5,∠ADE =∠CED ,∴DE 平分∠ADC ,∴∠ADE =∠CDE ,∴∠CDE =∠CED ,∴CD =CE =5=AB ,故答案为:5.9.如图,在ABC 中,ACB ∠的平分线交AB 于点D ,DE AC ⊥于点E .F 为BC 上一点,若DF AD =,6ACD CDF S S -=△△,则AED 的面积为______.【答案】3【分析】在CA 上截取CG =CF ,连接DG .根据题意易证()CDG CDF SAS ≅ ,得出DG DF =,CDG CDF S S = .即可求出AD DG =,6ADG S = .最后根据等腰三角形“三线合一”的性质即可求出ADE S .【解析】如图,在CA 上截取CG =CF ,连接DG,∵CD 平分ACB ∠,∴ACD BCD ∠=∠.在CDG 和CDF 中,CG CF GCD FCD CD CD =⎧⎪∠=∠⎨⎪=⎩,∴()CDG CDF SAS ≅ ,∴DG DF =,CDG CDF S S = .∵6ACD CDF S S -=△△,∴6ACD CDG S S -= ,即6ADG S = .∵AD DF =,∴AD DG=.∴AE=EG,∴132ADE GDE ADGS S S===.故答案为:3.10.如图,AB=BE,∠DBC=12∠ABE,BD⊥AC,则下列结论正确的是:_____.(填序号)①BC平分∠DCE;②∠ABE+∠ECD=180°;③AC=2BE+CE;④AC=2CD﹣CE.【答案】①②④【分析】根据已知∠DBC=12∠ABE,BD⊥AC,想到构造一个等腰三角形,所以延长CD,以B为圆心,BC长为半径画弧,交CD的延长线于点F,则BF=BC,就得到∠FBC=2∠DBC,然后再证明△FAB≌△CBE,就可以判断出BC平分∠DCE,再由角平分线的性质想到过点B作BG⊥CE,交CE的延长线于点G,从而证明△ABD≌△EBG,即可判断.【解析】解:延长CD,以B为圆心,BC长为半径画弧,交CD的延长线于点F,则BF=BC,过点B作BG⊥CE,交CE的延长线于点G,∵FB=BC,BD⊥AC,∴DF=DC,∠DBC=∠DBF=12∠FBC,∵∠DBC=12∠ABE,∴∠FBC=∠ABE,∴∠FBA=∠CBE,∵AB=AE,∴△FAB≌△CBE(SAS),∴∠F=∠BCE,∵BF=BC,∴∠F=∠BCD,∴∠BCD=∠BCE,∴BC平分∠DCE,故①正确;∵∠FBC+∠F+∠BCD=180°,∴∠ABE+∠BCE+∠BCD=180°,∴∠ABE+∠DCE=180°,故②正确;∵∠BDC=∠BGC=90°,BC=BC,∴△BDC≌△BGC(AAS),∴AD=GE,CD=CG,∵AC=AD+DC,∴AC=AD+CG=AD+GE+CE=2GE+CE,∵GE≠BE,∴AC≠2BE+CE,故③错误;∵AC=CF﹣AF,∴AC=2CD﹣CE,故④正确;故答案为:①②④.11.如图,在△ABC中,BD平分∠ABC交AC于点D,DE∥AB,交BC于点E,BE=2,则DE的长是___.【答案】2【分析】根据角平分线的定义得到∠ABD=∠CBD,根据平行线的性质得到∠ABD=∠BDE,等量代换得到∠DBE=∠BDE,得到DE=BE,于是得到结论.【解析】解:∵BD平分∠ABC,∴∠ABD=∠CBD,∵DE∥AB,∴∠ABD=∠BDE,∴∠DBE=∠BDE,∴DE=BE,∵BE=2,∴DE=2.故答案为:2.12.如图,△ABC中,AD、BD、CD分别平分△ABC的外角∠CAE、内角∠ABC、外角∠ACF,AD∥BC.以下结论:①∠ABC=∠ACB;②∠ADC+∠ABD=90°;③BD平分∠ADC;④2∠BDC=∠BAC.其中正确的结论有____________.(填序号)【答案】①②④【分析】根据角平分线的定义得到∠EAD=∠CAD,根据平行线的性质得到∠EAD=∠ABC,∠CAD=∠ACB,求得∠ABC=∠ACB,故①正确;根据角平分线的定义得到∠ADC=90°12-∠ABC,求得∠ADC+∠ABD=90°故②正确;根据全等三角形的性质得到AB=CB,与题目条件矛盾,故③错误,根据角平分线的定义和三角形外角的性质即可得到2∠BDC=∠BAC,故④正确.【解析】解:∵AD平分∠EAC,∴∠EAD=∠CAD,∵AD∥BC,∴∠EAD=∠ABC,∠CAD=∠ACB,∴∠ABC=∠ACB,故①正确;∵AD,CD分别平分∠EAC,∠ACF,∴可得∠ADC=90°12-∠ABC,∴∠ADC+12∠ABC=90°,∴∠ADC+∠ABD=90°,故②正确;∵∠ABD =∠DBC ,BD =BD ,∠ADB =∠BDC ,∴△ABD ≌△BCD (ASA ),∴AB =CB ,与题目条件矛盾,故③错误,∵∠DCF =∠DBC +∠BDC ,∠ACF =∠ABC +∠BAC ,∴2∠DCF =2∠DBC +2∠BDC ,2∠DCF =2∠DBC +∠BAC ,∴2∠BDC =∠BAC ,故④正确,故答案为:①②④.三、解答题13.如图,AC =BC ,∠1=∠2,求证:OD 平分∠AOB .【答案】见详解【分析】证明△ACO ≌△BCO 即可求证.【解析】证明:∵∠1=∠2,∠1+∠ACO =180°,∠2+∠BCO =180°,∴∠ACO =∠BCO ,∵AC =BC ,CO =CO ,∴△ACO ≌△BCO ,∴∠AOC =∠BOC ,∴OD 平分∠AOB .14.如图,在ABC 中,AE 平分BAC BE AE ∠⊥,于点E ,延长BE 交AC 于点D ,点F 是BC 的中点.若35AB AC ==,,求EF 的长.【答案】1【分析】根据角平分线的定义结合题意,即可利用“ASA”证明BAE DAE ≅ ,即得出3AD AB ==,BE DE =,从而可得出2CD =,点E 为BD 中点,从而可判定EF 为BCD △的中位线,进而可求出EF 的长.【解析】∵AE 平分BAC BE AE∠⊥,∴BAE DAE ∠=∠,90AEB AED ∠=∠=︒.又∵AE =AE ,∴BAE DAE ≅ (ASA),∴3AD AB ==,BE DE =,∴2CD AC AD =-=,点E 为BD 中点.∵F 是BC 的中点,∴EF 为BCD △的中位线,∴112EF CD ==.15.已知:如图,在△ABC 中,AB =AC ,∠A =100°,BD 是∠ABC 的平分线,BD =BE .求证:(1)△CED 是等腰三角形;(2)BD +AD =BC .【答案】(1)见解析;(2)见解析【分析】(1)由AB =AC ,∠A =100°求出∠ABC =∠C =40°,再由BD 是∠ABC 的平分线求出∠DBC =12∠ABC =20°,根据BD =BE 求出∠BED =∠BDE =80°,再根据三角形的外角等于与它不相邻的两个内角的和求得∠EDC =40°,则∠EDC =∠C ,从而证明ED =EC ,即△CED 是等腰三角形;(2)在BE 上截取BF =BA ,连结DF ,先证明△FBD ≌△ABD ,则FD =AD ,∠BFD =∠A =100°,可证明∠EFD =∠FED =80°,则AD =FD =ED =EC ,即可证明BD +AD =BE +EC =BC .【解析】(1)∵AB =AC ,∠A =100°,∴∠ABC =∠C =12×(180°-100°)=40°,∵BD 是∠ABC 的平分线,∴∠DBC =12∠ABC =20°,∵BD =BE ,∴∠BED =∠BDE =12×(180°-20°)=80°,∴∠EDC =∠BED -∠C =80°-40°=40°,∴∠EDC =∠C ,∴ED =EC ,∴△CED 是等腰三角形.(2)如图,在边BC 上取点F ,使BF BA =,在ABD △和FBD 中∵AB FB ABD FBD BD BD =⎧⎪∠=∠⎨⎪=⎩∴ABD FBD≌△△∴AD DF =,100BFD A ∠=∠=︒,∴18010080DFE ∠=︒-︒=︒,∴DFE DEF∠=∠∴DF DE=∴AD EC=∴BD AD BE EC BC +=+=.16.如图,AD 为△ABC的角平分线.(1)如图1,若CE ⊥AD 于点F ,交AB 于点E ,AB =8,AC =5.则BE =_______.(2)如图2,若∠C =2∠B ,点E 在AB 上,且AE =AC ,AB =a ,AC =b ,求CD 的长;(用含a 、b 的式子表示)(3)如图3,BG ⊥AD ,点G 在AD 的延长线上,连接CG ,若△ACG 的面积是7,求△ABC 的面积.【答案】(1)3;(2)CD =a -b ;(3)ABC S =14【分析】(1)利用ASA 证明△AEF ≌△ACF ,得AE =AC =5,得出答案;(2)利用ASA 证明△ADE ≌△ADC ,得∠C =∠AED ,DC =DE ,再证明∠B =∠BDE ,得出BE =DE ,即可得到结论;(3)利用ASA 证明△AGB ≌△AGH ,得出BG =HG ,即可得出△ABC 的面积.【解析】(1)∵AD 是△ABC 的平分线,∴∠BAD =∠CAD ,∵CE ⊥AD ,∴∠CFA =∠EFA ,∵在△AEF 和△ACF 中EAF CAF AF AF AFE AFC ∠∠⎧⎪⎨⎪∠∠⎩===,∴△AEF ≌△ACF (ASA ),∴AE =AC =5,∵AB =8,∴BE =AB −AC =8−5=3,故答案为:3;(2)∵AD 平分∠BAC ,∴∠BAD =∠CAD ,在△ADE 和△ADC 中AE AC EAD CAD AD AD =⎧⎪∠=∠⎨⎪=⎩∴△ADE ≌△ADC∴∠C =∠AED ,DC =DE又∵∠C =2∠B ,∠AED =∠B +∠BDE∴∠B =∠BDE∴DE =BE ,∴DC =DE =BE =AB -AE =AB -AC=a -b ;(3)如图,分别延长AC ,BG 交于点H ,∵AD 平分∠BAC ,∴∠BAD =∠CAD ,∵AG ⊥BH ,∴∠AGB =∠AGH =90°,∵在△AGB 和△AGH 中BAD CAD AG AG AGB AGH ∠=∠⎧⎪=⎨⎪∠=∠⎩,∴△AGB ≌△AGH ,∴BG =HG ,∴22BCH BCG HCG S S S == ,又∵2ABC BCH ACG CGH S S S S +=+ ()∴ABC S =14.17.已知:如图1,在Rt ABC 中,90ACB ∠=︒,60B ∠=︒,AD ,CE 是角平分线,AD 与CE 相交于点F ,FM AB ⊥,FN BC ⊥,垂足分别为M ,N .【思考说理】(1)求证:FE FD =.【反思提升】(2)爱思考的小强尝试将【问题背景】中的条件“90ACB ∠=︒”去掉,其他条件不变,观察发现(1)中结论(即FE FD =)仍成立.你认为小强的发现正确吗?如果不正确请举例说明,如果正确请仅就图2给出证明.【答案】(1)证明见详解;(2)正确,证明见详解;【分析】(1)由角平分线的性质、三角形内角和定理证()Rt FDN Rt FEM AAS ∆≅∆∠即可求解;(2)在AB 上截取CP =CD ,分别证()CDF CPF SAS ∆≅∆、()AFE AFP ASA ∆≅∆即可求证;【解析】证明:(1)∵AD 平分∠BAC ,CE 平分∠ACB ,∴点F 是ABC ∆的内心,∵FM AB ⊥,FN BC ⊥,∴FM FN =,∵90ACB ∠=︒,60ABC ∠=︒,∴30CAB ∠=︒∴15CAD ∠=︒∴75ADC ∠=︒∵45ACE ∠=︒∴75CEB ∠=︒∴ADC CEB∠=∠∴()Rt FDN Rt FEM AAS ∆≅∆∠∴FE FD=(2)如图,在AB 上截取CP =CD ,在CDF ∆和CPF ∆中,∵CD CP DCF PCF CF CF =⎧⎪∠=∠⎨⎪=⎩∴()CDF CPF SAS ∆≅∆∴FD FP =,∠CFD =∠CFP ,∵AD 平分∠BAC ,CE 平分∠ACB ,∴∠CAD =∠BAD ,∠ACE =∠BCE ,∵∠B =60°,∴∠ACB +∠BAC =120°,∴∠CAD +∠ACE =60°,∴∠AFC =120°,∵∠CFD =∠AFE =180°-∠AFC =60°,∵∠CFD =∠CFP ,∴∠AFP =∠CFP =∠CFD =∠AFE =60°,在AFE ∆和AFP ∆中,∵AFE AFP AF AF PAF EAF ∠=∠⎧⎪=⎨⎪∠=∠⎩∴()AFE AFP ASA ∆≅∆∴FP =EF∴FD =EF .18.如图,∠MAN 是一个钝角,AB 平分∠MAN ,点C 在射线AN 上,且AB =BC ,BD ⊥AC ,垂足为D.(1)求证:BAM BCA ∠=∠;(2)动点P ,Q 同时从A 点出发,其中点Q 以每秒3个单位长度的速度沿射线AN 方向匀速运动;动点P 以每秒1个单位长度的速度匀速运动.已知AC =5,设动点P ,Q 的运动时间为t 秒.①如图②,当点P 在射线AM 上运动时,若点Q 在线段AC 上,且52ABP BQC S S =△△,求此时t 的值;②如图③,当点P 在直线AM 上运动时,点Q 在射线AN 上运动的过程中,是否存在某个时刻,使得 APB 与 BQC 全等?若存在,请求出t 的值;若不存在,请说出理由.【答案】(1)见解析(2)①2517t =;②存在,54t =或52t =【分析】(1)①先证Rt △BDA ≌Rt △BDC (HL ),推出∠BAC =∠BCA .再由角平分线的定义得∠BAM =∠BAC ,等量代换即可证明BAM BCA ∠=∠;(2)①作BH ⊥AM ,垂足为M .先证△AHB ≌△ADB (AAS ),推出BH =BD ,再由S △ABP =52S △BQC ,推出52AP CQ =,结合P ,Q 运动方向及速度即可求解;②分“点P 沿射线AM 方向运动,点Q 在线段AC 上”,以及“点P 沿射线AM 反向延长线方向运动,点Q 在线段AC 延长线上”两种情况讨论,利用三角形全等得出AP 与CQ 的关系即可求解.【解析】(1)证明:∵BD ⊥AC ,∴90BDA BDC ∠=∠=︒,在Rt △BDA 和Rt △BDC 中,BD BD AB CB=⎧⎨=⎩,∴Rt △BDA ≌Rt △BDC (HL ),∴∠BAC =∠BCA .∵AB 平分∠MAN ,∴∠BAM =∠BAC ,∴∠BAM =∠BCA .(2)解:①如下图所示,作BH ⊥AM ,垂足为M .∵BH ⊥AM ,BD ⊥AC ,∴∠AHB =∠ADB =90°,在△AHB 和△ADB 中,AHB ADB BAH BAD AB AB ∠=∠⎧⎪∠=∠⎨⎪=⎩,,,∴△AHB ≌△ADB (AAS ),∴BH =BD ,∵S △ABP =52S △BQC ,∴151222AP BH CQ BD =⨯ ,∴52AP CQ =,∴5(53)2t t =-,∴2517t =.②存在,理由如下:当点P 沿射线AM 方向运动,点Q 在线段AC上时,如下图所示,∵AB =BC ,又由(1)得∠BAM =∠BCA ,∴当AP =CQ 时,△APB ≌△CQB ,∴53t t =-,∴54t =;当点P 沿射线AM 反向延长线方向运动,点Q 在线段AC 延长线上时,如下图所示,由(1)得∠BAM=∠BCA,∴∠BAP=∠BCQ,又∵AB=BC,∴当AP=CQ时,△APB≌△CQB,∴35t t=-,∴52 t=.综上所述,当54t=或52t=时,△APB和△CQB全等.。
初中几何常见辅助线及题型
一、角平分线半垂直,补全垂直试试看,角平分线加垂线,三线合一试试看1、已知,△ABC中,AD平分∠BAC,BE⊥AD交AD延长线于点E,EF∥AC交AB于点F.求证:AF =FB2、已知,如图△ABC中,BD平分∠ABC,AD⊥BD于D.求证:∠BAD=∠CAD +∠C3、已知,如图Rt△ABC中,AB=AC,BD平分∠ABC,CD⊥BE交BE延长线于点D.求证:BE=2CD4、已知,在△ABC中,点D是BC的中点,DE⊥AD,∠EAD=∠BAD.求证:AB=AE+CE5、已知,如图△ABC 中,∠ABC=3∠C ,AD 平分∠BAC ,BE ⊥AD 于E . 求证:)(21AB AC BE -=6、(2011•大连25)已知,在△ABC 中,∠A=90°,AB=AC ,点D 在线段BC 上,∠C=2∠EDB ,BE ⊥DE ,垂足为点E ,DE 与AB 相交于点F . (1)求∠EBF .(2)探究BE 与FD 的数量关系,并证明.二、证明线段和差倍,截长补短试试看1、如图,在△ABC 中,81BAC ∠=︒,AD 是BAC ∠的平分线,且AC AB BD =+.求ABC ∠的度数.2、已知△ABC 中,60A ∠=,BD 、CE 分别平分ABC ∠和.ACB ∠,BD 、CE 交于点O ,试判断BE 、CD 、BC 的数量关系,并加以证明.3、如图,点M 为正三角形ABD 的边AB 所在直线上的任意一点(点B 除外),作60DMN ∠=︒,射线MN 与DBA ∠外角的平分线交于点N ,试判断DM 与MN 有怎样的数量关系,并证明.4、如图,点M 为正方形ABCD 的边AB 上任意一点,MN DM ⊥且与ABC ∠外角的平分线交于点N ,MD 与MN 有怎样的数量关系?并证明你的结论.5、已知:如图,ABCD 是正方形,∠F AD =∠F AE . 求证:BE +DF =AE .6、如图所示,△ABC 是边长为1的正三角形,BDC ∆是顶角为120︒的等腰三角形,以D 为顶点作一个60︒的MDN ∠,点M 、N 分别在AB 、AC 上. 求AMN ∆的周长.7、五边形ABCDE 中,AB =AE ,BC +DE =CD ,∠ABC +∠AED =180°. 求证:AD 平分∠CDE .8、已知:如图,ABCD 是正方形,∠EAF=45°,且∠EAF 两边交BC 、CD 分别于E 、F 两点.求证:BE +DF =EF .9、如图,在直角梯形ABCD 中,AB ∥CD ,AB=BC=8,点E 为BC 边上一点,且BE=2,∠EAD=45°. 求DE 的长.10、如图,在△OAB 和△O ′CD 中(O ′ 在线段OA 上),∠A <90°,OB=O ′D ,∠AOB=∠CO ′D ,∠OAB 与∠O ′CD 互补,试探索线段AB 与CD 的数量关系,并证明你的结论.11、已知:∠BAC=90°,AB=AC ,AD=DC ,AE ⊥BD . 求证:∠ADB=∠CDE12、(2006•大连模拟26)如图,Rt △ABC 中,AB=AC ,点D 、E 是线段AC 上两动点,且AD=EC ,AM ⊥BD ,垂足为M ,AM 的延长线交BC 于点N ,直线BD 与直线NE 相交于点F .试判断△DEF 的形状,并加以证明.13、如图1-1,已知Rt △ABC 中,∠ACB=90°,AC=BC ,点D 、E 在边BC 上,且BD=CE ,连结AD ,当∠BAD=13∠BAC , CF ⊥AD ,交AB 于点F ,点G 为垂足,直线EF 交直线AD 、AC 分别于点H 、M . (1)在图1-1中,∠BAD= °,∠DAC= °. (2)如图1-1,猜想△HDE 的形状,并证明你的结论.(3)若点D 、E 在直线BC 上,如图1-2,其它条件不变,试判断△HAM 与(2)中△HDE 的形状是否相同,若不相同,说明理由;若相同,请证明.14、(2012•大连25)如图,梯形ABCD 中,AD ∥BC ,∠ABC=2∠BCD=2a ,点E在AD 上,点F 在DC 上,且∠BEF=∠A .(1)∠BEF=_____(用含a 的代数式表示);(2)当AB=AD 时,猜想线段EB 、EF 的数量关系,并证明你的猜想;(图1-2)七、要想证明是切线,半径垂线仔细添1、已知:如图,⊙O 的直径AB=8cm ,P 是AB 延长线上的一点,过点P 作⊙O 的切线,切点为C ,连接AC . (1) 若∠ACP=120°,求阴影部分的面积; (2)若点P 在AB 的延长线上运动,∠CP A 的平分线交AC 于点M ,∠CMP 的大小是否发生变化?若变化,请说明理由;若不变,求出∠CMP 的度数.2、已知:如图,点A 是⊙O 上一点,半径OC 的延长线与过点A 的直线交于点B ,OC=BC ,OB AC 21. (1)求证:AB 是⊙O 的切线; (2)若∠ACD=45°,OC=2,求弦CD 的长. (3)在(2)的条件下,求图中的阴影面积.3、如图,以等腰△ABC 中的腰AB 为直径作⊙O ,交底边BC 于点D ,交AC 边于点E .过点D 作DF ⊥AC ,垂足为F . (1)求证:DF 为⊙O 的切线; (2)若∠A=60°,AB=8,求DF 的长. (3)在(2)的条件下,求图中的阴影面积.4、如图,点A 、B 、F 在⊙O 上,∠AFB=30°,OB 的延长线交直线AD 于点D ,过点B 作BC ⊥AD 于C ,∠CBD=60°,连接AB . (1)求证:AD 是⊙O 的切线; (2)若BC=3,求⊙O 的直径.5、如图,已知AB 为⊙O 的弦,C 为⊙O 上一点,∠C =∠BAD ,且BD ⊥AB 于B . (1)求证:AD 是⊙O 的切线;(2)若⊙O 的半径为3,AB =4,求AD 的长.6、已知:如图,在△ABC 中,AB = AC ,点D 是边BC 的中点.以BD 为直径作⊙O ,交边AB 于点P ,联结PC ,交AD 于点E . (1)求证:AD 是⊙O 的切线;(2)若PC 是⊙O 的切线,BC = 8,求DE 的长.7、已知:如图,△ABC 中,AB =AC =5,BC =6,以AB 为直径作⊙O 交AC 于点D ,交BC 于点E ,EF ⊥AC 于F 交AB 的延长线于G . (1)求证:FG 是⊙O 的切线; (2)求AD 的长.8、如图,△ABC 中,AB =AE ,以AB 为直径作⊙O 交BE 于C ,过C 作CD ⊥AE 于D , DC 的延长线与AB 的延长线交于点P . (1)求证:PD 是⊙O 的切线; (2)若AE =5,BE =6,求DC 的长.9、如图,四边形ABCD 内接于⊙O ,BD 是⊙O 的直径,AE ⊥CD 于E ,DA 平分∠BDE . (1)求证:AE 是⊙O 的切线; (2)若∠DBC=30°,DE=1cm ,求BD 的长.10、在Rt△ABC中,∠C=90°,BC=9,CA=12,∠ABC的平分线BD交AC于点D,DE⊥DB交AB于点E,⊙O是△BDE的外接圆,交BC于点F.(1)求证:AC是⊙O的切线;(2)联结EF,求BDAC的值.11、如图,AB是⊙O的直径,⊙O交BC的中点于D,DE⊥AC,E是垂足.(1)求证:DE是⊙O的切线;(2)如果AB=5,12DECE,求CE的长.12、已知:在⊙O中,AB是直径,AC是弦,OE⊥AC于点E,过点C作直线FC,使∠FCA=∠AOE,交AB的延长线于点D.(1)求证:FD是⊙O的切线;(2)设OC与BE相交于点G,若OG=2,求⊙O半径的长;(3)在(2)的条件下,当OE=3时,求图中阴影部分的面积.与相似有关13、已知:如图,AB 为⊙O 的弦,过点O 作AB 的平行线,交⊙O 于点C ,直线OC 上一点D 满足∠D =∠ACB .(1)判断直线BD 与⊙O 的位置关系,并证明你的结论; (2)若⊙O 的半径等于5,AB=8,求CD 的长.14、已知:如图,在△ABC 中,∠ACB =90°,∠ABC 的平分线BD 交AC 于点D ,DE ⊥DB 交AB 于点E ,过B 、D 、E 三点作⊙O . (1)求证:AC 是⊙O 的切线;(2)设⊙O 交BC 于点F ,连结EF ,若BC =9,CA =12.求EFAC的值.15、已知:如图,AB 是⊙O 的直径,E 是AB 延长线上的一点,D 是⊙O 上的一点,且AD 平分∠F AE ,ED ⊥AF 交AF 的延长线于点C .(1)判断直线CE 与⊙O 的位置关系,并证明你的结论; (2)若AF ∶FC =5∶3,AE =16,求⊙O 的直径AB 的长.16、如图,点D是⊙O直径CA的延长线上一点,点B在⊙O上,且AB=AD=AO.(1)求证:BD是⊙O的切线;(2)若点E是劣弧BC上一点,弦AE与BC相交于点F,且CF=9,BF:AF=32,求EF的长.17、(2012•大连23) 如图,AB是⊙O的直径,点C在⊙O上,∠CAB的平分线交⊙O于点D,过点D作AC的垂线交AC的延长线于点E,连接BC交AD于点F.(1)猜想ED与⊙O的位置关系,并证明你的猜想;(2)若AB=6,AD=5,求AF的长.八、有k倍,比线段,截图相似平行线1、如图,点E是BC上一点,BE=k•EC,∠BAE=∠CDE.猜想AB、CD的数量关系,加以证明.2、如图,在△ABC 中,∠BAC=90°,AB= k •AC ,CD ∥BA ,点P 是BC 上一点,连结AP ,过点P 做PE ⊥AP 交CD 于E .探究PE 与P A 的数量关系,并加以证明.3、如图,在△ABC 中, AB= k •AC ,点D 在AB 上,点E 在AC 的延长线上,且BD=CE ,DE 交BC 于点P .探究PE 与PD 的数量关系,并加以证明.4、如图,在△ABC 中,∠DBC +∠ECB=∠A ,BD 、CE 交于点P ,P B= k •PC . 探究BE 与CD 的数量关系,并加以证明.5、如图,BD 平分∠EBC ,D ′是BD 上一点,且BD= k •BD ′,连结D ′C 、DE ,并延长DE 至点A ,使得EA=ED ,且∠ABE=∠C .探究AB 与CD ′的数量关系,并加以证明.6、如图,CB=CD ,∠ABC +∠CDE=180°,AB= k •DE . 探究AF 与EF 的数量关系,并加以证明.7、如图,在△ABC 中,AC=BC ,P 为AB 上一点,且AP= k •PB ,∠EPF +∠C=180°. 探究PE 与PF 的数量关系,并加以证明.8、如图,AD是△ABC的中线,AB= k•AC,点E是AC延长线上一点,且∠AEF=∠BAD,EF交BA延长线于点F.探究AE与AF的数量关系,并加以证明.9、(2012•大连25)如图1,梯形ABCD中,AD∥BC,∠ABC=2∠BCD=2a,点E在AD上,点F在DC上,且∠BEF=∠A.(1)∠BEF=_____(用含a的代数式表示);(2)当AB=AD时,猜想线段EB、EF的数量关系,并证明你的猜想;(3)当AB≠AD时,将“点E在AD上”改为“点E在AD的延长线上,且AE>AB,AB=mDE,AD=nDE”,其他条件不变(如图2),求EBEF的值(用含m、n的代数式表示)。
角平分线的性质(4种题型)-2023年新八年级数学核心知识点与常见题型(人教版)(解析版)

角平分线的性质(4种题型)【知识梳理】一、角的平分线的性质角的平分线的性质:角的平分线上的点到角两边的距离相等.要点诠释:用符号语言表示角的平分线的性质定理:若CD平分∠ADB,点P是CD上一点,且PE⊥AD于点E,PF⊥BD于点F,则PE=PF.二、角的平分线的逆定理角平分线的判定:角的内部到角两边距离相等的点在角的平分线上.要点诠释:用符号语言表示角的平分线的判定:三、角的平分线的尺规作图角平分线的尺规作图(1)以O为圆心,适当长为半径画弧,交OA于D,交OB于E.(2)分别以D 、E 为圆心,大于DE 的长为半径画弧,两弧在∠AOB 内部交于点C. (3)画射线OC.射线OC 即为所求. 【考点剖析】题型一:角平分线性质定理 例1.(2023春·陕西榆林·八年级校考期末)如图,在四边形ABCD 中,90B C ∠=∠=︒,点E 为BC 的中点,且AE 平分BAD ∠.求证:DE 是ADC ∠的平分线.【详解】证明:如图,过点E 作EF AD ⊥于点F ,∴90B Ð=°,AE 平分BAD ∠,∴BE EF =.∴点E 是BC 的中点,∴BE CE =,∴CE EF =.又∵90C ∠=︒,EF AD ⊥,∴DE 是ADC ∠的平分线.【变式1】(2023春·山西太原·七年级校考阶段练习)如图,ABC 中,90C ∠=︒,AD 平分BAC ∠,5AB =,2CD =,求ABD △的面积.12【答案】5【详解】解:作DE AB ⊥如图,∵AD 平分BAC ∠,90C ∠=︒,2CD =,∴=2CD DE =,1152522ABD S AB DE ∴=⨯⨯=⨯⨯=△.【变式2】(2023春·湖南常德·八年级统考期末)如图,点P 是ABC 的三个内角平分线的交点,若ABC 的周长为24cm ,面积为236cm ,则点P 到边BC 的距离是( )A .8cmB .3cmC .4cmD .6cm【答案】B 【详解】解:过点P 作PD AB ⊥于,PE BC ⊥于E ,PF AC ⊥于F ,如图,∵点P 是ABC 的内角平分线的交点,∴PE PF PD ==,又ABC 的周长为24cm ,面积为236cm ,∴()11112222ABC S AB PD BC PE AC PF PE AB BC AC =⋅+⋅+⋅=++,∴124363PE ⨯⨯=∴3cm PE =【变式3】(湖南省郴州市2022-2023学年八年级下学期期末数学试题)如图,在ABC 中,90ACB ∠=︒,BD 平分ABC ∠,DE AB ⊥于点E .如果8AC =,那么AD DE +=______.【答案】8【详解】解:∵在ABC 中,90ACB ∠=︒,BD 平分ABC ∠,DE AB ⊥,∴CD DE =,∵8AC =,∴8AD DE AD CD AC +=+==, 【变式4】(2023春·广东深圳·七年级统考期末)把两个同样大小的含30︒角的三角尺像如图所示那样放置,其中M 是AD 与BC 的交点,若4CM =,则点M 到AB 的距离为______.【答案】4【详解】解:由题意,得:90,30D C ABC DAB ∠=∠=︒∠=∠=︒,∴,60MC AC CAB ⊥∠=︒,∴30MAC BAC MAB MAB ∠=∠−∠=︒=∠,∴AM 平分DAB ∠,过点M 作MN AB ⊥,交AB 于点N ,∴4MN MC ==.故答案为:4.【变式5】如图,P 为ABC 三条角平分线的交点,PH 、PN 、PM 分别垂直于BC 、AC 、AB ,垂足分别为H 、N 、M .已知ABC 的周长为15cm ,3cm PH =,则ABC 的面积为______2cm .【答案】22.5【详解】解:连接PM 、PN 、PH ,P 为ABC 三条角平分线的交点,PH 、PN 、PM 分别垂直于BC 、AC 、AB ,3cm PM PN PH ∴===,ABC ∴∆的面积ΔAPB =的面积ΔBPC +的面积ΔAPC +的面积111222AB PM BC PH AC PN =⨯⨯+⨯⨯+⨯⨯ 1()32AB BC AC =++⨯222.5(cm )=.七年级校考期末)如图,在ABC 中,【答案】(1)32︒ (2)6【详解】(1)解:∵40B ∠=︒,76C ∠=︒,∴180407664BAC ∠=︒−︒−︒=︒,∵AD 平分BAC ∠, ∴1322BAD BAC ∠=∠=︒;(2)如图,过点D 作DF AB ⊥于点F ,∵AD 平分BAC ∠,DE AC ⊥,∴DF DE =,∵2DE =,6AB =,∴2DF =, ∴ABD △的面积12662=⨯⨯=.题型二:角平分线性质定理及证明 ,且PMN 与OMN 的面积分别是【答案】(1)证明过程见详解(2)20OM ON +=【详解】(1)证明:如图所示,过P 作PC MN PD OA PE OB ⊥⊥⊥,,,∵MP 平分AMN ∠,NP 平分MNB ∠,∴PD PE =,PC PE =,∴PD PE =,∵PD AO PE BO ⊥⊥,,∴OP 平分AOB ∠.(2)解:如图所示,过P 作PC MN PD OA PE OB ⊥⊥⊥,,,连接OP ,∵18162PMN MN S MN PC ===△,,∴4PC =,由(1)可知4PD PE PC ===,∵1624PMN OMN S S ==△△,,∴40MONP S =四边形,即1122OPM ONP MONP S S S OM PD ON PE =+=+△△四边形,∴1140442222OM ON OM ON =⨯+⨯=+,∴20OM ON +=. 【变式1】(2022秋·河南安阳·八年级校考阶段练习)如图,点E 是BC 的中点,AB BC DC BC ⊥⊥,,AE 平分BAD ∠.求证:(1)DE 平分ADC ∠;(2)AD AB CD +=.【详解】(1)证明:如下图,过E 作EF AD ⊥于F ,∵AB BC ⊥,AE 平分BAD ∠,∴EB EF =,∵点E 是BC 的中点,∴EB EC =,∴EF EC =,∵DC BC EF AD ⊥⊥,,∴90EFD ECD ∠∠︒==,在Rt EFD 和Rt ECD △中,EF EC ED ED =⎧⎨=⎩,∴Rt Rt HL EFD ECD ≌(),∴FDE CDE ∠∠=,∴DE 平分ADC ∠;(2)解:由(1)知,Rt Rt EFD ECD ≌,∴FD CD =,在Rt AEF 和Rt AEB 中,EF EB AE AE =⎧⎨=⎩,∴Rt Rt HL AEF AEB ≌(),∴AF AB =,∵AD AF FD +=,∴AD AB CD +=.【变式2】(2022秋·北京朝阳·八年级校考期中)如图,在ABC ∆中,90C ∠=︒,DE AB ⊥,于点E ,AD 平分CAB ∠,点F 在AC 上,BD DF =.求证:BE FC =.【详解】证明:∵AD 平分CAB ∠,90C ∠=︒,DE AB ⊥,∴DE DC =,90C DEB ∠=∠=︒,∴在Rt DEB ∆和Rt DCF ∆中,∵DE DC BD DF =⎧⎨=⎩,∴()HL DEB DCF ∆≅∆,∴BE FC =.(1)求证:BE =CD ;(2)判断点O 是否在∠BAC 的平分线上,并说明理由.(1)证明:BE 、CD 是ABC ∆的高,且相交于点O ,90∴∠=∠=︒BEC CDB ,在BDO ∆和CEO ∆中,90CDB BEC BOD COEBD CE ∠=∠=︒⎧⎪∠=∠⎨⎪=⎩,BOD COE ∴∆≅∆(AAS),OD OE ∴=,OB OC =,OD OC OE OB ∴+=+,即CD BE =;(2)解:点O 在BAC ∠的平分线上,理由如下: 连接AO ,如图所示:BE 、CD 是ABC ∆的高,且相交于点O , 90ADC AEB ∴∠=∠=︒,由(1)得BE CD =,∴在ABE ∆和ACD ∆中,90ADC AEB CAD BAE CD BE ∠=∠=︒⎧⎪∠=∠⎨⎪=⎩,ACD ABE ∴∆≅∆(AAS), AD AE ∴=,由(1)得OD OE =,∴在AOD ∆和AOE ∆中,90AD AE ADC AEB OD OE =⎧⎪∠=∠=︒⎨⎪=⎩,AOD AOE ∴∆≅∆(SAS),DAO EAO ∴∠=∠, ∴点O 在BAC ∠的平分线上.题型三:角平分线的判定定理 例3.如图,90B C ∠=∠=︒,M 是BC 的中点,AM 平分DAB ∠,求证:DM 平分ADC ∠.【详解】证明:如图:过点M 作ME AD ⊥,垂足为E ,AM 平分DAB ∠,MB AB ⊥,ME AD ⊥,ME MB =∴(角平分线上的点到角两边的距离相等),又MC MB =,ME MC ∴=,MC CD ⊥,ME AD ⊥,DM ∴平分ADC ∠(到角的两边距离相等的点在这个角的平分线上).【详解】(1)证明:如图,过点E 作EF DA ⊥于点F ,∵90C ∠=︒,DE 平分ADC ∠,∴CE EF =,∵E 是BC 的中点,∴BE CE =,∴BE EF =,又∵90B Ð=°,EF DA ⊥,∴AE 平分DAB ∠.(2)解:∵EF DA ⊥,90C ∠=︒,∴EFD △和ECD 都为Rt △,又∵DE 平分ADC ∠,∴EC EF =,在Rt EFD 和Rt ECD △中,ED ED EC EF =⎧⎨=⎩,∴()Rt Rt HL EFD ECD △≌△, ∴EFD ECD S S =△△,CED FED ∠=∠,∵EF DA ⊥,90B Ð=°,∴EFA △和EBA △都为Rt △,又∵AE 平分DAB ∠,∴EF EB =,在Rt EFA △和Rt EBA △中,EA EA EF EB =⎧⎨=⎩,∴()Rt Rt HL EFA EBA △≌△, ∴EFA EBA S S =△△,FEA BEA ∠=∠, ∴()111809022DEA DEF AEF CEF BEF ∠=∠+∠=∠+∠=⨯︒=︒, ∵4AE =,3DE =, ∴1143622AED S AE DE =⋅=⨯⨯=△, ∴EFD ECD EFA EBA ABCD S S S S S =+++△△△△四边形EFD EFD EFA EFA S S S S =+++△△△△()2EFD EFA S S =+△△2AED S =△ 26=⨯12=.∴四边形ABCD 的面积为12. 【变式2】如图,在AOB 和COD △中,OA OB =,OC OD =(OA OC <),AOB COD α∠=∠=,直线AC ,BD 交于点M ,连接OM .(1)求证:AC BD =;(2)用α表示AMB ∠的大小;(3)求证:OM 平分AMD ∠.【详解】(1)证明:AOB COD α∠=∠=,AOB BOC COD BOC ∴∠+∠=∠+∠,即AOC BOD ∠=∠,在AOC 和BOD 中,OA OB AOC BODOC OD =⎧⎪∠=∠⎨⎪=⎩,()SAS AOC BOD ∴≌, ∴AC BD =,(2)解:由三角形的外角性质得:AMB OBD OAC AOB ∠+∠=∠+∠,由(1)得()SAS AOC BOD ≌△△,∴OAC OBD ∠=∠,AMB AOB α∴∠=∠=,(3)证明:作OG AM ⊥于G ,OH DM ⊥于H ,如图所示,则90OGA OHB ∠=∠=︒,在OAG △和OBH △中,OGA OHB OAC OBDOA OB ∠=∠⎧⎪∠=∠⎨⎪=⎩,()AAS OAG OBH ∴≌, OG OH ∴=,OG AM ⊥于G ,OH DM ⊥于H ,MO ∴平分AMD ∠,是ABC 的角平分线,且交于点(1)APB ∠=______.(2)求证:点P 在C ∠的平分线上.【详解】(1)解:证明:60C ∠=︒,AE ,BD 是ABC 的角平分线,12ABP ABC ∴∠=∠,12BAP BAC ∠=∠,11()(180)6022BAP ABP ABC BAC C ∴∠+∠=∠+∠=︒−∠=︒, 120APB ∴∠=︒;(2)如图,过P 作PF AB ⊥,PG AC ⊥,PH BC ⊥,AE ,BD 分别平分CAB ∠,CBA ∠,PF PG ∴=,PF PH =,PH PG ∴=,∴点P 在C ∠的平分线上;(3)如图,在AB 上取点M 使AM AD =,连接PM ,AE 是BAC ∠的平分线,PAM PAD ∴∠=∠, 在AMP 与ADP △中,AP AP PAM PADAM AD =⎧⎪∠=∠⎨⎪=⎩,()SAS AMP ADP ∴≌, 18060APM APD APB ∴∠=∠=︒−∠=︒,180()60BPM APM APD ∴∠=︒−∠+∠=︒,60BPE APD ∠=∠=︒,BPM BPE ∴∠=∠,BD Q 是ABC ∠的角平分线,MBP EBP ∴∠=∠,在BPM △与BPE 中,MBP EBP BP BPBPE BPM ∠=∠⎧⎪=⎨⎪∠=∠⎩,()ASA BPM BPD ∴≌,BM BE ∴=, AB AM BM AD BE ∴=+=+. (1)如图1,连接AC BD ,,交点为G ,连接OG ,求证:①AC BD =;②OG 平分DGC ∠;(2)如图2,若90AOD BOC ∠=∠=︒,E 是CD 的中点,过点在同一条直线上.∴AOD AOB BOC AOB ∠+∠=∠+∠,∴AOB AOC ∠=∠,又∵OA OD =,OB OC =,∴()SAS DOB AOC V V ≌,∴AC BD =;②如图所示,过点O 作OH DB ⊥于点H ,OF AC ⊥于点F ,∵DOB AOC ≌,OH DB ⊥,OF AC ⊥∴OH OF =,∴点O 在DGC ∠的角平分线上,∴OG 是DGC ∠的角平分线,∴OG 平分DGC ∠;(2)证明:连接OE ,并延长到N ,使NE OE =,连接CN ,∵E 是CD 的中点,∴CE DE =,又∵CEN DEO ∠=∠,NE OE =,∴()SAS CEN DEO ∠V V ≌,∴NCE ODE ∠=∠,CN OD =,∴CN OD ∥,∴180OCN COD CN OA ∠+∠=︒=,,90AOD BOC ∠=∠=︒,180AOB COD ∴∠+∠=︒,OCN AOB ∴∠=∠,在ONC 和BAO 中,OC OB OCN AOBCN OA =⎧⎪∠=∠⎨⎪=⎩,()SAS ONC BAO ∴≌, NOC ABO ∴∠=∠,OF AB ⊥,90ABO BOF ∴∠+∠=︒,90NOC BOF ∴∠+∠=︒,180NOC BOF BOC ∴∠+∠+∠=︒,∴点E O F ,,在同一条直线上.题型四:尺规作图—作角平分线 例4.(2023春·陕西榆林·七年级校考期末)如图,已知ABC ,利用尺规,在AC 边上求作一点D ,使得ABD DBC ∠=∠.(保留作图痕迹,不写作法)【详解】解:如图点D 即为所求..【变式1】(2023春·福建福州·七年级福建省福州第十九中学校考期末)如图,Rt ABC △中,90BAC ∠=︒,AD 为BC 边上的高.(1)尺规作图,在AB 边上求作点P ,使得点P 到边BC 的距离等于AP (保留作图痕迹,不写做法):(2)连接CP (P 为所求作的点)交AD 于点Q ,若30B ∠=︒,求AQC ∠的度数.【详解】(1)解:如图:点P 即为所求;作法:作ACB ∠的角平分线,与AB 的交点P 即为所求;理由:∵CP 是ACB ∠的角平分线,∴点P 到AC 的距离等于点P 到BC 的距离,∵90BAC ∠=︒,∴点P 到AC 的距离即为PA 的值,故点P 到边BC 的距离等于AP .(2)解:如图:∵90BAC ∠=︒,30B ∠=︒,∴180903060ACB ∠=︒−−︒=︒,又∵AD 为BC 边上的高,∴90ADC ∠=︒,∴180906030DAC ∠=︒−−︒=︒,由(1)可知CP 是ACB ∠的角平分线, ∴1302ACQ QCD ACB ∠=∠=∠=︒,∴1803030128001ACQ DAC AQC ∠−∠=︒−︒−︒=︒∠=︒−. 【变式2】(2023·甘肃兰州·统考中考真题)综合与实践问题探究:(1)如图1是古希腊数学家欧几里得所著的《几何原本》第1卷命题9:“平分一个已知角.”即:作一个已知角的平分线,如图2是欧几里得在《几何原本》中给出的角平分线作图法:在OA 和OB 上分别取点C 和D ,使得OC OD =,连接CD ,以CD 为边作等边三角形CDE ,则OE 就是AOB ∠的平分线.请写出OE 平分AOB ∠的依据:____________;类比迁移:(2)小明根据以上信息研究发现:CDE 不一定必须是等边三角形,只需CE DE =即可.他查阅资料:我国古代已经用角尺平分任意角.做法如下:如图3,在AOB ∠的边OA ,OB 上分别取OM ON =,移动角尺,使角尺两边相同刻度分别与点M ,N 重合,则过角尺顶点C 的射线OC 是AOB ∠的平分线,请说明此做法的理由;拓展实践:(3)小明将研究应用于实践.如图4,校园的两条小路AB 和AC ,汇聚形成了一个岔路口A ,现在学校要在两条小路之间安装一盏路灯E ,使得路灯照亮两条小路(两条小路一样亮),并且路灯E 到岔路口A 的距离和休息椅D 到岔路口A 的距离相等.试问路灯应该安装在哪个位置?请用不带刻度的直尺和圆规..........在对应的示意图5中作出路灯E 的位置.(保留作图痕迹,不写作法)【详解】解:(1)∵OC OD =,CE DE =,DE DE =,∴()SSS OCE ODE ≌,∴AOE BOE ∠=∠,∴OE 是AOB ∠的角平分线;故答案为:SSS(2)∵OM ON =,CM CN =,OC OC =,∴()SSS OCM OCN ≌,∴AOC BOC ∠=∠,∴OC 是AOB ∠的角平分线;(3)如图,点E 即为所求作的点;. 【变式3】(2023春·重庆九龙坡·七年级校考期末)如图,已知在ABC 中,90BAC ∠=︒,AD BC ⊥于点D .(1)尺规作图:作ABC ∠的平分线交AC 于点E ,交AD 于点F ;(要求:保留作图痕迹,不写作法,不下结论)(2)在(1)的条件下,求证:AFE AEF ∠=∠.AD BC ⊥90ADB ∴∠=︒∴__________90BFD +∠=︒又BFD ∠=__________FBD ∴∠+__________90=︒90BAC ∠=︒ABF ∴∠+__________90=︒BF 平分ABC ∠ABF ∴∠=__________AFE AEF ∴∠=∠.【详解】(1)如图所示,(2)AD BC ⊥90ADB ∴∠=︒∴FBD ∠90BFD +∠=︒又BFD ∠=AEF ∠FBD ∴∠+AEF ∠90=︒90BAC ∠=︒ABF ∴∠+AFE ∠90=︒ BF 平分ABC ∠ABF ∴∠=FBD ∠AFE AEF ∴∠=∠.故答案为:FBD ∠;AEF ∠;AEF ∠;AFE ∠;FBD ∠.【过关检测】一、单选题 1.(2023春·四川泸州·八年级统考期末)如图,70AOB ∠=︒,点C 是AOB ∠内一点,CD OA ⊥于点D ,CE OB ⊥于点E .且CD CE =,则DOC ∠的度数是( )A .30︒B .35︒C .40︒D .45︒【答案】B【分析】根据角平分线的判定定理可得OC 平分AOB ∠,再计算角度.【详解】解:∵CD OA ⊥,CE OB ⊥,CD CE =,∴OC 平分AOB ∠, ∴1352DOC AOB ∠=∠=︒,故选C .【点睛】本题主要考查了角平分线的判定,注意:到角的两边距离相等的点在角平分线上. 2.(陕西省榆林市高新区2022-2023学年七年级下学期期末数学试题)如图,在Rt ABC △中,ABC ∠的平分线BD 交AC 于点D ,过点D 作DE AB ⊥交AB 于点E .若9cm CD =,则点D 到AB 的距离是( )A .9cmB .6cmC .4.5cmD .3cm【答案】A 【分析】根据角平分线的性质,角平分线上的点到角两边的距离相等,即可求解.【详解】∵BD 平分ABC ∠,DE AB ⊥,AC BC ⊥,∴9DC DE ==,∴点D 到AB 的距离是9cm .故选:A .【点睛】本题考查角平分线的性质,解题的关键是掌握角平分线的性质.3.(2023春·河南焦作·七年级校考期末)如图,在四边形ABCD 中,90A ∠=︒,3AD =,连接BD ,BD CD ⊥,ADB C ∠=∠.若P 是BC 边上一动点,则DP 的长不可能是( )【答案】A【分析】根据余角的性质可得ABD CBD ∠=∠,即BD 平分ABC ∠,作DE BC ⊥于E ,则3AD DE ==,再根据垂线段最短即可得到答案.【详解】解:∵90A ∠=︒,BD CD ⊥,∴90,90ABD ADB CBD C ∠+∠=︒∠+∠=︒,∵ADB C ∠=∠,∴ABD CBD ∠=∠,即BD 平分ABC ∠,作DE BC ⊥于E ,则3AD DE ==,∵P 是BC 边上一动点,则DP DE ≥,即3DP ≥,∴DP 的长不可能是52;故选:A .【点睛】本题考查了直角三角形的性质和角平分线的性质,得出BD 平分ABC ∠是解题的关键.A .12∠=∠且CM DM =B .13∠=∠且CM DM =C .12∠=∠且OD DM =D .23∠∠=且OD DM =【答案】A 【分析】由作图过程可得:,OD OC CM DM ==,再结合DM DM =可得()SSS COM DOM ≌,由全等三角形的性质可得12∠=∠即可解答.【详解】解:由作图过程可得:,OD OC CM DM ==,∵DM DM =,∴()SSS COM DOM ≌.∴12∠=∠.∴A 选项符合题意;不能确定OC CM =,则13∠=∠不一定成立,故B 选项不符合题意;不能确定OD DM =,故C 选项不符合题意,OD CM ∥不一定成立,则23∠∠=不一定成立,故D 选项不符合题意.故选A .【点睛】本题主要考查了角平分线的尺规作图、全等三角形的判定与性质等知识点,理解尺规作图过程是解答本题的关键. ,ABC 的面积为,则ABC 的周长为( A .4B .6C .24D .12【答案】C 【分析】过点E 作EF AB ⊥,垂足为F ,过点E 作EG AC ⊥,垂足为G ,根据角平分线的性质可得1EG EF ED ===,然后根据三角形的面积公式进行计算即可解答.【详解】解:过点E 作EF AB ⊥,垂足为F ,过点E 作EG AC ⊥,垂足为G ,∵BE 平分ABC ∠,ED BC ⊥,EF AB ⊥,∴1EF ED ==,∵CE 平分ACB ∠,ED BC ⊥,EG AC ⊥,∴1ED EG ==,∴ABC 的面积ABE =的面积BEC +△的面积AEC +△的面积()11111122222AB EF BC ED AC EG AB BC AC =⋅+⋅+⋅=⨯⨯++=,∴24AB BC AC ++=,即ABC 的周长为24.故选:C .【点睛】本题考查了角平分线的性质,根据题目的已知条件并结合图形添加适当的辅助线是解题的关键.A .3PD =B .3PD <C .3PD ≤ D .3PD ≥【答案】D 【分析】根据角平分线的性质得到3PF =,再根据垂线段最短即可解答.【详解】解:过点P 作PE AB ⊥于点E ,过点P 作PF BC ⊥于点F ,∵点P 在ABC ∠的平分线上,∴PE PF =, ∵3PE =,∴3PF =,∴根据垂线段最短可知:3PD ≥,故选D .【点睛】本题考查了角平分线的性质,垂线段最短,掌握角平分线的性质是解题的关键. 八年级统考期末)如图,在ABC 中, A .83 B .43 【答案】D【分析】由题意可求DC 的长,由角平分线的性质可求解.【详解】解:如图,过点D 作DH AB ⊥,垂足为H ,∵143AC DC AC ==,,∴1DC =,∵BD 平分ABC ∠,90C DH AB =︒∠,⊥,∴1CD DH ==,∴点D 到AB 的距离等于1,故选:D .【点睛】本题考查了角平分线的性质,熟练运用角平分线的性质是本题的关键.8.(2023春·湖南娄底·八年级统考期末)如图,三条公路把A ,B ,C 三个村庄连成一个三角形区域,现决定在这个三角形区域内修建一个集贸市场,要使集贸市场到三条公路的距离相等,则这个集贸市场应建在( )A .三角形三个内角的角平分线的交点B .三角形三条边的垂直平分线的交点C .三角形三条高的交点D .三角形三条中线的交点【答案】A 【分析】根据角平分线上的点到角的两边的距离相等解答即可.【详解】解:根据角平分线的性质,集贸市场应建在三个角的角平分线的交点处.故选:A .【点睛】本题主要考查了角平分线上的点到角的两边的距离相等的性质,熟记性质是解题的关键.9.(2023春·陕西榆林·八年级统考期末)如图,OD 平分AOB ∠,DE AO ⊥于点E ,5DE =,F 是射线OB 上的任意一点,则DF 的长度不可能是( )【答案】A 【分析】过D点作DH OB ⊥于H ,根据角平分线的性质得5DH DE ==,再利用垂线段最短得到5DF ≥,然后对各个选项进行判断即可,【详解】过D点作DH OB ⊥于H ,OD 平分AOB ∠,DE OA ⊥,DH OB ⊥,5DH DE ∴==,DF DH ≥,5DF ∴≥,故选A【点睛】本题考查了角平分线的性质:角的平分线上的点到角的两边的距离相等,也考查了垂线段最短,掌握角平分线的性质是解题的关键. 10.(2023春·河南开封·七年级统考期末)如图,在ABC 中,90C ∠=︒,AD 平分BAC ∠,DE AB ⊥于E ,则下列结论:①DE CD =;②AD 平分CDE ∠;③BAC BDE ∠=∠;④BE AC AB +=,其中正确的是( )A .1个B .2个C .3个D .4个【答案】D 【分析】①根据角平分线的性质得出结论:DE CD =;②证明ACD AED △≌△,得AD 平分CDE ∠;③由四边形的内角和为360︒得180CDE BAC ∠+∠=︒,再由平角的定义可得结论是正确的;④由ACD AED ∆≅∆得AC AE =,再由AB AE BE =+,得出结论是正确的.【详解】解:①90C ∠=︒,AD 平分BAC ∠,DE AB ⊥,DE CD ∴=;所以此选项结论正确;②DE CD =,AD AD =,90ACD AED ∠=∠=︒,ACD AED ∴≌,ADC ADE ∴∠=∠,AD ∴平分CDE ∠,所以此选项结论正确;③90ACD AED ∠=∠=︒,3609090180CDE BAC ∴∠+∠=︒−︒−︒=︒,180BDE CDE ∠+∠=︒,BAC BDE ∴∠=∠,所以此选项结论正确;④ACD AED ≌,AC AE ∴=,AB AE BE =+,BE AC AB ∴+=,所以此选项结论正确;本题正确的结论有4个,故选D .【点睛】本题考查了全等三角形性质和判定,同时运用角平分线的性质得出两条垂线段相等;本题难度不大,关键是根据HL 证明两直角三角形全等,根据等量代换得出线段的和,并结合四边形的内角和与平角的定义得出角的关系.二、填空题 七年级统考期末)如图,在ABC 中,ABC 的内部相交于点 【答案】5【分析】先根据尺规作图描述得出AD 为BAC ∠的角平分线,再根据角平分线的性质得到点D 到AB 的距离5DE =,进而求出三角形的面积.【详解】由作法得AD 平分BAC ∠,如图所示,过点D 作DE AB ⊥于E ,∵90ACB ∠=︒,根据角平分线的性质,得43DC DE ==,ABD ∴的面积114102233AB DE AB =⋅⋅=⨯⨯=. ∴5AB =,故答案为:5.【点睛】本题考查角平分线的性质,解决本题的关键是熟知角平分线的性质并灵活应用.【答案】2【分析】根据尺规作图可得BF 平分ABC ∠,再利用角平分线的性质定理可得出2DF CF ==,最后根据垂线段最短即可得出FH 的最小值是2.【详解】解:如图,过点F 作FD AB ⊥于D .由作图可知,BF 平分ABC ∠,∵FC BC ⊥,FD AB ⊥,∴2DF CF ==.根据垂线段最短可知,FH 的最小值为DF 的长,即为2.故答案为:2.【点睛】本题主要考查角平分线的性质,垂线段最短,解题的关键在于能够准确判断出BF 是ABC ∠的角平分线.13.(2023春·重庆沙坪坝·七年级重庆八中校考期末)如图,Rt ABC △中,90C ∠=︒,AD 平分BAC ∠交BC 于点D ,E 为线段AC 上一点,连接DE ,且B CED ∠=∠.若16AB =,6CE =,则AE 的长为________.【答案】4【分析】过点D 作DF AB ⊥于点F ,由角平分线的性质得出DC DF =,证明DCE DFB ≌,得出BF CE =,求出AF ,由HL 证明Rt Rt ADC ADF ≌,得出AC AF =,即可求出结果.【详解】解:过点D 作DF AB ⊥于点F ,如图所示:∵90C ∠=︒,AD 平分BAC ∠交BC 于点D ,,∴DC DF =,在DCE △和DFB △中,90=BFD DCE B CEDDC DF ∠=∠=︒⎧⎪∠=∠⎨⎪⎩,∴()AAS DCE DFB ≌,∴6BF CE ==,∴10AF AB BF =−=,在Rt ADC 与Rt ADF 中,==DC DF AD AD ⎧⎨⎩,∴Rt Rt ADC ADF ≌,∴10AC AF ==,∴1064AE AC CE =−=−=.故答案为:4.【点睛】此题考查全等三角形的判定和性质和角平分线的性质,解题的关键是作出辅助线,构造全等三角形,根据HL 证明直角三角形的全等解答.【答案】30【分析】由作图可知OC 是AOB ∠的角平分线,根据角平分线的定义即可得到答案.【详解】解:由题意可知,OC 是AOB ∠的角平分线,∴11603022AOC AOB ∠=∠=⨯︒=︒.故答案为:30【点睛】此题考查角平分线的作图、角平分线相关计算,熟练掌握角平分线的作图是解题的关键.,则POD 的面积是【答案】6【分析】过点P 作PF OB ⊥交OB 于点F ,由作图可知OP 是AOB ∠的平分线,根据角平分线的性质得3PF PC ==,即可求得POD 的面积.【详解】解:如图,过点P 作PF OB ⊥交OB 于点F ,由作图可知,OP 是AOB ∠的平分线,∵PC OA ⊥,PF OB ⊥,∴3PF PC ==,∴POD 的面积为:162OD PF ⋅=,故答案为:6.【点睛】本题考查了尺规作角平分线以及角平分线的性质定理:角平分线上的点到角两边的距离相等.16.(2023春·山东泰安·七年级统考期末)如图,在锐角ABC 中,60BAC ∠=︒,BE 、CD 为ABC 的角平分线.且BE 、CD 交于点F ,连接AF .有下列四个结论:①120BFC ∠=︒;②BD CE =;③BC BD CE =+;④FBD FEC FBC S S S +=△△△.其中结论正确的序号是__________ .【答案】①③④【分析】根据角平分线的定义和三角形内角和定理求出BFC ∠;在BC 上取BM BD =,证明()SAS DBF MBF ≌△△,再证明()ASA MCF ECF ≌△△;过点F 作FG AB ⊥于点G ,FH AC ⊥于点H ,FK BC ⊥于点K ,根据角平分线的性质和三角形面积公式分别对各个结论进行判断即可.【详解】解:∵ABC 的两条角平分线BE 和CD 交于点F ,60BAC ∠=︒,∴FBC FCB∠+∠()12ABC ACB =∠+∠()11802BAC ︒=−∠()1180602=⨯︒−︒60=︒, ∴()180********BFC FBC FCB ∠=︒−∠+∠=︒−︒=︒,故结论①正确; ∴18060BFD BFC CFE Ð=°-Ð=°=Ð,在BC 上取BM BD =,∵BE 平分ABC ∠,∴DBF MBF Ð=Ð,在DBF 和MBF V 中,BD BM DBF MBFBF BF =⎧⎪∠=∠⎨⎪=⎩, ∴()SAS DBF MBF ≌△△, ∴60BFD BFM ∠=∠=︒,∴1206060CFM BFC BFM ∠=∠−∠=︒−︒=︒,∴60CFM CFE ∠=∠=︒,∵CD 平分ACB ∠,∴MCF ECF ∠=∠,在MCF △和ECF △中,CFM CFE CF CFMCF ECF ∠=∠⎧⎪=⎨⎪∠=∠⎩, ∴()ASA MCF ECF ≌△△, ∴CM CE =,∴BC BM CM BD CE =+=+,故结论③正确;∵没有条件得出点M 是BC 的中点,∴不能得出BD 与CE 一定相等,故结论②错误;过点F 作FG AB ⊥于点G ,FH AC ⊥于点H ,FK BC ⊥于点K ,∵BE 、CD 为ABC 的角平分线,∴FG FK =,FK FH =,∴FG FK FE ==, ∵12FBD S BD FG =⋅△,12FEC S EC FH =⋅△,12FBC S BC FK =⋅△,∴FBD FEC S S +△△1122BD FG EC FH =⋅+⋅ 1122BM FK MC FK =⋅+⋅ ()12BM MC FK =+⋅ 12BC FK =⋅FBC S =△,∴FBD FEC FBC S S S +=△△△,故结论④正确,∴结论正确的序号是①③④.故答案为:①③④.【点睛】本题考查角平分线的性质,全等三角形的判定与性质,三角形内角和定理,三角形的面积,作出辅助线构造全等三角形是解题的关键.三、解答题 17.(2023春·重庆江北·七年级统考期末)完成下面的解答过程,并填上适当的理由.已知:如图,DE BC ∥,BD 平分ABC ∠,EF 平分AED ∠.解: ∵DE BC ∥(已知)∴ABC AED ∠=∠( ① ).∵BD 平分ABC ∠,EF 平分∠∴112ABC ∠=∠,122AED ∠=∠【答案】两直线平行,同位角相等 2∠ 等量代换 同位角相等,两直线平行【分析】先分析角的位置关系,根据平行线的性质及判定定理,即可写出答案.【详解】证明:∵DE BC ∥(已知),∴ABC AED ∠=∠.∵BD 平分ABC ∠,EF 平分AED ∠,∴112ABC ∠=∠,122AED ∠=∠.∴12∠=∠(等量代换).∴EF BD ∥(同位角相等,两直线平行).故答案为:两直线平行,同位角相等 ; 2∠ ;等量代换 同位角相等,两直线平行.【点睛】本题主要考查平行线的性质(两直线平行,同位角相等),及平行线的判定方法(同位角相等,两直线平行).牢记平行线的性质和判定方法是解题的关键.18.(2023春·山东泰安·七年级统考期末)如图,在AOB 和COD △中,OA OB =,OC OD =,OA OC <,36AOB COD ∠=∠=︒,连接AC 、BD 交于点M ,连接OM .求证:(1)36AMB ∠=︒;(2)MO 平分AMD ∠.【答案】(1)证明见解析 (2)证明见解析【分析】(1)证明()SAS AOC BOD ≌△△,由三角形全等的性质得出OAC OBD ∠=∠,由三角形的外角性质得:AMB OBD OAC AOB ∠+∠=∠+∠,可得出AMB ∠的度数;(2)作OG AC ⊥于G ,OH BD ⊥于H ,利用全等三角形对应边上的高相等,得出OG OH =,由角平分线的判定方法即可得证.【详解】(1)证明:∵36AOB COD ∠=∠=︒,∴AOB BOC COD BOC ∠+∠=∠+∠,即AOC BOD ∠=∠,在AOC 和BOD 中,OA OB AOC BODOC OD =⎧⎪∠=∠⎨⎪=⎩, ∴()SAS AOC BOD ≌△△, ∴OAC OBD ∠=∠,∵AEB ∠是AOE △和BME 的外角∴AEB AMB OBD AOB OAC ∠=∠+∠=∠+∠,∴36AMB AOB ∠=∠=︒;(2)如图所示,作OG AC ⊥于G ,OH BD ⊥于H ,∴OG 是AOC 中AC 边上的高,OH 是BOD 中BD 边上的高,由(1)知:AOC BOD ≌,∴OG OH =,∴点O 在AMD ∠的平分线上,即MO 平分AMD ∠.【点睛】本题考查全等三角形的判定与性质、三角形的外角性质、角平分线的判定等知识.证明三角形全等是解题的关键. 七年级统考期末)如图,在ABC 中, (2)18【分析】(1)根据BD 平分ABC ∠,CD 平分ACB ∠得12DBC ABC ∠=∠,12DCB ACB ∠=∠,根据40ABC ∠=︒,70ACB ∠=︒得140202DBC ∠=⨯︒=︒,170352DCB ∠=⨯︒=︒,根据三角形内角和定理即可得;(2)过点D 作DF BC ⊥于点F ,根据BD 平分ABC ∠,DE AB ⊥,DF BC ⊥得DE DF =,根据4DE =得4DF =,即可得.【详解】(1)解:∵BD 平分ABC ∠,CD 平分ACB ∠,∴12DBC ABC ∠=∠,12DCB ACB ∠=∠,∵40ABC ∠=︒,70ACB ∠=︒,∴140202DBC ∠=⨯︒=︒,170352DCB ∠=⨯︒=︒,∴在BCD △中,1802035125BDC ∠=︒−︒−︒=︒;(2)解:过点D 作DF BC ⊥于点F ,∵BD 平分ABC ∠,DE AB ⊥,DF BC ⊥,∴DE DF =,∵4DE =,∴4DF =,∵9BC =, ∴11S 941822BCD BC DF =⨯⨯=⨯⨯=△.【点睛】本题考查了角平分线,三角形内角和定理,三角形的面积,解题的关键是理解题意,掌握这些知识点. 八年级假期作业)如图,在ABC 中, 【答案】6cm CD =,34B ∠=︒【分析】根据角平分线的性质可得CD DE =,28BAD CAD ∠=∠=︒,再根据直角三角形的两个锐角互余即可求出B ∠的度数.【详解】解:∵ABC 中,90C ∠=︒,AD 平分BAC ∠,DE AB ⊥,∴6cm CD DE ==,28BAD CAD ∠=∠=︒,∴256BAC CAD ∠=∠=︒,∴9034B CAD ∠=︒−∠=︒.【点睛】本题考查了角平分线的性质定理和直角三角形的两个锐角互余,属于基础题型,熟练掌握角平分线的点到一个角的两边距离相等是解题关键.21.(2023春·广西南宁·七年级南宁十四中校考期末)如图,已知ABC .(1)尺规作图:作BAC ∠的角平分线交BC 于点G (不写作法,保留作图痕迹);(2)如果6AB =,10AC =,ABG 的面积为18,求ACG 的面积.【答案】(1)见解析(2)30【分析】(1)根据角平分线的尺规作图方法作图即可;(2)如图所示,过点G 作GE AB GF AC ⊥⊥,垂足分别为E 、F ,证明AEF AFG △≌△,得到EG FG =,根据面积法求出6EG FG ==,再根据三角形面积公式求解即可.【详解】(1)解:如图所示:(2)解:如图所示,过点G 作GE AB GF AC ⊥⊥,垂足分别为E 、F ,∴90AEG AFG ∠=∠=︒,∵AG 是BAC ∠的角平分线,∴EAG FAG ∠=∠,又∵AG AG =,∴()AAS AEF AFG △≌△,∴EG FG =;∵6AB =,ABG 的面积为18,∴1182AB EG ⋅=,即16182EG ⨯=,∴6EG =,∴6EG FG ==,∴111063022ACG S AC FG =⋅=⨯⨯=△.【点睛】本题主要考查了全等三角形的性质与判定,三角形面积,角平分线的尺规作图,角平分线的定义等等,灵活运用所学知识是解题的关键. 22.(2023春·山西太原·七年级统考期末)如图,在ABC 中,AD 是它的角平分线,DE AB ⊥于点,E DF AC ⊥于点F ,且BE CF =.线段BD 与CD 相等吗?说明理由.【答案】BD CD =,见解析【分析】根据角平分线的性质得出DE DF =,根据垂直定义得出90DEB DFC ∠=∠=︒,根据SAS 证明DFC △D E B ≌△,得出BD CD =即可.【详解】解:BD CD =;理由如下:∵AD 是BAC ∠的角平分线,DE AB ⊥,DF AC ⊥,∴DE DF =,∵DE AB ⊥,DF AC ⊥,∴90DEB DFC ∠=∠=︒,又∵BE CF =,∴DFC △DE B ≌△, ∴BD CD =.【点睛】本题主要考查了角平分线的性质,垂线定义理解,三角形全等的判定和性质,解题的关键是熟练掌握三角形全等的判定方法,证明DFC △DE B ≌△. 23.(重庆市大渡口区2022-2023学年七年级下学期期末数学试题)如图,AD BC ∥,180B BCD ∠+∠=︒.(1)用直尺和圆规完成以下基本作图:过点A 作BAD ∠的角平分线,交CD 于点F ,与BC 的延长线交于点E ;(不写做法,保留作图痕迹)(2)求证:CFE FEC ∠=∠.证明:∵AD BC ∥(已知),∴DAF FEC ∠=∠(①__________). ∵AE 平分BAD ∠,∴②__________(角平分线的定义). ∴BAE FEC ∠=∠(③__________). ∵180B BCD ∠+∠=︒(已知), ∴④__________(⑤__________). ∴BAE CFE ∠=∠(两直线平行,同位角相等). ∴CFE FEC ∠=∠(等量代换). 【答案】(1)见解析(2)见解析【分析】(1)利用基本作图作BAD ∠的平分线即可;(2)先根据平行线的性质得到DAF FEC ∠=∠,再利用角平分线的定义得到BAE DAF ∠=∠,则BAE FEC ∠=∠,接着证明AB CD ∥得到BAE CFE ∠=∠,然后利用等量代换得到CFE FEC ∠=∠.【详解】(1)解:如图,BE 为所作;(2)证明:AD BC ∥(已知), DAF FEC ∴∠=∠(两直线平行,内错角相等).AE 平分BAD ∠,BAE DAF ∴∠=∠(角平分线的定义),BAE FEC ∴∠=∠(等量代换).180B BCD ∠+∠=︒(已知),AB CD ∴∥(同旁内角互补,两直线平行).BAE CFE ∴∠=∠(两直线平行,同位角相等).CFE FEC ∴∠=∠(等量代换).【点睛】本题考查了作图−基本作图:熟练掌握5种基本作图是解决问题的关键.也考查了角平分线的性质和平行线的判定与性质. 七年级校考阶段练习)如图,ABC 中, 若BCG 的面积为,则ABC 的面积为【答案】(1)120︒(2)3(3)6【分析】(1)根据作图方法可得BG 是ABC ∠的角平分线,则1302ABG ABC ==︒∠∠,再由三角形外角的性质可得120BGC A ABG =+=︒∠∠;(2)如图所示,过点G 作GD BC ⊥于D ,先求出3AG AC CG =−=,再证明ABG DBG △≌△,得到3DG AG ==,根据垂线段最短可知线段H G 的最小值为3;(3)证明BDG CDG △≌△,得到122BDG CDG BCG S S S ===△△△,进而求出2BDG ABG S S ==△△,则6ABC ABG CBG S S S =+=△△△.【详解】(1)解:由作图方法可知BG 是ABC ∠的角平分线, ∴1302ABG ABC ==︒∠∠,∵90A ∠=︒,∴120BGC A ABG =+=︒∠∠,故答案为:120︒;(2)解:如图所示,过点G 作GD BC ⊥于D ,∴90BAG BDG ==︒∠∠,∵96AC CG ==,,∴3AG AC CG =−=,∵BG 是ABC ∠的角平分线,∴ABG DBG ∠=∠,又∵BG BG =,∴()AAS ABG DBG △≌△,∴3DG AG ==,∵H 是边BC 上一动点,∴当点H 与点D 重合时,HG 最小,∴线段HG 的最小值为3, 故答案为:3;(3)解:∵BG 是ABC ∠的角平分线,∴30ABG DBG ==︒∠∠,∵9030C ABC ∠=︒−∠=︒,∴GBD C ∠=∠,又∵90DG DG BDG CDG ===︒,∠∠,∴()AAS BDG CDG △≌△, ∴122BDG CDG BCG S S S ===△△△,∵ABG DBG △≌△,∴2BDG ABG S S ==△△,∴6ABC ABG CBG S S S =+=△△△,故答案为:6.【点睛】本题主要考查了全等三角形的性质与判定,三角形内角和定理,三角形外角的性质,角平分线的定义,角平分线的尺规作图等等,正确作出辅助线构造全等三角形是解题的关键. 七年级统考期末)ABC 中, (2)如图2,若ABC 是锐角三角形.过点FED ∠,EDB ∠与ABC ∠ (3)若ABC 是钝角三角形,其中FED ∠,EDB ∠与ABC ∠之间的数量关系.【答案】(1)45 (2)12BDE FED ABC ∠=∠+∠,证明见解析 (3)12ABC BDE DEF ∠=∠+∠【分析】(1)首先证明AED ABC ∠=∠得到DE BC ∥,得到EDB DBC ∠=∠,再根据角平分线的定义得到1452DBC ABC ∠=∠=︒,即可证明;(2)延长ED 、BC 交于G ,利用平行线的性质得FED G ∠=∠,再利用三角形外角的性质可得结论;(3)由(2)同理解决问题.【详解】(1)解:DE AB ∵⊥,90AED ∴∠=︒.90ABC ∠=︒,AED ABC ∴∠=∠.DE BC ∴∥.EDB DBC ∴∠=∠.BD Q 平分ABC ∠,1452DBC ABC ∴∠=∠=︒.45EDB ∴∠=︒.(2)如图,12BDE FED ABC ∠=∠+∠,理由如下:延长ED 、BC 交于G ,EF BC ∥,FED G ∴∠=∠,BD Q 平分ABC ∠,。
中考必会几何模型:角平分线四大模型

角平分线四大模型模型1 角平分线的点向两边作垂线如图,P是∠MON的平分线上一点,过点P作PA⊥OM于点A,PB⊥ON于点B,则PB=PA模型分析利用角平分线的性质:角平分线上的点到角两边的距离相等,构造模型,为边相等、角相等、三角形全等创造更多的条件,进而可以快速找到解题的突破口模型实例(1)如图①,在△ABC中,∠C=90°,AD平分∠CAB,BC=6,BD=4,那么点D到直线AB的距离是解答:如图,过点D作DE⊥AB于点E,∵AD平分∠CAB,∴CD=DE.∵CB=6,BD=4,∴DE=CD=2,即点D到直线AB的距离是2.(2)如图②,∠1=∠2,∠3=∠4,求证:AP平分∠BAC证明:如图,过点P作PD⊥AB于点D,PE⊥BC于点E,PF⊥AC于点F,∵∠1=∠2,∴PD=PE,∵∠3=∠4, ∴PE=PF,∴PD=PF又∵PD⊥AB,PF⊥AC,∴AP平分∠BAC(角平分线的判定)练习1、如图,在四边形ABCD中,BC>AB,AD=DC,BD平分∠ABC ,求证:∠BAD+∠BCD=180°证明:作DE⊥BC于E,作DF⊥BA的延长线于F,∴∠F=∠DEC=90°,∵BD平分∠ABC,∴DF=DE,又∵AD=DC,∴△DFA≌DEC,∴∠FAD=∠C∵∠FAD+∠BAD=180°,∴∠BAD+∠BCD=180°2.如图,△ABC的外角∠ACD∠的平分线CP与内角∠ABC的平分线BP相交于点P,若∠BPC=40°,则∠CAP=.解答:如图所示,作PN⊥BD于N,作PF⊥BA,交BA延长线于F,作PM⊥AC于M ∵BP、CP分别是∠CBA和∠DCA的角平分线,∴∠ABP=∠CBP,∠DCP=∠ACP,PF=PN=PM,∵∠BAC=∠ACD-∠ABC,∠BPC=∠PCD-∠PBC(外角性质)∴∠BAC=2∠PCD-2∠PBC=2(∠PCD-∠PBC)=2∠BPC=80°∴∠CAF=180°-∠BAC=100°,∵PF=PM∴AP是∠FAC的角平分线,∴∠CAP=∠PAF=50°模型2 截取构造对称全等如图,P是∠MON的平分线上的一点,点A是射线OM上任意一点,在ON上截取OB=OA,连接PB,则△OPB≌△OPA模型分析利用角平分线图形的对称性,在铁的两边构造对称全等三角形,可以得到对应边,对应角相等,利用对称性把一些线段或角进行转移,这是经常使用的一种解题技巧模型实例(1)如图①所示,在△ABC中,AD是△BAC的外角平分线,P是AD上异于点A的任意一点,试比较PB+PC与AB+AC的大小,并说明理由解题:PB+PC>AB+AC证明:在BA的延长线上取点E,使AE=AB,连接PE,∵AD平分∠CAE∴∠CAD=∠EAD,在△AEP与△ACP中,∵AE=AB,∠CAD=∠EAD,AP=AP,∴△AEP≌△ACP (SAS),∴PE=PC∵在△PBE中:PB+PE>BE,BE=AB+AE=AB+AC,∴PB+PC>AB+AC(2)如图②所示,AD是△ABC的内角平分线,其它条件不变,试比较PC-PB与AC-AB的大小,并说明理由解答:AC-AB>PC-PB证明:在△ABC中, 在AC上取一点E,使AE=AB ,∴AC-AE=AB-AC=BE∵AD平分∠BAC ,∴∠EAP=∠BAP ,在△AEP和△ACP中∴△AEP≌△ABP (SAS) ,∴PE=PB ,∵在△CPE中CE>CP-PE ,∴AC-AB>PC-PB练习1.已知,在△ABC中,∠A=2∠B,CD是∠ACB的平分线,AC=16,AD=8,求线段BC的长解:如图在BC边上截取CE=AC,连结DE,在△ACD和△ECD中⎪⎩⎪⎨⎧=∠=∠=CD CD ECD ACD EC AC∴△ACD ≌△ECD(SAS)∴AD =DE , ∠A =∠1 ,∵∠A =2∠B ,∴∠1=2∠B ,∵∠1=∠B +∠EDB , ∴∠B =∠EDB ,∴EBB =ED , ∴EB =DA =8,BC =EC +BE =AC +DA =16+8=242. 在△ABC 中,AB =AC,∠A =108°,BD 平分∠ABC ,求证:BC =AB +CD证明:在BC 上截取BE =BA ,连结DE ,∵BD 平分∠ABC,BE =AB,BD =BD∴△ABD ≌△EBD(SAS),∴∠DEB =∠A =108°,∴∠DEC =180°-108°=72°∵AB =AC ,∴∠C =∠ABC =12(180°-108°)=36°,∴∠EDC =72° , ∴∠DEC =∠EDC ,∴CE =CD ,∴BE +CE =AB +CD ,∴BC =AB +CD3.如图所示,在△ABC 中,∠A =100°,∠ABC =40°,BD 是∠ABC 的平分线,延长BD 至E ,使DE =AD ,求证:BC =AB +CE证明:在CB 上取点F ,使得BF =AB,连结DF ,∵BD 平分∠ABC ,BD =BD∴△ABD ≌△FBD ,∴DF =AD =DE,∠ADB =∠FDB ,∴BD 平分∠ABC∴∠ABD =20°,则∠ADB =180°-20°-100°=60°=∠CDE∠CDF =180°-∠ADB -∠FDB =60°,∴∠CDF =∠CDE ,在△CDE 和△CDF 中 ⎪⎩⎪⎨⎧=∠=∠=CD CD CDE CDF DF DE∴△CDE ≌CDF ,∴CE =CF ,∴BC =BF +FC =AB +CE模型3 角平分线+垂线构造等腰三角形如图,P 是∠MON 的平分线上一点,AP 丄OP 于P 点,延长AP 交ON 于点.B,则△AOB 是等腰三角形.模型分析构造此模型可以利用等腰三角形的"三线合一”,也可以得到两个全等的直角三角形.进而得到对应边.对应角相等.这个模型巧妙地把角平分线和三线合一联系了起来.模型实例如图.己知等腰直角三角形ABC中,∠A=90°, AB=AC, BD平分∠ABC, C£丄BD.垂足为E.求证:BD=2C£.解答:如图,延长CE、BA交于点F,∵CE丄BD于E, ∠BAC=90°,∴∠BAD=∠CED. ∴∠ABD=∠ACF.又∵AB=AC, ∠BAD=∠CAF=90°, ∴△ABD≌△ACF.∴ BD=CF.∵BD平分∠ABC, ∴∠CBE=∠FBE. 又BE=BE,∴△BCE≌△BFE.∴CE=EF. ∴BD=2CE.练习1.如图.在△ABC中.BE是角平分线.AD丄BE.垂足为D.求证:∠2=∠1+∠C.证明:延长AD交BC于F,∵AD⊥BE, ∴∠ADB=∠BDF=90°, ∵∠ABD=∠FBD,∴∠2=∠BFD. ∵∠BFD=∠1+∠C,∴∠2=∠1+∠C.2.如图.在△ABC中. ∠ABC=3∠C,AD是∠BAC的平分线, BE丄AD于点E.求证:1()2BE AC AB=-.(2)证明:延长BE 交AC 于点F.∵AD 为∠BAC 的角平分线,∴∠BAD=∠CAD.∵AE=AE, ∴∠BAE=∠FAE,则△AEB ≌△AEF ,∴AB=AF, BE=EF, ∠ 2=∠3.∴AC-AB=AC-AF=FC. ∵∠ABC=3∠C,∴∠2+∠1=∠3+∠1=∠1+∠C+∠1=3∠C.∴2∠1=2∠C即∠1=∠C ∴BF=FO=2BE.∴()1122BE FC AC AB ==-模型4 角平分线+平行线模型分析有角平分线时.常过角平分线上一点作角的一边的平行线. 构造等腰三角形.为证明结论提供更多的条件.体现了用平分线与等腰三角形之间的密切关系.模型实例解答下列问题:(1)如图①.△ABC 中,EF ∥BC,点D 在EF 上,BD 、CD 分别平分∠ABC 、∠ACB.写出线段EF 与BE 、CF 有什么数量关系?(2)如图②,BD 平分∠ABC,CD 平分外角∠ACG. DE//BC 交AB 于点E,交AC 于点F ,线段EF 与BE 、CF 有什么数量关系?并说明理由.(3)如图③,BD 、CD 为外角∠CBM 、∠BCN 的平分线,DE//BC 交AB 延长线于点E.交AC 延长线于点F,直接写出线段EF 与BE 、CF 有什么数关系?解答:(1) ∵EF//BC,∴∠EDB=∠DBC.∴BD平分∠EBC,∴∠EBD=∠DBC=EDB. ∴EB=ED. 同理:DF=FC. ∴EF=ED+DF=BE+CF.(2)图②中有EF=BE=CF,BD平分∠BAC,∴∠ABD=∠DBC.又DE//BC、∴∠EDB=∠DBC. ∴DE=EB.同理可证:CF=DF ∴EF=DE-DF=BE-CF.(3) EF=BE+CF.练习1.如图. 在△ABC中,∠ABC和∠ACB的平分线交于点E.过点E作MN∥BC交AB于M点. 交AC于N点.若BM+CN=9,则线段MN的长为.解答:∵∠ABC、∠ACB的平分线相交于点E,∴MBE=∠EBC,∠ECN=∠ECB.∵MN//BC, ∴∠EBC=∠MEB, ∠NEC=∠ECB. ∴∠MBE-∠MEB, ∠NEO=∠ECN.∴BM=ME, EN=CN. ∴MN=ME+EN,即MN=BM+CN.∵BM+CN=9,∴MN=9.2. 如图. 在△ABC中,AD平分∠BAC.点E、F分別在BD,AD上,EF∥AB.且DE=CD,求证:EF=AC.证明:如图,过点C作CM∥AB交AD的延长线于点M,∵AB∥EF,∴CM∥EF.∴∠3=∠4. ∵DE=CD, ∠5=∠6, ∴△DEF≌△DCM.∴EF=CM. ∵AB//CM,∴∠2=∠4. ∵∠1=∠2,∴∠1=∠4.∴CM=AC.∴EF=AC3.如图.梯形ABCD中,AD∥BC,点E在CD上,且AE平分∠BAD.BE平分∠ABC.求证:AD=AB-BC.证明:延长AD、BE交于点F.∵AD∥BC,∴∠2=∠F. ∵∠1=∠2,∴∠1=∠F.∴AB=AF. ∵AE平分∠BAD∴BE=EF. ∵∠DEF=∠CEB,∴△DEF≌△CEB.∴DF=BC.∴AD=AF-DF=AB-BC.。
适合初学者的角平分线几何初步题目带解答

一.解答题(共15小题)1.已知OC是∠AOB内部的一条射线,∠AOC=30°,OE是∠COB的平分线.当∠COE =40°时,求∠AOB的度数.解:∵OE是∠COB的平分线,∴∠COB=(理由:).∵∠COE=40°,∴.∵∠AOC=,∴∠AOB=∠AOC+ =110°.2.如图,已知∠BOC=2∠AOB,OD平分∠AOC,∠BOD=14°,求∠AOB的度数.3.已知:如图,∠AOB=150°,OC平分∠AOB,∠AOD是直角,求∠COD的度数.4.如图,已知∠AOC=90°,∠COB=50°,OD平分∠AOB,求∠COD等于多少度?5.已知:A、O、B三点在同一直线上,OE、OD分别平分∠AOC、∠BOC.(1)求∠EOD的度数;(2)若∠AOE=50°,求∠BOC的度数.6.如图,OB是∠AOC的平分线,OD是∠COE的平分线.(1)如果∠AOB=50°,∠DOE=30°,那么∠BOD是多少度?(2)如果∠AOE=160°,∠COD=30°,那么∠AOB是多少度?7.如图所示,∠AOB:∠BOC:∠COD=4:5:3,OM平分∠AOD,∠BOM=20°,求∠AOD和∠MOC.8.如图,∠AOC:∠BOC=1:4,OD平分∠AOB,且∠COD=36°,求∠AOB度数.9.如图,已知OB是∠AOC的平分线,OD是∠COE的平分线,如果∠AOE=140°,∠BOC比∠COD的2倍还多10°,那么∠AOB是多少度?10.如图,∠AOB是平角,射线OD平分∠AOC,射线OE平分∠BOD,且∠BOC=4∠AOD,求∠COE的度数.11.如图,OB是∠AOC的平分线,OD是∠EOC的平分线.(1)如果∠AOD=75°,∠BOC=19°,则∠DOE的度数为;(2)如果∠BOD=56°,求∠AOE的度数.12.如图,点A,O,B在同一条直线上,射线OD和射线OE分别平分∠AOC和∠BOC,求∠DOE的度数.13.如图,已知∠ABC是直角,∠DBC=30°,BF、BE分别是∠ABD、∠CBD的平分线,求∠EBF.14.如图,O为直线AB上一点,∠AOC=50°,OD平分∠AOC.(1)填空:∠BOD= 度;(2)当∠DOE=90°,请说明OE平分∠BOC.15.如图,已知∠AOB=90°,∠EOF=60°,OE平分∠AOB,OF平分∠BOC,求∠COB和∠AOC的度数.2018年03月13日吕泽文的初中数学组卷参考答案与试题解析一.解答题(共15小题)1.已知OC是∠AOB内部的一条射线,∠AOC=30°,OE是∠COB的平分线.当∠COE=40°时,求∠AOB的度数.解:∵OE是∠COB的平分线,∴∠COB= 2∠COE (理由:角平分线定义).∵∠COE=40°,∴∠COB=80°.∵∠AOC= 30° ,∴∠AOB=∠AOC+ ∠COB =110°.【分析】根据角平分线线的定义求得∠COB=80°.然后根据图中角与角间的和差关系得到∠AOB=∠AOC+∠COB=110°.【解答】解:∵OE是∠COB的平分线,∴∠COB=2∠COE(角平分线定义).∵∠COE=40°,∴∠COB=80°.∵∠AOC=30°,∴∠AOB=∠AOC+∠COB=110°.故答案是:2∠COE,角平分线定义,∠COB=80°,30°,∠COB.【点评】本题考查了角平分线的定义.从一个角的顶点出发,把这个角分成相等的两个角的射线叫做这个角的平分线.2.如图,已知∠BOC=2∠AOB,OD平分∠AOC,∠BOD=14°,求∠AOB的度数.【分析】此题可以设∠AOB=x,∠BOC=2x,再进一步表示∠AOC=3x,根据角平分线的概念表示∠AOD,最后根据已知角的度数列方程即可计算.【解答】解:设∠AOB=x,∠BOC=2x.则∠AOC=3x.又OD平分∠AOC,∴∠AOD=x.∴∠BOD=∠AOD﹣∠AOB=x﹣x=14°∴x=28°即∠AOB=28°.【点评】本题考查了角平分线的定义.此类题设恰当的未知数,根据已知条件进一步表示出相关的角,列方程计算较为简便.3.已知:如图,∠AOB=150°,OC平分∠AOB,∠AOD是直角,求∠COD的度数.【分析】根据∠AOB=150°,OC平分∠AOB,即可得到∠AOC=75°,进而得出∠C OD=∠AOD﹣∠AOC=90°﹣75°=15°.【解答】解:∵∠AOB=150°,OC平分∠AOB,∴∠AOC=∠AOB=×150°=75°,∴∠COD=∠AOD﹣∠AOC=90°﹣75°=15°.【点评】本题考查了角平分线的定义,解决本题的关键是根据根据∠AOB=150°,O C平分∠AOB,得出∠AOC=75°,再根据角之间和与差进行计算即可.4.如图,已知∠AOC=90°,∠COB=50°,OD平分∠AOB,求∠COD等于多少度?【分析】先根据题意得出∠AOB的度数,再由OD平分∠AOB得出∠AOD的度数,根据∠COD=∠AOC﹣∠AOD即可得出结论.【解答】解:∵∠AOC=90°,∠COB=50°,∴∠AOB=∠AOC+∠COB=140°,∵OD平分∠AOB,∴∠AOD=∠AOB=70°,∴∠COD=∠AOC﹣∠AOD=90°﹣70°=20°.【点评】本题考查的是角平分线的定义,熟知从一个角的顶点出发,把这个角分成相等的两个角的射线叫做这个角的平分线是解答此题的关键.5.已知:A、O、B三点在同一直线上,OE、OD分别平分∠AOC、∠BOC.(1)求∠EOD的度数;(2)若∠AOE=50°,求∠BOC的度数.【分析】(1)由于OE、OD分别平分∠AOC、∠BOC,所以∠EOC=∠AOC,∠COD=∠BOC,进而得出∠EOD=∠EOC+∠COD=∠AOB=90°;(2)由OE平分∠AOC,∠AOE=50°,得出∠AOC=2∠AOE=100°,再根据邻补角定义得出∠BOC=180°﹣∠AOC=80°.【解答】解:(1)∵OE、OD分别平分∠AOC、∠BOC,∴∠EOC=∠AOC,∠COD=∠BOC,∴∠EOD=∠EOC+∠COD=∠AOC+∠BOC=∠AOB,又∵A、O、B三点在同一直线上,∴∠AOB=180°,∴∠EOD=∠AOB=90°;(2)∵OE平分∠AOC,∠AOE=50°,∴∠AOC=2∠AOE=100°,∴∠BOC=180°﹣∠AOC=80°.【点评】本题考查了角平分线的定义:从一个角的顶点出发,把这个角分成相等的两个角的射线叫做这个角的平分线.也考查了角的和差,邻补角定义,准确识图是解题的关键.6.如图,OB是∠AOC的平分线,OD是∠COE的平分线.(1)如果∠AOB=50°,∠DOE=30°,那么∠BOD是多少度?(2)如果∠AOE=160°,∠COD=30°,那么∠AOB是多少度?【分析】(1)根据角平分线的性质可得∠DOE=∠COD,∠BOC=∠AOB,再根据条件∠AOB=50°,∠DOE=30°可得答案;(2)首先根据角平分线的性质可得∠DOE=∠COD,∠BOC=∠AOB,再根据条件∠COD=30°可得∠DOE=30°,然后可得答案.【解答】解:(1)∵OB是∠AOC的平分线,OD是∠COE的平分线,∴∠DOE=∠COD,∠BOC=∠AOB,∵∠AOB=50°,∠DOE=30°,∴∠DOC=30°,∠BOC=50°,∴∠BOD=80°;(2)∵OB是∠AOC的平分线,OD是∠COE的平分线,∴∠DOE=∠COD,∠BOC=∠AOB,∵∠COD=30°,∴∠DOE=30°,∴∠AOC=160°﹣30°﹣30°=100°,∵∠BOC=∠AOB,∴∠AOB=50°.【点评】此题主要考查了角平分线的定义,关键是掌握角平分线把角分成相等的两部分.7.如图所示,∠AOB:∠BOC:∠COD=4:5:3,OM平分∠AOD,∠BOM=20°,求∠AOD 和∠MOC.【分析】设∠AOB=4x,∠BOC=5x,∠COD=3x,得到∠AOD=12x,根据角平分线的定义得到∠AOM=∠AOD=6x,根据题意列出方程,解方程即可.【解答】解:设∠AOB=4x,∠BOC=5x,∠COD=3x,∴∠AOD=12x,∵OM平分∠AOD,∴∠AOM=∠AOD=6x,由题意得,6x﹣4x=20°,解得,x=10°,∴∠AOD=12x=120°,∠BOC=5x=50°,∴∠MOC=∠BOC﹣∠BOM=30°.【点评】本题考查的是角平分线的定义,掌握从一个角的顶点出发,把这个角分成相等的两个角的射线叫做这个角的平分线是解题的关键.8.如图,∠AOC:∠BOC=1:4,OD平分∠AOB,且∠COD=36°,求∠AOB度数.【分析】根据题意可以用∠AOB表示出∠AOC和∠AOD,然后根据∠COD=36°,即可求得∠AOB的度数.【解答】解:∵∠AOC:∠BOC=1:4,OD平分∠AOB,且∠COD=36°,∴∠AOC=,∠AOD=,∴∠COD=∠AOD﹣∠AOC=,∴,解得,∠AOB=120°,即∠AOB的度数是120°.【点评】本题考查角平分线的定义,解答本题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答.9.如图,已知OB是∠AOC的平分线,OD是∠COE的平分线,如果∠AOE=140°,∠BOC比∠COD的2倍还多10°,那么∠AOB是多少度?【分析】设∠COD的度数为x,则∠BOC=2x+10°,利用角平分线定义得到∠EOC=2∠COD=2x,∠BOC=2x+10°,再利用OB是∠AOC的平分线得到∠AOB=∠BOC,∠AOC=2∠BOC=4x+20°,所以2x+4x+20°=140°,解得x=20°,然后计算2x+10°即可.【解答】解:设∠COD的度数为x,∵OD是∠COE的平分线,∴∠EOC=2∠COD=2x,∵∠BOC比∠COD的2倍还多10°,∴∠BOC=2x+10°,∵OB是∠AOC的平分线,∴∠AOB=∠BOC,∠AOC=2∠BOC=4x+20°,∵∠AOE=140°,∴2x+4x+20°=140°,解得x=20°,∴∠BOC=2x+10°=50°∴∠AOB是50度.【点评】本题考查了角平分线的定义:灵活应用角平分线的定义进行角度的计算.10.如图,∠AOB是平角,射线OD平分∠AOC,射线OE平分∠BOD,且∠BOC=4∠AOD,求∠COE的度数.【分析】由OD平分∠AOC和∠BOC=4∠AOD,可求出∠AOC=60°,再求出∠COB 的度数,即可求出∠BOD,利用∠COE=∠DOE﹣∠COD即可求出.【解答】解:∵OD平分∠AOC,∴∠AOD=∠COD=∠AOC,∵∠BOC=4∠AOD,∴∠BOC=2∠AOC,∵∠BOC+∠AOC=180°,∴3∠AOC=180°,∴∠AOC=60°,∴∠COD=∠AOC=30°,∠BOC=2∠AOC=120°∴∠BOD=150°,∵OE平分∠BOD,∴∠EOD=∠BOE=75°,∴∠COE=∠DOE﹣∠COD=75°﹣30°=45°.【点评】本题主要考查了角平分线的定义,解题的关键是利用角平分线的定义找出各角之间的关系.11.如图,OB是∠AOC的平分线,OD是∠EOC的平分线.(1)如果∠AOD=75°,∠BOC=19°,则∠DOE的度数为37° ;(2)如果∠BOD=56°,求∠AOE的度数.【分析】(1)根据角平分线的定义求得∠AOC=38°,∠DOE=∠DOC=∠AOD﹣∠AOC=75°﹣38°=37°;(2)根据角平分线的定义易求∠AOE=2∠BOD.【解答】解:(1)∵OB是∠AOC的平分线,∠BOC=19°,∴∠AOC=2∠BOC=38°,∴∠DOC=∠AOD﹣∠AOC=75°﹣38°=37°.又∵OD是∠EOC的平分线,∴∠DOE=∠DOC=37°.故答案为:37°;(2)如图,∵OB是∠AOC的平分线,∴∠AOC=2∠BOC.∵OD是∠EOC的平分线,∴∠COE=2∠COD,∴∠AOE=∠AOC+∠COE=2∠BOC+2∠COD=2∠BOD=112°.【点评】本题考查了角平分线的定义.解题时,实际上是根据角平分线定义得出所求角与已知角的关系转化求解.12.如图,点A,O,B在同一条直线上,射线OD和射线OE分别平分∠AOC和∠BOC,求∠DOE的度数.【分析】根据角平分线的定义表示出∠COD和∠COE,再根据平角等于180°进行计算即可得解.【解答】解:∵射线OD和射线OE分别平分∠AOC和∠BOC,∴∠COD=∠AOC,∠COE=∠BOC,∴∠DOE=∠COD+∠COE=(∠AOC+∠BOC),∵点A,O,B在同一条直线上,∴∠AOC+∠BOC=180°,∴∠DOE=×180°=90°.【点评】本题考查了角平分线的定义,平角的定义,是基础题,熟记概念是解题的关键.13.如图,已知∠ABC是直角,∠DBC=30°,BF、BE分别是∠ABD、∠CBD 的平分线,求∠EBF.【分析】根据角平分线的定义得到∠FBD=∠ABD,∠EBD=∠CBD,计算即可.【解答】解:∵BF、BE分别是∠ABD、∠CBD的角平分线,∴∠FBD=∠ABD,∠EBD=∠CBD,∴∠EBF=∠FBD+∠EBD=(∠ABD+∠CBD)=∠ABC=45°.【点评】本题考查了角平分线的定义,熟练掌握此类题型是解题的关键.14.如图,O为直线AB上一点,∠AOC=50°,OD平分∠AOC.(1)填空:∠BOD= 155 度;(2)当∠DOE=90°,请说明OE平分∠BOC.【分析】(1)根据∠BOD=∠DOC+∠BOC,首先利用角平分线的定义和邻补角的定义求得∠DOC和∠BOC即可;(2)根据∠COE=∠DOE﹣∠DOC和∠BOE=∠BOD﹣∠DOE分别求得∠COE与∠BOE的度数即可说明.【解答】解:(1)∵∠AOC=50°,OD平分∠AOC,∴∠DOC=∠AOC=25°,∠BOC=180°﹣∠AOC=130°,∴∠BOD=∠DOC+∠BOC=155°;(2)∵∠DOE=90°,∠DOC=25°,∴∠COE=∠DOE﹣∠DOC=90°﹣25°=65°.又∵∠BOE=∠BOD﹣∠DOE=155°﹣90°=65°,∴∠COE=∠BOE,∴OE平分∠BOC.故答案为:155.【点评】本题主要考查了角的度数的计算,正确理解角平分线的定义,以及邻补角的定义是解题的关键.15.如图,已知∠AOB=90°,∠EOF=60°,OE平分∠AOB,OF平分∠BOC,求∠COB和∠AOC的度数.【分析】先根据角平分线,求得∠BOE的度数,再根据角的和差关系,求得∠BOF的度数,最后根据角平分线,求得∠BOC、∠AOC的度数.【解答】解:∵∠AOB=90°,OE平分∠AOB∴∠BOE=45°又∵∠EOF=60°∴∠FOB=60°﹣45°=15°∵OF平分∠BOC∴∠COB=2×15°=30°∴∠AOC=∠BOC+∠AOB=30°+90°=120°【点评】本题主要考查了角平分线的定义,根据角的和差关系进行计算是解题的关键.注意:也可以根据∠AOC的度数是∠EOF度数的2倍进行求解.。
2023年中考数学常见几何模型之角平分线非全等类模型

专题08 角平分线的重要模型(二)非全等类角平分线在中考数学中都占据着重要的地位,角平分线常作为压轴题中的常考知识点,需要掌握其各大模型及相应的辅助线作法,且辅助线是大部分学生学习几何内容中的弱点,,本专题就角平分线的非全等类模型作相应的总结,需学生反复掌握。
模型1.双角平分线模型(导角模型) 【模型解读】双角平分线模型(导角模型)指的是当三角形的内角(外角)的平分线相交时,可以导出平分线的夹角的度数。
【模型图示】条件:BD ,CD 是角平分线.结论:1902BDC A ∠=︒+∠1902BDC A ∠=︒−∠12BDC A ∠=∠1.(2022·广东·九年级专题练习)BP 是∠ABC 的平分线,CP 是∠ACB 的邻补角的平分线,∠ABP =20°,∠ACP =50°,则∠P =( )A.30°B.40°C.50°D.60°【答案】A【分析】据角平分线的定义以及一个三角形的外角等于与它不相邻的两个内角和,可求出∠P的度数.【详解】∵BP是△ABC中∠ABC的平分线,CP是∠ACB的外角的平分线,∴∠ABP=∠CBP=20°,∠ACP=∠MCP=50°,∵∠PCM是△BCP的外角,∴∠P=∠PCM−∠CBP=50°−20°=30°,故选:A.【点睛】本题考查三角形外角性质以及角平分线的定义,解题时注意:一个三角形的外角等于与它不相邻的两个内角的和.2.(2022·山东·济南中考模拟)如图1,在△ABC中,∠BAC的平分线AD与∠BCA的平分线CE交于点O.(1)求证:∠AOC=90°+1∠ABC;2(2)当∠ABC=90°时,且AO=3OD(如图2),判断线段AE,CD,AC之间的数量关系,并加以证明.3.(2022•蓬溪县九年级月考)某校七年级数学兴趣小组对“三角形内角或外角平分线的夹角与第三个内角的数量关系”进行了探究.(1)如图1,在△ABC中,∠ABC与∠ACB的平分线交于点P,∠A=64°,则∠BPC=;(2)如图2,△ABC的内角∠ACB的平分线与△ABC的外角∠ABD的平分线交于点E.其中∠A=α,求∠BEC.(用α表示∠BEC);(3)如图3,∠CBM、∠BCN为△ABC的外角,∠CBM、∠BCN的平分线交于点Q,请你写出∠BQC 与∠A的数量关系,并说明理由.(4)如图4,△ABC外角∠CBM、∠BCN的平分线交于点Q,∠A=64°,∠CBQ,∠BCQ的平分线交于点P,则∠BPC=°,延长BC至点E,∠ECQ的平分线与BP的延长线相交于点R,则∠R=°.【分析】(1)根据三角形的内角和角平分线的定义;(2)根据三角形的一个外角等于与它不相邻的两个内角的和,用∠A与∠1表示出∠2,再利用∠E与∠1表示出∠2,于是得到结论;(3)根据三角形的一个外角等于与它不相邻的两个内角的和以及角平分线的定义表示出∠EBC与∠ECB,然后再根据三角形的内角和定理列式整理即可得解;(4)结合(1)(2)(3)的解析即可求得.【解答】解:(1)∵PB、PC分别平分∠ABC和∠ACB,∴∠PBC=12∠ABC,∠PCB=12∠ACB(角平分线的性质),∴∠BPC+∠PBC+∠PCB=180°(三角形内角和定理),∴∠BPC=180°﹣(∠PBC+∠PCB)=180°﹣(12∠ABC+12∠ACB)=180°−12(∠ABC+∠ACB)=180°−12(180°﹣∠A)=180°﹣90°+12∠A=90°+12∠A=90°+12×64°=122°.故答案为:122°;(2)∵BE是∠ABD的平分线,CE是∠ACB的平分线,∴∠ECB=12∠ACB,∠ECD=12∠ABD.∵∠ABD是△ABC的外角,∠EBD是△BCE的外角,∴∠ABD=∠A+∠ACB,∠EBD=∠ECB+∠BEC,∴∠EBD=12∠ABD=12(∠A+∠ACB)=∠BEC+∠ECB,即12∠A+∠ECB=∠ECB+∠BEC,∴∠BEC=12∠A=12α;(3)结论∠BQC=90°−12∠A.∵∠CBM与∠BCN是△ABC的外角,∴∠CBM=∠A+∠ACB,∠BCN=∠A+∠ABC,∵BQ,CQ分别是∠ABC与∠ACB外角的平分线,∴∠QBC=12(∠A+∠ACB),∠QCB=12(∠A+∠ABC).∵∠QBC+∠QCB+∠BQC=180°,∴∠BQC=180°﹣∠QBC﹣∠EQB=180°−12(∠A+∠ACB)−12(∠A+∠ABC),=180°−12∠A−12(∠A+∠ABC+∠ACB)=180°−12∠A﹣90°=90°−12∠A;(4)由(3)可知,∠BQC=90°−12∠A=90°−12×64°=58°,由(1)可知∠BPC=90°+12∠BQC=90°+12×58°=119°;由(2)可知,∠R=12∠BQC=29°故答案为119,29.【点评】本题考查了三角形的外角性质与内角和定理,熟记三角形的一个外角等于与它不相邻的两个内角的和是解题的关键.4.(2022·辽宁沈阳·九年级期中)阅读下面的材料,并解决问题(1)已知在△ABC中,∠A=60°,图1-3的△ABC的内角平分线或外角平分线交于点O,请直接写出下列角度的度数,如图1,∠O=;如图2,∠O=;如图3,∠O=;(2)如图4,点O是△ABC的两条内角平分线的交点,求证:∠O=90°+12∠A(3)如图5,在△ABC中,∠ABC的三等分线分别与∠ACB的平分线交于点O1O2,若∠1=115°,∠2=135°,求∠A的度数.【答案】(1)120°,30°,60°(2)见解析(3)70°【分析】(1)由∠A的度数,在△ABC中,可得∠ABC与∠ACB的和,又BO、CO是内角平分线或外角平分线,利用角平分线的定义及三角形内角和定理、三角形的外角性质进而可求得答案;(2)由∠A的度数,在△ABC中,可得∠ABC与∠ACB的和,又BO、CO是角平分线,∴∠ABC+∠ACB=3α+2β=60°+50°=110°,∴∠A=70°.【点睛】本题主要考查了三角形内角和定理,角平分线的定义,三角形外角的性质等知识,熟练掌握三角形内角和定理,以及基本图形是解题的关键.模型2.角平分线加平行线等腰现(角平分线+平行线)【模型解读】1)过角平分线上一点作角的一边的平行线,构造等腰三角形;2)有角平分线时,过角一边上的点作角平分线的平行线,交角的另一边的直线于一点,也可构造等腰三角形。
初中数学经典几何模型04-角平分线模型在三角形中的应用(含答案)

初中数学经典几何模型专题04 角平分线模型在三角形中的应用在初中几何证明中,常会遇到与角平分线有关的问题。
不少同学遇到这类问题时,不清楚应该怎样去作辅助线。
实际上这类问题是有章可循的,其策略是:明确辅助线作用,记清相应模型辅助线作法,理解作辅助线以后的目的。
能做到这三点,就能在解题时得心应手。
【知识总结】【模型】一、角平分线垂两边 角平分线+外垂直当已知条件中出现OP 为OAB ∠的角平分线、PM OA ⊥于点M 时,辅助线的作法大都为过点P 作PN OB ⊥即可.即有PM PN =、OMP ∆≌ONP ∆等,利用相关结论解决问题.【模型】二、角平分线垂中间 角平分线+内垂直当已知条件中出现OP 为AOB ∠的角平分线,PM OP ⊥于点P 时,辅助线的作法大都为延长MP 交OB 于点N 即可.即有OMN ∆是等腰三角形、OP 是三线等,利用相关结论解决问题.【模型】三、角平分线构造轴对称 角平分线+截线段等当已知条件中出现OP 为AOB ∠的角平分线、PM 不具备特殊位置时,辅助线的作法大都为在OB 上截取ON OM =,连结PN 即可.即有OMP ∆≌ONP ∆,利用相关结论解决问题.【模型】四、角平分线加平行线等腰现 角平分线+平行线当已知条件中出现OP 为AOB ∠的角平分线,点P 角平分线上任一点时,辅助线的作法大都为过点P 作PM //OB 或PM //OA 即可.即有OMP ∆是等腰三角形,利用相关结论解决问题.1、如图, ABN CBN ∠=∠, P 为BN 上的一点,并且PD BC ⊥于点D ,2AB BC BD +=,求证:180BAP BCP ∠+∠=︒.2、如图,在ABC ∆中,CD 是ACB ∠的平分线,AD CD ⊥于点D ,DE //BC 交AB 于点E ,求证:EA EB =.3、已知:如图7,2,,AB AC BAD CAD DA DB =∠=∠=,求证:DC AC ⊥.4、如图,AB //CD ,AE 、DE 分别平分BAD ∠和ADC ∠.探究:在线段AD 上是否存在点M ,使得2AD EM =.【基础训练】1、如图所示,在四边形ABCD中,DC//AB,∠DAB=90°,AC⊥BC,AC=BC,∠ABC的平分线交AD,AC于点E、F,则BFEF的值是___________.2、如图,D是△ABC的BC边的中点,AE平分∠BAC,AE⊥CE于点E,且AB =10,AC =16,则DE的长度为______3、如图所示,在△ABC中,BC=6,E、F分别是AB、AC的中点,动点P在射线EF上,BP交CE于D,∠CBP的平分线交CE于Q,当CQ =13CE时,EP+BP =________.【巩固提升】1、如图,F,G是OA上两点,M,N是OB上两点,且FG =MN,S△PFG=S△PMN,试问点P是否在∠AOB 的平分线上?2、已知:在△ABC中,∠B的平分线和外角∠ACE的平分线相交于D,DG//BC,交AC于F,交AB于G,求证:GF =BG CF.3、在四边形ABCD中,∠ABC是钝角,∠ABC+∠ADC =180°,对角线AC平分∠BAD.(1)求证:BC =CD;(2)若AB +AD =AC,求∠BCD的度数;4、如图,在△ABC中,D、E、F分别为三边的中点,G点在边AB上,△BDG与四边形ACDG的周长相等,设BC =a、AC =b、AB =c.(1)求线段BG的长(2)求证:DG平分∠EDF.5、如图,BA⊥MN,垂足为A,BA=4,点P是射线AN上的一个动点(点P与点A不重合),∠B PC=∠BP A,BC⊥BP,过点C作CD⊥MN,垂足为D,设AP=x.CD的长度是否随着x的变化而变化?若变化,请用含x的代数式表示CD的长度;若不变化,请求出线段CD的长度.6、已知:平面直角坐标系中,四边形OABC的顶点分别为0(0,0)、A(5,0)、B(m,2)、C(m-5,2).(1)问:是否存在这样的m,使得在边BC上总存在点P,使∠OP A=90°?若存在,求出m的取值范围;若不存在,请说明理由.(2)当∠AOC与∠OAB的平分线的交点Q在边BC上时,求m的值.7、我们把由不平行于底边的直线截等腰三角形的两腰所得的四边形称为“准等腰梯形”。
中考数学常见几何模型角平分线的基本模型(一)全等类

专题07 角平分线的重要模型(一)全等类角平分线在中考数学中都占据着重要的地位,角平分线常作为压轴题中的常考知识点,需要掌握其各大模型及相应的辅助线作法,且辅助线是大部分学生学习几何内容中的弱点,本专题就角平分线的全等类模型作相应的总结,需学生反复掌握。
模型1.角平分线构造轴对称模型(角平分线+截线段等)【模型解读与图示】已知如图1,OP为AOB∠的角平分线、PM不具备特殊位置时,辅助线的作法大都为在OB上截取ON OM=,连结PN即可.即有OMP∆≌ONP∆,利用相关结论解决问题.图1 图21.(2022·湖北十堰·九年级期末)在△ABC中,△ACB=2△B,如图①,当△C=90°,AD为△BAC 的角平分线时,在AB上截取AE=AC,连结DE,易证AB=AC+CD.(1)如图②,当△C≠90°,AD为△BAC的角平分线时,线段AB,AC,CD又有怎样的数量关系?不需要证明,请直接写出你的猜想;(2)如图③,当AD为△ABC的外角平分线时,线段AB,AC,CD又有怎样的数量关系?请写出你的猜想,并对你的猜想给予证明.【答案】(1)AB AC CD=+;证明见解析;(2)AB AC CD+=;证明见解析.【分析】(1)首先在AB上截取AE=AC,连接DE,易证△ADE△△ADC(SAS),则可得△AED=△C,ED=CD,又由△AED=△ACB,△ACB=2△B,所以△AED=2△B,即△B=△BDE,易证DE=CD,则可求得AB=AC+CD;(2)首先在BA的延长线上截取AE=AC,连接ED,易证△EAD△△CAD,可得ED=CD,△AED =△ACD,又由△ACB=2△B,易证DE=EB,则可求得AC+AB=CD.【详解】(1)猜想:AB AC CD=+.AB∥CD⇒AB+CD=BCFDEBAC证明:如图②,在AB 上截取AE AC =,连结DE ,△AD 为ABC 的角平分线时,△BAD CAD ∠=∠,△AD AD =,△()SAS ADE ADC ≌△△, △AED C ∠=∠,ED CD =,△2ACB B ∠=∠,△2AED B ∠=∠.△B EDB ∠=∠,△EB ED =,△EB CD =,△AB AE DE AC CD =+=+.(2)猜想:AB AC CD +=.证明:在BA 的延长线上截取AE AC =,连结ED .△AD 平分FAC ∠,△EAD CAD ∠=∠.在EAD 与CAD 中,AE AC =,EAD CAD ∠=∠,AD AD =,△EAD CAD ≌△△.△ED CD =,AED ACD ∠=∠.△FED ACB ∠=∠.又2ACB B ∠=∠,FED B EDB ∠=∠+∠,EDB B ∠=∠.△EB ED =.△EA AB EB ED CD +===.△AC AB CD +=.【点睛】此题考查三角形综合题、全等三角形的判定与性质、等腰三角形的判定、角平分线的定义等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考常考题型.2.(2022·山东烟台·九年级期末)已知在ABC 中,满足2ACB B ∠=∠,(1)【问题解决】如图1,当90C ∠=︒,AD 为BAC ∠的角平分线时,在AB 上取一点E 使得AE AC =,连接DE ,求证:AB AC CD =+.(2)【问题拓展】如图2,当90C ∠≠︒,AD 为BAC ∠的角平分线时,在AB 上取一点E 使得AE AC =,连接DE ,(1)中的结论还成立吗?若成立,请你证明:若不成立,请说明理由.(3)【猜想证明】如图3,当AD 为ABC 的外角平分线时,在BA 的延长线上取一点E 使得AE AC =,连接DE ,线段AB 、AC 、CD 又有怎样的数量关系?请写出你的猜想,并对你的猜想给予证明. 【答案】(1)证明见解析(2)成立,证明见解析 (3)猜想AB AC CD +=,证明见解析【分析】(1)先根据SAS 定理证出AED ACD ≅,根据全等三角形的性质可得ED CD =,AED ACD ∠=∠,再根据三角形的外角性质可得45B BDE ∠=∠=︒,然后根据等腰三角形的判定可得EB ED =,从而可得EB CD =,最后根据线段和差、等量代换即可得证; (2)先根据SAS 定理证出AED ACD ≅,根据全等三角形的性质可得ED CD =,AED C ∠=∠,再根据三角形的外角性质可得B BDE ∠=∠,然后根据等腰三角形的判定可得EB ED =,从而可得EB CD =,最后根据线段和差、等量代换即可得证;(3)先根据SAS 定理证出AED ACD ≅,根据全等三角形的性质可得ED CD =,AED ACD ∠=∠,从而可得FED ACB ∠=∠,再根据三角形的外角性质可得B BDE ∠=∠,然后根据等腰三角形的判定可得EB ED =,从而可得EB CD =,最后根据线段和差、等量代换即可得证.(1)证明:△AD 为BAC ∠的角平分线,△EAD CAD ∠=∠,在AED 与ACD △中,AE AC EAD CAD AD AD =⎧⎪∠=∠⎨⎪=⎩,△()AED ACD SAS ≅,△ED CD =,AED ACD ∠=∠,又△90ACB ∠=︒,2ACB B ∠=∠,△45B ∠=︒,90AED ∠=︒,△45AED BDE B ∠=∠=∠-︒,△B BDE ∠=∠,△EB ED =,△EB CD =,△AB AE EB AC CD =+=+.(2)解:(1)中的结论还成立,证明如下:△AD 为BAC ∠的角平分线时,△EAD CAD ∠=∠,在AED 与ACD △中,AE AC EAD CAD AD AD =⎧⎪∠=∠⎨⎪=⎩,△()AED ACD SAS ≅,△AED C ∠=∠,ED CD =,△2ACB B ∠=∠,△2AED B ∠=∠,又△AED B EDB ∠=∠+∠,△B EDB ∠=∠,△EB ED =,△EB CD =,△AB AE EB AC CD =+=+.(3)解:猜想AB AC CD +=,证明如下:△AD 平分EAC ∠,△EAD CAD ∠=∠,在AED 与ACD △中,AE AC EAD CAD AD AD =⎧⎪∠=∠⎨⎪=⎩,△()AED ACD SAS ≅,△ED CD =,AED ACD ∠=∠,如图,△180180AED ACD ︒-∠=︒-∠,即FED ACB ∠=∠,△2ACB B ∠=∠,△2∠=∠,FED B又△FED B EDB∠=∠+∠,△EDB B∠=∠,△EB ED=,+===,△AB AE EB ED CD△AB AC CD+=.【点睛】本题主要考查了三角形全等的判定与性质、等腰三角形的判定,熟练掌握三角形全等的判定方法是解题关键.3.(2022·浙江·九年级期中)(1)如图1,在△ABC中,△ACB=2△B,△C=90°,AD为△BAC 的平分线交BC于D,求证:AB=AC+CD.(提示:在AB上截取AE=AC,连接DE)(2)如图2,当△C≠90°时,其他条件不变,线段AB、AC、CD又有怎样的数量关系,直接写出结果,不需要证明.(3)如图3,当△ACB≠90°,△ACB=2△B ,AD为△ABC的外角△CAF的平分线,交BC的延长线于点D,则线段AB、AC、CD又有怎样的数量关系?写出你的猜想,并加以证明.【答案】(1)见解析;(2)AB=AC+CD;(3)AB=CD﹣AC【分析】(1)在AB上截取AE=AC,连接DE,根据角平分线的定义得到△1=△2.推出△ACD△△AED (SAS).根据全等三角形的性质得到△AED=△C=90,CD=ED,根据已知条件得到△B=45°.求得△EDB=△B=45°.得到DE=BE,等量代换得到CD=BE.即可得到结论;(2)在AC取一点E使AB=AE,连接DE,易证△ABD△△AED,所以△B=△AED,BD=DE,又因为△B=2△C,所以△AED=2△C,因为△AED是△EDC的外角,所以△EDC=△C,所以ED=EC,BD=EC,进而可证明AB+BD=AE+EC=AC;(3)在AB的延长线AF上取一点E,使得AE=AC,连接DE.证明△ACD△△AED,根据全等三角形的性质得到DE=BE,BE=CD,即可得出结论.【详解】(1)证明:在AB上取一点E,使AE=AC△AD为△BAC的平分线△△BAD=△CAD.在△ACD和△AED中,AE ACBAD CADAD AD=⎧⎪∠=∠⎨⎪=⎩△△ACD△△AED(SAS).△△AED=△C=90°,CD=ED,又△△ACB=2△B,△C=90°,△△B=45°.△△EDB=△B=45°.△DE=BE,△CD=BE.△AB=AE+BE,△AB=AC+CD.(2)证明:在AB取一点E使AC=AE,在△ACD和△AED中,AC AEBAD EADAD AD===⎧⎪∠∠⎨⎪⎩,△△ACD△△AED,△△C=△AED,CD=DE,又△△C=2△B,△△AED=2△B,△△AED是△EDC的外角,△△EDB=△B,△ED=EB,△CD=EB,△AB=AC+CD;(3)猜想:AB=CD﹣AC证明:在BA的延长线上取一点E,使得AE=AC,连接DE,在△ACD和△AED中,AC AECAD EADAD AD=⎧⎪∠=∠⎨⎪=⎩,△△ACD△△AED(SAS),△△ACD=△AED,CD=DE,△△ACB=△FED,又△△ACB=2△B△△FED=2△B,又△△FED=△B+△EDB,△△EDB=△B,△DE=BE,△BE=CD,△AB=BE-AE△AB=CD﹣AC.【点睛】本题考查全等三角形的判定和性质,关于线段和差关系的证明,通常采用截长补短法.4.(2022·北京九年级专题练习)在四边形ABDE中,C是BD边的中点.(1)如图(1),若AC 平分BAE ∠,90ACE ∠=︒,则线段AE 、AB 、DE 的长度满足的数量关系为______;(直接写出答案)(2)如图(2),AC 平分BAE ∠,EC 平分AED ∠,若120ACE ∠=︒,则线段AB 、BD 、DE 、AE 的长度满足怎样的数量关系?写出结论并证明.【答案】(1)AE =AB +DE ;(2)AE =AB +DE +12BD ,证明见解析.【分析】(1)在AE 上取一点F ,使AF =AB ,由三角形全等的判定可证得△ACB ≌△ACF ,根据全等三角形的性质可得BC =FC ,∠ACB =∠ACF ,根据三角形全等的判定证得△CEF ≌△CED ,得到EF =ED ,再由线段的和差可以得出结论;(2)在AE 上取点F ,使AF =AB ,连结CF ,在AE 上取点G ,使EG =ED ,连结CG ,根据全等三角形的判定证得△ACB ≌△ACF 和△ECD ≌△ECG ,由全等三角形的性质证得CF =CG ,进而证得△CFG 是等边三角形,就有FG =CG =12BD ,从而可证得结论.【详解】解:(1)如图(1),在AE 上取一点F ,使AF =AB .∵AC 平分∠BAE ,∴∠BAC =∠FAC .在△ACB 和△ACF 中,AB AF BAC FAC AC AC ⎧⎪∠∠⎨⎪⎩===∴△ACB ≌△ACF (SAS ).∴BC =FC ,∠ACB =∠ACF .∵C 是BD 边的中点,∴BC =CD .∴CF =CD .∵∠ACE =90°,∴∠ACB +∠DCE =90°,∠ACF +∠ECF =90°.∴∠ECF =∠ECD .在△CEF 和△CED 中,CF CD ECF ECD CE CE ⎧⎪∠∠⎨⎪⎩===∴△CEF ≌△CED (SAS ).∴EF =ED .∵AE =AF +EF ,∴AE =AB +DE .故答案为:AE =AB +DE ;(2)AE =AB +DE +12BD .证明:如图(2),在AE 上取点F ,使AF =AB ,连结CF ,在AE 上取点G ,使EG =ED ,连结CG .∵C 是BD 边的中点,∴CB =CD =12BD .∵AC 平分∠BAE ,∴∠BAC =∠FAC . 在△ACB 和△ACF 中,AB AF BAC FAC AC AC ⎧⎪∠∠⎨⎪⎩===∴△ACB ≌△ACF (SAS ).∴CF =CB ,∠BCA =∠FCA .同理可证:△ECD ≌△ECG ∴CD =CG ,∠DCE =∠GCE .∵CB =CD ,∴CG =CF .∵∠ACE =120°,∴∠BCA +∠DCE =180°−120°=60°.∴∠FCA +∠GCE =60°.∴∠FCG =60°.∴△FGC 是等边三角形.∴FG =FC =12BD .∵AE =AF +EG +FG ,∴AE =AB +DE +12BD .【点睛】本题主要考查了全等三角形的判定与性质的运用,能熟练应用三角形全等的判定和性质是解决问题的关键.模型2.角平分线垂两边(角平分线+外垂直)【模型解读与图示】已知如图1,OP 为OAB ∠的角平分线、PM OA ⊥于点M 时,辅助线的作法大都为过点P 作PN OB ⊥即可.即有PM PN =、OMP ∆≌ONP ∆等,利用相关结论解决问题. 图1图2图3D B邻等对补模型:已知如图2,AP 是∠CAB 的角平分线,EP =DP辅助线:过点P 作PG ⊥AC 、PF ⊥AB结论:①︒=∠+∠180EPD BAC (D P E A 、、、四点共圆);②EG DF =;③DF AE AD 2+=1.(2022·北京·中考真题)如图,在ABC ∆中,AD 平分,.BAC DE AB ∠⊥若2,1,AC DE ==则ACD S ∆=____.【答案】1【分析】作DF AC ⊥于点F ,由角平分线的性质推出1DF DE ==,再利用三角形面积公式求解即可.【详解】解:如图,作DF AC ⊥于点F ,△AD 平分BAC ∠,DE AB ⊥,DF AC ⊥,△1DF DE ==, △1121122ACD S AC DF ∆=⋅=⨯⨯=.故答案为:1. 【点睛】本题考查角平分线的性质,通过作辅助线求出三角形ACD 中AC 边的高是解题的关键.2.(2022·山东泰安·中考真题)如图,△ABC 的外角∠ACD 的平分线CP 与内角∠ABC 的平分线BP 交于点P ,若∠BPC =40°,则∠CAP =( )A .40°B .45°C .50°D .60°【答案】C【分析】根据外角与内角性质得出∠BAC 的度数,再利用角平分线的性质以及直角三角形全等的判定,得出∠CAP =∠FAP ,即可得出答案.【详解】解:延长BA ,作PN ⊥BD ,PF ⊥BA ,PM ⊥AC ,设∠PCD =x °,∵CP 平分∠ACD ,∴∠ACP =∠PCD =x °,PM =PN ,∵BP 平分∠ABC ,∴∠ABP =∠PBC ,PF =PN ,∴PF =PM ,∵∠BPC =40°,∴∠ABP =∠PBC =∠PCD ﹣∠BPC =(x ﹣40)°,∴∠BAC =∠ACD ﹣∠ABC =2x °﹣(x °﹣40°)﹣(x °﹣40°)=80°,∴∠CAF =100°, 在Rt △PFA 和Rt △PMA 中,{PA PAPM PF ==,∴Rt △PFA ≌Rt △PMA (HL ),∴∠FAP =∠PAC =50°.故选C .【点睛】本题考查了角平分线的性质以及三角形外角的性质和直角三角全等的判定等知识,根据角平分线的性质得出PM =PN =PF 是解题的关键.3.(2022·江苏扬州·中考真题)如图,在ABCD 中,BE 、DG 分别平分ABC ADC ∠∠、,交AC 于点E G 、.(1)求证:,BE DG BE DG =∥;(2)过点E 作EF AB ⊥,垂足为F .若ABCD 的周长为56,6EF =,求ABC ∆的面积. 【答案】(1)见详解(2)84【分析】(1)由平行四边形的性质证()ABE CDG ASA ∆≅∆即可求证;(2)作EQ BC ⊥,由ΔΔΔABC ABE EBC S S S =+即可求解;(1)证明:在ABCD 中,△//AB CD ,△BAE DCG ∠=∠,△ABCD 的周长为56,AB BC +=BE 平分∠EQ EF ==ABC S S ∆∆=【点睛】本题主要考查平行四边形的性质、三角形的全等、角平分线的性质,掌握相关知识CD 交射线OA 于点F ,射线CE 交射线OB 于点G .(1)如图1,若CD △OA ,CE △OB ,请直接写出线段CF 与CG 的数量关系;(2)如图2,若△AOB =120°,△DCE =△AOC ,试判断线段CF 与CG 的数量关系,并说明理由.【答案】(1)CF=CG;(2)CF=CG,见解析【分析】(1)结论CF=CG,由角平分线性质定理即可判断.(2)结论:CF=CG,作CM△OA于M,CN△OB于N,证明△CMF△△CNG,利用全等三角形的性质即可解决问题.【详解】解:(1)结论:CF=CG;证明:△OP平分△AOB,CF△OA,CG△OB,△CF=CG(角平分线上的点到角两边的距离相等);(2)CF=CG.理由如下:如图,过点C作CM△OA,CN△OB,△OP平分△AOB,CM△OA,CN△OB,△AOB=120°,△CM=CN(角平分线上的点到角两边的距离相等),△△AOC=△BOC=60°(角平分线的性质),△△DCE=△AOC,△△AOC=△BOC=△DCE=60°,△△MCO=90°-60° =30°,△NCO=90°-60° =30°,△△MCN=30°+30°=60°,△△MCN=△DCE,△△MCF=△MCN-△DCN,△NCG=△DCE-△DCN,△△MCF=△NCG,在△MCF和△NCG中,CMF CNG CM CNMCF NCG ∠=∠⎧⎪=⎨⎪∠=∠⎩△△MCF △△NCG (ASA ),△CF =CG (全等三角形对应边相等).【点睛】本题考查三角形综合题、角平分线的性质、全等三角形的判定和性质,解题的关键是掌握角平分线的性质的应用,熟练证明三角形全等.模型3.角平分线垂中间(角平分线+内垂直)【模型解读与图示】已知如图1,OP 为AOB ∠的角平分线,PM OP ⊥于点P 时,辅助线的作法大都为延长MP 交OB 于点N 即可。
初三-几何问题之角平分线题型

学员编号: 年 级:初三 课 时 数: 3 学员姓名: 辅导科目:数学 学科教师: 授课类型 T —同步讲解C —专题 T —能力提升 星 级★★★★★★★★教学目标1.掌握角平分线的性质和判定;2.综合应用角的平分线的性质和判定解决相关问题;3。
综合应用垂直平分线、等腰三角形、四边形等知识解决相关问题; 4.学习分析问题、解决问题的能力。
授课时间教学内容——几何问题之角平分线题型1。
掌握角平分线的性质和判定;2.综合应用角的平分线的性质和判定解决相关问题;3。
综合应用垂直平分线、等腰三角形、四边形等知识解决相关问题; 4.学习分析问题、解决问题的能力。
知识结构一.知识要点详解:1。
角平分线的性质定理:(1)角平分线的性质定理:角平分线上的点到这个角的两边的距离相等。
(2)定理的数学表示:如图1,已知OE 是AOB ∠的平分线,F 是OE 上一点,若 CF OA ⊥于点C ,DF OB ⊥于点D ,则CF DF =。
(3)定理的作用:①证明两条线段相等;②用于几何作图问题; (4)角是一个轴对称图形,它的对称轴是角平分线所在的直线。
1.已知角平分线,构造全等三角形;2.已知一个点到角的一边的距离,过这个点作另一边的垂线段; 3。
已知角平分线和其上面的一点,过这一点作角的两边的垂线段。
DFEAB CNP E DCBAACEDB P三。
角平分线性质定理之联想:1.由角平分线的性质联想两线段相等; 2。
由角平分线的轴对称性构造全等三角形;3。
过角平分线上一点作一边的平行线,构成等腰三角形。
模块一。
角平分线的对称性:基本图形例1.如图,AD 是ABC ∆的角平分线,DE AB ⊥,DF AC ⊥,垂足分别是E F ,。
连接EF ,交AD 于点G 。
说出AD 与EF 之间有什么关系?证明你的结论。
例题1【分析】:两条线段之间的关系有长度和位置两种关系,因此我们可以从这两方面去猜测判断.角是以其平分线为对称轴的轴对称图形,此题可以利用这一点进行判断. 【解答】:EF AD ⊥,且EG FG =证明:AD 平分BAC ∠DE AB ⊥,DF AC ⊥,垂足分别是E F ,∴DE DF =在Rt DEA ∆和Rt DFA ∆中:DE DFAD AD =⎧⎨=⎩∴Rt DEA Rt DFA ∆≅∆ ∴ADE ADF ∠=∠ 在DGE ∆和DGF ∆中:DE DF GDE GDF DG DG =⎧⎪∠=∠⎨⎪=⎩∴DGE DGF ∆≅∆∴EG FG =,90DGE DGF ∠=∠= ∴EF AD ⊥,且EG FG =.►点评:通过此题我们知道,证明两条线段相等,除了利用全等三角形的性质外,还可以利用角平分线的性质。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
学员编号:年级:初三课时数: 3学员姓名:辅导科目:数学学科教师:授课类型T-同步讲解C-专题T-能力提升星级★★★★★★★★教学目标1.掌握角平分线的性质和判定;2.综合应用角的平分线的性质和判定解决相关问题;3.综合应用垂直平分线、等腰三角形、四边形等知识解决相关问题;4.学习分析问题、解决问题的能力。
授课时间教学内容——几何问题之角平分线题型1.掌握角平分线的性质和判定;2.综合应用角的平分线的性质和判定解决相关问题;3.综合应用垂直平分线、等腰三角形、四边形等知识解决相关问题;4.学习分析问题、解决问题的能力。
知识结构一.知识要点详解:1.角平分线的性质定理:(1)角平分线的性质定理:角平分线上的点到这个角的两边的距离相等。
(2)定理的数学表示:如图1,已知OE是AOB∠的平分线,F是OE上一点,若CF OA⊥于点C,DF OB⊥于点D,则CF DF=。
(3)定理的作用:①证明两条线段相等;②用于几何作图问题;(4)角是一个轴对称图形,它的对称轴是角平分线所在的直线。
O图1CDB A EFO图2CDBAF 图3DE FRIP Q ABC2.角平分线性质定理的逆定理:(1)角平分线性质定理的逆定理:在角的内部,且到角的两边距离相等的点在这个角的角平分线上。
(2)定理的数学表示:如图2,已知点F 在AOB ∠的内部,且FC OA ⊥于C ,FD OB ⊥于D ,若FD FC =,则点F 在AOB ∠的平分线上。
(3)定理的作用:用于证明两个角相等或证明一条射线是一个角的角平分线。
(4)注意角平分线的性质定理与逆定理的区别和联系。
3.关于三角形三条角平分线的定理: (1)关于三角形三条角平分线交点的定理:三角形三条角平分线相交于一点,并且这一点到三边的距离相等。
定理的数学表示:如图3,如果AP 、BQ 、CR 分别是ABC ∆的内角BAC ∠、ABC ∠、ACB ∠的平分线,那么:① AP 、BQ 、CR 相交于一点I ;② 若ID 、IE 、IF 分别垂直于BC 、CA 、AB 于点D 、E 、F ,则DI EI FI ==。
定理的作用:①用于证明三角形内的线段相等;②用于实际中的几何作图问题。
(2)三角形三条角平分线的交点位置与三角形形状的关系:三角形三个内角角平分线的交点一定在三角形的内部。
4.关于线段的垂直平分线和角平分线的作图:(1)会作已知线段的垂直平分线; (2)会作已知角的角平分线; (3)会作与线段垂直平分线和角平分线有关的简单综合问题的图形.二.角平分线定理使用中的几种辅助线作法:(如下图示)1.已知角平分线,构造全等三角形;2.已知一个点到角的一边的距离,过这个点作另一边的垂线段;3.已知角平分线和其上面的一点,过这一点作角的两边的垂线段。
DFEAB CNP E DCBAACEDB P三.角平分线性质定理之联想:1.由角平分线的性质联想两线段相等;2.由角平分线的轴对称性构造全等三角形;3.过角平分线上一点作一边的平行线,构成等腰三角形。
模块一.角平分线的对称性:基本图形例1.如图,AD 是ABC ∆的角平分线,DE AB ⊥,DF AC ⊥,垂足分别是E F ,。
连接EF ,交AD 于点G 。
说出AD 与EF 之间有什么关系?证明你的结论。
例题1【分析】:两条线段之间的关系有长度和位置两种关系,因此我们可以从这两方面去猜测判断。
角是以其平分线为对称轴的轴对称图形,此题可以利用这一点进行判断。
【解答】:EF AD ⊥,且EG FG =证明: AD 平分BAC ∠DE AB ⊥,DF AC ⊥,垂足分别是E F , ∴DE DF =在Rt DEA ∆和Rt DFA ∆中: DE DFAD AD =⎧⎨=⎩∴Rt DEA Rt DFA ∆≅∆ ∴ADE ADF ∠=∠在DGE ∆和DGF ∆中: DE DF GDE GDF DG DG =⎧⎪∠=∠⎨⎪=⎩∴DGE DGF ∆≅∆∴EG FG =,90DGE DGF ∠=∠= ∴EF AD ⊥,且EG FG =。
►点评:通过此题我们知道,证明两条线段相等,除了利用全等三角形的性质外,还可以利用角平分线的性质。
这样我们又多了一种证明线段相等的办法。
在利用角平分线的性质时,“角平分线”和“两个垂直”这两个条件缺一不可。
如图,BE CF =,DF AC ⊥于F ,DE AB ⊥于E ,BF 和CE 交于点D 。
求证:AD 平分BAC ∠。
例题2【分析】:要证AD 平分BAC ∠,已知条件中已经有两个垂直,即已经有点到角的两边的距离了,只要证明这两个距离相等即可。
而要证明两条线段相等,可利用全等三角形的性质来证明。
【证明】: DF AC ⊥于F ,DE AB ⊥于E ∴90DEB DFC ∠=∠= 在BDE ∆和CDF ∆中DEB DFC BDE CDF BE CF ∠=∠⎧⎪∠=∠⎨⎪=⎩∴BDE CDF ∆≅∆ ∴DE DF =又 DF AC ⊥于F ,DE AB ⊥于E ∴AD 平分BAC ∠。
►点评:判定角的平分线时若题目中只给出一个条件DE DF =或DF AC ⊥,DE AB ⊥,那么得出AD 平分BAC ∠这一结论是错误的。
例3.如图,在ABC ∆中,90C ∠= ,AD 平分BAC ∠,DE AB ⊥于E ,F 在AC 上,BD DF =。
求证:CF EB =。
【分析】:由已知条件很容易得到DC DE =;要证明CF EB =,只要证明其所在三角形全等即可,再由此去找全等条件。
【证明】:AD 平分BAC ∠,90C ∠= ,DE AB ⊥∴DC DE =在Rt FCD ∆与Rt BED ∆中例题3DC DEDF BD =⎧⎨=⎩∴Rt FCD Rt BED ∆≅∆ ∴CF EB =。
►点评:掌握角平分线的性质和判定固然重要,但学会分析题目所给条件更是解决问题的关键。
1.如图,12∠=∠,PD OA ⊥于D ,PE OB ⊥于E ,下列结论中错误的是(D ) ().A PD PE = ().B OD OE = ().C DPO EPO ∠=∠ ().C PD OD =2.如图,ABC ∆中,120ABC ∠= ,26C ∠=,且DE AB ⊥,DF AC ⊥,DE DF =求ADC ∠的度数。
1373.已知:12∠=∠,34∠=∠,求证:AP 平分BAC ∠。
【提示】过点P 作PE AB ⊥、PF AC ⊥,利用角平分线性质可得PE PF =。
4.如图,D 是ABC ∆的外角ACE ∠的平分线上一点,DF AC ⊥于F ,DE BC ⊥于E ,且交BC 的延长线于E 。
求证:CE CF =。
【证明】CD 是ACE ∠的平分线,DF AC ⊥于F ,DE BC ⊥于E∴90DEC DFC ∠=∠= ,DE DF = 在Rt DEC ∆和Rt DFC ∆中 DC DCDE DF =⎧⎨=⎩∴Rt DEC Rt DFC ∆≅∆ ∴CE CF =5.如图,在ABC ∆中,D 为BC 的中点,DE BC ⊥交BAC ∠的平分线AE 于E , EF AB ⊥于F ,EG AC ⊥交AC 延长线于G 。
求证:BF CG =\【证明】连接BE 、EC ,由DE BC ⊥,BD DC =,∴BE EC =,AE •平分BAC ∠,EF AB ⊥,EG AC ⊥, ∴EF EG =∴Rt BFE Rt CGE ∆∆≌,∴BF CG =6.如图,AB //CD ,90B ∠= ,E 是BC 的中点,DE 平分ADC ∠。
求证:AE 平分DAB ∠。
【证明】:过点E 作EF AD ⊥于FDE 平分ADC ∠,EC DC ⊥,EF FD ⊥∴CE EF = 又 CE BE = ∴EF BE =又 EF AF ⊥,BE AB ⊥∴AE 平分DAB ∠。
——角平分线性质定理的逆定理如图,已知在ABC ∆中,BD DC =,12∠=∠。
求证:AD 平分BAC ∠。
【分析】:有两种方法证明AD 平分BAC ∠:一是直接利用定义证明BAD CAD ∠=∠;二是利用角平分线的判定,证明点D 到角的两边距离相等。
仔细观察,前者需要证明三角形全等,但此题使用全等条件中的“边边角”,无法证明两个三角形全等。
后者通过作垂线构造出三角形,其条件足以证明两个三角形全等。
【证明】:过点D 作DE AB ⊥于E ,DF AC ⊥于F ∴90BED CFD ∠=∠=在BDE ∆与CDF ∆中: 12BED CFDBD CD ∠=∠⎧⎪∠=∠⎨⎪=⎩∴BDE CDF ∆≅∆ ∴DE DF =例题4又 DE AB ⊥于E ,DF AC ⊥于F ∴AD 平分BAC ∠。
►点评:1.当题目中有角平分线这一条件时,解题时常过角平分线上的点向角的两边作垂线;当有垂线这一条件时,常作辅助线得到角的平分线;2.用角平分线证明线段相等或角相等时,常常与证明三角形全等配合使用,证明时要先观察需证明的线段或角(或通过等量代换得到的线段或角)在哪两个可能全等的三角形中。
如图,已知在四边形ABCD 中,180B D ∠+∠= ,AC 平分BAD ∠,CE AD ⊥,E 为垂足。
求证:2AB AD AE +=。
【证明】:延长AB ,过C 作CH AB ⊥,H 为垂足AC 平分BAD ∠,且CE AD ⊥,CH AB ⊥∴CH CE =又 190HCA ∠+∠= ,290ECA ∠+∠= ,12∠=∠ ∴HCA ECA ∠=∠在ACH ∆与ACE ∆中: 90HCA ECAH AEC AC AC ∠=∠⎧⎪∠=∠=⎨⎪=⎩∴ACH ACE ∆≅∆ ∴AH AE =又 180ABC HBC ∠+∠= ,180ABC D ∠+∠= ∴HBC D ∠=∠在Rt BHC ∆与Rt DEC ∆中, 90HBC D BHC DEC HC EC ∠=∠⎧⎪∠=∠=⎨⎪=⎩∴Rt BHC Rt DEC ∆≅∆ ∴HB DE =∴AB AD AB AE ED +=++AB AE BH =++AH AE =+2AE = ∴2AB AD AE +=例题5如图1,Rt ABC ∆中,90ACB ∠=,CD AB ⊥,垂足为D 。
AF 平分CAB ∠,交CD 于点E ,交CB 于点F 。
(1)求证:CE CF =。
(2)将图2中的ADE ∆沿AB 向右平移到'''A D E ∆的位置,使点'E 落在BC 边上,其它条件不变,如图2所示。
试猜想:'BE 与CF 有怎样的数量关系?请证明你的结论。
图1E FD AC图2G E'D'E FDACA'B【解析】(1)证明:,90.90,90,90.CD AB ADC ACB CAF CFA DAE AED ⊥∴∠=∠=∴∠+∠=∠+∠=AF 平分CAB ∠....CAF DAE CFA AED CEF CE CF ∴∠=∠∴∠=∠=∠∴=(2)解:'BE CF =.证明:如图2,过点E 作EG AC ⊥于点G .又AF 平分CAB ∠,ED AB ⊥,ED EG ∴=. 由平移的性质可知:''D E DE =,''D E GE ∴=. 90ACB ∠=,90ACD DCB ∴∠+∠= .CD AB ⊥ 于.90.D B DCB ∴∠+∠= .ACD B ∴∠=∠在Rt CEG ∆与''Rt BE D ∆中,''''''',,,..GCE B CGE BD E EG E D CEG BE D CE BE ∠=∠∠=∠=∴∆≅∆∴=由(1)可知CE CF =,例题6'CF BE =.(1)如图1所示,在ABC ∆中,AD 是BAC ∆的外角平分线,P 是AD 上异于点A 的任意一点,试比较PB PC +与AB AC +的大小,并说明理由。
