线性代数厦门大学网络教育

合集下载

厦大《高代》讲义第6章+特征值

3. 对每个特征值0, 求齐次线性方程组 (0In A)X 0
的基础解系, Xs. 则k1 X1 +
k即2X20+的…特+征k子sX空s,即间是V对0的应基于, 特X1征, X值2, …λ0 ,
的全部特征向量, 其中ki为K上不全为零的数.
厦门大学数学科学学院网址:
• 掌握复数域上的矩阵可以相似于上三角矩阵并应用于讨论问题;
• 掌握判断和计算特征值和特征向量的方法; • 注意矩阵与线性变换的对应结论; • 注意特征值的概念与数域有关.
厦门大学数学科学学院网址:
IP: http://59.77.1.116
特征值和特征向量_1
厦门大学数学科学学院网址:
IP: http://59.77.1.116
例子
例5:设A Knn , g( x) K[x],
(1) 若是A的特征值, 则 g( )是 g( A)的特征值.
(2) 若1, 2 , ..., n是A的全部特征值, 则g(1 ),
厦门大学数学科学学院网址:
IP: http://59.77.1.116
特征值和特征向量_2
定义: 设λ是的一个特征值, 则 V { V | ( ) }
是V的子空间, 且是称为子空间, 称为的
属于特征值λ的特征子空间.
注: 设α是的关于λ的特征向量, β是的关于
IP: http://59.77.1.116
例子
1
例2:
求
a
b
的特征值与特征向量,
其中
d
a d,b 0,a 1,d 1.
3 1 1
例3:
求
2
2
1的特征值与特征向量.

《线性代数》模拟试卷(A)卷

厦门大学网络教育2008-2009学年第一学期《线性代数》模拟试卷（ A ）卷一、单项选择题(每小题3分，共24分).1. 若111221226a a a a =，则121122212020021a a a a --的值为( ). A ．12； B. －12； C. 18； D. 0. 2. 设A B 、为同阶方阵，则下面各项正确的是( ).A.若0AB =, 则0A =或0B =；B.若0AB =，则0A =或0B =；C.22()()A B A B A B -=-+；D.若A B 、均可逆，则111()AB A B ---=.3. 若方程组12312302403690x t x x ⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪= ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭　的基础解系含有两个解向量，则 t =( ). A ．2； B ．4； C ．6； D ．8.4. 已知方程组A x b =对应的齐次方程组为0Ax =，则下列命题正确的是( ).A ．若0Ax =只有零解，则Ax b =一定有唯一解；B ．若0Ax =有非零解，则Ax b =一定有无穷解；C ．若Ax b =有无穷解，则0Ax =一定有非零解；D ．若Ax b =有无穷解，则0Ax =一定只有零解.5. 设12, u u 是非齐次线性方程组Ax b =的两个解，则以下结论正确的是( ).A ．12u u +是Ax b =的解；B ．12u u -是Ax b =的解；C ．1ku 是Ax b =的解（1k ≠）；D ．12u u -是0Ax =的解. 6. 设123,,a a a 线性相关，则以下结论正确的是( ).A ．12,a a 一定线性相关；B ．13,a a 一定线性相关；C ．12,a a 一定线性无关；D ．存在不全为零的数123,,k k k ，使得1122330k a k a k a ++=.7. 若20000101A x ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦与200010001B ⎡⎤⎢⎥=⎢⎥⎢⎥-⎣⎦相似，则x =( ). A ．-1； B ．0； C ．1； D ．2.8. 二次型f(x 1,x 2,x 3)=32232221x x 12x 3x 3x +++是( ).A. 正定的；B. 半正定的；C. 负定的；D. 不定的.二、填空题(每小题4分，共24分)1. 设802020301A ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦，*A 为A 的伴随矩阵，则*A =_________. 2. 非齐次线性方程组m n A x b ⨯=有唯一解的充分必要条件是_________.3. 设方程组123131232 1 2 53(8)8x x x x x x x a x ++=⎧⎪+=⎨⎪+++=⎩，当a 取__________时，方程组无解.4. 设向量组1(1,3,)a k =-，2(1,0,0)a =，3(1,3,2)a =-线性相关，则k =_________.5. 二次型3231212322213214225),,(x x x x x tx x x x x x x f +-+++=为正定二次型，则t 的取值范围是_____________.6. 3阶方阵A 的特征值分别为1，-2，3，则21()A -的特征值为_________.三、计算题(共38分).1. (10分) 计算行列式 3112513420111533D ---=---.2. (10分) 求123221343A ⎛⎫ ⎪= ⎪ ⎪⎝⎭的逆矩阵1A -.3. (10分)求向量组)11,9,5,8(),2,1,1,3(),10,7,1,1(),1,1,1,2(4321=--=-==αααα的一个极大线性无关组，并将其余向量用此极大线性无关组线性表示.4. (8分)已知111131111A -⎡⎤⎢⎥=-⎢⎥⎢⎥⎣⎦，求A 的特征值. 四、证明题(每小题7分，共14分).1. 设列矩阵12(,,,)T n X x x x = 满足1T X X =，E 为n 阶单位阵，2T H E XX =-，证明: H 是对称阵，且T HH E =.2. 证明二次型22256444f x y z xy xz =---++是负定的.答案：一．1．A 1211121112111112222122212221212220220(1)22122021a a aa a a a a a a a a a a a a =-=-==--2. B 由矩阵的理论可得选项B3. C 基础解系含有两个解向量3()2()1r A r A ⇒-=⇒=,12312324006369000A t t ⎛⎫⎛⎫ ⎪ ⎪=→- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭,6t =时，()1r A =4. C 当()()r A r A =时，Ax b =有解5. D 1212()2A u u Au Au b b b +=+=+=，因此12u u +不是Ax b =的解，下面的选项类似讨论6. D 由线性相关的定义可得选项D7. B 相似矩阵具有相同的特征值8．D f 的矩阵是100036063A ⎛⎫ ⎪= ⎪ ⎪⎝⎭，A 的各阶主子式为：1110a =>，103003=>，10003613366270063A ==⋅⋅-⋅=-<，因此f 为不定的二．1．16 8022016124301A ==-=， 33***416A A A E A AA A ====⇒=2. n A r =)( 由方程组解的理论可得3. 0 方程组无解可得()(,)r A r A b ≠11211121112110120111011153880223001a a a ⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥→--→-⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥+--⎣⎦⎣⎦⎣⎦,(,)3r A b =，当0a =时，()2r A =。

《线性代数》复习题B

厦门大学网络教育2012-2013学年第一学期《线性代数》课程复习题（ B ）一、选择题1．设行列式 111222333a b c a b c d a b c =，则111111222222333333223223223c b c a b c c b c a b c c b c a b c ++++++=+++（）。

A ．2d -； B ．d -； C ．d ； D ．2d 。

1．B 。

解：由行列式的性质可知111111111111222222222222333333333333223223223c b c a b c c b a a b c c b c a b c c b a a b c d c b c a b c c b a a b c ++++++==-=-+++。

2．已知A 为n 阶非零方阵，E 为n 阶单位矩阵，若3A O =，则（）。

A ．A E +不可逆，E A -不可逆；B ．A E -不可逆，A E +可逆；C ．A E +可逆，E A -可逆；D ．AE +不可逆，E A -可逆。

2．C 。

解：由于23()()E A E A A E A E -++=-=，23()()E A E A A E A E +-+=+=，因此E A +，E A -均可逆，故选C 。

3．向量1α，2α，3α线性无关，则下列向量组线性相关的是（）。

A ．12αα+，23αα+，31αα+； B ．1α，12αα+，123ααα++； C ．12αα-，23αα-，31αα-； D ．12αα+，232αα+，313αα+。

3．C ．解：显然有1223311()1()1()0αααααα-+-+-=，所以12αα-，23αα-，31αα-线性相关，故选C 。

4．若3阶方阵2E A -及E A +，3A E -都不可逆，则A 的特征多项式中常数项为（）。

A ．23； B ．2 ； C ．23-； D ．43。

厦门大学线代期末试题及答案

一．（填空题（每小题4分，共20分）1．令 ()()1,0,3,5,2,8,6,9,TTA B ==-则T A B =_______， T AB =______________.2．若三元非齐次线性方程组的系数矩阵的秩为2，123,,βββ是它的三个解向量，且12(2,6,3),T ββ+=-23(6,8,5),T ββ+=-则该线性方程组的通解是__________.3. 设123625t A t t ⎛⎫⎪=- ⎪ ⎪-⎝⎭的行向量线性相关，则实数t 满足的条件是 _________.4．令ii A 是三阶矩阵A 的元素ii a 的代数余子式（i =1，2，3），若A 的特征值为3，4，5，则112233A A A ++=__________.5．若101020105A c c ⎛⎫ ⎪=+ ⎪ ⎪-⎝⎭是正定矩阵，则c 的取值范围为 ___________.二．选择题（每小题3分，共15分）1. 设A 、B 均为n 阶正交矩阵，则____________. （1）A+B 为正交矩阵（2）A-B 为正交矩阵（3） B AB 为正交矩阵（4）k AB 为正交矩阵(k >0为实数)厦门大学2009级《线性代数A 》课程试卷学院＿＿＿年级＿＿姓名＿＿＿＿学号＿＿＿＿主考教师：试卷类型：（A 卷） 2010.06.132．设A 为m 阶可逆矩阵，B 为n 阶可逆矩阵，则可逆分块矩阵 OA DB O ⎛⎫= ⎪⎝⎭的逆矩阵是____________.（1）11A O O B --⎛⎫⎪⎝⎭ （2）11O B A O --⎛⎫⎪⎝⎭ （3） 11B O OA --⎛⎫⎪⎝⎭ （4）11O A BO --⎛⎫ ⎪⎝⎭3．设α与β是线性无关的单位向量，则α与β的内积必 ____________.（1） >0 （2）<0 （3）>1 （4）<14.设A 为n 阶可逆矩阵，1*,,T A A A -分别是A 的转置矩阵，逆矩阵和伴随矩阵，若ξ是A 的特征向量，则下列命题中的不正确的是________.（1）ξ是T A 的特征向量（2）2ξ是1A -的特征向量（3）3ξ是*A 的特征向量（4） 4ξ是kA 的特征向量（k 为常数）5.设222623222,000222000A B ⎛⎫⎛⎫⎪ ⎪== ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭，则____ ____. （1）A 与B 是相似的且是合同的（2）A 与B 是相似的但不是合同的（3）A 与B 不是相似的但是合同的（4）A 与B 不是相似的也不是合同的三．（15分）试求五元齐次线性方程组123451234512345330,30,0x x x x x x x x x x x x x x x ++++=⎧⎪-++-+=⎨⎪+++-=⎩的解空间V(作为5R 的子空间)的一组规范（标准）正交基。

线性代数教学探讨

中国科教创新导刊I 中国科教创新导刊2008N O .36C hi na Educa t i on I nnov at i on H er al d 教育教学方法同微积分一样,线性代数是一门传统的数学课程,很多领域都有它的足迹,特别是随着计算机技术的飞速发展,线性代数对于科技人员已经是必不可少的。

但是线性代数课程内容抽象、概念多、定理多、证明方法独特,学生不易接受。

而且线性代数教材多是基于理论的准确和证明的严格,以及知识内容的相对独立性来编写的,要学好它并不太容易。

在教学过程中,笔者经常思考和探索如何教好这门课程。

下面谈谈笔者在线性代数教学中的一些体会。

1“交流”有利于提高学习成绩这里的“交流”包含三个方面:第一,教师应主动跟学生交流;第二,教师应努力调动气氛,使学生之间乐于交流;第三,教师之间经常交流可以促进教学水平的提高。

先谈谈教师跟学生的交流。

我们都知道,教师与学生相处是否融洽对学生的学习成绩有很大影响,而这主要取决于教师的表现。

一般来说,学生都是很乐意跟老师做好朋友的,教师如果能主动亲近学生,学生学习起来就会配合多了。

教师应鼓励学生多问问题,在答疑的时候,也可以在下课时间主动走到学生中去,找他们聊聊天,多了解下他们最近的学习情况,哪些知识点好学,哪些比较困难不好理解等等。

根据这些信息,教师可以相应地调整教学内容和进度,重点讲解那些“拦路虎”,不必浪费太多时间在简单的知识点上面。

特别地,面对那些“后进”学生,教师要努力发现他们的优点,多给他们一些赞美,态度一定要诚恳,只要他们有进步就要及时肯定,只有让他们自信起来,他们才会乐于读书,学习成绩才有可能提高。

而对于那些学有余力的“好学生”,教师可以鼓励他们站在更高些,看的更远些。

除了课下的交流,教师在课上跟学生的交流更加重要。

“满堂灌”、“填鸭式”教学模式不应该出现在大学课堂上,尤其是像线性代数这种抽象的理论课程。

教师应采取启发式、问题式教学模式,通过在引导、解惑和练习训练上下功夫,激发学生的学习兴趣,为学生创造充足的自主学习时间,调动学生自主学习的能动性,从而实现教学任务堂堂清。

厦门大学网络教育第一学期考试真题线性代数

1.下列排列中，（）是四级奇排列。

A 43212.若（-1）。

是五阶行列式【。

】的一项，则k,l之值及该项符号为（）B k=2,l=3,符号为负3.行列式【k-1 2。

】的充分必要条件是（）C k不等于-1且k不等于34.若行列式D=【a11 a12 a13。

】=M不等于0，则D1=【2a11 2a12 2a13。

】=（）C 8M5.行列式【0111】101111011110 =（）D -36.当a=（）时，行列式【-1 a 2…】=0B 17.如果行列式【a11 a12 a13 …】=d 则【3a31 3a32 3a33 …】=()B 6d8.当a=()时，行列式【a 1 1 …】=0A 19.行列式【125 64 27 8 。

】的值为（）A 1210.行列式【a 0 0 b …】中g元素的代数余子式为（）B bde-bcf11.设f(x)= 【1 1 2 。

】则f(x)=0的根为（）C 1，-1，2，-212.行列式【0 a1 0…0。

】=()D (-1)n+1 a1 a2…an-1 an113.行列式【a 0 b 0…】=()D (ad-bc)(xv-yu)14.~不能取（）时，方程组~X1+X2+X3=0…只有0解B 215.若三阶行列式D的第三行的元素依次为1，2，3它们的余子式分别为2，3，4，则D=()B 816.设行列式【a11 a12 a13…】=1,则【2a11 3a11-4a12 a13…】=()D -81.线性方程组x1+x2=1…解的情况是（）A 无解2.若线性方程组AX=B的增广矩阵A经初等行变换化为A- 【1234…】,当~不等于（）时，此线性方程组有唯一解B 0，13.已知n元线性方程组AX=B,其增广矩阵为A ，当（）时，线性方程组有解。

C r(A)=r(A)4.设A为m*n矩阵，则齐次线性方程组AX=0仅有零解的充分条件是（）A A的列向量线性无关5.非齐次线性方程组AX=B中，A和增广矩阵A的秩都是4，A是4*6矩阵，则下列叙述正确的是（）B 方程组有无穷多组解6.设线性方程组AX=B有唯一解，则相应的齐次方程AX=0（）C 只有零解7.线性方程组AX=0只有零解，则AX=B(B不等于0)B 可能无解8.设有向量组a1,a2,a3和向量BA1=(1,1,1) a2=(1,1,0) a3= (1,0,0) B=(0,3,1)则向量B由向量a1,a2,a3的线性表示是（）A B=a1+2a2-3a39.向量组a1=（1.1.1）（0.2.5）（1.3.6）是（）A 线性相关10.下列向量组线性相关的是（）C （7.4.1），（-2.1.2），（3.6.5）11.向量组a1.a2…ar 线性无关的充要条件是（）B 向量线的秩等于它所含向量的个数12.向量组B1.B2…Bt可由a1.a2…as线性表示出，且B1.B2…Bt线性无关，则s与t的关系为（）D s≥t13.n个向量a1.a2…an线性无关，去掉一个向量an，则剩下的n-1个向量（）B 线性无关14.设向量组a1.a2…as(s≥2)线性无关，且可由向量组B1.B2…Bs线性表示，则以下结论中不能成立的是（）C 存在一个aj，向量组aj，b2…bs线性无关15.矩阵【1 0 1 0 0…】的秩为（）A 516.向量组a1.a2…as（s≥2）线性无关的充分必要条件是（）C a1.a2…as每一个向量均不可由其余向量线性表示17.若线性方程组的增广矩阵为A=【1.~.2】则~=（）时，线性方程组有无穷多解。

厦门大学工商企业管理专业都学什么课程

厦门大学工商企业管理专业都学什么课程厦门大简称厦大(XMU)，由著名爱国华侨领袖陈嘉庚先生于1921年创办，是中国近代教育史上第一所华侨创办的大学，也是国家“211工程”和“985工程”重点建设的高水平大学。

今天店铺将在下文中为大家介绍厦门大学工商企业管理专业的课程，希望对大家有所帮助。

厦门大学工商企业管理专业介绍工商企业管理专业是自学考试学科调整后产生的新专业。

这一专业的设置是为了培养在社会主义市场经济条件下从事工商业及其他各类企业管理方面工作的专门人才。

经过专业学习，成绩合格者应系统地掌握现代管理理论、有广泛的知识。

熟悉各类管理的基本技能和科学方法，能够胜任企业管理工作。

厦门大学工商企业管理专业的培养目标为了满足工商企业管理专业培养目标的要求，选学工商管理专业的自考生应具有爱国主义和集体主义精神，有良好的道德情操，遵守法纪、法规，热爱并乐于从事各类管理工作，具有责任心。

工商管理专业专科层次的学习，以政治理论、经济理论。

基础课程和适用广泛的管理专业理论学习为主。

专科成绩合格者应能从事具有管理性质的基础工作和一般的经营活动。

工商管理专业本科层次的学习，是在专科知识的基础上，进一步扩展管理理论和管理知识的学习，增加中、高层次管理工作必须掌握的技能和方法，提高本科自考生的工作适应性。

厦门大学工商企业管理专业的课程设置厦门大学工商企业管理专业专科的课程03706 思想道德修养与法律基础 203707 毛泽东思想、邓小平理论和“三个代表”重要思想概论 400009 政治经济学(财经类) 604729 大学语文 400018 计算机应用基础 200019 计算机应用基础(实践) 200020 高等数学(一) 600041 基础会计学 500065 国民经济统计概论 600043 经济法概论(财经类) 4 00144 企业管理概论 500145 生产与作业管理 600058 市场营销学 500055 企业会计学 600146 中国税制 400147 人力资源管理(一) 600148 国际企业管理 6总学分 79厦门大学工商企业管理专业本科的课程03708 中国近现代史纲要03709 马克思主义基本原理概论 4 00015 英语(二)00016 日语(二) 三个语种任选一种00017 俄语(二)04183 概率论与数理统计(经管类) 5 04184 线性代数(经管类) 400051 管理系统中计算机应用 3 00052 管理系统中计算机应用(实践) 1 00054 管理学原理 600067 财务管理学 600149 国际贸易理论与实务 6 00150 金融理论与实务 600151 企业经营战略 60152 组织行为学 400153 质量管理(一) 400154 企业管理咨询 406999 毕业论文不计学分厦门大学报考条件1.热爱祖国，立志求学，遵纪守法2.应届高考毕业生，无文理科类型限制3.对口专业中专毕业生4.少量优秀往届高中毕业生工商企业管理专业就业前景随着管理教学的普及和不断深入，去年，我国各种管理人员总数达3800万人，其中包括了国家机关的公务员600万人，在未来20年内，即2020年前，我国将继续持管理人员数量大国的地位，中国所需各类管理人员1000-1300万人，是中国就业人数较多的行业和热门职业。

厦门大学高等代数课程试卷

必要性。对矩阵
A，存在可逆矩阵
P，Q
使得 A =
P
æ ç
I
r
è
ö
0
÷ ø
Q
=
æ Pç
è
Ir 0
ö ÷ ø
(Ir
, 0)Q
。令
S
=
æ Pç
è
Ir 0
ö ÷ ø
，
T = (Ir , 0)Q ，可证 P，Q 即为所求。显然， S 和T 分别是 n ´ r 矩阵和 r ´ n 矩阵，且因 P，Q 可逆，所以
P，使得
P-1 AP
=
æ ç
Ir
è
ö
0
÷ ø
。令 S
=
æ Pç
è
Ir 0
ö ÷ ,T ø
=
(Ir , 0)P-1 ，则
A
=
ST
， TS
=
Ir
，
r(S ) = r(T ) = r 。
由j(x1),...,j(xr ) 的线性无关性，得 k1 = ... = kr = 0 ，进而 kr+1 = ... = kn = 0 。因此
j
(j
(x1
),
...,
j
(xr
),
xr
+1
,
...,
xn
)
=
(j
(x1
),
...,
j
(x
r
),
x
r
+1
,
...,
xn
)
æ ç
I
r
è
0
ö ÷ ø
。
这说明存在可逆矩阵
(Ir

计算机科学与应用

主要课程：电路原理、模拟电子技术、数字逻辑、数字分析、计算机原理、微型计算机技术、计算机系统结构、计算机网络、高级语言、汇编语言、数据结构、操作系统、计算方法、离散数学、概率统计、线性代数以及算法设计与分析等。

主要实践性教学环节：包括电子工艺实习、硬件部件设计及调试、计算机基础训练、课程设计、计算机工程实践、生产实习、毕业设计(论文)。

修业年限：四年授予学位：工学或理学学士相近专业：微电子学自动化电子信息工程地理信息系统通信工程计算机科学与技术电子科学与技术生物医学工程电气工程与自动化信息工程信息科学技术影视艺术技术网络工程信息显示与光电技术集成电路设计与集成系统光电信息工程广播电视工程电气信息工程计算机软件电力工程与管理智能科学与技术数字媒体艺术探测制导与控制技术数字媒体技术信息与通信工程建筑电气与智能化电磁场与无线技术 2、软件工程方向就业前景十分广阔，学生毕业后可以到国内外众多软件企业、国家机关以及各个大、中型企、事业单位的信息技术部门、教育部门等单位从事软件工程领域的技术开发、教学、科研及管理等工作。

也可以继续攻读计算机科学与技术类专业研究生和软件工程硕士。

3、通信方向学生毕业后可到信息产业、财政、金融、邮电、交通、国防、大专院校和科研机构从事通信技术和电子技术的科研、教学和工程技术工作。

4、网络与信息安全方向宽口径专业，主干学科为信息安全和网络工程。

学生毕业后可为政府、国防、军队、电信、电力、金融、铁路等部门的计算机网络系统和信息安全领域进行管理和服务的高级专业工程技术人才。

并可继续攻读信息安全、通信、信息处理、计算机软件和其他相关学科的硕士学位。

发展趋势截至2005年底，全国电子信息产品制造业平均就业人数322．8万人，其中工人约占6 0％，工程技术人员和管理人员比例较低，远不能满足电子信息产业发展的需要。

软件业人才供需矛盾尤为突出。

2002年，全国软件产业从业人员59．2万人，其中软件研发人员为15．7万人，占26．52％。

厦门大学2012年硕士研究生入学考试高等代数试题参考解答

◇※☆■◇◇※☆■◇
4
高等代数资源网
厦门大学2012年硕士学位研究生入学考试高等代数试题参考解答

1 2 0 0 3 0 0 1 0 0 5.设4 × 5阶矩阵A经过一系列初等行变换后变为 0 0 0 1 −1 ,则A的列向量 0 0 0 0 0 组α1 , α2 , α3 , α4 , α5 的一个极大线性无关组是( ),其余向量用该极大线性无关组线性表示式为( ). 解:α1 , α3 , α4 , α2 = 2α1 , α5 = 3α1 − α3 . √ √ √ 6.设Q( 2) = {a + b 2|a, b ∈ Q},则Q( 2)是有理数域Q上( 是其一组基. √ 解:2;1, 2. )维线性空间,( ( )
) B C 有( CT 0
8.设p是素数,则xp + px + p和x2 + p的最大公因式为( ). x1 + x2 + x3 = 1 二.(20分)已知线性方程组 2x1 + (a + 2)x2 + (a + 1)x3 = a + 3 有无穷多解.又设A是 x1 + 2x2 + ax3 = 3 T T 三阶方阵,α1 = (1, a, 0) , α2 = (−a, 1, 0) , α3 = (0, 0, a)T 为A的属于特征值λ1 = 1, λ2 = −2, λ3 = −1的特征向量. (1)求矩阵A; (2)求行列式|A∗ + 2E |. 三.(15分)设多项式f (x), g (x)互素.证明:(f (x)g (x), f (x) + g (x)) = 1. 四.(12分)设A, B 分别为m × n, n × s矩阵,且r(A) = r(AB ).证明:存在s × n矩阵C 使得A = ABC. 五.(15分)设α, β 是不同的n(> 1)维单位列向量,A = αβ T ̸= 0,则 (1)0是A的一个特征值; (2)A可对角化的充要条件为α与β 不正交. { x1 + x2 − x3 = 1 六.(15分)设V1 是数域F 上的解空间.V2 是F 上x2 − x3 = 0的解空间. x2 + x3 = 0 证明:F 3 = V1 ⊕ V2 . 七.(15分)设ϕ, φ是n维线性空间V 的线性变换,且ϕ有n个互异特征值.证明: (1)ϕ的特征向量都是φ的特征向量的充要条件是ϕφ = φϕ; (2)若ϕφ = φϕ,则φ是ε, ϕ, ϕ2 , · · · , ϕn−1 的线性组合,其中ε是V 的恒等变换. 八.(10分)设A, A1 , A2 为n阶方阵,满足A2 = A, A = A1 + A2 , r(A) = r(A1 ) + r(A2 ),其中r(A)表示A的秩.求证:A2 i = Ai , i = 1, 2; Ai Aj = 0, 1 ≤ i ̸= j ≤ 2. 休息一下,来张美图欣赏一下吧.

厦门大学级会计学课程表

2+4
概论
中国近现代史纲要
2 34 34
2
军事理论
2 34 34
2
大学语文
2 34 34
2
微积分Ⅰ
3 68 52 16 3+1
微积分Ⅱ
3 68 56 12
3+1
概率统计(经济类)
3 50 50
3
体育Ⅰ
1 34
34 2
体育Ⅱ
1 34
34
2
七八 17 14
46 8周 12周
113
通识通必识修教课
块
114
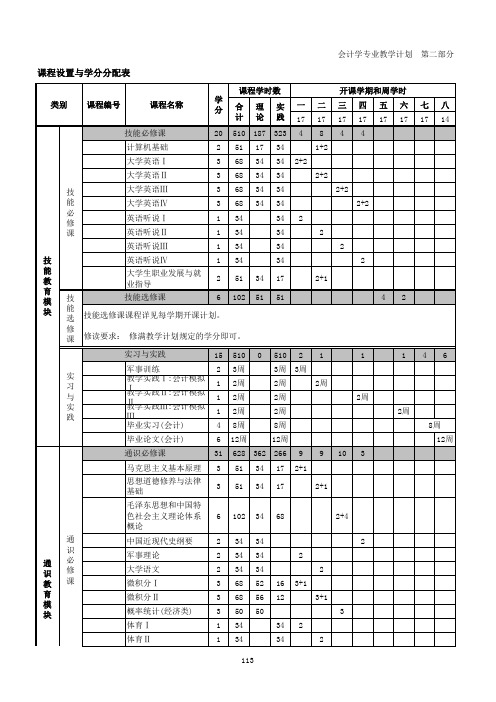
会计学专业教学计划第二部分
课程设置与学分分配表
专业类别教育模块
课程编号
课程名称
基础会计模拟高级财务管理
课程学时数
开课学期和周学时
学分
合
理
实
一
二
三
四
五
六
七
八
计论践 17 17 17 17 17 17 17 14
2 34 34
2
2 34 34
2
跨国公司财务管理
2 34 34
2 34 34
2
专
宏观经济学原理
2 34 34
业
统计学原理
3 50 50
必
修
中级财务会计(A)Ⅰ 3 50 50
课
中级财务会计(A)Ⅱ 3 50 50
2 3
3 3
高级财务会计
2 34 34
2
成本会计
3 50 50
3
财务管理(A)Ⅰ
3 50 50
3
财务管理(A)Ⅱ
3 50 50

(完整版)线性代数教案(正式打印版)

第（1）次课授课时间（）基本内容备注第一节二、三阶行列式的定义一、二阶行列式的定义从二元方程组的解的公式,引出二阶行列式的概念。

设二元线性方程组⎩⎨⎧=+=+22222211212111bxaxabxaxa用消元法,当021122211≠-aaaa时,解得211222111212112211222112121221,aaaababaxaaaababax--=--=令2112221122211211aaaaaaaa-=,称为二阶行列式,则如果将D中第一列的元素11a,21a换成常数项1b,2b,则可得到另一个行列式,用字母1D表示,于是有2221211ababD=按二阶行列式的定义,它等于两项的代数和：212221abab-,这就是公式（2）中1x的表达式的分子。

同理将D中第二列的元素a 12,a 22换成常数项b1,b2 ,可得到另一个行列式,用字母2D表示,于是有2121112babaD=按二阶行列式的定义,它等于两项的代数和：121211baba-,这就是公式（2）中2x的表达式的分子。

于是二元方程组的解的公式又可写为⎪⎪⎩⎪⎪⎨⎧==DDxDDx2211其中0≠D例1.解线性方程组.1212232121⎪⎩⎪⎨⎧=+=-xxxx同样,在解三元一次方程组⎪⎩⎪⎨⎧=++=++=++333323213123232221211313212111bxaxaxabxaxaxabxaxaxa时,要用到“三阶行列式”,这里可采用如下的定义.二、三阶行列式的定义设三元线性方程组⎪⎩⎪⎨⎧=++=++=++333323213123232221211313212111bxaxaxabxaxaxabxaxaxa用消元法解得定义设有9个数排成3行3列的数表333231232221131211aaaaaaaaa记333231232221131211aaaaaaaaaD=322113312312332211aaaaaaaaa++=332112322311312213aaaaaaaaa---,称为三阶行列式,则三阶行列式所表示的6项的代数和,也用对角线法则来记忆：从左上角到右下角三个元素相乘取正号,从右上角到左下角三个元素取负号,即例2. 计算三阶行列式243122421----=D.(-14)例3. 求解方程094321112=xx（32==xx或）例4. 解线性方程组.5573422⎪⎩⎪⎨⎧=+-=++-=++-zyxzyxzyx解先计算系数行列式573411112--=D069556371210≠-=----+-=第（ 2 ）次课授课时间（）第（ 3 ）次课授课时间（）基本内容备注第六节行列式按行（列）展开定义在n阶行列式中，把元素ija所处的第i行、第j列划去，剩下的元素按原排列构成的1-n阶行列式，称为ija的余子式，记为ijM；而ijjiijMA+-=)1(称为ij a的代数余子式.引理如果n阶行列式中的第i行除ija外其余元素均为零，即：nnnjnijnjaaaaaaaDΛΛMMMΛΛMMMΛΛ11111=.则：ijijAaD=.证先证简单情形：nnnnnaaaaaaaDΛMMMΛΛ212222111=再证一般情形：定理行列式等于它的任意一行（列）的各元素与对应的代数余子式乘积之和，即按行：()jiAaAaAajninjiji≠=+++02211Λ按列：()jiAaAaAanjnijiji≠=+++02211Λ证：（此定理称为行列式按行（列）展开定理）nnnniniinaaaaaaaaaDΛΛΛΛΛΛΛΛΛΛΛΛΛΛ2121112110+++++++++=nnnninnnnnninnnnninaaaaaaaaaaaaaaaaaaaaaΛΛΛΛΛΛΛΛΛΛΛΛΛΛΛΛΛΛΛΛΛΛΛΛΛΛΛΛΛΛΛΛΛΛ211121121211211211112110+++=).,2,1(2211niAaAaAaininiiiiΛΛ=+++=例1：335111243152113------=D.解:例2:21122112----=OOOOnD解:21122112----=OOOOnD2112211121---=+++OOOOΛn rr1+=nDn.从而解得1+=nDn.例3．证明范德蒙行列式112112222121111---=nnnnnnnxxxxxxxxxDΛΛΛΛΛΛΛΛ()1i jn i jx x≥>≥=-∏.其中，记号“∏”表示全体同类因子的乘积.证用归纳法因为=-==1221211xxxxD()21i ji jx x≥>≥-∏所以，当2=n n=2时，（4）式成立.现设（4）式对1-n时成立，要证对n时也成立.为此，设法把n D降阶；从第n行开始，后行减去前行的1x倍，有()()()()()()21311221331122222133111111nn nnn n nn nx x x x x xx x x x x x x x xDx x x x x x x x x---------=---LLLL L L LL（按第一列展开，并提出因子1xxi-）第（ 4 ）次课授课时间（）第（5）次课授课时间（）基本内容备注第一节矩阵一、矩阵的定义称m行、n列的数表mnmmnnaaaaaaaaaΛΛΛΛΛΛΛ212222111211为nm⨯矩阵，或简称为矩阵；表示为⎪⎪⎪⎪⎪⎭⎫⎝⎛=mnmmnnaaaaaaaaaAΛΛΛΛΛΛΛ212222111211或简记为nmijaA⨯=)(,或)(ijaA=或n m A⨯；其中ij a表示A中第i行，第j列的元素。

福建师范大学网络教育学位考试《高等代数选讲》学习小结论文小结

《高等代数选讲》学习小结《高等代数》是数学学科的一门传统课程。

在当今世界的数学内部学科趋于统一性和数学在其他学科的广泛应用性的今天，《高等代数》以追求内容结构的清晰刻画和作为数学应用的基础，是数学各个专业的主干基础课程。

它是数学在其它学科应用的必需基础课程，又是数学修养的核心课程。

高等代数是代数学发展到高级阶段的总称，它包括许多分支。

它是在初等代数的基础上研究对象进一步的扩充，引进了许多新的概念以及与通常很不相同的量，比如最基本的有集合、向量和向量空间等。

这些量具有和数相类似的运算的特点，不过研究的方法和运算的方法都更加繁复。

通过学习后，我们知道，不仅是数，还有矩阵、向量、向量空间的变换等，对于这些对象，都可以进行运算，虽然也叫做加法或乘法，但是关于数的基本运算定律，有时不再保持有效。

因此代数学的内容可以概括称为带有运算的一些集合，在数学中把这样的一些集合，叫做代数系统。

刚刚开始接触到高等代数的时候，对它一无所知，仅仅听其它同学谈论过线性代数这门课程。

在学习之前，我一直认为高等代数就是线性代数。

经过学习后，我发现，这两者之间区别还是挺大的。

高等代数是我们数学专业开设的专业课，更注重理论的分析，需要搞懂许多概念是怎么来的，而线性代数，只是一种运算工具，是供工科和部分医科专业开设的课程，更加注重应用。

经过课程和书本的学习，我对高等代数里面的知识有了个初步的认识和接触，特别是高等代数的一些思想，也从中收获不少。

下面就对高等代数的学习做一个回顾和总结。

一、行列式行列式是代数学中的一个基本概念，它不仅是讨论线性方程组理论的有力工具，而且还广泛的应用于数学及其他科学技术领域定义：设A=（a ij）为数域F上的n×n矩阵，规定A的行列式为|A|=∑(−1)τ(j1j2⋯j n)a1j1a2j2⋯a njnj1j2…j n其中，i1i2⋯i n为1,2，…，n的一个排列。

从定义，我们可以看出，行列式是F n×n到F的一个映射。

1-1 矩阵概念

注意
只有当两个矩阵是同维矩阵时，才能进行加法运算. 2、矩阵加法的运算规律 (1) A + B =B + A (交换律) (2) (A + B) + C = A + (B + C) (结合律)
二、数与矩阵相乘
1、定义数与矩阵 A (aij )的乘积记作 A或 A ，规定为
A aij
线性代数
主讲曹宵临
通知
1.线性代数课程中心。网址： 2.线性代数答疑安排: (第3周开始) 时间:周二晚18：00～20：30(助教); 双周三、单周四中午12：15～13：15 地点:教学A楼二楼教师休息室 3.习题册及自测练习: (自愿购买) 练习册(作业)每套8元，自测练习每套8元购买时间地点形式: 以自然班为单位于第一周周四上午10点～下午1点到理学院120室购买 .
行矩阵(或行向量)
b1 b2 B 列矩阵(或列向量) bm
注： ①行(列)向量常用小写字母表示. 为统一起见，一般向量均指列向量. ②向量的元素称为分量，分量个数称为向量的维数. 例： 1 a 2 5 3维列向量
1 2 4 2 3 1 5 4 5 4 0 2
一、矩阵定义
所谓矩阵就是由某些元素按行列排成的一个矩形阵列，一般总用大写字母A、B、 C……表示. 由 m n 个元素排成的m行n列矩阵就称为 m n维矩阵，简称 m n矩阵. 一般表示为：
a11 a12 a1n a21 a22 a2 n A am 1 am 2 amn
cij ai 1b1 j ai 2b2 j ais bsj aik bkj

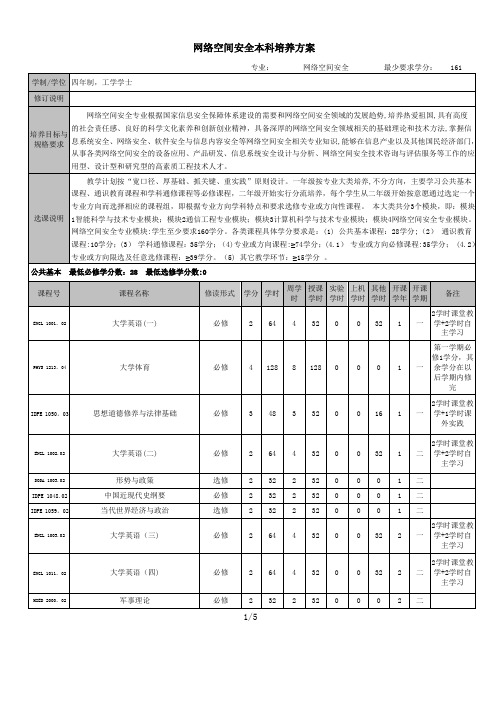
网络空间安全专业人才培养方案本科-厦门大学网络空间安全系

4
32
32
0
0
3
一
计算机网络
必修
4
70
4
56
14
0
0
3
一
计算机组成原理
必修
4
78
4
56
14
0
0
3
一
多媒体技术与应用
选修
2
32
2
16
16
0
0
3
一
数据库技术与应用（数据库系统原理）
必修
4
70
4
56
14
0
0
3
二
网络安全防护技术
必修
4
70
4
56
14
0
0
3
二
操作系统原理
必修
4
70
5
56
14
0
0
3
二
编译原理A
必修
课程号
课程名称
修读形式
学分
学时
周学时
授课学时
实验学时
上机学时
其他学时
开课学年
开课学期
备注
CHIN 1085.02
大学语文
必修
2
32
2
32
0
0
0
1
一
CSCI 1228.01
新生研讨课
必修
1
16
1
16
0
0
0
1
一
跨学科基本课程
选修
10
160
2
160
0
0
0
1
二
SOSA 3076。01

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

1.(1分)• A. A • B. B • C. C • D. D 纠错得分：0知识点：1展开解析答案D解析2.(1分)• A. A • B. B • C. C • D. D 纠错得分：0知识点：1答案B解析3.(1分)• A. A • B. B • C. C • D. D 纠错得分：0知识点：1展开解析答案B解析4.(1分)• A. A • B. B • C. C • D. D 纠错得分：0知识点：1展开解析答案A解析5.(1分)• A. A • B. B • C. C • D. D 纠错得分：0知识点：1展开解析答案D解析6.(1分)• A. A • B. B • C. C • D. D 纠错得分：0知识点：1展开解析答案A解析7.(1分)• A. A • B. B • C. C • D. D 纠错得分：0知识点：1展开解析答案C解析8.(1分)• A. A • B. B • C. C • D. D 纠错得分：0知识点：1展开解析答案B解析9.(1分)• A. A • B. B • C. C • D. D 纠错得分：0知识点：1展开解析答案B解析10.(1分)• A. A • B. B • C. C • D. D 纠错得分：0知识点：1展开解析答案D解析11.• A. A • B. B • C. C • D. D 纠错得分：0知识点：1展开解析答案C解析12.(1分)• A. A • B. B • C. C • D. D 纠错得分：0知识点：1展开解析答案C解析13.• A. A • B. B • C. C • D. D 纠错得分：0知识点：1展开解析答案B解析14.(1分)• A. A • B. B • C. C • D. D 纠错得分：0知识点：1展开解析答案B解析15.(1分)• A. A • B. B • C. C • D. D 纠错得分：0知识点：1展开解析答案D解析16.(1分)• A. A • B. B • C. C • D. D 纠错得分：0知识点：1展开解析答案A解析17.(1分)• A. A • B. B • C. C • D. D 纠错得分：0知识点：2展开解析答案D解析18.(1分)• A. A • B. B • C. C • D. D 纠错得分：0知识点：2展开解析答案B解析19.(1分)• A. A • B. B • C. C • D. D 纠错得分：0知识点：2展开解析答案C解析20.(1分)• A. A • B. B • C. C • D. D 纠错得分：0知识点：2展开解析答案B解析21.(1分)• A. A • B. B • C. C • D. D 纠错得分：0知识点：2展开解析答案D解析22.(1分)• A. A • B. B • C. C • D. D 纠错得分：0知识点：2展开解析答案B23.(1分)• A. A • B. B • C. C • D. D 纠错得分：0知识点：2展开解析答案D解析24.(1分)• A. A • B. B • C. C • D. D 纠错得分：0知识点：2展开解析答案A25.(1分)• A. A • B. B • C. C • D. D 纠错得分：0知识点：2展开解析答案C解析26.(1分)• A. A • B. B • C. C • D. D 纠错得分：0知识点：2展开解析答案A解析27.(1分)• A. A • B. B • C. C • D. D 纠错得分：0知识点：2展开解析答案C解析28.(1分)• A. A • B. B • C. C • D. D 纠错得分：0知识点：2展开解析答案C解析29.(1分)• A. A • B. B • C. C • D. D 纠错得分：0知识点：2展开解析答案C解析30.(1分)• A. A • B. B • C. C • D. D 纠错得分：0知识点：2展开解析答案C解析31.(1分)• A. A • B. B • C. C • D. D 纠错得分：0知识点：2展开解析答案C解析32.(1分)• A. A • B. B • C. C • D. D 纠错得分：0知识点：2展开解析答案C解析33.(1分)• A. A • B. B • C. C • D. D 纠错得分：0知识点：2展开解析答案C解析34.(1分)• A. A • B. B • C. C • D. D 纠错得分：0知识点：2展开解析答案D解析35.(1分)• A. A • B. B • C. C • D. D 纠错得分：0知识点：2展开解析答案B解析36.(1分)• A. A • B. B • C. C • D. D 纠错得分：0知识点：2展开解析答案B解析37.(1分)• A. A • B. B • C. C • D. D 纠错得分：0知识点：2展开解析答案B解析38.(1分)• A. A • B. B • C. C • D. D 纠错得分：0知识点：2展开解析答案A解析39.(1分)• A. A • B. B • C. C • D. D 纠错得分：0知识点：2展开解析答案A解析40.(1分)• A. A • B. B • C. C • D. D 纠错得分：0知识点：2展开解析答案B解析41.(1分)• B. B • C. C • D. D 纠错得分：0知识点：2展开解析答案B解析42.(1分)• A. A • B. B • C. C • D. D 纠错得分：0知识点：2展开解析答案D解析43.(1分)• A. A • B. B• D. D 纠错得分：0知识点：2展开解析答案A解析44.(1分)• A. A • B. B • C. C • D. D 纠错得分：0知识点：2展开解析答案B解析45.(1分)• A. A • B. B • C. C • D. D 纠错知识点：3展开解析答案A解析46.(1分)• A. A • B. B • C. C • D. D 纠错得分：0知识点：3展开解析答案A解析47.(1分)• A. A • B. B • C. C • D. D 纠错得分：0展开解析答案C解析48.(1分)• A. A • B. B • C. C • D. D 纠错得分：0知识点：3展开解析答案B解析49.(1分)• A. A • B. B • C. C • D. D 纠错得分：0展开解析答案D解析50.(1分)• A. A • B. B • C. C • D. D 纠错得分：0知识点：3展开解析答案B解析51.(1分)• A. A • B. B • C. C • D. D 纠错得分：0知识点：3展开解析答案B解析52.(1分)• A. A • B. B • C. C • D. D 纠错得分：0知识点：3展开解析答案C解析53.(1分)• A. A • B. B • C. C • D. D 纠错得分：0知识点：3展开解析答案D解析54.(1分)• A. A • B. B • C. C • D. D 纠错得分：0知识点：3展开解析答案C解析55.(1分)• A. A • B. B • C. C • D. D 纠错得分：0知识点：3展开解析答案A解析56.(1分)• A. A • B. B • C. C • D. D 纠错得分：0知识点：3展开解析答案D解析57.(1分)• A. A • B. B • C. C • D. D 纠错得分：0知识点：3展开解析答案D解析58.(1分)• A. A • B. B • C. C • D. D 纠错得分：0知识点：3展开解析答案C解析59.(1分)• A. A • B. B • C. C • D. D 纠错得分：0知识点：3展开解析答案C解析60.(1分)• A. A • B. B • C. C • D. D 纠错得分：0知识点：3展开解析答案A解析61.(1分)• A. A • B. B • C. C • D. D 纠错得分：0知识点：3展开解析答案C解析62.(1分)• A. A • B. B • C. C • D. D 纠错得分：0知识点：3展开解析答案C解析63.(1分)• A. A • B. B • C. C • D. D 纠错得分：0知识点：3展开解析答案C解析64.(1分)• A. A • B. B • C. C• D. D 纠错得分：0知识点：3展开解析答案A解析65.(1分)• A. A • B. B • C. C • D. D 纠错得分：0知识点：3展开解析答案C解析66.(1分)• A. A • B. B • C. C • D. D 纠错知识点：3展开解析答案C解析67.(1分)• A. A • B. B • C. C • D. D 纠错得分：0知识点：3展开解析答案B解析68.(1分)• A. A • B. B • C. C • D. D 纠错得分：0知识点：3答案D解析69.(1分)• A. A • B. B • C. C • D. D 纠错得分：0知识点：3展开解析答案D解析70.(1分)• A. A • B. B • C. C • D. D 纠错得分：0知识点：3答案B解析71.(1分)• A. A • B. B • C. C • D. D 纠错得分：0知识点：3展开解析答案C解析72.(1分)• A. A • B. B • C. C • D. D 纠错得分：0知识点：3答案B解析73.(1分)• A. A • B. B • C. C • D. D 纠错得分：0知识点：3展开解析答案B解析74.(1分)• A. A • B. B • C. C • D. D 纠错得分：0知识点：3展开解析答案D75.(1分)• A. A • B. B • C. C • D. D 纠错得分：0知识点：3展开解析答案C解析76.(1分)• A. A • B. B • C. C • D. D 纠错得分：0知识点：3展开解析答案C77.(1分)• A. A • B. B • C. C • D. D 纠错得分：0知识点：3展开解析答案B解析78.(1分)• A. A • B. B • C. C • D. D 纠错得分：0知识点：3展开解析答案A解析79.• A. A • B. B • C. C • D. D 纠错得分：0知识点：5展开解析答案A解析80.(1分)• A. A • B. B • C. C • D. D 纠错得分：0知识点：5展开解析答案A解析81.(1分)• A. A • B. B • C. C • D. D 纠错得分：0知识点：5展开解析答案C解析82.(1分)• A. A • B. B • C. C • D. D 纠错得分：0知识点：5展开解析答案B解析83.(1分)• A. A • B. B • C. C • D. D 纠错得分：0知识点：5展开解析答案A解析84.(1分)• A. A • B. B• C. C • D. D 纠错得分：0知识点：5展开解析答案A解析85.(1分)• A. A • B. B • C. C • D. D 纠错得分：0知识点：5展开解析答案C解析86.(1分)• A. A • B. B • C. C • D. D得分：0知识点：5展开解析答案C解析87.(1分)• A. A • B. B • C. C • D. D 纠错得分：0知识点：5展开解析答案B解析88.(1分)• A. A • B. B • C. C • D. D得分：0知识点：5展开解析答案C解析89.(1分)• A. A • B. B • C. C • D. D 纠错得分：0知识点：5展开解析答案C解析90.(1分)• A. A • B. B • C. C • D. D 纠错知识点：5展开解析答案B解析91.(1分)• A. A • B. B • C. C • D. D 纠错得分：0知识点：5展开解析答案D解析92.(1分)• A. A • B. B • C. C • D. D 纠错得分：0知识点：5答案C解析93.(1分)• A. A • B. B • C. C • D. D 纠错得分：0知识点：5展开解析答案C解析94.(1分)• A. A • B. B • C. C • D. D 纠错得分：0知识点：5展开解析解析95.(1分)• A. A • B. B • C. C • D. D 纠错得分：0知识点：5展开解析答案B解析96.(1分)• A. A • B. B • C. C • D. D 纠错得分：0知识点：5展开解析答案D97.(1分)• A. A • B. B • C. C • D. D 纠错得分：0知识点：5展开解析答案D解析98.(1分)• A. A • B. B • C. C • D. D 纠错得分：0知识点：5展开解析答案B解析99.(1分)• A. A • B. B • C. C • D. D 纠错得分：0知识点：5展开解析答案D解析100.(1分)• A. A • B. B • C. C • D. D 纠错得分：0知识点：5C。