圆锥曲线对偶的性质100条
圆锥曲线经典结论总结(教师版)

椭圆与双曲线的对偶性质--(必背的经典结论)高三数学备课组1. 点P 处的切线PT 平分△PF 1F 2在点P 处的外角.2. PT 平分△PF 1F 2在点P 处的外角,则焦点在直线PT 上的射影H 点的轨迹是以长轴为直径的圆,除去长轴的两个端点.3. 以焦点弦PQ 为直径的圆必与对应准线相离.4. 以焦点半径PF 1为直径的圆必与以长轴为直径的圆内切.5. 若000(,)P x y 在椭圆22221x y a b +=上,则过0P 的椭圆的切线方程是00221x x y y a b +=.6. 若000(,)P x y 在椭圆22221x y a b+=外 ,则过Po 作椭圆的两条切线切点为P 1、P 2,则切点弦P 1P 2的直线方程是00221x x y ya b+=.7. 椭圆22221x y a b+= (a >b >0)的左右焦点分别为F 1,F 2,点P 为椭圆上任意一点12F PF γ∠=,则椭圆的焦点角形的面积为122tan2F PF S b γ∆=.8. 椭圆22221x y a b+=(a >b >0)的焦半径公式:10||MF a ex =+,20||MF a ex =-(1(,0)F c -,2(,0)F c 00(,)M x y ).9. 设过椭圆焦点F 作直线与椭圆相交 P 、Q 两点,A 为椭圆长轴上一个顶点,连结AP和AQ 分别交相应于焦点F 的椭圆准线于M 、N 两点,则MF ⊥NF.10. 过椭圆一个焦点F 的直线与椭圆交于两点P 、Q, A 1、A 2为椭圆长轴上的顶点,A 1P 和A 2Q 交于点M ,A 2P 和A 1Q 交于点N ,则MF ⊥NF.11. AB 是椭圆22221x y a b +=的不平行于对称轴的弦,M ),(00y x 为AB 的中点,则22OM AB b k k a ⋅=-,即0202y a x b K AB -=。
12. 若000(,)P x y 在椭圆22221x y a b+=内,则被Po 所平分的中点弦的方程是2200002222x x y y x y a b a b+=+.13. 若000(,)P x y 在椭圆22221x y a b+=内,则过Po 的弦中点的轨迹方程是22002222x x y yx y a b a b+=+.1. 点P 处的切线PT 平分△PF 1F 2在点P 处的内角.2. PT 平分△PF 1F 2在点P 处的内角,则焦点在直线PT 上的射影H 点的轨迹是以长轴为直径的圆,除去长轴的两个端点. 3. 以焦点弦PQ 为直径的圆必与对应准线相交.4. 以焦点半径PF 1为直径的圆必与以实轴为直径的圆相切.(内切:P 在右支;外切:P 在左支)5. 若000(,)P x y 在双曲线22221x y a b-=(a >0,b >0)上,则过0P 的双曲线的切线方程是00221x x y ya b-=. 6. 若000(,)P x y 在双曲线22221x y a b-=(a >0,b >0)外 ,则过Po 作双曲线的两条切线切点为P 1、P 2,则切点弦P 1P 2的直线方程是00221x x y ya b-=.7. 双曲线22221x y a b-=(a >0,b >o )的左右焦点分别为F 1,F 2,点P 为双曲线上任意一点12F PF γ∠=,则双曲线的焦点角形的面积为122t2F PF S b co γ∆=.8. 双曲线22221x y a b-=(a >0,b >o )的焦半径公式:(1(,0)F c -,2(,0)F c当00(,)M x y 在右支上时,10||MF ex a =+,20||MF ex a =-.当00(,)M x y 在左支上时,10||MF ex a =-+,20||MF ex a =--9. 设过双曲线焦点F 作直线与双曲线相交 P 、Q 两点,A 为双曲线长轴上一个顶点,连结AP 和AQ 分别交相应于焦点F 的双曲线准线于M 、N 两点,则MF ⊥NF. 10. 过双曲线一个焦点F 的直线与双曲线交于两点P 、Q, A 1、A 2为双曲线实轴上的顶点,A 1P 和A 2Q 交于点M ,A 2P 和A 1Q 交于点N ,则MF ⊥NF.11. AB 是双曲线22221x y a b-=(a >0,b >0)的不平行于对称轴的弦,M ),(00y x 为AB的中点,则0202y a x b K K AB OM =⋅,即0202y a x b K AB =。
圆锥曲线对偶的性质100条

对偶圆锥曲线的性质:具有一系列特殊的 几何性质,如对称性、相似性等。
对偶圆锥曲线在几何中的应用:通过对偶 圆锥曲线,可以解决一些复杂的几何问题, 简化计算过程。
对偶圆锥曲线的起源与发展:起源于古代 数学家对几何图形的观察与研究,随着数 学的发展,对偶圆锥曲线逐渐成为数学领 域的一个重要分支。
对偶的性质
推导过程:利用坐标变换和参数方程,推导出新的圆锥曲线的方程,并证明其对偶性质
对偶的推广方法2
圆锥曲线对偶的推广方法:利用坐标变换和参数方程进行推导
圆锥曲线对偶的推广应用:在几何、代数和解析几何等领域有广泛的应用
圆锥曲线对偶的推广意义:丰富了数学理论体系,为解决实际问题提供了 更多思路和方法 圆锥曲线对偶的推广前景:随着数学和其他学科的发展,圆锥曲线对偶的 推广将有更广阔的发展前景
03
圆锥曲线对偶的性 质
对偶的性质1
定义:圆锥曲线上的点关于某 一直线对称的性质
性质:对偶性质在圆锥曲线中 具有普遍性,可以应用于椭圆、 双曲线和抛物线等
应用:在几何学、物理学等领 域有广泛的应用
证明:可以通过几何证明或代 数证明来证明对偶性质
对偶的性质2
定义:圆锥曲线 上的点关于某一 直线对称的性质
圆锥曲线中的 对偶形式:指 代几何图形中 的对称性质, 如椭圆和双曲 线的对称轴。
对偶在解析几 何中的应用: 通过对偶形式 描述几何图形 的性质,便于 进行解析和计
算。
对偶在几何证 明中的应用: 利用对偶性质 简化几何证明 过程,提高证
明效率。
对偶在几何作 图中的应用: 通过对偶形式 指导几何作图, 提高作图的准 确性和效率。
感谢观看
汇报人:XX
性质:对偶性质 在圆锥曲线中具 有普遍性,可以 应用于椭圆、双 曲线和抛物线等
高考数学圆锥曲线的常用性质

椭圆与双曲线的对偶性质--(必背的经典结论)椭 圆1. 点P 处的切线PT 平分△PF 1F 2在点P 处的外角.2. PT 平分△PF 1F 2在点P 处的外角,则焦点在直线PT 上的射影H 点的轨迹是以长轴为直径的圆,除去长轴的两个端点.3. 以焦点弦PQ 为直径的圆必与对应准线相离.4. 以焦点半径PF 1为直径的圆必与以长轴为直径的圆内切.5. 若000(,)P x y 在椭圆22221x y a b+=上,则过0P 的椭圆的切线方程是00221x x y y a b +=. 6.若000(,)P x y 在椭圆22221x y a b+=外 ,则过Po 作椭圆的两条切线切点为P 1、P 2,则切点弦P 1P 2的直线方程是00221x x y ya b +=. 7.椭圆22221x y a b+= (a >b >0)的左右焦点分别为F 1,F 2,点P 为椭圆上任意一点12F PF γ∠=,则椭圆的焦点角形的面积为122tan 2F PF S b γ∆=.8.椭圆22221x y a b+=(a >b >0)的焦半径公式:10||MF a ex =+,20||MF a ex =-(1(,0)F c - , 2(,0)F c 00(,)M x y ).9. 设过椭圆焦点F 作直线与椭圆相交 P 、Q 两点,A 为椭圆长轴上一个顶点,连结AP 和AQ 分别交相应于焦点F 的椭圆准线于M 、N 两点,则MF ⊥NF.10. 过椭圆一个焦点F 的直线与椭圆交于两点P 、Q, A 1、A 2为椭圆长轴上的顶点,A 1P 和A 2Q 交于点M ,A 2P和A 1Q 交于点N ,则MF ⊥NF.11. AB 是椭圆22221x y a b+=的不平行于对称轴的弦,M ),(00y x 为AB 的中点,则22OM AB b k k a ⋅=-,即0202y a xb K AB -=。
12. 若000(,)P x y 在椭圆22221x y a b+=内,则被Po 所平分的中点弦的方程是2200002222x x y y x y a b a b +=+. 13. 若000(,)P x y 在椭圆22221x y a b+=内,则过Po 的弦中点的轨迹方程是22002222x x y yx y a b a b +=+. 双曲线1. 点P 处的切线PT 平分△PF 1F 2在点P 处的内角.2. PT 平分△PF 1F 2在点P 处的内角,则焦点在直线PT 上的射影H 点的轨迹是以长轴为直径的圆,除去长轴的两个端点.3. 以焦点弦PQ 为直径的圆必与对应准线相交.4. 以焦点半径PF 1为直径的圆必与以实轴为直径的圆相切.(内切:P 在右支;外切:P 在左支)5. 若000(,)P x y 在双曲线22221x y a b -=(a >0,b >0)上,则过0P 的双曲线的切线方程是00221x x y y a b -=. 6. 若000(,)P x y 在双曲线22221x y a b-=(a >0,b >0)外 ,则过Po 作双曲线的两条切线切点为P 1、P 2,则切点弦P 1P 2的直线方程是00221x x y ya b-=.7. 双曲线22221x y a b-=(a >0,b >o )的左右焦点分别为F 1,F 2,点P 为双曲线上任意一点12F PF γ∠=,则双曲线的焦点角形的面积为122t 2F PF S b co γ∆=.8. 双曲线22221x y a b-=(a >0,b >o )的焦半径公式:(1(,0)F c - , 2(,0)F c当00(,)M x y 在右支上时,10||MF ex a =+,20||MF ex a =-.当00(,)M x y 在左支上时,10||MF ex a =-+,20||MF ex a =--9. 设过双曲线焦点F 作直线与双曲线相交 P 、Q 两点,A 为双曲线长轴上一个顶点,连结AP 和AQ 分别交相应于焦点F 的双曲线准线于M 、N 两点,则MF ⊥NF.10. 过双曲线一个焦点F 的直线与双曲线交于两点P 、Q, A 1、A 2为双曲线实轴上的顶点,A 1P 和A 2Q 交于点M ,A 2P 和A 1Q 交于点N ,则MF ⊥NF.11. AB 是双曲线22221x y a b -=(a >0,b >0)的不平行于对称轴的弦,M ),(00y x 为AB 的中点,则0202y a x b K K AB OM =⋅,即0202y a x b K AB =。
高考数学圆锥曲线的经典性质条

椭圆与双曲线的对偶性质--(必背的经典结论)椭 圆1. 点P 处的切线PT 平分△PF 1F 2在点P 处的外角.2.PT 平分△PF 1F 2在点P 处的外角,则焦点在直线PT 上的射影H 点的轨迹是以长轴为直径的圆,除去长轴的两个端点. 3. 以焦点弦PQ 为直径的圆必与对应准线相离.4. 以焦点半径PF 1为直径的圆必与以长轴为直径的圆内切.5.若000(,)P x y 在椭圆22221x y a b +=上,则过0P 的椭圆的切线方程是00221x x y ya b +=. 6.若000(,)P x y 在椭圆22221x y a b+=外 ,则过Po 作椭圆的两条切线切点为P 1、P 2,则切点弦P 1P 2的直线方程是00221x x y y a b +=.7.椭圆22221x y a b+= (a >b >0)的左右焦点分别为F 1,F 2,点P 为椭圆上任意一点12F PF γ∠=,则椭圆的焦点角形的面积为122tan2F PFS b γ∆=.8.椭圆22221x y a b+=(a >b >0)的焦半径公式:10||MF a ex =+,20||MF a ex =-(1(,0)F c - , 2(,0)F c 00(,)M x y ).9.设过椭圆焦点F 作直线与椭圆相交 P 、Q 两点,A 为椭圆长轴上一个顶点,连结AP 和AQ 分别交相应于焦点F 的椭圆准线于M 、N 两点,则MF ⊥NF.10. 过椭圆一个焦点F 的直线与椭圆交于两点P 、Q, A 1、A 2为椭圆长轴上的顶点,A 1P 和A 2Q 交于点M ,A 2P 和A 1Q 交于点N ,则MF ⊥NF. 11.AB 是椭圆22221x y a b +=的不平行于对称轴的弦,M ),(00y x 为AB 的中点,则22OM AB b k k a ⋅=-,即0202y a x b K AB -=。
12. 若000(,)P x y 在椭圆22221x y a b +=内,则被Po 所平分的中点弦的方程是2200002222x x y y x y a b a b +=+.13.若000(,)P x y 在椭圆22221x y a b+=内,则过Po 的弦中点的轨迹方程是22002222x x y yx y a b a b +=+. 双曲线1. 点P 处的切线PT 平分△PF 1F 2在点P 处的内角.2.PT 平分△PF 1F 2在点P 处的内角,则焦点在直线PT 上的射影H 点的轨迹是以长轴为直径的圆,除去长轴的两个端点.3. 以焦点弦PQ 为直径的圆必与对应准线相交.4. 以焦点半径PF 1为直径的圆必与以实轴为直径的圆相切.(内切:P 在右支;外切:P 在左支)5.若000(,)P x y 在双曲线22221x y a b-=(a >0,b >0)上,则过0P 的双曲线的切线方程是00221x x y ya b-=. 6.若000(,)P x y 在双曲线22221x y a b-=(a >0,b >0)外 ,则过Po 作双曲线的两条切线切点为P 1、P 2,则切点弦P 1P 2的直线方程是00221x x y ya b-=.7.双曲线22221x y a b-=(a >0,b >o )的左右焦点分别为F 1,F 2,点P 为双曲线上任意一点12F PF γ∠=,则双曲线的焦点角形的面积为122t2F PFS b co γ∆=.8.双曲线22221x y a b-=(a >0,b >o )的焦半径公式:(1(,0)F c - , 2(,0)F c当00(,)M x y 在右支上时,10||MF ex a =+,20||MF ex a =-.当00(,)M x y 在左支上时,10||MF ex a =-+,20||MF ex a =--9. 设过双曲线焦点F 作直线与双曲线相交 P 、Q 两点,A 为双曲线长轴上一个顶点,连结AP 和AQ 分别交相应于焦点F 的双曲线准线于M 、N 两点,则MF ⊥NF.10. 过双曲线一个焦点F 的直线与双曲线交于两点P 、Q, A 1、A 2为双曲线实轴上的顶点,A 1P 和A 2Q 交于点M ,A 2P 和A 1Q 交于点N ,则MF ⊥NF. 11.AB 是双曲线22221x y a b -=(a >0,b >0)的不平行于对称轴的弦,M ),(00y x 为AB 的中点,则0202y a x b K K AB OM =⋅,即0202y a x b K AB =。
圆锥曲线常用的二级结论和椭圆与双曲线对偶结论

圆锥曲线常用的二级结论:
1.零点定理:设F1,F2为椭圆E的两个焦点,P为椭圆上一点,则PF1 + PF2 = 2a(a
为椭圆长轴的一半);对于双曲线,PF1 - PF2 = 2a,其中a为双曲线的长轴的一半。
2.切线定理:设点P(x0,y0)在曲线C上,则C在点P处的切线方程为F_x(x0,y0)
x + F_y(x0,y0)y = F(x0,y0),其中F(x,y)为曲线C的方程,F_x和F_y为它的偏导数。
3.法线定理:设点P(x0,y0)在曲线C上,则C在点P处的法线方程为F_y(x0,y0)
x - F_x(x0,y0)y = F_y(x0,y0)x0 - F_x(x0,y0)y0。
4.离心率计算公式:设椭圆E的长轴为a,短轴为b,则椭圆的离心率为e = √(a² - b²)
/ a。
5.弦长定理:对于椭圆E,设以焦点F1,F2为端点的弦所对应的直角顶点为P,则弦PF1
+ PF2的长度等于椭圆长轴的长度;对于双曲线,弦PF1 - PF2的长度等于双曲线长轴的长度。
椭圆与双曲线的对偶结论:
1.椭圆E的对称中心为它所包围的正方形的中心,长、短半轴分别为正方形的对角线之
一和另外一边。
2.椭圆的纵轴端点为它所包围正方形的中心连通它上下角的一条直线,椭圆的焦点在这
条直线上。
3.双曲线的渐近线为对应椭圆的渐近线的转置。
4.对于椭圆E的焦点F和双曲线H的焦距f,有e² = 1 + f² / b²。
把椭圆的参数a,b
换成双曲线的参数a,b,即可得到双曲线的离心率计算公式。
(完整版)圆锥曲线经典结论总结(教师版)

椭圆与双曲线的对偶性质--(必背的经典结论)高三数学备课组1. 点P 处的切线PT 平分△PF 1F 2在点P 处的外角.2. PT 平分△PF 1F 2在点P 处的外角,则焦点在直线PT 上的射影H 点的轨迹是以长轴为直径的圆,除去长轴的两个端点.3. 以焦点弦PQ 为直径的圆必与对应准线相离.4. 以焦点半径PF 1为直径的圆必与以长轴为直径的圆内切.5. 若000(,)P x y 在椭圆22221x y a b +=上,则过0P 的椭圆的切线方程是00221x x y y a b +=.6. 若000(,)P x y 在椭圆22221x y a b+=外 ,则过Po 作椭圆的两条切线切点为P 1、P 2,则切点弦P 1P 2的直线方程是00221x x y ya b+=.7. 椭圆22221x y a b+= (a >b >0)的左右焦点分别为F 1,F 2,点P 为椭圆上任意一点12F PF γ∠=,则椭圆的焦点角形的面积为122tan2F PF S b γ∆=.8. 椭圆22221x y a b+=(a >b >0)的焦半径公式:10||MF a ex =+,20||MF a ex =-(1(,0)F c -,2(,0)F c 00(,)M x y ).9. 设过椭圆焦点F 作直线与椭圆相交 P 、Q 两点,A 为椭圆长轴上一个顶点,连结AP和AQ 分别交相应于焦点F 的椭圆准线于M 、N 两点,则MF ⊥NF.10. 过椭圆一个焦点F 的直线与椭圆交于两点P 、Q, A 1、A 2为椭圆长轴上的顶点,A 1P 和A 2Q 交于点M ,A 2P 和A 1Q 交于点N ,则MF ⊥NF.11. AB 是椭圆22221x y a b +=的不平行于对称轴的弦,M ),(00y x 为AB 的中点,则22OM AB b k k a ⋅=-,即0202y a x b K AB -=。
12. 若000(,)P x y 在椭圆22221x y a b+=内,则被Po 所平分的中点弦的方程是2200002222x x y y x y a b a b+=+.13. 若000(,)P x y 在椭圆22221x y a b+=内,则过Po 的弦中点的轨迹方程是22002222x x y yx y a b a b+=+.1. 点P 处的切线PT 平分△PF 1F 2在点P 处的内角.2. PT 平分△PF 1F 2在点P 处的内角,则焦点在直线PT 上的射影H 点的轨迹是以长轴为直径的圆,除去长轴的两个端点. 3. 以焦点弦PQ 为直径的圆必与对应准线相交.4. 以焦点半径PF 1为直径的圆必与以实轴为直径的圆相切.(内切:P 在右支;外切:P 在左支)5. 若000(,)P x y 在双曲线22221x y a b-=(a >0,b >0)上,则过0P 的双曲线的切线方程是00221x x y ya b-=. 6. 若000(,)P x y 在双曲线22221x y a b-=(a >0,b >0)外 ,则过Po 作双曲线的两条切线切点为P 1、P 2,则切点弦P 1P 2的直线方程是00221x x y ya b-=.7. 双曲线22221x y a b-=(a >0,b >o )的左右焦点分别为F 1,F 2,点P 为双曲线上任意一点12F PF γ∠=,则双曲线的焦点角形的面积为122t2F PF S b co γ∆=.8. 双曲线22221x y a b-=(a >0,b >o )的焦半径公式:(1(,0)F c -,2(,0)F c当00(,)M x y 在右支上时,10||MF ex a =+,20||MF ex a =-.当00(,)M x y 在左支上时,10||MF ex a =-+,20||MF ex a =--9. 设过双曲线焦点F 作直线与双曲线相交 P 、Q 两点,A 为双曲线长轴上一个顶点,连结AP 和AQ 分别交相应于焦点F 的双曲线准线于M 、N 两点,则MF ⊥NF. 10. 过双曲线一个焦点F 的直线与双曲线交于两点P 、Q, A 1、A 2为双曲线实轴上的顶点,A 1P 和A 2Q 交于点M ,A 2P 和A 1Q 交于点N ,则MF ⊥NF.11. AB 是双曲线22221x y a b-=(a >0,b >0)的不平行于对称轴的弦,M ),(00y x 为AB的中点,则0202y a x b K K AB OM =⋅,即0202y a x b K AB =。
高考数学圆锥曲线的经典性质50条
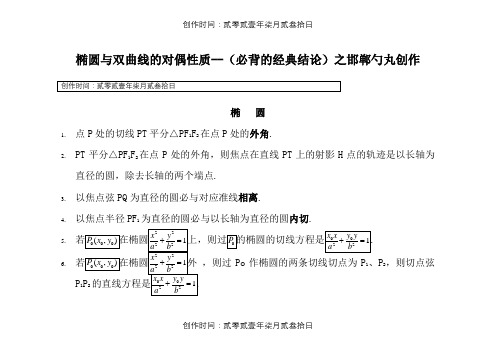
椭圆与双曲线的对偶性质--(必背的经典结论)之邯郸勺丸创作椭圆1.点P处的切线PT平分△PF1F2在点P处的外角.2.PT平分△PF1F2在点P处的外角,则焦点在直线PT上的射影H点的轨迹是以长轴为直径的圆,除去长轴的两个端点.3.以焦点弦PQ为直径的圆必与对应准线相离.4.以焦点半径PF1为直径的圆必与以长轴为直径的圆内切.5.6.,则过Po作椭圆的两条切线切点为P1、P2,则切点弦P1P27.>b>0)的左右焦点分别为F1,F2,点P为椭圆上任意一点8.)的焦半径公式:9.设过椭圆焦点F作直线与椭圆相交 P、Q两点,A为椭圆长轴上一个顶点,连结AP和AQ分别交相应于焦点F的椭圆准线于M、N两点,则MF⊥NF.10.过椭圆一个焦点F的直线与椭圆交于两点P、Q, A1、A2为椭圆长轴上的顶点,A1P和A2Q交于点M,A2P和A1Q交于点N,则MF⊥NF.11.AB12.Po13.Po双曲线1.点P处的切线PT平分△PF1F2在点P处的内角.2.PT平分△PF1F2在点P处的内角,则焦点在直线PT上的射影H点的轨迹是以长轴为直径的圆,除去长轴的两个端点.3.以焦点弦PQ为直径的圆必与对应准线相交.4.以焦点半径PF1为直径的圆必与以实轴为直径的圆相切.(内切:P在右支;外切:P在左支)5.a>0,b>06.a>0,b>0)外,则过Po作双曲线的两条切线切点为P1、P2,则切点弦P1P27.a>0,b>o)的左右焦点分别为F1,F 2,点P为双曲线上任意8.a>0,b>o)的焦半径公式:9.设过双曲线焦点F作直线与双曲线相交 P、Q两点,A为双曲线长轴上一个顶点,连结AP 和AQ分别交相应于焦点F的双曲线准线于M、N两点,则MF⊥NF.10.过双曲线一个焦点F的直线与双曲线交于两点P、Q, A1、A2为双曲线实轴上的顶点,A1P和A2Q交于点M,A2P和A1Q交于点N,则MF⊥NF.11.AB a>0,b>0)的不服行于对称轴的弦,AB的中12.a>0,b>0)内,则被Po所平分的中点弦的方程13.a>0,b>0)内,则过Po的弦中点的轨迹方程是椭圆与双曲线的对偶性质--(会推导的经典结论)高三数学备课组椭圆1.a>b>o y轴平行的直线交椭圆于P1、P2时A1P1与A2P22.>0, b>0)椭圆于B,C两点,则直线BC.3.若P a>b>0)上异于长轴端点的任一点,F1, F 2是焦点,4.a>b>0)的两个焦点为F1、F2,P(异于长轴端点)为椭圆上任意一点,在△PF1F2中,记, ,,则有5.a>b>0)的左、右焦点分别为F1、F2,左准线为L,则当0<e P,使得PF1是P到对应准线距离d与PF2的比例中项.6.P a>b>0)上任一点,F1,F2为二焦点,A为椭圆内一定点,则.7.有公共点的充要条件是8.P、Q为椭圆上两动点,且2(3)9.M,N两点,弦MN10.AB的垂直平分11.设P a>b>0)上异于长轴端点的任一点,F1、F2为其焦点12.设A、B a>b>0)的长轴两端点,P是椭圆上的一点,c、e焦距离心率,则有13. a>b>0x的直线与椭圆相交于A、B两点,AC经过线段EF 的中点.14.过椭圆焦半径的端点作椭圆的切线,与以长轴为直径的圆相交,则相应交点与相应焦点的连线必与切线垂直.15.过椭圆焦半径的端点作椭圆的切线交相应准线于一点,则该点与焦点的连线必与焦半径互相垂直.16.椭圆焦三角形中,内点到一焦点的距离与以该焦点为端点的焦半径之比为常数e(离心率).(注:在椭圆焦三角形中,非焦顶点的内、外角平分线与长轴交点分别称为内、外点.)17.椭圆焦三角形中,内心将内点与非焦顶点连线段分成定比e.18.椭圆焦三角形中,半焦距必为内、外点到椭圆中心的比例中项.椭圆与双曲线的对偶性质--(会推导的经典结论)高三数学备课组双曲线1.a>0,b>0y轴平行的直线交双曲线于P1、P2时A1P1与A2P22.a>0,b>o直线交双曲线于B,C两点,则直线BC.3.若P a>0,b>0)右(或左)支上除顶点外的任一点,F1,F 2是焦点.4.a>0,b>0)的两个焦点为F1、F2,P(异于长轴端点)为双曲线上任意一点,在△PF1F25.a>0,b>0)的左、右焦点分别为F1、F2,左准线为L,则当1<e P,使得PF1是P到对应准线距离d与PF2的比例中项.6.P a>0,b>0)上任一点,F1,F2为二焦点,A为双曲线内y轴同7.0,b>08.b>a >0),O为坐标原点,P、Q为双曲线上两动(1(2)|OP|2+|OQ|2(39.0,b>0)的右焦点F作直线交该双曲线的右支于M,N10. AB 的垂11.设P ,F 1、F 2为 12. 设A 、B有13. a >0,b >0xA 、B 两点,则直线AC经过线段EF 的中点.14.过双曲线焦半径的端点作双曲线的切线,与以长轴为直径的圆相交,则相应交点与相应焦点的连线必与切线垂直.15.过双曲线焦半径的端点作双曲线的切线交相应准线于一点,则该点与焦点的连线必与焦半径互相垂直.16.双曲线焦三角形中,外点到一焦点的距离与以该焦点为端点的焦半径之比为常数e(离心率).(注:在双曲线焦三角形中,非焦顶点的内、外角平分线与长轴交点分别称为内、外点).17.双曲线焦三角形中,其焦点所对的旁心将外点与非焦顶点连线段分成定比e.18.双曲线焦三角形中,半焦距必为内、外点到双曲线中心的比例中项.。
高考数学圆锥曲线的经典性质50条

椭圆与双曲线的对偶性质--(必背的经典结论)椭圆1.点P处的切线PT平分△PF1F2在点P处的外角.2.PT平分△PF1F2在点P处的外角,则焦点在直线PT上的射影H点的轨迹是以长轴为直径的圆,除去长轴的两个端点.3.以焦点弦PQ为直径的圆必与对应准线相离.4.以焦点半径PF1为直径的圆必与以长轴为直径的圆内切.5.若000(,)P x y 在椭圆22221x y a b +=上,则过0P 的椭圆的切线方程是00221x x y ya b +=.6.若000(,)P x y 在椭圆22221x y a b+=外 ,则过Po 作椭圆的两条切线切点为P 1、P 2,则切点弦P 1P 2的直线方程是00221x x y ya b+=.7.椭圆22221x y a b+= (a >b >0)的左右焦点分别为F 1,F 2,点P 为椭圆上任意一点12F PF γ∠=,则椭圆的焦点角形的面积为122tan2F PFS b γ∆=.8.椭圆22221x y a b+=(a >b >0)的焦半径公式:10||MF a ex =+,20||MF a ex =-(1(,0)F c -,2(,0)F c 00(,)M x y ).9.设过椭圆焦点F 作直线与椭圆相交 P 、Q 两点,A 为椭圆长轴上一个顶点,连结AP 和AQ 分别交相应于焦点F 的椭圆准线于M 、N 两点,则MF ⊥NF.10.过椭圆一个焦点F 的直线与椭圆交于两点P 、Q, A 1、A 2为椭圆长轴上的顶点,A 1P 和A 2Q 交于点M ,A 2P 和A 1Q 交于点N ,则MF ⊥NF.11.AB 是椭圆22221x y a b +=的不平行于对称轴的弦,M ),(00y x 为AB 的中点,则22OM AB b k k a ⋅=-,即0202y a x b K AB -=。
12.若000(,)P x y 在椭圆22221x y a b+=内,则被Po 所平分的中点弦的方程是2200002222x x y y x y a b a b+=+.13.若000(,)P x y 在椭圆22221x y a b+=内,则过Po 的弦中点的轨迹方程是22002222x x y yx y a b a b+=+. 双曲线1.点P 处的切线PT 平分△PF 1F 2在点P 处的内角.2.PT 平分△PF 1F 2在点P 处的内角,则焦点在直线PT 上的射影H 点的轨迹是以长轴为直径的圆,除去长轴的两个端点.3. 以焦点弦PQ 为直径的圆必与对应准线相交.4.以焦点半径PF 1为直径的圆必与以实轴为直径的圆相切.(内切:P 在右支;外切:P 在左支)5.若000(,)P x y 在双曲线22221x y a b-=(a >0,b >0)上,则过0P 的双曲线的切线方程是00221x x y ya b-=.6.若000(,)P x y 在双曲线22221x y a b-=(a >0,b >0)外 ,则过Po 作双曲线的两条切线切点为P 1、P 2,则切点弦P 1P 2的直线方程是00221x x y ya b-=.7.双曲线22221x y a b-=(a >0,b >o )的左右焦点分别为F 1,F 2,点P 为双曲线上任意一点12F PF γ∠=,则双曲线的焦点角形的面积为122t2F PFS b co γ∆=.8.双曲线22221x y a b-=(a >0,b >o )的焦半径公式:(1(,0)F c -,2(,0)F c当00(,)M x y 在右支上时,10||MF ex a =+,20||MF ex a =-.当00(,)M x y 在左支上时,10||MF ex a =-+,20||MF ex a =--9.设过双曲线焦点F 作直线与双曲线相交 P 、Q 两点,A 为双曲线长轴上一个顶点,连结AP 和AQ 分别交相应于焦点F 的双曲线准线于M 、N 两点,则MF ⊥NF.10.过双曲线一个焦点F 的直线与双曲线交于两点P 、Q, A 1、A 2为双曲线实轴上的顶点,A 1P 和A 2Q 交于点M ,A 2P 和A 1Q 交于点N ,则MF ⊥NF.11.AB 是双曲线22221x y a b-=(a >0,b >0)的不平行于对称轴的弦,M ),(00y x 为AB的中点,则0202y a x b K K AB OM =⋅,即0202y a x b K AB =。
高考数学圆锥曲线的经典性质50条之欧阳语创编

椭圆与双曲线的对偶性质--(必背的经典结论)椭 圆1. 点P 处的切线PT 平分△PF1F2在点P 处的外角.2.PT 平分△PF1F2在点P 处的外角,则焦点在直线PT 上的射影H 点的轨迹是以长轴为直径的圆,除去长轴的两个端点.3. 以焦点弦PQ 为直径的圆必与对应准线相离.4. 以焦点半径PF1为直径的圆必与以长轴为直径的圆内切.5.若000(,)P x y 在椭圆22221x y a b +=上,则过0P 的椭圆的切线方程是00221x x y ya b+=.6.若000(,)P x y 在椭圆22221x y a b+=外 ,则过Po 作椭圆的两条切线切点为P1、P2,则切点弦P1P2的直线方程是00221x x y ya b+=.7.椭圆22221x y a b += (a >b >0)的左右焦点分别为F1,F 2,点P 为椭圆上任意一点12F PF γ∠=,则椭圆的焦点角形的面积为122tan2F PF S b γ∆=.8.椭圆22221x y a b +=(a >b >0)的焦半径公式:10||MF a ex =+,20||MF a ex =-(1(,0)F c -,2(,0)F c 00(,)M x y ).9.设过椭圆焦点F 作直线与椭圆相交 P 、Q 两点,A 为椭圆长轴上一个顶点,连结AP 和AQ 分别交相应于焦点F 的椭圆准线于M 、N 两点,则MF⊥NF.10.过椭圆一个焦点F 的直线与椭圆交于两点P 、Q, A1、A2为椭圆长轴上的顶点,A1P 和A2Q 交于点M ,A2P 和A1Q 交于点N ,则MF⊥NF.11.AB 是椭圆22221x y a b +=的不平行于对称轴的弦,M ),(00y x 为AB 的中点,则22OM AB b k k a ⋅=-,即0202y a x b K AB -=。
12.若000(,)P x y 在椭圆22221x y a b +=内,则被Po 所平分的中点弦的方程是2200002222x x y y x y a b a b+=+.13.若000(,)P x y 在椭圆22221x y a b+=内,则过Po的弦中点的轨迹方程是22002222x x y yx y a b a b+=+.双曲线1. 点P 处的切线PT 平分△PF1F2在点P 处的内角.2.PT 平分△PF1F2在点P 处的内角,则焦点在直线PT 上的射影H 点的轨迹是以长轴为直径的圆,除去长轴的两个端点.3. 以焦点弦PQ 为直径的圆必与对应准线相交.4.以焦点半径PF1为直径的圆必与以实轴为直径的圆相切.(内切:P 在右支;外切:P 在左支)5.若000(,)P x y 在双曲线22221x y a b-=(a >0,b >0)上,则过0P 的双曲线的切线方程是00221x x y ya b-=.6.若000(,)P x y 在双曲线22221x y a b-=(a >0,b >0)外 ,则过Po 作双曲线的两条切线切点为P1、P2,则切点弦P1P2的直线方程是00221x x y ya b-=.7.双曲线22221x y a b-=(a >0,b >o )的左右焦点分别为F1,F 2,点P 为双曲线上任意一点12F PF γ∠=,则双曲线的焦点角形的面积为122t 2F PF S b co γ∆=.8.双曲线22221x y a b-=(a >0,b >o )的焦半径公式:(1(,0)F c -,2(,0)F c当00(,)M x y 在右支上时,10||MF ex a =+,20||MF ex a =-. 当00(,)M x y 在左支上时,10||MF ex a =-+,20||MF ex a =--9.设过双曲线焦点F 作直线与双曲线相交 P 、Q 两点,A 为双曲线长轴上一个顶点,连结AP 和AQ 分别交相应于焦点F 的双曲线准线于M 、N 两点,则MF⊥NF.10.过双曲线一个焦点F 的直线与双曲线交于两点P 、Q, A1、A2为双曲线实轴上的顶点,A1P 和A2Q 交于点M ,A2P 和A1Q 交于点N ,则MF⊥NF.11.AB 是双曲线22221x y a b-=(a >0,b >0)的不平行于对称轴的弦,M ),(00y x 为AB的中点,则0202y a x b K K AB OM =⋅,即0202y a x b K AB =。
圆锥曲线对偶的性质100条.doc.

椭圆与双曲线的对偶性质100条椭 圆1.12||||2PF PF a +=2.标准方程:22221x y a b+=3.11||1PF e d =< 4.点P 处的切线PT 平分△PF 1F 2在点P 处的外角.5.PT 平分△PF 1F 2在点P 处的外角,则焦点在直线PT 上的射影H 点的轨迹是以长轴为直径的圆,除去长轴的两个端点.6.以焦点弦PQ 为直径的圆必与对应准线相离.7.以焦点半径PF 1为直径的圆必与以长轴为直径的圆内切.8.设A 1、A 2为椭圆的左、右顶点,则△PF 1F 2在边PF 2(或PF 1)上的旁切圆,必与A 1A 2所在的直线切于A 2(或A 1).9.椭圆22221x y a b+=(a >b >0)的两个顶点为1(,0)A a -,2(,0)A a ,与y 轴平行的直线交椭圆于P 1、P 2时A 1P 1与A 2P 2交点的轨迹方程是22221x y a b -=.10.若000(,)P x y 在椭圆22221x y a b +=上,则过P 0的椭圆的切线方程是00221x x y ya b +=.11.若000(,)P x y 在椭圆22221x y a b+=外,则过P 0作椭圆的两条切线切点为P 1、P 2,则切点弦P 1P 2的直线方程是00221x x y ya b+=.12.AB 是椭圆22221x y a b +=的不平行于对称轴且过原点的弦,M 为AB 的中点,则22OM AB b k k a⋅=-.13.若000(,)P x y 在椭圆22221x y a b+=内,则被P 0所平分的中点弦的方程是2200002222x x y y x y a b a b +=+.14.若000(,)P x y 在椭圆22221x y a b+=内,则过P 0的弦中点的轨迹方程是22002222x x y yx y a b a b +=+.15.若PQ 是椭圆22221x y a b +=(a >b >0)上对中心张直角的弦,则122222121111(||,||)r OP r OQ r r a b +=+==.16.若椭圆22221x y a b+=(a >b >0)上中心张直角的弦L 所在直线方程为1Ax By +=(0)AB ≠,则:(1)222211A B a b +=+;(2)2222L a A b B=+.17.给定椭圆1C :222222b x a y a b +=(a >b >0), 2C :222222222()a b b x a y ab a b-+=+,则: (1)对1C 上任意给定的点000(,)P x y ,它的任一直角弦必须经过2C 上一定点M 2222002222(,)a b a b x y a b a b---++. (2)对2C 上任一点'''000(,)P x y 在1C 上存在唯一的点'M ,使得'M 的任一直角弦都经过'0P 点.18.设000(,)P x y 为椭圆(或圆)C : 22221x y a b+=(a >0,. b >0)上一点,P 1P 2为曲线C 的动弦,且弦P 0P 1, P 0P 2斜率存在,记为k 1, k 2, 则直线P 1P 2通过定点00(,)M mx my -(1)m ≠的充要条件是212211m b k k m a +⋅=-⋅-. 19.过椭圆22221x y a b+=(a >0, b >0)上任一点00(,)A x y 任意作两条倾斜角互补的直线交椭圆于B ,C 两点,则直线BC 有定向且2020BC b x k a y =(常数).20.椭圆22221x y a b+=(a >b >0)的左右焦点分别为F 1,F 2,点P 为椭圆上任意一点12F PF γ∠=,则椭圆的焦点角形的面积为122tan 2F PF S b γ∆=,2tan )2b P c γ . 21.若P 为椭圆22221x y a b+=(a >b >0)上异于长轴端点的任一点,F 1, F 2是焦点, 12PF F α∠=, 21PF F β∠=,则tan t 22a c co a c αβ-=+. 22.椭圆22221x y a b+=(a >b >0)的焦半径公式:10||MF a ex =+,20||MF a ex =-(1(,0)F c - , 2(,0)F c 00(,)M x y ).23.若椭圆22221x y a b+=(a >b >0)的左、右焦点分别为F 1、F 2,左准线为L ,则当0<e 1时,可在椭圆上求一点P ,使得PF 1是P 到对应准线距离d 与PF 2的比例中项. 24.P 为椭圆22221x y a b+=(a >b >0)上任一点,F 1,F 2为二焦点,A 为椭圆内一定点,则2112||||||2||a AF PA PF a AF -≤+≤+,当且仅当2,,A F P 三点共线时,等号成立.25.椭圆22221x y a b +=(a >b >0)上存在两点关于直线l :0()y k x x =-对称的充要条件是22220222()a b x a b k-≤+. 26.过椭圆焦半径的端点作椭圆的切线,与以长轴为直径的圆相交,则相应交点与相应焦点的连线必与切线垂直. 27.过椭圆焦半径的端点作椭圆的切线交相应准线于一点,则该点与焦点的连线必与焦半径互相垂直. 28.P 是椭圆cos sin x a y b ϕϕ=⎧⎨=⎩(a >b >0)上一点,则点P 对椭圆两焦点张直角的充要条件是2211sin e ϕ=+. 29.设A ,B 为椭圆2222(0,1)x y k k k a b +=>≠上两点,其直线AB 与椭圆22221x y a b+=相交于,P Q ,则AP BQ =.30.在椭圆22221x y a b+=中,定长为2m (0<m ≤a )的弦中点轨迹方程为2222222221()cos sin x y a b m a b αα-+=+,其中2222tan b x a y α=-,当0y =时, 90α=o .31.设S 为椭圆22221x y a b+=(a >b >0)的通径,定长线段L 的两端点A ,B 在椭圆上移动,记|AB |=l ,00(,)M x y 是AB 中点,则:当l S ≥Φ时,有20max ()2a l x c e =-222(c a b =-,ce a =); 当l S <Φ时,有0max ()x =0min ()0x =.32.椭圆22221x y a b+=与直线0Ax By C ++=有公共点的充要条件是22222A aB bC +≥.33.椭圆220022()()1x x y y a b--+=与直线0Ax By C ++=有公共点的充要条件是 2222200()A a B b Ax By C +≥++.34.设椭圆22221x y a b+=(a >b >0)的两个焦点为F 1、F 2,P (异于长轴端点)为椭圆上任意一点,在△PF 1F 2中,记12F PF α∠=, 12PF F β∠=,12F F P γ∠=,则有sin sin sin ce aαβγ==+. 35.经过椭圆222222b x a y a b+=(a >b >0)的长轴的两端点A 1和A 2的切线,与椭圆上任一点的切线相交于P 1和P 2,则212||||PA PA b ⋅=.36.已知椭圆22221x y a b +=(a >b >0),O 为坐标原点,P 、Q 为椭圆上两动点,且OP OQ ⊥.(1)22221111||||OP OQ a b +=+; (2)|OP |2+|OQ |2的最大值为22224a ba b +;(3)OPQ S ∆的最小值是2222a b a b+. 37.MN 是经过椭圆222222b x a y a b +=(a >b >0)过焦点的任一弦,若AB 是经过椭圆中心O 且平行于MN的弦,则2||2||AB a MN =.38.MN 是经过椭圆222222b x a y a b+=(a >b >0)焦点的任一弦,若过椭圆中心O 的半弦OP MN ⊥,则2222111||||a MN OP a b +=+.39.设椭圆22221x y a b+=(a >b >0),M (m ,0)或(0,m )为其对称轴上除中心,顶点外的任一点,过M 引一条直线与椭圆相交于P 、Q 两点,则直线A 1P 、A 2Q (A 1 ,A 2为对称轴上的两顶点)的交点N 在直线l :2a x m=(或2b y m=)上.40.设过椭圆焦点F 作直线与椭圆相交 P 、Q 两点,A 为椭圆长轴上一个顶点,连结AP 和AQ 分别交相应于焦点F 的椭圆准线于M 、N 两点,则MF ⊥NF .41.过椭圆一个焦点F 的直线与椭圆交于两点P 、Q , A 1、A 2为椭圆长轴上的顶点,A 1P 和A 2Q 交于点M ,A 2P 和A 1Q 交于点N ,则MF ⊥NF .42.设椭圆方程22221x y a b +=,则斜率为k (k ≠0)的平行弦的中点必在直线l :y kx =的共轭直线'y k x =上,而且2'2b kk a=-.43.设A 、B 、C 、D 为椭圆22221x y a b+=上四点,AB 、CD 所在直线的倾斜角分别为,αβ,直线AB 与CD 相交于P ,且P 不在椭圆上,则22222222||||cos sin ||||cos sin PA PB b a PC PD b a ββαα⋅+=⋅+.44.已知椭圆22221x y a b+=(a >b >0),点P 为其上一点F 1, F 2为椭圆的焦点,12F PF ∠的外(内)角平分线为l ,作F 1、F 2分别垂直l 于R 、S ,当P 跑遍整个椭圆时,R 、S 形成的轨迹方程是222x y a+=(2222222{[()()]}()[()]b y a ce x c x y cx ce x c +-+⋅++=+).45.设△ABC 内接于椭圆Γ,且AB 为Γ的直径,l 为AB 的共轭直径所在的直线,l 分别交直线AC 、BC 于E 和F ,又D 为l 上一点,则CD 与椭圆Γ相切的充要条件是D 为EF 的中点.46.过椭圆22221x y a b +=(a >b >0)的右焦点F 作直线交该椭圆右支于M ,N 两点,弦MN 的垂直平分线交x轴于P ,则||||2PF eMN =. 47.设A (x 1,y 1)是椭圆22221x y a b +=(a >b >0)上任一点,过A 作一条斜率为2121b x a y -的直线L ,又设d 是原点到直线 L 的距离, 12,r r 分别是Aab =.48.已知椭圆22221x y a b +=(a >b >0)和2222x y a bλ+=(01λ<< ),一直线顺次与它们相交于A 、B 、C 、D 四点,则│AB │=│CD │.49.已知椭圆22221x y a b+=(a >b >0),A 、B 、是椭圆上的两点,线段AB 的垂直平分线与x 轴相交于点0(,0)P x ,则22220a b a b x a a---<<. 50.设P 点是椭圆22221x y a b+=(a >b >0)上异于长轴端点的任一点,F 1、F 2为其焦点记12F PF θ∠=,则:(1)2122||||1cos b PF PF θ=+.(2) 122tan 2PF F S b γ∆=.51.设过椭圆的长轴上一点B (m ,0)作直线与椭圆相交于P 、Q 两点,A 为椭圆长轴的左顶点,连结AP和AQ 分别交相应于过B 点的直线MN :x n =于M ,N 两点,则90MBN ∠=o222()a m a a mb n a -⇔=++. 52.L 是经过椭圆22221x y a b+=(a >b >0)长轴顶点A 且与长轴垂直的直线,E 、F 是椭圆两个焦点,e 是离心率,点P L ∈,若EPF α∠=,则α是锐角且sin e α≤或sin arc e α≤(当且仅当||abPH c=时取等号).53.L 是椭圆22221x y a b+=(a >b >0)的准线,A 、B 是椭圆的长轴两顶点,点P L ∈,e 是离心率,EPF α∠=,H 是L 与X 轴的交点c 是半焦距,则α是锐角且sin e α≤或sin arc e α≤(当且仅当||abPH c=时取等号).54.L 是椭圆22221x y a b+=(a >b >0)的准线,E 、F 是两个焦点,H 是L 与x 轴的交点,点P L ∈,EPF α∠=,离心率为e ,半焦距为c ,则α为锐角且2sin e α≤或2sin arc e α≤(当且仅当||PH =. 55.已知椭圆22221x y a b+=(a >b >0),直线L 通过其右焦点F 2,且与椭圆相交于A 、B 两点,将A 、B 与椭圆左焦点F 1连结起来,则2222112(2)||||a b b F A F B a -≤⋅≤(当且仅当AB ⊥x 轴时右边不等式取等号,当且仅当A 、F 1、B 三点共线时左边不等式取等号).56.设A 、B 是椭圆22221x y a b+=(a >b >0)的长轴两端点,P 是椭圆上的一点,PAB α∠=,PBA β∠=,BPA γ∠=,c 、e 分别是椭圆的半焦距离心率,则有(1)22222|cos |||s ab PA a c co αγ=-. (2)2tan tan 1e αβ=-.(3)22222cot PAB a b S b a γ∆=-. 57.设A 、B 是椭圆22221x y a b +=(a >b >0)长轴上分别位于椭圆内(异于原点)、外部的两点,且A x 、B x 的横坐标2A B x x a ⋅=,(1)若过A 点引直线与这椭圆相交于P 、Q 两点,则PBA QBA ∠=∠;(2)若过B 引直线与这椭圆相交于P 、Q 两点,则180PBA QBA ∠+∠=o.58.设A 、B 是椭圆22221x y a b+=(a >b >0)长轴上分别位于椭圆内(异于原点),外部的两点.(1)若过A 点引直线与这椭圆相交于P 、Q 两点,(若BP 交椭圆于两点,则P 、Q 不关于x 轴对称),且PBA QBA ∠=∠,则点A 、B 的横坐标A x 、B x 满足2A B x x a ⋅=;(2)若过B 点引直线与这椭圆相交于P 、Q 两点,且180PBA QBA ∠+∠=o,则点A 、B 的横坐标满足2A B x x a ⋅=.59.设',A A 是椭圆22221x y a b+=的长轴的两个端点,'QQ 是与'AA 垂直的弦,则直线AQ 与''AQ 的交点P 的轨迹是双曲线22221x y a b -=.60.过椭圆22221x y a b+=(a >b >0)的左焦点F 作互相垂直的两条弦AB 、CD 则2222282()||||ab a b AB CD a b a+≤+≤+. 61.到椭圆22221x y a b +=(a >b >0)两焦点的距离之比等于a cb-(c 为半焦距)的动点M 的轨迹是姊妹圆222()x a y b ±+=.62.到椭圆22221x y a b +=(a >b >0)的长轴两端点的距离之比等于a cb -(c 为半焦距)的动点M 的轨迹是姊妹圆222()()a b x y e e±+=.63.到椭圆22221x y a b +=(a >b >0)的两准线和x 轴的交点的距离之比为a cb -(c 为半焦距)的动点的轨迹是姊妹圆22222()()a b x y e e±+=(e 为离心率).64.已知P 是椭圆22221x y a b+=(a >b >0)上一个动点,',A A 是它长轴的两个端点,且AQ AP ⊥,''AQ A P ⊥,则Q 点的轨迹方程是222241x b y a a+=.65.椭圆的一条直径(过中心的弦)的长,为通过一个焦点且与此直径平行的弦长和长轴之长的比例中项.66.设椭圆22221x y a b +=(a >b >0)长轴的端点为',A A ,11(,)P x y 是椭圆上的点过P 作斜率为2121b x a y -的直线l ,过',A A 分别作垂直于长轴的直线交l 于',M M ,则: (1)''2||||AM A M b =.(2)四边形''MAA M 面积的最小值是2ab .67.已知椭圆22221x y a b+=(a >b >0)的右准线l 与x 轴相交于点E ,过椭圆右焦点F 的直线与椭圆相交于A 、B 两点,点C 在右准线l 上,且BC x ⊥轴,则直线AC 经过线段EF 的中点.68.OA 、OB 是椭圆2222()1x a y a b-+=(a >0,b >0)的两条互相垂直的弦,O 为坐标原点,则 (1)直线AB 必经过一个定点2222(,0)ab a b+. (2)以OA 、OB 为直径的两圆的另一个交点Q 的轨迹方程是:222222222()()ab ab x y a b a b-+=++(0)x ≠.69.(,)P m n 是椭圆2222()1x a y a b-+=(a >b >0)上一个定点,P A 、P B 是互相垂直的弦,则 (1)直线AB 必经过一个定点2222222222()()(,)ab m a b n b a a b a b+--++. (2)以PA 、PB 为直径的两圆的另一个交点Q 的轨迹方程是22224222222222222[()]()()()ab a m b n a b n a b x y a b a b a b ++--+-=+++(x m ≠且y n ≠). 70.如果一个椭圆短半轴长为b ,焦点F 1、F 2到直线L 的距离分别为d 1、d 2,那么:(1)212d d b =,且F 1、F 2在L 同侧⇔直线L 和椭圆相切. (2)212d d b >,且F 1、F 2在L 同侧⇔直线L 和椭圆相离. (3)212d d b <,或F 1、F 2在L 异侧⇔直线L 和椭圆相交.71.AB 是椭圆22221x y a b+=(a >b >0)的长轴,N 是椭圆上的动点,过N 的切线与过A 、B 的切线交于C 、D两点,则梯形ABDC 的对角线的交点M 的轨迹方程是22241(0)x a y y +=≠.72.设点00(,)P x y 为椭圆22221x y a b +=(a >b >0)的内部一定点,AB 是椭圆22221x y a b+=过定点00(,)P x y 的任一弦,当弦AB 平行(或重合)于椭圆长轴所在直线时22222200max 2()(||||)a b a y b x PA PB b -+⋅=.当弦AB 垂直于长轴所在直线时, 22222200min 2()(||||)a b a y b x PA PB b -+⋅=.73.椭圆焦三角形中,以焦半径为直径的圆必与以椭圆长轴为直径的圆相内切. 74.椭圆焦三角形的旁切圆必切长轴于非焦顶点同侧的长轴端点. 75.椭圆两焦点到椭圆焦三角形旁切圆的切线长为定值a+c 与a-c. 76.椭圆焦三角形的非焦顶点到其内切圆的切线长为定值a-c.77.椭圆焦三角形中,内点到一焦点的距离与以该焦点为端点的焦半径之比为常数e (离心率). [注:在椭圆焦三角形中,非焦顶点的内、外角平分线与长轴交点分别称为内、外点.] 78.椭圆焦三角形中,内心将内点与非焦顶点连线段分成定比e. 79.椭圆焦三角形中,半焦距必为内、外点到椭圆中心的比例中项.80.椭圆焦三角形中,椭圆中心到内点的距离、内点到同侧焦点的距离、半焦距及外点到同侧焦点的距离成比例. 81.椭圆焦三角形中,半焦距、外点与椭圆中心连线段、内点与同侧焦点连线段、外点与同侧焦点连线段成比例. 82.椭圆焦三角形中,过任一焦点向非焦顶点的外角平分线引垂线,则椭圆中心与垂足连线必与另一焦半径所在 直线平行.83.椭圆焦三角形中,过任一焦点向非焦顶点的外角平分线引垂线,则椭圆中心与垂足的距离为椭圆长半轴的长.84.椭圆焦三角形中,过任一焦点向非焦顶点的外角平分线引垂线,垂足就是垂足同侧焦半径为直径的圆和椭圆 长轴为直径的圆的切点.85.椭圆焦三角形中,非焦顶点的外角平分线与焦半径、长轴所在直线的夹角的余弦的比为定值e. 86.椭圆焦三角形中,非焦顶点的法线即为该顶角的内角平分线. 87.椭圆焦三角形中,非焦顶点的切线即为该顶角的外角平分线.88.椭圆焦三角形中,过非焦顶点的切线与椭圆长轴两端点处的切线相交,则以两交点为直径的圆必过两焦点.89. 已知椭圆22221(0,0)x y a b a b +=>>(包括圆在内)上有一点P ,过点P 分别作直线b y x a =及by x a=-的平行线,与直线OP 分别交于,R Q ,O 为原点,则:.(1)222||||OM ON a +=; (2)222||||OQ OR b +=.90. 过平面上的P 点作直线1:b l y x a =及2:bl y x a=-的平行线,分别交x 轴于,M N ,交y 轴于,R Q . (1)若222||||OM ON a +=,则P 的轨迹方程是22221(0,0)x y a b a b +=>>.(2)若222||||OQ OR b +=,则P 的轨迹方程是22221(0,0)x y a b a b+=>>.91. 点P 为椭圆22221(0,0)x y a b a b+=>>(包括圆在内)在第一象限的弧上任意一点,过P 引x 轴、y 轴的平行线,交y 轴、x 轴于,M N ,交直线by x a=-于,Q R ,记 OMQ ∆与ONR ∆的面积为12,S S ,则:122ab S S +=. 92. 点P 为第一象限内一点,过P 引x 轴、y 轴的平行线,交y 轴、x 轴于,M N ,交直线by x a=-于,Q R ,记 OMQ ∆与ONR ∆的面积为12,S S ,已知122abS S +=,则P 的轨迹方程是22221(0,0)x y a b a b +=>>.双曲线1.12||||||2PF PF a -=2.标准方程:22221x y a b-=3.11||1PF e d => 4.点P 处的切线PT 平分△PF 1F 2在点P 处的内角.5.PT 平分△PF 1F 2在点P 处的内角,则焦点在直线PT 上的射影H 点的轨迹是以长轴为直径的圆,除去长轴的两个端点.6.以焦点弦PQ 为直径的圆必与对应准线相交.7.以焦点半径PF 1为直径的圆必与以实轴为直径的圆外切.8.设A 1、A 2为双曲线的左、右顶点,则△PF 1F 2在边PF 2(或PF 1)上的旁切圆,必与A 1A 2所在的直线切于A 2(或A 1).9.双曲线22221x y a b-=(a >0,b >0)的两个顶点为1(,0)A a -,2(,0)A a ,与y 轴平行的直线交双曲线于P 1、P 2时A 1P 1与A 2P 2交点的轨迹方程是22221x y a b+=.10.若000(,)P x y 在双曲线22221x y a b -=(a >0,b >0)上,则过0P 的双曲线的切线方程是00221x x y ya b -=.11.若000(,)P x y 在双曲线22221x y a b -=(a >0,b >0)外 ,则过P 0作双曲线的两条切线切点为P 1、P 2,则切点弦P 1P 2的直线方程是00221x x y ya b -=.12.AB 是双曲线22221x y a b-=(a >0,b >0)的不平行于对称轴且过原点的弦,M 为AB 的中点,则22OM AB b k k a⋅=.13.若000(,)P x y 在双曲线22221x y a b-=(a >0,b >0)内,则被P 0所平分的中点弦的方程是2200002222x x y y x y a b a b-=-. 14.若000(,)P x y 在双曲线22221x y a b-=(a >0,b >0)内,则过P 0的弦中点的轨迹方程是22002222x x y yx y a b a b -=-.15.若PQ 是双曲线22221x y a b -=(b >a >0)上对中心张直角的弦,则122222121111(||,||)r OP r OQ r r a b +=-==.16.若双曲线22221x y a b-=(b >a >0)上中心张直角的弦L 所在直线方程为1Ax By +=(0)AB ≠,则:(1)222211A B a b -=+;(2)2222||L a A b B =-. 17.给定双曲线1C :222222b x a y a b -=(a >b >0), 2C :222222222()a b b x a y ab a b+-=-,则: (1)对1C 上任意给定的点000(,)P x y ,它的任一直角弦必须经过2C 上一定点M (2222002222(,)a b a b x y a b a b++---. (2)对2C 上任一点'''000(,)P x y 在1C 上存在唯一的点'M ,使得'M 的任一直角弦都经过'0P 点.18.设000(,)P x y 为双曲线22221x y a b-=(a >0,b >0)上一点,P 1P 2为曲线C 的动弦,且弦P 0P 1, P 0P 2斜率存在,记为k 1, k 2, 则直线P 1P 2通过定点00(,)M mx my -(1)m ≠的充要条件是212211m b k k m a +⋅=⋅-. 19.过双曲线22221x y a b-=(a >0,b >0)上任一点00(,)A x y 任意作两条倾斜角互补的直线交双曲线于B ,C 两点,则直线BC 有定向且2020BC b x k a y =-(常数).20.双曲线22221x y a b-=(a >0,b >0)的左右焦点分别为F 1,F 2,点P 为双曲线上任意一点12F PF γ∠=,则双曲线的焦点角形的面积为122t 2F PF S b co γ∆=,2cot )2b P c γ . 21.若P 为双曲线22221x y a b -=(a >0,b >0)右(或左)支上除顶点外的任一点,F 1, F 2是焦点, 12PF F α∠=,21PF F β∠=,则tan t 22c a co c a αβ-=+(或tan t 22c a co c a βα-=+).22.双曲线22221x y a b-=(a >0,b >0)的焦半径公式:1(,0)F c -,2(,0)F c当00(,)M x y 在右支上时,10||MF ex a =+, 20||MF ex a =-.当00(,)M x y 在左支上时,10||MF ex a =-+,20||MF ex a =--.23.若双曲线22221x y a b-=(a >0,b >0)的左、右焦点分别为F 1、F 2,左准线为L ,则当1<e 1时,可在双曲线上求一点P ,使得PF 1是P 到对应准线距离d 与PF 2的比例中项.24.P 为双曲线22221x y a b-=(a >0,b >0)上任一点,F 1,F 2为二焦点,A 为双曲线内一定点,则21||2||||AF a PA PF -≤+,当且仅当2,,A F P 三点共线且P 和2,A F 在y 轴同侧时,等号成立.25.双曲线22221x y a b -=(a >0,b >0)上存在两点关于直线l :0()y k x x =-对称的充要条件是22220222()a b x a b k+>-.26.过双曲线焦半径的端点作双曲线的切线,与以长轴为直径的圆相交,则相应交点与相应焦点的连线必与切线垂直.27.过双曲线焦半径的端点作双曲线的切线交相应准线于一点,则该点与焦点的连线必与焦半径互相垂直.x a y b ϕϕ=⎧⎨=⎩(a>0,b>0)上一点,则点P对双曲线两焦点张直角的充要条件是2211taneϕ=-.28.P是双曲线sectan29.设A ,B 为双曲线2222x y k a b -= 上两点,其直线AB 与双曲线22221x y a b-=相交于,P Q ,则AP BQ =.30.在双曲线22221x y a b-=中,定长为2m 的弦中点轨迹方程为2222222221()cos sin x y a b m a bαα--=-,其中2222tan b x a yα=-,当0y =时, 90α=o.31.设S 为双曲线22221x y a b-=(a >0,b >0)的通径,定长线段L 的两端点A ,B 在双曲线上移动,记|AB |=l ,00(,)M x y 是AB 中点,则当l S ≥Φ时,有20min ()2a l x c e =+222(c a b =+,ce a=);当l S <Φ时,有0min ()x =32.双曲线22221x y a b-=(a >0,b >0)与直线0Ax By C ++=有公共点的充要条件是22222A aB bC -≤.33.双曲线220022()()1x x y y a b ---=(a >0,b >0)与直线0Ax By C ++=有公共点的充要条件是2222200()A a B b Ax By C -≤++.34.设双曲线22221x y a b-=(a >0,b >0)的两个焦点为F 1、F 2,P (异于长轴端点)为双曲线上任意一点,在△PF 1F 2中,记12F PF α∠=, 12PF F β∠=,12F F P γ∠=,则有sin (sin sin )ce a αγβ==±-. 35.经过双曲线22221x y a b-=(a >0,b >0)的实轴的两端点A 1和A 2的切线,与双曲线上任一点的切线相交于P 1和P 2,则212||||PA PA b ⋅=.36.已知双曲线22221x y a b-=(b >a >0),O 为坐标原点,P 、Q 为双曲线上两动点,且OP OQ ⊥.(1)22221111||||OP OQ a b +=-; (2)|OP |2+|OQ |2的最小值为22224a bb a -;(3)OPQ S ∆的最小值是2222a b b a -. 37.MN 是经过双曲线22221x y a b-=(a >0,b >0)过焦点的任一弦(交于两支),若AB 是经过双曲线中心O且平行于MN 的弦,则2||2||AB a MN =.38.MN 是经过双曲线22221x y a b-=(a >b >0)焦点的任一弦(交于同支),若过双曲线中心O 的半弦OP MN ⊥,(a >0,b >0,0,1k k >≠)则2222111||||a MN OP a b -=-.39.设双曲线22221x y a b-=(a >0,b >0),M (m ,0)为实轴所在直线上除中心,顶点外的任一点,过M 引一条直线与双曲线相交于P 、Q 两点,则直线A 1P 、A 2Q (A 1 ,A 2为两顶点)的交点N 在直线l :2a x m=上.40.设过双曲线焦点F 作直线与双曲线相交 P 、Q 两点,A 为双曲线长轴上一个顶点,连结AP 和AQ 分别交相应于焦点F 的双曲线准线于M 、N 两点,则MF ⊥NF .41.过双曲线一个焦点F 的直线与双曲线交于两点P 、Q , A 1、A 2为双曲线实轴上的顶点,A 1P 和A 2Q 交于点M ,A 2P 和A 1Q 交于点N ,则MF ⊥NF .42.设双曲线方程22221x y a b-=,则斜率为k (k ≠0)的平行弦的中点必在直线l :y kx =的共轭直线'y k x =上,而且2'2b kk a=.43.设A 、B 、C 、D 为双曲线22221x y a b-=(a >0,b >0)上四点,AB 、CD 所在直线的倾斜角分别为,αβ,直线AB 与CD 相交于P ,且P 不在双曲线上,则22222222||||cos sin ||||cos sin PA PB b a PC PD b a ββαα⋅-=⋅-.44.已知双曲线22221x y a b-=(a >0,b >0),点P 为其上一点F 1, F 2为双曲线的焦点,12F PF ∠的外(内)角平分线为l ,作F 1、F 2分别垂直l 于R 、S ,当P 跑遍整个双曲线时,R 、S 形成的轨迹方程是222x y a +=(322224223222{()[()]}[()]()a b x c a b x b c a c x c y ab c y -+-+-=).45.设△ABC 三顶点分别在双曲线Γ上,且AB 为Γ的直径,l 为AB 的共轭直径所在的直线,l 分别交直线AC 、BC 于E 和F ,又D 为l 上一点,则CD 与双曲线Γ相切的充要条件是D 为EF 的中点.46.过双曲线22221x y a b-=(a >0,b >0)的右焦点F 作直线交该双曲线的右支于M ,N 两点,弦MN 的垂直平分线交x 轴于P ,则||||2PF eMN =. 47.设A (x 1,y 1)是双曲线22221x y a b -=(a >0,b >0)上任一点,过A 作一条斜率为2121b x a y 的直线L ,又设d是原点到直线 L 的距离, 12,r r 分别是Aab =.48.已知双曲线22221x y a b -=(a >0,b >0)和2222x y a bλ-=(01λ<< ),一条直线顺次与它们相交于A 、B 、C 、D 四点,则│AB │=|CD │.49.已知双曲线22221x y a b -=(a >0,b >0),A 、B 是双曲线上的两点,线段AB 的垂直平分线与x 轴相交于点0(,0)P x , 则220a b x a+≥或220a b x a +≤-.50.设P 点是双曲线22221x y a b-=(a >0,b >0)上异于实轴端点的任一点,F 1、F 2为其焦点记12F PF θ∠=,则(1)2122||||1cos b PF PF θ=-;(2) 122cot 2PF F S b γ∆=.51.设过双曲线的实轴上一点B (m ,0)作直线与双曲线相交于P 、Q 两点,A 为双曲线实轴的左顶点,连结AP 和AQ 分别交相应于过B 点的直线MN :x n =于M ,N 两点,则90MBN ∠=o222()a m a a m b n a -⇔=-++. 52.L 是经过双曲线22221x y a b-=(a >0,b >0)焦点F 且与实轴垂直的直线,A 、B 是双曲线实轴的两个焦点,e是离心率,点P L ∈,若EPF α∠=,则α是锐角且1sin e α≤或1sin arc e α≤(当且仅当||abPH c=时取等号).53.L 是经过双曲线22221x y a b-=(a >0,b >0)的实轴顶点A 且与x 轴垂直的直线,E 、F 是双曲线的准线与x轴交点,点P L ∈,e 是离心率,EPF α∠=,H 是L 与X 轴的交点c 是半焦距,则α是锐角且1sin eα≤或1sin arc e α≤(当且仅当||abPA c=时取等号).54.L 是双曲线22221x y a b-=(a >0,b >0)焦点F 1且与x 轴垂直的直线,E 、F 是双曲线准线与x 轴交点,H 是L 与x 轴的交点,点P L ∈,EPF α∠=,离心率为e ,半焦距为c ,则α为锐角且21sin e α≤或21sin arc eα≤(当且仅当1||PF =.55.已知双曲线22221x y a b-=(a >0,b >0),直线L 通过其右焦点F 2,且与双曲线右支交于A 、B 两点,将A 、B与双曲线左焦点F 1连结起来,则222112(2)||||a b F A F B a +⋅≥(当且仅当AB ⊥x 轴时取等号).56.设A 、B 是双曲线22221x y a b-=(a >0,b >0)的长轴两端点,P 是双曲线上的一点,PAB α∠=,PBA β∠=,BPA γ∠=,c 、e 分别是双曲线的半焦距离心率,则有:(1) 22222|cos ||||s |ab PA a c co αγ=-. (2) 2tan tan 1e αβ=-.(3) 22222cot PAB a b S b a γ∆=+. 57.设A 、B 是双曲线22221x y a b-=(a >0,b >0)实轴上分别位于双曲线一支内(含焦点的区域)、外部的两点,且A x 、B x 的横坐标2A B x x a ⋅=,(1)若过A 点引直线与双曲线这一支相交于P 、Q 两点,则PBA QBA ∠=∠; (2)若过B 引直线与双曲线这一支相交于P 、Q 两点,则180PBA QBA ∠+∠=o.58.设A 、B 是双曲线22221x y a b-=(a >0,b >0)实轴上分别位于双曲线一支内(含焦点的区域),外部的两点,(1)若过A 点引直线与双曲线这一支相交于P 、Q 两点,(若BP 交双曲线这一支于两点,则P 、Q 不关于x轴对称),且PBA QBA ∠=∠,则点A 、B 的横坐标A x 、B x 满足2A B x x a ⋅=;(2)若过B 点引直线与双曲线这一支相交于P 、Q 两点,且180PBA QBA ∠+∠=o,则点A 、B 的横坐标满足2A B x x a ⋅=.59.设',A A 是双曲线22221x y a b -=的实轴的两个端点,'QQ 是与'AA 垂直的弦,则直线AQ 与''AQ 的交点P的轨迹是双曲线22221x y a b+=.60.过双曲线22221x y a b-=(a >0,b >0)的右焦点F 作互相垂直的两条弦AB 、CD ,则2228||||||ab AB CD a b ≤+-. 61.到双曲线22221x y a b -=(a >0,b >0)两焦点的距离之比等于c ab -(c 为半焦距)的动点M 的轨迹是姊妹圆222()()x ec y eb ±+=.62.到双曲线22221x y a b -=(a >0,b >0)的实轴两端点的距离之比等于c ab -(c 为半焦距)的动点M 的轨迹是姊妹圆222()x a y b ±+=.63.到双曲线22221x y a b -=(a >0,b >0)的两准线和x 轴的交点的距离之比为c ab-(c 为半焦距)的动点的轨迹是姊妹圆222()()b x a y e ±+=(e 为离心率).64.已知P 是双曲线22221x y a b -=(a >0,b >0)上一个动点,',A A 是它实轴的两个端点,且AQ AP ⊥,''AQ A P ⊥,则Q 点的轨迹方程是222241x b y a a-=.65.双曲线的一条直径(过中心的弦)的长,为通过一个焦点且与此直径平行的弦长和实轴之长的比例中项.66.设双曲线22221x y a b -=(a >0,b >0)实轴的端点为',A A ,11(,)P x y 是双曲线上的点过P 作斜率为2121b x a y 的直线l ,过',A A 分别作垂直于实轴的直线交l 于',M M ,则:(1)''2||||AM A M b =.(2)四边形''MAA M 面积的最小值是2ab .67.已知双曲线22221x y a b-=(a >0,b >0)的右准线l 与x 轴相交于点E ,过双曲线右焦点F 的直线与双曲线相交于A 、B 两点,点C 在右准线l 上,且BC x ⊥轴,则直线AC 经过线段EF 的中点.68.OA 、OB 是双曲线2222()1x a y a b--=(a >0,b >0,且a b ≠)的两条互相垂直的弦,O 为坐标原点,则: (1)直线AB 必经过一个定点2222(,0)ab b a-. (2)以OA 、OB 为直径的两圆的另一个交点Q 的轨迹方程是222222222()()ab ab x y b a b a -+=--(0)x ≠.69.(,)P m n 是双曲线2222()1x a y a b--=(a >0,b >0)上一个定点,PA 、PB 是互相垂直的弦,则: (1)直线AB 必经过一个定点2222222222()()(,)ab m b a n a b b a b a +-+--. (2)以PA 、PB 为直径的两圆的另一个交点Q 的轨迹方程是22224222222222222[()]()()()ab a m b n a b n a b x y b a b a b a -++-+-=---(x m ≠且y n ≠).70.如果一个双曲线虚半轴长为b ,焦点F 1、F 2到直线L 的距离分别为d 1、d 2,那么(1)212d d b =,且F 1、F 2在L 同侧⇔直线L 和双曲线相切,或L 是双曲线的渐近线. (2)212d d b >,且F 1、F 2在L 同侧⇔直线L 和双曲线相离. (3)212d d b <,或F 1、F 2在L 异侧⇔直线L 和双曲线相交.71.AB 是双曲线22221x y a b-=(a >0,b >0)的实轴,N 是双曲线上的动点,过N 的切线与过A 、B 的切线交于C 、D 两点,则梯形ABDC 的对角线的交点M 的轨迹方程是22241(0)x a y y -=≠.72.设点00(,)P x y 为双曲线22221x y a b-=(a >0,b >0)的内部((含焦点的区域))一定点,AB 是双曲线过定点00(,)P x y 的任一弦.(1)如a b ≥,则当弦AB 垂直于双曲线实轴所在直线时22222200min 2()(||||)b x a y a b PA PB a --⋅=.(2)如a b <,则当弦AB 平行(或重合)于双曲线实轴所在直线时,22222200min 2()(||||)b x a y a b PA PB b--⋅=. 73.双曲线焦三角形中,以焦半径为直径的圆必与以双曲线实轴为直径的圆相外切. 74.双曲线焦三角形的内切圆必切长轴于非焦顶点同侧的实轴端点. 75.双曲线两焦点到双曲线焦三角形内切圆的切线长为定值a+c 与a-c. 76.双曲线焦三角形的非焦顶点到其内切圆的切线长为定值a-c.77.双曲线焦三角形中,外点到一焦点的距离与以该焦点为端点的焦半径之比为常数e (离心率). [注:在双曲线焦三角形中,非焦顶点的内、外角平分线与长轴交点分别称为内、外点.] 78.双曲线焦三角形中,其焦点所对的旁心将外点与非焦顶点连线段分成定比e. 79.双曲线焦三角形中,半焦距必为内、外点到双曲线中心的比例中项.80.双曲线焦三角形中,双曲线中心到内点的距离、内点到同侧焦点的距离、半焦距及外点到同侧焦点的距离成比例.81.双曲线焦三角形中,半焦距、外点与双曲线中心连线段、内点与同侧焦点连线段、外点与同侧焦点连线段成比例.82.双曲线焦三角形中,过任一焦点向非焦顶点的内角平分线引垂线,则双曲线中心与垂足连线必与另一焦半径所在直线平行.83.双曲线焦三角形中,过任一焦点向非焦顶点内角平分线引垂线,则双曲线中心与垂足的距离为双曲线实半轴的长.84.双曲线焦三角形中,过任一焦点向非焦顶点的内角平分线引垂线,垂足就是垂足同侧焦半径为直径的圆和双曲线实轴为直径的圆的切点.85.双曲线焦三角形中,非焦顶点的内角平分线与焦半径、实轴所在直线的夹角的余弦的比为定值e.86.双曲线焦三角形中,非焦顶点的法线即为该顶角的外角平分线.87.双曲线焦三角形中,非焦顶点的切线即为该顶角的内角平分线.88.双曲线焦三角形中,过非焦顶点的切线与双曲线实轴两端点处的切线相交,则以两交点为直径的圆必过两焦点.89. 已知双曲线22221(0,0)x y a b a b-=>>上有一点P ,过P 分别引其渐近线的平行线,分别交x 轴于,M N ,交y 轴于,R Q , O 为原点,则:(1)2||||OM ON a ⋅=; (2)2||||OQ OR b ⋅=. 90. 过平面上的P 点作直线1:b l y x a =及2:b l y x a=-的平行线,分别交x 轴于,M N ,交y 轴于,R Q . (1)若2||||OM ON a ⋅=,则P 的轨迹方程是22221(0,0)x y a b a b-=>>. (2)若2||||OQ OR b ⋅=,则P 的轨迹方程是22221(0,0)x y a b a b-=>>. 91. 点P 为双曲线22221(0,0)x y a b a b-=>>在第一象限的弧上任意一点,过P 引x 轴、y 轴的平行线,交y 轴、x 轴于,M N ,交直线b y x a =-于,Q R ,记OMQ ∆与ONR ∆的面积为12,S S ,则:12||2ab S S -=. 92. 点P 为第一象限内一点,过P 引x 轴、y 轴的平行线,交y 轴、x 轴于,M N ,交直线b y x a=-于,Q R ,记OMQ ∆与ONR ∆的面积为12,S S ,已知12||2ab S S -=,则P 的轨迹方程是22221(0,0)x y a b a b -=>>或22221(0,0)y x a b b a -=>>.。
50条圆锥曲线性质和结论

椭圆与双曲线的对偶性质(必背的经典结论)1.2. 椭圆22221x y a b+=(a >b >0)的焦半径公式:10||MF a ex =+,20||MF a ex =-(1(,0)F c - , 2(,0)F c 00(,)M x y ).设过椭圆焦点F 作直线与椭圆椭 圆3. 点P 处的切线PT 平分△PF 1F 2在点P 处的外角.4. PT 平分△PF 1F 2在点P 处的外角,则焦点在直线PT 上的射影H 点的轨迹是以长轴为直径的圆,除去长轴的两个端点.5. 以焦点弦PQ 为直径的圆必与对应准线相离.6. 以焦点半径PF 1为直径的圆必与以长轴为直径的圆内切.7.若000(,)P x y 在椭圆22221x y a b +=上,则过0P 的椭圆的切线方程是00221x x y y a b+=. 8. 若000(,)P x y 在椭圆22221x y a b+=外 ,则过Po 作椭圆的两条切线切点为P 1、P 2,则切点弦P 1P 2的直线方程是00221x x y ya b+=. 9. 椭圆22221x y a b+= (a >b >0)的左右焦点分别为F 1,F 2,点P 为椭圆上任意一点12F PF γ∠=,则椭圆的焦点角形的面积为122tan2F PF S b γ∆=.相交 P 、Q 两点,A 为椭圆长轴上一个顶点,连结AP 和AQ 分别交相应于焦点F 的椭圆准线于M 、N 两点,则MF ⊥NF.10.过椭圆一个焦点F 的直线与椭圆交于两点P 、Q, A 1、A 2为椭圆长轴上的顶点,A 1P 和A 2Q 交于点M ,A 2P 和A 1Q 交于点N ,则MF ⊥NF.11.AB 是椭圆22221x y a b +=的不平行于对称轴的弦,M ),(00y x 为AB 的中点,则22OM AB b k k a⋅=-,即0202y a x b K AB-=。
12.若000(,)P x y 在椭圆22221x y a b+=内,则被Po 所平分的中点弦的方程是2200002222x x y y x y a b a b+=+. 13.若000(,)P x y 在椭圆22221x y a b +=内,则过Po 的弦中点的轨迹方程是22002222x x y y x y a b a b+=+.双曲线1. 点P 处的切线PT 平分△PF 1F 2在点P 处的内角.2. PT 平分△PF 1F 2在点P 处的内角,则焦点在直线PT 上的射影H 点的轨迹是以长轴为直径的圆,除去长轴的两个端点.3. 以焦点弦PQ 为直径的圆必与对应准线相交.4. 以焦点半径PF 1为直径的圆必与以实轴为直径的圆相切.(内切:P 在右支;外切:P 在左支)5. 若000(,)P x y 在双曲线22221x y a b-=(a >0,b >0)上,则过0P 的双曲线的切线方程是00221x x y ya b-=. 6. 若000(,)P x y 在双曲线22221x y a b-=(a >0,b >0)外 ,则过Po 作双曲线的两条切线切点为P 1、P 2,则切点弦P 1P 2的直线方程是00221x x y ya b-=. 7. 双曲线22221x y a b-=(a >0,b >o )的左右焦点分别为F 1,F 2,点P 为双曲线上任意一点12F PF γ∠=,则双曲线的焦点角形的面积为122t 2F PF S b co γ∆=.8. 双曲线22221x y a b-=(a >0,b >o )的焦半径公式:(1(,0)F c - , 2(,0)F c当00(,)M x y 在右支上时,10||MF ex a =+,20||MF ex a =-. 当00(,)M x y 在左支上时,10||MF ex a =-+,20||MF ex a =--9. 设过双曲线焦点F 作直线与双曲线相交 P 、Q 两点,A 为双曲线长轴上一个顶点,连结AP 和AQ 分别交相应于焦点F 的双曲线准线于M 、N 两点,则MF ⊥NF.10.过双曲线一个焦点F 的直线与双曲线交于两点P 、Q, A 1、A 2为双曲线实轴上的顶点,A 1P 和A 2Q 交于点M ,A 2P 和A 1Q 交于点N ,则MF ⊥NF.11.AB 是双曲线22221x y a b-=(a >0,b >0)的不平行于对称轴的弦,M ),(00y x 为AB 的中点,则0202y a x b K K ABOM =⋅,即0202y a x b K AB =。
高考数学圆锥曲线的经典性质50条之欧阳索引创编

椭圆与双曲线的对偶性质--(必背的经典结论)欧阳家百(2021.03.07)椭 圆1. 点P 处的切线PT 平分△PF1F2在点P 处的外角.2.PT 平分△PF1F2在点P 处的外角,则焦点在直线PT 上的射影H 点的轨迹是以长轴为直径的圆,除去长轴的两个端点.3. 以焦点弦PQ 为直径的圆必与对应准线相离.4. 以焦点半径PF1为直径的圆必与以长轴为直径的圆内切.5.若000(,)P x y 在椭圆22221x y a b +=上,则过0P 的椭圆的切线方程是00221x x y ya b +=.6.若000(,)P x y 在椭圆22221x y a b+=外 ,则过Po 作椭圆的两条切线切点为P1、P2,则切点弦P1P2的直线方程是00221x x y ya b+=.7.椭圆22221x y a b += (a >b >0)的左右焦点分别为F1,F 2,点P 为椭圆上任意一点12F PF γ∠=,则椭圆的焦点角形的面积为122tan2F PF S b γ∆=.8.椭圆22221x y a b+=(a >b >0)的焦半径公式:10||MF a ex =+,20||MF a ex =-(1(,0)F c -,2(,0)F c 00(,)M x y ).9.设过椭圆焦点F 作直线与椭圆相交 P 、Q 两点,A 为椭圆长轴上一个顶点,连结AP 和AQ 分别交相应于焦点F 的椭圆准线于M 、N 两点,则MF ⊥NF.10.过椭圆一个焦点F 的直线与椭圆交于两点P 、Q, A1、A2为椭圆长轴上的顶点,A1P 和A2Q 交于点M ,A2P 和A1Q 交于点N ,则MF ⊥NF.11.AB 是椭圆22221x y a b +=的不平行于对称轴的弦,M ),(00y x 为AB 的中点,则22OM ABb k k a⋅=-,即0202y a x b K AB -=。
12.若000(,)P x y 在椭圆22221x y a b +=内,则被Po 所平分的中点弦的方程是2200002222x x y y x y a b a b +=+.13.若000(,)P x y 在椭圆22221x y a b+=内,则过Po 的弦中点的轨迹方程是22002222x x y yx y a b a b+=+.双曲线1. 点P 处的切线PT 平分△PF1F2在点P 处的内角.2.PT 平分△PF1F2在点P 处的内角,则焦点在直线PT 上的射影H 点的轨迹是以长轴为直径的圆,除去长轴的两个端点.3. 以焦点弦PQ 为直径的圆必与对应准线相交.4.以焦点半径PF1为直径的圆必与以实轴为直径的圆相切.(内切:P 在右支;外切:P 在左支)5.若000(,)P x y 在双曲线22221x y a b-=(a >0,b >0)上,则过0P 的双曲线的切线方程是00221x x y ya b-=. 6.若000(,)P x y 在双曲线22221x y a b-=(a >0,b >0)外 ,则过Po 作双曲线的两条切线切点为P1、P2,则切点弦P1P2的直线方程是00221x x y ya b-=.7.双曲线22221x y a b-=(a >0,b >o )的左右焦点分别为F1,F 2,点P 为双曲线上任意一点12F PF γ∠=,则双曲线的焦点角形的面积为122t 2F PF S b co γ∆=.8.双曲线22221x y a b-=(a >0,b >o )的焦半径公式:(1(,0)F c -,2(,0)F c当00(,)M x y 在右支上时,10||MF ex a =+,20||MF ex a =-.当00(,)M x y 在左支上时,10||MF ex a =-+,20||MF ex a =--9.设过双曲线焦点F 作直线与双曲线相交 P 、Q 两点,A 为双曲线长轴上一个顶点,连结AP 和AQ 分别交相应于焦点F 的双曲线准线于M 、N 两点,则MF ⊥NF.10.过双曲线一个焦点F 的直线与双曲线交于两点P 、Q, A1、A2为双曲线实轴上的顶点,A1P 和A2Q 交于点M ,A2P 和A1Q 交于点N ,则MF ⊥NF.11.AB 是双曲线22221x y a b-=(a >0,b >0)的不平行于对称轴的弦,M ),(00y x 为AB 的中点,则0202y a x b K K AB OM =⋅,即0202y a x b K AB =。
高考数学圆锥曲线的经典性质50条之欧阳语创编

椭圆与双曲线的对偶性质--(必背的经典结论)椭 圆1. 点P 处的切线PT 平分△PF 1F 2在点P 处的外角.2.PT 平分△PF 1F 2在点P 处的外角,则焦点在直线PT 上的射影H 点的轨迹是以长轴为直径的圆,除去长轴的两个端点.3. 以焦点弦PQ 为直径的圆必与对应准线相离.4. 以焦点半径PF 1为直径的圆必与以长轴为直径的圆内切.5.若000(,)P x y 在椭圆22221x y a b +=上,则过0P 的椭圆的切线方程是00221x x y ya b+=.6.若000(,)P x y 在椭圆22221x y a b+=外 ,则过Po 作椭圆的两条切线切点为P 1、P 2,则切点弦P 1P 2的直线方程是00221x x y ya b+=.7.椭圆22221x y a b += (a >b >0)的左右焦点分别为F 1,F 2,点P 为椭圆上任意一点12F PF γ∠=,则椭圆的焦点角形的面积为122tan2F PF S b γ∆=.8.椭圆22221x y a b +=(a >b >0)的焦半径公式:10||MF a ex =+,20||MF a ex =-(1(,0)F c -,2(,0)F c 00(,)M x y ).9.设过椭圆焦点F 作直线与椭圆相交 P 、Q 两点,A 为椭圆长轴上一个顶点,连结AP 和AQ 分别交相应于焦点F 的椭圆准线于M 、N 两点,则MF ⊥NF.10.过椭圆一个焦点F 的直线与椭圆交于两点P 、Q, A 1、A 2为椭圆长轴上的顶点,A 1P 和A 2Q 交于点M ,A 2P 和A 1Q 交于点N ,则MF ⊥NF.11.AB 是椭圆22221x y a b +=的不平行于对称轴的弦,M ),(00y x 为AB 的中点,则22OM AB b k k a ⋅=-,即0202y a x b K AB -=。
12.若000(,)P x y 在椭圆22221x y a b +=内,则被Po 所平分的中点弦的方程是2200002222x x y y x y a b a b+=+.13.若000(,)P x y 在椭圆22221x y a b+=内,则过Po的弦中点的轨迹方程是22002222x x y yx y a b a b+=+.双曲线1. 点P 处的切线PT 平分△PF 1F 2在点P 处的内角.2.PT 平分△PF 1F 2在点P 处的内角,则焦点在直线PT 上的射影H 点的轨迹是以长轴为直径的圆,除去长轴的两个端点.3. 以焦点弦PQ 为直径的圆必与对应准线相交.4.以焦点半径PF 1为直径的圆必与以实轴为直径的圆相切.(内切:P 在右支;外切:P 在左支)5.若000(,)P x y 在双曲线22221x y a b-=(a >0,b >0)上,则过0P 的双曲线的切线方程是00221x x y ya b-=.6.若000(,)P x y 在双曲线22221x y a b-=(a >0,b >0)外 ,则过Po 作双曲线的两条切线切点为P 1、P 2,则切点弦P 1P 2的直线方程是00221x x y ya b-=.7.双曲线22221x y a b-=(a >0,b >o )的左右焦点分别为F 1,F 2,点P 为双曲线上任意一点12F PF γ∠=,则双曲线的焦点角形的面积为122t 2F PF S b co γ∆=.8.双曲线22221x y a b-=(a >0,b >o )的焦半径公式:(1(,0)F c -,2(,0)F c当00(,)M x y 在右支上时,10||MF ex a =+,20||MF ex a =-. 当00(,)M x y 在左支上时,10||MF ex a =-+,20||MF ex a =--9.设过双曲线焦点F 作直线与双曲线相交 P 、Q 两点,A 为双曲线长轴上一个顶点,连结AP 和AQ 分别交相应于焦点F 的双曲线准线于M 、N 两点,则MF ⊥NF.10.过双曲线一个焦点F 的直线与双曲线交于两点P 、Q, A 1、A 2为双曲线实轴上的顶点,A 1P 和A 2Q 交于点M ,A 2P 和A 1Q 交于点N ,则MF ⊥NF.11.AB 是双曲线22221x y a b-=(a >0,b >0)的不平行于对称轴的弦,M ),(00y x 为AB的中点,则0202y a x b K K AB OM =⋅,即0202y a x b K AB =。
高考数学圆锥曲线的经典性质50条之欧阳文创编

椭圆与双曲线的对偶性质--(必背的经典结论)椭 圆1. 点P 处的切线PT 平分△PF1F2在点P 处的外角.2.PT 平分△PF1F2在点P 处的外角,则焦点在直线PT 上的射影H 点的轨迹是以长轴为直径的圆,除去长轴的两个端点.3. 以焦点弦PQ 为直径的圆必与对应准线相离.4. 以焦点半径PF1为直径的圆必与以长轴为直径的圆内切.5.若000(,)P x y 在椭圆22221x y a b +=上,则过0P 的椭圆的切线方程是00221x x y y a b +=.6.若000(,)P x y 在椭圆22221x y a b+=外 ,则过Po 作椭圆的两条切线切点为P1、P2,则切点弦P1P2的直线方程是00221x x y ya b+=. 7.椭圆22221x y a b+= (a >b >0)的左右焦点分别为F1,F 2,点P 为椭圆上任意一点12F PF γ∠=,则椭圆的焦点角形的面积为122tan2F PF S b γ∆=.8.椭圆22221x y a b+=(a >b >0)的焦半径公式:10||MF a ex =+,20||MF a ex =-(1(,0)F c -,2(,0)F c 00(,)M x y ).9.设过椭圆焦点F 作直线与椭圆相交 P 、Q 两点,A 为椭圆长轴上一个顶点,连结AP 和AQ 分别交相应于焦点F 的椭圆准线于M 、N 两点,则MF⊥NF.10.过椭圆一个焦点F 的直线与椭圆交于两点P 、Q, A1、A2为椭圆长轴上的顶点,A1P 和A2Q 交于点M ,A2P 和A1Q 交于点N ,则MF⊥NF.11.AB 是椭圆22221x y a b +=的不平行于对称轴的弦,M ),(00y x 为AB 的中点,则22OM ABb k k a⋅=-,即0202y a x b K AB-=。
12.若000(,)P x y 在椭圆22221x y a b+=内,则被Po 所平分的中点弦的方程是2200002222x x y y x y a b a b+=+.13.若000(,)P x y 在椭圆22221x y a b+=内,则过Po的弦中点的轨迹方程是22002222x x y yx y a b a b+=+.双曲线1. 点P 处的切线PT 平分△PF1F2在点P 处的内角.2.PT 平分△PF1F2在点P 处的内角,则焦点在直线PT 上的射影H 点的轨迹是以长轴为直径的圆,除去长轴的两个端点.3. 以焦点弦PQ 为直径的圆必与对应准线相交.4.以焦点半径PF1为直径的圆必与以实轴为直径的圆相切.(内切:P 在右支;外切:P 在左支)5.若000(,)P x y 在双曲线22221x y a b-=(a >0,b >0)上,则过0P 的双曲线的切线方程是00221x x y ya b-=.6.若000(,)P x y 在双曲线22221x y a b-=(a >0,b >0)外 ,则过Po 作双曲线的两条切线切点为P1、P2,则切点弦P1P2的直线方程是00221x x y ya b-=.7.双曲线22221x y a b-=(a >0,b >o )的左右焦点分别为F1,F 2,点P 为双曲线上任意一点12F PF γ∠=,则双曲线的焦点角形的面积为122t2F PFS b co γ∆=.8.双曲线22221x y a b-=(a >0,b >o )的焦半径公式:(1(,0)F c -,2(,0)F c当00(,)M x y 在右支上时,10||MF ex a =+,20||MF ex a =-.当00(,)M x y 在左支上时,10||MF ex a =-+,20||MF ex a =--9.设过双曲线焦点F 作直线与双曲线相交 P 、Q 两点,A 为双曲线长轴上一个顶点,连结AP 和AQ 分别交相应于焦点F 的双曲线准线于M 、N 两点,则MF⊥NF.10.过双曲线一个焦点F 的直线与双曲线交于两点P 、Q, A1、A2为双曲线实轴上的顶点,A1P 和A2Q 交于点M ,A2P 和A1Q 交于点N ,则MF⊥NF.11.AB 是双曲线22221x y a b-=(a >0,b >0)的不平行于对称轴的弦,M ),(00y x 为AB的中点,则0202y a x b K K AB OM =⋅,即0202y a x b K AB =。
高考数学圆锥曲线的经典性质50条之欧阳文创编

椭圆与双曲线的对偶性质--(必背的经典结论)椭 圆1. 点P 处的切线PT 平分△PF 1F 2在点P 处的外角.2.PT 平分△PF 1F 2在点P 处的外角,则焦点在直线PT 上的射影H 点的轨迹是以长轴为直径的圆,除去长轴的两个端点.3. 以焦点弦PQ 为直径的圆必与对应准线相离.4. 以焦点半径PF 1为直径的圆必与以长轴为直径的圆内切.5.若000(,)P x y 在椭圆22221x y a b +=上,则过0P 的椭圆的切线方程是00221x x y y a b+=.6.若000(,)P x y 在椭圆22221x y a b+=外 ,则过Po 作椭圆的两条切线切点为P 1、P 2,则切点弦P 1P 2的直线方程是00221x x y ya b+=.7.椭圆22221x y a b += (a >b >0)的左右焦点分别为F 1,F 2,点P 为椭圆上任意一点12F PF γ∠=,则椭圆的焦点角形的面积为122tan2F PF S b γ∆=.8.椭圆22221x y a b+=(a >b >0)的焦半径公式:10||MF a ex =+,20||MF a ex =-(1(,0)F c -,2(,0)F c 00(,)M x y ).9.设过椭圆焦点F 作直线与椭圆相交 P 、Q 两点,A 为椭圆长轴上一个顶点,连结AP 和AQ 分别交相应于焦点F 的椭圆准线于M 、N 两点,则MF ⊥NF.10.过椭圆一个焦点F 的直线与椭圆交于两点P 、Q, A 1、A 2为椭圆长轴上的顶点,A 1P 和A 2Q 交于点M ,A 2P 和A 1Q 交于点N ,则MF ⊥NF.11.AB 是椭圆22221x y a b +=的不平行于对称轴的弦,M ),(00y x 为AB 的中点,则22OM ABb k k a⋅=-,即0202y a x b K AB-=。
12.若000(,)P x y 在椭圆22221x y a b+=内,则被Po 所平分的中点弦的方程是2200002222x x y y x y a b a b+=+.13.若000(,)P x y 在椭圆22221x y a b+=内,则过Po的弦中点的轨迹方程是22002222x x y yx y a b a b+=+.双曲线1. 点P 处的切线PT 平分△PF 1F 2在点P 处的内角.2.PT 平分△PF 1F 2在点P 处的内角,则焦点在直线PT 上的射影H 点的轨迹是以长轴为直径的圆,除去长轴的两个端点.3. 以焦点弦PQ 为直径的圆必与对应准线相交.4.以焦点半径PF 1为直径的圆必与以实轴为直径的圆相切.(内切:P 在右支;外切:P 在左支)5.若000(,)P x y 在双曲线22221x y a b-=(a >0,b >0)上,则过0P 的双曲线的切线方程是00221x x y ya b-=.6.若000(,)P x y 在双曲线22221x y a b-=(a >0,b >0)外 ,则过Po 作双曲线的两条切线切点为P 1、P 2,则切点弦P 1P 2的直线方程是00221x x y ya b-=.7.双曲线22221x y a b-=(a >0,b >o )的左右焦点分别为F 1,F 2,点P 为双曲线上任意一点12F PF γ∠=,则双曲线的焦点角形的面积为122t2F PFS b co γ∆=.8.双曲线22221x y a b-=(a >0,b >o )的焦半径公式:(1(,0)F c -,2(,0)F c当00(,)M x y 在右支上时,10||MF ex a =+,20||MF ex a =-.当00(,)M x y 在左支上时,10||MF ex a =-+,20||MF ex a =--9.设过双曲线焦点F 作直线与双曲线相交 P 、Q 两点,A 为双曲线长轴上一个顶点,连结AP 和AQ 分别交相应于焦点F 的双曲线准线于M 、N 两点,则MF ⊥NF.10.过双曲线一个焦点F 的直线与双曲线交于两点P 、Q, A 1、A 2为双曲线实轴上的顶点,A 1P 和A 2Q 交于点M ,A 2P 和A 1Q 交于点N ,则MF ⊥NF.11.AB 是双曲线22221x y a b-=(a >0,b >0)的不平行于对称轴的弦,M ),(00y x 为AB的中点,则0202y a x b K K AB OM =⋅,即0202y a x b K AB =。
高考数学圆锥曲线的经典性质50条之欧阳与创编

椭圆与双曲线的对偶性质--(必背的经典结论)椭圆1.点P处的切线PT平分△PF1F2在点P处的外角.2.PT平分△PF1F2在点P处的外角,则焦点在直线PT上的射影H点的轨迹是以长轴为直径的圆,除去长轴的两个端点.3.以焦点弦PQ为直径的圆必与对应准线相离.4.以焦点半径PF1为直径的圆必与以长轴为直径的圆内切.5.若000(,)P x y 在椭圆22221x y a b +=上,则过0P 的椭圆的切线方程是00221x x y ya b +=.6.若000(,)P x y 在椭圆22221x y a b+=外 ,则过Po 作椭圆的两条切线切点为P 1、P 2,则切点弦P 1P 2的直线方程是00221x x y ya b+=.7.椭圆22221x y a b+= (a >b >0)的左右焦点分别为F 1,F 2,点P 为椭圆上任意一点12F PF γ∠=,则椭圆的焦点角形的面积为122tan2F PFS b γ∆=.8.椭圆22221x y a b+=(a >b >0)的焦半径公式:10||MF a ex =+,20||MF a ex =-(1(,0)F c -,2(,0)F c 00(,)M x y ).9.设过椭圆焦点F 作直线与椭圆相交 P 、Q 两点,A 为椭圆长轴上一个顶点,连结AP 和AQ 分别交相应于焦点F 的椭圆准线于M 、N 两点,则MF ⊥NF.10.过椭圆一个焦点F 的直线与椭圆交于两点P 、Q, A 1、A 2为椭圆长轴上的顶点,A 1P 和A 2Q 交于点M ,A 2P 和A 1Q 交于点N ,则MF ⊥NF.11.AB 是椭圆22221x y a b +=的不平行于对称轴的弦,M ),(00y x 为AB 的中点,则22OM AB b k k a ⋅=-,即0202y a x b K AB -=。
12.若000(,)P x y 在椭圆22221x y a b+=内,则被Po 所平分的中点弦的方程是2200002222x x y y x y a b a b+=+.13.若000(,)P x y 在椭圆22221x y a b+=内,则过Po 的弦中点的轨迹方程是22002222x x y yx y a b a b+=+.双曲线1. 点P 处的切线PT 平分△PF 1F 2在点P 处的内角.2.PT 平分△PF 1F 2在点P 处的内角,则焦点在直线PT 上的射影H 点的轨迹是以长轴为直径的圆,除去长轴的两个端点.3. 以焦点弦PQ 为直径的圆必与对应准线相交.4.以焦点半径PF 1为直径的圆必与以实轴为直径的圆相切.(内切:P 在右支;外切:P 在左支)5.若000(,)P x y 在双曲线22221x y a b-=(a >0,b >0)上,则过0P 的双曲线的切线方程是00221x x y ya b-=.6.若000(,)P x y 在双曲线22221x y a b-=(a >0,b >0)外 ,则过Po 作双曲线的两条切线切点为P 1、P 2,则切点弦P 1P 2的直线方程是00221x x y ya b-=. 7.双曲线22221x y a b-=(a >0,b >o )的左右焦点分别为F 1,F 2,点P 为双曲线上任意一点12F PF γ∠=,则双曲线的焦点角形的面积为122t2F PF S b co γ∆=.8.双曲线22221x y a b-=(a >0,b >o )的焦半径公式:(1(,0)F c -,2(,0)F c当00(,)M x y 在右支上时,10||MF ex a =+,20||MF ex a =-.当00(,)M x y 在左支上时,10||MF ex a =-+,20||MF ex a =--9.设过双曲线焦点F 作直线与双曲线相交 P 、Q 两点,A 为双曲线长轴上一个顶点,连结AP 和AQ 分别交相应于焦点F 的双曲线准线于M 、N 两点,则MF ⊥NF.10.过双曲线一个焦点F 的直线与双曲线交于两点P 、Q, A 1、A 2为双曲线实轴上的顶点,A 1P 和A 2Q 交于点M ,A 2P 和A 1Q 交于点N ,则MF ⊥NF.11.AB 是双曲线22221x y a b-=(a >0,b >0)的不平行于对称轴的弦,M ),(00y x 为AB 的中点,则0202y a x b K K AB OM =⋅,即0202y a x b K AB =。
50条圆锥曲线性质和结论

椭圆与双曲线的对偶性质(必背的经典结论)1.2. 椭圆22221x y a b+=(a >b >0)的焦半径公式:10||MF a ex =+,20||MF a ex =-(1(,0)F c - , 2(,0)F c 00(,)M x y ).设过椭圆焦点F 作直线与椭圆椭 圆3. 点P 处的切线PT 平分△PF 1F 2在点P 处的外角.4. PT 平分△PF 1F 2在点P 处的外角,则焦点在直线PT 上的射影H 点的轨迹是以长轴为直径的圆,除去长轴的两个端点.5. 以焦点弦PQ 为直径的圆必与对应准线相离.6. 以焦点半径PF 1为直径的圆必与以长轴为直径的圆内切.7.若000(,)P x y 在椭圆22221x y a b +=上,则过0P 的椭圆的切线方程是00221x x y y a b+=. 8. 若000(,)P x y 在椭圆22221x y a b+=外 ,则过Po 作椭圆的两条切线切点为P 1、P 2,则切点弦P 1P 2的直线方程是00221x x y ya b+=. 9. 椭圆22221x y a b+= (a >b >0)的左右焦点分别为F 1,F 2,点P 为椭圆上任意一点12F PF γ∠=,则椭圆的焦点角形的面积为122tan2F PF S b γ∆=.相交 P 、Q 两点,A 为椭圆长轴上一个顶点,连结AP 和AQ 分别交相应于焦点F 的椭圆准线于M 、N 两点,则MF ⊥NF.10.过椭圆一个焦点F 的直线与椭圆交于两点P 、Q, A 1、A 2为椭圆长轴上的顶点,A 1P 和A 2Q 交于点M ,A 2P 和A 1Q 交于点N ,则MF ⊥NF.11.AB 是椭圆22221x y a b +=的不平行于对称轴的弦,M ),(00y x 为AB 的中点,则22OM AB b k k a⋅=-,即0202y a x b K AB-=。
12.若000(,)P x y 在椭圆22221x y a b+=内,则被Po 所平分的中点弦的方程是2200002222x x y y x y a b a b+=+. 13.若000(,)P x y 在椭圆22221x y a b +=内,则过Po 的弦中点的轨迹方程是22002222x x y y x y a b a b+=+.双曲线1. 点P 处的切线PT 平分△PF 1F 2在点P 处的内角.2. PT 平分△PF 1F 2在点P 处的内角,则焦点在直线PT 上的射影H 点的轨迹是以长轴为直径的圆,除去长轴的两个端点.3. 以焦点弦PQ 为直径的圆必与对应准线相交.4. 以焦点半径PF 1为直径的圆必与以实轴为直径的圆相切.(内切:P 在右支;外切:P 在左支)5. 若000(,)P x y 在双曲线22221x y a b-=(a >0,b >0)上,则过0P 的双曲线的切线方程是00221x x y ya b-=. 6. 若000(,)P x y 在双曲线22221x y a b-=(a >0,b >0)外 ,则过Po 作双曲线的两条切线切点为P 1、P 2,则切点弦P 1P 2的直线方程是00221x x y ya b-=. 7. 双曲线22221x y a b-=(a >0,b >o )的左右焦点分别为F 1,F 2,点P 为双曲线上任意一点12F PF γ∠=,则双曲线的焦点角形的面积为122t 2F PF S b co γ∆=.8. 双曲线22221x y a b-=(a >0,b >o )的焦半径公式:(1(,0)F c - , 2(,0)F c当00(,)M x y 在右支上时,10||MF ex a =+,20||MF ex a =-. 当00(,)M x y 在左支上时,10||MF ex a =-+,20||MF ex a =--9. 设过双曲线焦点F 作直线与双曲线相交 P 、Q 两点,A 为双曲线长轴上一个顶点,连结AP 和AQ 分别交相应于焦点F 的双曲线准线于M 、N 两点,则MF ⊥NF.10.过双曲线一个焦点F 的直线与双曲线交于两点P 、Q, A 1、A 2为双曲线实轴上的顶点,A 1P 和A 2Q 交于点M ,A 2P 和A 1Q 交于点N ,则MF ⊥NF.11.AB 是双曲线22221x y a b-=(a >0,b >0)的不平行于对称轴的弦,M ),(00y x 为AB 的中点,则0202y a x b K K ABOM =⋅,即0202y a x b K AB =。
高考数学圆锥曲线的经典性质50条之欧阳与创编

椭圆与双曲线的对偶性质--(必背的经典结论)椭圆1.点P处的切线PT平分△PF1F2在点P处的外角.2.PT平分△PF1F2在点P处的外角,则焦点在直线PT上的射影H点的轨迹是以长轴为直径的圆,除去长轴的两个端点.3.以焦点弦PQ为直径的圆必与对应准线相离.4.以焦点半径PF1为直径的圆必与以长轴为直径的圆内切.5.若000(,)P x y 在椭圆22221x y a b +=上,则过0P 的椭圆的切线方程是00221x x y ya b +=.6.若000(,)P x y 在椭圆22221x y a b+=外 ,则过Po 作椭圆的两条切线切点为P1、P2,则切点弦P1P2的直线方程是00221x x y ya b+=.7.椭圆22221x y a b+= (a >b >0)的左右焦点分别为F1,F 2,点P 为椭圆上任意一点12F PF γ∠=,则椭圆的焦点角形的面积为122tan2F PFS b γ∆=.8.椭圆22221x y a b+=(a >b >0)的焦半径公式:10||MF a ex =+,20||MF a ex =-(1(,0)F c -,2(,0)F c 00(,)M x y ).9.设过椭圆焦点F 作直线与椭圆相交 P 、Q 两点,A 为椭圆长轴上一个顶点,连结AP 和AQ 分别交相应于焦点F 的椭圆准线于M 、N 两点,则MF ⊥NF.10.过椭圆一个焦点F 的直线与椭圆交于两点P 、Q, A1、A2为椭圆长轴上的顶点,A1P 和A2Q 交于点M ,A2P 和A1Q 交于点N ,则MF ⊥NF.11.AB 是椭圆22221x y a b +=的不平行于对称轴的弦,M ),(00y x 为AB 的中点,则22OM AB b k k a ⋅=-,即0202y a x b K AB -=。
12.若000(,)P x y 在椭圆22221x y a b+=内,则被Po 所平分的中点弦的方程是2200002222x x y y x y a b a b+=+.13.若000(,)P x y 在椭圆22221x y a b+=内,则过Po 的弦中点的轨迹方程是22002222x x y yx y a b a b+=+.双曲线1. 点P 处的切线PT 平分△PF1F2在点P 处的内角.2.PT 平分△PF1F2在点P 处的内角,则焦点在直线PT 上的射影H 点的轨迹是以长轴为直径的圆,除去长轴的两个端点.3. 以焦点弦PQ 为直径的圆必与对应准线相交.4.以焦点半径PF1为直径的圆必与以实轴为直径的圆相切.(内切:P 在右支;外切:P 在左支)5.若000(,)P x y 在双曲线22221x y a b-=(a >0,b >0)上,则过0P 的双曲线的切线方程是00221x x y ya b-=.6.若000(,)P x y 在双曲线22221x y a b-=(a >0,b >0)外 ,则过Po 作双曲线的两条切线切点为P1、P2,则切点弦P1P2的直线方程是00221x x y ya b-=. 7.双曲线22221x y a b-=(a >0,b >o )的左右焦点分别为F1,F 2,点P 为双曲线上任意一点12F PF γ∠=,则双曲线的焦点角形的面积为122t2F PF S b co γ∆=.8.双曲线22221x y a b-=(a >0,b >o )的焦半径公式:(1(,0)F c -,2(,0)F c当00(,)M x y 在右支上时,10||MF ex a =+,20||MF ex a =-.当00(,)M x y 在左支上时,10||MF ex a =-+,20||MF ex a =--9.设过双曲线焦点F 作直线与双曲线相交 P 、Q 两点,A 为双曲线长轴上一个顶点,连结AP 和AQ 分别交相应于焦点F 的双曲线准线于M 、N 两点,则MF ⊥NF.10.过双曲线一个焦点F 的直线与双曲线交于两点P 、Q, A1、A2为双曲线实轴上的顶点,A1P 和A2Q 交于点M ,A2P 和A1Q 交于点N ,则MF ⊥NF.11.AB 是双曲线22221x y a b-=(a >0,b >0)的不平行于对称轴的弦,M ),(00y x 为AB 的中点,则0202y a x b K K AB OM =⋅,即0202y a x b K AB =。
高考数学圆锥曲线的经典性质50条之欧阳美创编

椭圆与双曲线的对偶性质--(必背的经典结论)椭 圆1. 点P 处的切线PT 平分△PF1F2在点P 处的外角.2.PT 平分△PF1F2在点P 处的外角,则焦点在直线PT 上的射影H 点的轨迹是以长轴为直径的圆,除去长轴的两个端点.3. 以焦点弦PQ 为直径的圆必与对应准线相离.4. 以焦点半径PF1为直径的圆必与以长轴为直径的圆内切.5.若000(,)P x y 在椭圆22221x y a b +=上,则过0P 的椭圆的切线方程是00221x x y ya b +=.6.若000(,)P x y 在椭圆22221x y a b+=外 ,则过Po 作椭圆的两条切线切点为P1、P2,则切点弦P1P2的直线方程是00221x x y ya b+=. 7.椭圆22221x y a b+= (a >b >0)的左右焦点分别为F1,F 2,点P 为椭圆上任意一点12F PF γ∠=,则椭圆的焦点角形的面积为122tan2F PF S b γ∆=.8.椭圆22221x y a b+=(a >b >0)的焦半径公式:10||MF a ex =+,20||MF a ex =-(1(,0)F c -,2(,0)F c 00(,)M x y ).9.设过椭圆焦点F 作直线与椭圆相交 P 、Q 两点,A 为椭圆长轴上一个顶点,连结AP 和AQ 分别交相应于焦点F 的椭圆准线于M 、N 两点,则MF⊥NF.10.过椭圆一个焦点F 的直线与椭圆交于两点P 、Q, A1、A2为椭圆长轴上的顶点,A1P 和A2Q 交于点M ,A2P 和A1Q 交于点N ,则MF⊥NF.11.AB 是椭圆22221x y a b +=的不平行于对称轴的弦,M ),(00y x 为AB 的中点,则22OM ABb k k a⋅=-,即0202y a x b K AB -=。
12.若000(,)P x y 在椭圆22221x y a b +=内,则被Po 所平分的中点弦的方程是2200002222x x y y x y a b a b +=+.13.若000(,)P x y 在椭圆22221x y a b+=内,则过Po的弦中点的轨迹方程是22002222x x y yx y a b a b+=+.双曲线1. 点P 处的切线PT 平分△PF1F2在点P 处的内角.2.PT 平分△PF1F2在点P 处的内角,则焦点在直线PT 上的射影H 点的轨迹是以长轴为直径的圆,除去长轴的两个端点.3. 以焦点弦PQ 为直径的圆必与对应准线相交.4.以焦点半径PF1为直径的圆必与以实轴为直径的圆相切.(内切:P 在右支;外切:P 在左支)5.若000(,)P x y 在双曲线22221x y a b-=(a >0,b >0)上,则过0P 的双曲线的切线方程是00221x x y ya b-=.6.若000(,)P x y 在双曲线22221x y a b-=(a >0,b >0)外 ,则过Po 作双曲线的两条切线切点为P1、P2,则切点弦P1P2的直线方程是00221x x y ya b-=.7.双曲线22221x y a b-=(a >0,b >o )的左右焦点分别为F1,F 2,点P 为双曲线上任意一点12F PF γ∠=,则双曲线的焦点角形的面积为122t2F PFS b co γ∆=.8.双曲线22221x y a b-=(a >0,b >o )的焦半径公式:(1(,0)F c -,2(,0)F c当00(,)M x y 在右支上时,10||MF ex a =+,20||MF ex a =-.当00(,)M x y 在左支上时,10||MF ex a =-+,20||MF ex a =--9.设过双曲线焦点F 作直线与双曲线相交 P 、Q 两点,A 为双曲线长轴上一个顶点,连结AP 和AQ 分别交相应于焦点F 的双曲线准线于M 、N 两点,则MF⊥NF.10.过双曲线一个焦点F 的直线与双曲线交于两点P 、Q, A1、A2为双曲线实轴上的顶点,A1P 和A2Q 交于点M ,A2P 和A1Q 交于点N ,则MF⊥NF.11.AB是双曲线22221x y a b-=(a >0,b >0)的不平行于对称轴的弦,M ),(00y x 为AB 的中点,则0202y a x b K K ABOM =⋅,即0202y a x b K AB=。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
椭圆与双曲线的对偶性质100条杨志明湖北省黄石二中 435003椭 圆1.2.标准方程:3.4.点P处的切线PT平分△PF1F2在点P处的外角.5.PT平分△PF1F2在点P处的外角,则焦点在直线PT上的射影H点的轨迹是以长轴为直径的圆,除去长轴的两个端点.6.以焦点弦PQ为直径的圆必与对应准线相离.7.以焦点半径PF1为直径的圆必与以长轴为直径的圆内切.8.设A1、A2为椭圆的左、右顶点,则△PF1F2在边PF2(或PF1)上的旁切圆,必与A1A2所在的直线切于A2(或A1).9.椭圆(a>b>o)的两个顶点为,,与y轴平行的直线交椭圆于P1、P2时A1P1与A2P2交点的轨迹方程是.10.若在椭圆上,则过的椭圆的切线方程是.11.若在椭圆外,则过Po作椭圆的两条切线切点为P1、P2,则切点弦P1P2的直线方程是.12.AB是椭圆的不平行于对称轴且过原点的弦,M为AB的中点,则. 13.若在椭圆内,则被Po所平分的中点弦的方程是.14.若在椭圆内,则过Po的弦中点的轨迹方程是.15.若PQ是椭圆(a>b>0)上对中心张直角的弦,则.16.若椭圆(a>b>0)上中心张直角的弦L所在直线方程为,则(1) ;(2) .17.给定椭圆:(a>b>0), :,则(i)对上任意给定的点,它的任一直角弦必须经过上一定点M(.(ii)对上任一点在上存在唯一的点,使得的任一直角弦都经过点. 18.设为椭圆(或圆)C: (a>0,. b>0)上一点,P1P2为曲线C的动弦,且弦P0P1, P0P2斜率存在,记为k1, k2, 则直线P1P2通过定点的充要条件是.19.过椭圆(a>0, b>0)上任一点任意作两条倾斜角互补的直线交椭圆于B,C两点,则直线BC有定向且(常数).20.椭圆(a>b>0)的左右焦点分别为F1,F2,点P为椭圆上任意一点,则椭圆的焦点角形的面积为, .21.若P为椭圆(a>b>0)上异于长轴端点的任一点,F1, F2是焦点, ,,则.22.椭圆(a>b>0)的焦半径公式:,( , ).23.若椭圆(a>b>0)的左、右焦点分别为F1、F2,左准线为L,则当0<e≤时,可在椭圆上求一点P,使得PF1是P到对应准线距离d与PF2的比例中项.24.P为椭圆(a>b>0)上任一点,F1,F2为二焦点,A为椭圆内一定点,则,当且仅当三点共线时,等号成立.25.椭圆(a>b>0)上存在两点关于直线:对称的充要条件是.26.过椭圆焦半径的端点作椭圆的切线,与以长轴为直径的圆相交,则相应交点与相应焦点的连线必与切线垂直.27.过椭圆焦半径的端点作椭圆的切线交相应准线于一点,则该点与焦点的连线必与焦半径互相垂直.28.P是椭圆(a>b>0)上一点,则点P对椭圆两焦点张直角的充要条件是.29.设A,B为椭圆上两点,其直线AB与椭圆相交于,则.30.在椭圆中,定长为2m(o<m≤a)的弦中点轨迹方程为,其中,当时, .31.设S为椭圆(a>b>0)的通径,定长线段L的两端点A,B在椭圆上移动,记|AB|=,是AB中点,则当时,有,);当时,有,.32.椭圆与直线有公共点的充要条件是.33.椭圆与直线有公共点的充要条件是.34.设椭圆(a>b>0)的两个焦点为F1、F2,P(异于长轴端点)为椭圆上任意一点,在△PF1F2中,记, ,,则有.35.经过椭圆(a>b>0)的长轴的两端点A1和A2的切线,与椭圆上任一点的切线相交于P1和P2,则.36.已知椭圆(a>b>0),O为坐标原点,P、Q为椭圆上两动点,且.(1);(2)|OP|2+|OQ|2的最大值为;(3)的最小值是.37.MN是经过椭圆(a>b>0)过焦点的任一弦,若AB是经过椭圆中心O且平行于MN的弦,则.38.MN是经过椭圆(a>b>0)焦点的任一弦,若过椭圆中心O的半弦,则.39.设椭圆(a>b>0),M(m,o) 或(o, m)为其对称轴上除中心,顶点外的任一点,过M引一条直线与椭圆相交于P、Q两点,则直线A1P、A2Q(A1 ,A2为对称轴上的两顶点)的交点N在直线:(或)上.40.设过椭圆焦点F作直线与椭圆相交P、Q两点,A为椭圆长轴上一个顶点,连结AP 和AQ分别交相应于焦点F的椭圆准线于M、N两点,则MF⊥NF.41.过椭圆一个焦点F的直线与椭圆交于两点P、Q, A1、A2为椭圆长轴上的顶点,A1P和A2Q交于点M,A2P和A1Q交于点N,则MF⊥NF.42.设椭圆方程,则斜率为k(k≠0)的平行弦的中点必在直线:的共轭直线上,而且.43.设A、B、C、D为椭圆上四点,AB、CD所在直线的倾斜角分别为,直线AB与CD相交于P,且P不在椭圆上,则.44.已知椭圆(a>b>0),点P为其上一点F1, F 2为椭圆的焦点,的外(内)角平分线为,作F1、F2分别垂直于R、S,当P跑遍整个椭圆时,R、S形成的轨迹方程是().45.设△ABC内接于椭圆,且AB为的直径,为AB的共轭直径所在的直线,分别交直线AC、BC于E和F,又D为上一点,则CD与椭圆相切的充要条件是D为EF的中点.46.过椭圆(a>b>0)的右焦点F作直线交该椭圆右支于M,N两点,弦MN的垂直平分线交x轴于P,则.47.设A(x1 ,y1)是椭圆(a>b>0)上任一点,过A作一条斜率为的直线L,又设d是原点到直线 L的距离, 分别是A到椭圆两焦点的距离,则.48.已知椭圆(a>b>0)和(),一直线顺次与它们相交于A、B、C、D四点,则│AB│=|CD│.49.已知椭圆( a>b>0) ,A、B、是椭圆上的两点,线段AB的垂直平分线与x轴相交于点, 则.50.设P点是椭圆(a>b>0)上异于长轴端点的任一点,F1、F2为其焦点记,则(1).(2) .51.设过椭圆的长轴上一点B(m,o)作直线与椭圆相交于P、Q两点,A为椭圆长轴的左顶点,连结AP和AQ分别交相应于过B点的直线MN:于M,N两点,则.52.L是经过椭圆(a>b>0)长轴顶点A且与长轴垂直的直线,E、F是椭圆两个焦点,e是离心率,点,若,则是锐角且或(当且仅当时取等号).53.L是椭圆(a>b>0)的准线,A、B是椭圆的长轴两顶点,点,e是离心率,,H是L与X轴的交点c是半焦距,则是锐角且或(当且仅当时取等号).54.L是椭圆(a>b>0)的准线,E、F是两个焦点,H是L与x轴的交点,点,,离心率为e,半焦距为c,则为锐角且或(当且仅当时取等号).55.已知椭圆(a>b>0),直线L通过其右焦点F2,且与椭圆相交于A、B两点,将A、B与椭圆左焦点F1连结起来,则(当且仅当AB⊥x 轴时右边不等式取等号,当且仅当A、F1、B三点共线时左边不等式取等号).56.设A、B是椭圆(a>b>0)的长轴两端点,P是椭圆上的一点,, ,,c、e分别是椭圆的半焦距离心率,则有(1).(2) .(3) .57.设A、B是椭圆(a>b>0)长轴上分别位于椭圆内(异于原点)、外部的两点,且、的横坐标,(1)若过A点引直线与这椭圆相交于P、Q两点,则;(2)若过B引直线与这椭圆相交于P、Q两点,则.58.设A、B是椭圆(a>b>0)长轴上分别位于椭圆内(异于原点),外部的两点,(1)若过A点引直线与这椭圆相交于P、Q两点,(若B P交椭圆于两点,则P、Q不关于x轴对称),且,则点A、B的横坐标、满足;(2)若过B点引直线与这椭圆相交于P、Q两点,且,则点A、B的横坐标满足.59.设是椭圆的长轴的两个端点,是与垂直的弦,则直线与的交点P的轨迹是双曲线.60.过椭圆( a>b>0)的左焦点作互相垂直的两条弦AB、CD则.61.到椭圆( a>b>0)两焦点的距离之比等于(c为半焦距)的动点M的轨迹是姊妹圆.62.到椭圆(a>b>0)的长轴两端点的距离之比等于(c为半焦距)的动点M的轨迹是姊妹圆.63.到椭圆(a>b>0)的两准线和x轴的交点的距离之比为(c为半焦距)的动点的轨迹是姊妹圆(e为离心率).64.已知P是椭圆(a>b>0)上一个动点,是它长轴的两个端点,且,,则Q点的轨迹方程是.65.椭圆的一条直径(过中心的弦)的长,为通过一个焦点且与此直径平行的弦长和长轴之长的比例中项.66.设椭圆(a>b>0)长轴的端点为,是椭圆上的点过P作斜率为的直线,过分别作垂直于长轴的直线交于,则(1).(2)四边形面积的最小值是.67.已知椭圆( a>b>0)的右准线与x轴相交于点,过椭圆右焦点的直线与椭圆相交于A、B两点,点在右准线上,且轴,则直线AC经过线段EF 的中点.68.OA、OB是椭圆(a>0,b>0)的两条互相垂直的弦,O为坐标原点,则(1)直线AB必经过一个定点.(2) 以O A、O B为直径的两圆的另一个交点Q的轨迹方程是.69.是椭圆(a>b>0)上一个定点,P A、P B是互相垂直的弦,则(1)直线AB必经过一个定点.(2)以P A、P B为直径的两圆的另一个交点Q的轨迹方程是(且).70.如果一个椭圆短半轴长为b,焦点F1、F2到直线的距离分别为d1、d2,那么(1),且F1、F2在同侧直线L和椭圆相切.(2),且F1、F2在L同侧直线和椭圆相离,(3),或F1、F2在L异侧直线L和椭圆相交.71.AB是椭圆(a>b>0)的长轴,是椭圆上的动点,过的切线与过A、B的切线交于、两点,则梯形ABDC的对角线的交点M的轨迹方程是.72.设点为椭圆( a>b>0)的内部一定点,AB是椭圆过定点的任一弦,当弦AB平行(或重合)于椭圆长轴所在直线时.当弦AB垂直于长轴所在直线时, .73.椭圆焦三角形中,以焦半径为直径的圆必与以椭圆长轴为直径的圆相内切.74.椭圆焦三角形的旁切圆必切长轴于非焦顶点同侧的长轴端点.75.椭圆两焦点到椭圆焦三角形旁切圆的切线长为定值a+c与a-c.76.椭圆焦三角形的非焦顶点到其内切圆的切线长为定值a-c.77.椭圆焦三角形中,内点到一焦点的距离与以该焦点为端点的焦半径之比为常数e(离心率). 注:在椭圆焦三角形中,非焦顶点的内、外角平分线与长轴交点分别称为内、外点.78.椭圆焦三角形中,内心将内点与非焦顶点连线段分成定比e.79.椭圆焦三角形中,半焦距必为内、外点到椭圆中心的比例中项.80.椭圆焦三角形中,椭圆中心到内点的距离、内点到同侧焦点的距离、半焦距及外点到同侧焦点的距离成比例.81.椭圆焦三角形中,半焦距、外点与椭圆中心连线段、内点与同侧焦点连线段、外点与同侧焦点连线段成比例.82.椭圆焦三角形中,过任一焦点向非焦顶点的外角平分线引垂线,则椭圆中心与垂足连线必与另一焦半径所在直线平行.83.椭圆焦三角形中,过任一焦点向非焦顶点的外角平分线引垂线,则椭圆中心与垂足的距离为椭圆长半轴的长.84.椭圆焦三角形中,过任一焦点向非焦顶点的外角平分线引垂线,垂足就是垂足同侧焦半径为直径的圆和椭圆长轴为直径的圆的切点.85.椭圆焦三角形中,非焦顶点的外角平分线与焦半径、长轴所在直线的夹角的余弦的比为定值e.86.椭圆焦三角形中,非焦顶点的法线即为该顶角的内角平分线.87.椭圆焦三角形中,非焦顶点的切线即为该顶角的外角平分线.88.椭圆焦三角形中,过非焦顶点的切线与椭圆长轴两端点处的切线相交,则以两交点为直径的圆必过两焦点.89.已知椭圆(包括圆在内)上有一点,过点分别作直线及的平行线,与直线分别交于,为原点,则:.(1);(2).90. 过平面上的点作直线及的平行线,分别交轴于,交轴于.(1)若,则的轨迹方程是.(2)若,则的轨迹方程是.91.点为椭圆(包括圆在内)在第一象限的弧上任意一点,过引轴、轴的平行线,交轴、轴于,交直线于,记与的面积为,则:.92.点为第一象限内一点,过引轴、轴的平行线,交轴、轴于,交直线于,记与的面积为,已知,则的轨迹方程是.双曲线1.2.标准方程:3.4.点P处的切线PT平分△PF1F2在点P处的内角.5.PT平分△PF1F2在点P处的内角,则焦点在直线PT上的射影H点的轨迹是以长轴为直径的圆,除去长轴的两个端点.6.以焦点弦PQ为直径的圆必与对应准线相交.7.以焦点半径PF1为直径的圆必与以实轴为直径的圆外切.8.设A1、A2为双曲线的左、右顶点,则△PF1F2在边PF2(或PF1)上的旁切圆,必与A1A2所在的直线切于A2(或A1).9.双曲线(a>0,b>0)的两个顶点为,,与y轴平行的直线交双曲线于P1、P2时A1P1与A2P2交点的轨迹方程是.10.若在双曲线(a>0,b>0)上,则过的双曲线的切线方程是. 11.若在双曲线(a>0,b>0)外,则过Po作双曲线的两条切线切点为P1、P2,则切点弦P1P2的直线方程是.12.AB是双曲线(a>0,b>0)的不平行于对称轴且过原点的弦,M 为AB的中点,则.13.若在双曲线(a>0,b>0)内,则被Po所平分的中点弦的方程是. 14.若在双曲线(a>0,b>0)内,则过Po的弦中点的轨迹方程是. 15.若PQ是双曲线(b>a >0)上对中心张直角的弦,则.16.若双曲线(b>a >0)上中心张直角的弦L所在直线方程为,则(1) ;(2) .17.给定双曲线:(a>b>0), :,则(i)对上任意给定的点,它的任一直角弦必须经过上一定点M(.(ii)对上任一点在上存在唯一的点,使得的任一直角弦都经过点. 18.设为双曲线(a>0,b>0)上一点,P1P2为曲线C的动弦,且弦P0P1, P0P2斜率存在,记为k1, k 2, 则直线P1P2通过定点的充要条件是.19.过双曲线(a>0,b>o)上任一点任意作两条倾斜角互补的直线交双曲线于B,C两点,则直线BC有定向且(常数).20.双曲线(a>0,b>o)的左右焦点分别为F1,F2,点P为双曲线上任意一点,则双曲线的焦点角形的面积为, .21.若P为双曲线(a>0,b>0)右(或左)支上除顶点外的任一点,F1, F 2是焦点, , ,则(或).22.双曲线(a>0,b>o)的焦半径公式:( ,当在右支上时,,.当在左支上时,,.23.若双曲线(a>0,b>0)的左、右焦点分别为F1、F2,左准线为L,则当1<e≤时,可在双曲线上求一点P,使得PF1是P到对应准线距离d与PF2的比例中项.24.P为双曲线(a>0,b>0)上任一点,F1,F2为二焦点,A为双曲线内一定点,则,当且仅当三点共线且和在y轴同侧时,等号成立.25.双曲线(a>0,b>0)上存在两点关于直线:对称的充要条件是.26.过双曲线焦半径的端点作双曲线的切线,与以长轴为直径的圆相交,则相应交点与相应焦点的连线必与切线垂直.27.过双曲线焦半径的端点作双曲线的切线交相应准线于一点,则该点与焦点的连线必与焦半径互相垂直.28.P是双曲线(a>0,b>0)上一点,则点P对双曲线两焦点张直角的充要条件是.29.设A,B为双曲线(a>0,b>0,)上两点,其直线AB与双曲线相交于,则.30.在双曲线中,定长为2m(m)0)的弦中点轨迹方程为,其中,当时, .31.设S为双曲线(a>0,b>o)的通径,定长线段L的两端点A,B在双曲线上移动,记|AB|=,是AB中点,则当时,有,);当时,有.32.双曲线(a>0,b>0)与直线有公共点的充要条件是.33.双曲线(a>0,b>0)与直线有公共点的充要条件是.34.设双曲线(a>0,b>0)的两个焦点为F1、F2,P(异于长轴端点)为双曲线上任意一点,在△PF1F2中,记, ,,则有.35.经过双曲线(a>0,b>0)的实轴的两端点A1和A2的切线,与双曲线上任一点的切线相交于P1和P2,则.36.已知双曲线(b>a >0),O为坐标原点,P、Q为双曲线上两动点,且.(1);(2)|OP|2+|OQ|2的最小值为;(3)的最小值是.37.MN是经过双曲线(a>0,b>0)过焦点的任一弦(交于两支),若AB是经过双曲线中心O且平行于MN的弦,则.38.MN是经过双曲线(a>b>0)焦点的任一弦(交于同支),若过双曲线中心O的半弦,则.39.设双曲线(a>0,b>0),M(m,o)为实轴所在直线上除中心,顶点外的任一点,过M引一条直线与双曲线相交于P、Q两点,则直线A1P、A2Q(A1 ,A2为两顶点)的交点N在直线:上.40.设过双曲线焦点F作直线与双曲线相交P、Q两点,A为双曲线长轴上一个顶点,连结AP 和AQ分别交相应于焦点F的双曲线准线于M、N两点,则MF⊥NF.41.过双曲线一个焦点F的直线与双曲线交于两点P、Q, A1、A2为双曲线实轴上的顶点,A1P和A2Q交于点M,A2P和A1Q交于点N,则MF⊥NF.42.设双曲线方程,则斜率为k(k≠0)的平行弦的中点必在直线:的共轭直线上,而且.43.设A、B、C、D为双曲线(a>0,b>o)上四点,AB、CD所在直线的倾斜角分别为,直线AB与CD相交于P,且P不在双曲线上,则.44.已知双曲线(a>0,b>0),点P为其上一点F1, F2为双曲线的焦点,的外(内)角平分线为,作F1、F2分别垂直于R、S,当P跑遍整个双曲线时,R、S形成的轨迹方程是().45.设△ABC三顶点分别在双曲线上,且AB为的直径,为AB的共轭直径所在的直线,分别交直线AC、BC于E和F,又D为上一点,则CD 与双曲线相切的充要条件是D为EF的中点.46.过双曲线(a>0,b>0)的右焦点F作直线交该双曲线的右支于M,N两点,弦MN的垂直平分线交x轴于P,则.47.设A(x1 ,y1)是双曲线(a>0,b>0)上任一点,过A作一条斜率为的直线L,又设d是原点到直线 L的距离, 分别是A到双曲线两焦点的距离,则.48.已知双曲线(a>0,b>0)和(),一条直线顺次与它们相交于A、B、C、D四点,则│AB│=|CD│.49.已知双曲线(a>0,b>0),A、B是双曲线上的两点,线段AB 的垂直平分线与x轴相交于点, 则或.50.设P点是双曲线(a>0,b>0)上异于实轴端点的任一点,F1、F2为其焦点记,则(1).(2) .51.设过双曲线的实轴上一点B(m,o)作直线与双曲线相交于P、Q两点,A为双曲线实轴的左顶点,连结AP和AQ分别交相应于过B点的直线MN:于M,N两点,则.52.L是经过双曲线(a>0,b>0)焦点F且与实轴垂直的直线,A、B是双曲线实轴的两个焦点,e是离心率,点,若,则是锐角且或(当且仅当时取等号).53.L是经过双曲线(a>0,b>0)的实轴顶点A且与x轴垂直的直线,E、F是双曲线的准线与x轴交点,点,e是离心率,,H是L与X轴的交点c是半焦距,则是锐角且或(当且仅当时取等号).54.L是双曲线(a>0,b>0)焦点F1且与x轴垂直的直线,E、F是双曲线准线与x轴交点,H是L与x轴的交点,点,,离心率为e,半焦距为c,则为锐角且或(当且仅当时取等号).55.已知双曲线(a>0,b>0),直线L通过其右焦点F2,且与双曲线右支交于A、B两点,将A、B与双曲线左焦点F1连结起来,则(当且仅当AB⊥x轴时取等号).56.设A、B是双曲线(a>0,b>0)的长轴两端点,P是双曲线上的一点,, ,,c、e分别是双曲线的半焦距离心率,则有(1).(2) .(3) .57.设A、B是双曲线(a>0,b>0)实轴上分别位于双曲线一支内(含焦点的区域)、外部的两点,且、的横坐标,(1)若过A点引直线与双曲线这一支相交于P、Q两点,则;(2)若过B引直线与双曲线这一支相交于P、Q两点,则.58.设A、B是双曲线(a>0,b>0)实轴上分别位于双曲线一支内(含焦点的区域),外部的两点,(1)若过A点引直线与双曲线这一支相交于P、Q两点,(若B P交双曲线这一支于两点,则P、Q不关于x 轴对称),且,则点A、B的横坐标、满足;(2)若过B点引直线与双曲线这一支相交于P、Q两点,且,则点A、B的横坐标满足.59.设是双曲线的实轴的两个端点,是与垂直的弦,则直线与的交点P的轨迹是双曲线.60.过双曲线(a>0,b>0)的右焦点作互相垂直的两条弦AB、CD,则.61.到双曲线(a>0,b>0)两焦点的距离之比等于(c为半焦距)的动点M的轨迹是姊妹圆.62.到双曲线(a>0,b>0)的实轴两端点的距离之比等于(c为半焦距)的动点M的轨迹是姊妹圆.63.到双曲线(a>0,b>0)的两准线和x轴的交点的距离之比为(c 为半焦距)的动点的轨迹是姊妹圆(e为离心率).64.已知P是双曲线(a>0,b>0)上一个动点,是它实轴的两个端点,且,,则Q点的轨迹方程是.65.双曲线的一条直径(过中心的弦)的长,为通过一个焦点且与此直径平行的弦长和实轴之长的比例中项.66.设双曲线(a>0,b>0)实轴的端点为,是双曲线上的点过P作斜率为的直线,过分别作垂直于实轴的直线交于,则(1).(2)四边形面积的最小值是.67.已知双曲线(a>0,b>0)的右准线与x轴相交于点,过双曲线右焦点的直线与双曲线相交于A、B两点,点在右准线上,且轴,则直线AC经过线段EF 的中点.68.OA、OB是双曲线(a>0,b>0,且)的两条互相垂直的弦,O为坐标原点,则(1)直线AB必经过一个定点.(2) 以O A、O B为直径的两圆的另一个交点Q的轨迹方程是.69.是双曲线(a>0,b>0)上一个定点,P A、P B是互相垂直的弦,则(1)直线AB必经过一个定点.(2)以P A、P B为直径的两圆的另一个交点Q的轨迹方程是(且).70.如果一个双曲线虚半轴长为b,焦点F1、F2到直线的距离分别为d1、d2,那么(1),且F1、F2在同侧直线L和双曲线相切,或是双曲线的渐近线.(2),且F1、F2在L同侧直线和双曲线相离,(3),或F1、F2在L异侧直线L和双曲线相交.71.AB是双曲线(a>0,b>0)的实轴,是双曲线上的动点,过的切线与过A、B的切线交于、两点,则梯形ABDC的对角线的交点M的轨迹方程是.72.设点为双曲线(a>0,b>0)的内部((含焦点的区域))一定点,AB是双曲线过定点的任一弦.(1)如,则当弦AB垂直于双曲线实轴所在直线时.(2)如,则当弦AB平行(或重合)于双曲线实轴所在直线时, .73.双曲线焦三角形中,以焦半径为直径的圆必与以双曲线实轴为直径的圆相外切.74.双曲线焦三角形的内切圆必切长轴于非焦顶点同侧的实轴端点.75.双曲线两焦点到双曲线焦三角形内切圆的切线长为定值a+c与a-c.76.双曲线焦三角形的非焦顶点到其内切圆的切线长为定值a-c.77.双曲线焦三角形中,外点到一焦点的距离与以该焦点为端点的焦半径之比为常数e(离心率).注:在双曲线焦三角形中,非焦顶点的内、外角平分线与长轴交点分别称为内、外点.78.双曲线焦三角形中,其焦点所对的旁心将外点与非焦顶点连线段分成定比e.79.双曲线焦三角形中,半焦距必为内、外点到双曲线中心的比例中项.80.双曲线焦三角形中,双曲线中心到内点的距离、内点到同侧焦点的距离、半焦距及外点到同侧焦点的距离成比例.81.双曲线焦三角形中,半焦距、外点与双曲线中心连线段、内点与同侧焦点连线段、外点与同侧焦点连线段成比例.82.双曲线焦三角形中,过任一焦点向非焦顶点的内角平分线引垂线,则双曲线中心与垂足连线必与另一焦半径所在直线平行.83.双曲线焦三角形中,过任一焦点向非焦顶点内角平分线引垂线,则双曲线中心与垂足的距离为双曲线实半轴的长.84.双曲线焦三角形中,过任一焦点向非焦顶点的内角平分线引垂线,垂足就是垂足同侧焦半径为直径的圆和双曲线实轴为直径的圆的切点.85.双曲线焦三角形中,非焦顶点的内角平分线与焦半径、实轴所在直线的夹角的余弦的比为定值e.86.双曲线焦三角形中,非焦顶点的法线即为该顶角的外角平分线.87.双曲线焦三角形中,非焦顶点的切线即为该顶角的内角平分线.88.双曲线焦三角形中,过非焦顶点的切线与双曲线实轴两端点处的切线相交,则以两交点为直径的圆必过两焦点.89. 已知双曲线上有一点,过分别引其渐近线的平行线,分别交轴于,交轴于,为原点,则:(1);(2).90. 过平面上的点作直线及的平行线,分别交轴于,交轴于.(1)若,则的轨迹方程是.(2)若,则的轨迹方程是.91. 点为双曲线在第一象限的弧上任意一点,过引轴、轴的平行线,交轴、轴于,交直线于,记与的面积为,则:.92.点为第一象限内一点,过引轴、轴的平行线,交轴、轴于,交直线于,记与的面积为,已知,则的轨迹方程是或.。
