正方体展开图规律
正方体展开图顺口溜

正方体展开图顺口溜
正方体展有规律,十一种类看仔细;中间四个成一行,两边各一无规矩;二三紧连错一个,三一相连一随意;两两相连各错一,三个两排一对齐。
一条线上不过四,田七和凹要放弃;相间之端是对面,间二拐角面相邻。
正方体简介
用六个完全相同的正方形围成的立体图形叫正方体。
侧面和底面均为正方形的直平行六面体叫正方体,即棱长都相等的六面体,又称“立方体”、“正六面体”。
正方体是特殊的长方体。
表面积
因为6个面全部相等,所以正方体的表面积=一个面的面积×6=棱长×棱长×6
设一个正方体的棱长为a,则它的表面积S:
S=6(a²)。
正方体展开图用“口诀”

正方体展开图用“口诀”我们在《丰富的图形世界》中掌握了“图形的展开与折叠”的技巧探索了立体图形与平面图形之间的转化规律但有的同学还不是很清楚为了使同学们更好地掌握其规律请同学们记住下列“口诀”“一线不过四田、凹应弃之相间、“Z”端是对面间二、拐角邻面知”下面结合中考题作一分析供同学们参考一、一线不过四是指在正方体展开图中一条直线上的小正方形不会超过四个如图1、图2都不是正方体的展开图例1.2004连云港下面每个图片都是由6个大小相同的正方形组成其中不能折成正方体的是分析因为一条直线上的小正方形不会超过四个所以应选B二、田、凹应弃之就是说在正方体表面展开图中不会有“田”字型、“凹”字型的形状如图3、图4、图5例2.2003天津在下列图形中每个小正方形皆为全等的正方形可以是一个正方体表面展开图的是分析通过观察、想象可以知道A、D含“田”字型、“凹”字型B也不能应选C三、相间、“Z”端是对面相间的两个小正方形中间隔着一个小正方形是正方体的两个对面如图6中的A面和B面“Z”字两端处的小正方形是正方体的对面如图7、图8的A面和B面例3.2005河南如图9一个正方体的每个面上都写有一个汉字其平面展开图如图9所示那么在该正方体中和“超”相对的字是分析自—信—沉—着—超构成了竖着的Z字型所以“自”与“超”对应故应填“自”四、间二、拐角邻面知中间隔着两个小正方形或拐角型的三个面是正方体的邻面例42004镇江如图10有一个正方体纸盒在它的三个侧面分别画有三角形、正方形和圆现用一把剪刀沿着它的棱剪开成一个平面图形则展开图可以是分析我们把画有圆的一面记为a面正方形阴影面记为b面三角形阴影面记为c面在选项A 中由Z字型结构知b与c对面与已知正方体bc相邻不符应排除在选项B中b面与c面隔着a 面b面与c面是对面也应排除在选项D中虽然a、b、c三面成拐角型是正方体的三个邻面b 面作为上面a面为正面则c面应在正方体的左面与原图不符应排除故应选C请你试一试吧1.2005年南宁如图11是正方体的平面展开图每个面上有一个汉字与“绿”字相对的面上的字是2.2005年黄冈水平放置的正方体六个面分别用“前面、后面、上面、下面、左面、右面”表达如图是一个正方体的平面展开图若图12中的“进”表示正方体的前面“步”表示右面“习”表示下面则“祝”、“你”、“学”分别表示正方体的3如图13是一个正方形纸盒的展开图若在其中的三个正方形 A、B、C内分别填入适当的数使得它们折成正方形后相对的面上的两个数互为相反数则填入正方形A、B、C内的三个数依次为() A、1、2、0 B、0、-2、1 C、-2、0、1 D、-2、1、04如图14是展开平面图的折叠过程请回答1号面、2号面、 3号面的对面是几号5猜一猜将一个正方体的纸盒沿某些棱剪开可以展成多少种不同的平面图形你能验证你的猜想吗请与同学交流你的收获与感悟答案1.应填“南”2. 后面、上面、左面3.A4. 1号面对面是4号2号面对面是6号3号面对面是5号5有11种情形。
正方体表面展开图的口诀

巧记口诀确定正方体表面展开图6个相连的正方形组成的平面图形,经折叠能否围城正方体问题,是近年来中考常考题型。
同学们在学习这一知识时常感到无从下手,现将确定正方体展开图的方法以口诀的方式总结出来,供大家参考:正方体盒巧展开,六个面儿七刀裁。
十四条边布周围,十一类图记分明:四方成线两相卫,六种图形巧组合;跃马失蹄四分开;两两错开一阶梯。
对面相隔不相连,识图巧排“7”、“凹”、“田”。
现将口诀的内涵解释如下:将一个正方体盒的表面沿某些棱剪开,展开成平面图形,需剪7刀,故平面展开图中周围有14条边长共有十一种展开图:一、四方成线两相卫,六种图形巧组合(1)(2)(3)(4)(5)(6)以上六种展开图可归结为四方连线,,另外两个小方块在四个方块的上下两侧,共六种情况。
二、跃马失蹄四分开(1)(2)(3)(4)以上四种情况可归结为五个小方块组成“三二相连”的基本图形(如图),另外一个小方块的位置有四种情况,即图中四个小方块中的任意一个,这一图形有点像失蹄的马,故称为“跃马失蹄”。
三、两两错开一阶梯这一种图形是两个小方块一组,两两错开,像阶梯一样,故称“两两错开一阶梯”。
四、对面相隔不相连这是确定展开图的又一种方法,也是确定展开图中的对面的一种方法。
如果出现三个相连,则1号面与3号面是对面,中间隔了一个2号面,并且是对面的一定不相连。
五、识图巧排“7”、“凹”、“田”(1) (2) (3)这里介绍的是一种排除法。
如果图中出现象图(1)中的“7”形结构的图形不可能是正方体展开图的,因为图中1号面与3号面是对面,3号面又与5号面是对面,出现矛盾。
如果图中出现象图(2)中的“田”形结构的图形不可能是正方体展开图的,因为同一顶点处不可能出现四个面的。
如果图中出现象图(3)中的“凹”形结构的图形不可能是正方体展开图的,因为如果把该图形折叠起来将有两个面重合。
现举例说明:例1.(2004海口市实验区)下面的平面图形中,是正方体的平面展开图的是( )解析:本题可用“识图巧排 ‘7’、‘田’、‘凹’”来解决。
正方体展开图16种口诀

正方体展开图16种口诀一、正方体一边展开图上边把下端抹,左右倒把先穿,里外两边搭叉,外边把右端搭在上。
二、正方体二边同时展开图上里先对搭,左右穿入侧边,外圈旋转搭至上,右边把下边压。
三、正方体三边展开图上里对搭又旋,左右同时进入,外圈围圈连搭,下边把右边压。
四、正方体四边展开图右上边倒进去,左下穿入侧边,外圈旋转连搭,左右把下边压。
五、正方体五边展开图先把左下边穿,右上边旋转压,里外两边再搭,最后右边把下边带。
六、正方体六边展开图上下先对搭,右边再进侧边,外圈旋转搭叉,最后把左端连上。
七、正方体七边展开图右上边穿入一,下底旋转压二,外边翻转三抹,最后里外两边搭。
八、正方体八边展开图右上倒入一,下底旋转压二,四边穿入三,右下把左上压。
九、正方体九边展开图右上倒进去一,里外把右下穿二,外边旋转三连,左右把左上压。
十、正方体十边展开图右上倒进去一,里外把右下穿二,外边四边带叉,最后把左上压三。
十一、正方体十一边展开图上下先对搭至,里外把右下穿,外层旋转向外翻,最后把左右上压进。
十二、正方体十二边展开图上下两边把对搭,进入正上倒一,里外又把右下穿,两边把最后四边带。
十三、正方体十三边展开图上下两边先搭,里外把右下穿,外用旋转六边带,最后把左右上压。
十四、正方体十四边展开图上下先对搭至,里外又把右下穿,外用旋转八边带,两边最后把上压。
十五、正方体十五边展开图上下两边先搭,里外八边穿一,外用旋转七边带,最后两边把可上压。
十六、正方体十六边展开图上下先对搭至,里外把右上倒,外用旋转九边连,最后把右下压住。
以上是学习正方体展开图的16种口诀,从展开图边数以1到16编号,每一种口诀中,描述了如何将正方体展开成平面图案的步骤。
巧记口诀确定正方体表面展开图

巧记⼝诀确定正⽅体表⾯展开图巧记⼝诀确定正⽅体表⾯展开图6个相连的正⽅形组成的平⾯图形,经折叠能否围城正⽅体问题,是近年来中考常考题型。
同学们在学习这⼀知识时常感到⽆从下⼿,现将确定正⽅体展开图的⽅法以⼝诀的⽅式总结出来,供⼤家参考:正⽅体盒巧展开,六个⾯⼉七⼑裁。
⼗四条边布周围,⼗⼀类图记分明:四⽅成线两相卫,六种图形巧组合;跃马失蹄四分开;两两错开⼀阶梯。
对⾯相隔不相连,识图巧排“7”、“凹”、“⽥”。
现将⼝诀的内涵解释如下:将⼀个正⽅体盒的表⾯沿某些棱剪开,展开成平⾯图形,需剪7⼑,故平⾯展开图中周围有14条边长共有⼗⼀种展开图:⼀、四⽅成线两相卫,六种图形巧组合(1)(2)(3)(4)(5)(6)以上六种展开图可归结为四⽅连线,即,另外两个⼩⽅块在四个⽅块的上下两侧,共六种情况。
⼆、跃马失蹄四分开(1)(2)(3)(4)以上四种情况可归结为五个⼩⽅块组成“三⼆相连”的基本图形(如图),另外⼀个⼩⽅块的位置有四种情况,即图中四个⼩⽅块中的任意⼀个,这⼀图形有点像失蹄的马,故称为“跃马失蹄”。
三、两两错开⼀阶梯这⼀种图形是两个⼩⽅块⼀组,两两错开,像阶梯⼀样,故称“两两错开⼀阶梯”。
四、对⾯相隔不相连这是确定展开图的⼜⼀种⽅法,也是确定展开图中的对⾯的⼀种⽅法。
如果出现三个相连,则1号⾯与3号⾯是对⾯,中间隔了⼀个2号⾯,并且是对⾯的⼀定不相连。
五、识图巧排“7”、“凹”、“⽥”(1)(2)(3)这⾥介绍的是⼀种排除法。
如果图中出现象图(1)中的“7”形结构的图形不可能是正⽅体展开图的,因为图中1号⾯与3号⾯是对⾯,3号⾯⼜与5号⾯是对⾯,出现⽭盾。
如果图中出现象图(2)中的“⽥”形结构的图形不可能是正⽅体展开图的,因为同⼀顶点处不可能出现四个⾯的。
如果图中出现象图(3)中的“凹”形结构的图形不可能是正⽅体展开图的,因为如果把该图形折叠起来将有两个⾯重合。
现举例说明:下⾯的平⾯图形中,是正⽅体的平⾯展开图的是()解析:本题可⽤“识图巧排 ‘7’、‘⽥’、‘凹’”来解决。
正方体的展开与折叠规律方法
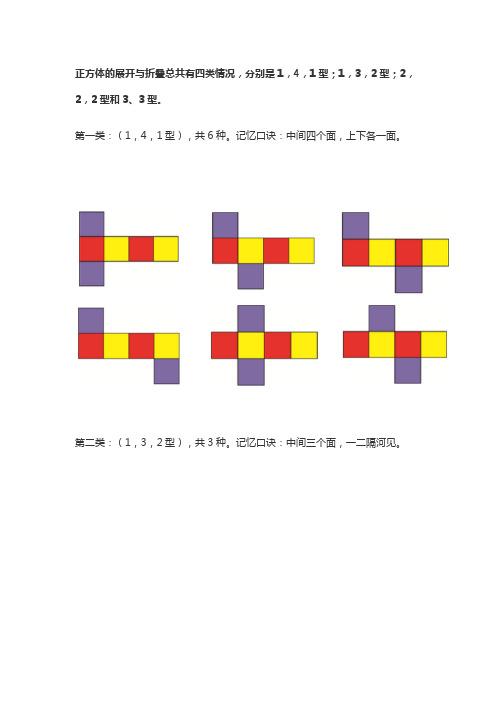
正方体的展开与折叠总共有四类情况,分别是1,4,1型;1,3,2型;2,2,2型和3、3型。
第一类:(1,4,1型),共6种。
记忆口诀:中间四个面,上下各一面。
第二类:(1,3,2型),共3种。
记忆口诀:中间三个面,一二隔河见。
第三类:(2,2,2型),共1种。
记忆口诀:中间两个面,楼梯天天见。
第四类:(3,3型),共1种。
记忆口诀:中间没有面,三三连一线。
解题技巧背一背
1、寻找正方体相对面
解题技巧:“I”型图不相连;“Z”型图在两端。
2、判断是否可以围成正方体
一线不过四(一条直线上的小正方形的个数不会超过四个);“7”、“田”、“凹”应弃之(在正方体展开图中,不会有“7”字型、“田”字型、“凹”字型)。
正方体的性质
1、正方体有有6个面,12条棱,8个顶点。
2、正方体一般指正六面体,用六个完全相同的正方形围成的立体图形叫正六面体,也称立方体、正方体。
3、且正方体的每个面都相等,展开之后的表面积也相等。
正方体表面展开图的口诀

巧记口诀确定正方体表面展开图6个相连的正方形组成的平面图形,经折叠能否围城正方体问题,是近年来中考常考题型。
同学们在学习这一知识时常感到无从下手,现将确定正方体展开图的方法以口诀的方式总结出来,供大家参考:正方体盒巧展开,六个面儿七刀裁。
十四条边布周围,十一类图记分明:四方成线两相卫,六种图形巧组合;跃马失蹄四分开;两两错开一阶梯。
对面相隔不相连,识图巧排“7”、“凹”、“田”。
现将口诀的内涵解释如下:将一个正方体盒的表面沿某些棱剪开,展开成平面图形,需剪7刀,故平面展开图中周围有14条边长共有十一种展开图:一、四方成线两相卫,六种图形巧组合(1)(2)(3)(4)(5)(6)以上六种展开图可归结为四方连线,即,另外两个小方块在四个方块的上下两侧,共六种情况。
二、跃马失蹄四分开(1)(2)(3)(4)以上四种情况可归结为五个小方块组成“三二相连”的基本图形(如图),另外一个小方块的位置有四种情况,即图中四个小方块中的任意一个,这一图形有点像失蹄的马,故称为“跃马失蹄”。
三、两两错开一阶梯这一种图形是两个小方块一组,两两错开,像阶梯一样,故称“两两错开一阶梯”。
四、对面相隔不相连这是确定展开图的又一种方法,也是确定展开图中的对面的一种方法。
如果出现三个相连,则1号面与3号面是对面,中间隔了一个2号面,并且是对面的一定不相连。
五、识图巧排“7”、“凹”、“田”(1) (2) (3)这里介绍的是一种排除法。
如果图中出现象图(1)中的“7”形结构的图形不可能是正方体展开图的,因为图中1号面与3号面是对面,3号面又与5号面是对面,出现矛盾。
如果图中出现象图(2)中的“田”形结构的图形不可能是正方体展开图的,因为同一顶点处不可能出现四个面的。
如果图中出现象图(3)中的“凹”形结构的图形不可能是正方体展开图的,因为如果把该图形折叠起来将有两个面重合。
现举例说明:例1.(2004海口市实验区)下面的平面图形中,是正方体的平面展开图的是( )解析:本题可用“识图巧排 ‘7’、‘田’、‘凹’”来解决。
正方体展开图口诀

正方体展开图口诀
正方体展有规律,十一种类看仔细;
中间四个成一行,两边各一无规矩;
二三紧连错一个,三一相连一随意;
两两相连各错一,三个两排一对齐。
一条线上不过四,田七和凹要放弃;
相间Z端是对面,间二拐角面相邻。
1.中间四个成一行,两边各一无规矩
"141"型,中间一行4个作侧面。
上下两个各作为上下底面,共有6种基本图形。
2.二三紧连错一个,三一相连一随意
“231”型,中间3个作侧面,共3种基本图形
3.两两相连各错一
"222"型,两行只能有1个正方形相连
4.三个两排一对齐
5.一条线上不过四
指在正方形展开图中,一条直线上的小正方形不会超过四个。
如以下的图形都不是正方体的展开图。
6.田七和凹要放弃
指在正方体展开图中,不会有“田”字型、“凹”字型的形状。
如以下的图形都不是正方体的展开图。
7.相间Z端是对面
相间的两个小正方形(中间隔着一个小正方形)是正方体的两个对面,“z”字端处的小正方形是正方体的对面。
如下面的展开图中,“1”对“5”,“2”对“4”,“3”对“6”。
8.间而拐角两面相邻
中间隔着两个小正方形或拐角型的三个面是正方形的邻面。
拐角型如下图所示。
正方体展开图16种口诀

正方体展开图16种口诀一、展开图的概念正方体是一种立体图形,它有六个面,每个面都是一个正方形。
展开图是将正方体展开成一个平面图形,使得每个面都能够呈现出来。
展开图有16种不同的排列方式,我们可以用口诀来记忆这些排列方式。
二、16种口诀1.上正下反,前正后反,左正右反,这是正方体的展开图排列方式之一。
2.上正下反,前正后反,左反右正,这是正方体的展开图排列方式之二。
3.上正下反,前反后正,左正右反,这是正方体的展开图排列方式之三。
4.上正下反,前反后正,左反右正,这是正方体的展开图排列方式之四。
5.上反下正,前正后反,左正右反,这是正方体的展开图排列方式之五。
6.上反下正,前正后反,左反右正,这是正方体的展开图排列方式之六。
7.上反下正,前反后正,左正右反,这是正方体的展开图排列方式之七。
8.上反下正,前反后正,左反右正,这是正方体的展开图排列方式之八。
9.左反右正,前正后反,上正下反,这是正方体的展开图排列方式之九。
10.左反右正,前正后反,上反下正,这是正方体的展开图排列方式之十。
11.左反右正,前反后正,上正下反,这是正方体的展开图排列方式之十一。
12.左反右正,前反后正,上反下正,这是正方体的展开图排列方式之十二。
13.左正右反,前正后反,上反下正,这是正方体的展开图排列方式之十三。
14.左正右反,前正后反,上正下反,这是正方体的展开图排列方式之十四。
15.左正右反,前反后正,上反下正,这是正方体的展开图排列方式之十五。
16.左正右反,前反后正,上正下反,这是正方体的展开图排列方式之十六。
三、口诀的用处这16种口诀可以帮助我们记忆正方体的展开图排列方式。
在解题时,我们可以根据这些口诀来确定展开图的排列方式,从而更加方便地计算正方体的表面积和体积。
口诀的使用可以提高我们的解题效率,确保我们能够正确地进行数学计算。
四、相关数学概念在学习正方体的展开图排列方式时,我们也需要了解一些相关的数学概念。
正方体展开图用“口诀”.

正方体展开图用“口诀”我们在《丰富的图形世界》中掌握了“图形的展开与折叠”的技巧探索了立体图形与平面图形之间的转化规律但有的同学还不是很清楚为了使同学们更好地掌握其规律请同学们记住下列“口诀”“一线不过四田、凹应弃之相间、“Z”端是对面间二、拐角邻面知”下面结合中考题作一分析供同学们参考一、一线不过四是指在正方体展开图中一条直线上的小正方形不会超过四个如图1、图2都不是正方体的展开图例1.2004连云港下面每个图片都是由6个大小相同的正方形组成其中不能折成正方体的是分析因为一条直线上的小正方形不会超过四个所以应选B二、田、凹应弃之就是说在正方体表面展开图中不会有“田”字型、“凹”字型的形状如图3、图4、图5例2.2003天津在下列图形中每个小正方形皆为全等的正方形可以是一个正方体表面展开图的是分析通过观察、想象可以知道A、D含“田”字型、“凹”字型B也不能应选C三、相间、“Z”端是对面相间的两个小正方形中间隔着一个小正方形是正方体的两个对面如图6中的A 面和B面“Z”字两端处的小正方形是正方体的对面如图7、图8的A面和B面例3.2005河南如图9一个正方体的每个面上都写有一个汉字其平面展开图如图9所示那么在该正方体中和“超”相对的字是分析自—信—沉—着—超构成了竖着的Z字型所以“自”与“超”对应故应填“自”四、间二、拐角邻面知中间隔着两个小正方形或拐角型的三个面是正方体的邻面例42004镇江如图10有一个正方体纸盒在它的三个侧面分别画有三角形、正方形和圆现用一把剪刀沿着它的棱剪开成一个平面图形则展开图可以是分析我们把画有圆的一面记为a面正方形阴影面记为b面三角形阴影面记为c 面在选项A 中由Z字型结构知b与c对面与已知正方体bc相邻不符应排除在选项B中b面与c面隔着a 面b面与c面是对面也应排除在选项D中虽然a、b、c三面成拐角型是正方体的三个邻面b 面作为上面a面为正面则c面应在正方体的左面与原图不符应排除故应选C请你试一试吧1.2005年南宁如图11是正方体的平面展开图每个面上有一个汉字与“绿”字相对的面上的字是2.2005年黄冈水平放置的正方体六个面分别用“前面、后面、上面、下面、左面、右面”表达如图是一个正方体的平面展开图若图12中的“进”表示正方体的前面“步”表示右面“习”表示下面则“祝”、“你”、“学”分别表示正方体的3如图13是一个正方形纸盒的展开图若在其中的三个正方形 A、B、C内分别填入适当的数使得它们折成正方形后相对的面上的两个数互为相反数则填入正方形A、B、C内的三个数依次为( A、1、2、0 B、0、-2、1 C、-2、0、1 D、-2、1、04如图14是展开平面图的折叠过程请回答1号面、2号面、 3号面的对面是几号5猜一猜将一个正方体的纸盒沿某些棱剪开可以展成多少种不同的平面图形你能验证你的猜想吗请与同学交流你的收获与感悟答案1.应填“南”2. 后面、上面、左面3.A4. 1号面对面是4号2号面对面是6号3号面对面是5号5有11种情形。
正方体的十一种平面展开图(宜兴 李保中)

11中正方体展开图正方体的十一种平面展开图可记忆成下面口诀:一三二,一四一,一在同层可任意,两个三,日状连,三个二,成阶梯,相邻必有日,整体没有田。
相对的两个面之间总隔着一个面正方体:中间四个面,上下各一面(6种摆法-141)中间三个面,一二隔河见(3种摆法-132/231)中间二个面,楼梯天天见(1种摆法-222)中间没有面,三三连一线(1种摆法-33)例1 在图13中(每个小四边形皆为全等的正方形),可以是一个正方体表面展开图的是( ).例2图14是一个正方体包装盒的表面展开图,若在其中的三个正方形A、B、C内分别填上适当的数,使得这个表面展开图沿虚线折成正方体后,相对面上的两个数互为相反数,则填在A、B、C内的三个数依次是( ).A.0,-2,1B.0,1,-2C.1,0,-2D.-2,0,1例3图15所示的是一个正方体包装盒的表面展开图,各个面上标注的数字分别为1,2,3,4,5,6。
现将表面展开图复原为正方体包装盒,则标注数字1和3的两个面是互相平行的,请你写出另一组相互平行的面上所对应的数字:_______。
注:例1、例2、例3的答案分别为:C;A;2与5或4与6。
是不是有点多此一举?例4 一个无盖的正方体纸盒,将它展开成平面图形,可能情况总共有()。
A.12种 B.11种 C.9种 D.8种千万注意,你可不要选B呦!选D才对。
我又在炫耀了,不过你能很快画出这8个平面展开图吗?下面是示意图,黑方块表示展开图,白方块表示空缺。
(一)□■□■■■□■□(二)■■■■■□□□(三)■■■■□■□□(四)■■■■□□■□(五)■■■■□□□■(六)□■□■■■□□■(七)□□■■■■□□■(八)■□□■■■□□■。
正方体的展开图与相对面分布规律

正方体的展开图与相对面分布规律正方体的展开与折叠是《图形的初步认识》这一章的重要内容,而探索正方体的展开图的相对面分布的规律更是其中的一个难点。
下面就谈一谈如何快速地确定相对面,供同学们学习时参考。
一、“141”型(共6种)展开图特点:在这类展开图中,最长的一行(或列)有四个正方形(如图1~6所示)在这种类型中,有4个正方形“直线”相连,其余2个正方形分别在“直线”两旁,位置任意。
相对面特点:图1~图6有四个面在同一层,可作为一类.确定相对面的方法是:一、三层的两个面是相对面,第二层四个面中不相邻的两个面是相对面.二、“231”型(共3种)展开图特点:在这类展开图中,最长的一行(或列)有3个正方形(如图7~9)。
在“231”型中,“3"所在的行(或列)必须在中间,“2"、“1"所在行(或列)分属两边(前后不分).也就是正方体展开后,如有三个面在“直线"相连,另2个面在“直线”相连面一旁,另一面在它另一旁。
故该种情况有3种。
相对面特点: 图7~图9有三个面在同一层,剩下的三个面分别在上下两侧,可作为一类.确定相对面的方法是:抓中间层;中间层中不相邻的两个面一定是相对面,中间的那个面与离它最远的面是相对面;余下的两个面是相对面.三、“222”型(只有1种)展开图特点:在展开图中,最多只有2个正方形“直线”相连.正如“二面三行,像楼梯”.如图10所示展开图相对面:,相邻两层不相邻的两个面一定是相对面,这样就可以先确定出两对不同的相对面,剩下的两个面一定是相对面.面A对面D,面B对E,面C对面F.四、“33”型(只有1种)犹如“三面两行,两台阶”如图中相对面每层中不相邻的两个面是相对面,剩下的两个面是相对面. 面A 对面C,面D对F,面B对面E。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
正方体展开图规律
一、基本知识
1.点、线、面、区域的关系---平面图形和立体图形的欧拉公式
2.截面形状的确定
①立方体被某平面所截,可以得到截面形状有:三角形、四边形、五边形、六边形。
②其他图形的截面。
例:圆锥被被某平面所截,可以得到截面形状有:三角形、圆、椭圆、抛物线、双曲线等。
尤其是圆锥被平行于轴对称面的竖直平面截取,截面形状不是三角形,而是抛物线。
二、正方体展开图规律的研究
试着将一个正方体的盒子剪开,我们会发现:随着剪纸的方向不同,展开图完全不同,似乎没有什么规律可遵循,但不要着急,换个角度来考虑问题。
我们知道,所有正方体都是六个面,同时找6个面展开图的分布规律的确很困难,我们能不能先找出其中4个面展开的分布规律,然后再研究其他两个面的分布规律呢?
4个面展开的分布规律有两个。
最容易想到的分布规律是第一个,如图1,我们称其为“长方形结构”
它组合起来恰好是一个无两个底的立方体桶状图形,仅缺少上下两个底面,而上下两个底面的位置恰好可由上图中的的上下两条边来定,图2中标号为1的面其位置有4个,代表上底面,标号为2的面其位置也有4个,代表下底面。
第2个分布规律如图3所示,我们可以形象地称它为“Z字结构”,大家一定能想象到,它拼合起来是个什么图形,对,应该是个类似撮箕的东西,现在缺少两个面:上边的面和前边
的面,我们现在研究如何把2个面补上。
经研究发现,当我们将一个面连接在AB、BC、DH边上时,恰好可以封闭上面的面,而将另一个面连接在AE、FG、GH边上时,可以封闭前面的面。
由于Z字结构可看成是由两个图形“┐”和“└”叠加而成,而拼合时,C和D两点重合,E和F两点重合,故AB、BC、DH恰好位于“┐”边上, AE、FG、GH则恰好是位于“└”边上。
找到规律后,我们便可以很方便的确定具有Z字结构的分布规律。
图4给出了两种具有
图1 分布规律一图2 展开图例
1 2 1 2 C
B A H
G F E
D 图3 Z字结构分布规律
var script = document.createElement('script'); script.src = '/resource/baichuan/ns.js'; document.body.appendChild(script);
Z字结构的正方体展开图,其中图4 A是正写的Z字,图4 B是反写的Z字。
反写的Z字,其分布规律和正写的Z字类似,区别仅仅是将反写Z看成是两个图形┌和叠加而成。
我们研究不难发现,如果展开图旋转、翻转,移动可以重合的算同一种情况,则正方体展开图不同的共有11种情况。
三、展开图的特点 1.对面的确定,
①Z字结构的头和尾属于对面,②对于
面1和面3为对面。
2.展开图中的垂直边,在组成正方体时会重合。
3.重合的顶点确定
图4 Z字结构展开图例 (A) 正写Z字结构 (B) 反写Z字结构 1 3
var script = document.createElement('script'); script.src = '/resource/baichuan/ns.js'; document.body.appendChild(script);
4.展开图中某些面上线的画法。
基本做法,先原图中按顺序读。
再在展开图中按顺序写出即可。
D C B
D1
B1
C1 A1
A
◎△
◎◎△
○○☉☆☉☆ A B C D B C B1
C1 D1 D A1 A D1 C1
A B C D
下载文档到电脑,查找使用更方便
2下载券 210人已下载
下载
还剩2页未读,继续阅读
四、右手法则:
面2、面3和面1的组成符合右手法则,因此不论立方体如何旋转,面2、面3和面1的组成符合右手法则的规律不变,通过右手法则,可以很容易判断立方体所对应的展开图。
例1:把正方体的表面沿某些棱剪开展成一个平面图形(如右下图),请根据各面上的图案判断这个正方体是()
例2:如图,有一个正方体纸盒,在它的三个侧面分别画有三角形、正方形和圆,现用一把剪刀沿着它的棱剪开成一个平面图形,则展开图可以是 ( )
五、视图的规律
将俯视图看做是一块地,地中长了很多麦子,将左视图和主视图想象为土地上长出的麦子的投影,因为麦子有高有低。
所以对应的左视图和主视图将不同。
例1. 下图是由一些相同的小正方体构成的几何体的三视图。
这些相同的小正方体的个数是()
例2. 由一些大小相同的小正方体组成的几何体的主视图和俯视图(如图7)。
2
3 1 1
2 3 (正方体纸盒)(A)(B)
(C)(D)
图7
(1)请你画出这个几何体的一种左视图;
(2)若组成这个几何体的小正方形的块数n,请你写出n的所有可能值。
