人教新课标版数学高二-数学B版选修2-2练习第一章《导数》习题课
人教课标版(B版)高中数学选修2-2第一章 导数及其应用导数

感悟高考
由 g′(x)=0,得 x1=1,x2=2. 所以当 x∈(-∞, 1)时, g′(x)<0, g(x)在(-∞, 1)上为减函数;
当 x∈(1,2)时,g′(x)>0,g(x)在(1,2)上为增函数; 当 x∈(2,+∞)时,g′(x)<0,g(x)在(2,+∞)上为减函数; 1 所以,当 x=1 时,g(x)取得极小值 g(1)= ,当 x=2 时函数取 e 3 得极大值 g(2)= 2. e 函数 y=k 与 y=g(x)的图象的大致形状如上, 1 3 由图象可知,当 k= 和 k= 2时,关于 x 的方程 f(x)=kex 恰有两 e e 个不同的实根.
1 1 ①当 x∈-2,0时,h′(x)>0,∴h(x)在-2,0上单调递增.
②当 x∈(0,+∞)时,h′(x)<0,∴h(x)在(0,+∞)上单调递减.
1 1 1-2ln 2 ∴当 x∈-2,0时,h(x)>h-2= . 4
g(3)<0, 即a+4-2ln 2<0, 解得 2ln 3-5≤a<2ln 2-4. g(4)≥0, a+5-2ln 3≥0,
综上所述,a 的取值范围是[2ln 3-5,2ln 2-4). 2 方法二 ∵f(x)=2ln(x-1)-(x-1) ,
∴f(x)+x2-3x-a=0 x+a+1-2ln(x-1)=0, 即 a=2ln(x-1)-x-1, 令 h(x)=2ln(x-1)-x-1, 3-x 2 ∵h′(x)= -1= ,且 x>1, x-1 x-1 由 h′(x)>0,得 1<x<3;由 h′(x)<0,得 x>3. ∴h(x)在区间[2,3]上单调递增,在区间[3,4]上单调递减.
人教新课标版数学高二人教数学B版选修2-2练习第一章《导数及其应用》测试

章末质量评估(一)(时间:100分钟 满分:120分)一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.曲线y =12x 2-2x 在点⎝ ⎛⎭⎪⎫1,-32处的切线的倾斜角为( ).A .-135°B .45°C .-45°D .135°解析 y ′=x -2,所以斜率k =1-2=-1,因此,倾斜角为135°. 答案 D2.下列求导运算正确的是( ).A.⎝ ⎛⎭⎪⎫x +3x ′=1+3x 2 B .(log 2x )′=1x ln 2 C .(3x )′=3x log 3eD .(x 2cos x )′=-2x sin x解析 ⎝ ⎛⎭⎪⎫x +3x ′=1-3x 2,所以A 不正确;(3x )′=3x ln 3,所以C 不正确;(x 2cosx )′=2x cos x +x 2·(-sin x ),所以D 不正确;(log 2x )′=1x ln 2,所以B 正确.故选B. 答案 B 3.|sin x |d x 等于( ).A .0B .1C .2D .4解析 |sin x |d x =sin x d x +(-sin x )d x =()-cos x ⎪⎪⎪π+cosx ⎪⎪⎪2ππ=1+1+1+1=4. 答案 D4.函数y =1+3x -x 3有( ).A .极小值-1,极大值1B .极小值-2,极大值3C .极小值-2,极大值2D .极小值-1,极大值3解析 y ′=-3x 2+3,令y ′=0得,x =1或x =-1, ∴f (1)=3,f (-1)=-1. 答案 D 5.函数f (x )=x 2x -1( ).A .在(0,2)上单调递减B .在(-∞,0)和(2,+∞)上单调递增C .在(0,2)上单调递增D .在(-∞,0)和(2,+∞)上单调递减 解析 f ′(x )=2x (x -1)-x 2(x -1)2=x 2-2x(x -1)2=x (x -2)(x -1)2. 令f ′(x )=0得x 1=0,x 2=2.∴x ∈(-∞,0)和(2,+∞)时,f ′(x )>0. x ∈(0,1)∪(1,2)时,f ′(x )<0. 答案 B6.函数y =x 4-4x +3在区间[-2,3]上的最小值为( ).A .72B .36C .12D .0解析y′=4x3-4,令y′=0,4x3-4=0,x=1,当x<1时,y′<0;当x>1时,y′>0得y极小值=y|x=1=0,而端点的函数值y|x=-2=27,y|x=3=72,得y min=0.答案 D7.一物体在力F(x)=3x2-2x+5(力单位:N,位移单位:m)作用力下,沿与力F(x)相同的方向由x=5 m直线运动到x=10 m处做的功是().A.925 J B.850 J C.825 J D.800 J解析W=F(x)d x=(3x2-2x+5)d x=(x3-x2+5x)⎪⎪105=(1 000-100+50)-(125-25+25)=825 (J).答案 C8.已知f(x)=x3+ax2+(a+6)x+1有极大值和极小值,则a的取值范围为().A.-1<a<2 B.-3<a<6C.a<-1或a>2 D.a<-3或a>6解析因为f(x)有极大值和极小值,所以导函数f′(x)=3x2+2ax+(a+6)有两个不等实根,所以Δ=4a2-12(a+6)>0,得a<-3或a>6.答案 D9.已知f(x)的导函数f′(x)图象如右图所示,那么f(x)的图象最有可能是图中的().解析∵x∈(-∞,-2)时,f′(x)<0,∴f(x)为减函数;同理f(x)在(-2,0)上为增函数,(0,+∞)上为减函数.答案 A10.由直线y=x,y=-x+1及x轴围成平面图形的面积为().解析画出图形,由定积分定义可知选C.答案 C11.设曲线y=x n+1(n∈N*)在(1,1)处的切线与x轴的交点的横坐标为x n,则log2 010x1+log2 010x2+…+log2 010x2 009的值为( ).A .-log 2 0102 009B .-1C .(log 2 0102 009)-1D .1解析 ∵y ′|x =1=n +1,∴切线方程为y -1=(n +1)(x -1), 令y =0,得x =1-1n +1=n n +1,即x n =nn +1.所以log 2 010x 1+log 2 010x 2+…+log 2 010x 2 009 =log 2 010(x 1·x 2·…·x 2 009)=log 2 010⎝ ⎛⎭⎪⎫12·23·…·2 0092 010=log 2 01012 010=-1. 答案 B12.由曲线y =x 2和直线x =0,x =1,y =t 2,t ∈(0,1)所围成的图形(阴影部分)的面积的最小值为 ( ) A.14 B.13 C.12D.23解析 面积为(t 2-x 2)d x + (x 2-t 2)d x=⎝ ⎛⎭⎪⎫t 2x -13x 3⎪⎪ t 0+⎝ ⎛⎭⎪⎫13x 3-t 2x ⎪⎪1t =43t 3-t 2+13, 下面求函数f (t )=43t 3-t 2+13在(0,1)上的最小值.f ′(x )=4t 2-2t ,在⎝⎛⎭⎪⎫0,12上f ′(t )<0,在⎝ ⎛⎭⎪⎫12,1上f ′(t )>0,所以f (t )=43t 3-t 2+13在⎝ ⎛⎭⎪⎫0,12上为减函数,在⎝ ⎛⎭⎪⎫12,1上为增函数,所以当t =12时,f (t )有最小值f ⎝ ⎛⎭⎪⎫12=43⎝ ⎛⎭⎪⎫123-⎝ ⎛⎭⎪⎫122+13=14.答案 A二、填空题(本大题共4小题,每小题5分,共20分.把答案填在题中横线上)13.若f (x )=x 3,f ′(x 0)=3,则x 0的值为________. 解析 f ′(x 0)=3x 20=3,∴x 0=±1. 答案 ±114.曲线y =ln x 在点M (e,1)处的切线的斜率是________,切线的方程为________. 解析 由于y ′=1x ,∴k =y ′|x =e =1e ,故切线的方程为y -1=1e (x -e),故y =1ex . 答案 1e x -e y =015.函数y =x 3+x 2-5x -5的单调递增区间是________. 解析 由y ′=3x 2+2x -5>0得x <-53,或x >1. 答案 ⎝ ⎛⎭⎪⎫-∞,-35,(1,+∞)16.若(x -k )d x =32,则实数k 的值为________.解析 ∫10(x -k )d x =⎝ ⎛⎭⎪⎫12x 2-k x ⎪⎪⎪10=12-k =32,∴k =-1. 答案 -1三、解答题(本大题共4小题,共40分.解答时应写出必要的文字说明、证明过程或演算步骤)17.(10分)设函数f (x )=2x 3-3(a +1)x 2+6ax +8,其中a ∈R .已知f (x )在x =3处取得极值. (1)求f (x )的解析式;(2)求f (x )在点A (1,16)处的切线方程. 解 (1)f ′(x )=6x 2-6(a +1)x +6a . ∵f (x )在x =3处取得极值,∴f′(3)=6×9-6(a+1)×3+6a=0,解得a=3.∴f(x)=2x3-12x2+18x+8.(2)A点在f(x)上,由(1)可知f′(x)=6x2-24x+18,f′(1)=6-24+18=0,∴切线方程为y=16.18.(10分)给定函数f(x)=x33-ax2+(a2-1)x和g(x)=x+a2x.(1)求证:f(x)总有两个极值点;(2)若f(x)和g(x)有相同的极值点,求a的值.(1)证明因为f′(x)=x2-2ax+(a2-1)=[x-(a+1)]·[x-(a-1)],令f′(x)=0,解得x1=a+1,x2=a-1.当x<a-1时,f′(x)>0;当a-1<x<a+1,f′(x)<0.所以x=a-1为f(x)的一个极大值点.同理可证x=a+1为f(x)的一个极小值点.所以f(x)总有两个极值点.(2)解因为g′(x)=1-a2x2=(x-a)(x+a)x2.令g′(x)=0,则x1=a,x2=-a.因为f(x)和g(x)有相同的极值点,且x1=a和a+1,a-1不可能相等,所以当-a=a+1时,a=-1 2;当-a=a-1时,a=1 2.经检验,当a=-12和a=12时,x1=a,x2=-a都是g(x)的极值点.19.(10分)已知函数f(x)=x3+ax2+bx+c在x=-1与x=2处都取得极值.(1)求a ,b 的值及函数f (x )的单调区间;(2)若对x ∈[-2,3],不等式f (x )+32c <c 2恒成立,求c 的取值范围. 解 (1)f ′(x )=3x 2+2ax +b ,由题意得⎩⎨⎧ f ′(-1)=0,f ′(2)=0,即⎩⎨⎧3-2a +b =0,12+4a +b =0,解得⎩⎪⎨⎪⎧a =-32,b =-6.∴f (x )=x 3-32x 2-6x +c ,f ′(x )=3x 2-3x -6. 令f ′(x )<0,解得-1<x <2; 令f ′(x )>0,解得x <-1或x >2. ∴f (x )的减区间为(-1,2),增区间为(-∞,-1),(2,+∞). (2)由(1)知,f (x )在(-∞,-1)上单调递增; 在(-1,2)上单调递减;在(2,+∞)上单调递增. ∴x ∈[-2,3]时,f (x )的最大值即为 f (-1)与f (3)中的较大者. f (-1)=72+c ,f (3)=-92+c . ∴当x =-1时,f (x )取得最大值. 要使f (x )+32c <c 2,只需c 2>f (-1)+32c , 即2c 2>7+5c ,解得c <-1或c >72. ∴c 的取值范围为(-∞,-1)∪⎝ ⎛⎭⎪⎫72,+∞.20.(10分)若函数f (x )=ax 3-bx +4,当x =2时,函数f (x )有极值-43. (1)求函数的解析式.(2)若方程f (x )=k 有3个不同的根,求实数k 的取值范围. 解 f ′(x )=3ax 2-b .(1)由题意得⎩⎪⎨⎪⎧f ′(2)=12a -b =0,f (2)=8a -2b +4=-43,解得⎩⎪⎨⎪⎧a =13,b =4,故所求函数的解析式为f (x )=13x 3-4x +4.(2)由(1)可得f ′(x )=x 2-4=(x -2)(x +2),令f ′(x )=0,得x =2或x =-2. 当x 变化时,f ′(x ),f (x )的变化情况如下表:x (-∞,-2)-2 (-2,2) 2 (2,+∞)f ′(x ) +0 -0 +f (x )283-43f (x )有极大值283,当x =2时,f (x )有极小值-43,所以函数f (x )=13x 3-4x +4的图象大致如图所示.若f (x )=k 有3个不同的根,则直线y =k 与函数f (x )的图象有3个交点,所以-43<k <283.。
高中数学选修2-2(人教B版)第一章导数及其应用1.2知识点总结含同步练习题及答案

′
解:(1)y ′ = (e3x+2 ) = e3x+2 ⋅ (3x + 2)′ = 3e3x+2 ; (2)y ′ = (ln(2x − 1))′ =
1 2 . ⋅ (2x − 1)′ = 2x − 1 2x − 1
2.利用导数求函数的切线方程 描述: 利用导数求函数的切线方程 步骤一:求出函数 y = f (x) 在点 x0 处的导数 f ′ (x0 ) ; 步骤二:根据直线方程的点斜式,得到切线方程为 y − f (x0 ) = f ′ (x0 )(x − x0 ). 例题: 求曲线 y = ex + 1 在 (0, 2) 处的切线方程. 解:因为 y = ex + 1,所以 y ′ = ex ,故曲线 y = ex + 1在 (0, 2)处的切线斜率为
解:(1)因为 y =
所以在点 P 处的切线的斜率等于 4 .所以在点 P 处的切线方程是
y−
即
8 = 4(x − 2), 3
12x − 3y − 16 = 0.
(2)设切点为 (x 0 , y 0 ),则由(1)知切线的斜率 k = x2 ,切线方程为 y − y 0 = x2 (x − x 0 ) . 0 0 又切线过点 P (2,
8 1 ) 且 (x0 , y 0 ) 在曲线 y = x3 上,所以 3 3 ⎧ ⎪ 8 − y = x2 (2 − x0 ), 0 0 ⎨3 1 ⎪ ⎩ y = x3 , ⎪ 0 3 0 − 3x2 + 4 = 0, x3 0 0
整理得
即
(x0 − 2)2 (x0 + 1) = 0.
人教新课标版数学高二-人教B版选修2-2练习 第一章 习题课
习题课一、基础过关1.函数f (x )=x cos x 的导函数f ′(x )在区间上的图象大致是 ( )2.函数y =x cos x -sin x 在下面哪个区间内是增函数( ) A.⎝⎛⎭⎫π2,3π2 B .(π,2π)C.⎝⎛⎭⎫3π2,5π2 D .(2π,3π)3.已知函数f (x )=x +ln x ,则有( ) A .f (2)<f (e)<f (3)B .f (e)<f (2)<f (3)C .f (3)<f (e)<f (2)D .f (e)<f (3)<f (2)4.函数y =f (x )的图象如下图所示,则导函数y =f ′(x )的图象可能是( )5.已知函数f(x)、g(x)均为上的可导函数,在上连续且f′(x)<g′(x),则f(x)-g(x)的最大值为()A.f(a)-g(a) B.f(b)-g(b)C.f(a)-g(b) D.f(b)-g(a)6.已知对任意实数x,有f(-x)=-f(x),g(-x)=g(x),且当x>0时,有f′(x)>0,g′(x)>0,则当x<0时,有() A.f′(x)>0,g′(x)>0B.f′(x)>0,g′(x)<0C.f′(x)<0,g′(x)>0D.f′(x)<0,g′(x)<07.已知函数f(x)=x3-ax2+3x+6,若x=3是f(x)的一个极值点,求f(x)在上的最值.二、能力提升8.若函数y =x 3+32x 2+m 在上的最大值为92,则m =________. 9.已知a >0,函数f (x )=x 3-ax 在0,+∞)内的最小值;(2)设曲线y =f (x )在点(2,f (2))处的切线方程为y =32x ,求a ,b 的值.三、探究与拓展12.已知a ∈R ,函数f (x )=(-x 2+ax )e x (x ∈R ).(1)当a =2时,求函数f (x )的单调区间;(2)若函数f (x )在(-1,1)上单调递增,求a 的取值范围.答案1.A 2.B 3.A 4.D 5.A 6.B7.解 f ′(x )=3x 2-2ax +3,由已知得f ′(3)=0,∴3×9-6a +3=0.∴a =5,∴f (x )=x 3-5x 2+3x +6.令f ′(x )=3x 2-10x +3=0,得x 1=13,x 2=3.当x 变化时,f ′(x ),f (x )的变化状态如下表:∴f (x )在上的最大值为f (5)=21,最小值为f (3)=-3.8.2 9.310.(1)解 f ′(x )=1+2ax +b x. 由已知条件得⎩⎪⎨⎪⎧ f (1)=0,f ′(1)=2, 即⎩⎪⎨⎪⎧ 1+a =0,1+2a +b =2. 解得⎩⎪⎨⎪⎧a =-1,b =3. (2)证明 因为f (x )的定义域为(0,+∞),由(1)知f (x )=x -x 2+3ln x .设g (x )=f (x )-(2x -2)=2-x -x 2+3ln x ,则g ′(x )=-1-2x +3x=-(x -1)(2x +3)x. 当0<x <1时,g ′(x )>0,当x >1时,g ′(x )<0.所以g (x )在(0,1)内单调递增,在(1,+∞)内单调递减. 而g (1)=0,故当x >0时,g (x )≤0,即f (x )≤2x -2.11.解 (1)f ′(x )=a e x -1a e x , 当f ′(x )>0,即x >-ln a 时,f (x )在(-ln a ,+∞)上递增;当f ′(x )<0,即x <-ln a 时,f (x )在(-∞,-ln a )上递减.①当0<a <1时,-ln a >0,f (x )在(0,-ln a )上递减, 在(-ln a ,+∞)上递增,从而f (x )在0,+∞)上递增, 从而f (x )在-x 2+(a -2)x +a -x 2+(a -2)x +a hslx3y3he x ≥0,注意到e x >0, 因此-x 2+(a -2)x +a ≥0在(-1,1)上恒成立,也就是a ≥x 2+2x x +1=x +1-1x +1在(-1,1)上恒成立. 设y =x +1-1x +1,则y ′=1+1(x +1)2>0, 即y =x +1-1x +1在(-1,1)上单调递增, 则y <1+1-11+1=32, 故a ≥32.。
高中数学新人教版选修2-2课时作业:第一章 导数及其应用1.5.3

1.5.3 定积分的概念明目标、知重点1.了解定积分的概念,会用定义求定积分.2.理解定积分的几何意义.3.掌握定积分的基本性质.探究点一定积分的概念思考1 分析求曲边梯形的面积和变速直线运动的路程,找一下它们的共同点.答两个问题均可以通过“分割、近似代替、求和、取极限”解决,都可以归结为一个特定形式和的极限.思考2 怎样正确认识定积分ʃb a f(x)d x?答(1)定积分ʃb a f(x)d x是一个数值(极限值).它的值仅取决于被积函数与积分上、下限,另外ʃb a f(x)d x与积分区间a,b]息息相关,不同的积分区间,所得值也不同.(2)定积分就是和的极限lim n →∞∑i =1nf (ξi )·Δx ,而ʃba f (x )d x 只是这种极限的一种记号,读作“函数f (x )从a 到b 的定积分”.(3)函数f (x )在区间a ,b ]上连续这一条件是不能忽视的,它保证了和的极限(定积分)的存在(实际上,函数连续是定积分存在的充分条件,而不是必要条件). 例1 利用定积分的定义,计算ʃ10x 3d x 的值. 解 令f (x )=x 3. (1)分割在区间0,1]上等间隔地插入n -1个分点,把区间0,1]等分成n 个小区间i -1n ,in](i =1,2,…,n ),每个小区间的长度为Δx =i n -i -1n =1n.(2)近似代替、求和取ξi =i n(i =1,2,…,n ),则ʃ10x 3d x ≈S n =∑ni =1f (in)·Δx =∑ni =1(i n )3·1n=1n 4∑ni =1i 3=1n 4·14n 2(n +1)2=14(1+1n)2. (3)取极限ʃ10x 3d x =lim n →∞S n =lim n →∞ 14(1+1n )2=14. 反思与感悟 (1)利用定积分定义求定积分的数值仍然是“分割、近似代替、求和、取极值”这一过程,需要注意的是在本题中将近似代替、求和一起作为步骤(2),从而省略了解题步骤. (2)从过程来看,当f (x )≥0时,定积分就是区间对应曲边梯形的面积. 跟踪训练1 用定义计算ʃ21(1+x )d x .解 (1)分割:将区间1,2]等分成n 个小区间⎣⎢⎡⎦⎥⎤1+i -1n ,1+in (i =1,2,…,n ),每个小区间的长度为 Δx =1n.(2)近似代替、求和:在⎣⎢⎡⎦⎥⎤1+i -1n ,1+i n 上取点ξi =1+i -1n(i =1,2,…,n ),于是f (ξi )=1+1+i -1n =2+i -1n ,从而得∑i =1n f (ξi )Δx =∑i =1n(2+i -1n )·1n =∑i =1n ⎝ ⎛⎭⎪⎫2n +i -1n 2=2n ·n +1n20+1+2+…+(n -1)]=2+1n 2·n (n -1)2=2+n -12n .(3)取极限:S =lim n →∞ ⎝⎛⎭⎪⎫2+n -12n =2+12=52. 因此ʃ21(1+x )d x =52.探究点二 定积分的几何意义思考1 从几何上看,如果在区间a ,b ]上函数f (x )连续且恒有f (x )≥0,那么ʃba f (x )d x 表示什么?答 当函数f (x )≥0时,定积分ʃba f (x )d x 在几何上表示由直线x =a ,x =b (a <b ),y =0及曲线y =f (x )所围成的曲边梯形的面积.思考2 当f (x )在区间a ,b ]上连续且恒有f (x )≤0时,ʃba f (x )d x 表示的含义是什么?若f (x )有正有负呢?答 如果在区间a ,b ]上,函数f (x )≤0时,那么曲边梯形位于x 轴的下方(如图①). 由于b -an>0,f (ξi )≤0,故 f (ξi )b -a n ≤0.从而定积分ʃb a f (x )d x ≤0,这时它等于如图①所示曲边梯形面积的相反值,即ʃbaf (x )d x =-S.当f (x )在区间a ,b ]上有正有负时,定积分ʃba f (x )d x 表示介于x 轴、函数f (x )的图象及直线x =a ,x =b (a ≠b )之间各部分面积的代数和(在x 轴上方的取正,在x 轴下方的取负).(如图②),即ʃba f (x )d x =-S 1+S 2-S 3. 例2 利用几何意义计算下列定积分: (1)ʃ3-39-x 2d x ;(2)ʃ3-1(3x +1)d x .解 (1)在平面上y =9-x 2表示的几何图形为以原点为圆心以3为半径的上半圆, 其面积为S =12·π·32.由定积分的几何意义知ʃ3-39-x 2d x =92π.(2)由直线x =-1,x =3,y =0,以及y =3x +1所围成的图形,如图所示: ʃ3-1(3x +1)d x 表示由直线x =-1,x =3,y =0以及y =3x +1所围成的图形在x 轴上方的面积减去在x 轴下方的面积,∴ʃ3-1(3x +1)d x =12×(3+13)×(3×3+1)-12(-13+1)×2=503-23=16. 反思与感悟 利用几何意义求定积分,关键是准确确定被积函数的图象,以及积分区间,正确利用相关的几何知识求面积.不规则的图象常用分割法求面积,注意分割点的准确确定. 跟踪训练2 根据定积分的几何意义求下列定积分的值: (1)ʃ1-1x d x ;(2)ʃ2π0cos x d x ;(3)ʃ1-1|x |d x . 解 (1)如图(1),ʃ1-1x d x =-A 1+A 1=0. (2)如图(2),ʃ2π0cos x d x =A 1-A 2+A 3=0.(3)如图(3),∵A 1=A 2,∴ʃ1-1|x |d x =2A 1=2×12=1.(A 1,A 2,A 3分别表示图中相应各处面积)探究点三 定积分的性质思考1 定积分的性质可作哪些推广? 答 定积分的性质的推广①ʃb a f 1(x )±f 2(x )±…±f n (x )]d x =ʃb a f 1(x )d x ±ʃb a f 2(x )d x ±…±ʃba f n (x )d x ; ②ʃb a f (x )d x =ʃc 1a f (x )d x +ʃc 2c 1f (x )d x +…+ʃb c n f (x )d x (其中n ∈N *). 思考2 如果一个函数具有奇偶性,它的定积分有什么性质? 答 奇、偶函数在区间-a ,a ]上的定积分①若奇函数y =f (x )的图象在-a ,a ]上连续不断,则ʃa-a f (x )d x =0. ②若偶函数y =g (x )的图象在-a ,a ]上连续不断,则ʃa -a g (x )d x =2ʃa0g (x )d x . 例3 计算ʃ3-3(9-x 2-x 3)d x 的值. 解 如图,由定积分的几何意义得ʃ3-39-x2d x=π×322=9π2,ʃ3-3x3d x=0,由定积分性质得ʃ3-3(9-x2-x3)d x=ʃ3-39-x2d x-ʃ3-3x3d x=9π2.反思与感悟根据定积分的性质计算定积分,可以先借助于定积分的定义或几何意义求出相关函数的定积分,再利用函数的性质、定积分的性质结合图形进行计算.跟踪训练3 已知ʃ10x3d x=14,ʃ21x3d x=154,ʃ21x2d x=73,ʃ42x2d x=563,求:(1)ʃ203x3d x;(2)ʃ416x2d x;(3)ʃ21(3x2-2x3)d x.解(1)ʃ203x3d x=3ʃ20x3d x=3(ʃ10x3d x+ʃ21x3d x)=3×(14+154)=12;(2)ʃ416x2d x=6ʃ41x2d x=6(ʃ21x2d x+ʃ42x2d x)=6×(73+563)=126;(3)ʃ21(3x2-2x3)d x=ʃ213x2d x-ʃ212x3d x=3ʃ21x2d x-2ʃ21x3d x=3×73-2×154=7-152=-12.1.下列结论中成立的个数是( )①ʃ10x3d x=∑i=1n i3n3·1n;②ʃ10x3d x=limn→∞∑i=1n(i-1)3n3·1n;③ʃ10x3d x=limn→∞∑i=1n i3n3·1n.A.0 B.1 C.2 D.3答案 C解析 ②③成立.2.定积分ʃba f (x )d x 的大小( )A .与f (x )和积分区间a ,b ]有关,与ξi 的取法无关B .与f (x )有关,与区间a ,b ]以及ξi 的取法无关C .与f (x )以及ξi 的取法有关,与区间a ,b ]无关D .与f (x )、积分区间a ,b ]和ξi 的取法都有关 答案 A3.根据定积分的几何意义,用不等号连接下列式子: ①ʃ10x d x ________ʃ10x 2d x ; ②ʃ204-x 2d x ________ʃ202d x . 答案 ①> ②<4.若ʃT 0x 2d x =9,则常数T 的值为________. 答案 3解析 令f (x )=x 2. (1)分割将区间0,T ]n 等分,则Δx =Tn. (2)近似代替、求和取ξi =T i n(i =1,2,…,n ),S n =∑i =1n(T i n )2·T n =T 3n 3∑i =1n i 2=T 3n 3(12+22+…+n 2)=T 3n 3·n (n +1)(2n +1)6=T 36(1+1n )(2+1n). (3)取极限S =lim n →∞T 36×2=T 33=9, ∴T 3=27,∴T =3. 呈重点、现规律]1.定积分ʃbaf (x )d x 是一个和式∑i =1nb -anf (ξi )的极限,是一个常数. 2.可以利用“分割、近似代替、求和、取极限”求定积分;对于一些特殊函数,也可以利用几何意义求定积分.3.定积分的几何性质可以帮助简化定积分运算.一、基础过关1.下列命题不正确的是( )A .若f (x )是连续的奇函数,则ʃa-a f (x )d x =0 B .若f (x )是连续的偶函数,则ʃa -a f (x )d x =2ʃa0f (x )d x C .若f (x )在a ,b ]上连续且恒正,则ʃba f (x )d x >0D .若f (x ) 在a ,b ]上连续且ʃba f (x )d x >0,则f (x )在a ,b ]上恒正 答案 D解析 对于A ,f (-x )=-f (x ),ʃa-a f (x )d x=ʃ0-a f (x )d x +ʃa 0f (x )d x =-ʃa 0f (x )d x +ʃa0f (x )d x =0,同理B 正确;由定积分的几何意义知,当f (x )>0时,ʃb a f (x )d x >0即C 正确;但ʃb a f (x )d x >0,不一定有f (x )恒正,故选D. 2.已知定积分ʃ60f (x )d x =8,且f (x )为偶函数,则ʃ6-6f (x )d x 等于( ). A .0 B .16 C .12 D .8 答案 B解析 偶函数图象关于y 轴对称, 故ʃ6-6f (x )d x =2ʃ60f (x )d x =16,故选B. 3.已知ʃt 0x d x =2,则ʃ0-t x d x 等于( ) A .0 B .2 C .-1 D .-2 答案 D解析 ∵f (x )=x 在-t ,t ]上是奇函数, ∴ʃt -t x d x =0.而ʃt -t x d x =ʃ0-t x d x +ʃt0x d x , 又ʃt0x d x =2,∴ʃ0-t x d x =-2.故选D.4.由曲线y =x 2-4,直线x =0,x =4和x 轴围成的封闭图形的面积(如图)是( ) A .ʃ40(x 2-4)d x B.||ʃ40(x 2-4)d x C .ʃ40|x 2-4|d xD .ʃ20(x 2-4)d x +ʃ42(x 2-4)d x 答案 C5.设a =ʃ10x 13d x ,b =ʃ10x 2d x ,c =ʃ10x 3d x ,则a ,b ,c 的大小关系是( )A .c >a >bB .a >b >cC .a =b >cD .a >c >b答案 B解析 根据定积分的几何意义,易知ʃ10x 3d x <ʃ10x 2d x <ʃ10x 13d x ,a >b >c ,故选B.6.若ʃa-a |56x |d x ≤2 016,则正数a 的最大值为( ) A .6 B .56 C .36 D .2 016 答案 A解析 由ʃa -a |56x |d x =56ʃa-a |x |d x ≤2 016, 得ʃa-a |x |d x ≤36,∴ʃa-a |x |d x =2ʃa0x d x =a 2≤36, 即0<a ≤6.故正数a 的最大值为6.7.lim n →∞ln n(1+1n )2(1+2n )2…(1+n n)2等于( )A .ʃ21ln 2x d x B .2ʃ21ln x d x C .2ʃ21ln(1+x )d x D .ʃ21ln 2(1+x )d x答案 B解析 lim n →∞ln n(1+1n )2(1+2n )2…(1+n n)2=lim n →∞2n ln ⎣⎢⎡⎦⎥⎤(1+1n )(1+2n)…(1+n n ) =2lim n →∞ ∑ni =1ln (1+i n )n =2ʃ21ln x d x (这里f (x )=ln x ,区间1,2]或者2lim n →∞ ∑ni =1ln (1+in )n=2ʃ10ln(1+x )d x ,区间0,1]).二、能力提升8.由y =sin x ,x =0,x =-π,y =0所围成图形的面积写成定积分的形式是S =________. 答案 -ʃ0-πsin x d x解析 由定积分的意义知,由y =sin x ,x =0,x =-π,y =0围成图形的面积为S =-ʃ0-πsinx d x .9.计算定积分ʃ1-14-4x 2d x =________. 答案 π解析 由于ʃ1-14-4x 2d x =2ʃ1-11-x 2d x 表示单位圆的面积π,所以ʃ1-14-4x 2d x =π. 10.设f (x )是连续函数,若ʃ10f (x )d x =1,ʃ20f (x )d x =-1,则ʃ21f (x )d x =________. 答案 -2解析 因为ʃ20f (x )d x =ʃ10f (x )d x +ʃ21f (x )d x ,所以ʃ21f (x )d x =ʃ20f (x )d x -ʃ10f (x )d x =-2.11.利用定积分的定义计算ʃ21(-x 2+2x )d x 的值,并从几何意义上解释这个值表示什么. 解 令f (x )=-x 2+2x . (1)分割在区间1,2]上等间隔地插入n -1个分点,把区间1,2]等分为n 个小区间1+i -1n ,1+in](i =1,2,…,n ),每个小区间的长度为Δx =i n -i -1n =1n.(2)近似代替、求和取ξi =1+in(i =1,2,…,n ),则S n =∑ni =1f (1+i n )·Δx =∑ni =1-(1+i n )2+2(1+i n )]·1n=-1n 3(n +1)2+(n +2)2+(n +3)2+…+(2n )2]+2n2(n +1)+(n +2)+(n +3)+…+2n ]=-1n 32n (2n +1)(4n +1)6-n (n +1)(2n +1)6]+2n 2·n (n +1+2n )2=-13(2+1n )(4+1n )+16(1+1n )(2+1n )+3+1n .(3)取极限ʃ21(-x 2+2x )d x =lim n →∞S n =lim n →∞-13(2+1n )(4+1n )+16(1+1n )(2+1n )+3+1n ]=23, ʃ21(-x 2+2x )d x =23的几何意义为由直线x =1,x =2,y =0与曲线f (x )=-x 2+2x 所围成的曲边梯形的面积.12.用定积分的意义求下列各式的值:(1)ʃ30(2x +1)d x ;(2)⎰x .解 (1)在平面上,f (x )=2x +1为一条直线,ʃ30(2x +1)d x 表示直线f (x )=2x +1,x =0,x =3与x 轴围成的直角梯形OABC 的面积,如图(1)所示,其面积为S =12(1+7)×3=12.根据定积分的几何意义知ʃ30(2x +1)d x =12.(2)由y =1-x 2可知,x 2+y 2=1(y ≥0)图象如图(2),由定积分的几何意义知⎰1-x 2d x等于圆心角为120°的弓形CED 的面积与矩形ABCD 的面积之和.S 弓形=12×23π×12-12×1×1×sin 23π=π3-34,S 矩形=|AB |·|BC |=2×32×12=32,∴⎰1-x 2d x =π3-34+32=π3+34.三、探究与拓展13.已知函数f (x )=⎩⎪⎨⎪⎧x 3, x ∈[-2,2)2x , x ∈[2,π)cos x , x ∈[π,2π],求f (x )在区间-2,2π]上的积分.解 由定积分的几何意义知 ʃ2-2x 3d x =0,ʃπ22x d x =(π-2)(2π+4)2 =π2-4, ʃ2ππcos x d x =0, 由定积分的性质得ʃ2π-2f (x )d x =ʃ2-2x 3d x +ʃπ22x d x +ʃ2ππcos x d x =π2-4.。
新课标高二数学选修2-2第一章导数及其应用测试题(含答案)

新课标高二数学选修2-2第一章导数及其应用测试题(含答案)案场各岗位服务流程销售大厅服务岗:1、销售大厅服务岗岗位职责:1)为来访客户提供全程的休息区域及饮品;2)保持销售区域台面整洁;3)及时补足销售大厅物资,如糖果或杂志等;4)收集客户意见、建议及现场问题点;2、销售大厅服务岗工作及服务流程阶段工作及服务流程班前阶段1)自检仪容仪表以饱满的精神面貌进入工作区域2)检查使用工具及销售大厅物资情况,异常情况及时登记并报告上级。
班中工作程序服务流程行为规范迎接指引递阅资料上饮品(糕点)添加茶水工作1)眼神关注客人,当客人距3米距离侯客迎询问客户送客户要求注意事项时,应主动跨出自己的位置迎宾,然后15度鞠躬微笑问候:“您好!欢迎光临!”2)在客人前方1-2米距离领位,指引请客人向休息区,在客人入座后问客人对座位是否满意:“您好!请问坐这儿可以吗?”得到同意后为客人拉椅入座“好的,请入座!”3)若客人无置业顾问陪同,可询问:请问您有专属的置业顾问吗?,为客人取阅项目资料,并礼貌的告知请客人稍等,置业顾问会很快过来介绍,同时请置业顾问关注该客人;4)问候的起始语应为“先生-小姐-女士早上好,这里是XX销售中心,这边请”5)问候时间段为8:30-11:30 早上好11:30-14:30 中午好 14:30-18:00下午好6)关注客人物品,如物品较多,则主动询问是否需要帮助(如拾到物品须两名人员在场方能打开,提示客人注意贵重物品);7)在满座位的情况下,须先向客人致歉,在请其到沙盘区进行观摩稍作等待;阶段工作及服务流程班中工作程序工作要求注意事项饮料(糕点服务)1)在所有饮料(糕点)服务中必须使用托盘;2)所有饮料服务均已“对不起,打扰一下,请问您需要什么饮品”为起始;3)服务方向:从客人的右面服务;4)当客人的饮料杯中只剩三分之一时,必须询问客人是否需要再添一杯,在二次服务中特别注意瓶口绝对不可以与客人使用的杯子接触;5)在客人再次需要饮料时必须更换杯子;下班程序1)检查使用的工具及销售案场物资情况,异常情况及时记录并报告上级领导;2)填写物资领用申请表并整理客户意见;3)参加班后总结会;4)积极配合销售人员的接待工作,如果下班时间已经到,必须待客人离开后下班;1.3.3.3吧台服务岗1.3.3.3.1吧台服务岗岗位职责1)为来访的客人提供全程的休息及饮品服务;2)保持吧台区域的整洁;3)饮品使用的器皿必须消毒;4)及时补充吧台物资;5)收集客户意见、建议及问题点;1.3.3.3.2吧台服务岗工作及流程阶段工作及服务流程班前阶段1)自检仪容仪表以饱满的精神面貌进入工作区域2)检查使用工具及销售大厅物资情况,异常情况及时登记并报告上级。
高中数学选修2-2(人教B版)第一章导数及其应用1.3知识点总结含同步练习题及答案

描述:例题:高中数学选修2-2(人教B版)知识点总结含同步练习题及答案
第一章 导数及其应用 1.3 导数的应用
一、学习任务
1. 理解函数的单调性与导数的关系;会利用导数研究函数的单调性;会求不超过三次的多项式
函数的单调区间.2. 了解函数的极大(小)值,最大(小)值的概念;了解函数的极值与最值的区别和联系;掌
握求函数的极值与最值的方法.
3. 体会导数在解决实际问题中的作用;会利用导数解决实际生活中的有关利润最大、用料最
省、效率最高等优化问题;掌握最优化问题的建模及求解.二、知识清单
导数与函数的图象
利用导数研究函数的单调性
利用导数求函数的极值
利用导数求函数的最值
利用导数处理生活中的优化问题
三、知识讲解
1.导数与函数的图象
(1)导数 表示函数 在点 处的切线斜率.当切线斜率为正值时,
切线的倾斜角小于 ,函数曲线呈上升状态;当切线的斜率为负值时,切线的倾斜角大于 且小于 ,函数曲线呈下降状态.
(2)如果在区间 内恒有 ,那么函数 在区间 内是常函数.
()f ′x 0y =f (x )(,f ()x 0x 090∘90∘180∘(a ,
b )
(x )=0f ′y =f (x )(a ,b ) 是函数 的导函数, 的图象如图所示,则 的图象最有可能是下列选
项中的( )
(x )f ′f (x )y =(x )f ′f (x )
y=f
(x)
已知函数 的图象如图所示,则导函数
f(x)(a,b)则函数 在开区间
0.001 m
)?
S
(2)求面积 的最大值.解:(1)依题意,以
y=f(x)(−3,1)
2。
(完整版)新课改高二数学选修2-2第一章导数及其应用测试题(含答案),推荐文档

x 2 +1 11a新课改高二数学选修 2-2 第一章导数及其应用测试题(时间 120 分钟,分值 150 分)说明:本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题).第Ⅰ卷(选择题,共 60 分)一、 选择题(本大题共 12 小题,每小题 5 分,共 60 分,在每小题给出的四个选项中,只有一项是符合题目要求的,请将所选答案写在答题卡上) 1.曲线 y = x 3 在点(2,8) 处的切线方程为().A . y = 6x - 12 C . y = 8x + 101 - x 24.设 y = sin x ,则 y ' = ( ).- 2x sin x - (1- x 2 ) cos xA .sin 2 x - 2x sin x + (1 - x 2 )B . y = 12x - 16 D . y = 2x - 32-2x sin x + (1- x 2 ) cos xB .sin 2 x- 2x sin x - (1 - x 2 )C.D .sin x sin x 5.设 f (x ) = ln ,则 f '(2) = ( ).4 2 1 3 A.B .C .D .55557. 函数 f (x ) =1 e x (sin x + cos x ) 在区间[0,]的值域为( ). 2 1 1 21 1A .[ , 2 e 2]2B. ( , 2 2e 2 )C .[1, e 2 ]D .(1, e 2 )8. 积分⎰a 2 - x 2 dx = ( ).-aA. a 24B. a 22C. a 2D. 2a 210. 由抛物线 y 2 = 2x 与直线 y = x - 4 所围成的图形的面积是( ).38 16 A .18B .C .D .1633第Ⅱ卷(非选择题,共90 分)二、填空题(每小题4 分,共16 分。
请将答案填在答题卷相应空格上。
)三、解答题:(本大题共5 小题,共74 分,解答应写出文字说明,证明过程或演算步骤)(17)(本小题满分10 分)已知向量a = (x 2 , x +1), b = (1-x, t) ,若函数f (x) =a ⋅b 在区间(-1,1) 上是增函数,求t 的取值范围。
新课标高二数学选修2-2第一章导数及其应用测试题(含答案)

新课标⾼⼆数学选修2-2第⼀章导数及其应⽤测试题(含答案)新课改⾼⼆数学选修2-2第⼀章导数及其应⽤测试题第Ⅰ卷(选择题,共40分)⼀、选择题(本⼤题共10⼩题,每⼩题4分,共40分)1.设xx y sin 12-=,则='y ().A .x x x x x 22sin cos )1(sin 2---B .xx x x x 22sin cos )1(sin 2-+- C .x x x x sin )1(sin 22-+- D .xx x x sin )1(sin 22---2.设1ln )(2+=x x f ,则=)2('f ().A .54 B .52 C .51 D .53 3.已知2)3(',2)3(-==f f ,则3)(32lim3--→x x f x x 的值为().A .4-B .0C .8D .不存在 4.曲线3x y =在点)8,2(处的切线⽅程为().A .126-=x yB .1612-=x yC .108+=x yD .322-=x y 5.满⾜()()f x f x '=的函数是A . f (x )=1-x B. f (x )=x C . f (x )=0D . f (x )=16.曲线34y x x =-在点(-1,-3)处的切线⽅程是A . 74y x =+ B. 72y x =+ C. 4y x =- D. 2y x =-7.若关于x 的函数2m n y mx -=的导数为4y x '=,则m n +的值为 A. -4 B. 1- C. D . 48.设ln y x x =-,则此函数在区间(0,1)内为A .单调递增, B.有增有减 C.单调递减, D.不确定 9.函数3()31f x x x =-+在闭区间[-3,0]上的最⼤值、最⼩值分别是A . 1,-1 B. 3,-17 C. 1,-17 D. 9,-1910.函数)(x f 的定义域为开区间),(b a ,导函数)(x f '在),(b a 内的图象如图所⽰,则函数)(x f 在开区间),(b a 内有极⼩值点 A 1个B 2个C 3个D 4个第Ⅱ卷(⾮选择题,共60分)⼆、填空题(每⼩题5分,共15分。
新课程人教版高中数学选修2-2课后习题解答(全)
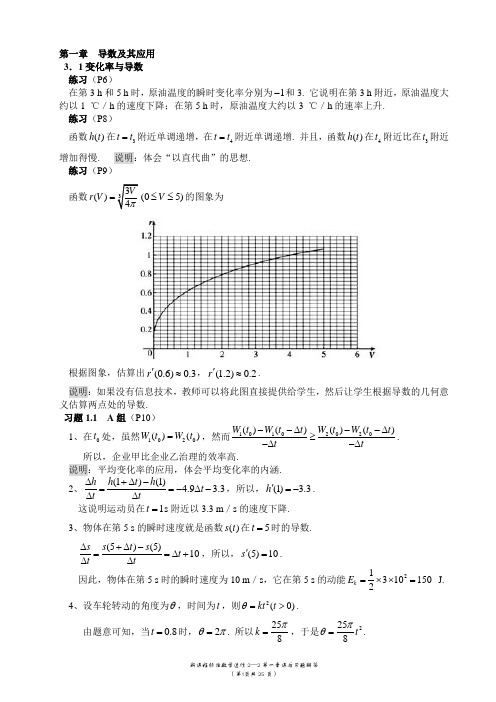
第一章 导数及其应用 3.1变化率与导数 练习(P6)在第3 h 和5 h 时,原油温度的瞬时变化率分别为1-和3. 它说明在第3 h 附近,原油温度大约以1 ℃/h 的速度下降;在第5 h 时,原油温度大约以3 ℃/h 的速率上升. 练习(P8)函数()h t 在3t t =附近单调递增,在4t t =附近单调递增. 并且,函数()h t 在4t 附近比在3t 附近增加得慢. 说明:体会“以直代曲”的思想. 练习(P9) 函数33()4Vr V π=(05)V ≤≤的图象为根据图象,估算出(0.6)0.3r '≈,(1.2)0.2r '≈.说明:如果没有信息技术,教师可以将此图直接提供给学生,然后让学生根据导数的几何意义估算两点处的导数. 习题1.1 A 组(P10)1、在0t 处,虽然1020()()W t W t =,然而10102020()()()()W t W t t W t W t t t t--∆--∆≥-∆-∆. 所以,企业甲比企业乙治理的效率高.说明:平均变化率的应用,体会平均变化率的内涵.2、(1)(1) 4.9 3.3h h t h t t t∆+∆-==-∆-∆∆,所以,(1) 3.3h '=-.这说明运动员在1t =s 附近以3.3 m /s 的速度下降. 3、物体在第5 s 的瞬时速度就是函数()s t 在5t =时的导数.(5)(5)10s s t s t t t∆+∆-==∆+∆∆,所以,(5)10s '=. 因此,物体在第5 s 时的瞬时速度为10 m /s ,它在第5 s 的动能213101502k E =⨯⨯= J. 4、设车轮转动的角度为θ,时间为t ,则2(0)kt t θ=>. 由题意可知,当0.8t =时,2θπ=. 所以258k π=,于是2258t πθ=.车轮转动开始后第3.2 s 时的瞬时角速度就是函数()t θ在 3.2t =时的导数.(3.2)(3.2)25208t t t t θθθππ∆+∆-==∆+∆∆,所以(3.2)20θπ'=. 因此,车轮在开始转动后第3.2 s 时的瞬时角速度为20π1s -. 说明:第2,3,4题是对了解导数定义及熟悉其符号表示的巩固.5、由图可知,函数()f x 在5x =-处切线的斜率大于零,所以函数在5x =-附近单调递增. 同理可得,函数()f x 在4x =-,2-,0,2附近分别单调递增,几乎没有变化,单调递减,单调递减. 说明:“以直代曲”思想的应用.6、第一个函数的图象是一条直线,其斜率是一个小于零的常数,因此,其导数()f x '的图象如图(1)所示;第二个函数的导数()f x '恒大于零,并且随着x 的增加,()f x '的值也在增加;对于第三个函数,当x 小于零时,()f x '小于零,当x 大于零时,()f x '大于零,并且随着x 的增加,()f x '的值也在增加. 以下给出了满足上述条件的导函数图象中的一种.说明:本题意在让学生将导数与曲线的切线斜率相联系. 习题3.1 B 组(P11)1、高度关于时间的导数刻画的是运动变化的快慢,即速度;速度关于时间的导数刻画的是速度变化的快慢,根据物理知识,这个量就是加速度.2、说明:由给出的()v t 的信息获得()s t 的相关信息,并据此画出()s t 的图象的大致形状. 这个过程基于对导数内涵的了解,以及数与形之间的相互转换.3、由(1)的题意可知,函数()f x 的图象在点(1,5)-处的切线斜率为1-,所以此点附近曲线呈下降趋势. 首先画出切线的图象,然后再画出此点附近函数的图象. 同理可得(2)(3)某点处函数图象的大致形状. 下面是一种参考答案.说明:这是一个综合性问题,包含了对导数内涵、导数几何意义的了解,以及对以直代曲思想的领悟. 本题的答案不唯一. 1.2导数的计算 练习(P18)1、()27f x x '=-,所以,(2)3f '=-,(6)5f '=.2、(1)1ln 2y x '=; (2)2x y e '=; (3)4106y x x '=-; (4)3sin 4cos y x x '=--;(5)1sin 33xy '=-; (6)21y x '=-.习题1.2 A 组(P18)1、()()2S S r r S r r r r r π∆+∆-==+∆∆∆,所以,0()lim(2)2r S r r r r ππ∆→'=+∆=.2、()9.8 6.5h t t '=-+.3、3213()34r V Vπ'=. 4、(1)213ln 2y x x '=+; (2)1n x n x y nx e x e -'=+; (3)2323sin cos cos sin x x x x x y x-+'=; (4)9899(1)y x '=+; (5)2x y e -'=-; (6)2sin(25)4cos(25)y x x x '=+++. 5、()822f x x '=-+. 由0()4f x '=有 04822x =-+,解得032x =. 6、(1)ln 1y x '=+; (2)1y x =-. 7、1xy π=-+.8、(1)氨气的散发速度()500ln 0.8340.834t A t '=⨯⨯.(2)(7)25.5A '=-,它表示氨气在第7天左右时,以25.5克/天的速率减少.习题1.2 B 组(P19) 1、(1)(2)当h 越来越小时,sin()sin x h xy h+-=就越来越逼近函数cos y x =.(3)sin y x =的导数为cos y x =.2、当0y =时,0x =. 所以函数图象与x 轴交于点(0,0)P . x y e '=-,所以01x y ='=-.所以,曲线在点P 处的切线的方程为y x =-.2、()4sin d t t '=-. 所以,上午6:00时潮水的速度为0.42-m /h ;上午9:00时潮水的速度为0.63-m /h ;中午12:00时潮水的速度为0.83-m /h ;下午6:00时潮水的速度为 1.24-m /h.1.3导数在研究函数中的应用 练习(P26)1、(1)因为2()24f x x x =-+,所以()22f x x '=-.当()0f x '>,即1x >时,函数2()24f x x x =-+单调递增; 当()0f x '<,即1x <时,函数2()24f x x x =-+单调递减. (2)因为()x f x e x =-,所以()1x f x e '=-.当()0f x '>,即0x >时,函数()x f x e x =-单调递增; 当()0f x '<,即0x <时,函数()x f x e x =-单调递减. (3)因为3()3f x x x =-,所以2()33f x x '=-.当()0f x '>,即11x -<<时,函数3()3f x x x =-单调递增; 当()0f x '<,即1x <-或1x >时,函数3()3f x x x =-单调递减. (4)因为32()f x x x x =--,所以2()321f x x x '=--.当()0f x '>,即13x <-或1x >时,函数32()f x x x x =--单调递增;当()0f x '<,即113x -<<时,函数32()f x x x x =--单调递减.2、3、因为2()(0)f x ax bx c a =++≠,所以()2f x ax b '=+. (1)当0a >时,()0f x '>,即2bx a >-时,函数2()(0)f x ax bx c a =++≠单调递增; ()0f x '<,即2bx a<-时,函数2()(0)f x ax bx c a =++≠单调递减.(2)当0a <时,()0f x '>,即2bx a <-时,函数2()(0)f x ax bx c a =++≠单调递增;()0f x '<,即2bx a>-时,函数2()(0)f x ax bx c a =++≠单调递减. 4、证明:因为32()267f x x x =-+,所以2()612f x x x '=-. 当(0,2)x ∈时,2()6120f x x x '=-<,因此函数32()267f x x x =-+在(0,2)内是减函数. 练习(P29)1、24,x x 是函数()y f x =的极值点,其中2x x =是函数()y f x =的极大值点,4x x =是函数()y f x =的极小值点. 2、(1)因为2()62f x x x =--,所以()121f x x '=-. 令()1210f x x '=-=,得112x =. 当112x >时,()0f x '>,()f x 单调递增;当112x <时,()0f x '<,()f x 单调递减. 所以,当112x =时,()f x 有极小值,并且极小值为211149()6()212121224f =⨯--=-.(2)因为3()27f x x x =-,所以2()327f x x '=-. 令2()3270f x x '=-=,得3x =±. 下面分两种情况讨论:①当()0f x '>,即3x <-或3x >时;②当()0f x '<,即33x -<<时. 当x 变化时,()f x ',()f x 变化情况如下表:注:图象形状不唯一.因此,当3x =-时,()f x 有极大值,并且极大值为54;当3x =时,()f x 有极小值,并且极小值为54-.(3)因为3()612f x x x =+-,所以2()123f x x '=-. 令2()1230f x x '=-=,得2x =±. 下面分两种情况讨论:①当()0f x '>,即22x -<<时;②当()0f x '<,即2x <-或2x >时. 当x 变化时,()f x ',()f x 变化情况如下表:因此,当2x =-时,()f x 有极小值,并且极小值为10-;当2x =时,()f x 有极大值,并且极大值为22(4)因为3()3f x x x =-,所以2()33f x x '=-. 令2()330f x x '=-=,得1x =±. 下面分两种情况讨论:①当()0f x '>,即11x -<<时;②当()0f x '<,即1x <-或1x >时. 当x 变化时,()f x ',()f x 变化情况如下表:因此,当1x =-时,()f x 有极小值,并且极小值为2-;当1x =时,()f x 有极大值,并且极大值为2练习(P31)(1)在[0,2]上,当112x =时,2()62f x x x =--有极小值,并且极小值为149()1224f =-. 又由于(0)2f =-,(2)20f =.因此,函数2()62f x x x =--在[0,2]上的最大值是20、最小值是4924-. (2)在[4,4]-上,当3x =-时,3()27f x x x =-有极大值,并且极大值为(3)54f -=;当3x =时,3()27f x x x =-有极小值,并且极小值为(3)54f =-;又由于(4)44f -=,(4)44f =-.因此,函数3()27f x x x =-在[4,4]-上的最大值是54、最小值是54-.(3)在1[,3]3-上,当2x =时,3()612f x x x =+-有极大值,并且极大值为(2)22f =.又由于155()327f -=,(3)15f =.因此,函数3()612f x x x =+-在1[,3]3-上的最大值是22、最小值是5527.(4)在[2,3]上,函数3()3f x x x =-无极值. 因为(2)2f =-,(3)18f =-.因此,函数3()3f x x x =-在[2,3]上的最大值是2-、最小值是18-. 习题1.3 A 组(P31)1、(1)因为()21f x x =-+,所以()20f x '=-<. 因此,函数()21f x x =-+是单调递减函数.(2)因为()cos f x x x =+,(0,)2x π∈,所以()1sin 0f x x '=->,(0,)2x π∈. 因此,函数()cos f x x x =+在(0,)2π上是单调递增函数. (3)因为()24f x x =--,所以()20f x '=-<. 因此,函数()24f x x =-是单调递减函数. (4)因为3()24f x x x =+,所以2()640f x x '=+>. 因此,函数3()24f x x x =+是单调递增函数.2、(1)因为2()24f x x x =+-,所以()22f x x '=+.当()0f x '>,即1x >-时,函数2()24f x x x =+-单调递增. 当()0f x '<,即1x <-时,函数2()24f x x x =+-单调递减. (2)因为2()233f x x x =-+,所以()43f x x '=-.当()0f x '>,即34x >时,函数2()233f x x x =-+单调递增. 当()0f x '<,即34x <时,函数2()233f x x x =-+单调递减.(3)因为3()3f x x x =+,所以2()330f x x '=+>. 因此,函数3()3f x x x =+是单调递增函数. (4)因为32()f x x x x =+-,所以2()321f x x x '=+-. 当()0f x '>,即1x <-或13x >时,函数32()f x x x x =+-单调递增. 当()0f x '<,即113x -<<时,函数32()f x x x x =+-单调递减.3、(1)图略. (2)加速度等于0.4、(1)在2x x =处,导函数()y f x '=有极大值; (2)在1x x =和4x x =处,导函数()y f x '=有极小值; (3)在3x x =处,函数()y f x =有极大值; (4)在5x x =处,函数()y f x =有极小值.5、(1)因为2()62f x x x =++,所以()121f x x '=+. 令()1210f x x '=+=,得112x =-. 当112x >-时,()0f x '>,()f x 单调递增; 当112x <-时,()0f x '<,()f x 单调递减.所以,112x =-时,()f x 有极小值,并且极小值为211149()6()212121224f -=⨯---=-.(2)因为3()12f x x x =-,所以2()312f x x '=-. 令2()3120f x x '=-=,得2x =±. 下面分两种情况讨论:①当()0f x '>,即2x <-或2x >时;②当()0f x '<,即22x -<<时. 当x 变化时,()f x ',()f x 变化情况如下表:因此,当2x =-时,()f x 有极大值,并且极大值为16;当2x =时,()f x 有极小值,并且极小值为16-.(3)因为3()612f x x x =-+,所以2()123f x x '=-+. 令2()1230f x x '=-+=,得2x =±. 下面分两种情况讨论:①当()0f x '>,即2x <-或2x >时;②当()0f x '<,即22x -<<时. 当x 变化时,()f x ',()f x 变化情况如下表:因此,当2x =-时,()f x 有极大值,并且极大值为22;当2x =时,()f x 有极小值,并且极小值为10-.(4)因为3()48f x x x =-,所以2()483f x x '=-. 令2()4830f x x '=-=,得4x =±. 下面分两种情况讨论:①当()0f x '>,即2x <-或2x >时;②当()0f x '<,即22x -<<时. 当x 变化时,()f x ',()f x 变化情况如下表:因此,当4x =-时,()f x 有极小值,并且极小值为128-;当4x =时,()f x 有极大值,并且极大值为128.6、(1)在[1,1]-上,当112x =-时,函数2()62f x x x =++有极小值,并且极小值为4724. 由于(1)7f -=,(1)9f =,所以,函数2()62f x x x =++在[1,1]-上的最大值和最小值分别为9,4724. (2)在[3,3]-上,当2x =-时,函数3()12f x x x =-有极大值,并且极大值为16; 当2x =时,函数3()12f x x x =-有极小值,并且极小值为16-. 由于(3)9f -=,(3)9f =-,所以,函数3()12f x x x =-在[3,3]-上的最大值和最小值分别为16,16-.(3)在1[,1]3-上,函数3()612f x x x =-+在1[,1]3-上无极值.由于1269()327f -=,(1)5f =-,所以,函数3()612f x x x =-+在1[,1]3-上的最大值和最小值分别为26927,5-.(4)当4x =时,()f x 有极大值,并且极大值为128.. 由于(3)117f -=-,(5)115f =,所以,函数3()48f x x x =-在[3,5]-上的最大值和最小值分别为128,117-. 习题3.3 B 组(P32)1、(1)证明:设()sin f x x x =-,(0,)x π∈. 因为()cos 10f x x '=-<,(0,)x π∈ 所以()sin f x x x =-在(0,)π内单调递减因此()sin (0)0f x x x f =-<=,(0,)x π∈,即sin x x <,(0,)x π∈. 图略 (2)证明:设2()f x x x =-,(0,1)x ∈. 因为()12f x x '=-,(0,1)x ∈所以,当1(0,)2x ∈时,()120f x x '=->,()f x 单调递增,2()(0)0f x x x f =->=;当1(,1)2x ∈时,()120f x x '=-<,()f x 单调递减,2()(1)0f x x x f =->=;又11()024f =>. 因此,20x x ->,(0,1)x ∈. 图略(3)证明:设()1x f x e x =--,0x ≠. 因为()1x f x e '=-,0x ≠所以,当0x >时,()10x f x e '=->,()f x 单调递增,()1(0)0x f x e x f =-->=;当0x <时,()10x f x e '=-<,()f x 单调递减,()1(0)0x f x e x f =-->=;综上,1x e x ->,0x ≠. 图略 (4)证明:设()ln f x x x =-,0x >. 因为1()1f x x'=-,0x ≠ 所以,当01x <<时,1()10f x x'=->,()f x 单调递增, ()ln (1)10f x x x f =-<=-<;当1x >时,1()10f x x'=-<,()f x 单调递减, ()ln (1)10f x x x f =-<=-<;当1x =时,显然ln11<. 因此,ln x x <. 由(3)可知,1x e x x >+>,0x >.. 综上,ln x x x e <<,0x > 图略2、(1)函数32()f x ax bx cx d =+++的图象大致是个“双峰”图象,类似“”或“”的形状. 若有极值,则在整个定义域上有且仅有一个极大值和一个极小值,从图象上能大致估计它的单调区间.(2)因为32()f x ax bx cx d =+++,所以2()32f x ax bx c '=++.下面分类讨论:当0a ≠时,分0a >和0a <两种情形: ①当0a >,且230b ac ->时,设方程2()320f x ax bx c '=++=的两根分别为12,x x ,且12x x <,当2()320f x ax bx c '=++>,即1x x <或2x x >时,函数32()f x ax bx cx d =+++单调递增; 当2()320f x ax bx c '=++<,即12x x x <<时,函数32()f x ax bx cx d =+++单调递减. 当0a >,且230b ac -≤时,此时2()320f x ax bx c '=++≥,函数32()f x ax bx cx d =+++单调递增. ②当0a <,且230b ac ->时,设方程2()320f x ax bx c '=++=的两根分别为12,x x ,且12x x <,当2()320f x ax bx c '=++>,即12x x x <<时,函数32()f x ax bx cx d =+++单调递增; 当2()320f x ax bx c '=++<,即1x x <或2x x >时,函数32()f x ax bx cx d =+++单调递减. 当0a <,且230b ac -≤时,此时2()320f x ax bx c '=++≤,函数32()f x ax bx cx d =+++单调递减 1.4生活中的优化问题举例 习题1.4 A 组(P37)1、设两段铁丝的长度分别为x ,l x -,则这两个正方形的边长分别为4x ,4l x -,两个正方形的面积和为 22221()()()(22)4416x l x S f x x lx l -==+=-+,0x l <<.令()0f x '=,即420x l -=,2lx =.当(0,)2l x ∈时,()0f x '<;当(,)2lx l ∈时,()0f x '>.因此,2lx =是函数()f x 的极小值点,也是最小值点.所以,当两段铁丝的长度分别是2l时,两个正方形的面积和最小.2、如图所示,由于在边长为a 的正方形铁片的四角截去 四个边长为x 的小正方形,做成一个无盖方盒,所以无 盖方盒的底面为正方形,且边长为2a x -,高为x .(1)无盖方盒的容积2()(2)V x a x x =-,02ax <<.(2)因为322()44V x x ax a x =-+,所以22()128V x x ax a '=-+.令()0V x '=,得2a x =(舍去),或6a x =. 当(0,)6a x ∈时,()0V x '>;当(,)62a ax ∈时,()0V x '<.因此,6ax =是函数()V x 的极大值点,也是最大值点.所以,当6ax =时,无盖方盒的容积最大.3、如图,设圆柱的高为h ,底半径为R , 则表面积222S Rh R ππ=+由2V R h π=,得2V h R π=. 因此,2222()222V V S R R R R R R ππππ=+=+,0R >. 令2()40VS R R Rπ'=-+=,解得R =.当R ∈时,()0S R '<;当)R ∈+∞时,()0S R '>.因此,R =是函数()S R 的极小值点,也是最小值点.此时,22V h R R π===. 所以,当罐高与底面直径相等时,所用材料最省.4、证明:由于211()()n i i f x x a n ==-∑,所以12()()n i i f x x a n ='=-∑.令()0f x '=,得11ni i x a n ==∑,可以得到,11ni i x a n ==∑是函数()f x 的极小值点,也是最小值点.这个结果说明,用n 个数据的平均值11ni i a n =∑表示这个物体的长度是合理的,这就是最小二乘法的基本原理.5、设矩形的底宽为x m ,则半圆的半径为2xm ,半圆的面积为28x π2m ,(第3题)矩形的面积为28x a π-2m ,矩形的另一边长为()8a xx π-m因此铁丝的长为22()(1)244xa x al x x x x xπππ=++-=++,0x <<令22()104al x xπ'=+-=,得x =.当x ∈时,()0l x '<;当x ∈时,()0l x '>.因此,x =()l x 的极小值点,也是最小值点.时,所用材料最省. 6、利润L 等于收入R 减去成本C ,而收入R 等于产量乘单价. 由此可得出利润L 与产量q 的函数关系式,再用导数求最大利润.收入211(25)2588R q p q q q q =⋅=-=-,利润2211(25)(1004)2110088L R C q q q q q =-=--+=-+-,0200q <<.求导得1214L q '=-+令0L '=,即12104q -+=,84q =.当(0,84)q ∈时,0L '>;当(84,200)q ∈时,0L '<;因此,84q =是函数L 的极大值点,也是最大值点.所以,产量为84时,利润L 最大,习题1.4 B 组(P37)1、设每个房间每天的定价为x 元,那么宾馆利润21801()(50)(20)7013601010x L x x x x -=--=-+-,180680x <<. 令1()7005L x x '=-+=,解得350x =.当(180,350)x ∈时,()0L x '>;当(350,680)x ∈时,()0L x '>. 因此,350x =是函数()L x 的极大值点,也是最大值点. 所以,当每个房间每天的定价为350元时,宾馆利润最大. 2、设销售价为x 元/件时,利润4()()(4)()(5)b x L x x a c cc x a x b b -=-+⨯=--,54ba x <<. 令845()0c ac bc L x xb b +'=-+=,解得458a bx +=. 当45(,)8a b x a +∈时,()0L x '>;当455(,)84a b bx +∈时,()0L x '<.当458a bx +=是函数()L x 的极大值点,也是最大值点.所以,销售价为458a b+元/件时,可获得最大利润.1.5定积分的概念 练习(P42) 83. 说明:进一步熟悉求曲边梯形面积的方法和步骤,体会“以直代曲”和“逼近”的思想. 练习(P45)1、22112()[()2]()i i i i i s s v t n n n n n n'∆≈∆=∆=-+⋅=-⋅+⋅,1,2,,i n =.于是 111()n n ni i i i i is s s v t n ==='=∆≈∆=∆∑∑∑2112[()]ni i n n n ==-⋅+⋅∑22211111()()()2n n n n n n n n -=-⋅--⋅-⋅+2231[12]2n n=-++++31(1)(21)26n n n n ++=-⋅+111(1)(1)232n n=-+++取极值,得1111115lim [()]lim [(1)(1)2]323nnn n i i i s v n n n n →∞→∞====-+++=∑∑说明:进一步体会“以不变代变”和“逼近”的思想.2、223km.说明:进一步体会“以不变代变”和“逼近”的思想,熟悉求变速直线运动物体路程的方法和步骤.练习(P48)2304x dx =⎰. 说明:进一步熟悉定积分的定义和几何意义.从几何上看,表示由曲线3y x =与直线0x =,2x =,0y =所围成的曲边梯形的面积4S =.习题1.5 A 组(P50) 1、(1)10021111(1)[(1)1]0.495100100i i x dx =--≈+-⨯=∑⎰; (2)50021111(1)[(1)1]0.499500500i i x dx =--≈+-⨯=∑⎰; (3)100021111(1)[(1)1]0.499510001000i i x dx =--≈+-⨯=∑⎰. 说明:体会通过分割、近似替换、求和得到定积分的近似值的方法.2、距离的不足近似值为:18112171310140⨯+⨯+⨯+⨯+⨯=(m ); 距离的过剩近似值为:271181121713167⨯+⨯+⨯+⨯+⨯=(m ).3、证明:令()1f x =. 用分点 011i i n a x x x x x b -=<<<<<<=将区间[,]a b 等分成n 个小区间,在每个小区间1[,]i i x x -上任取一点(1,2,,)i i n ξ=作和式11()nni i i b af x b a nξ==-∆==-∑∑, 从而11lim nban i b adx b a n→∞=-==-∑⎰, 说明:进一步熟悉定积分的概念. 4、根据定积分的几何意义,0⎰表示由直线0x =,1x =,0y =以及曲线y =所围成的曲边梯形的面积,即四分之一单位圆的面积,因此04π=⎰.5、(1)03114x dx -=-⎰.由于在区间[1,0]-上30x ≤,所以定积分031x dx -⎰表示由直线0x =,1x =-,0y =和曲线3y x =所围成的曲边梯形的面积的相反数.(2)根据定积分的性质,得1133311011044x dx x dx x dx --=+=-+=⎰⎰⎰.由于在区间[1,0]-上30x ≤,在区间[0,1]上30x ≥,所以定积分131x dx -⎰等于位于x 轴上方的曲边梯形面积减去位于x 轴下方的曲边梯形面积.(3)根据定积分的性质,得202333110115444x dx x dx x dx --=+=-+=⎰⎰⎰由于在区间[1,0]-上30x ≤,在区间[0,2]上30x ≥,所以定积分231x dx -⎰等于位于x 轴上方的曲边梯形面积减去位于x 轴下方的曲边梯形面积.说明:在(3)中,由于3x 在区间[1,0]-上是非正的,在区间[0,2]上是非负的,如果直接利用定义把区间[1,2]-分成n 等份来求这个定积分,那么和式中既有正项又有负项,而且无法抵挡一些项,求和会非常麻烦. 利用性质3可以将定积分231x dx -⎰化为02331x dx x dx -+⎰⎰,这样,3x 在区间[1,0]-和区间[0,2]上的符号都是不变的,再利用定积分的定义,容易求出031x dx -⎰,230x dx ⎰,进而得到定积分231x dx -⎰的值. 由此可见,利用定积分的性质可以化简运算.在(2)(3)中,被积函数在积分区间上的函数值有正有负,通过练习进一步体会定积分的几何意义.习题1.5 B 组(P50)1、该物体在0t =到6t =(单位:s )之间走过的路程大约为145 m.说明:根据定积分的几何意义,通过估算曲边梯形内包含单位正方形的个数来估计物体走过的路程. 2、(1)9.81v t =.(2)过剩近似值:8111899.819.8188.292242i i =⨯⨯⨯=⨯⨯=∑(m );不足近似值:81111879.819.8168.672242i i =-⨯⨯⨯=⨯⨯=∑(m ) (3)49.81tdt ⎰;49.81d 78.48t t =⎰(m ).3、(1)分割在区间[0,]l 上等间隔地插入1n -个分点,将它分成n 个小区间:[0,]l n ,2[,]l l n n ,……,(2)[,]n l l n -, 记第i 个区间为(1)[,]i l iln n-(1,2,i n =),其长度为 (1)il i l l x n n n-∆=-=.把细棒在小段[0,]l n ,2[,]l l n n ,……,(2)[,]n ll n-上质量分别记作:12,,,n m m m ∆∆∆,则细棒的质量1ni i m m ==∆∑.(2)近似代替当n 很大,即x ∆很小时,在小区间(1)[,]i l iln n-上,可以认为线密度2()x x ρ=的值变化很小,近似地等于一个常数,不妨认为它近似地等于任意一点(1)[,]i i l iln nξ-∈处的函数值2()i i ρξξ=. 于是,细棒在小段(1)[,]i l il n n -上质量 2()i i i lm x nρξξ∆≈∆=(1,2,i n =).(3)求和得细棒的质量 2111()nnni i i i i i l m m x nρξξ====∆≈∆=∑∑∑. (4)取极限细棒的质量 21lim ni n i lm n ξ→∞==∑,所以20l m x dx =⎰..。
高中数学选修2-2(人教B版)第一章导数及其应用1.4知识点总结含同步练习题及答案

1 1 1 25 . + +⋯+ < n+1 n+2 2n 36
即
2n 1 1 1 1 n + +⋯+ <∫ dx = ln x| 2 n = ln 2n − ln n = ln 2, n+1 n+2 2n x n
因为ln 2 ≈ 0.6931 , 25 ≈ 0.6944 ,所以ln 2 < 25 .所以
3 1
π 2 dx;(3)∫ 0 2 (sin x − cos x)dx. x
∫
(1 + x + x2 ) = ∫
3 1
1 2 3 1 x | 1 + x3 | 3 1 2 3 1 1 = (3 − 1) + (3 2 − 1 2 ) + (3 3 − 1 3 ) 2 3 44 = . 3 = x| 3 1 +
∑ f (ξi )Δx = ∑
i =1 i =1 n n
b−a f (ξi ), n
当 n → ∞ 时,上述和式无限接近某个常数,这个常数叫做函数 f (x) 在区间 [a, b] 上的定积分(definite integral),记作 ∫ ab f (x)dx,即
∫
b a
f (x)dx = lim ∑
∫
b a
f (x)dx = F (x)| b a = F (b) − F (a).
例题: 利用定积分定义计算: (1)∫ 1 (1 + x)dx;(2)∫ 0 xdx. 解:(1)因为 f (x) = 1 + x 在区间 [1, 2] 上连续,将区间 [1, 2] 分成 n 等份,则每个区间的
人教B版选修22高中数学第一章《导数及其应用》同步练习

导数的应用第1题、 2007海南、宁夏文)设函数错误!超链接引用无效. (Ⅰ)讨论错误!超链接引用无效。
的单调性;(Ⅱ)求错误!超链接引用无效。
在区间错误!超链接引用无效.的最大值和最小值.答案:解:错误!超链接引用无效。
的定义域为错误!超链接引用无效。
.(Ⅰ)错误!超链接引用无效。
.当错误!超链接引用无效。
时,错误!超链接引用无效。
;当错误!超链接引用无效。
时,错误!超链接引用无效。
;当错误!超链接引用无效.时,错误!超链接引用无效.. 从而,错误!超链接引用无效.分别在区间错误!超链接引用无效。
,错误!超链接引用无效.单调增加,在区间错误!超链接引用无效.单调减少.(Ⅱ)由(Ⅰ)知错误!超链接引用无效。
在区间错误!超链接引用无效.的最小值为错误!超链接引用无效。
又错误!超链接引用无效.错误!超链接引用无效。
. 所以错误!超链接引用无效。
在区间错误!超链接引用无效.的最大值为错误!超链接引用无效.. 第2题、 (2002海南、宁夏理)曲线错误!超链接引用无效。
在点错误!超链接引用无效.处的切线与坐标轴所围三角形的面积为( ) A。
错误!超链接引用无效。
B。
错误!超链接引用无效。
C。
错误!超链接引用无效.D.错误!超链接引用无效。
答案:D第3题、 (2007海南、宁夏理)设函数错误!超链接引用无效。
.(I )若当错误!超链接引用无效.时,错误!超链接引用无效。
取得极值,求错误!超链接引用无效。
的值,并讨论错误!超链接引用无效。
的单调性;(II )若错误!超链接引用无效。
存在极值,求错误!超链接引用无效。
的取值范围,并证明所有极值之和大于错误!超链接引用无效。
答案:解:(Ⅰ)错误!超链接引用无效。
,依题意有错误!超链接引用无效。
,故错误!超链接引用无效。
.从而错误!超链接引用无效.。
错误!超链接引用无效。
的定义域为错误!超链接引用无效。
.当错误!超链接引用无效。
时,错误!超链接引用无效.;当错误!超链接引用无效。
人教新课标版数学高二人教数学B版选修2-2练习第一章《导数及其应用》解读高考

命题趋势1. 导数是研究函数的重要工具,自从导数进入教材之后,给函数问题注入了生机和活力,开辟了许多解题新途径,拓展了高考对函数问题的命题空间,其中导数的概念和运算是导数的基础内容,在高考题中一般以容易题出现,并且在高考中所占的份量不大.2.由近三年的高考试题统计分析可以看出,导数的应用已经成为高考炙手可热的热点问题.每年全国及各省市的自主命题中都有导数应用的解答题出现,因此搞好导数应用的复习非常有必要. 常见的考查角度如下:(1)对导数与函数的单调性的考查,求导确定函数的单调区间,已知函数的某一单调区间探求参数的范围等.(2)对导数与函数的极(最)值的考查,如:求函数的极值及闭区间上的最值,以极值或最值为载体考查参数的范围;解题关键在于准确理解极值(最值)的定义,善于利用分类讨论思想,等价转化思想去解题.(3)对导数的综合应用的考查,与函数、方程、不等式、数列等联系进行综合考查,主要考查函数的最值或求参数的值或范围.解题时要善于把复杂的、生疏的、非规范化的问题转化为简单的、熟悉的、规范化的问题来解决.高考真题1.(2011·福建高考)(e x +2x )d x 等于( ).A .1B .e -1C .eD .e +1解析 (e x +2x )d x =(e x +x 2)⎪⎪⎪1=(e 1+12)-(e 0+02)=e.答案 C2.(2011·山东高考)曲线y =x 3+11在点P (1,12)处的切线与y 轴交点的纵坐标是( ).A .-9B .-3C .9D .15解析 ∵y =x 3+11,∴y ′=3x 2,∴y ′|x =1=3,∴曲线y =x 3+11在点P (1,12)处的切线方程为y -12=3(x -1).令x =0,得y =9. 答案 C3.(2010·辽宁高考)已知点P 在曲线y =4e x +1上,α为曲线在点P 处的切线的倾斜角,则α的取值范围是( ).A.⎣⎢⎡⎭⎪⎫0,π4 B.⎣⎢⎡⎭⎪⎫π4,π2 C.⎝ ⎛⎦⎥⎤π2,3π4 D.⎣⎢⎡⎭⎪⎫3π4,π 解析 y =4e x +1,∴y ′=-4e x (e x +1)2=-4e x e 2x +2e x +1=-4e x +1e x +2.≥-42e x ·1e x +2=-1,∵e x >0,∴e x +1e x ≥2, ∴y ′∈[-1,0),∴tan α∈[-1,0),又α∈[0,π), ∴α∈⎣⎢⎡⎭⎪⎫3π4,π.故选D.答案 D4.(2010·大纲全国高考)曲线y =e -2x +1在点(0,2)处的切线与直线y =0和y =x 围成的三角形的面积为( ).A.13B.12C.23D .1解析 ∵y ′=(-2x )′e -2x =-2e -2x ,k =y ′|x =0=-2e 0=-2, ∴切线方程为y -2=-2(x -0),即y =-2x +2. 如图,∵y =-2x +2与y =x 的交点 坐标为⎝ ⎛⎭⎪⎫23,23,y =-2x +2与x 轴的交点坐标为(1,0), ∴S =12×1×23=13 答案 A5.(2009·福建高考)若曲线f (x )=ax 3+ln x 存在垂直于y 轴的切线,则实数a 的取值范围是________. 解析 f ′(x )=3ax 2+1x , ∵f (x )存在垂直于y 轴的切线,∴f ′(x )=0有解,即3ax 2+1x =0有解, ∴3a =-1x 3,而x >0,∴a ∈(-∞,0). 答案 (-∞,0)6.(2011·安徽高考)设f (x )=e x1+ax 2,其中a 为正实数.(1)当a =43时,求f (x )的极值点;(2)若f (x )为R 上的单调函数,求a 的取值范围. 解 对f (x )求导得f ′(x )=e x1+ax 2-2ax(1+ax 2)2.①(1)当a =43时,若f ′(x )=0,则4x 2-8x +3=0, 解得x 1=32,x 2=12. 结合①,可知x ⎝ ⎛⎭⎪⎫-∞,12 12 ⎝ ⎛⎭⎪⎫12,32 32 ⎝ ⎛⎭⎪⎫32,+∞ f ′(x )+0 -0 +f (x )极大值极小值所以x 1=32是极小值点,x 2=12是极大值点.(2)若f (x )为R 上的单调函数,则f ′(x )在R 上不变号,结合①与条件a >0,知1+ax 2-2ax ≥0在R 上恒成立,即Δ=4a 2-4a =4a (a -1)≤0,由此并结合a >0,知0<a ≤1.所以a 的取值范围为{a |0<a ≤1}. 7.(2011·北京高考)已知函数f (x )=(x -k )e x . (1)求f (x )的单调区间;(2)求f (x )在区间[0,1]上的最小值. 解 (1)f ′(x )=(x -k +1)e x . 令f ′(x )=0,得x =k -1. f (x )与f ′(x )的变化情况如下:x ()-∞,k -1k -1 ()k -1,+∞f ′(x )-0 +f (x )-e k -1所以,f (x )的单调递减区间是-∞,k -1;单调递增区间是(k -1,+∞). (2)当k -1≤0,即k ≤1时, 函数f (x )在[0,1]上单调递增,所以f (x )在区间[0,1]上的最小值为f (0)=-k ; 当0<k -1<1,即1<k <2时, 由(1)知f (x )在[0,k -1)上单调递减, 在(k -1,1]上单调递增,所以f (x )在区间[0,1]上的最小值为f (k -1)=-e k -1; 当k -1≥1,即k ≥2时, 函数f (x )在[0,1]上单调递减,所以f (x )在区间[0,1]上的最小值为f (1)=(1-k )e. 8.(2011·江西高考)设f (x )=-13x 3+12x 2+2ax .(1)若f (x )在⎝ ⎛⎭⎪⎫23,+∞上存在单调递增区间,求a 的取值范围;(2)当0<a <2时,f (x )在[1,4]上的最小值为 -163,求f (x )在该区间上的最大值. 解 (1)由f ′(x )=-x 2+x +2a =-⎝ ⎛⎭⎪⎫x -122+14+2a ,当x ∈⎣⎢⎡⎭⎪⎫23,+∞时,f ′(x )的最大值为f ′⎝ ⎛⎭⎪⎫23=29+2a ;令29+2a >0,得a >-19, 所以,当a >-19时,f (x )在⎝ ⎛⎭⎪⎫23,+∞上存在单调递增区间.(2)令f ′(x )=0,得两根x 1=1-1+8a 2,x 2=1+1+8a2. 所以f (x )在(-∞,x 1),(x 2,+∞)上单调递减,在(x 1,x 2)上单调递增. 当0<a <2时,有x 1<1<x 2<4, 所以f (x )在[1,4]上的最大值为f (x 2). 又f (4)-f (1)=-272+6a <0, 即f (4)<f (1),所以f (x )在[1,4]上的最小值为 f (4)=8a -403=-163,得a =1,x 2=2,从而f (x )在[1,4]上的最大值为f (2)=103.9.(2011·福建高考)某商场销售某种商品的经验表明,该商场每日的销售量y (单位:千克)与销售价格x (单位:元/千克)满足关系式y =ax -3+10(x -6)2,其中3<x <6,a 为常数.已知销售价格为5元/千克时,每日可售出该商品11千克.(1)求a 的值;(2)若该商品的成本为3元/千克,试确定销售价格x 的值,使商品每日销售该商品所获得的利润最大. 解 (1)因为x =5时,y =11, 所以a2+10=11,a =2.(2)由(1)可知,该商品每日的销售量y =2x -3+10(x -6)2.所以商场每日销售该商品所获得的利润 f (x )=(x -3)⎣⎢⎡⎦⎥⎤2x -3+10(x -6)2=2+10(x -3)(x -6)2,3<x <6.从而,f ′(x )=10[(x -6)2+2(x -3)(x -6)]=30(x -4)(x -6). 于是,当x 变化时,f ′(x ),f (x )的变化情况如下表:所以,当x =4时,函数f (x )取得最大值, 且最大值等于42.答 当销售价格为4元/千克时,商场每日销售该商品所获得的利润最大.。
高中数学选修2-2(人教B版)第一章导数及其应用1.1知识点总结含同步练习题及答案

2. 一个物体的运动方程为 s (t) = 1 − t + t 2 ,其中 s 的单位是米,t 的单位是秒,那么物体在 3 秒时的瞬时速度是 ( A.7 米/秒
答案: C
B.6 米/秒
C.5 米/秒
D.8 米/秒
3. 如图,一个正五角星薄片(其对称轴与水面垂直)匀速地升出水面,记 t 时刻五角星露出水面部分的图形面积为
n→+∞
1 1 1 1 1 1 1 1 1 [( − ) + ( − ) + ( − )+⋯+ ( − )] 4 1 5 5 9 9 13 4n − 7 4n − 3 1 1 = lim (1 − ) n→+∞ 4 4n − 3 1 = . 4
(3)由
S n = 2n2 − n ,得 S1 +
Sn = 2n − 1 .所以 n S2 S S + 3 + ⋯ + n = 1 + 3 + 5 + 7 + ⋯ + (2n − 1) = n2 . 2 3 n
Δx→0
设函数 f (x) 在 x = x0 处可导,且 f ′ (x 0 ) = 2,求下列各极限的值.
f (x0 − Δx) − f (x0 ) ; Δx→0 Δx f ( x 0 + 2k ) − f ( x 0 ) (2) lim . k→0 k
(1) lim 解:(1)
原式 = lim
f (x0 − Δx) − f (x0 ) −(−Δx) f (x0 − Δx) − f (x0 ) = − lim Δx→0 −Δx = −f ′ (x0 ) = −2.
Δy f (x 2 ) − f (x 1 ) f (x1 + Δx) − f (x1 ) = = x2 − x1 Δx Δx
人教新课标版数学高二-人教B版选修2-2练习 第一章 导数及其应用 基础测试

第一章知能基础测试时间120分钟,满分150分.一、选择题(本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1.曲线y =12x 2-2x 在点⎝⎛⎭⎫1,-32 处的切线的倾斜角为( ) A .-1 B .45° C .-45° D .135°Dy ′=x -2,所以斜率k =1-2=-1,因此倾斜角为135°.故选D. 2.下列求导运算正确的是( ) A.⎝⎛⎭⎫x +3x ′=1+3x 2 B .(log 2x )′=1x ln2C .(3x )′=3x ·log 3eD .(x 2cos x )′=-2x sin x B⎝⎛⎭⎫x +3x ′=1-3x2,所以A 不正确; (3x )′=3x ln3,所以C 不正确;(x 2cos x )′=2x cos x +x 2·(-sin x ),所以D 不正确;(log 2x )′=1x ln2,所以B 对.故选B.3.如图,一个正五角星薄片(其对称轴与水面垂直)匀速地升出水面,记t 时刻五角星露出水面部分的图形面积为S (t )(S (0)=0),则导函数y =S ′(t )的图像大致为( )A由图象知,五角星露出水面的面积的变化率是增→减→增→减,其中恰露出一个角时变化不连续,故选A.4.已知函数f (x )=12x 4-2x 3+3m ,x ∈R ,若f (x )+9≥0恒成立,则实数m 的取值范围是( )A .m ≥32B .m >32C .m ≤32D .m <32A因为函数f (x )=12x 4-2x 3+3m ,所以f ′(x )=2x 3-6x 2.令f ′(x )=0,得x =0或x =3.经检验知x =3是函数的一个最小值点,所以函数的最小值点为f (3)=3m -272.不等式f (x )+9≥0恒成立,即f (x )≥-9恒成立,所以3m -272≥-9,解得m ≥32.5.直线y =4x 与曲线y =x 3在第一象限内围成的封闭图形的面积为( ) A .2 2 B .4 2 C .2 D .4 D 如图所示由⎩⎪⎨⎪⎧ y =4x ,y =x 3.解得⎩⎪⎨⎪⎧ x =2,y =8,或⎩⎪⎨⎪⎧x =-2,y =-8.∴第一象限的交点坐标为(2,8) 由定积分的几何意义得S =⎠⎛2(4x -x 3)dx =(2x 2-x 44)|2=8-4=4. 6.已知f (x )=x ln x ,若f ′(x 0)=2,则x 0=( ) A .e 2 B .e C.ln22 D .ln2Bf (x )的定义域为(0,+∞),f ′(x )=ln x +1, 由f ′(x 0)=2,得ln x 0+1=2,解得x 0=e.7.(2015·会宁县期中)曲线f (x )=x 3+x -2的一条切线平行于直线y =4x -1,则切点P 0的坐标为( )A .(0,-1)或(1,0)B .(1,0)或(-1,-4)C .(-1,-4)或(0,-2)D .(1,0)或(2,8)B由y =x 3+x -2,得y ′=3x 2+1, 由已知得3x 2+1=4,解之得x =±1. 当x =1时,y =0;当x =-1时,y =-4. ∴切点P 0的坐标为(1,0)或(-1,-4).8.函数f (x )=x 3-2x +3的图象在x =1处的切线与圆x 2+y 2=8的位置关系是( ) A .相切B .相交且过圆心C .相交但不过圆心D .相离C切线方程为y -2=x -1,即x -y +1=0.圆心到直线的距离为12=22<22,所以直线与圆相交但不过圆心.故选C.9.f ′(x )是f (x )的导函数,f ′(x )的图象如图所示,则f (x )的图象可能是( )D由图可知,当b >x >a 时,f ′(x )>0,故在上,f (x )为增函数.且又由图知f ′(x )在区间上先增大后减小,即曲线上每一点处切线的斜率先增大再减小,故选D.10.曲线y =e 12x 在点(4,e 2)处的切线与坐标轴所围三角形的面积为( )A.92e 2 B .4e 2 C .2e 2 D .e 2D∵y ′=12e x 2,∴在点(4,e 2)处的切线方程为y =12e 2x -e 2,令x =0得y =-e 2,令y =0得x =2, ∴围成三角形的面积为e 2.故选D.11.已知函数f (x )的导函数f ′(x )=a (x -b )2+c 的图象如图所示,则函数f (x )的图象可能是( )D由导函数图象可知,当x <0时,函数f (x )递减,排除A ,B ;当0<x <x 1时,f ′(x )>0,函数f (x )递增.因此,当x =0时,f (x )取得极小值,故选D.12.(2015·甘肃省会宁一中高二期中)对于任意的两个实数对(a ,b )和(c ,d ),规定:(a ,b )=(c ,d ),当且仅当a =c ,b =d ;运算“⊗”为:(a ,b )⊗(c ,d )=(ac -bd ,bc +ad );运算“⊕”为:(a ,b )⊕(c ,d )=(a +c ,b +d ),设p ,q ∈R ,若(1,2)⊗(p ,q )=(5,0),则(1,2)⊕(p ,q )=( )A .(4,0)B .(2,0)C .(0,2)D .(0,-4)B由(1,2)⊕(p ,q )=(5,0)得⎩⎪⎨⎪⎧ p -2q =52p +q =0⇒⎩⎪⎨⎪⎧p =1q =-2, 所以(1,2)⊕(p ,q )=(1,2)⊕(1,-2)=(2,0).二、填空题(本大题共4个小题,每小题4分,共16分.将正确答案填在题中横线上) 13.经过点(2,0)且与曲线y =1x相切的直线方程为______________.x +y -2=0设切点为⎝⎛⎭⎫x 0,1x 0,则1x 0x 0-2=-1x 20,解得x 0=1,所以切点为(1,1),斜率为-1,直线方程为x +y -2=0.14.若函数f (x )=ax 2-1x 在(0,+∞)上为增函数,则实数a 的取值范围是________.a ≥0f ′(x )=⎝⎛⎭⎫ax -1x ′=a +1x2, 由题意得,a +1x 2≥0对x ∈(0,+∞)恒成立,即a ≥-1x2,x ∈(0,+∞)恒成立.∴a ≥0.15.(2015·安徽理,15)设x 3+ax +b =0,其中a ,b 均为实数.下列条件中,使得该三次方程仅有一个实根的是________.(写出所有正确条件的编号)①a =-3,b =-3;②a =-3,b =2;③a =-3,b >2;④a =0,b =2;⑤a =1,b =2.①③④⑤令f (x )=x 3+ax +b ,求导得f ′(x )=3x 2+a ,当a ≥0时,f ′(x )≥0,所以f (x )单调递增,且至少存在一个数使f (x )<0,至少存在一个数使f (x )>0,所以f (x )=x 3+ax +b 必有一个零点,即方程x 3+ax +b =0仅有一根,故④⑤正确;当a <0时,若a =-3,则f ′(x )=3x 2-3=3(x +1)(x -1),易知,f (x )在(-∞,-1),(1,+∞)上单调递增,在上单调递减,所以f (x )极大=f (-1)=-1+3+b =b +2,f (x )极小=f (1)=1-3+b =b -2,要使方程仅有一根,则f (x )极大=f (-1)=-1+3+b =b +2<0或者f (x )极小=f (1)=1-3+b =b -2>0,解得b <-2或b >2,故①③正确.所以使得三次方程仅有一个实根的是①③④⑤.16.已知函数f (x )=x 3-3x ,若过点A (1,m )(m ≠-2)可作曲线y =f (x )的三条切线,则实数m 的取值范围为________.(-3,-2)f ′(x )=3x 2-3,设切点为P (x 0,y 0),则切线方程为y -(x 30-3x 0)=(3x 20-3)(x -x 0),∵切线经过点A (1,m ),∴m -(x 30-3x 0)=(3x 20-3)(1-x 0),∴m =-2x 30+3x 20-3,m ′=-6x 20+6x 0,∴当0<x 0<1时,此函数单调递增,当x 0<0或x 0>1时,此函数单调递减,当x 0=0时,m =-3,当x 0=1时,m =-2,∴当-3<m <-2时,直线y =m 与函数y =-2x 30+3x 20-3的图象有三个不同交点,从而x 0有三个不同实数根,故过点A (1,m )可作三条不同切线,∴m 的取值范围是(-3,-2).三、解答题(本大题共6个小题,共74分.解答应写出文字说明、证明过程或演算步骤) 17.(本题满分12分)设f (x )=a ln x +12x +32x +1,其中a ∈R ,曲线y =f (x )在点(1,f (1))处的切线垂直于y 轴.(1)求a 的值; (2)求函数f (x )的极值.(1)因为f (x )=a ln x +12x +32x +1,故f ′(x )=a x -12x 2+32.由于曲线y =f (x )在点(1,f (1))处的切线垂直于y 轴,故该切线斜率为0,即f ′(1)=0,从而a -12+32=0,解得a =-1.(2)由(1)知f (x )=-ln x =12x +32x +1(x >0),f ′(x )=-1x -12x 2+32=3x 2-2x -12x 2=(3x +1)(x -1)2x 2.令f ′(x )=0,解得x 1=1,x 2=-13(因为x 2=-13不在定义域内,舍去).当x ∈(0,1)时,f ′(x )<0,故f (x )在(0,1)上为减函数;当x ∈(1,+∞)时,f ′(x )>0,故f (x )在(1,+∞)上为增函数. 故f (x )在x =1处取得极小值f (1)=3.18.(本题满分12分)已知函数f (x )=ax 3+cx +d (a ≠0)是R 上的奇函数,当x =1时,f (x )取得极值-2.(1)求函数f (x )的解析式;(2)求函数f (x )的单调区间和极大值;(3)证明:对任意x 1、x 2∈(-1,1),不等式|f (x 1)-f (x 2)|<4恒成立. (1)∵f (x )是R 上的奇函数, ∴f (-x )=-f (x ),即-ax 3-cx +d =-ax 3-cx -d ,∴d =-d , ∴d =0(或由f (0)=0得d =0). ∴f (x )=ax 3+cx ,f ′(x )=3ax 2+c , 又当x =1时,f (x )取得极值-2,∴⎩⎪⎨⎪⎧f (1)=-2,f ′(1)=0,即⎩⎪⎨⎪⎧a +c =-2,3a +c =0,解得⎩⎪⎨⎪⎧a =1,c =-3.∴f (x )=x 3-3x .(2)f ′(x )=3x 2-3=3(x +1)(x -1),令f ′(x )=0,得x =±1, 当-1<x <1时,f ′(x )<0,函数f (x )单调递减; 当x <-1或x >1时,f ′(x )>0,函数f (x )单调递增;∴函数f (x )的递增区间是(-∞,-1)和(1,+∞);递减区间为(-1,1). 因此,f (x )在x =-1处取得极大值,且极大值为f (-1)=2.(3)由(2)知,函数f (x )在区间上单调递减,且f (x )在区间上的最大值为M =f (-1)=2.最小值为m =f (1)=-2.∴对任意x 1、x 2∈(-1,1),|f (x 1)-f (x 2)|<M -m =4成立.即对任意x 1、x 2∈(-1,1),不等式|f (x 1)-f (x 2)|<4恒成立. 19.(本题满分12分)计算定积分⎠⎛-40|x +3|d x .因为f (x )=|x +3|=⎩⎪⎨⎪⎧-x -3,x <-3,x +3,x ≥-3,所以原式=⎠⎜⎛-4-3(-x -3)d x +⎠⎛-30 (x +3)d x .分别取F 1(x )=-12x 2-3x ,F 2(x )=12x 2+3x ,则F ′1(x )=-x -3,F ′2(x )=x +3.所以⎠⎛-40|x +3|d x =⎠⎜⎛-4-3(-x -3)d x +⎠⎛-30 (x +3)d x =(-12x 2-3x )|-3-4+(12x 2+3x )|0-3=5. 20.(本题满分12分)某银行准备新设一种定期存款业务,经预测:存款量与存款利率的平方成正比,比例系数为k (k >0),借款的利率为4.8%.又银行吸收的存款能全部放贷出去.(1)若存款利率为x ,x ∈(0,0.048),试写出存款量g (x )及银行应支付给储户的利息h (x )与存款利率x 之间的关系式;(2)存款利率定为多少时,银行可获得最大收益?(1)由题意,存款量g (x )=kx 2.银行应支付的利息h (x )=xg (x )=kx 3. (2)设银行可获得收益为y ,则y =0.048kx 2-kx 3. ∴y ′=0.096kx -3kx 2.令y ′=0,得x =0(舍去)或x =0.032。
人教新课标版数学高二-人教B版选修2-2课时作业 1.2 导数的运算(1-2课时)

一、选择题1.已知函数f(x)=5,则f′(1)等于()A.5B.1C.0D.不存在【解析】∵f(x)=5,∴f′(x)=0,∴f′(1)=0.【答案】 C2.已知f(x)=x n且f′(-1)=-4,则n等于()A.4 B.-4C.5 D.-5【解析】∵f′(x)=nx n-1,∴f′(-1)=n(-1)n-1=-4.若(-1)n-1=-1,则n=4,此时满足(-1)n-1=-1;若(-1)n-1=1,则n=-4,此时不满足(-1)n-1=1.∴n=4【答案】 A3.正弦曲线y=sin x上一点P,以点P为切点的切线为直线l,则直线l的倾斜角的范围是()A.∪34π,π)B.π4,34π0,π4π2,34π0,π434π,π).【答案】 A4.已知直线y=kx是曲线y=e x的切线,则实数k的值为()A.1e B.-1eC.-e D.e【解析】设切点坐标为(x0,y0),∵y′=(e x)′=e x,【答案】 D5.若曲线y=在点(a,)处的切线与两个坐标轴围成的三角形的面积为18,则a=()A.64 B.32C.16 D.8【答案】 A二、填空题6.若y=10x,则y′|x=1=________.【解析】∵y′=10x ln 10,∴y′|x=1=10ln 10.【答案】10ln 107.直线y=12x+b是曲线y=ln x(x>0)的一条切线,则实数b=________.【解析】设切点坐标为(x0,y0),则y0=ln x0.∵y′=(ln x)′=1x,∴=1x0,由题意知1x0=12,∴x0=2,y0=ln 2.由ln 2=12×2+b,得b=ln 2-1.【答案】ln 2-18.抛物线y=x2上的点到直线x-y-2=0的距离的最小值为________.【解析】与直线x-y-2=0平行的抛物线的切线的切点到直线x-y-2=0距离最小.易知切点为(12,14),∴d=728.【答案】72 8三、解答题9.若质点P的运动方程是s=3t2(s的单位为m,t的单位为s),求质点P在t=8 s时的瞬时速度.∴质点P在t=8 s时的瞬时速度为13m/s.10.已知点P(-1,1),点Q(2,4)是曲线y=x2上的两点,求与直线PQ平行的曲线y=x2的切线方程.【解】∵y′=(x2)′=2x,设切点为M(x0,y0),则=2x0,又∵PQ的斜率为k=4-12+1=1,而切线平行于PQ,∴k=2x0=1,即x0=12,所以切点为M(12,1 4).∴所求的切线方程为y-14=x-12,即4x-4y-1=0.11.求证:曲线xy=1上任何一点处的切线与坐标轴构成的三角形面积为常数.【证明】由xy=1,得y=1 x ,所以y′=-1x2.在曲线xy=1上任取一点P(x0,1x0),则过点P的切线的斜率k=-1x20,切线方程为y-1x0=-1x20(x-x0),即y=-1x20x+2x0.设该切线与x轴、y轴分别相交于A、B两点,则A(2x0,0)、B(0,2x0),故S△OAB=12|OA|·|OB|=12|2x0|·|2x0|=2,所以曲线上任意一点处的切线与坐标轴构成的三角形面积为常数.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
习题课
一、基础过关
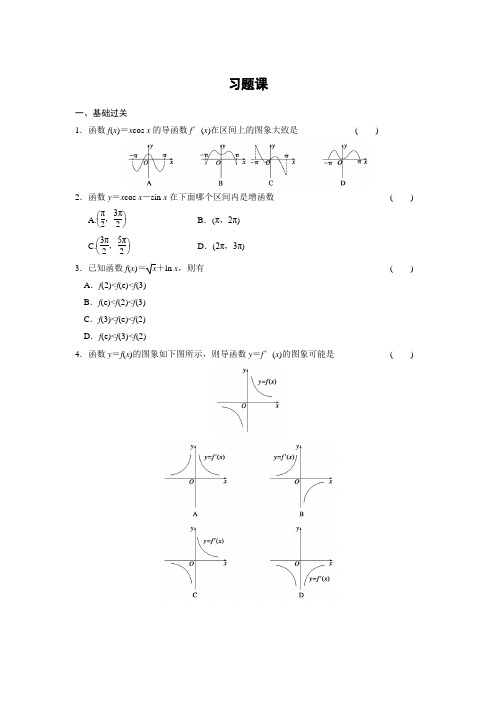
1.函数f (x )=x cos x 的导函数f ′(x )在区间[-π,π]上的图象大致是
( )
2.函数y =x cos x -sin x 在下面哪个区间内是增函数
( ) A.⎝⎛⎭⎫π2,3π
2 B .(π,2π)
C.⎝⎛⎭⎫3π2,5π
2 D .(2π,3π)
3.已知函数f (x )=x +ln x ,则有
( ) A .f (2)<f (e)<f (3)
B .f (e)<f (2)<f (3)
C .f (3)<f (e)<f (2)
D .f (e)<f (3)<f (2)
4.函数y =f (x )的图象如下图所示,则导函数y =f ′(x )的图象可能是
( )
5.已知函数f(x)、g(x)均为[a,b]上的可导函数,在[a,b]上连续且f′(x)<g′(x),则f(x)-g(x)的最大值为
()
A.f(a)-g(a) B.f(b)-g(b)
C.f(a)-g(b) D.f(b)-g(a)
6.已知对任意实数x,有f(-x)=-f(x),g(-x)=g(x),且当x>0时,有f′(x)>0,g′(x)>0,则当x<0时,有() A.f′(x)>0,g′(x)>0
B.f′(x)>0,g′(x)<0
C.f′(x)<0,g′(x)>0
D.f′(x)<0,g′(x)<0
7.已知函数f(x)=x3-ax2+3x+6,若x=3是f(x)的一个极值点,求f(x)在[0,a]上的最值.
二、能力提升
8.若函数y =x 3+32x 2+m 在[-2,1]上的最大值为92
,则m =________. 9.已知a >0,函数f (x )=x 3-ax 在[1,+∞)上单调递增,则a 的最大值为________.
10.设函数f (x )=x +ax 2+b ln x ,曲线y =f (x )过点P (1,0),且在P 点处的切线斜率为2.
(1)求a ,b 的值;
(2)证明:f (x )≤2x -2.
11.设函数f (x )=a e x +1a e x +b (a >0). (1)求f (x )在[0,+∞)内的最小值;
(2)设曲线y =f (x )在点(2,f (2))处的切线方程为y =32
x ,求a ,b 的值.
三、探究与拓展
12.已知a ∈R ,函数f (x )=(-x 2+ax )e x (x ∈R ).
(1)当a =2时,求函数f (x )的单调区间;
(2)若函数f (x )在(-1,1)上单调递增,求a 的取值范围.
答案
1.A 2.B 3.A 4.D 5.A 6.B
7.解 f ′(x )=3x 2-2ax +3,
由已知得f ′(3)=0,
∴3×9-6a +3=0.
∴a =5,∴f (x )=x 3-5x 2+3x +6.
令f ′(x )=3x 2-10x +3=0,得x 1=13
,x 2=3. 当x 变化时,f ′(x ),f (x )的变化状态如下表:
∴f (x )在[0,5]上的最大值为f (5)=21,最小值为f (3)=-3.
8.2 9.3
10.(1)解 f ′(x )=1+2ax +b x
. 由已知条件得⎩⎪⎨⎪⎧ f (1)=0,f ′(1)=2,
即⎩⎪⎨⎪⎧ 1+a =0,1+2a +b =2.
解得⎩⎪⎨⎪⎧
a =-1,
b =3. (2)证明 因为f (x )的定义域为(0,+∞),
由(1)知f (x )=x -x 2+3ln x .
设g (x )=f (x )-(2x -2)=2-x -x 2+3ln x ,
则g ′(x )=-1-2x +3x
=-(x -1)(2x +3)x
. 当0<x <1时,g ′(x )>0,当x >1时,g ′(x )<0.
所以g (x )在(0,1)内单调递增,在(1,+∞)内单调递减.
而g (1)=0,故当x >0时,g (x )≤0,即f (x )≤2x -2.
11.解 (1)f ′(x )=a e x -1a e x , 当f ′(x )>0,即x >-ln a 时,
f (x )在(-ln a ,+∞)上递增;
当f ′(x )<0,即x <-ln a 时,
f (x )在(-∞,-ln a )上递减.
①当0<a <1时,-ln a >0,f (x )在(0,-ln a )上递减,
在(-ln a ,+∞)上递增,从而f (x )在[0,+∞)上的最小值为f (-ln a )=2+b ; ②当a ≥1时,-ln a ≤0,f (x )在[0,+∞)上递增,
从而f (x )在[0,+∞)上的最小值为f (0)=a +1a
+b . (2)依题意f ′(2)=a e 2-1a e 2=32
, 解得a e 2=2或a e 2=-12
(舍去), 所以a =2e 2,代入原函数可得2+12+b =3,即b =12
, 故a =2e 2,b =12
. 12.解 (1)当a =2时,
f (x )=(-x 2+2x )e x ,
f ′(x )=(-x 2+2)e x .
当f ′(x )>0时,(-x 2+2)e x >0,注意到e x >0,
所以-x 2+2>0,解得-2<x < 2.
所以,函数f (x )的单调递增区间为(-2,2).
同理可得,函数f (x )的单调递减区间为(-∞,-2)和(2,+∞).
(2)因为函数f (x )在(-1,1)上单调递增,
所以f ′(x )≥0在(-1,1)上恒成立.
又f ′(x )=[-x 2+(a -2)x +a ]e x ,
即[-x 2+(a -2)x +a ]e x ≥0,注意到e x >0, 因此-x 2+(a -2)x +a ≥0在(-1,1)上恒成立,
也就是a ≥x 2+2x x +1=x +1-1x +1
在(-1,1)上恒成立. 设y =x +1-1x +1,则y ′=1+1(x +1)2
>0, 即y =x +1-1x +1
在(-1,1)上单调递增, 则y <1+1-11+1=32
, 故a ≥32
.。
