UG中规律曲线的画法

UG曲线建模

★
3.1 基本曲线
直线
绘制直线的方法有十三种，分别是：两点之间通过一个点并且保持水平或竖直的直线通过一个点并平行于 XC、YC 或 ZC 轴的直线通过一个点并与 XC 轴成一角度的直线
2015-2-9
通过一个点并平行或垂直于一条直线，或者与现有直线成一角度的直线通过一个点并与一条曲线相切或垂直的直线与一条曲线相切并与另一条曲线相切或垂直的直线
4
2015-2-9
2.1 点
【点】构造器
提供了在三维空间指定点和创建点对象和位置
的标准形式。【点】构造
器主要用于单独创建点或者配合其它功能（如创建
直线）。
5
★
2.1 点
捕捉点方法
2015年2月9日星期一
自动判断的点：该选项是最常用的选项，根据光标的位置自动判断是下列所述的哪种位置点，如端点、中点等。选择时鼠标右下角会显示相应类型的图标。光标位置：光标的位置，其实是当前光标所在位置投影至XC-YC平面内形成的点位置。现有点：在某个现有点上构造点，或通过选择某个现有点指定一个新点的位置。
端点：在现有的直线、圆弧、二次曲线以及其他曲线的端点指定一个位置。
控制点：在几何对象的控制点指定一个位置。
交点：在两条曲线的交点或一条曲线和一个曲面或平面的交点处指定一个位置。
6
★
2.1 点
捕捉点方法
2015-2-9
圆弧中心 /椭圆中心 /球心：圆弧、圆、椭圆的圆心和球的球心。圆弧/椭圆上的角度：在沿着圆弧或椭圆的成一定角度的地方指定一个位置。象限点：在一个圆弧或一个椭圆的四分点指定一个位置。点在曲线/边上：在选择的曲线上指定一个位置，并且可以通过设置U向参数来更改点在曲线上的位置。面上的点：在选择的曲面上指定一个位置，并且可以通过设置U向参数和V向参数来更改点在曲面上的位置。两点之间：在两点之间指定一个位置。

第三章UG NX 3.0的曲线操作

3.1.3 创建矩形和正多边形

1. 矩形（1）选择【插入】|【曲线】|【矩形】命令，或单击工具图标栏中的按钮，弹出如图3.5所示的【点构造器】对话框。（2）使用点构造功能指定第一角点和第二角点，指定两个点后，将完成创建一个矩形。
上一页下一页返回
3.1 基本曲线的创建

上一页下一页返回
3.3 曲线的功能特征

3.3.2 桥接功能

Leabharlann 选择【插入】|【曲线中的一条曲线】|【桥接】命令或者单击工具栏中的按钮，弹出如图3.14所示的【桥接曲线】对话框，其作用为融合或桥接两条不同位置的曲线。对话框中其他功能选项可用来设定桥接过程中桥接曲线的形成，下面对其进行说明。 1. 连续方式此选项可设置桥接曲线和欲桥接的第一条曲线、第二条曲线的连接点间的连续方式。 2. 开始/结束位置此选项可设定桥接曲线的起、止位置。首先选定起、止位置所在的曲线，即要桥接的第一条曲线或第二条曲线，然后通过下列方式来设定桥接点的位置。 3. 形状控制用于设定桥接曲线的形状控制方式。
下一页返回
3.1 基本曲线的创建

（2）在曲线上加点（3）曲线上的百分点（4）样条定义点（5）样条节点（6）样条极点（7）面上的点（8）曲面上的百分点（9）面（B曲面）极点（10）点成组-关

3.1.2 创建直线
单击图3.4所示的【基本曲线】对话框中的按钮，将进入直线绘制模式。下面介绍几种典型的直线创建方法。

1. 2. 3. 4. 5.
等分段根据边界对象分段输入弧长段在节点上在角上

ug正弦规律曲线表达

在UG NX中创建正弦规律曲线，你可以使用“表达式”功能来定义你的参数方程。

以下是一个基本的步骤说明：
1. 打开软件：启动UG NX软件。

2. 进入建模模式：按Ctrl+M键进入建模模式。

3. 打开表达式工具：按Ctrl+E键进入表达式输入界面。

4. 定义参数变量：
- 输入t=1作为时间或角度变量。

- 可以根据需要修改t的初始值和范围。

5. 定义坐标轴变量：
- 输入xt=50*t表示x轴方向的距离，其中50是乘法因子，可以根据实际需求调整。

- 输入yt=10*sin(t*360)表示y轴方向的距离，这里的10是振幅，也可以调整；t*360将角度从弧度转换为度数。

6. 定义z轴变量：
- 如果需要在三维空间中创建曲线，可以输入z=0或其他值。

7. 绘制规律曲线：
- 在建模环境下找到并点击“规律曲线”工具。

- 选择“F(X)”选项，并根据上述定义的表达式填写x、y、z坐标的表达式。

- 确定相应的起始点和结束点（或者步长）来定义曲线的范围。

- 点击“确定”按钮生成曲线。

8. 查看与编辑：
- 生成曲线后，可以通过切换视图来查看不同视角下的曲线。

- 如有需要，可以继续编辑曲线的属性，如颜色、线型等。

UG NX10.0中文版基础教程第4章创建和编辑曲线

28
2017/12/30
UG NX10.0
4.5 派生曲线
中 4.5.1偏置曲线文单击【曲线】工具条中的【偏置曲线】按钮或选择菜单【插入】版基 |【派生曲线】|【偏置】命令，系统弹出如图所示的【偏置曲线】对础话框，从而进入曲线偏移操作功能，用于生成原曲线的偏移曲线，当教前对话框状态下需要用户选取偏移曲线。程
4.5.7镜像曲线
单击【曲线】工具条中的【镜像曲线】按钮或者选择菜单【插入】|【派生曲线】|【镜像曲线】命令，系统弹出如图所示的【镜像曲线】对话框。选取需要镜像的曲线，然后选取镜像平面，最后单击【确定】或“应用】按钮即可。
35
2017/12/30
UG NX10.0 中文版基础教程
4.1.9样条
选择菜单【插入】|【曲线】|【样条】命令，系统弹出如图所示的【样条】对话框。
12
2017/12/30
UG NX10.0 中文版基础教程
4.1.10螺旋线
单击【曲线】工具条上的【螺旋线】按钮，或选择【插入】|【曲线】|【螺旋线】命令，系统弹出如图所示的【螺旋线】对话框。
19
2017/12/30
UG NX10.0 中文版基础教程
2.修剪角
单击【编辑曲线】工具条中的【修剪拐角】按钮，系统弹出如图所示的【修剪拐角】对话框并提示选取要修剪的拐角。在绘图区移动鼠标，在球半径之内选取交点。
20
2017/12/30
UG NX10.0 中文版基础教程
9
2017/12/30
UG NX10.0 中文版基础教程
4.1.7多边形
单击【曲线】工具条中的【多边形】按钮或选择菜单【插入】|【曲线】|【多边形】命令，系统弹出如图所示的【多边形】对话框。

120种ug表达式曲线画法(阿基米德螺旋线数学方程式)

120种UG表达式曲线画法（阿基米德螺旋线、数学方程式）在UG中利用【规律曲线】|【根据方程】绘制各种方程曲线：1、极坐标（或柱坐标r,θ,z）与直角坐标系(x,y,z)的转换关系：x=r*cos(θ)；y=r*sin(θ)；z=z2、球坐标系(r,θ,φ)与直角坐标系(x,y,z)的转换关系：x=rsinθcosφ；y=rsin θsinφ；z=rcosθ在UG表达式中输入的theta=θ；phi=φ；r=rho【注：所有UG表达式中，必须先在名称栏输入t，公式栏输入0，类型为恒定的，即无单位。

t是UG自带的系统变量，其取值为0~1之间的连续数】1.直线直线的数学方程为y-y0=tan(θ)*(x-x0)，若直线经过点（10,20），倾角θ为30°，长度L为40，即UG表达式为：theta=30L=40xt=10+L*cos(theta)*tyt=20+L*sin(theta)*tzt=0效果如图1 2.圆和圆弧圆的数学方程为(x-x0)^2+(y-y0)^2=r^2，若圆心坐标为（50,40），半径r为30，即UG表达式为：r=30theta=t*360xt=50+r*cos(theta)yt=40+r*sin(theta)zt=0效果如图23.椭圆和椭圆弧椭圆的数学方程为(x-x0)^2/a^2+(y-y0)^2/b^2=1，若椭圆中心坐标为（50,40），长半轴a为30（在X轴上），短半轴b为20，即UG表达式为：a=30b=20theta=t*360xt=50+a*cos(theta)yt=40+b*sin(theta)zt=0效果如图34.双曲线双曲线的数学方程为x2/a2-y2/b2=1，若中心坐标为（0,0），实长半轴a为4（在x轴上），虚半轴b为3，y的取值范围为-5~+5内的一段，即UG表达式为：a=4b=3yt=10*t-5xt=a/b*sqrt(b^2+yt^2)或xt=-a/b*sqrt(b^2+yt^2)zt=0做出一半后进行镜像复制，效果如图45.抛物线抛物线I的数学方程为y2=2px，若抛物线的顶点为（30,20）焦点到准线的距离p=8，y的取值范围为-25~+25，即UG表达式为：p=8yt=50*t-25+20xt=(yt-20)^2/(2*p)+30zt=0效果如图5-1抛物线II数学参数方程：x=2pt2，y=2pt（其中t为参数）。

UG NX 表达式规律曲线实例教程

我们要建立一个如下图中左侧一样的轴，它是用右侧的斜盘切割而成。

那么怎么做呢？范成法装配模拟无限逼近求差运算。

可不可以通过计算将右侧斜盘上点的运动数据转换求得左侧目标轴上对应点的轨迹数据呢？先做一个原理图看看.a圆与A圆向齿轮一样同步由C点向B点旋转相同角度c点与C点最终会在B点重合，那么ac的长度为ac=aA-CA，同步旋转的角度<bac=<BAC ,C点在右侧圆周线上的坐标X=DA=cos(<BAC)*r , (r为圆半径，r=CA=BA), Y=CD=sin(<BAC)*r , Zc=0现在要求C点对应的左侧圆c点的坐标则为Xc=cos(<BAC)*ac ,Yc=sin(<BAC)*ac, Zc=0以上为左右两侧平面圆上坐标转换原理。

我们注意到左右两个圆上C点Zc=0，Zc=0，如果C点在Z 轴上有值说明C点就是空间点，Z轴的值在左右圆的高度是一样的，不用转换，其他空间曲线只要投影到左右平面圆上就可以计算转换。

实战准备斜盘与水平夹角20度，斜盘截面图及数据，弧线上点到中间构造线距离为3.08mm图中显示为3.1mm旋转后的斜盘模型如下斜盘与被切轴之间的关系左边构造线部分是要求得的被切轴，被切轴与斜盘轴之间的轴心距aA=65mm，被切轴的半径r=50mm左侧被切轴数据如下：他被右侧斜盘切出5条规律曲线，下面我们就想法求出这些曲线。

求基本曲线如下图，y1他是右侧斜盘中间构造线旋转在左侧y4轴上切过形成的曲线。

左轴a右轴A，两轴间距aA=65mm 斜盘Y1与水平y3圆夹角20度，即<BAD=20Y4圆球逆时针与y1圆球顺时针同步旋转，求右边线段CE旋转到BD位置时，C点在y4圆球上形成的曲线。

y4圆球是由360度向180度方向旋转，y1圆球角<BAC是由180度向360度方向旋转。

但<BAC≠<DAE，<DAE的角度根据<BAC求出，因y4与y3同步且旋转方向相反所以<DAE=<eag 。

UG-基本曲线用法

可通过点子功能菜单或底部对话区确定点unigraphicssolutions给坐标值在已知点的基础上偏置点底部对话区可以输入数据生成曲线分第二部分ugcurve曲线1直线line画线的各种方法等距线点捕捉连续画线unigraphicssolutions连续画线平行坐标轴角度增量分第二部分ugcurve曲线作一条线和另外一条线成一个角度定义起点点取该直线注意不要选到端点和中点移动鼠标使鼠标拉动的直线和已知直线成一个角度按tab键把光标移动到框内输入角度值tap离开框unigraphicssolutions作和一条线有一定距离的平行线stringmode设为off选择原直线注意不要选到端点和中点按tab键把光标移动到框内输入偏置值回车分第二部分ugcurve曲线2画弧线的方法unigraphicssolutions分第二部分ugcurve曲线3圆倒圆unigraphicssolutions已知圆的圆心半径可在底部对话区内输入数值作圆分第二部分ugcurve曲线3曲线修剪及延伸unigraphicssolutions操作步骤
第二部分 UG/Curve曲线
一、概述
1、曲线功能（What)：用于建立遵循设计要求的点、直线、圆弧、样条、平面等几何要素，并可对这些几何要素进行编辑。 2、应用意义（When&Why)：通常按设计要求建立曲线，所建立的曲线作为构造3D模型的初始条件，用于生成扫描特征及构造空间曲面等。 3、应用入口（Where)：建立及编辑： Application—>Modeling—>Toolbox— >Curve 4、主界面：
第二部分 UG/Curve曲线
（八）、点组
操作步骤：
定义生成点组方法——> 定义控制参数——> 定义目标曲线

ug 规律曲线三项式曲线表达式

《探寻ug规律曲线：三项式曲线表达式》一、引言在工程设计和制造领域中，ug软件是一款功能强大的计算机辅助设计（CAD）和计算机辅助制造（CAM）软件，被广泛应用于各种行业。

在ug软件中，ug规律曲线是一种非常重要的数学曲线，它可以通过三项式曲线表达式进行描述。

在本文中，我们将深入探讨ug规律曲线的特点、应用以及三项式曲线表达式的原理和实际应用。

二、ug规律曲线的特点和应用1. ug规律曲线的特点ug规律曲线是一种特殊的曲线形状，具有以下特点：（在文章中多次提及ug规律曲线）（1）曲线平滑度高，能够准确描述复杂的曲线形状；（2）具有良好的数学特性，可以被数学公式准确描述和表达；（3）在CAD/CAM软件中具有广泛的应用，能够帮助工程师和设计师进行精确的曲线绘制和制造。

2. ug规律曲线的应用ug规律曲线在工程设计和制造中有着广泛的应用，例如：（在文章中多次提及ug规律曲线）（1）汽车外观设计和零部件制造；（2）航空航天器件的曲面设计和加工；（3）家电产品的曲线美学设计和生产制造。

三、三项式曲线表达式的原理和实际应用1. 三项式曲线表达式的原理三项式曲线是描述ug规律曲线的数学表达式，它具有以下形式：（在文章中多次提及三项式曲线表达式）y = ax^2 + bx + c其中，a、b、c为常数，x为自变量，y为因变量。

通过调整a、b、c 的数值，可以得到不同形状的曲线，从而准确描述ug规律曲线的特征。

2. 三项式曲线表达式的实际应用三项式曲线表达式在工程设计和制造中有着重要的应用价值，例如：（在文章中多次提及三项式曲线表达式）（1）通过调整三项式曲线的系数，可以精确描述复杂曲线形状，满足工程设计的需求；（2）在CAD/CAM软件中，三项式曲线表达式可以被高效地计算和绘制，提高工程设计和制造的效率；（3）工程师和设计师可以通过调整三项式曲线表达式的参数，实现对曲线形状的精确控制和调整。

四、个人观点和理解个人认为，ug规律曲线作为一种重要的数学曲线，具有着广泛的应用前景和研究价值。

ug规律曲线

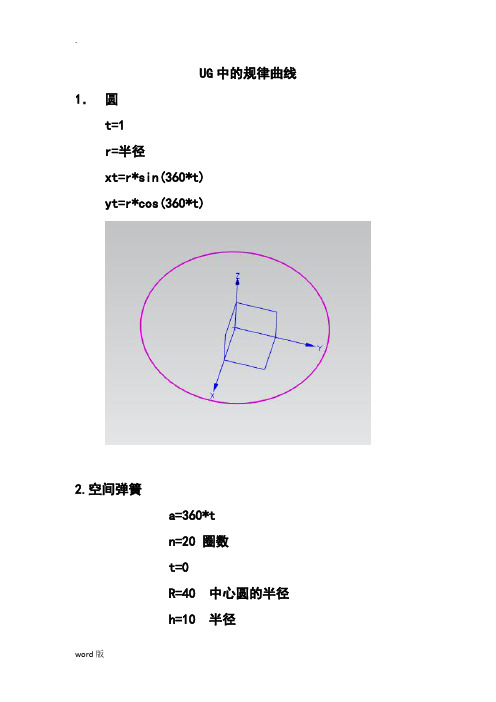
UG 中的规律曲线1. 圆t=1r= 半径xt=r*sin(360*t)yt=r*cos(360*t)2. 空间弹簧a=360*tn=20 圈数t=0R=40 中心圆的半径h=10 半径xt=(R+h*sin(a*n))*sin(a)yt=(R+h*sin(a*n))*cos(a)zt=h*cos(a*n)3. 渐开线方程R=40 起点到原点的直线距离a=720*tt=0xt=R*(cos(a)+a*sin(a))yt=R*(sin(a)-a*cos(a))4. 椭圆t=0a=1 x 方向椭圆半径b=1.5 y 方向椭圆半径r=1 放大倍数xt=a*r*sin(360*t)yt=b*r*cos(360*t)5. 若正弦曲线一个周期X 方向长度为50，振幅为10，即UG 表达式为：theta=t*360xt=50*tyt=10*sin(theta)zt=06. 余弦曲线若余弦曲线一个周期X 方向长度为50，振幅为10，即UG 表达式为：a=t*360xt=50*tyt=10*cos(a)zt=07. 螺旋线若圆柱螺旋线半径r 为20，螺距p 为10，圈数n 为5，即UG 表达式为：r=20p=10n=5a=t*360xt=r*cos(a*n)yt=r*sin(a*n)zt=p*n*t8. 星形线【四尖瓣线】星形线的数学方程：x=r*cos 3θ；y=r*sin 3θ。

【由n+1 尖瓣线通式：x=r(n*cos θ+cos(n* θ))；y=r(n*sin θ-sin(n*θ))当n=3 时的情况。

三角函数公式：sin3θ＝3sinθ－4sin3θ；cos3θ＝4cos3θ－3cosθ】若r=20 ，即UG 表达式为：r=20a=t*360xt=r*(cos(a))^3yt=r*(sin(a))^3zt=09. 抛物线Xt=t Yt=t^2Zt=010. 双曲余弦曲线双曲余弦曲线方程：x=6*t-3 ，y=(exp(x)+exp(0-x))/2 。

UG6.0 曲线完整版教程

提示：UGNX6.0中所指角度
默认的都是按逆时针与XC轴正方向所成的夹角，以后不再重述。
◆ 过一点创建与已知曲线相切或垂直的直
线
■ 步骤：
Step1:在绘图区任意选择一点作为起点。
Step2:将光标放在要与之相切或垂直的曲线上。
Step3:等待绘图区上方的提示行出现“相切”或“垂直”
字样
后单击左键即可。
■ 【平行于】选项组：只要点击
按钮就可画出平行于XC、 YC和ZC轴的直线。
直线的几种常见创建方法
◆ 过两点创建直线
步骤：
提示：
① 起点和终点可以使用点构造器
直接在图中选择。
② 也可以在【跟踪条】中输入
点的XC 、YC和ZC坐标值。
◆ 过一点创建与已知直线平行、垂直或成固定角度的直线
步骤：
step1:在绘图区任意选择一点
复选框取消的状
态下才能启用，如
下面对【直线】界面中的各个选项进行详细的介绍：
■
复选框：如果选中该复选框，不论生成方式如何，所
生成的任何直线都会被限制或延长在视图的
范围内。此时，
复选框被禁用。
■
复选框：如果选中该复选框，则系统会以增量的方式
来创建直线。即在选定一点后，分别在【跟踪栏】对话框中的XC、
◆ 创建与一曲线相切、与另一曲线相切或
垂直的直线
■ 步骤：
Step1:选择要与之相切的
第一条曲线。 Step2:将光标放在要与之
相切或垂直的第二条曲线上。 Step3:等待绘图区上方的
提示行出现“相切”或“法向” 字样
后单击该圆就可确定所需直线。
·提示：选择要相切的曲线时一定
要将【点方式】选择为【自动判断点】才能操作。

UG规律曲线公式大全[1]

t=1
theta=t*360*4
r=(cos(360*t*16)*0.5*t+1)*t
天蚕丝
t=1
theta=t*3600
r=(cos(360*t*20)*0.5*t+1)*t
人民币
t=1
theta=-t*360+180
r=cos(360*(t/(1+t^6))*6)*3+5
t=1
rho=360*t*10
yt=R*(sin(a)-a*cos(a))
阿基米德螺线（等进螺线）（用于凸轮）
a=360*t
t=0
xt=a*sin(a)
yt=a*cos(a)
UF_MODL_dissect_exp_string()
功能：将表达式的名称与数值分离，并得到表达式的标识；
UF_MODL_ask_exp()
功能：根据表达式的名称查找表达式是否存在，并取的表达式的全名；
形成圆了，如果再稍微复杂一点呢？
现在再来讲一个如下图的弹簧的方程。
我的方法是先分析曲线在x,y平面投影的曲线方程，显然该投影曲线是一个半径不断变化的圆，而半径
的变化规律为常数加上一个正弦曲线，即；r=a+b*sint.如是把圆的参数方程里的r替换一下，即
xt=(a+b*sint)*sint
yt=(a+b*sint)*cost
r=cos(360*t*5)*0.5+2.5
zt=cos(t*360*5+90)*0.5
心电图
t=1
r=sin(t*360*2)+0.2
theta=10+t*(6*360)
zt=t*3
ˉ燕尾剪
t=1

UG教学-2.2曲线操作

2．2曲线操作2．2．1偏置曲线在工具图标栏中单击或选择菜单命令插入⑥曲线操作⑥偏置，系统进入曲线偏移操作功能，它用于生成原曲线的偏移曲线。

在进行曲线偏移操作操作时，系统会弹出如下图所示的对象选取对话框，提示用户选取偏移曲线。

其中提供了四种对象选取方式：Solid Face（实体表面）、Solid Edge（实体边）、Curve（曲线）和Chain Curve（链接曲线）。

利用这些方式用户可以方便选择欲偏移的曲线，欲偏移的曲线可为直线、圆弧、二次曲线、样条曲线或对象的边。

确定了欲偏移的曲线后，系统又会弹出如右图所示的偏移曲线对话框。

同时，在所选择的曲线上出现一箭头，该箭头方向为偏移的方向，如果要取相反的偏移方向反向，可单击对话框中的“反向”按钮。

在设置好偏移方式以及相关参数后即可完成曲线的偏移操作。

下面介绍一下偏移曲线对话框中的各主要选项的用法。

1．偏置方式该选项用于设置曲线的偏移方式。

系统提供了4种偏移方式：距离、拔模角、规律控制和三维轴向。

●“距离”方式该方式是按给定的偏移距离来偏移曲线。

选择该方式后，其下方的“距离”文本框被激活，在“距离”和“拷贝数”文本框中分别输入偏移距离和产生偏移曲线的数量，并设定好其它参数后即可。

●“拔模角”方式该方式是将曲线按指定的“拔模角度”偏移到与曲线所在平面相距“拔模高度”的平面上。

拔模高度为原曲线所在平面和偏移后所在平面间的距离，拔模角度为偏移方向与原曲线所在平面的法线的夹角。

选择该方式后，“拔模高度”和“拔模角度”文本框被激活，在“拔模高度”和“拔模角度”文本框中分别输入拔模高度和拔模角度，然后再设置好其它参数即可。

如下图所示的就是这种方式的图例。

●“规律控制”方式该方式是按规律控制偏移距离来偏移曲线。

选择该方式后，会弹出如下图所示的规律控制方式对话框，从中选择相应的偏移距离的规律控制方式后，逐步响应系统提示即可。

●“三维轴向”方式该方式是通过“轴矢量”选项来控制偏置方向，选择该方式后，会弹出如下图所示的三维轴向方式对话框，从中选择相应的“三维偏置值”和“轴矢量”后，可完成偏置曲线。

UG教育训练之三-曲线

曲线（CURVE）曲线就是我们通常所说的Curve线Curve线的绘制与草图(SKETCH)的主要区别在于草图是构建在一个平面上的，而Curve可以直接绘制空间曲线。

因此草图适合构建比较规则的零件，而Curve适合构建较复杂，不规则的实体。

例如：有些实体是需要通过曲线的拉伸、旋转等去操作构造的。

Curve还有一大功能就是可以用曲线来创建曲面进行复杂实体造型。

例如：在天窗里有很多零件都要依据车顶弧度来构建，用草图就会觉得力不从心，用Curve就会解决空间曲线的构建问题。

当然这也要根据个人习惯喜好而定。

任何都不是绝对的。

另外要注意一点，创建的所有Curve都在XY平面内。

整个曲线功能分为：1.曲线的基本功能2.基本曲线3.高级曲线4.曲线的编辑5.曲线的操作一、曲线功能介绍我们常用的功能主要包括两个部分：一是基本曲线的生成；二是基本曲线的编辑。

基本操作可以在【Insert】下拉菜单中的【Curve】和【Curve Operation】两个菜单来完成。

也可用下图所示工具栏来完成。

曲线工具栏图标所示命令从左自右依次是：基本曲线，Spline曲线，由定义点生成Spline线，由控制点生成Spline线，点，点集，Curve线倒斜角，矩形，多边形，椭圆，抛物线，双曲线，圆锥曲线（二次曲线），螺旋线，规律曲线，偏移曲线，桥接曲线，简化曲线，连接曲线，投影曲线，组合投影曲线，交线，截面，析取曲线，在面上偏移曲线，绕线与展开，直线，圆弧线，平面。

编辑曲线工具栏所示命令从左自右依次是：编辑曲线，编辑曲线参数，修剪曲线，修剪相交线，分割曲线，编辑园角，拉伸曲线，编辑圆弧长度。

二、基本曲线的绘制点击工具栏的基本曲线图标或点击菜单【Insert】→【Curve】→【Basic Curves】命令，系统会出现如下图所示对话框。

其中包括了绘制曲线，圆弧，圆形，倒圆角，修剪曲线和编辑曲线的功能。

是基本曲线绘制的主要工具。

第一排为曲线方式，即几个基本绘制功能。

根据曲线规律作出规律函数：角度将360度分为若干，即a=360*t,半径
R=35.8+5t，X=R*cos(a)，Y=R*sin(a),
在UG中建立下列表达式，注意在建立表达式时要选择正确的类型，如角度变量需要选择角度，不能是长度；而常量变量t，需要选择恒定式，选择了其它的（如角度），在其它变量中就无法引用了，如长度变量就不能引用角度变量，否则会出现报错。

•设置好表达式后，运行规律曲线命令，进入规律曲线操作栏。

•在规律曲线操作栏中是按X、Y、Z顺序来输入规律曲线的变量关系的，如Z没有，可以在输入了X、Y之后确认。

选择“根据方程”来定义X、Y的
变量关系
第一次设定X方向
曲线的规律关系
第二次设定Y方向曲线的规律关系
第三次设定Y方向曲线的规律关系。

UG创建曲线

螺旋线
利用“螺旋线”对话框中的“使用规律曲线”单选钮，绘制半径值由规律曲线控制的螺旋线
利用“螺旋线” 对话框中的“定义方位”按钮，绘制以参考直线的方向为其轴线方向，以坐标原点为其中心起始点的螺旋线
一般二次曲线
一般二次曲线是由平面截取圆锥所得到的截面曲线。通过 “一般二次曲线”按钮可以绘制椭圆、椭圆弧、抛物线和双曲线等形状的曲线，也可绘制这几种类型曲线的混合曲线。
直线
“直线和圆弧”工具条中其他按钮的作用如下。
“直线（点-XYZ）”按钮：用于创建平行于X、Y或Z轴的直线。 “直线（点-垂直）”按钮：用于创建垂直于另外一条直线的直线。 “直线（点-相切）”按钮和“直线（相切-相切）”按钮：用于绘制与圆相切的直线。 “无界直线”按钮：用于绘制无限延伸的直线。
直线
圆和圆弧
①选择
绘制方式
④指定圆上
一点确定圆的半径
③指定
圆的中心点
②指定
绘制平面
圆和圆弧
圆弧
在UG中，圆弧可作放样物体的放样截面。在“圆弧/圆”对话框中选择一种绘制方式，在“圆弧/圆”对话框的“限制”标签栏中去掉“整圆”复选框的选择状态，然后指定相应的点和参数即可完成圆弧的绘制。
椭圆和椭圆弧
使用“椭圆”命令可以绘制椭圆或椭圆弧。单击“曲线”工具条中的“椭圆”按钮，利用打开的“点”对话框确定椭圆的圆心，然后在打开的“椭圆”对话框中设置椭圆的相关参数，即可绘制椭圆，如下图所示。
椭圆和椭圆弧
如果起始角和终止角不是“0”和“360”，将生成椭圆弧，如下图所示。
矩形和多边形
在UG中，矩形和多边形主要用于构建特征的剖截面，也可用作辅助平面。它们的绘制非常简单，下面以绘制多边形为例说明。

ug表达式之详细解规律曲线

信息” T 对象”来显示规律样条的非参数或特征信息。

Z 分量规律曲线通过X 、Y 及Z 分量的组合来定义一条规律样条。

必须指定每个组件的规律类型，可通过规律子函数进行指定。

可用的选项有：文档收集自网络，仅用于个人学习恒定允许您给整个规律函数定义一个常数值。

系统会提示您只输入一个规律值（即该常数）。

线性用于定义一个从起点到终点的线性变化率。

三次用于定义一个从起点到终点的三次变化率。

沿着样条的值-线性使用沿着脊线的两个或多个点来定义线性规律函数。

在选择脊线曲线后，可以沿着这条曲线指出多个点。

系统会提示您在每个点处输入一个值。

沿着样条的值-三次的使用沿着脊线的两个或多个点来定义一个三次规律函数。

在选择脊线曲线后，可以沿着该脊线指出多个点。

系统会提示您在每个点处输入一个值。

根据等式使用一个现有表达式及参数表达式变量”来定义一个规律。

允许您选择一条由光顺连接的曲线组成的线串来定义一个规律函数。

规律曲线2008-01-15 12:33:30作者：来源：互联网浏览次数：0文字大小：【大】【中】【小】简介：规律曲线”选项用于使用规律子函数创建样条。

规律样条定义为一组及Z 分量。

必须指定每个分量的规律。

要创建规律曲线：使用规律子函数，为 X 、Y 及Z 各分量选择并定义一个规律选项（可…文档收集自网络，仅用于个人学习规律曲线”选项用于使用规律子函数创建样条。

规律样条定义为一组的规律。

文档收集自网络，仅用于个人学习 X 、丫及Z 分量。

必须指定每个分量要创建规律曲线:1. 2.3.使用规律子函数，为X 、Y 及Z 各分量选择并定义一个规律选项。

（可选步骤）通过定义一个方位和/或基点，或指定一个参考坐标系来控制方位（样条的方位）用于个人学习选择确定”或应用”来创建曲线。

文档收集自网络，仅用于个人学习文档收集自网络，仅可以通过 la根据规律曲线如果使用编辑” T 变换” T 比例”或点拟合”来编辑规律样条，将会移除该样条的创建参数。

ug 规律曲线

UG中的规律曲线1．圆t=1r=半径xt=r*sin(360*t)yt=r*cos(360*t)2.空间弹簧a=360*tn=20 圈数t=0R=40 中心圆的半径 h=10 半径xt=(R+h*sin(a*n))*sin(a)yt=(R+h*sin(a*n))*cos(a)zt=h*cos(a*n)3.渐开线方程R=40 起点到原点的直线距离 a=720*tt=0xt=R*(cos(a)+a*sin(a))yt=R*(sin(a)-a*cos(a))4.椭圆t=0a=1 x方向椭圆半径b=1.5 y方向椭圆半径r=1放大倍数xt=a*r*sin(360*t)yt=b*r*cos(360*t)5.假设正弦曲线一个周期X方向长度为50，振幅为10，即UG表达式为：theta=t*360xt=50*tyt=10*sin(theta)zt=06.余弦曲线假设余弦曲线一个周期X方向长度为50，振幅为10，即UG 表达式为：a=t*360xt=50*tyt=10*cos(a)zt=07.螺旋线假设圆柱螺旋线半径r为20，螺距p为10，圈数n为5，即UG表达式为：r=20p=10n=5a=t*360xt=r*cos(a*n)yt=r*sin(a*n)zt=p*n*t8.星形线【四尖瓣线】星形线的数学方程：x=r*cos3θ；y=r*sin3θ。

【由n+1尖瓣线通式：x=r(n*cosθ+cos(n*θ))；y=r(n*sinθ-sin(n*θ))当n=3时的情况。

三角函数公式：sin3θ＝3sinθ－4sin3θ；cos3θ＝4cos3θ－3cosθ】假设r=20，即UG表达式为：r=20a=t*360xt=r*(cos(a))^3yt=r*(sin(a))^3zt=09.抛物线Xt=tYt=t^2Zt=010.双曲余弦曲线双曲余弦曲线方程：x=6*t-3，y=(exp(x)+exp(0-x))/2。

即UG表达式为：xt=t*6-3yt=(exp(xt)+exp(-xt))/2zt=011.双曲正切曲线双曲正切曲线方程：x=6*t-3，y=(exp(x)-exp(0-x))/(exp(x)+exp(0-x))。