牛二定律应用-连接体专题
牛二定律应用——连接体专题

牛顿第二定律——连接体问题(整体法与隔离法)命题:熊亮一、连接体:当两个或两个以上的物体通过绳、杆、弹簧相连,或多个物体直接叠放在一起的系统二、处理方法——整体法与隔离法系统运动状态相同 整体法问题不涉及物体间的内力使用原则系统各物体运动状态不同隔离法问题涉及物体间的内力三、连接体题型:1、连接体整体运动状态相同:(这类问题可以采用整体法求解)【例1】A、B两物体靠在一起,放在光滑水平面上,它们的质量分别为,,今用水平力推A,用水平力拉B,A、B间的作用力有多大?【练1】如图所示,质量为M的斜面A置于粗糙水平地面上,动摩擦因数为,物体B与斜面间无摩擦。
在水平向左的推力F作用下,A与B一起做匀加速直线运动,两者无相对滑动。
已知斜面的倾角为,物体B的质量为m,则它们的加速度a及推力F的大小为多少【练2】如图所示,质量为的物体2放在正沿平直轨道向右行驶的车厢底板上,并用竖直细绳通过光滑定滑轮连接质量为的物体,与物体1相连接的绳与竖直方向成角,则( )A. 车厢的加速度为B. 绳对物体1的拉力为C. 底板对物体2的支持力为D. 物体2所受底板的摩擦力为2、连接体整体内部各部分有不同的加速度:(不能用整体法来定量分析)【例2】如图所示,一个箱子放在水平地面上,箱内有一固定的竖直杆,在杆上套有一个环,箱和杆的总质量为M,环的质量为m。
已知环沿着杆向下加速运动,当加速度大小为a时(a<g),则箱对地面的压力为多大?【练3】如图所示,一只质量为m的小猴抓住用绳吊在天花板上的一根质量为M的竖直杆。
当悬绳突然断裂时,小猴急速沿杆竖直上爬,以保持它离地面的高度不变。
则杆下降的加速度为大?【练4】如图所示,在托盘测力计的托盘内固定一个倾角为30°的光滑斜面,现将一个重4 N的物体放在斜面上,让它自由滑下,那么测力计因4 N物体的存在,而增加的读数是()A.4 NB.2 NC.0 ND.3 N【练5】如图所示,A、B的质量分别为m A=0.2kg,m B=0.4kg,盘C的质量m C=0.6kg,现悬挂于天花板O处,处于静止状态。
高中物理牛顿第二定律连接体专题

高中物理牛顿第二定律连接体专题连接体问题连接件是相互关联的对象,它们之间的力与它们的运动和相对运动模式有关。
这些问题经常出现在各种各样的试题中,难度和难度各不相同。
这类问题很难分析和计算。
我们的目的是分析力量与运动之间的内在联系和规律,应用牛顿运动定律,运用逻辑关系来推导、训练、计算并获得结果。
有些问题更难解决。
我们不能用高中时所学的物理知识和数学知识来准确地描述它们。
我们可以用图像的方法来描述它们。
我们对物理问题的分析方法和解决方案做了一些研究和讨论。
与传统方法相比,上述方法的计算过程相对简单,但需要仔细思考。
我希望这本教科书的使用者会仔细思考。
为了便于研究,我们将连接器分为两种情况:相同加速度和不同加速度。
这种分类不是严格的科学分类,只是一种通用分类,便于分析。
由于运动情况不同,分析和解决问题的方法也会不同。
前者注重对加速度相同的物体“按质量等分外力”的概念;不同加速度的物体注重逻辑关系的推导、超重和失重的概念以及牛顿第二定律在系统中的应用;还有一些问题。
如果加速度发生变化,需要注意力、功、能关系的概念,以及运用图像方法解决问题的意识。
1加速度相同的连接体示例| 1在右图中,质量为M1和M2的物体通过弹簧连接,并在恒定力F下制造用下共同向右运动,弹簧的长度恒定,物块与水平面间动摩擦因数为?。
求:弹簧的弹力?M2m1f【指南】上述问题属于连接器问题。
根据传统的解法,老师会教你使用整体法和孤立法,在求解和计算之前,会按照“先整体后孤立”或“先孤立后整体”的方法推导方程。
如此相似,就像物体在水平面上的运动一样,水平面是平滑的或粗糙的;平衡力F 足够大,可以将物体沿着斜坡向上拉,并且斜坡光滑或粗糙;如果平衡力F足够大,可以沿垂直方向向上拉动物体,那么弹力的大小是多少?我们必须一个接一个地计算,而且没有规律可循吗?不妨来探索一下!【分析】解决方案1:常规方法(整体法和隔离法)以整体为研究对象,由牛顿第二定律得f-??m1?m2?Gm1?m2?A.解得a?f??(m1?m2)gfgm1?m2m1?M2以M2为研究对象ft??m2g?m2a解决方案是什么?m2fm1?m2质量分别为m1、m2的物体有弹簧相连接,在恒力f作用下共同向右运动。
牛顿第二定律的应用――连接体问题

专题: 牛顿第二定律的应用――― 连接体【知识讲解】一、连接体与隔离体(系统与质点)两个或两个以上物体,靠绳或接触面或电磁作用相互联系组成的物体系统,称为连接体(系统,多质点)。
如果把其中某个物体隔离出来,该物体即为隔离体(单质点)。
二、外力和内力如果以物体系为研究对象,受到系统之外的物体施加的作用力,这些力是系统受到的外 力,而系统内各物体间的相互作用力为内力。
应用牛顿第二定律列方程求合力时不考虑内力。
如果把物体隔离出来作为研究对象,则这些内力将转换为隔离体的外力。
三、连接体问题的分析方法1.整体法:整体法是物理中常用的一种思维方法。
它是将几个物体看作一个整体来作为研究对象即系统,这样就暂时回避了这些物体间的相互作用的内力,只考虑整体受到的外力,整体法列出的方程数目较少,解题变的简明快捷。
(1)连接体中的各物体如果加速度相同,求解时可以把连接体作为一个整体。
运用F 合=(m 1+m 2+m 3…..)a 列方程求解;题目只涉及内外力关系不需要求加速度时,也可以用牛顿定律在加速度相同情况下的推论:总合合合m m m 2211F F F ==(动力分配原理,即系统内各部分的合力与其质量成正比)。
(2)连接体中的各物体如果加速度不同,若系统内有几个物体,这几个物体的质量分别为m 1,m 2,m 3………m n ,,加速度分别为a 1,a 2,a 3......a n ,这个系统受到的合外力为F 合外,则对这个系统应用牛顿第二定律的表达式为1122n nF m a m a m a =++⋅⋅⋅+合外其正交分解表示式为11221122x x n nxy y n nyy F m a m a m a F m a m a m a=++⋅⋅⋅+=++⋅⋅⋅+x 外外(3)当系统内各个物体加速度均为零时,有的静止有的匀速运动,整个系统处于平衡状态,此时可用F 合外=0进行求解。
或者:0F 0F y x ==外外,联立求解。
高三物理牛顿运动定律应用——连接体问题ppt课件

的是
()
•
A 若水平面光滑,物块 A对B的作用力大小为F
D
•
B 若水平面光滑,物块 A对B的作用力大小为2F/3
•
C 若物块A与地面无摩擦,B与地面的动摩擦因数为μ,则物块A对B的作用力大小
为μmg。
•
D若物块A与地面无摩擦,B与地面的动摩擦因数为μ,则物块A对B的作用力大小
为(F+2 μmg)/3
牛顿第二定律应用 ——连接体问题
;.
1
连接体问题
一、连接体 当两个或两个以上的物体通过绳、杆、弹簧相连,或多个物体直接叠放在一起的系统——
连接体
二、处理方法——整体法与隔离法
系统运动状态相同 整体法
问题不涉及物体间的内力 使用原则
系统各物体运动状态不同 隔离法
问题涉及物体间的内力
2
平面均光滑 m1
F
A
B
5
斜面光滑 θ
6
斜面粗糙
θ 对整体分析:F-(m1+m2)gsinθ-μ(m1+m2)gcosθ=ma 对m1分析:T-m1gsinθ-μm1gcosθ=m1a
7
沿光滑斜面一起下滑 θ
8
沿粗糙 斜面一起下滑
θ 练习:17练1、2题, P50 / 4题 P52 例1
9
P52触类旁通1 质量为M,倾角为θ的楔形木块,静止在水平桌面上,与桌面间的动摩擦因数为μ,一质
量为m的木块置于楔形木块上,物块与斜面的接触面光滑,为了保持物体相对斜面静止, 可用一水平力F推楔形木块,如图所示,求此水平力的大小为多少?
对m分析:a=gtanθ 对整体分析:
F=(M+m)a+μ(M+m)g = (M+m)g(μ+tangθ)
牛顿运动定律专题——连接体

BD
F
D、支持力小于(M+m)g
例2、如图所示,两个相同的物体m和M,用 轻绳相连接,置于光滑水平面上,在M上施 一水平恒力F使两物体一起作匀加速直线运 动,求:细线的拉力?
F m M m
二、系统内物体有相同的加速度(关键词“一
起”) ,a1,a2相等。
用公式表示为:F合=(m1+m2)a
其中F合为系统所受的合外力,(m1+m2)为有系统 所有物体的总质量,a为系统的加速度,也是各 个物体的加速度。
练2、如图所示,A、B两物体之间用轻质弹 簧连接,用水平恒力F拉A,使A、B一起沿光 滑水平面做匀加速运动,这时弹簧的长度为 L1。若A、B将置于粗糙水平面上,且A、B与 粗糙水平面之间的动摩擦因数相同,用相同 水平恒力F拉A,使A、B一起做匀加速运动, 此时弹簧长度为L2,则( A ) A、L1=L2 B、L1>L2 C、L1<L2
对系统(两个物体为例)运用牛顿运动第二 定律,它的表达式可写成:
F合 m1a1 m2 a2
F合y m1a1 y m2 a2 y
F合x m1a1x m2 a2 x
其中F合为系统所受的合外力(不包括内力)的 矢量和,a1,a2,分别表示系统内各个物体的加速 度矢量,它们可能都等于零,也可能都不等于零, 还可能有的等于零,有的不等于零。
D、无法确定
例3、如图所示,圆环质量(包括直径)为M, 经过球心的直径上套有质量为m的小球。已知 小球沿直径向下做加速运动,当加速度大小为 a时,圆环对地面的压力是多大?
(M m) g ma
三、系统内只有一个物体有加速度,而其它物体
的加速度为零。
用公式表示为:F合=m1a1
牛顿第二定律专题1连接体问题

解:根据牛顿第二定律
整体的加速度 a F ①
F 1 2 3 ……… n
作以用从在第每4个个立小方立体方到体第n上nm的个合立力方体F的0 n-3m个a立方 体Fn组成②的系统为
研究对象,则第3个立方体对第4个立方体的作用力
F34
(n
3)ma
(n
3)F n
灵活选择研究对象
整体法求加速度,隔离法求相互作用力.
光滑,两物体之间的作用力为多大?
解:⑴ 对整体和m2分别根据牛顿第二定律
F (m1 m2 )g sin (m1 m2 )a1 ① N m2g sin m2a1 ②
联立①②式解出两物体之间的作用力
F
α
N1
m2 m1 m2
F
解:⑵对整体和m2分别根据牛顿第二定律
F (m1 m2 )g sin (m1 m2 )g cos (m1 m2 )a2 ③
3.引以为戒:
(l)例如F推M及m一起前进(如图),隔离m分析其 受力时,认为F通过物体M作用到m上,这是错误 的.不要把作用在其他物体上的力错误地认为通过 “力的传递”作用在研究对象上.
(2)用水平力F通过质量为m的弹簧秤拉物体M在光 滑水平面上加速运动时,往往会认为弹簧秤对物块M 的拉力也一定等于F.实际上此时弹簧秤拉物体M的力 F/=F—ma,显然F/<F.只有在弹簧秤质量可不计时, 才可认为F/=F.
2. 底座A上有一根直立长杆,其总质量为M,杆上 套有质量为m的环B, 它与杆有摩擦,设摩擦力的 大小恒定。当环从底座以初速度v向上飞起时,底 座保持静止,环的加速度大小为a,求环在升起过 程中,底座对水平面的压力分别是多大?
解:环向上做匀减速运动,底座连同直杆静止
高中物理牛顿运动定律的应用_牛顿运动定律的应用之连接体问题

牛顿运动定律的应用-牛顿运动定律的应用之连接体问题一、连接体概述两个或两个以上物体相互连接参与运动的系统称为连接体。
如几个物体叠放在一起,或并排挤放在一起,或用绳子、细杆等连在一起。
如下图所示:还有各种不同形式的连接体的模型图,不一一描述。
只以常见的模型为例。
连接体一般具有相同的运动情况(速度、加速度)。
二、连接体的分类根据两物体之间相互连接的媒介不同,常见的连接体可以分为三大类。
1. 接触连接:两个物体通过接触面的弹力或摩擦力的作用连接在一起。
2. 绳(杆)连接:两个物体通过轻绳或轻杆的作用连接在一起;3. 弹簧连接:两个物体通过弹簧的作用连接在一起;三、连接体的运动特点轻绳——轻绳在伸直状态下,两端的连接体沿绳方向的速度大小总是相等。
轻杆——轻杆平动时,连接体具有相同的平动速度;轻杆转动时,连接体具有相同的角速度,而线速度与转动半径成正比。
轻弹簧——在弹簧发生形变的过程中,两端连接体的速率不一定相等;在弹簧形变最大时,两端连接体的速率相等。
四、处理连接体问题的基本方法1. 内力和外力(1)系统:相互作用的物体称为系统。
系统由两个或两个以上的物体组成。
(2)系统内部物体间的相互作用力叫内力,系统外部物体对系统内物体的作用力叫外力。
2. 整体法(1)含义:所谓整体法就是将两个或两个以上物体组成的整个系统或整个过程作为研究对象进行分析研究的方法。
(2)理解:牛顿第二定律F=ma,F是指研究对象所受的合外力,将连接体作为整体看待,简化了受力情况,因为连接体间的相互作用力是内力.如图所示,用水平力F拉A使A、B保持相对静止沿粗糙水平面加速滑动时,若求它们的加速度,便可把它们看做一个整体,这样它们之间相互作用的静摩擦力便不需考虑。
题目不涉及连接体的内力问题时,应优先选用整体法(3)运用整体法解题的基本步骤:①明确研究的系统或运动的全过程.②画出系统的受力图和运动全过程的示意图.③寻找未知量与已知量之间的关系,选择适当的物理规律列方程求解.3. 隔离法(1)含义:所谓隔离法就是将所研究的对象--包括物体、状态和某些过程,从系统或全过程中隔离出来进行研究的方法。
牛顿第二定律的应用连接体问题

例2、如图所示,在水平铁轨上行驶的车厢里,用细 线悬挂一质量为m的小球,球与车保持相对静止,摆 线与竖直方向夹角为θ,求⑴列车的加速度;⑵车厢 的运动性质;⑶细线对小球的拉力.
θ
(1)a mg tan g tan
m
T
方向水平向左
θ
(2)向左匀加速运动或者向右匀减速运动
mg
练习1、如图所示,质量分别为M和m的物体A、B紧靠着 放在动摩因素为μ水平地面上,在水平力F的作用下一 起做匀加速运动,求:A对B的推力。
FAB
FAB
mF M m
练习3 、 一根质量为M的木棒,上端用细绳系在天花板上, 地面上有一只质量为m的小猴,小猴跳起抓住木板时, 绳子恰好断了,于是小候沿着木棒向上爬,结果它与地 面间的距离保持不变,求:这时 木棒下落的加速度。
解:由运动学公式v=at得:a= v 6 3m / s2 t2
如图所示建立直角坐标系:
X轴方向:F cos f ma Y轴方向:N F sin mg
f= N 解得:F= mg ma 10.89N
cos sin
练习1、一静止木箱质量为m=2kg,木箱与地面的动摩擦因
数为μ=0.2,现用斜向右下方与水平方向成θ=370角的力 F推木箱,推力大小为50N, 求经过2S时木箱的位移。
杆,杆上套着一个环,箱和杆的质量为M,环的质量为m
,已知环沿杆加速下滑,加速度大小为a,则此时箱对
地面的压力为多大?
F=(M+m)g–ma
m
M
例4、地面光滑,mA=2kg、mB=8kg、 µ=0.2,当F=50N 时,A、B的加速度各为多大?
µA B
F
a=(M+m)g/M
牛顿第二定律应用及连接体问题

牛顿第二定律应用及连接体问题(总12页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--牛顿定律的应用一 两类常用的动力学问题1. 已知物体的受力情况,求解物体的运动情况;2. 已知物体的运动情况,求解物体的受力情况上述两种问题中,进行正确的受力分析和运动分析是关键,加速度的求解是解决此类问题的纽带,思维过程可以参照如下:解决两类动力学问题的一般步骤根据问题的需要和解题的方便,选出被研究的物体,研究对象可以是单个物体,也可以是几个物体构成的系统 画好受力分析图,必要时可以画出详细的运动情景示意图,明确物体的运动性质和运动过程通常以加速度的方向为正方向 或者以加速度的方向为某一坐标的正方向若物体只受两个共点力作用,通常用合成法,若物体受到三个或是三个以上不在一条直线上的力的作用,一般要用正交分解法根据牛顿第二定律=ma F 合或者x x F ma = ;y y F ma =列方向求解,必要时对结论进行讨论解决两类动力学问题的关键是确定好研究对象分别进行运动分析跟受力分析,求出加速度 例1(新课标全国一2014 24 12分)公路上行驶的两汽车之间应保持一定的安全距离。
当前车突然停止时,后车司机以采取刹车措施,使汽车在安全距离内停下而不会与前车相碰。
通常情况下,人的反应时间和汽车系统的反明确研究对象受力分析和运动状态分析 选取正方向或建立坐标系 确定合外力F 合 列方程求解应时间之和为1s 。
当汽车在晴天干燥沥青路面上以108km/h 的速度匀速行驶时,安全距离为120m 。
设雨天时汽车轮胎与沥青路面间的动摩擦因数为晴天时的2/5,若要求安全距离仍为120m ,求汽车在雨天安全行驶的最大速度。
解:设路面干燥时,汽车与路面的摩擦因数为μ0,刹车加速度大小为a 0,安全距离为s ,反应时间为t 0,由牛顿第二定律和运动学公式得:ma mg =0μ ①020002a v t v s += ②式中,m 和v 0分别为汽车的质量和刹车钱的速度。
牛顿运动定律的应用——连接体问题

牛顿运动定律的应用——连接体问题一、连接体概述相互连接并且有共同的加速度的两个或多个物体组成的系统可以看作连接体。
如下图所示:还有各种不同形式的连接体的模型图,不一一描述。
只以常见的模型为例。
二、问题分类1.已知外力求内力(先整体后隔离)如果已知连接体在合外力的作用下一起运动,可以先把连接体系统作为一个整体,根据牛顿第二定律求出他们共同的加速度;再隔离其中的一个物体,求相互作用力。
2.已知内力求外力(先隔离后整体)如果已知连接体物体间的相互作用力,可以先隔离其中一个物体,根据牛顿第二定律求出他们共同的加速度;再把连接体系统看成一个整体,求解外力的大小。
2、木块A 和B 置于光滑的水平面上它们的质量分别为m m A B 和。
如图所示当水平力F 作用于左端A 上,两物体一起加速运动时,AB 间的作用力大小为N 1。
当同样大小的力F 水平作用于右端B 上,两物体一起加速运动时,AB 间作用力大小为N 2,则(ACD )A .两次物体运动的加速度大小相等;B .N N F 12+<;C .N N F 12+=;D .N N m m B A 12::= 18、如图所示,光滑水平桌面上,有甲、乙两个用细线相连的物体在水平拉力F 1和F 2的作用下运动,已知F 1<F 2,则以下说法中正确的有( ABD )A .若撤去F 1,则甲的加速度一定变大B .若撤去F 1,则细线上的拉力一定变小C .若撤去F 2,则乙的加速度一定变大D .若撤去F 2,则细线上的拉力一定变小6、在粗糙水平面上放一个三角形木块a ,有一滑块b 沿木块斜面匀速下滑,则下列说 F 图1 F 图2 θ 图3 θ 图4法中正确的是(A)a 保持静止,且没有相对于水平面运动的趋势;(B)a 保持静止,但有相对水平面向右运动的趋势;(C)a 保持静止,但有相对水平面向左运动的趋势;(D)没有数据,无法通过计算判断.4、质量为M 的斜面静止在水平地面上。
牛顿第二定律的应用(连接体问题)

牛顿第二定律的应用(连接体问题)
对于两个或多个相互连接的物体组成的物体系,若它们具有共同大小的加速度,则求出加速度往往是解决这类问题的关键。
既可以对单个物体使用隔离法运用牛顿第二定律求出加速度,也可以对整体运用牛顿第二定律求出加速度。
【例1】 光滑水平地面上有A 、B 两个滑
块,之间用细线相连,A 质量为2Kg ,B
质量为3Kg ,现用F=20N 的水平拉力拉
A ,求:
(1)A 、B 间细绳的张力。
(2)若把F 改为向左方向拉B ,A 、B 间细绳的张力又为多少?
【例2】 如图,质量为M 的光滑楔形小车在水平恒力F 的作用下向右做匀加速运动,斜面上相对静止一
质量为m 的光滑小球,倾斜角为θ,求F 的
大小
【例3】 质量为m 的重物通过细线与
质量为M 的小车连接,
求:
(1)小车加速度
(2)细线中的拉力
1
、光滑水平地面上有A 、B 两个滑块紧靠在一起,A 质量为3Kg ,B 质量为5Kg ,先用水平力F 向右
推B ,F 再改为向左推A ,求两种情况下A B 间的弹力大小之比。
2、如图,光滑水平地面上质量为M=5Kg 的小车在水平恒力F 的作用下向右匀加速运动,桅杆上用细线悬挂着质量为m=2Kg 的小球,细线与竖直方向的夹角为θ=370,求:
(1)细线拉力的大小。
(2)F 的大小
3、如图,物块A 、B 质量分别为3Kg 和2Kg ,不计摩擦,求:
(1)两物块加速度的大小
(2)绳中张力的大小。
4.7《牛顿第二定律应用:连接体问题》
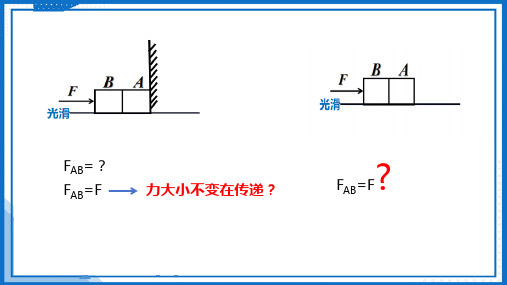
A. 两木块的加速度a 的大小为
B. 弹簧的形变量为
3
3
C. 两木块之间弹簧的弹力的大小为F
D.A 、B 两木块之间的距离为 0 +
AB
)
【作业2】(多选)如图所示, 5 块质量相同的木块并排放在水平地面上,它们
与地面间的动摩擦因数均相同, 当用力F 推第1 块木块使它们共同加速运动时,
【变式4】如图所示,质量分别为 mA、mB 的 A、B用弹簧相连 ,在恒
力 F 作用下 A B一起竖直向上 匀加速运动,求 A B 间的作用力。
【变式5】(多选)若将A、B 两物块用轻绳连接放在倾角为θ 的固定斜面上,用平
行于斜面向上的恒力F 拉A,使它们沿斜面匀加速上升,A、B与斜面间的动摩擦因
A.a1<a2
B.a1=a2
C.a1>a2
D.无法判断
【练习5】如图所示,在光滑的水平桌面上有一物体A,通过绳子与物体B相连,假设
绳子的质量以及绳子与定滑轮之间的摩擦力都可以忽略不计,绳子不可伸长.如果mB
=3mA,则绳子对物体A的拉力大小为( B )
A.mBg
C.3mAg
B.3mAg/4
D.3mBg /4
上的恒力F拉A,使它们沿斜面匀加速上升,A、B与斜面间的动摩擦因数均为μ,为
了增大AB间的作用力,可行的办法是(
)
AB
A. 增大A物块的质量
B. 减小B物块的质量
C. 增大倾角θ
D. 增大动摩擦因数μ
不管是光滑还是粗糙的水面、不管是水平面还是斜面、也不管是竖
直拉着连接体运动,只要推力F、MA、MB、µ(相同)一定,且A、
专题辅导 牛顿第二定律连接体问题(整体法与隔离法)
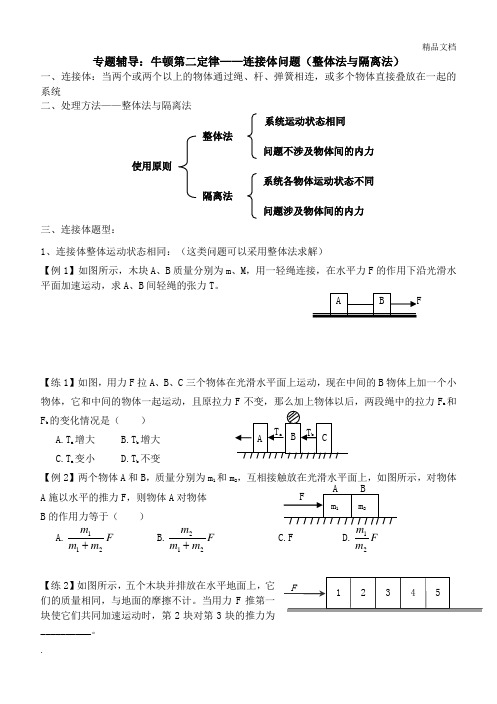
专题辅导:牛顿第二定律——连接体问题(整体法与隔离法)一、连接体:当两个或两个以上的物体通过绳、杆、弹簧相连,或多个物体直接叠放在一起的系统二、处理方法——整体法与隔离法系统运动状态相同整体法问题不涉及物体间的内力 使用原则系统各物体运动状态不同 隔离法问题涉及物体间的内力 三、连接体题型:1、连接体整体运动状态相同:(这类问题可以采用整体法求解)【例1】如图所示,木块A 、B 质量分别为m 、M ,用一轻绳连接,在水平力F 的作用下沿光滑水平面加速运动,求A 、B 间轻绳的张力T。
【练1】如图,用力F 拉A 、B 、C 三个物体在光滑水平面上运动,现在中间的B 物体上加一个小物体,它和中间的物体一起运动,且原拉力F 不变,那么加上物体以后,两段绳中的拉力F a 和F b 的变化情况是( ) A.T a 增大 B.T b 增大 C.T a 变小D.T b 不变【例2】两个物体A 和B ,质量分别为m 1和m 2,互相接触放在光滑水平面上,如图所示,对物体A 施以水平的推力F ,则物体A 对物体B 的作用力等于( ) A.F m m m 211+ B.F m m m 212+ C.FD.F m 21【练2】如图所示,五个木块并排放在水平地面上,它们的质量相同,与地面的摩擦不计。
当用力F 推第一块使它们共同加速运动时,第2块对第3块的推力为__________。
【练3】A、B两物体靠在一起,放在光滑水平面上,它们的质量分别为kgmA3=,kgmB6=,今用水平力NFA6=推A,用水平力NFB3=拉B,A、B间的作用力有多大?【例3】如图所示,质量为M的斜面A置于粗糙水平地面上,动摩擦因数为μ,物体B与斜面间无摩擦。
在水平向左的推力F作用下,A与B一起做匀加速直线运动,两者无相对滑动。
已知斜面的倾角为θ,物体B的质量为m,则它们的加速度a及推力F的大小为()A.)sin()(,sinθμθ++==gmMFga B. θθcos)(,cos gmMFga+==C.)tan()(,tanθμθ++==gmMFga D. gmMFga)(,cot+==μθ【练4】如图所示,质量为2m的物体2放在正沿平直轨道向右行驶的车厢底板上,并用竖直细绳通过光滑定滑轮连接质量为1m的物体,与物体1相连接的绳与竖直方向成θ角,则()A. 车厢的加速度为θsing B. 绳对物体1的拉力为θcos1gmC. 底板对物体2的支持力为gmm)(12- D. 物体2所受底板的摩擦力为θtan2gm【练5】如图所示,物体M、m紧靠着置于摩擦系数为μ的斜面上,斜面的倾角为θ,现施加一水平力F作用于M,M、m共同向上作加速运动,求它们之间相互作用力的大小。
牛顿第二定律的应用――连接体问题(详细答案)

牛顿第二定律的应用――― 连接体问题一、连接体与隔离体两个或两个以上物体相连接组成的物体系统,称为 。
如果把其中某个物体隔离出来,该物体即为 。
二、外力和内力如果以物体系为研究对象,受到系统之外的作用力,这些力是系统受到的 力,而系统内各物体间的相互作用力为 。
应用牛顿第二定律列方程不考虑 力。
如果把物体隔离出来作为研究对象,则这些内力将转换为隔离体的 力。
三、连接体问题的分析方法1.整体法:连接体中的各物体如果 ,求加速度时可以把连接体作为一个整体。
运用 列方程求解。
2.隔离法:如果要求连接体间的相互作用力,必须隔离其中一个物体,对该物体应用 求解,此法称为隔离法。
3.整体法与隔离法是相对统一,相辅相成的。
本来单用隔离法就可以解决的连接体问题,但如果这两种方法交叉使用,则处理问题就更加方便。
如当系统中各物体有相同的加速度,求系统中某两物体间的相互作用力时,往往是先用 法求出 ,再用 法求 。
【典型例题】例1.两个物体A 和B ,质量分别为m 1和m 2,互相接触放在光滑水平面上,如图所示,对物体A 施以水平的推力F ,则物体A 对物体B 的作用力等于( ) A.F m m m 211+ B.F m m m 212+ C.FD.F m21扩展:1.若m 1与m 2与水平面间有摩擦力且摩擦因数均为μ则对B 作用力等于。
2.如图所示,倾角为α的斜面上放两物体m 1和m 2,用与斜面平行的力F 推m 1,使两物加速上滑,不管斜面是否光滑,两物体 之间的作用力总为。
例2.如图所示,质量为M 的木板可沿倾角为θ的光滑斜面下滑, 木板上站着一个质量为m 的人,问(1)为了保持木板与斜面相 对静止,计算人运动的加速度?(2)为了保持人与斜面相对静止, 木板运动的加速度是多少?【针对训练】1.如图光滑水平面上物块A 和B 以轻弹簧相连接。
在水平拉力F 作用下以加速度a 作直线运动,设A 和B 的质量分别为m A 和m B ,当突然撤去外力F 时,A 和B 的加速度分别为( ) A.0、0B.a 、0C.B A A m m a m +、B A A m m am +-D.a 、a m m BA-V2.如图A 、B 、C 为三个完全相同的物体,当水平力F 作用 于B 上,三物体可一起匀速运动。
第六节 牛顿第二定律的应用(连接体问题)

牛顿第二定律的应用———连接体问题连接体是指在所研究的问题中涉及到的多个物体(或叠放在一起,或并排挤在一起,或用细绳,细杆联系在一起)组成的系统。
解连接体问题的基本方法是隔离法和整体法。
隔离法是把系统中的一个物体单独“取”出来,作为受力分析的对象,并对它应用牛顿第二定律列出方程,然后再对另外一个物体也单独“取”出来,进行同样的分析等。
整体法是把所有的物体作为一个整体分析,应用牛顿定律列方程。
这两种方法有时在同一个题目中可以同时采用。
不过整体法不能用来求系统内物体间的相互作用力。
如果求物体之间的相互作用力,必须要用到隔离法。
例一:在光滑的水平面上,有两个相互接触的物价,已知M>m,第一次用水平力F 向右推M,物体间相互作用力为N 1;第二次用同样大小的水平力F 向左推m,物体间的相互作用力为N 2,则N 1______ N 2练习:1. 两物体A 、B ,质量分别为m 1、m 2,互相接触,放在光滑的水平面上,对A 、B 分别施以水平推力F 1和F 2,且F>F,则A 对B 的作用力多大?若水平面粗糙,A 、B 是同种材料制成的,在推力F 1、F 2的作用下运动时,A 对B 的作用力又是多大?2.如图,A 、B 两个物体叠放在光滑的水平面上,AB 间动摩擦因数为μ用水平力F 1作用在A 上,AB 间恰好不发生相对滑动,若用水平力F 2作用在B 上,A 、B 间恰好不发生相对滑动,若m A :m B =2:3,则F 1:F 2=__________.3.一人在井下站在吊台上,用如图所示的定滑轮装置拉绳把吊台和自己提升上来,图中跨过滑轮的两面三刀段绳是竖直的且不计摩擦,跺台的质量是15kg,人的质量为55kg,起动时吊台向上的加速度是0.2m/s 2,求这时人对吊台的压力.4.如图,A 、B 两个物体用细绳连接在一起,用竖直向上的力F 将它们提起,细绳能承受的最大拉力为100N ,两个物体的质量m A =m B =5kg ,要使绳子在提起原来处于静止状态的物体时不被子拉断,拉力F 不能超过多少?(g=10m/s 2)。
3.8牛顿第二定律的应用(五)连接体、叠加体问题

牛顿第二定律的应用连接体、叠加体问题(教案)一、连接体、叠加体“连接体运动”是在生活和生产中常见的现象,也是运用牛顿运动定律解答的一种重要题型1.定义:通常是指某些通过相互作用力(绳子拉力、弹簧的弹力、摩擦力等)互相联系的几个物体所组成的物体系。
2.常见模型:(1)用轻绳连接( 2 )直接接触( 3 )靠摩檫接触3.特点:它们一般有着力学或者运动学方面的联系。
4.常见的三类问题:(1)连接体中各物体均处于平衡状态例1.如图已知Q和P之间以及P与桌面之间的动摩擦因数都是μ ,两物体的质量都是m,滑轮的质量和摩擦都不计。
若用一水平向右的力F拉P使它做匀速运动,则F的大小为多少?(答案4 μ mg)(2)各物体具有相同的加速度例2.如图水平面光滑,对M施加水平向右的推力F,则M对m的弹力为多大?(3)连接体中一个静止,另一个物体加速例3.如图中物块m沿斜面体M以加速度a下滑,斜面体不动.求地面对斜面体的静摩擦力的大小与方向。
解法一:对两个物体分别应用隔离法解法二:系统应用牛顿第二定律法f=macosθ+M×0=macosθ5.研究对象的选择和三种常用解题方法:(1)研究对象的选择(2)三种常用方法方法一:隔离法方法二:整体与隔离相结合(整体法求加速度,隔离法求相互作用力)方法三:系统应用牛顿第二定律法6. 解连接体问题时的常见错误:错误一:例如F推M及m一起前进(如图),隔离m分析其受力时,认为F通过物体M作用到m上,这是错误的.错误二:用水平力F通过质量为m的弹簧秤拉物体M在光滑水平面上加速运动时(如图所示.不考虑弹簧秤的重力),往往会认为弹簧秤对物块M的拉力也一定等于F.实际上此时弹簧秤拉物体M的力F/=F—ma,显然F/<F.只有在弹簧秤质量可不计时,才可认为F/=F.错误三:运用整体法分析问题时,认为只要加速度的大小相同就行,例如通过滑轮连接的物体,这是错误的.正确做法应产用分别隔离法求解。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
牛顿第二定律——连接体问题(整体法与隔离法) 命题:熊亮
一、连接体:当两个或两个以上的物体通过绳、杆、弹簧相连,或多个物体直接叠放在一起的系统 二、处理方法——整体法与隔离法
系统运动状态相同
整体法
问题不涉及物体间的内力 使用原则
隔离法
三、连接体题型:
1【例1】A 、B 水平力N F A 6=推A ,用水平力N F B 3=拉B ,A 、B 间的作用力有多大?
【练1】如图所示,质量为M 的斜面A 置于粗糙水平地面上,动摩擦因数为μ,物体B 与斜面间无摩擦。
在水平向左的推力F 作用下,A 与B 一起做匀加速直线运动,两者无相对滑动。
已知斜面的倾角为
θ,物体B 的质量为m ,则它们的加速度a 及推力F 的大小为多少
【练2】如图所示,质量为2m 的物体2滑定滑轮连接质量为1m 的物体,与物体1A. 车厢的加速度为θsin g
B. 绳对物体1的拉力为θ
cos 1g
m A
B
F A
F B
B θ
A
F
C. 底板对物体2的支持力为g m m )(12-
D. 物体2所受底板的摩擦力为θtan 2g m
2、连接体整体内部各部分有不同的加速度:(不能用整体法来定量分析)
【例2】如图所示,一个箱子放在水平地面上,箱内有一固定的竖直杆,在杆上套有一个环,箱和杆的总质量为M ,环的质量为m 。
已知环沿着杆向下加速运动,当加速度大小为a 时(a <g ),则箱对地面的压力为多大?
【练3】如图所示,一只质量为m 的小猴抓住用绳吊在天花板上的一根质量为M 的竖直杆。
当悬绳突然断裂时,小猴急速沿杆竖直上爬,以保持它离地面的高度不变。
则杆下降的加速度为大?
【练4】个重4 N 的读数是( )
A.4 N
B.23 N
C.0 N
D.3 N
【练5】如图所示,A 、B 的质量分别为m A =0.2kg ,m B =0.4kg ,盘C 的质量m C =0.6kg ,现悬挂于天花板O 处,处于静止状态。
当用火柴烧断O 处的细线瞬间,木块A 的加速度a A 多大?木块B 对盘C 的压力F BC 多大?(g 取10m/s 2)
【练6】水平桌面上放着质量为M 的滑块,用细绳通过定滑轮与质量为m 的物体相连,滑块向右加速运动。
已知滑块与桌面间的动摩擦因数为μ.试求滑块运动的加速度和细绳中的张力。
A B
C
O
M
m
m
连接体作业
1、如图所示,小车质量均为M ,光滑小球P 的质量为m ,绳的质量不计,水平地面光滑。
要使小球P 随车一起匀加速运动(相对位置如图所示),则施于小车的水平拉力F 各是多少?(θ已知)
球刚好离开斜面 球刚好离开槽底
F= F= F= F=
2、如图所示,A 、B 质量分别为m1,m2,它们在水平力F 的作用下均一起加速运动,甲、乙中水平面光滑,两物体间动摩擦因数为μ,丙中水平面光滑,丁中两物体与水平面间的动摩擦因数均为μ,求A 、B 间的摩擦力和弹力。
f= f= F AB = F AB = 3、如图所示,在光滑水平桌面上,叠放着三个质量相同的物体,用力推物体a ,使
三个物体保持静止,一起作加速运动,则各物体所受的合外力 ( )
A .a 最大
B .c 最大
C .同样大
D .b 最小
4、如图所示,小车的质量为M,前端相对于车保持静止,A.在竖直方向上,B.在水平方向上,C.若车的加速度变小,D.若车的加速度变大,
5、物体A 、B 叠放在斜面体C 向左匀加速运动的过程中,物体A 、B 体C 的摩擦力为
2
f F ,(
02≠f F A. 01=f F B. 2
f F C.
1
f F 水平向左 D.
2
f F F a b c
6、如图3所示,质量为M
面向上滑,至速度为零后加速返回,
A. 地面对物体M
B. 地面对物体M
C. 物块m
D. 地面对物体M
7、如图所示,质量M=8kg
达到1.5m/s时,
=0.2
8、如图所示,质量为A
m的物体A沿直角斜面C
滑轮与绳的质量及一切摩擦均忽略不计,
水平压力的大小。
9、如图所示,质量为M的滑块C
滑块上,与滑块间动摩擦因数为μ,细绳跨过滑轮后将B
摩擦力作用,水平推力F作用于滑块,为使A和B
B
A
m
F
μ<1
μ=0
.
10、在粗糙的水平面上有一质量为M
斜面上,有两个质量为1m、2m的物体分别以1a、2a
面静止,求三角形木块受到静摩擦力和支持力?
如有侵权请联系告知删除,感谢你们的配合!。
