一次函数与不等式PPT课件
人教版初二数学上册《一次函数与一元一次不等式》课件

y
y=3x-6
2
x
这时 y=3x-6 <0 ∴ 此不等式的解集为x <2
-6
解法二: 把 5x+4<2x+10 看做两个 一次函数y=5x+4和y=2x+10,
y 14
画出y=5x+4和y=2x+10的图像. 由图像可知
10
它们的交点的横坐标为2.
当x <2时直线y=5x+4 上的 点都在直线y=2x+10的下方.
试一试 :
1、如图是函数
y x x 2 的图象,则不等式
2
x x 2 0 ,则解是 问:若
2
x x2 0
2
y
x 2或x 1 的解集是___________
x 1或2
-1 0
2
x
,则解集是 问:若
x2 x 2 0
1 x 2
已知函数 y x 2 x 2 的图象与直线 问题2: 7 7 7 9 14 则不等式 y x 交与点( 3 , ),( , ) 10 10 2 4 5 25
0
2
x
随堂练习 2
1.若y1=-x+3,y2=3x+4,当x取何值时, y1>y2? 2.兄弟俩赛跑,哥哥先让弟弟跑9m,然后 自己才开始跑.已知弟弟每秒跑3m,哥哥每 秒跑4m.列出函数关系式,作出函数图象, 观察图象回答下列问题: (1)何时弟弟跑在哥哥前面? (2)何时哥哥跑在弟弟前面? (3)谁先跑过20m?谁先跑过100m?
y
y=3x-6 x
0
2
∴ 此不等式的解集为x <2
-6
3、如图,利用y=-2.5x+5 的图象, (1)求出-2.5x+5=0 的解; (2)求出-2.5x+5>0 的解集; (3)求出-2.5x+5≤0的解集; (4)你能求出-2.5x+5>3的解集吗? (5)你还能求出哪些不等式的解集呢?
一次函数与方程、不等式(共15张PPT)

04 综合练习与提高
综合练习题一
总结词
理解一次函数与方程、不等式之间的 关系
详细描述
通过解决一系列的练习题,理解一次 函数与方程、不等式之间的关系,掌 握将实际问题转化为数学模型的方法 。
综合练习题二
总结词
掌握一次函数的图像和性质
详细描述
通过绘制一次函数的图像,理解函数的增减性、截距等性质,掌握利用图像解决实际问题的技巧。
一次函数与不等式的实际应用
一次函数与不等式在实际生活中有着 广泛的应用。例如,在购物时,我们 可以通过比较商品的价格和折扣率来 选择最划算的购买方案,这需要用到 一元一次不等式的知识。
另外,在生产活动中,我们可以通过 控制生产成本和产量之间的关系来制 定最优的生产计划,这也需要用到一 元一次不等式R。
02 一次函数与方程
一次函数与一元一次方程的关系
一次函数是形如$y = kx + b$的函数,其中$k$和$b$是常数, 且$k neq 0$。一元一次方程是只含有一个变量的方程,其形式 为$ax + b = 0$,其中$a$和$b$是常数,且$a neq 0$。
一次函数与方程、不等式(共15张 ppt)
目录
• 一次函数的基本概念 • 一次函数与方程 • 一次函数与不等式 • 综合练习与提高 • 总结与回顾
01 一次函数的基本概念
一次函数的定义
一次函数
一般形式为y=kx+b(k≠0),其 中x为自变量,y为因变量,b为截 距,k为斜率。
线性函数
特殊的一次函数,形式为y=kx+b (k≠0,b=0)。
一次函数在实际问题中的应用
一次函数可以用于解决实际问题,如路程、速度和时间问题、价格和销售问题等。
一次函数与方程、不等式、方程组关系PPT课件

05
CHAPTER
总结与展望
总结一次函数与方程、不等式、方程组的关系
一次函数与方程的关系
一次函数与方程组的关系
一次函数是线性方程的几何表示,通 过将方程中的x替换为函数表达式,可 以得到相应的方程。
一次函数可以用于解决线性方程组问 题,通过消元法或代入法将方程组转 化为一次函数的交点问题。
一次函数与不等式的关系
斜率
一次函数图像的倾斜程度 由斜率k决定,k>0时,图 像为增函数;k<0时,图 像为减函数。
截距
b为y轴上的截距,表示函 数与y轴交点的纵坐标。
一次函数的图像
绘制方法
通过代入一组x值计算对应的y值 ,得到一系列点,将这些点连接 成线即可得到一次函数的图像。
图像特点
一次函数图像是一条直线,斜率为 k,截距为b。
一次函数与方程、不等式、方 程组关系ppt课件
目录
CONTENTS
• 一次函数的基本概念 • 一次函数与方程的关系 • 一次函数与不等式的关系 • 一次函数的应用 • 总结与展望
01
CHAPTER
一次函数的基本概念
一次函数的定义
01
02
03
一次函数
形如y=kx+b(k≠0)的 函数,其中x是自变量,y 是因变量。
一次函数与一元一次不等式组
一元一次不等式组
由两个或两个以上一元一次不等式组成的集合。
关系
对于一元一次不等式组,可以通过将其转化为一次函数的形式,利用函数的交点来求解。例如,解不等式组 $begin{cases} x + 2 > 0 x - 1 < 0 end{cases}$,可以将其转化为两个一次函数的形式,然后找到两个函数的 交点,即解集。
一次函数与方程不等式的关系 说课课件

80 70 60 50 40 30 20 10 0 1 2 3 4 t(小时) 乙 甲
---辅助练习--某单位用车,又不打算买车,他们准备和一个个体车主和一国营出租车公司中的一家签 定月租车合同.设汽车每月行驶x千米,应付给个体车主的月费用是y1元,应付给出租车公
司的月费用是y2元.y1’y2与x之间的函数的图象(两条射线)如图所示.观察图象,回答下列问
开始,如果设甲班的植树时间为t(小时),植树的棵数分别为y甲、y乙。你认为哪个
班植树比较多?结合函数图像的有关知识解决。.........(你还有其他方法吗?) y(棵)
由图像可知:2小时时一样多,不
足2小时时甲班多,超过2小时时 乙班多. y甲=20t(t≥o) y乙=40t-40(t≥1) y甲=y乙 、y甲≥y乙 、 y乙≥y甲
师真正成为学生学习的参与者和合作者;帮助者和引导者。
教学流程图
●复习回顾
教学过程
●动手动脑
●试着做做
●总结概括
●探索新知
●试试身手
●思维延伸
单击鼠标可按顺序播 点击●可进 一次函数的定义 ☆ ☆ 函数图像的概念 一次函数的图像的画法
k
(0,b) (1,k)
o
x
1
图像,联想结论。
(2)在讲课过程中可能会有一些学生不能很好的理解本节内容,一方面
我可以增加辅助练习,在实际的解决问题过程中让学生进一步体会它们之 间的联系;另一方面,我留给学生思考的时间,其间采取单独辅导予以补 救,尽量做到让每一个学生都能在本节课中有收获,有感悟。
板书设计
一、复习回顾
二、试着做做:问题引入(随堂练习)
(2)解不等式5x-1>3x+2时,我们除了可以直接求出解集以外,还可以借
第1讲-用一次函数看方程、不等式
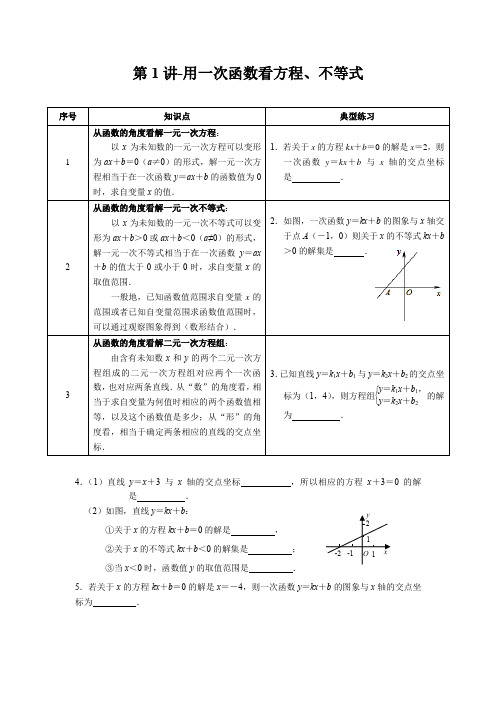
y2 1 1 O -2 -1x第1讲-用一次函数看方程、不等式序号知识点典型练习1从函数的角度看解一元一次方程:以x 为未知数的一元一次方程可以变形为ax +b =0(a ≠0)的形式,解一元一次方程相当于在一次函数y =ax +b 的函数值为0时,求自变量x 的值.1.若关于x 的方程kx +b =0的解是x =2,则一次函数y =kx +b 与x 轴的交点坐标是 .2从函数的角度看解一元一次不等式:以x 为未知数的一元一次不等式可以变形为ax +b >0或ax +b <0(a ≠0)的形式,解一元一次不等式相当于在一次函数y =ax+b 的值大于0或小于0时,求自变量x 的取值范围.一般地,已知函数值范围求自变量x 的范围或者已知自变量范围求函数值范围时,可以通过观察图象得到(数形结合). 2.如图,一次函数y =kx +b 的图象与x 轴交于点A (-1,0)则关于x 的不等式kx +b >0的解集是 .3从函数的角度看解二元一次方程组: 由含有未知数x 和y 的两个二元一次方程组成的二元一次方程组对应两个一次函数,也对应两条直线.从“数”的角度看,相当于求自变量为何值时相应的两个函数值相等,以及这个函数值是多少;从“形”的角度看,相当于确定两条相应的直线的交点坐标. 3.已知直线y =k 1x +b 1与y =k 2x +b 2的交点坐标为(1,4),则方程组⎩⎨⎧y =k 1x +b 1,y =k 2x +b 2的解为 .4.(1)直线y =x +3与x 轴的交点坐标 ,所以相应的方程x +3=0的解是 .(2)如图,直线y =kx +b :①关于x 的方程kx +b =0的解是 , ②关于x 的不等式kx +b <0的解集是 ; ③当x <0时,函数值y 的取值范围是 .5.若关于x 的方程kx +b =0的解是x =-4,则一次函数y =kx +b 的图象与x 轴的交点坐标为 .-21O yx-3Oxy -6 y 1=kx yy 2=ax+bx -2O -4 P6.已知一次函数y =kx +b 的图象,如图所示,当x <0时,y 的取值范围是( ).A .y >0B .y <0C .-2<y <0D .y <-27.如图,已知一次函数图象y =-2x -6,利用图象回答: (1)不等式-2x -6>0解集是 ,不等式-2x -6<0解集是 ;(2)函数图象与坐标轴围成的三角形的面积为 ; (3)当y =-4时,则x = ,当y =2时,则x = ;(4)如果y 的取值范围-4<y ≤2,则x 的取值范围 ;(5)如果x 的取值范围-3≤x ≤3,则y 的最大值是 ,最小值是 ; (6)若直线y =3x +4和直线y =-2x -6交于点A ,则点A 的坐标 .8.如图所示,已知直线y 2=ax +b 和直线y 1=kx 的图象交于点P ,利用图象回答:(1)关于二元一次方程组⎩⎨⎧y =ax+b ,y =kx的解是 ,则两直线的交点坐标是 ;(2)当y 2<y 1时,则x 的取值范围是 ; (3)当ax +b ≥kx 时,则x 的取值范围是 ; (4)当ax ≤kx -b 时,则x 的取值范围是 .9.(15海珠期末)直线y =x +1与直线y =-2x +a 的交点在第一象限,则a 的取值可以是( ). A .2B .1C .0D .-110.(15一中期末)如图,已知函数y1=3x+b和y2=ax-3的图象交于点P(-2,-5),则不等式3x+b>ax-3的解集为.11.(13太原期末改编)如图,直线l1:y1=x+1与直线l2:y2=mx+n相交于点P(1,b),直线y2与x轴交于点A(4,0).(1)求b的值并直接写出关于x,y的方程组1y xy mx n=+⎧⎨=+⎩的解;(2)求直线l2的表达式;(3)判断直线l3:y3=nx+m是否也经过点P?请说明理由.(4)若y3>y2>0,则x的取值范围是________________.12.已知一次函数y =kx+b的图象,如图所示,当y<0时,x的取值范围是().A.x>0B.x<0C.0<x<1D.x<113.(11广州)当实数x的取值使得x-2有意义时,函数y=4x+1中y的取值范围是().A.y≥-7B.y≥9 C.y>9D.y≤9 14.(15海珠期末)如图,直线y1=x+b与y2=kx-1相交于点P,点P的横坐标为-1,则关于x的不等式x+b>kx-1的解集在数轴上表示正确的是().A.B.C.D.15.如图,1l反映了某公司的销售收入与销售量的关系,2l反映了该公司产品的销售成本与销售量的关系,当该公司盈利(收入大于成本)时,销售量().A.小于3t B.大于3t C.小于4t D.大于4t第14题第15题16.(16天河期末)一次函数y1=kx+b与y2=x+a的图象如图,则下列结论①k<0;②a>0;③当x<4时,y1<y2;④b<0.其中正确的结论的个是().A.4个B.3个C.2个D.1个-2yO1x17.(16南充)小朱和爸爸从家步行去公园,爸爸先出发一直匀速前行,小朱后出发.家到公园的距离为2500m,如图是小明和爸爸所走的路程s(m)与步行时间t(min)的函数图象.(1)直接写出小朱所走路程s与时间t的函数关系式;(2)小朱出发多少时间与爸爸第三次相遇?(3)在速度都不变的情况下,小朱希望比爸爸早20min到达公园,则小朱在步行过程中停留的时间需作怎样的调整?18.(15衢州)高铁的开通,给衢州市民出行带来了极大的方便,“五一”期间,小卓卓和小越越相约到杭州市的某游乐园游玩,小卓卓乘私家车从衢州出发1小时后,小越越乘坐高铁从衢州出发,先到杭州火车站,然后再转出租车去游乐园(换车时间忽略不计),两人恰好同时到达游乐园,他们离开衢州的距离y(千米)与乘车时间t(小时)的关系如图所示.请结合图象解决下面问题:(1)高铁的平均速度是每小时多少千米?(2)当小越越达到杭州火车东站时,小卓卓距离游乐园还有多少千米?(3)若小卓卓要提前18分钟到达游乐园,问私家车的速度必须达到多少千米/小时?y (千米)游乐园t(小时)19.(14海珠期末)今年龙舟赛甲乙两队同时出发,其中甲、乙两队在比赛时,路程y (千米)与时间x (小时)的函数关系如图所示.甲队在出发2.5小时到达终点.(假设乙队速度不变)(1)写出比赛全程多少千米?谁先到达终点?乙队花多少时间到达终点? (2)求乙队何时追上甲队?(3)求在比赛过程中,甲乙两队何时相距最远?20.(1)(12恩施州)如图,直线y =kx +b 经过A (3,1)和B (6,0)两点,则不等式组0<kx +b<13x 的解集为 .(1) (2)(2)如图,直线y =kx +b 经过A (2,1),B (-1,-2)两点,则不等式组12x >kx +b >-2的解集为 .21.(15广雅期末)若直线y =-2x +m 与直线y =2x -1的交点在第四象限,则m 的取值范围是( ). A .m >-1 B .m <1C .-1<m <1D .-1≤m ≤1yA 2 1 xB 0 -1 -2 -3 -2-1 1 2 322.依照题意,解答下列问题:(1)如图①,已知直线y =2x +4与x 轴,y 轴分别交于A ,B 两点,请在图①中画出直线y =-12x +4,并探究两函数的图象与x 轴围成的三角形的特点;(2)如图②,已知点M 和点N 的坐标分别为(3,4)和(-2,-1),问在y 轴上是否存在一点P ,使△MNP 是以点M 或点N 为直角顶点的直角三角形?若存在,请求出P 的坐标;若不存在,请说明理由.y xB AO(图①))yx MN O(图②))第一讲-参考答案1.(2,0) 2.x >-13.⎩⎨⎧x =1,y =44.(1)(-3,0),x =-3; (2)①x =-2;②x <-2;③y <1. 5.(-4,0)6.D 7.(1)x <-3,x >-3; (2)9;(3)-1,-4; (4)-4≤x <-1;(5)0,-12;(6)(-2,-2).8.(1)⎩⎨⎧x =-4,y =-2,(-4,-2);(2)x >-4;(3)x ≤-4;(4)x ≥-4.9.A10.x >-211.(1)b =2,12x y =⎧⎨=⎩; (2)2833y x =-+;(3)由(2)可知m =23-,n =83,∴ y =83x -23,当x =1时,y =2.∴直线l 3:y =nx +m 也经过点P . (4)1<x <4.12.D 13.B 14.A 15.D 16.D17.解:(1)s =50(020)1000(2030)50500(3060)t t t t t ⎧⎪⎨⎪-⎩≤≤<≤<≤;(2)设小朱的爸爸所走的路程s 与步行时间t 的函数关系式为:s =kt +b ,则251000250k b b +=⎧⎨=⎩,解得30250k b =⎧⎨=⎩,则小朱的爸爸所走的路程与步行时间的关系式为:s =30t +250, 当50t -500=30t +250,即t =37.5min 时,小朱与爸爸第三次相遇; (3)30t +250=2500,解得,t =75,则小朱的爸爸到达公园需要75min , ∵小朱到达公园需要的时间是60min ,∴小朱希望比爸爸早20min 到达公园,则小朱在步行过程中停留的时间需减少5min .18.解:(1)v =2402-1=240(km/h ).答:高铁的平均速度是每小时240千米; (2)设乘坐高铁时路程与时间的关系式为y =kt +b ,当t =1时,y =0,当t =2时,y =240,得:⎩⎨⎧0=k +b 240=2k +b ,解得:⎩⎨⎧k =240b =-240,故把t =1.5代入y =240t -240,得y =120, 设乘坐私家车时路程与时间的关系式为y =at , 当t =1.5,y =120,得a =80,∴y =80t , 当t =2,y =160,216-160=56(千米), ∴小卓卓距离游乐园还有56千米; (3)把y =216代入y =80t ,得t =2.7,2.7-1860=2.4(小时),216 2.4=90(千米/时).∴小卓卓要提前18分钟到达游乐园,私家车的速度必须达到90千米/小时.19.解:(1)35千米;乙;3516小时; (2)对于乙队,x =1时,y =16,所以y =16x ,对于甲队,出发1小时后,设y 与x 关系为y =kx +b ,把x =1,y =20和x =2.5,y =35代入,得⎩⎨⎧20=k +b35=2.5k +b,则y =10x +10.联立方程组,⎩⎨⎧y =16x y =10x +10,得x =53,即:出发1小时40分钟后,乙队追上甲队; (3)1小时之内,两队相距最远距离是4千米,即当x =3516时,y 甲=10×3516+10=31.875,y 乙=35,y 甲-y 乙=35-31.875=3.125; 当x =1时,y 甲-y 乙=20-16=4;∵3.125<4,所以比赛过程中,甲、乙两队在出发后1小时相距最远.20.(1)3<x <6;(2)-1<x <2. 21.C22.(1)图略;用勾股定理的逆定理可以证明两函数与x 轴围成的三角形是一个直角三角形; (2)设P (0,y ),①当PM为斜边时,PN2+MN2=PM2,即(-2)2+(-1-y)2+25+25=32+(4-y)2,解得:y=-3,即P为(0,-3);②当PN为斜边时,PM2+MN2=PN2,即32+(4-y)2+25+25=(-2)2+(-1-y)2,解得:y=7,即P为(0,7);综上所述,在y轴上存在一点P,使△MNP是直角三角形,P为(0,-3)或(0,7).。
6.6 一次函数、一元一次方程和一元一次不等式 苏科版数学八年级上册课件(共20张PPT)

示例:如图6.6-2 所示,
方程k1x+b1=k2x+b2 的解为x=a; 不等式k1x+b1>k2x+b2 的解集为x > a; 不等式k1x+b1<k2x+b2 的解集为x < a.
感悟新知
知2-讲
特别提醒 利用图像解法解一元一次不等式的一般步骤: 1. 将不等式转化为kx+b > 0 或kx+b < 0(k ≠ 0)的形式; 2. 画出函数图像,并确定函数图像与x 轴的交点坐标; 3. 根据函数图像确定对应不等式的解集.
y=kx+b 当y=4 时对应的自变量的值.
知1-练
感悟新知
解:把点(4,0)和(3,2)的坐标分别代入y=kx+b,
得 4k+b=0,解得 k=-2,
3k+b=2,
b=8, 即y= - 2x+8.
当y=4 时,- 2x+8=4,解得x=2.
∴方程kx+b=4 的解为x=2.
知1-练
答案:B
感悟新知
感悟新知
知2-练
例 3 [三模·杭州] 如图6.6-3,已知函数y1=3x+b 和y2=ax
-3的图像交于点P(- 2, - 5),则根据图像可得不
等式3x+b > ax-3 的解集是( )
A. x > -2
B. x < -2
C. -2 < x < 0
D. x > 0
感悟新知
知2-练
解题秘方:求不等式3x+b >ax-3 的解集,就是看 当x 在什么范围时, 函数y1=3x+b 的图像在函 数y2=ax - 3 的图像上面.
答案:A
第6课时 一次函数与一元一次方程、一元一次不等式PPT课件(沪科版)

B.x<-3
C.x>3
D.x<3
11.如图所示,某公司市场营销部的营销人员的个人收入与 其每月的销售量成一次函数关系,由图中给出的信息,营销人 员没有销售量时的收入是( B )
A.310元 B.300元 C.290元 D.280元
12.已知关于x的方程ax-5=7的解为x=1, 则一次函数y=ax
解:(1)设大枣粽子的单价为 x 元/盒,普通粽子的单价为 y 元/盒, 根据题意得x2-x+y=4y1=5,300,解得xy==6405,. 答:大枣粽子的单价为 60 元/盒,普通粽子的单价为 45 元/盒
(2)①设买大枣粽子 x 盒,则购买普通粽子(20-x)盒,买水果共用了 w 元,根据题意得,w=1 240-60x-45(20-x)=1 240-60x-900+45x=- 15x+340,故 w 关于 x 的函数关系式为 w=-15x+340;
-12与x轴交点的坐标为 (1,0)
.
13.已知一次函数y=kx+b(k,b是常数,且k≠0),x与y的部分对 应值如下表所示,那么不等式kx+b<0的解集是____.x>1
x
- 2
- 1
0
1
2
3
y3
2
1
0
-- 12
14.如图,经过点B(-2,0)的直线y=kx+b与直线y=4x+2相
交于点A(-1,-2),则不等式4x+2<kx+b<0的
经过(D )
A.(2,0) B.(0,3) C.(0,4) D.(0,-3)
4.(4 分)如图,一次函数 y=kx+b 的图象经过点(2,0)与(0,3),
则关于 x 的不等式 kx+b>0 的Байду номын сангаас集是( A )
1一次函数与一元一次方程、不等式教学课件

合作探究
或者说,在直线y=3x+2上取纵坐标分别满足大于2、小于0、 小于-1的点,看它们的横坐标分别满足什么条件.
画出一次函数的图象,如图. 从图象 Nhomakorabea观察,上面的三个不等式可以看成 y=3x+2 的函数值y大于2、小于0、小于-1 时 自变量x的取值范围.
当y>2时, x>0;当y<0时, x< 2 ; 3
一次函数与方程、不等式
学习目标
1.认识一次函数与一元一次方程、一元一次不等式之间的联系. 2.会用函数观点解释方程和不等式及其解(解集)的意义.
新课导入
已知一次函数y=2x+1,求当函数值y =3,y =0,y = -1时,自变 量x的值.
自变量x的值依次是
1,
1 2
,-1
新课导入 当y=3时,2x+1等于几?当y =0,y = -1时,2x+1又等于几呢?你
典例精析
解:由3x-2=x+4得2x-6=0画函数y=2x-6的 图象,如图. 由图可知,直线y=2x-6与x轴的交点为(3,0), 所以x=3.
典例精析
利用函数图象解一元一次方程时,一般需将方程变形为ax+b= 0的形式,然后通过观察直线y=ax+b与x轴的交点坐标确定方程的 解,此求解对作图的准确性要求较高.
课堂总结
一次函数与一 元一次方程、
不等式
函数与方程 函数与不等式
函数值 函数图象
函数值 函数图象
y=0时x的值 与x轴交点横坐标 x的取值范围 x轴上方或下方
典例精析
已知函数y1=2x-5,y2=3-2x,求当x取何值时:
(1)y1>y2;
(2)y1=y2;
(3)y1<y2.
解:方法一:代数法.
一次函数与方程和不等式关系PPT课件

生产计划
在生产计划中,一次函数、 方程和不等式可以一起使 用,优化生产流程和提高 生产效率。
数据分析
在数据分析中,一次函数、 方程和不等式可以一起使 用,处理数据、建立数学 模型并解释结果。
05
总结与展望
一次函数、方程和不等式的重要性和意义
一次函数、方程和不等式是数学中的基础概念,对 于培养学生的逻辑思维、问题解决能力和数学素养 具有重要意义。
一次函数与方程和不等式关系 ppt课件
目
CONTENCT
录
• 一次函数的基本概念 • 一次函数与方程的关系 • 一次函数与不等式的关系 • 实际应用中的一次函数、方程和不
等式 • 总结与展望
01
一次函数的基本概念
一次函数的定义
一次函数
一般形式为y=kx+b(k≠0),其 中x是自变量,y是因变量,b是截 距,k是斜率。
随着数学与其他学科的交叉融 合,对于一次函数、方程和不 等式的研究也在不断深入,需 要加强与其他学科的合作与交 流,推动数学在各领域的应用 和发展。
随着信息技术的发展,数学教 育正面临着新的挑战和机遇, 需要加强信息技术与数学教育 的融合,利用信息技术手段提 高教学效果和学生的学习体验 。
THANK YOU
单调性
当k>0时,函数单调递增;当k<0时,函数单调递减 。
有界性
一次函数的值域为全体实数R。
02
一次函数与方程的关系
一次函数与一元一次方程
一次函数与一元一次方程具有密切的联系。一元一次方程可以看 作是y为常数的一次函数,其解即为函数的交点。通过对方程进行 求解,可以得到与一次函数交点的x坐标。
一次函数是代数函数中的基础,其图像为直线,通 过研究其性质可以帮助学生理解函数的增减性、单 调性等概念。
沪科版八年级数学上册1.5一次函数与一次方程、一次不等式课件

B(-3,0)
坐标x=-3就是方程2x+6=0的解.
•O
x
知识归纳
一次函数与一元一次方程的关系
一般地,一元一次方程 kx+b=0 的解就是一次函数y=kx+b的图象与x 轴交点的横坐标.
例题与练习
范例 利用函数图象解方程:3x-2=x+4.
分析:先将方程化为kx+b=0的情势,再在坐标系中画出函数
练习 1.画出一次函数 y=-2x-6 的图象,结合图象求:
(1)x__=_-_3__时,y=0; (2)x__<__-3__时,y>0; (3)x__>__-_3_时,y<0; (4)x__<__-6__时,y>6;
y=-2x-6
y
B(-6,6) •
6
4
2
A(-3,0) •
-6 -4 -2 O
2
y=kx+b的图象,然后视察出直线y=kx+b与x轴的交点坐标,
从而确定所求x的值.
解:由3x-2=x+4得2x-6=0. 令y=2x-6,画出函数y=2x-6的图象(如
y= 2x-6 y
O 1 234 5 x
-1
右图).
-2
由图象可以看出直线y=2x-6与x轴的交点坐标 -3
-4
为(3,0),
-5
O •B(3,0) x
• A(0,-9)
随堂练习
1.一次函数y=-x+2的图象如图,你能说出-x+2<0的解集吗?
解:x>2
y y=-x+2
0
2x
2.一次函数y=kx+b的图象如图,你能说出kx+b<0的解集吗? 解:x < -4
y
y=kx+b
一次函数与方程、不等式(共15张PPT)

1
整理方程
通过移项和合并同类项,将一次方程转化为形如ax = b的方程。
2பைடு நூலகம்
用除法解方程
通过将方程两边都除以系数a,得到x = b/a的解。
3
检验解
将求得的解代入原方程,验证方程两边是否相等。
一次方程的应用
经济学
一次方程可用于计算成本、利润和收入等经济指标。
工程学
在工程学中,一次方程可用于计算电路中的电流、电压和电阻。
平行线
具有相同斜率但不同截距的一次 函数将得到平行线。它们在平面 上永远不会相交。
相交线
具有不同斜率的一次函数将交叉 并在某个点相交。这个点是两条 直线的唯一交点。
一次方程的定义
一次方程是一个等式,其中包含至多一个未知数的一次项和常数项。例如, 2x + 3 = 7是一个一次方程。
一次方程的解法
物理学
一次方程可用于描述速度、加速度和力等物理量的关系。
一次不等式的定义和解法
一次不等式是一个包含未知数的一次项和常数项的不等式。例如,3x + 2 > 5是一个一次不等式。
一次函数与方程、不等式
一次函数与方程、不等式是数学中基础而重要的概念之一。通过本次演讲, 我们将深入探讨一次函数、方程和不等式的定义、性质和应用,使您对这些 概念有更深入的理解。
一次函数的表达式
标准形式
一次函数的标准形式为y = ax + b,其中a和b为常数。它描述了 直线的斜率和截距。
斜率截距形式
一次函数的斜率截距形式为y = mx + c,其中m是斜率,c是y轴 截距。这种形式更容易理解直 线的特征。
点斜式
一次函数的点斜式为y − y₁ = m(x − x₁),其中(x₁, y₁)是直线上的已 知点,m是斜率。这种形式方 便从已知点和斜率直接获得函 数。
一元一次不等式与一次函数课件

本章内容的总结
一元一次不等式的概念与性质
01
详细介绍了不等式的定义、性质以及解法,并通过实例进行说
明。
一次函数的定义与性质
02
深入探讨了一次函数的定义、性质、图像以及与一元一次不等
式的联系。
一元一次不等式与一次函数的实际应用
03
通过具体实例,展示了如何运用一元一次不等式和一次函数解
决实际问题。
对未来学习的展望
当k>0时,函数图像 为上升直线;当k<0 时,函数图像为下降 直线。
一次函数的性质
01
02
03
04
一次函数的单调性由斜率k决 定,k>0时单调递增,k<0时
单调递减。
一次函数的图像是直线,且过 定点(0,b)。
一次函数的斜截式方程 y=kx+b表示当x增加1时,y 增加k;当x减少1时,y减少k
方法2
对于题目2,代入 x = 2 到 y = 3x - 5 中得到 y = 1,因为 y 的 斜率为正,所以当 x < 2 时,y 的取值范围是 y < 1。
方法3
对于题目3,由解集的形式可知, 系数2a - 1必须小于0,即 2a - 1 < 0,解得 a < frac{1}{2}。
05
总结与展望
解题技巧与方法
技巧2
对于一次函数,根据一次函数的 性质,当斜率 k > 0 时,y 随 x 的增大而增大;当 k < 0 时,y 随 x 的增大而减小。
技巧1
解一元一次不等式时,首先移项 并合并同类项,然后根据不等式 的性质求解。
方法1
对于题目1,首先移项得到 -2x > -12,然后除以-2并反转不等号得 到 x < 6。
一次函数与一元一次方程不等式关系PPT课件

通过一元一次方程求得的函数 解析式可以用来描述函数的图 像。
函数图像与一元一次方程解的关系
函数图像与x轴的交点是一元一次方程的解,即当y=0时,对应的x值就是方程的解。 函数图像与x轴的交点个数与一元一次方程的解的个数相同,可能有1个或多个解。
通过观察函数图像与x轴的交点情况,可以直观地了解一元一次方程的解的情况。
一次函数与一元一次方程不 等式关系ppt课件
• 一次函数的基本概念 • 一元一次方程的基本概念 • 一次函数与一元一次方程的关系 • 一次函数与一元一次不等式的关系 • 实例分析
01
一次函数的基本概念
一次函数的定义
01
一次函数:一般形式为y=kx+b (k≠0),其中x为自变量,y为因 变量,k为斜率,b为截距。
详细描述
选取几个典型的一次函数,如 y=x、y=2x+1等,通过代入法或 消元法将其转化为对应的一元一 次方程,并解释转化过程和原理 。
一次函数与一元一次不等式的实例分析
总结词
通过具体实例展示一次函数与一元一 次不等式的关系
详细描述
选取几个典型的一次函数,如y=x、 y=2x+1等,通过移项或不等式性质 将其转化为对应的一元一次不等式, 并解释转化过程和原理。
一元一次方程的解法
总结词
解一元一次方程通常采用移项、合并同类项、系数化为1等方法。
详细描述
解一元一次方程的基本步骤包括去分母、去括号、移项、合并同类项和系数化 为1。例如,对于方程 3x - 5 = 2,可以通过移项和合并同类项得到 x = 3。
一元一次方程的应用
总结词
一元一次方程在实际生活中有广泛的应用如购物问题、行程问题等。02
斜率k决定了函数的增减性,k>0 时,函数单调递增;k<0时,函 数单调递减。
19.2.3一次函数与方程不等式课件人教版八年级数学下册

解:画函数y=5x-3与y=3x+1 的图象。
从图中看出,当x>2时,
·y y=3x+1
7
直线y=5x-3上的点在直线 y=3x+1上相应点的上方,即 5x-3>3x+1,所以不等式的
y=5x-3
o2
x
解集为x>2。
4、已知直线y=2x+k与直线y=kx-2的交点横坐标
为2,求k的值和交点纵坐标。
K=6
(2,10)
y
5. 已知直线y1=k1x+b1与直线y2=k2x+b2
3
相交于点P(-2,3)。如图所示,当
y1>y2时,x的取值范围是 x<-2
。y1
-2 O
y2
x
数(y=ax +b)值为k 时对应的
自变量的值.
2x
2x +1=0 的解 1
+1=-1-2的解-1
O -1
2x +1=3 的解 1 2 3x
归纳总结
一次函数与一元一次方程的关系
求一元一次方程 kx+b=0的解.
从“函数值”看
一次函数y= kx+b
中y=0时x的值.
求一元一次方程 kx+b=0的解. 从“函数图象”看
的取值范围是( D)
A.y>0 B.y<0 C.-2<y<0 D.y<-2
3.已知直线 y 2x k与x轴的交点为(-2,0),则关于x的不等式 2x k 0
C 的解集是( )
A.x 2
B.x 2
C.x 2
D.x 2
4.对于函数y=-x+4,当x>-2时,y的取值范围是( D)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2020年10月2日
4
自学指导:
教材40页到41页思考:
由40页两个问题的关系,能进一步 得到“解不等式 aX+b>0” 与“求 自变量X在什么范围内,一次函数 Y=ax+b的值大于0”有什么关系?
例2(略)
2020年10月2日
5
例2
0
2
-6
2020年10月2日
Y=2x+10
0
2
Y=5x+4
6
由于任何一元一次不等式都可 以转化为ax+b>0或ax+b<0(a, b为常数,a≠0)的形式,所 以解一元一次不等式可以看作: 当一次函数值大(小)于0时, 求自变量相应的取值范围。
11.3.2
一次函数与一元 一次不等式
2020年10月2日
1
学习目图象解决一元一次不等式的求 解问题。
学习用函数的观点看待不等式 的方法。
2020年10月2日
2
学习重点
一次函数与一元
一次不等式的关
系的理解
2020年10月2日
3
学习难点
利用一次函数图像 确定一元一次不等 式的解集。
2020年10月2日
7
本节课我们都学习了 什么?
2020年10月2日
8
演讲完毕,谢谢观看!
Thank you for reading! In order to facilitate learning and use, the content of this document can be modified, adjusted and printed at will after downloading. Welcome to download!
汇报人:XXX 汇报日期:20XX年10月10日
9
